Содержание
Разбор тренировочного теста
Разбор тренировочного теста интернет-олимпиады
по физике 2008/2009 года
11 класс. Кинематика
Вопрос № 1
По графику, представленному на рисунке, определите скорость
движения велосипедиста через три секунды после начала движения.
Решение.
На рисунке представлен график зависимости пути от времени.
График представляет собой прямую линию, значит, велосипедист двигался
равномерно. Определим по графику величину пути, пройденного велосипедистом за
фиксированный отрезок времени. Например, за 3 с велосипедист прошел 9 м.
Скорость велосипедиста V = L / t
= 9/3 = 3 м/с.
Вопрос № 2
Пешеход и велосипедист одновременно начали движение
навстречу. Их скорости равны V1 = 6 км/ч и V2 = 30 км/ч, соответственно.
Определите время движения до встречи, если начальное расстояние между ними L = 700 м.
Решение.
Определим скорость велосипедиста в системе отсчета пешехода V12
= V1 + V2 = 6 + 30 = 36 км/ч = 10 м/с. Итак, пешеход и
велосипедист сближаются со скоростью 10 м/с, тогда их время движения до встречи
t = L / V12 = 700/10 = 70 с.
Вопрос № 3
Автомобиль двигался со скоростью 15 м/с
в течение 5 с. Какой путь он проехал за это время?
Решение.
Автомобиль двигался равномерно, поэтому пройденный путь L = V∙t = 15∙5 = 75 м.
Вопрос № 4
Брошенный вертикально вверх мяч возвращается в исходное
положение. На рисунке представлен график его скорости от времени. В какой
момент времени мяч достиг максимальной высоты?
Решение.
В момент, когда мяч достиг максимальной высоты, его скорость
равна нулю.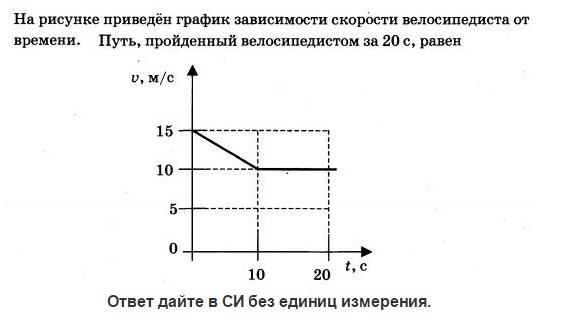 По графику, представленному на рисунке определяем, что скорость
По графику, представленному на рисунке определяем, что скорость
мяча равна нулю в момент времени t = 2 с.
Вопрос № 5
Какие из перечисленных выше величин векторные ? (Отметьте все векторные величины)
Решение.
Из перечисленных величин векторными являются скорость,
ускорение и перемещение. Путь — величина скалярная.
Вопрос № 6
Спортсмен пробежал дистанцию 400 м по дорожке стадиона и
возвратился к месту старта. Определите путь L, пройденный спортсменом, и модуль
его перемещения S.
Решение.
Пройденный спортсменом путь L = 400 м. Модуль перемещения S
= 0, так как спортсмен вернулся в точку, из которой он начал движение.
Вопрос № 7
Скорость тела, движущегося прямолинейно и равноускоренно,
изменилась при перемещении из точки 1 в точку 2 так, как показано на рисунке.
Какое направление имеет вектор ускорения на этом участке пути?
Решение.
Из рисунка видно, что модуль скорости тела при перемещении
уменьшается, значит, вектор ускорения направлен навстречу движению, то есть налево.
Вопрос № 8
По графику зависимости модуля скорости от времени определите
ускорение прямолинейно движущегося тела в момент времени t
= 2 с.
Решение.
По графику определим изменение скорости тела за
фиксированный момент времени. Например, за первые две секунды скорость тела
изменилась на 6 м/с (с V0
= 3 м/с до Vt = 9 м/с). Ускорение a = (Vt – V0) / t
= 6/2 = 3 м/с2.
Вопрос № 9
При равноускоренном движении автомобиля в течение пяти
секунд его скорость увеличилась от 10 до 15 м/с. Чему равен модуль ускорения автомобиля?
Решение.
Ускорение автомобиля a = (Vt – V0) / t = (15 – 10)/5 = 5/5 = 1 м/с2.
Вопрос № 10
Автомобиль стартует с места с постоянным ускорением а = 1
м/с2. Какой путь проходит автомобиль за
первые десять секунд движения?
Решение.
Автомобиль движется равноускоренно без начальной скорости —
пройденный путь L = a∙t2/2 = 1∙102/2
= 50 м.
Вопрос № 11
Плот равномерно плывет по реке со скоростью 3 км/ч. Сплавщик
движется поперек плота со скоростью 4 км/ч. Какова скорость сплавщика в системе отсчета, связанной с
берегом?
Решение.
Скорость сплавщика в в
системе отсчета, связанной с берегом
Вопрос № 12
Вертолет поднимается вертикально вверх c
постоянной скоростью. Какова траектория движения точки на конце лопасти винта
Какова траектория движения точки на конце лопасти винта
вертолета в системе отсчета, связанной с корпусом вертолета?
Решение.
Представьте себе, что вы находитесь в кабине вертолета, то
есть вы неподвижны относительно корпуса вертолета. В этом случае вы можете
видеть, что любая точка винта вертолета описывает окружность.
Вопрос № 13
Тело движется вдоль оси Х по закону, представленному на
рисунке, где х — координата в метрах, t — время в секундах. Определите модуль ускорения тела.
Решение.
Уравнение зависимости координаты от времени при
прямолинейном равноускоренном движении в общем виде имеет вид Х(t) = X0 + V0х∙t + aх∙t2/2, где X0 — начальная
координата, а V0х
и aх— проекции начальной скорости и ускорения на ось Х.
Приравнивая члены, в которые входит t2, получим aх∙t2/2 = –4,5∙t2. Откуда проекция ускорения aх
Откуда проекция ускорения aх
= –9 м/с2, а модуль ускорения a =
9 м/с2.
Вопрос № 14
На рисунке представлены графики зависимости модуля скорости
от времени для четырех тел. Какое из этих тел (или
какие тела) прошли наибольший путь?
Решение.
На рисунке показаны графики зависимости скорости движущихся
тел от времени. Как известно, пройденный телом путь представляет собой площадь,
лежащую под графиком скорости. Из рисунка видно, что фигура максимальной
площади лежит под графиком, для тела 4. Значит, за промежуток времени от 0 до t0
тело 4 прошло наибольший путь.
Вопрос № 15
Тело движется прямолинейно. На рисунке представлен график
скорости тела от времени. На каком промежутке (каких промежутках) времени
проекция ускорения отрицательна?
Решение.
Проанализируем график:
1. на
промежутке времени от 0 до 1с скорость тела постоянна, поэтому ах =
0;
2. на
промежутке времени от 1с до 2с скорость тела уменьшается, поэтому проекция
ускорения ах < 0;
3. на
промежутке времени от 2с до 3с тело покоится, поэтому ах = 0;
4. на
промежутке времени от 3с до 4с скорость тела увеличивается, поэтому проекция
ускорения ах > 0.
Итак, проекция ускорения отрицательна на промежутке времени
от 1с до 2с.
Вопрос № 16
Двигавшийся с начальной скоростью 20 м/с автомобиль
разгоняется с постоянным ускорением а = 2 м/с2
в течение 5 с. Какой путь он проехал за это время?
Решение.
Для расчета пути можно воспользоваться формулой L = V0∙t + a∙t2/2
= 20∙5 + 2∙52/2 = 125 м.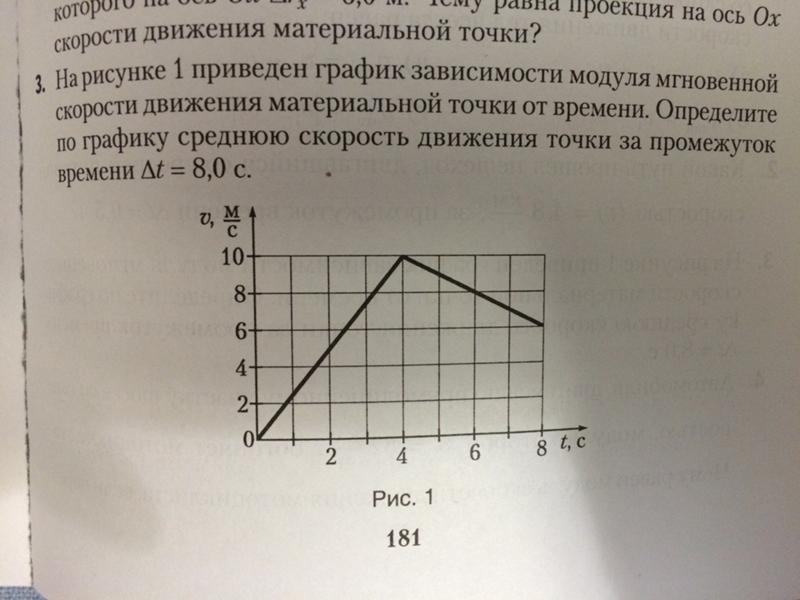
2. Графики
1.
Задание 1 № 101.
Может ли график зависимости
пути от времени иметь следующий
вид?
1)
да
2)
нет
3)
может, если траектория
прямолинейная
4)
может, если тело возвращается
в исходную точку
Решение.
Путь —
это физическая величина,
показывающая пройденное
телом расстояние. Иначе говоря,
это длина пройденного участка
траектории. По определению,
путь есть величина положительная,
которая может только возрастать
со временем, так что представленный
график не может изображать
зависимость пути от времени.
Правильный
ответ: 2.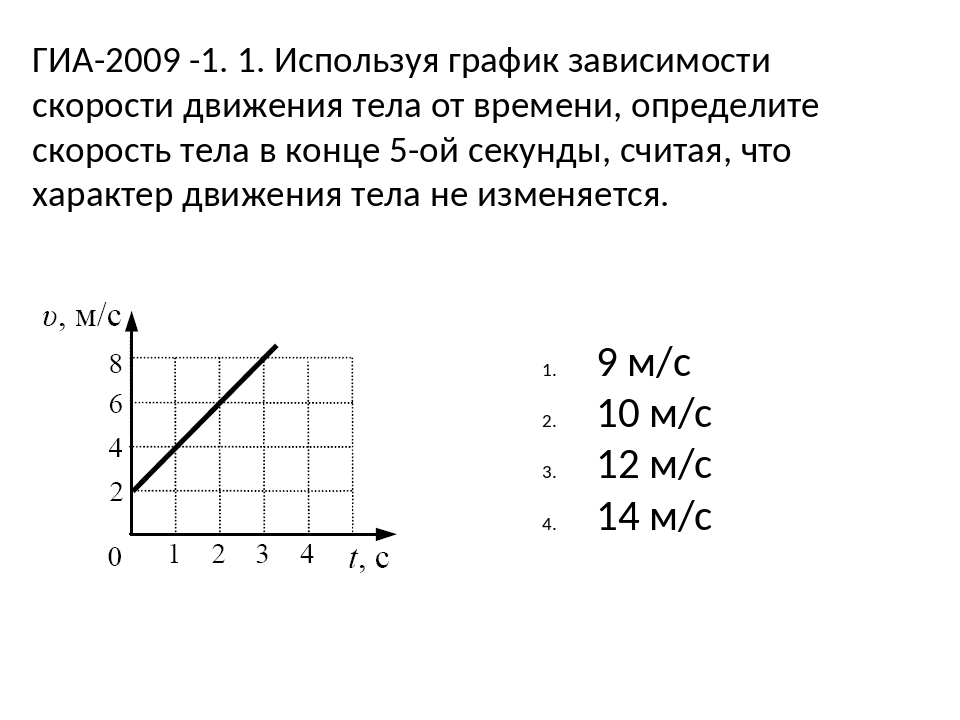
Ответ:
2
101
2
2.
Задание 1 № 102.
Мяч, брошенный вертикально
вверх, падает на землю. Найдите
график зависимости от
времени проекции скорости
на вертикальную ось, направленную
вверх.
1)
1
2)
2
3)
3
4)
4
Решение.
Мяч
после броска движется с
постоянным ускорением
свободного падения,
направленным вниз. Следовательно,
проекция скорости должна
уменьшаться со временем по
линейному закону,
,
график зависимости её от
времени представлен на
рисунке 2.
Правильный
ответ: 2.
Ответ:
2
102
2
3.
Задание 1 № 103.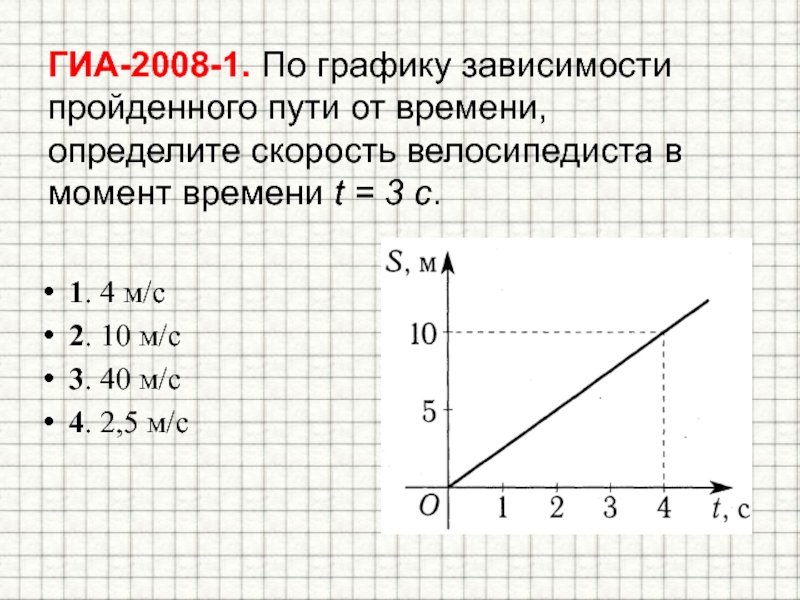
Мяч брошен с вершины скалы без
начальной скорости. Найдите
график зависимости модуля
перемещения от времени.
Сопротивлением воздуха
пренебречь.
1)
1
2)
2
3)
3
4)
4
Решение.
Поскольку
мяч брошен с вершины скалы без
начальной скорости, а
сопротивлением воздуха
можно пренебречь, зависимость
модуля перемещения от
времени должна иметь следующий
вид:
.
Искомая
зависимость представлена
на рисунке 4. Кроме того, модуль
есть величина положительная,
этому критерию также удовлетворяет
только график под номером
4.
Правильный
ответ: 4.
Ответ:
4
103
4
4.
Задание 1 № 104.
Автомобиль движется по
прямой улице. На графике
представлена зависимость
скорости автомобиля
от времени.
В
каком интервале времени
максимален модуль ускорения?
1)
от 0 до 10 с
2)
от 10 до 20 с
3)
от 20 до 30 с
4)
от 30 до 40 с
Решение.
На
всех рассматриваемых
интервалах времени
скорость автомобиля
меняется равномерно,
следовательно ускорение
на каждом интервале
постоянно. Все исследуемые
интервалы одинаковы
по длительности, поэтому
максимальному модулю
ускорения соответствует
максимальный модуль
изменения скорости в
течение интервала (самый
большой угол наклона). Из
графика видно, что это интервал
от 10 до 20 с.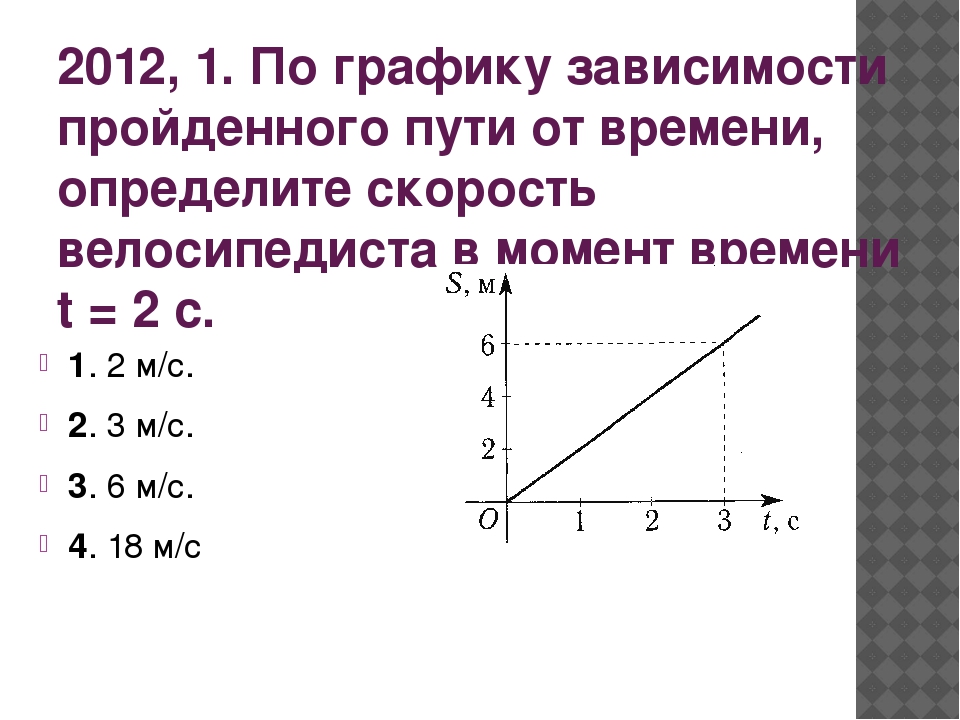
Правильный
ответ: 2.
Ответ:
2
104
2
5.
Задание 1 № 106.
По
графику зависимости
модуля скорости тела от
времени, представленного
на рисунке, определите
путь, пройденный телом от момента
времени 0 с до момента
времени 2 с.
1)
1 м
2)
2 м
3)
3 м
4)
4 м
Решение.
Для
того чтобы по графику модуля
скорости найти путь, пройденный
телом за некоторый интервал
времени, необходимо
вычислить площадь под частью
графика, соответствующей
этому интервалу времени
(в единицах произведения
величин, отложенных по
осям координат). В интервале
времени от 0 С до 2 с автомобиль
прошел путь
.
Примечание:
В принципе, интересующий
нас участок (от 0 до 2 с) не обязательно
разбивать на два, площадь под
графиком можно посчитать,
как площадь трапеции:
.
Правильный
ответ: 3.
Ответ:
3
106
3
6.
Задание 1 № 107.
На рисунке представлен
график зависимости модуля
скорости автомобиля
от времени. Определите по
графику путь, пройденный
автомобилем в интервале
от момента времени 0 с до
момента времени 5 с после
начала отсчета времени.
1)
6 м
2)
15 м
3)
17 м
4)
23 м
Решение.
Для
того чтобы по графику модуля
скорости найти путь, пройденный
автомобилем за некоторый
интервал времени, необходимо
вычислить площадь под частью
графика, соответствующей
этому интервалу времени
(в единицах произведения
величин, отложенных по
осям координат). В интервале
В интервале
от момента времени 0 с до
момента времени 5 с после
начала движения автомобиль
прошел путь
.
Другой
способ решения заключается
в анализе каждого участка
графика в отдельности,
определения из графика
начальных скоростей и
ускорений на каждом этапе и
использования стандартных
кинематических формул
для пути.
Правильный
ответ: 3.
Ответ:
3
107
3
7.
Задание 1 № 108.
На рисунке представлен
график зависимости модуля
скорости тела от времени.
Какой
путь пройден телом за вторую
секунду?
1)
0 м
2)
1 м
3)
2 м
4)
3 м
Решение.
Для
того чтобы по графику модуля
скорости найти путь, пройденный
телом за некоторый интервал
времени, необходимо
вычислить площадь под частью
графика, соответствующей
этому интервалу времени
(в единицах произведения
величин, отложенных по
осям координат). За вторую
секунду автомобиль прошел
путь
.
Правильный
ответ: 3.
Ответ:
3
108
3
8.
Задание 1 № 109.
На рисунке представлен
график зависимости модуля
скорости тела от времени.
Найдите
путь, пройденный телом за время
от момента времени 0 с до
момента времени 5 с.
1)
0 м
2)
15 м
3)
20 м
4)
30 м
Решение.
Для
того чтобы по графику модуля
скорости найти путь, пройденный
телом за некоторый интервал
времени, необходимо
вычислить площадь под частью
графика, соответствующей
этому интервалу времени
(в единицах произведения
величин, отложенных по
осям координат). В интервале
от момента времени 0 с до
момента времени 5 с после
начала движения тело прошло
путь
.
Другой
способ решения заключается
в анализе каждого участка
графика в отдельности,
определения из графика
начальных скоростей и
ускорений на каждом этапе и
использования стандартных
кинематических формул
для пути.
Правильный
ответ: 3.
Ответ:
3
109
3
9.
Задание 1 № 110.
На рисунке представлен
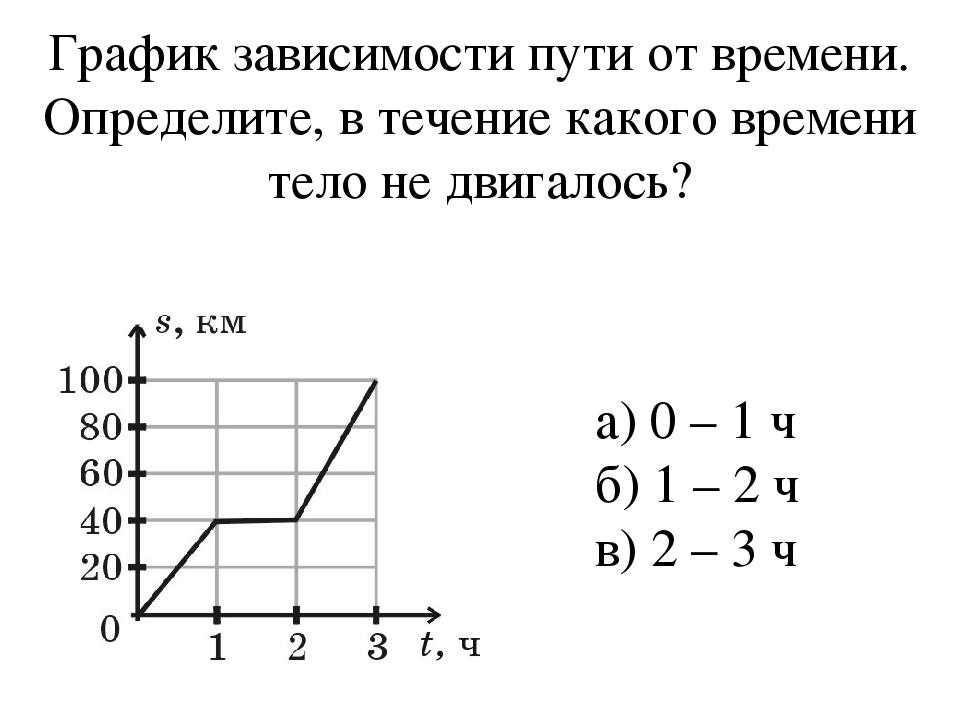
график зависимости пути
от времени.
Определите
по графику скорость движения
велосипедиста в интервале
от момента времени 1 с до
момента времени 3 с после
начала движения.
1)
2)
3)
4)
Решение.
Из
графика видно, что в интервале
от момента времени 1 с до
момента времени 3 с после
начала движения путь
велосипедиста не
изменялся. Следовательно
на этом интервале времени
велосипедист не двигался,
его скорость была равна нулю.
Правильный
ответ: 1.
Ответ:
1
110
1
10.
Задание 1 № 116.
На рисунке приведен график
зависимости проекции
скорости тела от времени.
На
каком графике представлена
проекция ускорения тела в
интервале времени от 10 до
20 с?
1)
1
2)
2
3)
3
4)
4
Решение.
Из
графика видно, что в интервале
времени от 10 до 20 с проекция
скорости тела не изменялась,
а значит, проекция ускорения
была равна нулю. Проекция ускорения
тела в этом интервале времени
представлена на графике
2.
Правильный
ответ: 2.
Ответ:
2
116
2
11.
Задание 1 № 117.
На рисунке приведен график
зависимости проекции
скорости тела от времени.
На
каком из графиков представлена
проекция ускорения тела в
интервале времени от 0 до
6 с?
1)
1
2)
2
3)
3
4)
4
Решение.
Из
графика видно, что ускорение
в интервале времени от 0
с до 10 с постоянно.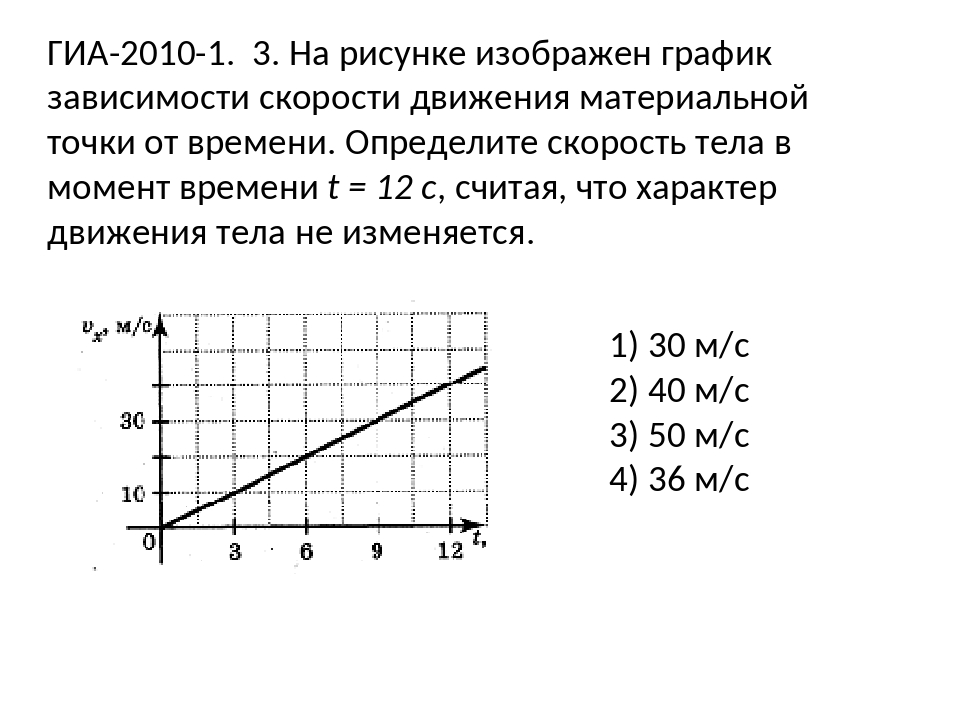 Значит,
Значит,
на этом интервале веремени
ускорение такое же, как и на
интервале от 0 с до 6 с. Найдём
это ускорение:
.
Проекция
ускорения тела в этом интервале
времени представлена на
графике 1.
Ответ:
1.
Ответ:
1
117
1
12.
Задание 1 № 118.
На рисунке приведен график
зависимости проекции
скорости тела от времени.
На
каком из графиков представлена
проекция ускорения тела в
интервале времени от 20 до
26 с?
1)
1
2)
2
3)
3
4)
4
Решение.
Из
графика видно, что в интервале
времени от 20 до 26 с проекция
скорости тела убывала
линейно со временем, а значит,
проекция ускорения была
постоянна и равнялась
.
Проекция
ускорения тела в этом интервале
времени представлена на
графике 3.
Правильный
ответ: 3.
Ответ:
3
118
3
13.
Задание 1 № 119.
На рисунке приведен график
зависимости проекции
скорости тела от времени.
На
каком из графиков представлена
проекция ускорения тела в
интервале времени от 54 до
60 с?
1)
1
2)
2
3)
3
4)
4
Решение.
Из
графика видно, что в интервале
времени от 54 до 60 с проекция
скорости тела не изменялась,
а значит, проекция ускорения
была равна нулю. Проекция ускорения
Проекция ускорения
тела в этом интервале времени
представлена на графике
2.
Правильный
ответ: 2.
Ответ:
2
119
2
14.
Задание 1 № 120.
На рисунке приведен график
зависимости проекции
скорости тела от времени.
На
каком из графиков представлена
проекция ускорения тела в
интервале времени от 42 до
48 с?
1)
1
2)
2
3)
3
4)
4
Решение.
Из
графика видно, что в интервале
времени от 42 до 48 с (и даже на более
большом интервале от 40 с до
50 с) проекция скорости тела
возрастала линейно со
временем, а значит, проекция
ускорения была постоянна
и равнялась
.
Проекция
ускорения тела в этом интервале
времени представлена на
графике 4.
Правильный
ответ: 4.
Ответ:
4
120
4
15.
Задание 1 № 121.
На рисунке представлен
график зависимости модуля
скорости
автомобиля
от времени t.
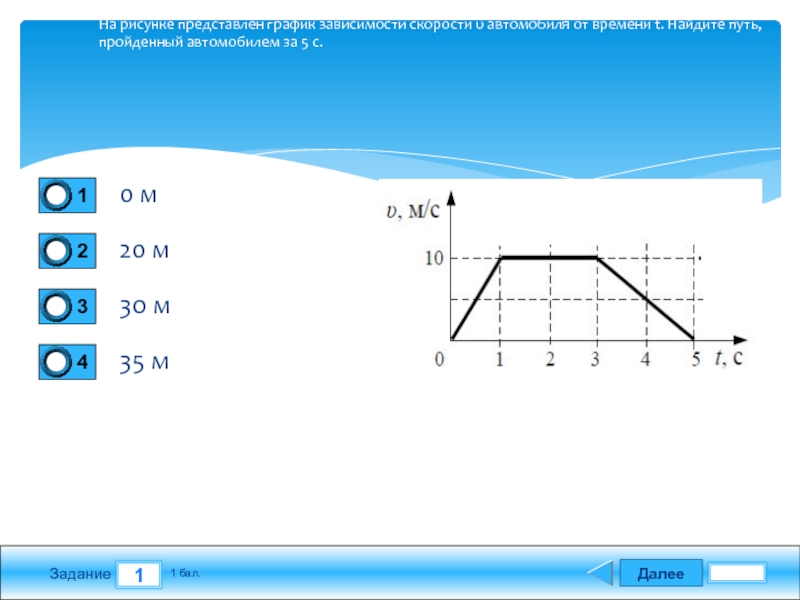
Найдите
путь, пройденный автомобилем
за 5 c.
1)
0 м
2)
20 м
3)
30 м
4)
35 м
Решение.
Для
того чтобы по графику модуля
скорости найти путь, пройденный
телом, необходимо вычислить
площадь под графиком (в единицах
произведения величин,
отложенных по осям координат).
За 5 c автомобиль прошел
путь
.
Другой
способ решения заключается
в анализе каждого участка
графика в отдельности,
определения из графика
начальных скоростей и
ускорений на каждом этапе и
использования стандартных
кинематических формул
для пути.
Правильный
ответ: 4.
Ответ:
4
121
4
16.
Задание 1 № 122.
Автомобиль движется по
прямой улице. На графике
представлена зависимость
его скорости от времени.
На
каком интервале времени
модуль ускорения автомобиля
максимален?
1)
от 0 с до 10 с
2)
от 10 с до 20 с
3)
от 20 с до 30 с
4)
от 30 с до 40 с
Решение.
На
всех рассматриваемых
интервалах времени
скорость автомобиля
меняется равномерно,
следовательно, ускорение
на каждом интервале
постоянно.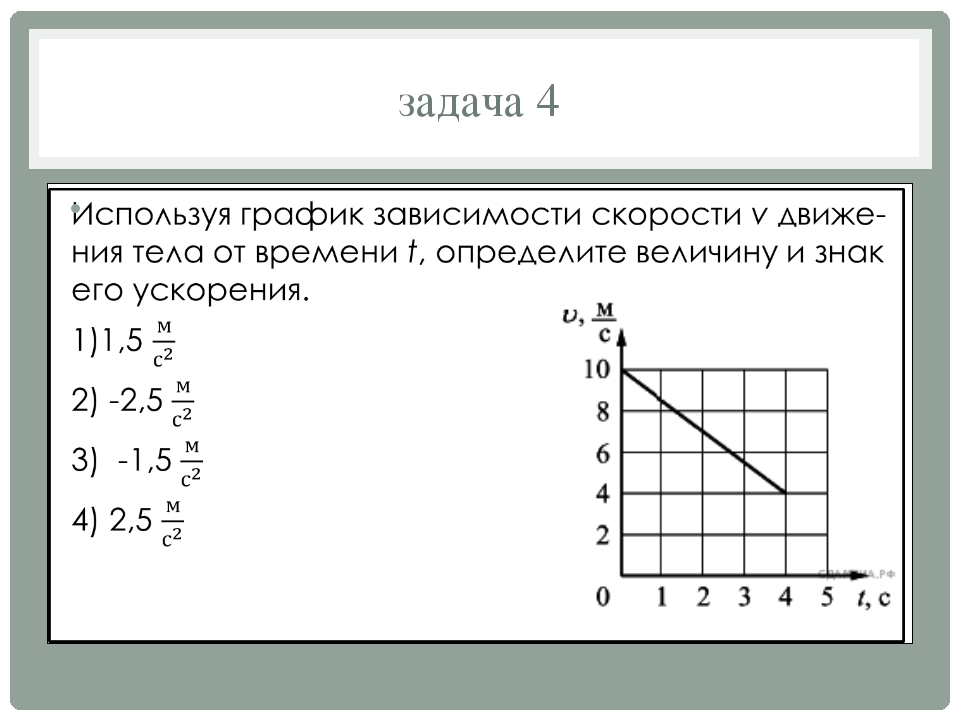 Все исследуемые
Все исследуемые
интервалы одинаковы
по длительности, поэтому
максимальному модулю
ускорения соответствует
максимальный модуль
изменения скорости в
течение интервала:
.
Из графика видно, что это интервал
от 20 до 30 с
(в
этом случае
,
на других интервалах
меньше).
Правильный
ответ: 3.
Ответ:
3
122
3
17.
Задание 1 № 128.
Тело движется по оси Ox.
На графике показана
зависимость проекции
скорости тела на ось Ox
от времени.
Каков
путь, пройденный телом к моменту
времени
1)
6 м
2)
8 м
3)
4 м
4)
5 м
Решение.
На
протяжении всего интервала
времени проекция скорости
тела на ось Ox
положительна.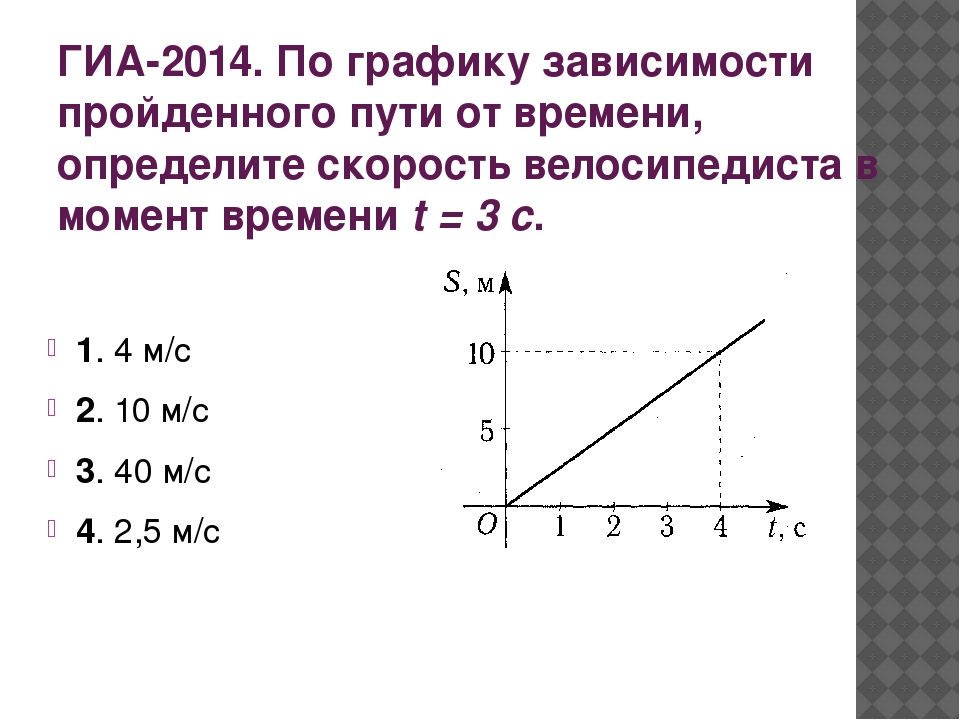 Поэтому,
Поэтому,
для того чтобы найти путь, пройденный
телом, необходимо вычислить
площадь под графиком (в единицах
произведения величин,
отложенных по осям координат).
К моменту времени
тело
прошло путь
.
Другой
способ решения заключается
в анализе каждого участка
графика в отдельности,
определения из графика
начальных скоростей и
ускорений на каждом этапе и
использования стандартных
кинематических формул
для пути.
Правильный
ответ: 1.
Ответ:
1
128
1
18.
Задание 1 № 130.
На рисунке приведен график
зависимости проекции
скорости тела
от
времени.
С
каким из графиков совпадает
график зависимости от
времени проекции ускорения
этого тела
в
интервале времени от 10 до
15 с?
1)
1
2)
2
3)
3
4)
4
Решение.
Из
графика видно, что в интервале
времени от 10 до 15 с проекция
скорости тела возрастала
линейно со временем, а значит,
проекция ускорения была
постоянна и равнялась
.
Проекция
ускорения тела в этом интервале
времени представлена на
графике 3.
Правильный
ответ: 3.
Ответ:
3
130
3
19.
Задание 1 № 132.
Автомобиль движется
прямолинейно. На графике
представлена зависимость
скорости автомобиля
от времени.
На
каком интервале времени
модуль его ускорения минимален?
1)
от 0 до 10 с
2)
от 10 с до 20 с
3)
от 20 с до 30 с
4)
от 30 до 40 с
Решение.
На
всех рассматриваемых
интервалах времени
скорость автомобиля
меняется равномерно,
следовательно ускорение
на каждом интервале
постоянно. Все исследуемые
интервалы одинаковы
по длительности, поэтому
минимальному модулю
ускорения соответствует
минимальный модуль изменения
скорости в течение интервала.
Из графика видно, что это интервал
от 0 до 10 с.
Правильный
ответ: 1.
Ответ:
1
132
1
20.
Задание 1 № 136.
На рисунке приведен график
зависимости проекции
скорости тела от времени.
На
каком из графиков представлена
проекция ускорения тела в
интервале времени от 24 до
30 с?
1)
1
2)
2
3)
3
4)
4
Решение.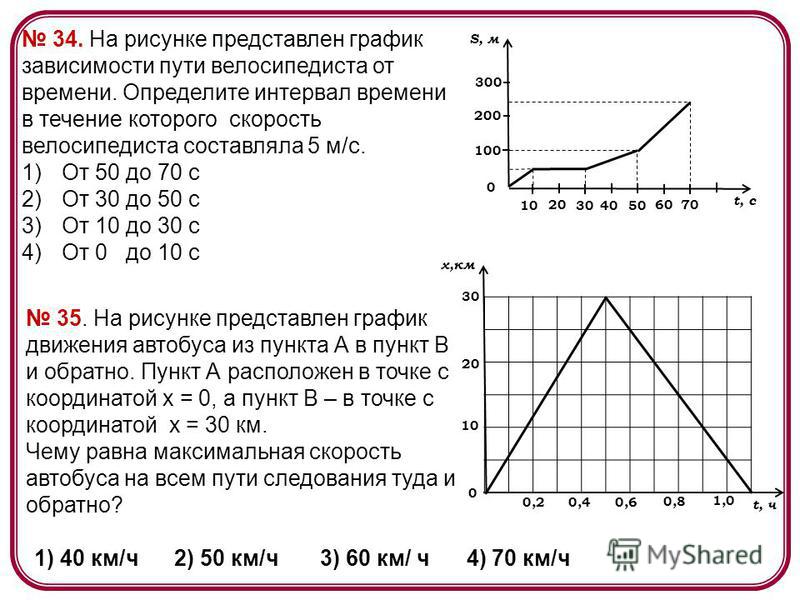
Из
графика видно, что в интервале
времени от 24 до 30 с проекция
скорости тела убывала
линейно со временем, а значит,
проекция ускорения была
постоянна и равнялась
.
Проекция
ускорения тела в этом интервале
времени представлена на
графике 3.
Правильный
ответ: 3.
Ответ:
3
136
3
21.
Задание 1 № 137.
На рисунке приведен график
зависимости проекции
скорости тела от времени.
На
каком из графиков представлена
проекция ускорения тела в
интервале времени от 4 до
10 с?
1)
1
2)
2
3)
3
4)
4
Решение.
Из
графика видно, что в интервале
времени от 0 до 6 с проекция
скорости тела возрастала
линейно со временем, а значит,
проекция ускорения была
постоянна и равнялась
.
Проекция
ускорения тела в этом интервале
времени представлена на
графике 1.
Правильный
ответ: 1.
Ответ:
1
137
1
22.
Задание 1 № 138.
На рисунке приведен график
зависимости проекции
скорости тела от времени.
На
каком графике представлена
проекция ускорения тела в
интервале времени от 30 до
40 с?
1)
1
2)
2
3)
3
4)
4
Решение.
Из
графика видно, что в интервале
времени от 30 до 40 с проекция
скорости тела не изменялась,
а значит, проекция ускорения
была равна нулю. Проекция ускорения
тела в этом интервале времени
представлена на графике
2.
Правильный
ответ: 2.
Ответ:
2
138
2
23.
Задание 1 № 140.
Тело начинает двигаться
из начала координат вдоль
оси Ox,
причем проекция скорости
меняется
с течением времени по
закону, приведенному
на графике.
Чему
будет равна проекция ускорения
тела
через
2 c?
1)
2)
3)
4)
Решение.
Из
графика видно, что проекция
скорости тела возрастала
со временем по линейному
закону, это означает, что
тело двигалось с постоянным
ускорением вдоль оси Ox.
Таким образом, проекция
ускорения тела через 2 c равна
.
Правильный
ответ: 2.
Ответ:
2
140
2
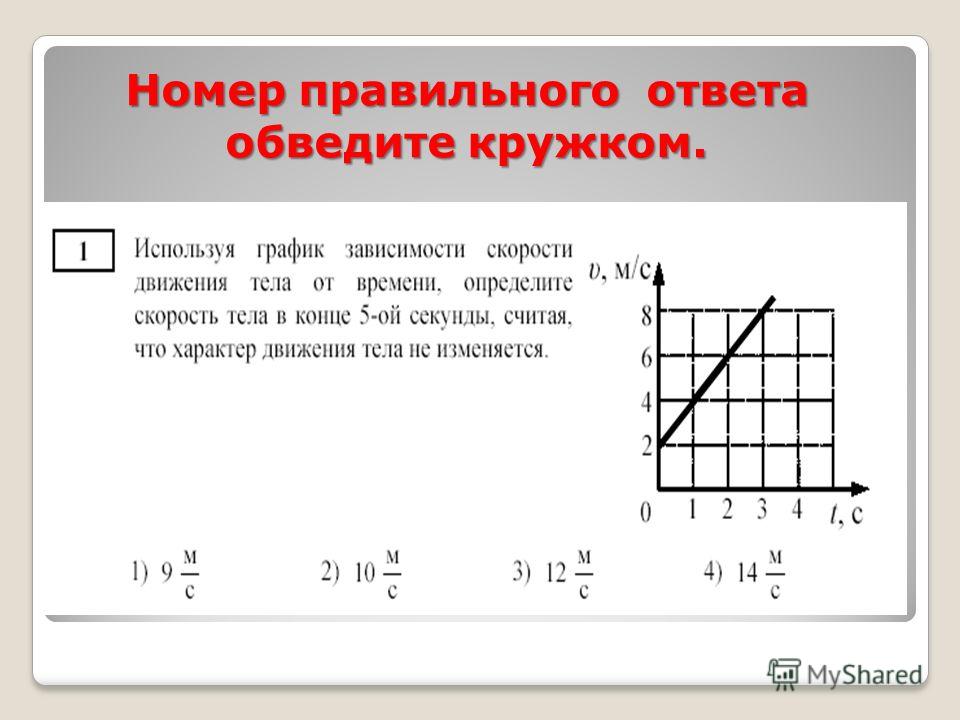
24.
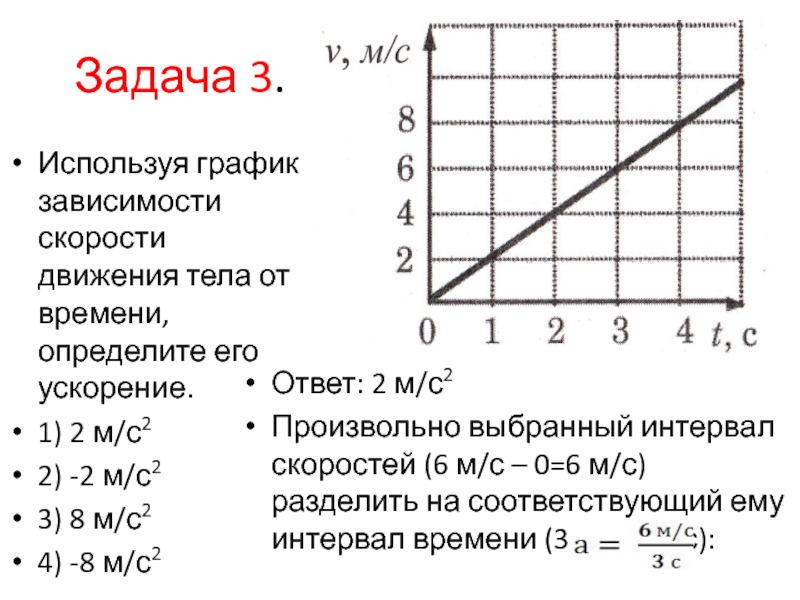
Задание 1 № 3323.
На
графике приведена
зависимость скорости
прямолинейного движущегося
тела от времени. Определите
модуль ускорения тела.
1)
2)
3)
4)
Решение.
Из
графика видно, что скорость
тела зависит линейно от
времени, а значит, его ускорение
постоянно. Для определения
модуля ускорения можно взять
любые две точки на графике:
.
Ответ:
1.
Ответ:
1
3323
1
25.
Задание 1 № 3324.
Тело
движется по оси х. По графику
зависимости проекции
скорости тела
от
времени t установите, какой
путь прошло тело за время от
до
.
1)
10 м
2)
15 м
3)
45 м
4)
20 м
Решение.
Необходимо
различать два понятия: путь
и перемещение. Путь —
величина строго положительная,
это длина пройденного телом
участка траектории. Под
перемещением же тела
понимается изменение
его координаты, перемещение
может быть отрицательным.
Пройденный телом путь определяется
зависимостью от времени
модуля скорости. Чтобы из
графика зависимости
проекции скорости тела от
времени получить график
модуля скорости, необходимо
зеркально отразить
относительно горизонтально
оси все отрицательные
участки. В данной задаче это
не столь принципиально,
поскольку на рассматриваем
интервале от
до
проекция
скорости тела остается
положительной, но в общем
случае это может привести к
нежелательной ошибке.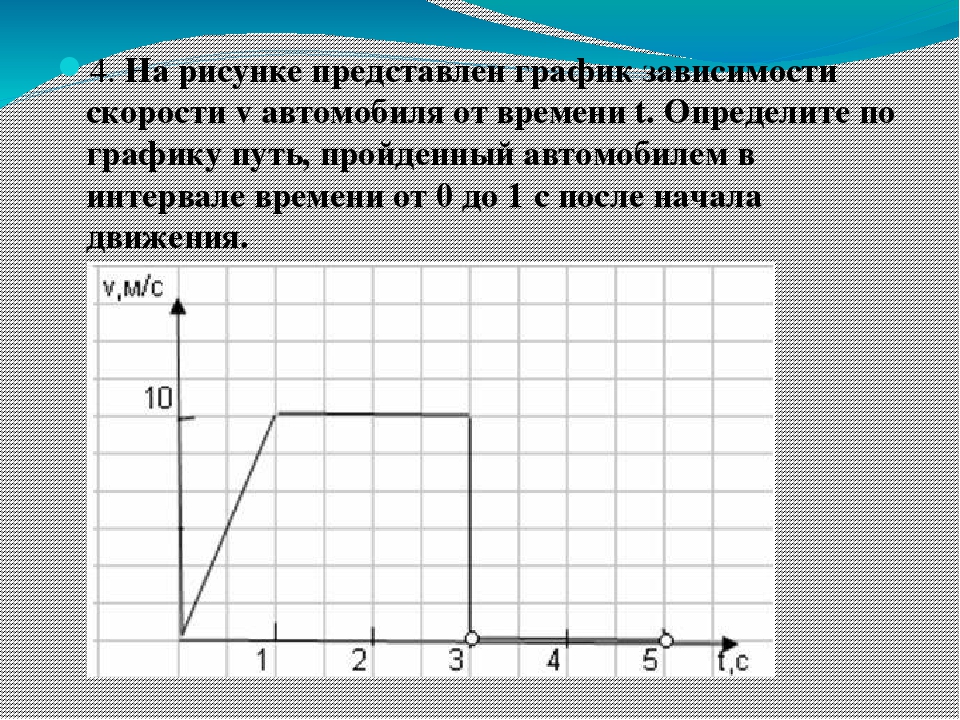
Тема «Кинематика». Задачи с графиками.
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ
1
По графику зависимости модуля
скорости тела от времени, представленного на рисунке, определите путь,
пройденный телом от момента времени 0 с до момента времени 2 с. (Ответ дайте в
метрах.)
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ
2
По графику зависимости модуля
скорости тела от времени, представленного на рисунке, определите путь,
пройденный телом от момента времени 0 с до момента времени 5 с. (Ответ дайте в
(Ответ дайте в
метрах.)
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ
3
На рисунке представлен график
зависимости модуля скорости тела от времени.
Найдите путь, пройденный телом за
время от момента времени 0 с до момента времени 5 с. (Ответ дайте в метрах.)
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ
4
На рисунке представлен график
зависимости модуля скорости υ автомобиля от времени t. Найдите путь,
Найдите путь,
пройденный автомобилем за 5 c. (Ответ дайте в метрах.)
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ
5
Тело движется по оси Ox. На графике
показана зависимость проекции скорости тела на ось Ox от времени. Каков путь,
пройденный телом к моменту времени t = 4 с? (Ответ дайте в метрах.)
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ
6
На рисунке представлен график
зависимости модуля скорости υ автомобиля от времени t. Определите по
Определите по
графику путь, пройденный автомобилем в интервале времени от 30 до 50 с после
начала движения. (Ответ дайте в метрах.)
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ
7
На рисунке представлен график
зависимости модуля скорости υ автомобиля от времени t. Определите по графику
путь, пройденный автомобилем в интервале времени от 0 до 30 с после начала
движения. (Ответ дайте в метрах.)
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ 8
Точечное тело движется вдоль горизонтальной
оси Ох.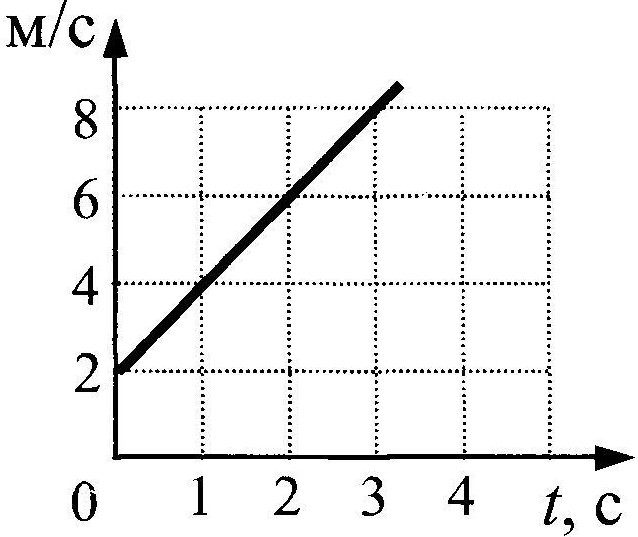 На рисунке представлен график зависимости проекции скорости υx
На рисунке представлен график зависимости проекции скорости υx
этого тела от времени t. Определите путь, пройденный телом за интервал времени
от 0 с до 4 с. Ответ выразите в метрах.
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ 9
Точечное тело движется вдоль
горизонтальной оси Ох. На рисунке представлен график зависимости проекции скорости
υx этого тела от времени t. Определите путь, пройденный телом
за интервал времени от 2 с до 6 с. Ответ выразите в метрах.
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ 10
Точечное тело движется вдоль
горизонтальной оси Ох. На рисунке представлен график зависимости
На рисунке представлен график зависимости
проекции скорости υx этого тела от времени t. Определите путь,
пройденный телом за интервал времени от 0 с до 4 с. Ответ выразите в метрах.
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ 11
Точечное тело движется вдоль
горизонтальной оси Ох. На рисунке представлен график зависимости
проекции скорости υx этого тела от времени t. Определите путь,
пройденный телом за интервал времени от 4 с до 7 с. Ответ выразите в метрах.
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ 12
Точечное тело движется вдоль
горизонтальной оси Ох. На рисунке представлен график зависимости
На рисунке представлен график зависимости
проекции скорости υx этого тела от времени t. Определите путь,
пройденный телом за интервал времени от 0 с до 6 с. Ответ выразите в метрах.
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ 13
Точечное тело движется вдоль
горизонтальной оси Ох. На рисунке представлен график зависимости
проекции скорости υx этого тела от времени t. Определите путь,
пройденный телом за интервал времени от 0 с до 10 с. Ответ выразите в метрах.
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ 14
Точечное тело движется вдоль
горизонтальной оси Ох.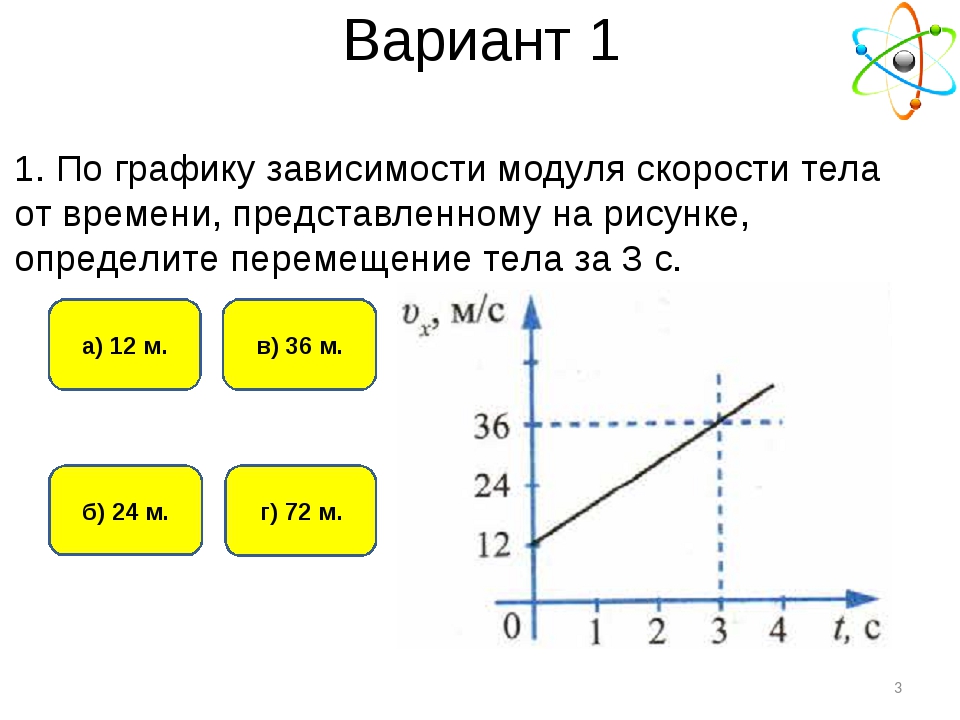 На рисунке представлен график зависимости
На рисунке представлен график зависимости
проекции скорости υx этого тела от времени t. Определите путь,
пройденный телом за интервал времени от 5 с до 20 с. Ответ выразите в метрах.
ТЕМА:
«КИНЕМАТИКА»
ЗАДАНИЕ:
АНАЛИЗ ГРАФИКОВ. ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
ВАРИАНТ 15
Точечное тело движется вдоль
горизонтальной оси Ох. На рисунке представлен график зависимости
проекции скорости υx этого тела от времени t. Определите путь,
пройденный телом за интервал времени от 1 с до 5 с. Ответ выразите в метрах.
Тест для 10 класса «Кинематика»
ФИЗИКА 10 КЛАСС Административная контрольная работа Вариант — №1 |
А1. А) если надо рассчитать период обращения ИСЗ вокруг Земли; Б) если надо рассчитать Архимедову силу, действующую на тело. В) оба случая правильные А2. Какая из величин скалярная? А) масса; Б) скорость; В) ускорение; Г) путь. А3. В каком случае движение тела равномерное? А). поезд в метро движется по прямолинейному пути. Он прибывает на станцию и отправляется от нее через одинаковые промежутки времени; Б). спутник движется по окружности вокруг Земли и за любые равные промежутки времени проходит одинаковые расстояния. В1. Скорость первого автомобиля относительно второго 30 км/ч, а относительно Земли 120 км/ч. Скорость второго автомобиля относительно Земли ____________ км/ч. (Автомобили движутся в одном направлении.) С1. Дан график зависимости скорости от времени. υ,м/с 15 10 5 1 2 3 t, с С2. Стрела выпущена из лука вертикально вверх со скоростью 20 м/с. Рассчитайте максимальную высоту подъема стрелы. С3. Мотоциклист совершает поворот по круговой траектории радиусом 50 м с постоянной по модулю скоростью 10 м/с. Каково ускорение и угловая скорость мотоциклиста? |
А1..Что образует систему отсчета? А) Тело Б) Система координат В) Часы Г) Тело отсчета, система координат, часы А2.Какая из величин векторная? А) время; Б) скорость; В) ускорение; Г) путь. А3.В каком случае движение тела равномерное? А) автобус движется по прямолинейному пути. Б) автомобиль движется по извилистой дороге и за любые равные промежутки времени проходит одинаковые расстояния. В1. По прямой дороге в одну сторону движутся легковой и грузовой автомобили со скоростями 72 км/ч и 54 км/ч соответственно. Скорость грузового автомобиля относительно легкового_______ км/ч. С1. Дан график зависимости скорости от времени. Определите путь пройденный телом за 3 секунды. υ, м/с 6 4 2 1 2 3 t, с С2. Тело брошено вертикально вверх со скоростью 30м/с. Какова максимальная высота подьема тела? С3. Трамвайный вагон движется на повороте по закруглению радиусом 40м. Рассчитайте линейную и угловую скорость трамвая, если центростремительное ускорение равно 0,4 м/с2. |
А1. А. Путь; Б. Перемещение; В. Скорость; Г. Ускорение. А2. Какое из уравнений описывает равноускоренное движение? А. Б. В. Г. А3. В каком из следующих случаев движение тела можно рассматривать как движение материальной точки? А. Вращение детали, обрабатываемой на токарном станке; Б. Движение поезда по мосту; В. Движение фигуриста на льду; Г. Полет самолета, совершающего рейс Минск – Москва. В1. Скорость движения теплохода вниз по реке 21 км/ч, а вверх — 17 км/ч. Скорость течения воды в реке _______ км/ч, собственная скорость теплохода ________ км/ч. С1. По заданному графику зависимости скорости от времени определите путь, пройденный телом за 4 секунды. С2. Рассчитайте время и скорость свободного падения тела с высоты 20 м. С3. Каковы центростремительное ускорение и угловая скорость поезда, движущегося по закруглению радиусом 800 м со скоростью 20м/с. ? |
А1. Какое из уравнений описывает равномерное движение? А. Б. В. Г. А2. Что называется перемещением? А. Путь, который проходит тело; Б. Вектор, соединяющий начальную и конечную точки траектории движения тела за данный промежуток времени; В. Длина траектории движения; Г. Путь, который проходит тело за единицу времени. А3. Основная задача кинематики … А. … установить причины движения тел; Б. … изучить условия равновесия тел; В. … определить положение тел в пространстве в любой момент времени. Г. … определить скорость движения. В1. Скорость течения реки 4 км/ч. Моторная лодка идет по течению со скоростью 15 км/ч (относительно воды). Со скоростью ________ км/ч она будет двигаться против течения (относительно берега). С1. По графику зависимости модуля скорости от времени определите путь, пройденный телом за 2 секунды. С2. Мяч упал на землю с высоты 80 м. Определите, сколько времени мяч находился в полете и с какой скоростью упал на землю. С3. Период обращения платформы карусельного станка 4с. Найдите линейную и угловую скорость крайних точек платформы, удаленных от оси вращения на 2м. |
Физика 10 класс
Административная контрольная работа по теме:
«Основы кинематики»
Цель: проверить усвоение знаний учащихся по кинематике.
П-и: понятия материальна точка, движение равномерное и неравномерное, прямолинейное, криволинейное,
формулы скорости, ускорения, перемещения, обозначение этих величин, их размерность.
Д-к: уметь читать графики, выражать неизвестные величины через известные
Ц-о: рационально распределять свое время, самооценка и саморазвитие уровня интеллектуальных способностей.
Количество баллов | Оценка | |
А1 теория «Механическое движение» | 1 б | 20-18 б — «5» 17-13 б — «4» 12-8 б — «3» менее 8б — «2» |
А2 теория «Механическое движение» | 1 б | |
А3 теория «Механическое движение» | 1 б | |
В1 Закон сложения скоростей | 2 б | |
С1 Равноускоренное движение | 5б | |
С2 Свободное падение тел | 5б | |
С3 Равномерное движение по окружности | 5б |
Ответы:
В-1 | В-2 | В-3 | В-4 | |
А1 | А | Г | А | Б |
А2 | А | Б. | Г | Б |
А3 | Б | Б | Г | В |
В1 | 90км/ч | -18км/ч | 2км/ч, 19 км/ч | 11 км/ч |
С1 | а=-3,3м/с2 s=15м | а=-1,3м/с2 s=6 м | А=-3 м/с2 s=24м | А= 0,5 м/с2 s=1м |
С2 | t=2c h=20м | t=3c h=45м | t=2c v=20м/c | t=4c v=40м/c |
С3 | а=2м/с2 ω=0,2 рад/с | v=4м/с ω=0,1 рад/с | а=0,5 м/с2 ω=0,025 рад/с | V=3,14 м/с ω=1,57 рад/с |
страница 1
Учебный материал Ответьте на вопросы:
Р З По графику пути (рис. 3) определите скорость движения тела. Задача 2. По графику скорости (рис. 4) определите путь, пройденный телом за 6 с. Как представить числовое значение пути, используя график скорости? З Скорость тела 20 м/с. Постройте график зависимости скорости от времени. Единицы масштаба выберите самостоятельно. З Д Задача 5. Какова скорость катера, график движения которого представлен на рис. 5? Задача 6. По графикам движений тел (рис. 6) можно утверждать, что: а) тела движутся по горкам разных наклонов; б) что скорости обоих тел одинаковы; в г) скорость первого тела в 2,5 раза больше скорости второго тела. Постройте графики скорости движения тел. Задача 7. Двигаясь с постоянными скоростями, пешеход прошел 5,4 км за час, а велосипедист 200 м проехал за 20 с. Постройте в одной системе координат: а) графики скорости названных тел; б) графики пути за 20 с движения. Задача 8. Н Задача 9. На рисунке 8 представлен график зависимости пути от времени. Как двигалось тело в течение времени движения? Определите путь s, пройденный телом, и скорости υ Задача 10. Используя график скорости движения тела (рис. 9), можно утверждать, что путь s 1 , пройденный за первые три секунды, и путь s 2 , пройденный за три последние секунды, связаны отношением: а) s 2 = 0,5s 1 ; б) s 2 = 1,5s 1 ; г) s 2 = 3s 1 . Задача 11. Упрощенный график скорости υ движения автомобиля приведен на рисунке 10. Охарактеризуйте движение автомобиля. Какие пути пройдены автомобилем на каждом участке движения? Какие детали графика опущены? Задача 12. Используя график скорости движения тела (рис. 11), можно доказать, что половина всего пути будет пройдена телом: а) к концу 10-й секунды; б) к концу 13-й секунды; в) к концу 18-й секунды; г) к концу 20-й секунды.
Наука никогда не решает вопроса, не поставив при этом десятка новых. Джорж Бернард Шоу ЛИСТ КОНТРОЛЯ
То, что должно вознестись на самый верх, начинается в самом низу. Гораций Человек, который попадает в цель, — талант; человек, который попадает в цель невидимую, — гений. Артур Шопенгауэр ДИФФЕРЕНЦИРОВАННОЕ ДОМАШНЕЕ ЗАДАНИЕ | |||
По графику зависимости модуля скорости от времени (см.рис2) определите ускорение прямолинейного движущегося тела ив момент времени t3с. Каково соответствующее уравнение проекции перемещения тела?
Контрольная работа№1 по теме : «Основы кинематики»
Вариант 1
Скорость тела, движущегося прямолинейно и равноускоренно, изменилась при перемещении из точки 1 в точку 2 так, как показано на рис.1. Какое направление имеет вектор ускорения на этом участке?
А) В)
Б) Г)направление может быть любым.
По графику зависимости модуля скорости от времени (см.рис2) определите ускорение прямолинейного движущегося тела ив момент времени t=3с.
А) 2м/с2 В)9 м/с2
Б)3 м/с2 Г)27 м/с2
По условию задачи 2 определите перемещение тела за 3с.
А)9м В)27м
Б)18м Г)36м
Уравнение зависимости проекции скорости движущегося тела от времени: Vx = 2+4t (м/с). Каково соответствующее уравнение проекции перемещения тела?
А) Sx = 2t + 3t2 В) Sx = 2t + 2t2
Б) Sx =1,5t2 Г) Sx = 3t + t2
Находящемуся на горизонтальной поверхности стола бруску сообщили скорость 5 м/с. Под действием сил трения брусок движется с ускорением 1м/с2. Чему равен путь, пройденный бруском за 6с?
А)5м Б)12м
В)12,5м Г)30м
6) Как, зная начальную и конечную скорость, ускорение, определить время?
А) t =(v/v0)/a B) t = S/v
Б) V = v0+at
_______________________________________________________________
Контрольная работа по теме : «Основы кинематики»
Вариант 2
Скорость тела, движущегося прямолинейно и равноускоренно, изменилась при перемещении из точки 1 в точку 2 так, как показано на рис.1. Какое направление имеет вектор ускорения на этом участке?
А) В)
Б) Г)направление может быть любым.
По графику зависимости модуля скорости от времени (см.рис2) определите ускорение прямолинейного движущегося тела ив момент времени t=2с.
А) 2м/с2 В) 7,5 м/с2
Б)5 м/с2 Г) 30 м/с2
По условию задачи 2 определите перемещение тела за 2с.
А)10м В)30м
Б)20м Г)40м
Уравнение зависимости проекции скорости движущегося тела от времени: Vx = 3+2t (м/с). Каково соответствующее уравнение проекции перемещения тела?
А) Sx = 2t + 3t2 В) Sx = 2t + 2t2
Б) Sx =1,5t2 Г) Sx = 3t + t2
Находящемуся на горизонтальной поверхности стола бруску сообщили скорость 4м/с. Под действием сил трения брусок движется с ускорением 1м/с2. Чему равен путь, пройденный бруском за 5с?
А)4м Б)7,5м
В)8м Г)20м
6) Как, зная начальную скорость тела и его ускорение, определить конечную скорость?
А) a =(v/v0)/t Б) v = s/t B) v = v0 + at
15
Приложенные файлы
- 24313231
Размер файла: 33 kB Загрузок: 0
6.2 Равномерное круговое движение — Физика
Задачи обучения разделу
К концу этого раздела вы сможете делать следующее:
- Описывать центростремительное ускорение и связывать его с линейным ускорением
- Опишите центростремительную силу и свяжите ее с линейной силой
- Решение проблем, связанных с центростремительным ускорением и центростремительной силой
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и кругов.
- (D) вычислить влияние сил на объекты, включая закон инерции, соотношение между силой и ускорением и характер пар сил между объектами.
Кроме того, Руководство лаборатории по физике для старших классов рассматривает содержание этого раздела лаборатории под названием «Круговое и вращательное движение», а также следующие стандарты:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях, используя уравнения, включая примеры снарядов и кругов.
Раздел Ключевые термины
| центробежная сила | центростремительное ускорение | центростремительная сила | равномерное круговое движение |
Центростремительное ускорение
Поддержка учителя
Поддержка учителя
[BL] [OL] Проверьте равномерное круговое движение.Попросите учащихся привести примеры кругового движения. Просмотрите линейное ускорение.
В предыдущем разделе мы определили круговое движение. Простейшим случаем кругового движения является равномерное круговое движение, когда объект движется по круговой траектории с постоянной скоростью . Обратите внимание, что, в отличие от скорости, линейная скорость объекта при круговом движении постоянно меняется, потому что он всегда меняет направление. Из кинематики мы знаем, что ускорение — это изменение скорости либо по величине, либо по направлению, либо по обоим направлениям.Следовательно, объект, совершающий равномерное круговое движение, всегда ускоряется, даже если величина его скорости постоянна.
Вы сами испытываете это ускорение каждый раз, когда едете в машине на повороте. Если во время поворота удерживать рулевое колесо неподвижно и двигаться с постоянной скоростью, вы совершаете равномерное круговое движение. Вы замечаете ощущение скольжения (или отбрасывания, в зависимости от скорости) от центра поворота. На вас действует не настоящая сила — это происходит только потому, что ваше тело хочет продолжать движение по прямой (согласно первому закону Ньютона), в то время как машина сворачивает с этого прямолинейного пути.Внутри машины создается впечатление, что вас оттесняют от центра поворота. Эта фиктивная сила известна как центробежная сила. Чем резче кривая и чем выше ваша скорость, тем заметнее становится этот эффект.
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Продемонстрируйте круговое движение, привязывая груз к веревке и вращая ее. Спросите студентов, что произойдет, если вы внезапно перережете веревку? В каком направлении движется объект? Почему? Что это говорит о направлении ускорения? Попросите учащихся привести примеры, когда они столкнулись с центростремительным ускорением.
На рис. 6.7 показан объект, движущийся по круговой траектории с постоянной скоростью. Направление мгновенной тангенциальной скорости показано в двух точках на пути. Ускорение происходит в направлении изменения скорости; в этом случае он указывает примерно на центр вращения. (Центр вращения находится в центре круговой траектории). Если мы представим, что ΔsΔs становится все меньше и меньше, тогда ускорение будет указывать точно на к центру вращения, но этот случай трудно изобразить.Мы называем ускорение объекта, движущегося в равномерном круговом движении, центростремительным ускорением a c , потому что центростремительное означает поиска центра .
Рисунок 6.7 Показаны направления скорости объекта в двух разных точках, и видно, что изменение скорости ΔvΔv указывает приблизительно на центр кривизны (см. Маленькую вставку). При очень малом значении ΔsΔs ΔvΔv указывает точно на центр круга (но это трудно изобразить).Поскольку ac = Δv / Δtac = Δv / Δt, ускорение также направлено к центру, поэтому a c называется центростремительным ускорением.
Поддержка учителей
Поддержка учителей
Обратите внимание на рисунок 6.7. На рисунке показан объект, движущийся по круговой траектории с постоянной скоростью, и направление мгновенной скорости двух точек на траектории. Ускорение происходит в направлении изменения скорости и указывает на центр вращения. Это строго верно только при стремлении ΔsΔs к нулю.
Теперь, когда мы знаем, что центростремительное ускорение направлено к центру вращения, давайте обсудим величину центростремительного ускорения. Для объекта, движущегося со скоростью по круговой траектории с радиусом , величина центростремительного ускорения составляет
.
Центростремительное ускорение больше на высоких скоростях и на крутых поворотах (меньший радиус), как вы могли заметить при вождении автомобиля, потому что автомобиль фактически толкает вас к центру поворота.Но немного удивительно, что a c пропорционально квадрату скорости. Это означает, например, что при повороте на 100 км / ч ускорение в четыре раза больше, чем при 50 км / ч.
Мы также можем выразить a c через величину угловой скорости. Подставляя v = rωv = rω в приведенное выше уравнение, мы получаем ac = (rω) 2r = rω2ac = (rω) 2r = rω2. Следовательно, величина центростремительного ускорения с точки зрения величины угловой скорости составляет
Советы для успеха
Уравнение, выраженное в форме a c = rω 2 , полезно для решения задач, в которых вам известна угловая скорость, а не тангенциальная скорость.
Virtual Physics
Движение божьей коровки в 2D
В этом моделировании вы экспериментируете с положением, скоростью и ускорением божьей коровки при круговом и эллиптическом движении. Переключите тип движения с линейного на круговое и наблюдайте за векторами скорости и ускорения. Затем попробуйте эллиптическое движение и обратите внимание, как векторы скорости и ускорения отличаются от векторов кругового движения.
Проверка захвата
Какой угол между ускорением и скоростью при равномерном круговом движении? Какое ускорение испытывает тело при равномерном круговом движении?
- Угол между ускорением и скоростью равен 0 °, и тело испытывает линейное ускорение.
- Угол между ускорением и скоростью равен 0 °, и тело испытывает центростремительное ускорение.
- Угол между ускорением и скоростью составляет 90 °, и тело испытывает линейное ускорение.
- Угол между ускорением и скоростью составляет 90 °, и тело испытывает центростремительное ускорение.
Центростремительная сила
Поддержка учителя
Поддержка учителя
[BL] [OL] [AL] Используя ту же демонстрацию, что и раньше, попросите учащихся предсказать отношения между величинами угловой скорости, центростремительного ускорения, массы, центростремительной силы.Предложите студентам поэкспериментировать, используя веревки разной длины и веса.
Поскольку объект в равномерном круговом движении испытывает постоянное ускорение (за счет изменения направления), мы знаем из второго закона движения Ньютона, что на объект должна действовать постоянная чистая внешняя сила.
Любая сила или комбинация сил могут вызвать центростремительное ускорение. Вот лишь несколько примеров: натяжение веревки на тросе, сила притяжения Земли на Луне, трение между дорогой и шинами автомобиля при движении по кривой или нормальная сила американских горок. следите за тележкой во время петли.
Любая чистая сила, вызывающая равномерное круговое движение, называется центростремительной силой. Направление центростремительной силы — к центру вращения, такое же, как и для центростремительного ускорения. Согласно второму закону движения Ньютона, чистая сила вызывает ускорение массы согласно F net = м a . Для равномерного кругового движения ускорение является центростремительным: a = a c . Следовательно, величина центростремительной силы F c равна Fc = macFc = mac.
Используя две разные формы уравнения для величины центростремительного ускорения, ac = v2 / rac = v2 / r и ac = rω2ac = rω2, мы получаем два выражения, включающих величину центростремительной силы F c . Первое выражение относится к тангенциальной скорости, второе — к угловой скорости: Fc = mv2rFc = mv2r и Fc = mrω2Fc = mrω2.
Обе формы уравнения зависят от массы, скорости и радиуса круговой траектории. Вы можете использовать любое более удобное выражение для центростремительной силы.Второй закон Ньютона также гласит, что объект будет ускоряться в том же направлении, что и чистая сила. По определению центростремительная сила направлена к центру вращения, поэтому объект также будет ускоряться к центру. Прямая линия, проведенная от круговой траектории к центру круга, всегда будет перпендикулярна тангенциальной скорости. Обратите внимание, что если вы решите первое выражение для r , вы получите
Из этого выражения мы видим, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть резкую кривую.
Рисунок 6.8 На этом рисунке сила трения f служит центростремительной силой F c . Центростремительная сила перпендикулярна тангенциальной скорости и вызывает равномерное круговое движение. Чем больше центростремительная сила F c , тем меньше радиус кривизны r и тем круче кривизна. Нижняя кривая имеет ту же скорость v , но большая центростремительная сила F c дает меньший радиус r’r ‘.
Watch Physics
Центростремительная сила и ускорение Intuition
В этом видео объясняется, почему центростремительная сила создает центростремительное ускорение и равномерное круговое движение. Он также охватывает разницу между скоростью и скоростью и показывает примеры равномерного кругового движения.
Поддержка учителей
Предупреждение о неправильном представлении
Поддержка учителей
Некоторые студенты могут запутаться между центростремительной силой и центробежной силой. Центробежная сила — это не реальная сила, а результат ускоряющейся системы отсчета, такой как вращающийся автомобиль или вращающаяся Земля.Центробежная сила относится к вымышленному центру , убегающему от силы .
Проверка захвата
Представьте, что вы качаете йойо по вертикальному кругу по часовой стрелке перед собой, перпендикулярно направлению, в которое вы смотрите. Если веревка порвется, когда йо-йо достигнет самого нижнего положения, ближайшего к полу. Что будет с йо-йо после разрыва струны?
- Йо-йо полетит внутрь в направлении центростремительной силы.
- Йо-йо полетит наружу в направлении центростремительной силы.
- Йо-йо полетит влево в направлении тангенциальной скорости.
- Йо-йо полетит вправо в направлении тангенциальной скорости.
Решение проблем центростремительного ускорения и центростремительной силы
Чтобы получить представление о типичных величинах центростремительного ускорения, мы проведем лабораторию по оценке центростремительного ускорения теннисной ракетки, а затем, в нашем первом рабочем примере, сравним центростремительное ускорение автомобиля, огибающего кривую, с ускорением свободного падения.Для второго рабочего примера мы вычислим силу, необходимую для поворота автомобиля на повороте.
Snap Lab
Оценка центростремительного ускорения
В этом упражнении вы будете измерять движение клюшки для гольфа или теннисной ракетки, чтобы оценить центростремительное ускорение конца клюшки или ракетки. Вы можете сделать это в замедленном режиме. Напомним, что уравнение центростремительного ускорения имеет вид ac = v2rac = v2r или ac = rω2ac = rω2.
- Одна теннисная ракетка или клюшка для гольфа
- Один таймер
- Одна линейка или рулетка
Порядок действий
- Работа с партнером.Стойте на безопасном расстоянии от вашего партнера, когда он или она размахивает клюшкой для гольфа или теннисной ракеткой.
- Опишите движение качелей — это равномерное круговое движение? Почему или почему нет?
- Постарайтесь сделать свинг как можно ближе к равномерному круговому движению. Какие корректировки нужно было внести вашему партнеру?
- Измерьте радиус кривизны. Что вы измерили физически?
- Используя таймер, найдите либо линейную, либо угловую скорость, в зависимости от того, какое уравнение вы решите использовать.
- Каково примерное центростремительное ускорение на основе этих измерений? Как вы думаете, насколько они точны? Почему? Как вы и ваш партнер можете сделать эти измерения более точными?
Подставка для учителя
Подставка для учителя
Размах клюшки или ракетки может быть очень близок к равномерному круговому движению. Для этого человек должен перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки — это радиус кривизны.Точность измерения угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки наблюдения человека. Размах клюшки или ракетки может быть очень близок к равномерному круговому движению. Для этого человек должен перемещать его с постоянной скоростью, не сгибая руки. Длина руки плюс длина клюшки или ракетки — это радиус кривизны. Точность измерения угловой скорости и углового ускорения будет зависеть от разрешающей способности используемого таймера и ошибки наблюдения человека.
Проверка захвата
Было ли более полезным использовать в этом упражнении уравнение ac = v2rac = v2r или ac = rω2ac = rω2? Почему?
- Должно быть проще использовать ac = rω2ac = rω2, потому что измерение угловой скорости путем наблюдения было бы проще.
- Должно быть проще использовать ac = v2rac = v2r, потому что измерение тангенциальной скорости посредством наблюдения было бы проще.
- Должно быть проще использовать ac = rω2ac = rω2, потому что измерение угловой скорости путем наблюдения было бы затруднительно.
- Должно быть проще использовать ac = v2rac = v2r, потому что измерение тангенциальной скорости посредством наблюдения было бы затруднительно.
Рабочий пример
Сравнение центростремительного ускорения автомобиля, огибающего кривую, с ускорением под действием силы тяжести
Автомобиль следует кривой радиусом 500 м со скоростью 25,0 м / с (около 90 км / ч). Какова величина центростремительного ускорения автомобиля? Сравните центростремительное ускорение для этой довольно пологой кривой, снятой на скорости по шоссе, с ускорением свободного падения ( g ).
Стратегия
Поскольку дана линейная, а не угловая скорость, наиболее удобно использовать выражение ac = v2rac = v2r, чтобы найти величину центростремительного ускорения.
Решение
Ввод данных значений v = 25,0 м / с и r = 500 м в выражение для a c дает
ac = v2r = (25,0 м / с) 2500 м = 1,25 м / с 2. ac = v2r = (25,0 м / с) 2500 м = 1,25 м / с2.
Обсуждение
Для сравнения с ускорением свободного падения ( g = 9.80 м / с 2 ), берем соотношение ac / g = (1,25 м / с2) / (9,80 м / с2) = 0,128 ac / g = (1,25 м / с2) / (9,80 м / с2) = 0,128. Следовательно, ac = 0,128gac = 0,128g, что означает, что центростремительное ускорение составляет примерно одну десятую ускорения свободного падения.
Рабочий пример
Сила трения на шинах автомобиля, огибающих кривую
- Рассчитайте центростремительную силу, действующую на автомобиль массой 900 кг, который движется по кривой радиусом 600 м на горизонтальной поверхности со скоростью 25,0 м / с.
- Статическое трение предотвращает скольжение автомобиля.Найдите величину силы трения между шинами и дорогой, которая позволяет автомобилю обогнуть поворот, не соскальзывая по прямой.
Стратегия и решение для (а)
Мы знаем, что Fc = mv2rFc = mv2r. Следовательно,
Fc = mv2r = (900 кг) (25,0 м / с) 2600 м = 938 Н. Fc = mv2r = (900 кг) (25,0 м / с) 2600 м = 938 Н.
Стратегия и решение для (b)
На изображении выше показаны силы, действующие на автомобиль при повороте кривой. На этой диаграмме автомобиль движется по странице, как показано, и поворачивает налево.Трение действует влево, ускоряя автомобиль к центру поворота. Поскольку трение — единственная горизонтальная сила, действующая на автомобиль, в этом случае оно обеспечивает всю центростремительную силу. Следовательно, сила трения является центростремительной силой в этой ситуации и направлена к центру кривой.
Обсуждение
Поскольку мы нашли силу трения в части (b), мы также можем найти коэффициент трения, поскольку f = μsN = μsmgf = μsN = μsmg.
Практические задачи
9.
Какое центростремительное ускорение ощущают пассажиры автомобиля, движущегося со скоростью 12 м / с по кривой радиусом 2,0 м?
- 3 м / с 2
- 6 м / с 2
- 36 м / с 2
- 72 м / с 2
10.
Вычислить центростремительное ускорение объекта, движущегося по траектории с радиусом кривизны 0,2 м и угловой скоростью 5 рад / с.
- 1 м / с
- 5 м / с
- 1 м / с 2
- 5 м / с 2
Проверьте свое понимание
11.
Что такое равномерное круговое движение?
- Равномерное круговое движение — это когда объект ускоряется по круговой траектории с постоянно увеличивающейся скоростью.
- Равномерное круговое движение — это когда объект движется по круговой траектории с переменным ускорением.
- Равномерное круговое движение — это когда объект движется по круговой траектории с постоянной скоростью.
- Равномерное круговое движение — это когда объект движется по круговой траектории с переменной скоростью.
12.
Что такое центростремительное ускорение?
- Ускорение объекта, движущегося по круговой траектории и радиально направленного к центру круговой орбиты
- Ускорение объекта, движущегося по круговой траектории и касательно направленного по круговой траектории
- Ускорение объекта, движущегося по линейной траектории и направленного в направлении движения объекта
- Ускорение объекта, движущегося по линейной траектории и направленного в направлении, противоположном движению объекта
13.
Существует ли чистая сила, действующая на объект при равномерном круговом движении?
- Да, объект ускоряется, поэтому на него должна действовать чистая сила.
- Да потому что разгона нет.
- Нет, потому что ускорение есть.
- Нет, потому что разгона нет.
14.
Укажите два примера сил, которые могут вызвать центростремительное ускорение.
- Сила притяжения Земли на Луну и нормальная сила
- Сила притяжения Земли на Луну и натяжение веревки на вращающемся тезерболе
- Нормальная сила и сила трения, действующие на движущийся автомобиль
- Нормальная сила и натяжение троса на тезерболе
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, усвоили ли учащиеся учебные цели этого раздела.Если учащиеся борются с определенной целью, формирующая оценка поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
Квадратичная Ячейки: Снаряд Для наших целей «снаряд»
Какая высота (вверху Затем т Обратите внимание на строительство s ( t ) …где « г » Запомните это уравнение
Хм … Не дали Они хотят, чтобы я нашел Но что это за вершина
Мои единицы на этот раз Так как это отрицательный Тогда объект находится на Не удивляйтесь, если многие
Наша начальная высота запуска В каждом случае мне нужно шахта: 0 Я проигнорирую негатив Время от времени они
Чтобы составить моё уравнение для Так « г » Затем т Примечание: на Земле это было бы Вверх
|
3.1.2: Распределения Максвелла-Больцмана — Химия LibreTexts
Уравнение Максвелла-Больцмана, лежащее в основе кинетической теории газов, определяет распределение скоростей газа при определенной температуре.Из этой функции распределения можно получить наиболее вероятную скорость, среднюю скорость и среднеквадратичную скорость.
Введение
Кинетическая молекулярная теория используется для определения движения молекулы идеального газа при определенных условиях. Однако, глядя на моль идеального газа, невозможно измерить скорость каждой молекулы в каждый момент времени. Следовательно, распределение Максвелла-Больцмана используется для определения количества молекул, движущихся между скоростями v и v + dv .2} {2k_BT}} дв \ label {1} \]
где
- dN / N — доля молекул, движущихся со скоростью от v до v + dv ,
- м — масса молекулы,
- k b — постоянная Больцмана, а
- T — абсолютная температура. 1
Кроме того, функция может быть записана в терминах скалярной количественной скорости c вместо векторной количественной скорости.2} {2k_BT}} \ label {2} \]
Наконец, распределение Максвелла-Больцмана можно использовать для определения распределения кинетической энергии для набора молекул. Распределение кинетической энергии идентично распределению скоростей для определенного газа при любой температуре. 2
Построение функции распределения Максвелла-Больцмана
На рисунке 1 показано распределение Максвелла-Больцмана скоростей для определенного газа при определенной температуре, например азота при 298 К.Скорость в верхней части кривой называется наиболее вероятной, потому что наибольшее количество молекул имеет эту скорость.
Рисунок 1 : Распределение Максвелла-Больцмана смещено в сторону более высоких скоростей и расширяется при более высоких температурах от OpenStax.
На рисунке 2 показано, как на распределение Максвелла-Больцмана влияет температура. При более низких температурах молекулы имеют меньше энергии. Следовательно, скорости молекул ниже, а распределение имеет меньший диапазон.По мере увеличения температуры молекул распределение выравнивается. Поскольку молекулы обладают большей энергией при более высокой температуре, молекулы движутся быстрее.
Рисунок 2 : Распределение Максвелла-Больцмана смещается в сторону более высоких скоростей и расширяется при более высоких температурах. из OpenStax.
На рис. 3 показана зависимость распределения Максвелла-Больцмана от массы молекулы. В среднем более тяжелые молекулы движутся медленнее, чем более легкие.Следовательно, более тяжелые молекулы будут иметь меньшее распределение скорости, в то время как более легкие молекулы будут иметь более широкое распределение скорости.
Рис. 3 : Функция плотности вероятности скорости для скоростей некоторых благородных газов при температуре 298,15 К (25 ° C). Ось Y находится в с / м, поэтому площадь под любым участком кривой (которая представляет вероятность того, что скорость находится в этом диапазоне) не имеет размеров. Рисунок используется с разрешения Википедии.
Выражения, связанные со скоростью
Три выражения скорости могут быть получены из распределения Максвелла-Больцмана: наиболее вероятная скорость, средняя скорость и среднеквадратичная скорость. Наиболее вероятная скорость — это максимальное значение на графике распределения. Это устанавливается путем определения скорости, когда следующая производная равна нулю
\ [\ dfrac {df (c)} {dc} | _ {C_ {mp}} = 0 \]
, что равно
\ [C_ {mp} = \ sqrt {\ dfrac {2RT} {M}} \ label {3a} \]
Средняя скорость — это сумма скоростей всех молекул, деленная на количество молекул.{\ infty} c f (c) dc = \ sqrt {\ dfrac {8RT} {\ pi M}} \ label {3b} \]
Среднеквадратичная скорость равна квадратному корню из квадрата средней скорости.
\ [C_ {rms} = \ sqrt {\ dfrac {3RT} {M}} \ label {3c} \]
где
- \ (R \) — газовая постоянная,
- \ (T \) — абсолютная температура, а
- \ (M \) — молярная масса газа.
Это всегда следует за таковым для газов, которые следуют распределению Максвелла-Больцмана (если термически обработаны)
\ [C_ {mp} 1.{20} \) молекулы аргона 3. C mp = 194,27 м / с C средн. = 219,21 м / с C rms = 237,93 м / с 4. Как указано выше, C mp является наиболее вероятной скоростью, поэтому она будет в верхней части кривой распределения. Справа от наиболее вероятной скорости будет средняя скорость, за которой следует среднеквадратичная скорость. 5. Совет: используйте соответствующие выражения для скорости, чтобы определить распределение молекул газа: гелий при 500 К.гелий при 300 К. аргон при 1000 К. Функция состояния — это свойство, значение которого не зависит от пути, выбранного для достижения этого конкретного значения. Напротив, функции, которые зависят от пути от двух значений, вызывают функции пути . Функции пути и состояния часто встречаются в термодинамике. При обсуждении соединений или химических реакций в первую очередь упоминается состояние конкретной молекулы или соединения. «Состояние» относится к температуре, давлению, количеству и типу присутствующего вещества. Как только государство установлено, можно определить функции состояния. Функции состояния — это значения, которые зависят от состояния вещества, а не от того, как это состояние было достигнуто. Например, плотность — это функция состояния, потому что на плотность вещества не влияет способ получения вещества.Рассмотрим количество H 2 O: не имеет значения, получен ли этот H 2 O из крана, из колодца или из бутылки, потому что, пока все три находятся в одинаковом состоянии, они имеют такая же плотность. Принимая решение о том, является ли определенное свойство функцией состояния или нет, помните следующее правило: влияет ли это свойство или значение на путь или способ его установления? Если ответ отрицательный, то это функция состояния, но если ответ положительный, то это не функция состояния. Другой способ представить функции состояния — интегралы. Интегралы зависят только от трех вещей: функции, нижнего предела и верхнего предела. Точно так же функции состояния зависят от трех вещей: свойства, начального значения и конечного значения. Другими словами, интегралы показывают, как функции состояния зависят только от конечного и начального значения, а не от истории объекта или пути, пройденного для перехода от начального к конечному значению.{t_1} \; H (t) dt = H (t_1) -H (t_o) \] Это эквивалентно знакомому определению энтальпии: \ [\ Delta H = H_ {final} — H_ {initial} \] Как представлено решением интеграла, энтальпия является функцией состояния, потому что она зависит только от начальных и конечных условий, а не от пути, выбранного для установления этих условий. Следовательно, интеграл функций состояния может быть взят только с двумя значениями: конечным и начальным значениями. С другой стороны, требуется несколько интегралов и несколько пределов интегрирования, чтобы взять интеграл от функции пути.Если интеграл определенного свойства можно вычислить, используя только свойство и его начальное и конечное значение, свойство является функцией состояния. Функции состояния определяются путем сравнения их с функциями пути. Как указывалось ранее, функция состояния — это свойство, значение которого не зависит от пути, пройденного для достижения этой конкретной функции или значения. По сути, если что-то не является функцией пути, это, вероятно, функция состояния. Чтобы лучше понять функции состояния, сначала определите функции пути, а затем сравните функции пути и состояния. Функции пути — это функции, которые зависят от пути, выбранного для достижения этого конкретного значения. Например, предположим, что на вашем сберегательном счете есть 1000 долларов. Предположим, вы хотите внести деньги на этот счет. Сумма, которую вы вносите, является функцией пути, потому что она зависит от пути, выбранного для получения этих денег. Другими словами, сумма денег, которую вы внесете на свой сберегательный счет, зависит от пути или способа получения этих денег. Если вы неделю работаете генеральным директором компании, а не неделю на заправке, в конце недели вы получите две разные суммы денег.Таким образом, функция пути — это свойство или значение, зависящее от пути, выбранного для установления этого значения. Функции состояния не зависят от пройденного пути. Используя тот же пример, предположим, что у вас есть 1000 долларов на сберегательном счете. Вы снимаете 500 долларов со своего сберегательного счета. Не имеет значения, снимаете ли вы 500 долларов за один прием или по ставке 50 долларов. В конце, когда вы получите свою ежемесячную выписку, вы заметите, что чистое снятие средств составляет 500 долларов, а итоговый баланс будет равен 500 долларам.Таким образом, банковский баланс является государственной функцией, потому что он не зависит от пути или способа снятия или внесения денег. В конце концов, независимо от того, делаете ли вы это за одну операцию или за несколько транзакций, ваш банковский счет останется неизменным. На рисунке ниже показаны функции состояния в виде энтальпии: Рисунок 1: Два разных пути из одного и того же начального и конечного состояний приводят к значениям переменных состояния На этом рисунке показаны два разных шага для формирования \ (NaCl _ {(s)} \). -_ {(g)} \ rightarrow NaCl _ {(s)} \ tag {5: формирование решетки} \] Когда добавляются энтальпии всех этих стадий, энтальпия образования \ (NaCl _ {(s)} \) все еще составляет -411 кДж / моль.Это прекрасный пример функции состояния: независимо от того, какой путь используется для образования \ (NaCl _ {(s)} \), в результате получается та же энтальпия образования -411 кДж / моль. 1 Последнее сравнение является обобщением, которое не обязательно справедливо для всех аспектов и расчетов, связанных с химией. Главное, что нужно помнить при попытке идентифицировать функцию состояния, — это определить, влияет ли путь, выбранный для достижения функции, на значение.Приведенная ниже аналогия показывает, как определить, является ли определенное свойство функцией состояния. Каждое утро миллионы людей должны решить, как добраться до своих офисов. Некоторые предпочитают подниматься по лестнице, а другие — на лифте. В этой ситуации ∆y, или изменение вертикального положения, одинаково независимо от того, поднимается ли человек по лестнице или на лифте. Расстояние от вестибюля до офиса остается неизменным, независимо от пути, по которому вы добираетесь до офиса. В результате ∆y является функцией состояния, поскольку ее значение не зависит от пути, по которому устанавливается ее значение. В той же ситуации время или ∆t не является функцией состояния. Если кто-то добирается до офиса более длинным путем (поднимается по лестнице), ∆t будет больше, а ∆t будет меньше, если воспользоваться лифтом. По этой аналогии ∆t не является функцией состояния, потому что его значение зависит от пути. Функции состояния обычно встречаются в термодинамике; многие уравнения термодинамики, такие как \ (\ Delta U \) и \ (\ Delta H \), являются функциями состояния.Кроме того, функции состояния имеют решающее значение в термодинамике, потому что они упрощают вычисления и позволяют вычислять данные, которые иначе могли бы быть получены только путем экспериментов. Более конкретно, функции состояния облегчают использование закона Гесса, который позволяет манипулировать (сложение, вычитание, умножение и т. Д.) Энтальпиями половинных реакций при добавлении нескольких полуреакций для образования полной реакции. Закон Гесса зависит от того факта, что энтальпия является функцией состояния.Если бы энтальпия не была функцией состояния, закон Гесса был бы намного сложнее, потому что нельзя было бы добавить энтальпии половинных реакций. Вместо этого потребуется несколько дополнительных вычислений. Кроме того, функции состояния и закон Гесса помогают вычислить энтальпию сложных реакций без необходимости фактически воспроизводить эти реакции в лаборатории. Все, что требуется, — это записать и просуммировать энтальпию полуреакций или гипотетических стадий, ведущих к химической реакции.Функции состояния также встречаются во многих других уравнениях, связанных с термодинамикой, таких как внутренняя энергия (∆U), свободная энергия Гибба, энтальпия и энтропия. Линейные функции применяются к задачам реального мира, которые связаны с постоянной скоростью. Применение линейных уравнений для решения задач о скорости изменения Линейные уравнения часто включают скорость изменения. Например, скорость, с которой расстояние изменяется во времени, называется скоростью. Если известны два момента времени и общее пройденное расстояние, можно определить скорость изменения, также известную как наклон. На основе этой информации можно написать линейное уравнение, а затем сделать прогнозы из уравнения линии. Если единица или количество, относительно которого что-то изменяется, не указаны, обычно ставка рассчитывается за единицу времени.Наиболее распространенный тип частоты — «в единицу времени», такой как скорость, частота сердечных сокращений и поток. Коэффициенты, не имеющие временного знаменателя, включают обменные курсы, уровень грамотности и электрическое поле (в вольтах на метр). При описании единиц частоты используется слово «per» для разделения единиц двух измерений, используемых для расчета частоты (например, частота пульса выражается «ударами в минуту»). Спортсмен начинает свою обычную тренировку перед следующим марафоном вечером.В 18:00 он начинает бежать и выходит из дома. В 19:30 спортсмен заканчивает забег дома и пробежал в общей сложности 7,5 миль. Какова была его средняя скорость во время бега? Скорость изменения — это скорость его бега; расстояние с течением времени. Следовательно, двумя переменными являются время [латекс] (x) [/ latex] и расстояние [latex] (y) [/ latex]. Первая точка находится в его доме, где его часы показывают 18:00. Это время начала, поэтому давайте установим его на [latex] 0 [/ latex]. Итак, наш первый пункт — [latex] (0,0) [/ latex], потому что он еще никуда не бегал.Давайте подумаем о нашем времени в часах. Наш второй пункт — [латекс] через 1,5 [/ латекс] часа спустя, и мы пробежали [латекс] 7,5 [/ латекс] миль. Второй пункт — [латекс] (1.5,7.5) [/ латекс]. Наша скорость (скорость изменения) — это просто наклон линии, соединяющей две точки. Наклон, определяемый выражением: [latex] m = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} [/ latex], становится [latex] m = \ frac {7.5} {1,5} = 5 [/ latex] миль в час. Чтобы построить график этой линии, нам нужен отрезок [latex] y [/ latex] и наклон для записи уравнения.Наклон составлял [латекс] 5 [/ латекс] миль в час, и поскольку начальная точка была в [латекс] (0,0) [/ латекс], интервал [латекс] y [/ латекс] равен [латекс] 0 [/латекс]. Итак, наша последняя функция [latex] y = 5x [/ latex]. График расстояния и времени: График [латекс] y = 5x [/ латекс]. Двумя переменными являются время [латекс] (x) [/ латекс] и расстояние [латекс] (y) [/ латекс]. Скорость бега составляет [латекс] 5 [/ латекс] миль в час. Используя график, можно делать прогнозы, предполагая, что его средняя скорость останется прежней. С помощью этой новой функции мы теперь можем ответить еще на несколько вопросов. Есть много таких приложений для линейных уравнений. Все, что связано с постоянной скоростью изменения, можно красиво представить линией с наклоном. В самом деле, если у вас есть только две точки, если вы знаете, что функция линейна, вы можете построить ее график и начать задавать вопросы! Просто убедитесь, что то, о чем вы спрашиваете, имеет смысл. Например, в примере с марафоном домен на самом деле только [latex] x \ geq0 [/ latex], поскольку нет смысла переходить в отрицательное время и терять мили! Линейные математические модели описывают реальные приложения с помощью линий. Применение линейных математических моделей к реальным задачам Математическая модель — это описание системы с использованием математических понятий и языка. Математические модели используются не только в естественных и инженерных дисциплинах, но и в социальных науках. Линейное моделирование может включать изменение численности населения, плату за телефонные звонки, стоимость аренды велосипеда, управление весом или сбор средств.Линейная модель включает скорость изменения [латекс] (м) [/ латекс] и начальную величину, точку пересечения по оси Y [латекс] b [/ латекс]. После того, как модель написана и построен график линии, любой из них можно использовать для прогнозирования поведения. Многие повседневные действия требуют использования математических моделей, возможно, неосознанно. Одна из трудностей математических моделей заключается в переводе реального приложения в точное математическое представление. Компания по аренде берет фиксированную плату в размере [латекс] 30 долларов [/ латекс] и дополнительно [латекс] 0,25 доллара [/ латекс] за милю за аренду движущегося фургона. Напишите линейное уравнение для аппроксимации стоимости [латекс] y [/ латекс] (в долларах) через [латекс] x [/ латекс], количество пройденных миль. Сколько будет стоить поездка на 75 миль? Использование формы линейного уравнения с пересечением наклона с общей стоимостью, обозначенной [латекс] y [/ латекс] (зависимая переменная), и милями, обозначенными [латекс] x [/ латекс] (независимая переменная): [латекс] \ displaystyle y = mx + b [/ латекс] Общая стоимость равна ставке за милю, умноженной на количество пройденных миль, плюс стоимость фиксированной платы: [латекс] \ displaystyle y = 0.25x + 30 [/ латекс] Чтобы рассчитать стоимость поездки [латекс] 75 [/ латекс] миль, подставьте [латекс] 75 [/ латекс] вместо [латекс] x [/ латекс] в уравнение: [латекс] \ displaystyle \ begin {align} y & = 0,25x + 30 \\ & = 0,25 (75) +30 \ & = 18,75 + 30 \\ & = 48,75 \ end {align} [/ latex] Также возможно моделировать несколько линий и их уравнения. Изначально поезда A и B находятся на расстоянии 325 [/ латексных] миль друг от друга.Поезд A движется в сторону B со скоростью [латекс] 50 [/ latex] миль в час, а поезд B движется в сторону A со скоростью [латекс] 80 [/ latex] миль в час. В какое время встретятся два поезда? В это время, как далеко проехали поезда? Во-первых, начните с исходных позиций поездов ([latex] y [/ latex] -tercepts, [latex] b [/ latex]). Начало поезда A — это источник, [latex] (0,0) [/ latex]. Поскольку поезд B находится в [латексе] 325 [/ latex] милях от поезда A изначально, его позиция — [латекс] (0,325) [/ латекс]. Во-вторых, чтобы написать уравнения, представляющие общее расстояние каждого поезда с точки зрения времени, вычислите скорость изменения для каждого поезда. Поскольку поезд A движется к поезду B, который имеет большее значение [latex] y [/ latex], скорость изменения поезда A должна быть положительной и равняться его скорости [latex] 50 [/ latex]. Поезд B движется к A, который имеет меньшее значение [latex] y [/ latex], что дает B отрицательную скорость изменения: [latex] -80 [/ latex]. Таким образом, две строки: [латекс] \ displaystyle y_A = 50x \\ [/ latex] А: [латекс] \ displaystyle y_B = -80x + 325 [/ латекс] Два поезда встретятся там, где пересекаются две линии.Чтобы найти место пересечения двух линий, приравняйте уравнения друг к другу и решите для [latex] x [/ latex]: [латекс] \ displaystyle y_ {A} = y_ {B} [/ latex] [латекс] \ displaystyle 50x = -80x + 325 [/ латекс] Решение для [latex] x [/ latex] дает: [латекс] \ displaystyle x = 2,5 [/ латекс] Два поезда встречаются через [латекс] 2,5 [/ латекс] часа. Чтобы найти его, подставьте [латекс] 2,5 [/ латекс] в любое уравнение. Подставляя его в первое уравнение, мы получаем [латекс] 50 (2.5) = 125 [/ latex], что означает, что он встречается после того, как A пролетит [latex] 125 [/ latex] миль. Вот графическая модель расстояния от времени для двух поездов: Поезда: поезд A (красная линия) представлен уравнением: [латекс] y = 50x [/ latex], а поезд B (синяя линия) представлен уравнением: [латекс] y = -80x + 325 [/ латекс]. Два поезда встречаются в точке пересечения [латекс] (2,5,125) [/ латекс], что через [латекс] 125 [/ латекс] миль за 2,5 [/ латекс] часа. Подгонка кривой с помощью линии пытается провести линию так, чтобы она «наилучшим образом соответствовала» всем данным. Используйте формулу регрессии наименьших квадратов для вычисления линии наилучшего соответствия для набора точек Аппроксимация кривой — это процесс построения кривой или математической функции, которая наилучшим образом соответствует ряду точек данных, возможно, с учетом ограничений. Аппроксимация кривой может включать либо интерполяцию, когда требуется точное соответствие данным, либо сглаживание, при котором строится «гладкая» функция, которая приблизительно соответствует данным.Подгонянные кривые можно использовать в качестве вспомогательного средства для визуализации данных, для вывода значений функции, когда данные недоступны, и для суммирования взаимосвязей между двумя или более переменными. Экстраполяция относится к использованию подобранной кривой за пределами диапазона наблюдаемых данных и подвержена большей степени неопределенности, поскольку она может отражать метод, использованный для построения кривой, в той же степени, в какой он отражает наблюдаемые данные. В этом разделе мы будем подгонять линии только к точкам данных, но следует отметить, что к данным можно подобрать полиномиальные функции, круги, кусочные функции и любое количество функций, и это широко используемая тема в статистике. . Линейная регрессия — это подход к моделированию линейной связи между зависимой переменной [latex] y [/ latex] и независимой переменной [latex] x [/ latex]. При линейной регрессии обнаруживается, что линия в форме пересечения наклона [латекс] y = mx + b [/ latex] «лучше всего соответствует» данным. Самая простая и, возможно, самая распространенная модель линейной регрессии — это обычное приближение наименьших квадратов. Это приближение пытается минимизировать суммы квадратов расстояния между линией и каждой точкой.{n} x_ {i} [/ латекс]. Используя эти значения [latex] m [/ latex] и [latex] b [/ latex], мы теперь имеем линию, которая аппроксимирует точки на графике. За [латекс] n = 8 [/ latex] баллов: [латекс] (- 1,0), (0,0), (1,1), (2,2), (3,1), (4 , 2,5), (5,3) [/ латекс] и [латекс] (6,4) [/ латекс].{n} x_ {i} \\ [/ latex]: [латекс] \ displaystyle b \ ок. 1,6875-0,554 (2,5) = 0,3025. [/ Латекс] Таким образом, наше окончательное уравнение [латекс] y = 0,554x + 0,3025 [/ латекс], и эта линия нанесена на график вместе с точками. Least Squares Fit Line: Линия, найденная методом наименьших квадратов, [латекс] y = 0,554x + 0,3025 [/ latex]. Обратите внимание на 4 точки над линией и 4 точки под линией. Если у нас есть точка, которая находится далеко от аппроксимирующей линии, это исказит результаты и сделает линию намного хуже.Например, в нашем исходном примере вместо точки [latex] (- 1,0) [/ latex] мы имеем [latex] (- 1,6) [/ latex]. Используя те же вычисления, что и выше, с новой точкой, результаты следующие: [латекс] m \ приблизительно0,0536 [/ латекс] и [латекс] b \ приблизительно2,3035 [/ латекс], чтобы получить новое уравнение [латекс] y = 0,0536x + 2,3035 [/ латекс]. Если посмотреть на точки и линию на новом рисунке ниже, эта новая линия не соответствует данным из-за выброса [latex] (- 1,6) [/ latex]. Действительно, попытка подогнать линейные модели к данным, которые являются квадратичными, кубическими или какими-либо нелинейными, или к данным со многими выбросами или ошибками, может привести к плохим приближениям. Приближенная линия выброса: вот приблизительная линия с учетом новой точки выброса в (-1, 6). Визуализация зависимостей модуля Python. Этот пакет устанавливает Из оболочки: Подробные примеры использования можно найти под историей версий. Примечание: pydeps находит импорт, ища коды операций импорта в Создание графика: Для создания графиков вам необходимо установить Graphviz. Следуйте инструкциям Отображение графика: Для отображения результирующих файлов Это можно изменить с помощью опции Вы также можете экспортировать имя такой программы просмотра в Запросы функций и отчеты об ошибках: Пожалуйста, сообщайте об ошибках и пожеланиях на GitHub по адресу Версия 1.9.10 Версия 1.9.8 Исправление для Версия 1.9.7 Проверьте Версия 1.9.6 Версия 1.9.1 Графики теперь стабильны и на Python 3.x — Версия 1.9.0 поддерживает Python 3.8. Версия 1.8.7 включает новый флаг Версия 1.8.5 С svg в качестве выходного формата (который используется по умолчанию), Версия 1.8.2 включает новый флаг Версия 1.8.0 включает 4 новых флага для рисования внешних зависимостей как Версия 1.7.3 включает новый флаг Версия 1.7.2 включает новый флаг Версия 1.7.1 исправлений исключены в файлах .pydeps (спасибо eqvis Версия 1.7.0 Новый флаг Версия 1.5.0 Поддержка Python 3 (спасибо восьмому за PR). Версия 1.3.4 Версия 1.2.8 Ярлык для поиска прямых внешних зависимостей , который выведет на экран список имен модулей в формате json, например: , что означает, что пакет Эта функция также доступна программно: Версия 1.2.5: Значения по умолчанию теперь разумны, например: , скорее всего, сделает то, что вы хотите. Это то же самое, что и Запуск pydeps pydeps –max-bacon = 4 на pydeps версии 1.8.0 дает следующий график: Если вас не интересует внутренняя структура внешних модулей, вы можете добавить флаг Чтобы увидеть внутреннюю структуру _и_ разграничить внешние модули, используйте флаг или, используя меньший максимальный размер кластера: Чтобы удалить кластеры со слишком небольшим количеством узлов, используйте флаг В некоторых ситуациях может быть полезно нарисовать целевой модуль как кластер: ..и поскольку поля кластера включают имя модуля, мы можем удалить эти префиксы: Каталожные номера Blalock, H. (Ed.) (1971). Причинные модели в социальных науках. Алдин-Атертон, Чикаго. Блэлок, Х. (1961). Причинные выводы в неэкспериментальных исследованиях. Пресса Университета Северной Каролины, Чапел-Хилл, Северная Каролина. Костнер, Х. (1971). Теория, дедукция и правила переписки. Причинные модели в социальных науках, Blalock, H. (ed.). Олдин, Чикаго. Гейгер Д. и Перл Дж. (1989b). Аксиомы и алгоритмы выводов с использованием условной независимости. Отчет CSD 8 , R-119-I, Лаборатория когнитивных систем, Калифорнийский университет, Лос-Анджелес. Гейгер Д., Верма Т. и Перл Дж. (1990) Определение независимости в байесовских сетях. Сети 20, 507-533. Глимур, К., Шайнс, Р., Спиртес, П., и Келли, К. (1987). Обнаружение причинной структуры. Academic Press, Сан-Диего, Калифорния. Кивери, Х. и Спид, Т. (1982). Структурный анализ многомерных данных: обзор. Социологическая методология, Лейнхард, С. (ред.). Джосси-Басс, Сан-Франциско. Перл, Дж. (1988). Вероятностное мышление в интеллектуальных системах. Морган и Кауфман, Сан-Матео. Перл, Дж. (1995). Причинно-следственные диаграммы для эмпирических исследований. Биометрика, 82, с. 669-710. Перл, Дж.и Dechter, R. (1989). Структура обучения на основе данных: опрос. Труды COLT ’89, 30–244. Перл, Дж., Гейгер, Д. и Верма, Т. (1990). Логика диаграмм влияния. Диаграммы влияния, сети убеждений и анализ решений. Р. Оливер и Дж. Смит, редакторы. John Wiley & Sons Ltd. Перл, Дж. И Верма, Т. (1991). Теория предполагаемой причинности. Принципы представления и рассуждения знаний: материалы второй международной конференции, Морган Кауфманн, Сан-Матео, Калифорния. Перл, Дж. И Верма, Т. (1990). Формальная теория индуктивной причинности. Технический отчет R-155, Лаборатория когнитивных систем, Департамент компьютерных наук Калифорнийского университета в Лос-Анджелесе. Перл, Дж. И Верма, Т. (1987). Логика представления зависимостей ориентированными графами. Отчет CSD 870004, R-79-II, Калифорнийский университет в лаборатории когнитивных систем Лос-Анджелеса. Ричардсон Т. (1994). Свойства циклических графических моделей. Магистерская диссертация, Ричардсон (1995).Полиномиальный алгоритм определения марковской эквивалентности Райхенбах, Х. (1956). Направление времени. Univ. из California Press, Беркли, Калифорния. Лосось, W. (1980). Вероятностная причинность. Pacific Philosophical Quarterly 61, 50-74. Спиртес, П. (1994a). «Условная независимость в ориентированных циклических графических моделях для обратной связи». Технический отчет CMU-PHIL-54, Департамент философии, Университет Карнеги-Меллона, Питтсбург, Пенсильвания. Spirtes, P., Glymour, C., & Scheines, R. (1993). Причинно-следственная связь, предсказание и поиск. Конспект лекций Springer-Verlag по статистике 81 ,. Спрингер-Верлаг, штат Нью-Йорк. Спиртес, П., Ричардсон, Т., Мик, К., Шайнс, Р., и Глимур, К. (1996). Использование d-разделения для вычисления нулевых частных корреляций в линейных моделях с коррелированными ошибками. Технический отчет CMU-PHIL-72, кафедра философии, Университет Карнеги-Меллона, Питтсбург, Пенсильвания, 15213. Suppes, P. (1970). Вероятностная теория причинности.Северная Голландия, Амстердам. . Список литературы
Проблемы
ответы
Авторы и авторство
Функции состояния и пути — Chemistry LibreTexts
Введение
Математика функций состояния
Функции состояния и функции пути
Состояние Функция Функция пути Независимо от пути, использованного для определения свойства или стоимости. Зависит от пути, по которому устанавливается свойство или стоимость. Возможна интеграция с использованием конечных и начальных значений. Требуются множественные интегралы и пределы интегрирования для интеграции. Несколько шагов приводят к одному и тому же значению. Несколько шагов приводят к разному значению. На основе установленного состояния системы (температура, давление, количество и идентичность системы). На основе того, как было установлено состояние системы. Обычно обозначается заглавной буквой. 1 Обычно обозначается строчной буквой. 1 Аналогия
Приложения
Проблемы
Решения
Список литературы
Авторы и авторство
приложений линейных функций | Безграничная алгебра
Скорость изменения
Цели обучения
Основные выводы
Ключевые моменты
Ключевые термины
Скорость изменения
Скорость изменения: приложение реального мира
Пример
Пример: Постройте линию, показывающую скорость
Линейные математические модели
Цели обучения
Основные выводы
Ключевые моменты
Ключевые термины
Математические модели
Линейная модель в реальной жизни
Пример: аренда фургона
Модель из реальной жизни с несколькими уравнениями
Пример
Подгонка по кривой
Цели обучения
Основные выводы
Ключевые моменты
Ключевые термины
Криволинейная арматура
Формула линейной регрессии
Использование приближения наименьших квадратов
Пример: напишите линию наименьших квадратов, а затем изобразите линию, которая наилучшим образом соответствует данным
Выбросы и регрессия методом наименьших квадратов
pydeps — документация pydeps 1.9.10
pydeps
команда, и обычное использование будет использовать ее из командной строки. оболочка> pydeps [флаги] каталог-модуля
байт-коды python (например, файлов .pyc, ). Поэтому только импортированные файлы
будут найдены (т.е. pydeps не будет искать файлы в вашем каталоге,
не импортируются). Кроме того, только файлы, которые можно найти с помощью
будет рассмотрен механизм импорта Python (т. е. если модуль
отсутствует или не установлен, он не будет включен независимо от того,
импортируется). Это можно изменить, используя --include-missing .
флаг, описанный ниже.
инструкции по установке, приведенные в ссылке на Graphviz (и
убедитесь, что на вашем пути есть команда dot ). .svg или .png , по умолчанию pydeps
вызывает соответствующий открыватель для платформы, например xdg-open foo.svg . --display PROGRAM , где PROGRAM — это
исполняемый файл, который может отображать файл изображения графика. PYDEPS_DISPLAY
или BROWSER переменная среды, которая изменяет поведение по умолчанию
когда --display не используется.
https://github.com/thebjorn/pydeps/issues no_show теперь учитывается при размещении в .pydeps файл.
Спасибо romain-dartigues за PR. превышение максимальной глубины рекурсии при использовании большого
frameworks (например, sympy ). Спасибо tanujkhattar за поиск исправления и
балопат за сообщение об этом. PYDEPS_DISPLAY и BROWSER , чтобы открыть программу
граф, PR jhermann --no-show и --no-dot как псевдонимы для --noshow
и - узел , PR jhermann
это уже имело место для Py2.7 (спасибо pawamoy за сообщение
и тестирование проблемы и киноу за помощь с тестированием). --rmprefix , который позволяет удалить
префиксы из меток узлов в графе. _Name_ узлов не влияет
так что это не вызывает слияния узлов и не меняет окраску — но это
может привести к нескольким узлам с одинаковой меткой (при наведении указателя мыши на узел
дайте полное название).Спасибо aroberge за запрос на улучшение.
пути теперь подсвечиваются при наведении курсора мыши (спасибо tomasito665 за
запрос об улучшении). - только , который заставляет pydeps
отчет только по указанным путям: оболочка> pydeps mypackage --only mypackage.a mypackage.b
кластеры.См. Примеры ниже.
Кроме того, стрелки теперь имеют цвет исходного узла. -xx или --exclude-точный , который
соответствует функциональности флага --exclude , за исключением того, что для этого требуется
точное совпадение, т.е. -xx foo.bar исключает foo.bar, но не
foo.bar.blob (спасибо AvenzaOleg за пиар). - no-output , который предотвращает
создание.svg / .png файл.
для отчета об ошибке). --reverse меняет направление
стрелок на графике зависимостей, поэтому они указывают _ на импортированный
модуль вместо _из_ импортированного модуля (спасибо goetzk за
отчет об ошибке и тобиасмайер для пиара!). --externals теперь будет включать модули,
не установлены ( modulefinder называет badmodules ).
пакета добавлено: pydeps --externals mypackage
(разработчик) перейти | c: \ srv \ lib \ dk-tasklib> pydeps --externals dktasklib
[
"dkfileutils"
]
dktasklib зависит только от пакета dkfileutils
упаковка. импорт ОС
из pydeps.pydeps импортировать внешние
# каталог, содержащий setup.py (на один уровень выше фактического пакета):
os.chdir ('каталог-пакета')
напечатать внешние ('mypackage')
pydeps --show --max-bacon = 2 mypackage , что означает отображение
график зависимостей в вашем браузере, но ограничьте его двумя прыжками (что
включает только те модули, которые импортирует ваш модуль, без продолжения
вниз по цепочке импорта).Старое поведение по умолчанию доступно с
pydeps --noshow --max-bacon = 0 mypackage . --cluster , который
сворачивает внешние модули в объекты в форме папок: оболочка> pydeps pydeps --max-bacon = 4 --cluster
--max-cluster-size , который управляет
сколько узлов может быть в кластере, прежде чем он будет свернут в значок папки: оболочка> pydeps pydeps --max-bacon = 4 --cluster --max-cluster-size = 1000
оболочка> pydeps pydeps --max-bacon = 4 --cluster --max-cluster-size = 3
--min-cluster-size : оболочка> pydeps pydeps --max-bacon = 4 --cluster --max-cluster-size = 3 --min-cluster-size = 2
оболочка> pydeps pydeps --max-bacon = 4 --cluster --max-cluster-size = 3 --min-cluster-size = 2 --keep-target-cluster
оболочка> pydeps pydeps --max-bacon = 4 --cluster --max-cluster-size = 3 --min-cluster-size = 2 --keep-target-cluster --rmprefix pydeps. stdlib_list.
D-разделение
Университет Карнеги Меллон.
направленных циклических графических моделей, Технический отчет PHIL-63,
Философский факультет Университета Карнеги-Меллона.
Ричард Шайнс ([email protected]) / Университет Карнеги-Меллона

 В каком случае тело можно считать материальной точкой?
В каком случае тело можно считать материальной точкой? Определите путь, пройденный телом за 3 секунды.
Определите путь, пройденный телом за 3 секунды. Он прибывает к остановке через одинаковые промежутки времени и через равные интервалы отбывает от них;
Он прибывает к остановке через одинаковые промежутки времени и через равные интервалы отбывает от них; Какие из перечисленных величин являются скалярными?
Какие из перечисленных величин являются скалярными?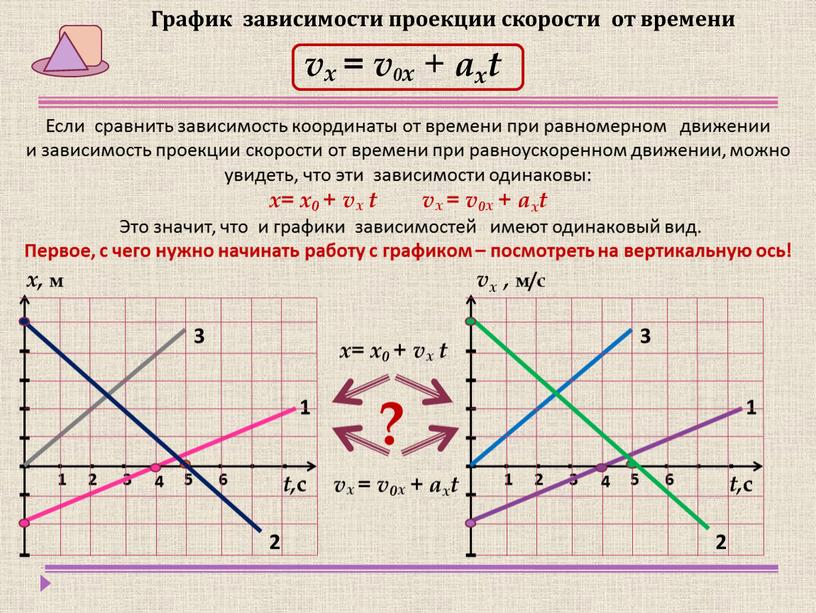

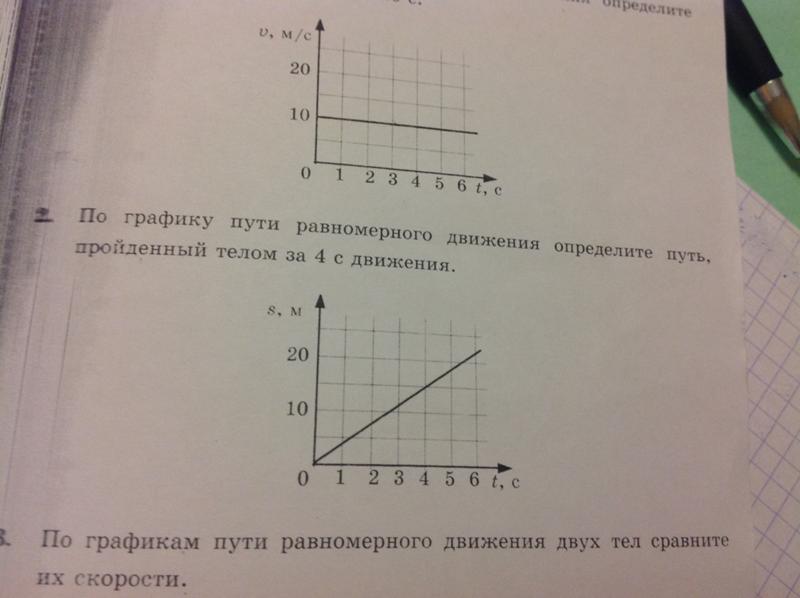 В
В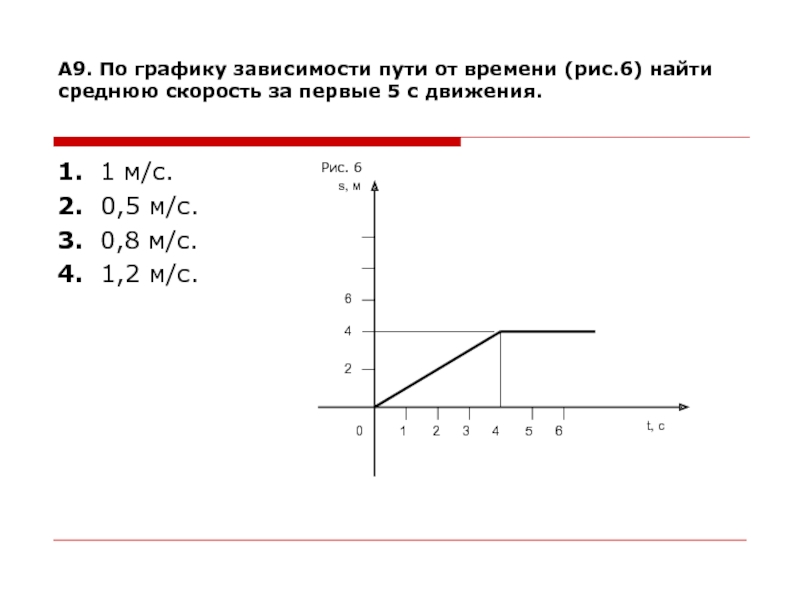 Определение кинематических характеристик движения с помощью графиков. Прямолинейное равноускоренное движение
Определение кинематических характеристик движения с помощью графиков. Прямолинейное равноускоренное движение