Как найти в равнобедренном треугольнике основание зная боковые стороны: Стороны равнобедренного треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

alexxlab

2 )

Содержание

Высота равнобедренного треугольника | Онлайн калькулятор

Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.

Соответственно, в таком треугольнике можно провести три высоты, две из которых будут равны между собой, аналогично сторонам — это высоты, опущенные на боковую сторону треугольника а, а третья высота опускается на основание. Высота треугольника проводится из угла треугольника к противолежащей стороне под прямым углом. Большинство задач с высотой треугольника решаются через прямоугольные треугольники, которые она образует.

Рассмотрим каждый случай по отдельности.

Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой, проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.

Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:

Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.

Площадь любого треугольника можно найти несколькими способами — например, через три стороны треугольника по формуле Герона, или через высоту, умножив ее на половину стороны, на которую она опущена. И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.

Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:

Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне

Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.

Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sin⁡α

Формула через боковую сторону и угол напротив основания β:

Формула через основание и угол при нем α:

через основание и угол противолежащий ему β:

Площадь равнобедренного треугольника

В данной статье приведены различные формулы нахождения площади равнобедренного треугольника: через его основание и высоту, через основание и сторону, через равные стороны и угол и через основание и угол.

Также прилагаются различные калькуляторы для вычисления площади рб. треугольника.

Для тех, кто сомневается, нужна ли ему эта страница или другая, напомним определение равнобедренного треугольника:

Определение 1

Равнобедренный треугольник — это треугольник, 2 стороны которого равны.

Для того чтобы воспользоваться онлайн-калькуляторами, введите значения величин из вашей задачи в поля для ввода.

Рассмотрим подробно, как вычислить площадь равнобедренного треугольника.

Площадь равнобедренного треугольника, зная основание и высоту

$S = \frac12 \cdot AC \cdot h$, где

$AC$ — основание равнобедренного треугольника;

$h$ — высота равнобедренного треугольника (перпендикуляр, опущенный из угла, лежащего напротив основания).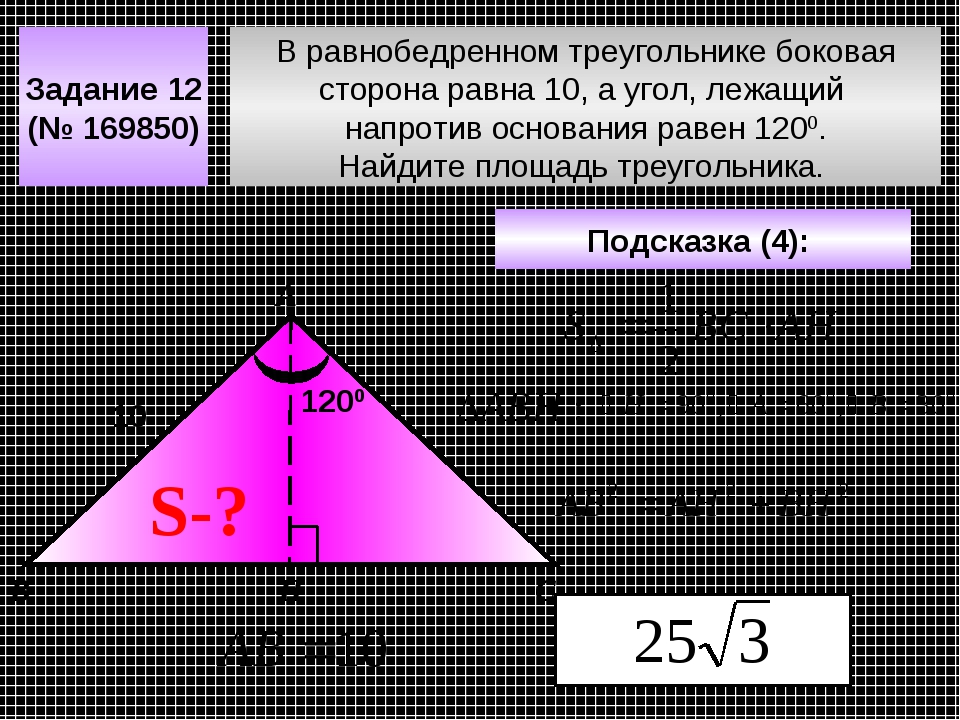 2}{4 \cdot \mathrm{tg}(\frac{y}{2})}$, где

$S$ — площадь треугольника,

$c$ — основание,

$y$ — угол между равными сторонами. 

Как найти стороны равнобедренного треугольника зная периметр. Периметр и площадь треугольника. Что мы узнали

Периметр – это сумма всех сторон фигуры. Эта характеристика, наравне с площадью, одинаково востребована для всех фигур. Формула периметра равнобедренного треугольника логично вытекает из его свойств, но формула не столь сложна, как получение и закрепление практических навыков.

Формула вычисления периметра

Боковые стороны равнобедренного треугольника равны между собой. Это проистекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и проистекает формула периметра:

P=2a+b, где b-это основание треугольника, a-значение боковой стороны.

Рис. 1. Равнобедренный треугольник

Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон. 2}=\sqrt{9+16}=\sqrt{25}=5$$

Найдем периметр: P=AC+AB*2=6+5*2=16

Задача 2

  • В равнобедренном треугольнике высота, проведенная к основанию, равна 10, а острый угол при основании 30 градусам. нужно найти периметр треугольника.

Рис. 3. Рисунок к задаче 2

Эта задача осложнена отсутствием сведений о сторонах треугольника, но, зная значение высоты и угла, в прямоугольном треугольнике ABH можно найти катет AH, а после решение пойдет по тому же сценарию, что и в задаче 1.

Найдем AH через значение синуса:

$$sin (ABH)={BH\over AB}={1\over2}$$ — синус 30 градусов является табличным значением.

Выразим нужную сторону:

$$AB={{BH\over {1\over 2}}} =BH*2=10*2=20$$

Через котангенс найдем значение AH:

$$ctg(BAH)={AH\over BH}={1\over\sqrt{3}}$$

$$AH={BH\over\sqrt{3}}=10*\sqrt{3}=17,32$$ — получившееся значение округлим до сотых.

Найдем основание:

AC=AH*2=17,32*2=34,64

Теперь, когда все требуемые значения найдены, определим периметр:

P=AC+2*AB=34,64+2*20=74,64

Задача 3

  • В равнобедренном треугольнике ABC известна площадь, которая равна $$16\over\sqrt{3}$$ и острый угол при основании в 30 градусов. Найти периметр треугольника.

Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений

При такой постановке задачи может показаться, что решений нет, ведь сложно выразить одну из сторон или высоту из имеющихся данных. Попробуем решить по-другому.

Обозначим высоту и половину основания латинскими буквами: BH=h и AH=a

Тогда основание будет равно: AC=AH+HC=AH*2=2a

Площадь: $$S={1\over 2}*AC*BH={1\over 2}*2a*h=ah$$

С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно тангенс? Потому что в треугольнике ABH мы уже обозначили два катета a и h. Нужно выразить одно через другое. Два катета вместе связывают тангенс и котангенс. Традиционно к котангенсу и косинусу обращаются, только если не подходит тангенс или синус. Это не правило, можно решать так, как удобно, просто так принято. 2}=4,62$$

Подставим значения в формулу периметра:

P=AB*2+AH*2=4,62*2+4*2=17,24

Что мы узнали?

Мы разобрались подробно во всех тонкостях нахождения периметра равнобедренного треугольника. Решили три задачи разного уровня сложности, показав на примере, как решаются типовые задачи на решение равнобедренного треугольника.

Тест по теме

Оценка статьи

Средняя оценка: 4.4
. Всего получено оценок: 83.

Предварительные сведения

Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон. Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.

Определение 1

Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками
(рис. 1).

Определение 2

Точки в рамках определения 1 будем называть вершинами треугольника.

Определение 3

Отрезки в рамках определения 1 будем называть сторонами треугольника.

Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.

В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.

Определение 4

Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.

Определение 5

Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.

Определение 6

Треугольник будем называть равносторонним, если все его стороны равняются друг другу.

Все виды этих треугольников Вы можете видеть на рисунке 2.

Как найти периметр разностороннего треугольника?

Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.

Вывод:
Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.

Пример 1

Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.

$P=34+12+11=57$ см

Ответ: $57$ см.

Пример 2

Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.

Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда

$α=10$
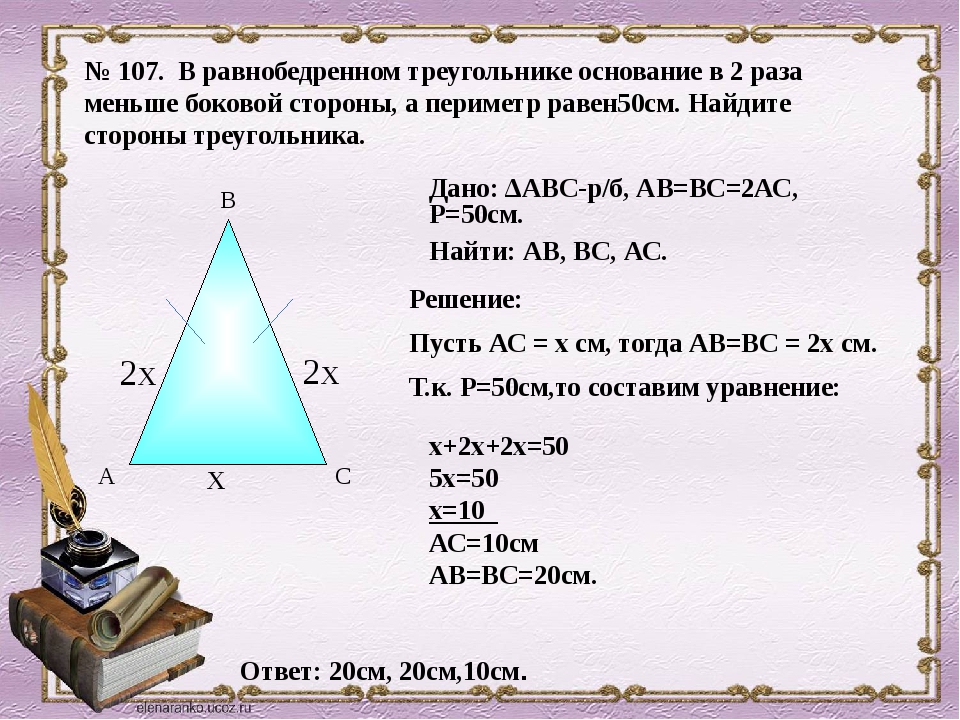
По правилу вычисления периметра разностороннего треугольника, получим

$P=10+8+6=24$ см

Ответ: $24$ см.

Как найти периметр равнобедренного треугольника?

Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+β=2α+β$

Вывод:
Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.

Пример 3

Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.

По рассмотренному выше примеру, видим, что

$P=2\cdot 12+11=35$ см

Ответ: $35$ см.

Пример 4

Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.

Рассмотрим рисунок по условию задачи:

Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.

По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда

По правилу вычисления периметра равнобедренного треугольника, получим

$P=2\cdot 10+12=32$ см

Ответ: $32$ см.

Как найти периметр равностороннего треугольника?

Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+α=3α$

Вывод:
 Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.

Пример 5

Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.

По рассмотренному выше примеру, видим, что

$P=3\cdot 12=36$ см

Предварительные сведения

Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон. Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.

Определение 1

Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками
(рис. 1).

Определение 2

Точки в рамках определения 1 будем называть вершинами треугольника.

Определение 3

Отрезки в рамках определения 1 будем называть сторонами треугольника.

Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.

В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.

Определение 4

Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.

Определение 5

Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.

Определение 6

Треугольник будем называть равносторонним, если все его стороны равняются друг другу.

Все виды этих треугольников Вы можете видеть на рисунке 2.

Как найти периметр разностороннего треугольника?

Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.

Вывод:
Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.

Пример 1

Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.

$P=34+12+11=57$ см

Ответ: $57$ см.

Пример 2

Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.

Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда

$α=10$
По правилу вычисления периметра разностороннего треугольника, получим

$P=10+8+6=24$ см

Ответ: $24$ см.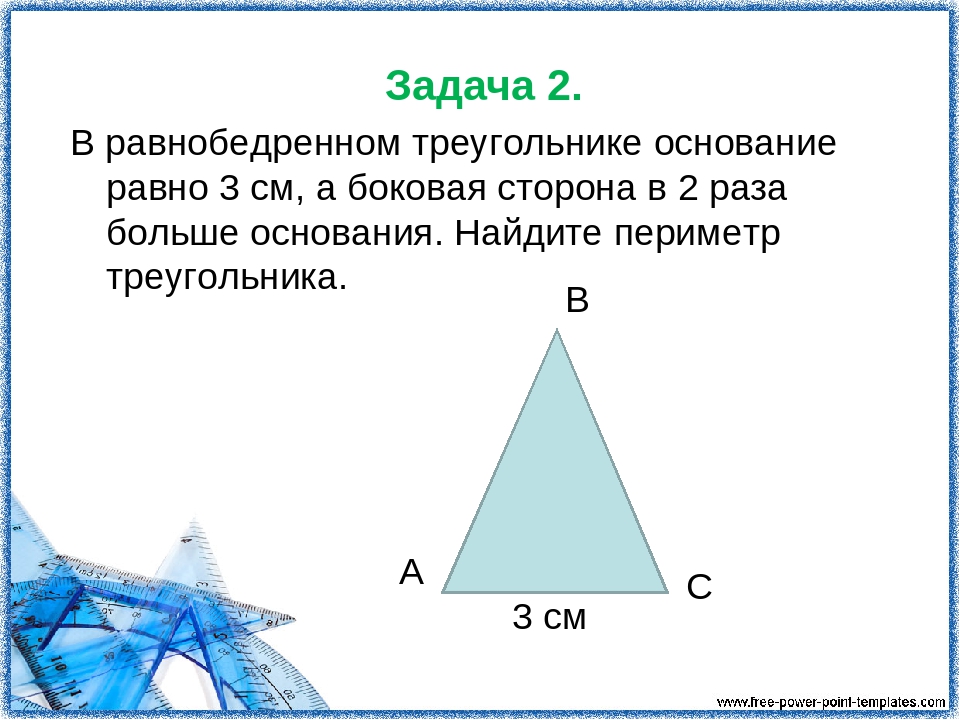

Как найти периметр равнобедренного треугольника?

Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+β=2α+β$

Вывод:
Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.

Пример 3

Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.

По рассмотренному выше примеру, видим, что

$P=2\cdot 12+11=35$ см

Ответ: $35$ см.

Пример 4

Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.

Рассмотрим рисунок по условию задачи:

Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.

По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда

По правилу вычисления периметра равнобедренного треугольника, получим

$P=2\cdot 10+12=32$ см

Ответ: $32$ см.

Как найти периметр равностороннего треугольника?

Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.

По определению периметра плоской геометрической фигуры, получим, что

$P=α+α+α=3α$

Вывод:
 Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.

Пример 5

Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.

По рассмотренному выше примеру, видим, что

$P=3\cdot 12=36$ см

Любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:

P
 = a
 + b
 + c

где P
 — это периметр треугольника, a
, b
 и c
 — его стороны.

Можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания.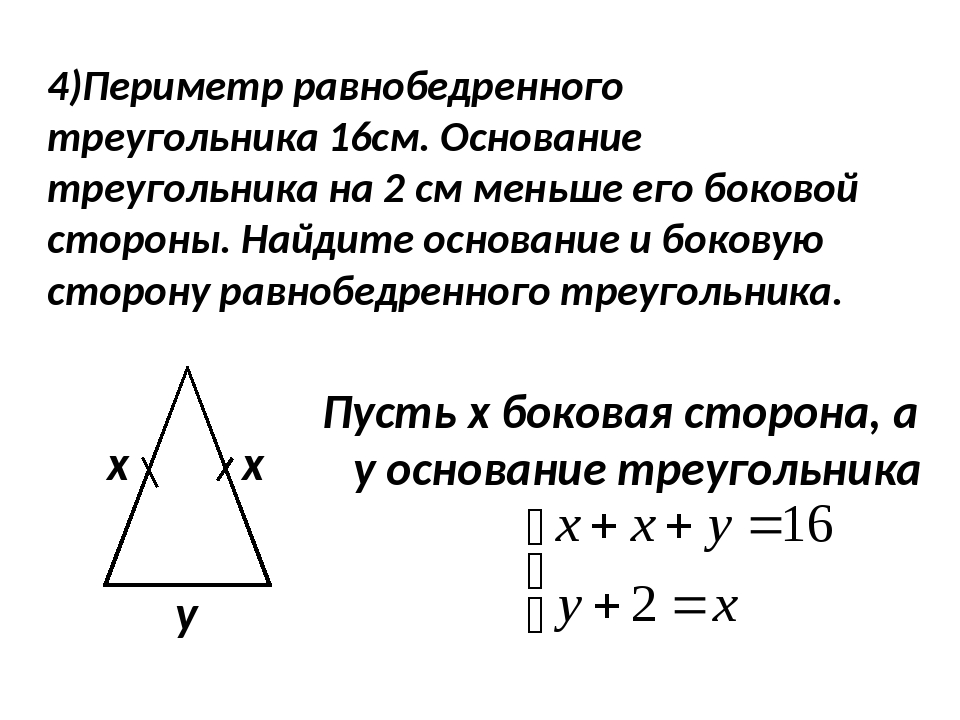 Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:

P
 = 2a
 + b

где P
 — это периметр равнобедренного треугольника, a
 — любая из боковых сторон, b
 — основание.

Можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:

P
 = 3a

где P
 — это периметр равностороннего треугольника, a
 — любая из его сторон.

Площадь

Для измерения площади треугольника можно сравнить его с параллелограммом . Рассмотрим треугольник ABC
:

Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:

В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.

Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC
 площадь будет равна

Теперь рассмотрим прямоугольный треугольник:

Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:

Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.

Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2
. Общая формула для нахождения площади треугольников будет выглядеть так:

где S
 — это площадь треугольника, a
 — его основание, h a
 — высота, опущенная на основание a
.

Как найти высоту в треугольнике abc: формулы, примеры задач

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.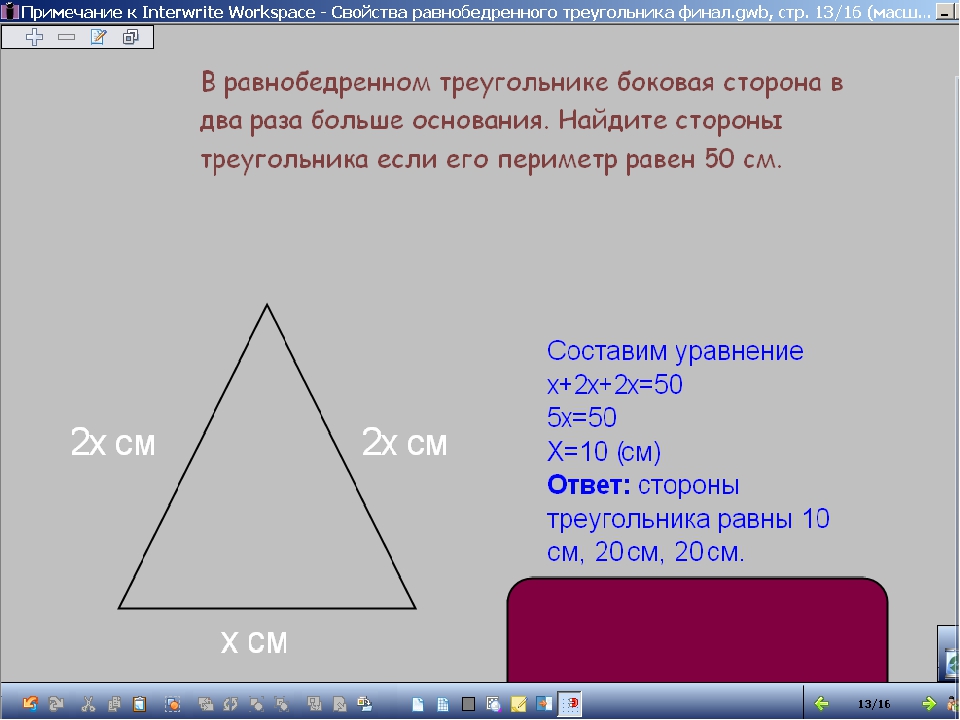

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

свойства, признаки и формулы / Блог / Справочник :: Бингоскул

Содержание:

  1. Свойства равнобедренного треугольника.
  2. Признаки равнобедренного треугольника.
  3. Формулы равнобедренного треугольника:
    • формулы длины стороны;
    • формулы длины равных сторон;
    • формулы высоты, медианы, биссектрисы равнобедренного треугольника.

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.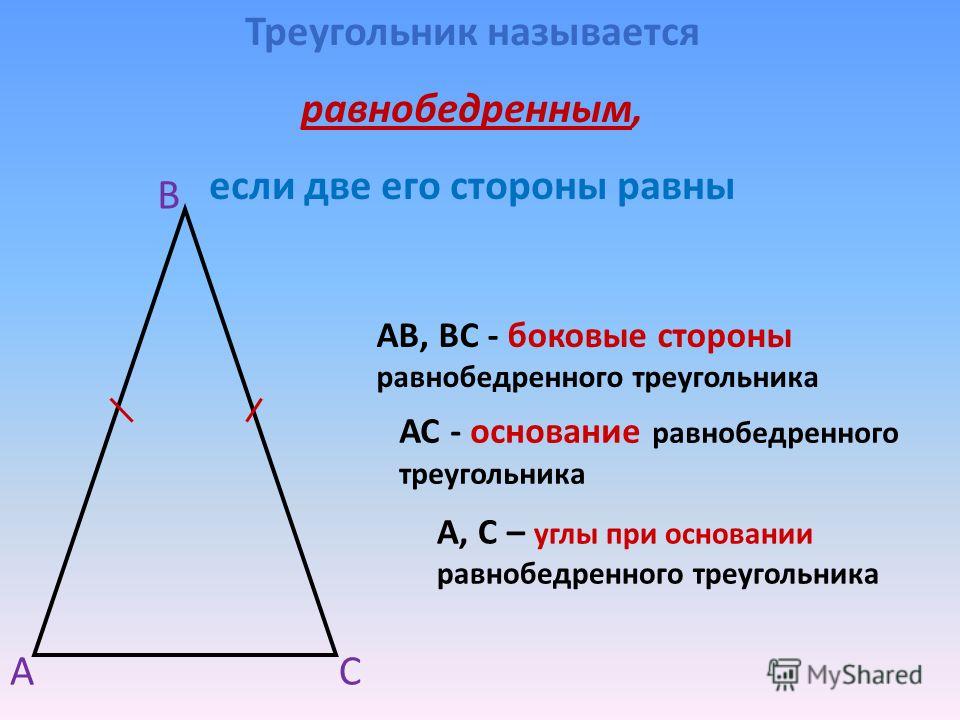

АВ = ВС — боковые стороны

АС — основание

Свойства равнобедренного треугольника

Свойства равнобедренного треугольника выражаются через 5 теорем:

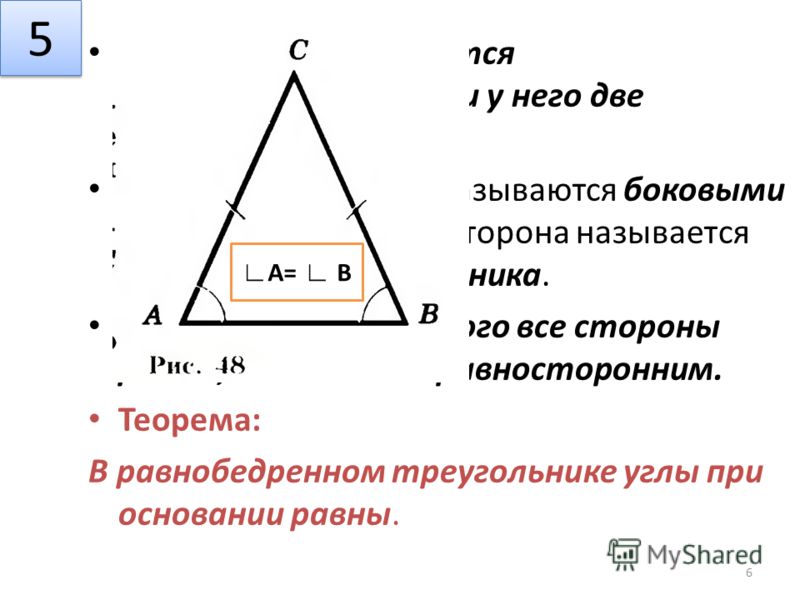
Теорема 1. В равнобедренном треугольнике углы при основании равны.

Доказательство теоремы:

Рассмотрим равнобедренный Δ ABC с основанием АС.

Боковые стороны равны АВ = ВС,

Следовательно углы при основании ∠ BАC = ∠ BСA.

Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника

  • Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
  • Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
  • Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Доказательство теоремы:

  • Дан Δ ABC.
  • Из точки В проведем высоту BD.
  • Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
  • Прямые АС и BD называются перпендикуляром.
  • В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
  • АВ = ВС — боковые стороны равны.
  • Стороны АD = СD, т.к. точка D отрезок делит пополам.
  • Следовательно Δ ABD = ΔBCD.
  • Биссектриса, высота и медиана это один отрезок — BD

Вывод:

  1. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
  2. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
  3. Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.

Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.

  • Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство теоремы:

Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.

Доказательство от противного.

  • Пусть треугольники не равны (а то треугольники были равны по первому признаку).
  • Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
  • Отсюда пришли к противоречию и теорему доказали.

Признаки равнобедренного треугольника

  1. Если в треугольнике два угла равны.
  2. Сумма углов треугольника 180°.
  3. Если в треугольнике биссектриса является медианой или высотой.
  4. Если в треугольнике медиана является биссектрисой или высотой.
  5. Если в треугольнике высота является медианой или биссектрисой.

Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

  • b — сторона (основание)
  • а — равные стороны
  • a — углы при основании
  • b — угол образованный равными сторонами

Формулы длины стороны (основания — b):

  • b = 2a \sin( \beta /2)= a \sqrt { 2-2 \cos \beta }
  • b = 2a \cos \alpha

Формулы длины равных сторон — (а):

  • a=\frac { b } { 2 \sin(\beta /2) } = \frac { b } { \sqrt { 2-2 \cos \beta } }
  • a=\frac { b } { 2 \cos\alpha }

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

  • L — высота=биссектриса=медиана
  • b — сторона (основание)
  • а — равные стороны
  • a — углы при основании
  • b — угол образованный равными сторонами

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

  • L = a sina
  • L = \frac { b } { 2 } *\tg\alpha
  • L = a \sqrt { (1 + \cos \beta)/2 } =a \cos (\beta)/2)

Формула высоты, биссектрисы и медианы, через стороны, (L):

  • L = \sqrt { a^ { 2 } -b^ { 2 } /4 }

Площадь равнобедренного треугольника

  • b — сторона (основание)
  • а — равные стороны
  • h — высота

Формула площади треугольника через высоту h и основание b, (S):

S=\frac { 1 } { 2 } *bh

 

Смотри также:

Площадь равнобедренного треугольника — формула, пример расчета, калькулятор

Равнобедренным треугольником называется фигура с двумя равными сторонами. В этом случае третья сторона считается основанием, а равные стороны – боковыми.

Если все стороны треугольника равны, то он считается правильным. Правильный треугольник также является равнобедренным.
Равнобедренный треугольник отличается следующими свойствами:

  • Углы (α) при основании равны;
  • Биссектрисы, медианы и высоты, исходящие из этих углов также равны между собой;
  • Центры описанной и вписанной окружности лежат на одной прямой;
  • Биссектриса, медиана и высота, проведенные из угла β к основанию b, равны между собой.

Существует множество способов нахождения площади равнобедренного треугольника. Для начала рассмотрим классический метод, для которого потребуется высота и основание. Зная эти параметры можно применить формулу площади равнобедренного треугольника:

То есть площадь равнобедренного треугольника равняется произведению высоты на половину длины основания.

Рассмотрим пример расчета площади равнобедренного треугольника.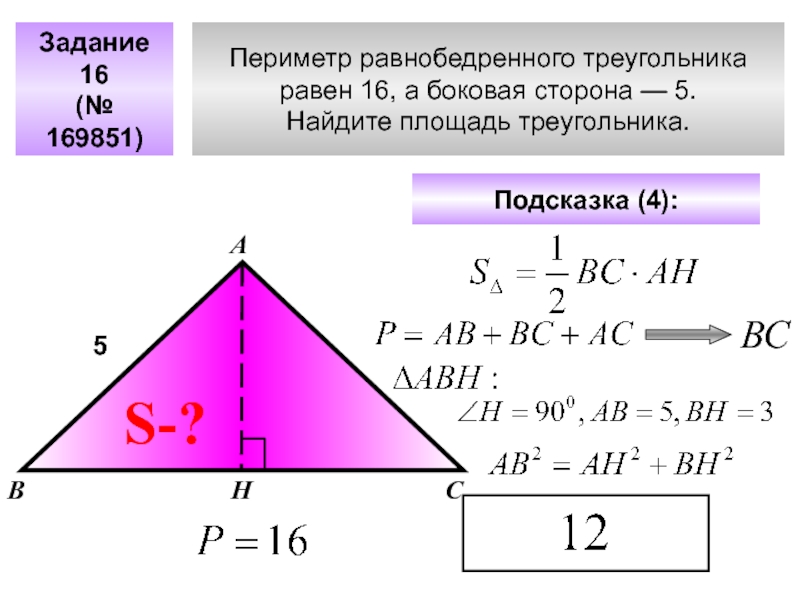
Задача: дан треугольник, в котором основание равно 4 см, а высота 6 см. Найдите площадь.
Подставляем данные в формулу:

Площадь треугольника равняется 12 кв. см

Также найти площадь можно по формуле площади через три стороны, или как еще говорят – формуле Герона. Во многих случаях это значение находится через радиус вписанной окружности.
Найти площадь фигуры через стороны, применив метод Герона, можно по этой формуле.

Это выражение можно преобразовать в сокращенную формулу:

Рассмотрим на примере.
В равнобедренном треугольнике основание b= 3 см, а сторона a= 6 см. Подставим значения в формулу:
или
Зная стороны, мы легко определили, что S = 8,7 кв. см

Для вычислений можно использовать две равные стороны и угол между ними.

И снова смотрим пример:
Стороны a = 6 см., а угол между ними 45°. По таблице синусов синус 45° равен 0.7071.
Рассчитываем площадь:
Площадь такого равнобедренного треугольника будет равна 12,6 квадратных сантиметра

Равнобедренный треугольник — определение математического слова

Равнобедренный треугольник — определение математического слова — Math Open Reference

Треугольник, две стороны которого равны.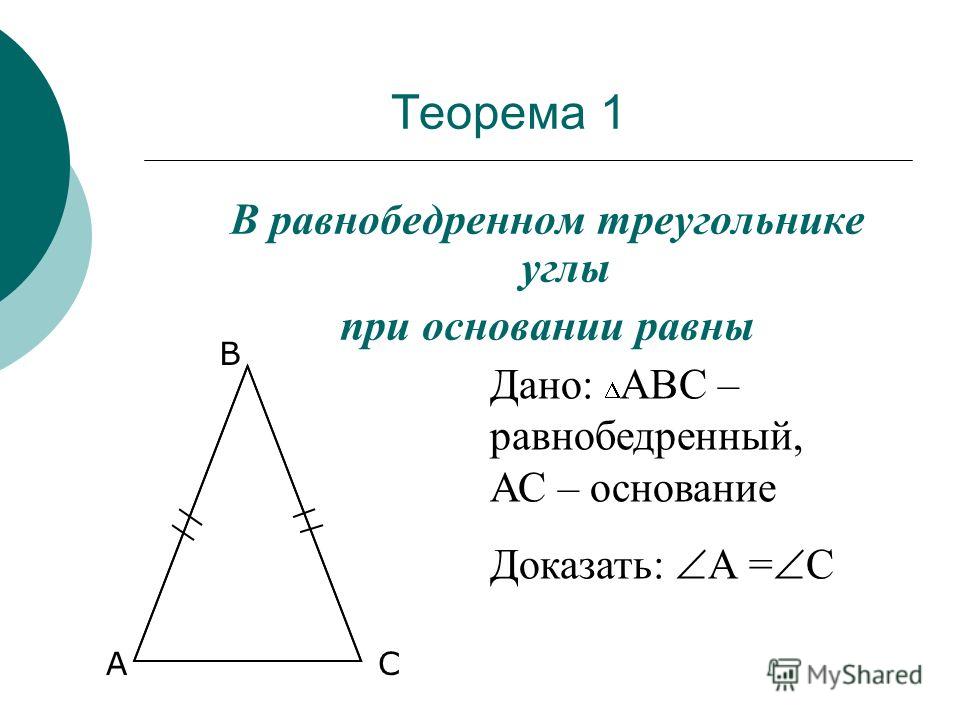

Попробуйте это Перетащите оранжевые точки на каждой вершине, чтобы изменить форму треугольника.
Обратите внимание, что он всегда остается равнобедренным треугольником, стороны AB и AC всегда равны по длине.

Слово «равнобедренный» произносится как «глаз- sos -ell-easy» с ударением на «sos». Это любой треугольник с двумя сторонами одинаковой длины.

Если все три стороны имеют одинаковую длину, это называется
равносторонний треугольник.
Очевидно, что все равносторонние треугольники также обладают всеми свойствами равнобедренного треугольника.

Недвижимость

  • Неравную сторону равнобедренного треугольника обычно называют «основанием» треугольника.
  • Углы основания равнобедренного треугольника всегда равны.
    На рисунке выше углы ∠ABC и ∠ACB всегда одинаковы.
  • Когда 3-й угол является прямым, он называется «прямоугольный равнобедренный треугольник».
  • Высота — это расстояние по перпендикуляру от основания до самой верхней вершины.

Построение равнобедренного треугольника

Можно построить равнобедренный треугольник заданных размеров, используя только циркуль и линейку. Посмотрите на эти три конструкции:

Решение равнобедренного треугольника

Основание, катет или высота равнобедренного треугольника можно найти, если вы знаете два других.
А
серединный перпендикуляр
базы образует
высота
треугольника, как показано справа.Это образует два
конгруэнтные прямоугольные треугольники
это может быть решено с помощью
Теорема Пифагора
как показано ниже.

Нахождение базы

Чтобы найти базу с учетом шага и высоты, используйте формулу:

где:
L — длина отрезка
A — высота

Нахождение отрезка

Чтобы найти длину ноги с учетом базы и высоты, используйте формулу:

где:
B — длина основания
A — высота

Высота

Чтобы найти высоту с учетом базы и ноги, используйте формулу:

где:
L — длина ножки
B — основание

Внутренние углы

Если вам дадут один
внутренний угол
равнобедренного треугольника можно найти два других.

Например, нам дан угол при вершине, как показано справа от 40 °.
Мы знаем, что внутренние углы всех треугольников составляют 180 °.
Таким образом, два базовых угла должны в сумме составлять 180-40 или 140 °. Поскольку два основных угла совпадают (одна и та же мера), каждый из них составляет 70 °.

Если нам дан базовый угол, скажем, 45 °, мы знаем, что базовые углы конгруэнтны (та же мера)
а внутренние углы любого треугольника всегда складываются в 180 °. Таким образом, угол при вершине должен составлять 180-45-45 или 90 °.

Другие темы треугольника

Общие

Периметр / Площадь

Типы треугольников

Центры треугольника

Конгруэнтность и сходство

Решение треугольников

Треугольник викторины и упражнения

(C) Открытый справочник по математике, 2011 г.

Все права защищены.

Равнобедренный треугольник Калькулятор — Расчет высокой точности

[1] 2021/04/21 10:12 Мужчина / Уровень 30 лет / Инженер / Очень /

Цель использования
Слишком долго не ходил в школу.Изготовление стола из эпоксидной смолы, необходимого для подрезки стальных ножек, пока смола мокрая Вырисовал ножки для прямоугольной основы, забыл некоторые геометрические доказательства. Смотрел их и вручную делал расчеты. Проверил с помощью этого калькулятора -> получилось с такими же точными числами и углами. Хороший инструмент для проверки, не ленитесь и полагайтесь на технологии, которые сделают все за вас. Вот почему у нас есть манекены, которые не могут решать математические уравнения Facebook.

[2] 2021/04/17 22:19 Женщина / 60 лет и старше / Пенсионер / Очень /

Цель использования
Пошив шторы для нашей горки для муниципального бассейна.Это пирамида, состоящая из 4-х треугольников. Стороны легко измерить, углы нужны.
Комментарий / запрос
Отлично и быстро. Спасибо.

[3] 2021/04/05 04:56 Женщина / Уровень 40 лет / Другое / Очень /

Цель использования
Рассчитать размер детской палатки для двора 🙂

[4] 2021/03/02 23:20 Женский / До 20 лет / Старшая школа / Университет / Аспирантка / Очень /

Цель использования
быстрее решать задачи

[5] 2021/02/26 02:15 Мужчина / Уровень 30 лет / Инженер / Очень /

Цель использования
Игра с периметром: отношения диаметров многоугольников с увеличивающимся числом сторон.Наблюдая, как отношение приближается к пи, когда многоугольник становится более круглым.

[6] 2021/02/10 22:40 Женщина / уровень 30 лет / Офисный работник / Государственный служащий / Очень /

Цель использования
Пытаюсь найти длины сторон, когда я знаю база — 48 дюймов, а базовый ангел — 30 градусов

[7] 2021/02/09 14:38 Мужчина / уровень 40 лет / Офисный работник / Государственный служащий / Очень /

Цель использования
Требуется дизайнерский угол «сделай сам», доступны только определенные размеры.Спасибо за калькулятор.

[8] 21.01.2021 17:17 Мужчина / До 20 лет / Высшая школа / Университет / аспирант / Очень /

Цель использования
школьный состав, сложное задание

[ 9] 2021.01.21 01:17 Женщина / До 20 лет / Офисный работник / Государственный служащий / Очень /

Цель использования
сложная вещь про сельскохозяйственные колеса

[10] 2020/12 / 19 00:09 Мужчина / Уровень 40 лет / Офисный работник / Государственный служащий / Полезно /

Цель использования
Расчет длины дуги сегмента окружности по линейной длине между конечными точками для обработанного стального кольца, которое будет быть разрезанным на сегменты.В конечном итоге приводит меня к тому, сколько сегментов я могу получить из одного кольца.

Калькулятор равнобедренного треугольника

Калькулятор равнобедренного треугольника — лучший выбор, если вы ищете быстрое решение ваших геометрических задач. Узнайте площадь равнобедренного треугольника, его периметр, внутренний радиус, окружной радиус, высоту и углы — все в одном месте. Если вы хотите построить питомник, узнать площадь равнобедренного фронтона греческого храма или просто выполнить домашнее задание по математике, этот инструмент здесь для вас.Поэкспериментируйте с калькулятором или продолжайте читать, чтобы узнать больше о формулах равнобедренного треугольника.

Что такое равнобедренный треугольник?

Равнобедренный треугольник — это треугольник с двумя сторонами равной длины, которые называются катетами. Третья сторона треугольника называется основанием. Угол при вершине — это угол между ножками и углами с основанием, так как одна из их сторон называется углами основания.

Свойства равнобедренного треугольника:

  • имеет ось симметрии по высоте вершины
  • два угла напротив ног равны по длине
  • равнобедренный треугольник может быть острым, прямым или тупым, но это зависит только от угла при вершине (углы основания всегда острые)

Равносторонний треугольник — частный случай равнобедренного треугольника.

Формулы равнобедренного треугольника для площади и периметра

Для вычисления площади равнобедренного треугольника можно использовать множество различных формул. Самыми популярными являются уравнения:

  1. Учитывая плечо a и основание b :

    площадь = (1/4) * b * √ (4 * a² - b²)

  2. Дано h высота от вершины и основания b или h3 высота от двух других вершин и плеча a :

    площадь = 0.5 * h * b = 0,5 * h3 * a

  3. Любой угол и плечо или основание

площадь = (1/2) * a * b * sin (base_angle) = (1/2) * a² * sin (vertex_angle)

Кроме того, вы можете воспользоваться нашим калькулятором площади треугольника, чтобы узнать другие уравнения, которые работают для всех типов треугольников, а не только для равнобедренных.

Чтобы вычислить периметр равнобедренного треугольника, просто сложите все стороны треугольника:
периметр = a + a + b = 2 * a + b

Теорема о равнобедренном треугольнике

Теорема о равнобедренном треугольнике, также известная как теорема об основных углах, утверждает, что , если две стороны треугольника равны, то углы, противоположные этим сторонам, равны .

Также существует обратная теорема, утверждающая, что , если два угла треугольника совпадают, то стороны, противоположные этим углам, равны .

Калькулятор золотого треугольника

Золотой треугольник, который также называют возвышенным треугольником, представляет собой равнобедренный треугольник, в котором ножка находится в золотом сечении по отношению к основанию:

a / b = φ ~ 1,618

Золотой треугольник обладает необычными свойствами:

  • Это единственный треугольник с тремя углами в пропорции 2: 2: 1
  • Форма треугольников в точках пентаграммы
  • Используется для формирования логарифмической спирали

Как найти площадь с помощью этого калькулятора равнобедренного треугольника?

Давайте разберемся, как пользоваться этим инструментом на простом примере.Взгляните на это пошаговое решение:

  1. Определите ваше первое данное значение . Предположим, мы хотим проверить свойства золотого треугольника. Наберите 1,681 дюйма в коробку , опора .
  2. Введите второй известный параметр . Например, возьмите основание, равное 1 дюйм.
  3. Все остальные параметры рассчитываются в мгновение ока! Мы проверили, например, что периметр равнобедренного треугольника равен 4,236 дюйма и что углы в золотом треугольнике равны 72 ° и 36 ° — соотношение действительно равно 2: 2: 1.

Вы можете использовать этот калькулятор для определения параметров, отличных от приведенных в примере, но помните, что обычно есть два разных равнобедренных треугольника с заданной площадью и другим параметром, например длина ноги. Наш калькулятор покажет одно из возможных решений.

Равнобедренных треугольников — Бесплатная справка по математике

В мире геометрии существует множество типов треугольников. Существует особый треугольник, называемый равнобедренным треугольником . В равнобедренном треугольнике базовые углы имеют одинаковую степень и, как следствие, равны (конгруэнтны).Точно так же, если два угла треугольника имеют одинаковую длину, тогда стороны , противоположные этим углам, имеют одинаковую длину. Самый простой способ определить равнобедренный треугольник — это у него две равные стороны .

В равнобедренном треугольнике есть две стороны, называемые ногами, и третья сторона, называемая основанием. Угол, расположенный напротив основания, называется вершиной.

Образец A:

Угол при вершине B равнобедренного треугольника ABC составляет 120 градусов.Найдите градус каждого базового угла.

Решение:

(1) Пусть x = мера каждого базового угла.
(2) Составьте уравнение и решите относительно x.

базовый угол + базовый угол + 120 градусов = 180 градусов
x + x + 120 градусов = 180 градусов
2x + 120 = 180
2x = 180 — 120
2x = 60
x = 60/2
x = 30

Каждый угол основания треугольника ABC составляет 30 градусов.

Образец B:

В равнобедренном треугольнике RST угол S — это угол при вершине.Базовые углы R и T равны 64 градусам. Найдите градус угла при вершине S.

Решение:

(1) Пусть x = мера угла при вершине S.
(2) Составьте уравнение и решите относительно x.

базовый угол + базовый угол + угол при вершине S = 180 градусов
64 градуса + 64 градуса + x = 180 градусов
128 + x = 180
x = 180 — 128
x = 52

Угол при вершине S в треугольнике RST составляет 52 градуса.

Образец C:

Угол основания равнобедренного треугольника XYZ в градусах в три раза превышает градус вершины Y на 60.Найдите градус угла при вершине Y. Обратите внимание, что трудно нарисовать картинку, не зная, какие углы наибольшие.

Нам нужно составить уравнение из этой проблемы, поэтому давайте разберемся, что она пытается нам сказать. Сначала мы читаем «Степень базового угла», поэтому начнем с X =

.

Наше уравнение на данный момент: X =

Теперь мы видим «превышает в три раза … Y … на 60», что означает 3Y + 60.

Теперь наше уравнение: X = 3Y + 60

Поскольку мы знаем, что X = Z, потому что это равнобедренный треугольник, мы можем найти меры всех углов.

базовый угол + базовый угол + вершина = 180
X + Y + Z = 180
(3Y + 60) + Y + (3Y + 60) = 180
7Y + 120 = 180
7Y = 60
Y = 60/7
Y = 8,57 градусов

Угол при вершине Y треугольника XYZ равен 8,57 градуса.

Урок, проводимый г-ном Фелизом

Основание равнобедренного треугольника

Привет, Тахрима.

Нарисуйте треугольник с общей вершиной вверху, и вы можете отбросить биссектрису от него на противоположную сторону.Это делит треугольник на два равных прямоугольных треугольника, с новой линией, равной высоте треугольника.

Площадь треугольника равна (1/2) основанию, умноженному на высоту. Пусть b = основание равнобедренного треугольника, а h — его высота. Тогда
12 = (1/2) bh

Вы также можете увидеть правые треугольники и заметить, что здесь должна работать теорема Пифагора, поэтому
5 2 = (b / 2) 2 + h 2 .

Итак, у вас есть два уравнения с двумя неизвестными значениями h и b (которые вы хотите знать).2 (это просто формальный способ сказать квадратичный, где значение переменной является квадратом того, что мы действительно хотим). Это то же самое, что и

x 2 — 100x + 2304 = 0, где x = b 2 .

Что мы можем решить, используя метод «завершения квадрата»:
x 2 — 100x + 2500 = 2500 — 2304
(x — 50) 2 = 196
x — 50 = +/- 14
x = 50 +/- 14 = {36, 64}

Но помните, что мы хотим b, а не x. и b = sqrt (x). Оба значения x положительны, поэтому мы должны принять в расчет две возможности:

b = sqrt ({36, 64}) = {6, 8}

Теперь мне нужно проверить эти значения.Сначала проверю b = 6 см:

ч = 24 / б = 24/6 = 4 см.

(b / 2) 2 + h 2 = 3 2 + 4 2 = 9 + 16 = 25.

И это то же самое, что и 5 2 , так что работает. Теперь проверьте b = 8 см:

h = 24 / b = 24/8 = 3 см.

(b / 2) 2 + h 2 = 4 2 + 3 2 = 16 + 9 = 25. Это верно.

Cheers,
Стивен Ла Рок.

Как найти длину стороны острого / тупого равнобедренного треугольника

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Что такое равнобедренный треугольник? — [Определение, факты и пример]

Что такое равнобедренный треугольник?

Треугольник с двумя сторонами равной длины является равнобедренным треугольником.Две равные стороны равнобедренного треугольника известны как «ноги», тогда как третья или неравная сторона известна как «основание».

Углы, противоположные равным сторонам в равнобедренном треугольнике, всегда равны. В данном равнобедренном треугольнике, если AB = AC, то ∠B = ∠C

Вот несколько примеров равнобедренного треугольника:

Примеры из жизни

Многие вещи в мире имеют форму равнобедренного треугольника.Некоторые популярные примеры равнобедренного треугольника в реальной жизни — кусок пиццы, пара серег.

Без примеров

Общая недвижимость

  • Равные стороны равнобедренного треугольника известны как «ноги».

  • Третья и неравная сторона равнобедренного треугольника известна как «основание».

  • Угол, образованный двумя равными сторонами равнобедренного треугольника, известен как «угол при вершине».’

  • Углы, составляющие основу равнобедренного треугольника, известны как «углы основания».

  • Углы, расположенные напротив равных сторон равнобедренного треугольника, всегда равны.

  • Все три угла, расположенные внутри равнобедренного треугольника, являются острыми, что означает, что углы меньше 90 °.

  • Сумма трех углов равнобедренного треугольника всегда равна 180 °, что означает, что мы можем определить третий угол треугольника, если известны два угла равнобедренного треугольника.

Интересные факты