Содержание
Доказать чему равна площадь треугольника
☰
Площадь треугольника равна половине от произведения его стороны на высоту, проведенную к этой стороне. Сторону, к которой проведена высота, принято в таком случае называть основанием. Таким образом, можно сказать, что площадь треугольника равна половине произведения его основания на высоту.
Если обозначить длину стороны-основания треугольника как a, высоту — как h, то получится формула площади треугольника:
S = ½ ah
Чтобы доказать эту формулу, следует рассмотреть все варианты расположения высоты в треугольнике. Их всего три. Это:
- Высота совпадает с одной из сторон треугольника. В этом случае мы имеем дело с прямоугольным треугольником, в котором за основание взят один из катетов. Высотой же, проведенной к этому катету, является другой катет.
- Высота находится внутри треугольника. В этом случае она пересекается с основанием и делит его на два отрезка.
 При этом данный треугольник делится на два прямоугольных треугольника.
При этом данный треугольник делится на два прямоугольных треугольника. - Высота проходит за пределами треугольника. В таком случае она пересекается не с самим основанием, а с его продолжением (прямой, на которой лежит основание).
Рассмотрим первый случай. Пусть дан треугольник ABC. В нем к основанию AC длиной a проведена высота h, которая совпала со стороной BC:
Как известно площадь прямоугольника равна произведению его смежных сторон. Если бы у нас был прямоугольник со сторонами, длины которых a и h, то его площадь была бы равна ah. Если в прямоугольнике провести диагональ, то она разбивает его на два равных прямоугольных треугольника (у них соответственно равны все три стороны). Площади этих треугольников также равны между собой и каждая составляет ½ от площади всего прямоугольника. Таким образом доказано, что площадь треугольника в данном случае будет равна ½ah.
Рассмотрим второй случай. Пусть в нем высота BH длиной h пересекает сторону AC длиной a.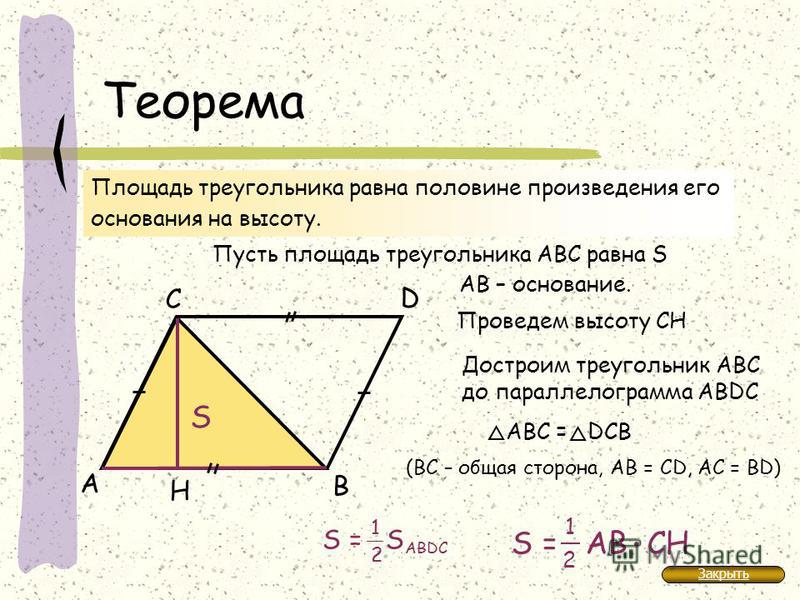
В этом случае мы получаем два прямоугольных треугольника: ABH и CBH. Из рассмотренного первого случая мы знаем, что их площади равны соответственно ½ · AH · h и ½ · CH · h.
Площадь же всего треугольника ABC представляет собой сумму этих двух площадей:
S = ½ · AH · h + ½ · CH · h
Вынесем за скобку общие множители:
S = ½ · h · (AH + CH)
Но ведь AH и CH в сумме составляют длину a. Таким образом, приходим к формуле, которую требовалось доказать:
S = ½ · h · a
Теперь рассмотрим третий случай, когда высота находится за пределами треугольника:
Здесь мы тоже можем увидеть два прямоугольных треугольника. Это ∆ABH и ∆CBH. Причем первый включает в себя второй. Искомый же треугольник ABC является дополнением к треугольнику CBH до треугольника ABH. Таким образом мы можем записать, что площадь ∆ABH равна сумме площадей ∆CBH и ∆ABC:
S∆ABH = S∆CBH + S∆ABC
Откуда находим площадь искомого треугольника ABC:
S∆ABC = S∆ABH – S∆CBH
Площадь треугольника ABH равна ½ · AH · h, площадь треугольника CBH равна ½ · CH · h:
S∆ABC = ½ · AH · h – ½ · CH · h
Выносим общие множители за скобку:
S∆ABC = ½ · h · (AH – CH)
Но ведь если из отрезка AH вычесть отрезок CH, то получится отрезок AC, длина которого равна a.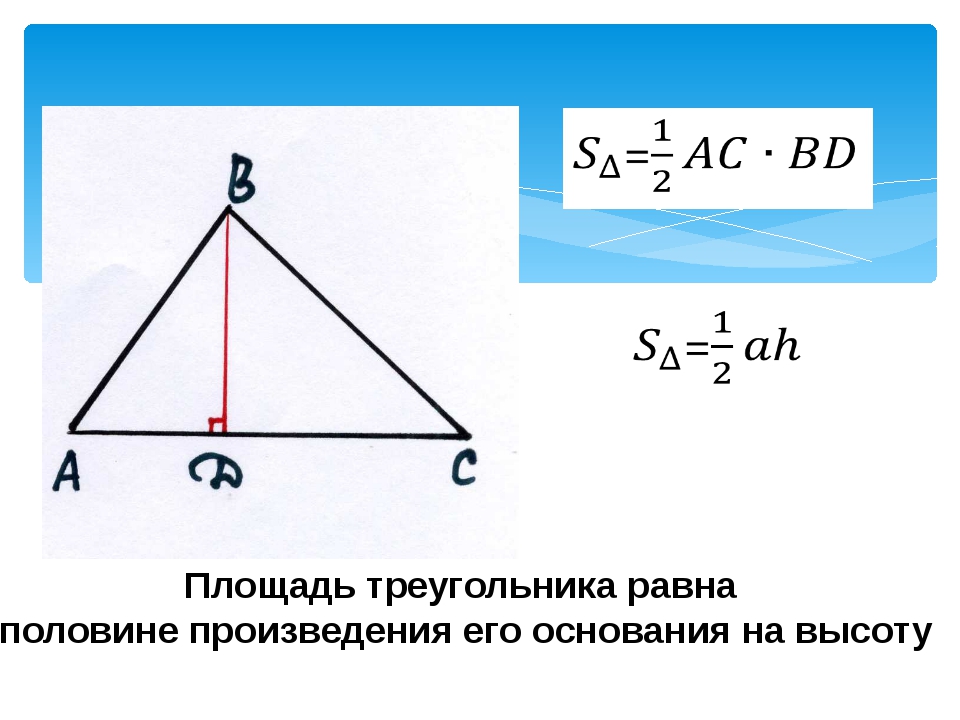 Следовательно, мы можем записать, что и в этом случае площадь треугольника равна также ½ ah.
Следовательно, мы можем записать, что и в этом случае площадь треугольника равна также ½ ah.
Формулы площади и программы для расчета площадей
Содержание:
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади выражается числом заключающихся в него квадратных единиц.
Формулы площади треугольника
1-ая формула
S — площадь треугольника
a, b — длины 2-х сторон треугольника
С — угол между сторонами a и b
2-ая формула
S — площадь треугольника
a — длина стороны треугольника
h — длина высоты, опущенной на сторону a
3-ья формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
p — полупериметр треугольника
4-ая формула
S — площадь треугольника
r — радиус вписанной окружности
p — полупериметр треугольника
5-ая формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
R — радиус описанной окружности
См.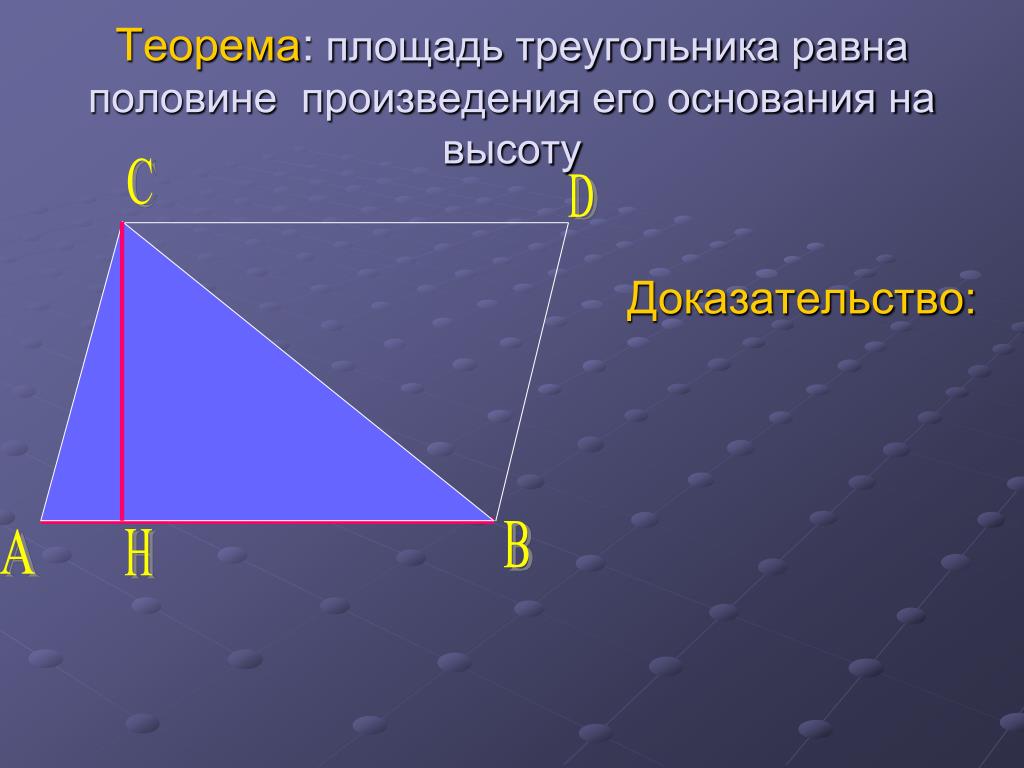 также: Программа для расчета площади треугольника.
также: Программа для расчета площади треугольника.
Формулы площади квадрата:
1) Площадь квадрата равна квадрату длины его стороны (a).
2) Площадь квадрата равна половине квадрата длины его диагонали (d).
S — площадь квадрата
a — длина стороны квадрата
d — длина диагонали квадрата
См. также: Программа для расчета площади квадрата.
Формула площади прямоугольника:
1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).
S — площадь прямоугольника
a — длина 1-ой стороны прямоугольника
b — длина 2-ой стороны прямоугольника
См. также: Программа для расчета площади прямоугольника.
Формула площади параллелограмма:
1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).
S — площадь параллелограмма
a — длина основания
h — длина высоты
См. также: Программа для расчета площади параллелограмма.
также: Программа для расчета площади параллелограмма.
Формула площади трапеции:
1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
S — площадь трапеции
a — длина 1-ого основания
b — длина 2-ого основания
h — длина высоты трапеции
См. также: Программа для расчета площади трапеции.
Формулы площади ромба:
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
S — площадь ромба
a — длина основания ромба
h — длина высоты ромба
d1 — длина 1-ой диагонали
d2 — длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
Формула площади круга:
1) Площадь круга равна произведению квадрата радиуса на число пи (3. 1415).
1415).
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
S — площадь круга
π — число пи (3.1415)
r — радиус круга
См. также: Программа для расчета площади круга.
Формула площади эллипса:
1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).
S — площадь эллипса
π — число пи (3.1415)
a — длина большой полуоси
b — длина малой полуоси
См. также: Программа для расчета площади эллипса.
Слишком сложно?
Формулы площади не по зубам? Тебе ответит эксперт через 10 минут!
Формулы площади и программы для расчета площадей
Содержание:
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры.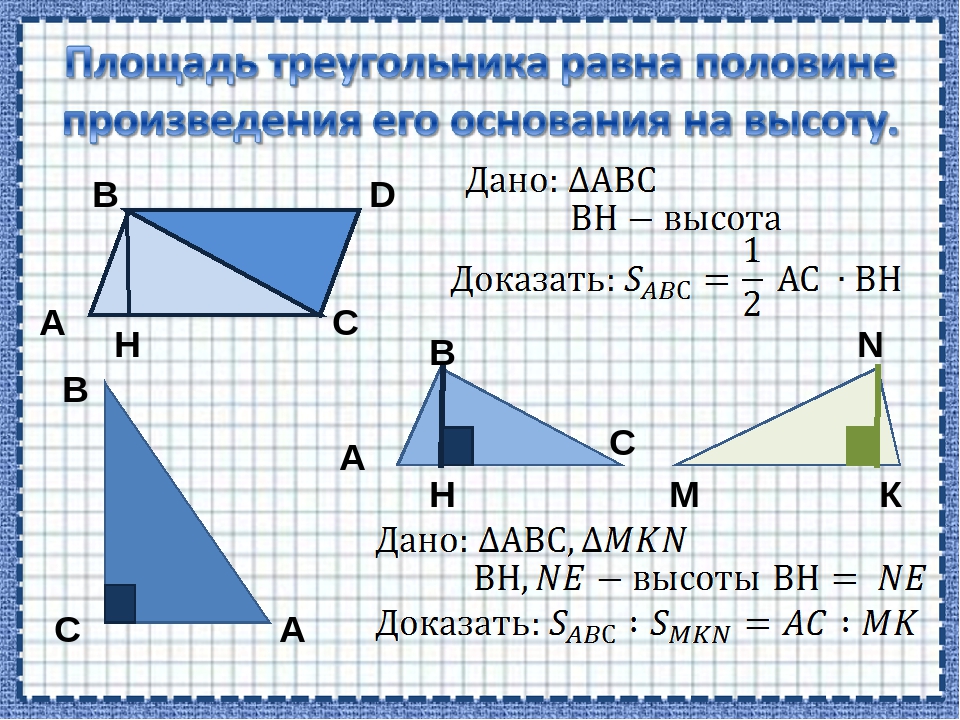
Величина площади выражается числом заключающихся в него квадратных единиц.
Формулы площади треугольника
1-ая формула
S — площадь треугольника
a, b — длины 2-х сторон треугольника
С — угол между сторонами a и b
2-ая формула
S — площадь треугольника
a — длина стороны треугольника
h — длина высоты, опущенной на сторону a
3-ья формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
p — полупериметр треугольника
4-ая формула
S — площадь треугольника
r — радиус вписанной окружности
p — полупериметр треугольника
5-ая формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
R — радиус описанной окружности
См.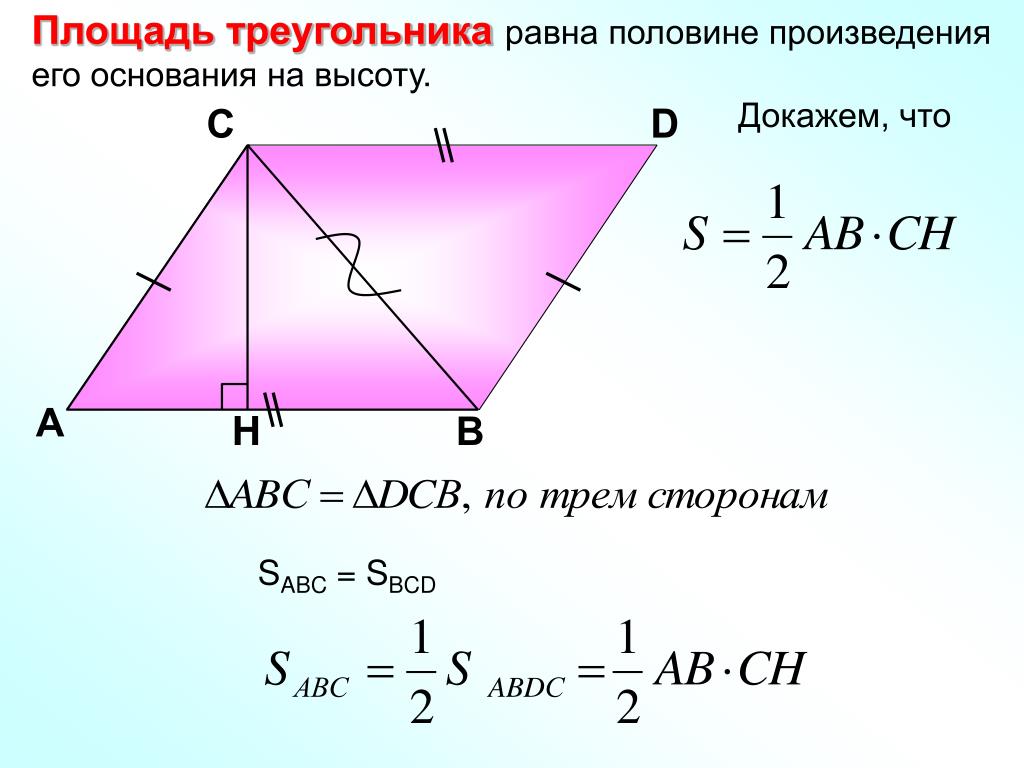 также: Программа для расчета площади треугольника.
также: Программа для расчета площади треугольника.
Формулы площади квадрата:
1) Площадь квадрата равна квадрату длины его стороны (a).
2) Площадь квадрата равна половине квадрата длины его диагонали (d).
S — площадь квадрата
a — длина стороны квадрата
d — длина диагонали квадрата
См. также: Программа для расчета площади квадрата.
Формула площади прямоугольника:
1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).
S — площадь прямоугольника
a — длина 1-ой стороны прямоугольника
b — длина 2-ой стороны прямоугольника
См. также: Программа для расчета площади прямоугольника.
Формула площади параллелограмма:
1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).
S — площадь параллелограмма
a — длина основания
h — длина высоты
См.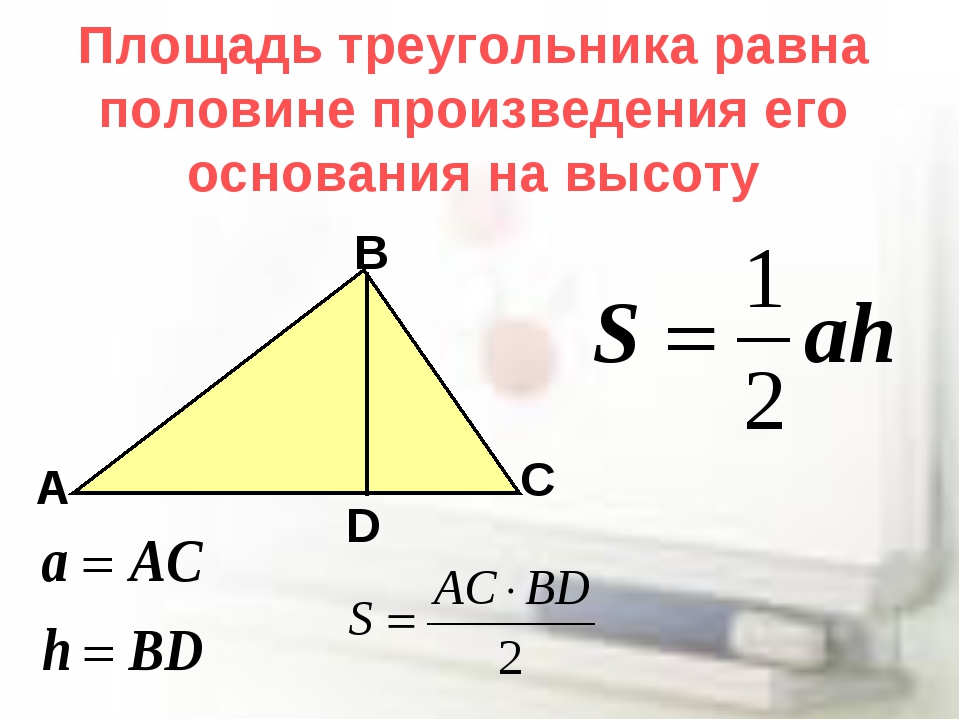 также: Программа для расчета площади параллелограмма.
также: Программа для расчета площади параллелограмма.
Формула площади трапеции:
1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
S — площадь трапеции
a — длина 1-ого основания
b — длина 2-ого основания
h — длина высоты трапеции
См. также: Программа для расчета площади трапеции.
Формулы площади ромба:
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
S — площадь ромба
a — длина основания ромба
h — длина высоты ромба
d1 — длина 1-ой диагонали
d2 — длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
Формула площади круга:
1) Площадь круга равна произведению квадрата радиуса на число пи (3.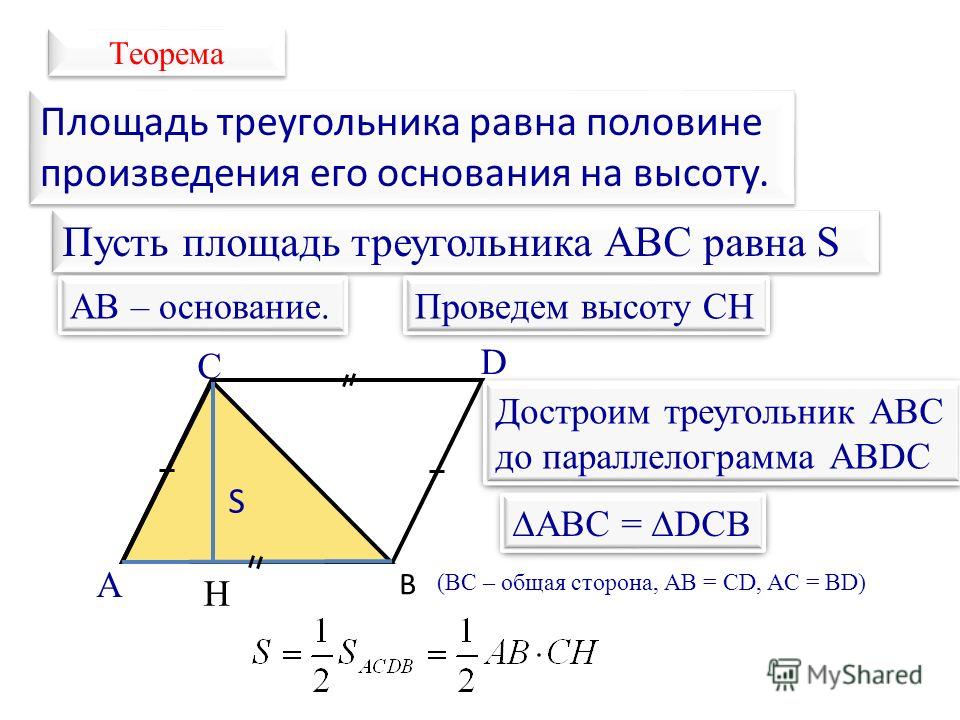 1415).
1415).
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
S — площадь круга
π — число пи (3.1415)
r — радиус круга
См. также: Программа для расчета площади круга.
Формула площади эллипса:
1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).
S — площадь эллипса
π — число пи (3.1415)
a — длина большой полуоси
b — длина малой полуоси
См. также: Программа для расчета площади эллипса.
Слишком сложно?
Формулы площади не по зубам? Тебе ответит эксперт через 10 минут!
Формулы площади и программы для расчета площадей
Содержание:
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади выражается числом заключающихся в него квадратных единиц.
Формулы площади треугольника
1-ая формула
S — площадь треугольника
a, b — длины 2-х сторон треугольника
С — угол между сторонами a и b
2-ая формула
S — площадь треугольника
a — длина стороны треугольника
h — длина высоты, опущенной на сторону a
3-ья формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
p — полупериметр треугольника
4-ая формула
S — площадь треугольника
r — радиус вписанной окружности
p — полупериметр треугольника
5-ая формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
R — радиус описанной окружности
См. также: Программа для расчета площади треугольника.
также: Программа для расчета площади треугольника.
Формулы площади квадрата:
1) Площадь квадрата равна квадрату длины его стороны (a).
2) Площадь квадрата равна половине квадрата длины его диагонали (d).
S — площадь квадрата
a — длина стороны квадрата
d — длина диагонали квадрата
См. также: Программа для расчета площади квадрата.
Формула площади прямоугольника:
1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).
S — площадь прямоугольника
a — длина 1-ой стороны прямоугольника
b — длина 2-ой стороны прямоугольника
См. также: Программа для расчета площади прямоугольника.
Формула площади параллелограмма:
1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).
S — площадь параллелограмма
a — длина основания
h — длина высоты
См. также: Программа для расчета площади параллелограмма.
также: Программа для расчета площади параллелограмма.
Формула площади трапеции:
1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
S — площадь трапеции
a — длина 1-ого основания
b — длина 2-ого основания
h — длина высоты трапеции
См. также: Программа для расчета площади трапеции.
Формулы площади ромба:
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
S — площадь ромба
a — длина основания ромба
h — длина высоты ромба
d1 — длина 1-ой диагонали
d2 — длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
Формула площади круга:
1) Площадь круга равна произведению квадрата радиуса на число пи (3. 1415).
1415).
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
S — площадь круга
π — число пи (3.1415)
r — радиус круга
См. также: Программа для расчета площади круга.
Формула площади эллипса:
1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).
S — площадь эллипса
π — число пи (3.1415)
a — длина большой полуоси
b — длина малой полуоси
См. также: Программа для расчета площади эллипса.
Слишком сложно?
Формулы площади не по зубам? Тебе ответит эксперт через 10 минут!
Площадь равнобедренного треугольника
В данном уроке размещены формулы и задачи на нахождение площади равнобедренного треугольника. Формулы снабжены пояснениями и комментариями.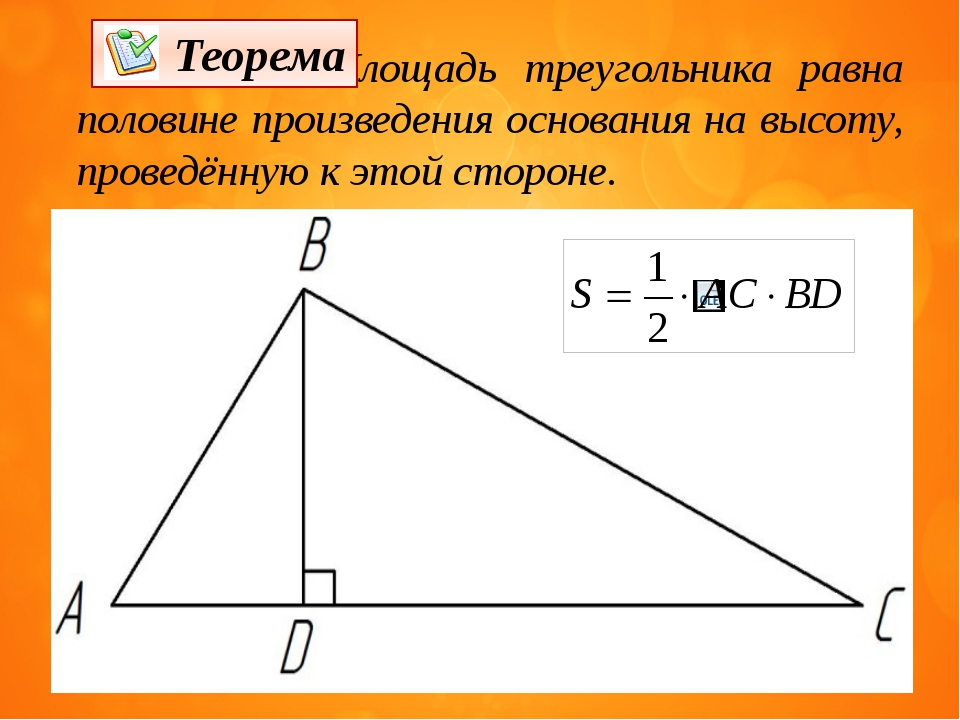 На отдельном рисунке приведено соответствие условных обозначений формул и элементов равнобедренного треугольника. Далее приведен раздел с примерами решения задач.
На отдельном рисунке приведено соответствие условных обозначений формул и элементов равнобедренного треугольника. Далее приведен раздел с примерами решения задач.
См. также:
Буквенные обозначения сторон и углов на приведенном рисунке соответствуют обозначениям, которые указаны в формулах. Таким образом, это поможет Вам сопоставить их с элементами равнобедренного треугольника. Из условия задачи определите, какие элементы известны, найдите на чертеже их обозначения и подберите подходящую формулу.
Формула площади равнобедренного треугольника
Далее приведены формулы нахождения площади равнобедренного треугольника: через стороны, боковую сторону и угол между ними, через боковую сторону, основание и угол при вершине, через сторону основания и угол при основании и т.д. Просто найдите наиболее подходящую на рисунке слева. Для самых любопытных в тексте справа поясняется, почему формула явяляется правильной и как именно с ее помощью находится площадь.
- Площадь равнобедренного треугольника можно найти, зная его сторону и основание. Данное выражение было получено путем упрощения более общей, универсальной формулы. Если за основу взять формулу Герона, а затем принять во внимание, что две стороны треугольника равны меду собой, то выражение упрощается до формулы, представленной на картинке.
Пример использования такой формулы приведен на примере решения задачи ниже. - Вторая формула позволяет найти его площадь через боковые стороны и угол между ними — это половина квадрата боковой стороны, умноженная на синус угла между боковыми сторонами
Если мысленно опустить высоту на боковую сторону равнобедренного треугольника, заметим, что ее длина будет равна a * sin β. Поскольку длина боковой стороны нам известна, высота, опущенная на нее теперь известна, половина их произведения и будет равна площади данного равнобедренного треугольника (Пояснение: полное произведение дает площадь прямоугольника, что очевидно. Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5
Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5 - Третья формула показывает нахождение площади через боковую сторону, основание и угол при вершине.
Строго говоря, зная один из углов равнобедренного треугольника, можно найти и остальные, поэтому применение данной или предыдущей формулы — вопрос вкуса (кстати, поэтому можно запомнить только одну из них).
У третьей формулы также есть еще одна интересная особенность — произведение a sin α даст нам длину высоты, опущенной на основание. В результате мы получим простую и очевидную формулу 5. - Площадь равнобедренного треугольника можно также найти через сторону основания и угол при основании (углы при основании равны) как квадрат основания, деленный на четыре тангенса половины угла, образованного его боковыми сторонами.
 Если присмотреться внимательнее, то станет очевидно, что половина основания (b/2) умноженная на tg(β/2) даст нам высоту треугольника. Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна.
Если присмотреться внимательнее, то станет очевидно, что половина основания (b/2) умноженная на tg(β/2) даст нам высоту треугольника. Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна. - Разумеется, площадь равнобедренного треугольника можно найти, опустив высоту из вершины на основание, в результате чего получится два прямоугольных треугольника. Далее — все очевидно. Половина произведения высоты на основание и есть искомая площадь. Пример использования данной формуле см. в задаче ниже (2-й способ решения)
- Эта формула получается, если попытаться найти площадь равнобедренного треугольника с помощью теоремы Пифагора. Для этого выразим высоту из предыдущей формулы, которая одновременно, является катетом прямоугольного треугольника, образованного боковой стороной, половиной его основания и высотой, через теорему Пифагора.
 Боковая сторона является гипотенузой, поэтому из квадрата боковой стороны (а) вычтем квадрат второго катета. Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Боковая сторона является гипотенузой, поэтому из квадрата боковой стороны (а) вычтем квадрат второго катета. Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Кстати, самые сообразительные могут увидеть, что если в Формуле 1 раскрыть скобки, то она превратиться в Формулу 6. Или наоборот, разность квадратов двух чисел, разложенная на множители, даст нам исходную, первую.
Обозначения, которые были применены в формулах на рисунке:
a — длина одной из двух равных сторон треугольника
b — длина основания
α — величина одного из двух равных углов при основании
β — величина угла между равными сторонами треугольника и противолежащего его основанию
h — длина высоты, опущенная из вершины равнобедренного треугольника на основание
Важно.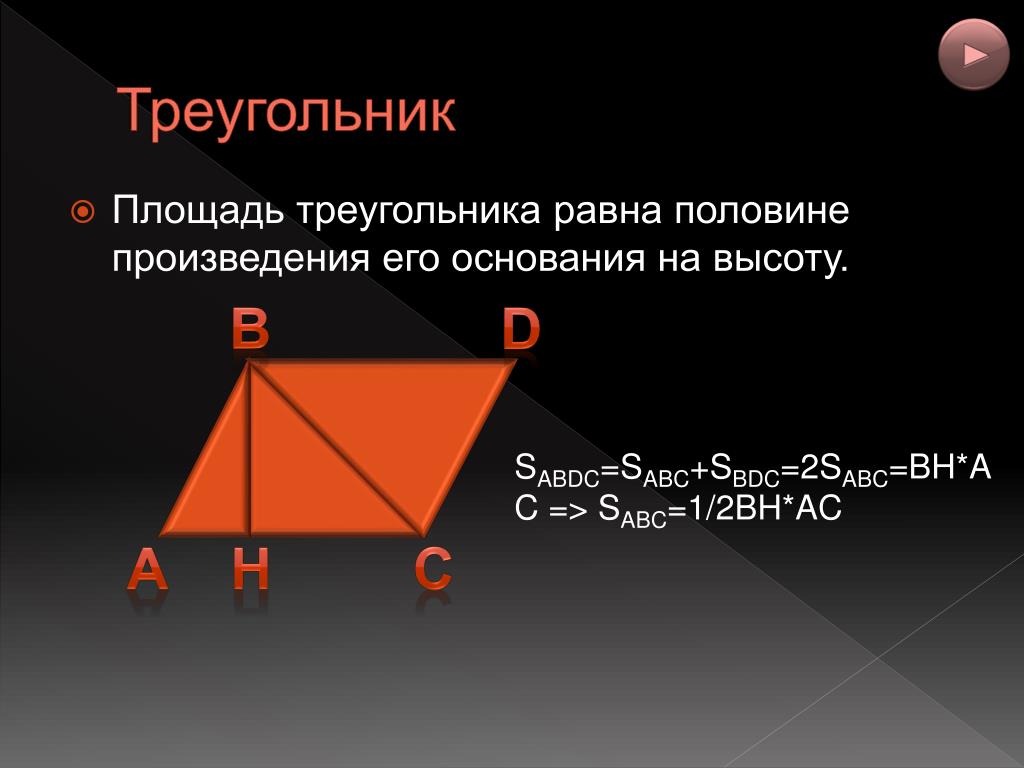 Обратите внимание на обозначения переменных! Не перепутайте α и β, а также a и b!
Обратите внимание на обозначения переменных! Не перепутайте α и β, а также a и b!
См. также: другие формулы и свойства равнобедренного треугольника
Примечание. Это часть урока с задачами по геометрии (раздел площадь равнобедренного треугольника). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Задача
Боковая сторона равнобедренного треугольника равна 13 см, а основание равно 10 см. Найдите площадь равнобедренного треугольника.
Решение.
1-й способ. Применим формулу Герона. Поскольку треугольник равнобедренный, то она примет более простой вид (см. формулу 1 в списке формул выше):
формулу 1 в списке формул выше):
где а — длина боковых сторон, а b — длина основания.
Подставив значения длин сторон треугольника из условия задачи, получим:
S = 1/2 * 10 * √ ((13 + 5 )( 13 — 5 )) = 5 √ (18 * 8) = 60 см2
2-й способ. Применим теорему Пифагора
Предположим, что мы не помним формулу, использованную в первом способе решения. Поэтому опустим из вершины B на основание AC высоту BK.
Поскольку высота равнобедренного треугольника делит его основание пополам, то длина половины основания будет равна
AK = AC / 2 = 10 / 2 = 5 см .
Высота с половиной основания и стороной равнобедренного треугольника образует прямоугольный треугольник ABK. В этом треугольнике нам известна гипотенуза AB и катет AK. Выразим длину второго катета через теорему Пифагора.
Соответственно, высота будет равна:
h = √ ( 132 — 52 ) = √144 = 12 см
Площадь исходного равнобедренного треугольника ABC будет равна площади двух прямоугольных треугольников ABK и CBK, образованных боковыми сторонами, высотой и половинами основания равнобедренного треугольника.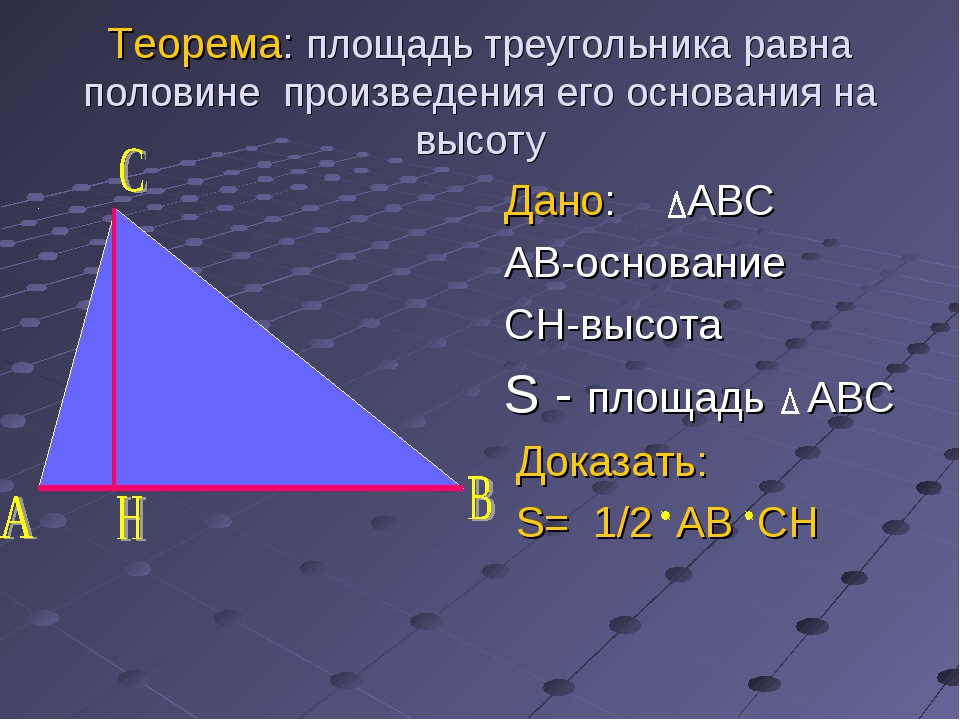 Оба прямоугольных треугольника равны между собой. Гипотенузы — это стороны равнобедренного треугольника, поэтому они равны, один из катетов — общий, а, поскольку, BK одновременно является и биссектрисой и высотой, то, соответствующие углы также равны. Поэтому нам будет достаточно найти площадь одного из них и умножить полученное число на два.
Оба прямоугольных треугольника равны между собой. Гипотенузы — это стороны равнобедренного треугольника, поэтому они равны, один из катетов — общий, а, поскольку, BK одновременно является и биссектрисой и высотой, то, соответствующие углы также равны. Поэтому нам будет достаточно найти площадь одного из них и умножить полученное число на два.
Площадь параллелограмма, треугольника и трапеции — урок. Геометрия, 8 класс.
Площадь параллелограмма
Необходимо определить, что такое высота параллелограмма.
Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону. Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.
Высота \(BE\), проведённая между длинными сторонами, короче высоты \(BF\), проведённой между короткими сторонами.
Так как стороны ромба одинаковы, то высоты ромба также одинаковы: \(BE = BF\).
Площадь произвольного параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.
Проведём высоты из двух вершин \(B\) и \(C\) к стороне \(AD\) .
Прямоугольные треугольники \(ABE\) и \(DCF\) равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
Параллелограмм \(ABCD\) и прямоугольник \(EBCF\) — равновеликие, так как состоят из равных фигур:
SABCD=SABE+SEBCD;SEBCF=SEBCD+SDCF.
Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
SEBCF=BE⋅BC;SABCD=BE⋅BC=BE⋅AD.
Если обозначить сторону через \(a\), высоту — через \(h\), то:
Sп−гр=a⋅h.
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
Площадь ромба
Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.
SABCD=4⋅SABO=4⋅BO⋅AO2=2⋅BO⋅AO.
Формула определения площади ромба:
Sромба=d1⋅d22.
Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.
Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали:
Sквадрата=d22.
Площадь произвольного треугольника
Так как диагональ параллелограмма делит его на два равных треугольника, то площадь треугольника равна половине площади параллелограмма.
Sтреуг=aha2, где \(h\) — высота (на рисунке — \(BE\)), проведённая к стороне \(a\) (на рисунке — \(AD\)).
Для определения площади треугольника можно использовать любую сторону и высоту, проведённую к этой стороне.
Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.
SΔ=pp−ap−bp−c;p=a+b+c2
— формула Герона, где \(a\), \(b\) и \(c\) — стороны треугольника, \(p\) — полупериметр треугольника.
Площадь прямоугольного треугольника
Так как катеты прямоугольного треугольника взаимно перпендикулярны, то один катет может быть высотой, а другой катет — стороной, к которой проведена высота. Получаем формулу:
S=a⋅b2, где \(a\) и \(b\) — катеты.
Для прямоугольного треугольника также можно применять формулы площади произвольного треугольника.
Пример:
1. вычислим площадь треугольника со сторонами \(17\) см, \(39\) см, \(44\) см.
Решение:
p=17+39+442=50;SΔ=50⋅50−17⋅50−39⋅50−44=50⋅33⋅11⋅6==25⋅2⋅3⋅11⋅11⋅2⋅3=5⋅2⋅3⋅11=330см2.
Чтобы легче было вычислить корень, необходимо не перемножать все числа, а раскладывать их на множители: a⋅a=a.
Формулу Герона можно использовать для вычисления высоты треугольника.
Пример:
2. вычислим меньшую высоту треугольника, стороны которого равны \(15\) см, \(13\) см, \(4\) см.
Решение:
используем две формулы вычисления площади: SΔ=aha2 и SΔ=pp−ap−bp−c.
Меньшая высота в треугольнике — та, которая проведена к большей стороне, поэтому \(a =\) \(15\) см.
SΔ=pp−ap−bp−c=16⋅1⋅3⋅12=24см2.
Составляем уравнение:
15⋅h3=24⋅215⋅h=48;h=4815=3,2(см).
Иногда формула Герона используется для вычисления площади параллелограмма, если даны стороны параллелограмма и его диагональ.
Пример:
3. дан параллелограмм со сторонами \(17\) см и \(39\) см, длина диагонали равна \(44\) см. Вычислим площадь параллелограмма.
Решение:
диагональ делит параллелограмм на два равных треугольника. Используем результат, полученный в первом примере:
Sпараллелограмма=2⋅SΔ=2⋅330=660(см2).
Площадь трапеции
Трапеция имеет одну пару параллельных сторон, следовательно, имеет одну высоту — перпендикуляр, проведённый между параллельными сторонами.
Чаще всего высоту трапеции проводят из вершин или через точку пересечения диагоналей.
Площадь трапеции определим как сумму площадей треугольников, на которые трапецию делит диагональ.
SABCD=SABD+SDBC;SABCD=AD⋅BE2+BC⋅DF2=AD⋅BE2+BC⋅BE2==AD+BC⋅BE2.
Если обозначить параллельные стороны (основания) трапеции через \(a\) и \(b\), высоту через \(h\), то:
Sтрап=a+b2⋅h.
Обрати внимание!
Важные следствия:
1. если высоты треугольников равны, то их площади относятся как длины оснований.
2. Если основания треугольников равны, то их площади относятся как длины высот.
3. Если высоты треугольников равны и их основания равны, то они равновелики, например, медиана делит треугольник на две равновеликие части.
Урок 11. площадь треугольника — Геометрия — 8 класс
Выведем формулу для вычисления площади треугольника и следствия из неё.
Одну из сторон треугольника будем называть основанием.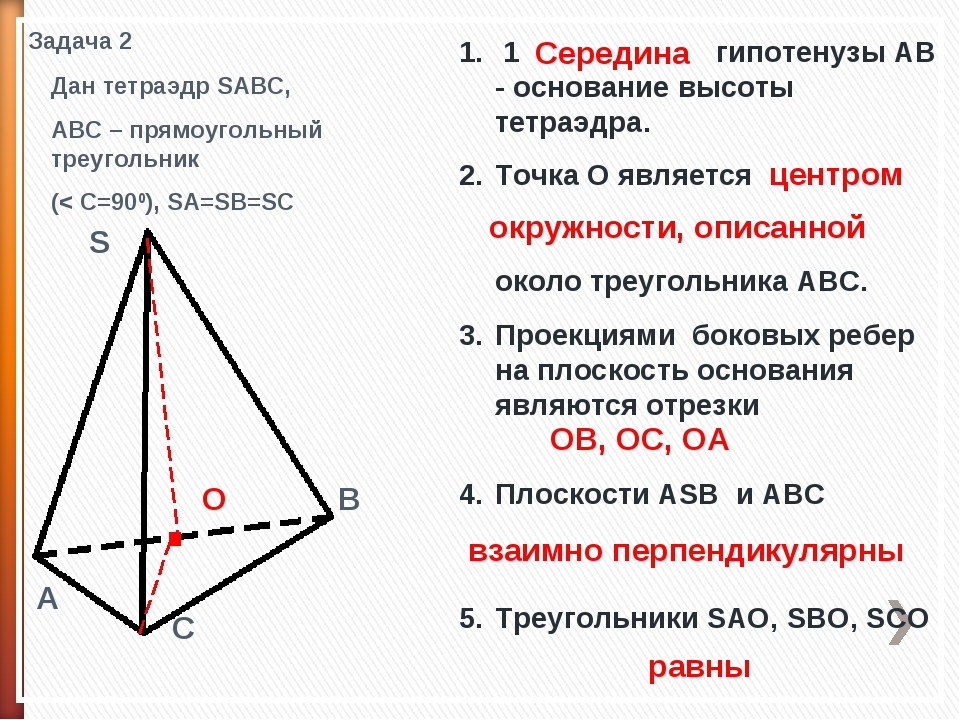 Например, сторону AC. Тогда высотой треугольника будем считать ту, которая проведена к основанию.
Например, сторону AC. Тогда высотой треугольника будем считать ту, которая проведена к основанию.
Достроим треугольник ABC до параллелограмма. Площадь параллелограмма равна сумме площадей треугольников ABC и BCD.
Sпараллелограмма = SABC + SBCD, SABC = SBCD, поэтому Sпараллелограмма = 2SABC
AC ∙ BH = 2SABC
SABC = 1/2 AC ∙ BH
Вывод
Sтреугольника = 1/2 a ∙ h
Площадь прямоугольного треугольника равна половине площади прямоугольника, т.е. половина произведения AB и BC.
SABC = 1/2 SABCD
SABC = 1/2 AB ∙ BC, но AB и BC – ab, поэтому
SABC = 1/2 ab, где a и b – катеты
Это первое следствие из теоремы о площади треугольника.
С другой стороны площадь прямоугольного треугольника равна половине произведения основания на высоту.
Пусть основанием является гипотенуза, а за высоту треугольника примем высоту, проведённую к гипотенузе.
SABC = 1/2 ch = 1/2 ab,
h = ab/c
Следствие второе:
Если высоты двух треугольников равны, то их площади относятся как основания.
Действительно, если h1 = h2 = h, то выражения для площадей примут вид
SABC = 1/2 AC ∙ hSA1B1C1 = 1/2A1C1 ∙ h
SABC/SA1B1C1 = (1/2 AC ∙ h)/(1/2 A1C1 ∙ h) = AC/A1C1
Тогда отношение площадей равно отношению оснований треугольников. Что и требовалось доказать.
Второе следствие помогает доказать утверждение:
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Пусть ∠A = ∠A1, тогда
SABC/SA1B1C1 = (AB ∙ AC)/(A1B1 ∙ A1C1)
Знание формулы для вычисления площади прямоугольного треугольника позволяет вывести формулу для вычисления площади ромба, отличную от формулы площади параллелограмма.
Известно, что диагонали ромба делят его на 4 равных прямоугольных треугольника. Поэтому площади этих треугольников равны. Значит, можно утверждать, что площадь ромба равна четырём площадям треугольника. Проведя дальнейшие рассуждения, получим, что площадь ромба равна половине произведения его диагоналей.
Sромба = 4 ∙ SABO = 4 ∙ 1/2 ∙ AO ∙ BO =(1)/2 ∙ 4 ∙ AO ∙ BO = 1/2 ∙ 2AO ∙ 2BO = 1/2 AC ∙ BD
Sромба = 1/2 ∙ d1 ∙ d2, где d1 ∙ d2 – диагонали ромба.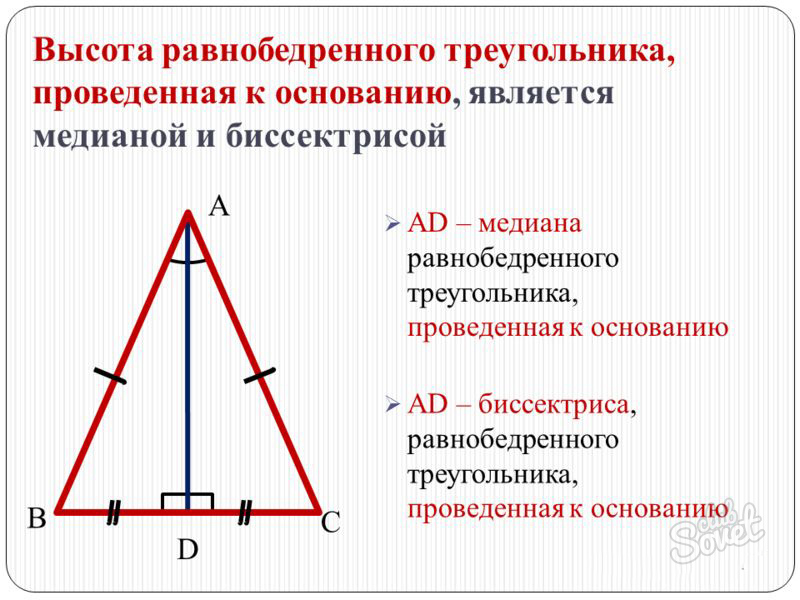
Площадь треугольника (традиционный метод) с помощью калькулятора
Площадь треугольника (традиционный метод) с помощью калькулятора — Math Open Reference
Количество квадратных единиц, необходимое для того, чтобы точно заполнить интерьер
треугольник.
Попробуйте это Перетащите оранжевые точки на каждую вершину
чтобы изменить форму треугольника. Показанная формула пересчитает площадь с использованием этого метода.
Самый распространенный метод
Площадь треугольника, обычно называемая «половина основания, умноженная на высоту», определяется по формуле, приведенной ниже. где
b — длина
база
a — длина соответствующего
высота
Вы можете выбрать любую сторону, чтобы быть
база.
Это не обязательно должен быть тот, который нарисован внизу треугольника.
Высота
должен быть тот, который соответствует выбранной вами базе.
Высота — это линия, перпендикулярная выбранному основанию от противоположной вершины.
На рисунке выше одна сторона была выбрана в качестве основания и показана соответствующая высота.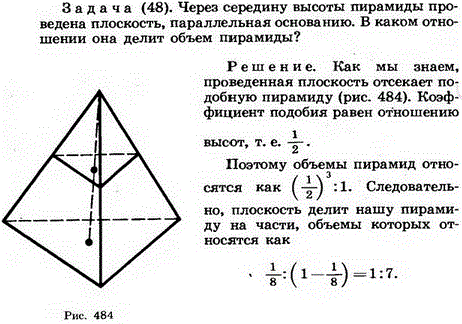
Калькулятор
Используйте калькулятор выше, чтобы вычислить площадь треугольника.
Введите любые два значения, и другое будет вычислено.Например: введите базу и высоту и нажмите «Рассчитать». Площадь будет рассчитана.
Точно так же, если вы войдете в область и базу, будет рассчитана высота, необходимая для получения этой области.
Методы определения площади треугольника
Что стоит попробовать
На рисунке выше нажмите «Высота замораживания».
Когда вы теперь перетаскиваете точку A, обратите внимание, что область не меняется.
Площадь зависит от основания и высоты, и ни один из них не меняется при перемещении верхней вершины из стороны в сторону.Следовательно, все треугольники, которые вы можете создать таким образом, имеют одинаковую площадь.
Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Центры треугольника
Соответствие и сходство
Решение треугольников
Треугольник викторины и упражнения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Как найти площадь треугольника
Как найти площадь треугольника
Чтобы найти площадь треугольника, умножьте основание на высоту и разделите на 2.В качестве альтернативы, разделите основание на 2, а затем умножьте на высоту или разделите высоту на 2, а затем умножьте на основание.
Не имеет значения, умножаете ли вы сначала основание и высоту, а затем делите ответ вдвое, или сначала уменьшаете вдвое основание или высоту, а затем умножаете.
Например, вот прямоугольный треугольник с основанием 8 см и высотой 3 см.
Умножая основание и высоту, получаем 8 × 3 = 24. Ответ вдвое равен 12.
Площадь 12 см 2 .
Площадь треугольника измеряется в квадратах. Возьмите единицу измерения сторон и запишите ее в квадрате после вашего ответа. Если стороны измеряются в см, то единицы площади равны 2 см. Если стороны измеряются в м, то единицы площади равны м 2 .
В этом расчете мы умножили сантиметры на сантиметры, поэтому единицы площади в этом примере равны см 2 .
Вместо того, чтобы сначала умножать основание на высоту, а затем делить на 2, мы можем сначала разделить пополам одну из длин основания или высоты.
Мы рассмотрим тот же пример и сначала разделим на 2 перед умножением.
Так как 8 см — это ровно, а 3 см — нет, то длину 8 см легче сократить вдвое.
Половина 8 равна 4, а затем 4 × 3 = 12. Площадь 12 см 2 .
Ответ один и тот же независимо от того, в каком порядке умножаются числа.
Формула площади треугольника: 1 / 2 × основание × высота. Эту формулу проще записать как Area = 1 / 2 bh.
Формула Area = 1 / 2 bh работает для всех треугольников, независимо от их размера и формы. Если известны высота и основание, эту формулу можно использовать для расчета площади.
Вот пример использования формулы для вычисления площади треугольника.
Основание этого треугольника составляет 11 м, а высота треугольника 8 м.
Значение b = 11 и значение h = 8.
1 / 2 × b × h становится 1 / 2 × 11 × 8.
Мы можем сначала умножить 11 на 8, а затем разделить ответ вдвое. 11 × 8 = 88, а затем 88 ÷ 2 = 44.
Длины сторон измеряются в метрах, поэтому площадь этого треугольника составляет 44 м 2 .
При обучении нахождению площади треугольника рекомендуется сначала разделить на 2 перед умножением, чтобы упростить расчет.
Проще сначала разделить 8 пополам, чтобы получить 4, а затем умножить это на 11, чтобы получить тот же ответ: 44 m 2 .
Делая сначала деление, в сумме умножения используются меньшие числа, которые легче вычислить. Этот метод также предполагает уменьшение вдвое меньшего числа, а не большего окончательного ответа.
При использовании формулы для определения площади треугольника важно убедиться, что основание и высота пересекаются под прямым углом.
Иногда вам могут быть даны все три стороны треугольника. Чтобы вычислить площадь треугольника, выберите две длины, расположенные под прямым углом друг к другу, в качестве основания и высоты.Умножьте эти длины и затем разделите на 2. Не обращайте внимания на другие длины сторон.
Почему площадь треугольника равна половине основания, умноженной на высоту
Любой треугольник можно нарисовать внутри прямоугольника, который в два раза больше его размера. Площадь прямоугольника равна основанию, умноженному на высоту, и поэтому площадь треугольника равна половине основания, умноженному на высоту.
Площадь прямоугольника равна основанию × высоте, также может быть записано как длина × ширина.
Чтобы из прямоугольника получился треугольник, разделите его пополам по диагонали.
Поскольку площадь прямоугольника равна основанию × высоте, площадь треугольника составляет 1 / 2 × основание × высота.
Вот еще один пример треугольника, который вдвое меньше прямоугольника.
Площадь прямоугольника составляет 10 × 6 = 60 мм 2 , а площадь треугольника составляет половину этой площади.
Площадь треугольника 30 мм 2
Помните, что при обучении площади треугольника проще всего сначала разделить высоту или основание на 2.
Половина 10 равна 5, а затем 5 × 6 = 30 мм 2 .
Обнаружение формул площади — элементарная математика
Формулы площади
Студенты, неформально относящиеся к области как к «количеству двумерного« материала », содержащегося внутри области, могут изобрести для себя большинство формул, которые их часто просят просто запомнить. Каждая формула, которую они изобретают заново, помогает укрепить их понимание (и память) о других формулах, которые они знают. (См. Также площадь поверхности.)
Площадь прямоугольников
Выбирая квадрат в качестве единицы площади, мы получаем интуитивное представление о площади прямоугольников.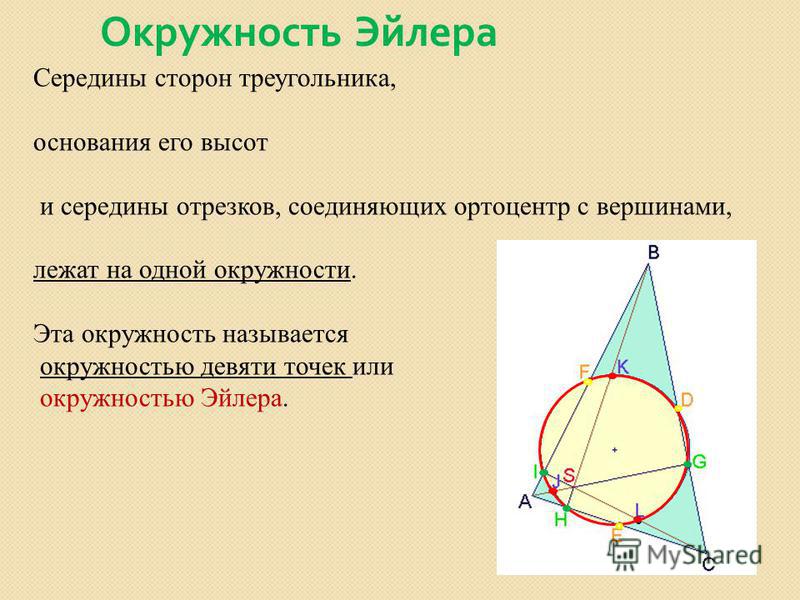 Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, который в 7 раз длиннее, будет иметь площадь 7 × 1.
Если мы решим, что площадь этого квадрата равна 1, то прямоугольник, который в 7 раз длиннее, будет иметь площадь 7 × 1.
Прямоугольник, который вдвое превышает высоту, будет иметь удвоенную площадь, поэтому площадь составляет 2 × 7 единиц площади. Мы можем сосчитать два ряда по семь квадратов. Точно так же он имеет 3 ряда по 7 квадратов (или 7 столбцов по 3 квадрата), всего 7 × 3 квадратов, поэтому его площадь составляет 21 квадратную единицу.
Количество квадратов в одном ряду — это длина прямоугольника. Количество строк — это высота прямоугольника. Таким образом, площадь равна длине × высоте.
Поскольку прямоугольник можно нарисовать под наклоном, «высота» определяется как «направление, перпендикулярное основанию», а «основание» определяется как, ну, с какой бы стороны вы его ни выбрали.
Это работает для подсчета чисел. Это работает даже для дробей. Показанный здесь синий прямоугольник измеряет половину единицы длины на пять с половиной единиц длины.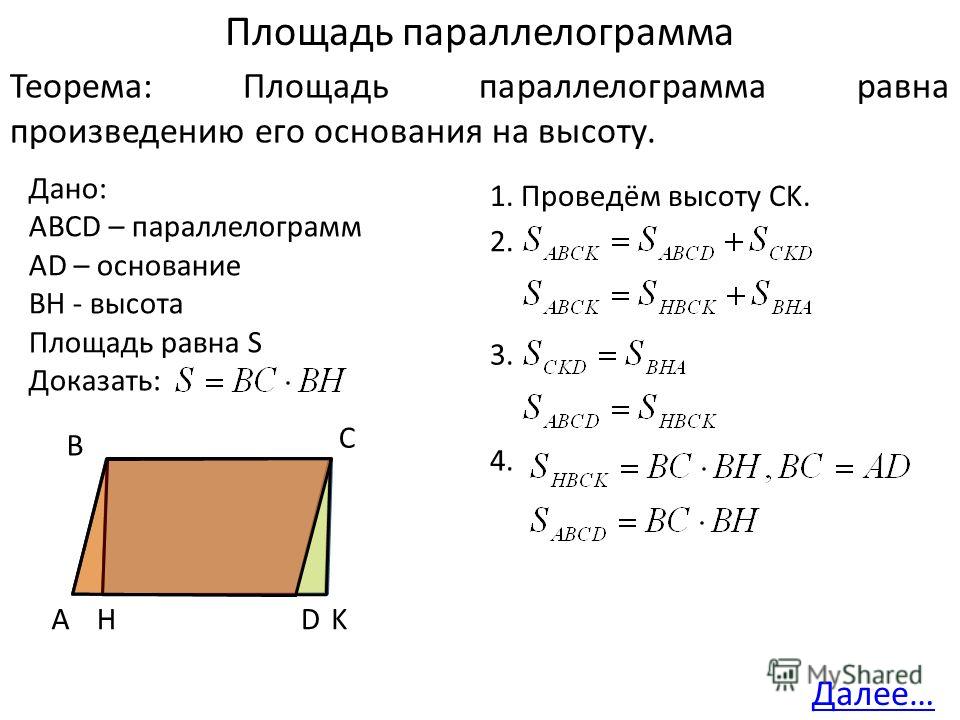 Если мы выберем соответствующий квадрат в качестве единицы площади, мы увидим, что синий прямоугольник содержит пять половин площади и одну четверть единицы площади, или всего две и три четверти единицы площади. (Розовые части показывают заполнение каждой квадратной единицы площади.)
Если мы выберем соответствующий квадрат в качестве единицы площади, мы увидим, что синий прямоугольник содержит пять половин площади и одну четверть единицы площади, или всего две и три четверти единицы площади. (Розовые части показывают заполнение каждой квадратной единицы площади.)
Чтобы включить всех чисел, мы определяем площадь прямоугольника как основание × высота (где «основание» и «высота» означают длины этих сторон, измеряется в те же единицы ).
Площадь параллелограммов
Идея
Мы можем вычислить формулу площади параллелограмма, рассекая параллелограмм и переставляя части, чтобы получился прямоугольник. Поскольку параллелограмм и прямоугольник состоят из одинаковых частей, они обязательно имеют одинаковую площадь. (См. Определение площади, чтобы узнать, почему эти области одинаковы.)
Мы видим, что они и имеют точно такую же длину основания (синий) и точно такую же высоту (зеленый). Поскольку основание × высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме, чтобы вычислить его площадь: основание × высота . (Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это та сторона, которую вы выбрали первой. См. Параллелограмм.)
Поскольку основание × высота дает площадь прямоугольника, мы можем использовать те же измерения на параллелограмме, чтобы вычислить его площадь: основание × высота . (Как и раньше, «высота» измеряется перпендикулярно основанию, а «основание» — это та сторона, которую вы выбрали первой. См. Параллелограмм.)
На разрезе, показанном выше, легко увидеть, что базовая длина не изменилась.Фактически, перпендикулярный разрез можно делать в любом месте основания.
Укрепление отверстий
Интуиция и доказательство
Это рассечение дает интуитивное понимание формулы площади параллелограмма, причина того, что он должен быть таким, какой есть. Но мы не сомневались, действительно ли рассечение «работает». То есть, когда мы разрезаем параллелограмм и переставляем его части, мы ожидаем, что получит , и результат определенно будет таким. Но внешность может быть обманчива. Что убеждает нас в том, что когда мы перемещаем этот треугольник, в результате получается прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если результат не всегда является идеальным прямоугольником, мы не можем использовать наши знания формулы площади прямоугольника, чтобы разработать формулу для параллелограмма. В старшей школе ученики смогут доказать, что две части параллелограмма, если правильно собрать их, действительно образуют прямоугольник. В классах K-8 учащиеся по большей части должны полагаться на визуальный эксперимент и получать интуитивное ощущение.Узнайте больше о том, почему эти вскрытия работают.
Но внешность может быть обманчива. Что убеждает нас в том, что когда мы перемещаем этот треугольник, в результате получается прямоугольник? Что, если это больше похоже (хотя и менее преувеличено)? Если результат не всегда является идеальным прямоугольником, мы не можем использовать наши знания формулы площади прямоугольника, чтобы разработать формулу для параллелограмма. В старшей школе ученики смогут доказать, что две части параллелограмма, если правильно собрать их, действительно образуют прямоугольник. В классах K-8 учащиеся по большей части должны полагаться на визуальный эксперимент и получать интуитивное ощущение.Узнайте больше о том, почему эти вскрытия работают.
Что, если мы выберем короткую сторону в качестве основания?
Мы можем выбрать любую сторону в качестве базы; «Высота» определяется как измеряемая перпендикулярно стороне, которую мы выбираем в качестве основания. Если мы возьмем за основу короткую сторону (синюю), то рассечение, показанное выше, не будет таким убедительным.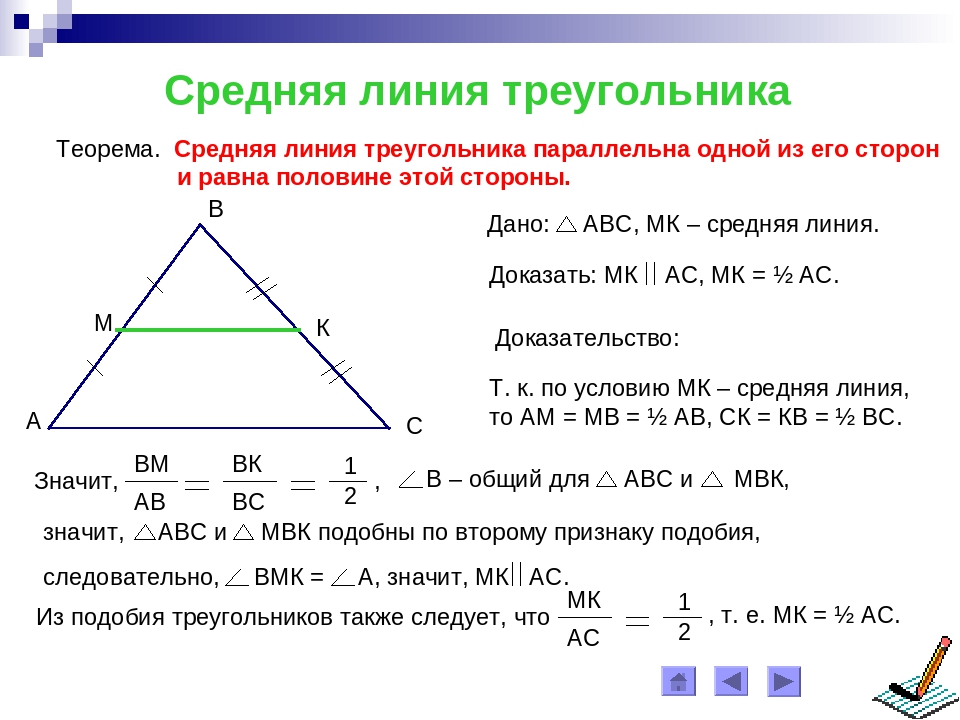 Резка на такой высоте и перестановка деталей оставляет беспорядок:
Резка на такой высоте и перестановка деталей оставляет беспорядок:
В этом конкретном примере мы можем спасти беспорядок, сделав еще один разрез, но что, если бы параллелограмм был еще длиннее и тоньше?
Оказывается, любой параллелограмм , независимо от того, насколько он длинный и тонкий, можно разрезать таким образом, чтобы части — возможно, многие из них — могли быть преобразованы в прямоугольник.Но нужно потрудиться, чтобы показать, что это всегда можно сделать. Нам нужна другая идея.
Немного другая идея рассечения в этом случае значительно упрощает жизнь. (Самостоятельно вы можете показать, что это работает и в исходном случае.)
- Заключите параллелограмм в прямоугольник.
- Две части прямоугольника, которые составляют , а не внутри параллелограмма, являются конгруэнтными треугольниками.
- Сдвиньте один из этих треугольников по направлению к другому, пока они не встретятся, образуя прямоугольник.Поскольку общая площадь внешнего прямоугольника не изменилась (это тот же прямоугольник, что и раньше), а желтая область не изменилась (части просто перемещались), разница между ними — фиолетовыми областями — должна быть такой же.
 Как и раньше, мы также можем видеть, что размеры прямоугольной фиолетовой области являются основанием и высотой исходного параллелограмма.
Как и раньше, мы также можем видеть, что размеры прямоугольной фиолетовой области являются основанием и высотой исходного параллелограмма.
Интуиция и доказательство, повтор: Опять же, рассечение дает существенное понимание, но требуется немного больше работы, чтобы убедиться, что два желтых треугольника, которые, безусловно, выглядят , как будто они подходят друг к другу, образуя прямоугольник, на самом деле точно подходят, а не просто почти .
Почему так важно быть осторожным?
При построении других формул площади (см. Ниже) мы захотим, чтобы использовал , как найти площадь параллелограмма, и поэтому мы хотим иметь возможность полагаться на найденное нами правило. Мы, , можем быть уверены, что перестановка частей не изменит площадь: то есть, в конце концов, то, как мы определяем область . Но мы также должны быть уверены, что детали подходят друг к другу, как мы заявляем, что они делают, или мы не можем полагаться на сделанные нами измерения. И мы должны быть уверены, что правило base × height не зависит от удачного выбора базы.
И мы должны быть уверены, что правило base × height не зависит от удачного выбора базы.
В большинстве учебных программ учащиеся не имеют достаточной систематической базы геометрических знаний до 8-го класса, чтобы убедительно доказать, что эти вскрытия работают. Но интуитивного понимания достаточно для объяснения и обоснования формул и хорошей основы для дальнейшего изучения геометрии.
Площадь треугольника
Знание того, как найти площадь параллелограмма, помогает нам найти площадь треугольника.
Рассекая треугольник
Мы можем разрезать треугольник на две части — одну из них треугольник, а другую — трапецию, разрезав его параллельно основанию. Если мы разрежем высоту ровно пополам с этим срезом, две части сложатся вместе, образуя параллелограмм с и тем же основанием , но половиной высоты .
Итак, основание × полувысота дает площадь треугольника. Аналогичный разрез показывает полубазовая × высота .Любой из них снижает до bh .
Аналогичный разрез показывает полубазовая × высота .Любой из них снижает до bh .
Удвоение треугольника и уменьшение полученной площади вдвое
Другой способ мышления: две копии треугольника образуют параллелограмм с тем же основанием, и той же высотой , что и треугольник.
Площадь параллелограмма равна основанию × высоте , но это вдвое больше площади треугольника, поэтому площадь треугольника составляет из основания × высоты , как мы видели с методом рассечения.
(Как всегда, выберите «основание» и измерьте высоту перпендикулярно этому основанию, от основания до противоположной вершины.)
Площадь трапеции
Удвоение трапеции и уменьшение полученной площади вдвое
Как и в случае с треугольником, две копии трапеции можно соединить вместе, чтобы получился параллелограмм.
Высота параллелограмма равна высоте трапеции, но его основание представляет собой сумму двух оснований трапеции.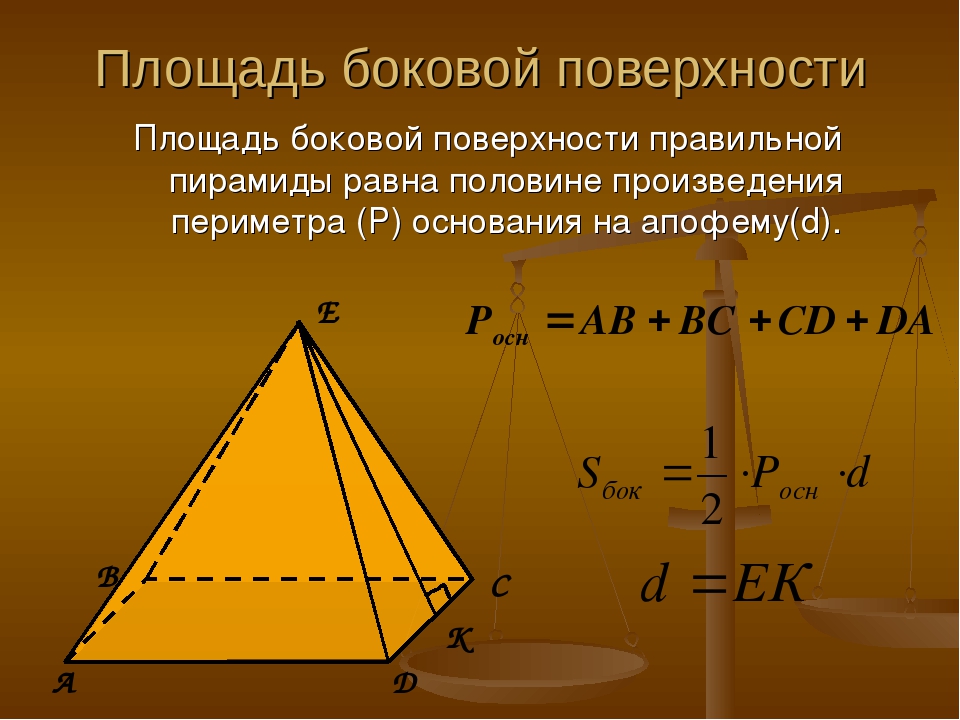 Таким образом, площадь параллелограмма равна по высоте × ( base1 + base2 ). Но эта площадь составляет две трапеции , поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.
Таким образом, площадь параллелограмма равна по высоте × ( base1 + base2 ). Но эта площадь составляет две трапеции , поэтому нам нужно разрезать ее пополам, чтобы получить площадь трапеции.
Рассечение трапеции
Мы также можем разрезать трапецию так же, как мы разрезали треугольник, с одним срезом, разрезающим ее высоту пополам. Две части соединяются вместе, образуя параллелограмм, основание которого является суммой двух оснований трапеции, но высота которого равна половине высоты трапеции.
В случае трапеции основания не могут быть выбраны произвольно. Две параллельные стороны являются основаниями, а высота, как всегда, представляет собой перпендикулярное расстояние от одного основания до противоположного.
Площадь этого параллелограмма равна его высоте (полувысоте трапеции), умноженной на его основание (сумма оснований трапеции), поэтому его площадь равна на полувысоте × ( base1 + base2 ).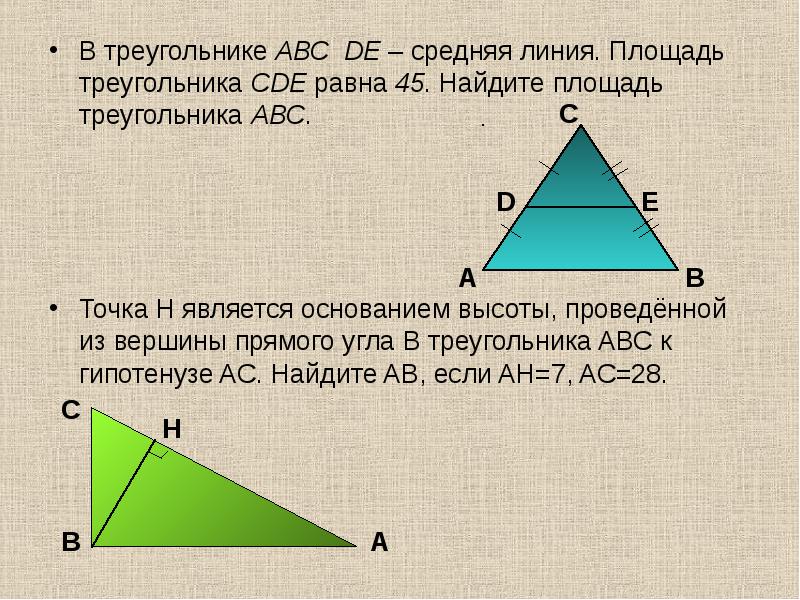 Поскольку параллелограмм состоит из того же материала, что и трапеция, это тоже площадь трапеции.
Поскольку параллелограмм состоит из того же материала, что и трапеция, это тоже площадь трапеции.
В любом случае площадь трапеции составляет × по высоте × ( base1 + base2 ) .
Площадь остальных четырехугольников
Площадь ромба
Площадь ромба можно найти, разрезав и переставив части, чтобы они образовали параллелограмм. Это можно сделать несколькими способами:
- Разрежьте более короткую диагональ (a), чтобы получились два совпадающих треугольника. Переместите нижнюю половину треугольника рядом с верхней половиной, чтобы получился параллелограмм.Более короткая диагональ (a) становится основанием параллелограмма, а половина более длинной диагонали (b) становится высотой параллелограмма. Таким образом, площадь ромба равна a * b или произведению диагоналей, что является стандартной формулой для ромба.
- Другой аналогичный способ — разрезать ромб на четыре равных треугольника и переставить их в прямоугольник с более короткой диагональю в качестве основания и половиной длинной диагонали в качестве высоты.

- После разрезания ромба на два равных треугольника мы можем вычислить площадь одного из треугольников, которая равна * основанию (a) * высоте (b) = ab.Затем умножьте на два, так как их два: 2 * ab = ab.
Площадь кайта
Площадь воздушного змея может быть похожа на площадь ромба. Если разрезать более длинную диагональ, получатся два равных треугольника. Если мы переставим их, мы можем сформировать параллелограмм с большей диагональю (b) в качестве основания и половиной более короткой диагонали (a) в качестве высоты. Итак, площадь становится b * a = ab. Более сложный подход требует немного алгебры. Разрежьте змей по более короткой диагонали, чтобы сформировать два треугольника с более короткой диагональю (a) в качестве основы.Таким образом, площадь первого треугольника — * волнистая, где волнистая — высота. Площадь второго треугольника равна a * (b — волнистый), где (b — волнистый) — оставшаяся часть большей диагонали. Таким образом, общая площадь становится (a * волнистая) + (a * (b — волнистая)). Вынося за скобки a, получаем a (волнистый + b — волнистый) = ab.
Вынося за скобки a, получаем a (волнистый + b — волнистый) = ab.
Ну что вы знаете. По сути, вам нужно только знать формулу для площади параллелограмма, а затем вывести формулу для других.
Площадь треугольников
Есть несколько способов найти площадь треугольника.
Зная базу и высоту
Когда мы знаем основание и высоту, это легко.
Это просто , половина b умноженная на h
Площадь = 1 2 bh
(Подробная информация на странице Треугольников)
Самое главное, чтобы основание и высота были под прямым углом. Поиграйте здесь:
Пример: Какова площадь этого треугольника?
(Примечание: 12 — это высота , а не длина левой стороны)
Высота = h = 12
База = b = 20
Площадь = ½ bh = ½ × 20 × 12 = 120
Знание трех сторон
Существует также формула для определения площади любого треугольника, когда мы знаем длины всех трех его сторон.
Это можно найти на странице формул Герона.
Зная две стороны и угол наклона
Когда мы знаем две стороны и включенный угол (SAS), мы можем использовать другую формулу (фактически, три эквивалентные формулы).
В зависимости от того, какие стороны и углы нам известны, формулу можно записать тремя способами:
Площадь = 1 2 ab sin C
Площадь = 1 2 до н.э. sin A
Площадь = 1 2 ca sin B
Это действительно та же формула, только с измененными сторонами и углом.
Пример: Найдите площадь этого треугольника:
Прежде всего мы должны решить, что мы знаем.
Мы знаем угол C = 25º, а стороны a = 7 и b = 10.
Итак, приступим:
Площадь = (½) ab sin C
Введите известные нам значения: ½ × 7 × 10 × sin (25º)
Сделайте некоторую работу с калькулятором: 35 × 0,4226 .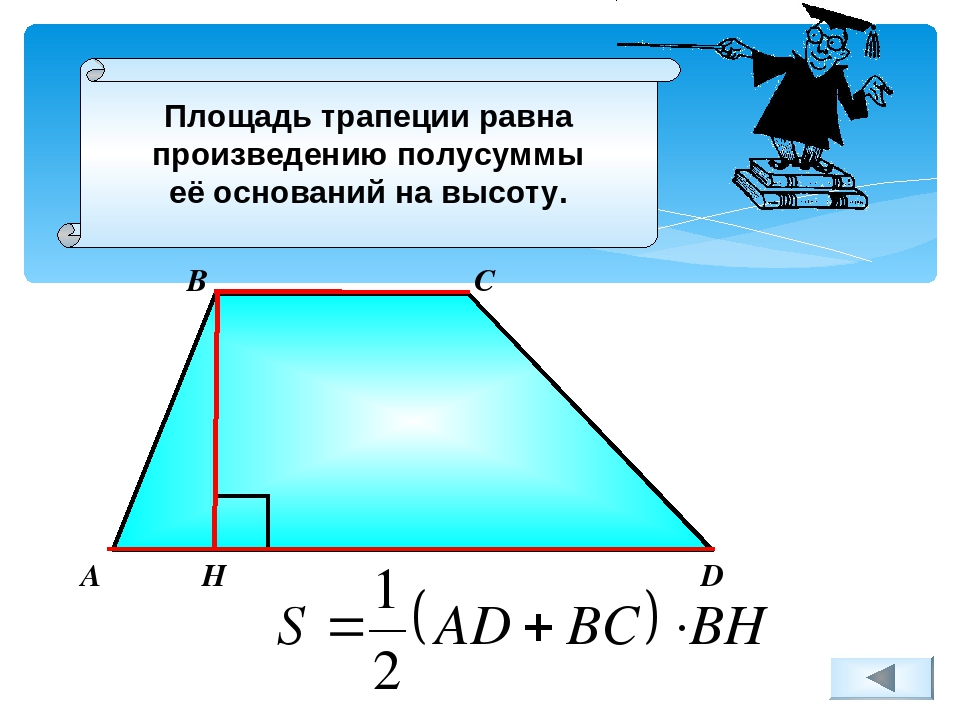 ..
..
Площадь = 14,8 с точностью до одного десятичного знака
Как помнить
Подумайте только о «abc»: Площадь = ½ a b sin C
Также хорошо помнить, что угол всегда составляет между двумя известными сторонами , что называется «включенным углом».
Как это работает?
Мы знаем, как найти область, когда знаем базу и высоту:
Площадь = ½ × основание × высота
В этом треугольнике:
|
Получаем:
Площадь = ½ × (c) × (b × sin A)
Что (проще):
Площадь = 1 2 до н.э. sin A
Изменив метки на треугольнике, мы также можем получить:
- Площадь = ½ ab sin C
- Площадь = ½ ca sin B
Еще один пример:
Пример: Найдите сколько земли
Фермер Джонс владеет треугольным участком земли.
Длина забора АВ составляет 150 м. Длина забора БЦ 231 м.
Угол между ограждением AB и ограждением BC составляет 123º.
Сколько земли принадлежит фермеру Джонсу?
Прежде всего мы должны решить, какие длины и углы нам известны:
- AB = c = 150 м,
- BC = a = 231 м,
- и угол B = 123º
Итак, мы используем:
Площадь = 1 2 ca sin B
Введите известные нам значения: ½ × 150 × 231 × sin (123º) м 2
Сделайте некоторую работу с калькулятором: 17,325 × 0.838 … м 2
Площадь = 14530 м 2
Фермер Джонс владеет 14530 м 2 земли
Площадь треугольника — пояснения и примеры
В этой статье вы узнаете площадь треугольника и определить площадь различных типов треугольников . Площадь треугольника — это пространство внутри треугольника.Он измеряется в квадратных единицах.
Площадь треугольника — это пространство внутри треугольника.Он измеряется в квадратных единицах.
Прежде чем перейти к теме о площади треугольника , давайте познакомимся с такими терминами, как основание и высота треугольника.
Основание — это сторона треугольника, которая считается нижней частью, а t высота треугольника — это перпендикулярная линия, опущенная на его основание из вершины, противоположной основанию. .
На приведенном выше рисунке пунктирными линиями показаны возможные высоты △ ABC. Обратите внимание, что у каждого треугольника, возможно, есть три высоты или высоты.
- Высота треугольника △ ABC равна h 1 , когда основание является стороной.
- Высота треугольника △ ABC равна h3 при основании AB.
- Высота треугольника △ ABC равна h 3 при основании
- Высота треугольника △ ABC может находиться вне треугольника ( h 4 ), что составляет такая же высота х 1 .

Из иллюстраций выше мы можем сделать следующие наблюдения:
- Высота треугольника зависит от его основания.
- Перпендикуляр к основанию треугольника равен высоте треугольника.
- Высота треугольника может быть вне треугольника.
Обсудив понятие высоты и основания треугольника, давайте теперь приступим к вычислению площади треугольника.
Как найти площадь треугольника?
Площадь прямоугольника нам хорошо известна, т.е.е., длина * ширина . Что будет, если прямоугольник разделить пополам по диагонали (разрезать пополам)? Какая будет его зона новостей? Например, в прямоугольнике с основанием и высотой 6 единиц и 12 единиц, соответственно, площадь прямоугольника составляет 72 квадратных единицы.
Теперь, если вы разделите на две равные половины (после деления прямоугольника пополам по диагонали), площадь двух новых фигур должна составлять 36 квадратных единиц каждая.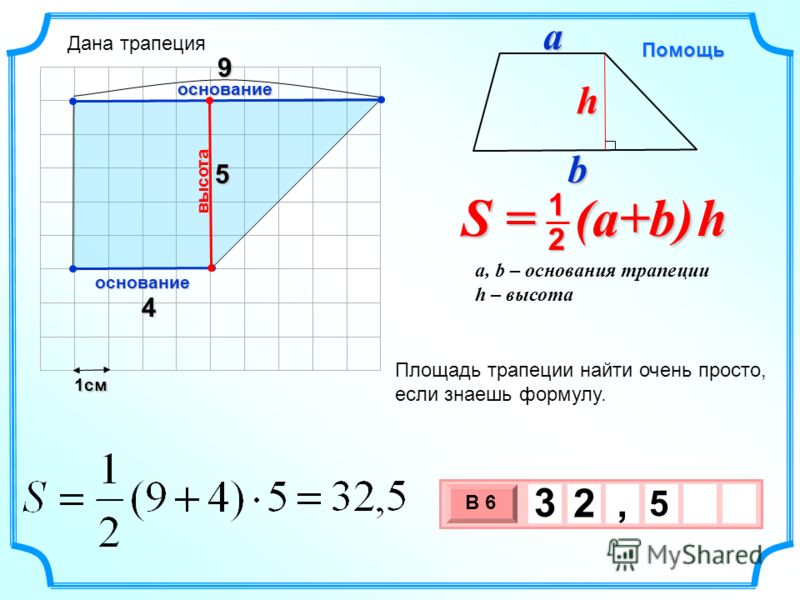 Две формы новостей представляют собой треугольники. Это означает, что если прямоугольник разрезан по диагонали на две равные половины, две новые формы образуются треугольниками, где каждый треугольник имеет площадь, равную ½ площади прямоугольника.
Две формы новостей представляют собой треугольники. Это означает, что если прямоугольник разрезан по диагонали на две равные половины, две новые формы образуются треугольниками, где каждый треугольник имеет площадь, равную ½ площади прямоугольника.
Площадь треугольника — это общее пространство или область, ограниченная определенным треугольником.
Площадь треугольника равна произведению основания и высоты на 2.
Стандартная единица измерения площади — квадратные метры (м 2 ).
Другие единицы включают:
- Квадратные миллиметры (мм 2 )
- Квадратные дюймы (дюймы 2 )
- Квадратные километры (км 2 )
- Квадратные ярды.
Формула площади треугольника
Общая формула для вычисления площади треугольника:
Площадь (A) = ½ (b × h) квадратных единиц, где; A — площадь, b — основание, h — высота треугольника. Треугольники могут быть разной природы, но важно отметить, что эта формула применима ко всем треугольникам.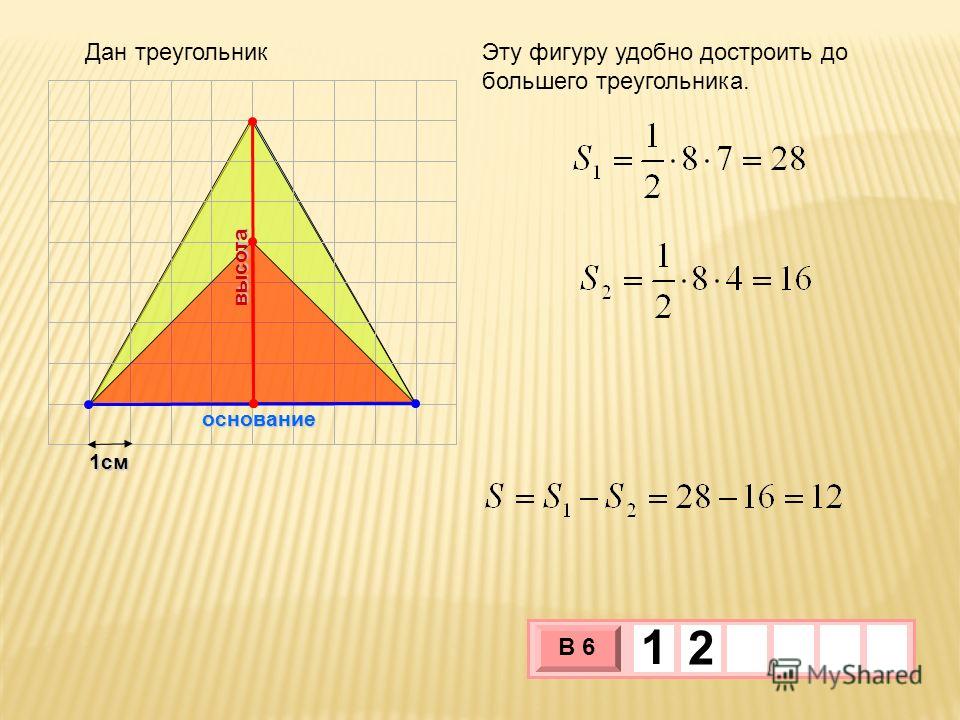 Различные типы треугольников имеют разные формулы площади.
Различные типы треугольников имеют разные формулы площади.
Примечание: база и высота должны быть в одних и тех же единицах измерения, то есть в метрах, километрах, сантиметрах и т. Д.
Площадь прямоугольного треугольника
Площадь треугольника = (½ × основание × высота) квадратных единиц.
Пример 1
Найдите площадь прямоугольного треугольника с основанием 9 м и высотой 12 м.
Решение
A = ¹ / ₂ × основание × высота
= ¹ / ₂ × 12 × 9
= 54 см²
Пример 2
Основание и высота прямоугольного треугольника равны 70 см и 8 м соответственно.Какая площадь у треугольника?
Решение
A = ½ × основание × высота
Здесь у нас 70 см и 8 м. Вы можете работать с cm или m. Давайте работать в метрах, заменив 70 см на метры.
Разделите 70 см на 100.
70/100 = 0,7 м.
⇒ A = (½ × 0,7 × 8) м 2
⇒ A = (½ x 5,6) м 2
⇒ A = 2,8 м 2
Площадь равнобедренного треугольника
An Равнобедренный треугольник — это треугольник, у которого две стороны равны, а также два угла равны. Формула площади равнобедренного треугольника:
Формула площади равнобедренного треугольника:
⇒A = ½ (основание × высота).
Если высота равнобедренного треугольника не указана, для нахождения высоты используется следующая формула:
Высота = √ (a 2 — b 2 /4)
Где;
b = основание треугольника
a = длина стороны двух равных сторон.
Следовательно, площадь равнобедренного треугольника может быть;
⇒A = ½ [√ (a 2 — b 2 /4) × b]
Кроме того, площадь равнобедренного прямоугольного треугольника определяется по формуле:
A = ½ × a 2 , где a = длина стороны двух равных сторон
Пример 3
Вычислите площадь равнобедренного треугольника с основанием 12 мм и высотой 17 мм.
Решение
⇒ A = ½ × основание × высота
⇒ 1/2 × 12 × 17
⇒ 1/2 × 204
= 102 мм 2
Пример 4
Найдите площадь равнобедренного треугольника, длина сторон которого составляет 5 м и 9 м.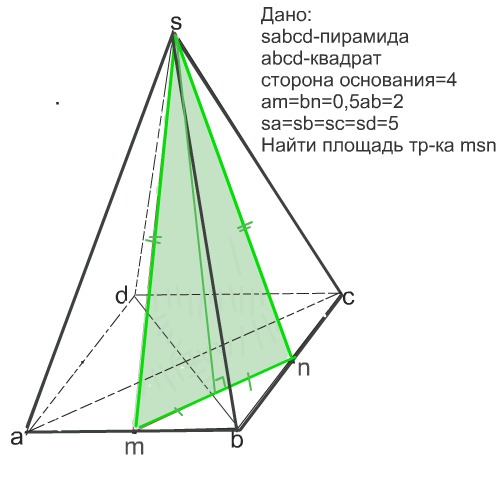
Решение
Пусть основание b = 9 м и a = 5 м.
⇒ A = ½ [√ (a 2 — b 2 /4) × b]
⇒ ½ [√ (5 2 — 9 2 /4) × 9]
= 9 .81m 2
Площадь равностороннего треугольника
Равносторонний треугольник — это треугольник, в котором три стороны равны и три внутренних угла равны. Площадь равностороннего треугольника:
A = (a 2 √3) / 4
, где a = длина сторон.
Пример 5
Вычислите площадь равностороннего треугольника со стороной 4 см.
Решение
⇒ A = (a 2 /4) √3
⇒ (4 2 /4) √3
⇒ (16/4) √3
= 4√3 см 2
Пример 6
Найдите площадь равностороннего треугольника с периметром 84 мм.
Решение
Периметр равностороннего треугольника = 3a.
⇒ 3a = 84 мм
⇒ a = 84/3
⇒ a = 28 мм
Площадь = (a 2 /4) √3
⇒ (28 2 /4) √3
= 196√3 мм 2
Площадь разностороннего треугольника
Разносторонний треугольник — это треугольник с 3 разными длинами сторон и 3 разными углами.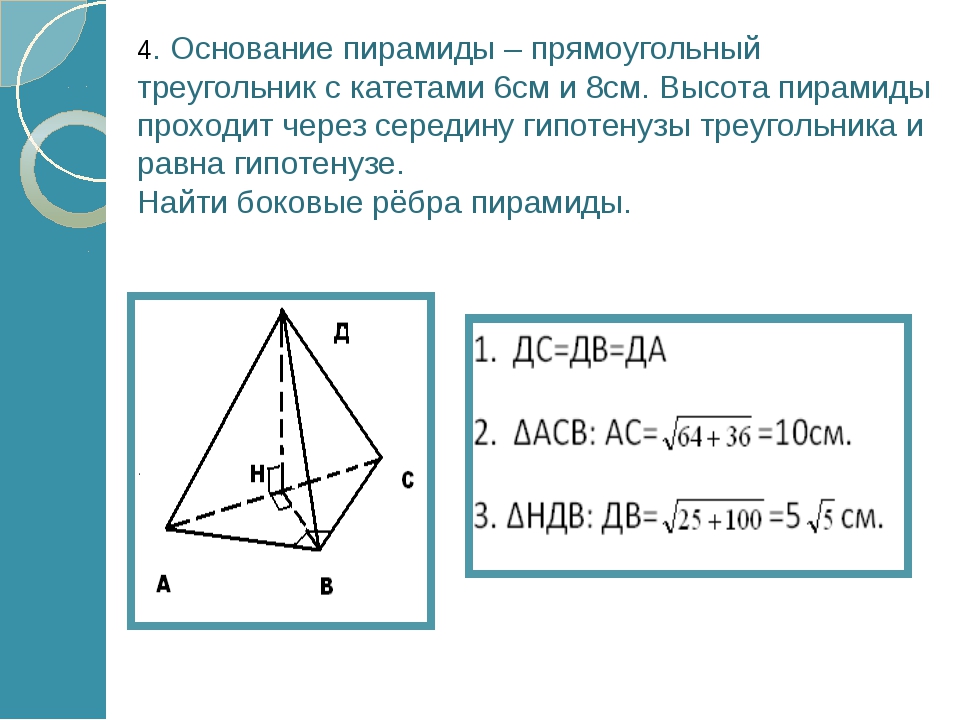 Площадь разностороннего треугольника можно рассчитать по формуле Герона.
Площадь разностороннего треугольника можно рассчитать по формуле Герона.
Формула Герона дается как;
⇒ Площадь = √ {p (p — a) (p — b) (p — c)}
где ‘p’ — полупериметр, а a, b, c — длины сторон.
⇒ p = (a + b + c) / 2
Пример 7
Вычислите площадь треугольника, длина сторон которого составляет 18 мм, 20 мм и 12 мм.
Решение
⇒ p = (a + b + c) / 2
Подставьте значения a, b и c.
⇒ p = (12 + 18 + 20) / 2
⇒ p = 50/2
⇒ p = 25
⇒ Площадь = √ {p (p — a) (p — b) (p — c)}
= √ {25 x (25 — 12) x (25 — 18) x (25 — 20)}
= √ (25 x 13 x 7 x 5)
= 5√455 мм 2
Предыдущий урок | Главная страница | Следующий урок
Формула области треугольника, примеры, рисунки и интерактивные практические задачи.
 Найти базу иногда непросто, но ..
Найти базу иногда непросто, но ..
Площадь треугольника всегда равна половине произведения высоты и основания.
$
Площадь = \ frac {1} {2} (базовая \ cdot высота)
$
Так с какой стороны основание?
Получение площади треугольника из прямоугольника
Пример 1
Какова площадь изображенного ниже треугольника?
Покажи ответ
Используйте формулу выше.
$$
A = \ frac {1} {2} (базовая высота \ cdot)
\\
A = \ frac {1} {2} (10 \ cdot 3)
\\ = \ frac {1} {2} (30)
\\ = \ frac {30} {2} = 15
$$
Найдите площадь каждого треугольника ниже. Округлите каждый ответ до ближайшей десятой доли.
Округлите каждый ответ до ближайшей десятой доли.
Задача 1
Какова площадь треугольника на следующем рисунке?
Покажи ответ
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу для площади.
$$
Площадь = \ frac {1} {2} (базовая \ cdot высота)
\\ = \ frac {1} {2} (3 \ cdot 3)
\\ = \ frac {1} {2} (9)
\\ = \ frac {9} {2}
\\ = 4.5 \ text {дюймы в квадрате}
$$
Задача 2
Вычислите площадь изображенного ниже треугольника.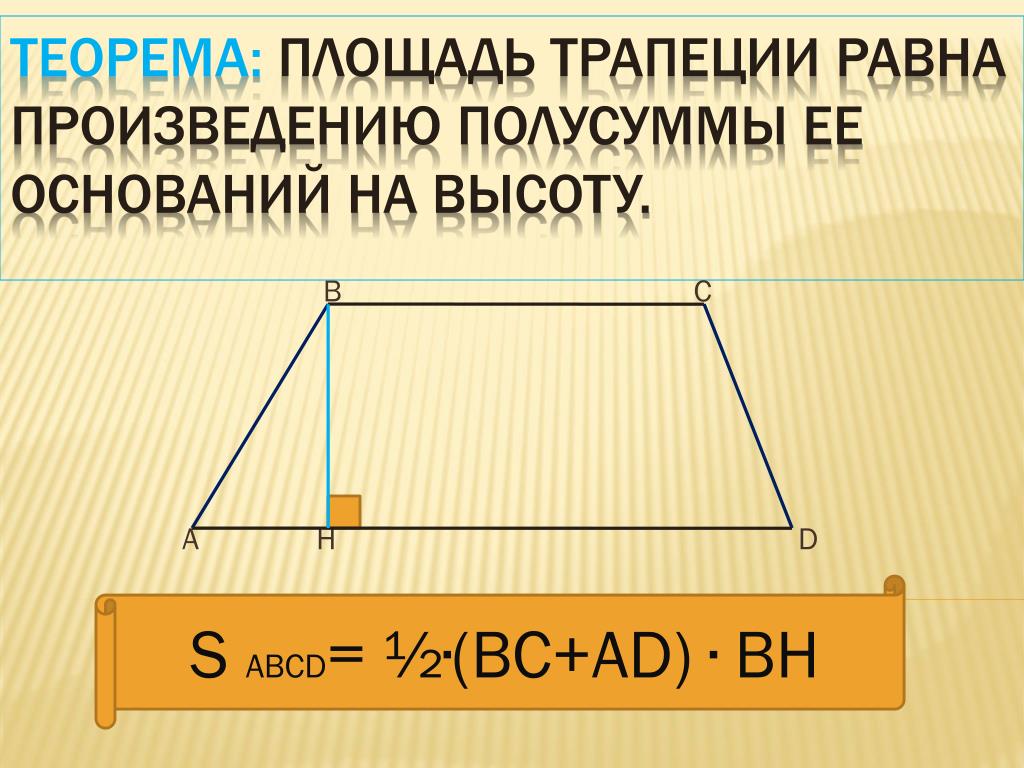
Покажи ответ
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу для площади.
$$
Площадь = \ frac {1} {2} (базовая \ cdot высота)
\\ = \ frac {1} {2} (24 \ cdot 27.6)
\\ = 331,2 \ text {дюймы в квадрате}
$$
Задача 3
Вычислите площадь изображенного ниже треугольника.
Покажи ответ
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу для площади.
$$
Площадь = \ frac {1} {2} (базовая \ cdot высота)
\\ = \ frac {1} {2} (12 \ cdot 2.5)
\\ = 15 \ text {дюймы в квадрате}
$$
Задача 4
Вычислите площадь изображенного ниже треугольника.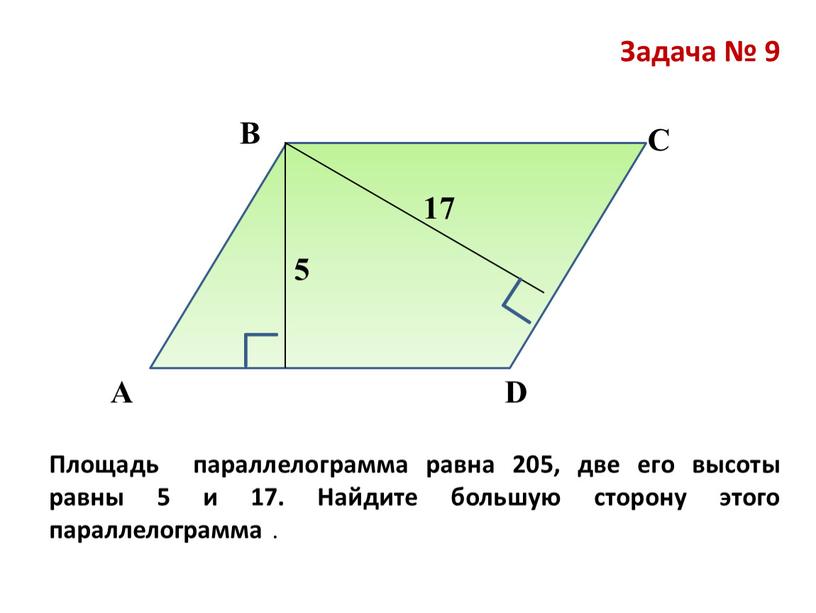
Покажи ответ
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу для площади.
$$
Площадь = \ frac {1} {2} (базовая \ cdot высота)
\\ = \ frac {1} {2} (12 \ cdot 3.9)
\\ = 23,4 \ text {дюймы в квадрате}
$$
Задача 5
Вычислите площадь изображенного ниже треугольника.
Покажи ответ
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу для площади.
$$
Площадь = \ frac {1} {2} (базовая \ cdot высота)
\\ = \ frac {1} {2} (14 \ cdot 4)
\\ = 28 \ text {дюймы в квадрате}
$$
Задача 6
Какова площадь следующего треугольника?
Покажи ответ
Эта задача включает в себя 1 небольшой поворот. Вы должны решить, какую из 3 баз использовать. Только помните, что основание и высота перпендикулярны. Следовательно, основание — 11, поскольку оно перпендикулярно высоте 13,4.
Вы должны решить, какую из 3 баз использовать. Только помните, что основание и высота перпендикулярны. Следовательно, основание — 11, поскольку оно перпендикулярно высоте 13,4.
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу для площади.
$$
Площадь = \ frac {1} {2} (базовая \ cdot высота)
\\ = \ frac {1} {2} (11 \ cdot 13.4)
\\ = 73,7 \ text {дюймы в квадрате}
$$
Задача 7
Какова площадь следующего треугольника?
Покажи ответ
Эта задача включает в себя 1 небольшой поворот. Вы должны решить, какую из 3 баз использовать. Только помните, что основание и высота перпендикулярны. Следовательно, основание — «12», поскольку оно перпендикулярно высоте 5,9.
Вы должны решить, какую из 3 баз использовать. Только помните, что основание и высота перпендикулярны. Следовательно, основание — «12», поскольку оно перпендикулярно высоте 5,9.
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу для площади.
$$
Площадь = \ frac {1} {2} (базовая \ cdot высота)
\\ = \ frac {1} {2} (12 \ cdot 5.9)
\\ = 35,4 \ text {дюймы в квадрате}
$$
Задача 8
Какова площадь следующего треугольника?
Покажи ответ
Как и в последней задаче, вы должны решить, какую из 3 баз использовать.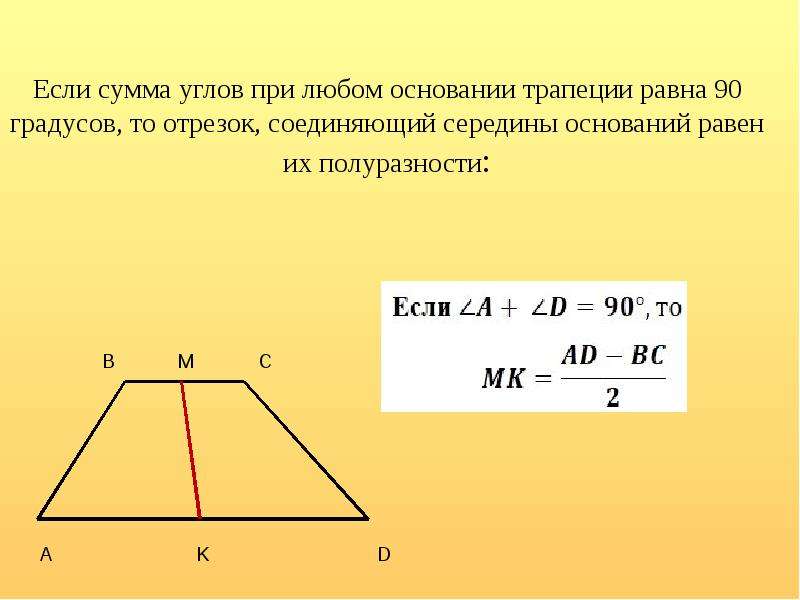 Только помните, что основание и высота перпендикулярны. Следовательно, основание — «4», поскольку оно перпендикулярно высоте 17,7.
Только помните, что основание и высота перпендикулярны. Следовательно, основание — «4», поскольку оно перпендикулярно высоте 17,7.
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу для площади.
$$
Площадь = \ frac {1} {2} (базовая \ cdot высота)
\\ = \ frac {1} {2} (4 \ cdot 17.7)
\\ = 35,4 \ text {дюймы в квадрате}
$$
Задача 9
Какова площадь следующего треугольника?
Покажи ответ
Опять же, вы должны решить, какую из 3 баз использовать.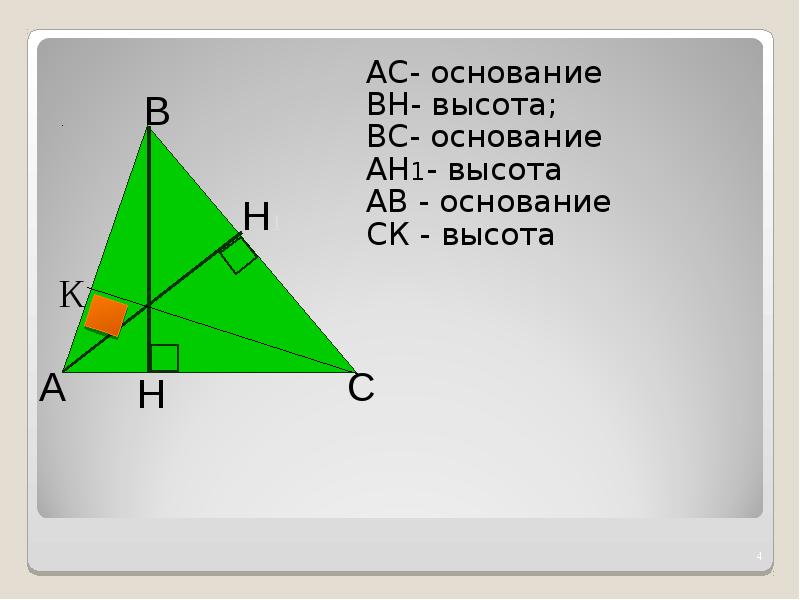 Только помните, что основание и высота перпендикулярны. Следовательно, основание — 22, поскольку оно перпендикулярно высоте 26,8.
Только помните, что основание и высота перпендикулярны. Следовательно, основание — 22, поскольку оно перпендикулярно высоте 26,8.
Чтобы найти площадь треугольника слева, подставьте основание и высоту в формулу для площади.
$$
Площадь = \ frac {1} {2} (базовая \ cdot высота)
\\ = \ frac {1} {2} (22 \ cdot 26.8)
\\ = 294,8 \ text {дюймы в квадрате}
$$
Использование свойств треугольников для решения задач
Результаты обучения
- Найдите площадь, основание и высоту треугольника
- Найдите длину одной стороны треугольника по периметру и двух других длин
Теперь мы знаем, как найти площадь прямоугольника. Мы можем использовать этот факт, чтобы визуализировать формулу площади треугольника. В прямоугольнике ниже мы обозначили длину [латекс] b [/ латекс] и ширину [латекс] h [/ латекс], поэтому его площадь равна [латекс] bh [/ латекс].
Мы можем использовать этот факт, чтобы визуализировать формулу площади треугольника. В прямоугольнике ниже мы обозначили длину [латекс] b [/ латекс] и ширину [латекс] h [/ латекс], поэтому его площадь равна [латекс] bh [/ латекс].
Площадь прямоугольника равна основанию [латекс] b [/ латекс], умноженному на высоту [латекс] h [/ латекс].
Мы можем разделить этот прямоугольник на два равных треугольника (см. Изображение ниже). Конгруэнтные треугольники имеют одинаковую длину сторон и углы, поэтому их площади равны.Площадь каждого треугольника составляет половину площади прямоугольника или [latex] \ Large \ frac {1} {2} \ normalsize bh [/ latex]. Этот пример помогает нам понять, почему формула для площади треугольника имеет вид [латекс] A = \ Large \ frac {1} {2} \ normalsize bh [/ latex].
Прямоугольник можно разделить на два треугольника равной площади. Площадь каждого треугольника составляет половину площади прямоугольника.
Формула площади треугольника: [латекс] A = \ Large \ frac {1} {2} \ normalsize bh [/ latex], где [latex] b [/ latex] — основа, а [латекс] h [/ latex] — высота.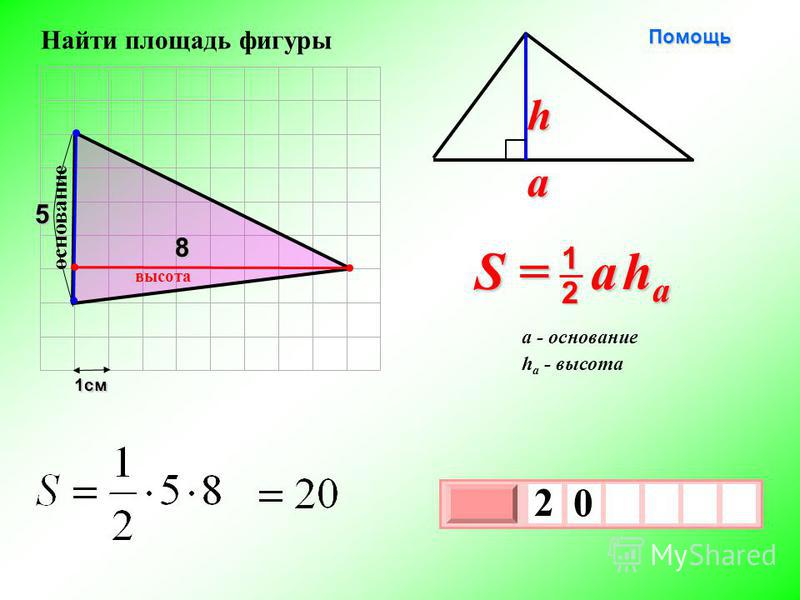 \ circ [/ latex]
\ circ [/ latex]
Периметр треугольника — это сумма длин сторон.
[латекс] P = a + b + c [/ латекс]
Площадь треугольника равна половине основания [латекс] b [/ латекс], умноженной на высоту [латекс] h [/ латекс].
[латекс] A = {\ Large \ frac {1} {2}} bh [/ латекс]
, пример
Найдите площадь треугольника с основанием [латекс] 11 [/ латекс] дюймов и высотой [латекс] 8 [/ латекс] дюймов.
Решение
| Шаг 1. Прочтите задачу. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите , что вы ищете. | площадь треугольника |
| Шаг 3. Имя. Выберите переменную для ее представления. | пусть A = площадь треугольника |
| Шаг 4. Translate. Напишите соответствующую формулу. Запасной. | |
| Шаг 5. Решите уравнение. | [латекс] A = 44 [/ латекс] квадратных дюйма. |
| Шаг 6. Проверка: [латекс] A = {\ Large \ frac {1} {2}} bh [/ латекс] [латекс] 44 \ stackrel {?} {=} {\ Large \ frac {1} {2}} (11) 8 [/ латекс] [латекс] 44 = 44 \ четырехугольник \ галочка [/ латекс] | |
| Шаг 7. Ответьте на вопрос. | Площадь [латекс] 44 [/ латекс] квадратных дюймов. |
В следующем видео представлен еще один пример использования формулы площади для треугольников.
, пример
Периметр треугольного сада составляет [латекс] 24 [/ латекс] фута. Длина двух сторон: [латекс] 4 [/ латекс] ножки и [латекс] 9 [/ латекс] ножек. Какова длина третьей стороны?
Длина двух сторон: [латекс] 4 [/ латекс] ножки и [латекс] 9 [/ латекс] ножек. Какова длина третьей стороны?
Показать решение
Решение
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите , что вы ищете. | длина третьей стороны треугольника |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть c = третья сторона |
| Шаг 4. Translate. Напишите соответствующую формулу. Заменить в данной информации. | |
| Шаг 5. Решите уравнение. | [латекс] 24 = 13 + c [/ латекс] [латекс] 11 = c [/ латекс] |
| Шаг 6. Чек: [латекс] P = a + b + c [/ латекс] [латекс] 24 \ stackrel {?} {=} 4 + 9 + 11 [/ латекс] [латекс] 24 = 24 \ галочка [/ латекс] | |
Шаг 7. Ответьте на вопрос. Ответьте на вопрос. | Третья сторона [латекс] длиной 11 [/ латекс] футов. |
, пример
Площадь треугольного церковного окна [латекс] 90 [/ латекс] квадратных метров. Основание окна [латекс] 15 [/ латекс] метров.Какая высота окна?
Показать решение
Решение
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию. | |
| Шаг 2. Определите , что вы ищете. | высота треугольника |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть h = высота |
| Шаг 4. Перевести. Напишите соответствующую формулу. Заменить в данной информации. | |
| Шаг 5. Решите уравнение. | [латекс] 90 = {\ Large \ frac {1} {2}} \ normalsize (15) h [/ latex] [латекс] 12 = h [/ латекс] |
Шаг 6. Проверка: Проверка: [латекс] A = {\ Large \ frac {1} {2}} \ normalsize bh [/ latex] [латекс] 90 \ stackrel {?} {=} {\ Large \ frac {1} {2}} \ normalsize \ cdot 15 \ cdot 12 [/ латекс] [латекс] 90 = 90 \ квадратик \ галочка [/ латекс] | |
| Шаг 7. Ответьте на вопрос. | Высота треугольника [латекс] 12 [/ латекс] метров. |
В следующем видео мы покажем еще один пример того, как найти высоту треугольника с учетом его площади.
Равнобедренные и равносторонние треугольники
Помимо прямоугольного треугольника, у некоторых других треугольников есть особые имена. Треугольник с двумя сторонами равной длины называется равнобедренным треугольником. Треугольник с тремя сторонами равной длины называется равносторонним треугольником.На изображении ниже показаны оба типа треугольников.
Треугольник с тремя сторонами равной длины называется равносторонним треугольником.На изображении ниже показаны оба типа треугольников.
В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона является основанием. В равностороннем треугольнике все три стороны имеют одинаковую длину.
Равнобедренные и равносторонние треугольники
Равнобедренный треугольник имеет две стороны одинаковой длины.
Равносторонний треугольник имеет три стороны равной длины.
, пример
Периметр равностороннего треугольника составляет [латекс] 93 [/ латекс] дюйма.Найдите длину каждой стороны.
Показать решение
Решение
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию. | Периметр = [латекс] 93 [/ латекс] дюйм |
Шаг 2. Определите , что вы ищете. | длина сторон равностороннего треугольника |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть s = длина каждой стороны |
| Шаг 4. Перевести. Напишите соответствующую формулу. Запасной. | |
| Шаг 5. Решите уравнение. | [латекс] 93 = 3с [/ латекс] [латекс] 31 = s [/ латекс] |
| Шаг 6. Проверка: [латекс] 93 \ stackrel {?} {=} 31 + 31 + 31 [/ латекс] [латекс] 93 = 93 \ четырехугольник \ галочка [/ латекс] | |
| Шаг 7. Ответьте на вопрос. | Каждая сторона [латекс] 31 [/ латекс] дюйм. |
, пример
У Арианны [латекс] 156 дюймов [/ latex] бусинок, которые можно использовать в качестве отделки вокруг шарфа.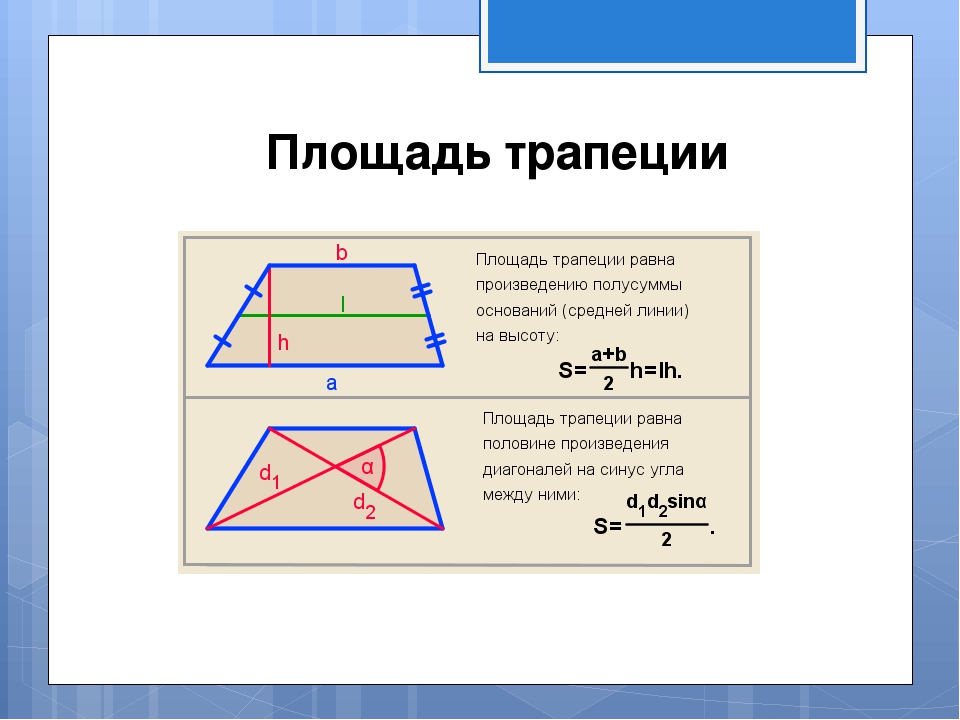 Шарф представляет собой равнобедренный треугольник с основанием [латекс] 60 [/ латекс] дюймов. Как долго она сможет сделать две равные стороны?
Шарф представляет собой равнобедренный треугольник с основанием [латекс] 60 [/ латекс] дюймов. Как долго она сможет сделать две равные стороны?
Показать решение
Решение
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и напишите на ней указанную информацию. | P = [латекс] 156 [/ латекс] дюйм |
| Шаг 2. Определите , что вы ищете. | длины двух равных сторон |
| Шаг 3. Имя. Выберите переменную для ее представления. | Пусть s = длина каждой стороны |
| Шаг 4. Translate. Напишите соответствующую формулу. Заменить в данной информации. | |
| Шаг 5. Решите уравнение. | [латекс] 156 = 2с = 60 [/ латекс] [латекс] 96 = 2с [/ латекс] [латекс] 48 = s [/ латекс] |
Шаг 6. |

 При этом данный треугольник делится на два прямоугольных треугольника.
При этом данный треугольник делится на два прямоугольных треугольника. Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5
Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5 Если присмотреться внимательнее, то станет очевидно, что половина основания (b/2) умноженная на tg(β/2) даст нам высоту треугольника. Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна.
Если присмотреться внимательнее, то станет очевидно, что половина основания (b/2) умноженная на tg(β/2) даст нам высоту треугольника. Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2) ). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна. Боковая сторона является гипотенузой, поэтому из квадрата боковой стороны (а) вычтем квадрат второго катета. Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Боковая сторона является гипотенузой, поэтому из квадрата боковой стороны (а) вычтем квадрат второго катета. Поскольку он равен половине основания (b/2) то его квадрат будет равен b2/4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».  Как и раньше, мы также можем видеть, что размеры прямоугольной фиолетовой области являются основанием и высотой исходного параллелограмма.
Как и раньше, мы также можем видеть, что размеры прямоугольной фиолетовой области являются основанием и высотой исходного параллелограмма.