Содержание
Вычитание отрицательных чисел — Kid-mama
Сейчас мы рассмотрим на примерах вычитание отрицательных чисел, и вы убедитесь, что это очень легко. Нужно просто помнить правило : два минуса, стоящие рядом, дают плюс.
Пример 1. Вычитание отрицательного числа из положительного числа
56 – (–34) = 56 + 34 = 90
Как видим, чтобы вычесть из положительного числа отрицательное число, нужно просто сложить их модули.
Пример 2. Вычитание отрицательного числа из отрицательного числа
– 60 – (– 25) = – 60 + 25 = – 35
– 15 – (– 30) = – 15 + 30 = 15
Таким образом, при вычитании отрицательного числа из отрицательного мы действуем по правилу сложения чисел с разными знаками, и у нас может получиться как положительное, так и отрицательное число.
Существует единое правило, определяющее вычитание любых чисел: как отрицательных, так и положительных, и звучит оно так:
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.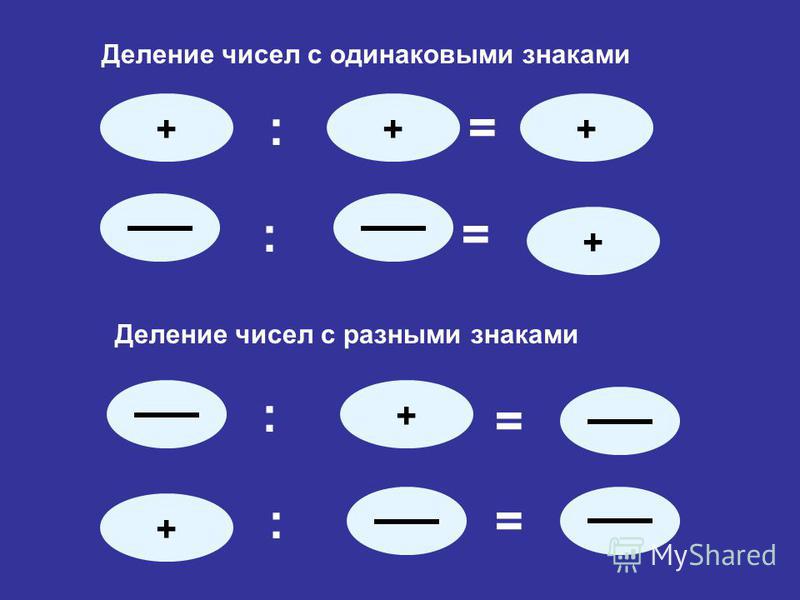 a — b = a + (-b) |
Для того, чтобы избавиться от лишних скобок при вычитании отрицательных чисел, мы можем воспользоваться правилом знаков. Это правило гласит:
| Если перед скобками стоит знак «+» , то при раскрытии скобок знак числа не изменяется. Если перед скобками стоит знак «-», то при раскрытии скобок знак числа меняется на противоположный. |
Например:
| 5 + (-7) = 5-7 | 9-(-5) = 9 + 5 | |
| -10 + (-6) = -10-6 | -4- (-6) = -4 + 6 |
Правило знаков действует также, если в скобках стоит несколько чисел. При этом,если перед скобками стоит минус, изменяются знаки у всех чисел:
Примеры:
a+(b-c-d)=a+b-c-d
a-(b-c-d)=a-b+c+d
a+(-b+c-d)=a-b+c-d
a-(-b+c-d)=a+b-c+d
Это правило обычно запоминают так:
| Минус на минус дает плюс, Плюс на минус дает минус |
А теперь пройдите тест и проверьте себя!
Сложение и вычитание отрицательных чисел
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
Выполните сложение или вычитание и введите ответ. Минус вводите при помощи дефиса (кнопка между «0» и «=» на клавиатуре). Ответ вводите без пробела (например: -3,4)
Минус вводите при помощи дефиса (кнопка между «0» и «=» на клавиатуре). Ответ вводите без пробела (например: -3,4)
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
С ответом
С отметкой о просмотре
Вычитание отрицательного числа, правило, примеры
Данная статья посвящена разбору такой темы, как выполнение вычитания отрицательных чисел. Материал представляет собой полезную информацию о правиле вычитания отрицательных чисел и других определениях. Для закрепления сути параграфа мы детально разберем примеры типичных упражнений и задач.
Материал представляет собой полезную информацию о правиле вычитания отрицательных чисел и других определениях. Для закрепления сути параграфа мы детально разберем примеры типичных упражнений и задач.
Правило вычитания отрицательных чисел
Для того, чтобы разобраться в данной теме, следует узнать основные определения и понятия.
Определение 1
Правило вычитания отрицательных чисел формулируется так: чтобы из числа a вычесть число b со знаком минус, необходимо к уменьшаемому a прибавить число −b, которое является противоположным вычитаемому b.
Если представить данное правило вычитания отрицательного числа b из произвольного числа a в буквенном виде, то оно будет выглядеть так: a−b=a+(−b).
Для того, чтобы использовать данное правило, необходимо доказать его справедливость.
Возьмем числа a и b. Чтобы вычесть из числа a число b, необходимо найти такое число с, которое в сумме с числом b будет равняться числу a. Другими словами, если найдено такое число c, что c+b=a, то разность a−b равна c.
Другими словами, если найдено такое число c, что c+b=a, то разность a−b равна c.
Для того, чтобы доказать правило вычитания, необходимо показать, что сложение суммы a+(−b) с числом b – это есть число a. Необходимо вспомнить о свойствах действий с действительными числами. Так как в этом случае работает сочетательное свойство сложения, то равенство (a+(−b)) +b=a+((−b) +b) будет верным.
Так, как сумма чисел с противоположными знаками равняется нулю, то a+((−b) +b) =a+0, а сумма a+0= а (если к числу прибавить нуль, то оно не изменится). Равенство a−b=a+(−b)считается доказанным, значит, доказана и справедливость приведенного правила вычитания чисел со знаком минус.
Мы рассмотрели, как работает данное правило для действительных чисел a и b. Но оно также считается справедливым для любых рациональных и целых чисел a и b. Действия с рациональными и целыми числами также обладают свойствами, использованными при доказательстве. Следует добавить, что с помощью разобранного правила можно выполнять действия числа со знаком минус как из положительного числа, так и из отрицательного или нуля.
Следует добавить, что с помощью разобранного правила можно выполнять действия числа со знаком минус как из положительного числа, так и из отрицательного или нуля.
Рассмотрим разобранное правило на типичных примерах.
Примеры использования правила вычитания
Рассмотрим примеры с вычитанием чисел. Для начала рассмотрим простой пример, который поможет легко разобраться со всеми тонкостями процесса.
Пример 1
Необходимо отнять от числа −13 число −7.
Возьмем число, противоположное вычитаемому −7. Это число 7. Тогда по правилу вычитания отрицательных чисел имеем (−13) −(−7) =(−13) +7. Выполняем сложение. Теперь получаем: (−13) +7=−(13−7) =−6.
Вот все решение: (−13) −(−7) =(−13) +7=−(13−7) =−6. (−13)−(−7)=−6. Вычитание дробных отрицательных чисел также можно выполнять. Необходимо перейти к обыкновенным дробям, смешанным числам или десятичным дробям. Выбор числа зависит от того, с каким вариантом вам удобнее работать.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 2
Необходимо выполнить вычитание из числа 3,4 числа -2323.
Применяем описанное выше правило вычитания, получаем 3,4—2323=3,4+2323. Заменяем дробь на десятичное число: 3,4=3410=175=325 (как переводить дроби, можно посмотреть в материале по теме), получаем 3,4+2323=325+2323. Выполняем сложение. На этом вычитание отрицательного числа -2323 из числа 3,4 завершено.
Приведем краткую запись решения: 3,4—2323=27115.
Пример 3
Необходимо выполнить вычитание числа −0,(326) от нуля.
По правилу вычитания, которое мы изучили выше, 0−(−0,(326))=0+0,(326)=0,(326).
Последний переход верен, так как здесь работает свойство сложения числа с нулем: 0−(−0,(326))=0,(326).
Из рассмотренных примеров видно, что при вычитании отрицательного числа может получиться как положительное, так и отрицательное число. Вычитание отрицательного числа может в результате дать и число 0, это происходит, когда уменьшаемое равно вычитаемому.
Вычитание отрицательного числа может в результате дать и число 0, это происходит, когда уменьшаемое равно вычитаемому.
Пример 4
Необходимо вычислить разность отрицательных чисел -5—5.
По правилу вычитания мы получаем -5—5=-5+5.
Мы пришли к сумме противоположных чисел, которая всегда равна нулю: -5—5=-5+5=0
Итак,-5—5=0.
В некоторых случаях результат вычитания необходимо записать в виде числового выражения. Это справедливо в тех случаях, когда уменьшаемое или вычитаемое является иррациональным числом. К примеру, вычитание из отрицательного числа −2 отрицательного числа –π проводится так: (−2)−(−π)=(−2)+π=π−2. Значение полученного выражения может быть вычислено максимально точно только в том случае, если это необходимо. Для подробной информации можно изучить другие разделы, связанные с данной темой.
Целые числа: положительные и отрицательные.
 Сравнение целых чисел
Сравнение целых чисел
Целые числа — это положительные и отрицательные числа, не имеющие дробной части и число нуль.
Число 0 целое, но не является ни положительным, ни отрицательным числом.
Ставить перед числом нуль какой-либо знак (+ или -) не имеет смысла, так как записи
+0, -0 и 0
представляют собой одно и тоже число:
+0 = -0 = 0.
Положительные и отрицательные числа
Существуют величины, отсчёт которых производиться в двух противоположных направлениях.
Пример. Температура отсчитывается в двух противоположных направлениях от температуры тающего льда, принимаемой за нулевую:
1) Уровень ртути при нулевой температуре (температуре тающего льда).
2) Уровень ртути при температуре, более низкой, чем нулевая.
3) Уровень ртути при температуре, более высокой, чем нулевая.
Если мы имеем какую-либо величину, отсчёт которой производится в двух противоположных направлениях, то одно из направлений, безразлично какое, принято называть положительным, а другое отрицательным.
Положительное число — это число, полученное в результате измерения величины, отсчитанной в положительном направлении. Положительное число изображается в виде числа со знаком +
(плюс) впереди. Например, +16 — положительное число.
Пример.
16 °C тепла
или +16 °C
.
Примечание: все градусы пишутся с буквой C
(Цельсия), знак градуса отделяется от числа пробелом. Например, +7 °C.
Наименьшее целое положительное число – это 1 (единица).
Отрицательное число — это число, полученное в результате измерения величины, отсчитанной в отрицательном направлении. Отрицательное число изображается в виде числа со знаком —
(минус) впереди. Например, -16 — отрицательное число.
Например, -16 — отрицательное число.
Пример.
16 °C мороза
или -16 °C
.
Наибольшее целое отрицательное число – это -1 (минус один).
Все числа, кроме нуля, записанные со знаком +
(плюс) впереди, являются положительными, а записанные со знаком —
(минус) — отрицательными.
Пример.
+1, +15, +57 и т. д. — положительные числа;
-1, -15, -57 и т. д. — отрицательные числа.
Положительные числа можно обозначать предшествующим знаком +
(плюс) или опускать его. Числа, перед которыми не стоит знака (+ или -), считаются положительными числами. Например, вместо
+8, +14, +100 и т. д.
можно написать просто
8, 14, 100 и т. д.
Сравнение целых чисел
Сравнить два целых числа — значит, узнать, какое из них больше, какое меньше, или определить, что числа равны.
Сравнивать целые числа можно с помощью ряда целых чисел, так как числа в нём расположены от меньшего к большему, если двигаться по ряду слева направо. Поэтому в ряду целых чисел можно заменить запятые на знак меньше:
… -5 < -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 < 5 < …
Следовательно, из двух целых чисел больше то число, которое в ряду стоит правее, и меньше то, которое стоит левее, значит:
1) Любое положительное число больше нуля и больше любого отрицательного числа:
1 > 0; 15 > -16.
2) Любое отрицательное число меньше нуля:
-7 < 0; -357 < 0.
3) Из двух отрицательных чисел больше то, которое в ряду целых чисел стоит правее:
-31 < -28.
Умножение отрицательного числа на положительное
Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.
Умножение чисел с одинаковыми знаками
Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.
Чтобы умножить два числа с одинаковыми знаками надо:
- перемножить модули чисел;
- перед полученным произведением поставить знак « + » (при записи ответа знак «плюс» перед первым числом слева можно опускать).
Примеры умножения отрицательных и положительных чисел.
Умножение чисел с разными знаками
Второй возможный случай — это умножение чисел с разными знаками.
Чтобы умножить два числа с разными знаками, надо:
- перемножить модули чисел;
- перед полученным произведением поставить знак « − ».
Примеры умножения отрицательных и положительных чисел.
Правила знаков для умножения
Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.
Минус на минус даёт плюс,
Плюс на минус даёт минус.
В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.
При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.
В примере пять отрицательных множителей. Значит, знак результата будет «минус».
Теперь вычислим произведение модулей, не обращая внимание на знаки.
Конечный результат умножения исходных чисел будет:
Умножение на ноль и единицу
Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.
Особую роль при умножении рациональных чисел играет отрицательная единица « −1 ».
При умножении на « −1 » число меняется на противоположное.
В буквенном выражении это свойство можно записать:
При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.
Пример умножения отрицательных и положительных чисел.
В данной статье сформулируем правило умножения отрицательных чисел и дадим ему объяснение. Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.
Умножение отрицательных чисел
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел – a , – b данное равенство считается верным.
Выше приведено правило умножения двух отрицательных чисел. Исходя из него, докажем выражение: ( – а ) · ( – b ) = a · b . Статья умножение чисел с разными знаками рассказывает о том, что равенств а · ( – b ) = – a · b справедливое, как и ( – а ) · b = – a · b . Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:
( – a ) · ( – b ) = ( – a · ( – b ) ) = – ( – ( a · b ) ) = a · b .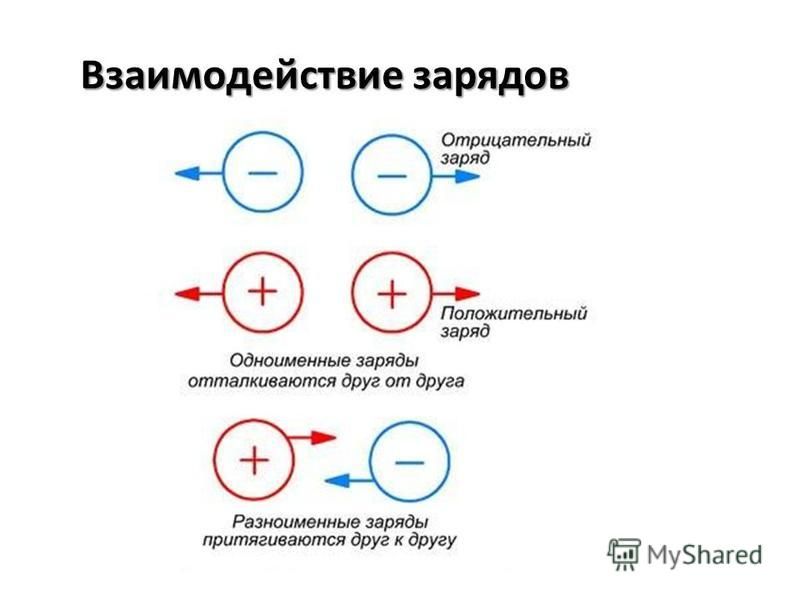
Тут явно видно доказательство правила умножения отрицательных чисел. Исходя из примеров явно, что произведение двух отрицательных чисел – положительное число. При перемножении модулей чисел результат всегда положительное число.
Данное правило применимо для умножения действительных чисел, рациональных чисел, целых чисел.
Примеры умножения отрицательных чисел
Теперь рассмотрим подробно примеры умножения двух отрицательных чисел. При вычислении необходимо пользоваться правилом, написанным выше.
Произвести умножение чисел – 3 и – 5 .
Решение.
По модулю умножаемые данные два числа равны положительным числам 3 и 5 . Их произведение дает в результате 15 . Отсюда следует, что произведение заданных чисел равно 15
Запишем кратко само умножение отрицательных чисел:
( – 3 ) · ( – 5 ) = 3 · 5 = 15
Ответ: ( – 3 ) · ( – 5 ) = 15 .
При умножении отрицательных рациональных чисел, применив разобранное правило, можно мобилизоваться к умножению дробей, умножению смешанных чисел, умножению десятичных дробей.
Вычислить произведение ( – 0 , 125 ) · ( – 6 ) .
Используя правило умножения отрицательных чисел, получим, что ( − 0 , 125 ) · ( − 6 ) = 0 , 125 · 6 . Для получения результата необходимо выполнить умножение десятичной дроби на натуральное число столбиков. Это выглядит так:
Получили, что выражение примет вид ( − 0 , 125 ) · ( − 6 ) = 0 , 125 · 6 = 0 , 75 .
Ответ: ( − 0 , 125 ) · ( − 6 ) = 0 , 75 .
В случае, когда множители – иррациональные числа, тогда их произведение может быть записано в виде числового выражения. Значение вычисляется только по необходимости.
Необходимо произвести умножение отрицательного – 2 на неотрицательное log 5 1 3 .
Находим модули заданных чисел:
– 2 = 2 и log 5 1 3 = – log 5 3 = log 5 3 .
Следуя из правил умножения отрицательных чисел, получим результат – 2 · log 5 1 3 = – 2 · log 5 3 = 2 · log 5 3 . Это выражение и является ответом.
Ответ: – 2 · log 5 1 3 = – 2 · log 5 3 = 2 · log 5 3 .
Для продолжения изучения темы необходимо повторить раздел умножение действительных чисел.
Умножение положительных и отрицательных чисел (то есть чисел с разными знаками) выполняется по следующему правилу:
Чтобы перемножить два числа с разными знаками (положительное и отрицательное число), надо перемножить их модули и перед полученным произведением поставить знак «минус».
Поскольку модуль положительного числа равен самому числу, модуль отрицательного числа равен противоположному числу, получаем:
То есть произведение двух чисел, одно из которых положительное, а другое — отрицательное, является отрицательным числом.
На практике при умножении чисел с разными знаками запись сокращают (модули находят устно):
Рассмотрим на конкретных примерах, как умножают положительные и отрицательные числа.
При умножении отрицательного числа на положительное получаем отрицательное число:
2) Применяем правила умножения чисел с разными знаками и умножения десятичных дробей:
По правилам умножения чисел с разными знаками и умножения дроби на натуральное число:
Используем правила умножения положительных и отрицательных чисел и умножения дробей:
По правилам умножения чисел с разными знаками и смешанных чисел:
При умножении нескольких чисел с разными знаками знак результата зависит от количества входящих в произведение отрицательных чисел.
При умножении двух отрицательных чисел получается положительное число. Поэтому если количество чисел со знаком «-» чётное, результат является числом положительным, если нечётное — отрицательным.
Положительные и отрицательные числа
Натуральные числа, противоположные им числа и число 0 называются целыми числами. Положительные числа (целые и дробные), отрицательные числа (целые и дробные) и число 0 составляют группу рациональных чисел.
Рациональные числа обозначаются большой латинской буквой R. Число 0 относится к целым рациональным числам. С натуральными и дробными положительными числами мы ознакомились ранее. Рассмотрим подробнее отрицательные числа в составе рациональных чисел.
Отрицательное число с древних времен ассоциируется со словом «долг», тогда как положительное число можно ассоциировать со словами «наличие» или «доход». Значит, положительные целые и дробные числа при вычислениях — это то, что мы имеем, а отрицательные целые и дробные числа — это то, что составляет долг. Соответственно, результат вычислений — это разность между имеющимся количеством и нашими долгами.
Соответственно, результат вычислений — это разность между имеющимся количеством и нашими долгами.
Отрицательные целые и дробные числа записываются со знаком «минус» («-») перед числом. Численная величина отрицательного числа — это его модуль. Соответственно, модуль числа — это значение числа (и положительного, и отрицательного) со знаком плюс. Модуль числа записывается так: |2|; |-2|.
Каждому рациональному числу на числовой оси соответствует единственная точка. Рассмотрим числовую ось (рисунок внизу), обозначим на ней точку О.
Точке О поставим в соответствие число 0. Число 0 служит границей между положительными и отрицательными числами: справа от 0 — положительные числа, величина которых изменяется от 0 до плюс бесконечности, а слева от 0 — отрицательные числа, величина которых тоже изменяется от 0 до минус бесконечности.
Правило. Всякое число, стоящее на числовой оси правее, больше числа, стоящего левее.
Исходя из этого правила, положительные числа растут слева направо, а отрицательные убывают справа налево (при этом модуль отрицательного числа увеличивается).
Свойства чисел на числовой оси
Всякое положительное число и 0 больше любого отрицательного числа.
Всякое положительное число больше 0. Всякое отрицательное число меньше 0.
Всякое отрицательное число меньше положительного числа. Положительное или отрицательное число, стоящее правее, больше положительного или отрицательного числа, стоящего левее на числовой оси.
Определение. Числа, которые отличаются друг от друга только знаком, называются противоположными.
Например, числа 2 и -2, 6 и -6. -10 и 10. Противоположные числа расположены на числовой оси в противоположных направлениях от точки О, но на одинаковом расстоянии от нее.
Дробные числа, представляющие собой в записи обыкновенную или десятичную дробь, подчиняются тем же правилам на числовой оси, что и целые числа. Из двух дробей больше та, которая стоит на числовой оси правее; отрицательные дроби меньше положительных дробей; всякая положительная дробь больше 0; всякая отрицательная дробь меньше 0.
Из двух дробей больше та, которая стоит на числовой оси правее; отрицательные дроби меньше положительных дробей; всякая положительная дробь больше 0; всякая отрицательная дробь меньше 0.
Например: Противоположные дроби: 0,5 и -0,5;
6 класс. Математика. Сложение чисел с разными знаками — Сложение чисел с разными знаками
Комментарии преподавателя
Найдем значение выражения:
Сначала к 5 прибавляем 7 – это будет 12, и из 12 вычитаем 10 – это будет 2:
Однако известно, что сложение и вычитание – это равноправные операции и их можно выполнять в любом порядке. Поэтому можно начать считать с вычитания:
Что же такое ? Увеличение числа на 7, а потом уменьшение на 10 в итоге означает уменьшение на 3. Поэтому считаем равным :
Далее к пяти прибавляем , то есть вычитаем 3:
Число не обозначает никакого реального количества. Такие числа называются отрицательными, они вводятся для упрощения механизма вычисления.
Такие числа называются отрицательными, они вводятся для упрощения механизма вычисления.
Следовательно, чтобы вычесть из меньшего числа большее, необходимо вычесть из большего числа меньшее, но в ответе поставит знак «–».
Пример
Найти значение выражения:
Можно сделать все действия подряд:
Однако из первого числа легче вычесть третье, а потом прибавить второе число:
Существует еще один способ пояснения, что такое отрицательное число.
Для каждого натурального числа, например 5, введем новое число, которое обозначим (–5), и определим, что оно обладает следующим свойством: сумма числа (–5) и 5 равна 0.
Число (–5) будем называть отрицательным, а числа (–5) и 5 – противоположными. Таким образом, мы получили бесконечное количество новых чисел, например:
(–1) – противоположное для числа 1;
(–10) – противоположное числу 10;
(–259) – противоположное числу 259;
(–1 000 000) – противоположное числу 1 000 000;
Вычтем из меньшего числа большее:
Прибавим к данному выражению 5:
Получили ноль. Однако, согласно свойству: число, которое в сумме с пятью дает ноль, обозначается минус пять (–5):
Однако, согласно свойству: число, которое в сумме с пятью дает ноль, обозначается минус пять (–5):
Следовательно, выражение можно обозначить как (–5):
У каждого положительного числа существует «число-близнец», которое отличается только тем, что перед ним стоит знак «–». Такие числа называются противоположными (см. Рис. 1).
Рис. 1. Примеры противоположных чисел
Свойства противоположных чисел
1. Сумма противоположных чисел равна нулю.
2. Если из нуля вычесть положительное число, то результатом будет противоположное отрицательное число.
1. Сложение отрицательных чисел
Для сложения отрицательных чисел необходимо сложить противоположные положительные числа и в ответе поставить знак «–».
2. Сложение чисел с разными знаками
Прибавление отрицательного числа можно считать как вычитание положительного.
Складывать числа можно проще, если использовать понятие модуля. У положительного числа модуль равен самому числу, а у отрицательного – противоположному положительному. То есть модули противоположных чисел равны.
1. Правило сложения отрицательных чисел
Чтобы сложить два отрицательных числа, нужно сложить их модули и поставить знак минус.
2. Правило сложения противоположных чисел
Чтобы сложить отрицательное и положительное число, нужно из большего модуля вычесть меньший модуль и поставить знак числа с большим модулем.
Решите примеры:
1.
Два данных числа отрицательные, следовательно, складываем их модули и ставим знак минус:
2.
Два числа с разными знаками, следовательно, из модуля числа 25 (больший модуль) вычитаем модуль числа 13 и ставим знак минус (знак числа с большим модулем):
3.
Два числа с разными знаками, следовательно, из модуля числа 25 (больший модуль) вычитаем модуль числа 13 и ставим знак плюс (знак числа с большим модулем):
У положительных и отрицательных чисел исторически разная роль.
Натуральные числа были введены для счета предметов, положительные дроби – для счета нецелых количеств, частей. Отрицательные же числа вводились не для счета каких-либо количеств, а как инструмент для упрощения расчетов. Однако они оказались настолько удобными, что им нашлось применение в быту.
Отрицательные величины в жизни используют только для сравнения. Например:
1. Отрицательная температура по Цельсию является отрицательной только по сравнению с нулем, который выбрал автор шкалы Андерс Цельсий. Есть другие шкалы, и та же самая температура уже может быть в них положительной.
2. Если в гостинице оборудовали подвал и туда пустили лифт, то, чтобы оставить привычную нумерацию этажей, может появиться минус первый этаж (см. Рис. 2). Этот минус первый означает всего лишь на этаж ниже уровня земли.
Рис. 2). Этот минус первый означает всего лишь на этаж ниже уровня земли.
Рис. 2. Минус первый и минус второй этажи
источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/tema/slozhenie-chisel-s-raznymi-znakami
источник видео — http://www.youtube.com/watch?v=bWLuAIf8B7I
источник видео — http://www.youtube.com/watch?v=-lGJFW3W54U
источник презентации — http://prezentacii.com/matematike/13647-slozhenie-chisel-s-raznymi-znakami-6-klass.html
Правила знаков
Минус и плюс – это признаки отрицательных и положительных чисел в математике. Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.
Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.
Рассмотрим подробней основные правила знаков.
Деление.
Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».
Умножение.
Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс». Тоже самое касается и двух отрицательных чисел. Если мы умножаем «минус» на «минус», то получим «плюс».
Вычитание и сложение.
Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.
Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.
Правила при умножении (делении) чисел | |||||||||||||||
| |||||||||||||||
Вычитание положительных и отрицательных чисел
Вычитание положительных чисел, таких как 4–2, несложно. Когда мы вычитаем отрицательные числа или вычитаем отрицательные числа из положительных, все становится сложнее.
Когда мы вычитаем отрицательные числа или вычитаем отрицательные числа из положительных, все становится сложнее.
Вот несколько простых правил, которым нужно следовать при вычитании отрицательных чисел.
Правило 1. Вычитание положительного числа из положительного — это обычное вычитание.
Например: это то, что вы узнали раньше. 6-3 — два положительных числа.Решите это уравнение, как всегда: 6 — 3 = 3.
Правило 2: Вычитание положительного числа из отрицательного числа — начните с отрицательного числа и считайте в обратном порядке.
Например: Допустим, у нас есть задача -2 — 3. Используя числовую линию, давайте начнем с -2.
Теперь сосчитайте назад на 3 единицы. Так что продолжайте отсчитывать три пробела от -2 в числовой строке.
Ответ: -2 — 3 = -5.
Правило 3: вычитание отрицательного числа из отрицательного числа — знак минус, за которым следует отрицательный знак, превращает два знака в знак плюс.
Итак, вместо вычитания отрицательного числа вы добавляете положительное. Обычно — (-4) становится +4, а затем вы складываете числа.
Например, допустим, у нас есть проблема -2 — –4. Это будет выглядеть как «два отрицательных минус 4 отрицательных». Итак, мы меняем два отрицательных знака на положительные, и теперь уравнение принимает вид -2 + 4.
На числовой строке он начинается с -2.
Затем продвигаемся на 4 единицы: +4.
class = «green-text»> Ответ -2 — (-4) = 2.
Правило 4: Вычитание отрицательного числа из положительного — превратите знак вычитания, за которым следует отрицательный знак, в знак плюс.
Итак, вместо того, чтобы вычитать отрицательное, вы добавляете положительное. Таким образом, уравнение превращается в простую задачу сложения.
Например: допустим, у нас есть проблема 2 — (-3). Это читается как «два минус три минус». — (-3) превращается в +3.
На числовой прямой мы начинаем с 2.
Затем продвигаемся на три части: 2 + 3.
Ответ 2 — (-3) = 5.
Вычитание положительных и отрицательных чисел
Вычесть
положительных и отрицательных чисел также может быть непросто, потому что есть несколько правил
, которые нужно запомнить и соблюдать.
Правило 1: Вычитание положительного числа из положительного — это нормальное вычитание
.
Пример 1: Не позволяйте разговорам о положительных и отрицательных числах сбить вас с пути — если вы видите положительное число минус положительное число, вычтите
, как обычно! Например, если вы видите 5 — 3, вычитайте как обычно! 5 — 3 = 2.
Правило 2: Вычитание положительного числа из отрицательного числа — начните с отрицательного числа
и отсчитайте в обратном порядке дополнительную сумму, которую вы вычитаете.
Пример 2: Допустим, у нас есть проблема -5 — 3. Это будет читаться как «отрицательное
Это будет читаться как «отрицательное
пять минус три». Это можно представить в виде числовой строки, что означает, что мы идем
, чтобы начать с отрицательного числа (-5) и продолжать обратный отсчет -3, получая
-8, например:
Большая красная точка над -5 показывает, что именно здесь мы начинаем нашу проблему.
Красная стрелка показывает, что мы считали в обратном порядке (вычитали) 3. Красный кружок вокруг
от –8 показывает, что это наш ответ.
Таким образом, -5 — 3 = -8.
Вы также можете думать об этих проблемах как о задачах сложения — вы складываете числа
вместе (5 + 3 = 8), а затем, поскольку оба числа имеют знак минус перед
, вы должны добавить отрицательный знак перед своим ответь вот так: -8. Если этот
имеет больше смысла, вы можете решать эти задачи, как это, но только задачи, которые записаны как
так: -5 — 3.Если есть другие признаки (сложение, вычитание,
и т. Д.), Вам необходимо следовать правилу для этого типа проблемы.
Д.), Вам необходимо следовать правилу для этого типа проблемы.
Правило 3: Вычитание отрицательного числа из отрицательного числа — когда вы видите
знак вычитания (минус), за которым следует отрицательный знак, превратите два знака в
, знак плюс. Таким образом, вместо того, чтобы вычитать отрицательное, вы добавляете положительное.
Итак, — -5 становится +5, и продолжается обычное добавление.
Пример 3: Допустим, у нас была проблема -6 — -3.Это будет читаться как «отрицательное
шесть минус отрицательное три». Это можно представить в виде числовой строки, что означает
, с которого мы собираемся начать, изменив — -3 на +3, например:
Теперь наша задача представляет собой -6 + 3, которую мы можем решить как обычную задачу сложения в числовой строке
, например:
Большая красная точка над -6 показывает, что именно здесь мы начинаем нашу проблему.
Синяя стрелка показывает, что мы посчитали вперед (прибавили) 3.Синий кружок вокруг
–3 показывает, что это наш ответ.
Правило 4: Вычитание отрицательного числа из положительного числа — когда вы видите
знак вычитания (минус), за которым следует отрицательный знак, превратите два знака в
знак плюс. Таким образом, вместо вычитания отрицательного числа вы добавляете положительное число
, поэтому у вас возникает простая задача сложения.
Пример 4: Допустим, у нас была проблема 5 — (-3). Это будет читаться как «пять
минус три минус.”Это будет работать так же, как и в предыдущем примере, поэтому
— (-3) изменится на +3; следовательно, ваша новая задача будет выглядеть так: 5 + 3, что означает
— простую задачу сложения, в результате чего получится 8.
Тест на вычитание положительных и отрицательных чисел
Проблемы
1. 4 — 2 4 — 2 | 2. -8 — 5 | 3.-4 — (-7) | 4. 6 — (-3) | 5. -9 — 1 |
| 6. -10 — (-8) | 7. 9 — 4 | 8. 2 — (-7) | 9. -7 — 8 | 10.-5 — (-6) |
Решения
| 1. 2 | 2. -13 | 3. 3 | 4. 9 | 5. -10 -10 |
| 6. -2 | 7.5 | 8. 9 | 9. -15 | 10. 1 |
положительных и отрицательных чисел | SkillsYouNeed
Стандартные числа, любые больше нуля, называются «положительными» числами. Мы не ставим перед ними знак плюса (+), потому что в этом нет необходимости, поскольку, по общему мнению, числа без знака положительны.
Числа меньше нуля известны как «отрицательные» числа. Перед ними стоит знак минус (-), указывающий на то, что они меньше нуля (например, -10 или « минус 10 »).
Визуализация отрицательных и положительных чисел
Вероятно, самый простой способ визуализировать отрицательные и положительные числа — использовать числовую линию, инструмент, с которым вы, возможно, хорошо знакомы, особенно если у вас есть дети в начальной школе.
Это выглядит примерно так:
Числовая линия может помочь вам визуализировать как положительные, так и отрицательные числа, а также операции (сложение и вычитание), которые вы можете с ними делать.
Когда вам нужно вычислить сложение или вычитание, вы начинаете с первого числа и перемещаете второе число разрядов вправо (для сложения) или влево (для вычитания).
Эта числовая линия является упрощенной версией, но вы можете нарисовать их с любым числом, если хотите. Большим преимуществом числовой линии является то, что ее очень легко нарисовать самостоятельно на обратной стороне конверта или клочка макулатуры, а также довольно сложно ошибиться в расчетах.Если вы внимательно подсчитываете количество мест, которые вы перемещаете, вы получите правильный ответ.
Рабочие примеры
Что такое 10-25?
Начиная с 10, вы перемещаете 25 чисел влево и сразу видите, что ответ — -15.
Что такое −17 + 23?
На этот раз вы начинаете с -17 и перемещаетесь на 23 позиции вправо. Сразу видно, что ответ — 6.
Сразу видно, что ответ — 6.
Вычитание отрицательных чисел
Если вы вычесть отрицательное число, два отрицательных числа объединятся, чтобы получить положительное.
−10 — (- 10) не равно −20. Вместо этого вы можете думать об этом как о том, чтобы повернуть один из отрицательных знаков вертикально, пересечь другой и получить плюс. Тогда сумма будет -10 + 10 = 0.
Краткое примечание по скобкам
Для наглядности, никогда нельзя писать два знака минус рядом без скобок.
Итак, если вас попросят вычесть отрицательное число, оно всегда будет заключено в скобки, чтобы вы могли увидеть, что использование двух отрицательных знаков было намеренным.
-10-10 неверно (и сбивает с толку)
-10 — (- 10) правильно (и яснее)
Умножение и деление на положительные и отрицательные числа
При умножении или делении с комбинациями положительных и отрицательных чисел вы можете упростить процесс, сначала игнорируя знаки (+/-) и просто умножая или деля числа, как если бы они оба были положительными. Получив числовой ответ, вы можете применить очень простое правило, чтобы определить знак ответа:
Получив числовой ответ, вы можете применить очень простое правило, чтобы определить знак ответа:
- Когда знаки двух чисел совпадают с , ответ будет положительным .
- Если знаки двух чисел разных , ответ будет отрицательным .
Итак:
(положительное число) × (положительное число) = положительное число
(отрицательное число) × (отрицательное число) = положительное число
Но:
(положительное число) × (отрицательное число) = отрицательное число
В качестве побочного вопроса это каким-то образом объясняет, почему у вас не может быть квадратного корня из отрицательного числа (подробнее об этом читайте на нашей странице в Special Numbers and Concepts ).Квадратный корень — это число, которое умножается само на себя, чтобы получить число. Вы не можете умножить число на само по себе, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Правило работает так же, когда вам нужно умножить или разделить более двух чисел. Четное число отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.
Рабочих примеров
Что такое −5 × 25?
5 x 25 равно 125.Но здесь у вас есть одно отрицательное и одно положительное число, поэтому знак ответа будет отрицательным. Следовательно, ответ будет −125 .
Что такое −40 ÷ 8?
40 ÷ 8 равно 5. Опять же, у вас есть одно положительное и одно отрицательное число, поэтому знак ответа будет отрицательным. Ответ: −5 .
Что такое −50 ÷ −5?
50 ÷ 5 равно 10. На этот раз у вас два отрицательных числа, поэтому знак ответа будет положительным. Ответ: 10 .
Ответ: 10 .
Что такое −100 × −2?
100 x 2 равно 200. Опять же, у вас два отрицательных числа, поэтому ответ положительный. Это 200 .
Что такое 10 x −2 × 3?
Для начала рассмотрим первую часть расчета. 10 x 2 = 20. У вас есть одно положительное и одно отрицательное число, поэтому знак ответа будет отрицательным, то есть −20.
Теперь возьмем вторую часть вычисления: −20 × 3.Итак, 20 × 3 = 60, но опять же, у вас есть отрицательное и положительное число, поэтому ответ будет отрицательным: −60 .
Почему умножение двух отрицаний дает положительный ответ?
Тот факт, что отрицательное число, умноженное на другое отрицательное число, дает положительный результат, часто может сбивать с толку и казаться нелогичным.
Чтобы объяснить, почему это так, вспомните числовые линии, использованные ранее в этой статье, поскольку они помогают объяснить это визуально.
- Во-первых, представьте, что вы стоите на числовой прямой в нулевой точке и обращены в положительном направлении, то есть в направлении 1, 2 и так далее. Вы делаете два шага вперед, делаете паузу, затем делаете еще два шага. Вы переместились 2 × 2 шага = 4 шага.
Следовательно, положительный × положительный = положительный - Теперь вернитесь к нулю и посмотрите в отрицательном направлении, то есть в сторону −1, −2 и т. Д. Сделайте два шага вперед, затем еще два. Теперь вы стоите на −4. Вы переместились на 2 × −2 шага = −4 шага.
Следовательно, отрицательный × положительный = отрицательный
В обоих этих примерах вы двигались вперед (то есть в том направлении, куда вы смотрели), что является положительным ходом.
- Вернитесь к нулю снова, но на этот раз вы собираетесь идти назад (отрицательное движение). Снова поверните голову в положительную сторону и сделайте два шага назад.
 Теперь вы стоите на -2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
Теперь вы стоите на -2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
Следовательно, положительный × отрицательный = отрицательный - Наконец, снова вернемся к нулю, повернемся в отрицательном направлении. Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись в отрицательном направлении и идя назад ( два отрицательных ), вы достигли положительного результата.
Следовательно, отрицательный × отрицательный = положительный
- Два негатива компенсируют друг друга. Вы можете увидеть это в речи:
- «Просто сделай это!» положительный стимул к чему-либо.
- «Не делай этого!» просит кого-то чего-то не делать. Это отрицательно.
- «Не делай этого» означает «пожалуйста». Два отрицания компенсируют и дают положительный результат как в математике, так и в речи.
- Знаки складываются физически. Когда у вас есть два отрицательных знака, один переворачивается, и они складываются, чтобы получить положительный. Если у вас есть положительный и отрицательный ответ, останется один штрих, и ответ будет отрицательным. Это простая и наглядная памятная записка, хотя она не обязательно удовлетворит тех, кто хочет понять правило.
Заключение
Отрицательные знаки могут выглядеть немного устрашающе, но правила, регулирующие их использование, просты и понятны. Помните об этом, и у вас не будет проблем.
Вычитание положительных и отрицательных чисел — видео и стенограмма урока
Вычитание положительных чисел
Во-первых, давайте посмотрим на положительное минус положительное. Хорошо, вы уже знаете, что 5 — 3 = 2, но как насчет 3 — 5? Странно, правда? Другими словами, странно, что большее число идет вторым, но такое бывает.Это как если бы у вас всего 3 доллара, но вы кому-то должны 5 долларов.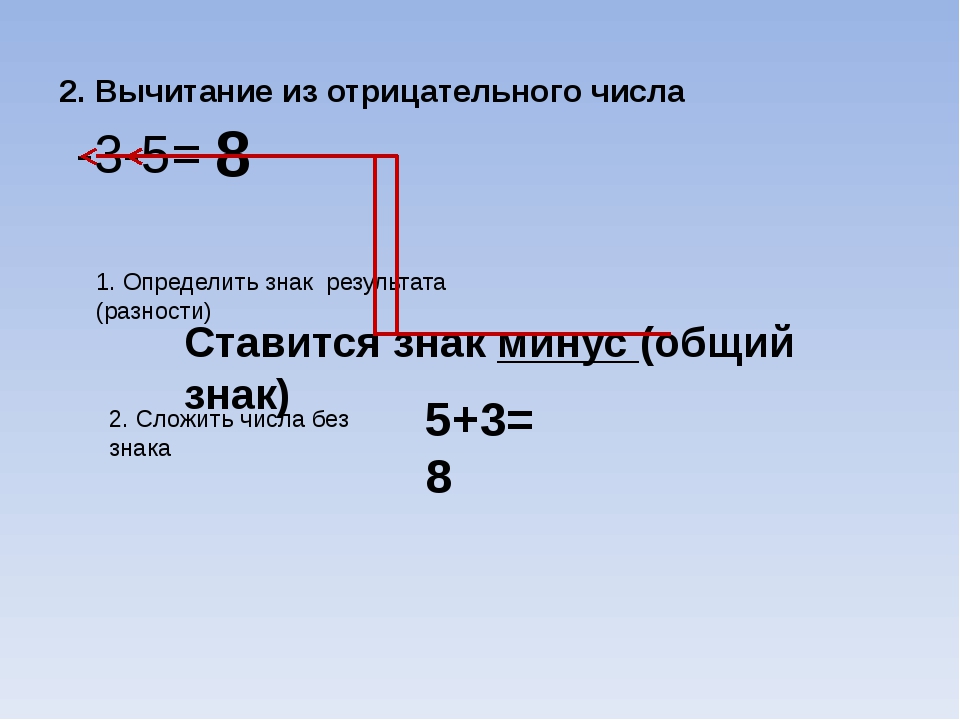 Начните с 3 на числовой прямой и отсчитайте 5 раз назад. Вы идете 2, 1, 0, -1, -2. Итак, 3-5 = -2. Это означает, что у вас 2 доллара в кармане; ты все еще должен 2 доллара.
Начните с 3 на числовой прямой и отсчитайте 5 раз назад. Вы идете 2, 1, 0, -1, -2. Итак, 3-5 = -2. Это означает, что у вас 2 доллара в кармане; ты все еще должен 2 доллара.
А как насчет 2–4? Вы начинаете с 2 и отсчитываете четыре позиции назад. Если хотите, используйте числовую строку. Начиная с 2, будет 1, 0, -1, -2.Итак, 2-4 = -2.
Теперь посмотрим на отрицательный минус положительный. Давайте попробуем -3 — 2. Ну, вы все еще вычитаете одно число из другого, так что вы все еще двигаетесь влево. Начните с -3, затем отсчитайте 2 разряда: -4, — 5. Наше окончательное уравнение: -3 — 2 = -5.
Вычитание отрицательных чисел
Как мы видели в начале этого урока, когда Томас использовал двойное отрицание, они вместе давали положительный результат. И «не надо», и «нет» отрицательны. Если вы говорите, что вы «не хотите» «нет» больше, это означает, что вы не хотите, чтобы ваша мама «не» дала вам больше. Итак, вы хотите большего. Хотя это кажется немного запутанным, с отрицательными числами дело обстоит именно так. Если вы вычесть отрицательное число, это то же самое, что добавить положительное число. Ага, правда!
Итак, вы хотите большего. Хотя это кажется немного запутанным, с отрицательными числами дело обстоит именно так. Если вы вычесть отрицательное число, это то же самое, что добавить положительное число. Ага, правда!
Во-первых, давайте посмотрим на положительный минус отрицательный. Как насчет того, чтобы попробовать? Попробуйте уравнение 1-2. Два отрицательных элемента дают положительный результат, что дает следующее уравнение: 1 + 2. Итак, начиная с 1, пройдите два пробела вперед: 1 + 2 = 3. Вы знаете, что 2 + 2 = 4, верно? Ну, 2 — -2 тоже равняется 4. Не забывайте, скажите это вслух: два отрицательных знака дают положительный результат.
Теперь, наконец, давайте посмотрим на минус минус минус. На этот раз давайте начнем с отрицательного числа. Как насчет -1 — -2. Ух ты! Там много отрицательных знаков, а? Помните, что два отрицательных знака дают положительный результат, поэтому это уравнение похоже на выражение -1 + 2. Посмотрите на числовую прямую и попробуйте. Начните с -1 и добавьте два разряда: 0, 1. Итак, -1 — -2 = 1.
Итак, -1 — -2 = 1.
Резюме урока
Хорошо, давайте ненадолго вспомним, что мы узнали.В этом уроке мы изучили лучшую стратегию вычитания положительных и отрицательных чисел, в частности, используя числовую строку , в которой числа увеличиваются при движении вправо и уменьшаются при движении влево. Другими словами, при вычитании чисел вы всегда будете перемещаться влево по числовой строке, если вы не вычитаете на отрицательное число. Тогда просто помните, что два отрицательных знака превращают положительный в проблему сложения!
Вычитание отрицательных чисел — лучшее объяснение
Учительница математики недавно спросила, как объяснить своему классу концепцию вычитания отрицательных чисел.Почему 8 — (-6) = 14 то же самое, что 8 + 6 = 14?
Я давно усвоил отрицательные значения как «противоположность», а вычитание как «противоположность сложению», поэтому в моей голове возникло понятие «противоположность противоположности сложению», которое упрощается до «сложения».
Но эта внутренняя вербализация все еще была довольно абстрактной. Подумав о лучшей интуиции, вот мой ответ:
Отличный вопрос! Пришлось немного подумать. Сложение и вычитание связаны, но немного отличаются от положительных и отрицательных чисел.
Представьте себе прогулку. Вы смотрите вперед и делаете 8 шагов вперед. Это действительно:
0 + 8
0 — ваша отправная точка. Знак «+» означает «лицом вперед», а «8» означает «8 шагов в том направлении, в котором вы смотрите». ОК.
Теперь предположим, что мы хотим продолжать смотреть вперед и сделать еще 6 шагов. Это будет:
8 + 6 = 14
Что дает нам 14 шагов от нашей отправной точки. Что, если бы мы повернулись назад и сделали 6 шагов?
8–6 = 2
Это означает, что мы довольно близко к нашей отправной точке, всего в 2 шагах от нас.Что, если бы мы смотрели назад, но шел назад на 6 шагов?
8 — (-6) = 14
А! Сложение / вычитание говорит нам, в какую сторону смотреть, а положительное / отрицательное говорит нам, будут ли наши шаги вперед или назад (независимо от того, куда мы смотрим).
В некотором смысле сложение / вычитание действует как глагол («лицом вперед» или «лицом назад»), а положительное / отрицательное действует как прилагательное («обычные шаги» или «шаги назад»). Или, может быть, это наречие, изменяющее то, как мы идем (идти вперед, идти назад).Вы уловили идею.
Для старших школьников «вычитание отрицательного результата» можно рассматривать как «списание долга». Если у меня есть долг в 30 долларов, и кто-то «вычитает его», я фактически получил 30 долларов. В целом, если вы убрали недостаток, вы улучшили свое положение — положительный момент.
Эти объяснения немного абстрактны, при ходьбе интереснее попробовать напрямую. Я действительно ходил, обдумывая интуицию. (Если вы любите приключения, вы можете начать думать о шагах в сторону или прыжках, и о том, как это будет представлено.)
Счастливая математика.
Приложение
Выполняя простую арифметику, мы отслеживаем только конечное местоположение, но не ориентацию. Если смотреть назад и идти назад, мы можем смотреть на 0, когда продвигаемся вперед. Но математически наша конечная точка такая же: 8 — (-6) = 8 + 6 = 14.
Если смотреть назад и идти назад, мы можем смотреть на 0, когда продвигаемся вперед. Но математически наша конечная точка такая же: 8 — (-6) = 8 + 6 = 14.
Если нам важно, куда мы смотрим, нам нужен более сложный математический объект (вектор), чтобы отслеживать нашу ориентацию, а также положение («14, лицом вперед» против «14, лицом назад»).Возможно, мы бы использовали линейный интеграл, двигаясь по пути и отслеживая направление, в котором мы движемся.
Подходящая аналогия приводит к вопросам о том, что еще возможно.
Другие сообщения этой серии
- Методы сложения чисел от 1 до 100
- Переосмысление арифметики: наглядное руководство
- Quick Insight: интуитивное значение подразделения
- Quick Insight: вычитание отрицательных чисел
- Удивительные узоры в квадратных числах (1, 4, 9, 16…)
- Развлечение с модульной арифметикой
- Учимся считать (как избежать проблемы со столбом)
- Причудливое введение в системы счисления
- Еще один взгляд на простые числа
- Интуиция для золотого сечения
- Различные интерпретации числа ноль
Размышление о плюсах и минусах
Возможно, вы слышали, как люди говорят: «Два минуса — плюс». Это не самый лучший способ думать о положительных и отрицательных числах.
Это не самый лучший способ думать о положительных и отрицательных числах.
Ниже приведены несколько различных способов сложения и вычитания положительных и отрицательных чисел. Мы надеемся, что они помогут вам понять, что происходит, когда у вас может возникнуть соблазн использовать правило вроде «Два минуса — плюс».
Есть четыре возможности, которые нам необходимо понять:
Добавление положительного числа
Добавление отрицательного числа
Вычитание положительного числа
Вычитание отрицательного числа
Воздушный шар
Первая предлагаемая нами модель — это модель воздушный шар, как показано в игре Up, Down, Flying Around.
В этой модели мы представляем положительные числа как «порывы» горячего воздуха, а отрицательные числа — как мешки с песком.
| Модель | Расчет | Результат |
| Добавление порций горячего воздуха | Добавление положительного числа | прибавка (по высоте) |
| Добавление мешков с песком | Добавление отрицательного числа | Понижение (по высоте) |
| Вычитание порывов горячего воздуха | Вычитание положительного числа | Понижение (по высоте) |
| Вычитание мешков с песком | Вычитание отрицательного числа | прибавка (по высоте) |
Теперь мы можем описать вычисление, такое как 4 + (-2) — (+5) — (-1) + (+7) , следующим образом:
Мой шарик начинается на высоте +4. Я складываю два мешка с песком (два вниз), вычитаю пять порций горячего воздуха (пять вниз), вычитаю один мешок с песком (на один вверх), затем добавляю семь порций горячего воздуха (семь вверх). Мой шар оказывается на высоте +5.
Я складываю два мешка с песком (два вниз), вычитаю пять порций горячего воздуха (пять вниз), вычитаю один мешок с песком (на один вверх), затем добавляю семь порций горячего воздуха (семь вверх). Мой шар оказывается на высоте +5.
Вы можете прочитать вычисление как «Четыре сложить два отрицательных, вычесть пять положительных, вычесть отрицательный один, добавить семь положительных» и подумать про себя «Четыре, два вниз, пять вниз, один вверх, семь вверх» или эквивалент .
Модель счастья
Вот описание учителя того, как она объясняет положительные и отрицательные числа своим классам:
«Я считаю, что сложение и вычитание с отрицательными числами имеет смысл.От -10 $ до 10 $, скажем) над или в верхней части моей доски. Вместе со студентами мы проводим мозговой штурм над положительными и отрицательными вещами. Мы говорим о том, что вы чувствуете, если кто-то дает вам положительный результат или кто-то его отнимает. Мы говорим о том, что вы чувствуете, если кто-то дает вам что-то негативное или кто-то уносит его.
Сегодня я чувствую себя нормально, может, я наберу 2 доллара (указывает на числовую линию) по этой шкале счастья.
Что бы я почувствовал, если бы кто-то дал мне шоколадные конфеты за 4 доллара (общий положительный результат!)? Да, я поднимаюсь с 4 до 6 долларов.-2 $.
Что, если вы позволите мне отказаться от моих задержек в размере 3 долларов? …
Добавление чего-то положительного или удаление чего-то отрицательного улучшает ситуацию (мы идем вверх по числовой строке).
Добавление чего-то отрицательного или удаление чего-то положительного ухудшает ситуацию (мы идем вниз по числовой линии).
Футбольная модель
В этой модели мы представляем положительные числа как хороших футболистов, которые забивают много голов, а отрицательные числа. как плохие футболисты, забивающие в собственные ворота.Когда наступает время трансферов, мы можем добавить новых игроков в нашу команду или исключить игроков из команды.
| Модель | Расчет | Результат |
| Купите хороших игроков | Добавление положительного числа | Повышение (в лиге) |
| Купить плохих игроков | Добавление отрицательного числа | Понижение (в лиге) |
| Продам хороших игроков | Вычитание положительного числа | Понижение (в лиге) |
| Продать плохих игроков | Вычитание отрицательного числа | Повышение (в лиге) |
Итак, представьте, что мы купили 5 хороших игроков, продали 2 хороших игроков, купили 3 плохих и продали 7 плохих игроков. -7) = 3 $
Студенты могут быть предложены чтобы создать еще несколько вычитаний, подобных приведенным выше.
Сбор различных результатов может дать учащимся возможность спросить, что они замечают.
Могут ли они подсказать, как вычитать отрицательные числа, не утруждая себя рисованием плюсов и минусов?
Если у вас есть SMART Board, вы можете загрузить этот файл записной книжки, которым поделился с нами Джон Турпин.
Правила использования положительных и отрицательных целых чисел
Целые числа, цифры, не имеющие дробей и десятичных знаков, также называются целыми числами.Они могут иметь одно из двух значений: положительное или отрицательное.
- Положительные целые числа имеют значения больше нуля.
- Отрицательные целые числа имеют значения меньше нуля.
- Ноль не является ни положительным, ни отрицательным.
Правила работы с положительными и отрицательными числами важны, потому что вы столкнетесь с ними в повседневной жизни, например, при балансировании банковского счета, вычислении веса или приготовлении рецептов.
Советы для успеха
Как и любой другой предмет, успех в математике требует практики и терпения. Некоторым людям легче работать с числами, чем другим. Вот несколько советов по работе с положительными и отрицательными целыми числами:
- Контекст может помочь вам разобраться в незнакомых концепциях. Попробуйте подумать о практическом приложении как о ведении счета, когда вы тренируетесь.
- Использование числовой линии , показывающей обе стороны нуля, очень полезно для понимания работы с положительными и отрицательными числами / целыми числами.
- Отрицательные числа легче отслеживать, если вы заключите их в скобки .
Дополнение
Независимо от того, добавляете ли вы положительные или отрицательные значения, это простейший расчет, который вы можете сделать с целыми числами. В обоих случаях вы просто вычисляете сумму чисел. Например, если вы складываете два положительных целых числа, это выглядит так:
Если вы вычисляете сумму двух отрицательных целых чисел, это выглядит так:
Чтобы получить сумму отрицательного и положительного числа, используйте знак большего числа и вычтите.Например:
- (–7) + 4 = –3
- 6 + (–9) = –3
- (–3) + 7 = 4
- 5 + (–3) = 2
Знак будет у большего числа. Помните, что добавление отрицательного числа равносильно вычитанию положительного.
Вычитание
Правила вычитания аналогичны правилам сложения. Если у вас есть два положительных целых числа, вы вычитаете меньшее из большего. Результатом всегда будет положительное целое число:
Точно так же, если вы вычтите положительное целое число из отрицательного, вычисление станет вопросом сложения (с добавлением отрицательного значения):
- (–5) — 3 = –5 + (–3) = –8
Если вы вычитаете отрицательные из положительных, два отрицательных результата уравновешиваются, и это становится сложением:
- 5 — (–3) = 5 + 3 = 8
Если вы вычитаете отрицательное число из другого отрицательного целого числа, используйте знак большего числа и вычтите:
- (–5) — (–3) = (–5) + 3 = –2
- (–3) — (–5) = (–3) + 5 = 2
Если вы запутались, часто помогает сначала написать положительное число в уравнении, а затем отрицательное.Это может упростить определение того, происходит ли смена знака.
Умножение
Умножение целых чисел довольно просто, если вы помните следующее правило: если оба целых числа либо положительные, либо отрицательные, сумма всегда будет положительным числом. Например:
- 3 x 2 = 6
- (–2) x (–8) = 16
Однако, если вы умножаете положительное целое число на отрицательное, результатом всегда будет отрицательное число:
- (–3) x 4 = –12
- 3 x (–4) = –12
Если вы умножаете большую серию положительных и отрицательных чисел, вы можете сложить, сколько положительных и отрицательных чисел.Последний знак будет лишним.
Отдел
Как и в случае с умножением, правила деления целых чисел следуют тому же положительному / отрицательному руководству. Разделение двух негативов или двух позитивов дает положительное число:
- 12/3 = 4
- (–12) / (–3) = 4
Деление одного отрицательного целого числа и одного положительного целого числа дает отрицательное число:
- (–12) / 3 = –4
- 12 / (–3) = –4
.
