Содержание
Латунная трубка, эфир налит в трубку, трубка закупорена.
Условие:
Латунная трубка, эфир налит в трубку, трубка закупорена.
Решение:
При быстром движении веревки, плотно обвитой вокруг латунной трубки, молекулы веревки взаимодействуют с молекулами металла (латуни). Отдельно взятая молекула веревки взаимодействует с молекулой латуни с силой F (эта сила проявляется как сила трения между веревкой и латунной трубкой), передает часть своей кинетической энергии молекуле латуни. Получив дополнительную энергию от молекулы веревки, молекула латуни начинает с большей амплитудой колебаться, оставаясь связанной с соседними молекулами латуни — кинетическая энергия молекулы веревки перешла в энергию колебаний молекулы латуни. Молекула латуни, за счет столкновений, передает свою энергию колебаний другим молекулам латуни, лежащим дальше от поверхности трубки. Эта энергия колебаний составляет внутреннюю энергию трубки. Значит внутренняя энергия трубки увеличивается за счет трения об неё веревки. Скорость движения молекул латуни во время колебаний увеличилась — значит увеличилась температура трубки. Трубка нагрелась. Увеличение скорости движения (амплитуды колебаний — обозначена «а» на рисунке) молекул латуни передалось самому внутреннему слою молекул латуни, непосредственно взаимодействующим с молекулами жидкого эфира. На рисунке, для простоты, нарисован только один слой молекул латуни. Молекула латуни взаимодействует (сталкивается) с молекулой эфира с силой f, передавая ей дополнительную энергию. Молекула эфира отскакивает от молекулы латуни с большей скоростью, приобретя дополнительную кинетическую энергию — внутренняя энергия эфира увеличилась, также как и температура. Температура кипения эфира низкая — у диметилового -23 градусов, а у диэтилового 34.4 градусов Цельсия. Поэтому при незначительном нагревании эфир кипит и испаряется. Пары эфира расширяются, т.к. кинетическая энергия молекул пара очень большая. Они с большой скоростью ударяются о стенки латунной трубки и о пробку, выталкивая её.
Скорость движения молекул латуни во время колебаний увеличилась — значит увеличилась температура трубки. Трубка нагрелась. Увеличение скорости движения (амплитуды колебаний — обозначена «а» на рисунке) молекул латуни передалось самому внутреннему слою молекул латуни, непосредственно взаимодействующим с молекулами жидкого эфира. На рисунке, для простоты, нарисован только один слой молекул латуни. Молекула латуни взаимодействует (сталкивается) с молекулой эфира с силой f, передавая ей дополнительную энергию. Молекула эфира отскакивает от молекулы латуни с большей скоростью, приобретя дополнительную кинетическую энергию — внутренняя энергия эфира увеличилась, также как и температура. Температура кипения эфира низкая — у диметилового -23 градусов, а у диэтилового 34.4 градусов Цельсия. Поэтому при незначительном нагревании эфир кипит и испаряется. Пары эфира расширяются, т.к. кинетическая энергия молекул пара очень большая. Они с большой скоростью ударяются о стенки латунной трубки и о пробку, выталкивая её. Кинетическая энергия молекул пара эфира перешла в кинетическую энергию пробки — внутренняя энергия эфира уменьшилась, также как и его температура.
Кинетическая энергия молекул пара эфира перешла в кинетическую энергию пробки — внутренняя энергия эфира уменьшилась, также как и его температура.
Советы:
Любое взаимодействие двух тел приводит к передаче энергии от одного к другому, что увеличивает внутреннюю энергию одного и уменьшает её у другого.
Виды теплопередачи. Теплопроводность. Конвекция. Излучение.
Урок 3. Тема: Виды теплопередачи. Теплопроводность. Конвекция. Излучение.
Примеры теплопередачи в природе и технике.
Цели: Познакомить учащихся с видами теплопередачи и привести примеры теплопередачи в природе и технике
Задачи:
— Образовательная: раскрыть понятия теплопроводность, конвекция, излучение. Познакомить с примерами теплопередачи в природе и технике.
— Развивающая: развивать внимание, воображение и память.
— Воспитательная: воспитывать самостоятельность, любовь к предмету.
Структура урока:
Организационный момент.

Проверка домашнего задания. (индивидуальные карточки).
Актуализация знаний. Объяснение нового материала .
Закрепление нового материала .
Домашнее задание.
Подведение итогов.
Рефлексия.
Ход урока.
1. Организационный момент. Приветствие. Выявление отсутствующих. Проверка готовности к уроку.
2. Проверка домашнего задания. Вопросы в конце параграфов 1-3.Карточки. в Приложении 1.
Вопросы:
1. Какие тепловые явления вы знаете? Что характеризует температура? Как связана температура тела со скоростью его молекул? Чем отличается движение молекул в газах, жидкостях и твердых телах?
2. Какие превращения энергии происходят при подъеме шара и при его падении? Как изменяется состояние свинцового шара и свинцовой плиты в результате их соударения? Какую энергию называют внутренней энергией тела? Зависит ли внутренняя энергия тела от его движения и положения относительно других тел?
Проверка упр. 1 №1 и2 стр. 8.
1 №1 и2 стр. 8.
3. Пользуясь рисунком 3, расскажите, как изменяется внутренняя энергия тела, когда над ним совершают работу. Опишите опыт, показывающий, что за счет внутренней энергии тело может совершить работу.
4. Объясните на основе молекулярного строения вещества нагревание спицы, опущенной в горячую воду.
5. Что такое теплопередача? Какими двумя способами можно изменить внутреннюю энергию.
3. Актуализация знаний. Объяснение нового материала.
Вспомним что называется теплопередачей? (Из прошлого урока вам известно, что процесс изменения внутренней энергии при теплообмене без совершения работы над телом или самим телом называется теплопередачей.)
Запишем тему урока. ( Слайд 1).
Частицы более нагретого тела, имея большую кинетическую энергию, при контакте с менее нагретым телом передают энергию непосредственно частицам менее нагретого тела.
Существуют 3 вида теплопередачи: теплопроводность, конвекция и излучение. ( Слайд 2).
( Слайд 2).
1) Рассмотрим 1 вид теплопередачи, теплопроводность. Запишем определение для теплопроводности. Явление передачи энергии от более нагретой части тела к менее нагретой или от более нагретого тела к менее нагретому через непосредственный контакт или промежуточные тела. В различных веществах(твердых, жидких, газообразных) она различна. Рассмотрим примеры на слайдах 2-7.
Прочитать два последних абзаца из параграфа 4 на странице 13 и ответить на вопрос.
Почему мех, пух, перья на теле животных и птиц, а также одежда человека защищают от холода? (слайд 8)
Ответим на вопросы: (слайд 9).
1. В стакан налит горячий чай. Как осуществляется теплообмен между чаем и стенками стакана?
2. Почему нагретые детали охлаждаются в воде быстрее, чем на воздухе?
3. Зачем ствол винтовки покрывают деревянной накладкой?
4. Почему вы обжигаете губы, когда пьете чай из металлической кружки, и не обжигаете, когда пьете чай из фарфоровой кружки? (Температура чая одинаковая. )
)
5. Если температура в комнате 16 °С, то нам не холодно, но если войти в воду, температура которой 20 °С, то мы ощущаем довольно сильный холод. Почему?
2) Еще один вид теплопередачи это конвекция. (слайд 11)
Конвекция – это процесс теплопередачи, при котором энергия переносится струями жидкости или газа. Она отсутствует в твердых телах и не имеет места в вакууме.
Различают два вида конвекции: естественную ( или свободную) и вынужденную.
3) Излучение. Процесс передачи энергии от одного тела к другому с помощью электромагнитных волн. Интенсивность излучения зависит от температуры, чем выше температура тела, тем больше излучение.
В каких средах происходит излучение? Привести примеры. Происходит во всех средах.
Закрепление материала.
Теплопередача это?
Виды теплопередач?
Примеры теплопроводности.
Объяснить процесс конвекция и излучения
Примеры теплопередачи в природе и технике.
Д/з параграф 4-6, упражнения в конце параграфов ( устно). Доклады или презентации по темам: «Устройство термоса», и «Теплопередача и растительный мир».
Подведение итогов. Выставление оценок за работу на уроке.
Рефлексия. Что нового, вы узнали сегодня на уроке? Какие были трудности? Удалось ли их преодолеть? Пригодятся ли вам знания, полученные сегодня на уроке
Резервное время. Самостоятельно ответим на вопросы. ( слайд 10 )
1. Какое из перечисленных ниже веществ имеет наибольшую теплопроводность?
А. Мех. Б. Дерево. В. Сталь.
1. Какое из перечисленных ниже веществ имеет наименьшую теплопроводность?
А. Воздух. Б. Чугун. В. Алюминий.
2. Какое из перечисленных ниже веществ имеет наименьшую теплопроводность?
А. Опилки. Б. Свинец. В. Медь.
Б. Свинец. В. Медь.
2. Какое из перечисленных ниже веществ имеет наибольшую теплопроводность?
А. Солома. Б. Вата. В. Железо.
3.В каком доме теплее зимой при одинаковой толщине стен: деревянном или кирпичном?
3. В какой одежде человеку теплее: хлопчатобумажной или шерстяной?
Приложение 1.
СР-1 Тема: Тепловое движение. Температура.
Вариант 1.
1. Какие явления называются тепловыми?
2. Какие из перечисленных ниже явлений относятся к тепловым явлениям:
а) таяние снега под лучами солнца;
б) движение автомобиля по дороге;
в) нагревание воды в электрическом чайнике;
г) появление радуги на небе?
3. Имеется три сосуда с холодной, теплой и горячей водой. Сравните скорости движения молекул воды в этих сосудах.
СР-1 Тема: Тепловое движение. Температура.
Вариант 2.
1. Какое из перечисленных ниже движений является тепловым:
а) движение Луны вокруг Земли;
б) беспорядочное движение молекул тела;
в) движение фигуриста на льду;
г) полет воздушного шара?
2. Как изменяется скорость движения молекул при повышении температуры?
Как изменяется скорость движения молекул при повышении температуры?
3. Имеется два сосуда с водой. В одном сосуде температура воды 20 С, в другом – 100 С. В каком сосуде средняя кинетическая энергия молекул воды больше?
СР-1 Тема: Тепловое движение. Температура.
Вариант 1.
1. Какие явления называются тепловыми?
2. Какие из перечисленных ниже явлений относятся к тепловым явлениям:
а) таяние снега под лучами солнца;
б) движение автомобиля по дороге;
в) нагревание воды в электрическом чайнике;
г) появление радуги на небе?
3. Имеется три сосуда с холодной, теплой и горячей водой. Сравните скорости движения молекул воды в этих сосудах.
СР-1 Тема: Тепловое движение. Температура.
Вариант 2.
1. Какое из перечисленных ниже движений является тепловым:
а) движение Луны вокруг Земли;
б) беспорядочное движение молекул тела;
в) движение фигуриста на льду;
г) полет воздушного шара?
2. Как изменяется скорость движения молекул при повышении температуры?
Как изменяется скорость движения молекул при повышении температуры?
3. Имеется два сосуда с водой. В одном сосуде температура воды 20 С, в другом – 100 С. В каком сосуде средняя кинетическая энергия молекул воды больше?
Большая Энциклопедия Нефти и Газа, статья, страница 1
Рисунком
Cтраница 1
Рисунком называется изображение на плоскости от руки ( без применения чертежных инструментов) объемных предметов. Рисование можно разделить на два вида: перспективное и техническое.
[1]
Рисунком называется изображение предметов, выполненное от руки на глаз в том виде, в каком они наблюдаются нами в действительности.
[2]
Рисунком называют изображение предмета от руки и на глаз с кажущимися относительными размерами и положениями отдельных его элементов.
[3]
Заполнение рисунком ( picture fill symbol) использует растровые рисунки или усовершенствованные метафайлы. Рисунки повторяются без зазора или с заданным интервалом.
Рисунки повторяются без зазора или с заданным интервалом.
[4]
Пользуясь рисунком 33, определите, какой процесс может совершаться в каждом из цилиндров, если в первом происходит впуск горючей смеси.
[5]
Пользуясь рисунком 8, расскажите, как определить цену деления изображенного на нем секундомера.
[6]
Пользуясь рисунком 64, объясните, как устроен силомер. Почему при сжатии стрелка этого динамометра поворачивается. Какую цену деления целесообразно придать такому динамометру.
[7]
Пользуясь рисунком 90, объясните на основе знаний о молекулах, почему жидкости и газы передают давление во все стороны одинаково.
[8]
Пользуясь рисунком 161, объясните, почему при гребле мы получаем проигрыш в силе и для чего это нужно.
[9]
Под рисунком 184 подписано: Сен-Жермен 10 октября 1906 г. Вес 44 золотника. Окраска светлозеленая ровная с мелкими коричнево-серыми точками.
[10]
Между рисунком и текстом должна существовать органическая связь: рисунок дополняет и обогащает тект, а текст разъясняет рисунок.
[11]
Пользуясь рисунком 4, расскажите, как изменяется внутренняя энергия тела, когда над ним совершают работу. Опишите опыт, показывающий, что за счет внутренней энергии тело может совершить работу.
[12]
Пользуясь рисунком 134, объясните, как строится изображение точки в зеркале. Почему изображение точки в плоском зеркале называется мнимым.
[13]
Пользуясь рисунком 31, а или рядом ( 41), легко найти электронную структуру любой молекулы указанного типа. Для этого суммарное число валентных электронов в атомах, составляющих молекулу, нужно расположить последовательно в ряду ( 41), соблюдая принцип Паули и правило Хупда.
Для этого суммарное число валентных электронов в атомах, составляющих молекулу, нужно расположить последовательно в ряду ( 41), соблюдая принцип Паули и правило Хупда.
[14]
Под рисунком понимается изображение предметов от руки, без помощи чертежных инструментов так, как их воспринимает наш глаз. Рисунок представляет собой графический образ натуры.
[15]
Страницы:
1
2
3
4
Принцип действия тепловых двигателей — Все уроки физики 8 класс — конспекты уроков — План урока — Конспект урока — Планы уроков — разработки уроков по физике
Урок 21/63. Принцип действия тепловых двигателей
Цель урока: рассмотреть применение закона сохранения и превращения энергии в тепловых двигателях; объяснить учащимся устройство и принцип работы паровой турбины.
Тип урока: урок изучения нового материала.
План урока
Демонстрации | 8 мин. | 1. Работа газа и пара при расширении. 2. Строение и действие паровой турбины. 3. Фрагменты видеофильма «Паровые турбины» |
Изучение нового материала | 30 мин. | 1. Знакомим с принципом действия тепловых двигателей. 2. Паровая турбина |
Закрепление изученного материала | 7 мин. | 1. Контрольные вопросы. 2. Учимся решать задачи. 3. Поразмысли и ответь |
Изучение нового материала
1. Знакомим с принципом действия тепловых двигателей
Знакомим с принципом действия тепловых двигателей
Внутренней энергией обладают все тела — земля, кирпичи, облака и так далее. Однако чаще всего удалить ее трудно, а порой и невозможно. Наиболее легко на нужды человека может быть использована внутренняя энергия лишь некоторых, образно говоря, «горючих» и «горячих» тел. К ним относятся: нефть, уголь, теплые источники вблизи вулканов и так далее.
Развитие техники зависит от умения использовать громадные запасы внутренней энергии, содержащейся в топливе. Использовать внутреннюю энергию — значит выполнить за счет ее полезную работу, то есть внутреннюю энергию необходимо превратить в механическую.
С тех пор как человечество познало природу тепловой энергии, ученые начали поиск способа преобразования тепловой энергии в механическую.
Над изобретением тепловых машин в XVII–XVIII веках трудились англичане Томас Севери, Джеймс Уатт, Томас Ньюкомен, француз Дени Папен, россиянин Иван Ползунов и многих других ученых.
Принцип работы всех тепловых двигателей очень прост: все они превращают внутреннюю энергию топлива в механическую энергию.
Но как превратить внутреннюю энергию в механическую?
Укрепим небольшую колбу с изогнутой трубкой над спиртівкою, а пар, выходящий из трубки, направим на колесо с лопастями. Ударяя в лопасти колеса, струя пара приводит колесо в движение.
При этом внутренняя энергия топлива частично превращается в механическую энергию колеса. В нашем опыте мы построили простейшую модель теплового двигателя.
· Тепловыми двигателями называют машины, в которых внутренняя энергия топлива частично превращается в механическую энергию.
Расширение рабочего тела — самый важный процесс в работе любого теплового двигателя. С помощью демонстраций нужно показать ученикам, что газ, имеющий избыточное давление по сравнению с окружающей средой, может выполнить работу расширения за счет изменения своей внутренней энергии.
Конечно в тепловом двигателе работу выполняет сила давления нагретого газа (пара) при расширении. Этот газ (или пар) называют рабочим телом теплового двигателя. Нагревают пар за счет сгорания топлива. Таким образом, в тепловом двигателе происходят следующие преобразования энергии:
Нагревают пар за счет сгорания топлива. Таким образом, в тепловом двигателе происходят следующие преобразования энергии:
1) при сгорании топлива его внутренняя энергия превращается во внутреннюю энергию нагретого пара;
2) расширяясь, пар выполняет работу, при этом внутренняя энергия пара частично переходит в механическую энергию.
2. Паровая турбина
Для преобразования тепловой энергии в механическую в тепловых и атомных электростанциях используют паровые турбины.
В основу действия турбины положено вращения колеса с лопастями под давлением водяного пара или газа.
Паровая турбина — тепловой двигатель, в котором внутренняя энергия водяного пара превращается в механическую энергию. Для получения водяного пара служат специальные паровые котлы, в которых за счет сжигания топлива получают водяной пар за поддержания слишком большого давления (до 3·107 Па ) и очень высокой температуры (до 600 °C ).
Выше на рисунке был показан принцип работы паровой турбины. Струи пара, вырывающиеся из сопел, оказывают значительное давление на лопатки и приводят диск турбины в быстрое вращательное движение.
Струи пара, вырывающиеся из сопел, оказывают значительное давление на лопатки и приводят диск турбины в быстрое вращательное движение.
В современных турбинах применяют не один, а несколько дисков, насаженных на общий вал. Пар последовательно проходит через лопатки всех дисков, отдавая каждому из них часть своей энергии.
Постепенно все большее применение приобретают газовые турбины, в которых вместо пара используются продукты сгорания газа.
Вопросы к учащимся в ходе изложения нового материала
1. Приведите примеры превращения внутренней энергии пара в механическую энергию.
2. Какие двигатели называют тепловыми?
3. Какие виды тепловых двигателей вам известны?
4. Что положено в основу действия паровой турбины?
5. Какие преобразования энергии происходят в паровой турбине?
6. Назовите основные элементы паровой турбины.
Закрепление изученного материала
1. Учимся решать задачи
1). Пользуясь рисунком, расскажите, из каких частей состоит паровая турбина и как она работает.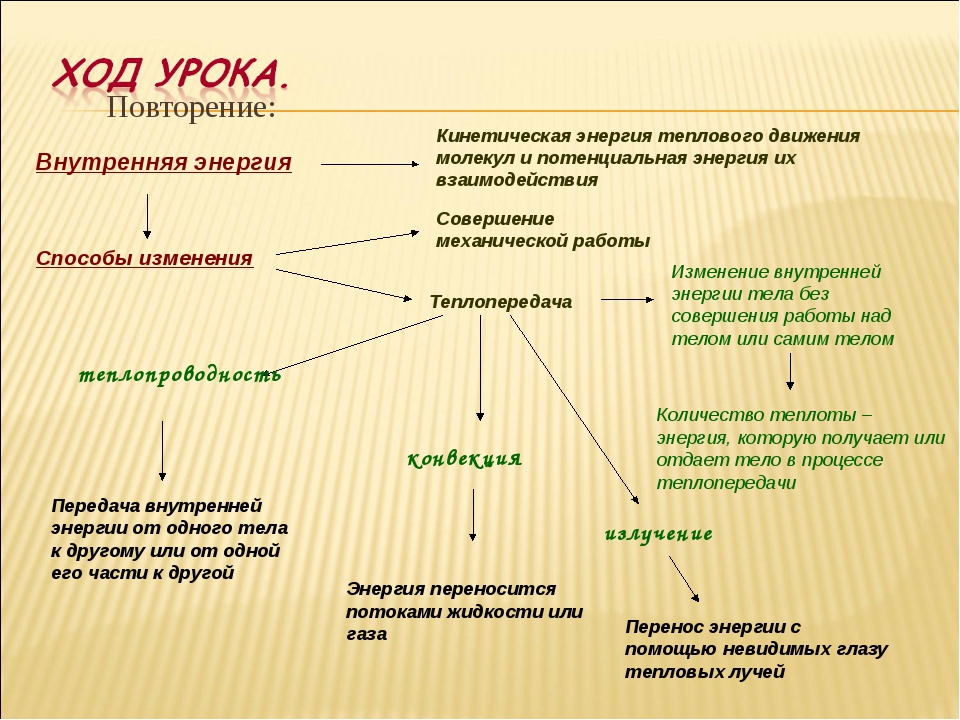
2). Изменяется ли давление пара в соплах паровой турбины? Меняется ли при этом скорость молекул пара?
Решение. Давление пара становится меньше. Скорость молекул увеличивается. Как известно, внутренняя энергия состоит из суммы потенциальной и кинетической энергий молекул. При снижении давления потенциальная энергия молекул уменьшается, она превращается в кинетическую.
2. Поразмысли и ответь
1). Отличается ли температура пара, выходящего из цилиндра паровой машины, от температуры пара, поступающего в этот цилиндр?
2). Какая форма механической энергии пара — потенциальная или кинетическая — используется в паровых турбинах?
3). Относится ли огнестрельное оружие к тепловым двигателям? Обоснуйте свой ответ.
Домашнее задание-1
1. В-1: § 28 (п. 1, 2).
2. Сб-1:
рів1— № 31.1, 31.2, 31.3, 32.9, 32.10.
рів2— № 31.13, 31.18, 32.14, 32.20, 32.21.
рів3— № 31.25, 31.26, 32.26, 32. 27, 32.29.
27, 32.29.
Домашнее задание-2
1. В-2: § 42 (п.1), 43 (п.1).
2. Сб-2:
рів1— № 31.1, 31.2, 31.5, 31.6.
рів2 — № 31.10, 31.11, 31.17.
Источники:
1. Все уроки физики. 8 класс./ Кирик Л. А.— Х.: Вид. группа «Основа», 2008.— 352 с.
2. Сайты: engine-market.ua
Презентация к уроку
Закон сохранения и превращения энергии в механических и тепловых процессах. Способы изменения внутренней энергии тела При натирании трубки с эфиром
Внутренняя энергия тела не является какой-то постоянной величиной. У одного и того же тела она может изменяться. При повышении температуры внутренняя энергия тела увеличивается, так как увеличивается средняя скорость движения молекул. Cледовательно, возрастает кинетическая энергия молекул этого тела. С понижением температуры, наоборот, внутренняя энергия тела уменьшается. Таким образом, внутренняя энергия тела меняется при изменении скорости движения молекул. Попытаемся выяснить, каким способом можно увеличить или уменьшить скорость движения молекул.
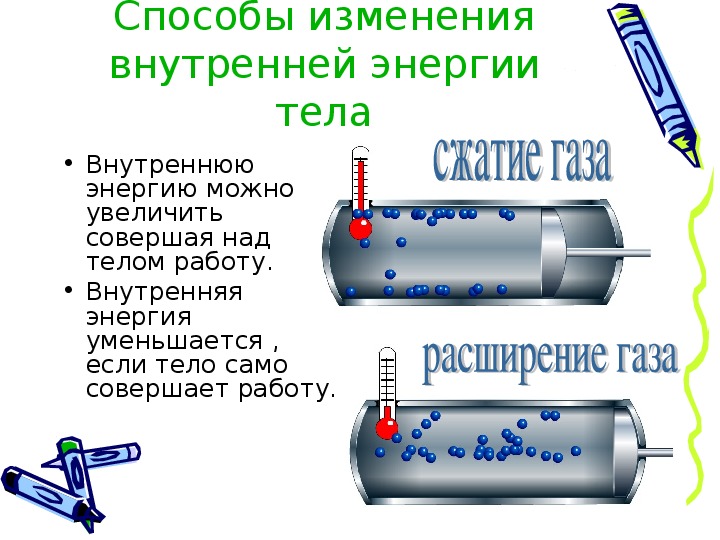
Для этого проделаем следующий опыт. Укрепим тонкостенную латунную трубку на подставке (рис. 4). Нальем в трубку немного эфира и закроем пробкой. Затем трубку обовьем веревкой и начнем быстро двигать ее то в одну сторону, то в другую. Через некоторое время эфир закипит, и пар вытолкнет пробку. Опыт показывает, что внутренняя энергия эфира увеличилась: ведь он нагрелся и даже закипел.Увеличение внутренней энергии произошло в результате совершения работы при натирании трубки веревкой.Нагревание тел происходит также при ударах, разгибании и сгибании, т. е. при деформации. Внутренняя энергия тела во всех приведенных примерах увеличивается. Следовательно, внутреннюю энергию тела можно увеличить, совершая над телом работу.Если же работу совершает само тело, то его внутренняя энергия уменьшается.
Проделаем следующий опыт. В толстостенный стеклянный сосуд, закрытый пробкой, накачаем воздух через специальное отверстие в ней (рис. 5). Через некоторое время пробка выскочит из сосуда. В момент, когда пробка выскакивает из сосуда, образуется туман. Его появление означает, что воздух в сосуде стал холоднее. Находящийся в сосуде сжатый воздух, выталкивая пробку, совершает работу. Эту работу он совершает за счет своей внутренней энергии, которая при этом уменьшается. Судить об уменьшении внутренней энергии можно по охлаждению воздуха в сосуде.Итак, внутреннюю энергию тела можно изменить путем совершения работы.
Его появление означает, что воздух в сосуде стал холоднее. Находящийся в сосуде сжатый воздух, выталкивая пробку, совершает работу. Эту работу он совершает за счет своей внутренней энергии, которая при этом уменьшается. Судить об уменьшении внутренней энергии можно по охлаждению воздуха в сосуде.Итак, внутреннюю энергию тела можно изменить путем совершения работы.
Внутреннюю энергию тела можно изменить и другим способом, без совершения работы.
Например, вода в чайнике, поставленном на плиту, закипает. Воздух и различные предметы в комнате нагреваются от радиатора центрального отопления. Внутренняя энергия в этих случаях увеличивается, так как повышается температура тел. Но при этом работа не совершается. Значит, изменение внутренней энергии может происходить не только в результате совершения работы.
Внутреннюю энергию тел можно изменить путем теплопередачи. Процесс изменения внутренней энергии без совершения работы над телом или самим телом называется теплопередачей.
Теплопередача всегда происходит в определенном направлении: от тел с более высокой температурой к телам с более низкой. Когда температуры тел выравняются, теплопередача прекращается.
Когда температуры тел выравняются, теплопередача прекращается.
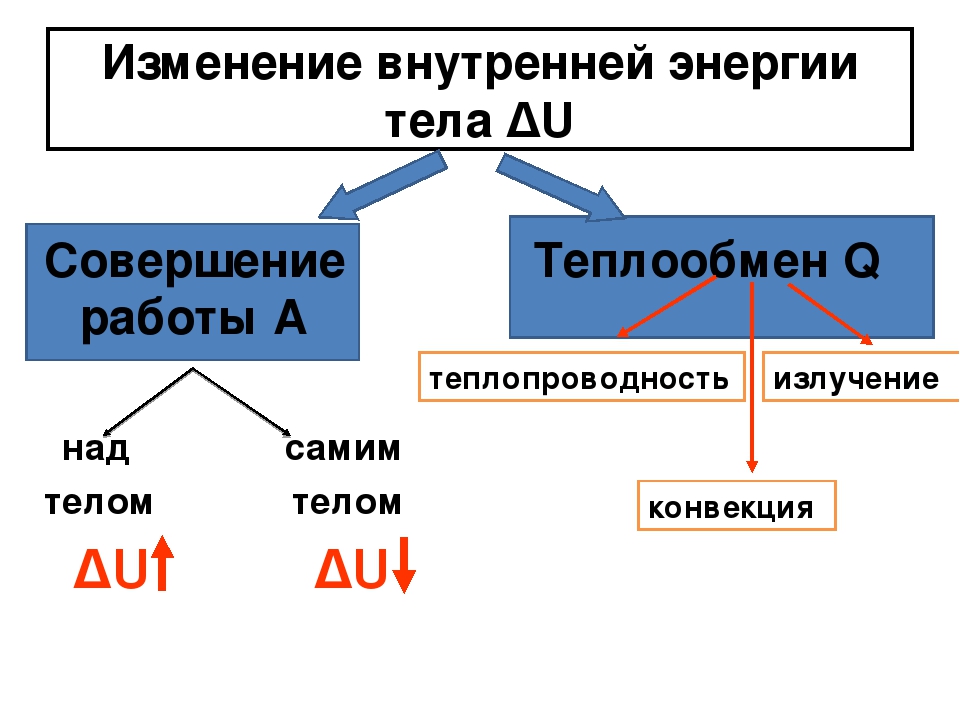
Внутреннюю энергию тела можно изменить двумя способами: совершая механическую работу или теплопередачей.
Теплопередача в свою очередь может осуществляться тремя способами: 1) теплопроводностью; 2) конвекцией; 3) излучением.
Внутренняя энергия тела не является какой-то постоянной величиной. У одного и того же тела она может изменяться.
При повышении температуры внутренняя энергия тела увеличивается
, так как увеличивается средняя скорость движения молекул.
Следовательно, возрастает кинетическая энергия молекул этого тела. С понижением температуры, наоборот, внутренняя энергия тела уменьшается
.
Таким образом, внутренняя энергия тела меняется при изменении скорости движения молекул
.
Попытаемся выяснить, каким способом можно увеличить или уменьшить скорость движения молекул. Для этого проделаем следующий опыт. Укрепим тонкостенную латунную трубку на подставке (рис. 3). Нальём в трубку немного эфира и закроем пробкой. Затем трубку обовьём верёвкой и начнём быстро двигать её то в одну сторону, то в другую. Через некоторое время эфир закипит, и пар вытолкнет пробку. Опыт показывает, что внутренняя энергия эфира увеличилась: ведь он нагрелся и даже закипел.
Затем трубку обовьём верёвкой и начнём быстро двигать её то в одну сторону, то в другую. Через некоторое время эфир закипит, и пар вытолкнет пробку. Опыт показывает, что внутренняя энергия эфира увеличилась: ведь он нагрелся и даже закипел.
Рис. 3. Увеличение внутренней энергии тела при совершении работы над ним
Увеличение внутренней энергии произошло в результате совершения работы при натирании трубки верёвкой.
Нагревание тел происходит также при ударах, разгибании и сгибании, т. е. при деформации. Внутренняя энергия тела во всех приведённых примерах увеличивается.
Следовательно, внутреннюю энергию тела можно увеличить, совершая над телом работу
.
Если же работу совершает само тело, то его внутренняя, энергия уменьшается
.
Проделаем следующий опыт.
В толстостенный стеклянный сосуд, закрытый пробкой, накачаем воздух через специальное отверстие в ней (рис. 4).
Рис. 4. Уменьшение внутренней энергии тела при совершении работы самим телом
Через некоторое время пробка выскочит из сосуда. В момент, когда пробка выскакивает из сосуда, образуется туман. Его появление означает, что воздух в сосуде стал холоднее. Находящийся в сосуде сжатый воздух, выталкивая пробку, совершает работу. Эту работу он совершает за счёт своей внутренней энергии, которая при этом уменьшается. Судить об уменьшении внутренней энергии можно по охлаждению воздуха в сосуде. Итак, внутреннюю энергию тела можно изменить путём совершения работы
.
Внутреннюю энергию тела можно изменить и другим способом, без совершения работы. Например, вода в чайнике, поставленном на плиту, закипает. Воздух и различные предметы в комнате нагреваются от радиатора центрального отопления, крыши домов нагреваются лучами солнца и т. п. Во всех этих случаях повышается температура тел, а значит, увеличивается их внутренняя энергия. Но при этом работа не совершается.
Значит, изменение внутренней энергии может происходить не только в результате совершения работы
.
Как можно объяснить увеличение внутренней энергии в этих случаях?
Рассмотрим следующий пример.
Опустим в стакан с горячей водой металлическую спицу. Кинетическая энергия молекул горячей воды больше кинетической энергии частиц холодного металла. Молекулы горячей воды при взаимодействии с частицами холодного металла будут передавать им часть своей кинетической энергии. В результате этого энергия молекул воды в среднем будет уменьшаться, а энергия частиц металла будет увеличиваться. Температура воды уменьшится, а температура металлической спицы постепенно увеличится. Через некоторое время их температуры выравняются. Этот опыт демонстрирует изменение внутренней энергии тел.
Итак, внутреннюю энергию тел можно изменить путём теплопередачи
.
Процесс изменения внутренней энергии без совершения работы над телом или самим телом называется теплопередачей.
Теплопередача всегда происходит в определённом направлении: от тел с более высокой температурой к телам с более низкой.
Когда температуры тел выравняются, теплопередача прекращается.
Внутреннюю энергию тела можно изменить двумя способами: совершая механическую работу или теплопередачей.
Теплопередача, в свою очередь, может осуществляться: 1) теплопроводностью; 2) конвекцией; 3) излучением
.
Вопросы
- Пользуясь рисунком 3, расскажите, как изменяется внутренняя энергия тела, когда над ним совершают работу.
- Опишите опыт, показывающий, что за счёт внутренней энергии тело может совершить работу.
- Приведите примеры изменения внутренней энергии тела способом теплопередачи.
- Объясните на основе молекулярного строения вещества нагревание спицы, опущенной в горячую воду.
- Что такое теплопередача?
- Какими двумя способами можно изменить внутреннюю энергию тела?
Упражнение 2
- Сила трения совершает над телом работу. Меняется ли при этом внутренняя энергия тела? По каким признакам можно судить об этом?
- При быстром спуске по канату нагреваются руки. Объясните, почему это происходит.
Задание
Положите монету на лист фанеры или деревянную доску. Прижмите монету к доске и двигайте её быстро то в одну, то в другую сторону. Заметьте, сколько раз надо передвинуть монету, чтобы она стала тёплой, горячей. Сделайте вывод о связи между выполненной работой и увеличением внутренней энергии тела.
При падении тела его потенциальная энергия превращается в кинетическую. При падении свинцового шара на свинцовую пластину механическая энергия превращается во
внутреннюю энергию шара и пластины. В двигателе автомобиля и трактора внутренняя энергия топлива превращается в механическую энергию движения.
Механическая и внутренняя энергии могут переходить от одного тела к другому. Кинетическая энергия текущей воды передается, например, колесам турбины, а энергия движущегося ветра — крыльям ветряного двигателя
. Переход внутренней энергии от одного тела к другому мы наблюдали при теплопередаче, когда внутренняя энергия от одного тела (например, нагретой печи) передавалась другому телу (воздуху комнаты).
Сохраняется ли энергия при переходе ее от одного тела к другому или при превращении из одного вида в другой?
Рассмотрев пример и проделав лабораторную работу по смешиванию горячей и холодной воды, мы убедились, что количество теплоты, отданное горячей водой, равнялось количеству теплоты, полученному холодной
водой. Значит, сколько внутренней энергии отдало одно тело, столько же получило и второе, т. е. значение внутренней энергии сохранилось при переходе от одного тела к другому.
Сделанный вывод относится не только к внутренней энергии.
Все другие, более сложные опыты, которые мы будем изучать в дальнейшем, показывают, что при любых превращениях энергии ее значение сохраняется.
Наблюдения и опыты привели к открытию одного из основных законов
физики — закона сохранения и превращения энергии.
Этот закон устанавливает, что энергия не исчезает и не создается. Она только превращается из одного вида в другой или переходит от одного тела к другому.
Энергия не может появиться у тела, если оно не получило ее от другого тела. Энергия текущей воды и ветра получается, как мы знаем, за счет энергии Солнца, потенциальная энергия взлетевшей вверх ракеты — за счет энергии
израсходованного при ее запуске топлива; воздух в комнате нагревается, т. е. его внутренняя энергия: увеличивается за счет энергии, полученной от печи или батареи отопления.
Закон сохранения энергии — один из величайших законов природы. Мы наблюдаем его проявление, как в живой, так и в неживой природе, он всегда учитывается в науке и технике.
Изучая различные механизмы, мы познакомились с «золотым правилом» механики, согласно которому ни один механизм не может дать выигрыша в работе. Это правило является одним из проявлений закона сохранения энергии.
Действительно, если бы мы, поднимая тело при помощи рычага, получили работу больше той, которую совершили, то и потенциальная энергия поднятого тела оказалась бы больше затраченной энергии, а это согласно закону сохранения энергии невозможно.
Закон сохранения энергии опровергает религиозные легенды о создании мира богом. Из него следует, что материальный мир никем не создан, он существует вечно, непрерывно развиваясь.
Вопросы.
1. Приведите примеры превращения механической энергии во внутреннюю и внутренней в механическую. 2. Приведите примеры перехода механической энергии от одного тела к другому. 3. Какой опыт показывает, что при переходе внутренней энергии от одного тела к другому ее значение сохраняется
? 4. В чем состоит закон сохранения энергий? 5. Какое значение имеет закон сохранения энергии в науке и технике?
Упражнения.
- Молот копра при падении ударяет о сваю и забивает ее в землю. Какие превращения и переходы энергии при этом происходят? (Следует учесть, что свая и почва нагреваются при ударе.)
- Какие превращения кинетической энергии автомобиля происходят при его торможении?
- Два одинаковых стальных шарика падают с одинаковой, высоты
. Один падает на стальную плиту и отскакивает вверх, другой попадает в песок и застревает в нем. Какие переходы энергии происходят в каждом случае? - Опишите все превращения и переходы энергии, которые происходят при натирании трубки с эфиром, закрытой пробкой.
Внутренняя энергия тела
не может являться постоянной величиной. Она может изменяться у любого тела. Если повысить температуру тела, то его внутренняя энергия увеличится, т.к. увеличится средняя скорость движения молекул. Таким образом, увеличивается кинетическая энергия молекул тела. И, наоборот, при понижении температуры, внутренняя энергия тела уменьшается.
Можно сделать вывод: внутренняя энергия тела изменяется, если меняется скорость движения молекул.
Попытаемся определить, каким методом можно увеличить или уменьшить скорость передвижения молекул. Рассмотрим следующий опыт. Закрепим на подставке латунную трубку с тонкими стенками. Наполним трубку эфиром и закроем его пробкой. Затем обвяжем его веревкой и начнем интенсивно двигать веревкой в разные стороны. Спустя определенное время, эфир закипит, и сила пара вытолкнет пробку. Опыт демонстрирует, что внутренняя энергия вещества (эфира) возросла: ведь он изменил свою температуру, при этом закипев.
Увеличение внутренней энергии произошло за счет совершения работы при натирании трубкой веревкой.
Как мы знаем, нагревание тел может происходить и при ударах, сгибании или разгибании, говоря проще, при деформации. Во всех приведенных примерах, внутренняя энергия тела возрастает.
Таким образом, внутреннюю энергию тела можно увеличить, совершая над телом работу.
Если же работу выполняет само тело, его внутренняя энергия уменьшается.
Рассмотрим еще один опыт.
В стеклянный сосуд, у которого толстые стенки и он закрыт пробкой, накачаем воздух через специально проделанное отверстие в ней.
Спустя некоторое время пробка вылетит из сосуда. В тот момент, когда пробка вылетает из сосуда, мы сможем увидеть образование тумана. Следовательно, его образование обозначает, что воздух в сосуде стал холодным. Сжатый воздух, который находится в сосуде, при выталкивании пробки наружу совершает определенную работу. Данную работу он выполняет за счет своей внутренней энергии, которая при этом сокращается. Делать выводы об уменьшении внутренней энергии можно исходя из охлаждения воздуха в сосуде. Таким образом, внутреннюю энергию тела можно изменять путем совершения определенной работы.
Однако, внутреннюю энергию возможно изменить и иным способом, без совершения работы. Рассмотрим пример, вода в чайнике, который стоит на плите закипает. Воздух, а также другие предметы в помещении нагреваются от радиатора центрального направления. В подобных случаях, внутренняя энергия увеличивается, т.к. увеличивается температура тел. Но работа при этом не совершается. Значит, делаем вывод, изменение внутренней энергии может произойти не из-за совершения определенной работы.
Рассмотрим еще один пример.
В стакан с водой опустим металлическую спицу. Кинетическая энергия молекул горячей воды, больше кинетической энергии частиц холодного металла. Молекулы горячей воды будут передавать часть своей кинетической энергии частицам холодного металла. Таким образом, энергия молекул воды будет определенным образом уменьшаться, тем временем как энергия частиц металла будет повышаться. Температуры воды понизится, а температуры спицы не спеша, будет увеличиваться. В дальнейшем, разница между температурой спицы и воды исчезнет. За счет этого опыта мы увидели изменение внутренней энергии различных тел. Делаем вывод: внутренняя энергия различных тел изменяется за счет теплопередачи.
Процесс преобразования внутренней энергии без совершения определенной работы над телом или самим телом называется теплопередачей.
Остались вопросы? Не знаете, как сделать домашнее задание?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
6.3: Первый закон термодинамики: внутренняя энергия
Цели обучения
- Для расчета изменений внутренней энергии
Чтобы изучить поток энергии во время химической реакции, нам нужно различать систему, небольшую, четко определенную часть вселенной, которая нас интересует (например, химическая реакция), и ее окружение, остальную часть Вселенная, включая контейнер, в котором происходит реакция (Рисунок \ (\ PageIndex {1} \)).В последующем обсуждении смесь химических веществ, которая вступает в реакцию, всегда является системой, а поток тепла может исходить от системы к окружающей среде или наоборот.
Рисунок \ (\ PageIndex {1} \): Система и ее окружение. Система — это та часть Вселенной, которую мы интересуемся изучением, например химическая реакция внутри колбы. Окружающая среда — это остальная часть Вселенной, включая контейнер, в котором происходит реакция.
В химии важны три типа систем.Открытая система может обмениваться материей и энергией с окружающей средой. Кастрюля с кипящей водой — это открытая система, потому что горелка подает энергию в виде тепла, а вещество в виде водяного пара теряется при кипении воды. Замкнутая система может обмениваться энергией, но не веществом, с окружающей средой. Запечатанный пакет готового обеда, брошенный в кастрюлю с кипящей водой, является закрытой системой, потому что тепловая энергия передается системе от кипящей воды, но не происходит обмен веществ (если пакет не протекает, и в этом случае это больше не закрытая система).Изолированная система не обменивается ни энергией, ни материей с окружающей средой. Между системой и ее окружением всегда происходит обмен энергией, хотя этот процесс может происходить очень медленно. По-настоящему изолированной системы на самом деле не существует. Изолированный термос, содержащий горячий кофе, напоминает изолированную систему, но в конечном итоге кофе остывает, поскольку тепло передается в окружающую среду. Во всех случаях количество тепла, теряемого системой, равно количеству тепла, полученного окружающей средой, и наоборот.То есть полная энергия системы плюс ее окружение постоянна , что должно быть истинным, если энергия сохраняется .
Состояние системы — это полное описание системы в данный момент времени, включая ее температуру и давление, количество вещества, которое она содержит, ее химический состав и физическое состояние вещества. Функция состояния — это свойство системы, величина которого зависит только от текущего состояния системы, а не от ее предыдущей истории.Температура, давление, объем и потенциальная энергия — все это функции состояния. Например, температура духовки не зависит от того, сколько шагов она могла предпринять для достижения этой температуры. Точно так же давление в шине не зависит от того, как часто воздух нагнетается в шину для достижения этого давления, как и конечный объем воздуха в шине. С другой стороны, тепло и работа не являются функциями состояния, поскольку они зависят от пути . Например, автомобиль, стоящий на верхнем уровне гаража, имеет одинаковую потенциальную энергию независимо от того, был ли он поднят краном, установлен там вертолетом, поднят или поднят группой студентов (Рисунок \ (\ PageIndex) {2} \)).Однако объем работы, затраченной на его получение, может сильно различаться в зависимости от выбранного пути. Если бы ученики решили перенести машину на вершину пандуса, они бы выполнили гораздо больше работы, чем если бы они просто подтолкнули машину вверх по пандусу (если, конечно, они не забыли отпустить стояночный тормоз, и в этом случае Затраченные работы существенно увеличились бы!). Однако потенциальная энергия автомобиля одинакова, независимо от того, какой путь они выберут.
Рисунок \ (\ PageIndex {2} \): Высота как пример функции состояния.Изменение высоты между состоянием 1 (внизу гаража) и состоянием 2 (на верхнем уровне гаража) одинаково для обоих путей A и B; это не зависит от того, какой путь идет снизу вверх. Напротив, пройденное расстояние и работа, необходимая для достижения вершины, действительно зависят от выбранного пути. Высота — это функция состояния, но расстояние и работа — это функции состояния , а не .
Направление теплового потока
Реакция порошкообразного алюминия с оксидом железа (III), известная как термитная реакция, генерирует огромное количество тепла — фактически достаточного для плавления стали (рис. \ (\ PageIndex {3} \)).Сбалансированное химическое уравнение реакции выглядит следующим образом:
\ [\ ce {2Al (s) + Fe_2O_3 (s) -> 2Fe (s) + Al_2O_3 (s)} \ label {5.2.1} \]
Рисунок \ (\ PageIndex {3} \): Реакция термитов выделяет столько тепла, что производимое ею железо выходит расплавленным, что делает эту реакцию полезной при сварке. Изображение предоставлено Kingfisher [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)] из Wikimedia Commons.
Мы также можем записать это химическое уравнение как
\ [\ ce {2Al (s) + Fe_2O_3 (s) \ rightarrow 2Fe (s) + Al_2O_3 (s)} + \ text {heat} \ label {5.2.2} \]
, чтобы указать, что тепло является одним из продуктов. Химические уравнения, в которых тепло отображается как реагент или продукт, называются термохимическими уравнениями . В этой реакции система состоит из атомов алюминия, железа и кислорода; все остальное, включая контейнер, составляет окружение. Во время реакции выделяется столько тепла, что железо разжижается. В конце концов, система остывает; железо затвердевает по мере передачи тепла в окружающую среду.Процесс, в котором тепло ( q ) передается от системы к ее окружению, описывается как экзотермический. По соглашению \ (q <0 \) для экзотермической реакции.
Когда вы держите кубик льда в руке, тепло из окружающей среды (включая вашу руку) передается в систему (лед), в результате чего лед тает, а ваша рука становится холодной. Мы можем описать этот процесс следующим термохимическим уравнением:
\ [\ ce {heat + H_2O (s) \ rightarrow H_2O (l)} \ label {5.2.3} \]
Когда тепло передается с на системе из ее окружения, процесс является эндотермическим. По соглашению \ (q> 0 \) для эндотермической реакции.
Тепло технически не является компонентом химических реакций
С технической точки зрения, наличие члена \ (тепло \) в химической реакции, как в Уравнениях \ (\ ref {5.2.2} \) и \ (\ ref {5.2.3} \), является плохой формой, поскольку это не настоящий вид в реакции. Однако это удобный подход для представления экзотермического и эндотермического поведения, который обычно используется химиками.
Первый Закон
Связь между изменением энергии системы и ее окружением задается первым законом термодинамики , который гласит, что энергия Вселенной постоянна. Математически этот закон можно выразить следующим образом:
\ [U_ {univ} = ΔU_ {sys} + ΔU_ {surr} = 0 \ label {5.2.4a} \]
\ [\ Delta {U_ {sys}} = — ΔU_ {surr} \ label {5.2.4b} \]
, где индексы univ, sys и surr относятся к вселенной, системе и окружению соответственно.Таким образом, изменение энергии системы идентично по величине, но противоположно по знаку изменению энергии ее окружения.
Все системы, химические или другие, имеют тенденцию двигаться к состоянию с наименьшей возможной энергией.
Важным фактором, определяющим исход химической реакции, является тенденция всех систем, химических или иных, двигаться к самому низкому возможному общему энергетическому состоянию. Когда кирпич падает с крыши, его потенциальная энергия преобразуется в кинетическую энергию; когда он достигает уровня земли, он достигает состояния с более низкой потенциальной энергией.Любой, кто находится поблизости, заметит, что энергия передается в окружающую среду, поскольку шум от удара отражается, и пыль поднимается, когда кирпич падает на землю. Точно так же, если искра воспламеняет смесь изооктана и кислорода в двигателе внутреннего сгорания, диоксид углерода и вода образуются спонтанно, в то время как потенциальная энергия (в виде относительного положения атомов в молекулах) выделяется в окружающую среду в виде тепла и Работа. Содержание внутренней энергии смеси продуктов \ (CO_2 / H_2O \) меньше, чем у смеси реагентов изооктан / \ (O_2 \).Однако эти два случая различаются по форме передачи энергии в окружающую среду. В случае падающего кирпича энергия передается как работа, выполняемая над всем, что оказывается на пути кирпича; в случае сжигания изооктана энергия может выделяться исключительно в виде тепла (если реакция осуществляется в открытом контейнере) или в виде смеси тепла и работы (если реакция осуществляется в цилиндре двигателя внутреннего сгорания. ). Поскольку тепло и работа — это единственные два способа передачи энергии между системой и ее окружением, любое изменение внутренней энергии системы является суммой переданного тепла (q) и проделанной работы (w):
\ [ΔU_ {sys} = q + w \ label {5.2.5} \]
Хотя \ (q \) и \ (w \) сами по себе не являются функциями состояния, их сумма (\ (ΔU_ {sys} \)) не зависит от пройденного пути и, следовательно, является функцией состояния. Основная задача разработчиков любой машины, преобразующей энергию в работу, состоит в том, чтобы максимально увеличить объем выполняемой работы и минимизировать количество энергии, выделяемой в окружающую среду в виде тепла. Примером может служить сжигание угля для производства электроэнергии. Хотя максимальное количество энергии, доступной в процессе, фиксируется содержанием энергии реагентов и продуктов, доля этой энергии, которая может быть использована для выполнения полезной работы, не фиксирована.
Поскольку мы фокусируемся почти исключительно на изменениях энергии системы, мы не будем использовать «sys» в качестве индекса, если нам не нужно явно различать систему и ее окружение.
Хотя \ (q \) и \ (w \) не являются функциями состояния, их сумма (\ (ΔU_ {sys} \)) не зависит от пройденного пути и, следовательно, является функцией состояния.
Таким образом, согласно первому закону, мы можем определить \ (ΔU \) для любого процесса, если мы можем измерить как \ (q \), так и \ (w \). Теплота \ (q \) может быть рассчитана путем измерения изменения температуры окружающей среды.Работа, \ (w \), может иметь разные формы, но ее тоже можно измерить. Одной из важных форм работы в химии является работа с объемом давления , выполняемая расширяющимся газом. При постоянном внешнем давлении (например, атмосферном)
\ [w = −PΔV \ label {5.2.6} \]
Отрицательный знак, связанный с выполненной работой \ (PV \), указывает на то, что система теряет энергию при увеличении объема. То есть расширяющийся газ действительно воздействует на свое окружение, в то время как газ, который сжимается, воздействует на него окружением.
Пример \ (\ PageIndex {1} \)
Проба идеального газа в цилиндре двигателя сжимается от 400 мл до 50,0 мл во время такта сжатия при постоянном давлении 8,00 атм. В то же время 140 Дж энергии передается от газа окружающей среде в виде тепла. Каково полное изменение внутренней энергии (ΔU) газа в джоулях?
Дано : начальный объем, конечный объем, внешнее давление и количество энергии, переданной в виде тепла
Запрошено: общее изменение внутренней энергии
Стратегия:
- Определите знак \ (q \) для использования в уравнении \ (\ ref {5.2.5} \).
- По формуле \ (\ ref {5.2.6} \) вычислите \ (w \) по заданным значениям. Подставьте это значение в уравнение \ (\ ref {5.2.5} \), чтобы вычислить \ (ΔU \).
Решение
A Из уравнения \ (\ ref {5.2.5} \) мы знаем, что ΔU = q + w. Нам дана величина q (140 Дж), и нам нужно только определить ее знак. Поскольку энергия передается от системы (газа) в окружающую среду, q по соглашению отрицательно.
B Поскольку газ сжимается, мы знаем, что в системе проводятся работы, поэтому \ (w \) должно быть положительным.Из уравнения \ (\ ref {5.2.5} \),
\ [w = -P _ {\ textrm {ext}} \ Delta V = -8,00 \ textrm {atm} (\ textrm {0,0500 L} — \ textrm {0,400 L}) \ left (\ dfrac {\ textrm {101,3 J}} {\ mathrm {L \ cdot atm}} \ right) = 284 \ textrm {J} \]
Таким образом,
\ [\ begin {align *} ΔU & = q + w \\ [4pt] & = −140 \, J + 284 \, J \\ [4pt] & = 144 \, J \ end {align *} \ ]
В этом случае, хотя с газом выполняется работа, увеличивая его внутреннюю энергию, тепло течет из системы в окружающую среду, уменьшая его внутреннюю энергию на 144 Дж.Проделанная работа и переданное тепло могут иметь противоположные знаки.
Упражнение \ (\ PageIndex {1} \)
Образец идеального газа расширяется от начального объема 0,200 л до конечного объема 3,50 л при постоянном внешнем давлении 0,995 атм. При этом 117 Дж тепла передается от окружающей среды к газу. Каково полное изменение внутренней энергии (ΔU) газа в джоулях?
- Ответ
−216 Дж
По соглашению (для химиков) и тепловой поток, и работа имеют отрицательный знак, когда энергия передается от системы к ее окружению и наоборот.
Сводка
В химии небольшая часть Вселенной, которую мы изучаем, — это система , а остальная часть Вселенной — это окружение . Открытые системы могут обмениваться как материей, так и энергией со своим окружением, закрытые системы могут обмениваться энергией, но не веществом со своим окружением, а изолированные системы не могут обмениваться ни материей, ни энергией со своим окружением. Функция состояния — это свойство системы, которое зависит только от ее текущего состояния , а не от ее истории.Реакция или процесс, в котором тепло передается от системы к ее окружению, — это экзотермический . Реакция или процесс, в котором тепло передается системе из окружающей среды, — это эндотермический . Первый закон термодинамики гласит, что энергия Вселенной постоянна. Изменение внутренней энергии системы — это сумма переданного тепла и проделанной работы. Тепловой поток равен изменению внутренней энергии системы плюс проделанная работа PV.Когда объем системы постоянен, изменения ее внутренней энергии можно рассчитать, подставив закон идеального газа в уравнение для ΔU.
Энергия, энтальпия и первый закон термодинамики
Энергия, энтальпия и первый закон
Термодинамика
Химическая термодинамика
Термодинамика определяется как отрасль науки, которая занимается
взаимосвязь между теплом и другими формами энергии, такими как работа.Часто бывает
обобщены в виде трех законов, которые описывают ограничения на то, как различные формы энергии могут
быть взаимопревращенными. Химическая термодинамика — это раздел термодинамики,
относится к химическим реакциям.
Законы термодинамики Первый закон: Энергия сохраняется; его нельзя ни создать, ни уничтожить. Второй закон: В изолированной системе естественные процессы являются спонтанными, когда они приводят к
увеличение беспорядка или энтропии.Третий закон: энтропия идеального кристалла равна нулю, когда температура
кристалл равен абсолютному нулю (0 К).
Было много попыток построить устройство, нарушающее законы
термодинамика. Все потерпели неудачу. Термодинамика — одна из немногих областей науки в мире.
для которых нет исключений.
Система и окружение
Одно из основных предположений термодинамики — это идея, что мы можем
произвольно разделите Вселенную на систему и ее окружение .В
граница между системой и ее окружением может быть такой же реальной, как стенки стакана
который отделяет решение от остальной вселенной (как на рисунке ниже).
Или это может быть так же воображаемо, как набор точек, которые просто разделяют воздух.
над поверхностью металла от остальной атмосферы (как на рисунке ниже).
Внутренняя энергия
Одним из термодинамических свойств системы является ее внутренняя энергия ,
E , который представляет собой сумму кинетической и потенциальной энергий частиц, которые
образуют систему.Внутреннюю энергию системы можно понять, исследуя
самая простая из возможных систем: идеальный газ. Поскольку частицы в идеальном газе не
взаимодействуют, эта система не имеет потенциальной энергии. Внутренняя энергия идеального газа равна
следовательно, сумма кинетических энергий частиц в газе.
Кинетическая молекулярная теория предполагает, что температура газа равна
прямо пропорциональна средней кинетической энергии его частиц, как показано на
рисунок ниже.
Следовательно, внутренняя энергия идеального газа прямо пропорциональна
температура газа.
E sys = 3 / 2 RT
В этом уравнении R — постоянная идеального газа в джоулях на моль.
кельвин (Дж / моль-К), а T — температура в кельвинах.
Внутренняя энергия систем, более сложных, чем идеальный газ
нельзя измерить напрямую. Но внутренняя энергия системы по-прежнему пропорциональна
его температура. Таким образом, мы можем отслеживать изменения внутренней энергии системы с помощью
наблюдая, что происходит с температурой системы. Когда температура
системы увеличивается, мы можем сделать вывод, что внутренняя энергия системы также
выросла.
Предположим пока, что термометр, погруженный в стакан с водой
на плитке показывает 73.5 o C, как показано на рисунке ниже. Это измерение может
описывать только состояние системы в данный момент времени. Он не может сказать нам,
воду нагревали непосредственно от комнатной температуры до 73,5 o C или нагревали из комнаты
температура до 100 o C, а затем дают остыть.
Температура, таким образом, является функцией состояния . Это зависит только от
состояние системы в любой момент времени, а не путь, по которому система
государственный.Поскольку внутренняя энергия системы пропорциональна ее температуре,
внутренняя энергия также является функцией состояния. Любое изменение внутренней энергии системы
равна разнице между его начальным и конечным значениями.
E sys
= E f — E i
Первый закон термодинамики
Первый закон термодинамики можно выразить в следующем уравнении:
который утверждает, что энергия Вселенной постоянна.Энергию можно передавать из
систему в ее окружение или наоборот, но она не может быть создана или уничтожена.
Первый закон термодинамики : E унив
= E sys
+ E surr
= 0
Более полезная форма первого закона описывает, как сохраняется энергия.Это
говорит, что изменение внутренней энергии системы равно сумме тепла
полученные или утраченные системой, а также работа, выполненная системой или в ней.
Первый закон термодинамики : E sys
= q + w
Знаковое соглашение о соотношении внутренней энергии
систему и тепло, получаемое или теряемое системой, можно понять, подумав о
конкретный пример, такой как стакан с водой на горячей плите.Когда плита повернута
при включении система получает тепло от окружающей среды. В результате и температура, и
внутренняя энергия системы увеличивается, а E составляет положительных . Когда конфорка выключена,
вода теряет тепло в окружающую среду при охлаждении до комнатной температуры, а E — отрицательное значение .
Взаимосвязь между внутренней энергией и работой можно понять с помощью
Рассмотрим другой конкретный пример: вольфрамовая нить внутри лампочки.Когда работаешь
осуществляется в этой системе путем пропускания электрического тока через вольфрамовую проволоку,
система нагревается и E , следовательно, положительный . (В конце концов, проволока становится достаточно горячей
светиться.) И наоборот, E
отрицательное значение , когда система работает со своим окружением.
Условные обозначения для тепла, работы и внутренней энергии кратко изложены в
рисунок ниже. Внутренняя энергия и температура системы уменьшаются ( E <0), когда система
либо теряет тепло, либо работает со своим окружением.И наоборот, внутренняя энергия и
повышение температуры ( E
> 0), когда система получает тепло от окружающей среды или когда она работает
в системе.
Система и работа
Система обычно определяется как химическая реакция, а граница
контейнер, в котором протекает реакция.В ходе реакции тепло либо
испускается или поглощается системой. Кроме того, система либо работает на нем.
окружение или какие-то работы, сделанные в его окрестностях. Любое из этих взаимодействий может
влияют на внутреннюю энергию системы.
E sys
= q + w
С химической реакцией обычно связаны два вида работы: электрическая
работа и работа расширения .Химические реакции могут повлиять на их
окружение, пропуская электрический ток по внешнему проводу. Реакции тоже делают
работать с их окружением, когда объем системы увеличивается в течение
реакция Количество работы расширения, совершаемой реакцией, равно произведению
давление, при котором система расширяется, умноженное на изменение объема
система.
w = — PV
Знаковое соглашение для этого уравнения отражает тот факт, что внутреннее
энергия системы уменьшается, когда система действительно работает со своим окружением.
Энтальпия относительно внутренней энергии
Что произойдет, если мы создадим набор условий, при которых работа не будет
что делает система в своем окружении или наоборот, во время химической реакции? Под
В этих условиях тепло, выделяемое или поглощаемое реакцией, будет равно
изменение внутренней энергии системы.
E sys
= q (тогда и только тогда, когда w = 0)
Самый простой способ достичь этих условий — запустить реакцию при
постоянный объем, при котором работа расширения невозможна.При постоянном объеме тепло
выделяется или поглощается реакцией, равно изменению внутренней энергии, которая
происходит во время реакции.
E sys
= q v (при постоянном объеме)
На рисунке ниже показан калориметр, в котором реакции могут проводиться при
постоянный объем. Однако большинство реакций проводят в открытых колбах и лабораторных стаканах. Когда это
сделано, объем системы не постоянный, потому что газ может входить или выходить из
контейнер во время реакции.Однако система находится под постоянным давлением, поскольку
общее давление внутри контейнера всегда равно атмосферному давлению.
Если во время реакции из колбы выходит газ, система
работать над его окрестностями. Если в результате реакции в колбу втягивается газ, окружающая среда
работать над системой. Мы все еще можем измерить количество тепла, выделяемого или поглощаемого во время
реакции, но она больше не равна изменению внутренней энергии
система, потому что часть тепла была преобразована в работу.
E sys
= q + w
Эту проблему можно обойти, введя понятие энтальпии
( H ), который представляет собой сумму внутренней энергии системы плюс произведение
давление газа в системе, умноженное на объем системы.
H sys = E sys + PV
Для простоты индекс «sys» будет опущен.
символ внутренней энергии системы и энтальпии системы из
сейчас на.Поэтому мы будем сокращать соотношение между энтальпией системы
и внутренняя энергия системы следующим образом.
H = E + PV
Изменение энтальпии системы во время химической реакции равно
равна изменению его внутренней энергии плюс изменение произведения давления
раз больше объема системы.
H
= E + ( PV )
Предположим, что реакция протекает в стакане из пенополистирола, как показано на
рисунок ниже.
Поскольку реакция протекает при постоянном давлении, изменение
энтальпия, возникающая во время реакции, равна изменению внутренней энергии
система плюс произведение постоянного давления на изменение объема
система.
H
= E + PV (при постоянном давлении)
Подстановка первого закона термодинамики в это уравнение дает
следующий результат.
H
= ( q p + w ) + PV
Предполагая, что единственная работа, совершаемая реакцией, — это работа расширения
дает уравнение, в котором члены PV сокращаются.
H
= ( q p — PV ) + PV
Таким образом, тепло, выделяемое или поглощаемое во время химической реакции при
постоянное давление равно изменению энтальпии системы.
H
= q p (при постоянном давлении)
Связь между изменением внутренней энергии системы
во время химической реакции и энтальпию реакции можно резюмировать следующим образом.
1. Тепло, выделяемое или поглощаемое при протекании реакции при константе
объем равен изменению внутренней энергии системы.
E sys
= q v
2.Тепло, выделяемое или поглощаемое при протекании реакции при константе
давление равно изменению энтальпии системы.
H sys
= q p
3. Изменение энтальпии системы во время химической реакции равно
равна изменению внутренней энергии плюс изменение произведения давления
количества газа в системе и его объема.
H sys
= E sys
+ ( PV )
4.Разница между E и H для системы небольшая
для реакций, в которых участвуют только жидкости и твердые вещества, потому что практически нет изменений
в объеме системы во время реакции. Разница может быть относительно большой,
однако для реакций, в которых участвуют газы, при изменении количества молей
газ в процессе реакции.
| Практическая задача 1: Какая из следующих (а) кислотно-основное титрование (б) разложение CaCo 3 путем нагревания известняка в тигле с бунзеном. (c) реакция между металлическим цинком и водным раствором ионов Cu 2+ до (d) измерение калорий в 1 унции.подача хлопьев для завтрака путем сжигания хлопьев Нажмите здесь, чтобы проверить свой ответ на «Практика» |
3.3 Первый закон термодинамики — Университетская физика, Том 2
Цели обучения
К концу этого раздела вы сможете:
- Изложите первый закон термодинамики и объясните, как его применять
- Объясните, как теплопередача, выполненная работа и изменение внутренней энергии связаны в любом термодинамическом процессе
Теперь, когда мы увидели, как рассчитать внутреннюю энергию, тепло и работу, проделанную для термодинамической системы, претерпевающей изменения во время некоторого процесса, мы можем увидеть, как эти величины взаимодействуют, чтобы повлиять на величину изменения, которое может произойти.Это взаимодействие задается первым законом термодинамики. Британскому ученому и писателю К. П. Сноу (1905–1980) приписывают шутку о четырех законах термодинамики. Его юмористическое заявление о первом законе термодинамики гласит: «Вы не можете победить», или, другими словами, вы не можете получить от системы больше энергии, чем вложили в нее. В этой главе мы увидим, как внутренняя энергия, тепло и работа играют роль в первом законе термодинамики.
Предположим, что Q представляет собой теплообмен между системой и окружающей средой, а W — это работа, выполняемая системой или над ней.Первый закон гласит, что изменение внутренней энергии этой системы задается Q − WQ − W. Поскольку добавленное тепло увеличивает внутреннюю энергию системы, Q является положительным, когда оно добавляется в систему, и отрицательным, когда оно удаляется из системы.
Когда газ расширяется, он работает, и его внутренняя энергия уменьшается. Таким образом, W является положительным, когда работа выполняется системой, и отрицательным, когда работа выполняется в системе. Это обозначение обозначено в Таблице 3.1. Первый закон термодинамики формулируется следующим образом:
Первый закон термодинамики
С каждым состоянием равновесия системы связана ее внутренняя энергия Eint.Eint. Изменение EintEint для любого перехода между двумя состояниями равновесия составляет
.
ΔEint = Q − WΔEint = Q − W
3,7
, где Q и W представляют собой, соответственно, тепло, передаваемое системой, и работу, выполняемую системой или над ней.
| Условные обозначения термодинамических знаков для тепла и работы | |
|---|---|
| Процесс | Конвенция |
| Тепло добавлено в систему | Q> 0Q> 0 |
| Отвод тепла из системы | Q <0Q <0 |
| Работа, выполненная системой | Вт> 0 Вт> 0 |
| Работа над системой | Вт <0 Вт <0 |
Таблица 3.1
Первый закон — это закон сохранения энергии. Он говорит нам, что система может обмениваться энергией с окружающей средой за счет передачи тепла и выполнения работы. Таким образом, обменная чистая энергия равна изменению полной механической энергии молекул системы (то есть внутренней энергии системы). Таким образом, если система изолирована, ее внутренняя энергия должна оставаться постоянной.
Хотя Q и W оба зависят от термодинамического пути, взятого между двумя состояниями равновесия, их разность Q-WQ-W не зависит.На рисунке 3.7 показана диаграмма pV системы, которая многократно совершает переход от A к B по различным термодинамическим путям. На пути 1 система поглощает тепло Q1Q1 и выполняет работу W1; W1; по пути 2 он поглощает тепло Q2Q2 и выполняет работу W2, W2 и так далее. Значения QiQi и WiWi могут варьироваться от пути к пути, но у нас
Q1 − W1 = Q2 − W2 = ⋯ = Qi − Wi = ⋯, Q1 − W1 = Q2 − W2 = ⋯ = Qi − Wi = ⋯,
или
ΔEint1 = ΔEint2 = ⋯ = ΔEinti = ⋯ .ΔEint1 = ΔEint2 = ⋯ = ΔEinti = ⋯.
То есть изменение внутренней энергии системы между A и B не зависит от пути.В главе о потенциальной энергии и сохранении энергии мы столкнулись с другой величиной, не зависящей от пути: изменением потенциальной энергии между двумя произвольными точками в пространстве. Это изменение представляет собой отрицательный результат работы, проделанной консервативной силой между двумя точками. Потенциальная энергия является функцией пространственных координат, тогда как внутренняя энергия является функцией термодинамических переменных. Например, мы могли бы написать Eint (T, p) Eint (T, p) для внутренней энергии. Такие функции, как внутренняя энергия и потенциальная энергия, известны как функции состояния , , потому что их значения зависят исключительно от состояния системы.
Рис. 3.7. Различные термодинамические пути, используемые системой при переходе из состояния A в состояние B . Для всех переходов изменение внутренней энергии системы ΔEint = Q − WΔEint = Q − W одинаково.
Часто первый закон используется в его дифференциальной форме, то есть
.
dEint = dQ − dW.dEint = dQ − dW.
3,8
Здесь dEintdEint — бесконечно малое изменение внутренней энергии, когда бесконечно малое количество тепла dQ обменивается с системой, и бесконечно малое количество работы dW выполняется (положительный знак) или (отрицательный знак) системой. .
Пример 3.2
Изменения государства и первый закон
Во время термодинамического процесса система переходит из состояния A в состояние B , она получает 400 Дж тепла и выполняет 100 Дж работы. (а) Каково изменение внутренней энергии системы при этом переходе? (b) Если система затем переходит из состояния B обратно в состояние A , каково изменение ее внутренней энергии? (c) Если при движении от A к B по другому пути, W′AB = 400JW′AB = 400J работы выполняется в системе, сколько тепла она поглощает?
Стратегия
Первый закон термодинамики связывает изменение внутренней энергии, работу, выполняемую системой, и тепло, передаваемое системе, в простом уравнении.Внутренняя энергия является функцией состояния и поэтому фиксируется в любой заданной точке независимо от того, как система достигает этого состояния.
Решение
- Из первого закона изменение внутренней энергии системы равно
ΔEintAB = QAB − WAB = 400 Дж − 100 Дж = 300 Дж. ΔEintAB = QAB − WAB = 400 Дж − 100 Дж = 300 Дж. - Рассмотрим замкнутый путь, который проходит через состояния A и B . Внутренняя энергия — это функция состояния, поэтому ΔEintΔEint равно нулю для замкнутого пути. Таким образом
ΔEint = ΔEintAB + ΔEintBA = 0, ΔEint = ΔEintAB + ΔEintBA = 0,
а также
ΔEintAB = −ΔEintBA.ΔEintAB = −ΔEintBA.
Это дает
ΔEintBA = −300J. ΔEintBA = −300J. - Изменение внутренней энергии одинаково для любого пути, поэтому
ΔEintAB = ΔE′intAB = Q′AB – W′AB; 300J = Q′AB — (- 400J), ΔEintAB = ΔE′intAB = Q′AB – W′AB; 300J = Q′AB — (- 400J),
и теплообменник
Q′AB = −100J. Q′AB = −100J.
Отрицательный знак указывает на то, что при этом переходе система теряет тепло.
Значение
Когда в качестве первого закона термодинамики рассматривается замкнутый цикл, изменение внутренней энергии на всем пути равно нулю.Если бы трение играло роль в этом примере, добавление тепла привело бы к меньшему объему работы. В примере 3.3 учитывается, что происходит, если трение играет роль.
Обратите внимание, что в примере 3.2 мы не предполагали, что переходы были квазистатическими. Это потому, что первый закон не подлежит такому ограничению. Он описывает переходы между состояниями равновесия, но не касается промежуточных состояний. Система не должна проходить только через состояния равновесия.Например, если газ в стальном контейнере при четко определенной температуре и давлении заставить взорваться с помощью искры, часть газа может конденсироваться, различные молекулы газа могут объединяться с образованием новых соединений, и могут быть все своего рода турбулентность в контейнере, но в конечном итоге система перейдет в новое состояние равновесия. Эта система явно не находится в равновесии во время своего перехода; однако его поведение по-прежнему определяется первым законом, потому что процесс начинается и заканчивается, когда система находится в состоянии равновесия.
Пример 3.3
Полировка фитинга
Машинист полирует медный фитинг весом 0,50 кг кусочком наждачной бумаги в течение 2,0 мин. Он перемещает ткань по фитингу с постоянной скоростью 1,0 м / с, прикладывая силу 20 Н по касательной к поверхности фитинга. (а) Какая общая работа, проделанная машинистом над фитингом? (б) Каково увеличение внутренней энергии фитинга? Предположим, что изменение внутренней энергии ткани незначительно и между фитингом и окружающей средой не происходит теплообмена.(c) Каково повышение температуры арматуры?
Стратегия
Сила машиниста на расстоянии, которое можно рассчитать, исходя из заданной скорости и времени, — это работа, проделанная над системой. Работа, в свою очередь, увеличивает внутреннюю энергию системы. Эту энергию можно интерпретировать как тепло, которое повышает температуру системы за счет ее теплоемкости. Будьте осторожны со знаком каждого количества.
Решение
- Мощность, создаваемая силой, действующей на объект, или скорость, с которой машинист выполняет работу трения с фитингом, равна F → · v → = −FvF → · v → = −Fv.Таким образом, за истекшее время ΔtΔt (2,0 мин) проделанная работа на фитинге составит
W = −FvΔt = — (20N) (1,0 м / с) (1,2 × 102 с) = — 2,4 × 103 Дж. W = −FvΔt = — (20N) (1,0 м / с) (1,2 × 102 с) = — 2,4 × 103J. - Предполагается, что между фитингом и окружающей средой не происходит теплообмена, поэтому первый закон дает изменение внутренней энергии фитинга:
ΔEint = −W = 2,4 × 103 Дж. ΔEint = −W = 2,4 × 103 Дж. - Так как ΔEintΔEint не зависит от пути, эффект работы 2,4 × 103 Дж 2,4 × 103 Дж такой же, как если бы он подавался при атмосферном давлении путем передачи тепла.Таким образом,
2,4 × 103Дж = mcΔT = (0,50 кг) (3,9 × 102Дж / кг · ° C) ΔT, 2,4 × 103Дж = mcΔT = (0,50 кг) (3,9 × 102Дж / кг · ° C) ΔT,
а повышение температуры фитинга равногде мы использовали значение удельной теплоемкости меди, c = 3,9 × 102Дж / кг · ° Cc = 3,9 × 102Дж / кг · ° C.
Значение
Если бы тепло выделялось, изменение внутренней энергии было бы меньшим и вызвало бы меньшее изменение температуры, чем то, что было рассчитано в задаче.
Проверьте свое понимание 3.2
Приведенные ниже величины представляют четыре разных перехода между одним и тем же начальным и конечным состоянием.Заполнить бланки.
| Q (Дж) | Вт (Дж) | ΔEint (Дж) ΔEint (Дж) |
|---|---|---|
| –80 | –120 | |
| 90 | ||
| 40 | ||
| –40 |
Таблица 3.2
Пример 3.4
Идеальный газ для перехода между двумя государствами
Рассмотрим квазистатическое расширение идеального газа между состояниями равновесия A и C на рисунке 3.6. Если к газу добавляется 515 Дж тепла при его прохождении по пути ABC , сколько тепла требуется для перехода по ADC ? Предположим, что p1 = 2,10 × 105 Н / м2, p2 = 1,05 × 105 Н / м2, V1 = 2,25 × 10–3 м3, p1 = 2,10 × 105 Н / м2, p2 = 1,05 × 105 Н / м2, V1 = 2,25 × 10–3 м3, и V2 = 4,50 × 10–3 м3. V2 = 4,50 × 10–3 м3.
Стратегия
Разница в работе, выполняемой между процессом ABC и процессом ADC , заключается в области, заключенной в ABCD . Поскольку изменение внутренней энергии (функция состояния) одинаково для обоих процессов, разница в работе, таким образом, такая же, как и разница в тепле, передаваемом системе.
Решение
Для пути ABC добавленное тепло составляет QABC = 515JQABC = 515 Дж, а работа, выполняемая газом, представляет собой площадь под путем на диаграмме pV , которая равна
WABC = p1 (V2 − V1) = 473J. WABC = p1 (V2 − V1) = 473J.
Вдоль ADC работа, выполняемая газом, снова находится в области под трактом:
WADC = p2 (V2-V1) = 236J. WADC = p2 (V2-V1) = 236J.
Затем, используя только что описанную стратегию, получаем
QADC-QABC = WADC-WABC, QADC-QABC = WADC-WABC,
, что приводит к
QADC = QABC + WADC − WABC = (515 + 236-473) J = 278J.QADC = QABC + WADC − WABC = (515 + 236-473) J = 278J.
Значение
Расчеты работы в этой задаче упрощены, поскольку работы по AD и BC , а также по AB и DC не выполняются; давление остается постоянным при изменении объема, поэтому проделанная работа просто равна pΔVpΔV. Изотермическая линия также могла быть использована, поскольку мы вывели работу для изотермического процесса как W = nRTlnV2V1W = nRTlnV2V1.
Пример 3.5
Изотермическое расширение идеального газа
Тепло добавляется к 1 моль идеального одноатомного газа, заключенного в цилиндр с подвижным поршнем на одном конце.Газ расширяется квазистатически при постоянной температуре 300 K, пока его объем не увеличится с V до 3 V . а) Как изменяется внутренняя энергия газа? б) Сколько работы выполняет газ? (c) Сколько тепла добавляется к газу?
Стратегия
(а) Поскольку система представляет собой идеальный газ, внутренняя энергия изменяется только при изменении температуры. (б) Тепло, добавленное к системе, поэтому используется исключительно для выполнения работы, которая была рассчитана в работе, тепле и внутренней энергии.(c) Наконец, первый закон термодинамики можно использовать для расчета тепла, добавляемого к газу.
Решение
- В предыдущем разделе мы видели, что внутренняя энергия идеального одноатомного газа является функцией только температуры. Поскольку ΔT = 0ΔT = 0, для этого процесса ΔEint = 0.ΔEint = 0.
- Квазистатическое изотермическое расширение идеального газа было рассмотрено в предыдущем разделе и оказалось
W = nRTlnV2V1 = nRTln3VV = (1,00 моль) (8,314 Дж / К · моль) (300 K) (ln3) = 2,74 × 103 Дж. W = nRTlnV2V1 = nRTln3VV = (1.00 моль) (8,314 Дж / К · моль) (300 К) (ln3) = 2,74 × 103 Дж. - Используя результаты частей (a) и (b), мы можем использовать первый закон для определения добавленного тепла:
ΔEint = Q − W = 0, ΔEint = Q − W = 0,
что приводит к
Q = W = 2,74 × 103 Дж. Q = W = 2,74 × 103 Дж.
Значение
Изотермический процесс не имеет изменения внутренней энергии. Исходя из этого, первый закон термодинамики сводится к Q = WQ = W.
Проверьте свое понимание 3.3
Почему нужно было указать, что процесс из Примера 3.5 квазистатический?
Пример 3.6
Испарение воды
Когда 1,00 г воды при 100 ° C и 100 ° C переходит из жидкой фазы в газовую при атмосферном давлении, ее изменение в объеме составляет 1,67 × 10–3 м3. 1,67 × 10–3 м3. а) Сколько тепла нужно добавить, чтобы вода испарилась? б) Сколько работы совершает вода против атмосферы при ее расширении? в) Как меняется внутренняя энергия воды?
Стратегия
Сначала мы можем выяснить, сколько тепла необходимо за счет скрытой теплоты испарения воды.По изменению объема мы можем рассчитать проделанную работу по формуле W = pΔVW = pΔV, потому что давление постоянно. Затем первый закон термодинамики дает нам изменение внутренней энергии.
Решение
- Если LvLv представляет скрытую теплоту парообразования, теплота, необходимая для испарения воды, равна
Q = mLv = (1,00 г) (2,26 × 103 Дж / г) = 2,26 × 103 Дж. Q = mLv = (1,00 г) (2,26 × 103 Дж / г) = 2,26 × 103 Дж. - Поскольку давление в системе постоянное и составляет 1,00 атм = 1,01 × 105 Н / м 21,00 атм = 1,01 × 105 Н / м2, работа, выполняемая водой при ее испарении, равна
W = pΔV = (1.01 × 105 Н / м2) (1,67 × 10–3 м3) = 169 Дж. W = pΔV = (1,01 × 105 Н / м2) (1,67 × 10–3 м3) = 169 Дж. - Из первого закона тепловая энергия воды при испарении изменяется на
ΔEint = Q − W = 2.26 × 103J − 169J = 2.09 × 103J. ΔEint = Q − W = 2.26 × 103J − 169J = 2.09 × 103J.
Значение
Отметим, что в части (c) мы видим изменение внутренней энергии, но при этом нет изменения температуры. Идеальные газы, не претерпевающие фазовых переходов, имеют внутреннюю энергию, пропорциональную температуре. Внутренняя энергия в целом — это сумма всей энергии в системе.
Проверьте свое понимание 3.4
Когда 1,00 г аммиака кипит при атмосферном давлении и -33,0 ° C, -33,0 ° C, его объем изменяется от 1,47 до 1130 см31130 см3. Его теплота испарения при этом давлении составляет 1,37 × 106 Дж / кг. 1,37 × 106 Дж / кг. Как изменяется внутренняя энергия аммиака при его испарении?
3.2 Работа, тепло и внутренняя энергия — University Physics Volume 2
Учебные цели
К концу этого раздела вы сможете:
- Опишите работу, выполняемую системой, теплопередачу между объектами и изменение внутренней энергии системы
- Расчет работы, теплопередачи и изменения внутренней энергии в простом процессе
Мы обсуждали концепции работы и энергии ранее в механике.Примеры и связанные с ними вопросы теплопередачи между различными объектами также обсуждались в предыдущих главах. Здесь мы хотим расширить эти концепции до термодинамической системы и окружающей ее среды. В частности, мы подробно остановились на концепциях теплопередачи и теплопередачи в предыдущих двух главах. Здесь мы хотим понять, как работа выполняется термодинамической системой или с ней; как тепло передается между системой и окружающей средой; и как общая энергия системы изменяется под влиянием проделанной работы и теплопередачи.
Работа, выполняемая системой
Сила, созданная из любого источника, может выполнять работу, перемещая объект через смещение. Тогда как же работает термодинамическая система? На рис. 3.4 показан газ, заключенный в цилиндр с подвижным поршнем на одном конце. Если газ расширяется относительно поршня, он передает силу на расстояние и действует на поршень. Если поршень сжимает газ при движении внутрь, работа также выполняется — в данном случае с газом. Работу, связанную с такими изменениями объема, можно определить следующим образом: Пусть давление газа на торце поршня равно p .Тогда сила, действующая на поршень за счет газа, составит pA , где A — площадь торца. Когда поршень выталкивается наружу на бесконечно малое расстояние dx , величина работы, совершаемой газом, составляет
.
Поскольку изменение объема газа dV = Adx, dV = Adx, это становится
Для конечного изменения объема от V1 кV2, V1toV2, мы можем проинтегрировать это уравнение от V1toV2V1toV2, чтобы найти чистую работу:
W = ∫V1V2pdV.W = ∫V1V2pdV.
3,4
Рисунок 3.4 Работа, совершаемая ограниченным газом при перемещении поршня на расстояние dx , определяется как dW = Fdx = pdV.dW = Fdx = pdV.
Этот интеграл имеет смысл только для квазистатического процесса, что означает процесс, который происходит бесконечно малыми шагами, поддерживая систему в тепловом равновесии. (Мы рассмотрим эту идею более подробно позже в этой главе.) Только тогда существует четко определенная математическая связь (уравнение состояния) между давлением и объемом. Это соотношение может быть отображено на графике pV зависимости давления от объема, где кривая представляет собой изменение состояния.Мы можем аппроксимировать такой процесс как процесс, который происходит медленно, через серию состояний равновесия. Интеграл графически интерпретируется как площадь под кривой pV (заштрихованная область на рис. 3.5). Работа, совершаемая газом, положительна для расширения и отрицательна для сжатия.
Рис. 3.5. Когда газ медленно расширяется от V1 до V2, от V1 до V2, работа, выполняемая системой, представлена заштрихованной областью под кривой pV .
Рассмотрим два процесса с участием идеального газа, которые представлены путями AC и ABC на рисунке 3.6. Первый процесс — это изотермическое расширение, при котором объем газа меняет свой объем с V1 на V2V1 на V2. Этот изотермический процесс представлен кривой между точками A и C . Газ поддерживается при постоянной температуре T , поддерживая его в тепловом равновесии с резервуаром тепла при этой температуре. Из уравнения 3.4 и закона идеального газа,
W = ∫V1V2pdV = ∫V1V2 (nRTV) dV.W = ∫V1V2pdV = ∫V1V2 (nRTV) dV.
Рисунок 3.6. Пути ABC , AC и ADC представляют три различных квазистатических перехода между состояниями равновесия A и C .
Расширение изотермическое, поэтому T остается постоянным на протяжении всего процесса. Поскольку n и R также постоянны, единственная переменная в подынтегральном выражении — V , поэтому работа, совершаемая идеальным газом в изотермическом процессе, составляет
.
W = nRT∫V1V2dVV = nRTlnV2V1.W = nRT∫V1V2dVV = nRTlnV2V1.
Обратите внимание, что если V2> V1V2> V1 (расширение), W положителен, как и ожидалось.
Прямые линии от A до B и затем от B до C представляют другой процесс.Здесь газ при давлении p1p1 сначала расширяется изобарически (постоянное давление) и квазистатически от V1 доV2V1toV2, после чего он охлаждается квазистатически при постоянном объеме V2V2, пока его давление не упадет до p2p2. От A до B давление постоянно на уровне p , поэтому работа на этой части пути составляет
.
W = ∫V1V2pdV = p1∫V1V2dV = p1 (V2 − V1). W = ∫V1V2pdV = p1∫V1V2dV = p1 (V2 − V1).
Объем с B до C не изменился, и поэтому работы не выполнялись.Тогда сеть по пути ABC равна
.
W = p1 (V2 − V1) + 0 = p1 (V2 − V1). W = p1 (V2 − V1) + 0 = p1 (V2 − V1).
Сравнение выражений для работы, совершаемой газом в двух процессах на рис. 3.6, показывает, что они совершенно разные. Это иллюстрирует очень важное свойство термодинамической работы: путь зависит от . Мы не можем определить работу, совершаемую системой при переходе из одного состояния равновесия в другое, если не знаем ее термодинамический путь. Разные ценности работы связаны с разными путями.
Пример 3.1
Изотермическое расширение газа Ван-дер-Ваальса
Исследования газа Ван-дер-Ваальса требуют корректировки закона идеального газа, который учитывает, что молекулы газа имеют определенный объем (см. Кинетическую теорию газов). Один моль газа Ван-дер-Ваальса имеет уравнение состояния
(p + aV2) (V − b) = RT, (p + aV2) (V − b) = RT,
, где a и b — два параметра для определенного газа. Предположим, что газ расширяется изотермически и квазистатически из объема V1V1 в объем V2.V2. Сколько работы совершает газ во время расширения?
Стратегия
Поскольку уравнение состояния задано, мы можем использовать уравнение 3.4, чтобы выразить давление через V и T . Кроме того, температура T является постоянной в изотермических условиях, поэтому V становится единственной изменяющейся переменной под интегралом.
Решение
Чтобы вычислить этот интеграл, мы должны выразить p как функцию от V .Из приведенного уравнения состояния давление газа равно
p = RTV-b-aV2.p = RTV-b-aV2.
Поскольку T постоянна в изотермических условиях, работа, совершаемая 1 моль газа Ван-дер-Ваальса при расширении из объема V1V1 в объем V2V2, таким образом, составляет
W = ∫V1V2 (RTV − b − aV2) dV = | RTln (V − b) + aV | V1V2 = RTln (V2 − bV1 − b) + a (1V2−1V1). W = ∫V1V2 (RTV − b− aV2) dV = | RTln (V − b) + aV | V1V2 = RTln (V2 − bV1 − b) + a (1V2−1V1).
Значение
С учетом объема молекул выражение для работы намного сложнее.Если, однако, мы установим a = 0a = 0 и b = 0, b = 0, мы увидим, что выражение для работы точно соответствует работе, совершаемой изотермическим процессом для одного моля идеального газа.
Проверьте свое понимание 3.1
Сколько работы совершает газ, как показано на рисунке 3.6, когда он квазистатически расширяется по пути ADC ?
Внутренняя энергия
Внутренняя энергия EintEint термодинамической системы по определению является суммой механических энергий всех молекул или объектов в системе.Если кинетическая и потенциальная энергии молекулы и равны KiKi и Ui, Ui, соответственно, то внутренняя энергия системы является средним значением полной механической энергии всех сущностей:
Eint = ∑i (K − i + U − i), Eint = ∑i (K − i + U − i),
3,5
, где суммирование ведется по всем молекулам системы, а столбцы над K и U указывают средние значения. Кинетическая энергия KiKi отдельной молекулы включает вклады из-за ее вращения и вибрации, а также ее поступательную энергию mivi2 / 2, mivi2 / 2, где vivi — скорость молекулы, измеренная относительно центра масс системы.Потенциальная энергия UiUi связана только с взаимодействиями между молекулой и и другими молекулами системы. Фактически, ни расположение системы, ни ее движение не имеют никакого значения с точки зрения внутренней энергии. На внутреннюю энергию системы не влияет перемещение ее из подвала на крышу 100-этажного дома или установка на движущийся поезд.
В идеальном одноатомном газе каждая молекула представляет собой отдельный атом. Следовательно, нет вращательной или колебательной кинетической энергии и Ki = mivi2 / 2Ki = mivi2 / 2.Кроме того, нет межатомных взаимодействий (несмотря на столкновения), поэтому Ui = constant Ui = constant, которую мы устанавливаем равной нулю. Следовательно, внутренняя энергия обусловлена только поступательной кинетической энергией и
Eint = ∑iK − i = ∑i12mivi2¯. Eint = ∑iK − i = ∑i12mivi2¯.
Из обсуждения в предыдущей главе мы знаем, что средняя кинетическая энергия молекулы в идеальном одноатомном газе равна
.
12mivi2− = 32kBT, 12mivi2− = 32kBT,
, где T — температура газа по Кельвину.Следовательно, средняя механическая энергия на молекулу идеального одноатомного газа также составляет 3kBT / 2,3kBT / 2, то есть
Ki + Ui¯ = Ki− = 32kBT.Ki + Ui¯ = Ki− = 32kBT.
Внутренняя энергия — это просто количество молекул, умноженное на среднюю механическую энергию на молекулу. Таким образом, для n моль идеального одноатомного газа
Eint = nNA (32kBT) = 32nRT.Eint = nNA (32kBT) = 32nRT.
3,6
Обратите внимание, что внутренняя энергия данного количества идеального одноатомного газа зависит только от температуры и полностью не зависит от давления и объема газа.Для других систем внутреннюю энергию нельзя выразить так просто. Однако увеличение внутренней энергии часто может быть связано с повышением температуры.
Из нулевого закона термодинамики мы знаем, что, когда две системы находятся в тепловом контакте, они в конечном итоге достигают теплового равновесия, при котором они имеют одинаковую температуру. В качестве примера предположим, что мы смешиваем два одноатомных идеальных газа. Теперь энергия, приходящаяся на молекулу идеального одноатомного газа, пропорциональна его температуре.Таким образом, когда два газа смешиваются, молекулы более горячего газа должны терять энергию, а молекулы более холодного газа должны получать энергию. Это продолжается до тех пор, пока не будет достигнуто тепловое равновесие, после чего температура и, следовательно, средняя кинетическая энергия поступательного движения, приходящаяся на одну молекулу, одинаковы для обоих газов. Подход к равновесию для реальных систем несколько сложнее, чем для идеального одноатомного газа. Тем не менее, мы все еще можем сказать, что между системами происходит обмен энергией до тех пор, пока их температуры не станут одинаковыми.
Работа, тепло и внутренняя энергия
Внутренняя энергия EintEint термодинамической системы по определению является суммой механических энергий всех молекул или объектов в системе. Если кинетическая и потенциальная энергии молекулы и равны KiKi и Ui, Ui, соответственно, то внутренняя энергия системы является средним значением полной механической энергии всех сущностей:
Eint = ∑i (K − i + U − i), Eint = ∑i (K − i + U − i),
, где суммирование ведется по всем молекулам системы, а полосы над K и U указывают средние значения.Кинетическая энергия KiKi отдельной молекулы включает вклады из-за ее вращения и вибрации, а также ее поступательную энергию mivi2 / 2, mivi2 / 2, где vivi — скорость молекулы, измеренная относительно центра масс системы. Потенциальная энергия UiUi связана только с взаимодействиями между молекулой i и другими молекулами системы. Фактически, ни расположение системы, ни ее движение не имеют никакого значения с точки зрения внутренней энергии.На внутреннюю энергию системы не влияет перемещение ее из подвала на крышу 100-этажного дома или установка на движущийся поезд.
В идеальном одноатомном газе каждая молекула представляет собой отдельный атом. Следовательно, нет вращательной или колебательной кинетической энергии и Ki = mivi2 / 2Ki = mivi2 / 2. Кроме того, нет межатомных взаимодействий (несмотря на столкновения), поэтому Ui = constant Ui = constant, которую мы устанавливаем равной нулю. Следовательно, внутренняя энергия обусловлена только поступательной кинетической энергией и
Eint = ∑iK − i = ∑i12mivi2¯.Eint = ∑iK − i = ∑i12mivi2¯.
Из обсуждения в предыдущей главе мы знаем, что средняя кинетическая энергия молекулы в идеальном одноатомном газе составляет
12mivi2− = 32kBT, 12mivi2− = 32kBT,
, где T — температура газа по Кельвину. Следовательно, средняя механическая энергия на молекулу идеального одноатомного газа также составляет 3kBT / 2,3kBT / 2, то есть
Ki + Ui¯ = Ki− = 32kBT.Ki + Ui¯ = Ki− = 32kBT.
Внутренняя энергия — это просто количество молекул, умноженное на среднюю механическую энергию на молекулу.Таким образом, для n моль идеального одноатомного газа,
Eint = nNA (32kBT) = 32nRT.Eint = nNA (32kBT) = 32nRT.
Обратите внимание, что внутренняя энергия данного количества идеального одноатомного газа зависит только от температуры и полностью не зависит от давления и объема газа. Для других систем внутреннюю энергию нельзя выразить так просто. Однако увеличение внутренней энергии часто может быть связано с повышением температуры.
Из нулевого закона термодинамики мы знаем, что, когда две системы находятся в тепловом контакте, они в конечном итоге достигают теплового равновесия, в этот момент они имеют одинаковую температуру.В качестве примера предположим, что мы смешиваем два одноатомных идеальных газа. Теперь энергия, приходящаяся на молекулу идеального одноатомного газа, пропорциональна его температуре. Таким образом, когда два газа смешиваются, молекулы более горячего газа должны терять энергию, а молекулы более холодного газа должны получать энергию. Это продолжается до тех пор, пока не будет достигнуто тепловое равновесие, после чего температура и, следовательно, средняя кинетическая энергия поступательного движения, приходящаяся на одну молекулу, одинаковы для обоих газов. Подход к равновесию для реальных систем несколько сложнее, чем для идеального одноатомного газа.Тем не менее, мы все еще можем сказать, что между системами происходит обмен энергией до тех пор, пока их температуры не станут одинаковыми.
Внутренняя энергия (физика): определение, формула и способы расчета
Обновлено 28 декабря 2020 г.
Ли Джонсон
Когда вы думаете о слове «энергия», вы, вероятно, думаете о чем-то вроде кинетической энергии движущийся объект или, возможно, потенциальная энергия, которой что-то может обладать из-за гравитации.
Однако в микроскопическом масштабе внутренняя энергия объекта более важна, чем эти макроскопические формы энергии.Эта энергия в конечном итоге является результатом движения молекул, и ее, как правило, легче понять и вычислить, если вы рассмотрите упрощенную замкнутую систему, такую как идеальный газ.
Что такое внутренняя энергия системы?
Внутренняя энергия — это полная энергия замкнутой системы молекул или сумма молекулярной кинетической энергии и потенциальной энергии в веществе. Макроскопическая кинетическая и потенциальная энергии не имеют значения для внутренней энергии — если вы переместите всю замкнутую систему или измените ее гравитационную потенциальную энергию, внутренняя энергия останется прежней.
Как и следовало ожидать от микроскопической системы, вычисление кинетической энергии множества молекул и их потенциальной энергии было бы сложной — если не практически невозможной — задачей. Таким образом, на практике вычисления внутренней энергии включают в себя средние значения, а не кропотливый процесс ее прямого вычисления.
Одним из особенно полезных упрощений является рассмотрение газа как «идеального газа», который, как предполагается, не имеет межмолекулярных сил и, следовательно, по существу не имеет потенциальной энергии.Это значительно упрощает процесс расчета внутренней энергии системы, и он не так уж и точен для многих газов.
Внутреннюю энергию иногда называют тепловой энергией, потому что температура, по сути, является мерой внутренней энергии системы — она определяется как средняя кинетическая энергия молекул в системе.
Уравнение внутренней энергии
Уравнение внутренней энергии — это функция состояния, что означает, что его значение в данный момент времени зависит от состояния системы, а не от того, как она туда попала.Для внутренней энергии уравнение зависит от количества молей (или молекул) в замкнутой системе и ее температуры в градусах Кельвина.
Внутренняя энергия идеального газа имеет одно из простейших уравнений:
U = \ frac {3} {2} nRT
Где n — количество молей, R — универсальная газовая постоянная и T — температура системы. Газовая постоянная имеет значение R = 8,3145 Дж моль — 1 K — 1 , или около 8.3 джоуля на моль на Кельвин. Это дает значение U в джоулях, как и следовало ожидать от значения энергии, и это имеет смысл, поскольку более высокие температуры и большее количество молей вещества приводят к более высокой внутренней энергии.
Первый закон термодинамики
Первый закон термодинамики — одно из самых полезных уравнений при работе с внутренней энергией, и в нем говорится, что изменение внутренней энергии системы равно количеству тепла, добавляемого к системе, за вычетом работа, выполненная системой (или плюс работа, выполненная в системе ).В символах это:
∆U = Q-W
С этим уравнением действительно просто работать, если вы знаете (или можете рассчитать) теплопередачу и проделанную работу. Однако многие ситуации еще больше упрощают ситуацию. В изотермическом процессе температура постоянна, а поскольку внутренняя энергия является функцией состояния, вы знаете, что изменение внутренней энергии равно нулю. В адиабатическом процессе отсутствует теплопередача между системой и ее окружением, поэтому значение Q равно 0, и уравнение принимает следующий вид:
∆U = -W
Изобарический процесс — это процесс, который происходит при постоянном давлении, а это означает, что проделанная работа равна давлению, умноженному на изменение объема: W = P ∆ V .Изохорные процессы происходят при постоянном объеме, и в этих случаях Вт = 0. Это оставляет изменение внутренней энергии равным теплу, добавленному в систему:
∆U = Q
Даже если вы можете ‘ • упростить задачу одним из этих способов, поскольку для многих процессов работа не выполняется или ее можно легко вычислить, поэтому определение количества полученного или потерянного тепла — это главное, что вам нужно сделать.
Перейти к основному содержанию
Поиск
Поиск
- Где угодно
Быстрый поиск где угодно
Поиск Поиск
Расширенный поиск
Войти | регистр
Пропустить основную навигацию Закрыть меню ящика Открыть меню ящика Дом
- Подписка / продление
- Учреждения
- Индивидуальные подписки
- Индивидуальное продление
- Библиотекари 9136
- Пакет для Чикаго
- Полный охват и охват содержимого
- Файлы KBART и RSS-каналы
- Разрешения и перепечатки
- Инициатива Чикаго для развивающихся стран
- Даты отправки и претензии
- Часто задаваемые вопросы библиотекарей
- , заказы
- и платежи
- О нас
- Публикация у нас
- Новые журналы
- tners
- Подпишитесь на уведомления eTOC
- Пресс-релизы
- СМИ
- Книги издательства Чикагского университета
- Распределительный центр в Чикаго
- Чикагский университет
- Положения и условия
- Заявление о публикационной этике
- Уведомление о конфиденциальности
- Доступность Chicago Journals
- Доступность университета
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
- Свяжитесь с нами
- Медиа и рекламные запросы
- Открытый доступ в Чикаго
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
.
