область определения, нули функции, четность функции и все остальные.

Функция — это одно из важнейших математических понятий.
Функция — зависимость переменной у от переменной x, если каждому значению
х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом.
Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции.
Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции.

Графиком функции называют множество всех точек
координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по
оси ординат откладываются значения переменной y.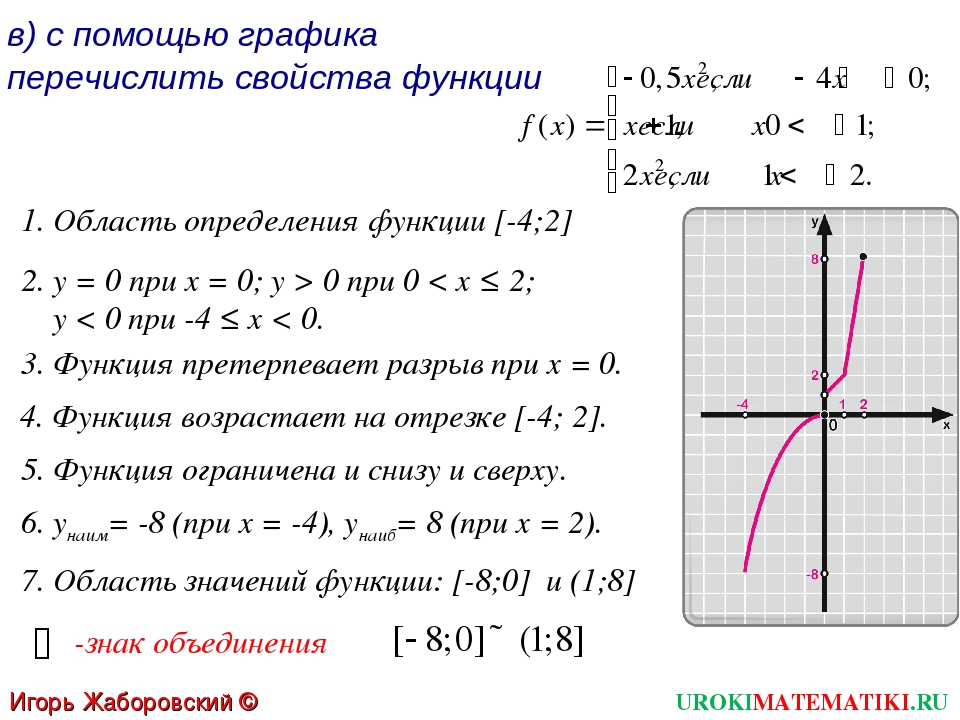 Для
построения графика функции необходимо знать свойства функции.
Основные свойства функции будут рассмотрены далее!

Для построения графика функции советуем использовать нашу программу —
Построение графиков функций онлайн.
Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем
форуме. Также на форуме Вам помогут
решить задачи по математике, химии,
геометрии,
теории вероятности
и многим другим предметам!

Основные свойства функций.

1) Область определения функции и область значений функции.

Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при
которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.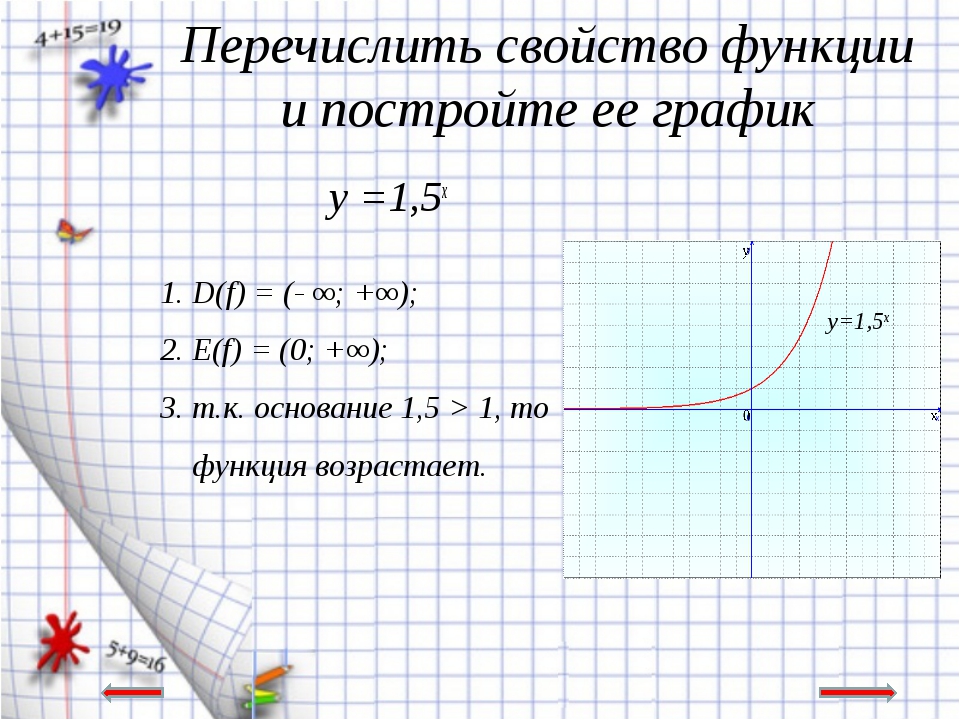

2) Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции.

Промежутки знакопостоянства функции – такие множества значений аргумента, на которых
значения функции только положительны или только отрицательны.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) — функция, у которой большему
значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) — функция, у которой большему значению
аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция — функция, у которой область определения симметрична относительно
начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен
относительно оси ординат.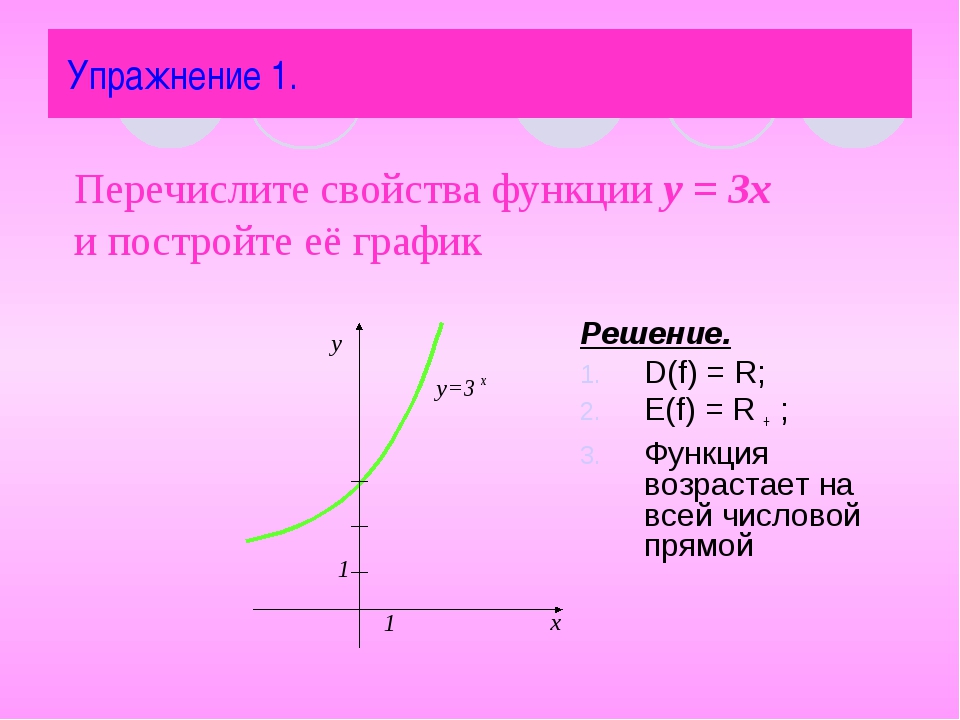

Нечетная функция — функция, у которой область определения симметрична относительно начала
координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен
относительно начала координат.

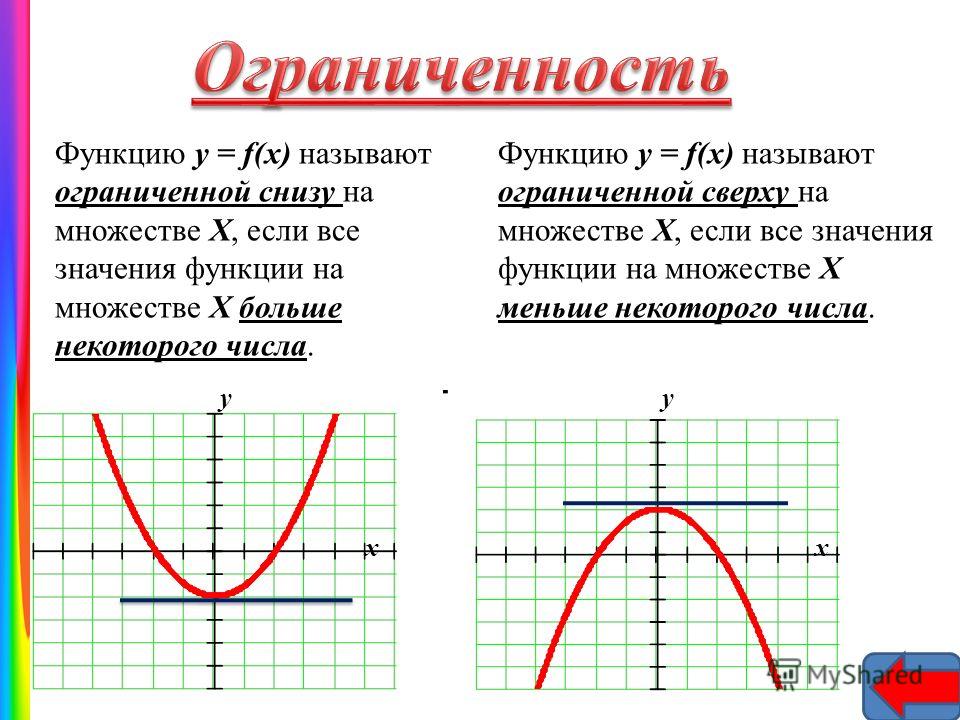
6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число
M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.

7) Периодическость функции.

Функция f(x) — периодическая, если существует такое отличное от нуля число T,
что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции.
Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по
свойствам функции сможете построить график функции.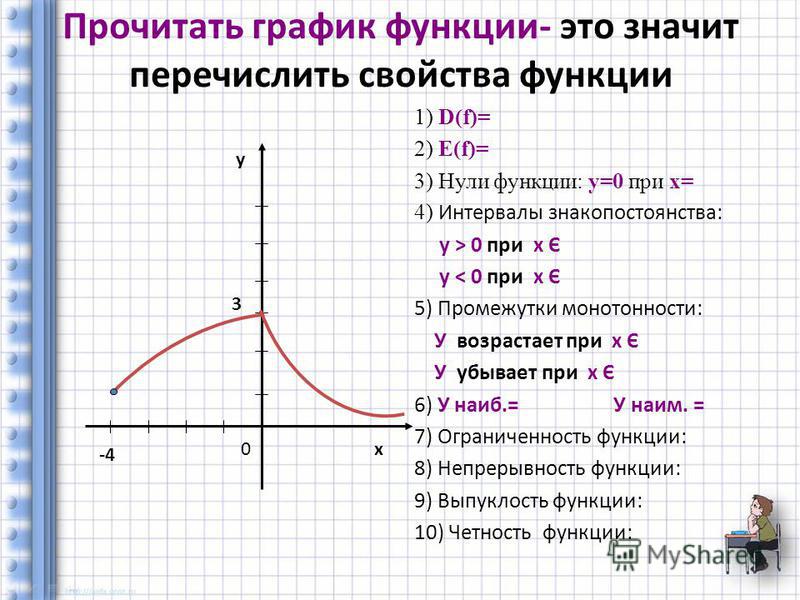 Также посмотрите материал про
таблицу истинности,
таблицу умножения,
таблицу Менделеева,
таблицу производных и
таблицу интегралов.

Слишком сложно?

Свойства функции не по зубам? Тебе ответит эксперт через 10 минут!

Свойства функций синуса, косинуса, тангенса и котангенса и их графики

Свойства функции y=sin(x) и ее график. 

График функции (синусоида)

Свойства функции

1.  Область определения: R (x — любое действительное число) т.е. 
2. Область значений:

3. Функция нечетная:

   (график симметричен относительно начала координат).

4. Функция периодическая с периодом 
5. Точки пересечения с осями координат:  
6. Промежутки знакопостоянства: 
7. Промежутки возрастания и убывания:   

Объяснение и обоснование

Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6)   промежутки знакопостоянства; 7) промежутки возрастания и убывания; 8) наибольшее и наименьшее значения функции.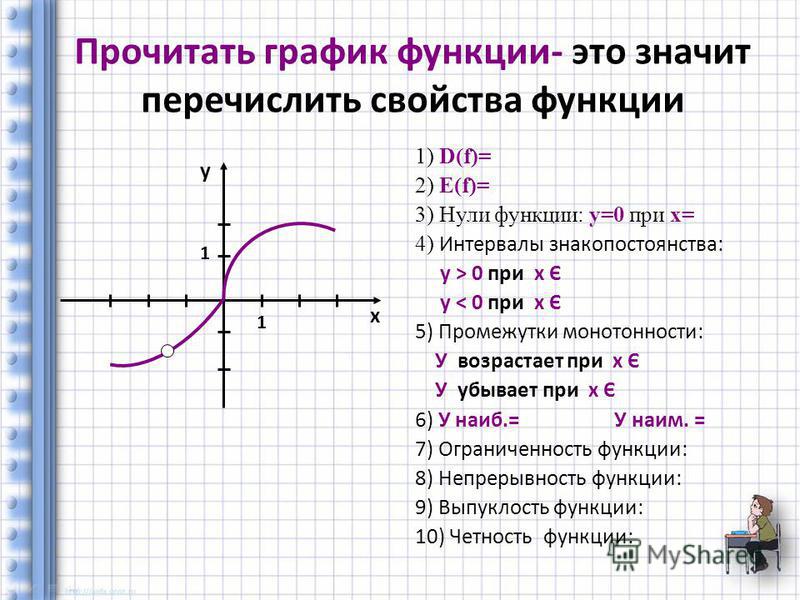

Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.

Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).

 Рис.1.

Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции — все действительные числа. Это можно записать так:

Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси орди­нат, и получить точку окружности, которая имеет рассматриваемую орди­нату. Таким образом, для функции область значений: .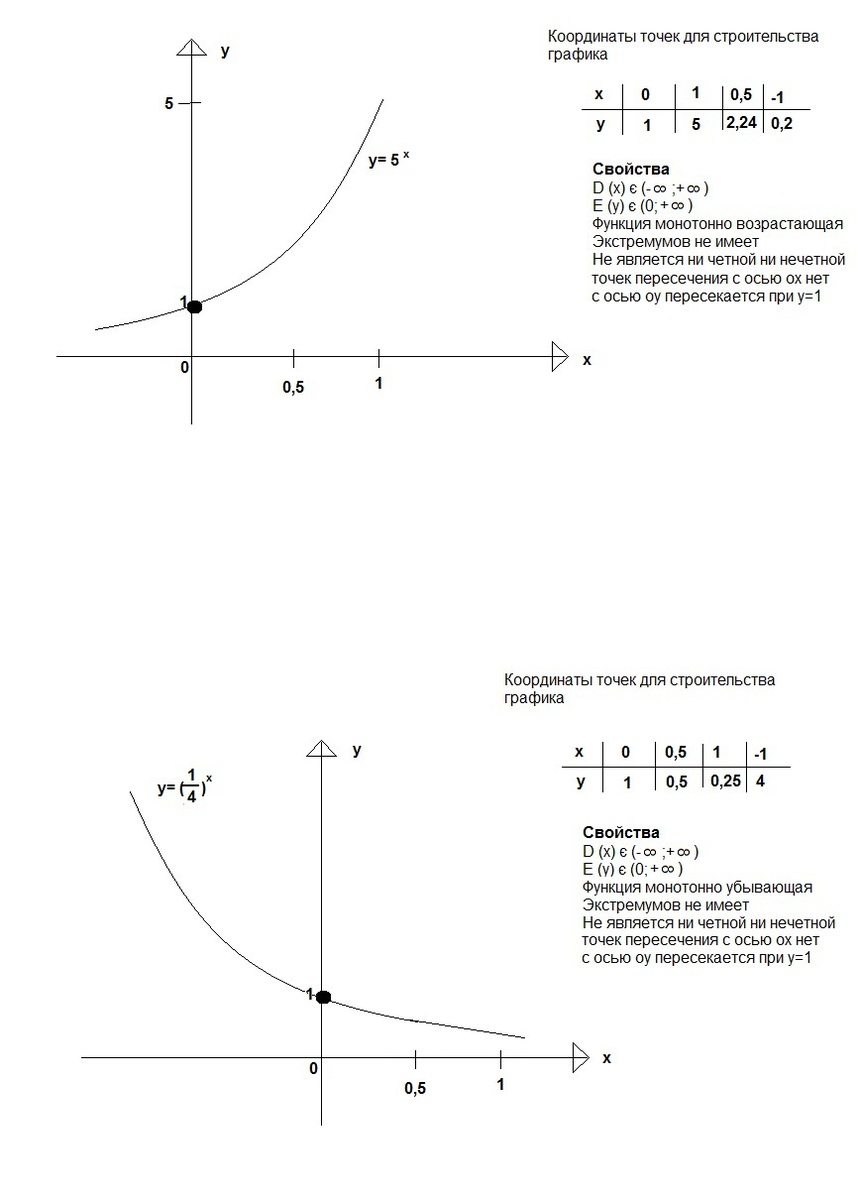 Это можно записать так:.Как видим, наибольшее значение функции sin x равно единице. Это зна­чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при Наименьшее значение функции равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окруж­ности является точка B, то есть при.

Синус — нечетная функция: , поэтому ее график симметричен относительно начала координат.

Синус — периодическая функция с наименьшим положительным периодом : , таким образом, через промежутки длиной вид графика функции повторя­ется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной , а потом полученную линию парал­лельно перенести вправо и влево вдоль оси Ox на расстояние , где k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение , то есть график функции проходит через начало координат.

На оси значение . Поэтому необходимо найти такие значения , при которых , то есть ордината соответствующей точки единичной окруж­ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж­ности будут выбраны точки C или D, то есть при (см. рис. 1).

Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, при всех , а также, учитывая период, при всех .

Значения функции синус отрицательны (то есть ордината соответствую­щей точки единичной окружности отрицательна) в III и IV четвертях, поэто­му при .

Промежутки возрастания и убывания. Учитывая периодичность функции с периодом , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке . 

Если (рис. 3, а), то при увеличении аргумента  ордината соответствующей точки единичной окружности увеличивается (то есть , следовательно, на этом промежутке функция возрас­тает. Учитывая периодичность функции , делаем вывод, что она также возрастает на каждом из промежутков 

Рис.2                                                                            Рис.3

Если  (рис.3,б), то при увеличении аргумента  ордината соответствующей точки единичной окружности уменьшается (то есть ), таким образом, на этом промежутке функция убыва­ет. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков 

Проведенное исследование позволяет обоснованно построить график функции . Учитывая периодичность этой функции (с периодом ), достаточно сначала построить график на любом промежутке длиной , на­пример на промежутке . Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината соответствующей точки единичной окружности. На рисунке 4 показано построение графика функции на промежутке . Учитывая нечетность функции  (ее график симметричен относительно начала координат), для построения графика на промежутке отображаем полученную кривую симметрич­но относительно начала координат (рис. 5).

Рис.4

Рис.5

Поскольку мы построили график на промежутке длиной , то, учитывая периодичность синуса (с периодом ), повторяем вид графика на каждом промежутке длиной (то есть переносим параллельно график вдоль оси на , где k — целое число). Получаем график, который называется синусоидой .(Рис.6)

Рис.6

Замечание. Тригонометрические функции широко применяются в ма­тематике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой . Та­кие процессы называют гармоническими колебаниями.

График функции можно получить из синусоиды сжатием или растяжением ее вдоль координатных осей и параллельным пере­носом вдоль оси . Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой , где А — амплитуда

колебания, — частота, — начальная фаза, — период колебания.

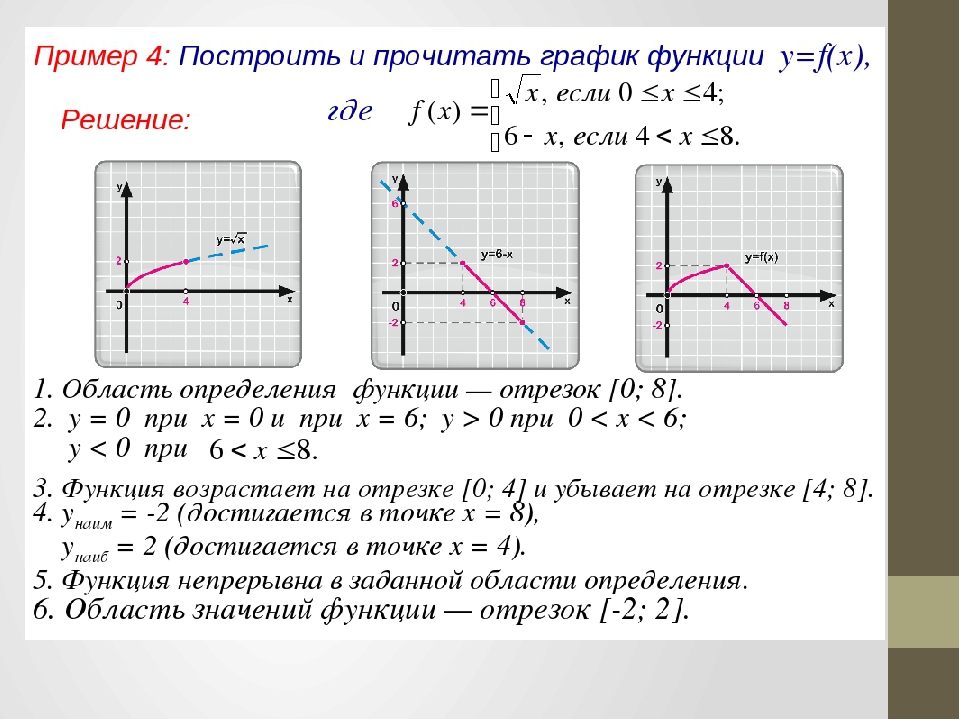
СВОЙСТВА ФУНКЦИИ И ЕЕ ГРАФИК

График функции  (косинусоида).

Свойства функции 

1. Область определения: R (x — любое действительное число).
2. Область значений: 

3. Функция четная:

   (график симметричен относительно оси ).

4. Функция периодическая с периодом  : 
5. Точки пересечения с осями координат 
6. Промежутки знакопостоянства: 
7. Промежутки возрастания и убывания: 

Объяснение и обоснование

Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции — все действительные числа. Это можно записать так:
.

Рис. 7

Для точек единичной окружности абсциссы находятся в промежутке и принимают все значения от -1 до 1, поскольку через любую точку отрезка оси абсцисс (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции . Это можно записать так: .

Как видим, наибольшее значение функции равно единице. Это зна­чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при .

Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окруж­ности является точка B, то есть при .

Косинус — четная функция: , поэтому ее график симметричен относительно оси .

Косинус — периодическая функция с наименьшим положительным периодом : . Таким об­разом, через промежутки длиной вид графика функции повторяется.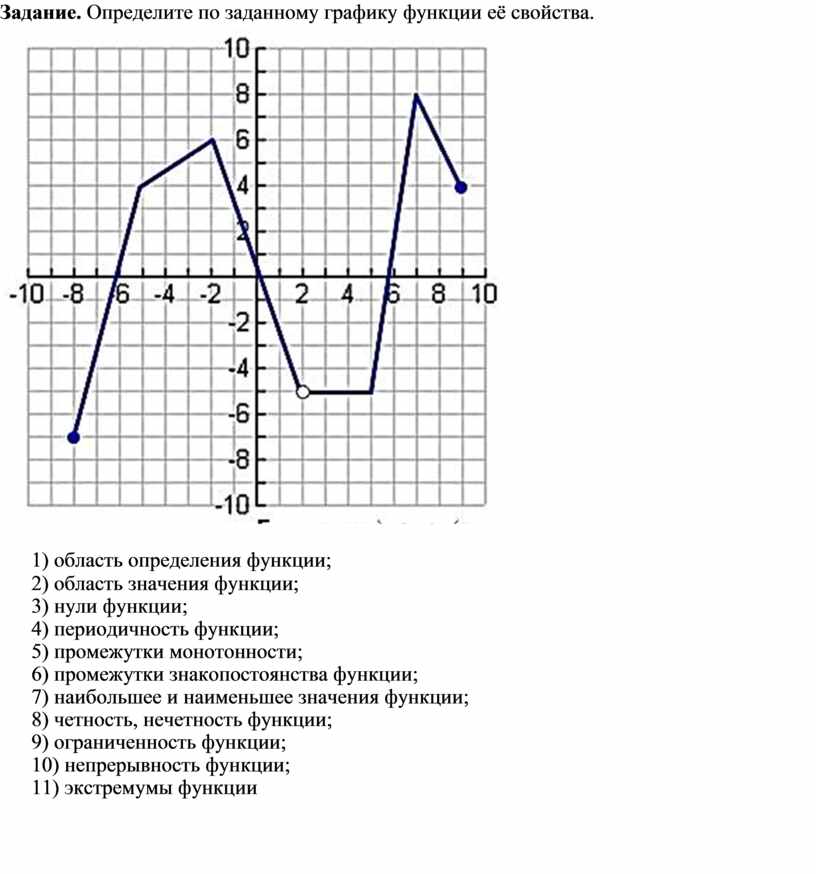

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение . На оси значение . Поэтому необходимо найти такие значения , при которых , то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при .

Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следова­тельно, 0 при , а также, учитывая период, при всех .

Значения функции косинус отрицательны (то есть абсцисса соответству­ющей точки единичной окружности отрицательна) во II и III четвертях, поэтому  при 

Промежутки возрастания и убывания. Учитывая периодичность функции , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .

Если (рис. 9, а), то при увеличении аргумента  абсцис­са соответствующей точки единичной окружности уменьшается (то есть ), следовательно, на этом промежутке функция убывает.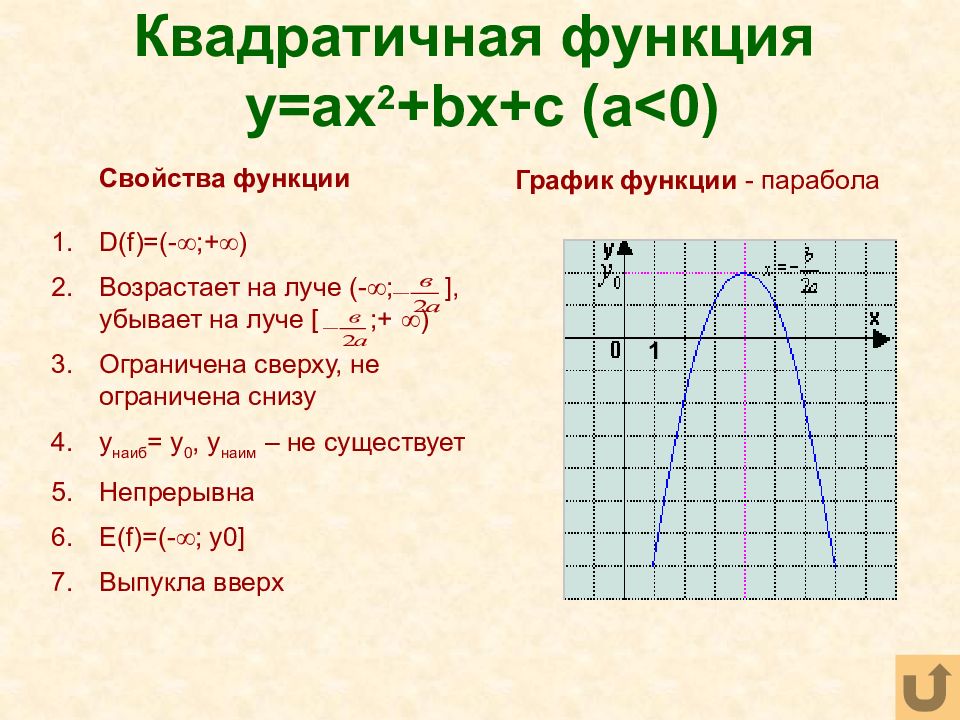 Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков .

Если (рис. 9, б), то при увеличении аргумента  аб­сцисса соответствующей точки единичной окружности увеличивается (то есть ), таким образом, на этом промежутке функция  возрастает. Учитывая периодичность функции , делаем вывод, что она возрастает также на каждом из промежутков . 

Рис.8                                                                                                                          Рис.9

Проведенное исследование позволяет построить график функции аналогично тому, как был построен график функции . Но график функции можно также получить с помощью геометрических преобразований графика функции , используя формулу

Рис.10

Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки а также

абсциссы и ординаты этих точек. Так как , то при повороте

прямоугольника  около точки на угол — против часовой стрел­ки он перейдет в прямоугольник .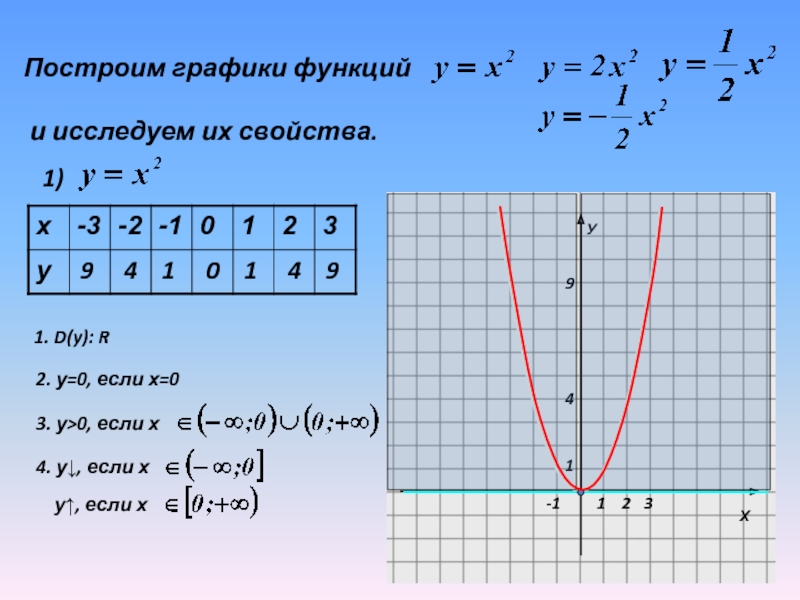 Но тогда . Следовательно, 00.

Укажем также формулы, которые нам понадобятся далее:.

Тогда,

Таким образом, .

Учитывая, что , график функции можно полу­чить из графика функции его параллельным переносом вдоль оси на  (рис. 11). Полученный график называется косинусоидой (рис. 12).

Рис.11

Рис.12

График функции  (тангенсоида) 

Свойства функции :

1. Область определения: 

2. Область значений: 

3. Функция нечетная: 

4. Функция периодическая с периодом 

5. Точки пересечения с осями координат:   

6. Промежутки знакопостоянства:

7. Промежутки возрастания и убывания:

8. Наибольшего и наименьшего значений функция не имеет.

График функции  (котангенсоида)

Свойства функции :

1. Область определения:

2. Область значений:

3. Функция нечетная: 

4. Функция переодическая с периодом 
5. Точки пересечения с осями координат: 

6. Промежутки знакопостоянства: 

7. Промежутки возрастания и убывания:

8. Наибольшего и наименьшего значений функция не имеет.

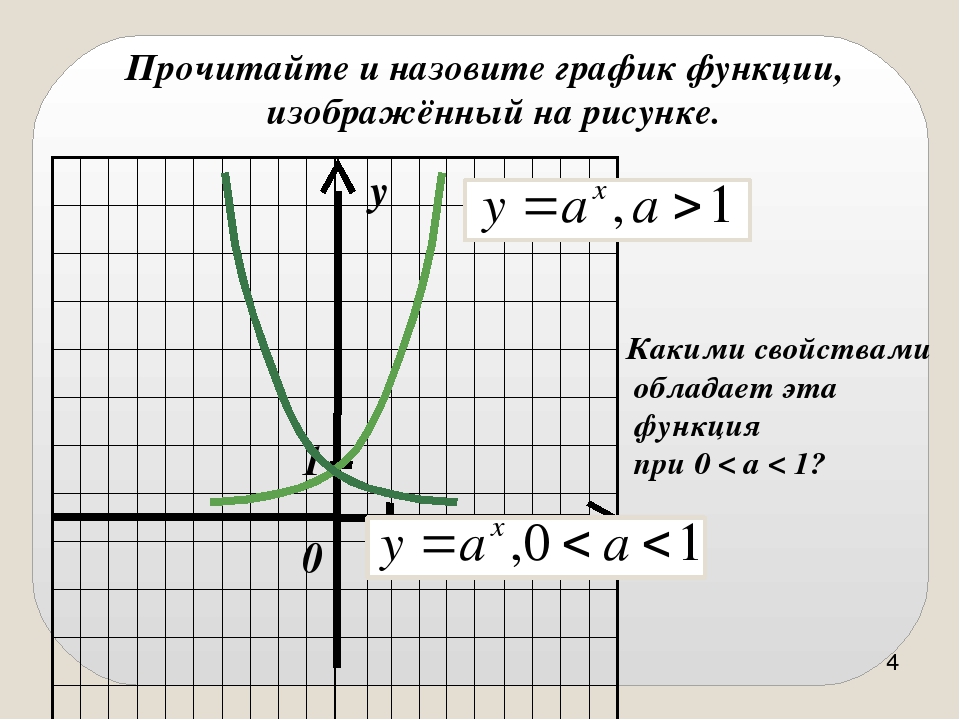
Урок 5. свойства и график функции y=tgx и y=ctg x — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №5. Свойства и график функции y=tgx и y=ctg x

Перечень вопросов, рассматриваемых в теме

• Изучение и объяснение свойств функций y=tgx и y=ctgx с помощью графика;
• Определение свойств и положения графика тригонометрических функций вида y=|tg(k|x|+b)| y=|ctg(k|x|+b|;
• Объяснение зависимости свойств и положения графика функции вида y=|tg(k|x|+b)| и y=|ctg(k|x|+b| от значения коэффициентов k,b.

Глоссарий по теме

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.

Тангенсоида –график функции у = tgx; плоская кривая, изображающая изменение тангенса в зависимости от изменения его аргумента (угла).

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.

Дополнительная литература:

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].–Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Актуализация знаний

Вычислите:

1. ;

2.

Ответ:

Объяснение нового материала

Изучение свойств функции y=tgx начнем с построения графика. Обратимся к единичной окружности:

рис.1 Тригонометрический круг

Переносим основные значения углов на координатную плоскость. По оси абсцисс откладываем угол в радианах, по оси ординат – значения тангенса угла.

рис.2 График y=tgx на промежутке

Как любая тригонометрическая функции, функция тангенса периодическая, делая параллельный перенос получаем:

рис.3 График y=tgx

Заметим, что график симметричен относительно начала координат, следовательно функция тангенса нечётная. Используя построенный нами график, выведем основные свойства y=tgx:

1. Область определения функции y = tgx все действительные числа, кроме чисел вида

2. Функция периодическая с периодом , т.к.

3. Функция нечётная, т.к. . График нечётной функции симметричен относительно начала координат;

4. Функция возрастает на всём интервале;

5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;

6.

7. Функция принимает:

• значение, равное 0, при ;
• положительные значения на интервале 
• отрицательные значения на интервале 

Для построения графика можно придерживаться алгоритму рассмотренному при построении графика , однако (формула приведения). Т.е. смещая тангенсоиду на единиц влево и делаем симметрию относительно оси Ох за счёт коэффициента –1, получаем:

рис.3 График y=сtgx

Основные свойства y=сtgx:

1. Область определения функции y = сtgx все действительные числа, кроме чисел вида

2. Функция периодическая с периодом ;

3. Функция нечётная. График нечётной функции симметричен относительно начала координат;

4. Функция убывает на всём интервале;

5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;

6. .

Примеры и разборы решения заданий тренировочного модуля:

Пример 1.

Найдем все корни уравнения , принадлежащие отрезку .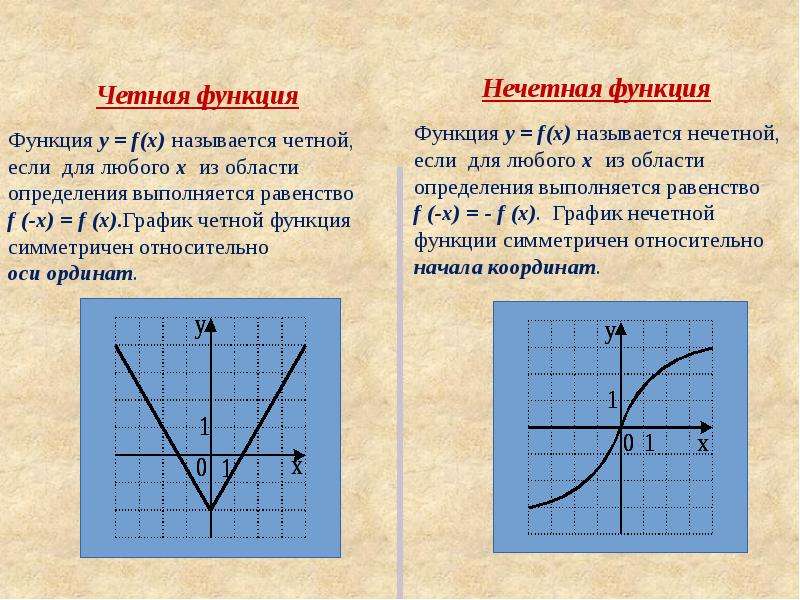 3+ 1$.

1. Составим таблицу значений:

2. Построим точки. Мы видим, что эти точки симметричны относительно точки с координатами (0,1). В итоге получаем кубическую параболу, смещенную вверх по оси OY (см. рис. 3).

Функция y = sin x, её свойства и график. 10-й класс

Тип урока: урок введения нового знания.

Педагогическая технология: проблемное обучение.

Формируемые результаты:

• Предметные: формировать умение строить график функции у = sin x, читать график и применять свойства при решении задач.
• Личностные: умение применять решение, применять независимость суждений.
• Метапредметные: формировать умение соотносить свои действия с планируемыми результатами.

Планируемые результаты: обучающиеся научатся применять свойства функции у = sin x и читать график.

Основные понятия: синусоида, свойства функции у = sin x.

Оборудование: ПК, проектор, Microsoft PowerPoint, презентация «Функция y = sin x, её свойства и график», таблица «Тригонометр».

Ход урока

1. Организационный момент

2. Целеполагание

— «Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.», писал Михаил Васильевич Остроградский (1801-1862, российский математик, механик). Как вы понимаете эти слова? (Слайд 1)

— Перед вами 4 графика. (Слайд 2)

— Как можно одним словом объединить эти графики? (функции)

— Опишите свойства графиков, представленных на слайде?

— Какие из предложенных графиков функций вам известны?

— Сформулируйте тему урока.

Тема урока: «Функция y = sin x, её свойства и график» (Слайд 3)

— Давайте попробуем определить цели нашего сегодняшнего урока, что мы уже знаем, и чему должны или можем научиться? (учитель вместе с обучающимися формирует цели, записывает их на доске).

— Познакомимся с историей возникновения слова синус (Слайд 4)

Синус (история имени)

Синус (sin) — название тригонометрической функции, появившееся благодаря удивительной цепочке искажений во время переводов математических трактатов. Древние индийские математики называли функцию «полу-тетивой», а затем просто «тетивой» — «джива», так как при геометрическом построении изображение напоминало лук. Арабские математики при знакомстве с трудами индийских коллег не стали переводить слово «джива» на арабский, а просто записали его по буквам. В процессе адаптации, устного использования и пр. оно превратилось в арабское выражение «джайб», которое можно перевести как пазуха, складка, карман, впадина. Когда, в свою очередь, арабские математические трактаты попали к европейским математикам, те перевели джайб на латинский, благо под рукой как раз было изящное слово, обозначающее складку или пазуху на римской тоге — слово sinus. Родственную функцию назвали complementi sinus, дополнительный синус. Позже утвердилось современное сокращение: sin и cos.

3. Планирование работы

— Составим план работы (перечень свойств, которые будут исследоваться).

Обучающиеся записывают план исследования синуса в тетрадях.

План

1. Область определения
2. Область значения
3. Нули функции
4. Промежутки возрастания, убывания функции
5. Промежутки знакопостоянства
6. Четность функции
7. Монотонность функции
8. Наименьшее и наибольшее значение функции

— Какую функцию называют периодической?

— Что такое период?

— Какое число является главным периодом функции  у = sin x?

4. Восприятие, осмысление, первичное закрепление

— Что происходит с ординатой точки при ее движении по первой четверти? (ордината увеличивается). Что происходит с ординатой точки при ее движении по второй четверти? (ордината постепенно уменьшается).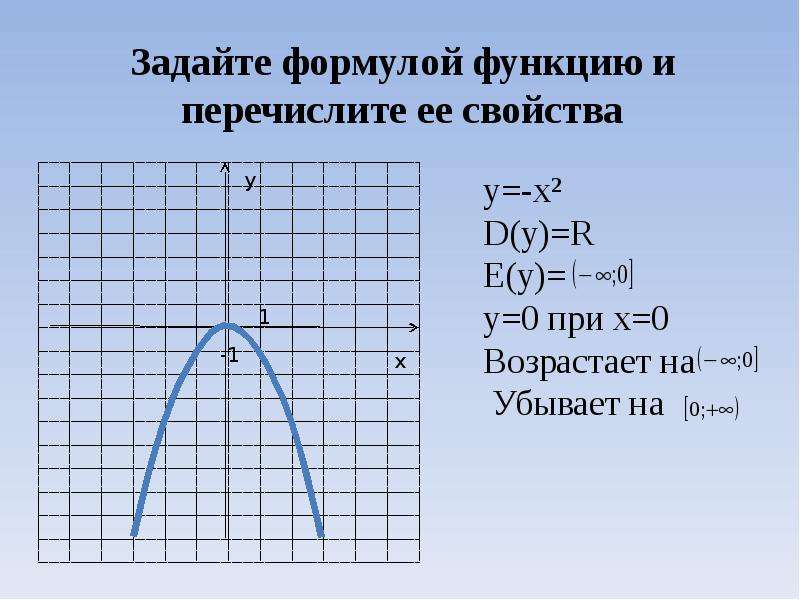 Как это связано с монотонностью функции? (функция у = sin t возрастает на отрезке  и убывает на отрезке ).

— Запишем функцию у = sin t в привычном для нас виде у = sin x (строить будем в привычной системе координат хОу) и составим таблицу значений этой функции.

Изучение нового материала (презентация, слайды 5-6).

Построение графика функции у = sin x и запись свойств функции в тетради. (Слайды 7–10)

1) D(y) = 

2) E (y) = 

3) функция ограничена и сверху, и снизу

4) унаиб = 1, унаим = -1

5) непрерывная функция

6) нечетная функция
7) возрастает на ; убывает на 

— Стихотворение (отрывок)

И линия эта волною качается,
И синусом график ее называется,
И через период она повторяется,
В периоде трижды она обнуляется,
Она полпериода вверх поднимается,
Придет в единицу и вниз опускается,
И так вдоль абсциссы все время болтается.
В системе, которую создал Декарт.

5. Применение знаний и способов при решении задач

— Постройте график функции (самостоятельно с проверкой, слайды 11-14):

а) у = sin x + 2

б) у = sin x — 1

в) у = sin 

г) у = sin 

—  Решите графически уравнение sin x =  (проверка слайд 15).

6. Первичная систематизация знаний и способов деятельности, их перенос и применение в новых ситуациях

№  21.5 (1), 21.9 (1)

7. Рефлексия

— Предлагаю оценить факт достижения цели урока: на все ли вопросы найдены ответы?

— Оцените свою работу на уроке. Закончите предложение. (Слайд 17)

Урок –

• заставил задуматься…
• навёл меня на размышления…
• Что нового вы узнали на уроке?
• Что вы считаете нужным запомнить?
• Над чем ещё надо поработать?

Домашняя работа

1. п. 21 (учить свойства функции у = sin x)
2. учебник № 21. 6 (1)
3. Построить график функции у = sin (x — )

— Спасибо за урок

Использованные материалы и ресурсы

1. Мерзляк А.Г., и др. Алгебра и начала математического анализа (углублённый уровень) 10 кл. – М.: «Вентана-Граф», 2017.
2. Мерзляк А.Г., и др. Дидактические материалы к учебнику Алгебра и начала математического анализа (углублённый уровень) – М.: «Вентана-Граф», 2017.
3. http://matematikam.ru/calculate-online/grafik.php

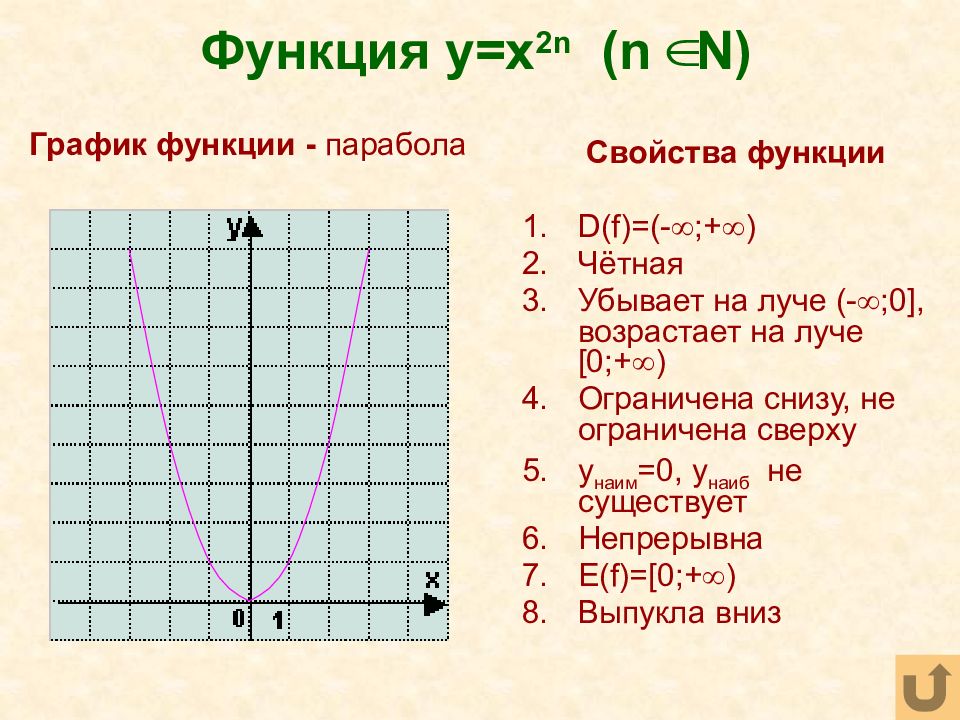
Внеклассный урок — Квадратичная функция. Функция y = ax2, ее график и свойства

Квадратичная функция. Функция y = ax², ее график и свойства

Квадратичная функция – это функция, которую можно задать формулой вида

                                                 y  =  ax²  +  bx  +  c,

где x – независимая переменная, a, b и c – некоторые числа, причем а ≠ 0.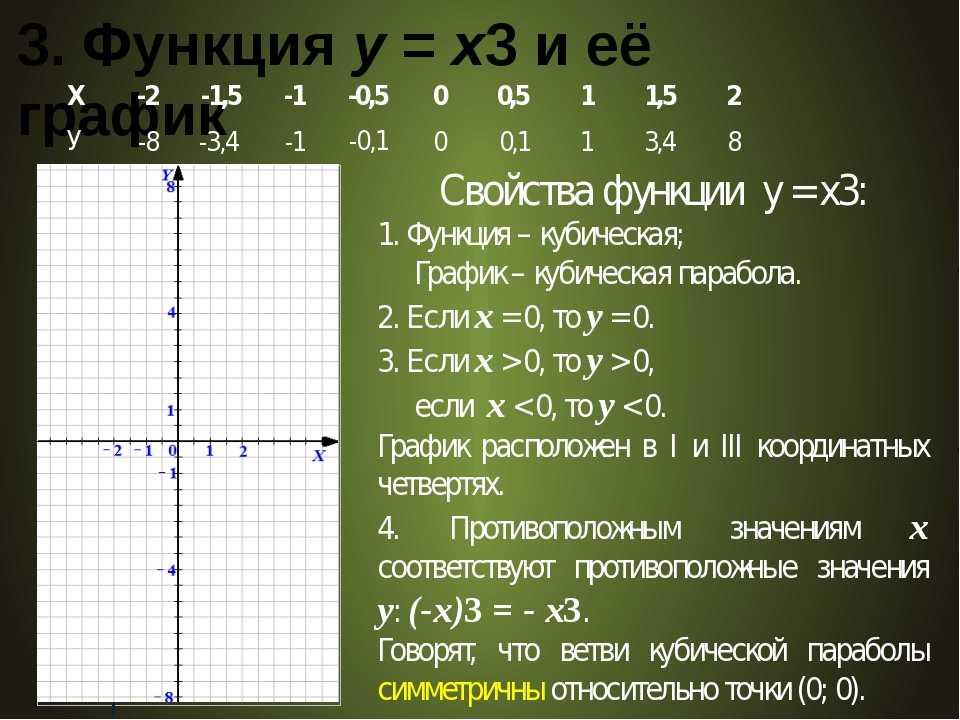

Областью определения квадратичной функции является множество всех чисел. (Напомним: областью определения функции называется совокупность значений независимой переменной, см.раздел «Функции и их графики»)

Функция  y = ax².

Функция y = ax² – это частный случай квадратичной функции.

Графиком функции y = ax² является парабола.

Свойства функции  y = ax² при a > 0:

Свойства функции  y = ax² при a < 0:

Свойства функции

В этой статье мы коротко суммируем сведения, которые касаются такого важного математического понятия, как функция. Мы поговорим о том, что такое  числовая функция и какие свойства функции необходимо знать и уметь исследовать.

Что такое  числовая функция? Пусть у нас есть два числовых множества: Х и Y, и  между этими множествами есть определенная зависимость. То есть каждому элементу х из множества Х по определенному правилу ставится в соответствие  единственный элемент  y из множества Y.

Важно, что каждому элементу х из множества Х соответствует один и только один элемент y из множества Y.

Правило, с помощью которого каждому элементу из множества Х мы ставим в соответствие единственный элемент из множества Y, называется числовой функцией. 

Множество Х называется областью определения функции.

Множество Y называется множеством значений значений функции.

Равенство   называется уравнением функции. В этом уравнении    — независимая переменная, или аргумент функции.   — зависимая переменная.

Если мы возьмем все пары и поставим им в соответствие соответствующие точки координатной плоскости, то  получим график функции. График функции — это графической изображение зависимости между множествами Х и Y.

Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график.

Основные свойства функций. 

1. Область определения функции.

Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции   имеет смысл. Другими словами, это область допустимых значений выражения .

Чтобы по графику функции найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.

2. Множество значений функции.

Множество значений функции  Е(y)— это множество всех значений, которые может принимать  зависимая переменная y.

Чтобы по графику функции  найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.

3.  Нули функции.

Нули функции — это те значения аргумента х, при которых значение функции (y) равно нулю.

Чтобы найти нули функции , нужно решить уравнение  . Корни этого уравнения и будут нулями функции .

Чтобы найти нули функции по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции  .

4. Промежутки знакопостоянства функции. 

Промежутки знакопостоянства функции — это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть  или .

Чтобы найти промежутки знакопостоянства функции , нужно решить неравенства и  .

Чтобы найти  промежутки знакопостоянства функции  по ее графику, нужно

• найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ — при этих значениях аргумента , 
• найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ — при этих значениях аргумента  .

5. Промежутки монотонности функции.

Промежутки монотонности функции — это такие промежутки значений  аргумента х, при которых функция возрастает или убывает.

Говорят, что функция   возрастает на промежутке I, если для любых двух значений аргумента  , принадлежащих промежутку I таких, что   выполняется соотношение:.

Другими словами, функция   возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.

Чтобы по графику функции определить промежутки возрастания функции, нужно, двигаясь  слева направо по линии графика функции, выделить промежутки значений аргумента х, на которых график идет вверх.

Говорят, что функция   убывает на промежутке I, если для любых двух значений аргумента  , принадлежащих промежутку I таких, что   выполняется соотношение: .

Другими словами, функция   убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.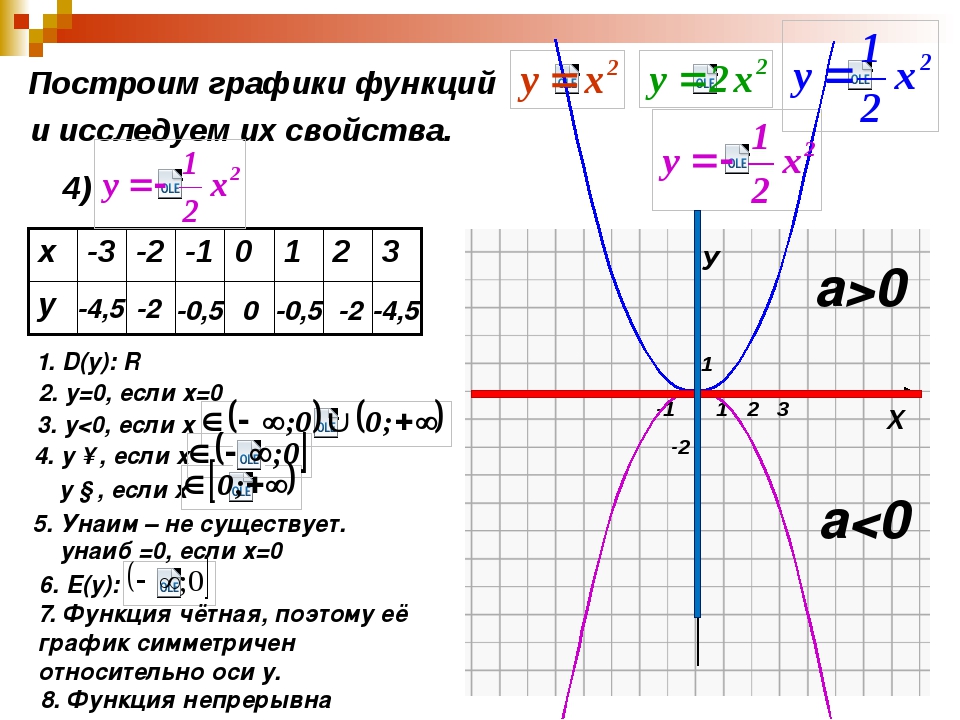  

Чтобы по графику функции определить промежутки убывания функции, нужно, двигаясь  слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которых график идет вниз.

6. Точки максимума и минимума функции.

Точка называется точкой максимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:

.

Графически это означает что точка с абсциссой  x_0 лежит выше других точек из окрестности I графика функции y=f(x).

Точка называется точкой минимума  функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:

Графически это означает что точка с абсциссой  лежит ниже других точек  из окрестности I графика функции .

Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.

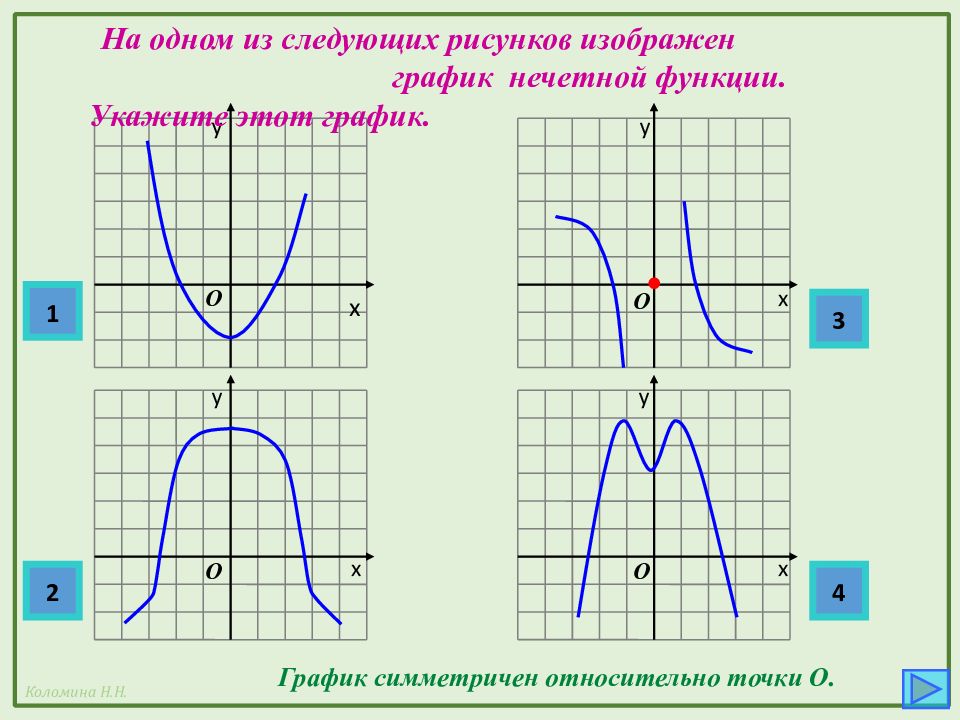
 7. Четность (нечетность) функции.

Функция  называется четной, если выполняются два условия:

а) Для любого значения аргумента , принадлежащего области определения функции,   также принадлежит области определения функции.

Другими словами, область определения  четной функции симметрична относительно начала координат.

б)  Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .

Функция называется нечетной, если выполняются два условия:

а) Для любого значения аргумента , принадлежащего области определения функции, также принадлежит области определения функции.

Другими словами, область определения нечетной функции симметрична относительно начала координат.

б)  Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .

Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.

Чтобы определить четность функции, нужно:

а). Найти область определения функции , и определить, является ли она симметричным множеством.

Если, например,  число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция — функция общего вида.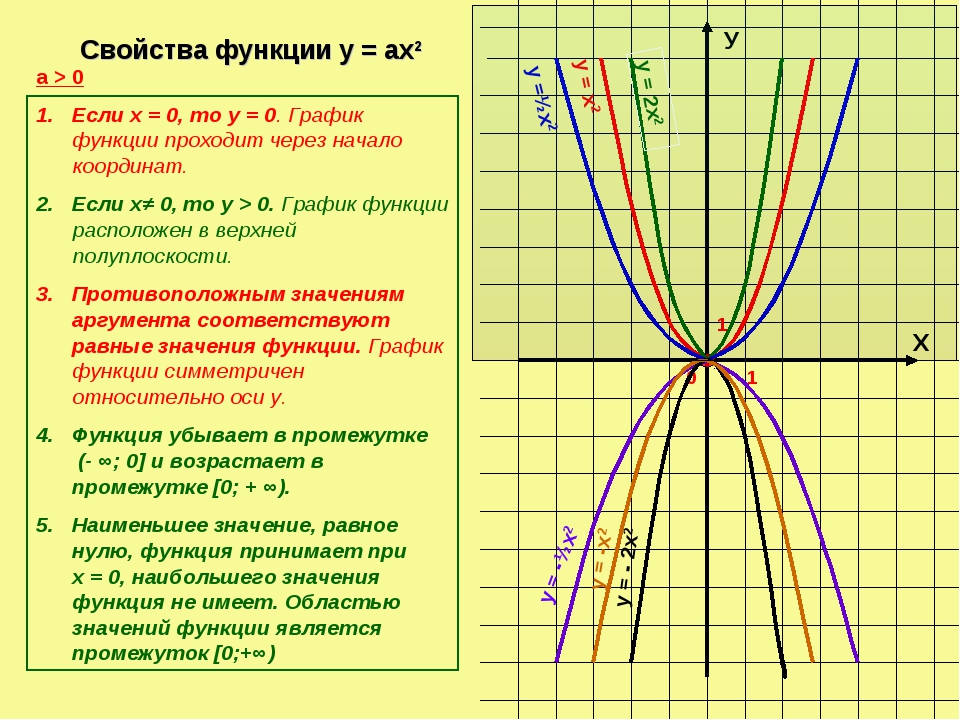

Если область определения  функции — симметричное множество, то проверяем п. б)

б). В уравнение функции  нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду  или .

Если , то функция четная.

Если , то функция нечетная.

Если не удалось привести ни к тому ни к другому, то наша функция — общего вида.

График четной функции симметричен относительно оси ординат ( прямой OY ).

График нечетной функции симметричен относительно начала координат ( точки (0,0) ).

8. Периодичность функции.

Функция называется периодической, если существует такое положительное число Т, что

• для любого значения х из области определения функции, х+Т также принадлежит D(x)

В программе средней школы из числа периодических функций изучают только тригонометрические функции.

Предлагаю вам посмотреть  ВИДЕОУРОК, в котором  я рассказываю, как определить свойства функции по ее графику.

И.В. Фельдман, репетитор по математике.

Свойства функций | Безграничная алгебра

Увеличивающие, убывающие и постоянные функции

Функции могут быть либо постоянными, либо увеличиваться при увеличении [latex] x [/ latex], либо уменьшаться при увеличении [latex] x [/ latex].

Цели обучения

Применить определения функций увеличения и уменьшения, чтобы определить, увеличивается ли функция, уменьшается или нет в заданном интервале

Основные выводы

Ключевые моменты

• Постоянная функция — это функция, значения которой не меняются независимо от ввода в функцию.
• Возрастающая функция — это функция, при которой для каждого [latex] x_ {1} [/ latex] и [latex] x_ {2} [/ latex], удовлетворяющих [latex] x_ {2} [/ latex]> [latex] x_ {1} [/ latex], затем [latex] f (x_ {2}) \ geq f (x_ {1}) [/ latex]. Если оно строго больше чем, то оно строго возрастает.
• Функция уменьшения — это функция, при которой для каждого [латекса] x_ {1} [/ latex] и [latex] x_ {2} [/ latex], удовлетворяющего [latex] x_ {2} [/ latex]> [latex] x_ {1} [/ latex], затем [latex] f (x_ {2}) \ leq f (x_ {1}) [/ latex]. Если он строго меньше, то он строго убывает.

Ключевые термины

• убывающая функция : Любая функция действительной переменной, значение которой уменьшается (или остается постоянным) по мере увеличения переменной.
• постоянная функция : функция, значение которой одинаково для всех элементов ее домена.
• возрастающая функция : Любая функция действительной переменной, значение которой увеличивается (или остается постоянным) при увеличении переменной.

Графическое поведение функций

В рамках исследования того, как изменяются функции, мы можем определить интервалы, в течение которых функция изменяется определенным образом.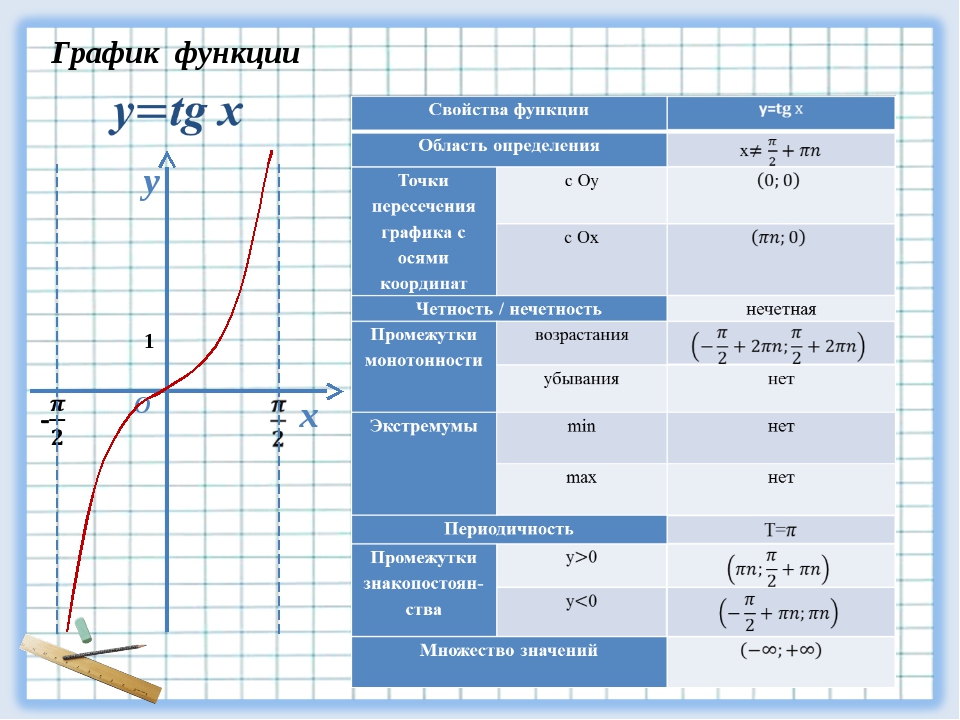 Мы говорим, что функция — это , увеличивающаяся на в интервале, если значения функции увеличиваются по мере увеличения входных значений в пределах этого интервала. Точно так же функция — это , уменьшающая на интервале, если значения функции уменьшаются по мере увеличения входных значений в течение этого интервала.

• Возрастающая функция — это функция, при которой для каждого [latex] x_1 [/ latex] и [latex] x_2 [/ latex], удовлетворяющих [latex] x_2> x_1 [/ latex], затем [latex] f (x_ {2} ) \ geq f (x_ {1}) [/ латекс]. Если оно строго больше, чем [latex] (f (x_2)> f (x_1)) [/ latex], то оно строго возрастает.
• Понижающая функция — это функция, при которой для каждого [латекса] x_1 [/ latex] и [latex] x_2 [/ latex], удовлетворяющего [latex] x_2> x_1 [/ latex], затем [latex] f (x_ {2}) \ leq f (x_ {1}) [/ латекс]. Если он строго меньше [latex] (f (x_2)

В терминах линейной функции [латекс] f (x) = mx + b [/ latex], если [latex] m [/ latex] положительное значение, функция увеличивается, если [latex] m [/ latex] отрицательное значение, оно уменьшается, и если [latex] m [/ latex] равно нулю, функция является постоянной функцией.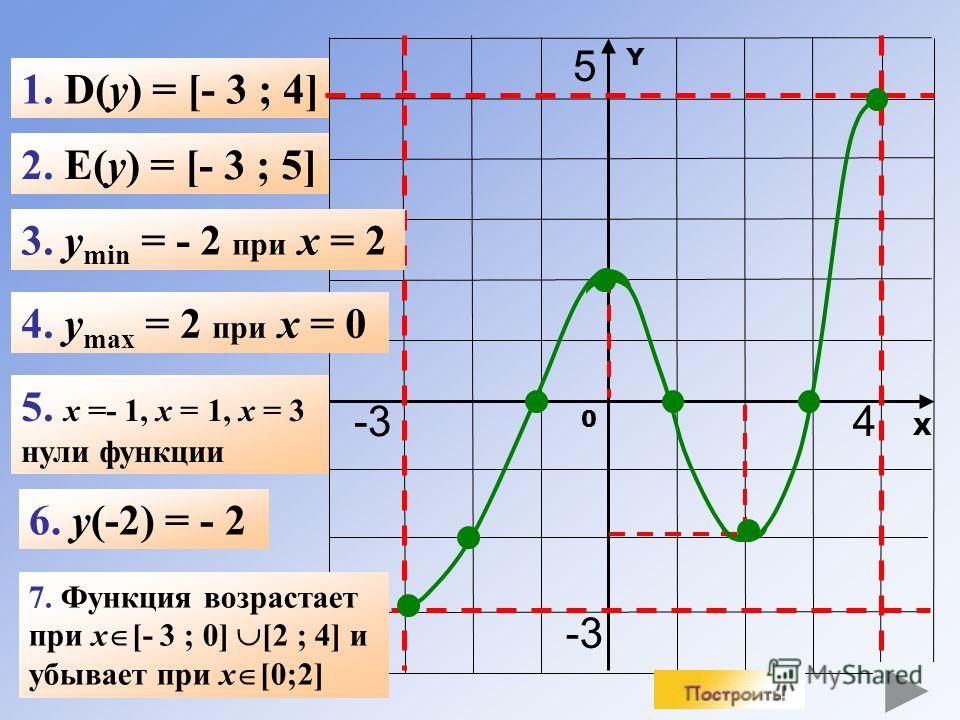 3−12x [/ latex] увеличивается по оси [latex] x [/ latex] от отрицательной бесконечности до [latex] -2 [/ latex], а также от [latex] 2 [/ latex] до положительной бесконечности. Обозначение интервалов записывается как: [latex] (- ∞, −2) ∪ (2, ∞) [/ latex]. Функция убывает на интервале: [latex] (−2, 2) [/ latex].

Постоянные функции

В математике постоянная функция ion — это функция, значения которой не меняются, независимо от ввода в функцию. Функция является постоянной функцией, если [latex] f (x) = c [/ latex] для всех значений [latex] x [/ latex] и некоторой константы [latex] c [/ latex].График постоянной функции [latex] y (x) = c [/ latex] представляет собой горизонтальную линию в плоскости, проходящую через точку [latex] (0, c). [/ Latex]

Константа Функция: График [latex] f (x) = 4 [/ latex] иллюстрирует постоянную функцию.

Определение функционального поведения

Пример 1: Определите интервалы, в которых функция увеличивается, уменьшается или остается постоянной.

Посмотрите на график слева направо по оси [latex] x [/ latex]; первая часть кривой убывает от бесконечности до [latex] x [/ latex] -значения [latex] -1 [/ latex], а затем кривая увеличивается.Кривая увеличивается на интервале от [латекс] -1 [/ латекс] до [латекс] 1 [/ латекс], а затем снова уменьшается до бесконечности.

График функции возрастания и убывания: Для функции, изображенной выше, кривая убывает в интервалах: [latex] (- \ infty, -1) \ cup (1, \ infty) [/ latex] и увеличивается в интервале [латекс] (-1,1) [/ латекс].

Относительные минимумы и максимумы

Относительные минимумы и максимумы — это точки наименьшего и наибольшего значений в их окрестностях соответственно.

Цели обучения

Определение локальных и глобальных максимумов и минимумов заданной функции

Основные выводы

Ключевые моменты

• Минимумы и максимумы вместе известны как экстремумы.
• Функция имеет глобальную (или абсолютную) точку максимума в [latex] x [/ latex] *, если [latex] f (x *) ≥ f (x) [/ latex] для всех [latex] x [/ latex] .
• Функция имеет глобальную (или абсолютную) точку минимума в [latex] x [/ latex] *, если [latex] f (x *) ≤ f (x) [/ latex] для всех [latex] x [/ latex] .
• Функция [latex] f [/ latex] имеет относительный (локальный) максимум r при [latex] x = b [/ latex], если существует интервал [latex] (a, c) [/ latex] с [латекс] a
• Функция [latex] f [/ latex] имеет относительный (локальный) минимум в [latex] x = b [/ latex], если существует интервал [latex] (a, c) [/ latex] с [latex] a
• Функции не обязательно имеют экстремумы. Например, любая строка [latex] f (x) = mx + b [/ latex], где [latex] m [/ latex] и [latex] b [/ latex] — константы, не имеет экстремумов, будь то локальные или глобальный.

Ключевые термины

• максимум : Наибольшее значение набора.
• экстремум : точка или значение, которое является максимумом или минимумом.
• минимум : наименьшее значение набора.

Минимумы и максимумы широко используются в задачах оптимизации и искусственного интеллекта, где, учитывая ряд ограничений на ресурсы, мы хотим наилучшим образом использовать наши ресурсы.Например, мы можем захотеть максимизировать нашу прибыль, учитывая предметы, которые мы можем производить, и наши доступные ресурсы. В области искусственного интеллекта мы можем захотеть выяснить, какой план действий наименее затратный для робота (т. Е. Кратчайший путь). В идеале вам нужно найти глобальные минимумы для планов. Однако, поскольку времени для определения правильного плана не существует, искусственный интеллект часто просто находит локальные минимумы.

Определения минимумов и максимумов: относительные и глобальные

В математике максимум и минимум функции (известные вместе как экстремумы ). — это наибольшее и наименьшее значение, которое функция принимает в точке либо в данной окрестности (локальный или относительный экстремум), либо в области функции в ее целостность (глобальный или абсолютный экстремум).

Примеры относительных и глобальных экстремумов : На этом графике представлены примеры всех четырех возможностей: относительного (локального) максимума и минимума, а также глобального максимума и минимума.

В то время как некоторые функции увеличиваются (или уменьшаются) во всей своей области, многие другие нет. Значение входа, при котором функция изменяется от увеличения к уменьшению (по мере того, как мы идем слева направо, то есть по мере увеличения входной переменной), называется относительным максимумом. Если функция имеет более одного, мы говорим, что у нее есть локальные максимумы.Точно так же значение входа, при котором функция изменяется от уменьшения к увеличению по мере увеличения входной переменной, называется относительным минимумом.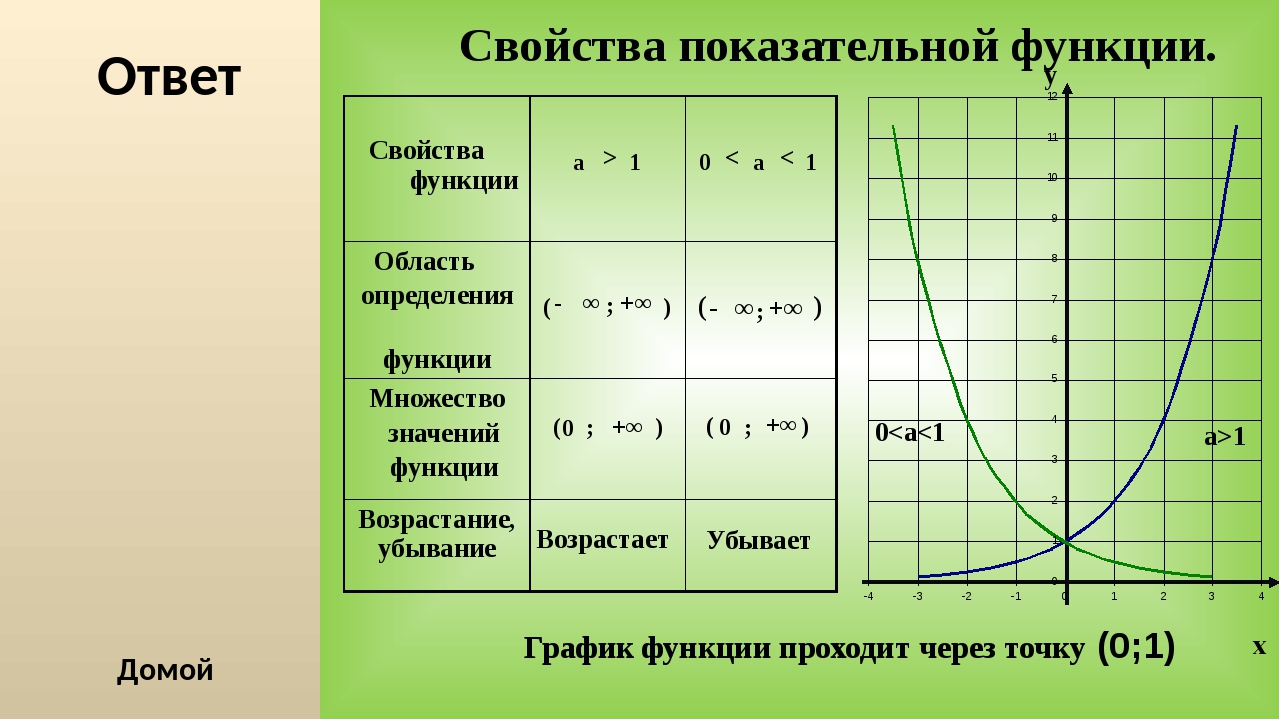 Форма множественного числа — локальные минимумы.

Функция также не возрастает и не убывает в экстремумах. Обратите внимание, что мы должны говорить о локальных экстремумах, потому что любой данный локальный экстремум, как здесь определено, не обязательно является наивысшим максимумом или наименьшим минимумом во всей области определения функции.

• Функция [latex] f [/ latex] имеет относительный (local) maximum at [latex] x = b [/ latex], если существует интервал [latex] (a, c) [/ latex ] С [латексом] a
• Аналогично, [latex] f [/ latex] имеет относительный (local) минимум at [latex] x = b [/ latex], если существует интервал [latex] (a, c) [/ latex] с [латексом] a

График минимума локального максимума: Для изображенной функции локальный максимум находится при значении [latex] y [/ latex], равном 16, и он возникает, когда [latex] x = -2 [/ latex]. Локальный минимум находится при значении [latex] y [/ latex], равном -16, и это происходит, когда [latex] x = 2 [/ latex].

Функция имеет глобальный (или абсолютный) максимум точки в [latex] x [/ latex] *, если [latex] f (x ∗) ≥ f (x) [/ latex] для всех [latex] x [/латекс]. Точно так же функция имеет глобальный (или абсолютный) минимум точки в [latex] x [/ latex], если [latex] f (x ∗) ≤ f (x) [/ latex] для всех [latex] x [/латекс]. Глобальные экстремумы также являются относительными экстремумами.

Функции не могут иметь экстремумов, таких как строка [latex] y = x [/ latex]. Эта линия увеличивается к бесконечности и убывает к отрицательной бесконечности и не имеет относительных экстремумов.

Разделение относительного и глобального максимума и минимума

Пример 1: Найдите все максимумы и минимумы на графике ниже:

График относительных максимумов и минимумов: Эта кривая показывает относительный минимум при [латексе] (- 1, -2) [/ латекс] и относительный максимум при [латексе] (1,2) [/ латексе].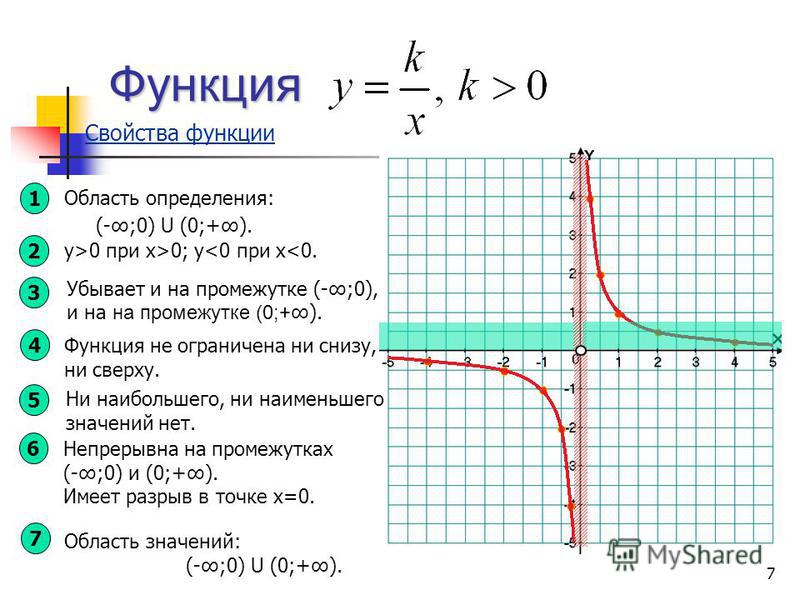

График достигает локального максимума в [latex] (1,2) [/ latex], потому что это наивысшая точка в открытом интервале около [latex] x = 1 [/ latex]. Локальный максимум — это координата y при [latex] x = 1 [/ latex], которая равна [latex] 2 [/ latex].

График достигает локального минимума в [latex] (- 1, -2) [/ latex], потому что это самая низкая точка в открытом интервале около [latex] x = -1 [/ latex]. Локальный минимум — это координата y [латекс] x = -1 [/ латекс], которая равна [латекс] -2 [/ латекс].

Пример 2:

Найдите все глобальные максимумы и минимумы на графике ниже:

Глобальный график максимальных и минимальных значений: Для функции, изображенной выше, абсолютный максимум происходит дважды при [latex] y = 16 [/ latex], а абсолютный минимум — при [latex] (3, -10) [/ latex] .

График достигает абсолютного максимума в двух местах, [latex] x = -2 [/ latex] и [latex] x = 2 [/ latex], потому что в этих местах график достигает своей наивысшей точки в домене. функции. Абсолютный максимум — координата y , которая равна [латекс] 16 [/ латекс].

На графике достигается абсолютный минимум при [latex] x = 3 [/ latex], потому что это самая низкая точка в области графика функции. Абсолютный минимум — координата y , которая равна [латекс] -10 [/ латекс].

Кусочные функции

Кусочная функция определяется несколькими подфункциями, каждая из которых применяется к отдельным интервалам входа

Цели обучения

Практика построения графиков кусочных функций и определение их областей и диапазонов

Основные выводы

Ключевые моменты

• Кусочные функции определяются с использованием общей функциональной нотации, где тело функции представляет собой массив функций и связанных поддоменов.
• Абсолютное значение, [латекс] \ left | x \ right | [/ latex] — очень распространенная кусочная функция. Для действительного числа его значение равно [latex] -x [/ latex], когда [latex] x <0 [/ latex], и его значение равно [latex] x [/ latex], когда [latex] x \ geq0 [/ latex ].
• Кусочные функции могут иметь горизонтальные или вертикальные пробелы (или и то, и другое) в своих функциях. Горизонтальный зазор означает, что функция не определена для этих входов.
• Открытый кружок в конце интервала означает, что конечная точка не включена в интервал, т.е.е. строго меньше или строго больше чем. Закрашенный кружок означает, что конечная точка включена.

Ключевые термины

• поддомен : домен, который является частью более крупного домена.
• абсолютное значение : Для действительного числа — его числовое значение без учета знака; формально [latex] -1 [/ latex] умноженное на число, если число отрицательное, и число без изменений, если оно равно нулю или положительно.
• кусочная функция : функция, в которой используется более одной формулы для определения вывода для разных частей домена.

В математике кусочная функция — это функция, в которой используется более одной формулы для определения выходных данных для разных частей домена. Кусочные функции определяются с использованием общей функциональной записи, где тело функции представляет собой массив функций и связанных интервалов. Мы используем кусочные функции для описания ситуаций, в которых правило или отношение изменяется, когда входное значение пересекает определенные «границы».

Построение графиков кусочных функций

Пример 1: Рассмотрим кусочное определение функции абсолютного значения:

[латекс] \ displaystyle \ left | x \ right | = \ left \ {\ begin {matrix} -x, & if \ x <0 \\ x, & if \ x \ geq0 \ end {matrix} \ right.[/ латекс]

Для всех значений [latex] x [/ latex] меньше нуля, используется первая функция [latex] (- x) [/ latex], которая отменяет знак входного значения, делая выходные значения положительными. Допустим [латекс] y = f (x) [/ latex], где [latex] f (x) = | x | [/ latex], некоторые примеры упорядоченных пар [latex] (x, | x |) [/ latex ]:

[латекс] \ displaystyle (-2,2) \\ (-1,1) \\ (-0,5,0,5) [/ латекс]

Для всех значений [latex] x [/ latex], больших или равных нулю, используется вторая функция [latex] (x) [/ latex], делая выходные значения равными входным значениям.Вот некоторые примеры заказанных пар:

[латекс] \ Displaystyle (2,2) \ (1,1) \\ (0,5,0,5) [/ латекс]

После нахождения и построения некоторых упорядоченных пар для всех частей («частей») функции результатом является V-образная кривая функции абсолютного значения, представленной ниже.

Кусочная функция: абсолютное значение: Кусочная функция, [латекс] \ left | x \ right | = \ left \ {\ begin {matrix} -x, & if \ x <0 \\ x, & if \ x \ geq0 \ end {matrix} \ right. [/ latex], является графиком функция абсолютного значения.2 [/ латекс]:

[латекс] \ displaystyle f (-2) = 4 \\ f (-1) = 1 \\ f (0) = 0 \ f (1) = 1 [/ latex]

Эти точки удовлетворяют первой части функции и образуют следующие упорядоченные пары:

[латекс] \ displaystyle (-2,4) \\ (-1,1) \\ (0,0) \\ (1,1) [/ латекс]

Для средней части (части), [latex] f (x) = 3 [/ latex] (постоянная функция) для области [latex] 1

[латекс] \ displaystyle (1.5,3) \ (1.8, 3) \ (2,3) [/ латекс]

Для последней части (кусок) [latex] f (x) = x [/ latex] для домена [latex] x> 2 [/ latex] несколько упорядоченных пар:

[латекс] \ displaystyle (2.2, & if \ x \ leq 1 \\ 3, & if \ 1 2 \\ \ end {matrix} \ right. [/ Latex] состоит из трех частей ( шт). В зависимости от стоимости домена каждый кусок отличается.

Обратите внимание на открытые и темные кружки на графике. Это связано с конкретными доменами для каждой части функции. Открытый кружок в конце интервала означает, что конечная точка не входит в интервал, т.е. строго меньше или строго больше чем. Закрашенный кружок означает, что конечная точка включена (равно).

Область определения функции начинается с отрицательной бесконечности и продолжается через каждую часть без пробелов до положительной бесконечности. Поскольку в [latex] x = 1 [/ latex] есть закрытая И открытая точка, функция там кусочно непрерывна. Когда [latex] x = 2 [/ latex], функция также кусочно-непрерывная. Следовательно, область определения этой функции — это набор всех действительных чисел, [latex] \ mathbb {R} [/ latex].

Диапазон начинается с самого низкого значения [latex] y [/ latex], [latex] y = 0 [/ latex] и продолжается до положительной бесконечности.2 [/ latex] включает эти значения. Следовательно, диапазон кусочной функции — это также набор всех действительных чисел, больших или равных [latex] 0 [/ latex], или всех неотрицательных значений: [latex] y \ geq 0 [/ latex].

Индивидуальные функции

Функция взаимно однозначного соответствия, также называемая инъективной функцией, никогда не отображает отдельные элементы своей области на один и тот же элемент ее кодомена.

Цели обучения

Используйте свойства взаимно-однозначных функций, чтобы определить, является ли данная функция взаимно-однозначной

Основные выводы

Ключевые моменты

• Функция «один к одному» имеет уникальный выход для каждого уникального входа.2 [/ latex] для [latex] x \ geq 0 [/ latex].
• Чтобы проверить, является ли функция взаимно однозначной, выполните тест горизонтальной линии. Если какая-либо горизонтальная линия пересекает график более чем в одной точке, функция не взаимно однозначна.
• Если каждый элемент диапазона функции соответствует ровно одному элементу ее домена, то функция называется взаимно однозначной.

Ключевые термины

• инъективная функция : функция, сохраняющая различимость: она никогда не отображает отдельные элементы своего домена в один и тот же элемент его кодомена.

Свойства однозначной функции

Однозначная функция , также называемая инъективной функцией, никогда не отображает отдельные элементы своей области в один и тот же элемент ее совместной области. Другими словами, каждый элемент диапазона функции соответствует ровно одному элементу ее домена. Иногда инъективная функция от [latex] X [/ latex] до [latex] Y [/ latex] обозначается [latex] f: X \ mapsto Y [/ latex] с помощью стрелки с заостренным хвостом. {2} [/ latex] (без ограничений домена) взаимно однозначной?

Один из способов проверить, является ли функция взаимно однозначной, — это построить график функции и выполнить тест горизонтальной линии.2 [/ latex] не проходит проверку горизонтальной линии и, следовательно, не является однозначной функцией. Если горизонтальная линия может проходить через две или более точек на графике функции, то функция не взаимно однозначна.

Другой способ определить, является ли функция взаимно однозначной, — это составить таблицу значений и проверить, соответствует ли каждый элемент диапазона ровно одному элементу домена. Список упорядоченных пар для функции:

[латекс] \ Displaystyle (-2,4) \\ (-1,1) \\ (0,0) \\ (1,1) \\ (2,4) [/ латекс]

Упорядоченные пары [latex] (- 2,4) [/ latex] и [latex] (2,4) [/ latex] не проходят определение один-к-одному, потому что элемент [latex] 4 [/ латекс] диапазона соответствует [латексу] -2 [/ латексу] и [латексу] 2 [/ латексу].Каждый уникальный вход должен иметь уникальный выход, поэтому функция не может быть взаимно однозначной. Также обратите внимание, что эти две упорядоченные пары образуют горизонтальную линию; что также означает, что функция не является взаимно однозначной, как было сказано ранее.

Пример 2: Функция [латекс] f (x) = \ left | x \ right | [/ latex] один к одному?

Это функция абсолютного значения, которая представлена ​​на графике ниже. Обратите внимание, что он не проходит тест горизонтальной линии. Поскольку каждый уникальный вход не имеет уникального выхода, эта функция не может быть взаимно однозначной.

График абсолютных значений: График функции, [латекс] f (x) = \ left | x \ right | [/ latex], не проходит проверку горизонтальной линии и, следовательно, не является однозначной функцией.

Симметрия функций

Два объекта обладают симметрией, если один объект может быть получен из другого преобразованием.

Цели обучения

Определить, демонстрирует ли данное отношение некоторую форму симметрии

Основные выводы

Ключевые моменты

• Функция имеет симметрию, если ее можно каким-либо образом преобразовать без изменения функции.
• Функция может быть симметричной относительно точки, если ее можно повернуть на фиксированную величину вокруг этой точки, не изменяя ее.
• Функция может быть симметричной относительно линии, если ее можно отразить над этой линией, не изменяя ее.

Ключевые термины

• симметрия : математическое свойство, при котором объект может подвергаться преобразованию при сохранении своих свойств.

Симметрия

В математике объект, такой как форма или функция, обладает симметрией, если он может быть преобразован каким-либо образом, сохраняющим свойства математического объекта.В геометрии геометрическая форма или объект являются симметричными, если их можно разделить на две или более идентичных части, которые расположены организованным образом. S означает, что объект является симметричным, если есть преобразование, которое перемещает отдельные части объекта, но не Не меняю общую форму.

Для функций функция демонстрирует симметрию, если каждая точка функции может быть изменена в соответствии с математическим правилом без изменения общей функции. Определение симметрии может включать построение графика функции или ее алгебраическое вычисление.

Типы симметричных функций

Функции и отношения могут быть симметричными относительно точки, линии или оси. Они также могут иметь симметрию после отражения.

Чтобы определить, имеет ли отношение симметрию, постройте график отношения или функции и посмотрите, является ли исходная кривая отражением самой себя над точкой, линией или осью. На изображении ниже показаны примеры отражения функции по оси [latex] x [/ latex] (вертикальное отражение) и по оси [latex] y [/ latex] (горизонтальное отражение).

Отражение : функция может быть отражена по оси [латекс] x [/ латекс] или [латекс] y [/ латекс]. Если функция выглядит так же после отражения, функция симметрична по этой оси.

На следующем графике ниже квадратичные функции обладают симметрией относительно линии, называемой осью симметрии. Ось делит U-образную кривую на две части кривой, которые отражаются над осью симметрии. 2 + 4x + 3 [/ latex] показывает ось симметрии относительно линии [latex] x = -2 [/ latex].Кривая разделена на две эквивалентные [латексные] 2 [/ латексные] половины. Обратите внимание, что точки пересечения [latex] x [/ latex] являются отраженными точками над осью симметрии и находятся на одинаковом расстоянии от оси.

Определение симметрии

Пример: Симметрия функции ниже?

Симметрия относительно точки: График выше имеет симметрию, поскольку помеченные точки отражаются над началом координат.

Граф имеет симметрию относительно начала координат или точки [latex] (0,0) [/ latex].Указанные точки [латекс] (1,3) [/ латекс] и [латекс] (- 1, -3) [/ латекс] отражаются поперек начала координат.

Четные и нечетные функции

Функции, которые имеют аддитивную инверсию, могут быть классифицированы как нечетные или четные в зависимости от их свойств симметрии.

Цели обучения

Определить, является ли функция четной, нечетной или ни одной

Основные выводы

Ключевые моменты

• Четность функции не обязательно показывает, является ли функция нечетной или четной.
• Четные функции алгебраически определяются как функции, в которых для всех значений выполняется следующее соотношение: [latex] f (x) = f (-x) [/ latex].
• Четная функция симметрична относительно оси [latex] y [/ latex]: для каждой точки [latex] (x, y) [/ latex] на графике соответствующая точка [latex] (- x, y) [/ latex] или наоборот тоже есть на графике.
• Нечетные функции алгебраически определяются как функции, в которых выполняется следующее соотношение для всех значений: [latex] -f (x) = f (-x) [/ latex].
• Нечетная функция симметрична относительно начала координат: для каждой точки [latex] (x, y) [/ latex] на графике соответствующая точка [latex] (- x, -y) [/ latex] или наоборот наоборот, тоже есть на графике. Другими словами, поворот графика [latex] на 180 [/ latex] градусов вокруг исходной точки приводит к тому же неизменному графику.

Ключевые термины

• четность : Набор со свойством того, что все его элементы принадлежат одному из двух непересекающихся подмножеств, особенно набор целых чисел, разделенных на подмножества четных и нечетных элементов.
• добавка обратная : Противоположная добавка.

Четные и нечетные определения

Функции могут быть классифицированы как «нечетные» или «четные» в зависимости от их состава. Эти метки коррелируют со свойствами симметрии функции.

Термины «нечетный» и «четный» могут применяться только к ограниченному набору функций. Чтобы функция была классифицирована как одна или другая, она должна иметь аддитивную обратную функцию. Следовательно, у него должен быть номер, который при добавлении к нему равен [latex] 0 [/ latex].3 \ right | [/ latex] имеет показатель степени, который является нечетным целым числом, [latex] 3 [/ latex], но также является четной функцией. Как мы можем проверить, четная или нечетная функция? Давайте посмотрим на их характеристики.

Четные функции

Четные функции алгебраически определяются как функции, в которых для всех значений [latex] x [/ latex] выполняется следующее соотношение:

[латекс] \ Displaystyle f (x) = f (-x) [/ латекс]

Чтобы проверить, является ли функция четной, любое выбранное значение [latex] x [/ latex] должно давать такое же выходное значение при замене в функцию как [latex] -x [/ latex].4 + 2x [/ latex], изображенный выше, не является даже потому, что график не является симметричным относительно оси [latex] y [/ latex]. Например, точка [latex] (- 1, -1) [/ latex] не отражается на точке [latex] (1, -1) [/ latex].

Мы можем подтвердить это графически: функции, удовлетворяющие требованию четности, симметричны относительно оси [latex] y [/ latex]. Следовательно, для каждой точки [latex] (x, y) [/ latex] на графике соответствующая точка [latex] (- x, y) [/ latex] или наоборот также находится на графике.

Нечетные функции

Нечетные функции алгебраически определяются как функции, в которых для всех значений [latex] x [/ latex] выполняется следующее соотношение:

[латекс] \ displaystyle -f (x) = f (-x) [/ latex]

Это отношение также может быть выражено как:

[латекс] \ displaystyle f (x) + f (-x) = 0 [/ латекс]

Чтобы проверить, является ли функция нечетной, отрицание функции (обязательно отрицание всех членов функции) должно давать тот же результат, что и замена значения [latex] -x [/ latex]. {2} -1 \).{2} -2 х-1 \)

Ответ

1. вниз
2. вверх

Найдите ось симметрии и вершину параболы

Посмотрите еще раз на Рисунок 9.6.10 . Вы видите, что мы можем сложить каждую параболу пополам, и тогда одна сторона окажется поверх другой? «Линия сгиба» — это линия симметрии. Мы называем ее осью симметрии параболы.

Мы снова показываем те же два графика с осью симметрии.{2} + b x + c \) равно \ (x = — \ frac {b} {2 a} \).

Итак, чтобы найти уравнение симметрии каждой из парабол, которые мы построили на графике выше, мы подставим в формулу \ (x = — \ frac {b} {2 a} \).

Обратите внимание, что это уравнения, изображенные пунктирными синими линиями на графиках.

Точка параболы, которая является самой низкой (парабола открывается вверх) или самой высокой (парабола открывается вниз), лежит на оси симметрии. Эта точка называется вершиной параболы.

Мы можем легко найти координаты вершины, потому что знаем, что она находится на оси симметрии.{2} -6 x + 2 \) найти:

1. ось симметрии
2. вершина

Решение :

а.

б.