| 1 | Найти точное значение | sin(30) | |||||||||||||||
| 2 | Найти точное значение | sin(45) | |||||||||||||||
| 3 | Найти точное значение | sin(30 град. ) | |||||||||||||||
| 4 | Найти точное значение | sin(60 град. ) | |||||||||||||||
| 5 | Найти точное значение | tan(30 град. ) | |||||||||||||||
| 6 | Найти точное значение | arcsin(-1) | |||||||||||||||
| 7 | Найти точное значение | sin(pi/6) | |||||||||||||||
| 8 | Найти точное значение | cos(pi/4) | |||||||||||||||
| 9 | Найти точное значение | sin(45 град. ) ) | |||||||||||||||
| 10 | Найти точное значение | sin(pi/3) | |||||||||||||||
| 11 | Найти точное значение | arctan(-1) | |||||||||||||||
| 12 | Найти точное значение | cos(45 град. ) | |||||||||||||||
| 13 | Найти точное значение | cos(30 град. ) | |||||||||||||||
| 14 | Найти точное значение | tan(60) | |||||||||||||||
| 15 | Найти точное значение | csc(45 град. ) | |||||||||||||||
| 16 | Найти точное значение | tan(60 град. ) ) | |||||||||||||||
| 17 | Найти точное значение | sec(30 град. ) | |||||||||||||||
| 18 | Найти точное значение | cos(60 град. ) | |||||||||||||||
| 19 | Найти точное значение | cos(150) | |||||||||||||||
| 20 | Найти точное значение | sin(60) | |||||||||||||||
| 21 | Найти точное значение | cos(pi/2) | |||||||||||||||
| 22 | Найти точное значение | tan(45 град. ) | |||||||||||||||
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |||||||||||||||
| 24 | Найти точное значение | csc(60 град. ) ) | |||||||||||||||
| 25 | Найти точное значение | sec(45 град. ) | |||||||||||||||
| 26 | Найти точное значение | csc(30 град. ) | |||||||||||||||
| 27 | Найти точное значение | sin(0) | |||||||||||||||
| 28 | Найти точное значение | sin(120) | |||||||||||||||
| 29 | Найти точное значение | cos(90) | |||||||||||||||
| 30 | Преобразовать из радианов в градусы | pi/3 | |||||||||||||||
| 31 | Найти точное значение | tan(30) | |||||||||||||||
| 32 | Преобразовать из градусов в радианы | 45 | |||||||||||||||
| 33 | Найти точное значение | cos(45) | |||||||||||||||
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |||||||||||||||
| 35 | Преобразовать из радианов в градусы | pi/6 | |||||||||||||||
| 36 | Найти точное значение | cot(30 град. ) ) | |||||||||||||||
| 37 | Найти точное значение | arccos(-1) | |||||||||||||||
| 38 | Найти точное значение | arctan(0) | |||||||||||||||
| 39 | Найти точное значение | cot(60 град. ) | |||||||||||||||
| 40 | Преобразовать из градусов в радианы | 30 | |||||||||||||||
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |||||||||||||||
| 42 | Найти точное значение | sin((5pi)/3) | |||||||||||||||
| 43 | Найти точное значение | sin((3pi)/4) | |||||||||||||||
| 44 | Найти точное значение | tan(pi/2) | |||||||||||||||
| 45 | Найти точное значение | sin(300) | |||||||||||||||
| 46 | Найти точное значение | cos(30) | |||||||||||||||
| 47 | Найти точное значение | cos(60) | |||||||||||||||
| 48 | Найти точное значение | cos(0) | |||||||||||||||
| 49 | Найти точное значение | cos(135) | |||||||||||||||
| 50 | Найти точное значение | cos((5pi)/3) | |||||||||||||||
| 51 | Найти точное значение | cos(210) | |||||||||||||||
| 52 | Найти точное значение | sec(60 град. ) ) | |||||||||||||||
| 53 | Найти точное значение | sin(300 град. ) | |||||||||||||||
| 54 | Преобразовать из градусов в радианы | 135 | |||||||||||||||
| 55 | Преобразовать из градусов в радианы | 150 | |||||||||||||||
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |||||||||||||||
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |||||||||||||||
| 58 | Преобразовать из градусов в радианы | 89 град. | |||||||||||||||
| 59 | Преобразовать из градусов в радианы | 60 | |||||||||||||||
| 60 | Найти точное значение | sin(135 град. ) ) | |||||||||||||||
| 61 | Найти точное значение | sin(150) | |||||||||||||||
| 62 | Найти точное значение | sin(240 град. ) | |||||||||||||||
| 63 | Найти точное значение | cot(45 град. ) | |||||||||||||||
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |||||||||||||||
| 65 | Найти точное значение | sin(225) | |||||||||||||||
| 66 | Найти точное значение | sin(240) | |||||||||||||||
| 67 | Найти точное значение | cos(150 град. ) ) | |||||||||||||||
| 68 | Найти точное значение | tan(45) | |||||||||||||||
| 69 | Вычислить | sin(30 град. ) | |||||||||||||||
| 70 | Найти точное значение | sec(0) | |||||||||||||||
| 71 | Найти точное значение | cos((5pi)/6) | |||||||||||||||
| 72 | Найти точное значение | csc(30) | |||||||||||||||
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |||||||||||||||
| 74 | Найти точное значение | tan((5pi)/3) | |||||||||||||||
| 75 | Найти точное значение | tan(0) | |||||||||||||||
| 76 | Вычислить | sin(60 град. ) ) | |||||||||||||||
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |||||||||||||||
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |||||||||||||||
| 79 | Найти точное значение | sin((7pi)/4) | |||||||||||||||
| 80 | Найти точное значение | arcsin(-1/2) | |||||||||||||||
| 81 | Найти точное значение | sin((4pi)/3) | |||||||||||||||
| 82 | Найти точное значение | csc(45) | |||||||||||||||
| 83 | Упростить | arctan( квадратный корень 3) | |||||||||||||||
| 84 | Найти точное значение | sin(135) | |||||||||||||||
| 85 | Найти точное значение | sin(105) | |||||||||||||||
| 86 | Найти точное значение | sin(150 град. ) ) | |||||||||||||||
| 87 | Найти точное значение | sin((2pi)/3) | |||||||||||||||
| 88 | Найти точное значение | tan((2pi)/3) | |||||||||||||||
| 89 | Преобразовать из радианов в градусы | pi/4 | |||||||||||||||
| 90 | Найти точное значение | sin(pi/2) | |||||||||||||||
| 91 | Найти точное значение | sec(45) | |||||||||||||||
| 92 | Найти точное значение | cos((5pi)/4) | |||||||||||||||
| 93 | Найти точное значение | cos((7pi)/6) | |||||||||||||||
| 94 | Найти точное значение | arcsin(0) | |||||||||||||||
| 95 | Найти точное значение | sin(120 град.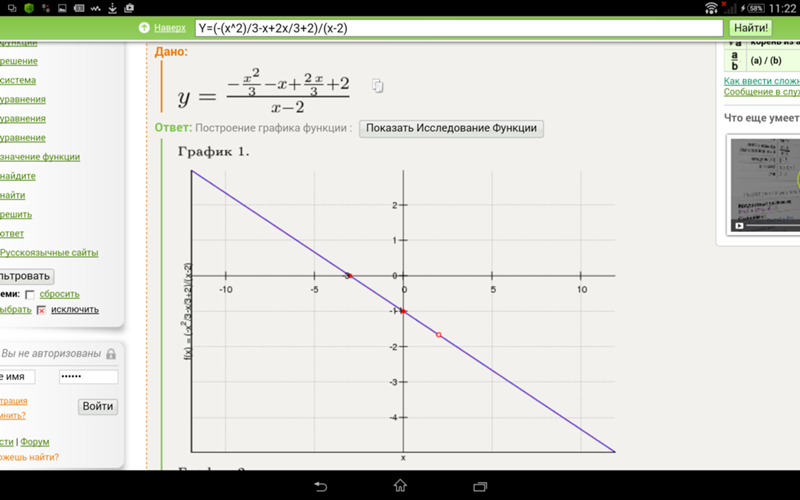 2 — x – 1 и построение графика. 2 — x – 1 и построение графика.Решение.
Ось Ох: при у = 0 нужно решить уравнение:
Преобразуем данное выражение, вынеся из двух первых слагаемых множитель х в квадрате, а из вторых двух слагаемых — минус:
Общий множитель выносим за скобки:
Решим полученное уравнение, разбив его на два более простых:
Получили две точки пересечения (—1; 0) и (1; 0).
Следовательно, функция не является ни четной, ни нечетной.
Найдем критические точки:
Рассмотрим поведение производной функции на трех полученных промежутках: Построение диаграммы «график»Давайте построим сначала график, он строится очень просто, практически в одно-два касания. Используем данные о курсе доллара за декабрь 2013 г. Таблица данных
Алгебра — Графические полиномыПоказать общее уведомление Показать мобильное уведомление Показать все заметки Скрыть все заметки Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST. Пол Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Раздел 5-3: Графические полиномы В этом разделе мы рассмотрим метод получения грубого наброска общего многочлена. В этом разделе мы либо дадим список нулей, либо их будет легко найти. В следующем разделе мы рассмотрим метод определения большой части списка для большинства многочленов. Сначала мы строим графики, поскольку метод нахождения всех нулей многочлена может быть немного длинным, и мы не хотим скрывать детали этого раздела в беспорядке нахождения нулей многочлена. Начнем с графика пары многочленов. Не беспокойтесь об уравнениях для этих многочленов. Мы приводим их только для того, чтобы мы могли использовать их для иллюстрации некоторых идей о многочленах. Во-первых, обратите внимание, что графики красивые и гладкие. На графике нет дыр или разрывов, и на графике нет острых углов. Графики многочленов всегда будут красивыми гладкими кривыми. Во-вторых, «неровности», на которых график меняет направление с увеличения на уменьшение или от уменьшения к увеличению, часто называют поворотными точками . Хотя это не сильно поможет с фактическим процессом построения графиков, это будет хорошей проверкой. Если у нас есть многочлен четвертой степени с 5 поворотными точками, мы будем знать, что сделали что-то не так, поскольку многочлен четвертой степени будет иметь не более трех поворотных точек. Затем нам нужно исследовать взаимосвязь между \ (x \) — перехватами графа многочлена и нулями многочлена.Напомним, что чтобы найти \ (x \) — точки пересечения функции, нам нужно решить уравнение \ [P \ left (x \ right) = 0 \] Также напомним, что \ (x = r \) является нулем многочлена \ (P \ left (x \ right) \) при условии \ (P \ left (r \ right) = 0 \). Но это означает, что \ (x = r \) также является решением \ (P \ left (x \ right) = 0 \). Другими словами, нули полинома также являются пересечениями графа размером x . Также обратите внимание на графики выше, что точки пересечения \ (x \) могут либо сгладиться, когда они пересекают ось \ (x \), либо они могут проходить через ось \ (x \) под углом. Следующий факт связывает все эти идеи с множественностью нуля. ФактЕсли \ (x = r \) является нулем многочлена \ (P \ left (x \ right) \) с кратностью \ (k \), то
Кроме того, если \ (k> 1 \), то график выровняется в точке \ (x = r \). Наконец, обратите внимание, что если мы позволяем \ (x \) увеличиваться как в положительном, так и в отрицательном смысле (, т. Мы не знаем, есть ли в полиноме какие-либо другие члены, но мы знаем, что первым членом должен быть тот, который указан в списке, поскольку он имеет степень \ (n \). Теперь у нас есть следующие факты о графике \ (P \ left (x \ right) \) на концах графа.
Хорошо, теперь, когда мы разобрались со всем этим, мы, наконец, можем дать процесс получения грубого наброска графика многочлена. Процесс построения многочлена
Мы должны быстро предупредить об этом процессе, прежде чем мы действительно попытаемся его использовать. Этот процесс предполагает, что все нули — действительные числа. Если есть какие-либо сложные нули, то этот процесс может упустить некоторые довольно важные особенности графика.2} — 20х — 40 \). Показать решение Мы нашли нули и кратности этого многочлена в предыдущем разделе, поэтому просто запишем их здесь для справки. \ [\ begin {align *} x & = — 1 & \ hspace {0,25 дюйма} & \ left ({{\ mbox {multiplicity 2}}} \ right) \\ x & = 2 & \ hspace {0,25 дюйма} & \ left ({{\ mbox {multiplicity 3}}} \ right) \ end {align *} \] Итак, из того факта, что мы знаем, что \ (x = — 1 \) просто коснется оси \ (x \), а не пересечет ее, и что \ (x = 2 \) пересечет \ (x \) -axis и будет плоской, так как кратность больше 1. Далее, точка пересечения \ (y \) — это \ (\ left ({0, — 40} \ right) \). Коэффициент при члене степени 5 -й степени положительный, и поскольку степень нечетная, мы знаем, что этот многочлен будет неограниченно увеличиваться на правом конце и неограниченно уменьшаться на левом конце. Наконец, нам просто нужно вычислить многочлен в нескольких точках.Пункты, которые мы выбираем, на самом деле не так уж и важны. Мы просто хотим выбрать точки в соответствии с указаниями в процессе, описанном выше, и точки, которые будет довольно легко оценить. Вот некоторые моменты. Мы предоставим вам возможность проверить оценки. \ [P \ left ({- 2} \ right) = — 320 \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} P \ left (1 \ right) = — 20 \ hspace {0,25 дюйма} \ hspace {0,25 дюйма } P \ left (3 \ right) = 80 \] Теперь, чтобы нарисовать график, мы начнем с левого конца и продвинемся к правому концу. Итак, по мере того, как мы перемещаемся вправо, функция фактически будет увеличиваться в точке \ (x = — 2 \), и мы будем продолжать увеличиваться, пока не достигнем первой точки пересечения x- в точке \ (x = — 1 \). На данный момент мы знаем, что график просто касается оси \ (x \), не пересекая ее, и при этом будет плоским.Это означает, что при \ (x = -1 \) график должен быть поворотной точкой. График теперь уменьшается по мере продвижения вправо. Опять же, это согласуется со следующей точкой, которую мы встретим, — точкой пересечения \ (y \). Теперь, согласно следующему пункту, который у нас есть, \ (x = 1 \), у графика должна быть другая поворотная точка где-то между \ (x = 0 \) и \ (x = 1 \), поскольку график выше при \ (x = 1 \), чем при \ (x = 0 \). Итак, движемся вправо и функция увеличивается. Следующая точка, в которую мы попадаем, — это точка пересечения \ (x \) в точке \ (x = 2 \), и эта точка пересекает ось \ (x \), поэтому мы знаем, что здесь не будет поворотной точки, как там. был на первом \ (x \) — перехвате. Кроме того, график будет плоским, поскольку он касается оси \ (x \), потому что кратность больше единицы. Таким образом, график будет продолжать увеличиваться через эту точку, на короткое время сглаживаясь при касании оси \ (x \), пока мы не достигнем последней точки, в которой мы оценили функцию в \ (x = 3 \). На этом этапе мы достигли всех точек пересечения \ (x \) — и знаем, что график будет неограниченно увеличиваться на правом конце, поэтому похоже, что все, что нам нужно сделать, это нарисовать увеличивающуюся кривую. Вот набросок многочлена. Обратите внимание, что одна из причин нанесения точек на концах — это увидеть, насколько быстро график увеличивается или уменьшается. Из оценок видно, что график убывает на левом конце намного быстрее, чем на правом конце.2} \ left ({x — 3} \ right) \ left ({x + 2} \ right) \] Вот список нулей и их кратностей. \ [\ begin {align *} x & = — 2 & \ hspace {0,25 дюйма} & \ left ({{\ mbox {multiplicity 1}}} \ right) \\ x & = 0 & \ hspace {0,25 дюйма} & \ left ({{\ mbox {multiplicity 2}}} \ right) \\ x & = 3 & \ hspace {0,25 дюйма} & \ left ({{\ mbox {multiplicity 1}}} \ right) \ end { выровнять*}\] Итак, нули в \ (x = — 2 \) и \ (x = 3 \) будут соответствовать \ (x \) — пересечениям, пересекающим ось \ (x \), поскольку их кратность нечетная и будет соответствовать так что под углом, поскольку их кратность НЕ меньше 2.Нуль в точке \ (x = 0 \) не будет пересекать ось \ (x \), поскольку его кратность четная, но будет плоской, когда он касается оси \ (x \), поскольку кратность больше единицы. Перехватчик \ (y \) — это \ (\ left ({0,0} \ right) \), и обратите внимание, что это также перехватчик \ (x \). Коэффициент при члене степени 4 -й степени положительный, и поэтому, поскольку степень четная, мы знаем, что многочлен будет неограниченно увеличиваться на обоих концах графика. Наконец, вот несколько оценок функций. \ [P \ left ({- 3} \ right) = 54 \ hspace {0,25 дюйма} P \ left ({- 1} \ right) = — 4 \ hspace {0,25in} P \ left (1 \ right) = — 6 \ hspace {0,25 дюйма} P \ left (4 \ right) = 96 \] Теперь, начиная с левого конца, мы знаем, что по мере того, как мы делаем \ (x \) все более и более отрицательным, функция должна неограниченно возрастать. Это означает, что по мере продвижения вправо график фактически будет уменьшаться. В \ (x = — 3 \) график будет уменьшаться и продолжит уменьшаться, когда мы коснемся первого \ (x \) — точки пересечения в \ (x = — 2 \), поскольку мы знаем, что это \ (x \ ) -перехват пересечет ось \ (x \) -. Далее, поскольку следующий \ (x \) — точка пересечения находится в точке \ (x = 0 \), мы должны где-то иметь точку поворота, чтобы график мог увеличиваться обратно до этого \ (x \) — точки пересечения. Опять же, мы не будем беспокоиться о том, где на самом деле находится этот поворотный момент. Как только мы достигли точки пересечения \ (x \) в точке \ (x = 0 \), мы знаем, что у нас должна быть точка поворота, поскольку эта точка пересечения \ (x \) не пересекает \ (x \ )-ось. Следовательно, справа от \ (x = 0 \) график теперь будет убывать. Напомним, однако, что, поскольку кратность больше единицы, она будет плоской, поскольку касается оси \ (x \). Он будет продолжать уменьшаться до тех пор, пока не достигнет другой поворотной точки (в какой-то неизвестной точке), так что график может вернуться к оси \ (x \) для следующего \ (x \) — точки пересечения в \ (x = 3 \).3} \ left ({x — 2} \ right) \ left ({x + 2} \ right) \] Обратите внимание, что мы сначала разложили знак минус, чтобы упростить остальную часть факторинга. Вот список всех нулей и их кратностей. \ [\ begin {align *} x & = — 2 & \ hspace {0,25 дюйма} & \ left ({{\ mbox {multiplicity 1}}} \ right) \\ x & = 0 & \ hspace {0,25 дюйма} & \ left ({{\ mbox {multiplicity 3}}} \ right) \\ x & = 2 & \ hspace {0.25 дюймов} & \ left ({{\ mbox {multiplicity 1}}} \ right) \ end {align *} \] Итак, все три нуля соответствуют \ (x \) — точкам пересечения, которые фактически пересекают ось \ (x \), поскольку все их кратности нечетны, однако только \ (x \) — точка пересечения в \ (x = 0 \) будет пересекать ось \ (x \) в плоском виде. Перехватчик \ (y \) — это \ (\ left ({0,0} \ right) \), и, как и в предыдущем примере, это также перехватчик \ (x \). В этом случае коэффициент при члене степени 5 -й отрицателен, и поэтому, поскольку степень нечетная, график будет неограниченно увеличиваться с левой стороны и неограниченно уменьшаться с правой стороны. Вот некоторые оценки функций. \ [P \ left ({- 3} \ right) = 135 \ hspace {0.25in} \, \, \, P \ left ({- 1} \ right) = — 3 \ hspace {0.25in} \, \ , \, \, \, P \ left (1 \ right) = 3 \ hspace {0,25 дюйма} P \ left (3 \ right) = — 135 \] Хорошо, этот график начнется так же, как и предыдущий. На левом конце график будет уменьшаться по мере продвижения вправо и будет уменьшаться через первую \ (x \) — точку пересечения в \ (x = — 2 \), поскольку известно, что эта \ (x \) — точка пересечения пересекает точку \ (x \) — ось. Теперь в какой-то момент мы получим поворотную точку, чтобы график мог вернуться к следующему \ (x \) — пересечению в \ (x = 0 \), и график продолжит увеличиваться через эту точку, поскольку он также пересекает ось \ (x \). Также обратите внимание, что в этой точке график должен быть плоским, поскольку кратность больше единицы. Наконец, график достигнет другой поворотной точки и начнет уменьшаться, так что он может вернуться к конечной точке пересечения \ (x \) в точке \ (x = 2 \).Поскольку мы знаем, что график будет неограниченно убывать на этом конце, мы закончили. Вот набросок этого многочлена. Процесс, который мы использовали в этих примерах, может быть трудным для освоения. Нужно время, чтобы научиться правильно интерпретировать результаты. Кроме того, как указывалось в различных местах, есть несколько ситуаций, с которыми мы не сможем справиться здесь.Чтобы найти большинство поворотных моментов, нам понадобится некоторый расчет, которого у нас явно нет. Кроме того, этот процесс требует, чтобы у нас были все нули и все они были действительными числами. Однако даже с этими недостатками процесс может, по крайней мере, дать нам представление о том, как будет выглядеть график многочлена. График на числовой прямойПостроение графика на числовой прямойЦелые и действительные числа могут быть представлены в числовой строке . Точка на этой линии, связанная с каждым числом, называется графиком числа. Обратите внимание, что числовые линии расположены одинаково или пропорционально (см. Рисунок 1). Рисунок 1. Числовые линии. График неравенствПри построении графиков неравенств, содержащих только целые числа, используются точки. Пример 1Изобразите набор x таким образом, чтобы 1 ≤ x ≤ 4 и x было целым числом (см. Рисунок 2). { x : 1 ≤ x ≤ 4, x — целое число} Рис. 2. График {x: 1 ≤ x ≤ 4, x является целым числом}. Когда графических неравенств, включающих действительные числа, используются линий, лучей и точек. Если номер включен, используется точка. Пустая точка используется, если номер не указан. Пример 2График, как показано (см. Рисунок 3).
Этот луч часто называют открытым лучом или полупрямой . Пустая точка отличает открытый луч от луча. Рис. 3. График { x : x ≥ 1}. Рис. 4. График { x : x > 1} Рис. 5. График { x : x <4} ИнтервалыИнтервал состоит из всех чисел, лежащих в двух определенных границах. Если включены две границы или фиксированные числа, то интервал называется закрытым интервалом . Если фиксированные числа не включены, то интервал называется открытым интервалом . Пример 3График.
Рис. 6. График, показывающий закрытый интервал { x : –1 ≤ x ≤ 2}. Рис. 7. График, показывающий открытый интервал { x : –2 < x <2}. Если интервал включает только одну из границ, то он называется полуоткрытым интервалом . Пример 4Постройте график полуоткрытого интервала (см. Рисунок 8). { x : –1 < x ≤ 2} Рис. 8. График, показывающий полуоткрытый интервал { x : –1 < x ≤ 2}. Графики неравенствЭтот урок научит вас построению графиков неравенств. Это может помочь напомнить вам, что такое неравенство, прежде чем показывать, как его построить. Например, утверждения x> 6 и x ≤ -5 являются примерами неравенств. Графическое изображение неравенств на пяти тщательно отобранных примерахExample # 1 Graph x> 2 Нарисуйте незатененный или открытый круг в точке 2 и закрасьте все справа от 2. Заштрихованная красным область — ваше решение. Это означает, что решением может быть любое число справа от 2. Обратите внимание, что 2 не закрашено, потому что 2 не включено в ваше решение. Также обратите внимание, что хотя последняя цифра в числовой строке — 9, ваше решение не ограничивается цифрой 9. Любое другое число больше 9 — это решение. Example # 2 Graph x Нарисуйте открытый круг с -3 и закрасьте все слева от -3.Обратите внимание, что -3 не закрашивается, потому что -3 не входит в ваше решение. Еще раз обратите внимание, что хотя последнее число в числовой строке -9, ваше решение не останавливается на -9. Пример # 3 График x ≥ 6 Нарисуйте закрашенный круг в точке 6, а затем закрасьте все, что находится справа от 6. Пример № 4 График x ≤ -1 Нарисуйте закрашенный круг в точке -1, а затем закрасьте все, что находится слева от -1.Еще раз обратите внимание, что круг закрашен, потому что x также равен -1. Пример № 5 График x ≠ 2 x ≠ 2 означает, что x равно любому числу, кроме 2. Нарисуйте круг на 2 и закрасьте все справа и слева от 2. Вы также можете записать x ≠ 2 как x> 2 или x <2. Обратите внимание на использование слова «или» вместо «и».Мы не могли использовать «и», потому что x не может быть больше 2 и меньше 2 одновременно.
поверхностей, часть 2поверхностей, часть 2 Поверхности и контурные графики Часть 2: Квадрические поверхности Квадрические поверхности — это графики квадратных уравнений с тремя декартовыми переменными. Сферы и эллипсоиды Сфера — это график
Параболоиды Поверхности, пересекающиеся с
Поверхность на следующем рисунке представляет собой график z = x 2 — y 2 .В этом случае пересечения с плоскостями, перпендикулярными к x- и
Гиперболоиды Гиперболоиды поверхности Эта поверхность называется гиперболоидом .
Другой тип — гиперболоид
|

 2.
2. к. тут еще много чего можно дорабатывать. Если вы хотите, чтобы график был у вас на листе, т.е., рядом с данными, то можно оставить так. Но я поменяю расположение листа. Правой кнопкой мыши тыкаем на диаграмму и выбираем «Переместить диаграмму».
к. тут еще много чего можно дорабатывать. Если вы хотите, чтобы график был у вас на листе, т.е., рядом с данными, то можно оставить так. Но я поменяю расположение листа. Правой кнопкой мыши тыкаем на диаграмму и выбираем «Переместить диаграмму». 2
2
 Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.
Будем надеяться, что единственное неудобство будет заключаться в периодическом «потерянном / разорванном» соединении, которое следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех. Единственная реальная информация, которая нам понадобится, — это полный список всех нулей (включая кратность) многочлена.
Единственная реальная информация, которая нам понадобится, — это полный список всех нулей (включая кратность) многочлена. Если мы знаем, что многочлен имеет степень \ (n \), тогда мы будем знать, что на графике будет не более \ (n — 1 \) точек поворота.
Если мы знаем, что многочлен имеет степень \ (n \), тогда мы будем знать, что на графике будет не более \ (n — 1 \) точек поворота.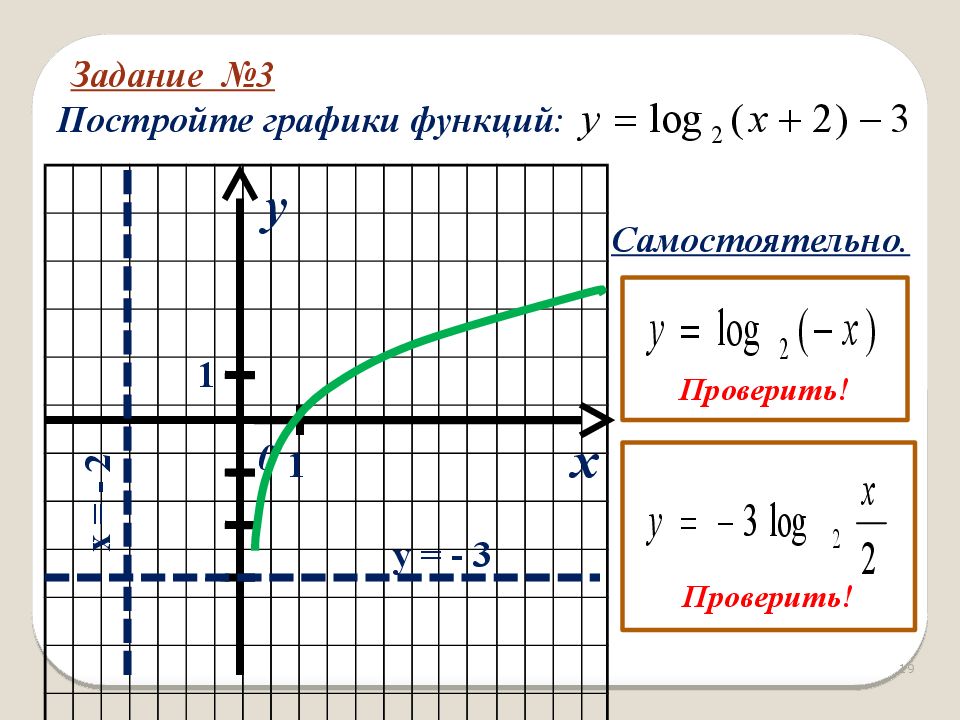 Также помните, что точки пересечения \ (x \) могут либо пересекать ось \ (x \), либо они могут просто касаться оси \ (x \), не пересекая ось.
Также помните, что точки пересечения \ (x \) могут либо пересекать ось \ (x \), либо они могут просто касаться оси \ (x \), не пересекая ось. е. на любом конце графика), то график будет либо неограниченно увеличиваться, либо уменьшаться без ограничений.n} + \ cdots \]
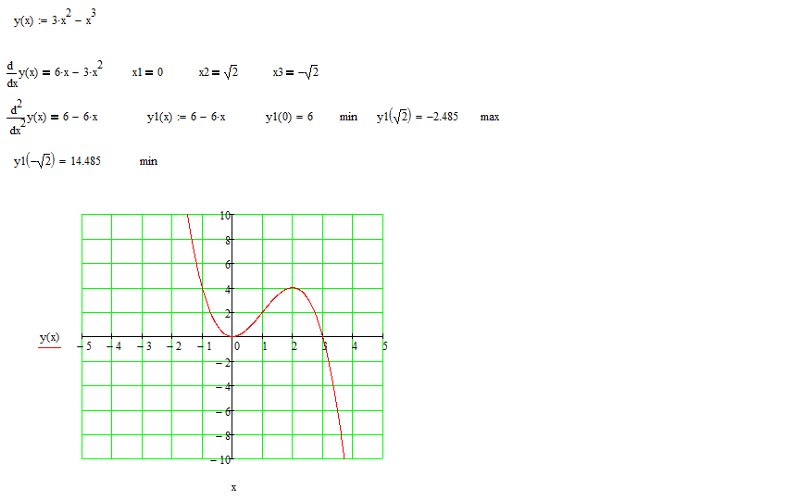
е. на любом конце графика), то график будет либо неограниченно увеличиваться, либо уменьшаться без ограничений.n} + \ cdots \] Хорошим примером этого является график — x 2 .
Хорошим примером этого является график — x 2 .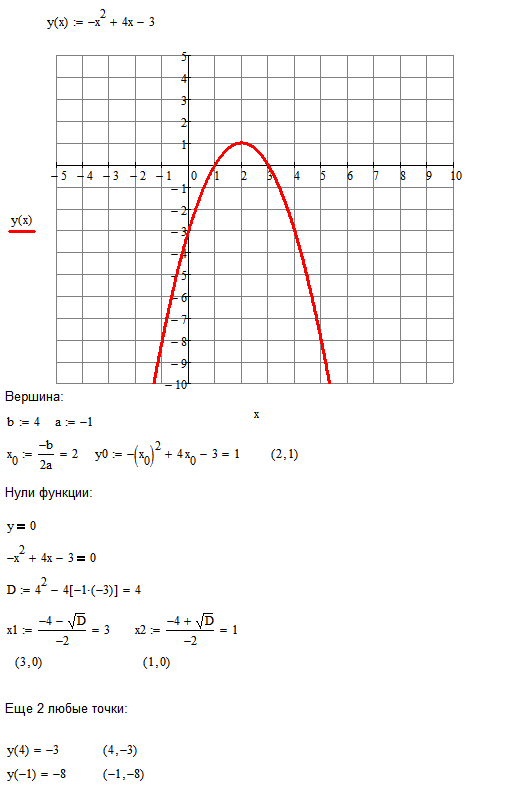
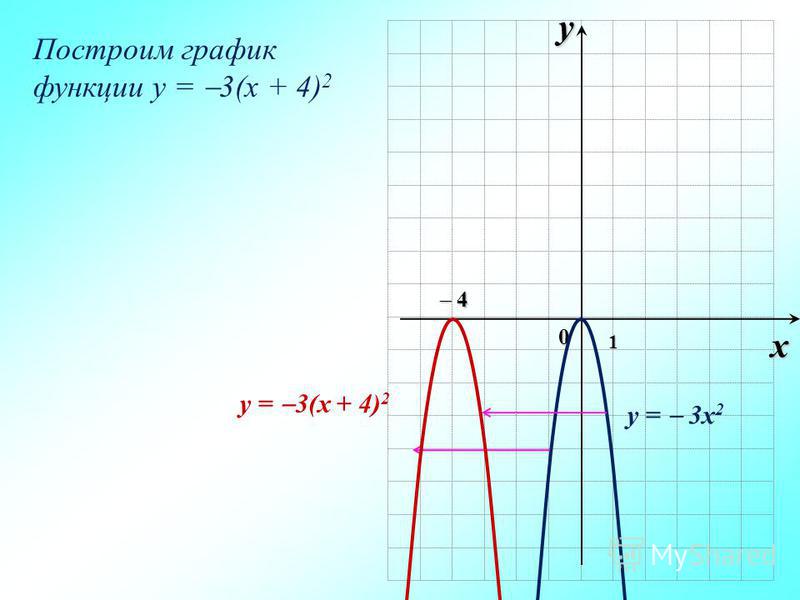 Кроме того, оба будут плоскими, поскольку они пересекают ось \ (x \), поскольку кратность для обоих больше 1.
Кроме того, оба будут плоскими, поскольку они пересекают ось \ (x \), поскольку кратность для обоих больше 1. Во-первых, мы знаем, что на левом конце график неограниченно уменьшается по мере того, как мы делаем \ (x \) все более и более отрицательным , и это согласуется с точкой, которую мы оценили как \ (x = — 2 \).
Во-первых, мы знаем, что на левом конце график неограниченно уменьшается по мере того, как мы делаем \ (x \) все более и более отрицательным , и это согласуется с точкой, которую мы оценили как \ (x = — 2 \). На этом уровне очень сложно определить, где именно произойдет этот поворотный момент, поэтому нам не нужно беспокоиться о попытках его найти.Фактически, определение этой точки обычно требует некоторого математического анализа.
На этом уровне очень сложно определить, где именно произойдет этот поворотный момент, поэтому нам не нужно беспокоиться о попытках его найти.Фактически, определение этой точки обычно требует некоторого математического анализа.