Содержание
Постройте график функции y = |-2
Задание.
Постройте график функции y = |-2 – |x + 5||.
Решение.
Страшная на первый взгляд функция на самом деле строиться не так уж сложно.
Чтобы разобраться в ее построении вспомним, что представляет собой модуль. Как известно из алгебры, модулем любого числа (то ли оно положительное, то ли отрицательное) всегда будет положительное число. Также модуль называют расстоянием, а как известно, расстояние не может быть отрицательным – это всегда положительное число.
Под знаком модуля в заданной функции стоит сумма неизвестного числа х и числа 5, которая может быть как положительной, так и отрицательной. Поэтому для построения графика этой функции нужно рассмотреть обе возможности.
Пусть сумма (х + 5) будет положительным числом. Тогда, при открытии знака модуля, функция примет следующий вид:
y = |–2 – |x + 5|| = |-2 – x – 5| = |– x – 7|
Здесь также возможны два варианта:
1) –х – 7 – положительное, тогда у = –х – 7
2) –х – 7 – отрицательное, тогда у = х + 7
Таким образом, при х > –5:
1) –х – 7 > 0
При x < –7 функция существовать не будет
2) –х – 7 < 0
При x > –7 функция будет существовать для х > –5, а тогда:
у (–4) = –4 + 7 = 3 – точка (–4; 3)
у (0) = 0 + 7 = 7 – точка (0; 7)
Пусть сумма (х + 5) будет отрицательным числом. Тогда, открыв знак модуля, получим:
Тогда, открыв знак модуля, получим:
y = |–2 – |x + 5|| = |-2 + x + 5| = |x + 3|
Здесь также возможны два варианта:
1) х + 3 – положительное, тогда у = х + 3
2) х + 3 – отрицательное, тогда у = – х – 3
Таким образом, при х < –5:
3) х + 3 > 0
При x > –3 функция у = х + 3 существовать не будет
4) х + 3 < 0
При x < –3 функция будет существовать для х < –5. Тогда:
у (–6) = –(–6) – 3 = 3 – точка (–6; 3)
у (–10) = –(–10) – 3 = 7 – точка (–10; 7)
Нанесем полученные точки на плоскость.
График кусочно заданной функции | Алгебра
Построить график кусочно заданной функции — один из видов задания 23 из ОГЭ по математике.
Рассмотрим примеры построения таких графиков.
1) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
Область определения функции D(y): x∈R.
График данной функции состоит из трёх частей.
Значения x=3 и x=4 разбивают числовую прямую на три промежутка, на каждом из которых рассмотрим отдельную функцию.
Соответственно, прямые x=3 и x=4 разбивают координатную плоскость на три области.
Каждый из графиков строится в своей области и не должен выходить за её пределы.
Чтобы не нарушить это правило, можно прямые x=3 и x=4 (прямые, параллельные оси Oy) выделить на черновике тонкой линией либо пунктиром. В чистовой вариант, разумеется, их переносить не нужно.
Итак, рассмотрим на трёх промежутках три различные функции.
1) Если x<4, y=2x-2.
y=2x-2 — линейная функция. Графиком линейной функции является прямая. Для построения прямой достаточно взять две точки.
При x=0 y=2·0-2=-2, получили точку (0;-2).
При x=2 y=2·2-2=2, получили точку (2;2).
Обычно для построения графика оформляют таблицу:
Значения x можно брать, вообще говоря, любые. Главное, не забыть, что данная прямая не должна выходить правее x=3. Поэтому всё же лучше выбирать x, удовлетворяющие условию x<3.
Главное, не забыть, что данная прямая не должна выходить правее x=3. Поэтому всё же лучше выбирать x, удовлетворяющие условию x<3.
2) Если 3≤x≤4, y=-3x+13.
y=-3x+13 — линейная функция. График — прямая. Для построения прямой берём две точки.
3) Если x>4, y=1,5x-5.
y=1,5x-5 — линейная функция. График — прямая. для построения прямой берём две точки.
Отметим каждую пару точек и проведём через них прямые, не забывая об ограничениях.
Получим график, состоящий их двух лучей и одного отрезка:
Прямая y=m имеет с графиком ровно две общие точки, если она проходит через точки соединения двух частей графика, то есть при m=1 и m=4:
Ответ: 1; 4.
2) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Если x≥4, y=x²-10x+27.
y=x²-10x+27 — квадратичная функция.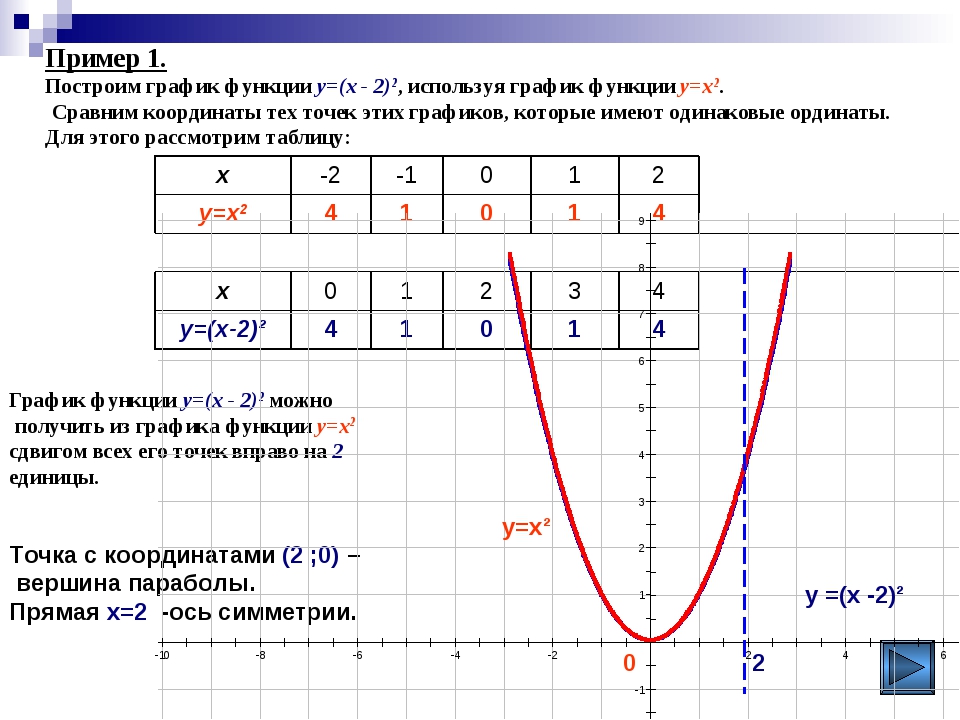 Её график — парабола, ветви которой направлены вверх (так как a=1>0).
Её график — парабола, ветви которой направлены вверх (так как a=1>0).
Ищем координаты вершины параболы.
Таким образом, (5;2) — вершина параболы.
Так как a=1, от вершины строим параболу y=x².
(Другой вариант — переписать правую часть формулы в виде y=(x²-10x+25)+2=(x-5)²+2 и построить график параллельным переносом графика y=x² на 5 единиц вправо вдоль оси Ox и на 2 единицы вверх вдоль оси Oy).
2) Если x<4, y=x-1.
y=x-1 — линейная функция. График — прямая. Для построения прямой берём две точки:
Хотя на x наложено условие x<4, для построения прямой можно брать любые значение. Главное — не забыть, что правее x=4 прямая не должна выходить.
Итак, график данной функции состоит из двух частей. Прямая x=4 разделяет плоскость на две полуплоскости. Справа от неё расположена часть параболы с вершиной в точке (5;2), слева — прямая:
Прямая y=m имеет с графиком ровно две общие точки, если она проходит через вершину параболы и через точку соединения параболы и прямой, то есть при m=2 и m=3:
Ответ: 2; 3.
3) Построить график функции
и определить, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Если x≥-3, y=x²+4x+4.
y=x²+4x+4 — квадратичная функция. График — парабола ветвями вверх. Можно найти координаты вершины параболы и от вершины построить график функции y=x².
(Если заметить в правой части формулу квадрата суммы и переписать формулу функции y=(x+4)², то можно построить параболу параллельным переносом параболы y=x² на 4 единицы влево вдоль оси Ox).
2) Если x<-3,
— функция обратной пропорциональности. График — гипербола. Для построения гиперболы нужно взять несколько точек:
Таким образом, график данной функции состоит из двух частей. Справа от прямой x=-3 строим параболу с вершиной в точке (-2;0), слева — ветвь гиперболы:
Прямая y=m имеет с графиком одну или две общие точки при m=0 и m≥1:
Ответ: m=0 и m∈[1;∞).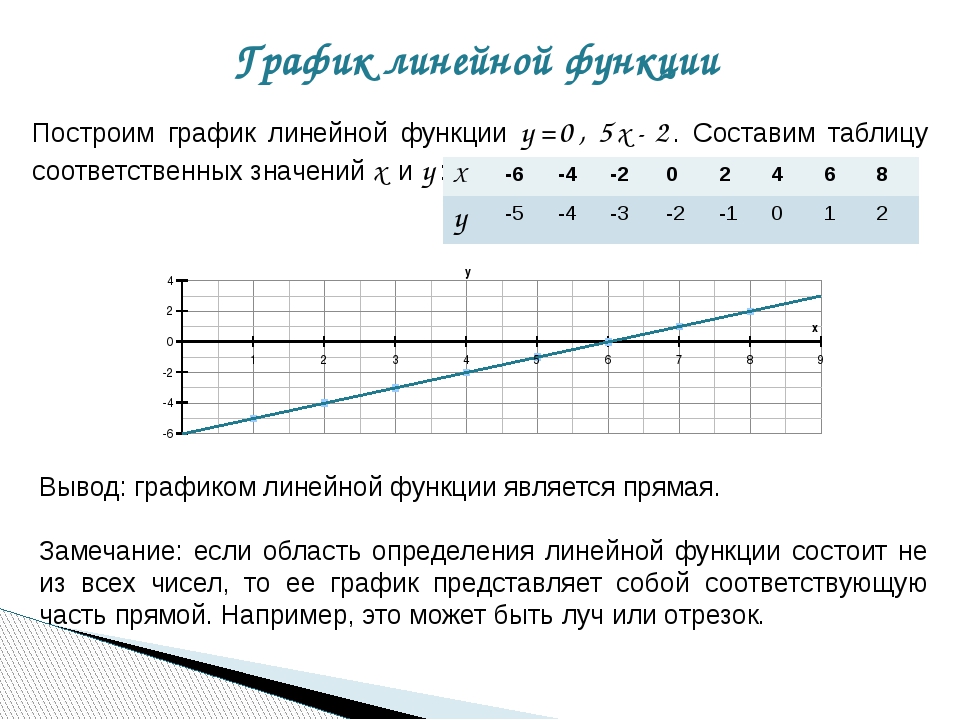
А-7 Контрольная работа №6 по теме «Функции». Вариант 1. Функция задана формулой y = -3x + 1. Определите: значение функции, если значение аргумента равно 4; значение аргумента, при котором значение функции равно -5; проходит ли график функции через точку А(-2; 7). Постройте график функции y = 2x – 5. Пользуясь графиком, найдите: значение функции, если значение аргумента равно 3; значение аргумента, при котором значение функции равно -1. Не выполняя построения, найдите координаты точек пересечения графика функции y = -0,6x+ 3 с осями координат. При каком значении k график функции y = kx+ 5 проходит через точку D(6; -19)? х, если х 3; Постройте график функции y = 1, если х 3. | А-7 Контрольная работа №6 по теме «Функции». Вариант 2. Функция задана формулой y = -2x + 3. Определите: значение функции, если значение аргумента равно 3; значение аргумента, при котором значение функции равно 5; проходит ли график функции через точку В(-1; 5). Постройте график функции y = 5x – 4. Пользуясь графиком, найдите: значение функции, если значение аргумента равно 1; значение аргумента, при котором значение функции равно 6. Не выполняя построения, найдите координаты точек пересечения графика функции y = 0,2x — 10 с осями координат. При каком значении k график функции y = kx — 15 проходит через точку С(-2; -3)? х, если х 4; Постройте график функции y = 2, если х 4. | А-7 Контрольная работа №6 по теме «Функции». Вариант 3. 1. Функция задана формулой y = 4x — 7. Определите: значение функции, если значение аргумента равно -3; значение аргумента, при котором значение функции равно 9; проходит ли график функции через точку С(2; 1). Постройте график функции y = -3x + 2. Пользуясь графиком, найдите: значение функции, если значение аргумента равно 2; значение аргумента, при котором значение функции равно 5. Не выполняя построения, найдите координаты точек пересечения графика функции y = -0,7x+ 14 с осями координат. При каком значении k график функции y = kx — 8 проходит через точку В(-2; -18)? , если х -6; Постройте график функции y = х, если х -6. | А-7 Контрольная работа №6 по теме «Функции». Вариант 4. 1. Функция задана формулой y = 6x — 5. Определите: значение функции, если значение аргумента равно -2; значение аргумента, при котором значение функции равно 13; проходит ли график функции через точку А(-1; -11). Постройте график функции y = 4x — 3. Пользуясь графиком, найдите: значение функции, если значение аргумента равно 1; значение аргумента, при котором значение функции равно -7. Не выполняя построения, найдите координаты точек пересечения графика функции y = -0,4x+ 2 с осями координат. При каком значении k график функции y = kx + 4 проходит через точку А(-3; -17)? 1, если х 5; Постройте график функции y = 0,2х, если х 5. |
постройте график функции y 2 5 x
Вы искали постройте график функции y 2 5 x? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и постройте график функции y 2 5x, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «постройте график функции y 2 5 x».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как постройте график функции y 2 5 x,постройте график функции y 2 5x. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и постройте график функции y 2 5 x. Просто введите задачу в окошко и нажмите
«решить» здесь (например, постройте график функции y 2 5 x).
Где можно решить любую задачу по математике, а так же постройте график функции y 2 5 x Онлайн?
Решить задачу постройте график функции y 2 5 x вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Урок 20. построение графиков функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №20.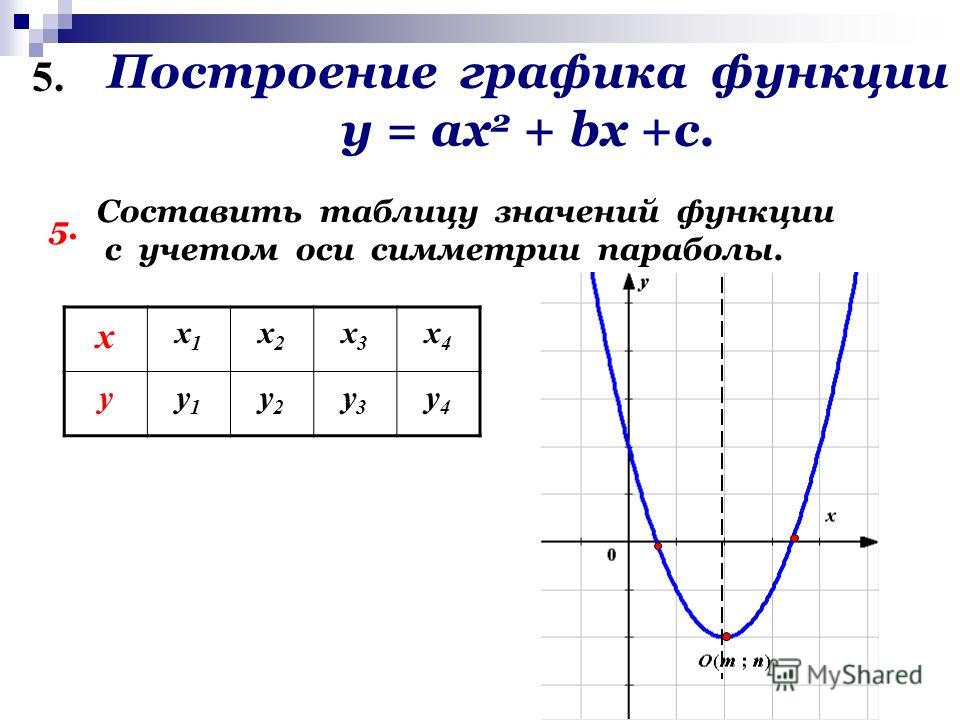 Построение графиков функций.
Построение графиков функций.
Перечень вопросов, рассматриваемых в теме
- Исследование функций;
- Построение графиков функций;
- Применение производной для решения графических задач.
Глоссарий по теме
Асимптота графика функции y = f(x) – прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1и х2, из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Выпуклость вверх. Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка.
Выпуклость вниз. Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.
Максимум функции. Значение функции в точке максимума называют максимумом функции.
Минимум функции. Значение функции в точке минимума называют минимумом функции.
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Производная второго порядка (вторая производная). Производная второго порядка есть первая производная от производной первого порядка.
Производную определяют, как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к 0, если такой предел существует.
Точка максимума функции. Точку х0называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство .
Точка перегиба.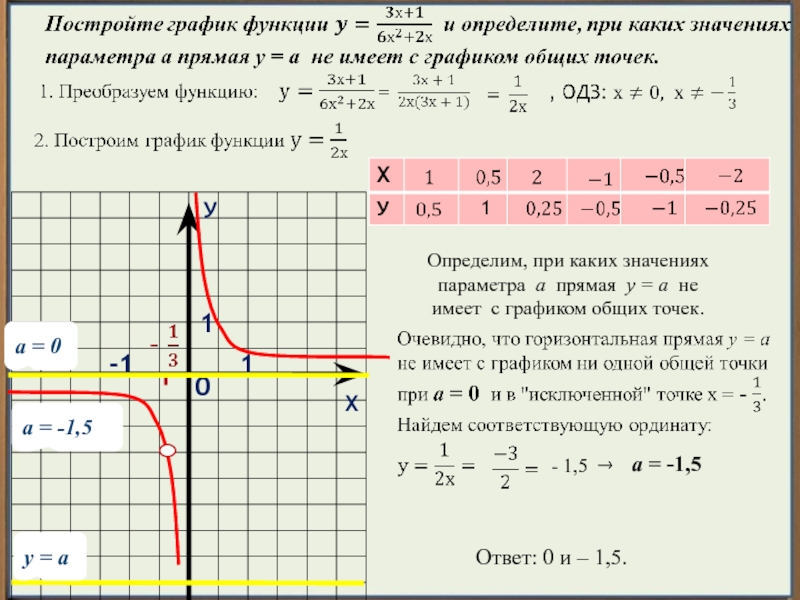 Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.
Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y=f(x) убывает на интервале X, если для любых х1 и х2 , из этого промежутка выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.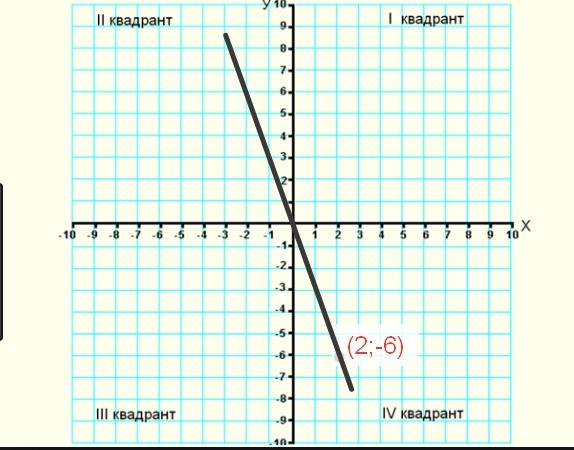
Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит вышепроведенного отрезка.
Полная схема построения графика функции:
- Найти область определения функции D(f).
- Исследовать функцию на четность (найти f(-x)).
- Найти асимптоты.
- Найти стационарные и критические точки.
- Найти промежутки монотонности.
- Найти интервалы выпуклости вверх и выпуклости вниз.
- Найти точки перегиба
- Составить таблицу значений функции для некоторых точек.
- По полученным данным построить график функции.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Постройте график функции у = х3 – 3х + 3, используя краткую схему построения. схему построения.
Решение:
1) D(y) = (-∞; +∞)
2) Функция не является ни четной, ни нечетной, т. к.
3) Асимптот нет
4) f’(x) = 3x2 – 3, f’(x) = 0 при х = 1, х = -1.
х = 1, х = -1 – стационарные точки.
5) f’(x)>0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки возрастания.
f’(x)<0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки убывания.
6) Так как в точке х = -1 производная меняет знак с «+» на «-», то х = -1 – точка максимума.
Так как в точке х = 1 производная меняет знак с «-» на «+», то х = 1 – точка минимума.
7) Результаты исследования представим в виде таблицы.
x | (-∞; -1) | -1 | (-1; 1) | 1 | (1; +∞) |
f’(x) | + | 0 | — | 0 | + |
f(x) | 5 | 1 | |||
max | min |
8) Координаты некоторых точек:
9) По полученным данным строим график (рис.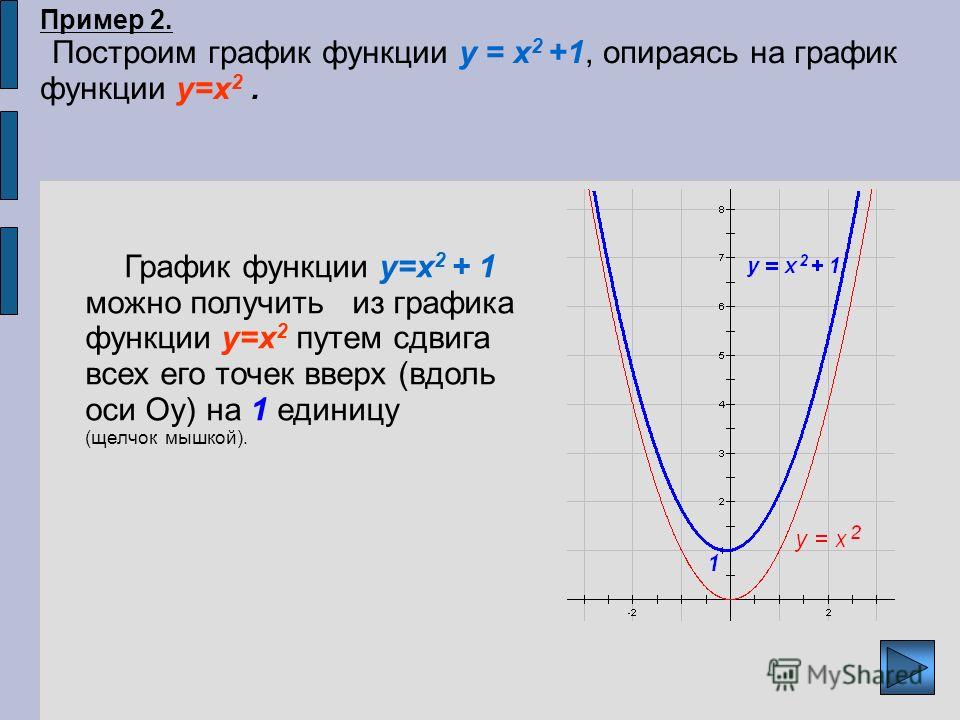 1)
1)
Рисунок 1 – график функции у = х3 – 3х + 3
Пример 2. Постройте график функции, используя подробную схему построения. схему построения.
Решение:
1)
2) Функция не является ни четной, ни нечетной, т. к.
3) х = 1 – вертикальная асимптота
4) , f’(x) = 0 при х = 2, х = 0.
х = 2, х = 0 – стационарные точки.
5) f’(x)>0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки возрастания.
f’(x)<0 при . Так как в точках х = 0, х = 2 функция непрерывна, то эти точки также включаются в промежутки убывания.
Так как в точке х = 0 производная меняет знак с «+» на «-», то х = 0 – точка максимума.
Так как в точке х = 2 производная меняет знак с «-» на «+», то х = 2 – точка минимума.
х = 1 – не является точкой экстремума
6) Найдем интервалы выпуклости функции.
; при функция выпукла вверх.
; при функция выпукла вниз.
7) Результаты исследования представим в виде таблицы.
x | (-∞; 0) | 0 | (0; 1) | 1 | (1; 2) | 2 | (2; +∞) |
f’(x) | + | 0 | — | Не сущ. | — | 0 | + |
f’’(x) | — | — | Не сущ. | + | + | ||
f(x) | -4 | Не сущ. | 0 | ||||
max | min |
8) Координаты некоторых точек:
x | -1 | 0,5 | 1,5 | 3 |
f(x) | -4,5 | -4,5 | 0,5 | 0,5 |
9) По полученным данным строим график (рис. 2)
2)
Рисунок 2 – график функции
Квадратичная функция, как построить Параболу
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.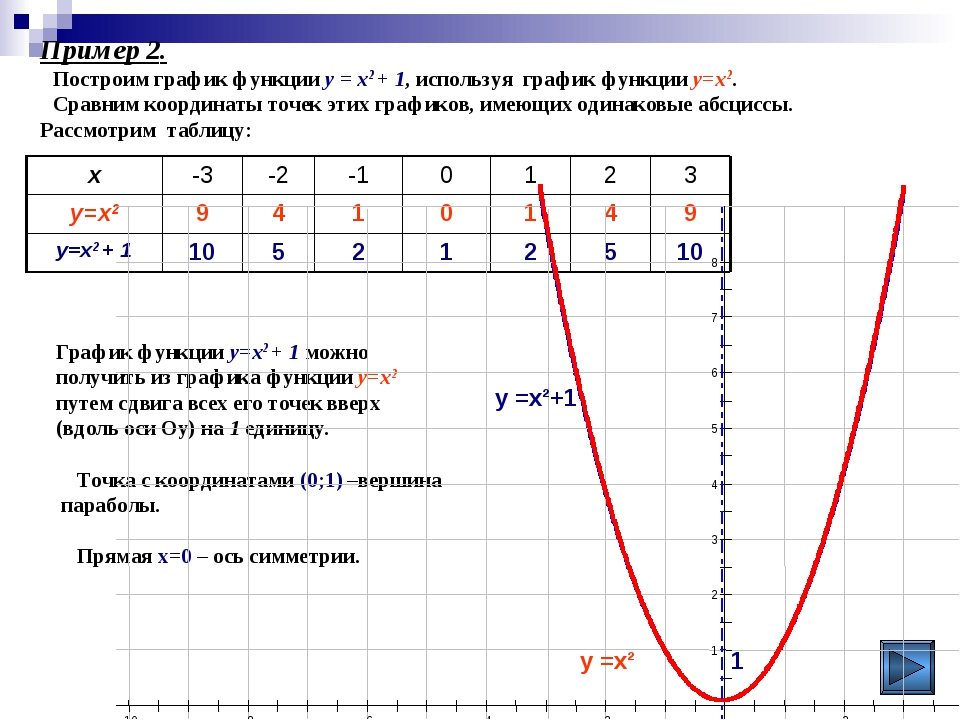
Построение квадратичной функции
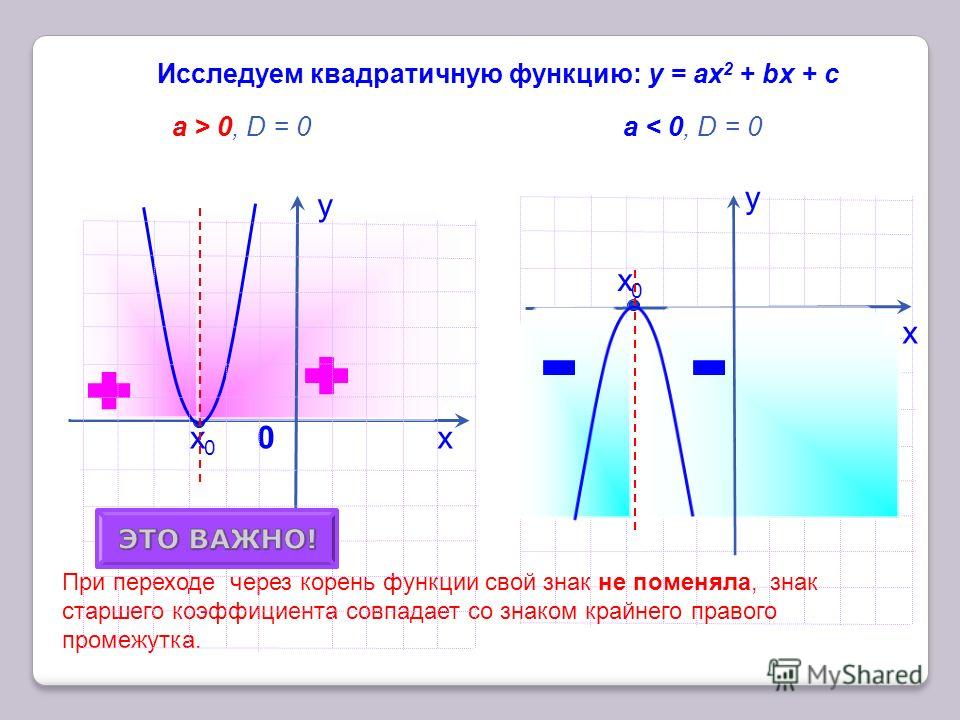
Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
|
График квадратичной функции — парабола, которая имеет следующий вид для y = x2:
Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:
x | -2 | -1 | 0 | 1 | 2 |
y | 4 | 1 | 0 | 1 | 4 |
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов.
График функции y = –x2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x | -2 | -1 | 0 | 1 | 2 |
y | -4 | -1 | 0 | -1 | -4 |
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.
Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.
На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.
Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.
Для наглядности возьмем функцию y = ax2 + bx + c, для построения которой нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax
2 + bx + c.
Разберем общий алгоритм на примере y = 2x2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x2 + 3x — 5.
D = b2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
√D = 7
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x2 + 3x — 5 = 0
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
- Нанести эти точки на координатную плоскость и построить график параболы:
Уравнение квадратичной функции имеет вид y = a * (x — x₀)
2 + y₀
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x — 1)2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить y = x2,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
- Построить график параболы для каждого случая.
Уравнение квадратичной функции имеет вид y = (x + a) * (x + b)
Рассмотрим следующий пример: y = (x — 2) * (x + 1).
Как строим:
- Данный вид уравнения позволяет быстро найти нули функции:
(x — 2) * (x + 1) = 0, отсюда х₁ = 2, х₂ = -1.
- Определим координаты вершины параболы:
- Найти точку пересечения с осью OY:
с = ab =(-2) * (1)= -2 и ей симметричная.
- Отметим эти точки на координатной плоскости и соединим плавной прямой.
11.3.1. Показательная функция, ее свойства и график.
Автор Татьяна Андрющенко На чтение 5 мин. Просмотров 7.6k. Опубликовано
data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»8834522701″
data-ad-format=»auto»>
- Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией.
- Область определения показательной функции: D (y)=R – множество всех действительных чисел.
- Область значений показательной функции: E (y)=R+ — множество всех положительных чисел.
- Показательная функция y=ax возрастает при a>1.
- Показательная функция y=ax убывает при 0<a<1.

Справедливы все свойства степенной функции:
- а0=1 Любое число (кроме нуля) в нулевой степени равно единице.
- а1=а Любое число в первой степени равно самому себе.
- ax∙ay=ax+y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
- ax:ay=ax- y При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
- (ax)y=axy При возведении степени в степень основание оставляют прежним, а показатели перемножают
- (a∙b)x=ax∙by При возведении произведения в степень возводят в эту степень каждый из множителей.

- (a/b)x=ax/by При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
- а-х=1/ax
- (a/b)-x=(b/a)x.
Примеры.
1) Построить график функции y=2x. Найдем значения функции
при х=0, х=±1, х=±2, х=±3.
x=0, y=20=1; Точка А.
x=1, y=21=2; Точка В.
x=2, y=22=4; Точка С.
x=3, y=23=8; Точка D.
x=-1, y=2-1=1/2=0,5; Точка K.
x=-2, y=2-2=1/4=0,25; Точка M.
x=-3, y=2-3=1/8=0,125; Точка N.
Большему значению аргумента х соответствует и большее значение функции у. Функция y=2x возрастает на всей области определения D (y)=R, так как основание функции 2>1.
2) Построить график функции y=(1/2)x. Найдем значения функции
при х=0, х=±1, х=±2, х=±3.
x=0, y=(½)0=1; Точка A.
x=1, y=(½)1=½=0,5; Точка B.
x=2, y=(½)2=¼=0,25; Точка C.
x=3, y=(½)3=1/8=0,125; Точка D.
x=-1, y=(½)-1=21=2; Точка K.
x=-2, y=(½)-2=22=4; Точка M.
x=-3, y=(½)-3=23=8; Точка N.
Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(1/2)x убывает на всей своей области определения: D (y)=R, так как основание функции 0<(1/2)<1.
3) В одной координатной плоскости построить графики функций:
y=2x, y=3x, y=5x, y=10x. Сделать выводы.
График функции у=2х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.
Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание а (если a>1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
4) В одной координатной плоскости построить графики функций:
y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x.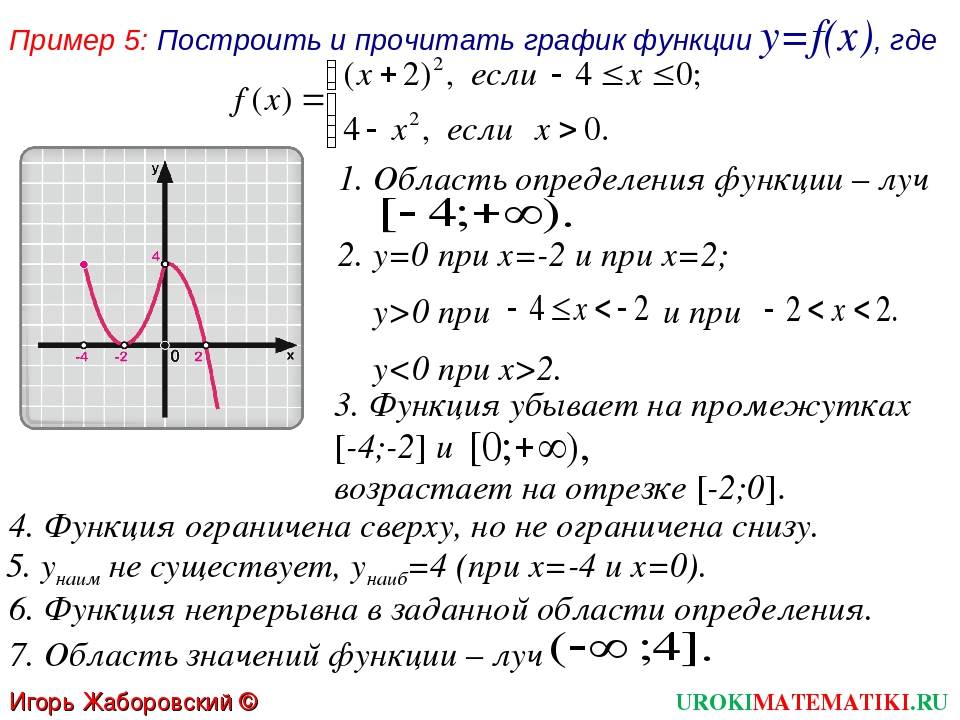 Сделать выводы.
Сделать выводы.
Смотрите построение графика функции y=(1/2)x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.
Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R+.
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
Чем меньше основание а (при 0<a<1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Решить графически уравнения:
1) 3x=4-x.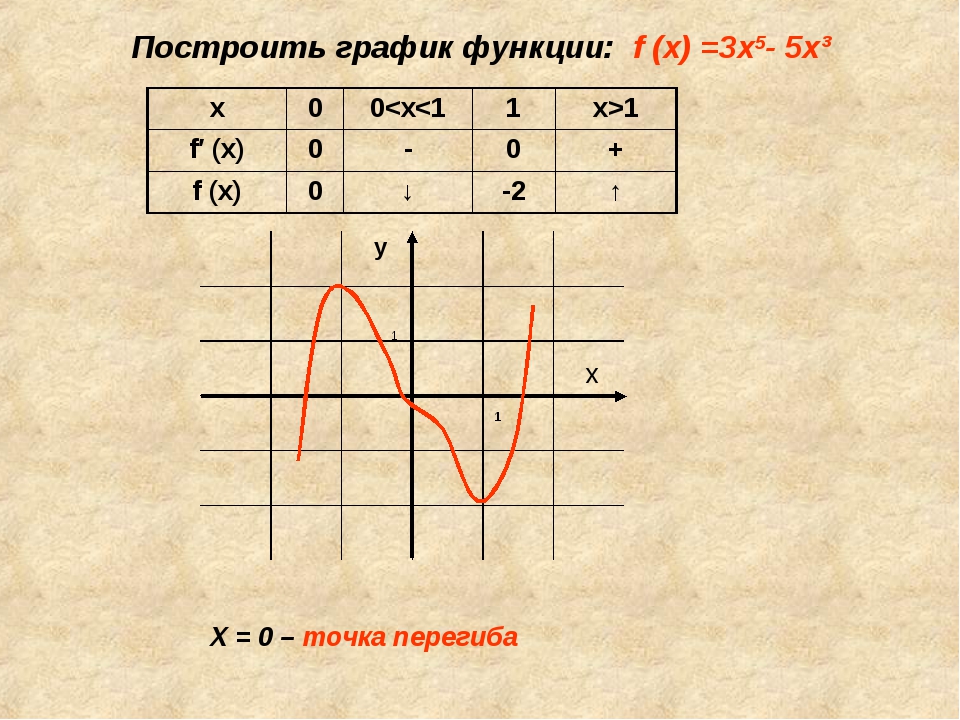
В одной координатной плоскости построим графики функций: у=3х и у=4-х.
Графики пересеклись в точке А(1; 3).
Ответ: 1.
2) 0,5х=х+3.
В одной координатной плоскости строим графики функций: у=0,5х
(y=(1/2)x )
и у=х+3.
Графики пересеклись в точке В(-1; 2).
Ответ: -1.
Найти область значений функции: 1) y=-2x; 2) y=(1/3)x+1; 3) y=3x+1-5.
Решение.
1) y=-2x
Область значений показательной функции y=2x – все положительные числа, т.е.
0<2x<+∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем:
— ∞<-2x<0.
Ответ: Е(у)=(-∞; 0).
2) y=(1/3)x+1;
0<(1/3)x<+∞, тогда, прибавляя ко всем частям двойного неравенства число 1, получаем:
0+1<(1/3)x+1<+∞+1;
1<(1/3)x+1<+∞.
Ответ: Е(у)=(1; +∞).
3) y=3x+1-5.
Запишем функцию в виде: у=3х∙3-5.
0<3x<+∞; умножаем все части двойного неравенства на 3:
0∙3<3x∙3<(+∞)∙3;
0<3x∙3<+∞; из всех частей двойного неравенства вычитаем 5:
0-5<3x∙3-5<+∞-5;
— 5<3x∙3-5<+∞.
Ответ: Е(у)=(-5; +∞).
Смотрите Карту сайта, и Вы найдете нужные Вам темы!
Графические линейные функции | Колледж алгебры
Результаты обучения
- Построение линейной функции путем нанесения точек
- Постройте линейную функцию, используя наклон и точку пересечения оси Y
- Построение линейной функции с помощью преобразований
Ранее мы видели, что график линейной функции представляет собой прямую линию. Мы также смогли увидеть точки функции, а также начальное значение на графике.
Мы также смогли увидеть точки функции, а также начальное значение на графике.
Есть три основных метода построения графиков линейных функций.Первый заключается в нанесении точек и затем проведении линии через точки. Второй — с использованием точки пересечения y- и наклона. Третий — применение преобразований к тождественной функции [латекс] f \ left (x \ right) = x [/ latex].
Построение графика функции по точкам
Чтобы найти точки функции, мы можем выбрать входные значения, оценить функцию по этим входным значениям и вычислить выходные значения. Входные значения и соответствующие выходные значения образуют пары координат.Затем мы наносим пары координат на сетку. В общем, мы должны оценивать функцию как минимум на двух входах, чтобы найти как минимум две точки на графике функции. Например, учитывая функцию [latex] f \ left (x \ right) = 2x [/ latex], мы можем использовать входные значения 1 и 2. Оценка функции для входного значения 1 дает выходное значение 2, которое представлена точкой (1, 2). Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4).Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что допустили ошибку.
Оценка функции для входного значения 2 дает выходное значение 4, которое представлено точкой (2, 4).Часто рекомендуется выбирать три точки, потому что, если все три точки не попадают на одну линию, мы знаем, что допустили ошибку.
Как сделать: для данной линейной функции построить график с помощью точек.
- Выберите минимум два входных значения.
- Оцените функцию для каждого входного значения.
- Используйте полученные выходные значения для определения пар координат.
- Нанесите пары координат на сетку.
- Проведите линию через точки.
Пример: построение графика по точкам
График [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex] путем нанесения точек.
Показать решение
Начните с выбора входных значений. Эта функция включает дробь со знаменателем 3, поэтому давайте выберем в качестве входных значений числа, кратные 3. Мы выберем 0, 3 и 6.
Оцените функцию для каждого входного значения и используйте выходное значение для определения пар координат.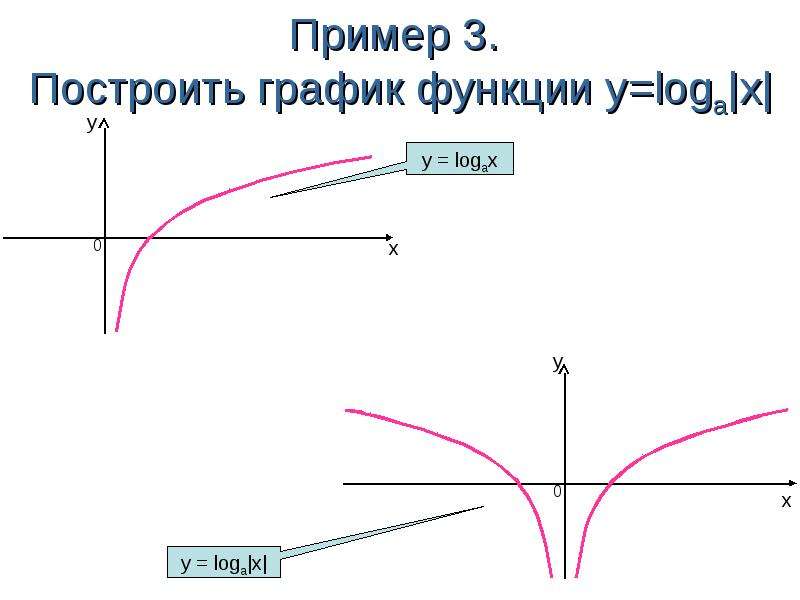
[латекс] \ begin {array} {llllll} x = 0 & & f \ left (0 \ right) = — \ frac {2} {3} \ left (0 \ right) + 5 = 5 \ Rightarrow \ left ( 0,5 \ right) \\ x = 3 & & f \ left (3 \ right) = — \ frac {2} {3} \ left (3 \ right) + 5 = 3 \ Rightarrow \ left (3,3 \ вправо) \\ x = 6 & & f \ left (6 \ right) = — \ frac {2} {3} \ left (6 \ right) + 5 = 1 \ Rightarrow \ left (6,1 \ right) \ end {array} [/ latex]
Постройте пары координат и проведите линию через точки.На приведенном ниже графике показана функция [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex].
Анализ решения
График функции представляет собой линию, как и ожидалось для линейной функции. Кроме того, график имеет наклон вниз, что указывает на отрицательный наклон. Это также ожидается от отрицательной постоянной скорости изменения уравнения для функции.
Попробуйте
График [латекс] f \ left (x \ right) = — \ frac {3} {4} x + 6 [/ latex] путем нанесения точек.
Показать решение
Построение линейной функции с использованием точки пересечения по оси Y и наклона
Другой способ построения графиков линейных функций — использование конкретных характеристик функции, а не точек.Первая характеристика — это точка пересечения y-, которая является точкой, в которой входное значение равно нулю. Чтобы найти точку пересечения y- , мы можем установить [latex] x = 0 [/ latex] в уравнении.
Другой характеристикой линейной функции является ее уклон м , который является мерой ее крутизны. Напомним, что наклон — это скорость изменения функции. Наклон линейной функции равен отношению изменения выходов к изменению входов.Другой способ подумать о наклоне — разделить вертикальную разницу или подъем между любыми двумя точками на горизонтальную разницу или бег. Наклон линейной функции будет одинаковым между любыми двумя точками. Мы столкнулись как с точкой пересечения y-, так и с наклоном в линейных функциях.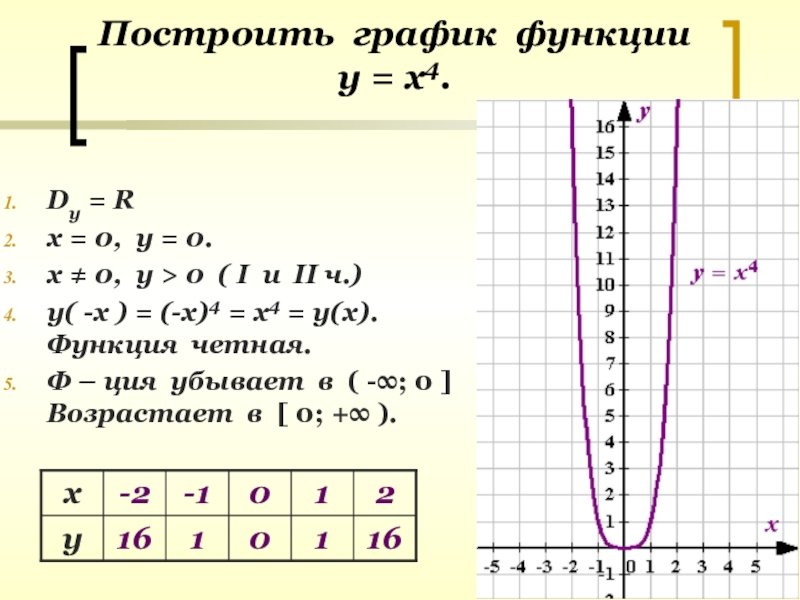
Рассмотрим следующую функцию.
[латекс] f \ left (x \ right) = \ frac {1} {2} x + 1 [/ latex]
Уклон [латекс] \ frac {1} {2} [/ latex]. Поскольку наклон положительный, мы знаем, что график будет наклоняться вверх слева направо.Пересечение y- — это точка на графике, когда x = 0. График пересекает ось y в точке (0, 1). Теперь мы знаем наклон и пересечение y . Мы можем начать построение графика с построения точки (0, 1). Мы знаем, что уклон возрастает над пробегом, [latex] m = \ frac {\ text {rise}} {\ text {run}} [/ latex]. В нашем примере [latex] m = \ frac {1} {2} [/ latex], что означает, что подъем равен 1, а диапазон равен 2. Начиная с нашего интервала y (0, 1) , мы можем подняться на 1 и затем пробежать 2 или пробежать 2 и затем подняться на 1.Мы повторяем, пока не получим несколько точек, а затем проводим линию через точки, как показано ниже.
Общее примечание: графическая интерпретация линейной функции
В уравнении [латекс] f \ left (x \ right) = mx + b [/ latex]
- b — пересечение графика y и указывает точку (0, b ), в которой график пересекает ось y .
- м — это наклон линии, указывающий вертикальное смещение (подъем) и горизонтальное смещение (пробег) между каждой последовательной парой точек.Напомним формулу наклона:
[латекс] m = \ frac {\ text {изменение на выходе (подъем)}} {\ text {изменение на входе (запуск)}} = \ frac {\ Delta y} {\ Delta x} = \ frac { {y} _ {2} — {y} _ {1}} {{x} _ {2} — {x} _ {1}} [/ latex]
Вопросы и ответы
Все ли линейные функции имеют точки пересечения y ?
Да. Все линейные функции пересекают ось Y и, следовательно, пересекаются по оси Y. (Примечание: Вертикальная линия, параллельная оси y, не имеет точки пересечения оси y.Имейте в виду, что вертикальная линия — единственная линия, которая не является функцией.)
Практическое руководство. Получив уравнение для линейной функции, постройте график функции, используя точку пересечения
y и наклон.
- Оцените функцию при нулевом входном значении, чтобы найти точку пересечения y-.
- Определите уклон.
- Постройте точку, представленную точкой пересечения y-.
- Используйте [latex] \ frac {\ text {rise}} {\ text {run}} [/ latex], чтобы определить еще как минимум две точки на линии.
- Проведите линию, проходящую через точки.
Пример: построение графика с использованием точки пересечения
y- и наклона
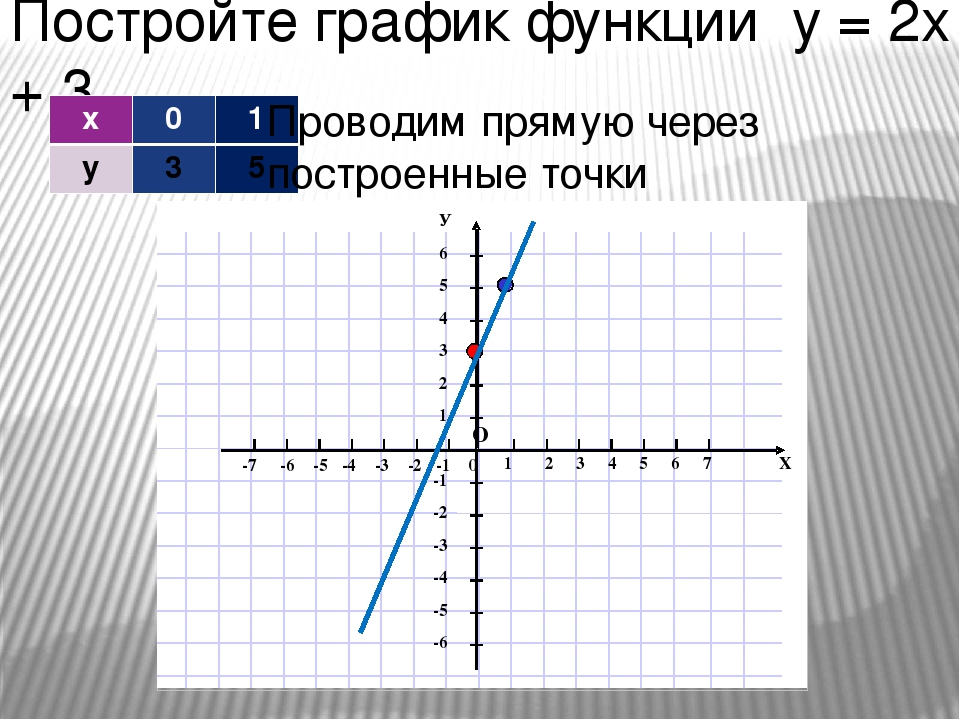
График [латекс] f \ left (x \ right) = — \ frac {2} {3} x + 5 [/ latex] с использованием точки пересечения y- и наклона.
Показать решение
Оцените функцию при x = 0, чтобы найти точку пересечения y-. Выходное значение, когда x = 0, равно 5, поэтому график пересечет ось y в точке (0, 5).
Согласно уравнению для функции, наклон линии составляет [латекс] — \ frac {2} {3} [/ latex].Это говорит нам о том, что для каждого вертикального уменьшения «подъема» на [латекс] –2 [/ латекс] единиц, «пробег» увеличивается на 3 единицы в горизонтальном направлении. Теперь мы можем построить график функции, сначала построив точку пересечения y . От начального значения (0, 5) мы перемещаемся вниз на 2 единицы и вправо на 3 единицы. Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.
Теперь мы можем построить график функции, сначала построив точку пересечения y . От начального значения (0, 5) мы перемещаемся вниз на 2 единицы и вправо на 3 единицы. Мы можем продлить линию влево и вправо, повторяя, а затем провести линию через точки.
Анализ решения
График наклонен вниз слева направо, что означает, что он имеет отрицательный наклон, как и ожидалось.
Попробуйте
Найдите точку на графике, который мы нарисовали в примере: построение графика с использованием точки пересечения y и угла наклона, имеющего отрицательное значение x .
Показать решение
Возможные ответы: [латекс] \ left (-3,7 \ right) [/ latex], [latex] \ left (-6,9 \ right) [/ latex] или [latex] \ left (-9, 11 \ справа) [/ латекс].
Построение линейной функции с помощью преобразований
Другой вариант построения графиков — использовать преобразования для функции идентичности [latex] f \ left (x \ right) = x [/ latex]. Функция может быть преобразована сдвигом вверх, вниз, влево или вправо. Функция также может быть преобразована с помощью отражения, растяжения или сжатия.
Функция может быть преобразована сдвигом вверх, вниз, влево или вправо. Функция также может быть преобразована с помощью отражения, растяжения или сжатия.
Вертикальное растяжение или сжатие
В уравнении [латекс] f \ left (x \ right) = mx [/ latex], m действует как вертикальное растяжение или сжатие функции идентичности. Когда м отрицательное, также имеется вертикальное отражение графика. Обратите внимание, что умножение уравнения [латекс] f \ left (x \ right) = x [/ latex] на m растягивает график f на коэффициент m единиц, если m > 1, и сжимает график f с коэффициентом м единиц, если 0 < м <1.Это означает, что чем больше абсолютное значение м , тем круче наклон.
Вертикальные растяжения, сжатия и отражения на функции [латекс] f \ left (x \ right) = x [/ latex].
Вертикальный сдвиг
В [latex] f \ left (x \ right) = mx + b [/ latex], b действует как вертикальный сдвиг , перемещая график вверх и вниз, не влияя на наклон линии. Обратите внимание, что добавление значения b к уравнению [latex] f \ left (x \ right) = x [/ latex] сдвигает график f всего на b единиц вверх, если b равно положительный и | b | единиц вниз, если значение b отрицательное.
Обратите внимание, что добавление значения b к уравнению [latex] f \ left (x \ right) = x [/ latex] сдвигает график f всего на b единиц вверх, если b равно положительный и | b | единиц вниз, если значение b отрицательное.
Этот график иллюстрирует вертикальные сдвиги функции [латекс] f \ влево (x \ вправо) = x [/ латекс].
Использование вертикального растяжения или сжатия вместе с вертикальным сдвигом — еще один способ определения различных типов линейных функций. Хотя это может быть не самый простой способ построить график функций такого типа, все же важно практиковать каждый метод.
Практическое руководство. Учитывая уравнение линейной функции, используйте преобразования, чтобы построить график линейной функции в виде [латекс] f \ left (x \ right) = mx + b [/ latex].
- График [латекс] f \ left (x \ right) = x [/ latex].
- Растянуть или сжать график по вертикали в м .

- Сдвинуть график вверх или вниз b единиц.
Пример: построение графиков с использованием преобразований
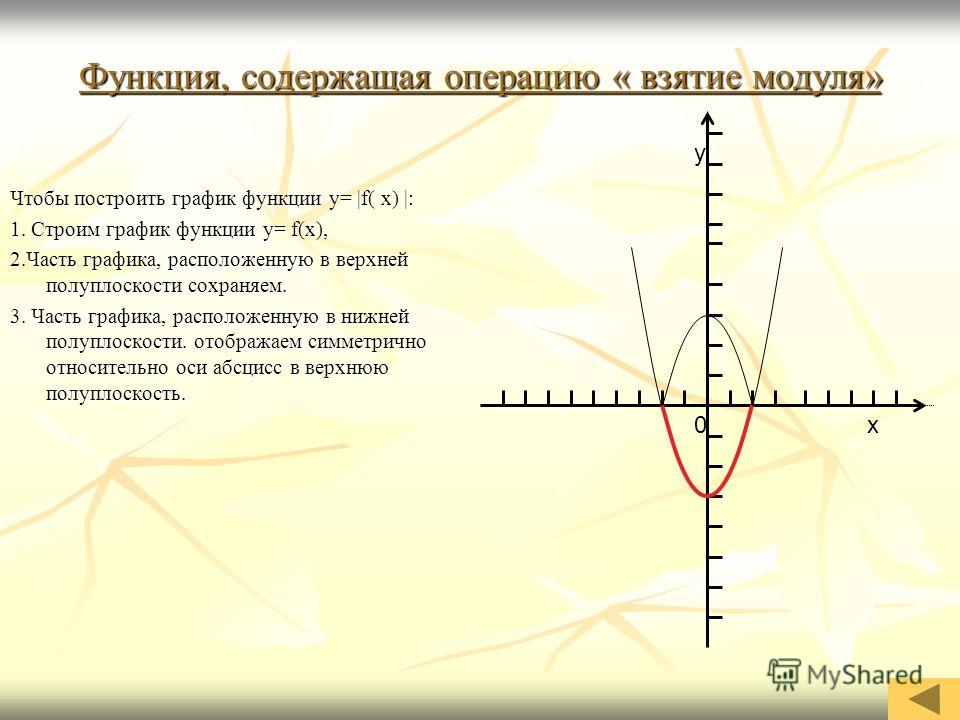
График [латекс] f \ left (x \ right) = \ frac {1} {2} x — 3 [/ latex] с использованием преобразований.
Показать решение
Уравнение для функции показывает, что [latex] m = \ frac {1} {2} [/ latex], поэтому функция идентичности сжимается по вертикали посредством [latex] \ frac {1} {2} [/ latex].Уравнение для функции также показывает, что [latex] b = -3 [/ latex], поэтому функция идентичности смещена по вертикали на 3 единицы.
Сначала изобразите функцию идентичности и покажите вертикальное сжатие.
Функция [latex] y = x [/ latex] сжимается с коэффициентом [latex] \ frac {1} {2} [/ latex].
Затем покажите вертикальный сдвиг.
Функция [latex] y = \ frac {1} {2} x [/ latex] сдвинута на 3 единицы вниз.
Попробуйте
График [латекс] f \ left (x \ right) = 4 + 2x [/ latex], с использованием преобразований.
Показать решение
Вопросы и ответы
В примере: построение графиков с помощью преобразований, могли бы мы изобразить график, изменив порядок преобразований на противоположный?
Нет. Порядок преобразований соответствует порядку операций. Когда функция оценивается на заданном входе, соответствующий выход вычисляется в соответствии с порядком операций. Вот почему мы сначала выполнили сжатие. Например, следуя порядку операций, пусть на входе будет 2.
[латекс] \ begin {array} {l} f \ text {(2)} = \ frac {\ text {1}} {\ text {2}} \ text {(2)} — \ text {3} \ hfill \\ = \ text {1} — \ text {3} \ hfill \\ = — \ text {2} \ hfill \ end {array} [/ latex]
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить страницуПодробнее
Инверсия функции — объяснение и примеры
Что такое обратная функция?
В математике обратная функция — это функция, отменяющая действие другой функции.
Например, , сложение и умножение являются инверсией соответственно вычитания и деления.
Обратную функцию можно рассматривать как отражение исходной функции по линии y = x. Проще говоря, обратная функция получается заменой (x, y) исходной функции на (y, x).
Мы используем символ f — 1 для обозначения обратной функции. Например, если f (x) и g (x) противоположны друг другу, то мы можем символически представить это утверждение как:
g (x) = f — 1 (x) или f (x) = g −1 (x)
Одна вещь, которую следует отметить в отношении обратной функции, заключается в том, что обратная функция не совпадает с ее обратной величиной, т.е.е., f — 1 (x) ≠ 1 / f (x). В этой статье мы обсудим, как найти обратную функцию.
Поскольку не все функции имеют инверсию, поэтому важно проверить, есть ли у функции инверсия, прежде чем приступать к определению инверсии.
Мы проверяем, есть ли у функции инверсия, чтобы не тратить время на поиск чего-то несуществующего.
Индивидуальные функции
Итак, как мы можем доказать, что данная функция имеет обратную? Функции, у которых есть обратные, называются взаимно однозначными функциями.
Функция называется взаимно однозначной, если для каждого числа y в диапазоне f существует ровно одно число x в области f такое, что f (x) = y.
Другими словами, область и диапазон однозначной функции имеют следующие отношения:
- Область f -1 = Диапазон f.
- Диапазон f −1 = Область f.
Например, чтобы проверить, является ли f (x) = 3x + 5 взаимно однозначной заданной функцией, f (a) = 3a + 5 и f (b) = 3b + 5.
⟹ 3a + 5 = 3b + 5
⟹ 3a = 3b
⟹ a = b.
Следовательно, f (x) является взаимно однозначной функцией, поскольку a = b.
Рассмотрим другой случай, когда функция f задается формулой f = {(7, 3), (8, –5), (–2, 11), (–6, 4)}. Эта функция взаимно однозначна, потому что ни одно из ее значений y не встречается более одного раза.
Что насчет этой другой функции h = {(–3, 8), (–11, –9), (5, 4), (6, –9)}? Функция h не является взаимно однозначной, потому что значение y, равное –9, встречается более одного раза.
Вы также можете графически проверить взаимно однозначную функцию, проведя вертикальную и горизонтальную линии через график функции. Функция взаимно однозначна, если и горизонтальная, и вертикальная линии проходят через график один раз.
Как найти обратную функцию?
Нахождение обратной функции — несложный процесс, хотя нам действительно нужно быть осторожными с парой шагов. В этой статье мы будем предполагать, что все функции, с которыми мы будем иметь дело, относятся друг к другу.
Порядок нахождения обратной функции f (x):
- Заменить обозначение функции f (x) на y.
- Поменять местами x на y и наоборот.
- Начиная с шага 2, решите уравнение относительно y. Будьте осторожны с этим шагом.
- Наконец, измените y на f −1 (x).
 Это обратная функция.
Это обратная функция. - Вы можете проверить свой ответ, проверив, верны ли следующие два утверждения:
⟹ (f ∘ f −1 ) (x) = x
⟹ (f −1 ∘ f) (x) = x
Давайте поработаем пару примеров.
Пример 1
Дана функция f (x) = 3x — 2, найдите ее обратную.
Решение
f (x) = 3x — 2
Замените f (x) на y.
⟹ y = 3x — 2
Поменять местами x на y
⟹ x = 3y — 2
Решить относительно y
x + 2 = 3y
Разделить на 3, чтобы получить;
1/3 (x + 2) = y
x / 3 + 2/3 = y
Наконец, заменим y на f −1 (x).
f −1 (x) = x / 3 + 2/3
Проверить (f ∘ f −1 ) (x) = x
(f ∘ f −1 ) (x) = f [f −1 (x)]
= f (x / 3 + 2/3)
⟹ 3 (x / 3 + 2/3) — 2
⟹ x + 2 — 2
= x
Следовательно, f −1 (x) = x / 3 + 2/3 — правильный ответ.
Пример 2
Дано f (x) = 2x + 3, найти f −1 (x).
Решение
f (x) = y = 2x + 3
2x + 3 = y
Поменять местами x и y
⟹2y + 3 = x
Теперь решите относительно y
⟹2y = x — 3
⟹ y = x / 2 — 3/2
Наконец, заменим y на f −1 (x)
⟹ f −1 (x) = (x– 3) / 2
Пример 3
Задайте функцию f (x) = log 10 (x), найдите f −1 (x).
Решение
f (x) = log₁₀ (x)
Заменено f (x) на y
⟹ y = log 10 (x) ⟹ 10 y = x
Теперь замените x на y получить;
⟹ y = 10 x
Наконец, заменим y на f −1 (x).
f -1 (x) = 10 x
Следовательно, обратное значение f (x) = log 10 (x) равно f -1 (x) = 10 x
Пример 4
Найдите обратную функцию следующей функции g (x) = (x + 4) / (2x -5)
Решение
g (x) = (x + 4) / ( 2x -5) ⟹ y = (x + 4) / (2x -5)
Заменить y на x и наоборот
y = (x + 4) / (2x -5) ⟹ x = (y + 4) / (2y -5)
⟹ x (2y − 5) = y + 4
⟹ 2xy — 5x = y + 4
⟹ 2xy — y = 4 + 5x
⟹ (2x — 1) y = 4 + 5x
Разделите обе части уравнения на (2x — 1).
⟹ y = (4 + 5x) / (2x — 1)
Заменить y на g — 1 (x)
= g — 1 (x) = (4 + 5x) / (2x — 1)
Проба:
(g g −1 ) (x) = g [g −1 (x)]
= g [(4 + 5x) / (2x — 1)]
= [(4 + 5x) / (2x — 1) + 4] / [2 (4 + 5x) / (2x — 1) — 5]
Умножьте числитель и знаменатель на (2x — 1).
⟹ (2x — 1) [(4 + 5x) / (2x — 1) + 4] / [2 (4 + 5x) / (2x — 1) — 5] (2x — 1).
⟹ [4 + 5x + 4 (2x — 1)] / [2 (4 + 5x) — 5 (2x — 1)]
⟹ [4 + 5x + 8x − 4] / [8 + 10x — 10x + 5]
⟹13x / 13 = x
Следовательно, g — 1 (x) = (4 + 5x) / (2x — 1)
Пример 5
Определите обратное для следующего function f (x) = 2x — 5
Решение
Замените f (x) на y.
f (x) = 2x — 5⟹ y = 2x — 5
Поменяйте местами x и y, чтобы получить;
⟹ x = 2y — 5
Изолировать переменную y.
2y = x + 5
⟹ y = x / 2 + 5/2
Измените y обратно на f –1 (x).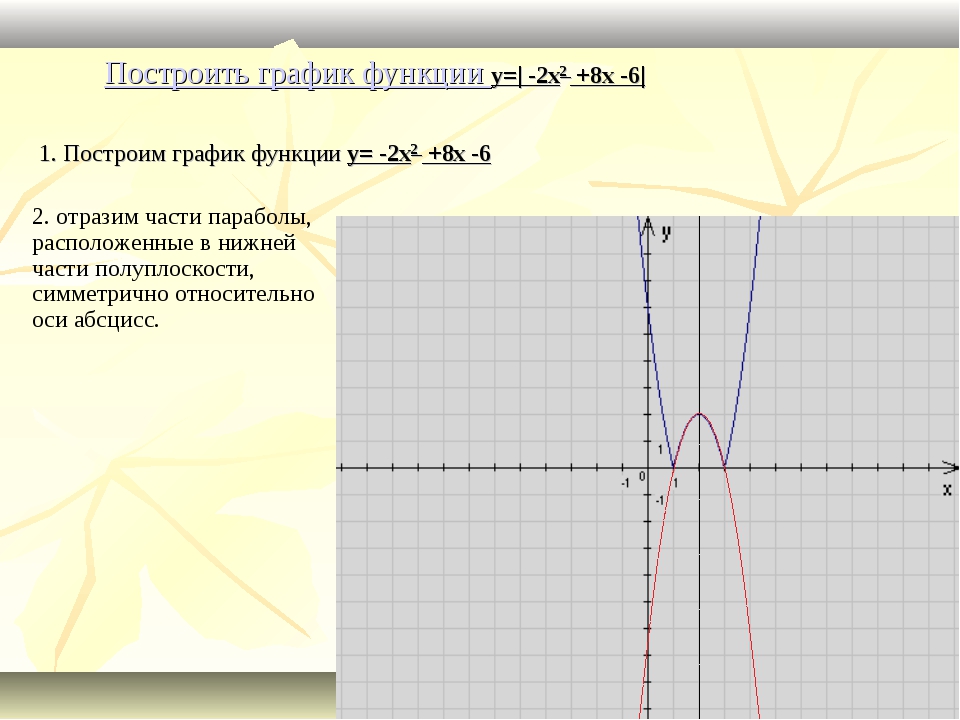
⟹ f –1 (x) = (x + 5) / 2
Пример 6
Найдите функцию, обратную h (x) = (x — 2) 3 .
Решение
Измените h (x) на y, чтобы получить;
h (x) = (x — 2) 3 ⟹ y = (x — 2) 3
Поменять местами x и y
⟹ x = (y — 2) 3
Изолировать y.
y 3 = x + 2 3
Найдите кубический корень из обеих частей уравнения.
3 √y 3 = 3 √x 3 + 3 √2 3
y = 3 √ (2 3 ) + 2
Заменить y на h — 1 (x)
h — 1 (x) = 3 √ (2 3 ) + 2
Пример 7
Найти обратное значение h (x) = ( 4x + 3) / (2x + 5)
Решение
Замените h (x) на y.
h (x) = (4x + 3) / (2x + 5) ⟹ y = (4x + 3) / (2x + 5)
Поменять местами x и y.
⟹ х = (4у + 3) / (2у + 5).
Решите относительно y в приведенном выше уравнении следующим образом:
⟹ x = (4y + 3) / (2y + 5)
Умножьте обе части на (2y + 5)
⟹ x (2y + 5) = 4y + 3
Распределить x
⟹ 2xy + 5x = 4y + 3
Изолировать y.
⟹ 2xy — 4y = 3 — 5x
⟹ y (2x — 4) = 3 — 5x
Разделим на 2x — 4, чтобы получить;
⟹ y = (3 — 5x) / (2x — 4)
Наконец, замените y на h -1 (x).
⟹ h — 1 (x) = (3 — 5x) / (2x — 4)
Практические вопросы
Найдите обратное из следующих функций:
- g (x) = (2x — 5) / 3.
- h (x) = –3x + 11.
- г (x) = — (x + 2) 2 — 1.
- г (x) = (5/6) x — 3/4
- f (x) = 3 x — 2.
- h (x) = x 2 + 1.
- g (x) = 2 (x — 3) 2 — 5
- f (x) = x 2 / (x 2 + 1)
- h (x) = √x — 3.
- f (x) = (x — 2) 5 + 3
- f (x) = 2 x 3 — 1
- f (x) = x 2 — 4 x + 5
- г (x) = 5 √ (2x + 11)
- h (x) = 4x / (5 — x)
Предыдущий урок | Главная страница | Следующий урок
Графические уравнения и системы уравнений с пошаговым решением математических задач
ВВЕДЕНИЕ В КВАДРАТИКУ
Цели
В этом разделе вы будете складывать, вычитать, умножать и строить квадратичные графики.
Словарь : Стандартный формат квадратного уравнения : y = ax 2 + bx + c ; a, b, c — постоянные; x — независимая переменная, а y — зависимая переменная. Квадраты также называются полиномами второй степени , потому что наивысший показатель степени равен 2. Уравнение пересечения наклона из второй главы y = mx + b называется полиномом первой степени , потому что наивысший показатель степени равен единице.
Зачем изучать квадратичность? Графики квадратных уравнений приводят к параболам (U-образные графики, которые открываются вверх или вниз).Эта особенность квадратичности делает их хорошими моделями для описания пути объекта в воздухе или описания прибыли компании (примеры чего вы можете увидеть в конечной математике или в микроэкономике).
Пример 1. Мальчик, лежащий на спине, выстрелом из пращи выстрелил в воздух камнем с начальной скоростью (силой, которую мальчик использует для выстрела камня) 64 фута в секунду. Квадратное уравнение, моделирующее высоту скалы, составляет
ч = -16т 2 + 64т.
а. Найдите высоту камня при t = 0.
В формуле h = -16t 2 + 64t, заменить t на 0.
h = -16 (0) 2 +64 (0)
h = 0
Камень находится на нулевом уровне в воздухе за 0 секунд. (Это точка прямо перед тем, как он выстрелит камнем в воздух.)
г. Найдите высоту камня при t = 1.
В формуле h = -16t 2 + 64t, заменить t на 1.
Скала находится на высоте 48 футов за одну секунду.
Объяснение : Возводится в квадрат только «1». -16 умножается на 1 2
г. Найдите высоту камня при t = 2.
В формуле h = -16t 2 + 64t, заменить t на 2.
Скала находится на высоте 64 фута за 2 секунды.
Объяснение : Порядок операций требует применения показателей перед умножением.
г. Найдите высоту камня при t = 3.
В формуле h = -16t 2 + 64t заменить t на 3.
Камень находится на высоте 48 футов за 3 секунды.
e. Найдите высоту камня при t = 4.
В формуле h = -16t 2 + 64t, заменить t на 4.
Камень находится на нулевом уровне в воздухе за 4 секунды; то есть камень ударился о землю.
ф. Постройте график точек, полученных в частях от a до e.
Высота камня зависит от времени, поэтому h — зависимая переменная, а t — независимая переменная.Точки имеют вид (t, h).
Согласно графику, скала достигает максимальной высоты за 2 секунды. Максимальная высота 64 фута. Точка максимума или минимума квадратичной называется вершиной. Вы узнаете, как найти вершину в Разделе 4.3, Квадратичные приложения и графики.
Согласно графику, камень оказывается на земле в 0 секунд (прямо перед тем, как мальчик стреляет в него) и в 4 секунды (когда камень приземляется). Эти точки являются отсечками времени.Вы узнаете, как их найти, в следующем разделе 4.2, «Применение квадратичной формулы».
Сложение и вычитание квадратичных:
Словарь : Чтобы добавить или вычесть квадратичные, объедините одинаковые термины. Подобные термины , первоначально представленные в разделе 1.3, «Упрощение алгебраических выражений», имеют одинаковую переменную и одинаковый показатель степени. Например, 2x 2 и 5x 2 похожи на термины, а 3x 2 и 7x — нет.
Коэффициент , первоначально представленный в Разделе 1.3, «Упрощение алгебраических выражений», является числом, умножающим переменную. Например, коэффициент при 2x равен 2, а коэффициент при -x 2 равен -1.
Правило: Чтобы объединить одинаковые термины, сложите их коэффициенты
Напомним о распределительном свойстве : Определение a (b + c) = ab + ac.
Не удалось объединить непохожие термины в скобках, поэтому мы использовали свойство распределения.После этого мы умножили 6x на 3, а затем -5 на 3.
Использовали свойство распределения и объединили похожие термины.
Пример 5. Уравнение прибыли: Прибыль = Выручка — Затраты
Если уравнение дохода для компании:
и уравнение стоимости:
найти уравнение прибыли для компании.
Подставил уравнения доходов и затрат в формулу прибыли. Необходимо использовать скобки.
Использовал свойство распределения и умножил уравнение доходов на 1, а уравнение затрат на -1.
Комбинированные одинаковые термины.
Подставил уравнения доходов и затрат в формулу прибыли. Необходимо использовать круглые скобки. Использовал распределительное свойство.
Умножил уравнение доходов на 1 и уравнение затрат на -1. Сочетание подобных терминов.
Умножение двух биномов.
Словарь : У бинома есть два члена (так же, как у велосипеда есть два колеса).
Правило: Чтобы умножить два бинома, умножьте каждый член первого члена на каждый член второго.
Пример 7. Умножаем (x + 2) (5x + 3).
Умножить x на 5x и 3 и умножить 2 на 5x и 3.
Объединить похожие термины.
FOIL — это простая мнемоника, чтобы запомнить, как умножить два бинома.
Пример 8. Умножить (8x + 6) (x + 7).
Учебный совет: Напишите карточку с объяснением мнемонической ФОЛЬГИ. Часто просматривайте карту.
Сводка
Квадраты — важные уравнения в физике и микроэкономике.Техника сложения и вычитания квадратиков такая же, как и мы практикуем весь семестр; то есть складывать или вычитать похожие термины. Для умножения используйте свойство распределения или FOIL. Вершина квадратичной будет объяснена более подробно в разделе «Графики квадратичных вычислений и приложения». Вершина — это точка максимума или минимума на квадратичном графике.
ПРИМЕНЕНИЕ КВАДРАТИЧЕСКОЙ ФОРМУЛЫ
Цель
В этом разделе показано, как решать квадратные уравнения.
Словарь : квадратное уравнение — это ax 2 + bx + c = 0. a, b и c — константы, а x — переменная.
Квадратичная формула ,, используется для решения квадратного уравнения.
Анализируем
Учебный совет: Напишите квадратное уравнение и квадратную формулу на карточках для заметок, чтобы вы могли ссылаться на них при выполнении домашнего задания.
Пример 1. Предположим, вы стоите на вершине утеса на высоте 375 футов над дном каньона и подбрасываете в воздух камень с начальной скоростью 82 фута в секунду.Уравнение, моделирующее высоту скалы над дном каньона:
ч = -16т 2 + 82т + 375.
Узнайте, сколько времени требуется камню, чтобы упасть на дно каньона.
Найдите t, когда h = 0.
Решите 0 = -16t 2 + 82t + 375.
Определите константы a, b и c.
Объяснение : Одна часть квадратного уравнения должна быть равна нулю.
a = -16, b = 82, c = 375
Пояснение :
a — коэффициент переменной, возведенный в квадрат.
b — коэффициент переменной в первой степени.
c — постоянная.
Используйте формулу корней квадратного уравнения
с a = -16, b = 82 и c = 375.
T = -2,916 — бессмысленный ответ, поскольку t — это время, за которое камень ударится о дно каньона, и время не может быть отрицательным.
T = 8,041 секунды — это время, за которое камень ударится о дно каньона.
Камень ударится о дно каньона за 8,041 секунды.
Пример 2. У владельца ранчо есть 500 ярдов ограждения, чтобы ограждать два соседних загона для свиней, которые упираются в сарай.Если площадь двух ручек должна составлять 20 700 квадратных ярдов, каковы должны быть размеры ручек?
L — длина обоих ручек.
а. Воспользуйтесь таблицей, чтобы найти уравнение для площади ручек.
г. Упростите уравнение для площади.
г. Найдите W, когда A = 20700.
Ширина 76,67 или 90 ярдов.
г. Найдите длину ручек.
Из таблицы в Части а, L = 500 — 3Вт.Подставляем W = 76,67 и W = 90 в уравнение для длины, L = 500 — 3w.
Размеры загона для свиней, площадь которого составляет 20 700 квадратных ярдов, составляют 76,67 на 270 ярдов и 90 на 230 ярдов.
Пример 3. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, следующая квадратичная функция может смоделировать температуру кислорода:
T = 0,26 м 2 -4,1 м + 7,9
, где T измеряется в градусах Цельсия, а m представляет собой минуты, в течение которых был проведен эксперимент.Определите, когда температура кислорода составляет 0 градусов Цельсия.
Задача просит вас найти m при T = 0.
Температура кислорода составит 0 градусов Цельсия через 2,246 минуты 13,52 минуты.
Учебный совет: Ключевая идея, продемонстрированная в примере 3, заключается в том, как обрабатывать отрицательное b в квадратном уравнении.
Сводка
В этом разделе показано, как решить новый тип уравнения — квадратное. У них есть важные приложения во многих областях, таких как бизнес, физика и инженерия.Учить
разница между квадратным уравнением и квадратной формулой.
Квадратное уравнение: ax 2 + bx + c = 0.
- Одна часть уравнения должна быть равна нулю.
- a — коэффициент при x.
- b — коэффициент при x.
- c — постоянный член.
Квадратичная формула решает квадратное уравнение.
- Формула дает два решения.
- Для поиска ответов используется калькулятор.
- Первым шагом в вычислении формулы является упрощение квадратного корня.
КВАДРАТИЧЕСКИЕ ПРИЛОЖЕНИЯ И ГРАФИКИ
Цели
В этом разделе исследуются дальнейшие ключевые точки квадратичного графика, вершины и пересечений. Эти моменты будут интерпретироваться в приложениях.
Пример 1. Мальчик, лежащий на спине, стреляет из пращи камнем прямо в воздух с начальной скоростью (силой, которую мальчик использует, чтобы выстрелить в камень) 64 фута в секунду.Квадратное уравнение, моделирующее высоту скалы, составляет
ч = -16т 2 + 64т.
(Этот пример взят из Раздела 4.1 «Введение в квадратику», стр. 317.)
На странице 318 мы сгенерировали следующие значения:
Мы использовали точки, чтобы получить график ниже. Вершина и пересечения также отмечены на графике.
Объяснение : Точка (0, 0) — это время и высота пересечения.
Вершина , (2,64) представляет максимальную высоту скалы. Скала достигает максимальной высоты 64 фута за 2 секунды.
Временные точки , (0, 0) и (4, 0) представляют, когда камень находится на земле. Камень оказывается на земле за 0 секунд до выстрела (это точка пересечения высоты ) и через 4 секунды, когда он возвращается на землю.
Чтобы построить квадратичный график, указанный уравнением, y = ax 2 + bx + c, усвойте следующие термины:
Словарь : Вершина: Вершина — это максимальная или минимальная точка на графике.Чтобы найти вершину:
а. Найдите координату x:
b. Найдите координату y: подставьте значение x, полученное в части a, в формулу y = ax 2 + bx + c.
X-пересечение : установите y = 0 и решите 0 = ax 2 + bx + c, используя формулу корней квадратного уравнения,
Y-точка пересечения : установите x = 0 и найдите y. y всегда будет c, константой.
Учебный совет: Напишите процедуру и определения на трех карточках для удобного использования.
Пример 2. Компания D +++ производит компьютерные игры. Стоимость создания g игр в месяц составляет C = 0,4g 2 — 32g + 625. Выручка от продажи игр g в месяц составляет R = -0,6g 2 + 52g. Единицы измерения g — сотни, C и R — тысячи долларов.
а. Найдите уравнение прибыли.
г. Найдите вершину и объясните, что эта вершина означает с точки зрения создания компьютерных игр.
Формула для координаты g:
Из уравнения прибыли a = -1, b = 84.
Вершина (42,1139). Если D +++ продаст 4200 игр, то они получат максимальную прибыль в размере 1 139 000 долларов США.
г. Найдите g перехватывает и объясните, что они означают с точки зрения создания компьютерных игр.
Чтобы найти точку пересечения g, установите P = 0.
Решить 0 = -g 2 + 84g — 625.
Используйте формулу корней квадратного уравнения, a = -1, b = 84, c = -625.
Перехваты g: (8.251, 0) и (75.75, 0).
Если они продадут 825 или 7 575 игр, они выйдут на уровень безубыточности.
г. Найдите P перехватывает и объясните, что они означают с точки зрения создания компьютерных игр.
Чтобы найти точку пересечения с P, установите g = 0.
P = -0 2 + 84 * 0-625
P = -625
Перехват по оси P равен (0, -625).
Стартовые затраты компании составляют 625 000 долларов.
e. Постройте график функции.
Постройте точки:
Вершина. (42, 1139).
Данный перехватывает. (8,251, 0) и (75,75, 0).
P-перехват. (0, -625).
Объяснение : Одно из объяснений того, что прибыль имеет две точки безубыточности, заключается в том, насколько эффективно компания производит продукт. Изготовление очень небольшого количества предметов обычно неэффективно. В какой-то момент фабрика становится очень эффективной в производстве продукта, но если фабрика пытается производить слишком много предметов, компания становится неэффективной в производстве своей продукции.
Помните, что единицы измерения g — сотни, а единицы P — тысячи.
Предположим, D +++ должен получать прибыль в размере 500 000 долларов (P = 500) в месяц. Нарисуйте эту линию на графике, полученном в Части b, и найдите, где линия пересекает график квадратичного. Напишите предложение, объясняющее, что означают ответы.
Эскиз P = 500 на предыдущем графике.
P = 500 — горизонтальная линия.
Если D +++ хочет получить прибыль в размере 500 000 долларов, им необходимо сделать и продать 1 672 или 6 728 игр.
Объяснение : График дает оценку того, где пересекаются горизонтальная линия P = 500 и уравнение прибыли P = -g 2 + 84g-625. Алгебра дает точную точку их пересечения.
г. Используя график и ответы к Части c, определите, сколько компьютерных игр необходимо сделать и продать, чтобы гарантировать прибыль, превышающую 500 000 долларов.
Компания получит прибыль более 500 000 долларов, если график прибыли будет выше горизонтальной линии P = 500.Эта проблема аналогична примеру 2d на стр. 203 в Разделе 2.9 «Приложения графиков».
Это происходит между точками g = 16,72 и g = 67,28 или
.
16,72
Компания заработает более 500 000 долларов, если будет производить и продавать от 1 672 до 6 728 компьютерных игр.
Пример 3. Оператор питомника хочет поставить три соседние загоны для собак одинакового размера у стены. У него 96 метров забора.
а. Найдите формулу площади.
Объяснение : Самая трудная часть таблицы — найти значение длины.Если фермер использует 10 метров для ширины загона, а есть 4 ширины, то он использовал 4 раза по 10, или 40 метров ограждения. Чтобы узнать, сколько ограждений осталось на эту длину, вычтите 40 из 96 — общего количества ограждений, доступных фермеру.
Формула площади загона для собак:
г. Найдите вершину и объясните, что это означает с точки зрения загонов для собак.
Формула для координаты W:
Из уравнения прибыли a = -4, b = 96.
Вершина равна (12, 576).
Вершина , (12, 576) представляет максимальную площадь трех загонов для собак. Когда W = 12, максимальная площадь будет 576. (Длина всех трех загонов будет 48 или длина одной собаки будет 16.) Будет три загона для собак 12 на 16 метров каждая.
г. Найдите W перехватывает и объясните, что они означают в терминах загонов для собак.
Чтобы найти точку пересечения с W, установите A = 0.
Решить 0 = -4 Вт 2 + 96 Вт.
Используйте формулу корней квадратного уравнения, a = -4, b = 96, c = 0.
W-точки перехвата: (0, 0) и (24, 0).
W-точки пересечения, (0, 0) и (24, 0) представляют ширину загона для собаки, которая даст нулевую площадь.
г. Найдите точку перехвата A и объясните, что это означает с точки зрения загонов для собак.
Чтобы найти точку пересечения A, установите W = 0.
Объяснение : Если ширина прямоугольника равна нулю, то площадь должна быть равна нулю.
Перехватчик A равен (0, 0).
Перехватчик A, (0, 0) — это область, когда W = 0.
e. Постройте уравнение
Постройте точки:
Вершина. (12, 576).
W перехватывает. (0, 0) и (24, 0).
Перехват. (0, 0).
ф. Предположим, общая площадь должна быть 400 квадратных метров. Изобразите график A = 400 и найдите размеры загонов для собак.
Эскиз A = 400 на предыдущем графике.
A = 400 — горизонтальная линия.
Поскольку W, ширина, известна, длину L можно определить по формуле A = LW.
Решите относительно L, разделив обе стороны на W.
Размеры загона для собак, дающего площадь 400 квадратных метров, составляют 5,367 на 74,53 и 18,63 на 21,47.
Пример 4. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, следующая квадратичная функция может смоделировать температуру кислорода:
Т = 0.26 м 2 -4,1 м + 7,9
, где T измеряется в градусах Цельсия, а m представляет собой минуты, в течение которых был проведен эксперимент. Постройте уравнение, найдя вершину и точки пересечения. Обозначьте эти точки на графике и объясните, что означают вершина и пересечения с точки зрения модели.
Вернуться назад: Это та же модель, что использовалась в примере 3 на стр. 332. Этот пример работал при нулевой температуре.
Найдите вершину из T = 0.26 м 2 — 4,1 м + 7,9.
Формула для координаты m вершины:
Вершина (7,885, -8,263).
Найдите точки пересечения м T = 0,26 м 2 -4,1 м + 7,9
Чтобы найти точки пересечения m, установите T = 0.
Решить 0 = 0,26 м 2 -4,1 м + 7,9.
Используйте формулу корней квадратного уравнения, a = 0,26, b = -4,1, c = 7,9.
М точки пересечения (13.52, 0) и (2.246, 0).
Найдите точки пересечения T T = 0,26 м 2 — 4,1 м + 7,9
Чтобы найти точку пересечения с Т, установите m = 0.
Т-образная точка пересечения (0, 7.9).
Vertex: Минимальная температура составляет 7,885 минут. Минимальная температура составит -8,263 градуса по Цельсию.
м пересекает: Температура будет ноль градусов Цельсия на отметках 2.246 и 13.52 мин.
T intercept: Температура в начале эксперимента составляла 7,9 градусов Цельсия.
Учебные советы: Квадраты — это U-образные графики. В некоторых случаях они имеют U-образную форму, как в примере выше, или форму, как в примерах с 1 по 3. Если a в уравнении, y = ax 2 + bx + c, положительно, тогда график имеет U-образную форму, что есть, открываясь. Если a отрицательно, график имеет форму, то есть раскрывается вниз. Этот факт следует записать на карточке для заметок.
Сводка
Графики квадратиков появляются по таким разнообразным предметам, как микроэкономика и физика. В этом разделе кратко излагаются основные идеи устройства.
Чтобы построить квадратичный график y = ax 2 + bx + c, вы должны найти:
- Вершина .
Формула для координаты x:Чтобы найти координату y, подставьте свой ответ вместо координаты x в уравнение y = ax 2 + bx + c.
- x перехватывает .Установите y = 0 и решите уравнение 0 = ax 2 + bx + c, используя формулу корней квадратного уравнения
- Перехватчик y .
Установите x = 0 в уравнении, y = ax 2 + bx + c, и найдите y. Обратите внимание, когда x = 0, y = c. - Если a отрицательное значение , обычно график выглядит следующим образом:
- Если a положительное значение , обычно график выглядит следующим образом:
.
ФАКТОРИНГ
Цели
Факторинг — это алгебраический метод, используемый для разделения выражения на составные части.Когда составные части умножаются вместе, результатом является исходное выражение. Иногда это можно использовать для решения квадратных уравнений. Факторинг — важный навык в MAT 100, Intermediate Algebra.
Словарь : Алгебраическое выражение учитывается, если последней операцией при вычислении выражения является умножение.
Пример 1. Какое выражение разложено на множители , x 2 — 5x — 24 или (x — 8) (x + 3)?
Выберите значение x и подставьте его в выражение.
Пусть x = 3.
Поскольку последней операцией для (x — 8) (x + 3) было умножение, то факторизуется (x — 8) (x + 3).
Объяснение : Менее формально алгебраическое выражение факторизуется, если оно заключено в круглые скобки.
Словарь : Распределительное свойство — это a (b + c) = ab + ac. Левая часть подвергается факторизации, и a является общим множителем.
У вас должна быть возможность проверить с помощью свойства distributive.
Объяснение : Хотя 8x 3 + 4x равно как 2x (4x 2 + 2), так и 4 (2x 3 + x), ни один из них не считается полностью разложенным, потому что в обоих случаях общее кратное 2, в 2x (4x 2 +2) и x в 4 (2x 3 + x) по-прежнему можно разложить на множители из членов в скобках.
Факторинг трехчленов: (Трехчлен состоит из трех членов.) Чтобы разложить на множители трехчлены, вспомните аббревиатуру FOIL.
Учебный совет: Проверьте свои карточки для заметок на предмет определения FOIL.
Пример 4. Умножаем (x + 3) (x + 5).
(x + 3) (x + 5) факторизуется, а x 2 + 8x +15 — нет. Чтобы разложить на множители трехчлены, вам нужно знать, как были вычислены 8x и 15. 8x произошло от сложения 5x и 3x, а 15 — от умножения 5 и 3.
Пример 5. Множитель x 2 + 8x +15. (Это из Примера 4.)
Нам нужны два числа, которые при сложении равны 8, а при умножении равны 15. 3 и 5 в сумме дают 8, а при умножении — 15.
Итак, x 2 + 8x +15 = (x + 3) (x + 5)
Пример 6. Фактор x 2 -4x- 12.
Нам нужны два числа, которые при сложении равны -4, а при умножении равны -12. -6 и 2 в сумме дают -4, а при умножении -12.
Итак, x 2 -4x -12 = (x-6) (x + 2).
Пример 7. Фактор x 2 — 64.
Это не трехчлен, но он может стать одним, добавив 0x.
x 2 -64 = x 2 + 0x -64
Нам нужны два числа, которые при сложении равны 0, а при умножении равны -64.
-8 и 8 прибавляются к 0, а при умножении — -64.
Итак, x 2 -64 = (x-8) (x + 8).
Этот пример называется факторизацией разности полных квадратов, и вы снова увидите это, если возьмете MAT 100, промежуточную алгебру.
Словарь : a 2 — b 2 — это разность полных квадратов .
Разность полных квадратов имеет специальную формулу факторизации: a 2 — b 2 = (a — b) (a + b)
Решение квадратных уравнений с помощью факторинга:
Если вы умножаете две величины и результат равен нулю, то вы знаете, что одна из величин должна быть равна нулю.В математической записи
, если a.b = 0, то a = 0 или b = 0.
Прежде чем вы подумаете, что разложение на множители для решения квадратичных уравнений намного проще, чем использование квадратичной формулы, вы должны знать, что разложение на множители не всегда работает. Рассмотрите возможность изменения примера 8 всего на единицу до x 2 — 11x + 31 = 0. Вы не можете найти два целых числа, которые при сложении равны -11, а при умножении равны 31. Чтобы разложить на множитель x 2 — 11x + 31, вы должны использовать квадратичная формула. Вы узнаете, как разложить на множители любое квадратное уравнение в Precalculus I, MAT 161.
Сводка
В этом модуле представлены два метода факторинга. Первый — это общие факторы, использующие свойство распределения, ab + ac = a (b + c). Другой — факторизация трехчленов. Чтобы разложить на множители трехчлены, вам нужно знать, как работает FOIL. Если вы возьмете MAT 100, промежуточную алгебру, вы увидите больше факторинга.
ОБЗОР ГЛАВЫ 4
Эта глава познакомила вас с квадратичностью. Две основные темы — это квадратичная формула и квадратичные графики.Эти темы имеют множество приложений в бизнесе, физике и геометрии. Факторинг — важная тема в MAT 100, Intermediate Algebra.
Раздел 4.1: Введение в квадратичность
Раздел 4.2: Приложения квадратичной формулы
Определение: ax 2 + bx + c = 0 — квадратное уравнение.
Определение: квадратная формула.
Пример 4. Фермер хочет ограждать два соседних курятника напротив сарая.У него 125 футов забора. Какие должны быть размеры, если он хочет, чтобы общая площадь составляла 700 квадратных футов.
а. Заполните таблицу, чтобы найти уравнение для площади.
г. Найдите W, когда A = 700.
Размеры курятника, который даст площадь 700 квадратных футов, составляют 35 на 20 футов и 6,667 на 105 футов.
(Чтобы получить длину, разделите 700 на 6,667 и 35.)
Раздел 4.3: Квадратичные приложения и графики
Для построения квадратичного графика y = ax 2 + bx + c необходимо найти:
- Вершина:
Координата x вычисляется по формуле
Координата y вычисляется путем замены координаты x на y = ax 2 + bx + c. - Пересечение x:
Установите y = 0 и решите 0 = ax 2 + bx + c, используя формулу корней квадратного уравнения. - Пересечение оси y:
Заменить x = 0 на y = ax 2 + bx + c. Обратите внимание, что когда x = 0, y = c.
Пример 5. Уравнение затрат на изготовление коробок для сока: C = 0,6B 2 — 24B + 36, а уравнение доходов — R = -0,4B 2 + 18B. B выражается в миллионах, а C и R — в тысячах долларов.
а. Найдите уравнение прибыли.
г. Изобразите уравнение прибыли и объясните, что точки пересечения B и P означают с точки зрения проблемы.
Вершина — (21, 405).
Найдите точку пересечения B. Установите P = 0.
B — точки пересечения (0.875, 0) и (41.13, 0).
Найдите точку пересечения P. Установите B = 0.
Перехватчик P равен (0, -36).
г. Предположим, компании нужно заработать 200 000 долларов прибыли (P = 200).Изобразите линию P = 200 и найдите, сколько коробок из-под сока нужно сделать компании, чтобы заработать 200 000 долларов.
Чтобы получить прибыль в размере 200 000 долларов, компании необходимо произвести 6 682 или 35,32 миллиона ящиков для сока.
Вершина (21,405) представляет максимальную прибыль. Компания получит максимальную прибыль в размере 405 000 долларов, продав 21 миллион коробок для сока.
Перехватчики B (0,875, 0) и (41,13, 0) говорят нам, что компания сломается, даже если они продадут.875 или 41,13 миллиона ящиков сока.
P-точка пересечения (0–36) представляет начальные затраты компании в размере 36 000 долларов.
Раздел 4.4: Факторинг
Общие факторы:
Триномы:
Решение квадратных уравнений на множители.
Если a. b = 0, тогда a = 0 или b = 0
Советы по обучению:
- Выполните повторный тест, начиная со следующей страницы, поместив себя в реалистичные условия экзамена.
- Найдите тихое место и используйте таймер, чтобы смоделировать продолжительность урока.
- Запишите свои ответы в домашнюю тетрадь или сделайте копию теста. Затем вы можете повторно сдать экзамен для дополнительной практики.
- Проверьте свои ответы.
- Дополнительный экзамен доступен на веб-странице MAT 011.
- НЕ ждите накануне, чтобы заняться изучением.
Узнайте, как построить график правила функции, построить график входов (x) и выходов (y)
В этом видео мы узнаем, как построить график функции.Чтобы построить график функции, вы должны выбрать значения x и подставить их в уравнение. Как только вы подставите эти значения в уравнение, вы получите значение y . Ваши значения x и y составляют ваши координаты для одной точки. Продолжайте вводить значения x, чтобы получить координаты для построения большего количества точек на графике, и тогда вы увидите свою графическую функцию, как только точки будут соединены. Обязательно пометьте свой график. После того, как вы закончите этот урок, просмотрите все наши уроки Алгебры 1 и попрактикуйтесь.
Пример построения графика функции-правила
Эти координаты будут выглядеть так:
и
Стенограмма видеоурока
Пример 1
Давайте выберем значения x, а затем решим соответствующие им значения y.
У нас есть значения x как.
Наша функция.
Итак, давайте заменим значения, чтобы получить значения.
А теперь нарисуем координаты.
Пример 2
Давайте выберем значения x, а затем решим соответствующие им значения y.
У нас есть значения x как.
Наша функция.
Итак, давайте заменим значения, чтобы получить значения.
А теперь нарисуем координаты.
Давайте рассмотрим график функции-правила.
Например:
Давайте выберем значения, а затем решим их соответствующие значения.
У нас есть значения as.
Наша функция.
Итак, давайте заменим значения, чтобы получить значения.
Если
, затем
так
Если
, затем
так
Если
, затем
так
Если
, затем
так
Если
, затем
так
Если
, затем
так
И на последок, если
, затем
так
Давайте также напишем наши координаты и
Теперь давайте изобразим это.
После соединения точек важно поставить стрелки на обоих концах отрезка линии.
Потому что мы знаем, что эти точки являются точками функции. Но дело не только в этом.
Функция может перемещаться на обоих концах, обозначенных стрелками.
А затем пометьте график.
Решите Свойства прямой y = 2x-5 Tiger Algebra Solver
Переставьте:
Переставьте уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения:
y- (2 * x -5) = 0
Шаг 1:
Уравнение прямой
1.1 Решите y-2x + 5 = 0
Тигр распознает, что здесь есть уравнение прямой. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании).
«y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось.
В этой формуле:
y говорит нам, как далеко идет линия.
x говорит нам, как далеко вдоль
м находится наклон или градиент, т.е. насколько крутой является линия.
b является пересечением по оси Y i.е. где линия пересекает ось Y
Пересечения X и Y и наклон называются свойствами линии. Теперь мы построим график линии y-2x + 5 = 0 и вычислим ее свойства
График прямой линии:
Вычислите точку пересечения Y:
Обратите внимание, что когда x = 0, значение y равно -5 / 1, поэтому эта линия «разрезает» ось y в точке y = -5,00000
y-intercept = -5/1 = -5,00000
Вычислить пересечение оси X:
Когда y = 0, значение x равно 5 / 2 Наша линия поэтому «разрезает» ось x в точке x = 2.50000
x-intercept = 5/2 = 2.50000
Вычислить наклон:
Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно -5,000, а для x = 2,000 значение y равно -1,000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на -1,000 — (-5,000) = 4.000 по y. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = RISE / RUN)
Наклон = 4.000 / 2.000 = 2.000
Геометрическая фигура: прямая
- Наклон = 4.000 / 2.000 = 2.000
- пересечение по оси x = 5/2 = 2,50000
- пересечение по оси y = -5/1 = -5,00000
Графики Разделы: Вводные Это может показаться немного Если степень в экспоненте
Это на самом деле полезный Иногда вы увидите На рассмотрение: ниже приведены некоторые <<
Предыдущий Топ
| 1 | 2
|
Графики смещения, отражения и растяжения
1.5 — Графики смещения, отражения и растяжения
Определения
- Абсцисса
- Координата x
- Ордината
- Координата Y
- Сдвиг
- Перевод, в котором размер и форма графика функции не изменены, но
расположение графика. - Масштаб
- Перевод, в котором изменен размер и форма графика функции.
- Отражение
- Перевод, в котором график функции отражается относительно оси.
Общие функции
Отчасти красота математики в том, что почти все основано на чем-то другом, и если
вы можете понять основы, а затем применить новые элементы к старым. Это способность
что делает возможным понимание математики.Если бы вы запомнили каждый кусок
математики, представленной вам без связи с другими частями, вы 1) станете
разочарованы в математике и 2) не очень разбираются в математике.
Есть несколько основных графиков, которые мы видели раньше. Применяя переводы к этим основным
графов, мы можем получить новые графы, которые по-прежнему обладают всеми свойствами старых. От
понимая основные графики и то, как к ним применяются переводы, мы узнаем каждый
новый график как небольшая вариация старого, а не как совершенно другой график, как у нас
никогда раньше не видел.Понимание этих переводов позволит нам быстро распознать и
нарисуйте новую функцию, не прибегая к построению точек.
Это общие функции, графики которых вы должны знать сейчас:
- Постоянная функция: y = c
- Линейная функция: y = x
- Квадратичная функция: y = x 2
- Кубическая функция: y = x 3
- Функция абсолютного значения: y = | x |
- Функция квадратного корня: y = sqrt (x)
- Наибольшая целочисленная функция: y = int (x) говорилось в предыдущем разделе.
Постоянная функция | Линейная функция | Квадратичная функция |
Кубическая функция | Функция абсолютного значения | Функция квадратного корня |
В вашем тексте линейная функция называется функцией тождества, а квадратичная функция — возведением в квадрат.
функция.
Переводы
Есть два типа переводов, которые мы можем сделать с графиком функции. Они меняются и
масштабирование. Если считать отражения, их три, но отражения — это всего лишь частный случай
второй перевод.
Смена
Сдвиг — это жесткий перевод, поскольку он не меняет форму или размер графика
функция. Все, что будет делать сдвиг, — это изменить положение графика. Вертикальный сдвиг
добавляет / вычитает константу к / из каждой координаты y, оставляя координату x неизменной.Горизонтальный сдвиг добавляет / вычитает константу к / из каждой координаты x, оставляя координату y неизменной. Вертикальные и горизонтальные сдвиги можно объединить в одно выражение.
Сдвиги добавляются / вычитаются к компонентам x или f (x). Если константа сгруппирована с x,
тогда это горизонтальный сдвиг, иначе это вертикальный сдвиг.
Весы (растяжение / сжатие)
Масштаб — это нежесткий перевод, поскольку он изменяет форму и размер графика
функция.Масштаб будет умножать / делить координаты, и это изменит внешний вид, а также
Местоположение. Вертикальное масштабирование умножает / делит каждую координату y на константу, оставляя
координата x не изменилась. Горизонтальное масштабирование умножает / делит каждую координату x на
константа, оставляя координату y неизменной. Вертикальные и горизонтальные масштабы могут быть
объединены в одно выражение.
Коэффициенты масштабирования умножаются / делятся на компоненты x или f (x). Если константа сгруппирована
с x, тогда это горизонтальное масштабирование, в противном случае это вертикальное масштабирование.
Отражения
Функция может быть отражена вокруг оси умножением на отрицательную единицу. Чтобы отразить ось Y, умножьте каждый x на -1, чтобы получить -x. Чтобы отразить ось x, умножьте f (x) на -1, чтобы получить -f (x).
Собираем все вместе
Рассмотрим основной график функции: y = f (x)
Все переводы можно выразить в форме:
y = a * f [b (x-c)] + d
| Вертикальный | Горизонтальный | |
|---|---|---|
| Масштаб | a | б |
| Сдвиг | д | c |
| действует нормально | действует наоборот |
Отступление
Понимание представленных здесь концепций является фундаментальным для понимания полиномиального и рационального
функции (ch 3) и особенно конические секции (ch 8).Это также будет играть очень большую роль в
Тригонометрия (Математика 117) и Исчисление (Математика 121, 122, 221 или 190).
Ранее в тексте (раздел 1.2, задачи 61-64) упоминалась серия задач, которые писали
уравнение линии как:
х / а + у / б = 1
Где a — точка пересечения по оси X, а b — точка пересечения по оси Y линии. «А» может
действительно быть
подумал о том, как далеко нужно пройти по оси x (масштабирование по оси x), и буква «b» могла бы
думать как
далеко идти в направлении «y» (масштабирование по оси y).Итак, «а» и «б» есть
собственно множители (даже если они появляются внизу). Что они
умножение
это 1
который находится с правой стороны. x + y = 1 будет иметь точки пересечения с координатами x и y
1.
Хорошо. Рассмотрим уравнение: y = f (x)
Это самый простой график функции. Но преобразования могут
применимо и к нему. Его можно записать в формате, показанном ниже.
В этом формате «a» — вертикальный множитель, а «b» — горизонтальный.
множитель.Мы знаем, что «a» влияет на y, потому что он сгруппирован с
y, а буква «b» влияет на
x, потому что он сгруппирован с x.
Буквы «d» и «c» — вертикальные и горизонтальные.
сдвигов соответственно. Мы знаем, что это смены, потому что они вычитаются
из переменной скорее
чем быть разделенными на переменные, что сделало бы их масштабными.
В этом формате все изменения кажутся противоположными ожидаемым. Если у вас есть
выражение (y-2) / 3, это вертикальный сдвиг на 2 вправо (хотя в нем указано y минус 2), и это
вертикальное растяжение на 3 (хотя там указано, что y делится на 3).Важно понимать, что в этом
формат, когда константы сгруппированы с переменной, на которую они влияют, перевод является
противоположное (обратное) тому, что думает большинство людей.
Однако этот формат не подходит для создания эскизов с помощью технологий,
потому что нам нравится писать функции как y =, а не (y-c) / d =.
Итак, если вы возьмете обозначение выше и решите его относительно y, вы получите обозначение ниже, которое
похоже, но не совсем в нашем базовом состоянии формы, приведенном выше.
y = a * f ((x-c) / b) + d
Обратите внимание, что для определения y вам нужно было инвертировать константы «a» и «d».Вместо деления на «а» вы теперь умножаете на «а». Ну, раньше
будь то ты
в любом случае пришлось применить обратную константу. Когда было сказано «разделить на»,
ты знал это
Это
означало «умножать
каждый y на «. Когда говорилось» вычесть d «, вы знали, что вам действительно нужно» добавить
d «. У вас есть
обратное уже было применено, так что больше не делайте этого! С константами, влияющими на
y, поскольку они были перемещены на другую сторону, принимайте их за чистую монету.
Если там написано «умножить на 2», делайте это, а не
разделить на 2.
Однако константы, влияющие на x, не изменились. Они по-прежнему противоположны
какими, по вашему мнению, они должны быть. И, что еще хуже, «x разделенное b» на самом деле означает
умножение каждой координаты x на «b» было перевернуто и записано как «b умножить на x», так что это действительно
означает разделить каждый x на «b». «X минус c» на самом деле означает прибавление c к каждой координате x.
Итак, окончательная форма (по технологии) такая же:
y = a * f [b (x-c)] + d
Хорошо, конец отступления.
Нормальное и обратное поведение
Вы заметите, что в таблице указано, что вертикальный перевод нормальный, а горизонтальный — нормальный.
переводы инвертированы. Объяснение причин читайте в отступлении выше. Концепции в
действительно важны для понимания многих графиков.
Примеры
- y = f (x)
- Нет перевода
- у = е (х + 2)
- +2 сгруппировано с x, поэтому это горизонтальный перевод.Поскольку он добавлен
к x, а не умноженному на x, это сдвиг, а не масштаб. Поскольку там написано плюс
и горизонтальные изменения инвертированы, фактический перевод заключается в перемещении всего
график слева на две единицы или «вычтите два из каждой координаты x», оставив
только координаты y. - у = е (х) +2
- +2 не сгруппирован с x, поэтому это вертикальный перевод. Поскольку он добавлен,
это не умножение, а сдвиг, а не масштаб.Поскольку там написано плюс и вертикальный
изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два
единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x. - y = f (x-3) +5
- На этот раз имеется сдвиг по горизонтали на три вправо и сдвиг по вертикали на пять вверх. Так
перевод будет заключаться в перемещении всего графика вправо на три и пять вверх или «добавить три
для каждой координаты x и пять для каждой координаты y « - у = 3f (х)
- 3 умножается, поэтому это масштабирование, а не сдвиг.3 не сгруппированы с
x, так что это вертикальное масштабирование. Вертикальные изменения происходят так, как вы думаете.
должно быть, поэтому в результате мы «умножим каждую координату y на три», оставив только координаты x. - у = -f (х)
- Y нужно умножить на -1. Это заставляет перенос «отражаться относительно оси x», оставляя только координаты x.
- y = f (2x)
- 2 умножается, а не складывается, поэтому это масштабирование, а не сдвиг.2 — это
сгруппированы с x, поэтому это горизонтальное масштабирование. Горизонтальные изменения противоположны
чем они кажутся, вместо того, чтобы умножать каждую координату x на два,
перевод заключается в «делении каждой координаты x на два», оставляя координаты y
без изменений. - у = f (-x)
- Х нужно умножить на -1. Это заставляет перемещение «отражаться относительно оси y», оставляя только координаты y.
- y = 1/2 f (x / 3)
- Здесь можно было бы перевести каждую координату y на 1/2 и умножить
каждую координату x на 3 дюйма. - у = 2f (х) +5
- Здесь может быть некоторая двусмысленность. Вы добавляете пять к каждой координате Y, а затем
умножьте на два «или вы» умножаете каждую координату y на два, а затем складываете пять «?
Вот тут-то и приходит мой предыдущий комментарий о математике, основанной на самой себе.
играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы помните это, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x. - y = f (2x-3)
- Теперь, когда порядок операций четко определен, двусмысленность
нужно сделать сначала снимается. Ответ не в том, чтобы «делить каждую координату x на два.
и добавьте три «, как и следовало ожидать. Причина в том, что проблема , а не , записанная в
стандартная форма. Стандартная форма — y = f [b (x-c)]. При написании в стандартной форме это
проблема становится y = f [2 (x-3/2)]. Это означает, что правильный перевод:
«разделить каждую координату x на два и добавить три половины», оставляя координаты y неизменными. - у = 3f (х-2)
- Перевод здесь означает «умножить каждую координату y на три и добавить два к каждой координате x». В качестве альтернативы вы можете изменить порядок. Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.
Переводы и влияние на домен и диапазон
Любой горизонтальный перевод повлияет на домен и оставит диапазон неизменным.Любая вертикаль
перевод повлияет на диапазон и оставит домен без изменений.
Примените тот же перевод к домену или диапазону, который вы применяете к координатам x или y. Это работает, потому что область может быть записана в обозначении интервала как интервал
между двумя координатами x. То же самое для диапазона, как интервал между двумя координатами y.
Помните, что в следующей таблице домен и диапазон даны в виде интервалов. Если ты
Если вы не знакомы с обозначением интервалов, обратитесь к главе о предварительных требованиях.Первая строка — это
формулировка определения и должна использоваться для определения остальных ответов.
| График | Перевод | Домен | Диапазон |
|---|---|---|---|
| y = f (x) | нет | (-2,5) | [4,8] |
| y = f (x-2) | правый 2 | (0,7) | [4,8] |
| y = f (x) -2 | вниз 2 | (-2,5) | [2,6] |
| y = 3f (x) | умножаем каждый y на 3 | (-2,5) | [12,24] |
| y = f (3x) | делим каждый x на 3 | (-2 / 3,5 / 3) | [4,8] |
| y = 2f (x-3) -5 | умножьте каждый y на 2 и вычтите 5; прибавьте 3 к каждому x | (1,8) | [3,11] |
| y = -f (x) | отразить относительно оси x | (-2,5) | [-8, -4] |
| y = 1 / f (x) | возьмите величину, обратную каждому y | (-2,5) | [1 / 8,1 / 4] |
Обратите внимание на последние два, что порядок в диапазоне изменился.Это потому, что в интервале
обозначение, меньшее число всегда идет первым.
Действительно хорошие вещи
Понимание переводов также может помочь при поиске домена и диапазона функции.
Допустим, ваша проблема — найти домен и диапазон функции y = 2-sqrt (x-3).
Начните с того, что вы знаете. Вы знаете, что основная функция — это sqrt (x), и вы знаете домен
и диапазон sqrt (x) равны [0, + бесконечность). Вы знаете это, потому что знаете эти шесть
общие функции на лицевой обложке вашего текста, которые будут использоваться в качестве строительных блоков
для других функций.
| Функция | Перевод | Домен | Диапазон | |
|---|---|---|---|---|
| Начать с чего ты знаешь | y = sqrt (x) | Нет | [0, + бесконечность) | [0, + бесконечность) |
| Примените переводы | y = -sqrt (x) | Отражение относительно оси x | [0, + бесконечность) | (-infinity, 0] |
| y = 2-sqrt (x) | Добавьте 2 к каждой ординате | [0, + бесконечность) | (-бесконечность, 2] | |
| y = 2-sqrt (x-3) | Добавьте 3 к каждой абсциссе | [3, + бесконечность) | (-бесконечность, 2] |
Итак, для функции y = 2-sqrt (x-3) домен равен x≥3, а диапазон — y≤2.
И лучшая часть в том, что вы это поняли! Вы не только поняли это, но вы были
в состоянии сделать это без построения графика на калькуляторе.
Нет ничего плохого в том, чтобы построить график, чтобы увидеть, что происходит, но вы должны уметь
понять, что происходит без графика, потому что мы узнали, что график
калькулятор не всегда точно показывает, что происходит. Это инструмент, который поможет вам понять
и понимание, а не инструмент для его замены.
Я хочу, чтобы все вы «поняли» именно эту связность математики. Все подходит
вместе так красиво.
.