Применение теоремы фалеса в жизни: Теорема Фалеса и ее применение в жизни | Математика — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Теорема Фалеса интересные факты. Интересные факты из жизни Фалеса

Интересные факты из жизни Фалеса. По легенде теорема была сформулирована в не сохранившейся «Морской астрономии» Фалеса или Фоки Самосского. Ни одно из античных свидетельств, касающихся Фалеса, с этой теоремой никак напрямую не связано. Возможно, что теорема приписана Фалесу опосредованно, поскольку известно, что он умел измерять высоту обелиска и расстояние до корабля в море; при этих измерениях можно использовать подобие треугольников, а утверждение о пропорциональности сторон подобных треугольников доказывается на основе «теоремы Фалеса». Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга. Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла. Основы геометрии Фалес постигал в Египте.

Слайд 4 из презентации «Математические открытия» к урокам математики на тему «История математики»

Размеры: 960 х 720 пикселей, формат: jpg.
Чтобы бесплатно скачать слайд для использования на уроке математики,
щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как…».
Скачать всю презентацию «Математические открытия.pptx» можно
в zip-архиве размером 622 КБ.

История математики

краткое содержание других презентаций об истории математики

«Математические открытия» — О теореме Пифагора. Теорема Пифагора. Великие открытия Архимеда. Открытия Архимеда. Фалес Милетский. Пифагорейцы. Творцы математики и их открытия. Сочинения Пифагора. Интересные факты из жизни Фалеса. Эратосфен Киренский. Труды Эратосфена. Мудрец. Решето Эратосфена. Теорема Фалеса. Начала Евклида. Описание монохорда.

«Математика в Греции» — Греческая математика поражает прежде всего красотой и богатством содержания.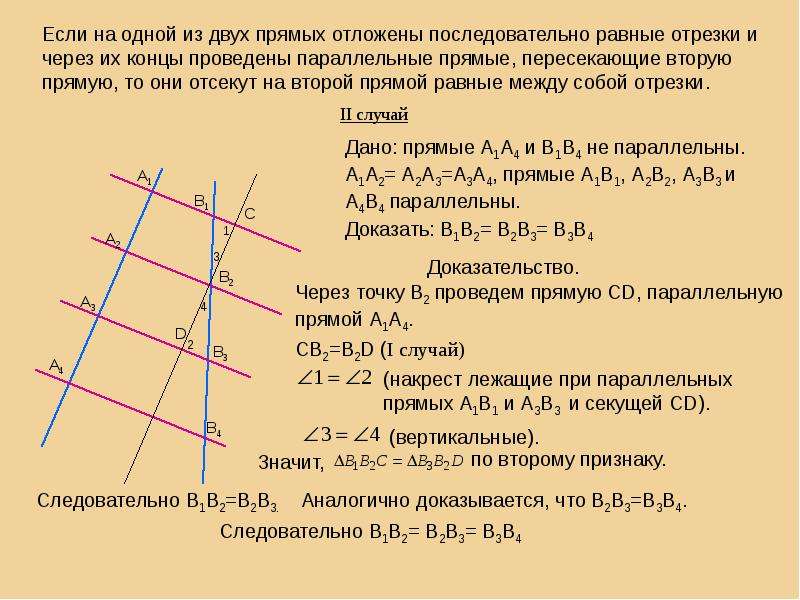 Успехи пифагорейцев в стереометрии были значительными. Математика в Древней Греции. Теэтет и Евклид установили классификацию квадратичных иррациональностей. Глава II. 1.2 Поворотный пункт в истории античной математики. Пифагорейцы заложили основы геометрической алгебры.

«Математика в США» — Джон фон Нейман. Чёрч стал профессором математики в Принстоне в 1929 году. Такой ответ поставил часового в тупик. Владимир Александрович Воеводский — российский и американский математик, преподаватель. Обозначение нуля также применялось для обозначения бесконечности. Американские премии в области математики.

«История математики в России» — Способ умножения с «помощью рук». Сухарева башня. Курбатов. Согласно показанию Курбатова, желающих учиться в школе было много. Материальная сторона дела была передана в Оружейную палату. Труд Магницкого. Первая математическая школа в Москве. Образование. А. Курбатов предложил Петру I математика. Арифметика.

«История появления математики» — Кипу, использовались инками для записи чисел. Рене Декарт. Листья на ветке растения. Математика в разное время. М.В.Остроградский. Интересные факты. Цифры майя. Математика. Математический закон Бенфорда. Великие математики. Исаак Ньютон. Разделы математики. История математики. Как появилась математика.

Источник: https://interesnyefakty.com/stati/fales-miletskiy-interesnye-fakty-geometriya-kratkaya-biografiya

Теорема Фалеса ударение. Замечания

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.

Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Доказательство в случае секущих

Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые A
A
1
|
|
B
B
1
|
|
C
C
1
|
|
D
D
1
{\displaystyle AA_{1}||BB_{1}||CC_{1}||DD_{1}} и при этом A
B
=
C
D
{\displaystyle AB=CD} .

Проведём через точки A
{\displaystyle A} и C
{\displaystyle C} прямые, параллельные другой стороне угла. A
B
2
B
1
A
1
{\displaystyle AB_{2}B_{1}A_{1}} и C
D
2
D
1
C
1
{\displaystyle CD_{2}D_{1}C_{1}} . Согласно свойству параллелограмма: A
B
2
=
A
1
B
1
{\displaystyle AB_{2}=A_{1}B_{1}} и C
D
2
=
C
1
D
1
{\displaystyle CD_{2}=C_{1}D_{1}} .

Как разделить отрезок на 3 равные части по теореме Фалеса. Теорема Фалеса и деление отрезка в заданном отношении

Давно о геометрии не говорили, а о теореме ФАлеса (или ФалЕса?) вообще мало говорят. Хотя она весьма полезна. Начнем с формулировки, которая весьма не вразумительна, чем и объясняется не популярность данной теоремы.

Мутно, долго, не понятно. Мне больше нравится другая формулировка.

Тоже не понятно, но элегантно и коротко.

Задачи, которые решаются с помощью данной теоремы, довольно специфичны. Но есть одна задача на построение, которую можно встретить в реальной жизни. Это задача о делении отрезка в заданном отношении.

Суть вопроса: Дан отрезок. Его нужно поделить на два куска, чтобы их длины относились, как 2 : 5. Кусков может быть сколько угодно и отношение, может быть каким угодно. Алгебраически задача решается крайне легко: находим общее количество частей (2 + 5 = 7), делим длину отрезка на общее количество частей, находим длину каждого куска.

Но алгебраическое решение не всегда прокатывает. Например, мы не можем найти длину отрезка, или при делении получаются не целые числа. Тогда можно воспользоваться геометрическим способом.

Во-первых, проводим луч из конца отрезка. Любой, в любую сторону.

Дальше, на этом луче от точки А откладываем 7 (общее количество частей) равных отрезков.

Последнюю получившуюся точку — J соединяем с точкой В, а затем через каждую точку луча проводим прямую параллельную JB.

Таким образом, мы разделили отрезок АВ на 7 равных частей (по теореме Фалеса). Отсчитываем две части и ставим точку. Получаем: AK : KB = 2 : 5.

Вот таким простым образом, вы можете поделить свою комнату с соседом в любом отношении. Если вам кажется, что построение такого количества параллельных прямых дело сложное, то подумайте о перпендикулярах.

Докажите теорему Фалеса. Обобщенная теорема Фалеса

Определение, которое мы сформулировали, является избыточным – чтобы треугольники были подобны, не нужно требовать и пропорциональности трех пар сторон, и равенства трех углов.

Для того чтобы убедиться в том, что два треугольника являются подобными, существуют признаки подобия треугольников (по аналогии с признаками равенства). И в них не требуется проверять все утверждения, перечисленные в определении.

Чтобы разобраться в этом, рассмотрим очень древний и очень удобный геометрический инструмент – теорему Фалеса. Фалес Милетский, именем которого названа теорема, жил более 2,5 тысяч лет назад.

Рис. 8. Фалес Милетский

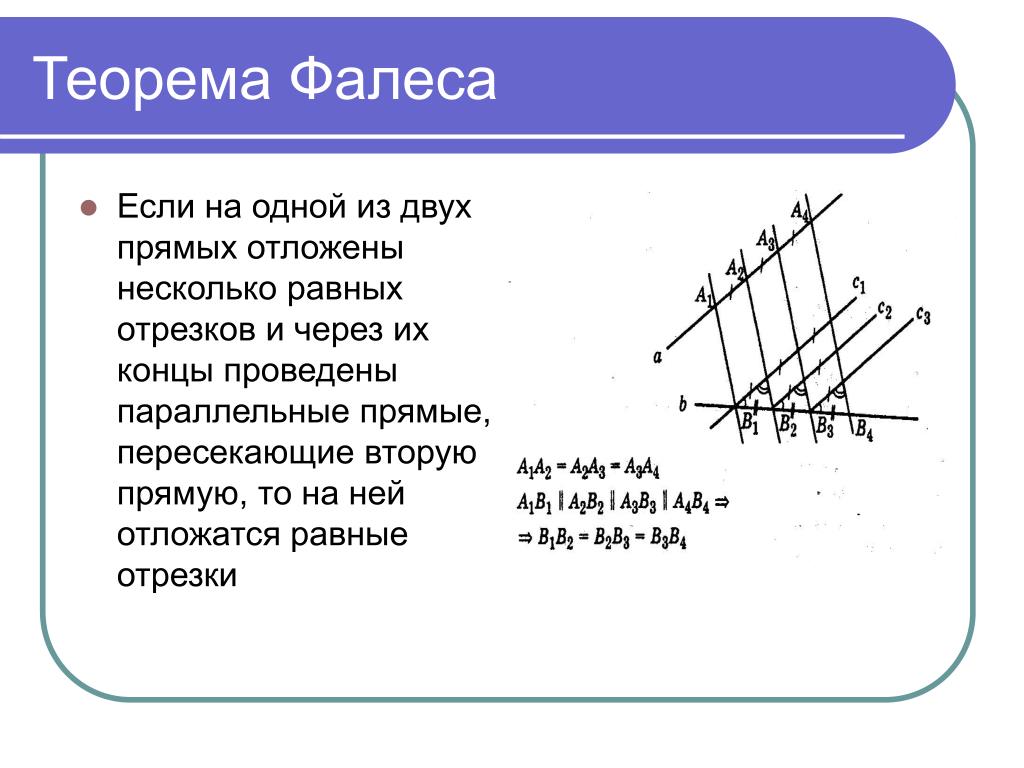
Теорема Фалеса достаточно наглядна и не вызывает особых сомнений даже без строгого доказательства: если параллельные прямые отсекают равные отрезки на одной стороне угла, то они отсекают равные отрезки и на другой стороне (см. рис. 9).

Рис. 9. Иллюстрация к теореме Фалеса

Более общая формулировка этой теоремы (ее еще называют обобщенной теоремой Фалеса или теоремой о пропорциональных отрезках ): параллельные прямые отсекают на сторонах угла пропорциональные отрезки .

Т. е. если пересечь угол несколькими параллельными прямыми (в отличие от классической формулировки можно начертить прямые на разных расстояниях друг от друга), то отношение двух отрезков на одной стороне угла будет равно отношению соответствующих отрезков на второй стороне (см. рис. 10):

Рис. 10. Иллюстрация к теореме Фалеса

Доказывать эти теоремы мы пока не умеем. Но обязательно сделаем это чуть позже. Пока возьмем их на вооружение как известные нам факты.

Теорема Фалеса в жизни

Чтобы проиллюстрировать применение теоремы Фалеса, рассмотрим такой пример.

Пусть два корабля движутся так, что их курс друг относительно друга не меняется (под курсом в данном случае мы понимаем угол между направлением движения судна и направлением на второе судно) (см.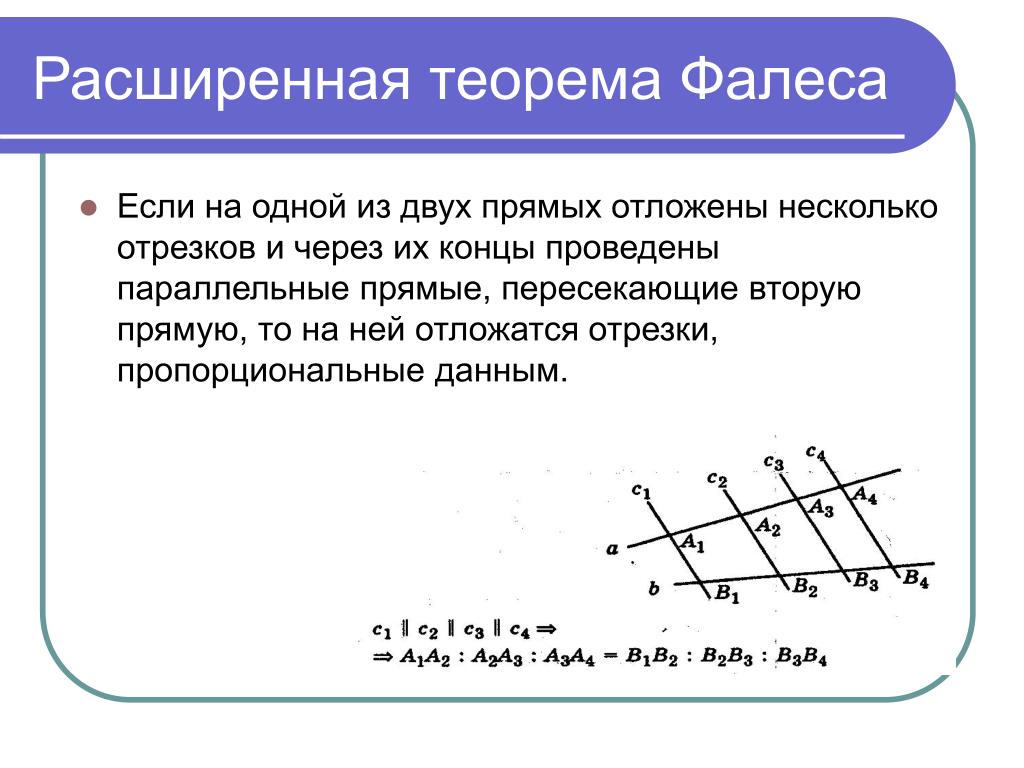 рис. 11).

Рис. 11. Курс двух движущихся кораблей друг относительно друга не меняется

Тогда ясно, что при неизменности ситуации, неизбежно столкновение (поскольку из равенства углов следует, что прямые, соединяющие корабли, параллельны друг другу, а значит, за равные промежутки времени они проходят одинаковые расстояния и должны сойтись в одной точке – вершине угла) (см. рис. 12).

Рис. 12. За равные промежутки времени корабли проходят одинаковые расстояния и должны сойтись в одной точке

Это можно использовать для предотвращения аварий в море. Ведь чем раньше капитаны кораблей узнают о вероятности столкновения, тем больше шансов его избежать.

В отличие от автомобилей большие грузовые суда имеют очень большой тормозной путь (т. к. сила сопротивления со стороны воды очень маленькая, а инертность из-за большой массы огромная). Так, у нефтяных танкеров тормозной путь может быть длиной несколько десятков километров.

Практическое применение теорем геометрии в жизни

1.

Автор: Боброва Елена Валентиновна Место работы: ГКОУ ВО «Специальная (коррекционная) общеобразовательная школа-интернат г.

Урок геометрии в 10-м классе

2. Автор: Боброва Елена Валентиновна Место работы: ГКОУ ВО «Специальная (коррекционная) общеобразовательная школа-интернат г.

Урок геометрии в 10-м классе по теме
«Практическое применение теорем
геометрии в жизни»
«Решение задач реальной математики
(подготовка к ОГЭ)»
A
а2+ b 2 =с 2
c
b
a
О теореме Пифагора
Пифагор (Pythagoras)
Самосский
(ок. 570 — 500 до н.э.)
Пребудет вечной истина, как скоро
Все познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
A.Шамиссо

4. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой с теченьем реки его

5. Задача Бхаскары

Решение.
Пусть CD – высота ствола.
BD = АВ
По теореме Пифагора имеем
АВ = 5 .
CD = CB + BD,
CD = 3 + 5 =8.
Ответ: 8 футов.
5

6. Какова глубина в современных единицах длины (1 фут приближённо равен 0,3 м) ?

Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”
Какова глубина в современных
единицах длины
(1 фут приближённо равен 0,3
6 м) ?
Решение:
Выполним чертёж к задаче и обозначим глубину озера АС =Х, тогда AD
= AB = Х + 0,5 .
Из треугольника ACB по теореме Пифагора имеем AB2 – AC2 = BC2,
(Х + 0,5)2 – Х2 = 22 ,
Х2 + Х + 0,25 – Х2 = 4,
Х = 3,75.
Таким образом, глубина озера составляет 3,75 фута.
3, 75 • 0,3 = 1,125 (м)
Ответ: 3,75 фута или 1, 125 м.
7
В 60 м одна от другой растут две сосны. Высота
одной 31 м, а другой – 6 м. Найдите расстояние
(в метрах) между их верхушками
?
25
31
60
6
60
+
=
4225
= 65
2. Лестница соединяет точки A и B и состоит из 40
ступеней. Высота каждой ступени равна 24 см, а
длина — 70 см. Найдите расстояние между
точками A и B (в метрах).
ПЛАН РЕШЕНИЯ
1.Найти гипотенузу в треугольнике
(ступеньке)
2.Умножить на количество
ступенек

10. Подобие в жизни

Определение подобных треугольников
В подобных треугольниках
сходственные стороны
пропорциональны, а углы
равны
В
AB AC ВС
=
A1B1 AC
В1С1
1 1
А
А1
В1
С
С

13. Историческая справка.

За шесть веков до нашей эры греческий мудрец Фалес
Милетский вычислил высоту египетской пирамиды,
измерив длину её тени.
Как это было, рассказывается в книге Я.И.Перельмана
«Занимательная геометрия».
Фалес, говорит предание, избрал день и час,
когда длина собственной его тени
равнялась его росту. В этот момент высота пирамиды
должна также равняться
длине отбрасываемой
его тени.
Вот, пожалуй, единственный
случай, когда человек
извлёк пользу из своей тени.
ПРИТЧА:
« Усталый чужеземец пришёл в страну Великого Хапи. Солнце
уже садилось, когда он подошёл к великолепному дворцу фараона.
Он что-то сказал слугам. По мановению руки распахнулись перед
ним двери и провели его в приёмную залу. И вот он стоит в
запылённом походном плаще, а перед ним на золоченом троне
сидит фараон. Рядом стоят высокомерные жрецы,
хранители великих тайн природы.
— Кто ты? – спросил верховный жрец.
— Зовут меня Фалес. Родом я из Милета.
Жрец надменно продолжал:
— Так это ты похвалялся, что сможешь измерить высоту
пирамиды, не взбираясь на неё? – Жрецы согнулись от хохота.
— Будет хорошо, — насмешливо продолжал жрец, — если ты
ошибёшься не более чем на 100 локтей.
— Я могу измерить высоту пирамиды и ошибусь не более чем на
пол-локтя. Я сделаю это завтра.
Лица жрецов потемнели. Какая наглость! Этот чужеземец
утверждает, что может вычислить то, чего не могут они – жрецы
великого Египта.
— Хорошо, — сказал фараон. – Около дворца стоит пирамида, мы
знаем её высоту. Завтра проверим твоё искусство».
На следующий день Фалес
нашёл длинную палку, воткнул
её в землю чуть поодаль
пирамиды. Дождался
определённого момента.
Провёл некоторые измерения,
сказал способ определения
высоты пирамиды и назвал её
высоту.

16. Способ Фалеса

Д
Н
В
h
А
С
Е

17. Способ Фалеса

Когда тень от палки будет той же длины,
что и сама палка, то длина тени от центра
основания пирамиды до её вершины будет
иметь ту же длину, что и сама пирамида.
СЕ=ED, т.е. H=b
Преимущества:
не требуются вычисления.
Недостатки:
нельзя измерить высоту предмета при отсутствии
солнца и, как следствие, тени.

20.

Способ Жуль Верна

Нахождения четвертого неизвестного члена
пропорции.
Преимущества:
можно производить измерения в любую
погоду;
простота формулы.
Недостатки:
нельзя
измерить высоту
предмета
не испачкавшись,
так как приходится
ложиться на землю.
Преимущества:
можно производить
измерения в любую погоду;
одежда будет чистой;
простота формулы;
Недостатки:
нужно специальное приспособление:
зеркало.
Нахождение ширины озера
Длина тени земного шара
1.Человек, рост которого равен 1,6 м, стоит на
расстоянии 17 м от уличного фонаря. При этом
длина тени человека равна 8 м. Определите
высоту фонаря (в метрах).
2. На рисунке изображён колодец с «журавлём».
Короткое плечо имеет длину 2 м, а длинное плечо
— 4 м. На сколько метров опустится конец
длинного плеча, когда конец короткого поднимется
на 1,5 м?
Литература
1. Л. С. Атанасян, В. Ф. Бутусов,С. Б. Кадомцев, Э. Г. Позняк, И. И.
Юдина 7-9. Учебник для общеобразоват. учреждений/ М.,Просвещение,2012.
2. Математика, 5-11 кл. Практикум-1С: Образование 3.0. ЗАО «1С», 20032004г. (электронное пособие, раздел Планиметрия→ Исследования и
практикумы→ Теорема Пифагора).
3. Г.И.Глейзер История математики в средней школе Просвещение 1970г.
4. Я.И.Перельман Занимательная геометрия Москва «Наука» 1976г
5. Зрительная гимнастика по Базарнову В.Ф.
6. Энциклопедический словарь юного математика /Сост.А. П. Савин. Педагогика, 1985
Интернет-ресурсы
wikikurgan.orbitel.ru/images/d/d3/Rechkalova_M.G.-prez10.ppt
www.all-biography.ru
http://www.zaitseva-irina.ru/
www.wiki.ciit.zp.ua
Источники иллюстраций
http://umrazum.ru/load/uchebnye_prezentacii/
http://www.rusedu.ru/detail_11537.html
http://www.rusedu.ru/detail_1744.html
http://www.rusedu.ru/detail_1744.html
http://www.rusedu.ru/detail_5014.html

Конспект «Теорема Фалеса» (8 класс)

Учебный проект

«Теорема Фалеса» в 8 классе

Учитель Гармаева Ц. Ц.

Цели урока:

Образовательная: доказать теорему Фалеса, научить применять её при решении задач по математике

Развивающая: развивать у учащихся познавательный интерес к учебным дисциплинам, умение применять свои знания на практике.

Воспитательная: воспитывать внимание, аккуратность, расширять кругозор учеников.

Оборудование и материалы:

Компьютер
Проектная работа “Теорема Фалеса”.
Плакат с рисунками 1,2,3.

Приложение

Задачи учителя

Показать практическое применение теоретических знаний учащихся при решении задач по геометрии и информатике.

Выявить глубокие связи между математикой и информатикой.

Название проекта: Теорема Фалеса

Тема проекта: Теорема Фалеса

Вид проекта: учебный.

Типология проекта: практико-ориентированный, индивидуально- групповой.

Предметные области: математика.

Гипотеза: Если человек знает как разделить отрезок на равные части, возникнет ли необходимость их применять в жизни?

Ход урока:

Приветствие и вступительное слово о целях урока.

Фронтальный опрос учащихся:

1. Какие отрезки называются равными?

2. Какие прямые называются параллельными? На рис. 1 покажите параллельные прямые.

3. Какие углы называются вертикальными, внутренними накрест лежащими? Покажите их на рис.2

4. Сформулируйте теорему о свойстве параллельных прямых, пересечённых третьей прямой.

5. Сформулируйте признаки равенства треугольников. По каким признакам равны треугольники на рис 3?

Объяснение нового материала (приложение)

Учащиеся вместе с учителем изучают и выполняют работу по новой теме с помощью просмотра презентации «Теорема Фалеса».

Сегодня мы докажем теорему, носящую имя древнегреческого учёного Фалеса, который жил в 624-547г.г. до н.э. Про древнегреческого ученого Фалеса расскажет ученица Дондокова Людмила.

Великий учёный Фалес Милетский основал одну из прекраснейших наук — геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Короче: он был то же для Греции, что Ломоносов для России.

Карьеру он начинал как купец и ещё в молодости попал в Египет. В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Считается, что геометрию и астрономию в Грецию привёз он.

Фалес — математик. Он измерил по тени высоту пирамиды; установил, что окружность диаметром делится пополам, что углы при основании равнобедренного треугольника равны. Ему же принадлежит теорема, что вписанный угол, опирающийся на диаметр окружности- прямой.

Фалес доказал теорему: “Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне”.

При активном участии учащихся разбирается доказательство теоремы с последовательным показом на экране каждого этапа построения чертежа и доказательства теоремы.

Из условия теоремы Фалеса делается вывод, что вместо сторон угла можно взять любые две прямые.

Затем ученики в парах выполняют в тетрадях практическую задачу на деление отрезка длиной в 7см. на 6 равных частей.

Греческие ученые открыли множество геометрических свойств и создали стройную систему геометрических знаний. В ее основу они положили простейшие геометрические свойства, подсказанные опытом. Остальные свойства выводились из простейших с помощью рассуждений.

Все этапы решения задачи учащиеся видят на экране. Это способствует зрительному запоминанию алгоритма решения и выполнения данной практической задачи

Вторую часть урока ведёт учитель информатики. Ученики вместе с учителем на компьютерах делят отрезок на три равные части.

Выполнение практического задания

Разделить данный отрезок на 3-равные части на компьютере

Используемые ИНСТРУМЕНТЫ

• стрелка;

• линейка (отрезок, луч).

Используемые КОМАНДЫ

• построения;

• правка;

Порядок работы:

1 .Построим данный отрезок АВ.

2.Проведем из т. А полупрямую а, не лежащую на прямой АВ.

3.Отложим на полупрямой а 3 равных отрезка.

Для этого используем команду ПОСТРОЕНИЯ— “окружность по центру и радиусу”; зададим произвольный радиус СО и построим на полупрямой а 3 окружности.

Они отсекают на полупрямой а равные отрезки АЕ=ЕР=РО.

4.Соединим точки В и О.

5. Проведем через точки Е и Р прямые, параллельные прямой ВО.

6. Они пересекают отрезок АВ в точках Н и I , которые делят отрезок АВ на 3 равные части; т.к. по теореме Фалеса:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Домашнее задание.

Задача: Разделить отрезок длиной 5 см. на 7 равных частей. Выучить теорему Фалеса.

Подведение итогов урока.

Общие выводы. Заключение

Осуществление данного учебного проекта позволило учащимся развить свои навыки работы не только с дополнительными источниками по математике, но и с компьютером, сформировать навыки работы в сети Интернет, а также коммуникативные способности учащихся.

Участие в осуществлении проекта позволило углубить знания по применению математики в различных областях, а также закрепить знания по указанной теме. Следует отметить, что полученные в ходе осуществления проекта знания извлекаются с конкретной целью и являются объектом заинтересованности ученика. Это способствует их глубокому усвоению.

В целом работа по проекту прошла успешно, в ней приняли участие практически все ученики 8 класса. Каждый был вовлечен в мыслительную деятельность по данной проблематике, приобрел новые знания путем самостоятельной работы.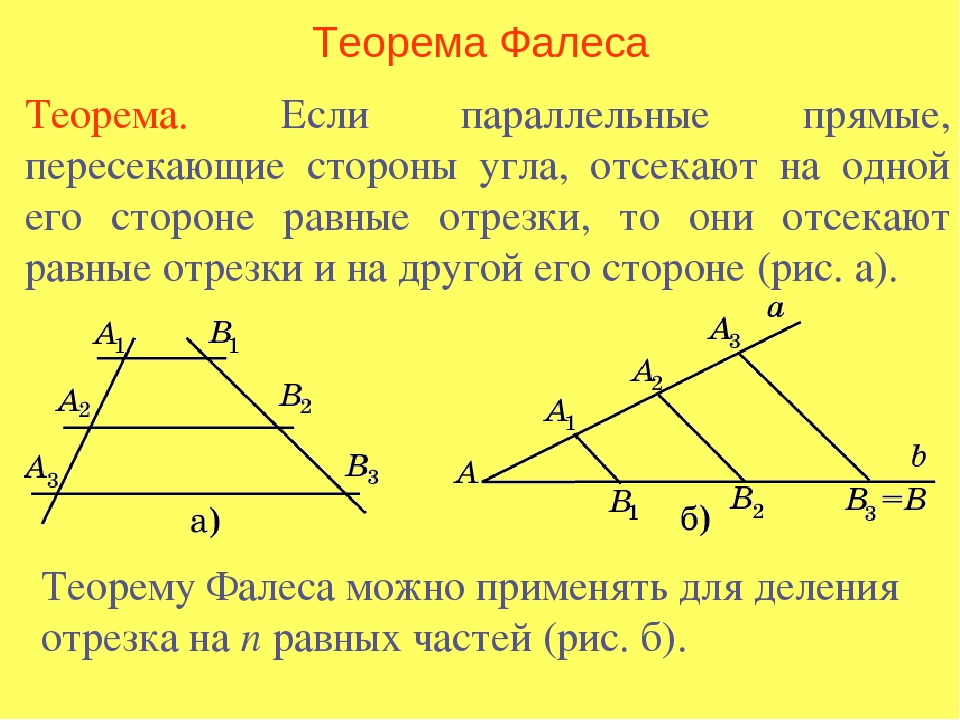 На защите своего проекта выступал каждый ученик. На заключительном этапе были апробированы практические приемы работы, проведен самоанализ в виде презентации.

Проектная деятельность учащихся способствует истинному обучению, т.к. она:

-Личностно ориентирована.

-Характеризуется возрастанием интереса и вовлеченности в работу по мере её выполнения.

-Позволяет реализовать педагогические цели на всех этапах.

-Позволяет учиться на собственном опыте, на реализации конкретного дела.

-Приносит удовлетворение ученикам, видящим продукт собственного труда.

Презентация.

Приложение

Теорема: если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Дано: угол, параллельные прямые пересекают стороны угла, А₁А₂=А₂А₃

Доказать: В₁В₂=В₂В₃

Доказательство.

Проведём через точку В₂ прямую ЕF, параллельную прямой А₁А₃.
По свойству параллелограмма А₁А₂=FВ₂, А₂А₃=В₂Е.
Так как А₁А₂=А₂А₃, то FВ₂=В₂Е
Треугольники В₂В₁F и В₂В₃Е равны по второму признаку ( у них В₂F=В₂Е по доказанному. Углы при вершине В₂ равны как вертикальные, а углы В₂FВ₃равны как внутренние накрест лежащие при параллельных А₁В₁ и А₃В₃ и секущей ЕF.)
Из равенства треугольников следует равенство сторон: В₁В₂=В₂В₃

ЗАДАЧА: РАЗДЕЛИТЕ ДАННЫЙ ОТРЕЗОК НА n РАВНЫХ ЧАСТЕЙ

1.Проведём из точки А полупрямую а, не лежащую на прямой АВ.

2.Отложим на полупрямой а равные отрезки:АА₁, А₁А₂, А₂А₃, …, А_n_-1А_n.

3.Соединим отрезком точку А_nс точкой В.

4.Через точки А₁,А₂, … А_n_-1проведём прямые, параллельные А_nВ.

5.По теореме Фалеса отрезки АВ₁, В₁В₂, …,В_n_-1В равны.

Доказать теорему фалеса. Теорема Фалеса

Эта гробница мала, но слава над ней необъятна.

В ней перед тобою сокрыт многоразумный Фалес.

Надпись на гробнице Фалеса Милетского

Представьте себе такую картину. 600 г. до н.э. Египет. Перед вами огромнейшая египетская пирамида. Чтобы удивить фараона и остаться у него в фаворитах вам нужно измерить высоту этой пирамиды. В распоряжении у вас… ничего. Можно пасть в отчаяние, а можно поступить, как Фалес Милетский
: использовать теорему подобия треугольников. Да, оказывается, все достаточно просто. Фалес Милетский подождал пока длина его тени и его рост совпадут, а затем с помощью теоремы о подобии треугольников нашел длину тени пирамиды, которая соответственно, была равна тени, отбрасываемой пирамидой.

Кто же такой этот Фалес Милетский
? Человек, который обрел славу одного из «семи мудрецов» древности? Фалес Милетский – древнегреческий философ, который отличился успехами в области астрономии, а также математики и физики. Годы его жизни были установлены только приблизительно: 625-645 гг до н.э.

Среди доказательств знания Фалесом астрономии можно привести следующий пример. 28 мая 585 г до н.э.
предсказание Милетским солнечного затмения помогло прекратить длившуюся уже 6 лет войну между Лидией и Мидией. Это явление настолько испугало мидян, что они согласились на невыгодные для себя условия заключения мира с лидийцами.

Довольно широко известна легенда, которая характеризует Фалеса как находчивого человека. Фалесу часто приходилось слышать нелестные отзывы о его бедности. Однажды он решил доказать то, что и философы могут при желании жить в достатке. Еще зимой Фалес по наблюдению за звездами определил, что летом будет хороший урожай маслин. Тогда же он нанял маслодавильни в Милете и на Хиосе. Это обошлось ему довольно дешево, так как зимой спрос на них практически отсутствует. Когда же маслины дали богатый урожай, свои маслодавильни Фалес начал сдавать внаем. Собранное большое количество денег таким методом расценивалось как доказательство того, что философы могут зарабатывать своим умом, но их призвание выше таких земных проблем. Эта легенда, кстати, повторялась самим Аристотелем.

Что же касается геометрии, то многое из его «открытий» было позаимствовано у египтян. И все же этот перенос знаний в Грецию считается одной из основных заслуг Фалеса Милетского.

Достижениями Фалеса считаются формулировка и доказательство следующих теорем:

вертикальные углы равны;
равными треугольниками признаются те, у которых сторона и два прилегающих угла соответственно равны;
углы при основании равнобедренного треугольника равны;
диаметр делит круг пополам;
вписанный угол, опирающийся на диаметр, является прямым.

Именем Фалеса названа еще одна теорема, которая полезна при решении геометрических задач. Существует ее обобщенный и частный вид, обратная теорема, формулировки также могут немного отличаться в зависимости от источника, но смысл их всех остается одним. Рассмотрим эту теорему.

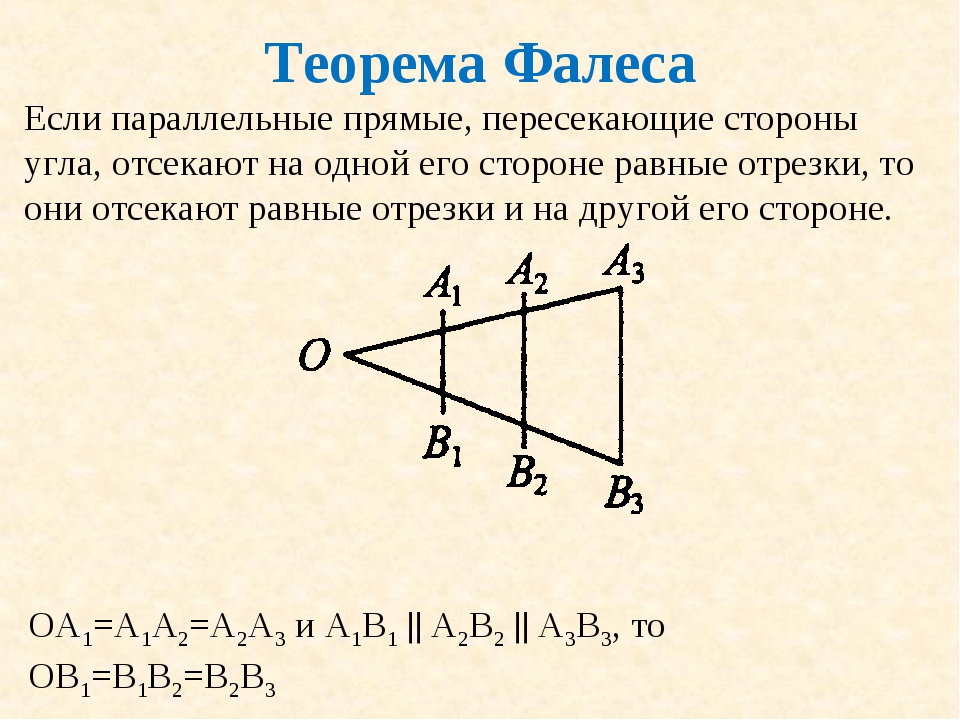
Если параллельные прямые пересекают стороны угла и отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Допустим, точки А 1 , А 2 , А 3 – точки пересечения параллельных прямых с одной из сторон угла, а В 1 , В 2 , В 3 – точки пересечения параллельных прямых с другой стороной угла. Необходимо доказать, что если А 1 А 2 = А 2 А 3 , то и В 1 В 2 = В 2 В 3 .

Через точку В 2 проведем прямую, параллельную прямой А 1 А 2 . Обозначим новую прямую С 1 С 2 . Рассмотрим параллелограммы A 1 C 1 B 2 A 2 и A 2 B 2 C 2 A 3 .

Свойства параллелограмма позволяют нам утверждать, что A1A2 = C 1 B 2 и A 2 A 3 = B 2 C 2 . А так как по нашему условию А 1 А 2 = А 2 А 3 , то и C 1 B 2 = В 2 С 2 .

И, наконец, рассмотрим треугольники Δ C 1 B 2 B 1 и Δ C 2 B 2 B 3 .

C 1 B 2 = B 2 C 2 (доказано выше).

А это значит, что Δ C 1 B 2 B 1 и Δ C 2 B 2 B 3 будут равны по второму признаку равенства треугольников (по стороне и прилегающим углам).

Таким образом, теорема Фалеса доказана.

Использование данной теоремы значительно облегчит и ускорит решение геометрических задач. Успехов в освоении этой занимательной науки математики!

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Эта гробница мала, но слава над ней необъятна.

В ней перед тобою сокрыт многоразумный Фалес.

Надпись на гробнице Фалеса Милетского

Достижениями Фалеса считаются формулировка и доказательство следующих теорем:

вертикальные углы равны;
равными треугольниками признаются те, у которых сторона и два прилегающих угла соответственно равны;
углы при основании равнобедренного треугольника равны;
диаметр делит круг пополам;
вписанный угол, опирающийся на диаметр, является прямым.

И, наконец, рассмотрим треугольники Δ C 1 B 2 B 1 и Δ C 2 B 2 B 3 .

C 1 B 2 = B 2 C 2 (доказано выше).

Таким образом, теорема Фалеса доказана.

blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Если стороны угла, пересекают прямые параллельные линии которые одну из сторон разделяют на несколько отрезков, то и вторую сторону, прямые так же разделят на равнозначны с другой стороной отрезки.

Теорему Фалеса
доказывает следующее: С 1 , С 2 , С 3 — это места где пересекаются прямые параллельные на любой стороне угла. С 2 находится посередине относительно С 1 и С 3 .. Точки D 1 , D 2 , D 3 — это места где пересекаются прямые, которые соответствуют прямым с другой стороной угла. Доказываем, что когда C 1 C 2 = C 2 C з, значит и D 1 D 2 =D 2 D 3 .
Проводим в месте D 2 прямой отрезок КР, параллельный участку C 1 C 3 . В свойствах параллелограмма C 1 C 2 =KD 2 , C 2 C 3 = D 2 P. Если C 1 C 2 =C 2 C 3 , то и KD 2 =D 2 P.

Полученные треугольные фигуры D 2 D 1 K и D 2 D 3 P равняются. И D 2 K=D 2 P по доказательству. Углы с верхней точкой D 2 равняются как вертикальные, а углы D 2 KD 1 и D 2 PD 3 равняются как внутренние накрест лежащие при параллельных C 1 D 1 и C 3 D 3 и разделяющей KP.
Так как D 1 D 2 =D 2 D 3 теорема доказана по равенству сторон треугольника

Заметка:

Если взять не стороны угла, а два прямых отрезка, доказательство будет такое же.
Любые прямые отрезки параллельные друг другу, которые пересекают две рассматриваемые нами прямые и разделяющие одну из них на одинаковые участки, тоже самое делают и со второй.

Рассмотрим несколько примеров

Первый пример

Условием задания требуется разбить прямую СD на п
одинаковых отрезков.
Проводим от точки С полу-прямую с, которая не лежит на прямой СD. Отметим на ней одинаковые по величине части. СС 1 , С 1 С 2 , С 2 С 3 …..С п-1 С п. Соединяем С п с D. Проводим прямые от точек С 1 ,С 2 ,….,С п-1 которые будут параллельны относительно С п D. Прямые будут пересекать СD в местах D 1 D 2 D п-1 и разделять прямую СD на п одинаковых отрезков.

Второй пример

На стороне АВ треугольника АВС отмечена точка СК. Отрезок СК пересекает медиану АМ треугольника в точке Р, при этом АК= АР. Требуется найти отношение ВК к РМ.
Проводим через точку М прямой отрезок, параллельный СК, который пересекает АВ в точке D

По теореме Фалеса
ВD=КD
По теореме пропорциональных отрезков получаем, что
РМ = КD = ВК/2, следовательно, ВК: РМ = 2:1
Ответ: ВК: РМ = 2:1

Третий пример

В треугольнике АВС, сторона ВС = 8 см. Прямая DE пересекает стороны АВ и ВС параллельно АС. И отсекает на стороне ВС отрезок ЕС = 4см. Доказать, что АD = DВ.

Так как ВС = 8 см и ЕС = 4см, то
ВЕ = ВС-ЕС, следовательно, ВЕ = 8-4 = 4(см)
По теореме Фалеса
, так как АС параллельна DE и ЕС = ВЕ то, следовательно, АD = DВ. Что и требовалось доказать.

В женском журнале — онлайн, Вы найдете много интересной информации для себя. Так же есть раздел, посвященный стихам которые написал Сергей Есенин . Заходите не пожалеете!

Тема урока

Цели урока

Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
Сформулировать и доказать свойства квадрата, доказать его свойства.
Научиться применять свойства фигур при решении задач.
Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока

Проверить умение учащихся решать задачи.

План урока

Историческая справка.
Фалес как математик и его труды.
Полезно вспомнить.

Историческая справка

Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.

Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Основы геометрии Фалес постигал в Египте.

Открытия и заслуги ее автора

А известно ли вам, что Фалес Милетский был одним из семи самых известных по тем временам, мудрецом Греции. Он основал Ионийскую школу. Идею, которую продвигал Фалес в этой школе, было единство всего сущего. Мудрец считал, что есть единое начало, от которого произошли все вещи.

Огромной заслугой Фалеса Милетского является создание научной геометрии. Этот великий учений сумел с египетского искусства измерения создать дедуктивную геометрию, базой которой есть общие основания.

Кроме огромных познаний в геометрии, Фалес еще и неплохо разбирался в астрономии. Эму первому удалось предсказать полное затмение Солнца. А ведь это происходило не в современном мире, а в далеком 585 году, еще до нашей эры.

Фалес Милетский был тем человеком, который сообразил, что север можно точно определить по созвездию Малой Медведицы. Но и это не было его последним открытием, так как он сумел в точности определить продолжительность года, разбить его на триста шестьдесят пять дней, а также установил время равноденствий.

Фалес на самом деле был всесторонне развитым и мудрым человеком. Кроме того, что он славился как прекрасный математик, физик, астроном, он еще и как настоящий метеоролог, смог довольно точно предсказать урожай оливок.

Но самое примечательное то, что Фалес никогда не ограничивался в своих познаниях только научно-теоретической областью, а всегда пытался закрепить доказательства своих теорий на практике. И самое интересное, то, что великий мудрец не сосредотачивался на какой-то одной области своих познаний, его интерес имел различные направленности.

Имя Фалеса стало нарицательным для мудреца уже тогда. Его важность и значимость для Греции была так велика, как для России имя Ломоносова. Конечно, его мудрость можно толковать по-разному. Но точно можно сказать, что ему были присущи и изобретательность, и практическая смекалка, и в какой-то степени отрешенность.

Фалес Милетский был отличным математиком, философом, астрономом, любил путешествовать, был купцом и предпринимателем, занимался торговлей, а также был неплохим инженером, дипломатом, провидцем и активно участвовал в политической жизни.

Он даже умудрился с помощью посоха и тени определить высоту пирамиды. А было это так. В один погожий солнечный день Фалес поставил свой посох на границе, где заканчивалась тень от пирамиды. Далее он дождался, когда длинна от тени его посоха сравнялась с его высотой, и замерил длину тени пирамиды. Вот так, казалось бы просто Фалес определил высоту пирамиды и доказал, что длина одной тени имеет отношение к длине другой тени, также, как и высота пирамиды относится к высоте посоха. Чем и поразил самого фараона Амасиса.

Благодаря Фалесу все известные в то время знания были переведены в область научного интереса. Он смог донести результаты до уровня, пригодного для научного потребления, выделив определенный комплекс понятий. И возможно с помощью Фалеса началось последующее развитие античной философии.

Теорема Фалеса играет одну важных ролей в математике. Она была известна не только в Древнем Египте и Вавилоне, но и в других странах и являлась почвой для развития математики. Да и в повседневной жизни, при строительстве зданий, сооружений, дорог и т.д., без теоремы Фалеса не обойтись.

Теорема Фалеса в культуре

Теорема Фалеса прославилась не только в математике, но ее приобщили еще и к культуре. Однажды аргентинская музыкальная группа Les Luthiers (исп.) на суд зрителей представила песню, которую посвятила известной теореме. Участники Les Luthiers в своем видеоклипе специально для этой песни предоставили доказательства
для прямой теоремы для пропорциональных отрезков.

Вопросы

Какие прямые называются параллельными?
Где практически применяется теорема Фалеса?
О чем гласит теорема Фалеса?

Список использованных источников

Энциклопедия для детей. Т.11. Математика/Глав.ред.М.Д.Аксенова.-м.:Аванта+,2001.
«Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»

Предмети > Математика > Математика 8 класс

Теорема планиметрии о параллельных и секущих.

Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том , что вписанный угол , опирающийся на диаметр окружности , является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла .

Формулировки
[
|
]

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.

Более общая формулировка, также называемая теорема о пропорциональных отрезках

Параллельные прямые отсекают на секущих пропорциональные отрезки :

A
1
A
2
B
1
B
2
=
A
2
A
3
B
2
B
3
=
A
1
A
3
B
1
B
3
.
{\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}

Замечания
[
|
]

Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Доказательство в случае секущих

Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые
A
A
1
|
|
B
B
1
|
|
C
C
1
|
|
D
D
1
{\displaystyle AA_{1}||BB_{1}||CC_{1}||DD_{1}}
и при этом
A
B
=
C
D
{\displaystyle AB=CD}
.

Доказательство в случае параллельных прямых

Проведем прямую BC
. Углы ABC
и BCD
равны как внутренние накрест лежащие при параллельных прямых AB
и CD
и секущей BC
, а углы ACB
и CBD
равны как внутренние накрест лежащие при параллельных прямых AC
и BD
и секущей BC
. Тогда по второму признаку равенства треугольников треугольники ABC
и DCB
равны. Отсюда следует, что AC
= BD
и AB
= CD
. ■

Вариации и обобщения
[
|
]

Обратная теорема
[
|
]

Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:

В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины

Таким образом (см. рис.) из того, что
C
B
1
C
A
1
=
B
1
B
2
A
1
A
2
=
…
{\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots }
, следует, что
A
1
B
1
|
|
A
2
B
2
|
|
…
{\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots }
.

Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).

Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.

Лемма Соллертинского
[
|
]

Следующее утверждение, двойственно к лемме Соллертинского :

Пусть
f
{\displaystyle f}

— проективное соответствие между точками прямой
l
{\displaystyle l}

и прямой
m
{\displaystyle m}

. Тогда множество прямых будет множеством касательных к некоторому коническому сечению (возможно, вырожденному).

В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.

Это утверждение, в свою очередь, является предельным случаем следующего утверждения:

Пусть
f
{\displaystyle f}

— проективное преобразование коники. Тогда огибающей множества прямых
X
f
(X)
{\displaystyle Xf(X)}
будет коника (возможно, вырожденная).

|
]

Теорема Фалеса

Тема урока: «Теорема Фалеса»

Класс : 8

Тип урока: получение и первичное закрепление новых знаний

Цели:

Образовательные:

— рассмотреть теорему Фалеса и её доказательство;

— закрепить теорему Фалеса в процессе решения задач;

— совершенствовать навыки решения задач на применение знаний по теме «Трапеция»

Воспитательные:

— формирование способностей анализировать свои действия, умения внимательно слушать

Развивающие:

Развитие логического мышления, воображения, памяти, кругозора, умения рассуждать и аргументировать.

Оборудование: доска, циркуль, линейка, треугольник, компьютер, проектор, экран, презентация.

Ход урока.

Сообщение темы и целей урока.

Французский писатель XIX столетия Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом”.

Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.

Тема сегодняшнего урока «Теорема Фалеса». Вы не только познакомитесь с этой теоремой, её доказательством, но также увидите, где можно ее применить.

Предлагаю выполнить такое задание: разделить отрезок на две, четыре, три части с помощью циркуля. (Учащиеся выходят к доске и показывают)

Перед вами стоит проблема деления отрезка на три равные части, а ученые столкнулись с проблемой деления отрезка на равные части много веков назад. И, конечно, они нашли выход из положения.

И чтобы нам сегодня справиться с возникшей задачей, докажем одну из важнейших теорем геометрии, которая называется Теорема Фалеса. Кем же был Фалес, что в его честь даже названа теорема в геометрии?

Фалес Милетский – древнегреческий философ из г. Милета (Малая Азия – территория современной Турции). Сведения о его жизни до сих пор носят противоречивый характер, но считается, что:

— именно он привез геометрию из Египта и познакомил с нею греков; его последователи и ученики основали Милетскую школу;

— именно его греки уже в древности называли «отцом философии»;

— именно он «открыл» для греков созвездие Малой Медведицы как путеводный инструмент;

— именно он ввёл календарь по египетскому образцу, в котором год состоял из 365 дней.

— одна из легенд гласит, что будучи в Египте, Фалес поразил фараона Амасиса тем, что сумел точно измерить высоту пирамиды. Как вы думаете, как он это сделал? Дождался пока длина тени от палки станет равной самой палке, значит и тень от пирамиды равна будет самой пирамиде;

— он предсказал солнечное затмение в мае 585 года до н. э.

Но одна из важнейших заслуг Фалеса в том, что ученый первый стал доказывать геометрические теоремы:

круг делится диаметром пополам;

в равнобедренном треугольнике углы при основании равны;

при пересечении двух прямых образуемые ими вертикальные углы равны;

два треугольника равны, если два угла и сторона одного из них равны двум углам и соответствующей стороне другого.

Вот такой был Фалес Милетский, в честь которого названа теорема в геометрии и эту теорему мы сегодня и рассмотрим.

Изучение нового материала.

Помощь в доказательстве Теоремы Фалеса нам окажет задача № 384, которую мы сейчас решим.

Задача. Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N. Докажите, что AN = NC.

Доказательство.

Проведем DC║АВ.

Рассмотрим Δ AMN и ΔNDC.

AM = MВ (по условию), МВ = DC (как противоположные стороны параллелограмма BMDC), поэтому AM = DC.

Угол 1 равен углу 2, угол 3 равен углу 4 (как накрест лежащие углы при пересечении параллельных прямых AB и CD секущими AC и MD)

Из 1) и 2) следует Δ AMN = ΔNDC, значит AN = NC, что и требовалось доказать.

Какой вывод из этой задачи мы можем сделать?

Если в треугольнике через середину одной стороны провести прямую, параллельную одной из двух других сторон, то эта прямая пройдет через середину третьей стороны.

Теорема Фалеса: «Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки».

Доказательство:

Пусть на прямой l₁ отложены равные отрезки А₁А₂, А₂А₃, А₃А₄, … и через их концы проведены параллельные прямые, которые пересекают прямую l₂в точках В₁, В₂, В₃, В₄, …. Требуется доказать, что отрезки В₁В₂, В₂В₃, В₃В₄, … равны друг другу. Докажем , например, что В₁В₂ = В₂В₃.

Пусть l₁║l_2.Тогда А₁А₂ = В₁В₂, А₂А₃ = В₂В₃, как противоположные стороны параллелограммов А₁ В₁В₂ А₂ и А₂В₂В₃А₃. Т.к. А₁А₂= А₂А₃, то и В₁В₂ = В₂В₃.

Если l₁и l₂ не параллельны, то через точку В₁ проведем прямую l║ l₁. Она пересечет прямые А₂В₂ и А₃В₃ в некоторых точках C и D. Так как А₁А₂= А₂А₃, то по ранее доказанному В₁С = СD. Отсюда получаем В₁В₂ = В₂В₃.

Теорема доказана.

Закрепление пройденного материала.

Решение задач на готовых чертежах.

Практическая работа.

Разделить отрезок на 5 равных частей.

Объяснить как это сделали

Итоги урока.

— С какой теоремой вы сегодня познакомились?

— На сколько частей вы теперь можете разделить данный отрезок?

Урок геометрії 8 клас теорема фалеса

Скачать урок геометрії 8 клас теорема фалеса rtf

Вы можете ознакомиться и скачать презентацию на тему «Теорема Фалеса» 8 класс. Урок №9 по геометрии. Доклад-сообщение содержит 24 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации. Слайд 1. Описание слайда: Теорема Фалеса Урок №9 по геометрии в 8 классе Учитель: Федорова Т.Ф. уч. год. Слайд 2. Описание слайда: Цели урока: Рассмотреть теорему Фалеса и закрепить ее в процессе реше. Данная разработка по геометрии на тему «Применение теоремы Фалеса к решению задач на установление отношений отрезков» может быть применена на уроках геометрии при изучении теоремы Фалеса в рамках изучения главы «Многоугольники».

Евгений Александрович Лисицын. учитель алгебры, математики, информатики, Архангельская область. Цели урока: Образовательная: доказать теорему Фалеса, научить применять её при решении задач. Развивающая: развивать у учащихся познавательный интерес к учебным дисциплинам, умение применять свои знания на практике. Воспитательная: воспитывать внимание, аккуратность, расширять кругозор учеников. Фалес – купец, политический деятель, астроном, математик, живший в Милете, первый доказал ряд геометрических теорем.

Эти положения были частично известны еще вавилонянам и египтянам, но в отличие от вавилонской и египетской геометрии, имевшей преимущественно практический характер, греческая геометрия характеризуется стремлением установить, что геометрические факты справедливы в любом случае. Алгебра. Геометрия. Элективный курс. 10 класс. Алгебра. Геометрия. 11 класс. Алгебра. Геометрия. Урок 5.

Теорема Фалеса (Геометрия 8 класс) Узнаем формулировку теоремы Фалеса, смоем применять ее на практике. Урок 5. Теорема Фалеса (Геометрия 8 класс) Узнаем формулировку теоремы Фалеса, смоем применять ее на практике.

Рассказывается теорема Фалеса и теорема о пропорциональных отрезках, а также приводятся примеры ее использования в реальной жизни. Если Вам понравился урок и появилось желание поддержать канал материально, то номера карт: Если у Вас нет такой возможности, то просто спасибо за то, что смотрите мои видеоуроки.

Предварительный просмотр: Урок геометрии в 8 классе. Тема: «Теорема Фалеса». Дата проведения: г. Учитель: Ярославцева Мария Николаевна. — закрепить теорему Фалеса в процессе решения задач; — совершенствовать навыки решения задач на применение знаний по теме «Трапеция». Воспитательные. Урок по теме Теорема Фалеса. Теоретические материалы и задания Геометрия, 8 класс. ЯКласс — онлайн-школа нового поколения. 3.

Теорема Фалеса. Теория: Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне. Теорему Фалеса используют, чтобы разделить отрезок на несколько равных частей. Необходимо разделить отрезок \(AB\) на \(7\) равных частей. Нарисуем угол, на одной стороне которого лежит отрезок \(AB\).

txt, fb2, EPUB, EPUB

Похожее:

Біологія 6 клас нова програма зошит гдз зошит андерсон

Природознавство 5 клас ярошенко бойко відповіді на тестові завдання

Графічний редактор paint урок 2 клас

Збірник наукових праць економіка. управління. інновації. серія економічні науки

Превентивне виховання в початкових класах презентація

Урок розвитку мовлення 4 клас вибірковий переказ тексту

Презентація кіммерійці та скіфи

Теорема фалеса 8 клас презентація

Скачать теорема фалеса 8 клас презентація PDF

Презентация Теорема Фалеса, 8 класс. Опубликовано: 19 июля , Презентация на тему «Теорема Фалеса» представляет практический и теоретический материал для работы на уроке геометрии в 8 классе. Используя данный ресурс, который можно бесплатно скачать с сайта для занятия, удастся познакомиться не только с доказательством теоремы, но и почерпнуть интересные сведения из биографии Фалеса, научиться решению задач, где необходимо применение выученного материала. Работа выполнена на 17 слайдах.

Практическая часть представлена тремя задачами. К ним имеется как готовое, правильно оформленное ре. Биография Фалеса Милетского Относительно времени жизни Фалеса существует несколько версий. Наиболее последовательно традиция утверждает, что он родился в период с й по ю олимпиаду, а умер в ю в возрасте 78 или 76 лет, то есть прибл.

с по до н. э.. Некоторые источники сообщают, что Фалес был известен уже в 7-ю олимпиаду (— до н. э.), но в целом время жизни Фалеса сводится. на период с — по — до н.

э., т.о. умереть Фалес мог в возрасте от 76 до 95 лет. 0. Благодаря этой рекламе сайт может продолжать свое существование, спасибо за просмотр. загрузить презентацию. 3. Высказывания. Формулировка теоремы Фалеса: Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Доказанная выше теорема является частным случаем общей теоремы Фалеса, так как равные отрезки пропорциональны с коэффициентом, равным единице. Теорема (теорема Фалеса). Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону угла, то на другой стороне угла отложатся равные отрезки.

Дано: АВ = ВС, АА1 1 ВВ1 1 СС1 Доказать: A1 B1 = B1 C1. Теорема (обратная теореме Фалеса). Если на сторонах угла от его вершины отложить равные отрезки (AB = BC, AB1 = B1 C1), то прямые, проходящие через их концы, будут параллельны (BB1 ∥ СС1). Номер слайда 5. Прокопчик Виктория Сергеевна. Геометрия, 8 класс, Презентации.

Скачать материал. Вам будет интересно. Презентация на тему «Площадь трапеции». Проект самоанализа урока по геометрии в 8 классе на тему «Площадь трапеции». Похожие материалы. Презентация » Трапеция» 8 класс. 0. Презентация к уроку геометрии по теме «Четырехугольники». 0. Четырехугольники. Разработка и презентация по геометрии на тему «Четырёхугольники и их свойства» (8 класс).

0. Уроки математики / Презентация / Презентация » Теорема Фалеса». Презентация » Теорема Фалеса». Бесплатно. Скачать материал.

Применение теоремы Фалеса для деления отрезка на n равных частей. Интерпретация теоремы о пропорциональных отрезках. Обоснование и доказательство правдивости теоремы Фалеса в планиметрии. Использование теоремы Фалеса в решении геометрических задач. Теория Фалеса. Теоремы второго и третьего признаков подобия и их доказательство. Пропорциональные отрезки в прямоугольном треугольнике. Формулировки теоремы Фалеса.

презентация, добавлен 2. Теорема Пифагора и способы ее доказательства. Обоснование значимости теоремы Пифагора, ее применение в геометрии. Урок 5. Теорема Фалеса (Геометрия 8 класс) Узнаем формулировку теоремы Фалеса, смоем применять ее на практике. Урок 5. Теорема Фалеса (Геометрия 8 класс) Узнаем формулировку теоремы Фалеса, смоем применять ее на практике. Вы можете изучить и скачать доклад-презентацию на тему «Теорема Фалеса» 8 класс.

Урок №9 по геометрии. Презентация на заданную тему содержит 24 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки! Презентации» Математика» «Теорема Фалеса» 8 класс. Урок №9 по геометрии. Слайды и текст этой презентации.

Слайд 1. Описание слайда: Теорема Фалеса Урок №9 по геометрии в 8 классе Учитель: Федорова Т.Ф. уч. год. Слайд 2. Описание слайда: Цели урока: Расс.

fb2, fb2, doc, txt

Похожее:

Презентація на тему сполучені посудини

Природознавство 4 клас савченко

Українська література 9 клас комплексний зошит для контролю знань

Відповіді до зошита для поточного та тематичного оцінювання 11 клас історія

Історія моєї родини в історії україни

Лабораторна робота з фізики 10 клас відповіді коршак

Все о математике Фалесе

Математика — это предмет, который часто поднимается в дебатах об образовательном секторе, где она постоянно является одним из предметов, по которым школьники борются больше всего. считается важным шагом в академической карьере учащихся, где Ожидается, что студенты будут укреплять свои знания каждый год, чтобы добиться успеха и понять новые математические понятия. Что входит в структуру и что лежит в основе этой дисциплины? Косинусы, обратные числа, дроби, четырехугольники, относительные числа, окружности, симметрия, касательные, неравенства — пересмотр курсов по математике может стать менее напряженным , если смотреть на это через призму истории.Один из многих прекрасных примеров — великий ученый и математик Фалес. Ознакомьтесь с его историей, чтобы разблокировать некоторые из стратегических концепций, с которыми вы, возможно, боретесь, и улучшить свои возможности в них!

Фалес Милетский: Жизнь математика

В жизни студента-математика есть два имени, которые невозможно забыть: Пифагор и Фалес. Последний, профессор первого, согласно историческим текстам, был философом, родившимся в Милете около 625 г. до н. Э.Удачно названный, греческий философ Фалес Милетский считается одним из семи мудрецов Древней Греции, наряду с другими греческими философами: Солоном, Хилоном Спарты, Питтаком Митиленским, Биасом Приенским, Клеобулом Линдосским и Периандром Коринфским. . Основатель школы милетцев, Фалес начал свою академическую карьеру как философ и ученый, отправившись в Египет в очень молодом возрасте благодаря хорошим отношениям, которые существовали между страной и его родным городом Милетом.Именно там молодой Фалес открыл знания египетских и вавилонских наук. Оказавшись там, он изучил геометрию, астрономию и философию — все знания, которые были основной частью образовательной подготовки египетских священников. По словам древнегреческих историков, эта поездка в Египет составляет , что не подтверждается данными . Фактически, только некоторые записи, написанные спустя годы после смерти Фалеса, смогли подтвердить жизнь ученого и поместить его в Египет в то время.Достигнув совершеннолетия, Фалес вернулся в греческий город Милет, чтобы создать Школу милетцев. Фалес использовал свое положение для распространения своих знаний в области математики и греческой философии, продолжая при этом проводить наблюдения и научные эксперименты. На протяжении всей своей жизни Фалес использовал свои наблюдения, чтобы понять, как устроен мир. Согласно легенде, он вычислил высоту великой пирамиды, помог предсказать лунное и солнечное затмения и применил на практике теоремы Фалеса.Узнайте об онлайн-курсах математики.

Древняя Греция, и особенно Милет, оказали глубокое влияние на западную философию.

Считается, что его математические и научные исследования произвели революцию во времени. Считающийся мудрецом, Фалес всегда гордился тем, что объяснял свои открытия с рациональной точки зрения , а не мифологической , это было традицией в то время. Для него процесс наблюдения и создания доказательств был основой научных рассуждений.Согласно некоторым отчетам, написанным через много лет после его смерти, Фалес умер около 547 г. до н.э. в Милете во время участия в гимнастических соревнованиях. Найденный на трибуне, он, очевидно, умер от голода, жажды и возраста. Среди других великих математиков и философов из этой области — Архимеда!

Как Фалес повлиял на курсы математики

Все слышали и даже узнали многие из теорем, открытых Фалесом. Фалес был первым, кто обозначил в истории математики , создав свою научную формулу и принцип.Вот пять геометрических теорем, которые ему приписывают:

Окружность делится пополам диаметром
Углы в треугольнике равны, если их противоположности — две стороны равной длины
Пересекающиеся прямые линии образуют противоположные углы, которые равны равно
Прямой угол и соответствующий ему прямоугольный треугольник можно нарисовать внутри и с использованием полукруга
Если даны основание треугольника и два угла, треугольник можно нарисовать

Хотя сегодня это может показаться слишком простым, чтобы когда-либо считались революционными , они фактически дают нам много информации и считались главным нововведением в то время.Теоремы Фалеса используются для вычисления определенных соотношений долготы и пропорций геометрических фигур, имеющих параллельные линии. Они также используются для вычисления многих понятий в тригонометрии, когда есть две параллельные линии. Согласно легенде, Фалес открыл эту теорему при вычислении высоты пирамиды. Для этого математик рассчитал тень пирамиды до пола. С помощью трости Фалес смог вычислить размеры пирамиды Египта по отношению к тени своей трости.Хотя Фалесу приписывают эти теоремы, они уже были известны вавилонянам и египтянам. Мы знаем это в первую очередь благодаря доказательству, разработанному в книге «Элементы Евклида», в которой рассматривается пропорциональность площадей треугольников одинаковой высоты. Однако Фалесу зачислили за то, что он поставил слова последнему. Фалес не получил во многих странах баллов за некоторые из своих теорем. Например, англичане называют одну из его теорем теоремой о перехвате, в то время как в отношении той же теоремы немцы называют ее теоремой лучей.Однако все они не полностью идентичны и больше напоминают теорию Пифагора.

История греческих математиков неполна без упоминания Фалеса

Фалеса От математики к астрономии

В течение своей жизни Фалес использовал математику, чтобы понять важные понятия реальной жизни. Математические упражнения, простые числа, десятичные дроби, уравнения, медианы, вычитание, сложение, философия, архитектура — математика служила инструментом для понимания окружающего мира.В начале своей карьеры Фалес увлекся астрономией и анализом неба. Из-за этого он считается одним из пионеров греческой астрономии. Подобно своим исследованиям в области математики, Фалес использовал метод наблюдения созвездий, чтобы понять, как функционирует Вселенная. Он сделал много открытий в этих областях :

Использовал ковш, чтобы направлять моряков в открытый океан
Вычислил продолжительность года благодаря интервалам солнцестояния и равноденствий
Указал путь сына между ними. два тропика
Перечислил эфемериды

Его открытия были лишь небольшой частью его наблюдений.В частности, он проанализировал количество дней в году и пришел к выводу, что год состоит не из 365 дней, а из 365 дней с четвертью. Это открытие позже станет базой високосных лет. Фалес также наблюдал звезды в движении, диаметр Солнца и Луны — все время используя ту же систему измерения объектов относительно тени трости. Он также определил позицию Плеяд, вычислил угол наклона орбиты зодиака и т. Д. Благодаря своим наблюдениям Фалес также мог предсказать большой урожай оливок согласно Аристотелю.Он применил эти наблюдения за природой, чтобы объяснить, как функционирует мир, но чаще всего в итоге просто улучшал жизнь окружающих его людей . Например, благодаря ему моряки научились ориентироваться, а навигация улучшилась в десять раз. Астрономия и все связанные с ней области многим обязаны Фалесу, который был простым математиком. Чтобы узнать больше о том, как эти открытия повлияли на работу другого великого математика, Рене Декарта, щелкните здесь!

Фалес в контексте великих

Все открытия Фалеса оставили особый след в области математики.Арифметика, сложные функции, целые числа, многоугольники, умножение, факторизация, вероятность — его знания и открытия все еще преподаются в наши дни и на наших курсах математики, что делает Фалеса одним из крупнейших математиков истории.

Древняя философия находилась под влиянием таких мыслителей, как Фалес.

Однако больше, чем его открытия, Фалес теоретизировал знаний, которые уже были установлены египтянами или вавилонянами. Математик не просто удовлетворился этими знаниями, изложенными в мифологических истинах, но попытался наблюдать и доказать все эти утверждения, с которыми он столкнулся во время своих занятий по математике.Таким образом Фалес сбивал своих современников с толку. В книге Жана Вуалкена научный французский редактор объяснил, что Фалес хотел «заменить мифологическое объяснение» явлений «физическим объяснением». Это то, что побуждает Вуалкина, наряду со многими другими, называть его «одним из предшественников греческой науки». Научное наследие Фалеса усиливается открытиями его Милетской школы. Их работа, получившая название милетской школы или «ионийской школы», произвела революцию в области науки, и они стали известны как досократические философы.Его учение, характерное для Фалеса, благоприятствовало зрительному восприятию и наблюдению, чтобы придать знаниям практичность. Школа включала в себя в основном геометрию и астрономию, две любимые области Фалеса, но в школе также работали над предметами , такими как биология, физика и метафизика. Они были первыми студентами, которых назвали физиками, и они изучали все о природе. Ученики Милетской школы использовали такие понятия, как четыре элемента, для объяснения функции среды .Все эти исследования считаются первыми научными исследованиями природы и оставили неизгладимый вклад в науку. Фалес обозначил не только область математики в древности, но и историю науки в целом, вдохновляя работы даже сэра Исаака Ньютона. Для этого мы должны помнить его имя вместе с его достижениями.

Здесь можно найти хорошие уроки математики.

Как Фалес Милетский изменил мир

Неудивительно, что Фалес Милетский был назван первым из семи мудрецов Греции.На протяжении всей своей жизни ему удавалось навязать научное мышление во многих областях, от математики до философии. Бесспорный ученый, он жил между 624 и 546 годами до нашей эры и внес колоссальный вклад в знания человечества. Во многих смыслах можно сказать, что Фалес изменил мир, но то, что делает его широко популярным, — это теоремы, которые произвели революцию в математике.

Фалес Милетский

Философские идеи

Большая часть того, что мы знаем о философии Фалеса сегодня, исходит от Аристотеля.Некоторые считают, что Фалес не оставил никаких произведений, но это все еще предмет споров. Сом думает, что он написал две работы: «В день солнцестояния», и «В день равноденствия», , но ни одна из них до сих пор не существует.

Самый первый философ-досократик, главной заботой Фалеса было определение субстанции (веществ), которые формируют окружающий нас мир. По этой причине многие называют его первым в мире ученым . Он был одним из первых, кто попытался натуралистически объяснить материальные явления, используя научный метод, не прибегающий к мистическим или мифологическим объяснениям.

Фалес также имел громкие религиозные взгляды: он верил в единого трансцендентного Бога без начала и конца, который выражается через других богов. Идея справедливости философа вращалась вокруг буквы закона и духа закона — для него были важны и справедливость, и честность. Его представление о счастье включало три основных направления: здоровое тело, находчивую душу и обучаемую натуру.

[Читайте также: Познакомьтесь с Да Винчи Ислама: Аль-Бируни, отец геодезии, антропологии и магистр фармации]

Среди его основных идей одна была особенно важной.Сегодня это может показаться здравым смыслом, но при его жизни это было весьма противоречиво: идея о том, что мы должны ожидать от наших детей такой же поддержки, как и наши родители .

Однако Фалес известен прежде всего своими достижениями в области науки и математики. Размышляя о влиянии магнетизма и статического электричества, он полагал, что сама способность перемещать предметы без изменения самого движителя является характеристикой жизни; другими словами, магнит тоже в некотором роде живой.Если это так, полагал он, то не было бы никакой разницы между живыми и мертвыми — если бы все существа были живыми, то предполагалось, что они имеют души или божества. Заключение этого аргумента подразумевало почти полное удаление разума от субстанции, что впервые открыло дверь небожественному принципу действия. Философы работают над этой идеей и по сей день.

Математика

Фалес считается одним из самых блестящих математиков в истории.Сегодня мы явно приписываем Фалесу пять теорем, и две из них он успешно применил к решению практических задач.

Определение : Диаметр окружности делится пополам.
Утверждение : В равнобедренных треугольниках углы при основании равны друг другу, и, если равные прямые образуются дальше, то углы под основанием равны друг другу.
Утверждение : Вертикальный и противоположный углы равны.
Предложение : Равенство треугольников (двумя углами и стороной)
Утверждение : Угол в полукруге прямой.

Теорема Фалеса через wikipedia.org

Теории о Земле

Вода как основной принцип

Космологический изречение Фалеса утверждает, что вода является основным элементом (первичным принципом) во всем. Идея о том, что весь мир произошел из воды, является примером материального монизма (примерно аналогична более поздней идее Анаксимена о том, что все в мире состоит из воздуха).Согласно Аристотелю, метод, с помощью которого Фалес объяснил свою теорию, заключался в анализе биологических принципов. В биологическом мире Фалес обратился к трем вещам:

вся жизнь зависит от воды — удалите воду из растения, и оно погибнет; лишают животных воды, и они умирают;
все семена сами по себе не что иное, как влага;
тепло (в форме солнца и луны) создается из влаги и поддерживается ею.

Эта последняя идея была основана на связи между небесными телами и океанами.

Земля, плывущая по воде через philipkay.wordpress.com

Фалес считал, что вода была источником всех вещей , субстанцией, из которой все возникает и в которую все вещи вернутся; более того, он считал, что вещи — это в конечном итоге вода. Аристотель объясняет в «De Caelo», что «[его] вера является самым древним дошедшим до нас объяснением и приписывается Фалесу Милетскому».

Считается, что Фалес был первым, кто заявил, что Земля имеет сферическую форму, хотя свидетельств, подтверждающих это, нет.В своей работе Аристотель упомянул некоторые идеи Фалеса, но почему-то упустил эту идею, поэтому фактических доказательств этой географической философии нет.

Что мы знаем об этой теории, так это то, что, во-первых, она очень согласуется с гипотезой о том, что Земля плавает на воде. Этот принцип применялся и для объяснения природы землетрясений. Сенека приписал Фалесу следующую теорию: в тех случаях, когда Земля испытывает землетрясение, оно действительно колеблется из-за неровностей океана.Это объяснение, хотя и неверное, является первым, которое объясняет природный феномен без привлечения каких-либо сверхъестественных или мистических сущностей.

Астрономия

Изображение через греческие имена.

Считается, что Фалес предвидел солнечное затмение, которое, по словам Геродота, произошло 28 мая 585 г. до н. Э. Евдем также упомянул Фалеса как первого, кто открыл «солнечное затмение и что его период относительно солнцестояний не всегда постоянен».

Диоген Лаэртий упомянул, что Фалес «был первым, кто определил курс солнца от солнцестояния до солнцестояния», а также признал астрономию Евдема своим источником.Неизвестно, как Фалес пришел к заключению о солнцестоянии как повторяющемся явлении, но Флавий Филострат пишет, что: «[t] hales наблюдал небесные тела с горы Микале, которая находилась недалеко от его дома».

Диоген Лаэртий написал, что «Он (Фалес), как говорят, открыл времена года и разделил их на 365 дней». Объяснение этому вполне разумное. Из-за определения солнцестояний и равноденствий будет справедливо предположить, что Фалес мог также знать длину солнечного года.Конечно, было бы неправдой сказать, что он открыл времена года как таковые, учитывая, что египтяне знали о них тысячелетиями. Но благодаря своему пониманию солнечного года он, возможно, поделился информацией, таким образом, будучи первым, кто научно объяснил времена года в том виде, в каком мы их знаем.

Задачи по математике

Математические задачи на слова позволяют вам применять свои математические знания в повседневных задачах.Задачи со словами учатся понимать, переводить на математический язык (например, уравнения), решать их и проверять точность и обсуждение решения.

Выберите тему, по которой вы хотите посчитать и улучшить.

Из нашей базы данных математических задач и примеров мы предлагаем:

Рыбацкая лодка
Рыболовная лодка поймала 14 рыб за один день. Сколько рыбы поймают четыре рыбацкие лодки за 8 дней?
Льдина
Какой объем льдины массой 326 кг? Плотность льда всего 920 кг / м ³.
ВПП
Рассчитайте направление, противоположное взлетно-посадочной полосе 13. Взлетно-посадочные полосы обозначаются числом от 01 до 36, что обычно составляет одну десятую азимута курса ВПП в градусах: взлетно-посадочная полоса пронумерована 09 точками на восток (90 °), ВПП 18 находится на юге (180 °), ВПП 2
Расчет CN
Рассчитайте: (789 выберите 786) — (789 выберите 3)
Равнобедренный треугольник
Рассчитайте размер внутренних углов и длину основания равнобедренный треугольник, если длина руки 17 см, а высота до основания 12 см.
Четырехугольная призма
Четырехугольная призма имеет объем 648 см ³. Трапеция, являющаяся его основанием, имеет размеры основания: a = 10 см, c = 5 и высоту v = 6 см. Какая высота призмы?
Вторая сторона
Вычислите длину другой стороны прямоугольника, если его окружность составляет 60 см, а длина одной стороны — 10 см.
Алопеция
В медицинской литературе указано, что 45% мужчин страдают облысением. Для случайной выборки из 8 мужчин рассчитайте вероятность того, что: (а) ровно четыре мужчины страдают алопецией.(б) не более двух мужчин страдают алопецией.
Наполовину наполненный
Цилиндрический горшок диаметром 24 см наполовину наполнен водой. На сколько сантиметров поднимется уровень, если мы добавим в него литр воды?
Обратная матрица
Найдите, во сколько раз больший определитель равен матрице A, которая равна 9 как определитель своей обратной матрицы.
Периметр
Треугольник имеет одну сторону 5 см, а другую — 11 см. Что может быть наименьшим и каков наибольший периметр?
Crimson Lynx
У капитана Эмили есть корабль H.M. S Crimson Lynx. Корабль находится в пяти стадиях от ужасного пирата Умаймы и ее безжалостной банды воров. Если ее корабль еще не был поражен, капитан Эмили имеет вероятность 3/5 поразить пиратский корабль. Если ее корабль имеет размер
Максимальная площадь ромба
Вычислите внутренние углы, при которых равносторонний ромб имеет максимальную площадь.
Море
Как далеко вы можете видеть с мачты корабля, пик которой находится на высоте 14 метров над уровнем моря? (Радиус Земли 6370 км).
Три зернохранилища
Три зернохранилища вмещают 7 800 центов зерна.В первом на 70 тонн зерна было больше, чем во втором, а в третьем — на 120 тонн меньше, чем во втором. Сколько зерна было в каждом зернохранилище?
Прямоугольный
Из прямоугольного треугольника с ножками 12 см и 20 см мы построили квадрат с тем же содержанием, что и треугольник. Какова длина стороны квадрата?
Дорожное падение
На прямом участке дороги отмечается 12-процентное падение. Какой угол образует направление дороги с горизонтальной плоскостью?

следующие задачи по математике »

Thales — Биография, факты и изображения

г.624 г. до н.э. — ок. 546 г. до н.э.

Фалес Милетский жил в Древней Греции. Он был первым ученым в истории.

Фалес искал закономерности в природе, чтобы объяснить, как устроен мир, вместо того, чтобы полагать, что все произошло только потому, что это велел один из греческих богов. Он заменил суеверия наукой.

Он был первым, кто применил дедуктивную логику для поиска новых результатов в геометрии и, потребовав доказательства теорем, вывел математику на новый, более высокий уровень.

Вообще то, что мы знаем о нем, было написано через сотни лет после его жизни, например, Аристотелем.

Произнося его имя, мы говорим thail-eez , делая ударение на первом слоге.

До Фалеса могли быть и другие ученые, но если и были, то мы не знаем их имен.

Объявления

Ранняя жизнь и образование

Фалес родился в привилегированной семье в древнегреческом городе Милет примерно в 624 году до нашей эры.Его отца звали Экзэмиес, а мать — Клеобулин. Он родился в ту же эпоху, что и Эзоп, известный своими баснями.

Когда родился Фалес, Милет был одним из самых богатых и могущественных городов Греции. Сегодня он расположен на побережье Турции.

Фалес родился в греческом обществе, менее развитом в интеллектуальном плане, чем те, что к востоку и югу от него — например, вавилоняне и древние египтяне. Вавилоняне были искусными астрономами и математиками, в то время как египтяне также намного опережали греков в этих областях.

В Египте и Вавилоне математика использовалась в торговле, астрономии и строительстве. Это была чисто практическая наука. Астрономия использовалась для изучения неба, чтобы понять, о чем могут думать боги.

В молодости Фалес стал купцом, что, вероятно, было бизнесом его семьи.

В последние годы своей жизни Фалес отправился в Египет, где узнал об астрономии и математике. Возможно, он отправился в Вавилон; если бы он это сделал, то это было бы во время правления Навуходоносора.

Когда Фалес вернулся в Милет, он сменил карьеру, сильно упал в доходах и стал первым ученым Древней Греции.

Время жизни избранных древнегреческих ученых и философов

Фалес: наука

В какой-то момент, после того как он вернулся в Милет, Фалес пошел на шаг впереди своих учителей. (Конечно, его учителя могли пойти на этот шаг сами, но если они и сделали, то исторических свидетельств об этом нет.)

Хапи не нужен, чтобы развести Нил

Фалес понял, что у природных явлений есть разумные причины, которые можно изучить и понять.Например, ежегодное разливание реки Нил можно объяснить без Хапи, речного бога, изображенного выше.

В Египте ежегодное повышение уровня реки Нил было жизненно важным для успешного сбора урожая в Королевстве. Каждый год заиленная река поднималась и наполняла землю вокруг себя питательными веществами и влагой. Затем река спадет, и египтяне возделывают новые плодородные земли. Без Нила не могло быть царства Египта, потому что там почти никогда не выпадал дождь.

Египтяне полагали, что наводнения Нила были вызваны Хапи , одним из их многочисленных богов.Если бы боги были недовольны, река не разлилась бы, и наступил бы голод. Боги должны быть счастливы любой ценой.

Фалес сказал, что Нил разлился по естественным причинам, а не из-за Хапи.

В наши дни, конечно, мы знаем о наводнениях Нила, потому что сезонные дожди идут дальше на юг в Африке: на самом деле, это был другой древний грек, Эратосфен, который первым понял это, хотя сам Фалес, кажется, размышлял об истинной причине .

Переключение между верой в то, что боги ответственны за повседневные события, и верой в то, что если бы мы понимали природные явления, мы действительно могли бы объяснить и предсказать событий, было величайшим достижением Фалеса.

Он развязал способность людей думать об основных причинах того, что мы наблюдаем. Это было первое известное нам научное мышление: Фалес отказался от суеверий в пользу науки.

Ботан с головой в облаках, разбогатевший!

Однажды темным вечером Фалес гулял по Милету и смотрел на ночное небо. Он споткнулся в канаву, после чего старушка, которая знала его как «мыслителя», засмеялась и спросила: «Как ты можешь видеть то, что тебе говорят небеса, если ты даже не можешь видеть то, что у тебя под ногами?»

Фалес, кажется, был первым ученым в Древней Греции — фактически, его первым ботаником! И над ним издевались за это.В богатом городе Милет люди говорили Фалесу, что никто никогда не сможет добиться процветания, просто думая, и поэтому он не был богатым.

Фалес, однако, доказал, что его недоброжелатели ошибались.

Он изучал погодные условия в районе Ионии, где находился город Милет. Погода одной зимой показала, что урожай оливок в следующем сезоне будет рекордным. Еще была зима, он сделал небольшой залог, чтобы арендовать все оливковые прессы в Милете для следующего урожая.Летом, когда оливковые производители начали понимать, что собирается огромный урожай оливок, они обнаружили, что Фалес нанял все оливковые прессы.

Фалес заработал состояние, продав свои права на прессы производителям оливок. Он не выполнял никакой физической работы. Он разбогател только благодаря силе разума, применяя свои наблюдения за погодными условиями, чтобы предсказать, насколько велик будет урожай оливок. Он не нуждался в помощи Аристея , греческого бога оливковых рощ.

Землетрясения

Древние люди считали землетрясения мерой гнева их богов.Жертвоприношения, включая человеческие жертвоприношения в некоторых культурах, стали нормальным способом умиротворить разгневанных богов.

Древние люди считали землетрясения мерой гнева их богов.

Фалес искал рациональное объяснение землетрясений. Он предположил, что вся наша планета Земля представляет собой плоский диск, плавающий в бесконечном море воды, и что землетрясения происходят, когда на планету ударяет волна, проходящая через воду. С помощью современной науки мы знаем, что Фалес ошибся.

Его теория, однако, была огромным шагом вперед по сравнению с утверждением, что Земля дрожала оттого, что Зевс чем-то был раздражен. Фалес как минимум пытался найти рациональное объяснение землетрясений.

Еще одним преимуществом идей Фалеса (к счастью) было то, что они не требовали жертв.

Из чего сделаны вещи?

Фалес глубоко задумался о материи. Он решил, что, по сути, все должно быть сделано из одного и того же — почти так же, как сегодня мы считаем, что вся материя состоит из атомов.Его идея заключалась в том, что в своей самой фундаментальной форме вся материя — это вода. Потребовалось около 200 лет, чтобы идея Фалеса была преобразована его соотечественником Демокритом в формулировку «вся материя — это атомы».

Древнегреческий историк Плутарх, живший через 600 лет после Фалеса, писал, что египетские жрецы утверждали, что теория Фалеса «все есть вода» первоначально пришла из Египта.

Астрономия

Фалес узнал об астрономии в Египте и, возможно, в Вавилоне.

Когда Архимед был убит во время римского завоевания Сиракуз в 212 г. до н.э., римский историк Цицерон написал об этом событии.Он сообщает нам, что римляне обнаружили у Архимеда машину, которая точно предсказывала движение Луны и планет и предсказывала солнечные и лунные затмения. (Такая машина действительно была обнаружена археологами — это удивительно сложное устройство, названное «антикиферским механизмом».)

Римляне также нашли более простой глобус с изображением небесной сферы — предшественника антикиферского механизма — который впервые был изготовлен Фалесом.

Фалес построил сферу, показывающую планеты и звезды в их созвездиях вокруг Земли.Позже греки — возможно, Архимед — развили это дальше и построили удивительно сложный небесный калькулятор — антикиферский механизм.

Новаторская математика

Как и в астрономии, Фалес узнал о математике в Египте и, возможно, в Вавилоне.

Вернувшись в Милет, он опирался на полученные знания и был первым человеком, применившим дедуктивную логику в математике, что привело к новым результатам в геометрии.

Он впервые установил, что математические теоремы требуют доказательства, прежде чем они будут приняты за истину.

Он начал превращать математику из практической области обучения в ту, которую можно было изучать, не беспокоясь о практических приложениях. Таким образом, Фалес сделал большой шаг вперед в сторону современной чистой математики, предмета, основанного на дедукции и доказательствах, не заботясь о практическом использовании ее результатов. (Как ни странно, хотя чистая математика выполняется без каких-либо мыслей о практическом использовании, открытия в чистой математике часто оказываются важными в реальном мире!)

Фалес основал милетскую школу, где преподавал математику, заложив основу для процветания математики в Древней Греции.

Вера в богов

Фалес не отвергал богов. Он верил, что боги присутствуют во всем. В результате вся материя имела в себе какой-то аспект жизни. Он думал, что, понимая фундаментальные принципы природы, люди действительно лучше узнают и поймут своих богов.

«Для Фалеса главный вопрос был не в том, что мы знаем, а в том, как мы это узнаем?»

Аристотель, 384 — 322 гг. До н.э.

г.

Наследие

Фалес был основоположником науки в Древней Греции.Он основал милетскую школу, которая передала его знания, в первую очередь, Анаксимандру и Пифагору. Пик развития греческой науки и математики пришелся на 300 лет спустя, в эпоху Архимеда.

Повторное открытие древнегреческих знаний стало той искрой, которая зажгла в Европе Возрождение и научную революцию, направив науку на путь, ведущий в наш современный технологический мир.

Отказ от суеверий в пользу науки начался с Фалеса.

Семейная жизнь и конец

Счета древних историков расходятся во мнениях относительно того, был ли Фалес когда-либо женат.Некоторые говорят, что он женился и имел сына. Другие говорят, что он не женился, а относился к одному из своих племянников, как к своему сыну.

Фалес умер в возрасте 78 лет примерно в 546 году до нашей эры.

Объявления

Процитируйте эту страницу

Используйте следующую ссылку, соответствующую требованиям MLA:

 "Фалес". Известные ученые.famousscientists.org. 22 января 2015 г. Web.
.

Опубликовано FamousScientists.org

Теорема Пифагора | Определение и история

Теорема Пифагора , хорошо известная геометрическая теорема о том, что сумма квадратов на катетах прямоугольного треугольника равна квадрату на гипотенузе (сторона, противоположная прямому углу) — или, как известно алгебраическая запись, a ² + b ² = c ².Хотя теорема давно ассоциируется с греческим математиком-философом Пифагором (около 570–500 / 490 гг. До н. Э.), На самом деле она намного старше. Четыре вавилонских таблички примерно 1900–1600 гг. До н.э. указывают на некоторое знание теоремы, с очень точным вычислением квадратного корня из 2 (длина гипотенузы прямоугольного треугольника с длиной обоих катетов, равной 1) и списками специальные целые числа, известные как тройки Пифагора, которые ему удовлетворяют (например, 3, 4 и 5; 3 ² + 4 ² = 5 ², 9 + 16 = 25).Эта теорема упоминается в индийской Баудхаяне Сульба-сутре , написанной между 800 и 400 годами до нашей эры. Тем не менее, теорема была приписана Пифагору. Это также предложение номер 47 из Книги I Евклида Элементы .

Британская викторина

36 вопросов из самых популярных научных викторин «Британники»

Насколько хорошо вы знаете астрономию? А как насчет квантовой механики? В этой викторине вы ответите на 36 самых сложных вопросов из самых популярных викторин «Британника» о науках.Его завершат только лучшие мастера викторины.

Согласно сирийскому историку Ямвлиху (ок. 250–330 гг. Н. Э.), Пифагор был представлен математике Фалесом Милетским и его учеником Анаксимандром. В любом случае известно, что Пифагор отправился в Египет около 535 г. до н.э. для дальнейшего изучения, был схвачен во время вторжения Персии Камбиза II в 525 г. до н.э. и доставлен в Вавилон, и, возможно, посетил Индию, прежде чем вернуться в Средиземное море. Вскоре Пифагор поселился в Кротоне (ныне Кротоне, Италия) и основал школу или, говоря современным языком, монастырь ( см. пифагореизм), где все члены дали строгую клятву секретности, и все новые математические результаты за несколько столетий были приписаны его имя.Таким образом, неизвестно не только первое доказательство теоремы, но и некоторые сомнения в том, что сам Пифагор действительно доказал теорему, носящую его имя. Некоторые ученые предполагают, что первое доказательство было показано на рисунке. Вероятно, он был независимо обнаружен в нескольких разных культурах.

Теорема Пифагора

Наглядная демонстрация теоремы Пифагора. Это может быть оригинальным доказательством древней теоремы, которая гласит, что сумма квадратов на сторонах прямоугольного треугольника равна квадрату на гипотенузе ( a ² + b ² = c ²).В поле слева заштрихованные зеленым цветом a ² и b ² представляют квадраты на сторонах любого из идентичных прямоугольных треугольников. Справа четыре треугольника переставлены, остается c ², квадрат на гипотенузе, площадь которого с помощью простой арифметики равна сумме a ² и b ². Чтобы доказательство работало, нужно только увидеть, что c ² действительно квадрат.Это делается путем демонстрации того, что каждый из его углов должен составлять 90 градусов, поскольку все углы треугольника должны составлять в сумме 180 градусов.

Encyclopædia Britannica, Inc.

Книга I Elements заканчивается знаменитым «ветряным» доказательством Евклида теоремы Пифагора. ( См. Врезку : Ветряная мельница Евклида.) Позже в Книге VI Элементов Евклид предлагает еще более простую демонстрацию, используя утверждение, что площади подобных треугольников пропорциональны квадратам их соответствующих сторон.По-видимому, Евклид изобрел доказательство ветряной мельницы, чтобы поместить теорему Пифагора в качестве завершающей в Книгу I. Он еще не продемонстрировал (как он сделал это в Книге V), что длинами строк можно изменять пропорции, как если бы они были соизмеримыми числами ( целые числа или отношения целых чисел). Проблема, с которой он столкнулся, объясняется на боковой панели: несоизмеримые.

Было изобретено очень много различных доказательств и расширений теоремы Пифагора. Сам Евклид, сначала взяв расширения, показал в теореме, восхваляемой в древности, что любые симметричные правильные фигуры, нарисованные на сторонах прямоугольного треугольника, удовлетворяют пифагорейскому соотношению: фигура, нарисованная на гипотенузе, имеет площадь, равную сумме площадей фигур. нарисовано на ногах.Полукруги, определяющие луны Гиппократа Хиосского, являются примерами такого расширения. ( См. Врезку : Квадратура Луны.)

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

В девяти главах по математическим процедурам (или девяти главах ), составленных в I веке нашей эры в Китае, дается несколько задач вместе с их решениями, которые включают определение длины одной из сторон прямоугольный треугольник, если учесть две другие стороны.В комментарии Лю Хуэй , относящемся к 3-м веку, Лю Хуэй предложил доказательство теоремы Пифагора, которая призывает разрезать квадраты на катетах прямоугольного треугольника и переставлять их («стиль танграм»), чтобы они соответствовали квадрат на гипотенузе. Хотя его первоначальный рисунок не сохранился, на следующем рисунке показана возможная реконструкция.

«танграмное» доказательство теоремы Пифагора Лю Хуэй

Это реконструкция доказательства китайского математика (основанного на его письменных инструкциях) о том, что сумма квадратов на сторонах прямоугольного треугольника равна квадрату на гипотенузе.Начинают с ² и b ², квадратов на сторонах прямоугольного треугольника, а затем разрезают их на различные формы, которые можно переставить, чтобы получить c ², квадрат на гипотенузе.

Британская энциклопедия, Inc.

Теорема Пифагора очаровывала людей почти 4000 лет; в настоящее время существует более 300 различных доказательств, в том числе от греческого математика Паппа Александрийского (процветание ок. 320 г. н. э.), арабского математика-врача Табита ибн Курры (ок.836–901), итальянского художника-изобретателя Леонардо да Винчи (1452–1519) и даже президента США. Джеймс Гарфилд (1831–81).

Биография Фалеса — Жизнь греческого математика

г.

Thales

Математик и философ
Специальность	Этика, метафизика, математика, астрономия
Родился	г. 624 г. до н.э.
Умер	г.547–546 до н.э.
Гражданство	Греческий

Фалес родился более чем за 600 лет до Рождества Христова. Он вошел в жизнь, пропитанную культурой, определяемой древними мифологиями. Но именно Фалес считается одним из первых, кто отбросил столетия ненаучных систем верований. Вместо этого он попытался объяснить физическую реальность с точки зрения объективного наблюдения, измерения, тестирования и разработки твердой математики.

Ранние годы Фалеса

Считается, что Фалес родился около 624 г. до н. Э.C. в ионическом городе Милет, который сегодня расположен на западном побережье Турции. Из-за обширных временных рамок конкретные детали того, где и когда родился Фалес, отрывочны. Некоторые древние источники называют его родителей Экзамьесом и Клеобулином. Возможно и вероятно, что его семья была из высшего сословия и, возможно, даже из богатых купцов. Некоторые проследили происхождение семьи Фалеса до важного финикийского принца.

Следует признать, однако, что возможно, что Фалес родился в Афинах, а затем переселился в Милет.Это потому, что Фалеса часто считают «первым мудрецом» из знаменитых семи мудрецов. Это была школа элитных философов, которая, как известно, была основана в Афинах в период, приписываемый жизни Фалеса.

Философ Фалес

Вплоть до времен Фалеса древние греки обычно объясняли природные явления «действиями богов». Например, грозу можно отнести к гневу Зевса, а землетрясение — к действиям богов подземного мира.

Но Фалес был достаточно смел, чтобы выйти за рамки этого образа мышления в пользу более логичных и рациональных объяснений. Что касается землетрясений, например, Фалес предположил, что массивы суши Земли плавают в океанах, и поэтому сильное воздействие волн может быть истинной причиной сотрясения Земли.

Материалы по математике

Невозможно переоценить важность вклада Фалеса в понимание математики. Его теоретические работы в области геометрии окажут огромное влияние на всю последующую западную науку.Фалес предшествовал Евклиду, в честь которого названа евклидова геометрия. Но без Фалеса, возможно, никогда не было бы Евклида.

Считается, что Фалес был первым, кто описал основные принципы деления окружностей пополам, и, возможно, он был первым, кто математически продемонстрировал, что углы в основании равнобедренного треугольника равны. Фалес также показал, что треугольники, имеющие два угла и одну сторону, равны, делят равенство. Это было больше, чем просто возвышенная теория, поскольку эти принципы можно было использовать в практических целях, например, для определения расстояния кораблей в море.

Без такого фундаментального понимания геометрии многое из того, что мы сегодня считаем само собой разумеющимся, было бы невозможным. Математические разработки Фалеса стимулировали развитие множества практических дисциплин, от навигации и архитектуры до инженерии и более глубокого понимания астрономии.

Фалес известен важной теоремой, названной в его честь. Теорема Фалеса гласит: «Если A, B и C — точки на окружности, а прямая AC — это диаметр окружности, то угол ABC — прямой угол.”

Фалес и материализм

Величайшие философы современности обсуждали влияние Фалеса с энтузиазмом, но также и с большим разногласием. Многие указывают на Фалеса как на человека, который породил материализм — идею о том, что наша реальность состоит из чего-то «твердого». Это выводит основы физики из области мистицизма или сверхъестественных объяснений в «жесткую реальность».

Фалес также считается одним из первых «натуралистов», что означает, что он в основном пытался объяснить «природу самой природой».То есть, вместо того, чтобы приписывать создание воды, скал или деревьев богам, традиционно приписываемым каждому из них, Фалес стремился смотреть на все с точки зрения фундаментальных свойств веществ, а не накладывать на это ссылку на нефизические свойства. или трансцендентный источник.

Таким образом, Фалес был одним из первых, кто радикально отказался от традиционного образа мышления, господствовавшего в течение нескольких столетий. Это делает его значимой и важной фигурой в мировой истории.

Фалес Милетский — Хронология математики — Матигон

c. 300 г. до н. Э .: Индийский математик Пингала пишет о нуле, двоичных числах, числах Фибоначчи и треугольнике Паскаля.

г. 260 г. до н. Э .: Архимед доказывает, что π находится между 3,1429 и 3,1408.

г. 235 г. до н.э.: Эратосфен использует алгоритм сита, чтобы быстро находить простые числа.

г. 200 г. до н. Э .: «Суан шу шу» (Книга о числах и вычислениях) — один из старейших китайских текстов по математике.

г. 100 г. н. Э.: Никомах ставит самую старую нерешенную проблему в математике: существуют ли какие-либо нечетные совершенные числа.

г. 250 г. н.э .: культура майя в Центральной Америке процветает, и в ней используется система счисления с основанием 20.

г. 830 г. н.э .: Аль-Хорезми издает «Китаб аль-джабр ва аль-мукабала», первую книгу об алгебре и тезку по ней.

1202: Liber Abaci Фибоначчи вводит арабские цифры в Европу, а также простую алгебру и числа Фибоначчи.

1482: Первое печатное издание «Элементов» Евклида

1545: Кардано задумал идею комплексных чисел.

1609: Кеплер публикует «Astronomia nova», в которой объясняет, что планеты движутся по эллиптическим орбитам.

1618: Napier публикует первые упоминания числа e в книге по логарифмам.

1637: Ферма утверждает, что доказал Великую теорему Ферма.

1654: Паскаль и Ферма развивают теорию вероятностей.

1684: Лейбниц публикует первую статью по исчислению.

1687: Ньютон издает «Основы математики», содержащие законы гравитации и движения, а также свою версию исчисления.

1736: Эйлер решает проблему Кенигсбергских мостов, изобретая теорию графов.

1761: Ламберт доказывает, что π иррационально

1799: Гаусс доказывает основную теорему алгебры.

1829: Бойяи, Гаусс и Лобачевский изобретают гиперболическую неевклидову геометрию.

1832: Галуа находит общее условие для решения алгебраических уравнений, тем самым основывая теорию групп и теорию Галуа.

1858: Август Фердинанд Мебиус изобретает ленту Мебиуса.

1874: Кантор доказывает, что существуют разные «размеры» бесконечности и что действительные числа неисчислимы.

1895: Статья Пуанкаре «Analysis Situs» положила начало современной топологии.

1905: Эйнштейн объясняет фотоэлектрический эффект и броуновское движение, открывает специальную теорию относительности и E = mc².

1915: Нётер показывает, что каждый закон сохранения в физике соответствует симметрии Вселенной.

1931: Теорема Гёделя о неполноте устанавливает, что математика всегда будет неполной.

1939: Группа французских математиков издает свою первую книгу по теории множеств под псевдонимом Николя Бурбаки.

1961: Лоренц обнаруживает хаотическое поведение в моделировании погоды — эффект бабочки.

1976: Аппель и Хакен доказывают гипотезу четырех цветов с помощью компьютера.

1977: Адельман, Ривест и Шамир вводят криптографию с открытым ключом с использованием простых чисел.

1994: Эндрю Уайлс доказывает Великую теорему Ферма.

2000: Институт математики Клэя опубликовал семь задач Премии тысячелетия.

2003: Перельман доказывает гипотезу Пуанкаре, единственную из семи решенных на сегодняшний день проблем тысячелетия.

г. 9100 г. до н.э.: старейшее известное сельскохозяйственное поселение на Кипре.

г. 2030 г. до н.э.: шумерский город Ур — самый большой город в мире.

г. 3500 г. до н.э .: первые автомобили с колесами появляются в Месопотамии и Восточной Европе.

г. 3200 г. до н.э .: первые системы письма появляются в Месопотамии, Египте и долине Инда.

г. 3000 г. до н.э .: первые свидетельства плавки железной руды для производства кованого железа.

г. 2560 г. до н.э .: Великая пирамида Гизы построена в Древнем Египте для фараона Хуфу.

г. 1754 г. до н.э .: вавилонский царь Хаммурапи издает Кодекс Хаммурапи, один из первых юридических документов.

776 г. до н.э .: Первые Олимпийские игры проходят в Греции.

753 г. до н. Э .: Легендарная дата основания Рима.

г. 563 г. до н.э .: Будда родился в Индии. Его учение стало основой буддизма.

г. 551 г. до н. Э .: Конфуций родился в Китае. Его учение стало основой конфуцианства.

490 г. до н.э .: Греция остановила персидское вторжение в битве при Марафоне. Начинается классический период.

432 г. до н. Э.: Акрополь построен в Афинах во время их золотого века при Перикле.

399 до н.э .: Сократ приговорен к смерти, отказывается бежать и выпивает чашу яда.

327 г. до н.э .: Александр Великий вторгается в Индию, создав огромную империю в Азии.

г. 221 г. до н.э.: Цинь Шихуанди объединяет Китай и начинает строительство Великой стены.

146 г. до н. Э .: Римская армия разрушает Карфаген, положив конец Третьей Пунической войне.

44 г. до н. Э .: Юлий Цезарь убит.

4 г. до н. Э.: Иисус из Назарета родился в Вифлееме, утверждая христианство.

180 г. н. Э.: Смертью Марка Аврелия завершился Pax Romana, 200-летний период мира в Европе.

476 н.э .: падение Римской империи

570 н.э .: Мухаммад, основатель ислама, родился в Мекке.

г. 641 г. н.э .: Александрийская библиотека разрушена.

800 г. н.э .: Карл Великий коронован как первый император Священной Римской империи.

г. 870 г. н.э.: норвежские исследователи открывают и колонизируют Исландию.

1066: Вильгельм Завоеватель побеждает в битве при Гастингсе и становится королем Англии.

1088: Первый университет открыт в Болонье, Италия.

1096: Первый крестовый поход инициирован Папой Урбаном II.

1206: Чингисхан побеждает своих соперников и получает титул «Вселенский правитель монголов».

1215: король Англии Иоанн вынужден подписать Великую хартию вольностей, ограничивая его полномочия.

1266: Марко Поло прибывает ко двору Хубилай-хана в Пекине.

г. 1347 год: Черная смерть убивает миллионы людей по всей Европе.

1439: Иоганнес Гутенберг изобретает печатный станок.

1453 г .: Османские турки завоевывают Константинополь, отмечая падение Византийской империи.

1492: Христофор Колумб прибывает в Америку, начиная новую эру европейских завоеваний.

1517: Мартин Лютер публикует свои 95 тезисов, положив начало протестантской реформации.

1522: Экспедиция Фердинанда Магеллана облетает Землю.

1543: Польский ученый Николай Коперник пишет, что Земля вращается вокруг Солнца.

1588: При королеве Елизавете I Англия побеждает испанскую армаду.

1603: Впервые исполняется «Гамлет» Уильяма Шекспира.

1633: Католическая инквизиция судит Галилео Галилея за его научные труды.

1649: Король Карл I предан суду и обезглавлен во время Гражданской войны в Англии.

1756: Вольфганг Амадей Моцарт родился в Австрии.

г. 1765: Джеймс Ватт изобретает более эффективный паровой двигатель, который станет двигателем промышленной революции.

1776: Америка издает Декларацию независимости от Великобритании.

1789: Революционеры штурмуют Бастилию в Париже, начиная Французскую революцию.

1804: Наполеон становится императором Франции.

1819: Симон Боливар побеждает Испанию в битве при Бояке, что приводит к независимости многих стран Южной Америки.

1837: Сэмюэл Морс и другие разрабатывают электрические телеграфы.

1859: Чарльз Дарвин публикует «Происхождение видов», вводя естественный отбор.

1865: Авраам Линкольн убит в конце Гражданской войны в США.

1876: Александр Белл изобретает телефон.

1903: Братья Райт создают первый самолет с двигателем тяжелее воздуха.

1914: Франц Фердинанд из Австрии убит в Сараево, в начале Первой мировой войны.

1929: Обвал фондового рынка в «черный вторник» положил начало великой депрессии.

1939: Адольф Гитлер вторгается в Польшу, начиная Вторую мировую войну.

1953: Уотсон и Крик открывают двойную спиральную структуру ДНК.

1957: Советский Союз запускает в космос Спутник-1, первый искусственный спутник Земли.

1969: Астронавты Аполлона-11 Нил Армстронг и Базз Олдрин приземляются и идут по Луне.

Теорема Фалеса интересные факты. Интересные факты из жизни Фалеса

Теорема Фалеса интересные факты. Интересные факты из жизни Фалеса

История математики

Теорема Фалеса ударение. Замечания

Как разделить отрезок на 3 равные части по теореме Фалеса. Теорема Фалеса и деление отрезка в заданном отношении

Докажите теорему Фалеса. Обобщенная теорема Фалеса

Теорема Фалеса в жизни

Практическое применение теорем геометрии в жизни

1.

2. Автор: Боброва Елена Валентиновна Место работы: ГКОУ ВО «Специальная (коррекционная) общеобразовательная школа-интернат г.

4. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой с теченьем реки его

5. Задача Бхаскары

6. Какова глубина в современных единицах длины (1 фут приближённо равен 0,3 м) ?

10. Подобие в жизни

13. Историческая справка.

16. Способ Фалеса

17. Способ Фалеса

20.

Конспект «Теорема Фалеса» (8 класс)

Доказать теорему фалеса. Теорема Фалеса

Тема урока

Цели урока

Задачи урока

План урока

Историческая справка

Открытия и заслуги ее автора

Теорема Фалеса в культуре

Вопросы

Список использованных источников

Формулировки [ | ]

Замечания [ | ]

Вариации и обобщения [ | ]

Обратная теорема [ | ]

Лемма Соллертинского [ | ]

Теорема Фалеса

Урок геометрії 8 клас теорема фалеса

Теорема фалеса 8 клас презентація

Все о математике Фалесе

Фалес Милетский: Жизнь математика

Как Фалес повлиял на курсы математики

Фалеса От математики к астрономии

Фалес в контексте великих

Как Фалес Милетский изменил мир

Философские идеи

Математика

Теории о Земле

Астрономия

Задачи по математике

Из нашей базы данных математических задач и примеров мы предлагаем:

Thales — Биография, факты и изображения

Ранняя жизнь и образование

Время жизни избранных древнегреческих ученых и философов

Фалес: наука

Хапи не нужен, чтобы развести Нил

Ботан с головой в облаках, разбогатевший!

Землетрясения

Из чего сделаны вещи?

Астрономия

Новаторская математика

Вера в богов

Наследие

Семейная жизнь и конец

Процитируйте эту страницу

Теорема Пифагора | Определение и история

Биография Фалеса — Жизнь греческого математика

Ранние годы Фалеса

Философ Фалес

Материалы по математике

Фалес и материализм

Фалес Милетский — Хронология математики — Матигон

Добавить комментарий Отменить ответ

Формулировки
[
|
]

Замечания
[
|
]

Вариации и обобщения
[
|
]

Обратная теорема
[
|
]

Лемма Соллертинского
[
|
]