Примеры нод с ответами: Наибольший общий делитель. Наименьшее общее кратное. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Нахождение наименьшего общего кратного: способы, примеры нахождения НОК

Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.

Вычисление наименьшего общего кратного (НОК) через НОД

Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.

Определение 1

Найти наименьшее общее кратное через наибольший общий делитель можно по формуле НОК(a, b)=a·b:НОД(a, b).

Пример 1

Необходимо найти НОК чисел 126 и 70.

Решение

Примем a=126, b=70. Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК(a, b)=a·b:НОД(a, b).

Найдет НОД чисел 70 и 126. Для этого нам понадобится алгоритм Евклида: 126=70·1+56, 70=56·1+14, 56=14·4, следовательно, НОД(126, 70)=14.

Вычислим НОК: НОК(126, 70)=126·70:НОД(126, 70)=126·70:14=630.

Ответ: НОК(126, 70)=630.

Пример 2

Найдите нок чисел 68 и 34.

Решение

НОД в данном случае нейти несложно, так как 68 делится на 34. Вычислим наименьшее общее кратное по формуле: НОК(68, 34)=68·34:НОД(68, 34)=68·34:34=68.

Ответ: НОК(68, 34)=68.

В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b: если первое число делится на второе, что НОК этих чисел будет равно первому числу.

Нахождение НОК с помощью разложения чисел на простые множители

Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.

Определение 2

Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:

составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
исключаем их полученных произведений все простые множители;
полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК(a, b)=a·b:НОД(a, b). Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.

Пример 3

У нас есть два числе 75 и 210. Мы можем разложить их на множители следующим образом: 75=3·5·5 и 210=2·3·5·7. Если составить произведение всех множителей двух исходных чисел, то получится: 2·3·3·5·5·5·7.

Если исключить общие для обоих чисел множители 3 и 5, мы получим произведение следующего вида: 2·3·5·5·7=1050. Это произведение и будет нашим НОК для чисел 75 и 210.

Пример 4

Найдите НОК чисел 441 и 700, разложив оба числа на простые множители.

Решение

Найдем все простые множители чисел, данных в условии:

44114749713377

700350175357122557

Получаем две цепочки чисел: 441=3·3·7·7 и 700=2·2·5·5·7.

Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2·2·3·3·5·5·7·7·7. Найдем общие множители. Это число 7. Исключим его из общего произведения: 2·2·3·3·5·5·7·7. Получается, что НОК(441, 700)=2·2·3·3·5·5·7·7=44 100.

Ответ: НОК(441, 700)= 44 100.

Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.

Определение 3

Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:

разложим оба числа на простые множители:
добавим к произведению простых множителей первого числа недостающие множители второго числа;
получим произведение, которое и будет искомым НОК двух чисел.

Пример 5

Вернемся к числам 75 и 210, для которых мы уже искали НОК в одном из прошлых примеров. Разложим их на простые множители: 75=3·5·5 и 210=2·3·5·7. К произведению множителей 3, 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210. Получаем: 2·3·5·5·7. Это и есть НОК чисел 75 и 210.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Пример 6

Необходимо вычислить НОК чисел 84 и 648.

Решение

Разложим числа из условия на простые множители: 84=2·2·3·7 и 648=2·2·2·3·3·3·3. Добавим к произведению множителей 2, 2, 3 и 7 числа 84 недостающие множители 2, 3, 3 и
3 числа 648. Получаем произведение 2·2·2·3·3·3·3·7=4536. Это и есть наименьшее общее кратное чисел 84 и 648 .

Ответ: НОК(84, 648)=4 536.

Нахождение НОК трех и большего количества чисел

Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.

Теорема 1

Предположим, что у нас есть целые числа a1, a2, …, ak. НОК mk этих чисел находится при последовательном вычислении m2=НОК(a1, a2), m3=НОК(m2, a3), …, mk=НОК(mk−1, ak).

Теперь рассмотрим, как можно применять теорему для решения конкретных задач.

Пример 7

Необходимо вычислить наименьшее общее кратное четырех чисел 140, 9, 54 и 250.

Решение

Введем обозначения: a1=140, a2=9, a3=54, a4=250.

Начнем с того, что вычислим m2=НОК(a1, a2)=НОК(140, 9). Применим алгоритм Евклида для вычисления НОД чисел 140 и 9: 140=9·15+5, 9=5·1+4, 5=4·1+1, 4=1·4. Получаем: НОД(140, 9)=1, НОК(140, 9)=140·9:НОД(140, 9)=140·9:1=1 260. Следовательно, m2=1 260.

Теперь вычислим по тому е алгоритму m3=НОК(m2, a3)=НОК(1 260, 54). В ходе вычислений получаем m3=3 780.

Нам осталось вычислить m4=НОК(m3, a4)=НОК(3 780, 250). Действуем по тому же алгоритму. Получаем m4=94 500.

НОК четырех чисел из условия примера равно 94500.

Ответ: НОК(140, 9, 54, 250)=94 500.

Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.

Определение 4

Предлагаем вам следующий алгоритм действий:

раскладываем все числа на простые множители;
к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
полученное произведение будет наименьшим общим кратным всех чисел из условия.

Пример 8

Необходимо найти НОК пяти чисел 84, 6, 48, 7, 143.

Решение

Разложим все пять чисел на простые множители: 84=2·2·3·7, 6=2·3, 48=2·2·2·2·3, 7, 143=11·13. Простые числа, которым является число 7, на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.

Теперь возьмем произведение простых множителей 2, 2, 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3. Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.

Продолжаем добавлять недостающие множители. Переходим к числу 48, из произведения простых множителей которого берем 2 и 2. Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2·2·2·2·3·7·11·13=48 048. Это и есть наименьшее общее кратное пяти исходных чисел.

Ответ: НОК(84, 6, 48, 7, 143)=48 048.

Нахождение наименьшего общего кратного отрицательных чисел

Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.

Пример 9

НОК(54, −34)=НОК(54, 34), а НОК(−622, −46, −54, −888)=НОК(622, 46, 54, 888).

Такие действия допустимы в связи с тем, что если принять, что a и −a – противоположные числа,

то множество кратных числа a совпадает со множеством кратных числа −a.

Пример 10

Необходимо вычислить НОК отрицательных чисел −145 и −45.

Решение

Произведем замену чисел −145 и −45 на противоположные им числа 145и 45. Теперь по алгоритму вычислим НОК(145, 45)=145·45:НОД(145, 45)=145·45:5=1 305, предварительно определив НОД по алгоритму Евклида.

Получим, что НОК чисел −145 и −45 равно 1 305.

Ответ: НОК(−145, −45)=1 305.

Решение задач по теме «НОК и НОД»

Цель урока: показать обучающимся, что понятия
наибольшего общего делителя и наименьшего
общего кратного применимы в обычной жизни.

Задачи:

Актуализация и обобщение знаний обучающихся по
теме, рефлексия.

Формирование личностных УУД посредством
самооценки различных видов деятельности.

Формирование коммуникативных УУД (работа в
группе).

Развитие презентативных умений (презентация
работы в группе).

Повышение интереса обучающихся к предмету,
активизация познавательной деятельности.

Ход урока

Приложение 1

Приложение 2

Приветствуем гостей. Садимся.

Делители, кратные, НОКи и НОДы,

Как много приходится вам изучать!

Признаки, свойства, и вечные дроби,

В них можно попасть, если правил не знать!

Уже целый месяц мы с вами изучаем главу
“Делимость чисел”. Запутываемся, распутываемся,
и запутываемся снова. Но, как гласит закон
философии, количество всегда переходит в
качество. И сегодня мы снова запутаемся, или
распутаемся, но главное, мы попытаемся сами
оценить, что мы уже знаем, а что нам стоит еще
подучить. Перед вами на парте – оценочный лист
урока (слайд №2 приложения 1), и я надеюсь, что вы
уже достаточно взрослые, чтобы оценивать себя
честно.

Ф.И.________________________		самооценка
1.	“Верите ли вы?”
	“Установи соответствие”
	“Сократи дробь”
	“Собери цепочку по алгоритму Евклида”
	Решение задач.
Итоговая оценка за урок.
Изобрази настроение (смайлик)

I. Играем в “Верите ли вы”. Как обычно, 7
цифр в столбик.

Верите ли вы, что делители числа делятся на это
число без остатка?

Верите ли вы, что кратные числа делятся на это
число без остатка?

Верите ли вы, что наименьшее общее кратное двух
чисел всегда больше меньшего из этих чисел?

Верите ли вы, что единица может быть наибольшим
общим делителем каких-либо чисел?

Верите ли вы, что сократить дробь – это
разделить числитель и знаменатель дроби на их
наименьший общий делитель?

Верите ли вы, что натуральные числа, имеющие
только два делителя, называют простыми?

Верители вы, что разложение на простые
множители может помочь в нахождении наибольшего
общего делителя?

Проверка, самооценка.

№ задания	1	2	3	4	5	6	7
ответ	нет	да	да	да	нет	да	да

Верно:

7 заданий – “5”,

6 заданий – “4+”,

5 заданий – “4”,

4 задания – “3”,

менее 4-х заданий – “Учи правила!”

Сделать запись в оценочном листе урока.

II. Установи соответствие.

Задание

Ответ

НОК (2; 12)=

НОД(4;20)=

НОК(3;23)=

НОД(3;23)=

НОК(50;75)=

НОД(50;75)=

НОД(25;26)=

2; 12; 24; 4; 20; 80; 3; 23; 69; 1; 50; 75; 25; 150; 3750

1 человек устанавливает соответствие с помощью
интерактивной доски.

Самооценка, критерии те же. Внесение в
оценочный лист урока.

III. Индивидуальная работа “Сократи дробь”.

Проверка по образцу. Самооценка по количеству
правильно выполненных заданий. Запись в
оценочном листе урока. Листики передаем вперед.

IV. Соберите цепочку по алгоритму Евклида
(работа на интерактивной доске).

НОД (235;150)=НОД(150;85)=НОД(85;65)=НОД(65;20)=НОД(20;5)=5

Оценка по количеству правильно подобранных
звеньев (знаки равенства). Запись в оценочном
листе урока.

V. Проблемная ситуация.

Итак, мы с вами порешали, дроби посокращали,
себя оценили… А я тут как-то встретила в магазине
бывшую ученицу, у нее сын Миша в 6-м классе другой
школы учится. Приходит домой, жалуется, как
трудно и скучно ему эти НОКи и НОДы считать, ведь
в жизни это нигде не нужно. “Как ответить сыну?”-
спрашивает моя ученица. Я обещала ей подумать, да
и задалась тем же вопросом; “А моим
шестиклассникам тоже, наверное, скучно и
непонятно?” Вот и подобрала я вам задачки,
которые и предлагаю в группах решить. Может, мы
сможем ответить на вопрос Миши: “Зачем все это
надо?”

Каждая группа получает задачи. Кружочком
отмечена задача, за которую отвечает данная
группа. На обсуждение и решение – 5 минут.
Потом каждая группа представляет свою задачу.
Если вы решили быстрее, и во всем уверены, каждый
может решать любую понравившуюся задачу и затем
оценить свое решение и внести оценку в оценочный
лист.

Группируемся, как обычно: вторая парта 1 вариант
пересаживается на 1 парту, 2 вариант – на третью,
четвертая парта 1 и третьего ряда – на пятую,
четвертая и пятая парта среднего ряда – на
шестую. Молодцы.

Приступаем к работе.

№	задача	решение
	Заместитель директора Вера Александровна организует проведение дня здоровья. 424 человека повезут на стадион “Спартак” для проведения эстафет, а 477 человек – в плавательный бассейн с морской водой. Для перевозки нужно заказать автобусы. Перевозчик имеет автобусы с одинаковым количеством мест, все места должны быть заняты. Сколько автобусов надо заказать и сколько пассажиров будет в каждом автобусе?	НОД(424,477)=НОД(424;53)=53 53 человека в автобусе, 424:53=8 автобусов, 477:53=9 автобусов Всего 17 автобусов.
	Бегун Коля знает, что через каждые 400 м от старта стоит наблюдатель, а через каждые 700 м от старта можно попить воды. На каком минимальном расстоянии от старта можно попить воды и задать вопрос наблюдателю?	НОК(400;700)=2800 м
	Марина Николаевна, член родительского комитета, закупила для новогодних подарков 84 мандарина, 56 апельсинов, 112 вкуснейших шоколадных конфет, и передала все это для упаковки Светлане Алексеевне, сын которой совсем недавно учится в этом классе и не помнит точно, сколько в нем человек, но знает, что больше 25. Сможет ли Светлана Алексеевна определить, на сколько человек ей распаковывать подарки?	НОД (84; 56; 112) = 28 В классе 28 человек.
	Длина шага Бори 50 см, а его отца – 70 см. Боря утверждает, что первый раз, сделав целое количество шагов, они с папой окажутся на одинаковом расстоянии от начала пути через 3 метра, а папа не соглашается. Кто прав в этом споре?	НОК(50;70)= 350 см. а не 3 метра Прав папа.
	Заведующая хозяйством Раиса Максимовна дала поручение учителю труда Ильдару Олеговичу закупить доски, которые можно распилить на равные части и по 30 см, и по 40 см. Какой длины и сколько потребуется досок, если нужно 16 кусочков по 30 см и 12 кусочков по 40 см.	НОК(30; 40) = 120 см 16:(120:30)=4 доски 12:(120:40)=4 доски Всего 8 досок по 120 см.
	На празднике “Последнего звонка” выступающим первоклассникам принято дарить подарки. Ученики 11 “а” класса купили 58 конфет, ученики 11 “б” класс – 116 “чупа-чупсов”, а ученики 11 “в” класса – по одной мягкой игрушке. Сколько куплено мягких игрушек?	НОД (58;116)=29 Куплено 29 мягких игрушек.
	Родители Артема – люди очень интересных профессий. Мама – стюардесса, а папа – машинист скорого поезда. Мама бывает дома один раз в четыре дня, а папа – один раз в семь дней. Так получилось, что оба они 1 января 2015 года уходят в рейс. Когда Артем увидит своих родителей дома вместе?	НОК(4;7)=28 Семья будет дома вместе 28 января.
	Продавец цветочного магазина к 8 марта получила с базы 45 тюльпанов, 30 нарциссов и 60 веточек мимозы. Из этих цветов ей надо составить максимально возможное количество одинаковых букетов. Зашедшая к ней в магазин дочка-шестиклассница быстро решила эту задачу, сообщив, сколько надо сделать букетов и какое количество каждого вида цветов в них войдет. Как рассуждала дочь Маша?	НОД(45;30;60)=15 букетов 45:15=3 тюльпана, 30:15=2 нарцисса 60:15=4 веточки мимозы.
	Друзья Алексей Николаевич и Борис Петрович решили заняться гостиничным бизнесом. Для своей гостиницы Алексей Николаевич завез 108 кроватей и 72 шкафа, а Борис Петрович – 128 кроватей и 64 шкафа. Кровати и шкафы распределяются по комнатам поровну. Сколько комнат в гостиницах каждого из друзей? У кого из них остановиться третьему другу Александру Ивановичу, если он отдыхает с семьей, состоящей вместе с ним из 8 человек?	НОД(108;72)=36 – комнат у Алексей Николаевича; 108:36=3 кровати в номере; НОД(128;64)=32- комнат у Бориса Петровича. 128:32=4 кровати в номере. Александру Ивановичу лучше остановиться у Бориса Петровича (2 номера по 4 человека).

Решенная группой задача – “5” в оценочный
лист. Аналогично за каждую задачу, решенную
индивидульно.

При ответе групп ребята записывают задачи в
свой лист с задачами (в презентации представлены
задачи для лучшего восприятия при ответе групп).

После ответа группы учащиеся сразу садятся на
свои места.

VI. Учитель. Ребята, мы с вами решили 9
задач, в которых нет ни слова про делители и
кратные, но именно эти понятия помогли вам их
решить. Могу я передать эти задачи своей ученице
для сына? Поверит он, что не зря учит НОКи и НОДы?

Хорошо. Подведем итоги. Посмотрите на свой
оценочный лист и выставите итоговую оценку за
урок. Это может быть “пять”, “четыре”, “три”
или просто фраза “тема не понята”.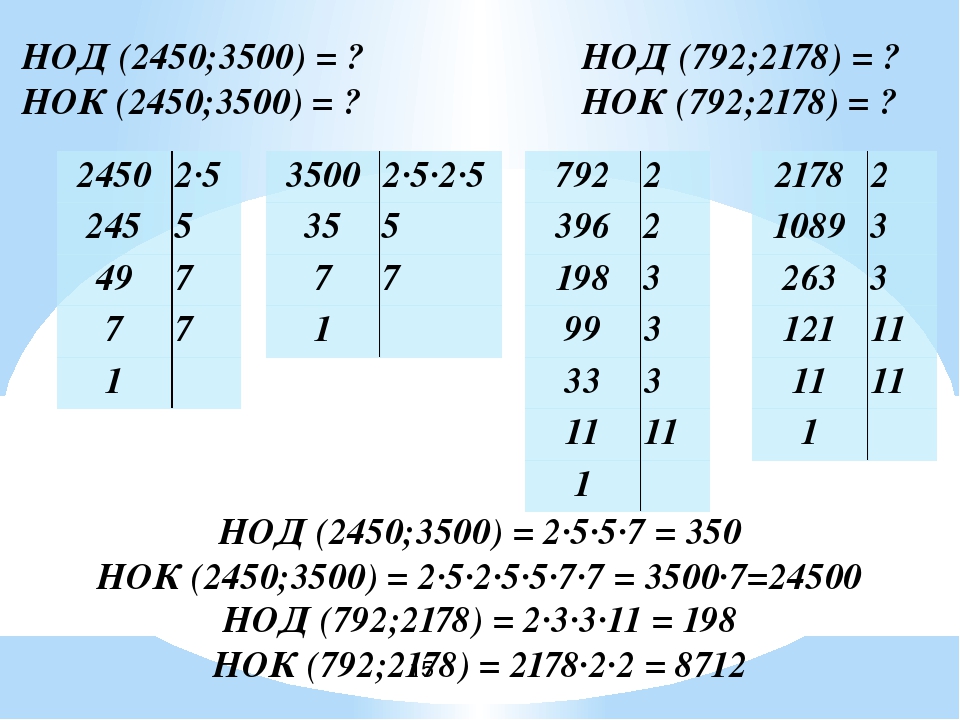 И в последней
строчке нарисуйте свое настроение, веселый,
грустный или равнодушный смайлик.

Передаем мне оценочные листы, открываем
дневники и записываем домашнее задание:

Придумать три интересные задачи, которые
решаются с помощью НОК и НОД, и решить их. Задание
выполнять на двойном листочке.

Всем спасибо за работу. Урок окончен.
Попрощаемся с нашими гостями.

Урок 43. наибольший общий делитель (нод) — Математика — 5 класс

Математика

5 класс

Урок № 43

Наибольший общий делитель (НОД)

Перечень рассматриваемых вопросов:

– делители числа;

– кратные числа;

– разложение на простые множители;

– НОД.

Тезаурус

Простое число – это натуральное число, которое больше 1 и делится только на 1 и само на себя.

Составные числа – это непростые натуральные числа больше 1.

Взаимно простые числа – это числа, которые не имеют общих простых делителей.

Обязательная литература:

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература:

Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Начнём наше занятие словами известной поговорки: «Учить – ум точить». Сегодня мы будем оттачивать умение находить общие делители сразу нескольких чисел.

Итак, рассмотрим два числа: 12 и 15. Выпишем все делители этих чисел. 12 – делители 1, 2, 3, 4, 6, 12.

15 – делители 1, 3, 5, 15.

Найдём общие делители этих чисел – это числа 1 и 3. Введём новое понятие – «наибольший общий делитель», который кратко обозначают НОД.

У этих чисел наибольший общий делитель равен 3.

Записывается – НОД (12; 15) = 3. НОД чисел двенадцать и пятнадцать равен трём.

Правило нахождения НОД:

разложим числа на простые множители;
подчеркнём одинаковые множители этих чисел;
перемножим общие множители одного из чисел, это и будет НОД заданных чисел.

Найдём НОД чисел 15 и 16.

НОД (15; 16) = ?

Разложим числа на простые множители.

Видно, что из всех множителей – общий лишь 1.

Такие числа, которые не имеют общих простых делителей, называются взаимно простыми числами. Любые два простых числа или два соседних натуральных числа будут взаимно простыми.

Найдём НОД (10; 100).

Разложим числа на простые множители.

Выделим общие делители у этих чисел, это 2 и 5.

Умножим их и получим наибольший общий делитель: НОД (10; 100) = 2 · 5 = 10.

Обратите внимание на то, что 100 делится нацело на 10 и НОД тоже равен 10. Поэтому можно сделать вывод: если одно из двух чисел делится нацело на другое, то НОД этих чисел равен меньшему из них.

Найдём наибольший общий делитель трёх чисел.

НОД (42; 70; 98) = ?

Разложим числа на простые множители:

Выделим общие делители у этих чисел, это 2 и 7.

Умножим их и получим наибольший общий делитель: НОД (42; 70; 98) = 2 · 7 = 14

Некоторые задачи можно решить при помощи НОД проще, чем каким-либо другим способом.

Например, решим такую задачу.

Для участия в соревнованиях нужно разделить 35 детей в возрасте 14 лет и 21 ребёнка в возрасте 12 лет на команды так, чтобы они состояли только из одновозрастных спортсменов. Какое наибольшее число участников одного возраста может быть в команде?

Решение: чтобы решить эту задачу нужно найти НОД (21; 35).

Разложим числа на простые множители:

Следовательно, НОД (21; 35) = 7 – это и будет наибольшим числом участников в команде.

Ответ: 7 человек.

Тренировочные задания

№ 1. Какую цифру нужно подставить в число НОД (7; 2_) вместо пропуска, чтобы получить НОД = 7?

Варианты ответов: 1, 2, 3.

Решение: разложим на множители оба числа, при этом вместо пропуска подставим по порядку все цифры. А далее найдём подходящий НОД этих чисел, равный 7. Получим следующее разложение:

Из всех разложений на множители под НОД (7; 2) = 7 подходит только число 21.

Ответ: искомая цифра – 1.

№ 2. В продуктовых наборах должно быть одинаковое количество груш и апельсинов. Всего приготовили 120 груш и 126 апельсинов. В какое наибольшее количество наборов можно разложить их поровну?

Решение: чтобы решить эту задачу, нужно найти НОД заданных чисел, он и будет являться искомым ответом, т. е. наибольшим количеством наборов при равном разложении фруктов.

НОД (120; 126) = 2 · 3 = 6

Ответ: 6 наборов.

НАХОЖДЕНИЕ И ПРИМЕНЕНИЕ НОД И НОК

Мульмин В.Н. 1

1ГБОУ ООШ с.Заволжье м.р. Приволжский Самарской области

Шишина И. А. 1

1ГБОУ ООШ с.Заволжье м.р. Приволжский Самарской области

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение.

В каждодневной жизни человеку приходится решать большое число разного рода задач, которые требуют применения определённых алгоритмов. Когда мы приготавливаем чай, пользуемся определённым алгоритмом (иногда заданным инструкцией, напечатанной на упаковке).

Слово алгоритм стало широко употребляться в последнее время. Оно означает описание совокупности действий, составляющих некоторый процесс. Обычно здесь подразумевают процесс решения некоторой задачи, но и кулинарный рецепт, и инструкция по пользованию стиральной машиной, и ещё многие другие правила, не имеющие отношения к математике, являются алгоритмами

Данная работа знакомит с алгоритмами вычисления НОД и НОК. Знакомство с ними не только дополняет и углубляет математические знания, но и развивает интерес к предмету, любознательность и логическое мышление. Предлагаемая работа рассчитана на учеников, желающих повысить уровень математической подготовки, увидеть красоту математических выкладок и эстетику алгоритма Евклида.

Гипотеза:Есть алгоритмы нахождения НОД и НОК, которые являются удобными и не требующие громоздкого способа вычисления.

Цель исследования: изучить разные алгоритмы вычисления НОД и НОК, выявить наиболее рациональные способы решения, красиво и сравнительно просто приводящие к ответу.

Достижение поставленной цели требует решения следующих основных задач:

Рассмотреть несколько алгоритмов вычисления НОД и НОК

Сравнить алгоритмы для вычисления НОД и НОК

Провести анкетирование «Знание и использование НОД и НОК»

Составить список памятку «Применение НОД И НОК»

Предмет исследования: Алгоритмы вычисления НОД и НОК

Объект исследования: умения и навыки вычисления НОД и НОК

Методы исследования: Изучение специальной литературы по данному вопросу: энциклопедии, справочники и учебные пособия. Анкетирование. Сравнение и анализ. Обработка полученных данных (составление обобщающих таблиц, диаграмм). Для решения поставленных задач я изучал как литературные источники, так и интернет-источники, в том числе учебник под редакцией Н. Я. Виленкина «Математика. 6 класс».

Глава 1. Алгоритмы вычисления НОД и НОК 1.1. «Прадедушка» всех алгоритмов

Алгоритм Евклида — эффективный алгоритм для нахождения наибольшего общего делителя двух целых чисел. Алгоритм назван в честь греческого математика Евклида, который впервые описал его в VII и X книгах «Начал».

В самом простом случае алгоритм Евклида применяется к паре положительных целых чисел и формирует новую пару, которая состоит из меньшего числа и разницы между большим и меньшим числом. Процесс повторяется, пока числа не станут равными. Найденное число и есть наибольший общий делитель исходной пары.

Первое описание алгоритма находится в «Началах Евклида» (около 300 лет до н.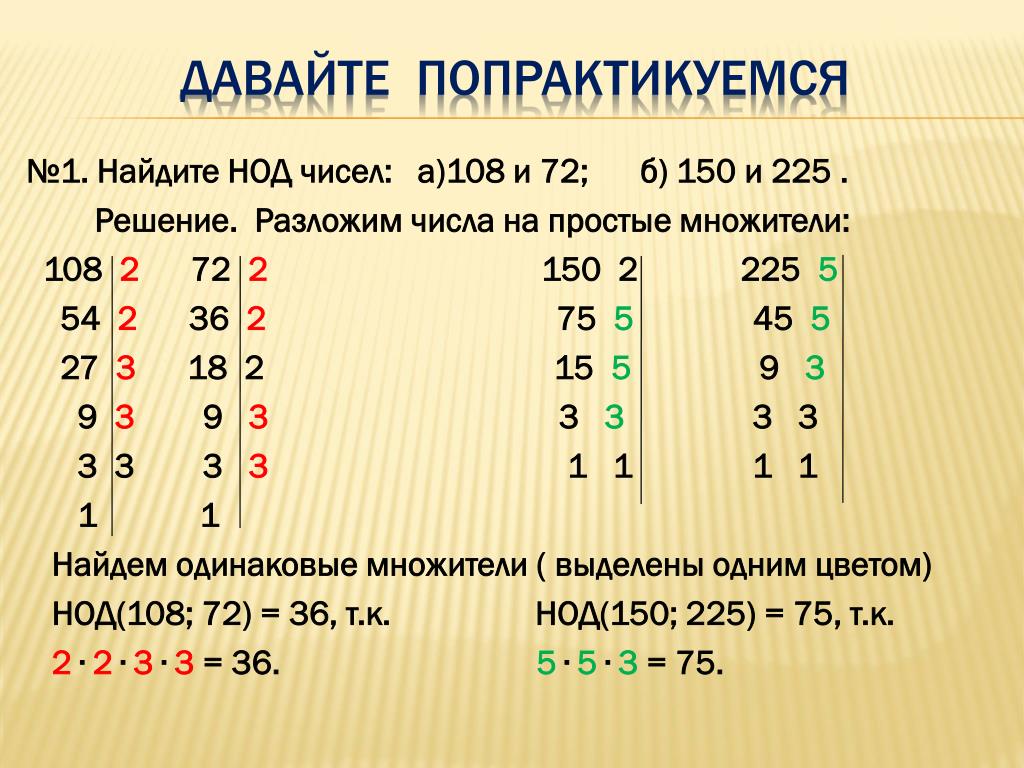 э.), что делает его одним из старейших численных алгоритмов, используемых в наше время. Оригинальный алгоритм был предложен только для натуральных чисел и геометрических длин (вещественных чисел). Позже алгоритм Евклида также был обобщен на другие математические структуры, такие как узлы и многомерные полиномы (многочлен от нескольких переменных) [2.2].

Для данного алгоритма существует множество теоретических и практических применений. В частности он широко распространён в электронной коммерции. Также алгоритм используется при решении диофантовых уравнений (Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами). Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, например: Решить в целых числах уравнение x² – xy – 2y² = 7), при построении непрерывных дробей. Алгоритм Евклида является основным инструментом для доказательства теорем в современной теории чисел. [2.3]

Долгое время алгоритм Евклида был самым эффективным способом отыскания наибольшего общего делителя, однако с появлением электронно-вычислительных машин ситуация изменилась Учет специфических особенностей выполнения арифметических операций компьютером позволил построить более эффективную (для программной реализации) версию алгоритма Евклида.

1. 2. Алгоритмы вычисления НОД 1.2.1 Алгоритм простого перебора

Чтобы найти наибольший общий делитель двух данных натуральных чисел можно действовать по определению: выписать все делители этих чисел, выделить среди них общие и выбрать среди всех общих делителей наибольший.

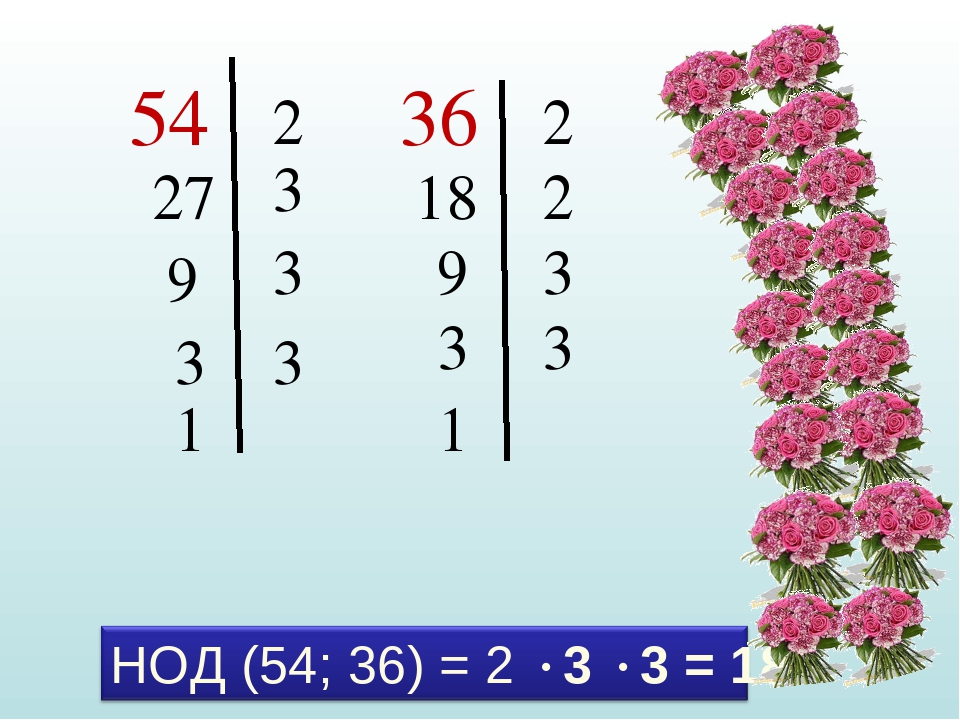
Пример. Найдем все делители чисел 54 и 36.

54 делится на 1; 2; 3; 6; 9; 18; 27; 54.

36 делится на 1; 2; 3; 4; 6; 9; 18; 36.

Общими делителями являются числа: 1, 2, 3, 6, 9, 18.

Значит НОД(54; 36)=18

1.2.2 Нахождение НОД с помощью разложения чисел на простые множители

Рассмотрим еще один способ нахождения НОД. Наибольший общий делитель может быть найден по разложениям чисел на простые множители.

Что такое разложение на множители? Это способ превращения неудобного и сложного примера в простой и симпатичный. Встречается на каждом шагу и в элементарной математике, и в высшей. Подобные превращения на математическом языке называются тождественными преобразованиями выражений. Смысл любого тождественного преобразования — это запись выражения в другом виде с сохранением его сути.

Смысл разложения на множители предельно прост и понятен. Прямо из самого названия. Например, надо разложить число 12. Можно смело записать: 12=3·4

А можно разложить 12 по-другому: 12=3·4=2·6=3·2·2=0,5·24=……..

Вариантов разложения — бесконечное количество.

Сформулируем правило: НОД двух целых положительных чисел a и b равен произведению всех общих простых множителей, находящихся в разложениях чисел a и b на простые множители.

Приведем пример для пояснения правила нахождения НОД.

Пусть нам известны разложения чисел 220 и 600 на простые множители, они имеют вид 220=2·2·5·11 и 600=2·2·2·3·5·5. Общими простыми множителями, участвующими в разложении чисел 220 и 600, являются 2, 2 и 5. Следовательно, НОД(220, 600)=2·2·5=20.

Таким образом, если разложить числа a и b на простые множители и найти произведение всех их общих множителей, то будет найден наибольший общий делитель чисел a и b.

Пример. Найдите наибольший общий делитель чисел 72 и 96.

Решение. Разложим числа 72 и 96 на простые множители.

72=2·2·2·3·3 и 96=2·2·2·2·2·3. Общими простыми множителями являются 2, 2, 2 и 3. Таким образом, НОД(72, 96)=2·2·2·3=24.

Ответ: НОД(72, 96)=24.

В заключение этого пункта заметим, что справедливость приведенного правила нахождения НОД следует из свойства наибольшего общего делителя, которое утверждает, что

НОД(m·a, m·b)=m·НОД(a, b), где m – любое целое положительное число.

1.2.3. Алгоритм Евклида

Одним из простейших алгоритмов нахождения наибольшего общего делителя является Алгоритм Евклида. Он может быть реализован, как при помощи вычитания, так и деления. Рассмотрим каждый из этих двух способов.

а) Описание алгоритма нахождения НОД вычитанием:

Из большего числа вычитаем меньшее. Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла). Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.

Переходим к пункту 1.

Пример:

Найти НОД для 30 и 18.

30 — 18 = 12

18 — 12 = 6

12 — 6 = 6

6 – 6 = 0 Конец: НОД – это уменьшаемое или вычитаемое. НОД (30, 18) = 6

б) Описание алгоритма нахождения НОД делением:

Большее число делим на меньшее. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла). Если есть остаток, то большее число заменяем на остаток от деления. Переходим к пункту 1.

Пример.

Пусть требуется найти НОД(102;84). Разделим одно число на другое и определим остаток.

102=84*1+18 0

Просмотров работы: 4358

Составьте 5 примеров на НОК и НОД

Наибольший общий делитель

Общим делителем нескольких чисел называется число, служащее делителем для каждого из них. Например, числа 12, 18, 30 имеют общий делитель 3; число 2 — тоже их общий делитель. Среди всех общих делителей всегда имеется наибольший, в нашем примере — число 6. Это число называется наибольшим общим делителем (НОД).

Примеры. Для чисел 16, 20, 28 НОД есть 4; для чисел 5, 30, 60, 90 НОД есть 5.

Пример 1. Найти НОД чисел 252, 441, 1080. Разлагаем на простые множители

252 = 22 · 32-7; 441 = 32 · 72; 1080 = 23 · З2 · 5.

Общим для чисел является только простой множитель 3; наименьший из показателей, с которыми он входит в данные числа, есть 2. НОД равен З2 = 9.

Пример 2. Найти НОД чисел 234, 1080, 8100.

234 = 2 · З2-13; 1080 = 23 · З2 · 5; 8100 = 22 · З4 · 52. НОД = 2 · 32 = 18.

Может случиться так, что простых множителей, общих для всех данных чисел, не будет вовсе. Тогда наибольший общий делитель есть 1. Например, для чисел 15 = 3 · 5, 10 = 2 · 5, 6 = 2 · 3 НОД = 1. Два числа, НОД которых равен 1, называются взаимно простыми. Например, 15 и 22 взаимно простые числа.

Наименьшее общее кратное

Общим кратным нескольких чисел называется число, служащее кратным для каждого из них. Например, числа 15, 6, 10 имеют общее кратное 180; число 90 — также общее кратное этих чисел. Среди всех общих кратных всегда есть наименьшее, в данном случае число 30. Это число называется наименьшим общим кратным (НОК). Для небольших чисел НОК находится легко по догадке. Если числа большие, поступаем так: разлагаем данные числа на простые множители; выписываем все простые множители, входящие хотя бы в одно из данных чисел; каждый из
взятых множителей возводим в наибольшую из тех степеней, с которыми он входит в данные числа. Производим умножение.

Пример 1. Найти НОК чисел 252, 441, 1080.

Разлагаем на простые множители: 252 = 22 · З2 · 7; 441 = З2 · 72; 1080 = 23 · З3 · 5. Перемножаем 23 · З3 · 72 х 5. НОК = 52 920.

Пример 2. Найти НОК чисел 234, 1080, 8100 НОК = 23 · З4 · 52 · 13 = 210 600.

Задание в картинках по теме «Задача на нахождение НОК и НОД». К1

Данный модуль представляет собой задание в картинках. Задание направлено на отработку умений учащихся решать задачи на находжение наибольшего общего делителя и еаименьшего общего кратного. При решении задания учащемуся предоставляется возможность прочитать условие задания в классическом виде. В случае затруднения учащийся может посмотреть развернутое решение с ответом. Задание данного учебного модуля параметризировано. Это позволяет формировать индивидуальные задания для каждого учащегося.

Категория пользователей
Обучаемый, Преподаватель

Дисциплины
Математика
/ Наибольший общий делитель. Наименьшее общее кратное

Уровень образования
Профессионально-техническая подготовка, повышение квалификации

Статус
Завершенный вариант (готовый, окончательный)

Тип ИР сферы образования
информационный модуль

Ключевые слова
делитель

Издатель

ООО «Кирилл и Мефодий»

Россия, 127549, Москва, стр. 1, ул. Пришвина, 8

Тел. — +7-495- 787-2610, +7-495- 787-2610
Сайт —
http://www.nmg.ru

Правообладатель

ООО «Кирилл и Мефодий»

Россия, 127549, Москва, стр.1, ул. Пришвина, 8

Тел. — +7-495- 787-2610, +7-495- 787-2610
Сайт —
http://www.nmg.ru

Внимание! Для воспроизведения модуля необходимо установить на компьютере проигрыватель ресурсов.

Характеристики информационного ресурса

Тип используемых данных:
text/plain, text/html, image/jpeg

Объем цифрового ИР
548 636 байт

Проигрыватель

Категория модифицируемости компьютерного ИР

Признак платности
бесплатный

Наличие ограничений по использованию
нет ограничений

Рубрикация

Ступени образования
Основное общее образование

Целевое назначение
Учебное

Тип ресурса
Открытая образовательная модульная мультимедийная система (ОМС)

Классы общеобразовательной школы
5

Уровень образовательного стандарта
Федеральный

Характер обучения
Базовое

Нок и нод примеры для решения.

Нахождение наименьшего общего кратного, способы, примеры нахождения НОК. Как проверить, что число делится на другое число без остатка

Представленный ниже материал является логическим продолжением теории из статьи под заголовком НОК — наименьшее общее кратное, определение, примеры, связь между НОК и НОД . Здесь мы поговорим про нахождение наименьшего общего кратного (НОК)
, и особое внимание уделим решению примеров. Сначала покажем, как вычисляется НОК двух чисел через НОД этих чисел. Дальше рассмотрим нахождение наименьшего общего кратного с помощью разложения чисел на простые множители. После этого остановимся на нахождении НОК трех и большего количества чисел, а также уделим внимание вычислению НОК отрицательных чисел.

Навигация по странице.

Вычисление наименьшего общего кратного (НОК) через НОД

Один из способов нахождения наименьшего общего кратного основан на связи между НОК и НОД . Существующая связь между НОК и НОД позволяет вычислять наименьшее общее кратное двух целых положительных чисел через известный наибольший общий делитель. Соответствующая формула имеет вид НОК(a, b)=a·b:НОД(a, b)

. Рассмотрим примеры нахождения НОК по приведенной формуле.

Пример.

Найдите наименьшее общее кратное двух чисел 126
и 70
.

Решение.

В этом примере a=126
, b=70
. Воспользуемся связью НОК с НОД, выражающуюся формулой НОК(a, b)=a·b:НОД(a, b)
. То есть, сначала нам предстоит найти наибольший общий делитель чисел 70
и 126
, после чего мы сможем вычислить НОК этих чисел по записанной формуле.

Найдем НОД(126, 70)
, используя алгоритм Евклида: 126=70·1+56
, 70=56·1+14
, 56=14·4
, следовательно, НОД(126, 70)=14
.

Теперь находим требуемое наименьшее общее кратное: НОК(126, 70)=126·70:НОД(126, 70)=
126·70:14=630
.

Ответ:

НОК(126, 70)=630
.

Пример.

Чему равно НОК(68, 34)
?

Решение.

Так как 68
делится нацело на 34
, то НОД(68, 34)=34
. Теперь вычисляем наименьшее общее кратное: НОК(68, 34)=68·34:НОД(68, 34)=
68·34:34=68
.

Ответ:

НОК(68, 34)=68
.

Заметим, что предыдущий пример подходит под следующее правило нахождения НОК для целых положительные чисел a
и b
: если число a
делится на b
, то наименьшее общее кратное этих чисел равно a
.

Нахождение НОК с помощью разложения чисел на простые множители

Другой способ нахождения наименьшего общего кратного базируется на разложении чисел на простые множители . Если составить произведение из всех простых множителей данных чисел, после чего из этого произведения исключить все общие простые множители, присутствующие в разложениях данных чисел, то полученное произведение будет равно наименьшему общему кратному данных чисел
.

Озвученное правило нахождения НОК следует из равенства НОК(a, b)=a·b:НОД(a, b)
. Действительно, произведение чисел a
и b
равно произведению всех множителей, участвующих в разложениях чисел a
и b
. В свою очередь НОД(a, b)
равен произведению всех простых множителей, одновременно присутствующих в разложениях чисел a
и b
(о чем написано в разделе нахождение НОД с помощью разложения чисел на простые множители).

Приведем пример. Пусть мы знаем, что 75=3·5·5
и 210=2·3·5·7
. Составим произведение из всех множителей данных разложений: 2·3·3·5·5·5·7
. Теперь из этого произведения исключим все множители, присутствующие и в разложении числа 75
и в разложении числа 210
(такими множителями являются 3
и 5
), тогда произведение примет вид 2·3·5·5·7
. Значение этого произведения равно наименьшему общему кратному чисел 75
и 210
, то есть, НОК(75, 210)= 2·3·5·5·7=1 050
.

Пример.

Разложив числа 441
и 700
на простые множители, найдите наименьшее общее кратное этих чисел.

Решение.

Разложим числа 441
и 700
на простые множители:

Получаем 441=3·3·7·7
и 700=2·2·5·5·7
.

Теперь составим произведение из всех множителей, участвующих в разложениях данных чисел: 2·2·3·3·5·5·7·7·7
. Исключим из этого произведения все множители, одновременно присутствующие в обоих разложениях (такой множитель только один – это число 7
): 2·2·3·3·5·5·7·7
. Таким образом, НОК(441, 700)=2·2·3·3·5·5·7·7=44 100
.

Ответ:

НОК(441, 700)= 44 100
.

Правило нахождения НОК с использованием разложения чисел на простые множители можно сформулировать немного иначе. Если ко множителям из разложения числа a
добавить недостающие множители из разложения числа b
, то значение полученного произведения будет равно наименьшему общему кратному чисел a
и b

Для примера возьмем все те же числа 75
и 210
, их разложения на простые множители таковы: 75=3·5·5
и 210=2·3·5·7
. Ко множителям 3
, 5
и 5
из разложения числа 75
добавляем недостающие множители 2
и 7
из разложения числа 210
, получаем произведение 2·3·5·5·7
, значение которого равно НОК(75, 210)
.

Пример.

Найдите наименьшее общее кратное чисел 84
и 648
.

Решение.

Получаем сначала разложения чисел 84
и 648
на простые множители. Они имеют вид 84=2·2·3·7
и 648=2·2·2·3·3·3·3
. К множителям 2
, 2
, 3
и 7
из разложения числа 84
добавляем недостающие множители 2
, 3
, 3
и 3
из разложения числа 648
, получаем произведение 2·2·2·3·3·3·3·7
, которое равно 4 536
. Таким образом, искомое наименьшее общее кратное чисел 84
и 648
равно 4 536
.

Ответ:

НОК(84, 648)=4 536
.

Нахождение НОК трех и большего количества чисел

Наименьшее общее кратное трех и большего количества чисел может быть найдено через последовательное нахождение НОК двух чисел. Напомним соответствующую теорему, дающую способ нахождения НОК трех и большего количества чисел.

Теорема.

Пусть даны целые положительные числа a 1 , a 2 , …, a k
, наименьшее общее кратное m k
этих чисел находится при последовательном вычислении m 2 =НОК(a 1 , a 2)
, m 3 =НОК(m 2 , a 3)
, …, m k =НОК(m k−1 , a k)
.

Рассмотрим применение этой теоремы на примере нахождения наименьшего общего кратного четырех чисел.

Пример.

Найдите НОК четырех чисел 140
, 9
, 54
и 250
.

Решение.

В этом примере a 1 =140
, a 2 =9
, a 3 =54
, a 4 =250
.

Сначала находим m 2 =НОК(a 1 , a 2)=НОК(140, 9)
. Для этого по алгоритму Евклида определяем НОД(140, 9)
, имеем 140=9·15+5
, 9=5·1+4
, 5=4·1+1
, 4=1·4
, следовательно, НОД(140, 9)=1
, откуда НОК(140, 9)=140·9:НОД(140, 9)=
140·9:1=1 260
. То есть, m 2 =1 260
.

Теперь находим m 3 =НОК(m 2 , a 3)=НОК(1 260, 54)
. Вычислим его через НОД(1 260, 54)
, который также определим по алгоритму Евклида: 1 260=54·23+18
, 54=18·3
. Тогда НОД(1 260, 54)=18
, откуда НОК(1 260, 54)=
1 260·54:НОД(1 260, 54)=
1 260·54:18=3 780
. То есть, m 3 =3 780
.

Осталось найти m 4 =НОК(m 3 , a 4)=НОК(3 780, 250)
. Для этого находим НОД(3 780, 250)
по алгоритму Евклида: 3 780=250·15+30
, 250=30·8+10
, 30=10·3
. Следовательно, НОД(3 780, 250)=10
, откуда НОК(3 780, 250)=
3 780·250:НОД(3 780, 250)=
3 780·250:10=94 500
. То есть, m 4 =94 500
.

Таким образом, наименьшее общее кратное исходных четырех чисел равно 94 500
.

Ответ:

НОК(140, 9, 54, 250)=94 500
.

Во многих случаях наименьшее общее кратное трех и большего количества чисел удобно находить с использованием разложений данных чисел на простые множители. При этом следует придерживаться следующего правила. Наименьшее общее кратное нескольких чисел равно произведению, которое составляется так: ко всем множителям из разложения первого числа добавляются недостающие множители из разложения второго числа, к полученным множителям добавляются недостающие множители из разложения третьего числа и так далее
.

Рассмотрим пример нахождения наименьшего общего кратного с использованием разложения чисел на простые множители.

Пример.

Найдите наименьшее общее кратное пяти чисел 84
, 6
, 48
, 7
, 143
.

Решение.

Сначала получаем разложения данных чисел на простые множители: 84=2·2·3·7
, 6=2·3
, 48=2·2·2·2·3
, 7
(7
– простое число , оно совпадает со своим разложением на простые множители) и 143=11·13
.

Для нахождения НОК данных чисел к множителям первого числа 84
(ими являются 2
, 2
, 3
и 7
) нужно добавить недостающие множители из разложения второго числа 6
. Разложение числа 6
не содержит недостающих множителей, так как и 2
и 3
уже присутствуют в разложении первого числа 84
. Дальше к множителям 2
, 2
, 3
и 7
добавляем недостающие множители 2
и 2
из разложения третьего числа 48
, получаем набор множителей 2
, 2
, 2
, 2
, 3
и 7
. К этому набору на следующем шаге не придется добавлять множителей, так как 7
уже содержится в нем. Наконец, к множителям 2
, 2
, 2
, 2
, 3
и 7
добавляем недостающие множители 11
и 13
из разложения числа 143
. Получаем произведение 2·2·2·2·3·7·11·13
, которое равно 48 048
.

НОД — это наибольший общий делитель.

Чтобы найти наибольший общий делитель нескольких чисел необходимо:

определить множители, общие для обоих чисел;
найти произведение общих множителей.

Пример нахождения НОД:

Найдем НОД чисел 315 и 245.

315 = 5 * 3 * 3 * 7;

245 = 5 * 7 * 7.

2. Выпишем множители, общие для обоих чисел:

3. Найдем произведение общих множителей:

НОД(315; 245) = 5 * 7 = 35.

Ответ: НОД(315; 245) = 35.

Нахождение НОК

НОК — это наименьшее общее кратное.

Чтобы найти наименьшее общее кратное нескольких чисел необходимо:

разложить числа на простые множители;
выписать множители, входящие в разложение одного из чисел;
допишем к ним недостающие множители из разложения второго числа;
найти произведение получившихся множителей.

Пример нахождения НОК:

Найдем НОК чисел 236 и 328:

1. Разложим числа на простые множители:

236 = 2 * 2 * 59;

328 = 2 * 2 * 2 * 41.

2. Выпишем множители, входящие в разложение одного из чисел и допишем к ним недостающие множители из разложения второго числа:

2; 2; 59; 2; 41.

3. Найдем произведение получившихся множителей:

НОК(236; 328) = 2 * 2 * 59 * 2 * 41 = 19352.

Ответ: НОК(236; 328) = 19352.

Для нахождения НОД (наибольшего общего делителя) двух чисел необходимо:

2. Найти (подчеркнуть) все общие простые множители в полученных разложениях.

3. Найти произведение общих простых множителей.

Для нахождения НОК (наименьшего общего кратного) двух чисел необходимо:

1. Разложить данные числа на простые множители.

2. Разложение одного из них дополнить теми множителями разложения другого числа, которых нет в разложении первого.

3. Вычислить произведение полученных множителей.

Сейчас и в дальнейшем мы будем подразумевать, что хотя бы одно из данных чисел отлично от нуля. Если все данные числа равны нулю, то их общим делителем является любое целое число, а так как целых чисел бесконечно много, то мы не можем говорить о наибольшем из них. Следовательно, нельзя говорить о наибольшем общем делителе чисел, каждое из которых равно нулю.

Теперь мы можем дать определение наибольшего общего делителя
двух чисел.

Определение.

Наибольший общий делитель
двух целых чисел – это наибольшее целое число, делящее два данных целых числа.

Для краткой записи наибольшего общего делителя часто используют аббревиатуру НОД – Наибольший Общий Делитель. Также наибольший общий делитель двух чисел a
и b
часто обозначают как НОД(a, b)
.

Приведем пример наибольшего общего делителя (НОД)
двух целых чисел. Наибольший общий делитель чисел 6
и −15
равен 3
. Обоснуем это. Запишем все делители числа шесть: ±6
, ±3
, ±1
, а делителями числа −15
являются числа ±15
, ±5
, ±3
и ±1
. Теперь можно найти все общие делители чисел 6
и −15
, это числа −3
, −1
, 1
и 3
. Так как −3

Определение наибольшего общего делителя трех и большего количества целых чисел аналогично определению НОД двух чисел.

Определение.

Наибольший общий делитель
трех и большего количества целых чисел – это наибольшее целое число, делящее одновременно все данные числа.

Наибольший общий делитель n
целых чисел a 1 , a 2 , …, a n
мы будем обозначать как НОД(a 1 , a 2 , …, a n)
. Если найдено значение b
наибольшего общего делителя этих чисел, то можно записать НОД(a 1 , a 2 , …, a n)=b
.

В качестве примера приведем НОД четырех целых чисел −8
, 52
, 16
и −12
, он равен 4
, то есть, НОД(−8, 52, 16, −12)=4
. Это можно проверить, записав все делители данных чисел, выбрав из них общие и определив наибольший общий делитель.

Отметим, что наибольший общий делитель целых чисел может быть равен одному из этих чисел. Это утверждение справедливо в том случае, если все данные числа делятся на одно из них (доказательство приведено в следующем пункте этой статьи). Например, НОД(15, 60, −45)=15
. Это действительно так, так как 15
делит и число 15
, и число 60
, и число −45
, и не существует общего делителя чисел 15
, 60
и −45
, который превосходит 15
.

Особый интерес представляют так называемые взаимно простые числа , — такие целые числа, наибольший общий делитель которых равен единице.

Свойства наибольшего общего делителя, алгоритм Евклида

Наибольший общий делитель обладает рядом характерных результатов, иными словами, рядом свойств. Сейчас мы перечислим основные свойства наибольшего общего делителя (НОД)
, формулировать их мы будем в виде теорем и сразу приводить доказательства.

Все свойства наибольшего общего делителя мы будем формулировать для положительных целых чисел, при этом будем рассматривать лишь положительные делители этих чисел.

Наибольший общий делитель чисел a
и b
равен наибольшему общему делителю чисел b
и a
, то есть, НОД(a, b)=НОД(a, b)
.

Это свойство НОД напрямую следует из определения наибольшего общего делителя.

Если a
делится на b
, то множество общих делителей чисел a
и b
совпадает со множеством делителей числа b
, в частности, НОД(a, b)=b
.

Доказательство.

Любой общий делитель чисел a
и b
является делителем каждого из этих чисел, в том числе и числа b
. С другой стороны, так как a
кратно b
, то любой делитель числа b
является делителем и числа a
в силу того, что делимость обладает свойством транзитивности, следовательно, любой делитель числа b
является общим делителем чисел a
и b
. Этим доказано, что если a
делится на b
, то совокупность делителей чисел a
и b
совпадает с совокупностью делителей одного числа b
. А так как наибольшим делителем числа b
является само число b
, то наибольший общий делитель чисел a
и b
также равен b
, то есть, НОД(a, b)=b
.

В частности, если числа a
и b
равны, то НОД(a, b)=НОД(a, a)=НОД(b, b)=a=b
. К примеру, НОД(132, 132)=132
.

Доказанное свойство наибольшего делителя позволяет нам находить НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число. Например, НОД(8, 24)=8
, так как 24
кратно восьми.

Если a=b·q+c
, где a
, b
, c
и q
– целые числа, то множество общих делителей чисел a
и b
совпадает со множеством общих делителей чисел b
и c
, в частности, НОД(a, b)=НОД(b, c)
.

Обоснуем это свойство НОД.

Так как имеет место равенство a=b·q+c
, то всякий общий делитель чисел a
и b
делит также и c
(это следует из свойств делимости). По этой же причине, всякий общий делитель чисел b
и c
делит a
. Поэтому совокупность общих делителей чисел a
и b
совпадает с совокупностью общих делителей чисел b
и c
. В частности, должны совпадать и наибольшие из этих общих делителей, то есть, должно быть справедливо следующее равенство НОД(a, b)=НОД(b, c)
.

Сейчас мы сформулируем и докажем теорему, которая представляет собой алгоритм Евклида
. Алгоритм Евклида позволяет находить НОД двух чисел (смотрите нахождение НОД по алгоритму Евклида). Более того алгоритм Евклида позволит нам доказать приведенные ниже свойства наибольшего общего делителя.

Прежде чем дать формулировку теоремы, рекомендуем освежить в памяти теорему из раздела теории , которая утверждает, что делимое a
может быть представлено в виде b·q+r
, где b
– делитель, q
– некоторое целое число, называемое неполным частным, а r
– целое число, удовлетворяющее условию , называемое остатком.

Итак, пусть для двух ненулевых целых положительных чисел a
и b
справедлив ряд равенств

заканчивающийся, когда r k+1 =0
(что неизбежно, так как b>r 1 >r 2 >r 3 , …
— ряд убывающих целых чисел, и этот ряд не может содержать более чем конечное число положительных чисел), тогда r k
– это наибольший общий делитель чисел a
и b
, то есть, r k =НОД(a, b)
.

Доказательство.

Докажем сначала, что r k
является общим делителем чисел a
и b
, после чего покажем, что r k
не просто делитель, а наибольший общий делитель чисел a
и b
.

Будем двигаться по записанным равенствам снизу вверх. Из последнего равенства можно сказать, что r k−1
делится на r k
. Учитывая этот факт, а также предыдущее свойство НОД, предпоследнее равенство r k−2 =r k−1 ·q k +r k
позволяет утверждать, что r k−2
делится на r k
, так как и r k−1
делится на r k
и r k
делится на r k
. По аналогии из третьего снизу равенства заключаем, что r k−3
делится на r k
. И так далее. Из второго равенства получаем, что b
делится на r k
, а из первого равенства получаем, что a
делится на r k
. Следовательно, r k
является общим делителем чисел a
и b
.

Осталось доказать, что r k =НОД(a, b)
. Для достаточно показать, что любой общий делитель чисел a
и b
(обозначим его r 0
) делит r k
.

Будем двигаться по исходным равенствам сверху вниз. В силу предыдущего свойства из первого равенства следует, что r 1
делится на r 0
. Тогда из второго равенства получаем, что r 2
делится на r 0
. И так далее. Из последнего равенства получаем, что r k
делится на r 0
. Таким образом, r k =НОД(a, b)
.

Из рассмотренного свойства наибольшего общего делителя следует, что множество общих делителей чисел a
и b
совпадает с множеством делителей наибольшего общего делителя этих чисел. Это следствие из алгоритма Евклида позволяет найти все общие делители двух чисел как делители НОД этих чисел.

Пусть a
и b
– целые числа, одновременно не равные нулю, тогда существуют такие целые числа u 0
и v 0
, то справедливо равенство НОД(a, b)=a·u 0 +b·v 0
. Последнее равенство представляет собой линейное представление наибольшего общего делителя чисел a
и b
, это равенство называют соотношением Безу, а числа u 0
и v 0
– коэффициентами Безу.

Доказательство.

По алгоритму Евклида мы можем записать следующие равенства

Из первого равенства имеем r 1 =a−b·q 1
, и, обозначив 1=s 1
и −q 1 =t 1
, это равенство примет вид r 1 =s 1 ·a+t 1 ·b
, причем числа s 1
и t 1
— целые. Тогда из второго равенства получим r 2 =b−r 1 ·q 2 =
b−(s 1 ·a+t 1 ·b)·q 2 =−s 1 ·q 2 ·a+(1−t 1 ·q 2)·b
. Обозначив −s 1 ·q 2 =s 2
и 1−t 1 ·q 2 =t 2
, последнее равенство можно записать в виде r 2 =s 2 ·a+t 2 ·b
, причем s 2
и t 2
– целые числа (так как сумма, разность и произведение целых чисел является целым числом). Аналогично из третьего равенства получим r 3 =s 3 ·a+t 3 ·b
, из четвертого r 4 =s 4 ·a+t 4 ·b
, и так далее. Наконец, r k =s k ·a+t k ·b
, где s k
и t k
— целые. Так как r k =НОД(a, b)
, и, обозначив s k =u 0
и t k =v 0
, получим линейное представление НОД требуемого вида: НОД(a, b)=a·u 0 +b·v 0
.

Если m
– любое натуральное число, то НОД(m·a, m·b)=m·НОД(a, b)
.

Обоснование этого свойства наибольшего общего делителя таково. Если умножить на m
обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД(m·a, m·b)=m·r k
, а r k
– это НОД(a, b)
. Следовательно, НОД(m·a, m·b)=m·НОД(a, b)
.

На этом свойстве наибольшего общего делителя основан способ нахождения НОД с помощью разложения на простые множители .

Пусть p
– любой общий делитель чисел a
и b
, тогда НОД(a:p, b:p)=НОД(a, b):p
, в частности, если p=НОД(a, b)
имеем НОД(a:НОД(a, b), b:НОД(a, b))=1
, то есть, числа a:НОД(a, b)
и b:НОД(a, b)
— взаимно простые.

Так как a=p·(a:p)
и b=p·(b:p)
, и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД(a, b)=НОД(p·(a:p), p·(b:p))=
p·НОД(a:p, b:p)
, откуда и следует доказываемое равенство.

Только что доказанное свойство наибольшего общего делителя лежит в основе .

Сейчас озвучим свойство НОД, которое сводит задачу нахождения наибольшего общего делителя трех и большего количества чисел к последовательному отысканию НОД двух чисел.

Наибольший общий делитель чисел a 1 , a 2 , …, a k
равен числу d k
, которое находится при последовательном вычислении НОД(a 1 , a 2)=d 2
, НОД(d 2 , a 3)=d 3
, НОД(d 3 , a 4)=d 4
, …, НОД(d k-1 , a k)=d k
.

Доказательство базируется на следствии из алгоритма Евклида. Общие делители чисел a 1
и a 2
совпадают с делителями d 2
. Тогда общие делители чисел a 1
, a 2
и a 3
совпадают с общими делителями чисел d 2
и a 3
, следовательно, совпадают с делителями d 3
. Общие делители чисел a 1
, a 2
, a 3
и a 4
совпадают с общими делителями d 3
и a 4
, следовательно, совпадают с делителями d 4
. И так далее. Наконец, общие делители чисел a 1 , a 2 , …, a k
совпадают с делителями d k
. А так как наибольшим делителем числа d k
является само число d k
, то НОД(a 1 , a 2 , …, a k)=d k
.

На этом закончим обзор основных свойств наибольшего общего делителя.

Список литературы.

Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
Виноградов И.М. Основы теории чисел.
Михелович Ш.Х. Теория чисел.
Куликов Л.Я. и др. Сборник задач по алгебре и теории чисел: Учебное пособие для студентов физ.-мат. специальностей педагогических институтов.

Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем
этих чисел. Обозначают НОД(a, b).

Рассмотрим нахождения НОД на примере двух натуральных чисел 18 и 60:

1 Разложим числа на простые множители:
18
= 2 × 3 × 3

60
= 2 × 2 × 3 × 5

2 Вычеркнуть из разложения первого числа все множители которые не входят в разложения второго числа, получим 2 × 3 × 3
.

3 Перемножаем оставшиеся простые множители после вычеркивания и получаем наибольший общий делитель чисел: НОД(18
, 60
)=2 × 3
= 6
.

4 Заметим что не важно из первого или второго числа вычеркиваем множители, результат будет одинаков:
18
= 2 × 3 × 3

60
= 2 × 2 × 3 × 5

324
, 111
и 432

Разложим числа на простые множители:

324
= 2 × 2 × 3 × 3 × 3 × 3

111
= 3 × 37

432
= 2 × 2 × 2 × 2 × 3 × 3 × 3

Вычеркнуть из первого числа, множители которых нету во втором и третьем числе, получим:

2 × 2 × 2 × 2 × 3 × 3 × 3 = 3

В результате НОД(324
, 111
, 432
)=3

Нахождение НОД с помощью алгоритма Евклида

Второй способ нахождения наибольшего общего делителя с помощью алгоритма Евклида
. Алгоритм Евклида является наиболее эффективным способом нахождения НОД
, используя его нужно постоянно находить остаток от деления чисел и применять рекуррентную формулу
.

Рекуррентная формула
для НОД, НОД(a, b)=НОД(b, a mod b)
, где a mod b — остаток от деления a на b.

Алгоритм Евклида

Пример Найти наибольший общий делитель чисел

7920
и 594

Найдем НОД(7920
, 594
) с помощью алгоритма Евклида, вычислять остаток от деления будем с помощью калькулятора.

НОД(7920
, 594
)

НОД(594
, 7920
mod 594
) = НОД(594
, 198
)

НОД(198
, 594
mod 198
) = НОД(198
, 0
)

НОД(198
, 0
) = 198

7920 mod 594 = 7920 — 13 × 594 = 198
594 mod 198 = 594 — 3 × 198 = 0

В результате получаем НОД(7920
, 594
) = 198

Наименьшее общее кратное

Для того, чтобы находить общий знаменатель при сложении и вычитании дробей с разными знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное
(НОК).

Кратное числу « a » — это число, которое само делится на число « a » без остатка.

Числа кратные 8 (то есть, эти числа разделятся на 8 без остатка): это числа 16, 24, 32 …

Кратные 9: 18, 27, 36, 45 …

Чисел, кратных данному числу a бесконечно много, в отличии от делителей этого же числа. Делителей — конечное количество.

Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело
.

Наименьшим общим кратным
(НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.

Как найти НОК

НОК можно найти и записать двумя способами.

Первый способ нахождения НОК

Данный способ обычно применяется для небольших чисел.

Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
Кратное числа « a » обозначаем большой буквой «К».

Пример. Найти НОК 6 и 8 .

Второй способ нахождения НОК

Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.

Количество одинаковых множителей в разложениях чисел может быть разное.

Подчеркнуть в разложении меньшего числа (меньших чисел) множители, которые не вошли в разложение бóльшего числа (в нашем примере это 2) и добавить эти множители в разложение бóльшего числа.
НОК (24, 60) = 2 · 2 · 3 · 5 · 2

Полученное произведение записать в ответ.
Ответ: НОК (24, 60) = 120

Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24) .

24 = 2 · 2 · 2 · 3

Как видим из разложения чисел, все множители 12 вошли в разложение 24 (самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из разложения числа 16 .

НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48

Ответ: НОК (12, 16, 24) = 48

Особые случаи нахождения НОК

Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.

Например, НОК (60, 15) = 60
Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее кратное равно произведению этих чисел.

На нашем сайте вы также можете с помощью специального калькулятора найти наименьшее общее кратное онлайн, чтобы проверить свои вычисления.

Если натуральное число делится только на 1 и на само себя, то оно называется простым.

Любое натуральное число всегда делится на 1 и на само себя.

Число 2 — наименьшее простое число. Это единственное чётное простое число, остальные простые числа — нечётные.

Простых чисел много, и первое среди них — число 2 . Однако нет последнего простого числа. В разделе «Для учёбы» вы можете скачать таблицу простых чисел до 997 .

Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.

число 12 делится на 1 , на 2 , на 3 , на 4 , на 6 , на 12 ;
число 36 делится на 1 , на 2 , на 3 , на 4 , на 6 , на 12 , на 18 , на 36 .

Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12) называются делителями числа.

Делитель натурального числа a — это такое натуральное число, которое делит данное число « a » без остатка.

Натуральное число, которое имеет более двух делителей называется составным.

Обратите внимание, что числа 12 и 36 имеют общие делители. Это числа: 1, 2, 3, 4, 6, 12 . Наибольший из делителей этих чисел — 12 .

Общий делитель двух данных чисел « a » и « b » — это число, на которое делятся без остатка оба данных числа « a » и « b ».

Наибольший общий делитель
(НОД) двух данных чисел « a » и « b » — это наибольшее число, на которое оба числа « a » и « b » делятся без остатка.

Кратко наибольший общий делитель чисел « a » и « b » записывают так
:

Пример: НОД (12; 36) = 12 .

Делители чисел в записи решения обозначают большой буквой «Д».

Числа 7 и 9 имеют только один общий делитель — число 1 . Такие числа называют взаимно простыми числами
.

Взаимно простые числа
— это натуральные числа, которые имеют только один общий делитель — число 1 . Их НОД равен 1 .

Как найти наибольший общий делитель

Чтобы найти НОД двух или более натуральных чисел нужно:

разложить делители чисел на простые множители;

Вычисления удобно записывать с помощью вертикальной черты. Слева от черты сначала записываем делимое, справа — делитель. Далее в левом столбце записываем значения частных.

Поясним сразу на примере. Разложим на простые множители числа 28 и 64 .

64 = 2 · 2 · 2 · 2 · 2 · 2
Находим произведение одинаковых простых множителей и записать ответ;
НОД (28; 64) = 2 · 2 = 4

Ответ: НОД (28; 64) = 4

Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».

Первый способ записи НОД

Найти НОД 48 и 36 .

НОД (48; 36) = 2 · 2 · 3 = 12

Второй способ записи НОД

Теперь запишем решение поиска НОД в строчку. Найти НОД 10 и 15 .

На нашем информационном сайте вы также можете с помощью программы помощника найти наибольший общий делитель онлайн, чтобы проверить свои вычисления.

Нахождение наименьшего общего кратного, способы, примеры нахождения НОК.

Представленный ниже материал является логическим продолжением теории из статьи под заголовком НОК — наименьшее общее кратное, определение, примеры, связь между НОК и НОД. Здесь мы поговорим про нахождение наименьшего общего кратного (НОК)
, и особое внимание уделим решению примеров. Сначала покажем, как вычисляется НОК двух чисел через НОД этих чисел. Дальше рассмотрим нахождение наименьшего общего кратного с помощью разложения чисел на простые множители. После этого остановимся на нахождении НОК трех и большего количества чисел, а также уделим внимание вычислению НОК отрицательных чисел.

Навигация по странице.

Вычисление наименьшего общего кратного (НОК) через НОД

Один из способов нахождения наименьшего общего кратного основан на связи между НОК и НОД. Существующая связь между НОК и НОД позволяет вычислять наименьшее общее кратное двух целых положительных чисел через известный наибольший общий делитель. Соответствующая формула имеет вид НОК(a, b)=a·b:НОД(a, b)
. Рассмотрим примеры нахождения НОК по приведенной формуле.

Найдите наименьшее общее кратное двух чисел 126 и 70 .

В этом примере a=126 , b=70 . Воспользуемся связью НОК с НОД, выражающуюся формулой НОК(a, b)=a·b:НОД(a, b) . То есть, сначала нам предстоит найти наибольший общий делитель чисел 70 и 126 , после чего мы сможем вычислить НОК этих чисел по записанной формуле.

Найдем НОД(126, 70) , используя алгоритм Евклида: 126=70·1+56 , 70=56·1+14 , 56=14·4 , следовательно, НОД(126, 70)=14 .

Теперь находим требуемое наименьшее общее кратное: НОК(126, 70)=126·70:НОД(126, 70)= 126·70:14=630 .

Чему равно НОК(68, 34) ?

Так как 68 делится нацело на 34 , то НОД(68, 34)=34 . Теперь вычисляем наименьшее общее кратное: НОК(68, 34)=68·34:НОД(68, 34)= 68·34:34=68 .

Заметим, что предыдущий пример подходит под следующее правило нахождения НОК для целых положительные чисел a и b: если число a делится на b , то наименьшее общее кратное этих чисел равно a .

Нахождение НОК с помощью разложения чисел на простые множители

Другой способ нахождения наименьшего общего кратного базируется на разложении чисел на простые множители. Если составить произведение из всех простых множителей данных чисел, после чего из этого произведения исключить все общие простые множители, присутствующие в разложениях данных чисел, то полученное произведение будет равно наименьшему общему кратному данных чисел
.

Озвученное правило нахождения НОК следует из равенства НОК(a, b)=a·b:НОД(a, b) . Действительно, произведение чисел a и b равно произведению всех множителей, участвующих в разложениях чисел a и b . В свою очередь НОД(a, b) равен произведению всех простых множителей, одновременно присутствующих в разложениях чисел a и b (о чем написано в разделе нахождение НОД с помощью разложения чисел на простые множители).

Приведем пример. Пусть мы знаем, что 75=3·5·5 и 210=2·3·5·7 . Составим произведение из всех множителей данных разложений: 2·3·3·5·5·5·7 . Теперь из этого произведения исключим все множители, присутствующие и в разложении числа 75 и в разложении числа 210 (такими множителями являются 3 и 5), тогда произведение примет вид 2·3·5·5·7 . Значение этого произведения равно наименьшему общему кратному чисел 75 и 210 , то есть, НОК(75, 210)= 2·3·5·5·7=1 050 .

Разложив числа 441 и 700 на простые множители, найдите наименьшее общее кратное этих чисел.

Разложим числа 441 и 700 на простые множители:

Получаем 441=3·3·7·7 и 700=2·2·5·5·7 .

Теперь составим произведение из всех множителей, участвующих в разложениях данных чисел: 2·2·3·3·5·5·7·7·7 . Исключим из этого произведения все множители, одновременно присутствующие в обоих разложениях (такой множитель только один – это число 7): 2·2·3·3·5·5·7·7 . Таким образом, НОК(441, 700)=2·2·3·3·5·5·7·7=44 100 .

НОК(441, 700)= 44 100 .

Правило нахождения НОК с использованием разложения чисел на простые множители можно сформулировать немного иначе. Если ко множителям из разложения числа a добавить недостающие множители из разложения числа b , то значение полученного произведения будет равно наименьшему общему кратному чисел a и b
.

Для примера возьмем все те же числа 75 и 210 , их разложения на простые множители таковы: 75=3·5·5 и 210=2·3·5·7 . Ко множителям 3 , 5 и 5 из разложения числа 75 добавляем недостающие множители 2 и 7 из разложения числа 210 , получаем произведение 2·3·5·5·7 , значение которого равно НОК(75, 210) .

Найдите наименьшее общее кратное чисел 84 и 648 .

Получаем сначала разложения чисел 84 и 648 на простые множители. Они имеют вид 84=2·2·3·7 и 648=2·2·2·3·3·3·3 . К множителям 2 , 2 , 3 и 7 из разложения числа 84 добавляем недостающие множители 2 , 3 , 3 и 3 из разложения числа 648 , получаем произведение 2·2·2·3·3·3·3·7 , которое равно 4 536 . Таким образом, искомое наименьшее общее кратное чисел 84 и 648 равно 4 536 .

Нахождение НОК трех и большего количества чисел

Пусть даны целые положительные числа a 1 , a 2 , …, a k , наименьшее общее кратное m k этих чисел находится при последовательном вычислении m 2 =НОК(a 1 , a 2) , m 3 =НОК(m 2 , a 3) , …, m k =НОК(m k−1 , a k) .

Рассмотрим применение этой теоремы на примере нахождения наименьшего общего кратного четырех чисел.

Найдите НОК четырех чисел 140 , 9 , 54 и 250 .

Сначала находим m 2 =НОК(a 1 , a 2)=НОК(140, 9) . Для этого по алгоритму Евклида определяем НОД(140, 9) , имеем 140=9·15+5 , 9=5·1+4 , 5=4·1+1 , 4=1·4 , следовательно, НОД(140, 9)=1 , откуда НОК(140, 9)=140·9:НОД(140, 9)= 140·9:1=1 260 . То есть, m 2 =1 260 .

Теперь находим m 3 =НОК(m 2 , a 3)=НОК(1 260, 54) . Вычислим его через НОД(1 260, 54) , который также определим по алгоритму Евклида: 1 260=54·23+18 , 54=18·3 . Тогда НОД(1 260, 54)=18 , откуда НОК(1 260, 54)= 1 260·54:НОД(1 260, 54)= 1 260·54:18=3 780 . То есть, m 3 =3 780 .

Осталось найти m 4 =НОК(m 3 , a 4)=НОК(3 780, 250) . Для этого находим НОД(3 780, 250) по алгоритму Евклида: 3 780=250·15+30 , 250=30·8+10 , 30=10·3 . Следовательно, НОД(3 780, 250)=10 , откуда НОК(3 780, 250)= 3 780·250:НОД(3 780, 250)= 3 780·250:10=94 500 . То есть, m 4 =94 500 .

Таким образом, наименьшее общее кратное исходных четырех чисел равно 94 500 .

НОК(140, 9, 54, 250)=94 500 .

Найдите наименьшее общее кратное пяти чисел 84 , 6 , 48 , 7 , 143 .

Сначала получаем разложения данных чисел на простые множители: 84=2·2·3·7 , 6=2·3 , 48=2·2·2·2·3 , 7 (7 – простое число, оно совпадает со своим разложением на простые множители) и 143=11·13 .

Для нахождения НОК данных чисел к множителям первого числа 84 (ими являются 2 , 2 , 3 и 7) нужно добавить недостающие множители из разложения второго числа 6 . Разложение числа 6 не содержит недостающих множителей, так как и 2 и 3 уже присутствуют в разложении первого числа 84 . Дальше к множителям 2 , 2 , 3 и 7 добавляем недостающие множители 2 и 2 из разложения третьего числа 48 , получаем набор множителей 2 , 2 , 2 , 2 , 3 и 7 . К этому набору на следующем шаге не придется добавлять множителей, так как 7 уже содержится в нем. Наконец, к множителям 2 , 2 , 2 , 2 , 3 и 7 добавляем недостающие множители 11 и 13 из разложения числа 143 . Получаем произведение 2·2·2·2·3·7·11·13 , которое равно 48 048 .

Следовательно, НОК(84, 6, 48, 7, 143)=48 048 .

НОК(84, 6, 48, 7, 143)=48 048 .

Нахождение наименьшего общего кратного отрицательных чисел

Иногда встречаются задания, в которых требуется найти наименьшее общее кратное чисел, среди которых одно, несколько или все числа являются отрицательными. В этих случаях все отрицательные числа нужно заменить противоположными им числами, после чего находить НОК положительных чисел. В этом и состоит способ нахождения НОК отрицательных чисел. Например, НОК(54, −34)=НОК(54, 34) , а НОК(−622, −46, −54, −888)= НОК(622, 46, 54, 888) .

Мы можем так поступать, потому что множество кратных числа a совпадает со множеством кратных числа −a (a и −a – противоположные числа). Действительно, пусть b – какое-то кратное числа a , тогда b делится на a , и понятие делимости утверждает существование такого целого числа q , что b=a·q . Но будет справедливо и равенство b=(−a)·(−q) , которое в силу того же понятия делимости означает, что b делится на −a , то есть, b есть кратное числа −a . Справедливо и обратное утверждение: если b – какое-то кратное числа −a , то b является кратным и числа a .

Найдите наименьшее общее кратное отрицательных чисел −145 и −45 .

Заменим отрицательные числа −145 и −45 на противоположные им числа 145 и 45 . Имеем НОК(−145, −45)=НОК(145, 45) . Определив НОД(145, 45)=5 (например, по алгоритму Евклида), вычисляем НОК(145, 45)=145·45:НОД(145, 45)= 145·45:5=1 305 . Таким образом, наименьшее общее кратное отрицательных целых чисел −145 и −45 равно 1 305 .

www.cleverstudents.ru

Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД
и НОК
.

НОД
— это наибольший общий делитель.

НОК
— это наименьшее общее кратное.

Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.

Наибольший общий делитель

Определение. Наибольшим общим делителем чисел a
и b
a
и b
делятся без остатка.

Чтобы хорошо понять это определение, подставим вместо переменных a
и b
любые два числа, например, вместо переменной a
подставим число 12, а вместо переменной b
число 9. Теперь попробуем прочитать это определение:

Наибольшим общим делителем чисел 12
и 9
называется наибольшее число, на которое 12
и 9
делятся без остатка.

Из определения понятно, что речь идёт об общем делителе чисел 12 и 9, причем этот делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.

Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.

Второй и третий способы довольны просты и дают возможность быстро найти НОД. Мы с вами рассмотрим все три способа. А какой применять на практике — выбирать вам.

Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9
.

Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.

12: 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)

12: 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)

12: 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)

12: 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)

12: 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)

12: 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)

12: 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)

12: 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)

12: 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)

12: 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)

12: 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)

12: 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)

Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9

9: 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)

9: 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)

9: 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)

9: 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)

9: 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)

9: 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)

9: 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)

9: 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)

9: 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)

Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить, какой является наибольшим и общим.

Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3

И число 12 и число 9 делятся на 3 без остатка:

Значит НОД (12 и 9) = 3

Второй способ нахождения НОД

Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.

Пример 1
. Найти НОД чисел 24 и 18

Сначала разложим оба числа на простые множители:

Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.

Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:

Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.

Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.

Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:

Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:

Значит НОД (24 и 18) = 6

Третий способ нахождения НОД

Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.

Например, найдём НОД для чисел 28 и 16 этим способом. В первую очередь, раскладываем эти числа на простые множители:

Получили два разложения: и

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семерка. Её и вычеркнем из первого разложения:

Теперь перемножаем оставшиеся множители и получаем НОД:

Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:

Пример 2.
Найти НОД чисел 100 и 40

Раскладываем на множители число 100

Раскладываем на множители число 40

Получили два разложения:

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения

Перемножим оставшиеся числа:

Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:

НОД (100 и 40) = 20.

Пример 3.
Найти НОД чисел 72 и 128

Раскладываем на множители число 72

Раскладываем на множители число 128

2 × 2 × 2 × 2 × 2 × 2 × 2

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:

Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:

НОД (72 и 128) = 8

Нахождение НОД для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

Например, найдём НОД для чисел 18, 24 и 36

Разложим на множители число 18

Разложим на множители число 24

Разложим на множители число 36

Получили три разложения:

Теперь выделим и подчеркнём общие множители в этих числах. Общие множители должны входить во все три числа:

Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:

НОД (18, 24 и 36) = 6

Пример 2.
Найти НОД для чисел 12, 24, 36 и 42

Разложим на простые множители каждое число. Затем найдём произведение общих множителей этих чисел.

Разложим на множители число 12

Разложим на множители число 42

Получили четыре разложения:

Теперь выделим и подчеркнём общие множители в этих числах. Общие множители должны входить во все четыре числа:

Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:

НОД (12, 24 , 36 и 42) = 6

Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.

Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, при этом оно должно быть максимально маленьким.

Определение. Наименьшее общее кратное (НОК) чисел a
и b —
a
и b
a
и число b
.

Определение содержит две переменные a
и b
. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a
подставим число 9, а вместо переменной b
подставим число 12. Теперь попробуем прочитать определение:

Наименьшее общее кратное (НОК) чисел 9
и 12 —
это наименьшее число, которое кратно 9
и 12
. Другими словами, это такое маленькое число, которое делится без остатка на число 9
и на число 12
.

Из определения понятно, что НОК это наименьшее число, которое делится без остатка на 9 и на 12. Этот НОК требуется найти.

Для нахождения наименьшего общего кратного (НОК) можно пользоваться двумя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.

В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9. Итак, начнём. Кратные будем выделять красным цветом:

Теперь находим кратные для числа 12. Для этого, поочерёдно умножаем 12 на все числа 1 до 12.

Но многие натуральные числа делятся нацело ещё и на другие натуральные числа.

Например
:

Число 12 делится на 1, на 2, на 3, на 4, на 6, на 12;

Число 36 делится на 1, на 2, на 3, на 4, на 6, на 12, на 18, на 36.

Числа, на которые число делится нацело (для 12 это 1, 2, 3, 4, 6 и 12) называются делителями числа
. Делитель натурального числа a
— это такое натуральное число, которое делит данное число a
без остатка. Натуральное число, которое имеет более двух делителей, называется составным
. Обратите внимание, что числа 12 и 36 имеют общие делители. Это числа: 1, 2, 3, 4, 6, 12. Наибольший из делителей этих чисел — 12.

Общий делитель двух данных чисел a
и b
— это число, на которое делятся без остатка оба данных числа a
и b
. Общий делитель нескольких чисел (НОД)
— это число, служащее делителем для каждого из них.

Кратко наибольший общий делитель чисел a
и b
записывают так:

Пример
: НОД (12; 36) = 12.

Делители чисел в записи решения обозначают большой буквой «Д».

Пример:

НОД (7; 9) = 1

Числа 7 и 9 имеют только один общий делитель — число 1. Такие числа называют взаимно простыми
чи слами
.

Наибольший общий делитель (НОД), свойства.

Основное свойство: наибольший общий делитель m
и n
делится на любой общий делитель этих чисел. Пример
: для чисел 12 и 18 наибольший общий делитель равен 6; он делится на все общие делители этих чисел: 1, 2, 3, 6.
Следствие 1: множество общих делителей m
и n
совпадает с множеством делителей НОД(m
, n
).
Следствие 2: множество общих кратных m
и n
совпадает с множеством кратных НОК (m
, n
).

Это означает, в частности, что для приведения дроби к несократимому виду надо разделить её числитель и знаменатель на их НОД.

Наибольший общий делитель чисел m
и n
может быть определён как наименьший положительный элемент множества всех их линейных комбинаций:

и поэтому представим в виде линейной комбинации чисел m
и n
:

Это соотношение называется соотношением Безу
, а коэффициенты u
и v
— коэффициентами Безу
. Коэффициенты Безу эффективно вычисляются расширенным алгоритмом Евклида. Это утверждение обобщается на наборы натуральных чисел — его смысл в том, что подгруппа группы , порождённая набором , — циклическая и порождается одним элементом: НОД (a
1 , a
2 , … , a n
).

Вычисление наибольшего общего делителя (НОД).

Эффективными способами вычисления НОД двух чисел являются алгоритм Евклида
и бинарный
алгоритм
. Кроме того, значение НОД (m
,n
) можно легко вычислить, если известно каноническое разложение чисел m
и n
на простые множители:

где — различные простые числа, а и — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда НОД (m
,n
) и НОК (m
,n
) выражаются формулами:

Если чисел более двух: , их НОД находится по следующему алгоритму:

— это и есть искомый НОД.

Также, для того, чтобы найти наибольший общий делитель
, можно разложить каждое из заданных чисел на простые множители . Потом выписать отдельно только те множители, которые входят во все заданные числа. Потом перемножаем между собой выписанные числа — результат перемножения и есть наибольший общий делитель.

Разберем пошагово вычисление наибольшего общего делителя:

1. Разложить делители чисел на простые множители:

Вычисления удобно записывать с помощью вертикальной черты. Слева от черты сначала записываем делимое, справа — делитель. Далее в левом столбце записываем значения частных. Поясним сразу на примере. Разложим на простые множители числа 28 и 64.

2. Подчёркиваем одинаковые простые множители в обоих числах:

28 = 2
. 2
. 7

64 = 2
. 2
. 2 . 2 . 2 . 2

3. Находим произведение одинаковых простых множителей и записываем ответ:

НОД (28; 64) = 2 . 2 = 4

Ответ: НОД (28; 64) = 4

Оформить нахождение НОД можно двумя способами: в столбик (как делали выше) или «в строчку».

Первый способ записи НОД:

Найти НОД 48 и 36.

НОД (48; 36) = 2 . 2 . 3 = 12

Второй способ записи НОД:

Теперь запишем решение поиска НОД в строчку. Найти НОД 10 и 15.

Д (10) = {1, 2, 5, 10}

Д (15) = {1, 3, 5, 15}

Д (10, 15) = {1, 5}

Учебное пособие по физике: узлы и анти-узлы

Как упоминалось ранее в Уроке 4, картина стоячей волны — это явление интерференции. Он образуется в результате идеально синхронизированной интерференции двух волн, проходящих через одну и ту же среду. Модель стоячей волны на самом деле не является волной; скорее, это картина, возникающая из-за присутствия двух волн одной и той же частоты с разными направлениями движения в одной и той же среде.

Что такое узлы и пучности?

Одной из характерных черт каждой модели стоячей волны является то, что в среде есть точки, которые кажутся неподвижными.Эти точки, иногда описываемые как точки отсутствия смещения, обозначаются как узлов . Есть и другие точки вдоль среды, которые испытывают колебания между большим положительным и большим отрицательным смещением. Это точки, которые подвергаются максимальному смещению во время каждого колебательного цикла стоячей волны. В некотором смысле эти точки противоположны узлам, поэтому они называются пучностями , . Картина стоячей волны всегда состоит из чередования узлов и пучностей.На анимации, показанной ниже, изображена веревка, колеблющаяся в виде стоячей волны. Узлы и пучности отмечены на схеме. Когда в среде устанавливается картина стоячей волны, узлы и пучности всегда располагаются в одном и том же положении вдоль среды; они стоят на месте . Именно эта характеристика и принесла модели название Standing wav e.

Flickr Physics Фотография

Стоячая волна создается на колеблющейся струне с помощью гармонического осциллятора и генератора частоты.Строб используется для освещения струны несколько раз в течение каждого цикла. Палец указывает на узловую позицию.

Диаграммы стоячей волны

Расположение узлов и пучностей в структуре стоячей волны можно объяснить, сосредоточив внимание на интерференции двух волн. Узлы производятся в местах, где возникает деструктивная интерференция. Например, узлы образуются в местах, где вершина одной волны встречается с впадиной второй волны; или полувысок одной волны встречает полувысок второй волны; или четверть гребня одной волны встречает четверть-впадину второй волны; и т.п.С другой стороны, пучности образовываются в местах, где происходит конструктивное вмешательство. Например, если гребень одной волны встречается с гребнем второй волны, получается точка большого положительного смещения. Точно так же, если впадина одной волны встречает впадину второй волны, возникает точка большого отрицательного смещения. Пучины всегда колеблются между этими точками большого положительного и большого отрицательного смещения; это потому, что во время полного цикла вибрации гребень встретится с гребнем; а затем через половину цикла желоб встретится с желобом.Поскольку пучности колеблются взад и вперед между большим положительным и большим отрицательным смещением, диаграмма стоячей волны иногда изображается путем рисования формы среды в определенный момент времени и в мгновение ока на половину колебательного цикла позже. Это сделано на схеме ниже.

Узлы и пучности не следует путать с гребнями и впадинами. При обсуждении движения бегущей волны принято называть точку большого максимального смещения гребнем, а точку большого отрицательного смещения — впадиной.Они представляют точки возмущения , которые перемещаются из одного места в другое через среду. С другой стороны, пучность — это точка на среде , которая остается в том же месте. Более того, пучность колеблется взад и вперед между большим смещением вверх и большим смещением вниз. И, наконец, узлы и пучности на самом деле не являются частью волны. Напомним, что стоячая волна на самом деле не волна, а скорее картина, возникающая в результате интерференции двух или более волн.Поскольку стоячая волна технически не является волной, пучность технически не является точкой на волне. Узлы и пучности — это просто уникальные точки в среде, которые составляют волновую картину.

Смотри!

Инструктор по физике демонстрирует и объясняет формирование продольной стоячей волны в пружине.

Хотим предложить…

Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие — это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного шаблона стоячих волн. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивная программа «Модели стоячей волны» предоставляет учащемуся среду для изучения формирования стоячих волн, моделей стоячих волн и математических соотношений для моделей стоячих волн.

Проверьте свое понимание

1. Предположим, что в парке развлечений «Стоячая волна » был аттракцион «». Какое место — узел или пучность — во время поездки вызовет наибольшее волнение?

2. Стоячая волна образуется при ____.

а. волна преломляется из-за изменения свойств среды.
г. волна отражается от стены каньона и слышится вскоре после ее образования.
г. красные, оранжевые и желтые волны огибают взвешенные атмосферные частицы.
г. две одинаковые волны, движущиеся в разных направлениях по одной и той же среде, интерферируют.

3. Количество узлов в стоячей волне, показанной на диаграмме справа, равно ____.

4. Число пучностей в стоячей волне, показанной на диаграмме вверху справа, равно ____.

Рассмотрите образец стоячей волны справа, отвечая на следующие два вопроса.

5. Количество узлов во всем шаблоне ___.

6. Из всех отмеченных точек деструктивная интерференция происходит в точке (ах) ____.

а. B, C и D
г.A, E и F
г. А только
г. C только
e. все точки

48+ Top Node.js Интервью Вопросы и ответы в 2021 году

Node.js — суперпопулярная серверная платформа, которую используют все больше и больше организаций. Если вы готовитесь к смене карьеры и у вас предстоящее собеседование, всегда полезно заранее подготовиться и освежить свои навыки собеседования. Хотя есть несколько часто задаваемых вопросов на собеседовании по Node.js, которые всплывают во время всех типов собеседований, мы также рекомендуем вам подготовиться, сосредоточившись на эксклюзивных вопросах для вашей конкретной отрасли.

Мы составили исчерпывающий список распространенных Node.js вопросы интервью, которые часто возникают на собеседовании, и лучшие способы ответить на эти вопросы. Это также поможет вам понять фундаментальные концепции Node.js.

Вопросы собеседования по Node.js сгруппированы в следующие категории:

Вопросы на собеседовании для начинающих по Node.js
Intermediate Node.js Вопросы на собеседовании
Расширенные вопросы на собеседовании по Node.js

Full Stack Java Developer Course

The Gateway to Master Web DevelopmentExplore курс

Узел для начинающих.js Вопросы для интервью

1. Что такое Node.js? Где это можно использовать?

Node.js — это кроссплатформенная среда выполнения JavaScript с открытым исходным кодом и библиотека для запуска веб-приложений вне клиентского браузера . Используется для создания серверных веб-приложений.

Node.js идеально подходит для приложений с интенсивным использованием данных, поскольку он использует асинхронную модель, управляемую событиями. Вы можете использовать веб-приложения с интенсивным вводом-выводом, такие как сайты потокового видео. Вы также можете использовать его для разработки: веб-приложений реального времени, сетевых приложений, приложений общего назначения и распределенных систем.

2. Зачем использовать Node.js?

Node.js упрощает создание масштабируемых сетевых программ. Некоторые из его преимуществ включают:

Обычно быстро
Редко блокирует
Он предлагает унифицированный язык программирования и тип данных
Все асинхронно
Обеспечивает отличный параллелизм

3. Как работает Node.js?

Веб-сервер, использующий Node.js, обычно имеет рабочий процесс, очень похожий на схему, показанную ниже.Давайте подробно рассмотрим этот поток операций.

Выделитесь среди сверстников в этом сезоне аттестации

Начните учиться с наших БЕСПЛАТНЫХ курсов

Клиенты отправляют запросы на веб-сервер для взаимодействия с веб-приложением. Запросы могут быть неблокирующими или блокирующими:
Запрос данных
Удаление данных
Обновление данных
Node.js получает входящие запросы и добавляет их в очередь событий
Затем запросы передаются один за другим через цикл событий.Он проверяет, достаточно ли просты запросы, чтобы не требовать никаких внешних ресурсов
Цикл событий обрабатывает простые запросы (неблокирующие операции), такие как опрос ввода-вывода, и возвращает ответы соответствующим клиентам

Один поток из пула потоков назначается одному сложному запросу. Этот поток отвечает за выполнение конкретного запроса на блокировку путем доступа к внешним ресурсам, таким как вычисления, база данных, файловая система и т. Д.

После того, как задача выполнена полностью, ответ отправляется в цикл событий, который отправляет этот ответ обратно клиенту.

4. Почему Node.js однопоточный?

Node.js является однопоточным для асинхронной обработки. Выполняя асинхронную обработку в однопоточном режиме при типичных веб-нагрузках, можно достичь большей производительности и масштабируемости вместо типичной реализации на основе потоков.

5. Объясните обратный вызов в Node.js.

Функция обратного вызова вызывается после данной задачи. Тем временем он позволяет запускать другой код и предотвращает любые блокировки. Являясь асинхронной платформой, Node.js сильно зависит от обратного вызова. Все API-интерфейсы Node написаны для поддержки обратных вызовов.

6. Как бы вы определили термин «ввод / вывод»?

Термин «ввод-вывод» используется для описания любой программы, операции или устройства, которые передают данные на носитель или с носителя и на другой носитель или с другого носителя
Каждая передача — это выход из одного носителя и вход в другой. Носитель может быть физическим устройством, сетью или файлами в системе

7. Как чаще всего используется Node.js?

Узел.js широко используется в следующих приложениях:

Чаты в реальном времени
Интернет вещей
Комплексные СПА (одностраничные приложения)
Инструменты для совместной работы в реальном времени
Потоковые приложения
Архитектура микросервисов

8. Объясните разницу между фронтенд-разработкой и бэкэнд-разработкой?

Интерфейс	Серверная часть
Frontend относится к клиентской стороне приложения	Backend относится к серверной части приложения
Это часть веб-приложения, которую пользователи могут видеть и взаимодействовать с .	Он составляет все, что происходит за кулисами
Обычно он включает в себя все, что связано с визуальными аспектами веб-приложения.	Обычно включает в себя веб-сервер, который взаимодействует с базой данных для обслуживания запросов
HTML, CSS, JavaScript, AngularJS и ReactJS — это некоторые из основных элементов веб-разработки.	Java, PHP, Python и Node.js — это некоторые из технологий бэкэнд-разработки

9. Что такое NPM?

NPM означает диспетчер пакетов узла, отвечающий за управление всеми пакетами и модулями для Node.js.

Node Package Manager предоставляет две основные функции:

Предоставляет онлайн-репозитории для пакетов / модулей node.js, которые доступны для поиска на search.nodejs.org
Предоставляет утилиту командной строки для установки пакетов Node.js, а также управляет Node.js версии и зависимости

10. Какие модули есть в Node.js?

Модули

похожи на библиотеки JavaScript, которые можно использовать в приложении Node.js для включения набора функций. Чтобы включить модуль в приложение Node.js, используйте функцию require () с круглыми скобками, содержащими имя модуля.

Node.js имеет множество модулей для обеспечения базовой функциональности, необходимой для веб-приложения. Некоторые из них включают:

Основные модули	Описание
HTTP	Включает классы, методы и события для создания узла.js HTTP-сервер
, утилита	Включает служебные функции, полезные для разработчиков
фс	Включает события, классы и методы для работы с файловыми операциями ввода-вывода
url	Включает методы анализа URL-адресов
строка запроса	Включает методы для работы со строкой запроса
поток	Включает методы для обработки потоковых данных
злиб	Включает методы сжатия или распаковки файлов

11.Почему Node.js предпочтительнее других серверных технологий, таких как Java и PHP?

Некоторые из причин, по которым предпочтение отдается Node.js:

Node.js очень быстрый
Node Package Manager имеет в распоряжении разработчика более 50 000 пакетов
Идеально подходит для веб-приложений, работающих в режиме реального времени с интенсивным использованием данных, поскольку Node.js никогда не ждет, пока API вернет данные
Лучшая синхронизация кода между сервером и клиентом благодаря той же кодовой базе
Веб-разработчикам легко начать использовать Node.js в своих проектах, поскольку это библиотека JavaScript

12. В чем разница между Angular и Node.js?

Угловой	Node.js
Это среда разработки внешнего интерфейса	Это серверная среда
Написан на TypeScript	Написан на языках C, C ++
Используется для создания одностраничных клиентских веб-приложений	Используется для создания быстрых и масштабируемых серверных сетевых приложений
Разбивает веб-приложение на компоненты MVC	Создает запросы к базе данных

13.Какая база данных чаще используется с Node.js?

MongoDB — самая распространенная база данных, используемая с Node.js. Это кроссплатформенная документно-ориентированная база данных NoSQL, обеспечивающая высокую производительность, доступность и простую масштабируемость.

14. Какие библиотеки наиболее часто используются в Node.js?

В Node.js есть две часто используемые библиотеки:

ExpressJS — Express — это гибкая платформа веб-приложений Node.js, которая предоставляет широкий набор функций для разработки веб-приложений и мобильных приложений.
Mongoose — Mongoose также является фреймворком веб-приложений Node.js, который упрощает подключение приложения к базе данных.

15. Каковы плюсы и минусы Node.js?

Node.js Профи	Node.js Минусы
Быстрая обработка и модель на основе событий	Не подходит для тяжелых вычислительных задач
Использует JavaScript, хорошо известный разработчикам.	Использование обратного вызова сложно, так как вы получаете несколько вложенных обратных вызовов
Node Package Manager содержит более 50 000 пакетов, которые обеспечивают функциональность приложения	Работа с реляционными базами данных — не лучший вариант для Node.js
Лучше всего подходит для потоковой передачи огромных объемов данных и операций с интенсивным вводом-выводом	Поскольку Node.js является однопоточным, задачи с интенсивным использованием ЦП не являются его сильной стороной

БЕСПЛАТНЫЙ тренинг по сертификации Java

Изучите Java от А до Я, как никогда раньше

16. Какая команда используется для импорта внешних библиотек?

Команда «require» используется для импорта внешних библиотек.Например — «var http = require (« HTTP »)». Это загрузит библиотеку HTTP и единственный экспортированный объект через переменную HTTP.

Теперь, когда мы рассмотрели некоторые важные вопросы собеседования по Node.js для начинающих, давайте рассмотрим некоторые из вопросов собеседования по Node.js среднего уровня.

Промежуточные вопросы на собеседовании по Node.js

17. Что означает программирование, управляемое событиями?

Подход к программированию, управляемому событиями, использует события для запуска различных функций.Событием может быть что угодно, например нажатие клавиши или нажатие кнопки мыши. Функция обратного вызова уже зарегистрирована в элементе, который выполняется всякий раз, когда запускается событие.

18. Что такое цикл событий в Node.js?

Циклы событий обрабатывают асинхронные обратные вызовы в Node.js. Это основа неблокирующего ввода / вывода в Node.js, что делает его одной из наиболее важных функций среды.

19. Что такое EventEmitter в Node.js?

EventEmitter — это класс, содержащий все объекты, которые могут генерировать события
Каждый раз, когда объект из класса EventEmitter генерирует событие, все присоединенные функции вызываются синхронно

20.Какие два типа функций API есть в Node.js?

В Node.js есть два типа API-функций:

Асинхронные неблокирующие функции
Синхронный, функции блокировки

Научитесь быстро и эффективно создавать сетевые приложения с использованием JavaScript с помощью Node.js Training. Нажмите, чтобы зарегистрироваться сейчас!

21. Что такое файл package.json?

Файл package.json — это сердце системы Node.js. Этот файл содержит метаданные для конкретного проекта.Файл package.json находится в корневом каталоге любого приложения Node или модуля

Так выглядит файл package.json сразу после создания проекта Node.js с помощью команды: npm init

Вы можете редактировать параметры при создании проекта Node.js.

22. Как бы вы использовали модуль URL в Node.js?

Модуль URL в Node.js предоставляет различные утилиты для разрешения и анализа URL. Это встроенный модуль, который помогает разделить веб-адрес в читаемый формат.

23. Что такое пакет Express.js?

Express — это гибкая платформа веб-приложений Node.js, которая предоставляет широкий набор функций для разработки как веб-приложений, так и мобильных.

24. Как создать простое приложение Express.js?

Объект запроса представляет HTTP-запрос и имеет свойства для строки запроса запроса, параметров, тела, заголовков HTTP и т. Д.
Объект ответа представляет HTTP-ответ, который приложение Express отправляет при получении HTTP-запроса

25.Что такое потоки в Node.js?

Потоки — это объекты, которые позволяют вам непрерывно читать или записывать данные.

Есть четыре типа потоков:

Читаемый — Используется для операций чтения

с возможностью записи — Используется для операций записи

Дуплекс — Может использоваться как для чтения, так и для записи

Преобразование — Тип дуплексного потока, в котором вывод вычисляется на основе ввода

26.Как установить, обновить и удалить зависимость?

27. Как создать в Node.js простой сервер, возвращающий Hello World?

Импортировать модуль HTTP
Используйте функцию createServer с функцией обратного вызова, используя запрос и ответ в качестве параметров.
Введите «привет, мир».
Настройте сервер на прослушивание порта 8080 и назначьте IP-адрес

28. Объясните асинхронные и неблокирующие API в Node.js.

Все API библиотеки Node.js являются асинхронными, что означает, что они также не блокируют
Сервер на основе Node.js никогда не ждет, пока API вернет данные. Вместо этого он переходит к следующему API после его вызова, и механизм уведомления от события Node.js отвечает серверу на предыдущий вызов API

29. Как реализовать асинхронность в Node.js?

Как показано ниже, асинхронный код просит движок JavaScript, выполняющий код, дождаться запроса.get () для завершения перед переходом к следующей строке для выполнения.

30. Для чего нужен module.exports?

Модуль в Node.js используется для инкапсуляции всех связанных кодов в единый блок кода, который можно интерпретировать, сдвигая все связанные функции в один файл. Вы можете экспортировать модуль с помощью module.exports, что позволяет импортировать его в другой файл, используя необходимое ключевое слово.

31. Что такое функция обратного вызова в Node.js?

Обратный вызов — это функция, вызываемая после данной задачи. Это предотвращает любую блокировку и позволяет одновременно запускать другой код.

В последнем разделе мы рассмотрим некоторые из вопросов собеседования по Node.js продвинутого уровня.

Курс веб-разработчика Full Stack

Чтобы стать экспертом в курсе MEAN StackView

Advanced Node.js Вопросы на собеседовании

32. Что такое REPL в Node.js?

REPL расшифровывается как Read Eval Print Loop и представляет компьютерную среду.Это похоже на консоль Windows или оболочку Unix / Linux, в которой вводится команда. Затем система отвечает выводом

33. Что такое функция потока управления?

Функция потока управления — это фрагмент кода, который выполняется между вызовами нескольких асинхронных функций.

34. Как поток управления управляет вызовами функций?

35. В чем разница между методами fork () и spawn () в Node.js?

вилка ()	возрождение ()

fork () — это частный случай spawn (), который генерирует новый экземпляр движка V8.	Spawn () запускает новый процесс с доступным набором команд.
Несколько рабочих процессов работают на базе кода одного узла для выполнения нескольких задач.	Этот метод не создает новый экземпляр V8, и на процессоре активна только одна копия модуля узла.

36. Что такое класс буфера в Node.js?

Класс Buffer хранит необработанные данные, аналогичные массиву целых чисел, но соответствует выделению необработанной памяти за пределами кучи V8.Класс буфера используется, потому что чистый JavaScript несовместим с двоичными данными

37. Что такое конвейер в Node.js?

Конвейер — это механизм, используемый для подключения вывода одного потока к другому потоку. Обычно он используется для извлечения данных из одного потока и передачи вывода в другой поток

38. Какие флаги используются в операциях чтения / записи в файлах?

39. Как открыть файл в Node.js?

40. Что такое ад обратного вызова?

Ад обратных вызовов, также известный как пирамида гибели, является результатом интенсивно вложенных, нечитаемых и неуправляемых обратных вызовов, что, в свою очередь, затрудняет чтение и отладку кода
неправильная реализация асинхронной логики вызывает ад обратного вызова

41.Что такое шаблон реактора в Node.js?

Схема реактора — это концепция неблокирующих операций ввода-вывода. Этот шаблон предоставляет обработчик, связанный с каждой операцией ввода-вывода. Как только сгенерирован запрос ввода / вывода, он передается на демультиплексор

42. Что такое тестовая пирамида в Node.js?

43. Опишите коды выхода Node.js.

44. Объясните концепцию промежуточного программного обеспечения в Node.js.

Middleware — это функция, которая получает объекты запроса и ответа.Большинство задач, которые выполняют функции промежуточного программного обеспечения:

Выполнить любой код
Обновить или изменить объекты запроса и ответа
Завершить цикл запрос-ответ
Вызвать следующее промежуточное ПО в стеке

45. Какие существуют типы HTTP-запросов?

HTTP определяет набор методов запроса, используемых для выполнения желаемых действий. Методы запроса включают:

GET: Используется для получения данных

POST: Обычно используется для изменения состояния или реакции на сервере

HEAD: Аналогичен методу GET, но запрашивает ответ без тела ответа

DELETE: Используется для удаления заранее определенного ресурса

46.Как бы вы подключили базу данных MongoDB к Node.js?

Для создания базы данных в MongoDB:

Начните с создания объекта MongoClient
Укажите URL-адрес подключения с правильным IP-адресом и именем базы данных, которую вы хотите создать

47. Какова цель NODE_ENV?

48. Перечислите различные временные особенности Node.js.

По мере того, как вы готовитесь к предстоящему собеседованию, мы надеемся, что это подробное руководство поможет лучше понять, какие типы вопросов вам будут задавать.

Я считаю, что эти вопросы на собеседовании Node.js помогут вам понять, какие вопросы могут быть заданы вам на собеседовании, и, пройдя эти вопросы на собеседовании на Node.js, вы сможете подготовиться и взломать свое следующее собеседование за один раз.

Для более глубокого обучения этой набирающей популярность среде разработки веб-приложений зарегистрируйтесь сегодня на учебном курсе Simplilearn по Node.js, который подготовит вас еще больше к любым предстоящим собеседованиям по Node.js.

Удачи на предстоящем собеседовании!

центральность

центральность

Упражнение
для главы 6: Центральность

Ответы

Упражнение 1

(а) Рассчитать
градусов
центральность баллов каждого узла в сети выше, и завершите
Таблица ниже.

Относится к степени центральности узла
к количеству ребер, прикрепленных к узлу. Чтобы узнать
стандартизированная оценка, вам нужно разделить каждую оценку на n-1 (n = число
узлов). Поскольку в графе 7 узлов, знаменатель — 6 (7-1).
по этому вопросу.

Центральность в градусах

Узел	Оценка	Стандартизированный Оценка
1	1	1/6
2	1	1/6
3	3	3/6 = 1/2
4	2	2/6 = 1/3
5	3	3/6 = 1/2
6	2	2/6 = 1/3
7	2	2/6 = 1/3

(б) Рассчитать
Близость
центральность баллов каждого узла в сети выше, и завершите
Таблица ниже.( Не забудьте взять обратный .)

Вам нужно вычислить перевернутую
оценка после подсчета общего количества шагов до узла. Чтобы
чтобы узнать стандартизированный балл, вам нужно разделить балл на (n-1), затем
взять обратное. Обратите внимание, что самый центральный узел — это узел 4, в то время как
Самый центральный узел для степени центральности — это узлы 3 и 5.

Центральность по близости

Узел	Оценка	Стандартизированный Оценка
1	1/16	6/16 = 3/8
2	1/16	6/16 = 3/8
3	1/11	6/11
4	1/10	6/10 = 3/5
5	1/11	6/11
6	1/15	15.06 = 2/5
7	1/15	15.06 = 2/5

Чтобы вычислить центральность промежуточности,
вы берете каждую пару сети и подсчитываете, сколько раз узел может
прервать кратчайшие пути (геодезическое расстояние) между двумя узлами
пары. Для стандартизации отмечу, что знаменатель равен (n-1) (n-2) / 2.
Для этой сети (7-1) (7-2) / 2 = 15. Обратите внимание, что узел 5 имеет небольшой
меньшая оценка центральности узлов 3 и 4, потому что связь между
узел 6 и 7 снижает управляемость узла 5.

Центральность по промежуточности

Узел	Оценка	Стандартизированный Оценка
1	0	0
2	0	0
3	16/3	16/45
4	13/3	13/45
5	13/3	13/45
6	0	0
7	0	0

По следующим вопросам (d),
(e) и (f), вам нужно запомнить лекцию на

Мотоки.Вы должны прочитать
краткое изложение каждого центрального места в ваших заметках. (Я написал это на
самый конец лекции). Если вы это хорошо понимаете, у вас нет
трудности с ответом на три вопроса.

(d) Предположим, что
сеть относится к сети дружбы. Каждый узел представляет человека,
и каждое ребро олицетворяет дружбу между людьми на концах.
Если вы заинтересованы в поиске самого популярного человека в сети,
какая мера центральности является наиболее подходящей? Дать ответ
с указанием причин, по которым он является наиболее подходящим.

Самый популярный человек должен
иметь наибольшее количество друзей. Таким образом, центральность степени — это
наиболее подходящая мера.

(e) Предположим, что
Сеть относится к сети информационных потоков организации. Каждый
узел представляет раздел в организации, а каждое ребро представляет
возможен обмен информацией между секциями на концах. Если
вы заинтересованы в поиске раздела, который может наиболее эффективно
получить информацию из всех остальных разделов , которые измеряют центральность
самый подходящий? Дайте ответ с причинами, почему это
наиболее подходящий.

Для получения информации необходимо
быть рядом со всеми. В этом смысле узел в ближайшей позиции
в среднем может наиболее эффективно получать информацию. Таким образом, близость
центральность является наиболее подходящей.

(f) Снова предположим
Вышеупомянутая сеть относится к сети информационных потоков организации.
Если вы хотите найти , раздел, в котором чаще всего
управлять информационным потоком в сети , мера центральности которого
самый подходящий? Дайте ответ с причинами, почему это
наиболее подходящий.

Для управления информационным потоком,
узел должен находиться между другими узлами, потому что узел может прервать передачу информации
течь между ними. Таким образом, центральность посредничества является наиболее подходящей.
мера.

Упражнение 2

(a) Для каждой сети,
рассчитать три индекса центральности (степень, близость и промежуточность)
для каждого всего графа (Не для каждого узла графа) .Который
граф более централизованный?

Используйте уравнения 6.8, 6.9 и 6.10
на стр. 171 учебника по этому вопросу. Основная идея
центральность для всего графа заключается в вычислении среднего отклонения каждого узла
от самого центрального узла.

Степень центральности (уравнение 6.8)

Сеть A

Узел 1 — оценка центральности
3

Узел 2 — оценка центральности 1

Узел 3 — оценка центральности
1

Узел 4 — оценка центральности
1

Максимальный балл — 3.

Используйте уравнение 6.8

((3-3) + (3-1) + (3-1) + (3-1)) / (16-12 + 2)
= (0 + 2 + 2 + 2) / 6 = 1

Оценка степени центральности
Сеть A — 1.

Сеть B

Узел 1 — оценка центральности
3

Узел 2 — оценка центральности
3

Узел 3 — оценка центральности
3

Узел 4 — оценка центральности
3

Максимальный балл — 3.

Используйте уравнение.6,8

((3-3) + (3-3) + (3-3) + (3-3)) / (16-12 + 2)
= (0 + 0 + 0 + 0) / 6 = 0

Оценка степени центральности
Сеть B — 0.

Таким образом, сеть A более централизована
чем сеть B по степени центральности.

Центральность близости (Уравнение
6,9)

* Вам необходимо использовать стандартизированные
счет.

Сеть A

Узел 1 — оценка центральности
3/3 = 1

Узел 2 — оценка центральности
3/5

Узел 3 — оценка центральности
3/5

Узел 4 — оценка центральности
3/5

Максимальный балл 3/3 = 1.

Используйте уравнение 6.9.

((1-1) + (1-3 / 5) + (1-3 / 5) + (1-3 / 5)) / ((16-12 + 2) / (8-3))

= (0 + 2/5 + 2/5 + 2/5) / (6/5)

= (6/5) / (6/5) = 1.

Оценка центральности близости
сети A — 1.

Сеть B

Узел 1 — оценка центральности
3/3 = 1

Узел 2 — оценка центральности
3/3 = 1

Узел 3 — оценка центральности
3/3 = 1

Узел 4 — оценка центральности
3/3 = 1

Максимальный балл — 1.

Используйте уравнение 6.9.

((1-1) + (1-1) + (1-1) + (1-1)) / ((16-12 + 2) / (8-3))
= (0 + 0 + 0 + 0) / (6/5) = 0

Оценка центральности близости
сети B — 0.

Таким образом, сеть A более централизована
чем сеть B для центральности близости.

Центральность посредничества (Уравнение
6.10)

* Вам необходимо использовать стандартизированные
счет.

Сеть A

Узел 1 — оценка центральности
3/3 = 1

Узел 2 — оценка центральности
0

Узел 3 — оценка центральности
0

Узел 4 — оценка центральности
0

Максимальный балл 3/3 = 1.

Используйте уравнение 6.10.

((1-1) + (1-0) + (1-0) + (1-0)) / (4-1)
= (0 + 1 + 1 + 1) / 3 = 1.

Оценка центральности близости
сети A — 1.

Сеть B

Узел 1 — оценка центральности
0

Узел 2 — оценка центральности
0

Узел 3 — оценка центральности
0

Узел 4 — оценка центральности
0

Максимальный балл — 0.

Используйте уравнение.6.10.

((0-0) + (0-0) + (0-0) + (0-0)) / (4-1)
= (0 + 0 + 0 + 0) / 3 = 0

Оценка центральности близости
сети B — 0.

Таким образом, сеть A более централизована
чем Сеть B по центральности между промежуточными звеньями.

Замечу, что оценка центральности
сети A равен 1 для любых показателей центральности, в то время как оценка центральности
Сеть B равна 0 для любых мер центральности, потому что сеть A максимально
централизованная сеть с четырьмя узлами, а сеть B — нецентрализованная
сеть с четырьмя узлами.

(б) Сравнение централизованных
и нецентрализованный график выше, обсудите преимущества и недостатки
централизованная сеть.

Это открытый вопрос.
Задача вопроса — дать вам представление о некоторых централизованных и нецентрализованных
сетей в реальном мире и сравните их. Поскольку этот курс
курс социологии, важно, чтобы вы применяли математический подход
к актуальному социальному явлению. Я даю вам образец ответа.

Пример ответа

Если сеть представляет информацию
flow, узел 1 в сети A обладает огромной управляемостью информационного потока.
Если узел 1 работает очень хорошо, сеть очень эффективна, потому что там
нет избыточных ребер в сети. Однако, если узел 1 не
работы, узлы 2, 3 и 4 изолированы. В этом смысле сеть A рискованна.
в том, что эффективность информационного потока полностью зависит от производительности узла 1.
С другой стороны, сеть B более гибкая.Даже если узел 1
не работает, все остальные узлы могут общаться друг с другом. Тем не мение,
в другом смысле эта сеть имеет много избыточных ребер. Если потребуется
стоит сделать ребра, эта сеть очень дорогая.

Упражнение 3

Можно использовать центральность
как показатель мощности в сетях, потому что самый центральный узел больше
вероятно, займет самую сильную позицию. Как вы думаете, это правда?
Укажите причины, по которым вы так думаете.

Ответ на самом деле
«нет». Экспериментальное исследование Cook et. al. (1983) демонстрирует, что
центральность не обязательно является показателем власти. Тебе не нужно знать
об этом исследовании, но вам нужно подумать, является ли влиятельная позиция
всегда центральное место в сети. Я не объясняю детали этого исследования.
Если вам это интересно, свяжитесь со мной. Я объясню это. С
основная цель этого вопроса — дать вам возможность подумать о значении
центральность, вы можете написать свою собственную идею.

Если есть вопросы, задавайте
Мотоки. [email protected]

Примеры вопросов о структурах данных — Глава 10

Примеры вопросов о структурах данных — Глава 10

Примеры вопросов о структурах данных

Глава 10

Деревья

Структуры данных и другие объекты с использованием C ++

от

Майкл Мэйн

а также

Уолтер Сэвич

Второе издание ISBN 0-201-70297-5, Мягкая обложка, 816 страниц, 2000 г.

Цель этих вопросов

Это типичные экзаменационные вопросы из 10-й главы учебника.Эти
точные вопросы могут не входить в ваш экзамен, но если вы исследуете и найдете
правильные ответы на эти вопросы, это должно быть хорошей подготовкой
для настоящего экзамена. (Также возможно, что часть этого материала была
не охвачены в вашем классе.) На данный момент есть
20 короткие ответы на вопросы
а также
20 вопросов с несколькими вариантами ответов
в этом файле.

Короткие ответы

Короткие ответы
Раздел 10.1
Введение
в Деревья

Вот небольшое двоичное дерево:
14 / \ 2 11 / \ / \ 1 3 10 30 / / 7 40
Обведите все листочки. Поместите квадратную коробку вокруг корня. Нарисуйте звезду
вокруг каждого предка узла, содержащего 10. Поместите большой X через
каждый потомок узла содержит 10.
Нарисуйте полное двоичное дерево как минимум с 6 узлами.
Короткие ответы
Раздел 10.2
Дерево
Представления
Нарисуйте полное двоичное дерево ровно с шестью узлами. Поставить другой
значение в каждом узле. Затем нарисуйте массив из шести компонентов и покажите
где каждое из шести значений узлов будет помещено в массив (используя
обычное представление массива полного двоичного дерева).
Напишите частные переменные-члены для
новое определение узла, которое можно использовать для узла в дереве
где: (1) Каждый узел содержит данные типа int, (2) Каждый узел имеет до четырех
дочерние элементы и (3) Каждый узел также имеет указатель на своего родителя.Хранить
указатели на дочерние элементы в массиве из четырех указателей.
Краткие ответы
Раздел 10.3
Набор инструментов для узлов двоичного дерева
Нарисуйте двоичное дерево таксономии, которое можно использовать для этих четырех животных:
Кролик, Лошадь, Кит, Змея.

Используя binary_tree_node из Раздела 10.3,
напишите функцию, соответствующую следующей спецификации. Проверить как
большая часть предусловия, насколько это возможно.Рекурсия не требуется.
шаблон <элемент класса> void subswap (binary_tree_node * root_ptr) // Предварительное условие: root_ptr - это корневой указатель непустого двоичного дерева. // Постусловие: исходное левое поддерево было перемещено и теперь является правым // поддерево, а исходное правое поддерево теперь является левым поддеревом. // Пример исходного дерева: Пример нового дерева: // 1 1 // / \ / \ // 2 3 3 2 // / \ / \ // 4 5 4 5

шаблон <элемент класса>
Использование binary_tree_node из Раздела 10.3,
напишите рекурсивную функцию в соответствии со следующей спецификацией. Проверить как
большая часть предусловия, насколько это возможно.
шаблон <элемент класса> void flip (binary_tree_node <элемент> * root_ptr) // Предварительное условие: root_ptr - это корневой указатель непустого двоичного дерева. // Постусловие: теперь дерево является зеркальным отображением своего исходного значения. // Пример исходного дерева: Пример нового дерева: // 1 1 // / \ / \ // 2 3 3 2 // / \ / \ // 4 5 5 4
Короткие ответы
Раздел 10.4
Дерево
Обходы

Вот небольшое двоичное дерево:
14 / \ 2 11 / \ / \ 1 3 10 30 / / 7 40
Запишите порядок посещаемых узлов в:

A. Обход по порядку:

Б. Обход предварительного заказа:

C. Обход после заказа:

Использование binary_tree_node из Раздела 10.3,
Напишите рекурсивную функцию, соответствующую следующей спецификации. Ты не
необходимо проверить предварительное условие.
шаблон <элемент класса> увеличение недействительности (binary_tree_node * root_ptr) // Предварительное условие: root_ptr - корневой указатель двоичного дерева. // Постусловие: данные каждого узла дерева увеличены на единицу.

Используя binary_tree_node из Раздела 10.3,
напишите рекурсивную функцию в соответствии со следующей спецификацией.Ты не
необходимо проверить предварительное условие.
шаблон <элемент класса> size_t many_nodes (binary_tree_node <элемент> * root_ptr) // Предварительное условие: root_ptr - корневой указатель двоичного дерева. // Постусловие: возвращаемое значение - количество узлов в дереве. // ПРИМЕЧАНИЯ: пустое дерево имеет 0 узлов, а дерево только с корнем имеет // 1 узел.

Используя binary_tree_node из Раздела 10.3,
напишите рекурсивную функцию в соответствии со следующей спецификацией.Ты не
необходимо проверить предварительное условие.
шаблон <элемент класса> int tree_depth (binary_tree_node <элемент> * root_ptr) // Предварительное условие: root_ptr - корневой указатель двоичного дерева. // Постусловие: возвращаемое значение - глубина двоичного дерева. // ПРИМЕЧАНИЯ: пустое дерево имеет глубину -1, а дерево только с корнем // имеет глубину 0.

Используя binary_tree_node из Раздела 10.3,
напишите функцию, соответствующую следующей спецификации.Ты не
необходимо проверить предварительное условие.
шаблон <элемент класса> size_t count42 (binary_tree_node * root_ptr) // Предварительное условие: root_ptr - это корневой указатель двоичного дерева (но // НЕ ОБЯЗАТЕЛЬНО дерево поиска). // Постусловие: возвращаемое значение указывает, сколько раз появляется 42 // в дереве. ПРИМЕЧАНИЕ. Если дерево пусто, функция возвращает ноль.

Использование binary_tree_node из Раздела 10.3,
напишите функцию, соответствующую следующей спецификации. Ты не
необходимо проверить предварительное условие.
шаблон <элемент класса> bool has_42 (binary_tree_node <элемент> * root_ptr) // Предварительное условие: root_ptr - это корневой указатель двоичного дерева (но // НЕ ОБЯЗАТЕЛЬНО дерево поиска). // Постусловие: возвращаемое значение указывает, появляется ли где-нибудь 42 // в дереве. ПРИМЕЧАНИЕ. Если дерево пусто, функция возвращает false.

Использование binary_tree_node из Раздела 10.3,
напишите функцию, соответствующую следующей спецификации. Ты не
необходимо проверить предварительное условие.
шаблон <элемент класса> bool all_42 (binary_tree_node <элемент> * root_ptr) // Предварительное условие: root_ptr - это корневой указатель двоичного дерева (но // НЕ ОБЯЗАТЕЛЬНО дерево поиска). // Постусловие: возвращаемое значение истинно, если каждый узел в дереве // содержит 42. ПРИМЕЧАНИЕ. Если дерево пусто, функция возвращает значение true.

Использование binary_tree_node из Раздела 10.3,
напишите рекурсивную функцию в соответствии со следующей спецификацией. Ты не
необходимо проверить предварительное условие.
шаблон <элемент класса> int sum_all (binary_tree_node <элемент> * root_ptr) // Предварительное условие: root_ptr - корневой указатель двоичного дерева. // Постусловие: возвращаемое значение - это сумма всех данных во всех узлах. // ПРИМЕЧАНИЯ: возвращаемое значение для пустого дерева - ноль.
Короткие ответы
Раздел 10.5
Двоичный поиск
Деревья

Предположим, мы хотим создать двоичное дерево поиска, в котором каждый узел содержит
информация некоторого типа данных
называется Item (который имеет конструктор по умолчанию и правильную семантику значения).
Какой дополнительный коэффициент требуется для типа данных Item?
Предположим, что двоичное дерево поиска содержит число 42 в узле с
двое детей. Напишите два или три четких предложения, чтобы описать процесс
требуется удалить 42 из дерева.
Используя binary_tree_node из Раздела 10.3,
напишите функцию, соответствующую следующей спецификации. Ты не
необходимо проверить предварительное условие. Сделайте функцию такой же эффективной, как
возможно (без необходимости не посещать узлы):
шаблон <элемент класса> size_t count42 (binary_tree_node * root_ptr) // Предварительное условие: root_ptr - это корневой указатель двоичного ПОИСКОВОГО дерева. // Постусловие: возвращаемое значение указывает, сколько раз появляется 42 // в дереве.
Используя binary_tree_node из Раздела 10.3,
напишите функцию, соответствующую следующей спецификации. Ты не
необходимо проверить предварительное условие. Сделайте функцию такой же эффективной, как
возможно (без необходимости не посещать узлы):
шаблон <элемент класса> int max (binary_tree_node <элемент> * root_ptr) // Предварительное условие: root_ptr - корневой указатель непустого двоичного ПОИСКА // дерево. // Постусловие: возвращаемое значение - наибольшее значение в дереве.

Используя binary_tree_node из Раздела 10.3,
напишите функцию, соответствующую следующей спецификации. Ты не
необходимо проверить предварительное условие.
шаблон <элемент класса> void insert_one_42 (binary_tree_node * & root_ptr) // Предварительное условие: root_ptr - это корневой указатель двоичного ПОИСКОВОГО дерева. // Постусловие: одна копия числа 42 добавлена в двоичный файл // дерево поиска.

Множественный выбор
Раздел 10.1
Введение
в Деревья

В поле вверху этого раздела есть дерево. Сколько листьев делает
это есть?
В поле вверху этого раздела есть дерево. Сколько из
у узлов есть хотя бы один брат?
В поле вверху этого раздела есть дерево.Какая ценность
хранится в родительском узле узла, содержащего 30?
А. 10
Б. 11
С. 14
Д. 40
E. Ничего из вышеперечисленного
В поле вверху этого раздела есть дерево. Сколько потомков
рут есть?
В поле вверху этого раздела есть дерево. Какая глубина
дерево?
В поле вверху этого раздела есть дерево.Сколько детей делает
рут есть?
Рассмотрим двоичное дерево в поле вверху этого раздела.
Какое утверждение является правильным?
A. Дерево не полное и не полное.
B. Дерево полное, но не полное.
C. Дерево полное, но не целое.
D. Дерево полное и законченное.
Какое минимальное количество узлов в полном двоичном дереве с глубиной 3?
А.3
Б. 4
С. 8
Д. 11
E. 15
Какое минимальное количество узлов в полном двоичном дереве с глубиной 3?
А. 3
Б. 4
С. 8
Д. 11
E. 15
Выберите одно верное утверждение.
A. Каждое двоичное дерево является полным или полным.
B. Каждое полное двоичное дерево также является полным двоичным деревом.
C. Каждое полное двоичное дерево также является полным двоичным деревом.
D. Никакое двоичное дерево не является одновременно полным и полным.
Предположим, что T — двоичное дерево с 14 узлами. Какая минимально возможная глубина
Т?
Выберите один оператор FALSE о двоичных деревьях:
A. Каждое двоичное дерево имеет хотя бы один узел.
B. Каждое непустое дерево имеет ровно один корневой узел.
C. Каждый узел имеет не более двух дочерних узлов.
D. Каждый некорневой узел имеет ровно одного родителя.
Множественный выбор
Раздел 10.2
Дерево
Представления
Рассмотрим binary_tree_node из Раздела 10.3.
Какое выражение указывает на то, что t представляет собой пустое дерево?
А.(t == NULL)
Б. (t-> data () == 0)
С. (t-> data () == NULL)
D. ((t-> left () == NULL) && (t-> right () == NULL))
Рассмотрим узел полного двоичного дерева, значение которого хранится в
data [i] для реализации массива. Если у этого узла есть правый дочерний элемент,
где будет храниться ценность правильного ребенка?
A. данные [i + 1]
B. данные [i + 2]
С.данные [2 * i + 1]
D. данные [2 * i + 2]
Множественный выбор
Раздел 10.3
Набор инструментов для узлов двоичного дерева
Сколько рекурсивных вызовов обычно происходит при реализации
функция tree_clear для двоичного дерева?
Предположим, что бинарное таксономическое дерево включает 8 животных. Что это
минимальное количество NONLEAF узлов в дереве?
Множественный выбор
Раздел 10.4
Дерево
Обходы
14 / \ 2 11 / \ / \ 1 3 10 30 / / 7 40
В поле вверху этого раздела есть дерево. Каков порядок
узлы, посещенные с использованием обхода предварительного заказа?
А. 1 2 3 7 10 11 14 30 40
Б. 1 2 3 14 7 10 11 40 30
С.1 3 2 7 10 40 30 11 14
Д. 14 2 1 3 11 10 7 30 40
В поле вверху этого раздела есть дерево. Каков порядок
узлы, посещенные с помощью обхода по порядку?
А. 1 2 3 7 10 11 14 30 40
Б. 1 2 3 14 7 10 11 40 30
В. 1 3 2 7 10 40 30 11 14
Д. 14 2 1 3 11 10 7 30 40
В поле вверху этого раздела есть дерево.Каков порядок
узлы, посещенные с помощью обхода после заказа?
А. 1 2 3 7 10 11 14 30 40
Б. 1 2 3 14 7 10 11 40 30
В. 1 3 2 7 10 40 30 11 14
Д. 14 2 1 3 11 10 7 30 40
Множественный выбор
Раздел 10.5
Двоичный поиск
Деревья
Рассмотрим это двоичное дерево поиска:
14 / \ 2 16 / \ 1 5 / 4
Допустим убираем рут, заменяя на что-то слева
поддерево.Какой будет новый рут?
А. 1
Б. 2
С. 4
Д. 5
E. 16

003

Структуры данных и другие объекты с использованием C ++

Майкл Мэйн
(main @ colorado.edu)

а также

Уолтер Сэвич
([email protected])
Спасибо за посещение
http://www.cs.colorado.edu/~main/questions/chap10q.html

Авторские права © 2000
Addison-Wesley Computer and Engineering Publishing Group
Основы сетевых технологий | IBM
Из этого введения в сети вы узнаете, как работают компьютерные сети, об архитектуре, используемой для проектирования сетей, и о том, как обеспечить их безопасность.
Что такое компьютерная сеть?
Компьютерная сеть состоит из двух или более компьютеров, которые соединены кабелем (проводным) или Wi-Fi (беспроводным) с целью передачи, обмена или совместного использования данных и ресурсов. Вы строите компьютерную сеть, используя оборудование (например, маршрутизаторы, коммутаторы, точки доступа и кабели) и программное обеспечение (например, операционные системы или бизнес-приложения).
Географическое положение часто определяет компьютерную сеть.Например, LAN (локальная сеть) соединяет компьютеры в определенном физическом пространстве, таком как офисное здание, тогда как WAN (глобальная сеть) может соединять компьютеры на разных континентах. Интернет — крупнейший пример глобальной сети, соединяющей миллиарды компьютеров по всему миру.
Вы можете дополнительно определить компьютерную сеть по протоколам, которые она использует для связи, физическому расположению ее компонентов, способам управления трафиком и ее назначению.
Компьютерные сети позволяют общаться в любых деловых, развлекательных и исследовательских целях.Интернет, онлайн-поиск, электронная почта, обмен аудио и видео, онлайн-торговля, потоковое вещание и социальные сети — все это существует благодаря компьютерным сетям.
Типы компьютерных сетей
По мере развития сетевых потребностей менялись и типы компьютерных сетей, удовлетворяющие этим потребностям. Вот наиболее распространенные и широко используемые типы компьютерных сетей:
LAN (локальная сеть): LAN соединяет компьютеры на относительно небольшом расстоянии, позволяя им обмениваться данными, файлами и ресурсами.Например, LAN может соединить все компьютеры в офисном здании, школе или больнице. Обычно локальные сети находятся в частной собственности и управляются.
WLAN (беспроводная локальная сеть): WLAN похожа на локальную сеть, но соединения между устройствами в сети выполняются по беспроводной сети.
WAN (глобальная сеть): Как следует из названия, WAN соединяет компьютеры на большой территории, например, от региона к региону или даже от континента к континенту.Интернет — это крупнейшая глобальная сеть, соединяющая миллиарды компьютеров по всему миру. Обычно вы видите модели коллективного или распределенного владения для управления WAN.
MAN (городская сеть): MAN обычно больше, чем LAN, но меньше, чем WAN. Города и государственные учреждения обычно владеют и управляют MAN.
PAN (персональная сеть): PAN обслуживает одного человека. Например, если у вас есть iPhone и Mac, вполне вероятно, что вы настроили PAN, который обменивается и синхронизирует контент — текстовые сообщения, электронные письма, фотографии и многое другое — на обоих устройствах.
SAN (сеть хранения данных): SAN — это специализированная сеть, которая обеспечивает доступ к хранилищу на уровне блоков — общей сети или облачному хранилищу, которое для пользователя выглядит и работает как накопитель, физически подключенный к компьютеру. (Для получения дополнительной информации о том, как SAN работает с блочным хранилищем, см. Блочное хранилище: полное руководство.)
CAN (сеть кампуса): CAN также называется корпоративной сетью.CAN больше LAN, но меньше WAN. CAN обслуживают такие объекты, как колледжи, университеты и бизнес-городки.
VPN (виртуальная частная сеть): VPN — это безопасное двухточечное соединение между двумя конечными точками сети (см. «Узлы» ниже). VPN устанавливает зашифрованный канал, по которому личность пользователя и учетные данные для доступа, а также любые передаваемые данные остаются недоступными для хакеров.
Важные термины и понятия
Ниже приведены некоторые общие термины, которые следует знать при обсуждении компьютерных сетей:
IP-адрес : IP-адрес — это уникальный номер, присваиваемый каждому устройству, подключенному к сети, которая использует Интернет-протокол для связи.Каждый IP-адрес идентифицирует хост-сеть устройства и местоположение устройства в хост-сети. Когда одно устройство отправляет данные другому, данные включают «заголовок», который включает IP-адрес отправляющего устройства и IP-адрес целевого устройства.
Узлы : Узел — это точка подключения внутри сети, которая может принимать, отправлять, создавать или хранить данные. Каждый узел требует, чтобы вы предоставили некоторую форму идентификации для получения доступа, например IP-адрес.Несколько примеров узлов включают компьютеры, принтеры, модемы, мосты и коммутаторы. Узел — это, по сути, любое сетевое устройство, которое может распознавать, обрабатывать и передавать информацию любому другому сетевому узлу.
Маршрутизаторы : Маршрутизатор — это физическое или виртуальное устройство, которое отправляет информацию, содержащуюся в пакетах данных, между сетями. Маршрутизаторы анализируют данные в пакетах, чтобы определить наилучший способ доставки информации к месту назначения. Маршрутизаторы пересылают пакеты данных, пока они не достигнут узла назначения.
Коммутаторы : Коммутатор — это устройство, которое соединяет другие устройства и управляет межузловой связью в сети, гарантируя, что пакеты данных достигают конечного пункта назначения. Пока маршрутизатор отправляет информацию между сетями, коммутатор отправляет информацию между узлами в одной сети. При обсуждении компьютерных сетей «переключение» относится к тому, как данные передаются между устройствами в сети. Три основных типа переключения следующие:
Коммутация цепей , которая устанавливает выделенный канал связи между узлами в сети.Этот выделенный путь гарантирует, что во время передачи будет доступна вся полоса пропускания, что означает, что никакой другой трафик не может проходить по этому пути.
Коммутация пакетов включает разбиение данных на независимые компоненты, называемые пакетами, которые из-за своего небольшого размера предъявляют меньше требований к сети. Пакеты проходят через сеть до конечного пункта назначения.
Коммутация сообщений полностью отправляет сообщение от исходного узла, перемещаясь от коммутатора к коммутатору, пока не достигнет своего узла назначения.
Порты : порт определяет конкретное соединение между сетевыми устройствами. Каждый порт обозначается номером. Если вы считаете IP-адрес сопоставимым с адресом отеля, то порты — это номера или апартаменты в этом отеле. Компьютеры используют номера портов, чтобы определить, какое приложение, служба или процесс должны получать определенные сообщения.
Типы сетевых кабелей : Наиболее распространенными типами сетевых кабелей являются витая пара Ethernet, коаксиальный и оптоволоконный.Выбор типа кабеля зависит от размера сети, расположения сетевых элементов и физического расстояния между устройствами.
Примеры компьютерных сетей
Проводное или беспроводное соединение двух или более компьютеров с целью совместного использования данных и ресурсов образуют компьютерную сеть. Сегодня почти каждое цифровое устройство принадлежит компьютерной сети.
В офисе вы и ваши коллеги можете использовать общий доступ к принтеру или к системе группового обмена сообщениями.Вычислительная сеть, которая позволяет это сделать, скорее всего, будет LAN или локальной сетью, которая позволяет вашему отделу совместно использовать ресурсы.
Правительство города может управлять общегородской сетью камер наблюдения, которые отслеживают движение транспорта и инциденты. Эта сеть будет частью MAN или городской сети, которая позволит городскому персоналу службы экстренной помощи реагировать на дорожно-транспортные происшествия, сообщать водителям об альтернативных маршрутах движения и даже отправлять штрафы водителям, которые едут на красный свет.
The Weather Company работала над созданием одноранговой ячеистой сети, которая позволяет мобильным устройствам напрямую связываться с другими мобильными устройствами, не требуя подключения к Wi-Fi или сотовой связи.Проект Mesh Network Alerts позволяет доставлять жизненно важную информацию о погоде миллиардам людей даже без подключения к Интернету.
Компьютерные сети и Интернет
Интернет — это сеть сетей, соединяющая миллиарды цифровых устройств по всему миру. Стандартные протоколы обеспечивают связь между этими устройствами. Эти протоколы включают протокол передачи гипертекста («http» перед всеми адресами веб-сайтов). Интернет-протокол (или IP-адреса) — это уникальные идентификационные номера, необходимые для каждого устройства, имеющего доступ к Интернету.IP-адреса сопоставимы с вашим почтовым адресом, предоставляя уникальную информацию о местоположении, чтобы информация могла быть доставлена правильно.
Интернет-провайдеры (ISP) и сетевые сервис-провайдеры (NSP) предоставляют инфраструктуру, которая позволяет передавать пакеты данных или информации через Интернет. Не каждый бит информации, отправляемой через Интернет, попадает на все устройства, подключенные к Интернету. Это комбинация протоколов и инфраструктуры, которая сообщает информацию, куда именно нужно идти.
Как они работают?
Компьютерные сети соединяют такие узлы, как компьютеры, маршрутизаторы и коммутаторы, с помощью кабелей, оптоволокна или беспроводных сигналов. Эти соединения позволяют устройствам в сети обмениваться информацией и ресурсами, а также обмениваться ими.
Сети
следуют протоколам, которые определяют способ отправки и получения сообщений. Эти протоколы позволяют устройствам обмениваться данными. Каждое устройство в сети использует Интернет-протокол или IP-адрес, строку чисел, которая однозначно идентифицирует устройство и позволяет другим устройствам распознавать его.
Маршрутизаторы
— это виртуальные или физические устройства, которые облегчают обмен данными между различными сетями. Маршрутизаторы анализируют информацию, чтобы определить наилучший способ доставки данных к месту назначения. Коммутаторы подключают устройства и управляют межузловой связью внутри сети, гарантируя, что пакеты информации, передаваемые по сети, достигают конечного пункта назначения.
Архитектура
Архитектура компьютерной сети определяет физическую и логическую структуру компьютерной сети.В нем описывается, как компьютеры организованы в сети и какие задачи им назначены. Компоненты сетевой архитектуры включают оборудование, программное обеспечение, среду передачи (проводную или беспроводную), топологию сети и протоколы связи.
Основные типы сетевой архитектуры
Существует два типа сетевой архитектуры: одноранговая (P2P) и клиент / сервер . В архитектуре P2P два или более компьютера соединены как «одноранговые узлы», что означает, что они имеют одинаковую мощность и привилегии в сети.P2P-сеть не требует центрального сервера для координации. Вместо этого каждый компьютер в сети действует как клиент (компьютер, которому требуется доступ к службе) и как сервер (компьютер, который обслуживает потребности клиента, обращающегося к службе). Каждый одноранговый узел делает некоторые из своих ресурсов доступными для сети, разделяя хранилище, память, пропускную способность и вычислительную мощность.
В сети клиент / сервер центральный сервер или группа серверов управляют ресурсами и предоставляют услуги клиентским устройствам в сети.Клиенты в сети общаются с другими клиентами через сервер. В отличие от модели P2P, клиенты в архитектуре клиент / сервер не разделяют свои ресурсы. Этот тип архитектуры иногда называют многоуровневой моделью, потому что он разработан с несколькими уровнями или уровнями.
Топология сети
Сетевая топология — это то, как устроены узлы и ссылки в сети. Сетевой узел — это устройство, которое может отправлять, получать, хранить или пересылать данные. Сетевой канал соединяет узлы и может быть кабельным или беспроводным.
Понимание типов топологии обеспечивает основу для построения успешной сети. Существует несколько топологий, но наиболее распространенными являются шина, кольцо, звезда и сетка:
Топология сети с шиной — это когда каждый сетевой узел напрямую подключен к основному кабелю.
В кольцевой топологии узлы соединены в петлю, поэтому каждое устройство имеет ровно двух соседей. Смежные пары подключаются напрямую; несмежные пары связаны косвенно через несколько узлов.
В звездообразной топологии сети все узлы подключены к одному центральному концентратору, и каждый узел косвенно подключен через этот концентратор.
Ячеистая топология определяется перекрывающимися соединениями между узлами. Вы можете создать топологию полной сетки, в которой каждый узел в сети подключен ко всем остальным узлам. Вы также можете создать частичную топологию сетки, в которой только некоторые узлы подключены друг к другу, а некоторые подключены к узлам, с которыми они обмениваются наибольшим объемом данных.Полная ячеистая топология может быть дорогостоящей и трудоемкой для выполнения, поэтому ее часто резервируют для сетей, требующих высокой избыточности. Частичная сетка обеспечивает меньшую избыточность, но более экономична и проста в исполнении.
Безопасность
Безопасность компьютерной сети защищает целостность информации, содержащейся в сети, и контролирует, кто имеет доступ к этой информации. Политики сетевой безопасности уравновешивают необходимость предоставления услуг пользователям с необходимостью контролировать доступ к информации.
Есть много точек входа в сеть. Эти точки входа включают оборудование и программное обеспечение, из которых состоит сама сеть, а также устройства, используемые для доступа к сети, такие как компьютеры, смартфоны и планшеты. Из-за этих точек входа сетевая безопасность требует использования нескольких методов защиты. Защита может включать брандмауэры — устройства, которые отслеживают сетевой трафик и предотвращают доступ к частям сети на основе правил безопасности.
Процессы аутентификации пользователей с помощью идентификаторов пользователей и паролей обеспечивают еще один уровень безопасности.Безопасность включает в себя изоляцию сетевых данных, так что служебная или личная информация труднее получить доступ, чем менее важная информация. Другие меры сетевой безопасности включают обеспечение регулярного обновления аппаратного и программного обеспечения и исправлений, информирование пользователей сети об их роли в процессах безопасности и постоянную осведомленность о внешних угрозах, создаваемых хакерами и другими злоумышленниками. Сетевые угрозы постоянно развиваются, что делает безопасность сети бесконечным процессом.
Использование общедоступного облака также требует обновления процедур безопасности для обеспечения постоянной безопасности и доступа.Для безопасного облака требуется защищенная базовая сеть.
Прочтите о пяти основных рекомендациях (PDF, 298 КБ) по обеспечению безопасности общедоступного облака.
Ячеистые сети
Как отмечалось выше, ячеистая сеть — это тип топологии, в котором узлы компьютерной сети подключаются к как можно большему количеству других узлов. В этой топологии узлы взаимодействуют для эффективной маршрутизации данных к месту назначения. Эта топология обеспечивает большую отказоустойчивость, поскольку в случае отказа одного узла существует множество других узлов, которые могут передавать данные.Mesh-сети самонастраиваются и самоорганизуются, ища самый быстрый и надежный путь для отправки информации.
Тип ячеистых сетей
Есть два типа ячеистых сетей — полная и частичная:
В полносвязной топологии каждый сетевой узел подключается ко всем остальным сетевым узлам, обеспечивая высочайший уровень отказоустойчивости. Однако выполнение этого стоит дороже. В топологии с частичной сеткой подключаются только некоторые узлы, обычно те, которые обмениваются данными наиболее часто.
Беспроводная ячеистая сеть может состоять из десятков и сотен узлов. Этот тип сети подключается к пользователям через точки доступа, расположенные на большой территории.
Балансировщики нагрузки и сети
Балансировщики нагрузки
эффективно распределяют задачи, рабочие нагрузки и сетевой трафик между доступными серверами. Думайте о балансировщиках нагрузки, как о диспетчере воздушного движения в аэропорту. Балансировщик нагрузки наблюдает за всем входящим в сеть трафиком и направляет его к маршрутизатору или серверу, который лучше всего оборудован для управления им.Цели балансировки нагрузки — избежать перегрузки ресурсов, оптимизировать доступные ресурсы, улучшить время отклика и максимизировать пропускную способность.
Полный обзор балансировщиков нагрузки см. В разделе «Балансировка нагрузки: полное руководство».
Сети доставки контента
Сеть доставки контента (CDN) — это распределенная серверная сеть, которая доставляет временно сохраненные или кэшированные копии контента веб-сайта пользователям в зависимости от их географического положения. CDN хранит этот контент в распределенных местах и предоставляет его пользователям, чтобы сократить расстояние между посетителями вашего веб-сайта и сервером вашего веб-сайта.Кэширование контента ближе к конечным пользователям позволяет вам обслуживать контент быстрее и помогает веб-сайтам лучше охватить глобальную аудиторию. Сети CDN защищают от скачков трафика, уменьшают задержку, уменьшают потребление полосы пропускания, ускоряют время загрузки и уменьшают влияние взломов и атак, создавая слой между конечным пользователем и инфраструктурой вашего веб-сайта.
Потоковое мультимедиа в реальном времени, мультимедиа по запросу, игровые компании, создатели приложений, сайты электронной коммерции — по мере роста цифрового потребления все больше владельцев контента обращаются к CDN, чтобы лучше обслуживать потребителей контента.
Компьютерные сетевые решения и IBM
Компьютерные сетевые решения помогают предприятиям увеличивать трафик, делать пользователей счастливыми, защищать сеть и легко предоставлять услуги. Лучшее компьютерное сетевое решение — это обычно уникальная конфигурация, основанная на вашем конкретном виде бизнеса и потребностях.
Сети доставки контента (CDN), балансировщики нагрузки и сетевая безопасность — все упомянутые выше — являются примерами технологий, которые могут помочь предприятиям создавать оптимальные компьютерные сетевые решения.IBM предлагает дополнительные сетевые решения, в том числе:
Устройства шлюза — это устройства, которые дают вам расширенный контроль над сетевым трафиком, позволяют повысить производительность вашей сети и повысить безопасность вашей сети. Управляйте своими физическими и виртуальными сетями для маршрутизации нескольких VLAN, межсетевых экранов, VPN, формирования трафика и т. Д.
Direct Link защищает и ускоряет передачу данных между частной инфраструктурой, мультиоблаком и IBM Cloud.
Cloud Internet Services — это возможности обеспечения безопасности и производительности, предназначенные для защиты общедоступного веб-контента и приложений до того, как они попадут в облако.Получите защиту от DDoS-атак, глобальную балансировку нагрузки и набор функций безопасности, надежности и производительности, предназначенных для защиты общедоступного веб-контента и приложений до того, как они попадут в облако.
Сетевые службы в IBM Cloud предоставляют сетевые решения для увеличения трафика, удовлетворения ваших пользователей и легкого предоставления ресурсов по мере необходимости.
Развивайте навыки работы в сети и получите профессиональную сертификацию IBM на курсах профессиональной программы Cloud Site Reliability Engineers (SRE).
Зарегистрируйтесь в IBMid и создайте свою учетную запись IBM Cloud.
Страница не найдена | MIT
Перейти к содержанию ↓
Образование
Исследовать
Инновации
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О MIT
Подробнее ↓
Прием + помощь
Студенческая жизнь
Новости
Выпускников
О MIT
Меню ↓
Поиск
Меню
Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!
Что вы ищете?
Увидеть больше результатов
Предложения или отзывы?
Узловой анализ
Узловой анализ
Найдите эффективный метод определения напряжения в цепи, используя метод узлового анализа, применяя KCL в данном узле.

Процедура решения :
Определите все экстраординарные узлы, выбрав один из них в качестве опорного узла (землю), и назначьте узловые напряжения остальным необычным узлам (N-1). Необычный узел
— это подключенный
до трех и более
элементы вместе
Примените форму KCL, требующую, чтобы сумма всего тока, выходящего из узла, была равна нулю в каждом узле.
Решите (N-1) независимое одновременное уравнение, чтобы определить узловые напряжения.
Пример 1: V ₁, V ₂, V ₃ как исключительные узлы, V ₃ относится к (заземлению)
г. Применить KCL на узлах 1 и 2
Узел 1
Следовательно,
Узел 2
i ₄, i ₅ и i ₆
Следовательно,
Решение одновременных уравнений
Решение одновременного уравнения
Пример 2: Применение узлового анализа для определения узлового напряжения V в следующей схеме
Пример 3: Для следующей цепи:
Найдите общее значение резистора R _T
Найдите текущий i
Найдите напряжение на отдельных резисторах
Проверить закон напряжения Кирхгофа
Пример 4: Для следующей цепи:
Найти V ₁
Найти V ₂
Проверить закон напряжения Кирхгофа вокруг замкнутого контура
Практические задачи :
(Щелкните изображение, чтобы просмотреть решение)
Задача 1: Используйте узловой анализ для определения i ₀ и V _R.
Просмотреть решение
Раствор:
В ₁
В ₂
Использование Wolfram Alpha:
Задача 2: Используя узловой анализ, получите V ₀ по следующей схеме.
Просмотреть решение
Проблема 3: Найдите приложенное напряжение к следующей цепи, используя предоставленную информацию
Просмотреть решение
Раствор:
Задача 4: Найдите значение резистора R , используя предоставленную информацию
Просмотреть решение
Задача 5 : Найти V _x
Просмотреть решение
Операции:
.

а. B, C и D	г.A, E и F	г. А только
г. C только	e. все точки