Примеры теорема пифагора: формула, доказательство и примеры решений — ошкольное образовательное учреждение № 4 «Алёнушка»

{2}$ было известно уже египтянам ещё около
2300 г. до н.э. По мнению ученого, строители строили тогда прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте приводится приближённое вычисление гипотенузы равнобедренного
прямоугольного треугольника.

Содержание

Теорема Пифагора — формула, доказательство, задачи

Основные понятия

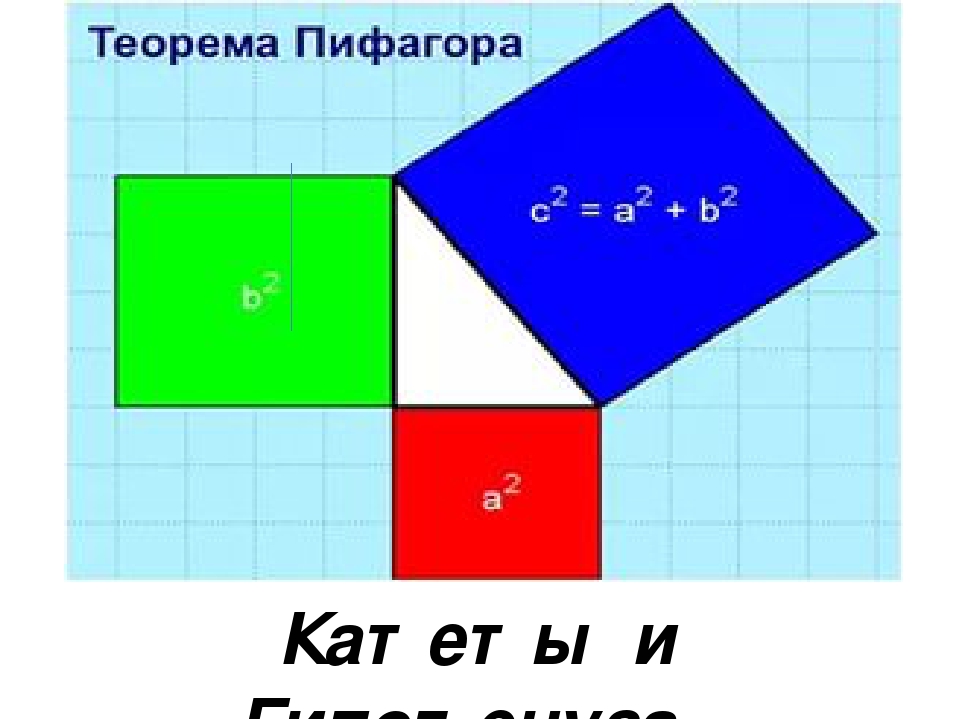
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

a² + b² = c²,

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

a = √c²− b²
b = √c² − a²
c = √a² + b²

Запоминаем

в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.

Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:

если c²< a²+ b² , значит угол, обращенный к стороне c, является острым.
если c²= a²+ b² , значит угол, обращенный к стороне c, является прямым.
если c²> a²+b² , значит угол, обращенный к стороне c, является тупым.

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a² + b² = c².

Пошаговое доказательство:

Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

∠ACB =∠CHA = 90º,

∠A — общий.

Также прямоугольная фигура ∆CBH подобна ∆ABC:

∠ACB =∠CHB = 90º,

∠B — общий.

Введем новые обозначения: BC = a, AC = b, AB = c.

Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

Значит a²= c * HB, b² = c * AH.
Сложим полученные равенства:

a²+ b²= c * HB + c * AH

a²+ b²= c * (HB + AH)

a²+ b²= c * AB

a²+ b²= c * c

a² + b² = c²

Теорема доказана.

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такая фигура является прямоугольной.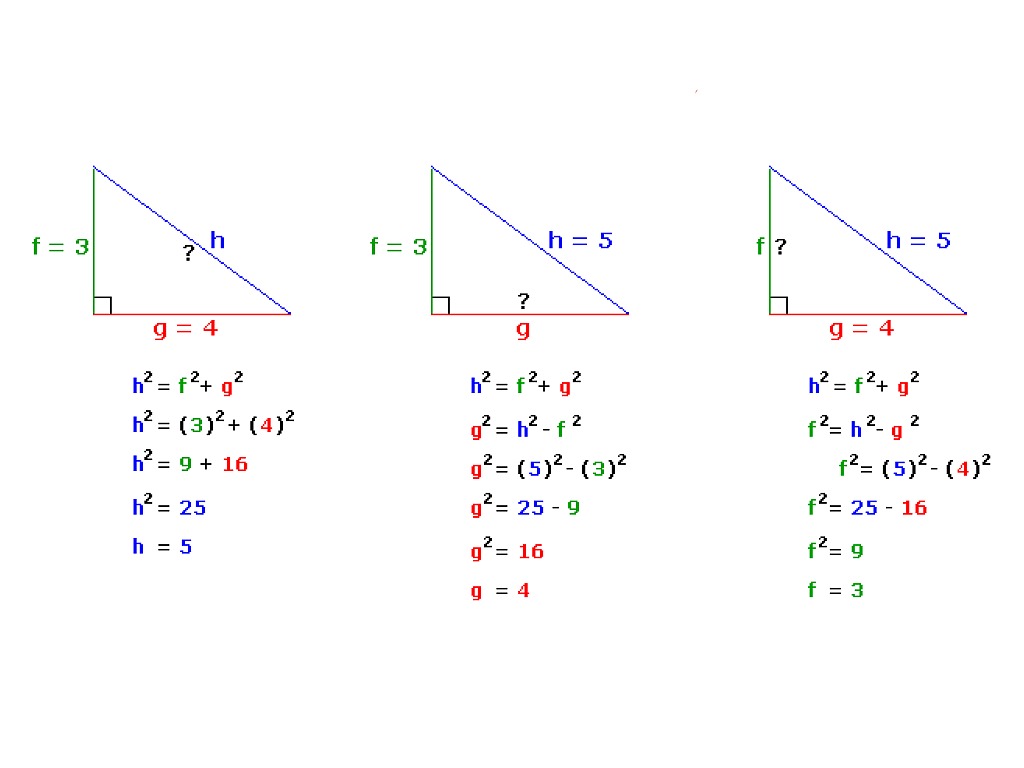

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

Построим прямой угол с вершиной в точке C₁.
Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

Проведём отрезок A₁B₁.
Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁² = A₁C₁² + B₁C₁².
Таким образом получится:

Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

C₁A₁ = CA и C₁B₁ = CB по результату построения,
A₁B₁ = AB по доказанному результату.

Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см.

Какое значение у гипотенузы?

Как решаем:

значит c²= a²+ b² = 6²+ 10² = 36 + 100 = 136

Ответ: 11,7.

Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?

Как решаем:

Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

11²= 8²+ 9²

121 ≠ 146

Ответ: треугольник не является прямоугольным.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до теоремы Пифагора — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Теорема Пифагора — формула с доказательством

Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Вы узнаете, как доказать теорему, формула Пифагора и как решать задачи.

История теоремы

Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.

Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.

Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище – это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.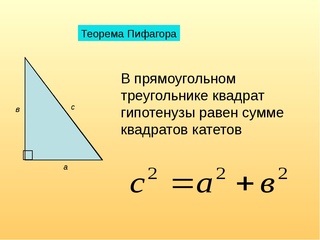

Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.

Нужна работа? Есть решение!

Более 70 000 экспертов: преподавателей и доцентов вузов готовы помочь вам в написании работы прямо сейчас.

Подробнее Гарантии Отзывы

Теорема Пифагора, формула

Как уже говорилось, есть много разнообразных доказательств теоремы с разносторонними математическими подходами. Однако, более часто используют теоремы, связанные с площадями.

Построим на треугольнике квадраты (синий, зеленый, красный)

То есть сумма площадей квадратов, построенных на катетах равняется площади квадрата, построенном на гипотенузе. Соответственно, площади этих квадратов равны – . Это и есть геометрическое объяснение Пифагора.

Доказательство теоремы методом площадей: 1 способ

Докажем, что .

Рассмотрим всё тот же треугольник с катетами a, b и гипотенузой c.

Достраиваем прямоугольный треугольник до квадрата. От катета “а” продолжаем линию вверх на расстояние катета “b” (красная линия).
Далее ведём линию нового катета “а” вправо (зелёная линия).
Два катета соединяем гипотенузой “с”.

Получается такой же треугольник, только перевёрнутый.

Аналогично строим и с другой стороны: от катета “а” проводим линию катета “b” и вниз “а” и “b” А снизу от катета “b” проводим линию катета “а”. В центре от каждого катета провели гипотенузы “с”. Таким образом гипотенузы образовали квадрат в центре.

Этот квадрат состоит из 4-х одинаковых треугольников. А площадь каждого прямоугольного треугольника = половина произведения его катетов. Соответственно, . А площадь квадрата в центре = , так как все 4 гипотенузы со стороной . Стороны четырёхугольника равны, а углы прямые. Как нам доказать, что углы прямые? Очень просто. Возьмём всё тот же квадрат:

Мы знаем, что эти два угла, показаны на рисунке, являются 90 градусам. Так как треугольники равны, значит следующий угол катета “b” равен предыдущему катету “b”:

Сумма этих двух углов = 90 градусов. Соответственно, предыдущий угол тоже 90 градусов. Конечно же, аналогично и с другой стороны. Соответственно, у нас действительно квадрат с прямыми углами.

Так как острые углы прямоугольного треугольника в общей сложности равняются 90 градусам, то угол четырёхугольника так же будет равен 90 градусов, ведь 3 угла в сумме = 180 градусов.

Соответственно, площадь квадрата складывается из четырёх площадей одинаковых прямоугольных треугольников и площади квадрата, который образован гипотенузами.

Таким образом, получили квадрат со стороной . Мы знаем, что площадь квадрата со стороной – это будет квадрат его стороны. То есть . Этот квадрат состоит из четырёх одинаковых треугольников.

Запишем: .
Далее смотрим, что площадь прямоугольного треугольника – это половина произведения его катетов. Поэтому дальше записываем:т
Также надо прибавить площадь квадрата, который находится в центре между треугольниками со стороной “с”. И теперь получим:

Раскрываем скобки и получаем:
Сокращаем . Получается:

И это значит, что мы доказали теорему Пифагора.

ВАЖНО!!! Если находим гипотенузу, тогда складываем два катета, а затем ответ выводим из корня. При нахождении одного из катетов: из квадрата длины второго катета вычитаем квадрат длины гипотенузы и находим квадратный корень.

Примеры решения задач

Пример 1

Задача

Дано: прямоугольный треугольник с катетами 4 и 5.

Найдите гипотенузу. Пока её обозначим “с”

Решение

Сумма квадратов катетов равняется квадрату гипотенузы. В нашем случае – .

Воспользуемся теоремой Пифагора:

Итак, , а . Катеты в сумме получают 41.

Тогда . То есть квадрат гипотенузы равен 41.

Квадрат числа 41 = 6,4.

Мы нашли гипотенузу.

Ответ

Гипотенуза = 6,4

Пример 2

Задача

Дано: прямоугольный треугольник, где гипотенуза = 12, один катет = 10

Найдите второй катет.

Решение

Обозначим неизвестный катет – b.

Воспользуемся теоремой Пифагора:

, а

Запишем:

Находим

Если , тогда просто

Ответ

Второй катет (b) равен 6,6.

Заключение

Итак, мы рассмотрели теорему Пифагора, смогли привести ее доказательство и привели несколько примеров задач и их решений.

Запомните раз и навсегда: квадраты гипотенузы равен суммы квадратов катетов: (это вся теорема Пифагора).

Теорема Пифагора обновлено: 16 апреля, 2020 автором: Научные Статьи. Ру

Теорема Пифагора, формула и доказательство

ТЕОРЕМА

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Геометрическая формулировка теоремы Пифагора

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах (рис. 1).

Доказательство теоремы Пифагора

Площадь прямоугольного треугольника вычисляется по формуле

С другой стороны для вычисления площади произвольного треугольника справедлива формула: . В этой формуле – полупериметр , а – радиус вписанной окружности и для прямоугольника он равен . Далее приравнивая правые части обеих формул для площади треугольника, получим

Что и требовалось доказать.

Примеры решения задач

ПРИМЕР 1

Задание

Катеты прямоугольного треугольника равны 12 см и 5 см.

Найти гипотенузу.

Решение

Обозначим катеты см и см, а гипотенузу – . По теореме Пифагора гипотенуза будет равна

Подставляя длины катетов, получим

(см)

Ответ

Гипотенуза прямоугольного треугольника равна 13 см

ПРИМЕР 2

Задание

Диагональ прямоугольника равна 5 см, а одна из его сторон – 3 см. Найти вторую сторону прямоугольника.

Решение

Сделаем рисунок (рис. 2).

Обозначим см, см. Рассмотрим прямоугольный треугольник . Запишем для него теорему Пифагора:

Выразим из последнего равенства неизвестную сторону :

Подставляя известные значения сторон, получим

(см)

Ответ

Вторая сторона прямоугольника равна 4 см

Разные способы доказательства теоремы Пифагора: примеры, описание и отзывы

В одном можно быть уверенным на все сто процентов, что на вопрос, чему равен квадрат гипотенузы, любой взрослый человек смело ответит: «Сумме квадратов катетов». Эта теорема прочно засела в сознании каждого образованного человека, но достаточно лишь попросить кого-либо ее доказать, и тут могут возникнуть сложности. Поэтому давайте вспомним и рассмотрим разные способы доказательства теоремы Пифагора.

Краткий обзор биографии

Теорема Пифагора знакома практически каждому, но почему-то биография человека, который произвел ее на свет, не так популярна. Это поправимо. Поэтому прежде чем изучить разные способы доказательства теоремы Пифагора, нужно кратко познакомиться с его личностью.

Пифагор – философ, математик, мыслитель родом из Древней Греции. Сегодня очень сложно отличить его биографию от легенд, которые сложились в память об этом великом человеке. Но как следует из трудов его последователей, Пифагор Самосский родился на острове Самос. Его отец был обычный камнерез, а вот мать происходила из знатного рода.

Судя по легенде, появление на свет Пифагора предсказала женщина по имени Пифия, в чью честь и назвали мальчика. По ее предсказанию рожденный мальчик должен был принести много пользы и добра человечеству. Что вообще-то он и сделал.

Рождение теоремы

В юности Пифагор переехал с острова Самос в Египет, чтобы встретиться там с известными египетскими мудрецами. После встречи с ними он был допущен к обучению, где и познал все великие достижения египетской философии, математики и медицины.

Вероятно, именно в Египте Пифагор вдохновился величеством и красотой пирамид и создал свою великую теорию. Это может шокировать читателей, но современные историки считают, что Пифагор не доказывал свою теорию. А лишь передал свое знание последователям, которые позже и завершили все необходимые математические вычисления.

Как бы там ни было, сегодня известна не одна методика доказательства данной теоремы, а сразу несколько. Сегодня остается лишь гадать, как именно древние греки производили свои вычисления, поэтому здесь рассмотрим разные способы доказательства теоремы Пифагора.

Теорема Пифагора

Прежде чем начинать какие-либо вычисления, нужно выяснить, какую теорию предстоит доказать. Теорема Пифагора звучит так: «В треугольнике, у которого один из углов равен 90^о, сумма квадратов катетов равна квадрату гипотенузы».

Всего существует 15 разных способов доказательства теоремы Пифагора. Это достаточно большая цифра, поэтому уделим внимание самым популярным из них.

Способ первый

Сначала обозначим, что нам дано. Эти данные будут распространяться и на другие способы доказательств теоремы Пифагора, поэтому стоит сразу запомнить все имеющееся обозначения.

Допустим, дан прямоугольный треугольник, с катетами а, в и гипотенузой, равной с. Первый способ доказательства основывается на том, что из прямоугольного треугольника нужно дорисовать квадрат.

Чтобы это сделать, нужно к катету длиной а дорисовать отрезок равный катету в, и наоборот. Так должно получиться две равные стороны квадрата. Остается только нарисовать две параллельные прямые, и квадрат готов.

Внутри получившейся фигуры нужно начертить еще один квадрат со стороной равной гипотенузе исходного треугольника. Для этого от вершин ас и св нужно нарисовать два параллельных отрезка равных с. Таким образом, получиться три стороны квадрата, одна из которых и есть гипотенуза исходного прямоугольного треугольники. Остается лишь дочертить четвертый отрезок.

На основании получившегося рисунка можно сделать вывод, что площадь внешнего квадрата равна (а+в)². Если заглянуть внутрь фигуры, можно увидеть, что помимо внутреннего квадрата в ней имеется четыре прямоугольных треугольника. Площадь каждого равна 0,5ав.

Поэтому площадь равна: 0,5ав+с²=2ав+с²

Отсюда (а+в)²=2ав+с²

И, следовательно, с²=а²+в²

Теорема доказана.

Способ два: подобные треугольники

Данная формула доказательства теоремы Пифагора была выведена на основании утверждения из раздела геометрии о подобных треугольниках. Оно гласит, что катет прямоугольного треугольника – среднее пропорциональное для его гипотенузы и отрезка гипотенузы, исходящего из вершины угла 90^о.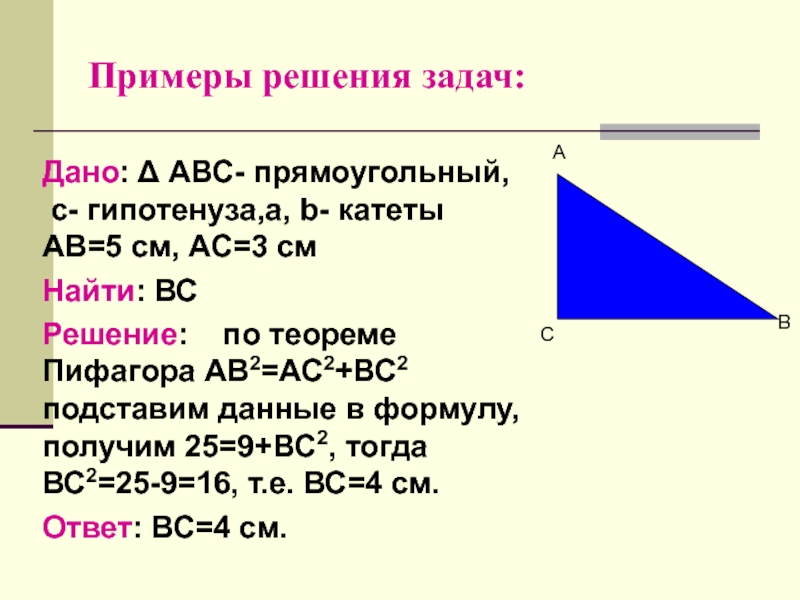

Исходные данные остаются те же, поэтому начнем сразу с доказательства. Проведем перпендикулярный стороне АВ отрезок СД. Основываясь на вышеописанном утверждении катеты треугольников равны:

АС=√АВ*АД, СВ=√АВ*ДВ.

Чтобы ответить на вопрос, как доказать теорему Пифагора, доказательство нужно проложить возведением в квадрат обоих неравенств.

АС²=АВ*АД и СВ²=АВ*ДВ

Теперь нужно сложить получившиеся неравенства.

АС²+ СВ²=АВ*(АД*ДВ), где АД+ДВ=АВ

Получается, что:

АС²+ СВ²=АВ*АВ

И, следовательно:

АС²+ СВ²=АВ²

Доказательство теоремы Пифагора и различные способы ее решения нуждаются в разностороннем подходе к данной задаче. Однако этот вариант является одним из простейших.

Еще одна методика расчетов

Описание разных способов доказательства теоремы Пифагора могут ни о чем не сказать, до тех самых пор пока самостоятельно не приступишь к практике. Многие методики предусматривают не только математические расчеты, но и построение из исходного треугольника новых фигур.

В данном случае необходимо от катета ВС достроить еще один прямоугольный треугольник ВСД. Таким образом, теперь имеется два треугольника с общим катетом ВС.

Зная, что площади подобных фигур имеют соотношение как квадраты их сходных линейных размеров, то:

S_авс *^{с²— S_авд*в² =S_авд*а²— S_всд*а²}

S_авс*(с²-в²)=а²*(S_авд-S_всд)

с²-в²=а²

с²=а²+в²

Поскольку из разных способов доказательств теоремы Пифагора для 8 класса этот вариант едва ли подойдет, можно воспользоваться следующей методикой.

Самый простой способ доказать теорему Пифагора. Отзывы

Как полагают историки, этот способ был впервые использован для доказательства теоремы еще в древней Греции. Он является самым простым, так как не требует абсолютно никаких расчетов. Если правильно начертить рисунок, то доказательство утверждения, что а²+в²=с², будет видно наглядно.

Условия для данного способа будет немного отличаться от предыдущего. Чтобы доказать теорему, предположим, что прямоугольный треугольник АВС – равнобедренный.

Гипотенузу АС принимаем за сторону квадрата и дочерчиваем три его стороны. Кроме этого необходимо провести две диагональные прямые в получившемся квадрате. Таким образом, чтобы внутри него получилось четыре равнобедренных треугольника.

К катетам АВ и СВ так же нужно дочертить по квадрату и провести по одной диагональной прямой в каждом из них. Первую прямую чертим из вершины А, вторую – из С.

Теперь нужно внимательно всмотреться в получившийся рисунок. Поскольку на гипотенузе АС лежит четыре треугольника, равные исходному, а на катетах по два, это говорит о правдивости данной теоремы.

Кстати, благодаря данной методике доказательства теоремы Пифагора и появилась на свет знаменитая фраза: «Пифагоровы штаны во все стороны равны».

Доказательство Дж. Гарфилда

Джеймс Гарфилд – двадцатый президент Соединенных Штатов Америки. Кроме того, что он оставил свой след в истории как правитель США, он был еще и одаренным самоучкой.

В начале своей карьеры он был обычным преподавателем в народной школе, но вскоре стал директором одного из высших учебных заведений. Стремление к саморазвитию и позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения выглядит следующим образом.

Сначала нужно начертить на листе бумаги два прямоугольных треугольника таким образом, чтобы катет одного из них был продолжением второго. Вершины этих треугольников нужно соединить, чтобы в конечном итоге получилась трапеция.

Как известно, площадь трапеции равна произведению полусуммы ее оснований на высоту.

S=а+в/2 * (а+в)

Если рассмотреть получившуюся трапецию, как фигуру, состоящую из трех треугольников, то ее площадь можно найти так:

S=ав/2 *2 + с²/2

Теперь необходимо уравнять два исходных выражения

2ав/2 + с/2=(а+в)²/2

с²=а²+в²

О теореме Пифагора и способах ее доказательства можно написать не один том учебного пособия. Но есть ли в нем смысл, когда эти знания нельзя применить на практике?

Практическое применение теоремы Пифагора

К сожалению, в современных школьных программах предусмотрено использование данной теоремы только в геометрических задачах. Выпускники скоро покинут школьные стены, так и не узнав, а как они могут применить свои знания и умения на практике.

На самом же деле использовать теорему Пифагора в своей повседневной жизни может каждый. Причем не только в профессиональной деятельности, но и в обычных домашних делах. Рассмотрим несколько случаев, когда теорема Пифагора и способы ее доказательства могут оказаться крайне необходимыми.

Связь теоремы и астрономии

Казалось бы, как могут быть связаны звезды и треугольники на бумаге. На самом же деле астрономия – это научная сфера, в которой широко используется теорема Пифагора.

Например, рассмотрим движение светового луча в космосе. Известно, что свет движется в обе стороны с одинаковой скоростью. Траекторию АВ, которой движется луч света назовем l. А половину времени, которое необходимо свету, чтобы попасть из точки А в точку Б, назовем t. И скорость луча – c. Получается, что: c*t=l

Если посмотреть на этот самый луч из другой плоскости, например, из космического лайнера, который движется со скоростью v, то при таком наблюдении тел их скорость изменится. При этом даже неподвижные элементы станут двигаться со скоростью v в обратном направлении.

Допустим, комический лайнер плывет вправо. Тогда точки А и В, между которыми мечется луч, станут двигаться влево. Причем, когда луч движется от точки А в точку В, точка А успевает переместиться и, соответственно, свет уже прибудет в новую точку С. Чтобы найти половину расстояния, на которое сместилась точка А, нужно скорость лайнера умножить на половину времени путешествия луча (t’).

d= t’*v

А чтобы найти, какое расстояние за это время смог пройти луч света, нужно обозначить половину пути новой буковой s и получить следующее выражение:

s=c* t’

Если представить, что точки света С и В, а также космический лайнер – это вершины равнобедренного треугольника, то отрезок от точки А до лайнера разделит его на два прямоугольных треугольника. Поэтому благодаря теореме Пифагора можно найти расстояние, которое смог пройти луч света.

s² =l² + d²

Этот пример, конечно, не самый удачный, так как только единицам может посчастливиться опробовать его на практике. Поэтому рассмотрим более приземленные варианты применения этой теоремы.

Радиус передачи мобильного сигнала

Современную жизнь уже невозможно представить без существования смартфонов. Но много ли было бы от них прока, если бы они не могли соединять абонентов посредством мобильной связи?!

Качество мобильной связи напрямую зависит от того, на какой высоте находиться антенна мобильного оператора. Для того чтобы вычислить, каком расстоянии от мобильной вышки телефон может принимать сигнал, можно применить теорему Пифагора.

Допустим, нужно найти приблизительную высоту стационарной вышки, чтобы она могла распространять сигнал в радиусе 200 километров.

АВ (высота вышки) = х;

ВС (радиус передачи сигнала) = 200 км;

ОС (радиус земного шара) = 6380 км;

Отсюда

ОВ=ОА+АВОВ=r+х

Применив теорему Пифагора, выясним, что минимальная высота вышки должна составить 2,3 километра.

Теорема Пифагора в быту

Как ни странно, теорема Пифагора может оказаться полезной даже в бытовых делах, таких как определение высоты шкафа-купе, например. На первый взгляд, нет необходимости использовать такие сложные вычисления, ведь можно просто снять мерки с помощью рулетки. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все мерки были сняты более чем точно.

Дело в том, что шкаф-купе собирается в горизонтальном положении и только потом поднимается и устанавливается к стене. Поэтому боковина шкафа в процессе подъема конструкции должна свободно проходить и по высоте, и по диагонали помещения.

Предположим, имеется шкаф-купе глубиной 800 мм. Расстояние от пола до потолка – 2600 мм. Опытный мебельщик скажет, что высота шкафа должна быть на 126 мм меньше, чем высота помещения. Но почему именно на 126 мм? Рассмотрим на примере.

При идеальных габаритах шкафа проверим действие теоремы Пифагора:

АС=√АВ²+√ВС²

АС=√2474²+800²=2600 мм – все сходится.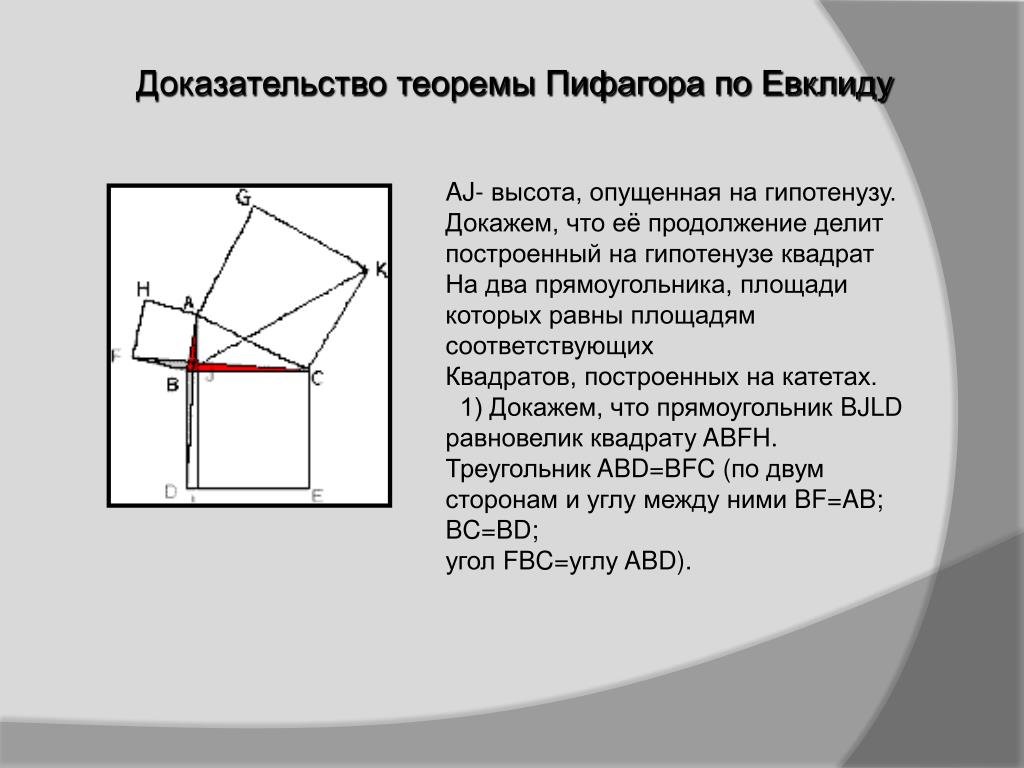

Допустим, высота шкафа равна не 2474 мм, а 2505 мм. Тогда:

АС=√2505²+√800²=2629 мм.

Следовательно, этот шкаф не подойдет для установки в данном помещении. Так как при поднятии его в вертикальное положение можно нанести ущерб его корпусу.

Пожалуй, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что она более чем правдива. Теперь можно использовать полученную информацию в своей повседневной жизни и быть полностью уверенным, что все расчеты будут не только полезны, но и верны.

Урок на тему «Примеры решения задач с помощью теоремы Пифагора с применением электронного учебника»

Тема урока: «Примеры решения задач с помощью теоремы

Пифагора с применением электронного учебника»

Образовательная: формирование умений находить неизвестные элементы с помощью теоремы Пифагора, навыков в решении задач по названной теме с применением электронного учебника.

Развивающая: развитие наблюдательности, догадки, формирования математического мышления, самостоятельности на доступном задачном материале с использованием электронного учебника.

Воспитательная: воспитание внимания, имения работать самостоятельно и интереса к учебной работе за счет сочетания обычных форм работы с работой на компьютере.

1.Актуализация теоретических знаний.

2. Решение задачи №1.

3. Решение задачи №3.

4. Решение задачи №4 самостоятельно.

5. Задание на дом.

1. Актуализация теоретических знаний.

Урок проводится с применение электронного учебника по геометрии, 8 класс.

— Ребята, сформулируйте теорему Пифагора.

[-Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов].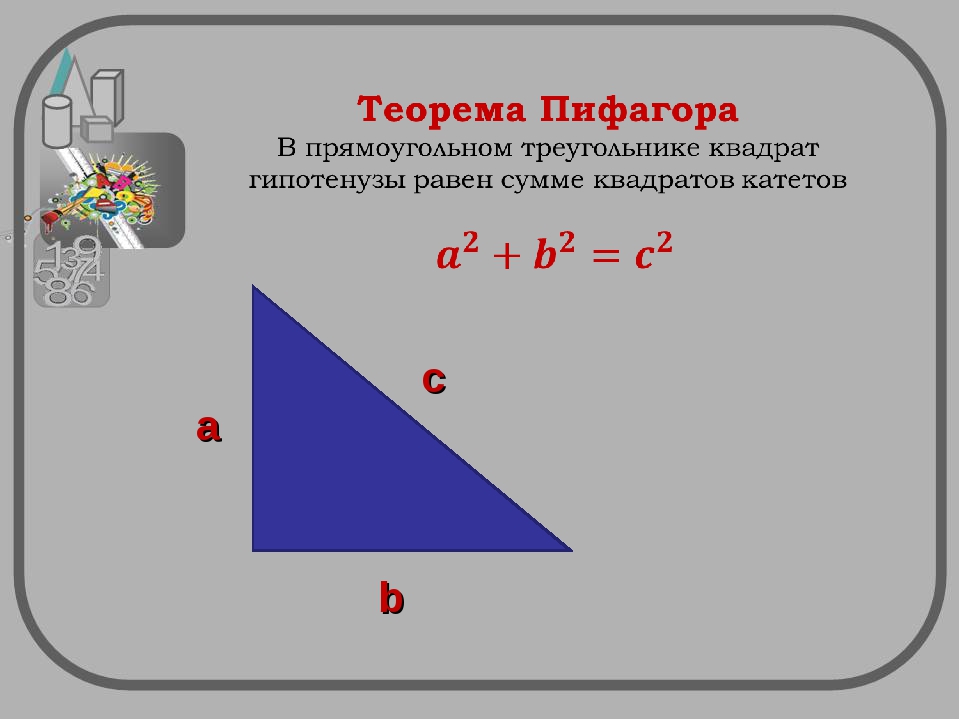

— Сформулируйте обратную теорему Пифагора. [Если в треугольнике квадрат некоторой стороны равен сумме квадратов двух других сторон, то этот треугольник — прямоугольный.]

— Посмотрите на монитор, и проверьте сами себя, правильно ли вы сформулировали обе теоремы.

2. Решение задачи №1

— Откройте в электронном учебнике Главе 3.Треугольники, §22. Примеры решения задач с помощью теоремы Пифагора, п. 22.1. Задачи на прямоугольный треугольник.

— Решим задачу №1.

— Нажмите на Задача №1 и прочитайте условие.

Задача №1.

Стороны треугольника равны 60 cм, 91 см и 109 см. Найдите медиану, проведенную к большей стороне.

Ученики читают условие задачи.

— Обратите внимание, что эту задачу мы будем решать без выполнения чертежа.

Анализ условия задачи

-Что нам известно по условию задачи?

[- Треугольник и его стороны равные 60 см, 91см и 109см. ]

— Что нужно найти?

[-Найти медиану ,проведенную к боковой стороне.]

— Нажмем на экране «Краткую запись задачи» и проверим, правильно ли мы установили что нам дано и что нужно найти.

— Как мы поступим, что бы решить эту задачу?

[1.Установим вид треугольника, для этого воспользуемся теоремой Пифагора]

— Мы нашли замысел решения.

— Предположим, что мы установили вид треугольника, что дальше?

[2.Найдите медиану, проведенную к большей стороне.]

-Каким свойством медианы мы воспользуемся?

[-Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.]

Решение

1. Так как 60² + 91² = 109² это прямоугольный треугольник.

2. По свойству медианы, получим 109 : 2 = 54,5 (см).

Ответ: 54,5 см.

— Теперь, что бы проверить наше решения на экране нажмем «Решение».

— Перейдем к решению задачи №3, для этого в нижней части экрана нажмите на правый треугольник 2 раза. Далее нажмите на слово Задача №3 и прочитайте условие задачи.

3. Решение задачи №3

В прямоугольном треугольнике АВС катет АС = 2, А = 30°. Найдите:
1) неизвестные стороны;
2) высоту, медиану и биссектрису, проведенные из вершины В.

Анализ условия задачи

— Что нам известно по условию задачи?

[- Дан прямоугольный треугольник АВС, катет АС = 2, А = 30°.]

— Что нужно найти?

[ — Стороны треугольника, высоту медиану и биссектрису, проведенные из вершины В. ]

— Нажмем на карандашик в нижней части окна. В открывшемся окне сделаем рисунок и запишем дано.

— Нажмем на слово «рис. 140, а» и сравним его с тем рисунком, который сделали мы. Правильно сделали рисунок? [Правильно.]

Ход решения

— Прежде чем начать решать задачу давайте проанализируем решения. Рисунок сделали, дано записали. Что будем искать в первую очередь?

[Найдем одну из сторон треугольника ABC, — гипотенузу]

— Как мы будем ее искать?

[Воспользуемся теоремой Пифагора]

— Следующий шаг…

[Найдем высоту, медиану и биссектрису]

— Чем является высота в прямоугольном треугольнике?

[-В прямоугольном треугольнике высота является один из катетов]

— Чем необходимо воспользоваться что бы найти биссектрису?

[Необходимо воспользоваться свойствами биссектрисы (соотношением сторон)]

Решение

— Сделаем рисунок.

— Для простоты решения введем обозначения: BC = x.

[1.По условию задачи А = 30°, а мы знаем что сторона лежащая против угла в 30º, равна половине гипотенузы. Значит, АВ = 2·х;

2. Теперь по теореме Пифагора найдем гипотенузу: 4х² = х² + 4. Отсюда

х²=, х =

3. подставим х, получим, ВС = , AB = 2

— Мы решили первую часть задачи, перейдем ко второй.

[ 4.Высота ВС =, т.к. она является катетом.]

— Для нахождения медианы необходимо ее провести. Проведем медиану на нашем рисунке.

[5.Медиана делит сторону на две равные части, значит из треугольника СВВ₁ можем найти и сторону ВВ_1.По теореме Пифагора имеем: ВВ₁ =.]

— Проводим биссектрису.

[Биссектриса треугольника делит угол на два равных угла и противоположную сторону на части, пропорциональные прилежащим сторонам]

— Обозначим нашу биссектрису BL.

[6.По свойствам биссектрисы имеем: , 4 – 2AL = AL, AL =.

7. Так как АВL = 30°, то АВL = САВ. Поэтому труегольник АВL – равнобедренный и BL = AL =.]

Ответ: ВС = , AB = 2, h_b =, m_b =., l_b =.

4. Решение задачи №4 самостоятельно.

Т. к. задача №4 аналогична задачи №3, то ученики решают самостоятельно.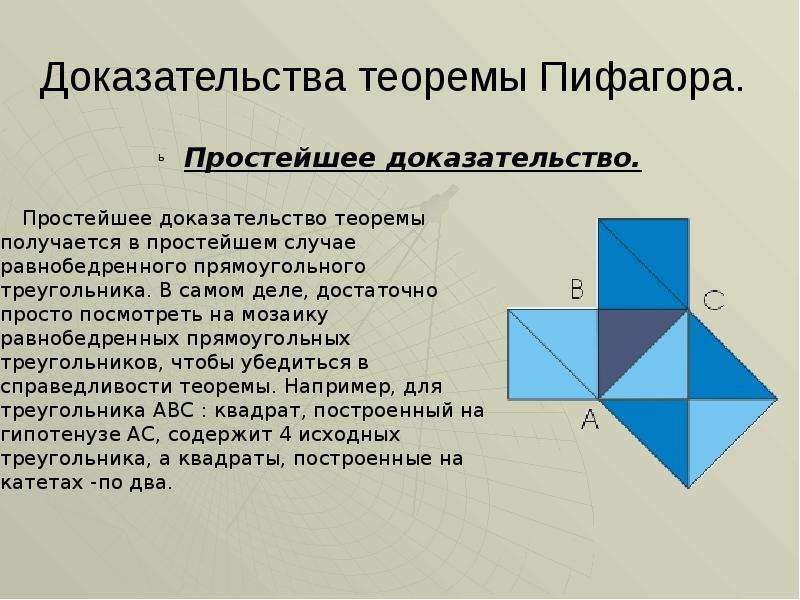

Анализ условия задачи

— Что нам известно по условию задачи?

[- Дан прямоугольный треугольник АВС, катета = СВ = 4 и гипотенузас = АВ =5.]

— Что нужно найти?

[ — Неизвестный катет, высоту медиану и биссектрису, проведенные из вершины прямого угла.]

— Нажмем на карандашик в нижней части окна. В открывшемся окне сделаем рисунок и запишем дано. Сравним его с рисунком на мониторе.

[Найдем одну из сторон треугольника ABC, — катет]

[Найдем высоту, воспользуемся теоремой Пифагора.Найдем медиану.]

— Чем необходимо воспользоваться что бы найти биссектрису?

[Необходимо воспользоваться свойствами биссектрисы (соотношением сторон):биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам. {2}

Обратная теорема Пифагора:

Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. То есть для всякой тройки положительных чисел a, b
и c
, такой, что

a 2 + b 2 = c 2
,

существует прямоугольный треугольник с катетами a
и b
и гипотенузой c
.

Теорема Пифагора
— одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Доказана она ученым математиком и философом Пифагором.

Значение теоремы
в том, что с ее помощью можно доказать другие теоремы и решать задачи.

Дополнительный материал:

Тем, кто интересуется историей теоремы Пифагора, которую изучают в школьной программе, будет также любопытен такой факт, как публикация в 1940 году книги с трехсот семьюдесятью доказательствами этой, казалось бы, простой теоремы. Но она интриговала умы многих математиков и философов разных эпох. В книге рекордов Гиннеса она зафиксирована, как теорема с самым максимальным числом доказательств.

История теоремы Пифагора

Связанная с именем Пифагора, теорема была известна задолго до рождения великого философа. Так, в Египте, при строительстве сооружений, учитывалось соотношение сторон прямоугольного треугольника пять тысячелетий назад. В вавилонских текстах упоминается о все том же соотношении сторон прямоугольного треугольника за 1200 лет до рождения Пифагора.

Возникает вопрос, почему тогда гласит история — возникновение теоремы Пифагора принадлежит ему? Ответ может быть только один — он доказал соотношение сторон в треугольнике. Он сделал то, что века назад не делали те, кто просто пользовался соотношением сторон и гипотенузы, установленным опытным путем.

Из жизни Пифагора

Будущий великий ученый, математик, философ родился на острове Самосе в 570 году до нашей эры. Исторические документы сохранили сведения об отце Пифагора, который был резчиком по драгоценным камням, а вот о матери сведений нет. О родившемся мальчике говорили, что это незаурядный ребенок, проявивший с детского возраста страсть к музыке и поэзии. К учителям юного Пифагора историки относят Гермодаманта и Ферекида Сиросского. Первый ввел мальчика в мир муз, а второй, будучи философом и основателем итальянской школы философии, направил взор юноши к логосу.

В 22 года от роду (548 г. до н. э.) Пифагор отправился в Навкратис для изучения языка и религии египтян. Далее его путь лежал в Мемфис, где благодаря жрецам, пройдя через их хитроумные испытания, он постиг египетскую геометрию, которая, возможно натолкнула пытливого юношу на доказательство теоремы Пифагора. История в дальнейшем припишет теореме именно это имя.

В плену царя Вавилона

По пути домой в Элладу, Пифагор попадает в плен царя Вавилона. Но нахождение в плену принесло пользу пытливому уму начинающего математика, ему было чему поучиться. Ведь в те годы математика в Вавилоне была более развитой чем в Египте. Двенадцать лет он провел за изучением математики, геометрии и магии. И, возможно, именно вавилонская геометрия причастна к доказательству соотношения сторон треугольника и истории открытия теоремы. У Пифагора было для этого достаточно полученных знаний и времени. Но, что это произошло в Вавилоне, документального подтверждения или опровержения тому нет.

В 530 г. до н.э. Пифагор бежит из плена на родину, где живет при дворе тирана Поликрата в статусе полураба. Такая жизнь Пифагора не устраивает, и он удаляется в пещеры Самоса, а затем отправляется на юг Италии, где в то время располагалась греческая колония Кротон.

Тайный монашеский орден

На базе этой колонии Пифагор организовал тайный монашеский орден, представлявший собой религиозный союз и научное общество одновременно. Это общество имело свой устав, в котором говорилось о соблюдении особого образа жизни.

Пифагор утверждал, чтобы понять Бога, человек должен познать такие науки как алгебра и геометрия, знать астрономию и понимать музыку. Исследовательская работа сводилась к познанию мистической стороны чисел и философии. Следует отметить, что проповедованные в то время Пифагором принципы, имеют смысл в подражании и в настоящее время.

Многие из открытий, которые делали ученики Пифагора, приписывались ему. Тем не менее, если говорить кратко, история создания теоремы Пифагора древними историками и биографами того времени, связывается непосредственно с именем этого философа, мыслителя и математика.

Учение Пифагора

Возможно, на мысль о связи теоремы с именем Пифагора натолкнуло историков высказывание великого грека, что в пресловутом треугольнике с его катетами и гипотенузой зашифрованы все явления нашей жизни. А этот треугольник является «ключом» к решению всех возникающих проблем. Великий философ говорил, что следует узреть треугольник, тогда можно считать, что задача на две трети решена.

О своем учении Пифагор рассказывал только своим ученикам устно, не делая никаких записей, держа его в тайне. К великому сожалению, учение величайшего философа не сохранилось до наших дней.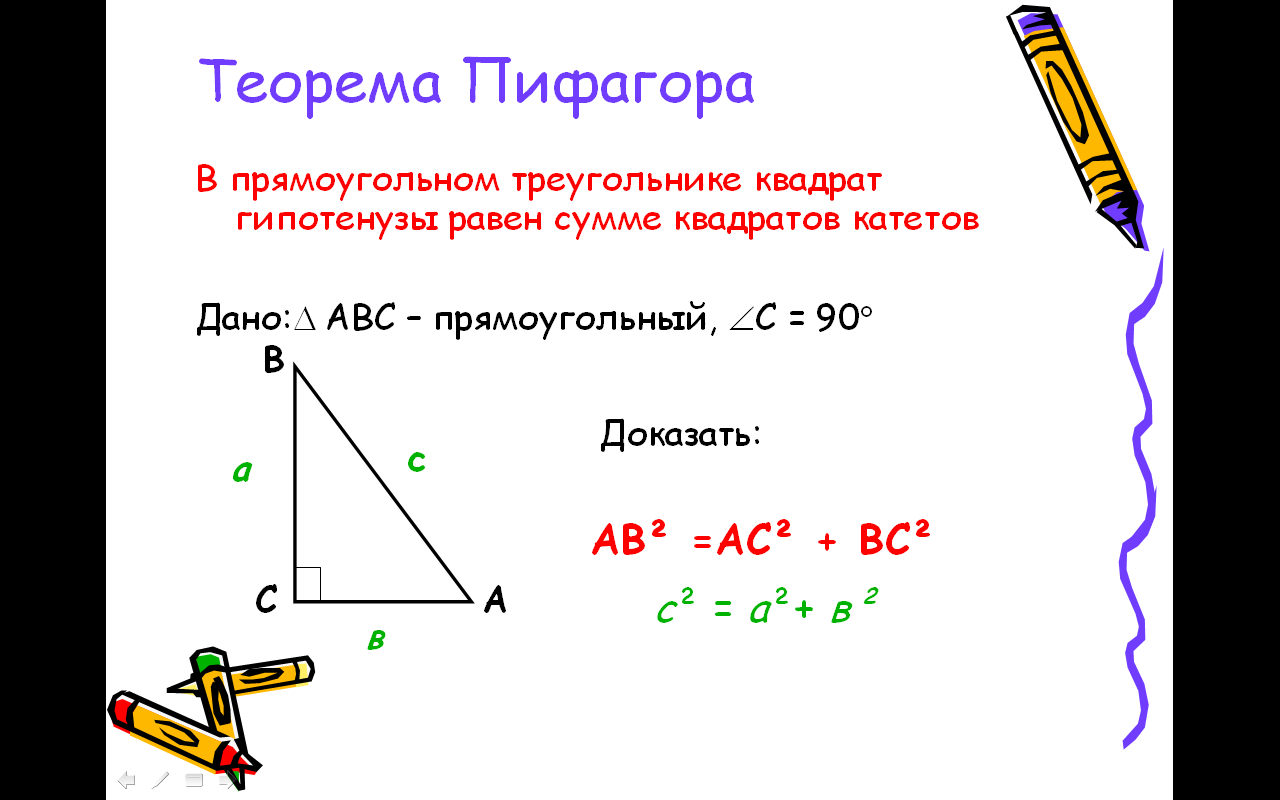 Что-то из него просочилось, но нельзя сказать сколько истинного, а сколько ложного в том, что стало известно. Даже с историей теоремы Пифагора не все бесспорно. Историки математики сомневаются в авторстве Пифагора, по их мнению теоремой пользовались за много веков до его рождения.

Теорема Пифагора

Может показаться странным, но исторических фактов доказательства теоремы самим Пифагором нет — ни в архивах, ни в каких-либо других источниках. В современной версии считается, что оно принадлежит не кому иному, как самому Евклиду.

Есть доказательства одного из крупнейших историков математики Морица Кантора, обнаружившего на папирусе, хранящемся в Берлинском музее, записанное египтянами примерно в 2300 году до н. э. равенство, которое гласило: 3² + 4² = 5².

Кратко из истории теоремы Пифагора

Формулировка теоремы из евклидовых «Начал», в переводе звучит также как и в современной интерпретации. Нового в ее прочтении нет: квадрат стороны противолежащей прямому углу, равен сумме квадратов сторон, прилегающих к прямому углу. О том, что теоремой пользовались древние цивилизации Индии и Китая подтверждает трактат «Чжоу — би суань цзинь». Он содержит сведения об египетском треугольнике, в котором описано соотношение сторон как 3:4:5.

Не менее интересна еще одна китайская математическая книга «Чу-пей», в которой также упоминается о пифагоровом треугольнике с пояснением и рисунками, совпадающими с чертежами индусской геометрии Басхары. О самом треугольнике в книге написано, что если прямой угол можно разложить на составные части, тогда линия, которая соединяет концы сторон, будет равна пяти, если основание равно трем, а высота равна четырем.

Индийский трактат «Сульва сутра», относящийся примерно к VII-V векам до н. э., рассказывает о построении прямого угла при помощи египетского треугольника.

Доказательство теоремы

В средние века ученики считали доказательство теоремы слишком трудным делом. Слабые ученики заучивали теоремы наизусть, без понимания смысла доказательства. В связи с этим они получили прозвище «ослы», потому что теорема Пифагора была для них непреодолимым препятствием, как для осла мост. В средние века ученики придумали шутливый стих на предмет этой теоремы.

Чтобы доказать теорему Пифагора самым легким путем, следует просто измерить его стороны, не используя в доказательстве понятие о площадях. Длина стороны, противолежащая прямому углу — это c, а прилежащие к нему a и b, в результате получаем уравнение: a 2 + b 2 = c 2 . Данное утверждение, как говорилось выше, проверяется путем измерения длин сторон прямоугольного треугольника.

Если начать доказательство теоремы с рассмотрения площади прямоугольников, построенных на сторонах треугольника, можно определить площадь всей фигуры. Она будет равна площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырех треугольников и внутреннего квадрата.

(a + b) 2 = 4 x ab/2 + c 2 ;

a 2 + 2ab + b 2 ;

c 2 = a 2 + b 2 , что и требовалось доказать.

Практическое значение теоремы Пифагора заключается в том, что с ее помощью можно найти длины отрезков, не измеряя их. При строительстве сооружений рассчитываются расстояния, размещение опор и балок, определяются центры тяжести. Применяется теорема Пифагора и во всех современных технологиях. Не забыли о теореме и при создании кино в 3D-6D-измерениях, где кроме привычных нам 3-х величин: высоты, длины, ширины — учитываются время, запах и вкус. Как связаны с теоремой вкусы и запахи — спросите вы? Все очень просто — при показе фильма нужно рассчитать, куда и какие запахи и вкусы направлять в зрительном зале.

То ли еще будет. Безграничный простор для открытия и создания новых технологий ждет пытливые умы.

Своеобразна судьба иных теорем и задач… Как объяснить, например, столь исключительное внимание со стороны математиков и любителей математики к теореме Пифагора? Почему многие из них не довольствовались уже известными доказательствами, а находили свои, доведя за двадцать пять сравнительно обозримых столетий количество доказательств до нескольких сотен?
Когда речь идет о теореме Пифагора, необычное начинается уже с ее названия. Считается, что сформулировал ее впервые отнюдь не Пифагор. Сомнительным полагают и то, что он дал ее доказательство. Если Пифагор — реальное лицо (некоторые сомневаются даже в этом!), то жил он, скорее всего, в VI-V в. до н. э. Сам он ничего не писал, называл себя философом, что значило, в его понимании, «стремящийся к мудрости», основал пифагорейский союз, члены которого занимались музыкой, гимнастикой, математикой, физикой и астрономией. По-видимому, был он и великолепным оратором, о чем свидетельствует следующая легенда, относящаяся к пребыванию его в городе Кротоне: «Первое появление Пифагора пред народом в Кротоне началось речью к юношам, в которой он так строго, но вместе с тем и так увлекательно изложил обязанности юношей, что старейшие в городе просили не оставить и их без поучения. В этой второй речи он указывал на законность и на чистоту нравов, как на основы семейства; в следующих двух он обратился к детям и женщинам. Последствием последней речи, в которой он особенно порицал роскошь, было то, что в храм Геры доставлены были тысячи драгоценных платьев, ибо ни одна женщина не решалась более показываться в них на улице.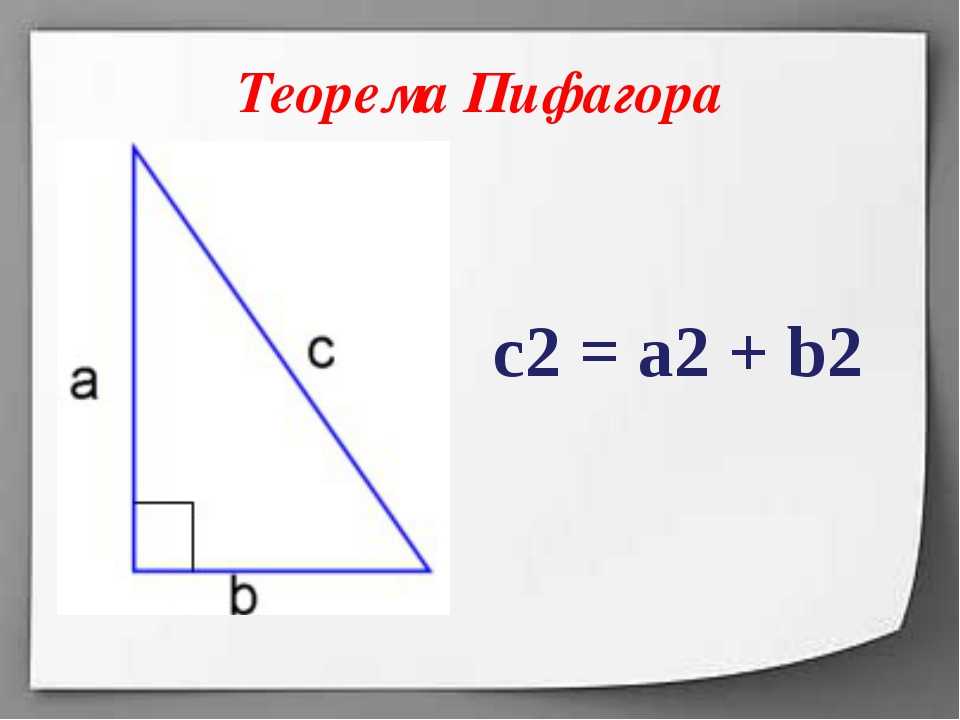 ..» Тем не менее еще во втором столетии нашей эры, т. е. спустя 700 лет, жили и творили вполне реальные люди, незаурядные ученые, находившиеся явно под влиянием пифагорейского союза и относящиеся с большим уважением к тому, что согласно легенде создал Пифагор.
Несомненно также, что интерес к теореме вызывается и тем, что она занимает в математике одно из центральных мест, и удовлетворением авторов доказательств, преодолевших трудности, о которых хорошо сказал живший до нашей эры римский поэт Квинт Гораций Флакк: «Трудно хорошо выразить общеизвестные факты».
Первоначально теорема устанавливала соотношение между площадями квадратов, построенных на гипотенузе и катетах прямоугольного треугольника:

.
Алгебраическая формулировка:

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
a 2 +b 2 =c 2 .
Обе формулировки теоремы эквивалентны, но вторая формулировка более элементарна, она не требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника.

Обратная теорема Пифагора.
Для всякой тройки положительных чисел a, b и c, такой, что
a 2 + b 2 = c 2 , существует прямоугольный треугольник с катетами a и b и гипотенузой c.

Доказательства

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства (например с помощью дифференциальных уравнений).

Через подобные треугольники

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом.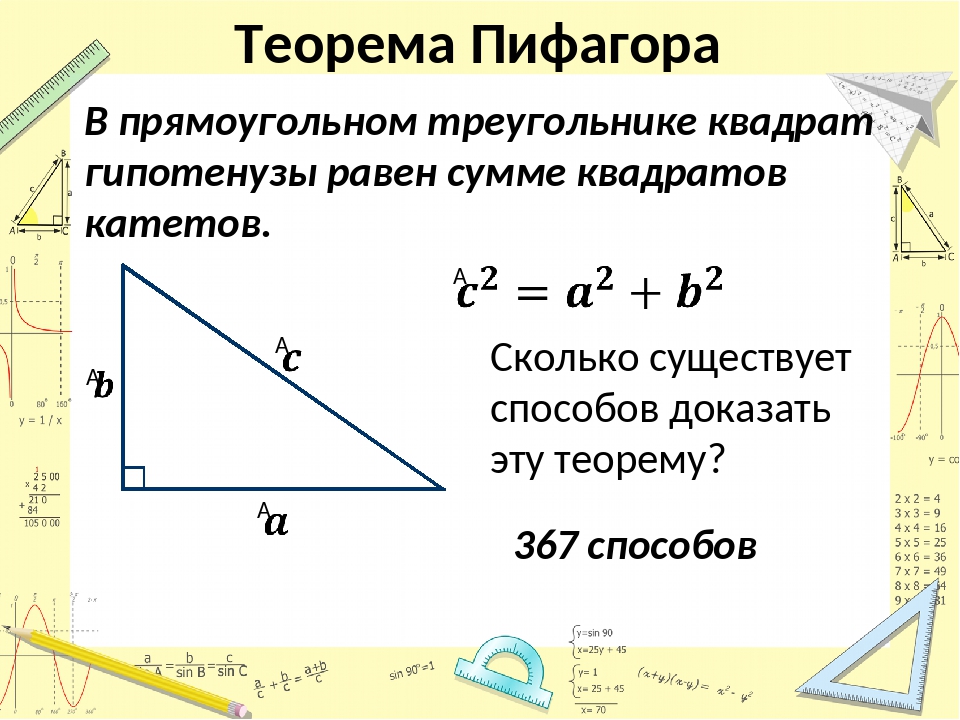 В частности, оно не использует понятие площади фигуры.
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам.
Аналогично, треугольник CBH подобен ABC. Введя обозначения

получаем

Что эквивалентно

Сложив, получаем

или

Доказательства методом площадей

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость

1. Расположим четыре равных прямоугольных треугольника так, как показано на рисунке.
2. Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
3. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и внутреннего квадрата.

Что и требовалось доказать.

Доказательства через равносоставленность

Пример одного из таких доказательств указан на чертеже справа, где квадрат, построенный на гипотенузе, перестановкой преобразуется в два квадрата, построенных на катетах.

Доказательство Евклида

Идея доказательства Евклида состоит в следующем: попробуем доказать, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов, построенных на катетах, а тогда и площади большого и двух малых квадратов равны.
Рассмотрим чертеж слева. На нём мы построили квадраты на сторонах прямоугольного треугольника и провели из вершины прямого угла С луч s перпендикулярно гипотенузе AB, он рассекает квадрат ABIK, построенный на гипотенузе, на два прямоугольника — BHJI и HAKJ соответственно. Оказывается, что площади данных прямоугольников в точности равны площадям квадратов, построенных на соответствующих катетах.
Попытаемся доказать, что площадь квадрата DECA равна площади прямоугольника AHJK Для этого воспользуемся вспомогательным наблюдением: Площадь треугольника с той же высотой и основанием, что и данный прямоугольник, равна половине площади заданного прямоугольника. Это следствие определения площади треугольника как половины произведения основания на высоту. Из этого наблюдения вытекает, что площадь треугольника ACK равна площади треугольника AHK (не изображённого на рисунке), которая, в свою очередь, равна половине площади прямоугольника AHJK.
Докажем теперь, что площадь треугольника ACK также равна половине площади квадрата DECA. Единственное, что необходимо для этого сделать, — это доказать равенство треугольников ACK и BDA (так как площадь треугольника BDA равна половине площади квадрата по указанному выше свойству). Равенство это очевидно, треугольники равны по двум сторонам и углу между ними. Именно — AB=AK,AD=AC — равенство углов CAK и BAD легко доказать методом движения: повернём треугольник CAK на 90° против часовой стрелки, тогда очевидно, что соответствующие стороны двух рассматриваемых треугольников совпадут (ввиду того, что угол при вершине квадрата — 90°).
Рассуждение о равенстве площадей квадрата BCFG и прямоугольника BHJI совершенно аналогично.
Тем самым мы доказали, что площадь квадрата, построенного на гипотенузе, слагается из площадей квадратов, построенных на катетах.

Доказательство Леонардо да Винчи

Главные элементы доказательства — симметрия и движение.

Рассмотрим чертёж, как видно из симметрии, отрезок CI рассекает квадрат ABHJ на две одинаковые части (так как треугольники ABC и JHI равны по построению). Пользуясь поворотом на 90 градусов против часовой стрелки, мы усматриваем равенство заштрихованных фигур CAJI и GDAB. Теперь ясно, что площадь заштрихованной нами фигуры равна сумме половин площадей квадратов, построенных на катетах, и площади исходного треугольника. С другой стороны, она равна половине площади квадрата, построенного на гипотенузе, плюс площадь исходного треугольника. Последний шаг в доказательстве предоставляется читателю.

Шаповалова Л.А. (ст. Егорлыкская, МБОУ ЕСОШ № 11)

1. Глейзер Г.И. История математики в школе VII – VIII классы, пособие для учителей, – М: Просвещение, 1982.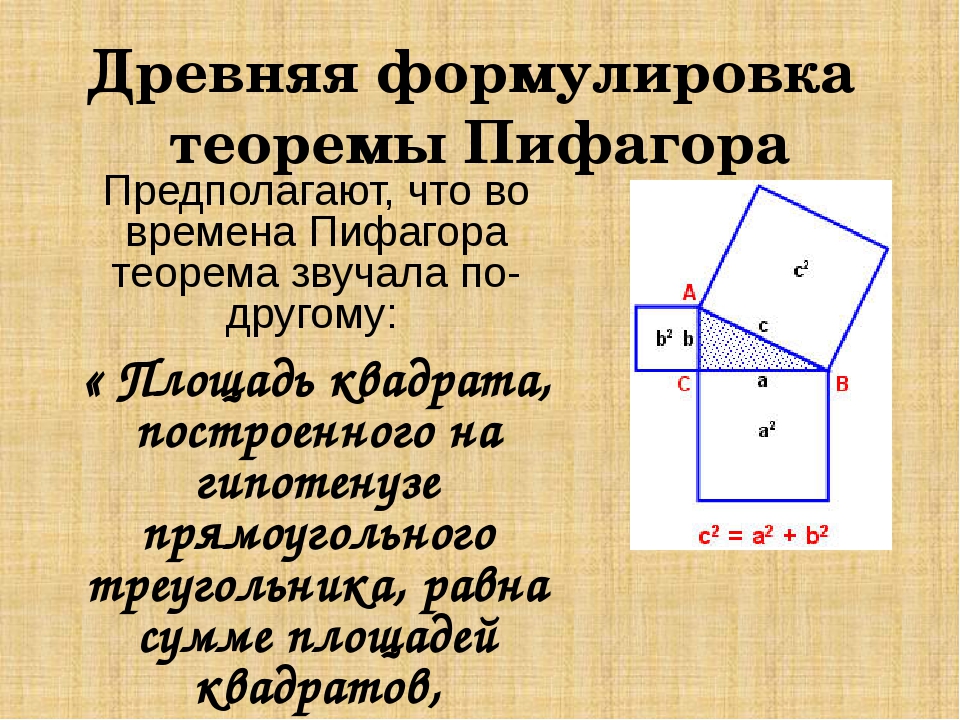

2. Демпан И.Я., Виленкин Н.Я. «За страницами учебника математики» Пособие для учащихся 5-6 классов. – М.: Просвещение, 1989.

3. Зенкевич И.Г. «Эстетика урока математики». – М.: Просвещение, 1981.

4. Литцман В. Теорема Пифагора. – М., 1960.

5. Волошинов А.В. «Пифагор». – М., 1993.

6. Пичурин Л.Ф. «За страницами учебника алгебры». – М., 1990.

7. Земляков А.Н. «Геометрия в 10 классе». – М., 1986.

8. Газета «Математика» 17/1996.

9. Газета «Математика» 3/1997.

10. Антонов Н.П., Выгодский М.Я., Никитин В.В., Санкин А.И. «Сборник задач по элементарной математики». – М., 1963.

11. Дорофеев Г.В., Потапов М.К., Розов Н.Х. «Пособие по математике». – М., 1973.

12. Щетников А.И. «Пифагорейское учение о числе и величине». – Новосибирск, 1997.

13. «Действительные числа. Иррациональные выражения» 8 класс. Издательство Томского университета. – Томск, 1997.

14. Атанасян М.С. «Геометрия» 7-9 класс. – М.: Просвещение, 1991.

15. URL: www.moypifagor.narod.ru/

16. URL: http://www.zaitseva-irina.ru/html/f1103454849.html.

В этом учебном году я познакомились с интересной теоремой, известной, как оказалось с древнейших времён:

«Квадрат, построенный на гипотенузе прямоугольного треугольника равновелик сумме квадратов построенных на катетах».

Обычно открытие этого утверждения приписывают древнегреческому философу и математику Пифагору (VI век до н.э). Но изучение древних рукописей показало, что это утверждение было известно задолго до рождения Пифагора.

Я заинтересовались, почему в таком случае её связывают с именем Пифагора.

Актуальность темы: Теорема Пифагора имеет огромное значение: применяется в геометрии буквально на каждом шагу. Я считаю, что труды Пифагора до сих пор актуальны, ведь куда бы мы ни посмотрели, везде можно увидеть плоды его великих идей, воплощенные в различные отрасли современной жизни.

Целью моего исследования было: узнать, кто такой был Пифагор, и какое отношение он имеет к этой теореме.

Изучая историю теоремы, я решила выяснить:

Существуют ли другие доказательства этой теоремы?

Каково значение этой теоремы в жизни людей?

Какую роль сыграл Пифагор в развитии математики?

Из биографии Пифагора

Пифагор Самосский — великий греческий учёный. Его известность связана с названием теоремы Пифагора. Хотя сейчас уже мы знаем, что эта теорема была известна в древнем Вавилоне за 1200 лет до Пифагора, а в Египте за 2000 лет до него был известен прямоугольный треугольник со сторонами 3, 4, 5, мы по-прежнему называем её по имени этого древнего учёного.

Про жизнь Пифагора достоверно почти ничего неизвестно, но с его именем связано большое количество легенд.

Пифагор родился в 570 году до н.э на острове Самос.

Пифагор имел красивую внешность, носил длинную бороду, а на голове золотую диадему. Пифагор — это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор — «убеждающий речью»).

В 550 году до н.э Пифагор принимает решение и отправляется в Египет. Итак, перед Пифагором открывается неизвестная страна и неведомая культура. Многое поражало и удивляло Пифагора в этой стране, и после некоторых наблюдений за жизнью египтян Пифагор понял, что путь к знаниям, охраняемым кастой жрецов, лежит через религию.

После одиннадцати лет обучения в Египте Пифагор отправляется на родину, где по пути попадает в Вавилонский плен. Там он знакомится с вавилонской наукой, которая была более развита, чем египетская. Вавилоняне умели решать линейные, квадратные и некоторые виды кубических уравнений. Сбежав из плена, он не смог долго оставаться на родине из-за царившей там атмосферы насилия и тирании. Он решил переселиться в Кротон (греческая колония на севере Италии).

Именно в Кротоне начинается самый славный период в жизни Пифагора. Там он учредил нечто вроде религиозно-этического братства или тайного монашеского ордена, члены которого обязывались вести так называемый пифагорейский образ жизни.

Пифагор и пифагорейцы

Пифагор организовал в греческой колонии на юге Апенинского полуострова религиозно-этическое братство, типа монашеского ордена, который впоследствии назовут пифагорейским союзом. Члены союза должны были придерживаться определённых принципов: во-первых, стремиться к прекрасному и славному, во-вторых, быть полезными, в-третьих, стремиться к высокому наслаждению.

Система морально-этических правил, завещанная Пифагором своим ученикам, была собрана в своеобразный моральный кодекс пифагорейцев «Золотые стихи», которые пользовались большой популярностью в эпоху Античности, эпоху Средневековья и эпоху Возрождения.

Пифагорейская система занятий состояла из трёх разделов:

Учения о числах — арифметике,

Учения о фигурах — геометрии,

Учения о строении Вселенной — астрономии.

Система образования, заложенная Пифагором, просуществовала много веков.

Школа Пифагора много сделала, чтобы придать геометрии характер науки. Основной особенностью метода Пифагора было объединение геометрии с арифметикой.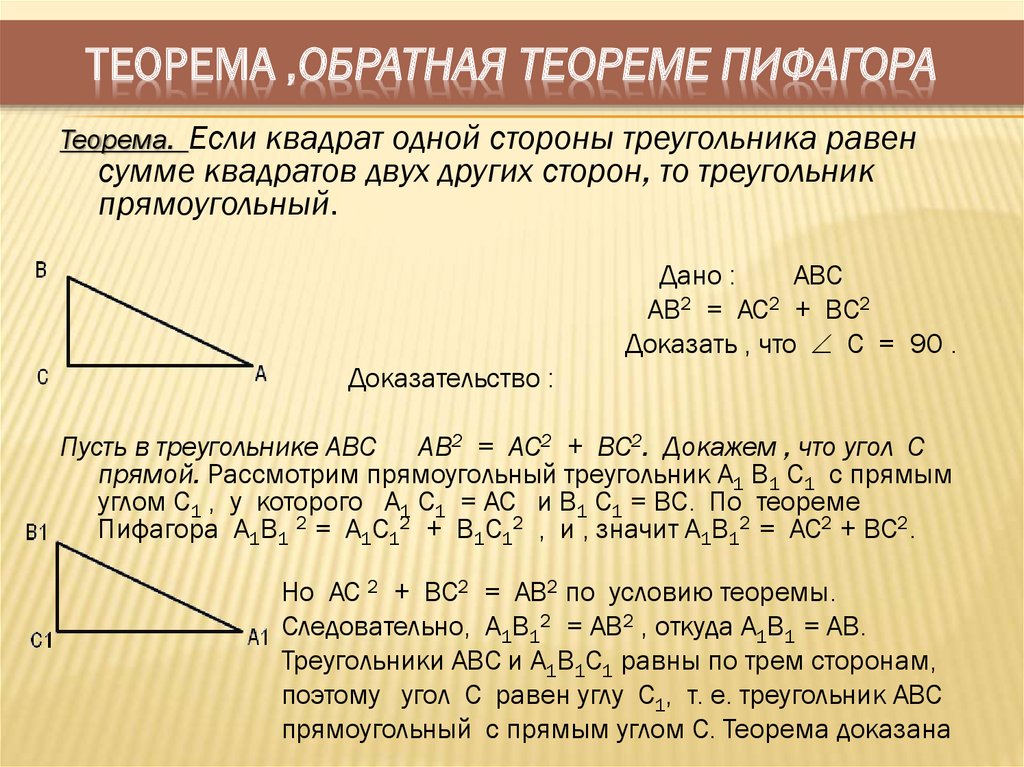

Пифагор много занимался пропорциями и прогрессиями и, вероятно, подобием фигур, так как ему приписывают решение задачи: «По данным двум фигурам построить третью, равновеликую одной из данных и подобную второй».

Пифагор и его ученики ввели понятие о многоугольных, дружественных, совершенных числах и изучали их свойства. Арифметика как практика вычислений не интересовала Пифагора, и он с гордостью заявил, что «поставил арифметику выше интересов торговца».

Членами пифагорейского союза были жители многих городов Греции.

В своё общество пифагорейцы принимали и женщин. Союз процветал более двадцати лет, а потом начались гонения на его членов, многие из учеников были убиты.

О смерти самого Пифагора ходило много самых разных легенд. Но учение Пифагора и его учеников продолжало жить.

Из истории создания теоремы Пифагора

В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что именно Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих «Начал». С другой стороны, Прокл утверждает, что доказательство в «Началах» принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных конкретных данных о жизни Пифагора и его математической деятельности.

Исторический обзор теоремы Пифагора начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:

«Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4».

Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра.

Геометрия у индусов была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 8 века до нашей эры. Наряду с чисто ритуальными предписаниями, существуют и сочинения геометрически теологического характера. В этих сочинениях, относящихся к 4 или 5 веку до нашей эры, мы встречаемся с построением прямого угла при помощи треугольника со сторонами 15, 36, 39.

В средние века теорема Пифагора определяла границу, если не наибольших возможных, то, по крайней мере, хороших математических знаний. Характерный чертеж теоремы Пифагора, который ныне иногда превращается школьниками, например, в облаченного в мантию профессора или человека цилиндре, в те времена нередко употреблялся как символ математики.

В заключение приведем различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.

Евклида эта теорема гласит (дословный перевод):

«В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол».

Как видим, в разных странах и разных языках существуют различные варианты формулировки знакомой нам теоремы. Созданные в разное время и в разных языках, они отражают суть одной математической закономерности, доказательство которой также имеет несколько вариантов.

Пять способов доказательства теоремы Пифагора

Древнекитайское доказательство

На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами a, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной a + b, а внутренний — квадрат со стороной с, построенный на гипотенузе

a2 + 2ab + b2 = c2 + 2ab

Доказательство Дж. Гардфилда (1882 г.)

Расположим два равных прямоугольных треугольника так, чтобы катет одного из них был продолжением другого.

Площадь рассматриваемой трапеции находится как произведение полусуммы оснований на высоту

C другой стороны, площадь трапеции равна сумме площадей полученных треугольников:

Приравнивая данные выражения, получаем:

Доказательство простейшее

Это доказательство получается в простейшем случае равнобедренного прямоугольного треугольника.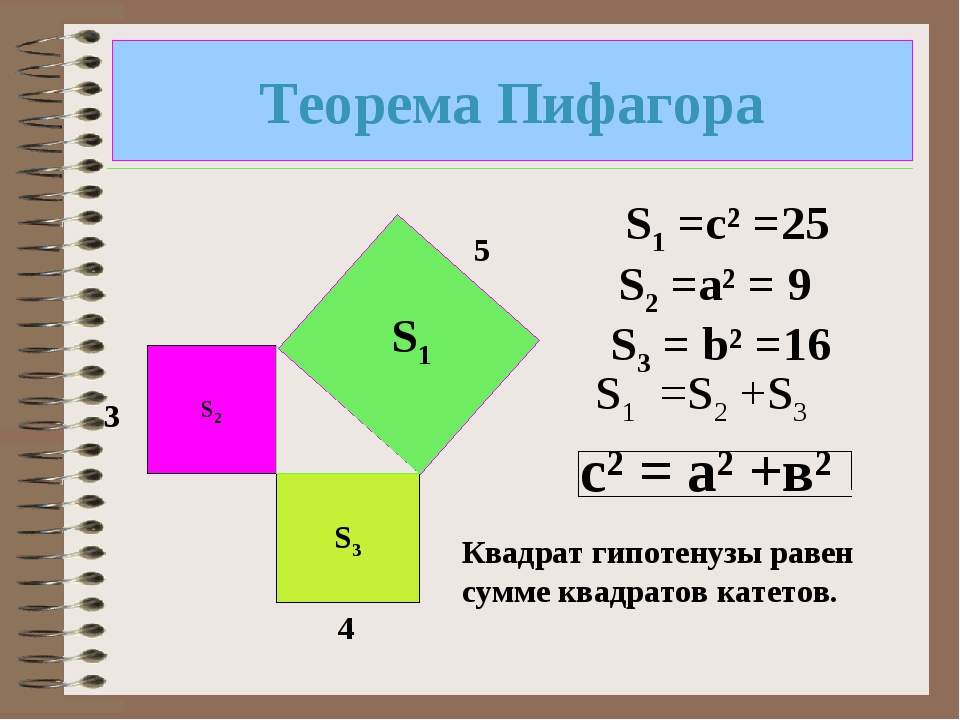

Вероятно, с него и начиналась теорема.

В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы.

Например, для треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, — по два. Теорема доказана.

Доказательство древних индусов

Квадрат со стороной (a + b), можно разбить на части либо как на рис. 12. а, либо как на рис. 12, б. Ясно, что части 1, 2, 3, 4 на обоих рисунках одинаковы. А если от равных (площадей) отнять равные, то и останутся равные, т.е. с2 = а2 + b2.

Доказательство Евклида

В течение двух тысячелетий наиболее распространенным было доказательство теоремы Пифагора, придуманное Евклидом. Оно помещено в его знаменитой книге «Начала».

Евклид опускал высоту BН из вершины прямого угла на гипотенузу и доказывал, что её продолжение делит достроенный на гипотенузе квадрат на два прямоугольника, площади которых равны площадям соответствующих квадратов, построенных на катетах.

Чертёж, применяемый при доказательстве этой теоремы, в шутку называют «пифагоровы штаны». В течение долгого времени он считался одним из символов математической науки.

Применение теоремы Пифагора

Значение теоремы Пифагора состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии и решить множество задач. Кроме этого, практическое значение теоремы Пифагора и обратной ему теоремы заключается в том, что с их помощью можно найти длины отрезков, не измеряя самих отрезков. Это как бы открывает путь от прямой к плоскости, от плоскости к объемному пространству и дальше. Именно по этой причине теорема Пифагора так важна для человечества, которое стремится открывать все больше измерений и создавать технологии в этих измерениях.

Заключение

Теорема Пифагора настолько известна, что трудно представить себе человека, не слышавшего о ней. Я узнала, что существует несколько способов доказательства теоремы Пифагора. Я изучила ряд исторических и математических источников, в том числе информацию в Интернете, и поняла, что теорема Пифагора интересна не только своей историей, но и тем, что она занимает важное место в жизни и науке. Об этом свидетельствуют приведённые мной в данной работе различные трактовки текста этой теоремы и пути её доказательств.

Итак, теорема Пифагора — одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Теорема Пифагора замечательна и тем, что сама по себе она вовсе не очевидна. Например, свойства равнобедренного треугольника можно видеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: c2 = a2 + b2. Поэтому для её доказательства часто используют наглядность. Заслуга же Пифагора состояла в том, что он дал полноценное научное доказательство этой теоремы. Интересна личность самого учёного, память о котором неслучайно сохранила эта теорема. Пифагор — замечательный оратор, учитель и воспитатель, организатор своей школы, ориентированной на гармонию музыки и чисел, добра и справедливости, на знания и здоровый образ жизни.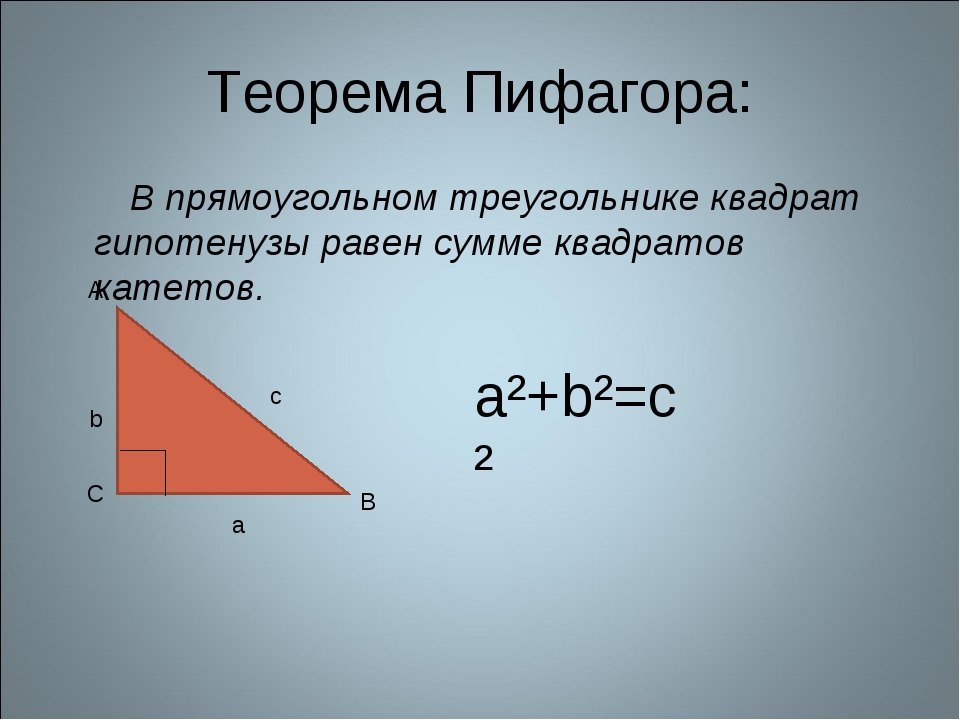 {2}$ было известно уже египтянам ещё около
2300 г. до н.э. По мнению ученого, строители строили тогда прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте приводится приближённое вычисление гипотенузы равнобедренного
прямоугольного треугольника.

Теорема Пифагора с примерами

Теорема Пифагора — это способ соотнести длины катетов прямоугольного треугольника с длиной гипотенузы, которая является стороной, противоположной прямому углу. Несмотря на то, что он написан в этих терминах, его можно использовать для поиска любой стороны, если вам известны длины двух других сторон. В этом уроке мы рассмотрим несколько различных типов примеров применения этой теоремы.

Содержание

Примеры использования теоремы Пифагора
Решение прикладных задач (текстовых задач)
Решение алгебраических задач
Сводка

объявление

Применение теоремы Пифагора (примеры)

В приведенных ниже примерах мы увидим, как применить это правило, чтобы найти любую сторону прямоугольного треугольника.Как и в приведенной ниже формуле, пусть a и b будут длинами катетов, а c — длиной гипотенузы. Однако помните, что вы можете использовать любые переменные для представления этих длин.

В каждом примере обращайте пристальное внимание на предоставленную информацию и на то, что мы пытаемся найти. Это поможет вам определить правильные значения для использования в различных частях формулы.

Пример

Найдите значение \ (x \).

Решение

Сторона, противоположная прямому углу, — это сторона с меткой \ (x \).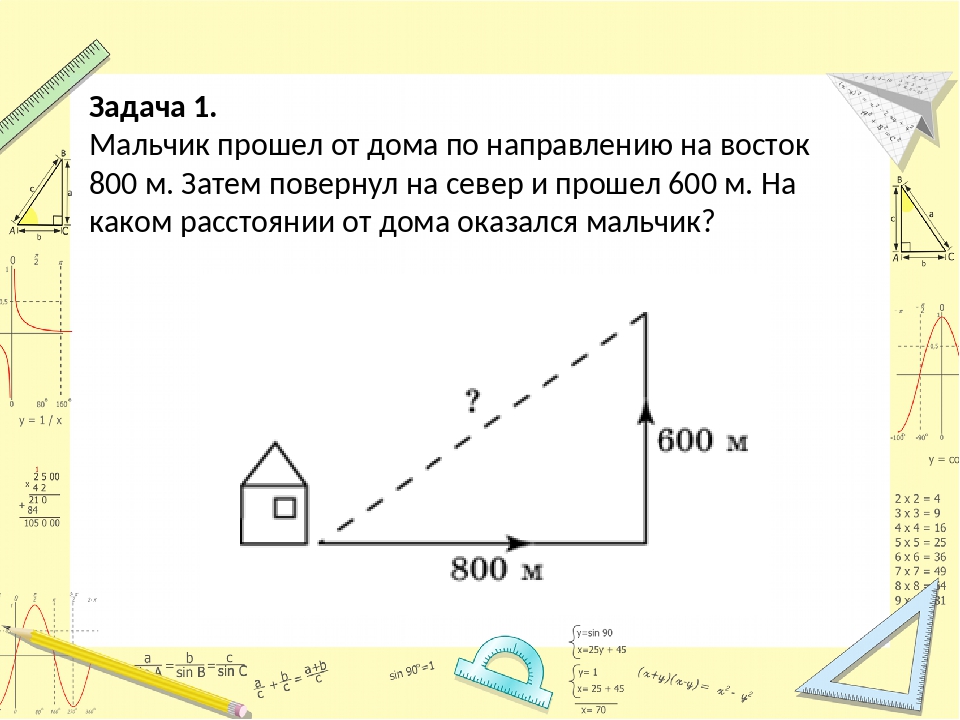 2 \)

Следовательно, можно написать:

\ (\ begin {align} x & = \ sqrt {100} \\ & = \ bbox [граница: сплошной черный 1 пиксель; отступ: 2 пикселя] {10} \ end {align} \)

Возможно, вы помните, что в таком уравнении \ (x \) также может быть –10, поскольку –10 в квадрате также равно 100. Но длина любой стороны треугольника никогда не может быть отрицательной, и поэтому мы рассматриваем только положительный квадратный корень.

В других ситуациях вы будете пытаться найти длину одного из катетов прямоугольного треугольника.2 = 80 \)

Следовательно:

\ (\ begin {align} y & = \ sqrt {80} \\ & = \ sqrt {16 \ times 5} \\ & = \ bbox [граница: 1 пиксель сплошной черный; отступ: 2 пикселя] {4 \ sqrt {5 }} \ end {align} \)

В этом последнем примере мы оставили ответ в точной форме, а не в десятичном приближении. Это обычное дело, если вы не работаете над прикладной проблемой.

Приложения (проблемы с текстом) с теоремой Пифагора

Существует множество различных типов реальных проблем, которые можно решить с помощью теоремы Пифагора. Самый простой способ убедиться в том, что вам следует применять эту теорему, — это нарисовать картину любой описанной ситуации.

Пример

Два туриста покидают хижину одновременно: один направляется на юг, а другой — на запад. Через час турист, идущий на юг, преодолел 2,8 мили, а пешеход, идущий на запад, — 3,1 мили. Какое в данный момент самое короткое расстояние между двумя туристами?

Решение

Сначала нарисуйте изображение предоставленной информации.2 \)

Теперь воспользуйтесь калькулятором, чтобы извлечь квадратный корень. Вероятно, вам придется округлить свой ответ.

\ (\ begin {align} x & = \ sqrt {17,45} \\ & \ приблизительно 4,18 \ text {miles} \ end {align} \)

Как видите, вам решать, что прямой угол является частью ситуации, заданной в слове «проблема». Если это не так, то вы не можете использовать теорему Пифагора.

Задачи в стиле алгебры с теоремой Пифагора

Есть еще одна проблема, с которой вы можете столкнуться, когда вы используете теорему Пифагора для написания некоторого типа алгебраических выражений. 2 \)

Когда в задаче написано «значение \ (y \)», это означает, что вы должны решить для \ (y \).2} \)

Наконец, это упрощает выражение, которое мы ищем:

\ (y = \ bbox [граница: сплошной черный 1 пиксель; отступ: 2 пикселя] {x \ sqrt {3x}} \)

объявление

Сводка

Теорема Пифагора позволяет вам найти длину любой из трех сторон прямоугольного треугольника. Это одна из тех вещей, которые вам следует запомнить, поскольку она встречается во всех областях математики, и, следовательно, вы, вероятно, пройдете множество различных математических курсов.Не забывайте избегать распространенной ошибки, заключающейся в том, чтобы путать ноги в формуле с гипотенузой, и всегда рисовать картинку, когда она не указана.

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

Теорема Пифагора — объяснение и примеры

Теорема Пифагора, , также известная как « теорема Пифагора, », возможно, самая известная математическая формула , , которая определяет отношения между сторонами прямоугольного треугольника.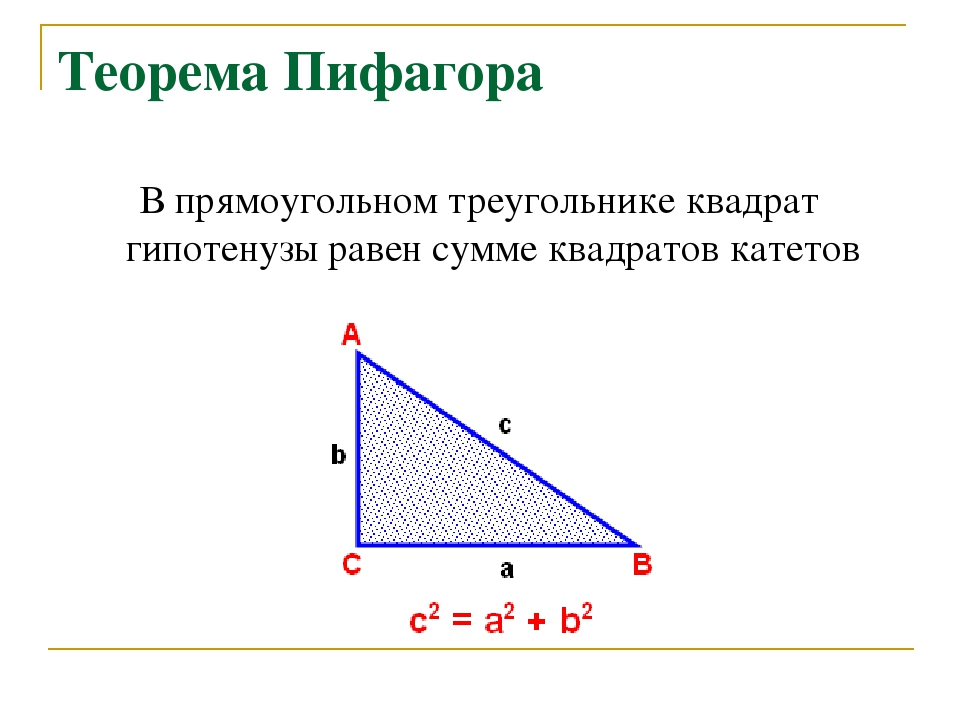

Приписывают теорему греческому математику и философу по имени Пифагор (569-500 до н. Э.). Он внес большой вклад в математику, но теорема Пифагора является наиболее важной из них.

Пифагору приписывают несколько вкладов в математику, астрономию, музыку, религию, философию и т. Д. Одним из его заметных вкладов в математику является открытие теоремы Пифагора. Пифагор изучил стороны прямоугольного треугольника и обнаружил, что сумма квадрата двух более коротких сторон треугольников равна квадрату самой длинной стороны.

В этой статье e будет обсуждаться, что такое теорема Пифагора , ее обратная формула и формула теоремы Пифагора. Прежде чем углубляться в тему, вспомним прямоугольный треугольник. Прямоугольный треугольник — это треугольник, внутренний угол которого равен 90 градусам. В прямоугольном треугольнике две короткие ножки встречаются под углом 90 градусов. Гипотенуза треугольника противоположна углу в 90 градусов.

Что такое теорема Пифагора?

Теорема Пифагора — это математический закон, который гласит, что сумма квадратов длин двух коротких сторон прямоугольного треугольника равна квадрату длины гипотенузы .

Теорема Пифагора алгебраически записывается как:

a ² + b ² = c ²

Как составить теорему Пифагора?

Рассмотрим прямоугольный треугольник выше.

Учитывая, что:

∠ ABC = 90 °.

Пусть BD — прямая, перпендикулярная стороне AC.

Подобные ∆s:

∆ADB и ∆ABC — подобные треугольники.

Из правила подобия,

⇒ AD / AB = AB / AC

⇒ AD × AC = (AB) ² —————– (i)

Аналогично;

∆BDC и ∆ABC — подобные треугольники.Следовательно;

⇒ DC / BC = BC / AC

⇒ DC × AC = (BC) ² —————– (ii)

Объединив уравнения (i) и (ii), мы получим
AD × AC + DC × AC = (AB) ² + (BC) ²

⇒ (AD + DC) × AC = (AB) ² + (BC) ²

⇒ (AC) ² = (AB) ² + (BC) ²

Следовательно, если мы положим AC = c; AB = b и BC = b, тогда;

⇒ c ² = a ² + b ²

Есть много демонстраций теоремы Пифагора , данных разными математиками.

Другая распространенная демонстрация — это нарисовать 3 квадрата таким образом, чтобы они образовывали прямоугольный треугольник между ними, а площадь большего квадрата (тот, который находится в гипотенузе) равна сумме площадей двух меньших. квадраты (те, что с двух сторон).

Рассмотрим 3 квадрата ниже:

Они нарисованы таким образом, что образуют прямоугольный треугольник. Мы можем записать их площади в форме уравнения:

Площадь квадрата III = Площадь квадрата I + Площадь квадрата II

Предположим, что длина квадрата I , квадрата II, и квадрата III равна a, b и c соответственно.

Затем,

Площадь квадрата I = a ²

Площадь квадрата II = b ²

Площадь квадрата III = c ²

Следовательно, мы можем записать это как:

a ² + b ² = c ²

, который является теоремой Пифагора.

Обращение теоремы Пифагора

Преобразование теоремы Пифагора — это правило, которое используется для классификации треугольников как прямоугольный, острый или тупой.

Учитывая теорему Пифагора, a ² + b ² = c ², тогда:

Для острого треугольника c ² 2 + b ², где c — сторона, противоположная острому углу.
Для прямоугольного треугольника c ² = a ² + b ², где c — сторона угла в 90 градусов.
Для тупого треугольника c ²> a ² + b ², где c — сторона, противоположная тупому углу.

Пример 1

Классифицируйте треугольник с размерами; a = 5 м, b = 7 м и c = 9 м.

Решение

Согласно теореме Пифагора, тогда a ² + b ² = c ²;

a ² + b ² = 5 ² + 7 ² = 25 + 49 = 74

Но, c ² = 9 ² = 81
Сравните: 81> 74

Следовательно, c ²> a ² + b ² (тупой треугольник).

Пример 2

Классифицируйте треугольник, длина сторон a, b, c которого равна 8 мм, 15 мм и 17 мм соответственно.

Решение
a ² + b ² = 8 ² + 15 ² = 64 + 225 = 289
Но, c ² = 17 ² = 289
Сравнить: 289 = 289

Следовательно, c ² = a ² + b ² (прямоугольный треугольник).

Пример 3

Классифицируйте треугольник, длина сторон которого равна: 11 дюймов, 13 дюймов и 17 дюймов.

Решение
a ² + b ² = 11 ² + 13 ² = 121 + 169 = 290
c ² = 17 ² = 289
Сравнить: 289 <290

Следовательно, c ² 2 + b ² (острый треугольник)

Формула теоремы Пифагора

Формула теоремы Пифагора имеет следующий вид:

⇒ c ² = a ² + b ²

где;

c = длина гипотенузы;

a = длина одной стороны;

b = длина второй стороны.

Эту формулу можно использовать для решения различных задач, связанных с прямоугольными треугольниками. Например, мы можем использовать формулу для определения третьей длины треугольника, когда известны длины двух сторон треугольника.

Применение формулы теоремы Пифагора в реальной жизни

Мы можем использовать теорему Пифагора, чтобы проверить, является ли треугольник прямоугольным или нет.
В океанографии формула используется для расчета скорости звуковых волн в воде.
Теорема Пифагора используется в метеорологии и авиакосмической промышленности для определения источника звука и его дальности.
Мы можем использовать теорему Пифагора для расчета электронных компонентов, таких как экраны телевизоров, компьютерные экраны, солнечные панели и т. Д.
Мы можем использовать теорему Пифагора для вычисления градиента определенного ландшафта.
В навигации теорема используется для вычисления кратчайшего расстояния между заданными точками.
В архитектуре и строительстве мы можем использовать теорему Пифагора для расчета уклона крыши, водосточной системы, плотины и т. Д.

Рабочие примеры теоремы Пифагора:

Пример 4

Две короткие стороны прямоугольного треугольника — 5 см и 12 см. Найдите длину третьей стороны

Решение

Учитывая, a = 5 см

b = 12 см

c =?

Из формулы теоремы Пифагора; c ² = a ² + b ², имеем;

Следовательно, третий равен 13 см.

Пример 5

Длина диагонали и одной стороны треугольной стороны составляет 25 см и 24 см соответственно. Каков размер третьей стороны?

Решение

Использование теоремы Пифагора,

c ² = a ² + b ².

Пусть b = третья сторона

25 ² = 24 ² + b ²
625 = 576 + b ²
625-576 = 576-576 + b ²
49 = b ²
b ² = 49

b = √49 = 7 см

Пример 6

Найдите размер экрана компьютера 8 и 14 дюймов.

Подсказка: диагональ экрана равна его размеру .

Решение

Размер экрана компьютера равен диагонали экрана.

Использование теоремы Пифагора,

с ² = 8 ² + 15 ²

Решить относительно c.

с ² = 64 + 225

с ² = 289

с = √289

с = 17

Следовательно, размер экрана компьютера 17 дюймов.

Пример 7

Найдите площадь прямоугольного треугольника, учитывая, что диагональ и основание составляют 8,5 см и 7,7 см соответственно.

Решение

Использование теоремы Пифагора,

8,5 ² = ² + 7,5 ²

Решите для a.

72,25 = ² + 56,25

72,25 — 56,25 = к ² + 56,25 — 56,25

16 = ²

a = √16 = 4 см

Площадь прямоугольного треугольника = (½) x основание x высота

= (½ х 7.7 x 4) см ²

= 15,4 см ²

Практические вопросы

Канат длиной 20 м натянут от вершины 12-метрового дерева до земли. Какое расстояние между деревом и концом веревки на земле?
К стене прислонена лестница длиной 13 м. Если расстояние от основания лестницы до стены составляет 5 м, какова высота стены?

Предыдущий урок | Главная страница | Следующий урок

Примеры теоремы Пифагора

Применение теоремы Пифагора в сценариях реальной жизни

Использование теоремы Пифагора

Возможно, вы слышали о теореме Пифагора (или теореме Пифагора) на уроках математики, но вы можете не осознавать, что теорема Пифагора часто используется в реальных жизненных ситуациях.Получите лучшее понимание концепции с помощью этих реальных примеров. Согласно теореме Пифагора сумма квадратов двух сторон прямоугольного треугольника равна квадрату гипотенузы. Пусть одна сторона прямоугольного треугольника равна a, другая сторона — b, а гипотенуза равна c. Согласно теореме Пифагора: a2 + b2 = c2 Этому учат в каждом классе по всему миру, но не учат тому, как его можно применять вне класса.

Реальное применение теоремы Пифагора

Некоторые практические приложения для ознакомления учащихся средней школы с концепцией теоремы Пифагора приведены ниже: 1) Road Trip: Допустим, двое друзей встречаются на детской площадке.Мэри уже в парке, но ее другу Бобу нужно добраться туда по кратчайшему пути. У Боба есть два пути — он может следовать по дорогам, ведущим к парку — сначала на юг на 3 мили, затем на запад на 4 мили. Общее расстояние, пройденное по дорогам, составит 7 миль. Другой способ добраться туда — это пройти через открытое поле и пройти прямо в парк. Если мы применим теорему Пифагора для вычисления расстояния, вы получите: (3) 2 + (4) 2 = 9 + 16 = C2 √25 = C 5 миль.= C Прогулка по полю будет на 2 мили короче, чем прогулка по дорогам. . 2) Рисование на стене: Художники используют лестницы для рисования на высоких зданиях и часто используют теорему Пифагора для завершения своей работы. Маляр должен определить, какой высоты должна быть лестница, чтобы безопасно разместить основание подальше от стены, чтобы оно не опрокинулось. В этом случае гипотенузой будет сама лестница. Возьмем, к примеру, художника, который должен красить стену высотой около 3 метров.Маляр должен поставить основание лестницы на расстоянии 2 м от стены, чтобы она не опрокинулась. Какой длины будет лестница, необходимая художнику для завершения работы? Вы можете вычислить его, используя теорему Пифагора: (3) 2 + (2) 2 = C2 9 + 4 = C2 √13 = C 3,6 м. = C Таким образом, маляру понадобится лестница высотой около 3,6 метра. 3) Покупка чемодана: Мистер Гарри хочет купить чемодан. Владелец магазина сообщает мистеру Гарри, что в настоящее время у него есть 30-дюймовый чемодан, а высота чемодана 18 дюймов.Рассчитайте фактическую длину чемодана для мистера Гарри, используя теорему Пифагора. Он рассчитывается следующим образом: (18) 2 + (b) 2 = (30) 2 324 + b2 = 900 B2 = 900 — 324 b = √576 = 24 дюйма 4) Телевизор какого размера следует покупать? Г-н Джеймс увидел рекламу телевизора в газете, где упоминалось, что телевизор имеет высоту 16 дюймов и ширину 14 дюймов. Вычислите диагональ экрана мистера Джеймса. Используя теорему Пифагора, его можно рассчитать как: (16) 2 + (14) 2 = 256 + 196 = C2 √452 = C примерно 21 дюйм.= C 5) В поисках компьютера подходящего размера: Мэри хочет получить компьютерный монитор для своего стола, на котором можно разместить 22-дюймовый монитор. Она нашла монитор шириной 16 дюймов и высотой 10 дюймов. Подходит ли компьютер в каюту Мэри? Используйте теорему Пифагора, чтобы узнать: (16) 2 + (10) 2 = 256 + 100 = C2 √356 = C примерно 19 дюймов. = C Щелкните здесь, чтобы узнать больше о теореме Пифагора и ее доказательстве. Практические идеи

Теперь напишите свою задачу, основанную на возможной реальной жизненной ситуации.

Список литературы

Теорема Пифагора — задачи, примеры и формулы

В 1960-х годах был показан мюзикл «Веселый Эндрю» об учителе математики, который присоединился к цирку. В этой истории есть песня, объясняющая теорему Пифагора. Пифагор сказал: «Интересно, как далеко можно было бы пройти отсюда туда, не обойдя вокруг этого дерева?» Согласно Пифагору, квадрат гипотенузы равен сумме квадратов двух других сторон треугольника.Хотя Пифагор — гений, он вызвал немало споров, особенно в том, что касается того, что бросили человека в море за утверждение, что квадратный корень из 2 иррационален. Однако речь идет не о жизни Пифагора, а о теореме.

В этом уроке вы узнаете о теореме Пифагора, ее выводах и уравнениях, за которыми следуют решения реальных задач о треугольнике и квадратах теоремы Пифагора.

Что такое теорема Пифагора?

Теорема Пифагора утверждает, что если треугольник прямоугольный (90 градусов), то квадрат гипотенузы равен сумме квадратов двух других сторон.В данном треугольнике ABC, , имеем BC ² = AB ² + AC ². Здесь AB — основание, AC — высота или высота, а BC — гипотенуза.

Теорема Пифагора Уравнение

Уравнение теоремы Пифагора поможет вам решить задачи прямоугольного треугольника, используя уравнение Пифагора: c ² = a ² + b ² (‘c’ = гипотенуза прямоугольного треугольника, тогда как ‘a’ и ‘b ‘- две другие ноги.). Следовательно, любой треугольник с одним углом, равным 90 градусам, сможет создать треугольник Пифагора. Мы можем использовать это уравнение Пифагора: c ² = a ² + b ².

История теоремы Пифагора

Теорема Пифагора была введена греческим математиком Пифагором из Самоса. Он был древнегреческим ионийским философом. Он основал группу математиков, которые религиозно работали с числами и жили как монахи. Наконец, греческий математик сформулировал теорему, поэтому она названа по его имени «теоремой Пифагора».«Хотя он был введен много веков назад, его применение в нынешнюю эпоху обязательно в прагматических ситуациях.

Хотя Пифагор представил и популяризировал эту теорему, существует достаточно свидетельств, подтверждающих ее существование в других цивилизациях, за 1000 лет до рождения Пифагора. Самые старые известные свидетельства датируются 20-16 веками до нашей эры в древневавилонский период.

Теорема Пифагора Формула

Формула теоремы Пифагора утверждает, что в прямоугольном треугольнике ABC квадрат гипотенузы равен сумме квадратов двух других катетов.Если AB, BC и AC — стороны треугольника, то: BC ² = AB ² + AC ². Тогда как если a, b и c — стороны треугольника, то c ² = a ² + b ². В этом случае мы можем сказать, что AB — основание, AC — высота или высота, а BC — гипотенуза.

Доказательство теоремы Пифагора

Теорема Пифагора может быть доказана многими способами. Некоторые из наиболее распространенных и наиболее широко используемых методов заключаются в использовании доказательства алгебраического метода и использовании аналогичного метода треугольников для их решения.Давайте рассмотрим оба этих метода по отдельности, чтобы понять доказательство этой теоремы.

Алгебраический метод Доказательство теоремы Пифагора
Доказательство теоремы Пифагора с использованием подобных треугольников

Алгебраический метод Доказательство теоремы Пифагора

Доказательство теоремы Пифагора алгебраическим методом поможет нам получить доказательство теоремы Пифагора, используя значения a, b и c (значения мер длин сторон, соответствующих сторонам BC, AC и AB соответственно).Рассмотрим четыре прямоугольных треугольника ABC, где b — основание, a — высота и c — гипотенуза. Расположите эти четыре равных прямоугольных треугольника в данном квадрате со стороной a + b.

Площадь квадрата, образованного четырьмя треугольниками, равна c ². Площадь квадрата со стороной (a + b) = Площадь четырех треугольников + Площадь квадрата со стороной c. Отсюда следует (a + b) ² = 4 × 1/2 × (a × b) + c ², a ² + b ² + 2ab = 2ab + c ^2. Следовательно, a ² + b ² = c ². Следовательно, доказано.

Доказательство теоремы Пифагора с использованием подобных треугольников

Два треугольника называются подобными, если их соответствующие углы имеют одинаковую меру и их соответствующие стороны находятся в одинаковом соотношении. Кроме того, если углы имеют одинаковую меру, то мы можем сказать, используя закон синуса, что соответствующие стороны также будут в одинаковом соотношении. Следовательно, соответствующие углы в подобных треугольниках приведут нас к равному соотношению сторон.

В треугольнике ABD и треугольнике ACB:

∠A = ∠A (общий)
∠ADB = ∠ABC (оба прямые углы)

Таким образом, треугольник ABD и треугольник ACB равноугольны, что означает, что они похожи по критерию сходства AA. Точно так же мы можем доказать треугольник BCD аналогично треугольнику ACB. Поскольку треугольники ABD и ACB подобны, имеем AD / AB = AB / AC. Таким образом, мы можем сказать, что AD × AC = AB ². Точно так же похожи треугольники BCD и ACB.Это дает нам CD / BC = BC / AC. Таким образом, мы также можем сказать, что CD × AC = BC ². Теперь, используя оба этих уравнения подобия, мы можем сказать, что AC ² = AB ² + BC ². Следовательно, доказано.

Теорема Пифагора Треугольники

Правые треугольники подчиняются правилу теоремы Пифагора и называются треугольниками теоремы Пифагора. Длина всех трех сторон вместе называется тройкой Пифагора. Например, 3, 4 и 5 можно назвать одним из наборов таких треугольников.Есть намного больше прямоугольных треугольников, которые называются треугольниками Пифагора. Все такие треугольники подчиняются одному общему правилу: c ² = a ² + b ².

Теорема Пифагора Квадраты

Согласно теореме Пифагора Гипотенуза ² = Перпендикуляр ² + основание ² или c ² = a ² + b ² , что дополнительно оправдывает , площадь квадрата, построенного на гипотенузе прямоугольного треугольника, будет равна сумме площадей квадратов, построенных на двух других сторонах.И эти квадраты известны как квадраты Пифагора.

Приложения теоремы Пифагора

Хотя необходимо изучить основные концепции, такие как формулировка теоремы и ее математическое представление, нам было бы более любопытно понять приложения теоремы Пифагора, которые мы обезглавливаем в повседневных жизненных ситуациях.

Вот некоторые из приложений теоремы Пифагора

Инженерные и строительные отрасли

Большинство архитекторов используют технику теоремы Пифагора, чтобы найти значение, а также, когда длина или ширина известны, очень легко вычислить диаметр конкретного сектора.В основном он используется в двух измерениях в инженерных областях.

Распознавание лиц в камерах видеонаблюдения

Сегодня мы больше знакомы с распознаванием лиц, оно снижает беспорядок при расследовании преступлений в зонах безопасности. Он подчиняется концепции теоремы Пифагора, то есть расстояние между камерой наблюдения и местом, где заметили человека, хорошо проецируется через объектив с использованием этой концепции.

Деревообработка и дизайн интерьеров

Поскольку основная концепция указывает, что если квадратные картоны можно легко превратить в треугольник, разрезая их по диагонали, то можно очень легко применить концепцию Пифагора.В основном изделия из дерева делаются по стратегии, что упрощает работу дизайнеров.

Это очень удивительный факт, но люди, путешествующие по морю, используют эту технику, чтобы найти кратчайшее расстояние и путь к интересующим их местам.

Обычно геодезисты используют эту технику для поиска крутых горных областей, зная горизонтальную область, им было бы легче вычислить остальную часть, используя концепцию Пифагора. Фиксированное и изменяющееся расстояние может быть просмотрено геодезистом в телескоп, что облегчает путь.

Обращение теоремы Пифагора

Мы предполагаем, что вы знакомы с теоремой Пифагора.

Обратное к теореме Пифагора:

Если квадрат длины самой длинной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.

То есть в
ΔABC, если c2 = a2 + b2, то
∠C — прямоугольный треугольник,
ΔPQR — прямой угол.

Мы можем доказать это от противного.

Предположим, что c2 = a2 + b2 в ΔABC и треугольник , а не прямоугольный.

Теперь рассмотрим другой треугольник.
ΔPQR.

Мы строим
ΔPQR так, чтобы
PR = a, QR = b и ∠R — прямой угол.

По теореме Пифагора (PQ) 2 = a2 + b2.

Но мы знаем, что a2 + b2 = c2, a2 + b2 = c2 и c = AB.

Итак, (PQ) 2 = a2 + b2 = (AB) 2.

То есть (PQ) 2 = (AB) 2.

Поскольку PQ и AB — длины сторон, мы можем взять положительные квадратные корни.

PQ = AB

То есть, все три стороны ΔPQR конгруэнтны трем сторонам ΔABC.

Итак, два треугольника конгруэнтны по свойству конгруэнтности сторона-сторона-сторона.

Поскольку ΔABC конгруэнтно ΔPQR, а ΔPQR — прямоугольный треугольник, ΔABC также должен быть прямоугольным треугольником.

Получили противоречие. Следовательно, наше предположение должно быть неверным.

Пример 1:

Проверьте, является ли треугольник со сторонами 6 см, 10 см и 8 см прямоугольным.

Проверьте, является ли квадрат длины самой длинной стороны суммой квадратов двух других сторон.

(10) 2 =? (8) 2+ (6) 2100 =? 64 + 36 100 = 100

Примените обратную теорему Пифагора.

Поскольку квадрат длины самой длинной стороны является суммой квадратов двух других сторон, согласно обратной теореме Пифагора, треугольник является прямоугольным.

Следствие теоремы подразделяет треугольники на острые, правые и тупые.

В треугольнике с длинами сторон a, b и c, где c — длина самой длинной стороны,

, если c2

если c2> a2 + b2, то треугольник тупой.

Пример 2:

Проверьте, является ли треугольник с длинами сторон 5, 7 и 9 единиц острым, прямым или тупым треугольником.

Самая длинная сторона треугольника имеет длину 9 единиц.

Сравните квадрат длины самой длинной стороны и сумму квадратов двух других сторон.

Квадрат длины самой длинной стороны 92 = 81 кв. Ед.

Сумма квадратов двух других сторон равна

52 + 72 = 25 + 49 = 74 кв. Единицы

То есть 92> 52 + 72.

Следовательно, согласно следствию, обратному теореме Пифагора, треугольник является тупым треугольником.

Решение задач, связанных с теоремой Пифагора

Решение задач, связанных с теоремой Пифагора
Вот шаги, необходимые для решения задач комбинированной вариации:

Шаг 1 :	Нарисуйте прямоугольный треугольник и снова прочитайте задачи, чтобы определить длину катетов и гипотенузу.
Шаг 2 :	Используйте теорему Пифагора (a ² + b ² = c ²), чтобы написать уравнение, которое нужно решить. Помните, что a и b — это катеты, а c — гипотенуза (самая длинная сторона или сторона, противоположная углу 90º).
Шаг 3 :	Упростите уравнение, распределяя и комбинируя одинаковые термины по мере необходимости.
Шаг 4 :	Решите уравнение.Если уравнение содержит x ², приравняйте уравнение к нулю и решите уравнение на множители. Если уравнение не содержит x ², решите уравнение, получив переменные с одной стороны и числа с другой.
Шаг 5 :	Ответьте на вопрос, заданный в исходном вопросе, и убедитесь, что ответ имеет смысл. Не забудьте указать единицы в своем окончательном ответе.

Пример 1 — Гипотенуза прямоугольного треугольника на 1 дюйм длиннее его более длинного катета.Более короткая нога на 7 дюймов короче более длинной. Найдите длину гипотенузы.

Пример 2 — Кэрри работает в счет к югу от своей квартиры. Ее подруга Сара работает к востоку от квартиры. Они уходят на работу одновременно. К тому времени, как Кэрри находится в 5 милях от их квартиры, расстояние между ними будет на 1 милю больше, чем расстояние Сары от квартиры. Как далеко от квартиры Сара?

Щелкните здесь для практических задач

Пример 3 — Оттяжка прикреплена к телефонной опоре.Расстояние от точки соприкосновения провода с землей до основания телефонной опоры на 4 фута меньше длины провода. На каком расстоянии от телефонного столба расположен провод, если расстояние от земли до места, где провод прикреплен к столбу, на 2 фута меньше длины провода?

Щелкните здесь для практических задач

Пример 4 — Основание лестницы находится на расстоянии 10 футов от стены. Лестница на 2 фута длиннее, чем высота, которую она достигает на стене.Какая длина лестницы?

Щелкните здесь для практических задач

Теорема Пифагора — формула, доказательство, задачи

Основные понятия

Теорема Пифагора: доказательство

Обратная теорема Пифагора: доказательство

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см.

Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?

Теорема Пифагора — формула с доказательством

История теоремы

Теорема Пифагора, формула

Доказательство теоремы методом площадей: 1 способ

Примеры решения задач

Заключение

Теорема Пифагора, формула и доказательство

Геометрическая формулировка теоремы Пифагора

Доказательство теоремы Пифагора

Примеры решения задач

Разные способы доказательства теоремы Пифагора: примеры, описание и отзывы

Краткий обзор биографии

Рождение теоремы

Теорема Пифагора

Способ первый

Способ два: подобные треугольники

Еще одна методика расчетов

Самый простой способ доказать теорему Пифагора. Отзывы

Доказательство Дж. Гарфилда

Практическое применение теоремы Пифагора

Связь теоремы и астрономии

Радиус передачи мобильного сигнала

Теорема Пифагора в быту

Урок на тему «Примеры решения задач с помощью теоремы Пифагора с применением электронного учебника»

История теоремы Пифагора

Из жизни Пифагора

В плену царя Вавилона

Тайный монашеский орден

Учение Пифагора

Теорема Пифагора

Кратко из истории теоремы Пифагора

Доказательство теоремы

Теорема Пифагора с примерами

Применение теоремы Пифагора (примеры)

Пример

Решение

Приложения (проблемы с текстом) с теоремой Пифагора

Пример

Решение

Задачи в стиле алгебры с теоремой Пифагора

Сводка

Подпишитесь на нашу рассылку новостей!

Теорема Пифагора — объяснение и примеры

Что такое теорема Пифагора?

Как составить теорему Пифагора?

Обращение теоремы Пифагора

Добавить комментарий Отменить ответ