Содержание
Виды уравнений и способы их решения
Цели урока:
Обучающие:
- Обобщить знания по всем видам уравнений,
подчеркнуть значимость всех способов,
применяемых при решении уравнений. - Активизирование работы учащихся за счет,
разнообразных приемов на уроке. - Проверить теоретические и практические навыки
при решении уравнений. - Заострить внимание на том, что, одно уравнение
можно решить несколькими способами
Развивающие:
- Повысить интерес учащихся к предмету, через
использование ИКТ. - Ознакомление учащихся с историческим
материалом по теме. - Развитие мыслительной деятельности при
определении вида уравнения и способов его
решения.
Воспитательные:
- Воспитать дисциплину на уроке.

- Развитие способности к восприятию прекрасного,
в себе самом, в другом человеке и в окружающем
мире.
Тип урока:
- Урок обобщения и систематизации знаний.
Вид урока:
- Комбинированный.
Материально-техническое оснащение:
- Компьютер
- Экран
- Проектор
- Диск с презентацией темы
Методы и приемы:
- Использование презентации
- Фронтальная беседа
- Устная работа
- Игровые моменты
- Работа в парах
- Работа у доски
- Работа в тетрадях
План урока:
- Организационный момент (1минуты)
- Расшифровка темы урока (3минуты)
- Сообщение темы и цели урока (1минута)
- Теоретическая разминка (3минут)
- Исторический экскурс (3минуты)
- Игра “Убери лишнее” (2минуты)
- Творческая работа (2минуты)
- Задание “Найди ошибку” (2минуты)
- Решение одного уравнения несколькими способами
(на слайде) (3минуты) - Решение одного уравнения несколькими способами
(у доски) (24 минут) - Самостоятельная работа в парах с последующим
объяснением (5минут) - Индивидуальное домашнее задание(1минуты)
- Итог урока рефлексия (1минута)
Эпиграф урока:
“Учиться можно только весело, чтобы
переваривать знания, нужно поглощать их с
аппетитом”.
А.Франс
Конспект урока
Организационная часть
Проверяю готовность учащихся к уроку, отмечаю
отсутствующих на уроке. Ребята, Французский
писатель 19 века А.Франс однажды заметил “
Учиться можно только весело, чтобы переваривать
знания, нужно поглощать их с аппетитом”. Так
давайте на нашем уроке следовать совету,
писателя и переваривать знания с большим
аппетитом, ведь они пригодятся в нашей жизни.
Расшифровка темы урока
Для того, чтобы перейти к более сложном
заданием, давайте разомнем свои мозги простыми
заданиями. Тема нашего урока зашифрована, решив
устные задания и найдя к ним ответ, зная, что
каждый ответ имеет свою букву, мы раскроем тему
урока. Презентация слайд 3
Сообщение темы и цели урока
Вы, сегодня сами назвали тему урока
“Виды уравнений и способы их решения”. Презентация
Презентация
слайд 4
Цель: Вспомнить и обобщить все виды уравнений и
способы их решения. Решить одно уравнение всеми
способами. Презентация слайд 5 Прочитать
высказывание Эйнштейна Презентация слайд 5
Теоретическая разминка
Вопросы Презентация слайд 7
Ответы
- Равенство, содержащее переменную величину,
обозначенную какой-то буквой. - Это значит найти все его корни, или доказать, что
корней нет. - Значение переменной, при котором уравнение
обращается в верное равенство. - После этого определения прочесть стихотворение
об уравнении Презентация слайд 12,13,14
Ответы на 2 последних вопроса Презентация слайд
9,10,11
Исторический экскурс
Историческая справка, о том “Кто и когда
придумал уравнение” Презентация слайд 15
Представим себе, что первобытная мама по
имени. .. впрочем, у неё, наверно, и имени то не было,
.. впрочем, у неё, наверно, и имени то не было,
сорвала с дерева 12 яблок, чтобы дать каждому из
своих 4 детей. Вероятно, она не умела считать не
только до 12, но и до четырёх, и уж несомненно не
умела делить 12 на 4.А яблоки она поделила, наверно,
так: сначала дала каждому ребёнку по яблоку,
потом ещё по яблоку, потом ещё по одному и тут
увидела, что яблок больше нет и дети довольны.
Если записать эти действия на современном
математическом языке, то получается х4=12, то есть
мама решила задачу на составление уравнение.
По-видимому, ответить на поставленный выше
вопрос невозможно. Задачи, приводящие к решению
уравнений, люди решили на основе здравого смысла
с того времени, как они стали людьми. Ещё за 3-4
тысячи лет до нашей эры египтяне и вавилоняне
умели решать простейшие уравнения, вид которых и
приёмы решения были не похожи на современные.
Греки унаследовали знания египтян, и пошли
дальше. Наибольших успехов в развитие учения об
Наибольших успехов в развитие учения об
уравнениях достиг греческий учёный Диофант(III
век), о котором писали:
Он уйму всяких разрешил проблем.
И запахи предсказывал, и ливни.
Поистине, его познанья дивны.
Большой вклад в решение уравнений внёс
среднеазиатский математик Мухаммед ал Хорезми
(IХ век). Его знаменитая книга ал-Хорезми
посвящена решению уравнений. Она называется
“Китаб ал-джебр вал-мукабала”, т. е. “Книга о
восполнении и противопоставлении”. Эта книга
стала известна европейцам, а от слова “ал-джебр”
из ее заглавия произошло слово “алгебра” –
название одной из главных частей математики. В
дальнейшем многие математики занимались
проблемами уравнений. Общее правило решений
квадратных уравнений приведённых к виду х2+вх=0
было сформулировано немецким математиком
Штифелем, проживавшим в ХV веке. После трудов
нидерландского математика Жирара (ХVI век), а
также Декарта и Ньютона, способ решения принял
современный вид. Формулы, выражающие зависимости
Формулы, выражающие зависимости
корней уравнения от его коэффициентов была
введена Виетом. Франсуа Виет жил в ХVI веке. Он
внёс большой вклад в изучение различных проблем
в математике и астрономии; в частности, он ввёл
буквенные обозначения коэффициентов уравнения.
А сейчас познакомимся с интересным эпизодом из
его жизни. Громкую славу Виет получил при короле
Генрихе III, вовремя франко-испанской войны.
Испанские инквизиторы изобрели очень сложную
тайнопись, благодаря которой испанцы вели
переписку с врагами Генриха III даже в самой
Франции.
Напрасно французы пытались найти ключ к шифру,
и тогда король обратился к Виету. Рассказывают,
что Виет нашёл за две недели непрерывной работы
ключ к шифру, после чего, неожиданно для Испании,
Франция стала выигрывать одно сражение за
другим. Будучи уверенным, что шифр разгадать не
возможно, испанцы обвинили Виета в связи с
дьяволом и приговорили к сожжению на костре.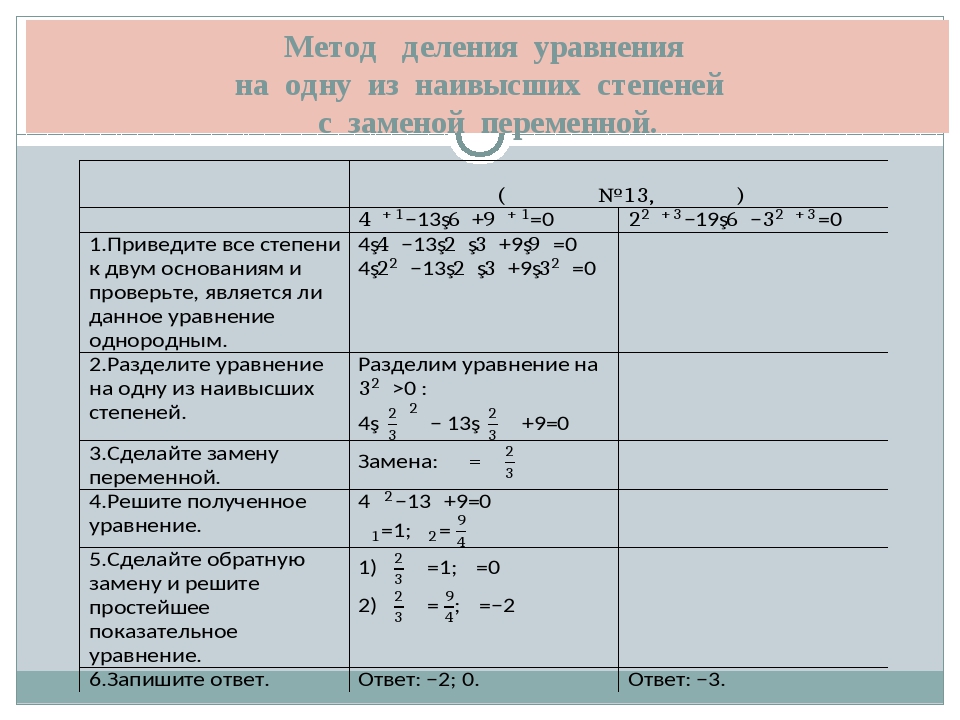 К
К
счастью, он не был выдан инквизиции и вошёл в
историю как великий математик.
Игра “Убери лишнее”
Цель игры ориентирование в видах
уравнений.
У нас даны три столбика уравнений ,в каждом из
них, уравнения определены по какому-то признаку
,но одно из них лишнее ваша задача его найти и
охарактеризовать. Презентация слайд 16
Творческая работа
Цель этого задания: Восприятие на слух
математической речи ориентировании детей в
видах уравнений .
На экране вы видите 9 уравнений. Каждое
уравнение имеет свой номер, я буду называть вид
этого уравнения, а вы должны найти уравнение
этого вида, и поставить только номер, под которым
оно стоит, в результате вы получите 9-значное
число Презентация слайд 17
- Приведенное квадратное уравнение.
- Дробно-рациональное уравнение
- Кубическое уравнение
- Логарифмическое уравнение
- Линейное уравнение
- Неполное квадратное уравнение
- Показательное уравнение
- Иррациональное уравнение
- Тригонометрическое уравнение
Задание “Найди ошибку”
Один ученик решал уравнения, но весь класс
смеялся, в каждом уравнении он допустил ошибку,
ваша задача найти ее и исправить. Презентация
Презентация
слайд 18
Решение одного уравнения несколькими
способами
А теперь решим одно уравнение всеми возможными
способами, для экономии времени на уроке одно
уравнение на экране. Сейчас вы назовете вид этого
уравнения, и объясните какой способ используется
, при решении этого уравнения Презентация слайды
19-27
Решение одного уравнения несколькими
способами (у доски)
Мы посмотрели пример, а теперь давайте решим
уравнение у доски всевозможными способами.
=x-2 -
иррациональное уравнение
Возведем в квадрат обе части уравнения.
2x-1=(x-2)2
2x-1=x2-4x+4
-x2+2x+4x-1-4=0
x2-6x+5=0
Решаем это уравнение у доски 9 способами.
Самостоятельная работа в парах с
последующим объяснением у доски
А сейчас вы поработаете в парах, на парту я даю
уравнение, ваша задача определить вид уравнения,
перечислить все способы решения этого уравнения,
решить 1-2 наиболее рациональными для вас
способами. (2 минуты)
(2 минуты)
Задания для работы в парах
Решите уравнение
- =x-2
- =6
- 36-x=33x-2
- 9x-83x-9=0
- 23x+1-3x=15
- = 4
После самостоятельной работы в парах один
представитель выходит к доске представляет свое
уравнение, решает одним способом
Индивидуальное домашнее задание
(дифференцируемо)
Решите уравнение
- =x-2
- =6
- 36-x=33x-2
- 9x-83x-9=0
- 23x+1-3x=15
- =4
- 3x5=96
- |x+2|=
(определить вид уравнения, решить всеми
способами на отдельном листе)
Итог урока рефлексия.
Подвожу итог урока, заостряю внимание на том,
что одно уравнение можно решить многими
способами, выставляю оценки, делаю вывод, кто был
активным кому надо быть поактивнее. Зачитываю
высказывание Калинина Презентация слайд 28
Посмотрите внимательно на те цели которые мы с
вами поставили для сегодняшнего урока:
- Что на ваш взгляд нам удалось сделать?
- Что получилось не очень хорошо?
- Что вам особенно понравилось и запомнилось?
- Сегодня я узнал новое…
- На уроке мне пригодились знания…
- Для меня было сложно…
- На уроке мне понравилось…
Литература.
- Дорофеев Г.В. “Сборник заданий для проведения
письменного экзамена по математике за курс
средней школы” — М.: Дрофа, 2006. - Гарнер Мартин. Математические головоломки и
развлечения.
- Ивлев Б.М., Саакян С.М. Дидактические материалы
по алгебре и началам анализа для 10 кл., 11 кл. М.:
Просвещение. 2002.
Презентация на тему «Виды уравнений и способы их решения. Урок без ручки и тетради»
Слайд 1
Виды уравнений и способы их решений
35 минут без ручки и тетради
9 класс, алгебра
Учитель КОУ «В(С)ОШ №3», г. Омск, Валентина Федоровна Краус
Слайд 2
Решите уравнения
Слайд 3
Слайд 4
Слайд 5
Слайд 6
Слайд 7
Слайд 8
Слайд 9
Установите соответствие
Слайд 10
Поехали!!!
Слайд 11
Решите графически уравнение
Слайд 12
Форма клумбы
Слайд 13
Определите вид уравнений
Слайд 14
Решите уравнения
Слайд 15
Слайд 16
Слайд 17
Слайд 18
Определите вид уравнений
Слайд 19
Решите уравнения
Слайд 20
Слайд 21
Слайд 22
Слайд 23
Слайд 24
Слайд 25
Определите вид уравнений
Слайд 26
Решите уравнения
Слайд 27
Слайд 28
Слайд 29
Слайд 30
Слайд 31
Определите вид уравнений
Слайд 32
Решите уравнения
Слайд 33
Слайд 34
Слайд 35
Определите вид уравнений
Слайд 36
Решите уравнения
Слайд 37
Слайд 38
Слайд 39
Слайд 40
Слайд 41
Определите вид уравнений
Слайд 42
Решите уравнения
Слайд 43
Слайд 44
Слайд 45
Слайд 46
Определите вид уравнений
Слайд 47
Слайд 48
Решите уравнения
Слайд 49
Слайд 50
Решить уравнения, фиксируя на листе только ответы
Слайд 51
Проверьте, каждое верное решение приносит вам 1 балл
Слайд 52
-Молодцы, ребята!!! Путешествие окончено.
 Возвращаемся домой!
Возвращаемся домой!
Слайд 53
Домашнее задание
составьте 2 варианта контрольной работы по теме «Виды уравнений и различные способы их решений»
или
составьте кроссворд, содержащий слова прозвучавшие сегодня на уроке, связанные с уравнением
или
подберите из учебника по 1 примеру к различным видам уравнений и решите их
Различные способы решения квадратных уравнений
В процессе работы над индивидуальным проектом по математике «Различные способы решения квадратных уравнений» учениками 9 класса школы была поставлена и реализована цель, изучить различные методы решения квадратных уравнений.
Подробнее о проекте:
В ученической исследовательской работе по математике «Различные способы решения квадратных уравнений» автор проводит анализ учебно-методической литературы по решению квадратных уравнений, анализирует различные способы решения квадратных уравнений, изучает возможные варианты решения квадратных уравнений и апробирует их на практике, собирает дидактический материл для дальнейшего его использования на уроках математики и во время самостоятельных занятий по предмету.
В готовом творческом и исследовательском проекте по математике «Различные способы решения квадратных уравнений» автор выполняет практические задания по решению квадратных уравнений разными способами, подробно описывает их. Также в работе представлен интересный блок из истории развития квадратных уравнений в разных странах и в разные временные отрезки, объясняется теорема Виета. В практической части работы продемонстрированы способы решения квадратных уравнений, некоторые из которых в школе не изучаются.
Оглавление
Введение
1. История развития квадратных уравнений.
2. О теореме Виета.
3. Способы решения квадратных уравнений.
Заключение
Литература
Приложение
Введение
Актуальность. Практически все, что окружает современного человека — это все так или иначе связано с математикой. А достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем решение многих практических задач сводится к решению квадратных уравнений.
Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Они представляют собой большой и важный класс уравнений, которые решаются как с помощью формул, так и с помощью нестандартных способов. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств.
В школьном курсе математики мы изучили квадратные уравнения, узнали различные способы решения уравнений второй степени. Этот материал нас заинтересовал, и мы решили узнать, существуют ли другие способы решения квадратных уравнений. Это определило тему нашего исследования: «Квадратные уравнения и методы их решения».
В учебниках мы знакомимся с несколькими видами квадратных уравнений, и отрабатываем решение по формулам. Нам пришла идея рассмотреть те способы решения квадратных уравнений, на которые недостаточно времени уделено на уроках или совсем не рассматриваются в школьном курсе.
Вместе с тем, современные научно-методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.
Цель исследования: изучение различных методов решения квадратных уравнений.
Задачи:
- Произвести анализ учебно-методической литературы по решению квадратных уравнений.
- Произвести анализ различных способов решения квадратных уравнений.
- Изучить различные способы решения квадратных уравнений, апробировать их на практике, собрать дидактический материла.
Гипотеза: существуют методы решения квадратных уравнений не изучаемые в школе.
Новизна исследования состоит в комплексном рассмотрении способов решения уравнений второй степени.
Объект исследования: квадратные уравнения.
Предмет исследования: методы решения квадратных уравнений.
Практическая значимость работы состоит в приобретении навыка решения квадратных уравнений различными способами.
Применяемые методы исследования:
- эмпирические: изучение литературы, обработка материалов.
- теоретические: сравнение, классификация, анализ, обобщение.
Структура работы: работа состоит из введения, теоретической и практической частей, заключения, списка литературы и приложения.
История развития квадратных уравнений
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Уравнения — это наиболее объёмная тема всего курса математики.
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37.», — поучал во II тысячелетии до новой эры египетский писец Ахмес.
«Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37.», — поучал во II тысячелетии до новой эры египетский писец Ахмес.
В древних математических задачах Междуречья, Индии . [4, c.23], Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри», «Делай так», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) — собрание задач на составление уравнений с систематическим изложением их решений.
Уравнения второй степени умели решать еще в древнем Вавилоне. Математики Древней Греции решали квадратные уравнения с помощью геометрических построений [4, c.21]; например, Евклид — при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактах.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.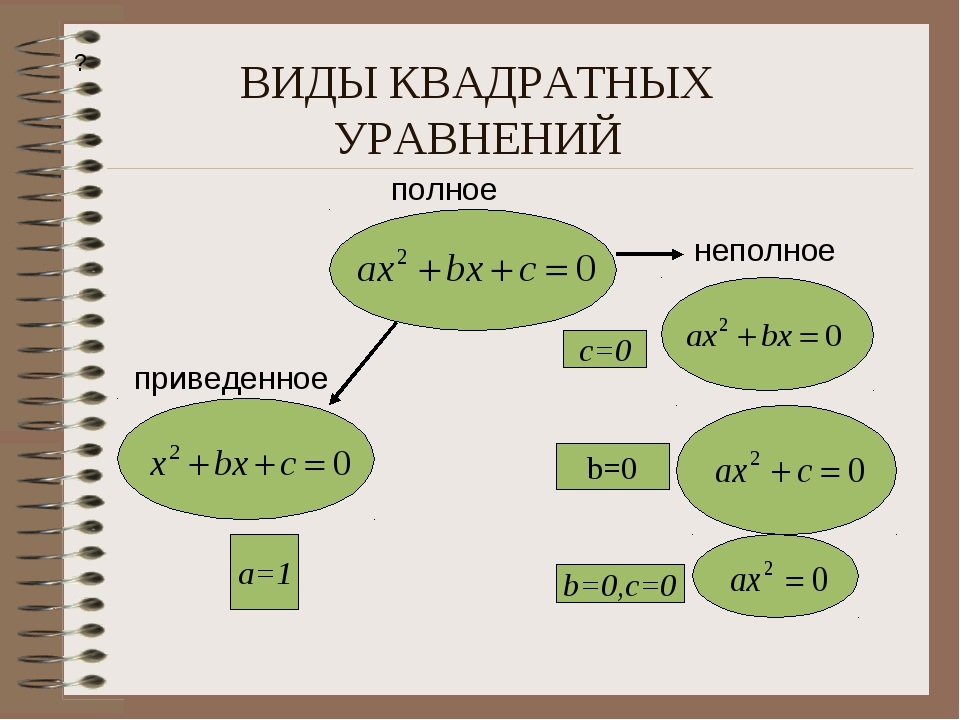 Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения: X2 + X = ѕ; X2 — X = 14,5.
Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения: X2 + X = ѕ; X2 — X = 14,5.
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Как составлял и решал Диофант квадратные уравнения
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней. При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные. Вот, к примеру, одна из его задач.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные. Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение — 96»
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 — х. Разность между ними 2х. Отсюда уравнение: (10 + х)(10 — х) = 96
или же: 100 — х2 = 96, х2 — 4 = 0 (1) Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа. Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения: у(20 — у) = 96,
у2 — 20у + 96 = 0. (2)
(2)
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам» [4, c.23], составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ах2 + bх = с, а > 0. (1)
В уравнении (1) коэффиценты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму. Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задачи часто облекались в стихотворную форму. Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача 13.
«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений.
Соответствующее задаче 13 уравнение: (x/8)2 + 12 = x.
Бхаскара пишет под видом: х2 — 64х = -768 и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем:
х2 — 64х + 322 = -768 + 1024,
(х — 32)2 = 256, х — 32 = ± 16, х1 = 16, х2 = 48.
Квадратные уравнения у ал – Хорезми
В алгебраическом трактате ал — Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корнями», т. е. ах2 + с = bх.
е. ах2 + с = bх.
2) «Квадраты равны числу», т.е. ах2 = с.
3) «Корни равны числу», т.е. ах = с.
4) «Квадраты и числа равны корням», т.е. ах2 + с = bх.
5) «Квадраты и корни равны числу», т.е. ах2 + bx = с.
6) «Корни и числа равны квадратам», т.е. bx + с = ах2.
Для ал — Хорезми, избегавшего употребления отрицательных чисел, члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал — джабр и ал — мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал — Хорезми, как и все математики до XVII в., е учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал — Хорезми на частных числовых примерах излагает правила решения, а затем и геометрические доказательства.
Задача 14. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат ал — Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
Квадратные уравнения в Европе XIII — XVII вв.
Формулы решения квадратных уравнений по образцу ал — Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения.
Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII.
Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду: х2 + bx = с, при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
О теореме Виета
Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D, умноженное на A — A2, равно BD, то A равно В и равноD».
следующим образом: «Если B + D, умноженное на A — A2, равно BD, то A равно В и равноD».
Чтобы понять Виета, следует вспомнить, что А, как и всякая гласная буква, означало у него неизвестное (наше х), гласные же В,D — коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место (а + b)х — х2 = ab, т.е. х2 — (а + b)х + аb = 0,то х1 = а, х2 = b.
Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. [4, c.25]
Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и поэтому при решении уравнений рассматривал лишь случаи, когда все корни положительны.
Перейти к разделу: 2. Способы решения квадратных уравнений
Исследовательская работа «Алгебраические уравнения высших степеней»
LnRiLWZpZWxke21hcmdpbi1ib3R0b206MC43NmVtfS50Yi1maWVsZC0tbGVmdHt0ZXh0LWFsaWduOmxlZnR9LnRiLWZpZWxkLS1jZW50ZXJ7dGV4dC1hbGlnbjpjZW50ZXJ9LnRiLWZpZWxkLS1yaWdodHt0ZXh0LWFsaWduOnJpZ2h0fS50Yi1maWVsZF9fc2t5cGVfcHJldmlld3twYWRkaW5nOjEwcHggMjBweDtib3JkZXItcmFkaXVzOjNweDtjb2xvcjojZmZmO2JhY2tncm91bmQ6IzAwYWZlZTtkaXNwbGF5OmlubGluZS1ibG9ja311bC5nbGlkZV9fc2xpZGVze21hcmdpbjowfQ==
LnRiLWhlYWRpbmcuaGFzLWJhY2tncm91bmR7cGFkZGluZzowfQ==
LnRiLWJ1dHRvbntjb2xvcjojZjFmMWYxfS50Yi1idXR0b24tLWxlZnR7dGV4dC1hbGlnbjpsZWZ0fS50Yi1idXR0b24tLWNlbnRlcnt0ZXh0LWFsaWduOmNlbnRlcn0udGItYnV0dG9uLS1yaWdodHt0ZXh0LWFsaWduOnJpZ2h0fS50Yi1idXR0b25fX2xpbmt7Y29sb3I6aW5oZXJpdDtjdXJzb3I6cG9pbnRlcjtkaXNwbGF5OmlubGluZS1ibG9jaztsaW5lLWhlaWdodDoxMDAlO3RleHQtZGVjb3JhdGlvbjpub25lICFpbXBvcnRhbnQ7dGV4dC1hbGlnbjpjZW50ZXI7dHJhbnNpdGlvbjphbGwgMC4zcyBlYXNlfS50Yi1idXR0b25fX2xpbms6aG92ZXIsLnRiLWJ1dHRvbl9fbGluazpmb2N1cywudGItYnV0dG9uX19saW5rOnZpc2l0ZWR7Y29sb3I6aW5oZXJpdH0udGItYnV0dG9uX19saW5rOmhvdmVyIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazpmb2N1cyAudGItYnV0dG9uX19jb250ZW50LC50Yi1idXR0b25fX2xpbms6dmlzaXRlZCAudGItYnV0dG9uX19jb250ZW50e2ZvbnQtZmFtaWx5OmluaGVyaXQ7Zm9udC1zdHlsZTppbmhlcml0O2ZvbnQtd2VpZ2h0OmluaGVyaXQ7bGV0dGVyLXNwYWNpbmc6aW5oZXJpdDt0ZXh0LWRlY29yYXRpb246aW5oZXJpdDt0ZXh0LXNoYWRvdzppbmhlcml0O3RleHQtdHJhbnNmb3JtOmluaGVyaXR9LnRiLWJ1dHRvbl9fY29udGVudHt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7dHJhbnNpdGlvbjphbGwgMC4zcyBlYXNlfS50Yi1idXR0b25fX2ljb257ZGlzcGxheTppbmxpbmUtYmxvY2s7dmVydGljYWwtYWxpZ246bWlkZGxlO2ZvbnQtc3R5bGU6bm9ybWFsICFpbXBvcnRhbnR9LnRiLWJ1dHRvbl9faWNvbjo6YmVmb3Jle2NvbnRlbnQ6YXR0cihkYXRhLWZvbnQtY29kZSk7Zm9udC13ZWlnaHQ6bm9ybWFsICFpbXBvcnRhbnR9LnRiLWJ1dHRvbl9fbGlua3tiYWNrZ3JvdW5kLWNvbG9yOiM0NDQ7Ym9yZGVyLXJhZGl1czowLjNlbTtmb250LXNpemU6MS4zZW07bWFyZ2luLWJvdHRvbTowLjc2ZW07cGFkZGluZzowLjU1ZW0gMS41ZW0gMC41NWVtfSAudGItYnV0dG9uW2RhdGEtdG9vbHNldC1ibG9ja3MtYnV0dG9uPSIzOTA4OTI3NmJjZGIwOGQxMGY4ZjhlMmViODBjNmM2ZiJdIHsgdGV4dC1hbGlnbjogY2VudGVyOyB9IC50Yi1idXR0b25bZGF0YS10b29sc2V0LWJsb2Nrcy1idXR0b249IjM5MDg5Mjc2YmNkYjA4ZDEwZjhmOGUyZWI4MGM2YzZmIl0gLnRiLWJ1dHRvbl9fbGluayB7IGJhY2tncm91bmQtY29sb3I6IHJnYmEoIDI1NSwgMjU1LCAyNTUsIDEgKTtib3JkZXItcmFkaXVzOiAyMXB4O2NvbG9yOiByZ2JhKCAwLCAwLCAwLCAxICk7Ym9yZGVyOiAycHggc29saWQgcmdiYSggOTksIDEyOSwgMjQwLCAxICk7Zm9udC1zaXplOiAxNnB4O2NvbG9yOiByZ2JhKCAwLCAwLCAwLCAxICk7IH0gLnRiLWJ1dHRvbltkYXRhLXRvb2xzZXQtYmxvY2tzLWJ1dHRvbj0iMzkwODkyNzZiY2RiMDhkMTBmOGY4ZTJlYjgwYzZjNmYiXSAudGItYnV0dG9uX19pY29uIHsgZm9udC1mYW1pbHk6IGRhc2hpY29uczsgfSAudGItZmllbGRbZGF0YS10b29sc2V0LWJsb2Nrcy1maWVsZD0iZTM0M2ZjNmUzZTgzOWQ5MWIxNmFjMzA0NTFjZGI2ZTUiXSB7IGZvbnQtc2l6ZTogMTNweDtmb250LXN0eWxlOiBpdGFsaWM7IH0gIC50Yi1maWVsZFtkYXRhLXRvb2xzZXQtYmxvY2tzLWZpZWxkPSJlMzQzZmM2ZTNlODM5ZDkxYjE2YWMzMDQ1MWNkYjZlNSJdIGEgeyB0ZXh0LWRlY29yYXRpb246IG5vbmU7IH0gLnRiLWNvbnRhaW5lciAudGItY29udGFpbmVyLWlubmVye3dpZHRoOjEwMCU7bWFyZ2luOjAgYXV0b30gLndwLWJsb2NrLXRvb2xzZXQtYmxvY2tzLWNvbnRhaW5lci50Yi1jb250YWluZXJbZGF0YS10b29sc2V0LWJsb2Nrcy1jb250YWluZXI9IjZmN2QzNjU3NDcwNzUyMzI0MmI2MWFiNDc3NzM3NDY2Il0geyBwYWRkaW5nOiAyNXB4OyB9IC50Yi1ncmlkLC50Yi1ncmlkPi5ibG9jay1lZGl0b3ItaW5uZXItYmxvY2tzPi5ibG9jay1lZGl0b3ItYmxvY2stbGlzdF9fbGF5b3V0e2Rpc3BsYXk6Z3JpZDtncmlkLXJvdy1nYXA6MjVweDtncmlkLWNvbHVtbi1nYXA6MjVweH0udGItZ3JpZC1pdGVte2JhY2tncm91bmQ6I2QzOGEwMztwYWRkaW5nOjMwcHh9LnRiLWdyaWQtY29sdW1ue2ZsZXgtd3JhcDp3cmFwfS50Yi1ncmlkLWNvbHVtbj4qe3dpZHRoOjEwMCV9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tdG9we3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6ZmxleC1zdGFydH0udGItZ3JpZC1jb2x1bW4udGItZ3JpZC1hbGlnbi1jZW50ZXJ7d2lkdGg6MTAwJTtkaXNwbGF5OmZsZXg7YWxpZ24tY29udGVudDpjZW50ZXJ9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tYm90dG9te3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6ZmxleC1lbmR9IC53cHYtdmlldy1vdXRwdXRbZGF0YS10b29sc2V0LXZpZXdzLXZpZXctZWRpdG9yPSJlMjNiZTRiNjZhNjA3ODkwMzAyMmFiMDgxODJmYzU0OSJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDRuICsgMSkgeyBncmlkLWNvbHVtbjogMSB9IC53cHYtdmlldy1vdXRwdXRbZGF0YS10b29sc2V0LXZpZXdzLXZpZXctZWRpdG9yPSJlMjNiZTRiNjZhNjA3ODkwMzAyMmFiMDgxODJmYzU0OSJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDRuICsgMikgeyBncmlkLWNvbHVtbjogMiB9IC53cHYtdmlldy1vdXRwdXRbZGF0YS10b29sc2V0LXZpZXdzLXZpZXctZWRpdG9yPSJlMjNiZTRiNjZhNjA3ODkwMzAyMmFiMDgxODJmYzU0OSJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDRuICsgMykgeyBncmlkLWNvbHVtbjogMyB9IC53cHYtdmlldy1vdXRwdXRbZGF0YS10b29sc2V0LXZpZXdzLXZpZXctZWRpdG9yPSJlMjNiZTRiNjZhNjA3ODkwMzAyMmFiMDgxODJmYzU0OSJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDRuICsgNCkgeyBncmlkLWNvbHVtbjogNCB9IC53cHYtdmlldy1vdXRwdXRbZGF0YS10b29sc2V0LXZpZXdzLXZpZXctZWRpdG9yPSJlMjNiZTRiNjZhNjA3ODkwMzAyMmFiMDgxODJmYzU0OSJdIC5qcy13cHYtbG9vcC13cmFwcGVyID4gLnRiLWdyaWQgeyBncmlkLXRlbXBsYXRlLWNvbHVtbnM6IG1pbm1heCgwLCAwLjI1ZnIpIG1pbm1heCgwLCAwLjI1ZnIpIG1pbm1heCgwLCAwLjI1ZnIpIG1pbm1heCgwLCAwLjI1ZnIpO2dyaWQtYXV0by1mbG93OiByb3cgfSAud3B2LXBhZ2luYXRpb24tbmF2LWxpbmtzW2RhdGEtdG9vbHNldC12aWV3cy12aWV3LXBhZ2luYXRpb24tYmxvY2s9ImNkZmQ0YzQ3MzdiMjg5OGViYTQ0NDNkZDU5YTFiZjUwIl0geyB0ZXh0LWFsaWduOiBsZWZ0O2p1c3RpZnktY29udGVudDogZmxleC1zdGFydDsgfSAudGItYnV0dG9ue2NvbG9yOiNmMWYxZjF9LnRiLWJ1dHRvbi0tbGVmdHt0ZXh0LWFsaWduOmxlZnR9LnRiLWJ1dHRvbi0tY2VudGVye3RleHQtYWxpZ246Y2VudGVyfS50Yi1idXR0b24tLXJpZ2h0e3RleHQtYWxpZ246cmlnaHR9LnRiLWJ1dHRvbl9fbGlua3tjb2xvcjppbmhlcml0O2N1cnNvcjpwb2ludGVyO2Rpc3BsYXk6aW5saW5lLWJsb2NrO2xpbmUtaGVpZ2h0OjEwMCU7dGV4dC1kZWNvcmF0aW9uOm5vbmUgIWltcG9ydGFudDt0ZXh0LWFsaWduOmNlbnRlcjt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9fbGluazpob3ZlciwudGItYnV0dG9uX19saW5rOmZvY3VzLC50Yi1idXR0b25fX2xpbms6dmlzaXRlZHtjb2xvcjppbmhlcml0fS50Yi1idXR0b25fX2xpbms6aG92ZXIgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOmZvY3VzIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVkIC50Yi1idXR0b25fX2NvbnRlbnR7Zm9udC1mYW1pbHk6aW5oZXJpdDtmb250LXN0eWxlOmluaGVyaXQ7Zm9udC13ZWlnaHQ6aW5oZXJpdDtsZXR0ZXItc3BhY2luZzppbmhlcml0O3RleHQtZGVjb3JhdGlvbjppbmhlcml0O3RleHQtc2hhZG93OmluaGVyaXQ7dGV4dC10cmFuc2Zvcm06aW5oZXJpdH0udGItYnV0dG9uX19jb250ZW50e3ZlcnRpY2FsLWFsaWduOm1pZGRsZTt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9faWNvbntkaXNwbGF5OmlubGluZS1ibG9jazt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7Zm9udC1zdHlsZTpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19pY29uOjpiZWZvcmV7Y29udGVudDphdHRyKGRhdGEtZm9udC1jb2RlKTtmb250LXdlaWdodDpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19saW5re2JhY2tncm91bmQtY29sb3I6IzQ0NDtib3JkZXItcmFkaXVzOjAuM2VtO2ZvbnQtc2l6ZToxLjNlbTttYXJnaW4tYm90dG9tOjAuNzZlbTtwYWRkaW5nOjAuNTVlbSAxLjVlbSAwLjU1ZW19IC50Yi1idXR0b25bZGF0YS10b29sc2V0LWJsb2Nrcy1idXR0b249ImFkYjAyMDVlYjkwZjFiMmFmZWU3ZDE1OWNmYjQyZmMxIl0geyB0ZXh0LWFsaWduOiBjZW50ZXI7IH0gLnRiLWJ1dHRvbltkYXRhLXRvb2xzZXQtYmxvY2tzLWJ1dHRvbj0iYWRiMDIwNWViOTBmMWIyYWZlZTdkMTU5Y2ZiNDJmYzEiXSAudGItYnV0dG9uX19saW5rIHsgYmFja2dyb3VuZC1jb2xvcjogcmdiYSggMjU1LCAyNTUsIDI1NSwgMSApO2JvcmRlci1yYWRpdXM6IDIxcHg7Y29sb3I6IHJnYmEoIDAsIDAsIDAsIDEgKTtib3JkZXI6IDJweCBzb2xpZCByZ2JhKCA5OSwgMTI5LCAyNDAsIDEgKTtmb250LXNpemU6IDE2cHg7Y29sb3I6IHJnYmEoIDAsIDAsIDAsIDEgKTsgfSAudGItYnV0dG9uW2RhdGEtdG9vbHNldC1ibG9ja3MtYnV0dG9uPSJhZGIwMjA1ZWI5MGYxYjJhZmVlN2QxNTljZmI0MmZjMSJdIC50Yi1idXR0b25fX2ljb24geyBmb250LWZhbWlseTogZGFzaGljb25zOyB9IC50Yi1maWVsZFtkYXRhLXRvb2xzZXQtYmxvY2tzLWZpZWxkPSJjYThjNDY0NWQ0OTBhMmM2ZjE0N2JjYTY4MmQ1YjRlYiJdIHsgZm9udC1zaXplOiAxM3B4O2ZvbnQtc3R5bGU6IGl0YWxpYzsgfSAgLnRiLWZpZWxkW2RhdGEtdG9vbHNldC1ibG9ja3MtZmllbGQ9ImNhOGM0NjQ1ZDQ5MGEyYzZmMTQ3YmNhNjgyZDViNGViIl0gYSB7IHRleHQtZGVjb3JhdGlvbjogbm9uZTsgfSBoMy50Yi1oZWFkaW5nW2RhdGEtdG9vbHNldC1ibG9ja3MtaGVhZGluZz0iNWZkYjdlM2Y5ODY1NDRjNGZlMTMwNDhkZmYzZDM2ZTYiXSAgeyBmb250LXNpemU6IDE2cHg7Y29sb3I6IHJnYmEoIDAsIDAsIDAsIDEgKTsgfSAgaDMudGItaGVhZGluZ1tkYXRhLXRvb2xzZXQtYmxvY2tzLWhlYWRpbmc9IjVmZGI3ZTNmOTg2NTQ0YzRmZTEzMDQ4ZGZmM2QzNmU2Il0gYSAgeyBjb2xvcjogcmdiYSggMCwgMCwgMCwgMSApO3RleHQtZGVjb3JhdGlvbjogbm9uZTsgfSBoMi50Yi1oZWFkaW5nW2RhdGEtdG9vbHNldC1ibG9ja3MtaGVhZGluZz0iMDg1ZGJiYmMwZGVmZWFkYzI3YjIzYjU3MzdhY2U2NDUiXSAgeyBjb2xvcjogcmdiYSggMjU1LCAyNTUsIDI1NSwgMSApO2JhY2tncm91bmQtY29sb3I6IHJnYmEoIDYsIDE0NywgMjI3LCAxICk7cGFkZGluZy10b3A6IDIwcHg7cGFkZGluZy1ib3R0b206IDIwcHg7cGFkZGluZy1sZWZ0OiAyNXB4O21hcmdpbi10b3A6IDIwcHg7bWFyZ2luLWJvdHRvbTogMjBweDsgfSAgaDIudGItaGVhZGluZ1tkYXRhLXRvb2xzZXQtYmxvY2tzLWhlYWRpbmc9IjA4NWRiYmJjMGRlZmVhZGMyN2IyM2I1NzM3YWNlNjQ1Il0gYSAgeyBjb2xvcjogcmdiYSggMjU1LCAyNTUsIDI1NSwgMSApO3RleHQtZGVjb3JhdGlvbjogbm9uZTsgfSAudGItZ3JpZCwudGItZ3JpZD4uYmxvY2stZWRpdG9yLWlubmVyLWJsb2Nrcz4uYmxvY2stZWRpdG9yLWJsb2NrLWxpc3RfX2xheW91dHtkaXNwbGF5OmdyaWQ7Z3JpZC1yb3ctZ2FwOjI1cHg7Z3JpZC1jb2x1bW4tZ2FwOjI1cHh9LnRiLWdyaWQtaXRlbXtiYWNrZ3JvdW5kOiNkMzhhMDM7cGFkZGluZzozMHB4fS50Yi1ncmlkLWNvbHVtbntmbGV4LXdyYXA6d3JhcH0udGItZ3JpZC1jb2x1bW4+Knt3aWR0aDoxMDAlfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLXRvcHt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtc3RhcnR9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tY2VudGVye3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6Y2VudGVyfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLWJvdHRvbXt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtZW5kfSAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC50Yi1ncmlkW2RhdGEtdG9vbHNldC1ibG9ja3MtZ3JpZD0iOGM2NzkxNTZjMTRlODFhZDQ5NjBhYWM1MzQ4NWUyNjEiXSB7IGdyaWQtdGVtcGxhdGUtY29sdW1uczogbWlubWF4KDAsIDAuNzJmcikgbWlubWF4KDAsIDAuMjhmcik7Z3JpZC1hdXRvLWZsb3c6IHJvdyB9IC53cC1ibG9jay10b29sc2V0LWJsb2Nrcy1ncmlkLnRiLWdyaWRbZGF0YS10b29sc2V0LWJsb2Nrcy1ncmlkPSI4YzY3OTE1NmMxNGU4MWFkNDk2MGFhYzUzNDg1ZTI2MSJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDJuICsgMSkgeyBncmlkLWNvbHVtbjogMSB9IC53cC1ibG9jay10b29sc2V0LWJsb2Nrcy1ncmlkLnRiLWdyaWRbZGF0YS10b29sc2V0LWJsb2Nrcy1ncmlkPSI4YzY3OTE1NmMxNGU4MWFkNDk2MGFhYzUzNDg1ZTI2MSJdID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDJuICsgMikgeyBncmlkLWNvbHVtbjogMiB9IC50Yi1idXR0b257Y29sb3I6I2YxZjFmMX0udGItYnV0dG9uLS1sZWZ0e3RleHQtYWxpZ246bGVmdH0udGItYnV0dG9uLS1jZW50ZXJ7dGV4dC1hbGlnbjpjZW50ZXJ9LnRiLWJ1dHRvbi0tcmlnaHR7dGV4dC1hbGlnbjpyaWdodH0udGItYnV0dG9uX19saW5re2NvbG9yOmluaGVyaXQ7Y3Vyc29yOnBvaW50ZXI7ZGlzcGxheTppbmxpbmUtYmxvY2s7bGluZS1oZWlnaHQ6MTAwJTt0ZXh0LWRlY29yYXRpb246bm9uZSAhaW1wb3J0YW50O3RleHQtYWxpZ246Y2VudGVyO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19saW5rOmhvdmVyLC50Yi1idXR0b25fX2xpbms6Zm9jdXMsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVke2NvbG9yOmluaGVyaXR9LnRiLWJ1dHRvbl9fbGluazpob3ZlciAudGItYnV0dG9uX19jb250ZW50LC50Yi1idXR0b25fX2xpbms6Zm9jdXMgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOnZpc2l0ZWQgLnRiLWJ1dHRvbl9fY29udGVudHtmb250LWZhbWlseTppbmhlcml0O2ZvbnQtc3R5bGU6aW5oZXJpdDtmb250LXdlaWdodDppbmhlcml0O2xldHRlci1zcGFjaW5nOmluaGVyaXQ7dGV4dC1kZWNvcmF0aW9uOmluaGVyaXQ7dGV4dC1zaGFkb3c6aW5oZXJpdDt0ZXh0LXRyYW5zZm9ybTppbmhlcml0fS50Yi1idXR0b25fX2NvbnRlbnR7dmVydGljYWwtYWxpZ246bWlkZGxlO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19pY29ue2Rpc3BsYXk6aW5saW5lLWJsb2NrO3ZlcnRpY2FsLWFsaWduOm1pZGRsZTtmb250LXN0eWxlOm5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2ljb246OmJlZm9yZXtjb250ZW50OmF0dHIoZGF0YS1mb250LWNvZGUpO2ZvbnQtd2VpZ2h0Om5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2xpbmt7YmFja2dyb3VuZC1jb2xvcjojNDQ0O2JvcmRlci1yYWRpdXM6MC4zZW07Zm9udC1zaXplOjEuM2VtO21hcmdpbi1ib3R0b206MC43NmVtO3BhZGRpbmc6MC41NWVtIDEuNWVtIDAuNTVlbX0gLnRiLWJ1dHRvbltkYXRhLXRvb2xzZXQtYmxvY2tzLWJ1dHRvbj0iMzRmMGE0ZDQ1MjcyYTczOTQ1NmM5MmYwZDlmZjdkYTAiXSB7IHRleHQtYWxpZ246IGNlbnRlcjsgfSAudGItYnV0dG9uW2RhdGEtdG9vbHNldC1ibG9ja3MtYnV0dG9uPSIzNGYwYTRkNDUyNzJhNzM5NDU2YzkyZjBkOWZmN2RhMCJdIC50Yi1idXR0b25fX2xpbmsgeyBiYWNrZ3JvdW5kLWNvbG9yOiByZ2JhKCAyNTUsIDI1NSwgMjU1LCAxICk7Ym9yZGVyLXJhZGl1czogMjFweDtjb2xvcjogcmdiYSggMCwgMCwgMCwgMSApO2JvcmRlcjogMnB4IHNvbGlkIHJnYmEoIDgwLCAxMTMsIDIxOCwgMSApO2ZvbnQtc2l6ZTogMTZweDtsaW5lLWhlaWdodDogMjNweDtjb2xvcjogcmdiYSggMCwgMCwgMCwgMSApOyB9IC50Yi1idXR0b25bZGF0YS10b29sc2V0LWJsb2Nrcy1idXR0b249IjM0ZjBhNGQ0NTI3MmE3Mzk0NTZjOTJmMGQ5ZmY3ZGEwIl0gLnRiLWJ1dHRvbl9faWNvbiB7IGZvbnQtZmFtaWx5OiBkYXNoaWNvbnM7IH0gLnRiLWJ1dHRvbltkYXRhLXRvb2xzZXQtYmxvY2tzLWJ1dHRvbj0iMzRmMGE0ZDQ1MjcyYTczOTQ1NmM5MmYwZDlmZjdkYTAiXSAudGItYnV0dG9uX19pY29uOjpiZWZvcmUgeyBjb250ZW50OiAnXGY0NjcnOyB9ICAudGItZmllbGRbZGF0YS10b29sc2V0LWJsb2Nrcy1maWVsZD0iNjY4YWUxODU1YjI1YjE2MmViOGU0NjAyN2U4NGVlZDYiXSBhIHsgdGV4dC1kZWNvcmF0aW9uOiBub25lOyB9ICAudGItZmllbGRbZGF0YS10b29sc2V0LWJsb2Nrcy1maWVsZD0iYTA5M2Y4MGI5ODk4OGY0NDg2N2JjOTJiYzhiMmJjY2UiXSBhIHsgdGV4dC1kZWNvcmF0aW9uOiBub25lOyB9ICAudGItZmllbGRbZGF0YS10b29sc2V0LWJsb2Nrcy1maWVsZD0iYjIwN2JlMWYwOWI1Y2ZlYWVkZTZhNzE5ODhhNzQyNzUiXSBhIHsgdGV4dC1kZWNvcmF0aW9uOiBub25lOyB9ICAudGItZmllbGRbZGF0YS10b29sc2V0LWJsb2Nrcy1maWVsZD0iNjYwNzcwMDhmOGIzODIyNjg4ZTQyN2Q5ZTAzOWYyMWYiXSBhIHsgdGV4dC1kZWNvcmF0aW9uOiBub25lOyB9IGgzLnRiLWhlYWRpbmdbZGF0YS10b29sc2V0LWJsb2Nrcy1oZWFkaW5nPSI0MDIzN2JiYTNhYjRmMjdjYmJiYWY4ZmRlZDk1ZGQ0ZSJdICB7IGZvbnQtc2l6ZTogMTZweDtjb2xvcjogcmdiYSggMCwgMCwgMCwgMSApOyB9ICBoMy50Yi1oZWFkaW5nW2RhdGEtdG9vbHNldC1ibG9ja3MtaGVhZGluZz0iNDAyMzdiYmEzYWI0ZjI3Y2JiYmFmOGZkZWQ5NWRkNGUiXSBhICB7IGNvbG9yOiByZ2JhKCAwLCAwLCAwLCAxICk7dGV4dC1kZWNvcmF0aW9uOiBub25lOyB9IC53cC1ibG9jay10b29sc2V0LWJsb2Nrcy1ncmlkLWNvbHVtbi50Yi1ncmlkLWNvbHVtbltkYXRhLXRvb2xzZXQtYmxvY2tzLWdyaWQtY29sdW1uPSIzMDM0ZmJlODg2YzExMDU0ZTk1YjQ2YjA5ZDNlNDExMiJdIHsgZGlzcGxheTogZmxleDsgfSAudGItY29udGFpbmVyIC50Yi1jb250YWluZXItaW5uZXJ7d2lkdGg6MTAwJTttYXJnaW46MCBhdXRvfSAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtY29udGFpbmVyLnRiLWNvbnRhaW5lcltkYXRhLXRvb2xzZXQtYmxvY2tzLWNvbnRhaW5lcj0iNzk5MDAxN2I5ZDJhNjk3MTQ5OTcxOTJkMTJjZGY5MzAiXSB7IHBhZGRpbmc6IDI1cHg7Ym94LXNoYWRvdzogNXB4IDVweCAxMHB4IDAgcmdiYSggMCwgMCwgMCwgMC41ICk7IH0gLnRiLWZpZWxkW2RhdGEtdG9vbHNldC1ibG9ja3MtZmllbGQ9Ijc5MzY1OWQ4MmY4Zjk2YjU1NmE1NzY3YmQzMDM2Njc4Il0geyBtYXJnaW4tdG9wOiAzMHB4O21hcmdpbi1ib3R0b206IDMwcHg7IH0gIC50Yi1maWVsZFtkYXRhLXRvb2xzZXQtYmxvY2tzLWZpZWxkPSI3OTM2NTlkODJmOGY5NmI1NTZhNTc2N2JkMzAzNjY3OCJdIGEgeyB0ZXh0LWRlY29yYXRpb246IG5vbmU7IH0gIGgxLnRiLWhlYWRpbmdbZGF0YS10b29sc2V0LWJsb2Nrcy1oZWFkaW5nPSI0ZjVhNjYwNTg5ZjhhMmViOGU3YTg1MDIwOTBkODFkYyJdIGEgIHsgdGV4dC1kZWNvcmF0aW9uOiBub25lOyB9IC50Yi1jb250YWluZXIgLnRiLWNvbnRhaW5lci1pbm5lcnt3aWR0aDoxMDAlO21hcmdpbjowIGF1dG99IC53cC1ibG9jay10b29sc2V0LWJsb2Nrcy1jb250YWluZXIudGItY29udGFpbmVyW2RhdGEtdG9vbHNldC1ibG9ja3MtY29udGFpbmVyPSJlZDM4MzJhYTYyMDFjYmVjNWIxZTViOTAyZGMwNjdlMiJdIHsgcGFkZGluZzogMjVweDsgfSBAbWVkaWEgb25seSBzY3JlZW4gYW5kIChtYXgtd2lkdGg6IDc4MXB4KSB7IC50Yi1idXR0b257Y29sb3I6I2YxZjFmMX0udGItYnV0dG9uLS1sZWZ0e3RleHQtYWxpZ246bGVmdH0udGItYnV0dG9uLS1jZW50ZXJ7dGV4dC1hbGlnbjpjZW50ZXJ9LnRiLWJ1dHRvbi0tcmlnaHR7dGV4dC1hbGlnbjpyaWdodH0udGItYnV0dG9uX19saW5re2NvbG9yOmluaGVyaXQ7Y3Vyc29yOnBvaW50ZXI7ZGlzcGxheTppbmxpbmUtYmxvY2s7bGluZS1oZWlnaHQ6MTAwJTt0ZXh0LWRlY29yYXRpb246bm9uZSAhaW1wb3J0YW50O3RleHQtYWxpZ246Y2VudGVyO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19saW5rOmhvdmVyLC50Yi1idXR0b25fX2xpbms6Zm9jdXMsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVke2NvbG9yOmluaGVyaXR9LnRiLWJ1dHRvbl9fbGluazpob3ZlciAudGItYnV0dG9uX19jb250ZW50LC50Yi1idXR0b25fX2xpbms6Zm9jdXMgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOnZpc2l0ZWQgLnRiLWJ1dHRvbl9fY29udGVudHtmb250LWZhbWlseTppbmhlcml0O2ZvbnQtc3R5bGU6aW5oZXJpdDtmb250LXdlaWdodDppbmhlcml0O2xldHRlci1zcGFjaW5nOmluaGVyaXQ7dGV4dC1kZWNvcmF0aW9uOmluaGVyaXQ7dGV4dC1zaGFkb3c6aW5oZXJpdDt0ZXh0LXRyYW5zZm9ybTppbmhlcml0fS50Yi1idXR0b25fX2NvbnRlbnR7dmVydGljYWwtYWxpZ246bWlkZGxlO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19pY29ue2Rpc3BsYXk6aW5saW5lLWJsb2NrO3ZlcnRpY2FsLWFsaWduOm1pZGRsZTtmb250LXN0eWxlOm5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2ljb246OmJlZm9yZXtjb250ZW50OmF0dHIoZGF0YS1mb250LWNvZGUpO2ZvbnQtd2VpZ2h0Om5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2xpbmt7YmFja2dyb3VuZC1jb2xvcjojNDQ0O2JvcmRlci1yYWRpdXM6MC4zZW07Zm9udC1zaXplOjEuM2VtO21hcmdpbi1ib3R0b206MC43NmVtO3BhZGRpbmc6MC41NWVtIDEuNWVtIDAuNTVlbX0gLnRiLWNvbnRhaW5lciAudGItY29udGFpbmVyLWlubmVye3dpZHRoOjEwMCU7bWFyZ2luOjAgYXV0b30udGItZ3JpZCwudGItZ3JpZD4uYmxvY2stZWRpdG9yLWlubmVyLWJsb2Nrcz4uYmxvY2stZWRpdG9yLWJsb2NrLWxpc3RfX2xheW91dHtkaXNwbGF5OmdyaWQ7Z3JpZC1yb3ctZ2FwOjI1cHg7Z3JpZC1jb2x1bW4tZ2FwOjI1cHh9LnRiLWdyaWQtaXRlbXtiYWNrZ3JvdW5kOiNkMzhhMDM7cGFkZGluZzozMHB4fS50Yi1ncmlkLWNvbHVtbntmbGV4LXdyYXA6d3JhcH0udGItZ3JpZC1jb2x1bW4+Knt3aWR0aDoxMDAlfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLXRvcHt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtc3RhcnR9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tY2VudGVye3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6Y2VudGVyfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLWJvdHRvbXt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtZW5kfSAud3B2LXZpZXctb3V0cHV0W2RhdGEtdG9vbHNldC12aWV3cy12aWV3LWVkaXRvcj0iZTIzYmU0YjY2YTYwNzg5MDMwMjJhYjA4MTgyZmM1NDkiXSA+IC50Yi1ncmlkLWNvbHVtbjpudGgtb2YtdHlwZSgybiArIDEpIHsgZ3JpZC1jb2x1bW46IDEgfSAud3B2LXZpZXctb3V0cHV0W2RhdGEtdG9vbHNldC12aWV3cy12aWV3LWVkaXRvcj0iZTIzYmU0YjY2YTYwNzg5MDMwMjJhYjA4MTgyZmM1NDkiXSA+IC50Yi1ncmlkLWNvbHVtbjpudGgtb2YtdHlwZSgybiArIDIpIHsgZ3JpZC1jb2x1bW46IDIgfSAud3B2LXZpZXctb3V0cHV0W2RhdGEtdG9vbHNldC12aWV3cy12aWV3LWVkaXRvcj0iZTIzYmU0YjY2YTYwNzg5MDMwMjJhYjA4MTgyZmM1NDkiXSAuanMtd3B2LWxvb3Atd3JhcHBlciA+IC50Yi1ncmlkIHsgZ3JpZC10ZW1wbGF0ZS1jb2x1bW5zOiBtaW5tYXgoMCwgMC41ZnIpIG1pbm1heCgwLCAwLjVmcik7Z3JpZC1hdXRvLWZsb3c6IHJvdyB9IC50Yi1idXR0b257Y29sb3I6I2YxZjFmMX0udGItYnV0dG9uLS1sZWZ0e3RleHQtYWxpZ246bGVmdH0udGItYnV0dG9uLS1jZW50ZXJ7dGV4dC1hbGlnbjpjZW50ZXJ9LnRiLWJ1dHRvbi0tcmlnaHR7dGV4dC1hbGlnbjpyaWdodH0udGItYnV0dG9uX19saW5re2NvbG9yOmluaGVyaXQ7Y3Vyc29yOnBvaW50ZXI7ZGlzcGxheTppbmxpbmUtYmxvY2s7bGluZS1oZWlnaHQ6MTAwJTt0ZXh0LWRlY29yYXRpb246bm9uZSAhaW1wb3J0YW50O3RleHQtYWxpZ246Y2VudGVyO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19saW5rOmhvdmVyLC50Yi1idXR0b25fX2xpbms6Zm9jdXMsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVke2NvbG9yOmluaGVyaXR9LnRiLWJ1dHRvbl9fbGluazpob3ZlciAudGItYnV0dG9uX19jb250ZW50LC50Yi1idXR0b25fX2xpbms6Zm9jdXMgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOnZpc2l0ZWQgLnRiLWJ1dHRvbl9fY29udGVudHtmb250LWZhbWlseTppbmhlcml0O2ZvbnQtc3R5bGU6aW5oZXJpdDtmb250LXdlaWdodDppbmhlcml0O2xldHRlci1zcGFjaW5nOmluaGVyaXQ7dGV4dC1kZWNvcmF0aW9uOmluaGVyaXQ7dGV4dC1zaGFkb3c6aW5oZXJpdDt0ZXh0LXRyYW5zZm9ybTppbmhlcml0fS50Yi1idXR0b25fX2NvbnRlbnR7dmVydGljYWwtYWxpZ246bWlkZGxlO3RyYW5zaXRpb246YWxsIDAuM3MgZWFzZX0udGItYnV0dG9uX19pY29ue2Rpc3BsYXk6aW5saW5lLWJsb2NrO3ZlcnRpY2FsLWFsaWduOm1pZGRsZTtmb250LXN0eWxlOm5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2ljb246OmJlZm9yZXtjb250ZW50OmF0dHIoZGF0YS1mb250LWNvZGUpO2ZvbnQtd2VpZ2h0Om5vcm1hbCAhaW1wb3J0YW50fS50Yi1idXR0b25fX2xpbmt7YmFja2dyb3VuZC1jb2xvcjojNDQ0O2JvcmRlci1yYWRpdXM6MC4zZW07Zm9udC1zaXplOjEuM2VtO21hcmdpbi1ib3R0b206MC43NmVtO3BhZGRpbmc6MC41NWVtIDEuNWVtIDAuNTVlbX0gICAudGItZ3JpZCwudGItZ3JpZD4uYmxvY2stZWRpdG9yLWlubmVyLWJsb2Nrcz4uYmxvY2stZWRpdG9yLWJsb2NrLWxpc3RfX2xheW91dHtkaXNwbGF5OmdyaWQ7Z3JpZC1yb3ctZ2FwOjI1cHg7Z3JpZC1jb2x1bW4tZ2FwOjI1cHh9LnRiLWdyaWQtaXRlbXtiYWNrZ3JvdW5kOiNkMzhhMDM7cGFkZGluZzozMHB4fS50Yi1ncmlkLWNvbHVtbntmbGV4LXdyYXA6d3JhcH0udGItZ3JpZC1jb2x1bW4+Knt3aWR0aDoxMDAlfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLXRvcHt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtc3RhcnR9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tY2VudGVye3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6Y2VudGVyfS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLWJvdHRvbXt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmZsZXgtZW5kfSAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC50Yi1ncmlkW2RhdGEtdG9vbHNldC1ibG9ja3MtZ3JpZD0iOGM2NzkxNTZjMTRlODFhZDQ5NjBhYWM1MzQ4NWUyNjEiXSB7IGdyaWQtdGVtcGxhdGUtY29sdW1uczogbWlubWF4KDAsIDAuNWZyKSBtaW5tYXgoMCwgMC41ZnIpO2dyaWQtYXV0by1mbG93OiByb3cgfSAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC50Yi1ncmlkW2RhdGEtdG9vbHNldC1ibG9ja3MtZ3JpZD0iOGM2NzkxNTZjMTRlODFhZDQ5NjBhYWM1MzQ4NWUyNjEiXSA+IC50Yi1ncmlkLWNvbHVtbjpudGgtb2YtdHlwZSgybiArIDEpIHsgZ3JpZC1jb2x1bW46IDEgfSAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC50Yi1ncmlkW2RhdGEtdG9vbHNldC1ibG9ja3MtZ3JpZD0iOGM2NzkxNTZjMTRlODFhZDQ5NjBhYWM1MzQ4NWUyNjEiXSA+IC50Yi1ncmlkLWNvbHVtbjpudGgtb2YtdHlwZSgybiArIDIpIHsgZ3JpZC1jb2x1bW46IDIgfSAudGItYnV0dG9ue2NvbG9yOiNmMWYxZjF9LnRiLWJ1dHRvbi0tbGVmdHt0ZXh0LWFsaWduOmxlZnR9LnRiLWJ1dHRvbi0tY2VudGVye3RleHQtYWxpZ246Y2VudGVyfS50Yi1idXR0b24tLXJpZ2h0e3RleHQtYWxpZ246cmlnaHR9LnRiLWJ1dHRvbl9fbGlua3tjb2xvcjppbmhlcml0O2N1cnNvcjpwb2ludGVyO2Rpc3BsYXk6aW5saW5lLWJsb2NrO2xpbmUtaGVpZ2h0OjEwMCU7dGV4dC1kZWNvcmF0aW9uOm5vbmUgIWltcG9ydGFudDt0ZXh0LWFsaWduOmNlbnRlcjt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9fbGluazpob3ZlciwudGItYnV0dG9uX19saW5rOmZvY3VzLC50Yi1idXR0b25fX2xpbms6dmlzaXRlZHtjb2xvcjppbmhlcml0fS50Yi1idXR0b25fX2xpbms6aG92ZXIgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOmZvY3VzIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVkIC50Yi1idXR0b25fX2NvbnRlbnR7Zm9udC1mYW1pbHk6aW5oZXJpdDtmb250LXN0eWxlOmluaGVyaXQ7Zm9udC13ZWlnaHQ6aW5oZXJpdDtsZXR0ZXItc3BhY2luZzppbmhlcml0O3RleHQtZGVjb3JhdGlvbjppbmhlcml0O3RleHQtc2hhZG93OmluaGVyaXQ7dGV4dC10cmFuc2Zvcm06aW5oZXJpdH0udGItYnV0dG9uX19jb250ZW50e3ZlcnRpY2FsLWFsaWduOm1pZGRsZTt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9faWNvbntkaXNwbGF5OmlubGluZS1ibG9jazt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7Zm9udC1zdHlsZTpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19pY29uOjpiZWZvcmV7Y29udGVudDphdHRyKGRhdGEtZm9udC1jb2RlKTtmb250LXdlaWdodDpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19saW5re2JhY2tncm91bmQtY29sb3I6IzQ0NDtib3JkZXItcmFkaXVzOjAuM2VtO2ZvbnQtc2l6ZToxLjNlbTttYXJnaW4tYm90dG9tOjAuNzZlbTtwYWRkaW5nOjAuNTVlbSAxLjVlbSAwLjU1ZW19ICAgICAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC1jb2x1bW4udGItZ3JpZC1jb2x1bW5bZGF0YS10b29sc2V0LWJsb2Nrcy1ncmlkLWNvbHVtbj0iMzAzNGZiZTg4NmMxMTA1NGU5NWI0NmIwOWQzZTQxMTIiXSB7IGRpc3BsYXk6IGZsZXg7IH0gLnRiLWNvbnRhaW5lciAudGItY29udGFpbmVyLWlubmVye3dpZHRoOjEwMCU7bWFyZ2luOjAgYXV0b30gIC50Yi1jb250YWluZXIgLnRiLWNvbnRhaW5lci1pbm5lcnt3aWR0aDoxMDAlO21hcmdpbjowIGF1dG99IH0gQG1lZGlhIG9ubHkgc2NyZWVuIGFuZCAobWF4LXdpZHRoOiA1OTlweCkgeyAudGItYnV0dG9ue2NvbG9yOiNmMWYxZjF9LnRiLWJ1dHRvbi0tbGVmdHt0ZXh0LWFsaWduOmxlZnR9LnRiLWJ1dHRvbi0tY2VudGVye3RleHQtYWxpZ246Y2VudGVyfS50Yi1idXR0b24tLXJpZ2h0e3RleHQtYWxpZ246cmlnaHR9LnRiLWJ1dHRvbl9fbGlua3tjb2xvcjppbmhlcml0O2N1cnNvcjpwb2ludGVyO2Rpc3BsYXk6aW5saW5lLWJsb2NrO2xpbmUtaGVpZ2h0OjEwMCU7dGV4dC1kZWNvcmF0aW9uOm5vbmUgIWltcG9ydGFudDt0ZXh0LWFsaWduOmNlbnRlcjt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9fbGluazpob3ZlciwudGItYnV0dG9uX19saW5rOmZvY3VzLC50Yi1idXR0b25fX2xpbms6dmlzaXRlZHtjb2xvcjppbmhlcml0fS50Yi1idXR0b25fX2xpbms6aG92ZXIgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOmZvY3VzIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVkIC50Yi1idXR0b25fX2NvbnRlbnR7Zm9udC1mYW1pbHk6aW5oZXJpdDtmb250LXN0eWxlOmluaGVyaXQ7Zm9udC13ZWlnaHQ6aW5oZXJpdDtsZXR0ZXItc3BhY2luZzppbmhlcml0O3RleHQtZGVjb3JhdGlvbjppbmhlcml0O3RleHQtc2hhZG93OmluaGVyaXQ7dGV4dC10cmFuc2Zvcm06aW5oZXJpdH0udGItYnV0dG9uX19jb250ZW50e3ZlcnRpY2FsLWFsaWduOm1pZGRsZTt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9faWNvbntkaXNwbGF5OmlubGluZS1ibG9jazt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7Zm9udC1zdHlsZTpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19pY29uOjpiZWZvcmV7Y29udGVudDphdHRyKGRhdGEtZm9udC1jb2RlKTtmb250LXdlaWdodDpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19saW5re2JhY2tncm91bmQtY29sb3I6IzQ0NDtib3JkZXItcmFkaXVzOjAuM2VtO2ZvbnQtc2l6ZToxLjNlbTttYXJnaW4tYm90dG9tOjAuNzZlbTtwYWRkaW5nOjAuNTVlbSAxLjVlbSAwLjU1ZW19IC50Yi1jb250YWluZXIgLnRiLWNvbnRhaW5lci1pbm5lcnt3aWR0aDoxMDAlO21hcmdpbjowIGF1dG99LnRiLWdyaWQsLnRiLWdyaWQ+LmJsb2NrLWVkaXRvci1pbm5lci1ibG9ja3M+LmJsb2NrLWVkaXRvci1ibG9jay1saXN0X19sYXlvdXR7ZGlzcGxheTpncmlkO2dyaWQtcm93LWdhcDoyNXB4O2dyaWQtY29sdW1uLWdhcDoyNXB4fS50Yi1ncmlkLWl0ZW17YmFja2dyb3VuZDojZDM4YTAzO3BhZGRpbmc6MzBweH0udGItZ3JpZC1jb2x1bW57ZmxleC13cmFwOndyYXB9LnRiLWdyaWQtY29sdW1uPip7d2lkdGg6MTAwJX0udGItZ3JpZC1jb2x1bW4udGItZ3JpZC1hbGlnbi10b3B7d2lkdGg6MTAwJTtkaXNwbGF5OmZsZXg7YWxpZ24tY29udGVudDpmbGV4LXN0YXJ0fS50Yi1ncmlkLWNvbHVtbi50Yi1ncmlkLWFsaWduLWNlbnRlcnt3aWR0aDoxMDAlO2Rpc3BsYXk6ZmxleDthbGlnbi1jb250ZW50OmNlbnRlcn0udGItZ3JpZC1jb2x1bW4udGItZ3JpZC1hbGlnbi1ib3R0b217d2lkdGg6MTAwJTtkaXNwbGF5OmZsZXg7YWxpZ24tY29udGVudDpmbGV4LWVuZH0gLndwdi12aWV3LW91dHB1dFtkYXRhLXRvb2xzZXQtdmlld3Mtdmlldy1lZGl0b3I9ImUyM2JlNGI2NmE2MDc4OTAzMDIyYWIwODE4MmZjNTQ5Il0gID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDFuKzEpIHsgZ3JpZC1jb2x1bW46IDEgfSAud3B2LXZpZXctb3V0cHV0W2RhdGEtdG9vbHNldC12aWV3cy12aWV3LWVkaXRvcj0iZTIzYmU0YjY2YTYwNzg5MDMwMjJhYjA4MTgyZmM1NDkiXSAuanMtd3B2LWxvb3Atd3JhcHBlciA+IC50Yi1ncmlkIHsgZ3JpZC10ZW1wbGF0ZS1jb2x1bW5zOiBtaW5tYXgoMCwgMWZyKTtncmlkLWF1dG8tZmxvdzogcm93IH0gLnRiLWJ1dHRvbntjb2xvcjojZjFmMWYxfS50Yi1idXR0b24tLWxlZnR7dGV4dC1hbGlnbjpsZWZ0fS50Yi1idXR0b24tLWNlbnRlcnt0ZXh0LWFsaWduOmNlbnRlcn0udGItYnV0dG9uLS1yaWdodHt0ZXh0LWFsaWduOnJpZ2h0fS50Yi1idXR0b25fX2xpbmt7Y29sb3I6aW5oZXJpdDtjdXJzb3I6cG9pbnRlcjtkaXNwbGF5OmlubGluZS1ibG9jaztsaW5lLWhlaWdodDoxMDAlO3RleHQtZGVjb3JhdGlvbjpub25lICFpbXBvcnRhbnQ7dGV4dC1hbGlnbjpjZW50ZXI7dHJhbnNpdGlvbjphbGwgMC4zcyBlYXNlfS50Yi1idXR0b25fX2xpbms6aG92ZXIsLnRiLWJ1dHRvbl9fbGluazpmb2N1cywudGItYnV0dG9uX19saW5rOnZpc2l0ZWR7Y29sb3I6aW5oZXJpdH0udGItYnV0dG9uX19saW5rOmhvdmVyIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazpmb2N1cyAudGItYnV0dG9uX19jb250ZW50LC50Yi1idXR0b25fX2xpbms6dmlzaXRlZCAudGItYnV0dG9uX19jb250ZW50e2ZvbnQtZmFtaWx5OmluaGVyaXQ7Zm9udC1zdHlsZTppbmhlcml0O2ZvbnQtd2VpZ2h0OmluaGVyaXQ7bGV0dGVyLXNwYWNpbmc6aW5oZXJpdDt0ZXh0LWRlY29yYXRpb246aW5oZXJpdDt0ZXh0LXNoYWRvdzppbmhlcml0O3RleHQtdHJhbnNmb3JtOmluaGVyaXR9LnRiLWJ1dHRvbl9fY29udGVudHt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7dHJhbnNpdGlvbjphbGwgMC4zcyBlYXNlfS50Yi1idXR0b25fX2ljb257ZGlzcGxheTppbmxpbmUtYmxvY2s7dmVydGljYWwtYWxpZ246bWlkZGxlO2ZvbnQtc3R5bGU6bm9ybWFsICFpbXBvcnRhbnR9LnRiLWJ1dHRvbl9faWNvbjo6YmVmb3Jle2NvbnRlbnQ6YXR0cihkYXRhLWZvbnQtY29kZSk7Zm9udC13ZWlnaHQ6bm9ybWFsICFpbXBvcnRhbnR9LnRiLWJ1dHRvbl9fbGlua3tiYWNrZ3JvdW5kLWNvbG9yOiM0NDQ7Ym9yZGVyLXJhZGl1czowLjNlbTtmb250LXNpemU6MS4zZW07bWFyZ2luLWJvdHRvbTowLjc2ZW07cGFkZGluZzowLjU1ZW0gMS41ZW0gMC41NWVtfSAgIC50Yi1ncmlkLC50Yi1ncmlkPi5ibG9jay1lZGl0b3ItaW5uZXItYmxvY2tzPi5ibG9jay1lZGl0b3ItYmxvY2stbGlzdF9fbGF5b3V0e2Rpc3BsYXk6Z3JpZDtncmlkLXJvdy1nYXA6MjVweDtncmlkLWNvbHVtbi1nYXA6MjVweH0udGItZ3JpZC1pdGVte2JhY2tncm91bmQ6I2QzOGEwMztwYWRkaW5nOjMwcHh9LnRiLWdyaWQtY29sdW1ue2ZsZXgtd3JhcDp3cmFwfS50Yi1ncmlkLWNvbHVtbj4qe3dpZHRoOjEwMCV9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tdG9we3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6ZmxleC1zdGFydH0udGItZ3JpZC1jb2x1bW4udGItZ3JpZC1hbGlnbi1jZW50ZXJ7d2lkdGg6MTAwJTtkaXNwbGF5OmZsZXg7YWxpZ24tY29udGVudDpjZW50ZXJ9LnRiLWdyaWQtY29sdW1uLnRiLWdyaWQtYWxpZ24tYm90dG9te3dpZHRoOjEwMCU7ZGlzcGxheTpmbGV4O2FsaWduLWNvbnRlbnQ6ZmxleC1lbmR9IC53cC1ibG9jay10b29sc2V0LWJsb2Nrcy1ncmlkLnRiLWdyaWRbZGF0YS10b29sc2V0LWJsb2Nrcy1ncmlkPSI4YzY3OTE1NmMxNGU4MWFkNDk2MGFhYzUzNDg1ZTI2MSJdIHsgZ3JpZC10ZW1wbGF0ZS1jb2x1bW5zOiBtaW5tYXgoMCwgMWZyKTtncmlkLWF1dG8tZmxvdzogcm93IH0gLndwLWJsb2NrLXRvb2xzZXQtYmxvY2tzLWdyaWQudGItZ3JpZFtkYXRhLXRvb2xzZXQtYmxvY2tzLWdyaWQ9IjhjNjc5MTU2YzE0ZTgxYWQ0OTYwYWFjNTM0ODVlMjYxIl0gID4gLnRiLWdyaWQtY29sdW1uOm50aC1vZi10eXBlKDFuKzEpIHsgZ3JpZC1jb2x1bW46IDEgfSAudGItYnV0dG9ue2NvbG9yOiNmMWYxZjF9LnRiLWJ1dHRvbi0tbGVmdHt0ZXh0LWFsaWduOmxlZnR9LnRiLWJ1dHRvbi0tY2VudGVye3RleHQtYWxpZ246Y2VudGVyfS50Yi1idXR0b24tLXJpZ2h0e3RleHQtYWxpZ246cmlnaHR9LnRiLWJ1dHRvbl9fbGlua3tjb2xvcjppbmhlcml0O2N1cnNvcjpwb2ludGVyO2Rpc3BsYXk6aW5saW5lLWJsb2NrO2xpbmUtaGVpZ2h0OjEwMCU7dGV4dC1kZWNvcmF0aW9uOm5vbmUgIWltcG9ydGFudDt0ZXh0LWFsaWduOmNlbnRlcjt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9fbGluazpob3ZlciwudGItYnV0dG9uX19saW5rOmZvY3VzLC50Yi1idXR0b25fX2xpbms6dmlzaXRlZHtjb2xvcjppbmhlcml0fS50Yi1idXR0b25fX2xpbms6aG92ZXIgLnRiLWJ1dHRvbl9fY29udGVudCwudGItYnV0dG9uX19saW5rOmZvY3VzIC50Yi1idXR0b25fX2NvbnRlbnQsLnRiLWJ1dHRvbl9fbGluazp2aXNpdGVkIC50Yi1idXR0b25fX2NvbnRlbnR7Zm9udC1mYW1pbHk6aW5oZXJpdDtmb250LXN0eWxlOmluaGVyaXQ7Zm9udC13ZWlnaHQ6aW5oZXJpdDtsZXR0ZXItc3BhY2luZzppbmhlcml0O3RleHQtZGVjb3JhdGlvbjppbmhlcml0O3RleHQtc2hhZG93OmluaGVyaXQ7dGV4dC10cmFuc2Zvcm06aW5oZXJpdH0udGItYnV0dG9uX19jb250ZW50e3ZlcnRpY2FsLWFsaWduOm1pZGRsZTt0cmFuc2l0aW9uOmFsbCAwLjNzIGVhc2V9LnRiLWJ1dHRvbl9faWNvbntkaXNwbGF5OmlubGluZS1ibG9jazt2ZXJ0aWNhbC1hbGlnbjptaWRkbGU7Zm9udC1zdHlsZTpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19pY29uOjpiZWZvcmV7Y29udGVudDphdHRyKGRhdGEtZm9udC1jb2RlKTtmb250LXdlaWdodDpub3JtYWwgIWltcG9ydGFudH0udGItYnV0dG9uX19saW5re2JhY2tncm91bmQtY29sb3I6IzQ0NDtib3JkZXItcmFkaXVzOjAuM2VtO2ZvbnQtc2l6ZToxLjNlbTttYXJnaW4tYm90dG9tOjAuNzZlbTtwYWRkaW5nOjAuNTVlbSAxLjVlbSAwLjU1ZW19ICAgICAud3AtYmxvY2stdG9vbHNldC1ibG9ja3MtZ3JpZC1jb2x1bW4udGItZ3JpZC1jb2x1bW5bZGF0YS10b29sc2V0LWJsb2Nrcy1ncmlkLWNvbHVtbj0iMzAzNGZiZTg4NmMxMTA1NGU5NWI0NmIwOWQzZTQxMTIiXSB7IGRpc3BsYXk6IGZsZXg7IH0gLnRiLWNvbnRhaW5lciAudGItY29udGFpbmVyLWlubmVye3dpZHRoOjEwMCU7bWFyZ2luOjAgYXV0b30gIC50Yi1jb250YWluZXIgLnRiLWNvbnRhaW5lci1pbm5lcnt3aWR0aDoxMDAlO21hcmdpbjowIGF1dG99IH0g
Способы решения квадратных уравнений | Статья в журнале «Юный ученый»
Наш проект посвящен способам решения квадратных уравнений. Цель проекта: научиться решать квадратные уравнения способами, не входящими в школьную программу. Задача: найти все возможные способы решения квадратных уравнений и научиться их использовать самим и познакомить одноклассников с этими способами.
Что же такое «квадратные уравнения»?
Квадратное уравнение — уравнение вида ax2+ bx + c = 0, где a, b, c — некоторые числа (a ≠ 0), x — неизвестное.
Числа a, b,c называются коэффициентами квадратного уравнения.
- a называется первым коэффициентом;
- b называется вторым коэффициентом;
- c — свободным членом.
А кто же первый «изобрёл» квадратные уравнения?
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до н.э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений.
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Вавилонские математики примерно с IV века до н.э. использовали метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 года до н.э. Эвклид придумал более общий геометрический метод решения. Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был индийский ученый Брахмагупта (Индия, VII столетие нашей эры).
Брахмагупта изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ax2 + bх = с, а>0
В этом уравнении коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корням», т. е. ах2 = bх.
2) «Квадраты равны числу», т. е. ах2 = с.
3) «Корни равны числу», т. е. ах2 = с.
4) «Квадраты и числа равны корням», т. е. ах2 + с = bх.
5) «Квадраты и корни равны числу», т. е. ах2 + bх =с.
6) «Корни и числа равны квадратам», т. е. bх + с == ах2.
Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.
Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья,Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
Рассмотрим несколько способов решения квадратных уравнений.
Стандартные способы решения квадратных уравнений из школьной программы:
- Разложение левой части уравнения на множители.
- Метод выделения полного квадрата.
- Решение квадратных уравнений по формуле.
- Графическое решение квадратного уравнения.
- Решение уравнений с использованием теоремы Виета.
Остановимся подробнее на решение приведенных и не приведенных квадратных уравнений по теореме Виета.
Напомним, что для решения приведенных квадратных уравнений достаточно найти два числа такие, произведение которых равно свободному члену, а сумма — второму коэффициенту с противоположным знаком.
Пример.x2-5x+6=0
Нужно найти числа, произведение которых равно 6, а сумма 5. Такими числами будут 3 и 2.
Ответ: x1=2, x2=3.
Но можно использовать этот способ и для уравнений с первым коэффициентом не равным единице.
Пример.3x2+2x-5=0
Берём первый коэффициент и умножаем его на свободный член: x2+2x-15=0
Корнями этого уравнения будут числа, произведение которых равно — 15, а сумма равна — 2. Эти числа — 5 и 3. Чтобы найти корни исходного уравнения, полученные корни делим на первый коэффициент.
Ответ: x1=-5/3, x2=1
6. Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение ах2 + bх + с = 0, где а≠0.
Умножая обе его части на а, получаем уравнение а2х2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению у2 + by + ас = 0, равносильному данному. Его корни у1 и у2 найдем с помощью теоремы Виета.
Окончательно получаем х1 = у1/а и х2 = у2/а.
При этом способе коэффициент a умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример.2х2 — 11х + 15 = 0.
«Перебросим» коэффициент 2 к свободному члену и сделав замену получим уравнение у2 — 11у + 30 = 0.
Согласно обратной теореме Виета
у1 = 5, х1 = 5/2, х1=2,5 ;у2 = 6, x2 = 6/2, x2 = 3.
Ответ: х1=2,5; х2= 3.
7. Свойства коэффициентов квадратного уравнения.
Пусть дано квадратное уравнение ах2 + bх + с = 0, а ≠ 0.
1. Если a+ b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х1 = 1.
2. Если а — b + с = 0, или b = а + с, то х1 = — 1.
Пример.345х2 — 137х — 208 = 0.
Так как а + b + с = 0 (345 — 137 — 208 = 0), то х1 = 1, х2 = -208/345.
Ответ: х1=1; х2 = -208/345 .
Пример.132х2 + 247х + 115 = 0
Т.к. a-b+с = 0 (132 — 247 +115=0), то х1= — 1, х2= — 115/132
Ответ: х1= — 1; х2=- 115/132
Существуют и другие свойства коэффициентов квадратного уравнения. но ихиспользование более сложное.
8. Решение квадратных уравнений с помощью номограммы.
Рис 1. Номограмма
Это старый и в настоящее время забытый способ решения квадратных уравнений, помещенный на с.83 сборника: Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам (рис. 1):
ОВ =AB =
Полагая ОС = р, ED = q, ОЕ = а (все в см), из рис.1 подобия треугольников САН и CDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение z2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.
Рис. 2 Решение квадратных уравнения с помощью номограммы
Примеры.
1) Для уравнения z2 — 9z + 8 = 0 номограмма дает корни z1 = 8,0 и z2 = 1,0
Ответ:8,0; 1,0.
2) Решим с помощью номограммы уравнение
2z2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение z2 — 4,5z + 1 = 0.
Номограмма дает корни z1 = 4 и z2 = 0,5.
Ответ: 4; 0,5.
9. Геометрический способ решения квадратных уравнений.
Пример.х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».
Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5x. Полученную фигуру дополняют затем до нового квадрата АВСD, достраивая в углах четыре равных квадрата, сторона каждого из них 2,5, а площадь 6,25
Рис. 3 Графический способ решения уравнения х2 + 10х = 39
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4∙2,5x = 10х) и четырех пристроенных квадратов (6,25∙ 4 = 25) , т.е. S = х2 + 10х = 25. Заменяя х2 + 10х числом 39, получим что S = 39+ 25 = 64, откуда следует, что сторона квадрата АВСD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
10. Решение уравнений с использованием теоремы Безу.
Теорема Безу. Остаток от деления многочлена P(x) на двучлен x — α равен P(α) (т.е. значению P(x) при x = α).
Если число α является корнем многочлена P(x), то этот многочлен делится на x -α без остатка.
Пример.х²-4х+3=0
Р(x)= х²-4х+3, α: ±1,±3, α =1, 1-4+3=0. Разделим Р(x) на (х-1):(х²-4х+3)/(х-1)=х-3
х²-4х+3=(х-1)(х-3), (х-1)(х-3)=0
х-1=0; х=1, или х-3=0, х=3; Ответ: х1=2, х2=3.
Вывод: Умение быстро и рационально решать квадратные уравнения просто необходимо для решения более сложных уравнений, например, дробно-рациональных уравнений, уравнений высших степеней, биквадратных уравнений, а в старшей школе тригонометрических, показательных и логарифмических уравнений. Изучив все найденные способы решения квадратных уравнений, мы можем посоветовать одноклассникам, кроме стандартных способов, решение способом переброски (6) и решение уравнений по свойству коэффициентов (7), так как они являются более доступными для понимания.
Литература:
- Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990.
- Алгебра 8 класс: учебник для 8 кл. общеобразоват. учреждений Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. под ред. С. А. Теляковского 15-е изд., дораб. — М.: Просвещение, 2015
- https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
- Глейзер Г.И. История математики в школе. Пособие для учителей. / Под ред. В.Н. Молодшего. — М.: Просвещение, 1964.
Основные термины (генерируются автоматически): уравнение, квадратное уравнение, свободный член, решение уравнений, корень, число, способ решения, квадрат, коэффициент, решение.
Решение уравнений третьей степени различными способами
1. Проект по алгебре: «Решение уравнений третьей степени различными способами».
Выполнила ученица 9 класса
Зингейской СОШ
Пушкарева Марина
2. Цель проекта:
• Совершенствовать свои умения и навыки
при решении уравнений;
• Познакомиться с историческими
сведениями о решении уравнений;
• Представить материал в виде презентации.
3. Омар Хайям (ок. 1048- ок. 1123)
Описал всевозможные виды
уравнений третьей степени и
рассмотрел сложные и
красивые способы
геометрических построений
для отыскания их решения.
3
2
аx bx cx d 0
• В начале XVI века в крупных
торговых городах Северной Италии
были популярны математические
состязания. Математики публично
вызывали соперников на поединок,
причем на победителя обычно
делались денежные ставки. В это
время быстро распространялось
преподавание арифметики,
необходимой в торговле, и
публичные состязания обеспечивали
соперничающим преподавателям
известность и привлекали учеников.
Задачи формулировались для
числовых значений, но иногда
требовали решения алгебраических
уравнений более высокого порядка.
Результаты состязаний
обнародовались, но методы
решения математических задач —
оружие в борьбе за репутацию и
доходы — каждый из участников
противоборства предпочитал
держать в секрете.
• Николо Тарталья (ребёнок
из очень бедной семьи,
мать не могла платить за
образование, поэтому
мальчик в школе узнал
только половину азбуки,
всеми остальными
знаниями он овладел
самостоятельно). В 6 лет
он получил удар мечом в
гортань от французского
воина и с тех пор говорил
с трудом, отсюда и
прозвище Тарталья
(заика). Он вывел
формулы для решения
уравнений 3-ей степени,
но своё открытие держал
в тайне.
Никколо Тарталья
(1499-1557)
• Джероламо Кардано (медик)
занимался астрологией,
составлял гороскопы.
Кардано неоднократно
обращался к Тарталье с
просьбой сообщить ему
формулу для решения
кубических уравнений и
обещал хранить её в
секрете. Он не сдержал
слово и опубликовал
формулу, указав, что
Тарталье принадлежит честь
открытия «такого
прекрасного и
удивительного,
превосходящего все таланты
человеческого духа».
Джероламо Кардано
(1501-1576)
7. x³-3x-2=0 1) Разложение на множители:
x³-3x-2=x³+x²-x²-x-2x-2=0
x²(x+1)-x(x+1)-2(x+1)=0
(x+1)(x²-x-2)=0
x=-1
D=1+8=9
x₁=2
x₂=-1
Ответ: -1; 2.
8. 2) Решение с помощью теоремы Безу: x³-3x-2=0
x³-3x-2=0
(-1)³ -3(-1)-2=0
x=-1
x³-3x-2 x+1
x³+x²
x²-x-2
-x²-3x
-x²-x
-2x-2
-2x-2
0
• x³-3x-2 =(x+1)(x²-x-2)=0
Ответ: -1; 2.
9. 3) Графический способ решения:
• x³-3x-2=0
• Ответ: -1; 2.
10. x³-7x+6=0 1) Разложение на множители:
x³-7x+6=0
x(x²-1)-6(x-1)=0
x(x-1)(x+1)-6(x-1)=0
(x²+x-6)(x-1)=0
D=1+24=25
x-1=0
x₁=2
x=1
x₂=3
Ответ: -3; 1; 2.
11. 2) Решение с помощью теоремы Безу: 1³-7+6=0
• 1³-7+6=0
• x³-7x+6 x-1
• x³-x²
x²+x-6
x²-7x
-x²+x
-6x+6
-6x+6
0
x³-7x+6=(x-1)(x²+x-6)
x=1
x²+x-6=0
D=1+24=25
x₁=2
x₂=-3
Ответ: -3; 1; 2.
12. 3) Графический способ решения:
• Ответ: -3; 1; 2.
13. x³-13x+12=0 1) Разложение на множители:
x³-13x+12=0
x³-x-12x+12=0
x(x²-1)-12(x-1)=0
x(x-1)(x+1)-12(x-1)=0
(x²+x-12)(x-1)=0
D=1+48=49
x=1
x₁=3
x₂=-4
Ответ: -4; 1; 3.
14. 2) Решение с помощью теоремы Безу: x³-13x+12=0
x³-13x+12=0
1-13+12=0
x=1
x³-13x+12 x-1
x³-x²
x²+x-12
x²-13x
x²-x
-12x+12
-12x+12
0
• x³-13x+12=(x-1)(x²+x12)=0
• x=1
D=1+48=49
x₁=3
x₂=-4
Ответ: -4; 1; 3.
15. 3) Графический способ решения:
• Ответ: -4; 1; 3.
16. 2x³+x²-3=0 1) Разложение на множители:
2x³+x²-3=0
3x³-x³+x²-3=0
3(x³-1)-x²(x-1)=0
3(x-1)(x²+x+1)-x²(x-1)=0
(x-1)(3x²+3x+3-x²)=0
(x-1)(2x²+3x+3)=0
x=1
2x²+3x+3=0
D=9-24=-15
Ответ: 1.
17. 2) Решение с помощью теоремы Безу: 2x³+x²-3=0
• 2x³+x²-3 x-1
• 2x³-2x² 2x²+3x+3
3x²-3
3x²-3x
3x-3
3x-3
0
• (x-1)(2x²+3x+3)=0
• x=1 или 2x²+3x+3=0
D=9-24=-15
Ответ: 1.
18. 3) Графический способ решения:
• Ответ: 1.
Темы исследовательских проектов по математике в 9 классе
В этом разделе можно выбрать тему исследовательской работы по математике для 9 класса школы. По данным темам предполагается проведение исследовательских работ, связанных с аналитическим и графическим способами решения уравнений и неравенств с одной и с двумя переменными.
Представленные темы проектов по математике для 9 класса позволяют ученикам в процессе проведения исследовательской деятельности изучить квадратичную функцию и её свойства, арифметическую и геометрическую прогрессии, элементы комбинаторики и теории вероятности, освоить различные способы решения уравнений второй степени.
Любую из тем проектов по математике для 9 класса учащимся можно расширить или упростить в зависимости от сложности и объемности темы. Необходимо внимательно выбирать тему исследовательской проектной работы по математике, представляя объем предстоящей работы и цель проекта.
Темы исследовательских работ по математике в 9 классе
Примерные темы исследовательских работ по математике для учащихся 9 класса:
Алгоритмический подход к решению геометрических задач.
Вероятность получения положительной отметки при написании тестовой контрольной работы путем угадывания правильного ответа.
Виды уравнений и способы их решения.
Вписанные и описанные окружности. Вневписанные окружности.
График дробно-линейной функции.
Загадки арифметической прогрессии.
Замечательные точки треугольника.
Золотое сечение
Информация, кибернетика и математика.
Иррациональные неравенства.
Иррациональные уравнения.
Использование тригонометрических формул при измерительных работах
История развития учения об уравнениях.
Летопись открытий в мире чисел и фигур.
Математика – царица или слуга для других наук.
Метод подобия в задачах на построение.
Методы решения текстовых задач.
Методы решения уравнений 4 степени.
Можно ли считать мир геометрически правильным.
На правильном пути по ступенькам прогрессии.
Неравенства и системы неравенств с двумя переменными.
Неравенства с параметром.
Нестандартные задачи по алгебре.
Нестандартные задачи по геометрии.
Нестандартные решения уравнений
Нестандартные способы нахождения площадей некоторых многоугольников.
Нестандартные способы решения квадратных уравнений.
О среднем арифметическом, о среднем гармоничном, о среднем геометрическом, о среднем квадратичном.
Парабола и я
Последовательности и прогрессии в жизни.
Построение графиков сложных функций
Презентации избранных вопросов алгебры или геометрии.
Приложения математики в экономике.
Применение векторов к доказательству свойств и признаков параллелограмма.
Применение векторов к доказательству теорем о треугольниках.
Применение подобия к доказательству и решению задач.
Применение свойств квадратичной функции при решении задач.
Прогрессии в нашей жизни
Простые и сложные проценты
Путешествие в историю математики.
Темы проектов по математике для 9 классе
Примерные темы проектов по математике для учащихся 9 класса:
Равносильные преобразования неравенств: теория и практика.
Равносильные преобразования уравнений: теория и практика.
Равносоставленные многоугольники.
Развитие понятия числа. Понятие о действительных числах и действиях над ними.
Различные способы доказательства теоремы Пифагора
Решение задач на смеси и сплавы
Сложные проценты
Способы решения систем уравнений с двумя переменными.
Стандартные и нестандартные методы решения неравенств.
Стандартные и нестандартные методы решения уравнений.
Статистические исследования.
Сценарий математического праздника, викторины, нетрадиционного урока с использованием мультимедийных технологий.
Теория игр. Кубик Рубика.
Теория чисел
Треугольник Паскаля
Треугольник Эйлера-Бернулли
Уравнения высших степеней.
Уравнения с параметром.
Уравнения с переменной под знаком модуля.
Функции в окружающем мире
Характеристические свойства окружности.
Частота и вероятность событий.
Чем геометрия Лобачевского отличается от геометрии Евклида.
Перейти к разделу:
Ученические проекты по математике
Тему исследовательской работы по математике
Если страница Вам понравилась, поделитесь в социальных сетях:
лабораторных занятий по математике с заданием — решение системы линейных уравнений
лабораторных занятий по математике с заданием — решение системы линейных уравнений
ЦЕЛЬ
Использовать графический метод для получения условий согласованности и, следовательно, для решения заданной системы линейных уравнений с двумя переменными
Необходимые материалы
- Три листа миллиметровой бумаги
- Линейка
- Карандаш
Теория
Линии, соответствующие каждому из уравнений, заданных в системе линейных уравнений, нарисованы на миллиметровой бумаге.Сейчас,
- Если две линии пересекаются в одной точке, система согласована и имеет уникальное решение.
- , если две линии совпадают, то система непротиворечива и имеет бесконечно много решений.
- , если две линии параллельны друг другу, то система несовместима и не имеет решения.
Процедура
Рассмотрим пару линейных уравнений с двумя переменными типа
a 1 x + b 1 y = c 1
a 2 x + b 2 y = c 2
Шаг 1: Пусть первая система линейных уравнений имеет вид
x + 2y = 3… (i)
4x + 3y = 2… (ii)
Шаг 2: Из уравнения (i), у нас есть
y = ½ (3 — x).
Найдите значения y для двух разных значений x, как показано ниже.
Аналогично, из уравнения (ii) имеем
y = 1/3 (2 — 4x).
Затем
Шаг 3: Нарисуйте линию, представляющую уравнение x + 2y = 3, на миллиметровой бумаге I, нанеся точки (1,1) и (3,0) и соединив их.
Аналогичным образом нарисуйте линию, представляющую уравнение 4x + 3y = 2, построив точки (-1, 2) и (2, -2) и соединив их.
Шаг 4: Запишите свои наблюдения в первую таблицу наблюдений.
Шаг 5: Рассмотрим вторую систему линейных уравнений:
x — 2y = 3… (iii)
-2x + 4y = -6… (iv)
Шаг 6: Из уравнения (iii) получаем
Из уравнения (iv) получаем
Нарисуйте линии на миллиметровой бумаге II, используя эти точки, и запишите свои наблюдения во вторую таблицу наблюдений.
Шаг 7: Рассмотрим третью систему линейных уравнений:
2x — 3y = 5… (v)
-4x + 6y = 3… (vi)
Шаг 8: Из уравнения (v) получаем
Из уравнения (vi) получаем
Нарисуйте линии на миллиметровой бумаге III, используя эти точки, и запишите свои наблюдения в третью таблицу наблюдений.
Наблюдения
I. Для первой системы уравнений
II. Для второй системы уравнений
III. Для третьей системы уравнений
Выводы
- Первая система уравнений представлена пересекающимися линиями, которые показывают, что система непротиворечива и имеет единственное решение, то есть x = -1, y = 2 (см. Первую таблицу наблюдений).
- Вторая система уравнений представлена совпадающими линиями, что показывает, что система непротиворечива и имеет бесконечно много решений (см. Вторую таблицу наблюдений).
- Третья система уравнений представлена параллельными линиями, которые показывают, что система несовместима и не имеет решения (см. Третью таблицу наблюдений).
Примечания: Учитель должен предоставить студентам дополнительные задачи для практики каждого из трех типов систем уравнений.
Математические лаборатории с активностьюМатематические лабораторииНаучные практические навыкиНаучные лаборатории
Урок в девятом классе Создание линейных уравнений в одной переменной
После создания новых групп мы пересматриваем учебную цель учащихся:
SLT 1.4: я могу создавать уравнения и неравенства для одной переменной и использовать их для решения проблем.
Вот как это работает. Я прошу добровольца прочитать SLT вслух. Как только кто-то его прочитает, я прошу студентов выкрикивать самые важные слова SLT. Я подчеркиваю каждое слово, которое они говорят: уравнений, неравенств, переменных, решений, задач . Когда кто-то говорит, что создает , я обводил его. «Это глагол», — говорю я. «Это то, что вы собираетесь делать сейчас. Обратите внимание, что этот SLT не просто говорит, что вы должны получить правильный ответ .В нем говорится, что вам нужно создать уравнения . Это то, над чем мы собираемся работать в течение следующих нескольких дней ». Мы также отмечаем, что в SLT указано одна переменная , что означает, что на данный момент для каждой решаемой проблемы будет одна неизвестная.
Чтобы отработать эту новую учебную цель, я говорю, что у нас есть две проблемы, которые нужно решить. Мне нравится рассказывать каждому классу, что мы собираемся «поработать над задачей под названием Vanessa’s Raise , которая касается женщины по имени Ванесса, которая получает прибавку, и другой задачей под названием Ed’s Book , которая касается парня по имени Эд. кто читает книгу.»В мире, полном надуманных вводных задач по алгебре — все из которых служат ясной цели в учебном смысле, но могут нарушить законы повседневной реальности ребенка — этот вид юмора привлекает студентов, позволяя приостановить недоверие и поиграть с математикой.
Я использую четвертый слайд сегодняшних заметок, чтобы представить структуру сегодняшнего класса. Это тот, который будет становиться все более распространенным с течением года. Объясняю, что сейчас собираюсь выставить каждому по наблюдению.«Я ищу, чтобы каждый из вас работал над тем, чтобы помочь своей группе понять смысл каждой проблемы, и чтобы вы помогли своей группе упорствовать », — говорю я. Мы обсуждаем, как это может выглядеть: задавать вопросы, вовлекать всех, объяснять свои мысли, записывать вещи и не сдаваться — все это возможности. «Ответы на эти проблемы не будут очевидны сразу, — говорю я, — поэтому убедитесь, что вы делаете все возможное, чтобы понять все, что вы можете.«
Я раздаю по одной копии «Подъема Ванессы» (из CME Algebra 1) на каждый стол и проецирую ее на экран в передней части комнаты. Все работают в группах по 4 человека, хотя может быть группа или две или меньше студентов, если так получается.
Я говорю: «Я дам вам 10 минут, чтобы поработать над этим в группе. Будьте настойчивы и постарайтесь понять все, что вы можете. Через 10 минут я дам вам подсказку о том, как решить эту проблему.
Подсказка: как угадать и проверить
В эти первые 10 минут происходят отличные беседы, и я часто вижу новую и отличную сторону многих студентов в этом контексте.Однако обычно у меня не так много групп, которые могут с уверенностью сказать, что они решили проблему, и еще меньше групп могут создать уравнение для ее представления. Вот почему я пользуюсь этой возможностью, чтобы представить высоко структурированную форму предположений и проверок, которая поможет студентам развить способность составлять уравнения.
Я говорю, что намекну, показывая всем неправильный ответ. Это привлекает всеобщее внимание. Я говорю, что хочу отгадать ответ на этот вопрос и проверить его.«Когда я угадаю, я хочу выбрать реалистичное число, с которым легко работать», — говорю я. «Разумно ли говорить, что Ванесса может зарабатывать 10 долларов в час?» Мы решаем, что это так, и я продолжаю: «Я выбираю это число, потому что с ним легко работать. Я думаю, что его легко умножить на 10». Если студенты колеблются, я могу сравнить это с умножением на 13,75 доллара в час, и они поймут идею.
Я также представляю идею «до» и «после», которую я обычно нахожу в той или иной форме в работе одного или двух студентов.Если у студентов возникла эта идея, я воздаю им должное, сказав, что я получил идею, используя эти слова от этих студентов, и я напишу эти два слова на доске. Итак, до и после чего? Студенты задумываются об этом и понимают, что Ванессе предложили повышение. Она зарабатывала одну сумму до повышения, а другую — после. «Я надеюсь, что это случится со всеми вами», — говорю я. «И когда это произойдет, я бы хотел, чтобы вы смогли проанализировать ситуацию, как это делает Ванесса здесь.«Я записываю свое предположение и проверяю, как вы можете видеть здесь, и вы можете представить, как после еще пары предположений это приведет к правильному ответу. Как только эта структура будет создана, дети будут рады попробовать свои собственные предположения. Мои их задача — распространить и убедиться, что они все еще обсуждают проблему, записывают свои попытки в свои заметки и имеют хорошие идеи о том, что делать дальше.
Еще два очка, если время позволяет
- Когда я вижу, что студенты на правильном пути, я мог бы воспользоваться возможностью, чтобы продолжить развитие функционального мышления, проанализировав пару неправильных ответов, чтобы увидеть, как работают догадки и проверка.Сравнивая входные и выходные данные, учащиеся могут увидеть, каким может быть следующее разумное предположение.
- Мне также нравится подчеркивать силу того, что Ванесса делает в этой проблеме. Я спрашиваю всех, как бы они были взволнованы, если бы их начальник предложил им надбавку на 2 доллара в час и 8 часов в неделю. Звучит захватывающе? Затем мы расширяем его: как звучат 200 долларов в неделю? Как звучит 800 долларов в месяц? Как звучит 9600 долларов в год? Изменение этих контекстов может действительно подчеркнуть силу подобного мышления и может лучше проинформировать кого-то о том, насколько он должен быть взволнован.Это интересный разговор.
Формы линейных уравнений — Урок
Быстрый просмотр
Уровень оценки: 8
(7-9)
Требуемое время: 45 минут
Зависимость урока:
Тематические области:
Алгебра
Резюме
Учащиеся узнают о четырех формах уравнений: прямое изменение, форма пересечения наклона, стандартная форма и форма точки-наклона.Они составляют график и завершают наборы задач для каждого, конвертируя одну форму уравнения в другую и изучая преимущества и способы использования каждой из них.
Инженерное соединение
Идея наклона как скорости изменения важна для понимания того, как изображаются линии. Инженеры должны уметь создавать и понимать графики, которые могут объяснять наборы данных. Инженеры-механики читают и понимают графики, показывающие смещение, скорость и ускорение, чтобы затем проанализировать данные с испытательных площадок, чтобы узнать, как проектировать свои продукты (например, автомобили и самолеты), чтобы они были более эффективными и безопасными.В вопросах журнала 5-6 итоговой оценки студенты думают как инженеры, учитывая значение ключевых точек данных и цель использования линий для моделирования данных.
Цели обучения
После этого урока учащиеся должны уметь:
- Различайте различные формы уравнений, включая прямую вариацию, форму пересечения наклона, стандартную форму и форму точки-наклона.
- Объясните, что подразумевается под термином эквивалентные уравнения.
- Преобразование из одной формы уравнения в другую.
- Сообщите, когда каждая форма полезна и как построить график с использованием каждой формы.
- Используйте наклон параллельной или перпендикулярной линии вместе с точкой на прямой, чтобы написать уравнение прямой в любой из трех основных форм.
Образовательные стандарты
Каждый урок или задание TeachEngineering соотносится с одним или несколькими научными предметами K-12,
образовательные стандарты в области технологий, инженерии или математики (STEM).
Все 100000+ стандартов K-12 STEM, охватываемых TeachEngineering , собираются, обслуживаются и упаковываются сетью стандартов Achievement Standards Network (ASN) ,
проект D2L (www.achievementstandards.org).
В ASN стандарты иерархически структурированы: сначала по источникам; например , по штатам; внутри источника по типу; например , естественные науки или математика;
внутри типа по подтипу, затем по классу, и т. д. .
Государственные стандарты Common Core — математика
- Решите, находятся ли две величины в пропорциональном отношении, например, проверив эквивалентные отношения в таблице или построив график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.
(Оценка
7)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Используйте аналогичные треугольники, чтобы объяснить, почему угол наклона m одинаков между любыми двумя разными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для линии, проходящей через начало координат, и уравнение y = mx + b для линии, пересекающей вертикальную ось в точке b.(Оценка
8)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Создайте функцию для моделирования линейной зависимости между двумя величинами.Определите скорость изменения и начальное значение функции по описанию взаимосвязи или по двум (x, y) значениям, включая чтение их из таблицы или графика. Интерпретируйте скорость изменения и начальное значение линейной функции в терминах моделируемой ситуации, а также в терминах ее графика или таблицы значений.
(Оценка
8)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Опишите качественно функциональную взаимосвязь между двумя величинами, проанализировав график (например,g., где функция возрастающая или убывающая, линейная или нелинейная). Нарисуйте график, демонстрирующий качественные характеристики функции, которая была описана устно.
(Оценка
8)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Решите линейные уравнения с одной переменной.(Оценка
8)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Анализируйте и решайте пары одновременных линейных уравнений.(Оценка
8)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Выберите и создайте эквивалентную форму выражения, чтобы раскрыть и объяснить свойства величины, представленной выражением.(Оценки
9 —
12)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Создавайте уравнения с двумя или более переменными, чтобы представить отношения между величинами; графические уравнения на координатных осях с надписями и шкалами.(Оценки
9 —
12)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Графические функции выражаются символически и показывают ключевые особенности графа вручную в простых случаях и с использованием технологий для более сложных случаев.(Оценки
9 —
12)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Создавайте уравнения и неравенства для одной переменной и используйте их для решения задач.Включите уравнения, возникающие из линейных и квадратичных функций, а также простых рациональных и экспоненциальных функций.
(Оценки
9 —
12)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Решите линейные уравнения и неравенства с одной переменной, включая уравнения с коэффициентами, представленными буквами.(Оценки
9 —
12)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии — Технология
- Используйте компьютеры и калькуляторы в различных приложениях.(Оценки
6 —
8)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
- Знания, полученные в других областях исследований, имеют прямое влияние на разработку технологических продуктов и систем.(Оценки
6 —
8)Подробнее
Посмотреть согласованную учебную программу
Вы согласны с таким раскладом?
Спасибо за ваш отзыв!
ГОСТ
Предложите выравнивание, не указанное выше
Какое альтернативное выравнивание вы предлагаете для этого контента?
Предпосылки и концепции урока для учителей
Начните с возврата строки из последнего класса, прошедшего между точками (0,3) и (6,5).Напомните учащимся, что они определили этот наклон как 1/3. Однако было бы неплохо узнать эту линию не только по ее наклону. Что действительно было бы здорово, так это создать связь между двумя переменными x и y. Напомните учащимся, что для любой данной линейной функции каждое значение x имеет ровно одно соответствующее значение y. Для другой линейной функции это значение x может иметь другое соответствующее значение y. Итак, часть того, что нам нужно сделать, — это охарактеризовать линию так, чтобы мы указали связь между x и y, независимо от того, какие числовые значения для этой функции.
Один из «особых случаев», с которого интересно начать, — это взаимосвязь переменных, которые имеют прямое изменение друг с другом. То есть они следуют соотношению y = k x, где k — «постоянная вариации». Это видно по соотношению между расстоянием, скоростью и временем, где скорость поддерживается постоянной, поскольку y и x изменяются напрямую друг от друга. Поскольку учащиеся хорошо знакомы с взаимосвязью между скоростью, расстоянием и временем, попросите их выполнить практическое задание, чтобы продемонстрировать эту взаимосвязь (см. Ниже упражнение «Сопоставление движений»).Эти отношения, обнаруженные в деятельности, важны для инженеров при анализе данных. Например, инженеры-механики должны понимать различные отношения между скоростью, расстоянием и временем, чтобы лучше и безопаснее проектировать такие продукты, как автомобили и самолеты. На данный момент учащиеся должны знать, как определить постоянную вариации (которая представляет собой наклон линии) по паре значений (x, y). Им также необходимо знать, как определить одно значение с учетом другого значения и постоянной вариации.Например, «y изменяется прямо как x. Y = 4, когда x = 0,5. Что такое k? Напишите уравнение. Когда y = 2, что такое x?» Пример работы показан ниже.
Прямая вариационная зависимость на самом деле является просто частным случаем следующей формы уравнений, которые будут изучать учащиеся, — формы наклон-пересечение. Единственное отличие состоит в том, что он всегда имеет точку пересечения оси Y, равную 0 (пересекает начало координат).
Первой широко принятой формой уравнения является форма с пересечением наклона. Для этой формы нам нужно знать — как вы уже догадались — наклон линии и ее пересечение по оси Y.(Отсечка по оси Y — это место, где линия пересекает ось y.) Уравнения точки пересечения наклона принимают следующую форму: y = m x + b, где m — наклон, а b — точка пересечения оси y. Итак, если вы знаете наклон линии, как обсуждалось в нашем предыдущем уроке, и знаете, где она пересекает ось Y (точка пересечения оси Y), то вы можете написать уравнение линии. Например, y = 2x + 3 имеет наклон 2 и пересекает ось Y при положительном значении 3. Учащиеся должны иметь возможность взять уравнение в любой другой форме и преобразовать его в форму с пересечением наклона, переставив уравнение с помощью свойства равенства.Пример показан ниже.
Учащиеся также должны уметь легко перемещаться между алгебраическим и графическим представлениями линейных отношений.
Вторая важная форма уравнений — это стандартная форма , которая записывается как Ax + By = C. Учащиеся должны знать, что, в отличие от формы с пересечением наклона, эту форму сложнее получить непосредственно из графика, потому что A, B и C не являются наклоном, пересечениями или какой-либо другой характеристикой линии.Наилучший способ написать уравнение этого типа из построенной на графике линии — найти линию в другой форме, например, в форме пересечения наклона, а затем перестроить уравнение так, чтобы оно было в стандартной форме. Красота стандартной формы уравнения состоит в том, что по нему можно легко определить пересечения по осям x и y и использовать эти точки для построения графика. Для этого предложите студентам составить таблицу x-y, как показано ниже. Вставьте 0 вместо x и посмотрите, что такое y. Затем вставьте 0 для y и посмотрите, что такое x. С помощью этих двух точек студенты могут легко построить график линейной функции.Студенты также должны уметь преобразовывать уравнение в стандартную форму.
Третье уравнение формы, о котором должны знать учащиеся, — это точка-наклон, форма прямой, где m — наклон, а (x1, y1) — точка на прямой. Эта форма уравнения полезна, потому что, если кто-то знает точку на графике и наклон, он / она может легко построить линию. Учащиеся должны уметь смотреть на график и определять форму точки-наклона уравнения линии, а также брать уравнение в форме точки-наклона и рисовать график.Кроме того, они должны иметь возможность конвертировать между этой формой и другими формами уравнений. Интересно отметить сходство между этой формулой и формулой для наклона прямой.
Завершите уроки, связав их с контрольным вопросом. Попросите учащихся достать свои листы бумаги или журналы, в которых они записывали идеи. Попросите их записать, как эта информация о формах уравнений может помочь им решить сложный вопрос.
Для домашнего задания каждый вечер попросите учащихся заполнить прилагаемые рабочие листы.Раздайте им раздаточный материал « форм линий » для изучения.
занятий, которые сделают практику многоступенчатых уравнений потрясающей
Моя история обучения многоступенчатым уравнениям была не из приятных, но внимание спойлера, есть счастливый конец. Несколько лет назад я преподавал вместе с относительно новым учителем, и я чувствовал сильное давление, чтобы показать ему основы. Я был новичком в математических стандартах 8-го класса. В течение первого месяца в школе все шло хорошо, пока мы не приступили к решению многоступенчатых уравнений.Мы работали в течение двух полных недель и учили студентов тому, как нас учили многоступенчатым уравнениям. Ребята провалили модульный тест. Это было ужасно. Затем у нас была возможность переучить большинство детей, и мы попробовали кое-что еще. Это тоже не удалось. Это был по меньшей мере унизительный опыт.
Я отступил и посмотрел на концепт. Я потратил много времени, пытаясь понять, где дети сбиты с толку. Для стольких детей нужно было запомнить очень много вещей. Итак, я придумал способ решения этих уравнений, названный методом ящиков.Через несколько недель мы снова научили студентов решать многоступенчатые уравнения, на этот раз с помощью ящиков, но на это у нас было всего два дня. Даже за два дня это было самым успешным из того, что мы сделали.
Я знал, что в следующем году, когда придет время преподавать многоступенчатые уравнения, мы с самого начала будем обучать этому методу ящиков. И я был уверен, что у нас все получится. Удивительно, но это оказалось даже более правильным, чем я надеялся. На второй год мы начали обучение по этому методу, и подавляющее большинство детей освоили его с первого раза.Мы использовали этот метод в течение всего года, и наши ученики были намного лучше, чем когда-либо прежде. Чтобы увидеть пошаговое руководство по обучению с помощью этого метода ящиков, ознакомьтесь с публикацией «Как обучать многоступенчатым уравнениям, как босс».
Независимо от того, как вы учите студентов многоступенчатым уравнениям, как только они научатся решать многоступенчатые уравнения, у них появится множество различных способов практиковаться. И как бы вы ни выбрали практику, студентам нужно много возможностей для отработки этого навыка.Вот подборка некоторых занятий, которые мне нравится использовать в классе.
Решение лабиринтов с многоступенчатыми уравнениями (печатные и цифровые)
Переменные прогулки по галерее с обеих сторон
Целевая игра с картами задач
Доска с листами
Модель интерактивных весов
Опасность умения работать с многоступенчатыми уравнениями
Бинго
Cootie Catchers
Шмооп Видео
Иллюстративное упражнение по математике
Онлайн-игра Algebra Meltdown
Действия по решению многоступенчатых уравнений
Указанные ниже задания можно использовать в разных частях урока.Некоторые из них хорошо работают в качестве упреждающих сетов, в то время как другие отлично подходят для практики. Все они интересны, и многие из них поощряют сотрудничество. Некоторые действия выполняются на компьютере, в то время как другие используют бумагу.
Вот описание каждого из действий и несколько советов по их использованию:
В моем классе мы делаем много лабиринтов. Это отличный способ начать день. Их можно использовать для колоколов после вводного урока или в качестве циклического обзора.У этих конкретных лабиринтов есть переменные с обеих сторон. Кроме того, они становятся сложнее от лабиринта к лабиринту. В решаемых уравнениях есть целые числа и дроби. Студентам нравится их выполнять, и они даже не осознают, что завершают работу.
У этих лабиринтов теперь есть и цифровая версия! Эта версия встроена в Google Slides и может быть легко назначена в Google Classroom (или другой LMS). Они просты в использовании и интерактивны для учащихся, с перетаскиваемыми стрелками, чтобы отмечать их путь.
Между прочим, это отличный шанс зарегистрироваться в БЕСПЛАТНОМ клубе «Лабиринт месяца», если вы еще этого не сделали. Я отправляю членам MotM Club бесплатный эксклюзивный лабиринт по различным математическим концепциям средней школы прямо на их почтовые ящики каждый месяц (как в цифровой, так и в печатной версии!) Присоединяйтесь сегодня и попробуйте несколько математических лабиринтов в своем классе:
Нажмите здесь, чтобы присоединиться к клубу «Лабиринт месяца».
Это мероприятие по прогулке по галерее является бесплатным ресурсом (перейдите по ссылке здесь).Когда вы попадаете на веб-сайт, вам нужно прокрутить вниз, а затем загрузить Gallery Walk. На этом веб-сайте показано множество других занятий. Самое замечательное в этом занятии то, что все готово к работе. 30 задач, включенных в эту галерею, становятся все сложнее, и многие из них можно использовать как задачи-вызовы. Некоторые из задач бросят вызов быстрым финишерам или могут быть полезны для использования в продвинутом классе. Наконец, прогулки по галерее действительно увлекают детей и заставляют их перемещаться по классной комнате.
Карты заданий можно использовать по-разному. Один из способов — использовать их со всем классом и играть с ним в игру. Вы можете сделать это с помощью Target Game на доске или Trashketball с помощью мусорной корзины. Обе игры требуют от учащихся решить задачу, а затем вы моделируете ответ для класса. Затем кто-то может бросить липкий мяч в мишень на доске или выстрелить из скомканной бумаги в мусорное ведро. Им нравится задача целевой части, и обычно весь класс действительно в нее входит.Так просто, но так весело.
Я использую некоторые карточки задач из этого набора карточек с многоэтапными уравнениями в качестве задач для этой игры (она поставляется как в печатной, так и в цифровой версии). Это просто, и тогда у меня есть все задачи, которые мне нужны для игры. Я даю баллы всем детям, которые правильно ответили на вопрос. Количество очков зависит от того, как бросил мяч или сделал бросок. Несмотря на то, что я не уделяю особого внимания пунктам, дети все равно воодушевляются.
4- Доска с рабочими листами
Мне нравится, когда ученики работают над досками. В моем классе у меня есть набор из 6 больших досок, и ученики любят над ними работать. Они могут быть на стене, или студенты могут снимать их, чтобы поработать над ними. Перейдите по этой ссылке, чтобы перейти к серии рабочих листов. Вы найдете 15 рабочих листов, которые переходят от простого к сложному и работают с десятичными и дробными числами.
Мы редко просто делаем рабочий лист в моем классе, но мне нравится, что эти задачи готовы к использованию.Например, когда я занимаюсь доской, у меня есть группа из двух или трех человек, которые вместе работают над одной и той же задачей. Я моделирую математическую беседу, которую хочу, и стараюсь хорошо понимать, как я группирую студентов. Затем учащиеся вместе решают на доске, демонстрируя на доске свои математические рассуждения и обсуждая свою стратегию решения проблем со своими одноклассниками. Это упражнение хорошо работает в качестве упражнения, упреждающего набора или упражнения с губкой.
Иногда вы хотите, чтобы студенты работали с уравнениями конкретным образом.Эта модель баланса из Math Playground помогает вашим детям увидеть, что они делают, решая уравнения. Им потребуется немного знаний по уравнениям, прежде чем вы назначите эту модель. Одна из замечательных частей состоит в том, что для них устанавливаются уравнения, а затем ученики работают над ними на весах. Это предварительный набор для меня на 3-й или 4-й день занятия по решению многоступенчатых уравнений.
Jeopardy существует уже давно как способ пересмотра концепций. Мы играли в Jeopardy еще в младших классах (а это было в 80-е годы!).Вы можете играть в Jeopardy всем классом, где каждый должен ответить на вопрос. Учащиеся отслеживают свои индивидуальные баллы.
Эта конкретная игра Jeopardy от Jeopardy Labs основана на предварительных навыках для многошаговых уравнений, включая свойство распределения и комбинирование подобных терминов. Это довольно быстрая игра для моих восьмиклассников. Мне нравится использовать такие игры как предварительный набор. Мы не доделываем всю игру, но играем в нее примерно 5-7 минут. Это идеальный способ активизировать предыдущие знания и вовлечь детей в урок.
Бинго — один из моих любимых способов обсудить любую тему. Обычно мы делаем это в день теста или за день до теста. Это зависит от того, сколько времени продлится тест. Вы можете попросить учащихся положить карточки бинго в конверт SmartPal или сделать так, чтобы они пометили свой лист разными символами. На решение 30 задач уходит много времени, и мы обычно не решаем их все. Обычно я выбираю уравнения, которые, как мне кажется, вселяют в учеников уверенность и помогают отработать ключевые камни преткновения.Эта игра Бинго включает уравнения с дробями и уравнения с переменными с обеих сторон.
Bingo — отличная игра с циклическим обзором. Редко есть тот, кто не хочет играть в Бинго. Я даю призы победителям. Часто приз — это Веселый ранчо, маленький карандаш или ластик. Удивительно, как усердно дети будут работать ради этого маленького поощрения.
Использование кути-ловцов или того, что некоторые называют гадалками, — интересный способ привлечь студентов. Я считаю, что эти упражнения хорошо подходят для детей, которые опасаются темы многоступенчатых уравнений.Эта тема может быть немного сложной для многих студентов, и когда они решают уравнения с партнером, играя в небольшую игру, они, кажется, теряют бдительность.
У каждого партнера есть кути-ловец с разными проблемами. Затем каждый партнер работает над своей проблемой. Студенты могут играть лицом к лицу и видеть, кто получит наиболее правильные ответы за определенное время.
Проблемы в этой конкретной деятельности по улавливанию хлопьев включают фракции и свойство распределения.Я узнал, что ученикам нужны разные ситуации, когда дело касается уравнений. В противном случае они просто запоминают некоторые шаги, а затем, после модульного теста, они быстро забывают, что делают.
(добавление 2020 г. — недавно у нас была учительница, которая рассказала, что она заставляла своих учеников практиковаться в этом упражнении, чтобы убедиться, что они были социально дистанцированы, чтобы они «на самом деле не ловили кути». Так весело!)
Это глупое видео от Shmoop дает пример того, почему вы должны выполнять какие-либо операции с обеих сторон при решении уравнения.В ролике используется история Рудольфа Красноносого оленя. Это видео — отличный выбор для предварительного просмотра через пару дней после установки. Кроме того, это можно было бы использовать в конце раздела, чтобы увидеть, что понимают учащиеся.
Мне нравится, когда студенты получают возможность делать больше, чем просто решать практические задачи, когда они действительно применяют то, что они изучают. Что ж, это упражнение из Иллюстративной математики идеально подходит для этого. Он дает студентам простой пример того, как мы моделируем математику.Затем он предлагает студентам решить уравнение математически и символически. Это действительно бросает вызов мышлению учащихся, особенно если математика дается им легко. Что-то подобное действительно может вывести их из зоны комфорта.
Это задание представляет собой расширенный ответ, на выполнение которого учащимся потребуется 15–45 минут. Есть несколько частей, и если у вас меньше времени, они могут использовать часть этого. Те, кто быстро заканчивает, могут работать над этим по мере продвижения модуля, когда они заканчивают классную работу. Ниже начало задания.Щелкнув по картинке, вы перейдете ко всей задаче.
Algebra Meltdown — это онлайн-игра, которая делает изучение алгебры интересным и конкретным. Студенты должны перемещаться по ряду уравнений и внутри лаборатории ученого. По мере выполнения задачи становятся все сложнее и сложнее, и они сводятся к многоступенчатым уравнениям. Поначалу это может быть непросто для некоторых студентов. Поскольку это игра, это отличный способ напомнить учащимся, что, как и когда они играют в видеоигры, нормально потерпеть неудачу и попробовать еще раз.Так мы узнаем новое.
Студенты любят играть в подобные игры и имеют в классе доску лидеров. Вы можете отслеживать лидеров в течение дня или недели. Вы также можете вручить пятерке лучших победителей какой-нибудь небольшой приз — просто удивительно, как далеко может зайти Jolly Rancher или симпатичный ластик!
Попробуйте одно…
Этот сборник идей может показаться занятием большим, если вы попытаетесь реализовать их все сразу. Просто попробуйте одно задание и посмотрите, как оно проходит в вашем классе.После этого вы можете попробовать другой. Чем больше стратегий взаимодействия вы попробуете, тем легче будет увлечься поиском еще большего количества способов добавить изюминки в упражнения по математике.
Спасибо за чтение! До скорого.
Связанные
Решение вопросов Word
МНОГО примеров!
В алгебре мы часто задаем словесные вопросы, например:
Пример: Сэм и Алекс играют в теннис.
В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр.
Сколько игр сыграл Алекс?
Как мы их решаем?
Уловка состоит в том, чтобы разбить решение на две части:
Превратите английский в алгебру.
Затем решите с помощью алгебры.
Превращение английского в алгебру
Превратить английский в алгебру помогает:
- Прочтите сначала все
- Сделайте эскиз , если возможно
- Назначьте буквы для значений
- Найдите или разработайте формулы
Вам также следует записать , что на самом деле требуется для , чтобы вы знали, куда вы собираетесь и когда вы прибыли!
Также ищите ключевые слова:
| Когда вы видите | Думаю | |
|---|---|---|
сложить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более | + | |
минус, меньше, разница, меньше, уменьшилась, уменьшилась | – | |
умноженное на умножение на произведение, множитель | × | |
разделенное, частное, на, из, соотношение, соотношение, процент, ставка | ÷ | |
| увеличить или уменьшить | геометрия формулы | |
| Скорость, скорость | расстояние формулы | |
| Сколько дней, часов, минут, секунд | раз |
Ясное мышление
Некоторые формулировки могут быть хитрыми, из-за чего трудно думать «правильно», например:
$
Пример: У Сэма на 2 доллара меньше, чем у Алекса.Как это записать в виде уравнения?
- Пусть S = долларов, у Сэма
- Пусть A = долларов у Алекса
Теперь … вот что: S — 2 = A
или должно быть: S = A — 2
или должно быть: S = 2 — A
Правильный ответ: S = A — 2
( S — 2 = A — распространенная ошибка, так как в вопросе написано «Сэм … на 2 меньше … Алекс»)
Пример: на нашей улице собак вдвое больше, чем кошек.Как это записать в виде уравнения?
- Пусть D = количество собак
- Пусть C = количество кошек
Теперь … это то, что: 2D = C
или должно быть: D = 2C
Подумайте внимательно!
Правильный ответ: D = 2C
( 2D = C — распространенная ошибка, так как в вопросе написано «дважды … собаки … кошки»)
Примеры
Давайте начнем с очень простого примера , чтобы увидеть, как это делается:
Пример: прямоугольный сад размером 12 м на 5 м, какова его площадь?
Превратите английский в алгебру:
Эскиз:
.
букв:
- Используйте w для ширины прямоугольника: w = 12 м
- Используйте h для высоты прямоугольника: h = 5m
Формула для площади прямоугольника: A = w × h
Нас спрашивают о Районе.
Решить:
A = ш × в = 12 × 5 = 60 м 2
Площадь кв.м. 60 кв.м. .
Теперь давайте попробуем пример сверху страницы:
Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алекс?
Превратите английский в алгебру:
букв:
- Используйте S , чтобы узнать, сколько игр Сэм сыграл
- Используйте A , чтобы узнать, сколько игр сыграл Алекс
Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4
И мы знаем, что вместе они сыграли 12 игр: S + A = 12
Нас спрашивают, сколько игр сыграл Алекс: A
Решить:
Начать с: S + A = 12
S = A + 4 , поэтому мы можем
заменить S на «A + 4»: (A + 4) + A = 12
Упростить: 2A + 4 = 12
Вычтем 4 с обеих сторон: 2A = 12-4
Упростить: 2A = 8
Разделите обе части на 2: A = 4
Это означает, что Алекс сыграл 4 игры в теннис.
Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр.
Вместе они сыграли 8 + 4 = 12 игр. Да!
Немного более сложный пример:
Пример: Алекс и Сэм также создают таблицы.
Вместе они делают 10 столов за 12 дней.
Алекс, работая в одиночку, может заработать 10 за 30 дней.
Сколько времени потребуется Сэму, работая в одиночку, чтобы сделать 10 столов?
Превратите английский в алгебру:
букв:
- Используйте и для скорости работы Алекса
- Используйте с для скорости работы Сэма
12 дней Алекса и Сэма — это 10 столов, поэтому: 12a + 12s = 10
30 дней одного Алекса — это тоже 10 столов: 30a = 10
Нас спрашивают, сколько времени потребуется Сэму, чтобы сделать 10 столов.
Решить:
30a = 10 , поэтому ставка Алекса (столов в день) составляет: a = 10/30 = 1/3
Начать с: 12a + 12s = 10
Положите «1/3» для a: 12 (1/3) + 12s = 10
Упростить: 4 + 12 = 10
Вычтем 4 с обеих сторон: 12s = 6
Разделите обе стороны на 12: s = 6/12
Упростить: с = 1/2
Это означает, что ставка Сэма составляет половину стола в день (быстрее, чем у Алекса!).
Итак, 10 столов займет у Сэма всего 20 дней.
Интересно, стоит ли Сэму платить больше?
И еще пример «подстановки»:
Пример: Дженна усиленно тренируется, чтобы пройти квалификацию к Национальным играм.
У нее обычный еженедельный распорядок дня: в одни дни она тренируется по пять часов в день, а в другие — по 3 часа в день.
В общей сложности она тренируется 27 часов в семидневную неделю. Сколько дней она тренируется по пять часов?
Письма:
- Количество «5 часовых» дней: d
- Количество «3-х часовых» дней: e
Мы знаем, что в неделе семь дней, поэтому: d + e = 7
И она тренируется 27 часов в неделю, из которых d 5 часов в день и e 3 часа в день: 5d + 3e = 27
Нас спрашивают, сколько дней она тренируется по 5 часов: d
Решить:
d + e = 7
Итак: e = 7 — d
Положим, что в 5d + 3e = 27 5d + 3 (7 − d) = 27
Упростить: 5d + 21 — 3d = 27
Вычтем 21 с обеих сторон: 5d — 3d = 6
Упростить: 2d = 6
Разделим обе части на 2: d = 3
Количество «5 часовых» дней — 3
Проверка : Она тренируется по 5 часов 3 дня в неделю, поэтому она должна тренироваться по 3 часа в день в остальные 4 дня недели.
3 × 5 часов = 15 часов, плюс 4 × 3 часа = 12 часов дает в сумме 27 часов
Некоторые примеры из Geometry:
Пример: круг имеет площадь 12 мм
2 , каков его радиус?
букв:
- Используйте A для Area: A = 12 мм 2
- Используйте r для радиуса
И формула для площади: A = π r 2
У нас спрашивают радиус.
Решить:
Нам нужно переставить формулу, чтобы найти площадь
Начать с: A = π r 2
Поменять местами стороны: π r 2 = A
Разделим обе стороны на π : r 2 = A / π
Извлечь квадратный корень из обеих частей: r = √ (A / π)
Теперь мы можем использовать формулу: r = √ (12/ π)
И получаем: r = 1.954 (до 3-х мест)
Пример: куб имеет объем 125 мм
3 , какова его площадь поверхности?
Сделайте быстрый набросок:
букв:
- Используйте V для объема
- Используйте A для Area
- Используйте s для длины стороны куба
Формулы:
- Объем куба: В = с 3
- Площадь куба: A = 6s 2
У нас спрашивают площадь.
Решить:
Первая отработка с по формуле объема:
Начать с: В = с 3
Поменять местами стороны: s 3 = V
Извлечь кубический корень с обеих сторон: s = ∛ (V )
И получаем: s = ∛ (125 ) = 5
Теперь мы можем рассчитать площадь поверхности:
Начать с: A = 6s 2
И получаем: A = 6 (5) 2
A = 6 × 25 = 150 мм 2
Пример о деньгах:
Пример: Джоэл работает в местной пиццерии.Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычного.
Одна неделя Джоэл проработал 40 часов по обычной ставке, а также 12 часов сверхурочно. Если Джоэл заработал за эту неделю 660 долларов, какова его нормальная ставка заработной платы?
букв:
- Обычная ставка оплаты труда Джоэля: N $ в час
Формулы:
- Джоэл работает 40 часов по цене N $ в час = 40N
- Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1 доллар.25N в час
- Джоэл работает 12 часов по цене 1,25 доллара США в час = (12 × 1 доллар США) = 15 долларов США
- А вместе он заработал 660 долларов, итак:
$ 40N + $ (12 × 1¼N) = 660 $
У нас спрашивают нормальную ставку заработной платы Джоэла в $ N.
Решить:
Начните с 40N $ + (12 × 1¼N) = 660 $
Упростить: 40N + 15N = 660 $
Еще более упростите: 55 долларов США = 660 долларов США
Разделим обе стороны на 55: $ N = 12 $
Итак, обычная ставка оплаты труда Джоэла составляет 12 долларов в час.
Чек
Обычная ставка оплаты труда Джоэла составляет 12 долларов в час, поэтому его сверхурочная ставка составляет 1¼ × 12 долларов в час = 15 долларов в час.Таким образом, его обычная зарплата 40 × 12 = 480 долларов плюс его сверхурочная работа в размере 12 × 15 долларов = 180 долларов дает нам в общей сложности 660 долларов
.
Подробнее о деньгах на этих двух примерах, связанных со сложным процентом
Пример: Алекс вкладывает 2000 долларов в банк под 11% годовых. Сколько это будет стоить через 3 года?
Это формула сложных процентов:
Итак, мы будем использовать эти буквы:
- Текущая стоимость PV = 2000 долларов США
- Процентная ставка (в десятичном формате): r = 0.11
- Количество периодов: n = 3
- Будущее значение (значение, которое мы хотим): FV
Нас спрашивают о будущей стоимости: FV
Решить:
Начать с: FV = PV × (1 + r) n
Добавьте то, что мы знаем: FV = $ 2000 × (1 + 0,11) 3
Вычислить: FV = $ 2000 × 1,367631
Вычислим: FV = 2735 долларов.26 (с точностью до цента)
Пример: Роджер положил 1000 долларов на сберегательный счет. На заработанные деньги ежегодно начислялись проценты по той же ставке. Через девять лет депозит Роджера вырос до 1 551,33 доллара США
Какова была годовая процентная ставка по сберегательному счету?
Формула сложных процентов:
С:
- Текущая стоимость PV = 1000 долларов США
- Процентная ставка (желаемое значение):
- Количество периодов: n = 9
- Будущая стоимость: FV = 1551 доллар.33
р.
Нас спрашивают о процентной ставке:
р.
Решить:
Начать с: FV = PV × (1 + r) n
Добавьте то, что мы знаем: 1551,33 доллара = 1000 долларов × (1 + r) 9
Обменивать стороны: 1000 $ × (1 + r) 9 = 1551,33 $
Разделите обе стороны на 1000: (1 + r) 9 = 1551,33 доллара США / 1000 долларов США
Упростить: (1 + r) 9 = 1.55133
Корень 9-й степени: 1 + r = 1,55133 (1/9)
Вычислить: 1 + r = 1.05
Вычислить: r = 0,05 = 5%
Таким образом, годовая процентная ставка составляет 5%
Чек : 1000 долларов × (1,05) 9 = 1000 долларов × 1,55133 = 1551,33 доллара
И пример вопроса о соотношении:
Пример: В начале года соотношение мальчиков и девочек в классе было 2: 1
Но теперь, полгода спустя, четыре мальчика покинули класс и появились две новые девочки.Соотношение мальчиков и девочек сейчас составляет 4: 3
Сколько всего студентов сейчас?
Письма:
- Кол-во мальчиков сейчас: б
- Количество девочек сейчас: г
Коэффициент текущей ликвидности 4: 3
б г = 4 3
Что можно переставить на 3b = 4g
На начало года было (b + 4) мальчиков и (g — 2) девочек, и соотношение было 2: 1
б + 4 г — 2 = 2 1
Которая может быть преобразована в b + 4 = 2 (g — 2)
Нас спрашивают, сколько всего студентов сейчас: b + g
Решить:
Начать с: b + 4 = 2 (г — 2)
Упростить: b + 4 = 2g — 4
Вычтем 4 с обеих сторон: b = 2g — 8
Умножаем обе стороны на 3 (получаем 3b): 3b = 6g — 24
Помните 3b = 4g : 4g = 6g — 24
Вычесть 6g с обеих сторон : −2g = -24
Разделим обе части на −2: г = 12
Всего девушек !
И 3b = 4g , поэтому b = 4g / 3 = 4 × 12/3 = 16 , то есть 16 мальчиков
Таким образом, сейчас в классе 12 девочек и 16 мальчиков, что составляет человек из 28 человек, всего человек.
Чек
Сейчас 16 мальчиков и 12 девочек, поэтому соотношение мальчиков и девочек составляет 16: 12 = 4: 3.
В начале года было 20 мальчиков и 10 девочек, поэтому соотношение было 20: 10 = 2: 1
А теперь некоторые квадратные уравнения:
Пример: произведение двух последовательных четных целых чисел равно 168. Что такое целые числа?
Последовательные означают один за другим. И это , даже , так что они могут быть 2 и 4, или 4 и 6 и т. Д.
Мы назовем меньшее целое число n , поэтому большее целое число должно быть n + 2
И нам говорят, что произведение (то, что мы получаем после умножения) равно 168, поэтому мы знаем:
п (п + 2) = 168
Нас спрашивают целые числа
Решить:
Начать с: n (n + 2) = 168
Развернуть: n 2 + 2n = 168
Вычтем 168 с обеих сторон: n 2 + 2n — 168 = 0
Это квадратное уравнение, и есть много способов его решить.Используя метод решения квадратного уравнения, мы получаем −14 и 12.
Проверка −14: −14 (−14 + 2) = (−14) × (−12) = 168 ДА
Проверка 12: 12 (12 + 2) = 12 × 14 = 168 ДА
Итак, есть два решения: -14 и -12 — одно, 12 и 14 — другое.
Примечание: мы также могли попробовать «угадать и проверить»:
- Мы могли бы попробовать, скажем, n = 10: 10 (12) = 120 NO (слишком мало)
- Затем мы могли бы попробовать n = 12: 12 (14) = 168 ДА
Но если мы не вспомним, что умножение двух отрицаний дает положительный результат, мы можем пропустить другое решение (−14) × (−12).
А:
Пример: вы архитектор. Вашему клиенту нужна комната вдвое больше ширины. Им также нужна веранда шириной 3 метра по длинной стороне.
У вашего клиента 56 квадратных метров красивой мраморной плитки для покрытия всей площади.
Какой должна быть длина комнаты?
Давайте сначала сделаем набросок, чтобы все было правильно !:
букв:
- длина помещения: л
- ширина помещения: Вт
- Общая площадь с верандой: А,
Мы знаем:
- ширина комнаты равна половине ее длины: W = ½L
- общая площадь равна (ширина помещения + 3), умноженная на длину: A = (W + 3) × L = 56
Нас спрашивают о длине комнаты: L
Решить:
Начать с: (Ш + 3) × Д = 56
Заменитель W = ½L : (½L + 3) × L = 56
Упростить: ½L 2 + 3L = 56
Умножьте все члены на 2: L 2 + 6L = 112
Вычесть 112 с обеих сторон : L 2 + 6L — 112 = 0
Это квадратное уравнение , есть много способов его решить, на этот раз давайте воспользуемся факторингом:
Начать с: L 2 + 6L — 112 = 0
Два числа, которые умножаются, чтобы получить ac = −112,
и
сложить, чтобы получить b = 6, 14 и −8: L 2 + 14L — 8L — 112 = 0
Группа: L (L +14) — 8 (L + 14) = 0
Группа: (L — 8) (L + 14) = 0
Итак, L = 8 или −14
Есть два решения квадратного уравнения, но только одно из них возможно, так как длина комнаты не может быть отрицательной!
Итак, длина помещения 8 м
Чек
L = 8, поэтому W = ½L = 4
Итак, площадь прямоугольника = (W + 3) × L = 7 × 8 = 56
Вот и мы…
… Я надеюсь, что эти примеры помогут вам понять, как отвечать на словесные вопросы. А как насчет практики?
Глава 2: ПРИРОДА МАТЕМАТИКИ Математика опирается как на логику, так и на творческий потенциал, и ей занимаются В этой главе математика рассматривается как часть научного МОДЕЛИ И ОТНОШЕНИЯ Математика — это наука о закономерностях и отношениях. Как теоретический Центральным направлением исследований теоретической математики является определение Математика — это еще и прикладная наука. Многие математики сосредотачиваются Результаты теоретической и прикладной математики часто влияют на МАТЕМАТИКА, НАУКА, Из-за своей абстрактности математика в некотором смысле универсальна.
МАТЕМАТИЧЕСКИЙ ЗАПРОС Использование математики для выражения идей или решения проблем предполагает: Абстракция и символическое представление Математическое мышление часто начинается с процесса абстракции, т.е. Такая абстракция позволяет математикам сосредоточиться на некоторых особенностях. Манипулирование математическими утверждениями После того, как были сделаны абстракции и символические изображения Обычно строки символов объединяются в утверждения, которые выражают Математическое понимание абстрактных отношений переросло Заявка Математические процессы могут привести к некой модели предмета из Иногда здравого смысла достаточно, чтобы решить, стоит ли Часто один раунд математических рассуждений не дает удовлетворительных результатов. Но какая степень точности достаточно хороша? Ответ зависит от |
Ремесленные проекты для математического класса
Учитель рисования Мелинда Нгуен проводила утро в своей бывшей школе, начальной школе Несбит в Такере, штат Джорджия, помогая в программе расширения знаний по математике под названием Mighty Minds.В рамках программы она работала с учителем второго класса, чтобы объяснить сложение «сделай 10», но ученики не уловили эту концепцию. Поэтому Нгуен решил попробовать что-то другое. Она руководила учениками в создании мозаики, для чего требовалось понимание сложения 10. Урок застрял.
Уроки, интегрированные в искусство, могут прояснить абстрактные концепции, создать запоминающиеся визуальные эффекты и помочь преодолеть разрыв между классными уроками и реальными приложениями. И, как отмечает Сара Джейкобсон из Хадсона, Нью-Гэмпшир, учительница первого класса, эти проекты могут стимулировать кинестетическое обучение, давая ученикам возможность «потрогать и манипулировать».”Вот восемь математических поделок, которые помогут привнести искусство в ваш класс, чтобы научить всему — от умножения до радиальной симметрии.
Сделайте мозаику
Прислал: Мелинда Нгуен, K – 5 art, элементарная школа Баггетта, Лоуренсвилл, Джорджия. Блогер в Art с миссис Нгуен.
Материалы: Игральные карты, листы плотной бумаги размером 1 x 1 дюйм разных цветов, клей, диаграмма сотен
Когда это использовать: Нгуен разработал это задание, чтобы научить прибавлять 10 детей к находящимся в затруднительном положении второклассникам.Это делает концепцию «конкретной, визуальной и забавной», — говорит Нгуен.
Указания: «Попросите каждого ученика вытащить карту из модифицированной колоды, без валетов, дам и королей», — говорит Нгуен. «Выпавшее число будет числом, которое они укажут для первого добавления в своем первом пустом математическом предложении. Учащиеся выбирают бумажные квадраты одного цвета для обозначения числа и наклеивают соответствующее количество квадратов на первую строку таблицы. Затем ученики должны выяснить, сколько еще квадратов им понадобится, чтобы завершить ряд из 10.Как только они это сделают, попросите детей указать это число во втором дополнении и выбрать новый цвет квадратов, чтобы завершить ряд. Повторите то же самое для всех 10 рядов, поощряя детей создавать творческие узоры, меняя порядок цветов. Нгуен отмечает: «Независимо от заказа сумма будет одинаковой!»
Город Умножения
Представлено: Анной Мари Шевалье, классы 1-2, католическая начальная школа Святого Габриэля, Кембридж, Онтарио. Блогер в Elementary AMC.
Материалы: Черная или синяя плотная бумага (9 «x 12»), желтая плотная бумага (8.5 «x 11»), бумага разных цветов, клей
Когда это использовать: Используйте этот проект, чтобы научить студентов использовать массивы для демонстрации концепций умножения.
Направления: Вдохновленный книгой Мэрилин Бернс Удивительный сон Аманды Бин, , в которой Аманда находит массивы для подсчета по всему городу, Шевалье начинает урок с того, что направляет учеников в школьную экскурсию по обнаружению массивов умножения, прежде чем предложить им создать свои собственные. города, построенные из массивов.Затем ученики вырезают прямоугольники и приклеивают их к фоновому листу, чтобы создать линию горизонта. Они используют желтую бумагу, чтобы вырезать окна и прикрепить их к своему зданию рядами. Затем ученики обмениваются рисунками с одноклассниками и решают массивы умножения на каждой картинке. Для дополнительного прикосновения создайте дополнительные массивы звезд или снежинок на небе.
Колониальный граф
Прислал: Стефани Мурман, 5 класс, Лос-Анджелес. Блогер на уроке в аудитории 6.
Материалы: Листы миллиметровой бумаги размером 20 дюймов на 20 дюймов размером 1 дюйм, мелки, ламинат, клейкая лента, лист для записи
Когда это использовать: «В этом уроке я попытался объединить математические стандарты, которые мы изучали в то время (дроби и проценты), и некоторые прошлые стандарты (многоугольники, периметр, площадь, симметрия) с нашим отделом социальных исследований Колониальная Америка, — говорит Мурман.
Направления: «Студенты читают документы, относящиеся к колониальному и раннему американскому дизайну лоскутных одеял, затем создают свои собственные геометрические рисунки, используя комбинации от трех до пяти цветов», — говорит Мурман, который попросил, чтобы каждый рисунок содержал хотя бы один полный прямоугольник. Когда квадраты были готовы, Мурман ламинировал их и соединил каждый квадрат изолентой, чтобы получилось лоскутное одеяло. Затем она предложила студентам вычислить долю и процентное содержание каждого цвета, представленного на их квадрате лоскутного одеяла, а также периметр и площадь различных участков квадрата.Чтобы усложнить задачу, повторите эти вычисления для квилта в целом.
Flying Fact Families
Прислал: Келли Доллинг, 1-й класс, начальная школа Антилопы, Ред-Блафф, Калифорния. Блогер на фабрике идей учителей.
Материалы: Листы миллиметровой бумаги размером 20 x 20 дюймов с размером 1 дюйм, мелки, ламинат, клейкая лента, шаблоны для записи (доступны здесь)
Когда это использовать: Знакомьте своих подающих надежды математиков с семьями фактов с помощью дружелюбного лица.
Указания: Перед началом урока скопируйте шаблоны формул на цветную бумагу и распечатайте столько наборов, чтобы каждый ребенок получил четыре. Затем раздайте каждому ученику четыре круга, два глаза, полоску цветной бумаги (примерно 8,5 x 1,5 дюйма) и лист цветной бумаги. Направляйте детей в создании крыльев, складывая бумагу на четверти и используя ножницы, чтобы закруглить углы, удерживая складку. Затем назначьте учащимся группы фактов и попросите их написать свои числа на красочной полоске, прикрепить глаза к верхней части полоски и приклеить ее к центру их бабочки.(Добавьте усики и улыбку для забавного прикосновения.) Дети завершают своих бабочек, записывая различное уравнение, созданное их семьей фактов, в каждом круге и приклеивая круги к крыльям.
Большой аллигатор
Прислал: Сара Джейкобсон, 1-й класс, школа доктора Х. О. Смита, Хадсон, Нью-Гэмпшир. Блогер в солнечный день в первом классе.
Материалы: Зелено-белая плотная бумага, ножницы, клей, черные маркеры
Когда это использовать: Знакомьте своих начинающих математиков с семьями фактов с помощью символа го », — говорит Якобсон.«Изображение аллигатора, жующего большее количество, действительно помогает детям увидеть и понять».
Направления: Сначала вырежьте два зеленых прямоугольника и склейте их в форме буквы V, чтобы сформировать голову. Затем создайте зубы, вырезав два белых прямоугольника и сделав зигзагообразный узор на одной из длинных сторон каждого прямоугольника. Завершите своего аллигатора, вырезав белые круги вместо глаз, добавив зрачки черным маркером и приклеив по одному с обеих сторон головы аллигатора. Наконец, напишите «больше чем» с одной стороны и «меньше чем» с другой.Завершите задание, раздайте своих аллигаторов ученикам и разрешите классу использовать их при работе в небольших группах или за доской. «Это дает им возможность потрогать и манипулировать», — говорит Якобсон.
Супер симметрия
Прислал: Ханна Маззуто, учитель рисования, Центральный школьный округ Вест-Вэлли, Нью-Йорк. Блогер в Art. Бумага. Ножницы. Клей!
Материалы: Строительная бумага черного цвета (18 x 18 дюймов) и разных цветов (5 x 5 дюймов), клей
Когда это использовать: В этом трехмерном художественном проекте оригами используется для обучения радиальной симметрии или симметрии вокруг центральной оси.
Указания: Начните с того, что попросите учащихся сложить фоновый лист пополам по горизонтали и вертикали, чтобы создать складки. Повторите по диагоналям. Эти линии сгиба, образующие восемь треугольников, служат ориентиром для создания симметричного дизайна. Затем научите студентов четырем простым складкам, которые традиционно используются в дизайнах оригами. (Мацзуто использовал излюбленные новичками, такие как дизайн воздушного змея.) Вооруженные новыми техниками, ученики выбирают цвета и типы складок, создают элементы, необходимые для их дизайна, и выстраивают их в радиально-симметричном узоре.Если после завершения дизайна вы разделите фоновый лист пополам в любом направлении, он должен быть идентичным с обеих сторон (включая цвета). Увеличьте активность, найдя примеры радиальной симметрии в природе.
Умноженный на Клее
Прислал: Эйми Фрезия, K – 6 art, Prairie View Elementary, Lee’s Summit, штат Миссури. Блогер в One Happy Art Teacher. (Оригинальная идея от бывшего учителя Мэри Франко.)
Материалы: Пауль Клее Однажды вышедший из серой ночи, миллиметровая бумага размером 1 дюйм, цветной картон, карандаши, ножницы, клей
Когда это использовать: Сыграйте в геометрический стиль художника Пауля Клее, чтобы закрепить факты умножения.
Как добраться: Покажите студентам картины Клее. Дайте им лист миллиметровой бумаги размером 1 дюйм и попросите их выбрать факт умножения, с которым они борются (например, 6 x 8 = 48). Студенты заполняют каждый квадрат числом или символом из своего уравнения, чтобы каждое число Символ / касается краев поля. В верхней строке начните уравнения до упора влево. Для каждой из следующих трех строк переместите уравнение на один квадрат вправо. Для последних трех строк переместите каждое уравнение на один квадрат назад. слева, чтобы создать тесселяцию перевода или мозаику.Заполните отрицательные поля в каждом поле цветом или рисунком, чтобы совпадали числа и символы. Затем вырежьте мозаику.
Фракция рыбы
Прислал: Эми Убеле Браун, K – 5 art, начальная школа Хеменуэй, Фрамингхэм, Массачусетс. Блогер художественного класса миссис Браун.
Материалы: Цветная бумага разных цветов, круги для обводки, ножницы, карандаши, клей
Когда это использовать: «Студенты изучают математику и дроби, а также навыки резки и композиции при проектировании своего подводного мира», — говорит Браун.
Указания: Раздайте материалы, прежде чем предлагать учащимся обвести и вырезать несколько кругов одинакового размера на бумаге разного цвета. Затем попросите учащихся сложить круги на части по своему выбору и вырезать те части, которые они складывают. (Например, сложив четверти, получится четыре треугольника.) Дети могут использовать эти части для создания подводной сцены. «Создавая сами фракции, они могут увидеть, как две половинки составляют единое целое», — говорит Браун.
