Прямая формула график: Линейная функция и ее график — ошкольное образовательное учреждение № 4 «Алёнушка»

2+cx+d\) выглядит, например, как $(3)$.

Факт 4.
$\bullet$ Функция корня – функция $f(x)=\sqrt x$.
$\bullet$ График функции $y=\sqrt x$:

$\bullet$ Заметим, что $y=\sqrt x$ определена при $x\geqslant 0$ и принимает значения $y\geqslant 0$.

Факт 5.
$\bullet$ Графиком функции $y=\sin x$ является синусоида

$\bullet$ Графиком функции $y=\cos x$ также является синусоида, но сдвинутая на $\frac{\pi}2$ единиц влево по оси $Ox$

$\bullet$ Обе функции $y=\sin x$ и $y=\cos x$ периодичны с периодом $2\pi$. Обе функции могут принимать значения $y\in [-1;1]$.
$\bullet$ Функция $y=\sin x$ – нечетная, функция $y=\cos x$ – четная.

Факт 6.
$\bullet$ График функции $y=\mathrm{tg} \,x$

Прямые $x=k\cdot \frac{\pi}2$, где $k$ – нечетное число, являются асимптотами графика (то есть график их не пересекает).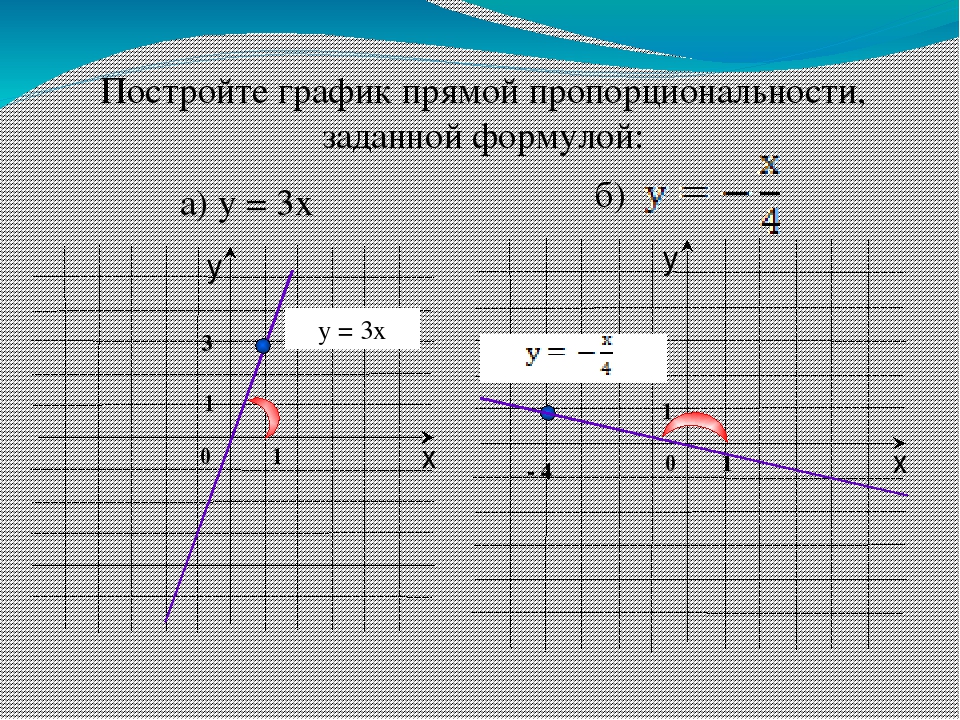 x\in (0;+\infty)\):

Ее график всегда проходит через точку $(0;1)$.

Факт 8.
$\bullet$ Логарифмическая функция $y=\log_ax$ при $a>1$ является возрастающей, ее область определения $x>0$, ее область значений $(-\infty;+\infty)$:

Ее график всегда проходит через точку $(1;0)$.

$\bullet$ Логарифмическая функция $y=\log_ax$ при $0<a<1$ является убывающей, ее область определения $x>0$, ее область значений $(-\infty;+\infty)$:

Ее график всегда проходит через точку $(1;0)$.

Содержание

Линейная функция — подготовка к ЕГЭ по Математике

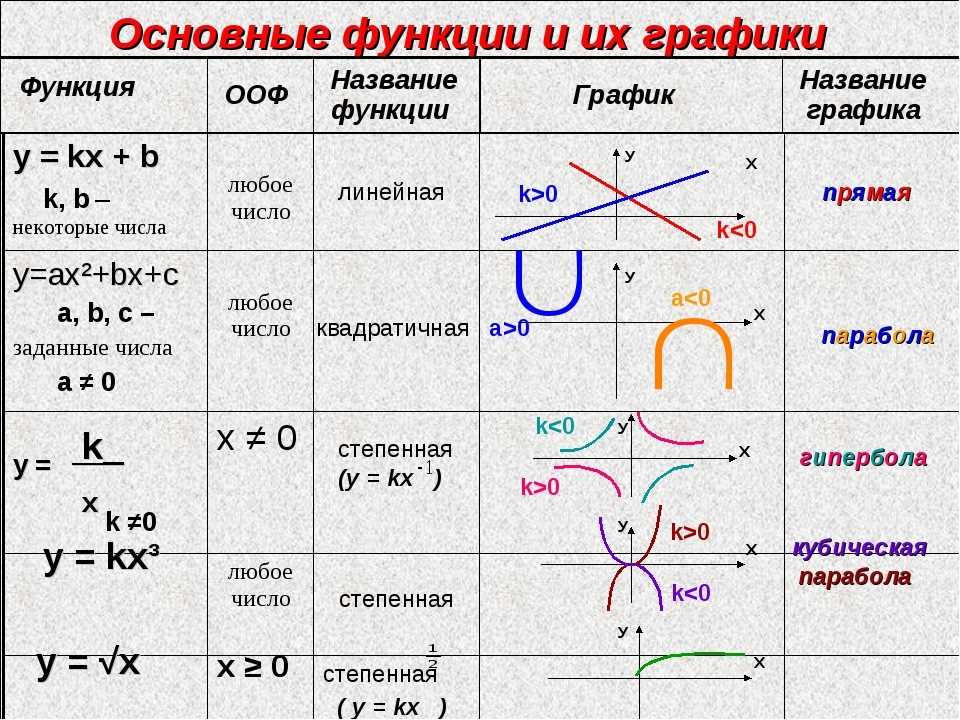
Линейная функция — функция вида График линейной функции — прямая.

Для построения графика линейной функции достаточно двух точек — потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.

Угловой коэффициент прямой

Величина k в формуле линейной функции называется угловым коэффициентом прямой

Если , линейная функция возрастает. Чем больше х, тем больше у, то есть график идет вправо и вверх.

Если , линейная функция убывает. Чем больше х, тем меньше у, то есть график идет вправо и вниз.

Угловой коэффициент k равен тангенсу угла наклона графика линейной функции к положительному направлению оси Х.

Пусть Чем больше k, тем круче вверх идет график функции.

А что же будет, если ? Мы получим горизонтальную прямую На рисунке показан график функции

Заметим, что прямая (также изображенная на рисунке) не является графиком функции в нашем обычном, школьном смысле слова. В самом деле — мы помним, что функция — это соответствие между двумя множествами, причем каждому элементу множества Х соответствует один и только один элемент множества Y.

Для прямой это не выполняется: значению соответствует бесконечно много значений у.

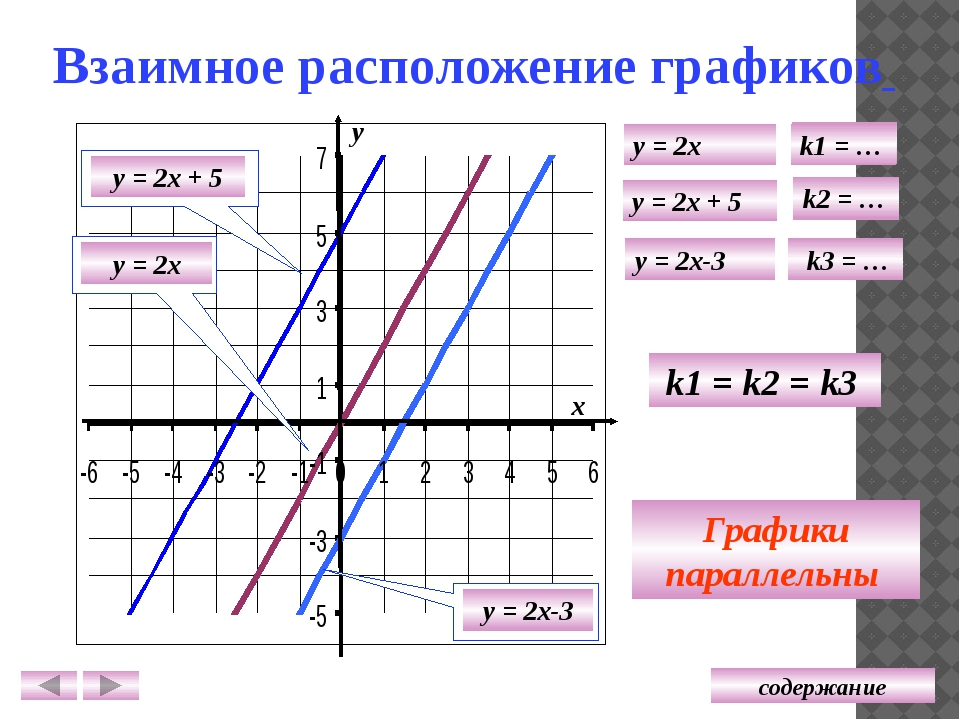
Если прямые параллельны.

При этом, чем больше b, тем выше расположен на координатной плоскости график функции.

Например, прямые и параллельны. Их угловые коэффициенты равны.

Если прямые перпендикулярны. Например, прямые и пересекаются под прямым углом. Произведение их угловых коэффициентов равно — 1.

Построение графика линейной функции

График линейной функции построить легко — достаточно двух точек.

Оказывается, что привычный нам вид уравнения прямой — не единственно возможный.

Уравнение прямой можно записать также в виде

Построим, например, прямую, заданную уравнением

При получаем, что

Значит, наша прямая проходит через точки и

Выразив у из уравнения , получим уравнение прямой вида

Если вы поступаете в вуз на специальность, связанную с математикой, — уже на первом курсе вы познакомитесь и с другими видами уравнения прямой.

Зачем изучать линейную функцию?

Дело в том, что многие зависимости в природе и технике описываются формулой виде

Например, закон Ома для участка цепи: Напряжение U прямо пропорционально силе тока I.

Формула для равномерного прямолинейного движения: . Пройденное расстояние S прямо пропорционально времени.

Закон теплового расширения , который вам встретится в одной из задач под номером 10 варианта Профильного ЕГЭ по математике — тоже линейная функция. И таких примеров можно привести очень много.

Обратите внимание, что в формулу линейной функции аргумент х входит в первой степени. Мы просто умножаем х на угловой коэффициент k и прибавляем b.

Если в формулу функции входит аргумент в любой другой степени — например, в квадрате или в кубе, если мы делим на х, если в формуле присутствует или , или показательные или логарифмические выражения, зависящие от х, — график функции уже не будет прямой линией.

3.Линейная функция вида y = kx + b

Линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.

В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b).

Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью.

Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат.

Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.

Свойства линейной функции:

1) Область определения линейной функции есть вся вещественная ось;

2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось. Если k = 0, то область значений линейной функции состоит из числа b;

3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.

a) b ≠ 0, k = 0, следовательно, y = b – четная;

b) b = 0, k ≠ 0, следовательно y = kx – нечетная;

c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;

d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.

4) Свойством периодичности линейная функция не обладает;

5) Точки пересечения с осями координат:

Ox: y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс.

Oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.

Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.

6) Промежутки знакопостоянства зависят от коэффициента k.

a) k > 0; kx + b > 0, kx > -b, x > -b/k.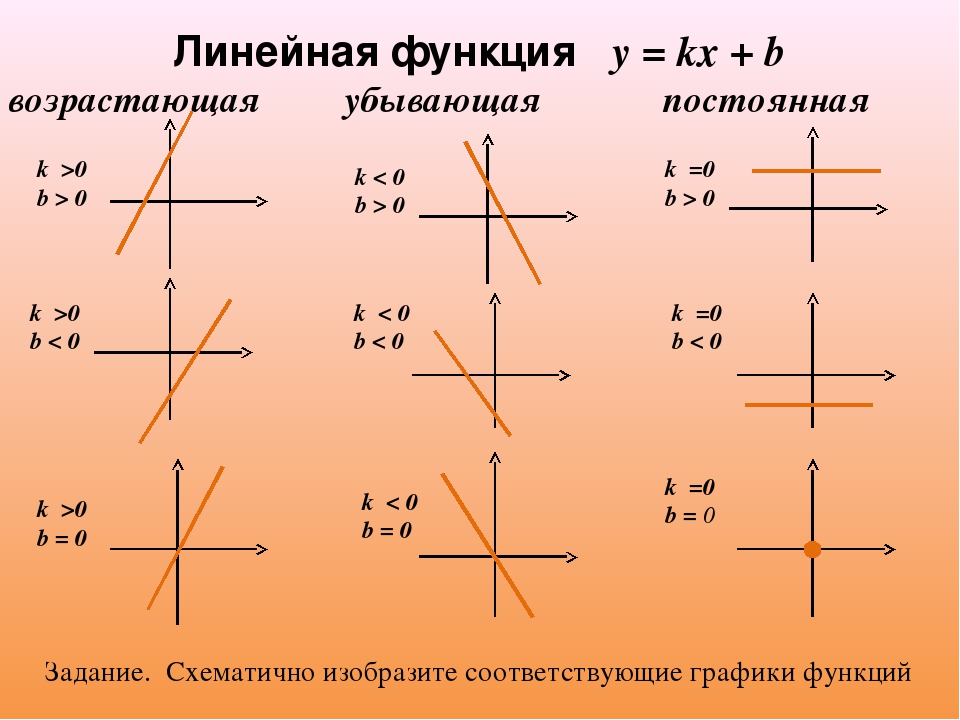

y = kx + b – положительна при x из (-b/k; +∞),

y = kx + b – отрицательна при x из (-∞; -b/k).

b) k < 0; kx + b < 0, kx < -b, x < -b/k.

y = kx + b – положительна при x из (-∞; -b/k),

y = kx + b – отрицательна при x из (-b/k; +∞).

c) k = 0, b > 0; y = kx + b положительна на всей области определения,

k = 0, b < 0; y = kx + b отрицательна на всей области определения.

7) Промежутки монотонности линейной функции зависят от коэффициента k.

k > 0, следовательно y = kx + b возрастает на всей области определения,

k < 0, следовательно y = kx + b убывает на всей области определения.

8) Графиком линейной функции является прямая. Для построения прямой
достаточно знать две точки. Положение прямой на координатной плоскости
зависит от значений коэффициентов k и b. Ниже приведена таблица, которая наглядно это иллюстрирует.

Прямая пропорциональность y = kx свойства и график функции

Определение прямой пропорциональности

Если машина движется со скоростью 50 км/ч, пройденное расстояние (в километрах) в зависимости от времени (в часах) s = 50t. Время мы определяем как $t\geq0$. Но механика позволяет нам рассчитать не только будущее положение тела, но и прошлое, подставив в формулу $t \lt 0$ и запросто «прокрутив» время назад. Поэтому в общем случае, если движение было и остаётся постоянным, мы получаем:

$${\left\{ \begin{array}{c} — \infty \lt t\lt + \infty \\ s = 50t \end{array} \right.}$$

Можно представить себе не только отрицательное время («поход в прошлое»). Ещё проще ввести отрицательные координаты: направо идём – координата растёт, становится положительной, поворачиваем налево – уменьшается, становится отрицательной.

В задачах, связанных с экономикой, величины также могут уходить в «плюс» и «минус»: покупки/продажи, кредиты/депозиты, доходы/затраты, прибыли/убытки . Часто эти величины изменяются на какую-то постоянную сумму с течением времени.

Если обобщить формулы, описывающие подобные зависимости, то получаем:

$${\left\{ \begin{array}{c}- \infty \lt x \lt + \infty — аргумент, \quad любое \quad действительное \quad число \\ k = const ≠ 0 \quad — параметр, \quad константа \\ y = kx \quad — функция\end{array} \right.}$$

Функция такого вида называется прямой пропорциональностью.

Если $k \gt 0$, то чем больше x, тем больше y – функция возрастает.

Если $k \lt 0$, то чем больше x, тем больше y – функция убывает.

График прямой пропорциональности

Графиком прямой пропорциональности является прямая, проходящая через начало координат.

Согласно аксиоме планиметрии, через любые две точки можно провести прямую и притом только одну. Значит, положение прямой на плоскости полностью определяется двумя точками . Получаем:

Алгоритм построения графика прямой пропорциональности

Выбрать произвольное значение аргумента $x_*\neq 0$
Вычислить соответствующее значение функции $y_*=kx_*$
Отметить на координатной плоскости точку $(x_*,y_* )$
Провести прямую через начало координат (0;0) и точку $(x_*,y_* )$

Эта прямая – график прямой пропорциональности y=kx.

Например: построим график функции y = 2x

Примеры

Пример 1. Постройте графики прямых пропорциональностей.

Укажите, возрастает или убывает функция.

$k = 1 \gt 0$ – функция возрастает

$k = 3 \gt 0$ – функция возрастает

$k = \frac{1}{3} \gt 0$ – функция возрастает

$k = -1 \lt 0$ – функция убывает

$k = -2 \lt 0$ – функция убывает

е) $y = — \frac{1}{2} x$

$k = -\frac{1}{2} \lt 0$ – функция убывает

Пример 2. Известно, что график прямой пропорциональности проходит через точку A(5;22). Проходит ли этот график через точки B(7;32,4)и C(9;39,6)?

Точка A определяет коэффициент пропорциональности:

$$ k= \frac{y_A}{x_A} = \frac{22}{5} = 4,4 $$

При $x = 7:y = 4,4 \cdot 7 = 30,8 \neq 32,4 \Rightarrow$ B не принадлежит графику.

При $x = 9:y = 4,4 \cdot 9 = 39,6 \Rightarrow C$ принадлежит графику.

Пример 3. Является ли прямой пропорциональностью функция, проходящая через точки:

а) A(1,5;2,75) и B(12;22)

Найдём коэффициенты пропорциональностей для каждой из точек:

$$ k_A = \frac{y_A}{x_A} = \frac{2,75}{1,5} \stackrel{\text{ × 4}}{=} \frac{11}{6} = \frac{15}{6} $$

$$ k_B = \frac{y_B}{x_B} = \frac{22}{12} = \frac{11}{6} = \frac{15}{6} $$

$k_A = k_B \Rightarrow$ прямая AB $y=1 \frac{5}{6} x$ является прямой пропорциональностью.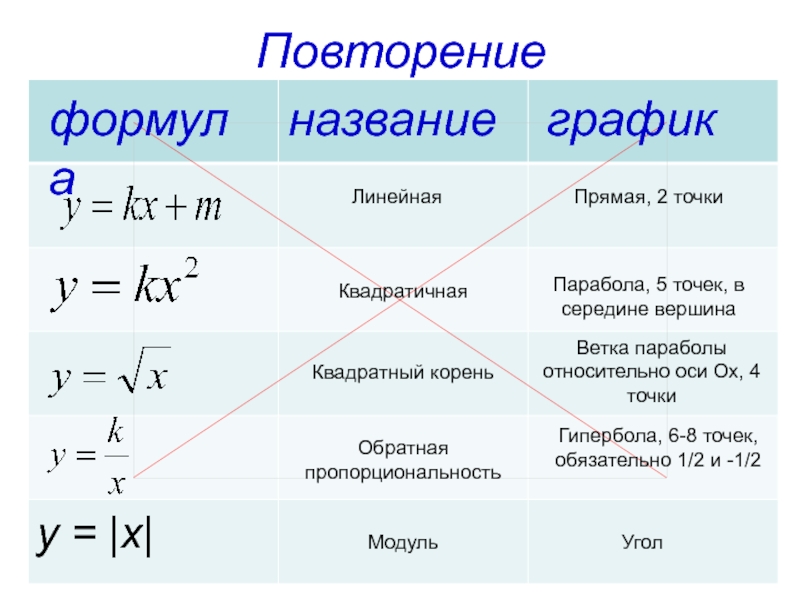

б) A(3;4,5) и B(5;8)

Найдём коэффициенты пропорциональностей для каждой из точек:

$$ k_A = \frac{y_A}{x_A} = \frac{2,75}{1,5} = \frac{4,5}{3} = 1,5 $$

$$ k_B = \frac{y_B}{x_B} = \frac{8}{5} = 1,6 $$

$k_A \neq k_B \Rightarrow$ прямая AB не является прямой пропорциональностью.

Функция прямой

Линейная функция – это функция вида

f(x)=k∙x+b

или

y(x)=k∙x+b,

где

x-аргумент (независимая переменная),

y- функция (зависимая переменная),

k и b- некоторые постоянные числа

k=const

b=const

Графиком линейной функции является прямая.

Для построения графика достаточно двух точек, т.к. через две точки можно провести прямую и притом только одну.

Если k˃0, то график расположен в 1-й и 3-й координатных четвертях. Если k˂0, то график расположен в 2-й и 4-й координатных четвертях.

Число k называют угловым коэффициентом прямой графика функции y(x)=kx+b. Если k˃0, то угол наклона прямой y(x)= kx+b к положительному направлению Ох — острый; если k˂0, то этот угол- тупой.

Коэффициент b показывает точку пересечения графика с осью ОУ (0; b).

a) k≠0; b=0,

тогда

y(x)=k∙x+0,

или

y(x)=k∙x

y(x)=k∙x— частный случай типичной функции носит название прямая пропорциональность. Графиком является прямая, проходящая через начало координат, поэтому для построения этого графика достаточно одной точки.

График линейной функции

y=kx

Где коэффициент k = 3, следовательно

y=3x

График функции будет возрастать и иметь острый угол с осью Ох т. к. коэффициент k имеет знак плюс.

ООФ линейной функции

X∈R

D(f)=R

ОЗФ линейной функции

Y∈R

E(f)=R

Кроме случая, где

Y(x)=b

Так же линейная функция вида

y=kx+b

Является функцией общего вида.

Б) Если k=0; b≠0,

тогда

y(x)=0∙x+b,

или

y(x)=b

В этом случае графиком является прямая параллельная оси Ох и проходящая через точку (0;b).

В) Если k≠0; b≠0, то линейная функция имеет вид y(x)=k∙x+b.

Пример 1. Построить график функции y(x)= -2x+5

Пример 2. Найдём нули функции у=3х+1, у=0;

3х+1=0;

– нули функции.

Ответ: или (;0)

Пример 3. Определить значение функции y=-x+3 для x=1 и x=-1

Решение:

y(1)=-1+3=2

y(-1)=-(-1)+3=1+3=4

Ответ: y_1=2; y_2=4.

Пример 4. Определить координаты их точки пересечения или доказать, что графики не пересекаются. Пусть даны функции y₁=10∙x-8 и y₂=-3∙x+5.

Если графики функций пересекаются, то значение функций в этой точке равны

x₁=x₂

y₁=y₂

т.е.

10х-8=-3х+5;

13х=13;

x=1

Подставим х=1, то y₁ (1)=10∙1-8=2.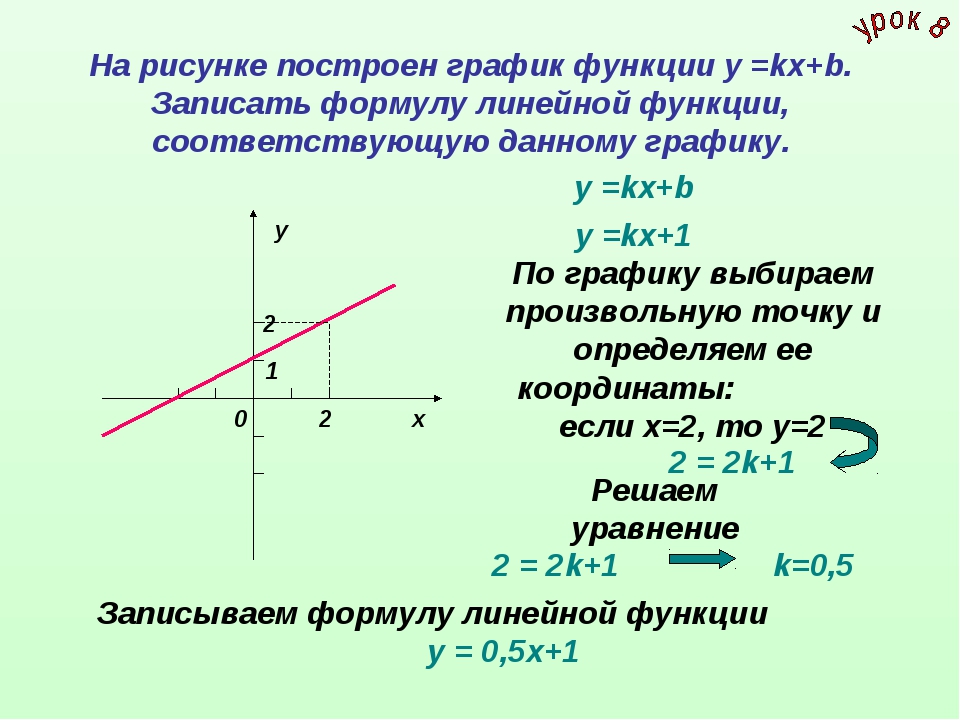

Замечание. Подставить полученное значение аргумента можно и в функцию y₂=-3∙x+5, тогда получим тот же самый ответ y₂ (1)=-3∙1+5=2.

y=2- ордината точки пересечения.

(1;2)- точка пересечения графиков функций у=10х-8 и у=-3х+5.

Ответ: (1;2)

Пример 5.

Построить графики функций y₁(x)= x+3 и y₂(x)= x-1.

Решение:

Можно заметить, что коэффициент k=1 для обеих функций.

Из выше сказанного следует, что если коэффициенты линейной функции равны, то их графики в системе координат расположены параллельно.

Пример 6.

Построим два графика функции.

Первый график имеет формулу

y₁= -2x+4

Второй график имеет формулу

у₂=0,5х+4

В данном случае перед нами график двух прямых, пересекающихся в точке (0;4).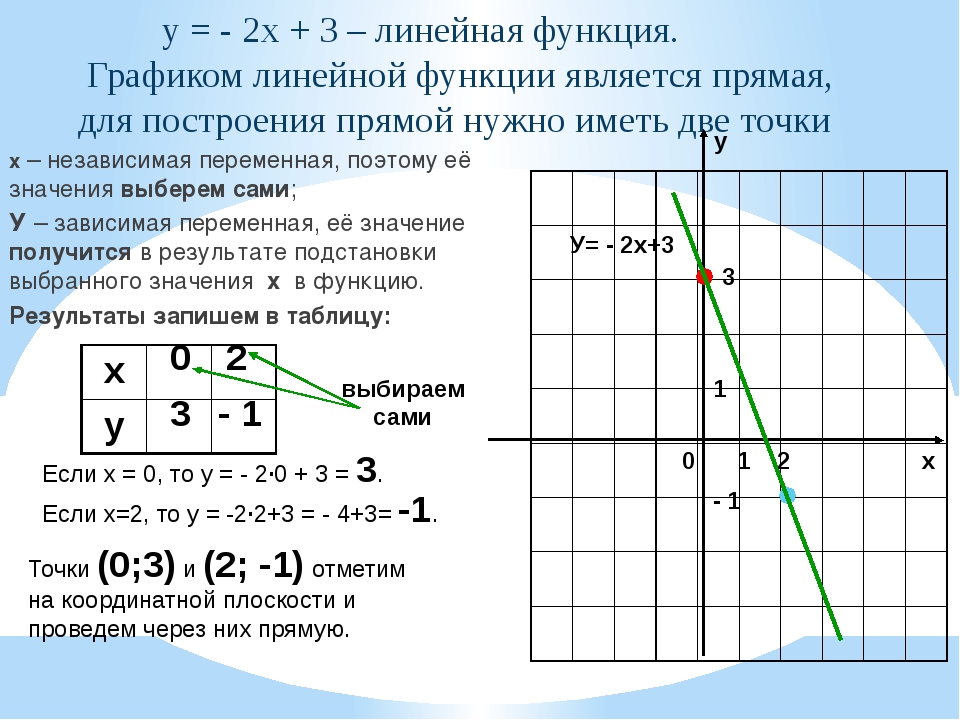 Это значит, что коэффициент b, отвечающий за высоту подъёма графика над осью Ох, если х=0. Значит мы может полагать, что коэффициент bу обоих графиков равен 4.

Автор статьи: Глотов Василий Максимович

Редакторы: Агеева Любовь Александровна, Гаврилина Анна Викторовна

Внеклассный урок — Линейная функция. Прямая пропорциональность. Обратная пропорциональность

Линейная функция. Прямая пропорциональность. Обратная пропорциональность.

Линейная функция

Линейная функция – это функция, которую можно задать формулой y = kx + b,

где x – независимая переменная, k и b – некоторые числа.

Графиком линейной функции является прямая.

Число k называют угловым коэффициентом прямой – графика функции y = kx + b.

Если k > 0, то угол наклона прямой y = kx + b к оси х острый; если k < 0, то этот угол тупой.

Если угловые коэффициенты прямых, являющихся графиками двух линейных функций, различны, то эти прямые пересекаются. А если угловые коэффициенты одинаковы, то прямые параллельны.

График функции y = kx + b, где k ≠ 0, есть прямая, параллельная прямой y = kx.

Прямая пропорциональность.

Прямой пропорциональностью называется функция, которую можно задать формулой y = kx, где х – независимая переменная, k – не равное нулю число. Число k называют коэффициентом прямой пропорциональности.

График прямой пропорциональности представляет собой прямую, проходящую через начало координат (см.рисунок).

Прямая пропорциональность является частным случаем линейной функции.

Свойства функции y = kx:

1. Область определения функции — множество всех действительных чисел.

2. Это нечетная функция.

3. Переменные изменяются прямо пропорционально на всей числовой прямой: при возрастании аргумента функция пропорционально возрастает, при убывании аргумента функция пропорционально убывает.

Обратная пропорциональность

Обратной пропорциональностью называется функция, которую можно задать формулой:

k
y = —
x

где x – независимая переменная, а k – не равное нулю число.

Графиком обратной пропорциональности является кривая, которую называют гиперболой (см.рисунок).

Для кривой, которая является графиком этой функции, оси x и y выступают в роли асимптот. Асимптота – это прямая, к которой приближаются точки кривой по мере их удаления в бесконечность.

k
Свойства функции y = —:
x

1. Область определения функции — множество всех действительных чисел, кроме нуля.

2. Это нечетная функция.

3. При возрастании аргумента функция пропорционально убывает, при убывании аргумента функция пропорционально возрастает.

Графики прямой, параболы, гиперболы, с модулем

Пошаговое построение графиков.

«Навешивание» модулей на прямые, параболы, гиперболы.

Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.

Для понимания друг друга введу немного «обзываний» системы координат:

Для начала построим график прямой y = 2x − 1.

Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.

Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1

Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:

А если теперь добавить модуль y = |2x − 1|.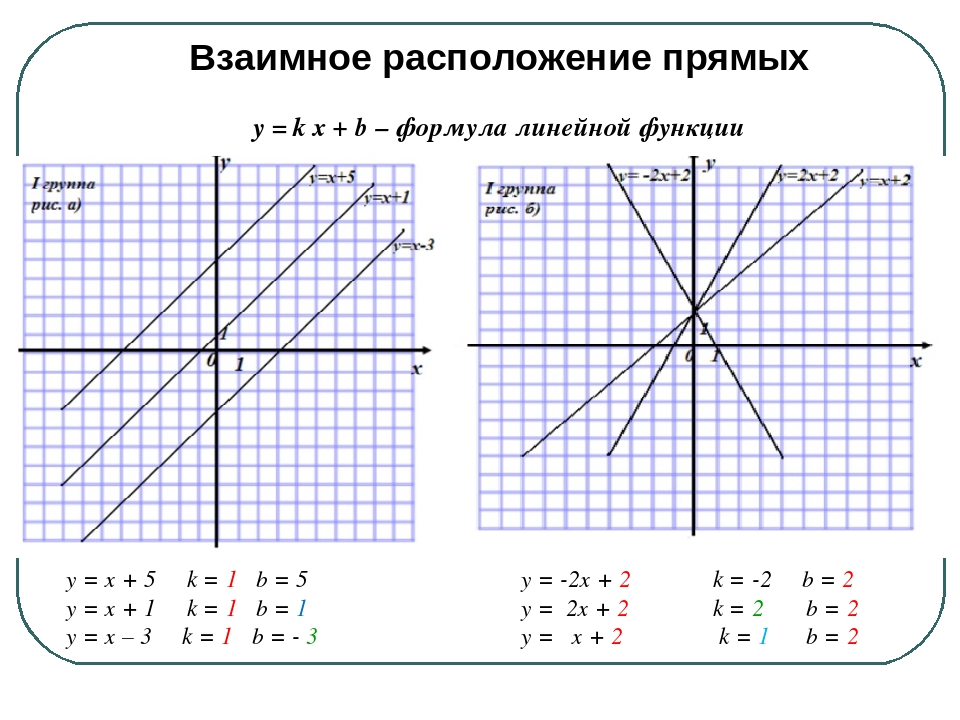

Модуль — это всегда положительное значение, получается, что «y» должен быть всегда положительным.

Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).

Получается такая зеленая «галочка».

Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?

Одна строчка рассуждений и рисуем:

Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.

Здесь отражаем относительно оси «y». Такая же галочка, только теперь через другую ось.

Смертельный номер: y = |2|x| − 1|.

Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.

В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!

А после этого отражаем относительно оси «y» то, что мы получили справа налево:

Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.

Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x₁ = 1 и x₂ = -2.

Можно найти вершину у параболы и взять пару точек для точного построения.

А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.

При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:

А дальше что мелочиться: рассмотри сразу остальные графики с модулем!

Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.

При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!

Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.

А теперь сразу комбо:

Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.

Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.

Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.

Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.

y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:

А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:

А что будет, если мы добавим в знаменателе «−1»? График сдвинется вправо на единицу.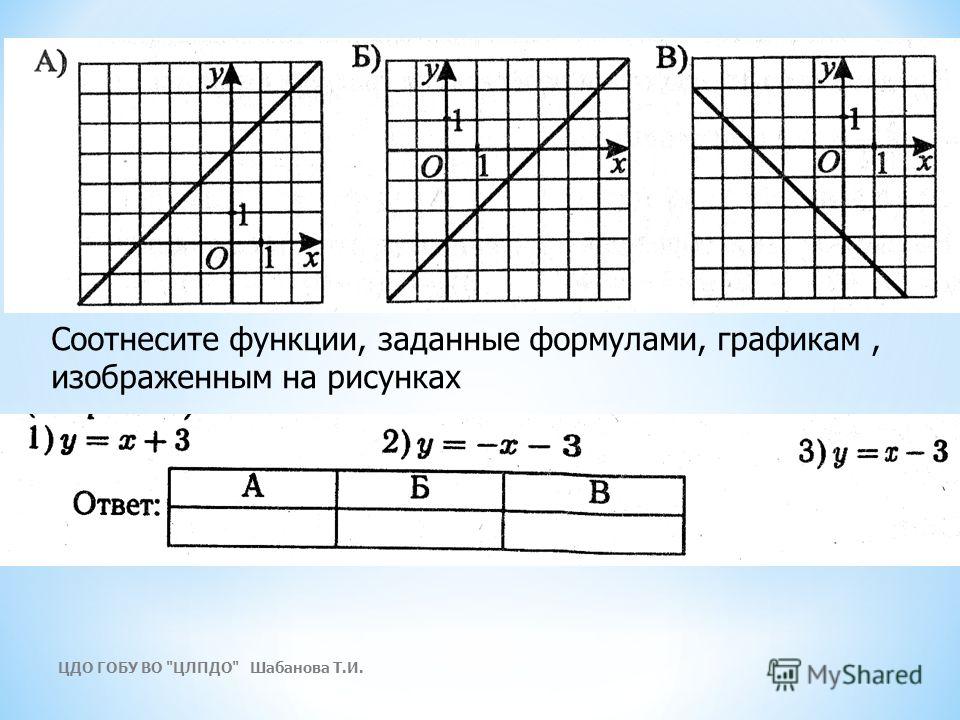

А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!

Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!

Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.

Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.

Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.

Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.

Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.

Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.

Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:

И построить график, разбив его на кусочно-заданные функции.

Например для прямой:

Для параболы с одним модулем будет два кусочно-заданных графика:

C двумя модулями кусочно-заданных графиков будет четыре:

Таким способом, медленно и кропотливо можно построить любой график!

Выводы:

Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.
Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:

Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
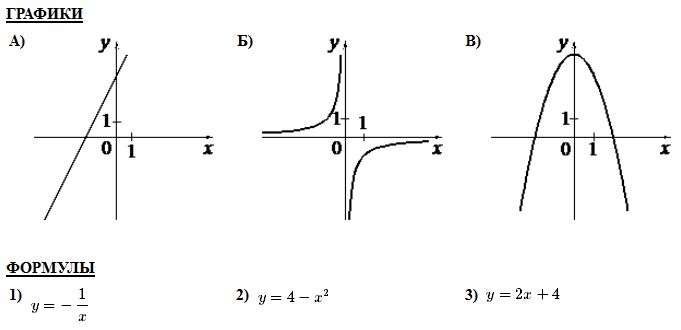
Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.

Будь в курсе новых статеек, видео и легкого математического юмора.

Прямая вариация — ChiliMath

Концепция прямого изменения резюмируется приведенным ниже уравнением.

Мы говорим, что y напрямую зависит от x, если y выражается как произведение некоторого постоянного числа k и x.

Случаи прямого изменения

Однако значение k не может равняться нулю , т.е. k \ ne 0.

Случай 1: k> 0 (k положительно)

Если x увеличивается, значение y также увеличивается, или если x уменьшается, значение y также уменьшается.

Случай 2: k

<0 (k отрицательно)

Если x увеличивается, значение y уменьшается, или если x уменьшается, значение y увеличивается.

Если мы изолировать k с одной стороны, это показывает, что k — постоянное отношение между y и x. Другими словами, деление y на x всегда дает постоянный результат.

k также известно как постоянная вариации или константа пропорциональности.

Примеры прямого изменения

Пример 1: Укажите, изменяется ли y напрямую с x в таблице ниже.Если да, напишите уравнение, чтобы представить прямую вариацию.

Решение :

Чтобы показать, что y напрямую зависит от x, нам нужно проверить, всегда ли деление y на x дает нам одно и то же значение.

Поскольку при делении y на x мы всегда получали одно и то же значение 2, мы можем утверждать, что y напрямую зависит от x. Фактически, это постоянное число является нашим k = 2.

Чтобы написать уравнение прямой вариации, заменим букву k на цифру 2 в уравнении y = kx.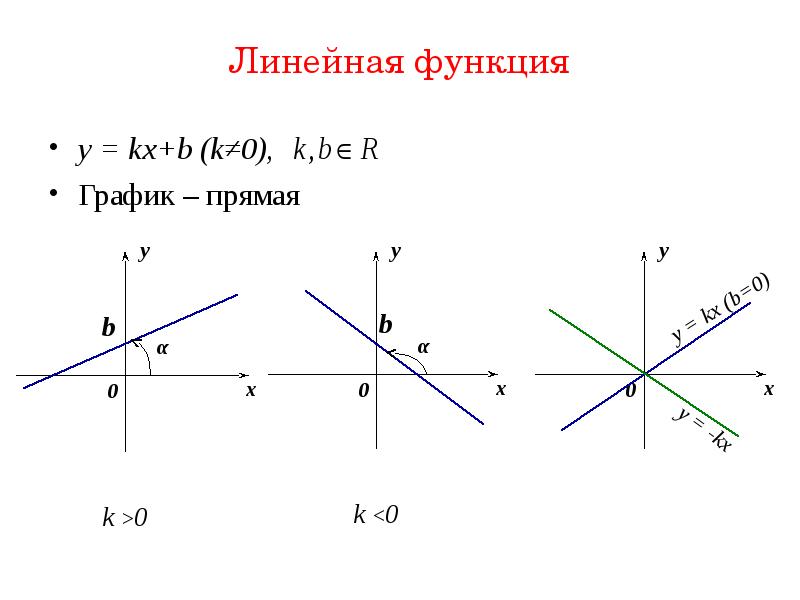

Когда уравнение, представляющее прямую вариацию, строится на декартовой плоскости, это всегда прямая линия , проходящая через начало координат.

Думайте об этом как о форме пересечения наклона линии, записанной как

y = mx + b , где b = 0

Вот график найденного выше уравнения.

Пример 2: Укажите, изменяется ли y напрямую с x в таблице ниже. Если да, напишите уравнение, чтобы представить прямую вариацию.

Решение :

Разделите каждое значение y на соответствующее значение x.

Частное y и x всегда равно k = — \, 0,25. Это означает, что y напрямую зависит от x. Вот уравнение, представляющее его прямую вариацию.

Вот график. Отрицательное значение k означает, что линия имеет отрицательный наклон. Как видите, линия убывает слева направо.

Кроме того, поскольку k отрицательно , мы видим, что, когда x увеличивается, значение y уменьшается.

Пример 3: Сообщите, изменяется ли y напрямую с x в таблице. Если да, напишите уравнение, показывающее прямое изменение.

Решение :

Найдите отношение y и x и посмотрите, сможем ли мы получить общий ответ, который мы назовем константой k.

Похоже, значение k в третьей строке отличается от остальных. Чтобы это была прямая вариация, все они должны иметь одинаковое значение k.

Таблица не представляет прямого изменения, поэтому мы не можем написать уравнение для прямого изменения.

Пример 4: При условии, что y напрямую зависит от x. Если x = 12, то y = 8.

Напишите уравнение прямого изменения, которое связывает x и y.

Каково значение y, когда x = — \, 9?

a) Напишите уравнение прямого изменения, которое связывает x и y.

Поскольку y напрямую зависит от x, я бы сразу записал формулу, чтобы увидеть, что происходит.

Нам дана информация, что когда x = 12, тогда y = 8.Подставьте значения x и y в формулу и решите k.

Замените «k» в формуле значением, решенным выше, чтобы получить уравнение прямого изменения, которое связывает x и y.

б) Каково значение y при x = — \, 9?

Чтобы найти y, подставьте x = — \, 9 в уравнение, найденное в части a).

Пример 5: Если y напрямую зависит от x, найдите недостающее значение x в

Решение :

Мы будем использовать первую точку, чтобы найти константу пропорциональности k и составить уравнение y = kx.

Подставьте значения x и y, чтобы найти k.

Уравнение прямой пропорциональности, связывающее x и y, равно…

Теперь мы можем найти x в (x, — \, 18), подставив y = — \, 18.

Пример 6: Длина окружности (C) напрямую зависит от ее диаметра. Если круг диаметром 31,4 дюйма имеет радиус 5 дюймов,

Напишите уравнение прямого изменения, которое связывает длину окружности и диаметр круга.

Каков диаметр окружности с радиусом 7 дюймов?

a) Напишите уравнение прямого изменения, которое связывает длину и диаметр окружности.

Нам не нужно постоянно использовать формулу y = k \, x. Но мы можем использовать его для создания аналогичной настройки в зависимости от того, что задает проблема.

Задача говорит нам, что длина окружности напрямую зависит от ее диаметра. Вместо этого мы можем написать следующее уравнение прямой пропорциональности.

Диаметр не указан, но радиус есть. Поскольку радиус задан как 5 дюймов, это означает, что мы можем найти диаметр, потому что он равен удвоенной длине радиуса. Это дает нам диаметр 10 дюймов.

Уравнение прямой пропорциональности, которое связывает окружность и диаметр, показано ниже. Обратите внимание, k заменяется числовым значением 3.14.

б) Каков диаметр окружности с радиусом 7 дюймов?

Поскольку уравнение требует диаметра, а не радиуса, нам нужно сначала преобразовать значение радиуса в диаметр. Помните, что диаметр в два раза больше радиуса, поэтому 7 дюймов радиуса равны 14 дюймам в диаметре.

Теперь мы подставляем d = 14 в формулу, чтобы получить ответ для длины окружности.

Возможно, вас заинтересует:

Обратная вариация

Прямое изменение

Прямая вариация

описывает простые отношения между двумя

переменные

. Мы говорим

y

напрямую меняется

с участием

Икс

(или же

в виде

Икс

, в некоторых учебниках), если:

знак равно

Икс

для некоторых

постоянный

, называется

постоянная вариации

или же

константа пропорциональности

.(Некоторые учебники описывают прямое изменение, говоря »

изменяется прямо как

Икс

«,»

изменяется пропорционально как

Икс

«, или же »

прямо пропорциональна

Икс

. «)

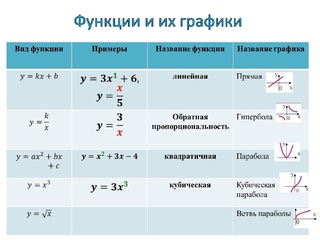Это означает, что как

Икс

увеличивается,

увеличивается и как

Икс

уменьшается,

уменьшается — и что

соотношение

между ними всегда остается неизменным.

График уравнения прямого изменения представляет собой прямую линию, проходящую через начало координат.

Уравнение прямого изменения

для

разные значения

Пример 1:

Учитывая, что

изменяется прямо как

Икс

, с постоянной вариации

знак равно

, найти

когда

Икс

знак равно

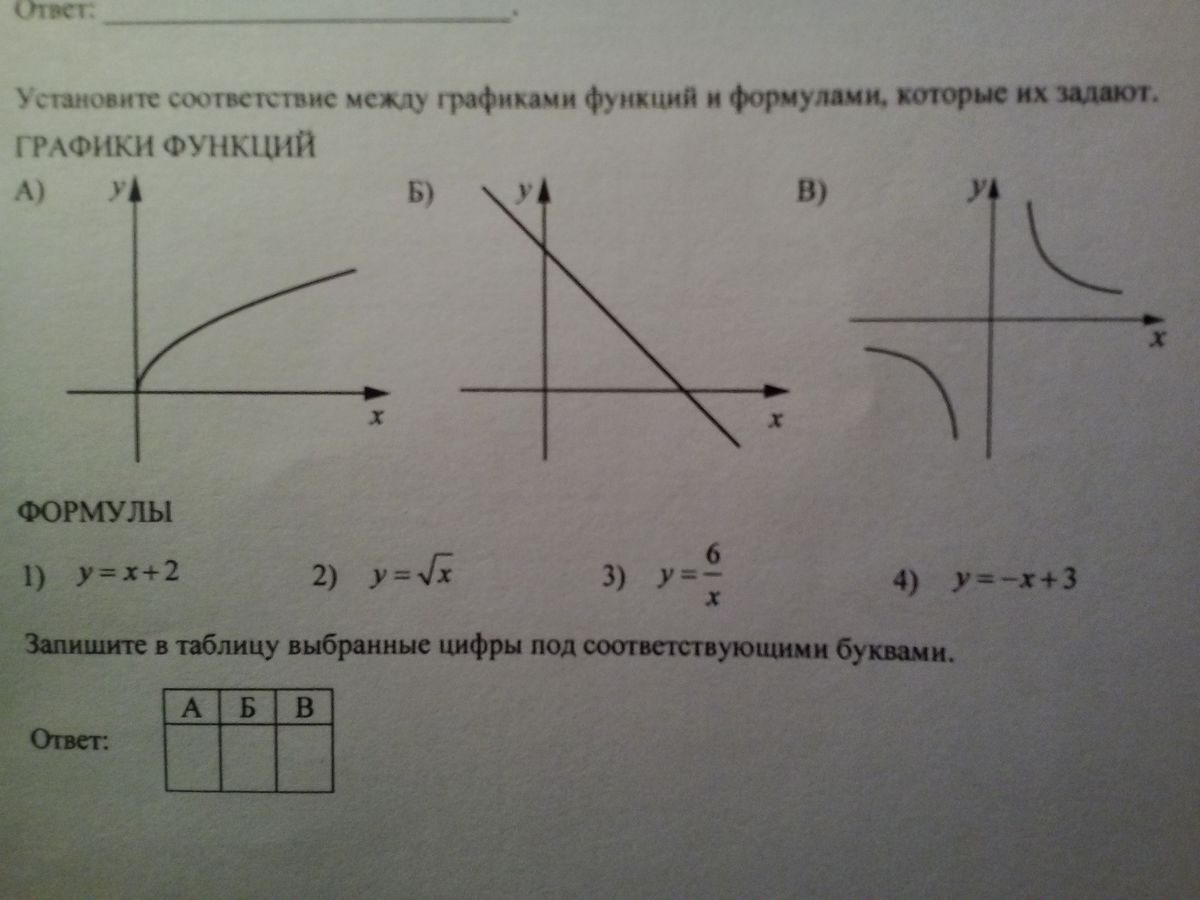
Напишите уравнение прямой вариации.

знак равно

Икс

Заменить данный

Икс

значение.

знак равно

⋅

знак равно

Пример 2:

Учитывая, что

изменяется прямо как

Икс

, найти постоянную вариации, если

знак равно

а также

Икс

знак равно

Напишите уравнение прямой вариации.

знак равно

Икс

Заменить данный

Икс

а также

значения и решить для

знак равно

⋅

знак равно

Пример 3:

Предполагать

изменяется прямо как

Икс

, а также

знак равно

когда

Икс

знак равно

. В чем ценность

когда

Икс

знак равно

100

Напишите уравнение прямой вариации.

знак равно

Икс

Заменить данный

Икс

а также

значения и решить для

знак равно

⋅

знак равно

Уравнение

знак равно

Икс

.Теперь замените

Икс

знак равно

100

и найти

знак равно

⋅

100

знак равно

500

Прямая вариация | Колледж алгебры

Результаты обучения

Решить прямую вариационную задачу
Используйте постоянную вариации для описания взаимосвязи между двумя переменными

Компания по производству подержанных автомобилей только что предложила своему лучшему кандидату, Николь, должность в отделе продаж. Позиция предлагает 16% комиссионных от ее продаж. Ее заработок зависит от объема продаж. Например, если она продаст автомобиль за 4600 долларов, она заработает 736 долларов. Она хочет оценить предложение, но не знает, как это сделать. В этом разделе мы рассмотрим отношения, подобные этой, между доходами, продажами и ставкой комиссии.

В приведенном выше примере заработок Николь можно определить, умножив объем продаж на ее комиссионные. Формула [latex] e = 0,16s [/ latex] говорит нам, что ее заработок, [latex] e [/ latex], получен от произведения 0.16, ее комиссия и продажная цена транспортного средства, [латекс] [/ латекс]. Если мы создадим таблицу, мы увидим, что по мере увеличения продажной цены увеличивается и прибыль, что должно быть интуитивно понятным.

[latex] s [/ latex], отпускные цены	[латекс] e = 0,16s [/ латекс]	Интерпретация
4 600 долл. США	[латекс] e = 0,16 (4600) = 736 [/ латекс]	Продажа автомобиля за 4600 долларов приносит 736 долларов прибыли.
9 200 долл. США	[латекс] е = 0.16 (9 200) = 1,472 [/ латекс] 90 204	Продажа автомобиля за 9 200 долларов приносит прибыль 1472 доллара.
18 400 долл. США	[латекс] e = 0,16 (18 400) = 2 944 [/ латекс]	Продажа автомобиля за 18 400 долларов приносит прибыль 2944 доллара.

Обратите внимание, что прибыль кратна продажам. По мере увеличения продаж прибыль предсказуемо увеличивается. Удвойте продажи автомобиля с 4600 до 9 200 долларов, и мы удвоим прибыль с 736 до 1472 долларов. По мере увеличения входа выход увеличивается как кратное входное.{n}} [/ latex], где [latex] k [/ latex] называется константой вариации , которая помогает определить взаимосвязь между переменными.

Практическое руководство. Учитывая описание задачи прямого изменения, решите неизвестное.

Определите вход, [latex] x [/ latex], и выход, [latex] y [/ latex].

{3} [/ latex].{3} \\ [1 мм] & = 675 \ hfill \ end {align} [/ latex]

Анализ решения

График этого уравнения представляет собой простую кубическую форму, как показано ниже.

Вопросы и ответы

Графики всех уравнений прямой вариации выглядят как Пример 1?

Нет. Уравнения прямой вариации являются степенными функциями — они могут быть линейными, квадратичными, кубическими, квартическими, радикальными и т. Д. Но все графики проходят через [latex] (0, 0) [/ latex] .

Попробуй

Количество [латекс] y [/ латекс] напрямую зависит от площади [латекса] y [/ латекса]. Если [latex] y = 24 [/ latex], когда [latex] x = 3 [/ latex], найдите [latex] y [/ latex], когда [latex] x [/ latex] равно 4.

Показать решение

[латекс] \ dfrac {128} {3} [/ латекс]

Посмотрите это видео, чтобы получить быстрый урок по прямым вариациям. Вы увидите больше отработанных примеров.

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

Прямая вариация — Бесплатная справка по математике

Когда две переменные связаны таким образом, что соотношение их значений всегда остается неизменным, говорят, что эти две переменные находятся в прямом изменении.

Проще говоря, это означает, что если A всегда вдвое больше, чем B, то они напрямую изменяют . Если галлон молока стоит 3 доллара, а я покупаю 1 галлон, общая стоимость составляет 3 доллара. Если я куплю 10 галлонов, цена составит 30 долларов.В этом примере общая стоимость молока и количество купленных галлонов могут быть напрямую изменены — отношение стоимости к количеству галлонов всегда равно 3.

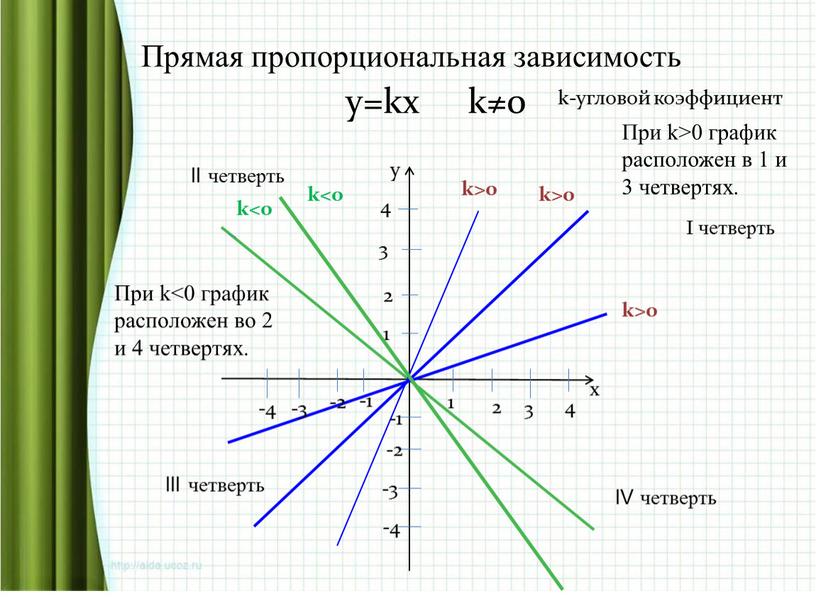
Чтобы быть более «геометрическим», если y изменяется прямо как x, то график всех точек, описывающих эту взаимосвязь, представляет собой линию, проходящую через начало координат (0, 0), наклон которой называется постоянной вариации. Это потому, что каждая из переменных является постоянным кратным другой, как на графике, показанном ниже:

Ключевые понятия прямого изменения:

Как распознать прямую вариацию в уравнении?

Уравнение \ (\ frac {y} {x} = 6 \) утверждает, что y изменяется прямо как x, поскольку отношение y к x (также обозначаемое как y: x) никогда не меняется.Число 6 в уравнении \ (\ frac {y} {x} = 6 \) называется постоянной вариации. Уравнение \ (\ frac {y} {x} = 6 \) также может быть записано в эквивалентной форме \ (y = 6x \). Эта форма показывает, что y всегда в 6 раз больше x.

Аналогично, для уравнения \ (y = \ frac {x} {3} \) постоянная вариации равна \ (\ frac {1} {3} \). Уравнение говорит нам, что для любого значения x y всегда будет 1/3 от этого значения.

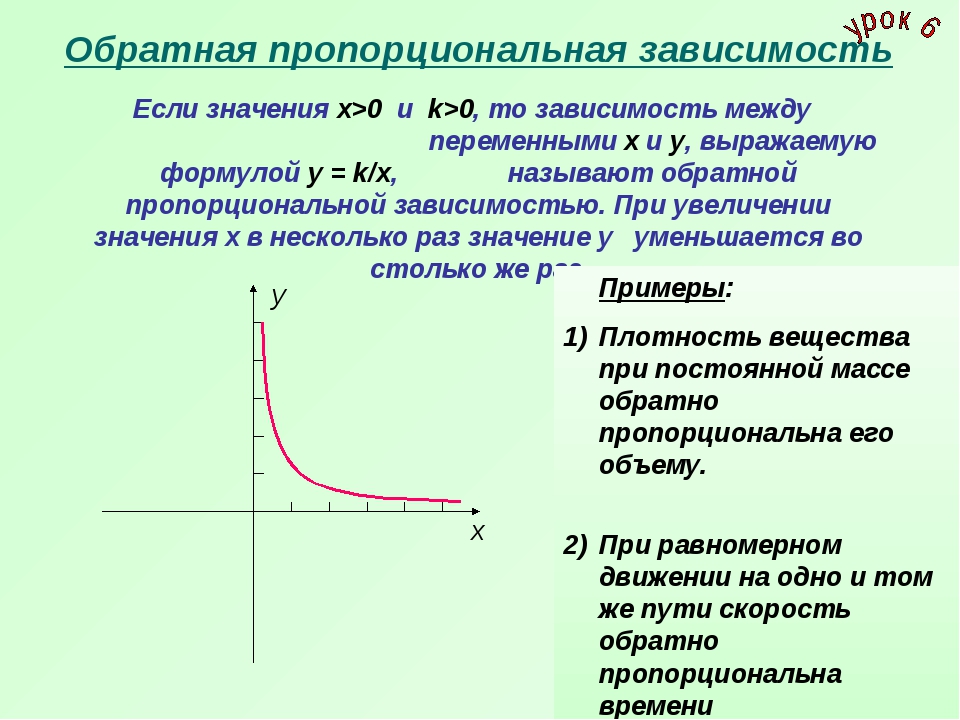
Алгебраическая интерпретация прямой вариации

Для уравнения вида \ (y = kx \), умножение x на некоторую фиксированную величину также умножает y на ТАКУЮ ФИКСИРОВАННУЮ СУММУ.Если мы удвоим x, мы также удвоим соответствующее значение y. Что это значит? Например, поскольку периметр P квадрата напрямую зависит от длины одной стороны квадрата, мы можем сказать, что P = 4s, где число 4 представляет четыре стороны квадрата, а s представляет длину одной стороны. Это уравнение говорит нам, что периметр всегда в четыре раза больше длины одной стороны (имеет смысл, верно?), Но также говорит нам, что удвоение длины сторон удваивает периметр (который все равно будет в четыре раза больше в итоге).

Геометрическая интерпретация прямого изменения

Уравнение \ (y = kx \) является частным случаем линейного уравнения (\ (y = mx + b \)), где точка пересечения y равна 0. (Примечание: уравнение \ (y = mx + b \) — форма пересечения наклона, где m — наклон, а b — точка пересечения по оси Y). 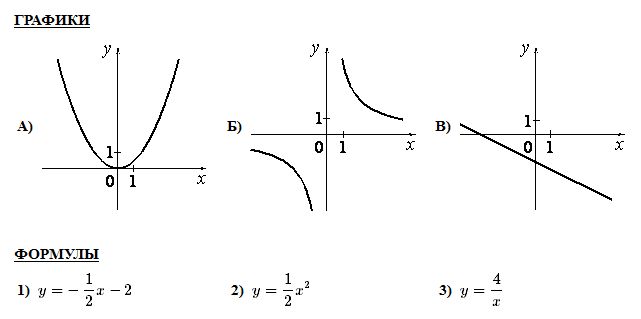В любом случае прямая линия через начало координат (0,0) всегда представляет прямую вариацию между y и x. Наклон этой линии — постоянная вариации. Другими словами, в уравнении \ (y = mx \) m — постоянная вариации.

Пример A:

Если y изменяется прямо как x и \ (y = 8 \), когда \ (x = 12 \), найдите k и напишите уравнение, которое выражает это изменение.

План атаки:

Подставьте указанные значения в уравнение \ (y = kx \).

Решите относительно k.

Затем замените k его значением в уравнении \ (y = kx \).

Пошаговая инструкция:

Начнем с нашего стандартного уравнения: \ (y = kx \)

Вставьте наши известные значения: \ (8 = k * 12 \)

Разделите обе части на 12, чтобы найти k: \ (\ frac {8} {12} = k \)

\ (\ frac {2} {3} = k \)

Далее: вернитесь к \ (y = kx \) и замените k на \ (\ frac {2} {3} \).

Результат:

$$ y = \ frac {2} {3} * x $$

Пример B:

Если y изменяется прямо как x и \ (y = 24 \), когда \ (x = 16 \), найдите y, когда \ (x = 12 \).

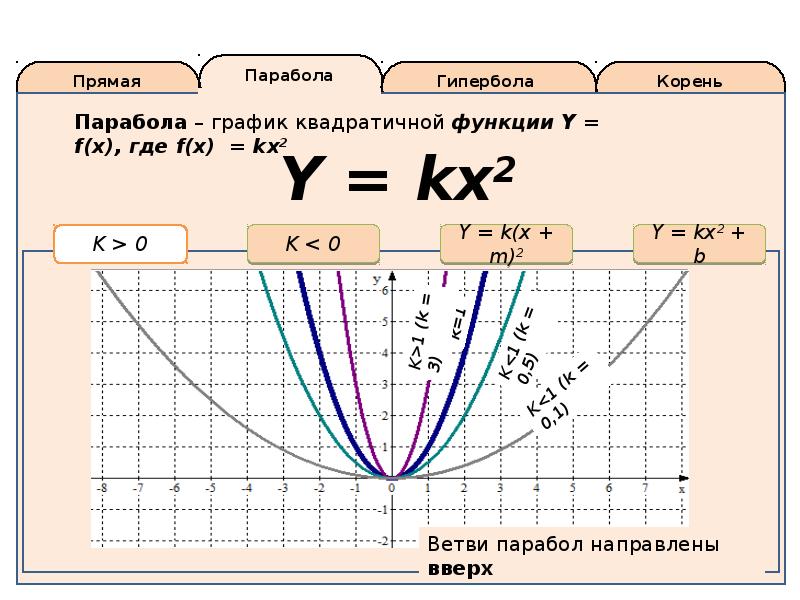
План атаки:

Когда две величины изменяются напрямую, их соотношение всегда одинаково. Мы создадим два отношения, установим их равными друг другу, а затем найдем недостающее количество.

Пошаговая инструкция:

Указанные числа образуют одно соотношение, которое мы можем записать как \ (\ frac {y} {x} \): \ (\ frac {24} {16} \)

Чтобы найти y при \ (x = 12 \), мы устанавливаем другое соотношение: \ (\ frac {y} {12} \)

Решить:

По определению, оба отношения равны:

$$ \ frac {24} {16} = \ frac {y} {12} $$

Умножьте каждую сторону на 12, чтобы найти y:

$$ \ frac {24} {16} * 12 = y $$ $$ y = \ frac {3} {2} * 12 $$

Результат:

Теперь у вас есть базовые представления о прямой вариации? Если вам все еще нужна дополнительная помощь, попробуйте поискать на нашем веб-сайте (вверху страницы) более конкретный вопрос или просмотрите другие наши уроки алгебры.Иногда помогает объяснение предмета кем-то другим (свежий взгляд!), Поэтому вас также может заинтересовать другой урок, посвященный прямым вариациям, например, эта страница, на которой приведены примеры решения прямых вариаций.

Интерактивный решатель алгебры

Прямые и обратные отношения

Прямые и обратные отношения
Эта страница была посещена

раз с 2 апреля 2001 г.

ПРЯМО И ОБРАТНО
ВЗАИМООТНОШЕНИЯ

Часто отношения между переменными можно увидеть, просто изучив математическое
уравнение.Поскольку многие физические соотношения в электростатике, электродинамике,
термодинамика и т. д. выражаются математическими уравнениями, позволяющими качественно видеть
отношения между переменными часто имеют решающее значение для понимания многих технологий.
Следующее объяснение может помочь вам «увидеть» эти отношения.

Давайте посмотрим на следующее уравнение:

Y = 4X

Это уравнение достаточно просто решить для нескольких значений X. Например, если мы позволим
X = 1, тогда Y = 4.Если X = 2, то Y = 8 и так далее. Каковы значения Y, когда X = 3? Икс
= 4? Теперь посмотрим на график изменения Y при изменении X.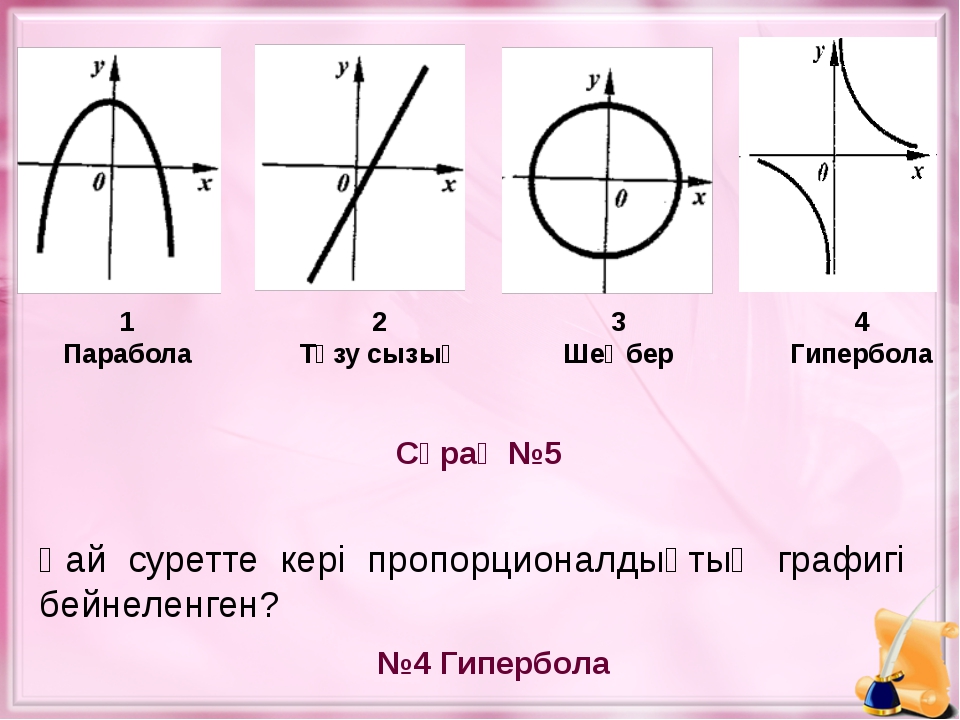 По мере увеличения величины X Y
увеличивается линейно. Это называется прямой связью . (в
уравнение, такое как Y =
-X, связь по-прежнему прямая, хотя Y уменьшается с увеличением X, потому что
X ₁ / X ₂ = Y ₁ / Y ₂)

Один из способов изобразить эти отношения без математических расчетов — это подумать о
качели или качели, которые находятся в равновесии с одним ребенком на каждом конце.Если мы дадим книгу одному
ребенок, что мы должны сделать с другим ребенком, если мы хотим, чтобы баланс сохранялся? Конечно,
мы также должны дать другому ребенку книгу такого же веса. Верно и обратное, если мы возьмем
вес с одной стороны, мы также должны снять вес с другой стороны, чтобы сохранить
равенство. Это «прямая связь».

Теперь давайте посмотрим на следующее уравнение:

Y = 20 / X

Если X = 1, то Y = 20. Если X = 2, то Y = 10. Если X = 3, то Y = 6.7. Если X = 4, то Y = 5.
Примечание
что по мере увеличения X Y уменьшается нелинейным образом. Это обратное увеличение, Y убывает нелинейным образом. Это обратная зависимость, где
X ₁ / X ₂ = Y ₂ / Y ₁. График показан
ниже:

(Между Y и 1 / X существует прямая связь. Вы можете убедиться в этом, если вы нанесете на график значения
Y против 1 / X.)

Вот новое уравнение:

A x B = 15

Рассчитайте несколько значений для B, используя произвольные значения для A.Что это за отношения?
Верно! Обратный. Либо подставив несколько значений, либо узнав форму уравнения,
вы можете легко определить, прямые или обратные отношения.

Примечание: Приведенное выше обсуждение не применяется, когда переменные возводятся в квадрат и т. Д., Но
как один
переменная будет меняться, когда изменяется другая, часто может быть легко определена путем замены
значения и графики.

афинг.

Аппроксимация

кривой — гипертекст по физике

Обсуждение

введение

Я украл это у «Triple A-S» (Американской ассоциации содействия развитию науки). Они знают, как это делать правильно, так зачем это менять.

Из-за своей абстрактности математика универсальна в том смысле, что другие области человеческой мысли — нет. Он находит полезные применения в бизнесе, промышленности, музыке, исторической науке, политике, спорте, медицине, сельском хозяйстве, инженерии, а также в социальных и естественных науках. Связь между математикой и другими областями фундаментальной и прикладной науки особенно сильна.

Я вижу одиннадцать различных полей, упомянутых в этом единственном предложении.Я занимаюсь только одним из них ежедневно, но я согласен с тем, что все они обязаны математике. Если вы принимаете решения о том, чему посвятите свою жизнь (или, по крайней мере, чему вы будете учиться профессионально), основываясь на каком-то понятии «важности», тогда откажитесь от всего, кроме математики. Это одна из древнейших областей человеческого знания. Единственное, что старше, — это сельское хозяйство… ммм… да… а еще есть инструменты, огонь и… ну, язык очень важен, а математика — прямо там. Ага по математике!

Что это значит для вас прямо сейчас?

Работает как обычно.Предполагается, что между отображаемыми на графике величинами существует некоторая математическая связь. Данные стремятся к этому математическому идеалу, но из-за ограниченности людей и их инструментов они только приближаются к нему. Точки данных на графике образуют облако вокруг кривой функции. Если бы только у нас было лучшее «зрение». Если бы только наши устройства лучше записывали фактические значения. Если бы только мы действительно знали, в чем заключается сущность природы, чтобы мы могли назначить эти устройства их предназначенной задаче.Потом. Тогда мы увидим, что каждая точка данных попадает в точную аналитическую кривую. Ах, какой это был бы прекрасный мир. К сожалению, реальные данные никогда не выглядят в точности как идеальные кривые математики.

горизонтальная ось ( x )	вертикальная ось ( y )
независимая переменная	зависимая переменная
объясняющая переменная	переменная ответа

∞	∝	α
бесконечность	пропорционально	Греческая «альфа»

Также.

категориальные переменные — представлены разными символами в одной системе координат
скрытые переменные или скрытые переменные — источник некоторых экспериментальных ошибок

В поисках отношений.

Ваш друг — символ соразмерности.

независимый

Посмотрите на кривую справа. Независимо от того, какое значение принимает переменная x на кривой, переменная y остается неизменной.Это классический пример отношений под названием независимость . Две величины являются независимыми , если одна не влияет на другую. Кривая представляет собой горизонтальную прямую линию, представленную уравнением общего вида…

и = к

, где k — постоянная.

Подходящим выводом из такой взаимосвязи будет то, что…

y не зависит от x .
y не зависит от x .
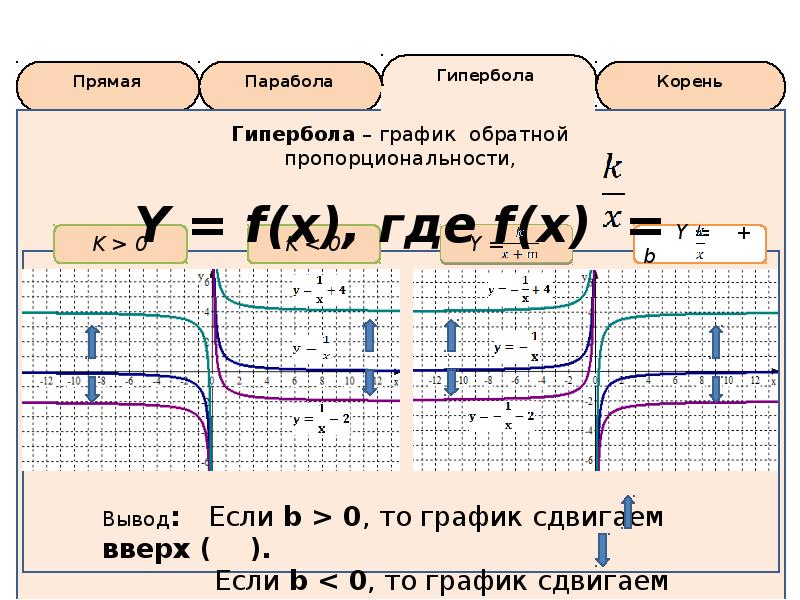
y постоянна для всех значений x .
y не зависит от x .
y и x независимы.

Например…

Ускорение свободного падения не зависит от массы. При отсутствии сопротивления воздуха тяжелые предметы падают так же быстро, как и легкие.
Период простого маятника не зависит от его массы. Простые маятники, которые идентичны во всех отношениях, за исключением веса груза на конце, будут качаться взад и вперед одинаковым образом.
Скорость света в вакууме c постоянна для всех значений v , скорость опорного кадра. Независимо от того, как я двигаюсь, скорость света в вакууме всегда остается неизменной.
На силу сухого трения не влияет площадь двух соприкасающихся поверхностей. Перетаскивание прямоугольника за его нижнюю или боковую часть приводит к той же силе трения.
Масса и местоположение не зависят. Если замороженная индейка имеет массу 10 кг в Нью-Йорке, она будет иметь массу 10 кг в Нью-Джерси, в Нью-Дели, на горе Эверест, в самолете, на орбите, на поверхности Луны, в Галактика Андромеды, в…Ну вы поняли.

Независимые отношения могут быть как скучными, так и глубокими. Скучно, когда мы понимаем, что между двумя величинами нет связи. Глубоко, когда мы понимаем, что определили фундаментальный принцип или основополагающую концепцию, имеющую большое значение. Независимость скорости света и скорости системы отсчета — одно из этих утверждений. Скорость света — фундаментальная постоянная, одна из трех или четырех в физике.

прямой

А теперь взгляните на эту кривую.По мере увеличения переменной x увеличивается и переменная y . Но есть много кривых, которые это делают. Что делает его уникальным? Что отличает его от всех остальных кривых, которые монотонно увеличиваются (как говорят математики) на на ? Ключ в форме — прямой негоризонтальной линии, проходящей через начало координат. С этой конкретной формой происходит нечто особенное.

Укажите точку на линии и запишите ее координаты. Удвойте значение переменной x и посмотрите, как отреагирует переменная y . 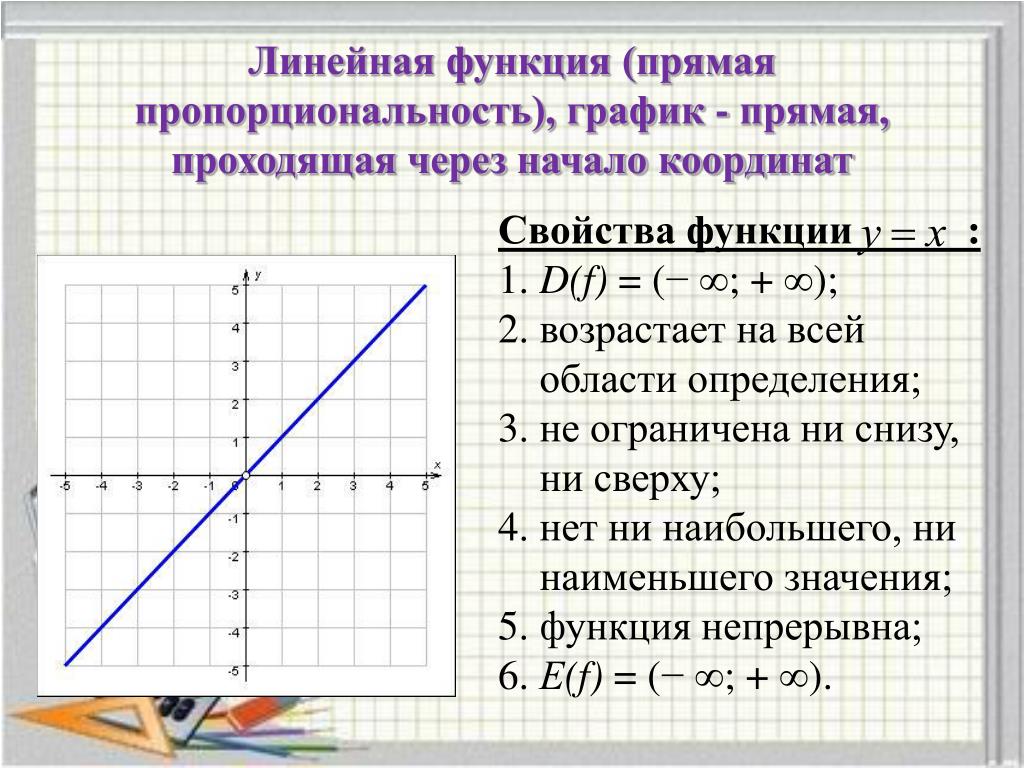Новое значение и также должно удвоиться. Попробуйте снова. Только на этот раз сократите переменную x пополам. Переменная y должна была отреагировать таким же образом; то есть его тоже нужно разрезать пополам. Что бы ни делал x , y делает то же самое. Это иллюстрирует простейшую, нетривиальную форму пропорциональности — прямая пропорциональность . Две величины прямо пропорциональны , если их соотношение является постоянным.

Изменив это определение, мы получим уравнение в общем виде…

y = kx

, где k — постоянная пропорциональности, которую каждый должен распознать как наклон прямой в плоскости xy .

Подходящим выводом из такой взаимосвязи будет то, что…

y прямо пропорционально x .
y напрямую зависит от x
y и x прямо пропорциональны.
y ∝ x

Например,

Регулярная заработная плата прямо пропорциональна количеству отработанных часов. За сорок часов работы оплачивается в четыре раза больше, чем за десять часов работы.За один час работы оплачивается одна десятая десяти часов работы.
Вес напрямую зависит от массы. В три раза больше массы означает в три раза больше веса. Точно так же половина массы означает половину веса.
Расстояние и время прямо пропорциональны, когда скорость постоянна. За два часа езды вы уедете вдвое дальше, чем за час, но только на половину до четырех часов.

Внимание! Не думайте, что прямо пропорциональный означает «когда одно увеличивается, другое увеличивается» или «когда одно уменьшается, другое уменьшается».Это более конкретные отношения, чем эти. Приведу противоположный пример. Рабочий, который работает 60 часов, работает в 1,5 раза больше, чем тот, кто затрачивает 40 часов.

Но рабочие, работающие в США более 40 часов в неделю, должны получать сверхурочную работу, которая обычно в полтора раза превышает их обычную заработную плату. Таким образом, 60-часовой рабочий зарабатывает в 1,75 раза больше, чем 40-часовой рабочий.

1 × 40 обычных часов + 1,5 × 20 сверхурочных часов)	= 1.75
1 × 40 в обычное время

Поскольку изменения не совпадают…

1,75 ≠ 1,5

заработная плата в этом примере не прямо пропорциональна отработанному времени. Прямые отношения гораздо более специфичны, чем общее утверждение «когда одно увеличивается, другое увеличивается». Это больше похоже на то, что «когда один изменяется в определенном соотношении, другой изменяется в таком же соотношении».

обратный

Идем дальше.Взгляните на эту кривую. Эта форма называется прямоугольной гиперболой — гиперболой, поскольку она имеет асимптоты (линии, к которым кривая приближается, но никогда не пересекает), и прямоугольной, поскольку асимптоты представляют собой оси x и y (которые расположены под прямым углом. для другого).

Некоторые говорят, что эта кривая показывает поведение, противоположное предыдущему; то есть, когда переменная x увеличивается, переменная y уменьшается, а при уменьшении переменной x увеличивается переменная y . Но, как и в случае с предыдущей кривой, происходит более конкретное изменение. Убедитесь сами. Выберите удобную точку на кривой. Обратите внимание на значения координат в этой точке. Теперь удвойте координату x и посмотрите, что произойдет с координатой y . Он разрезан пополам. А теперь попробуйте обратное. Укажите точку на кривой и разрежьте ее координату x пополам. Координата y теперь в два раза больше исходного значения. Трижды x , вы получите одну треть от y .Уменьшите x до одной четвертой и посмотрите, как y увеличится на четыре. Однако вы меняете одну из переменных, а другая изменяется на обратную величину. Это иллюстрирует другой простой вид пропорциональности — обратная пропорциональность . Две величины называются обратно пропорциональными , если их произведение является константой.

xy = к

Преобразование этого определения дает нам уравнение общей формы…

, где k — константа пропорциональности.

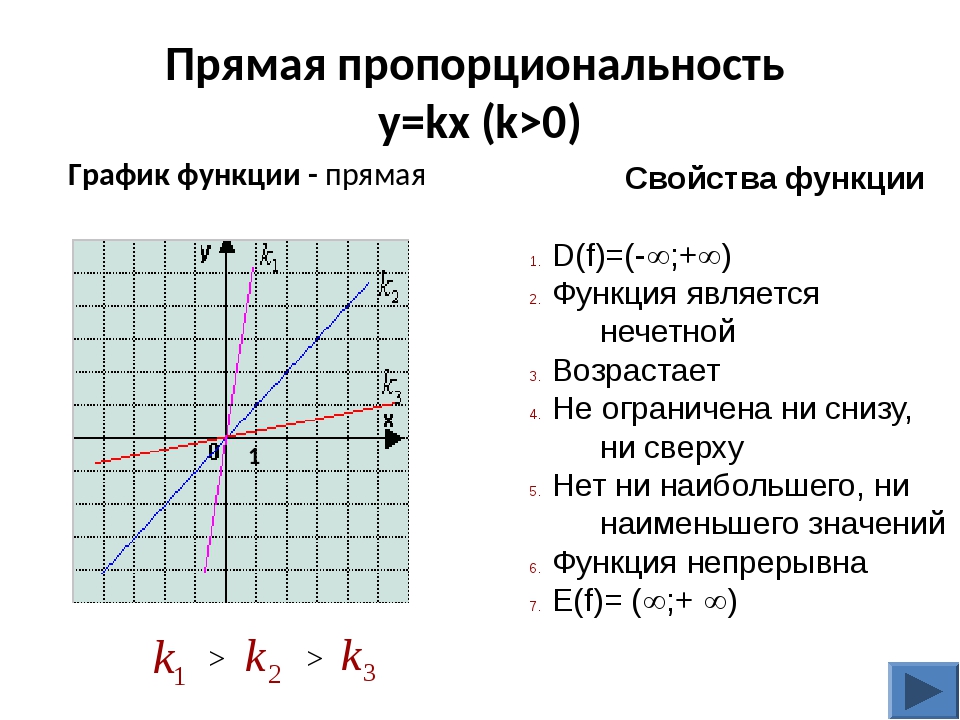
Подходящим выводом из такой взаимосвязи будет то, что…

y обратно пропорционально x .
y изменяется обратно пропорционально x .
y и x обратно пропорциональны.
y ∝ 1/ x
y ∝ x ⁻¹

Например…

Время, необходимое для завершения работы, обратно пропорционально количеству рабочих.Больше рабочих означает меньше времени на выполнение работы. (В два раза больше означает половину времени.) Меньше рабочих означает больше времени. (Если появится только одна треть от нормального количества рабочих, работа займет в три раза больше.)
Объем массы газа обратно пропорционален действующему на него давлению. Поместите воздушный шар в барокамеру и увеличьте давление вдвое — воздушный шар сократится до половины своего первоначального объема. Поместите баллон в вакуумную камеру и уменьшите давление до одной десятой атмосферного — баллон расширится в десять раз в объеме (при условии, что он не сломается первым).

квадрат

Что у нас здесь? Почему это парабола с вершиной в начале координат. Вы получаете такую кривую, когда одна величина пропорциональна квадрату другой. Поскольку эта парабола симметрична относительно оси y , это делает ее вертикальной параболой , и мы знаем, что квадрат получает горизонтальная переменная. Вот уравнение общего вида для такой кривой…

y = kx ²

Подходящим выводом из такой зависимости было бы то, что…

y пропорционально квадрату x .
y ∝ x ²

Например…

Расстояние, пройденное объектом, упавшим из состояния покоя, пропорционально квадрату времени. Сколько времени нужно, чтобы упасть на один метр? Удвойте это время, и вы упадете на 4 метра, утроите его, и вы упадете на 9 метров, и так далее.
Скорость, с которой электрическая цепь производит тепло, пропорциональна квадрату силы тока. Удвоение тока в тостере увеличивает ее тепловыделение в четыре раза.Уменьшите ток в процессоре компьютера до половины его предыдущего значения, и вы уменьшите тепловыделение до четверти от предыдущего значения.

корень квадратный

Вот еще одна парабола с вершиной в начале координат. Эта парабола наклонена на бок и симметрична относительно оси x . Для горизонтальной параболы , подобной этой, квадрат получает вертикальная переменная. Уравнение общего вида для такой кривой…

y = k √ x

Подходящим выводом из такой зависимости было бы то, что…

y пропорционально квадратному корню из x .
y ∝ √ x
y ∝ x ^½

Например…

Скорость пропорциональна квадратному корню из расстояния для свободно падающих объектов. Как быстро движется объект после падения на один метр? На четырёх метрах он будет иметь вдвое большую скорость; на девяти метрах — тройной; шестнадцать, четырехместные; и так далее.

Что нужно запомнить — квадратный корень не является явной функцией. Это не однозначно.Каждое число имеет два квадратных корня: положительный и отрицательный. Типичное программное обеспечение для построения кривой игнорирует отрицательный корень, поэтому я нарисовал только половину параболы на диаграмме выше. Еще кое-что нужно запомнить — область квадратного корня ограничена неотрицательными значениями. Это причудливый способ сказать, что вы не можете найти квадратный корень из отрицательного числа (то есть не без расширения вашего понятия «число»).

мощность

На данный момент у нас есть пять кривых и пять уравнений общего вида…

• независимый	y = к
• прямой	y = kx
• обратный	y = k / x
• квадрат	y = kx ²
• корень квадратный	y = k √ x

У них есть три общих компонента…

х =	независимая переменная (или объясняющая переменная)
y =	зависимая переменная (или переменная ответа)
к =	константа пропорциональности

и один изменяемый компонент…

n =	степень независимой переменной

Мы могли бы переписать эти общие уравнения с двумя переменными, константой пропорциональности и такой степенью…

• независимый	y = kx ⁰
• прямой	y = kx ¹
• обратный	y = kx ⁻¹
• квадрат	y = kx ²
• корень квадратный	y = kx ^½

Мы могли бы даже пойти дальше и написать уравнение общего вида для всего семейства уравнений…

y = kx ⁿ

Говорят, что любые две переменные, которые связаны друг с другом уравнением этой формы, имеют отношение мощности между ними.

Обобщенные властные отношения
мощность	общая форма	описание	внешний вид
0	y = к	независимый	горизонтальный, прямой
1	y = kx	прямой	негоризонтальная прямая линия, проходящая через начало координат
2	y = kx ²	квадрат	вертикальная парабола с вершиной в начале координат
3	y = kx ³	куб
-1	y = k / x	обратный	прямоугольная гипербола
−2	y = k / x ²	обратный квадрат
−3	y = k / x ³	обратный куб
½	y = k √ x	корень квадратный	горизонтальная парабола с вершиной в начале координат
⅓	y = k ∛ x	кубический корень

линейный

Описание: Комбинация постоянного и прямого.Фиксированная сумма добавляется (или вычитается) через равные промежутки времени.

Общий вид.

y = ax + b

Подходящим выводом из такой зависимости будет то, что…

y линейно с x .
y изменяется линейно с x .
y является линейной функцией x .

Внешний вид: любая прямая линия, независимо от наклона или точки пересечения оси Y

Пример (ы): счета за коммунальные услуги (всегда есть плата за обслуживание)

квадратичный

Описание: Комбинация квадрата, прямого и постоянного.

Общая форма

y = ax ² + bx + c

Подходящим выводом из такой связи будет следующее:

y квадратично с x .
y изменяется квадратично с x .
y — квадратичная функция x .

Внешний вид: Вертикальная парабола на графике. Его вершина может быть где угодно.Его также можно было перевернуть вверх дном.

Пример (ы): расстояние при равномерном ускорении

полином

Описание: Комбинация постоянного, прямого, квадрата, куба,…. Продолжайте идти так далеко, как хотите.

Общий вид.

y = a + bx + cx ² + dx ³ +…

Подходящим выводом из такой связи будет то, что…

y может быть аппроксимируется полиномом n-го порядка x .
Полином n-го порядка x соответствовал y .

Внешний вид: любая непериодическая функция без асимптот

Пример (ы): Полиномиальные функции могут использоваться для аппроксимации многих непрерывных однозначных кривых

Обобщенные полиномиальные отношения
заказ	общая форма	название
0	и = а	постоянная
1	y = a + bx	линейный
2	y = a + bx + cx ²	квадратичный
3	y = a + bx + cx ² + dx ³	куб.
4	y = a + bx + cx ² + dx ³ + ex ⁴	квартика
5	y = a + bx + cx ² + dx ³ + ex ⁴ + fx ⁵	квинтик
⋮	⋮	⋮
№	y = a ₀ x ⁰ + a ₁ x ¹ + a ₂ x 2 909 3 909 x ³ +… + a _n x ⁿ	Многочлен n-го порядка

экспоненциальный рост

Описание:

Общий вид.

y = an ^bx

Подходящим выводом из такой зависимости было бы то, что…

y увеличивается экспоненциально с x .
y экспоненциально растет с x .
y ∝ n ^x

Отношение последовательных итераций является постоянным. Количество умножается на фиксированное количество через равные промежутки времени.

Внешний вид: асимптотика с отрицательной осью x , за которой следует неконтролируемое расширение

Пример (ы): неограниченный рост населения, магия сложных процентов

экспоненциальный спад

Описание:

Общий вид.

y = an ^{— bx}

Подходящим выводом из такой зависимости было бы то, что…

y уменьшается экспоненциально с x .
y экспоненциально затухает с x .
y ∝ n ^{— x}

Отношение последовательных итераций является константой. Количество делится на фиксированное количество через равные промежутки времени.

Внешний вид: большое начальное значение с последующим резким коллапсом, асимптотически приближается к положительной оси x

Пример (ы): радиоактивный распад, разряд конденсатора, обесточивание катушки индуктивности

экспоненциальный подход

Описание:

Общий вид.

y = a (1 — n ^{— bx}) + c

Подходящим выводом из такой зависимости будет то, что…

y приближается к окончательному значению экспоненциально .

Внешний вид: асимптотически приближается к горизонтальной прямой

Пример (ы): зарядка конденсатора, включение индуктора, обучение (половина студентов получает его, затем половина оставшихся студентов получает его, затем половина оставшихся студентов и так далее…)

периодический

Описание:

Общий вид.

y = a sin ( bx + c )

Подходящим выводом из такой связи будет следующее:

y периодически изменяется на x .
y периодичен с x .

Внешний вид: Синусоидальная кривая — это типичный, а не единственный пример. Любая повторяющаяся кривая периодична.

Пример (ы): Любое ежедневное (суточное), ежемесячное (лунное), годовое (годовое, сезонное) или другое периодическое изменение.

Нахождение наклона прямой по уравнению — задача 2

Чтобы найти наклон прямой по уравнению прямой, сначала запишите его в форме пересечения наклона. Используйте обратные операции, чтобы найти y, чтобы оно было записано как y = mx + b. Тогда вы можете легко увидеть наклон, поскольку это коэффициент переменной x или число перед x. Не забудьте указать правильный знак наклона.

Когда вас просят найти наклон прямой для данного уравнения, это может быть очень просто, если линия уже находится в форме y, равной mx плюс b.Если вы помните, когда y сам по себе, и у нас есть уравнение, которое решает для y, наклон — это просто коэффициент для x, поэтому, если я могу взять эту линию и решить для y, так что y изолирован, тогда мои числа наклона будут прыгнет на меня. Это будет коэффициент x. Так что давай сделаем это.

Если я хочу решить для y, это означает получить y сам по себе, я собираюсь вычесть x из обеих сторон. Я собираюсь переписать эту задачу здесь, чтобы у меня было больше места. Хорошо, вычтите x из обеих частей, так что у меня -2y равно -x плюс 6, и я все еще не совсем там, потому что y умножается на -2, противоположность умножения — это деление.

Итак, я собираюсь разделить все на -2, и теперь у меня y = равно -x / -2 становится + x / 2, или вы можете думать об этом как о 1/2 плюс, давайте посмотрим, что 6 делится на -2 равно -3. Хорошо, это то же самое уравнение, только что переписанное, я просто переставил материал. Я не менял никаких значений, но теперь я вижу, что коэффициент наклона равен любому коэффициенту x, и это довольно сложно, потому что x / 2 означает ли это, что наклон равен 2? Не совсем, наклон будет 1/2; Я постараюсь обернуть его рамкой.Наклон — это весь коэффициент, есть секрет x, извините, секрет 1 перед x, так что ваше число наклона не просто x / 2. Это не 2, ваш номер наклона 1/2, это ваш окончательный ответ, наклон равен 1/2.

Опять же, способ решения этих задач, если вам задали уравнение и попросили найти наклон, — это получить уравнение таким образом, чтобы оно было решено относительно y. Поместите его в форму y, равную mx плюс b, и тогда число наклона будет просто коэффициентом перед x.

Линейная функция — подготовка к ЕГЭ по Математике

3.Линейная функция вида y = kx + b

Прямая пропорциональность y = kx свойства и график функции

Определение прямой пропорциональности

График прямой пропорциональности

Примеры

Функция прямой

Внеклассный урок — Линейная функция. Прямая пропорциональность. Обратная пропорциональность

Графики прямой, параболы, гиперболы, с модулем

Будь в курсе новых статеек, видео и легкого математического юмора.

Прямая вариация — ChiliMath

Случаи прямого изменения

Случай 1: k> 0 (k положительно)

Случай 2: k

Примеры прямого изменения

Прямое изменение

Прямая вариация | Колледж алгебры

Результаты обучения

Практическое руководство. Учитывая описание задачи прямого изменения, решите неизвестное.

Анализ решения

Вопросы и ответы

Попробуй

Внесите свой вклад!

Прямая вариация — Бесплатная справка по математике

Ключевые понятия прямого изменения:

Как распознать прямую вариацию в уравнении?

Алгебраическая интерпретация прямой вариации

Геометрическая интерпретация прямого изменения

Пример A:

План атаки:

Пошаговая инструкция:

Результат:

Пример B:

План атаки:

Пошаговая инструкция:

Решить:

Результат:

Интерактивный решатель алгебры

Прямые и обратные отношения

кривой — гипертекст по физике

Обсуждение

введение

независимый

прямой

обратный

квадрат

корень квадратный

мощность

линейный

квадратичный

полином

экспоненциальный рост

экспоненциальный спад

экспоненциальный подход

периодический

Нахождение наклона прямой по уравнению — задача 2

Добавить комментарий Отменить ответ