Содержание
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Равнобедренный треугольник | Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство | Углы при основании равнобедренного треугольника | Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак | Два равных угла треугольника | Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство | Медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают.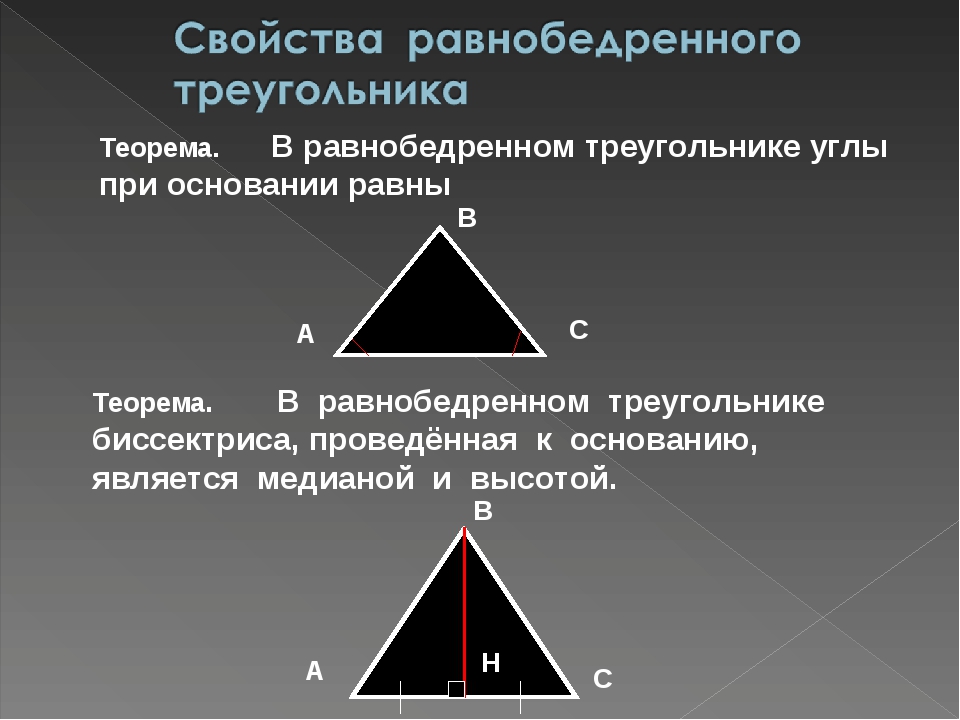 | |
| Признак | Высота треугольника, совпадающая с медианой | Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак | Высота треугольника, совпадающая с биссектрисой | Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак | Биссектриса треугольника, совпадающая с медианой | Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
| Определение: равнобедренный треугольник | |
Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. | |
| Свойство: углы при основании равнобедренного треугольника | |
Если треугольник является равнобедренным треугольником, то углы при его основании равны. | |
| Признак: два равных угла треугольника | |
Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. | |
| Свойство: медиана, биссектриса и высота, проведённые к основанию равнобедренного треугольника | |
| В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. | |
| Признак: высота треугольника, совпадающая с медианой | |
Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным | |
| Признак: высота треугольника, совпадающая с биссектрисой | |
Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным | |
| Признак: биссектриса треугольника, совпадающая с медианой | |
Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным | |
| Определение равнобедренного треугольника |
Определение: Равнобедренным треугольником называют треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами равнобедренного треугольника, третью сторону называют основанием равнобедренного треугольника. |
| Свойство углов при основании равнобедренного треугольника |
Свойство: Если треугольник является равнобедренным треугольником, то углы при его основании равны. |
| Признак равнобедренного треуголька: два равных угла треугольника |
Признак: Если у треугольника два угла равны, то этот треугольник является равнобедренным треугольником. |
| Свойство медианы, биссектрисы и высоты, проведённых к основанию равнобедренного треугольника |
Свойство: В равнобедренном треугольнике медиана, биссектриса и высота, проведённые из вершины, противолежащей основанию, совпадают. |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с медианой |
Признак: Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: высота треугольника, совпадающая с биссектрисой |
Признак: Если в треугольнике высота совпадает с биссектрисой, то этот треугольник является равнобедренным |
| Признак равнобедренного треугольника: биссектриса треугольника, совпадающая с медианой |
Признак: Если в треугольнике биссектриса совпадает с медианой, то этот треугольник является равнобедренным |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Мерзляк. Учебник 5 класс. Страница 92
Страница 92
Вопросы к параграфу
1. Какие бывают виды треугольников в зависимости от вида их углов?
Остроугольные – все углы острые.
Прямоугольные один из углов треугольника прямой – равен 90°.
Тупоугольные – один из углов треугольника тупой.
2. Какой треугольник называют остроугольным? Прямоугольным? Тупоугольным?
Остроугольные прямоугольники – это треугольники, у которых все углы острые (меньше 90°).
Прямоугольные треугольники – это прямоугольники, у которых один из углов прямой (90°).
Тупоугольные треугольники – это треугольники, у которых один из углов тупой (больше 90°).
3. Какие бывают виды треугольников в зависимости от количества равных сторон?
Равнобедренные треугольники – 2 стороны равны.
Равносторонние треугольники – 3 стороны равны.
4. Какой треугольник называют равнобедренным? Равносторонним? Разносторонним?
Равнобедренный треугольник – это треугольник, у которого две стороны равны.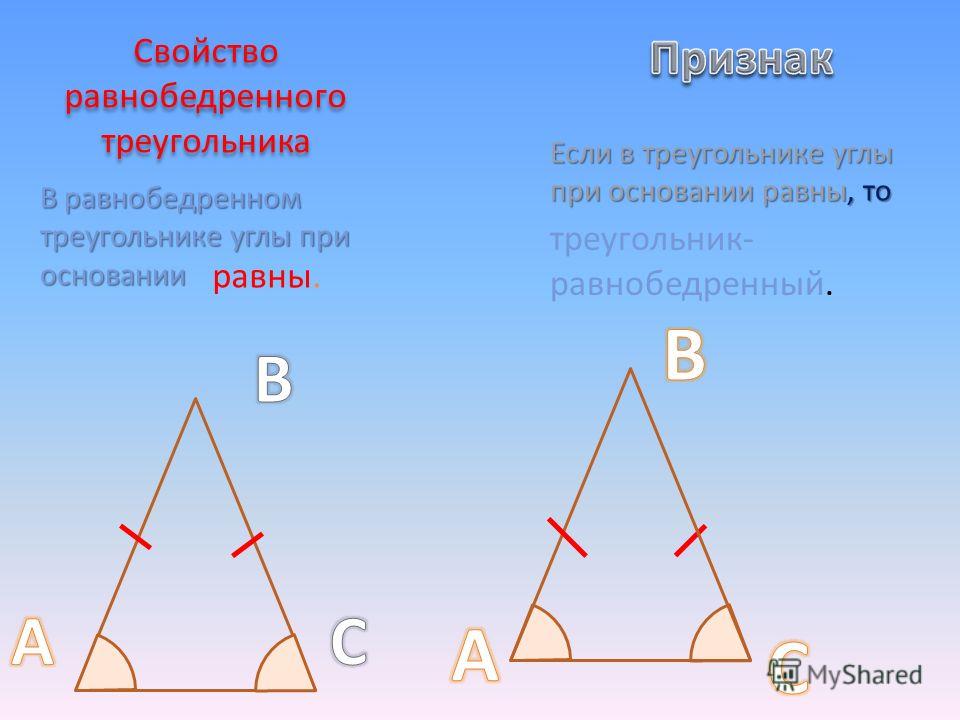
Равносторонний треугольник – это треугольник, у которого три стороны равны.
Разносторонний треугольник – это треугольник, у которого все стороны имеют различную длину.
5. Как называют стороны равнобедренного треугольника?
- равные стороны равнобедренного треугольника называют боковыми сторонами;
- отличающуюся по длине сторону равнобедренного треугольника называют основанием.
6. По какой формуле вычисляют периметр равностороннего треугольника?
Периметр равностороннего треугольника равен произведению числа 3 и длины его стороны : P = 3a.
Решаем устно
1. Чему равен периметр восьмиугольника, каждая сторона которого равна 4 см?
8 • 4 = 32 (см) – периметр восьмиугольника.
Ответ: 32 см.
2. Вычислите сумму 27 + 16 + 33 + 24.
27 + 16 + 33 + 24 = (27 + 33) = (16 + 24) = 60 + 40 = 100
Ответ: 100.
3. Каких чисел не хватает в цепочке вычислений?
Каких чисел не хватает в цепочке вычислений?
4. На трёх кустах расцвело 15 роз. Когда на одном из этих кустов распустились ещё 3 розы, то на всех кустах роз стало поровну. Сколько роз было на каждом кусте вначале?
1) Мы знаем, что вначале на всех кустах было 15 роз, но потом на одной розе распустилось ещё 3 цветка:
15 + 3 = 18 (цветов) – стало на всех кустах в конце.
2) Мы знаем, что в конце на каждом из трёх кустов роз было поровну:
18 : 3 = 6 (цветов) – стало на каждом кусте в конце.
3) Мы знаем, что на одном из кустов роз вначале было на 3 меньше:
6 – 3 = 3 (цветка) – было на одном из кустов вначале.
4) Мы знаем, что количество роз на остальных кустах не изменилось, то есть было и осталось по 6 цветков.
Ответ: 6, 6 и 3 розы.
Упражнения
338. Определите вид треугольника, изображённого на рисунке 121, в зависимости от вида его углов и количества равных сторон.
а) треугольник ABC – это разносторонний остроугольный треугольник;
б) треугольник MNK – это разносторонний прямоугольный треугольник;
в) треугольник PEF – это равнобедренный остроугольный треугольник;
г) треугольник QSR – это равнобедренный тупоугольный треугольник;
д) треугольник OTR – это разносторонний тупоугольный треугольник;
е) треугольник DAB – это равнобедренный прямоугольный треугольник.
339. Начертите:
1) RTQ – разносторонний остроугольный треугольник;
2) JLD – равнобедренный прямоугольный треугольник;
3) POS – равнобедренный тупоугольный треугольник.
Хотите сказать спасибо?
Подпишитесь на нашу группу вк!
Треугольники и их углы. Виды треугольников. Углы треугольника. Различия в названиях по углам
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис.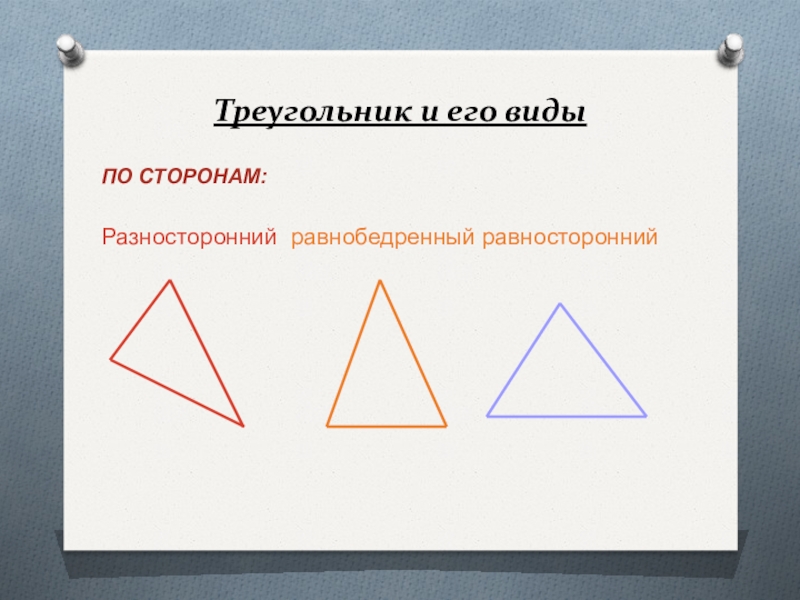 1).
1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника
, отрезки — его сторонами
. Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла.
По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис.
5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
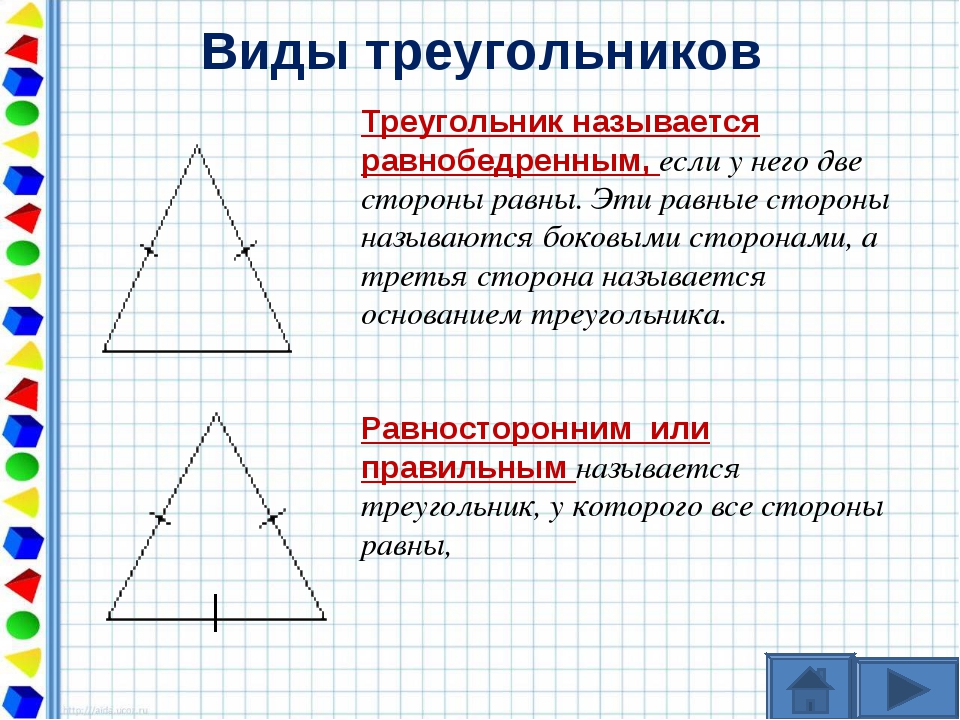
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми
, третья сторона — основанием
. В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными
(рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
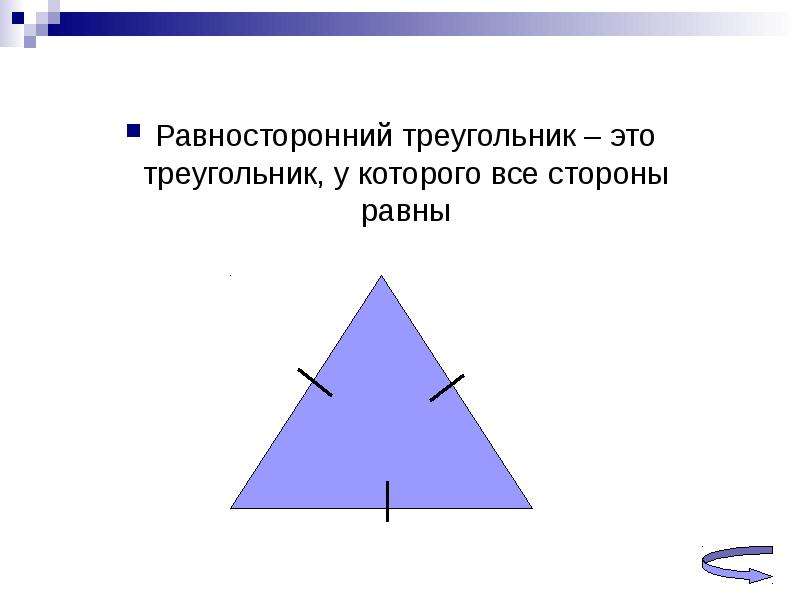
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны
. Равносторонние треугольники
Равносторонние треугольники
всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник.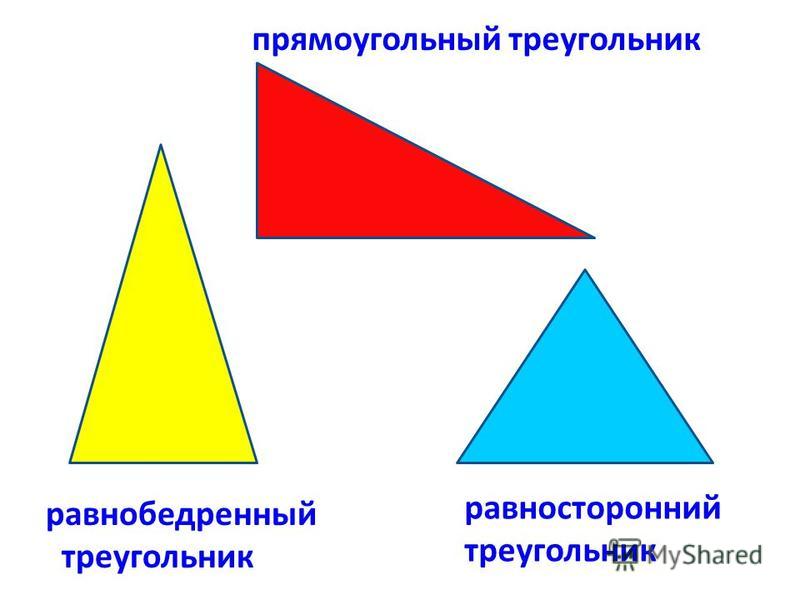 На рисунке он изображен третьим.
На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются …
, отрезки — его …
. Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
Предмет: математика
Класс: 3 класс
Учебник: «Математика» 2 часть.
Тема:
Виды треугольников
Тип урока:
открытие новых знаний
Цель:
Научить определять виды треугольников по измерениям длин их сторон.
Задачи
:
1)Актуализировать знания о геометрических фигурах — прямоугольник, квадрат, треугольник.
2)Актуализировать сложение и вычитание трёхзначных чисел, деление двузначного числа на однозначное, двузначное и круглое; умножение двузначного на однозначное число.
3)Ввести термины: равнобедренный, равносторонний, разносторонний треугольник.
Ход урока
1.Мотивация к учебной деятельности
Посмотрите, скажите, что это такое?
(пирамида)
Скажите, из чего она состоит? (из частей, уровней …)
Можно ли эту пирамиду сравнить с нашим знанием? (да)
Каждый день вы строите всё новые и новые пирамиды, каждый уровень пирамиды- это новое знание, которое вы получаете на уроке. А что будет с пирамидой, если мы уберём синий уровень? (Она разрушиться, станет меньше. )
)
А как из-за чего может разрушиться наша пирамида знаний? (Из-за не выполненного д/з, пропусков уроков, не внимательно слушать учителя.)
Что нужно делать, чтобы наша пирамида становилась прочнее, росла? (Учить уроки, хорошо работать на уроке, выполнять д/з, не прогуливать школу.)
Ребята, вы сказали всё верно. А теперь давайте представим, что наша пирамида отбросила тень. Скажите, на какую геометрическую фигуру тень похожа?
(На треугольник.)
Сегодня мы продолжим работать с такой геометрической фигурой, как треугольник.
2.Актуальзация знаний и фиксация затруднений в проблемной ситуации
С какими геометрическими фигурами вы знакомы? (квадрат, прямоугольник, треугольник).
На доске таблица, заполните её, опираясь на свои знания (у каждого обучающегося карточка с такой таблицей):
Как называются первые две геометрические фигуры? (прямоугольник и квадрат, одним словом это четырёхугольники.)
Скажите, какие виды четырёхугольников вы знаете? Ответить на этот вопрос вам поможет изображение их на слайде.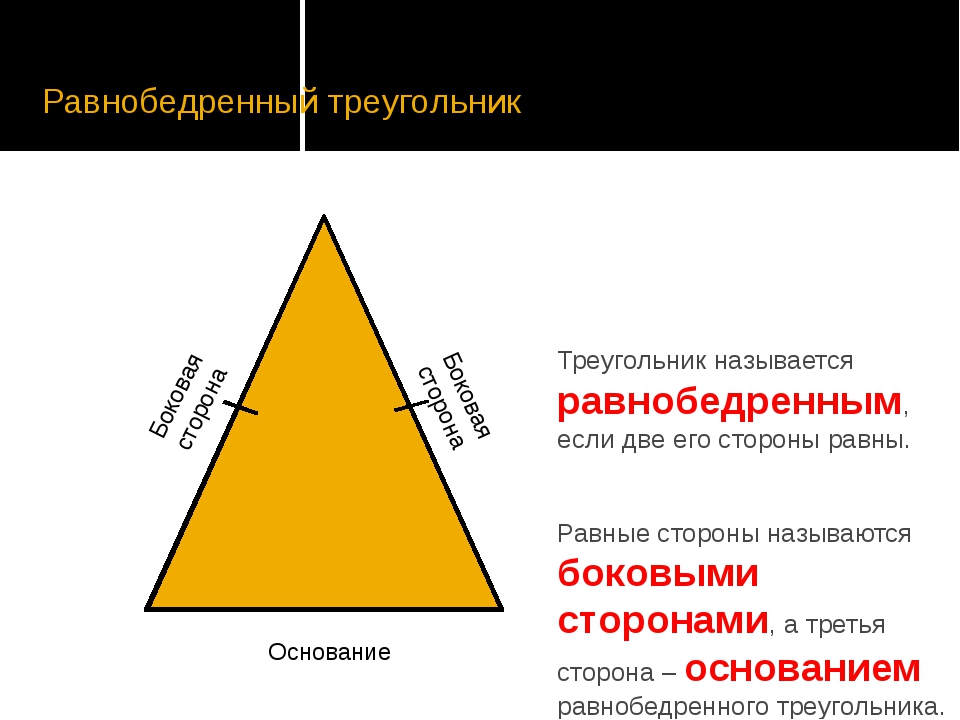
Названия четырёхугольников появляются после ответов детей.
(ромб, квадрат, прямоугольник, трапеция, параллелограмм — называют их по изображениям на слайде или доске.)
Можете ли вы сказать, что такое прямоугольник, а что такое квадрат?
(Прямоугольник — четырёхугольник, у которого все углы прямые.
Квадрат — это прямоугольник, у которого все стороны равны)
Найдите лишнюю геометрическую фигуру, опираясь на результаты таблицы. (Треугольник).
Хорошо, четырёхугольники все очень разные, а что вы знаете о треугольнике? (Треугольники бывают: остроугольные, тупоугольные, прямоугольные.)
Что вы ещё знаете о треугольнике? (Определение)
Треугольник — это геометрическая фигура, у которой 3 угла, 3 вершины, 3 стороны.
Заполните следующую таблицу, опираясь на свои знания:
(Учитель заполняет таблицу в соответствии ответам детей. В колонках «название» возникают разные мнения, а некоторые дети оставляют их пустыми.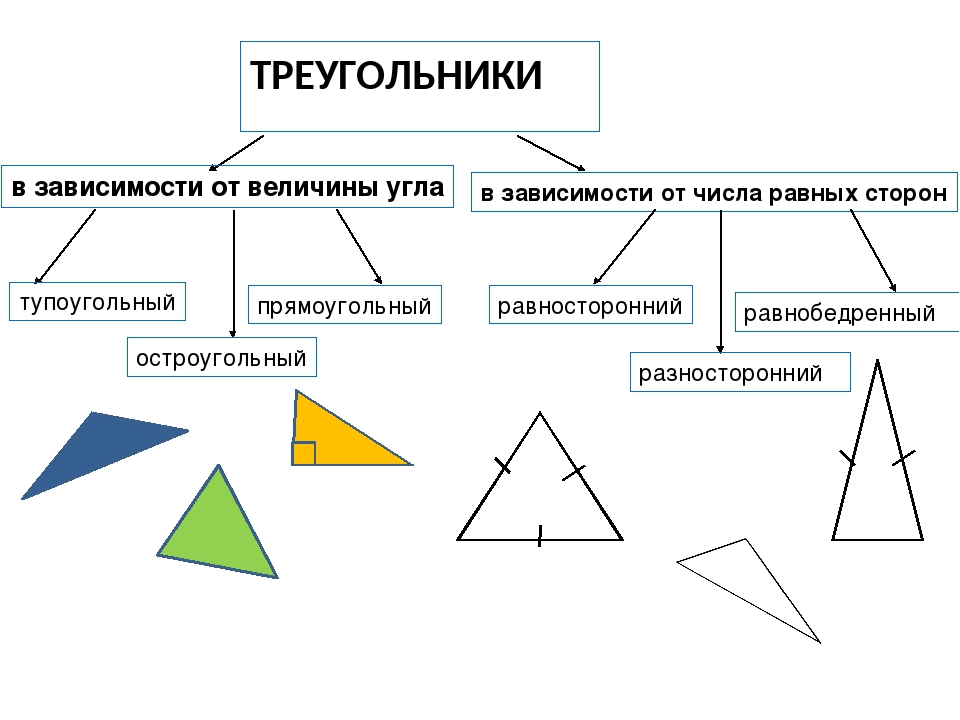 )
)
3.Выявление места и причины затруднения.
Какое задание вы выполняли? (Заполни таблицу.)
Где возникло затруднение? (При записи названий треугольников)
Почему возникло затруднение? (Не знаем как они называются)
Какую цель урока нужно поставить? (Узнать, какие ещё есть виды треугольников кроме изученных (тупоугольный, остроугольный, прямоугольный) , научиться определять эти виды у треугольников.)
Какая тема нашего урока? (Виды треугольников)
4.Открытие нового знания.
Давайте вернёмся к таблице.
Впишем размеры сторон треугольников. (Вписывают.)
Хорошо, а сейчас посмотрите и скажите, что вы заметили? (У первого треугольника все стороны равны, у второго 2 стороны равны, а у третьего все стороны разные.)
Верно, а можете ли вы придумать названия этим треугольникам, основываясь на том объяснении, которое вы сейчас дали? (Да)
Как вы назовёте треугольник, у которого все стороны равные? Придумай прилагательное, состоящее из 2х слов: равные стороны.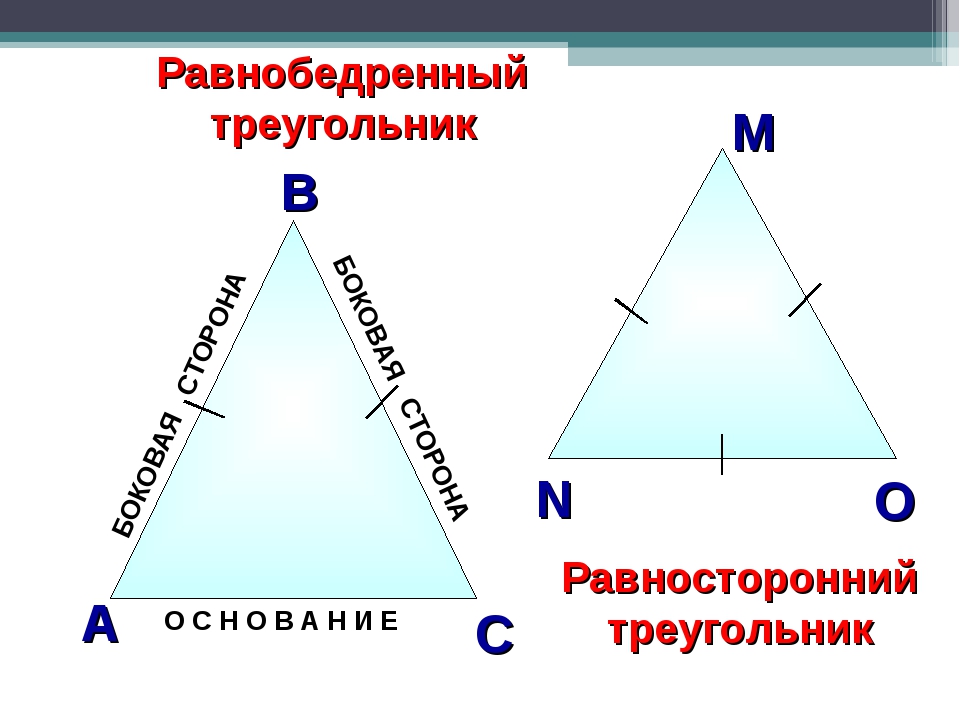 (Равносторонний)
(Равносторонний)
Как назвать треугольник, у которого все стороны различные? (Разносторонний)
Как называется треугольник, у которого 2 стороны равные? (Дети сомневаются, чтобы ответить на этот вопрос они пользуются учебником с.73) (Равнобедренный) А какой ещё треугольник можем назвать равнобедренным? (Равносторонний)
Заполните таблицу самостоятельно, опираясь на новые знания.
А можем ли сейчас дать определение видам треугольников? (Да)
Равносторонний
— треугольник, у которого все три стороны равны.
Равнобедренный
— треугольник, у которого равны хотя бы две стороны. Равнобедренным треугольником является и равносторонний треугольник.
Разносторонний
— треугольник, у которого все стороны разные.
Проверьте свои определения с.73 -учебник. (Проверяют.)
Верно ли вы составили определения? (Да.)
5.Первичное закрепление с проговариванием во внешней речи
Выполните задание из учебника с. 74 (под?)
74 (под?)
1)Разносторонние: 2,3,5
2)Равнобедренные: 1,
4
, 6,
7
(Учащиеся записывают в тетради. По очереди говорят ответы, аргументируя. Образец фиксируется на доске).
6.Самостоятельная работа с самопроверкой по эталону.
Выполнение задания самостоятельно. По окончанию работы — самопроверка по образцу (на доске или на индивидуальных карточках).
№1.Заполни таблицу
, схематично изобрази треугольники.
№2.Выпиши номера:
1)Разносторонних треугольников.
2)Равнобедренных, из выписанных номеров подчеркни номера равносторонних треугольников.
Эталон:
Задание №1:
Задание №2:
1)Разносторонние треугольники: 2,3,4
2)Равнобедренные треугольники (подчеркнут номер равностороннего треугольника): 1,
5
7.Включение в систему знаний и повторение
На песке мальчик нарисовал треугольники и зашифровал слова, найди значения выражений, записанные в треугольниках. Сначала решай те, которые записаны в разносторонних треугольниках, а потом в равнобедренных треугольниках. И отгадаешь зашифрованные слова.
Сначала решай те, которые записаны в разносторонних треугольниках, а потом в равнобедренных треугольниках. И отгадаешь зашифрованные слова.
Подсказка: Запиши числа в порядке возрастания и слова у тебя получатся.
Карточка:
Решение:
Ответ: Виды треугольников
8.Рефлексия учебной деятельности.
Нарисуй соответственно пирамиду знаний, состоящую из 7 уровней. Каждый уровень — это ответ на вопрос.
Ответьте на вопросы:
1)Ребята, что такое вы записали «виды треугольников»? (Тему нашего урока)
2)Какова была наша цель? (Узнать, как называются все 3 вида треугольников, научиться определять эти виды по измерениям длин сторон.)
3)Какие виды треугольников вы узнали? (разносторонний, равнобедренный, равносторонний)
4) А почему они так называются?
(
Равносторонний
— треугольник, у которого все стороны равны.
Равнобедренный
— треугольник, у которого хотя бы две стороны равны, в том числе и равносторонний треугольник, потому что у него есть две равные стороны.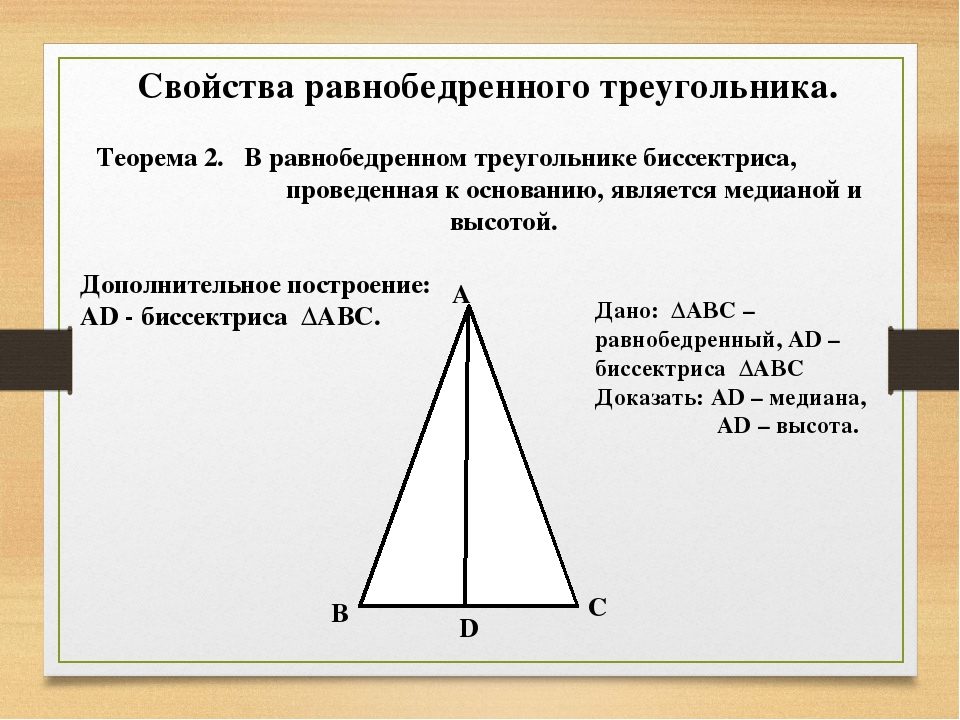 )
)
Разносторонний
— треугольник, у которого все стороны разные.)
5) Научились схематично изображать все виды треугольников? (Да, на самостоятельной работе.)
6) Какие открытия вы сегодня сделали? (Новые виды треугольников, их названия.)
7) Ребята, а вы сможете определить вид треугольника по его измерениям? (Да) Я вам сейчас буду говорить измерения, а вы поднимать вверх карточку с названием вида треугольника (карточки выданы дополнительно- по 3 карточки.)
1. 2см, 3см,5 см.- разносторонний
2. 4см, 4см, 2 см — равнобедренный
3.6см, 6см,6см — равносторонний, равнобедренный
Поднимите руки, кто сегодня достиг вершины этого знания? (Поднимают)
А поднимите руки, кому не хватило 1, 2 уровней. (Поднимают.)
(Учитель анализирует «пирамиды знаний у детей, делает выводы — какой уровень западает и на следующем уроке начинает актуализацию знаний с этого.)
Треугольник — определение и общие понятия
Треугольник – это такой простой многоугольник, состоящий из трех сторон и имеющий столько же углов. Его плоскости ограничиваются 3 точками и 3 отрезками, попарно соединяющими даные точки.
Его плоскости ограничиваются 3 точками и 3 отрезками, попарно соединяющими даные точки.
Все вершины любого треугольника, независимо от его разновидности, обозначаются заглавными латинскими буквами, а его стороны изображаются соответствующими обозначениями противоположных вершин, только не большими буквами, а малыми. Так, например, треугольник с вершинами обозначенными буквами А, В и С имеет стороны a, b, c.
Если рассматривать треугольник в евклидовом пространстве, то это такая геометрическая фигура, которая образовалась с помощью трех отрезков, соединяющих три точки, которые не лежат на одной прямой.
Посмотрите внимательно на рисунок, который изображен вверху. На нем точки А, В и С являются вершинами этого треугольника, а его отрезки носят названия сторон треугольника. Каждая вершина этого многоугольника образует внутри его углы.
Виды треугольников
Согласно величины, углов треугольников, они делятся на такие разновидности, как:
Прямоугольные;
Остроугольные;
Тупоугольные.
К прямоугольным принадлежат такие треугольники, у которых в наличии есть один прямой угол, а остальные два имеют острые углы.
Остроугольные треугольники – это те, у которых все его углы острые.
А если у треугольника имеется один тупой угол, а два остальных угла острые, то такой треугольник относится к тупоугольным.
Каждый из вас прекрасно понимает, что не все треугольники имеют равные стороны. И соответственно тому, какую длину имеют его стороны, треугольники можно поделить на:
Равнобедренные;
Равносторонние;
Разносторонние.
Задание: Нарисуйте разные виды треугольников. Дайте им определение. Какое между ними отличие вы видите?
Основные свойства треугольников
Хотя эти простые многоугольники могут отличаться друг от друга величиной углов или сторон, но в каждом треугольнике есть основные свойства, характерны для этой фигуры.
В любом треугольнике:
Общая сумма всех его углов равняется 180º.
Если он принадлежит к равносторонним, то каждый его угол равен 60º.
Равносторонний треугольник имеет одинаковые и ровные между собой углы.
Чем меньше сторона многоугольника, тем меньший угол расположен напротив него и наоборот напротив большей стороны находиться больший угол.
Если стороны равные, то напротив них расположены равные углы, и наоборот.
Если взять треугольник и продлить его сторону, то в итоге мы образуется внешний угол. Он равен сумме внутренних углов.
В любом треугольнике его сторона, независимо от того, какую бы вы не выбрали, все равно будет меньше, чем сумма 2-х других сторон, но больше чем их разность:
1. a b – c;
2. b a – c;
3. c a – b.
Задание
В таблице приведены уже известные два угла треугольника. Зная общую сумму всех углов найдите, чему равен третий угол треугольника и занесите в таблицу:
1. Сколько градусов имеет третий угол?
2. К какому виду треугольников он относится?
Признаки равности треугольников
I признак
II признак
III признак
Высота, биссектриса и медиана треугольника
Высота треугольника — перпендикуляр, проведенный из вершины фигуры к его противоположной стороне, называется высотой треугольника. Все высоты треугольника пересекаются в одной точке. Точка пересечения всех 3-х высот треугольника является его ортоцентром.
Все высоты треугольника пересекаются в одной точке. Точка пересечения всех 3-х высот треугольника является его ортоцентром.
Отрезок, проведенный из данной вершины и соединяющий ее на средине противоположной стороны, является медианой. Медианы, также как и высоты треугольника, имеют одну общую точку пересечения, так называемый центр тяжести треугольника или центроид.
Биссектриса треугольника — отрезок, соединяющий вершину угла и точку противоположной стороны, а также делящий этот угол пополам. Все биссектрисы треугольника пересекаются в одной точке, которую называют центром окружности, вписанной в треугольник.
Отрезок, который соединяет середины 2-х сторон треугольника, называется средней линией.
Историческая справка
Такая фигура, как треугольник, была известна еще в Древние времена. Об этой фигуре и ее свойствах упоминалось на египетских папирусах четырех тысячелетней давности.
Немного позже, благодаря теореме Пифагора и формуле Герона, изучение свойства треугольника, перешло на более высокий уровень, но все же, это происходило более двух тысяч лет назад.
В XV – XVI веках стали проводить много исследований о свойствах треугольника и в итоге возникла такая наука, как планиметрия, которая получила название «Новая геометрия треугольника».
Ученый из России Н. И.Лобачевский внес огромный вклад в познание свойств треугольников. Его труды в дальнейшем нашли применение как в математике, так и физике и кибернетике.
Благодаря знаниям свойств треугольников возникла и такая наука, как тригонометрия. Она оказалась необходимой для человека в его практических потребностях, так как ее применение просто необходимо при составлении карт, измерении участков, да и при конструировании различных механизмов.
А какой самый известный треугольник вы знаете? Это конечно же Бермудский треугольник! Он получил такое название в 50-х годах из-за географического расположения точек (вершин треугольника), внутри которых, согласно существующей теории, возникали связанные с ним аномалии. Вершинами Бермудского треугольника выступают Бермудские острова, Флорида и Пуэрто-Рико.
Задание: А какие теории о Бермудском треугольнике слышали вы?
А известно ли вам, что в теории Лобачевского при сложении углов треугольника их сумма всегда имеет результат меньший, чем 180º. В геометрии Римана, сумма всех углов треугольника больше 180º, а в трудах Эвклида она равна 180 градусам.
Домашнее задание
Решите кроссворд на заданную тему
Вопросы к кроссворду:
1. Как называется перпендикуляр, который провели из вершины треугольника к прямой, расположенной на противоположной стороне?
2. Как, одним словом можно назвать сумму длин сторон треугольника?
3. Назовите треугольник, у которого две стороны равны?
4. Назовите треугольник, у которого есть угол, равный 90°?
5. Какое название носит большая, из сторон треугольника?
6. Название стороны равнобедренного треугольника?
7. Их всегда три в любом треугольнике.
8. Какое название носит треугольник, у которого один из углов превышает 90°?
9. Название отрезка, соединяющего вершину нашей фигуры со срединой противоположной стороны?
Название отрезка, соединяющего вершину нашей фигуры со срединой противоположной стороны?
10. В простом многоугольнике АВС, заглавная буква А является …?
11. Какое название носит отрезок, делящий угол треугольника пополам.
Вопросы к теме треугольников:
1. Дайте определение.
2. Сколько высот он имеет?
3. Сколько биссектрис у треугольника?
4. Чему равна его сумма углов?
5. Какие виды этого простого многоугольника вам известны?
6. Назовите точки треугольников, которые носят название замечательных.
7. Каким прибором можно измерить величину угла?
8. Если стрелки часов показывают 21 час. Какой угол образуют часовые стрелки?
9. На какой угол поворачивается человек, если ему дана команда «налево», «кругом»?
10. Какие еще определения вам известны, которые связанные с фигурой, имеющей три угла и три стороны?
Предмети > Математика > Математика 7 класс
Пожалуй, самой основной, простой и интересной фигурой в геометрии является треугольник. В курсе средней школы изучаются его основные свойства, однако иногда знания по этой теме формируются неполными. Виды треугольников изначально определяют их свойства. Но подобное представление остается смешанным. Поэтому сейчас разберем немного подробнее эту тему.
В курсе средней школы изучаются его основные свойства, однако иногда знания по этой теме формируются неполными. Виды треугольников изначально определяют их свойства. Но подобное представление остается смешанным. Поэтому сейчас разберем немного подробнее эту тему.
Виды треугольников зависят от градусной меры углов. Эти фигуры бывают остро-, прямо- и тупоугольными. Если все углы не превышают значения в 90 градусов, то фигуру смело можно назвать остроугольной. Если хотя бы один угол треугольника равен 90 градусам, то вы имеете дело с прямоугольным подвидом. Соответственно, во всех остальных случаях рассматриваемую называют тупоугольной.
Существует множество задач для остроугольных подвидов. Отличительной чертой является внутреннее местонахождение точек пересечения биссектрис, медиан и высот. В других случаях это условие может не выполняться. Определить тип фигуры “треугольник” нетрудно. Достаточно знать, например, косинус каждого угла. Если какие-нибудь значения меньше нуля, значит, треугольник в любом случае является тупоугольным. В случае нулевого показателя фигура обладает прямым углом. Все положительные значения гарантированно подскажут вам о том, что перед вами остроугольный вид.
В случае нулевого показателя фигура обладает прямым углом. Все положительные значения гарантированно подскажут вам о том, что перед вами остроугольный вид.
Нельзя не сказать о правильном треугольнике. Это самый идеальный вид, где совпадают все точки пересечения медиан, биссектрис и высот. Центр вписанной и описанной окружности лежит также в одном месте. Для решения задач необходимо знать только одну сторону, так как вам углы изначально заданы, а две другие стороны известной. То есть фигура задается только одним параметром. Существуют Их главная особенность — равенство двух сторон и углов при основании.
Иногда встречается вопрос о том, существует ли треугольник с заданными сторонами. На самом деле вас спрашивают, подходит ли данное описание под основные виды. Например, если сумма двух сторон меньше третьей, то в реальности такой фигуры не существует вообще. Если в задании просят найти косинусы углов треугольника со сторонами 3,5,9, то здесь очевидный можно объяснить без сложных математических приемов. Предположим, вы хотите из пункта A попасть в пункт B. Расстояние по прямой равно 9 километрам. Однако вы вспомнили, что необходимо зайти в пункт C в магазин. Расстояние от А до С равно 3 километрам, а от С до В — 5. Таким образом получается, что, двигаясь через магазин, вы пройдете на один километр меньше. Но так как пункт C не расположен на прямой AB, то вам придется пройти лишнее расстояние. Здесь возникает противоречие. Это, конечно, условное объяснение. Математика знает не один способ доказательства того, что все виды треугольников подчиняются основному тождеству. Оно гласит о том, что сумма двух сторон больше длины третьей.
Предположим, вы хотите из пункта A попасть в пункт B. Расстояние по прямой равно 9 километрам. Однако вы вспомнили, что необходимо зайти в пункт C в магазин. Расстояние от А до С равно 3 километрам, а от С до В — 5. Таким образом получается, что, двигаясь через магазин, вы пройдете на один километр меньше. Но так как пункт C не расположен на прямой AB, то вам придется пройти лишнее расстояние. Здесь возникает противоречие. Это, конечно, условное объяснение. Математика знает не один способ доказательства того, что все виды треугольников подчиняются основному тождеству. Оно гласит о том, что сумма двух сторон больше длины третьей.
Любой вид обладает следующими свойствами:
1) Сумма всех углов равняется 180 градусам.
2) Всегда существует ортоцентр — точка пересечения всех трех высот.
3) Все три медианы, проведенные из вершин внутренних углов, пересекаются в одном месте.
4) Вокруг любого треугольника можно описать окружность. Также можно вписать круг так, чтобы он имел только три точки соприкосновения и не выходил за внешние стороны.
Теперь вы познакомились с основными свойствами, которыми обладают различные виды треугольников. В будущем важно понимать, с чем вы имеете дело при решении задачи.
Самый простой многоугольник, который изучается в школе — это треугольник. Он более понятен для учащихся и встречает меньше трудностей. Несмотря на то что существуют различные виды треугольников, у которых имеются особенные свойства.
Какая фигура называется треугольником?
Образованная тремя точками и отрезками. Первые называются вершинами, вторые — сторонами. Причем все три отрезка должны быть соединены, чтобы между ними образовывались углы. Отсюда и название фигуры «треугольник».
Различия в названиях по углам
Поскольку они могут быть острыми, тупыми и прямыми, то и виды треугольников определяются по этим названиям. Соответственно, групп таких фигур три.
- Первая. Если все углы треугольника острые, то он будет иметь название остроугольного. Все логично.
- Вторая.
 Один из углов тупой, значит треугольник тупоугольный. Проще некуда.
Один из углов тупой, значит треугольник тупоугольный. Проще некуда.
- Третья. Имеется угол, равный 90 градусам, который называется прямым. Треугольник становится прямоугольным.
Различия в названиях по сторонам
В зависимости от особенностей сторон выделяют такие виды треугольников:
общий случай — разносторонний, в котором все стороны имеют произвольную длину;
равнобедренный, у двух сторон которого имеются одинаковые числовые значения;
равносторонний, длины всех его сторон одинаковые.
Если в задаче не указан конкретный вид треугольника, то нужно чертить произвольный. У которого все углы острые, а стороны имеют разную длину.
Свойства, общие для всех треугольников
- Если сложить все углы треугольника, то получится число, равное 180º. И неважно, какого он вида. Это правило действует всегда.
- Числовое значение любой стороны треугольника меньше, чем сложенные вместе две другие. При этом она же больше, чем их разность.
- Каждый внешний угол имеет значение, которое получается при сложении двух внутренних, не смежных с ним. Причем он всегда больше, чем смежный с ним внутренний.
- Напротив меньшей стороны треугольника всегда лежит самый маленький угол. И наоборот, если сторона большая, то и угол будет самым большим.
Эти свойства справедливы всегда, какие бы виды треугольников ни рассматривались в задачах. Все остальные вытекают из конкретных особенностей.
Свойства равнобедренного треугольника
- Углы, которые прилегают к основанию, равны.
- Высота, которая проведена к основанию, является также медианой и биссектрисой.
- Высоты, медианы и биссектрисы, которые построены к боковым сторонам треугольника, соответственно равны друг другу.
Свойства равностороннего треугольника
Если имеется такая фигура, то будут верны все свойства, описанные немного выше. Потому что равносторонний всегда будет равнобедренным. Но не наоборот, равнобедренный треугольник не обязательно будет равносторонним.
- Все его углы равны друг другу и имеют значение 60º.
- Любая медиана равностороннего треугольника является его высотой и биссектрисой. Причем они все равны друг другу. Для определения их значений существует формула, которая состоит из произведения стороны на квадратный корень из 3, деленного на 2.
Свойства прямоугольного треугольника
- Два острых угла дают в сумме значение в 90º.
- Длина гипотенузы всегда больше, чем у любого из катетов.
- Числовое значение медианы, проведенной к гипотенузе, равно ее половине.
- Этому же значению равен катет, если он лежит напротив угла в 30º.
- Высота, которая проведена из вершины со значением 90º, имеет определенную математическую зависимость от катетов: 1/н 2 = 1/а 2 + 1/в 2 . Здесь: а, в — катеты, н — высота.
Задачи с разными видами треугольников
№1. Дан равнобедренный треугольник. Его периметр известен и равен 90 см. Требуется узнать его стороны.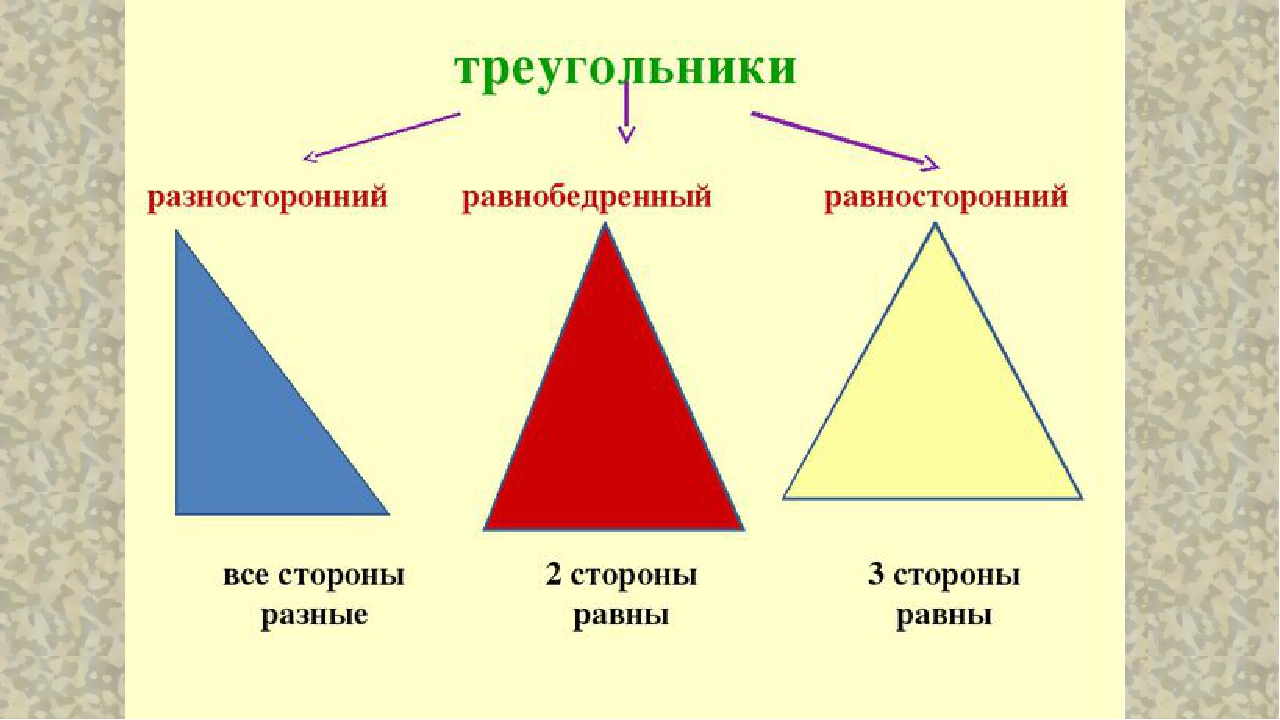 В качестве дополнительного условия: боковая сторона меньше основания в 1,2 раза.
В качестве дополнительного условия: боковая сторона меньше основания в 1,2 раза.
Значение периметра напрямую зависит от тех величин, которые нужно найти. Сумма всех трех сторон и даст 90 см. Теперь нужно вспомнить признак треугольника, по которому он является равнобедренным. То есть две стороны равны. Можно составить уравнение с двумя неизвестными: 2а + в = 90. Здесь а — боковая сторона, в — основание.
Настала очередь дополнительного условия. Следуя ему, получается второе уравнение: в = 1,2а. Можно выполнить подстановку этого выражения в первое. Получится: 2а + 1,2а = 90. После преобразований: 3,2а = 90. Отсюда а = 28,125 (см). Теперь несложно узнать основание. Лучше всего это сделать из второго условия: в = 1,2 * 28,125 = 33,75 (см).
Для проверки можно сложить три значения: 28,125 * 2 + 33,75 = 90 (см). Все верно.
Ответ: стороны треугольника равны 28,125 см, 28,125 см, 33,75 см.
№2. Сторона равностороннего треугольника равна 12 см. Нужно вычислить его высоту.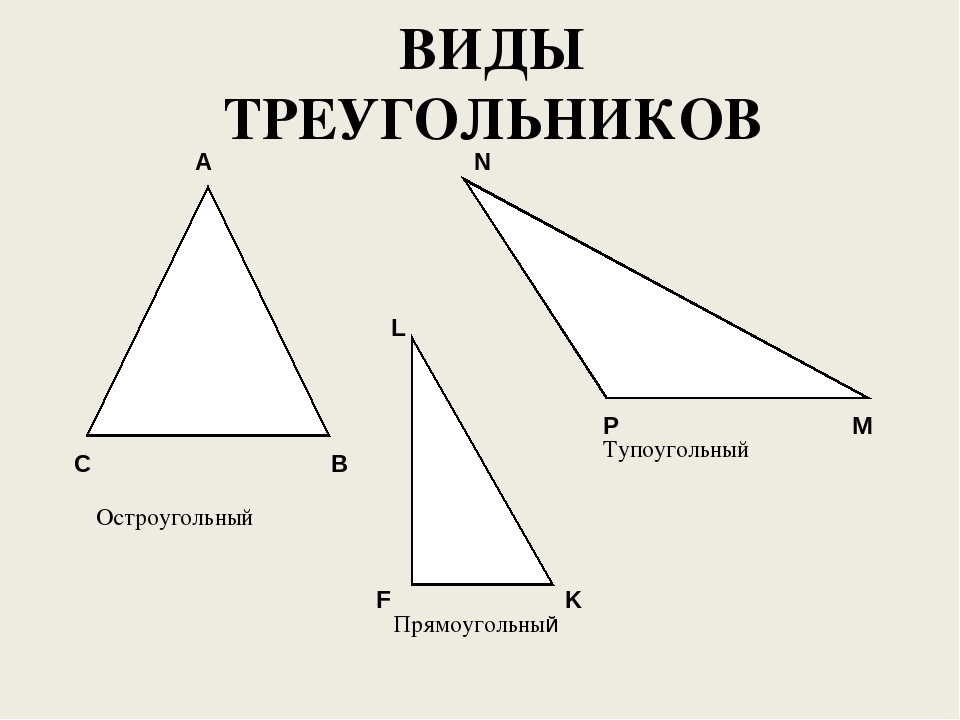
Решение. Для поиска ответа достаточно вернуться к тому моменту, где были описаны свойства треугольника. Так указана формула для нахождения высоты, медианы и биссектрисы равностороннего треугольника.
н = а * √3 / 2, где н — высота, а — сторона.
Подстановка и вычисление дают такой результат: н = 6 √3 (см).
Эту формулу необязательно запоминать. Достаточно вспомнить, что высота делит треугольник на два прямоугольных. Причем она оказывается катетом, а гипотенуза в нем — это сторона исходного, второй катет — половина известной стороны. Теперь нужно записать теорему Пифагора и вывести формулу для высоты.
Ответ: высота равна 6 √3 см.
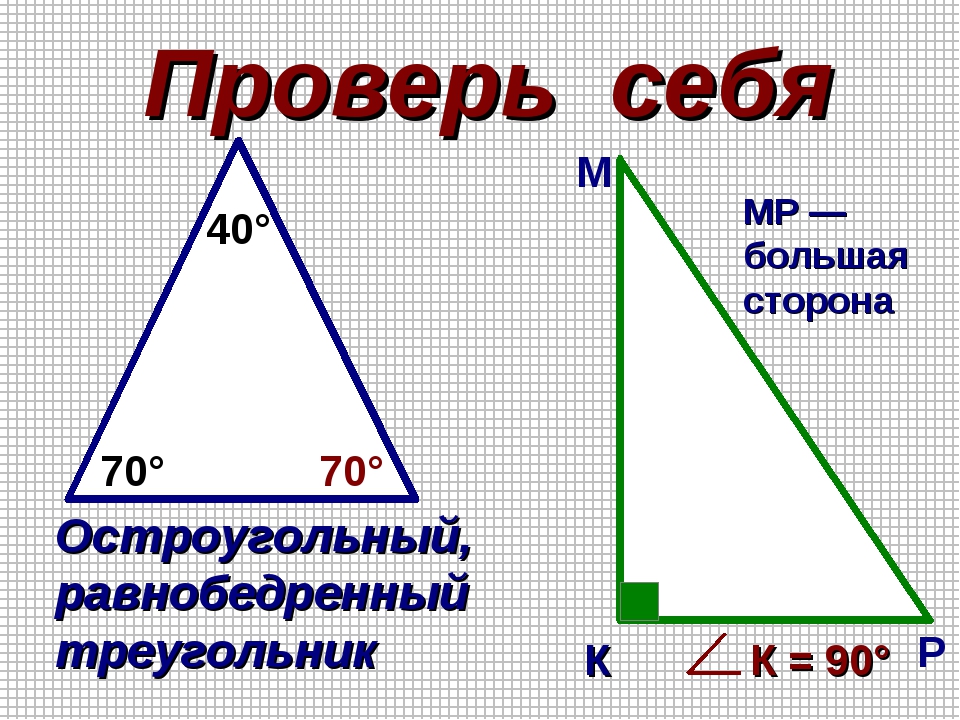
№3. Дан МКР — треугольник, 90 градусов в котором составляет угол К. Известны стороны МР и КР, они равны соответственно 30 и 15 см. Нужно узнать значение угла Р.
Решение. Если сделать чертеж, то становится ясно, что МР — гипотенуза. Причем она в два раза больше катета КР. Снова нужно обратиться к свойствам. Одно из них как раз связано с углами. Из него понятно, что угол КМР равен 30º. Значит искомый угол Р будет равен 60º. Это следует из другого свойства, которое утверждает, что сумма двух острых углов должна равняться 90º.
Из него понятно, что угол КМР равен 30º. Значит искомый угол Р будет равен 60º. Это следует из другого свойства, которое утверждает, что сумма двух острых углов должна равняться 90º.
Ответ: угол Р равен 60º.
№4. Нужно найти все углы равнобедренного треугольника. Про него известно, что внешний угол от угла при основании равен 110º.
Решение. Поскольку дан только внешний угол, то этим и нужно воспользоваться. Он образует с внутренним углом развернутый. Значит в сумме они дадут 180º. То есть угол при основании треугольника будет равен 70º. Так как он равнобедренный, то второй угол имеет такое же значение. Осталось вычислить третий угол. По свойству, общему для всех треугольников, сумма углов равна 180º. Значит, третий определится как 180º — 70º — 70º = 40º.
Ответ: углы равны 70º, 70º, 40º.
№5. Известно, что в равнобедренном треугольнике угол, лежащий напротив основания, равен 90º. На основании отмечена точка. Отрезок, соединяющий ее с прямым углом, делит его в отношении 1 к 4.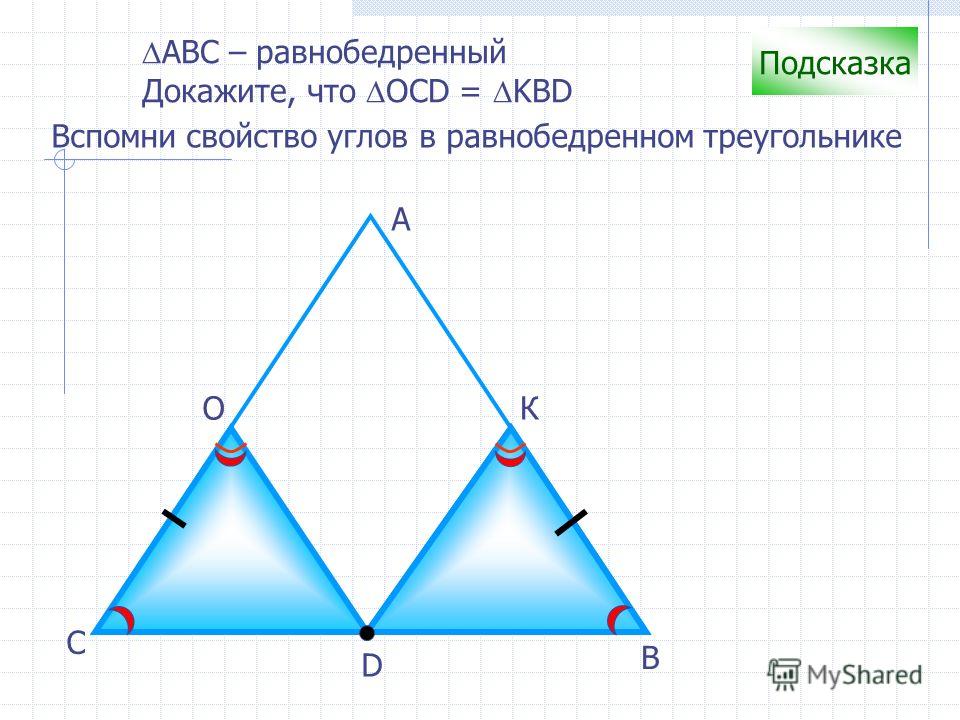 Нужно узнать все углы меньшего треугольника.
Нужно узнать все углы меньшего треугольника.
Решение. Один из углов можно определить сразу. Поскольку треугольник прямоугольный и равнобедренный, то те, что лежат у его основания, будут по 45º, то есть по 90º/2.
Второй из них поможет найти известное в условии отношение. Поскольку оно равно 1 к 4, то частей, на которые он делится получается всего 5. Значит, чтобы узнать меньший угол треугольника нужно 90º/5 = 18º. Осталось узнать третий. Для этого из 180º (суммы всех углов треугольника) нужно вычесть 45º и 18º. Вычисления несложные, и получится: 117º.
Презентация «Равнобедренный, разносторонний и равносторонний треугольники» 3 класс
Урок математики
в 3 классе
Улыбнитесь друг другу,
и удобнее садитесь.
Руки? На месте!
Ноги? На месте!
Локти? У края!
Спина? Прямая!
Девиз урока
Шарада
СУМКА
СУММА
С «К» — для продуктов годна,
С «М» — для сложенья нужна.
Шарада
ШЕСТЬ
МЕСТЬ
С «Ш» — для счёта я нужна,
С «М» — обидчикам страшна!
??????
Треугольник, у которого есть прямой угол, называется прямоугольным
Правило
??????
Треугольник, у которого есть тупой угол, называется тупоугольным
Правило
??????
Треугольник, у которого все углы острые, называется остроугольным
Правило
1. Начерти прямоугольный треугольник
Начерти прямоугольный треугольник
2. Начерти остроугольный треугольник
3. Начерти тупоугольный треугольник
Самостоятельная работа
4. Начерти любой прямоугольный треугольник, одна сторона которого на 2 см больше другой
Самостоятельная работа
?????
Равнобедренный, разносторонний и равностроннний треугольники
Тема урока
Узнать, что такое…
Уметь чертить…
Задачи урока
Начертите треугольник так, чтобы все стороны были разные
Треугольник, у которого все стороны разные, называется разностронним
Правило
Начертите треугольник так, чтобы 2 стороны были равные
Треугольник, у которого 2 стороны равные, называется равнобедренным
Правило
Начертите треугольник так, чтобы 3 стороны были равные
Треугольник, у которого все стороны равные, называется равностронним
Правило
№440,441. с. 133
№448. с. 135
(для желающих)
Домашнее задание
Изобразите разносторонний треугольник
Физминутка
Изобразите равносторонний треугольник
Может ли равнобедренный треугольник быть остроугольным?
Является ли равнобедренный треугольник симметричной фигурой?
Можно ли равнобедренный треугольник разбить на 2 равных прямоугольных треугольника?
Можно ли равносторонний треугольник назвать равнобедренным?
Определи вид треугольника
по сторонам
Определи вид треугольника
по углам
Ещё остались вопросы
Самооценка
Всё усвоил(а)
Пока всё сложно
Треугольники бывают…
Равнобедренный – это…
Разносторонний – это…
Равносторонний — это
Итог урока
Презентация «Виды треугольников» 3 класс
60
180
1100
950
52
32
320
2500
590
422
554
40 ∙ 80 : 100= О 200 ∙ 7 – 300 = Е
3 ∙ 26 – 18 = Т 649 – 40 – 19 = Н
250 + 700 = У 880 : 44 ∙ 9 = Р
4 + 96 : 2 = Г 482 – 60 = И
560 : 7 ∙ 4 = Л 300 ∙ 9 – 200 = Ь
902 – 348 = К
Какие виды треугольников вы знаете?
Проверка. Треугольники бывают:
Треугольники бывают:
- прямоугольные
- тупоугольные
- остроугольные
- равнобедренные
- равносторонние
1. Прямоугольные треугольники
Треугольник, у которого есть прямой угол, называется прямоугольным.
Каждый из таких треугольников называют прямоугольным.
2.Тупоугольные треугольники
Треугольник, у которого есть тупой угол, называется тупоугольным.
Это – тупоугольные треугольники.
`
3. Остроугольные треугольники
Треугольник, у которого все углы острые, называется остроугольным.
Это – остроугольные треугольники.
4. Равнобедренные треугольники
Треугольник, у которого есть равные стороны, называется равнобедренным.
Каждый из таких треугольников — равнобедренный.
5.Равносторонние треугольники
Треугольник, у которого все стороны равны, называется равносторонним
Это равносторонние треугольники
6.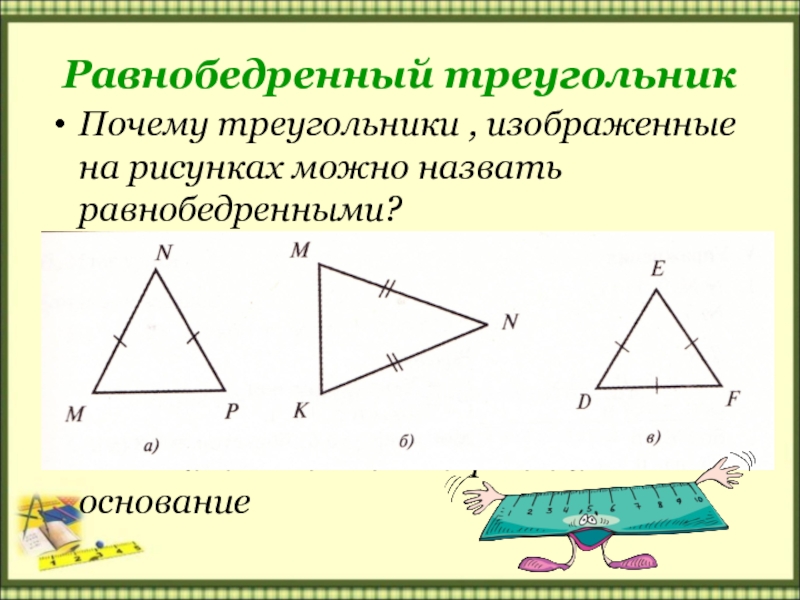 Разносторонние треугольники
Разносторонние треугольники
Треугольник, у которого все стороны имеют разную длину, называется разносторонним
- Это разносторонние треугольники
1
3
7. Задание:
Определить виды треугольников, изображённых ниже
Почему они так называются?
2
4
Как определить вид угла?
Острый угол – это угол, который меньше прямого.
Тупой угол – это угол, который больше прямого.
В
А
С
— Догадайся из какого куска проволоки (1,2,3) сделали каждый треугольник.
— Найди периметры этих треугольников.
Задача:
Е
Д
В
К
М
С
А
О
Т
50
50
20
1
30
30
30
2
10
40
35
3
1. 50+50+20=120(см) — Р
50+50+20=120(см) — Р
2. 30 • 3=90(см) — Р
3. 10+40+35=85(см) — Р
- 1. 50+50+20=120(см) — Р 2. 30 • 3=90(см) — Р 3. 10+40+35=85(см) — Р
КДЕ
АВС
ОМТ
Реши задачу
Для изготовления геометрической аппликации на уроках труда ученики 3 класса вырезали 130 красных треугольников, синих на 27 больше, чем красных , а зеленых – на 17 меньше, чем синих.
Сколько всего треугольников вырезали ?
- 130+27 = 157 ( т ) – синих
2) 157- 17 = 140 ( т ) – зеленых
3) 130 + 157 + 140 = 427 ( т )
Виды треугольников
по сторонам
по углам
У меня всё получилось, я доволен свой работой.
У меня не всё получилось, но я доволен своей работой.
Я хорошо знаю теоретический материал, но в практической работе у меня получилось не всё.
Мне было сложно и малопонятно.
Виды треугольников по соотношению сторон
Привет,
ребята!
А
я приготовил вам загадку.
Злая рыба, хвост-лопата, откусила полквадрата –
Целый угол, верь не верь! Кто ж
он, бедненький, теперь?
Догадались, что это? Ну конечно, треугольник!
Три вершины тут видны,
Три угла, три стороны, —
Ну, пожалуй, и довольно!
Перед нами треугольник.
И
действительно, сегодня я хочу поговорить с вами о треугольниках.
Посмотрите, я нарисовал несколько разных треугольников – и больших, и маленьких.
Обратите
внимание вот на эти треугольники.
Как
вы думаете, что между ними общего? Ну, конечно, у каждого из них по три вершины,
по три стороны и по три угла.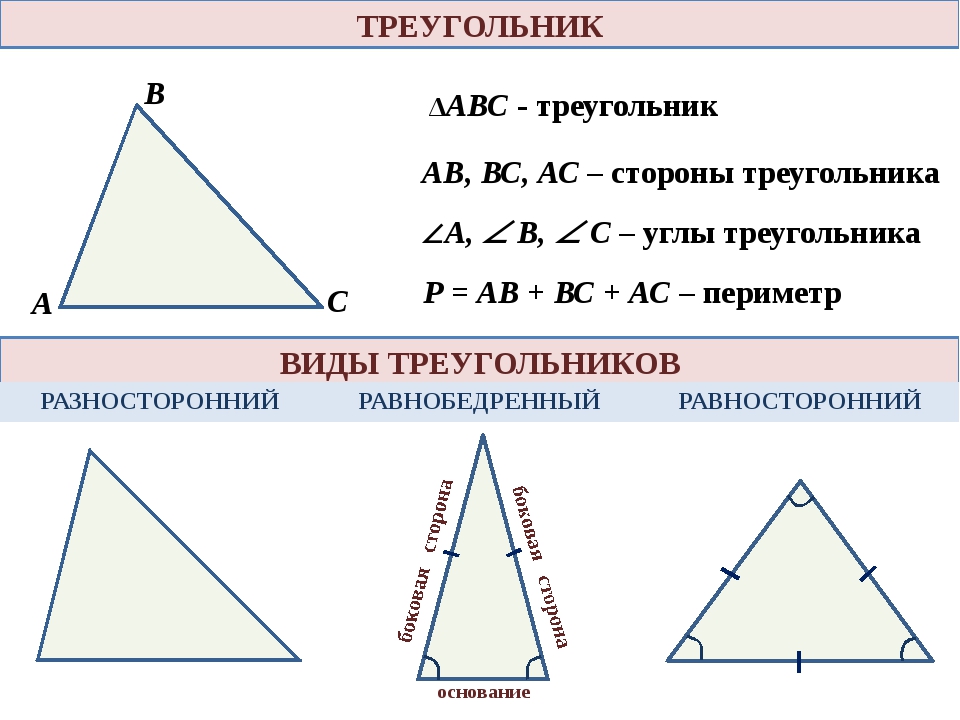 А ещё у каждого из
А ещё у каждого из
них все углы острые. Да и высота этих треугольников одинакова. Но
можно ли сказать, что все эти треугольники одинаковые? Я думаю, вы прекрасно
видите, что они разные. Обратите внимание на первый треугольник. Давайте
измерим все его стороны. Что можно сказать? У этого треугольника все стороны разные
по длине. То есть, это – разносторонний треугольник.
Попробуем
измерить стороны второго треугольника. У него есть две равные стороны. Такие
треугольники, у которых две стороны равны между собой, принято называть равнобедренными.
Эти
равные стороны называются боковыми, а третья сторона – основанием
равнобедренного треугольника.
В
равнобедренном треугольнике и углы, которые находятся при основании,
между собой равны.
Измеряем
стороны третьего треугольника. Здесь все стороны между
собой равны. Такие треугольники, у которых все стороны равны между собой,
Такие треугольники, у которых все стороны равны между собой,
называются равносторонними. А как вы думаете, что можно
сказать про углы равностороннего треугольника? В равностороннем треугольнике все
углы между собой равны.
Итак,
мы выделили три группы треугольников по соотношению сторон – разносторонние,
равнобедренные и равносторонние.
Кстати,
вы знаете? Такая классификация треугольников по видам была создана древними
греками. Примерно две тысячи триста лет назад древнегреческий математик Евклид
в одной из книг своего сборника «Начала» писал:
«Из
трёхсторонних фигур равносторонний треугольник есть фигура, имеющая три равные
стороны, равнобедренный же – имеющий только две равные стороны, разносторонний
же – имеющий три неравные стороны».
Ну
вот и всё, что я сегодня хотел вам рассказать. Я надеюсь, вы слушали
внимательно и теперь знаете, что: треугольники по соотношению сторон
могут делиться на три вида – разносторонние, равнобедренные и равносторонние.
А
теперь я предлагаю вам внимательно посмотреть вот на эти треугольники.
Видите,
на каждом из них есть номер. Я предлагаю вам определить, какие из этих
треугольников разносторонние, какие равнобедренные, и какие – равносторонние.
А
сейчас проверьте, зоркие ли у вас глаза, внимательно ли вы меня слушали.
Разносторонние
треугольники под номерами один и семь.
К
равнобедренным треугольникам относятся треугольники под номерами два, пять и
восемь. А треугольники под номерами один, четыре, есть – равносторонние.
Ну
что, вы так выполнили задание?
Какие
молодцы!
А
теперь пришло время нам попрощаться. До свидания, ребята!
Определение вида треугольника. Треугольник
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника
, отрезки — его сторонами
. Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла.
По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис.
5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
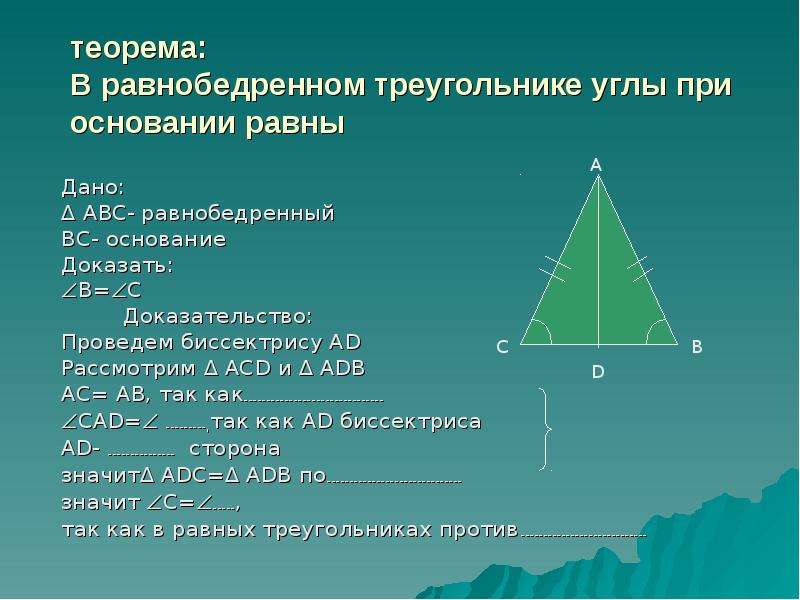
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми
, третья сторона — основанием
. В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными
(рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны
. Равносторонние треугольники
Равносторонние треугольники
всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.

- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются …
, отрезки — его …
. Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
Треугольник — определение и общие понятия
Треугольник – это такой простой многоугольник, состоящий из трех сторон и имеющий столько же углов.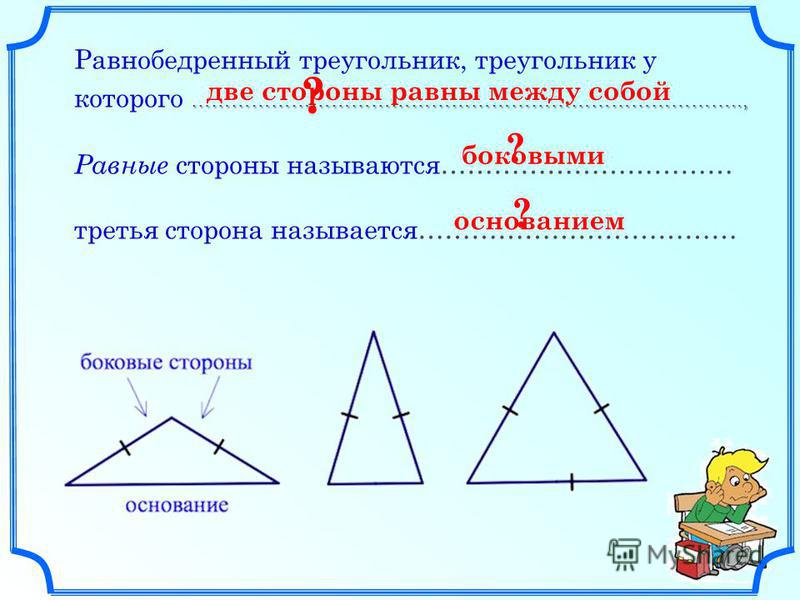 Его плоскости ограничиваются 3 точками и 3 отрезками, попарно соединяющими даные точки.
Его плоскости ограничиваются 3 точками и 3 отрезками, попарно соединяющими даные точки.
Все вершины любого треугольника, независимо от его разновидности, обозначаются заглавными латинскими буквами, а его стороны изображаются соответствующими обозначениями противоположных вершин, только не большими буквами, а малыми. Так, например, треугольник с вершинами обозначенными буквами А, В и С имеет стороны a, b, c.
Если рассматривать треугольник в евклидовом пространстве, то это такая геометрическая фигура, которая образовалась с помощью трех отрезков, соединяющих три точки, которые не лежат на одной прямой.
Посмотрите внимательно на рисунок, который изображен вверху. На нем точки А, В и С являются вершинами этого треугольника, а его отрезки носят названия сторон треугольника. Каждая вершина этого многоугольника образует внутри его углы.
Виды треугольников
Согласно величины, углов треугольников, они делятся на такие разновидности, как:
Прямоугольные;
Остроугольные;
Тупоугольные.
К прямоугольным принадлежат такие треугольники, у которых в наличии есть один прямой угол, а остальные два имеют острые углы.
Остроугольные треугольники – это те, у которых все его углы острые.
А если у треугольника имеется один тупой угол, а два остальных угла острые, то такой треугольник относится к тупоугольным.
Каждый из вас прекрасно понимает, что не все треугольники имеют равные стороны. И соответственно тому, какую длину имеют его стороны, треугольники можно поделить на:
Равнобедренные;
Равносторонние;
Разносторонние.
Задание: Нарисуйте разные виды треугольников. Дайте им определение. Какое между ними отличие вы видите?
Основные свойства треугольников
Хотя эти простые многоугольники могут отличаться друг от друга величиной углов или сторон, но в каждом треугольнике есть основные свойства, характерны для этой фигуры.
В любом треугольнике:
Общая сумма всех его углов равняется 180º.
Если он принадлежит к равносторонним, то каждый его угол равен 60º.
Равносторонний треугольник имеет одинаковые и ровные между собой углы.
Чем меньше сторона многоугольника, тем меньший угол расположен напротив него и наоборот напротив большей стороны находиться больший угол.
Если стороны равные, то напротив них расположены равные углы, и наоборот.
Если взять треугольник и продлить его сторону, то в итоге мы образуется внешний угол. Он равен сумме внутренних углов.
В любом треугольнике его сторона, независимо от того, какую бы вы не выбрали, все равно будет меньше, чем сумма 2-х других сторон, но больше чем их разность:
1. a b – c;
2. b a – c;
3. c a – b.
Задание
В таблице приведены уже известные два угла треугольника. Зная общую сумму всех углов найдите, чему равен третий угол треугольника и занесите в таблицу:
1. Сколько градусов имеет третий угол?
2. К какому виду треугольников он относится?
Признаки равности треугольников
I признак
II признак
III признак
Высота, биссектриса и медиана треугольника
Высота треугольника — перпендикуляр, проведенный из вершины фигуры к его противоположной стороне, называется высотой треугольника. Все высоты треугольника пересекаются в одной точке. Точка пересечения всех 3-х высот треугольника является его ортоцентром.
Отрезок, проведенный из данной вершины и соединяющий ее на средине противоположной стороны, является медианой. Медианы, также как и высоты треугольника, имеют одну общую точку пересечения, так называемый центр тяжести треугольника или центроид.
Биссектриса треугольника — отрезок, соединяющий вершину угла и точку противоположной стороны, а также делящий этот угол пополам. Все биссектрисы треугольника пересекаются в одной точке, которую называют центром окружности, вписанной в треугольник.
Отрезок, который соединяет середины 2-х сторон треугольника, называется средней линией.
Историческая справка
Такая фигура, как треугольник, была известна еще в Древние времена. Об этой фигуре и ее свойствах упоминалось на египетских папирусах четырех тысячелетней давности.
Немного позже, благодаря теореме Пифагора и формуле Герона, изучение свойства треугольника, перешло на более высокий уровень, но все же, это происходило более двух тысяч лет назад.
В XV – XVI веках стали проводить много исследований о свойствах треугольника и в итоге возникла такая наука, как планиметрия, которая получила название «Новая геометрия треугольника».
Ученый из России Н. И.Лобачевский внес огромный вклад в познание свойств треугольников. Его труды в дальнейшем нашли применение как в математике, так и физике и кибернетике.
Благодаря знаниям свойств треугольников возникла и такая наука, как тригонометрия. Она оказалась необходимой для человека в его практических потребностях, так как ее применение просто необходимо при составлении карт, измерении участков, да и при конструировании различных механизмов.
А какой самый известный треугольник вы знаете? Это конечно же Бермудский треугольник! Он получил такое название в 50-х годах из-за географического расположения точек (вершин треугольника), внутри которых, согласно существующей теории, возникали связанные с ним аномалии. Вершинами Бермудского треугольника выступают Бермудские острова, Флорида и Пуэрто-Рико.
Задание: А какие теории о Бермудском треугольнике слышали вы?
А известно ли вам, что в теории Лобачевского при сложении углов треугольника их сумма всегда имеет результат меньший, чем 180º. В геометрии Римана, сумма всех углов треугольника больше 180º, а в трудах Эвклида она равна 180 градусам.
Домашнее задание
Решите кроссворд на заданную тему
Вопросы к кроссворду:
1. Как называется перпендикуляр, который провели из вершины треугольника к прямой, расположенной на противоположной стороне?
2. Как, одним словом можно назвать сумму длин сторон треугольника?
3. Назовите треугольник, у которого две стороны равны?
4. Назовите треугольник, у которого есть угол, равный 90°?
5. Какое название носит большая, из сторон треугольника?
6. Название стороны равнобедренного треугольника?
7. Их всегда три в любом треугольнике.
8. Какое название носит треугольник, у которого один из углов превышает 90°?
9. Название отрезка, соединяющего вершину нашей фигуры со срединой противоположной стороны?
10. В простом многоугольнике АВС, заглавная буква А является …?
11. Какое название носит отрезок, делящий угол треугольника пополам.
Вопросы к теме треугольников:
1. Дайте определение.
2. Сколько высот он имеет?
3. Сколько биссектрис у треугольника?
4. Чему равна его сумма углов?
5. Какие виды этого простого многоугольника вам известны?
6. Назовите точки треугольников, которые носят название замечательных.
7. Каким прибором можно измерить величину угла?
8. Если стрелки часов показывают 21 час. Какой угол образуют часовые стрелки?
9. На какой угол поворачивается человек, если ему дана команда «налево», «кругом»?
10. Какие еще определения вам известны, которые связанные с фигурой, имеющей три угла и три стороны?
Предмети > Математика > Математика 7 класс
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника
, отрезки — его сторонами
. Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла.
По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми
, третья сторона — основанием
. В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными
(рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны
. Равносторонние треугольники
всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются …
, отрезки — его …
. Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
Треугольник (с точки зрения пространства Эвклида) – это такая геометрическая фигура, которая образована тремя отрезками, соединяющими три точки, не лежащими на одной прямой. Три точки, которые образовали треугольник, называются его вершинами, а отрезки соединяющие вершины называются сторонами треугольника. Какие есть треугольники?
Равные треугольники
Существует три признака равенства треугольников. Какие треугольники называются равными? Это те, у которых:
- равны две стороны и угол между этими сторонами;
- равна одна сторона и два прилежащие к ней угла;
- равны все три стороны.
У прямоугольных треугольников существуют следующие признаки равенства:
- по острому углу и гипотенузе;
- по острому углу и катету;
- по двум катетам;
- по гипотенузе и катету.
Какие бывают треугольники
По числу равных сторон треугольник может быть:
- Равносторонним. Это треугольник с тремя равными сторонами. Все углы в равностороннем треугольнике равны 60 градусов. Кроме этого, совпадают центры описанной и вписанной окружностей.
- Неравносторонним. Треугольник, не имеющий равных сторон.
- Равнобедренным. Это треугольник с двумя равными сторонами. Две одинаковые стороны – боковые, а третья сторона – основание. В таком треугольнике совпадают биссектриса, медиана и высота, если их опустить на основание.
По величине углов треугольник может быть:
- Тупоугольным — когда один из углов имеет величину более 90 градусов, то есть когда он тупой.
- Остроугольным – если все три угла в треугольнике острые, то есть они имеют величину менее 90 градусов.
- Какой треугольник называется прямоугольным? Это такой, у которого есть один прямой угол равный 90 градусов. Катетами в нем будут назваться две стороны, которыми образован этот угол, а гипотенузой – противолежащая прямому углу сторона.
Основные свойства треугольников
- Против меньшей стороны всегда лежит меньший угол, а больший угол всегда лежит против большей стороны.
- Равные углы всегда лежат против равных сторон, а против разных сторон всегда лежат разные углы. В частности, в равностороннем треугольнике все углы имеют одинаковое значение.
- В любом треугольнике сумма углов равняется 180 градусов.
- Внешний угол можно получить, если у треугольника продолжить одну из его сторон. Величина внешнего угла будет равняться сумме не смежных с ним внутренних углов.
- Сторона треугольника больше, чем разность его двух других сторон, но меньше, чем их сумма.
В пространственной геометрии Лобачевского сумма углов треугольника будет всегда меньше, чем 180 градусов. На сфере это значение больше 180 градусов. Разность между 180 градусов и суммой углов треугольника называется дефектом.
Треугольник
— это выпуклый многоугольник с наименьшим числом углов и сторон. Треугольник образуется замкнутой ломаной , состоящей из трёх звеньев, и той частью плоскости, которая находится внутри ломаной.
В тексте треугольники обозначаются символом Δ и тремя прописными латинскими буквами, стоящими при вершинах — ΔABC
:
В треугольнике ABC
точки A
, B
и C
— это вершины треугольника
, отрезки AB
, BC
и CA
— стороны треугольника
. Углы, образованные сторонами треугольника, называются углами треугольника
.
Нижнюю сторону треугольника обычно называют основанием
. В треугольнике ABC
сторона AC
— основание.
Виды треугольников
Треугольники различаются между собой, во-первых, по характеру углов, во-вторых, по характеру сторон.
По характеру углов треугольник называется:
- Остроугольным
, если все его углы являются острыми. - Прямоугольным
, если один угол прямой. В прямоугольном треугольнике стороны, образующие прямой угол, называются катетами
, а сторона, лежащая напротив прямого угла — гипотенузой
. - Тупоугольным
, если один из его углов тупой.
По характеру сторон треугольник называется:
- Разносторонним
, если все его стороны имеют различную длину. - Равнобедренным
, если две его стороны равны между собой. Равные стороны называются боковыми сторонами
, а третья сторона — основанием
. В равнобедренных треугольниках углы при основании равны. - Равносторонним
, если все три его стороны равны между собой. В равносторонних треугольниках все три угла равны.
Равные стороны стороны на чертежах отмечаются одинаковым количеством чёрточек.
треугольников — равносторонние, равнобедренные и чешуйчатые
Треугольник имеет три стороны и три угла | ||
Три угла всегда складываются в 180 ° |
Равносторонний, равнобедренный и чешуйчатый
Треугольникам даны три специальных имени, которые показывают, сколько сторон (или углов) равны.
Может быть 3 , 2 или Нет равных сторон / углов:
Равносторонний треугольник Три равных стороны | |
Равнобедренный треугольник Две равные стороны | |
Скаленовый треугольник Нет равные стороны |
Как запомнить? По алфавиту идут 3, 2, нет:
- Равносторонний : «равный» — боковой (боковой означает сторона), поэтому все стороны имеют равные стороны
- Равнобедренный : означает «равноногие», а у нас две ноги , верно? Также i SOS celes имеет два одинаковых «S ides», соединенных стороной « O dd».
- Скален : означает «неровный» или «нечетный», поэтому нет равных сторон.
Какой тип угла?
Треугольники также могут иметь имена, которые сообщают вам, какой тип угла находится внутри :
Острый треугольникВсе углы меньше 90 ° | |
Прямой треугольникИмеет прямой угол (90 °) | |
Тупой треугольникИмеет угол более 90 ° |
Объединение имен
Иногда у треугольника будет два имени, например:
Правый равнобедренный треугольникИмеет прямой угол (90 °), а также два равных угла. Вы можете угадать, каковы равные углы? |
Поиграй с ним…
Попробуйте перетащить точки и составить разные треугольники:
Вы также можете поиграть с Интерактивным треугольником.
Уголки
Три внутренних угла всегда составляют 180 °
Периметр
Периметр — это расстояние по краю треугольника: просто сложите три стороны:
Площадь
Площадь составляет , половина базовой, умноженная на высоту .
- «b» — расстояние по основанию
- «h» — высота (измеренная под прямым углом к основанию)
Площадь = ½ × b × h
Формула работает для всех треугольников.
Примечание: более простой способ записать формулу — bh / 2
Пример: Какова площадь этого треугольника?
(Примечание: 12 — это высота , а не длина левой стороны)
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Основание может быть любой стороной. Убедитесь, что «высота» измеряется под прямым углом к »основанию». :
(Примечание: вы также можете рассчитать площадь, исходя из длин всех трех сторон, используя формулу Герона.)
Почему область «половина bh»?
Представьте, что вы «удвоили» треугольник (перевернули его вокруг одного из верхних краев), чтобы получилась квадратная форма (параллелограмм), которую можно преобразовать в простой прямоугольник:
ЗАТЕМ вся площадь составляет bh , что соответствует обоим треугольникам, поэтому только один будет ½ × bh .
Что такое равнобедренный треугольник?
Математик Евклид, известный как «отец геометрии», жил около 300 г. до н.э.Он придумал правила, касающиеся равнобедренных треугольников. Но что такое равнобедренный треугольник? Чем он отличается от других треугольников? А как можно рассчитать его высоту, периметр и площадь? Вот ответы на эти и другие вопросы. И обязательно посмотрите другие видео из нашей серии «Геометрия»!
Что такое равнобедренный треугольник?
«Равнобедренный» происходит от греческих слов «isos» (что означает равный) и «skelos» (что означает нога). Как следует из этого названия, равнобедренный треугольник имеет две равные стороны с двумя равными углами, противоположными этим сторонам.Некоторые из других типов треугольников включают:
- Каждый равносторонний треугольник может также считается равнобедренным треугольником, но не каждый равнобедренный треугольник является равносторонним.
Следовательно, в зависимости от размера стороны и угла, ваш равнобедренный треугольник может быть острым, тупым, прямым или равносторонним треугольником.
Части равнобедренного треугольника
Две равные стороны равнобедренного треугольника — ноги, а третья сторона — основание. Угол между равными сторонами называется углом при вершине. При сложении все углы должны равняться 180 градусам.
Высота
Если бы вы провели воображаемую линию от угла вершины к основанию (под углом 90 градусов от основания), вы бы получили высоту вашего равнобедренного треугольника. Для расчета высоты используйте следующее уравнение:
«a» — это длина ноги, а «b» — это базовая длина.После ввода этих чисел в уравнение вы можете упростить его, используя порядок операций для определения длины высоты.
Периметр
Периметр — это размер вокруг внешней части формы. Чтобы рассчитать это, вам просто нужно добавить длину каждой стороны. Однако, поскольку есть две стороны одинаковой длины, вы можете упростить его до следующего уравнения:
p = 2a + b
Площадь
Площадь — это количество единичных квадратов, которые могут уместиться в данной форме.Чтобы определить площадь равнобедренного треугольника, вы можете использовать следующую формулу:
Как показано в уравнении, вам потребуются измерения для основания и высоты. Если высота не указана, вы можете сначала использовать уравнение высоты. Затем введите числа и решите область.
Чтобы вычислить высоту, периметр и площадь треугольника, вам необходимо сначала определить тип треугольника. Таким образом, вы можете использовать правильные уравнения для получения точных результатов.
О Джейми Гудвине
Джейми окончил Университет Бригама Янга в Айдахо по специальности «Английский язык». Она провела несколько лет, обучая и обучая учеников начальной, средней школы и колледжа. В настоящее время она работает писателем по контракту и разработчиком учебных программ для онлайн-курсов. В свободное время она любит бегать и проводить время со своими мальчиками!
Равнобедренный треугольник | Свойства и теоремы
Равнобедренные треугольники — это треугольники, у которых две стороны равны, а у третьего — разная.Мы знаем, что треугольники — это трехсторонние замкнутые многоугольники, и они классифицируются как равносторонние, равнобедренные или разносторонние в зависимости от длины их сторон. В этом разделе мы узнаем об определении равнобедренного треугольника и его свойствах.
Что такое равнобедренный треугольник?
Равнобедренный треугольник — это треугольник, у которого две стороны равны. Давайте сделаем небольшое упражнение, чтобы лучше понять это. Возьмите прямоугольный лист бумаги и сложите его пополам. Проведите линию от верхнего загнутого угла к нижнему краю.Вы можете увидеть треугольник, когда открываете лист. Отметьте вершины треугольников как A, B и C. Теперь измерьте AB и AC. Повторите это упражнение с разными тактами и проследите за закономерностью. Мы можем заметить, что AB и AC всегда равны. Этот тип треугольника, в котором две стороны равны, называется равнобедренным треугольником .
Свойства равнобедренного треугольника
Каждая геометрическая фигура обладает некоторыми свойствами, которые делают ее отличной от других.Вот список некоторых свойств равнобедренных треугольников:
- Две равные стороны равнобедренного треугольника называются ногами , а угол между ними называется углом при вершине или углом при вершине.
- Сторона, противоположная углу при вершине, называется основанием, а углы основания равны.
- Перпендикуляр от угла при вершине делит пополам основание , и угол при вершине.
Теорема о равнобедренном треугольнике
В равнобедренном треугольнике, если две стороны треугольника равны, то углы, противоположные этим сторонам, совпадают.И наоборот, если два угла треугольника равны, соответствующие стороны также совпадают. Таким образом, мы можем сказать, что ABC = ∠ACB, а AB = AC на данном рисунке:
Теперь мы также знаем, что в равнобедренном треугольнике высота от угла при вершине (перпендикуляре) делит пополам основание и угол при вершине. Итак, можно сказать, что ∠BAD = ∠DAC, а BD = DC. Имея эту информацию, мы можем сказать, что ΔADB и ΔCDB совпадают.
Формула площади равнобедренного треугольника
Площадь равнобедренного треугольника можно вычислить разными способами на основе его известных элементов.2} {4}} \]
Часто задаваемые вопросы о равнобедренном треугольнике
Каковы углы в равнобедренном треугольнике?
Равнобедренный треугольник имеет угол при вершине и два угла при основании. Углы основания равнобедренного треугольника равны.
Что такое равнобедренный треугольник?
Треугольник, в котором две стороны равны, называется равнобедренным треугольником. Следуя этому факту, если две стороны треугольника равны, то и углы, противоположные этим сторонам, также равны.
Объясните свойство равнобедренного треугольника.
Свойство равнобедренного треугольника утверждает, что, когда две стороны равны, углы основания также равны, а перпендикуляр от угла при вершине делит основание пополам.
Как узнать, является ли треугольник равнобедренным?
Треугольник может быть разносторонним, равнобедренным или равносторонним, если его классифицировать по длине его сторон.В треугольнике, если любые две стороны равны, он считается равнобедренным треугольником.
Суммируются ли равнобедренные треугольники 180?
Сумма внутренних углов всех треугольников всегда равна 180 °. Следовательно, в сумме углы равнобедренного треугольника составляют 180 °.
Какой треугольник является прямым равнобедренным треугольником?
В прямоугольном равнобедренном треугольнике равные стороны образуют прямой угол. Другими словами, любой треугольник с углами 90 °, 45 °, 45 ° является правильным равнобедренным треугольником.
Могут ли быть правильными равнобедренные треугольники?
Да, равнобедренные треугольники могут быть прямоугольными, если их три угла составляют 90 °, 45 ° и 45 ° соответственно. В прямоугольном равнобедренном треугольнике равные стороны соединяются, образуя прямой угол.
Равносторонний и равнобедренный треугольники
На этом уроке геометрии 5-го класса рассматриваются равносторонние, равнобедренные и разносторонние треугольники, а также предлагаются различные упражнения, включая рисование.
упражнения на эти темы для студентов.
Если все три стороны треугольника равны Equi — относится к «одинаковым» или | Если только две стороны треугольника равны Подумай об этом Отметьте два совпадающих |
Наконец, если ни одна из сторон треугольника |
1.Классифицируйте треугольники по Каждую можно маркировать |
2. Заполните таблицу, классифицируя треугольники, помеченные как (a), (d), (e) и
(g) выше как «острый», «правый»,
или «тупые» (по углам), а также как
«Равносторонний», «равнобедренный» или «разносторонний» (по бокам).
| Треугольник | Классификация по сторонам | Классификация по углам |
| а | ||
| г | ||
| e | ||
| г |
3.Постройте точки и соедините их Треугольник 1: (0, 0), (4, 0), (0, 4) ___________________________ и ___________________________ Треугольник 2: (5, 5), (1, 8), (9, 4) ___________________________ и ___________________________ |
4.Нарисуйте в координатной сетке острый разносторонний треугольник.
6. а. Нарисуйте разносторонний тупой треугольник, одна сторона которого равна 3 см, а другая — 7 см.
Подсказка:
Сначала нарисуйте 7-сантиметровую сторону, затем 3-сантиметровую, образуя любой тупой угол с
первая сторона.
г.
Измерьте третью сторону.
Сравните свой треугольник с треугольниками одноклассников или нарисуйте другой
один себе.
Вы можете нарисовать несколько
разные треугольники с этой информацией,
или все они идентичны
(конгруэнтно)?
7. а. Нарисуйте равнобедренный прямоугольный треугольник, две стороны которого
отмерьте 5 см.
Подсказка: сначала нарисуйте прямой угол. Затем отмерьте стороны по 5 см. Затем втяните
последняя сторона.
г. Измерьте третью сторону. Это ____________ см.
Сравните свой треугольник с
те из ваших одноклассников, или нарисуйте другой
один себе.
Вы можете нарисовать несколько
разные треугольники с этой информацией,
или все они идентичны
(конгруэнтно)?
8. а. Нарисуйте любой равнобедренный треугольник.
Подсказка:
Нарисуйте любой угол. Затем отмерьте две совпадающие стороны, убедившись, что они
такой же длины.
Затем нарисуйте последнюю сторону.
г. Измерьте углы вашего треугольника. Они
Измерьте ________ °, ________ ° и ________ °.
Сумма углов равна ________ °.
9. Измерьте все углы в
равнобедренные треугольники (а) и (б).
При необходимости продолжайте их стороны.
| а. | г. |
| _________ °, _________ ° и ________ °. Сумма углов составляет ________ °. | _________ °, _________ ° и ________ °. Сумма углов составляет ________ °. |
Что ты заметил?
__________________________________________________________________________________
__________________________________________________________________________________
Там Остающийся угол | Вы можете найти верхний угол и |
10. Угол при A составляет 40 °.
Нарисуйте еще один угол 40 ° в точке B, а затем продолжите его стороной
.
так что вы получите равнобедренный треугольник с углами основания 40 °.
Измерьте верхний угол. Это _______ °. Сумма трех угловых мер составляет
_______ °.
11.
а. Нарисуйте равнобедренный треугольник с углами в основании 75 °. (Длина
стороны могут быть любыми.)
Подсказка: начните с рисования
сторона основания (любой длины). Затем нарисуйте углы 75 °.
г. Измерьте верхний угол. Это _______ °.Сумма трех угловых мер составляет
_______ °.
г. Сравните ваш треугольник с
те из ваших одноклассников, или нарисуйте другой
один себе.
Вы можете нарисовать несколько
разные на вид треугольники с этой информацией, или все они идентичны?
| 14. а. Может ли равносторонний треугольник быть прямоугольным? Если да, нарисуйте пример. Если нет, объясните почему нет. |
г. Может ли разносторонний треугольник быть тупым?
Если да, нарисуйте пример. Если нет, объясните
почему нет.
г. Может ли острый треугольник быть разносторонним?
Если да, нарисуйте пример. Если нет, объясните
почему нет.
г. Может ли прямоугольный треугольник быть разносторонним?
Если да, нарисуйте пример.Если нет, объясните
почему нет.
e. Может ли тупой треугольник быть равносторонним?
Если да, нарисуйте пример. Если нет, объясните
почему нет.
Этот урок взят из книги Марии Миллер Math Mammoth Geometry 1 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
| Телефон : | 780-427-5318 | |
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | ||
| Телекопье: | 780-427-1179 | |
| Adresse de Courriel: | cshelpdesk @ gov.ab.ca | |
Что такое равнобедренный треугольник? — Определение, свойства и теорема — Видео и стенограмма урока
Свойства равнобедренных треугольников
Конечно, главное свойство равнобедренных треугольников — это их две совпадающие стороны. Кроме того, все равнобедренные треугольники также имеют совпадающие углы при основании.
Это свойство справедливо для всех равнобедренных треугольников, независимо от направления их вершин.
Если нам известна величина любого из углов основания, то мы можем определить меру третьего (при вершине) угла. Поскольку в сумме углы треугольника равны 180 градусам, третий угол равен 180 минус двукратному основному углу, в результате получается формула для измерения угла при вершине равнобедренного треугольника:
A = 180-2 b
Где A — это размер при вершине, а b — это размер одного базового угла.
Итак, если базовый угол в равнобедренном треугольнике составлял 58 градусов, мы могли бы включить это в нашу формулу, чтобы определить меру угла при вершине:
A = 180 — (2 * 58)
A = 180 — 116
A = 64
Угол при вершине треугольника составляет 64 градуса.
Точно так же, если мы знаем меру угла при вершине, мы можем найти меры обоих базовых углов на основе того же понимания. В сумме углы составляют 180 градусов, 180 минус угол при вершине приведет к сумме обоих базовых углов.Затем мы просто делим это на два, чтобы найти размер каждого базового угла.
2 b = (180 — A )
Если угол при вершине равнобедренного треугольника составляет 72 градуса, мы могли бы использовать это в нашей формуле для определения меры обоих углов основания.
2 b = (180 — 72)
2 b = 108
b = 108/2
b = 54
Размер каждого угла основания в треугольнике составляет 54 градуса .
Теорема о равнобедренном треугольнике
Теорема о равнобедренном треугольнике включает три утверждения:
Утверждение 1. Высота равнобедренного треугольника или отрезок прямой, который простирается от вершины треугольника до середины его основания, перпендикулярен его основанию.
Эта часть теоремы верна, потому что конгруэнтные стороны равнобедренного треугольника помещают его вершину (точка A) прямо над серединой основания (точка D). Итак, когда мы рисуем высоту, получается прямая линия, пересекающая основание под прямым углом.
Положение 2. Высота равнобедренного треугольника делит пополам или равномерно пополам угол его вершины.
Поскольку высота совпадает со средней точкой основания (точка D), она служит линией симметрии треугольника. Два результирующих угла при вершине (точка A) совпадают.
Утверждение 3. Два результирующих треугольника, образованных высотой равнобедренного треугольника, совпадают.
Поскольку высота соответствует основанию в его средней точке (точка D), отрезки BD и CD также совпадают друг с другом.
И поскольку оба новых треугольника имеют третью сторону, у нас также есть совпадение. Итак, два треугольника, образованные из исходного равнобедренного треугольника, конгруэнтны, потому что все три стороны одного совпадают со всеми тремя сторонами другого.
Резюме урока
Равнобедренный треугольник — это треугольник, который:
- Имеет две равные стороны.
- Имеет совпадающие углы основания.
- Имеет высоту, которая: (1) пересекает основание под прямым углом, (2) делит угол при вершине пополам и (3) разделяет исходный равнобедренный треугольник на две равные половины.
Если ваш треугольник соответствует всем этим требованиям, он равнобедренный!
Ключевые точки на равнобедренных треугольниках
- Равнобедренный треугольник имеет две равные стороны и два равных угла при основании
- Теорема о равнобедренных треугольниках состоит из трех компонентов
- Формула для определения угла при вершине: A = 180-2 b
Результаты обучения
Закончив, вы должны уметь:
- Описать равнобедренный треугольник
- Напомним утверждения, составляющие теорему о равнобедренных треугольниках
Скален, равнобедренный и равносторонний треугольники — математика для 3-го класса
Научитесь определять чешуйчатые, равнобедренные и равносторонние треугольники
Вы помните, как определять треугольники по их углам? 🤔
Мы также можем идентифицировать треугольники, сравнивая длины сторон и углов.
Другие типы треугольников
Давайте узнаем еще несколько типов треугольников! 🤗
Треугольники шкалы не имеют равных сторон и равных углов.
Вы видите, что все три стороны имеют разную длину?
А все три угла разные?
Отлично! Посмотрим на другое! 👇
Равнобедренные треугольники имеют две равные стороны и два равных угла.
У нас есть два угла по 70 градусов и две стороны, длина которых равна 8.
Последний! 👇
Равносторонние треугольники имеют три равные стороны и три равных угла.
👉 Совет : равные углы всегда равны 60 °.
Совет: Сумма трех углов во всех треугольниках составляет 180 °.
Итак, если вы не можете вспомнить углы в равностороннем треугольнике, просто разделите 180 ° на 3!
Теперь давайте попробуем определить треугольники как разносторонние, равнобедренные или равносторонние.
Определение скален, равнобедренных и равносторонних треугольников.
Что это за треугольник? 👇
Вот и все!
✅ Это равнобедренный треугольник . У него 2 равные стороны и 2 равных угла.
Давай попробуем еще. 🤔
Что это за треугольник?
Молодец!
✅ Это разносторонний треугольник . Ни одна из сторон или углов не равны. Каждая сторона и угол имеют разные размеры.
Попробуем еще!
Что это за треугольник?
Верно!
✅ Это равносторонний треугольник.


