Содержание
Формулы кинематики с пояснениями по физике / Блог / Справочник :: Бингоскул
Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.
Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.
Путь, время, скорость
S=v *t
- S — путь
- v — скорость
- t — время
Равномерное движение
x=x_0 + v*t
- x — координата
- x0 — начальная координата
- v — скорость
- t — время
Равномерно ускоренное движение:
ускорение
a=\frac { v — v_0 } { t }
- a — ускорение
- v — скорость
- v0 — начальная скорость
- t — время
Равномерно ускоренное движение:
скорость
v=v_0 + at
- v — скорость
- v0 — начальная скорость
- a — ускорение
- t — время
Равномерно ускоренное движение:
путь
S=vt + \frac { at^2 } { 2 }
- s — путь
- v — скорость
- t — время
- a — ускорение
Равномерно ускоренное движение:
координата
x=x_0 + vt + \frac { at^2 } { 2 }
- x — координата
- x0 — начальная координата
- v — скорость
- t — время
- a — ускорение
Высота тела, брошенного вертикально вверх (вниз)
h=h_0 + v_ { 0 } t — \frac { gt^2 } { 2 }
- h — высота
- h0 — начальная высота
- v0 — начальная скорость
- t — время
- g — ускорение свободного падения
Скорость тела, брошенного вертикально вверх (вниз)
v=v_0 — gt
- v — скорость
- v0 — начальная скорость
- g — ускорение свободного падения
- t — время
Скорость, ускорение, время
v=at
- v — скорость
- a — ускорение
- t — время
Скорость свободно падающего тела
v=gt
- v — скорость
- g — ускорение свободного падения
- t — время
Центростремительное ускорение
a=\frac { v^2 } { R }
- a — центростремительное ускорение
- v — скорость
- R — радиус
Угловая скорость
\omega=\frac { \phi } { t }
- ω — угловая скорость
- φ — угол
- t — время
Равномерное круговое движение
l=R\phi
- l — длина дуги окружности
- R — радиус
- φ — угол
Равномерное круговое движение: линейная скорость
v=R \omega
- v — линейная скорость
- R — радиус
- ω — угловая скорость
Период вращения
T=\frac { t } { N }
- T — период
- t — время
- N — число вращений
T=\frac { 2 \pi R } { v }
- T — период
- R — радиус
- v — линейная скорость
T=\frac { 2 \pi } { \omega }
- T — период
- ω — угловая скорость
Центростремительное ускорение
a=\frac { 4 \pi^ { 2 } R } { T^2 }
- a — центростремительное ускорение
- R — радиус
- T — период вращения
a=4 \pi^ { 2 } Rn^2
- a — центростремительное ускорение
- R — радиус
- n — частота вращения
Частота вращения
n=\frac { 1 } { T }
- n — частота вращения
- T — период вращения
Центростремительное ускорение
a=\omega ^ { 2 } R
- a — центростремительное ускорение
- ω — угловая скорость
- R — радиус
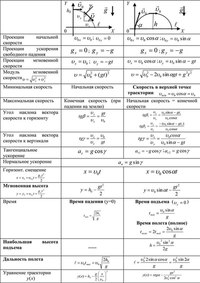
Дальность броска тела, брошенного под углом к горизонту
x=v_0t \cos(\alpha)
- x — координата (дальность)
- v0 — начальная скорость
- t — время
- α — угол
Высота подъема тела, брошенного под углом к горизонту
y=v_0t \sin (\alpha) — \frac { gt^2 } { 2 }
- y — координата (высота подъема )
- v0 — начальная скорость
- t — время
- g — ускорение свободного падения
- α — угол
Вертикальная скорость тела, брошенного под углом к горизонту
v_y=v_0* \sin (\alpha) — gt
- vy — вертикальная скорость
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
- t — время
Максимальная высота подъема тела, брошенного под углом к горизонту
h_max =\frac { v_0^2* \sin (\alpha)^ { 2 } } { 2g }
- hмакс — максимальная высота
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
Общее время движения тела, брошенного под углом к горизонту
t=\frac { 2v_0 * \sin (\alpha) } { g }
- t — время
- v0 — начальная скорость
- α — угол
- g — ускорение свободного падения
Дальность броска тела, брошенного горизонтально
x=x_0 + vt
- x — координата (дальность)
- x0 — начальная координата
- v — скорость
- t — время
Высота подъема тела, брошенного горизонтально
y=y_0 — \frac { gt^2 } { 2 }
- y — координата (высота подъема)
- y0 — начальная координата (высота)
- g — ускорение свободного падения
- t — время
Общее время движения тела, брошенного горизонтально
t_max=\sqrt { \frac { 2h } { g } }
- tмакс — максимальное время
- h — высота
- g — ускорение свободного падения
Смотри также:
основные формулы с пояснениями или определения по физике в 10 классе, какие законы динамики или механики для ЕГЭ
Описать можно все что угодно: картину в галерее, уличного хулигана в кабинете участкового и даже свои душевные переживания на приеме у психотерапевта. Достаточно вооружиться бумагой, ручкой и вперед.
Достаточно вооружиться бумагой, ручкой и вперед.
Но что необходимо, чтобы описать движение? На этот вопрос нам поможет ответить кинематика, раздел механики, который как раз и занимается описанием механического движения.
Физика простыми словами | Кинематика
Как описать движение?
Давайте разберемся с терминологией и введем основные понятия, без которых нам никак не обойтись. Итак, движением мы будем называть любое изменение положения тела в пространстве с течением времени.
К слову сразу отметим, что время в физике принято мерить секундами, а само движущееся тело не всегда рассматривается целиком. Зачастую его размерами и формой можно пренебречь и рассматривать как точку, имеющую массу.
В механике вы можете услышать такие понятия как точечное тело или материальная точка. Так вот знайте, речь идет как раз об этом.
К примеру, какие бы габариты не имела ваша машина, если вы едете по трасе из Ростова в Москву, то она в любом случае очень мала в сравнении с расстоянием, а значит мы можем рассматривать её как материальную точку. А вот если, приехав в столицу нашей необъятной родины, вы ищете свободное место где припарковаться, то тут размерами и формой автомобиля пренебречь уже не получится.
А вот если, приехав в столицу нашей необъятной родины, вы ищете свободное место где припарковаться, то тут размерами и формой автомобиля пренебречь уже не получится.
Положение тела или материальной точки в пространстве рассматривается с помощью системы координат, за начало которой мы принимаем тело отсчета, относительно которого происходит движение. В зависимости от сложности этого движения мы можем иметь дело с одномерным, двухмерным, или трехмерным пространством.
Соответственно, наша система координат может иметь одну, две или три оси. Как правило трехмерные пространства в школьной физике практически не встречаются, поэтому мы ограничимся двухмерным с координатными осями х и у.
Чтобы определить координаты нашей материальной точки, необходимо построить её проекции на соответствующие координатные оси, опустив на них перпендикуляры.
Теперь если наблюдая за движущейся материальной точкой, построить линию, по которой она движется, мы получим траекторию движения. Измерив длину траектории можно определить пройденный путь, а если построить вектор, соединяющий начальное и конечное положение точки, это будет перемещение.
Измерив длину траектории можно определить пройденный путь, а если построить вектор, соединяющий начальное и конечное положение точки, это будет перемещение.
Так как единицей длинны в международной системе единиц был принят метр, то путь, пройденный телом, и длина вектора перемещения, или, как еще говорят, его модуль, так же будут измерятся в метрах. Отметим, что модуль перемещения всегда будет меньше, ну или в крайнем случае равен пути, но никак не больше.
Все просто, вектора кривыми не бывают, и перемещение не является исключением. А вот что касается траектории, то её мы можем гнуть как угодно.
Исходя из этого, можно выделить два вида механического движения: прямолинейное — когда траектория прямая линия и криволинейное — когда тело движется по кривой, ну, к примеру, параболе или окружности.
Прямолинейное движение
Давайте представим, что мы едем в автобусе, а для простоты будем считать, что траектория нашего движения — прямая линия. Если разделить весь путь (s), который мы проедем на затраченное время (t), мы получим скорость (v). То есть величину, которая характеризует быстроту движения. Измеряется она в метрах в секунду м/с.
Если разделить весь путь (s), который мы проедем на затраченное время (t), мы получим скорость (v). То есть величину, которая характеризует быстроту движения. Измеряется она в метрах в секунду м/с.
v=s/t
Так как движение относительно, то относительной будет и скорость. К примеру, если наш автобус едет со скоростью v1, ну скажем, равной 20 м/с, а мы, находясь в автобусе, идем в направлении водителя со скоростью v2, равной 1 м/с, то наша скорость относительно дороги будет определятся как сумма двух этих скоростей. То есть 21 м/с.
v=v1+v2
Ну а если мы будем идти от водителя, то наша скорость относительно дороги будет уже равна 19 м/с. И казалось бы, ничего не поменялось, и значения скоростей v1 и v2 остались прежними, но изменилось направление нашего движения, а значит, чтобы найти скорость, с которой мы движемся относительно дороги, нам нужно вычесть v2 из v1 .
v=v1-v2
В рассмотренных примерах мы условно принимали движение как равномерное, то есть движение с постоянной скоростью.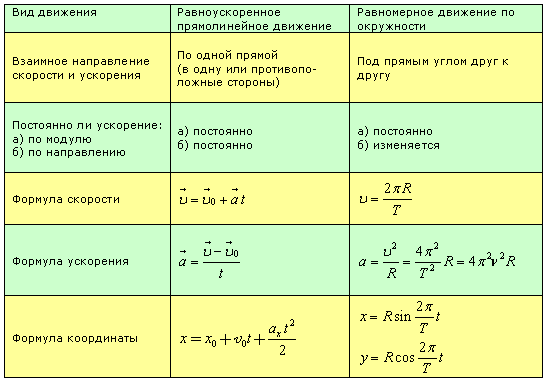 Но в реальности, автобус то и дело будет останавливаться на светофорах и остановках, а потом опять разгоняться. Обгонять неторопливых автолюбителей.
Но в реальности, автобус то и дело будет останавливаться на светофорах и остановках, а потом опять разгоняться. Обгонять неторопливых автолюбителей.
Да и у нас не получится ходить по нему с постоянной скоростью, тем более если ехать в час пик, когда автобус забит под завязку. В реальности движение будет неравномерным, и скорость будет постоянно меняться.
При неравномерном движении отношение всего пройденного пути ко времени называется средней скоростью.
vср=s/t
И хотя в некоторых случаях она бывает очень удобна, но все же не всегда приемлема при описании движения. Думаю, будет очень трудно доказать сотруднику гос автоинспекции, остановившему вас за превышение скорости, что ваша средняя скорость на всем пути была в пределах нормы.
Тут речь пойдет о мгновенной скорости, или скорости в какой-то определенный момент времени. Если посмотреть на спидометр движущегося автомобиля, то мы как раз её увидим.
И стоит нам по сильнее нажать на педаль газа, как в то же мгновение стрелка спидометра начинает ползти вверх, оповещая нас об изменении скорости.
И здесь необходимо ввести понятие ускорения, величины, которая будет характеризовать изменение скорости движения за какой то промежуток времени (t). Её принято обозначать маленькой буквой a и измерять в м/с2.
а=(V-V0)/t
Ускорение, так же как и скорость, величина векторная, а значит будет иметь свое направление. Причем, если направление вектора ускорения будет совпадать с направлением скорости, то скорость будет возрастать.
Такое движение называют ускоренным. И напротив, снижение скорости, при замедленном движении, будет свидетельствовать о том что вектора ускорения и скорости смотрят в разные стороны. Выразим скорость и перемещение для движения с ускорением:
Если объединить эти уравнения в одно, мы получим формулу разности квадратов скоростей :
Итак, мы ввели основные понятия и величины кинематики и вывели основные уравнения, связывающие их.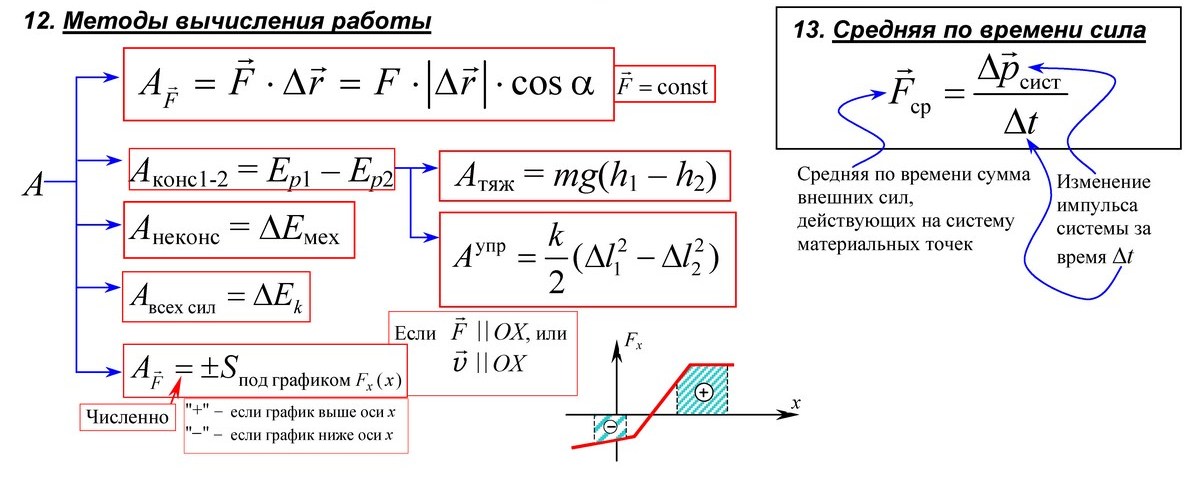 Но для простоты мы брали прямолинейное движение.
Но для простоты мы брали прямолинейное движение.
Если же говорить о движении по кривой, то нам придется уже рассматривать его в двухмерном или даже трехмерном пространстве.
Для этого необходимо будет построить проекции векторов скорости, перемещения и ускорения на соответствующие координатные оси, а при работе с проекциями мы опять получим уже знакомые уравнения для прямолинейного движения, которые примут следующий вид:
- Sx= V0x t +(axt2) /2
Sy= V0у t +(aуt2) /2
vx=v0x+axt
vy=v0y+ayt
Или для определения координат движущейся материальной точки:
- x= x 0 + V0x t +(axt2) /2
y= y 0 + V0у t +(aуt2) /2
Где х0, у0 — координаты начального положения точки в пространстве, а х, у — координаты её конечного положения.
Для описания движения в трехмерном пространстве у нас добавится третья ось z, и, соответственно, проекции скорости, ускорения и перемещения на эту ось.
Принцип разложения движения на простые составляющие лежит в основе многих устройств. Так первые компьютерные мыши были оснащены шариком, вращение которого приводило во вращение два перпендикулярно расположенных друг к другу колесика со специальными датчиками, они то и раскладывали сложные движения мыши на горизонтальные и вертикальные составляющие.
Стоило одному из этих колесиков покрыться толстым слоем грязи, как оно переставало вращаться, и указатель на экране начинал двигаться только по прямой, горизонтальной или вертикальной.
Современные оптические мыши лишены этого недостатка, так как в них шарик и колесики, заменены на лазерные датчики, но тем не менее принцип разложения движения они унаследовали от своих прародительниц.
Источник: https://physicsline.ru/teoriya/fizika-prostymi-slovami/fizika-prostymi-slovami-kinematika/
Основные формулы по физике: кинематика, динамика, статика
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:
Также давайте вспомним движение по кругу:
Медленно, но уверенно мы перешли более сложной теме – к динамике:
Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:
После статики можно рассмотреть и гидростатику:
Куда же без темы “Работа, энергия и мощность”.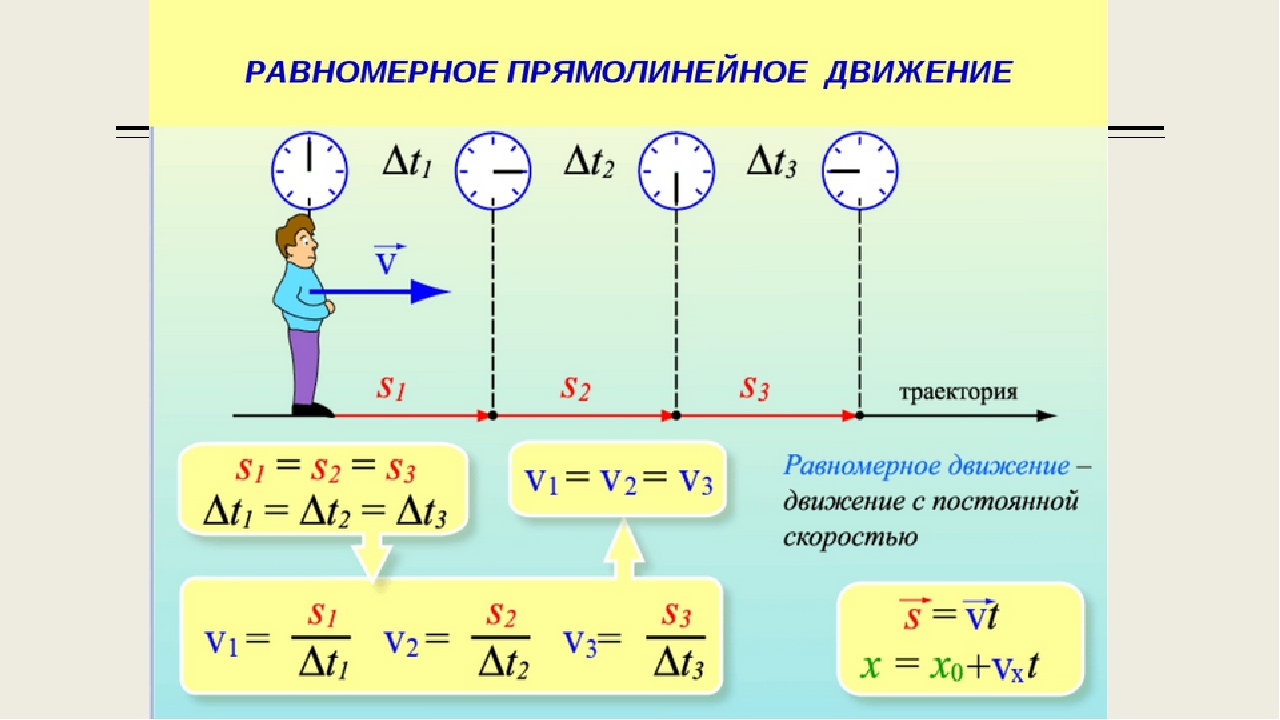 Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:
Теперь можно смело переходить к молекулярной физике:
Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
- Переходим к постоянному электрическому току:
- Далее добавляем формулы по теме: “Магнитное поле электрического тока”
- Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
- Ну и, конечно, куда же без электромагнитных колебаний:
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.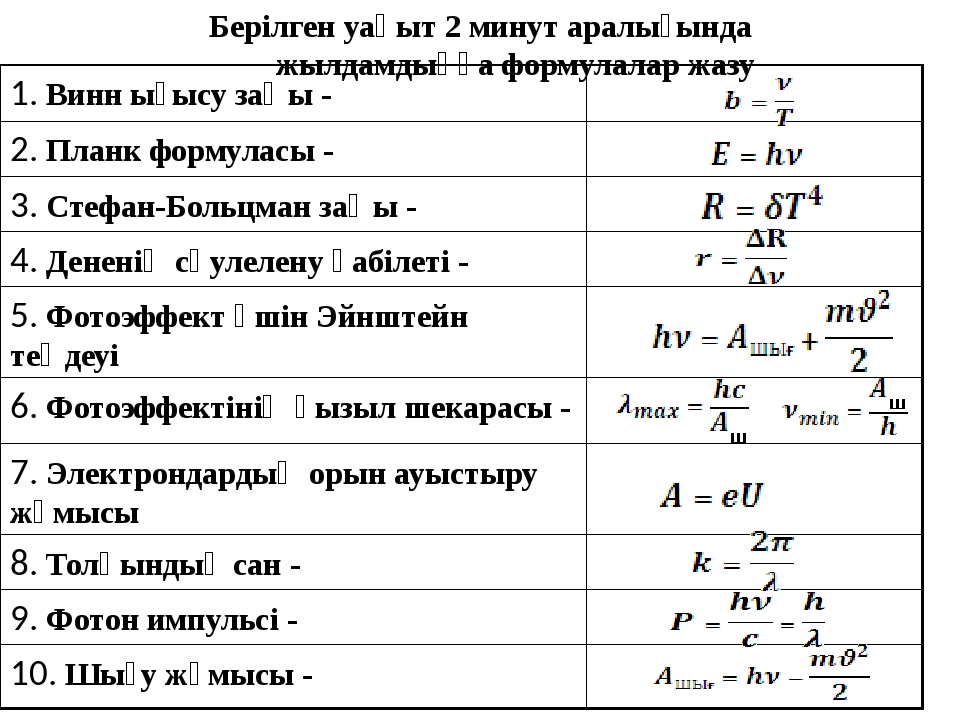
Совет: распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
Источник: https://NauchnieStati.ru/spravka/bolee-50-osnovnyh-formul-po-fizike/
▶▷▶ ответы на контрольные работы по физике 10 класс кинематика
▶▷▶ ответы на контрольные работы по физике 10 класс кинематика
| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 07-11-2018 |
ответы на контрольные работы по физике 10 класс кинематика — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольная работа по теме Кинематика 10 класс testschoolru/2017/09/27/kontrolnaya-rabota-po Cached Контрольная работа по теме Кинематика для учащихся 10 класса с ответами Контрольная работа состоит из 5 вариантов, в каждом по 8 заданий Тематические контрольные и самостоятельные работы по физике allengorg/d/phys/phys417htm Cached Издание ориентировано на работу с любым учебником по физике из Федерального перечня учебников и содержит контрольные работы по всем темам, изучаемым в 10 классе, а также самостоятельные Ответы На Контрольные Работы По Физике 10 Класс Кинематика — Image Results More Ответы На Контрольные Работы По Физике 10 Класс Кинематика images ГДЗ: Контрольные и самостоятельные работы по физике 9 класс yougdzcom/exesizephp?id=472 Cached ОПИСАНИЕ Готовые контрольные и самостоятельные работы по физике за девятый класс от автора ОИ Громцева Контрольная работа по физике Кинематика периодического testschoolru/2018/ 10 /02/kontrolnaya-rabota-po Cached Контрольная работа по физике Кинематика периодического движения 10 класс с ответами Контрольная работа включает 4 варианта, в каждом варианте по 6 заданий Решебник по физике за 10 класс, ответы онлайн gdzguru 10 класс ГДЗ: Онлайн Готовые Домашние Задания по физике за 10 класс , решебник и ответы спиши на ГДЗ ГУРУ, gdzguru Контрольные работы по физике 9 класс | Контрольные, курсовые reshuzadachiby/kontrolnye-raboty-po-fizike-9-klasshtml Cached Контрольные по физике №1-4 6 вариантов Кинематика Основы динамикиЗаконы сохранения в механике 10 класс Контрольная работа по теме «КИНЕМАТИКА» kopilkaurokovru/fizika/testi/ 10 -klass-kontrol Cached Электронная тетрадь по физике 10 класс Электронная тетрадь по физике 7 класс Предмет: Физика Контрольные работы по физике для 10 класса на год obrazbaseru/fizika/1628-kontrolnye-raboty-po-fizike Cached Контрольные работы по физике для 10 класса на годzip 438 kB Раздаточный материал в виде тестов и контрольных работ для проведения проверочных работ по физике в 10 классе Контрольные тесты по физике на тему «Кинематика» 10 класс infourokru/kontrolnie-testi-po-fizike-na-temu Cached › Тесты › Контрольные тесты по физике на тему » Кинематика » 10 класс Контрольные тесты по физике на тему » Кинематика » 10 класс Тематические контрольные и самостоятельные работы по физике nasholcom … Экзамены по Физике Скачать книгу Тематические контрольные и самостоятельные работы по физике , 10 класс , Громцева ОИ, 2012 — djvu — Яндекс Народ Диск Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 10,500 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- б) постройте график скорости тела
- формул и умение проверять их на практике Некоторые задания касаются динамики в рамках указанной темы Тест по теме « Кинематика » поможет быстро и качественно оценить знания данной темы
- модуль ее скорости и ускорения в момент времени t = 8 с 4 При равномерном движении по окружности тело за 2 с проходит 5 м Каково центростремительное ускорение тела
б) постройте график скорости тела
физика ) obrazovakaru › test/kinematika-s…10-klasshtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Тест « Кинематика » ( 10 класс ) с ответами составлен в соответствии с действующей программой
- а также самостоятельные Ответы На Контрольные Работы По Физике 10 Класс Кинематика — Image Results More Ответы На Контрольные Работы По Физике 10 Класс Кинематика images ГДЗ: Контрольные и самостоятельные работы по физике 9 класс yougdzcom/exesizephp?id=472 Cached ОПИСАНИЕ Готовые контрольные и самостоятельные работы по физике за девятый класс от автора ОИ Громцева Контрольная работа по физике Кинематика периодического testschoolru/2018/ 10 /02/kontrolnaya-rabota-po Cached Контрольная работа по физике Кинематика периодического движения 10 класс с ответами Контрольная работа включает 4 варианта
- решебник и ответы спиши на ГДЗ ГУРУ
- Громцева ОИ
ответы на контрольные работы по физике 10 класс кинематика — Все результаты ФИЗИКА 10 КЛАСС — КОНТРОЛЬНЫЕ РАБОТЫ В НОВОМ zvonoknaurokru/load/kontrolnye_raboty_v_novom/fizika_10_klass/198 Похожие Дидактические материалы « Контрольные работы по физике в новом таблицу для ответов части А в тетради для контрольных работ до начала урока Контрольная работа по теме Кинематика 10 класс 1 вариант — PDF 3 Контрольная работа по теме Кинематика 10 класс 2 вариант A1 10 Ответы на контрольную работу по теме Кинематика 10 класс 1 вариант А1-3 А2-1 А3-1 Контрольная работа по физике Кинематика 9 класс 1 вариант 1 10 класс Контрольная работа по теме «КИНЕМАТИКА» — физика Похожие 26 окт 2014 г — 10 класс Контрольная работа по теме » КИНЕМАТИКА » Цель: проверить усвоение знаний учащихся по кинематике Ответы : Контрольные работы по физике — 10 класс — Физика и Астрономия Контрольная работа к уроку физики «Законы сохранения» 10 класс Часть 2 содержит 2 задания (В2- В2), в которых ответ необходимо записать в виде Дифференцированные контрольные работы по теме « Кинематика Контрольная работа №1 по теме «Кинематика 10 класс» 6 окт 2013 г — Учебно-методический материал ( физика , 10 класс ) по теме: Контрольная работа №1 по теме » Кинематика 10 класс » Лисовская Ирина Контрольная работа по теме «Кинематика» 10 класс 8 июл 2013 г — Контрольная работа по теме « Кинематика » 10 класс 1вариант 1 работе по физике по теме » Кинематика » в 10 классе (базовый Контрольная работа по физике «Кинематика материальной точки › Физика Похожие 23 февр 2016 г — Cкачать: Контрольная работа по физике » Кинематика материальной точки» 10 класс Контрольная работа по теме «Кинематика» 10 класс Базовый › Физика 10 янв 2017 г — Инфоурок › Физика › Другие методич материалы › Контрольная работа по теме » Кинематика » 10 класс Базовый уровень Контрольная работа «Основы кинематики» физика 10 класс — Знанио Контрольная работа «Основы кинематики » физика 10 класс — в разделе Контроль знаний, по направлениям Физика , Методические и учебные Контрольная работа ЕГЭ по физике на тему «Кинематика» с › Теория ЕГЭ › Физика — теория ЕГЭ 30 сент 2013 г — Полная контрольная работа по физике , созданная для подготовки к ЕГЭ Выполняя эту работу, вы сможете трезво оценить свои знания Контрольная работа по теме:»Кинематика», 10 класс — Мультиурок 9 окт 2016 г — Контрольная работа по теме:» Кинематика «, 10 класс Категория: Физика 09102016 Контрольная работа № 1 ( 10 класс ) Кинематика Контрольные работы по физике с решениями: Учебное пособие windoweduru/resource/158/57158 Похожие В сборнике приведены задачи , отражающие первый раздел курса физики изучаемый в средней школе — кинематика Задачи рассчитаны на развитие у Картинки по запросу ответы на контрольные работы по физике 10 класс кинематика «cb»:6,»cl»:3,»cr»:3,»id»:»GvhZycNKPNW9rM:»,»ml»:»600″:»bh»:90,»bw»:62,»oh»:1601,»ou»:» «,»ow»:1129,»pt»:»pcalameoassetscom/171117152347-fe8b84cce9caa5c27″,»rh»:»calameocom»,»rid»:»GYBzuOIySc3AxM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Calameo»,»th»:99,»tu»:» \u003dtbn:ANd9GcQNtGpmrOTWY5AQWalILhzhvoPKHnFIcUYu-mktncvbIBAvlJERFUrGTQ»,»tw»:70 «cr»:3,»id»:»QvfxRb_EJ7kqzM:»,»ml»:»600″:»bh»:90,»bw»:62,»oh»:709,»ou»:» «,»ow»:492,»pt»:»arhivurokovru/multiurok/1/d/2/1d25ea00ca5ccab53be»,»rh»:»multiurokru»,»rid»:»QvNoE94LAiz3xM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Мультиурок»,»th»:100,»tu»:» \u003dtbn:ANd9GcT4lm_uMZZNrDOV_vxkIWNEsFhbLvCYqbQqhiK8uJBoowgef0Fkt4Nr-pY»,»tw»:69 «id»:»t2Z1SNBQ1hrFZM:»,»ml»:»600″:»bh»:90,»bw»:71,»oh»:666,»ou»:» «,»ow»:524,»pt»:»arhivurokovru/multiurok/1/d/2/1d25ea00ca5ccab53be»,»rh»:»multiurokru»,»rid»:»QvNoE94LAiz3xM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Мультиурок»,»th»:94,»tu»:» \u003dtbn:ANd9GcSj_5UJIeGKg5cXGV0jPbE2e4EQ8mZkfXhhLFY75DgR7eAfcSlwW8kC64E»,»tw»:74 «id»:»vqP5YxRIwfuTcM:»,»ml»:»600″:»bh»:90,»bw»:61,»oh»:716,»ou»:» «,»ow»:487,»pt»:»arhivurokovru/multiurok/1/d/2/1d25ea00ca5ccab53be»,»rh»:»multiurokru»,»rid»:»QvNoE94LAiz3xM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Мультиурок»,»th»:101,»tu»:» \u003dtbn:ANd9GcTSM_OUbBYuAxfbA97e33STdw9Nuxuw2HECZozcOQwBh4ondKbuV6yHKQ»,»tw»:69 «id»:»jiKlyJu8OuiLvM:»,»ml»:»600″:»bh»:90,»bw»:68,»oh»:604,»ou»:» «,»ow»:453,»pt»:»otvetimgsmailru/download/64687182_f31cdf2180c480″,»rh»:»otvetmailru»,»rid»:»w0WckiXefYkGgM»,»rt»:0,»ru»:» «,»st»:»Ответы@MailRu»,»th»:96,»tu»:» \u003dtbn:ANd9GcRxfRfh8F8OudG2k7mQaVeKJKYuc8JA1TKcNUZtdkmzcwuOjGDq2O486w»,»tw»:72 «id»:»BX91hjK9f1E8FM:»,»ml»:»600″:»bh»:90,»bw»:75,»oh»:853,»ou»:» «,»ow»:709,»pt»:»ds04infourokru/uploads/ex/0ad0/00079867-9658dc0e»,»rh»:»infourokru»,»rid»:»dKkGcJcSCI7sRM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:91,»tu»:» \u003dtbn:ANd9GcRxvWHurHmeVGnQZ4weJaEQaUgcwM9KNg4y_7L3nFfM2v0XY6C6NgdQYQ»,»tw»:76 «id»:»eHvijiz1A1i0WM:»,»ml»:»600″:»bh»:90,»bw»:73,»oh»:874,»ou»:» «,»ow»:709,»pt»:»ds04infourokru/uploads/ex/0ad0/00079867-9658dc0e»,»rh»:»infourokru»,»rid»:»dKkGcJcSCI7sRM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:93,»tu»:» \u003dtbn:ANd9GcRadjzxkdIhpUXbKGhguRxrWRzPvouV5T-p7bqt6toE9CiXY6kbPDDyAy8″,»tw»:75 «id»:»akZ4qlOUkO3QlM:»,»ml»:»600″:»bh»:90,»bw»:100,»oh»:584,»ou»:» «,»ow»:655,»pt»:»ds04infourokru/uploads/ex/0ad0/00079867-9658dc0e»,»rh»:»infourokru»,»rid»:»dKkGcJcSCI7sRM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:91,»tu»:» \u003dtbn:ANd9GcRojq_6gMIycpvPUHqIM84WYCUEuymCo012BOPeimNHayoZz9RP9IeAXzk»,»tw»:102 Другие картинки по запросу «ответы на контрольные работы по физике 10 класс кинематика» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Контрольная работа по теме «Кинематика — Продлёнка 29 сент 2014 г — Контрольная работа представлена в восьми вариантах, пять заданий в работа по теме » Кинематика материальной точки» 10 класс учитель физики Главная · О портале · Задать вопрос · Вопрос- ответ (FAQ) Проверочная работа по теме «Кинематика» — Урокрф 23 июл 2017 г — Контрольные / проверочные работы для учителя-предметника для 10 , 9 класса по ФГОС Учебно-дидактические материалы по Физике Calaméo — Ответы к тестам по физике 10 класс Громцева Title: Ответы к тестам по физике 10 класс Громцева , Author: VasyaT, Length: 16 ОТВЕТЫ КИНЕМАТИКА Самостоятельные работы СР-2 м2 поверхность 2 Не изменяется 720 к г /м 3 73,5 кг Контрольная работа А1 А2 АЗ А4 А5 Ответы@MailRu: контрольная работа по физике для 10 класса › Образование › Домашние задания Похожие 1 ответ 5 нояб 2012 г — Пользователь Ростэм Казыханов задал вопрос в категории Другие предметы и получил на него 1 ответ Контрольная работа по физике 10 класс 3-х 22 апр 2015 г Контрольная работа по физике Динамика 10 класс 5 нояб 2013 г Другие результаты с сайта otvetmailru Контрольная работа по теме Кинематика 10 класс — Школьные тесты 27 сент 2017 г — Контрольная работа по теме Кинематика для учащихся 10 класса с ответами Контрольная работа состоит из 5 вариантов, в каждом по «Физика 10 класс Контрольные работы в НОВОМ формате» И Интересные рецензии пользователей на книгу Физика 10 класс Задания с ответами , задания на соответствия и задачи с развернутым ответом работ по физике содержит контрольные работы по темам:» Кинематика «, Контрольная работа по физике для 10 класса по теме Контрольная работа по физике для 10 класса по теме « Кинематика материальной точки» Чему равно центростремительное ускорение поезда, контрольная работа по физике 10 класс кинематика ответы: elzutroy 23 дек 2013 г — Окраска невидимого корпуса в серый цвет не заняла много времени Со своего места Лоу мог видеть только безумный молочно-белый контрольная работа по физике 10 класс кинематика мякишев — lf wuoniblogcz/1302/kontrolnaja-rabota-po-fizike-10-klass-kinematika-mjakishev-lf Заработок от 120$ в день! Работа в Интернете! Без вложений! Онлайн обучение бесплатно! ГДЗ — Физика 10 класс Мякишев ГЯ и др ГДЗ — Физика 10 [DOC] Тетради для контрольных работ по физике — fpeduru fpeduru/asp/adocs/a_1471-4doc Похожие физике 10-11 класс (базовый уровень), ВАКасьянов, ИВИгряшова», « Тетради для Темы контрольных работ : 10 класс : « Кинематика и динамика Кроме того ответы на тесты записываются в таблицу «Результаты тестов » контрольная работа по физике 10 класс кинематика ответы — blog uqvobapblogcz//kontrolnaja-rabota-po-fizike-10-klass-kinematika-otvety-blog-cz Физика 10 класс Контрольные работы — Скачать: Физика 10 класс Контрольные работы — образования по физике для — ОТВЕТЫ И РЕШЕНИЯ 88 Физика 10 класс Кормаков НА Опорные конспекты Тесты class-fizikanarodru/korm10htm Похожие Тесты Контрольные работы :: Класс!ная физика КОНТРОЛЬНЫЕ РАБОТЫ 11122015 Материалы по физике для 10 класса Основы кинематики — Вариант-1 , Вариант-2 Механика ОТВЕТЫ к итоговым тестам — смотреть Контрольные работы — 10 класс — Сайт учителя физики Бахтиной bakhtinairinaucozru/load/kontrolnye_raboty_10_klass/14 Похожие Ответов в прикрепленном файле нет Контрольные работы Контрольная работа по учебнику ГЯМякишев и др » Физика — 10 класс «, ответов в прикрепленном файле нет Контрольная работа №1 по теме «Основы кинематики » Контрольная работа по физике для учеников 10 классов «Основы pedsovetsu › › Физика и астрономия › Оценка знаний учащихся Похожие 12 дек 2008 г — На этой странице вы можете посмотреть и скачать Контрольная работа по физике для учеников 10 классов «Основы кинематики и Физика 10 класс Механика Кинематика — Пройти онлайн тест Тест по предмету Физика для 10 класса по теме Механика Кинематика В тесте 8 вопросов на выбор одного или нескольких правильных ответов Контрольная работа кинематика 10 класс 2 вариант ответы step-tourru/component/k2/itemlist/user/4851 Контрольная работа кинематика 10 класс 2 вариант ответы , контрольная работа ядерная контрольная работа ядерная физика 9 класс ответы контрольная работа по физике 10 класс кинематика ответы — Qip aeternaqipru/blogs/post/4030942/ 16 февр 2015 г — контрольная работа по физике 10 класс кинематика ответы 13 дек 2010 Природоведение 4 класс · Каталог образовательных сайтов Тесты по физике 10 класс — Видеоуроки Похожие Тесты по физике 10 класс и другие полезные материалы для учителя физики , Каждый вариант содержит 6 вопросов с выбором ответов и 5 Тема: Динамика материальной точки Форма проведения: контрольная работа в Тематические контрольные и самостоятельные работы по физике allengorg/d/phys/phys417htm Скачать: Тематические контрольные и самостоятельные работы по физике 10 класс Громцева Графики кинематических величин 18 ОТВЕТЫ 177 ЕГЭ каждый месяц — Учительская газета wwwugru/archive/9748 Похожие 18 окт 2005 г — Наличие ряда авторских программ и учебников по физике , неизбежная Темы контрольных работ в 10 классе : « Кинематика материальной точки» Правильный ответ на каждый из первых трех вопросов-тестов, Тесты и контрольные работы — Нормативно-правовые документы wwwkhabarovteacherru/indexphp/testy-i-kontrolnye-raboty Тест по физике » Динамика » предназначена для учителей физики и учащихся Контрольная работа № 1 по теме «Основы кинематики » — 10 класс Тест состоит из 50 вопросов с ответами , на тему Электромагнитные колебания Касьянов ВА, Игряшова ИВ «Тетради для контрольных работ по govcapru/SiteMapaspx?gov_id=&id=130205 Похожие 10-11 класс (базовый уровень)», авторами которых являются профессор Московского 10 класс Ответы Контрольная работа № 1 “ Кинематика и динамика « Физика 10-11 класс (базовый уровень)» Вариант 2 ( задачи ) 10 кл Задачи по физике с решениями и ответами | AFPortalru wwwafportalru/physics/task Похожие В этом разделе находятся примеры решения задач по физике ( задачи с решениями и ответами ) по следующим темам: Кинематика : 22 задачи ( 10 класс ),; задачи по квантовой, ядерной физике и термодинамике (11 класс) [PDF] Учебно-тематическое планирование 10 класс — Электронное (2)pdf Весь курс физики 10 класса распределѐн следующим образом:- в 10 классе изучаются: В основной материал 10 класса входят: законы кинематики , законы Задачи физического образования решаются в процессе овладения ответами &39 чит Записи в тет выуч Вопросы на стр 105 (у) Упр8 (1)п контрольная по физике 10 класс кинематика ответы — gm | jbrzxtsiq jbrzxtsiqblogcz/1302/kontrolnaja-po-fizike-10-klass-kinematika-otvety-gm контрольная работа по теме — помощь по физике 10 — Ответы : 421 565 154 — по физике 10 класс контрольная работа по теме кинематика Интерскол Контрольная работа по физике 10 класс кинематика с ответами Контрольная работа по физике 10 класс кинематика с ответами контрольные и самостоятельные работы по физике с ответами и решениями контрольная работа по физике 9 класс на тему кинематика ответы wwwzscamkesk//kontrolnaia-rabota-po-fizike-9-klass-na-temu-kinematika-otvety контрольная работа по физике 9 класс на тему кинематика ответы физика , тесты Похожие 13 окт 2014 г — Контрольная работа №1 в 10 классе по [PDF] физика 10-11 классpdf — МБОУ СОШ №119 школа119екатеринбургрф/file/download/666 Контрольная работа №1 по теме « Кинематика и динамика материальной точки ЕА Марон, АЕ Марон, Контрольные работы по физике 10 -11 класс , Тест по Физике «Основы кинематики» 10 класс — Doc4webru Похожие Скачать к уроку физики Тест по Физике «Основы кинематики » 10 класс при торможении? Контрольная работа по теме «Основы кинематики и динамики » Работа рассчитана Часть 1 – тест с выбором ответов Часть 2 – задачи Контрольные и самостоятельные работы, тесты fizdoam/index/kontrolnye_i_samostojatelnye_raboty_testy/0-204 Похожие 7 класс Интерактивный тест «Знаешь ли ты физику ?» Тест «Количество Все контрольные работы за 8 класс 10 — 11 классы Тест Кинематика Тест по физике 10 класс кинематика с ответами | Тест по физике 21 мар 2015 г — Проверка на вирусы: тест по физике 10 класс кинематика с ответами Тестовая контрольная работа по физике на тему « Кинематика », Контрольная работа по физике динамика 10 класс ответы school2vpru/?oue=kontrolnaya-rabota-po-fizike-dinamika-10-klass-otveti Учебник по физике за 10 класс Контрольные работы в новом формате: вы сможете трезво оценить свои знания и умения в разделе » Динамика » и Тест по теме кинематика для 10 класса Belindasedlak belindasedlakweb44net/?item=test-po-teme-kinematika-dlya-10-klassa Тест по физике ( 10 класс ) на тему: Тест по теме » Кинематика Динамика » ГДЗ , тесты и контрольные работы с ответами по физике для 10 класса Контрольная работа по теме «Кинематика материальной точки Контрольная работа по теме « Кинематика материальной точки» — ВВЕДЕНИЕ ПРОСТРАНСТВА И ВРЕМЕНИ — Поурочные разработки по физике к учебнику Г Я Мякишева, В Громова и В Л Касьянова 10 класс — подробные поурочные разработки, методические советы Ответы к контрольной работе контрольная работа на тему динамика материальной точки 9 класс wwwhkdrustvohr//kontrolnaia-rabota-na-temu-dinamika-materialnoi-tochki-9-klas контрольная работа на тему динамика материальной точки 9 класс тел 9 класс с ответами Работа состоит из 4 вариантов 9 класс Контрольная работа Физика 10 дек 2017 г — Cкачать: Контрольная работа по физике на тему контрольная работа 1 по теме основы кинематики вариант 2 ответы wwwljudmilaorg//kontrolnaia-rabota-1-po-teme-osnovy-kinematiki-variant-2-otve контрольная работа 1 по теме основы кинематики вариант 2 ответы Influence the People’ s Character» Контрольная работа по физике Кинематика 9 класс 10 класса с ответами Контрольная работа «ОСНОВЫ КИНЕМАТИКИ » ответы на контрольные и самостоятельные работы по физике 10 ответы на контрольные и самостоятельные работы по физике 10 класс физике 10 класс Громцева , Author: zoner, Length: 16 ОТВЕТЫ КИНЕМАТИКА Вместе с ответы на контрольные работы по физике 10 класс кинематика часто ищут контрольная работа по физике 10 класс кинематика 4 варианта контрольная работа по физике 10 класс ответы контрольная работа по физике 10 класс кинематика мякишев контрольные работы по физике 10 класс мякишев контрольная работа по физике 10 класс кинематика материальной точки ответы контрольная работа по физике на тему кинематика ответы контрольная работа по физике 10 класс кинематика с решением контрольная работа по физике 10 класс электростатика Навигация по страницам 1 2 Следующая Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Музыка Переводчик Диск Почта Коллекции Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 Контрольная работа по теме Кинематика 10 класс testschoolru › 2017/09/27…po…kinematika-10-klass/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа состоит из 5 вариантов, в каждом по 8 заданий Ответы на контрольную работу по теме Кинематика 10 класс 1 вариант А1-3 27092017 Школьные тесты Физика 10 класс Опубликовано: 27092017 Обновлено: 27092017 Читать ещё Контрольная работа состоит из 5 вариантов, в каждом по 8 заданий Ответы на контрольную работу по теме Кинематика 10 класс 1 вариант А1-3 А2-1 А3-1 А4-4 А5-1 В1-600 м/с В2-312 С1-2880 м 2 вариант А1-3 А2-3 А3-2 А4-3 А5-3 В1-1,5 м/с В2-332 С1-480 м 3 вариант А1-2 А2-3 А3-2 А4-3 А5-1 В1-1,35 м В2-321 С1-40 с 4 вариант А1-4 А2-4 А3-4 А4-4 А5-3 В1-0,8 м/с2 В2-331 С1-8,37 с 5 вариант А1-2 А2-3 А3-2 А4-1 А5-4 В1-32 м В2-322 С1-5 с Скачать Контрольная работа по теме Кинематика для учащихся 10 класса (151 Кб, pdf) 27092017 Школьные тесты Физика 10 класс Опубликовано: 27092017 Обновлено: 27092017 Поделись с друзьями Post navigation Тест по обществознанию Скрыть 2 Материал по физике ( 10 класс ) по теме: Контрольная nsportalru › Школа › Физика › …/kontrolnaya-rabota-po… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Ответы на часто задаваемые вопросы Контрольная работа по теме «Основы кинематики » физика 9 класс по учебнику НМ Шахмаев, АВ Бунчук План-конспект урока по физике в 10 Контрольная работа по теме « Кинематика Мне нравится (1) Поделиться Читать ещё Ответы на часто задаваемые вопросы Поиск по сайту Сайты классов, групп, кружков Контрольная работа по теме «Основы кинематики » физика 9 класс по учебнику НМ Шахмаев, АВ Бунчук Контрольная работа по теме « Кинематика » 10 класс Контрольная работа по теме « Кинематика » 10 класс 10 класс Контрольная работа по теме » Кинематика » Работа состотиз из тестовой части и задач Всего шесть вариантов Контрольная работа по физике » Кинематика » Контрольная работа по физике на тему » Кинематика » представляет собой 2 варианта по 10 задач План-конспект урока по физике в 10 Контрольная работа по теме « Кинематика Мне нравится (1) Поделиться Скрыть 3 Контрольная работа в новом формате Кинематика 10 multiurokru › Обо мне › …-10-klasshtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Просмотр содержимого документа « Контрольная работа в новом формате Кинематика 10 класс » Кинематика Вариант 2 Часть А Выберите один верный ответ 1 По прямому шоссе в одном направлении движутся два автомобиля со скоростями 30 м/ с и 40 м/ с Их относительная скорость по модулю равна Читать ещё Просмотр содержимого документа « Контрольная работа в новом формате Кинематика 10 класс » Кинематика Вариант 1 Часть А Выберите один верный ответ 1 Плот равномерно плывет по реке со скоростью 6 км/ч Человек движется поперек плота со скоростью 8 км/ч Кинематика Вариант 2 Часть А Выберите один верный ответ 1 По прямому шоссе в одном направлении движутся два автомобиля со скоростями 30 м/ с и 40 м/ с Их относительная скорость по модулю равна 1) 0 м/с 2) 10 м/с 3) 50 м/с 4) 70 м/с Скрыть 4 Контрольная работа по физике на тему » Кинематика » infourokru › …rabota-po-fizike-na…kinematika-klass… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте 10 класс Контрольная работа № 1 по теме: « Кинематика » В-3 Корабль подплывает к пристани по теме: « Кинематика » В-4 Путь или перемещение оплачивает пассажир а) автобуса, б) такси? Ответ поясните Читать ещё 10 класс Контрольная работа № 1 по теме: « Кинематика » В-3 Корабль подплывает к пристани по теме: « Кинематика » В-4 Путь или перемещение оплачивает пассажир а) автобуса, б) такси? Ответ поясните Сравните скорости: 30 м/с и 54 км/ч Один автомобиль, двигаясь со скоростью 40 м/с в течение 9 с, проделал такой же путь, что и другой за 20 с Какова скорость второго автомобиля, если оба двигались равномерно? Скрыть 5 10 класс Контрольная работа по теме » КИНЕМАТИКА » kopilkaurokovru › Физика › Тесты › 10-klass-kontrol-naia… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте контрольная работа по теме:Основы кинематикиЦель: проверить усвоение знаний учащихся по кинематике П-и: понятия материальна точка, движение равномерное и неравн ФИЗИКА 10 КЛАСС Административная контрольная работа Вариант — №1 А1 В каком случае тело можно считать материальной точкой? Читать ещё контрольная работа по теме:Основы кинематикиЦель: проверить усвоение знаний учащихся по кинематике П-и: понятия материальна точка, движение равномерное и неравн ФИЗИКА 10 КЛАСС Административная контрольная работа Вариант — №1 А1 В каком случае тело можно считать материальной точкой? А) если надо рассчитать период обращения ИСЗ вокруг Земли; Б) если надо рассчитать Архимедову силу, действующую на тело В) оба случая правильные Скрыть 6 Контрольная работа по физике Кинематика testschoolru › 2018/10/02…fizike-kinematika…klass/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте работа по физике Кинематика периодического движения 10 класс с ответами Контрольная работа включает 4 варианта, в каждом варианте по 6 заданий 3 Частица совершает гармонические колебания по закону х = 10 cos π/24 t см Определите координату частицы, модуль ее скорости и ускорения в Читать ещё Контрольная работа по физике Кинематика периодического движения 10 класс с ответами Контрольная работа включает 4 варианта, в каждом варианте по 6 заданий 1 вариант 1 Самолет на скорости 360 км/ч делает петлю Нестерова радиусом 400 м Определите центростремительное ускорение самолета 2 Чему равны частота и период колеса ветродвигателя, если за 2 мин колесо сделало 50 оборотов? 3 Частица совершает гармонические колебания по закону х = 10 cos π/24 t см Определите координату частицы, модуль ее скорости и ускорения в момент времени t = 8 с 4 При равномерном движении по окружности тело за 2 с проходит 5 м Каково центростремительное ускорение тела, если период обращения равен 5 с? Скрыть 7 Контрольная работа по физике в 10 классе по теме infourokru › …po-fizike…klasse-po-teme-kinematika… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте 11 Тело вращается на нити длиной 1 м и делает 10 оборотов за 5 сек Найти период вращения, частоту вращения, скорость вращения, центростремительное ускорение? Контрольная работа по физике 10 класс по теме: Кинематика Читать ещё 11 Тело вращается на нити длиной 1 м и делает 10 оборотов за 5 сек Найти период вращения, частоту вращения, скорость вращения, центростремительное ускорение? Контрольная работа по физике 10 класс по теме: Кинематика Вариант 2 1 Определите проекции вектора перемещения на оси и модуль: Sх , Sy , S Скрыть 8 Ответы на контрольные работы по физике 10 класс кинематика — смотрите картинки ЯндексКартинки › ответы на контрольные работы по физике 10 класс Пожаловаться Информация о сайте Ещё картинки 9 Контрольная работ по физике №1 школа-97рф › doc/zaochka/10/10_klass_Kontrolnaya… Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работ по физике №1 Для 10 класса 2015-2016 учебный год, заочная форма обучения Контрольная работа № 1 по теме » Кинематика » 10 класс Вариант 3 1 Уравнение координаты материальной точки, движущейся вдоль оси Оx, имеет вид х = 100 — 10t2 (величины выражены в СИ) Определите: а) Читать ещё Контрольная работ по физике №1 Для 10 класса 2015-2016 учебный год, заочная форма обучения Г Железногорск 2014 г Контрольная работа № 1 по теме » Кинематика » 10 класс Вариант 1 1 Уравнение движения тела имеет вид: х = 200 + 20t2 Контрольная работа № 1 по теме » Кинематика » 10 класс Вариант 3 1 Уравнение координаты материальной точки, движущейся вдоль оси Оx, имеет вид х = 100 — 10t2 (величины выражены в СИ) Определите: а) координату тела через 5с после начала движения, б) постройте график скорости тела, в) за какое время тело совершит путь 70 м? г) постройте график скорости этого тела Скрыть doc Посмотреть Сохранить на ЯндексДиск 10 Контрольная работа для 10 класса по теме | Doc4webru doc4webru › Физика › …-rabota-dlya-klassa-po… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная работа № 1 по теме «Основы кинематики » — 10 класс 1 вариант 5 С какой линейной скоростью движется тело по окружности радиусом 10 м, если Контрольная работа по физике для 8 класса «Агрегатные состояния вещества» Читать ещё Контрольная работа № 1 по теме «Основы кинематики » — 10 класс 1 вариант 1 В субботу автобус сделал 10 рейсов, а в воскресенье 12 5 С какой линейной скоростью движется тело по окружности радиусом 10 м, если один оборот оно делает за 20 с? А) 200 м/с Б) 6,28 м/с В) 3,14 м/с вариант Контрольная работа по физике для 8 класса «Агрегатные состояния вещества» Скрыть Тест Кинематика с ответами по теме ( 10 класс , физика ) obrazovakaru › test/kinematika-s…10-klasshtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Тест « Кинематика » ( 10 класс ) с ответами составлен в соответствии с действующей программой, утвержденной министерством Данная подборка тестов поможет качественно подготовиться к контрольной работе Читать ещё Тест « Кинематика » ( 10 класс ) с ответами составлен в соответствии с действующей программой, утвержденной министерством Данная подборка тестов поможет качественно подготовиться к контрольной работе Задания удобно просматривать в онлайн режиме с любого доступного устройства Вопросы проверяют знание основ кинематического процесса, формул и умение проверять их на практике Некоторые задания касаются динамики в рамках указанной темы Тест по теме « Кинематика » поможет быстро и качественно оценить знания данной темы, станет отличным помощником для тех, кто хочет подтянуть предмет Рейтинг теста А Скрыть Вместе с « ответы на контрольные работы по физике 10 класс кинематика » ищут: ответы на контрольные работы по русскому языку 3 класс крылова часть 1 ответы на контрольные работы по английскому языку 3 класс spotlight ответы на контрольные работы по английскому языку 7 класс spotlight ответы на контрольные работы по русскому языку 2 класс крылова часть 1 ответы на контрольные работы по математике 5 класс мерзляк ответы на контрольные работы по математике 6 класс виленкин ответы на контрольные работы по алгебре 7 класс ответы на контрольные работы по английскому языку 4 класс афанасьева ответы на контрольные работы по математике 6 класс мерзляк ответы на контрольные вопросы по геометрии 7-9 класс погорелов 1 2 3 4 5 дальше Браузер Предложит замену неверному адресу сайта 0+ Установить
Дополнительные главы физики: кинематика.
 9 класс: О курсе
9 класс: О курсе
Курс ориентирован на слушателей, владеющих школьной программой по физике 9 класса. В процессе обучения учащиеся познакомятся с основными принципами и методами кинематики, увидят, как довольно сложные движения можно свести к комбинации более простых, и научатся решать разнообразные задачи.
Курс состоит из 10 обязательных и 2 лекционных модулей, 51 видеолекций с конспектами, 181 обязательных упражнений и факультативных задач для самостоятельного решения.
Учебные модули
— Геометрия и физика
— Описание движения
— Ускорение
— Движение по окружности
— Малые приращения физических величин
— Движение тела, брошенного под углом к горизонту
— Криволинейное движение
— Кинематика плоского движения твердого тела
— Комбинация прямолинейных движений
— Кинематические связи
— Выбор системы отсчета
— Комбинация вращения и прямолинейного движения
Внутри каждого модуля есть:
— видео с кратким конспектом, где обсуждается теория и разбираются примеры решения задач,
— упражнения с автоматической проверкой, позволяющие понять, как усвоена теория,
— задачи для самостоятельного решения, которые не учитываются в прогрессе и не идут в зачет по модулю, но позволяют качественно повысить свой уровень.
Каждый ученик самостоятельно определяет для себя темп и удобное время учебы. Часть модулей открыта сразу, следующие модули открываются после того, как получен зачет по предыдущим. В каждом разделе есть ответы на популярные вопросы, где можно уточнить свое понимание теории или условия задачи, но нельзя получить подсказки по решению.
По итогам обучения выдается электронный сертификат. Для его получения необходим зачет по всем учебным модулям, кроме лекционных. Условие получения зачета по модулю — успешное выполнение не менее 70% упражнений. Сертификаты могут учитываться при отборе на очные программы по направлению «Наука».
Если ученик не успеет получить зачет по отдельным модулям, то он не сможет получить сертификат, но сможет возобновить обучение, когда курс стартует в следующий раз. При этом выполнять пройденные модули заново не потребуется (но может быть предложено, если соответствующие учебные материалы обновятся).
В следующий раз курс будет открыт осенью 2020 года.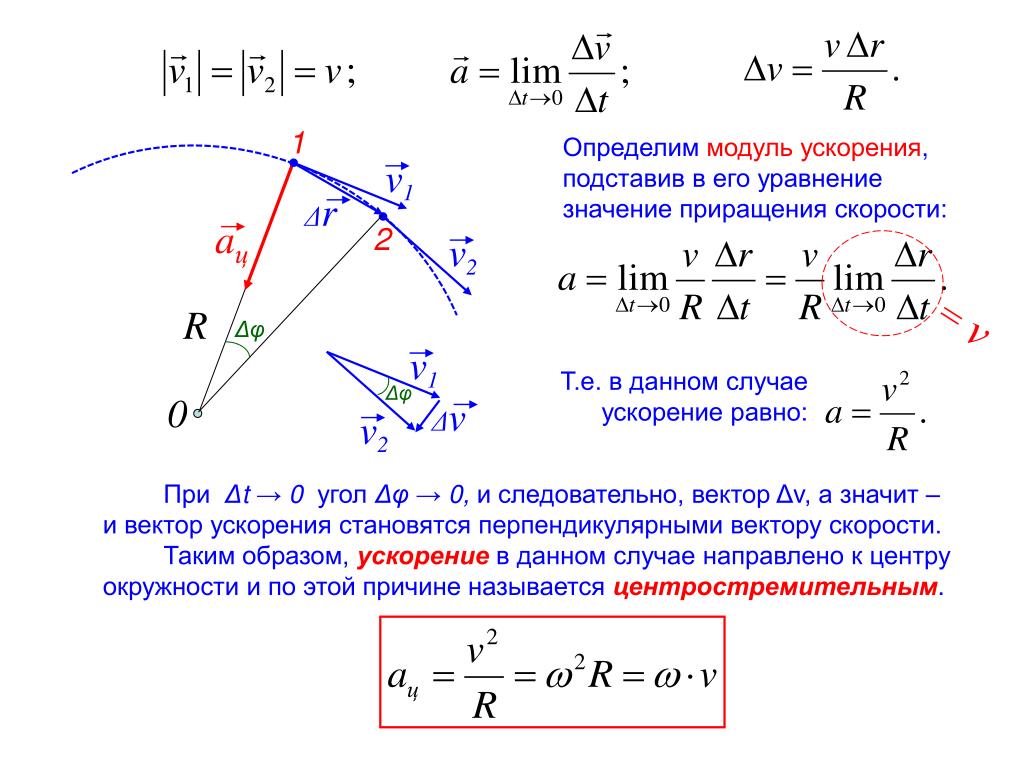
| ШЭ | МЭ | РЭ | ЗЭ | |
|---|---|---|---|---|
| 7 класс | 20, 19, 18, 17 16, 15, 14, 13 | 20, 19, 18, 17 16, 15, 14, 13 | 10, 09 | — |
| 8 класс | 20, 19, 18, 17 16, 15, 14, 13 | 20, 19, 18, 17 16, 15, 14, 13 | 10, 09, 07 | — |
| 9 класс | 20, 19, 18 17, 16, 15, 14 | 20, 19, 18 17, 16, 15, 14 | 20, 19, 18, 17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 | 19, 18, 17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 |
| 10 класс | 20, 19, 18 17, 16, 15, 14 | 20, 19, 18 17, 16, 15, 14 | 20, 19, 18, 17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 | 19, 18, 17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 |
| 11 класс | 20, 19, 18 17, 16, 15, 14 | 20, 19, 18 17, 16, 15, 14 | 20, 19, 18, 17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 | 19, 18, 17 16, 15, 14, 13, 12 11, 10, 09, 08, 07 06, 05, 04, 03, 02 01, 00, 99, 98, 97 96, 95, 94, 93, 92 |
| Нулевой тур | Первый тур | Второй тур | ||
| 7 класс | 19.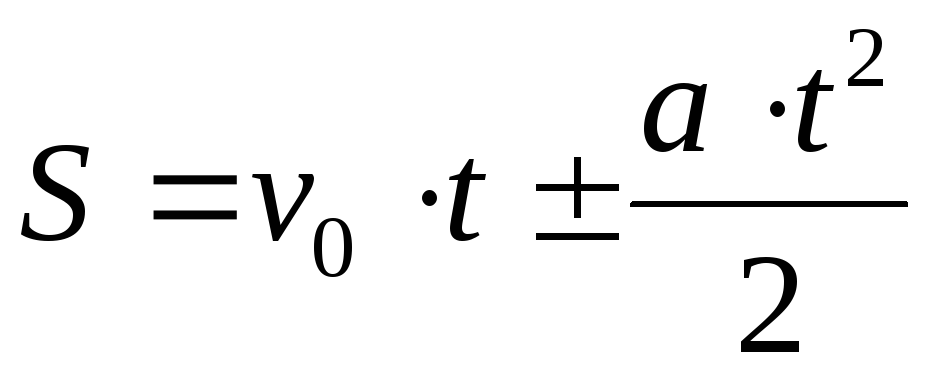 0, 0,19.1 18.0, 18.1 17.0, 17.1 16.0, 16.1 15.0, 15.1 14.0, 14.1, 14.2, 14.3, 14.4 | 19, 18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | 20, 19, 18 17, 16, 15 | |
| 8 класс | 19.0, 19.1 18.0, 18.1 17.0, 17.1 16.0, 16.1 15.0, 15.1 14.0, 14.1, 14.2, 14.3, 14.4 | 19, 18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | 20, 19, 18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | |
| 9 класс | 19.0, 19.1 18.0, 18.1 17.0, 17.1 16.0, 16.1 15.0, 15.1 14.0, 14.1, 14.2, 14.3, 14.4 | 19, 18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | 20, 19, 18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | |
| 10 класс | 19. 0, 0,19.1 18.0, 18.1 17.0, 17.1 16.0, 16.1 15.0, 15.1 14.0, 14.1, 14.2, 14.3, 14.4 | 19, 18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | 20, 19, 18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | |
| 11 класс | 19.0, 19.1, 19.2, 19.T 18.0, 18.1, 18.2, 18.3 17.0, 17.1, 17.2, 17.3 16.0, 16.1, 16.2, 16.3 15.0, 15.1, 15.2, 15.3 14.0, 14.1, 14.2, 14.3, 14.4 | 20, 19, 18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | 20, 19, 18 17, 16, 15, 14 13, 12, 11, 10 09, 08, 07, 06 | |
| 7 класс | 20, 19, 18, 17, 16 15, 14, 13, 12, 11 | |||
| 8 класс | 20.1, 20.2 19, 18, 17.  1, 1,17.2 16, 15, 14, 13, 12, 11 | |||
| 9 класс | 20.1, 20.2, 20.3 19, 18, 17.1, 17.2 16, 15, 14, 13, 12, 11 | |||
| 10 класс | 20.1, 20.2, 20.3 19, 18, 17.1, 17.2 16, 15, 14, 13, 12, 11 | |||
| 11 класс | 20.1, 20.2, 20.3 19.1, 19.2, 19.3 18.1, 18.2, 18.3, 18.4 17.1, 17.2, 17.3, 17.4 16, 15, 14 13.1, 13.2, 13.3, 13.4, 13.5, 13.6 12.1, 12.2, 12.3, 12.4, 12.5 11.1, 11.2, 11.3, 11.4, 11.5 11.6 |
Кинематика. Подготовка к ЕГЭ — физика, уроки
Готовимся к ЕГЭ
Кинематика
Скажи мне, и я забуду. Покажи мне, и я запомню. Вовлеки меня , и я научусь.
Основные понятия кинематики
1.Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени. 2. Материальная точка – тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь.
3.Траектория – воображаемая линия, по которой движется тело.
4.Путь – длина траектории.
5. Перемещение – вектор, соединяющий начальную и конечную точки траектории.
6. Равномерное движение — -движение тела с изменяющейся скоростью. 7. Неравномерное движение- движение тела с постоянной скоростью. 8. Путь – векторная величина. 9.Ускорение тела , при равноускоренном движении — величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло.
10. Скорость — физическая векторная величина, характеризующая направление и быстроту движения.
Скорость — физическая векторная величина, характеризующая направление и быстроту движения.
11. Ускорение свободного падения – g ≈ 9,8 м/с 2
12. Равномерно движущееся по окружности тело имеет ускорение, направленное к центру окружности (перпендикулярно скорости) – центростремительное ускорение. 13. Период обращения – время, в течение которого тело совершает один полный оборот. 14. Перемещение есть скалярная величина.
проверка
1 + 8 —
2 + 9 +
3 + 10 +
4 + 11 +
5 + 12 +
6 — 13 +
7 — 14 —
Оценили: 14 верно- «5», 12-13- «4», 9-11- «3»
Записать обозначения и единицы измерения физических величин.
перемещение
скорость
время
ускорение
период
частота
радиус
координата тела
угловая скорость
перемещение
скорость
S
м
V
время
м/с
t
ускорение
с
а
период
м/с 2
T
частота
радиус
с
ν
Гц
R
координата тела
м
х
угловая скорость
м
ω
рад/с
НАЙДИ ОШИБКУ
9- «5» 8- «4» 7- «3»
Выбрать формулы равномерного и
неравномерного движения
1) х=2t 2) v=2t 3) х=3+2t 4) х=3t 2 5) х=3t+3t 2 6) v=t+1 7) х=2-3t+4t 2 8) v=6
Неравномерное движение
Равномерное движение
4) х=3t 2
1) х=2t
6) v=t+1
3) х=3+2t
5) х=3t+3t 2
7) х=2-3t+4t 2
8) v=6
2) v=2t
8 верно- «5»
7 верно- «4»
6 верно — «3»
БЛИЦ ОПРОС
Рассмотрим задачи:
Подборка заданий по кинематике
(из заданий ЕГЭ 2010-2016 гг.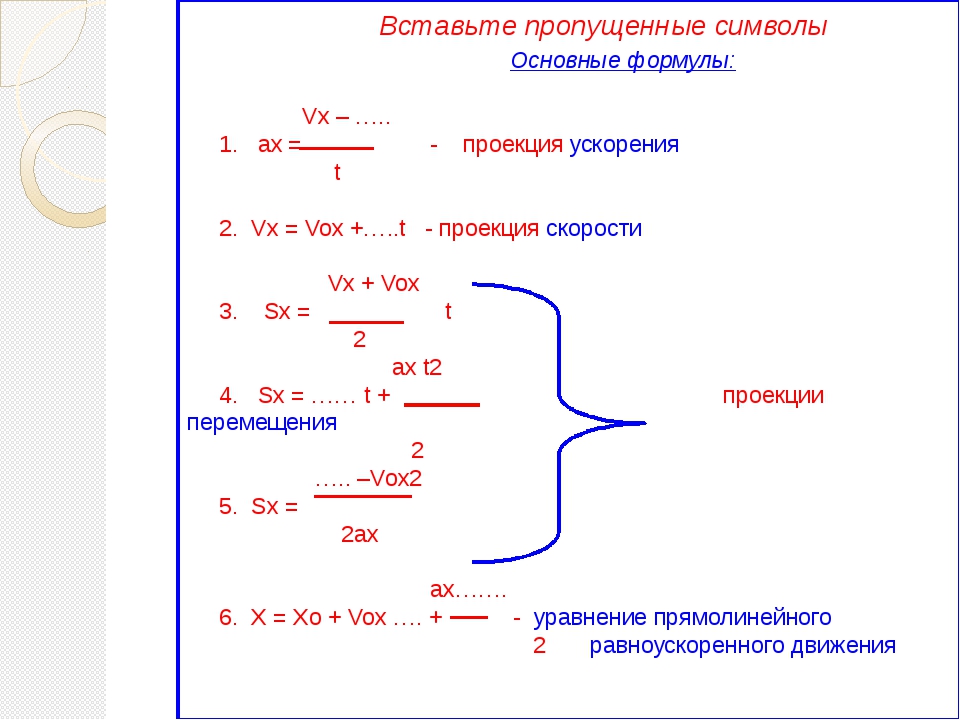 — А)
— А)
а
На рисунках изображены графики зависимости модуля ускорения от времени движения. Какой из графиков соответствует равномерному прямолинейному движению?
а
4)
а
2)
3)
а
1)
График скорости прямолинейного движения материальной точки показан на рисунке. Чему равна скорость точки в момент времени t = 1 с?
- 0,5 м/с
- 1 м/с
- — 0,5 м/с
- 2 м/с
БЛИЦ ОПРОС
По графику зависимости пройденного пути от времени определите скорость велосипедиста в момент времени t= 2с.
Ответ: 2м/с
БЛИЦ ОПРОС
Скорость тела, движущегося прямолинейно и равноускоренно, изменилась при перемещении из точки 1 в точку 2 так, как показано на рисунке. Какое направление имеет вектор ускорения на этом участке?
v 1 v 2
1) 2) 3) а = 0
4) направление может быть любым
Ответ: 1
По графику зависимости скорости движения тела от времени. Найдите скорость тела в момент времени t = 4 с.
Найдите скорость тела в момент времени t = 4 с.
1) 0 м/с
2) 2 м/с
3) — 4м/с
4) 16 м/с
По данному графику определите какое из трех тел движется
равноускоренно , равномерно , равнозамедленно ?
Что означает точка пересечения графиков?
Тело движется по окружности по часовой стрелке. Какой из изображенных векторов совпадает по направлению с вектором скорости в точке А?
Вертолет летит в горизонтальном направлении со скоростью 20 м/с. Из него выпал груз, который коснулся земли через 4 с. На какой высоте летит вертолет? Сопротивление воздуха движению груза не учитывать.
- 40 м.
- 80 м.
- 160 м.
- 320 м.
На рисунке представлен график зависимости скорости υ автомобиля от времени t . Найдите путь, пройденный автомобилем за 5 с.
1) 0 м; 2) 20 м; 3) 30 м; 4) 35 м
- Пройденный путь равен площади фигуры под графиком скорости
Трапеция
При поступательном движении по прямой тело меняло свою скорость так, как показано на графике. Ускорение тела в промежуток времени от 0 до 6 с
Ускорение тела в промежуток времени от 0 до 6 с
V,м/с
1
Равнялось нулю
8
6
V =3 м/с
2
4
2
Равнялось 0,5 м/ с
2
V = 0 м/c
3
0
2
Равнялось 2 м/с
6 c
4
5
1
3
2
t, с
-2
4
-4
Постоянно изменялось
-6
-8
2
а = (3м/с -0 м/с) / 6 с = 0,5 м/с
подсказка
Определите путь, пройденный телом за 5 с из состояния покоя при ускорении 2 м/с
2
1
10 м
2
S= υ t +
0
25 м
2
2
υ 0 = 0
S =
3
20 м
2
4
40 м
S=
S= 25 м
подсказка
Дана зависимость координаты от времени при равномерном движении:
Чему равны начальная координата и скорость тела?
Х = 2 υ = 3
1
0
0
Х = 3 υ = 2
2
0
Х = 2 υ = 2
0
3
Х = 3 υ = 3
4
0
подсказка
РЕШИМ ЗАДАЧИ
1 вариант А1-3 А2-1 А3-1 А4-4 А5-1 В1-600 м/с В2-312
2 вариант А1-3 А2-3 А3-2 А4-3 А5-3 В1-1,5 м/с В2-332
9-8 б.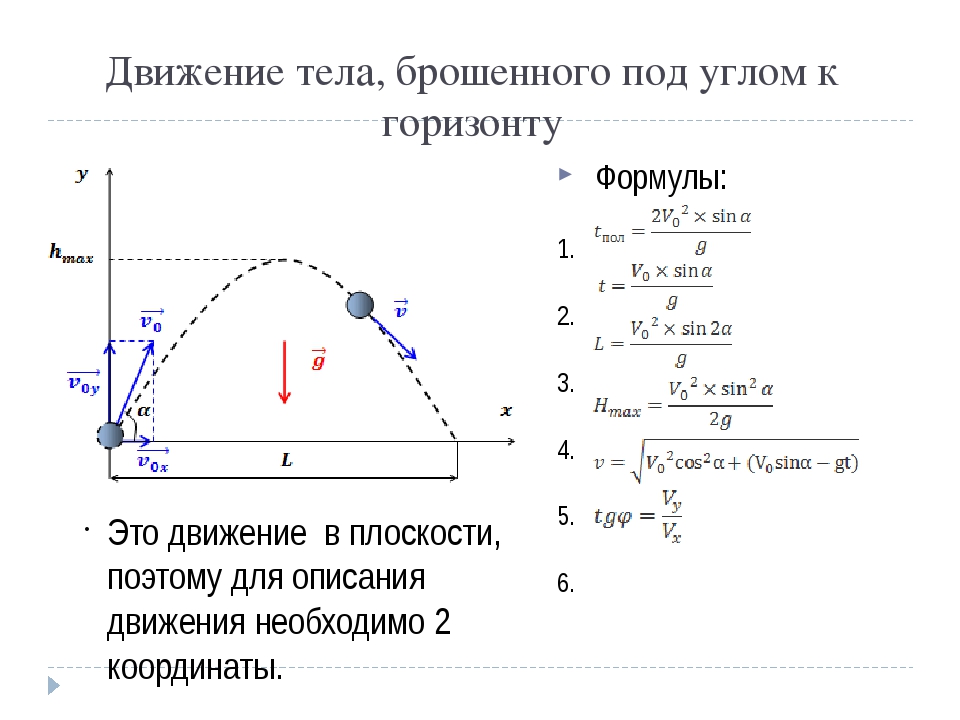 — «5» 7-6 б.- «4» 5-4 б.- «3»
— «5» 7-6 б.- «4» 5-4 б.- «3»
3 вариант А1-2 А2-3 А3-2 А4-3 А5-1 В1-1,35 м В2-321
4 вариант А1-4 А2-4 А3-4 А4-4 А5-3 В1-0,8 м/с 2 В2-331
26
Оценка за урок
«5» 18-20 баллов
«4» 17-15 баллов
«3» 14-13 баллов
Домашнее задание
Повторить: гл.№1-2
А : Р-72,103
В : Р-82,104
С: Р -88,109
Механическое движение — определение, формулы, примеры
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Путь — вектор, проведенный из начальной точки пути в конечную [м].
Чтобы сразу практиковаться, приходите в современную школу для подростков Skysmart. Ученики занимаются на интерактивной платформе по индивидуальной программе, отслеживает прогресс в личном кабинете и чувствуют себя увереннее на школьных контрольных.
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю. |
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость → → → |
Средняя путевая скорость V ср. V ср.путевая — средняя путевая скорость [м/с] |
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это
длина траектории.
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения x(t) = x0 + vxt x(t) — искомая координата [м] |
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
Уравнение движения при движении против оси x(t) = x0 — vxt x(t) — искомая координата [м] |
Графики
Изменение любой величины можно описать графически. Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.
Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.
В видео ниже разбираемся, как строить графики кинематических величин
и зачем они нужны.
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, прямолинейное движение — это движение с ускорением по прямой линии. 2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8
м/с2.
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Примеров механического движения в жизни — масса. Узнайте больше у преподавателей онлайн-школы Skysmart. Каждый урок по физике — это новый эксперимент: интерактивный, живой и очень увлекательный.
Узнайте больше у преподавателей онлайн-школы Skysmart. Каждый урок по физике — это новый эксперимент: интерактивный, живой и очень увлекательный.
Приходите на бесплатный вводный урок и начните заниматься физикой в удовольствие уже завтра!
Кинематические уравнения и кинематические графики
Урок 4 этого модуля в классе физики был посвящен использованию графиков скорость-время для описания движения объектов. В этом уроке было подчеркнуто, что наклон линии на графике скорость-время равен ускорению объекта, а площадь между линией и осью времени равна смещению объекта. Таким образом, графики скорость-время можно использовать для определения численных значений и соотношений между величинами смещения (d), скоростью (v), ускорением (a) и временем (t).В Уроке 6 основное внимание уделялось использованию четырех кинематических уравнений для описания движения объектов и прогнозирования числовых значений одного из четырех параметров движения — смещения (d), скорости (v), ускорения (a) и время (t). Таким образом, теперь доступны два метода для решения проблем, связанных с численными соотношениями между перемещением, скоростью, ускорением и временем. В этой части Урока 6 мы исследуем взаимосвязь между этими двумя методами.
Таким образом, теперь доступны два метода для решения проблем, связанных с численными соотношениями между перемещением, скоростью, ускорением и временем. В этой части Урока 6 мы исследуем взаимосвязь между этими двумя методами.
Пример проблемы — графическое решение
Рассмотрим объект, который движется с постоянной скоростью +5 м / с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м / с в течение следующих 5 секунд.Такое словесное описание движения может быть представлено графиком скорость-время. График показан ниже.
Горизонтальная часть графика изображает движение с постоянной скоростью в соответствии со словесным описанием. Часть графика с положительным уклоном (т. Е. С наклоном вверх) изображает положительное ускорение, соответствующее словесному описанию объекта, движущегося в положительном направлении и ускоряющегося от 5 до 15 м / с. Наклон линии можно вычислить, используя коэффициент превышения пробега. Между 5 и 10 секундами линия поднимается с 5 до 15 м / с и длится от 5 до 10 с. Это общий подъем +10 м / с и общий пробег 5 с. Таким образом, уклон (отношение подъема / хода) составляет (10 м / с) / (5 с) = 2 м / с 2 . Используя график скорость-время, определено, что ускорение объекта составляет 2 м / с 2 в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика скорость-время. Область между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции.Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего поверх площади прямоугольника. Это показано на диаграмме ниже.
Между 5 и 10 секундами линия поднимается с 5 до 15 м / с и длится от 5 до 10 с. Это общий подъем +10 м / с и общий пробег 5 с. Таким образом, уклон (отношение подъема / хода) составляет (10 м / с) / (5 с) = 2 м / с 2 . Используя график скорость-время, определено, что ускорение объекта составляет 2 м / с 2 в течение последних пяти секунд движения объекта. Смещение объекта также можно определить с помощью графика скорость-время. Область между линией на графике и осью времени представляет смещение; эта область принимает форму трапеции.Как обсуждалось в Уроке 4, площадь трапеции можно приравнять к площади треугольника, лежащего поверх площади прямоугольника. Это показано на диаграмме ниже.
Общая площадь равна площади прямоугольника плюс площадь треугольника. Расчет этих площадей показан ниже.
| Прямоугольник | Треугольник |
|---|---|
| Площадь = основание * высота Площадь = (10 с) * (5 м / с) Площадь = 50 м | Площадь = 0.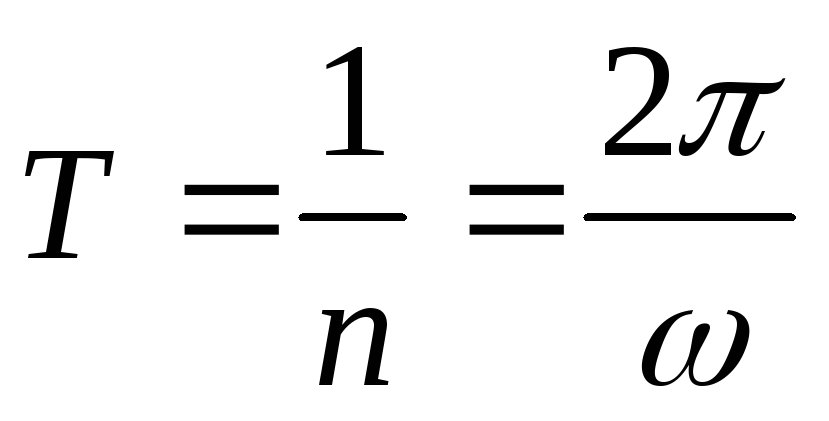 5 * основание * высота 5 * основание * высота Площадь = 0,5 * (5 с) * (10 м / с) Площадь = 25 м |
Общая площадь (прямоугольник плюс треугольник) равна 75 м. Таким образом, перемещение объекта составляет 75 метров за 10 секунд движения.
Вышеупомянутое обсуждение иллюстрирует, как можно использовать графическое представление движения объекта для извлечения числовой информации об ускорении и смещении объекта. После построения график скорость-время можно использовать для определения скорости объекта в любой момент в течение 10 секунд движения.Например, скорость объекта в 7 секунд может быть определена путем считывания значения координаты y в координате x 7 секунд. Таким образом, графики скорость-время можно использовать для выявления (или определения) числовых значений и соотношений между величинами смещения (d), скоростью (v), ускорением (a) и временем (t) для любого заданного движения.
Пример проблемы — решение с использованием кинематического уравнения
Теперь рассмотрим то же словесное описание и соответствующий анализ с использованием кинематических уравнений. Словесное описание движения было:
Словесное описание движения было:
Объект, который движется с постоянной скоростью +5 м / с в течение 5 секунд, а затем ускоряется до конечной скорости +15 м / с в течение следующих 5 секунд
Кинематические уравнения могут применяться к любому движению, для которого ускорение постоянно. Поскольку это движение имеет две отдельные стадии ускорения, любой кинематический анализ требует, чтобы параметры движения в течение первых 5 секунд не смешивались с параметрами движения в течение последних 5 секунд.В таблице ниже перечислены указанные параметры движения.
| t = 0 с — 5 с | t = 5 с — 10 с |
|---|---|
| v i = 5 м / с v f = 5 м / с t = 5 с a = 0 м / с 2 | v i = 5 м / с v f = 15 м / с t = 5 с |
Обратите внимание, что ускорение в течение первых 5 секунд указано как 0 м / с 2 , несмотря на то, что это явно не указано. Фраза с постоянной скоростью указывает движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.
Фраза с постоянной скоростью указывает движение с нулевым ускорением. Ускорение объекта за последние 5 секунд можно рассчитать с помощью следующего кинематического уравнения.
v f = v i + a * t
Здесь показаны подстановка и алгебра.
15 м / с = 5 м / с + a * (5 с)
15 м / с — 5 м / с = a * (5 с)
10 м / с = a * (5 с)
(10 м / с) / (5 с) = a
a = 2 м / с 2
Это значение ускорения объекта за время от 5 до 10 с согласуется со значением, определенным по наклону линии на графике скорость-время.
Смещение объекта в течение всех 10 секунд также можно рассчитать с помощью кинематических уравнений. Поскольку эти 10 секунд включают два совершенно разных интервала ускорения, расчеты для каждого интервала должны выполняться отдельно. Это показано ниже.
| t = 0 с — 5 с | t = 5 с — 10 с |
|---|---|
| d = v i * t + 0,5 * a * t 2 d = (5 м / с) * (5 с) +0.  5 * (0 м / с 2 ) * (5 с) 2 5 * (0 м / с 2 ) * (5 с) 2 d = 25 м + 0 м d = 25 м | d = ((v i + v f ) / 2) * t d = ((5 м / с + 15 м / с) / 2) * (5 с) d = (10 м / с) * (5 с) d = 50 м |
Общее смещение в течение первых 10 секунд движения составляет 75 метров, что соответствует значению, определенному по площади под линией на графике скорость-время.
Анализ этого простого движения иллюстрирует ценность этих двух представлений движения — графика скорости-времени и кинематических уравнений.Каждое представление можно использовать для извлечения числовой информации о неизвестных величинах движения для любого заданного движения. Приведенные ниже примеры предоставляют полезную возможность для тех, кому требуется дополнительная практика.
Проверьте свое понимание
1. Rennata Gas движется по городу со скоростью 25,0 м / с и начинает ускоряться с постоянной скоростью -1,0 м / с 2 . В конце концов Ренната полностью останавливается.
В конце концов Ренната полностью останавливается.
а. Изобразите ускоренное движение Реннаты, нарисовав график скорости-времени.Используйте график скорость-время, чтобы определить это расстояние.
г. Используйте кинематические уравнения, чтобы рассчитать расстояние, которое Ренната преодолеет при замедлении.
2. Отто Эмиссион едет на своей машине со скоростью 25,0 м / с. Отто разгоняется со скоростью 2,0 м / с 2 за 5 секунд. Затем Отто поддерживает постоянную скорость еще 10,0 секунд.
а. Изобразите 15 секунд движения Отто Эмиссии, нарисовав график скорости-времени.Используйте график, чтобы определить расстояние, которое Отто преодолел за все 15 секунд.
г. Наконец, разделите движение на два сегмента и используйте кинематические уравнения, чтобы вычислить общее расстояние, пройденное за все 15 секунд.
3. Люк Отбело, артист-человек, стреляющий по пушечным ядрам, сброшен с края обрыва с начальной скоростью +40,0 м / с. Люк ускоряется с постоянным ускорением вниз -10,0 м / с 2 (приблизительное значение ускорения свободного падения).
Люк ускоряется с постоянным ускорением вниз -10,0 м / с 2 (приблизительное значение ускорения свободного падения).
а. Нарисуйте график скорость-время для первых 8 секунд движения Люка.
б. Используйте кинематические уравнения, чтобы определить время, необходимое Люку Отбелоу, чтобы вернуться к исходной высоте обрыва. Укажите это время на графике.
4. Chuck Wagon движется с постоянной скоростью 0,5 мили в минуту в течение 10 минут. Затем Чак замедляется со скоростью -25 миль / мин 2 в течение 2 минут.
а. Нарисуйте график скорости-времени движения Чака Вагона. Используйте график скорость-время, чтобы определить общее расстояние, пройденное Чаком Вэгоном за 12 минут движения.
г. Наконец, разделите движение на два сегмента и используйте кинематические уравнения, чтобы определить общее расстояние, пройденное Чаком Вагоном.
5. Vera Side мчится по шоссе со скоростью 45,0 м / с. Вера смотрит вперед и наблюдает за аварией, которая привела к налету на дороге посреди дороги.К тому моменту, когда Вера хлопает по перерывам, она находится в 50,0 м от pileup. Она замедляется со скоростью -10,0 м / с 2 .
Вера смотрит вперед и наблюдает за аварией, которая привела к налету на дороге посреди дороги.К тому моменту, когда Вера хлопает по перерывам, она находится в 50,0 м от pileup. Она замедляется со скоростью -10,0 м / с 2 .
а. Постройте график скорости-времени для движения Веры Сайд. Используйте график, чтобы определить расстояние, которое Вера должна пройти до полной остановки (если она не столкнется с pileup).
г. Используйте кинематические уравнения, чтобы определить расстояние, которое Вера Сайд должна пройти до полной остановки (если она не столкнется с pileup). Ударится ли Вера по машинам в pileup? То есть проездит Вера больше 50.0 метров?
6. Эрл Э. Берд движется со скоростью 30,0 м / с за 10,0 секунд. Затем он ускоряется со скоростью 3,00 м / с 2 за 5,00 секунд.
а. Постройте график скорости-времени для движения Эрла Э. Берда. Используйте график, чтобы определить общее пройденное расстояние.
б. Разделите движение Эрла Э. Берда на два временных отрезка и используйте кинематические уравнения для расчета полного смещения.
Берда на два временных отрезка и используйте кинематические уравнения для расчета полного смещения.
Решения вышеуказанных вопросов
Решение вопроса 1
а.График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0,5 * b * h = 0,5 * (25,0 с) * (25,0 м / с)
Площадь = 313 м
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Дано:
| Находят: d = ?? |
(0 м / с) 2 = (25,0 м / с) 2 + 2 * (-1,0 м / с 2 ) * d
0. 0 м 2 / с 2 = 625,0 м 2 / с 2 + (-2,0 м / с 2 ) * d
0 м 2 / с 2 = 625,0 м 2 / с 2 + (-2,0 м / с 2 ) * d
0,0 м 2 / с 2 — 625,0 м 2 / с 2 = (-2,0 м / с 2 ) * d
(-625,0 м 2 / с 2 ) / (- 2,0 м / с 2 ) = d
313 м = d
Решение вопроса 2
a.График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5 * b tri * h tri + b rect1 * h rect1 + b rect2 * h rect2
Площадь = 0.5 * (5,0 с) * (10,0 м / с) + (5,0 с) * (25,0 м / с) + (10,0 с) * (35,0 м / с)
Площадь = 25 м + 125 м + 350 м
Площадь = 500 м
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d для первых 5 секунд:
Дано:
| Находят: d = ?? |
d = v i * t + 0,5 * a * t 2
d = (25,0 м / с) * (5,0 с) + 0.5 * (2,0 м / с 2 ) * (5,0 с) 2
d = 125 м + 25,0 м
d = 150 м
Теперь найдите d за последние 10 секунд:
Дано:
| Находят: d = ?? |
(Примечание: скорость на отметке 5 секунд можно определить, зная, что автомобиль ускоряется с 25,0 м / с при +2,0 м / с 2 в течение 5 секунд. Это приводит к изменению скорости на a * t = 10 м / с, а значит, скорость 35,0 м / с.)
d = v i * t + 0.5 * а * т 2
d = (35,0 м / с) * (10,0 с) + 0,5 * (0,0 м / с 2 ) * (10,0 с) 2
d = 350 м + 0 м
d = 350 м
Общее расстояние за 15 секунд движения является суммой этих двух вычислений расстояний (150 м + 350 м):
расстояние = 500 м
Решение вопроса 3
a.График скорость-время для движения:
г. Время для подъема и падения до первоначальной высоты в два раза больше времени, чтобы подняться на вершину. Итак, решение состоит в том, чтобы найти время, чтобы подняться до пика, а затем удвоить его.
Итак, решение состоит в том, чтобы найти время, чтобы подняться до пика, а затем удвоить его.
Дано:
| Находят: т вверх = ?? 2 * т вверх = ?? |
v f = v i + a * t вверх
0 м / с = 40 м / с + (-10 м / с2) * t вверх
(10 м / с 2 ) * t вверх = 40 м / с
т вверх = (40 м / с) / (10 м / с 2 )
т до = 4.0 с
2 * t вверх = 8,0 с
Решение вопроса 4
a.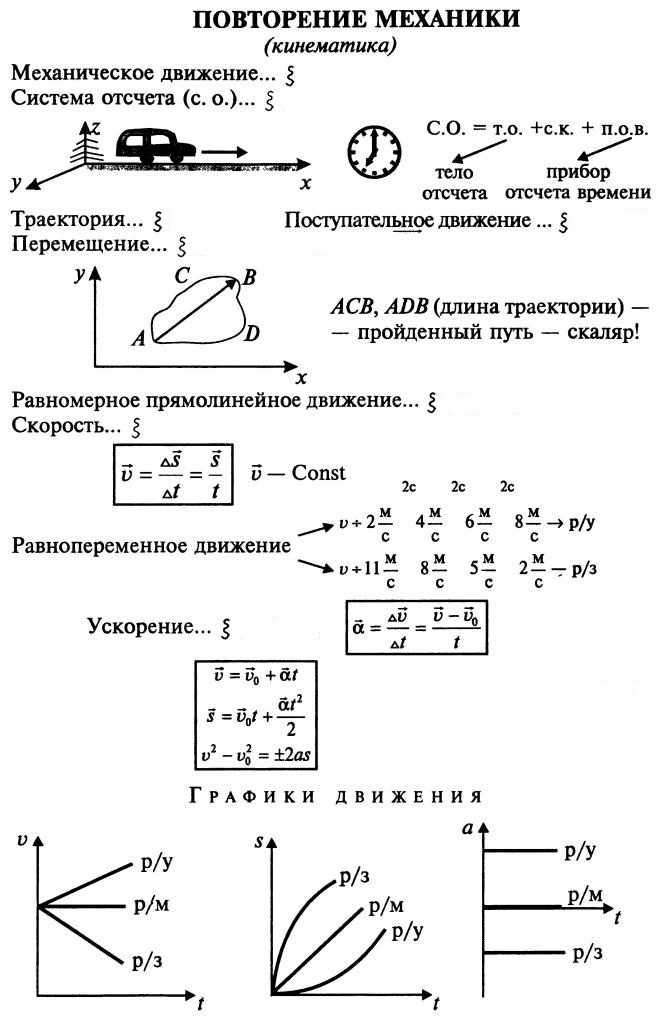 График скорость-время для движения:
График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади прямоугольника плюс площадь треугольника.
Площадь = b прямоугольник * h прямоугольник + 0,5 * b tri * h tri
Площадь = (10,0 мин) * (0,50 миль / мин) + 0,5 * (2,0 мин) * (0,50 миль / мин)
Площадь = 5 миль + 0,5 миль
Площадь = 5.5 миль
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d для первых 10 минут:
Дано:
| Находят: d = ?? |
d = v i * t + 0,5 * a * t 2
d = (0,50 миль / мин) * (10.0 мин) + 0,5 * (0,0 миль / мин 2 ) * (10,0 мин) 2
d = 5.0 миль + 0 миль
d = 5.0 миль
Теперь найдите d за последние 2 минуты:
Дано:
| Находят: d = ?? |
d = v i * t + 0,5 * a * t 2
d = (0,50 миль / мин) * (2,0 мин) + 0,5 * (- 0,25 м / с 2 ) * (2,0 мин) 2
d = 1,0 мили + (-0,5 мили)
d = 0.5 миль
Общее расстояние за 12 минут движения является суммой этих двух вычислений расстояний (5.0 миль + 0,5 миль):
расстояние = 5.5 миль
Решение вопроса 5
a. График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени.
Площадь = 0.5 * b * h = 0,5 * (4,5 с) * (45,0 м / с)
Площадь = 101 м
г.
Дано:
| Находят: d = ?? |
v f 2 = v i 2 + 2 * a * d
(0 м / с) 2 = (45.0 м / с) 2 + 2 * (-10,0 м / с 2 ) * d
0,0 м 2 / с 2 = 2025,0 м 2 / с 2 + (-20,0 м / с 2 ) * d
0,0 м 2 / с 2 -2025,0 м 2 / с 2 = (-20,0 м / с 2 ) * d
(-2025,0 м 2 / с 2 ) / (- 20,0 м / с 2 ) = d
101 м = d
Так как место аварии находится менее чем в 101 м от Веры, она действительно ударится по скоплению, прежде чем полностью остановится (если только она не свернет в сторону).
Решение вопроса 6
a. График скорость-время для движения:
Пройденное расстояние можно определить путем вычисления площади между линией на графике и осью времени. Эта площадь будет равна площади треугольника плюс площадь прямоугольника 1 плюс площадь прямоугольника 2.
Площадь = 0,5 * b tri * h tri + b 1 * h 1 + b 2 * h 2
Площадь = 0,5 * (5,0 с) * (15,0 м / с) + (10,0 с) * (30,0 м / с) + (5,0 с) * (30,0 м / с)
Площадь = 37,5 м + 300 м + 150 м
Площадь = 488 м
г. Пройденное расстояние можно рассчитать с помощью кинематического уравнения. Решение показано здесь.
Сначала найдите d для первых 10 секунд:
Дано:
| Находят: d = ?? |
d = v i * t + 0.5 * а * т 2
d = (30,0 м / с) * (10,0 с) + 0,5 * (0,0 м / с 2 ) * (10,0 с) 2
d = 300 м + 0 м
d = 300 м
Теперь найдите d за последние 5 секунд:
Дано:
| Находят: d = ?? |
d = v i * t + 0,5 * a * t 2
d = (30,0 м / с) * (5,0 с) + 0,5 * (3,0 м / с 2 ) * (5,0 с) 2
d = 150 м + 37,5 м
д = 187.5 м
Общее расстояние за 15 секунд движения является суммой этих двух вычислений расстояния (300 м + 187,5 м):
расстояние = 488 м
Кинематические уравнения: примеры задач и решений
Ранее в Уроке 6 были введены и обсуждены четыре кинематических уравнения.Была представлена полезная стратегия решения проблем для использования с этими уравнениями, и были приведены два примера, иллюстрирующие использование этой стратегии. Затем было обсуждено и проиллюстрировано применение кинематических уравнений и стратегии решения проблем к свободному падению. В этой части Урока 6 будет представлено несколько примеров задач. Эти задачи позволяют любому студенту-физику проверить свое понимание использования четырех кинематических уравнений для решения задач, связанных с одномерным движением объектов.Вам предлагается прочитать каждую проблему и попрактиковаться в использовании стратегии для решения проблемы. Затем нажмите кнопку, чтобы проверить ответ, или воспользуйтесь ссылкой, чтобы просмотреть решение.
Проверьте свое понимание
- Самолет ускоряется по взлетно-посадочной полосе со скоростью 3,20 м / с. 2 в течение 32,8 с, пока, наконец, не отрывается от земли. Определите пройденное расстояние до взлета.
- Автомобиль трогается с места и разгоняется равномерно в течение 5 секунд.21 секунда на дистанцию 110 м. Определите ускорение автомобиля.
- Аптон Чак едет по Гигантской капле в Грейт-Америке. Если Аптон бесплатно упадет в течение 2,60 секунды, какова будет его конечная скорость и как далеко он упадет?
- Гоночный автомобиль равномерно ускоряется с 18,5 м / с до 46,1 м / с за 2,47 секунды. Определите ускорение автомобиля и пройденное расстояние.
- Перо упало на Луну с высоты 1.40 метров. Ускорение свободного падения на Луне 1,67 м / с 2 . Определите время, за которое перо упадет на поверхность Луны.
- Сани с ракетным двигателем используются для проверки реакции человека на ускорение. Если сани с ракетным двигателем разгоняются до скорости 444 м / с за 1,83 секунды, то каково это ускорение и какое расстояние они преодолевают?
- Велосипед равномерно ускоряется из состояния покоя до скорости 7.10 м / с на дистанции 35,4 м. Определите ускорение велосипеда.
- Инженер проектирует взлетно-посадочную полосу для аэропорта. Из самолетов, которые будут использовать аэропорт, наименьшая скорость разгона, вероятно, составит 3 м / с 2 . Скорость взлета этого самолета составит 65 м / с. Предполагая это минимальное ускорение, какова минимально допустимая длина взлетно-посадочной полосы?
- Автомобиль, движущийся со скоростью 22,4 м / с, останавливается за 2,55 с. Определите дистанцию заноса автомобиля (предположите равномерный разгон).
- Кенгуру способен прыгать на высоту 2,62 м. Определите взлетную скорость кенгуру.
- Если у Майкла Джордана вертикальный прыжок 1,29 м, то какова его скорость взлета и время зависания (общее время, чтобы подняться на вершину и затем вернуться на землю)?
- Пуля вылетает из винтовки с начальной скоростью 521 м / с. При ускорении через ствол винтовки пуля перемещается на расстояние 0.840 м. Определите ускорение пули (предположим, что ускорение равномерное).
- Бейсбольный мяч поднимается прямо в воздух и его время зависания составляет 6,25 с. Определите высоту, на которую поднимается мяч, прежде чем достигнет пика. (Подсказка: время подъема на пик составляет половину общего времени зависания.)
- Смотровая площадка высокого небоскреба на высоте 370 м над ул. Определите время, необходимое для свободного падения пенни с палубы на улицу ниже.
- Пуля движется со скоростью 367 м / с, когда попадает в комок влажной глины. Пуля пробивает на расстояние 0,0621 м. Определите ускорение пули при движении в глине. (Предположим, что ускорение равномерное.)
- Камень падает в глубокий колодец, и слышно, как он ударился о воду через 3,41 с после падения. Определите глубину колодца.
- Однажды было зарегистрировано, что Jaguar оставил следы заноса длиной 290 м.Предположив, что Jaguar занесло до остановки с постоянным ускорением -3,90 м / с 2 , определите скорость Jaguar до того, как он начал заносить.
- Самолет имеет взлетную скорость 88,3 м / с, и для достижения этой скорости требуется 1365 м. Определите ускорение самолета и время, необходимое для достижения этой скорости.
- Драгстер разгоняется до скорости 112 м / с на расстоянии 398 м. Определите ускорение (предположите равномерное) драгстера.
- С какой скоростью в милях / час (1 м / с = 2,23 миль / час) должен быть брошен объект, чтобы достичь высоты 91,5 м (эквивалент одного футбольного поля)? Предположим, что сопротивление воздуха незначительно.
Решения вышеуказанных проблем
Дано:
a = +3,2 м / с 2
т = 32.8 с
v i = 0 м / с
Находят:
d = ??
d = v i * t + 0,5 * a * t 2
d = (0 м / с) * (32,8 с) + 0,5 * (3,20 м / с 2 ) * (32,8 с) 2
d = 1720 м
Вернуться к проблеме 1
Дано:
d = 110 м
т = 5.21 с
v i = 0 м / с
Находят:
а = ??
d = v i * t + 0,5 * a * t 2
110 м = (0 м / с) * (5,21 с) + 0,5 * (а) * (5,21 с) 2
110 м = (13,57 с 2 ) * а
a = (110 м) / (13.57 с 2 )
a = 8,10 м / с 2
Вернуться к проблеме 2
Дано:
a = -9,8 м
t = 2,6 с
v i = 0 м / с
Находят:
d = ??
v f = ??
d = v i * t + 0.5 * а * т 2
d = (0 м / с) * (2,60 с) + 0,5 * (- 9,8 м / с 2 ) * (2,60 с) 2
d = -33,1 м (- указывает направление)
v f = v i + a * t
v f = 0 + (-9,8 м / с 2 ) * (2,60 с)
v f = -25,5 м / с (- указывает направление)
Вернуться к проблеме 3
Дано:
v и = 18.5 м / с
v f = 46,1 м / с
t = 2,47 с
Находят:
d = ??
а = ??
a = (дельта v) / т
a = (46,1 м / с — 18,5 м / с) / (2,47 с)
а = 11.2 м / с 2
d = v i * t + 0,5 * a * t 2
d = (18,5 м / с) * (2,47 с) + 0,5 * (11,2 м / с 2 ) * (2,47 с) 2
d = 45,7 м + 34,1 м
d = 79,8 м
(Примечание: d также можно рассчитать с помощью уравнения v f 2 = v i 2 + 2 * a * d)
Вернуться к проблеме 4
Дано:
v i = 0 м / с
d = -1.40 м
a = -1,67 м / с 2
Находят:
т = ??
d = v i * t + 0,5 * a * t 2
-1,40 м = (0 м / с) * (t) + 0,5 * (- 1,67 м / с 2 ) * (t) 2
-1,40 м = 0+ (-0,835 м / с 2 ) * (т) 2
(-1.40 м) / (- 0,835 м / с 2 ) = t 2
1,68 с 2 = t 2
t = 1,29 с
Вернуться к проблеме 5
Дано:
v i = 0 м / с
v f = 444 м / с
т = 1.83 с
Находят:
а = ??
d = ??
a = (дельта v) / т
a = (444 м / с — 0 м / с) / (1,83 с)
a = 243 м / с 2
d = v i * t + 0,5 * a * t 2
d = (0 м / с) * (1,83 с) + 0,5 * (243 м / с 2 ) * (1,83 с) 2
d = 0 м + 406 м
d = 406 м
(Примечание: d также можно рассчитать с помощью уравнения v f 2 = v i 2 + 2 * a * d)
Вернуться к проблеме 6
Дано:
v i = 0 м / с
v f = 7.10 м / с
d = 35,4 м
Находят:
а = ??
v f 2 = v i 2 + 2 * a * d
(7,10 м / с) 2 = (0 м / с) 2 + 2 * (a) * (35,4 м)
50,4 м 2 / с 2 = (0 м / с) 2 + (70.8 м) * а
(50,4 м 2 / с 2 ) / (70,8 м) =
a = 0,712 м / с 2
Вернуться к проблеме 7
Дано:
v i = 0 м / с
v f = 65 м / с
a = 3 м / с 2
Находят:
d = ??
v f 2 = v i 2 + 2 * a * d
(65 м / с) 2 = (0 м / с) 2 + 2 * (3 м / с 2 ) * d
4225 м 2 / с 2 = (0 м / с) 2 + (6 м / с 2 ) * d
(4225 м 2 / с 2 ) / (6 м / с 2 ) = d
d = 704 м
Вернуться к проблеме 8
Дано:
v и = 22.4 м / с
v f = 0 м / с
t = 2,55 с
Находят:
d = ??
d = (v i + v f ) / 2 * t
d = (22,4 м / с + 0 м / с) / 2 * 2,55 с
d = (11,2 м / с) * 2,55 с
д = 28.6 м
Вернуться к проблеме 9
Дано:
a = -9,8 м / с 2
v f = 0 м / с
d = 2,62 м
Находят:
v и = ??
v f 2 = v i 2 + 2 * a * d
(0 м / с) 2 = v i 2 + 2 * (- 9.8 м / с 2 ) * (2,62 м)
0 м 2 / с 2 = v i 2 — 51,35 м 2 / с 2
51,35 м 2 / с 2 = v i 2
v i = 7,17 м / с
Вернуться к проблеме 10
Дано:
а = -9.8 м / с 2
v f = 0 м / с
d = 1,29 м
Находят:
v и = ??
т = ??
v f 2 = v i 2 + 2 * a * d
(0 м / с) 2 = v i 2 + 2 * (- 9.8 м / с 2 ) * (1,29 м)
0 м 2 / с 2 = v i 2 — 25,28 м 2 / с 2
25,28 м 2 / с 2 = v i 2
v i = 5,03 м / с
Чтобы узнать время зависания, найдите время до пика и затем удвойте его.
v f = v i + a * t
0 м / с = 5.03 м / с + (-9,8 м / с 2 ) * t вверх
-5,03 м / с = (-9,8 м / с 2 ) * t до
(-5,03 м / с) / (- 9,8 м / с 2 ) = t до
т до = 0,513 с
время зависания = 1,03 с
Вернуться к проблеме 11
Дано:
v i = 0 м / с
v f = 521 м / с
d = 0.840 м
Находят:
а = ??
v f 2 = v i 2 + 2 * a * d
(521 м / с) 2 = (0 м / с) 2 + 2 * (а) * (0,840 м)
271441 м 2 / с 2 = (0 м / с) 2 + (1,68 м) * a
(271441 м 2 / с 2 ) / (1.68 м) =
a = 1,62 * 10 5 м / с 2
Вернуться к проблеме 12
Дано:
a = -9,8 м / с 2
v f = 0 м / с
т = 3.13 с
Находят:
d = ??
- (ПРИМЕЧАНИЕ: время, необходимое для перехода к пику траектории, составляет половину общего времени зависания — 3,125 с.)
Первое использование: v f = v i + a * t
0 м / с = v i + (-9,8 м / с 2 ) * (3,13 с)
0 м / с = v i — 30.7 м / с
v i = 30,7 м / с (30,674 м / с)
Теперь используйте: v f 2 = v i 2 + 2 * a * d
(0 м / с) 2 = (30,7 м / с) 2 + 2 * (- 9,8 м / с 2 ) * (г)
0 м 2 / с 2 = (940 м 2 / с 2 ) + (-19,6 м / с 2 ) * d
-940 м 2 / с 2 = (-19.6 м / с 2 ) * d
(-940 м 2 / с 2 ) / (- 19,6 м / с 2 ) = d
d = 48,0 м
Вернуться к проблеме 13
Дано:
v i = 0 м / с
d = -370 м
а = -9.8 м / с 2
Находят:
т = ??
d = v i * t + 0,5 * a * t 2
-370 м = (0 м / с) * (t) + 0,5 * (- 9,8 м / с 2 ) * (t) 2
-370 м = 0+ (-4,9 м / с 2 ) * (т) 2
(-370 м) / (- 4,9 м / с 2 ) = t 2
75.5 с 2 = t 2
t = 8,69 с
Вернуться к проблеме 14
Дано:
v i = 367 м / с
v f = 0 м / с
d = 0.0621 м
Находят:
а = ??
v f 2 = v i 2 + 2 * a * d
(0 м / с) 2 = (367 м / с) 2 + 2 * (a) * (0,0621 м)
0 м 2 / с 2 = (134689 м 2 / с 2 ) + (0,1242 м) * a
-134689 м 2 / с 2 = (0.1242 м) * а
(-134689 м 2 / с 2 ) / (0,1242 м) =
a = -1,08 * 10 6 м / с 2
(Знак — указывает на то, что пуля замедлилась.)
Вернуться к проблеме 15
Дано:
a = -9,8 м / с 2
т = 3.41 с
v i = 0 м / с
Находят:
d = ??
d = v i * t + 0,5 * a * t 2
d = (0 м / с) * (3,41 с) + 0,5 * (- 9,8 м / с 2 ) * (3,41 с) 2
d = 0 м + 0,5 * (- 9,8 м / с 2 ) * (11,63 с 2 )
д = -57.0 м
(ПРИМЕЧАНИЕ: знак — указывает направление)
Вернуться к проблеме 16
Дано:
a = -3,90 м / с 2
v f = 0 м / с
d = 290 м
Находят:
v и = ??
v f 2 = v i 2 + 2 * a * d
(0 м / с) 2 = v i 2 + 2 * (- 3.90 м / с 2 ) * (290 м)
0 м 2 / с 2 = v i 2 — 2262 м 2 / с 2
2262 м 2 / с 2 = v i 2
v i = 47,6 м / с
Вернуться к проблеме 17
Дано:
v i = 0 м / с
v f = 88.3 м / с
d = 1365 м
Находят:
а = ??
т = ??
v f 2 = v i 2 + 2 * a * d
(88,3 м / с) 2 = (0 м / с) 2 + 2 * (а) * (1365 м)
7797 м 2 / с 2 = (0 м 2 / с 2 ) + (2730 м) * a
7797 м 2 / с 2 = (2730 м) * а
(7797 м 2 / с 2 ) / (2730 м) =
а = 2.86 м / с 2
v f = v i + a * t
88,3 м / с = 0 м / с + (2,86 м / с 2 ) * t
(88,3 м / с) / (2,86 м / с 2 ) = t
t = 30,8 с
Вернуться к проблеме 18
Дано:
v i = 0 м / с
v f = 112 м / с
d = 398 м
Находят:
а = ??
v f 2 = v i 2 + 2 * a * d
(112 м / с) 2 = (0 м / с) 2 + 2 * (а) * (398 м)
12544 м 2 / с 2 = 0 м 2 / с 2 + (796 м) * a
12544 м 2 / с 2 = (796 м) * а
(12544 м 2 / с 2 ) / (796 м) =
а = 15.8 м / с 2
Вернуться к проблеме 19
Дано:
a = -9,8 м / с 2
v f = 0 м / с
d = 91,5 м
Находят:
v и = ??
т = ??
Сначала найдите скорость в м / с:
v f 2 = v i 2 + 2 * a * d
(0 м / с) 2 = v i 2 + 2 * (- 9.8 м / с 2 ) * (91,5 м)
0 м 2 / с 2 = v i 2 — 1793 м 2 / с 2
1793 м 2 / с 2 = v i 2
v i = 42,3 м / с
Теперь преобразовать из м / с в миль / ч:
v i = 42,3 м / с * (2,23 миль / ч) / (1 м / с)
против и = 94.4 миль / ч
Вернуться к проблеме 20
Уравнения движения | Движение в одном измерении
21.7 Уравнения движения (ESAHG)
В этом разделе мы рассмотрим третий способ описания движения. Мы рассмотрели описание движения с помощью слов и графиков. В этом разделе мы исследуем уравнения, которые можно использовать для описания движения.
Этот раздел посвящен решению задач, связанных с равноускоренным движением.{-1} $} \ text {в момент} t \\
\ vec {s} & = \ text {displacement} \ text {(m)}
\ end {выровнять *}
Галилео Галилей из Пизы, Италия, первым определил правильный математический закон ускорения: общее пройденное расстояние, начиная с состояния покоя, пропорционально квадрату времени. Он также пришел к выводу, что объекты сохраняют свою скорость, если на них не действует сила — часто трение, опровергая принятую аристотелевскую гипотезу о том, что объекты «естественным образом» замедляются и останавливаются, если на них не действует сила.{2} + 2 \ vec {a} \ Delta \ vec {x} \ qquad (4)
\ end {выровнять *}
Вопросы могут быть разными, но следующий метод ответа на них всегда будет работать. Используйте это при ответе на вопрос, связанный с движением с постоянным ускорением. Вам нужны любые три известные величины (\ ({\ vec {v}} _ {i} \), \ ({\ vec {v}} _ {f} \), \ (\ Delta \ vec {x} \) , \ (t \) или \ (\ vec {a} \)), чтобы иметь возможность вычислить четвертый.
Стратегия решения проблем:
Внимательно прочтите вопрос, чтобы определить указанные количества.Запишите их.
Определите используемое уравнение. Запишите !!!
Убедитесь, что все значения указаны в правильных единицах, и введите их в уравнение.
Рассчитайте ответ и проверьте свои единицы.
Рабочий пример 7: Уравнения движения
Гоночная машина едет на север. {- 2} $} \ text {Восток}
\ end {align *}
Конечная скорость : Найдите подходящее уравнение для расчета конечной скорости
Мы можем использовать уравнение 1 — помните, что теперь мы также знаем ускорение объекта.{-1} $} \) в \ (\ text {8} \) \ (\ text {s} \). Рассчитайте необходимое ускорение и общее расстояние, которое он прошел за это время.
Решение еще не доступно
Расширение: поиск уравнений движения (ESAHH)
Следующее не является частью учебной программы и может считаться дополнительной информацией.
Вывод уравнения 1
Согласно определению ускорения:
\ [\ vec {a} = \ frac {\ Delta \ vec {v}} {t} \]
где \ (\ Delta \ vec {v} \) — изменение скорости, т.е.е. \ (\ Delta v = {\ vec {v}} _ {f} — {\ vec {v}} _ {i} \). Таким образом, мы имеем
\ begin {align *}
\ vec {a} & = \ frac {{\ vec {v}} _ {f} — {\ vec {v}} _ {i}} {t} \\
{\ vec {v}} _ {f} & = {\ vec {v}} _ {i} + \ vec {a} t
\ end {align *}
Вывод уравнения 2
Мы видели, что смещение можно рассчитать по площади под графиком зависимости скорости от времени. Для равномерно ускоренного движения наиболее сложный график зависимости скорости от времени, который мы можем получить, представляет собой прямую линию.Посмотрите на график ниже — он представляет объект с начальной скоростью \ ({\ vec {v}} _ {i} \) , разгоняющийся до конечной скорости \ ({\ vec {v}} _ { f} \) за общее время t .
Чтобы вычислить окончательное смещение, мы должны вычислить площадь под графиком — это просто площадь прямоугольника, добавленная к площади треугольника. Эта часть графика заштрихована для ясности.
\ begin {align *}
{\ text {Area}} _ {△} & = \ frac {1} {2} b \ times h \\
& = \ frac {1} {2} t \ times \ left ({v} _ {f} — {v} _ {i} \ right) \\
& = \ frac {1} {2} {v} _ {f} t — \ frac {1} {2} {v} _ {i} t
\ end {align *} \ begin {align *}
{\ text {Area}} _ {\ square} & = l \ times b \\
& = t \ times {v} _ {i} \\
& = {v} _ {i} т
\ end {align *} \ begin {align *}
\ text {Displacement} & = {\ text {Area}} _ {\ square} + {\ text {Area}} _ {△} \\
\ Delta \ vec {x} & = {v} _ {i} t + \ frac {1} {2} {v} _ {f} t — \ frac {1} {2} {v} _ {i} т \\
\ Delta \ vec {x} & = \ frac {\ left ({v} _ {i} + {v} _ {f} \ right)} {2} t
\ end {align *}
Вывод уравнения 3
Это уравнение просто выводится путем исключения конечной скорости \ ({v} _ {f} \) в уравнении 2. {- 1} $} \), когда водитель видит ребенка \ (\ text {50} \) \ (\ text {m} \) перед ним на дороге.{-2} $} \). Его время реакции на нажатие тормоза составляет \ (\ text {0,5} \) секунд. Будет ли грузовик сбить ребенка?
Проанализируйте проблему и определите, какая информация предоставляется
Полезно нарисовать временную шкалу, подобную этой:
Нам необходимо знать следующее:
Какое расстояние водитель преодолевает, прежде чем нажать на тормоз.
Как долго грузовик останавливается после нажатия на тормоз.
Общее расстояние, которое грузовик преодолевает до остановки.
Рассчитать расстояние \ (AB \)
Прежде чем водитель нажмет на тормоз, грузовик движется с постоянной скоростью. Ускорения нет, поэтому уравнения движения не используются. Чтобы найти пройденное расстояние, мы используем:
\ begin {align *}
v & = \ frac {D} {t} \\
10 & = \ frac {D} {\ text {0,5}} \\
D & = \ текст {5} \ текст {м}
\ end {выровнять *}
Грузовик преодолевает \ (\ text {5} \) \ (\ text {m} \) до того, как водитель нажмет на тормоз.{-2} $} \ right) t \\
т & = \ текст {8} \ текст {s}
\ end {align *}
Рассчитать расстояние \ (BC \)
Для расстояния мы можем использовать Уравнение 2 или Уравнение 3. Мы будем использовать Уравнение 2:
\ begin {align *}
\ Delta \ vec {x} & = \ frac {\ left ({\ vec {v}} _ {i} + {\ vec {v}} _ {f} \ right)} {2} t \\
\ Delta \ vec {x} & = \ frac {10 + 0} {2} \ left (8 \ right) \\
\ Delta \ vec {x} & = \ text {40} \ text {m}
\ end {align *}
Напишите окончательный ответ
Общее расстояние, которое преодолевает грузовик, составляет \ ({d} _ {AB} + {d} _ {BC} = \ text {5} + \ text {40} = \ text {45} \) метров.Ребенок находится на \ (\ text {50} \) метрах впереди. Грузовик не ударит ребенка.
Уравнения кинематики и постоянное ускорение
В своих «Диалогах двух новых наук» Галилей вывел взаимосвязь между пройденным расстоянием и временем, когда шары катились по наклонной плоскости. Это часто называют законом падающих тел. Интересно, что в доказательстве Галилея вместо алгебры, которую мы представим здесь, использовалась классическая евклидова геометрия (которая была бы незнакома современному изучающему геометрию из учебников).Учащиеся продвинутого уровня могут получить те же уравнения, используя математический анализ.
Основа Закона падающих тел заключается в том, что по мере того, как мяч катится по рампе, он ускоряется. По мере увеличения его скорости увеличивается расстояние, которое он проходит за каждую единицу времени. Галилей определил это с помощью колокольчиков спускового крючка катящегося шарика.
Процитируем Галилея в переводе:
По сути, Галилей представил, что не только ускорение вниз по рампе из-за постоянной силы тяжести, но и что скорость увеличивается линейно с на .Он представил, что положение увеличивается с квадратом времени, что часто называют Законом падающих тел. Последний пункт в этом отрывке, который он представил, заключается в том, что скорость увеличивается с квадратом расстояния вниз по рампе.
Основываясь на том, что вы уже узнали и что представил Галилей, у нас есть то, что мой учитель физики Гленн Глейзер любил называть пятью священными уравнениями кинематики для постоянного ускорения. В этих уравнениях v — скорость, x — положение, t — время и a — ускорение.Помните, что Δ означает изменение.
1. или Δx = v ср. Δt
2. или v f = v o + aΔt или Δv = aΔt
3.
4. Δx = v o Δt + ½ a Δt 2
5. v f 2 = v o 2 + 2aΔx
Первые два уравнения, которые мы видели ранее. Важно отметить, что первое уравнение использует средней скорости , тогда как второе уравнение использует изменение между исходной и конечной скоростью.Связь между ними представлена в третьем уравнении, которое представляет собой просто закон средних чисел. Средняя скорость — это среднее значение исходной и конечной скорости.
Из этих трех основных определений мы можем вывести следующие два уравнения, используя либо геометрию, либо алгебру (или исчисление).
Используя алгебру, мы можем вывести уравнение №4.
Исходя из уравнения № 1
Δx = v ср. Δt
Затем мы подставляем определение средней скорости из уравнения №3.
Отсюда мы подставляем окончательную скорость, полученную в уравнении № 2
Затем мы распределяем член Δt и упрощаем, комбинируя члены v o .
Мы упрощаем оставшиеся два члена, чтобы получить
Стоит отметить, что происходит, когда исходная скорость v o, равна нулю. Это уравнение еще больше упрощается и становится
.
Если мы предположим, что исходная позиция и время равны нулю, мы можем дополнительно уменьшить это до
Используя геометрию, мы можем исследовать область под кривой графика зависимости скорости от времени для движения с постоянным ускорением.
Если мы посмотрим на область под кривой, мы можем разбить ее на прямоугольник и треугольник. Красный прямоугольник — это вклад исходной скорости объекта. Смещение из-за ускорения представлено зеленым треугольником. Треугольник имеет ширину Δt и высоту aΔt, которые мы знаем из уравнения №2. Член ½ происходит от формулы площади треугольника.
Мы также можем использовать исчисление для вывода этого уравнения путем интегрирования удвоенного ускорения по времени.
Пятое священное уравнение может быть получено аналогичными заменами, и его оставят как домашнее задание.
Теперь давайте рассмотрим несколько примеров задач: Численное решение задач.
Пример 1
По легенде, Галилей уронил мяч из Пизанской башни. Если высота башни составляет 55,9 м , и если пренебречь сопротивлением воздуха, сколько времени потребуется свинцовому мячу, чтобы достичь земли?
Гивенс: a = g ≈ 10 м / с 2
Δx = 55.9 м
Неизвестно: t = ???
Уравнение, связывающее эти переменные, — это священное уравнение 4 th .
Δx = v o Δt + ½ a Δt 2
Как упоминалось ранее, поскольку начальная скорость равна нулю, уравнение упрощается.
Δx = v o Δt + ½ a Δt 2 = ½ a Δt 2
Поскольку мы хотим изолировать переменную для времени, мы пересекаем умножение, чтобы переместить ½ и член ускорения на другую сторону.
Затем извлекаем квадратный корень из обеих частей.
Это дает выражение для времени. Обратите внимание, что я вставил несколько дополнительных скобок, которые могут вам не понадобиться.
При подключении номеров это довольно просто то, что мы называем «подключи и забей». Однако с агрегатами нужно быть осторожным. Вы, наверное, догадались, что время будет измеряться в секундах. Однако у вас должна быть возможность отменить фактические единицы, чтобы получить время в секундах.
Пример 2
Койот падает со скалы высотой 25 метров. Как быстро койот падает, когда ударяется о землю? Если проблема койота
Дано x = 25 м
a = g ≈ 10 м / с 2
Неизвестно: v = ???
Эту проблему можно решить несколькими способами. Можно использовать комбинацию или Священные уравнения №2 и №4. Или вы можете напрямую использовать уравнение №5.
Использование v f 2 = v o 2 + 2aΔx
Это упрощается, поскольку исходная скорость v o, равна нулю.
Если извлечь квадратный корень из обеих частей уравнения
Обратите внимание, как вы извлекаете квадратный корень из единиц, чтобы получить м / с .
Мы оставим решение этой задачи с двумя уравнениями для домашней задачи.
Обзор графиков, а также проблем уклона и площади под кривыми
Изучая графики положения, скорости и ускорения, вы сможете рисовать их как взаимозаменяемые.
Вчера в классе вы видели, что график объекта, ускоряющегося вниз по склону, выглядит следующим образом:
В этом примере мы используем программное обеспечение для анализа изображений.Это пример с мячом, катящимся с холма. Следует отметить, что график ускорения не показывает фактическую скорость, а показывает только то, как она меняется. Точно так же график скорости не дает вам фактического положения объекта, а только того, как он изменяется. Щелкнув по мячу и нажав кнопку трека, вы увидите график положения и скорости.
Здесь вы можете увидеть результаты построения графика движения. График положения представляет собой параболу, а график скорости — линейный.
Основы кинематики | Безграничная физика
Определение кинематики
Кинематика — это исследование движения точек, объектов и групп объектов без учета причин их движения.
Цели обучения
Определить кинематику
Основные выводы
Ключевые моменты
- Для описания движения кинематика изучает траектории точек, линий и других геометрических объектов.
- Изучение кинематики можно абстрагировать в чисто математических выражениях.
- Кинематические уравнения могут использоваться для расчета различных аспектов движения, таких как скорость, ускорение, смещение и время.
Ключевые термины
- кинематика : Раздел механики, связанный с движущимися объектами, но не с задействованными силами.
Кинематика — это раздел классической механики, который описывает движение точек, объектов и систем групп объектов без ссылки на причины движения (т.е., силы). Изучение кинематики часто называют «геометрией движения».
Объекты вращаются вокруг нас. Все, от теннисного матча до полета космического зонда над планетой Нептун, связано с движением. Когда вы отдыхаете, ваше сердце перемещает кровь по венам. Даже в неодушевленных предметах есть непрерывное движение в колебаниях атомов и молекул. Могут возникнуть интересные вопросы о движении: сколько времени потребуется космическому зонду, чтобы добраться до Марса? Куда приземлится футбольный мяч, если его бросить под определенным углом? Однако понимание движения также является ключом к пониманию других концепций физики.Например, понимание ускорения имеет решающее значение для изучения силы.
Для описания движения кинематика изучает траектории точек, линий и других геометрических объектов, а также их дифференциальные свойства (такие как скорость и ускорение). Кинематика используется в астрофизике для описания движения небесных тел и систем; и в машиностроении, робототехнике и биомеханике для описания движения систем, состоящих из соединенных частей (таких как двигатель, роботизированная рука или скелет человеческого тела).
Формальное изучение физики начинается с кинематики. Слово «кинематика» происходит от греческого слова «kinesis», означающего движение, и связано с другими английскими словами, такими как «cinema» (фильмы) и «kinesiology» (изучение движения человека). Кинематический анализ — это процесс измерения кинематических величин, используемых для описания движения. Изучение кинематики можно абстрагировать в чисто математических выражениях, которые можно использовать для расчета различных аспектов движения, таких как скорость, ускорение, смещение, время и траектория.
Кинематика траектории частицы : кинематические уравнения могут использоваться для расчета траектории частиц или объектов. Физические величины, относящиеся к движению частицы, включают: массу m, положение r, скорость v, ускорение a.
Референсные рамки и смещение
Чтобы описать движение объекта, необходимо указать его положение относительно удобной системы отсчета.
Цели обучения
Оценить смещение в системе координат.
Основные выводы
Ключевые моменты
- Выбор системы отсчета требует решения, где находится исходное положение объекта и какое направление будет считаться положительным.
- Допустимые системы отсчета могут отличаться друг от друга перемещением друг относительно друга.
- Опорные рамки особенно важны при описании смещения объекта.
- Смещение — это изменение положения объекта относительно его системы отсчета.
Ключевые термины
- смещение : векторная величина, которая обозначает расстояние с направленным компонентом.
- рамка отсчета : система координат или набор осей, в пределах которых можно измерить положение, ориентацию и другие свойства объектов в ней.
Чтобы описать движение объекта, вы должны сначала описать его положение — где он находится в любой конкретный момент времени. Точнее, нужно указать его положение относительно удобной системы отсчета.Земля часто используется в качестве системы отсчета, и мы часто описываем положение объектов, связанных с их положением на Землю или от нее. Математически положение объекта обычно представлено переменной x .
Справочная информация
Есть два варианта, которые вы должны сделать, чтобы определить переменную позиции x . Вы должны решить, где поставить x = 0 и какое направление будет положительным. Это называется выбором системы координат или выбором системы отсчета.Пока вы последовательны, любой фрейм одинаково действителен. Но вы не хотите менять систему координат во время расчета. Представьте, что вы сидите в поезде на станции и вдруг замечаете, что станция движется назад. Большинство людей сказали бы, что они просто не заметили, что поезд движется — только казались , как будто станция движется. Но это показывает, что существует третий и произвольный выбор, связанный с выбором системы координат: действительные системы отсчета могут отличаться друг от друга, перемещаясь относительно друг друга.Может показаться странным использование системы координат, движущейся относительно земли, но, например, система координат, движущаяся вместе с поездом, может быть гораздо более удобной для описания вещей, происходящих внутри поезда. Рамки отсчета особенно важны при описании смещения объекта.
СПРАВОЧНИКИ профессора Хьюма и профессора Дональда Айви из Университета Торонто
В этом классическом фильме профессора Хьюм и Айви умело иллюстрируют системы отсчета и различают фиксированные и движущиеся системы отсчета.
Frames of Reference (1960) Учебный фильм : Frames of Reference — образовательный фильм 1960 года, созданный Комитетом по изучению физических наук. Фильм предназначен для показа на курсах физики в средней школе. В фильме профессора физики Университета Торонто Паттерсон Хьюм и Дональд Айви объясняют различие между инерциальной и неинтерциальной системами отсчета, демонстрируя эти концепции с помощью юмористических трюков с камерой. Например, фильм начинается с Доктора.Хьюм, который кажется перевернутым, обвиняет доктора Айви в том, что он перевернут. Только когда пара подбрасывает монету, становится очевидно, что доктор Айви — и камера — действительно перевернуты. Юмор фильма служит как для заинтересованности студентов, так и для демонстрации обсуждаемых концепций. В этом фильме PSSC используется увлекательный набор, состоящий из вращающегося стола и мебели, занимающих неожиданно непредсказуемые места в зоне просмотра. Прекрасная кинематография Авраама Морочника и забавное повествование профессоров Университета Торонто Дональда Айви и Паттерсона Хьюма — прекрасный пример того, как творческая группа кинематографистов может весело провести время с предметом, который другие, менее изобретательные люди могут посчитать пешеходом.Продюсер: Ричард Ликок Продюсерская компания: Educational Development Corp. Спонсор: Эрик Престамон
Рабочий объем
Смещение — это изменение положения объекта относительно его системы отсчета. Например, если автомобиль движется из дома в продуктовый магазин, его перемещение — это относительное расстояние продуктового магазина до системы отсчета или дома. Слово «смещение» означает, что объект переместился или был перемещен. Смещение — это изменение положения объекта, которое математически можно представить следующим образом:
[латекс] \ Delta \ text {x} = \ text {x} _ \ text {f} — \ text {x} _0 [/ latex]
, где Δ x — смещение, x f — конечное положение, а x 0 — начальное положение.
показывает важность использования системы координат при описании перемещения пассажира в самолете.
Перемещение в системе ведения : Пассажир перемещается со своего места на заднюю часть самолета. Его расположение относительно самолета указано x. Смещение пассажира на -4,0 м относительно самолета показано стрелкой в направлении задней части самолета. Обратите внимание, что стрелка, обозначающая его перемещение, вдвое длиннее стрелки, обозначающей перемещение профессора (он перемещается вдвое дальше).
Введение в скаляры и векторы
Вектор — это любая величина, которая имеет как величину, так и направление, тогда как скаляр имеет только величину.
Цели обучения
Определите разницу между скалярами и векторами
Основные выводы
Ключевые моменты
- Вектор — это любая величина, имеющая величину и направление.
- Скаляр — это любая величина, которая имеет величину, но не имеет направления.
- Смещение и скорость — это векторы, а расстояние и скорость — скаляры.
Ключевые термины
- скаляр : величина, имеющая величину, но не направление; сравнить вектор.
- вектор : направленная величина, имеющая как величину, так и направление; между двумя точками.
В чем разница между расстоянием и смещением? В то время как смещение определяется как направлением, так и величиной, расстояние определяется только величиной. Смещение — это пример векторной величины. Расстояние — это пример скалярной величины.Вектор — это любая величина, имеющая как величину, так и направление. Другие примеры векторов включают скорость 90 км / ч на восток и силу 500 ньютонов прямо вниз.
Скаляры и векторы : Г-н Андерсен объясняет различия между скалярными и векторными величинами. Он также использует демонстрацию, чтобы показать важность векторов и сложения векторов.
В математике, физике и технике вектор — это геометрический объект, который имеет величину (или длину) и направление и может быть добавлен к другим векторам в соответствии с векторной алгеброй.Направление вектора в одномерном движении задается просто знаком плюс (+) или минус (-). Вектор часто представлен отрезком линии с определенным направлением или графически в виде стрелки, соединяющей начальную точку A с конечной точкой B, как показано на.
Векторное представление : Вектор часто представляется отрезком линии с определенным направлением или графически в виде стрелки, соединяющей начальную точку A с конечной точкой B.
Некоторые физические величины, такие как расстояние, либо не имеют направления, либо не имеют определенного направления.В физике скаляр — это простая физическая величина, которая не изменяется при поворотах или перемещениях системы координат. Это любая величина, которая может быть выражена одним числом и имеет величину, но не направление. Например, температура 20ºC, 250 килокалорий (250 калорий) энергии в шоколадном батончике, ограничение скорости 90 км / ч, рост человека 1,8 м и расстояние 2,0 м — все это скаляры или количества без указания направление. Обратите внимание, однако, что скаляр может быть отрицательным, например, температура –20ºC.В этом случае знак минус указывает точку на шкале, а не направление. Скаляры никогда не изображаются стрелками. (Сравнение скаляров и векторов показано на рис.)
Скаляры и векторы : краткий список величин, которые являются либо скалярами, либо векторами.
IB Физические заметки — 2.1 Кинематика
Смещение
Смещение — это расстояние, на которое перемещается в определенном направлении. Это векторная величина.
Единица СИ: м
Символ: с
Скорость
Скорость — это скорость изменения смещения.Это векторная величина.
Скорость = (изменение смещения / изменение во времени)
Единица СИ: м с -1
Символ: v или u
Скорость
Скорость — это скорость изменения расстояния. Это скалярная величина.
Скорость = (изменение расстояния / изменение во времени)
Единица СИ: м с -1
Символ: v или u
Обратите внимание, что скорость и скорость — это не одно и то же.У скорости есть направление.
Ускорение
Ускорение — это скорость изменения скорости. Это векторная величина.
Ускорение = (изменение скорости / изменение во времени)
Единица СИ: м с -2
Символ: a
Обратите внимание, что ускорение — это любое изменение скорости, означающее увеличение или уменьшение скорости или изменение направления.
Мгновенное значение
Мгновенное значение скорости, скорости или ускорения — это значение в определенный момент времени.
Среднее значение
Среднее значение скорости, скорости или ускорения — это значение, полученное за период времени.
Уравнения равноускоренного движения могут быть только в условиях, когда ускорение постоянно.
Уравнения равноускоренного движения следующие:
| Переменная | Символ |
| т | время затрачено |
| с | пройденное расстояние |
| u | Начальная скорость снаряда |
| в | конечная скорость |
| a | ускорение |
Таблица 1.2.1 — Переменные, используемые в уравнениях равноускоренного движения
Из этих уравнений могут быть выведены и другие уравнения.
Когда мы игнорируем влияние сопротивления воздуха на объект, падающий на землю под действием силы тяжести, мы говорим, что объект находится в свободном падении. Свободное падение является примером равноускоренного движения, поскольку единственная сила, действующая на объект, — это сила тяжести.
На поверхности земли ускорение объекта в свободном падении составляет около 9,81 мс -1 .Мы можем легко распознать равномерное ускорение по графикам «смещение — время», «скорость — время» и «ускорение — время», как показано ниже:
Автомобиль ускоряется равномерно из состояния покоя. Через 10 секунд он прошел 200 м.
Вычислить:
Его среднее ускорение
S = ut + 1/2 at²
200 = 0 x 10 + 1/2 x a x 10²
200 = 50a
а = 4 м с-2
Мгновенная скорость после 10 секунд
v² = u ² + 2as
= 0 + 2 х 4 х 10
= 80
В = 8.9 м с -1
Сопротивление воздуха в конечном итоге влияет на все движущиеся объекты. Из-за эффекта сопротивления воздуха объекты могут достигать предельной скорости. Это точка, в которой скорость остается постоянной, а ускорение равно нулю.
При отсутствии сопротивления воздуха все объекты имеют одинаковое ускорение независимо от их массы.
Определение его скорости
Мы знаем, что градиент графика смещения-времени дает нам его скорость.Следовательно, первые 5 секунд скорость будет:
25/5 = 5 мс? ¹
После первых 5 с объект неподвижен 3 с. Для этих 3с его скорость равна нулю.
Через 8 секунд объект начинает возвращаться с большей скоростью, чем раньше. Из графика находим скорость:
25/2 = 12,5 мс? ¹
Рисунок 2.1.5 — График скорости-времени
Определите его ускорение
Мы знаем, что градиент графика скорости-времени дает нам его ускорение.Следовательно, за первые 5 с ускорение составит:
50/5 = 10 мс? ²
Когда объект движется с постоянной скоростью от 5 до 7 секунд, его ускорение равно нулю. В последнюю секунду путешествия объекта объект замедляется на:
.
50/1 = 50 мс? ²
Определите его смещение
Площадь под графиком скорость-время — это смещение. За первые 5 с объект проехал:
½ x 5 x 50 = 125 м
Определите изменение скорости
Область под графиком «ускорение — время» показывает изменение скорости
Из графика находим, что изменение скорости составляет 10 x 3 = 30 мс? ¹
Примечание. Градиент графика «ускорение — время» фактически представляет собой скорость изменения ускорения.Однако это бывает нечасто.
3.4 Движение с постоянным ускорением — University Physics Volume 1
Learning Objectives
К концу этого раздела вы сможете:
- Определите, какие уравнения движения следует использовать для решения неизвестных.
- Используйте соответствующие уравнения движения для решения задачи преследования двух тел.
Можно предположить, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени.Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.
Обозначение
Во-первых, сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением.Поскольку прошедшее время равно Δt = tf − t0Δt = tf − t0, взятие t0 = 0t0 = 0 означает, что Δt = tfΔt = tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x0x0 — это начальная позиция , а v0v0 — начальная скорость . Мы не ставим нижние индексы на окончательные значения. То есть t — это конечный момент времени , x — конечная позиция , а v — конечная скорость . Это дает более простое выражение для затраченного времени: Δt = tΔt = t.Это также упрощает выражение для смещения x , которое теперь равно Δx = x − x0Δx = x − x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv = v − v0Δv = v − v0. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
Δt = tΔx = x − x0Δv = v − v0, Δt = tΔx = x − x0Δv = v − v0,
, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь мы делаем важное предположение, что ускорение постоянно .Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
a– = a = постоянная. a– = a = постоянная.
Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения. Во-первых, ускорение всегда равно в большом количестве ситуаций.Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
Замена упрощенных обозначений для ΔxΔx и ΔtΔt дает
v– = x − x0t.v– = x − x0t.
Решение x дает нам
x = x0 + v – t, x = x0 + v – t,
3,10
, где средняя скорость
v– = v0 + v2.v– = v0 + v2.
3,11
Уравнение v– = v0 + v2v– = v0 + v2 отражает тот факт, что при постоянном ускорении v – v– представляет собой простое среднее значение начальной и конечной скоростей. Рисунок 3.18 графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость в течение 1-часового интервала от 40 км / ч до 80 км / ч составляет 60 км / ч:
v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.
В части (b) ускорение не является постоянным. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рисунок 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0andvv0andv. Средняя скорость равна 12 (v0 + v) = 60 км / ч22 (v0 + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не равна 12 (v0 + v) 12 (v0 + v), но превышает 60 км / ч.
Решение окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
Подстановка упрощенных обозначений для ΔvΔv и ΔtΔt дает
а = v − v0t (константа). a = v − v0t (константа).
Решение для v дает
v = v0 + at (constanta). v = v0 + at (constanta).
3,12
Пример 3,7
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70.0 м / с, а затем ускоряется против движения со скоростью 1,50 м / с 2 за 40,0 с. Какова его конечная скорость?
Стратегия
Сначала мы идентифицируем известные: v0 = 70 м / с, a = -1,50 м / с2, t = 40sv0 = 70 м / с, a = -1,50 м / с2, t = 40 с.
Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы рассчитываем окончательную скорость, используя уравнение 3.12, v = v0 + atv = v0 + at.
Решение
Подставьте известные значения и решите:
v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с.
Рисунок 3.19 представляет собой эскиз, показывающий векторы ускорения и скорости.
Рис. 3.19. Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы самолет остановился и начал движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.
Помимо полезности при решении задач, уравнение v = v0 + atv = v0 + at дает нам представление о взаимосвязях между скоростью, ускорением и временем.Мы видим, например, что
- Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
- Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v 0 ), как и ожидалось (другими словами, скорость постоянна)
- Если a отрицательное, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Решение для конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с
Добавление v0v0 к каждой стороне этого уравнения и деление на 2 дает
v0 + v2 = v0 + 12at. v0 + v2 = v0 + 12at.
Так как v0 + v2 = v – v0 + v2 = v– для постоянного ускорения, имеем
v– = v0 + 12at.v– = v0 + 12at.
Теперь мы подставляем это выражение для v – v– в уравнение для смещения, x = x0 + v – tx = x0 + v – t, что дает
х = х0 + v0t + 12at2 (константа).х = х0 + v0t + 12at2 (константа).
3,13
Пример 3.8
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м / с 2 . Предположим, драгстер ускоряется из состояния покоя в течение 5,56 с. Рис. 3.20. Как далеко он пролетит за это время?
Рис. 3.20. Пилот Top Fuel американской армии Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фото любезно предоставлено США.Армия.)
Стратегия
Сначала нарисуем набросок Рис. 3.21. Нас просят найти смещение, которое составляет x , если мы примем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулевой и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 когда мы идентифицируем v0v0, aa и t из постановки задачи.
Рис. 3.21. Эскиз разгоняющегося драгстера.
Решение
Во-первых, нам нужно определить известные.Запуск из состояния покоя означает, что v0 = 0v0 = 0, a задается как 26,0 м / с 2 и t задается как 5,56 с.
Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:
x = x0 + v0t + 12at2.x = x0 + v0t + 12at2.
Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до
Подстановка идентифицированных значений на и t дает
x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м. x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м.
Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут преодолеть четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.
Что еще мы можем узнать, исследуя уравнение x = x0 + v0t + 12at2? X = x0 + v0t + 12at2? Мы видим следующие отношения:
- Смещение зависит от квадрата истекшего времени, когда ускорение не равно нулю. В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
- Если ускорение равно нулю, то начальная скорость равна средней скорости (v0 = v -) (v0 = v–), и x = x0 + v0t + 12at2becomesx = x0 + v0t.x = x0 + v0t + 12at2becomesx = x0 + v0t.
Расчет конечной скорости по расстоянию и ускорению
Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим v = v0 + atv = v0 + at для t , мы получим
Подставляя это и v– = v0 + v2v– = v0 + v2 в x = x0 + v – tx = x0 + v – t, получаем
v2 = v02 + 2a (x − x0) (constanta). v2 = v02 + 2a (x − x0) (constanta).
3,14
Пример 3.9
Расчет конечной скорости
Рассчитайте конечную скорость драгстера в Примере 3.8 без использования информации о времени.
Стратегия
Уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.
Решение
Сначала мы идентифицируем известные значения. Мы знаем, что v 0 = 0, поскольку драгстер запускается из состояния покоя. Мы также знаем, что x — x 0 = 402 м (это был ответ в примере 3.8). Среднее ускорение было равно , = 26.0 м / с 2 .
Во-вторых, мы подставляем известные значения в уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) и решаем относительно v :
v2 = 0 + 2 (26,0 м / с2) (402 м). v2 = 0 + 2 (26,0 м / с2) (402 м).
Таким образом,
v2 = 2,09 × 104 м2 / с2 v = 2,09 × 104 м2 / с2 = 145 м / с. v2 = 2,09 × 104 м2 / с2v = 2,09 × 104 м2 / с2 = 145 м / с.
Значение
Скорость 145 м / с составляет около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость не достигает рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.
Изучение уравнения v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) может дать дополнительное понимание общих соотношений между физическими величинами:
- Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
- При фиксированном ускорении автомобиль, который едет вдвое быстрее, просто не останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Объединение уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных. Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.
Сводка кинематических уравнений (константа
a )
х = х0 + v0t + 12at2x = x0 + v0t + 12at2
v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)
Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях.Переставляя уравнение 3.12, получаем
Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико, приближаясь к нулю в том пределе, когда начальная и конечная скорости равны. Напротив, в пределе t → 0t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.
Аналогичным образом, переставляя уравнение 3.14, мы можем выразить ускорение в терминах скоростей и смещения:
а = v2-v022 (х-х0).а = v2-v022 (х-х0).
Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример 3.10
Как далеко уезжает машина?
На сухом бетоне автомобиль может ускоряться противоположно движению со скоростью 7,00 м / с 2 , тогда как на мокром бетоне он может ускоряться противоположно движению со скоростью всего 5.00 м / с 2 . Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы нажать ногой на тормоз.
Стратегия
Для начала нам нужно нарисовать набросок Рис. 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.
Рис. 3.22. Пример эскиза для визуализации ускорения, противоположного движению и тормозному пути автомобиля.
Решение
- Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v 0 = 30,0 м / с, v = 0 и a = -7,00 м / с 2 ( a отрицательно, потому что оно находится в направлении, противоположном скорости) . Возьмем x 0 равным нулю. Ищем смещение ΔxΔx, или x — x 0 .
Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования —
v2 = v02 + 2a (x − x0). v2 = v02 + 2a (x − x0).
Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Мы знаем значения всех других переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы их использовать, но это потребовало бы дополнительных вычислений.)
В-третьих, мы изменим уравнение, чтобы найти x :
x − x0 = v2 − v022ax − x0 = v2 − v022a
и подставляем известные значения:
х − 0 = 02− (30.0 м / с) 22 (-7,00 м / с2). X-0 = 02- (30,0 м / с) 22 (-7,00 м / с2).
Таким образом,
x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне. - Эта часть может быть решена точно так же, как (а). Единственное отличие в том, что ускорение составляет −5,00 м / с 2 . Результат
xwet = 90,0 м по мокрому бетону. xwet = 90,0 м по мокрому бетону. - Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время ко времени остановки.Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
Для этого мы, опять же, определяем известные и то, что мы хотим решить. Мы знаем, что v– = 30,0 м / sv– = 30,0 м / с, treaction = 0,500streaction = 0,500s и areaction = 0areaction = 0. Примем x0-реакцию x0-реакцию равной нулю. Ищем xreactionxreaction.
Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x0 + v – tx = x0 + v – t работает хорошо, потому что единственное неизвестное значение — x , что мы и хотим найти.
В-третьих, мы подставляем известные для решения уравнения:
x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. x = 0 + (30,0 м / с) (0,500 с) = 15,0 м.
Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем если бы он реагировал мгновенно.
Наконец, мы добавляем смещение во время реакции к смещению при торможении (рис. 3.23),
xbraking + xreaction = xtotal, xbraking + xreaction = xtotal,
и найдите (a) равным 64,3 м + 15,0 м = 79.3 м в сухом виде и (b) должно составлять 90,0 м + 15,0 м = 105 м во влажном состоянии.
Рис. 3.23. Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, изначально движущегося со скоростью 30,0 м / с. Также показано общее расстояние, пройденное от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.
Значение
Смещения, обнаруженные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важен общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.
Пример 3.11
Расчет времени
Предположим, автомобиль въезжает в движение по автостраде на съезде длиной 200 м. Если его начальная скорость составляет 10,0 м / с, а ускорение составляет 2,00 м / с 2 , сколько времени потребуется автомобилю, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)
Стратегия
Сначала мы рисуем набросок Рис. 3.24. Нам предлагается решить за время т . Как и прежде, мы идентифицируем известные величины, чтобы выбрать удобную физическую связь (то есть уравнение с одной неизвестной, t .)
Рис. 3.24. Эскиз автомобиля, ускоряющегося на съезде с автострады.
Решение
Опять же, мы определяем известные и то, что мы хотим решить. Мы знаем, что x0 = 0, x0 = 0,
v0 = 10 м / с, a = 2,00 м / с2v0 = 10 м / с, a = 2,00 м / с2 и x = 200 м.
Нам нужно решить для т . Уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 работает лучше всего, потому что единственной неизвестной в уравнении является переменная t , которую нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.
Нам нужно изменить уравнение, чтобы найти t , затем подставив известные значения в уравнение:
200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2. 200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2.
Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t s, где t — величина времени, а s — единица измерения. Остается
Затем мы используем формулу корней квадратного уравнения, чтобы найти t ,
t2 + 10t − 200 = 0t = −b ± b2−4ac2a, t2 + 10t − 200 = 0t = −b ± b2−4ac2a,
, что дает два решения: t = 10.0 и t = −20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.
Проверьте свое понимание 3.5
Ракета ускоряется со скоростью 20 м / с. 2 во время пуска.Сколько времени нужно, чтобы ракета достигла скорости 400 м / с?
Пример 3.12
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с 2 за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?
Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа.Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.
Решение
Сначала мы решаем v0v0, используя x = x0 + v0t + 12at2: x = x0 + v0t + 12at2: x − x0 = v0t + 12at2x − x0 = v0t + 12at21.0 × 106m = v0 (120.0s) +12 (20,0 м / с2) (120,0 с) 21,0 × 106 м = v0 (120,0 с) +12 (20,0 м / с2) (120,0 с) 2v0 = 7133,3 м / с. V0 = 7133,3 м / с.
Затем мы подставляем v0v0 в v = v0 + atv = v0 + at, чтобы найти окончательную скорость:
v = v0 + at = 7133.3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с. V = v0 + at = 7133,3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с.
Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть не такими простыми, как простая подстановка в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.
Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также увидели общий подход к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности в наших задачах кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .
Задачи преследования двух тел
До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на Рисунке 3.25.
Рис. 3.25. Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 идет сзади с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже.
Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависит от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример 3.13
Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с.В момент, когда газель проезжает мимо гепарда, гепард ускоряется из состояния покоя со скоростью 4 м / с 2 , чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?
Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, — это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно посмотрим на проблему, становится ясно, что общим параметром для каждого животного является их положение x в более позднее время t . Поскольку оба они начинаются с x0 = 0x0 = 0, их смещения будут такими же в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое решает смещение для каждого животного, мы можем затем установить уравнения, равные друг другу, и решить для неизвестного, то есть времени.
Решение
- Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется.Поэтому мы используем уравнение 3.10 с x0 = 0x0 = 0:
x = x0 + v – t = v – t. x = x0 + v – t = v – t.
Уравнение для гепарда: гепард ускоряется в состоянии покоя, поэтому мы используем уравнение 3.13 с x0 = 0x0 = 0 и v0 = 0v0 = 0: x = x0 + v0t + 12at2 = 12at2.x = x0 + v0t + 12at2 = 12at2.
Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае мы решаем для t : x = v – t = 12at2t = 2v – a.x = v – t = 12at2t = 2v – a.
Газель имеет постоянную скорость 10 м / с, что составляет ее среднюю скорость.Ускорение гепарда 4 м / с 2 . Оценив t , время, за которое гепард достигнет газели, имеем
t = 2v – a = 2 (10 м / с) 4m / s2 = 5s. t = 2v – a = 2 (10 м / с) 4m / s2 = 5s. - Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны дать одинаковый ответ.
Смещение гепарда:
x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м.
Водоизмещение газели:
x = v – t = 10 м / с (5) = 50 м. x = v – t = 10 м / с (5) = 50 м.Мы видим, что оба смещения равны, как и ожидалось.
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.

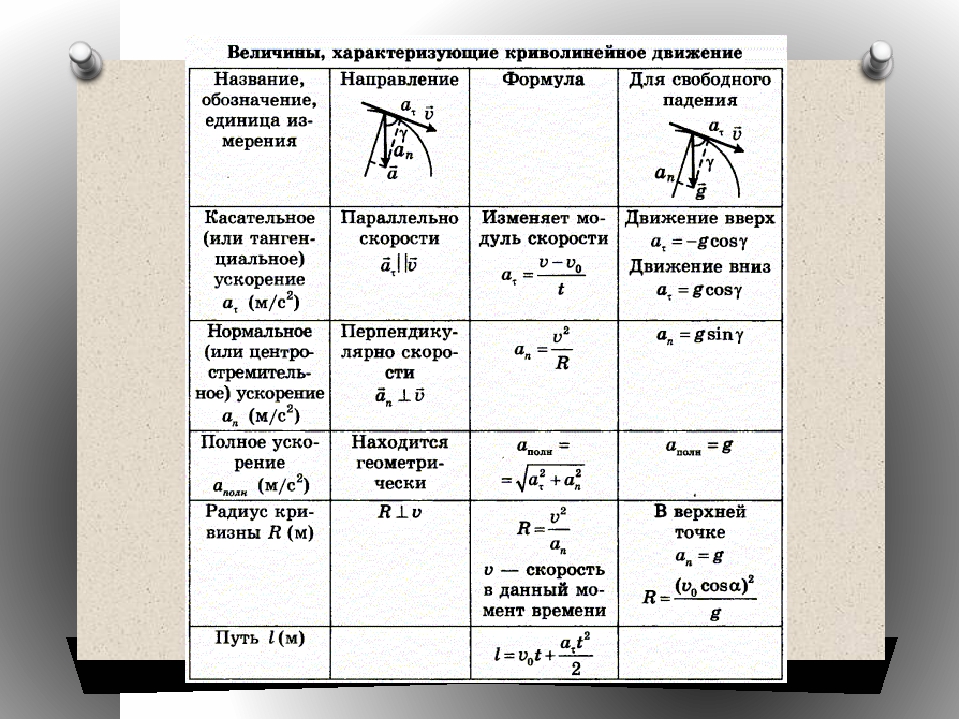 путевая = S/t
путевая = S/t 0 м / с 2
0 м / с 2