Содержание
11.3.1. Показательная функция, ее свойства и график.
Автор Татьяна Андрющенко На чтение 5 мин. Просмотров 3.6k. Опубликовано
data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»8834522701″
data-ad-format=»auto»>
- Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией.
- Область определения показательной функции: D (y)=R – множество всех действительных чисел.
- Область значений показательной функции: E (y)=R+ — множество всех положительных чисел.
- Показательная функция y=ax возрастает при a>1.
- Показательная функция y=ax убывает при 0<a<1.
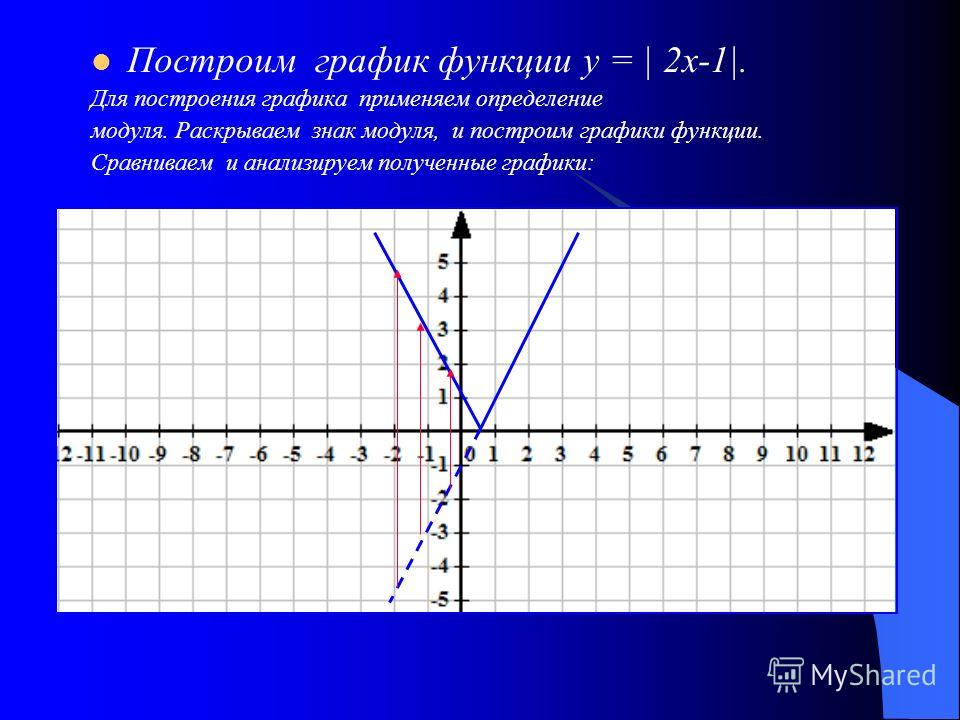
Справедливы все свойства степенной функции:
- а0=1 Любое число (кроме нуля) в нулевой степени равно единице.
- а1=а Любое число в первой степени равно самому себе.
- ax∙ay=ax+y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
- ax:ay=ax- y При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
- (ax)y=axy При возведении степени в степень основание оставляют прежним, а показатели перемножают
- (a∙b)x=ax∙by При возведении произведения в степень возводят в эту степень каждый из множителей.
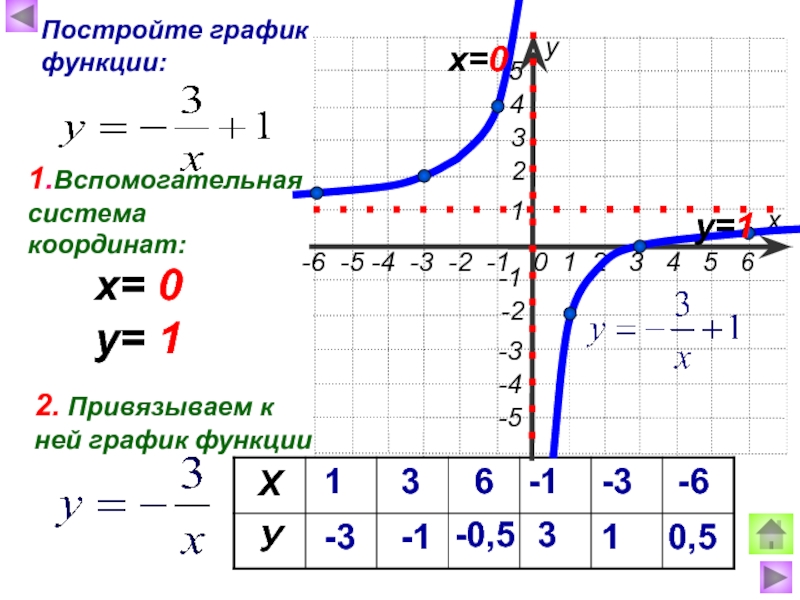
- (a/b)x=ax/by При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
- а-х=1/ax
- (a/b)-x=(b/a)x.
Примеры.
1) Построить график функции y=2x. Найдем значения функции
при х=0, х=±1, х=±2, х=±3.
x=0, y=20=1; Точка А.
x=1, y=21=2; Точка В.
x=2, y=22=4; Точка С.
x=3, y=23=8; Точка D.
x=-1, y=2-1=1/2=0,5; Точка K.
x=-2, y=2-2=1/4=0,25; Точка M.
x=-3, y=2-3=1/8=0,125; Точка N.
Большему значению аргумента х соответствует и большее значение функции у. Функция y=2x возрастает на всей области определения D (y)=R, так как основание функции 2>1.
2) Построить график функции y=(1/2)x. Найдем значения функции
при х=0, х=±1, х=±2, х=±3.
x=0, y=(½)0=1; Точка A.
x=1, y=(½)1=½=0,5; Точка B.
x=2, y=(½)2=¼=0,25; Точка C.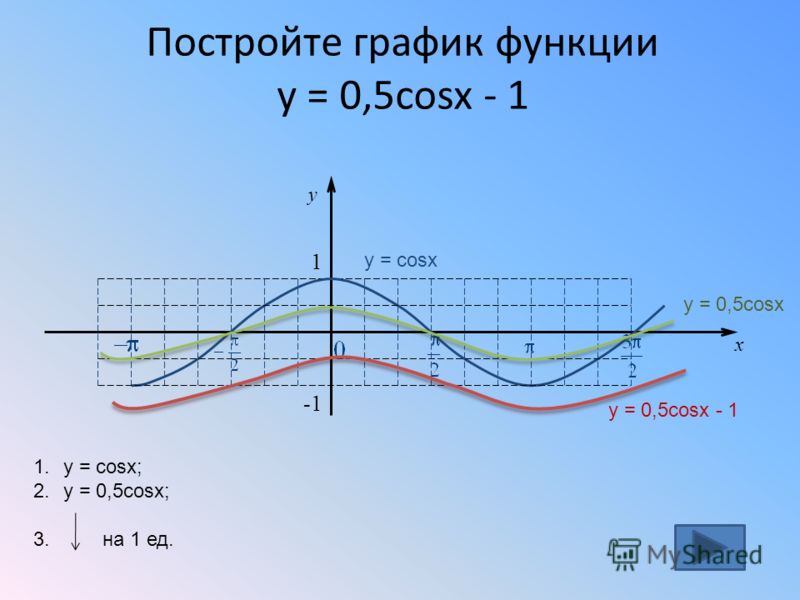
x=3, y=(½)3=1/8=0,125; Точка D.
x=-1, y=(½)-1=21=2; Точка K.
x=-2, y=(½)-2=22=4; Точка M.
x=-3, y=(½)-3=23=8; Точка N.
Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(1/2)x убывает на всей своей области определения: D (y)=R, так как основание функции 0<(1/2)<1.
3) В одной координатной плоскости построить графики функций:
y=2x, y=3x, y=5x, y=10x. Сделать выводы.
График функции у=2х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.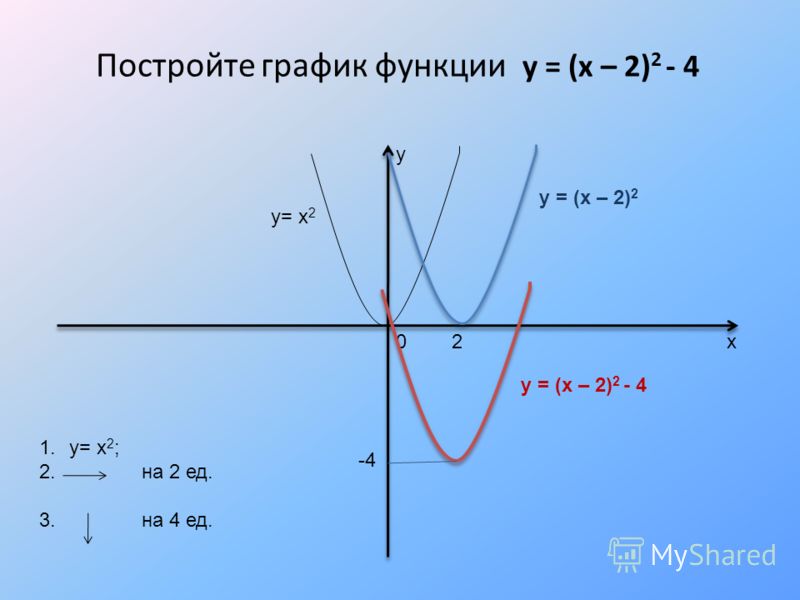
Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание а (если a>1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
4) В одной координатной плоскости построить графики функций:
y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x. Сделать выводы.
Сделать выводы.
Смотрите построение графика функции y=(1/2)x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.
Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R+.
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
Чем меньше основание а (при 0<a<1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Решить графически уравнения:
1) 3x=4-x.
В одной координатной плоскости построим графики функций: у=3х и у=4-х.
Графики пересеклись в точке А(1; 3).
Ответ: 1.
2) 0,5х=х+3.
В одной координатной плоскости строим графики функций: у=0,5х
(y=(1/2)x )
и у=х+3.
Графики пересеклись в точке В(-1; 2).
Ответ: -1.
Найти область значений функции: 1) y=-2x; 2) y=(1/3)x+1; 3) y=3x+1-5.
Решение.
1) y=-2x
Область значений показательной функции y=2x – все положительные числа, т.е.
0<2x<+∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем:
— ∞<-2x<0.
Ответ: Е(у)=(-∞; 0).
2) y=(1/3)x+1;
0<(1/3)x<+∞, тогда, прибавляя ко всем частям двойного неравенства число 1, получаем:
0+1<(1/3)x+1<+∞+1;
1<(1/3)x+1<+∞.
Ответ: Е(у)=(1; +∞).
3) y=3x+1-5.
Запишем функцию в виде: у=3х∙3-5.
0<3x<+∞; умножаем все части двойного неравенства на 3:
0∙3<3x∙3<(+∞)∙3;
0<3x∙3<+∞; из всех частей двойного неравенства вычитаем 5:
0-5<3x∙3-5<+∞-5;
— 5<3x∙3-5<+∞.
Ответ: Е(у)=(-5; +∞).
Смотрите Карту сайта, и Вы найдете нужные Вам темы!
Построить график функции у=-x²+2x+8 (парабола) – решение и ответ
Формулировка задания: Построить график функции у = -x² + 2x + 8.
Решение:
Для построения графика параболы нужно построить таблицу значений x и y.
Для удобства начнем с точек, находящихся на осях Ox и Oy.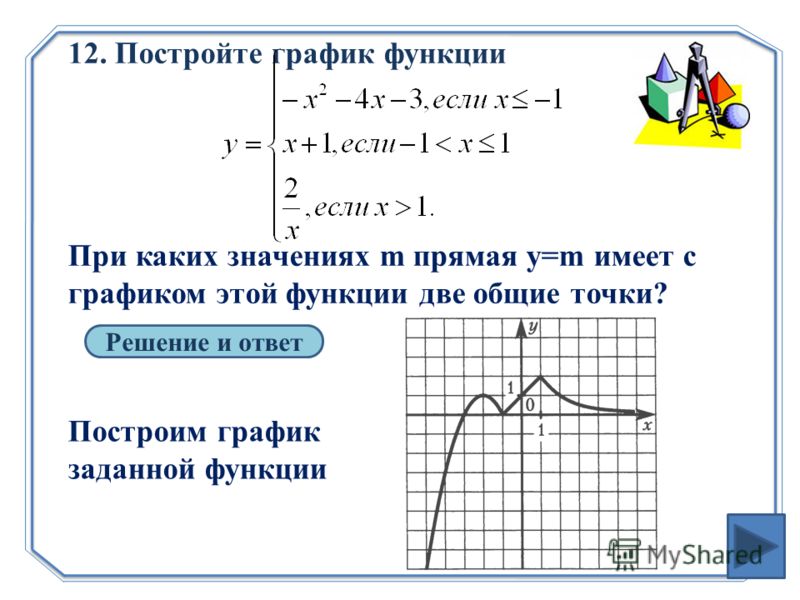 Если точка лежит на оси Oy (x = 0), тогда:
Если точка лежит на оси Oy (x = 0), тогда:
x = 0 ⇒
y = -0² + 2 ⋅ 0 + 8 = 8
Если точка лежит на оси Ox (y = 0), нужно решить квадратное уравнение:
y = 0 ⇒
-x² + 2x + 8 = 0
a = -1, b = 2, c = 8
D = 2² – 4 ⋅ (-1) ⋅ 8 = 36
x1 = (-2 + 6) / (-2) = -2
x2 = (-2 – 6) / (-2) = 4
Таким образом, мы получили 3 точки пересечения с осями. Заполняем ими таблицу:
Возьмем еще пару точек, которые будет просто посчитать, например, x = 1 и x = -1:
x = 1 ⇒
y = -1² + 2 ⋅ 1 + 8 = 9
x = -1
y = -(-1)² + 2 ⋅ (-1) + 8 = 5
Таблица значений теперь выглядит следующим образом:
Отметим полученные точки на координатной плоскости:
Координату x вершины параболы можно определить по любым 2 точкам параболы, у которых равно значение y: она лежит точно между ними.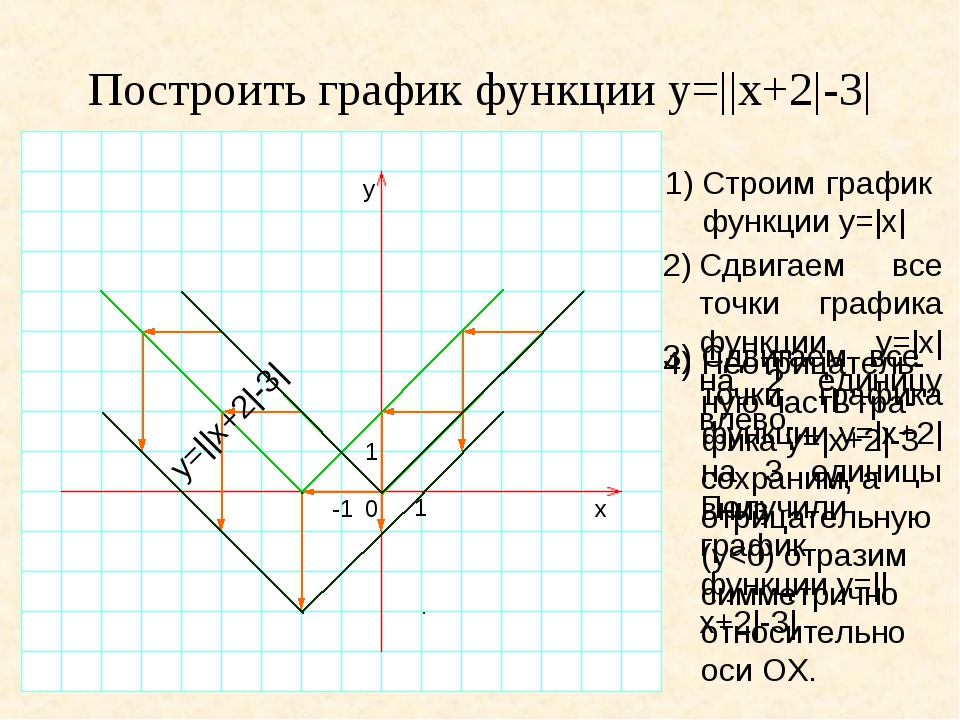 Например, найдем координату x вершины параболы по точкам (-2;0) и (4;0):
Например, найдем координату x вершины параболы по точкам (-2;0) и (4;0):
(4 – (-2)) / 2 = 6 / 2 = 3
xв = -2 + 3 = 1
Точка с таким значением x уже есть в таблице значений. Осталось построить график:
Поделитесь статьей с одноклассниками «Построить график функции у=-x²+2x+8 (парабола) – решение и ответ».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
«График квадратичной функции». 9-й класс
Цель урока:
- научить изображать схематически графики функций y = ax2 + n и y = a(x-m)2;
- уметь указывать на рисунке соответствующую формулу для графика функций;
- строить с помощью шаблона параболы графики функций.
Задачи урока:
Образовательные:
- расширить сведения о свойствах квадратичной функции;
- ознакомить учащихся с графиками частных видов квадратичной;
- научить строить и выполнять преобразования графиков квадратичной функции.
Развивающие:
- развитие у учащихся аналитического мышления;
- развитие речи (расширение математического словаря).
Воспитательные:
- привитие практических умений и навыков по построению графиков;
- воспитание познавательной активности;
- воспитание ответственности;
- воспитание культуры диалога.
Тип урока: формирование новых знаний и умений.
План урока:
- Организационный момент.
- Устная работа.
- Изучение нового материала.
- Тренировочные упражнения.
- Самостоятельная работа.
- Итог урока.
- Сообщение домашнего задания.
Ход урока
I. Организационный момент
II. Устная работа
- Дайте определение функции.
- Какая функция называется квадратичной? Приведите примеры.
- Что представляет собой график функции y = ax2?
- В каких четвертях расположен график функции y = ax2 при а>0 и при а< 0?
III. Изучение нового материала
Пример 1
Построим графики функций y = x2 и y = — x2.
| X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| Y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| Y = -x2 | -9 | -4 | -1 | 0 | -1 | -4 | -9 |
При любом значении х значения функций y = x2 и y = — x2 являются противоположными числами, значит соответствующие точки графиков симметричны относительно оси х (см. рис.1).
рис.1).
рис. 1
Вывод: График функции y= — ax2 можно получить из графика функции y = ax2 c помощью симметрии относительно оси х.
Пример 2
Построим графики функций y = x2 и y = x2 + 2.
Составим таблицу значений этих функций при одних и тех же значениях аргумента.
| X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y=x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| y=x2+ 2 | 11 | 6 | 3 | 2 | 3 | 6 | 11 |
Эта таблица подсказывает, что каждой точке (x0;y0) графика функции y = x2 соответствует точка (xo;y0+2) графика функции y = x2 + 2. Следовательно, график функции y = x2 + 2 получен в результате параллельного переноса графика функции y = x2 на две единицы вверх (см. рис. 2).
Следовательно, график функции y = x2 + 2 получен в результате параллельного переноса графика функции y = x2 на две единицы вверх (см. рис. 2).
рис 2.
Аналогично график функции y = x2 — 4 можно получить в результате параллельного переноса графика функции y = x2 на 4 единицы вниз (см. рис.3).
рис. 3
Вывод: График функции y= ax2 + n можно получить в результате параллельного переноса графика функции y = ax2 на n единиц вверх, если n > 0 и на — n единиц вниз, если n <0.
Пример 3. Построим графики функций y = (x + 2)2 и y = (x — 2)2.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y=x2 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
| y=(x+ 2)2 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
| y= (x-2)2 | 36 | 25 | 16 | 9 | 4 | 1 | 0 | 1 | 4 |
По таблице видим, что график функции y=(x+2)2 получен в результате параллельного графика функции y = x2 на две единицы влево; график функции y=(x-2)2 получен в результате переноса на две единицы вправо (см.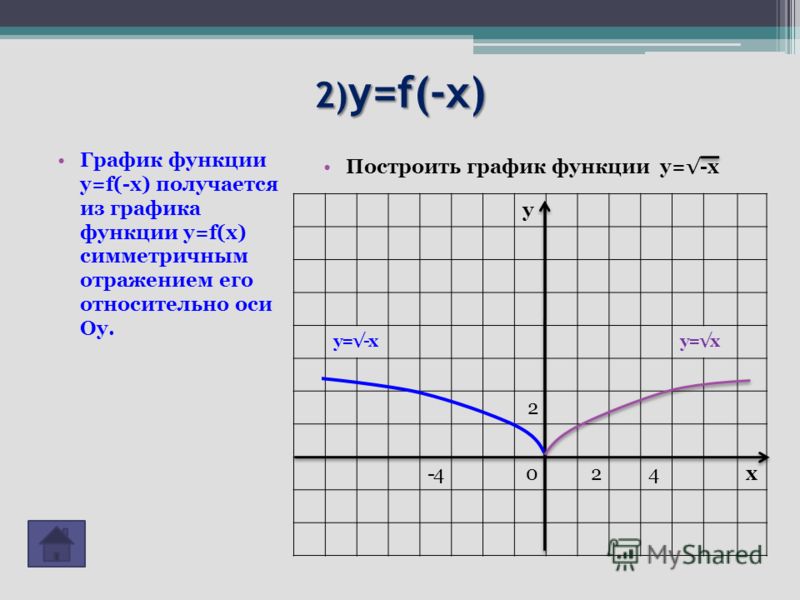 рис. 4 и рис. 5).
рис. 4 и рис. 5).
рис. 4
рис. 5
Вывод: График функции y=а(х-m)2 можно получить в результате параллельного переноса графика функции y = ax2 на m единиц влево, если — m < 0 и на m единиц вправо, если m > 0.
Пример 4. Построим график функции y = (x -1)2 +3.
Решение:
Построим шаблон графика функции y = x2.
Параллельно перенесем график функции y=x2 на 1 единицу вправо. Получим график функции y = (x-1)2.
Параллельно перенесем график функции y= (x-1)2 на 3 единицы вверх. Получим график функции y = (x-1)2 +3 (см. рис. 6).
рис. 6
IV. Тренировочные упражнения
1. График какой функции получим, если график функции y = x2 параллельно перенесем:
- на 6 единиц вверх;
- на 9 единиц вправо;
- на 12 единиц вниз;
- на 7 единиц влево;
- на 2 единицы вправо и на 3 единицы вниз;
- на 1 единицу влево и на 1 единицу вверх?
2.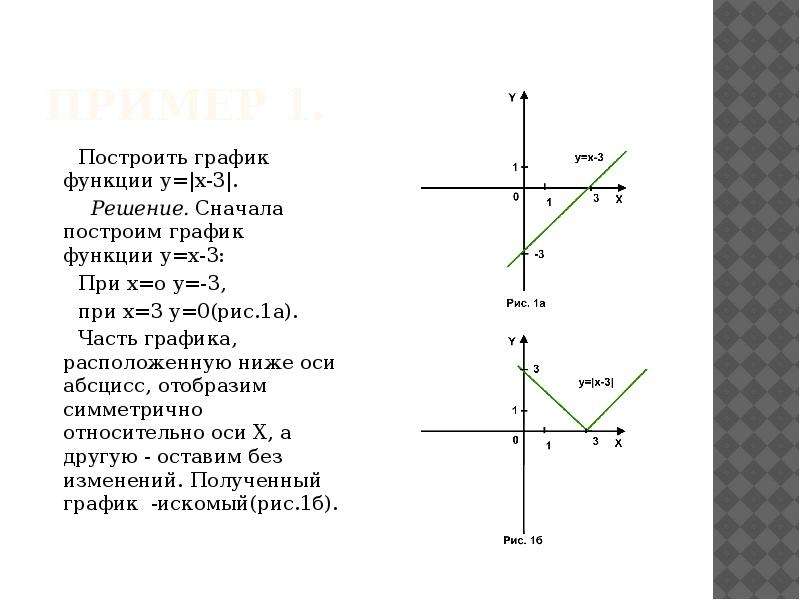 Задайте формулами вида y = ax2 + n, y = a(x — m)2 , y = a(x — m)2 + n функции, графики которых изображены на рисунках:
Задайте формулами вида y = ax2 + n, y = a(x — m)2 , y = a(x — m)2 + n функции, графики которых изображены на рисунках:
рис. 7
рис. 8
рис. 9
рис. 10
рис. 11
рис. 12
V. Самостоятельная работа с последующей проверкой
(Учащимся раздаются карточки с индивидуальными заданиями).
Вариант 1
1. Используя шаблон параболы y = x2 постройте график функции:
а) y = x2 – 4;
б) y = (x-3)2;
в) y = -x2 +3;
г) y = (x + 3)2 – 3
д) y = — (x + 1)2 + 2;
2. Дополнительное задание: изобразите схематически график функции: y=¼(x — 2)2 – 3.
Вариант 2
1. Используя шаблон параболы y = x2 постройте график функции:
Используя шаблон параболы y = x2 постройте график функции:
а) y = x2 – 3;
б) y = (x+1)2;
в) y = — x2 + 2;
г) y = — (x — 1)2 + 3;
д) y = — (x + 2)2 + 4.
2. Дополнительное задание: изобразите схематически график функции: y= -¼(x + )2+3.
VI. Итог урока
Ответьте на вопросы:
- Как можно получить график функции y = ax2 + n, используя график функции y = ax2?
- Как можно получить график функции y = a(x — m)2, используя график функции y = ax2?
- Как можно получить график функции y = a(x — m)2 + n, используя график функции y = ax2?
VII. Задание на дом
Учебник «Алгебра 9» , авторы Ю.Н. Макарычев и др.
П. 6 №№ 107,108,110, на повторение № 119.
Урок №1. «Функция у=х^2 и ее график.
 «
«
Алгебра. 8 класс.
Урок № 1 § 11
Тема: Функция и ее график.
Цель урока:
Образовательная: рассмотреть функцию и ее свойства, уметь строить график функции, решать уравнения с использованием графика функции .
Развивающая: развитие вычислительных и графических навыков.
Воспитательная: воспитание прилежности, аккуратности .
Тип урока: урок усвоения новых знаний и умений
Оборудование: мел, доска, учебник, линейка.
Х о д у р о к а
- Организационный момент.
Добрый день! Добрый час!
Как я рада видеть вас.
Прозвенел уже звонок
Начинается урок.
Улыбнулись. Подровнялись.
Друг на друга поглядели
И тихонько дружно сели.
- Мотивация урока.
Выдающийся французский философ, ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя.
Анализ контрольной работы
- Объяснение нового материала
Рассмотрим функцию, заданную формулой у = х2. Область её определения — множество всех чисел.
Составим таблицу значений функции для некоторых значений аргумента х:
х | -3 | -2,5 | -2 | -1,5 | -1 | 0 | 1 | 1,5 | 2 | 2,5 | 3 |
у | 9 | 6,25 | 4 | 2,25 | 1 | 0 | 1 | 2,25 | 4 | 6,25 | 9 |
Нанесём точки, координаты которых приведены в этой таблице.
-3 -2 -1 0 1 2 4 -3 -2 -1 0 1 2 4
Если на координатной плоскости нанести больше точек с координатами х и у, удовлетворяющих формулу у = х2, то они разместились бы так, как показано на втором рисунке. Если для каждого действительного значения х по формуле у = х2 вычислить соответствующее значение у и обозначить точки с такими координатами на координатной плоскости, то получим непрерывную кривую линию, которую называют параболой. Парабола имеет две бесконечных ветви, плавно сходящиеся в одной точке — вершине параболы.
Для функции у = х2 вершиной параболы является точка (0; 0). То есть график функции у = х2 проходит через начало координат. Поскольку противоположным значениям аргумента соответствуют равные значения функции, то её график симметричен относительно оси у. Построенный график даёт возможность наглядно выразить свойства функции у = х2.
То есть график функции у = х2 проходит через начало координат. Поскольку противоположным значениям аргумента соответствуют равные значения функции, то её график симметричен относительно оси у. Построенный график даёт возможность наглядно выразить свойства функции у = х2.
Рассматривая график мы можем сказать, что функция у = х2 обладает такими свойствами:
Область определения – любое число.
Область значения – все неотрицательные числа (у ≥ 0)
Промежутки убывания – когда х < 0
Промежутки возрастания – когда х > 0
Нули функции (значение аргумента, при котором значение функции равно 0) – х=0
Для чего надо знать, каков график функции? Подробнее об этом вы узнаете в старших классах. А сейчас обратите внимание на то, что с помощью графиков функций можно решать уравнения, которые иными способами решить сложно либо невозможно.
А сейчас обратите внимание на то, что с помощью графиков функций можно решать уравнения, которые иными способами решить сложно либо невозможно.
Сколько решений имеет уравнение х2 = 9? Прямая (её уравнение у = 9) пересекает график функции у = х2 в двух точках (рис. 3).
х2 = 9
х = 3 или х = — 3
Их абсциссы х = 3 и х = — 3 — решения уравнения.
Так же можно решить более сложное уравнение х2 – 3х – 4 = 0.
Сначала представим это уравнение в виде х2 = 3х + 4.
Графики функций
у = х2 и у = 3х + 4.
пересекаются в точках с
абсциссами х = -1 и х = 4,
которые в свою очередь являются
решениями данного уравнения.
4. Закрепление изученного материала.
Опираясь на график функции у = х2 , весь класс отвечает на вопросы задания № 350.
Вопрос классу. Как можно определить проходит ли график функции через ту или иную точку?
После выполнения задания рассматриваем свойства функции у = — х2
5. Физкультурная пауза.
Почти 90% всей информации человек воспринимает глазами. Если устают глаза, снижается наше внимание и активность. Давайте перед следующей задачей дадим отдых глазам и себе.
1. Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы.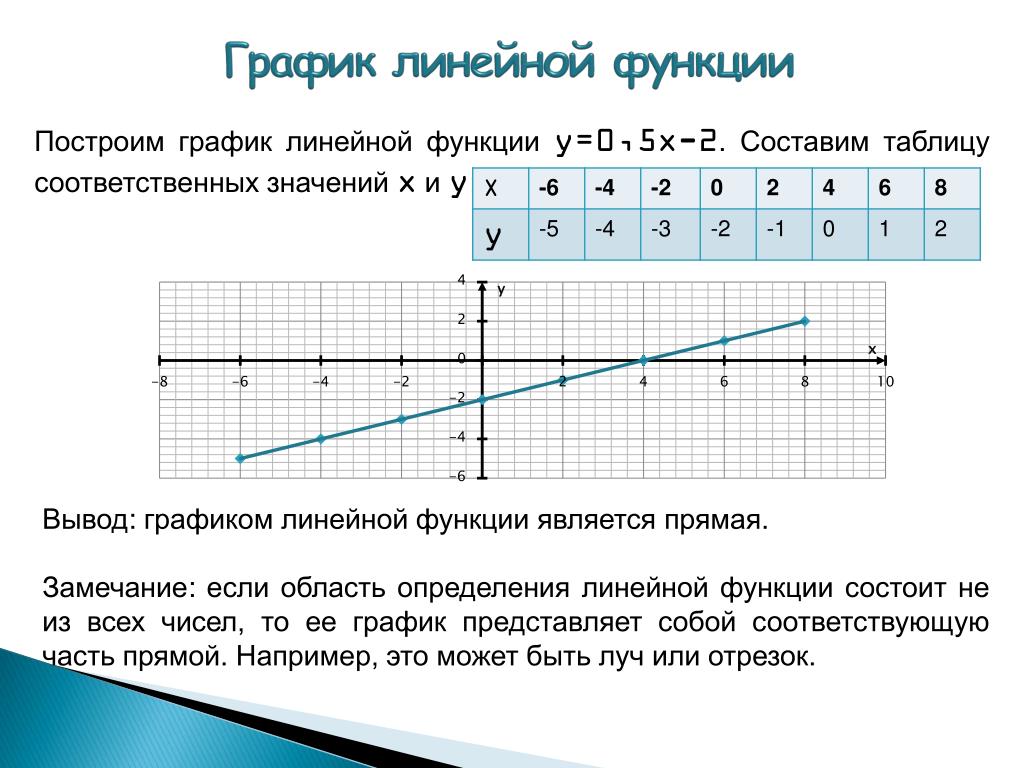 Повторите 3-4 раза.
Повторите 3-4 раза.
2. Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3—4 раза.
3. Медленно наклоняйте голову: вперед—влево— вправо — назад. Повторите 3-4 раза.
4. Поморгайте несколько раз глазами, не напрягая мышц. Сделайте глубокий вздох и медленный выдох.
6. Проблемная ситуация:
Сколько решений имеет уравнение х2 =5, и как их найти? Попробуем ответить на этот вопрос самостоятельно, учащиеся приходят к мысли, что корни они могут найти приближенно.
7. Итоги урока. Рефлексия.
Что мы узнали нового?
Как называется график функции у = х2 ?
Какими свойствами она обладает?
8. Домашнее задание § 11, № 351, 352, на повторение №368
2
Если вы не добавите знак равенства, предполагается, что вы имеете в виду « = 0 »
Он не был хорошо протестирован, поэтому получайте удовольствие , но ему не доверяют .
Если возникнут проблемы, дайте мне знать.
Примечание: для завершения может потребоваться несколько секунд, потому что для этого требуется много вычислений.
Если вы просто хотите построить график функции в стиле «y = …», вы можете предпочесть Function Grapher и Calculator
Масштабирование
Используйте ползунок масштабирования (влево увеличивает масштаб, вправо уменьшает).
Чтобы сбросить масштаб до исходных границ, нажмите кнопку Сбросить .
Перетаскивание
Щелкните и перетащите, чтобы переместить график. Если вы просто щелкнете и отпустите (без перетаскивания), то место, на котором вы щелкнули, станет новым центром
.
Примечание: на графиках использовано компьютерных расчетов . Округление может вызвать ошибки или значения могут быть полностью упущены.
Все функции
Операторы
| + | Оператор сложения | |
|---|---|---|
| – | Оператор вычитания | |
| * | Оператор умножения | |
| / | Оператор отдела | |
| ^ | Оператор экспоненты (степени) |
Функции
кв.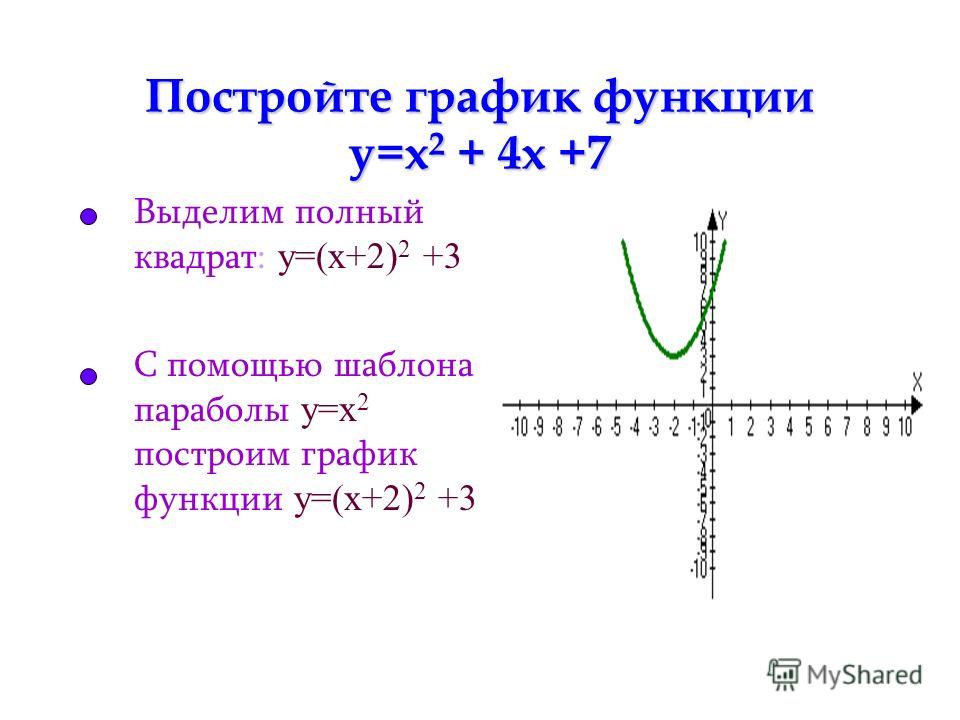 | Квадратный корень значения или выражения. | |
|---|---|---|
| грех | синус значения или выражения | |
| cos | Косинус значения или выражения | |
| желто-коричневый | тангенс значения или выражения | |
| asin | обратный синус (арксинус) значения или выражения | |
| acos | обратный косинус (arccos) значения или выражения | |
| атан | Арктангенс (арктангенс) значения или выражения | |
| синх | Гиперболический синус (sinh) значения или выражения | |
| cosh | Гиперболический косинус (cosh) значения или выражения | |
| танх | Гиперболический тангенс (tanh) значения или выражения | |
эксп.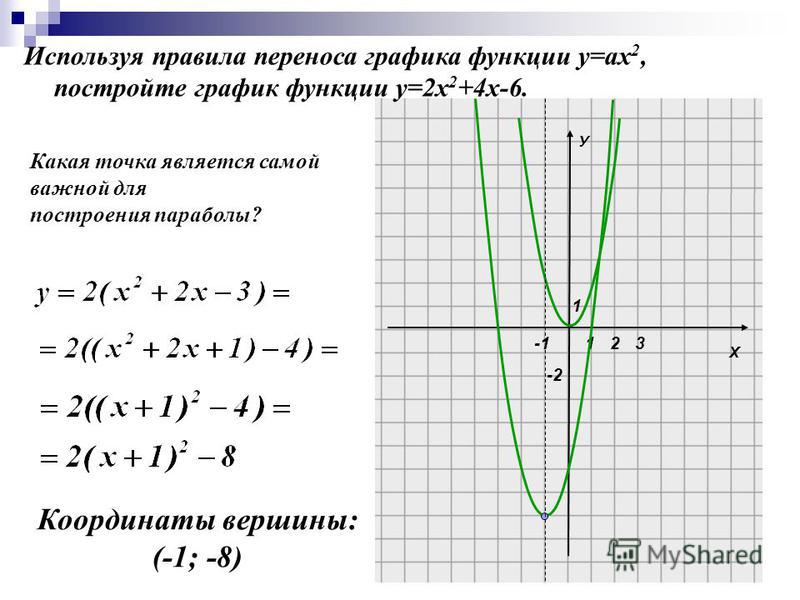 | e (константа Эйлера) в степени значения или выражения | |
| пер. | Натуральный логарифм значения или выражения | |
| журнал | Логарифм по основанию 10 значения или выражения | |
| этаж | Возвращает наибольшее (ближайшее к положительной бесконечности) значение, которое не больше аргумента и равно математическому целому числу. | |
| потолок | Возвращает наименьшее (ближайшее к отрицательной бесконечности) значение, которое не меньше аргумента и равно математическому целому числу. | |
| круглый | Округлить до ближайшего целого числа. Примеры: округление (−2,5) = −2, округление (-0,1) = 0, округление (0,1) = 0, округление (2,5) = 3 | |
| абс | Абсолютное значение (расстояние от нуля) значения или выражения | |
| знак | Знак (+1 или -1) значения или выражения | |
Константы
| пи | Константа π (3.141592654 …) | |
|---|---|---|
| e | Число Эйлера (2,71828 …), основание натурального логарифма |
3D поверхностный плоттер | Academo.org
Эта демонстрация позволяет вам ввести математическое выражение в терминах x и y. Когда вы нажмете кнопку «Рассчитать», демонстрация будет
вычислить значение выражения в предоставленных диапазонах x и y, а затем отобразить результат в виде поверхности.График можно увеличивать, прокручивая мышью, и вращать, перетаскивая. Щелчок по графику покажет значения x, y и z в этой конкретной точке.
В таблице ниже перечислены функции, которые можно вводить в поле выражения.
| Выражение | Описание |
|---|---|
| грех (х) | Синус x в радианах |
| cos (x) | Косинус x в радианах |
| желто-коричневый (x) | Тангенс x в радианах |
| asin (x), acos (x), atan (x) | Обратная из трех тригонометрических функций, перечисленных выше |
| sqrt (x) | Квадратный корень из x (только для положительного x) |
| журнал (x) | Натуральный логарифм x |
| pow (x, y) | Степень x к y |
Вы также можете применить к графику определенные ограничения / неравенства.2 \) во всех областях, где \ (x \) больше, чем \ (y \), и \ (x \) во всех областях, где x равен , а не больше, чем y.
Ползунок разрешения можно использовать для увеличения количества точек данных, отображаемых на графике, что дает более плавный конечный результат, но поскольку для этого требуется больше вычислительной мощности, вы можете заметить небольшое снижение частоты кадров при взаимодействии с графиком.
Каждый раз, когда вы нажимаете кнопку «Рассчитать», URL-адрес обновляется с вашими текущими настройками, что означает, что вы можете поделиться ссылкой прямо на график по вашему выбору, не набирая значения в настройках.2-2x-1 — график квадратичной функции. обозначить вершину и ось полутуры.
Содержание:
Шаг 1: Поиск вершины
Шаг 2: Поиск двух точек слева от оси симметрии
Шаг 3: Отражение двух точек для получения точек справа от оси симметрии
Шаг 4: Построение точек (с таблицей)
Шаг 5: Построение параболы
Чтобы построить график, мы можем выполнить следующие шаги:
Шаг 1) Найдите вершину (вершина — это либо самая высокая, либо самая низкая точка на графике).Также вершина находится на оси симметрии параболы (т.е. делит ее пополам).
Шаг 2) Когда у вас есть вершина, найдите две точки слева от оси симметрии (линия, которая вертикально проходит через вершину).
Шаг 3) Отразите эти две точки над осью симметрии, чтобы получить еще две точки справа от оси симметрии.
Шаг 4) Постройте все найденные точки (включая вершину).
Шаг 5) Проведите кривую через все точки, чтобы построить параболу.
Давайте подробно рассмотрим эти шаги
Перейти к началу страницы
Шаг 1)
Нахождение вершины:
Чтобы найти вершину, нам сначала нужно найти x-координату вершины.
Чтобы найти координату x вершины, используйте эту формулу:.
Начните с данной формулы.
Из, мы видим, что, и.
Подключите и.
Отменить получить.
Умножаем 2 и получаем.
Разделить.
Итак, координата x вершины равна. Примечание: это означает, что ось симметрии тоже.
Теперь, когда мы знаем координату x вершины, мы можем использовать ее, чтобы найти координату y вершины.
Начните с данного уравнения.
Подключите.
Квадрат
пр.
Умножаем и получаем.
Умножаем и получаем.
Объедините похожие термины.
Итак, y-координата вершины.
Так вершина есть.
———————————————— ———————
Перейти к началу страницы
Шаг 2)
Найдите две точки слева от оси симметрии:
Давайте найдем значение y, когда
Начнем с данного уравнения.
Подключите.
Квадрат
пр.
Умножаем и получаем.
Умножаем и получаем.
Объедините похожие термины.
Итак, первая точка слева от оси симметрии (-1,2)
———————
Давайте найдем значение y, когда
Начнем с данного уравнения.
Подключите.
Квадрат
пр.
Умножаем и получаем.
Умножаем и получаем.
Объедините похожие термины.
Итак, вторая точка слева от оси симметрии (0, -1)
———————————————— ———————
Перейти к началу страницы
Шаг 3)
Отражение двух точек по оси симметрии:
Теперь запомните, парабола симметрична относительно оси симметрии (которая есть)
Это означает, что значение y для (которое находится на расстоянии одной единицы от оси симметрии) равно значению y (которое также находится на расстоянии одной единицы от оси симметрии).Итак, когда, что дает нам точку (2, -1). Таким образом, мы по существу отразили точку (0, -1) на (2, -1).
Кроме того, значение y для (которое находится в двух единицах от оси симметрии) равно значению y (которое также находится на расстоянии двух единиц от оси симметрии). Итак, когда, что дает нам точку (3,2). Таким образом, мы по существу отразили точку (-1,2) на (3,2).
———————————————— ———————
Перейти к началу страницы
Шаг 4)
Нанесение точек:
Теперь давайте составим таблицу вычисленных нами значений:
х | y = x 2 | (х, у) |
0 | 0 | (0,0) |
1 | 1 | (1,1) |
2 | 4 | (2,4) |
3 | 9 | (3,9) |
–1 | 1 | (-1,1) |
-2 | 4 | (-2,4) |
-3 | 9 | (-3,9) |
Х | у = 1 / х | (х, у) |
1/3 | 3 | (1 / 3,3) |
1/2 | 2 | (1 / 2,2) |
1 | 1 | (1, 1) |
2 | 1/2 | (2,1 / 2) |
3 | 1/3 | (3,1 / 3) |
-1/3 | -3 | (-1/3, -3) |
-1/2 | -2 | (-1/2, -2) |
–1 | –1 | (-1, -1) |
-2 | -1/2 | (-2, -1/2) |
-3 | -1/3 | (-3, -1 / 3) |
| | x | знак равно | x, если x ≥ 0, т.е.е. x неотрицателен -x, если x |
График совпадает с линией y = x для x > 0 и с линией y = -x
для x <0.
график f (x) = -x
Объединяя эти два графика, получаем
график f (x) = | x |
Пример: 4 Нарисуйте график
t (x) = (x 2 — 4) / (x — 2) =
= ((х — 2) (х + 2) / (х — 2)) =
= (х + 2) х ≠ 2
Следовательно, эту функцию можно записать как
y = x + 2 x ≠ 2
График h (x) = x 2 — 4 Или x — 2
график y = x + 2 x ≠ 2
Пример: 4 Нарисуйте график
| г (х) = | 1, если x ≤ 2 x + 2, если x> 2 |
Графические функции по переводам
— Предположим, что график f (x) известен
— Тогда мы можем найти графики
у = е (х) + с
у = f (х) — с
y = f (x + c)
y = f (x — c)
y = f (x) + c график f (x) переводит
UP по c единиц
y = f (x) — c график f (x) переводит
ВНИЗ по c единиц
y = f (x + c) график f (x) переводит
СЛЕВА по c единиц
y = f (x — c) график f (x) переводит
СПРАВА по ц
Пример: 5 Нарисуйте
график y = f (x) = | x — 3 | + 2
Перевести график y = | x | 3 единицы ВПРАВО, чтобы получить график
y = | x-3 |
Перевести график y = | x — 3 | 2 единицы к UP, чтобы получить график y = | x — 3 | + 2
Пример: 8
Нарисуйте график
y = x 2 — 4x + 5
— завершить квадрат
y + 4 = (x 2 — 4x + 5) + 4 y = (x 2 — 4x + 4) + 5-4
у = (х — 2) 2 + 1
В этой форме мы видим, что график можно получить, переведя график y = x 2 вправо на 2 единицы из-за x — 2 и на 1 единицу вверх из-за +1.
y = x 2 — 4x + 5
Отражения
(-x, y) — отражение (x, y) относительно оси y
(x, -y) — отражение (x, y) относительно оси x
Графики y = f (x) и y = f (-x) являются отражениями друг друга относительно оси y
Графики y = f (x) и y = -f (x) являются отражениями друг друга относительно оси x
График можно получить путем отражения и перевода:
— Нарисуйте график
— Отразите его вокруг оси Y, чтобы получить график
.
— Переведите этот график вправо на 2 единицы, чтобы получить график
Вот график
Если f (x) умножить на положительную константу c
График f (x) сжимается по вертикали, если 0 График f (x) растягивается по вертикали, если c> 1
Кривая не является графиком y = f (x) для любой функции f
Графические квадратные уравнения с использованием факторинга
Квадратное уравнение
это
многочлен
уравнение
степень
2
.Стандартная форма квадратного уравнения:
0
знак равно
а
Икс
2
+
б
Икс
+
c
где
а
,
б
а также
c
все реальные числа и
а
≠
0
.
Если мы заменим
0
с участием
y
, то получаем
квадратичная функция
y
знак равно
а
Икс
2
+
б
Икс
+
c
чей график будет
парабола
.
Точки пересечения графика
Икс
-оси будут решениями уравнения,
а
Икс
2
+
б
Икс
+
c
знак равно
0
. То есть, если многочлен
а
Икс
2
+
б
Икс
+
c
может быть учтен на
(
Икс
—
п
)
(
Икс
—
q
)
, мы знаем по
свойство нулевого продукта
что если
(
Икс
—
п
)
(
Икс
—
q
)
знак равно
0
, либо
(
Икс
—
п
)
знак равно
0
или же
(
Икс
—
q
)
знак равно
0
.потом
п
а также
q
являются решениями уравнения
а
Икс
2
+
б
Икс
+
c
знак равно
0
и поэтому
Икс
-перехваты квадратного уравнения.
Поскольку
Икс
-координата
вершина параболы
это точно середина
Икс
-перехватывает
, то
Икс
-координата вершины будет
п
+
q
2
.
Вы можете использовать
Икс
-координата вершины для нахождения
y
-координат.
Теперь у вас есть вершина и
2
другие точки параболы (а именно
Икс
-перехватывает). Вы можете использовать эти три точки для построения графика.
Пример 1:
Постройте график функции
y
знак равно
Икс
2
—
8
Икс
+
12
с использованием факторинга.
Сравните уравнение со стандартной формой,
y
знак равно
а
Икс
2
+
б
Икс
+
c
. Поскольку значение
а
положительный, парабола открывается.
Разложите на множители трехчлен,
Икс
2
—
8
Икс
+
12
.
Идентифицировать
2
числа, сумма которых
—
8
и продукт
12
.Цифры
—
2
а также
—
6
. Это,
Икс
2
—
8
Икс
+
12
знак равно
(
Икс
—
2
)
(
Икс
—
6
)
.
Икс
2
—
8
Икс
+
12
знак равно
0
⇒
(
Икс
—
2
)
(
Икс
—
6
)
знак равно
0
Итак, по свойству нулевого продукта либо
(
Икс
—
2
)
знак равно
0
или же
(
Икс
—
6
)
знак равно
0
.Тогда корни уравнения равны
2
а также
6
.
Следовательно
Икс
-перехваты функции
6
а также
2
.
В
Икс
-координата вершины — это середина х-точек пересечения. Итак, вот
Икс
-координата вершины будет
2
+
6
2
знак равно
4
.
Заменять
Икс
знак равно
4
в уравнении
y
знак равно
Икс
2
—
8
Икс
+
12
найти
y
-координата вершины.
y
знак равно
(
4
)
2
—
8
(
4
)
+
12
знак равно
16
—
32
+
12
знак равно
—
4
То есть координаты вершины равны
(
4
,
—
4
)
.
Теперь у нас 3 очка
(
4
,
—
4
)
,
(
2
,
0
)
а также
(
6
,
0
)
которые находятся на параболе. Нанесите точки.
Соедините их плавной кривой и продолжите параболу.
Пример 2:
Постройте график функции
y
знак равно
—
Икс
2
—
2
Икс
+
8
с использованием факторинга.
Сравните уравнение со стандартной формой,
y
знак равно
а
Икс
2
+
б
Икс
+
c
. Поскольку значение
а
положительный, парабола открывается.
Разложите на множители трехчлен,
—
Икс
2
—
2
Икс
+
8
.
Во-первых, фактор вне
—
1
.
—
Икс
2
—
2
Икс
+
8
знак равно
—
1
(
Икс
2
+
2
Икс
—
8
)
Разложите выражение на множители в скобках. Идентифицировать
2
числа, сумма которых
2
и продукт
—
8
.Цифры
4
а также
—
2
. Это,
Икс
2
+
2
Икс
—
8
знак равно
(
Икс
+
4
)
(
Икс
—
2
)
.
Тогда данная функция принимает вид
y
знак равно
—
(
Икс
+
4
)
(
Икс
—
2
)
.
Так,
y
знак равно
0
следует, в силу свойства нулевого продукта,
Икс
+
4
знак равно
0
или же
Икс
—
2
знак равно
0
.
Следовательно
Икс
-перехваты графика
—
4
а также
2
.
В
Икс
-координата вершины параболы — середина
Икс
-перехватывает.Итак, вот
Икс
-координата вершины будет
—
4
+
2
2
знак равно
—
1
.
Заменять
Икс
знак равно
—
1
в уравнении
y
знак равно
—
Икс
2
—
2
Икс
+
8
найти
y
-координата вершины.
y
знак равно
—
(
—
1
)
2
—
2
(
—
1
)
+
8
знак равно
—
1
+
2
+
8
знак равно
9
Итак, координаты вершины равны
(
—
1
,
9
)
.
Теперь у нас есть
3
точки
(
—
1
,
9
)
,
(
—
4
,
0
)
а также
(
2
,
0
)
которые находятся на параболе. Нанесите точки.
Соедините их плавной кривой и продолжите параболу.
Эскиз кривой
В процессе построения кривой выполняются следующие шаги:
\ (1.\) Домен
Найдите область определения функции и определите точки разрыва (если есть).
\ (2. \) Перехватывает
Определите точки пересечения \ (x- \) и \ (y — \) функции, если это возможно. Чтобы найти точку пересечения \ (x — \), мы устанавливаем \ (y = 0 \) и решаем уравнение для \ (x. \). Точно так же мы устанавливаем \ (x = 0 \), чтобы найти \ (y- \ ) перехват. Найдите интервалы, в которых функция имеет постоянный знак \ (\ left ({f \ left (x \ right) \ gt 0} \ right. \) И \ (\ left. {F \ left (x \ right) \ lt 0} \ вправо).\)
\ (3. \) Симметрия
Определите, является ли функция четной, нечетной или ни одной, и проверьте периодичность функции. Если \ (f \ left ({- x} \ right) = f \ left (x \ right) \) для всех \ (x \) в области, то \ (f \ left (x \ right) \) является четное и симметричное относительно оси \ (y — \). Если \ (f \ left ({- x} \ right) = -f \ left (x \ right) \) для всех \ (x \) в домене, то \ (f \ left (x \ right) \) нечетное и симметричное относительно начала координат.
\ (4. \) Асимптоты
Найдите вертикальную, горизонтальную и наклонную (наклонную) асимптоты функции.\ prime \ left (x \ right) \) и найдите критические точки функции. (Помните, что критические точки — это точки, в которых первая производная равна нулю или не существует.) Определите интервалы, в которых функция увеличивается и уменьшается с помощью теста первой производной.
\ (6. \) Локальный максимум и минимум
Используйте первый или второй производный тест, чтобы классифицировать критические точки как локальный максимум или локальный минимум. Вычислите значения \ (y — \) локальных экстремальных точек.
\ (7.2} — 6x + 2 = 0, \; \;} \ Rightarrow
{D = 36-4 \ cdot 3 \ cdot 2 = 12, \; \;} \ Rightarrow
{{x_ {1,2}} = \ frac {{6 \ pm \ sqrt {12}}} {6}} = {1 \ pm \ sqrt 3 \ приблизительно 0,42; \; 1,58. 2}} \ right]}
+ {2 — \ frac {{2 \ sqrt 3}} {3}}
= {\ cancel {1} - \ sqrt 3 + \ cancel {1}}
— {\ frac {{\ sqrt 3}} {9} — \ cancel {3}}
+ {2 \ sqrt 3 — \ cancel {1} + \ cancel {2}}
— {\ frac {{2 \ sqrt 3}} {3}}
= {\ frac {{9 \ sqrt 3 — \ sqrt 3 — 6 \ sqrt 3}} {9}}
= {\ frac {{2 \ sqrt 3}} {9} \ приблизительно 0,38;}
\]
Аналогично находим, что
\ [
{y \ left ({1 + \ frac {{\ sqrt 3}} {3}} \ right)}
= — {\ frac {{2 \ sqrt 3}} {9} \ приблизительно -0 , 38.}
\]
Таким образом, функция имеет локальный максимум в точке
.
\ [\ left ({1 — \ frac {{\ sqrt 3}} {3}, \ frac {{2 \ sqrt 3}} {9}} \ right) \ приблизительно \ left ({0,42; \ ; 0,38} \ вправо). \]
Соответственно, локальный минимум достигается в точке
.
\ [\ left ({1 + \ frac {{\ sqrt 3}} {3}, — \ frac {{2 \ sqrt 3}} {9}} \ right) \ приблизительно \ left ({1,58; \; — 0,38} \ вправо) \]
Интервалы увеличения / уменьшения следуют из рисунка \ (1a. \)
Рассмотрим вторую производную:
\ [
{y ^ {\ prime \ prime} \ left (x \ right) = {\ left ({3 {x ^ 2} — 6x + 2} \ right) ^ \ prime}}
= {6x — 6;}
\]
\ [
{y ^ {\ prime \ prime} \ left (x \ right) = 0, \; \;} \ Rightarrow
{6x — 6 = 0, \; \;} \ Rightarrow
{x = 1 .2}}
= {\ left ({x + 2} \ right) \ left ({2x — \ cancel {2} + x + \ cancel {2}} \ right)}
= {3x \ left ({x + 2} \ вправо).}
\]
Стационарных точек
\ [
{y ‘\ left (x \ right) = 0, \; \;} \ Rightarrow
{3x \ left ({x + 2} \ right) = 0, \; \;} \ Rightarrow
{ {x_1} = 0, \; {x_2} = — 2.}
\]
Производная меняет знак, как показано на рисунке \ (3a. \). Следовательно, \ (x = -2 \) — точка максимума, а \ (x = 0 \) — точка минимума. В этих экстремальных точках функция имеет следующие значения:
\ [
{y \ left ({- 2} \ right) = — 4,} \; \; \; \ kern-0.3}}} = 0, \; \;} \ Rightarrow
{{x_1} = — \ sqrt 3, \; {x_2} = \ sqrt 3.}
\]
При прохождении через эти точки вторая производная меняет знак. Следовательно, обе точки являются точками перегиба. Функция строго выпуклая вниз в интервалах \ (\ left ({- \ infty, — \ sqrt 3} \ right) \) и \ (\ left ({\ sqrt 3, + \ infty} \ right) \) и соответственно, строго выпукло вверх в интервале \ (\ left ({- \ sqrt 3, \ sqrt 3} \ right). 2} + 1}} {{\ cancel {1} - \ sqrt 2 — \ cancel {1}}}} = {\ frac {{1 — 2 \ sqrt 2 + 2 + 1}} {{- \ sqrt 2}}} = {\ frac {{4 — 2 \ sqrt 2}} {{- \ sqrt 2}}} = {\ frac {{4 — 4 \ sqrt 2}} {2}} = {2 \ left ({1 — \ sqrt 2} \ right) \ приблизительно {- 0.2} + 1}} {{\ cancel {1} + \ sqrt 2 — \ cancel {1}}}} = {\ frac {{1 + 2 \ sqrt 2 + 2 + 1}} {{\ sqrt 2} }} = {\ frac {{4 + 2 \ sqrt 2}} {{\ sqrt 2}}} = {\ frac {{4 + 4 \ sqrt 2}} {2}} = {2 \ left ({1 + \ sqrt 2} \ right) \ приблизительно {4.83}} \]
Теперь мы можем нарисовать график функции (рисунок \ (5b \)).
Графики смещения, отражения и растяжения
1.5 — Графики смещения, отражения и растяжения
Определения
- Абсцисса
- Координата x
- Ордината
- Координата Y
- Сдвиг
- Перевод, в котором размер и форма графика функции не изменены, но
расположение графика. - Шкала
- Перевод, в котором размер и форма графика функции изменены.
- Отражение
- Перевод, в котором график функции отражается относительно оси.
Общие функции
Отчасти красота математики в том, что почти все основано на чем-то другом, и если
вы можете понять основы, а затем применить новые элементы к старым. Это способность
что делает возможным понимание математики.Если бы вы запомнили каждый кусок
математики, представленной вам без связи с другими частями, вы 1) станете
разочарованы в математике и 2) не очень разбираются в математике.
Есть несколько основных графиков, которые мы видели раньше. Применяя переводы к этим основным
графов, мы можем получить новые графы, которые по-прежнему обладают всеми свойствами старых. От
понимая основные графики и то, как к ним применяются переводы, мы узнаем каждый
новый график как небольшая вариация старого, а не как совершенно другой график, как у нас
никогда раньше не видел.Понимание этих переводов позволит нам быстро распознать и
нарисуйте новую функцию, не прибегая к построению точек.
Это общие функции, графики которых вы должны знать сейчас:
- Постоянная функция: y = c
- Линейная функция: y = x
- Квадратичная функция: y = x 2
- Кубическая функция: y = x 3
- Функция абсолютного значения: y = | x |
- Функция квадратного корня: y = sqrt (x)
- Наибольшая целочисленная функция: y = int (x) говорилось в предыдущем разделе.
Постоянная функция | Линейная функция | Квадратичная функция |
Кубическая функция | Функция абсолютного значения | Функция квадратного корня |
В вашем тексте линейная функция называется функцией тождества, а квадратичная функция — возведением в квадрат.
функция.
Переводы
Есть два типа переводов, которые мы можем сделать с графиком функции. Они меняются и
масштабирование. Если считать отражения, их три, но отражения — это всего лишь частный случай
второй перевод.
Смена
Сдвиг — это жесткий перевод, поскольку он не меняет форму или размер графика
функция. Все, что будет делать сдвиг, — это изменить положение графика. Вертикальный сдвиг
добавляет / вычитает константу к / из каждой координаты y, оставляя координату x неизменной.Горизонтальный сдвиг добавляет / вычитает константу к / из каждой координаты x, оставляя координату y неизменной. Вертикальные и горизонтальные сдвиги можно объединить в одно выражение.
Сдвиги добавляются / вычитаются из компонентов x или f (x). Если константа сгруппирована с x,
тогда это горизонтальный сдвиг, иначе — вертикальный сдвиг.
Весы (растяжение / сжатие)
Масштаб — это нежесткий перевод, поскольку он изменяет форму и размер графика
функция.Масштаб будет умножать / делить координаты, и это изменит внешний вид, а также
Местоположение. Вертикальное масштабирование умножает / делит каждую координату y на константу, оставляя
координата x не изменилась. Горизонтальное масштабирование умножает / делит каждую координату x на
константа, оставляя координату y неизменной. Вертикальные и горизонтальные масштабы могут быть
объединены в одно выражение.
Коэффициенты масштабирования умножаются / делятся на компоненты x или f (x). Если константа сгруппирована
с x, тогда это горизонтальное масштабирование, в противном случае это вертикальное масштабирование.
Отражения
Функция может быть отражена относительно оси умножением на отрицательную единицу. Чтобы отразить ось Y, умножьте каждый x на -1, чтобы получить -x. Чтобы отразить ось x, умножьте f (x) на -1, чтобы получить -f (x).
Собираем все вместе
Рассмотрим основной график функции: y = f (x)
Все переводы могут быть выражены в форме:
y = a * f [b (x-c)] + d
| Вертикальный | горизонтальный | |
|---|---|---|
| Масштаб | а | б |
| Сдвиг | д | c |
| действует нормально | действует наоборот |
отступление
Понимание представленных здесь концепций является фундаментальным для понимания полиномиального и рационального
функции (ch 3) и особенно конические секции (ch 8).Это также будет играть очень большую роль в
Тригонометрия (Математика 117) и Исчисление (Математика 121, 122, 221 или 190).
Ранее в тексте (раздел 1.2, задачи 61-64) была серия задач, в которых
уравнение линии как:
х / а + у / б = 1
Где a — точка пересечения по оси X, а b — точка пересечения по оси Y линии. «А» может
действительно быть
подумал о том, как далеко нужно пройти по оси x (масштабирование по оси x), и «b» может
думать как
далеко идти в направлении «y» (масштабирование по оси y).Итак, «а» и «б» есть
собственно множители (даже если они появляются внизу). Что они
умножение
это 1
который находится с правой стороны. x + y = 1 будет иметь точки пересечения с координатами x и y
1.
Хорошо. Рассмотрим уравнение: y = f (x)
Это самый простой график функции. Но преобразования могут
применимо и к нему. Его можно записать в формате, показанном ниже.
В этом формате «a» — вертикальный множитель, а «b» — горизонтальный.
множитель.Мы знаем, что «a» влияет на y, потому что он сгруппирован с
y и «b» влияет на
x, потому что он сгруппирован с x.
Буквы «d» и «c» — вертикальное и горизонтальное.
сдвигов соответственно. Мы знаем, что это сдвиги, потому что они вычитаются
из переменной скорее
чем быть разделенными на переменные, что сделало бы их масштабными.
В этом формате все изменения кажутся противоположными ожидаемым. Если у вас есть
выражение (y-2) / 3, это вертикальный сдвиг на 2 вправо (даже если в нем указано y минус 2), и это
вертикальное растяжение на 3 (хотя там указано, что y делится на 3).Важно понимать, что в этом
формат, когда константы сгруппированы с переменной, на которую они влияют, перевод является
противоположное (обратное) тому, что думает большинство людей.
Однако этот формат не подходит для создания эскизов с помощью технологий,
потому что нам нравится писать функции как y =, а не (y-c) / d =.
Итак, если вы возьмете обозначение выше и решите его относительно y, вы получите обозначение ниже, которое
похоже, но не совсем в нашем базовом состоянии формы, приведенном выше.
y = a * f ((x-c) / b) + d
Обратите внимание, что для определения y вам нужно было инвертировать константы «a» и «d».Вместо деления на «а» вы теперь умножаете на «а». Ну, раньше
будь то ты
в любом случае пришлось применить обратную константу. Когда было сказано «разделить на»,
ты знал это
Это
означало «умножать
каждый y на «. Когда говорилось» вычесть d «, вы знали, что вам действительно нужно» добавить
d «. У вас есть
обратное уже было применено, так что больше не делайте этого! С константами, влияющими на
y, поскольку они были перемещены на другую сторону, принимайте их за чистую монету.
Если там написано «умножить на 2», делайте это, а не
разделить на 2.
Однако константы, влияющие на x, не изменились. Они по-прежнему противоположны
какими, по вашему мнению, они должны быть. И, что еще хуже, «x разделенное b», что на самом деле означает
умножение каждой координаты x на «b» было перевернуто и записано как «b умножить на x», так что это действительно
означает разделить каждый x на «b». «X минус c» на самом деле означает прибавление c к каждой координате x.
Итак, окончательная форма (для технологии) такая же, как указано выше:
y = a * f [b (x-c)] + d
Хорошо, конец отступления.
Нормальное и обратное поведение
Вы заметите, что в таблице указано, что вертикальный перевод нормальный, а горизонтальный — нормальный.
переводы инвертированы. Объяснение причин читайте в отступлении выше. Концепции в
действительно важны для понимания многих графиков.
Примеры
- y = f (x)
- Нет перевода
- у = е (х + 2)
- +2 сгруппировано с x, поэтому это горизонтальный перевод.Поскольку он добавлен
к x, а не умноженному на x, это сдвиг, а не масштаб. Поскольку там написано плюс
и горизонтальные изменения инвертированы, фактический перевод заключается в перемещении всего
график слева на две единицы или «вычтите два из каждой координаты x», оставив
только координаты y. - у = е (х) +2
- +2 не сгруппирован с x, поэтому это вертикальный перевод. Поскольку он добавлен,
это не умножение, а сдвиг, а не масштаб.Поскольку он говорит плюс и вертикальный
изменения действуют так, как выглядят, фактический перевод заключается в перемещении всего графа на два
единиц вверх или «прибавьте два к каждой координате y», не трогая координаты x. - y = f (x-3) +5
- На этот раз имеется сдвиг по горизонтали на три вправо и сдвиг по вертикали на пять вверх. Так
перевод будет заключаться в перемещении всего графика вправо на три и пять вверх или «добавить три
для каждой координаты x и пять для каждой координаты y « - у = 3f (х)
- 3 умножается, поэтому это масштабирование, а не сдвиг.3 не сгруппированы с
x, так что это вертикальное масштабирование. Вертикальные изменения происходят так, как вы думаете.
должно быть, поэтому в результате мы «умножим каждую координату y на три», оставив только координаты x. - у = -f (х)
- Y нужно умножить на -1. Это заставляет перенос «отражаться относительно оси x», оставляя только координаты x.
- y = f (2x)
- 2 умножается, а не складывается, поэтому это масштабирование, а не сдвиг.2 — это
сгруппированы с помощью x, поэтому это горизонтальное масштабирование. Горизонтальные изменения противоположны
чем они кажутся, вместо того, чтобы умножать каждую координату x на два,
перевод заключается в «делении каждой координаты x на два», оставляя координаты y
без изменений. - у = f (-x)
- x нужно умножить на -1. Это заставляет перемещение «отражаться относительно оси y», оставляя только координаты y.
- y = 1/2 f (x / 3)
- Здесь можно перевести как «умножить каждую координату y на 1/2 и умножить
каждую координату x на 3 дюйма. - у = 2f (х) +5
- Здесь может быть некоторая двусмысленность. Вы добавляете пять к каждой координате Y, а затем
умножьте на два «или вы» умножаете каждую координату y на два, а затем складываете пять «?
Вот тут-то и приходит мой предыдущий комментарий о математике, основанной на самой себе.
играть. Существует порядок операций, который гласит, что умножение и деление
выполняется перед сложением и вычитанием. Если вы это помните, то решение
легкий. Правильное преобразование — «умножить каждую координату y на два, а затем
добавьте пять дюймов, не трогая координаты x. - y = f (2x-3)
- Теперь, когда порядок операций четко определен, двусмысленность здесь
нужно сделать сначала снимается. Ответ не в том, чтобы «делить каждую координату x на два.
и добавьте три «, как и следовало ожидать. Причина в том, что проблема , а не , записанная в
стандартная форма. Стандартная форма — y = f [b (x-c)]. При написании в стандартной форме это
проблема становится y = f [2 (x-3/2)]. Это означает, что правильный перевод —
«разделить каждую координату x на два и добавить три половины», оставляя координаты y неизменными. - у = 3f (х-2)
- Перевод здесь означает «умножить каждую координату y на три и добавить два к каждой координате x». В качестве альтернативы вы можете изменить порядок. Изменения x или y
можно сделать независимо друг от друга, но при наличии масштабов и сдвигов на одинаковые
переменной, важно сначала выполнить масштабирование, а затем — сдвиг.
Переводы и влияние на домен и диапазон
Любой горизонтальный перевод повлияет на домен и оставит диапазон неизменным.Любая вертикаль
перевод повлияет на диапазон и оставит домен без изменений.
Примените тот же перевод к домену или диапазону, который вы применяете к x-координатам или y-координатам. Это работает, потому что область может быть записана в обозначении интервала как интервал
между двумя координатами x. То же самое для диапазона как интервал между двумя координатами y.
Помните, что в следующей таблице домен и диапазон даны в виде интервалов. Если ты
Если вы не знакомы с обозначением интервалов, обратитесь к главе о предварительных требованиях.Первая строка — это
формулировка определения и должна использоваться для определения остальных ответов.
| График | Перевод | Домен | Диапазон |
|---|---|---|---|
| y = f (x) | нет | (-2,5) | [4,8] |
| y = f (x-2) | правый 2 | (0,7) | [4,8] |
| y = f (x) -2 | вниз 2 | (-2,5) | [2,6] |
| y = 3f (x) | умножить каждый y на 3 | (-2,5) | [12,24] |
| y = f (3x) | делим каждый x на 3 | (-2 / 3,5 / 3) | [4,8] |
| y = 2f (x-3) -5 | умножить каждый y на 2 и вычесть 5; добавить 3 к каждому x | (1,8) | [3,11] |
| y = -f (x) | отразить относительно оси x | (-2,5) | [-8, -4] |
| y = 1 / f (x) | — величина, обратная каждому y | (-2,5) | [1 / 8,1 / 4] |
Обратите внимание на последние два, что порядок в диапазоне изменился.Это потому, что в интервале
обозначение, меньшее число всегда идет первым.
Действительно хорошие вещи
Понимание переводов также может помочь при поиске домена и диапазона функции.
Допустим, ваша проблема — найти домен и диапазон функции y = 2-sqrt (x-3).
Начните с того, что вы знаете. Вы знаете, что основная функция — это sqrt (x), и вы знаете домен
и диапазон sqrt (x) равны [0, + бесконечность). Вы знаете это, потому что знаете эти шесть
общие функции на лицевой обложке вашего текста, которые будут использоваться в качестве строительных блоков
для других функций.
| Функция | Перевод | Домен | Диапазон | |
|---|---|---|---|---|
| Начать с чего ты знаешь | y = sqrt (x) | Нет | [0, + бесконечность) | [0, + бесконечность) |
| Примените переводы | y = -sqrt (x) | Отражение относительно оси x | [0, + бесконечность) | (-infinity, 0] |
| y = 2-sqrt (x) | Добавьте 2 к каждой ординате | [0, + бесконечность) | (-бесконечность, 2] | |
| y = 2-sqrt (x-3) | Добавьте 3 к каждой абсциссе | [3, + бесконечность) | (-бесконечность, 2] |
Итак, для функции y = 2-sqrt (x-3) домен равен x≥3, а диапазон — y≤2.
И лучшая часть этого в том, что вы это поняли! Вы не только поняли это, но вы были
в состоянии сделать это без построения графика на калькуляторе.
Нет ничего плохого в том, чтобы построить график, чтобы увидеть, что происходит, но вы должны уметь
понять, что происходит без графика, потому что мы узнали, что график
калькулятор не всегда точно показывает, что происходит. Это инструмент, который поможет вам понять
и понимание, а не инструмент для его замены.
Я хочу, чтобы все вы «поняли» именно эту связность математики. Все подходит
вместе так красиво.
.
