Решатель квадратных уравнений: Онлайн калькулятор. Решение квадратных уравнений. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Квадратное уравнение

— это уравнение вида a x² + b x + c = 0, где a не равно 0.

Геометрический смысл

Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют точки пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня.

Если коэффициент a положительный, ветви параболы направлены вверх, если отрицательный — ветви параболы направлены вниз. Если коэффициент b положительный, то вершина параболы лежит в левой полуплоскости, если отрицательный — в правой полуплоскости.

Вывод формулы для решения квадратного уравнения

Формулу для решения квадратного уравнения a x² + b x + c = 0 можно получить так:

перенесем c в правую часть a x² + b x = — c

умножим уравнение на 4a (2a x)² + 4a b x = — 4a c

добавим b² к обоим частям (2a x)² + 4a b x + b² = b² — 4a c

в левой части выделим полный квадрат (2a x + b)² = b² — 4a c

извлечем квадратный корень 2a x + b = ± √b² — 4a c

перенесем b в правую часть 2a x = — b ± √b² — 4a c

разделим уравнение на 2a

x = -b ± √b² — 4a c
2 a

Дискриминант квадратного уравнения

Дискриминантом

квадратного уравнения называют число равное D = b² − 4ac

Квадратное уравнение с вещественными коэффициентами может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта:

при D > 0 корней два, и они вычисляются по формуле

x_1,2 = -b ± √D
2 a

при D = 0 корень один (два равных или совпадающих корня), кратности 2:

при D
x_1,2 =

-b ± i√-D

2 a

Теорема Виета

Приведенным квадратным уравнением

называется уравнение, в котором коэффициент при x² равен единице. Такое уравнение может быть получено делением всего выражения на коэффициент a: x² + px + q = 0,
где p = ba, q = ca

Сумма корней приведённого квадратного уравнения

x² + px + q = 0 равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:
x₁ + x₂ = -p, x₁x₂ = q.

Разложение квадратного уравнения на множители

Если известны оба корня квадратного уравнения, его можно разложить по формуле

ax² + bx + c = a(x — x₁)(x — x₂)

Примеры решения квадратных уравнений

Например. Найти корни квадратного уравнения: 2x² + 5x + 3 = 0

D = 5² — 4·3·2 = 25 — 24 = 1

x₁ =	—5 + √1	= -1,
	2·2

x₂ =	—5 — √1	= -1	1
	2·2		2

Упражнения. Квадратные уравнения.

Как решать неполные квадратные уравнения? Примеры и Формулы

Основные понятия

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

если D < 0, корней нет;
если D = 0, есть один корень;
если D > 0, есть два различных корня.

Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю.

Неполные квадратные уравнения бывают трех видов:

Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.
Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.

Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три формулы неполных квадратных уравнений:

ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax² + c = 0, при b = 0;
ax² + bx = 0, при c = 0.

Давайте рассмотрим каждый случай отдельно и решим примеры неполных квадратных уравнений. А еще лучше — приходите сразу практиковаться в современную школу Skysmart.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Как решить уравнение ax² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −5x² = 0.

Как решаем:

Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.

По шагам решение выглядит так:
−5x² = 0
x² = 0
x = √0
x = 0
Ответ: 0.

Как решить уравнение ax² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

перенесем c в правую часть: ax² = — c,
разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x² = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р² = — c/а не является верным.

Если — c/а > 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах

Неполное квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое:

не имеет корней при — c/а < 0;
имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

Пример 1.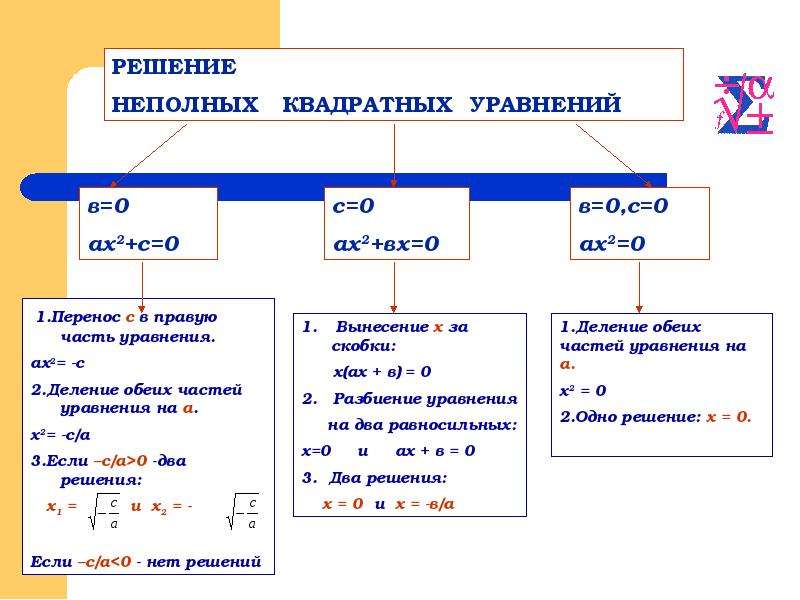 Найти решение уравнения 9x² + 4 = 0.

Как решать:

Перенесем свободный член в правую часть:
9x² = — 4

Разделим обе части на 9:
x² = — 4/9

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 9x² + 4 = 0 не имеет корней.

Пример 2. Решить -x² + 9 = 0.

Как решаем:

Перенесем свободный член в правую часть:
-x² = -9

Разделим обе части на -1:
x² = 9

Найти корни:
x = √9
x = -3
x = 3

Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3.

Как решить уравнение ax² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

Пример 1. Решить уравнение 2x² — 32x = 0

Как решать:

Вынести х за скобки
х(2x — 32) = 0

Это уравнение равносильно х = 0 и 2x — 32 = 0.

Решить линейное уравнение:
2x = 32,
х = 32/2

Разделить:
х = 16

Значит корни исходного уравнения — 0 и 16.

Ответ: х = 0 и х = 16.

Пример 2. Решить уравнение 3x² — 12x = 0

Как решать:

Разложить левую часть уравнения на множители и найти корни:

Ответ: х = 0 и х = 4.

Алгебра 7-9 классы. 20. Решение квадратных уравнений

Подробности: Категория: Алгебра 7-9 классы

ФОРМУЛЫ КОРНЕЙ КВАДРАТНЫХ УРАВНЕНИЙ

Пусть дано квадратное уравнение Применим к квадратному трехчлену те же преобразования, которые мы выполняли ранее, когда доказывали теорему о том, что графиком функции с является парабола.

Имеем

Обычно выражение обозначают буквой D и называют дискриминантом квадратного уравнения (или дискриминантом квадратного трехчлена ).

Таким образом,

Значит, квадратное уравнение можно переписать в виде

и далее

Любое квадратное уравнение можно преобразовать к виду (1), удобному, как мы сейчас убедимся, для того, чтобы определять число корней квадратного уравнения и находить эти корни.

Теорема 1

Если D <0, то квадратное уравнение не имеет корней.

Доказательство. Если D < 0, то правая часть уравнения (1) — отрицательное число; в то же время левая часть уравнения (1) при любых значениях х принимает неотрицательные значения. Значит, нет ни одного значения х, которое удовлетворяло бы уравнению (1), а потому уравнение (1) не имеет корней.

Пример 1. Решить уравнение

Решение. Здесь а = 2, b = 4, с = 7,

Так как D < 0, то по теореме 1 данное квадратное уравнение не имеет корней.

Теорема 2

Если D = О, то квадратное уравнение имеет один корень, который находится по формуле

Доказательство. Если D = 0, то уравнение (1) принимает вид Значит, единственный корень уравнения.

Замечание 1. Помните ли вы, что абсцисса вершины параболы, которая служит графиком функции ? Почему именно это значение оказалось единственным корнем квадратного уравнения ? «Ларчик» открывается просто: если D = 0, то, как мы установили ранее,

Графиком же функции является парабола с вершиной в точке (см., например, рис. 98). Значит, абсцисса вершины параболы и единственный корень квадратного уравнения при D = 0 — одно и то же число.

Пример 2. Решить уравнение 4х² — 20х + 25 = 0.

Решение. Здесь а = 4, b = -20, с = 25, D = b² — 4ас = (-20)² — 4 • 4 • 25 = 400 — 400 = 0.

Так как D = 0, то по теореме 2 данное квадратное уравнение имеет один корень. Этот корень находится по формуле

Значит, .

Ответ: 2,5.

Замечание 2. Обратите внимание, что 4х² — 20х +25 — полный квадрат: 4Х² — 20х + 25 = (2х — 5)². Если бы мы это заметили сразу, то решили бы уравнение так: (2х — 5)² = 0, значит, 2х — 5 = 0, откуда получаем х = 2,5. Вообще, если D = 0, то ах² + bх + с =
— это мы отметили ранее в замечании 1.

Теорема 3. Если D > О, то квадратное уравнение ах² + bх + с = О имеет два корня, которые находятся по формулам

Доказательство. Перепишем квадратное уравнение в виде (1)

Положим тогда уравнение (1) примет вид

По условию, D > О, значит, правая часть уравнения положительное число. Тогда из уравнения (2) получаем, что

Ho , таким образом, задача свелась к решению двух уравнений:

Из первого уравнения находим

Из второго уравнения находим

Итак, заданное квадратное уравнение имеет два корня:

Замечание 3. в математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Возьмем новое понятие — дискриминант. Вспомните слово «дискриминация». Что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отношение к различным людям. Оба слова (и дискриминант, и дискриминация) происходят от латинского discriminans — «различающий». Дискриминант различает квадратные уравнения по числу корней.

Пример 3. Решить уравнение Зх² + 8x — 11 = 0. Решение. Здесь а = 3, b = 8, с = —11,

D = b² — 4ас = 8² — 4 • 3 • (—11) = 64 4- 132 = 196.

Так как D > 0, то по теореме 3 данное квадратное уравнение имеет два корня. Эти корни находятся по формулам (3)

Ответ: 1,

Фактически мы с вами выработали следующее правило:

Калькулятор квадратных уравнений — решение квадратных уравнений онлайн

Этот калькулятор квадратных формул работает как решить квадратное уравнение решатель квадратных уравнений, который помогает решить квадратное уравнение заданное квадратное уравнение с помощью формулы квадратного уравнения.

Что ж, прежде чем узнать об этом калькулятор квадратных уравнений квадратных уравнений, давайте начнем с некоторых основ!

Что такое квадратичная формула?

Квадратичная формула считается одним из самых эффективных инструментов математики. 2 – 4ac}} {2a} \]

Наш калькулятор квадратных формул также использует ту же формулу для [решения квадратного уравнения].

Есть три возможности получить корни (квадратного уравнения), но помните, что эти возможности зависят от значения Дискриминанта.

Если b2 – 4ac = 0, то будет только один корень
Если b2 – 4ac> 0, то будет только два действительных корня
Если b2 – 4ac <0, то будет два комплексных корня

Коэффициенты квадратного уравнения:

Также важно отметить, что числа, то есть a, b и c, считаются коэффициентами уравнения и не могут быть «0». Все они действительные числа, не зависящие от x. Если A = 0, то уравнение называется не квадратичным, а линейным.
Если B² <4AC, то определитель Δ будет отрицательным, как решать квадратные уравнения уравнение это уравнение не имеет действительных корней.

Наш квадратичный калькулятор также может вам помочь, если вы можете записать уравнение в такой форме:

ax2 bx c = 0

Калькулятор квадратной формулы:

Этот калькулятор квадратных уравнений квадратной формулы представляет собой инструмент, который помогает решить квадратное уравнение квадратное уравнение, используя квадратную формулу или завершив метод квадратов. Вам просто нужно сформировать уравнение, метод вычисления и ввести параметры уравнения; этот решатель квадратной формулы лучше всего подойдет вам!

Как пользоваться калькулятором квадратной формулы:

Не волнуйтесь; этот решатель решение квадратного уравнения квадратных уравнений онлайн довольно прост в использовании и имеет продуманный и удобный интерфейс!

Входы:
Форма уравнения:

Вы должны выбрать форму уравнения; это форма, в соответствии с которой вы должны ввести значения в обозначенные поля нашего калькулятора квадратичных функций.

В этом калькулятор квадратных уравнений используется следующая форма:

Ax2 Bx C = 0 (стандартная форма)
A (x – H) 2 K = 0 (форма вершины)
A (x-x₁) (x-x₂) = 0 (Факторная форма)

Метод вычисления:

Наш калькулятор квадратных уравнений квадратного уравнения позволяет вам решить квадратное уравнение квадратное уравнение, используя формулу корней квадратного уравнения и завершив метод квадратов.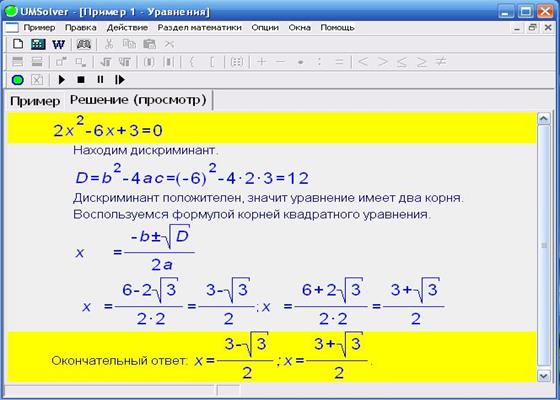

Введите значения:

Если вы выбрали форму Ax2 Bx C = 0, вам необходимо ввести значения A, B и C

Если вы выбрали форму A (x – H) 2 K = 0, то вам необходимо ввести значения A, H и K

Если вы выбрали форму A (x-x₁) (x-x₂) = 0, вам необходимо ввести значения A, x1 и x2

Вывод:

После того, как решить квадратное уравнение указанные выше значения, наш решатель (квадратного уравнения) покажет следующее:

Показать корни:

Этот калькулятор квадратного корня показывает корень или корни вашего данного уравнения.

Покажите упрощение:

Калькулятор шаг за шагом упростит данное уравнение.

Показать дискриминант:

Если вы решите решение квадратных уравнений онлайн с помощью формулы квадратичного, то наш калькулятор квадратичного дискриминанта покажет дискриминант

Покажите квадратичный график:

Этот калькулятор квадратичных графиков показывает вам полный квадратичный график для данного уравнения!

Как решать квадратные уравнения?

Когда дело доходит до решения квадратных уравнений, квадратная формула используется для выполнения вычислений.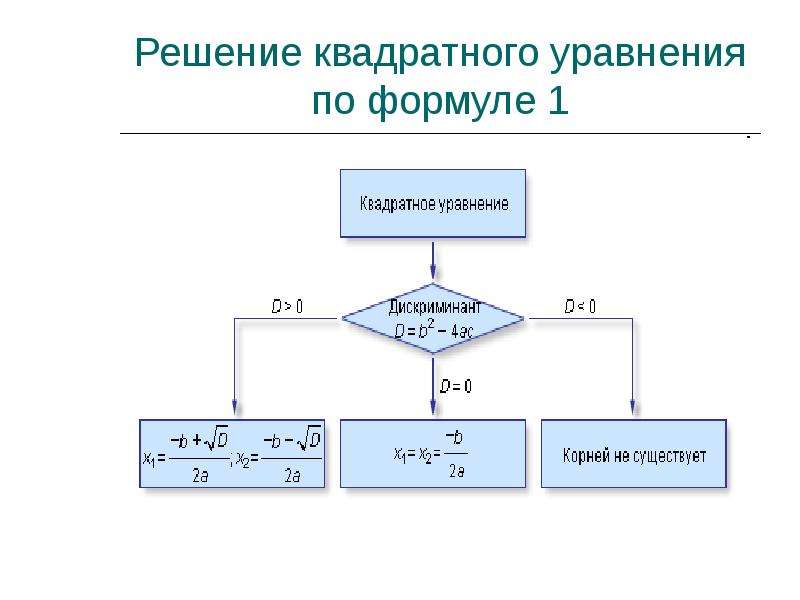 2x. Говорят, что «b» является коэффициентом, который появляется при умножении линейного члена x, а коэффициент «c» считается постоянным.

Пример №1:

как решать квадратные уравнения следующего выражения x2 3x 1?

В этом случае a = 1 (это коэффициент умножения на квадратный член x2), b = 3b = 3 (коэффициент, умноженный на линейный член x) и c = 1 (константа).

Пример №2:

Какие сейчас коэффициенты, если у вас есть следующее выражение: 5/4 3/4 x 1/2 x2

В этом случае a = 1/2 (это коэффициент умножения на квадратичный член x2), b = 3/4 (коэффициент, умноженный на линейный член x) и c = 5/4 (константа).

Пример №3:

Какие коэффициенты, если у вас есть следующее выражение: -3 1/2

В этом случае a = 0, поскольку данное выражение не содержит квадратичного члена x2. Итак, это не считается квадратичным выражением.

Подставьте коэффициенты, которые вы нашли в формуле (шаг 2):

Формула:

\ [x = \ dfrac {-b \ pm \ sqrt {b ^ 2 – 4ac}} {2a} \]

Теперь вам нужно заменить значения коэффициентов a, b и c. 2 – 4 (-3) (1)}} {2 (-3)} \]

Упростите значения в уравнении (шаг 3):

После того, как вы подставили значения a, b и c, вы должны упростить значения в уравнении. Из предыдущего примера у вас есть:

\ [x = \ dfrac {-2 \ pm \ sqrt {4 – 12}} {(- 6)} \]

\ [x = \ dfrac {-2 \ pm \ sqrt {-8}} {(- 6)} \]

Загляните внутрь квадратного корня (шаг 4):

Если значение положительное, то уравнение имеет два действительных корня. Если значение равно 0, то существует только один действительный корень, а если значение внутри квадратного корня отрицательное, то будет два комплексных корня. В предыдущем примере у вас есть -8 внутри квадратного корня, что означает, что у вас есть два сложных решения (как показано ниже):

\ [x = \ dfrac {-2 \ pm \ sqrt {4 – 12}} {(- 6)} \]

\ [x = \ dfrac {-2 \ pm \ sqrt {-8}} {(- 6)} \]

\ [x = \ dfrac {-2 \ pm \ sqrt {8} \, i} {(- 6)} \]

К счастью, вы узнали, как решать квадратные уравнения (вручную). 2 – 4ac}} {2a} \]

Имейте в виду, поскольку b2 – 4ac <0, квадратный корень из определителя будет мнимым значением. Отсюда:

Re (x) = -B / 2A

Im (x) = ± (√Δ) / 2A

Решение квадратного уравнения методом построения графиков:

Итак, из графика параболы узнайте вершину, ось симметрии, точку пересечения по оси y, точку пересечения с x.

Задача имеет два решения, и они демонстрируют точки пересечения уравнения, которые являются точкой пересечения с осью x (это точка, в которой ось x пересекается кривой. При этом составляется график данного уравнения x2 3x – 4 = 0, можно рассматривать как решить квадратное уравнение:

Вершина:

Это демонстрация пика. Итак, вершина (квадратного уравнения) указывает точку пика параболы. Если парабола открывается вверх, то говорят, что вершина – это самая высокая точка, а если парабола открывается вниз, то вершина называется самой низкой точкой.

Ось симметрии:

Ось симметрии делит параболу на две равные половины; он всегда проходит через вершину параболы.

X-перехват:

Корни также называют пересечением по оси x. Он расположен ниже оси x или выше оси x на графике. Поэтому для определения корня квадратичной функции положим y = 0

Y-перехват:

Каждая парабола имеет точку пересечения с осью y, и говорят, что это точка, в которой функция пересекает ось y. Это вычисляется путем установки переменной x в уравнении на 0.

Итак, давайте начнем решать графически,

Сначала возьмем уравнение f (x) = 2×2 – 4x-1 или Y = 2×2 – 4x-1.

Здесь a = 2, b = -4 и c = -1.

Если «a» имеет положительное значение, то помните, что парабола открывается вверх на графике. Сначала вам нужно найти вершину x:

х = (- Ь) / 2а

х = (- (- 4)) / 2 (2)

х = 1

Теперь вам нужно найти вершину Y:

Вы должны подставить значение x в уравнение 2×2 – 4x-1

у = 2 (1) 2-4 (1) -1

у = 2 – 4 – 1

у = 3

Итак, у вас есть ось симметрии: x = 1

Теперь вам нужно найти точку пересечения по оси x, используя формулу корней квадратного уравнения:

\ [x = \ dfrac {- (- 4) \ pm \ sqrt {(- 4) ^ 2 – 4 (2) (- 1)}} {2 (2)} \]

\ [x = \ dfrac {4 \ pm \ sqrt {16 8}} {4} \]

\ [x = \ dfrac {4 \ pm \ sqrt {24}} {4} \]

\ [x = \ dfrac {4 \ pm 4.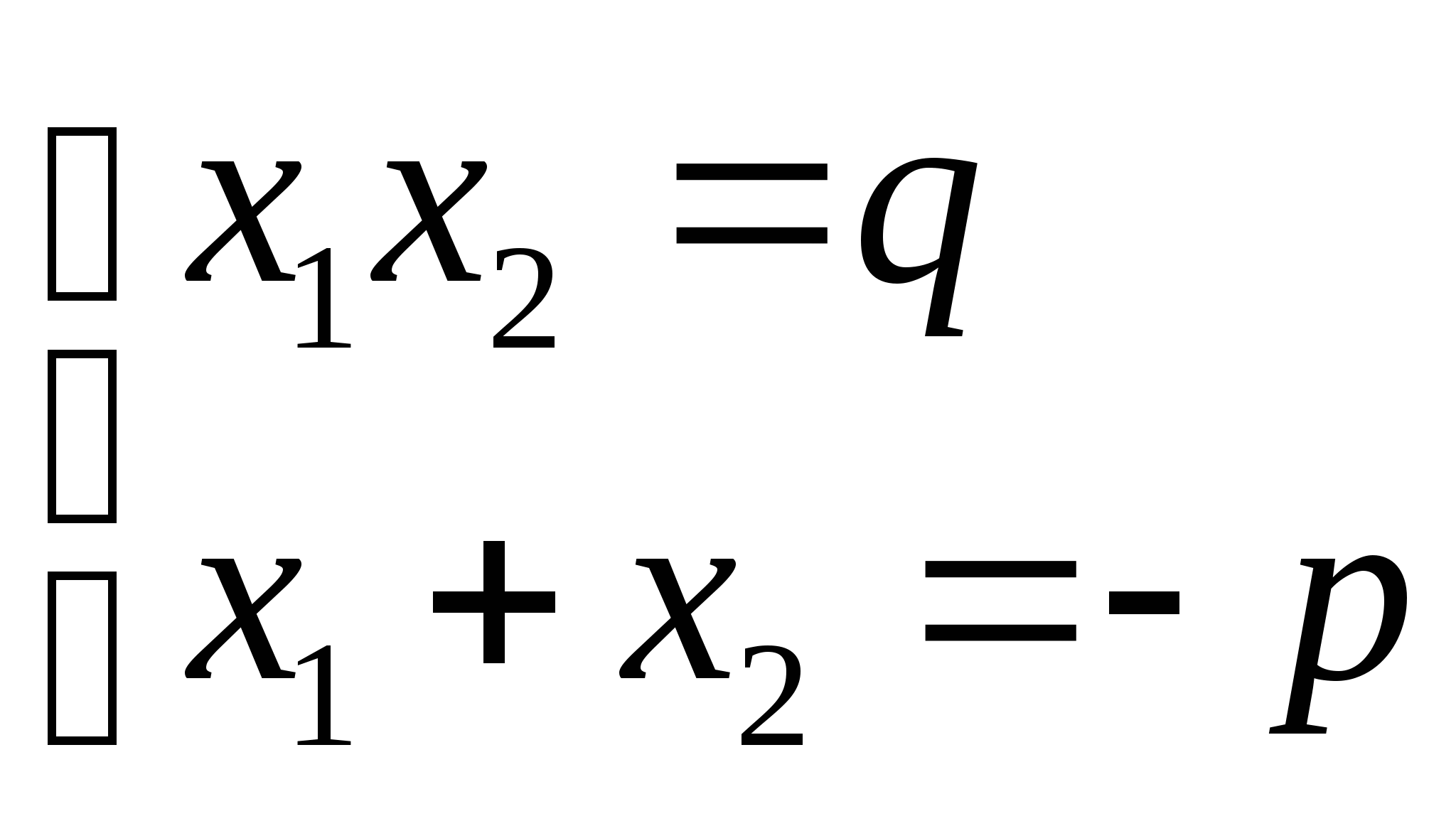 2 – 4 (-1) (1)}} {2 (-1)} \]

\ [x = \ dfrac {-2 \ pm \ sqrt {8}} {-2} \]

х1 = – 0,414214

х2 = 2,414214

Теперь найдите y-точку пересечения:

х2 2х 1 = 0

(0) 2 2 (0) 1 = 0

y-intercept = 1, теперь вам нужно нанести значения на график!

Для чего используется квадратичная формула?

Квадратичная формула – это хорошо известная формула, которая встречается повсюду в математике. Он часто учитывается при решении всевозможных геометрических задач, таких как:

Увеличение площади
Учитывая фиксированный периметр
Многочисленные проблемы с Word

Есть много людей, которые задаются вопросом, есть ли какая-либо связь между этой формулой (квадратным уравнением) и методом завершения квадрата. Проще говоря, вы получите квадратную формулу, просто решив решение квадратных уравнений онлайн, заполнив квадрат. Это в точности та же идея, которая вытекает из известной всем нам формулы квадратичных уравнений!

Важность квадратного уравнения в реальной жизни:

Будучи студентом, вас могут принимать во внимание по различным вопросам математики. Кроме того, студенты обычно используют это уравнение в таких предметах, как решать квадратные уравнения инженерия и физика. Есть и другие профессии, которые используют (квадратные уравнения):

Военные и правоохранительные органы – (для определения траектории ракет, выпущенных артиллерией)
Инженеры – (относится к гражданскому строительству)
Уравнение движения (как на игровой площадке, так и в игровых ситуациях, оно описывает траекторию полета мяча и определяет высоту брошенного мяча)
Наука (Астрономы – описывают орбиту планет, солнечных систем и галактик)
Сферы сельского хозяйства (оптимальное расположение границ для производства самого большого поля)

Часто задаваемый вопрос:

Как найти формулу корней квадратного уравнения?

Проще говоря, вам просто нужно заполнить квадрат ax2 bx c = 0, чтобы получить формулу корней
квадратного уравнения

Вам следует разделить обе части уравнения на «а», чтобы коэффициент при x2 был равен 1.

2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.

Как узнать, имеет ли квадратное уравнение одно решить квадратное уравнение онлайн, два или нет?

Это помогает определить, сколько существует решений (квадратного уравнения). Если дискриминант положительный, говорят, что есть 2 корня. Если он равен нулю, значит есть только 1 корень. Если дискриминант отрицательный, то говорят, что корней 0.

Other Languages: Quadratic Formula Calculator, Løs Andengradsligning, Quadratische Gleichungen Lösen, Kinci Dereceden Denklem Çözücü, Rozwiązywanie Równań Kwadratowych, Kalkulator Persamaan Kuadrat, Risolvere Equazioni Di Secondo Grado, Résoudre Une Équation Du Second Degré, Equazioni Di Secondo Grado, Resolver Ecuaciones De Segundo Grado, Toisen Asteen Yhtälön Ratkaisu, Řešení Kvadratické Rovnice, 二次方程式の解, حل المعادلات التربيعية, 이차방정식 계산기

Решить квадратное уравнение онлайн

Предлагаем вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Вы сможете быстро получить решение квадратного уравнения онлайн и разобраться, как они решаются, на понятных примерах.

Чтобы произвести решение квадратного уравнения онлайн, вначале приведите уравнение к общему виду:
ax² + bx + c = 0
Заполните соответственно поля формы:

Как решить квадратное уравнение

Как решить квадратное уравнение:

Виды корней:

1. Привести квадратное уравнение к общему виду:
Общий вид Аx²+Bx+C=0
Пример : 3х — 2х²+1=-1 Приводим к -2х²+3х+2=0

2. Находим дискриминант D.
D=B²-4*A*C .

Для нашего примера D= 9-(4*(-2)*2)=9+16=25.

3. Находим корни уравнения.
x1=(-В+D^1/2)/2А .

Для нашего случая x1=(-3+5)/(-4)=-0,5
x2=(-В-D^1/2)/2А.

Для нашего примера x2=(-3-5)/(-4)=2
Если В — четное число, то дискриманант и корни удобнее считать по формулам:
D=К²-ac
x1=(-K+D^1/2)/А
x2=(-K-D^1/2)/А,
Где K=B/2

1. Действительные корни. Причем. x1 не равно x2
Ситуация возникает, когда D>0 и A не равно 0.

2. Действительные корни совпадают. x1 равно x2
Ситуация возникает, когда D=0. Однако при этом, ни А, ни В, ни С не должны быть равны 0.

3. Два комплексных корня. x1=d+ei, x2=d-ei, где i=-(1)^1/2
Ситуация возникает, когда D

4. Уравнение имеет одно решение.
A=0, B и C нулю не равны. Уравнение становиться линейным.

5. Уравнение имеет бесчисленное множество решений.
A=0, B=0, C=0.

6. Уравнение решений не имеет.
A=0, B=0, C не равно 0.

Для закрепления алгоритма, вот еще несколько показательных примеров решений квадратных уравнений.

Пример 1. Решение обычного квадратного уравнения с разными действительными корнями.

x² + 3x -10 = 0
В этом уравнении
А=1, B = 3, С=-10
D=B²-4*A*C = 9-4*1*(-10) = 9+40 = 49
квадратный корень будем обозначать, как число^1/2!
x1=(-В+D^1/2)/2А = (-3+7)/2 = 2
x2=(-В-D^1/2)/2А = (-3-7)/2 = -5

Для проверки подставим:
(x-2)*(x+5) = x2 -2x +5x – 10 = x2 + 3x -10

Пример 2. Решение квадратного уравнения с совпадением действительных корней.

х²– 8x + 16 = 0
А=1, B = -8, С=16
D = k² – AC = 16 – 16 = 0
X = -k/A = 4

Подставим
(x-4)*(x-4) = (x-4)2 = X² – 8x + 16

Пример 3. Решение квадратного уравнения с комплексными корнями.
13х² – 4x + 1 = 0
А=1, B = -4, С=9
D = b²– 4AC = 16 – 4*13*1 = 16 — 52 = -36
Дискриминант отрицательный – корни комплексные.

x1=(-В+D^1/2)/2А = (4+6i)/(2*13) = 2/13+3i/13
x2=(-В-D^1/2)/2А = (4-6i)/(2*13) = 2/13-3i/13
, где I – это квадратный корень из -1

Вот собственно все возможные случаи решения квадратных уравнений.
Надеемся, что наш онлайн калькулятор окажется весьма полезным для вас.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Квадратные уравнения (8 класс)

Примеры:

$3x^2-26x+5=0$

$(4-x)(4x-3)=3$
$\frac{x^2}{2}$$+$ $\frac{2x}{3}$$=$$\frac{x-2}{6}$

В первом примере $a=3$, $b=-26$, $c=5$. 2-4·3·2=1-24=-23\)

Найдем корни уравнения по формулам $x_1=\frac{-b + \sqrt{D}}{2a}$ и $x_1=\frac{-b — \sqrt{D}}{2a}$.

$x_1=\frac{-1 + \sqrt{-23}}{2·3}$

$x_2=\frac{-1- \sqrt{-23}}{2·3}$

Оба корня невычислимы, так как арифметический квадратный корень из отрицательного числа не извлекается.

Ответ: нет корней.

Обратите внимание, в первом уравнении у нас два корня, во втором – один, а в третьем – вообще нет корней. Это связано со знаком дискриминанта (подробнее смотри тут).

Также многие квадратные уравнения могут быть решены с помощью обратной теоремы Виета. Это быстрее, но требует определенного навыка. 2-7x+6=0\).
Решение: Согласно обратной теореме Виета, корнями уравнения будут такие числа, которые в произведении дадут $6$, а в сумме $7$. Простым подбором получаем, что эти числа: $1$ и $6$. Это и есть наши корни (можете проверить решением через дискриминант).
Ответ: $x_1=1$, $x_2=6$.

Данную теорему удобно использовать с приведенными квадратными уравнениями, имеющими целые коэффициенты $b$ и $c$.

Примеры решения полных, неполных и приведенных квадратных уравнений

Смотрите также:
Квадратные уравнения (шпаргалка)

Скачать статью

Как решать квадратное уравнение

Как решать квадратные уравнения

Алгоритм решения квадратного уравнения

Речь идет о поиске только действительных корней квадратного уравнения.

Шаг 1: Записываем уравнение в стандартном виде

В общем виде квадратное уравнение можно записать так:

Здесь — любое ненулевое число, — любые числа, a — то число, которое необходимо найти. Такой вид уравнения называют стандартным. Например, — квадратное уравнение в стандартном виде, причем , и . Число называют старшим коэффициентом, число — свободным коэффициентом. А все выражение вида называют квадратным трехчленом.

Типичная ошибка: считать, что , то есть забыть про знак «-«.

Cтоит заметить, что все коэффициенты уравнения можно уменьшить в раза. Уравнение примет вид . Числа , и , естественно, изменились (уменьшились!). Зато корни уравнения остались прежними. Поэтому всегда стоит проверять, а нельзя ли таким образом упростить уравнение, чтобы легче было далее находить корни.

Итак, первым делом необходимо привести квадратное уравнение к стандартному виду. Для этого можно раскрывать скобки, приводить подобные слагаемые, переносить слагаемые из одной части уравнения в другую (при этом слагаемые меняют знак). Например, . Раскрываем скобки: . Приводим подобные слагаемые: . Переносим все слагаемые из правой части в левую: (повторю: такие слагаемые меняют свой знак). И опять приводим подобные слагаемые: . Получим квадратное уравнение в стандартном виде. Причем , и .

Типичная ошибка: забыть поменять знак слагаемого при переносе.

Типичная ошибка: перепутать слагаемые местами и неправильно определить коэффициенты. Например, . И кажется, что , и . На самом деле, , и .

Интересный случай: предположим, что получилось уравнение . Чему равно ? На этот вопрос не каждый может ответить уверенно. Ответ: .

Интересный случай: дано уравнение . Мы смело раскрываем скобки и переносим и из правой части в левую. Но после приведения подобных слагаемых получается уравнение . Нет ! Ни о каком стандартном виде квадратного уравнения здесь не может быть и речи просто потому, что это не квадратное уравнение, а совсем другая история под названием «Линейное уравнение».

Замечание: опытные в квадратных уравнениях математики советуют всегда делать коэффициент положительным. Для этого левую и правую части уравнения всегда можно домножить на . Например, заменим на . По-простому говоря, каждое слагаемое меняет знак. Да, это другое уравнение и коэффициенты другие. Но корни у него такие же, как и у исходного уравнения. Поэтому далее спокойно можно работать с новым. Зачем делать положительным? Например, затем, чтобы было меньше арифметических ошибок, когда будем находить дискриминант. Что такое дискриминант, узнаем в следующем шаге.

Шаг 2: Находим дискриминант.

У нас есть квадратное уравнение в виде . Вычисляем число , которое называется дискриминантом квадратного уравнения. Например, для уравнения дискриминант равен .

Типичная ошибка: часто вместо пишут , то есть забывают скобки, но это уже , а не .

Типичная ошибка: неправильно определяют коэффициенты , и

Типичная ошибка: в слагаемом неправильно определяют окончательный знак. Например, в все-таки в итоге получается , а не .

Редкая ошибка: дискриминант пишут с большой буквы, видимо, из уважения или считая, что это фамилия.

Шаг 3: Находим корни уравнения

У нас есть дискриминант . Далее все зависит от его знака.

Если , то корней у уравнения нет. Ответ: корней нет. Вот так внезапно решение закончилось. Например, в уравнении дискриминант равен . Поэтому корней нет. Кстати, что это значит? Это значит, что какое бы число вы не выбрали, подстановка его в выражение вместо никогда не даст . Проверим число , например: . Не ноль. То есть — не корень. Аналогично с любым другим числом: ноль никогда не получится.

Если , то . Числа и — это как раз те коэффициенты из стандартной записи уравнения. Например, в уравнении дискриминант . Тогда . Ответ: .

Типичная ошибка: неправильно подставляют в формулу . Ошибаются со знаком. Ведь если , например, то .

Если . То в ответе будет два корня, которые можно найти по формулам и . Например, в уравнении дискриминант . Тогда и . Так как , то и . Ответ: .

Замечание: часто для сокращения пишут две формулы в одной: .

Замечание: иногда дискриминант может оказаться «некрасивым», например, . Такое может быть, и терять самообладание не стоит. Совет один: перепроверить решение и, если ошибка не найдена, со спокойной совестью решать дальше. Чаще всего задачи придумывают так, чтобы дискриминант были полным квадратом (кстати, полезно выучить таблицу квадратов чисел от 1 до 20). Но иногда попадаются ответы вида .

Типичная ошибка: неправильно находят . Например, считают, что . На самом деле, . Отрицательным выражение быть не может (по определению арифметического квадратного корня).

Вот и весь алгоритм. Конечно, есть еще много деталей. Например, есть неполные квадратные уравнения, когда лучше решать способами без дискриминанта. Есть еще уравнения, сводящиеся к квадратным. Есть еще поиск комплексных корней квадратного уравнения (для ЕГЭ это излишне). Кстати, проверить свое решение квадратного уравнения всегда можно здесь. Далее стоит изучить теорему Виета, понять, а как возникает формула для дискриминанта, как быть с уравнением третьей степени.

Полный пример решения квадратного уравнения.

Условие

Решить уравнение

Решение

Согласно алгоритму, раскрываем скобки: .
На всякий случай, расписал все подробно. Но вообще такие действия надо научиться делать почти устно. Более того, лучше заметить, что к первому слагаемому применима формула сокращенного умножения, точнее, разность квадратов. Такие формулы позволяют значительно экономить время и силы (потренироваться можно здесь).
Но продолжим решение: . Приводим подобные слагаемые и переносим в левую часть уравнения: .
Изменим знак : .
Находим дискриминант. Так как , и , то . Дискриминант , поэтому у уравнения два корня: и .
Осталось заметить, что корни можно упростить, ведь .
Получаем окончательный ответ, который запишем одной формулой: .
Как видите, малейшая неточность в арифметических вычислениях — и весь труд в итоге напрасен.
Поэтому стоит потренироваться выполнять арифметические вычисления устно и без ошибок.

Ответ:

Задачи для самостоятельного решения

Номера 41, 42, 43, 51, 52, 53 (ответы находятся после условий)

все статьи по математике

Решите квадратное уравнение с помощью программы «Пошаговое решение математических задач»

Решение уравнений — центральная тема алгебры. Все приобретенные навыки в конечном итоге приводят к способности решать уравнения и упрощать решения. В предыдущих главах мы решали уравнения первой степени. Теперь у вас есть необходимые навыки для решения уравнений второй степени, которые известны как квадратных уравнений .

КВАДРАТИКА, РЕШЕННАЯ ФАКТОРИНГОМ

ЗАДАЧИ

По завершении этого раздела вы сможете:

Определите квадратное уравнение.
Приведите квадратное уравнение в стандартную форму.
Решите квадратное уравнение, вычислив множители.

Квадратное уравнение — это полиномиальное уравнение, которое содержит вторую, но не более высокую степень переменной.

Стандартная форма квадратного уравнения — ax ² + bx + c = 0, когда a ≠ 0 и a, b и c — действительные числа.

Все квадратные уравнения могут быть представлены в стандартной форме, и любое уравнение, которое может быть преобразовано в стандартную форму, является квадратным уравнением.Другими словами, стандартная форма представляет все квадратные уравнения.

Решение уравнения иногда называют корнем уравнения.

Эта теорема доказана в большинстве учебников по алгебре в колледжах.

Важная теорема, которую невозможно доказать на уровне этого текста, гласит: «Каждое полиномиальное уравнение степени n имеет ровно n корней». Использование этого факта говорит нам, что квадратные уравнения всегда будут иметь два решения.Возможно, что два решения равны.

Квадратное уравнение будет иметь два решения, потому что оно имеет степень два.

Самый простой метод решения квадратичных вычислений — факторинг. Этот метод не всегда можно использовать, потому что не все многочлены факторизуемы, но он используется всякий раз, когда факторизация возможна.

Метод решения с помощью факторизации основан на простой теореме.

Если AB = 0, то либо A = 0, либо B = 0.

Другими словами, если произведение двух факторов равно нулю, то по крайней мере один из факторов равен нулю.

Мы не будем пытаться доказывать эту теорему, но внимательно отметим, что в ней говорится. Мы никогда не сможем перемножить два числа и получить ответ ноль, если хотя бы одно из чисел не равно нулю. Конечно, оба числа могут быть нулевыми, поскольку (0) (0) = 0.

Решение Шаг 1 Приведите уравнение в стандартную форму.

Мы должны вычесть 6 с обеих сторон.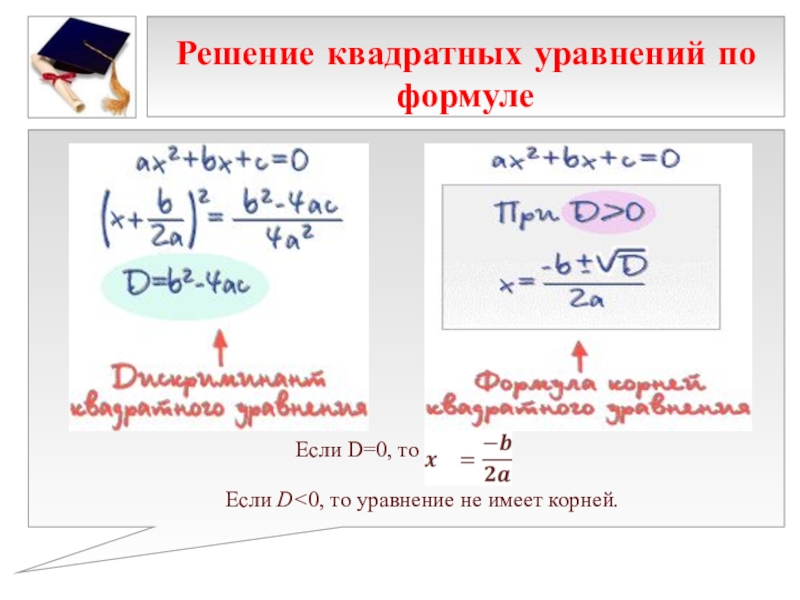

Шаг 2 Полностью разложить на множители.

Вспомните, как разложить на множители трехчлены.

Шаг 3 Установите каждый коэффициент равным нулю и решите относительно x. Поскольку у нас (x — 6) (x + 1) = 0, мы знаем, что x — 6 = 0 или x + 1 = 0, и в этом случае x = 6 или x = — 1.

Здесь применяется приведенная выше теорема, согласно которой хотя бы один из факторов должен иметь нулевое значение.

Шаг 4 Проверьте решение в исходном уравнении. Если x = 6, то x ² — 5x = 6 становится

Проверка ваших решений — верный способ узнать, правильно ли вы решили уравнение.

Следовательно, x = 6 является решением. Если x = — 1, то x ² — 5x = 6 становится

Следовательно, — 1 — решение.

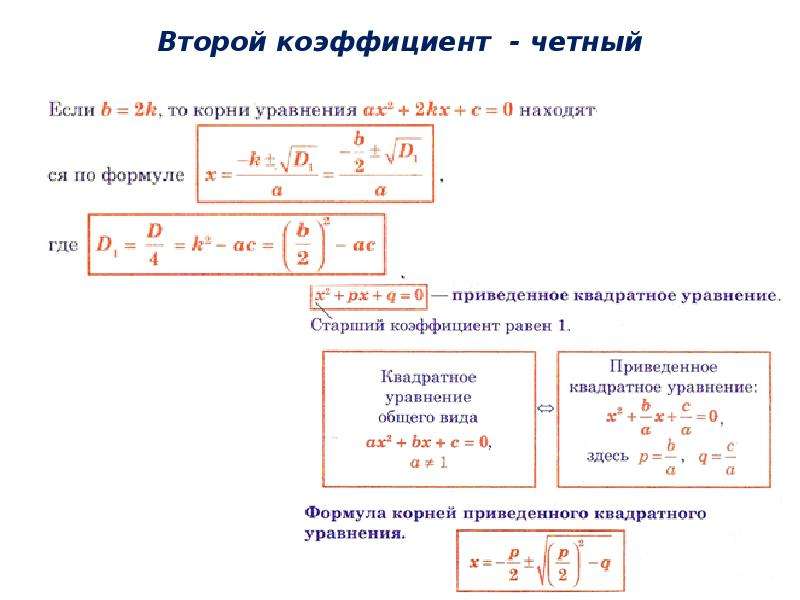
Решения могут быть указаны либо записью x = 6 и x = — 1, либо использованием обозначения набора и записи {6, — 1}, что мы читаем: «набор решений для x равен 6 и — 1.«В этом тексте мы будем использовать обозначение набора.

В этом примере 6 и -1 называются элементами набора.

Обратите внимание, что в этом примере уравнение уже имеет стандартную форму.

Опять же, проверка решений убедит вас, что вы не допустили ошибки при решении уравнения.
также называют корнями уравнения.

(x + 1) — наименьший общий знаменатель всех дробей в уравнении.
Помните, что каждый член уравнения нужно умножить на (x + 1).

Проверьте решения в исходном уравнении.

Проверьте исходное уравнение, чтобы убедиться, что знаменатель не равен нулю.

Обратите внимание, что здесь два решения равны. Это происходит только тогда, когда трехчлен является полным квадратом.

НЕПОЛНАЯ КВАДРАТИКА

ЗАДАЧИ

По завершении этого раздела вы сможете:

Определите неполное квадратное уравнение.
Решите неполное квадратное уравнение.

Если, когда уравнение помещено в стандартную форму ax ² + bx + c = 0, либо b = 0, либо c = 0, уравнение представляет собой неполное квадратичное .

Пример 1

5x ² — 10 = 0 является неполным квадратичным, так как средний член отсутствует и, следовательно, b = 0.

Когда вы встречаетесь с неполной квадратичной с c — 0 (отсутствует третий член), ее все же можно решить с помощью факторизации.

x — общий множитель. Произведение двух факторов равно нулю. Поэтому мы используем теорему из предыдущего раздела.
Проверьте эти решения.

Обратите внимание, что если член c отсутствует, вы всегда можете множить x из других членов. Это означает, что во всех таких уравнениях нуль будет одним из решений.
Неполная квадратичная с отсутствующим членом b должна быть решена другим методом, так как факторизация будет возможна только в особых случаях.

Пример 3 Решить относительно x, если x ² — 12 = 0.

Решение Поскольку x ² — 12 не имеет общего множителя и не является разностью квадратов, его нельзя разложить на рациональные множители. Но из предыдущих наблюдений мы имеем следующую теорему.

Обратите внимание, что есть два значения, которые в квадрате будут равны A.

Используя эту теорему, мы имеем

Проверьте эти решения.

Добавьте 10 с каждой стороны. Проверьте эти решения.

Здесь 7x — общий множитель. Проверьте эти решения.

Обратите внимание, что в этом примере у нас есть квадрат числа, равного отрицательному числу. Это никогда не может быть правдой в действительной системе счисления, и поэтому у нас нет реального решения.

ЗАВЕРШЕНИЕ ПЛОЩАДИ

ЗАДАЧИ

По завершении этого раздела вы сможете:

Определите трехчлен полного квадрата.
Завершите третий член, чтобы получить трехчлен в виде полного квадрата.
Решите квадратное уравнение, заполнив квадрат.

Из вашего опыта факторинга вы уже понимаете, что не все многочлены факторизуемы. Следовательно, нам нужен метод решения квадратичных вычислений, которые не подлежат факторизации. Необходимый метод называется «завершение квадрата».

Сначала давайте рассмотрим значение «трехчлена полного квадрата». Когда мы возводим двучлен в квадрат, мы получаем полный квадрат трехчлена.Общая форма: (a + b) ² = a ² + 2ab + b ².

Помните, возведение бинома в квадрат означает его умножение на само себя.

Из общей формы и этих примеров мы можем сделать следующие наблюдения относительно трехчлена полного квадрата.

Два из трех членов являются точными квадратами. 4x ² и 9 в первом примере, 25x ² и 16 во втором примере, а также ² и b ² в общем виде.

Другими словами, первый и третий члены — это полные квадраты.
Другой член — это два плюс или минус произведение квадратных корней из двух других членов.

Член -7 сразу говорит о том, что это не может быть трехчлен с полным квадратом. Задача при заполнении квадрата состоит в том, чтобы найти число, которое заменит -7 так, чтобы получился идеальный квадрат.

Рассмотрим эту задачу: заполните пробел так, чтобы «x ² + 6x + _______» было трехчленом в виде полного квадрата.Из двух условий для трехчлена полного квадрата мы знаем, что пробел должен содержать полный квадрат и что 6x должно быть удвоенным произведением квадратного корня x ² и числа в пробеле. Поскольку x уже присутствует в 6x и представляет собой квадратный корень из x ², то 6 должно быть в два раза больше квадратного корня из числа, которое мы помещаем в пробел. Другими словами, если мы сначала возьмем половину 6, а затем возведем этот результат в квадрат, мы получим необходимое число для бланка.

Следовательно, x ² + 6x + 9 — это трехчлен полного квадрата.

Теперь давайте рассмотрим, как мы можем использовать завершение квадрата для решения квадратных уравнений.

Пример 5 Решите x ² + 6x — 7 = 0, заполнив квадрат.

Напомним, что вместо -7, +9 сделает выражение идеальным квадратом.

Решение Сначала мы замечаем, что член -7 необходимо заменить, если мы хотим получить трехчлен в виде полного квадрата, поэтому мы перепишем уравнение, оставив пробел для нужного числа.

Здесь будьте осторожны, чтобы не нарушить никаких правил алгебры. Например, обратите внимание, что вторая форма появилась в результате добавления +7 к обеим сторонам уравнения. Никогда не добавляйте что-то с одной стороны, не добавляя то же самое с другой стороны.

Теперь мы находим половину 6 = 3 и 3 ² = 9, чтобы получить число для пробела. Опять же, если мы поместим 9 в пустое поле, мы также должны добавить 9 к правой стороне.

Помните, что если 9 добавляется к левой части уравнения, это также должно быть добавлено к правой части.

Теперь разложите на множитель полного квадрата трехчлена, что дает

Теперь x ² + 6x + 9 можно записать как (x + 3) ².

Таким образом, 1 и -7 являются решениями или корнями уравнения.

Пример 6 Решите 2x ² + 12x — 4 = 0, заполнив квадрат.

Решение Эта проблема порождает еще одну трудность.Первый член, 2x ², не является полным квадратом.
Мы исправим это, разделив все члены уравнения на 2, и получим

Другими словами, получите коэффициент 1 для члена x ².

Теперь добавим 2 к обеим сторонам, получив

Опять же, это более лаконично.

Пример 7 Решите 3x ² + 7x — 9 = 0, заполнив квадрат.

Решение Шаг 1 Разделите все члены на 3.

Опять же, получите коэффициент 1 для x ², разделив на 3.

Шаг 2 Перепишите уравнение, оставив пробел для члена, необходимого для завершения квадрата.

Шаг 3 Найдите квадрат половины коэффициента при x и прибавьте к обеим сторонам.

Это выглядит сложно, но мы следуем тем же правилам, что и раньше.

Шаг 4 Разложите квадрат на множители.

Факторинг никогда не должен быть проблемой, поскольку мы знаем, что у нас есть полный квадратный трехчлен, что означает, что мы находим квадратные корни из первого и третьего членов и используем знак среднего члена.

Если у вас возникнут затруднения, вам следует еще раз повторить арифметику при сложении чисел справа.
Теперь у нас

Шаг 5 Извлеките квадратный корень из каждой части уравнения.

Шаг 6 Решите относительно x (два значения).

нельзя упростить. Мы могли бы также записать решение этой проблемы в более сжатой форме как

Выполните шаги, описанные в предыдущем вычислении, а затем обратите особое внимание на последнее значение. Каков вывод, когда квадрат количества равен отрицательному числу? «Нет реального решения».

Какое действительное число возведем в квадрат и получим -7?

Таким образом, чтобы решить квадратное уравнение путем заполнения квадрата, следуйте этому пошаговому методу.

Шаг 1 Если коэффициент при x2 не равен 1, разделите все члены на этот коэффициент.
Шаг 2 Перепишите уравнение в виде x2 + bx + _______ = c + _______.
Шаг 3 Найдите квадрат половины коэффициента члена x и добавьте эту величину к обеим сторонам уравнения.
Шаг 4 Разложите заполненный квадрат на множители и сложите числа в правой части уравнения.
Шаг 5 Найдите квадратный корень из каждой части уравнения.
Шаг 6 Решите относительно x и упростите.
Если шаг 5 невозможен, уравнение не имеет реального решения.

Эти шаги помогут решить уравнения в следующем упражнении.

КВАДРАТИЧЕСКАЯ ФОРМУЛА

ЗАДАЧИ

По завершении этого раздела вы сможете:

Решите общее квадратное уравнение, заполнив квадрат.
Решите любое квадратное уравнение, используя формулу корней квадратного уравнения.
Решите квадратное уравнение, заполнив квадрат.

Стандартная форма квадратного уравнения — ax ² + bx + c = 0. Это означает, что каждое квадратное уравнение может быть представлено в этой форме. В некотором смысле ax ² + bx + c = 0 представляет все квадратичные системы. Если вы сможете решить это уравнение, у вас будет решение всех квадратных уравнений.

Решим общее квадратное уравнение методом завершения квадрата.

Это необходимо для получения члена x ² с коэффициентом 1.
Это мы делали в предыдущем разделе много раз.

Надо прибавить с каждой стороны.

Эта форма называется квадратной формулой и представляет собой решение всех квадратных уравнений.

Запомните это выражение.

Чтобы использовать формулу квадратного уравнения, вы должны указать a, b и c. Для этого данное уравнение всегда необходимо оформлять в стандартном виде.

Осторожно подставьте значения a, b и c в формулу.

Не каждое квадратное уравнение имеет реальное решение.

Это уравнение уже имеет стандартную форму.

Реального решения нет, так как -47 не имеет действительного квадратного корня.

Опять же, это уравнение в стандартной форме.

Теперь это решение следует упростить.

ПРОБЛЕМЫ СО СЛОВОМ

ЗАДАЧИ

По завершении этого раздела вы сможете:

Определите проблемы со словами, для решения которых требуется квадратное уравнение.
Решать текстовые задачи, связанные с квадратными уравнениями.

Некоторые типы задач со словами можно решить с помощью квадратных уравнений. Процесс обрисовки и постановки проблемы такой же, как описано в главе 5, но с проблемами, решаемыми квадратичными методами, вы должны быть очень осторожны, проверяя решения в самой проблеме. Физические ограничения внутри проблемы могут устранить одно или оба решения.

Пример 1 Если длина прямоугольника на 1 единицу больше, чем в два раза больше ширины, а его площадь составляет 55 квадратных единиц, найдите длину и ширину.

Решение Формула площади прямоугольника: Площадь = Длина X Ширина. Пусть x = ширина, 2x + 1 = длина.

Если x представляет ширину, то 2x представляет удвоенную ширину, а 2x + 1 представляет единицу более чем удвоенную ширину.

Приведите квадратное уравнение в стандартную форму.
Эта квадратичная величина может быть решена путем факторизации.

На этом этапе вы можете видеть, что решение x = -11/2 недействительно, поскольку x представляет собой измерение ширины, а отрицательные числа не используются для таких измерений.Следовательно, решение

ширина = x = 5, длина = 2x + 1 = 11.

Измерение не может быть отрицательным.

Величина, обратная x.
Помните, что ЖК-дисплей означает наименьший общий знаменатель.

Каждый член нужно умножить в 10 раз.
Опять же, эту квадратичную величину можно разложить на множители.

Оба решения проверяют. Следовательно, набор решений есть.

Есть два решения этой проблемы.

Пример 3 Если определенное целое число вычитается из его квадрата, умноженного на 6, получается 15. Найдите целое число.

Решение Пусть x = целое число. Тогда

Поскольку ни одно из решений не является целым числом, проблема не имеет решения.

У вас может возникнуть соблазн указать эти значения в качестве решения, если вы не обратили пристальное внимание на тот факт, что проблема запрашивала целое число.

Пример 4 Управляющий фермой имеет под рукой 200 метров забора и хочет ограждать прямоугольное поле так, чтобы его площадь составляла 2400 квадратных метров. Какими должны быть размеры поля?

Решение Здесь задействованы две формулы. P = 2l + 2w для периметра и A = lw для площади.
Сначала используя P = 2l + 2w, получаем

Теперь мы можем использовать формулу A = lw и подставить (100 — l) вместо w, получив

Поле должно быть шириной 40 метров и длиной 60 метров.

Мы могли бы точно так же решить для l, получив l = 100 — w. Тогда

Обратите внимание, что в этой задаче мы фактически используем систему уравнений

P = 2 l + 2 w
A = l w.

В общем случае система уравнений, в которой участвует квадратичная функция, будет решаться методом подстановки. (См. Главу 6.)

РЕЗЮМЕ

Ключевые слова

Квадратное уравнение — это полиномиальное уравнение от одной неизвестной, которое содержит вторую степень, но не более высокую степень переменной.
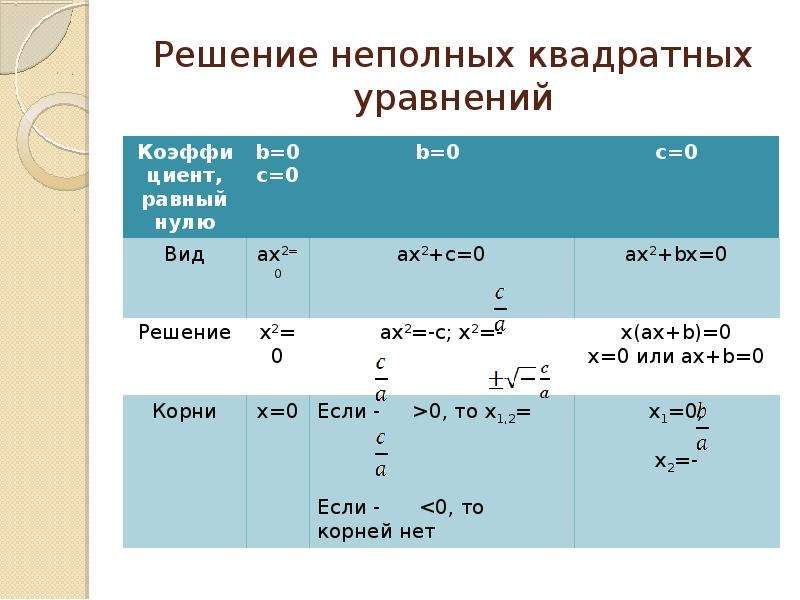
Стандартная форма квадратного уравнения: ax ² + bx + c = 0, когда a 0.
Неполное квадратное уравнение имеет вид ax ² + bx + c = 0, и либо b = 0, либо c = 0.
Квадратичная формула :

Процедуры

Самый прямой и, как правило, самый простой метод поиска решений квадратного уравнения — это факторизация. Этот метод основан на теореме: если AB = 0, то A = 0 или B = 0. Чтобы использовать эту теорему, мы приводим уравнение в стандартную форму, коэффициент и устанавливаем каждый коэффициент равным нулю.

Чтобы решить квадратное уравнение, заполнив квадрат, выполните следующие действия:
Шаг 1 Если коэффициент при x ² не равен 1, разделите все члены на этот коэффициент.
Шаг 2 Перепишите уравнение в виде x ² + bx + _____ = c + _____
Шаг 3 Найдите квадрат половины коэффициента члена x и прибавьте это количество к обеим сторонам.

2 + 33x — 378 = 0 $$
Значения a , b и c равны,
$$ \ bbox [4pt, граница: сплошной серый 1px] {a = 1, \; b = 33, \; c = -378} $$

Калькулятор квадратичных формул | Комплексный

Если вам нужно решить уравнение вида Ax² + Bx + C = 0 , этот калькулятор квадратной формулы здесь, чтобы помочь вам.Всего за несколько кликов вы сможете решить даже самые сложные задачи. В этой статье подробно описывается, что такое квадратная формула и что обозначают символы A, B и C. Здесь также объясняется, как решать квадратные уравнения, которые имеют отрицательный определитель и не имеют действительных корней.

Что такое квадратная формула?

Квадратичная формула является решением полиномиального уравнения второй степени следующего вида:

Ax² + Bx + C = 0

Если вы можете переписать свое уравнение в этой форме, это означает, что оно может быть решено с помощью формулы корней квадратного уравнения. Решение этого уравнения также называется корнем уравнения.

Квадратичная формула имеет следующий вид:

x = (-B ± √Δ) / 2A

где:

Используя эту формулу, вы можете найти решения любого квадратного уравнения. Учтите, что есть три возможных варианта получения результата:

Квадратное уравнение имеет два уникальных корня, когда Δ> 0. Тогда первое решение квадратной формулы: x₁ = (-B + √Δ) / 2A , а второе — x₂ = (-B - √ Δ) / 2А .
Квадратное уравнение имеет только один корень, когда Δ = 0. Решение равно x = -B / 2A . Иногда его называют повторным или двойным корнем.
Квадратное уравнение не имеет реальных решений при Δ <0.

Вы также можете построить график функции y = Ax² + Bx + C . Его форма представляет собой параболу, а корни квадратного уравнения являются точками пересечения по оси x этой функции.

Коэффициенты квадратного уравнения

A, B и C — коэффициенты квадратного уравнения. Все они действительные числа, не зависящие от x. Если A = 0, то уравнение не квадратичное, а линейное.

Если B² <4AC , то определитель Δ будет отрицательным. Это означает, что у такого уравнения нет реальных корней.

Как использовать решатель квадратичных формул

Запишите уравнение. Предположим, это 4x² + 3x - 7 = -4 - x .
Приведите уравнение к виду Ax² + Bx + C = 0 . В этом примере мы сделаем это в следующие шаги:
4x² + 3x - 7 = -4 - x
4x² + (3 + 1) x + (-7 + 4) = 0
4x² + 4x - 3 = 0
Вычислить определитель.
Δ = B² - 4AC = 4² - 4 * 4 * (- 3) = 16 + 48 = 64 .
Решите, будет ли определитель больше, равен или меньше нуля. В нашем случае определитель больше 0, что означает, что это уравнение имеет два уникальных корня.
Вычислите два корня по формуле корней квадратного уравнения.
x₁ = (-B + √Δ) / 2A = (-4 + √64) / (2 * 4) = (-4 + 8) / 8 = 4/8 = 0,5
x₂ = (-B - √Δ) / 2A = (-4 -√64) / (2 * 4) = (-4-8) / 8 = -12/8 = -1.5
Корни вашего уравнения: x₁ = 0,5 и x₂ = -1,5 .

Вы также можете просто ввести значения A, B и C в наш калькулятор квадратного уравнения и позволить ему выполнять все вычисления за вас.

Убедитесь, что вы записали правильное количество цифр с помощью нашего калькулятора значащих цифр.

Решение квадратных уравнений с отрицательным определителем

Даже если калькулятор квадратной формулы указывает, что уравнение не имеет действительных корней, можно найти решение квадратного уравнения с отрицательным определителем.Эти корни будут комплексными числами.

Комплексные числа имеют действительную и мнимую части. Мнимая часть всегда равна числу i = √ (-1) , умноженному на действительное число.

Квадратичная формула в этом случае остается прежней.

x = (-B ± √Δ) / 2A

Обратите внимание, что при Δ <0 квадратный корень из определителя будет мнимым значением. Отсюда:

Re (x) = -B / 2A
Im (x) = ± (√Δ) / 2A

Если, узнав все о решении квадратных уравнений, вы все еще захотите больше математики? В Omni есть более 240 математических калькуляторов.Мы также рекомендуем вам посетить веб-страницу Computer Technology For Math Excellence. У них есть обширная коллекция ресурсов, чтобы узнать все о математике, с особым вниманием к учебной программе Common Core.

Решение квадратных уравнений

Квадратное уравнение - это уравнение, которое можно записать как

ось ² + bx + c = 0

, когда а 0.

Существует три основных метода решения квадратных уравнений: факторинг, использование формулы квадратиков и завершение квадрата.

Факторинг

Чтобы решить квадратное уравнение на множители,

Поместите все члены с одной стороны от знака равенства, оставив ноль с другой стороны.
Коэффициент
.
Установите каждый коэффициент равным нулю.
Решите каждое из этих уравнений.
Проверьте, подставив свой ответ в исходное уравнение.

Пример 1

Решить x ² - 6 x = 16.

Следуя инструкциям,

x ² - 6 x = 16 становится x ² - 6 x - 16 = 0

Коэффициент

( x - 8) ( x + 2) = 0

Установка каждого коэффициента на ноль,

Затем проверить,

Оба значения, 8 и –2, являются решениями исходного уравнения.

Пример 2

Решить y ² = - 6 y - 5.

Устанавливая все члены равными нулю,

y ² + 6 y + 5 = 0

Коэффициент

( y + 5) ( y + 1) = 0

Установка каждого коэффициента на 0,

Для проверки, y ² = –6 y - 5

Квадратичный с отсутствующим членом называется неполным квадратичным (при условии, что член ax ² не пропущен).

Пример 3

Решить x ² - 16 = 0.

Коэффициент

Для проверки, x ² - 16 = 0

Пример 4

Решить x ² + 6 x = 0.

Коэффициент

Для проверки, x ² + 6 x = 0

Пример 5

Решить 2 x ² + 2 x - 1 = x ² + 6 x - 5.

Во-первых, упростите, поместив все термины в одну сторону и комбинируя одинаковые термины.

А теперь фактор.

Для проверки, 2 x ² + 2 x - 1 = x ² + 6 x - 5

Квадратичная формула

Многие квадратные уравнения не могут быть решены факторизацией. Обычно это верно, когда корни или ответы не являются рациональными числами. Второй метод решения квадратных уравнений включает использование следующей формулы:

a, b, и c взяты из квадратного уравнения, записанного в его общей форме

ось ² + bx + c = 0

, где a - это число перед x ², b - это число перед x , а c - это число без переменной рядом с ним (a .k.a., «постоянная»).

При использовании формулы корней квадратного уравнения вы должны знать о трех возможностях. Эти три возможности различаются частью формулы, называемой дискриминантом. Дискриминант - это значение под знаком корня, b ² - 4 ac . Квадратное уравнение с действительными числами в качестве коэффициентов может иметь следующее:

Два разных действительных корня, если дискриминант b ²-4 ac является положительным числом.
Один действительный корень, если дискриминант b ² - 4 ac равен 0.
Нет действительного корня, если дискриминант b ²-4 ac является отрицательным числом.

Пример 6

Решите относительно x : x ² - 5 x = –6.

Устанавливаем все члены равными 0,

x ² - 5 x + 6 = 0

Затем замените 1 (который, как предполагается, стоит перед x ²), –5 и 6 вместо a , b и c, соответственно в формуле корней квадратного уравнения и упростите.

Поскольку дискриминант b ² - 4 ac положительный, вы получаете два разных действительных корня.

Пример
производит рациональные корни. В примере
, квадратная формула используется для решения уравнения, корни которого нерациональны.

Пример 7

Решить относительно y : y ² = –2y + 2.

Устанавливаем все члены равными 0,

y ² + 2 y - 2 = 0

Затем замените 1, 2 и –2 на a , b и c, соответственно в формуле корней квадратного уравнения и упростите.

Обратите внимание, что два корня иррациональны.

Пример 8

Решить относительно x : x ² + 2 x + 1 = 0.

Подставляя в формулу корней квадратного уравнения,

Поскольку дискриминант b ²-4 ac равен 0, уравнение имеет один корень.

Квадратичная формула также может использоваться для решения квадратных уравнений, корни которых являются мнимыми числами, то есть они не имеют решения в действительной системе счисления.

Пример 9

Найдите x : x ( x + 2) + 2 = 0 или x ² + 2 x + 2 = 0.

Подставляя в формулу корней квадратного уравнения,

Поскольку дискриминант b ² - 4 ac отрицателен, это уравнение не имеет решения в действительной системе счисления.

Но если бы вы выразили решение с помощью мнимых чисел, решения были бы такими.

Завершение квадрата

Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.

Запишите уравнение в виде ax ² + bx = - c .
Убедитесь, что a = 1 (если a ≠ 1, умножьте уравнение на, прежде чем продолжить).
Используя значение b из этого нового уравнения, добавьте к обеим сторонам уравнения, чтобы получить полный квадрат в левой части уравнения.
Найдите квадратный корень из обеих частей уравнения.
Решите полученное уравнение.

Пример 10

Решить относительно x : x ² - 6 x + 5 = 0.

Оформить в виде

Поскольку a = 1, прибавьте или 9 к обеим сторонам, чтобы завершить квадрат.

Извлеките квадратный корень из обеих частей.

х - 3 = ± 2

Решить.

Пример 11

Решить относительно y : y ² + 2 y - 4 = 0.

Оформить в виде

Поскольку a = 1, прибавьте или 1 к обеим сторонам, чтобы завершить квадрат.

Извлеките квадратный корень из обеих частей.

Решить.

Пример 12

Решите относительно x : 2 x ² + 3 x + 2 = 0.

Оформить в виде

Поскольку - это ≠ 1, умножаем уравнение на.

Добавьте или с обеих сторон.

Извлеките квадратный корень из обеих частей.

В действительной системе счисления нет решения. Вам может быть интересно узнать, что завершение квадратного процесса для решения квадратных уравнений использовалось для уравнения ax ² + bx + c = 0 для вывода формулы квадратичного уравнения.

TI-83/84 Plus BASIC Math Programs (Quadratic Solvers)

42 1k

04-08

42 03 -08-26

	Имя	Размер	Дата	Рейтинг Рейтинг
	(родительский каталог)	папка			До TI-83/84 Plus BASIC математические программы
	advquads.zip	3k	04-06-07		Программа расширенных квадратичных формул Квадратичный решатель и многое другое!
	abc.zip	3k	04-06-09		ABC-Formula 3. 1 Это последнее обновление моего популярного квадратичного решателя. Теперь программа полностью идеальна. Я знаю, что это не единственный квадратичный решатель, но он уникален, потому что он дает не только решения, но и весь расчет! Смотрите скриншоты!
	квадратич.3.2.zip	1k	03-07-11		Quadratic v.3.2 Программа Jamaica Bay. Это лучшая квадратичная программа. Он дает вам ответы в упрощенной дробной форме для тестов и домашних заданий или может дать ответ в десятичной форме. Включает режим построения графиков, точечное построение, управление осями и управление окнами. Прост в использовании и протестирован на наличие ошибок.
	2nddegreesolver.zip	1k	11-01-01		Решатель уравнений 2-й степени Эта программа использует квадратичную формулу и дает вам точные ответы.
	abc1.8xp	1k	02-03-01		ABC Formular v1.1 Фиксированная версия v1.0
	abc_69.zip	1k	12-05-29		ABC Program Проверено только на TI 84 Plus Будет отредактировано позже
	abcformule.zip	1k	05-03-20		ABC Formule На голландском языке.С указанием того, как вы можете рассчитать эту сумму. (Не только ответ, что делает большинство программ). Итак, отлично подходит для математики!
	abcfull. zip	1k	04-10-07		abc-Formel Это формула abc. Если хотите, он показывает вам все этапы расчета. Язык главного меню - немецкий, но в любом случае, должно быть легко понять, как пользоваться программой.
	abcpq_english.2 + px + q ABCPQ - довольно полезная и удобная программа, которая удаляет все использованные переменные после выхода и которую также можно использовать с такой ОС, как MirageOS.
	abcpq_german.zip	2k	05-05-07		ABCPQ (немецкий) [EN] ABCPQ - это простая в использовании программа для решения квадратичных формул. [DE] ABCPQ ist ein sehr leicht zu benutzendes Programme, mit dessen Hilfe sich quadratische Formeln lösen lassen. 2 + px + q (ABC-Formel und PQ-Formel ABCPQ ist ein leicht zu benutzendes Programm. Es löscht nach dem Verlassen all benötigten Variablen und kann auch mit einem OS wie MirageOS benutzt werden.	15k	19-03-21	ADVQUAD, QUAD, QUADLIT1 & QUADLITE ПЕРВЫЕ ПРОЧИТАЙТЕ README! Последнее обновление: v1.6.0 от 18.03.2019 (вероятно, последнее обновление). Вот лучшие программы квадратичных формул, которые вы можете получить.Программа ADVQUAD имеет больше возможностей, чем любая другая программа с квадратными формулами. Обычный QUAD имеет все отношения на основе алгебры для квадратичного, QUADLIT1 удобен для хранения, но все же упрощает квадратичную формулу, а QUADLITE помогает вам сэкономить место, но по-прежнему видеть квадратную формулу в prettyprint.
	adamquad.zip	1k	99-11-19		AdamQuad Эта программа дает вам пересечение по оси x (действительное или мнимое), точку пересечения по оси Y и координаты вершины и в каком направлении она открывается, линия симметрии, область, диапазон и дискриминант. Он также регулирует окно, чтобы оно соответствовало вашему графику. Все ранее введенные графики и настройки окон восстанавливаются после выхода из программы, если пользователь не выберет «График и выход». Вы можете переключаться между отображением результатов в виде дроби (по умолчанию) или десятичной дроби (некоторые из них имеют 3 десятичных знака), выбрав «Параметры» в главном меню. Он также сообщает вам формулы (квадратичные и дискриминантные), чтобы вы могли записать их на тестах, а затем показать замену.
	advquad.zip	5k	08-12-15		Усовершенствованный четырехъядерный решатель Pretty-print Этот четырехъядерный решатель отображает результат в довольно-печатном виде, если это «уродливое» число с плавающей запятой, например -1.26653589
	allaboutquadratics8x. zip	60k	10-06-10		Все о квадратиках Как видно из скриншотов, это один из лучших квадратичных решателей, когда-либо созданных в TI- БАЗОВЫЙ.Это НЕ просто еще одна программа с квадратными формулами, которая делает то же самое, что и сотни других. Вместо этого он запрашивает у вас стандартное квадратное уравнение, а затем показывает вам абсолютно все, что вам нужно знать об уравнении - его общие, вершинные и факторизованные формы, его пересечения по осям X и Y и его вершины, ВСЕ В ПРЕДВАРИТЕЛЬНОЙ ПЕЧАТИ, ВСЕ В УМЕНЬШЕННОЙ ФОРМЕ - все НА ОДНОМ ЭКРАНЕ! Автоматически определяет, существуют ли решения, поэтому нет случайных ошибок. Никакого беспорядка - всего одна крошечная программа, которая вам все расскажет.
	aquad2.zip	7k	09-04-19		Exact Quadratic Это расширенный квадратичный решатель, разработанный, чтобы позволить вам использовать ответ, введенный на экране, и поставить это правильный ответ. 2 + bx + c = 0) .2 + bx + c форма для x. Эта программа дает вам различение, два решения, координаты (x, y) вершины сформированной параболы и направление, в котором парабола открывается! Он даже позволяет вам ввести значение y, если вы хотите найти решения в этих точках !!! Попытайся!
	aquad.zip	1k	99-11-14		AQUAD Final Квадратичная программа, которая решит в радикальной форме.
	basicquad.zip	1k	03-03-12		Квадратичная формула Эта программа использует квадратичную формулу для нахождения рациональных, действительных или мнимых нулей квадратичного полинома .
	benquad.zip	3k	01-02-23		Полная программа квадратичных формул v5.5 Математическая программа, в которой пользователь вводит коэффициенты квадратного уравнения и выясняет, какие X равно и как уравнение учитывается.Если X не является рациональным числом, оно будет отображаться точно так, как оно выглядело бы упрощенно в квадратном уравнении. Также показан график, дискриминант и вершина уравнения. Вы также можете просмотреть значение X в десятичной форме. Может правильно обрабатывать отрицательное значение для A и дробные значения для A, B или C.
	bestalgebra1.zip	2k	12-03-22		Best Algebra 1 Program v2 .1! Версия 2.Наконец-то выпущена первая из лучших программ по алгебре 1. Как и просили, я обновил ключ учителя, чтобы он не содержал ошибок. Также добавлено бортовое руководство по эксплуатации. В этой версии используется совершенно новый формат, с использованием клавиш-графиков и привлекательного титульного экрана (как показано на скриншоте) вместо утомительного старого меню. Он выполняет те же математические функции, но улучшается, а также включает такие функции, как обновленный ключ учителя и файл чтения. Эта программа не только полезна для чего-либо в Алгебре 1, но также может использоваться для большинства тем, связанных с Алгеброй 2.2 + bx + c.
	cquadratic.zip	1k	00-04-15		Quadratic v.1B Это начало моих математических программ серии C, которые я выйду как как только они мне понадобятся для выполнения домашних заданий. Эта программа предлагает реальные и воображаемые решения и даст точный ответ, а также решение. Он также показывает различение.
	dcsquad83p.zip	1k	10-08-19		DCSQuad Solver v1.0 DCSQuad Solver - это стандартный квадратичный решатель, способный решать как действительные, так и мнимые корни квадратного уравнения. Его уникальная особенность заключается в том, что он построен с использованием библиотек Doors CS BASIC (DCSB Libs) для ввода текста, движения и щелчка мышью, а также визуализации интерфейса. Требуется Doors CS 6.9 beta или выше.
	Discriminants.zip	1k	10-02-05		Дискриминантный решатель Введите B, A, C, и он даст вам числовой ответ и есть ли у него 2 мнимых решения, 2 реальных решения или 1 реальное решение.
	discriminant.zip	1k	02-02-10		Дискриминантная программа Быстро находит значение дискриминанта, чтобы вы могли анализировать квадратичную функцию.
	dis.zip	1k	02-03-06		Discriminant Finder Введите A, B и C, и он сообщит вам дискриминант И он описывает корни.
	equal2.zip	1k	02-10-15		Equation Математическая программа, которая использует квадратное уравнение при задании A, B и C.
	equalplusdp.zip	1k	03-03-06		Super Quadratics plus Отлично подходит для алгебры 2 в квадратиках
	equsolve.2 + bx + c и показывает, где он пересекает ось Y, вершину, ось симметрии, направление графика и факторы. Также включен вариант графика, чтобы увидеть окончательный результат.
	evilquad.zip	1k	11-04-01		EVILQUAD Это похоже на обычный четырехъядерный решатель . 2 + bx + c) и использует квадратную формулу, чтобы найти точки пересечения по оси x.2 + bx + c), и вы получите факторизацию в линейном выражении.
	formreso.zip	1k	14-03-19		Fórmula Resolvente v1.1 Mostra passos e resultados da resolução de equações de 2º grau. Совместимость с MirageOS.
	fresolve.zip	1k	03-03-06		Fórmula resolvente Это грандиозная программа, используемая на разрешении плавных переходов.Наслаждаться!!!
	grayquad.zip	7k	06-03-26		Решатель квадратичных уравнений в градациях серого Ваш окончательный спаситель здесь, единственный квадратичный решатель в своем роде! Требуется xLIB.
	guessquadratic.zip	1k	11-04-01		Number Guesser and Quadratic Solver Эта забавная игра сочетает в себе познавательную ценность квадратичного решателя с развлечением числа угадывающий.Учите математику и получайте удовольствие одновременно! * Батарейки в комплект не входят. за свои корни. Программа дополнена линией симметрии и вершиной. Вы можете написать мне со своими пожеланиями, если вы хотите, чтобы я что-то еще добавил.
	улучшенная квадратичная формула.zip	3k	12-03-29		Улучшенная квадратичная формула Эта программа является улучшением по сравнению с моей предыдущей программой, поскольку она показывает результаты в символической, а не в десятичной форме. См. Снимки экрана, чтобы получить представление. Наслаждаться!
	mathic.zip	1k	02-10-12		Mathic Это небольшая программа под названием Mathic. Решает уравнения второй степени.Легко использовать.
	maxmin.zip	1k	05-12-10		Поиск максимума / минимума Найдет максимальное или минимальное квадратное уравнение и расскажет, какое из них. Просто введите коэффициенты, в зависимости от уравнения отобразятся минимальные или максимальные значения и вы получите координаты! Чрезвычайно простой и легкий в использовании! Совместим с MirageOS.
	neoquad.zip	1k	02-09-05		Neo Quadratic Это идеальная программа для всех, у кого проблемы с квадратичными формулами. Очень проста в использовании
	nfactor.zip	1k	05-04-03		Программа факторинга Nfactor Это (на мой взгляд) одна из лучших программ факторинга. Он также может решить квадратную формулу за вас.Он показывает квадратичную в факторизованной форме, а также нули сами по себе. Это ранняя версия, которая включает в себя функции более высокого уровня и больше сопутствующих.
	polyroot.zip	1k	10-10-15		Polyroot Эта небольшая программа вычисляет корни многочлена методом Ньютона, включая квадратные уравнения.
	pqformula.zip	1k	04-10-07		PQ-Formel Эта программа вычисляет pq-формулу и показывает шаги, необходимые для расчет, если хотите.Идеально подходит для любого экзамена по математике. Сама программа написана на немецком языке, но я думаю, что в формуле на всех языках используется одна и та же буква (p и q), так что вы, возможно, все равно ее поймете, если не говорите по-немецки.
	qe01.zip	2k	05-03-20		Квадратичные уравнения Программа занимает 700 Б, решает и рисует квадратичные функции, не стирает ваши функции в Y1 или других (резервное копирование), находит ноль также в линейных функциях, дает вам вершину.Эта версия занимает меньше места, но имеет больше возможностей. Результаты (корни, вершина) отображаются на одном экране. Вы можете изменить число с плавающей запятой (при отображении результатов), указав 1,2,3 или 4.
	qes.zip	1k	03-08-07		Решатель квадратного уравнения Это лучшая программа для решения квадратных уравнений, написанная на BASIC для TI-83 +. Он мгновенно дает все решения, реальные или мнимые, в простейшей радикальной, интегральной или дробной форме!
	кв.8xp	1k	03-05-25		Квадратичная формула Эта простая программа решает квадратную формулу. Он использует только 56 БАЙТОВ.
	qforms.zip	1k	10-01-31		QForm 0.1 QForm - это пара замечательных программ, которые я написал. Один из них - решатель квадратной формулы, другой - программа установки квадратной формулы. У них чистый, простой в использовании интерфейс.Это только первый выпуск, скоро будут новые. См. Readme для получения дополнительной информации.
	qformula.zip	3k	03-03-06		QFormula Решатель квадратичных формул
	qform.zip		Qform Еще один, чтобы добавить ко многим программам квадратичных формул в этом архиве. Преимущество этой программы в том, что она проста в использовании и дает воображаемые тенты.
	quad1.zip	1k	06-10-27		Квадратичная формула BASIC Это очень простая квадратичная формула. Это даст вам воображаемые решения в дополнение к реальным решениям. Самым большим преимуществом моей программы перед другими является ее простота и внешний вид. В моей программе нет лишних ненужных функций, которые есть в других квадратичных программах; в начале нет назойливых экранов, сообщающих вам, кто это написал.Все, что делает моя программа, - это дает вам два значения x самым простым и быстрым из возможных способов. Исходный код включен в текстовый файл, поэтому, если у вас нет кабеля для передачи данных, вы можете вручную ввести код.
	quad2001.zip	2k	01-02-22		Quad 2001 v3.0 Решатель квадратного уравнения с действительными / мнимыми корнями в десятичной / дробной форме, интерактивное построение графиков, таблица значений, дескриминант, вершина и Y-int.2+ BX + C = 0. Он состоит из трех ступеней. Во-первых, он дает вам числовые значения, во-вторых, он дает вам формулу плюс формулу со вставленными значениями, и в-третьих, он дает вам упрощенные точные значения как для действительных, так и для комплексных / мнимых корней плюс вершина. A, B и C не изменяются во время расчета. QUAD2: это более простая версия QUAD1. У него те же три шага, но без вершины на третьем шаге. Представление результатов проще для экономии байтов. Все сделано максимально просто.Это более чем на 300 байт меньше, чем QUAD1, но в целом медленнее. A, B и C не изменяются во время расчета. QUAD3: Это очень простая программа, из которой вы получаете: ROOTS (числовые и точные), VERTEX, DISCRIMINANT и GRAPH.
	quad3.zip	2k	00-05-26		Quad3 Quad3 позволяет легко решать квадратные уравнения. Встроенная поддержка мнимых чисел, упрощающих радикалов и т. Д... Прочтите Quad3.txt для получения дополнительной информации. Вы вводите значения A, B и C, и я покажу работу для проблемы и покажу ответы в десятичном формате. Также будут отображаться воображаемые ответы. Очень просто и быстро использовать
	quad4.zip	1k	02-06-01		Квадратичная формула Эдмонда Введите значения A, B и C, и эта программа решит X в десятичной и радикальной форме. Работает и с мнимыми числами.
	quad5.zip	1k	02-11-20		Квадратичная формула Решает квадратичную формулу
	quad6.zip		QUAD.ZIP Я пробовал многие другие квадратичные программы, и для моих целей это лучшая. Он отображает решения как в наиболее упрощенной дробной, так и в десятичной форме. Посмотрите на скриншот, если вы не понимаете, в какой форме он находится, значит, вас учат не так, как меня. Спасибо, наслаждайтесь программой.
	quad7.zip	1k	08-08-11		Ultimate Quadratic Formula Program Действительно лучшая программа для решения квадратичных формул.2 + Bx + C. Все, что вам нужно сделать, это ввести A, B и C
	quad8.zip	1k	08-08-11		Ultimate Quadratic Solver дает вам простейшую радикальную форму, Комплексные ответы и дискриминант, всего 440 байт.
	quad_92.zip	1k	12-01-21		Квадратичная формула Простая квадратичная формула.Я оставил программу разблокированной, как всегда, чтобы люди могли изучить сценарий, изучить и изменить его, чтобы он соответствовал вашим потребностям. Наслаждайтесь; D Не стесняйтесь присылать мне электронное письмо для обратной связи: [email protected]
	quadcub.zip	1k	08-11-30		Quadriatic & Cubic Solver Вставьте три последовательных термина для quad. или четыре члена для кубики, и он расскажет вам формулу для переменных A, B и C (D для кубической).Он использует следующие уравнения: Quad: AX2 + BX + C Кубический: AX3 + BX2 + CX + D Наслаждайтесь!
	quaddisc.zip	1k	02-02-25		Quadratic Discriminant Finder Находит дискриминант в задаче квадратичности
	quadequa.zip	3k	02-04-06		Квадратичное уравнение Он разрывает уравнение, сообщающее вам все, что вам нужно знать
	quadextr.2 + Bx + C = 0, когда вы вводите его корни. Если, например, вы учитель и хотите убедиться, что уравнения, которые вы приводите, имеют правильную сложность, с рациональными, иррациональными и / или воображаемыми решениями.
	quadform_12.zip	1k	09-05-12		Квадратичная формула Noob quad form
	quadform20037
1k -05-07		Quadform Средство решения квадратного уравнения.
	quadform2.zip	1k	99-12-24		Квадратичная формула Быстрое и легкое решение для x
	quadform_35.zip	1k	12-05-29		Квадратичная формула Использует квадратичную формулу. Буду делать мнимые числа.
	quadform3.zip	1k	00-09-27		Квадратичная формула Вычисляет ответы на квадратную формулу.
	quadform4.zip	2k	02-02-21		Квадратичная формула 2 Самая обширная на сегодняшний день программа с квадратными формулами. Для реальных многочленов эта программа полностью факторизует их, помещая их в простейшую форму, дает вам точки графика для параболы, рисует параболу и решает обе возможности X. Для нереального многочлена она дает вам (в очень хороший макет) упрощенная формула, а затем упрощает исходный бином.Есть небольшая ошибка с биномами с иррациональными ответами, но она содержится в файле readme.
	quadform_58.zip	1k	10-10-26		Квадратичная формула Это может быть просто, но это работает, также дает вершину.
	quadform5.zip	4k	03-08-06		Квадратное уравнение V1.4b Это моя первая * хорошая * математическая программа.Другие предыдущие программы (которых не так много) были довольно бесполезны. Надеюсь, вы найдете это полезным!
	quadform8xp.zip	1k	03-06-03		Квадратичная формула Полезная программа для алгебры 1. Просто введите уравнение, и калькулятор будет использовать квадратную формулу чтобы отобразить корни и дать вам вершину.
	quadformfastnez.zip	1k	03-03-31		Самая быстрая и простая программа по квадратичной формуле! Как и все другие квадратичные программы, решает сам знаешь что, вводя a, b, c. Простой S ***. Но то, что отличает эту программу от других, - это ее скорость и размер. Менее 1000 байт, один из самых маленьких. Я разработал усовершенствованную программу упрощения и могу пообещать, что она самая быстрая из существующих. Это делает то же самое, что и большинство других, но намного быстрее, проще, эффективнее и меньше, чем кто-либо другой.Поверьте, вы не будете использовать другую квадратичную программу после того, как воспользуетесь моей.
	quadformsolver.zip	1k	10-02-03		Решение квадриатических формул Введите A, B, C, и вы получите как положительный, так и отрицательный ответ. 2 + BX + C = 0.2-5x + 6 ", и тогда он будет очень быстро уложен.
	quadfunc.zip	1k	01-02-20		Quadfunc Это очень хорошая программа для поиска полиномиальной формы квадратного уравнения, если у вас есть 2 корня ... она также может работать с мнимыми числами и дробями, и все это упростит для вас! Очень удобный .... любые вопросы, e -пишите мне
	quadf.zip	1k	05-09-30		QUADF Эта программа представляет собой расширенную форму квадратичной формулы. В нем есть графики, дискриминант, центр, таблица, повтор и выход, все из которых удобно расположены в одном меню. Он также удобен для использования со строками.
	quadgs.zip	1k	00-04-05		Quad GS v1.1 Очень хороший решатель квадратных уравнений.Решает реальные или ненастоящие решения.
	quadplus3.zip	1k	99-11-10		QuadPlus Программа расчета квадратичных формул, которая дает вам значения X в долях, когда это возможно, и значения вершин для параболы.
	quadplus.zip	2k	03-05-01		Квадратичный решатель Это квадратичный решатель.(да) Он небольшой по размеру и полезный. Он также имеет функцию, которая отображает формулу
	quadprogs.zip	14k	19-02-22		ADVQUAD, QUAD и QUADLITE СНАЧАЛА ПРОЧИТАЙТЕ README! Последний файл теперь находится под именем abcsolver. Последнее обновление: v1.3.1 от 17.02.2019. Вот лучшие программы квадратичных формул, которые вы можете получить. Программа ADVQUAD имеет больше возможностей, чем любая другая программа с квадратными формулами.2 + BX + C = 0, где A, B и C - рациональные числа. Таким образом, даже простые уравнения подвергаются факторизации, что означает, что при необходимости используются i и знак квадратного корня. Вы можете разложить уравнение, например, где A = 2,5, B = 3,25 и C = 4,75. Посмотрите скриншоты.
	quadra6.zip	1k	09-10-20		Quadratic Factorer Plus Эта программа факторизует все квадратные уравнения, которые можно разложить на множители с использованием целых чисел и i.Даже с ненастоящими решениями, где вы получаете мнимые и комплексные числа. (Попробуйте, например: A = 1,5, B = 5, C = 4 и A = 1, B = 3, C = 2,5). Если уравнение не может быть учтено таким образом, программа сообщает вам об этом. В обоих случаях вы также получаете числовые значения.
	quadra9.zip	1k	11-03-16		Standard Quadratic Factorer Это стандартная программа факторизации, которая множит квадратные уравнения с действительными рациональными корнями.Если уравнение нельзя разложить на множители таким образом, программа сообщит вам об этом. В обоих случаях вы получаете числовые значения.
	quadrad83p.zip	1k	03-04-30		Quadrad v2.01 Это оригинальный, простой для понимания и эффективный инструмент для решения квадратных уравнений на вашем компьютере. . Версия 2.00 принесла ОГРОМНОЕ исправление ошибки и теперь показывает дискриминант (я обнаружил, что некоторые учителя хотят знать это в обсуждениях в классе и на тестах).2.01 исправляет сделанную мной опечатку (вы, вероятно, этого не заметили).
	quadradc.8xp	1k	02-10-23		Квадратичная формула Очень хорошая программа, очень проста в использовании, просто определите A, B и C и он сообщает вам ответ ..... ДАЖЕ ЕСЛИ ЭТО НЕ РЕАЛЬНО, он покажет правильную форму !!!!! ДОЛЖЕН ИМЕТЬ ДЛЯ ЛЮБЫХ, ИСПОЛЬЗУЮЩИХ КВАДРАТИЧЕСКУЮ ФОРМУЛУ
	quadrad.zip	1k	03-03-04		Quadrad v.3.2 Это программа * отличного * квадратного уравнения. Она работает НАМНОГО больше, чем средняя программа, и используется учителями и учениками по всей моей школе. Он может упростить большинство квадратных уравнений, показать работы, которые учителя хотят видеть, И дать обычный старый десятичный ответ. Если вам нужна хорошая программа по квадратичному уравнению, не соглашайтесь ни на что меньшее. Будут новые версии!
	quadraform.zip	1k	03-03-28		Решение квадратного уравнения Эта программа не делает ничего особенного.Его единственная функция - решение X. Нет никаких дополнительных бесполезных инструментов, которые другие авторы добавляют в свои программы. У вас не будет проблем с этой программой. Он каждый раз дает вам точные ответы. Чрезвычайно быстро.
	quadralong.zip	6k	03-04-01		QuadraLong Это простая, но полезная программа решения квадратичных решений. Он решает для X, выводит формулу за 3 шага (примерно все, что вам действительно нужно) и дает ответы в дробной форме после выхода.Посмотрите скриншоты.
	quadrat2.8xp	1k	02-09-05		Quadratic Simplify Упрощает квадратные уравнения
	quadrat37.8xp	1k 02 -08-28		Quad Рассчитывает квадратичную формулу с максимальной точностью. Он может обрабатывать мнимые числа, но не все ответы хороши и изящны из-за того, как они отображаются.Но все они ПРАВИЛЬНЫЕ. Если вы обнаружите какие-либо проблемы, неправильные ответы или что-то, о чем я должен знать, пожалуйста, дайте мне знать.
	quadratc2.zip	1k	02-01-01		Квадратичная формула Эта программа отображает ответ на квадратную формулу в радикол и десятичной форме. 2 + Bx + C = 0.2 + K. 4. Также указаны дискриминант D и фокус.
	quadrate.zip	1k	02-11-01		Quadrate Другая программа, которая выполняет квадратную формулу, но занимает всего 49 байт. (Называется "Q")
	quadrati_29.zip	28k	10-02-17		Квадратичное уравнение Одна из лучших квадратичных электронных программ.Это решает корни, дискриминант, вершину и линию симметрии. Прочтите README для получения дополнительной информации.
	quadratibyjonbush.zip	1k	11-02-01		QUADRATI от Джона Буша QUADTRATI - это программа, которая может выполнять несколько действий, связанных с квадратичной формулой.
	quadratic1.zip	7k	02-03-05		Квадратичная формула v1.2 Я знаю, что последнее, что нужно этому архиву, - это еще одна программа с квадратными формулами, но эта отличается от других. Эта программа даст вам корни, реальные или ненастоящие, различит и поможет найти корни. Работа? Да, работа. Он отобразит всю работу, чтобы получить корни, поэтому, если вам нужно показать свою работу или получить точный ответ, это идеально подходит для этого.
	quadratic_22.zip	1k	10-05-18		Quadratic Quarto Short and Sweet; РАБОЧИЙ квадратичный решатель.Хотите, чтобы я добавил что-нибудь еще? Пришлите мне электронное письмо по выходным или в понедельник. & Вторник.
	quadratic_34.zip	1k	11-11-02		QuadraticJL Эта программа вычислит вершину квадратичной функции, а также решения квадратных уравнений, действительные или сложные корни могут быть сообщены и автоматически преобразованы в дроби, если это возможно. Наслаждаться!
	четырехканальный лист.zip	1k	12-07-01		Quadratic / FOIL Включает квадратный решатель и FOILer (первый внешний внутренний последний)
	quadraticformula_99.8xp.zip	1k	11-09-19		Quad Решает квадратные уравнения. Работает с нереальными цифрами. Расскажу вам ответы, линию симметрии, детерминант и многое другое.
	quadraticformula_99.zip	1k	11-01-15		Квадратичная формула Простая в использовании программа, которая решает квадратичную формулу с использованием квадратичной формулы. Последнее обновление также допускает ненастоящие ответы.
	quadraticformula.zip	1k	06-09-08		Квадратичная формула На этом сайте есть тонна программ квадратичных формул, но я решил бросить свою все равно там.Хорошая программа, дисплей неплохой. Скриншоты немного показывают, на что он способен.
	quadraticform.zip	1k	03-03-05		Квадратичная формула Эта программа вычисляет квадратичную формулу. Это может быть распространено в других местах, если мне это придают должное.
	quadratichelper.zip	15k	09-04-01		Quadratic Helper Эта программа позаботится обо всех ваших квадратичных потребностях! Теперь можно взять три точки и построить из них формулу корней квадратного уравнения!
	quadraticjl2.zip	2k	14-04-06		Квадратичная формула 2JL Обновленная версия моей предыдущей программы.
	quadraticquarto.zip	1k	10-05-28		Quadratic Quarto Short and Sweet; РАБОЧИЙ квадратичный решатель. Хотите, чтобы я добавил что-нибудь еще? Пришлите мне электронное письмо по выходным или в понедельник. & Вторник.
	quadratic_roots.zip	1k	03-05-04		Корни Эта программа находит корни квадратичной функции.
	quadraticsolver.zip	2k	03-05-05		Quadrasolver Plus Version 1.6 Новое и последнее улучшение! Я исправил несколько мелких ошибок и две большие. Эта программа - лучший инструмент для решения круговых / квадратичных вычислений. Он работает с действительными и комплексными числами, может отображать работу и позволяет рисовать круги! Сейчас перенесен на TI-83
	quadratic.zip	1k	00-06-08		Квадратичный решатель Сделайте свою жизнь проще с квадратичным решателем v5.78. Эта программа находит значение X в формуле корней квадратного уравнения. Он также поддерживает нереальные числа. Это упрощает радикалы и дроби в ответе! ДОСТОЙНАЯ ЗАГРУЗКА!
	quadrati.zip	1k	10-12-19		QUADFORM Простая, легкая программа с квадратными формулами.
	quadratv10.zip	9k	11-02-27		Квадратичная формула (V1.0) Наконец, программа, которую все так ждали, Quadrat. Самая удобная программа в этой группе, она решает квадратное уравнение [b ± √ (b2-4ac)] / 2a для любого квадратичного уравнения, введенного для нахождения пересечений по оси x (если они существуют). Если он сокращается посредством деления, он должен это сделать; в противном случае пользователь получит и мнимое (ι) число, или сумасшедшую десятичную дробь.Пользователь должен сам проверить упрощение, чтобы убедиться, что у него лучший х-перехват! Кроме того, чтобы предотвратить «ошибку нереального ответа», которая возникает, когда радикал становится воображаемым, перейдите к  и затем измените REAL на a + bι. Самое главное, у этой программы есть дополнительная ссылка на Pardat, чтобы найти точку пересечения по оси Y, симметричную точку и вершину! Тогда у пользователя будет вся информация о квадратичном!
	quadra.zip	1k	11-03-16		Программа квадратичных формул Эта программа решает квадратное уравнение в форме AX ^ 2 + BX + C = 0 .Значения даны как в числовой, так и в упрощенной точной форме, как для действительных, так и для мнимых решений. Я постарался сделать программу максимально простой с минимумом байтов. Например, в конце нет меню с вопросом: СНОВА?, 1: ДА, 2: НЕТ. Если вы хотите снова запустить программу, просто нажмите ENTER. На вашем экране нет парабол, и вам не нужно выбирать, сколько цифр вы хотите, чтобы в ответе было. Нет экрана, чтобы сказать вам, кто это сделал, только мой адрес электронной почты внутри.
	quadreqbymelo.zip	1k	18-05-15		Sassy Quadratic Equation Solver Показывает квадратичную формулу и решает ее за вас после того, как вы попросите ввести запрошенные переменные . Два возможных ответа сохраняются на вашем калькуляторе как переменные D и E.
	quadriat.zip	20k	03-06-26		QUADRIAT QUADRIAT - еще одна программа Quadriatic Formula, но в отличие от других программ Quadriatic Formula, она отличается простой в использовании -использовать интерфейс, а также другие функции, такие как поиск оси симметрии, вершины и y-перехвата (извините, мне просто пришлось вставить это туда).Он также сообщает вам значение дескриминанта и на основе этого сообщает вам, сколько корней (или решений, или x-перехватов, если хотите) имеет квадриатическая функция.
	quadritics.zip	1k	03-03-15		Ultra-Small Quadratic Equation Solver QUAD - это программа, которая решает квадратные уравнения, действительные и мнимые корни отображаются. САМЫЙ МАЛЕНЬКИЙ !!!
	quadrtc.8xp	1k	02-02-27		Программа для решения квадратного уравнения Эрика Уэльсебуша Эта очень простая программа решит квадратное уравнение за вас. Сначала вам будет предложено ввести A, B и C. После нажатия клавиши ввода будет отображаться любое возможное значение X. Эта программа отличается от других решателей квадратного уравнения, потому что она может обрабатывать воображаемые числа.
	quadrtic.zip	1k	02-09-09		Решение квадратного уравнения Используется для факторизации квадратных уравнений, а также для поиска корней.
	quadr.zip	15k	07-12-31		Квадратичная формула v1.1 Это моя четвертая программа, которую я сделал. Эта программа показывает всю работу для каждого шага и даже упрощает последний радикал (с установленным omnicalc (в комплекте)). Наслаждаться!
	quadsolv_02.zip	1k	09-06-10		Решатель квадратичных формул Реапекса Детально решает оба корня.Останавливается на нереальном ответе. Исправлена ошибка кодировки. Наслаждаться!
	quadsolv2.zip	1k	03-03-17		Квадратичный решатель Введите переменные A, B и C, и он даст вам дискриминант (сохраненный к D) и решения для X (сохраненные в list5), если они вообще есть.
	quadsolv_39.zip	1k	15-05-19		Решение квадратичных формул v1.0 С легкостью решите любые квадратные задачи, потому что эта программа может решить их за вас, используя формулу корней квадратного уравнения. Эта программа ДАЖЕ ПОКАЗЫВАЕТ ВСЕ ВАШИ РАБОТЫ !!! * Только для образовательных целей !!!
	quadsolver.zip	1k	03-04-27		QuadSolver Решает квадратные уравнения для обоих ответов Ничего сложного, простой в использовании интерфейс, напишите мне на [email protected] TO ПОЗВОЛЬТЕ МНЕ УЗНАТЬ, КАК ЭТО ДЕЙСТВУЕТ, И УЗНАТЬ, ЧТО ДЕЙСТВИТЕЛЬНО ИСПОЛЬЗУЮТ ЭТО
	quadsolv.zip	1k	02-04-05		Quadratic Equation Master Эта отличная программа решит квадратное уравнение и отобразит график и таблицу. Ридми включен.
	quadsupdated.zip	1k	03-09-20		Quads Эта программа находит дискриминант, пересекает x, строит уравнение, находит точку поворота и преобразует в Форма ТП.ПОКАЗЫВАЕТ ПОЛНУЮ РАБОТУ !!!!!!!!
	quads.zip	1k	03-09-19		quads Эта программа находит дискриминант, TP, пересекает x и преобразует уравнение в форму точки поворота . Он показывает, что все работает полностью.
	quadti84plussilveredition.zip	1k	10-01-08		Квадратичный решатель v.1 Решает квадратные уравнения как для действительных, так и для ненастоящих ответов.
	quadwork83p.zip	6k	02-03-12		QuadWork v1.0 Замечательная программа, которая показывает работу для вашего квадратного уравнения, поэтому все, что вам нужно сделать, это скопировать что на экране
	quadworks.zip	1k	02-06-04		Квадратичный решатель, демонстрирующий работу Название говорит само за себя.Это решает квадратное уравнение и показывает работу. Не обрабатывает воображаемые, но не отображает РЕАЛЬНЫХ РЕШЕНИЙ
	quadx.zip	1k	02-09-05		Basic Quad Solver Не так хорошо, как Neo Quad, но говорит вы, что такое соло
	quad.zip	7k	00-09-28		Окончательная квадратичная формула v4.1 Эта программа делает с квадратичными все, что только можно вообразить. Он имеет несколько вариантов ввода и определяет для вас такие вещи, как directix, root, focus и latus Rectum среди других. Корни показаны в иррациональной форме, как вы могли бы увидеть, когда решали задачу вручную.
	quaraticpro.zip	1k	09-11-01		Quadratic Pro Показывает пошаговую работу по решению квадратного уравнения.Окончательный ответ иногда можно упростить еще больше, чем это делает программа. Однако эта программа дала мне 100% тест по математике как по алгебре, так и по предварительному исчислению.
	secongr.8xp	1k	02-05-27		secongr (Полностью расширенная квадратичная программа) Полностью улучшенная квадратичная программа [Ax² + Bx + C = 0] . Включает нули (да), сгибание и уменьшение, канонический от [A (xh) ² + K], вершину, мин / макс, домен [R] / изображение, SymeAxe, положительные и отрицательные координаты и, наконец, вариант ввода Y для поиска 2 значения X на этой высоте.Для удобного использования EZ введите ABC, а затем нажмите клавишу ВВОД, чтобы просмотреть все данные. --- Что-то пропало? : ppp
	small_quad.zip	1k	03-03-06		Quadratic Fourmula Самая маленькая полная квадратичная программа четырехмулы за всю историю. Его всего 67 байт. Проверено и работает.
	решатель. 8xp	1k	02-10-23		Решатель квадратного уравнения Эта программа решает квадратные уравнения.Просто введите A, B и C, и он решит для X.
	solvers.8xg.zip	1k	10-02-28		Solvers Включает два из них (Но не для одного и того же.)
	resolve.zip	1k	02-05-12		Решите уравнение Это то же самое, что и у Calc, но больше просто.
	суперкар.zip	1k	02-03-08		Super Quadratic v1.0 Это лучшая программа для работы с квадратными уравнениями. Он будет делать корни, дискриминант, вершину, строить график, отображать таблицу, корни в уравнении, стандартную и завершенную квадратную форму, фокус, значение / функцию директрисы и длину прямой латуса. Он также будет обрабатывать мнимые числа.
	tenchiquad83p.zip	1k	03-01-01		Квадратичный решатель Все, что вам нужно сделать, это ввести три числа для A, B и C.Затем программа решит его и решит, есть ли у него 0, 1 или 2 решения. Затем, если у него нулевое решение, он поставит Номер воображения, если у него одно решение, он даст вам 1 ответ, а если у него 2 решения, он даст вам оба. Наконец, в конце он также отобразит его в виде графика. Он не округляется, поэтому дает максимально возможную точность.
	trinomep.zip	6k	10-03-20		Trinome + Программа для восстановления полиномов 2./ Программа для разрешения многочлена степеней 2.
	trinome.zip	2k	10-03-22		Trinome Ce degrés 2. (Moins complete que trinôme +). Эта программа позволяет разрешить корни многочлена 2-й степени (менее полный, чем trinome +).
	trinom.zip	11k	17-11-16		Trinom Дуга Factor5 - новейшая программа трехчленного факторинга, которая может обрабатывать числа от 100000+ и множить все трехчлены состоящий из целых чисел, самый быстрый.Кроме того, у него простой, интуитивно понятный и ненавязчивый интерфейс. Это показывает GCF (даже если его невозможно было разложить на множители) и два числа, которые складываются для «B» и умножаются для «C».
	triquad3.zip	4k	04-12-16		TriQuad3 Улучшенная версия, на мой взгляд, моей предыдущей программы. Эта новая версия упрощает все намного лучше, чем предыдущая, и я изменил все для удобства использования.2 + bx + c = 0, но вы также можете ввести его в форме AHK и FOIL. Затем эта программа возьмет уравнение и преобразует его, разложит на множители, решит, построит график и так далее. Это результат двухлетней работы. Первоначально я создал его, потому что не смог найти программу Quadratic, которая была бы свободна от ошибок и проста в использовании, так что, надеюсь, я это выполнил. Здесь нет надоедливых заставок, только простые меню.
	vertexfm.zip	1k	03-06-14		VERTEXFM Эта математическая программа преобразует стандартную форму QUADRATIC FORMULA в vetex-форму QUADRATIC FORMULA.Это действительно удобно, потому что тогда вы можете легко найти вершину параболы. Если возникнут проблемы с этой программой, напишите мне!

Решение квадратных уравнений с помощью факторинга

Purplemath

Этот урок охватывает множество способов решения квадратичных вычислений, таких как извлечение квадратного корня, вычисление квадрата и использование квадратичной формулы.Но начнем с решения по факторингу.

(Прежде чем перейти к решению квадратных уравнений, вы должны уже знать, как разложить квадратные выражения на множители. Если нет, сначала просмотрите, как разложить квадратичные уравнения на множители.)

Вы уже разложили квадратные выражения на множители. Новым здесь является то, что квадратное выражение является частью уравнения, и вам предлагается найти значения переменной, которые делают уравнение истинным. Вот как это работает:

MathHelp.com

Решите (
x - 3) ( x - 4) = 0 путем факторизации.

Хорошо, эта квадратичная для меня уже учтена.Но как мне использовать эту факторизацию для решения уравнения?

Для решения квадратичных вычислений путем факторинга мы используем то, что называется «Свойство нулевого произведения». Это свойство говорит о том, что кажется довольно очевидным, но только после того, как нам на это указали; а именно:

Свойство нулевого произведения: если мы умножаем две (или более) вещи вместе и результат равен нулю, то мы знаем, что по крайней мере один из тех вещей, которые мы умножили, также должен был быть равен нулю.Другими словами, единственный способ получить ноль при умножении двух (или более) множителей состоит в том, чтобы один из множителей был равен нулю.

Итак, если мы умножаем два (или более) множителя и получаем нулевой результат, то мы знаем, что по крайней мере один из множителей сам был равен нулю. В частности, мы можем установить каждый из факторов равным нулю и решить полученное уравнение для одного решения исходного уравнения.

Мы можем сделать полезный вывод о множителях (а именно, что один из этих множителей должен был быть равен нулю, поэтому мы можем установить множители равными нулю), только если сам продукт равен нулю.Если произведение коэффициентов равно на любое ненулевое значение , то мы не можем сделать какое-либо заявление о значениях факторов.

Следовательно, при решении квадратных уравнений путем факторизации мы должны всегда иметь уравнение в форме «(квадратное выражение) равно (нулю)», прежде чем предпринимать какие-либо попытки решить квадратное уравнение путем факторизации.

Возвращение к упражнению:

Принцип нулевого фактора говорит мне, что хотя бы один из факторов должен быть равен нулю.Поскольку хотя бы один из коэффициентов должен быть равен нулю, я могу установить каждый из коэффициентов равным нулю:

x - 3 = 0 или x - 4 = 0

Это дает мне простые линейные уравнения, которые легко решить:

И эти два значения - то решение, которое они ищут:

Обратите внимание, что « x = 3, 4» означает то же самое, что и « x = 3 или x = 4»; единственная разница - это форматирование.Формат « x = 3, 4» является более распространенным.

Решите
x ² + 5 x + 6 = 0 и проверьте.

Это уравнение уже имеет форму «(квадратичное) равно (нулю)», но, в отличие от предыдущего примера, оно еще не учтено. Я ДОЛЖЕН сначала разложить на множители квадратичный, потому что только когда я УМНОЖДАЮ и получаю ноль, я могу что-либо сказать о факторах и решениях.Я не могу сделать никаких выводов об отдельных членах квадратичной функции без факторизации (например, 5 x или 6), потому что я могу добавить много всего, что в сумме равно нулю.

Итак, первое, что мне нужно сделать, это фактор:

x ² + 5 x + 6 = ( x + 2) ( x + 3)

Теперь я могу переформулировать исходное уравнение в терминах произведения факторов, при этом произведение равно нулю:

Теперь я могу решить каждый фактор, установив каждый из них равным нулю и решив получившиеся линейные уравнения:

x + 2 = 0 или x + 3 = 0

x = –2 или x = - 3

Эти два значения являются решением исходного квадратного уравнения.Итак, мой ответ:

Я еще не закончил, потому что в исходном упражнении мне было сказано «проверить», а это означает, что мне нужно вставить свои ответы обратно в исходное уравнение и убедиться, что оно получилось правильным. В этом случае я буду вставлять выражение в левой части исходного уравнения и проверять, что я получаю правую часть; а именно с 0:

проверка x = –3:

[–3] ² + 5 [–3] + 6

9–15 + 6

9 + 6–15

15–15

проверка x = –2:

[–2] ² + 5 [–2] + 6

4–10 + 6

4 + 6 - 10

10–10

Когда в упражнении указано, что вы должны решить «и проверить» вышеуказанное «plug-n-chug», они ищут вас, чтобы показать, что вы включили свой ответ в исходное упражнение и получили что-то, что сработало правильно.Выше, где я показал свои чеки, все, что им нужно. Но делайте свою работу аккуратно!

Между прочим, вы можете использовать эту технику «проверки», чтобы проверить свои ответы на любое «решающее» упражнение. Так, например, если вы не уверены в своем ответе на вопрос «фактор и решение» в следующем тесте, попробуйте включить свои ответы в исходное уравнение и убедиться, что ваши решения приводят к истинным утверждениям.

Это уравнение не имеет форму «(квадратичное) равно (нулю)», поэтому я пока не могу его решить.Первое, что мне нужно сделать, это перебрать все термины с одной стороны, а с другой - ноль. Только тогда я могу разложить на множители и решить:

x ² - 3 = 2 x

x ² - 2 x - 3 = 0

( x - 3) ( x + 1) = 0

x - 3 = 0, x + 1 = 0

x = 3, x = –1

Тогда мое решение:

Решите (
x + 2) ( x + 3) = 12.

Студенты часто видят уравнения такого типа и говорят:

«Круто! Это уже учтено! Я установлю множители равными 12 и решу, чтобы получить x = 10 и x = 9. Это было легко!»

Да, это было легко; это тоже было неправильно. Очень-очень неправильно.

Помимо того факта, что ни (10 + 2) (10 + 3), ни (9 + 2) (9 + 3) не равно 12, мы никогда не должны забывать, что мы должны иметь «(квадратичное) равно (нулю)», прежде чем мы сможем решить по факторингу.

Возвращение к упражнению:

Каким бы заманчивым это ни казалось, я не могу приравнять каждый из множителей в левой части уравнения к другой части уравнения и решить. В противном случае я бы получил совершенно неправильную путаницу.

Вместо этого я сначала должен умножить и упростить левую часть, затем вычесть 12 из левой и повторно разложить на множители. Только тогда я смогу решить.

( x + 2) ( x + 3) = 12

x ² + 5 x + 6 = 12

x ² + 5 x - 6 = 0

( x + 6) ( x - 1) = 0

x + 6 = 0, x - 1 = 0

x = –6, x = 1

Тогда мое решение:

Эту двухчленную квадратичную легче разложить на множители, чем предыдущие квадратичные: я сразу вижу, что могу вынести x из обоих членов, взяв x вперед.Это дает мне:

Очень распространенная ошибка, которую делают ученики на этом этапе, - это «решить» уравнение для « x + 5 = 0», разделив его на x . Но это неверный шаг. Почему? Потому что мы не можем делить на ноль. Как это здесь играет роль?

При делении на коэффициент x делается неявное предположение, что x не равно нулю.Для такого предположения нет абсолютно никаких оснований! И такое предположение привело бы к потере половины нашего решения этого уравнения.

Возвращение к упражнению:

Мне нужно помнить, что фактор может содержать только переменную без добавления к другим терминам; в частности, « x » - вполне допустимый коэффициент. Мне нужно установить и из коэффициентов равными нулю, а затем решить два результирующих линейных уравнения:

x ( x + 5) = 0

x = 0, x + 5 = 0

x = 0, x = –5

Тогда мое решение:

В предыдущем примере было два члена, и его легко разложить на множители.Есть еще один случай двухчленной квадратичной системы, который мы можем разложить на множители. Это только немного сложнее:

Это уравнение имеет форму «(квадратичное) равно (нулю)», поэтому я могу решить его путем факторизации. Но как это учесть? Заметив, что это разница квадратов. Применим формулу разности квадратов, которую выучил:

x ² - 4 = 0

( x -2) ( x + 2) = 0

x - 2 = 0, x + 2 = 0

x = 2, x = –2

Тогда мое решение:

Примечание. Приведенное выше решение также можно отформатировать как « x = ± 2».Это произносится как « x равно плюс-минус 2».

В последнем примере, приведенном выше, на следующей странице показано, как решить, извлекая квадратный корень. 2 + bx + c = 0 $.2–4 \ cdot 2 \ cdot (-15)}} {2 \ cdot2} $$

$$ x_ {1,2} = \ frac {-7 \ pm \ sqrt {49 + 120}} {4} $$

$$ x_ {1,2} = \ frac {-7 \ pm \ sqrt {169}} {4} $$

$$ x_ {1,2} = \ frac {-7 \ pm 13} {4} $$

Для вычисления первого решения мы используем знак «+»:

Для вычисления второго решения мы используем знак «-»:

$$ x_ {1} = \ frac {-7 + 13} {4} $$

$$ x_ {1} = \ frac {6} {4} $$

$$ x_ {1} = \ frac {3} {2} $$

$$ x_ {2} = \ frac {-7–13} {4} $$

$$ x_ {2} = \ frac {-20} {4} $$

$$ x_ {2} = -5 $$

Осуществление:

Решите уравнение 3x ² + 2x - 5 = 0 . 2 + \ frac {7} {2} x - \ frac {15} {2} = 0 $$

Шаг 1: Разделите все члены на коэффициент x ².2 = \ frac {169} {16} $$

Шаг 5: Напишите полный квадрат слева.

$$ x + \ frac {7} {4} = \ pm \ sqrt {\ frac {169} {16}} $$

$$ x + \ frac {7} {4} = \ pm \ frac {13} {4} $$

Шаг 6: Извлеките квадратный корень из обеих частей уравнения.

$$ x_1 = - \ frac {7} {4} + \ frac {13} {4} = \ frac {3} {2} $$

$$ x_2 = - \ frac {7} {4} - \ frac {13} {4} = -5 $$

Шаг 7: Решите относительно x.

x =	-b ± √b² — 4a c
	2 a

x_1,2 =	-b ± √D
	2 a

Квадратное уравнение

Геометрический смысл

Вывод формулы для решения квадратного уравнения

Дискриминант квадратного уравнения

Теорема Виета

Разложение квадратного уравнения на множители

Примеры решения квадратных уравнений

Как решать неполные квадратные уравнения? Примеры и Формулы

Основные понятия

Решение неполных квадратных уравнений

Как решить уравнение ax² = 0

Как решить уравнение ax² + с = 0

В двух словах

Как решить уравнение ax² + bx = 0

Алгебра 7-9 классы. 20. Решение квадратных уравнений

Алгебра 7-9 классы. 20. Решение квадратных уравнений

ФОРМУЛЫ КОРНЕЙ КВАДРАТНЫХ УРАВНЕНИЙ

Калькулятор квадратных уравнений — решение квадратных уравнений онлайн

Решить квадратное уравнение онлайн

Как решить квадратное уравнение

Квадратные уравнения (8 класс)

Примеры решения полных, неполных и приведенных квадратных уравнений

Как решать квадратное уравнение

Как решать квадратные уравнения

Алгоритм решения квадратного уравнения

Решите квадратное уравнение с помощью программы «Пошаговое решение математических задач»

КВАДРАТИКА, РЕШЕННАЯ ФАКТОРИНГОМ

ЗАДАЧИ

НЕПОЛНАЯ КВАДРАТИКА

ЗАДАЧИ

ЗАВЕРШЕНИЕ ПЛОЩАДИ

ЗАДАЧИ

КВАДРАТИЧЕСКАЯ ФОРМУЛА

ЗАДАЧИ

ПРОБЛЕМЫ СО СЛОВОМ

ЗАДАЧИ

РЕЗЮМЕ

Ключевые слова

Процедуры

Калькулятор квадратичных формул | Комплексный

Что такое квадратная формула?

Коэффициенты квадратного уравнения

Как использовать решатель квадратичных формул

Решение квадратных уравнений с отрицательным определителем

Решение квадратных уравнений

Решение квадратных уравнений

Факторинг

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

Квадратичная формула

Пример 6

Пример 7

Пример 8

Пример 9

Завершение квадрата

Пример 10

Пример 11

Пример 12

TI-83/84 Plus BASIC Math Programs (Quadratic Solvers)

Решение квадратных уравнений с помощью факторинга

Purplemath

MathHelp.com

Решите (

Решите

Решите (

Добавить комментарий Отменить ответ