Решение систем методом подстановки: Способ подстановки — урок. Алгебра, 7 класс. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Примеры решения систем методом подстановки

Рассмотрим конкретные примеры решения систем линейных уравнений методом подстановки.

В данном случае удобно из второго уравнения системы выразить x через y и подставить полученное выражение вместо x в первое уравнение:

Первое уравнение — уравнение с одной переменной y. Решаем его:

5(7-3y)-2y = -16

35-15y-2y= -16

-17y= -51

y=3.

Полученное значение y подставляем в выражение для x:

Ответ: (-2; 3).

В данной системе проще из первого уравнения выразить y через x и подставить полученное выражение вместо y во второе уравнение:

Второе уравнение — уравнение с одной переменной x. Решим его:

3x-4(-1,5-3,5x)=23

3x+6+14x=23

17x=17

x=1.

В выражение для y вместо x подставляем x=1 и находим y:

Ответ: (1; -5).

Здесь удобнее из второго уравнения выразить y через x (поскольку делить на 10 проще, чем на 4, -9 или 3):

Решаем первое уравнение:

4x-9(1,6-0,3x)= -1

4x-14,4+2,7x= -1

6,7x=13,4

x=2.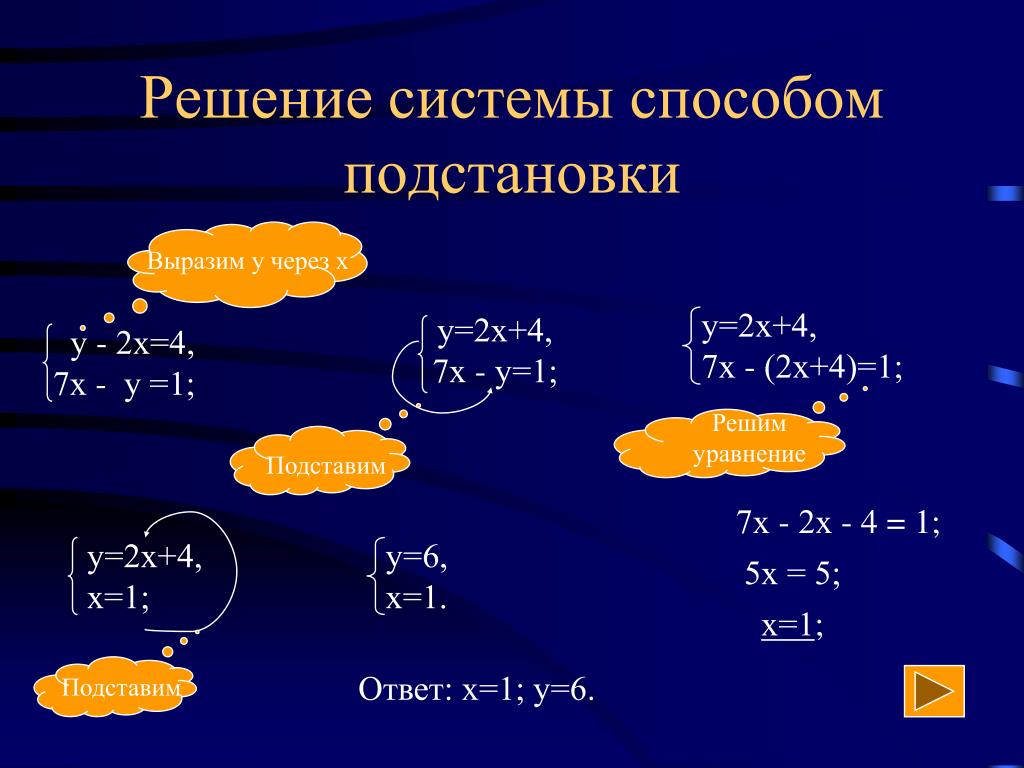

Подставляем x=2 и находим y:

Ответ: (2; 1).

Прежде чем применить метод подстановки, эту систему следует упростить. Обе части первого уравнения можно умножить на наименьший общий знаменатель, во втором уравнении раскрываем скобки и приводим подобные слагаемые:

Получили систему линейных уравнений с двумя переменными. Теперь применим подстановку. Удобно из второго уравнения выразить a через b:

Решаем первое уравнение системы:

3(21,5 + 2,5b) — 7b = 63

64,5+7,5b-7b=63

0,5b= -1,5

b= -3.

Осталось найти значение a:

Согласно правилам оформления, ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.

Ответ: (14; -3).

Выражая одну переменную через другую, иногда удобнее оставлять её с некоторым коэффициентом.

В данном случае удобно выразить y через x из второго уравнения. При этом лучше не делить обе части уравнения на 3, а оставить коэффициент 3 рядом с y, поскольку в первом уравнении 12y кратно 3:

9x-4(43-4x)=78

9x-172+16x=78

25x=250

x=10.

Ответ: (10;1).

Из всех способов решения систем уравнений метод подстановки в алгебре используется чаще других. С помощью этого метода могут быть решены не только системы линейных уравнений, но и системы уравнений других видов.

Решение системы линейных уравнений методом подстановки: алгоритм, правило, примеры

Алгоритм решения системы линейных уравнений методом подстановки

Из любого уравнения системы выразить одну переменную через другую.
Подставить во второе уравнение системы вместо переменной выражение, полученное на первом шаге.
Решить второе уравнение относительно выраженной переменной.
Подставить найденное значение переменной в выражение, полученное на первом шаге.
Найти значение второй переменой.
Записать ответ в виде упорядоченной пары найденных значений переменных.

Например: ${\left\{ \begin{array}{c} 3x+y = 5 \\ y-x = 1 \end{array} \right.}$

Шаг 1

Из второго уравнения выражаем y:

y = x+1

Шаг 2

Подставляем выражение для y в первое уравнение:

3x+(x+1) = 5

Шаг 3 Решаем первое уравнение:

4x = 5-1

x = 1

Шаг 4

Подставляем значение x в выражение для y:

y = 1+1

Шаг 5

Находим y:

y = 2

Шаг 6

Записываем ответ:

(1;2)

В последовательной записи:

$$ {\left\{ \begin{array}{c} 3x+y = 5 \\ y-x = 1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3x+y = 5 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3x+(x+1) = 5 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x = 5-1 \\ y = x+1 \end{array} \right. } \Rightarrow $$ $$ \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 2\end{array} \right.} $$

Ответ: (1;2)

Примеры

Пример 1. Решите систему уравнений методом подстановки:

$ а) {\left\{ \begin{array}{c} 5x-4y = 3 \\ 2x-3y = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x-4y = 3 \\ x = \frac{3y+4}{2} = 1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(1,5y+2)-4y = 3 \\ x = 1,5y+2 \end{array} \right.} \Rightarrow $

$ \Rightarrow {\left\{ \begin{array}{c} 7,5y+10-4y = 3 \\ x=1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3,5y = -7 \\ x = 1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = -2 \\ x = 1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = -1 \\ y = -2\end{array} \right.} $

Ответ: (-1;-2)

$ б) {\left\{ \begin{array}{c} 4x-3y = 7 \\ 3x-4y = 0 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 4x-3y = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x-3\cdot \frac{3}{4} x = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} (4- \frac{9}{4})x = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow $

$\Rightarrow {\left\{ \begin{array}{c} x = 7 \cdot \frac{4}{7} = 4 \\ y = \frac{3}{4} x = \frac{3}{4} \cdot 4 = 3 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}x = 4 \\ y = 3 \end{array} \right.} $

Ответ: (4;3)

$ в) {\left\{ \begin{array}{c} 5a-4b = 9 \\ 2a+3b = -1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5a-4b = 9 \\ a = \frac{-3b-1}{2} = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(-1,5b-0,5)-4b = 9 \\ a = -1,5b-0,5 \end{array} \right.} \Rightarrow $

$ \Rightarrow {\left\{ \begin{array}{c} -7,5b-2,5-4b = 9 \\ a = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}-11,5b = 11,5 \\ a = -1,5b-0,5 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = -1 \end{array} \right.} $

Ответ: (1;-1)

$ г) {\left\{ \begin{array}{c} 7a+4b = 5 \\ 3a+2b = 1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7a+4b = 5 \\ b = \frac{-3a+1}{2} = -1,5a+0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7a+4(-1,5a+0,5) = 5 \\ b = -1,5a+0,5 \end{array} \right.} \Rightarrow $

$ \Rightarrow {\left\{ \begin{array}{c} 7a-6a+2 = 5 \\ b = -1,5a+0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 3 \\ b = -1,5\cdot3+0,5 = -4 \end{array} \right.} $

Ответ: (3;-4)

Пример 2. Найдите решение системы уравнений:

$а) {\left\{ \begin{array}{c} \frac{x}{4}-y = 7 | \times 4 \\ 3x+ \frac{y}{2} = 9 | \times 2\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x-4y = 28 \\ 6x+y = 18 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 4y+28 = 4(y+7) \\ 6 \cdot 4(y+7)+y = 18 \end{array} \right.} \Rightarrow $

$\Rightarrow {\left\{ \begin{array}{c} x = 4(y+7) \\ 24y+168+y = 18 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} x = 4(y+7) \\ 25y = -150 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}x = 4(-6+7) = 4 \\ y = -6 \end{array} \right.}$

Ответ: (4;-6)

$б) {\left\{ \begin{array}{c} \frac{x}{2}+ \frac{y}{3} = \frac{1}{6} |\times 6 \\ \frac{x}{3}+ \frac{y}{2} = -\frac{1}{6}| \times 6 \end{array} \right.}\Rightarrow {\left\{ \begin{array}{c} 3x+2y = 1 \\ 2x+3y = -1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = \frac{-3x+1}{2} = -1,5x+0,5 \\ 2x+3(-1,5x+0,5) = -1\end{array} \right.} \Rightarrow$

$ \Rightarrow {\left\{ \begin{array}{c} y = -1,5x+0,5 \\ 2x-4,5x+1,5 = -1\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = -1,5x+0,5 \\ -2,5x = -2,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = -1 \end{array} \right.} $

Ответ: (1;-1)

$ в) {\left\{ \begin{array}{c} 3(5x-y)+14 = 5(x+y) \\ 2(x-y)+9 = 3(x+2y)-16 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end{array} \right. } \Rightarrow $

$ \Rightarrow {\left\{ \begin{array}{c} 10x-8y = -14 |:2 \\ x+8y = 25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(-8y+25)-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow $

$ \Rightarrow {\left\{ \begin{array}{c} -40y+125-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} -44y = -132 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 3 \end{array} \right.} $

Ответ: (1;3)

$ г) {\left\{ \begin{array}{c} 5-3(2x+7y) = x+y-52 \\ 4+3(7x+2y) = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5-6x-21y = x+y-52 \\ 4+21x+6y = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ 2x-6y = 4 |:2 \end{array} \right.}$

$$ \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x-3y = 2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x = 3y+2 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 7(3y+2)+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow $$

$$ \Rightarrow {\left\{ \begin{array}{c} 21y+14+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 43y = 43 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 5 \\ y = 1 \end{array} \right.}$$

Ответ: (5;1)

Пример 3*. Найдите решение системы уравнений:

$ {\left\{ \begin{array}{c} \frac{3}{2x-5y} + \frac{8}{x+y} = 5 \\ \frac{12}{x+y} — \frac{1}{2x-5y} = 2 \end{array} \right.} $

Введём новые переменные: $ {\left\{ \begin{array}{c} a = \frac{1}{2x-5y} \\ b = \frac{1}{x+y} \end{array} \right.} $

Перепишем систему и найдём решение для новых переменных:

$$ {\left\{ \begin{array}{c} 3a+8b = 5 \\ 12b-a = 2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3(12b-2)+8b = 5 \\ a = 12b-2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 36b-6+8b = 5 \\ a = 12b-2 \end{array} \right. } \Rightarrow $$

$$ \Rightarrow {\left\{ \begin{array}{c} 44b = 11 \\ a = 12b-2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = \frac{1}{4} \end{array} \right.} $$

Получаем:

$$ {\left\{ \begin{array}{c} 2x-5y = \frac{1}{a} = 1 \\ x+y = \frac{1}{b} = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 2x-5(4-x) = 1 \\ y = 4-x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 2x-20+5x = 1 \\ y = 4-x \end{array} \right.} \Rightarrow $$

$$ \Rightarrow {\left\{ \begin{array}{c} 7x = 21 \\ y = 4-x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 3 \\ y = 1 \end{array} \right.} $$

Ответ: (3;1)

Способы решения систем уравнений с двумя неизвестными

Линейные системы уравнений

Системы линейных уравнений. Метод подстановки

+ показать

• Выражаем одну переменную через другую.

• Выраженную из одного уравнения переменную подставляем во второе уравнение. Получаем уравнение относительно одной переменной, которое и решаем.

• Опираясь на найденное значение одной переменной, находим значение второй, подставляя в оставшееся уравнение.

Решить систему уравнений:

Решение: + показать

Системы линейных уравнений. Метод сложения

+ показать

• Добиваемся, путем равносильных преобразований, наличия равных (или противоположных) коэффициентов при одной из неизвестных переменных в уравнениях.

• Вычитаем (или складываем) полученные уравнения с целью выхода на уравнение с одной неизвестной.

• Решаем полученное уравнение с одной неизвестной.

• Найденное значение одной переменной подставляем в любое из уравнений системы, находим значение второй.

1. Решить систему уравнений:

Решение: + показать

Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

Ответ:

2. Решить систему уравнений:

Решение: + показать

Нелинейные системы уравнений

Системы уравнений, сводящихся к линейным

1. Решить систему уравнений:

Решение: + показать

Можно сделать замену и Тогда выходим на систему линейных уравнений:

Систему можно решить методом сложения, например.

Но приведем решение без замены.

Умножим первое уравнение системы на , второе – на и произведем сложение полученных уравнений, оставим при этом в системе, например, первое уравнение исходной системы.

Ответ:

2. Решить систему уравнений:

Решение: + показать

Можно сделать замену и выйти на систему линейных уравнений:

Приведем решение без замены.

Выражаем из второго уравнения системы и подставляем в первое.

Ответ:

Нелинейные системы уравнений. Метод подстановки

Решить систему уравнений:

Решение: + показать

Выражаем из первого уравнения системы и подставляем во второе.

Ответ:

Нелинейные системы уравнений. Метод сложения

Решить систему уравнений:

Решение: + показать

Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

Ответ:

Нелинейные системы уравнений. Метод почленного умножения (деления)

1. Решить систему уравнений:

Решение: + показать

Производим деление первой строки на вторую, оставляем в системе вторую строку без изменений.

Ответ:

Симметрические системы. Метод введения переменной

Симметрическая система – система, все уравнения которой симметрические. Симметрическое уравнение от двух переменных и – уравнение, которое не изменяется при замене на и на .

Для таких систем удобно использовать замену

Решить систему уравнений:

Решение: + показать

При замене приходим к следующей системе

которую будем решать способом подстановки:

Производим обратную замену:

Ответ:

Системы однородных уравнений и приводящиеся к ним системы

Однородным уравнением с двумя неизвестными будем называть уравнение вида

1. Решить систему уравнений:

Решение: + показать

2. Решить систему уравнений:

Решение: + показать

Применим прежде к системе метод сложения. После чего выйдем на однородное уравнение.

Ответ:

Графический метод решения систем уравнений

1. Решите графически систему уравнений:

Решение: + показать

Выразим в обеих строках системы через :

Первое уравнение системы задает прямую, второе – гиперболу. Строим графики в одной системе координат, находим координаты точек пересечения графиков.

Ответ:

2. Решите графически систему уравнений:

Решение: + показать

3. Решите графически систему уравнений:

Решение: + показать

Задания для самостоятельной работы

+ показать

Решите системы уравнений:

Ответ:

Решите графически системы уравнений:

Ответ:

10.

Ответ:

Метод подстановки при решении системы линейных уравнений

☰

При решении системы линейных уравнений с двумя переменными можно использовать графический метод. Однако алгебраический является более надежным. Одним из алгебраических методов является метод подстановки.

Суть метода подстановки заключается в следующем. В одном уравнении (не важно каком) системы одна переменная выражается через другую. После этого во второе уравнение системы вместо соответствующей переменной подставляется выражение, которому равна эта переменная, полученное ранее. Приведем пример; допустим, дана система уравнений:

| 10x + 10y + 10 = 0
| –2x – 4y – 8 = 0

Выразим во втором уравнении y через x:
–4y = 2x + 8
y = (2x + 8) / –4
y = –0. 5x – 2

Теперь подставим в первое уравнение вместо y выражение –0.5x – 2. Это допустимо, так как y равен этому выражению, то есть y и это выражение эквивалентны. Получим:
10x + 10(–0.5x – 2) + 10 = 0

Теперь решим полученное уравнение с одной переменной, то есть найдем значение x.
10x – 5x – 20 + 10 = 0
5x – 10 = 0
5x = 10
x = 2

Для того, чтобы найти y надо подставить значение x в любое линейное уравнение из системы, но проще в то, где y уже выражен через x:
y = –0.5x – 2 = y = –0.5 * 2 – 2 = –1 – 2 = –3

Таким образом решением заданной системы уравнений являются значения x = 2, y = –3.

Проверим это, подставив соответствующие значения в одно или оба линейных уравнения системы:
10x + 10y + 10 = 10 * 2 + 10 * (–3) + 10 = 20 – 30 + 10 = 0 — верное равенство
–2x – 4y – 8 = –2 * 2 – 4 * (–3) – 8 = –4 + 12 – 8 = 0 — верное равенство

При использовании метода подстановки не важно выражать ли x через y или как в приведенном примере y через x. При выборе исходить надо из удобства: что проще из чего выразить. Например, в уравнении 4.35x + y – 1.5 проще выразить y через x: y = 1.5 – 4.35x. А вот в уравнении 2x – 4y = 0 лучше выразить x через y: x = 2y.

Как отмечалось выше уравнение, которое подвергается преобразованию, также можно выбрать произвольно, исходя из принципа удобства.

Система линейных уравнений с двумя переменными. Методы решения систем уравнений.

Решением системы линейных уравнений двух переменных является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.

Как можно решить систему уравнений с двумя переменными?

Системы уравнений с двумя переменными можно решить методом подстановки:

Системы уравнений с двумя переменными можно решить методом сложения:

Пример. Решить систему методом сложения: $\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}$.

Решение:

Система уравнений состоящее из двух переменных должно удовлетворять всем решениям одновременно. Система линейных уравнений из двух переменных рассматривается одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям системы одновременно. Некоторые линейные системы могут не иметь решения, и это будет их решением, другие системы могут иметь бесконечное число решений. Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальное решение.

Выводы:

Система линейных уравнений из двух переменных решается совместно методом подстановки или методом сложения.

Чтобы найти решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям в системе одновременно.

Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных.

Решить систему уравнений это значит найти численное значение для каждой переменной в системе либо доказать что решений нет.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Геометрия с нуля

— Индивидуальные занятия

— В любое удобное для вас время

— Бесплатное вводное занятие

Математика по Skype

— Индивидуальные занятия

— В любое удобное для вас время

— Бесплатное вводное занятие

Записаться на бесплатный урок

Конспект урока по алгебре «Решение систем линейных уравнений методом подстановки» (7 класс)

Конспект урока по теме:

«Решение систем линейных уравнений методом подстановки»

7 класс

Составила:

Учёнова Наталья Николаевна

учитель математики МОУ СОШ № 22

Тема урока: Решение систем линейных уравнений методом подстановки.

Учебник: Алгебра: 7 класс: учебник для учащихся образовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.

Тип урока: урок изучения нового материала.

Цель урока: формирование у учащихся умения решать системы линейных уравнений с двумя неизвестными способом подстановки.

Задачи:

Образовательные: повторить понятие, что называется решением системы линейный уравнений, что значит, решить систему линейных уравнений с двумя неизвестными, познакомиться с алгоритмом решения системы двух линейных уравнений с двумя неизвестными методом подстановки, обобщить и систематизировать знания и умения обучающихся при решении систем линейных уравнений с двумя переменными.

Развивающие: развивать математический и общий кругозор, мышление и речь обучающихся, способствовать формированию умений применять приёмы: обобщения, сравнения, выделения главного.

Воспитательные: формировать интерес к математике, к познанию нового, умению анализировать, сравнивать, организованности и взаимопомощи через работу в парах.

Планируемые результаты:

Предметные:

Знать, что такое решить систему линейных уравнений с двумя переменными, что называется решением системы уравнений с двумя переменными, умение применять на практике графический метод решения систем двух линейных уравнений и метод подставки;

уметь выражать одну переменную через другую, полученный результат подставлять в другое уравнение, решать уравнение с одной переменной.

Мета предметные:

Познавательные: умение работать с новой информацией, умение анализировать, синтезировать, сравнивать полученный результат;

Регулятивные: осуществлять контроль своих знаний и умений в процессе достижения результата в форме сравнений решений различными способами и его результата с заданным образцом с целью обнаружения ошибок, корректировать свои действия в случае расхождения

Коммуникативные: обнаружение и формулирование обучающимися учебной проблемы совместно с учителем; высказывание своего предположения, умение определить и сформулировать цель урока с помощью учителя, умение вступать в диалог с учителем и одноклассниками, участвовать в коллективном обсуждении;

Личностные:

формировать желание учиться и приобретать новые знания, не останавливаться перед трудностями и искать пути их решения, умение осуществлять самооценку успешности своей учебной деятельности.

Методы: фронтальный, частично–поисковый, коллективный, индивидуальный.

Оборудование: учебник, проектор, экран, раздаточный материал.

Ход урока

Организационный момент

Учащиеся перед началом урока делятся на группы.

Деятельность учителя

Учитель приветствует учащихся, проверяет их готовность к уроку, создает положительный настрой и выбирает ответственного ученика в каждой группе.

Деятельность учащихся

Приветствуют учителя. Проверяют готовность к уроку, настраиваются на получение новых знаний.

Проверка домашнего задания

Деятельность учителя

Включает слайд 1, 2. Отвечает на вопросы учащихся, если что-то непонятное встретилось в домашней работе.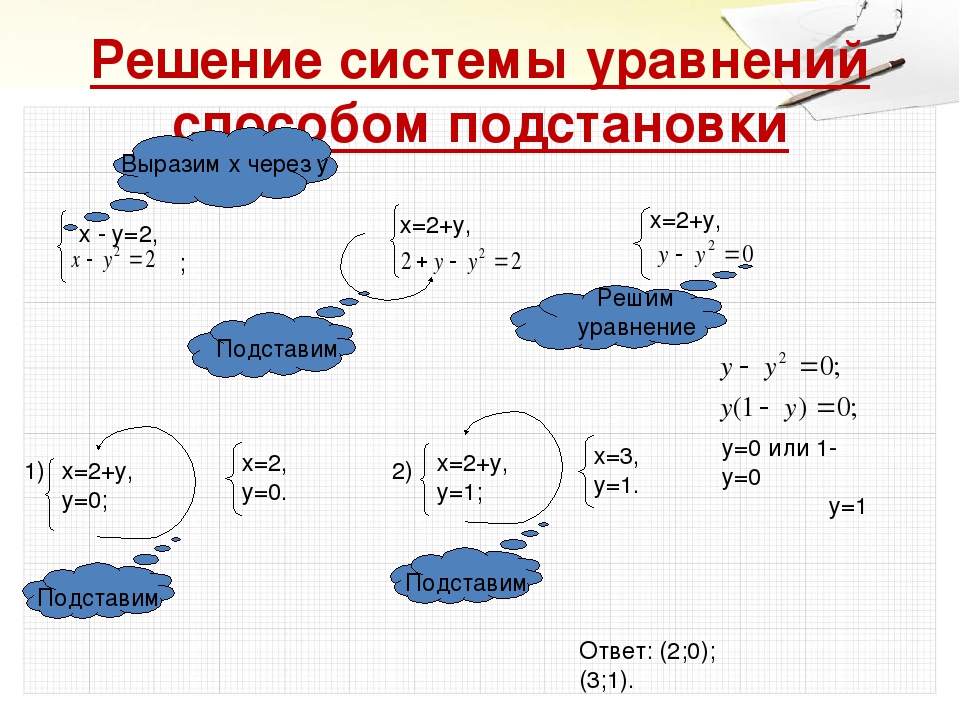

Деятельность учащихся

Самопроверка по готовым ответам. Задают вопросы по домашней работе. Обсуждают. Самооценка. Исправление ошибок. Сдают работы на проверку.

Слайд 1.

№ 1. Решить графически систему уравнений:

Построим график первого уравнения линейной функции

Построим график второго уравнения линейной функции

Мы видим по графику, что точка пересечения графиков имеет координаты (0;4). Эта пара чисел и будет решение этой системы уравнений.

Ответ: (0;4).

Слайд 2.

№ 2. Решить графически систему уравнений:

преобразуем 2-ое уравнение, разделив обе части уравнения на -2, получим:

у= — 5 это прямая, параллельная оси абсцисс

Построим график второго уравнения линейной функции

Мы видим по графику, что точка пересечения графиков имеет координаты (-1;-5). Эта пара чисел и будет решение этой системы уравнений.

Ответ: (-1;-5).

Устный счёт

Деятельность учителя

Учитель предлагает учащимся найти пару чисел, которая является решением системы. Выводит на экран слайд 3.

Деятельность учащихся

Учащиеся подставляют поочередно пары чисел в систему уравнений, считают, поднимают руку и называют ответ. Обосновывают решения.

Слайд 3

Какая из пар чисел (-5;1), (1;4), (2;3) является решением системы уравнений

Актуализация знаний

Деятельность учителя

Учитель предлагает учащимся вспомнить основные понятия из ранее изученного материала, задаёт вопросы:

Что будет решением уравнения с двумя переменными?

Что значит решить уравнение с двумя переменными?

Свойства уравнений с двумя переменными?

Что будет решением системы?

Что значит решить систему?

Деятельность учащихся

Учащиеся отвечают на вопросы учителя. Повторяют основные понятия, которые им понадобятся для изучения новой темы.

Постановка целей, задач урока, мотивация учебной деятельности учащихся

Деятельность учителя

Учитель задает наводящие вопросы:

Мы научились решать системы уравнений графическим способом, строив графики.

Мы знаем свойства уравнений с двумя переменными и умеем их применять.

Как вы думаете, что можно сделать с уравнениями в системе?

Как вы думаете, как можно другим способом решить систему уравнений?

Как называется такой метод?

С каким методом решения системы уравнений мы познакомимся?

Чему мы должны научиться на этом уроке?

Деятельность учащихся

Отвечают на вопросы.

Формулируют цели и задачи урока.

Формулируют тему урока.

Изучение нового материала.

Алгоритм решения системы двух уравнений с двумя переменными методом подстановки

Деятельность учителя

Учитель вводит новый способ решения системы двух уравнений с двумя переменными методом подстановки. Объясняет учащимся алгоритм решения методом подстановки. Решает вместе с учащимися у доски задание с помощью алгоритма решения системы уравнений методом подстановки.

Алгоритм:

Выразить из любого уравнения системы одну переменную через другую

2. Подставить в другое уравнение системы вместо этой переменной выражение, полученное на первом шаге;

3. Решить уравнение с одной переменной, полученное на втором шаге;

4. Подставить найденное значение переменной в выражение, полученное на первом шаге;

5. Вычислить значение другой переменной;

6. Записать ответ.

Деятельность учащихся

Учащиеся внимательно слушают объяснения учителя, записывают себе схематично алгоритм. Один из учащихся по желанию выходит к доске, остальные в это время работают в тетрадях.

№ 1.

1 шаг. Из уравнения (1) выразим х:

2 и 3 шаг. Подставим х в уравнение (2):

2х+4у=30

16 + 10у + 4у = 30

14у = 30 – 16

14у = 14

У =14 : 14

У=1

4 и 5 шаг. Найденное значение у=1 подставим в

Получим .

Пара чисел (х;у) будет решением системы, в данном случае (13;1)

Проверка

6 шаг. Ответ: (13;1)

Первичное закрепление материала

Деятельность учителя

Решает вместе с учащимися у доски несколько заданий с помощью алгоритма решения системы уравнений методом подстановки.

Деятельность учащихся

Учащиеся внимательно слушают объяснения учителя. Один из учащихся по желанию выходит к доске, остальные в это время работают в тетрадях.

Ответ: (4;2)

№ 3

Ответ: (2;3)

Самостоятельная работа

Деятельность учителя

Раздает карточки с заданиями. Объясняет в чем заключается задание. Выдает образец решение и ответы, по которым ответственный группы оценит работы учащихся.

Деятельность учащихся

Учащиеся внимательно слушают объяснения учителя. Выполняют задание в тетрадях. Ответственный учащийся каждой группы проверят работу по образцу и оценивает работу.

Вариант 1

Решить систему линейных уравнений графическим методом и методом подстановки

Вариант 2

Решить систему линейных уравнений графическим методом и методом подстановки

Вариант 3

Решить систему линейных уравнений графическим методом и методом подстановки

Вариант 4

Решить систему линейных уравнений графическим методом и методом подстановки

Рефлексия деятельности

Деятельность учителя

Организует фронтальную работу по контролю теоретических знаний и подведение итогов урока. Оценивание деятельности учащихся.

Задает вопросы:

Понравился ли вам метод подстановки?

Какой метод на ваш взгляд проще: графический или метод подстановки?

Все ли осталось понятным?

Деятельность учащихся

Учащиеся высказывают свое мнение.

Называют основные позиции нового материала и как они их усвоили, что не получилось и почему

Домашняя работа

Деятельность учителя

Учитель задает домашнее задание. Объясняет, как его выполнить.

Домашнее задание дифференцированное по выбору:

1)с. 203-204, № 1034.

2)выполнить задание по карточкам, решить двумя способами

3) подготовить презентацию «Способы решения системы уравнений». Изобразить решение системы с помощью графического редактора http://www.yotx.ru и решить систему методом подстановки.

Деятельность учащихся

Записывают домашнее задание к себе в дневник.

Технологическая карта урока

личностные

умение контролировать внимание, уважение к окружающим; развитие познавательного интереса

Приветствует учащихся; делит учащихся на группы, выбирает ответственного в группе, проверяет готовность класса к уроку; озвучивает тему и цели урока

Приветствуют учителя, подготавливаются к уроку, слушают и обсуждают тему урока

Проверка домашнего задания

личностные

умение контролировать внимание, умение находить ошибки в работе, умение оценивать работу, умение уважать мнение товарища, вступать в диалог

Организует проверку домашнего задания,

Учащиеся обмениваются тетрадями, проверяют домашнюю работу своего одноклассника и оценивают

Устный счёт

личностные

умение концентрироваться на своих знаниях, умение выделять главную мысль, умение вступать в диалог, умение уважать мнение товарища

Задает задачи для устного счета, для закрепления основных понятий

Учащиеся самостоятельно анализируют и решают задания

Актуализация знаний

личностные

умение концентрироваться на своих знаниях, умение выделять главную мысль уважать мнение товарища, вступать в диалог

Задает вопросы по предыдущему материалу, проверка знаний и уровня усвояемости изученного материала

Учащиеся участвуют в беседе, отвечают на поставленные вопросы, отвечают основные определения и понятия

Постановка целей, задач урока, мотивация учебной деятельности учащихся

личностные

умение строить логические рассуждения, умение выражать свои мысли в соответствии с поставленными задачами,

Участвует в беседе.

Подводит к проблемной ситуации.

Подводит к постановке целей, задач, теме урока

Участвуют в беседе, отвечают на вопросы, высказывают свое мнение формулирует цели, задачи, тему урока

Изучения нового материала

коммуникативные

выявление проблемы, поиск и оценка способов разрешения конфликта, принятие решения и его реализация;

планирование своей деятельности для решения поставленной задачи

Вводит алгоритм решения системы двух линейных уравнений с двумя неизвестными методом подстановки

Конспект.

Первичное закрепление материала

коммуникативные

выявление проблемы, поиск и оценка способов разрешения конфликта, принятие решения и его реализация;

планирование своей деятельности для решения поставленной задачи

Организация коллективной и индивидуальной работы учащихся

Выполняют задания у доски и в рабочих тетрадях, выполняют по вариантам самостоятельную работу

Самостоятельная работа

личностные

умение концентрироваться на своих знаниях

коммуникативные

выявление проблемы, поиск и оценка способов разрешения конфликта, принятие решения и его реализация

Раздает ответственным в группах карточки по вариантам.

После окончания выдает лист с ответами

Ответственный каждой группы выдает учащимся по кругу карточки с самостоятельной работой. После окончания работы сравнивает ответ с образцом и оценивает работу товарища

Рефлексия деятельности

личностные

нравственно-этическая ориентация

регулятивные

оценка промежуточных результатов и саморегуляция для повышения учебной мотивации

Подводит итоги урока.

Выводит на экран ответы к самостоятельной работе

Проставляют оценки за самостоятельную работу, делают выводы о достигнутых результатах

10.

Домашнее задание

Задает дозированное домашнее задание

1) с. 203-204, № 1034.

2) выполнить задание по карточкам, решить двумя способами.

Записывают домашнее задание в дневник

Решение системы линейных уравнений. Метод подстановки, сложения, графический. Особые случаи, тесты

Тестирование онлайн

Система линейных уравнений

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.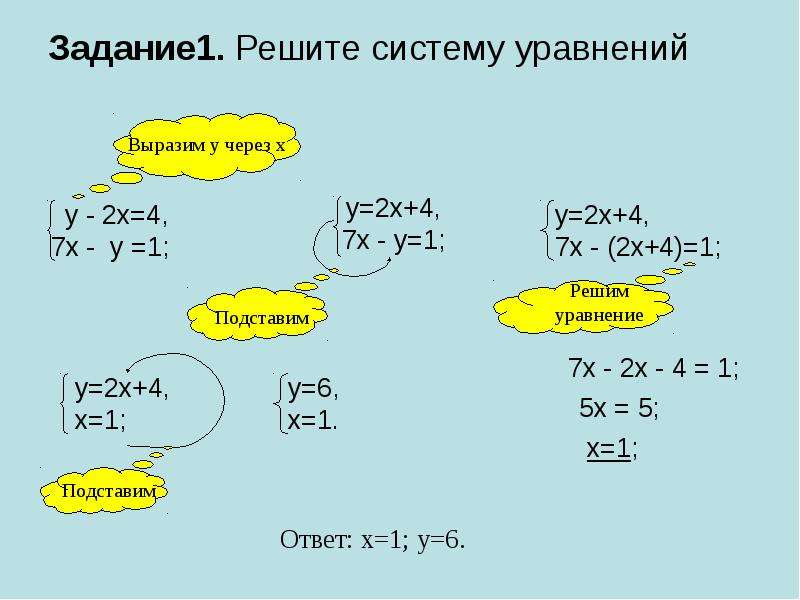

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену , тогда

Переходим к первоначальным переменным

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если , то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.

Решение систем линейных уравнений с использованием подстановки

Системы линейных уравнений:

А

система

линейные уравнения

представляет собой просто набор из двух или более линейных уравнений.

В двух переменных

(

Икс

а также

)

, график системы двух уравнений представляет собой пару прямых на плоскости.

Есть три возможности:

Линии пересекаются в нулевых точках. (Линии параллельны.)
Линии пересекаются ровно в одной точке. (Большинство случаев.)
Прямые пересекаются в бесконечном множестве точек. (Два уравнения представляют собой одну и ту же линию.)

Как решить систему с помощью

Метод замены

Шаг
1
:

Сначала решите одно линейное уравнение относительно
у
с точки зрения
Икс
.
Шаг
2
:

Затем замените это выражение на
у
в другом линейном уравнении. Вы получите уравнение в
Икс
.
Шаг
3
:

Решите это, и у вас будет
Икс
-координата перекрестка.
Шаг
4
:

Затем подключите
Икс
к любому уравнению, чтобы найти соответствующее
у
-координат.

Примечание

:

Если это проще, вы можете начать с решения уравнения для

Икс

с точки зрения

, и — такая же разница!

Пример:

Решите систему

{

Икс

знак равно

Икс

знак равно

Решите второе уравнение относительно

знак равно

—

Икс

Заменять

—

Икс

для

в первом уравнении и решить для

Икс

(

—

Икс

)

знак равно

Икс

—

Икс

знак равно

—

Икс

знак равно

—

Икс

знак равно

Заменять

для

Икс

знак равно

—

Икс

и решить для

знак равно

—

(

)

знак равно

Решение

(

)

Примечание

:

Если линии параллельны, ваш

Икс

-условия будут отменены в шаге

, и вы получите невозможное уравнение, что-то вроде

знак равно

Примечание

:

Если два уравнения представляют одну и ту же строку, все будет отменено на шаге

, и вы получите избыточное уравнение,

знак равно

Решение линейных систем заменой

Метод замены

В этом разделе мы определим полностью алгебраический метод решения систем. Идея состоит в том, чтобы решить одно уравнение относительно одной из переменных и подставить результат в другое уравнение.После выполнения этого шага замены у нас останется одно уравнение с одной переменной, которое можно решить с помощью алгебры. Это называется методом подстановки. Средство решения линейной системы путем решения для одной из переменных и подстановки результата в другое уравнение. , И шаги описаны в следующем примере.

Пример 1: Решить заменой: {2x + y = 73x − 2y = −7.

Решение:

Шаг 1: Решите для любой переменной в любом уравнении.Если вы выберете первое уравнение, вы можете выделить и за один шаг.

Шаг 2: Подставьте выражение −2x + 7 для переменной y в другое уравнение .

Это оставляет вам эквивалентное уравнение с одной переменной, которое можно решить, используя методы, изученные до этого момента.

Шаг 3: Найдите оставшуюся переменную. Чтобы найти x , сначала распределите −2:

Шаг 4: Обратная подстановка После того, как значение переменной найдено, подставьте его обратно в одно из исходных уравнений или их эквивалентных уравнений, чтобы определить соответствующее значение другой переменной. чтобы найти значение другой координаты. Подставьте x = 1 в исходные уравнения или их эквиваленты. Обычно мы используем эквивалентное уравнение, которое мы нашли при выделении переменной на шаге 1.

Решение системы: (1, 5). Обязательно представляйте решение в виде заказанной пары.

Шаг 5: Проверка. Убедитесь, что эти координаты решают оба уравнения исходной системы:

График этой линейной системы следующий:

Метод подстановки для решения систем является полностью алгебраическим методом.Таким образом, графическое отображение линий не требуется.

Ответ: (1, 5)

Пример 2: Решить заменой: {2x − y = 12x − y = 3.

Решение: В этом примере мы видим, что x имеет коэффициент 1 во втором уравнении. Это означает, что его можно изолировать за один этап следующим образом:

Замените 3 + y на x в первом уравнении. Используйте круглые скобки и позаботьтесь о распространении.

Используйте x = 3 + y, чтобы найти x .

Ответ: (9, 6). Чек предоставляется читателю.

Пример 3: Решить заменой: {3x − 5y = 17x = −1.

Решение: В этом примере переменная x уже изолирована. Следовательно, мы можем подставить x = −1 в первое уравнение.

Ответ: (−1, −4).Построение графика этой конкретной системы — хорошее упражнение для сравнения метода подстановки с методом построения графиков для решения систем.

Попробуй! Решить заменой: {3x + y = 48x + 2y = 10.

Ответ: (1, 1)

Алгебраическое решение систем часто требует работы с дробями.

Пример 4: Решить заменой: {2x + 8y = 524x − 4y = −15.

Решение: Начните с решения относительно x в первом уравнении.

Затем подставляем во второе уравнение и решаем относительно y .

Обратная подстановка в уравнение, использованное на этапе замены:

Ответ: (−1/2, 3/4)

Как известно, не все линейные системы имеют только одно упорядоченное парное решение. Напомним, что некоторые системы имеют бесконечно много упорядоченных парных решений, а некоторые не имеют решений.Затем мы исследуем, что происходит при использовании метода подстановки для решения зависимой системы.

Пример 5: Решить заменой: {−5x + y = −110x − 2y = 2.

Решение: Поскольку в первом уравнении есть член с коэффициентом 1, мы решаем сначала решить это уравнение.

Затем замените это выражение на y во втором уравнении.

Этот процесс привел к истинному утверждению; следовательно, уравнение является тождественным, а любое действительное число является решением.Это указывает на то, что система зависима. Одновременные решения принимают форму ( x , mx + b ) или, в данном случае, ( x , 5 x — 1), где x — любое действительное число.

Ответ: (x, 5x − 1)

Чтобы лучше понять предыдущий пример, перепишите оба уравнения в форме пересечения наклона и изобразите их на одном и том же наборе осей.

Мы видим, что оба уравнения представляют одну и ту же линию, и, следовательно, система является зависимой.Теперь исследуем, что происходит при решении противоречивой системы с помощью метода подстановки.

Пример 6: Решить заменой: {−7x + 3y = 314x − 6y = −16.

Решение: Решите относительно и в первом уравнении.

Подставляем во второе уравнение и решаем.

Решение приводит к ложному утверждению. Это указывает на противоречие между уравнением.Нет решения для x и, следовательно, нет решения для системы.

Ответ: Нет решения, Ø

Ложное утверждение указывает на то, что система несовместима, или, говоря геометрическими терминами, что линии параллельны и не пересекаются. Чтобы проиллюстрировать это, определите форму пересечения наклона каждой линии и изобразите их на одном и том же наборе осей.

В форме пересечения наклона легко увидеть, что две линии имеют одинаковый наклон, но разные точки пересечения y .

Попробуй! Решить с помощью замены: {2x − 5y = 34x − 10y = 6.

Ответ: (x, 25x − 35)

Ключевые выводы

Метод подстановки — это полностью алгебраический метод решения системы уравнений.
Метод подстановки требует, чтобы мы решили одну из переменных, а затем подставили результат в другое уравнение. После выполнения шага подстановки результирующее уравнение имеет одну переменную и может быть решено с использованием методов, изученных до этого момента.
Когда значение одной из переменных определено, вернитесь и подставьте его в одно из исходных уравнений или их эквивалентных уравнений, чтобы определить соответствующее значение другой переменной.
Решения систем двух линейных уравнений с двумя переменными, если они существуют, представляют собой упорядоченные пары ( x , y ).
Если процесс решения системы уравнений приводит к ложному утверждению, то система несовместима и решения нет, Ø.
Если процесс решения системы уравнений приводит к истинному утверждению, то система является зависимой и существует бесконечно много решений, которые можно выразить с помощью формы ( x , mx + b ).

Тематические упражнения

Часть A: Метод замещения

Решить заменой.

1. {y = 4x − 1−3x + y = 1

2.{y = 3x − 84x − y = 2

3. {x = 2y − 3x + 3y = −8

4. {x = −4y + 12x + 3y = 12

5. {y = 3x − 5x + 2y = 2

6. {y = x2x + 3y = 10

7. {y = 4x + 1−4x + y = 2

8. {y = −3x + 53x + y = 5

9. {y = 2x + 32x − y = −3

10. {y = 5x − 1x − 2y = 5

11. {y = −7x + 13x − y = 4

12. {x = 6y + 25x − 2y = 0

13. {y = −2−2x − y = −6

14.{x = −3x − 4y = −3

15. {y = −15x + 37x − 5y = 9

16. {y = 23x − 16x − 9y = 0

17. {y = 12x + 13x − 6y = 4

18.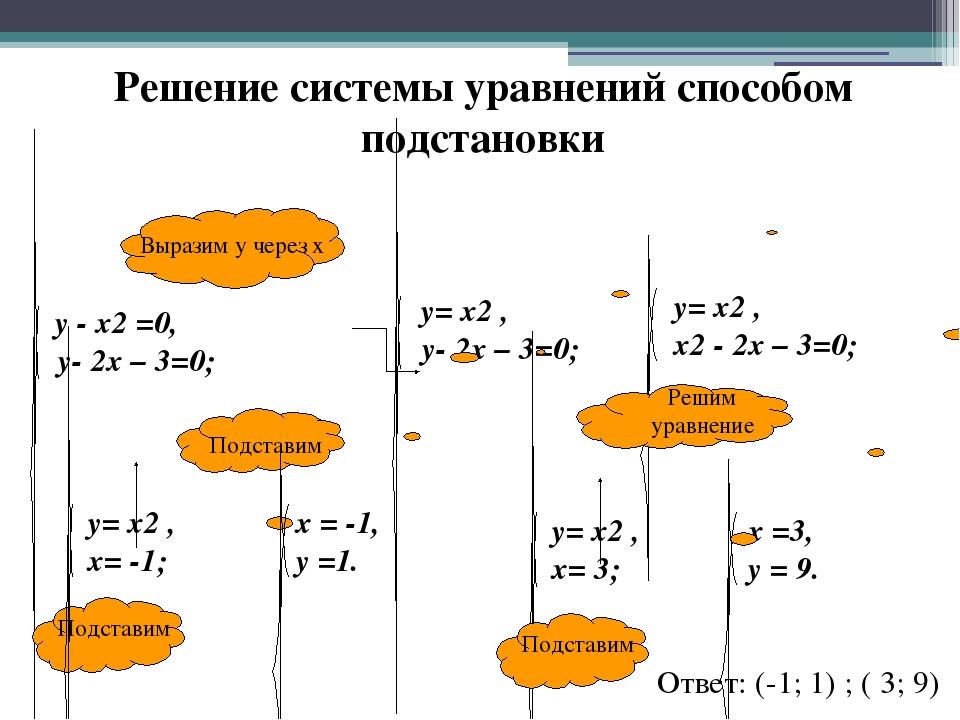 {y = −38x + 122x + 4y = 1

19. {x + y = 62x + 3y = 16

20. {x − y = 3−2x + 3y = −2

21. {2x + y = 23x − 2y = 17

22. {x − 3y = −113x + 5y = −5

23. {x + 2y = −33x − 4y = −2

24. {5x − y = 129x − y = 10

25.{x + 2y = −6−4x − 8y = 24

26. {x + 3y = −6−2x − 6y = −12

27. {−3x + y = −46x − 2y = −2

28. {x − 5y = −102x − 10y = −20

29. {3x − y = 94x + 3y = −1

30. {2x − y = 54x + 2y = −2

31. {−x + 4y = 02x − 5y = −6

32. {3y − x = 55x + 2y = −8

33. {2x − 5y = 14x + 10y = 2

34. {3x − 7y = −36x + 14y = 0

35. {10x − y = 3−5x + 12y = 1

36.{−13x + 16y = 2312x − 13y = −32

37. {13x + 23y = 114x − 13y = −112

38. {17x − y = 1214x + 12y = 2

39. {−35x + 25y = 1213x − 112y = −13

40. {12x = 23yx − 23y = 2

41. {−12x + 12y = 5814x + 12y = 14

42. {x − y = 0 − x + 2y = 3

43. {y = 3x2x − 3y = 0

44. {2x + 3y = 18−6x + 3y = −6

45. {−3x + 4y = 202x + 8y = 8

46. {5x − 3y = −13x + 2y = 7

47.{−3x + 7y = 22x + 7y = 1

48. {y = 3y = −3

49. {x = 5x = −2

50. {y = 4y = 4

Создайте линейную систему и решите ее с помощью метода подстановки.

51. Сумма двух чисел равна 19. Чем больше число, тем на 1 меньше, чем в три раза меньшее.

52. Сумма двух чисел равна 15. Чем больше 3, тем меньше в два раза.

53. Разница двух чисел равна 7, а их сумма равна 1.

54. Разница двух чисел равна 3, а их сумма равна −7.

55. Где на графике −5x + 3y = 30 координата x совпадает с координатой y ?

56. Где на графике 12x − 13y = 1 координата x совпадает с координатой y ?

Часть B: Темы дискуссионной доски

57. Опишите, что движет выбором переменной для решения в начале процесса решения путем подстановки.

58. Обсудите достоинства и недостатки метода замены.

ответы

1: (2, 7)

3: (−5, −1)

5: (2, 6)

9: (x, 2x + 3)

11: (1/2, −5/2)

13: (4, −2)

15: (3, 12/5)

17: (−3, −7/6)

19: (2, 4)

21: (3, −4)

23: (−8/5, −7/10)

25: (х, −12x − 3)

27:

29: (2, −3)

31: (−8, −2)

33: (1/2, 0)

35:

37: (1, 1)

39: (−11/10, −2/5)

41: (-1/2, 3/4)

43: (0, 0)

45: (−4, 2)

47: (-1/5, 1/5)

49:

51: два числа — 5 и 14.

53: два числа — 4 и −3.

55: (−15, −15)

3.3: Алгебраические методы решения систем

Решите систему уравнений, используя метод подстановки

В последних парах разделов мы проверили, что упорядоченные пары являются решениями систем, и использовали графики, чтобы классифицировать, сколько решений имеет система двух линейных уравнений. Что, если нам не дана точка пересечения или она не очевидна из графика? Можем ли мы еще найти решение этой системы? Конечно, можно, используя алгебру!

В этом разделе мы изучим метод подстановки для нахождения решения системы линейных уравнений с двумя переменными.На протяжении всего курса мы использовали подстановку по-разному, например, когда мы использовали формулы для площади треугольника и простых процентов. Мы подставили значения, которые мы знали, в формулу, чтобы найти значения, которых мы не знали. Идея аналогична применительно к системам решения, в этом процессе всего несколько этапов. Сначала вы решите одну переменную, а затем подставите это выражение в другое уравнение. Чтобы понять, что это означает, давайте начнем с примера.

Пример

Найдите значение x для этой системы.

Уравнение A: \ (4x + 3y = −14 \)

Уравнение B: \ (y = 2 \)

[show-answer q = ”478211 ″] Показать решение [/ show-answer]
[hidden-answer a =” 478211 ″] Задача требует решения для x . Уравнение B дает вам значение y , \ (y = 2 \), поэтому вы можете подставить 2 в уравнение A для y.

\ (\ begin {array} {r} 4x + 3y = −14 \\ y = 2 \, \, \, \, \, \, \, \ end {array} \)

Подставьте \ (y = 2 \) в уравнение A.

\ (4x + 3 \ влево (2 \ вправо) = — 14 \)

Упростите и решите уравнение для x.

\ (\ begin {array} {r} 4x + 6 = −14 \\ 4x = −20 \\ x = −5 \, \, \, \ end {array} \)

Ответ

\ (х = -5 \)

[/ hidden-answer]

Вы можете заменить значение переменной, даже если это выражение. Вот пример.

Пример

Решите относительно x и y .

Уравнение A: \ (y + x = 3 \)

Уравнение B: \ (x = y + 5 \)

[показать-ответ q = ”300993 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 300993 ″] Цель метода подстановки — переписать одно из уравнений в терминах одной переменной. Уравнение B говорит нам, что \ (y + 5 \) в уравнение A для x .

\ (\ begin {array} {l} y + x = 3 \\ x = y + 5 \ end {array} \)

Подставьте \ (y + 5 \) в уравнение A для x .

\ (\ begin {array} {r} y + x = 3 \\ y + \ left (y + 5 \ right) = 3 \ end {array} \)

Упростите и решите уравнение для y.

\ (\ begin {array} {r} 2y + 5 = \, \, \, \, 3 \\\ подчеркивание {−5 \, \, \, \, \, — 5} \\ 2y = −2 \ \ y = −1 \ end {массив} \)

Теперь найдите x , подставив это значение для y в любое уравнение, и решите относительно x . Здесь мы будем использовать уравнение А.

\ (\ begin {array} {r} y + x = 3 \\ — 1 + x = 3 \\\ подчеркивание {+1 \, \, \, \, \, \, \, \, \, + 1 } \\ x = 4 \ end {array} \)

Наконец, проверьте решение \ (y = −1 \), подставив эти значения в каждое из исходных уравнений.

\ (\ begin {array} {r} y + x = 3 \\ — 1 + 4 = 3 \\ 3 = 3 \\\ text {TRUE} \ end {array} \)

\ (\ begin {array} {l} x = y + 5 \\ 4 = −1 + 5 \\ 4 = 4 \\\ text {TRUE} \ end {array} \)

Ответ

\ (у = -1 \)

Решение: \ ((4, −1) \).

[/ hidden-answer]

Помните, решение системы уравнений должно быть решением каждого из уравнений внутри системы. Упорядоченная пара \ ((4, −1) \) действительно работает для обоих уравнений, поэтому вы знаете, что это также решение системы.

Давайте посмотрим на другой пример, замена которого включает свойство распределения.

Пример

Решите относительно x и y .

\ (\ begin {array} {l} y = 3x + 6 \\ — 2x + 4y = 4 \ end {array} \)

[раскрыть-ответ q = ”240040 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 240040 ″] Выберите уравнение, которое будет использоваться для замены.

Первое уравнение говорит вам, как выразить y через x , поэтому имеет смысл подставить 3 x + 6 во второе уравнение для y .

\ (\ begin {array} {l} y = 3x + 6 \\ — 2x + 4y = 4 \ end {array} \)

Подставьте \ (3x + 6 \) вместо y во второе уравнение.

\ (\ begin {array} {r} −2x + 4y = 4 \\ — 2x + 4 \ left (3x + 6 \ right) = 4 \ end {array} \)

Упростите и решите уравнение для x.

\ (\ begin {array} {r} −2x + 12x + 24 = 4 \, \, \, \, \, \, \, \\ 10x + 24 = 4 \, \, \, \, \, \ , \, \\\ подчеркивание {−24 \, \, — 24 \, \, \, \,} \\ 10x = −20 \\ x = −2 \, \, \, \ end {array} \)

Чтобы найти y , подставьте это значение вместо x обратно в одно из исходных уравнений.

\ (\ begin {array} {l} y = 3x + 6 \\ y = 3 \ left (−2 \ right) +6 \\ y = −6 + 6 \\ y = 0 \ end {array} \)

Проверьте решение \ (y = 0 \), подставив его в каждое из исходных уравнений.

\ (\ begin {array} {l} y = 3x + 6 \\ 0 = 3 \ left (−2 \ right) +6 \\ 0 = −6 + 6 \\ 0 = 0 \\\ text {TRUE} \ конец {массив} \)

\ (\ begin {array} {r} −2x + 4y = 4 \\ — 2 \ left (−2 \ right) +4 \ left (0 \ right) = 4 \\ 4 + 0 = 4 \\ 4 = 4 \\\ текст {ИСТИНА} \ end {массив} \)

Ответ

\ (у = 0 \)

Решение: (−2, 0).

[/ hidden-answer]

В приведенных выше примерах одно из уравнений уже было дано нам в терминах переменной x или y . Это позволило нам быстро подставить это значение в другое уравнение и найти одно из неизвестных.

Иногда вам, возможно, придется сначала переписать одно из уравнений в терминах одной из переменных, прежде чем вы сможете произвести замену. В приведенном ниже примере вам сначала нужно изолировать одну из переменных, прежде чем вы сможете заменить ее в другое уравнение.

Пример

Решите относительно x и y .

\ (\ begin {array} {r} 2x + 3y = 22 \\ 3x + y = 19 \ end {array} \)

[показать-ответ q = ”344538 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 344538 ″] Выберите уравнение, которое будет использоваться для замены. Второе уравнение,

\ (3x + y = 19 \), можно легко переписать в терминах y , поэтому имеет смысл начать с этого.

\ (\ begin {array} 2x + 3y = 22 \\ 3x + y = 19 \ end {array} \)

Записываем \ (3x + y = 19 \) в виде y .

\ (\ begin {array} 3x + y = 19 \\ y = 19–3x \ end {array} \)

Подставьте \ (19–3x \) вместо y в другое уравнение.

\ (\ begin {array} {r} 2x + 3y = 22 \\ 2x + 3 (19–3x) = 22 \ end {array} \)

Упростите и решите уравнение для x.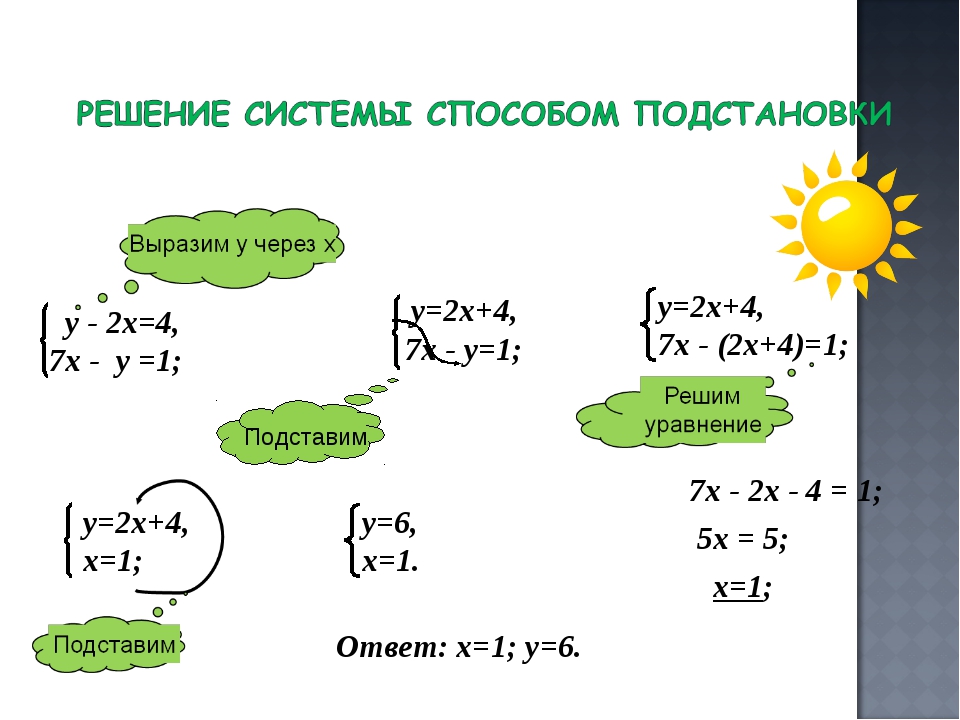

\ (\ begin {array} {r} 2x + 57–9x = 22 \, \, \, \, \\ — 7x + 57 = 22 \, \, \, \, \\ — 7x = −35 \\ х = 5 \, \, \, \, \, \, \, \ end {array} \)

Подставьте \ (x = 5 \) обратно в одно из исходных уравнений, чтобы найти y.

\ (\ begin {array} {r} 3x + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ 3 \ left (5 \ right) + у = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ 15 + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ y = 19−15 \\ y = 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ end {массив} \)

Проверьте оба решения, подставив их в каждое из исходных уравнений.

\ (\ begin {array} {r} 2x + 3y = 22 \\ 2 (5) +3 \ left (4 \ right) = 22 \\ 10 + 12 = 22 \\ 22 = 22 \\\ text {TRUE } \\\\ 3x + y = 19 \\ 3 \ left (5 \ right) + 4 = 19 \\ 19 = 19 \\\ text {TRUE} \ end {array} \)

Ответ

\ (у = 4 \)

Решение (5, 4).

[/ hidden-answer]

В следующем видео вам будет показан пример решения системы двух уравнений с использованием метода подстановки.

Элемент YouTube был исключен из этой версии текста. Вы можете просмотреть его онлайн здесь: pb.libretexts.org/ba/?p=80

Если бы вы выбрали другое уравнение для начала в предыдущем примере, вы все равно смогли бы найти такое же решение. Это действительно вопрос предпочтений, потому что иногда решение для переменной приводит к необходимости работать с дробями.По мере того, как вы приобретете больший опыт в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.

Распознавать системы уравнений, не имеющие решения или бесконечное количество решений

Когда мы изучили методы решения линейных уравнений с одной переменной, мы обнаружили, что некоторые уравнения не имеют решений, а другие имеют бесконечное количество решений. Мы снова увидели это поведение, когда начали описывать решения систем уравнений с двумя переменными.

Вспомните этот пример из модуля 1 для решения линейных уравнений с одной переменной:

Решите относительно x . \ (12 + 2x – 8 = 7x + 5–5x \)

\ (\ Displaystyle \ begin {array} {l} 12 + 2x-8 = 7x + 5-5x \\\, \, \, \, \, \, \, \, \, \, \, \, \ , \, 2x + 4 = 2x + 5 \ end {array} \)

\ (\ begin {array} {l} \, \, \, \, \, \, \, \, \, \, \, \, 2x + 4 = 2x + 5 \\\, \, \, \ , \, \, \, \, \ underline {-2x \, \, \, \, \, \, \, \, \, \, — 2x \, \, \, \, \, \, \, \,} \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, 4 = \, 5 \ end {array} \)

Это ложное утверждение подразумевает, что не существует решений этого уравнения.Таким же образом вы можете увидеть такой результат, если воспользуетесь методом подстановки, чтобы найти решение системы линейных уравнений с двумя переменными. В следующем примере вы увидите пример системы двух уравнений, не имеющей решения.

Пример

Решите относительно x и y .

\ (\ begin {array} {l} y = 5x + 4 \\ 10x − 2y = 4 \ end {array} \)

[показать-ответ q = ”787022 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 787022 ″] Поскольку первое уравнение равно \ (5x + 4 \) для y во втором уравнение.

\ (\ begin {array} {r} y = 5x + 4 \\ 10x − 2y = 4 \, \, \, \, \, \, \, \, \, \, \, \, \\ 10x– 2 \ left (5x + 4 \ right) = 4 \, \, \, \, \, \, \, \, \, \, \, \, \ end {array} \)

Разверните выражение слева.

\ (10x – 10x – 8 = 4 \)

Объедините похожие члены в левой части уравнения.

\ (- 8 = 4 \).

\ (\ begin {array} {r} 0–8 = 4 \\ — 8 = 4 \ end {array} \)

Ответ

Утверждение \ (- 8 = 4 \) неверно, поэтому решения нет.

[/ hidden-answer]

Вы получаете ложное утверждение \ (- 8 = 4 \). Что это значит? График этой системы проливает свет на то, что происходит.

Прямые параллельны, они никогда не пересекаются, и у этой системы линейных уравнений нет решения. Обратите внимание, что результат \ (- 8 = 4 \) — это , а не решение. Это просто ложное утверждение, и оно указывает на то, что не существует решения .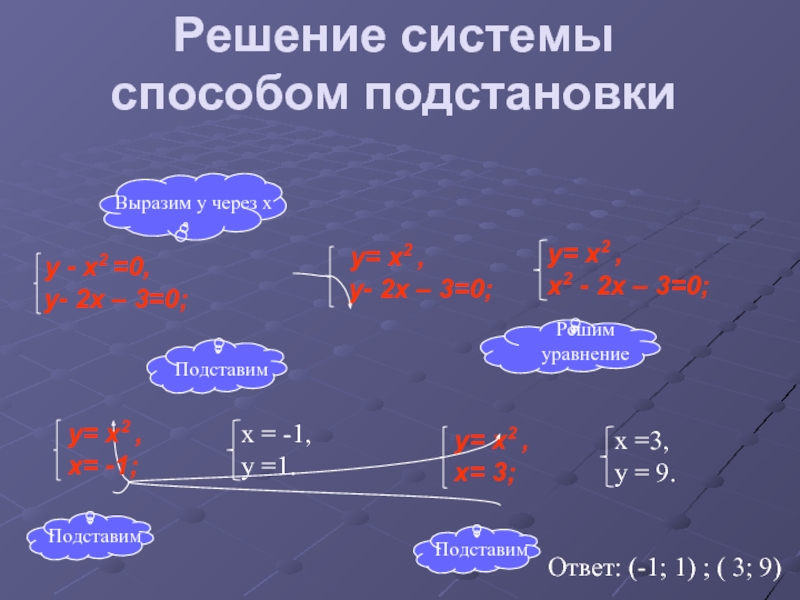

Мы также видели линейные уравнения с одной переменной и системы уравнений с двумя переменными, которые имеют бесконечное количество решений.В следующем примере вы увидите, что происходит, когда вы применяете метод подстановки к системе с бесконечным числом решений.

Пример

Решите относительно x и y.

\ (\ begin {array} {l} \, \, \, y = −0,5x \\ 9y = −4,5x \ end {array} \)

[show-answer q = ”683508 ″] Показать решение [/ show-answer]
[hidden-answer a =” 683508 ″]

Подставляя -0,5 x вместо y во втором уравнении, вы получаете следующее:

\ (\ begin {array} {r} 9y = −4.5x \\ 9 (−0.5x) = — 4.5 \, \, \, \\ — 4.5x = −4.5x \ end {array} \)

[/ hidden-answer]

На этот раз вы получите верное утверждение: \ (- 4,5x = −4,5x \). Но что означает такой ответ? Опять же, построение графиков может помочь вам разобраться в этой системе.

Эта система состоит из двух уравнений, которые представляют одну и ту же линию; две линии коллинеарны. Каждая точка на линии будет решением системы, и поэтому метод подстановки дает верное утверждение.В этом случае существует бесконечное количество решений.

В следующем видео вы увидите пример решения системы, которая имеет бесконечное количество решений.

Элемент YouTube был исключен из этой версии текста. Вы можете просмотреть его онлайн здесь: pb.libretexts.org/ba/?p=80

В следующем видео вы увидите пример решения системы уравнений, не имеющей решений.

Элемент YouTube был исключен из этой версии текста.Вы можете просмотреть его онлайн здесь: pb.libretexts.org/ba/?p=80

Решите систему уравнений методом исключения

Метод исключения для решения систем линейных уравнений использует добавочное свойство равенства. Вы можете добавить одно и то же значение к каждой стороне уравнения, чтобы исключить один из переменных членов. В этом методе вам может потребоваться, а может и не потребоваться сначала умножить члены в одном уравнении на число. Сначала мы рассмотрим примеры, в которых умножение не требуется для использования метода исключения.В следующем разделе вы увидите примеры использования умножения после того, как познакомитесь с идеей метода исключения.

С помощью этого метода легче показать, чем рассказать, поэтому давайте сразу же рассмотрим несколько примеров.

Если сложить два уравнения,

\ (x + y = 8 \) вместе, смотрите, что происходит.

\ (\ Displaystyle \ begin {array} {l} \, \, \, \, \, xy = \, — 6 \\\ подчеркивание {+ \, x + y = \, \, \, 8} \\ \, 2x + 0 \, = \, \, \, \, 2 \ end {array} \)

Вы исключили член y , и это уравнение можно решить, используя методы решения уравнений с одной переменной.

Давайте посмотрим, как эта система решается методом исключения.

Пример

Используйте устранение, чтобы решить систему.

\ (\ begin {array} {r} x – y = −6 \\ x + y = \, \, \, \, 8 \ end {array} \)

[показать-ответ q = ”403819 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 403819 ″] Добавьте уравнения.

\ (\ Displaystyle \ begin {array} {r} xy = \, \, — 6 \\ + \ underline {\, \, x + y = \, \, \, \, \, 8} \\\, \, \, \, \, \, 2x \, \, \, \, \, = \, \, \, \, \, \, 2 \ end {array} \)

Решите относительно x .

\ (\ begin {array} {r} 2x = 2 \\ x = 1 \ end {array} \)

Подставьте \ (x = 1 \) в одно из исходных уравнений и решите относительно y .

\ (\ begin {array} {l} x + y = 8 \\ 1 + y = 8 \\\, \, \, \, \, \, \, \, \, \, y = 8–1 \ \\, \, \, \, \, \, \, \, \, \, y = 7 \ end {array} \)

Обязательно проверьте свой ответ в обоих уравнениях!

\ (\ begin {array} {r} x – y = −6 \\ 1–7 = −6 \\ — 6 = −6 \\\ text {TRUE} \\\\ x + y = 8 \\ 1 + 7 = 8 \\ 8 = 8 \\\ текст {ИСТИНА} \ end {array} \)

Проверяйте ответы.

Ответ

Решение (1, 7).

[/ hidden-answer]

К сожалению, не все системы справляются с этим легко. Как насчет такой системы, как \ (- 3x + y = 2 \). Если вы сложите эти два уравнения вместе, никакие переменные не будут исключены.

\ (\ Displaystyle \ begin {array} {l} \, \, \, \, 2x + y = 12 \\\ подчеркивание {-3x + y = \, \, \, 2} \\ — x + 2y = 14 \ end {array} \)

Но вы хотите исключить переменную. Итак, давайте добавим противоположность одного из уравнений к другому уравнению.Это означает умножение каждого члена в одном из уравнений на -1, чтобы знак каждого члена был противоположным.

\ (\ begin {array} {l} \, \, \, \, 2x + \, \, y \, = 12 \ rightarrow2x + y = 12 \ rightarrow2x + y = 12 \\ — 3x + \, \, y \ , = 2 \ rightarrow− \ left (−3x + y \ right) = — (2) \ rightarrow3x – y = −2 \\\, \, \, \, 5x + 0y = 10 \ end {array} \)

Вы удалили переменную y , и теперь проблема может быть решена.

В следующем видео описывается аналогичная проблема, при которой можно исключить одну переменную, сложив два уравнения вместе.

Элемент YouTube был исключен из этой версии текста. Вы можете просмотреть его онлайн здесь: pb.libretexts.org/ba/?p=80

Осторожность! Когда вы добавляете противоположность одного целого уравнения к другому, не забудьте изменить знак КАЖДОГО члена с обеих сторон уравнения. Это очень распространенная ошибка.

Пример

Используйте устранение, чтобы решить систему.

\ (\ begin {array} {r} 2x + y = 12 \\ — 3x + y = 2 \, \, \, \ end {array} \)

[Показать-ответ q = ”702178 ″] Показать решение [/ Показать-ответ]
[hidden-answer a =” 702178 ″] Переменную y можно исключить, если к одному из уравнений добавить противоположное. другое уравнение.

\ (\ begin {array} {r} 2x + y = 12 \\ — 3x + y = 2 \, \, \, \ end {array} \)

Перепишите второе уравнение как противоположное.

Доп. Решите относительно x .

\ (\ begin {array} {r} 2x + y = 12 \, \\ 3x – y = −2 \\ 5x = 10 \, \\ x = 2 \, \, \, \, \ end {array} \)

Подставьте \ (y = 2 \) в одно из исходных уравнений и решите относительно y .

\ (\ begin {array} {r} 2 \ left (2 \ right) + y = 12 \\ 4 + y = 12 \\ y = 8 \, \, \, \ end {array} \)

Обязательно проверьте свой ответ в обоих уравнениях!

\ (\ begin {array} {r} 2x + y = 12 \\ 2 \ left (2 \ right) + 8 = 12 \\ 4 + 8 = 12 \\ 12 = 12 \\\ text {TRUE} \\ \\ — 3x + y = 2 \\ — 3 \ left (2 \ right) + 8 = 2 \\ — 6 + 8 = 2 \\ 2 = 2 \\\ текст {ИСТИНА} \ end {array} \)

Проверяйте ответы.

Ответ

Решение (2, 8).

[/ hidden-answer]

Ниже приведены еще два примера, показывающих, как решать линейные системы уравнений с использованием исключения.

Пример

Используйте устранение, чтобы решить систему.

\ (\ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = \, 25 \ end {array} \)

[раскрыть-ответ q = ”438400 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 438400 ″] Обратите внимание на коэффициенты каждой переменной в каждом уравнении.Если вы сложите эти два уравнения, член x будет удален, поскольку \ (- 2x + 2x = 0 \).

\ (\ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = \, 25 \ end {array} \)

Сложите и решите относительно и .

\ (\ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = 25 \, \\ 8y = 24 \, \\ y = 3 \, \, \, \, \ end {массив } \)

Подставьте \ (y = 3 \) в одно из исходных уравнений.

\ (\ begin {array} {r} 2x + 5y = 25 \\ 2x + 5 \ left (3 \ right) = 25 \\ 2x + 15 = 25 \\ 2x = 10 \\ x = 5 \, \, \, \ end {массив} \)

Проверить решения.

\ (\ begin {array} {r} −2x + 3y = −1 \\ — 2 \ left (5 \ right) +3 \ left (3 \ right) = — 1 \\ — 10 + 9 = −1 \ \ -1 = -1 \\\ текст {ИСТИНА} \\\\ 2x + 5y = 25 \\ 2 \ left (5 \ right) +5 \ left (3 \ right) = 25 \\ 10 + 15 = 25 \\ 25 = 25 \\\ текст {ИСТИНА} \ end {array} \)

Проверяйте ответы.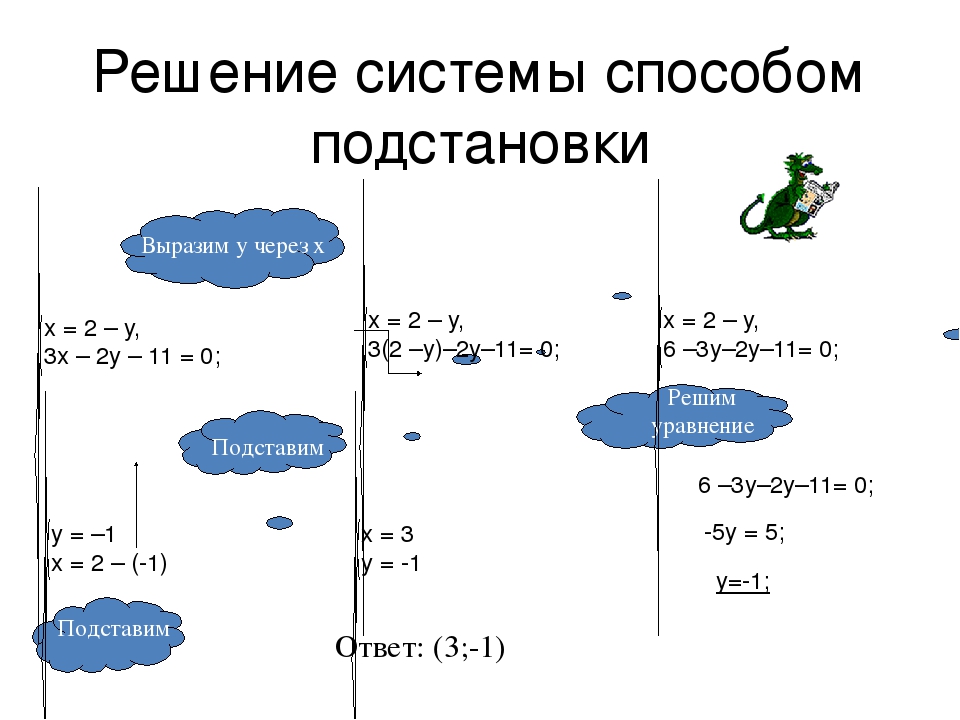

Ответ

Решение: (5, 3).

[/ hidden-answer]

Пример

Используйте исключение, чтобы найти x и y.

\ (\ begin {array} {r} 4x + 2y = 14 \\ 5x + 2y = 16 \ end {array} \)

[показать-ответ q = ”776093 ″] Показать решение [/ показать-ответ]
[скрытый-ответ a =” 776093 ″] Обратите внимание на коэффициенты каждой переменной в каждом уравнении.Вам нужно будет добавить противоположное одному из уравнений, чтобы исключить переменную y , как \ (2y + \ left (−2y \ right) = 0 \).

\ (\ begin {array} {r} 4x + 2y = 14 \\ 5x + 2y = 16 \ end {array} \)

Замените одно из уравнений на противоположное, сложите и решите для x .

\ (\ begin {array} {r} 4x + 2y = 14 \, \, \, \, \\ — 5x – 2y = −16 \\ — x = −2 \, \, \, \\ x = 2 \, \, \, \, \, \, \, \ end {array} \)

Подставьте \ (x = 2 \) в одно из исходных уравнений и решите относительно y .

\ (\ begin {array} {r} 4x + 2y = 14 \\ 4 \ left (2 \ right) + 2y = 14 \\ 8 + 2y = 14 \\ 2y = 6 \, \, \, \\ y = 3 \, \, \, \ end {array} \)

Ответ

Решение: (2, 3).

[/ hidden-answer]

Проверьте последний пример — подставьте (2, 3) в оба уравнения. Получается два верных утверждения: 14 = 14 и 16 = 16!

Обратите внимание, что вы могли бы использовать противоположное первому уравнению, а не второе уравнение, и получить тот же результат.

Распознавать системы, у которых нет решения или бесконечное количество решений

Как и в случае с методом подстановки, метод исключения иногда удаляет и v ariables, и вы получаете либо истинное, либо ложное утверждение. Напомним, ложное утверждение означает, что решения нет.

Давайте посмотрим на пример.

Пример

Решите относительно x и y.

\ (\ begin {array} {r} -x – y = -4 \\ x + y = 2 \, \, \, \, \ end {array} \)

[раскрыть-ответ q = ”101540 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 101540 ″] Добавьте уравнения, чтобы исключить член x .

\ (\ begin {array} {r} -x – y = -4 \\\ underline {x + y = 2 \, \, \,} \\ 0 = −2 \ end {array} \)

Ответ

Нет решения.

[/ hidden-answer]

Построение этих линий показывает, что они являются параллельными линиями и как таковые не имеют общих точек, подтверждая отсутствие решения.

Если обе переменные исключены и у вас осталось истинное утверждение, это означает, что существует бесконечное количество упорядоченных пар, которые удовлетворяют обоим уравнениям.По сути, уравнения — это одна и та же линия.

Пример

Решите относительно x и y .

\ (\ begin {array} {r} x + y = 2 \, \, \, \, \\ — x − y = -2 \ end {array} \)

[показать-ответ q = ”328100 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 328100 ″] Добавьте уравнения, чтобы исключить член x .

\ (\ begin {array} {r} x + y = 2 \, \, \, \, \\\ подчеркивание {-x − y = -2} \\ 0 = 0 \, \, \, \, \ , \ end {array} \)

Ответ

Существует бесконечное количество решений.

[/ hidden-answer]

Построение этих двух уравнений поможет проиллюстрировать, что происходит.

Решите систему уравнений, когда необходимо умножение, чтобы исключить переменную

Много раз сложение уравнений или добавление противоположности одного из уравнений не приведет к удалению переменной. Посмотрите на систему ниже.

\ (\ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} \)

Если вы сложите приведенные выше уравнения или сложите противоположное одному из уравнений, вы получите уравнение, в котором по-прежнему есть две переменные.Итак, давайте теперь сначала воспользуемся свойством умножения равенства. Вы можете умножить обе части одного уравнения на число, которое позволит вам исключить ту же переменную из другого уравнения.

Мы делаем это с умножением. Обратите внимание, что первое уравнение содержит член 4 y , а второе уравнение содержит член y . Если вы умножите второе уравнение на −4, то при сложении обоих уравнений переменные y в сумме дадут 0.

В следующем примере показаны все шаги по поиску решения для этой системы.

Пример

Решите относительно x и y .

Уравнение A:
\ (3х + 4у = 52 \)

Уравнение B:
\ (5x + y = 30 \)

[show-answer q = ”815377 ″] Показать решение [/ show-answer]
[hidden-answer a =” 815377 ″] Найдите термины, которые можно исключить. В уравнениях нет членов x или y с одинаковыми коэффициентами.

\ (\ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} \)

Умножьте второе уравнение на \ (- 4 \), чтобы у них был одинаковый коэффициент.

\ (\ begin {array} {l} \, \, \, \, \, \, \, \, \, 3x + 4y = 52 \\ — 4 \ left (5x + y \ right) = — 4 \ left (30 \ right) \ end {array} \)

Перепишите систему и добавьте уравнения.

\ (\ begin {array} {r} 3x + 4y = 52 \, \, \, \, \, \, \, \\ — 20x – 4y = −120 \ end {array} \)

Решите относительно x .

\ (\ begin {array} {l} −17x = -68 \\\, \, \, \, \, \, \, \, \, \, x = 4 \ end {array} \)

Подставьте \ (x = 4 \) в одно из исходных уравнений, чтобы найти y .

\ (\ begin {array} {r} 3x + 4y = 52 \\ 3 \ left (4 \ right) + 4y = 52 \\ 12 + 4y = 52 \\ 4y = 40 \\ y = 10 \ end { множество}\)

Проверьте свой ответ.

\ (\ begin {array} {r} 3x + 4y = 52 \\ 3 \ left (4 \ right) +4 \ left (10 \ right) = 52 \\ 12 + 40 = 52 \\ 52 = 52 \ \\ текст {ИСТИНА} \\\\ 5x + y = 30 \\ 5 \ left (4 \ right) + 10 = 30 \\ 20 + 10 = 30 \\ 30 = 30 \\\ текст {TRUE} \ end {множество}\)

Проверяйте ответы.

Ответ

Решение (4, 10).

[/ hidden-answer]

Осторожность! Когда вы используете умножение для исключения переменной, вы должны умножить КАЖДЫЙ член в уравнении на выбранное вами число. Забыть умножить каждый член — распространенная ошибка.

Есть и другие способы решить эту систему. Вместо умножения одного уравнения, чтобы исключить переменную при добавлении уравнений, вы могли бы умножить обоих уравнений на разные числа.

На этот раз удалим переменную x . Умножьте уравнение A на 5 и уравнение B на \ (- 3 \).

Пример

Решите для x и y .

\ (\ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} \)

[показать-ответ q = ”40585 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 40585 ″] Найдите термины, которые можно исключить.В уравнениях нет членов x или y с одним и тем же коэффициентом.

\ (\ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} \)

Чтобы использовать метод исключения, вы должны создать переменные с одинаковым коэффициентом — тогда вы можете их исключить. Умножьте верхнее уравнение на 5.

\ (\ begin {array} {r} 5 \ left (3x + 4y \ right) = 5 \ left (52 \ right) \\ 5x + y = 30 \, \, \, \, \, \, \ , \, \, \, \, \, \\ 15x + 20y = 260 \, \, \, \, \, \, \\ 5x + y = 30 \, \, \, \, \, \, \ , \, \, \ end {массив} \)

Теперь умножьте нижнее уравнение на −3.

\ (\ begin {array} {r} 15x + 20y = 260 \, \, \, \, \, \, \, \, \\ — 3 (5x + y) = — 3 (30) \\ 15x + 20y = 260 \, \, \, \, \, \, \, \, \\ — 15x – 3y = −90 \, \, \, \, \, \, \, \ end {array} \)

Затем сложите уравнения и решите относительно y .

\ (\ begin {array} {r} 15x + 20y = 260 \\ — 15x – 3y = \, — 90 \\ 17y = 170 \\ y = \, \, \, 10 \ end {array} \)

Подставьте \ (y = 10 \) в одно из исходных уравнений, чтобы найти x .

\ (\ begin {array} {r} 3x + 4y = 52 \\ 3x + 4 \ left (10 \ right) = 52 \\ 3x + 40 = 52 \\ 3x = 12 \\ x = 4 \, \ , \, \ end {array} \)

Вы пришли к тому же решению, что и раньше.

Ответ

Решение (4, 10).

[/ hidden-answer]

Эти уравнения были умножены на 5 и \ (- 3 \) соответственно, потому что это дало вам члены, которые в сумме дают 0. Не забудьте умножить все члены уравнения.

В следующем видео вы увидите пример использования метода исключения для решения системы уравнений.

Элемент YouTube был исключен из этой версии текста.Вы можете просмотреть его онлайн здесь: pb.libretexts.org/ba/?p=80

Можно использовать метод исключения с умножением и получить результат, который не указывает никаких решений или бесконечно много решений, точно так же, как с другими методами, которые мы изучили для поиска решений систем. В следующем примере вы увидите систему, которая имеет бесконечно много решений.

Пример

Решите относительно x и y .

Уравнение A:
\ (х-3у = -2 \)

Уравнение B:
\ (- 2х + 6у = 4 \)

[show-answer q = ”815327 ″] Показать решение [/ show-answer]
[hidden-answer a =” 815327 ″] Найдите термины, которые можно исключить. В уравнениях нет членов x или y с одинаковыми коэффициентами.

\ (\ begin {array} {r} x-3y = -2 \\ — 2x + 6y = 4 \ end {array} \)

Умножьте первое уравнение на \ (2 \), чтобы члены x уменьшились.

\ (\ begin {array} {l} \, \, \, \, \, \, \, \, \, 2 \ left (x-3y \ right) = 2 \ left (-2 \ right) \ \ -2x + 6y = 4 \ end {array} \)

Перепишите систему и добавьте уравнения.

\ (\ begin {array} {r} 2x-6y = -4 \\ — 2x + 6y = 4 \\ 0x + 0y = 0 \\\, \, \, \, \, \, \, \, 0 = 0 \ конец {массив} \)

Вам знакомо такое решение? Это представляет собой решение всех действительных чисел для линейных уравнений, и это представляет то же самое, когда вы получаете такой результат с системами.Если мы решим оба этих уравнения относительно y, вы увидите, что это одно и то же уравнение.

Решите уравнение A относительно y:

\ (\ begin {array} {r} x-3y = -2 \\ — 3y = -x-2 \\ y = \ frac {1} {3} x + \ frac {2} {3} \ end { множество}\)

Решите уравнение B относительно y:

\ (\ begin {array} -2x + 6y = 4 \\ 6y = 2x + 4 \\ y = \ frac {2} {6} x + \ frac {4} {6} \ end {array} \)

Уменьшите дроби, разделив числитель и знаменатель обеих дробей на 2:

\ (y = \ frac {1} {3} + \ frac {2} {3} \)

Оба уравнения одинаковы, если записаны в форме пересечения наклона, и поэтому набором решений для системы являются все действительные числа.

Ответ

Решение: все x и y могут быть действительными числами.

[/ hidden-answer]

В следующем видео метод исключения используется для решения системы уравнений. Обратите внимание, что сначала нужно умножить одно из уравнений на отрицательное. Вдобавок у этой системы есть бесконечное количество решений.

Элемент YouTube был исключен из этой версии текста. Вы можете просмотреть его здесь: pb.libretexts.org / ba /? p = 80

Решение систем уравнений подстановкой

Решение линейной системы с двумя переменными с помощью построения графиков хорошо работает, когда решение состоит из целочисленных значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод. Мы рассмотрим еще два метода решения системы линейных уравнений , которые более точны, чем построение графиков. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение, чтобы найти вторую переменную.Напомним, что мы можем решать только одну переменную за раз, поэтому метод подстановки является одновременно ценным и практичным.

Как сделать: дана система двух уравнений с двумя переменными, решите, используя метод подстановки.

Решите одно из двух уравнений относительно одной из переменных через другую.
Подставьте выражение для этой переменной во второе уравнение, затем решите для оставшейся переменной.
Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной.Если возможно, запишите решение в виде упорядоченной пары.
Проверьте решение в обоих уравнениях.

Пример 3: Решение системы уравнений с двумя переменными подстановкой

Решите следующую систему уравнений путем подстановки.

[латекс] \ begin {массив} {l} \ text {} -x + y = -5 \ hfill \\ \ text {} 2x — 5y = 1 \ hfill \ end {array} [/ latex]

Решение

Сначала мы решим первое уравнение для [латекс] y [/ латекс].

[латекс] \ begin {массив} {l} -x + y = -5 \ hfill \\ \ text {} y = x — 5 \ hfill \ end {array} [/ latex]

Теперь мы можем заменить выражение [latex] x — 5 [/ latex] на [latex] y [/ latex] во втором уравнении.

[латекс] \ begin {array} {l} \ text {} 2x — 5y = 1 \ hfill \\ 2x — 5 \ left (x — 5 \ right) = 1 \ hfill \\ \ text {} 2x — 5x + 25 = 1 \ hfill \\ \ text {} -3x = -24 \ hfill \\ \ text {} x = 8 \ hfill \ end {array} [/ latex]

Теперь мы подставляем [latex] x = 8 [/ latex] в первое уравнение и решаем относительно [latex] y [/ latex].

[латекс] \ begin {array} {l} — \ left (8 \ right) + y = -5 \ hfill \\ \ text {} y = 3 \ hfill \ end {array} [/ latex]

Наше решение — [латекс] \ left (8,3 \ right) [/ latex].

Проверьте решение, подставив [latex] \ left (8,3 \ right) [/ latex] в оба уравнения.

[латекс] \ begin {array} {llll} -x + y = -5 \ hfill & \ hfill & \ hfill & \ hfill \\ — \ left (8 \ right) + \ left (3 \ right) = — 5 \ hfill & \ hfill & \ hfill & \ text {True} \ hfill \\ 2x — 5y = 1 \ hfill & \ hfill & \ hfill & \ hfill \\ 2 \ left (8 \ right) -5 \ left ( 3 \ right) = 1 \ hfill & \ hfill & \ hfill & \ text {True} \ hfill \ end {array} [/ latex]

Попробуй 3

Решите следующую систему уравнений путем подстановки.

[латекс] \ begin {array} {l} x = y + 3 \ hfill \\ 4 = 3x — 2y \ hfill \ end {array} [/ latex]

Вопросы и ответы

Можно ли методом подстановки решить любую линейную систему с двумя переменными?

Да, но этот метод работает лучше всего, если одно из уравнений содержит коэффициент 1 или –1, чтобы нам не приходилось иметь дело с дробями.

Методы замены и добавления

Результаты обучения

Используйте метод подстановки, чтобы найти решение (я) системы двух линейных уравнений.
Используйте метод сложения, чтобы найти решение (я) системы линейных уравнений.

Решение систем уравнений подстановкой

Решение линейной системы с двумя переменными с помощью построения графиков хорошо работает, когда решение состоит из целочисленных значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод.Мы рассмотрим еще два метода решения системы линейных уравнений , которые более точны, чем построение графиков. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение, чтобы найти вторую переменную. Напомним, что мы можем решать только одну переменную за раз, поэтому метод подстановки является одновременно ценным и практичным.

Как сделать: дана система двух уравнений с двумя переменными, решите, используя метод подстановки.

Решите одно из двух уравнений относительно одной из переменных через другую.
Подставьте выражение для этой переменной во второе уравнение, затем решите для оставшейся переменной.
Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
Проверьте решение в обоих уравнениях.

Пример: решение системы уравнений с двумя переменными подстановкой

Решите следующую систему уравнений путем подстановки.

[латекс] \ begin {align} -x + y & = — 5 \\ 2x-5y & = 1 \ end {align} [/ latex]

Показать решение

Сначала мы решим первое уравнение для [латекс] y [/ латекс].

[латекс] \ begin {align} -x + y & = — 5 \\ y & = x — 5 \ end {align} [/ latex]

Теперь мы можем заменить выражение [latex] x — 5 [/ latex] на [latex] y [/ latex] во втором уравнении.

[латекс] \ begin {align} 2x — 5y & = 1 \\ 2x — 5 \ left (x — 5 \ right) & = 1 \\ 2x — 5x + 25 & = 1 \\ -3x & = — 24 \\ x & = 8 \ end {align} [/ latex]

Теперь мы подставляем [latex] x = 8 [/ latex] в первое уравнение и решаем относительно [latex] y [/ latex].

[латекс] \ begin {align} — \ left (8 \ right) + y & = — 5 \\ y & = 3 \ end {align} [/ latex]

Наше решение — [латекс] \ left (8,3 \ right) [/ latex].

Проверьте решение, подставив [latex] \ left (8,3 \ right) [/ latex] в оба уравнения.

[латекс] \ begin {align} -x + y & = — 5 \\ — \ left (8 \ right) + \ left (3 \ right) & = — 5 && \ text {True} \\ [3mm] 2x — 5y & = 1 \\ 2 \ left (8 \ right) -5 \ left (3 \ right) & = 1 && \ text {True} \ end {align} [/ latex]

Попробуйте

Вы можете использовать онлайн-инструмент построения графиков, который поможет вам решить систему уравнений путем подстановки.Мы будем использовать следующую систему, чтобы показать вам, как:

[латекс] \ begin {align} x & = y + 3 \\ 4 & = 3x — 2y \ end {align} [/ latex]

Сначала решите оба уравнения относительно y:

[латекс] \ begin {align} y & = x-3 \\ y & = \ frac {3} {2} x — 2 \ end {align} [/ latex]

Теперь введите [latex] x-3 = \ frac {3} {2} x — 2 [/ latex] в Desmos. Вы увидите, что Desmos предоставил вам [латекс] x = -2 [/ latex].

Теперь вы можете заменить [latex] x = -2 [/ latex] в оба уравнения. Если вы получите одинаковый результат для обоих, вы нашли решение для упорядоченной пары.Попробуйте.

Показать решение

[латекс] \ влево (-2, -5 \ вправо) [/ латекс]

Вопросы и ответы

Можно ли методом подстановки решить любую линейную систему с двумя переменными?

Следующее видео длится ~ 10 минут и представляет собой мини-урок по использованию метода подстановки для решения системы линейных уравнений.Мы представляем три разных примера, а также используем инструмент построения графиков, чтобы подытожить решение для каждого примера.

Решение систем уравнений с двумя переменными методом сложения

Третий метод решения систем линейных уравнений — это метод сложения , этот метод также называется методом исключения . В этом методе мы складываем два члена с одинаковой переменной, но с противоположными коэффициентами, так что сумма равна нулю.Конечно, не все системы созданы с двумя членами одной переменной, имеющими противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения умножением, чтобы одна переменная была исключена сложением.

Как: решить систему уравнений методом сложения.

Запишите оба уравнения с переменными x и y слева от знака равенства и константами справа.
Запишите одно уравнение над другим, выровняв соответствующие переменные.Если одна из переменных в верхнем уравнении имеет коэффициент, противоположный той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную. Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
Решите полученное уравнение для оставшейся переменной.
Подставьте это значение в одно из исходных уравнений и решите для второй переменной.
Проверьте решение, подставив значения в другое уравнение.

Пример: решение системы методом сложения

Решите данную систему уравнений сложением.

[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \ end {align} [/ latex]

Показать решение

Оба уравнения уже установлены равными константе. Обратите внимание, что коэффициент [латекс] x [/ латекс] во втором уравнении, –1, противоположен коэффициенту [латекс] x [/ латекс] в первом уравнении, 1.Мы можем сложить два уравнения, чтобы исключить [latex] x [/ latex] без умножения на константу.

[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \\ \ hline 3y & = 2 \ end {align} [/ latex]

Теперь, когда мы удалили [latex] x [/ latex], мы можем решить полученное уравнение для [latex] y [/ latex].

[латекс] \ begin {align} 3y & = 2 \\ y & = \ dfrac {2} {3} \ end {align} [/ latex]

Затем мы подставляем это значение для [latex] y [/ latex] в одно из исходных уравнений и решаем для [latex] x [/ latex].

[латекс] \ begin {align} -x + y & = 3 \\ -x + \ frac {2} {3} & = 3 \\ -x & = 3- \ frac {2} {3} \\ -x & = \ frac {7} {3} \\ x & = — \ frac {7} {3} \ end {align} [/ latex]

Решение этой системы — [латекс] \ left (- \ frac {7} {3}, \ frac {2} {3} \ right) [/ latex].

Проверьте решение в первом уравнении.

[латекс] \ begin {align} x + 2y & = — 1 \\ \ left (- \ frac {7} {3} \ right) +2 \ left (\ frac {2} {3} \ right) & = \\ — \ frac {7} {3} + \ frac {4} {3} & = \\ — \ frac {3} {3} & = \\ -1 & = — 1 && \ text {True} \ end { align} [/ латекс]

Анализ решения

Мы получаем важное представление о системах уравнений, глядя на графическое представление.Посмотрите на график ниже, чтобы увидеть, что уравнения пересекаются в решении. Нам не нужно спрашивать, может ли быть второе решение, потому что наблюдение за графиком подтверждает, что система имеет ровно одно решение.

Пример: использование метода сложения, когда требуется умножение одного уравнения

Решите данную систему уравнений методом сложения .

[латекс] \ begin {align} 3x + 5y & = — 11 \\ x — 2y & = 11 \ end {align} [/ latex]

Показать решение

Добавление этих уравнений в представленном виде не устраняет переменную.Однако мы видим, что в первом уравнении есть [latex] 3x [/ latex], а во втором уравнении — [latex] x [/ latex]. Итак, если мы умножим второе уравнение на [latex] -3, \ text {} [/ latex], термины x прибавятся к нулю.

[латекс] \ begin {align} x — 2y & = 11 \\ -3 \ left (x — 2y \ right) & = — 3 \ left (11 \ right) && \ text {Умножаем обе стороны на} -3 \ \ -3x + 6y & = — 33 && \ text {Использовать свойство распределения}. \ end {align} [/ latex]

А теперь добавим их.

[латекс] \ begin {align} 3x + 5y & = — 11 \\ −3x + 6y & = — 33 \\ \ hline 11y & = — 44 \\ y & = — 4 \ end {align} [/ latex]

На последнем этапе мы подставляем [latex] y = -4 [/ latex] в одно из исходных уравнений и решаем для [latex] x [/ latex].

[латекс] \ begin {align} 3x + 5y & = — 11 \\ 3x + 5 \ left (-4 \ right) & = — 11 \\ 3x — 20 & = — 11 \\ 3x & = 9 \\ x & = 3 \ end {align} [/ latex]

Наше решение — упорядоченная пара [латекс] \ left (3, -4 \ right) [/ latex]. Проверьте решение в исходном втором уравнении.

[латекс] \ begin {align} x — 2y & = 11 \\ \ left (3 \ right) -2 \ left (-4 \ right) & = 3 + 8 \\ & = 11 && \ text {True} \ конец {align} [/ latex]

Попробуйте

Решите систему уравнений сложением.

[латекс] \ begin {align} 2x — 7y & = 2 \\ 3x + y & = — 20 \ end {align} [/ latex]

Показать решение

[латекс] \ влево (-6, -2 \ вправо) [/ латекс]

Пример: использование метода сложения, когда требуется умножение обоих уравнений

Решите данную систему уравнений с двумя переменными сложением.

[латекс] \ begin {align} 2x + 3y & = — 16 \\ 5x — 10y & = 30 \ end {align} [/ latex]

Показать решение

Одно уравнение имеет [латекс] 2x [/ латекс], а другое — [латекс] 5x [/ латекс].Наименьшее общее кратное — [latex] 10x [/ latex], поэтому нам придется умножить оба уравнения на константу, чтобы исключить одну переменную. Давайте удалим [latex] x [/ latex], умножив первое уравнение на [latex] -5 [/ latex], а второе уравнение на [latex] 2 [/ latex].

[латекс] \ begin {align} -5 \ left (2x + 3y \ right) & = — 5 \ left (-16 \ right) \\ -10x — 15y & = 80 \\ [3 мм] 2 \ left (5x — 10y \ right) & = 2 \ left (30 \ right) \\ 10x — 20y & = 60 \ end {align} [/ latex]

Затем мы складываем два уравнения.

[латекс] \ begin {align} -10x-15y & = 80 \\ 10x-20y & = 60 \\ \ hline -35y & = 140 \\ y & = — 4 \ end {align} [/ latex]

Подставьте [латекс] y = -4 [/ latex] в исходное первое уравнение.

[латекс] \ begin {align} 2x + 3 \ left (-4 \ right) & = — 16 \\ 2x — 12 & = — 16 \\ 2x & = — 4 \\ x & = — 2 \ end {align} [ / латекс]

Решение: [латекс] \ left (-2, -4 \ right) [/ latex]. Проверьте это в другом уравнении.

[латекс] \ begin {align} 5x — 10y & = 30 \\ 5 \ left (-2 \ right) -10 \ left (-4 \ right) & = 30 \\ -10 + 40 & = 30 \\ 30 & = 30 \ end {align} [/ latex]

Пример: использование метода сложения в системах уравнений, содержащих дроби

Решите данную систему уравнений с двумя переменными сложением.

[латекс] \ begin {align} \ frac {x} {3} + \ frac {y} {6} & = 3 \\ [1 мм] \ frac {x} {2} — \ frac {y} {4 } & = 1 \ end {align} [/ latex]

Показать решение

Сначала очистите каждое уравнение от дробей, умножив обе части уравнения на наименьший общий знаменатель.

[латекс] \ begin {align} 6 \ left (\ frac {x} {3} + \ frac {y} {6} \ right) & = 6 \ left (3 \ right) \\ [1 мм] 2x + y & = 18 \\ [3 мм] 4 \ left (\ frac {x} {2} — \ frac {y} {4} \ right) & = 4 \ left (1 \ right) \\ [1 мм] 2x-y & = 4 \ end {align} [/ latex]

Теперь умножьте второе уравнение на [latex] -1 [/ latex], чтобы мы могли исключить x .

[латекс] \ begin {align} -1 \ left (2x-y \ right) & = — 1 \ left (4 \ right) \\ [1 мм] -2x + y & = — 4 \ end {align} [/ латекс]

Добавьте два уравнения, чтобы исключить x , и решите полученное уравнение относительно y .

[латекс] \ begin {align} 2x + y & = 18 \\ −2x + y & = — 4 \\ \ hline 2y & = 14 \\ y & = 7 \ end {align} [/ latex]

Подставьте [латекс] y = 7 [/ латекс] в первое уравнение.

[латекс] \ begin {align} 2x + \ left (7 \ right) & = 18 \\ 2x & = 11 \\ x & = \ frac {11} {2} \\ & = 7.5 \ end {align} [/ latex]

Решение: [латекс] \ left (\ frac {11} {2}, 7 \ right) [/ latex]. Проверьте это в другом уравнении.

[латекс] \ begin {align} \ frac {x} {2} — \ frac {y} {4} & = 1 \\ [1 мм] \ frac {\ frac {11} {2}} {2} — \ frac {7} {4} & = 1 \\ [1 мм] \ frac {11} {4} — \ frac {7} {4} & = 1 \\ [1 мм] \ frac {4} {4} & = 1 \ end {align} [/ latex]

Попробуйте

Решите систему уравнений сложением.

[латекс] \ begin {align} 2x + 3y & = 8 \\ 3x + 5y & = 10 \ end {align} [/ latex]

Показать решение

[латекс] \ влево (10, -4 \ вправо) [/ латекс]

в следующем видео мы представляем больше примеров того, как использовать метод сложения (исключения) для решения системы двух линейных уравнений.

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

Промежуточная алгебра
Урок 19: Решение систем линейных уравнений
в двух переменных

WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня

Цели обучения

По завершении этого руководства вы сможете:

Узнайте, является ли упорядоченная пара решением системы линейных уравнений
в
две переменные или нет.
Решите систему линейных уравнений от двух переменных с помощью построения графиков.
Решите систему линейных уравнений с двумя переменными заменой
метод.
Решите систему линейных уравнений с двумя переменными методом исключения
метод.

Введение

В этом уроке мы будем специально рассматривать
системы, которые имеют
два уравнения и две неизвестные. Урок 20: Решение систем
Линейный
Уравнения в трех переменных будут охватывать системы, которые имеют три
уравнения
и три неизвестных. Мы рассмотрим их решение трех разных
способы: построение графиков, метод подстановки и метод исключения.
Это приведет нас к решению проблем со словами с системами, которые
быть
показано в Урок 21: Системы линейных уравнений и задачи
Решение .
Вот где мы должны ответить на печально известный вопрос, когда мы будем использовать
это? Но сначала мы должны научиться работать с системами в
Генеральная.
Вот почему на этом этапе мы используем общие переменные, такие как x и y . Если
вы знаете, как это решить в целом, тогда, когда у вас есть конкретный
проблема
что вы решаете, где переменные принимают значение, такое как время или
Деньги
(две вещи, которых нам, кажется, никогда не бывает достаточно), вы будете готовы к
идти. Итак, давайте посмотрим на
системы в целом, чтобы подготовить нас к решению предстоящих проблем
из нас.

Учебник

Система линейных уравнений

Система линейных уравнений состоит из двух или более линейных
уравнения, которые
решаются одновременно.

В этом руководстве мы рассмотрим системы, которые
имеют только два линейных
уравнения и две неизвестные.

В общем, решение системы двух переменных
заказанный
пара, которая делает ОБЕИХ уравнениями истинными.

Другими словами, здесь пересекаются два графика,
что у них есть
в общем. Итак, если упорядоченная пара является решением одного уравнения,
но
не другой, то это НЕ решение системы.

Согласованная система — это система, в которой
хотя бы одно решение.

Несогласованная система — это система, имеющая
нет решения .

Уравнения системы зависимы если ВСЕ
решения
одного уравнения являются решениями другого уравнения. В
Другие
словами, они в итоге оказываются той же строкой .

Уравнения системы независимы , если
они не разделяют
ВСЕ решения . У них может быть одна общая черта, только не
все
их.

Одно решение
Если система с двумя переменными имеет одно решение, это
заказанный
пара, которая является решением ОБЕИХ уравнений. Другими словами,
когда
вы вставляете значения упорядоченной пары, она делает ОБА уравнения
ПРАВДА.

Если вы получите одно решение для окончательного ответа, будет
эта система непротиворечива или непоследовательна?
Если вы сказали «последовательный», похлопайте себя по плечу!

Если вы получите одно решение для окончательного ответа, будет
уравнения быть зависимыми или независимыми?
Если вы сказали независимый, вы правы!

График ниже иллюстрирует систему двух уравнений.
и два неизвестных
у которого есть одно решение:

Нет решения
Если две линии параллельны друг другу, они будут
никогда не пересекаются.
Значит, у них нет ничего общего. В этом
ситуация
у вас не будет решения.

Если окончательного ответа нет, — это
эта система непротиворечива или непоследовательна?
Если вы сказали непоследовательно, вы правы!

Если вы не получите окончательного ответа, будет
уравнения быть зависимыми или независимыми?
Если вы сказали независимый, вы правы!

График ниже иллюстрирует систему двух уравнений.
и два неизвестных
без решения:

Бесконечный
Решения
Если две линии в конечном итоге лежат друг на друге, тогда
Там есть
бесконечное количество решений. В этой ситуации они
было бы
в конечном итоге будут одной строкой, поэтому любое решение, которое будет работать в одном
уравнение
будет работать в другом.

Если вы получите бесконечное количество решений для
ваш окончательный ответ, я с
эта система непротиворечива или непоследовательна?
Если вы сказали «последовательный», вы правы!

Если вы получите бесконечное количество решений для
ваш окончательный ответ, будет
уравнения быть зависимыми или независимыми?
Если вы сказали иждивенец, вы правы!

График ниже иллюстрирует систему двух уравнений.
и два неизвестных
имеющий бесконечное количество решений:

Пример
1 : Определите, является ли каждая упорядоченная пара решением
из
система.
(3, -1) и (0, 2)

Давайте проверим упорядоченную пару (3, -1) в первом
уравнение:

* Вставка 3 для x и -1 для y

* Истинное утверждение

Пока все хорошо, (3, -1) является решением
первое уравнение x + y = 2.

Теперь давайте проверим (3, -1) во втором уравнении:

* Вставка 3 для x и -1 для y

* Истинное утверждение

Эй, мы закончили с еще одним верным утверждением, которое
означает, что (3, -1) является
также решение второго уравнения x — y = 4.

Вот большой вопрос, является ли (3, -1) решением
данная система ?????
Поскольку это было решение ОБЕИХ уравнений в системе,
Затем это
это решение всей системы.

Теперь поместим (0, 2) в первое уравнение:

* Вставка 0 для x и 2 для y
* Истинное заявление

Это истинное утверждение, поэтому (0, 2) является решением
первое уравнение x + y = 2.

Наконец, поместим (0,2) во второе уравнение:

* Вставка 0 для x и 2 для y
* Ложное заявление

На этот раз мы получили ложное заявление, вы знаете, что это
средства.
(0, 2) НЕ является решением второго уравнения x — y = 4.

Вот большой вопрос, является ли (0, 2) решением
данная система ?????
Поскольку это не было решением ОБЕИХ уравнений в
система, то
это не решение всей системы.

Три способа Решение систем линейных
Уравнений с двумя переменными

Шаг 1. Постройте первое уравнение.

Шаг 2: Изобразите второе уравнение на
та же координата
система как первая.

Вы изобразите второе уравнение так же, как и любое другое.
уравнение.
Обратитесь к первому шагу, если вам нужно рассмотреть различные способы
график
линия.

Отличие в том, что на такой же ставишь
система координат
как первый. Это как две задачи с графиком в одной.

Шаг 3. Найдите решение.

Если две линии пересекаются в одном месте , то
точка
перекресток — решение системы.

Если две линии параллельны , то они никогда не
пересекаются, так что
нет решения.

Если у две строки лежат друг на друге , то
они
та же строка , и у вас есть бесконечное количество решений. .
В этом случае вы можете записать любое уравнение как решение
указывать
это одна и та же линия.

Шаг 4: Проверьте предложенный заказанный
парное решение в
ОБА уравнения.

Предлагаемое решение можно подключить к ОБА
уравнения. Если
это делает ОБЕИЕ уравнения истинными, тогда у вас есть решение
система.

Если хотя бы одно из них становится ложным, вам нужно идти
назад и повторить
проблема.

Пример
2 : Решите систему уравнений, построив график.

* Вставка 0 для y для x -int
* x -intercept

Перехват x — (3, 0).

y -перехват

* Вставка 0 для x для y -int
* y -intercept

Перехват y — (0, 3).

Найдите другого
решение, положив x = 1.

* Вставка 1 для x

Другое решение — (1, 2).

Решения:

х	y	(х, у)
3	0	(3, 0)
0	3	(0, 3)
1	2	(1, 2)

Построение упорядоченных парных решений и построение
линия:

* Вставка 0 для y для x -int
* x -intercept

Перехват x — (1, 0).

Y-перехват

* Вставка 0 для x для y -int

* инверсия мульт. на -1 — это div.
по -1

* y -перехват

Перехват y — (0, -1).

Найдите другого
решение, положив x = 2.

* Вставка 2 для x
* Сумма, обратная сумме 2, является вспомогательной. 2

* инверсия мульт. на -1 это div
по -1

Другое решение — (2, 1).

Решения:

х	y	(х, у)
1	0	(1, 0)
0	-1	(0, -1)
2	1	(2, 1)

Построение упорядоченных парных решений и построение
линия:

Мы должны спросить себя, есть ли место, где
две линии пересекаются,
и если да, то где?

Ответ — да, они пересекаются в (2, 1).

Вы обнаружите, что если вы подключите заказанную пару (2, 1)
в ОБЕИХ уравнения
исходной системы, что это решение ОБЕИХ из них.

Решение этой системы — (2, 1).

Пример
3 : Решите систему уравнений, построив график.

* Вставка 0 для y для x -int
* x -intercept

Перехват x — (5, 0).

y -перехват

* Вставка 0 для x для y -int

* y -перехват

Перехват y — (0, 5).

Найдите другого
решение, положив x = 1.

* Вставка 1 для x
* Сумма, обратная сумме 1, является вспомогательной. 1

Другое решение — (1, 4).

Решения:

х	y	(х, у)
5	0	(5, 0)
0	5	(0, 5)
1	4	(1, 4)

Построение упорядоченных парных решений и построение
линия:

* Вставка 0 для y для x -int
* Сумма, обратная сумме 3, является sub.3

* инверсия мульт. на -1 — это div.
по -1

* x -перехват

Перехват x — (3, 0).

y -перехват

* Вставка 0 для x для y -int
* y -intercept

Перехват y — (0, 3).

Найдите другого
решение, положив x = 1.

* Вставка 1 для x

Другое решение — (1, 2).

Решения:

х	y	(х, у)
3	0	(3, 0)
0	3	(0, 3)
1	2	(1, 2)

Построение упорядоченных парных решений и построение
линия:

Мы должны спросить себя, есть ли место, где
две линии пересекаются,
и если да, то где?

Ответ — нет, они не пересекаются.Мы
иметь два параллельных
линий.

Нет заказанных пар для проверки.

Ответа нет.

Решить методом подстановки

Шаг 1. При необходимости упростите.

Это может включать в себя такие вещи, как удаление () и
удаление фракций.

Чтобы удалить (): просто используйте свойство distributive.

Чтобы удалить дроби: поскольку дроби — это еще один способ
написать деление,
а обратное деление — умножение, дробь удаляется на
умножение
обе стороны ЖК-дисплеем всех ваших фракций.

Шаг 2. Решите одно уравнение для
любая переменная.

Неважно, какое уравнение вы используете или какое
переменная, которую вы выбираете
решить для.

Вы хотите сделать это как можно проще.Если один
уравнений
уже решено для одной из переменных, это быстро и легко
способ
идти.

Если вам нужно найти переменную, попробуйте выбрать
тот, у которого есть
1 как коэффициент. Таким образом, когда вы идете решать это, вы
не будет
делить на число и рисковать работать с
доля
(фу !!).

Шаг 3. Замените то, что вы получаете, на
шаг 2 в
другое уравнение.

Вот почему он называется методом подстановки.
Убедись в том, что
вы подставляете выражение в ДРУГОЕ уравнение, то, которое вы
не сделал
использовать на шаге 2.

Это даст вам одно уравнение с одним неизвестным.

Шаг 4. Решите для
оставшаяся переменная.

Шаг 5: Решите для второго
Переменная.

Если вы нашли значение переменной на шаге
4, что означает
два уравнения имеют одно решение. Вставьте значение, найденное в
шаг 4 в любое уравнение задачи и решить для другого
Переменная.

Если ваша переменная выпадает, и у вас есть ЛОЖЬ
заявление, что означает
ваш ответ не решение.

Если ваша переменная выпадает и у вас есть ИСТИНА
заявление, что означает
ваш ответ — бесконечные решения, которые были бы уравнением
линия.

Шаг 6: Проверьте предложенный заказанный
парное решение в
ОБЕ исходные уравнения.

Предлагаемое решение можно подключить к ОБА
уравнения. Если
это делает ОБЕИХ уравнения истинными, тогда у вас есть решение
система.

Если хотя бы одно из них становится ложным, вам нужно идти
назад и повторить
проблема.

Пример
4 : Решите систему уравнений заменой
метод.

Оба эти уравнения уже упрощены.
Нет необходимости в работе
делать здесь.

Обратите внимание, что второе уравнение уже решено для y .
Мы можем использовать его на этом этапе.

Неважно, какое уравнение или какую переменную вы
выбрать решение
для. Но в ваших интересах, чтобы это было так просто, как
возможный.

Второе уравнение, решенное относительно y :

* Решено для y

Подставьте выражение 2 x + 4 вместо y в первое уравнение и решите относительно x :
(когда вы вставляете такое выражение, это похоже на то, как вы подключаете
в номере вашей переменной)

* Под.2 x + 4 дюйма
для y
* Расст. -5 через ()
* Объединить похожие термины

* Обратное от sub. 20 добавлено 20

* Значение, обратное div. by -7 есть мульт.
по -7

Вставьте -5 для x в
уравнение в
шаг 2, чтобы найти значение y .

* Вставка -5 для x

Вы обнаружите, что если вы подключите заказанную пару (-5,
-6) в ОБЕИХ
уравнения исходной системы, что это решение ОБЕИХ из
их.

(-5, -6) — это решение нашей системы.

Пример
5 : Решите систему уравнений заменой
метод.

Оба эти уравнения уже упрощены.
Нет необходимости в работе
делать здесь.

На этот раз проблема была не так хороша для нас, мы
придется
проделайте небольшую работу, чтобы решить одно уравнение для одной из наших переменных.

Неважно, какое уравнение или какую переменную вы
выбрать решение
для.Просто будьте проще.

Так как x в первом
уравнение имеет
коэффициент 1, это означало бы, что нам не нужно было бы делить на
номер
решить эту проблему и рискнуть работать с дробями
(УРА !!)
Самый простой способ — решить первое уравнение для x ,
и мы определенно хотим выбрать легкий путь. Ты бы не был
неправильный
чтобы выбрать другое уравнение и / или решить для y, снова вы хотите
чтобы сделать его максимально простым.

Решая первое уравнение для x , получаем:

* Обратное от sub. 2 y добавлено 2 y

* Решено для x

Подставьте выражение 5 + 2 y вместо x во второе уравнение и решите относительно y :
(когда вы вставляете такое выражение, это похоже на то, как вы подключаете
в номере вашей переменной)

* Под.5 + 2 y для x

* Переменная выпала И ложь

Погодите, а где наш
переменная go ????

Как упоминалось выше, если ваша переменная выпадает, и вы
иметь оператор FALSE,
тогда решения нет. Если бы мы изобразили эти два графика,
они будут параллельны друг другу.

Поскольку мы не получили значение для y ,
там
здесь нечего подключать.

Нет заказанных пар для проверки.

Ответа нет.

Решить методом исключения

Этот метод также известен как сложение или
исключение добавлением
метод.

Шаг 1. Упростите и поместите оба
уравнения в виде
A x + B y = C, если необходимо.

Это может включать в себя такие вещи, как удаление () и
удаление фракций.

Чтобы удалить (): просто используйте свойство distributive.

Шаг 2: Умножьте один или оба
уравнения по числу
который при необходимости создаст противоположные коэффициенты для x или y .

Забегая вперед, мы добавим эти два
уравнения вместе .
В этом процессе нам нужно убедиться, что одна из переменных падает
вне,
оставив нам одно уравнение и одно неизвестное. Единственный способ, которым мы можем
гарантия, что если мы добавляем противоположности . Сумма
противоположности
равно 0.

Если ни одна из переменных не выпадает, мы застреваем с
уравнение с
две неизвестные, которые неразрешимы.

Неважно, какую переменную вы выберете для удаления
вне.
Вы хотите, чтобы это было как можно проще. Если переменная уже
имеет противоположные коэффициенты, чем при добавлении двух уравнений
все вместе.
В противном случае вам нужно умножить одно или оба уравнения на число.
что
создаст противоположные коэффициенты в одной из ваших переменных.Ты
может
думайте об этом как о ЖК-дисплее. Подумайте, какой номер оригинал
коэффициенты
оба входят и соответственно умножают каждое отдельное уравнение.
Делать
убедитесь, что одна переменная положительна, а другая отрицательна, прежде чем вы
Добавлять.

Например, если у вас есть 2 x в одном уравнении
и 3 x в другом уравнении, мы могли бы
умножать
первое уравнение на 3 и получаем 6 x и
в
второе уравнение на -2, чтобы получить -6 x .
Так
когда вы собираетесь сложить эти два вместе, они выпадут.

Сложите два уравнения вместе.

Переменная с противоположными коэффициентами будет
выпадать из этого
шаг, и у вас останется одно уравнение с одним неизвестным.

Шаг 4: Найдите оставшуюся переменную.

Решите уравнение, найденное на шаге 3, для переменной
что осталось.

Если вам нужен обзор по этому поводу, перейдите к руководству
7: Линейные уравнения с одной переменной.

Если выпадают обе переменные и вы получаете ЛОЖЬ
заявление, что означает
ваш ответ не решение.

Если выпадают обе переменные и у вас есть ИСТИНА
заявление, что означает
ваш ответ — бесконечные решения, которые были бы уравнением
линия.

Шаг 5: Найдите вторую переменную.

Шаг 6: Проверьте предложенный заказанный
парное решение в
ОБЕ исходные уравнения.

Предлагаемое решение можно подключить к ОБА
уравнения.Если это
делает ОБЕИХ уравнения истинными, тогда у вас есть решение
система.

Если хотя бы одно из них становится ложным, вам нужно идти
назад и повторить
проблема.

Пример
6 : Решите систему уравнений методом исключения
метод.

В этом уравнении полно неприятных дробей.
Мы можем упростить
оба уравнения, умножив каждое в отдельности на его ЖК-дисплей, как
вы можете сделать это, когда работаете с одним уравнением. До тех пор, как вы
проделайте то же самое с обеими сторонами уравнения, оставив обе стороны
равны друг другу.

Умножая каждое уравнение на соответствующий ЖК-дисплей, мы
получить:

* Мног. по ЖК из 15

* Мульт. по ЖК из 6

Опять же, вы хотите сделать это так просто, как
возможный.Обратите внимание, как
коэффициенты как для , так и для равны
3. Мы
должны быть противоположности, поэтому, если один из них равен 3, а другой -3,
Они
будут взаимно отменять друг друга, когда мы перейдем к их добавлению.

Если бы мы сложили их вместе, как сейчас, мы бы
закончить с
одно уравнение и две переменные, ничего бы не выпало. И мы
было бы
не смогу ее решить.

Предлагаю умножить второе уравнение на -1,
это будет
создайте -3 перед x , и мы будем
имеют
наши противоположности.

Обратите внимание, что мы могли бы так же легко умножить первое
уравнение на -1
а не второй. В любом случае работа будет выполнена.

Умножая второе уравнение на -1, получаем:

* Мног.обе стороны 2-го ур. по -1

* y х
иметь противоположное
коэффициенты

* Обратите внимание, что и
выпал

* Инверсная по отношению к мульт.на 3 — div. по 3

Вы можете выбрать любое уравнение, используемое в этой задаче, чтобы
вставьте найденное значение x .

Я выбираю подключить 11 для x в
первое упрощенное уравнение (найдено на шаге 1), чтобы найти y ’s
значение.

* Вставка 11 для x

* Сумма, обратная сумме 55, является вспомогательной.55

* инверсия мульт. на 3 — div.
по 3

Вы обнаружите, что если вы подключите заказанную пару (11,
-25/3) в ОБЕИХ
уравнения исходной системы, что это решение ОБЕИХ из
их.

(11, -25/3) — это решение для нашей системы.

Пример
7 : Решите систему уравнений методом исключения
метод.

Эта задача уже упрощена.Однако второй
уравнение
не записывается в виде Ax + By = C. Другими словами, нам нужно
написать
это в этой форме, чтобы все было готово к работе, когда мы добавим
два
уравнения вместе.

Переписывая второе уравнение, получаем:

* Инверсия сложения 6 x является вспомогательным.6 x

* Все в порядке

Обратите внимание, что если мы умножим первое уравнение на 2, то
Мы будем иметь
-6 x , что является противоположностью 6 x , найденным во втором уравнении.

Умножая первое уравнение на 2, получаем:

* Мног.1-й экв. по 2

* x имеют противоположные коэффициенты

* Переменные выпали И истинно

Эй, откуда у нас переменные
идти??

Как упоминалось выше, если переменная выпадает И мы
иметь ИСТИННОЕ заявление,
тогда когда есть бесконечное количество решений.Они в конечном итоге
та же линия.

Здесь нет никакой ценности для подключения.

Когда они оказываются в одном уравнении, у вас есть
бесконечное число
решений.Вы можете написать свой ответ, написав либо
уравнение, чтобы указать, что это одно и то же уравнение.

Два способа написать ответ: {( x , y ) | 3 x — 2 y = 1} OR {( x , y )
| 4 y = 6 x —
2}.

Практические задачи

Это практические задачи, которые помогут вам
следующий уровень.
Это позволит вам проверить и понять, понимаете ли вы
эти
типы проблем. Math работает так же, как
что-нибудь
иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться
Это.
Даже лучшие спортсмены и музыканты получали помощь и много
практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте.
На самом деле не бывает слишком много практики.

Чтобы получить максимальную отдачу от них, вы должны работать
проблема на
свой собственный, а затем проверьте свой ответ, щелкнув ссылку для
ответ / обсуждение
для этой проблемы . По ссылке вы найдете ответ
а также любые шаги, которые привели к поиску этого ответа.

Практика
Задача 1a: Решите систему, построив график.

Практика
Задача 2а: Решите систему подстановкой
метод.

Практика
Задача 3a: Решите систему
метод устранения.

Нужна дополнительная помощь по этим темам?

3 Методы решения систем уравнений

Три метода, наиболее часто используемые для решения систем уравнений, — это подстановка, исключение и расширенные матрицы. Замена и исключение — это простые методы, с помощью которых можно эффективно решить большинство систем двух уравнений за несколько простых шагов. Метод расширенных матриц требует большего количества шагов, но его применение распространяется на большее количество систем.

Замена

Замена — это метод решения систем уравнений путем удаления всех переменных, кроме одной, в одном из уравнений, а затем решения этого уравнения. Это достигается путем выделения другой переменной в уравнении и последующей подстановки значений этих переменных в другое уравнение. Например, чтобы решить систему уравнений x + y = 4, 2x — 3y = 3, выделите переменную x в первом уравнении, чтобы получить x = 4 — y, затем подставьте это значение y во второе уравнение, чтобы получить 2 (4 — у) — 3у = 3.Это уравнение упрощается до -5y = -5 или y = 1. Подставьте это значение во второе уравнение, чтобы найти значение x: x + 1 = 4 или x = 3.

Исключение

Исключение — еще один способ решения системы уравнений, переписав одно из уравнений в терминах только одной переменной. Метод исключения достигает этого путем сложения или вычитания уравнений друг из друга, чтобы сократить одну из переменных. Например, сложение уравнений x + 2y = 3 и 2x — 2y = 3 дает новое уравнение 3x = 6 (обратите внимание, что члены y сокращены).Затем система решается с использованием тех же методов, что и для замены. Если невозможно сократить переменные в уравнениях, необходимо будет умножить все уравнение на коэффициент, чтобы коэффициенты совпали.

Расширенная матрица

Расширенные матрицы также могут использоваться для решения систем уравнений. Расширенная матрица состоит из строк для каждого уравнения, столбцов для каждой переменной и расширенного столбца, который содержит постоянный член с другой стороны уравнения.Например, расширенная матрица для системы уравнений 2x + y = 4, 2x — y = 0 имеет вид [[2 1], [2 -1] … [4, 0]].

Определение решения

Следующий шаг включает использование элементарных операций со строками, таких как умножение или деление строки на константу, отличную от нуля, и добавление или вычитание строк. Цель этих операций — преобразовать матрицу в форму строки-эшелона, в которой первая ненулевая запись в каждой строке равна 1, записи выше и ниже этой записи — все нули, а первая ненулевая запись для каждого row всегда находится справа от всех таких записей в строках над ней.Строчно-эшелонированная форма для указанной выше матрицы — [[1 0], [0 1] … [1, 2]]. Значение первой переменной задается первой строкой (1x + 0y = 1 или x = 1). Значение второй переменной задается второй строкой (0x + 1y = 2 или y = 2).

Приложения

Подстановка и исключение — это более простые методы решения уравнений, которые используются гораздо чаще, чем расширенные матрицы в базовой алгебре.