Содержание
Найти уравнение четвертой степени онлайн
Равенство, содержащее неизвестное число, которое обозначено буквой, называется уравнением. Решение уравнения предполагает нахождение всех значений неизвестного (неизвестных), при которых соблюдается верное равенство. Такие значения неизвестного (неизвестных) являются корнями или решением уравнения.
Уравнение вида ах4 + bх3 + сх2 + dх + е = 0 называется уравнением 4-й степени с одним неизвестным. В результате решения уравнения получается 4 комплексных или вещественных корня.
Для решения приведенного уравнения 4-й степени вида: х4 + Ах3 + Вх2 +Сх + D = 0 можно воспользоваться методом Феррари.
Составим кубическое уравнение: у3 — Ву2 + (АС — 4D)у — А2D + 4ВD — С2 = 0.
Решаем полученное уравнение, находим один из его вещественных корней у0, который используем для дальнейшего нахождения корней квадратных уравнений.
Получаем и решаем два квадратных уравнения: . Корни уравнений будут корнями первоначального уравнения 4-й степени.
Если дано биквадратное уравнение 4-й степени вида: Ах4 + Вх2 + С = 0 и нужно найти его корни, можно свести его к квадратному, заменив переменную х2 на у (у = х2). В результате получим уравнение вида: Ау2 + Ву + С = 0. Далее решаем квадратное уравнение через дискриминант.
Если дано возвратное уравнение 4-й степени вида: Ах4 + Вх3 + Сх2 + Вх + А = 0 и нужно найти его корни, следует разделить уравнение на х2, получим:
Ах2 + Вх + С + В / х + А / х2 = 0.
Группируем и выносим коэффициенты за скобки: Ах2 + А / х2 + Вх + В / х + С = 0; А(х2 + 1 / х2) + В(х + 1 / х) + С = 0.
Произведем замену переменных: х + 1 / х = у; х2 + 1 / х2 = у2 — 2, получим: А(у2 — 2) + Ву + С = 0.
Сводим уравнение 4-й степени к квадратному уравнению и решаем его через дискриминант Ау2 + Ву + С — 2А = 0.
Находим у1 и у2, после чего возвращаемся к замене и находим корни.
Быстро решить любое уравнение вы сможете с помощью представленного на сайте онлайн калькулятора.
42
42. РЕШЕНИЕ УРАВНЕНИЯ 4-ой СТЕПЕНИ
Тип игры: граф
Класс: 8, 9
Тема: Уравнения, приводящиеся к квадратным
Комментарий. Эта игра
интересна тем, что важными и полезными являются различные пути получения
результата. Это как раз пример на воплощение дидактической идеи – процесс
важнее результата.
Кроме обычной организации
игры с разбивкой учащихся на группы, идущие различными путями, можно предложить
и фронтальный вариант, в котором учитель показывает и комментирует различные
этапы решения. Разумеется, при этом ослабляется игровой характер задания, не
Разумеется, при этом ослабляется игровой характер задания, не
появляется возможность в деятельностной форме ознакомить учащихся с несколькими
важными алгебраическими идеями.
Тип
игры: граф (выбор пути решения).
Дано
уравнение x(x + 1)(x + 2)(x + 3) = 360.
Шаг
1
Выберите
один из возможных способов преобразования уравнения.
1. Перемножить
сомножители в левой части.
2. Сгруппировать
сомножители по два.
3. Использовать
симметрию множителей и сделать замену .
4. Воспользоваться
известным тождеством для преобразования произведения четырех подряд идущих
целых чисел.
Реакция
на выбор способа преобразования
1. Этот
способ самый прямой, однако не ясно, приведет ли он к цели. Тем не менее,
попробуйте перемножить и получить уравнение 4-ой степени вида x4 + ax3 + bx2 + cx + d = 0.
Закончив
вычисления, перейдите к шагу 2.
Сверьте
свои вычисления с правильным ответом.
Шаг
2
x4 + 6x3 + 11x2 + 6x – 360 = 0
Выберите
один из двух известных вам типов решения уравнения 4-ой степени.
1.1. Приведение
к биквадратному уравнению с помощью удачной замены неизвестного.
1.2. Приведение
к возвратному уравнению, используя симметрию коэффициентов.
Реакция
на второй шаг
1.1. Это
хороший путь. Чтобы подобрать замену, советуем выделить полный квадрат,
используя первые два слагаемых.
Предлагайте
выкладки, подберите необходимую замену и сверьте с ответом.
Шаг
3
1.1.1. У
вас должно получиться следующее уравнение:
(x2 + 3x)2 + 2(x2 + 3x) –360 = 0.
Теперь
замена ясна. Обозначьте новое неизвестное через y и сверьте
Обозначьте новое неизвестное через y и сверьте
ответ.
Шаг
4
y2 + 2y – 360 = 0
Решите
это квадратное уравнение и запишите два его корня: y1 = (–20), y2 = (18).
Реакция:
верно – неверно.
Для
каждого найденного значения y решите уравнение x2 + 3x = y.
До записи ответа укажите число корней.
Шаг
5
Уравнение
имеет (2) корня.
Запишите
ответ.
Шаг
6
x1 = (–6), x2 = (3)
1.2. Этот
путь хороший, но нелегкий. Мешает свободный член – 360. Советуем продолжить
путь обычным образом – поделить на x2 и заменить . Не пугайтесь того, то x не исчезнет – останется
слагаемое вида .
Сверьте
с правильным ответом.
Шаг
2
Слева
и справа стоят полные квадраты. Воспользуйтесь этим, извлеките корни из обеих
частей и перейдите к следующему шагу.
Шаг
3
Проверьте
себя, что вы не забыли извлечь корень с двумя знаками и получить два уравнения:
и .
Вернитесь
к неизвестному x и получите два квадратных
уравнения.
Шаг
4
x2 + 3x + 20 = 0
x2 + 3x – 18 = 0
До
записи ответа укажите число корней исходного уравнения.
Шаги
5 и 6 совпадают с этими шагами в пути 1.1.
2. Этот
путь самый естественный. Решите, какие пары множителей вы будете объединять.
Шаг
2
|
Первый и второй
|
|
Неудачно, попробуйте другой способ
|
|
Третий и четвертый
|
| |
|
Первый и третий
|
| |
|
Второй и четвертый
|
|
|
Первый и четвертый
|
|
Это удачный способ, подсказанный соображениями симметрии.
|
|
Второй и третий
|
|
Шаг
3
(x2 + 3x)(x2 + 3x + 2) = 360
Сделайте
замену.
2.1. y = (x2 + 3x)
2.2. y = (x2 + 3x + 1)
2.1. Эта замена
естественная, хотя и не самая лучшая. Лучше было бы заменить x2 + 3x + 1 = y.
Продолжите свой способ и получите квадратное уравнение относительно y.
Шаг
4
Совпадает
с шагом 4 в 1.1 и дальше до конца.
2.2. Это
очень толково. Сразу замечаете симметрию. Сверьте уравнение.
Шаг
4
y2 – 1 = 360; y2 = 361
До
записи окончательного ответа укажите число корней исходного уравнения.
Шаг
5
как
в 1.1
3. Это
способ наиболее короткий. Сверьте запись получающегося биквадратного уравнения.
Шаг
2
Запишите
квадратное уравнение относительно z2 = y.
Шаг
3
Решите
это квадратное уравнение. Сверьте корни.
Шаг
4
,
Вспомните,
что y = z2.
До
записи ответа найдите число корней исходного уравнения.
Шаг
5 и далее – тот же, что и в 1.1
4. Этот
способ хорош, если вы действительно помните тождество x(x + 1)(x + 2)(x + 3) + 1 = (x2 + ___x + ___)2
Сверьте
ответ.
Шаг
2
x(x + 1)(x + 2)(x + 3) + 1 = (x2 + 3x + 1)2
Извлеките
корень и перейдите к двум уравнениям относительно x.
Сверьте
ответ.
Шаг
3
x2 + 3x + 1 = –19
x2 + 3x + 1 = +19
До
записи окончательного ответа укажите число корней исходного уравнения.
Шаг
4 = Шаг 5 в 1.1
________________________
Граф
Решение уравнения четвертой степени одной переменной
Решение уравнения четвертой степени одной переменной
0 Предисловие
В процессе обучения необходимо решить квадратное уравнение одной переменной.
Поскольку он имеет неизвестные параметры, я хотел использовать MATLAB для решения своего аналитического решения и записать его в C ++ для расчета. Позже было обнаружено, что решение было слишком длинным.
Если вы поместите его непосредственно в C ++, то даже на решение в реальном времени с помощью аналитического решения потребуется больше времени, чем на решение унарного квартичного уравнения. Так что найдите другой способ выяснить, как решить унарное уравнение квартики.
Так что найдите другой способ выяснить, как решить унарное уравнение квартики.
1. Способ первый
Метод Ferrari, который также является самым простым способом попасть в Google.
Я перестал смотреть на принцип ограничения времени и пошел прямо, чтобы узнать. По совпадению, есть код на энциклопедии.Link.
Ferrari.cpp
#include <math.h>
#include <float.h>
#include <complex>
#include <iostream>
std::complex<double> sqrtn(const std::complex<double>&x,double n)
{
double r = hypot(x.real(),x.imag());
if(r > 0.0)
{
double a = atan2(x.imag(),x.real());
n = 1.0 / n;
r = pow(r,n);
a *= n;
return std::complex<double>(r * cos(a),r * sin(a));
}
return std::complex<double>();
}
std::complex<double> Ferrari(std::complex<double> x[4]
,std::complex<double> a
,std::complex<double> b
,std::complex<double> c
,std::complex<double> d
,std::complex<double> e)
{
a = 1. 0 / a;
b *= a;
c *= a;
d *= a;
e *= a;
std::complex<double> P = (c * c + 12.0 * e - 3.0 * b * d) / 9.0;
std::complex<double> Q = (27.0 * d * d + 2.0 * c * c * c + 27.0 * b * b * e - 72.0 * c * e - 9.0 * b * c * d) / 54.0;
std::complex<double> D = sqrtn(Q * Q - P * P * P,2.0);
std::complex<double> u = Q + D;
std::complex<double> v = Q - D;
if(v.real() * v.real() + v.imag() * v.imag() > u.real() * u.real() + u.imag() * u.imag())
{
u = sqrtn(v,3.0);
}
else
{
u = sqrtn(u,3.0);
}
std::complex<double> y;
if(u.real() * u.real() + u.imag() * u.imag() > 0.0)
{
v = P / u;
std::complex<double> o1(-0.5,+0.86602540378443864676372317075294);
std::complex<double> o2(-0.5,-0.86602540378443864676372317075294);
std::complex<double>&yMax = x[0];
double m2 = 0.0;
double m2Max = 0.0;
int iMax = -1;
for(int i = 0;i < 3;++i)
{
y = u + v + c / 3.
0 / a;
b *= a;
c *= a;
d *= a;
e *= a;
std::complex<double> P = (c * c + 12.0 * e - 3.0 * b * d) / 9.0;
std::complex<double> Q = (27.0 * d * d + 2.0 * c * c * c + 27.0 * b * b * e - 72.0 * c * e - 9.0 * b * c * d) / 54.0;
std::complex<double> D = sqrtn(Q * Q - P * P * P,2.0);
std::complex<double> u = Q + D;
std::complex<double> v = Q - D;
if(v.real() * v.real() + v.imag() * v.imag() > u.real() * u.real() + u.imag() * u.imag())
{
u = sqrtn(v,3.0);
}
else
{
u = sqrtn(u,3.0);
}
std::complex<double> y;
if(u.real() * u.real() + u.imag() * u.imag() > 0.0)
{
v = P / u;
std::complex<double> o1(-0.5,+0.86602540378443864676372317075294);
std::complex<double> o2(-0.5,-0.86602540378443864676372317075294);
std::complex<double>&yMax = x[0];
double m2 = 0.0;
double m2Max = 0.0;
int iMax = -1;
for(int i = 0;i < 3;++i)
{
y = u + v + c / 3. 0;
u *= o1;
v *= o2;
a = b * b + 4.0 * (y - c);
m2 = a.real() * a.real() + a.imag() * a.imag();
if(0 == i || m2Max < m2)
{
m2Max = m2;
yMax = y;
iMax = i;
}
}
y = yMax;
}
else
{
y = c / 3.0;
}
std::complex<double> m = sqrtn(b * b + 4.0 * (y - c),2.0);
if(m.real() * m.real() + m.imag() * m.imag() >= DBL_MIN)
{
std::complex<double> n = (b * y - 2.0 * d) / m;
a = sqrtn((b + m) * (b + m) - 8.0 * (y + n),2.0);
x[0] = (-(b + m) + a) / 4.0;
x[1] = (-(b + m) - a) / 4.0;
a = sqrtn((b - m) * (b - m) - 8.0 * (y - n),2.0);
x[2] = (-(b - m) + a) / 4.0;
x[3] = (-(b - m) - a) / 4.0;
}
else
{
a = sqrtn(b * b - 8.0 * y,2.0);
x[0] =
x[1] = (-b + a) / 4.0;
x[2] =
x[3] = (-b - a) / 4.0;
}
return x[4];
}
int main()
{
std::complex<double> x[4];
x[4] = Ferrari(x,1,2,3,4,5);
std::cout<<"root1: "<<x[0]<<std::endl<<"root2: "<<x[1]<<std::endl<<"root3: "<<x[2]<<std::endl<<"root4: "<<x[3]<<std::endl;
return true;
}
0;
u *= o1;
v *= o2;
a = b * b + 4.0 * (y - c);
m2 = a.real() * a.real() + a.imag() * a.imag();
if(0 == i || m2Max < m2)
{
m2Max = m2;
yMax = y;
iMax = i;
}
}
y = yMax;
}
else
{
y = c / 3.0;
}
std::complex<double> m = sqrtn(b * b + 4.0 * (y - c),2.0);
if(m.real() * m.real() + m.imag() * m.imag() >= DBL_MIN)
{
std::complex<double> n = (b * y - 2.0 * d) / m;
a = sqrtn((b + m) * (b + m) - 8.0 * (y + n),2.0);
x[0] = (-(b + m) + a) / 4.0;
x[1] = (-(b + m) - a) / 4.0;
a = sqrtn((b - m) * (b - m) - 8.0 * (y - n),2.0);
x[2] = (-(b - m) + a) / 4.0;
x[3] = (-(b - m) - a) / 4.0;
}
else
{
a = sqrtn(b * b - 8.0 * y,2.0);
x[0] =
x[1] = (-b + a) / 4.0;
x[2] =
x[3] = (-b - a) / 4.0;
}
return x[4];
}
int main()
{
std::complex<double> x[4];
x[4] = Ferrari(x,1,2,3,4,5);
std::cout<<"root1: "<<x[0]<<std::endl<<"root2: "<<x[1]<<std::endl<<"root3: "<<x[2]<<std::endl<<"root4: "<<x[3]<<std::endl;
return true;
}
Коэффициент испытаний: 1, 2, 3, 4, 5
Убедитесь, что результат правильный, используйте matlab для проверки:
p = [1 2 3 4 5];
x = roots(p)
Результаты соответствуют, хорошо. {n-2}+\cdots+c_1x+c_0
{n-2}+\cdots+c_1x+c_0
P(x)=xn+cn−1xn−1+cn−2xn−2+⋯+c1x+c0
Сопутствующая матрица:
M
x
=
[
0
0
.
.
.
0
−
c
0
1
0
.
.
.
0
−
c
1
0
1
.
.
.
0
−
c
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0
0
.
.
.
1
−
c
n
−
1
]
M_x = \left[\begin{array}{ccccc} 0 & {0} & {…} & {0} & {-c_0} \\ 1 &0 & {…} & {0} & {-c_1} \\ {0} & {1} & {…} & {0} & {-c_2} \\ { …} & {…} & {…} & {…} & {…} \\ {0} & {0} & {…} & {1} & {-c_{n-1}} \end{array}\right]
Mx=⎣⎢⎢⎢⎢⎡010…0001…0……………000…1−c0−c1−c2…−cn−1⎦⎥⎥⎥⎥⎤
Характеристическое значение равно
P
(
x
)
P(x)
P(x)Корнеплоды.
Так что используйте Eigen для решения полинома:
#include <iostream>
#include <Eigen/Core>
#include <Eigen/Dense>
using namespace std;
int main( int argc, char** argv )
{
Eigen::Matrix<double, 4, 4> matrix_44;
Eigen::Matrix<complex<double>, Eigen::Dynamic, Eigen::Dynamic> matrix_eigenvalues;
matrix_44 << 0, 0, 0, -5,
1, 0, 0, -4,
0, 1, 0, -3,
0, 0, 1, -2;
std::cout<<"matrix_44: "<<std::endl<<matrix_44<<std::endl<<std::endl;
matrix_eigenvalues = matrix_44. eigenvalues();
std::cout<<"matrix_eigenvalues: "<<std::endl<<matrix_eigenvalues<<std::endl;
return 0;
}
eigenvalues();
std::cout<<"matrix_eigenvalues: "<<std::endl<<matrix_eigenvalues<<std::endl;
return 0;
}
Результат такой же, как указано выше:
3. Вывод
Чем глубже математические навыки, тем ниже сложность кода! !
Формула решения уравнения 4 степени
Существует несколько методов нахождения корней полиномиального уравнения 4-ой степени.
Однако они не очень удобны при решении уравнений с коэффициентами, которые представляют собой выражения с параметрами.
Инстаграм
1. Формула решения уравнения 4 степени.
Рассмотрим уравнение 4-ой степени, сумма корней которого равна нулю. Коэффициенты могут быть вещественными или комплексными.
Произведение следующих двух квадратов тождественно рассматриваемому уравнению 4-ой степени.
Значение R является решением следующего кубического уравнения.
Почти такое же уравнение появляется при решении уравнения 4-ой степени путем разложения на разность полных квадратов. 3 заменяется на
3 заменяется на
Получается выражение
В общем описанные в п.2 преобразования не являются тождественными. Но если считать интересными только значения x, которые являются корнями исходного уравнения, то данные преобразования можно считать квазитождественными. И тогда y представляется выражением, соответствующим корням исходного уравнения.
3. Для кубического уравнения операция в п.2 производится еще один раз. В итоге получается система из 3 уравнений по x, которая имеет три ненулевых решения, соответствующих корням исходного уравнения. Из коэффициентов x формируем матрицу
4. Находим определитель матрицы, который представляется кубическим выражением по y.
Вычисляем значения, обеспечивающие равенство определителя нулю.
5. В уравнении по y имеются два параметра P и Q. Вычислим их так, чтобы нулю равнялись коэффициенты при второй и первой степени y.
Любое P
, где
6. В итоге имеем уравнение c тремя кратными корнями для y
7. Остается решить квадратное уравнение с известными y, P, Q
Остается решить квадратное уравнение с известными y, P, Q
Одно из решений будет решением исходного уравнения.
3. Параметры решения вспомогательного кубического уравнения.
Для конкретных значений коэффициентов все выглядит не таким страшным образом.
Отметим, что для формулы решения уравнения 4-ой степени требуется только один корень R вспомогательного кубического уравнения.
Для конкретных коэффициентов вспомогательного уравнения имеем
При использовании формулы решения уравнения 4-ой степени необходимо ссылаться — «Метод ftvmetrics».
Интересные задачи присылайте в Direct Инстаграмм.
“Методы решения уравнений четвертой степени”
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №1 г. Южи Ивановской области
Педагогический проект по теме:
“Методы решения уравнений четвертой степени”
Работа Чуриной
Елена Вениаминовна,
учитель математики первой
квалификационной категории
Г. Южа
Южа
2021 год
Содержание
Актуальность
Цель и задачи работы:………………………………
1. Исторические сведения об уравнениях четвёртой степени……стр.
2. Определение уравнения 4 степени………………………….стр.
3. Способы решения уравнений 4 степени……………………………стр.
3.1. Схема метода Феррари……………………….стр.
3.2. Разложение на множители. Кубическая резольвента……………стр.
3.3. Теорема Виета для уравнения 4 степени……………………..стр.
3.4. Решение уравнений 4 степени по схеме Горнера……………………стр.
4.Решение некоторых уравнений 4 степени……………………………стр.
4.1. Решение биквадратного уравнения………………………………стр.
4.2. Решение уравнения способом группировки………………….стр.
4.3. Решение уравнения по свободному члену……………………стр.
4.4. Графический метод………………………………………..стр.
4.5. Применение формул сокращенного умножения. Выделение полного квадрата………………………………………………. .стр.
.стр.
5. Исследование………………………………………………стр.
6. Выводы
7. Заключение
8. Тренировочные задания для отработки различных способов решения уравнений высших степеней……………………………………………стр.
Список литературы
Актуальность
Как все знают, в математике одна из важнейших вещей — это уравнения. Чаще всего решаются линейные либо квадратные уравнения, но не мало важны уравнения 4 степени, которые решить сможет не каждый учащийся 9 класса. Чтобы решать такие уравнения было проще, нужно выбрать тот способ, который тебе более понятен.
Задания с уравнениями высших степеней есть в контрольных измерительных материалах при проведении государственной итоговой аттестации. Значит, ученики должны уметь решать уравнения не только 2 степени, но и выше. А это умеет делать далеко не каждый.
Цель работы: узнать и разобрать методы решения уравнений высших степеней.
Задачи:
Изучить литературу по истории приемов решения уравнений 4-й стпени
Обобщить накопленные знания об уравнениях4-й степени и способах их решения.
Сделать выводы.
Разработать дидактический материал для проведения практикума по решению уравнений 4-й степени с использованием новых приемов в помощь ученикам, увлеченным математикой и учителям, ведущим факультативные занятия.
Проблемный вопрос: существуют ли кроме общепринятых приемов решения квадратных уравнений другие, которые позволяют быстро и рационально решать уравнения 4-й степени?
Гипотеза: существует универсальный способ для решения всех видов уравнений 4-степеней.
Объект исследования: уравнения 4-й степени
Предмет изучения: методы и приемы решениях уравнений 4-й степени, в том числе
1.Исторические сведения об уравнениях четвёртой степени
Решение уравнений высших степеней – история полная драматизма, разочарования и радости открытия. В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.
Необходимость решать уравнения не только первой, но и второй и высших степеней ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне.
Однако уже при решении уравнений третей степени математики столкнулись с большими трудностями. История открытия способа решения кубических уравнений полна тайн, так как в древности учёные часто на открытых диспутах соревновались в решении трудных задач. От исхода этих состязаний зависела их научная репутация и материальное благополучие.
Тот, кто первым овладел решением кубических уравнений, мог легко победить своих соперников давая им задачи, сводящиеся к кубическим уравнениям. Поэтому способы решения уравнения тщательно скрывались. Историки полагают, что первым нашёл способ решения кубических уравнений известный итальянский алгебраист Специна дель Ферро (1465-1576), но впервые опубликовал общую формулу решения кубических уравнений итальянский математик Джераламо Кордано (1501-1576г. ). Эта формула носит теперь название формулы Кордано, хотя предполагают, что эту формулу ему передал итальянский математик Николо Тарталья ( 1500-1557). С именами этих же математиков связано открытие способов решения уравнений четвёртой степени.
). Эта формула носит теперь название формулы Кордано, хотя предполагают, что эту формулу ему передал итальянский математик Николо Тарталья ( 1500-1557). С именами этих же математиков связано открытие способов решения уравнений четвёртой степени.
В дальнейшем математики активно пытались найти формулы вычисления корней уравнений пятой и более степени. И только почти через три столетия впервые итальянский учёный Паоло Руффини (1765-1822), а затем норвежский математик Нильс Хенрих Абель (1802-1829г.) доказали, что не существует формулы, выражающей корни любого целого уравнения пятой степени через конечное число алгебраических операций над его коэффициентами. Да и найденные формулы вычисления корней для уравнений третьей и четвёртой степени столь сложны, что ими практически не пользуются. Поэтому в современной математике разработаны методы, позволяющие находить с любой степенью точности приближенные значения корней уравнений. Использование компьютеров значительно облегчают эту работу.
2. Определение уравнения 4 степени
Уравнение четвёртой степени —алгебраическое уравнение вида:
,
при этом a≠0 и где a,b,c,d,e- любые числа.
Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любых значениях коэффициентов).
3. Способы решения уравнений 4 степени.
3.1 Схема метода Феррари
a0x4 + a1x3 + a2x2 + a3x + a4 = 0, | (1) |
где a0, a1, a2, a3, a4 – произвольные вещественные числа, причем
Метод Феррари состоит из двух этапов.
На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.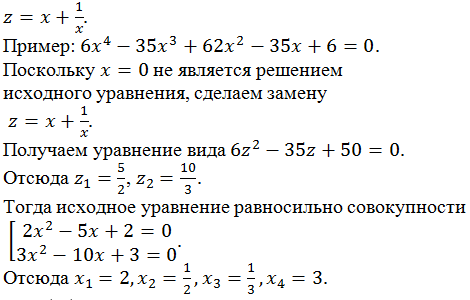
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Приведение уравнений 4-ой степени
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
x4 + ax3 + bx2 + cx + d = 0, | (2) |
где a, b, c, d – произвольные вещественные числа.
Сделаем в уравнении (2) замену
(3) |
где y – новая переменная.
Тогда, поскольку
то уравнение (2) принимает вид
(4) |
Если ввести обозначения
то уравнение (4) примет вид
y4 + py2 + qy + r = 0, | (5) |
где p, q, r – вещественные числа.
Первый этап метода Феррари завершён.
3.2.Разложение на множители. Кубическая резольвента
Добавив и вычитая в левой части уравнения (5) выражение
2sy2 + s2,
где s – некоторое число, которое мы определим чуть позже, из (5) получим
Следовательно, уравнение (5) принимает вид
(6) |
Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения
(7) |
то уравнение (6) примет вид
(8) |
Избавляясь от знаменателя, уравнение (7) можно переписать в виде
или, раскрыв скобки, — в виде
(9) |
Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).
Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».
Действительно,
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение
(10) |
а также квадратное уравнение
(11) |
Вывод метода Феррари завершен.
Пример решения уравнения 4-ой степени
Пример. Решить уравнение
x4 + 4x3 – 4x2 – 20x – 5 = 0. | (12) |
Решение. В соответствии с (3) сделаем в уравнении (12) замену
Поскольку
x4 + 4x3 – 4x2 – 20x – 5 = (y – 1)4 + 4(y – 1)3 – 4(y – 1)2 – 20(y – 1)– 5 =
= y4 – 4y3 + 6y2 – 4y + 1 + 4y3 – 12y2 + 12y – 4 – 4y2 + 8y – 4 – 20y + 20 – 5 =
= y4 – 10y2 – 4y + 8,
то в результате замены (13) уравнение (12) принимает вид
y4 – 10y2 – 4y + 8 = 0. | (14) |
В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства
p = – 10, q = – 4, r = 8. | (15) |
В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение
2s3 + 10s2 – 16s – 84 = 0,
которое при сокращении на 2 принимает вид:
s3 + 5s2 – 8s – 42 = 0. | (16) |
Проверяя, какой из делителей свободного члена уравнения (16) является целым корнем этого уравнения, находим, что целым корнем кубической резольвенты является число
Подставляя значения (15) и (17) в формулу (10), получаем уравнение
y2 – 2y – 4 = 0,
корни которого имеют вид:
(18) |
Подставляя значения (15) и (17) в формулу (11), получаем уравнение
y2 + 2y – 2 = 0,
корни которого имеют вид:
(19) |
В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):
Ответ.
Но эти способы очень сложны. Рассмотрю более простые способы, с помощью которых можно решить некоторые уравнения 4-й четверти.
3.3Теорема Виета для уравнения четвёртой степени
Корни уравнения четвёртой степени {\displaystyle x_{1},\,x_{2},\,x_{3},\,x_{4}} связаны с коэффициентами {\displaystyle a,\,b,\,c,\,d,\,e}следующим образом:
{\displaystyle x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}},}
3.4.Решение уравнений четвертой степени по схеме Горнера
2x4 + 5x3 — 11x2 — 20x + 12 = 0
Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди:
1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1 не является корнем многочлена
-1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена
Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки. | |
2 ∙ 2 + 5 = 9 | |
2 ∙ 9 — 11 = 7 | |
2 ∙ 7 — 20 = -6 | |
2 ∙ (-6) + 12 = 0 | |
2 | 5 | -11 | -20 | 12 | |
2 | 2 | 9 | 7 | -6 | 0 |
Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.
Таким образом, мы исходный многочлен разложили на множители и переходим к уравнению.
(х-2)(2х3+9х2+7х-6)=0
Многочлен, являющийся вторым множителем попробуем разложить на множители подобным образом.
Отыщем опять делители свободного члена. В данном случае делителями числа -6: ±1, ±2, ±3, ±4, ±6.
Число -2 является корнем многочлена. Напишем найденный корень в схему Горнера и начнем заполнять ячейки:
2 | 5 | -11 | -20 | 12 | |
2 | 2 | 9 | 7 | -6 | 0 |
-2 |
Во вторую ячейку третьей строки запишем число 2, просто перенеся его из соответствующей ячейки второй строки. |
-2 ∙ 2 + 9 = 5 |
-2 ∙ 5 + 7 = -3 |
-2 ∙ (-3) — 6 = 0 |
2 | 5 | -11 | -20 | 12 | |
2 | 2 | 9 | 7 | -6 | 0 |
-2 | 2 | 5 | -3 | 0 |
Таким образом, мы исходный многочлен разложили на множители и переходим к уравнению.{2}-4ac}}}{2a}}}.}
Пример.
Решить уравнение
Замена
из этого следует, что уравнение имеет два корня.
Обратная замена
т.е. невозможно
Ответ: .
4.2. Решение уравнения способом группировки
Способом группировки можно решить уравнение 4 степени.
Чтобы разложить уравнение на множители, надо сгруппировать слагаемые по парам. Мы должны сгруппировать слагаемые по парам таким образом, чтобы при вынесении общего множителя за скобки у слагаемых был одинаковый множитель.
Решим на примере.
2х4-5х3+2х2-5х=0
(2х4-5х3)+( 2х2-5х)=0
х3(2х-5)+х(2х-5)=0
(2х-5)(х3-х)=0
х(2х-5)(х2-1)=0
х(2х-5)(х-1)(х+1)=0
х=0 или 2х-5=0 или х-1=0 или х+1=0
х1=0 х2=2,5 х3=1 х4=-1
4.3. Решение уравнения по свободному члену
Любое уравнение вида можно свести к приведенному уравнению той же степени, домножив обе его части на и выполнив замену переменной вида :
Полученные коэффициенты тоже будут целыми.
Таким образом, будем решать приведенное уравнение степени n с целыми коэффициентами вида .
Алгоритм решения.
Находим целые корни уравнения.
Целые корни уравнения , i=1, 2, …, m (m – количество целых корней уравнения) находятся среди делителей свободного члена . То есть, первым делом выписываем делители свободного члена и подставляем их по очереди в исходное равенство для проверки. Перебираем их по очереди, пока не получим тождество. Как только тождество получено, то первый целый корень уравнения найден и уравнение предстает в виде , где — корень уравнения, а — частное от деления на .
Продолжаем подставлять выписанные ранее делители в уравнение , начиная с (так как корни могут повторяться). Как только получаем тождество, то корень найден и уравнение предстает в виде , где — частное от деления на .
И так продолжаем перебор делителей, начиная с . В итоге найдем все m целых корней уравнения и оно представится в виде , где — многочлен степени n-m. Весь этот процесс удобно проводить по схеме Горнера.
Дробных корней приведенное уравнение с целыми коэффициентами иметь не может.
Находим оставшиеся корни (иррациональные и/или комплексные) из уравнения любым способом.
Решить уравнение .
Во-первых, найдем все целые корни данного уравнения.
Свободным членом является -3. Его делителями являются числа 1, -1, 3 и -3.
Будем подставлять их по очереди в исходное равенство до получения тождества.
При х=1 имеем . То есть х=1 является корнем уравнения.
Разделим многочлен на (х-1) столбиком:
Следовательно, .
Продолжим перебор делителей, но уже для равенства :
При х = -1 получили верное равенство, следовательно, -1 является корнем уравнения.
Разделим на (х+1) столбиком:
Таким образом,
Продолжаем перебор делителей для равенства , начиная с х = -1:
Получили неверные равенства, следовательно, целых корней уравнение больше не имеет.
Оставшиеся корни исходного уравнения являются корнями квадратного трехчлена .
, то есть, действительных корней трехчлен не имеет, но имеет пару комплексно сопряженных.
4.4.Графический метод.
Иногда полезно рассмотреть эскизы графиков функций у=ƒ(x) и у=g(x), входящих в уравнение ƒ(x) = g(x). Это может помочь выяснить:
1) на какие множества надо разбить числовую ось, чтобы на каждом из этих множеств использовать свой способ решения;
2) наличие или отсутствие корней, их количество.
Пример: (материал взят из ОГЭ 2016г.)
x4=(3x-10)2
Решение №3: x4=(3x-10)2
1) Рассмотрим две функции: у = х4 и у =(3х-10)2.
2) Построим график функции у = х4 — график парабола ветви направлены вверх.
3) Построим график линейной функции у = (3х-10)2. Это парабола ветви, которой направлены вверх.
4) В данном примере наглядно видна только одна точка пересечения В(2;16) (см. приложение рис.3), хотя очевидно, что графики пересекаются еще в одной точке (т.е. имеется еще одно решение).
Как видим, что графический способ в данном случае не удобен, так как ограниченный размер листа тетради не позволяет увидеть все точки пересечения.
Графическое решение уравнения- наглядный способ, он хорош при необходимости определения наличия или отсутствия корней и их количества.
4.5. Применение формул сокращенного умножения. Выделение полного квадрата.
Этот метод основан на использовании формул:
а2-b2=(а-b)(а+b)a2+2ab+b2=(a+b)2a2−2ab+b2=(a−b)2
а3+b3=(а+b)(а2-аb+b2)а3-b3=(а-b)(а2+аb+b2)(а+b)3=а3+3а2b+3аb2+b3
(а-b)3= а3-3а2b+3аb2-b3,
Пример: х4=(3х-10)2
Способ 1: Используем формулу сокращенного умножения х4-(3х-10)2=0
(х2-3х+10)(х2+3х-10)=0
х2-3х+10=0 или х2+3х-10=0
D=9-40=-31 D=9+40=49
корней нет х1=-5, х2=2.
Ответ: х1=-2, х2=5.
6. Выводы:
1. Уравнения высших степеней решали еще более 500 тыс. лет назад.
2. Есть много способов решения уравнений 4-й степеней. Некоторые из них довольно сложные, а некоторые помогут быстро решить задания на ОГЭ.
3. Уравнения 4-й степеней играют немалую роль в развитии математики. Лишь немногие из учащихся умеют решать такие уравнения. Эти методы решения уравнений высших степеней непросты в применении, но они всё равно могут заинтересовать увлекающихся математикой учеников.
7. Заключение
В данной работе рассмотрены способы решения уравнений 4-й степени.
А также рассмотрены приёмы решения уравнений 4-й степени, которые позволяют быстрее и проще решить такие уравнения.
Данные приёмы решения заслуживают внимания, поскольку каждые из них интересны и уникальны. Овладение данными приёмами поможет экономить время и эффективно решать уравнения. Потребность в быстром и упрощенном решении обусловлена применением этих навыком на экзаменах.
Таким образом, цель работы — узнать и разобрать методы решения уравнений высших степеней- достигнуты. Гипотеза доказана, существует универсальный способ решения уравнений 4-й степени, способ Феррари.
Литература
Алгебра. 9 класс:учебник для общеобразовательных организаций / А45 Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под редакцией С. А. Теляковского. – 4-е издание – М.: Просвещение, 2017. – 287 с.: ил. – ISBN 978-5-09-046396-6.
. М.Л. Галицкий, А.М. Гольдман, Л.М. Звавич «Сборник задач по алгебре для 8-9 классов». Учебное пособие для учащихся школ и классов с углубленным изучением математики -Москва «Просвещение», 1999.
В.В. Бардушкин, И.Б. Кожухов, А.А. Прокофьев, А.М. Ревякин,
А.М. Терещенко «Письменный вступительный экзамен по математике» — Москва «Лист», 1998.
Н.В. Бурмистрова, Н.Г. Старостенкова «Функции и их графики». Учебное пособие — Саратов «Лицей», 2003.
М.А.Еремин «Уравнения высших степеней» — Арзамас, 2003.
А.Г.Курош «Алгебраические уравнения произвольных степеней» — М.:Наука, 1975.
Л.М.Лоповок «1000 проблемных задач по математике» — М.: Просвящение, 1995.
И.Р.Шафаревич «Популярные лекции по математике. О решении уравнений высших степеней» Вып.15 – М.: Наука, 1954.
10.https://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/
11. http://www.cleverstudents.ru/equations/equations_of_higher_degree.html
12. https://ru.wikipedia.org/wiki/Уравнение_четвёртой_степени
Приложение 1
Тренировочные задания для отработки различных способов решения уравнений 4-й степени.
№1 Решите уравнения способом замены: , б) X4-2x2-8=0,
в) x4-8x2-9=0, г) x4-7x2+12=0, д) 3x4-13x2+4=0, е) 2x4-19x2+9=0,
ж) 3x4-13x2+4=0, з) (x2+4x)(x2+4x-17)=60=0, и) (x2-5x)(x2-5x+10)+24=0,
к)(x2-3x)2-2(x2-3x)=8, л) (x2+x)2-11(x2+x)=12, 1
м) ( )+10=0, н) ( )=3; о)
№2 Решите уравнения, раскладывая левую часть на множители способом группировки:
а) 2x4-5x3+2x2-5x=0,
б) 6x4-3x3+12x2-6x=0,
в) 2x4+3x3-8x2-12x=0,
г) 2x4-5x3-18x2+45x=0.
№3 Решите уравнения по свободному члену
а) 2x4 – 3x3 – 7x2 –15x + 50 =0 б)х4-4х2 +3х+2=0
в) х4+2х3-7х2 -8х+12=0
№4 Решить уравнения, применения формулы сокращенного умножения
а) б) .
Уравнение 4 степени с примерами решения
Содержание:
- Решение методом Лагранжа уравнений четвертой степени
- Пример с решением
- Решение методом Эйлера уравнений четвертой степени
Уравнение четвертой степени при Биквадратное уравнение: при Замена переменной приводит биквадратное уравнение к квадратному Корни биквадратного уравнения: где — дискриминант.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Пример:
Решение методом Лагранжа уравнений четвертой степени
Попытаемся обобщить метод предыдущего параграфа на случай 4-й степени. Рассмотрим выражение где — корень 4-й степени из — корни уравнения то есть Сколько значений принимает выражение при различных перестановках корней? Очевидно, 24 значения — столько же, сколько всех возможных перестановок.
Однако заметим, что некоторые перестановки дают выражения, пропорциональные , причем коэффициенты пропорциональности являются корнями четвертой степени из 1.
Это происходит при циклической перестановке и, следовательно, еще при двух перестановках, являющихся ее степенями, а именно при перестановках (перестановка уже является тождественной). Можно это проверить и непосредственно, например, заметив, что перестановка меняет местами переменные и а также переменные и и выражение при этом меняет знак на противоположный.
Возможно вам будут полезны данные страницы:
Заметим, что при этих перестановках выражение вообще не меняется.
Упражнение 107. Проверьте, что любая другая перестановка не обладает этим свойством.
Упражнение 108. Проверьте, что при всех 24 перестановках выражение принимает ровно 24/4 = 6 значений:
Эти значения являются корнями уравнения шестой степени, коэффициенты которого полиномиально выражаются через коэффициенты исходного уравнения. Получившееся уравнение шестой степени можно разложить на два кубических. Однако этот способ требует слишком много вычислений.
Попытаемся найти более удобные выражения, чем Для этого рассмотрим подробнее метод разложения на два множителя, примененный Феррари.
Его идея состоит в том, чтобы представить левую часть уравнения в виде разности двух квадратов. Тогда ее можно будет разложить на два множителя второй степени, и решение уравнения приведется к решению двух квадратных уравнений.
Для этого левую часть представим в виде
где — вспомогательная неизвестная, которую подберем так, чтобы выражение в квадратных скобках оказалось квадратом линейного двучлена. Для этого необходимо и достаточно выполнения условия
Это условие есть кубическое уравнение относительно . Оно называется резольвентой Феррари.
После раскрытия скобок уравнение преобразуется к виду
Пусть — один из корней этого уравнения. Тогда при условие будет выполнено, так что имеет место
при некоторых и Исходное уравнение примет вид
или
Приравняв к нулю каждый из сомножителей, находим четыре корня исходного уравнения.
Пусть и — корни первого сомножителя, и — корни второго. Тогда Сложив эти равенства, получим, что Таким образом, мы получим выражение корня вспомогательного кубического уравнения через корни исходного уравнения четвертой степени.
Другими корнями кубического уравнения будут Таким образом, мы нашли такое выражение от корней что при их всевозможных перестановках получается только два новых выражения. Поэтому эти выражения являются корнями уравнения третьей степени, коэффициенты которого полиномиально выражаются через коэффициенты исходного уравнения четвертой степени.
Данный результат можно было получить и двигаясь от этих выражений к уравнению третьей степени.
Действительно, согласно теореме Виета для уравнения Аналогично
и также
Значит, — корни уравнения После решения этого уравнения остается справиться с системой
Пример с решением
Рассмотрим еще один метод решения уравнения 4-й степени Возьмем другое выражение от корней которое тоже принимает при переставлении корней всего 3 значения: Найдем кубическое уравнение с корнями Другими словами, выразим его коэффициенты через коэффициенты Используя теорему Виета, имеем Найдя из этого уравнения можно определить и корни Для этого используем равенство из которого следует, что
Значит
Отсюда можно выразить
Решение методом Эйлера уравнений четвертой степени
Существуют и другие способы решения уравнения четвертой степени. Один из наиболее изящных принадлежит Эйлеру. Этот способ состоит в следующем. Полное уравнение четвертой степени (5) подстановкой приводится к более простому виду: (6) Полагаем: (7) В равенство (7) введено три неизвестных. Чтобы определить их, нужно будет дать три уравнения. Возводя обе части равенства (7) два раза в квадрат, получаем: (8)
Подставляя в уравнение (6) вместо их выражения из равенств (7) и (8), после упрощения получим: (9)
Для того чтобы выполнялось равенство где — корень уравнения (6), необходимо и достаточно выполнение уравнения (9).
Оно содержит три неизвестных. Чтобы определить их, нужны еще два уравнения, которые можно выбрать произвольно. Свободой выбора следует воспользоваться для наибольшего упрощения уравнения.
Руководствуясь этим, положим (10) При этом выборе величин и уравнение (9) обращается в уравнение (11) Из (10) и (11) заключаем, что и удовлетворяют системе уравнений (12) Отсюда следует, что числа и являются корнями уравнения: (13) Оно совпадает с резольвентой Феррари, полученной ранее. Пусть —корни резольвенты. Положим Извлекая корни, имеем (14) При этом, в силу равенства (10), выполняется равенство (15)
У двух радикалов в равенствах (14) можно взять любое из их значений. После этого значение третьего радикала следует взять определенное — оно находится из равенства (15). Подставляя полученные выражения для в уравнение (7), приходим к следующей теореме.
Теорема 100 (Эйлер). Корни приведенного уравнения четвертой степени выражаются через корни резольвенты Феррари
по формулам: При этом значения радикалов и должны быть выбраны так, чтобы выполнялось равенство:
Уравнение четвертой степени — это… Что такое Уравнение четвертой степени?
- Уравнение четвертой степени
Уравнение четвёртой степени — в математике алгебраическое уравнение вида:
.
Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).
Решения
Решение Декарта — Эйлера
Сделав подстановку , получим уравнение в следующем виде (он называется «неполным»):
- y4 + py2 + qy + r = 0.
Корни y1, y2, y3, y4 такого уравнения равны одному из следующих выражений:
в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:
- ,
причём z1, z2 и z3 — это корни кубического уравнения
Решение Феррари
Основная статья: Метод Феррари
Представим уравнение четвёртой степени в виде:
- Ax4 + Bx3 + Cx2 + Dx + E = 0,
Его решение может быть найдено из следующих выражений:
- если β = 0, решив u4 + αu2 + γ = 0 и, сделав подстановку , найдём корни:
- .
- если β = 0, решив u4 + αu2 + γ = 0 и, сделав подстановку , найдём корни:
- , (любой знак квадратного корня подойдёт)
- , (три комплексных корня, один из которых подойдёт)
- Два ±s должны иметь одинаковый знак, ±t — независимы. Для того, чтобы найти все корни, надо найти x для знаковых комбинаций ±s,±t = +,+ для +,− для −,+ для −,−. Двойные корни появятся два раза, тройные корни — три раза и корни четвёртого порядка — четыре раза. Порядок корней зависит от того, какой из кубических корней U выбран.
См. также
Литература
- Корн Г., Корн Т. (1974) Справочник по математике.
Ссылки
Wikimedia Foundation.
2010.
- Уравнение состояния газа Ван-дер-Ваальса
- Уравнение третьей степени
Смотреть что такое «Уравнение четвертой степени» в других словарях:
уравнение четвертой степени — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN quartic equation … Справочник технического переводчика
Уравнение четвёртой степени — График многочлена 4 ой степени с четырьмя корнями и тремя критическими точками. Уравнение четвёртой степени в математике алгебраическое уравнение вида: Четвёртая степень для алгебраических уравнений является наивысшей, при которой… … Википедия
Возвратное уравнение четвёртой степени — Уравнение вида: anxn + an − 1xn − 1 + … + a1x + a0 = 0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, то есть если an − k = ak, при k = 0, 1, …, n. Содержание 1 Уравнение четвёртой степени … Википедия
БИКВАДРАТНОЕ УРАВНЕНИЕ — в котором неизвестный член в четвертой степени. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907. БИКВАДРАТНОЕ УРАВНЕНИЕ от лат. bis, дважды, и quadratum, квадрат. Уравнение, в котором наибольшая степень… … Словарь иностранных слов русского языка
Алгебра — вместе с арифметикой есть наука о числах и через посредство чисел о величинах вообще. Не занимаясь изучением свойств каких нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин как таковых, независимо от… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ПОЛЕТА ТЕОРИЯ И ПРАКТИКА — совокупность прикладных знаний, позволяющих авиационным инженерам на занятий в области аэродинамики, проблем прочности, двигателестроения и динамики полета летательных аппаратов (т.е. теории) создать новый летательный аппарат или улучшить… … Энциклопедия Кольера
МАТЕМАТИКИ ИСТОРИЯ — Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… … Энциклопедия Кольера
Важнейшие открытия в физике — История технологий По периодам и регионам: Неолитическая революция Древние технологии Египта Наука и технологии древней Индии Наука и технологии древнего Китая Технологии Древней Греции Технологии Древнего Рима Технологии исламского мира… … Википедия
УРАВНЕНИЯ — Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида… … Энциклопедия Кольера
Теорема Абеля — Теорема Абеля Руффини утверждает, что общее уравнение степени при неразрешимо в радикалах. Содержание 1 Подробности … Википедия
Уравнение четвертой степени
Подстановками всегда можно получить каноническое уравнение:
x 4 + ax 2 + bx + c = 0.
Затем мы ищем, чтобы записать это как (метод Декарта):
(x 2 + px-u) (x 2 -px-v) = 0
Раскрытие и приравнивание двух выражений приводит к:
-a = (u + v) + p 2 и (u + v) 2 = (a + p 2 ) 2
b = p (uv) и b 2 = p 2 (uv) 2 = p 2 ((u + v) 2 -4uv)
c = уф
Пусть Z = p 2 и исключим (u + v) 2 и uv из предыдущей системы, это дает:
б 2 = Z ((a + Z) 2 -4c)
И резольвантное уравнение третьей степени:
| Z 3 + 2aZ 2 + (a 2 -4c) Z-b 2 = 0 |
Каждый из корней этого уравнения дает набор значений для p, u и v.Но глобально это то же самое, что поменять местами корни уравнения 4 -й степени ,
и мы можем выбрать любой корень, а именно Z 1 .
Тогда (x 1 , x 2 ) являются корнями x 2 + px-u = 0 и
(x 3 , x 4 ) корни из x 2 -px-v = 0
Конкретно x 1 + x 2 = -p = -√Z 1
и x 3 + x 4 = p = √Z 1
Обмен корнями дает аналогично:
x 1 + x 3 = -√Z 2 ,
х 2 + х 4 = √Z 2
а также
x 1 + x 4 = -√Z 3 ,
x 2 + x 3 = √Z 3
Путем линейной комбинации этих выражений мы получаем корни уравнения 4 -й степени :
| x 1 = 1/2 (-√Z 1 -√Z 2 -√Z 3 ) x 2 = 1/2 (-√Z 1 + √Z 2 + √Z 3 ) x 3 = 1/2 (√Z 1 -√Z 2 + √Z 3 ) x 4 = 1/2 (√Z 1 + √Z 2 -√Z 3 ) с Z i решениями Z 3 + 2aZ 2 + (a 2 -4c) Z-b 2 = 0 |
Что касается уравнения 3 градуса , то эти формулы на практике бесполезны.На практике решение уравнения 4 -й степени осуществляется с помощью числовых приближений,
кроме частных случаев или тривиальных решений.
Скрипт для решения методом Ньютона.
Обратите внимание, что хотя формулы с квадратными и кубическими корнями существуют для общих
уравнения степени 2, 3 и 4,
не может быть такой формулы для общих уравнений степени 5 и выше (см. теорию Абеля и Галуа).
(PDF) Простой метод решения уравнений четвертой степени
Aust.J. Basic & Appl. Sci., 6 (6): 331-336, 2012
336
СПИСОК ЛИТЕРАТУРЫ
Abramowitz, M. and I.A. Стегун, 1972. (Ред.). «Решения уравнений четвертой степени». §3.8.3 в Справочнике по математическим функциям
с формулами, графиками и математическими таблицами, 9-е издание. Нью-Йорк: Довер, стр:
17-18.
Бергер М., 1987. §16.4.1-16.4.11.1 в геометрии I. Нью-Йорк: Springer-Verlag.
Бейер, W.H., 1987a. Стандартные математические таблицы CRC, 28-е изд.Бока-Ратон, Флорида: CRC Press, стр. 12.
Beyer, W.H., 1987b. Справочник по математическим наукам, 6-е изд. Бока-Ратон, Флорида: CRC Press.
Биркгоф, Г. и С.А. Мак-Лейн, 1996. Обзор современной алгебры, 5-е изд. Нью-Йорк: Macmillan, стр:
107-108.
Borwein, P. and T. Erdélyi, 1995. «Quartic Equations». §1.1.E.1e в многочленах и многочленах
Неравенства. Нью-Йорк: Springer-Verlag, p: 4.
Boyer, C.B. and U.C.A. Мерцбах, 1991.История математики, 2-е изд. Нью-Йорк: Wiley, стр: 286-287.
Эрлих, Г. 1991. §4.16 в Основные понятия абстрактной алгебры. Бостон, Массачусетс: PWS-Kent.
Faucette, W.M., 1996. «Геометрическая интерпретация решения общего многочлена четвертой степени».
амер. Математика. Ежемесячно, 103: 51-57.
Геллерт, В., С. Готвальд, М. Хелвич, Х. Кестнер и Х. Кюнстнер, 1989 г. (ред.). ВНР Краткая
Математическая энциклопедия, 2-е изд. Нью-Йорк: Ван Ностранд Рейнхольд.
Hazewinkel, M., 1988. (Управляющий ред.). Энциклопедия математики: обновленная и аннотированная
Перевод советской «Математической энциклопедии». Дордрехт, Нидерланды: Рейдел.
Стюарт И., 2004. «Теория Галуа», изд: Chapman & Hall / CRC Mathematics.
О’Коннор, Дж. Дж. и Э.Ф. Робертсон, «Лодовико Феррари», в архиве истории математики MacTutor, под ред.
Школа математики и статистики Университета Сент-Эндрюс, Шотландия.
MathPages. 2006. «Преобразование квартиков в кубики». http://www.mathpages.com/home/kmath396.htm.
Джейкобсон, Н., «Базовая алгебра», 1, 2-е изд: Довер, 2009.
Смит, Д.Е.А., 1994. Справочник по математике. Нью-Йорк: Дувр.
ван дер Варден, Б.Л., 1993. §64 по алгебре, т. 1. Нью-Йорк: Спрингер-Верлаг.
Решение уравнений Полиномиальные уравнения 4-й степени
Калькулятор позволяет вычислять корни любого многочлена четвертой степени.
Коэффициенты могут быть как действительными, так и комплексными числами.
Использовалась некая методика, которая нигде не описана и не отсортирована.
Формулы Феррари использовать не стал — не интересно.
Несмотря на свой путь, вы все равно утыкаетесь в задаче решения вспомогательного уравнения третьей степени, так называемой кубической резольвенты. И скорее всего избежать этого никак не получится.
Но дальше все идет по другому.
По любому из значений корня резольвенты, вычисляем три вспомогательных параметра.
Зная эти три параметра, мы легко можем найти все четыре корня исходного уравнения.
Есть только один нюанс, с которым столкнулись предшественники, мне иногда приходится некоторым определять знак + или тоже — для одного вспомогательного параметра.
Теперь в виде формул
Замена подстановки получаем так называемый заданный многочлен
Ищем решение этого уравнения в виде сумм двух функций
Три вспомогательных параметра связаны с коэффициентами данного полинома следующими соотношениями
Выражая любой из вспомогательных параметров, получаем, в том или ином виде кубическая резольвента
Например, если мы выразим F2
Это кубическое уравнение, подстановка которого превращается в классическую кубическую резольвенту.
Теперь о нюансе которого говорили ранее. Какой знак использовать при вычислении корней?
Критерий получается очень простой. Берем любой корень резольвенты и сравниваем его
если это условие истинно ставится + (плюс), если условие некорректно — (минус)
Далее все эти параметры подставляются в формулу
также определены корни уравнения 4 степени.
Еще хотелось бы поговорить о критерии.Вдумчивый читатель спросит: «А что, если какой-то корень резольвенты является комплексным числом? Каков в данном случае критерий?»
Наилучшим образом, я рассчитывал на подстановку корня в исходное уравнение. Для этого существует легкий алогритический способ, описанный в статье Значение производной многочлена по методу Хорнера. Если адрес выражения равен нулю, то есть истина, то знак не меняется. Если иначе то знак ставим минус.
Теперь можно легко и быстро решать сложные уравнения 4 степени.Вы не найдете его в онлайн-сервисах.
Попробуйте решить уравнение
Один из корней равен
Кто считает, что действительной частью можно пренебречь и отвергнуть как «почти нулевую», глубоко заблуждается. Отказавшись от него, мы будем иметь значение функции, а не ноль.
И только с учетом «такой маленькой» действительной части уравнение стать идентичным. Поэтому точность расчетов очень важна. Если вдруг заметили ошибку в расчетах (а вдруг?) Просьба сообщить.Но я надеюсь, что этого не произойдет.
Несколько примеров:
Новый классический метод решения уравнений четвертой степени :: Science Publishing Group
Прикладная и вычислительная математика
Том 2, Выпуск 2, апрель 2013 г., Страницы: 24-27
Поступила: 25 декабря 2012 г .;
Опубликовано: 2 апреля 2013 г.
Просмотры Загрузки
Авторы
Амир Фатхи, Департамент электротехники, филиал Урмия, Исламский университет Азад, Урмия, Иран
Настаран Шарифан, юридический факультет, филиал Варамин-Пишва, Исламский университет Азад, Варамин, Пишва, Иран
Полиномы высоких степеней часто встречаются во многих задачах, например в задачах оптимизации.Уравнения четвертой степени или так называемые квартики являются одним из типов этих многочленов. В этой статье мы даем новый классический метод решения полиномиального уравнения четвертой степени (Quartic). Мы покажем, как легко представить формулу четвертой степени на уровне предварительного вычисления.
Амир Фатхи,
Настаран Шарифан,
Классический новый метод решения уравнений четвертой степени, Прикладная и вычислительная математика .Vol. 2, №2,
2013, с. 24-27.
DOI: 10.11648 / j.acm.20130202.11
[1]
«Простой метод решения уравнений четвертой степени» Амир Фати, Пуйя Мобадерсани, Рахим Фатхи, Австралийский журнал фундаментальных и прикладных наук, 6 (6): 331-336, 2012, ISSN 1991-8178.
[2]
Кардано, Джироламо, (перевод Т. Ричарда Витмера), Ars Magna или Правила алгебры, Дувр, Нью-Йорк, Нью-Йорк, 1993.
[3]
Смеситель, W.М. «Геометрическая интерпретация решения общего многочлена четвертой степени». Амер. Математика. Месяц 103, 51-57, 1996.
[4]
Gellert, W .; Gottwald, S .; Hellwich, M .; Kästner, H .; и Кюнстнер, Х. (ред.). Краткая энциклопедия математики ВНР, 2-е изд. Нью-Йорк: Ван Ностранд Рейнхольд, 1989.
[5]
Хазевинкель, М.(Управляющий ред.). Энциклопедия математики: обновленный и аннотированный перевод советской «Математической энциклопедии». Дордрехт, Нидерланды: Рейдел, 1988.
[6]
MathPages. «Преобразование квартиков в кубики». http://www.mathpages.com/home/kmath396.htm.
[7]
Смит, Д.E. Справочник по математике. Нью-Йорк: Дувр, 1994.
[8]
ван дер Варден, Б. Л. §64 по алгебре, т. 1. Нью-Йорк: Springer-Verlag, 1993.
.
[9]
Бейер, В.H. Стандартные математические таблицы CRC, 28-е изд. Бока-Ратон, Флорида: CRC Press, стр. 12, 1987а.
[10]
Бейер, У. Х. Справочник по математическим наукам, 6-е изд. Бока-Ратон, Флорида: CRC Press, 1987b.
[11]
Биркгоф, Г.и Мак Лейн, С. Обзор современной алгебры, 5-е изд. Нью-Йорк: Macmillan, стр. 107-108, 1996.
.
[12]
Борвейн П. и Эрдейи Т. «Уравнения четвертой степени». §1.1.E.1e в полиномах и полиномиальных неравенствах. Нью-Йорк: Springer-Verlag, стр. 4, 1995.
[13]
Бойер, К.Б. и Мерцбах, У. С. История математики, 2-е изд. Нью-Йорк: Wiley, стр. 286-287, 1991.
[14]
И. Стюарт, «Теория Галуа», изд: Chapman & Hall / CRC Mathematics, 2004.
[15]
Дж.Дж. О’Коннор и Э. Ф. Робертсон, «Лодовико Феррари», в архиве истории математики MacTutor, под ред. Школа математики и статистики Университета Сент-Эндрюс, Шотландия.
[16]
ЛЕГКИЙ ВЗГЛЯД НА КУБИЧЕСКУЮ ФОРМУЛУ. Томас Дж. Ослер, Математический факультет, Университет Роуэн, Глассборо, штат Нью-Джерси, 08028.
Почему я ненавижу физику: Решение четвертой степени: Часть II
Когда мы остановились, мы только что достигли середины нашего решения уравнения четвертой степени.Что мы сделали, так это показать шаги, необходимые для написания явных выражений p, q и r для этих трех специфических функций альфа, бета, гамма и дельта:
P, q и r оказались корнями кубики с рациональными коэффициентами, которые мы можем легко вычислить. Наши альфы, бета и т. Д., Конечно же, являются корнями нашей квартики. Теперь давайте посмотрим, как мы можем извлечь их по отдельности из наших p и q и т. Д.
Следующий шаг — рассмотреть все возможные комбинации альфа- и бета-версий и т. Д.с переменным знаком:
Есть еще всего три возможных комбинации, но они равны тому, что у нас уже есть с противоположными знаками. Сейчас я хочу показать вам, что наши A, B и C на самом деле являются квадратным корнем из чисел, к которым у нас есть доступ через наши p, q и т. Д.! Вы можете проверить это, возведя в квадрат A, например:
Посмотрите, что у нас есть. Первая строка в альфа-квадрате и т. Д. Симметрична в альфа-бета-гамма-дельта, поэтому это просто рациональное число. Вторая строка в альфа-бета и т. Д.также симметрична … фактически, это просто коэффициент при линейном члене в уравнении четвертой степени. Так что это тоже рациональное число. Третья строка — это наш p , число, которое мы сказали, было решением кубического уравнения, для которого мы знаем коэффициенты. Другими словами, наш A — это просто квадратный корень из (p + b), где b — рациональное число.
Очевидно, что наши B и C также являются квадратными корнями из аналогичных функций, которые мы можем записать в радикалах. Таким образом, мы можем явно писать A, B и C… по крайней мере до двусмысленности знака минус. Но посмотрите, что мы получаем для суммы A, B и C:
Сложив A, B и C, мы изолируем альфа! Помните, что второй коэффициент в любом полиноме легко сделать равным нулю с помощью простого линейного сдвига, который выбивает член в квадратных скобках в приведенном выше выражении. (Это называется «завершение квадрата», когда мы делаем это для квадратного уравнения.) Мы показали явное выражение, которое решает уравнение четвертой степени.
А как насчет бета, гаммы и дельты? Помните, когда мы извлекали квадратный корень, возникла двусмысленность.В каждом случае мы могли выбрать альтернативные знаки. Различные варианты знака квадратного корня приводят к суммам A, B и C, которые могут быть бета, гамма и дельта в зависимости от нашего выбора.
Вот как вы решаете уравнение четвертой степени.
Калькулятор уравнений четвертой степени | Калькулятор уравнений четвертой степени
Калькулятор уравнений четвертой степени, также известный как калькулятор уравнений четвертой степени, позволяет вычислять корни уравнения четвертой степени. Эта страница включает онлайн-калькулятор уравнений 4-й степени, который вы можете использовать со своего мобильного телефона, устройства, настольного компьютера или планшета, а также включает вспомогательное руководство и инструкции по использованию калькулятора.
| x 1 : | + | i | ||
| x 2 : | + | i | ||
| x 3 : | + | i | ||
| x 4 : | + | i |
Если вы нашли Калькулятор Quartic Equation Calculator полезным, было бы здорово, если бы вы любезно предоставили оценку для калькулятор и, если у вас есть время, поделитесь в своей любимой социальной сети netowrk.Это помогает нам сосредоточить наши ресурсы и поддерживать текущие калькуляторы, а также разрабатывать дополнительные математические калькуляторы для поддержки нашего глобального сообщества.
★ ★ ★ ★ ★ [3 голосов]
Чем мне полезен этот калькулятор?
Калькулятор уравнения четвертой степени Это математический онлайн-калькулятор, разработанный калькулятором для поддержки развития ваших математических знаний. Вы можете использовать его, чтобы проверять домашние задания и помогать при расчетах уравнений четвертой степени.Это особенно полезно, если вы плохо знакомы с уравнениями четвертой степени или вам нужно освежить свои математические знания, поскольку калькулятор уравнений четвертой степени точно вычислит вычисления, так что вы можете проверить свои собственные математические вычисления вручную.
Как рассчитать корень четвертой степени?
Вы можете вычислить корень четвертой степени вручную, используя уравнение четвертой степени ниже, или вы можете использовать калькулятор уравнений четвертой степени и сэкономить время и нервы, связанные с вычислением математики вручную.Вы также можете использовать калькулятор, чтобы проверить свои собственные математические вычисления, сделанные вручную, чтобы убедиться, что ваши вычисления верны, и чтобы вы могли проверить любые ошибки в вычислениях уравнений четвертой степени.
Формула уравнения четвертой степени:
ax 4 + bx 3 + cx 2 + dx + e = 0
p = sqrt (y1)
q = sqrt (y3) 7
r = — g / ( 8pq)
s = b / (4a)
x1 = p + q + r — s
x2 = p — q — r — s
x3 = -p + q — r — s
x4 = -p — q + r — s
Как вычислить корень четвертой степени с помощью калькулятора уравнений четвертой степени?
Для тех, кто уже знает, как рассчитать уравнение четвертой степени и хочет сэкономить время или проверить свои результаты, вы можете использовать калькулятор уравнения четвертой степени, выполнив следующие шаги:
- Введите значение для ax 4
- Введите a значение для xb 3
- Введите значение для cx 2
- Введите значение для dx
- Введите значение для e
- Калькулятор уравнения 4-й степени вычислит корни введенного вами уравнения 4-й степени
История уравнения 4-й степени
Формула уравнения четвертой степени была впервые открыта Лодовико Феррари в 1540 году, хотя утверждалось, что в 1486 году испанский математик якобы сказал Томас де Торквемада, главный инквизитор испанской инквизиции, что «это было волей бога, чтобы такое решение было недоступно человеческому разумению», в результате чего математик был сожжен на костре.
Несмотря на то, что Лодовико обнаружил решение квартики в 1540 году, оно не было опубликовано до 1545 года, поскольку решение также требовало решения кубики, которая была обнаружена и опубликована вместе с решением четвертой степени наставником Лодовико Джероламо Кардано в книге Ars Magna.
Как эта формула применима в жизни?
Уравнения четвертой степени на самом деле довольно распространены в вычислительной геометрии, они используются в таких областях, как компьютерная графика, оптика, дизайн и производство.Они также могут быть полезны для расчета соотношений.
Например, при автоматизированном производстве концевых фрез, если они часто связаны с формой тора, требуется решение четвертой степени для расчета его положения относительно триангулированной поверхности.
Математические калькуляторы
Вам также могут пригодиться следующие математические калькуляторы.
КАЛЬКУЛЯТОР КВАРТИЧНЫХ УРАВНЕНИЙ
КАЛЬКУЛЯТОР КВАРТИЧНЫХ УРАВНЕНИЙ
Калькулятор квадратного уравнения
Калькулятор кубического уравнения
Калькулятор четвертого уравнения
1,080 = 0 -123 D = -126 E = 1080 Щелкните E N T E R, и ваши ответы должны быть 5 3–4 и -6.
И Н С Т Р У К Т И О Н С 1) НЕ вводите запятые. 4) Если в уравнении есть член без коэффициента, введите его как 1 (а не 0 или пробел). Для 0 A = 1 B = 6 C = 10 D = 1 E = 0 Чтобы увидеть метод решения уравнений четвертой степени, щелкните ЗДЕСЬ. Если вы хотите использовать метод «длинной руки» для решения квартик, вы можете |

