| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град.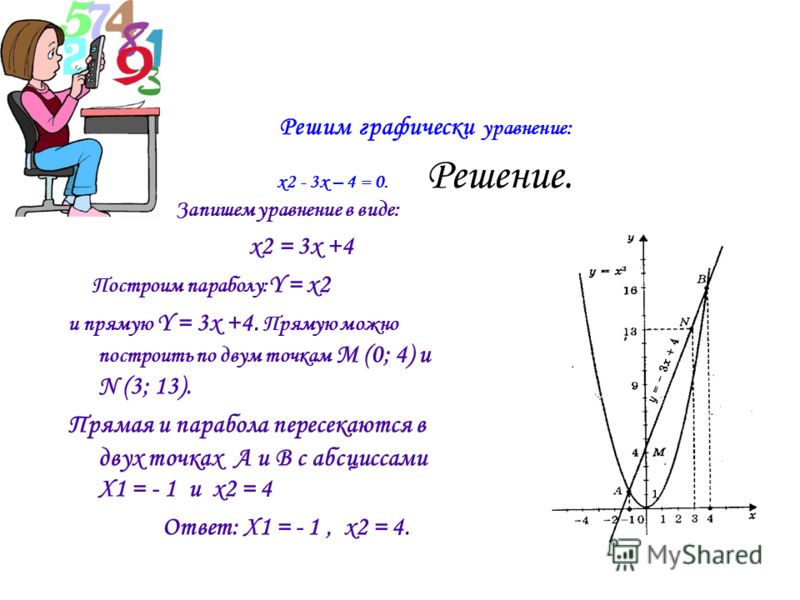 ) ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Алгебра 8 Мордкович (упр. 25.1
Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). § 25. Графическое решение квадратных уравнений. ОТВЕТЫ на упражнения 25.1 — 25.24. ГЛАВА 3. Квадратичная функция. Функция у = k/x. Нажмите на спойлер, чтобы посмотреть ответ на задание.
ОТВЕТЫ на упражнения 25.1 — 25.24. ГЛАВА 3. Квадратичная функция. Функция у = k/x. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 25.1 — 25.24)
§ 25. Графическое решение квадратных уравнений
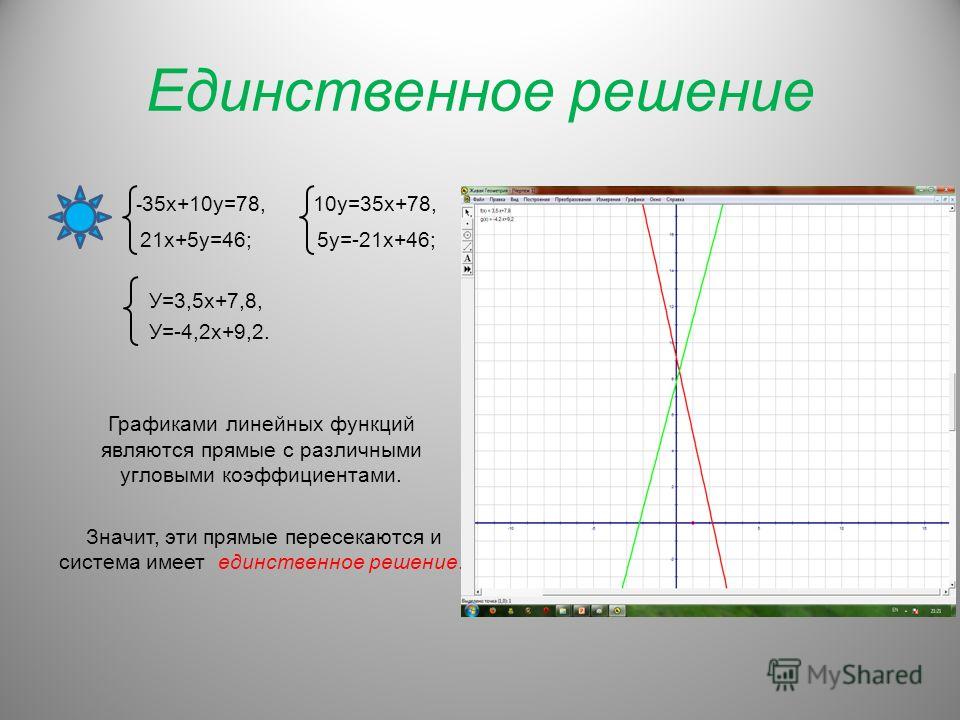
Решите уравнение двумя способами – графическим и аналитическим:
Задание № 25.1. а) х2 – 2х = 0; в) х2 + 4х = 0;
б) –х2 + 6х = 0; г) –х2 – 8х = 0.
Смотреть ответы на № 25.1
Задание № 25.2. а) х2 – 4 = 0; в) х2 – 9 = 0;
б) –х2 + 1 = 0; г) –х2 + 16 = 0.
Смотреть ответы на № 25.2
Задание № 25.3. а) 2х2 – 2 = 0; в) 0,5х2 –2 = 0;
б) –3х2 + 6х = 0; г) –х2 – 2х = 0.
Смотреть ответы на № 25.3
Решите графически уравнение:
Задание № 25. 4. а) х2 + 2х – 3 = 0; в) х2 + 4х – 5 = 0;
4. а) х2 + 2х – 3 = 0; в) х2 + 4х – 5 = 0;
б) х2 – 4х + 3 = 0; г) х2 – 2х – 3 = 0.
Смотреть ответы на № 25.4
Задание № 25.5. а) х2 – х – 2 = 0; в) х2 + 3x + 2 = 0;
б) х2 – 3х – 4 = 0; г) х2 + х – 6 = 0.
Смотреть ответы на № 25.5
Задание № 25.6. а) –х2 + 6х – 5 = 0; в) –х2 – 6x – 8 = 0;
б) –х2 – 3х + 4 = 0; г) –х2 + х + 6 = 0.
Смотреть ответы на № 25.6
Задание № 25.7. а) х2 – 5х + 6 = 0; в) х2 – х – 6 = 0;
б) –х2 – х + 6 = 0; г) –х2 – bx – 6 = 0.
Смотреть ответы на № 25.7
Задание № 25.8. Докажите, что уравнение не имеет корней:
а) 3х2 – 6х + 11 = 0; в) х2 + 2х + 4 = 0;
б) х2 – 3х + 5 = 0; г) 2х2 + 5х + 9 = 0.
Смотреть ответы на № 25. 8
8
Задание № 25.9. Найдите стороны прямоугольника, если известно, что его площадь равна 8 см2, а длина на 2 см больше ширины.
Смотреть ответы на № 25.9
Задание № 25.10. Найдите стороны прямоугольника, если известно, что его периметр равен 14 дм, а площадь равна 12 дм2.
Смотреть ответы на № 25.10
Задание № 25.11. Найдите катеты прямоугольного треугольника, если его гипотенуза равна 5 см, а один из его катетов на 1 см больше другого.
Смотреть ответы на № 25.11
Задание № 25.12.
Смотреть ответы на № 25.12
Задание № 25.13.
Смотреть ответы на № 25.13
Задание № 25.14.
Смотреть ответы на № 25.14
Задание № 25.15.
Смотреть ответы на № 25.15
Задание № 25.16.
Смотреть ответы на № 25.16
Задание № 25.17.
Смотреть ответы на № 25.17
Задание № 25.18.
Смотреть ответы на № 25.18
Задание № 25. 19.
19.
Смотреть ответы на № 25.19
Задание № 25.20.
Смотреть ответы на № 25.20
Задание № 25.21.
Смотреть ответы на № 25.21
Задание № 25.22.
Смотреть ответы на № 25.22
Задание № 25.23.
Смотреть ответы на № 25.23
Задание № 25.24.
Смотреть ответы на № 25.24
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 3. Квадратичная функция. Функция у = k/x. § 25. Графическое решение квадратных уравнений. ОТВЕТЫ на упражнения 25.1 — 25.24. Вернуться в ОГЛАВЛЕНИЕ.
Просмотров:
14 739
Решите графически уравнение: √x = 4
15+16 =31 -шаров в первой корзине, 14+7=21 -шаров во второй.
Вероятность, что из первой корзины достали белый шар = 15/31.
Белый из второй корзины = 14/21 = 2/3.
Вероятность, что оба шара белые равна произведению 15/31 · 2/3 =10/31.
Второй вопрос решается так. Возможны 4 варианта: белый из первой корзины и черный из второй, черный из первой и белый из второй, оба белые, оба черные. Благоприятные — три первые варианта. Надо найти вероятность каждого и сложить. Неблагоприятный последний. можно найти вероятность последнего варианта и ее вычесть из 1.
16/31 · 7/21 = 0,172 — вероятность, что оба шара черные.
1-0,172 = 0,828. — вероятность, что хотя бы один шар белый
Решение в прикрепленном файле.
Использовано правило дифференцирования, взаимосвязь функции и производной
Раскроем скобки
a^4+2a^2b^2+b^4+7a^2b^2=(a^4-2a^2b^2+b^4)+4a^2b^2+7a^2b^2=(a^2-b^2)^2+11a^2b^2=((a-b)(a+b))^2+11a^2b^2
Теперь несложно заметить, что первое слагаемое кратно 11 по условию, а второе очевидно кратно 11, так как содержит множитель 11. Следовательно, сумма также делится на 11. Что требовалось доказать
Следовательно, сумма также делится на 11. Что требовалось доказать
Задача №1256 (построение уравнения регрессии)
По семи территориям Уральского федерального округа за 2006 г. известны значения двух признаков:
Исходные данные:
| Номер региона | Регион | Расходы на покупку продовольственных товаров в общих расходах, %, y | Среднедневная заработная плата одного работающего, усл. ед., x |
| 1 | Удмуртская область | 68,8 | 45,1 |
| 2 | Свердловская область | 61,2 | 59,0 |
| 3 | Башкортостан | 59,9 | 57,2 |
| 4 | Челябинская область | 56,7 | 61,8 |
| 5 | Пермский край | 55,0 | 58,8 |
| 6 | Курганская область | 54,3 | 47,2 |
| 7 | Оренбургская область | 49,3 | 55,2 |
Каким видом задается уравнение линейной регрессии, характеризующей зависимость расходов на покупку продовольственных товаров в общих расходах?
Рекомендуемые задачи по дисциплине
Решение задачи:
Заполняем вспомогательную таблицу:
| № | x | y | y*x | x2 | y2 |
| 1 | 45,1 | 68,8 | 3102,88 | 2034,01 | 4733,44 |
| 2 | 59,0 | 61,2 | 3610,80 | 3481,00 | 3745,44 |
| 3 | 57,2 | 59,9 | 3426,28 | 3271,84 | 3588,01 |
| 4 | 61,8 | 56,7 | 3504,06 | 3819,24 | 3214,89 |
| 5 | 58,8 | 55,0 | 3234,00 | 3457,44 | 3025,00 |
| 6 | 47,2 | 54,3 | 2562,96 | 2227,84 | 2948,49 |
| 7 | 55,2 | 49,3 | 2721,36 | 3047,04 | 2430,49 |
| Итого | 384,3 | 405,2 | 22162,34 | 21338,41 | 23685,76 |
Решение линейно-квадратичных систем
Вы, наверное, решили системы линейных уравнений. Но как насчет системы двух уравнений, в которой одно уравнение является линейным, а другое — квадратичным?
Но как насчет системы двух уравнений, в которой одно уравнение является линейным, а другое — квадратичным?
Мы можем использовать вариант метода подстановки для решения систем этого типа.
Помните, что уравнение прямой имеет вид y = mx + b, а стандартная форма уравнения параболы с вертикальной осью симметрии — y = ax2 + bx + c, a ≠ 0.
Чтобы избежать путаницы с переменными, запишем линейное уравнение в виде y = mx + d, где m
наклон и d
является точкой пересечения оси Y линии.
Подставляем выражение для y
из линейного уравнения в квадратное уравнение. То есть подставляем mx + d
для тебя
в y = ax2 + bx + c
.
мх + д = ах2 + Ьх + с
Теперь перепишите новое квадратное уравнение в стандартной форме.
Вычесть
mx + d
с обеих сторон.
(mx + d) — (mx + d) = (ax2 + bx + c) — (mx + d) 0 = ax2 + (b − m) x + (c − d)
.
Теперь у нас есть квадратное уравнение с одной переменной, решение которого можно найти с помощью формулы корней квадратного уравнения.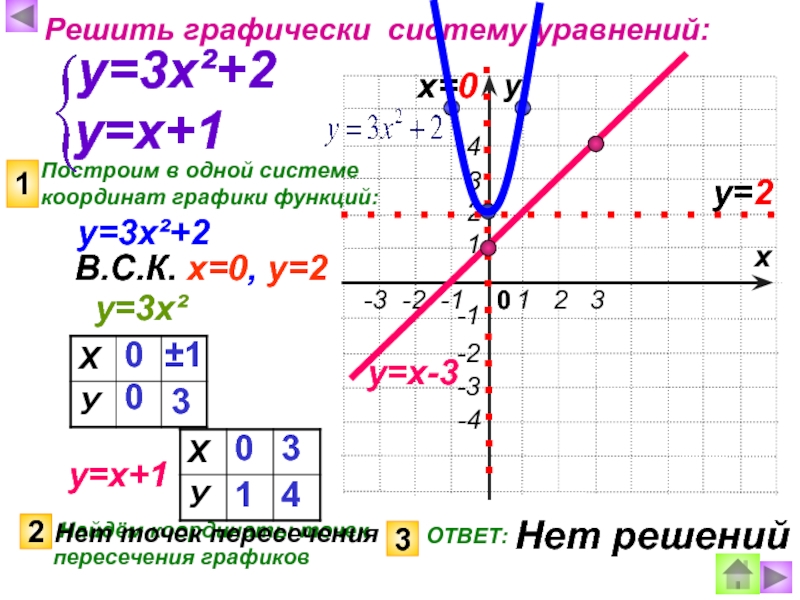
Решения уравнения ax2 + (b − m) x + (c − d) = 0
даст x-координаты точек пересечения графиков прямой и параболы. Соответствующие координаты y могут быть найдены с помощью линейного уравнения.
Другой способ решения системы — построить график двух функций на одной и той же координатной плоскости и определить точки пересечения.
Пример 1:
Найдите точки пересечения прямой y = 2x + 1
и парабола y = x2−2.
Замена 2x + 1
для y в y = x2−2.
2x + 1 = x2−2
Запишите квадратное уравнение в стандартной форме.
2x + 1−2x − 1 = x2−2−2x − 10 = x2−2x − 3
Используйте формулу корней квадратного уравнения, чтобы найти корни квадратного уравнения.
Здесь a = 1, b = −2, c = −3.
x = — (- 2) ± (−2) 2-4 (1) (- 3) 2 (1) = 2 ± 4 + 122 = 2 ± 42 = 3, −1
Подставьте значения x в линейное уравнение, чтобы найти соответствующие значения y.
x = 3⇒y = 2 (3) +1 = 7x = −1⇒y = 2 (−1) +1 = −1
Следовательно, точки пересечения равны (3,7)
и (−1, −1).
Постройте параболу и прямую линию на координатной плоскости.
Аналогичный метод можно использовать для поиска точек пересечения прямой и окружности.
Пример 2:
Найдите точки пересечения прямой y = −3x
и окружность x2 + y2 = 3.
Заменитель −3x
для тебя
в x2 + y2 = 3
.
x2 + (- 3x) 2 = 3
Упростить.
x2 + 9×2 = 310×2 = 3×2 = 310
Извлечение квадратного корня, x = ± 310.
Подставьте значения x в линейное уравнение, чтобы найти соответствующие значения y.
x = 310⇒y = −3 (310) = −3310x = −310⇒y = −3 (−310) = 3310
Следовательно, точки пересечения (310, −3310)
и (-310, 3310).
Постройте окружность и прямую линию на координатной плоскости.
… или линия и эллипс.
Пример 3:
Решите систему уравнений y = −5.
и x29 + y24 = 1.
Заменитель −5
для тебя
в −5.
x29 + (- 5) 24 = 1
Упростить.
x29 + (- 5) 24 = 14×236 + 9 (25) 36 = 14×2 + 225 = 364×2 = −189×2 = −1894
Здесь у нас есть отрицательное число как квадрат числа. Итак, два уравнения не имеют реальных решений.
Постройте эллипс и прямую линию на координатной плоскости.
Мы видим, что они не пересекаются.
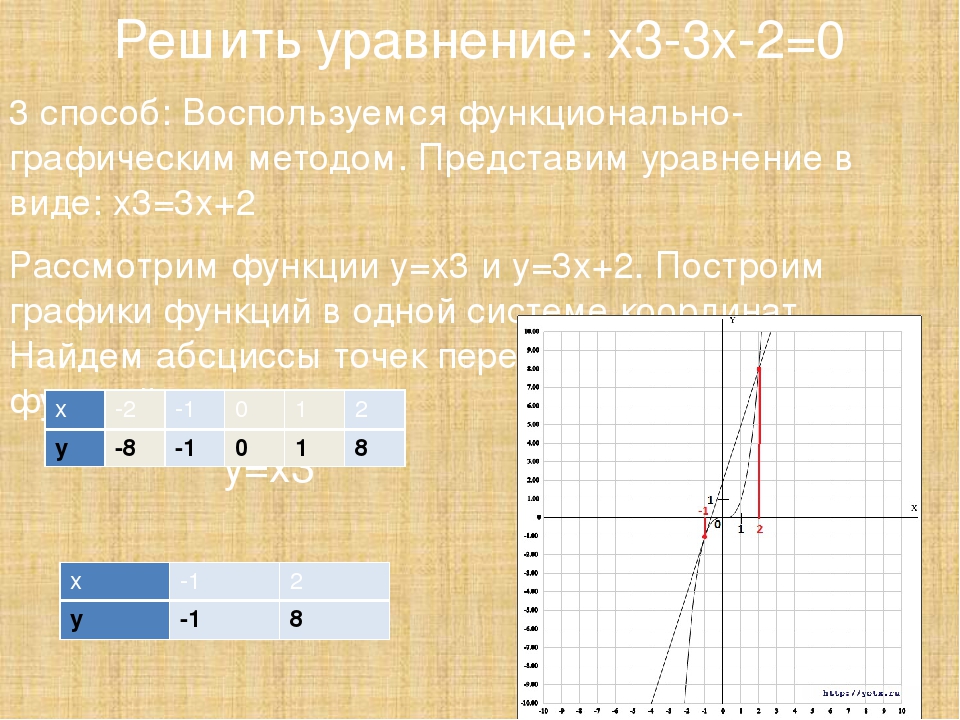
Решение квадратных уравнений с помощью графических примеров
Сначала мы должны построить график для данного квадратного уравнения.Чтобы решить второе квадратное уравнение с использованием первого, мы должны вычесть второе уравнение из первого уравнения. Так получаем прямую.
Мы можем определить корни квадратного уравнения графически, выбрав соответствующую параболу и пересекая ее желаемой прямой линией.
(i) Если прямая линия пересекает параболу в двух различных точках, то координаты x этих точек будут корнями данного квадратного уравнения.
(ii) Если прямая линия касается параболы только в одной точке, то координата x общей точки будет единственным корнем квадратного уравнения.
(iii) Если прямая линия не пересекает параболу и не касается параболы, то квадратное уравнение не будет иметь действительных корней.
Пример 1:
Нарисуйте график y = x 2 + 3x — 4 и, следовательно, решите x 2 + 3x — 4 = 0
Решение:
Теперь давайте нарисуем график y = x 2 + 3x — 4
x -4 -3 -2 -1 0 1 2 3 4 | x 2 16 9 4 1 0 1 4 9 16 | 3x -12 -9 -8 -3 0 3 6 9 12 | -4 -4 -4 -4 -4 -4 -4 -4 -4 -4 | л 0 -4 -8 -6 -4 0 6 14 24 |
Точки для построения:
(-4, 0) (-3, -4) (-2, -8) (-1, -6) (0, -4) (1, 0) (2 , 6) (3, 14) (4, 24)
Чтобы найти x-координату вершины параболы, мы можем использовать формулу x = -b / 2a
x = -3/2 (1) = -3/2
Применяя x = -3/2, мы получаем значение y.
y = (-3/2) 2 + 3 (-3/2) — 4
y = 9/4 — (9/4) — 4
y = -4
Вершина (- 3/2, -4)
y = x 2 + 3x — 4 —— (1)
0 = x 2 + 3x — 4 —— (2)
(1) — (2)
y = x 2 + 3x — 4 —— (1)
0 = x 2 + 3x — 4 —— (2)
(-) (-) (-) (-)
——————-
y = 0
y = 0 означает ось абсцисс.Парабола пересекает ось x в двух точках -4 и 1.
Следовательно, решения равны -4 и 1.
Пример 2:
Нарисуйте график y = x 2 −5x −6 и следовательно, решите x 2 −5x −14 = 0
Решение:
Теперь давайте нарисуем график y = x 2 — 5x — 6
x -4 -3 -2 -1 0 1 2 3 4 | x 2 16 9 4 1 0 1 4 9 16 | -5x 20 15 10 5 0 -5 -10 -15 -20 | -6 -6 -6 -6 -6 -6 -6 -6 -6 -6 | л 30 18 8 0 -6 -10 -12 -12 -10 |
Точки для построения:
(-4, 30) (-3, 18) (-2, 8) (-1, 0) (0, -6) (1, -10) (2, — 12) (3, -12) (4, -10)
Чтобы найти x-координату вершины параболы, мы можем использовать формулу x = -b / 2a
x = — (- 5) / 2 (1) = 5/2
Применяя x = 5/2, мы получаем значение y.
y = (5/2) 2 — 5 (5/2) — 6
y = 25/4 — (25/2) — 6
y = (25-50 — 24) / 4
y = -49/4
Вершина (5/2, -49/4)
y = x 2 −5x −6 —— (1)
0 = x 2 −5x −14 —— (2)
(1) — (2)
y = x 2 −5x −6 —— (1)
0 = x 2 −5x −14 —— (2)
(-) (-) (+) (+)
——————-
y = 8
Следовательно, парабола и прямая пересекаются в двух точках -2 и 7 на оси абсцисс.
Следовательно, решения равны -2 и 7.
Пример 3:
Нарисуйте график y = 2x 2 — 3x — 5 и, следовательно, решите 2x 2 — 4x — 6 = 0
Решение:
Построим график y = 2x 2 — 3x — 5
x -2 -1 0 1 2 3 4 | 2x 2 8 2 0 2 8 18 32 | -3x 6 3 0 -3 -6 -9 -12 | -5 -5 -5 -5 -5 -5 -5 -5 | л 9 0 -5 -6 -3 4 15 |
Точки для построения:
(-2, 9) (-1, 0) (0, -5) (1, -6) (2, -3) (3, 4) (4, 15)
Чтобы найти x-координату вершины параболы, мы можем использовать формулу x = -b / 2a
x = — (- 3) / 2 (2) = 3/4
Применяя x = 3/4, получаем значение y.
y = 2 (3/4) 2 — 3 (3/4) — 5
y = 18/16 — (12/4) — 5
y = (18 — 48 — 80) / 16
y = -110/16
Вершина (3/4, -110/16)
y = 2x 2 — 3x — 5 —— (1)
0 = 2x 2 — 4x — 6 —— (2)
(1) — (2)
y = 2x 2 — 3x — 5 —— (1)
0 = 2x 2 — 4x — 6 —— (2)
(-) (-) (+) (+)
——————-
y = x + 1
Проведя линию на том же графике, мы получим
Парабола и прямая пересекаются в двух точках -1 и 3.Следовательно, решения равны -1 и 3.
Пример 4:
Нарисуйте график y = (x — 1) (x + 3) и, следовательно, решите x 2 — x — 6 = 0
Решение:
y = (x — 1) (x + 3)
y = x 2 + 3x — x — 3
y = x 2 + 2x — 3
x -2 -1 0 1 2 3 4 | x 2 4 1 0 1 4 9 16 | 2x -4 -2 0 2 4 6 8 | -3 -3 -3 -3 -3 -3 -3 -3 | л -3 -4 -3 0 5 12 21 |
Точки для построения:
(-2, -3) (-1, -4) (0, -3) (1, 0) (2, 5) (3, 12) (4, 21)
Чтобы найти координату x вершины параболы, мы можем использовать формулу x = -b / 2a
x = -2/2 (1) = -1
Применяя x = -1, мы получить значение y.
y = (-1) 2 + 2 (-1) — 3
y = 1-2-3
y = -4
Вершина (-1, -4)
y = x 2 + 2x — 3 —— (1)
0 = x 2 — x — 6 —— (2)
(1) — (2)
y = x 2 + 2x — 3 —— (1)
0 = x 2 — x — 6 —— (2)
(-) (-) (+) (+)
——————-
y = 3x + 3
y = 3 (x + 1)
Рисуя линии на том же графике, получаем
Парабола и прямая пересекаются в двух точках -2 и 7.Следовательно решения -2 и 7.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Проблемы со словами на квадратных уравнениях
23
задачи на слова
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по количеству слов
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойным фактом
Проблемы со словами тригонометрии
Проблемы со словами в процентах
задачи
задачи с десятичными числами
задачи со словами на дроби
задачи со словами на смешанные фракции
одностадийные задачи на слова с уравнениями
задачи на слова с линейным неравенством и пропорциями
Задачи со словами
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами на возрастах
Проблемы со словами из теоремы Пифагора
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами на сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
000 Домен и диапазон рациональных функций 9122 функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск корня из длинного квадрата видение
Л. 2-3x-2 = 0 Tiger Algebra Solver
2-3x-2 = 0 Tiger Algebra Solver Пошаговое решение:
Шаг 1:
Попытка разложить на множители путем разделения среднего члена
1.1 Факторинг x 2 -3x-2
Первый член равен x 2 , его коэффициент равен 1.
Средний член равен -3x, его коэффициент равен -3.
Последний член, «константа», равен -2
Шаг-1: Умножьте коэффициент первого члена на константу 1 • -2 = -2
Шаг-2: Найдите два множителя -2, сумма которых равен коэффициенту среднего члена, который равен -3.
| -2 | + | 1 | = | -1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -1 | + | 2 |
|
|
Ответ:
| x | 3 | -2 | 0 |
| y | 0 | 5 | 3 |
| ( x , y ) | (3, 0) | -2, 5 | (0, 3) |
| x | 4 | –1 | 0 |
| y | 0 | -5 | –4 |
| ( x , y ) | 4,0 | -1, -5 | (0, –4) |
Страница № 8:
Вопрос 2:
Решите следующие одновременные уравнения графически.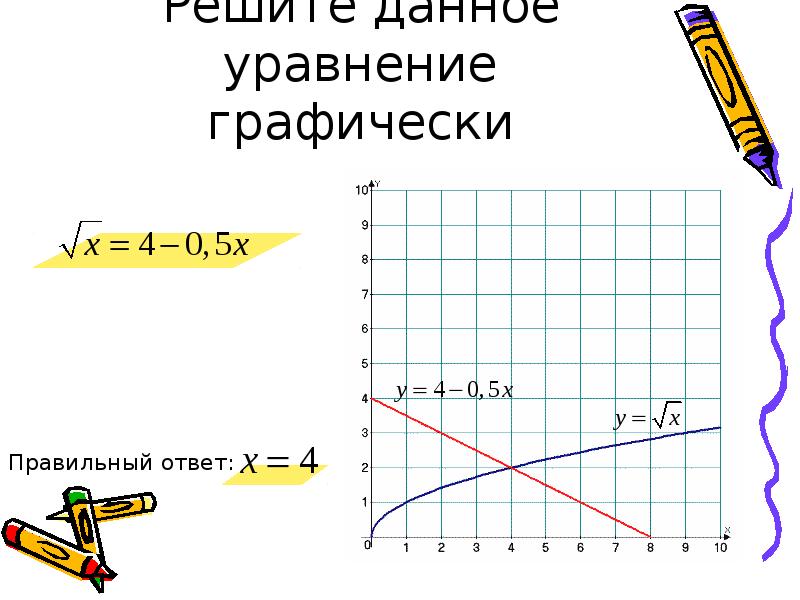
(1) x + y = 6; x — y = 4
(2) x + y = 5; x — y = 3
(3) x + y = 0; 2 x — y = 9
(4) 3 x — y = 2; 2 x — y = 3
(5) 3 x — 4 y = –7; 5 x — 2 y = 0
(6) 2 x — 3 y = 4; 3 y — x = 4
Ответ:
(1) x + y = 6;
x — y = 4
Точка пересечения двух линий — (5, 1).
(2) x + y = 5
x — y = 3
Точка пересечения двух линий — (4, 1)
(3) x + y = 0
2 x — y = 9
Точка пересечения двух прямых — (3, −3).
(4) 3 x — y = 2
2 x — y = 3
Точка пересечения двух прямых — (−1, −5).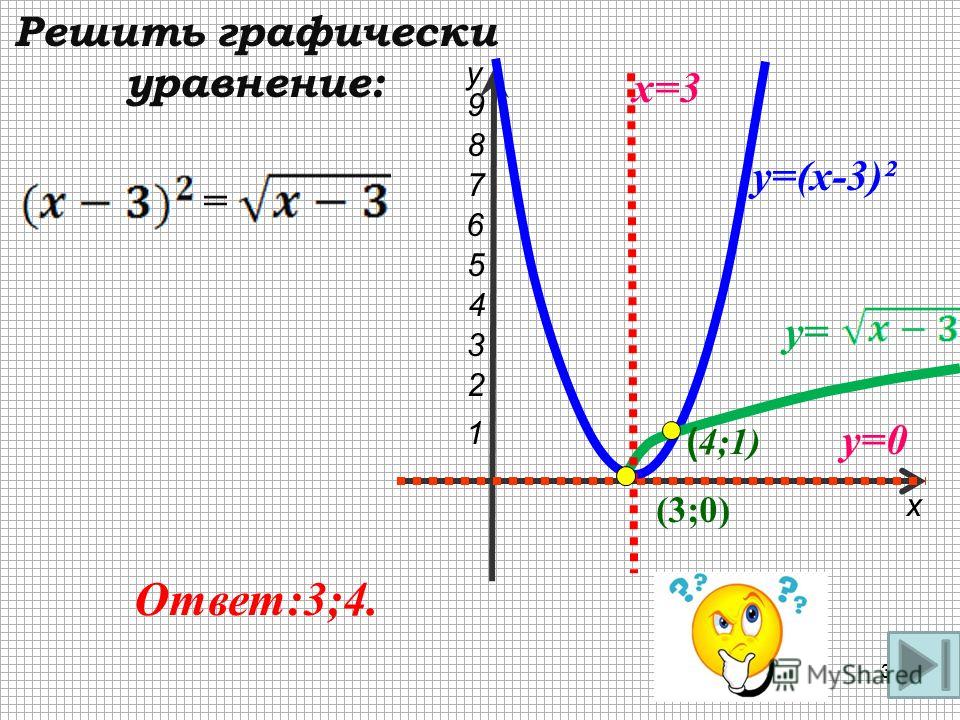
(5) 3 x — 4 y = –7
| x | 1 | 0 | −2,3 |
| y | 2,5 | 1,75 | 0 |
5 x — 2 y = 0
Точка пересечения двух прямых — (1, 2.5).
(6) 2 x — 3 y = 4
3 y — x = 4
Точка пересечения двух прямых — (8, 4).
Страница № 16:
Вопрос 1:
Заполните пропуски правильным номером
3 24 5 = 3 × — × 4 = –8 =
Ответ:
3 24 5 = 35-24 = 15-8 = 7
Таким образом, имеем
3 24 5 = 3 × 5 — 2 × 4 = 15 –8 = 7
Страница № 16:
Вопрос 2:
Найдите значения следующих определителей.
(1) -1 7 2 4
(2) 5 3-7 0
(3) 73533212
Ответ:
(1) -1 7 2 4
= -14-72 = -4-14 = -18
(2) 5 3-7 0 = 5 × 0-3 × -7 = 0 + 21 = 21
(3) 73533212 = 73 × 12-53 × 32 = 76-52 = 7-156 = -86 = -43
Страница № 16:
Вопрос 3:
Решите следующие одновременные уравнения, используя правило Крамера.
(1) 3 x — 4 y = 10; 4 x + 3 y = 5
(2) 4 x + 3 y — 4 = 0; 6 x = 8 — 5 y
(3) x + 2 y = –1; 2 x — 3 y = 12
(4) 6 x — 4 y = –12; 8 x — 3 y = –2
(5) 4 м + 6 n = 54; 3 м + 2 n = 28
(6) 2x + 3y = 2; х-у2 = 12
Ответ:
(1) 3 x — 4 y = 10
4 x + 3 y = 5
D = 3-443 = 3 × 3—4 × 4 = 9 + 16 = 25Dx = 10 -453 = 10 × 3—4 × 5 = 30 + 20 = 50Dy = 31045 = 3 × 5-10 × 4 = 15-40 = -25
x = DxD = 5025 = 2y = DyD = -2525 = -1x , y = 2, -1
(2) 4 x + 3 y — 4 = 0; 6 x = 8-5 y
D = 4365 = 4 × 5-6 × 3 = 20-18 = 2Dx = 4385 = 4 × 5-3 × 8 = 20-24 = -4Dy = 4468 = 4 × 8-6 × 4 = 32-24 = 8
x = DxD = -42 = -2y = DyD = 82 = 4x, y = -2,4
(3) x + 2 y = — 1; 2 x — 3 y = 12
D = 122-3 = 1 × -3-2 × 2 = -3-4 = -7Dx = -1212-3 = -1 × -3-2 × 12 = 3-24 = -21Dy = 1-1212 = 1 × 12—1 × 2 = 12 + 2 = 14
x = DxD = -21-7 = 3y = DyD = 14-7 = -2x, y = 3, -2
(4) 6 x — 4 y = –12; 8 x — 3 y = –2
D = 6-48-3 = 6 × -3-4 × 8 = -18 + 32 = 14Dx = -12-4-2-3 = — 12 × -3—4 × -2 = 36-8 = 28Dy = 6-128-2 = 6 × -2—12 × 8 = -12 + 96 = 84
x = DxD = 2814 = 2y = DyD = 8414 = 6x, y = 2,6
(5) 4 м + 6 n = 54; 3 м + 2 n = 28
D = 4632 = 4 × 2-6 × 3 = 8-18 = -10Dx = 546282 = 54 × 2-6 × 28 = 108-168 = -60Dy = 454328 = 4 × 28-54 × 3 = 112-162 = -50
x = DxD = -60-10 = 6y = DyD = -50-10 = 5x, y = 6,5
(6) 2x + 3y = 2; x-y2 = 12
D = 231-12 = 2 × -12-3 × 1 = -1-3 = -4Dx = 2312-12 = 2 × -12-3 × 12 = -1-32 = -52Dy = 22112 = 2 × 12-2 × 1 = 1-2 = -1
x = DxD = -52-4 = 58y = DyD = -1-4 = 14x, y = 58,14
Страница № 19:
Вопрос 1:
Решите следующие одновременные уравнения.
1 2x-3y = 15; 8x + 5y = 772 · 10x + y + 2x-y = 4; 15x + y-5x-y = -23 27x-2 + 31y + 3 = 85; 31x-2 + 27y + 3 = 894 13x + y + 23x-y = 34; 123x + y-123x-y = -18
Ответ:
1 2x-3y = 15; 8x + 5y = 77
Пусть 1x = u и 1y = v
Итак, уравнение принимает вид
2u-3v = 15 ….. I8u + 5v = 77 ….. II
Умножьте (I) на 4 we получаем
8u-12v = 60 ….. III
(II) — (III)
8u-8u + 5v — 12v = 77-60⇒17v = 17⇒v = 1 Вставляем значение v в I2u-31 = 15⇒2u = 15 + 3 = 18⇒u = 9
Таким образом,
1x = u = 9⇒x = 191y = v = 1⇒y = 1x, y = 19,1
2 10x + y + 2x- у = 4; 15x + y-5x-y = -2
Пусть 1x + y = u и 1x-y = v
Итак, уравнение принимает вид
10u + 2v = 4….. I15u-5v = -2 ….. II
Умножая (I) на 5 и (II) на 2, получаем
50u + 10v = 20 ….. III30u-10v = -4 .. … IV
Складывая (III) и (IV), получаем
u = 1680 = 15
Подставляя это значение в (I)
10 × 15 + 2v = 4⇒2 + 2v = 4⇒v = 1
1x + y = 15 и 1x-y = 1⇒x + y = 5 и xy = 1 Решая эти уравнения, мы получаем x = 3 и y = 2
3 27x-2 + 31y + 3 = 85; 31x-2 + 27y + 3 = 89
Пусть 1x-2 = u и 1y + 3 = v
27u + 31v = 85 . …. I31u + 27v = 89….. IIСложив I и II58u + 58v = 174u + v = 3 ….. III Вычтя II из I4u-4v = 4⇒uv = 1 ….. IV
…. I31u + 27v = 89….. IIСложив I и II58u + 58v = 174u + v = 3 ….. III Вычтя II из I4u-4v = 4⇒uv = 1 ….. IV
Складывая (III) и (IV), получаем
2u = 4⇒u = 2
Подставляем значение u в III
2 + v = 3⇒v = 1
1x-2 = u = 2⇒x-2 = 12⇒x = 52
1y + 3 = 1⇒y + 3 = 1⇒y = -2
x, y = 52, -2
4 13x + y + 23x-y = 34; 123x + y-123x-y = -18
Пусть 13x + y = u и 13x-y = v
u + 2v = 34 и 12u-12v = -18
Итак, уравнения становятся
4u + 4v = 3 .. … I4u-4v = 1….. II
Складываем (I) и (II)
8u = 4⇒u = 12
Подставляем значение u в (I)
12 + 2v = 34⇒v = 14
13x + y = u и 13x-y = v⇒13x + y = 123x + y = 2 ….. III Также, 13x-y = 14⇒3x-y = 4 ….. IV
(III) + (IV) получаем
6x = 6⇒x = 1y = -1
Страница № 26:
Вопрос 1:
Два числа отличаются на 3. Сумма удвоенного меньшего числа и троекратного большего числа равна 19. Найдите числа.
Найдите числа.
Ответ:
Пусть меньшее число будет x , а большее число будет y .
Учитывая, что два числа отличаются на 3, поэтому
yx = 3 ….. (I)
Кроме того, сумма удвоенного меньшего числа и троекратного большего числа равна 19
Итак, 2x + 3y = 19 … … (II)
Два полученных уравнения:
yx = 3
2x + 3y = 19
Умножая (I) на 3, получаем
3y-3x = 9….. (III)
Складывая (III) и (II), получаем
4 y = 28
⇒y = 284 = 7
Подставляя значение y = 7 в (I), получаем
7 -x = 3⇒-x = 3-7⇒-x = -4⇒x = 4
Таким образом, два числа — 4 и 7.
Страница № 26:
Вопрос 2:
Выполните следующее.
Ответ:
Длина данного прямоугольника равна 2x + y + 8 и 4x-y
2x + y + 8 = 4x-y⇒y + y + 8 = 4x-2x⇒8 + 2y = 2x⇒2x-2y = 8 Делим на 2х-у = 4. …. I
…. I
Ширина прямоугольника 2 y и x + 4.
2y = x + 4⇒x-2y = -4 ….. II
Вычитание (II) из (I)
xxy — 2y = 4—4⇒-y + 2y = 8⇒y = 8 Подставляя значение y = 8 в (I), получаем x-8 = 4⇒x = 4 + 8 = 12
Length = 4x- y = 412-8 = 40
Ширина = 2 × 8 = 16
Периметр = 2 длина + ширина = 240 + 16 = 112 единиц
Площадь = длина × ширина = 40 × 16 = 640 единиц2
Страница № 26:
Вопрос 3:
Сумма возраста отца и двойного возраста его сына составляет 70 лет.Если мы удвоим возраст отца и прибавим его к возрасту его сына, получится 95. Найдите их нынешний возраст.
Ответ:
Пусть возраст отца составляет x года, а возраст сына — y года.
Сумма возраста отца и удвоенного возраста его сына равна 70, так что
x + 2y = 70 …… (I)
Удвоенный возраст отца, добавленный к возрасту его сына, сумма составляет 95
2х + у = 95. …. (II)
…. (II)
Складывая (I) и (II), получаем
3x + 3y = 165 Делим на 3x + y = 55 ….. III
Вычитая (I) из (II)
2x-x + y-2y = 95-70⇒xy = 25 ….. IV
Складывая (III) и (IV), получаем
2x = 80⇒x = 40 Подставляя значение x = 40 в III40 + y = 55⇒y = 55-40⇒y = 15
Таким образом, возраст отца — 40 лет, а возраст сына — 15 лет.
Страница № 26:
Вопрос 4:
Знаменатель дроби на 4 больше, чем ее числитель.Знаменатель становится в 12 раз больше числителя, если и числитель, и знаменатель уменьшаются на 6. Найдите дробь.
Ответ:
Пусть дробь будет xy.
Знаменатель дроби на 4 раза больше ее числителя.
Итак,
y = 4 + 2x⇒2x-y = -4 ….. I
Кроме того, знаменатель становится в 12 раз больше числителя, если и числитель, и знаменатель уменьшаются на 6.
Итак,
y-6 = 12x-6⇒y-6 = 12x-72⇒12x-y = 72-6 = 66⇒12x-y = 66 . …. II
…. II
Вычитание (I) из (II)
12x-2x-y — y = 66—4⇒10x = 70⇒x = 7010 = 7⇒x = 7
Подставляем значение x = 7 в (I)
27-y = -4⇒ 14-y = -4⇒y = 14 + 4 = 18
Таким образом, полученная дробь равна 718.
Страница № 26:
Вопрос 5:
Два типа ящиков A, B должны быть помещены в грузовик грузоподъемностью 10 тонн.Когда в грузовик загружается 150 ящиков типа А и 100 ящиков типа В, он весит 10 тонн. Но когда в грузовик загружено 260 ящиков типа A, он все еще может вместить 40 ящиков типа B, так что он полностью загружен. Найдите вес каждого типа коробки.
Ответ:
Пусть вес коробки A составляет x , а вес коробки B — y .
Когда 150 ящиков типа A и 100 ящиков типа B загружены в грузовик, он весит 10 тонн i.е 10000 кг.
Итак,
150x + 100y = 10000⇒15x + 10y = 1000⇒3x + 2y = 200 . …. I
…. I
Когда 260 ящиков типа A загружены в грузовик, он все еще может вместить 40 ящиков типа B, чтобы он был полностью загружен.
260x + 40y = 10000⇒26x + 4y = 1000⇒13x + 2y = 500 ….. II
Вычитая (I) из (II), получаем
13x-3x + 2y-2y = 500-200⇒10x = 300⇒x = 30 Подставляем значение x = 30 в I330 + 2y = 200⇒90 + 2y = 200⇒2y = 200-90 = 110⇒y = 1102 = 55
Таким образом, вес коробки A = 30 кг, а вес коробки ящик Б = 55 кг.
Страница № 26:
Вопрос 6:
Из 1900 км Вишал проехал какое-то расстояние на автобусе, а часть на самолете. Автобус движется со средней скоростью 60 км / час, а средняя скорость самолета составляет 700 км / час. Путешествие занимает 5 часов. Определив расстояние, Вишал ехал на автобусе.
Ответ:
Мы знаем скорость = расстояние и время
Средняя скорость автобуса = 60 км / ч.
Пусть время, проведенное в автобусе, составит x часа.
Средняя скорость автобуса = 700 км / ч.
Пусть время в автобусе составит и часов.
Общее пройденное расстояние = 1900 км
60x + 700y = 1900⇒6x + 70y = 190⇒3x + 35y = 95 ….. I
Путешествие занимает 5 часов, поэтому
x + y = 5 .. … II
Умножая (II) на 3
3x + 3y = 15 ….. III
Вычитая (III) из (I), получаем
3x-3x + 35y-3y = 95-15⇒32y = 80 ⇒y = 2,5
Положив значение y = 2.5 в (II) получаем
x + 2,5 = 5⇒x = 2,5
Расстояние, пройденное Vishal на автобусе = скорость × время = 60 × 2,5 = 150 км.
Страница № 27:
Вопрос 1:
Выберите правильный вариант для каждого из следующих вопросов
(1) Чтобы нарисовать график 4 x +5 y = 19, найдите y , когда x = 1.
| А) 4 | (В) 3 | (К) 2 | (Д) –3 |
(2) Для одновременных уравнений в переменных x и y , D x = 49, D y = –63, D = 7, тогда что будет x ?
| А) 7 | (В) –7 | (К) 17 | (Д) -17 |
(3) Найдите значение 53-7-4
| A) –1 | (В) –41 | (К) 41 | (Г) 1 |
(4) Решить x + y = 3; 3 x -2 y -4 = 0 методом определителя найти D.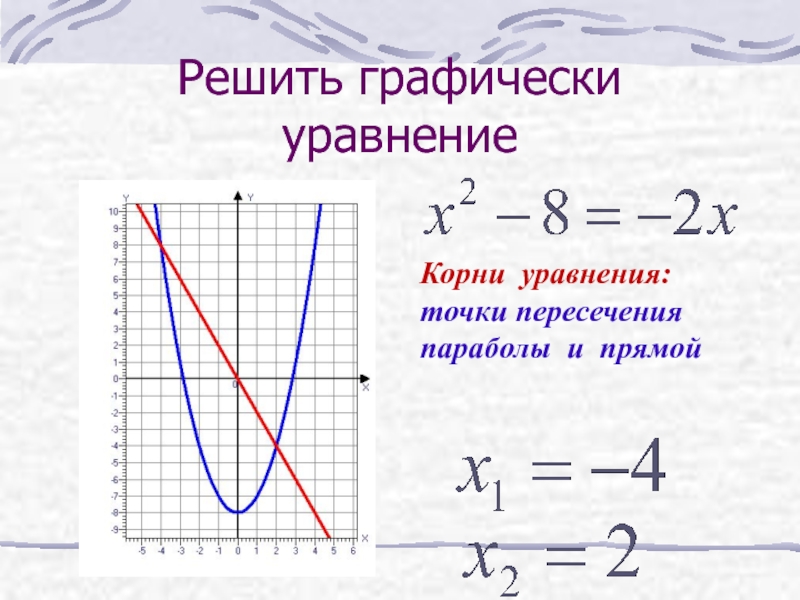
| А) 5 | (В) 1 | (К) –5 | (Д) –1 |
(5) ax + на = c и mx + ny = d и an ≠ bm , тогда эти одновременные уравнения имеют —
| (А) | Только одно общее решение. | (А) | Нет решения. |
| (К) | Бесконечное количество решений. | (Г) | Только два решения. |
Ответ:
(1) 4 x +5 y = 19
Когда x = 1, тогда y будет
41 + 5y = 19⇒4 + 5y = 19⇒5y = 19-4 = 15⇒ 5y = 15⇒y = 155 = 3
Следовательно, правильный ответ — вариант (B).
(2) x = DxD = 497 = 7
Следовательно, правильный ответ — вариант (A).
(3) 53-7-4 = 5 × -4-3 × -7 = -20 + 21 = 1
Следовательно, правильный ответ — вариант (D).
(4) x + y = 3; 3 x — 2 y — 4 = 0
D = 113-2 = 1 × -2-1 × 3 = -2-3 = -5
Следовательно, правильный ответ — вариант (C).
(5) ax + by = c и mx + ny = d
D = abmn = an-bm
an ≠ bm
So, D ≠ 0.
Итак, данные уравнения имеют единственное решение или только одно общее решение.
Следовательно, правильный ответ — вариант А.
Страница № 27:
Вопрос 2:
Заполните следующую таблицу, чтобы построить график 2 x — 6 y = 3
| x | –5 | х |
| y | х | 0 |
| ( х, ) | х | х |
Ответ:
2 x — 6 y = 3
| x | –5 | 32 |
| y | -136 | 0 |
| ( х, ) | -5, -136 | 32,0 |
Страница № 27:
Вопрос 3:
Решите следующие одновременные уравнения графически.
(1) 2 x + 3 y = 12; x — y = 1
(2) x — 3 y = 1; 3 x — 2 y + 4 = 0
(3) 5 x — 6 y + 30 = 0; 5 x + 4 y — 20 = 0
(4) 3 x — y — 2 = 0; 2 x + y = 8
(5) 3 x + y = 10; x — y = 2
Ответ:
(1) 2 x + 3 y = 12
x — y = 1
Решением данных уравнений является точка пересечения двух прямых i.е (3, 2).
(2) x — 3 y = 1
3 x -2 y + 4 = 0
Решение данных уравнений — точка пересечения двух прямых, т.е. (-2, -1).
(3) 5 x — 6 y + 30 = 0
5 x + 4 y -20 = 0
Решением данных уравнений является точка пересечения двух прямых, т. е. (0, 5).
е. (0, 5).
(4) 3 x — y — 2 = 0
2 x + y = 8
Решением данных уравнений является точка пересечения двух прямых, т.е. (2, 4).
(5) 3 x + y = 10
x — y = 2
Решением данных уравнений является точка пересечения двух прямых, т.е. (3, 1).
Страница № 27:
Вопрос 4:
Найдите значения каждого из следующих определителей.
| (1) 4327 | (2) 5-2-31 | (3) 3-114 |
Ответ:
(1) 4327 = 4 × 7-3 × 2 = 28-6 = 22
(2) 5-2-31 = 5 × 1-2 × -3 = 5-6 = -1
(3 ) 3-114 = 3 × 4—1 × 1 = 12 + 1 = 13
Страница № 28:
Вопрос 5:
Решите следующие уравнения методом Крамера.
(1) 6 x — 3 y = –10; 3 x + 5 y — 8 = 0
(2) 4 м — 2 n = –4; 4 м + 3 n = 16
(3) 3 x — 2 y = 52; 13x + 3y = -43
(4) 7 x + 3 y = 15; 12 y -5 x = 39
(5) x + y-82 = x + 2y-143 = 3x-y4
Ответ:
(1) 6 x — 3 y = –10; 3 x + 5 y — 8 = 0
D = 6-335 = 6 × 5—3 × 3 = 30 + 9 = 39Dx = -10-385 = -10 × 5—3 × 8 = -50 + 24 = -26Dy = 6-1038 = 6 × 8—10 × 3 = 48 + 30 = 78x = DxD = -2639 = -23y = DyD = 7839 = 2x, y = -23,2
( 2) 4 м — 2 n = –4; 4 м + 3 n = 16
D = 4-243 = 4 × 3—2 × 4 = 12 + 8 = 20Dx = -4-2163 = -4 × 3—2 × 16 = -12 + 32 = 20Dy = 4-4416 = 4 × 16—4 × 4 = 64 + 16 = 80x = DxD = 2020 = 1y = DyD = 8020 = 4x, y = 1,4
(3) 3 x — 2 y = 52; 13x + 3y = -43
D = 3-2133 = 9 + 23 = 293Dx = 52-2-433 = 152-83 = 296Dy = 35213-43 = -4-56 = -296x = DxD = 296293 = 12y = DyD = -296293 = -12x, y = 12, -12
(4) 7 x + 3 y = 15; 12 y — 5 x = 39
D = 73-512 = 7 × 12-5 × 3 = 84 + 15 = 99Dx = 1533912 = 15 × 12-39 × 3 = 180-117 = 63Dy = 715 -539 = 7 × 39—5 × 15 = 273 + 75 = 348x = DxD = 6399 = 711y = DyD = 34899 = 11633x, y = 711,11633
(5) x + y-82 = x + 2y- 143 = 3x-y4
x + y-82 = x + 2y-143⇒3x + 3y-24 = 2x + 4y-28⇒xy = -4. …. I и x + 2y-143 = 3x-y4⇒4x + 8y-56 = 9x-3y⇒5x-11y = -56 ….. II
…. I и x + 2y-143 = 3x-y4⇒4x + 8y-56 = 9x-3y⇒5x-11y = -56 ….. II
Из (I) и (II)
D = 1-15-11 = -11 × 1—1 × 5 = -11 + 5 = -6Dx = -4-1-56-11 = -11 × -4—1 × -56 = 44-56 = — 12Dy = 1-45-56 = -56 × 1-4 × 5 = -56 + 20 = -36x = DxD = -12-6 = 2y = DyD = -36-6 = 6x, y = 2,6
Страница № 28:
Вопрос 6:
Решите следующие одновременные уравнения.
(1) 2x + 23y = 16; 3x + 2y = 0
(2) 72x + 1 + 13y + 2 = 27; 132x + 1 + 7y + 2 = 33
(3) 148x + 231y = 527xy; 231x + 148y = 610xy
(4) 7x-2yxy = 5; 8x + 7yxy = 15
(5) 123x + 4y + 152x-3y = 14; 53x + 4y-22x-3y = -32
Ответ:
(1) 2х + 23у = 16; 3x + 2y = 0
Пусть 1x = u и 1y = v
2u + 23v = 16 12u + 4v = 1….. I3u + 2v = 0 ….. II
Умножьте (II) на 2
6u + 4v = 0 ….. III
I-III
6u = 1⇒u = 16
Ввод значения и во II.
3 × 16 + 2v = 0⇒12 + 2v = 0⇒v = -14
1x = u⇒x = 61y = v⇒y = -4x, y = 6, -4
(2) 72x + 1 + 13лет + 2 = 27; 132x + 1 + 7y + 2 = 33
Пусть 12x + 1 = u и 1y + 2 = v
7u + 13v = 27 ….. I13u + 7v = 33 ….. II
(I) + ( II)
20u + 20v = 60u + v = 3 ….. III
(II) — (I)
6u-6v = 6 uv = 1….. IV
(III) + (IV)
2u = 4⇒u = 2 Подставляем значение u в (IV) 2-v = 1⇒v = 1
12x + 1 = u = 2 ⇒2x + 1 = 12⇒x = -14 и 1y + 2 = v = 1⇒y + 2 = 1⇒y = -1x, y = -14, -1
(3) 148x + 231y = 527xy; 231x + 148y = 610xy
Умножить на xy
148y + 231x = 527 ….. I 231y + 148x = 610 ….. II Сложить I и II 379y + 379x = 1137⇒x + y = 3 … ..IIIII-I83y-83x = 83⇒yx = 1 ….. IVIII + IV2y = 4⇒y = 2
Подставляем значение y в (IV)
2-x = 1⇒x = 1x , y = 1,2
(4) 7x-2yxy = 5; 8x + 7yxy = 15
⇒ 7y-2x = 5 и 8y + 7x = 15
Пусть 1x = u, 1y = v
7v-2u = 5….. I8v + 7u = 15 ….. II
Умножьте (I) на 7 и (II) на 2
49v-14u = 35 . …. III16v + 14u = 30 ….. IV
…. III16v + 14u = 30 ….. IV
Складываем (III) и (IV)
65v = 65⇒v = 1 и 1y = v = 1⇒y = 1
Подставляем значение v в (I)
71-2u = 5⇒u = 11x = u = 1⇒x = 1x, y = 1,1
(5) 123x + 4y + 152x-3y = 14; 53x + 4y-22x-3y = -32
13x + 4y = u, 12x-3y = v12u + 15v = 14 ⇒10u + 4v = 5 ….. I5u-2v = -32⇒10u-4v = -3 ….. II
(I) + (II)
20u = 2⇒u = 110
Подставляем значение u в (II)
10 × 110-4v = -3⇒1 + 3 = 4v⇒ v = 1
13x + 4y = u = 110⇒3x + 4y = 10….. III12x-3y = v = 1⇒2x-3y = 1 ….. IV
Умножаем (III) на 2 и (IV) на 3
6x + 8y = 20 ….. V6x-9y = 3 ….. VI
(V) — (VI)
17y = 17⇒y = 1
Подставляем значение y в (VI)
6x-9 = 3⇒6x = 12⇒x = 2x , у = 2,1
Страница № 28:
Вопрос 7:
Решите следующие задачи со словами.
(1) Двухзначное число и число с замененными цифрами в сумме дают 143.В данном номере цифра в разряде единиц на 3 больше, чем цифра в разряде десятков. Найдите исходный номер.
(2) Кантабай купил в магазине 112 кг чая и 5 кг сахара. Она заплатила 50 рупий в качестве обратного проезда на рикше. Общие расходы составили 700 рупий. Затем она поняла, что, заказывая товары в Интернете, товары можно купить с бесплатной доставкой на дом по той же цене. Поэтому в следующем месяце она разместила онлайн-заказ на 2 кг чая и 7 кг сахара. Она заплатила за это 880 рупий. Найдите норму сахара и чая на кг.
(3) Чтобы узнать количество записей, которые были у Анушки, выполните следующее задание.
(4) Сумма нынешнего возраста Маниша и Савиты составляет 31 год. Возраст Маниша 3 года назад был в 4 раза старше возраста Савиты. Найдите их нынешний возраст.
(5) На фабрике соотношение заработной платы квалифицированных и неквалифицированных рабочих составляет 5: 3. Общая заработная плата за один день для обоих составляет 720 рупий. Найдите дневную заработную плату квалифицированных и неквалифицированных рабочих.
(6) Пункты A и B находятся на расстоянии 30 км друг от друга и находятся на прямой дороге. Хамид едет из пункта А в пункт Б. на велосипеде. В то же время Джозеф стартует из точки B на велосипеде и едет в сторону A.Они встречаются через 20 минут. Если бы Джозеф стартовал из B в то же время, но в противоположном направлении (а не в направлении A), Хамид догнал бы его через 3 часа. Найдите скорость Хамида и Джозефа.
Ответ:
(1) Пусть число на месте единицы будет x , а цифра на месте десяти будет y.
Таким образом, число равно 10 y + x
После перестановки цифр число становится 10 x + y.
Учитывая, что двузначное число и число с замененными цифрами дают в сумме 143.
Итак, 10 y + x + 10 x + y = 143
⇒11x + 11y = 143⇒x + y = 13. …. I
Также в данном номере цифра в месте единицы на 3 больше, чем цифра в разряде десятков.
Итак, xy = 3 ….. II
Складывая (I) и (II), мы получаем
2x = 16⇒x = 8
Подставляя значение x в (I), получаем
8 + y = 13⇒y = 13-8 = 5
Таким образом, число 58.
(2) Пусть ставка чая будет x рупий за кг, а сахар — y рупий за кг.
Когда Кантабай покупал товары в магазине,
32x + 5y + 50 = 700⇒3x + 10y = 1300 ….. I
Когда Кантабай покупал товары в Интернете, тогда
2x + 7y = 880 …. .II
Умножая (I) на 2 и (II) на 3, получаем
6x + 20y = 2600 ….. III6x + 21y = 2640 ….. IV
(IV) — (III)
y = 40
Подставляем значение y = 40 в (II)
2x + 740 = 880⇒2x = 880-280 = 600⇒x = 300
Таким образом, чай стоит 300 рупий за кг, а сахар — 40 рупий за кг. .
(3) Заявление об отказе от ответственности: В данном вопросе есть ошибка. Вместо банкнот по 10 рупий должны быть банкноты по 100 рупий.
Пусть количество банкнот в 100 рупий составляет x , а количество банкнот в размере 50 составляет y .
100x + 50y = 2500⇒2x + y = 50 ….. I
Когда количество нот меняется местами,
50x + 100y = 2000⇒x + 2y = 40 ….. II
Умножение (I) с 2
4x + 2y = 100 ….. III
Вычитая (III) из (II), получаем
3x = 60⇒x = 203x = 60⇒x = 20
Подставляя значение x в (I ) получаем
y = 10
Таким образом, получается 20 банкнот по 100 рупий и 10 банкнот по 50 рупий.
(4) Пусть нынешний возраст Маниша будет x года, а возраст Савиты — y года.
Сумма их нынешнего возраста = 31
x + y = 31 ….. I
Их возраст 3 года назад был
Возраст Маниша = x-3
Возраст Савиты = y-3
Возраст Маниша 3 года назад был в 4 раза больше эпоха Савиты.
x-3 = 4y-3⇒x-3 = 4y-12⇒x-4y = -9 ….. II
(I) — (II) получаем
5y = 40⇒y = 8
Положив значение y в (I) получаем
x + 8 = 31⇒x = 23
Таким образом, возраст Маниша составляет 23 года, а возраст Савиты — 8 лет.
(5) Отношение заработной платы квалифицированного к неквалифицированному рабочему = 5: 3
Пусть дневная заработная плата квалифицированного специалиста составит x , а неквалифицированного — y.
Их общая дневная заработная плата 720
x + y = 720 ….. I
Кроме того,
xy = 53⇒3x = 5y⇒3x-5y = 0 ….. II
Умножение (I) на 3 получаем
3x + 3y = 2160 ….. III
(III) — (II)
8y = 2160⇒y = 270
Подставляя значение y в (I), получаем
x = 450
One дневная заработная плата квалифицированного специалиста 450 рупий, неквалифицированного человека 270 рупий.
(6) Пусть скорость Хамида составляет x км / ч, а скорость Джозефа — y км / ч.
Когда оба едут в одном направлении, расстояние, которое они преодолевают вместе, составит 30 км.
Мы знаем Скорость = Расстояние Время
Они встречаются через 20 минут = 2060 = 13 часов
x3 + y3 = 30⇒x + y = 90 ….. I
Когда Джозеф стартовал из точки B, но двигался в противоположном направлении.
Расстояние, пройденное Хамидом — Расстояние, пройденное Джозефом = 30
⇒3x-3y = 30⇒x-y = 10….. II
Складывая (I) и (II), получаем
2x = 100⇒x = 50
Подставляя значение x в (II), получаем
50-y = 10⇒y = 40
Таким образом скорость Хамида — 50 км / ч, Иосифа — 40 км / ч.

 1 Найдите вершину y = x 2 -3x-2
1 Найдите вершину y = x 2 -3x-2
 Сложение (8/4) + (9/4) дает 17/4
Сложение (8/4) + (9/4) дает 17/4  3 Решение x 2 -3x-2 = 0 по квадратичной формуле.
3 Решение x 2 -3x-2 = 0 по квадратичной формуле. Итак, две линии не имеют общей точки. Следовательно, данная система не имеет решений.
Итак, две линии не имеют общей точки. Следовательно, данная система не имеет решений.



 Итак, две линии не имеют общей точки.
Итак, две линии не имеют общей точки.
 Следовательно, система уравнений имеет бесконечно много решений.
Следовательно, система уравнений имеет бесконечно много решений.



 Вычислите площадь, ограниченную этими линиями и осью абсцисс.
Вычислите площадь, ограниченную этими линиями и осью абсцисс.
 Единиц
Единиц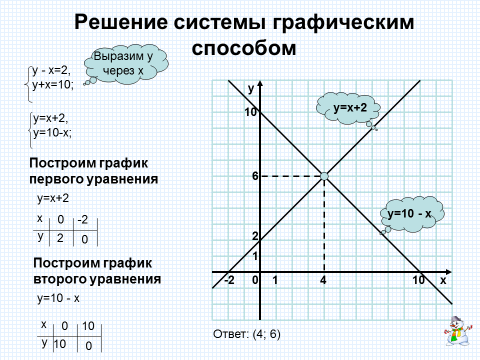
 н.э. = 4 — 2 = 2
н.э. = 4 — 2 = 2


 Они приведены в следующей таблице.
Они приведены в следующей таблице.


 …. (I)
…. (I)  …. (I)
…. (I)  …. IV
…. IV  …. III
…. III