Решение задач на подобие прямоугольных треугольников: Решение задач на подобие. Подобные треугольники. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Решение задач на подобие. Подобные треугольники.

Рассмотрим задачи, при решении которых мы будем использовать подобие треугольников. Уделим внимание как базовым задачам, так и задачам посложней. В конце статье вы найдете задачи для самостоятельной работы.

Задача 1.

Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4 и АС = 9.

Решение: + показать

Задача 2.

Прямая, параллельная основанию треугольника, делит его на треугольник и трапецию, площади которых относятся как 4:5. Периметр образовавшегося треугольника равен 20 см. Найдите периметр данного треугольника.

Решение: + показать

Задача 3.

Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислите площади образовавшихся треугольников.

Решение: + показать

Задача 4.

Из одной точки проведены к кругу две касательные. Длина касательной равна 156, а расстояние между точками касания равно 120. Найдите радиус круга.

Решение: + показать

Задача 5.

В трапеции меньшая диагональ , равная 6, перпендикулярна основаниям и . Найдите сумму тупых углов и .

Решение:+ показать

Задача 6.

Основания трапеции равны a и b. Определите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.

Решение: + показать

Задачи для самостоятельной работы

1. Через точки E и F, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая EF, параллельная стороне АС. Найдите длину BС, если EF = 10, AC = 15 и FC = 9. (Ответ: 27).

2. В прямоугольном треугольнике проведена высота к гипотенузе. , Найдите катет . (Ответ: 20/3).

3. Прямая, параллельная основанию треугольника, отсекает от него треугольник, площадь которого в 8 раз меньше площади оставшейся части. Периметр большего треугольника равен 27. Найдите периметр меньшего треугольника. (Ответ: 9).

4. Основание треугольника 15 см, а боковые стороны 13 и 14 см. Высота разделена в отношении 2:3 (считая от вершины) и через точку деления проведена прямая, параллельная основанию. Найдите площадь образовавшейся при этом трапеции. (Ответ: 70,56 (возможно, вам потребуется формула Герона)).

5. В трапеции с основаниями и диагонали пересекаются в точке . Площадь треугольника равна 4, площадь треугольника равна 9. Найдите площадь трапеции. (Ответ: 25).

6. Трапеция разделена диагоналями на четыре части. Определить ее площадь, если известны площади ее частей, прилежащих к основаниям и . (Ответ: ).

Задачи на подобие треугольников

Рассмотрим некоторые задачи на подобие треугольников.

I. В треугольнике проведен отрезок, параллельный стороне. Концы отрезка лежат на других сторонах треугольника.

Рассмотрим треугольники ABC и A1BC1.

Решать задачи на подобие треугольников удобнее, используя цветовую визуализацию, поэтому выделим данные треугольники разными цветами:

1) ∠B — общий;

2)∠ BAC=∠BA1C1 (как соответственные углы при AC∥A1C1 и секущей AB).

Следовательно, треугольники ABC и A1BC1 подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Задача

Прямая, параллельная стороне АС треугольника АВС, пересекает сторону АВ в точке А1, а сторону ВС — в точке В1. Найти длину отрезка А1С1, если АС=35, АА1: А1В=2:5.

Решение:

Доказываем подобие треугольников ABC и A1BC1.

Ответ: 25.

II. В треугольник вписан ромб.

Рассмотрим треугольники AFK и BFC.

Выделим данные треугольники в цвете.

1) ∠F — общий;

2)∠ FAK=∠FBC (как соответственные углы при AD∥BC и секущей AB).

Следовательно, треугольники AFK и BFC подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

Задача.

В треугольник AFK вписан ромб ABCD так, что угол A у них общий, в вершина C принадлежит стороне FK. Найти сторону ромба, если AF=21 см, AK=24 см.

Решение.

Доказываем подобие треугольников AFK и BFC. Из трех соотношений выбираем те, в которых нам что-либо известно:

Примем сторону ромба за x:

Тогда BF=AF-AB=21-x см. Отсюда

Разделив обе части уравнения на 3, получаем:

Ответ: 11,2 см.

В следующий раз рассмотрим задачи на подобные треугольники в трапеции.

Подобные треугольники. Геометрия, 8 класс: уроки, тесты, задания.

Вход

Вход

Регистрация

Начало

Новости

ТОПы

Учебные заведения

Предметы

Проверочные работы

Обновления

Переменка

Поиск по сайту

Отправить отзыв

org/BreadcrumbList»>

Предметы

Геометрия

8 класс

Подобные треугольники. Пропорциональные отрезки

Признаки подобия треугольников

Применение подобия.
Решение задач

Тригонометрические функции острого угла прямоугольного треугольника

Отправить отзыв

Нашёл ошибку?

Сообщи нам!

Пользовательское соглашение

Геометрия «Подобные треугольники» — презентация по Геометрии

Презентация на тему: Геометрия «Подобные треугольники»

Скачать эту презентацию

№ слайда 1

Описание слайда:

Подобные треугольники. Геометрия, 8 класс. 5klass.net

№ слайда 2

Описание слайда:

Урок 32. Пропорциональные отрезки. Рассмотрим пропорцию: Отрезки называются пропорциональными, если равны отношения их длин. К Е Н Х А В Р Т Решение задач: № 533 (устно) № 534.

№ слайда 3

Описание слайда:

Свойство биссектрисы треугольника. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. А В С К Решение задач: № 536(а), 538. Домашнее задание: п.56, № 536(б), 537.

№ слайда 4

Описание слайда:

Урок 33. Подобные треугольники. Два треугольника называются подобными, если их углы соответственно равны, и стороны од- ного треугольника пропорциональны соответ- ствующим сторонам другого треугольника. где k – коэффициент подобия. Говорят, что ∆АВС ~ ∆МРК А В С М Р К

№ слайда 5

Описание слайда:

№ 541. А В С D E F 106 34 106 40 4,4 5,2 7,6 15,6 22,8 13,2 Решение задач: № 542. Домашнее задание: п.56-57, № 540.

№ слайда 6

Описание слайда:

Урок 34. Теорема об отношении площадей подобных треугольников. ТЕОРЕМА. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. где k – коэффициент подобия. Отношение периметров двух подобных треугольников равно коэффициенту подобия. А В С М Р К Решение задач: № 545, 549. Домашнее задание: п. 56-58, № 544, 548.

№ слайда 7

Описание слайда:

Урок 35. Первый признак подобия треугольников. А В С А1 В1 С1 ТЕОРЕМА. Если 2 угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны. Доказательство: Так как углы А=А1 и С=С1, то угол В=В1. Так как угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих эти углы. Следовательно, ∆АВС ~ ∆А1В1С1

№ слайда 8

Описание слайда:

№ 550. 8 12 а а 6 x y 20 8 10 Домашнее задание: п. 59, № 553, 561.

№ слайда 9

Описание слайда:

Урок 36. Первый признак подобия треугольников. № 551(а) A B C D E F 10 4 8 ? ? 7

№ слайда 10

Описание слайда:

№ 552(а) A B C D O 25 10 4

№ слайда 11

Описание слайда:

№ 557(в). A B D C E 12 Домашнее задание: стр.160, вопросы 1-5, п.56-59, №552(в).

№ слайда 12

Описание слайда:

Урок 37. Второй признак подобия треугольников. ТЕОРЕМА. Если 2 стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны. Доказательство: Достаточно доказать, что углы С = С1. Рассмотрим ∆АВ2С, у которого углы 1=А1, 2=С1. ∆А1В1С1 ~∆АВ2С по 2 углам, следовательно Значит АВ2 = АВ и ∆АВ2С = ∆АВС по 2 сторонам и углу между ними => угол С=2, но угол 2=С1 => угол С1 = С => ∆А1В1С1 ~∆АВС по 2 углам Самостоятельная работа: стр.120, вариант А1,А2, №1. А1 В1 С1 А В С В2 1 2

№ слайда 13

Описание слайда:

Задача 1. D B O A C 5 9 6 15 12 ?

№ слайда 14

Описание слайда:

Задача 2. D C O B A 15 5 1 часть 3 части ? ? Домашнее задание: п. 59, 60, № 559.

№ слайда 15

Описание слайда:

Задача. А В С К Р М Стороны треугольника АВС в 2,5 раза больше сторон треугольника КРМ, углы В = Р, АС + КМ = 4,2. Найти АС и КМ.

№ слайда 16

Описание слайда:

Урок 38. Третий признак подобия треугольников. ТЕОРЕМА. Если 3 стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Доказательство: Достаточно доказать, что углы А = А1. Рассмотрим ∆АВ2С, у которого углы 1=А1, 2=С1. ∆А1В1С1 ~∆АВ2С по 2 углам, следовательно Но мы знаем, что Значит АВ2 = АВ, СВ2=СВ и ∆АВ2С = ∆АВС по 2 сторонам и углу между ними => угол А=1, но угол 1=А1 => угол С1 = С => ∆А1В1С1 ~∆АВС по 2 признаку А1 В1 С1 А В С В2 1 2

№ слайда 17

Описание слайда:

Задачи. Подобны ли ∆АВС и ∆КРМ, если АВ = 1м, АС = 2м, ВС = 1,5 м, КР = 8 дм, КМ = 16 дм, РМ = 12 дм. Стороны треугольника равны 0,8 м, 1,6 м, 2 м. Найти стороны подобного ему треугольника, периметр которого равен 5,5 м. Домашнее задание: п. 59-61, № 560.

№ слайда 18

Описание слайда:

Математический диктант. Третий признак подобия треугольников. Второй признак подобия треугольников. У двух треугольников по одному равному углу. Какого условия недостает, чтобы треугольники были подобны по 1 признаку? Стороны одного треугольника равны 3 см, 6 см и 7 см, а 2 стороны подобного ему треугольника равны 15 см и 35 см. Найти третью сторону. Соответствующие катеты двух подобных треугольников 6 дм и 18 дм. Найти гипотенузу меньшего треугольника, если гипотенуза большего 27 дм. Первый признак подобия треугольников. Третий признак подобия треугольников. У двух треугольников по одному равному углу. Какого условия недостает, чтобы треугольники были подобны по 2 признаку? Соответствующие катеты двух подобных треугольников 5 дм и 10 дм. Найти гипотенузу большего треугольника, если гипотенуза меньшего 7 дм. Стороны одного треугольника равны 15 см, 35 см и 30 см, а 2 стороны подобного ему треугольника равны 6 см и 7 см. Найти третью сторону.

№ слайда 19

Описание слайда:

Ответы. По 3 пропорциональ-ным сторонам. По 2 пропорциональ-ным сторонам и углу между ними. Пара равных углов. 30 см. 9 дм. По 2 равным углам. По 3 пропорциональным сторонам. Пропорциональность сторон угла. 14 дм. 3 м.

№ слайда 20

Описание слайда:

Подобие прямоугольных треугольников. Два прямоугольных треугольника подобны, если: У них есть по равному острому углу. Катеты одного треугольника пропорциональны катетам другого треугольника. Гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого треугольника.

№ слайда 21

Описание слайда:

Задача. A B C D O 18 12 15 10 Доказать, что ABCD – трапеция.

№ слайда 22

Описание слайда:

№ 554. A B M C D 8 3,6 3,9 5 Домашнее задание: п. 59-61, Стр. 160, вопросы 1-7, задача Задача. Продолжение боковых сторон АВ и CD трапеции ABCD пересекаются в точке Е. Найти стороны ∆АЕD, если АВ = 5 см, ВС = 10 см, АD = 15 см, СD = 8 см.

№ слайда 23

Описание слайда:

Урок 39. Средняя линия треугольника. ТЕОРЕМА. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Доказательство: ∆АВС ~ ∆КВР, так как угол В-общий, а стороны АВ и КВ, СВ и РВ пропорциональны => угол А=ВКР, но это соответственные углы => КР ll АС. А В С К Р Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. ТЕОРЕМА. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

№ слайда 24

Описание слайда:

Решение задач. № 564. № 570. 8 7 5 А В С D M O 18 Домашнее задание: п. 62, № 566.

№ слайда 25

Описание слайда:

Математический диктант. Две стороны треугольника соединили отрезком, непараллельным третьей стороне. Является ли этот отрезок средней линией треугольника? Сторона АВ ∆АВС равна 6 см. Чему равна средняя линия треугольника, параллельная этой стороне? Точки М, Р и О – середины сторон ∆АВС. Найти стороны ∆АВС, если стороны ∆МРО равны 3 см, 4 см и 5 см. Концы отрезка АВ лежат на двух сторонах треугольника, а длина этого отрезка равна половине третьей стороны. Обязательно ли этот отрезок является средней линией треугольника? Точки А и В являются серединами двух сторон треугольника.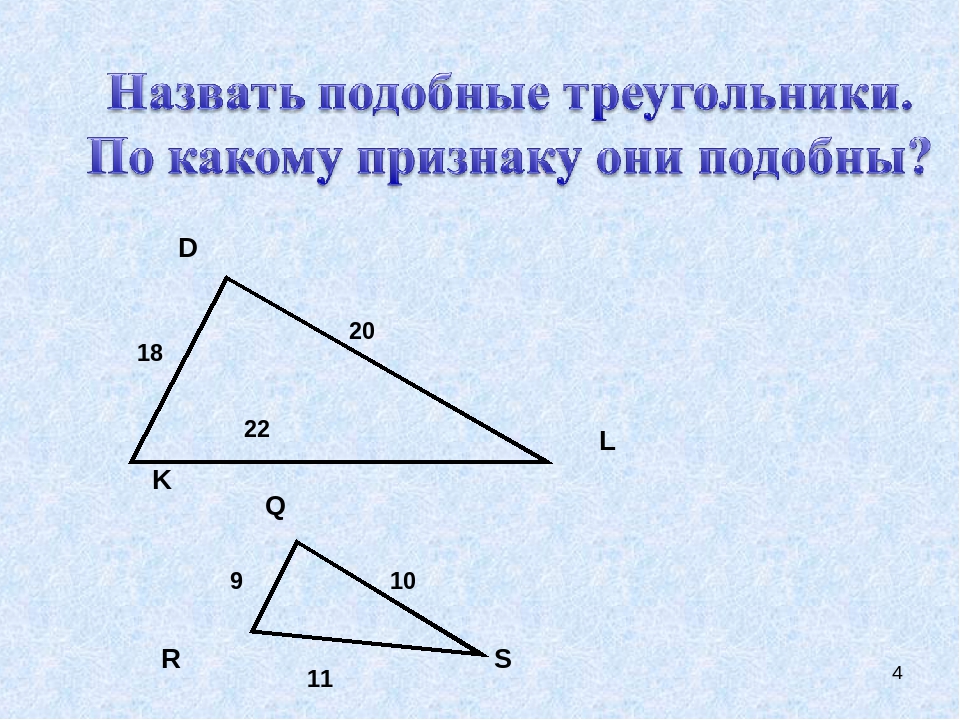 Как называется отрезок АВ? Средней линией ∆АВС, параллельная стороне ВС, равна 4 см. Найти сторону ВС. Точки А, В, С – середины сторон ∆МРО. Найти периметр ∆АВС, если отрезки МР, РО и МО равны 3 дм, 4 дм и 5 дм. Концы отрезка КР лежат на двух сторонах треугольника, он параллелен третьей стороне треугольника и равен ее половине. Является ли КР средней линией?

№ слайда 26

Описание слайда:

Ответы. Нет Средняя линия 24 см Нет Средняя линия 8 см 6 дм Нет

№ слайда 27

Описание слайда:

Задачи. Дано: РАВС= 12 см Найти: РМРО А В С М Р О 2. Дано: AD=2BC, MB=MK, NC=NK, BC=6 см Найти PQ A P B C Q D M N 6 3. Дано: АС=10см, BD=8см Найти РMNPK A B C D K M N P

№ слайда 28

Описание слайда:

Урок 40. Пропорциональные отрезки в прямоугольном треугольнике. Признак подобия прямоугольных треугольников. Два прямоугольных треугольника подобны, если у них есть по равному острому углу.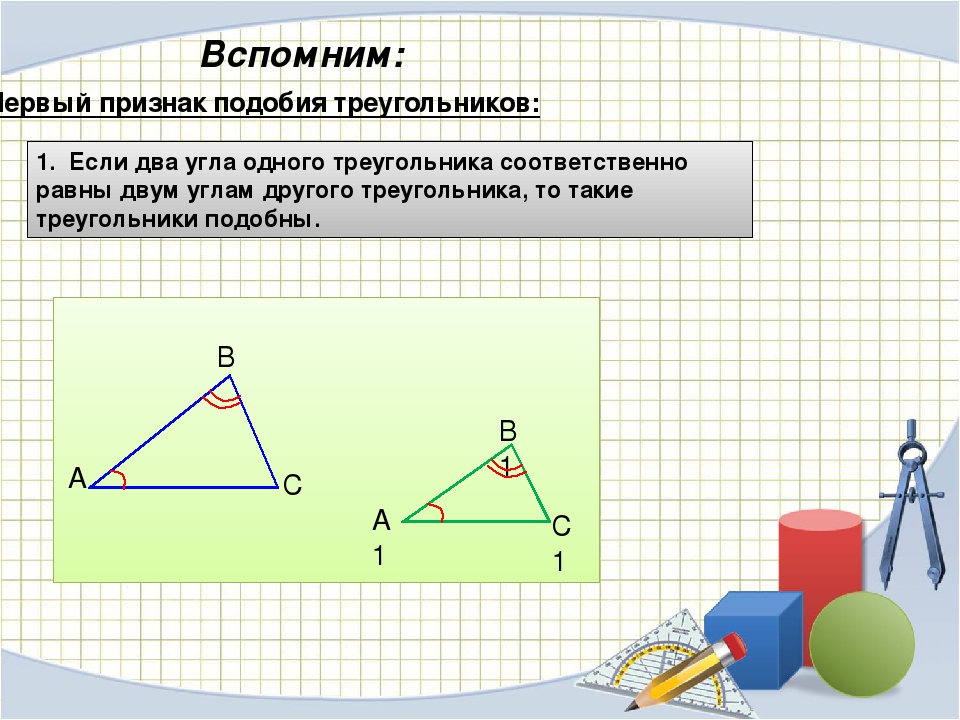 Отрезок XY называется средним пропорциональным (средним геометрическим) для отрезков АВ и CD, если Свойство 1. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу. Свойство 2. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. А С В Н Высота прямоугольного треугольника, проведенная из вершины прямого угла, делит треугольник на 2 подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. с bc ac a b h

№ слайда 29

Описание слайда:

Решение задач: № 572, 575, 577. Домашнее задание: стр.160, вопросы 8-11, принести циркуль, № 576, 578-в общую тетрадь. Проверочная работа. стр. 124, вариант А1, А2, задачи 1, 2.

№ слайда 30

Описание слайда:

Урок 42. Синус, косинус и тангенс острого угла прямоугольного треугольника. А В С Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Тангенс угла равен отношению синуса к косинусу этого угла. α β

№ слайда 31

Описание слайда:

Основное тригонометрическое тождество. Решение задач: № 591(а,б), 592(а,в,д), 593(а,в). Домашнее задание: п.66, № 593(б,г), 592(б,г,е), 591(в,г).

№ слайда 32

Описание слайда:

Урок 43. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°. А В С 30° 60°

№ слайда 33

Описание слайда:

Урок 43. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°. А В С 45° Пусть АС = ВС = а, тогда а а

№ слайда 34

Описание слайда:

Решение задач. Найти площадь равнобедренного прямоугольного треугольника с основанием 10 см и углом при основании 45°. Найти катеты прямоугольного треугольника, гипотенуза которого 2 см, один из острых углов 30°. В треугольнике АВС угол А=45°, угол С=60°, ВС=2 см. Найти АС. № 600. Домашнее задание: п. 66, 67, № 602.

№ слайда 35

Описание слайда:

Контрольная работа № 4. Средняя линия равнобед-ренного треугольника, параллельная боковой стороне, равна 13 см, а медиана, проведенная к основанию — 24 см. Найти среднюю линию, парал-лельную основанию треугольника. Найти sin α и tg α, если cosα=8/17. Найти синус, косинус тангенс большего острого угла прямоугольного треугольника с катетами 7 см и 24 см. Средняя линия равнобед-ренного треугольника, параллельная основанию, равна 16 см, а биссект-риса, проведенная к основанию — 30 см. Найти среднюю линию, парал-лельную боковой стороне треугольника. Найти cos α и tg α, если sinα=5/12. Найти синус, косинус тангенс меньшего острого угла прямоугольного треугольника с катетом 40 см и гипотенузой 41 см.

№ слайда 36

Описание слайда:

Подобие треугольников. Решение задач с практическим содержанием.

Приветствую вас на уроке геометрии в 9 классе

Девиз урока

«Любопытный отыскивает редкости только затем, чтобы им удивляться, любознательный же затем, чтобы узнать их и перестать удивляться»

Р. Декарт.

Так будьте же сегодня на уроке очень любознательными

Цель урока : обобщение знаний по теме «Признаки подобия треугольников».

Задачи урока:

Обобщить и систематизировать теоретические знания ;
Формировать навыки применения признаков подобия треугольников при решении задач.
Формировать правильную математическую речь,
воспитание культуры личности, отношения к геометрии, как к части общечеловеческой культуры, играющей огромную роль в общественном развитии;
Повысить интерес к предмету.

Экспресс-опрос по теории

Дайте определение преобразования подобия.

2. Назовите свойства подобных треугольников.

В 1

Свойства

подобных треугольников

А 1

С 1

Подобие прямоугольных треугольников

достаточно по одному равному острому углу

Ключевая задача

высота, проведённая из вершины прямого угла в прямоугольном треугольнике разбивает его на 2 треугольника, подобных данному и

АС =

следствие

ВС =

Найдите среди треугольников пары подобных и докажите почему они подобны

Найдите и назовите подобные треугольники

Решаем задачи в группах

(по рядам)

1 группа Отрезки АВ и ДС лежат на параллельных прямых, а отрезки АС и ВД пересекаются в точке М. Найдите МС, если АВ =14, ДС=56, АС=40.

2 группа Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и Н соответственно. Найдите СН, если МН=13, АС=65, НВ=7.

3 группа В трапеции АВСД с основаниями АД=21 и ВС=14 продолжения боковых сторон пересекаются в точке М. Найти длину отрезка МС, если боковая сторона трапеции СД=10

Проверка

Решение:

160-4х=х

5х=160

Х=32

Ответ: 32

Проверка

2 группа Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и Н соответственно. Найдите ВН, если МН=13, АС=65, НС=28.

Решение:

ВС= 35,

НС= 35-7=28

Ответ: 28

Проверка

Решение:

3х=2х+20

Х=20

Ответ: 20

Игра «Гусеница»

Решение задач

по карточкам

ПРОВЕРЬ И ОЦЕНИ РАБОТУ СОСЕДА ПО ПАРТЕ

Карточка №1 Ответ: 3,5

Карточка №2 Ответ: 300

Карточка №3 Ответ: 20

Карточка №4 Ответ: 1,8

Карточка №5 Ответ: треугольники подобны по 2 –му пр. под. треугольников

Карточка №6 Ответ: 9

Геометрия в природе

Подобия из жизни

Геометрия – это целый мир.

Некоторые открытия в нём ждут именно вас

Фалес

… ПО ЛЕГЕНДЕ ФАЛЕС ИЗМЕРИЛ ВЫСОТУ ОДНОЙ ИЗ ЕГИПЕТСКИХ ПИРАМИД, ИСПОЛЬЗУЯ МЕТОД ПОДОБИЯ ТРЕУГОЛЬНИКОВ.

Когда тень от палки, воткнутой вертикально в землю, будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды.

… ПО ЛЕГЕНДЕ ФАЛЕС ИЗМЕРИЛ ВЫСОТУ ОДНОЙ ИЗ ЕГИПЕТСКИХ ПИРАМИД,

ИСПОЛЬЗУЯ МЕТОД ПОДОБИЯ ТРЕУГОЛЬНИКОВ.

Высота шеста — 4 локтя Длина тени шеста — 6 локтей Длина тени пирамиды — 200 локтей

Ширина квадратного основания пирамиды — 600 локтей

1 Локоть =45 см

В 1

300

200

С 1

А 1

Тень от палки

Тень от пирамиды

[приблизительно 333,3 локтя (333 1/3)]

Пирамида Хеопса

14985 см

Высота 146,6 м

Задачи

Что нужно измерить, чтобы вычислить

ширину озера

высоту башни

Домашнее задание.

1) Длина тени дерева равна 10,2 м, а длина тени человека, рост которого 1,7 м, равна 2,5 м. Найдите высоту дерева.

2) Определить ширину реки , если АС = 100 м, АМ = 32 м, АК = 34 м.

3) Практическая работа по группам.

ПРАКТИЧЕСКАЯ РАБОТА

1 группа Определение высоты дерева с помощью равнобедренного прямоугольного треугольника

2 группа Определение ширины озера

3 группа Определение высоты дерева с помощью зеркала.

ИТОГИ урока

Не делай никогда того, чего не знаешь,

но научись всему, что следует

знать

ПИФАГОР

Красный цвет — настроение восторженное, радостное, теплое. Я доволен своей работой на уроке.

Желтый цвет — настроение светлое, приятное, спокойное. Я хорошо работал, но могу лучше.

Синий цвет — настроение неудовлетворенное, грустное, тревожное. Работа не получилась, было трудно.

Спасибо за урок!

Урок геометрии «Решение задач на признаки подобия треугольников» » 8 класс

Урок разработан в соответствии с УМК А.С. Атанасян, соответствует ФГОС ООО

Просмотр содержимого документа

«Урок геометрии «Решение задач на признаки подобия треугольников» » 8 класс»

«Признаки подобия треугольников» 8 класс

Докажите, что треугольники подобны. Напишите отношения сходственных сторон

№ 1. Выпишите номера верных утверждений:

В подобных треугольниках стороны равны.
Треугольники подобны по двум углам.
Отношения сходственных сторон подобных треугольников равны коэффициенту подобия.
Отношение площадей подобных треугольников равно коэффициенту подобия.
Все квадраты подобны.
Все треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Для доказательства подобия треугольников достаточно найти две пары пропорциональных сторон у этих треугольников.

Взаимопроверка. Каждый верный ответ – 1 балл.

№ 1. 2357

2. Треугольники подобны по двум углам.

3. Отношения сходственных сторон подобных треугольников равны коэффициенту подобия.

5. Все квадраты подобны.

7. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Блиц-опрос «Признаки подобия треугольников» 8 класс

Тема «Признаки подобия треугольников»

1 вариант

1)Стороны одного треугольника равны 6дм, 12дм и 14дм, а две стороны подобного ему треугольника равны 12 дм и 28дм. Вычислите длину третьей стороны.

2) Соответствующие катеты двух подобных прямоугольных треугольников 12 см и 36 см. Найдите гипотенузу меньшего треугольника, если гипотенуза большего равна 54 см.

3)У треугольников АВС и МРК равны углы А и М. Какого условия не хватает для того, чтобы эти треугольники были подобны по первому признаку?
4) Подобны ли треугольники АВС и МРК, если АВ=1,2м, ВС=3,5м, АС=7м, МР=24м, РК=70м, МК=140м
5)Подобны ли равнобедренные треугольники, если они имеют по равному тупому углу

2 вариант

1)Соответствующие катеты двух подобных прямоугольных треугольников 5 см и 10 см. Найдите гипотенузу большего треугольника, если гипотенуза меньшего равна 7 см.
2) Стороны одного треугольника равны 15дм, 35дм и 30дм, а две стороны подобного ему треугольника равны 7 дм и 6 дм. Вычислите длину третьей стороны.

3)Подобны ли треугольники АВС и МРК, если АВ=3см, ВС=5см, АС=7см, МР=7,5см, РК=12,5см, МК=17,5см

4) У треугольников АВС и МРК равны углы А и М. Какого условия не хватает для того, чтобы эти треугольники были подобны по второму признаку?
5) Подобны ли равнобедренные треугольники, если они имеют по прямому углу

Ответ:

2 вариант

1 вариант

1)14 см

24 дм
18 см
Равенства второй пары углов , например, равенство углов В и Р или С и К
подобны
да

2)3 дм

3)подобны

4)АВ=МР, АС=МК

5)да

Подобие прямоугольных треугольников. Применение презентаций для иллюстрирования теорем Подобные треугольники презентация савченко е м

«Задачи на подобие» — Подобные треугольники. Найти x, y, z. Пример № 4. Решение задач по геометрии на готовых чертежах. Условие задачи: Дано: ?ABC ~ ?A1B1C1. Темы задач. Пример № 2. Автор: Скурлатова Г.Н. МОУ «СОШ № 62». Первый признак подобия треугольников. Завершить презентацию. Пример № 1. Второй и третий признаки подобия треугольников.

«Урок Признаки подобия треугольников» — В подобных фигурах стороны пропорциональны. А. А1. Урок геометрии «Признаки подобия треугольников». В1. Цель урока: Обобщение по теме «Признаки подобия треугольников». Когда. В. В подобных фигурах углы равны. Подобные фигуры. Задачи урока: Треугольники подобны?

«Практические приложения подобия треугольников» — Какие существуют способы для определения высоты предмета? Вопрос учебной темы: Применение подобия треугольников. Презентация-реферат, буклет, информационный бюллетень по способам определения высоты предмета. Как с помощью простых приспособлений можно измерять высоту предмета? Учебные предметы: геометрия, литература, физика.

«Признаки подобия» — A. Подобные треугольники. C. АВС и А1 В1С1 –треугольники

«Подобие треугольников 8 класс» — 1 признак подобия треугольника. Подготовил ученик 8 «б» класса Михальченко Дмитрий. 3 признак подобия треугольника. Задача № 1. 2 признак подобия треугольника. Стороны a и d, b и c – сходственные. Применение подобия в жизни человека.

«Применение подобия треугольников» — Пропорциональные отрезки в прямоугольном треугольнике. Деление отрезка в заданном отношении. Разделить отрезок в отношении 2/3. Практическое применение подобия треугольников. В. Применение подобия треугольников при доказательстве теорем. Измерительные работы на местности. Теорема о средней линии треугольника.

Изобразим: а) две неравные окружности; б) два неравных квадрата; в) два неравных равнобедренных прямоугольных треугольника; г) два неравных равносторонних треугольника. а) две неравные окружности; б) два неравных квадрата; в) два неравных равнобедренных прямоугольных треугольника; г) два неравных равносторонних треугольника. Чем отличаются фигуры в каждой представленной паре? Что у них общего? Почему они не равны?

В подобных треугольниках АВС и А 1 В 1 С 1 АВ = 8 см, ВС = 10 см, А 1 В 1 = 5,6 см, А 1 С 1 = 10,5 см. Найдите АС и В 1 С 1. А В С А1А1 В1В1 С1С,6 10,5 подобных,6 10,5 x y Ответ: AC = 14 м, B 1 C 1 = 7 м.

Физкультминутка: Долго тянется урок Много вы решали Не поможет тут звонок, Раз глаза устали. Занимаемся все сразу Повторим четыре раза. – Пройдите глазами по знаку подобия. – Закройте глаза. – Расслабьте мышцы лба. – Медленно переведите глазные яблоки в крайнее левое положение. – Почувствуйте напряжение глазных мышц. – Зафиксируйте положение – Теперь медленно с напряжением переведите глаза вправо. – Повторите четыре раза. – Откройте глаза. – Пройдите глазами по знаку подобия.

Первый признак подобия Теорема. (Первый признак подобия.) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. А В С С1С1 В1В1 А1А1 C»C» В»

Слайд 2
. На этом слайде показано, как представлена теорема Пифагора
в учебнике. Текст и готовый чертеж. В презентации статический чертеж из учебника
мы можем «оживить», т.е. показать последовательные шаги построения, показать
динамику дополнительных построений, необходимых для доказательства.

Я работаю в классе с
дистанционной мышью, поэтому я могу управлять презентацией и одновременно
индивидуально работать с обучающимися. Я считаю это главным преимуществом
применения презентаций на уроке геометрии. Я не «привязана» к доске, к компьютеру, имею дополнительное время
для индивидуальной работы. Появившееся свободное время позволяет мне обойти
всех детей и проверить правильность выполнения чертежа в тетрадях. Бывает ощущение,
что в классе два учителя. Первый работает «в реале» индивидуально
–

это я. Второй
виртуальный учитель, показывает шаги построения – это компьютер. У меня есть
возможность по просьбе детей повторить шаги построения, прокрутить колесико
мышки назад.

Слайд 3
. Теорема Пифагора. Алгоритм работы на уроке с модулем.

— Читаем теорему, выделяем
условие и заключение теоремы.

— Для доказательства нам
необходимо достроить треугольник до квадрата. Учитель демонстрирует построение
на слайде, работая с дистанционной мышью, и ведет индивидуальную работу с
обучающимися.

-Для доказательства
вычисляем площадь построенного квадрата двумя способами.
Как можно вычислить
площадь квадрата? Фронтальная работа над идеей доказательства.

Первый способ. S = а². Сторона
квадрата равна (a+b), тогда S = (a+b)².

Второй способ вычисления с применением свойства
площадей: площадь квадрата равна сумме площадей четырех прямоугольных
треугольников и площади квадрата со стороной с.

Приравняем правые
части этих равенств. Вызываю к доске ученика. Преобразования оформляем мелом на
доске.

Слайд 4.
Технически более сложный слайд. Использованы анимации:
вращения, пути перемещения. В этом модуле используется анимационный герой для
сопровождения объяснения.

Слайд 5.
Используя презентацию можно дать значительно больший объем
информации на уроке. Например, представить другие способы доказательства
теоремы.

А сколько задач для отработки
доказанных теорем можно предложить! Вот например, какие задачи я составила для
отработки записи формулировки теоремы Пифагора.

Слайды 6, 7
для устной работы. Технически эти модули достаточно
простые.
Алгоритм работы на уроке.

Учитель. Какие прямоугольные
треугольники вы видите на чертеже?

Обучающиеся должны
сформулировать свойство диагоналей ромба и назвать все треугольники. А затем
для каждого треугольника составить запись теоремы Пифагора.

Внеся небольшие изменения на
слайдах, эти задания можно предложить на следующем уроке, как задания с
последующей проверкой.

Алгоритм организации работы на
уроке. Слайды 8, 9.

Слайд 8.
Математический диктант. Записать последовательно теорему
Пифагора для каждого треугольника. Треугольники появляются по щелчку мыши в
любой части слайда (но не по
шторке). Переходим на слайд 9. Еще для четырех треугольников записываем
теорему. По кнопке возвращаемся назад на слайд 8. Щелчком по шторке открываем
ответы. Самопроверка или взаимопроверка. Переходим на слайд 9, щелчком по
шторке открываем ответы. В ходе урока можно запланировать 1 или более слайдов с
самостоятельной работой с последующей самопроверкой.

Слайд 10.

Алгоритмы организации работы на
уроке над теоремой могут быть разными. В одном классе мы отработаем с теоремой
одним способом, в другом классе организуем работу иначе. Например. Я рассмотрю
свойство углов равнобедренного треугольника.

1 способ организации
работы над теоремой.

Учитель. Выделяем условие и
заключение теоремы.

Обучающиеся формулируют, что «дано» в теореме и что надо «доказать».

Учитель. Прошу закончить мои
предложения-подсказки. Равенство углов следует обычно из … Учащиеся продолжают …
из равенства треугольников.

Учитель. Значит, нам нужны
треугольники. Чтобы треугольники появились, сделаем дополнительное построение. Придумайте,
как разбить треугольник на два равные треугольника? Построим биссектрису ВD. (На этом построении показ презентации останавливаю).

Ученики обычно сразу видят
равные треугольники. Докажем равенство треугольников.
Один ученик приглашается к доске
и мелом на доске записывает доказательство равенства треугольников. Выписывает
равные элементы. Делает вывод, о равенстве треугольников, называет признак.
Итоговый вывод, о равенстве углов при основании.

Учитель. Проверим и повторим
доказательство. (Продолжает показ
презентации).

Таким образом, доказательство
выполнено обучающимся самостоятельно, а через проектор учитель показывает его
еще раз, идет пошаговый разбор доказательства.

2 способ работы над
теоремой.

Если в классе нет учеников,
которые могут доказать теорему самостоятельно и сделать грамотные
последовательные записи шагов доказательства от начала до конца.

Просматриваем весь ход
доказательства от начала до конца. Делаем чертеж, формулируем условие и
заключение теоремы. Оформляем в тетради чертеж, дано, доказать.

Обсуждаем доказательство фронтально. Вместе ищем равные элементы появившихся на
чертеже треугольников. После устного разбора теоремы, вызываем к доске ученика,
который сможет восстановить доказательство. Так и формулируем перед ним задачу
«Восстановить доказательство». Колесиком на мышке возвращаемся на начало
доказательства (Дано, доказать, ДП – биссектриса).

Итак, в первом случае учащиеся
доказывают теорему самостоятельно

. После этого показываем доказательство через
проектор, обобщаем. Во втором случае сначала просматриваем доказательство через
проектор, а затем просим восстановить доказательство

.

Но бывают теоремы, которые
ученикам не под силу доказать самостоятельно. Здесь учителю придет на помощь
компьютер. В презентации можно «оживить» чертеж, анимировать последовательные
шаги доказательства, используя выделение цветом фигур, сделать более доступным
для понимания доказательство.

Слайды 11 – 13.

На слайде 11 дана визуальная
подсказка компьютера – красным цветом выделены слова «Если» и «то». Не сложно
сформулировать условие и заключение теоремы.

На слайде 12 анимированное
доказательство. В подготовленном классе можно сначала просмотреть теорему, а
затем предложить восстановить доказательство мелом на доске. После просмотра
доказательства можно ПКМ выбрать Экран-Черный экран.

В другом классе можно одновременно
с показом оформлять доказательство в тетради. На слайде приведены записи,
которые должны быть оформлены в тетради.

Также можно привести и еще два
случая, которые предложим для самостоятельного доказательства (например, выполнить по желанию дома). После оформления записей в тетради, просматриваем
доказательство повторно. Учитель повторяет все шаги.

Я использовала еще такой
алгоритм. Например, одновременно с демонстрацией, ученики записали
доказательство в тетради. Т.е. одновременно смотрим, обсуждаем фронтально,
записываем в тетради доказательство. После завершения этой работы, колесиком на
мышке возвращаюсь на начало теоремы. Приглашаю к экрану ученика. С указкой в
руке он доказывает теорему. А учитель, делая клик мышкой, раскрывает каждый
верный шаг рассуждения.

Этот неплохой алгоритм я
перестала использовать. Т.к. проектор в классе стоит на парте. В этом случае
луч проектора светит в глаза ребенку, он зажмуривается, испытывает дискомфорт.
Это очень вредно для глаз! Оптимальное место расположения проектора – на
потолке. Тогда луч проектора идет у нас над головой, а не светит нам в глаза.
Приглашая учеников к доске во время работы проектора, подбирайте удаленное
место от экрана. Дорогие коллеги, берегите и свои глаза! Избегайте прямого
попадания луча проектора в глаза.

На слайдах 14 -17
приведены игровые задания. Как сделать такие
модули, описано в ресурсе «Геометрия. Применение презентаций для
иллюстрирования определений». Используя время записи начала анимации с помощью
триггера, можно делать игровые модули. Эти маленькие тестовые задания удачно предложить на любом этапе урока. Главное – мера.

Авторский прием.
При изучении
многих тем геометрии полезно давать «Парные задачи». Опять преимущество
презентации в том, что можно заранее подготовить слайд. На доске мелом к уроку
подготовить такие «пары» достаточно сложно, требуется время.

Цель составления «Парных задач»
— это систематизация знаний по теме.

На слайде 18
приводится пример. Задачи по теме «Свойства
параллелограмма» и «Признаки параллелограмма». Как организовать работу?

Учитель. На слайде даны две
задачи. В первой задаче Дано: АВСD – параллелограмм, а во второй
задаче надо доказать, что АВСD – параллелограмм. В какой задаче нам потребуются
свойства параллелограмма, а в какой признаки параллелограмма?

Ученики. Дают ответ.

Устно решаем две задачи.
Проговаривая формулировки применяемых свойств.

Слайд 19
– домашняя задача № 383.

Учитель. А вот ваша домашняя
задача. Давайте разберемся, что вам потребуется для решения этой задачи: свойства или признаки параллелограмма.

Ученики. Дан параллелограмм АВСD, значит можно применить
свойства параллелограмма. Чтобы доказать, что APCQ является параллелограммом потребуются признаки
параллелограмма.

Мои ученики сразу увидели, что
можно доказать равенство треугольников АВР и СDQ,
DQ и СВР по 1
признаку равенства треугольников. Тогда, АР=СQ, PC=AQ, а если в 4-угольнике
противолежащие стороны равны, то АРСQ параллелограмм.

А вот еще один способ, который
заложен в анимациях слайда, пришлось им показать. Тогда они догадались, что
есть и еще способ доказать, что АВСQ параллелограмм. Используя признак 3º, через
диагонали.

Мы обсудили две дороги для
решения этой задачи дома.

Слайд 20.
Еще пример задач-пар. В 7 классе важно научить детей
различать, в каких задачах потребуются признаки параллельности прямых, а в
каких задачах необходимо применить обратные теоремы.

На этом слайде для парных задач
дана визуальная подсказка – красным цветом на слайде выделено ключевое различие
между задачами. В первой задаче цветом выделено «AB II CD»,
а во второй задаче «a II b». Если предложить подобные парные задачи на следующем уроке, то
визуальную подсказку цветом уже можно не давать.

Учитель. Ключевое различие между
задачами выделено на слайде цветом. В первой задаче требуется доказать,
что прямые параллельны

. А во второй задаче даны две параллельные прямые

. В
какой задаче потребуются признаки параллельности прямых. А в какой обратные
теоремы – о пересечении двух параллельных прямых секущей?

Первую задачу решаем устно, с
комментированием. Кстати, в первой задаче можно обосновать решение иначе: по
признаку параллельности через односторонние углы.

Вторую задачу решаем в тетради.
Начинаем рассуждать устно все вместе. Если никто не вспомнит, что такие задачи
решаем алгебраическим способом, обозначив за «х» одну часть, то выводим визуальную подсказку
сопровождающего героя «Пусть х – 1 часть». Далее дети вспомнят: тогда углы соответственно
равны 5х и 4х, а сумма односторонних углов при пересечении двух параллельных
прямых третей равна 180º. Значит, можно составить уравнение.

Пусть (х)º – 1 часть

Составлю и решу уравнение…

Замечание.
При записи решения в
тетради я часто использую аббревиатуры. Например, ОУ – односторонние углы,
аналогично, НЛУ, СУ. Теорема о трех
перпендикулярах ТТП и т.д.

Слайды 21 – 23
. На этапе подготовки к новой теореме можно создать
модули для организации повторения. Пример из курса геометрии 8 класса. Для
доказательства теоремы о площади трапеции, мне потребовалось напомнить детям о
свойстве площадей. Я решила рассмотреть задачу из учебника, чтобы доказательство
теоремы дети затем смогли бы придумать сами.

Слайд 21.
Повторили свойство площадей. С помощью этого свойства
можно вычислять площади различных фигур, разбивая их на части.

Слайд 22.
Рассмотрим задачу из учебника №478. На слайде показан
способ построения четырехугольника. Начать построение удобно с диагоналей! А
затем построить стороны четырехугольника. Никогда не вывожу на экран визуальных
подсказок, сначала слушаю идеи учеников. Одна ученица предложила вычислить
площадь для каждого из четырех прямоугольных треугольников, а затем их сложить.
Других идей, к сожалению, предложено не было. Я пригласила девочку к доске, она
решила задачу своим способом.

Снова предлагаю детям подумать.
Ведь можно рассмотреть и другие треугольники и решить задачу проще. Теперь
догадались. Назвали треугольники КМB, ВРК и МВР, МКР. Второй вариант рассмотрели устно. Какой способ
более красивый? Тот, который мы записали в тетради или тот, который нам
предлагает компьютер? Сделали выбор. Выгодно разбить фигуру на меньшее число
частей. Мы начали чертеж с диагоналей, возможно, это и помешало детям мыслить. Но, тем не
менее, мы подготовились к восприятию теоремы о вычислении площади трапеции.

Слайд 23
. Итак, предложите способ, как разбить фигуру на части, для
которых мы можем найти площадь по известным нам формулам. Предложили диагональ
ВD или АС.

С комментированием просматриваем
анимации дополнительных построений, доказательства. Затем щелчок ПКМ, выбираем
«черный экран». Оформите доказательство в тетради. Один ученик приглашается к
доске.

Слайды 24 – 29.
Фрагмент урока. Теорема об отношении площадей
треугольников, имеющих по равному углу. Актуальны знания: следствие 2 об
отношении площадей треугольников, имеющих равные высоты. Слайды 24, 25
актуализация знаний. Повторили, закрепили на примере. На слайде 25 обратили
внимание, что для треугольника АВС высота лежит во внутренней области
треугольника, а для треугольника FBR высота прошла во внешней области. Например, можно задать детям вопрос:
чем различается расположение высоты для каждого треугольника?

В теореме очень сложный чертеж.
Учителю сложно на доске начертить и одновременно оказать индивидуальную помощь детям. Работать
над теоремой с заготовленным заранее модулем более удобно. Учитель показывает
анимации, работая с дистанционной мышью, и одновременно работает индивидуально
с обучающимися. Строим чертеж и доказываем вместе с компьютером.

Оговариваем, что вершину А 1
будем называть А. Поэтому А 1 запишем в скобках. После каждой
анимации задаем детям вопрос. Например, вышла на экран высота СН. Для каких
треугольников эта высота является общей?…
Ответ. Как записать отношение площади треугольника АВС к площади АВ 1 С.
Ответ… Выводим на экран высоту СН 1 . Для каких треугольников эта
высота является общей?… Ответ. Как
записать отношение площади треугольника АВ 1 С к площади АВ 1 С 1 .
Ответ… Умножим равенства… и т.д.

Слайды 28, 29
для закрепления
доказанной теоремы.
Согласитесь, что выполнить всю
эту работу мелом на доске учителю сложно. А значит, есть еще важное
преимущество применения модулей: облегчить тяжелый труд учителя.

Геометрия

глава 7

Подготовила Кириллова Дарья, ученица 9 класса

Учитель Денисова Т.А.

1.Определение подобных треугольников

а)пропорциональные отрезки

б)определение подобных треугольников

в)Отношение площадей

а)Первый признак подобия

б)Второй признак подобия

в)Третий признак подобия

а)Средняя линия треугольника

б)Пропорциональные отрезки в прямоугольном треугольнике

в)Практические приложения подобия треугольников

б)Значение синуса, косинуса и тангенса для углов 30 0 , 45 0 и 60 0

Отношением отрезков АВ и СD
называется отношение их длин, т.е. АВ:CD

АВ = 8 см

СD = 11,5 см

Отрезки АВ и CD пропорциональны отрезкам А
1
В
1
и С
1
D
1
, если:

АВ= 4 см

CD= 8 см

С
1
D
1
= 6 см

А
1
В
1
=3 см

Подобные фигуры-
это фигуры одинаковой формы

Если в треугольниках все углы соответственно равны, то стороны, лежащие напротив равных углов, называются
сходственными

Пусть в треугольниках АВС и А
1
В
1
С
1
углы соответственно равны

То АВ и А
1
В
1
,ВС и В
1
С
1
,СА и С
1
А
1
-сходственные

Два треугольника называются подобными
, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника

K- коэффициент подобия

назад

Стороны одного треугольника равны 15 см, 20 см, и 30 см. Найдите стороны треугольника, подобного данному, если периметр равен 26 см

Отношение площадей двух подобных
треугольников
равно квадрату коэффициента подобия

Доказательство:

Коэффициент подобия равен К

S и S 1 — площади треугольников, то

По формуле имеем

Первый признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны

Доказать:

Доказательство

1)По теореме о сумме углов треугольника

2)Докажем, что стороны треугольников пропорциональны

Аналогично и с углами

Итак, стороны

пропорциональны сходственным сторонам

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны

Доказать:

Доказательство

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны

Доказать:

Доказательство

Средней линией
называется отрезок, соединяющий середины двух его сторон

Теорема:

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны

Доказать:

Доказательство

Теорема:

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины

Доказать:

Доказательство

В треугольнике АВС медианы АА
1
и ВВ
1
пересекаются в точке О. Найдите площадь треугольника АВС, если площадь треугольника АВО равна S

Теорема:

Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику

Доказать:

Доказательство

Теорема:

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой

Доказать:

Доказательство

Определение высоты предмета:

Определить высоту телеграфного столба

Из подобия треугольников следует:

Практические приложения подобия треугольников

Определение расстояния до недопустимой точки:

Синус

—
отношение противолежащего катета к гипотенузе в прямоугольном треугольнике

Косинус —

отношение прилежащего катета к гипотенузе в прямоугольном треугольнике

Тангенс-

отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике

0
, 45
0
, 60
0

Значение синуса, косинуса и тангенса для углов 30
0
, 45
0
, 60
0

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Подобные треугольники

Подобные фигуры Фигуры принято называть подобными, если они имеют одинаковую форму (похожи по виду).

Подобие в жизни(карты местности)

Пропорциональные отрезки Определение: отрезки называются пропорциональными, если пропорциональны их длины. 12 6 8 4 А 1 В 1 АВ С 1 К 1 СК Говорят, что отрезки А 1 В 1 и С 1 К 1 пропорциональны отрезкам АВ и СК. Пропорциональны ли отрезки АВ и СК отрезкам ЕР и НТ, если: а) АВ = 15 см, СК = 2,5 см, ЕР = 3 см, НТ = 0,5 см? б) АВ = 12 см, СК = 2,5 см, ЕР = 36 см, НТ = 5 см? в) АВ = 24см, СК = 2,5 см, ЕР = 12 см, НТ = 5 см? да нет нет А В 6 см С К 4 см А 1 В 1 12 см С 1 8 см К 1

б Пропорциональные отрезки Тест 1. Указать верное утверждение: а) отрезки АВ и РН пропорциональны отрезкам СК и МЕ; б) отрезки МЕ и АВ пропорциональны отрезкам РН и СК; в) отрезки АВ и МЕ пропорциональны отрезкам РН и СК. А В 3 см С К 2см М Е 9 см Р Н 6 см Приложение: равенство МЕ АВ РН СК можно записать ещё тремя равенствами: РН СК МЕ АВ; МЕ РН АВ СК; АВ СК МЕ РН.

Пропорциональные отрезки 2 . Тест F Y Z R L S N 1 c м 2 см 4 см 2 см 3 см Какой отрезок нужно вписать, чтобы было верным утверждение: отрезки FY и YZ пропорциональны отрезкам LS и ……. а) RL ; б) RS ; в) SN а) RL

Пропорциональные отрезки (нужное свойство) Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. Н Дано: АВС, АК – биссектриса. Доказательство: 1 А В К С 2 Т. к. АК – биссектриса, то 1 = 2, значит, АВК и АСК имеют по равному углу, поэтому Доказать: ВК АВ КС АС S АВК S АСК АВ ∙ АК АС ∙ АК AB AC АВК и АСК имеют общую высоту АН, значит, S АВК S АСК ВК К C AB А C BK K С ВК АВ КС АС Следовательно, Проведём АН ВС.

Подобные треугольники Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны одного треугольника пропорциональны сходственным сторонам другого. А 1 В 1 С 1 А В С Сходственными сторонами в подобных треугольниках называются стороны, лежащие против равных углов. А 1 = А, В 1 = В, С 1 = С А 1 В 1 В 1 С 1 А 1 С 1 АВ ВС АС k A 1 B 1 C 1 ABC K – коэффициент подобия ~

Подобные треугольники А 1 В 1 С 1 А В С Нужное свойство: А 1 = А, В 1 = В, С 1 = С, АВ ВС АС А 1 В 1 В 1 С 1 А 1 С 1 1 k ABC ~ A 1 B 1 C 1 , – коэффициент подобия 1 k A 1 B 1 C 1 ABC , K – коэффициент подобия ~

Реши задачи 3. По данным на чертеже найти стороны АВ и В 1 С 1 подобных треугольников АВС и А 1 В 1 С 1: А В С А 1 С 1 В 1 6 3 4 2,5 ? ? Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 3 . 2. Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 1/3.

Теорема 1. Отношение периметров подобных треугольников равно коэффициенту подобия. М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: Р МКЕ: Р АВС = k Доказательство: K , МК АВ КЕ ВС МЕ АС Значит, МК = k ∙ АВ, КЕ = k ∙ ВС, МЕ = k ∙ АС. Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то Р МКЕ = МК + КЕ + МЕ = k ∙ АВ + k ∙ ВС + k ∙ АС = k ∙ (АВ + ВС + АС) = k ∙ Р АВС. Значит, Р МКЕ: Р АВС = k .

Теорема 2. Отношение площадей подобных треугольников равно квадрату коэффициент a подобия. М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: S МКЕ: S АВС = k 2 Доказательство: Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то M = A, k, MK AB ME AC значит, МК = k ∙ АВ, МЕ = k ∙ АС. S MKE S ABC MK ∙ ME AB ∙ AC k ∙ АВ ∙ k ∙ АС АВ ∙ АС k 2

Реши задачи Две сходственные стороны подобных треугольников равны 8 см и 4 см. Периметр второго треугольника равен 12 см. Чему равен периметр первого треугольника? 24 см 2. Две сходственные стороны подобных треугольников равны 9 см и 3 см. Площадь второго треугольника равна 9 см 2 . Чему равна площадь первого треугольника? 81 см 2 3. Две сходственные стороны подобных треугольников равны 5 см и 10 см. Площадь второго треугольника равна 32 см 2 . Чему равна площадь первого треугольника? 8 см 2 4. Площади двух подобных треугольников равны 12 см 2 и 48 см 2 . Одна из сторон первого треугольника равна 4 см. Чему равна сходственная сторона второго треугольника? 8 см

Решение задачи Площади двух подобных треугольников равны 50 дм 2 и 32 дм 2 , сумма их периметров равна 117 дм. Найдите периметр каждого треугольника. Найти: Р АВС, Р РЕК Решение: Т. к. по условию треугольники АВС и РЕК подобны, то: Дано: АВС, РЕК подобны, S АВС = 50 дм 2 , S РЕК = 32 дм 2 , Р АВС + Р РЕК = 117дм. S АВС S РЕК 50 32 25 16 K 2 . Значит, k = 5 4 K , Р АВС Р РЕК Р АВС Р РЕК 5 4 1,25 Значит, Р АВС = 1,25 Р РЕК Пусть Р РЕК = х дм, тогда Р АВС = 1,25 х дм Т. к. по условию Р АВС + Р РЕК = 117дм, то 1,25 х + х = 117, х = 52. Значит, Р РЕК = 52 дм, Р АВС = 117 – 52 = 65 (дм). Ответ: 65 дм, 52 дм.

« Математику уже затем учить следует, что она ум в порядок приводит» М. В. Ломоносов Желаю успехов в учёбе! Михайлова Л. П. ГОУ ЦО № 173.

Использование теоремы Пифагора для решения задач

Результаты обучения

Используйте теорему Пифагора, чтобы найти неизвестную длину прямоугольного треугольника с учетом двух других длин

Теорема Пифагора — это особое свойство прямоугольных треугольников, которое использовалось с древних времен. \ circ [/ latex], который мы обычно отмечаем маленьким квадратом в углу.{2} = 25 [/ латекс].
Мы будем использовать это определение квадратных корней, чтобы найти длину стороны прямоугольного треугольника.

пример

Используйте теорему Пифагора, чтобы найти длину гипотенузы.

Решение

Шаг 1. Прочтите о проблеме.
Шаг 2. Определите , что вы ищете.	длина гипотенузы треугольника
Шаг 3.{2}} [/ латекс] [латекс] 9 + 16 \ stackrel {?} {=} 25 [/ латекс] [латекс] 25 + 25 \ галочка [/ латекс]
Шаг 7. Ответьте на вопрос.	Длина гипотенузы [латекс] 5 [/ латекс].

пример

Используйте теорему Пифагора, чтобы найти длину более длинной ноги.

Показать решение

Решение

Шаг 1. {2} [/ latex]

Шаг 5.{2} [/ латекс]

[латекс] 25 + 144 \ stackrel {?} {=} 169 [/ латекс]

[латекс] 169 = 169 \ галочка [/ латекс]

Шаг 7. Ответьте на вопрос.

Длина штанины [латекс] 12 [/ латекс].

пример

Кельвин строит беседку и хочет укрепить каждый угол, поставив деревянную скобу [латекс] \ text {10 дюймов} [/ латекс] по диагонали, как показано. Как далеко ниже угла он должен закрепить скобу, если он хочет, чтобы расстояния от угла до каждого конца скобки были одинаковыми? Примерно с точностью до десятых долей дюйма.

Показать решение

Решение

Шаг 1. Прочтите о проблеме.
Шаг 2. Определите , что вы ищете.	расстояние от угла, на котором должен крепиться кронштейн
Шаг 3. Имя. Выберите переменную для ее представления.	Пусть x = расстояние от угла
Шаг 4.{2} [/ латекс] Да.
Шаг 7. Ответьте на вопрос.	Кельвин должен закрепить каждый кусок дерева примерно на [латекс] 7,1 ″ [/ латекс] от угла.

специальных прямоугольных треугольников — объяснения и примеры

Теперь вы знаете, что треугольник — это двумерный многоугольник с тремя сторонами, , , тремя углами, и , тремя вершинами, .В этой статье мы собираемся изучить другие типы треугольников, известные как специальные прямоугольные треугольники. Прежде чем мы начнем, давайте вспомним прямоугольный треугольник.

Что такое прямоугольный треугольник?

Термин « right » относится к латинскому слову « rectus, », означающему прямо. Следовательно, прямоугольный треугольник — это треугольник, один угол которого равен 90 градусам ( прямой угол ). Правые треугольники обозначаются прямоугольником в месте расположения прямого угла.

Самая длинная сторона прямоугольного треугольника на противоположной стороне от прямого угла известна как гипотенуза. Две другие стороны треугольника называются ногами. Горизонтальная ножка — это основа, а вертикальная ножка — это высота прямоугольного треугольника.

Иллюстрация:

Что такое специальный прямоугольный треугольник?

Специальные прямоугольные треугольники — это треугольники, стороны которых находятся в определенном соотношении, известные как тройки Пифагора. В геометрии теорема Пифагора — это утверждение, которое показывает соотношение сторон прямоугольного треугольника.

Уравнение прямоугольного треугольника задается следующим образом: a ² + b ² = c ² , где a или b — высота и основание треугольника, а c — гипотенуза. Используя теорему Пифагора, найти недостающую сторону треугольника довольно просто и легко.

Два специальных прямоугольных треугольника включают:

45 °; 45 °; Треугольник 90 °
30 °; 60 °; Треугольник 90 °

Давайте сделаем краткий обзор этих специальных прямоугольных треугольников, поскольку мы подробно рассмотрим их в следующих статьях.

45 °; 45 °; Треугольник 90 °

Это специальный прямоугольный треугольник с углами 45 °, 45 ° и 90 °. Отношение основания к высоте для гипотенузы этого треугольника составляет 1: 1: √2.

База: Высота: Гипотенуза = x: x: x√2 = 1: 1: √2.

Другими словами, 45 °; 45 °; Треугольник 90 ° тоже может быть равнобедренным. Равнобедренный треугольник — это треугольник, в котором две длины двух сторон равны, а также два его угла равны.

Используя уравнение прямоугольного треугольника a ² + b ² = c ², мы можем вычислить гипотенузу a 45 °; 45 °; Треугольник 90 ° следующим образом:

Т.к., а 45 °; 45 °; Треугольник 90 ° также является равнобедренным треугольником;

пусть a = b = x;

x ² + x ² = 2x ²

Найдите квадратный корень из каждого члена уравнения

√x ² + √x ² = √ (2x ²)

х + х = х √2

Следовательно, гипотенуза 45 °; 45 °; Треугольник 90 ° равен x √2

30 °; 60 °; Треугольник 90 °

Это особый тип прямоугольного треугольника с углами 30 °; 60 °; 90 °.Отношение длин сторон x: x√3: 2x.

Как решать специальные прямоугольные треугольники?

Решить специальные прямоугольные треугольники — значит найти недостающие длины сторон. Вместо использования теоремы Пифагора мы можем использовать специальные соотношения прямоугольного треугольника для выполнения вычислений.

Давайте разберемся с парой примеров.

Пример 1

Более длинная сторона 30 °; 60 °; Прямоугольный треугольник 90 ° равен 8√3 см.Какова мера его высоты и гипотенузы?

Решение

Лучший способ решить подобные проблемы — нарисовать треугольники:

Передаточное отношение 30 °; 60 °; Правый треугольник 90 ° равен x: x√3: 2x. В этом случае x и x√3 — соответственно более короткая и длинная стороны, а 2x — гипотенуза.

Следовательно, x√3 = 8√3 см

Возведите обе части уравнения в квадрат.

⇒ (x√3) ² = (8√3) ²

⇒ 3x ² = 64 * 3

⇒ x ² = 64

Найдите квадрат обеих сторон.

√x ² = √64

x = 8 см

Запасной.

2x = 2 * 8 = 16 см.

Следовательно, более короткая сторона равна 8 см, а гипотенуза — 16 см.

Пример 2

Гипотенуза 45 °; 45 °; Треугольник 90 ° равен 6√2 мм. Рассчитайте длину его основания и высоту.

Решение

Передаточное отношение 45 °; 45 °; Треугольник 90 ° равен x: x: x√2. Итак, у нас есть;

⇒x√2 = 6√2 мм

Возведите обе части уравнения в квадрат.

⇒ (x√2) ² = (6√2) ² мм

⇒ 2x ² = 36 * 2

⇒ 2x ² = 72

х ² = 36

Найдите квадратный корень.

x = 6 мм

Заменить x = 6 мм в соотношении.

Следовательно, основание и высота прямоугольного треугольника равны 6 мм каждая.

Пример 3

Если диагональ прямоугольного треугольника равна 8 см, найдите две другие стороны треугольника, учитывая, что один из его углов равен 30 градусам.

Решение

Это треугольник 30 ° -60 ° -90 °. Поэтому мы используем соотношение x: x√3: 2x.

Учитывая, что диагональ = гипотенуза = 8 см.

⇒2x = 8 см

⇒ x = 4 см

Запасной.

x√3 = 4√3 см

Короткая сторона прямоугольного треугольника 4 см, а длинная сторона 4√3 см.

Пример 4

Найдите гипотенузу треугольника 30 ° — 60 ° — 90 °, длинная сторона которого 6 дюймов.

Решение

Соотношение = x: x√3: 2x.

⇒ x√3 = 6 дюймов.

Квадрат с двух сторон

⇒ (x√3) ² = 36

⇒ 3x ² = 36

х ² = 12

x = 2√3 дюйма.

Пример 5

Лестница, прислоненная к стене, составляет угол 30 градусов с землей. Если длина лестницы 9 м, найти;

Высота стены.
Рассчитайте длину между основанием лестницы и стеной.

Решение

Учитывая, что один угол равен 30 градусам, это должен быть прямоугольный треугольник 60 ° — 60 ° — 90 °.

Соотношение = x: x√3: 2x.

⇒ 2x = 9

⇒ х = 9/2

= 4,5

Запасной.

Высота стены = 4,5м
x√3 = 4,5√3м

Практические вопросы

Если длина одной стороны равностороннего треугольника составляет 15 м, какова высота этого треугольника?
Если длина диагонали квадрата равна 10 единицам, какова площадь квадрата?
Если высота равностороннего треугольника 22 см, какова длина стороны равностороннего треугольника?

Предыдущий урок | Главная страница | Следующий урок

3 4 5 Правые треугольники — объяснение и примеры

Правые треугольники очень полезны в нашей повседневной жизни.Чем проще размеры прямоугольного треугольника, тем проще его использование.

Способность распознавать специальные прямоугольные треугольники — это быстрый способ решения задач, связанных с прямоугольными треугольниками. Вместо использования теоремы Пифагора вы можете использовать специальные соотношения прямоугольного треугольника для вычисления недостающих длин.

Они могут иметь различных размеров, , но самый распространенный из них — это прямоугольный треугольник 3-4-5 . В этой статье мы обсудим, что такое прямоугольный треугольник 3-4-5 и как решить задачи, связанные с прямоугольным треугольником 3-4-5.

Треугольник — это двумерный многоугольник с тремя углами, тремя вершинами и тремя углами, соединенными вместе, образуя замкнутую диаграмму в геометрии. Существуют разные типы треугольников в зависимости от длины сторон и величины их внутренних углов. Более подробно о треугольниках вы можете прочитать в предыдущих статьях.

Что такое прямоугольник 3-4-5?

Прямоугольный треугольник 3-4-5 — это треугольник, длина сторон которого составляет 3: 4: 5. Другими словами, треугольник 3-4-5 имеет отношение сторон в целых числах, называемых тройками Пифагора.

Это соотношение можно представить как:

Сторона 1: Сторона 2: Гипотенуза = 3n: 4n: 5n = 3: 4: 5

Мы можем доказать это, используя теорему Пифагора следующим образом:

⇒ a ² + b ² = c ²

⇒ 3 ² + 4 ² = 5 ²

⇒ 9 + 16 = 25

25 = 25

Прямоугольный треугольник 3-4-5 имеет три внутренних угла: 36,87 °, 53.13 ° и 90 °. Следовательно, прямоугольный треугольник 3 4 5 можно классифицировать как разносторонний, потому что длина всех трех его сторон и внутренние углы различны

Помните, что треугольник 3-4-5 не означает, что соотношение равно 3: 4: 5; это может быть любой общий множитель этих чисел. Например, треугольник 3-4-5 также может принимать следующие формы:

6-8-10
9-12-15
12-16-20
15-20-25

Как решить треугольник 3-4-5

Решение прямоугольного треугольника 3-4-5 — это процесс нахождения недостающих длин сторон треугольника.Соотношение 3: 4: 5 позволяет быстро вычислять различные длины в геометрических задачах, не прибегая к таким методам, как таблицы или теорема Пифагора.

Пример 1

Найдите длину одной стороны прямоугольного треугольника, в котором длина гипотенузы и другой стороны равны 30 см и 24 см соответственно.

Решение

Проверьте соотношение, чтобы убедиться, что оно соответствует 3n: 4n: 5n

?: 24: 30 =?: 4 (6): 5 (6)

Это должен быть прямоугольный треугольник 3-4-5, так что у нас есть;

п = 6

Следовательно, длина другой стороны равна;

3n = 3 (6) = 18 см

Пример 2

Самый длинный край и нижний край треугольного паруса парусника составляют 15 ярдов и 12 ярдов соответственно.Какая высота у паруса?

Решение

Проверить соотношение

⇒?: 12: 15 =? : 4 (3): 5 (3)

Следовательно, значение n = 3

Запасной.

⇒ 3n = 3 (3) = 9

Следовательно, высота паруса — 9 ярдов.

Пример 3

Найдите прямоугольный треугольник 3-4-5 из следующего списка треугольников.

Треугольник A ⇒ 8, 8, 25

Треугольник B ⇒ 9, 12, 15

Треугольник C ⇒ 23, 27, 31

Треугольник D ⇒ 12, 16, 20

Треугольник E ⇒ 6, 8, 10

Решение

Проверьте соотношение каждого треугольника.

А ⇒ 8: 8: 25

Б ⇒ 9: 12: 15 (каждый член разделите на 3)

= 3: 4: 5

К ⇒ 23: 27: 31

D ⇒ 12:16: 20 (разделите каждый член на 4)

= 3: 4: 5

E ⇒6: 8: 10 (разделить на 2)

= 3: 4: 5

Следовательно, треугольники B, D и E являются 3-4-5 прямыми треугольниками.

Пример 4

Найдите значение x на рисунке, показанном ниже. Предположим, что это прямоугольный треугольник 3-4-5.

Решение

Найдите множитель «n» в прямоугольном треугольнике 3-4-5.

?: 80: 100 =?: 4 (20): 5 (20)

Следовательно, n = 20

Заменить в 3н: 4н: 5н.

3n = 3 (20) = 60

Следовательно, x = 60 м

Пример 5

Вычислите длину диагонали прямоугольного треугольника с длинами сторон 6 и 8 дюймов.

Решение

Проверьте соотношение, соответствует ли оно соотношению 3n: 4n: 5n.

6: 8:? = 3 (2): 4 (2) 😕

п = 2

Заменить n = 2 на 5n.

5n = 5 (2) = 10.

Следовательно, длина диагонали 10 дюймов.

Предыдущий урок | Главная страница | Следующий урок

Решение прямоугольных треугольников

Треугольники состоят из трех отрезков прямых. Они встречаются, образуя три угла. Размеры углов и длины сторон связаны друг с другом. Если вы знаете размер (длину) трех из шести частей треугольника (должна быть включена хотя бы одна сторона), вы можете найти размеры остальных сторон и углов.Если треугольник прямоугольный, вы можете использовать простые тригонометрические соотношения, чтобы найти недостающие части. В общем треугольнике (остром или тупом) вам нужно использовать другие методы, включая закон косинусов и закон синусов. Вы также можете найти площадь треугольников, используя тригонометрические соотношения.

Все треугольники состоят из трех сторон и трех углов. Если три угла треугольника обозначены как ∠ A , ∠ B и ∠ C , то три стороны треугольника должны быть обозначены как a , b и c .На рисунке 1 показано, как строчные буквы используются для обозначения сторон треугольника, противоположных углам, названным соответствующими прописными буквами. Если известны какие-либо три из этих шести измерений (кроме измерения трех углов), то вы можете рассчитать значения трех других измерений. Процесс поиска недостающих измерений известен как решение треугольника . Если треугольник прямоугольный, то один из углов равен 90 °. Следовательно, вы можете решить прямоугольный треугольник, если вам даны размеры двух из трех сторон или если вам даны размеры одной стороны и одного из двух других углов.

Рисунок 1
Чертеж для примера 1.

Пример 1 : Решите прямоугольный треугольник, показанный на рисунке (b), если ∠ B = 22 °

Поскольку сумма трех углов треугольника должна составлять 180 °, ∠ A = 90 ∠ B, следовательно, ∠ A = 68 °.

Ниже приводится альтернативный способ решения для сторон a и c:

Это альтернативное решение может быть проще, поскольку не требует разделения.

Пример 2 : Решите прямоугольный треугольник, показанный на рисунке (b), если b = 8 и a = 13.

Вы можете использовать теорему Пифагора, чтобы найти недостающую сторону, но вместо этого используются тригонометрические отношения. Сначала будут найдены два отсутствующих угловых измерения, а затем — отсутствующая сторона.

Во многих приложениях определенные углы обозначаются специальными именами. Два из этих специальных названий: угол наклона и угол наклона .В примерах, показанных на Рисунке 2, используются эти термины.

Рисунок 2
а) угол возвышения и б) угол падения.

Пример 3: Большой самолет (самолет A) , летящий на высоте 26 000 футов, видит меньший самолет (самолет B) , летящий на высоте 24 000 футов. Угол депрессии 40 °. Какое расстояние прямой видимости ( x ) между двумя плоскостями?

Рисунок 3 иллюстрирует условия этой проблемы.

Рисунок 3
Чертеж для примера 3.

Из рисунка 3 вы можете найти решение, используя синус 40 °:

Пример 4: Лестница должна достигать вершины здания. Основание лестницы будет на расстоянии 25 футов от основания здания. Угол подъема от основания лестницы до вершины здания — 64 °. Найдите высоту здания (h) и длину лестницы ( м ).

Рисунок 4 иллюстрирует условия этой проблемы.

Рисунок 4
Чертеж для примера 4.

Пример 5: Дровосек хочет определить высоту высокого дерева. Он встает на некотором расстоянии от дерева и определяет, что угол подъема к вершине дерева равен 40 °. Он приближается к дереву на 30 футов, и теперь угол подъема составляет 50 °.Если глаза дровосека находятся на высоте 5 футов над землей, какова высота дерева?

Рисунок 5 поможет вам визуализировать проблему.

Рисунок 5
Чертеж для примера 5.

Из маленького прямоугольного треугольника и из большого прямоугольного треугольника очевидны следующие соотношения:

Подставляя первое уравнение во второе, получаем:

Обратите внимание, что 5 ′ необходимо добавить к значению x , чтобы получить высоту дерева, или 90.06 ′ высотой.

Пример 6: Используя рисунок 6, найдите длину сторон x и y и площадь большого треугольника.

Рисунок 6
Чертеж для примера 6.

Поскольку это равнобедренный треугольник, и равные стороны имеют противоположные равные углы, значения x и y совпадают. Если треугольник разделен на два прямоугольных, основание каждого будет 6.Следовательно,

Решайте реальные проблемы с прямоугольными треугольниками.

MA.912.G.5.4 — Решение реальных задач с использованием прямоугольных треугольников.

Веб-сайт несовместим с используемой вами версией браузера. Не все функции могут быть доступны. Пожалуйста, обновите ваш браузер до последней версии.

Решайте реальные проблемы с использованием прямоугольных треугольников.

Разъяснения

Пример: расстояние между основанием лестницы и стеной, к которой она опирается, должно составлять не менее 1/3 общей длины лестницы. Предположим, что 12-футовая лестница размещена в соответствии с этими рекомендациями.Приведите минимальное расстояние основания лестницы от стены. Насколько высоко по стене поднимется лестница? Объясните и включите набросок в свое объяснение.

Общая информация

Предметная область: X-Mathematics (бывшие стандарты — 2008)

Класс: 912

Свод знаний: Геометрия

Идея: Уровень 3: Стратегическое мышление и комплексное мышление

Стандарт : Прямоугольники. Применяйте теорему Пифагора для решения задач, в том числе связанных с высотами прямоугольных треугольников и треугольников с особыми угловыми отношениями.Используйте специальные прямоугольные треугольники для решения задач, используя свойства треугольников.

Дата принятия или изменения: 09/07

Дата последней оценки: 06/07

Статус: Утверждено Государственным советом — Архивировано

Оценено: Да

Характеристики тестового объекта

Тип товара:
Этот эталонный показатель можно оценить с помощью:
MC
,
FR
Предметы)

Также оценивает:

MA.912.G.5.1 Докажите и примените метод Пифагора.
Теорема и обратное.

MA.912.G.5.2 Укажите и примените отношения, которые
существуют, когда высота проводится к гипотенузе прямоугольного треугольника.

MA.912.G.5.3 Используйте специальные прямоугольные треугольники
(30 ° — 60 ° — 90 ° и 45 ° — 45 ° — 90 °) для решения проблем.

Уточнение:
Учащиеся будут применять свойства прямоугольных треугольников для решения реальных задач.
проблемы.
Ограничения по содержанию:
Элементы могут потребовать от студентов применения теоремы Пифагора, специальной
отношения прямоугольного треугольника и / или характеристики треугольников
в результате высоты прямоугольного треугольника, нарисованного справа
угол к гипотенузе.
Элементы могут включать применение среднего геометрического.
Атрибуты стимула:
Пункты, оценивающие MA.912.G.5.2, могут быть заданы либо математически, либо
контексты реального мира.Все остальные элементы должны быть настроены в реальном контексте.
Любые радикальные выражения в основе элемента должны быть в упрощенном или
рационализированная форма.
Графика должна использоваться в большинстве этих элементов по мере необходимости.
Атрибуты ответа:
Будут предоставлены любые радикальные выражения в вариантах с множественным выбором
в упрощенном или рационализированном виде.

Образцы тестовых заданий (2)

Тестовый элемент №: Образец теста 2
Вопрос:
Нара создал два прямоугольных треугольника.Она начала с LJKL и нарисовала высоту от точки K в сторону.
JL. На диаграмме ниже показан LJKL и некоторые его размеры в сантиметрах (см).
Основываясь на информации на диаграмме, какова мера x с точностью до десятых долей?
сантиметр?
Сложность: НЕТ
Тип: FR: Заполняющий ответ

Связанные точки доступа

Альтернативная версия этого теста для учащихся со значительными когнитивными нарушениями.

Связанные ресурсы

Проверенные ресурсы преподаватели могут использовать для обучения концепциям и навыкам, связанным с этим тестом.

Ресурсы для учащихся

Проверенные ресурсы учащиеся могут использовать для изучения концепций и навыков в этом тесте.

Ресурсы для родителей

Проверенные ресурсы, которые могут использовать опекуны, чтобы помочь учащимся изучить концепции и навыки, используемые в этом тесте.

Загрузка. {\ circ} $$ ($$ \ angle $$ B на рисунке слева) и множество часто изучаемых формул, таких как:

SOHCAHTOA применяется только к прямоугольным треугольникам (подробнее здесь) .

Картинка 2

Гипотенуза прямоугольного треугольника

Гипотенуза — наибольшая сторона прямоугольного треугольника, всегда противоположная прямому углу.

(Только прямоугольные треугольники имеют гипотенузу).Две другие стороны треугольника, AC и CB, называются «ногами».

В треугольнике выше гипотенуза — это сторона AB, противоположная прямому углу $$ \ angle C $$.

Калькулятор гипотенузы

Онлайн-инструмент вычисляет гипотенузу (или катет) с помощью теоремы Пифагора.

(Также рисует бесплатно загружаемое изображение вашего правого Треугольника!) .

Ниже приведены несколько практических задач, связанных с теоремой Пифагора, вы также можете получить более подробный урок о том, как использовать теорему Пифагора здесь.

Задача 1

Найдите длину стороны t треугольника слева.

Покажи ответ

Задача 2

Какое значение x на картинке слева?

Покажи ответ

Задача 3

Какое значение x на картинке слева?

Покажи ответ

$$
х ^ 2 = 21 ^ 2 + 72 ^ 2
\\
х ^ 2 = 5625
\\
х = \ sqrt {5625}
\\
х = 75
$$

Задача 4

Найдите длину стороны X в треугольнике слева?

Покажи ответ

Задача 5

Что такое x в треугольнике слева?

Покажи ответ

х ² + 4 ² = 5 ²
х ² + 16 = 25
х ² = 25 — 16 = 9
х = 3

Калькулятор прямоугольного треугольника
—

Онлайн-инструмент для определения размеров сторон и углов прямоугольного треугольника.Также рисует загружаемое изображение треугольника на основе вашего ввода.

прямоугольных треугольников

прямоугольных треугольников

Давайте снова согласимся со стандартным соглашением для обозначения частей прямоугольного треугольника. Обозначим прямой угол C , а гипотенузу c. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им, соответственно.

Решение прямоугольных треугольников

Мы можем использовать теорему Пифагора и свойства синусов, косинусов и касательных, чтобы решить треугольник, то есть найти неизвестные части в терминах известных частей.

Теорема Пифагора: a ² + b ² = c ².
Синусы: sin A = a / c, sin B = b / c.
Косинусы: cos A = b / c, cos B = a / c.
Касательные: tan A = a / b, tan B = b / a.

Давайте сначала рассмотрим некоторые случаи, когда мы не знаем всех сторон. Предположим, мы не знаем гипотенузу, но знаем две другие стороны. Теорема Пифагора даст нам гипотенузу. Например, если a = 10 и b = 24, то c ² = a ² + b ² = 10 ² + 24 ² = 100 + 576 = 676.Квадратный корень из 676 равен 26, поэтому c = 26 (неплохо привести примеры, когда квадратные корни получаются из целых чисел; в жизни обычно этого не происходит).

Теперь предположим, что мы знаем гипотенузу и одну сторону, но должны найти другую. Например, если b = 119 и c = 169, то a ² = c ² — b ² = 169 ²-119 ² = 28561 — 14161 = 14400, квадратный корень из 14400 равен 120, поэтому a = 120.

Мы можем знать только одну сторону, но мы также знаем угол. Например, если сторона a = 15 и угол A = 41 °, мы можем использовать синус и касательную, чтобы найти гипотенузу и другую сторону. Так как sin A = a / c, мы знаем c = a / sin A = 15 / sin 41. Используя калькулятор, это 15 / 0,6561 = 22,864. Кроме того, tan A = a / b, , поэтому b = a / tan A = 15 / tan 41 = 15/0.8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.

Обратные триггерные функции: арксинус, арккозинус и арктангенс

Теперь давайте посмотрим на проблему определения углов, если вы знаете стороны. Опять же, вы используете триггерные функции, но в обратном порядке. Вот пример. Предположим, что a = 12,3 и b = 50,1. Тогда tan A = a / b = 12,3 / 50,1 = 0,2455. Раньше, когда люди использовали таблицы тригонометрических функций, они просто смотрели в таблицу касательных, чтобы увидеть, какой угол имеет тангенс 0.2455. На калькуляторе мы используем обратные триггерные функции, называемые арктангенсом, арксинусом и арккосинусом. Обычно на калькуляторе есть кнопка с надписью inv или arc, которую вы нажимаете перед нажатием соответствующей триггерной кнопки. Арктангенс 0,2455 равен 13,79, поэтому угол A равен 13,79 °. (Если хотите, можете преобразовать 0,79 градуса в минуты и секунды.)

Вот и все.

Остальные три тригонометрические функции: котангенс, секанс и косеканс

Для большинства целей достаточно трех триггерных функций: синуса, косинуса и тангенса.Однако бывают случаи, когда нужны другие. В исчислении часто используется секанс. Вы можете спросить: «Почему шесть триггерных функций?» Это своего рода симметрия. Есть шесть способов соотношения двух сторон прямоугольного треугольника, и это дает шесть функций:

sin A = кондиционер (opp / hyp)
cos A = b / c (прил / гип)
желто-коричневый A = a / b (опп / прил)
детская кроватка A = b / a (прил. / Опп)
сек A = c / b (hyp / adj)
csc A = c / a (hyp / opp)

Из списка видно, что котангенс (сокращенно cot, или иногда ctn) является обратной величиной тангенса, секанс (сокращенно sec) является обратной величиной косинуса, а косеканс (сокращенно csc или иногда cosec) является обратной величиной синуса.Они в значительной степени избыточны, но стоит знать, что они из себя представляют, на случай, если вы с ними столкнетесь. Обратите внимание, что котангенсы — это тангенсы дополнительных углов, что означает, что кроватка A = tan B, и косеканс являются секущими дополнительных углов, и это означает, что csc A = sec B.

Эти три другие функции также можно интерпретировать с помощью круговой диаграммы.

Мы рассматриваем угол AOB. Напомним, что его касательной является линия AC. По симметрии тангенс угла FOB является линией FG, , но FOB является дополнительным углом AOB, , следовательно, котангенс AOB равен FG.

Затем, чтобы интерпретировать секущие геометрически. Угол AOB появляется в треугольнике COA как угол AOC, , поэтому sec AOB = sec AOC = hyp / adj = OC / OA = OC. Вот и все — секущая — это линия от центра окружности до касательной AC. Причина, по которой он называется секущей, заключается в том, что она разрезает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».

Аналогично, косеканс угла AOB является линией OG от центра окружности до линии котангенса FG.

Упражнения

Примечание: как обычно, во всех упражнениях на прямоугольные треугольники c обозначает гипотенузу, a и b — перпендикулярные стороны, а A и B — углы, противоположные a и b соответственно.

26. В каждом из следующих прямоугольных треугольников, у которых даны две стороны, вычислите sin, cos и tan углов A, и B. Выразите результаты в виде общих дробей.

(i). c = 41, a = 9.

(ii). c = 37, a = 35.

(iii). a = 24, b = 7.

31. В прямоугольном треугольнике c = 6 футов 3 дюйма и загар B = 1.2. Найдите a и b.

34. a = 1,2, b = 2,3. Найдите A и c.

42. a = 10,11, b = 5,14. Найдите B и c.

В следующих нескольких задачах треугольники не являются прямоугольными, но вы можете решить их, используя то, что вы знаете о прямоугольных треугольниках.

61. В наклонном треугольнике ABC, A = 30 °, B = 45 °, а длина перпендикуляра от C до AB составляет 12 дюймов. Найдите длину AB.

67. Если сторона равностороннего треугольника равна a, найдите высоту и радиусы описанных и вписанных окружностей.

202. От вершины здания высотой 50 футов углы подъема и понижения верха и низа другого здания составляют 19 ° 41 ‘и 26 ° 34’ соответственно.Какая высота и расстояние до второго дома.

207. От вершины маяка высотой 175 футов углы падения верха и низа флагштока составляют 23 ° 17 ‘и 42 ° 38’ соответственно. Какой высоты у шеста?

214. В двух точках на расстоянии 65 футов на одной стороне дерева и на одной линии с ним углы подъема вершины дерева составляют 21 ° 19 ‘и 16 ° 20’. Найдите высоту дерева.

215. Когда воздушный шар проходит между двумя точками A, и B, на расстоянии 2 миль друг от друга, углы подъема воздушного шара в этих точках составляют 27 ° 19 ‘и 41 ° 45’ соответственно. Найдите высоту воздушного шара. Возьмем A и B на одном уровне.

233. Вершина маяка находится на высоте 230 футов над уровнем моря. Как далеко находится объект, который находится только «на горизонте»? [Предположим, что Земля — это сфера радиусом 3956 миль.]

234. Какая должна быть высота наблюдателя, чтобы он мог видеть объект на Земле в тридцати милях от него? Предположим, что Земля представляет собой гладкую сферу.

На каждом из рисунков, упомянутых в следующих нескольких задачах, объект должен выразить свою площадь (i) через радиус R, то есть радиус описанной окружности, (ii) через apothem r, , то есть радиус вписанной окружности, и (iii) относительно стороны a.

251. Равносторонний треугольник. [См. Проблему 67 выше.]

252. пл.

253. Правильный пятиугольник.

254. Правильный шестигранник.

255. Правильный восьмиугольник.

Подсказки

26. Вам нужны только sin, cos и tan углов A и B ; сами углы не нужны.Итак, вам нужна только третья сторона, которую вы можете вычислить с помощью теоремы Пифагора, а затем вычислить отношения двух сторон.

31. Вы знаете c и tan B. К сожалению, tan B — это соотношение двух сторон, которых вы не знаете, а именно b / a. Эту проблему можно решить несколькими способами. Вот два.

Метод 1. Возьмите уравнение 1.2 = tan B = b / a, , чтобы получить связь между a и b, а именно b = 1.2 а. Теорема Пифагора тогда дает 6,25 ² = a ² + 1,44 a ², из которого вы можете определить a, , а затем найти b.

Метод 2. Из tan B, вы можете определить угол B (используйте arctan). Отсюда вы можете найти cos B, , а затем a, , и вы можете найти sin B, , а затем b.

34. Поскольку у вас есть a и b, вы можете использовать касательные, чтобы найти A , и теорему Пифагора, чтобы найти c.

42. Найдите B по касательным и c по теореме Пифагора.

61. Начните с рисования рисунка. Хотя треугольник ABC не является прямоугольным, он разбивается на два прямоугольных треугольника. Вы можете использовать касательные, чтобы найти две части стороны AB и сложить их.

67. Равносторонний треугольник ABC имеет три угла при вершине 60 °. Отбросьте перпендикуляр из одной вершины, скажем, C, , и вы получите два конгруэнтных прямоугольных треугольника ACF, и BCF, , и вы можете найти длину этого перпендикуляра, то есть высоту равностороннего треугольника. Описанная окружность — это круг, проходящий через три вершины, а вписанный круг — это круг, касающийся всех трех сторон.Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и используя триггер на полученных маленьких треугольниках, вы можете найти радиусы этих двух окружностей.

202. Поскольку вы знаете высоту своего здания и угол наклона основания другого здания, вы можете определить, как далеко оно находится. Тогда угол подъема к вершине другого здания покажет вам, насколько оно выше вашего.

207. Подсказка похожа на 202. Видите ли, триггер может быть полезен, если вы одинокий смотритель маяка и не знаете, что делать!

214. Это полезная задача. Вы можете использовать его, чтобы найти высоты недоступных вещей. Нарисуйте фигуру. Есть два неизвестных: высота x дерева и расстояние x ближайшей точки к дереву. Дальнейшая точка будет x + 65 футов от дерева. Используя тангенсы известных углов, вы можете составить два уравнения, которые можно решить, чтобы определить y, и x.

215. Это похоже на 214, но в этой задаче баллон находится между двумя точками. Нарисуйте фигуру. Определитесь с вашими переменными. Составьте уравнения и решите их.

233. Очень интересная задача. На протяжении веков для вычисления радиуса Земли использовались различные обратные величины. В этой задаче мы предполагаем, что знаем о Земле. Все, что вам здесь нужно, это теорема Пифагора. Одна сторона прямоугольного треугольника равна r, радиус Земли, а гипотенуза — r + h , где h — высота маяка.Теорема Пифагора о третьей стороне треугольника.

234. Задайте эту задачу аналогично 233, но известны разные переменные.

251–255. Вы можете сделать все это сразу, оставив вычисления напоследок. Пусть n — количество сторон правильного многоугольника. Проведите линии от центра фигуры к вершинам и серединам сторон. У вас получится 2 n маленьких треугольников. Каждый из них представляет собой прямоугольный треугольник с гипотенузой R, с одним катетом r, и другим катетом a /2.Угол в центре равен 360 ° / (2 n ) = 180 ° / n. Используя тригонометрию, вы можете легко написать уравнения, связывающие площадь правильного многоугольника, как требуется.

ответы

26. (i). b = 40. Итак sin A = cos B = 9/41, cos A = sin B = 40/41, tan A = 9/40, tan B = 40 / 9.

(ii). b = 12. Итак sin A = cos B = 35/37, cos A = sin B = 12/37, tan A = 35/12, tan B = 12 / 37.
(iii). c = 25. Итак sin A = cos B = 24/25, cos A = sin B = 7/25, tan A = 24/7, tan B = 7 / 24.

31. a = 4 фута, b = 4,8 фута, около 4 футов 10 дюймов.

34. A = 27,55 °, примерно 28 °. c = 2,6.

42. B = 26,95 ° или 26 ° 57 ‘. с = 11.3.

61. AB = 12 / tan A + 12 / tan B = 12 (√3 + 1) дюймов, около 33 дюймов.

67. ( a √3) / 2, ( a √3) / 3 и ( a √3) / 6 соответственно.

202. Расстояние = 50 / тангаж 26 ° 34 ‘= 100 футов. Высота = 50 + 100 см. 19 ° 41 ‘= 85,8’ = 85’9 дюймов.

207. Расстояние = 175 / тангенс угла 42 ° 38 ‘= 190 футов. Рост = 175 — 190 см. 23 ° 17 ‘= 93.23 ‘= 9’3 «.

214. Два уравнения:

0,293052 = загар 16 ° 20 ‘= ч / (65 + x ), и

0,3
= загар 21 ° 19 ‘= ч / x .

где x — расстояние от ближайшей точки до основания дерева. Вы можете решить их одновременно для x и ч.

Расстояние x = 196 футов. Высота ч = 76,5 футов.

215. Если h — это высота воздушного шара, а x — это расстояние по земле от A до точки непосредственно под воздушным шаром, то два уравнения равны

tan 27 ° 19 ‘= h / x , и

загар 41 ° 45 ‘= ч / (2 — x )

Вы можете решить эту пару уравнений для x и h.

Высота = 0,654 мили = 3455 футов.

233. Мелочь больше 18.5 миль.

234. 600 футов.

251–255. Площадь обычного n -угольника равна A = nra /2. Чтобы найти A в терминах R, r, или a, используйте отношения

cos 180 & deg / n = r / R, и

загар 180 ° / n = a / (2 r ).

потом

(i) в единицах R, площадь A = nR ² cos 180 ° / n sin 180 ° / n ,

(ii) в единицах r, площадь A = nr ² tan 180 & deg / n , и

(iii) в единицах a, площадь A = na ² / (4tan 180 & deg / n ).
Проблема форма (i) R (ii) r (iii) a
251 треугольник (3 р ² √3) / 4 3 r ² √3 ( a ² √3) / 4
252 квадрат 2 R ² 4 r ² a ²
253 пятиугольник (5 R ² sin 108 °) / 2 5 r ² загар 36 ° (5 a ² загар 54 °) / 4
254 шестигранник (3 р ² √3) / 2 2 r ² √3 (3 a ² √3) / 2
255 восьмиугольник 2 R ² √2 8 r ² загар 22 ° 30 ‘ 2 a ² tan 67 ° 30 ‘

Проблема	форма	(i) R	(ii) r	(iii) a
251	треугольник	(3 р ² √3) / 4	3 r ² √3	( a ² √3) / 4
252	квадрат	2 R ²	4 r ²	a ²
253	пятиугольник	(5 R ² sin 108 °) / 2	5 r ² загар 36 °	(5 a ² загар 54 °) / 4
254	шестигранник	(3 р ² √3) / 2	2 r ² √3	(3 a ² √3) / 2
255	восьмиугольник	2 R ² √2	8 r ² загар 22 ° 30 ‘	2 a ² tan 67 ° 30 ‘

Кроме того, пифагоровы тройки

Это не имеет отношения к тригонометрии, но интересно.Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника как целые числа, а третья также оказывается целым числом. Как и в задаче 26, где у всех трех прямоугольных треугольников стороны имеют целые числа, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3: 4: 5.

Итак, существуют ли другие специальные прямоугольные треугольники, все стороны которых представляют собой целые числа? Да, и они давно изучаются.Три числа a, b, и c такие, что a ² + b ² = c ², как говорят, образуют тройку Пифагора , в честь Пифагора. Он жил около 550 г. до н. Э. и, наверное, знаю немало из них. Но древние вавилоняне примерно 1800 г. до н. Э. знал их всех, и многие из них были известны в других древних цивилизациях, таких как Китай и Индия.

Прежде чем читать абзац, посмотрите, сможете ли вы найти еще несколько троек Пифагора.Не считайте те, у которых есть общий множитель, как новые, например 6: 8: 10, поскольку они будут похожи на меньшие.

В книге Евклида Элементы есть описание всех возможных пифагоровых троек. Вот современный пересказ Евклида. Возьмем любые два нечетных числа m, и n, с m, n и взаимно простые числа (то есть без общих множителей). Пусть a = mn, пусть b = ( n ² — m ²) / 2, и пусть c = ( n ² + m ²) / 2.Тогда a : b : c — тройка Пифагора. Например, если взять м = 1 и n = 3, то получится наименьшая тройка Пифагора 3: 4: 5.

Решение задач на подобие. Подобные треугольники.

Задача 1.

Задача 2.

Задача 3.

Задача 4.

Задача 5.

Задача 6.

Задачи для самостоятельной работы

Задачи на подобие треугольников

Подобные треугольники. Геометрия, 8 класс: уроки, тесты, задания.

Подобные треугольники. Пропорциональные отрезки

Признаки подобия треугольников

Применение подобия.

Тригонометрические функции острого угла прямоугольного треугольника

Геометрия «Подобные треугольники» — презентация по Геометрии

Подобие треугольников. Решение задач с практическим содержанием.

Урок геометрии «Решение задач на признаки подобия треугольников» » 8 класс

Подобие прямоугольных треугольников. Применение презентаций для иллюстрирования теорем Подобные треугольники презентация савченко е м

Подписи к слайдам:

Использование теоремы Пифагора для решения задач

Результаты обучения

пример

пример

пример

специальных прямоугольных треугольников — объяснения и примеры

Что такое специальный прямоугольный треугольник?

Как решать специальные прямоугольные треугольники?

3 4 5 Правые треугольники — объяснение и примеры

Что такое прямоугольник 3-4-5?

Как решить треугольник 3-4-5

Решение прямоугольных треугольников

Решайте реальные проблемы с прямоугольными треугольниками.

Веб-сайт несовместим с используемой вами версией браузера. Не все функции могут быть доступны. Пожалуйста, обновите ваш браузер до последней версии.

Разъяснения

Связанные точки доступа

Связанные ресурсы

Ресурсы для учащихся

Ресурсы для родителей

Загрузка. {\ circ} $$ ($$ \ angle $$ B на рисунке слева) и множество часто изучаемых формул, таких как:

Гипотенуза прямоугольного треугольника

Задача 1

Задача 2

Задача 3

Задача 4

Задача 5

прямоугольных треугольников

Решение прямоугольных треугольников

Обратные триггерные функции: арксинус, арккозинус и арктангенс

Остальные три тригонометрические функции: котангенс, секанс и косеканс

Упражнения

Подсказки

ответы

Кроме того, пифагоровы тройки

Добавить комментарий Отменить ответ