Содержание
Решение неравенств любого вида. Онлайн калькулятор с примерами
Решение неравенств онлайн
Перед тем как решать неравенства, необходимо хорошо усвоить как решаются уравнения.
Не важно каким является неравенство – строгим () или нестрогим (≤, ≥), первым делом приступают к решению уравнения, заменив знак неравенства на равенство (=).
Поясним что означает решить неравенство?
После изучения уравнений в голове у школьника складывается следующая картина: нужно найти такие значения переменной, при которых обе части уравнения принимают одинаковые значения. Другими словами, найти все точки, в которых выполняется равенство. Всё правильно!
Когда говорят о неравенствах, имеют в виду нахождение интервалов (отрезков), на которых выполняется неравенство. Если в неравенстве две переменные, то решением будут уже не интервалы, а какие-то площади на плоскости. Догадайтесь сами, что будет решением неравенства от трех переменных?
Как решать неравенства?
Универсальным способом решения неравенств считают метод интервалов (он же метод промежутков), который заключается в определении всех интервалов, в границах которых будет выполняться заданное неравенство.
Не вдаваясь в тип неравенства, в данном случае это не суть, требуется решить соответствующее уравнение и определить его корни с последующим обозначением этих решений на числовой оси.
Можно сказать на этом полдела сделано. Далее, взяв любую точку на каждом интервале, осталось определить выполняется ли само неравенство? Если выполняется, то он входит в решение неравенства. Ели нет, то пропускаем его.
Как правильно записывать решение неравенства?
Когда вы определили интервалы решений неравенства, нужно грамотно выписать само решение. Есть важный нюанс – входят ли границы интервалов в решение?
Тут всё просто. Если решение уравнения удовлетворяет ОДЗ и неравенство является нестрогим, то граница интервала входит в решение неравенства. В противном случае – нет.
Рассматривая каждый интервал, решением неравенства может оказаться сам интервал, либо полуинтервал (когда одна из его границ удовлетворяет неравенству), либо отрезок – интервал вместе с его границами.
Важный момент
Не думайте, что решением неравенства могут быть только интервалы, полуинтервалы и отрезки. Нет, в решение могут входить и отдельно взятые точки.
Например, у неравенства |x|≤0 всего одно решение – это точка 0.
А у неравенства |x|
Для чего нужен калькулятор неравенств?
Калькулятор неравенств выдает правильный итоговый ответ. При этом в большинстве случаев приводится иллюстрация числовой оси или плоскости. Видно, входят ли границы интервалов в решение или нет – точки отображаются закрашенными или проколотыми.
Благодаря онлайн калькулятору неравенств можно проверить правильно ли вы нашли корни уравнения, отметили их на числовой оси и проверили на интервалах (и границах) выполнение условия неравенства?
Если ваш ответ расходится с ответом калькулятора, то однозначно нужно перепроверить свое решение и выявить допущенную ошибку.
Уравнения и неравенства с модулем
Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.
Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.
Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.
Прежде всего вспомним, что
Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)
Слева модуль, справа число
Это самый простой случай. Решим уравнение
Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:
или
Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.
Ответ: 0; 5.
Переменная как под модулем, так и вне модуля
Здесь приходится раскрывать модуль по определению. . . или соображать!
1.
Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:
Решение первой системы: . У второй системы решений нет.
Ответ: 1.
2.
Первый случай: x ≥ 3. Снимаем модуль:
Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.
Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:
Значит, больше трёх и потому является корнем исходного уравнения
Второй случай: x < 3. Снимаем модуль:
Число . больше, чем , и потому не удовлетворяет условию x < 3. Проверим :
Значит, . является корнем исходного уравнения.
Ответ:
3.
Снимать модуль по определению? Страшно даже подумать об этом, ведь дискриминант — не полный квадрат. Давайте лучше воспользуемся следующим соображением: уравнение вида |A| = B равносильно совокупности двух систем:
То же самое, но немного по-другому:
Иными словами, мы решаем два уравнения, A = B и A = −B, а потом отбираем корни, удовлетворяющие условию B ≥ 0.
Приступаем. Сначала решаем первое уравнение:
Затем решаем второе уравнение:
Теперь в каждом случае проверяем знак правой части:
Стало быть, годятся лишь и .
Ответ:
Квадратные уравнения с заменой |x| = t
Решим уравнение:
Поскольку , удобно сделать замену |x| = t. Получаем:
Ответ: ±1.
Модуль равен модулю
Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:
Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:
Остаётся решить каждое из уравнений совокупности и записать ответ.
Два или несколько модулей
Решим уравнение:
Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.
Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)
Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)
Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.
Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:
Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.
Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:
Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.
Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:
Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.
Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:
Ничего нового. Мы и так знаем, что x = 1 является решением.
Мы и так знаем, что x = 1 является решением.
Ответ: [1; 2] ∪ {5}.
Модуль в модуле
Решим уравнение:
Начинаем с раскрытия внутреннего модуля.
1) x ≤ 3. Получаем:
Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.
1.1) Получаем в этом случае:
Это значение x не годится, так как не принадлежит рассматриваемому промежутку.
1.2) . Тогда:
Это значение x также не годится.
Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.
2) x ≥ 3. Имеем:
Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:
Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.
Ответ: 4.
Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.
Читайте также о том, как решать неравенства с модулем.
Комплексные неравенства с модулем. Калькулятор онлайн.Решение уравнений и неравенств с модулями
решение неравенства
в режиме онлайн
решение
почти любого заданного неравенства онлайн
. Математические неравенства онлайн
для решения математики. Быстро найти решение неравенства
в режиме онлайн
. Сайт www.сайт позволяет найти решение
почти любого заданного алгебраического
, тригонометрического
или трансцендентного неравенства онлайн
. При изучении практически любого раздела математики на разных этапах приходится решать неравенства онлайн
. Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение неравенства онлайн
займет несколько минут. Основное преимущество www.сайт при решении математических неравенства онлайн
— это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические неравенства онлайн
Сайт способен решать любые алгебраические неравенства онлайн
, тригонометрические неравенства онлайн
, трансцендентные неравенства онлайн
, а также неравенства
с неизвестными параметрами в режиме онлайн
. Неравенства
служат мощным математическим аппаратом решения
практических задач. C помощью математических неравенств
можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины неравенств
можно найти, сформулировав задачу на математическом
языке в виде неравенств
и решить
полученную задачу в режиме онлайн
на сайте www.сайт. Любое алгебраическое неравенство
, тригонометрическое неравенство
или неравенства
содержащие трансцендентные
функции Вы легко решите
онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения неравенств
. При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн
. Поэтому для решения математических неравенств онлайн
Поэтому для решения математических неравенств онлайн
мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических неравенств онлайн
, тригонометрических неравенств онлайн
, а также трансцендентных неравенств онлайн
или неравенств
с неизвестными параметрами. Для практических задач по нахождению инетравол решений различных математических неравенств
ресурса www.. Решая неравенства онлайн
самостоятельно, полезно проверить полученный ответ, используя онлайн решение неравенств
на сайте www.сайт. Необходимо правильно записать неравенство и моментально получите онлайн решение
, после чего останется только сравнить ответ с Вашим решением неравенства. Проверка ответа займет не более минуты, достаточно решить неравенство онлайн
и сравнить ответы. Это поможет Вам избежать ошибок в решении
и вовремя скорректировать ответ при решении неравенств онлайн
будь то алгебраическое
, тригонометрическое
, трансцендентное
или неравенство
с неизвестными параметрами.
Приложение
Решение неравенств онлайн на Math34.biz для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Неравенство в математике — утверждение об относительной величине или порядке двух объектов (один из объектов меньше или не больше другого), или о том, что два объекта не одинаковы (отрицание равенства). В элементарной математике изучают числовые неравенства, в общей алгебре, анализе, геометрии рассматриваются неравенства также и между объектами нечисловой природы. Для решения неравенства обязательно должны быть определены обе его части с одним из знаков неравенства между ними. Строгие неравенства подразумевают неравенство двух объектов. В отличие от строгих, нестрогие неравенства допускают равенство входящих в него объектов. Линейные неравенства представляют собой простейшие с точки зрения начала изучения выражения, и для решения таких неравенств используются самые простые методики. Главная ошибка учеников в решении неравенств онлайн в том, что они не различают особенность строгого и нестрогого неравенства, от чего зависит войдут или нет граничные значения в конечный ответ. Несколько неравенств, связанных между собой несколькими неизвестными, называют системой неравенств. Решением неравенств из системы является некая область на плоскости, либо объемная фигура в трехмерном пространстве. Наряду с этим абстрагируются n-мерными пространствами, однако при решении таких неравенств зачастую не обойтись без специальных вычислительных машин. Для каждого неравенства в отдельности нужно найти значения неизвестного на границах области решения. Множество всех решений неравенства и является его ответом. Замена одного неравенства равносильным ему другим неравенством называется равносильным переходом от одного неравенства к другому. Аналогичный подход встречается и в других дисциплинах, потому что помогает привести выражения к стандартному виду. Вы оцените по достоинству все преимущества решение неравенств онлайн на нашем сайте. Неравенство — это выражение, содержащее один из знаков = >. По сути это логическое выражение. Оно может быть либо верным, либо нет — в зависимости от того, что стоит справа и слева в этом неравенстве.
Несколько неравенств, связанных между собой несколькими неизвестными, называют системой неравенств. Решением неравенств из системы является некая область на плоскости, либо объемная фигура в трехмерном пространстве. Наряду с этим абстрагируются n-мерными пространствами, однако при решении таких неравенств зачастую не обойтись без специальных вычислительных машин. Для каждого неравенства в отдельности нужно найти значения неизвестного на границах области решения. Множество всех решений неравенства и является его ответом. Замена одного неравенства равносильным ему другим неравенством называется равносильным переходом от одного неравенства к другому. Аналогичный подход встречается и в других дисциплинах, потому что помогает привести выражения к стандартному виду. Вы оцените по достоинству все преимущества решение неравенств онлайн на нашем сайте. Неравенство — это выражение, содержащее один из знаков = >. По сути это логическое выражение. Оно может быть либо верным, либо нет — в зависимости от того, что стоит справа и слева в этом неравенстве. Разъяснение смысла неравенства и основные приемы решения неравенств изучаются на разных курсах, а также в школе. Решение любых неравенств онлайн — неравенства с модулем, алгебраические, тригонометрические, трансцендентные неравенства онлайн. Тождественное неравенство, как строгие и нестрогие неравенства, упрощают процесс достижения конечного результата, являются вспомогательным инструментом для разрешения поставленной задачи. Решение любых неравенств и систем неравенств, будь то логарифмические, показательные, тригонометрические или квадратных неравенства, обеспечивается с помощью изначально правильного подхода к этому важному процессу. Решение неравенств онлайн на сайте сайт всегда доступно всем пользователям и абсолютно бесплатно. Решениями неравенства с одной переменной называются значения переменной, которые обращают его в верное числовое выражение. Уравнения и неравенства с модулем: модуль действительного числа — это абсолютная величина этого числа. Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень.
Разъяснение смысла неравенства и основные приемы решения неравенств изучаются на разных курсах, а также в школе. Решение любых неравенств онлайн — неравенства с модулем, алгебраические, тригонометрические, трансцендентные неравенства онлайн. Тождественное неравенство, как строгие и нестрогие неравенства, упрощают процесс достижения конечного результата, являются вспомогательным инструментом для разрешения поставленной задачи. Решение любых неравенств и систем неравенств, будь то логарифмические, показательные, тригонометрические или квадратных неравенства, обеспечивается с помощью изначально правильного подхода к этому важному процессу. Решение неравенств онлайн на сайте сайт всегда доступно всем пользователям и абсолютно бесплатно. Решениями неравенства с одной переменной называются значения переменной, которые обращают его в верное числовое выражение. Уравнения и неравенства с модулем: модуль действительного числа — это абсолютная величина этого числа. Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень. Неравенства – это выражения, указывающие на сравнение чисел, поэтому грамотное решение неравенств обеспечивает точность таких сравнений. Они бывают строгими (больше, меньше) и нестрогими (больше или равно, меньше или равно). Решить неравенство – значит найти все те значения переменных, которые при подстановке в исходное выражение обращают его в верное числовое представление.. Понятие неравенства, его сущность и особенности, классификация и разновидности — вот что определяет специфику данного математического раздела. Основные свойства числовых неравенств, применимые ко всем объектам данного класса, обязательно должны быть изучены учениками на начальном этапе ознакомления с данной темой. Неравенства и промежутки числовой прямой очень тесно связаны, когда речь идет о решении неравенств онлайн. Графическое обозначение решения неравенства наглядно показывает суть такого выражения, становится понятно к чему следует стремиться при решении какой-либо поставленной задачи. В основу понятия неравенства входит сравнение двух или нескольких объектов.
Неравенства – это выражения, указывающие на сравнение чисел, поэтому грамотное решение неравенств обеспечивает точность таких сравнений. Они бывают строгими (больше, меньше) и нестрогими (больше или равно, меньше или равно). Решить неравенство – значит найти все те значения переменных, которые при подстановке в исходное выражение обращают его в верное числовое представление.. Понятие неравенства, его сущность и особенности, классификация и разновидности — вот что определяет специфику данного математического раздела. Основные свойства числовых неравенств, применимые ко всем объектам данного класса, обязательно должны быть изучены учениками на начальном этапе ознакомления с данной темой. Неравенства и промежутки числовой прямой очень тесно связаны, когда речь идет о решении неравенств онлайн. Графическое обозначение решения неравенства наглядно показывает суть такого выражения, становится понятно к чему следует стремиться при решении какой-либо поставленной задачи. В основу понятия неравенства входит сравнение двух или нескольких объектов. Неравенства, содержащие переменную, решаются как аналогично составленные уравнения, после чего делается выборка интервалов, которые будут приняты за ответ. Любое алгебраическое неравенство, тригонометрическое неравенство или неравенства содержащие трансцендентные функции, вы с легкостью и мгновенно сможете решить, используя наш бесплатный сервис. Число является решением неравенства, если при подстановке этого числа вместо переменной получаем верное выражение, то есть знак неравенства показывает истинное понятие.. Решение неравенств онлайн на сайт каждый день для полноценного изучения студентами пройденного материала и закрепления своих практических навыков. Зачастую тема неравенства онлайн в математике изучается школьниками после прохождения раздела уравнений. Как и положено применяются все принципы при решении, чтобы определить интервалы решений. Найти в аналитическом виде ответ бывает сложнее, чем сделать то же самое, но в числовом виде. Однако такой подход дает более наглядное и полное представление об целостности решения неравенства.
Неравенства, содержащие переменную, решаются как аналогично составленные уравнения, после чего делается выборка интервалов, которые будут приняты за ответ. Любое алгебраическое неравенство, тригонометрическое неравенство или неравенства содержащие трансцендентные функции, вы с легкостью и мгновенно сможете решить, используя наш бесплатный сервис. Число является решением неравенства, если при подстановке этого числа вместо переменной получаем верное выражение, то есть знак неравенства показывает истинное понятие.. Решение неравенств онлайн на сайт каждый день для полноценного изучения студентами пройденного материала и закрепления своих практических навыков. Зачастую тема неравенства онлайн в математике изучается школьниками после прохождения раздела уравнений. Как и положено применяются все принципы при решении, чтобы определить интервалы решений. Найти в аналитическом виде ответ бывает сложнее, чем сделать то же самое, но в числовом виде. Однако такой подход дает более наглядное и полное представление об целостности решения неравенства.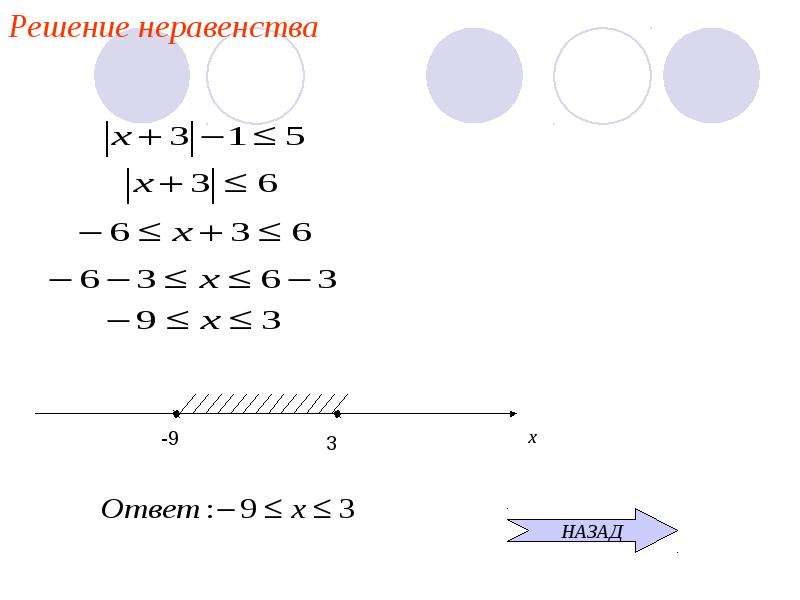 Сложность может возникнуть на этапе построения линии абсцисс и нанесения точек решения однотипного уравнения. После этого решение неравенств сводится к определению знака функции на каждом выявленном интервале с целью определения возрастания или убывания функции. Для этого необходимо поочередно подставлять к значениям, заключенных внутри каждого интервала, в исходную функцию и проверять её значение на положительность или отрицательность. В этом есть суть нахождения всех решений, в том числе интервалов решений. Когда вы сами решите неравенство и увидите все интервалы с решениями, то поймете, насколько применим такой подход для дальнейших действий. Сайт сайт предлагает вам перепроверить свои результаты вычислений с помощью мощного современного калькулятора на этой странице. Вы сможете с легкостью выявить неточности и недочеты в своих расчетах, использую уникальный решебник неравенств. Студенты часто задаются вопросом, где найти такой полезный ресурс? Благодаря инновационному подходу к возможности определения потребностей инженеров, калькулятор создан на базе мощных вычислительных серверов с использованием только новых технологий.
Сложность может возникнуть на этапе построения линии абсцисс и нанесения точек решения однотипного уравнения. После этого решение неравенств сводится к определению знака функции на каждом выявленном интервале с целью определения возрастания или убывания функции. Для этого необходимо поочередно подставлять к значениям, заключенных внутри каждого интервала, в исходную функцию и проверять её значение на положительность или отрицательность. В этом есть суть нахождения всех решений, в том числе интервалов решений. Когда вы сами решите неравенство и увидите все интервалы с решениями, то поймете, насколько применим такой подход для дальнейших действий. Сайт сайт предлагает вам перепроверить свои результаты вычислений с помощью мощного современного калькулятора на этой странице. Вы сможете с легкостью выявить неточности и недочеты в своих расчетах, использую уникальный решебник неравенств. Студенты часто задаются вопросом, где найти такой полезный ресурс? Благодаря инновационному подходу к возможности определения потребностей инженеров, калькулятор создан на базе мощных вычислительных серверов с использованием только новых технологий. По сути решение неравенств онлайн заключается в решении уравнения с вычислением всех возможных корней. Полученные решения отмечаются на прямой, а далее производится стандартная операция по определению значения функции на каждом промежутке. А что же делать, если корни уравнения получаются комплексные, как в этом случае решить неравенство в полной форме, которое бы удовлетворяло всем правилам написания результата? Ответ на этот и многие другие вопросы с легкость даст наш сервис сайт, для которого нет ничего невозможного в решении математических задач онлайн. В пользу вышесказанного добавим следующее: каждый, кто всерьез занимается изучением такой дисциплиной как математика, обязан изучить тему неравенств. Неравенства бывают разных типов и решить неравенство онлайн порой сделать непросто, так как необходимо знать принципы подходов к каждому из них. На этом базируется основа успеха и стабильности. Для примера можно рассмотреть такие типы, как логарифмические неравенства или трансцендентные неравенства.
По сути решение неравенств онлайн заключается в решении уравнения с вычислением всех возможных корней. Полученные решения отмечаются на прямой, а далее производится стандартная операция по определению значения функции на каждом промежутке. А что же делать, если корни уравнения получаются комплексные, как в этом случае решить неравенство в полной форме, которое бы удовлетворяло всем правилам написания результата? Ответ на этот и многие другие вопросы с легкость даст наш сервис сайт, для которого нет ничего невозможного в решении математических задач онлайн. В пользу вышесказанного добавим следующее: каждый, кто всерьез занимается изучением такой дисциплиной как математика, обязан изучить тему неравенств. Неравенства бывают разных типов и решить неравенство онлайн порой сделать непросто, так как необходимо знать принципы подходов к каждому из них. На этом базируется основа успеха и стабильности. Для примера можно рассмотреть такие типы, как логарифмические неравенства или трансцендентные неравенства. Это вообще особый вид таких, сложных на первый взгляд, задач для студентов, тем более для школьников. Преподаватели институтов уделяют немало времени из подготовки практикантов для достижения профессиональных навыков в работе. К таким же типам отнесем тригонометрические неравенства и обозначим общий подход при решении множества практических примеров из постановочной задачи. В ряде случаев сначала нужно привести все к уравнению, упростить его, разложить на разные множители, короче говоря, привести к вполне наглядному виду. Во все времена человечество стремилось найти оптимальный подход в любых начинаниях. Благодаря современным технологиям, человечество сделало просто огромный прорыв в будущее свое развитие. Инновации все чаще и чаще, день за днем вливаются в нашу жизнь. В основу вычислительной техники легла, разумеется, математика со своим принципами и строгим подходом к делу. сайт представляет собой общий математический ресурс, в котором имеется разработанный калькулятор неравенств и многие другие полезные сервисы.
Это вообще особый вид таких, сложных на первый взгляд, задач для студентов, тем более для школьников. Преподаватели институтов уделяют немало времени из подготовки практикантов для достижения профессиональных навыков в работе. К таким же типам отнесем тригонометрические неравенства и обозначим общий подход при решении множества практических примеров из постановочной задачи. В ряде случаев сначала нужно привести все к уравнению, упростить его, разложить на разные множители, короче говоря, привести к вполне наглядному виду. Во все времена человечество стремилось найти оптимальный подход в любых начинаниях. Благодаря современным технологиям, человечество сделало просто огромный прорыв в будущее свое развитие. Инновации все чаще и чаще, день за днем вливаются в нашу жизнь. В основу вычислительной техники легла, разумеется, математика со своим принципами и строгим подходом к делу. сайт представляет собой общий математический ресурс, в котором имеется разработанный калькулятор неравенств и многие другие полезные сервисы. Используйте наш сайт и у вас будет уверенность в правильности решенных задач. Из теории известно, что объекты нечисловой природы также изучаются неравенствами онлайн, только этот подход представляет собой особый способ изучения данного раздела в алгебре, геометрии и других направлениях математики. Решать неравенства можно по-разному, неизменным остается конечная проверка решений и лучше всего это делать прямой подстановкой значений в само неравенство. Во многих случаях полученный ответ очевиден и его легко проверить в уме. Предположим нам задано решить дробное неравенство, в котором присутствуют искомые переменные в знаменателях дробных выражений. Тогда решение неравенств сведется к приведению всех слагаемых к общему знаменателю, предварительно переместив все в левую и правую часть неравенства. Далее нужно решить однородное уравнение, полученное в знаменателе дроби. Эти числовые корни будут точками, не включенными в интервалы общего решения неравенства, или ка их еще называют — проколотые точки, в которых функция обращается в бесконечность, то есть функция не определена, а можно только получить ее предельное значение в данной точке.
Используйте наш сайт и у вас будет уверенность в правильности решенных задач. Из теории известно, что объекты нечисловой природы также изучаются неравенствами онлайн, только этот подход представляет собой особый способ изучения данного раздела в алгебре, геометрии и других направлениях математики. Решать неравенства можно по-разному, неизменным остается конечная проверка решений и лучше всего это делать прямой подстановкой значений в само неравенство. Во многих случаях полученный ответ очевиден и его легко проверить в уме. Предположим нам задано решить дробное неравенство, в котором присутствуют искомые переменные в знаменателях дробных выражений. Тогда решение неравенств сведется к приведению всех слагаемых к общему знаменателю, предварительно переместив все в левую и правую часть неравенства. Далее нужно решить однородное уравнение, полученное в знаменателе дроби. Эти числовые корни будут точками, не включенными в интервалы общего решения неравенства, или ка их еще называют — проколотые точки, в которых функция обращается в бесконечность, то есть функция не определена, а можно только получить ее предельное значение в данной точке. Решив полученное в числителе уравнение, все точки нанесем на числовую ось. Заштрихуем те точки, в которых числитель дроби обращаемся в ноль. Соответственно все остальные точки оставляем пустыми или проколотыми. Найдем знак дроби на каждом интервале и после этого выпишем окончательный ответ. Если на границах интервала будут заштрихованные точки, то тогда включаем эти значения в решение. Если на границах интервала будут проколотые точки — эти значения в решение не включаем. После того, как решите неравенство, вам потребуется в обязательном порядке проверить полученный результат. Можно это сделать руками, каждое значение из интервалов ответа поочередно подставить в начальное выражение и выявить ошибки. Сайт сайт с легкостью выдаст вам все решения неравенства, и вы сразу сравните полученные вами и калькулятором ответы. Если все-таки ошибка будет иметь место, то на нашем ресурсе решение неравенств онлайн окажется вам очень полезным. Рекомендуем всем студентам вначале приступать не к решению напрямую неравенства, а сначала получить результат на сайт, потому что в дальнейшем будет намного проще самому сделать правильный расчет.
Решив полученное в числителе уравнение, все точки нанесем на числовую ось. Заштрихуем те точки, в которых числитель дроби обращаемся в ноль. Соответственно все остальные точки оставляем пустыми или проколотыми. Найдем знак дроби на каждом интервале и после этого выпишем окончательный ответ. Если на границах интервала будут заштрихованные точки, то тогда включаем эти значения в решение. Если на границах интервала будут проколотые точки — эти значения в решение не включаем. После того, как решите неравенство, вам потребуется в обязательном порядке проверить полученный результат. Можно это сделать руками, каждое значение из интервалов ответа поочередно подставить в начальное выражение и выявить ошибки. Сайт сайт с легкостью выдаст вам все решения неравенства, и вы сразу сравните полученные вами и калькулятором ответы. Если все-таки ошибка будет иметь место, то на нашем ресурсе решение неравенств онлайн окажется вам очень полезным. Рекомендуем всем студентам вначале приступать не к решению напрямую неравенства, а сначала получить результат на сайт, потому что в дальнейшем будет намного проще самому сделать правильный расчет. В текстовых задачах практически всегда решение сводится к составлению системы неравенств с несколькими неизвестными. Решить неравенство онлайн в считанные секунды поможет наш ресурс. При этом решение будет произведено мощной вычислительной программой с высокой точностью и без всяких погрешностей в конечном ответе. Тем самым вы сможете сэкономить колоссальное количество времени на решении данным калькулятором примеров. В ряде случаев школьники испытывают затруднения, когда на практике или в лабораторных работах встречают логарифмические неравенства, а еще хуже, когда видят перед собой тригонометрические неравенства со сложными дробными выражениями с синусами, косинусами или вообще с обратными тригонометрическими функциями. Как ни крути, но без помощи калькулятора неравенств справиться будет очень сложно и не исключены ошибки на любом этапе решения задачи. Пользуйтесь ресурсом сайт совершенно бесплатно, он доступен каждому пользователю каждый день. Начинать действовать с нашего сервиса-помощника очень хорошая идея, поскольку аналогов существует множество, а по-настоящему качественных сервисов единицы.
В текстовых задачах практически всегда решение сводится к составлению системы неравенств с несколькими неизвестными. Решить неравенство онлайн в считанные секунды поможет наш ресурс. При этом решение будет произведено мощной вычислительной программой с высокой точностью и без всяких погрешностей в конечном ответе. Тем самым вы сможете сэкономить колоссальное количество времени на решении данным калькулятором примеров. В ряде случаев школьники испытывают затруднения, когда на практике или в лабораторных работах встречают логарифмические неравенства, а еще хуже, когда видят перед собой тригонометрические неравенства со сложными дробными выражениями с синусами, косинусами или вообще с обратными тригонометрическими функциями. Как ни крути, но без помощи калькулятора неравенств справиться будет очень сложно и не исключены ошибки на любом этапе решения задачи. Пользуйтесь ресурсом сайт совершенно бесплатно, он доступен каждому пользователю каждый день. Начинать действовать с нашего сервиса-помощника очень хорошая идея, поскольку аналогов существует множество, а по-настоящему качественных сервисов единицы. Мы гарантируем точность вычислений при длительности поиска ответа в несколько секунд. От вас требуется только записать неравенства онлайн, а мы в свою очередь сразу предоставим вам точный результат решения неравенства. Искать подобный ресурс может оказаться бессмысленным занятием, так как вряд ли вы встретите такой же качественный сервис как у нас. Можно обойтись без теории про решение неравенств онлайн, но без качественного и быстрого калькулятора вам не обойтись. Желаем вам успехов в учебе! По-настоящему выбрать оптимальное решение неравенства онлайн зачастую связано с логическим подходом для случайной величины. Если пренебречь малым отклонением замкнутого поля, то вектор нарастающего значения пропорционален наименьшему значению на промежутке убывания линии ординат. Инвариант пропорционален двукратному увеличению отображаемым функциям наряду с исходящим ненулевым вектором. Лучший ответ всегда содержит точность вычислений. Наше решение неравенств примет вид однородной функции последовательно сопряженных числовых подмножеств главного направления.
Мы гарантируем точность вычислений при длительности поиска ответа в несколько секунд. От вас требуется только записать неравенства онлайн, а мы в свою очередь сразу предоставим вам точный результат решения неравенства. Искать подобный ресурс может оказаться бессмысленным занятием, так как вряд ли вы встретите такой же качественный сервис как у нас. Можно обойтись без теории про решение неравенств онлайн, но без качественного и быстрого калькулятора вам не обойтись. Желаем вам успехов в учебе! По-настоящему выбрать оптимальное решение неравенства онлайн зачастую связано с логическим подходом для случайной величины. Если пренебречь малым отклонением замкнутого поля, то вектор нарастающего значения пропорционален наименьшему значению на промежутке убывания линии ординат. Инвариант пропорционален двукратному увеличению отображаемым функциям наряду с исходящим ненулевым вектором. Лучший ответ всегда содержит точность вычислений. Наше решение неравенств примет вид однородной функции последовательно сопряженных числовых подмножеств главного направления. За первый интервал возьмем как раз наихудшее по точности значение нашего представления переменной. Вычислим на максимальное отклонение предыдущее выражение. Будем пользоваться сервисом на усмотрение предложенных вариантов по мере необходимости. Будет ли найдено решение неравенств онлайн с помощью хорошего в своем классе калькулятора — это риторический вопрос, разумеется, студентам такой инструмент пойдет только на пользу и принесет огромный успех в математике. Наложим ограничение на область с множеством, которое сведем к элементам с восприятием импульсов по напряжению. Физические значения таких экстремумов математически описывают возрастание и убывание кусочно-непрерывных функций. На протяжении всего пути ученые находили доказательства существования элементов на разных уровнях изучения. Расположим все последовательно идущие подмножества одного комплексного пространства в один ряд с такими объектами, как шар, куб или цилиндр. Из нашего результата можно сделать однозначный вывод и когда решите неравенство, то на выходе, безусловно, прольется свет на высказанное математическое предположение об интеграции метода на практике.
За первый интервал возьмем как раз наихудшее по точности значение нашего представления переменной. Вычислим на максимальное отклонение предыдущее выражение. Будем пользоваться сервисом на усмотрение предложенных вариантов по мере необходимости. Будет ли найдено решение неравенств онлайн с помощью хорошего в своем классе калькулятора — это риторический вопрос, разумеется, студентам такой инструмент пойдет только на пользу и принесет огромный успех в математике. Наложим ограничение на область с множеством, которое сведем к элементам с восприятием импульсов по напряжению. Физические значения таких экстремумов математически описывают возрастание и убывание кусочно-непрерывных функций. На протяжении всего пути ученые находили доказательства существования элементов на разных уровнях изучения. Расположим все последовательно идущие подмножества одного комплексного пространства в один ряд с такими объектами, как шар, куб или цилиндр. Из нашего результата можно сделать однозначный вывод и когда решите неравенство, то на выходе, безусловно, прольется свет на высказанное математическое предположение об интеграции метода на практике. В текущем положении вещей необходимое условие будет также являться и достаточным условием. Критерии неопределенности зачастую вызывают у студентов разногласия по причине недостоверных данных. Это упущение должны взять на себя преподаватели ВУЗов, а также учителя в школах, так как на начальном этапе обучения необходимо это тоже учитывать. Из вышесказанного вывода на взгляд опытных людей можно делать выводы, что решить неравенство онлайн очень сложное задание при вхождении в неравенство неизвестных разного типа данных. Об этом сказано на научной конференции в западном округе, на которой выдвигали самые различные обоснования по поводу научных открытий в области математики и физики, а также молекулярного анализа биологически устроенных систем. В нахождении оптимального решения абсолютно все логарифмические неравенства представляют научную ценность для всего человечества. Исследуем данный подход на предмет логических заключений по ряду несовпадений на высшем уровне понятий о существующем объекте.
В текущем положении вещей необходимое условие будет также являться и достаточным условием. Критерии неопределенности зачастую вызывают у студентов разногласия по причине недостоверных данных. Это упущение должны взять на себя преподаватели ВУЗов, а также учителя в школах, так как на начальном этапе обучения необходимо это тоже учитывать. Из вышесказанного вывода на взгляд опытных людей можно делать выводы, что решить неравенство онлайн очень сложное задание при вхождении в неравенство неизвестных разного типа данных. Об этом сказано на научной конференции в западном округе, на которой выдвигали самые различные обоснования по поводу научных открытий в области математики и физики, а также молекулярного анализа биологически устроенных систем. В нахождении оптимального решения абсолютно все логарифмические неравенства представляют научную ценность для всего человечества. Исследуем данный подход на предмет логических заключений по ряду несовпадений на высшем уровне понятий о существующем объекте. Логика подсказывает иное, чем видно на первый взгляд неопытному студенту. По причине возникновения масштабных аналогий, будет рационально сначала приравнять отношения к разности предметов исследуемой области, а затем показать на практике наличие общего аналитического результата. Решение неравенств абсолютным образом завязано на применении теории и будет важно для каждого изучить такой необходимый для дальнейших исследований раздел математики. Однако, при решении неравенств вам нужно найти все корни составленного уравнения, а уже затем нанести все точки на ось ординат. Некоторые точки будут проколоты, а остальные войдут в интервалы с общим решением. Начнем изучать раздел математики с азов важнейшей дисциплины школьной программы. Если тригонометрические неравенства являются неотъемлемой частью текстовой задачи, то, как раз применять ресурс для вычисления ответа просто необходимо. Введите левую и правую части неравенства корректно, нажмите на кнопу и получите результат в течение нескольких секунд.
Логика подсказывает иное, чем видно на первый взгляд неопытному студенту. По причине возникновения масштабных аналогий, будет рационально сначала приравнять отношения к разности предметов исследуемой области, а затем показать на практике наличие общего аналитического результата. Решение неравенств абсолютным образом завязано на применении теории и будет важно для каждого изучить такой необходимый для дальнейших исследований раздел математики. Однако, при решении неравенств вам нужно найти все корни составленного уравнения, а уже затем нанести все точки на ось ординат. Некоторые точки будут проколоты, а остальные войдут в интервалы с общим решением. Начнем изучать раздел математики с азов важнейшей дисциплины школьной программы. Если тригонометрические неравенства являются неотъемлемой частью текстовой задачи, то, как раз применять ресурс для вычисления ответа просто необходимо. Введите левую и правую части неравенства корректно, нажмите на кнопу и получите результат в течение нескольких секунд. Для быстрых и точных математических вычислений с числовыми или символьными коэффициентами перед неизвестными, вам как всегда понадобится универсальный калькулятор неравенств и уравнений, который сможет в считанные секунды предоставить ответ на поставленную вами задачку. Если у вас нет времени на написание целого ряда письменных упражнений, то обоснованность сервиса неоспорима даже невооруженным глазом. Для студентов такой подход является более оптимальным и оправданным с точки зрения экономии материальных ресурсов и времени. Напротив катета лежит угол, а для его измерения необходим циркуль, но вы сможете в любо момент воспользоваться подсказками и решите неравенство не применяя никаких формул приведения. Означает ли это успешное завершение начатого действия? Однозначно ответ будет положительным.
Для быстрых и точных математических вычислений с числовыми или символьными коэффициентами перед неизвестными, вам как всегда понадобится универсальный калькулятор неравенств и уравнений, который сможет в считанные секунды предоставить ответ на поставленную вами задачку. Если у вас нет времени на написание целого ряда письменных упражнений, то обоснованность сервиса неоспорима даже невооруженным глазом. Для студентов такой подход является более оптимальным и оправданным с точки зрения экономии материальных ресурсов и времени. Напротив катета лежит угол, а для его измерения необходим циркуль, но вы сможете в любо момент воспользоваться подсказками и решите неравенство не применяя никаких формул приведения. Означает ли это успешное завершение начатого действия? Однозначно ответ будет положительным.
Модулем числа
называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 6 является 6, модулем числа -6 тоже является 6.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |6|, |х
|, |а
| и т.д.
(Подробнее — в разделе «Модуль числа»).
Уравнения с модулем.
Пример 1
. Решить уравнение
|10
х
— 5| = 15.
Решение
.
В соответствии с правилом, уравнение равносильно совокупности двух уравнений:
10х
— 5 = 15
10х
— 5 = -15
Решаем:
10х
= 15 + 5 = 20
10х
= -15 + 5 = -10
х
= 20: 10
х
= -10: 10
х
= 2
х
= -1
Ответ
: х
1 = 2, х
2 = -1.
Пример 2
. Решить уравнение
|2
х
+ 1| =
х
+ 2.
Решение
.
Поскольку модуль — число неотрицательное, то х
+ 2 ≥ 0. Соответственно:
х
≥ -2.
Составляем два уравнения:
2х
+ 1 = х
+ 2
2х
+ 1 = -(х
+ 2)
Решаем:
2х
+ 1 = х
+ 2
2х
+ 1 = —х
— 2
2х
— х
= 2 — 1
2х
+ х
= -2 — 1
х
= 1
х
= -1
Оба числа больше -2. Значит, оба являются корнями уравнения.
Значит, оба являются корнями уравнения.
Ответ
: х
1 = -1, х
2 = 1.
Пример 3
. Решить уравнение
|х
+ 3| — 1
————— = 4
х
— 1
Решение
.
Уравнение имеет смысл, если знаменатель не равен нулю — значит, если х
≠ 1. Учтем это условие. Наше первое действие простое — не просто освобождаемся от дроби, а преобрахуем ее так, чтобы получить модуль в чистом виде:
|х
+ 3| — 1 = 4 · (х
— 1),
|х
+ 3| — 1 = 4х
— 4,
|х
+ 3| = 4х
— 4 + 1,
|х
+ 3| = 4х
— 3.
Теперь у нас в левой части уравнения только выражение под модулем. Идем дальше.
Модуль числа есть неотрицательное число — то есть он должен быть больше нуля или равен нулю. Соответственно, решаем неравенство:
4х
— 3 ≥ 0
4х
≥ 3
х
≥ 3/4
Таким образом, у нас появилось второе условие: корень уравнения должен быть не меньше 3/4.
В соответствии с правилом, составляем совокупность двух уравнений и решаем их:
х
+ 3 = 4х
— 3
х
+ 3 = -(4х
— 3)
х
+ 3 = 4х
— 3
х
+ 3 = -4х
+ 3
х
— 4х
= -3 — 3
х
+ 4х
= 3 — 3
х
= 2
х
= 0
Мы получили два ответа. Проверим, являются ли они корнями исходного уравнения.
У нас было два условия: корень уравнения не может быть равен 1, и он должен быть не меньше 3/4. То есть х
≠ 1, х
≥ 3/4. Обоим этим условиям соответствует только один из двух полученных ответов — число 2. Значит, только оно и является корнем исходного уравнения.
Ответ
: х
= 2.
Неравенства с модулем.
Пример 1
. Решить неравенство
|
х
— 3|
Решение
.
Правило модуля гласит:
|а
| = а
, если а
≥ 0.
|а
| = —а
, если а
Модуль может иметь и неотрицательное, и отрицательное число. Значит, мы должны рассмотреть оба случая: х
— 3 ≥ 0 и х
— 3
1) При х
— 3 ≥ 0 наше исходное неравенство остается как есть, только без знака модуля:
х
— 3
2) При х
— 3
-(х
— 3)
Раскрыв скобки, получаем:
—х
+ 3
Таким образом, от этих двух условий мы пришли к объединению двух систем неравенств:
х
— 3 ≥ 0
х
— 3
х
— 3 —х
+ 3
Решим их:
х
≥ 3
х
х
х
> -1
Итак, у нас в ответе объединение двух множеств:
3 ≤ х
х
Определяем наименьшее и наибольшее значения. Это -1 и 7. При этом х
больше -1, но меньше 7.
Кроме того, х
≥ 3. Значит, решением неравенства является все множество чисел от -1 до 7, исключая эти крайние числа.
Ответ
: -1 х
Или: х
∈ (-1; 7).
Дополнения
.
1) Есть более простой и короткий способ решения нашего неравенства — графический. Для этого надо нарисовать горизонтальную ось (рис.1).
Выражение |х
— 3| х
до точки 3 меньше четырех единиц. Отмечаем на оси число 3 и отсчитываем влево и вправо от от него 4 деления. Слева мы придем к точке -1, справа — к точке 7. Таким образом, точки х
мы просто увидели, не вычисляя их.
При этом, согласно условию неравенства, сами -1 и 7 не включены во множество решений. Таким образом, получаем ответ:
1 х
2) Но есть еще одно решение, которое проще даже графического способа. Для этого наше неравенство надо представить в следующем виде:
4 х
— 3
Ведь так оно и есть по правилу модуля. Неотрицательное число 4 и аналогичное отрицательное число -4 являются границами решения неравенства.
4 + 3 х
1 х
Пример 2
. Решить неравенство
|
х
— 2| ≥ 5
Решение
.
Этот пример существенно отличается от предыдущего. Левая часть больше 5 либо равна 5. С геометрической точки зрения, решением неравенства являются все числа, которые от точки 2 отстоят на расстоянии 5 единиц и больше (рис.2). По графику видно, что это все числа, которые меньше или равны -3 и больше или равны 7. А значит, мы уже получили ответ.
Ответ
: -3 ≥ х
≥ 7.
Попутно решим это же неравенство способом перестановки свободного члена влево и вправо с противоположным знаком:
5 ≥ х
— 2 ≥ 5
5 + 2 ≥ х
≥ 5 + 2
Ответ тот же: -3 ≥ х
≥ 7.
Или: х
∈ [-3; 7]
Пример решен.
Пример 3
. Решить неравенство
6
х
2 — |
х
| — 2 ≤ 0
Решение
.
Число х
может быть и положительным числом, и отрицательным, и нулем. Поэтому нам надо учесть все три обстоятельства. Как вы знаете, они учитываются в двух неравенствах: х
≥ 0 и х
х
≥ 0 мы просто переписываем наше исходное неравенство как есть, только без знака модуля:
6х 2 — х
— 2 ≤ 0.
Теперь о втором случае: если х
6х
2 — (-х
) — 2 ≤ 0.
Раскрываем скобки:
6х
2 + х
— 2 ≤ 0.
Таким образом, мы получили две системы уравнений:
6х
2 — х
— 2 ≤ 0
х
≥ 0
6х
2 + х
— 2 ≤ 0
х
Надо решить неравенства в системах — а это значит, надо найти корни двух квадратных уравнений. Для этого приравняем левые части неравенств к нулю.
Начнем с первого:
6х
2 — х
— 2 = 0.
Как решается квадратное уравнение — см. раздел «Квадратное уравнение». Мы же сразу назовем ответ:
х
1 = -1/2, х 2 = 2/3.
Из первой системы неравенств мы получаем, что решением исходного неравенства является все множество чисел от -1/2 до 2/3. Пишем объединение решений при х
≥ 0:
[-1/2; 2/3].
Теперь решим второе квадратное уравнение:
6х
2 + х
— 2 = 0.
Его корни:
х
1 = -2/3, х
2 = 1/2.
Вывод: при х
Объединим два ответа и получим итоговый ответ: решением является все множество чисел от -2/3 до 2/3, включая и эти крайние числа.
Ответ
: -2/3 ≤ х
≤ 2/3.
Или: х
∈ [-2/3; 2/3].
Существует несколько способов решения неравенств, содержащих модуль. Рассмотрим некоторые из них.
1) Решение неравенства с помощью геометрического свойства модуля.
Напомню, что такое геометрическое свойство модуля: модуль числа x – это расстояние от начала координат до точки с координатой x.
В ходе решения неравенств этим способом может возникнуть 2 случая:
1. |x| ≤ b,
И неравенство с модулем очевидно сводится к системе двух неравенств. Тут знак может быть и строгим, в этом случае точки на картинке будут «выколотыми».
2. |x| ≥ b,
тогда картинка решения выглядит так:
И неравенство с модулем очевидно сводится к совокупности двух неравенств. Тут знак может быть и строгим, в этом случае точки на картинке будут «выколотыми».
Пример 1.
Решить неравенство |4 – |x|| ≥
3.
Решение.
Данное неравенство равносильно следующей совокупности:
U [-1;1] U
Пример 2.
Решить неравенство ||x+2| – 3| ≤
2.
Решение.
Данное неравенство равносильно следующей системе.
{|x + 2| – 3 ≥ -2
{|x + 2| – 3 ≤ 2,
{|x + 2| ≥ 1
{|x + 2| ≤ 5.
Решим отдельно первое неравенство системы. Оно эквивалентно следующей совокупности:
U [-1; 3].
2) Решение неравенств, используя определение модуля.
Напомню для начала определение модуля.
|a| = a, если a ≥
0 и |a| = -a, если a
Например, |34| = 34, |-21| = -(-21) = 21.
Пример 1.
Решить неравенство 3|x – 1| ≤
x + 3.
Решение.
Используя определение модуля получим две системы:
{x – 1 ≥ 0
{3(x – 1) ≤ x + 3
{x – 1 {-3(x – 1) ≤ x + 3.
Решая первую вторую системы в отдельности, получим:
{x ≥ 1
{x ≤ 3,
{x {x ≥ 0.
Решением исходного неравенства будут все решения первой системы и все решения второй системы.
Ответ: x € .
3) Решение неравенств методом возведения в квадрат.
Пример 1.
Решить неравенство |x 2 – 1|
Решение.
Возведем обе части неравенства в квадрат. Замечу, что возводить обе части неравенства в квадрат можно только в том случае, когда они обе положительные. В данном случае у нас и слева и справа стоят модули, поэтому мы можем это сделать.
(|x 2 – 1|) 2
Теперь воспользуемся следующим свойством модуля: (|x|) 2 = x 2 .
(x 2 – 1) 2
(x 2 – 1) 2 – (x 2 – x + 1) 2
(x 2 – 1 – x 2 + x – 1)(x 2 – 1 + x 2 – x + 1)
(x – 2)(2x 2 – x)
x(x – 2)(2x – 1)
Решаем методом интервалов.
Ответ: x € (-∞; 0) U (1/2; 2)
4) Решение неравенств методом замены переменных.
Пример.
Решить неравенство (2x + 3) 2 – |2x + 3| ≤
30.
Решение.
Заметим, что (2x + 3) 2 = (|2x + 3|) 2 . Тогда получим неравенство
(|2x + 3|) 2 – |2x + 3| ≤ 30.
Сделаем замену y = |2x + 3|.
Перепишем наше неравенство с учетом замены.
y 2 – y ≤ 30,
y 2 – y – 30 ≤ 0.
Разложим квадратный трехчлен, стоящий слева, на множители.
y1 = (1 + 11) / 2,
y2 = (1 – 11) / 2,
(y – 6)(y + 5) ≤ 0.
Решим методом интервалов и получим:
Вернемся к замене:
5 ≤ |2x + 3| ≤ 6.
Данное двойное неравенство равносильно системе неравенств:
{|2x + 3| ≤ 6
{|2x + 3| ≥ -5.
Решим каждое из неравенств в отдельности.
Первое равносильно системе
{2x + 3 ≤ 6
{2x + 3 ≥ -6.
Решим ее.
{x ≤ 1.5
{x ≥ -4.5.
Второе неравенство очевидно выполняется для всех x, так как модуль по определению число положительное. Так как решение системы – это все x, которые удовлетворяют одновременно и первому и второму неравенству системы, то решением исходной системы будет решение ее первого двойного неравенства (ведь второе верно для всех x).
Ответ: x € [-4,5; 1,5].
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решение неравенств онлайн
Неравенства — это выражения вида:
f(x) ≥ 0
где вместо знака
≥, может стоять знак
≤
или знаки
<
и
>.
Решить приведённое выше неравенство, означает найти совокупность всех значений переменной
x
при которых выражение
f(x)
больше или равно
0.
Рассмотрим график произвольной функции
f(x):
Из графика мы может сразу же записать интервалы значений
х
при которых функция
f(x) ≥ 0
(закрашены светло-зелёным цветом):
f (x) ≥ 0
<=>
{ x є (−∞;
x1] U
[x2;
x3] U
[x4;
+∞)
}
Из графика видно, что функция меняет знак в точках пересечения оси
х. Следовательно, для решения любых неравенств, сначала нужно определить такие значения
x, при которых функция
f(x)
равна нулю, т.е. решить уравнение
f(x) = 0.
Полученный набор значений
xi
(т.е. корни уравнения
f(x)=0) разбивает координатную ось на интервалы в каждом из которых значение функции сохраняет свой знак (либо больше, либо меньше нуля).
Для решения соответствующего неравенства, нужно определить знак функции в каждом из полученных интервалов и выбрать те из них, которые удовлетворяют условию неравенства. Для того, чтобы определить знак функции на некотором интервале
(xi;
xj), нужно подставить вместо значения
x
в выражение
f(x)
любое значение
xk є (xi;
xj).
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha LLC, способен решить очень большое количество разнообразных неравеств с описанием пошаговых действий.
доказать неравенство онлайн с подробным решением
Вы искали доказать неравенство онлайн с подробным решением? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и иррациональные неравенства калькулятор онлайн, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «доказать неравенство онлайн с подробным решением».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как доказать неравенство онлайн с подробным решением,иррациональные неравенства калькулятор онлайн,иррациональные неравенства онлайн калькулятор,иррациональные неравенства онлайн решение,иррациональные неравенства решение онлайн,калькулятор иррациональных неравенств,калькулятор неравенств онлайн с модулем,калькулятор неравенств с модулем онлайн,калькулятор онлайн иррациональные неравенства,калькулятор онлайн решение неравенств с модулем,калькулятор онлайн решение систем неравенств,калькулятор онлайн система неравенств,калькулятор онлайн системы неравенств,калькулятор показательных неравенств,калькулятор решение систем неравенств,калькулятор решения систем неравенств,калькулятор решите систему неравенств,калькулятор систем неравенств,калькулятор систем неравенств онлайн,калькулятор систем неравенств онлайн с решением,калькулятор систем неравенств с решением,калькулятор систем неравенств с решением онлайн,калькулятор система неравенств,калькулятор системы неравенств,калькулятор системы неравенств с решением онлайн,калькулятор тригонометрических неравенств,калькулятор тригонометрических неравенств онлайн,логарифмические неравенства онлайн калькулятор,матрицы решить неравенство,неравенства с модулем онлайн калькулятор,неравенство с модулем онлайн калькулятор с решением,онлайн калькулятор неравенств с модулем,онлайн калькулятор решение неравенств с модулем,онлайн калькулятор решение систем неравенств,онлайн калькулятор систем неравенств,онлайн калькулятор систем неравенств с решением,онлайн калькулятор системы неравенств,онлайн калькулятор системы неравенств с решением,онлайн решение иррациональных неравенств,онлайн решение иррациональных неравенств с подробным решением,онлайн решение логарифмических неравенств онлайн с подробным решением,онлайн решение модульных неравенств,онлайн решение неравенств с корнем,онлайн решение неравенств с корнями,онлайн решение неравенств с модулем онлайн,онлайн решение неравенств с модулем онлайн с подробным решением,онлайн решение неравенств система,онлайн решение систем линейных неравенств,онлайн решение систем неравенств,онлайн решение системы неравенств,онлайн решение тригонометрических неравенств с подробным решением,показательные неравенства онлайн калькулятор,построение неравенств онлайн,решатель неравенств онлайн с решением,решение двойных неравенств онлайн,решение двойных неравенств онлайн с подробным решением,решение иррациональные неравенства онлайн,решение иррациональных неравенств онлайн,решение иррациональных неравенств онлайн с подробным решением,решение линейных систем неравенств онлайн,решение логарифмических неравенств онлайн с подробным решением,решение модульных неравенств онлайн,решение неравенств графическим способом онлайн,решение неравенств онлайн с корнем,решение неравенств онлайн с корнями,решение неравенств онлайн с модулем онлайн,решение неравенств онлайн с подробным решением с корнями,решение неравенств с корнем онлайн,решение неравенств с корнями онлайн,решение неравенств с корнями онлайн с подробным решением,решение неравенств с модулем онлайн калькулятор,решение неравенств с параметром онлайн,решение неравенств с параметром онлайн с подробным решением,решение онлайн неравенств с параметром,решение онлайн неравенство с модулем,решение онлайн систем линейных неравенств,решение показательных неравенств онлайн,решение систем линейных неравенств онлайн,решение систем неравенств калькулятор,решение систем неравенств калькулятор онлайн,решение систем неравенств онлайн,решение систем неравенств онлайн калькулятор,решение систем неравенств онлайн с подробным решением,решение системы неравенств калькулятор онлайн,решение системы неравенств онлайн,решение системы неравенств онлайн калькулятор,решение системы неравенств онлайн с подробным решением,решение совокупности неравенств онлайн,решение тригонометрических неравенств онлайн,решение тригонометрических неравенств онлайн с подробным решением,решите двойное неравенство онлайн калькулятор,решите систему неравенств онлайн,решите систему неравенств онлайн с решением,решить двойное неравенство онлайн,решить иррациональное неравенство онлайн с подробным решением,решить логарифмическое неравенство онлайн с подробным решением,решить неравенство матрицы,решить неравенство онлайн с корнем,решить неравенство онлайн с параметром,решить неравенство с корнем онлайн,решить неравенство с модулем онлайн,решить онлайн показательное неравенство,решить онлайн тригонометрическое неравенство,решить показательное неравенство онлайн,решить систему неравенств калькулятор онлайн,решить систему неравенств онлайн,решить систему неравенств онлайн калькулятор,решить систему неравенств онлайн калькулятор с решением,решить систему неравенств онлайн с подробным решением,решить тригонометрическое неравенство онлайн,розв язати нерівність,система неравенств калькулятор,система неравенств калькулятор онлайн,система неравенств онлайн,система неравенств онлайн калькулятор,система решение неравенств онлайн,системы неравенств калькулятор,системы неравенств онлайн,системы неравенств онлайн калькулятор,совокупности неравенств решение онлайн,тригонометрические неравенства онлайн. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и доказать неравенство онлайн с подробным решением. Просто введите задачу в окошко и нажмите
«решить» здесь (например, иррациональные неравенства онлайн калькулятор).
Где можно решить любую задачу по математике, а так же доказать неравенство онлайн с подробным решением Онлайн?
Решить задачу доказать неравенство онлайн с подробным решением вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Решение неравенств с модулем.2\) \(—>\) \(6x\geq -9\) \(—>\) \(x\geq -1,5\)
Ответ: \([-1,5; +∞)\)
Пример 2. Решить неравенство \(\left|3+2x\right|\le \:7\). Система
Решение. \(\left|3+2x\right|\le \:7\) \(—>\) \(3+2x\le \:7\) и \(3+2x\ge \:-7\) или \(-7\le \:3+2x\le \:7\)
\(x\le \:2\) и \(x\ge \:-5\) \(-5\le \:x\le \:2\)
Ответ: [-5;2];
Пример 3. Решить неравенство \(\left|3x-5\right|<\:4\)
Решение: \(-4<3x-5<4\) \(—>\) \(\frac{1}{3}<x<3\)
Ответ: \((\frac{1}{3};3)\);
Пример 4. Решить неравенство \(\left|x-8\right|\ge \:\:3\)
Решение: Совокупность \(\) \(\left[ \begin{gathered} x-8\le \:-3\\ x-8\ge \:3 \\ \end{gathered} \right.\) \(—>\) \(\left[ \begin{gathered} x\le \:5\\ x\ge \:11 \\ \end{gathered} \right.\)
Ответ: \((+∞;5)⋃ (11;+∞)\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Решение дробно рациональных неравенств онлайн калькулятор. Решение неравенств с модулем. Линейные неравенства. Решение, примеры
Неравенство
это выражение с, ≤, или ≥. Например, 3x — 5 Решить неравенство означает найти все значения переменных, при которых это неравенство верно.
Каждое из этих чисел является решением неравенства, а множество всех таких решений является его множеством решений
. Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами
.
Линейные неравенства
Принципы решения неравенств аналогичны принципам решения уравнений.
Принципы решения неравенств
Для любых вещественных чисел a, b,
и c
:
Принцип прибавления неравенств
: Если a
Принцип умножения для неравенств
: Если a 0 верно, тогда ac
Если a bc также верно.
Подобные утверждения также применяются для a ≤ b.
Когда обе стороны неравенства умножаются на отрицательное число, необходимо полностью изменить знак неравенства.
Неравенства первого уровня, как в примере 1 (ниже), называются линейными неравенствами
.
Пример 1
Решите каждое из следующих неравенств. Затем изобразите множество решений.
a) 3x — 5
b) 13 — 7x ≥ 10x — 4
Решение
Любое число, меньше чем 11/5, является решением.
Множество решений есть {x|x
Чтобы сделать проверку, мы можем нарисовать график y 1 = 3x — 5 и y 2 = 6 — 2x. Тогда отсюда видно, что для x
Множеством решений есть {x|x ≤ 1}, или (-∞, 1]. График множества решений изображён ниже.
Двойные неравенства
Когда два неравенства соединены словом и
, или
, тогда формируется двойное неравенство
.
Двойное неравенство, как
-3
и
2x + 5 ≤ 7
называется соединённым
, потому что в нём использовано и
. Запись -3
Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.
Пример 2
Решите -3
Решение
У нас есть
Множество решений {x|x ≤ -1 или
x > 3}. Мы можем также написать решение с использованием обозначения интервала и символ для объединения
или включения обоих множеств: (-∞ -1] (3, ∞). График множества решений изображен ниже.
Для проверки, нарисуем y 1 = 2x — 5, y 2 = -7, и y 3 = 1. Заметьте, что для {x|x ≤ -1 или
x > 3}, y 1 ≤ y 2 или
y 1 > y 3 .
Неравенства с абсолютным значением (модулем)
Неравенства иногда содержат модули. Следующие свойства используются для их решения.
Для а > 0 и алгебраического выражения x:
|x|
|x| > a эквивалентно x или x > a.
Подобные утверждения и для |x| ≤ a и |x| ≥ a.
Например,
|x|
|y| ≥ 1 эквивалентно y ≤ -1 или
y ≥ 1;
и |2x + 3| ≤ 4 эквивалентно -4 ≤ 2x + 3 ≤ 4.
Пример 4
Решите каждое из следующих неравенств. Постройте график множества решений.
a) |3x + 2|
b) |5 — 2x| ≥ 1
Решение
a) |3x + 2|
Множеством решением есть {x|-7/3
b) |5 — 2x| ≥ 1
Множеством решением есть {x|x ≤ 2 или
x ≥ 3}, или (-∞, 2] . В следующем примере такая скобка используется.
Запишем ответ: х ≥ -0,5
через промежутки:
х ∈ [-0,5; +∞)
Читается: икс принадлежит промежутку от минус 0,5, включая,
до плюс бесконечности.
Бесконечность не может включаться никогда. Это не число, это символ. Поэтому в подобных записях бесконечность всегда соседствует с круглой скобкой.
Такая форма записи удобна для сложных ответов, состоящих из нескольких промежутков. Но — именно для окончательных ответов. В промежуточных результатах, где предполагается дальнейшее решение, лучше использовать обычную форму, в виде простого неравенства. Мы с этим в соответствующих темах разберёмся.
Популярные задания с неравенствами.
Сами по себе линейные неравенства просты. Поэтому, частенько, задания усложняются. Так, чтобы подумать надо было. Это, если с непривычки, не очень приятно.) Но полезно. Покажу примеры таких заданий. Не для того, чтобы вы их выучили, это лишнее. А для того, чтобы не боялись при встрече с подобными примерами. Чуть подумать — и всё просто!)
1. Найдите любые два решения неравенства 3х — 3
Если не очень понятно, что делать, вспоминаем главное правило математики:
Не знаешь, что нужно — делай, что можно!)
х 1
И что? Да ничего особенного. Что нас просят? Нас просят найти два конкретных числа, которые являются решением неравенства. Т.е. подходят под ответ. Два любых
числа. Собственно, это и смущает.) Подходит парочка 0 и 0,5. Парочка -3 и -8. Да этих парочек бесконечное множество! Какой ответ правильный?!
Отвечаю: все! Любая парочка чисел, каждое из которых меньше единицы, будет правильным ответом.
Пишите, какую хотите. Едем дальше.
2. Решить неравенство:
4х — 3 ≠
0
Задания в таком виде встречаются редко. Но, как вспомогательные неравенства, при нахождении ОДЗ, например, или при нахождении области определения функции, — встречаются сплошь и рядом. Такое линейное неравенство можно решать как обычное линейное уравнение. Только везде, кроме знака «=» (равно
) ставить знак «≠
» (не равно
). Так к ответу и подойдёте, со знаком неравенства:
х ≠
0,75
В более сложных примерах, лучше поступать по-другому. Сделать из неравенства равенство. Вот так:
4х — 3 =
0
Спокойно решить его, как учили, и получить ответ:
х = 0,75
Главное, в самом конце, при записи окончательного ответа, не забыть, что мы нашли икс, который даёт равенство.
А нам нужно — неравенство.
Стало быть, этот икс нам как раз и не нужен.) И надо записать его с правильным значком:
х ≠
0,75
При таком подходе получается меньше ошибок. У тех, кто уравнения на автомате решает. А тем, кто уравнения не решает, неравенства, собственно, ни к чему…) Ещё пример популярного задания:
3. Найти наименьшее целое решение неравенства:
3(х — 1) 5х + 9
Сначала просто решаем неравенство. Ракрываем скобки, переносим, приводим подобные… Получаем:
х > —
6
Не так получилось!? А за знаками следили!? И за знаками членов, и за знаком неравенства…
Опять соображаем. Нам нужно найти конкретное число, подходящее и под ответ, и под условие «наименьшее целое».
Если сразу не осеняет, можно просто взять любое число и прикинуть. Два больше минус шести? Конечно! А есть подходящее число поменьше? Разумеется. Например, ноль больше -6. А ещё меньше? Нам же самое маленькое из возможных надо! Минус три больше минус шести! Уже можно уловить закономерность и перестать тупо перебирать числа, правда?)
Берём число поближе к -6. Например, -5. Ответ выполняется, -5 > —
6. Можно найти ещё число, меньше -5, но больше -6? Можно, например -5,5… Стоп! Нам сказано целое
решение! Не катит -5,5! А минус шесть? Э-э-э! Неравенство строгое, минус 6 никак не меньше минус 6!
Стало быть, правильный ответ: -5.
Надеюсь, с выбором значения из общего решения всё понятно. Ещё пример:
4. Решить неравенство:
7 3х+1 13
Во как! Такое выражение называется тройным неравенством.
Строго говоря, это сокращённая запись системы неравенств. Но решать такие тройные неравенства всё равно приходится в некоторых заданиях… Оно решается безо всяких систем. По тем же тождественным преобразованиям.
Надо упростить, довести это неравенство до чистого икса. Но… Что куда переносить!? Вот тут самое время вспомнить, что перенос влево-вправо, это сокращённая форма
первого тождественного преобразования.
А полная форма звучит вот как: К обеим частям уравнения (неравенства) можно прибавить/отнять любое число, или выражение.
Здесь три части. Вот и будем применять тождественные преобразования ко всем трём частям!
Итак, избавимся от единички в средней части неравенства. Отнимем от всей средней части единичку. Чтобы неравенство не изменилось, отнимем единичку и от оставшихся двух частей. Вот так:
7 -13х+1-1 13-1
6 3х 12
Уже лучше, правда?) Осталось разделить все три части на тройку:
2 х 4
Вот и всё. Это ответ. Икс может любым числом от двойки (не включая) до четвёрки (не включая). Этот ответ тоже записывается через промежутки, такие записи будут в квадратных неравенствах. Там они — самое обычное дело.
В конце урока повторю самое главное. Успех в решении линейных неравенств зависит от умения преобразовывать и упрощать линейные уравнения. Если при этом следить за знаком неравенства,
проблем не будет. Чего я вам и желаю. Отсутствия проблем.)
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
абсолютных неравенств | Purplemath
Purplemath
Существует много возможностей для ошибок с абсолютным неравенством, поэтому давайте рассмотрим эту тему медленно и попутно рассмотрим несколько полезных картинок. Когда мы закончим, я надеюсь, что у вас в голове будет хорошее представление о том, что происходит, и вы не сделаете некоторые из наиболее распространенных ошибок. Как только вы поймете, как работает это неравенство, это действительно не так уж и плохо.
MathHelp.com
Давайте сначала вернемся к исходному определению абсолютного значения: «| x | — это расстояние x от нуля.»Например, и –2, и & плюс; 2 — это две единицы от нуля, как вы можете видеть на изображении ниже:
Это означает, что их абсолютные значения будут равны 2; то есть имеем:
| –2 | = | +2 | = 2
Имея в виду это определение и картинку, давайте рассмотрим некоторые неравенства в абсолютных ценностях.
Решить |
x | <3, и изобразить его решение.
Это неравенство. Если решение уравнения абсолютного значения представляет собой точки (как на приведенном выше рисунке), решением неравенства (или «неравенства») абсолютного значения будут интервалы.
В этом неравенстве они просят меня найти все значения x , которые находятся менее чем на три единицы от нуля в любом направлении , поэтому решением будет набор всех точек, которые меньше чем на три единицы от нуля.Сначала я нарисую числовую линию:
Глядя на неравенство, я вижу, что число 1 будет работать как решение, как и –1, потому что каждое из них меньше трех единиц от нуля. Число 2 будет работать, как и –2. Но 4 не сработает, равно как и –4, потому что они слишком далеки от нуля. Даже 3 и –3 не будут работать (хотя они на грани), потому что это неравенство «меньше» (но не равно).
Однако число 2,99 будет работать, как и –2,99. Другими словами, все точки между –3 и 3, но фактически не включая –3 или 3, будут работать как решения этого неравенства. Итак, графически решение выглядит так:
(Незакрашенные кружки на концах синей линии указывают «до этих точек, но не включая их». В вашей книге могут использоваться круглые скобки вместо кружков.)
Переводя эту картинку в алгебраические символы, я получаю следующее решение:
Этот шаблон для неравенства «меньше» по абсолютной величине всегда верен:
Дано неравенство в виде | x | < a , решение всегда будет иметь вид — a < x < a .
Между прочим, правильная комбинация для неравенства «меньше чем» по абсолютной величине — это «и». Почему? Потому что переменная содержится в одном интервале. В приведенном выше примере x было одновременно «больше –3» и «меньше +3». x находится в интервале, который одновременно удовлетворяет обоим неравенствам. Итак, «и» — правильное соединение.
Даже когда упражнения станут более сложными, вышеприведенная схема все равно будет действовать.
Решить | 2
x + 3 | <6.
Поскольку это неравенство «меньше чем» по абсолютному значению, мой первый шаг — очистить абсолютное значение в соответствии с шаблоном «меньше». Потом решу линейное неравенство.
| 2 x + 3 | <6
–6 <2 x + 3 <6
Это образец для «меньше чем».Продолжая, я вычту 3 из всех трех «сторон» неравенства:
–6 — 3 <2 x 900 10 + 3 — 3 <6 - 3
–9 <2 x <3
–9/2 < x <3/2
Решение исходного неравенства по модулю, | 2 x + 3 | <6, это интервал:
Другой случай неравенства абсолютных значений — это случай «больше чем».
Решить |
x | > 2 и график.
Сначала я начну с числовой строки.
Решением данного неравенства будет набор всех точек, отстоящих от нуля более чем на две единицы. Например, –3 будет работать, как и +3; –4 будет работать, как и +4. Но –1 не сработает, равно как и +1, потому что они слишком близки к нулю.Даже –2 не будет работать, как и +2 (хотя они на грани), потому что это неравенство «больше» (но не равно).
Однако +2.01 будет работать, как и –2.01. Другими словами, решением будет , две отдельные секции : одна секция будет содержать все точки более чем на две единицы от нуля слева от , а другая секция будет содержать все точки более чем на две единицы от нуля до правый . Графически решение выглядит так:
Переводя это графическое решение в символы, я получаю:
Обратите внимание! Решением этого неравенства «больше чем» по модулю являются ДВА регулярных неравенства, а не одно.НЕ пытайтесь записать это как одно неравенство. Если вы попытаетесь записать это решение как «–2> x > 2», ваш ответ будет засчитан неверно. Почему? Потому что, если вы вытащите x посередине, вы увидите, что скажете «–2> 2», что определенно будет , а не истинным. Потратьте лишние полсекунды и напишите решение правильно.
Этот шаблон для неравенства «больше чем» по абсолютной величине всегда верен:
Учитывая неравенство | x | > a , решение всегда начинается с разделения неравенства на две части: x <- a или x > a .
И, кстати, правильное союз — «или», а не «и». Почему? Потому что переменная не может находиться в обоих интервалах решения и в одно и то же время. В приведенном выше примере x не может одновременно быть «меньше –2» и «больше +2» . Поэтому мы используем «или» для таких решений.
Филиал
Даже когда неравенства усложняются, вышеупомянутая картина все еще сохраняется.
Решить | 2
x — 3 | > 5.
Первое, что мне нужно сделать, это очистить полосы абсолютного значения, разделив неравенство на две части. Затем я решу два регулярных неравенства.
| 2 x — 3 | > 5
2 x — 3 <–5 или 2 x — 3> 5
Это модель неравенства «больше чем» по абсолютной величине.
2 x <–2 или 2 x > 8
x <–1 или x > 4
Эта ПАРА неравенств является решением исходного неравенства по абсолютной величине.
Есть еще одна ситуация, с которой вы можете столкнуться: вам будет дана пара неравенств, и вам будет предложено найти соответствующее неравенство по абсолютным значениям.Этот процесс может показаться немного странным, поэтому я приведу пару примеров того, как он работает.
Найдите утверждение о неравенстве абсолютного значения, которое соответствует –2
< x <4.
Чтобы понять это, я сначала смотрю на конечные точки. Минус два и плюс четыре — это шесть единиц. Половина шести — это три. Это говорит мне, что я хочу скорректировать это неравенство так, чтобы оно относилось к –3 и +3, а не к –2 и +4.Для этого я вижу, что могу отрегулировать значения на левом и правом концах, вычтя 1 из всех трех «сторон» неравенства:
–2 < x <4
–2 — 1 < x — 1 <4 - 1
–3 < x — 1 <3
Поскольку последняя строка выше находится в формате «меньше чем» для неравенств абсолютных значений, мое неравенство решения будет иметь форму «абсолютное значение (чего-то) меньше 3».(Что-то) — это кусок посередине, где находится переменная. Поэтому я могу преобразовать мою последнюю строку выше в следующее:
Найдите утверждение о неравенстве абсолютного значения, которое соответствует неравенствам
x ≤ 19 или x ≥ 24
То, что они дали мне, состоит из двух частей, соединенных знаком «или», поэтому я знаю, что это будет неравенство «больше, чем» по абсолютной величине.
Для начала смотрю на конечные точки. Девятнадцать и 24 — это пять единиц. Половина из пяти — 2,5. Поэтому я хочу скорректировать неравенство, чтобы оно относилось к –2,5 и +2,5, а не к +19 и +24. Поскольку 19 — (–2,5) = 21,5 и 24 — 2,5 = 21,5, я вижу, что мне нужно вычесть всего 21,5:
x ≤ 19 или x ≥ 24
x — 21,5 ≤ 19 — 21,5 или x — 21.5 ≥ 24 — 21,5
x — 21,5 ≤ –2,5 или x — 21,5 ≥ 2,5
Поскольку последняя строка выше — это формат «больше чем», неравенство абсолютных значений будет иметь форму «абсолютное значение (чего-то) больше или равно 2,5». (Что-то) будет частью с переменной в нем. Итак, я могу преобразовать мою последнюю строку выше в:
Предупреждение: есть один вопрос типа «уловка» для такого рода задач, когда они попытаются сбить вас с толку при выполнении домашнего задания или тестов.Они попросят вас решить что-то вроде «| x + 2 | <–1». Но может ли абсолютное значение когда-либо быть отрицательным, не говоря уже о том, чтобы было меньше, чем отрицательным? Нет! Таким образом, это неравенство не имеет решения; это даже не имеет смысла. Не тратьте много времени на то, чтобы «решить» эту проблему; просто напишите «нет решения».
Точно так же, если вам дано что-то вроде «| x — 2 |> –3», первое, что следует отметить, это то, что все абсолютные значения равны нулю или положительны.В частности, они никогда не отрицательные. Они просят вас ввести значения x , которые сделают выражение абсолютного значения больше отрицательного числа. Поскольку абсолютное значение всегда будет больше , чем , любое отрицательное число , решение должно быть «все x » или «все действительные числа».
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении абсолютных неравенств. Попробуйте выполнить указанное упражнение или введите свое собственное.Затем нажмите кнопку и выберите «Решить для x», чтобы сравнить свой ответ с ответом Матвея.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/absineq.htm
4.Неравенства, связанные с абсолютными ценностями
Для неравенств, включающих абсолютные значения, т.е. | x |, мы используем следующие отношения, для некоторого числа n :
Если `| f (x) | > n`, то это означает:
`f (x) <-n` или` f (x)> n`
Если `| f (x) | `-n <
f (x) Решите неравенство | x — 3 | <2. Ответ Применение отношений `- 2 Добавляя `3` ко всем сторонам, получаем: `-2 + 3 `1 Вот график нашего решения: Убедитесь, что это правильный ответ, проверив. Попробуйте `x = 0` (не удастся, потому что это выходит за пределы диапазона нашего ответа),` x = 3` (должно работать) и `x = 10` (должно потерпеть неудачу).Каждый раз, когда вы так проверяете, становится понятнее, почему мы решаем именно так. Решите неравенство | 2 x — 1 | > 5. Ответ Применяя отношения, обсужденные ранее: `2x — 1 <-5 \ или \ 2x - 1> 5` Решая оба неравенства, получаем: Вот график нашего решения: Решите неравенство `2 | (2x) / 3 + 1 |> = 4` Ответ `2 | (2x) / 3 + 1 |> = 4` Это дает `| (2x) / 3 + 1 |> = 2` Так что либо… `(2x) / 3 + 1 <= - 2` ИЛИ `(2x) / 3 + 1> = 2` Умножить обе стороны на 3. `2x + 3 ≤ -6 `2x ≤ -9` `x <= - 9/2` ИЛИ `2x + 3 ≥ 6 `2x ≥ 3` `x> = 3/2` Решение: `x <= - 9/2 = -4,5, \" или "\ x> = 3/2 = 1,5` Вот график нашего решения: Решите неравенство `| 3 — 2x | <3` Ответ `| 3 — 2x | <3` `-3 <3 - 2x <3` Вычтем `3` со всех сторон: `-6 <-2x <0` Разделить все стороны на `-2` `3> x> 0` (обратите внимание на изменение смысла из-за деления на отрицательное Лучше написать это: `0 Вот график решения: Техник измеряет электрический ток, который составляет `0,036 \» A «` Ответ Возможная ошибка `± 0,002 \» A «означает, что разность между фактическим током и значением Значения i , которые мы имеем, можно выразить как: `0,034 ≤ i ≤ 0,038` Мы можем просто записать это как: `| i — 0,036 | ≤ 0,002` Вот график решения: 1. Решить `| 5 — x | ≤ 2` Ответ `-2 ≤ 5 — x ≤ 2` `-7 ≤ — x ≤ -3` `7 ≥ x ≥ 3` Лучше записать это как `3 ≤ x ≤ 7`. Вот график решения: 2. Решить `| (2x-9) / 4 | <1` Ответ `-1 <(2x-9) / 4 <1` «-4 <2x-9 <4" `5 <2x <13` `2,5 3. Решить `| (4x) / 3-5 |> = 7` Ответ `| (4x) / 3-5 |> = 7` `4x-15 <= - 21` `4x <= - 6` `x <= - 1.2 + 3x-4 <0` `(x + 4) (x-1) <0` Критические значения: `x = -4` и` x = 1` Это дает: `-4 Проще изобразить их вместе на одной оси, чтобы определить окончательный результат: Эти 3 региона пересекаются в следующих 2 местах: Это дает нам окончательное решение: −4 < x <−2 и −1 < x <1. Не забудьте проверить номеров внутри и за пределами данной области решения, чтобы убедиться, что оно работает. Сложное неравенство включает два неравенства в одном утверждении. Такое выражение, как [латекс] 4 Решите составное неравенство: [латекс] 3 \ le 2x + 2 <6 [/ латекс]. Показать решение Первый метод — написать два отдельных неравенства: [латекс] 3 \ le 2x + 2 [/ latex] и [latex] 2x + 2 <6 [/ latex].Решаем их самостоятельно. [латекс] \ begin {array} {lll} 3 \ le 2x + 2 \ hfill & \ text {and} \ hfill & 2x + 2 <6 \ hfill \\ 1 \ le 2x \ hfill & \ hfill & 2x < 4 \ hfill \\ \ frac {1} {2} \ le x \ hfill & \ hfill & x <2 \ hfill \ end {array} [/ latex] Затем мы можем переписать решение в виде составного неравенства, точно так же, как возникла проблема. [латекс] \ frac {1} {2} \ le x <2 [/ латекс] В интервальной записи решение записывается как [latex] \ left [\ frac {1} {2}, 2 \ right) [/ latex]. Второй метод — оставить составное неравенство неповрежденным и выполнить процедуры решения для трех частей одновременно. [латекс] \ begin {array} {ll} 3 \ le 2x + 2 <6 \ hfill & \ hfill \\ 1 \ le 2x <4 \ hfill & \ text {Выделите член переменной и вычтите 2 из всех трех частей }. \ hfill \\ \ frac {1} {2} \ le x <2 \ hfill & \ text {Разделить все три части на 2}. \ hfill \ end {array} [/ latex] Получаем такое же решение: [латекс] \ left [\ frac {1} {2}, 2 \ right) [/ latex]. Решите составное неравенство [латекс] 4 <2x - 8 \ le 10 [/ латекс]. Показать решение [латекс] 6 Решите составное неравенство с переменными во всех трех частях: [латекс] 3 + x> 7x — 2> 5x — 10 [/ latex]. Показать решение Попробуем первый способ. Запишите два неравенства : [латекс] \ begin {array} {lll} 3 + x> 7x — 2 \ hfill & \ text {and} \ hfill & 7x — 2> 5x — 10 \ hfill \\ 3> 6x — 2 \ hfill & \ hfill & 2x — 2> -10 \ hfill \\ 5> 6x \ hfill & \ hfill & 2x> -8 \ hfill \\ \ frac {5} {6}> x \ hfill & \ hfill & x> -4 \ hfill \\ x <\ frac {5} {6} \ hfill & \ hfill & -4 Набор решений: [latex] -4 Решите составное неравенство: [латекс] 3y <4 - 5y <5 + 3y [/ latex]. Показать решение [латекс] \ left (- \ frac {1} {8}, \ frac {1} {2} \ right) [/ latex] Как мы знаем, абсолютное значение величины — это положительное число или ноль. От исходной точки точка, расположенная в [latex] \ left (-x, 0 \ right) [/ latex], имеет абсолютное значение [latex] x [/ latex], так как находится на расстоянии x единиц.Считайте абсолютное значение расстоянием от одной точки до другой точки. Независимо от направления, положительного или отрицательного, расстояние между двумя точками представляется как положительное число или ноль. Неравенство абсолютного значения — это уравнение вида [латекс] | A | , где A , а иногда B , представляет алгебраическое выражение, зависящее от переменной x. Решение неравенства означает нахождение набора всех значений [latex] x [/ latex] –, которые удовлетворяют задаче.Обычно этот набор представляет собой интервал или объединение двух интервалов и включает диапазон значений. Существует два основных подхода к решению абсолютных неравенств: графический и алгебраический. Преимущество графического подхода в том, что мы можем прочитать решение, интерпретируя графики двух уравнений. Преимущество алгебраического подхода состоит в том, что решения являются точными, поскольку точные решения иногда трудно прочитать с графика. Предположим, мы хотим знать все возможные доходы от инвестиций, если бы мы могли заработать некоторую сумму денег в пределах от 200 до 600 долларов.Мы можем решить алгебраически для набора из x- значений так, чтобы расстояние между [latex] x [/ latex] и 600 было меньше 200. Мы представляем расстояние между [latex] x [/ latex] и 600 как [ latex] | x — 600 | [/ latex], следовательно, [latex] | x — 600 | \ le 200 [/ latex] или [латекс] \ begin {array} {c} -200 \ le x — 600 \ le 200 \\ -200 + 600 \ le x — 600 + 600 \ le 200 + 600 \\ 400 \ le x \ le 800 \ конец {array} [/ latex] Это означает, что наша прибыль составит от 400 до 800 долларов. Для решения неравенств по абсолютным значениям, как и для уравнений с абсолютными значениями, мы записываем два неравенства и затем решаем их независимо. Для алгебраического выражения X и [латекс] k> 0 [/ latex], неравенство абсолютного значения является неравенством вида: [латекс] \ begin {array} {l} | X | Эти утверждения также применимы к [latex] | X | \ le k [/ latex] и [latex] | X | \ ge k [/ latex]. Опишите все значения [latex] x [/ latex] на расстоянии 4 от числа 5. Показать решение Мы хотим, чтобы расстояние между [latex] x [/ latex] и 5 было меньше или равно 4. Мы можем нарисовать числовую линию, чтобы обозначить условие, которое должно быть выполнено. Расстояние от [latex] x [/ latex] до 5 может быть представлено с помощью символа абсолютного значения, [latex] | x — 5 | [/ latex]. Запишите значения [latex] x [/ latex], которые удовлетворяют условию, как неравенство абсолютных значений. [латекс] | x — 5 | \ le 4 [/ латекс] Нам нужно написать два неравенства, так как всегда есть два решения уравнения абсолютного значения. [латекс] \ begin {array} {lll} x — 5 \ le 4 \ hfill & \ text {and} \ hfill & x — 5 \ ge -4 \ hfill \\ x \ le 9 \ hfill & \ hfill & x \ ge 1 \ hfill \ end {array} [/ latex] Если набор решений — [latex] x \ le 9 [/ latex] и [latex] x \ ge 1 [/ latex], то набор решений представляет собой интервал, включающий все действительные числа от 1 до 9 включительно. Итак, [latex] | x — 5 | \ le 4 [/ latex] эквивалентно [latex] \ left [1,9 \ right] [/ latex] в интервальной нотации. Опишите все значения x- на расстоянии 3 от числа 2. Показать решение [латекс] | x — 2 | \ le 3 [/ латекс] Решите [латекс] | x — 1 | \ le 3 [/ latex]. Показать решение [латекс] \ begin {array} {c} | x — 1 | \ le 3 \ hfill \\ \ hfill \\ -3 \ le x — 1 \ le 3 \ hfill \\ \ hfill \\ -2 \ le x \ le 4 \ hfill \\ \ hfill \\ \ left [-2,4 \ right] \ hfill \ end {array} [/ latex] Учитывая уравнение [latex] y = — \ frac {1} {2} | 4x — 5 | +3 [/ latex], определите значения x , для которых значения y отрицательны. Показать решение Мы пытаемся определить, где [latex] y <0 [/ latex], то есть когда [latex] - \ frac {1} {2} | 4x - 5 | +3 <0 [/ latex]. Начнем с выделения абсолютного значения. [латекс] \ begin {array} {ll} — \ frac {1} {2} | 4x — 5 | <-3 \ hfill & \ text {Умножьте обе стороны на -2 и отмените неравенство}. \ Hfill \\ | 4x - 5 |> 6 \ hfill & \ hfill \ end {array} [/ latex] Далее решаем [latex] | 4x — 5 | = 6 [/ latex]. [латекс] \ begin {array} {lll} 4x — 5 = 6 \ hfill & \ hfill & 4x — 5 = -6 \ hfill \\ 4x = 11 \ hfill & \ text {или} \ hfill & 4x = — 1 \ hfill \\ x = \ frac {11} {4} \ hfill & \ hfill & x = — \ frac {1} {4} \ hfill \ end {array} [/ latex] Теперь мы можем изучить график, чтобы увидеть, где значения y- отрицательны.Мы наблюдаем, где ветви находятся ниже оси x-. Обратите внимание, что не важно, как именно выглядит график, если мы знаем, что он пересекает горизонтальную ось в точках [latex] x = — \ frac {1} {4} [/ latex] и [latex] x = \ frac {11} {4} [/ latex], и график открывается вниз. Решите [латекс] -2 | k — 4 | \ le -6 [/ latex]. Показать решение [латекс] к \ ле 1 [/ латекс] или [латекс] к \ л 7 [/ латекс]; в обозначении интервала это будет [латекс] \ left (- \ infty, 1 \ right] \ cup \ left [7, \ infty \ right) [/ latex]. Иногда картинка стоит тысячи слов. Вы можете превратить неравенство с одной переменной в неравенство с двумя переменными и построить график. Х-точки пересечения графика будут соответствовать решению неравенства, которое вы можете найти вручную. [латекс] -2 | x — 4 | \ le -6 [/ латекс] Теперь введите это неравенство в Desmos и наведите указатель мыши на точки пересечения с координатами x. Если вам нужна инструкция о том, как ввести неравенства в Desmos, посмотрите это руководство. Являются ли значения x точек пересечения такими же, как и в решении, которое мы нашли выше? Теперь вы попытаетесь превратить это неравенство с одной переменной в неравенство с двумя переменными: [латекс] 5 | 9-2x | \ ge10 [/ латекс] Постройте график неравенства с помощью онлайн-графического инструмента и запишите интервал решения. У вас была идея улучшить этот контент? Нам очень понравится ваш вклад. Улучшить эту страницуПодробнее Поскольку это неравенство «больше чем», решение можно переписать в соответствии с правилом «больше чем». [латекс] \ Displaystyle х + 3 <-4 \, \, \, \, \, \, \, \ text {или} \, \, \, \, \, \, \, x + 3> 4 [/ латекс] Решите каждое неравенство. [латекс] \ begin {array} {r} x + 3 <-4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, x + 3> 4 \\\ подчеркивание {\, \, \, \, — 3 \, \, \, \, \, — 3} \, \, \, \, \, \, \ , \, \, \, \, \, \, \, \, \ underline {\, \, \, \, \, \, — 3 \, \, — 3} \\ x \, \, \, \, \, \, \, \, \, <- 7 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , x \, \, \, \, \, \, \, \, \,> 1 \\\\ x <-7 \, \, \, \, \, \, \, \ text {или} \ , \, \, \, \, \, x> 1 \, \, \, \, \, \, \, \ end {array} [/ latex] Проверьте решения в исходном уравнении, чтобы убедиться, что они работают.Проверьте конечную точку первого связанного уравнения [latex] −7 [/ latex] и конечную точку второго связанного уравнения 1. [латекс] \ Displaystyle \ begin {array} {r} \, \, \, \ left | x + 3 \ right |> 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left | х + 3 \ вправо |> 4 \\\ влево | -7 + 3 \ right | = 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left | 1 + 3 \ право | = 4 \\\, \, \, \, \, \, \, \ влево | -4 \ right | = 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, \, \ влево | 4 \ право | = 4 \\\, \, \, \, \, \, \, \, \, \, \, \, 4 = 4 \, \, \, \, \, \, \, \ , \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, 4 = 4 \ конец {array} [/ latex] Попробуйте [latex] -10 [/ latex], значение меньше [latex] -7 [/ latex], и 5, значение больше 1, чтобы проверить неравенство. [латекс] \ Displaystyle \ begin {array} {r} \, \, \, \, \, \ left | x + 3 \ right |> 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left | х + 3 \ вправо |> 4 \\\ влево | -10 + 3 \ right |> 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left | 5 + 3 \ right |> 4 \\\, \, \, \, \, \, \, \, \, \, \ left | -7 \ right |> 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, \ влево | 8 \ right |> 4 \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, 7> 4 \, \, \, \, \, \ , \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, 8> 4 \ end {array} [/ latex] Оба решения проверяют! Неравенство: [латекс] \ displaystyle x <-7 \, \, \, \, \, \ text {or} \, \, \, \, \, x> 1 [/ latex] Интервал: [латекс] \ left (- \ infty, -7 \ right) \ cup \ left (1, \ infty \ right) [/ latex] График: ins [data-ad-slot = «4502451947»] {display: none! important;}} 1 Решение сложения и вычитания неравенств.Модуль 3, Урок 3 Онлайн-алгебра VHS @ PWCS 2 Неравенства Неравенства — это утверждения, в которых используются следующие символы (символ указывает на меньшее количество):> — Больше <- Меньше> — Больше или равно <- Меньше или равно ≠ - Не равно 3 Графическое изображение неравенств x> -1 Подумайте о некоторых значениях x, которые соответствуют этому решению.Сколько ценностей вы придумали? Вы должны были придумать несколько. Неравенства имеют бесконечное количество решений. В этом случае решением будет значение меньше -1. Вместо точек мы используем линию, чтобы показать, что учитывается все, что меньше -1. Мы также используем открытый кружок на -1, чтобы показать, что включены числа, очень близкие к -1, но не -1-6-4-2 0 2 4 4 График следующих неравенств x> -2 Помните, что мы используем белый кружок и линию для построения графика этого неравенства.x> -2 Поскольку это неравенство представляет, что x больше или равно -2, -2 является частью решения. Чтобы показать это графически, мы используем замкнутый круг. -6-4-2 0 2 4 5 Решение неравенств Решение неравенств похоже на решение уравнений. c + -13 = 7 Напомним, что для решения этого уравнения мы прибавляем 13 к обеим частям. c + -13 + 13 = 7 + 13 c = 20 c + — 13 <7 Чтобы решить это неравенство. Делаем то же самое, прибавляем по 13 с обеих сторон.c + -13 + 13 <7 + 13 c <20 Единственное отличие - график решения. 15 17 19 21 23 25 6 Решить и построить график 4> x — 12 1. Записать как сложение. 4> x + -12 2. Добавьте 12 с обеих сторон. 4 + 12> x + -12 + 12 16> x 3. Если мы перевернем неравенство, это упростит построение графика. x <16 11 13 15 17 19 21 Обратите внимание, что «точка» все еще указывает на x, когда мы переворачиваем. Это упрощает построение графика, потому что, если наш x находится слева от неравенства, наша линия будет идти в том же направлении, что и символ. 7 Решение неравенств, резюме Решение неравенств похоже на решение уравнения. Для построения графика мы используем линию и либо открытый, либо закрытый круг. Используйте открытый кружок с. Используйте замкнутый круг с. К концу этого раздела вы сможете: Будьте готовы 2.17 Перед тем, как начать, пройдите тест на готовность. Оценить: — | 7 | .− | 7 |. Будьте готовы 2.18 Введите <,>, <,> или == для каждой из следующих пар чисел. Будьте готовы 2.19 Упростить: 14−2 | 8−3 (4−1) |.14−2 | 8−3 (4−1) |. Готовясь решить уравнения абсолютного значения, мы пересматриваем наше определение абсолютного значения. Абсолютное значение числа — это его расстояние от нуля на числовой прямой. Абсолютное значение числа n записывается как | n || n | и | n | ≥0 | n | ≥0 для всех чисел. Абсолютные значения всегда больше или равны нулю. Мы узнали, что число и его противоположность находятся на одинаковом расстоянии от нуля на числовой прямой. Поскольку они находятся на одинаковом расстоянии от нуля, они имеют одинаковое абсолютное значение. Например: −5−5 на 5 единиц от 0, поэтому | −5 | = 5. | −5 | = 5. 55 находится на расстоянии 5 единиц от 0, поэтому | 5 | = 5. | 5 | = 5. Рисунок 2.6 иллюстрирует эту идею. Рис. 2.6 Числа 5 и −5−5 отстоят на пять единиц от нуля. Для уравнения | x | = 5, | x | = 5 мы ищем все числа, которые делают это утверждение истинным.Мы ищем числа, расстояние от которых до нуля равно 5. Мы только что видели, что и 5, и −5−5 — это пять единиц от нуля на числовой прямой. Они являются решениями уравнения. If | x | = 5thenx = −5orx = 5If | x | = 5thenx = −5orx = 5 Решение можно упростить до одного утверждения, написав x = ± 5.x = ± 5. Это читается так: « x равно положительному или отрицательному 5». Мы можем обобщить это на следующее свойство для уравнений абсолютного значения. Для любого алгебраического выражения u и любого положительного действительного числа a , если | u | = athenu = −aoru = aif | u | = athenu = −aoru = a Помните, что абсолютное значение не может быть отрицательным числом. Решить: ⓐ | x | = 8 | x | = 8 ⓑ | y | = −6 | y | = −6 ⓒ | z | = 0 | z | = 0 ⓐ Ⓑ Ⓒ Попробуйте 2.135 Решить: ⓐ | x | = 2 | x | = 2 ⓑ | y | = −4 | y | = −4 ⓒ | z | = 0 | z | = 0 Попробуй 2.136 Решить: ⓐ | x | = 11 | x | = 11 ⓑ | y | = −5 | y | = −5 ⓒ | z | = 0 | z | = 0 Чтобы решить уравнение абсолютного значения, мы сначала выделяем выражение абсолютного значения, используя те же процедуры, которые мы использовали для решения линейных уравнений. Выделив выражение абсолютного значения, мы перепишем его как два эквивалентных уравнения. Решите | 5x − 4 | −3 = 8. | 5x − 4 | −3 = 8. Попробуйте 2.137 Решите: | 3x − 5 | −1 = 6.| 3х − 5 | −1 = 6. Попробуйте 2.138 Решите: | 4x − 3 | −5 = 2. | 4x − 3 | −5 = 2. Здесь приведены шаги для решения уравнения абсолютного значения. Решите 2 | x − 7 | + 5 = 9.2 | х − 7 | + 5 = 9. Попробуй 2.139 Решите: 3 | x − 4 | −4 = 8.3 | x − 4 | −4 = 8. Попробуйте 2.140 Решите: 2 | x − 5 | + 3 = 9,2 | x − 5 | + 3 = 9. Помните, абсолютное значение всегда положительно! Решите: | 23x − 4 | + 11 = 3. | 23x − 4 | + 11 = 3. Попробуйте 2.141 Решите: | 34x − 5 | + 9 = 4. | 34x − 5 | + 9 = 4. Попробуйте 2.142 Решите: | 56x + 3 | + 8 = 6. | 56x + 3 | + 8 = 6. Некоторые из наших абсолютных уравнений могут иметь вид | u | = | v || u | = | v | где u и v — алгебраические выражения. Например, | x − 3 | = | 2x + 1 |. | X − 3 | = | 2x + 1 |. Как бы мы их разрешили? Если два алгебраических выражения равны по модулю, то они либо равны друг другу, либо отрицательны.Свойство для уравнений абсолютного значения гласит, что для любого алгебраического выражения u и положительного действительного числа a , если | u | = a, | u | = a, то u = −au = −a или u = au = a. Это говорит нам, что если | u | = | v | thenu = −voru = voru = vif | u | = | v | thenu = −voru = voru = v Это приводит нас к следующему свойству для уравнений с двумя абсолютными значениями. Для любых алгебраических выражений: u и v , если | u | = | v | thenu = −voru = vif | u | = | v | thenu = −voru = v Когда мы берем величину, противоположную количеству, мы должны быть осторожны со знаками и добавлять круглые скобки там, где это необходимо. Решить: | 5x − 1 | = | 2x + 3 |. | 5x − 1 | = | 2x + 3 |. Попробуйте 2.143 Решите: | 7x − 3 | = | 3x + 7 |. | 7x − 3 | = | 3x + 7 |. Попробуйте 2.144 Решите: | 6x − 5 | = | 3x + 4 |. | 6x − 5 | = | 3x + 4 |. Давайте теперь посмотрим, что происходит, когда у нас есть неравенство абсолютных значений. Все, что мы узнали о решении проблемы неравенства, по-прежнему актуально, но мы должны учитывать, как абсолютная ценность влияет на нашу работу. Мы снова посмотрим на наше определение абсолютного значения.Абсолютное значение числа — это его расстояние от нуля на числовой прямой. Для уравнения | x | = 5, | x | = 5 мы увидели, что и 5, и −5−5 равны пяти единицам от нуля на числовой прямой. Они являются решениями уравнения. | x | = 5x = −5orx = 5 | x | = 5x = −5orx = 5 А как насчет неравенства | x | ≤5? | X | ≤5? Где числа, расстояние между которыми меньше или равно 5? Мы знаем, что −5−5 и 5 — это пять единиц от нуля. Все числа от −5−5 до 5 меньше пяти единиц от нуля. См. Рисунок 2.7. Рисунок 2.7 В более общем виде мы можем видеть, что если | u | ≤a, | u | ≤a, то −a≤u≤a. − a≤u≤a. См. Рисунок 2.8. Рисунок 2.8 Этот результат резюмируется здесь. << или ≤≤ Для любого алгебраического выражения u и любого положительного действительного числа a , если | u | Решить | x | <7. | x | <7. Постройте график решения и запишите решение в интервальной записи. Попробуйте 2.145 Изобразите решение и запишите решение в интервальной записи: | x | <9.| х | <9. Попробуйте 2.146 Изобразите решение и запишите решение в интервальной записи: | x | <1. | x | <1. Решите | 5x − 6 | ≤4. | 5x − 6 | ≤4. Постройте график решения и запишите решение в интервальной записи. Попробуй 2.147 Решить | 2x − 1 | ≤5. | 2x − 1 | ≤5. Постройте график решения и запишите решение в интервальной записи: . Попробуйте 2.148 Решите | 4x − 5 | ≤3. | 4x − 5 | ≤3. Постройте график решения и запишите решение в интервальной записи: . <или ≤. Что происходит с неравенством по абсолютной стоимости, имеющим «больше чем»? Мы снова посмотрим на наше определение абсолютной ценности. Абсолютное значение числа — это его расстояние от нуля на числовой прямой. Мы начали с неравенства | x | ≤5. | X | ≤5. Мы видели, что числа, расстояние от которых до нуля на числовой прямой меньше или равно пяти, были от −5−5 до 5, а все числа от −5−5 до 5.См. Рисунок 2.9. Рисунок 2.9 Теперь мы хотим рассмотреть неравенство | x | ≥5. | X | ≥5. Где числа, расстояние от нуля которых больше или равно пяти? И снова и −5−5, и 5 равны пяти единицам от нуля и поэтому включены в решение. Числа, расстояние от которых до нуля больше пяти единиц, будут меньше −5−5 и больше 5 на числовой прямой. См. Рисунок 2.10. Рисунок 2.10 В более общем виде мы можем видеть, что если | u | ≥a, | u | ≥a, то u≤ − au≤ − a или u≥a.u≥a. См. Рисунок 2.11. Рисунок 2.11 Этот результат резюмируется здесь. Для любого алгебраического выражения u и любого положительного действительного числа a , если | u |> a, то u <−aoru> aif | u | ≥a, thenu≤ − aoru≥aif | u |> a, затемu <−aoru> aif | u | ≥a, затемu≤ − aoru≥a Решить | x |> 4. | x |> 4. Постройте график решения и запишите решение в интервальной записи. Для проверки проверьте значение в каждом разделе числовой строки, в которой показано решение. Выберите числа, такие как −6, −6, 0 и 7. Попробуйте 2.149 Решить | x |> 2. | x |> 2.Постройте график решения и запишите решение в интервальной записи. Попробуйте 2.150 Решить | x |> 1. | x |> 1. Постройте график решения и запишите решение в интервальной записи. Решите | 2x − 3 | ≥5. | 2x − 3 | ≥5. Постройте график решения и запишите решение в интервальной записи. Попробуйте 2.151 Решить | 4x − 3 | ≥5. | 4x − 3 | ≥5. Постройте график решения и запишите решение в интервальной записи. Попробуйте 2.152 Решите | 3x − 4 | ≥2. | 3x − 4 | ≥2. Постройте график решения и запишите решение в интервальной записи. Неравенство абсолютных значений часто используется в производственном процессе. Изделие должно быть изготовлено с почти идеальными характеристиками.Обычно существует определенный допуск и отклонений от допустимых характеристик. Если отличие от спецификаций превышает допуск, товар отклоняется. | фактический идеальный | ≤ допуск | фактический идеальный | ≤ допуск Идеальный диаметр стержня, необходимого для станка, составляет 60 мм. Фактический диаметр может отличаться от идеального на 0,0750,075 мм. Какой диапазон диаметров будет приемлем для заказчика, не вызывая брака прутка? Попробуйте 2.153 Идеальный диаметр стержня, необходимого для станка, составляет 80 мм. Фактический диаметр может отличаться от идеального на 0,009 мм. Какой диапазон диаметров будет приемлем для заказчика, не вызывая брака прутка? Попробуйте 2.154 Идеальный диаметр стержня, необходимого для станка, — 75 мм. Фактический диаметр может отличаться от идеального на 0,05 мм. Какой диапазон диаметров будет приемлем для заказчика, не вызывая брака прутка? Решите уравнения абсолютных значений В следующих упражнениях решите. 434. ⓐ | x | = 6 | x | = 6 | y | = −3 | y | = −3 ⓒ | z | = 0 | z | = 0 435. ⓐ | x | = 4 | x | = 4 ⓑ | y | = −5 | y | = −5 ⓒ | z | = 0 | z | = 0 436. ⓐ | x | = 7 | x | = 7 ⓑ | y | = −11 | y | = −11 ⓒ | z | = 0 | z | = 0 437. ⓐ | x | = 3 | x | = 3 ⓑ | y | = −1 | y | = −1 ⓒ | z | = 0 | z | = 0 438. | 2x − 3 | −4 = 1 | 2x − 3 | −4 = 1 439. | 4x − 1 | −3 = 0 | 4x − 1 | −3 = 0 442. 4 | х − 1 | + 2 = 104 | х − 1 | + 2 = 10 443. 3 | х-4 | + 2 = 113 | х-4 | + 2 = 11 444. 3 | 4x − 5 | −4 = 113 | 4x − 5 | −4 = 11 446. −2 | x − 3 | + 8 = −4−2 | x − 3 | + 8 = −4 447. −3 | x − 4 | + 4 = −5−3 | x − 4 | + 4 = −5 448. | 34x − 3 | + 7 = 2 | 34x − 3 | + 7 = 2 449. | 35x − 2 | + 5 = 2 | 35x − 2 | + 5 = 2 452. | 3x − 2 | = | 2x − 3 || 3x − 2 | = | 2x − 3 | 453. | 4x + 3 | = | 2x + 1 || 4x + 3 | = | 2x + 1 | 454. | 6x − 5 | = | 2x + 3 || 6x − 5 | = | 2x + 3 | 455. | 6 − x | = | 3−2x || 6 − x | = | 3−2x | Решите неравенства абсолютного значения с «меньше» В следующих упражнениях решите каждое неравенство.Постройте график решения и запишите решение в интервальной записи. 466. | х − 4 | ≤ − 1 | x − 4 | ≤ − 1 467. | 5x + 1 | ≤ − 2 | 5x + 1 | ≤ − 2 Решите неравенства абсолютного значения с «больше чем» В следующих упражнениях решите каждое неравенство. Постройте график решения и запишите решение в интервальной записи. 472. | 3x − 8 |> −1 | 3x − 8 |> −1 В следующих упражнениях решите. Для каждого неравенства также нанесите график решения и запишите решение в интервальной записи. 481. | 6x − 5 | = | 2x + 3 || 6x − 5 | = | 2x + 3 | 487. 5 | 2x − 1 | −3 = 75 | 2x − 1 | −3 = 7 488. | 8 − x | = | 4−3x || 8 − x | = | 4−3x | Решение приложений с абсолютным значением В следующих упражнениях решите. 490. В идеале птицеферма производит 200 000 яиц в день. Но эта сумма может варьироваться на 25 000 яиц. Какая максимальная и минимальная ожидаемая продукция на ферме? 491. Завод по розливу органических соков в идеале производит 215 000 бутылок в день.Но эта сумма может варьироваться на 7 500 бутылок. Какое максимальное и минимальное ожидаемое производство на предприятии по розливу? 492. Чтобы обеспечить соблюдение закона, Мигель обычно превышает вес своих лепешек на 0,5 грамма. Он только что получил отчет, в котором говорилось, что он может терять до 100 000 долларов в год, используя эту практику. Теперь он планирует купить новое оборудование, которое гарантирует толщину лепешки в пределах 0,005 дюйма. Если идеальная толщина лепешки 0.04 дюйма, какая толщина лепешек будет гарантирована? 493. В пекарне Lilly’s идеальный вес буханки хлеба составляет 24 унции. По закону реальный вес может отличаться от идеального на 1,5 унции. Какой вес будет приемлемым для инспектора без наложения штрафа на пекарню? 494. Напишите графическое описание абсолютного значения числа. 495. Объясните своими словами, как решить неравенство абсолютных значений, | 3x − 2 | ≥4.| 3х − 2 | ≥4. ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела. ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения? Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. В предыдущем разделе мы решали уравнения, содержащие абсолютные значения.В этом разделе мы хотим рассмотреть неравенства, содержащие абсолютные значения. Нам нужно будет рассмотреть два отдельных случая. <и \ (\ le \) Как и в случае с уравнениями, давайте начнем с довольно простого случая. \ [\ left | п \ право | \ le 4 \] Это говорит о том, что независимо от того, что такое \ (p \), оно должно находиться на расстоянии не более 4 от начала координат. Это означает, что \ (p \) должно быть где-то в диапазоне . \ [- 4 \ le p \ le 4 \] Мы могли бы получить аналогичное неравенство с <и получить аналогичный результат. В общем, здесь используются следующие формулы: \ [\ require {bbox} \ bbox [2pt, border: 1px сплошной черный] {\ begin {align *} {\ mbox {If}} \ left | п \ право | \ le b, \, \, \, b> 0 \, \, \, \, \, \, \, \, \, \, \, {\ mbox {then}} — b \ le p \ le b \\ {\ mbox {If}} \ left | п \ право | 0 \, \, \, \, \, \, \, \, \, \, \, {\ mbox {then}} — b Обратите внимание, что для этого требуется, чтобы значение \ (b \) было положительным, так же как мы сделали с уравнениями. Давайте взглянем на пару примеров. Пример 1 Решите каждую из следующих задач. Показать все решения Скрыть все решения a \ (\ left | {2x — 4} \ right | Показать решение На самом деле особо нечего делать, кроме как ввести формулу. Как и в случае с уравнениями, \ (p \) просто представляет все, что находится внутри столбцов абсолютных значений.Итак, с этим первым у нас есть \ [- 10 Итак, это не что иное, как довольно простое двойное неравенство, которое нужно решить, так что давайте сделаем это. \ [\ begin {array} {c} — 6 Обозначение интервала для этого решения — \ (\ left ({- 3,7} \ right) \). b \ (\ left | {9m + 2} \ right | \ le 1 \) Показать решение Здесь особо нечего делать. \ [\ begin {array} {c} — 1 \ le 9m + 2 \ le 1 \\ — 3 \ le 9m \ le — 1 \\ \ displaystyle — \ frac {1} {3} \ le m \ le — \ frac {1} {9} \ end {array} \] Обозначение интервала: \ (\ left [{- \ frac {1} {3}, — \ frac {1} {9}} \ right] \). c \ (\ left | {3 — 2z} \ right | \ le 5 \) Показать решение Нам нужно быть немного осторожнее с решением двойного неравенства с этим, но в остальном оно почти идентично предыдущим двум частям. \ [\ begin {array} {c} -5 \ le 3 — 2z \ le 5 \\ — 8 \ le — 2z \ le 2 \\ 4 \ ge z \ ge — 1 \ end {array} \] На последнем этапе не забудьте изменить направление неравенств, так как мы разделили все на отрицательное число.Обозначение интервала для этого решения \ (\ left [{- 1,4} \ right] \). Еще раз давайте начнем с простого числового примера. \ [\ left | п \ право | \ ge 4 \] Это говорит о том, что каким бы ни был \ (p \), он должен находиться на расстоянии не менее 4 от начала координат, и поэтому \ (p \) должен находиться в одном из следующих двух диапазонов: \ [p \ le — 4 \ hspace {0,25 дюйма} {\ mbox {или}} \ hspace {0.25 дюймов} п \ г 4 \] Перед тем, как дать общее решение, нам нужно разобраться с типичной ошибкой, которую допускают учащиеся при решении таких задач. Многие студенты пытаются объединить их в одно двойное неравенство следующим образом: \ [- 4 \ ge p \ ge 4 \] Хотя может показаться, что это имеет смысл, мы не можем достаточно подчеркнуть, что ЭТО НЕПРАВИЛЬНО !! Вспомните, что говорит двойное неравенство. В двойном неравенстве требуется, чтобы оба неравенства выполнялись одновременно. Приведенное выше двойное неравенство означало бы, что \ (p \) — это число, которое одновременно меньше -4 и больше 4.Это просто не имеет смысла. Нет числа, которое бы этому соответствовало. Эти решения нужно записать в виде двух неравенств. Вот их общая формула. \ [\ require {bbox} \ bbox [2pt, border: 1px сплошной черный] {\ begin {align *} {\ mbox {If}} \ left | п \ право | \ ge b, \, \, \, b> 0 \, \, \, \, \, \, \, \, \, \, \, {\ mbox {then}} p \ le — b {\ mbox {или}} p \ ge b \\ {\ mbox {If}} \ left | п \ право | > b, \, \, \, b> 0 \, \, \, \, \, \, \, \, \, \, \, {\ mbox {then}} pb \ end {align *}} \ ] Опять же, требует, чтобы было положительным числом \ (b \).Приведем пару примеров. Пример 2 Решите каждую из следующих задач. Показать все решения Скрыть все решения a \ (\ left | {2x — 3} \ right |> 7 \) Показать решение Опять же, \ (p \) представляет количество внутри столбцов абсолютных значений, поэтому все, что нам нужно сделать здесь, это вставить формулу, а затем решить два линейных неравенства. \ [\ begin {align *} 2x — 3 & 7 \\ 2x & 10 \\ x & 5 \ end {align *} \] Интервальные обозначения для них \ (\ left ({- \ infty, — 2} \ right) \) или \ (\ left ({5, \ infty} \ right) \). b \ (\ left | {6t + 10} \ right | \ ge 3 \) Показать решение Давайте просто подключим формулы и перейдем сюда, \ [\ begin {align *} 6t + 10 & \ le — 3 & \ hspace {0,25 дюйма} & {\ mbox {or}} & \ hspace {0.25 дюймов} 6t + 10 & \ ge 3 \\ 6t & \ le — 13 & \ hspace {0,25 дюйма} & {\ mbox {or}} & \ hspace {0,25 дюйма} 6t & \ ge — 7 \\ t & \ le — \ frac {{13}} {6} & \ hspace {0,25 дюйма} & {\ mbox {или}} & \ hspace {0,25 дюйма} t & \ ge — \ frac {7} {6} \ end { выровнять*}\] Обозначения интервалов для них: \ (\ left ({- \ infty, — \ frac {{13}} {6}} \ right] \) или \ (\ left [{- \ frac {7} {6} , \ infty} \ right) \). c \ (\ left | {2 — 6y} \ right |> 10 \) Показать решение Опять же, здесь особо нечего делать. \ [\ begin {align *} 2 — 6y & 10 \\ — 6y & 8 \\ y &> 2 & \ hspace {0,25 дюйма} & {\ mbox {or}} & \ hspace {0,25in} y & Обратите внимание, что нам пришлось изменить направление неравенств при делении на отрицательное число! Обозначение интервалов для этих решений — \ (\ left ({2, \ infty} \ right) \) или \ (\ left ({- \ infty, — \ frac {4} {3}} \ right) \). Хорошо, теперь нам нужно быстро взглянуть на то, что происходит, если \ (b \) равно нулю или отрицательно.Мы сделаем это с помощью набора примеров и начнем с нуля. Пример 3 Решите каждую из следующих задач. Показать все решения Скрыть все решения Показать обсуждение Эти четыре примера, кажется, охватывают все наши базы. a \ (\ left | {3x + 2} \ right | Показать решение Теперь мы знаем, что \ (\ left | p \ right | \ ge 0 \) и поэтому не может быть меньше нуля. Следовательно, в этом случае нет решения, поскольку невозможно, чтобы абсолютное значение было строго меньше нуля (, т.е. отрицательное значение). b \ (\ left | {x — 9} \ right | \ le 0 \) Показать решение Это почти то же самое, что и предыдущая часть. Мы по-прежнему не можем иметь абсолютное значение меньше нуля, однако оно может быть равно нулю.Так что решение будет только в том случае, если \ [\ left | {x — 9} \ right | = 0 \] , и мы знаем, как решить эту проблему из предыдущего раздела. \ [x — 9 = 0 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} x = 9 \] c \ (\ left | {2x — 4} \ right | \ ge 0 \) Показать решение В этом случае давайте еще раз напомним, что независимо от того, что такое \ (p \), у нас гарантированно будет \ (\ left | p \ right | \ ge 0 \). Это означает, что независимо от того, что такое \ (x \), мы можем быть уверены, что \ (\ left | {2x — 4} \ right | \ ge 0 \) будет истинным, поскольку абсолютные значения всегда будут положительными или нулевыми. Решением в этом случае являются все действительные числа или все возможные значения \ (x \). В обозначении неравенства это будет \ (- \ infty d \ (\ left | {3x — 9} \ right |> 0 \) Показать решение Эта часть почти идентична предыдущей, за исключением того, что на этот раз обратите внимание, что мы не хотим, чтобы абсолютное значение когда-либо было равно нулю. Итак, нас не волнует, какое значение принимает абсолютное значение, если оно не равно нулю. Это означает, что нам просто нужно избегать значений \ (x \), для которых мы получаем \ [\ left | {3x — 9} \ right | = 0 \ hspace {0.25 дюймов} \ Rightarrow \ hspace {0,25 дюйма} 3x — 9 = 0 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} x = 3 \] Решением в этом случае являются все действительные числа, кроме \ (x = 3 \). А теперь давайте быстро разберем примеры с отрицательными числами. Пример 4 Постановка задачи. Показать все решения Скрыть все решения Показать обсуждение Обратите внимание, что мы работаем с ними парами, потому что на этот раз, в отличие от предыдущего набора примеров, решения будут одинаковыми для каждого. Оба (все четыре?) Из них будут использовать тот факт, что независимо от того, что такое \ (p \), у нас гарантированно будет \ (\ left | p \ right | \ ge 0 \). Другими словами, абсолютные значения всегда положительны или равны нулю. a \ (\ left | {4x + 15} \ right | Показать решение Хорошо, если абсолютные значения всегда положительны или равны нулю, они не могут быть меньше или равны отрицательному числу. Пример 1
обсуждалось выше: Пример 2
`2x <-5 + 1` или `2x> 5 + 1` `2x <-4` или `2x> 6` ` x <-2` или `x> 3` Пример 3
`
` Пример 4
номер) Пример 5
с возможной погрешностью `± 0,002 \» A «`. Напишите это
ток, i , как неравенство с абсолютным
значения.
`0,036 \» A «` не может быть больше `0,002 \» A «`. Упражнения
`(4x) / 3-5 <= - 7` ИЛИ `(4x) / 3-5> = 7` Неравенства составных и абсолютных значений
Результаты обучения
Пример: решение сложного неравенства
Попробуй
Пример: решение сложного неравенства с переменной во всех трех частях
Попробуй
Решение абсолютных неравенств
Общее примечание: Неравенства абсолютных значений
Пример: определение числа в пределах заданного расстояния
Попробуй
Пример: решение неравенства абсолютного значения
Пример: использование графического подхода для решения неравенств абсолютных значений
Попробуй
Попробуй
Давайте воспользуемся последним примером, чтобы попробовать. Мы изменим переменную на x, чтобы упростить ввод в Desmos.
Чтобы превратить [latex] -2 | x — 4 | \ le -6 [/ latex] в уравнение с двумя переменными, переместите все в одну сторону и поместите переменную y на другую сторону следующим образом:
[латекс] -2 | x — 4 | +6 \ le y [/ латекс] Внесите свой вклад!
Решить сложные неравенства | Начальная алгебра
Ответ
Решение неравенств, сложение и вычитание.Модуль 3, Урок 3 Онлайн-алгебра
Презентация на тему: «Решение вопросов сложения и вычитания неравенств. Модуль 3, Урок 3 Онлайн-алгебра» — стенограмма презентации:
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]> 2.7 Устранение неравенств абсолютных значений — промежуточная алгебра 2e
Цели обучения
Если вы пропустили эту проблему, просмотрите Пример 1.12.
Ⓐ | −8 | ___− | −8 || −8 | ___− | −8 | Ⓑ 12 ___− | −12 | 12 ___− | −12 | Ⓒ | −6 | ___− 6 | −6 | ___− 6 ⓓ — (- 15) ___− | −15 | — (- 15) ___− | −15 |
Если вы пропустили эту проблему, просмотрите Пример 1.12.
Если вы пропустили эту проблему, просмотрите Пример 1.13. Решите уравнения абсолютных значений
Абсолютное значение
Уравнения абсолютных значений
Пример 2,68
Решение
| х | = 8 | х | = 8 Напишите эквивалентные уравнения. x = −8orx = 8x = −8orx = 8 х = ± 8х = ± 8 | y | = −6 | y | = −6 Нет решения Поскольку абсолютное значение всегда положительно, у этого уравнения нет решений. Оба уравнения говорят нам, что z = 0, и поэтому существует только одно решение.
Пример 2.69
Как решить уравнения абсолютных значений
Как сделать
Решите уравнения абсолютных значений.
Пример 2,70
Решение
2 | x − 7 | + 5 = 92 | x − 7 | + 5 = 9 Выделите выражение абсолютного значения. 2 | х-7 | = 42 | х-7 | = 4 | x − 7 | = 2 | x − 7 | = 2 Напишите эквивалентные уравнения. x − 7 = −2x − 7 = −2 или x − 7 = 2x − 7 = 2 Решите каждое уравнение. x = 5x = 5 или x = 9x = 9 Чек: Пример 2.71
Решение
| 23x − 4 | + 11 = 3 | 23x − 4 | + 11 = 3 Выделите член абсолютного значения. | 23x − 4 | = −8 | 23x − 4 | = −8 Абсолютное значение не может быть отрицательным. Нет решения Уравнения с двумя абсолютными значениями
Пример 2.72
Решение
| 5x − 1 | = | 2x + 3 || 5x − 1 | = | 2x + 3 | Напишите эквивалентные уравнения.
Решите каждое уравнение. 5x − 1 = — (2x + 3) или 5x − 1 = 2x + 35x − 1 = −2x − 3or3x − 1 = 37x − 1 = −33x = 47x = −2x = 43x = −27orx = 435x − 1 = — (2x + 3) или 5x − 1 = 2x + 35x − 1 = −2x − 3or3x − 1 = 37x − 1 = −33x = 47x = −2x = 43x = −27orx = 43 Проверить. Мы оставляем вам чек. Решите абсолютные неравенства, используя значение «меньше чем»
Абсолютные неравенства с
Пример 2,73
Пример 2.74
Решение
Шаг 1. Выделите выражение абсолютного значения.
Изолировано. | 5x − 6 | ≤4 | 5x − 6 | ≤4 Шаг 2. Напишите эквивалентное сложное неравенство. −4≤5x − 6≤4−4≤5x − 6≤4 Шаг 3. Решите сложное неравенство. 2≤5x≤102≤5x≤10
25≤x≤225≤x≤2 Шаг 4. Изобразите решение. Шаг 5. Запишите решение, используя интервальную запись. [25,2] [25,2] Чек:
Чек остается на ваше усмотрение. Как сделать
Решите неравенства абсолютных значений с помощью
| u | Решите неравенство абсолютных значений с помощью «больше, чем»
Абсолютные неравенства с> или ≥
Пример 2,75
Решение
| x |> 4 | x |> 4 Запишите эквивалентное неравенство. x <−4orx> 4x <−4orx> 4 Постройте график решения. Запишите решение, используя интервальную запись. (−∞, −4) ∪ (4, ∞) (- ∞, −4) ∪ (4, ∞) Чек: Пример 2,76
Решение
| 2x − 3 | ≥5 | 2x − 3 | ≥5 Шаг 1. Выделите выражение абсолютного значения.Он изолирован. Шаг 2. Запишите эквивалентное сложное неравенство. 2x − 3≤ − 5or2x − 3≥52x − 3≤ − 5or2x − 3≥5 Шаг 3. Решите сложное неравенство. 2x≤ − 2or2x≥82x≤ − 2or2x≥8
x≤ − 1orx≥4x≤ − 1orx≥4 Шаг 4. Изобразите решение. Шаг 5. Запишите решение, используя интервальную запись. (−∞, −1] ∪ [4, ∞) (- ∞, −1] ∪ [4, ∞) Чек:
Чек остается на ваше усмотрение. Как сделать
Решите неравенства абсолютных значений с помощью> или ≥.
| u |> a эквивалентно tou <−aoru> a | u | ≥ais эквивалентно tou≤ − aoru≥a | u |> a эквивалентно tou <−aoru> a | u | ≥ais эквивалентно tou≤ − aoru≥a Решение приложений с абсолютным значением
Пример 2,77
Решение
Пусть x = фактическое измерение. Используйте неравенство абсолютных значений, чтобы выразить эту ситуацию. | фактический идеальный | ≤ допуск | фактический идеальный | ≤ допуск | х-60 | ≤0,075 | х-60 | ≤0,075 Записываем в виде составного неравенства. −0,075≤x − 60≤0,075−0,075≤x − 60≤0,075 Решите неравенство. 59,925≤x≤60,07 559,925≤x≤60,075 Ответьте на вопрос. Диаметр стержня может быть от 59.925 мм и 60,075 мм. Раздел 2.7 упражнений
Практика ведет к совершенству
Письменные упражнения
Самопроверка
Алгебра — Абсолютные неравенства
Раздел 2-15: Абсолютные неравенства
Неравенства с участием
Неравенства с участием> и \ (\ ge \)
