Содержание
«Решение уравнений с модулем и параметром»
Пояснительная записка
1 Пояснительная записка Профильное обучение в гимназии направлено на обеспечение углубленного изучения математики, а, значит, прежде всего, на осознанное изучение данного предмета, на развитие математического
Подробнее
Пояснительная записка.
Пояснительная записка. методов решения уравнений и неравенств с модулем и своим содержанием привлекает внимание учащихся 10 классов, которым интересна математика. Предлагаемый курс является развитием системы
Подробнее
Пояснительная записка.

1 2 Пояснительная записка. Курс «Решение задач с параметрами» является предметно-ориентированным и предназначен для обучающихся 10 и 11 классов, сориентированных на получение высшего профессионального
Подробнее
Cрок реализации программы 1 год
Управление образования городского округа «Охинский» Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа г. Охи РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА ОБЪЕДИНЕНИЯ ДОПОЛНИТЕЛЬНОГО
Подробнее
b, где x, y переменные, k, b параметры.
1 Пояснительная записка Основная функция курса по выбору «Решение задач с параметром» направлена на повышение интереса к математике. Общеизвестно, что на вступительных экзаменах в ВУЗы довольно часто предлагаются
Подробнее
Элективный курс «Задачи с параметром»
Элективный курс «Задачи с параметром» Неделя Тема урока неделя Задачи с параметром. Первое знакомство 2 неделя Типы задач с параметрами 3 2 неделя Параметр и поиск решений уравнений, неравенств и их систем
Первое знакомство 2 неделя Типы задач с параметрами 3 2 неделя Параметр и поиск решений уравнений, неравенств и их систем
Подробнее
Знакомые и незнакомые функции
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА 2» Рекомендовано Председатель методсовета Ф. И. О. Протокол от 2016 г. Утверждаю Директор школы О. А.Сорокина
Подробнее
Требования к знаниям и умениям учащихся:
2 Пояснительная записка Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной
Подробнее
Пояснительная записка
Пояснительная записка Программа данного курса предназначена для учащихся 11 класса. Основная цель курса: Создание условий для развития логического мышления, математической культуры и интуиции учащихся
Подробнее
Пояснительная записка
Пояснительная записка 1 Профильное обучение в гимназии направлено на обеспечение углубленного изучения математики, а, значит, прежде всего, на осознанное изучение данного предмета, на развитие математического
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа составлена на основе: — Федерального компонента государственного образовательного стандарта среднего (полного) общего образования (профильный уровень) по математике
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
2 ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Программа разработана на основе авторской программы Шарыгина И. Ф. «Факультативный курс по математике, 8 класс», с учетом требований Обязательного минимума содержания программ по
Ф. «Факультативный курс по математике, 8 класс», с учетом требований Обязательного минимума содержания программ по
Подробнее
Виды деятельности на занятиях:
Пояснительная записка программы платной образовательной услуге «Избранные вопросы математики» для учащихся 0-классов Платная образовательная программа «Избранные вопросы математики» для учащихся 0- классов
Подробнее
«Решение уравнений и неравенств»
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа 32 городского округа Тольятти ПРОГРАММА СПЕЦКУРСА ПО МАТЕМАТИКЕ «Решение уравнений и неравенств» ДЛЯ УЧАЩИХСЯ 9-Х КЛАССОВ
Подробнее
Пояснительная записка
2 Пояснительная записка Рабочая программа элективного курса «Решение задач с параметрами» 9 класса разработана с учетом нормативно-правовых документов: -Закон Российской Федерации от 29. 12.2012г. 273-ФЗ
12.2012г. 273-ФЗ
Подробнее
Powered by TCPDF (
Powered by TCPDF (www.tcpdf.org) Элективный курс «Элементарная алгебра в ЕГЭ » Элективный курс «Элементарная алгебра в ЕГЭ» рассчитан на 34 часа для учащихся 11 классов. Данная программа курса сможет привлечь
Подробнее
<т 2016 г. Рабочая программа
Министерство образования и науки Российской Федерации Экономический лицей Федерального государственного бюджетного образовательного учреждения высшего образования «Российский экономический университет
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа по элективному курсу «Избранные вопросы математики» для учащихся 10 классов составлена на основе примерной программы среднего общего образования (профильный уровень)
Подробнее
Рабочая программа Факультативный курс
Согласовано Утверждаю Руководитель МО математического цикла Директор МОБУ «Боровая СОШ» Дементьева Е. Г. Ерѐмина Т.Н. «26» августа 2015г. 2015г. Рабочая программа Факультативный курс Подготовка к ЕГЭ по
Г. Ерѐмина Т.Н. «26» августа 2015г. 2015г. Рабочая программа Факультативный курс Подготовка к ЕГЭ по
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Статус документа
1 ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Статус документа Элективный курс «Углубленное изучение отдельных тем курса математики» соответствует целям и задачам обучения в старшей школе. Основная функция данного элективного
Подробнее
учебный год
Муниципальное бюджетное общеобразовательное учреждение «Гимназия 1» «Согласовано» Принято решением «Утверждаю» заместитель директора по УВР педагогического совета Директор МБОУ Гимназия 1 Тропина И.А.
Подробнее
Пояснительная записка. Цели предмета:
Пояснительная записка. Основная задача обучения математике в школе — обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой
Подробнее
Пояснительная записка
Пояснительная записка Концепция профильного обучения подразумевает, что реализация идеи профилизации обучения на старшей ступени ставит выпускника основной ступени перед необходимостью совершения ответственного
Подробнее
Пояснительная записка
Пояснительная записка Рабочая программа элективного курса «Задачи с модулями и параметрами», реализуемая в рамках профильного обучения, носит предметно ориентированный характер и предназначена для учащихся
Подробнее
Пояснительная записка
Пояснительная записка Основная задача обучения математике в школе обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Факультативный курс Квадратный трехчлен и его неравенства рассчитан на 34 часа (1 час в неделю), предназначен для учащихся 9-го класса общеобразовательной школы, является предметно-ориентированным.
Подробнее
РАБОЧАЯ ПРОГРАММА. Класс 9
Муниципальное казенное общеобразовательное учреждение Ханты-Мансийского района «Средняя общеобразовательная школа с. Елизарово» Рассмотрена на заседании ШМО Протокол от 20 г. Согласовано Заместитель директора
Подробнее
Пояснительная записка.
Пояснительная записка. Рабочая программа элективного учебного предмета составлена на основе: — авторской программы элективного предмета «Методы решения уравнений» Дрогаченко Т.В., учителя МОУ «СОШ с углубленным
Подробнее
Пояснительная записка
Пояснительная записка Итоговый письменный экзамен по алгебре за курс основной школы сдают все учащиеся 9х классов. Особенности такого экзамена: состоит из двух частей; на выполнение каждой части дается
Подробнее
ПРОГРАММА ЭЛЕКТИВНОГО КУРСА
Приложение к основной образовательной программе основного общего образования муниципального бюджетного общеобразовательного учреждения муниципального образования город Нягань «Средняя общеобразовательная
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры школьника, но их решение вызывает у них значительные затруднения. Это связано
Это связано
Подробнее
«Практикум решения уравнений с модулем»
Аттестационная работа слушателя курсов повышения квалификации по программе: «Проектная и исследовательская деятельность как способ формирования метапредметных результатов обучения в условиях реализации ФГОС»
Кугушева Наталья Ивановна
КГБ ПОУ «Минусинский сельскохозяйственный колледж» г. Минусинск, Красноярский край.
На тему:
Методическая разработка
«Практикум решения уравнений с модулем»
Краткая характеристика методической разработки
- Данная разработка может быть предложена обучающимся 9-11 классов, студентам 1 курса средне-специальных учреждений в рамках урочной деятельности и элективного курса.
- Изучение материала построено по принципу «от простого к сложному». В начале рассматриваются задания на преобразование выражений, содержащих модуль, затем простейшие уравнения с модулем.

- В рамках изучения темы, рассматриваются следующие вопросы: определение и свойства модуля; преобразования выражений, содержащих модуль; решение простейших уравнений с модулем; общие методы решения уравнений с модулем; метод интервалов.
Краткая характеристика КГБ ПОУ «Минусинского сельскохозяйственного колледжа»
- Колледж готовит студентов по специальностям: Механизация сельского хозяйства; Электрификация и автоматизация сельского хозяйства; Теплоснабжение и теплотехническое оборудование; Экономика и бухгалтерский учет; Технология хлебопечения, кондитерских и макаронных изделий.
- Отделение, на котором я работаю, образовалось при объединении колледжа с сельским профессиональным училищем, и готовит для сельского хозяйства рабочих по профессиям: тракторист-машинист сельскохозяйственного производства; повар-кондитер;
портной. Срок обучения на данном отделении 2года 10 месяцев.
Цель и задачи методической разработки
Цель: обобщение и систематизация знаний, связанных с определением и свойствами модуля.
Задачи:
- Повысить интерес к математике за счет дифференцированного подхода к решению математических заданий с модулем.
- Способствовать развитию практического опыта решения уравнений, неравенств и систем уравнений и неравенств, содержащих модули.
- Помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их применения.
- Формировать умение работать со справочной литературой, находить и использовать информацию в рекомендованных изданиях.
Формы работы
В процессе изучения темы «Решение уравнений с модулем» учащиеся могут включиться в такие виды деятельности, как:
- поиск и анализ необходимой информации, в том числе с помощью Интернета;
- работа в группах при составлении и решении заданий;
- устные выступления по способам решения с последующей дискуссией;
- оформление результатов деятельности в форме набора уравнений и неравенств, а также их систем или компьютерной презентации.

Основное содержание работы
Задание 1. Вспомнить или найти в справочной литературе определение модуля.
Модулем (абсолютной величиной) действительного числа называется само это число, если a≥ 0, и противоположное число – a , если a
Основное содержание работы
Задание 2. Работа в группе. Найдите и запишите свойства модуля.
- |a|≥0
- |a|=|-a|
- |a·b|=|a|·|b|
- |a:b|=|a|:|b|
- |a|²=a²
- |a-b| есть расстояние между точками a и b числовой оси.
Основное содержание работы
Презентация основных способов решения уравнений с модулем.
- По определению.
- Возведение обеих частей уравнения в квадрат.
- Замена переменной.
- «Раскрытие» модуля на промежутке знакопостоянства.
- Использования геометрического смысла модуля.
Основное содержание работы
Задание 3. Выбрать, к какому способу решения уравнений с модулем относится каждый из предложенных алгоритмов.
Алгоритм 1.
1. Решить уравнение | а | = а.
2. Решить уравнение | а | = -а.
3. Сделать проверку найденных корней.
4. Записать ответ.
Алгоритм 2.
1. Обозначить | х | = t .
2. Решить полученное уравнение относительно t .
3. Сделать замену на х.
4. Сделать проверку найденных значений х.
5. Записать ответ.
Основное содержание работы
Алгоритм 3.
1. Возвести левую и правую части уравнения в квадрат.
2. В полученном равносильном уравнении найти корни.
3. Сделать проверку. Записать ответ.
Алгоритм 4.
1. Найти нули всех подмодульных выражений,
расположить их по мере возрастания на числовой оси.
2. На полученных интервалах определить знак всех
подмодульных выражений и раскрыть модули по
определению.
3. Найти решение уравнения на каждом интервале.
4. Объединить эти решения. Записать ответ.
Основное содержание работы
Задание 4. Выясните, к какому способу
Выясните, к какому способу
решения уравнений с модулем алгоритм не
предложен. Найдите к этому способу
соответствующие примеры. Составьте
алгоритм решения.
Задание 5. Подберите по 3 примера к каждому
из рассмотренных способов. Решите их,
объясняя каждый этап решения.
- Гайдуков И.И. Абсолютная величина. Пособие для учителей.Изд.2-е.М. «Просвещение»,1995.
- Семенко Е.А. Готовимся к ЕГЭ. Обобщающее повторение курса алгебры и начала анализа. Краснодар: «Просвещение — Юг»,2005, 1 часть.
- Сканави М.И. Сборник задач по математике для поступающих в вузы. М.: ООО «Издательский дом» ОНИКС 21 век.2003.
- Никольский С.М. Алгебра и начала анализа. Изд. «Просвещение», 2009.
- Под ред.Фальке Л.Я.Изучение сложных тем курса алгебры в средней школе. Пособие по математике. Изд.2-е.- М.: Народное образование; Илекса; Ставрополь: Сервисшкола, 2004.
Методы диагностики образовательных результатов
Если учащийся:
- принимал активное участие в практикумах,
- успешно выполнил индивидуальные домашние
задания,
- продемонстрировал умение использовать
справочную литературу,
- научился работать в группах,
- находить и использовать информацию в
рекомендованных изданиях.
То он набирает от 30 до 50 баллов (максимальное
количество 50 баллов) и получает зачет. Каждое
задание 10 баллов.
Перспективы развития исследовательской деятельности в профессиональной работе
1. Систематизация имеющегося материала по темам.
Корректировка групповых и домашних заданий,
используя приемы исследовательской деятельности.
2. Презентация образовательных результатов учащихся
на дистанционных и очных олимпиадах по математике
разного уровня (очная межрегиональная олимпиада
«Ищем Ломоносовых», международная дистанционная
олимпиада научно-образовательного центра
«Эрудит»).
3. Составление групповых и индивидуальных проектов
по математике со студентами 1-2 курсов Минусинского
сельскохозяйственного колледжа.
Решение задач вычислительной электродинамики, или Какой модуль расширения использовать для э/м расчётов?
Вопрос, который постоянно задают сотрудникам технической поддержки нашей компании: «Какой из продуктов COMSOL следует использовать для моделирования конкретного электромагнитного устройства или приложения?» В настоящее время доступно шесть модулей линейки «Электродинамика и оптика», которые расширяют возможности базовой платформы COMSOL Multiphysics®. Кроме того, есть еще шесть модулей из других линеек, которые в той или иной мере также используют различные следствия из уравнений Максвелла в сочетании с другими физиками. Давайте попробуем систематизировать информацию о них.
Кроме того, есть еще шесть модулей из других линеек, которые в той или иной мере также используют различные следствия из уравнений Максвелла в сочетании с другими физиками. Давайте попробуем систематизировать информацию о них.
Примечание: Этот блогпост был первоначально опубликован 10 сентября 2013 года. С тех пор он был дополнен дополнительной информацией и примерами.
Вычислительная электродинамика: Уравнения Максвелла
Уравнения Максвелла связывают плотность электрического заряда, \rho; электрическое поле, \mathbf{E}; электрическое поле смещения, \mathbf{D}; и ток, \mathbf{J}; а также магнитное поле, \mathbf{H}, и магнитную индукцию, \mathbf{B}:
\nabla \cdot \mathbf{D} = \rho | \nabla \cdot \mathbf{J} = 0 |
\nabla \times \mathbf{E} = -\frac{\partial}{\partial t} \mathbf{B} | \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial}{\partial t} \mathbf{D} |
Для решения этих уравнений нам нужен набор граничных условий, а также материальные уравнения (уравнения состояния), которые связывают поле \mathbf{E} с полем \mathbf{D}, поле\mathbf{J} с полем \mathbf{E}, а поле \mathbf{B}с полем \mathbf{H}. Эти уравнения решаются и сопрягаются с другими физиками при различных допущениях в различных модулях линейки расширений COMSOL.
Эти уравнения решаются и сопрягаются с другими физиками при различных допущениях в различных модулях линейки расширений COMSOL.
Примечание: Большинство уравнений, представленных здесь, приведены в сокращенной форме, чтобы передать ключевую концепцию. Полная форму всех управляющих уравнений и материальных соотношения приведена в справочных руководствах и документации по продуктам пакета.
Для начала давайте разберем несколько основополагающих концепций…
Стационарная задача, задача в динамике во временной или частотной области?
Решая уравнения Максвелла, мы обычно стараемся сделать как можно больше корректных предположений с целью сократить вычислительную нагрузку. Уравнения Максвелла могут быть решены для любых произвольно изменяющихся во времени входных данных, но мы часто можем разумно допустить, что входные данные и вычисленные решения являются либо стационарными, либо синусоидально изменяющимися во времени. Первый вариант в литературе часто обозначают как DC (direct current – постоянный ток), а второй – как AC (alternating current – переменный ток) или FD (frequency domain – частотная область).
Предположение стационарного DC режима справедливо, если поля вообще не изменяются во времени или изменяются настолько незначительно, что это не имеет практического значения. Математически это равносильно занулению всех производных по времени в уравнениях Максвелла. Например, если ваше устройство подключено к батарее (которая может заметно разрядиться лишь по прошествии трех и более часов), то это будет очень разумным предположением. Более формально, мы допускаем, что: \frac{\partial \mathbf{B}}{\partial t} = \frac{\partial \mathbf{D}}{\partial t} = 0, что сразу же «убирает» два члена из уравнений Максвелла.
Предположение о AC-режиме справедливо, если любое возбуждение или нагрузка в системе изменяются синусоидально и если отклик системы также изменяется синусоидально на той же частоте. Другими словами – реакция системы линейна. В таких случаях вместо решения задачи во временной области мы можем решить её в частотной области, используя соотношение: \mathbf{E}(\mathbf{x},t) = \Re \left( \exp ^{j \omega t }\mathbf{E_c(x)} \right), где \mathbf{E}(\mathbf{x},t) – поле, изменяющееся в пространстве и времени; \mathbf{E_c(x)}– комплекснозначное поле, изменяющееся в пространстве; и \omega – угловая частота. Решение уравнений Максвелла на множестве дискретных частот очень вычислительно эффективно по сравнению с пошаговым расчётом во временной области, хотя вычислительные требования растут пропорционально числу различных частот, для которых решается задача (с некоторыми оговорками, которые мы обсудим позже).
Решение уравнений Максвелла на множестве дискретных частот очень вычислительно эффективно по сравнению с пошаговым расчётом во временной области, хотя вычислительные требования растут пропорционально числу различных частот, для которых решается задача (с некоторыми оговорками, которые мы обсудим позже).
Расчёт во временной области необходим, когда решение произвольно изменяется во времени или когда отклик системы нелинеен (хотя и здесь есть некоторые исключения, о которых мы еще поговорим). Моделирование во временной области является более сложным с вычислительной точки зрения, чем моделирование в стационарной постановке или в частотной области, поскольку время решения увеличивается пропорционально длительности интересующего нас промежутка времени и при наличии нелинейностей в задаче. При решении задач во временной области полезно заранее оценивать спектральные характеристики вашего входного сигнала, в т.ч. определить самую высокую частоту, которая присутствует в системе и значима.
Электрические поля, магнитные поля или же их совокупность?
Хотя мы можем решить уравнения Максвелла сразу и совместно для электрического и для магнитного полей, но часто возможно и разумно пренебречь одним или другим, особенно в DC постановке. Например, если токи достаточно малы по величине, то магнитные поля будут малы. Даже в тех случаях, когда токи высоки, мы можем не беспокоиться о результирующих магнитных полях. С другой стороны, иногда в системе существует только магнитное поле, но нет электрического поля, как в случае устройства, состоящего только из магнитов и магнитных материалов.
Однако во временной и частотной областях мы должны быть немного осторожнее. Первая характеристика, которую стоит при этом проверить, – это толщина скин-слоя для материалов в нашей модели. Толщина скин-слоя для металла обычно аппроксимируется следующим эмпирическим соотношением \delta = \sqrt{2/{\omega \mu \sigma} }, где \mu – проницаемость, а \sigma– проводимость материала. Если толщина скин-слоя намного больше характерного (электрического) размера объекта, то разумно предположить, что скин-эффект пренебрежимо мал, а решать задачу можно только для электрических полей. Однако, если толщина скин-слоя равна или меньше размера объекта, то индуктивные эффекты важны, и мы должны учитывать как электрические, так и магнитные поля. Полезно сделать быструю проверку толщины скин-слоя перед началом любого э/м расчёта.
Если толщина скин-слоя намного больше характерного (электрического) размера объекта, то разумно предположить, что скин-эффект пренебрежимо мал, а решать задачу можно только для электрических полей. Однако, если толщина скин-слоя равна или меньше размера объекта, то индуктивные эффекты важны, и мы должны учитывать как электрические, так и магнитные поля. Полезно сделать быструю проверку толщины скин-слоя перед началом любого э/м расчёта.
По мере увеличения частоты возбуждения важно также знать первую резонансную частоту устройства или системы. На этой фундаментальной резонансной частоте энергия в электрических и магнитных полях находится точно в равновесии, а мы можем считать, что находимся в высокочастотном режиме. Хотя обычно трудно предварительно оценить резонансную частоту, хорошим эмпирическим правилом является сравнение характерного размера объекта, L_c, с длиной волны, \lambda = c/f. Если размер объекта приближается к значительной доле от длины волны, L_c \approx \lambda/100, то мы приближаемся к высокочастотному режиму. В этом режиме энергия передается в основном посредством излучения через диэлектрические среды, а не через токи внутри проводящих материалов. Это приводит к несколько иной форме управляющих уравнений. Частоты значительно ниже первого резонанса часто называют низкочастотным режимом работы.
В этом режиме энергия передается в основном посредством излучения через диэлектрические среды, а не через токи внутри проводящих материалов. Это приводит к несколько иной форме управляющих уравнений. Частоты значительно ниже первого резонанса часто называют низкочастотным режимом работы.
Давайте теперь посмотрим, как эти различные предположения применяются к уравнениям Максвелла и дают нам различные наборы итоговых расчётных уравнений. Кроме того, мы определимся с тем, какие модули нам нужно будет использовать для каждой из получаемых формулировок.
Моделирование стационарных электрических полей и токов
В предположении стационарного режима можно далее допустить, что мы имеем дело исключительно с проводящими материалами или же с совершенными изоляторами. В первом случае мы можем предположить, что ток течет во всех областях, и уравнения Максвелла могут быть переписаны как:
\nabla \cdot \left( – \sigma \nabla V \right ) = 0
Это уравнение решается для электрического потенциала V, через которых можно выразить электрическое поле, как \mathbf{E} = -\nabla V, а ток, как \mathbf{J} = \sigma \mathbf{E}. Эта формулировка считается базовой и может быть реализована с помощью базовой платформы COMSOL Multiphysics, её решение демонстрируется в т.ч. во вводном демонстрационном примере к программному обеспечению. Модуль AC/DC и модуль MEMS расширяют возможности базовой платформы. При их использовании доступно условие Terminal, упрощающее настройку модели, а также граничные условия для моделирования относительно тонких проводящих и диэлектрических областей, а также отдельные физические интерфейсы для моделирования течения тока через геометрически тонкие, в т.ч. многослойные, структуры.
Эта формулировка считается базовой и может быть реализована с помощью базовой платформы COMSOL Multiphysics, её решение демонстрируется в т.ч. во вводном демонстрационном примере к программному обеспечению. Модуль AC/DC и модуль MEMS расширяют возможности базовой платформы. При их использовании доступно условие Terminal, упрощающее настройку модели, а также граничные условия для моделирования относительно тонких проводящих и диэлектрических областей, а также отдельные физические интерфейсы для моделирования течения тока через геометрически тонкие, в т.ч. многослойные, структуры.
С другой стороны, в предположении, что нас интересуют электрические поля в идеальных изоляторах, описываемых диэлектрической проницаемостью материала \epsilon, мы можем решить уравнение:
\nabla \cdot \left( – \epsilon \nabla V \right ) = 0
Оно позволяет вычислить напряженность электрического поля в диэлектрических областях между объектами (электродами) с различным электрическим потенциалом. Это уравнение также может быть решено с помощью базовой платформы COMSOL Multiphysics, и опять же, модули AC/DC и MEMS расширяют эти возможности, например, с помощью условия Terminal, граничных условий для моделирования тонких диэлектрических областей и тонких зазоров в диэлектрических материалах. Кроме того, эти два продукта дополнительно предлагают формулировку на основе метода граничных элементов, в которой решается то же управляющее уравнение, но имеются некоторые преимущества для моделей, состоящих только из проводов и проводящих поверхностей, как обсуждалось в одной из заметок нашего корпоративного блога.
Это уравнение также может быть решено с помощью базовой платформы COMSOL Multiphysics, и опять же, модули AC/DC и MEMS расширяют эти возможности, например, с помощью условия Terminal, граничных условий для моделирования тонких диэлектрических областей и тонких зазоров в диэлектрических материалах. Кроме того, эти два продукта дополнительно предлагают формулировку на основе метода граничных элементов, в которой решается то же управляющее уравнение, но имеются некоторые преимущества для моделей, состоящих только из проводов и проводящих поверхностей, как обсуждалось в одной из заметок нашего корпоративного блога.
Моделирование электрических полей и токов в динамике во временной и частотной областях
При наличии задачи смоделировать изменяющиеся во времени электрические поля, в формулировке сразу появятся токи проводимости и смещения, и вам потребуются интерфейсы и инструменты, входящие в состав либо модуля AC/DC, либо модуля MEMS. Уравнения немного отличаются от первого уравнения, приведенного выше, и в случае формулировки для временной области записываются как:
\nabla \cdot \left( \mathbf{J_c +J_d} \right ) = 0
Это уравнение решается как для токов проводимости, \mathbf{J}_c = \sigma \mathbf{E}, так и для токов смещения, \mathbf{J}_d = \frac{ \partial \mathbf{D}}{\partial t}. Такой подход целесообразно использовать, когда исходные сигналы негармоничны и вы хотите мониторить реакцию системы с течением времени. Пример такой задачи можно увидеть в учебной модели «Моделирование переходных процессов в конденсатора, подключенного в электрическую цепь».
Такой подход целесообразно использовать, когда исходные сигналы негармоничны и вы хотите мониторить реакцию системы с течением времени. Пример такой задачи можно увидеть в учебной модели «Моделирование переходных процессов в конденсатора, подключенного в электрическую цепь».
В частотной области мы можем использовать следующую стационарную формулировку:
\nabla \cdot \left( – \left( \sigma + j \omega \epsilon \right) \nabla V \right ) = 0
Токи смещения в этом случае определяются как \mathbf{J}_d = j \omega \epsilon \mathbf{E}. Примером использования этого уравнения является модель «Моделирование работы конденсатора в частотной области».
Держите в уме, что при моделировании только электрических полей не учитываются вихревые токи. При необходимости их рассмотрения следует решать магнитную задачу в динамике.
Моделирование магнитных полей с помощью модуля AC/DC
Моделирование магнитных полей в стационарном, динамическом или низкочастотном режиме реализуется с помощью модуля AC/DC. 2 \epsilon \mathbf{A}, и начинает выглядеть довольно похоже на волновое уравнение. Фактически, это уравнение можно использовать до и в окрестности резонанса системы в предположении, что излучение пренебрежимо мало, см. пример: Моделирование 3D-индуктора.
2 \epsilon \mathbf{A}, и начинает выглядеть довольно похоже на волновое уравнение. Фактически, это уравнение можно использовать до и в окрестности резонанса системы в предположении, что излучение пренебрежимо мало, см. пример: Моделирование 3D-индуктора.
Более полный обзор использования приведенных выше наборов уравнений для моделирования магнитных полей представлен в нашей серии видеолекций по моделированию электромагнитных катушек.
Также можно смешивать уравнения относительно магнитного скалярного потенциала и векторного потенциала, что актуально и применимо для расчета электродвигателей и генераторов.
В дополнение к вышеприведенным уравнениям относительно магнитного векторного потенциала и скалярного потенциала существует также отдельная формулировка в терминах магнитного поля, которая подходит для моделирования сверхпроводящих материалов. См. демонстрационную модель сверхпроводящего провода.
Моделирование электромагнитных волн в частотной и временной областях с помощью модулей Радиочастоты или Волновая оптика
Когда мы выходим на высокочастотный режим, электромагнитные поля становятся волнообразными по своей природе, что учитывается при моделировании антенн, микроволновых контуров, оптических волноводов, микроволнового нагрева и рассеяния в свободном пространстве, а также рассеяния от объектов, интегрированных на подложке. 2 \epsilon_0 \mu_0 \left(\epsilon_r – j \sigma/\omega \epsilon_0 \right) \mathbf{E} = 0
2 \epsilon_0 \mu_0 \left(\epsilon_r – j \sigma/\omega \epsilon_0 \right) \mathbf{E} = 0
Это уравнение записывается в терминах электрического поля, \mathbf{E}, а магнитное поле вычисляется как j \omega \mathbf{B} = \nabla \times \mathbf{E} . В такой формулировка задача может быть решена либо для заданного набора частот, либо как задача на поиск собственных частот, в рамках которой определяются резонансные моды устройства. Из примеров анализа собственных частот можно отметить несколько эталонных моделей расчёта замкнутых полостей, катушек и резонатора Фабри–Перо, при этом доступен расчет как непосредственно резонансных частот, так и добротности таких систем.
При исследовании отклика системы в диапазоне заданных частот можно непосредственно решать задачу на множестве дискретных частот, и в этом случае вычислительные затраты линейно масштабируются с числом заданных частот. Альтернативно можно использовать распараллеливание на отдельных компьютерах, так и на кластерах для ускорения решений. {-1} \nabla \times \mathbf{A} \right)+ \mu_0 \sigma \frac{ \partial \mathbf{A}}{\partial t} +\mu_0 \frac{ \partial}{\partial t}\left( \epsilon_0 \epsilon_r \frac{ \partial \mathbf{A}}{\partial t} \right) = 0
{-1} \nabla \times \mathbf{A} \right)+ \mu_0 \sigma \frac{ \partial \mathbf{A}}{\partial t} +\mu_0 \frac{ \partial}{\partial t}\left( \epsilon_0 \epsilon_r \frac{ \partial \mathbf{A}}{\partial t} \right) = 0
Это уравнение также решается для магнитного векторного потенциала, но включает в себя как первую, так и вторую производные по времени, таким образом, позволяя учитывать как токи проводимости, так и токи смещения. Такая формулировка применима для моделирования оптических нелинейностей, дисперсионных материалов и распространения сигналов. Результаты во временной области также могут быть преобразованы в частотную область с помощью специального решателя, проводящего быстрое преобразования Фурье, как показано в этом примере.
Вычислительные требования для решения волновых уравнений с точки зрения потребления памяти вызывают беспокойство. Устройство, представляющее интерес, и пространство вокруг него дискретизируются с помощью сетки конечных элементов, и эта сетка должна быть достаточно подробной для разрешения длины волны. То есть, как минимум, потребуется выполнение критерия Найквиста (теоремы Котельникова). На практике это означает, что расчет задачи при размере домена около 10 x 10 x 10 длин волн (независимо от рабочей частоты) потребует рабочей станции, на которой доступно не менее 64 ГБ оперативной памяти. По мере увеличения размера области (или увеличения частоты) требования к памяти будут расти пропорционально количеству кубических длин волн, для которых решается задача. Это означает, что данная формулировка хорошо подходит для структур, характерный размер которых примерно не превышает 10-кратной длины волны на самой высокой рабочей частоте, представляющей интерес. Однако есть два способа обойти этот предел.
То есть, как минимум, потребуется выполнение критерия Найквиста (теоремы Котельникова). На практике это означает, что расчет задачи при размере домена около 10 x 10 x 10 длин волн (независимо от рабочей частоты) потребует рабочей станции, на которой доступно не менее 64 ГБ оперативной памяти. По мере увеличения размера области (или увеличения частоты) требования к памяти будут расти пропорционально количеству кубических длин волн, для которых решается задача. Это означает, что данная формулировка хорошо подходит для структур, характерный размер которых примерно не превышает 10-кратной длины волны на самой высокой рабочей частоте, представляющей интерес. Однако есть два способа обойти этот предел.
Одним из подходов к расчету э/м полей вокруг объекта, значительно меньшего длины волны, является явная формулировка Time Explicit. Она основа на другой форме записи уравнений Максвелла для временной области, которые могут быть решены с использованием гораздо меньшего объема памяти. Данная формулировка в первую очередь предназначена для моделирования линейных задач и будет полезна в ряде ситуаций, например, для исследования широкополосного рассеяния фонового поля на объекте. 2 \epsilon_0 \mu_0 \left(\epsilon_r – j \sigma/\omega \epsilon_0 \right) \mathbf{E_e} = 0
2 \epsilon_0 \mu_0 \left(\epsilon_r – j \sigma/\omega \epsilon_0 \right) \mathbf{E_e} = 0
Где электрическое поле представляется как \mathbf{E} = \mathbf{E_e} \exp \left (-i \phi \right), а \mathbf{E_e} – огибающая электрического поля.
Дополнительная переменная, \phi, представляет собой так называемую фазовую функцию, которая должна быть известна, по крайней мере приблизительно, и задана как входная информация. К счастью, для многих оптических волноводных задач это действительно так. Можно решать задачу для одного или двух таких полей огибающей пучка одновременно. Преимущество этого подхода заключается в том, что требования к памяти намного ниже, чем для полноволнового уравнения, представленного в начале данного раздела. Примеры его использования: расчёты направленного ответвителяи моделирование самофокусировки в оптическом стержне.
Выбор между модулями AC/DC, Радиочастоты и Волновая оптика
Разделение областей использования модулей AC/DC и Радиочастоты достаточно нечеткое. Полезно задать себе несколько следующих вопросов:
Полезно задать себе несколько следующих вопросов:
- Излучают ли устройства, для которых планируется исследование, значительное количество энергии? Интересен ли расчёт резонансов? Если это так, то более подходящим является модуль Радиочастоты.
- Как соотносится размер устройства с длиной волны? Он намного меньше длины волны на самой высокой рабочей длине волны? И в первую очередь интересуют магнитные поля? Если это так, то более подходящим является модуль AC/DC.
Если вы находитесь в пограничной ситуации, то может быть разумно иметь оба продукта в вашей конфигурации лицензии.
Выбор между модулями Радиочастоты и Волновая оптика подразумевает конкретизацию области применения. Между этими модулями существует много совпадений и пересечений по функциональным возможностям в контексте полноволнового моделирования на основе уравнений Максвелла во временной и частотной областях, однако есть некоторые небольшие различия в граничных условиях. Так называемые граничные условия типа Lumped Port (Сосредоточенный порт) и Lumped Element (Сосредоточенный элемент) актуальны для моделирования СВЧ-устройств и поэтому доступны при наличии именно модуля Радиочастоты. Также имейте в виду, что только в модуле Волновая оптика доступна формулировка Beam Envelopes.
Также имейте в виду, что только в модуле Волновая оптика доступна формулировка Beam Envelopes.
Кроме того, эти два продукта поставляются с различными библиотеками материалов: модуль Радиочастоты включает набор стандартных диэлектрических подложек, в то время как модуль Волновая Оптика включает данные о показателе преломления более тысячи различных материалов в оптическом и ИК-диапазоне. Для получения более подробной информации об этих и других доступных библиотеках материалов см. наш исчерпывающий обзор.
Конечно, если у вас есть дополнительные уточняющие вопросы, то свяжитесь с нами. Краткое описание логики разделения функционала этих модулей приведено на рисунке ниже.
Трассировка оптических лучей с помощью модуля Геометрическая оптика
Если вы моделируете устройства, размер которых во много тысяч раз превышающие длину волны, то уже нереалистично разрешить длину волны с помощью сетки конечных элементов. В таких случаях мы также предлагаем использовать модуль Геометрическая оптика. Реализованный в нем подход не решает напрямую уравнения Максвелла, а вместо этого позволяет трассировать оптические лучи в расчётной области. Этот подход требует построения сетки только на отражающих поверхностях и диэлектрических областях, но не на однородном свободном пространстве. Указанная технология применима для моделирования линз, телескопов, больших лазерных резонаторов, а также для сопряженного анализа механических, тепловых и оптических эффектов в больших оптических системах (STOP-analysis). Трассировку лучей и полноволновый анализ пожно сопрягать так, как показано в следующей учебной модели.
Реализованный в нем подход не решает напрямую уравнения Максвелла, а вместо этого позволяет трассировать оптические лучи в расчётной области. Этот подход требует построения сетки только на отражающих поверхностях и диэлектрических областях, но не на однородном свободном пространстве. Указанная технология применима для моделирования линз, телескопов, больших лазерных резонаторов, а также для сопряженного анализа механических, тепловых и оптических эффектов в больших оптических системах (STOP-analysis). Трассировку лучей и полноволновый анализ пожно сопрягать так, как показано в следующей учебной модели.
Мультифизическое моделирование электродинамических систем
Помимо решения непосредственно уравнений Максвелла, одной из основных сильных сторон программы COMSOL Multiphysics является решение задач, где есть связи между несколькими физиками. Одним из наиболее распространенных примеров является связь между уравнениями Максвелла и уравнениями теплопередачи, при которой повышение температуры влияет на электрические (а также тепловые) свойства системы. Обзор способов решения подобных электротермических проблем можно найти в этом блоге.
Обзор способов решения подобных электротермических проблем можно найти в этом блоге.
Также важно сочетать механические расчеты и исследования электрических и магнитных полей. Иногда это просто связано с учётом деформаций электронных компонентов, но в ряде случаев требуется анализ пьезоэлектрических, пьезорезистивных, магнитострикционных или даже оптомеханических эффектов и материалов. Все указанные связки реализуются в программе. Модуль MEMS также предлагает специальный физический интерфейс для расчета кремниевых микромеханических резонаторов с электростатической актуацией. Механические контакты и протекание тока между контактирующими частями также могут быть рассмотрены в контексте моделирования электрических токов.
Помимо сопряжения с тепловым и механическим анализом, вы также можете решать уравнения Максвелла для электрического тока с учетом химических процессов в электролитах, что реализовано в модулях Электрохимия, Электрохимические аккумуляторы, Электроосаждение и Коррозия. В модуле Плазма вы даже можете исследовать физико-химические процессы, лежащие в основе электрических разрядов, а с помощью модуля Трассировка частиц вы можете исследовать движение заряженных частиц в электрических и магнитных поля. Наконец наш модуль Полупроводники рассчитан на моделирование динамики электронов и дырок в полупроводниковых системах в дрейфово-диффузионном приближении. Каждый из этих модулей определенно достоин отдельного обзора, поэтому мы не будем пытаться рассмотреть их их функционал прямо здесь.
В модуле Плазма вы даже можете исследовать физико-химические процессы, лежащие в основе электрических разрядов, а с помощью модуля Трассировка частиц вы можете исследовать движение заряженных частиц в электрических и магнитных поля. Наконец наш модуль Полупроводники рассчитан на моделирование динамики электронов и дырок в полупроводниковых системах в дрейфово-диффузионном приближении. Каждый из этих модулей определенно достоин отдельного обзора, поэтому мы не будем пытаться рассмотреть их их функционал прямо здесь.
Если вы хотите обсудить любой из этих модулей более подробно и узнать, как он применим к интересующему вас устройству или процессу, не стесняйтесь обращаться к нам с помощью контактной формы по нажатию на кнопку ниже.
Решение уравнений с модулем — презентация онлайн
1. Решение уравнений с модулем
Учителя МОУ СОШ №23
Сурмалян Л.М.
Кущевский район.
2. Обучение- это ремесло, использующее бесчисленное количество маленьких трюков.
3.
 Задание 1. IХ-3I=5 Отметьте точки, координаты которых удовлетворяют указанному условию. Запишите их координаты.
Задание 1. IХ-3I=5 Отметьте точки, координаты которых удовлетворяют указанному условию. Запишите их координаты.
Отметим точки, удаленные от точки А на 5 единичных
отрезков. Запишем их координаты.
4. Геометрическая интерпретация
Уравнение Iх – аI = b, где b > 0, допускает простую
геометрическую интерпретацию.
Решить уравнение Iх – 1I = 3 – значит найти все
точки числовой оси, которые отстоят от точки с
координатой (1) на расстоянии 3.
Ответ: -2 ; 4.
5. Геометрическая интерпретация
Решить уравнение Iх + 2I = 3 – значит найти все
точки числовой оси, которые отстоят от точки
с координатой (-2) на расстоянии 3.
Ответ: -5 ; 1.
6. Задание 2. Решите уравнения
IХ – 4I = 3
I х + 2 I= 7
ответ 1; 7
5; -9
7. Метод интервалов
Уравнение вида:
b1I x – a1I + … + bnI x – anI = b,
где a1
решается методом интервалов.
Суть: точки a1 , a2 , …, an числовую ось делят на
непересекающиеся промежутки знакопостоянства.
Решаем уравнение на каждом промежутке;
совокупность решений на всех промежутках и
составит решение исходного уравнения.
8. Решение уравнений.
Ⅰ
x
-x+2-x-3=7
X=-4
Iх — 2I + Iх + 3I = 7
Ⅱ
-3
-x+2+x+3=7
решений нет
Ответ: -4; 3.
Ⅲ
x>2
x-2+x+3=7
x=3
9. Решение уравнений.
Ⅰ
x
-x+5+x-2=3
X
Iх — 5I — Iх — 2I = 3
Ⅱ
2
-x+5-x+2=3
x=2
Ответ: x
Ⅲ
x>5
x-5-x+2=3
решений нет
10. Геометрическая интерпретация
Уравнения
Ix – aI + Ix – bI =c и Ix – aI — Ix – bI =c
имеют простую геометрическую интерпретацию.
Вернемся к предыдущим уравнениям.
11. Пример 1.
Решить уравнение
Iх — 2I + Iх + 3I = 7 – это
значит найти все точки на числовой оси Ох, для
каждой из которых сумма расстояний до точек с
координатами (2) и (-3) равна 7. Внутри отрезка
таких точек нет, так как длина меньше семи, значит
точки вне отрезка.
Ответ: -4; 3.
12. Пример 2.
Решить уравнение
Iх — 5I — Iх — 2I = 3 – это
значит найти все точки на числовой оси Ох, для
каждой из которых разность расстояний от нее до
точки с координатой (5) и расстояний от нее до
точки с координатой (2) равнялось 3. Длина отрезка
равна 3 следовательно любая точка левее (2) будет
решением уравнения.
Ответ: x
13. Пример 3.
IX — 1I + IX — 2I + IX — 3I =2
Построим графики функций:
Y=IX — 1I +
y
4
0
2
4
IX — 3I и Y= 2 — IX — 2I
пересечение графиков
точка (2;2)
Ответ: 2.
6
x
14. Обобщение.
Если в уравнении Ix – aI + Ix – bI =c,
Iа – bI
отрезка [a;b];
а если Ia – bI=c, то отрезок [a;b] будет
решением уравнения;
если Ia – bI>c, то уравнение решений иметь
не будет.
15. Обобщение.
Если в уравнении Ix – aI — Ix – bI =c,
Iа – bI = c, то при a b
a > b, x
если Ia – bI
если Ia – bI>c, то решение лежит внутри
отрезка [a;b].
16. Домашняя работа.
IX + 3I + IX — 3I =6
IX — 1I + IXI = 9
IX — 3I + IX — 1I =3
IX + 6I + IX + 4I =5
IX — 1I – IX + 1I = 3
I5 + XI – Iх – 8I = 13
IX — 3I + 2IX + 1I =4
IX — 4I + IX — 2I = IX+ 1I
IX+1I +IX-2I+IX-5I=6
Графический метод решения модуль содержащих задач с параметрами Текст научной статьи по специальности «Математика»
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ МОДУЛЬ СОДЕРЖАЩИХ ЗАДАЧ С ПАРАМЕТРАМИ Григорян К.М. Email: [email protected]
Григорян Карине Микитовна — ассистент, кафедра ИТ и естественных наук, Шушинский технологический университет, г. Шуши, Республика Армения
Аннотация: в статье рассмотрены примеры применения графического метода решения модуль содержащих задач с параметрами. Для построения графической модели задачи в зависимости от особенностей задачи используется координатная плоскость или параметрические плоскости. При этом плоскость построения разбивается на области, в каждом из которых выражения, стоящие под знаком модуля, сохраняют свой знак. В каждой из этих областей строится соответствующий график. Решение задачи определяется по графику с исследованием семейства кривых, зависящих от параметра
При этом плоскость построения разбивается на области, в каждом из которых выражения, стоящие под знаком модуля, сохраняют свой знак. В каждой из этих областей строится соответствующий график. Решение задачи определяется по графику с исследованием семейства кривых, зависящих от параметра
Ключевые слова: задача, модуль, параметр, плоскость построения, разбиение, решение.
GRAPHICAL METHOD OF SOLUTION OF THE CONTAINING MODULE TASK WITH PARAMETERS Grigoryan K.M.
Grigoryan Karine Mikitovna — assistant, CHAIR OF IT AND NATURAL SCIENCES, SHUSHI UNIVERSITY OF TECHNOLOGY, SHUSHI, REPUBLIC OF ARMENIA
Abstract: the article describes the examples of the graphical method of solving the module problems with parameters. To build a graphical model of the problem, depending on the features of the problem, a coordinate plane or parametric planes are used. In this case, the plot plane is divided into areas, in each of which the expressions under the module sign retain their sign. In each of these areas, a corresponding graph is drawn. The solution of the problem is determined by the graph with the study of a family of curves that depend on the parameter. Keywords: task, module, option, plane, build, split, chart, decision.
In this case, the plot plane is divided into areas, in each of which the expressions under the module sign retain their sign. In each of these areas, a corresponding graph is drawn. The solution of the problem is determined by the graph with the study of a family of curves that depend on the parameter. Keywords: task, module, option, plane, build, split, chart, decision.
УДК 512. 1
При решении модуль содержащих уравнений, неравенств и их систем с параметрами часто применяется графический метод, преимущество которого в наглядности и краткости решения. Аналитическое решение подобных задач, основанное на определении модуля, сводится к решению совокупности различных систем, что может быть более длинным и громоздким, особенно, если алгебраическое выражение задачи содержит несколько модулей. Суть графического метода состоит в условном разбиении координатной плоскости на области, в каждом из которых выражения, находящиеся под знаком модуля, сохраняют свой знак и последующем построении в каждой области соответствующих графиков.
проходит через точку ( — ~~~;О ) или через точку ( О ;2 а 2 ) .
а2
В первом случае, при х — — — , у — О из уравнения прямой получим:
а2 а
—-=0оа+а = 0оа = —1
2 2
Итак.
графику определяя знаки корней (они положительны) и выражения, содержащегося под знаком внешнего модуля.
2
хх — — — Для нахождения двух других корней, рещим уравнение (1), по
х + — = |4х ■
■2 фф
х + — = 4х ■
2
х + — = 2 — 4х
2
5
X = —
6
Х ю
Во втором случае, при , из уравнения прямой получим:
а ‘ 1
2а2 =—ФФа = —
2 4
Аналогично, найдем два других корня, решив уравнение (1) с учетом знаков корней и выражения, содержащегося под знаком модуля ( они определяются по
граф
)ику). Уравнение (1) равносильно следующей совокупности:
Уравнение (1) равносильно следующей совокупности:
х Н— = |—4х — 2а 8 1
х + — = |4х — 2а21
х + — = —4х — 2 а
8
1 9
х + — = 4х — 2 аг
х = —-
х = —
12
Итак, при
— ,х7 — —,хо — — при а — — х, ——,х7 — о , х-, — —.
2 10 л 6 г 4 х 20 -3 12
Пример 2,Найти все значения параметра а, при каждом из которых неравенство 3 — | х — а | > х 2 имеет хотя бы одно отрицательное решение.
Решение.Перепишем искомое неравенство в виде 3—х 2 > | х —а | (2) и построим в координатной плоскости хОу графики функций у=3 — х 2 и у = | х — а | (рис.2).
У , у = \х-а\
у = \х — я1
£1! -т/3 \ о \л/3 а2 у = 3-х2 X
Рис. 2. Графики функций
Неравенство (2) имеет хотя бы одно отрицательное решение при (см.
рис.2). Очевидно, что а2=3. Так как при ах < а < — //3 отрицательные корни неравенства больше , то выражение принимает положительные значения, и,
следовательно, неравенство (2) примет вид: х2+х — а — 3<О
Последнее неравенство имеет корни, если дискриминант положителен, то есть 4а + 1 3 > О о а > — —. о
о
при — — < а < 3 .
Пример 3.Найти все значения параметров а и Ь, при каждом из которых система уравнений
(\х + у\=х — у + а (1)
||х-у|=х + у + Ь (2)
имеет бесчисленное множество решений,
Решение. Построим в координатной плоскости х0у графики уравнений (1) и(2) .Прямая у=-х разбивает координатную плоскость на две полуплоскости, в каждом из которых выражение, стоящее под знаком модуля в уравнении (1), сохраняет свои знак.Если у>-х, то у=а/2, если у<-х, то х=-а/2. Таким образом, графиком уравнения (1) являются два параллельных координатным осям луча, исходящие из точки (-а/2;а/2). Аналогично, прямая у=х разбивает координатную плоскость на две полуплоскости, в каждом из которых выражение, стоящее под знаком модуля уравнения (2), сохраняет свой знак. При у>х имеем у=-Ь/2, а при у<х , х=-Ь/2. Итак, графиком уравнения (2) являются два параллельных осям координат луча, исходящие из точки (-Ь/2;-Ь/ 2).
При у>х имеем у=-Ь/2, а при у<х , х=-Ь/2. Итак, графиком уравнения (2) являются два параллельных осям координат луча, исходящие из точки (-Ь/2;-Ь/ 2).
Искомая система имеет бесчисленное множество решений при взаимном расположении графиков уравнений (1) и (2), показанных на рисунках 3 и 4, соответствующих случаям и .
/
/
N /
Ч /
ч а ;
ч — У
ч 2 /
ч /
ч ?
ч /
ч /
ч /
у? 9″
а 2 у У / / / / / /■ \ ч ч ч 1 X 2 \ ч ч ч ч
/ ч ч
Рис. (рис.4).
(рис.4).
Заключение. Особенностью графического метода решения модуль содержащих задач с псрсметрами является разбиение плоскости построения на области, в каждом из которых выражения, находящиеся под знаком модуля, сохраняют свой знак.Построив в этих областях соответствующие графики, можно определить решение задачи в зависимости от значений параметра. Наличие параметра обусловливает рассмотрение множества кривых у=Дх) в плоскости хОу.Во многих случаях более рационалзно применение параметрических плоскостей а0х или х0а (см. [1]).
Список литературы /References
1. Григорян К.М., Арутюнян Р.М Модуль содержащие уравнения с параметрами.Ученые записки Арцахского государственного университета,1/2017, стр.33-39
2. Старков В.Н. 165 задач с параметрами (в помощь абитуриенту) // Методические указания. СПб. Изд. СПБГУ, 2004. 25 с.
СПб. Изд. СПБГУ, 2004. 25 с.
3. Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.И. Задачи по математике. Уравнения и неравенства. М.: Наука, 1987. 240 с.
Модуль 5: Процесс решения проблемы
Исходя из информации, полученной на этапах 1 и 2 (см. Таблица 1: Процесс решения проблем ), вы должны быть готовы выбрать подход к разрешению жалобы, действовать и оценивать результат. Помните о потенциальных препятствиях, выявленных на этапе 2, и будьте достаточно гибкими, чтобы использовать другой подход, если ваш первоначальный выбор не дает ожидаемых результатов.
Разрешение означает просто найти решение. Иногда вы будете разрабатывать решение, чтобы попытаться «продать» соответствующим сторонам; в других случаях вам, возможно, придется объединить людей и помочь им выработать значимые решения.Важным моментом является то, что решение должно «исправлять» проблему. Например, помощь жителю в поиске утерянной одежды может быть приятным делом, но это не является долгосрочным решением проблемы неправильного обращения со стиркой или личными вещами. В другом случае у вас может быть помощница медсестры, которая согласится позволить ординатору не ложиться спать допоздна, что является обычным делом ординатора. Для достижения долгосрочного решения, возможно, потребуется пересмотреть план ухода за жильцом или сделать отметку в ее записях о том, что она предпочитает более поздний отход ко сну.Об этом изменении необходимо уведомить весь персонал, работающий в ночное время с этим резидентом. Без этих дополнительных шагов более позднее время отхода ко сну могло бы быть лишь достижением на одну ночь; тогда вам придется столкнуться с той же проблемой во второй раз.
Например, помощь жителю в поиске утерянной одежды может быть приятным делом, но это не является долгосрочным решением проблемы неправильного обращения со стиркой или личными вещами. В другом случае у вас может быть помощница медсестры, которая согласится позволить ординатору не ложиться спать допоздна, что является обычным делом ординатора. Для достижения долгосрочного решения, возможно, потребуется пересмотреть план ухода за жильцом или сделать отметку в ее записях о том, что она предпочитает более поздний отход ко сну.Об этом изменении необходимо уведомить весь персонал, работающий в ночное время с этим резидентом. Без этих дополнительных шагов более позднее время отхода ко сну могло бы быть лишь достижением на одну ночь; тогда вам придется столкнуться с той же проблемой во второй раз.
Важно распознать, когда было достигнуто решение проблемы или соглашение. . Некоторые люди настолько вовлекаются в расследование или переговоры, что не понимают, что они добились своего или решили проблему. С другой стороны, вы также должны распознавать, когда удовлетворительное решение не было достигнуто, и проблема продолжает повторяться.Если удовлетворительное соглашение не достигнуто, пора обсудить проблему с вашим руководителем LTCO или с омбудсменом штата по долгосрочному уходу (SLTCO).
С другой стороны, вы также должны распознавать, когда удовлетворительное решение не было достигнуто, и проблема продолжает повторяться.Если удовлетворительное соглашение не достигнуто, пора обсудить проблему с вашим руководителем LTCO или с омбудсменом штата по долгосрочному уходу (SLTCO).
ВИДЕО: Решение проблем до разрешения
Проследите за решением проблемы Мэри до разрешения в видеоролике ниже.
Страница не найдена — PHI
НовостиМнениеРазработка государстваРесурсКейсыИстория воздействияЭкспертКлиент / Партнер / Сторонник / Система города Нью-ЙоркаВакансииСтраница
Расширенные роли Дизайн учебной программыМодели домохозяйстваОрганизационная деятельность и развитие лидерских качествPHI Coaching Approach® Общественное образование и обмен сообщениямиНабор и удержаниеИсследования и анализ политикиОбучение
Эллисон Кук, Стивен Кэмпбелл, Мария, Елена Дель Валле, Роберт Эспиноза, Пегги Пауэлл, Кезия Скейлс, доктор философии, Джоди М. SturgeonAngelina Del Rio DrakeSandra E. SmithErica Brown-MyrieMartha MedinaIrma RiveraAbigail BarriosMichael ElsasDonna CalameDenise ClarkAnne GeggieKaren KulpJerry PhilipAdria PowellEmily DieppaLois MorganArielle AltmanKathleen GrahamCassandra Мартин-Himmons, LMSWYarissa SorianoBrian DiPaoloMandy TownsendSweta AdhikariBettyRose GreenAmy SohnJenny Фридлер
SturgeonAngelina Del Rio DrakeSandra E. SmithErica Brown-MyrieMartha MedinaIrma RiveraAbigail BarriosMichael ElsasDonna CalameDenise ClarkAnne GeggieKaren KulpJerry PhilipAdria PowellEmily DieppaLois MorganArielle AltmanKathleen GrahamCassandra Мартин-Himmons, LMSWYarissa SorianoBrian DiPaoloMandy TownsendSweta AdhikariBettyRose GreenAmy SohnJenny Фридлер
AlabamaAlaskaArizonaArkansasCaliforniaColoradoConnecticutDelawareDistrict из ColumbiaFloridaGeorgiaHawaiiIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaOhioOklahomaOregonPennsylvaniaRhode IslandSouth CarolinaTennesseeTexasUnited StatesUtahVermontVirginiaWashingtonWest VirginiaWisconsinWyoming
Сбор данных и качество Расширенный доступ и культурная компетентностьУход в семьеУход за людьмиОбучение и повышенные роли Заработная плата и льготы
Ресурсный центр по болезни АльцгеймераCaledonian House at Scottish HomeЦентры для услуг Medicare и Medicaid Центр общественной политики в области жизниЦентр еврейской реабилитацииLorettoПартнеры в CareTrinity Health Сообщества пожилых людейWestminster Canterbury
1199SEIU и 1199SEIU Фонд обучения и образованияАмериканское общество по проблемам старенияАспенский институтЗабота о разных поколенияхЦентр по продвижению паллиативной помощиАльянс работников по уходу за престарелымиСотрудники по уходу за детьмиПоддержки по уходу за домомВакансии
Каталог модулей
— Университет Ньюкасла
MAS1801: Решение проблем и вычисления I (неактивный)
- Неактивен в течение года: 2021/22
- Руководители модуля: Доктор Эндрю Флетчер
- Лектор: Доктор Стюарт Холл, доктор Крис Грэм
- Собственная школа: Математика, статистика и физика
- Место преподавания: Кампус Ньюкасл-Сити
Семестры
| Стоимость кредита за семестр 1: | 10 |
| Кредиты ECTS: | 5. 0 0 |
Цели
Цель модуля — помочь учащимся обдумать и решить проблемы, которые не были им непосредственно продемонстрированы и которые можно сформулировать математически
Краткое описание модуля
Хотя формально следует рассматривать два отдельных модуля, MAS1801 и MAS1802 как пара. Цель состоит в том, чтобы позволить студентам испытать независимое мышление и критическую оценку, а не более традиционное преподавание и изучение математики.Это будет достигнуто путем представления незнакомых проблем для решения с минимальным указанием методов или без них. Некоторые проблемы могут быть выражены уже на математическом языке, тогда как другие будут основаны на сценариях реального мира, и первая задача будет заключаться в том, чтобы логически осмыслить смысл проблемы и то, как выразить ее таким образом, чтобы это могло быть решено. Студенты будут работать над разными задачами в одиночку или в группах, модуль будет побуждать студентов писать и представлять математику ясно и точно, а также потребуется использование компьютеров для поддержки обучения и решения задач.
План программы
Использование Python для математических вычислений. Начало работы, ввод и вывод, типы данных, построение графиков и простые вычисления, управляющие операторы, функции.
Индивидуальные и групповые задачи, основанные на существующих математических знаниях (например, исчисление, последовательности и серии, функции одного значения, построение кривых и простой численный анализ, линейная алгебра, матричные манипуляции, перестановки и комбинации).
Математические задачи и головоломки из логики, теории чисел, геометрии, алгебры, вероятности, стратегии.
Методы преподавания
Обратите внимание, , что руководители модулей пересматривают методы обучения и оценки модулей для модулей семестра 2 в свете ограничений Covid-19. Также могут быть внесены некоторые дальнейшие изменения в модули семестра 1. Окончательная информация будет доступна к концу августа 2020 года для модулей 1-го семестра и к концу октября 2020 г. для модулей 2-го семестра.
Педагогическая деятельность
| Категория | Действия | Номер | Длина | Студенческие часы | Комментарий |
|---|---|---|---|---|---|
| Запланированная учебная и преподавательская деятельность | Лекция | 13 | 1:00 | 13:00 | Официальные лекции |
| Запланированная учебная и преподавательская деятельность | Лекция | 10 | 2:00 | 20:00 | Проблемные классы |
| Независимое управляемое исследование | Подготовка и завершение оценки | 1 | 1:30 | 1:30 | Невидимый экзамен |
| Независимое управляемое исследование | Подготовка к оценке и завершение | 1 | 13:00 | 13:00 | Ревизия для невидимого экзамена |
| Управляемое независимое исследование | Подготовка и завершение оценки | 1 | 7:30 | 7:30 | Подготовка проекта |
| Плановая учебно-педагогическая деятельность | D rop-in / хирургия | 12 | 0:10 | 2:00 | Часы работы |
| Независимое исследование под руководством | Независимое исследование | 1 | 43:00 | 43:00 | Обучение, практика и понимание материала курса |
| Итого | 100: 00 |
Обоснование преподавания и взаимосвязь
После первой недели лекций, посвященных модулю, объясняющему ожидания студентов, организацию модуля, распределение студентов по командам и распространение материалов курса, будет одна часовая лекция и одна две лекции. -часовое занятие по проблемам в неделю в течение десяти недель.Лекции будут адресованы всем студентам, в то время как каждый проблемный класс будет включать группы примерно из пяти студентов. Каждую неделю лекция предоставляет материал для недельного изучения, и студенты будут работать в группах в проблемном классе. На 2–6 неделях студенты представят свои работы в конце каждого проблемного класса, а на 7–11 неделях они представят командный проект по этому материалу. Кроме того, рабочие часы (два в неделю) предоставят возможность для более прямого контакта между отдельными студентами и лекцией: типичный студент может потратить в общей сложности один или два часа в течение модуля, индивидуально или как часть лекции. группа.
-часовое занятие по проблемам в неделю в течение десяти недель.Лекции будут адресованы всем студентам, в то время как каждый проблемный класс будет включать группы примерно из пяти студентов. Каждую неделю лекция предоставляет материал для недельного изучения, и студенты будут работать в группах в проблемном классе. На 2–6 неделях студенты представят свои работы в конце каждого проблемного класса, а на 7–11 неделях они представят командный проект по этому материалу. Кроме того, рабочие часы (два в неделю) предоставят возможность для более прямого контакта между отдельными студентами и лекцией: типичный студент может потратить в общей сложности один или два часа в течение модуля, индивидуально или как часть лекции. группа.
Методы оценки
Обратите внимание, , что руководители модулей пересматривают методы обучения и оценивания модулей для модулей 2 семестра в свете ограничений Covid-19. Также могут быть внесены некоторые дальнейшие изменения в модули семестра 1. Окончательная информация будет доступна к концу августа 2020 года для модулей 1-го семестра и к концу октября 2020 г. для модулей 2-го семестра.
Окончательная информация будет доступна к концу августа 2020 года для модулей 1-го семестра и к концу октября 2020 г. для модулей 2-го семестра.
Формат повторных экзаменов определяется экзаменационной комиссией
Экзамены
| Описание | Длина | семестр | при установке | В процентах | Комментарий |
|---|---|---|---|---|---|
| Письменный экзамен | 90 | 1 | A | 40 | Н / Д |
Прочая оценка
| Описание | семестр | при установке | В процентах | Комментарий |
|---|---|---|---|---|
| Упражнения по вероятному решению | 1 | M | 10 | Решение вычислительных задач |
| Упражнения по вероятному решению | 1 | M | 20 | Решение письменных задач |
| Письменное упражнение | 1 | M | 30 | Командный проект (максимум восемь страниц) |
Обоснование оценки и взаимосвязь
Для сдачи модуля необходимо будет сдать и экзамен, и командный проект (не более 34 баллов будет выставлен студенту, который не сдал экзамен и / или командный проект. ).
).
Формальный невидимый экзамен важен для проверки индивидуального понимания.
На 2–6 неделе еженедельные оценки будут поощрять участие и поощрять командную работу; каждая еженедельная оценка проблемного класса составляет примерно 4%. В течение недель с 7 по 11 будет примерно четыре вычислительных упражнения примерно одинакового веса и командный проект; командный проект представляет собой письменный отчет, который будет отмечен лектором модуля одной третью балла, выставленной путем экспертной оценки.
Списки чтения
Расписание
Решение проблем с помощью алгоритмов — COMP3830 — Модули
Обзор
Этот модуль направлен на укрепление у студентов основополагающих способностей «программирование в малом» за счет сильной практической ориентации на решение проблем. Конкретные темы будут включать вводные алгоритмы, правильность алгоритма, время выполнения алгоритма, а также нотацию большого O. Будут рассмотрены основные структуры данных и навыки алгоритмического программирования, такие как массивы, списки и деревья, поиск и сортировка, рекурсия и разделяй и властвуй.
Детали
Часы работы
Общее количество часов: 32
Часы индивидуального обучения: 118
Общее количество часов: 150
Метод оценки
Основные методы оценки
100% Курсовая работа
Методы переоценки
аналогичный
Ориентировочное значение
Скиена, Стивен С., «Руководство по разработке алгоритмов», Springer, 2008 г.
См. Список чтения библиотеки для этого модуля (Кентербери)
Результаты обучения
Предполагаемые результаты обучения по конкретному предмету.
После успешного завершения модуля студенты смогут:
1 Прочтите описание проблемы и примените соответствующий алгоритм для решения этой проблемы.
2 Сформулируйте решение проблемы в алгоритмической форме с использованием псевдокода.
3 Причина правильности алгоритма.
4 Причина времени выполнения алгоритма.
5 Реализуйте алгоритм как часть исполняемой программы.
6 Реализуйте базовые структуры данных (например, массивы, списки, деревья) и используйте алгоритмические методы (рекурсия и разделяй и властвуй) для решения хорошо известных проблем (поиск и сортировка), а также как применять их принципы к вновь возникшим проблемам.
Предполагаемые общие результаты обучения.
После успешного завершения модуля студенты смогут:
1 Работа в командах.
2 Сообщите о своем понимании технических проблем и их решениях.
3 Эффективно используйте ИТ-возможности.
4 Эффективно распоряжайтесь своим временем и ресурсами.
Банкноты
Уровень кредита 4 . Модуль уровня сертификата обычно берется на первом этапе бакалавриата.
- Кредиты ECTS признаны во всем ЕС и позволяют легко переводить кредиты из одного университета в другой.
- Названный организатор является организатором текущей академической сессии.
Наверх
Университет Кента прилагает все усилия для обеспечения точности информации модуля для соответствующей академической сессии и для предоставления образовательных услуг, как описано. Однако курсы, услуги и другие вопросы могут быть изменены. Пожалуйста, прочтите наш полный отказ от ответственности.
MA3E7 Решение проблем
Лектор: Сири Чонгчитнан
Срок (ы): Срок 2
Статус студентов-математиков: Список A для 3-го курса G100 (и 4-го курса G101), Список B для третьего курса G103 (G105).Если позволяют числа, четвертый год может рассматривать этот модуль как необычный вариант, но подтверждение будет дано только в начале семестра 2.
Обязательства: 10 двухчасовых и 10 одночасовых семинаров (включая некоторые оценочные решения проблем)
Оценка: 10% от еженедельных семинаров, 40% от задания, 50% двухчасового экзамена в июне
Предварительные требования: модулей Core Maths для 1-го и 2-го классов
Введение
Этот модуль дает вам возможность участвовать в решении математических задач и развивать навыки решения проблем путем анализа набора эвристик. Вы будете работать как индивидуально, так и в группах над математическими задачами, вырабатывая стратегии, которые вы используете, и сравнивая их с другими подходами.
Вы будете работать как индивидуально, так и в группах над математическими задачами, вырабатывая стратегии, которые вы используете, и сравнивая их с другими подходами.
Общие цели
Этот модуль позволит вам развить навыки решения проблем; использовать явные стратегии для начала, работы и размышления над математическими проблемами; объединить математические методы и методы рассуждений для исследования открытых проблем; использовать и разрабатывать схему эвристики для решения проблем.
Этот модуль обеспечивает основу для последующих математических модулей.Он должен дать вам уверенность в том, что вы сможете решать незнакомые проблемы, продумывать решения и представлять строгие и убедительные аргументы в пользу своих предположений. Хотя в этом курсе будет использоваться только небольшое количество математического содержания, которое будет распространено непосредственно на другие курсы, полученные навыки должны иметь широкий диапазон применимости.
Ожидаемые результаты
Цели обучения
Предполагаемые результаты заключаются в том, что к концу модуля вы должны:
- Используйте явную схему решения задач, чтобы контролировать свой подход к математическим задачам
- Объясните роль, которую играют разные этапы решения проблем
- Критически оценивайте свою практику решения проблем
Организация
Модуль работает во 2 семестре, недели 1-10. Обычно проводится еженедельная сессия для решения задач, составляющих 10% от модуля (см. Ниже), и вторая, более длительная сессия, на которой обсуждается теория и совместная работа над проблемами.
Обычно проводится еженедельная сессия для решения задач, составляющих 10% от модуля (см. Ниже), и вторая, более длительная сессия, на которой обсуждается теория и совместная работа над проблемами.
Ожидается, что вы будете присутствовать в любое время по расписанию.
Сведения об оценке
- Плоская ставка 10% предоставляется за серьезные попытки решить задачи во время курса. Каждую неделю вам будет назначаться задача для семинара. В конце семинара вы должны представить рубрику вашей работы над этой проблемой на данный момент.Если вы отправите хотя бы 7 рубрик, которые считаются серьезными попытками, вы получите 10%.
- Задание (40%) со сроком погашения в марте.
- 2-часовой экзамен в летнем семестре (50%).
Модуль 3: Решение проблем и их эскалация — Заметки для ведущего
Слайд 1: Практики управления для устойчивого развития Модуль 3: Решение проблем и эскалация
Скажи:
В этом модуле мы сосредоточимся на двух элементах в системе непосредственного управления, которые мы обозначили — наличие хорошо понятных методов решения проблем и эскалации проблем, доступных и регулярно используемых сотрудниками и руководителями.
Слайд 2: Передовая система управления для продвижения стандартных работ по безопасности
Скажи:
Как показано на рисунке, система непосредственного управления основана на способности сотрудников и руководителей распознавать проблемы и либо решать их напрямую, либо получать помощь для их решения.
Есть много способов решения проблем. Есть ли у вашей организации предпочтительный метод? Какие у вас есть договоренности о том, когда и как обострять проблемы и проблемы, чтобы привлечь внимание и помощь старших менеджеров?
Слайд 3: В чем проблема? Что есть решение?
Скажи:
У вас могут быть проблемы, влекущие за собой такие последствия, как причинение вреда или предвидение ситуации.Центры амбулаторной хирургии обычно имеют формальные методы исследования и решения таких проблем, документируя анализ первопричин и контрмеры для предотвращения рецидивов.
У вас также могут быть проблемы, связанные с методами, например, разрыв между стандартным способом проведения тайм-аута в операционной и прямым наблюдением за тайм-аутом. Например, при наблюдении за 190 часами работы медсестер в четырех больницах исследователи обнаружили 120 проблем. Из этих 120 проблем 110 были рассмотрены и решены как решения первого типа, которые устраняют немедленный разрыв, но не обязательно предотвращают повторение в будущем. 1 Решения 2-го типа предотвращают рецидив, часто затрагивая более глубокие причины. Эти цифры соответствуют вашему опыту?
Например, при наблюдении за 190 часами работы медсестер в четырех больницах исследователи обнаружили 120 проблем. Из этих 120 проблем 110 были рассмотрены и решены как решения первого типа, которые устраняют немедленный разрыв, но не обязательно предотвращают повторение в будущем. 1 Решения 2-го типа предотвращают рецидив, часто затрагивая более глубокие причины. Эти цифры соответствуют вашему опыту?
Часто бывает уместно применить решение проблемы типа 2, чтобы понять, почему проблема возникла, а затем попытаться предотвратить ее повторение. Чтобы предотвратить повторение ошибки, иногда решение очевидное, а иногда приходится пробовать другие идеи.
1 Такер А.Л., Эдмондсон А.С., Спир С. Когда решение проблем мешает организационному обучению. Журнал управления организационными изменениями 2002 15 (2): 122-37.
Slide 4: Как помечаются проблемы?
Скажи:
Большинство проблем выявляются персоналом или наблюдаются руководителями.
Ежедневная беседа дает вам место и время каждый день говорить о проблемах, замеченных членами команды. Еще одним основным источником является еженедельное наблюдение супервайзером за процедурами и методами работы в том виде, в каком они выполняются на самом деле. Наблюдатель также может вносить наблюдения в ежедневную беседу.
Слайд 5: Четыре ящика с проблемами
Скажи:
Некоторые проблемы и вопросы требуют немедленного внимания со стороны руководства, например, срочные и важные вопросы, такие как случай причинения вреда.В этих случаях вы можете разработать «SBAR», в котором излагается ситуация, предыстория, ваша оценка ситуации и рекомендация. Это решение проблемы и эскалация в действии.
Однако многие проблемы не требуют такого немедленного внимания. Мы делим несрочные вопросы на четыре категории.
Давайте посмотрим на блок 1. Если не срочная проблема связана с людьми, не соблюдающими согласованные методы или установленный протокол, тогда напоминаний и информации может быть достаточно для решения проблемы. Иногда метод необходимо изменить, а дальнейшие шаги не ясны, поэтому вы переходите к блоку 3.
Иногда метод необходимо изменить, а дальнейшие шаги не ясны, поэтому вы переходите к блоку 3.
Во вставке 2 мы описываем другой подход под названием «просто сделай это». «Просто сделай это» уместно, если у вас есть четкое представление о том, как предотвратить повторение проблемы, и нет риска непредвиденных последствий. Изменить метод работы или рабочую среду можно немедленно. Если ваше понимание нечеткое или вас беспокоят непредвиденные последствия, переходите к блоку 3.
Вставка 3 применима, если вы не уверены, что делать, и вам нужно потратить время и силы, чтобы предотвратить повторение. Анализ — это один из способов двигаться вперед. Вы можете использовать инструменты анализа первопричин, такие как таблицы «есть / нет» или причинно-следственные диаграммы, для разработки идей изменений, которые вы можете протестировать и которые могут привести к повышению производительности.
Если проблема кажется более серьезной, чем то, что команда и руководитель могут решить в рамках подразделения в течение недели, то проблема является кандидатом для эскалации в более формальный проект повышения качества.
Вставка 4 относится к проблемам изменения процесса или проблем с потоком между отделами, которые требуют дополнительного внимания и могут быть более крупными, межфункциональными проектами повышения качества.
Подумайте о применимости этой классификации к вашему текущему процессу решения проблем.
Слайд 6: Применение модели для улучшения для улучшения решения проблем
Скажи:
Чтобы внедрить более систематическое решение проблем в своей организации, вы можете использовать Модель улучшения, так же, как мы это делали для других методов управления, которые мы обсуждали.
Модель улучшения начинается с трех вопросов:
Спросите:
Во-первых, какова ваша цель? Другими словами, чего вы пытаетесь достичь?
Во-вторых, каковы ваши меры? Другими словами, как вы узнаете, что изменение — это улучшение?
Наконец, какие изменения вы собираетесь протестировать? Что конкретно вы сделаете по-другому, чтобы добиться улучшения?
Скажи:
Давайте рассмотрим пример.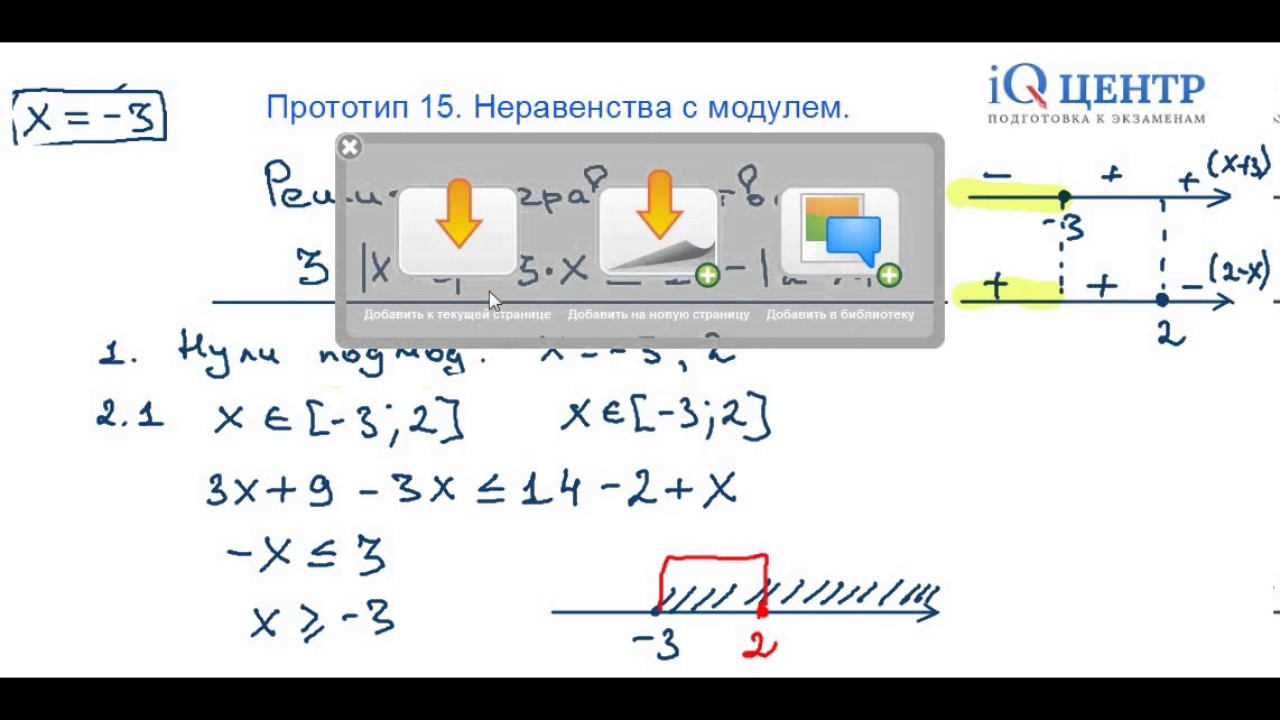 Менеджер центра заметил, что та же проблема повторяется, и хочет глубже понять, как ее улучшить. Таким образом, она пытается уменьшить количество повторяющихся проблем. Она будет знать, что это успешно, когда возникнет меньше подобных проблем. Чтобы определить правильный курс действий, менеджер будет использовать алгоритм сортировки проблем.
Менеджер центра заметил, что та же проблема повторяется, и хочет глубже понять, как ее улучшить. Таким образом, она пытается уменьшить количество повторяющихся проблем. Она будет знать, что это успешно, когда возникнет меньше подобных проблем. Чтобы определить правильный курс действий, менеджер будет использовать алгоритм сортировки проблем.
Использование этих вопросов в качестве руководства поможет четко определить проблему и предполагаемый конечный результат.
Слайд 7: Применение модели для улучшения для улучшения решения проблем – 2
Скажи:
Основным способом, который мы используем для применения модели улучшения, является цикл «планирование-выполнение-исследование-действие» или «PDSA», как описано в предыдущих модулях.
Вот напоминание о PDSA. Когда вы «планируете», вы излагаете спецификации или детали вашего теста. Кто, когда, где, как, почему. Когда вы «делаете», вы фактически запускаете тест. Когда вы «учитесь», вы анализируете, как прошел тест и чему вы научились, а также размышляете о том, что вы могли бы сделать по-другому. Когда вы «действуете», вы используете эти размышления и идеи для информирования ваших следующих тестов или вашего нового согласованного способа выполнения работы.
Когда вы «действуете», вы используете эти размышления и идеи для информирования ваших следующих тестов или вашего нового согласованного способа выполнения работы.
Обращение к решению проблем:
- Первый тест — можете ли вы назначить проблему одному из четырех полей и довести ее до разрешения?
- Второй тест — можете ли вы назначить каждую из пяти проблем для коробки и продолжить ее решение?
Эти тесты должны выявить возможности для разработки руководящих принципов, которым должны следовать ваши сотрудники.
Слайд 8: Решение передовых клинических проблем
Скажи:
Большая часть дискуссий до сих пор была посвящена решению проблем и эскалации проблем в целом.
Мы также хотим напомнить вам, что существуют ресурсы для облегчения эскалации критических проблем, связанных с безопасностью, которые могут возникнуть на переднем крае клинической помощи. На веб-сайте AHRQ вы можете найти ресурсы, связанные с тем, как использовать один инструмент, в частности, CUS, который может помочь выявить проблемы безопасности. В устном общении CUS может быть сигнальной фразой для всех членов команды о том, что проблема серьезна и требует внимания.
В устном общении CUS может быть сигнальной фразой для всех членов команды о том, что проблема серьезна и требует внимания.
Чтобы использовать CUS, сначала укажите, что вас беспокоит, а затем укажите, почему вам неудобно. Если конфликт не разрешен, укажите, что существует проблема безопасности, и обсудите, каким образом эта проблема связана с безопасностью. Если проблема безопасности не обнаружена, необходимо уведомить руководителя.
Если во время оказания помощи происходит событие, которое беспокоит сотрудника, этот простой протокол предполагает, что сотрудник выразит эту озабоченность.Если проблема не решена, сотрудник заявляет, что ему неудобно.
Если заявление о дискомфорте все еще не решено, то сотрудник объявляет, что существует проблема безопасности, требующая действий — например, вызвать дополнительный медицинский персонал или остановить процедуру.
В комплекте компонентов, прилагаемом к этому модулю, который доступен через веб-сайт AHRQ, вы можете найти дополнительную информацию о CUS, а также политику шаблона, которую вы можете адаптировать к своему объекту, чтобы помочь жестко использовать инструмент CUS в вашем центре. .
.
Слайд 9: Советы
Скажи:
Как и в случае с другими практиками, которые мы обсуждали в предыдущих модулях, мы хотим дать вам несколько практических советов, которые помогут вам во внедрении улучшенного решения проблем и эскалации проблем в вашей организации. Решение проблем, как мы описали, направлено на достижение и поддержание надежной работы
Во-первых, если в вашей организации есть стандартный метод решения проблем, научитесь его использовать. Во-вторых, разберитесь с инструментами анализа первопричин, которые ваш центр применяет для расследования и документирования случаев причинения вреда.В-третьих, включите использование протокола связи CUS в повседневное использование на вашем предприятии. Важно обеспечить широкое понимание персонала и удобство его использования.
Для получения дополнительной информации о решении проблем и эскалации см. Комплекты компонентов, также доступные на веб-сайте AHRQ, которые сопровождают эти презентации.
Благодарим вас за просмотр этого модуля по решению и эскалации проблем. Не забудьте просмотреть модули и комплекты компонентов по другим элементам системы первичного управления, чтобы продвигать устойчивые стандарты безопасности при работе в центрах амбулаторной хирургии, которые также доступны на веб-сайте AHRQ: Инструментарий для повышения безопасности в центрах амбулаторной хирургии.
Мышление, рассуждение и решение проблем — Введение в психологию
Этот модуль о том, как твердое практическое знание психологических принципов может помочь вам мыслить более эффективно, чтобы вы могли добиться успеха в школе и в жизни. Вы можете быть склонны верить в это — потому что вы думали столько, сколько себя помните, потому что вы можете найти решение многих проблем, потому что вы чувствуете себя способным использовать логику, чтобы аргументировать точку зрения, потому что вы можете оценивать имеет ли смысл то, что вы читаете и слышите, — вам не нужна особая тренировка мышления. Но это, конечно, одно из основных препятствий на пути людей к лучшему мышлению. Если вы не верите, что что-то не так, зачем пытаться это исправить?
Но это, конечно, одно из основных препятствий на пути людей к лучшему мышлению. Если вы не верите, что что-то не так, зачем пытаться это исправить?
Человеческий мозг — действительно замечательная мыслящая машина, способная к удивительным, сложным, творческим и логическим мыслям. Почему же тогда мы говорим вам, что вам нужно научиться думать? Главным образом потому, что один из основных уроков когнитивной психологии состоит в том, что эти возможности человеческого мозга относительно нечасто реализуются. Многие психологи считают, что люди по сути своей «скупердяи».«Дело не в том, что мы ленивы, а в том, что мы склонны тратить минимум необходимых умственных усилий. Хотя вы можете этого не осознавать, на самом деле для размышлений требуется много энергии. Тщательное, обдуманное рассуждение и критическое мышление очень сложны. Поскольку мы, кажется, добиваемся успеха, даже не пытаясь правильно использовать эти навыки, мы не чувствуем необходимости развивать их. Однако, как вы увидите, в когнитивных процессах, описанных в этом модуле, есть много подводных камней. Когда люди не прилагают дополнительных усилий к обучению и совершенствованию навыков рассуждения, решения проблем и критического мышления, они совершают множество ошибок.
Когда люди не прилагают дополнительных усилий к обучению и совершенствованию навыков рассуждения, решения проблем и критического мышления, они совершают множество ошибок.
Как и в случае с памятью, если вы разовьете когнитивные навыки, представленные в этом модуле, вы добьетесь большего успеха в школе. Однако важно, чтобы вы понимали, что эти навыки помогут вам далеко за пределами школы, даже больше, чем хорошая память. Хотя в некоторой степени полезно иметь хорошую память, через десять лет ни один потенциальный работодатель не будет заботиться о том, сколько вопросов вы правильно ответили на экзаменах с несколькими вариантами ответов во время учебы в колледже.Однако все они узнают, являетесь ли вы логическим, аналитическим и критическим мыслителем. Обладая этими навыками мышления, вы станете эффективным и убедительным коммуникатором и отлично решите проблемы.
Модуль начинается с описания различных видов мысли и знаний, особенно концептуальных знаний и критического мышления. Понимание этих различий будет полезно по мере того, как вы будете учиться в школе и столкнетесь с различными заданиями, которые потребуют от вас использования разных видов знаний.Второй раздел посвящен дедуктивным и индуктивным рассуждениям — процессам, которые мы используем для построения и оценки сильных аргументов. Это важные навыки, которыми нужно обладать всякий раз, когда вы пытаетесь убедить кого-то (включая себя) в какой-то точке зрения или реагировать на чьи-то попытки убедить вас. Модуль заканчивается разделом о решении проблем. Четкое понимание ключевых процессов, связанных с решением проблем, поможет вам справиться со многими повседневными проблемами.
7.1. Разные мысли
7.2. Рассуждения и суждения
7.3. Решение проблем
Помните и поймите
Прочитав и изучив Модуль 7, вы должны уметь запомнить и описать:
- Концепции и выводы (7.1)
- Знание процедуры (7.1)
- Метапознание (7.1)
- Характеристики критического мышления: скептицизм; выявлять предубеждения, искажения, упущения и предположения; навыки рассуждения и решения проблем (7.1)
- Рассуждение: дедуктивное рассуждение, дедуктивно действительный аргумент, индуктивное рассуждение, индуктивно сильный аргумент, эвристика доступности, эвристика репрезентативности (7.2)
- Фиксация: функциональная неподвижность, ментальная установка (7,3)
- Алгоритмы, эвристика и роль систематической ошибки подтверждения (7.3)
- Эффективная последовательность решения проблем (7.3)
Применить
Читая и размышляя о том, как концепции Модуля 6 применимы к реальной жизни, вы должны уметь:
- Определите, к какому типу знаний относится информация (7.1)
- Распознавать примеры дедуктивного и индуктивного рассуждений (7.2)
- Признать суждения, на которые, вероятно, повлияла эвристика доступности (7.2)
- Распознавать примеры эвристик и алгоритмов решения проблем (7.3)
Анализировать, оценивать и создавать
Читая и размышляя о Модуле 6, участвуя в классных занятиях и выполняя внеклассные задания, вы должны уметь:
- Используйте принципы критического мышления для оценки информации (7.1)
- Объясните, являются ли примеры аргументов дедуктивно верными или индуктивно сильными (7.2)
- Обрисуйте, как вы могли бы попытаться решить проблему из своей жизни, используя эффективную последовательность решения проблем (7.3)
7.1. Разные мысли и знания
- Потратьте несколько минут, чтобы записать все, что вы знаете о собаках.
- Вы верите, что:
- Психические способности существуют?
- Гипноз — это измененное состояние сознания?
- Магнитотерапия эффективна для снятия боли?
- Аэробные упражнения — эффективное лечение депрессии?
- НЛО из космоса побывали на Земле?
На чем вы основываете свое убеждение или недоверие в ответах на приведенные выше вопросы?
Конечно, все мы знаем, что означают слова , думаю, и , знания, .Вы, вероятно, также понимаете, что это не единые концепции; есть разные виды мысли и знания. В этом разделе давайте рассмотрим некоторые из этих различий. Если вы знакомы с этими различными видами мысли и обращаете на них внимание на уроках, это поможет вам сосредоточиться на правильных целях, более эффективно учиться и добиваться успехов в школе. Различные задания и требования в школе призывают вас использовать разные виды знаний или мыслей, поэтому вам будет очень полезно научиться их распознавать (Андерсон и др.2001).
Фактические и концептуальные знания
Модуль 5 представил идею декларативной памяти, которая состоит из фактов и эпизодов. Если вы когда-либо играли в викторину или смотрели Jeopardy по телевизору, вы понимаете, что человеческий мозг способен хранить невероятное количество фактов. Точно так же вы понимаете, что у каждого из нас есть огромный запас эпизодов, по сути, фактов о событиях, произошедших в нашей жизни. Однако может быть трудно помнить об этом, когда мы изо всех сил пытаемся извлечь один из этих фактов во время сдачи экзамена.Частично проблема заключается в том, что, вопреки совету из Модуля 5, многие студенты продолжают пытаться запоминать материал курса как серию несвязанных фактов (представьте, что студент-историк просто пытается запомнить историю как набор несвязанных дат без каких-либо связанных история, связывающая их вместе). Однако факты в реальном мире не случайны и неорганизованы. То, как они организованы, составляет второй ключевой вид знания — концептуальный.
Концепции — это не что иное, как наши ментальные представления категорий вещей в мире.Например, подумайте о собаках. Когда вы это сделаете, вы можете вспомнить конкретные факты о собаках, например, у них есть шерсть и они лают. Вы также можете вспомнить собак, с которыми столкнулись, и представить их себе в уме. Вся эта информация (и многое другое) составляет ваше представление о собаке. У вас могут быть понятия простых категорий (например, треугольник), сложных категорий (например, маленьких собак, которые спят весь день, едят из мусора и лают на листья), типов людей (например, профессора психологии), событий (например,, дни рождения) и абстрактные идеи (например, справедливость). Грегори Мерфи (2002) называет концепции «клеем, который скрепляет нашу ментальную жизнь» (стр. 1). Проще говоря, обобщение мира с помощью концепций — одна из самых важных когнитивных задач, которые мы выполняем. Наши концептуальные знания — это наших знаний о мире. Отдельные концепции связаны друг с другом и образуют богатую взаимосвязанную сеть знаний. Например, подумайте, как следующие понятия могут быть связаны друг с другом: собака, домашнее животное, игра, фрисби, жевательная игрушка, обувь.Или, что для вас более очевидно, как эти концепции связаны между собой: рабочая память, долговременная память, декларативная память, процедурная память и репетиция? Поскольку наш разум имеет естественную тенденцию систематизировать информацию концептуально, когда студенты пытаются запомнить материал курса как отдельные факты, они работают против своих сильных сторон.
Последний важный момент, связанный с концепциями, заключается в том, что они позволяют мгновенно узнать большой объем информации о чем-либо. Например, если кто-то протягивает вам небольшой красный предмет и говорит: «Вот яблоко», им не нужно говорить вам: «Это то, что вы можете съесть».«Вы уже знаете, что можете съесть это, потому что это правда в силу того факта, что это яблоко; это называется выводом , при условии, что что-то верно на основе ваших предыдущих знаний (например, о принадлежности к категории или о том, как устроен мир) или логических рассуждений.
Процедурные знания
Физические навыки, такие как завязывание обуви, вращение колеса телеги и вождение автомобиля (или выполнение всех трех одновременно, но не пытайтесь делать это дома), безусловно, являются своего рода знаниями.Это процедурные знания, та же идея, что и процедурная память, которую вы видели в Модуле 5. Психические навыки, такие как чтение, обсуждение и планирование психологического эксперимента, также являются процедурными знаниями. Короче говоря, процедурное знание — это знание того, как что-то делать (Cohen & Eichenbaum, 1993).
Метакогнитивные знания
Флойд раньше думал, что у него отличная память. Теперь у него лучшая память. Почему? Потому что он наконец понял, что его память не так хороша, как он когда-то думал.Поскольку Флойд со временем узнал, что он часто забывает, куда кладет вещи, он, наконец, выработал привычку складывать вещи в одно и то же место. (К сожалению, он не усвоил этот урок, прежде чем потерял по крайней мере 5 часов и обручальное кольцо.) Поскольку он наконец понял, что часто забывает что-то делать, он наконец начал использовать приложение To Do list на своем телефоне. И так далее. Понимание Флойда реальных ограничений его памяти позволило ему вспомнить то, что он раньше забывал.
Все мы знаем, как работает наш собственный разум.Возможно, вы знаете, что у вас хорошая память на имена людей и плохая память на математические формулы. Кто-то другой может понять, что ему трудно что-то вспомнить, например, останавливаться в магазине по дороге домой. Другие до сих пор знают, что они склонны упускать из виду детали. Это знание о нашем собственном мышлении на самом деле очень важно; это называется метакогнитивным знанием, или метапознанием , . Как и другие виды мышления, он подвержен ошибкам. Например, в неопубликованном исследовании один из авторов опросил около 120 студентов-психологов в первый день семестра.Среди других вопросов учащихся попросили предсказать свою оценку в классе и сообщить свой текущий средний балл. Две трети студентов предсказали, что их оценка по курсу будет выше, чем их средний балл. (Реальность такова, что в нашем колледже студенты, как правило, получают более низкие оценки по психологии, чем их общий средний балл.) Другой пример: студенты обычно сообщают, что, по их мнению, хорошо сдали экзамен, но, к своему ужасу, обнаруживают, что они были неправы (подробнее об этой важной проблеме чуть позже).Обе ошибки указывают на нарушение метапознания.
Эффект Даннинга-Крюгера
В целом, большинство студентов, вероятно, недостаточно учатся. Например, используя данные Национального исследования вовлеченности студентов, Fosnacht, McCormack и Lerma (2018) сообщили, что студенты-первокурсники 4-летних колледжей в США в среднем готовятся к занятиям менее 14 часов в неделю. Типичное предложение состоит в том, что вы должны проводить два часа вне класса каждый час в классе или 24–30 часов в неделю для студентов очного отделения.Ясно, что студенты в целом далеки от рекомендованной отметки. Многие наблюдатели, в том числе некоторые преподаватели, считают, что этот дефицит является результатом того, что студенты слишком заняты или ленивы. Возможно, правда, что многие студенты слишком заняты, например, работой и семейными обязанностями. Другие не особо заинтересованы в учебе, и поэтому их можно правильно назвать ленивыми. Однако третье возможное объяснение состоит в том, что некоторые студенты могут не думать, что им нужно тратить так много времени. И это вопрос метапознания.Рассмотрим сценарий, упомянутый выше, когда студенты думают, что они хорошо сдали экзамен, но обнаруживают, что они этого не сделали. Джастин Крюгер и Дэвид Даннинг исследовали очень похожие сценарии в 1999 году. Крюгер и Даннинг давали участникам исследования тесты на юмор, логику и грамматику. Затем они попросили участников оценить свои способности и проверить свои способности в этих областях. Они обнаружили, что участники в целом склонны переоценивать свои способности, что уже является проблемой для метапознания.Важно отметить, что участники, набравшие наименьшее количество баллов, больше всего переоценили свои способности. В частности, студенты, набравшие в нижней четверти (в среднем в 12-м процентиле), думали, что они набрали 62-й процентиль. Это стало известно как эффект Даннинга-Крюгера . Многие отдельные преподаватели повторили эти результаты со своими студентами на экзаменах по курсу, включая авторов этой книги. Подумай об этом. Некоторые студенты, которые только что сдавали экзамен и плохо успели сдать экзамен, полагают, что они сдали хорошо, еще до того, как увидят свою оценку.Кажется весьма вероятным, что это те самые студенты, которые прекратили занятия накануне вечером, потому что думали, что они «закончили». Проще говоря, дело не только в том, что они не знали материала. Они не знали, что не знали материала. Это плохое метапознание.
Чтобы развить хорошие метакогнитивные навыки, вы должны постоянно следить за своим мышлением и получать частые отзывы о его точности (Medina, Castleberry, & Persky, 2017). Например, на уроках возьмите за привычку предсказывать свои экзаменационные оценки.Как можно скорее после сдачи экзамена постарайтесь выяснить, какие вопросы вы пропустили, и постарайтесь выяснить, почему. Если вы сделаете это достаточно скоро, вы сможете вспомнить, что чувствовали, когда изначально ответили на вопрос. Вы были уверены, что ответили на вопрос правильно? Тогда вы только что открыли возможность улучшить свое метапознание. Следите за этим чувством и отвечайте осторожно.
концепция: мысленное представление категории вещей в мире
Эффект Даннинга-Крюгера : менее компетентные люди склонны переоценивать свои способности больше, чем более компетентные люди
вывод: предположение об истинности чего-то, о чем не говорится.Выводы основаны на наших предварительных знаниях и опыте, а также на основе логических рассуждений
метапознание: знаний о собственных когнитивных процессах; думая о своем мышлении
Критическое мышление
Одним из конкретных видов знаний или навыков мышления, связанных с метапознанием, является критическое мышление (Chew, 2020). Возможно, вы заметили, что критическое мышление является целью многих курсов колледжа, и поэтому это может быть законная тема для обсуждения практически в любом курсе колледжа.Однако это особенно уместно в психологии. Как наука о (поведении и) психических процессах, психология, очевидно, хорошо подходит в качестве дисциплины, с помощью которой вы должны познакомиться с этим важным способом мышления.
Что еще более важно, в психологии особенно важно использовать критическое мышление. Мы все в каком-то смысле эксперты в области человеческого поведения и психических процессов, занимаясь ими буквально с рождения. Таким образом, возможно, больше, чем в любом другом классе, студенты обычно подходят к психологии с очень четкими идеями и мнениями по ее предмету.То есть студенты уже много «знают» о психологии. Проблема в том, что «проблемы возникают не столько из-за того, чего мы не знаем. Это то, что мы знаем, но это не так »(Уорд, цитата по Гиловичу, 1991). В самом деле, многие предубеждения студентов о психологии просто ошибочны. Рэндольф Смит (2002) написал книгу о критическом мышлении в психологии под названием «, бросая вызов своим предубеждениям», подчеркнув этот факт. С другой стороны, многие предубеждения студентов о психологии совершенно верны! Но подождите, как узнать, какие из ваших предубеждений верны, а какие нет? И когда вы натолкнетесь на результаты исследования или теории в этом классе, которые противоречат вашим предубеждениям, что вы сделаете? Будете ли вы придерживаться своей первоначальной идеи, не принимая во внимание информацию из класса? Вы сразу передумаете? Критическое мышление может помочь нам разобраться в этой запутанной неразберихе.
Но что такое критическое мышление? Цель критического мышления легко сформулировать (но чрезвычайно трудно достичь): это быть правым, делать правильные выводы, верить в то, что истинно, и не верить в то, что ложно. Мы дадим два определения критического мышления (или, если хотите, одно большое определение с двумя отдельными частями). Во-первых, более концептуальный: критическое мышление — это мыслить как ученый в повседневной жизни (Schmaltz, Jansen, & Wenckowski, 2017).Наше второе определение более оперативное; это просто список навыков, необходимых для критического мышления. Критическое мышление требует твердого мышления и навыков решения проблем; скептицизм; и способность выявлять предубеждения, искажения, упущения и предположения. Отличные дедуктивные и индуктивные рассуждения и навыки решения проблем способствуют развитию критического мышления. Итак, вы можете рассматривать содержание разделов 7.2 и 7.3 как часть критического мышления. Поскольку мы будем уделять этим концепциям значительное время в оставшейся части модуля, давайте начнем с обсуждения других аспектов критического мышления.
критическое мышление : Мыслить как ученый в повседневной жизни с целью делать правильные выводы. Это влечет за собой скептицизм; способность выявлять предубеждения, искажения, упущения и предположения; отличные дедуктивные и индуктивные рассуждения и навыки решения проблем.
Обратимся к первой части определения. Ученые формируют гипотезы или прогнозы о некоторых возможных будущих наблюдениях. Затем они собирают данные или информацию (думайте об этом как о будущих наблюдениях).Они делают все возможное, чтобы делать беспристрастные наблюдения, используя надежные методы, проверенные другими. Тогда и только тогда они делают вывод о том, что означают эти наблюдения. Да, и не забывайте о самой важной части. «Заключение», вероятно, не самое подходящее слово, потому что этот вывод носит предварительный характер. Ученый всегда готов к тому, что кто-то другой может прийти и произвести новые наблюдения, которые потребуют нового вывода. Ух ты! Если вы хотите быть правым, вы могли бы сделать намного хуже, чем использовать такой процесс.
Инструментарий критического мыслителя
Теперь о второй части определения. Хорошие критические мыслители (и ученые) полагаются на множество инструментов для оценки информации. Возможно, самый узнаваемый инструмент критического мышления — это скептицизм (и этот термин обеспечивает наиболее четкую связь с таким мышлением, как определение ученого, как вы сейчас увидите). Некоторые люди, называя кого-то скептиком, воспринимают это как оскорбление. Но если кто-то называет вас скептиком, если они правильно используют этот термин, вы должны считать это отличным комплиментом.Проще говоря, скептицизм — это образ мышления, при котором вы воздерживаетесь от вывода или изменения своего мнения до тех пор, пока не будут предоставлены убедительные доказательства. Люди из Миссури должны признать этот принцип, так как штат Миссури известен как Штат Show-Me. Как скептик, вы не склонны верить чему-либо только потому, что кто-то так сказал, потому что кто-то этому верит или потому, что это звучит разумно. Вас должны убедить доказательства высокого качества.
Конечно, если такие доказательства будут представлены, вы, как скептик, обязаны изменить свое мнение.Неспособность изменить убеждение перед лицом убедительных доказательств не является скептицизмом; в основе скептицизма лежит непредубежденность. М. Нил Браун и Стюарт Кили (2018) используют термин критическое мышление со слабым чувством, чтобы описать поведение критического мышления, которое используется только для укрепления предшествующего убеждения. С другой стороны, сильное критическое мышление направлено на достижение наилучшего результата. Иногда это означает укрепление вашего предыдущего убеждения, но иногда это означает изменение вашего убеждения, чтобы приспособиться к лучшим свидетельствам.
Часто неспособность мыслить критически или слабое критическое мышление связано с предубеждением , склонностью, склонностью, склонностью или предубеждением. У всех есть предубеждения, но многие люди о них не подозревают. Осознание собственных предубеждений дает вам возможность контролировать их или противодействовать им. К сожалению, однако, многие люди счастливы позволить своим предубеждениям закрасться в их попытки убедить других; действительно, это ключевая часть их стратегии убеждения. Чтобы увидеть, как эти предубеждения влияют на сообщения, просто посмотрите на различные описания и объяснения одних и тех же событий, данные людьми разного возраста или разного уровня дохода, или консервативными и либеральными комментаторами, или комментаторами из разных частей мира.Конечно, чтобы добиться успеха, эти люди, сознательно использующие свои предубеждения, должны их замаскировать. Иногда бывает трудно выявить даже неприкрытые предубеждения, поэтому замаскированные почти невозможно.
Вот несколько распространенных источников предубеждений:
- Личные ценности и убеждения. Некоторые люди считают, что люди в основном стремятся к власти и что они обычно соревнуются друг с другом за ограниченные ресурсы. Эти убеждения похожи на мировоззрение, которое политологи называют «реализмом».Другие люди верят, что люди предпочитают сотрудничать и что, если представится возможность, они это сделают. Эти убеждения похожи на мировоззрение, известное как «идеализм». Для многих людей эти глубоко укоренившиеся убеждения могут влиять или предвзято относиться к их интерпретациям таких разнообразных ситуаций, как поведение наций и их лидеров или поведение водителя в машине впереди вас. Например, если ваше мировоззрение таково, что люди обычно соревнуются и кто-то подрезает вас на шоссе, вы можете предположить, что водитель сделал это намеренно, чтобы опередить вас.Другие типы убеждений о том, каков мир или каким он должен быть, например, политические убеждения, также могут стать значительным источником предвзятости.
- Расизм, сексизм, эйджизм и другие формы предрассудков и фанатизма. К сожалению, это распространенный источник предвзятости у многих людей. По сути, они представляют собой особый вид «веры в то, каков мир». Эти убеждения — например, что женщины не могут быть эффективными лидерами — побуждают людей игнорировать противоречивые доказательства (примеры эффективных женщин-лидеров или исследования, которые оспаривают это убеждение) и интерпретировать неоднозначные доказательства в соответствии с их убеждениями.
- Личная выгода. Когда определенные люди извлекают выгоду из того, что все складывается определенным образом, они иногда могут быть очень восприимчивыми к тому, чтобы позволить этому интересу влиять на них. Например, компания, которая получит прибыль, если продаст свой продукт, может иметь предвзятость в способах предоставления информации о своем продукте. Профсоюз, который выиграет, если его члены получат щедрый контракт, может иметь предвзятость в том, как он представляет информацию о зарплатах в конкурирующих организациях. (Обратите внимание, что включение примеров, описывающих как компании, так и профсоюзы, является явной попыткой контролировать наши личные предубеждения).Покупатели жилья часто с тревогой обнаруживают, что они купили дом своей мечты у кого-то, чьи интересы заставили их солгать о проблемах с наводнением в подвале или на заднем дворе. Этот принцип, подстраховка личного интереса, вероятно, привел к знаменитой фразе Caveat Emptor (пусть покупатель остерегается) .
Знание о существовании подобных предубеждений поможет вам более критически оценивать доказательства. Однако не забывайте, что люди не всегда стремятся позволить вам обнаружить источники предвзятости в их аргументах.Например, компании или политические организации могут иногда замаскировать свою поддержку исследования, заключив контракт с университетским профессором, который, казалось бы, имеет беспристрастную институциональную принадлежность, для проведения исследования.
Сознательные или бессознательные предубеждения людей могут привести к тому, что они будут делать упущения, искажения и предположения, которые подрывают нашу способность правильно оценивать доказательства. Вы должны искать эти элементы. Всегда спрашивайте, чего не хватает, чего не так, как кажется, и что здесь предполагается? Например, рассмотрите эту (вымышленную) диаграмму из рекламного сообщения об удовлетворенности клиентов в 4 местных клубах здоровья.
Очевидно, что, судя по результатам таблицы, можно было бы испытать желание попробовать клуб C, поскольку удовлетворенность клиентов намного выше, чем у остальных трех клубов.
Однако в этой таблице так много искажений и упущений, что на самом деле она совершенно бессмысленна. Во-первых, как измерялось удовлетворение? Представляют ли полосы ответы на опрос? Если да, то как задавались вопросы? Самое главное, где отсутствует масштаб графика? Хотя различия выглядят довольно большими, действительно ли они?
Ну, вот та же диаграмма, но в другом масштабе, на этот раз обозначенная:
.
Club C уже не так впечатляет, правда? Фактически, все клубы здоровья имеют рейтинг удовлетворенности клиентов (что бы это ни значило) от 85% до 88%.На первой диаграмме вся шкала графика включала только проценты от 83 до 89. Этот «разумный» выбор шкалы — некоторые назвали бы это искажением — и отсутствие этой шкалы в таблице делают крошечные различия между клубами. кажутся важными, однако.
Кроме того, чтобы мыслить критически, вам необходимо научиться обращать внимание на предположения, лежащие в основе сообщения. Давайте кратко проиллюстрируем роль предположений, коснувшись взглядов некоторых людей на систему уголовного правосудия в США.Некоторые считают, что главная проблема нашей судебной системы заключается в том, что многие преступники освобождаются из-за юридических формальностей. Другие считают, что главная проблема заключается в том, что многие невиновные люди осуждены за преступления. Простой факт в том, что возникают оба типа ошибок. Вывод человека о том, какая ошибка в нашей судебной системе является большей трагедией, основывается на предположении о том, какая из них является более серьезной ошибкой (освобождение виновных или осуждение невиновных). Этот тип предположения называется ценностным предположением (Browne and Keeley, 2018).Он отражает различия в ценностях, которые развиваются у людей, различия, которые могут привести к игнорированию достоверных свидетельств, которые не соответствуют нашим конкретным ценностям.
Да, кстати, некоторые студенты, вероятно, заметили это, но семь советов по оценке информации, которыми мы поделились в Модуле 1, связаны с этим. Собственно, они часть этого раздела. Советы в значительной степени представляют собой набор идей, которые вы можете использовать, чтобы помочь вам выявить предубеждения, искажения, упущения и предположения. Если вы не помните этот раздел, мы настоятельно рекомендуем вам потратить несколько минут на его изучение.
скептицизм: образ мышления, при котором вы воздерживаетесь от вывода или изменения своего мнения до тех пор, пока не будут предоставлены веские доказательства
предубеждение: склонность, склонность, склонность или предубеждение
- Какие из ваших убеждений (или неверия) в упражнении Activate для этого раздела возникли в результате процесса критического мышления? Если некоторые из ваших убеждений не были основаны на критическом мышлении, готовы ли вы пересмотреть эти убеждения? Если ответ отрицательный, почему вы так думаете? Если «да», какие конкретные шаги вы предпримете?
7.2 Рассуждения и суждения
- Какой процент похищений совершается незнакомцами?
- Какая часть дома наиболее опасна: кухня, ванная или лестница?
- Какой вид рака наиболее распространен в США?
- Какой процент убийств на рабочем месте совершается коллегами?
Важным набором навыков процедурного мышления является рассуждения , способность генерировать и оценивать твердые выводы из набора утверждений или доказательств.Вы должны отметить, что эти выводы (когда они генерируются, а не оцениваются) являются одним из ключевых типов вывода, который мы описали в Разделе 7.1. Есть два основных типа рассуждений: дедуктивный и индуктивный.
Дедуктивное рассуждение
Предположим, ваш учитель говорит вам, что если вы получите пятерку на заключительном экзамене курса, вы получите пятерку за весь курс. Тогда вы получите пятерку на выпускном экзамене. Какая будет ваша итоговая оценка за курс? Большинство людей сразу понимают, что вы можете с уверенностью сказать, что получите пятёрку за курс.Это тип рассуждения, называемый дедуктивным рассуждением , который определяется как рассуждение, в котором заключение гарантированно будет истинным, пока утверждения, ведущие к нему, истинны. Три утверждения могут быть перечислены как аргумент с двумя начальными утверждениями и заключением:
Утверждение 1. Если вы получите пятерку на выпускном экзамене, вы получите пятерку за курс
.
Утверждение 2: Вы получите пятерку на выпускном экзамене
Заключение: по курсу
вы получите пятерку.
Эта конкретная схема, в которой истинные начальные утверждения приводят к гарантированно истинному заключению, известна как дедуктивно действительный аргумент .Хотя дедуктивное рассуждение часто является предметом абстрактных, дразнящих мозг, похожих на головоломки словесных задач, на самом деле это чрезвычайно важный тип повседневных рассуждений. Иногда это просто сложно распознать. Например, представьте, что вы ищете ключи от машины и понимаете, что они либо в кухонном ящике, либо в сумке с книгами. Заглянув в кухонный ящик, сразу понимаешь, что они должны быть в твоей сумке с книгами. Этот вывод является результатом простого дедуктивного аргумента.Кроме того, твердые навыки дедуктивного мышления необходимы вам для успеха в науках, философии, математике, компьютерном программировании и в любых усилиях, связанных с использованием логики для убеждения других в вашей точке зрения или для оценки аргументов других.
Когнитивные психологи, а до них философы, были весьма заинтересованы в дедуктивных рассуждениях не столько из-за их практического применения, сколько из-за того, что оно могло дать им понимание способов мышления людей. Одна из первых идей, которые возникли при изучении дедуктивного мышления, заключается в том, что люди изучают (или разрабатывают) ментальные версии правил, которые позволяют им решать эти типы задач рассуждения (Braine, 1978; Braine, Reiser, & Rumain, 1984).Лучший способ увидеть эту точку зрения — понять, что существуют разные возможные правила, и некоторые из них очень простые. Например, рассмотрим это правило логики:
p или q
не п
следовательно q
Логические правила часто представлены абстрактно в виде букв, чтобы показать, что их можно использовать в очень многих конкретных ситуациях. Вот конкретная версия того же правила:
У меня сегодня на ужин пиццу или гамбургер (p или q)
Я не буду пиццы (не p)
Значит, я буду гамбургер (значит, q)
Подобные рассуждения кажутся настолько естественными и легкими, что вполне вероятно, что мы будем использовать версию этого правила в нашей повседневной жизни.По крайней мере, это кажется более правдоподобным, чем некоторые из альтернативных возможностей — например, что нам нужно иметь опыт работы с конкретной ситуацией (в данном случае пицца или гамбургер), чтобы легко решить этот тип проблемы. Так что, возможно, существует форма естественной логики (Rips, 1990), которая содержит очень простые версии логических правил. Когда мы сталкиваемся с проблемой рассуждений, которая соответствует одному из этих правил, мы используем это правило.
Но будьте очень осторожны; не всегда все бывает так просто, как кажется.Даже эти простые правила не так просты. Например, рассмотрим следующее правило. Многие люди не понимают, что это правило так же верно, как и правило пиццы или гамбургера, приведенное выше.
если p, то q
не q
следовательно, а не р
Бетонная версия:
Если ужинаю, то и десерт
У меня не было десерта
Следовательно, я не обедал
Простой факт в том, что людям может быть очень трудно правильно применять правила дедуктивной логики; в результате они делают много ошибок, пытаясь это сделать.Это дедуктивно верный аргумент или нет?
Студенты, которые любят школу, много учатся
Студенты, которые много учатся, получают хорошие оценки
Джейн не любит школу
Следовательно, Джейн не получает хороших оценок
Многие люди с удивлением обнаруживают, что это логически неверный аргумент; заключение не гарантируется с самого начала. Хотя в первом утверждении говорится, что ученики, которым нравится школа, много учатся, в нем НЕ говорится, что ученики, которым не нравится школа, учатся мало.Другими словами, вполне возможно, что можно много учиться, не любя школу. Даже люди, которые иногда сталкиваются с подобными проблемами правильно, могут не использовать правила дедуктивного мышления. Вместо этого они могут просто выносить суждения на основе известных им примеров, в данном случае вспоминая случаи, когда люди получали хорошие оценки, несмотря на то, что им не нравилась школа.
Еще более трудным дедуктивное рассуждение является тот факт, что есть два важных свойства, которыми может обладать аргумент. Во-первых, он может быть действительным или недействительным (это означает, что вывод логически следует или не следует из утверждений, которые к нему привели).Во-вторых, аргумент (вернее, его вывод) может быть истинным или ложным. Вот пример аргумента, который логически верен, но имеет ложный вывод (по крайней мере, мы думаем, что он ложный).
Либо вы ростом одиннадцать футов, либо Гранд-Каньон был создан космическим кораблем, врезавшимся в землю.
Ваш рост не одиннадцать футов
Следовательно, Гранд-Каньон был создан космическим кораблем, врезавшимся в землю
Этот аргумент имеет ту же форму, что и аргумент о пицце или гамбургере, приведенный выше, что делает его дедуктивно верным.Однако это заключение настолько ложно, что абсурдно (конечно, причина, по которой это заключение является ложным, состоит в том, что первое утверждение ложно). Когда люди оценивают аргументы, они, как правило, не замечают разницы между дедуктивной достоверностью и эмпирической истинностью утверждений или выводов. Если элементы аргумента верны, люди, вероятно, сочтут аргумент логически достоверным; если элементы ложны, они, скорее всего, сочтут его недействительным (Markovits & Bouffard-Bouchard, 1992; Moshman & Franks, 1986).Таким образом, кажется преувеличением сказать, что люди используют эти логические правила для оценки обоснованности аргументов. Многие психологи считают, что у большинства людей на самом деле очень ограниченные навыки дедуктивного мышления (Johnson-Laird, 1999). Они утверждают, что, сталкиваясь с проблемой, для решения которой требуется дедуктивная логика, люди прибегают к более простым методам, таким как сопоставление терминов, которые появляются в утверждениях и заключении (Evans, 1982). Это может показаться не проблемой, но что, если рассуждающие верят, что элементы верны, а они ошибаются; они будут полагать, что они используют форму рассуждений, гарантирующую, что они верны, но в то же время ошибаются.
дедуктивное рассуждение: тип рассуждения, при котором заключение гарантированно будет истинным в любое время, когда утверждения, приведшие к нему, верны
аргумент: набор утверждений, в которых начальные утверждения приводят к заключению
дедуктивно действительный аргумент: аргумент, для которого истинные начальные утверждения гарантируют верность заключения
Индуктивное рассуждение и суждение
Каждый день вы делаете множество суждений о вероятности того или иного.Осознаёте вы это или нет, но ежедневно практикуете индуктивное мышление . В аргументах с индуктивным рассуждением вывод вероятен, если предшествующие ему утверждения верны. Первое, на что следует обратить внимание в отношении индуктивного рассуждения, — это то, что по определению вы никогда не можете быть уверены в своем заключении; вы можете только оценить, насколько вероятен такой вывод. Индуктивные рассуждения могут побудить вас сосредоточиться на кодировании и кодировании памяти при подготовке к экзамену, но возможно, что вместо этого инструктор задаст больше вопросов о восстановлении памяти.В отличие от дедуктивного мышления, выводы, к которым вы пришли с помощью индуктивного мышления, только вероятны, но не уверены. Вот почему ученые считают индуктивные рассуждения более слабыми, чем дедуктивные. Но представьте, как трудно нам было бы действовать, если бы мы не могли действовать, пока не были уверены в результате.
Индуктивные рассуждения могут быть представлены как логические аргументы, состоящие из утверждений и заключения, точно так же, как дедуктивные рассуждения. В индуктивном аргументе вам даются некоторые утверждения и вывод (или вам даются некоторые утверждения и вы должны сделать вывод).Аргумент индуктивно сильный , если заключение было бы очень вероятным, когда утверждения верны. Так, например, вот индуктивно сильный аргумент:
- Заявление №1: Синоптик 2-го канала сказал, что сегодня пойдет дождь.
- Заявление № 2: Синоптик 5 канала сказал, что сегодня пойдет дождь.
- Положение № 3: Очень пасмурно и влажно.
- Заявление №4: Вы только что услышали гром.
- Заключение (или суждение): Сегодня пойдет дождь.
Считайте заявления доказательствами, на основании которых вы сделаете вывод. Итак, основываясь на доказательствах, представленных в четырех заявлениях, весьма вероятно, что сегодня пойдет дождь. Сегодня обязательно пойдет дождь? Конечно нет. Мы все можем вспомнить времена, когда синоптик ошибался.
Правдивая история: Несколько лет назад студент-психолог смотрел бейсбольный матч плей-офф между «Сент-Луис Кардиналс» и «Лос-Анджелес Доджерс». Графика на экране только что проинформировала аудиторию о том, что кардинал на летучей мыши (шорт-стоп Зала славы) Оззи Смит, нападающий на стрелку, отбивающий левую руку в этом выступлении на пластине, ни разу за почти 3000 карьерных летучих мышей не ударил хоумран левша.Студент, который только что узнал об индуктивном мышлении на уроке психологии, повернулся к своему товарищу (фанату Кардиналов) и самодовольно сказал: «Это индуктивно сильный аргумент, что Оззи Смит не добьется успеха». Он повернулся к телевизору как раз вовремя, чтобы посмотреть, как мяч пересекает правое ограждение поля для хоумрана. Хотя в то время студент чувствовал себя глупо, он не ошибался. Это был сильный индуктивный аргумент; 3000 ат-летучих мышей — это ужасно много свидетельств того, что Волшебник Озза (как он был известен) не стал бы ударить одного из парка (подумайте о каждой летучей мыши без хоум-ран как утверждение в индуктивном аргументе) .К сожалению (для стойкого фаната Детёнышей и студента, ненавидящего кардиналов), несмотря на силу аргументов, вывод был неверным.
Учитывая возможность того, что мы можем сделать неверный вывод даже с помощью сильного индуктивного аргумента, мы действительно хотим быть уверены, что действительно приводим индуктивно сильные аргументы. Если мы судим о чем-то вероятном, лучше быть вероятным. Если мы будем судить о чем-то почти невозможном, лучше этого не случится. Думайте об индуктивных рассуждениях, как о достаточно точных суждениях о вероятности того или иного вывода при наличии набора свидетельств.
Многие решения в нашей жизни основываются на индуктивных рассуждениях. Например:
Утверждение №1: Психология — не лучший предмет для меня
Утверждение № 2: Мой преподаватель психологии имеет репутацию специалиста по сдаче сложных экзаменов
Утверждение № 3: Мой первый экзамен по психологии был намного сложнее, чем я ожидал
Суждение: Следующий экзамен, вероятно, будет очень трудным.
Решение: сегодня вечером буду учиться, а не смотреть Netflix.
Некоторые другие примеры суждений, которые люди обычно принимают в школьном контексте, включают суждения о вероятности того, что:
- Конкретный класс будет интересен / полезен / сложен
- Вы сможете закончить писать доклад к следующей неделе, если выйдете сегодня вечером
- Батареи вашего ноутбука хватит на следующий поход в библиотеку
- Вы не пропустите ничего важного, если пропустите завтра
- Ваш инструктор не заметит, если вы завтра пропустите занятия
- Вы сможете найти книгу, которая вам понадобится для бумаги
- На следующем экзамене будет задан вопрос о кодировании памяти.
Тверски и Канеман (1983) признали, что есть два общих способа, с помощью которых мы можем делать эти суждения; они назвали их экстенсиональными (т.е., следуя законам вероятности) и интуитивно понятным (т. е. с использованием ярлыков или эвристик, см. ниже). Мы будем использовать аналогичное различие между мышлением типа 1 и типа 2, как описано Китом Становичем и его коллегами (Evans and Stanovich, 2013; Stanovich and West, 2000). Мышление типа 1 — быстрое, автоматическое, требующее усилий и эмоциональное мышление. На самом деле, вряд ли справедливо называть это рассуждением, поскольку суждения просто приходят в голову. Мышление типа 2 , с другой стороны, работает медленно, требует усилий и логично.Таким образом, очевидно, что это с большей вероятностью приведет к правильному или оптимальному решению. Проблема в том, что мы склонны чрезмерно полагаться на Тип 1. Теперь мы не говорим, что Тип 2 — это правильный путь для каждого нашего решения или суждения. Например, это кажется немного сложным, чтобы участвовать в пошаговой процедуре логических рассуждений, чтобы решить, будем ли мы сегодня вечером есть на ужин курицу или рыбу.
Однако многие неверные решения в некоторых очень важных контекстах могут быть связаны с неправильными суждениями о вероятности определенных рисков или результатов, которые возникают в результате использования Типа 1, когда более уместным был бы более логичный процесс рассуждений.Например:
Заявление №1: Поздняя ночь.
Заявление № 2: Альберт последние пять часов пил пиво на вечеринке.
Заявление № 3: Альберт не совсем уверен, где он находится и как далеко от дома.
Решение: Альберту не составит труда дойти до дома.
Решение: Он идет домой один.
Как вы можете видеть в этом примере, три утверждения, подтверждающие суждение, на самом деле его не поддерживают. Другими словами, этот аргумент не является индуктивно сильным, потому что он основан на суждениях, игнорирующих законы вероятности.Каковы шансы, что кто-то, столкнувшийся с этими условиями, сможет легко добраться домой один? И не нужно быть пьяным, чтобы принимать неверные решения на основе суждений, которые только что приходят нам в голову.
Истина в том, что многие из наших вероятностных суждений не очень близки к тому, чем они должны быть по законам вероятности. Подумай об этом. Чтобы рассуждать в соответствии с этими законами, нам необходимо знать законы вероятности, которые позволят нам вычислить взаимосвязь между конкретными доказательствами и вероятностью некоторого исхода (т.е., насколько вероятность должна измениться при наличии доказательства), и нам пришлось бы проделывать эти тяжелые математические вычисления в уме. В конце концов, это то, что требует Тип 2. Излишне говорить, что даже если бы мы были мотивированы, мы часто даже не знали, как применять рассуждение типа 2 во многих случаях.
Итак, что нам делать, если у нас нет знаний, навыков или времени, необходимых для правильного математического суждения? Не будем ли мы задерживаться и ждать, пока не получим более убедительные доказательства? Читаем ли мы о вероятности и запускаем наше приложение-калькулятор, чтобы вычислить правильную вероятность? Конечно нет.Мы полагаемся на мышление Типа 1. Мы «крылатые». То есть мы делаем оценку вероятности, используя имеющиеся в нашем распоряжении средства. Психологи используют термин «эвристика» для описания того типа «крылатого крыла», о котором мы говорим. Эвристика — это сокращенная стратегия, которую мы используем, чтобы сделать какое-то суждение или решить некоторую проблему (см. Раздел 7.3). Эвристики просты и быстры, считайте их основными процедурами, характерными для Типа 1. Они могут абсолютно точно привести к разумным суждениям и решениям в некоторых ситуациях (например, выбор между курицей и рыбой на ужин).Однако они далеко не надежны. На самом деле существует довольно много ситуаций, в которых эвристика может привести нас к неправильным суждениям, и во многих случаях решения, основанные на этих суждениях, могут иметь серьезные последствия.
Давайте вернемся к деятельности, с которой начинается этот раздел. Вас попросили оценить вероятность (или частоту) определенных событий и рисков. Вы могли свободно придумывать свои собственные доказательства (или заявления), чтобы выносить эти суждения. Вот где возникает эвристика.В качестве кратчайшего пути суждения мы склонны приводить конкретные примеры тех самых событий, чтобы помочь нам определить их вероятность или частоту. Например, если нас просят судить, насколько распространен, часто или вероятен тот или иной тип рака, многие из наших утверждений будут примерами конкретных случаев рака:
Заявление № 1: Энди Кауфман (комик) болел раком легких.
Заявление № 2: Колин Пауэлл (государственный секретарь США) болел раком простаты.
Заявление № 3: Боб Марли (музыкант) страдал от рака кожи и мозга
Заявление № 4: Сандра Дэй О’Коннор (судья Верховного суда) болела раком груди.
Заявление № 5: Фред Роджерс (детский артист) болел раком желудка.
Заявление № 6: Робин Робертс (ведущий новостей) болел раком груди.
Заявление № 7: Бетт Дэвис (актриса) болела раком груди.
Суждение: рак груди — самый распространенный тип.
Ваш собственный опыт или память также могут сказать вам, что рак груди является наиболее распространенным типом. Но это не так (хотя это обычное дело). На самом деле рак кожи — самый распространенный тип в США. Мы все время делаем одни и те же неверные суждения, потому что мы не генерируем примеры или доказательства в соответствии с их фактической частотой или вероятностью.Вместо этого у нас есть тенденция (или предвзятость) искать примеры в памяти; если их легко найти, мы предполагаем, что они обычны. Перефразируя это на языке эвристики, события кажутся более вероятными в той степени, в которой они доступны в памяти. Это смещение получило название эвристики доступности (Канеман и Тверски, 1974).
Тот факт, что мы используем эвристику доступности, не означает автоматически, что наше суждение неверно. Причина, по которой мы используем эвристики в первую очередь, заключается в том, что они во многих случаях работают достаточно хорошо (и, конечно же, их легко использовать).Итак, самые простые примеры иногда оказываются самыми распространенными. Является ли более вероятным, что членом Сената США является мужчина или женщина? Большинству людей гораздо легче создавать примеры мужчин-сенаторов. И, как оказалось, в Сенате США мужчин намного больше, чем женщин (от 74 до 26 в 2020 году). В этом случае эвристика доступности приведет вас к правильному суждению; гораздо более вероятно, что сенатором будет мужчина.
Однако во многих других случаях эвристика доступности сбивает нас с пути.Это потому, что события могут быть запоминающимися по многим причинам, помимо их частоты. В разделе 5.2, «Кодирование значения» было высказано предположение, что хороший способ закодировать значение некоторой информации — это сформировать ее мысленный образ. Таким образом, информация, которая была мысленно отображена, будет более доступной для памяти. В самом деле, яркое и легко изображаемое событие заставит многих людей предположить, что события такого типа встречаются чаще, чем они есть на самом деле. Повторение информации также сделает ее более запоминающейся.Итак, если одно и то же событие описано вам в журнале, в вечерних новостях, в подкасте, который вы слушаете, и в вашей ленте Facebook; это будет очень доступно памяти. Опять же, эвристика доступности приведет к неправильному восприятию частоты событий такого типа.
Самое интересное, что необычная информация более запоминающаяся. Предположим, мы даем вам следующий список слов для запоминания: ящик, цветок, письмо, утконос, печь, лодка, газета, кошелек, барабан, машина. Скорее всего, проще всего запомнить слово «утконос», необычное.То же самое и с воспоминаниями о событиях. Событие может быть доступно в памяти, потому что оно необычно, но эвристика доступности позволяет нам сделать вывод, что событие является обычным. Вы это уловили? В этих случаях эвристика доступности заставляет нас думать, прямо противоположно истинной частоте. В конечном итоге мы думаем, что что-то обычное , потому что необычно (и поэтому запоминается). Ой.
Неправильное применение эвристики доступности иногда приводит к неудачным результатам.Например, если вы за последние 10 лет ходили в школу K-12 в США, весьма вероятно, что вы участвовали в тренировках по изоляции и активной стрельбе. Конечно, все пытаются предотвратить трагедию очередной стрельбы в школе. И, поверьте, мы не пытаемся преуменьшить масштабы трагедии. Но правда в том, что расстрелы в школах случаются крайне редко. Поскольку федеральное правительство не ведет базы данных о стрельбе в школах, газета Washington Post ведет собственный подсчет.В период с 1999 г. по январь 2020 г. (дата последней стрельбы в школе со смертью в США на момент написания этого абзаца) Post сообщила, что в общей сложности в результате стрельбы в школах в США погибло 254 человека. Не 254 в год, всего 254. Это в среднем 12 в год. Конечно, это 254 человека, которым не следовало умирать (особенно потому, что многие из них были детьми), но для страны с примерно 60 миллионами студентов и учителей это очень небольшой риск.
Но многие ученики и учителя боятся, что они станут жертвами стрельбы в школах, из-за эвристики доступности.Придумывать примеры настолько легко (они легко запоминаются), что люди считают, что это очень обычное событие. Нет. И у этого есть обратная сторона. Мы случайно считаем, что в Соединенных Штатах существует огромная проблема насилия с применением огнестрельного оружия. По данным Центров по контролю и профилактике заболеваний, в 2017 году в США произошло 39 773 смертельных случая, связанных с огнестрельным оружием. Пятнадцать из этих смертей произошли в результате стрельбы в школах, сообщает Post. 60% этих смертей были самоубийствами. Когда люди обращают внимание на риск стрельбы в школе (низкий), они часто не замечают гораздо большего риска.
И подобные примеры отнюдь не уникальны. Авторы этой книги преподают психологию с 1990-х годов. Мы смогли привести те же самые аргументы относительно неправильного применения эвристик доступности и поддерживать их актуальность, просто заменив их на «страх дня». В 1990-х годах это было похищение детей незнакомцами (это было известно как «опасность для незнакомцев»), несмотря на то, что похищения составляли только 2% насильственных преступлений, совершаемых против детей, и только 24% похищений совершаются незнакомцами (США. Министерство юстиции, 2007 г.).Этот страх перекликается со страхом перед терроризмом, охватившим страну после террористических атак 2001 г. на Всемирный торговый центр и Пентагон США и до сих пор отравляющим население США в 2020 г. После широко разрекламированного сенсационного акта насилия люди чрезвычайно вероятно, что они увеличат свои оценки шансов, что они тоже станут жертвами террора. Однако подумайте о реальности. В октябре 2001 года террорист разослал споры сибирской язвы членам правительства США и ряду медиа-компаний.В результате этого нападения погибло пять человек. Нация была почти парализована страхом умереть от нападения; в действительности вероятность смерти отдельного человека составляла 0,00000002.
Эвристика доступности также может привести к неправильным суждениям в школе. Например, предположим, что вы пытаетесь решить, следует ли вам брать урок у определенного профессора математики. Вы можете попытаться оценить, насколько она хороша в качестве учителя, вспомнив случаи, когда друзья и знакомые комментировали ее навыки преподавания.У вас может быть несколько примеров, которые предполагают, что она плохой учитель, очень доступный для запоминания, поэтому на основе эвристики доступности вы судите ее как плохую учительницу и решаете взять урок у кого-то другого. Что, если бы все случаи, которые вы вспомнили, принадлежали одному и тому же человеку, а этот человек оказался очень ярким рассказчиком? Последующая легкость запоминания примеров может не указывать на то, что профессор в конце концов плохой учитель.
Хотя эвристика доступности, очевидно, важна, это не единственная эвристика оценки, которую мы используем.Амос Тверски и Дэниел Канеман исследовали роль эвристики в индуктивном мышлении в длинной серии исследований. Канеман получил Нобелевскую премию по экономике за это исследование в 2002 году, и Тверски, несомненно, получил бы ее, если бы он не умер от меланомы в возрасте 59 лет в 1996 году (Нобелевские премии не вручаются посмертно). Канеман и Тверски неоднократно демонстрировали, что люди не рассуждают так, как это согласуется с законами вероятности. Они определили несколько эвристических стратегий, которые люди используют вместо этого, чтобы судить о вероятности.Важность этой работы для экономики (и причина того, что Канеман был удостоен Нобелевской премии) заключается в том, что более ранние экономические теории предполагали, что люди действительно выносят суждения рационально, то есть в соответствии с законами вероятности.
Еще одна распространенная эвристика, которую люди используют для вынесения суждений, — это эвристика репрезентативности (Канеман и Тверски, 1973). Предположим, мы описываем вам человека. Он тихий и застенчивый, непритязательный, любит работать с числами.Этот человек, скорее всего, будет бухгалтером или адвокатом? Если вы сказали бухгалтер, вы, вероятно, использовали эвристику репрезентативности. Считается, что наш воображаемый человек скорее всего будет бухгалтером, потому что он похож на бухгалтера или является его представителем. Когда участников исследования просят высказать подобные суждения, кажется, что единственное, что имеет значение, — это репрезентативность описания. Например, если будет сказано, что описанный человек находится в комнате, в которой находятся 70 юристов и 30 бухгалтеров, участники все равно будут считать, что он бухгалтер.
индуктивное рассуждение: тип рассуждения, в котором мы делаем суждения о вероятности на основе наборов доказательств
индуктивно сильный аргумент: индуктивный аргумент, в котором начальные утверждения приводят к заключению, которое, вероятно, верно
эвристика: сокращенная стратегия, которую мы используем для вынесения суждений и решения проблем. Хотя они просты в использовании, они не гарантируют правильных суждений и решений.
эвристика доступности: оценка частоты или вероятности события определенного типа в зависимости от того, насколько легко можно вспомнить примеры события (т.е., насколько они доступны в памяти)
эвристика репрезентативности: оценка вероятности того, что что-то является членом категории, на основе того, насколько оно похоже на типичного члена категории (то есть насколько репрезентативно для категории)
Мышление типа 1: быстрое, автоматическое и эмоциональное мышление.
Мышление типа 2 : медленное, требующее усилий и логическое мышление.
- Напомните свои ответы на эти вопросы из раздела «Активировать»:
- Какой процент похищений совершается незнакомцами?
- Какая часть дома наиболее опасна: кухня, ванная или лестница?
- Какой вид рака наиболее распространен в США?
- Какой процент убийств на рабочем месте является насилием со стороны коллег?
Многие люди неправильно задают эти вопросы.Ответы — 10%; лестница; кожа; 6%. Насколько близки были ваши ответы? Объясните, как эвристика доступности могла привести вас к неверным суждениям.
- Можете ли вы вспомнить какие-то другие суждения, которые вы сделали (или убеждения, которые у вас есть), на которые могла повлиять эвристика доступности?
7.3 Решение проблем
- Уделите несколько минут, чтобы перечислить ряд проблем, с которыми вы сталкиваетесь прямо сейчас.
- Теперь напишите о проблеме, которую вы недавно решили.
- Как вы определяете проблему?
У Мэри проблема. Ее дочь, которая обычно очень стремится доставить удовольствие, кажется, рада быть последним, кто что-то сделает. Собирается ли она в школу, ходит на уроки игры на фортепиано или уроки карате, или даже гуляет с друзьями, она, похоже, не хочет или не может подготовиться вовремя. У других людей разные проблемы. Например, многие студенты работают на работе, имеют многочисленные семейные обязанности и сталкиваются с расписанием курса, полным сложных экзаменов, заданий, работ и выступлений.Как они могут найти достаточно времени, чтобы посвятить себя учебе, и при этом выполнять свои другие обязанности? Говоря об учениках и их проблемах: покажите, что мячу, брошенному вертикально вверх с начальной скоростью v0, требуется в два раза больше времени для возврата, чем для достижения наивысшей точки (из Spiegel, 1981).
Это три очень разные ситуации, но все мы назвали их проблемами. Что делает их все одинаковыми, несмотря на различия? Психолог может определить проблему как ситуацию с начальным состоянием, целевым состоянием и набором возможных промежуточных состояний.В несколько более значимом смысле мы могли бы рассматривать проблему как ситуацию, в которой вы находитесь здесь в одном состоянии (например, дочь всегда опаздывает), вы хотите быть там в другом состоянии (например, дочь не всегда опаздывает) и без очевидных способ добраться отсюда туда. При таком определении каждую из трех описанных нами ситуаций теперь можно рассматривать как пример одной и той же общей концепции — проблемы. На этом этапе вы можете начать задаваться вопросом, что не является проблемой, учитывая такое общее определение. Кажется, что почти каждую нестандартную задачу, которую мы выполняем, можно квалифицировать как проблему.Пока вы понимаете, что проблемы не обязательно плохие (принять вызов и решить проблему может быть довольно весело и приятно), это может быть полезным способом подумать об этом.
Можем ли мы определить набор навыков решения проблем, которые можно было бы применить в этих самых разных ситуациях? Вкратце, эта задача — основная цель этого раздела. Давайте попробуем разобраться в большом разнообразии способов решения проблем, сделав одно важное наблюдение: процесс решения проблем можно разделить на две ключевые части.Во-первых, люди должны заметить, понять и правильно представить проблему в уме (так называемое представление проблемы , ). Во-вторых, они должны применить какую-то стратегию решения проблемы. Психологи подробно изучили обе эти ключевые части процесса.
Когда вы впервые думаете о процессе решения проблем, вы можете предположить, что большинство наших трудностей возникает из-за того, что мы терпим неудачу на втором этапе, применении стратегии. Хотя большую часть времени это может быть значительной трудностью, более важным источником трудностей, вероятно, является представление проблемы.Короче говоря, нам часто не удается решить проблему, потому что мы смотрим на нее или думаем о ней неправильно.
проблема: ситуация, в которой мы находимся в начальном состоянии, имеем желаемое целевое состояние и есть ряд возможных промежуточных состояний (т.е. нет очевидного способа перейти от начального к целевому состоянию)
представление проблемы: обнаружение, осмысление и формирование мысленного представления о проблеме
Определение и мысленное представление проблем для их решения
Итак, главное препятствие к решению проблемы состоит в том, что мы не совсем ясно понимаем, в чем проблема.Вспомните проблему с дочерью Мэри, которая всегда опаздывает. Один из способов представить или подумать об этой проблеме — это то, что она сопротивляется. Она отказывается вовремя подготовиться. Этот тип представления или определения предлагает конкретный тип решения. Однако еще один способ подумать о проблеме — это рассмотреть возможность того, что она просто отвлекается на интересные развлечения. Эта другая концепция проблемы (то есть другое представление) предполагает совершенно другую стратегию решения.Например, если Мэри определяет проблему как неповиновение, у нее может возникнуть соблазн решить проблему с помощью какой-либо тактики принуждения, то есть утвердить свой авторитет как своей матери и заставить ее слушать. С другой стороны, если Мэри определяет проблему как отвлечение, она может попытаться решить ее, просто удалив отвлекающие объекты.
Как вы могли догадаться, когда проблема представлена односторонним образом, решение может показаться очень трудным или даже невозможным. С другой стороны, решение может быть очень простым.Например, рассмотрим следующую задачу (из Насара, 1998 г.):
Два велосипедиста начинают движение на расстоянии 20 миль друг от друга и направляются друг к другу, каждый со стабильной скоростью 10 миль в час. В то же время муха, которая движется со стабильной скоростью 15 миль в час, стартует от переднего колеса велосипеда, идущего на юг, и летит к переднему колесу велосипеда, движущегося на север, затем разворачивается и снова летит к переднему колесу велосипеда, движущегося на юг. , и так продолжается до тех пор, пока он не оказывается зажат между двумя передними колесами.Вопрос: какое общее расстояние пролетела муха?
Уделите несколько минут, чтобы попытаться решить эту проблему.
Большинство людей представляют эту проблему как вопрос о мухе, потому что, ну, вот как задается вопрос. Решение, используя это представление, состоит в том, чтобы выяснить, как далеко пролетит муха на первом этапе своего путешествия, а затем прибавить эту сумму к тому, как далеко она пролетит на втором этапе своего путешествия (когда она развернется и вернется к первому этапу путешествия). велосипед), затем продолжайте прибавлять меньшее расстояние от каждого отрезка пути до тех пор, пока не найдете правильный ответ.Чтобы решить эту задачу, вам потребуется достаточно хорошо разбираться в математике, и для этого вам, вероятно, потребуется время, карандаш и бумага.
Однако, если вы рассмотрите другое представление, вы можете решить эту проблему в уме. Вместо того, чтобы думать об этом как о вопросе о мухе, подумайте об этом как о вопросе о велосипедах. Между ними 20 миль, и каждый движется со скоростью 10 миль в час. Как долго велосипеды доберутся до друг друга? Хорошо, один час. Муха движется со скоростью 15 миль в час; следовательно, он проедет в общей сложности 15 миль туда и обратно за час до встречи велосипедов.Представленная в одностороннем порядке (в виде задачи о мухе) задача довольно сложная. Представить по-другому (как задачу о двух велосипедах) легко. Изменение вашего представления о проблеме иногда является лучшим, а иногда и единственным способом ее решения.
Однако, к сожалению, изменить представление проблемы — не самое легкое дело. Часто специалисты по решению проблем застревают, глядя на проблему с одной стороны. Это называется фиксацией . Большинство людей, которые представляют предыдущую проблему как проблему с мухой, вероятно, не останавливаются, чтобы пересмотреть и, следовательно, изменить свое представление.Родитель, который думает, что его дочь ведет себя вызывающе, вряд ли рассмотрит возможность того, что ее поведение гораздо менее целенаправленно.
Привязка к решению проблем была исследована группой немецких психологов, называемых гештальт-психологами, в 1930-х и 1940-х годах. Карл Дункер, например, обнаружил важный тип неспособности принять другую точку зрения, названный функциональной фиксированностью . Представьте себя участником одного из его экспериментов. Вас просят выяснить, как установить две свечи на дверь, и вам дадут набор всяких лишних вещей, включая небольшую пустую картонную коробку и несколько канцелярских кнопок.Возможно, вы уже придумали решение: прикрепите коробку к двери, чтобы она образовала платформу, а затем поставьте свечи на коробку. Большинство людей могут прийти к этому решению. Однако представьте себе небольшое изменение процедуры. Что, если бы коробка была не пустой, а в ней лежали спички? Большинство людей, которым предлагается эта версия проблемы, не приходят к решению, приведенному выше. Почему? Потому что людям кажется, что когда коробка содержит совпадения, у нее уже есть функция; это спичечный коробок.Люди вряд ли будут рассматривать новую функцию для объекта, у которого уже есть функция. Это функциональная неподвижность.
Ментальный набор — это тип фиксации, при котором решатель проблем застревает, используя ту же стратегию решения, которая была успешной в прошлом, даже если решение больше не может быть полезным. Обычно это наблюдается, когда ученики решают математические задачи для домашнего задания. Часто несколько проблем подряд требуют повторного применения одной и той же стратегии решения. Затем, без предупреждения, следующая задача в наборе требует новой стратегии.Многие студенты пытаются применить ранее успешную стратегию к новой проблеме и поэтому не могут найти правильный ответ.
Следует помнить, что вы не можете решить проблему, если правильно не определите, с чего она должна начинаться (начальное состояние) и каким должен быть конечный результат (состояние цели). Это может означать, что нужно взглянуть на проблему под другим углом и по-новому представить ее. Правильное представление не гарантирует успешного решения, но, безусловно, направит вас на правильный путь.
Более оптимистично то, что гештальт-психологи открыли то, что можно считать противоположностью фиксации, а именно инсайт . Иногда решение проблемы просто приходит в голову. Вольфганг Колер исследовал способность проникновения в суть, поставив перед шимпанзе множество различных проблем, в основном связанных с получением ими недоступной пищи. По одной из версий, банан помещали вне клетки шимпанзе, а короткую палку помещали внутрь клетки. Палка была слишком короткой, чтобы достать банан, но достаточно длинной, чтобы достать более длинную палку, также находящуюся за пределами клетки.Эта вторая палка была достаточно длинной, чтобы достать банан. После неудачной попытки дотянуться до банана более короткой палкой шимпанзе делал пару случайных попыток, реагировал с некоторым явным разочарованием или гневом, а затем внезапно бросался к более длинной палке, при этом правильное решение было полностью реализовано. точка. Это внезапное появление решения, которое неоднократно наблюдалось с множеством различных проблем, было названо Колером прозрением.
Чтобы вы не подумали, что это относится только к шимпанзе, Карл Дункер продемонстрировал, что дети также решают проблемы с помощью проницательности в 1930-х годах.Что еще более важно, вы, вероятно, сами испытали озарение. Вспомните время, когда вы пытались решить сложную проблему. После некоторой борьбы вы сдались. Через несколько часов раствор просто пришел вам в голову, возможно, когда вы гуляли, ужинали или лежали в постели.
фиксация: , когда решатель проблем застревает, глядя на проблему определенным образом и не может изменить свое представление о ней (или его или ее предполагаемую стратегию решения)
функциональная неподвижность: особый тип фиксации, при котором решатель проблем не может придумать новое использование для объекта, который уже имеет функцию
ментальная установка: особый тип фиксации, при которой решающий проблемы застревает, используя ту же стратегию решения, которая была успешной в прошлом
озарение: внезапное осознание решения проблемы
Решение проблем методом проб и ошибок
Правильное определение проблемы и цель ее решения — хорошее начало, но вспомните определение проблемы, данное психологом: оно включает в себя набор возможных промежуточных состояний.С этой точки зрения проблема может быть решена удовлетворительно, только если можно найти путь через некоторые из этих промежуточных состояний к цели. Представьте себе довольно обычную задачу: найти новый маршрут в школу, когда ваш обычный маршрут заблокирован (например, из-за строительства дороги). На каждом перекрестке вы можете повернуть налево, повернуть направо или ехать прямо. Удовлетворительное решение проблемы (добраться до школы) — это последовательность выбора на каждом перекрестке, которая позволяет вам закончить школу.
Если бы у вас было все время в мире, чтобы добраться до школы, вы могли бы попробовать случайным образом выбрать промежуточные состояния.В одном углу вы поворачиваете налево, затем идете прямо, затем снова налево, затем направо, затем направо, затем прямо. К сожалению, метод проб и ошибок не обязательно приведет вас туда, куда вы хотите, и даже если это произойдет, это не самый быстрый способ добраться туда. Например, когда наш друг учился в колледже, он заблудился по дороге на концерт и попытался найти место, случайно выбрав улицы для поворота (это было задолго до использования GPS). Удивительно, но стратегия сработала, хотя в итоге он пропустил две из трех групп, которые играли в тот вечер.
Метод проб и ошибок — это не все плохо. Б.Ф. Скиннер, известный психолог-бихевиорист, предположил, что люди часто ведут себя случайным образом, чтобы увидеть, какое влияние это поведение оказывает на окружающую среду и какое последующее влияние на них оказывает это изменение окружающей среды. Это кажется особенно актуальным для очень молодого человека. Представьте, например, ребенка, который наполняет домашний аквариум туалетной бумагой. Для ребенка, пытающегося развить репертуар творческих стратегий решения проблем, странное и случайное поведение может быть только билетом.В конце концов, как надеется разгневанный родитель, ребенок обнаружит, что многие из этих случайных форм поведения не решают проблемы; фактически, во многих случаях они создают проблемы. Таким образом, можно было бы ожидать уменьшения этого случайного поведения по мере взросления ребенка. Однако вы должны понимать, что противоположная крайность столь же контрпродуктивна. Если дети становятся слишком жесткими, никогда не пробуют что-то неожиданное и новое, их навыки решения проблем могут стать слишком ограниченными.
Для эффективного решения проблем, кажется, нужна золотая середина, которая устанавливает баланс между использованием хорошо обоснованных старых стратегий и попытками освоить новую территорию и территорию.Человек, который распознает ситуацию, в которой старая стратегия решения проблем будет работать лучше всего, и который также может распознать ситуацию, в которой необходима новая непроверенная стратегия, находится на полпути к успеху.
Решение проблем с помощью алгоритмов и эвристики
Для многих проблем существует возможная стратегия, которая гарантирует правильное решение. Например, подумайте о математических задачах. Уроки математики часто состоят из пошаговых инструкций, которые можно использовать для решения задач.Если вы примените стратегию без ошибок, вы гарантированно придете к правильному решению проблемы. Этот подход называется с использованием алгоритма , термина, который обозначает пошаговую процедуру, гарантирующую правильное решение. Поскольку алгоритмы иногда доступны и поставляются с гарантией, вы можете подумать, что большинство людей используют их часто. К сожалению, это не так. Как показывает опыт многих студентов, которые с трудом проходили уроки математики, алгоритмы могут быть чрезвычайно сложными в использовании, даже если решатель проблем знает, какой алгоритм должен работать при решении проблемы.В задачах за пределами математического класса мы часто даже не знаем, доступен ли алгоритм. В таком случае, вероятно, будет справедливо сказать, что алгоритмы редко используются, когда люди пытаются решить проблемы.
Поскольку алгоритмы настолько сложны в использовании, люди часто упускают возможность гарантировать правильное решение в пользу стратегии, которая намного проще в использовании и дает разумные шансы придумать правильное решение. Эти стратегии называются эвристикой решения проблем .Подобно тому, что вы видели в разделе 6.2 с эвристикой рассуждения, эвристика решения проблем — это сокращенная стратегия, которую люди используют при попытке решить проблемы. Обычно это работает неплохо, но не гарантирует правильного решения проблемы. Например, одним из эвристических методов решения проблем может быть «всегда двигаться к цели» (поэтому, пытаясь добраться до школы, когда ваш обычный маршрут заблокирован, вы всегда будете поворачивать в том направлении, в котором, по вашему мнению, находится школа). Эвристика, которую люди могут использовать при выполнении домашнего задания по математике, — это «использовать ту же стратегию решения, которую вы только что использовали для предыдущей задачи.”
Между прочим, мы надеемся, что эти последние два абзаца покажутся вам знакомыми. Похоже, они совпадают с различием, которое вы недавно узнали. Действительно, алгоритмы и эвристика решения проблем — еще один пример различия между мышлением типа 1 и мышлением типа 2.
Хотя, вероятно, не стоит описывать большое количество конкретных эвристик, стоит упомянуть два наблюдения об эвристиках. Во-первых, эвристика может быть очень общей или очень конкретной, относящейся только к определенному типу проблемы.Например, «всегда двигаться к цели» — это общая стратегия, которую можно применять в бесчисленных проблемных ситуациях. С другой стороны, «когда вы заблудились без работающего GPS, выберите самый дорогой автомобиль, который вы видите, и следите за ним» — это специфическая проблема потери. Во-вторых, не все эвристики одинаково полезны. Многие студенты знают одну эвристику: «Если сомневаетесь, выберите c для вопроса на экзамене с несколькими вариантами ответов». Это ужасная стратегия, потому что многие преподаватели намеренно случайным образом меняют порядок ответов.Еще одна эвристика при прохождении теста, несколько более полезная, — это «поищите ответ на один вопрос где-нибудь еще на экзамене».
Вам действительно стоит обратить внимание на применение эвристики при прохождении тестов. Представьте, что, просматривая свои ответы на экзамен с несколькими вариантами ответов перед тем, как сдать его, вы сталкиваетесь с вопросом, на который, как вы изначально думали, ответ был c. Поразмыслив, вы теперь думаете, что ответ может быть b. Следует ли вам изменить ответ на b или вам следует придерживаться своего первого впечатления? Большинство людей будут применять эвристическую стратегию, чтобы «придерживаться своего первого впечатления».«Чего они, конечно, не понимают, так это того, что это очень плохая стратегия (Lilienfeld et al, 2009). Большинство ошибок на экзаменах возникает из-за вопросов, на которые изначально были даны неправильные ответы и которые не были изменены (поэтому они остаются неправильными). Гораздо меньше ошибок, когда мы меняем правильный ответ на неправильный. И, конечно, иногда мы меняем неправильный ответ на правильный. Фактически, исследования показали, что чаще менять неправильный ответ на правильный, чем наоборот (Bruno, 2001).
Вера в эту плохую стратегию сдачи теста (придерживайтесь своего первого впечатления) основана на предвзятости подтверждения (Никерсон, 1998; Уэйсон, 1960). Вы впервые увидели предвзятость подтверждения в Модуле 1, но, поскольку это очень важно, мы повторим эту информацию здесь. У людей есть предубеждение или склонность замечать информацию, которая подтверждает то, во что они уже верят. Кто-то когда-то сказал вам придерживаться своего первого впечатления, поэтому, когда вы посмотрите на результаты сданного экзамена, вы будете склонны замечать случаи, которые соответствуют этому убеждению.То есть вы заметите случаи, когда изначально вы дали правильный ответ и изменили его на неправильный ответ. Вы, как правило, не замечаете два других важных (и более распространенных) случая, меняя ответ с неправильного на правильный и оставляя неправильный ответ неизменным.
Поскольку эвристика по определению не гарантирует правильного решения проблемы, ошибки неизбежны, когда мы их применяем. Неправильный выбор конкретной эвристики приведет к еще большей вероятности ошибки.
алгоритм: пошаговая процедура, гарантирующая правильное решение проблемы
эвристика решения проблем: сокращенная стратегия, которую мы используем для решения проблем. Хотя они просты в использовании, они не гарантируют правильных суждений и решений.
систематическая ошибка подтверждения: людей склонны замечать информацию, которая подтверждает то, во что они уже верят
Последовательность эффективного решения проблем
У вас может возникнуть большой вопрос: если алгоритмы сложно использовать, а эвристика часто не работает, как я должен решать проблемы? Роберт Штернберг (1996) в рамках своей теории того, что делает людей успешными интеллектуальными (Модуль 8), описал последовательность решения проблем, которая, как было показано, работает довольно хорошо:
- Определите наличие проблемы. В школе выявить проблему часто легко; Например, проблемы, с которыми вы сталкиваетесь на уроках математики, для вас удобно обозначать как задачи. Однако за пределами школы осознание того, что у вас есть проблема, — это ключевая трудность, которую вы должны преодолеть, чтобы начать ее решать. Вы должны быть очень чувствительны к симптомам, указывающим на проблему.
- Определите проблему. Предположим, вы понимаете, что в последнее время у вас много головных болей. Скорее всего, вы определили бы это как проблему.Если вы определяете проблему как «головные боли», решением, вероятно, будет прием аспирина, ибупрофена или других противовоспалительных препаратов. Однако, если головные боли продолжают возвращаться, вы на самом деле не решили проблему — вероятно, потому, что вы ошибочно приняли симптом за саму проблему. Вместо этого вы должны найти первопричину головных болей. Стресс может быть настоящей проблемой. Для успешного решения многих проблем вам может потребоваться преодолеть свои фиксации и представить проблемы по-другому.Одна конкретная стратегия, которая может оказаться полезной, — это попытаться определить проблему с чужой точки зрения. Как бы ваши родители, супруга, вторая половинка, врач и т. Д. Определили бы проблему? Где-то в этих разных точках зрения может скрываться ключевое определение, которое позволит вам найти более легкое и постоянное решение.
- Сформулируйте стратегию. Теперь пора начать планировать, как именно будет решена проблема. Есть ли у вас алгоритм или эвристика? Помните, что эвристика по самой своей природе гарантирует, что иногда вам не удастся решить проблему.Следует иметь в виду, что вам следует искать долгосрочные решения, которые с большей вероятностью устранят основную причину проблемы, чем краткосрочные решения.
- Представляйте и систематизируйте информацию. Подобно тому, как сама проблема может быть определена или представлена множеством способов, информация внутри проблемы открыта для различных интерпретаций. Предположим, вы готовитесь к большому экзамену. У вас есть главы из учебника и дополнительных материалов для чтения, а также конспекты лекций, которые необходимо изучить.Как вы должны (представлять и) организовывать эти материалы? Следует ли разделять их по типу материала (текст, читатель или конспект лекций) или следует разделять их по темам? Чтобы эффективно решать проблемы, вы должны научиться находить наиболее полезное представление и организацию информации.
- Распределить ресурсы. Это, пожалуй, самый простой принцип последовательности решения проблем, но для многих он чрезвычайно труден. Во-первых, вы должны решить, помогут ли время, деньги, навыки, усилия, добрая воля или какой-либо другой ресурс решить проблему.Затем вы должны сделать трудный выбор, решив, какие ресурсы использовать, понимая, что вы не можете выделить максимум ресурсов для каждого. проблема.Очень часто решение проблемы — просто изменить способ распределения ресурсов (например, тратить больше времени на обучение, чтобы улучшить оценки).
- Отслеживайте и оценивайте решения. Обратите внимание на стратегию решения, когда вы ее применяете. Если это не работает, вы можете выбрать другую стратегию. Еще один факт, который вы должны понимать в отношении решения проблем, — это то, что оно никогда не заканчивается. Решение одной проблемы часто приводит к возникновению новых. Хороший мониторинг и оценка решений ваших проблем может помочь вам предвидеть неизбежные новые проблемы, которые могут возникнуть, и быстро приступить к их решению.
Обратите внимание, что это как эффективная последовательность решения проблем, а не как эффективная последовательность решения проблем. Точно так же, как вы можете зациклиться и в конечном итоге неправильно представить проблему или попытаться найти неэффективное решение, вы можете застрять, применяя последовательность решения проблем негибким образом. Ясно, что есть проблемные ситуации, которые можно решить, не используя эти навыки в указанном порядке.
Кроме того, для решения многих реальных проблем может потребоваться, чтобы вы возвращались и переопределяли проблему несколько раз по мере изменения ситуации (Sternberg et al.2000). Например, в последний раз рассмотрим проблему с дочерью Мэри. Сначала Мэри представляла проблему как проблему неповиновения. Когда ее ранняя стратегия умолять и угрожать наказанием не увенчалась успехом, Мэри начала более внимательно наблюдать за своей дочерью. Она заметила, что действительно внимание ее дочери будет привлечено неотразимым отвлечением или книгой. Только что переосмыслив проблему, она начала новую стратегию решения. Она начала напоминать дочери каждые несколько минут, чтобы она оставалась на работе, и напоминала ей, что если она будет готова до того, как пора уходить, она может вернуться к книге или другому отвлекающему объекту в это время.К счастью, эта стратегия оказалась успешной, поэтому Мэри не пришлось возвращаться и заново определять проблему.
Выберите одну или две проблемы, которые вы указали, когда впервые начали изучать этот раздел, и попытайтесь выработать для каждой из них шаги последовательности решения проблем, предложенные Штернбергом.
.
