Содержание
Урок по математике «Решение задач разными способами»
Тема “Решение задач разными способами”
Вид: закрепление умения решать задачи
на основе расширения способа действия.
Цели:
- научить решать задачи арифметическим и
алгебраическим способом; - научить решать усложненные уравнения.
Ход урока
1. Орг. момент.
(Пальчиковая гимнастика)
Эмоционально-психологический настрой на урок.
(Цель: создать эмоционально-психологический
контроль)
Мне вспомнилась одна пословица “Корень ученья
горек, да плод его сладок”. Как вы понимаете эту
пословицу?
Она очень подходит к нашему уроку и вы это
поймете.
2. Сообщение темы и цели урока.
— Тема нашего урока “Решение задач разными
способами”
— Запишите число и тему урока.
3. Актуализация знаний.
— Мы с вами уже решали очень много самых разных
задач, а сегодня я предлагаю вам решить необычные
задачи, а задачи в которых есть буквенное
значение.
(Дети записывают решение в тетради.)
- В зале занято 6 рядов по в мест. Сколько мест
занято? - А сколько свободных мест, если в зале а мест?
- Длина прямоугольника 8 см. Найдите периметр
квадрата.
— Можно решить эту задачу? (Эта задача требует
пояснения при решении. Если прямоугольник
является квадратом, то задача имеет решение, а
если нет, то задачу решить нельзя) - Скоро Новый Год и я предлагаю вам задание
составить задачу с такими данными.Масса подарка
800 граммов.
4. Решение задачи.
Для ремонта школы привезли в одинаковых банках
90 кг зеленой краски и 180 кг белой краски. Зеленой
Зеленой
краски было 18 банок. Сколько купили банок с белой
краской?
Работа над задачей идет по плану:
- 1 этап – восприятие задачи.
- 2 этап – поиск плана решения (прикидка ответа)
- 3 этап – выполнение плана.
- 4 этап – проверка (сравнить с прикидкой)
1 способ.
1) 90 : 18 = 5 (кг) – в 1 банке.
2) 180 : 5 = 36 (б)
2 способ.
1) 180 : 90 = 2 (раза) – во сколько раз за белую краску
заплатили больше, чем за зеленую.
2) 18 х 2 = 36 (банок.)
— Ребята, что обозначает часть или целое число 90?
18? 180?
— Где мы еще с вами можем встретить часть и
целое? (В уравнении)
5. Физминутка.
Если неизвестное число находится сложением –
приседаете,
Вычитанием – руки вверх,
Умножением – хлопаем,
Делением – руки вперед.
А – 7 = 18
35 : а = 7
а + 6 = 10
30 – а = 13
а : 12 = 5
а х 4 = 24
— Назовите уравнения, где а – целое.
Решите уравнения второго столбика (по
вариантам)
— Ребята, а что такое уравнение?
— А попробуйте теперь решить в паре такое
уравнение:
а : 4 = 17 х 3
6. Расширение способа действия.
— Мы с вами решали задачу двумя способами. Это
были арифметические способы решения. А
давайте попробуем решить эту задачу еще одним
способом – с помощью уравнения.
— Что мы возьмем за х?
— Вы уже говорили, что уравнение это равенство.
Какая величина в нашей задаче равна, одинаковая?
— Исходя из этих данных составьте в группах
уравнение по этой задаче. (180 : х = 90 : 18)
— Молодцы! Это алгебраический способ
решения задачи.
7. РРО.
— Мы с вами уже решали задачи разными способами,
а сейчас попробуйте записать решение задачи в
виде уравнения.
Уровень 1.
Реши задачу, составив уравнение.
На крыше сидело 7 голубей. Когда к ним прилетело
еще несколько, их стало 15. Сколько голубей
прилетело?
Уровень 2.
Реши задачу, составив уравнение.
В 7 одинаковых коробках 21 кг винограда. Сколько
килограммов винограда в 4 таких же коробках?
8. Итог урока.
— Разрешите закончить наш урок, задав вам
несколько вопросов.
— С чем мы сегодня познакомились на уроке?
Чему вы научились?
9. Домашнее задание.
1 уровень. Найдите в учебнике задачи, которые
можно решить уравнением.
2 уровень. Составьте 2 задачи, которые можно
решить уравнением – простым и усложненным.
Урок 28. решение задач. проверка решения задачи — Математика — 2 класс
Математика, 2 класс
Урок №28. Решение задач. Проверка решения задачи
Перечень вопросов, рассматриваемых в теме:
— Как проверить решение задачи?
— Как моделировать текст задачи табличным способом?
Глоссарий по теме:
Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.
Выражение – формула, выражающая какие–либо математические отношения.
Обратные задачи – это задачи, в которых число и результат меняются местами (известное становится неизвестным, а неизвестное известным).
Основная и дополнительная литература по теме урока:
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 8-е изд. – М.: Просвещение, 2017. – с88, 89.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1/М. И. Моро, М.А.Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.62.
- Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.23, 24.
- Математика. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. С. И. Волкова – М.: Просвещение, 2017. – с.34, 35.
Теоретический материал для самостоятельного изучения
Действия сложение и вычитание связаны друг с другом, являются взаимно обратными действиями.
СЛОЖЕНИЕ
ВЫЧИТАНИЕ
Вы помните, что в математике существуют обратные задачи. Они нам помогут при проверке решения. Обратные задачи должны обладать следующими признаками: сходный сюжет задач, число и результат меняются местами (известное становится неизвестным, а неизвестное известным).
Вы уже умеете выполнять проверку сложения и вычитания двумя способами. Вспомним эти правила.
Для проверки сложения надо из значения суммы вычесть одно из слагаемых. Если в результате вычитания получается другое слагаемое, значит, сложение выполнено верно
Для проверки вычитания, надо к значению разности прибавить вычитаемое. Если в результате сложения получается уменьшаемое, значит, вычитание выполнено верно.
Для проверки вычитания, надо из уменьшаемого вычесть разность. Если в результате получается вычитаемое, значит, вычитание выполнено верно.
Решим задачу и на её примере выполним проверку решения.
Папа поймал на рыбалке 6 окуней и 8 лещей. Сколько всего рыб поймал папа?
Чтобы узнать, сколько всего рыбы поймал папа, сложим количество окуней и лещей.
8 + 6 = 14 (р.) всего поймал папа.
Выполним проверку обратным действием.
Проверка: 14 – 6 = 8 (р.)
8 – это количество лещей, которых поймал папа. Значит, задачу решили верно.
Это действие является решением обратной задачи:
Папа поймал на рыбалке 14 окуней и лещей. Окуней было 6. Сколько лещей поймал папа?
Значит, чтобы проверить решение задачи, можно решить обратную задачу.
Теперь рассмотрим, как представить текст задачи в таблице. Прочитайте задачу.
Выделим главные слова в этой задаче, которые показывают действия, совершаемые с карандашами. Это слова: было, взяли, положили, стало.
Начертим таблицу из четырёх столбиков и двух строк. Запишем главные слова и вставим данные и вопрос.
БЫЛО | ВЗЯЛИ | ПОЛОЖИЛИ | СТАЛО |
24 к. | ? к. | 3 к. | 17 к. |
Решим задачу. Сначала узнаем, сколько стало карандашей, когда их положила сестра.
Сначала узнаем, сколько стало карандашей, когда их положила сестра.
24 + 3 = 27 (к.)
Теперь узнаем, сколько карандашей взял брат, если их осталось только семнадцать.
27 – 17 = 10 (к.)
Выполним проверку другим способом. Подставим в таблицу все данные и запишем выражение к задаче.
БЫЛО | ВЗЯЛИ | ПОЛОЖИЛИ | СТАЛО |
24 к. | 10 к. | 3 к. | 17 к. |
Проверка: 24 – 10 + 3 = 17 (к.)
Получили верное равенство, значит, задачу решили верно.
Вывод: Чтобы выполнить проверку решения задачи можно подставить полученные данные в условие или проверить правильность вычислений обратным действием. Текст задачи можно моделировать разными способами: в виде схематического чертежа, таблицы, диаграммы.
Тренировочные задания.
1.Подберите обратные задачи к задаче: «В книге 48 страниц. Таня прочитала 30 страниц. Сколько страниц этой книги осталось прочитать Тане?»
Таня прочитала 30 страниц. Сколько страниц этой книги осталось прочитать Тане?»
Правильные ответы:
1 задача и 3 задача
2. Выберите для каждой задачи все выражения для её решения.
13 – (7 + 5)
13 – 5 + 7
7 – 5 + 13
13 – 7 – 5
(13 + 7) – 5
Правильные ответы:
13 – 5 + 7
7 – 5 + 13
13 – 7 – 5
13 – (7 + 5)
(13 + 7) – 5
Урок 38. решение задач. часть 2. — Математика — 2 класс
Математика, 2 класс
Урок № 38. Решение задач
Перечень вопросов, рассматриваемых в теме:
— решение текстовых задач арифметическим способом, представление текста задачи в виде модели.
Глоссарий по теме:
Задача — упражнение, которое выполняется посредством умозаключения, вычисления.
Простая задача — задача, которая решается при помощи одного действия.
Составная задача — задача, в решении которой используют два или более действий.
Основная и дополнительная литература по теме урока:
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. – 8-е изд. – М.: Просвещение, 2017. – с.17.
2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова – 7-е изд., дораб. – М.: Просвещение, 2016. – с.23.
Теоретический материал для самостоятельного изучения
Приступая к решению любой задачи, необходимо знать её составные части.
Части задачи: условие, вопрос, решение, ответ.
Давайте выясним, который текст будет являться задачей.
Первый текст:
Дети нашли 9 грибов. Игорь нашёл 7 грибов, а Миша 2 гриба.
Второй текст:
Игорь нашёл 7 грибов, а Миша 2 гриба. Сколько грибов нашли дети?
Сколько грибов нашли дети?
Мы уже знаем, что в задаче должны быть обязательно условие и вопрос.
Разберемся, какие составные части можно выделить в этих текстах.
Первый текст: дети нашли 9 грибов. Игорь нашёл 7 грибов, а Миша 2 гриба-не содержит вопроса. Значит, он не может быть задачей.
Второй текст:
Игорь нашёл 7 грибов, а Миша 2 гриба. Сколько грибов нашли дети? -состоит из двух частей.
Игорь нашёл 7 грибов, а Миша 2 гриба — это условие нашей задачи.
Сколько всего грибов нашли дети?- это вопрос задачи.
Условие и вопрос задачи можно представить в виде схемы. Для этого изобразим грибы, которые находили дети, отрезками.
Игорь — 7 грибов, Миша — 2 гриба
И. 7гр
М. 2 гр
В вопросе спрашивалось, сколько всего грибов нашли дети. Слово «всего» мы передадим в схеме при помощи фигурной скобки. Поставим знак вопроса.
И. 7гр
М. 2 гр ?
2 гр ?
Решим эту задачу. Рассуждаем: в задаче неизвестно целое, поэтому для нахождения целого мы выполним действие сложения.
7 + 2 = 9 (гр.)
Мы узнали, что дети нашли 9 грибов. Теперь необходимо записать ответ. Вопрос был: «Сколько всего грибов нашли дети?»
Ответ: 9 грибов.
После решения проверим, все ли элементы записаны. Мы записали краткое условие и вопрос в виде схемы, решение задачи и ответ.
Сделаем вывод.
Чтобы решить задачу, нужно:
1) Прочитать ее условие.
2) Подумать, с помощью какого действия вы ответите на вопрос задачи.
3) Решить задачу по действиям или выражением.
4) Правильно записать ответ.
Тренировочные задания.
1. Решите задачу: В корзине лежало 36 лимонов. Продали 20 лимонов. Сколько лимонов осталось?
Правильный ответ: 36 — 20 = 16 (л)
2. Решите задачу: С одной берёзы упало 10 листиков, а с другой 7 листиков. Сколько всего листиков упало с двух берёз?
Сколько всего листиков упало с двух берёз?
Правильный ответ: 10 + 7 = 17 (л)
Конспект урока математики во 2 классе «Решение задач разными способами» | План-конспект урока по математике (2 класс) на тему:
-Поработаем в группах.
(на каждую группу задача, которую можно решить двумя способами)
1)В одной бочке было 20 вёдер воды, а в другой – 15 вёдер. Для полива взяли 5 вёдер воды. Сколько вёдер воды осталось в бочках?
1)20+15=35(в.)-всего ведёр
2)35-5=30(в.)-осталось
1)20-5=15(в.)-осталось в 1 бочке, после того,как взяли
2)15+15=30(в.)-осталось
Ответ: осталось 30 вёдер.
2)В кувшине было 12 стаканов молока. На кашу пошло 5 стаканов молока, а на омлет – 2 стакана. Сколько стаканов молока осталось в кувшине?
1)5+2=7(ст.)-ушло на кашу и омлет
2)12-7=5(ст.)-осталось
1)12-5=7(ст.)-осталось после того, как взяли на кашу
2)7-2=5(ст.)-осталось
Ответ:5 стаканов осталось.
3)На двух полках было 47 книг. С первой взяли 9 книг, а со второй – 7 книг. Сколько книг осталось на полках?
С первой взяли 9 книг, а со второй – 7 книг. Сколько книг осталось на полках?
1)9+7=16(кн.)-взяли с двух полок
2)47-16=31(кн.)-осталось на полках
1)47-9=38(кн.)-осталось, после того, как взяли с 1 полки
2)38-7=31(кн.)-осталось на полках
Ответ: 31 книга.
4)В троллейбусе ехали 47 пассажиров. На остановке 12 пассажиров вышли и 15 вошли. Сколько стало пассажиров в троллейбусе?
1)47-12=35(п.)-осталось в троллейбусе
2)35+15=50(п.) – стало в троллейбусе
(47-12)+15=50(п.)-стало в троллейбусе
Ответ:50 пассажиров стало в троллейбусе.
5)В школьную столовую привезли 35 кг помидоров и 15 кг огурцов. На завтрак ученикам раздали 16 кг овощей. Сколько кг овощей осталось?
1)35+15=50(кг)-привезли
2)50-16=34(кг) –осталось
(35+15)-16=34 (кг)
Ответ:34 кг.
6)У Феди в аквариуме было 23 рыбки. Мальчик подарил 6 рыбок Ване и 4 рыбки Максиму. Сколько рыбок осталось в аквариуме у Феди?
1)6+4=10(р.)-Максим подарил всего
2)23-10=13(р. )-осталось
)-осталось
1)23-6=17(р.)-осталось, после того, как подарил Ване
2)17-4=13(р.)-осталось
Ответ:13 рыбок.
Презентация к уроку математики во 2 классе «Решение составных задач разными способами»
Просмотр содержимого документа
«Презентация к уроку математики во 2 классе «Решение составных задач разными способами»»
Решение составных задач разными способами
Реши задачу разными способами У Полины было 30 шоколадных конфет и 14 карамелек. Она съела 9 конфет. Сколько конфет осталось у Полины?
Было – 30 к. и 14 к. Съела – 9 к. Ост. — ? I способ 1) 30 + 14 = 44 (к.) – было 2) 44 – 9 = 35 (к.) 30 + 14 – 9 = 35 (к. )
)
Было – 30 к. и 14 к. Съела – 9 к. Ост. — ? II способ 1) 30 – 9 = 21 (к.)-ост. шок. 2) 21 + 14 = 35 (к.) 30 – 9 + 14 = 35 (к.)
Было – 30 к. и 14 к. Съела – 9 к. Ост. — ? III способ 1) 14 – 9 = 5 ( к.) – ост. кар. 2) 5 + 30 = 35 (к.) 14 – 9 + 30 = 35 (к.) Ответ: 35 конфет.
Задача За время дистанционного обучения Саша получил 61 пятерку. Их них 25 пятерок – по математике, 28 – по русскому языку, а остальные – по чтению. Сколько пятерок по чтению получил Саша за время дистанционного обучения?
Вова предложил решить задачу разными способами так: I способ 1) 25 + 28 = 53 (п.)- пятерок по мат. и рус.яз. 2) 61 – 53 = 8 (п.) II способ 1) 61 – 25 = 36 ( п.) – пятерок по рус.яз. и чтен. 2) 36 – 28 = 8 (п. ) III способ 61 – 25 – 28 = 8 (п.) Согласен ли ты с Вовой? Почему? Какую ошибку он допустил?
) III способ 61 – 25 – 28 = 8 (п.) Согласен ли ты с Вовой? Почему? Какую ошибку он допустил?
II и III способы одинаковые. Разница только в форме записи: по действиям и выражением. II способ 1) 61 – 25 = 36 ( п.) – пятерок по рус.яз. и чтен. 2) 36 – 28 = 8 (п.) III способ 61 – 25 – 28 = 8 (п.)
Марина предложила решить задачу разными способами так: I способ 1) 25 + 28 = 53 (п.) 2) 61 – 53 = 8 (п.) II способ 61 – (25 + 28) = 8 (п.) III способ 61 – (28 + 25) = 8 (п.) Согласен ли ты с Мариной? Почему? Какую ошибку допустила Марина?
Все три способа Марины одинаковые.
Никита предложил решить задачу разными способами так: I способ 1) 25 + 28 = 53 (п.) 2) 61 – 53 = 8 (п.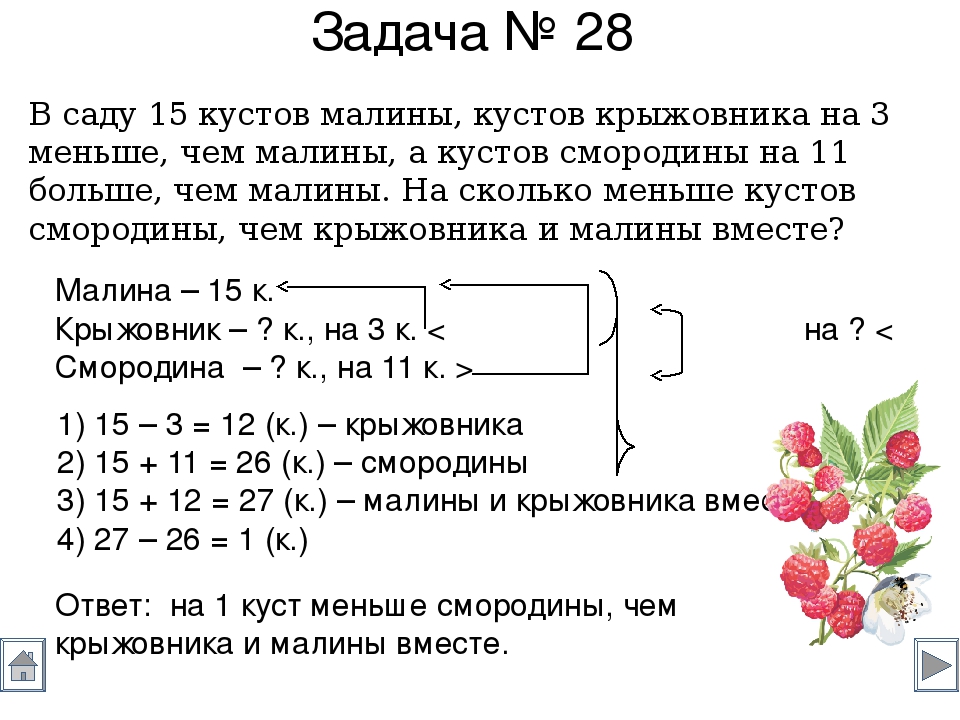 ) II способ 1) 61 – 25 = 36 ( п.) 2) 36 – 28 = 8 (п.) III способ 1) 61 – 28 = 33(п.) 2) 33 – 25 = 8 (п.) Согласен ли ты с Никитой?
) II способ 1) 61 – 25 = 36 ( п.) 2) 36 – 28 = 8 (п.) III способ 1) 61 – 28 = 33(п.) 2) 33 – 25 = 8 (п.) Согласен ли ты с Никитой?
Никита – молодец! Он верно решил задачу тремя разными способами.
Арина предложила решить задачу разными способами так: I способ 61 – (25 + 28) = 8 (п.) II способ 61 – 25 – 28 = 8 (п.) III способ 61 – 28 – 25 = 8 (п.) Согласен ли ты с Ариной?
Арина– молодец! Она тоже верно решила задачу тремя разными способами.
Спасибо за работу!
Решение составных задач разными способами
Цель: Закрепить умение решать задачи изученного вида разными способами
Задачи: Рассматривая и сравнивая разные виды задач и способы их решения, используя метод моделирования, совершенствовать мыслительные навыки; закреплять навыки счета в пределах 100.
Развивать гибкость мышления, математическую речь.
Продолжить работу над развитием профиля студента и всех видов навыков, организовав работу в группах по уровням и предоставив возможность презентовать работу.
Оборудование: задания на листах для каждой уровневой группы, кубики, клей, цветная бумага, фломастеры, линейки, формат А3.
Ход урока:
I.Орг. момент. Приветствие.
— Сегодня девизом нашего урока будет китайская мудрость:
«Я слышу — и забываю,
я вижу — и запоминаю,
я делаю – и понимаю».
— Почему говорится, что когда делаешь сам, то понимаешь?
II. Устный счёт
А) «мозговой штурм»
-Какое число было 3 дня назад?
-Какой день недели будет послезавтра?
У жука 3 пары ног. Сколько всего ног у жука?
— В семье двое детей. Саша брат Жени, но Женя Саше не брат. Может ли так быть? Кто Женя?
Саша брат Жени, но Женя Саше не брат. Может ли так быть? Кто Женя?
Б) Впиши число вместо знака:
7 3 6 4 9 5 6 5 4
16 18 ?
В) — А сейчас проверим, как вы можете «на слух» решать задачи. Я читаю задачу, а вы в тетрадь записываете только ответ.
Задачи:
1. На одном проводе сидело 8 ласточек, а на другом на 4 ласточек больше. Сколько ласточек сидело на втором проводе?
2. В корзине лежит 14 яблок и 6 груш. Сколько всего фруктов лежит в корзине?
3. У Ромы было 20 марок. Папа подарил ему ещё 7 марок. Сколько марок стало у Ромы?
4.В I коробке 8 ручек, во II – 10 ручек. А в III коробке столько ручек, сколько в I и во II коробках вместе. Сколько ручек в III коробке?
5. У Саши было 80 тенге. Он потратил 50 тенге. Сколько тенге осталось у Саши?
6. У Юли было 11 кукол, а зайчат на 6 меньше. Сколько зайчат было у Юли?
У Юли было 11 кукол, а зайчат на 6 меньше. Сколько зайчат было у Юли?
7. Альбом стоит 100 тенге, а блокнот 80 тенге. На сколько тенге альбом дороже блокнота?
Проверка: 16, 20, 27, 18, 30, 5, 20.
— Какие виды задач встретились?
(Учитель выставляет в глоссарий слова: задача, нахождение суммы, на увеличение, на уменьшение, нахождение остатка, на сравнение)
_ Сколько действий надо было выполнить, чтобы ответить на вопрос задачи? (Одно).
— Что можно сделать, чтобы задачи решались двумя действиями?
Ответ: 1.Изменить вопрос, чтобы действий стало больше.
2. Дополнить условие (добавить числа), не изменяя вопроса.
3.Изменить текст задачи.
III.Постановка проблемы.
— Сегодня мы будем решать задачи в 2 действия и постараемся доказать такую гипотезу:
Задачу можно решить разными способами.
IV. План урока:
1. Определение структуры задачи
Определение структуры задачи
2. Исследование способов решения задачи
3. Презентация
Актуализация знаний. Работа с глоссарием.
— Из каких частей состоит задача? ( В глоссарий выставляются слова: условие, вопрос, схема, модель, решение, ответ)
-Как можно доказать гипотезу? (Решить задачи разными способами).
Определение знаний по континууму и деление на группы
1 группа – начинающий уровень
2 группа – базовый уровень
3 группа – творческий уровень
V. Исследование способов решения
Каждая группа получает простую задачу, преобразовывает её в составную, решает разными способами, сопровождая моделью или схемой.
1 группа (работает под руководством учителя)
Задача: На одном проводе сидело 8 ласточек, а на другом на 4 ласточек больше. Сколько ласточек сидело на втором проводе?
— Измените вопрос задачи так, чтобы она решалась двумя действиями. Решите задачу разными способами.
Изменяют вопрос – Сколько всего ласточек сидело на проводе? В ходе исследования получается на листе продукт:
Условие:
1провод -8 ласт. ?
2 провод -?л., на4 больше
Схема:
Решение: 1 способ
1) 8+4=12 (л) — на 2 проводе
2) 8+12=20(л) – всего
2 способ
1) 8+8=16 (л) – если бы было поровну
2) 16+4=20(л) – всего
Ответ: 20 птиц всего
2 группа
Задача: У Саши было 80 тенге. Он потратил 50 тенге на ручку. Сколько тенге осталось у Саши?
( Дополните условие так, чтобы задача решалась двумя действиями. Решите задачу разными способами).
(Добавляют условие: он потратил 50 тенге на ручку и 20 тенге на ластик)
Условие:
Было – 80 тг
Потратил 50 тг и 20 тг
Осталось -?тг
Схема:
Решение:
1способ
1)50+20=70 (тг)-потратил
2)80 – 70 = 10(тг)- осталось
2 способ
1)80-50=30(тг)-осталось после покупки ручки
2) 30-20=10(тг) – осталось
3способ
1)80-20=60(тг)-осталось после покупки ластика
2) 60-50=10(тг) – осталось
Ответ: 10 тенге осталось у Саши.
3 группа
Задача: На фотоплёнке а кадров. В первый день Юра сделал в снимков, а во второй день на 4 больше. Сколько не отснятых кадров осталось на фотоплёнке?
— Определите, какие способы решения подходят к этой задаче: А, Б, В.
А) 1) + 2) + 3) –
Б) 1) + 2) — 3) –
В) 1) — 2) + 3) –
(Начертите чертёж к задаче, вставьте подходящие числа и решите её разными способами)
Чертеж: а
в в+4 ? тг
VI. Презентация. Каждая группа презентует задачу, называя из каких простых задач она состоит и способы решения.
VII. Какие концепции помогли нам доказать гипотезу?
(виды задач- функция,
способы решения – размышление, изменение)
VIII. Оценивание по континууму:
Оценивание по континууму:
1)Гипотезу доказали.
Всё понятно.
Умею решать задачи разными способами.
2)Гипотезу доказали частично.
Затрудняюсь в понимании.
3) Мне было трудно. Нужна помощь.
Итог урока:
— Какое задание было трудным?
— А какое задание было наиболее интересным?
— Как оцените работу своей группы? Какими вы были на уроке?
Просмотр содержимого документа
«Решение составных задач разными способами»
Открытый урок
по математике во 2 классе
Тема: Решение составных задач разными способами
Составила Шемолина О. А.
А.
Алматы
МКНО
2013 год
Цель: Закрепить умение решать задачи изученного вида разными способами
Задачи: Рассматривая и сравнивая разные виды задач и способы их решения, используя метод моделирования, совершенствовать мыслительные навыки; закреплять навыки счета в пределах 100.
Развивать гибкость мышления, математическую речь.
Продолжить работу над развитием профиля студента и всех видов навыков, организовав работу в группах по уровням и предоставив возможность презентовать работу.
Оборудование: задания на листах для каждой уровневой группы, кубики, клей, цветная бумага, фломастеры, линейки, формат А3.
Ход урока:
I.Орг. момент. Приветствие.
— Сегодня девизом нашего урока будет китайская мудрость:
«Я слышу — и забываю, я вижу — и запоминаю, я делаю – и понимаю». |
— Почему говорится, что когда делаешь сам, то понимаешь?
II. Устный счёт
А) «мозговой штурм»
-Какое число было 3 дня назад?
-Какой день недели будет послезавтра?
У жука 3 пары ног. Сколько всего ног у жука?
— В семье двое детей. Саша брат Жени, но Женя Саше не брат. Может ли так быть? Кто Женя?
Б) Впиши число вместо знака
7 3 4 9 6 5
?
18
166
6 5 4
В) — А сейчас проверим, как вы можете «на слух» решать задачи. Я читаю задачу, а вы в тетрадь записываете только ответ.
Задачи:
1. На одном проводе сидело 8 ласточек, а на другом на 4 ласточек больше. Сколько ласточек сидело на втором проводе?
2. В корзине лежит 14 яблок и 6 груш. Сколько всего фруктов лежит в корзине?
3. У Ромы было 20 марок. Папа подарил ему ещё 7 марок. Сколько марок стало у Ромы?
4. В I коробке 8 ручек, во II – 10 ручек. А в III коробке столько ручек, сколько в I и во II коробках вместе. Сколько ручек в III коробке?
В I коробке 8 ручек, во II – 10 ручек. А в III коробке столько ручек, сколько в I и во II коробках вместе. Сколько ручек в III коробке?
5. У Саши было 80 тенге. Он потратил 50 тенге. Сколько тенге осталось у Саши?
6. У Юли было 11 кукол, а зайчат на 6 меньше. Сколько зайчат было у Юли?
7. Альбом стоит 100 тенге, а блокнот 80 тенге. На сколько тенге альбом дороже блокнота?
Проверка: 16, 20, 27, 18, 30, 5, 20.
— Какие виды задач встретились?
(Учитель выставляет в глоссарий слова: задача, нахождение суммы, на увеличение, на уменьшение, нахождение остатка, на сравнение)
_ Сколько действий надо было выполнить, чтобы ответить на вопрос задачи? (Одно).
— Что можно сделать, чтобы задачи решались двумя действиями?
Ответ: 1.Изменить вопрос, чтобы действий стало больше.
2. Дополнить условие (добавить числа), не изменяя вопроса.
3.Изменить текст задачи.
III.Постановка проблемы.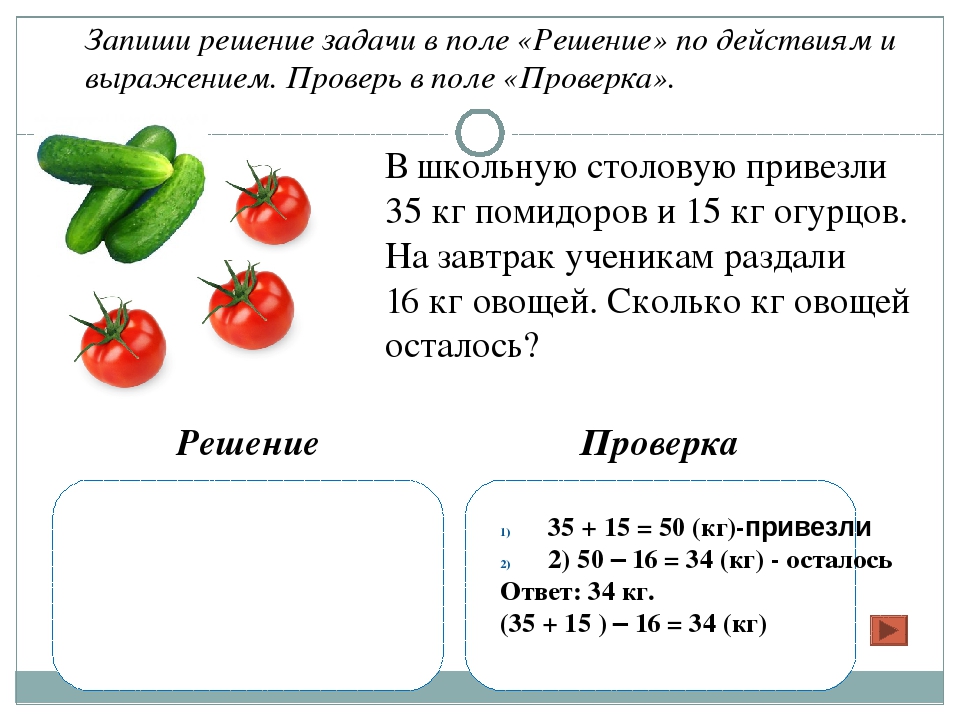
— Сегодня мы будем решать задачи в 2 действия и постараемся доказать такую гипотезу:
Задачу можно решить разными способами.
IV. План урока:
1.Определение структуры задачи
2. Исследование способов решения задачи
3. Презентация
Актуализация знаний. Работа с глоссарием.
— Из каких частей состоит задача? ( В глоссарий выставляются слова: условие, вопрос, схема, модель, решение, ответ)
-Как можно доказать гипотезу? (Решить задачи разными способами).
Определение знаний по континууму и деление на группы
1 группа – начинающий уровень
2 группа – базовый уровень
3 группа – творческий уровень
V. Исследование способов решения
Каждая группа получает простую задачу, преобразовывает её в составную, решает разными способами, сопровождая моделью или схемой.
1 группа (работает под руководством учителя)
Задача: На одном проводе сидело 8 ласточек, а на другом на 4 ласточек больше. Сколько ласточек сидело на втором проводе?
Сколько ласточек сидело на втором проводе?
( Измените вопрос задачи так, чтобы она решалась двумя действиями. Решите задачу разными способами).
Изменяют вопрос – Сколько всего ласточек сидело на проводе? В ходе исследования получается на листе продукт:
Условие:
1провод -8 ласт.
?
2 провод -?л., на4 больше
Схема:
?
Решение: 1 способ
1) 8+4=12 (л) — на 2 проводе
2) 8+12=20(л) – всего
2 способ
1) 8+8=16 (л) – если бы было поровну
2) 16+4=20(л) – всего
Ответ: 20 птиц всего
2 группа
Задача: У Саши было 80 тенге. Он потратил 50 тенге на ручку. Сколько тенге осталось у Саши?
( Дополните условие так, чтобы задача решалась двумя действиями. Решите задачу разными способами).
(Добавляют условие: он потратил 50 тенге на ручку и 20 тенге на ластик)
Условие:
Было – 80 тг
Потратил 50 тг и 20 тг
Осталось -?тг
Схема:
Решение:
1способ
1)50+20=70 (тг)-потратил
2)80 – 70 = 10(тг)- осталось
2 способ
1)80-50=30(тг)-осталось после покупки ручки
2) 30-20=10(тг) – осталось
3способ
1)80-20=60(тг)-осталось после покупки ластика
2) 60-50=10(тг) – осталось
Ответ: 10 тенге осталось у Саши.
3 группа
Задача: На фотоплёнке а кадров. В первый день Юра сделал в снимков, а во второй день на 4 больше. Сколько не отснятых кадров осталось на фотоплёнке?
— Определите, какие способы решения подходят к этой задаче: А, Б, В.
А) 1) + 2) + 3) –
Б) 1) + 2) — 3) –
В) 1) — 2) + 3) –
(Начертите чертёж к задаче, вставьте подходящие числа и решите её разными способами)
Чертеж: а
в в+4 ? тг
VI. Презентация. Каждая группа презентует задачу, называя из каких простых задач она состоит и способы решения.
VII. Какие концепции помогли нам доказать гипотезу?
(виды задач- функция,
способы решения – размышление, изменение)
VIII. Оценивание по континууму
Гипотезу доказали. Всё понятно. Умею решать задачи разными способами. | Гипотезу доказали частично. Затрудняюсь в понимании . | Мне было трудно. Нужна помощь. |
Итог урока:
— Какое задание было трудным?
— А какое задание было наиболее интересным?
— Как оцените работу своей группы? Какими вы были на уроке?
Задачи на уравнивание: примеры и решение
Рассмотрим задачи на уравнивание. В таких задачах дана общая сумма двух чисел, одно из которых больше или меньше другого. Задачи на уравнивание решаются в три действия.
Задача 1. В двух стопках всего 70 журналов, причём в первой стопке на 10 журналов больше чем во второй. Сколько журналов в каждой стопке?
Решение: Если бы в первой стопке было бы столько же журналов сколько и во второй, то сумма журналов была бы:
70 — 10 = 60 — общее количество журналов в двух одинаковых стопках.
Таким образом мы уравняли
количество журналов в обеих стопках. Теперь, разделив 60 на количество стопок, можно узнать сколько журналов во второй стопке:
60 : 2 = 30 журналов.
Чтобы узнать, сколько журналов в первой стопке, надо вернуть
обратно 10 журналов в первую стопку:
30 + 10 = 40 журналов.
Решение задачи по действиям можно записать так:
1) 70 — 10 = 60 — общее количество журналов в двух одинаковых стопках.
2) 60 : 2 = 30 — количество журналов во второй стопке.
3) 30 + 10 = 40 — количество журналов в первой стопке.
Можно выполнить проверку и убедиться, что задача решена правильно:
40 + 30 = 70 — общее количество журналов,
40 — 30 = 10 — разница в количестве журналов между стопками.
Ответ: В первой стопке 40 журналов, а во второй — 30.
Задача 2. В коробке лежит 117 ручек, причём синих ручек на 39 больше, чем красных. Сколько синих и сколько красных ручек лежит в коробке.
Сколько синих и сколько красных ручек лежит в коробке.
Решение: Чтобы уравнять
количество синих и красных ручек, мы можем к общему количеству добавить ещё 39 красных ручек:
117 + 39 = 156 ручек.
Так как теперь количество ручек одинаковое, то каждого вида ручек в коробке будет по:
156 : 2 = 78 ручек.
Таким образом мы выяснили сколько синих ручек в коробке, узнав большую часть общей суммы. Чтобы узнать сколько красных ручек, надо забрать обратно 39 красных ручек, которые мы доложили для уравнивания
:
78 — 39 = 39 ручек.
Решение задачи по действиям можно записать так:
1) 117 + 39 = 156 — количество ручек, если их будет поровну.
2) 156 : 2 = 78 — количество синих ручек.
3) 78 — 39 = 39 — количество красных ручек.
Можно выполнить проверку и убедиться, что задача решена правильно:
78 + 39 = 117 — общее количество ручек,
78 — 39 = 39 — разница в количестве ручек.
Ответ: В коробке лежит 78 синих ручек и 39 красных.
Из решения данных задач можно сделать вывод, что решать задачи на уравнивание можно двумя способами:
- Вычитать разницу для уравнивания между двумя количествами.
- Прибавлять разницу для уравнивания между двумя количествами.
Решение задач: 2 класс по математике
Приборная панель
Математика 2 класс
Решение проблем
Перейти к содержанию
Приборная панель
Авторизоваться
Приборная панель
Календарь
Входящие
История
Помощь
Закрывать
-
Мой Dashboard
- 2 класс Математика
- Страницы
- Решение задач
NE
- Дом
- Процедуры
- Закрытие
- Банк ресурсов
- Курс 1-го класса
- Курс 3-го класса
- Учебный план 2-го класса Сообщество
- Семья и сообщество 2-го класса
- Сотрудничество
- Google Drive
Способы решения задач сложения многозначных чисел
Одним из наиболее важных аспектов «новой» математики Common Core является идея о том, что учащиеся разрабатывают несколько стратегий для решения задач. Я говорю о том, почему я учу студентов нескольким стратегиям для глубокого решения проблем, в другом сообщении в блоге. Вот краткий пример диаграммы привязки, которую я составил со студентами, чтобы проиллюстрировать все стратегии в одном месте.
Я говорю о том, почему я учу студентов нескольким стратегиям для глубокого решения проблем, в другом сообщении в блоге. Вот краткий пример диаграммы привязки, которую я составил со студентами, чтобы проиллюстрировать все стратегии в одном месте.
На днях наш класс сравнил стратегии двух- и трехзначного сложения. Ранее в этом году мы тщательно практиковали стратегии сложения двузначных чисел в различных мероприятиях. Недавно мы начали работать над сложением трехзначных чисел, и студентам нужно было освежить некоторые из стратегий, которые они усвоили ранее в этом году.
Мне нравится эта таблица, потому что она связывает то, что мы узнали ранее в этом году, и помогает студентам установить связь между тем, что они уже узнали, и тем, над чем они работают прямо сейчас.
Мне нравится учить студентов гибко думать о том, как решать проблемы, и помогая им, я предпочитаю использовать веселье на месте. Используя эти стратегии, учащиеся получают гораздо более глубокое понимание концепций позиционной ценности.
Я не создаю эту диаграмму привязки, если учащиеся не проработали каждую стратегию индивидуально и глубоко.
Мои студенты хорошо понимали каждую из этих стратегий до того, как мы создали диаграмму привязки, и моей целью при ее создании было помочь студентам увидеть сходство в применении стратегий между двузначным и трехзначным сложением. Я также всегда составляю эту таблицу немного по-другому каждый год, в зависимости от потребностей моих учеников, сложности их мышления и слов, которые они выбрали для обозначения стратегий. Это действительно о студентах, которые находят смысл и устанавливают связи.
Некоторые ученики тяготеют к использованию алгоритма, потому что это то, чем занимаются их родители и где они получают наибольшую индивидуальную помощь. Однако есть несколько, которые используют альтернативную стратегию, и, как правило, именно те студенты, которые обладают наибольшей гибкостью и сложностью в своем математическом мышлении.
Дополнительную информацию о каждой нетрадиционной стратегии можно найти, перейдя по ссылкам ниже.
Если вы преподаете во втором классе, вам могут понравиться несколько страниц из некоторых моих двузначных продуктов сложения и вычитания.Я собрал этот PDF-файл с ресурсами в качестве выборки из нескольких различных продуктов, которые действительно подчеркивают всю работу, которую мы делаем в нашем классе для углубленной разработки этих стратегий. Различные компоненты сэмплера могут использоваться всей группой или небольшой группой и идеально подходят для того, чтобы помочь вашим ученикам мыслить нестандартно, когда дело доходит до решения сложения и вычитания многозначных чисел.
Возможно, вас заинтересует. . .
Преподавание задач со словами для 2-х классов
Задачи со словами были одним из самых больших разделов, которые я преподавал в 2 классе и , и я не понаслышке знаю, что преподавать задачи со словами для второклассников может быть непросто.Но как бы сложно это ни было, это также чрезвычайно важно. Задачи со словами — ключевой навык для студентов, и их следует изучать и повторять в течение всего года.
Задачи со словами — ключевой навык для студентов, и их следует изучать и повторять в течение всего года.
Прежде чем мы поговорим об обучении задачам со словами во 2-м классе, давайте посмотрим, где должны быть ученики, когда они пойдут во 2-й класс, и как обращаться с учениками более низкого уровня.
Что должны знать первоклассники
Учащиеся, поступающие во 2 класс, должны обладать следующими навыками:
- Решите до 20 задач со словами, используя сложение и вычитание;
- Типы задач со словами: сложение, взятие, сложение, разборка и сравнение с неизвестными во всех позициях.
В начале года полезно оценить понимание учащимися того, как складывать и вычитать до 20. Если они могут плавно складывать и вычитать до 20, переходите к числам 20–50. Если есть большая группа учащихся, которые все еще испытывают трудности, найдите время, чтобы изучить стандарт 1.OA.A.1 для 1-го класса задачи со словами.
Используйте сложение и вычитание в пределах 20 для решения словесных задач, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях.
Единственное различие между 1 st и 2 стандартами nd состоит в том, что 1 st решает до 20, а 2 nd — до 100. Так что, если вам нужно просмотреть 1 st , вы по-прежнему охватываете практические концепции стандарта, только в ограниченном диапазоне.
Сколько времени вы потратите на проверку, будет зависеть от уровня ваших учеников. Если вашим ученикам это нужно, полезно выделить на повторение весь первый цикл обучения текстовым задачам, что займет около двух недель.Может показаться, что у вас много времени для повторения, но имейте в виду, что в это время вы учите студентов различным типам задач со словами и процессу их решения. Работа с числами меньше 20 делает вычисления более управляемыми и позволяет учащимся сосредоточиться на изучении типов проблем и процессе их решения.
Преподавание задач по слову во 2-х классах: день 1
Подготовка к уроку:
- Создайте плакат для моделирования задачи со словом.
 Вы можете использовать мои задачи с плакатом из моего пакета задач 2 nd Grade Word или написать свои собственные.
Вы можете использовать мои задачи с плакатом из моего пакета задач 2 nd Grade Word или написать свои собственные. - Распечатайте и ламинируйте плакаты «Процесс решения проблем». Прикрепите их к ленте и повесьте в удобном месте, где их будут видеть все ученики. Убедитесь, что вы можете легко получить доступ к плакату или переместить его для уроков.
- Начните создавать плакат «Типы проблем со словами». В первый день вы должны включить задачи со словами «Добавление к». Вы добавите навыки к этому плакату по мере того, как познакомите их с учениками.
- Подготовьте по одному плакату с групповой задачей для каждой группы, чтобы ученики использовали его во время групповой работы. Вы можете написать свои собственные задачи или распечатать одну из задач «добавить к» в моем пакете задач Word. Отличный способ заинтересовать ваших учеников — это написать вместе с их именами словесные задачи. Я также сделал свой пакет задач Word редактируемым, так что вы можете ввести свой список класса, и задачи будут автоматически сгенерированы вместе со списком классов!
Открытие урока:
1) Ввести стандарт
Представьте стандарт. Сообщите учащимся, что вы начинаете с рассмотрения задач со словами, которые они выучили в первом классе. Сегодня студенты будут работать над задачами «Дополнения». «Добавление к» задачам означает, что вы начинаете с нескольких вещей, и в вашу группу добавляется еще больше.
Сообщите учащимся, что вы начинаете с рассмотрения задач со словами, которые они выучили в первом классе. Сегодня студенты будут работать над задачами «Дополнения». «Добавление к» задачам означает, что вы начинаете с нескольких вещей, и в вашу группу добавляется еще больше.
2) Расскажите о проблеме
Покажите плакат со словом «проблема». Объясните, что вы собираетесь показать им, как решить эту проблему.
Плакат с инструкциями по устранению проблем
- Покажите плакат с инструкциями по решению проблем. Укажите на первый шаг.Объясните, что сначала нам нужно прочитать проблему и визуализировать ее. Затем смоделируйте навык, прочитав задачу, а затем объяснив картину, которую вы видите в уме.
- «В Sweet Delights было 33 клубничных кекса. Испекли еще 6 штук. Сколько клубничных кексов сейчас в Sweet Delights? »
- Я представляю себе магазин кексов с подносами кексов на прилавке. У них есть поднос с 33 кексами, который состоит из 3 рядов по 10 и 1 ряда по 3.
 Затем я представляю, как пекарь выходит с еще шестью клубничными кексами и добавляет их в ряд из трех.
Затем я представляю, как пекарь выходит с еще шестью клубничными кексами и добавляет их в ряд из трех. - Теперь я визуализировал проблему (укажите на первый шаг на схеме процесса).
3) Перескажите для понимания
Далее я перескажу проблему.
- Закройте проблему руками и перескажите историю своему классу. Спросите: «Я понял суть проблемы?»
4) Определите ключевые слова
Теперь, когда я пересказал проблему, я знаю, что понимаю ее, поэтому я готов обвести и подчеркнуть ключевые слова.Модель обведет цифры в задаче и подчеркнет ключевые слова.
- «Sweet Delights » было (33) клубничных кексов. Испекли (6) еще . Сколько клубничных кексов в Sweet Delights сейчас ? »
- Проверить! Я обвел и подчеркнул ключевые слова и числа, которые помогут мне решить проблему.
5) Стратегия решения
Далее я собираюсь решить проблему, используя стратегию. Для этой задачи я нарисую картинку.
Для этой задачи я нарисую картинку.
- Нарисуйте противень для кексов с 3 рядами из десяти кругов и одним рядом из 3 кругов, используя черный маркер.
- «Я начал с 33 кексов Sweet Delights. Теперь я добавлю еще 6 ». На подносе нарисуйте 6 розовых кружков.
- Теперь у меня есть все клубничные кексы, поэтому, чтобы ответить на вопрос «Сколько клубничных кексов сейчас в Sweet Delights?» Я собираюсь пересчитать все кексы. У меня 39 кексов.
* Примечание * В начале класса 2 и рисование изображений и диаграмм для решения проблем является подходящим методом решения проблем. По мере того, как учащиеся осваивают процесс решения проблем, цифры будут усложняться, и учащимся следует перейти к более эффективным стратегиям.
6) Запишите уравнение
Теперь, когда я решил проблему, я собираюсь написать уравнение.
- Это была проблема «сложения», поэтому я знаю, что это уравнение сложения.
______ + _______ = ________
- Sweet Delights началось с 33 клубничных кексов, поэтому я знаю, что это будет первое число в моем уравнении.

- Затем они добавили еще 6 клубничных кексов, так что я знаю, что это будет мой второй номер.
- Я знаю, что после того, как они добавили 6 кексов, у них было всего 39 клубничных кексов, так что 39 — это то, что стоит после знака равенства.
7) Ответ на ярлык
На следующем шаге предлагается пометить мой ответ.
- Что значит 39? Есть 39 щенков? Или 39 детей? Может, 39 карандашей? Нет, значит 39 клубничных кексов.
8) Проверить работу
Теперь, когда у меня есть ответ, вы, наверное, думаете, что я закончил, верно? Нет! Математика прекрасна, потому что мы знаем, что часто есть правильный или неправильный ответ. Есть много шансов на ошибку, но если мы проверим свою работу, мы будем намного увереннее, что не сделали ошибки.
- Смоделируйте, как проверить свою работу, используя другую стратегию.Стратегия может заключаться в использовании манипуляторов, создании другой картинки или подсчете на пальцах.
 После того, как вы смоделировали проверку своей работы, поставьте большую галочку рядом с ответом, чтобы показать, что этот шаг выполнен.
После того, как вы смоделировали проверку своей работы, поставьте большую галочку рядом с ответом, чтобы показать, что этот шаг выполнен.
Работа в группе:
Теперь у учащихся будет возможность попробовать шаги по решению проблем с добавлением задачи в своих группах. Они сделают свой собственный плакат со своими группами, показывая всю их работу. Студенты любят работать с диаграммной или крупной цветной бумагой.
(Примечание: важно установить ожидания для групповой работы, включая всех учащихся, участвующих и помогающих друг другу. Когда учитель подходит, чтобы задать вопрос, все члены группы должны иметь возможность ответить.)
По мере того, как каждая группа работает над своей проблемой, по очереди задавайте вопросы для проверки понимания. Если учащиеся совершают ошибки, не говорите им прямо. Вместо этого ожидайте, что студенты «поймут это», когда они проверит свою работу. После того, как учащиеся выполнили все шаги, просмотрите свой плакат и дайте им возможность просмотреть свою работу маркерами, чтобы он выделялся. Затем я выбираю одну группу, чтобы рассказать классу, как они решили проблему.
Затем я выбираю одну группу, чтобы рассказать классу, как они решили проблему.
Образец плаката о групповой работе
Самостоятельная работа:
Рабочий лист Word Problem со всеми шагами по решению проблем.
Затем ученики самостоятельно работают над одной из задач второго класса из моего пакета задач со словами. Вытяните учащихся, которые испытывают трудности, в один на один. Повторное обучение в малых группах также может быть эффективным, но обычно достаточно, чтобы учащиеся работали независимо, в то время как вы наблюдаете и задаете вопросы, чтобы направлять их в правильном направлении.Не забывайте, что цель — сделать их более независимыми!
Непосредственно перед окончанием рабочего периода еще раз обойдите комнату, чтобы понаблюдать за работой студентов. Выберите одного учащегося, который выполнил указанные шаги и получил правильный ответ, чтобы рассказать, как они решили проблему. (Примечание: в начале раздела мне нравилось целенаправленно отбирать студентов, которые «понимают», но по мере продвижения модуля я думаю, что важно, чтобы учащиеся рассказали, кто, возможно, пропустил шаг или получил неправильный ответ.
В начале этого раздела я предлагал студентам выполнять только 1-2 задачи каждый день. Это крайне важно. Лучше меньше, да лучше, потому что цель состоит в том, чтобы научить студентов овладевать процессом решения проблем. Задавая учащимся слишком много задач на раннем этапе, можно перегрузить их учебный процесс и слишком много внимания уделять получению ответов только для того, чтобы сделать это.
Закрытие:
Начните со сбора всей самостоятельной работы. Затем попросите выбранного учащегося рассказать, как они решили проблему.Изначально важно, чтобы учащийся поделился всем процессом, но по мере того, как блок и год продолжаются и учащиеся овладевают процессом, вы можете сократить это, попросив учащегося рассказать об одном шаге, который они сделали.
Чтобы убедиться, что учащиеся усвоили стратегию решения проблем, я всегда проводил короткую викторину в последний день или перед тем, как приступить к следующей стратегии. Мой пакет задач по словам также включает короткие викторины с двумя вопросами, так что убедитесь, что ваши ученики на правильном пути.
Навыки решения проблем со словом:
Продолжайте этот распорядок каждый день, решая разные типы сюжетных задач.Вот пример расписания:
| День 1 | Добавление к |
| День 2 | Взять от |
| День 3 | Собираем вместе |
| День 4 | Разрушение |
| День 5 и 6 | Сравнение |
| День 7 и 8 | Неизвестно |
| День 9 и 10 | Многоступенчатый |
| День 12 и 13 | Обзор всех типов |
Типы сюжетных задач для 2.OA.A.1
Сложение, извлечение, объединение и разборка проблем, как правило, легче усвоить учащимся, потому что они больше всего сталкиваются с ними. Сравнивать, неизвестные и многоступенчатые задачи гораздо сложнее, поэтому вам может потребоваться несколько дней, чтобы сосредоточиться на них.
После изучения всех типов задач я оцениваю студентов по 2.OA.A.1 с диапазоном чисел, который я преподавал. Вы можете найти оценки на 20–50, 50–100 и 100–1000 в текстовом пакете задач.
Общая картина:
При обучении задачам со словами во 2-м классе в течение года используйте тот же процесс, чтобы развить у учащихся навыки решения проблем.
Когда учащиеся учатся складывать и вычитать до 100, выполните еще один блок по решению проблем с числами до 100. Когда учащиеся учатся складывать и вычитать до 1000, вы можете расширить свои навыки и выполнить блок по решению проблем с числами. до 1000, хотя стандарт собирается только до 100.
Другие мысли
- Обучая задачи второго класса со словами, я уделяю большое внимание процессу решения проблем. По мере того, как учащиеся начинают понимать шаги и развивать свои навыки решения проблем, важно дать им гибкость.Мозг каждого человека работает по-разному, и мы можем выполнять некоторые действия в разном порядке. Например, для некоторых учеников может быть разумнее написать уравнение до того, как они решат задачу, но другим, возможно, потребуется сначала решить проблему. Некоторые студенты могут обводить ключевые слова во время чтения задачи, потому что это помогает им понять. Не забывайте проявлять гибкость с учениками и не бойтесь предлагать различные подходы, чтобы помочь им усвоить концепции.
Якорная диаграмма, отображающая типы словесных задач, которые следует усвоить второклассникам.Уроки задач, идей, советов и приемов для 2-го класса.
Урок второго класса Счет до решения задач
Чтобы начать урок, я снова ввожу пустую числовую строку. Я даю каждому студенту пустую числовую строку на полосе предложений. Прошу сделать отметку прямо у левого края. Затем я приказываю им положить 2 пальца и сделать еще одну отметку. Я прошу их повторять это до тех пор, пока числовая строка у них не будет отмечена четными пробелами.
Затем я прошу их поставить цветную фишку на отметку у левого края.Я предлагаю им представить, что эта метка — число 18. Я прошу их использовать числовую линию, чтобы сосчитать 10 и найти на 10 больше 18. Мы проверяем наши ответы. Теперь прошу переместить фишку на отметку в правом конце строки. Я прошу их представить, что это число равно 25. Я прошу их сосчитать 10 и найти 10 меньше 25.
Я повторяю это еще с несколькими числами. Я хочу усилить концепцию «десять больше, десять меньше» как способ понять сложение и вычитание десятков.
Затем я разбиваю класс на 3 группы в зависимости от их понимания числовой линии из неформальных оценок предыдущего урока.
Группе, которая может использовать числовую прямую для решения задач, выдается контрольный документ с задачами со словами, которые требуют сложения двухзначных чисел. Их просят работать вместе с партнерами или в одиночку, чтобы решать проблемы, используя свою цифровую линию, если это необходимо для поддержки их мышления.
Группа, которая имеет некоторое представление о числовой строке, но испытывает трудности с пустой строкой, будет работать с родителем, чтобы найти число в строке, а затем добавить к нему второе число. Здесь цель состоит в том, чтобы учащиеся поняли, что им не всегда нужно начинать с отметки на левом конце.Им нужно подумать о том, какое число они добавляют, то есть далеко ли оно от числа, с которого они начинают, или очень близко. Если он далеко, они должны считать по 2 или 10. Группа вместе примет некоторые решения об отправных точках, а затем решит проблемы.
Группа, которая до сих пор не понимает, как работает числовая линия (они всегда хотят начинать с 1, даже если они ищут число 89), будет работать со мной, чтобы найти одно число относительно другого, считая единицы или Комбинации 2 и установка фишек на два числа.Если учащиеся овладеют этим навыком, мы попробуем начать с однозначного числа и добавить второе однозначное число.
Решение реальных задач по математике для второго класса
Edgewood Magnet School в Нью-Хейвене, штат Коннектикут, — это школа-магнит, которая объединяет искусство в учебную программу. Студентам в этой среде рекомендуется использовать стратегии наблюдения, интерпретации и анализа, чтобы улучшить свои мыслительные способности по каждому предмету.Выполняя эту миссию, и учителя, и ученики используют уникальные и захватывающие подходы к «основам» и работают вместе, чтобы обеспечить включение всех учащихся.
Для большинства второклассников начало года — время освежить знания и навыки первого класса. Лето вдали от прямого обучения и возможностей для практики и руководства иногда означает потерю твердого понимания усвоенных концепций в математике. Этот трех-четырехнедельный блок предназначен для обзора и построения нового понимания одноэтапного решения словесных задач с использованием сложения и вычитания по мере того, как учащиеся развивают навыки и стратегии, которые они будут использовать в течение всего года.Учащиеся с помощью серии математических сценариев будут использовать типы задач, указанные в Таблице 1 Общего основного математического глоссария, который охватывает сложение и вычитание. 1
Common Core концентрируется на четком наборе математических навыков и концепций. Учащиеся изучают концепции организованным образом в течение учебного года, а также между классами. Стандарты побуждают студентов решать реальные проблемы. 2
Common Core требует большего внимания к математике.Вместо того, чтобы стремиться охватить множество тем в учебной программе шириной в милю и глубиной в дюйм, стандарты просят учителей математики значительно сузить и углубить то, как время и энергия тратятся в классе. Это означает четкое сосредоточение внимания на основной работе каждого класса, которая для классов от детского сада до второго класса включает в себя концепции, навыки и решение проблем, связанных со сложением и вычитанием.
В округе государственных школ Нью-Хейвена используется сингапурский подход «Математика в фокусе», — учебная программа на основе Common Core для учащихся от детского сада до пятого класса.Учебники и рабочие тетради для учащихся следуют учебному плану, который включает изучение концепций и навыков с помощью наглядных уроков и инструкций учителя для понимания того, как и почему; объединение концепций и навыков посредством практики, занятий и математических журналов для глубокого понимания математики, практической работы в парах и в небольших группах; и, , применение концепций и навыков посредством обширной практики решения проблем и задач для создания специалистов по решению проблем в реальном мире. 3
Этот подход включает решение проблем на протяжении каждого урока и поощряет частую практику как в вычислениях, так и в решении проблем. Словесные задачи появляются в каждой главе и переходят от 1-го шага к 2-шагному и многоступенчатому. Каждая глава завершается сложной задачей или набором задач, которые требуют от студентов решения некоторых нестандартных вопросов. Для решения этих проблем учащимся необходимо использовать свои глубокие предыдущие знания, а также недавно приобретенные концепции и навыки, сочетая стратегии решения проблем с навыками критического мышления, включая классификацию, сравнение, упорядочение, идентификацию частей и целого, выявление закономерностей и взаимосвязей, индукция и дедукция и пространственная визуализация.
Текст для второго класса начинается с цифр до 1000. Учащиеся начинают с выражения чисел в стандартной форме (231), развернутой форме (200 + 30 + 1) и словарной форме (двести тридцать один). Это сопровождается конкретными представлениями через базовые десять блоков, а для двухзначных чисел и нескольких трехзначных чисел — представление цепочками стержней длиной 1, 10 и 100. Эта начальная глава также включает в себя последовательность чисел и сравнение с использованием большего, чем и меньше терминологии, а затем сразу перейдем к сложению и вычитанию двух- и трехзначных чисел.Здесь должен быть вывод, если у вас еще сотни, десятки и единицы не имеют никакого / большого значения; и если у вас столько же сотен, но больше десятков, то единицы не имеют большого значения. Большинство моих учеников (если не все) борются с самого начала! Похоже, у них нет прочного основания для понимания чисел до 100 или концепции разряда в целом. Этот модуль разработан для того, чтобы опередить разочарование, которое студенты испытывают, когда их слишком быстро подталкивают, прежде чем они получат твердое представление о принципах позиционной ценности и свойствах операций.
Этот модуль открывает учебный год с одноступенчатых задач сложения и вычитания всех типов с использованием чисел до 10. Цель состоит в том, чтобы потратить время на отработку основных вычислений с числами, с которыми ученик может комфортно работать, прежде чем сразу перейти к школьной программе. Когда будет достигнут уровень понимания этих наборов задач (числа до 10), учащиеся перейдут к решению одноэтапных задач с использованием чисел для подростков, а затем к числам до 100. Большинство задач по учебной программе в начале года требуют добавления и вычитание 3-значных чисел.Некоторые учащиеся быстро перейдут к заданиям с числами до 100 и будут готовы работать по обычной учебной программе.
На протяжении всего курса основное внимание будет уделяться решению, а затем и построению набора словесных задач, обеспечивающих надежную и сбалансированную практику. Наборы задач будут основаны на сценарии, который раскрывает суть истории. Каждый сценарий позволит нам решить несколько проблем, изменив числа и убедившись, что каждый набор чисел представляет собой разумную проблему.Эта идея выглядит так: У Джона в коробке 8 мелков. Он делит 3 с Сэмом. Сколько мелков осталось у Джона в коробке? В коробке у Джона есть мелки. Он делит 3 с Сэмом. В коробке у Джона осталось 5 мелков. Со скольких мелков Джон начал? У Джона 5 цветных карандашей. У Сэма на 2 меньше, чем у Джона. Сколько мелков у Сэма? Джон и Сэм делятся мелками. У Джона их 5, а у Сэма 3. Сколько мелков у друзей вместе? Двое учащихся участвуют в нескольких рассказах об обмене цветными карандашами, в которых используется один и тот же набор чисел, но в немного разных ситуациях.Некоторые ситуации более очевидны и понятны, в то время как другие требуют больше размышлений. Важно предоставить учащимся возможность работать и решать различные типы задач, которые можно создать из одного набора чисел. 4
Таксономия типов задач на сложение и вычитание, определенная в Глоссарии общих основных государственных стандартов математики, представляет собой структуру, которая разделяет одноэтапные задачи на три широких класса: изменить , сравнение и частично частично полностью .Затем каждый из трех классов разделяется на 14 типов задач, отсортированных следующим образом: изменение , в котором некоторое количество либо добавляется к другому количеству, либо отнимается от него с течением времени; сравнение , в котором одна сумма описывается как больше или меньше другой суммы; и частично-частично-целое , в котором сумма состоит из двух частей. 5
В группе проблем изменения есть две подгруппы: изменение-увеличение , в котором количество добавляется к начальной сумме, и изменение-уменьшение , в котором количество берется из начальной суммы.Мы могли бы узнать эти подгруппы более привычно как «добавить к» или «взять от». Кроме того, в каждой из этих подгрупп существует три возможных неизвестных величины. Один сценарий, показывающий изменение-увеличение : 2 котенка играли с пряжей. К ним присоединяются еще 3 котенка. Сейчас 5 котят играют с пряжей. Используя эти количества, неизвестное может быть результатом (2 + 3 =?), Неизвестной величиной изменения (2 +? = 5) или неизвестной начальной суммой (? + 3 = 5). В подгруппе изменение-уменьшение снова есть три возможных неизвестных.Сценарий для этого примера: на ветке сидят 5 птиц. 2 улетают. Теперь на ветке сидят 3 птицы. Здесь ученики снова могут решить окончательную сумму (5 — 2 =?), Сумму сдачи (5 -? = 3) или начальную сумму (? — 2 = 3). Это дает все шесть типов проблем с изменениями.
Точно так же сравнение проблемы также можно разделить на две подгруппы: сравнение-больше , в котором одна величина описывается как больше или больше, чем другая, и сравнение-меньше, , в которой одна величина описывается как меньше или меньше чем другой.Здесь снова каждая из этих двух подгрупп имеет три возможных неизвестных, всего 6 типов. У Сэма 6 шариков. У Джеймса 8 шариков. У Джеймса на 2 шарика больше, чем у Сэма. Неизвестным количеством может быть меньшее количество (? + 2 = 8), неизвестное большее количество
(6 + 2 =?), Или неизвестная разница (8-6 =?), Одна величина больше, а другая меньше. Используя тот же сценарий для набора задач без сравнения , язык необходимо изменить с «больше чем» на «меньше чем».Вот как можно представить этот набор с языковыми настройками: у Сэма 6 шариков. У Джеймса 8 шариков. У Сэма на 2 шарика меньше, чем у Джеймса.
Часть-часть-целое задачи — это набор двух величин, частей, которые вместе составляют целое количество. Этот тип проблемы очень похож на изменение категории , но в этом типе проблемы нет никаких изменений с течением времени. Две части играют эквивалентные роли, что позволяет использовать только две возможные неизвестные категории: либо часть неизвестна, либо неизвестно целое.Есть 4 большие собаки и 3 маленькие собаки. Всего 7 собак. Одна из частей может быть неизвестной (4 +? = 7 или? + 3 = 7) или неизвестным может быть размер целого (4 + 3 =?). Поскольку детали взаимозаменяемы, в этом классе задач всего 2 типа.
Следующая диаграмма сортирует эти классы и категории в структуру. В Приложении А к этому модулю приведен набор примеров проблем, иллюстрирующих каждый из этих 14 типов.
Тип проблемы | Сумма неизвестна | ||||
Изменение | Увеличение Дополнение к | Начальный | Изменение | Финал | |
Уменьшение Вычесть из | Начальный | Изменение | Финал | ||
Сравнение | Большой / Подробнее | Меньший | Большой | Разница | |
Меньше / Меньше | Меньший | Большой | Разница | ||
Частично-частично-целое | Часть | Всего | |||
Сценарии проблем
Для второклассников школьная жизнь — это большая часть их мира.Большинство моих учеников приехали в Эджвуд на год детского сада и остались там до первого класса, так что год во втором классе, по сути, стал их третьим годом в той же школе. Им комфортно в здании, и они знают многих других студентов. Они станут активными участниками математических историй, которые мы будем строить вместе. Действия, которые происходят в классе, в кафетерии, на детской площадке и в автобусе, кажутся узнаваемыми ситуациями, которые помогут в базовом понимании контекста.
Кроме того, у учащихся есть возможность включить темы и изучить другие предметы, такие как наука, общественные науки, грамотность, искусство, музыка и, в нашей школе, танцы и драма. Одним из примеров может быть создание набора задач-рассказов, посвященных жизненному циклу бабочки, единице изучения каждый год во втором классе. Обладая общими знаниями, которые получат учащиеся, этот контент может стать сценарием текстовых задач. Примером может быть: Семь гусениц поднялись по ветке и образовали куколки.Позже в тот же день еще три гусеницы поднялись по ветке и образовали куколки. Сколько кукол свешивается с ветки? Точно так же использование персонажей в книге, прочитанной вместе как класс, может дать персонажей новый набор задач. Любопытный Джордж съел связку бананов. Он съел 4 из них. Теперь у него 3. Сколько бананов начал любопытный Джордж? Использование общего или тематического контента не только объединит все мышление и практику, но и предоставит осязаемые и реальные ситуации.При наличии установленного сценария учащиеся будут работать с набором чисел, определяя неизвестное в рамках каждого типа задач.
Создание проблем
Часто задаваемый вопрос: «Что нам делать, чтобы ответить на вопрос, чтобы решить проблему со словом?» Фундаментальное понимание того, что задают, не очевидно для студентов, что делает решение недоступным. Большинство первоклассников, поступающих во второй класс, имеют базовое понимание, когда история (проблема) классифицируется как окончательное неизвестное или целое неизвестное , но большинство других компонентов таксономии им незнакомы или слишком трудны для декодирования.Чтобы начать помогать им в их мышлении, они будут использовать конкретные модели, такие как они сами (2 ребенка сидят за столом для чтения, еще 4 присоединяются к ним), разыгрывая сценарии. Многие основные материалы в классе — карандаши, записные книжки, папки, мелки — можно использовать для создания и разработки сценариев с учетом каждого типа проблемы.
Решение проблем
Следуя общему плану сингапурской математической программы, студенты будут решать задачи, используя конкретный, графический и абстрактный подход.Поскольку это стандартный подход к преподаванию математики в нашем округе в течение года, ученики начнут с этого набора стратегий для решения наборов задач.
Задачи со словом пишутся в виде рассказов и сценариев, поэтому язык необходимо учитывать при составлении задач для начинающих второклассников. Задачи со словами связаны с языком и чтением так же, как и с математикой. Если рассказ непонятен, как студенты могут начать понимать, что им делать с числами, которые им дали, и вопросом, который им задали? Таким образом, слова и словарный запас должны быть подходящими и полезными для разных уровней чтения поступающих студентов.Структура словесных задач должна быть понятной и ясной, доступной как в языке, так и в цифрах. Кроме того, следует обсудить язык, особенно слова, которые выражают взаимосвязь между задействованными величинами, чтобы убедиться, что он знаком всем учащимся.
Это явная интеграция языковых искусств и математики и метода, с помощью которого учащиеся могут связать математику с реальным миром, в данном случае, посредством занятий, которыми они занимаются в школе. Навыки чтения и вычисления сочетаются даже с простейшими задачами со словами.
Структура коллекции задач
Введение в содержание этого раздела включает в себя определенную последовательность и основы, которые помогут студентам решить 14 типов задач. Чтобы начать раздел, учащиеся будут работать только с числами до 10. Это важная отправная точка для обеспечения понимания. Большинство моих второклассников умеют складывать и вычитать до 10, но не очень хорошо владеют языком проблемных слов. Итак, во-первых, ученикам будет больше интересна язык, чем арифметика.Студенты будут практиковаться в выяснении того, что именно задают проблемы, с проблемами, с которыми они знакомы, прежде чем переходить к новому этапу. Выполнение всех типов задач улучшит и увеличит стратегию и уверенность!
После того, как освоено сложение и вычитание в пределах 10, следующая фаза единицы переходит к числам до 20. Ключевым моментом является продолжение сценариев, которые очевидны и повторяются по мере введения новых чисел. Примером этого перехода могут быть следующие параллельные задачи:
На первой остановке в автобус сели 6 студентов.На второй остановке в автобус сели 3 студента. Сколько студентов в автобусе после второй остановки? ( изменение-увеличение, окончательное неизвестно)
Некоторые студенты сели в автобус на первой остановке. На второй остановке в автобус сели 3 студента. Сейчас в автобусе 9 студентов. Сколько студентов сели на первую остановку? ( сдача-прибавка, изначально неизвестно)
Теперь они становятся:
На первой остановке в автобус сели 11 студентов. На второй остановке в автобус сели 7 студентов.Сколько студентов в автобусе после второй остановки? ( изменение-увеличение, окончательное неизвестно)
Некоторые студенты сели в автобус на первой остановке. На второй остановке в автобус сели 7 студентов. Сейчас в автобусе 18 студентов. Сколько студентов сели на первую остановку? ( сдача-прибавка, изначально неизвестно)
При работе с числами до 20 важно, чтобы учащиеся понимали, что «подростковые» числа (11-19) на самом деле равны 10 и некоторым единицам. Студенты должны работать с числами в пределах 20, составляя уравнения, используя свои знания и умение составлять первую десятку.В случае 7 + 6 создание новой десятки выглядит так:
7 + 6 = 7 + 3 + 3 = 10 + 3 = 13
Поскольку 7 требует 3, чтобы получить десять, а 6 состоит из 3 + 3, это уравнение показывает последовательность создания 10 и некоторых других. Практика этого метода с использованием двух десятков фреймов наглядно демонстрирует процесс. В приведенном выше примере учащиеся используют десять кадров, чтобы показать 7 и 6 отдельно. Чтобы получить новые 10, ученики переместят 3 из 6, которые теперь показывают 10 и еще 3 или 13.
Как упоминалось ранее, очевидно, что наиболее доступными типами задач для учеников, поступающих во второй класс, являются изменение-увеличение или изменение-уменьшение, результат неизвестен и часть-часть-целое, целое неизвестно. Общая стратегия решения задачи со словами, кажется, состоит в том, чтобы просто взять два числа, которые вы видите, и сложить их вместе или, возможно, вычесть их, но часто ученики просто не уверены. Похоже, что это наиболее часто используемые типы задач, что оставляет учащихся без сбалансированного опыта работы со всеми 14 типами и, в конечном итоге, без некоторых стратегий, которые они могли бы использовать при решении задач.Студентам необходимо увидеть широкий круг задач, чтобы получить четкое представление о том, как используются сложение и вычитание и как они связаны друг с другом. Понятие достаточности примеров означает, что учащимся следует познакомиться с широким спектром примеров, чтобы обеспечить всестороннюю практику с концепцией. 6
Подходы к данной учебной программе различаются в зависимости от стиля обучения всех учащихся.
Общий формат основан на модели мастерской. Концепции и навыки преподаются с помощью серии мини-уроков, посвященных цели, с использованием следующих методов:
Эмпирическое обучение: Большинству молодых студентов необходимо начинать с практического обучения.Использование конкретных моделей для разработки математических историй позволяет учащимся увидеть проблему и манипулировать элементами по мере развития рассказа. Этот тип обучения — важный первый шаг.
Дифференцированное обучение: уроки и упражнения будут нацелены на максимальное обучение. Студенты будут использовать различные подходы, работая иногда индивидуально, а иногда в небольших группах, в зависимости от сложности работы. Некоторые студенты будут двигаться быстрее по мере овладения навыками, а некоторым потребуется больше возможностей для практики.
Совместное обучение: учащимся будет предоставлена возможность работать в совместных группах над созданием математических рассказов для представления классу. Эта стратегия позволит студентам работать совместно, выполняя различные роли, необходимые для завершения работы, с акцентом на успех для всех.
Задание 1: Упорядоченные типы проблем — Проблемы к 10
Вводная (и обзорная) часть модуля охватывает все типы проблем, но в определенной последовательности. Цель состоит в том, чтобы учащиеся прочитали и интерпретировали словесную задачу с помощью инструкций, а затем самостоятельно попрактиковались.Из-за множества типов задач эта часть займет несколько дней, прежде чем студенты научатся писать свои собственные наборы задач. В зависимости от потребностей учащихся и темпа понимания, я ожидаю, что этот раздел будет продолжаться от четырех до шести дней, а при необходимости — и больше.
Последовательность следующая: часть-часть-целое ; изменение-увеличение и изменение-уменьшение ; и, наконец, сравнить больше и сравнить меньше .Следующие вводные занятия разработаны как групповое мероприятие, когда студенты сидят за партами или собираются на ковре рядом с доской или мольбертом. Вся групповая часть должна составлять максимум 20 минут. В конце каждой сессии я предлагаю студентам решить от 5 до 10 похожих задач. Более способные студенты могут начать создавать свои собственные проблемы во время самостоятельной работы.
Начало с основ дает хорошую возможность познакомиться с навыками студентов, что помогает при подготовке дифференцированной работы и создании групп,
На этом уроке учащиеся будут интерпретировать проблемы реального мира и с помощью манипуляций и картинок решать истории отчасти-части-целого, используя сложение и вычитание.
Играют 6 девочек
С ними играют 3 мальчика.
Сколько всего детей играет?
Начните рассказ со всего неизвестного, как в этом примере. Этот тип историй идеально подходит для того, чтобы ученики разыгрывали прямо в классе. Напишите историю на доске или листе с диаграммами и попросите учащихся выступить в качестве актеров. Когда ученики решат задачу, напишите математическое предложение, чтобы показать, что произошло: 6 + 3 = 9 учеников. Объясните, что две части (мальчики и девочки) составили одно целое (детей).Пока студенты все еще находятся в актерской позиции, представьте новый подход к этому сценарию:
Играют 9 учеников.
Из них 6 девочек.
Сколько мальчиков играет?
На этом наглядном примере ученики должны сразу увидеть, сколько. Важная концепция, которую следует продемонстрировать, заключается в том, что части могут быть определены, когда известны целое и одна часть, в этом случае 9 известно как целое, а 6 — как одна часть. Опять же, напишите математическое предложение, чтобы показать этот расчет: 6 +? = 9 и включите стратегию начала с целого, чтобы определить недостающую часть как предложение вычитания 9-6 = 3.Практика обоих подходов к решению поможет учащимся соединить сложение и вычитание и понять, как они используются вместе.
Поскольку на этом уроке учащиеся должны читать задачи-рассказы, я объединю беглых читателей с теми, кто не владеет свободно, предоставлю счетчики тем, кто их хочет, и позволю партнерам работать вместе над решением проблем и поделиться стратегиями, которые они использовали.
Я воспользуюсь еще двумя примерами, подобными приведенным ниже, чтобы продемонстрировать, не забывая писать на доске слово «задача», а также математическое предложение.Я также перефразирую проблемы, чтобы часть была неизвестной.
У Ханны 5 красных маркеров.
У нее 3 синих маркера
Сколько всего маркеров у Ханны?
7 учеников рисуют мелками.
2 ученика рисуют цветными карандашами.
Сколько учеников рисуют?
Продолжая эту же идею, следующий набор типов проблем включает изменение-увеличение и изменение-уменьшение .Хотя часть-часть-целое — это язык, который учащиеся могут усвоить и использовать при обсуждении своей работы, язык изменение-увеличение и изменение уменьшение немного сложнее. Использование слова изменение больше подходит для студентов, чтобы продемонстрировать, что некоторая сумма была либо добавлена, либо вычтена из начальной суммы.
Введите слово «проблема» ниже, которое является примером неизвестного результата в категории «изменение-увеличение».
У Джейсона в начале дня на графике было 8 наклеек «пойманный на хорошем».
За школьный день он заработал еще 2 стикера.
Сколько наклеек у Джейсона на графике в конце дня?
Студент может решить задачу, как написано, и, используя тот же сценарий, предложить им создать историю неизвестное изменение и начальное неизвестное рассказ. Одним из примеров может быть:
У Джейсона было несколько наклеек «пойманный на хорошем» на графике
.
начало дня.
За школьный день он заработал еще 2 стикера.
В итоге у него 10 наклеек.
Сколько наклеек было у Джейсона в начале дня?
Это устное задание, в котором я напишу скорректированную версию по всем направлениям, поместив математическое предложение внизу. Важно позволить студентам поработать над составлением задачи, чтобы они могли начать видеть взаимосвязь между проблемами и тем, что они задают.
Результат Неизвестно Версия 8 + 2 =? | Изменение Неизвестно Версия 8+? = 10 | Начальный Неизвестно Версия ? + 2 = 10 |
Цель состоит в том, чтобы учащиеся понимали, а не просто решали.Я могу неформально оценить во время обсуждения переписывания текста слово «проблема», с более формальной оценкой позже в разделе.
Следующая категория, которую следует представить, — это типы задач изменение-уменьшение . Следуя тому же формату, что и раньше, я представлю результат неизвестный, заменим неизвестное , а затем начальное неизвестное.
Кристалл собрала 7 листов для своего проекта.
2 листа унесло ветром.
Сколько листьев у Кристалл осталось для своего проекта?
Результат Неизвестно 7 — 2 =? | Изменение Неизвестно 7 -? = 5 | Начальный Неизвестно ? — 2 = 5 |
Опять же, цель — понять, а не просто решить.
Третий широкий класс, сравните, сложнее для моих 2 учеников и . Это требует, чтобы текст словесных задач был очень простым. Студенты не должны путаться, когда учатся извлекать данные из задачи. Помните, что использование точной терминологии — это не цель, а, скорее, понимание сути проблемы. Вот три способа, которыми я представлю сценарий, который показывает типы задач сравнение-больше , и три способа показать без сравнения. Студенты должны иметь возможность практиковать все типы. Конечно, не все эти примеры следует использовать одновременно. Когда я записываю задачи на листе с диаграммами и вывешиваю их в классе, ученики могут начать видеть и проводить собственные сравнения и противопоставления, поскольку один сценарий объясняется по-разному. Использование слов «больше» и «меньше» должно быть выделено и объяснено по мере введения и работы над набором проблем. Моя роль здесь состоит в том, чтобы позволить ученикам начать замечать тонкие различия в формулировках и в том, как они меняют мышление.Лучше начать с простого!
У Оливии на 4 ластика больше, чем у Джона. У Джона 2 ластика. Сколько ластиков у Оливии? (сравнение-больше, большее неизвестно) 2 + 4 =? | У Джона на 4 ластика меньше, чем у Оливии. У Джона 2 ластика. Сколько ластиков у Оливии? (без сравнения, большее неизвестно) 4 + 2 =? |
У Оливии на 4 ластика больше, чем у Джона. У Оливии 6 ластиков. Сколько ластиков у Джона? (сравнение больше, меньше неизвестно) 6 — 4 =? | У Джона на 4 ластика меньше, чем у Оливии. У Оливии 6 ластиков. Сколько ластиков у Джона? (без сравнения, меньше неизвестно) 6 — 4 =? |
У Оливии 6 ластиков. У Джона 2 ластика. На сколько ластиков у Оливии больше, чем у Джона (сравнение-больше, разница неизвестна 6 — 2 =? 2+? = 6 | У Джона 2 ластика. У Оливии 6 ластиков. На сколько ластиков у Джона меньше, чем у Оливии? (без сравнения, разница неизвестна) 6 — 2 =? |
На протяжении этих вводных занятий мы со студентами будем обсуждать сценарии, которые в конечном итоге могут быть использованы в собственных задачах со словами.Идеи должны генерироваться на основе школьных мероприятий и материалов, побуждая учащихся думать о том, что ученики могут фактически использовать для манипуляций или, как в первом сценарии, уметь действовать, чтобы решить. Сохраняя список идей на бумаге с диаграммами в качестве справочного материала, учащиеся не будут испытывать затруднений со словарным запасом или подходящими сценариями; им предстоит решить свои проблемы. Этот список подготовит студентов ко второй части модуля.
Мероприятие 2: Классные / школьные сценарии
Как указывалось ранее, слова и словарный запас должны быть доступны для учащихся, а не должны быть проблемой или препятствием.Цель состоит в том, чтобы обдумать истории и использовать информацию, собранную во время мозгового штурма. Чтобы начать эту часть, просмотрите диаграммы и добавьте больше, если у учащихся появятся новые идеи. Для составления задач со словами может быть полезно иметь информацию в категориях, например:
Используемые нами материалы
Занятия, которые мы посещаем
Занятия в школе
Имена одноклассников
Я создам группы из двух или трех учеников, чтобы они написали собственные задачи и поделились с классом.Поскольку этот урок требует, чтобы учащиеся читали и писали задачи-рассказы, опять же, беглые читатели и писатели с теми, кто не владеет свободно, предоставляют счетчики для тех, кто их хочет, и позволяют партнерам работать вместе над решением проблем и делиться стратегиями, которые они использовали. .
Цель в течение этого периода времени — предложить учащимся написать ту же задачу, но попробовать ее по-другому, выбрать другой тип, когда они рассказывают историю. Время для совместной работы студенческих групп будет во время прибытия в качестве утренней работы и во время части математического семинара по математике.Это позволит учащимся работать со своими партнерами по 30 минут в день над созданием математических рассказов.
Я подчеркну, что важно хранить их коллекцию вместе, поскольку большая часть их работы станет частью рабочей тетради, которую они создадут в конце этого раздела. Папки и математические журналы могут быть полезны, или мой ежедневный сбор незавершенной работы — еще один вариант.
Мероприятие 3: Научные сценарии
Первым разделом в науке 2 классов и является исследование жизненного цикла бабочки.Студенты получают гусениц в начале семестра и наблюдают и записывают изменения в жизни гусениц. Работа, которую студенты выполняют на уроках естествознания, может стать информацией и сценариями, которые они могут использовать для составления текстовых задач.
Используя все типы задач, мы напишем несколько вместе как класс. Это дополнительная возможность очень конкретно интегрировать математику в наши научные исследования и работу. Студентам важно осознавать, что, хотя их обучение было разделено на предметные области, по существу невозможно разделить все это на категории.Таким образом, в этой части модуля используются математика, естественные науки и чтение, чтобы помочь учащимся узнать о жизненном цикле бабочки (а также других животных).
Студенты будут создавать наборы задач, которые используют свой ежедневный опыт отслеживания своих гусениц. У каждого ученика есть 2-3 гусеницы, за которыми можно наблюдать и записывать информацию, что может стать началом словесных задач. Примеры для начала: если в таблице 3 8 гусениц и 2 гусеницы присоединяются к этой группе, сколько гусениц наблюдается в таблице 3? В классе 28 учеников.Каждому ученику понадобится одна чашка еды для гусениц. Есть 30 чашек корма для гусениц. На сколько чашек еды больше, чем у студентов?
Часто встречаются студенты, которые проявляют большой интерес к другим областям науки. Это область, которую следует поощрять, если учащиеся рады поделиться своими знаниями. Некоторые учащиеся будут более склонны использовать единицу обучения, проводимую в классе, но в течение дня, посвященного грамотности, учащиеся знакомятся с большим количеством научно-популярной литературы или информационного текста, который, безусловно, может обогатить наши научные словесные задачи. .
На протяжении всего раздела по естествознанию студенты будут продолжать писать текстовые задачи различных типов, чтобы в конечном итоге включить их в наш последний проект — рабочую тетрадь. Эти задачи можно писать во время утренней рабочей сессии, во время семинара по математике и в конце урока естествознания. К концу раздела у каждого студента должно быть две задачи, которые нужно добавить в главу «Наука» в учебном пособии.
Мероприятие 4: Создание Рабочей тетради / Празднование публикации
Цель этой части модуля состоит в том, чтобы отсортировать словарные задачи по «главам» и создать рабочую тетрадь, которой можно поделиться на Празднике публикации.Главы будут названы по предметам или категориям, в зависимости от выбора ученика и предложения учителя. Идеи включают в себя рассказы для начинающих, занятия в классе, развлечения на детской площадке, науку и математику и связи с общественными исследованиями. Пусть студенты творчески подходят к названиям!
Студенты представят свои работы, которые будут включать как минимум одно словесное задание для каждой главы. Они также должны представить решения своих проблем, чтобы их можно было включить в ключ ответа. В каждой главе будет не менее 25 задач с примерами всех типов и с разным уровнем сложности.Задачи со словами могут быть напечатаны или написаны от руки для окончательной рабочей тетради, в зависимости от того, что учащиеся решат в классе. Для празднования необходимо будет скопировать и каким-либо образом переплести одну рабочую тетрадь на каждого учащегося.
За две недели до Праздника публикации студенты создадут приглашение, чтобы передать его семье и друзьям, приглашая их прийти на «Праздник решения проблем». Родители и другие VIP-гости потратят некоторое время на работу над задачами со словами, перемещаясь по комнате, навещая многих учеников.Студенты поделятся с гостями своей конкретной работой (словесные задачи, которые они сами создали) и «помогут» посетителям найти ответы.
У каждого студента будет лист «Комментарии», который гости смогут подписать и оставить комментарии о своем опыте работы со студентом. Я рекомендую посетителям остановиться, чтобы поговорить с каждым студентом или с любым другим учеником во время их посещения.
Кроме того, это возможность предложить студентам работать редакторами и издателями.Создание рабочей книги потребует времени на просмотр и сборку, и эти задачи могут быть делегированы заинтересованным учащимся и разделены с ними.
Общие основные государственные стандарты по математике,
http://www.corestandards.org/the-standards/mat Mathematics.
Фонг, Хо Кхеонг. Математика в фокусе Сингапурская математика Маршалла Кавендиша . Итоговая ред. Сингапур: образование Маршалла Кавендиша, 2015 г.
Фусон, Карен К. Математические выражения . Издание 2011 г. Орландо, Флорида: Houghton Mifflin Harcourt;, 2011.
Хау, Роджер. Три столпа математики для первого класса и не только
Howe, Roger, Самое важное, что нужно знать вашему ребенку об арифметике
Хау, Роджер и Гарольд Рейтер, Пять стадий разложения места
Ma, L. Знание и преподавание элементарной математики , Erlbaum Associates, Mahwah, NJ, 1999.
Московские головоломки: 359 математических увлечений . Нью-Йорк: Dover Publications, 1992.
Поля, Георгий. Как решить: новый аспект математического метода . Издание Новой Принстонской научной библиотеки, 2014.
Изменение Увеличение / Результат Неизвестен
На занятиях 7 учеников. К ним присоединяются еще 2 студента. Сколько учеников сейчас в классе?
Изменение Увеличение / Изменение Неизвестно
На занятиях 7 учеников.К ним присоединяются еще несколько студентов. Тогда было 9 учеников. Сколько студентов попадает в первые 7 человек?
Увеличение изменения / начальное значение неизвестно
Некоторые ученики на занятиях. К ним присоединились еще 2 студента. Тогда было 9 учеников. Сколько студентов было в классе вначале?
Изменение Уменьшение / Результат Неизвестен
На занятиях находилось
учеников 9 человек. 2 студента ушли домой. Сколько учеников сейчас в классе?
Изменение Уменьшение / Изменение Неизвестно
На занятиях находилось
учеников 9 человек.Некоторые студенты разошлись по домам. Сейчас здесь 7 студентов. Сколько студентов ушли домой?
Изменение Уменьшение / Исходное значение Неизвестно
Несколько учеников были в классе. 2 студента ушли домой. Тогда в классе было 7 учеников. Сколько студентов было в классе вначале?
Сравнить больше / Разница неизвестна
У Сэма 10 картошек фри. У Эмили 6 картошек фри. Насколько больше у Сэма, чем у Эмили?
Сравнить Больше / Больше неизвестно
У Сэма на 4 картофеля фри больше, чем у Эмили.У Эмили 6 картошек фри. Сколько картофеля фри у Сэма?
Сравнить Больше / Меньше Неизвестно
У Сэма на 4 картофеля фри больше, чем у Эмили. У Сэма есть 10 картошек фри. Сколько картофеля фри у Эмили?
Сравнить Меньше / Различий неизвестно
У Сэма 10 картошек фри. У Эмили 6 картошек фри. Насколько у Эмили меньше, чем у Сэма?
Сравнить Меньше / Меньше Неизвестно
У Эмили на 4 картофеля фри меньше, чем у Сэма. У Сэма есть 10 картошек фри.Сколько картошки фри у Эмили?
Сравнить Меньше / больше Неизвестно
У Эмили на 4 картофеля фри меньше, чем у Сэма. У Эмили 6 картошек фри. Сколько картофеля фри у Сэма?
Частично-Частично-Целое / Целое Неизвестно
У Сэма 4 печенья на обед. У него есть еще 2 на ужин. Сколько файлов cookie у Сэма?
Частично-Частично-Целое / Целое Неизвестно
Сэм сегодня съел 6 печенек. У него было 4 штуки на обед. Сколько он ел на обед?
Этот модуль, естественно, объединяет грамотность и математику.Как чтение, так и письмо являются неотъемлемой частью способности учащихся решать словесные задачи, включающие как сложение, так и вычитание.
Ученики будут работать в соответствии с Общим основным государственным стандартом по математике, 2.OA.A.1, который гласит, что второклассники должны к концу года уметь «представлять и решать задачи, включающие сложение и вычитание, в пределах 100». для решения одноэтапных задач со словами, включающих ситуации сложения, взятия из, объединения, разборки и сравнения с неизвестными во всех позициях.Во время этого раздела учащиеся начнут решать и составлять словесные задачи с числами до 10, переходить к числам до 20 и переходить к сотням и до 1000 по мере того, как они усваивают концепции с числовым значением.
В этом разделе также рассматриваются общие основные государственные стандарты чтения информационного текста, RI.2.1, в которых учащиеся работают над поиском ключевых идей и деталей, задавая и отвечая на такие вопросы, как кто, что, где, когда, почему и как продемонстрировать понимание ключевых деталей текста.На протяжении этого раздела, посвященного задачам со словами, учащиеся будут работать, задавая эти вопросы, чтобы определить, какую информацию дает математический рассказ. Когда они начнут писать свои собственные текстовые задачи, им нужно будет рассмотреть эти вопросы, чтобы составить содержательный рассказ для текста своей проблемы.
- Общие основные государственные стандарты по математике, http://www.corestandards.org/the-standards/mat Mathematics.
- Общие государственные стандарты по математике
- Ho Kheong Fong, Math in Focus Singapore Math by Marshall Cavendish , 8.
- Роджер Хоу, Три столпа математики для первого класса и не только, 2 .
- Роджер Хоу, Три столпа математики для первого класса и не только, 1 . Общие основные государственные стандарты по математике
- Роджер Хоу, Три столпа математики для первого класса и не только, 2
Решая задачи с многоступенчатым словом, как босс
Напоминание о решении проблем со словами
Сначала я рассмотрел со своим классом, как решать обычные задачи с текстом.Я научил их стратегии «Обведите, Круг, Подчеркните» (обведите информацию и подчеркните, что они хотят, чтобы они вычислили), чтобы сосредоточить внимание на важных вещах. Мы решили проблему и были готовы двигаться дальше. Затем я добавил второй вопрос к нашему предыдущему. Я показал студентам, как использовать информацию, полученную на первом этапе, для решения второго вопроса. Как только мы решили, мы вернулись на свои места, чтобы сделать заметки о трехэтапном методе.
Вы можете узнать больше о нашем простом пении, помогающем решить односложные задачи со словами здесь!
Я использовал процесс постепенного выпуска в качестве структуры обучения для этого метода, и он очень хорошо сработал.
Моделирование двухэтапных задач со словами
Сначала дети выписали 3 шага, которые нужно предпринять для решения многоступенчатой задачи со словами.
Практика с приятелем
Затем настала их очередь практиковаться с приятелем. У меня есть класс по группам в стиле Каган, поэтому я попросил их повернуться к своему партнеру по плечу для этой части.
Они обсудили это со своим приятелем, а затем приклеили.
Независимая практика
Наконец, они были готовы опробовать процесс самостоятельно.Они решали задачи со словами так же, как и со своим приятелем. И поскольку их приятель все еще сидел рядом с ними, они также могли дважды проверить, есть ли у них проблема.
Я проверял записные книжки каждого ученика, когда они заканчивали. Для меня это была прекрасная возможность увидеть, кому все еще нужна помощь в решении многоэтапных задач.
Моя проверка маркером с запахом апельсиновой газировки была их билетом в математические центры. Если ученики все еще боролись, я перетаскивал их в свою небольшую группу, пока другие ученики работали в своих ваннах в течение недели.На следующий день мы продолжили использовать трехэтапный процесс для решения многоэтапных задач. Я хотел, чтобы студенты снова попробовали этот процесс самостоятельно. Я раздал другую половину листа и приклеил к их блокнотам.
Я дал им 10 минут на решение проблемы. Это было НАМНОГО больше времени, чем им действительно могло бы понадобиться, но я хотел, чтобы они действительно поработали над проблемой, и это дало мне возможность провести выборочную проверку со студентами, которые испытывали трудности в предыдущий день.
Число, говорящее о наших ответах
Когда все ученики были готовы, мы снова собрались вместе и поделились способами решения проблемы каждым человеком.Я хотел, чтобы каждый студент нашел момент и объяснил свой мыслительный процесс. В конце концов, мы перейдем к написанию того, почему и как, но пока разговор — это наш первый шаг!
Я записал на доске все методы. (Да… в моей новой школе есть наполовину классная и наполовину белая доска… так грустно!)
Результаты были впечатляющими! Если студенты использовали тот же самый метод, я писал их имена рядом с показанной работой. Это было отличное начало для объяснения наших мыслей. Вместе наш маленький класс из 15 человек смог придумать 9 различных способов решения этой одной проблемы! Мне нравились разговоры, которые вспыхивали потом: «Зачем ты это сделал?» «Зачем ты это сделал?» «Это было бы проще…»
Это была одна из самых эффективных стратегий, которые я когда-либо использовал для решения текстовых задач! Больше не интересно… подождите… я сделал все шаги? Решено, выполнено, БАМ! Если вам нужно еще несколько упражнений с задачами, состоящими из нескольких этапов, обязательно ознакомьтесь с этими карточками задач со словами!
Эти дифференцированные карточки ИДЕАЛЬНЫ для всех учащихся вашего 2-го или 3-го класса, поскольку у них есть задачи со словами для сложения, вычитания, простого умножения и деления из 2–3 цифр.Они также включают многоэтапные задачи для каждого раздела!
Итак, у вас есть небольшой трюк для решения многоэтапных задач? Этот способ отлично работал с моими учениками! Вы можете получить листы, которые я использовал здесь, БЕСПЛАТНО! Просто подтвердите свой адрес электронной почты, чтобы я знал, что вы не робот, а затем вы можете скачать бесплатно!
Дополнение
со стратегиями перегруппировки — Lucky Little Learners
Я большой сторонник обучения студентов ПОЧЕМУ до ПРОЦЕДУРА при изучении новой математической концепции.Я твердо верю, что учителя обязаны своим ученикам научить их множеству способов решения математических задач. Все мы изучаем концепции по-разному, и математика не исключение. С учетом сказанного, в этом посте будет объяснено несколько различных дополнений к стратегиям перегруппировки, которым вы можете научить своих учеников, чтобы они могли лучше понять эту концепцию.
Добавление с перегруппировкой — это очень систематическая концепция для обучения учащихся, и без твердого понимания числовой ценности нет смысла продолжать обучение.Важно, чтобы учащиеся твердо придерживались своих практических навыков, прежде чем переходить к сложению с перегруппировкой. В зависимости от того, где вы преподаете, вам может потребоваться обучать сложению 2-х и 3-х цифр немного по-разному. Итак, я предлагаю вам множество стратегий, которые вы можете попробовать со своими учениками. Если вы видите стратегию, которую не можете использовать, продолжайте прокручивать. Я обещаю, что будет кое-что, что вам будет полезно.
Коврики с разметкой
Прежде, чем я начну свое добавление с перегруппировкой единицы, я провожу месяц, обучая разряду.Учащиеся должны твердо понимать свое месторасположение, чтобы по-настоящему понять, ЧТО и ПОЧЕМУ добавляются при перегруппировке. В первый день обучения этому навыку мои ученики получают кубики unifix и узнают, как выглядит перегруппировка. Вы также можете использовать блоки с числовыми значениями, но мне нравится, что кубы unifix можно разделить и сдвинуть вместе. Мы всегда начинаем с двузначного числа вверху и однозначного числа внизу. Вот как я этому учу:
Пока я прохожу этот урок, у меня есть ученики, которые, кажется, способны понять концепцию, подходят и показывают классу, как все это делать, одновременно объясняя, что они делают.Когда студенты объясняют свое мышление и мыслительный процесс, это очень действенно.
Через день или два обучения этой концепции с использованием циновки с числовыми значениями, я попрошу их перейти к решению задач на бумаге и карандаше, но все же предоставлю им их кубики unifix и мат с числовыми значениями для построения и решения каждой задачи. Не забудьте взять свой БЕСПЛАТНЫЙ коврик с оценкой стоимости, прежде чем идти дальше! Зарегистрируйтесь ниже, чтобы получить халяву.
Успех! Теперь проверьте свою электронную почту, чтобы подтвердить подписку и получить бесплатную информацию о размещаемой стоимости.Если письма нет в вашем почтовом ящике, проверьте папку со спамом! -Angie 🙂 Lucky Little Learners
Один совет — дайте своим ученикам маркеры, пусть они просмотрят свой рабочий лист и выделят нужные места, чтобы у них было визуальное напоминание о том, с чего начать решать свои математические задачи.
Остерегайтесь тех, кто просто хочет взять двузначное число и рассчитывать на него. Хотя это практический способ решения этих проблем, вы также должны думать о концепции, которой вы пытаетесь их научить… перегруппировке.
Далее мы переходим к двузначным числам сверху и снизу. Конечно, мы возвращаемся к математическим манипуляциям, чтобы помочь им увидеть и понять процесс перегруппировки.
Продолжаем выделять единичные места на данном этапе. Я хочу, чтобы мои ученики всегда начинали с первых мест. Для них эта концепция сложнее, чем мы думаем. Их учат читать и писать слева направо, поэтому включение их с правой стороны задачи, как правило, вызывает у некоторых учеников затруднения.
Как я уже говорил в начале этого поста, я твердо верю в то, что нужно обучать студентов нескольким способам решения проблем, потому что никогда не знаешь, что с ними связано. Вот еще несколько способов, с помощью которых я показал своим ученикам, как решать сложение с помощью задач перегруппировки.
Метод стикера
Метод Break It Up
Метод нарезки и разделения
Как только ваши ученики найдут один или два метода, которые им комфортно использовать, важно предоставить множество возможностей для практики! Вот несколько ресурсов, которые вы можете начать использовать в своем классе уже сегодня! (ссылки под изображением)
МАТЕМАТИЧЕСКИЕ РЕСУРСЫ ДЛЯ ВАШЕГО КЛАССА
2-значные карты задач сложения
3-значные карты задач сложения
2-значные цвета по номеру годовой пакет
Добавление с перегруппировкой Math Notebook
2-значное добавление с помощью карт задач QR-кодов
Добавление трех цифр с помощью карточек с QR-кодами
Math Toothy ® Task Kit Bundle
Math Puzzles Bundle
2 Grade Math Centres Bundle
Успех! Теперь проверьте свою электронную почту, чтобы подтвердить подписку.

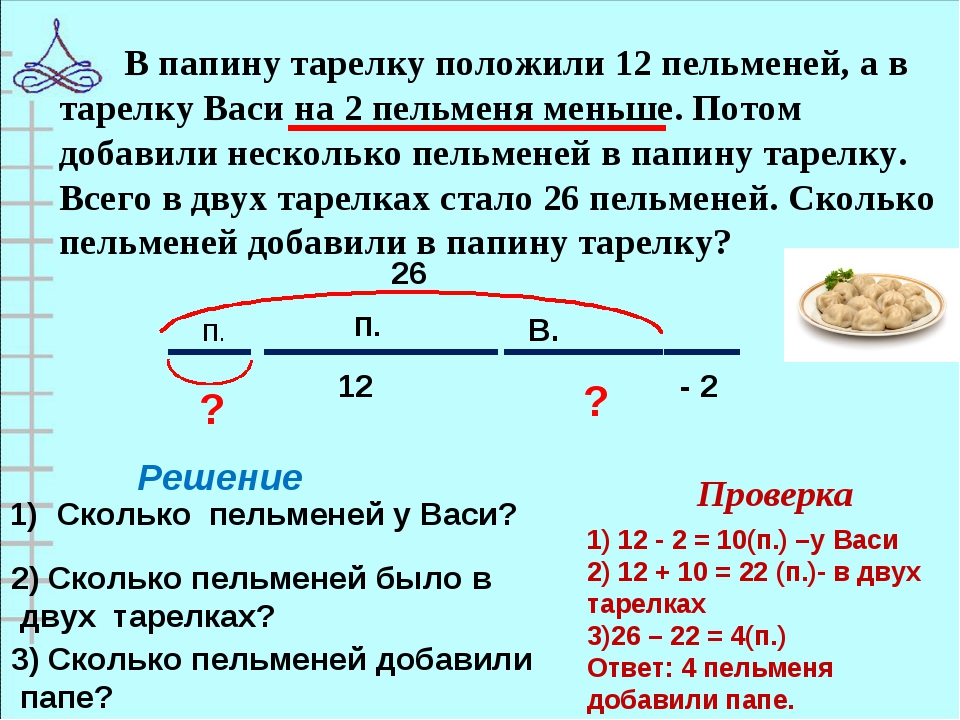
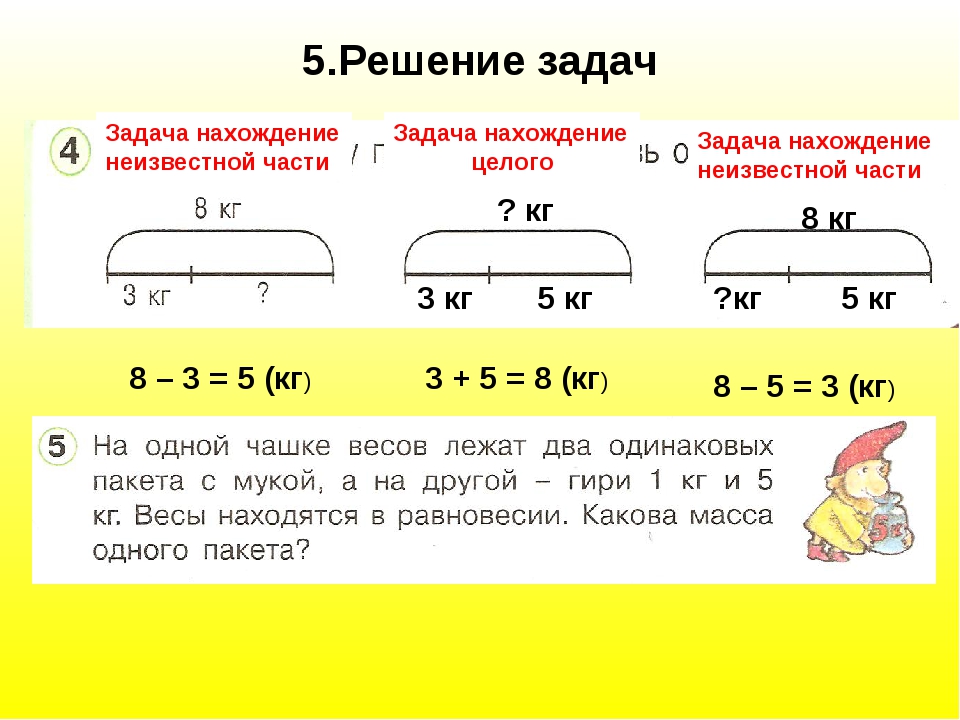
 Вы можете использовать мои задачи с плакатом из моего пакета задач 2 nd Grade Word или написать свои собственные.
Вы можете использовать мои задачи с плакатом из моего пакета задач 2 nd Grade Word или написать свои собственные. Затем я представляю, как пекарь выходит с еще шестью клубничными кексами и добавляет их в ряд из трех.
Затем я представляю, как пекарь выходит с еще шестью клубничными кексами и добавляет их в ряд из трех.
 После того, как вы смоделировали проверку своей работы, поставьте большую галочку рядом с ответом, чтобы показать, что этот шаг выполнен.
После того, как вы смоделировали проверку своей работы, поставьте большую галочку рядом с ответом, чтобы показать, что этот шаг выполнен.