Содержание
Решение задач на проценты. Решение задач по теме проценты.
Решение задач на проценты
Задача 1. Найди какой процент числа \(80\) от \(160\)?
Решение:
\(\frac{80}{160}* 100=50\%\)
Ответ: \(50\%\).
Процент: увеличение и уменьшение
Когда число увеличивается до другого числа, то сумма увеличения вычисляется по формуле:
\(Увеличение = новое \quadчисло-старое \quadчисло \)
Когда число уменьшается до другого числа, то сумма уменьшения задается как:
\(Уменьшение = старое \quadчисло-новое \quadчисло \)
Процент увеличения или уменьшения числа всегда выражается на основании старого числа.
\( Увеличение = 100\frac{ новое \quadчисло-старое \quadЧисло} {старое \quad число}\)
\( Уменьшение = 100\frac{ старое \quadчисло-новое \quadЧисло} {старое \quad число}\)
Задача 2. У вас есть \(80 \) почтовых марок, и вы начинаете собирать больше в течение этого месяца до тех пока общее количество марок не достигнет 120. Процент увеличения количества марок, которые у вас есть в настоящее время:
У вас есть \(80 \) почтовых марок, и вы начинаете собирать больше в течение этого месяца до тех пока общее количество марок не достигнет 120. Процент увеличения количества марок, которые у вас есть в настоящее время:
Решение:
\(\frac{120-80}{80}×100=50\%\)
Ответ: \(50\%\).
Задача 3. У тебя 120 марок. Некоторые из них ты отдал другу в обмен на игру Lego , так что осталось 100 марок. Чему в этом случае равно процентное уменьшение.
Решение:
\(\frac{120-100}{120}*100\)\(=\frac{20}{120}*100=16,67\%\)
Ответ: \(16,67\%\).
Задача 4. Сергей начал бизнес в сфере торговли. В первый месяц он купил продукты за \(650$\) и продал их за \(800$\), а во второй месяц он купил за \(800$\) и продал за \(1200$\). Сколько получил прибыли Сергей.
Решение:
Мы не можем сразу сказать увеличивается ли прибыль Сергея или нет, так как количество его расходов и прибыли отличаются каждый месяц. Для того, чтобы решить эту задачу, мы нужно отнести все значения к фиксированному базовому значению, которое составляет \(100\). Выразим процент прибыли относительно расходов Сергея за первый месяц:
Для того, чтобы решить эту задачу, мы нужно отнести все значения к фиксированному базовому значению, которое составляет \(100\). Выразим процент прибыли относительно расходов Сергея за первый месяц:
\( \frac{800\: -\: 650} { 650} *100 = 23,08\%\)
Это означает, что, если бы Сергей потратил \(100$\), он бы получил прибыль \(23,08\%\) за первый месяц.
Теперь расчитаем прибыль за второй месяц:
\(\frac{1200 — 800} {800} *100 = 50\%\)
Итак, на второй месяц, если бы Сергей потратил \(100$\), он получил бы прибыль в \(50$\). Теперь ясно, что прибыль Сергея растет.
Задача 5. Райан любит собирать крышки от coca-cola. Он собрал 32 крышки от fanta, 25 крышек от sprite и 47 крышек от cola. Каков процент от общего количества крышек?
Решение:
- \(32 + 25 + 47 = 104\) — общее количество
- \(\frac{32}{104} * 100 = 30,8\%\) — крышки от fanta
- \(\frac{25}{104} *100 = 24\%\) — крышки от sprite
- \(\frac{47}{104} *100 = 45.
 2\%\) — крышки от cola
2\%\) — крышки от cola
Задача 6. У тебя была математическая викторина на уроке. В викторине было \(5\) вопросов; три из них по \(3\) бала, а два по \(4\) бала . Вам удалось правильно решить \(2\) вопроса по \(3\) бала и один вопрос с 4 баллами. Каков процент оценок, которые вы получили в этой викторине?
Решение:
- \(3*3 + 2х4 = 17-\)общая оценки
- \(2*3 + 4 = 10-\)количество баллов за правильные ответы
- \(3*3 + 2*4 = 17-\) максимальное количество баллов
- \(\frac{10}{17} *100 = 58,8\%-\)процент полученных баллов
Математика 5-6 классы. 17. Проценты. Решение задач на проценты
Математика 5-6 классы. 17. Проценты. Решение задач на проценты
- Подробности
- Категория: Математика 5-6 классы
Понятие о проценте
В метрической системе мер, и вообще в десятичной системе счисления, широко используются сотые части.
Сотая часть называется процентом (от латинского pro cento—на сотню, из сотни, с сотни) и обозначается %. Поэтому пишут 1 % = 0,01.
Например; 1) 1 % рубля = 0,01 рубля = 1 копейке;
2) 1 % метра = 0,01 метра = 1 сантиметру.
Запись «2 %» читается «два процента» или «две сотые». Вместо того чтобы говорить «тридцать девять сотых», говорят «тридцать девять процентов» и пишут «39 %».
Задача 1. Найти 25% от 36.
Решение.
I способ.
1) Найдем 1 % от 36:
2) Найдем 25 % от 36. Это в 25 раз больше:
II способ.
Так как 25%= 0,25, то задача сводится к нахождению 0,25 числа от 36:
Ответ. 9.
Задача 2. Найти число, 30 % которого равны 7.
Решение.
I способ.
1) Если 30% числа равны 7, то 1 % числа равен 7:30 =
2) Если 1 %,числа равен , то само число в 100 раз больше:
II способ.
Обозначим неизвестное число через тогда 0,30 • x= 7,
Ответ:
Решение задач на проценты
С процентами связаны задачи трех основных типов:
— нахождение процентов данного числа;
— нахождение числа по его процентам;
— нахождение процентного отношения чисел.
Задачи первых двух типов уже рассмотрены выше. Для их решения достаточно знать, что процент—сотая часть. Задачи третьего типа связаны с выражением в процентах отношения двух чисел.
Пример. Из 300 учеников IV и V классов школы в различных кружках занимается 138. Сколько процентов учащихся IV и V классов занимается в кружках?
Решение.
I способ. Вопрос задачи сводится к определению числа процентов, которое составляет 138 от 300. Примем 300 человек за 100%. Тогда 3 человека составляют 1 %, так как 300:100 = 3.
Определим, сколько-процентов составляют 138 учеников:
138:3=46 (%).
II способ. Отношение 138 к 300 равно
Решение обычно записывают короче:
Ответ. 46 %.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100.
Все три типа задач на проценты можно решать с помощью одного приема как задачи на прямую пропорциональную зависимость.
Примеры.
1) Найдем 7 % от 35.
Решение. Пусть х—искомое число; тогда
Ответ.
2) Найдем число, 12 % которого равны 3.
Решение. Пусть х—искомое число; тогда
Ответ. 25.
3) Найдем процентное отношение чисел 8 и 35.
Решение. Пусть х—искомое число процентов; тогда
Ответ.
Решение задач на проценты (урок изучения нового материала). 5-й класс
Цели:
- научить решать основные задачи на проценты:
нахождение процента от величины, нахождение
величины по её проценту, нахождение процента
одной величины от другой; - способствовать развитию творческой активности
учащихся; - развивать познавательный интерес к предмету
путем применения информационных технологий; - способствовать развитию математической речи.

Метод обучения: лекция, объяснение,
устные упражнения, письменные упражнения,
самостоятельная работа.
Формы контроля: проверка
самостоятельно решенных задач.
Оборудование: мультимедийный
проектор (презентация на тему » Проценты»)
Учебник: Математика: Учеб. Для 5 кл.
общеобразоват. Учреждений/ Н.Я. Виленкин, В.И.
Жохов, А.С. Чесноков, С. И. Шварцбурд.
Ход урока
I. Актуализация прежних знаний.
1. Устная работа (на закрепление
понятия «процент») Предлагаются упражнения по
переводу дроби в проценты, а процентов в
десятичные дроби.
| 1. Представьте данные десятичные
дроби в процентах: (слайд №2) | ||
| 0,5= : (50%) | 0,01=: (1%) | 0,42=: (42%) |
| 123=: (12300%) | 0,123=: (12,3%) | 7,2=: (720%) |
| 0,045=: (4,5%) | 70,5=: (7050%) | 1,5=: (150%) |
| 0,6=: (60%) | 0,0035=: (0,35%) | 10= : (1000%) |
2. Представьте проценты Представьте проценты
десятичными дробями: (слайд №3) | ||
| 100%=: | 1000%=: | 72,1%=: |
| 230%=: | 3,17%=: | 0,5%=: |
| 0,08%=: | 133%=: | 94,8%=: |
3. Заполнить таблицу: (слайд №4)
| Обыкновенная дробь | 1/2 | 1/5 | 4/5 | ||||||
| Десятичная дробь | 0,25 | 0,4 | 0,75 | ||||||
| Проценты | 10% | 60% | 100% |
II. Изучение нового материала
Изучение нового материала
1). Простейшие задачи на проценты. Существует
три типа задач на проценты. Сегодня на уроке вы
научитесь их различать и решать, используя
определение процента.
1 тип. Нахождение процентов данного
числа (дано все и процент, найти часть). (Слайд №5)
В книге 600 страниц. Мальчик прочитал 23% книги.
Сколько страниц прочитал мальчик?
2 тип. Нахождение числа по его
процентам (дана часть и процент, найти всё). (Слайд
№6)
Мальчик прочитал 138 страниц — это 23% всей книги.
Сколько страниц в книге?
3 тип. Нахождение процентного
отношения чисел (дано два числа, найти процент
одного от другого) (слайд №7)
В книге 600 страниц. Мальчик прочитал 138 страниц.
Сколько процентов всей книги он прочитал?
(Учащимся раздаются памятки, в которых написаны
три типа задач на проценты и их признаки).
Задание 1. Устно определить тип задачи:
№1536, №1543, №1544, №1555, №1540 (учебника)
При решении задач на проценты удобно
пользоваться следующим алгоритмом (слайд 8):
- Попытаться определить тип задачи;
- Определить, что принимаем за 100%;
- Первым действием находим, сколько приходится на
1%.
Учащиеся вместе с учителем решают задачи 1-3.
Задача 1. (Слайд 9)
Решение. Задача на нахождение процента от
числа.
600стр. — 100%
?стр. — 23%
600 : 100 = 6 (стр.) — 1% книги
6 x 23 = 138 (стр.) — прочитал мальчик
Ответ: 138 страниц.
Задача 2. (Слайд 10)
Решение. Задача на нахождение числа по
проценту.
?стр. — 100%
138стр. — 23%
138 : 23 = 6 (стр.) — 1% книги.
6 x 100 = 600 (стр.) — в книге.
Ответ: 600 страниц.
Задача 3. (Слайд 11)
Решение. Задача на процентное отношение.
600стр. — 100%
138стр. — ?%
600 : 100 = 6 (стр.) — 1% книги
138 : 6 = 23 % книги прочитал мальчик
Ответ: 23%.
III. Тренировочные упражнения
№1538 (учебника) На поле, площадь
которого 620 га, работали хлопкоуборочные машины.
За сутки они убрали 15% всего поля. Сколько
гектаров поля убрали за сутки?
Решение. Задача на нахождение процента от
числа.
620 га — 100%
? га — 15%
620 : 100 = 6,2(га) — 1% поля
6,2x 15 = 93 (га) — убрали за сутки.
Ответ: 93га.
№1548 (учебника) Масса медвежонка
составляет 15% массы белого медведя. Найдите массу
белого медведя, если масса медвежонка 120 кг.
Решение. Задача на нахождение числа по
проценту.
? кг — 100%
120 кг — 15%
120 :15 = 8 (кг)- 1% массы белого медведя.
8 x 100 = 800 (кг) — масса белого медведя.
Ответ: 800 кг.
№1551 (учебника) В школе 700 учащихся.
Среди них 357 мальчиков. Сколько процентов
учащихся этой школы составляют мальчики?
Решение. Задача на процентное отношение.
700 учащихся — 100%
357 учащихся — ?%
700 : 100 = 7(уч.) — 1 % учащихся школы.
357 : 7 = 51 (%) — составляют мальчики.
Ответ: 51%.
IV. Обучающая самостоятельная работа (7
минут) (Слайд №12)
Вариант №1.
1. Из сахарного тростника получается 18% сахара.
Сколько тонн сахара получится из 42,5 т сахарного
тростника?
2. Засеяли 65% поля, что составило 325 га. Найдите
Найдите
площадь всего поля.
Вариант №2.
1. Площадь поля 450 га. В первую смену засеяли 270
га. Сколько процентов всей площади засеяли в
первую смену?
2. Из овса получается 40% муки. Сколько муки
получится из 26,5 т овса?
Работу сдают на проверку.
V. Подведение итогов урока, выставление
отметок.
VI. Домашнее задание. п.40; №1571, 1575. (Слайд
13)
Решение проблем со сложными процентами
При решении задач со сложными процентами первым важным шагом является визуализация проблемы в виде временной шкалы. При создании временной шкалы необходимо соблюдать два важных соглашения. Во-первых, денежные потоки должны быть представлены, приближаясь к читателю (указывая вниз), тогда как денежные потоки уходят (указывает вверх). Во-вторых, PV всегда раньше (слева) от FV.
Мы продемонстрируем, как решить эти проблемы с помощью уравнения, а также с помощью финансового калькулятора и программного обеспечения для работы с электронными таблицами. Обратите внимание, что при использовании калькулятора или электронной таблицы приток денежных средств будет представлен с использованием положительных значений, а отток будет отрицательным. Кроме того, несмотря на то, что входные данные довольно стандартизированы для разных брендов, см. Приложение к этой главе, чтобы узнать о различиях между популярными брендами калькуляторов и электронных таблиц.
Обратите внимание, что при использовании калькулятора или электронной таблицы приток денежных средств будет представлен с использованием положительных значений, а отток будет отрицательным. Кроме того, несмотря на то, что входные данные довольно стандартизированы для разных брендов, см. Приложение к этой главе, чтобы узнать о различиях между популярными брендами калькуляторов и электронных таблиц.
Решение для FV
Сьюзан кладет 2000 долларов на сберегательный счет. Если процентная ставка составляет 2% годовых, каков ее ожидаемый баланс через пять лет?
Поскольку Сьюзен передает свои деньги в банк, это отток наличности.Через пять лет она потенциально может вывести деньги, что вызовет их приток.
Рисунок 6.3 Пример временной шкалы FV
Обратите внимание, что если мы решаем проблему с точки зрения банка, разница только в направлении денежных потоков. Цифры обязательно должны совпадать!
Цифры обязательно должны совпадать!
Рисунок 6.4 Пример временной шкалы FV (вид банка)
Мы можем решить эту проблему, не прибегая к формулам или технологиям, путем анализа балансов на конец каждого года.После первого ее 2000 долларов вырастут на 2%: 2000 долларов + (2000 долларов × 2%) = 2000 долларов + 40 долларов = 2040 долларов. В течение второго года весь баланс вырастет еще на 2%: 2040 долларов США + (2040 долларов США × 2%) = 2040 долларов США + 40,80 долларов США = 2080,80 долларов США. И так до тех пор, пока мы не достигнем баланса в размере 2208,16 долларов за пятый год.
Рисунок 6.5 Конечное сальдо
Решение по формуле дает результат быстрее, но очень важно понять, почему формула работает! Используя PV = 2000 долларов США, n = 5 лет, r = 2% в год, получаем: 2000 долларов США × (1+.02) 5 = 2208,16 доллара. Обратите внимание, что мы должны использовать десятичное представление процентной ставки (0,02 вместо 2%), чтобы формула работала правильно.
Проверка работоспособности
Поскольку разница между простым процентом и сложным процентом относительно невелика, мы можем быстро использовать простой процент, чтобы «проверить работоспособность» нашей работы на наличие ошибок. 2% от 2000 долларов составляют 40 долларов, поэтому с простыми процентами мы получим 40 долларов в год, или 5 × 40 долларов = 200 долларов общей суммы процентов. Компаундирование должно приносить немного больше, чем простой процент, который, как мы можем проверить, добавляет только 8 долларов.Еще 16. Конечно, чем выше процентная ставка или чем больше периодов будет, тем больше разница, но это полезный ориентир для проверки того, что мы находимся на приблизительной отметке.
Решение с помощью финансового калькулятора довольно просто, если вы определили правильные исходные данные и учли несколько незначительных отличий. Во-первых, приток денежных средств представлен положительными числами, а отток — отрицательными. Таким образом, чтобы точно представить нашу проблему, PV следует вводить как отрицательное число (поскольку Сьюзен кладет деньги в банк, что является оттоком наличности.Конечно, если мы решим эту проблему с точки зрения банка, с положительным PV, мы получим такой же ответ для FV, только с перевернутым знаком!). Другое важное отличие финансовых калькуляторов заключается в том, что они рассчитывают процентную ставку в процентах, а не в десятичной дроби. На данный момент вы можете игнорировать ключ pmt .
Таким образом, чтобы точно представить нашу проблему, PV следует вводить как отрицательное число (поскольку Сьюзен кладет деньги в банк, что является оттоком наличности.Конечно, если мы решим эту проблему с точки зрения банка, с положительным PV, мы получим такой же ответ для FV, только с перевернутым знаком!). Другое важное отличие финансовых калькуляторов заключается в том, что они рассчитывают процентную ставку в процентах, а не в десятичной дроби. На данный момент вы можете игнорировать ключ pmt .
должен показать правильное решение 2 208,16.
Использование функции электронной таблицы очень похоже на финансовый калькулятор. pmt , вероятно, будет обязательным вводом, поэтому пока просто введите 0; мы объясним, для чего это используется, в следующей главе.
= БС (ставка, кпер, пт, пв)
= FV (2%, 5, 0, −2000)
2 208,16
Кроме того, при определении входных данных для проблемы, независимо от того, какой метод вы используете, рекомендуется записывать единицы времени для n и r , поскольку они должны соответствовать периоду сложения . Традиционно процентные ставки указываются как годовая процентная ставка (APR). Ставка определяется путем умножения процентной ставки за период начисления сложных процентов на количество периодов в году., или процентную ставку периода начисления сложных процентов, умноженную на количество периодов в году. Поскольку период начисления сложных процентов в нашей пробной задаче был годовым, нам не нужно было это учитывать, но в большинстве реальных примеров периоды начисления сложных процентов обычно короче (раз в полгода, месяц или день). Если специально не указано иное, предполагается, что все последующие процентные ставки в этой книге указаны как годовые.
Традиционно процентные ставки указываются как годовая процентная ставка (APR). Ставка определяется путем умножения процентной ставки за период начисления сложных процентов на количество периодов в году., или процентную ставку периода начисления сложных процентов, умноженную на количество периодов в году. Поскольку период начисления сложных процентов в нашей пробной задаче был годовым, нам не нужно было это учитывать, но в большинстве реальных примеров периоды начисления сложных процентов обычно короче (раз в полгода, месяц или день). Если специально не указано иное, предполагается, что все последующие процентные ставки в этой книге указаны как годовые.
Уравнение 6.7 Периодическая процентная ставка от
годовых
Годовая процентная ставка / количество периодов в году = периодическая процентная ставка
Как бы изменился наш ответ, если бы проценты начислялись ежемесячно? PV по-прежнему будет составлять 2000 долларов, но r должно составлять 2% / (12 месяцев в год) = 0. 1667% в месяц, а n должно быть (5 лет × 12 месяцев в году) = 60 месяцев. Теперь, когда r и n соответствуют периоду начисления сложных процентов, мы можем использовать наше уравнение: 2000 долларов × (1 + .001667) 60 = 2210,20 доллара. Более частое начисление процентов принесет Сьюзан примерно на 2 доллара больше процентов; Это может показаться небольшой разницей, но для более высоких процентных ставок или более продолжительного срока более частое начисление сложных процентов может иметь большее влияние.
1667% в месяц, а n должно быть (5 лет × 12 месяцев в году) = 60 месяцев. Теперь, когда r и n соответствуют периоду начисления сложных процентов, мы можем использовать наше уравнение: 2000 долларов × (1 + .001667) 60 = 2210,20 доллара. Более частое начисление процентов принесет Сьюзан примерно на 2 доллара больше процентов; Это может показаться небольшой разницей, но для более высоких процентных ставок или более продолжительного срока более частое начисление сложных процентов может иметь большее влияние.
Распространенные ошибки формул
Обращайте внимание на детали при использовании формулы, так как есть множество способов сделать ошибки.Два самых больших используют процентное соотношение, когда необходимо десятичное число, и не соответствуют периоду начисления сложных процентов. Поскольку числа, с которыми мы имеем дело для процентных ставок, могут быть небольшими, хорошим практическим правилом является сохранение четырех цифр (не считая ведущих нулей!) Процентной ставки перед округлением. Ежедневная начисленная процентная ставка в 2% составляет 0,005479% годовых. Преобразование в десятичную форму (еще один потенциальный источник ошибок — подсчитайте эти десятичные разряды!) Дает r = 0,00005479.
Ежедневная начисленная процентная ставка в 2% составляет 0,005479% годовых. Преобразование в десятичную форму (еще один потенциальный источник ошибок — подсчитайте эти десятичные разряды!) Дает r = 0,00005479.
Другой распространенный источник путаницы может исходить от ярлыков «настоящее» и «будущее», поскольку сегодняшний день не всегда совпадает с PV.Рассмотрим следующий пример:
Пять лет назад Сьюзан положила 2000 долларов на сберегательный счет. Если процентная ставка составляет 2% годовых, каков ее баланс сегодня?
Этот пример в точности эквивалентен первому в этом разделе, несмотря на то, что сегодня это FV! Если бы кто-то всегда предполагал, что «текущая стоимость» должна быть «сегодняшней», установка на проблему пошла бы совсем не так. Однако при рисовании временной шкалы метки надежно размещаются там, где они должны быть.Вот почему, кстати, мы почти всегда будем использовать метки PV и FV вместо полных слов.
Рисунок 6.6 График FV с течением времени для различных процентных ставок
Решение для PV
На сберегательном счете Сьюзан осталось 3 312,24 доллара. Если процентная ставка составляла 2% годовых, сколько она внесла на депозит пять лет назад, когда открывала счет?
Рисунок 6.7 PV Пример временной шкалы
Очень важно отметить, что, хотя ее текущий баланс составляет 3312,24, это наша БС, поскольку нам нужно вычислить сумму ранее на временной шкале (которая должна быть PV). Перефразируя ту же задачу, можно сказать:
.
Сьюзен хочет, чтобы на ее сберегательном счете было 3 312,24 доллара через пять лет. Если процентная ставка составляет 2% годовых, какую сумму она должна внести сейчас?
PV × (1+.02) 5 = 3312,24
Решение для PV дает решение в размере 3000 долларов.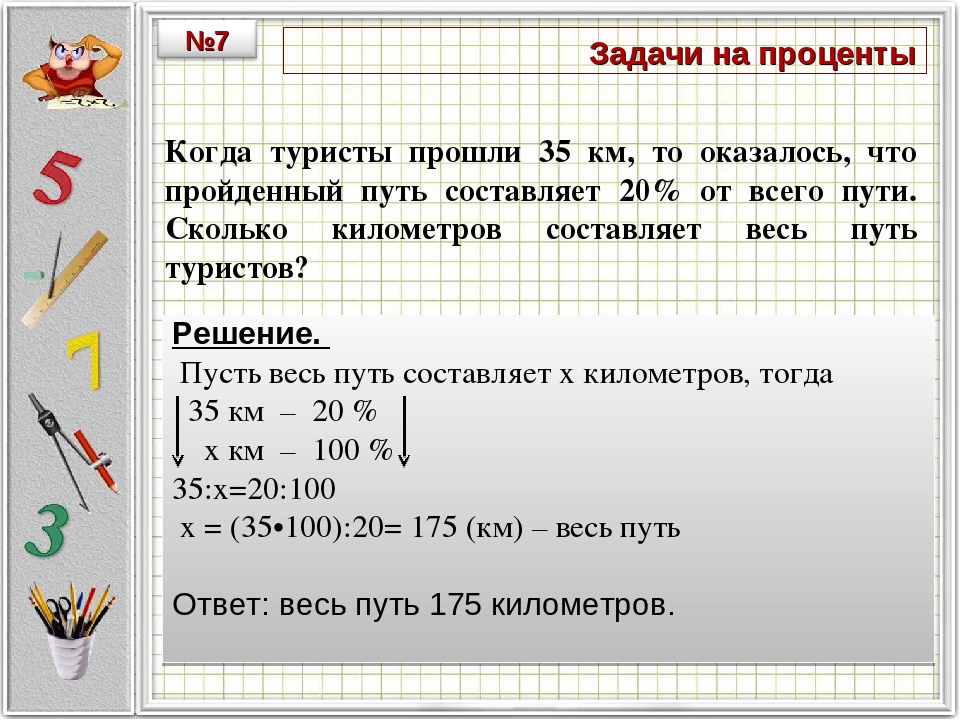 Поскольку решение для PV — такая частая задача в финансах, стоит изменить уравнение.
Поскольку решение для PV — такая частая задача в финансах, стоит изменить уравнение.
Уравнение 6.8 Сложные проценты за n периодов (изменено)
PV × (1 + r) ⁿ = FV
PV = FV (1 + r) n
С помощью финансового калькулятора:
должен показать правильное решение -3,000.
Таблица:
= ПС (ставка; кпер; пт; бс)
= ТС (2%, 5, 0, 3312,24)
-3,000.00
Рисунок 6.8 График PV с течением времени для различных процентных ставок
Решение по процентной ставке
У Дэвида в настоящее время 100 тысяч долларов, и он хотел бы удвоить эти деньги за счет инвестиций, планируя выйти на пенсию через 10 лет. По какой процентной ставке он должен инвестировать для достижения этой цели?
Поскольку у Дэвида 100 тысяч долларов, и он хочет удвоить свои деньги, он должен захотеть получить 200 тысяч долларов через 10 лет.
Рисунок 6.9 Пример временной шкалы скорости
Так много нулей….
Иногда в сфере финансов мы имеем дело с очень большими суммами наличных: тысячами, миллионами или даже миллиардами! Вместо того, чтобы каждый раз вводить все эти нули (и, возможно, оставлять один из них по ошибке), мы все равно можем использовать эти формулы, обрабатывая все наши денежные числа в соответствующих единицах. Например, эта проблема все еще может быть решена правильно с PV = 100 и FV = 200, поскольку наши единицы теперь стоят тысячи долларов.Только не забывай быть последовательным!
100000 × (1+ r) 10 = 200000. Решение для r (вам нужно взять корень 10-й степени) дает решение 0,07177 или 7,177%.
С помощью финансового калькулятора:
должен показать правильное решение 7,177%. Обратите внимание, что один из денежных потоков должен быть отрицательным, а другой — положительным, иначе калькулятор выдаст ошибку.
Таблица:
= СТАВКА (кпер; пт; пв; бс)
= СТАВКА (10; 0; −100000; 200000)
0,07177
Скорость роста
Обратите внимание, что мы можем использовать эту формулу для определения любой скорости роста, например, роста выручки или роста дивидендов по акции!
Решение для количества периодов
У Дэвида сейчас 100 тысяч долларов, и он хотел бы удвоить эти деньги за счет инвестиций до выхода на пенсию.Если лучшая процентная ставка, которую он может найти, — 6%, как долго ему придется ждать, чтобы выйти на пенсию?
Рисунок 6.10 Пример временной шкалы количества периодов
100000 × (1+ 0,06) n = 200000. Решить для n немного сложно: нам нужно будет использовать логарифмы. Большинство профессионалов просто используют финансовый калькулятор или электронную таблицу для решения подобных проблем.
С помощью финансового калькулятора:
Таблица:
= КПЕР (ставка; pmt; pv; fv)
= КПЕР (6%; 0; −100000; 200000)
11,90
Правило 72
Определение времени удвоения настолько распространено, что есть быстрый способ получить приблизительный ответ. Просто разделите 72 на процентную ставку, и это ваше время (разумеется, в совпадающие периоды). Так что, если мой бизнес растет на 9% в месяц, он удвоится примерно через (72/9) = 8 месяцев.Он также помогает найти процентную ставку для заданного количества периодов: если я хочу, чтобы мои деньги удвоились к моему выходу на пенсию через 20 лет, тогда мне нужна ставка (72/20) = 3,6%.
Основные выводы
- Всегда составляйте график.
 PV находится слева от FV.
PV находится слева от FV. - При использовании финансового калькулятора или электронной таблицы приток денежных средств является положительным, а отток — отрицательным. При решении относительно r или n всегда должен быть хотя бы один представитель каждого типа.
Упражнения
- Если 300 долларов инвестируются под 4% годовых, сколько процентов будет заработано через 10 лет с начислением годовых? Сложный ежемесячно? Ежедневно?
- Если ростовщик предлагает дать вам 5000 долларов сегодня в обмен на 8000 долларов через три недели, какова подразумеваемая недельная процентная ставка? Какова эта ставка как годовая процентная ставка?
- На банковском счете в настоящее время имеется остаток в размере 7 400 долларов США.Если первоначальный депозит был сделан четыре года назад, а процентная ставка составляет 5% годовых, какой был первоначальный депозит? Если процентная ставка вместо этого составляет 5% годовых, начисленных ежемесячно, каков был первоначальный депозит?
Проблемы со сложными процентными словами и их решения
Мы будем использовать формулу сложных процентов для решения этих задач со сложными процентами.
Пример № 1
Депозит в размере 3000 долларов приносит 2% годовых, начисляемых раз в полгода.Сколько денег будет в банке через 4 года?
Решение
B = P (1 + r) n
P = 3000 долларов США
r = 2% годовая процентная ставка / 2 процентных периода = 1% годовая процентная ставка
n = количество периодов выплат = количество процентных периодов, умноженное на количество лет
n = 2 раза 4 = 8
B = 3000 (1 + 1%) 8 = 3000 (1 + 0,01) 8 = 3000 (1.01) 8
B = 3000 (1.082856)
B = 3248,57
Через четыре года на банковском счете будет 3248,57 доллара.
Пример № 2
Депозит в размере 2150 долларов приносит 6% процентов, начисляемых ежеквартально. Сколько денег будет в банке через 6 лет?
Решение
B = P (1 + r) n
P = 2150 долларов США
r = 6% годовая процентная ставка / 4 процентных периода = 1,5% квартальная процентная ставка
n = количество периодов выплат = количество процентных периодов, умноженное на количество лет
n = 4 умноженное на 6 = 24
B = 2150 (1 + 1.5%) 24 = 2150 (1 + 0,015) 24 = 2150 (1,015) 24
B = 2150 (1,4295)
B = 3073,425
Через 6 лет в банковский счет.
Пример № 3
Депозит в размере 495 долларов приносит 3% годовых, начисляемых ежегодно. Сколько денег будет в банке через 3 года?
Решение
B = P (1 + r) n
P = 495 долларов США
r = 3% годовая процентная ставка / 1 процентный период = 3% годовая процентная ставка
n = количество периодов выплат = количество процентных периодов, умноженное на количество лет
n = 1 умноженное на 3 = 3
B = 495 (1 + 3%) 3 = 495 (1 + 0.03) 3 = 495 (1.03) 3
B = 495 (1.092727)
B = 540,89
Через 3 года на банковском счете будет 540,89 долларов.
Шесть советов для успешного решения проблем на основе интересов
Майкл Херли в течение нескольких лет был директором по образованию Коалиции профсоюзов Kaiser Permanente, и он и его команда разработали многие программы LMP, используемые для поддержки командного обучения подразделений.
1. Знайте, почему мы используем решение проблем на основе интересов
Решение проблем на основе интересов (IBPS) — это совместный подход к решению проблем, процесс мирного урегулирования разногласий без уступок. Когда вы находитесь в постоянном партнерстве — будь то партнерство между сотрудниками и руководством или, скажем, брак — у вас, вероятно, есть несколько целей, которых вы хотите достичь при разрешении разногласий. К ним относятся не только желание решить проблему таким образом, который отвечает вашим потребностям, но и желание решить ее не слишком дорого (по времени, деньгам или эмоциональному износу), и это разрывает отношения. нетронутой или даже улучшенной.Потому что в будущем вы знаете, что снова будете работать вместе, чтобы решить следующую проблему, которая возникнет.
2.
Основные термины
Четыре слова лежат в основе процесса, основанного на интересах. Проблема — это проблема или предметная область, которую необходимо решить. Позиция — это предлагаемое решение. Интерес — это основная потребность, мотивация или беспокойство, которые, возможно, придется решить для достижения решения; Вы можете сказать об интересе отчасти, потому что обычно существует несколько способов удовлетворить его.Вариант — это потенциальный способ решить проблему полностью или частично.
Ваша должность говорит нам, чего вы хотите, но не обязательно, почему вы этого хотите.
- Супруг (а) хочет положить 5 процентов дохода на пенсионный сберегательный счет.
- Родитель хочет, чтобы ребенок ложился спать до 9:30 в будний день.
- Профсоюз требует повышения заработной платы на 3% в коллективных переговорах.
Ваши интересы говорят нам о том, что для вас важно.
- Супруг (а) хочет накопить достаточно средств для комфортной пенсии.
- Родители хотят, чтобы на следующий день ребенок хорошо отдохнул и пойдет в школу.
- Профсоюзный представитель хочет компенсационный пакет для членов, который помогает при найме и удержании.
3. Спросите: действительно ли этот «интерес» — это позиция?
Что вы делаете, когда ваша должность маскируется под интерес? Обычно вы можете понять интересы, лежащие в основе позиции, если внимательно выслушаете и зададите правильные вопросы.Узнайте потребности и проблемы, стоящие за этой позицией. Вот пример:
Заявление жены: «Ненавижу жить в Лос-Анджелесе. Мы должны переехать в Орегон ».
Реакция на себя: «Отлично, мы снова».
Вопрос жене: «Почему мы должны переехать в Орегон?»
Ответ: «Мы в колее. Мы прожили здесь всю жизнь. Я устал от этого.»
Вопрос: «Что еще вам нравится в штате Орегон?»
Ответы: «Погода здесь слишком жаркая, и мы так много времени проводим в пробках.Мы должны делать все упражнения здесь, в тренажерном зале. В Орегоне прохладнее, и есть более красивые дороги для езды на велосипеде. Мы можем быстрее добраться до леса и хороших пеших прогулок. Там люди более расслаблены. «
Интересы: Перемена погоды, уменьшение трафика, более легкий доступ к малолюдным улицам, меньше стресса.
Начиная с обсуждения интересов, стороны могут говорить о том, что для них важно, не делая ставки на то, каким они хотят видеть результат. Это открывает дверь к совместному решению проблем, а не к конкуренции или компромиссу.
4. Согласуйте информацию
Найдите соглашение о том, какие данные собирать и как их собирать, проанализируйте и сообщите — или вы просто будете спорить о данных.
5. Составьте план действий
Создайте план действий для воплощения решений в жизнь. Четко укажите, кто за что отвечает. Установите график.
6. Установите основные правила
Помните, что процессы, основанные на интересах, не всегда работают. По моему опыту, у них больше шансов на успех, если стороны договорятся:
- Сосредоточьтесь на проблеме, а не на личностях.
- Обменивайтесь информацией как можно раньше.
- Слушайте активно.
- Упорно работайте, чтобы удовлетворить интересы, а не продавать позиции.
- Будьте открыты для выбора.
- Ищите способы укрепить доверие.
Как решать простые проблемы, связанные с процентами
Узнайте, как решать простые задачи по процентам, используя простую формулу процентов.
Связанные темы
Пошаговое руководство по решению простых процентов
- Простые проценты: плата за заем денег или возврат за их ссуду.
- Чтобы решить простую задачу по процентам, используйте эту формулу:
Проценты \ (= \) основная сумма \ (\ times \) ставка \ (\ times \) время \ (⇒ \ color {blue} {I = p \ × \ r \ × \ t} \)
Простой процент
Простой процент — Пример 1:
Найдите простой процент для инвестиций в \ ($ 450 \) по ставке \ (7 \% \) на \ (8 \) лет.
Решение:
Используйте формулу процента: \ (\ color {blue} {I = prt} \)
P \ (= $ 450 \), r \ (= 7 \% = \ frac {7} {100} = 0.07 \) и t \ (= 8 \)
Тогда: I \ (= 450 \ × \ 0,07 \ × \ 8 = 252 доллара \)
Простой процент — Пример 2:
Найдите простой процент на инвестиции в размере \ (5200 долларов США) по ставке \ (4 \% \) в течение \ (3 \) лет.
Решение:
Используйте простую формулу процента: \ (\ color {blue} {I = prt} \)
P \ (= 5200 $ \), r \ (= 4 \% = \ frac {4} {100} = 0,04 \) и t \ (= 3 \)
Тогда: I \ (= 5200 \ × \ 0,04 \ × \ 3 = 624 доллара \)
Простой процент — Пример 3:
Найдите простой процент для инвестиций в \ ($ 5,000 \) по ставке \ (3 \% \) на \ (4 \) лет.
Решение:
Используйте простую формулу процента: \ (\ color {blue} {I = prt} \)
\ (P = 5 000 долларов США, r = 3 \% = \ frac {3} {100} = 0,03 \) и \ (= 4 \)
Тогда: \ (I = 5000 × 0,03 × 4 = 600 долларов США \)
Простой процент — Пример 4:
Найдите простой процент на \ (900 $ \) по цене \ (3.5 \% \) на \ (5 \) лет.
Решение:
Используйте простую формулу процента: \ (\ color {blue} {I = prt} \)
\ (P = 900 $, r = 3,5 \% = 0,035 \) и \ (t = 5 \)
Тогда: \ (I = 900 × 0.035 × 5 = 157,50 $ \)
Упражнения для расчета простых процентов
Простой интерес
Используйте простой процент, чтобы найти конечный баланс.
- \ (1300 $ \) при \ (5 \% \) на \ (6 \) лет.
- \ (5400 долларов США \) по ставке \ (7,5 \% \) на \ (6 \) месяцев.
- \ (25 600 $ \) при \ (9,2 \% \) на \ (5 \) лет.
- \ (240 $ \) проценты начисляются на основную сумму \ (1500 $ \) по простой процентной ставке \ (4 \% \) годовых. На сколько лет был вложен основной капитал?
- Новый автомобиль, оцененный в \ (28 000 долларов США), амортизируется из расчета \ (9 \% \) в год от первоначальной цены.Определите стоимость автомобиля через \ (3 \) года после покупки.
- Сара вкладывает \ (2000 долларов \) в инвестицию, приносящую \ (5 \% \) годовой простой процент; она оставила деньги на пять лет. Сколько процентов получает Сара по прошествии этих пяти лет?
Скачать лист простых процентов
ответов
- \ (\ color {blue} {1,690,00 $} \)
- \ (\ color {blue} {5,602,50} \)
- \ (\ color {blue} {37 376,00 $} \)
- \ (\ color {blue } {4 \ years} \)
- \ (\ color {blue} {$ 20,440} \)
- \ (\ color {blue} {$ 500} \)
Реза — опытный преподаватель математики и специалист по подготовке к экзаменам, который занимается со студентами с 2008 года.Он помог многим студентам поднять результаты стандартизированных тестов и поступить в колледжи своей мечты. Он работает со студентами индивидуально и в группах, преподает как живые, так и онлайн-курсы по математике и математическую часть стандартизированных тестов. Он предоставляет индивидуальный индивидуальный план обучения и индивидуальное внимание, которое влияет на то, как учащиеся относятся к математике.
Относится к «Как решать простые проблемы, связанные с интересом»
Личный интерес человека и проблема решения долгосрочных проблем — блог долгого времени
Мы эгоистичные и недальновидные люди.Как показали многие эксперименты по теории игр, мы не так мотивированы обещанием коллективных будущих выгод, как удовлетворением мгновенных частных вознаграждений.
Группа исследователей из Нью-Йоркского университета сейчас утверждает, что такая личная заинтересованность может создать серьезные препятствия на пути решения долгосрочных проблем, связанных с разными поколениями, таких как изменение климата. Как сообщалось в октябрьском выпуске Nature Climate Change , команда провела исследование, в котором измерялась готовность участников вкладывать личные ресурсы в групповые усилия, которые приведут к вознаграждению в будущем: каждому предмету дали 40 евро, а затем попросили внести 0, 2 или 4 евро на коллективный «климатический счет», который будет финансировать рекламу экологической осведомленности.Если каждый участник внесет на счет достаточно средств, чтобы общая сумма на счете достигла 120 евро, все получат дополнительные 45 евро.
Однако вознаграждение за сотрудничество — пожертвование в размере 45 евро на члена группы за достижение цели в 120 евро — было распределено по трем различным временным горизонтам. В одном случае (T 1 ) пожертвование в размере 45 евро было выплачено на следующий день; во втором сеансе лечения (T 2 ) пожертвование в размере 45 евро было выплачено через 7 недель; в третьем варианте (T 3 ) пожертвования в размере 45 евро были вложены в посадку дубов, которые будут связывать углерод (а также обеспечивать среду обитания и зелень) и, следовательно, приносить наибольшую пользу будущим поколениям, хотя и в валюте, отличной от денежные пожертвования предлагаются в T 1 и T 2 .
Как и предполагали ученые, готовность участников инвестировать была самой высокой в сценарии T 1 и самой низкой для T 3 . Другими словами: чем дальше будет вознаграждение в будущем — и чем меньше вероятность того, что индивид сам извлечет из него выгоду — тем меньше у него мотивации отдать свои личные ресурсы ради общего блага. Исследовательская группа заключает:
Результаты показывают, что дисконтирование между поколениями может подорвать сотрудничество….Немедленное денежное вознаграждение кажется наиболее важным. Применение наших результатов к международным переговорам по изменению климата рисует отрезвляющую картину. Из-за дисконтирования между поколениями сотрудничество будет сильно подорвано, если, как в наших условиях, краткосрочные выгоды могут быть получены только в результате отступничества. Это предполагает необходимость введения мощных краткосрочных стимулов к сотрудничеству, таких как наказание, вознаграждение или репутация, в экспериментальных исследованиях, а также в международных усилиях по смягчению последствий изменения климата.
В статье объясняется, что немедленное и отложенное вознаграждение запускает совершенно разные части человеческого мозга, предполагая, что долгосрочная и краткосрочная стратегия включает в себя различные когнитивные процессы. Таким образом, кажется, что нашим лучшим шансом развить чувство ответственности за будущее может быть создание сценариев, в которых обе части мозга стимулируются одновременно: путем объединения стимула долгосрочного вознаграждения с стимулом краткосрочного вознаграждения. последствия.
Простой калькулятор процентов — WebMath
Быстро! Мне нужна помощь с:
Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLines Theotation, The Equation from slopeLines Theotation и Y-intation , Поиск шансов, Математика, Практика многочленов, Математика, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание чисел Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторинг триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
Решение проблем на основе интересов | Главный сайт FWC
Решение проблем на основе интересов (IBPS) — это совместный подход к решению проблем на рабочем месте.Его можно использовать для разрешения существующих споров на рабочем месте и для предотвращения будущих.
Подход направлен на решение проблем интересов . Традиционные подходы к вопросам рабочего места сосредоточены на должностях.
Позиции — это требования или требования в отношении вещей, которые, по мнению стороны, устранят проблему.
Интересы — это вещи, лежащие в основе любого запроса или требования.
Подход, основанный на интересах, вовлекает людей, которых затронула проблема.Сотрудничество между всеми заинтересованными сторонами позволяет получить больше точек зрения и более полную картину имеющихся проблем и может привести к более разнообразному набору возможных решений: в подавляющем большинстве случаев это приводит к лучшим результатам.
IBPS может помочь на рабочих местах:
- Внедряйте инновации и находите лучшие и творческие решения
- Формируйте более крепкие постоянные отношения между сторонами, основанные на доверии и уважении
- Получение большего признания среди затронутых сторон необходимых изменений
- Повышение гибкости и способности решать проблемы на рабочем месте
Как проявлять интерес к решению проблем
Когда возникает цель или проблема, соберите стороны вместе.Сюда входят все, кого затрагивает цель или проблема, а также любые представители.
Разъясните и согласитесь с проблемой, чтобы все были на одной странице.
Определите интересы заинтересованных сторон.
Проведите мозговой штурм и найдите возможные решения проблемы.
Протестируйте возможные решения по набору критериев (например, является ли возможное решение доступным, законно, соответствует ли оно ценностям компании и т. Д.).
Наконец, стороны вместе должны выбрать результат, который наилучшим образом достигнет цели или решит проблему.
Подходит ли решение проблем на основе интересов для нашего рабочего места?
Работодатели и сотрудники, у которых есть хорошие отношения, должны рассмотреть вопрос о IBPS.
Основные требования к IBPS — творческий подход и командная работа. IBPS предполагает высокий уровень обмена информацией и искреннее общение, поэтому доверие и уважение между сторонами важны.
IBPS сложнее на рабочих местах с натянутыми отношениями или недоверием между руководством и персоналом.Однако IBPS также может быть способом улучшения сложных отношений.
С чего начать
В нашем руководстве по решению проблем, основанном на интересах, описывается, как применить этот подход, включая предложенную нами модель того, как работать с любой заданной проблемой или проблемой. Вы также можете узнать больше о том, как подход, основанный на интересах, улучшает рабочие места.
Если вы решили использовать подход к решению проблем, основанный на интересах, вы можете использовать наш:
Мы также предлагаем поддержку в рамках нашей программы «Совместные рабочие места».Программа предназначена для рабочих мест, которые хотят попробовать подходы, основанные на интересах. Член комиссии будет работать с вами, чтобы провести обучение и помочь вам облегчить процесс. Они также предложат рекомендации и советы, когда вы перейдете к использованию подхода, основанного на интересах. Программа бесплатна.
.
