2-1)≥0\\x<3\end{cases}\)

Решение системы неравенств

Чтобы

решить систему неравенств нужно найти значения иксов, которые подойдут всем неравенствам в системе – это и значит, что они выполняются одновременно.

Пример. Решим систему \(\begin{cases}x>4\\x\leq7\end{cases}\)
Решение: Первое неравенство становится верным, если икс больше \(4\). То есть, решения первого неравенства – все значения иксов из интервала \((4;\infty)\), или на числовой оси:

Второму неравенству подойдут значения иксов меньшие чем 7, включая саму семерку, то есть любой икс  из интервала \((-\infty;7]\) или на числовой оси:

А какие значения подойдут обоим неравенствам? Те, которые принадлежат обоим промежуткам, то есть где промежутки пересекаются.

Ответ: \((4;7]\)

Как вы могли заметить для пересечения решений неравенств в системе удобно использовать числовые оси.

Общий принцип решения систем неравенств: нужно найти решение каждого неравенства, а потом пересечь эти решения с помощью числовой прямой.

Пример: (Задание из ОГЭ)  Решить систему \(\begin{cases} 7(3x+2)-3(7x+2)>2x\\(x-5)(x+8)<0\end{cases}\)

Решение:

\(\begin{cases} 7(3x+2)-3(7x+2)>2x\\(x-5)(x+8)<0\end{cases}\)	Давайте каждое неравенство решим отдельно от другого.
1) \(7(3x+2)-3(7x+2)>2x\)	Раскроем скобки.
\(21x+14-21x-6>2x\)	Приведем подобные слагаемые.
\(8>2x\)	Перевернем получившееся неравенство.
\(2x<8\)	Поделим все неравенство на \(2\).
\(x<4\)	Отметим решение на числовой прямой.
	Запишем ответ для первого неравенства.
\(x∈(-∞;4)\)	Теперь решим второе неравенство.
2) \((x-5)(x+8)<0\)	Неравенство уже в идеальном виде для применения метода интервалов.
	Запишем ответ для второго неравенства. 2\)
\(10-2x≥0\)	Перед нами обычное линейное неравенство – выразим \(x\). Для этого перенесем \(10\) в правую часть.
\(-2x≥-10\)	Поделим неравенство на \(-2\). Так как число отрицательное меняем знак неравенства.
\(x≤5\)	Отметим решение на числовой прямой.
	Запишем ответ к первому неравенству.
\(x∈(-∞;5]\)	На данном этапе главное не забыть, что есть второе неравенство.
2) \(2-7x≤14-3x\)	Опять линейное неравенство – опять выражаем \(x\). 2-28x+196\\(x-5)(x-50)≥0\\x>14\end{cases}\)	В первом перенесем все слагаемые в левую часть. И приведем подобные слагаемые.
\(\begin{cases}-27x+54<0\\(x-5)(x-50)≥0\\x>14\end{cases}\)	Теперь в нем же перенесем \(54\) в левую сторону и поделим обе части на \((-27)\), не забыв при этом перевернуть знак сравнения.
\(\begin{cases}x>2\\(x-5)(x-50)≥0\\x>14\end{cases}\)	Отметим решения неравенств на числовых прямых.
	Решения подходящие всем неравенствам системы находятся от \(50\) и дальше. Запишем ответ.

Ответ: \([50;+∞)\)

Смотрите также:

Системы линейных неравенств
Совокупности неравенств

Скачать статью

Системы линейных неравенств с одной переменной

Предварительные навыки

Примеры решения систем линейных неравенств с одной переменной

Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.

Рассмотрим простейший пример. Система состоит из двух неравенств, которые уже решены.

Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.

Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:

Но дело в том, что неравенства x > 4 и x < 9 соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями, как захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.

Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.

Значит решениями системы  являются числа от 4 до 9. Границы 4 и 9 не включаются во множество решений системы, поскольку неравенства x > 4 и x < 9 строгие. Ответ можно записать в виде числового промежутка:

x ∈ ( 4 ; 9 )

Также, нужно изобразить множество решений системы на координатной прямой.

Для системы линейных неравенств решение на координатной прямой изображают так:

Сначала указывают границы обоих неравенств:

На верхней области отмечают множество решений первого неравенства x > 4

На нижней области отмечают множество решений второго неравенства x < 9

Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 4 до 9. Для наглядности выделим эту область красным цветом:

Для проверки можно взять любое число из этого промежутка и подставить его в исходную систему . Возьмем, например, число 6

Видим, что решение 6 удовлетворяет обоим неравенствам. Возьмём ещё какое-нибудь число из промежутка (4; 9), например, число 8

Видим, что решение 8 удовлетворяет обоим неравенствам.

Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:

Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.

Пример 2. Решить систему неравенств 

Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.

Решениями же обоих неравенств являются все числа, которые больше 17.

Изобразим множество решений системы  на координатной прямой и запишем ответ в виде числового промежутка.

Для начала отметим на координатной прямой границы обоих неравенств:

На верхней области отметим множество решений первого неравенства x > 17

На нижней области отметим множество решений второго неравенства x > 12

Нас интересует область, которая отмечена штрихами с обеих сторон.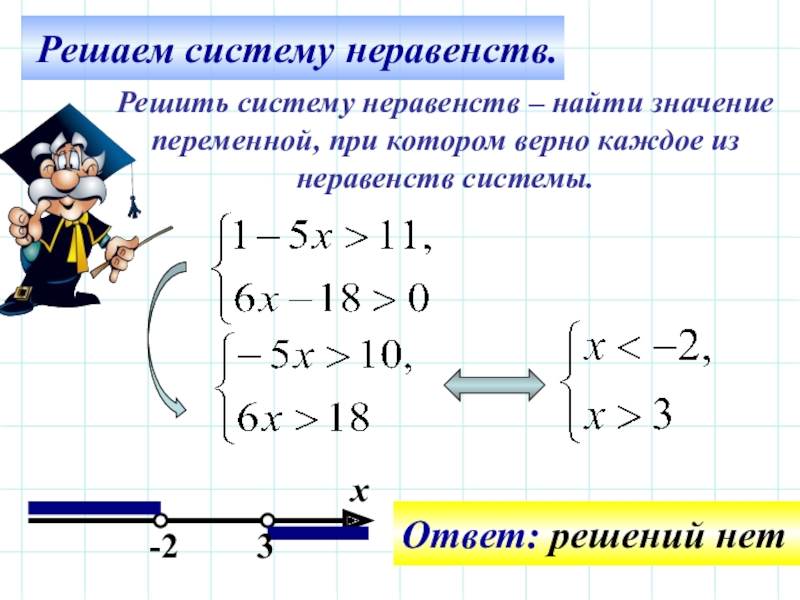 В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 17 до плюс бесконечности. Запишем ответ в виде числового промежутка:

x ∈ ( 17 ; +∞ )

---

Пример 3. Решить систему неравенств 

Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок

Получили систему . На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.

Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства (x > 6 и x > 3). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы 

x ∈ ( 6 ; + ∞ )

---

Пример 4. Решить систему неравенств 

Решим каждое неравенство по отдельности:

Изобразим множество решений системы  на координатной прямой и запишем ответ в виде числового промежутка:

---

Пример 5. Решить неравенство 

Решим каждое неравенство по отдельности:

Изобразим множество решений системы  на координатной прямой и запишем ответ в виде числового промежутка:

---

Когда решений нет

Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.

Пример 1. Решить неравенство 

Решим каждое неравенство по отдельности:

Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.

Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:

На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система 

А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система 

Ответ: решений нет.

---

Пример 2. Решить систему неравенств 

Решим каждое неравенство по отдельности:

Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:

Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система 

А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система

Ответ: решений нет.

---

Пример 3.  Решить систему неравенств 

Решим каждое неравенство по отдельности:

Получили неравенства 0 < −0,2 и a > 5. Первое неравенство не является верным и не имеет решений. Решением второго неравенство a > 5 являются все числа, которые больше 5. Но поскольку первое неравенство не будет верным ни при каком a, то можно сделать вывод, что у неравенств нет общих решений. А значит не имеет решений исходная система 

Ответ: решений нет.

---

Задания для самостоятельного решения

Задание 1. Решите неравенство:

Решение:

Задание 2. Решите неравенство:

Задание 3. Решите неравенство:

Задание 4. Решите неравенство:

Задание 5. Решите неравенство:

Задание 6. Решите неравенство:

Задание 7. Решите неравенство:

Задание 8. Решите неравенство:

Решение:

Решений нет

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Математика по полочкам: 13.

Системы неравенств

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Если ставится задача найти множество общих решений двух или более неравенств, то говорят, что надо решить систему неравенств.

Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда системы неравенств записывают в виде двойного неравенства:

-5<x<12 или 

Решением системы неравенств называется число, которое при его подстановке в систему обращает каждое неравенство в верное числовое неравенство.

Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет.

Чтобы решить систему неравенств с одной переменной, надо:

1) отдельно решить каждое неравенство;

2) найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.

Это пересечение и является множеством решений системы неравенств.

Пример:
Решить систему неравенств:

Решим каждое неравенство в отдельности
1) 5x-x2≥0,
5x-x2=0,
x(5-x)=0,
x=0 или 5-x=0,
-x=-5,
x=5.
Находим решение с помощью метода интервалов:

2) 6-2x<-2,
-2x<-2-6,
-2x<-8,
x>-8:(-2),
x>4.

Объединим оба решения:

Ответ: (4; 5].

---

Говорят, что несколько неравенств с одной переменной образуют совокупность, если необходимо найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств. Совокупность неравенств обозначается квадратной скобкой.

Решением совокупности неравенств называют такие значения переменной, которые являются верными хотя бы для одного из этих неравенств.

Чтобы решить совокупность неравенств с одной переменной, надо:

1) отдельно решить каждое неравенство;

2) найти объединение найденных решений, отметив решение каждого неравенства на числовой прямой.

Это объединение и является решением совокупности неравенств.

Пример:
Решить совокупность неравенств:

Решим каждое неравенство в отдельности
1) 5х+6≤1,
     5х≤ -5,
     х≤ -1.

2) 2х+1≥3,
    2х≥2,
    х≥1.

Объединим оба решения:

Ответ: (-∞; -1]U[1;+∞).

---

УПРАЖНЕНИЯ

1. Решите систему неравенств:

Решение:
а)

Ответ: (5; 7]

---

2. Решите систему неравенств:

Решение:

Ответ: (1; 10].

---

3. Найдите целые решения системы неравенств:

Решение:
а)

Ответом являются все целые числа, которые принадлежат промежутку (-15; 5).
Ответ: -14; -13; -12; -11; -10; -9; -8; -7; -6.

---

4. Решите систему неравенств:

Решение:

Ответ: (-1; 3).

---

5. Решите систему неравенств:

Решение:

Ответ: (-1;2).

---

6. Решите систему неравенств:

Решение:

Ответ: нет решений.

---

7. Решите систему неравенств:

Решение:

Ответ: (0; +∞).

---

8. Решите неравенство:

а) -2<3x+5≤10;    б) 2<4x+6≤12.

Решение:

Ответ: (-2 1/3; 1 2/3].

---

9. Решите систему неравенств:

Решение:

Ответ: [0,4; 0,5).

---

10. Решите систему неравенств (№ 3.4.52 [7]):

Решение:

Ответ: (-1; 2).

---

11. Решите систему неравенств:

Решение:

Ответ: [-9; 3)U(3; 9].

---

12. Решите систему неравенств:

Решение:

Ответ: (-7; -6)U(1;7).

---

13. Решите систему неравенств:

Решение:

Ответ: (2; 4).

---

14. Решите систему неравенств:

Решение:

Ответ: (-7; -2)U(0; 2).

---

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Решите систему неравенств:

2. Решите систему неравенств:

3. Решите систему неравенств:

4. Решите систему неравенств:

5. Решите систему неравенств:

6. Решите систему неравенств:

7. Решите систему неравенств:

8. Решите систему неравенств:

9. Решите систему неравенств:

10. Решите систему неравенств:

---

Проверь себя

---

Решите систему неравенств и укажите все целые числа, которые являются ее решениями

1. 2.Решите систему неравенств и укажите все целые числа, которые являются ее решениями

12 6 x 0,
3x 1 25 x;
МЕНЮ

2. Решение 2

12 6 x 0,
3x 1 25 x;
6 x 12,
4 x 24;
x 2,
x 6.
2
6
[2;6]
Ответ: 2,3,4,5,6.
МЕНЮ
x

3. 3. Найдите целые решения системы неравенств

12a 37 0,
6a 42;
МЕНЮ

4. Решение 3

12a 37 0,
6a 42;
12a 37,
a 7;
1
a
3
,
12
a 7.
3
МЕНЮ
1
12
7
(3 ;7].
x
Ответ: 4,5,6,7.

5. 4. Решите системы неравенств

x x
7,
1. 3 4
1 x 0;
6
y 1
y
1,
2.
2
y 5;
3
3x 1
5. 2 1,
x 1 x;
2
МЕНЮ
3x 1
3. 2 x 2,
2 x x 1;
3
x 1 x 3
2,
6. 2
3
13x 1 0;
2
p 2
2
p
4,
4.
5
p p 6;
2 8
5 y 1 2 y 1
0,
7. 6
2
1 y 4 0;
3

6. Решение 4.1

x x
3 4 7,
1 x 0;
6
*12
*6
4 x 3x 7,
6 x 0;
7 x 84,
x 6;
x 12,
x 6.
6
Ответ: (- ;6).
МЕНЮ
12
x

7. Решение 4.2

y 1
y
1,
2
y 5;
3
2 y y 1 2,
y 15;
y 1,
y 15.
Ответ: (1;15).

8. Решение 4.3

3x 1
2 x 2,
2 x x 1;
3
3x 1 2 x 4,
6 x x 3;
x 5,
5 x 3;
Ответ: [0,6;5].

9. Решение 4.4

p 2
2
p
4,
5
p p 6;
2 8
10 p p 2 20,
4 p p 48;
9 p 18,
3 p 48;
Ответ: (2;16].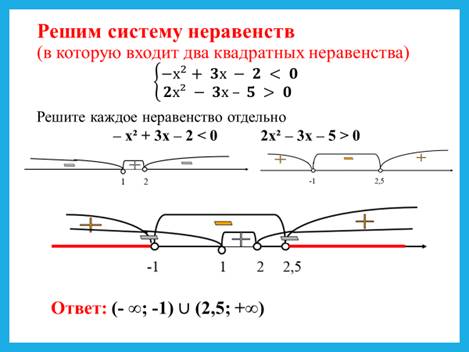

10. Решение 4.5

3x 1
2 1,
x 1 x;
2
3x 1 2,
x 2 2 x;
3x 3,
x 2;
Ответ: (-2;-1).

11. Решение 4.6

x 1 x 3
2 3 2,
13x 1 0;
2
3x 3 2 x 6 12,
13x 1 0;
x 3 12,
13 x 1;
x 9,
1
x
.
13
1
; 9).
13
Ответ : (

12. Решение 4.7

5 y 1 2 y 1
6 2 0,
1 y 4 0;
3
5 y 1 6 y 3 0,
3 y 4 0;
y 2,
y 1.
Ответ: (-1; 2).

13. 5. Решите двойное неравенство:

2 6 2 y 5;
МЕНЮ

14. Решение 5

2 6 2 y 5;
6 2 y 2,
6 2 y 5;
2 y 4,
2 y 1;
y 2,
1
y
.
2
2
1
2
Ответ:1( ; 2).
МЕНЮ
2
х

15. 6. При каких у значения двучлена 3у-5 принадлежат промежутку (-1;1)?

МЕНЮ

16. Решение 6

1 3y 5 1
3 y 5 1,
3 y 5 1;
3 y 4,
3 y 6;
1
y 1 ,
3
y 2.
1
МЕНЮ
1
3
Ответ:
y
2
(1
1
;
3
2).

17. 7. Решите систему неравенств

x 8,
x 7,
x 4.
МЕНЮ

18. Решение 7

x 8,
x 7,
x 4.
-4
7
Ответ: (8; + )
МЕНЮ
8
х

19. 8. Решите систему неравенств

2 x 1 x 3,
5 x 1 6 2 x,
x 5 0;
МЕНЮ

20. Решение 8

2 x 1 x 3,
5 x 1 6 2 x,
x 5 0;
x 4,
7 x 7,
x 5;
x 4,
x 1,
x 5.
Ответ: (1; 4).
МЕНЮ
1
4
5
х
• Домашнее задание
• Выполнить № 875,877,879.

Системы линейных неравенств и выпуклые множества точек

Неравенство — это два числа или математических выражения, соединённых
одним из знаков: > (больше, в случае строгих неравенств), < (меньше, в случае
строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤
(меньше или равно, в случае нестрогих неравенств).

Неравенство является линейным при тех же условиях, что и
уравнение: оно содержит переменные только в первой степени и не содержит произведений переменных.

Решение линейных неравенств и систем линейных неравенств неразрывно связано
с их геометрическим смыслом: решением линейного неравенства является некоторая полуплоскость,
на которые всю плоскость делит прямая, уравнением которой задано линейное неравенство. Эту
полуплоскость, а в случае системы линейных неравенств — часть плоскости, ограниченную
несколькими прямыми, требуется найти на чертеже.

К решению систем линейных неравенств с большим числом переменных сводятся
многие экономические задачи, в частности, задачи линейного программирования, в которых
требуется найти максимум или минимум функции.

Одно неравенство с двумя неизвестными, так же как и уравнение, имеет
бесчисленное множество решений. Решением данного неравенства назовём пару чисел
,
удовлетворяющих этому неравенству. Геометрически множество решений неравенства изображается
в виде полуплоскости, ограниченной прямой

,

которую назовём граничной прямой.

Шаг 1. Построить прямую, ограничивающую множество решений линейного
неравенства

Для этого надо знать какие-либо две точки этой прямой. Найдём точки
пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1).
Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу
после этого теретического экскурса.

Абсциссу найдём, решая как систему уравнение прямой с уравнением оси .

Найдём пересечение с осью :

Подставляя значение
в первое уравнение, получаем

,
откуда .

Таким образом, нашли абсциссу точки A .

Найдём координаты точки пересечения с осью .

Абсцисса точки B равна нулю. Решим уравнение граничной прямой с уравнением
оси координат:

Решение:

,

следовательно, координаты точки B: .

Шаг 2. Начертить прямую, ограничивающую множество решений неравенства. Зная точки A и B пересечения граничной прямой с осями
координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две
части, лежащие справа и слева (выше и ниже) от этой прямой.

Шаг 3. Установить, которая из полуплоскостей является решением данного
неравенства. Для этого нужно в это неравенство подставить начало координат (0; 0). Если координаты начала
удовлетворяют неравенству, то решением неравенства является полуплоскость, в которой
находится начало координат. Если же координаты не удовлетворяют неравенству, то решением
неравенства является полуплоскость, которая не содержит начала координат. Полуплоскость
решения неравенства будем обозначать штрихами от прямой внутрь полуплоскости, как на рисунке 1.

Если решаем систему линейных неравенств, то каждый шаг выполняется для
каждого из неравенств системы.

Пример 1. Решить неравенство

Решение. Начертим прямую

Подставив в уравнение прямой ,
получим , а
подставив ,
получим .
Следовательно, координаты точек пересечения с осями будут A(3; 0),
B(0; 2). Через эти точки проведём прямую (опять рисунок 1).

Выберем полуплоскость решений неравенства. Для этого в неравенство подставим
координаты начала (0; 0):

,

получим ,
т. е. координаты начала удовлетворяют данному неравенству. Следовательно, решением неравенства
является полуплоскость, содержащая в себе начало координат, т. е. левая (она же нижняя) полуплоскость.

Если бы данное неравенство было строгим, то есть имело бы вид

,

то точки граничной прямой не являлись бы решением, так как они не
удовлетворяют неравенству.

Теперь рассмотрим систему линейных неравенств с двумя неизвестными:

Каждое из неравенств этой системы на плоскости определяет полуплоскость.
Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и
несовместной, если она не имеет решений. Решением системы линейных неравенств называется
любая пара чисел (),
удовлетворяющая всем неравенствам данной системы.

Геометрически решением системы линейных неравенств является множество
точек, удовлетворяющих всем неравенствам системы, то есть, общая часть получаемых
полуплоскостей. Поэтому геометрически в общем случае решение может быть изображено в виде
некоторого многоугольника, в частном случае — может быть линия, отрезок и даже точка. Если
система линейных неравенств несовместна, то на плоскости не существует ни одной точки,
удовлетворяющей всем неравенствам системы.

Пример 2. Решить систему линейных неравенств

Решение. Итак, требуется найти многоугольник решений этой системы неравенств.
Построим граничную прямую для первого неравенства, то есть прямую ,
и граничную прямую для второго неравенства, то есть прямую .

Делаем это пошагово, как было показано в теоретической справке и в примере 1,
тем более, что в примере 1 строили граничную прямую для неравенства, которое является первым
в данной системе.

Полуплоскости решений, соответствующие неравенствам данной системы, на
рисунке 2 заштрихованы вовнутрь. Общая часть полуплоскостей решений представляет собой
открытый угол ABC. Это означает, что множество точек
плоскости, составляющих открытый угол ABC, является
решением как первого, так и второго неравенства системы, то есть, является решением системы
двух линейных неравенств. Иначе говоря, кординаты любой точки из этого множества
удовлетворяют обоим неравенствам системы.

Пример 3. Решить систему линейных неравенств

Решение. Построим граничные прямые, соответствующие неравенствам системы.
Делаем это, выполняя шаги, данные в теоретической справке, для каждого неравенства. Теперь
определим полуплоскости решений для каждого неравенства (рисунок 3).

Полуплоскости решений, соответствующие неравенствам данной системы,
заштрихованы вовнутрь. Пересечение полуплоскостей решений изображается, как показано на
рисунке, в виде четырёхугольника ABCE. Получили, что
многоугольник решений системы линейных неравенств с двумя переменными является
четырёхугольником ABCE.

Всё описанное выше о системах линейных неравенств с двумя неизвестными
относится и к системе неравенств с любым числом неизвестных, с той лишь разницей, что решением
неравенства с n неизвестными будет совокупность n чисел (),
удовлетворяющих всем неравенствам, а вместо граничной прямой будет граничная гиперплоскость
n-мерного пространства. Решением будет многогранник решений (симплекс), ограниченный
гиперплоскостями.

Так же, как и в двухмерном пространстве (на плоскости), каждое из
неравенств системы определяет n-мерное полупространство. Пересечение всех этих
полупространств образует многогранник решений. Но изобразить этот многогранник (называемый
симплексом) геометрически невозможно. Лишь в случае, когда число неизвестных не больше трёх, то есть
в действительном пространстве, многогранник решений можно изобразить геометрически.

Множество решений линейных неравенств геометрически составляет выпуклый
многогранник или выпуклое множество точек.

Как уже отмечалось, системы линейных неравенств играют важную роль в
линейном программировании. Теоремы линейного программирования содержат такие понятия, как
выпуклые множества и крайние точки. Разберёмся бегло, о чём речь.

Множество точек называется выпуклым, если вместе с его любыми двумя
точками ему принадлежит и весь отрезок, соединяющий их. Если же существует хотя бы такая
пара точек множества, что отрезок, соединяющий эти точки, не принадлежит целиком этому
множеству, то такое множество называется невыпуклым. На рисунке 4 слева изображено
выпуклое множество, а справа — невыпуклое.

Выпуклые множества обладают важным свойством, которое устанавливается
следующей теоремой.

Теорема. Пересечение двух выпуклых множеств — также
выпуклое множество.

Через любую внутреннюю точку выпуклого множества можно провести отрезок,
для которого она является внутренней, а сам отрезок целиком принадлежит этому множеству.
Но есть точки (для выпуклого многоугольника это его вершины), для которых такое построение
выполнить нельзя: нет ни одного отрезка, для которого вершина являлась бы внутренней, а
отрезок целиком бы принадлежал мноргоугольнику.

Точка выпуклого множества называется угловой (или крайней), если через
неё нельзя провести ни одного отрезка, состоящего только из точек данного множества и для
которого она была бы внутренней.

Продолжение темы «Систем уравнений и неравенств»

Начало темы «Линейная алгебра»

Поделиться с друзьями

Как решать систему неравенств 8 класс

Основные понятия

Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.

Числовое неравенство — в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Типы неравенств

Строгие — используют только больше (>) или меньше (<)

• a < b — это значит, что a меньше, чем b.
• a > b — это значит, что a больше, чем b.
• a > b и b < a означают одно и тоже, то есть равносильны.

Нестрогие — используют сравнения ≥ (больше или равно) или ≤ (меньше или равно)

• a ≤ b — это значит, что a меньше либо равно b.
• a ≥ b — это значит, что a больше либо равно b.
• знаки ⩽ и ⩾ являются противоположными.

Другие типы

• a ≠ b — означает, что a не равно b.
• a ≫ b — означает, что a намного больше, чем b.
• a ≪ b — означает, что a намного меньше, чем b.
• знаки >> и << противоположны.

Система неравенств

Чтобы щелкать задачки, нам пригодятся свойства числовых неравенств. Вот они:

 

1. Если а > b , то b < а. Также наоборот: а < b, то b > а.

2. Если а > b и b > c, то а > c. И также если а < b и b < c, то а < c.

3. Если а > b, то а + c > b+ c (и а – c > b – c).
   Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям можно прибавлять или вычитать одну и ту же величину.

4. Если а > b и c > d, то а + c > b + d.
   Если а < b и c < d, то а + c < b + d.
   Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять, т.к. возможны исключения. Например, если из 12 > 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

5. Если а > b и c < d, то а – c > b – d.
   Если а < b и c > d, то а – c < b – d.
   Из одного неравенства можно почленно вычесть другое противоположного смысла, оставляя знак того, из которого вычиталось.

6. Если а > b, m — положительное число, то mа > mb и

   .

   Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
   Если же а > b, n — отрицательное число, то nа < nb и

   .

   Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.

7. Если а > b и c > d, где а, b, c, d > 0, то аc > bd.
   Если а < b и c < d, где а, b, c, d > 0, то аc < bd.
   Неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
   Следствием является: если а > b, где а, b > 0, то а² > b², и если а < b, то а² < b². На множестве положительных чисел обе части можно возвести в квадрат.

8. Если а > b, где а, b > 0, то .
   Если а < b , то .

Таблица числовых промежутков

Полезна тем, что с ее помощью удобно записывать множество решений.

Неравенство	Графическое решение	Форма записи ответа
x < c		x ∈ (−∞; c)
x ≤ c		x ∈ (−∞; c]
x > c		x ∈ (c; +∞)
x ≥ c		x ∈ (c; +∞)

Еще один важный шаг — запись ответа. Вот, как правильно это делать:

• Если знак строгий (>, <), точка на оси будет не закрашена, а скобка — круглой.

• Если знак нестрогий (≥, ≤), точка на оси будет закрашена, а скобка — квадратной.

• Скобка, рядом со знаком бесконечности всегда круглая.

Решение системы неравенств

Линейное неравенство — то, в котором неизвестное представлено в первой степени. Для его решения нужно, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице. Алгоритм решения:

1. Раскрыть скобки, перенести неизвестное в левую часть, числа в правую и привести подобные слагаемые. Получится одно из следующих видов:

• ax < b,
• ax ≤ b,
• ax > b,
• ax ≥ b.

2. Если получилось ax ≤ b.Для его решения необходимо поделить левую и правую часть на коэффициент перед неизвестным a.

3. Если a > 0, то x ≤ ba.
Если a < 0, то знак меняется на противоположный.
Получаем x ≥ ba.

4. Записываем ответ как он есть или в соответствии с таблицей числовых промежутков.

Решим пример

3 * (2 − x) > 18

Как решаем Раскрываем скобки, оставляем неизвестное слево, числа перемещаем вправо, приводим подобные слагаемые. 6 − 3x > 18 −3x > 18 − 6 −3x > 12 Делим обе части на коэффициент, который стоит перед неизвестным. Так как −3 < 0, знак меняется на противоположный.  x < 12−3 x < −4 Ответ: x < −4 или в числовом промежутке x ∈ (−∞; −4).

И еще один

Как решаем Оставляем неизвестное слева, избавляемся от знаменателя через умножение на это число обеих частей. Делим обе части на коэффициент, который стоит перед неизвестным. Так как — 2 < 0, знак меняется на противоположный.  Ответ: х < – 2.

Последний, чтобы разобраться наверняка

Как решаем Проверим, что неизвестное находится слева. Делим обе части на коэффициент, который стоит перед неизвестным в каждом из них.  Ответ: числовой промежуток x ∈ (– 2; 0].

Запомнить все правила и научиться быстро их применять помогут на уроках математики в детской школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

калькулятор системы неравенств онлайн

Вы искали калькулятор системы неравенств онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и решить графически систему неравенств онлайн, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «калькулятор системы неравенств онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как калькулятор системы неравенств онлайн,решить графически систему неравенств онлайн,решить систему неравенств графически онлайн,решить систему неравенств онлайн графически. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор системы неравенств онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь (например, решить систему неравенств графически онлайн).

Где можно решить любую задачу по математике, а так же калькулятор системы неравенств онлайн Онлайн?

Решить задачу калькулятор системы неравенств онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Графические неравенства с программой «Пошаговое решение математических задач»

В предыдущих главах мы решали уравнения с одной неизвестной или переменной. Теперь мы изучим методы решения систем уравнений, состоящих из двух уравнений и двух переменных.

ТОЧКИ НА САМОЛЕТЕ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Представьте декартову систему координат и определите начало координат и оси.
2. Для упорядоченной пары найдите эту точку в декартовой системе координат.
3. Для данной точки в декартовой системе координат укажите связанную с ней упорядоченную пару.

Мы уже использовали числовую прямую, на которой мы представили числа в виде точек на прямой.

Обратите внимание, что это понятие содержит элементы из двух областей математики, строки из геометрии и чисел из алгебры. Рене Декарт (1596-1650) разработал метод соотношения точек на плоскости с алгебраическими числами. Эта схема называется декартовой системой координат (от Декарта) и иногда упоминается как прямоугольная система координат.

Эта система состоит из двух числовых линий, перпендикулярных в своих нулевых точках.

Перпендикуляр означает, что две прямые расположены под прямым углом друг к другу.

Внимательно изучите диаграмму, отмечая каждый из следующих фактов.

Числовые линии называются осями . Горизонтальная линия — это ось x , а вертикальная — ось y . Нулевая точка, в которой они перпендикулярны, называется исходной точкой .

Оси множественного числа. Ось особенная.

Положительный — справа и вверх ; отрицательный — к слева и вниз .

Стрелки указывают, что числовые линии продолжаются бесконечно. Таким образом, плоскость бесконечно простирается во всех направлениях.

Самолет разделен на четыре части, называемые квадрантами . Они пронумерованы в направлении против часовой стрелки, начиная с верхнего правого угла.

Точки на плоскости обозначаются упорядоченными парами чисел, записанными в скобках с запятой между ними, например (5,7). Это называется упорядоченной парой, потому что важен порядок, в котором написаны числа. Заказанная пара (5,7) — это , а не , как заказанная пара (7,5). Точки расположены на плоскости следующим образом.

Сначала начните с начала координат и посчитайте слева или справа количество пробелов, обозначенных первым числом в упорядоченной паре.Во-вторых, от точки на оси x, заданной первым числом, отсчитайте вверх или вниз количество пробелов, обозначенных вторым числом упорядоченной пары. Упорядоченные пары всегда сначала пишутся с x, а затем y, (x, y). Числа, представленные x и y, называются координатами и точки (x, y).

Это важно. Первое число упорядоченной пары всегда относится к горизонтальному направлению, а второе число всегда относится к вертикальному направлению.

Пример 1 В следующей декартовой системе координат точки A (3,4), B (0,5), C (-2,7), D (-4,1), E (-3 , -4), F (4, -2), G (0, -5) и H (-6,0) обозначены. Проверьте каждый, чтобы определить, как они расположены.

Каковы координаты начала координат?

ГРАФИЧЕСКИЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Найдите несколько упорядоченных пар, которые делают данное линейное уравнение истинным.
2. Найдите эти точки в декартовой системе координат.
3. Проведите прямую линию через те точки, которые представляют график этого уравнения.

График — это графическое изображение пронумерованных фактов. Есть много типов графиков, таких как гистограммы, круговые графики, линейные графики и так далее. Примеры таких графиков обычно можно найти в финансовом разделе газеты. Графики используются, потому что изображение обычно упрощает понимание числовых фактов.

В этом разделе мы обсудим метод построения графика уравнения с двумя переменными. Другими словами, мы нарисуем картину уравнения с двумя переменными.
Рассмотрим уравнение x + y — 7 и заметим, что мы легко можем найти множество решений. Например, если x = 5, то y — 2, поскольку 5 + 2 = 7. Кроме того, если x = 3, то y = 4, поскольку 3 + 4 = 7. Если мы представим эти ответы в виде упорядоченных пар (x, y) , то у нас есть (5,2) и (3,4) как две точки на плоскости, которые представляют ответы на уравнение x + y = 7.

Все возможные ответы на это уравнение, расположенные в виде точек на плоскости, дадут нам график (или картинку) уравнения.

Конечно, мы никогда не сможем найти все числа x и y такие, что x + y = 7, поэтому мы должны довольствоваться наброском графика. Эскиз можно охарактеризовать как «кривую наилучшего соответствия». Другими словами, необходимо найти достаточно точек, чтобы получить достаточно точную картину уравнения.

Помните, существует бесконечно много упорядоченных пар, которые удовлетворяли бы уравнению.

Пример 1 Нарисуйте график 2x + y = 3.

Решение Мы хотим найти несколько пар чисел, которые сделают это уравнение истинным. Мы добьемся этого, выбрав число для x, а затем найдя соответствующее значение для y. Таблица значений используется для записи данных.

В верхней строке (x) мы разместим числа, которые мы выбрали для x. Затем в нижней строке (y) мы поместим соответствующее значение y, полученное из уравнения.

Конечно, мы также могли бы начать с выбора значений для y, а затем найти соответствующие значения для x.

В этом примере мы позволим x принимать значения -3, -2, -1,0, 1,2,3.

Эти значения произвольны. Мы могли выбирать любые ценности.

Обратите внимание, что после того, как мы выбрали значение для x, значение для y определяется с помощью уравнения.

Эти значения x дают целые числа для значений y.Таким образом, это хороший выбор. Предположим, мы выбрали

Эти факты дают нам следующую таблицу значений:

Теперь мы находим упорядоченные пары (-3,9), (-2,7), (-1,5), (0,3), (1,1), (2, -1), (3, -3) на координатной плоскости и соедините их линией.

Теперь у нас есть график 2x + y = 3.

Линия указывает, что все точки на линии удовлетворяют уравнению, а также точки из таблицы.Стрелки указывают, что линия продолжается бесконечно.

Графики всех уравнений первой степени с двумя переменными будут прямыми линиями. Этот факт будет использован здесь, хотя в математике будет гораздо позже, прежде чем вы сможете доказать это утверждение. Такие уравнения первой степени называются линейными уравнениями .

Таким образом, любое уравнение вида ax + by — c, где a, b и c — действительные числа, является линейным уравнением.

Уравнения с двумя неизвестными более высокой степени дают графики, которые представляют собой кривые разных типов.Вы изучите их на будущих курсах алгебры.

Поскольку график уравнения первой степени с двумя переменными представляет собой прямую линию, необходимо иметь только две точки. Однако ваша работа будет более точной, если вы найдете хотя бы три точки. Ошибки можно найти и исправить, если найденные точки не лежат на одной линии. Таким образом, мы называем третью точку «контрольной точкой».

Это важно. Не пытайтесь сократить свою работу, найдя только два момента.Вы удивитесь, как часто вы обнаружите ошибку, обнаружив все три точки.

Пример 2 Нарисуйте график 3x — 2y — 7.

Решение Сначала составьте таблицу значений и выберите три числа, которые будут заменять x. Попробуем 0, 1,2.

Опять же, вы также могли начать с произвольными значениями y.

Ответ не так легко найти на графике, как целое число.Похоже, что x = 0 был не очень удачным выбором. Иногда можно заглянуть вперед и сделать лучший выбор для x.

Поскольку и x, и y являются целыми числами, x = 1 был хорошим выбором.

Точку (1, -2) будет легче найти. Если x = 2, у нас будет другая дробь.

Точку (3,1) легко найти.

x = 3 был еще одним хорошим выбором.

Скорректируем таблицу значений и будем использовать точки, дававшие целые числа. Это не всегда возможно, но попытка получить целые значения даст более точный набросок. Теперь у нас есть таблица для 3x — 2y = 7.

Мы можем это сделать, поскольку выбор x был произвольным.

Расположение точек (1, -2), (3,1), (- 1, -5) дает график 3x — 2y = 7.

Сколько упорядоченных пар удовлетворяют этому уравнению?

НАКЛОН ЛИНИИ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Свяжите уклон линии с ее крутизной.
2. Запишите уравнение прямой в форме пересечения наклона.
3. Постройте прямую линию, используя ее наклон и точку пересечения по оси Y.

Теперь мы хотим обсудить важную концепцию, называемую наклоном линии. Интуитивно мы можем думать об уклоне как о крутизне линии по отношению к горизонту.

Ниже приведены графики из нескольких линий. Внимательно изучите их и мысленно ответьте на следующие вопросы.

Какая линия круче?

Как выглядит связь между коэффициентом при x и крутизной Какой график будет круче: линии, когда уравнение имеет вид y = mx?

Какой график будет круче: y = 3x или y = 7x?

Теперь изучите следующие графики.

Какая линия круче?

Как отрицательное значение m влияет на график?

Какой график будет круче: y = 3x или y = 7x?

Для графика y = mx необходимо было сделать следующие наблюдения.

1. Если m> 0, то
   • по мере увеличения значения m крутизна линии увеличивается и
   • линия поднимается вправо и опускается влево.
2. Если м
3. по мере увеличения значения m крутизна линии уменьшается и
4. линия поднимается влево и опускается вправо

Помните, m> 0 означает, что «m больше нуля. «

Другими словами, в уравнении вида y — mx, m управляет крутизной линии. В математике мы используем слово наклон для обозначения крутизны и формируем следующее определение:

В уравнении вида y = mx, m — это наклон графика уравнения.

Пример 1 Нарисуйте график y = 6x и укажите наклон линии.

Решение Сначала мы составим таблицу, показывающую три набора упорядоченных пар, которые удовлетворяют уравнению.

Помните, нам нужны только две точки для определения линии, но мы используем третью точку в качестве проверки.

Затем мы делаем набросок графика.

Значение m равно 6, следовательно, наклон равен 6. Мы можем просто написать m — 6.

Пример 2 Нарисуйте график и укажите наклон

.

Решение Выбирая значения x, которые делятся на 3, получаем таблицу

Зачем использовать значения, которые делятся на 3?

Тогда график

Склон

Теперь мы хотим сравнить графики двух уравнений, чтобы установить другую концепцию.

Пример 3 Нарисуйте графики y 3x и y — 3x + 2 на одном и том же наборе координатных осей.

Сравните коэффициенты при x в этих двух уравнениях.

Решение

В примере 3 посмотрите на таблицы значений и обратите внимание, что для данного значения x,
значение y в уравнении y = 3x + 2 на два больше, чем соответствующее значение y в уравнении y = 3x.

Теперь посмотрите на графики двух уравнений и обратите внимание, что график y = 3x + 2, кажется, имеет тот же наклон, что и y = 3x.Также обратите внимание, что если весь график y = 3x перемещается вверх на две единицы, он будет идентичен графику y = 3x + 2. График y = 3x пересекает ось y в точке (0,0). , а график y = 3x + 2 пересекает ось y в точке (0,2).

Снова сравните коэффициенты при x в двух уравнениях.

Сравните эти таблицы и графики, как в примере 3.

Обратите внимание: когда две линии имеют одинаковый наклон, они параллельны.

Наклон от одной точки на линии к другой определяется отношением изменения y к изменению x. То есть

Если вы хотите произвести впечатление на своих друзей, вы можете написать , где греческая буква (дельта) означает «изменение».

Обратите внимание, что изменение x равно 3, а изменение y равно 2.

Изменение x равно -4, а изменение y равно 1.

Можно также сказать, что изменение x равно 4, а изменение y равно -1.Это приведет к той же строке.

Пример 7 На графике y = 3x — 2 наклон равен 3.

Изменение x равно 1, а изменение y равно 3.

y = mx + b называется формой с пересечением наклона уравнения прямой линии. Если уравнение имеет такую ​​форму, m — это наклон линии, а (0, b) — точка, в которой график пересекает (пересекает) ось y.

Точка (0, b) называется точкой пересечения по оси y.

Если уравнение прямой имеет форму пересечения наклона, можно нарисовать его график, не составляя таблицу значений. Используйте точку пересечения оси Y и наклон, чтобы нарисовать график, как показано в примере 8.

Обратите внимание, что это уравнение имеет вид y = mx + b.

Сначала найдите точку (0, -2). Это одна из точек на линии. Наклон показывает, что изменение x равно 4, поэтому из точки (0, -2) мы перемещаем четыре единицы в положительном направлении параллельно оси x.Поскольку изменение y равно 3, мы перемещаем три единицы в положительном направлении параллельно оси y. Получившаяся точка тоже на линии. Поскольку две точки определяют прямую линию, мы рисуем график.

Всегда начинайте с точки пересечения оси Y. Распространенная ошибка, которую допускают многие студенты, — это путать точку пересечения по оси Y с точкой пересечения по оси x (точка, в которой линия пересекает ось x).

Пример 9 Задайте наклон и точку пересечения по оси Y и нарисуйте график y = 3x + 4.

Решение m = -3, точка пересечения по оси y = (0,4).

Чтобы выразить наклон в виде отношения, мы можем написать -3 как или. Если мы запишем наклон как, то из точки (0,4) мы перемещаем одну единицу в положительном направлении параллельно оси x, а затем перемещаем три единицы в отрицательном направлении параллельно оси y. Затем мы проводим линию через эту точку и (0,4).

Предположим, уравнение не имеет формы y = mx + b. Сможем ли мы найти наклон и точку пересечения по оси Y? Ответ на этот вопрос — да. Однако для этого мы должны изменить форму данного уравнения, применив методы, использованные в разделе 4-2.

Раздел 4-2 посвящен решению буквальных уравнений. Вы можете просмотреть этот раздел.

Пример 10 Найдите наклон и точку пересечения оси Y для 3x + 4y = 12.

Решение Во-первых, мы понимаем, что уравнение не находится в форме пересечения наклона, необходимой для ответа на заданные вопросы. Чтобы получить эту форму, решите данное уравнение относительно y.

Нарисуйте здесь график.

Пример 11 Найдите наклон и точку пересечения оси y для 2x — y = 7.

Решение Помещая уравнение в форму пересечения наклона, получаем

Нарисуйте график линии на сетке ниже.

ГРАФИК ЛИНЕЙНЫХ НЕРАВЕНСТВ

ЗАДАЧИ

По завершении этого раздела вы сможете построить график линейных неравенств.

В главе 4 мы построили линейные графики неравенств, например

Это были неравенства с участием только одной переменной. Мы обнаружили, что во всех таких случаях график представлял собой некоторую часть числовой прямой. Поскольку уравнение с двумя переменными дает график на плоскости, кажется разумным предположить, что неравенство с двумя переменными будет отображаться как некоторая часть или область плоскости. На самом деле это так. Решение неравенства x + y

Пример 1 Каждая из следующих пар чисел в наборе решений x + y

Решение

Набор решений состоит из всех упорядоченных пар, которые делают утверждение верным.

Подводя итог, следующие упорядоченные пары дают верное утверждение. (2,1), (3, -4), (0,0), (- 1,4)

Следующие упорядоченные пары дают ложное утверждение. (5,6), (3,2), (- 2,8)

Ниже приведен график прямой x + y = 5. Точки из примера 1 указаны на графике с ответами на вопрос «Является ли x + y

Обратите внимание, что все точки, удовлетворяющие уравнению, находятся слева и ниже линии, а все точки, которые не соответствуют, находятся сверху и справа.

Обратите внимание, что все ответы «да» лежат на одной стороне линии x + y = 5, а все ответы «нет» лежат на другой стороне линии или на самой строке.

График прямой x + y = 5 делит плоскость на три части: саму линию и две стороны линий (называемые полуплоскостями).

х + у
х + у

Если одна точка полуплоскости находится в наборе решений линейного неравенства, то все точки в этой полуплоскости входят в набор решений. Это дает нам удобный метод построения графиков линейных неравенств.

Построение графика линейного неравенства
1. Замените символ неравенства знаком равенства и нанесите на график полученную линию.
2. Отметьте одну точку, которая, очевидно, находится в определенной полуплоскости этой прямой, чтобы увидеть, входит ли она в набор решений неравенства.
3. Если выбранная точка находится в наборе решений, то вся эта полуплоскость является набором решений. Если выбранная точка не входит в набор решений, тогда другая полуплоскость является набором решений.

Почему нужно проверять только одну точку?

Пример 2 Нарисуйте график 2x 4- 3y> 7.

Решение Шаг 1. Сначала нарисуйте график линии 2x + 3y = 7, используя таблицу значений или форму пересечения наклона.

Шаг 2: Затем выберите точку, которая не находится на прямой 2x + 3y = 7. [Если линия не проходит через начало координат, то точка (0,0) всегда будет хорошим выбором.] Теперь обратимся к неравенство 2x + 3y>> 7, чтобы увидеть, находится ли выбранная точка в наборе решений.

Шаг 3: Точка (0,0) не входит в набор решений, поэтому полуплоскость, содержащая (0,0), не является набором решений. Следовательно, другая полуплоскость, определяемая линией 2x + 3y = 7, является множеством решений.
Поскольку сама линия не является частью решения, она показана пунктирной линией, а полуплоскость заштрихована, чтобы показать набор решений.

Набор решений — это полуплоскость сверху и справа от линии.

Пример 3 Изобразите график решения линейного неравенства 2x — y ≥ 4.

Решение Шаг 1. Первый график 2x — y = 4. Поскольку линейный график для 2x — y = 4 не проходит через начало координат (0,0), проверьте эту точку в линейном неравенстве.

Шаг 2:

Шаг 3: Поскольку точка (0,0) не входит в набор решений, полуплоскость, содержащая (0,0), отсутствует в наборе. Следовательно, решение — другая полуплоскость. Обратите внимание, однако, что строка 2x — y = 4 включена в набор решений. Поэтому нарисуйте сплошную линию, чтобы показать, что это часть графика.

Набор решений — это линия и полуплоскость ниже и справа от линии.

Пример 4 График x

Решение Первый график x = y. Затем проверьте точку не на линии. Обратите внимание, что график линии содержит точку (0,0), поэтому мы не можем использовать ее в качестве контрольной точки. Чтобы определить, какая полуплоскость является набором решений, используйте любую точку, которая явно не находится на прямой x = y. Точка (- 2,3) является такой точкой.

Используя эту информацию, построить график x

Когда график линии проходит через начало координат, любая другая точка на оси x или y также будет хорошим выбором.

ГРАФИЧЕСКОЕ РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Нарисуйте графики двух линейных уравнений в одной и той же системе координат.
2. Найдите общее решение двух графиков.

Пример 1 Пара уравнений называется системой линейных уравнений.

Мы заметили, что каждое из этих уравнений имеет бесконечно много решений, и каждое из них будет образовывать прямую линию, когда мы построим его в декартовой системе координат.

Теперь мы хотим найти решения для системы. Другими словами, нам нужны все точки (x, y), которые будут на графике обоих уравнений.

Решение Мы рассуждаем следующим образом: если все решения 2x — y = 2 лежат на одной прямой, а все решения x + 2y = 11 лежат на другой прямой, то решение обоих уравнений будет их точками пересечение (если две прямые пересекаются).

В этой таблице мы позволяем x принимать значения 0, 1 и 2. Затем мы находим значения для y, используя уравнение. Сделайте это перед тем, как продолжить. В этой таблице мы позволяем y принимать значения 2, 3 и 6. Затем мы находим x, используя уравнение. Также проверьте эти значения.

Две прямые пересекаются в точке (3,4).

Обратите внимание, что точка пересечения выглядит как (3,4). Теперь мы должны проверить точку (3,4) в обоих уравнениях, чтобы убедиться, что это решение системы.

В качестве проверки мы подставляем упорядоченную пару (3,4) в каждое уравнение, чтобы увидеть, получим ли мы истинное утверждение. Существуют ли другие точки, которые удовлетворяли бы обоим уравнениям? Почему?

Следовательно, (3,4) является решением системы.

Не все пары уравнений дают единственное решение, как в этом примере. На самом деле существует три возможности, и вы должны знать о них.

Поскольку мы имеем дело с уравнениями, которые представляют собой прямые линии, мы можем исследовать эти возможности, наблюдая за графиками.

1. Независимые уравнения Две прямые пересекаются в одной точке. В этом случае есть единственное решение.

Приведенный выше пример представляет собой систему независимых уравнений.

2. Несогласованные уравнения Две линии параллельны. В этом случае решения нет.

Независимо от того, как далеко протянуты эти линии, они никогда не пересекутся.

3. Зависимые уравнения Два уравнения дают одну и ту же линию. В этом случае любое решение одного уравнения является решением другого.

В этом случае общих решений будет бесконечно много.

На более поздних курсах алгебры будут изучены методы распознавания несовместных и зависимых уравнений. Однако на этом уровне мы будем иметь дело только с независимыми уравнениями. Тогда вы можете ожидать, что для всех проблем, приведенных в этой главе, будут найдены уникальные решения.

Это означает, что графики всех систем в этой главе будут пересекаться в одной точке.

Чтобы решить систему двух линейных уравнений с помощью построения графиков
1. Составьте таблицу значений и нарисуйте график каждого уравнения в той же системе координат.
2. Найдите значения (x, y), которые называют точку пересечения линий.
3. Отметьте эту точку (x, y) в обоих уравнениях.

Опять же, в этой таблице wc произвольно выбрал значения x равными — 2, 0 и 5. Здесь мы выбрали для x значения 2, 4 и 6. Вы можете выбрать любые значения, которые хотите. Мы говорим «кажущийся», потому что мы еще не проверили упорядоченную пару в обоих уравнениях. Как только он проверит, это определенно решение.

Поскольку (3,2) проверяет оба уравнения, это решение системы.

ГРАФИЧЕСКОЕ РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Постройте два или более линейных неравенства на одном и том же наборе осей координат.
2. Определите область плоскости, которая является решением системы.

Более поздние занятия по математике будут включать тему линейного программирования. Несмотря на то, что сама тема выходит за рамки этого текста, одна техника, используемая в линейном программировании, вполне доступна вам — построение графиков систем линейных неравенств — и мы обсудим это здесь.

В предыдущем разделе вы обнаружили, что решение системы линейных уравнений — это пересечение решений каждого из уравнений. Таким же образом решение системы линейных неравенств представляет собой пересечение полуплоскостей (и, возможно, прямых), которые являются решениями каждого отдельного линейного неравенства.

Другими словами, x + y> 5 имеет множество решений и 2x — y

имеет в качестве своего решения область плоскости, которая находится в наборе решений обоих неравенств.

Для построения графика решения этой системы мы наносим на график каждое линейное неравенство на одном и том же наборе координатных осей и указываем пересечение двух наборов решений.

Обратите внимание, что решением системы линейных неравенств будет набор точек.

Опять же, используйте либо таблицу значений, либо форму уравнения с пересечением наклона для построения графика линий.

Проверка точки (0,0) в неравенстве x + y> 5 показывает, что точка (0,0) не входит в набор ее решений. Мы указываем набор решений x + y> 5 экраном справа от пунктирной линии.

Эта область находится справа и выше линии x + y = 5.

Проверка точки (0,0) в неравенстве 2x — y

Эта область находится слева и выше линии 2x — y = 4.

Пересечение двух наборов решений — это та область плоскости, в которой пересекаются два экрана. Этот регион показан на графике.

Еще раз обратите внимание, что решение не включает строки.Если, например, нас попросили построить график решения системы , который указывает, что решение включает точки на линии x + y = 5.

Результаты показывают, что все точки в заштрихованной части графика будут в наборах решений x + y> 5 и 2x — y.

РЕШЕНИЕ СИСТЕМЫ ПУТЕМ ЗАМЕНЫ

ЗАДАЧИ

По завершении этого раздела вы должны уметь решать систему двух линейных уравнений методом подстановки.

В разделе 6-5 мы решили систему двух уравнений с двумя неизвестными с помощью построения графиков. Графический метод очень полезен, но он был бы непрактичным, если бы решения были дробными. Фактическую точку пересечения может быть очень сложно определить.
Существуют алгебраические методы решения систем. В этом разделе мы обсудим метод подстановки.

Пример 1 Решить методом подстановки:

Решение
Шаг 1 Мы должны решить одну неизвестную в одном уравнении.Мы можем выбрать либо x, либо y либо в первом, либо во втором уравнении. Наш выбор может быть основан на получении простейшего выражения. В этом случае мы решим относительно x во втором уравнении, получив x = 4 + 2y, потому что любой другой выбор привел бы к дроби.

Посмотрите на оба уравнения и посмотрите, есть ли в одном из них переменная с коэффициентом, равным единице.

Шаг 2 Подставьте значение x в другое уравнение. В этом случае уравнение
2х + 3у = 1.
Подставляя (4 + 2y) вместо x, мы получаем 2 (4 + 2y) + 3y = 1, уравнение только с одной неизвестной.

Причина этого в том, что если x = 4 + 2y в одном из уравнений, то x должен быть равен 4 + 2y в другом уравнении.

Шаг 3 Решите неизвестное.

Помните, сначала удалите скобки.

Шаг 4 Подставьте y = — 1 в любое уравнение, чтобы найти соответствующее значение для x.Поскольку мы уже решили второе уравнение относительно x через y, мы можем его использовать.

Мы можем подставить y = — 1 в любое уравнение, поскольку y имеет одинаковое значение в обоих.

Таким образом, у нас есть решение (2, -1).

Помните, что x записывается первым в упорядоченной паре.

Шаг 5 Проверьте решение в обоих уравнениях. Помните, что решение системы должно быть верным для каждого уравнения в системе.С

решение (2, -1) действительно проверяет.

Это проверяет: 2x + 3y = 1 и x — 2y = 4.

Проверьте эту упорядоченную пару в обоих уравнениях. Ни в одном из этих уравнений не было переменной с коэффициентом, равным единице. В этом случае решение заменой — не лучший метод, но мы сделаем это так, чтобы показать, что это возможно. В следующем разделе будет предложен более простой метод.

РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ ДОПОЛНЕНИЕМ

ЗАДАЧИ

По завершении этого раздела вы должны уметь решать систему двух линейных уравнений методом сложения.

Метод сложения для решения системы линейных уравнений основан на двух фактах, которые мы использовали ранее.

Во-первых, мы знаем, что решения уравнения не меняются, если каждый член этого уравнения умножается на ненулевое число. Во-вторых, мы знаем, что если мы добавим одинаковые или равные количества к обеим сторонам уравнения, результаты все равно будут одинаковыми.

Пример 1 Решить сложением:

Обратите внимание, что мы можем решить эту систему методом подстановки, решив первое уравнение относительно y.Решите эту систему методом подстановки и сравните свое решение с решением, полученным в этом разделе.

Решение
Шаг 1 Наша цель — сложить два уравнения и исключить одно из неизвестных, чтобы мы могли решить полученное уравнение с одним неизвестным. Если мы сложим уравнения как есть, мы не удалим неизвестное. Это означает, что мы должны сначала умножить каждую сторону одного или обоих уравнений на число или числа, что приведет к исключению одного из неизвестных при сложении уравнений.
Внимательно изучив проблему, мы замечаем, что проще всего устранить неизвестное y. Это делается путем умножения каждой стороны первого уравнения на -2.

Обратите внимание, что каждый член необходимо умножить на (- 2).

Шаг 2 Добавьте уравнения.

Шаг 3 Решите полученное уравнение.

В этом случае мы просто умножаем каждую сторону на (-1).

Шаг 4 Найдите значение другой неизвестной, подставив это значение в одно из исходных уравнений.Используя первое уравнение,

Подставьте x = 4 во второе уравнение и посмотрите, получите ли вы такое же значение для y.

Шаг 5 Если мы проверим упорядоченную пару (4, -3) в обоих уравнениях, мы увидим, что это решение системы.

Пример 2 Решить сложением:

Обратите внимание, что в этой системе ни одна переменная не имеет коэффициента, равного единице. Поэтому лучший метод решения — метод сложения.

Решение
Шаг 1 Необходимо изменить оба уравнения, чтобы исключить одно из неизвестных. Ни одно из неизвестных не будет проще другого, поэтому удалите либо x, либо y.
Чтобы исключить x, умножьте каждую сторону первого уравнения на 3 и каждую сторону второго уравнения на -2.

Если вы решили исключить y, умножьте первое уравнение на — 2, а второе уравнение на 3. Сделайте это и решите систему.Сравните ваше решение с полученным в примере.

Шаг 2 Сложив уравнения, мы получаем

Шаг 3 Решение для урожайности

Шаг 4 Использование первого уравнения в исходной системе для нахождения значения другой неизвестной дает

Шаг 5 Убедитесь, что упорядоченная пара (- 1,3) является решением системы.

Чек остается на ваше усмотрение.

СТАНДАРТНАЯ ФОРМА

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Напишите линейное уравнение в стандартной форме.
2. Решите систему двух линейных уравнений, если они заданы в нестандартной форме.

Уравнения в предыдущих разделах не содержали дробей, как неизвестные в левой части уравнения, так и неизвестные в том же порядке.
Такие уравнения называются стандартными. То есть они имеют вид ax + by = c, где a, b и c — целые числа. Перед решением методом сложения уравнения необходимо привести к стандартному виду.

Пример 1 Измените 3x = 5 + 4y на стандартную форму.

Решение 3x = 5 + 4y не в стандартной форме, потому что одно неизвестное находится справа. Если мы прибавим -4y к обеим сторонам, мы получим 3x — 4y = 5, что в стандартной форме.

Будьте осторожны здесь. Многие студенты забывают умножить правую часть уравнения на 24.

Снова убедитесь, что каждый член умножен на 12.

Теперь прибавьте — 24x к обеим сторонам, получив — 24x + 9y = -10, что в стандартной форме.Обычно уравнения пишутся так, что первый член положительный. Таким образом, мы умножаем каждый член этого уравнения на (- 1).

Вместо того, чтобы говорить «первый член положительный», мы иногда говорим «ведущий коэффициент положительный».

ПРОБЛЕМЫ СО СЛОВОМ С ДВУМЯ НЕИЗВЕСТНЫМИ

ЗАДАЧИ

По завершении этого раздела вы сможете:

1. Определите, когда проблема со словом может быть решена с использованием двух неизвестных.
2. Составьте уравнения и решите словесную задачу.

Многие проблемы со словами можно обрисовать и решить, используя два неизвестных.

Пример 1 Сумма двух чисел равна 5. Трижды первое число, умноженное на пять, второе число равно 9. Найдите числа.

Решение Пусть x = первое число
y = второе число
Первое утверждение дает нам уравнение
x + y = 5.
Второе утверждение дает нам уравнение
3x + 5 y = 9.
Теперь у нас есть система

, которую мы можем решить любым из известных нам методов, давая
x = 8 и y = — 3.

Решите систему с помощью подстановки.

Пример 2 Два работника получают в общей сложности 136 долларов за 8-часовую работу. Если одному работнику платят на 1 доллар в час больше, чем другому, найдите почасовую ставку для каждого.

Решение Пусть x = почасовая ставка одного работника
y = почасовая ставка другого работника.

Обратите внимание, что очень важно сказать, что представляют x и y.

Первое утверждение дает нам уравнение
8x + 8y = 136.
Второе утверждение дает уравнение
х = у + 1.
Теперь у нас есть система (в стандартном виде)

Решение дает x = 9 и y = 8. Ставка одного рабочего составляет 9 долларов в час, а другого — 8 долларов в час.

Решите эту систему методом сложения.

РЕЗЮМЕ

Ключевые слова

• Декартова система координат — это метод наименования точек на плоскости.
• Упорядоченные пары чисел используются для обозначения точек на плоскости.
• Линейное уравнение представляет собой прямую линию.
• Наклон от одной точки на линии до другой — это отношение.
• Угол наклона-пересечения уравнения прямой имеет вид y = mx + b.
• Линейное неравенство отображается как часть плоскости.
• Система двух линейных уравнений состоит из линейных уравнений, для которых мы хотим найти одновременное решение.
• Независимые уравнения имеют уникальные решения.
• Противоречивые уравнения не имеют решения.
• Зависимые уравнения имеют бесконечно много решений.
• Система двух линейных неравенств состоит из линейных неравенств, для которых мы хотим найти одновременное решение.
• Стандартная форма линейного уравнения — это ax + by = c, где a, b и c — действительные числа.

Процедуры

• Чтобы нарисовать график линейного уравнения, найдите упорядоченные пары чисел, которые являются решениями этого уравнения.Найдите эти точки в декартовой системе координат и соедините их линией.
• Чтобы нарисовать график линии, используя ее наклон:
  Шаг 1 Запишите уравнение прямой в форме y — mx + b.
  Шаг 2 Найдите точку пересечения j (0, b).
  Шаг 3 Начиная с (0, b), используйте наклон m, чтобы найти вторую точку.
  Шаг 4 Соедините две точки прямой линией.
• Чтобы построить график линейного неравенства:
  Шаг 1 Замените символ неравенства знаком равенства и нанесите на график полученную линию.
  Шаг 2 Проверьте одну точку, которая явно находится в определенной полуплоскости этой прямой, чтобы увидеть, входит ли она в набор решений неравенства.
  Шаг 3 Если выбранная точка находится в наборе решений, то вся эта полуплоскость является набором решений. Если выбранная точка не входит в набор решений, тогда другая полуплоскость является набором решений.
• Чтобы решить систему двух линейных уравнений с помощью построения графиков, тщательно изобразите уравнения в одной и той же системе координат.Их точка пересечения и будет решением системы.
• Чтобы решить систему двух линейных неравенств с помощью построения графиков, определите область плоскости, которая удовлетворяет обоим утверждениям неравенства.
• Чтобы решить систему двух уравнений с двумя неизвестными путем подстановки, решите одну неизвестную одного уравнения через другую неизвестную и подставьте эту величину в другое уравнение. Затем подставьте полученное таким образом числовое значение в любое уравнение, чтобы найти значение другого неизвестного.Наконец, проверьте решение в обоих уравнениях.
• Чтобы решить систему двух уравнений с двумя неизвестными путем сложения, умножьте одно или оба уравнения на необходимые числа так, чтобы при сложении уравнений одно из неизвестных было удалено. Решите оставшиеся неизвестные и подставьте это значение в одно из уравнений, чтобы найти другое неизвестное. Проверьте оба уравнения.
• Чтобы решить словесную задачу с двумя неизвестными, найдите два уравнения, которые показывают связь между неизвестными.Затем решите систему. Всегда проверяйте решение указанной проблемы.

Система линейных неравенств — объяснение и примеры

Прежде чем решит системы линейных неравенств , давайте посмотрим, что означает неравенство. Слово неравенство означает математическое выражение, в котором стороны не равны друг другу.

Как правило, для представления уравнений неравенства используются пять символов неравенства.

Это меньше (<), больше (>), меньше или равно (≤), больше или равно (≥) и символ «не равно» (≠).Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной.

Что такое система линейных неравенств?

Система линейных неравенств — это система уравнений линейных неравенств, содержащих одинаковые переменные.

Несколько методов решения систем линейных уравнений переводятся в систему линейных неравенств. Однако решение системы линейных неравенств несколько отличается от линейных уравнений, потому что знаки неравенства мешают нам решить с помощью метода замены или исключения.Возможно, лучший метод решения систем линейных неравенств — это графическое отображение неравенств.

Как решать системы линейных неравенств?

Ранее вы научились решать простое линейное неравенство с помощью построения графиков. В этой статье мы узнаем, как найти решения для системы линейных неравенств путем одновременного построения графиков двух или более линейных неравенств.

Решением системы линейных неравенств является область, в которой графики всех линейных неравенств в системе перекрываются.

Чтобы решить систему неравенств, изобразите каждое линейное неравенство в системе на одной оси x-y, выполнив следующие шаги: :

• Изолируйте переменную y в каждом линейном неравенстве.
• Нарисуйте и заштрихуйте область над линией границы, используя пунктирные и сплошные линии для символов> и ≥ соответственно.
• Аналогичным образом нарисуйте и закрасьте область под линией границы, используя пунктирные и сплошные линии для символов <и ≤ соответственно.
• Закрасьте область, где все уравнения перекрываются или пересекаются.Если нет области пересечения, то делаем вывод, что система неравенств не имеет решения.

Давайте рассмотрим пару примеров, чтобы понять эти шаги.

Пример 1

Изобразите следующую систему линейных неравенств:

y ≤ x — 1 и y <–2x + 1

Решение

Изобразите первое неравенство y ≤ x — 1.

• Из-за символа «меньше или равно» мы нарисуем сплошную границу и сделаем штриховку под линией.
• Также изобразите второе неравенство y <–2x + 1 на той же оси x-y.
• В этом случае наша граница будет пунктирной или пунктирной из-за символа «меньше». Заштрихуйте область ниже границы.

Следовательно, решением этой системы неравенств является более темная заштрихованная область, продолжающаяся вечно в направлении вниз, как показано ниже.

Пример 2

Решите следующую систему неравенств:

x — 5y ≥ 6

3x + 2y> 1

Решение

• Сначала выделите переменную y слева в каждом неравенстве.

Для x — 5y ≥ 6;

=> x ≥ 6 + 5y

=> 5y ≤ x — 6

=> y ≤ 0,2 x — 1,2

И для 3x + 2y> 1;

=> 2y> 1 — 3x

=> y> 0,5 — 1,5x

• Мы построим график y ≤ 2 x — 1,2 и y> 0,5 — 1,5x, используя сплошную и ломаную линии соответственно .

Решение системы неравенства — более темная заштрихованная область, которая является перекрытием двух отдельных областей решения.

Пример 3

Изобразите следующую систему линейных неравенств.

y ≤ (1/2) x + 1,

y ≥ 2x — 2,

y ≥ — (1/2) x — 3.

Решение

Эта система неравенств имеет три уравнения, которые все связаны символом «равно». Это говорит нам о том, что все границы будут прочными. График трех неравенств показан ниже.

Заштрихованная область трех уравнений перекрывается прямо в средней части.Следовательно, решения системы лежат в ограниченной области, как показано на графике.

Пример 4

Изобразите следующую систему линейных неравенств:

x + 2y <2, y> –1,

x ≥ –3.

Решение

Выделите переменную y в первом неравенстве, чтобы получить;

y <- x / 2 +1 Обратите внимание, что неравенства y> –1 и x ≥ –3 будут иметь горизонтальные и вертикальные граничные линии соответственно.Давайте изобразим три неравенства, как показано ниже.

Более темная заштрихованная область, окруженная двумя сегментами пунктирной линии и одним сегментом сплошной линии, дает три неравенства.

Пример 5

Решите следующую систему линейных неравенств:

–2x -y <-1

4x + 2y ≤-6

Решение

Изолировать переменную y неравенство.

–2x -y <-1 => y> –2x + 1

4x + 2y ≤ -6 => y ≤ -2x -3

Давайте продолжим и построим график y> –2x + 1 и y ≤ — 2x -3:

Поскольку заштрихованные области двух неравенств не перекрываются, мы можем сделать вывод, что система неравенств не имеет решения.

Предыдущий урок | Главная страница | Следующий урок

Решение систем неравенств — Бесплатная справка по математике

Сначала нам нужно рассмотреть символы неравенства:

• Символ <означает меньше чем.
• Символ> означает больше чем.
• Символ \ (\ leq \) означает меньше или равно. Обычно на компьютерах это пишется как <=, потому что это легче вводить.
• Символ \ (\ geq \) означает больше или равно.Иногда на компьютерах это пишется как> =, потому что так легче набирать.

Есть бесконечные решения для неравенства. В свете этого факта может быть проще всего найти набор решений для неравенств, решив систему графически.

Как решить системы неравенств графически

1) Запишите неравенство в форме пересечения наклона или в форме \ (y = mx + b \).

Например, если вас попросят решить \ (x + y \ leq 10 \), мы сначала перепишем как \ (y \ leq -x + 10 \).

2) Временно замените данный символ неравенства (в данном случае \ (\ leq \)) на просто равный символ. При этом вы можете рассматривать неравенство как уравнение. НО НЕ забудьте заменить символ равенства на исходный символ неравенства в КОНЕЦ задачи!

Итак, \ (y \ leq -x + 10 \) на данный момент становится \ (y = -x + 10 \).

3) Изобразите линию, найденную на шаге 2. Это сформирует «границу» неравенства — с одной стороны линии условие будет истинным, с другой — нет.Посмотрите, как построить линию здесь.

4) Вернемся к найденному ранее неравенству как \ (y \ leq -x + 10 \). Обратите внимание, что это верно, когда y меньше или равно. На шаге 3 мы построили линию (случай равенства), поэтому теперь нам нужно учесть случай «меньше чем». Поскольку y меньше определенного значения в нижней части оси, мы закрасим область ниже линии, чтобы указать, что неравенство верно для всех точек ниже линии:

5) Проверить. Вставьте точку не на линии, например (0,0).Убедитесь, что неравенство выполнено. В данном случае это означает \ (0 \ leq -0 + 10 \), что явно верно. Мы заштриховали правильную сторону линии.

Пример:

Найдите все значения x и y, которые удовлетворяют: \ (y \ geq \ frac {-3} {2} x + 6 \).

Обратите внимание, что это неравенство уже имеет форму пересечения наклона. Я заменю данный символ неравенства на символ равенства для построения линии.

\ (y \ geq \ frac {-3} {2} x + 6 \) становится \ (y = \ frac {-3} {2} x + 6 \). Теперь постройте эту линию, как показано:

Так как это случай, когда неравенство истинно для значений y, которые больше или равны чему-то, мы закрасили область над линией.Все точки на этой линии графика или ВЫШЕ будут удовлетворять нашему неравенству. Опять же, выберите любую точку над линией графика, чтобы убедиться, что она удовлетворяет или раскрывает ИСТИННОЕ утверждение с точки зрения исходного неравенства. Например, (5,3). Подключите это, и у нас будет \ (3 \ geq \ frac {-3} {2} * 5 + 6 \). Упростив его до \ (3 \ geq -1.5 \), мы увидим, что неравенство верно в точке (5,3). Поскольку эта точка находилась над нашей линией, она должна быть заштрихована, что подтверждает наше решение.

Множественные неравенства — система неравенств

Система неравенств содержит более одного утверждения неравенства, которое должно быть выполнено.Графически это означает, что нам нужно сделать то, что мы только что сделали — построить линию, представленную каждым неравенством, — а затем найти область графика, которая верна для ОБОИХ неравенств. Для двух приведенных выше примеров мы можем объединить оба графика и построить площадь, разделяемую двумя неравенствами.

Какой набор решений? Набор решений для ОБЕИХ неравенств будет ЛЮБОЙ ТОЧКОЙ, где ОБЕИ области закрашены вместе или где встречаются ОБЕ заштрихованные области.

Первоначально принадлежит г-ну Фелизу, © 2005

Определите решения для систем линейных неравенств

Результаты обучения

• Определить решения систем линейных неравенств

Изобразите систему двух неравенств

Помните из модуля построения графиков, что график одного линейного неравенства разбивает координатную плоскость на две области.По одну сторону лежат все решения неравенства. С другой стороны, решений нет. Рассмотрим график неравенства [латекс] y <2x + 5 [/ latex].

Пунктирная линия [латекс] y = 2x + 5 [/ latex]. Каждая упорядоченная пара в заштрихованной области под линией является решением [latex] y <2x + 5 [/ latex], поскольку все точки под линией делают неравенство истинным. Если вы сомневаетесь в этом, попробуйте подставить координаты x и y точек A и B в неравенство; вы увидите, что они работают.Итак, заштрихованной областью показаны все решения этого неравенства.

Граничная линия делит координатную плоскость пополам. В этом случае он показан пунктирной линией, поскольку точки на линии не удовлетворяют неравенству. Если бы неравенство было [латекс] y \ leq2x + 5 [/ латекс], то граница была бы сплошной.

Теперь изобразите другое неравенство: [latex] y> −x [/ latex]. Вы можете проверить пару точек, чтобы определить, какую сторону границы нужно заштриховать. Контрольные точки M и N дают верные утверждения.Итак, заштриховываем область над линией. Линия пунктирна, поскольку точки на линии не соответствуют действительности.

Чтобы создать систему неравенств, вам нужно построить график двух или более неравенств вместе. Давайте использовать [latex] y <2x + 5 [/ latex] и [latex] y> −x [/ latex], поскольку мы уже изобразили каждый из них.

Фиолетовая область показывает, где перекрываются решения двух неравенств. Эта область — решение системы неравенств. Любая точка в этой фиолетовой области будет верна как для [latex] y> −x [/ latex], так и для [latex] y <2x + 5 [/ latex].

В следующих видео-примерах мы покажем, как построить график системы линейных неравенств и определить область решения.

В следующем разделе мы увидим, что точки могут быть решениями систем уравнений и неравенств. Проверим алгебраически, является ли точка решением линейного уравнения или неравенства.

Определить, является ли упорядоченная пара решением системы линейных неравенств

На приведенном выше графике вы можете видеть, что точки B и N являются решениями для системы, потому что их координаты делают оба неравенства истинными.

Напротив, точки M и A лежат вне области решения (фиолетовый). Хотя точка M является решением неравенства [latex] y> −x [/ latex], а точка A является решением неравенства [latex] y <2x + 5 [/ latex], ни одна из точек не является решением для система . В следующем примере показано, как проверить точку, чтобы увидеть, является ли она решением системы неравенств.

Пример

Является ли точка [латекс] (2, 1) [/ латекс] решением системы [латекс] x + y> 1 [/ латекс] и [латекс] 2x + y <8 [/ latex]?

Показать решение

Отметьте точку с каждым неравенством.Замените [латекс] 2 [/ латекс] на x и [латекс] 1 [/ латекс] вместо y . Является ли дело решением обоих неравенств?

[латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex]

[latex] (2, 1) [/ latex] — решение для [латекса] x + y> 1 [/ latex].

[латекс] \ begin {array} {r} 2x + y <8 \\ 2 \ left (2 \ right) +1 <8 \\ 4 + 1 <8 \\ 5 <8 \\\ text {TRUE} \ end {array} [/ latex]

[латекс] (2, 1) [/ латекс] — решение для [латекса] 2x + y <8.[/ латекс]

Поскольку [latex] (2, 1) [/ latex] является решением каждого неравенства, он также является решением системы.

Вот график системы в примере выше. Обратите внимание, что [latex] (2, 1) [/ latex] находится в фиолетовой области, которая является областью перекрытия для двух неравенств.

Пример

Является ли точка [латекс] (2, 1) [/ латекс] решением системы [латекс] x + y> 1 [/ латекс] и [латекс] 3x + y <4 [/ латекс]?

Показать решение

Отметьте точку с каждым неравенством.Замените [латекс] 2 [/ латекс] на x и [латекс] 1 [/ латекс] вместо y . Является ли дело решением обоих неравенств?

[латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex]

[latex] (2, 1) [/ latex] — решение для [латекса] x + y> 1 [/ latex].

[латекс] \ begin {array} {r} 3x + y <4 \\ 3 \ left (2 \ right) +1 <4 \\ 6 + 1 <4 \\ 7 <4 \\\ text {FALSE} \ end {array} [/ latex]

[латекс] (2, 1) [/ латекс] — это , а не решение для [латекса] 3x + y <4 [/ latex].

Поскольку [latex] (2, 1) [/ latex] — это , а не как решение одного из неравенств, это не решение системы.

Вот график системы выше. Обратите внимание, что [latex] (2, 1) [/ latex] не находится в фиолетовой области, которая является областью перекрытия; это решение одного неравенства (красная область), но не решение второго неравенства (синяя область).

В следующем видео мы показываем еще один пример определения, находится ли точка в решении системы линейных неравенств.

Как показано выше, нахождение решений системы неравенств может быть выполнено путем графического отображения каждого неравенства и определения общей для них области. Ниже приведены дополнительные примеры, показывающие весь процесс определения области решений на графике для системы двух линейных неравенств. Общие шаги описаны ниже:

• Изобразите каждое неравенство в виде линии и определите, будет ли оно сплошным или пунктирным.
• Определите, с какой стороны каждой граничной линии представлены решения неравенства, проверив точку с каждой стороны.
• Закрасьте область, которая представляет решения для обоих неравенств.

Системы без решений

В следующем примере мы покажем решение системы двух неравенств, граничные линии которых параллельны друг другу. Когда графики системы двух линейных уравнений параллельны друг другу, мы обнаружили, что у системы нет решения. Мы получим аналогичный результат для следующей системы линейных неравенств.

Примеры

Изобразите систему [latex] \ begin {array} {c} y \ ge2x + 1 \\ y \ lt2x-3 \ end {array} [/ latex]

Показать решение

Границы этой системы параллельны друг другу.Обратите внимание, как у них одинаковые уклоны.

[латекс] \ begin {array} {c} y = 2x + 1 \\ y = 2x-3 \ end {array} [/ latex]

Построение граничных линий даст график ниже. Обратите внимание, что неравенство [latex] y \ lt2x-3 [/ latex] требует рисования пунктирной линии, а неравенство [latex] y \ ge2x + 1 [/ latex] требует сплошной линии.

Теперь нам нужно заштриховать области, представляющие неравенства. Для неравенства [латекс] y \ ge2x + 1 [/ latex] мы можем проверить точку по обе стороны от линии, чтобы увидеть, какую область затенять.Протестируйте [латекс] \ left (0,0 \ right) [/ latex], чтобы облегчить задачу.

Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ ge2x + 1 [/ latex]

[латекс] \ begin {array} {c} y \ ge2x + 1 \\ 0 \ ge2 \ left (0 \ right) +1 \\ 0 \ ge {1} \ end {array} [/ latex]

Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [latex] y \ ge2x + 1 [/ latex]. График теперь будет выглядеть так:

Теперь закрасьте область, которая показывает решения неравенства [latex] y \ lt2x-3 [/ latex].Опять же, мы можем выбрать [latex] \ left (0,0 \ right) [/ latex] для тестирования, потому что это упрощает алгебру.

Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ lt2x-3 [/ latex]

[латекс] \ begin {array} {c} y \ lt2x-3 \\ 0 \ lt2 \ left (0, \ right) x-3 \\ 0 \ lt {-3} \ end {array} [/ latex ]

Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [латекс] y \ lt2x-3 [/ latex]. График теперь будет выглядеть так:

Эта система неравенств не имеет общих точек, поэтому не имеет решения.

Сводка

• Решениями систем линейных неравенств являются целые области точек.
• Вы можете проверить, является ли точка решением системы линейных неравенств, точно так же, как вы проверяете, является ли точка решением системы уравнений.
• Системы неравенств не могут иметь решений, если граничные линии параллельны.

Системы линейных неравенств

Пожалуйста, включите скрипты (или JavaScript) в вашем веб-браузере, и
затем перезагрузите эту страницу.

Система неравенства — это список из двух или более неравенств, которые должны выполняться. Для Например, пара неравенств, показанная справа, представляет собой систему линейных неравенств. В этом урок вы узнаете о решениях систем линейных неравенства и как их найти с помощью графиков.

$$ \ {\, \ cl «плотно» {\ table x, +, 2y, <, -7; 2x, -, 3y,>, 0} $$

---

Мы хотим решить эту систему линейных неравенств:

$$ \ {\, \ cl «плотно» {\ table y≥-2x-2; y≥-2} $$

То есть мы хотим найти пары $ (x, y) $, которые являются решениями для и
неравенства.Во-первых, нам нужно построить график линий $ y = -2x-2 $
и $ y = -2 $. Посмотрите на сетки слева. В левой сетке вы
смотрите на график $ y = -2x-2 $. На
справа вы смотрите на график $ y = -2 $.

Вот способ узнать, является ли точка $ (1,2) $ решением
первое неравенство:

$ y≥-2x-2 $ за $ (1,2) $?

$ 2≥-2 (1) -2 $?

$ 2≥-2-2 $?

$ 2≥-4 $?

ДА

Проверьте каждую точку в таблице ниже в обоих неравенствах.Также укажите, какие точки
решения системы двух неравенств (то есть, какие точки являются решением обеих
первое неравенство и второе неравенство ).

Точка	Решение для $ y≥-2x-2 $?	Решение для $ y≥-2 $?	Решение для обоих?

Нажмите посмотреть графики неравенств. Являются ли синие точки, которые являются решениями $ y≥-2x-2 $ в заштрихованной области на левой сетке?

Синие точки — это решения $ y≥-2 $ в заштрихованной области справа?

Назовите синие точки на сетке, которые являются решениями для всего система (оба неравенства).

Нажмите, чтобы увидеть
$ y≥-2x-2 $ и $ y≥-2 $ построены вместе. В
темно-синий участок — это область, где
решение устанавливает перекрытие.
Светло-синий участок — это остальная часть набора решений.
$ y≥-2 $, а розовое сечение — это остальная часть набора решений
$ y≥-2x-2 $.

Найдите на графике только что перечисленные точки. Они в темноте синий, голубой или розовый раздел?

Какой цветной участок графика представляет множество решений всей системы неравенство?

Теперь решим систему линейных неравенств:

$$ \ {\, \ cl «плотно» {\ table y≥-4x-2; 3x + 4y≤18} $$

Красная линия — это график $ y = -4x-2 $ и
синяя линия — график
$ 3x + 4y = 18 $.

Для каждой точки в таблице ниже найдите точку на сетке и
определить, является ли это решением каждого неравенства.

Точка	Решение для $ y≥-4x-2 $?	Решение для $ 3x + 4y≤18 $?	Решение для обоих?

Нажмите посмотреть на график неравенств. Помните, что темно-синий область — график множества решений системы линейных неравенств.Назовите точка на сетке, лежащая в наборе решений.

Ваш ответ совпадает с ответом из таблицы?

Теперь ваша очередь решать систему линейных неравенств, показанную здесь:

$$ \ {\, \ cl «плотно» {\ table x, +, y, ≥, -2; 2x, -, 3y, ≤, 6} $$

Графики линий $ x + y = -2 $
и $ 2x-3y = 6 $ указаны на
сетка ниже. Как видите, графики этих двух линий делят сетку
на четыре секции, которые были обозначены A, B, C и D.

Выберите точку в каждом разделе сетки выше (A, B, C и D) и заполните таблицу ниже.

Раздел	Пункт	Решение для $ x + y≥-2 $?	Решение для $ 2x-3y≤6 $?	Решение для обоих?

Какие разделы (A, B, C или D) являются решениями для $ x + y≥-2 $?

Какие разделы являются решениями для $ 2x-3y≤6 $?

В каком разделе задано решение системы линейных неравенств?

Щелкните, чтобы построить график двух неравенств.Есть ли темно-синий участок сетки слева соответствует к только что найденному набору решений?

В верхней сетке слева показана система двух неравенств. Нижняя сетка показывает другой система, включающая неравенство $ y

Графическая система линейных неравенств

Ранее вы узнали, как изобразить одно линейное неравенство на плоскости xy .В этом уроке мы будем иметь дело с системой линейных неравенств. Слово «система» означает, что мы собираемся построить график двух или более линейных неравенств одновременно. Решением системы будет область или область, где пересекаются графики всех линейных неравенств в системе.

ПРИМЕЧАНИЕ: Для успешного построения графиков линейных неравенств необходимо знать, как построить линию на плоскости xy. В противном случае найдите время, чтобы просмотреть материал.

---

шагов Как построить график системы линейных неравенств

Шаг 1: Изобразите каждое линейное неравенство в системе на той же оси xy . Помните ключевые шаги при построении графика линейного неравенства:

• Выделите переменную « y » слева от неравенства.
• Если символы> и ≥, мы закрашиваем область над линией границы пунктирной и сплошной линиями соответственно.
• С другой стороны, если символы <и ≤, мы закрашиваем область под линией границы пунктирными и сплошными линиями соответственно.

Шаг 2: Закрасьте область, где все области линейных неравенств пересекаются или перекрываются. Если нет области пересечения, мы говорим, что система не имеет решения.

Давайте рассмотрим несколько примеров, чтобы проиллюстрировать процедуру.

---

Примеры графической системы линейных неравенств

Пример 1: Изобразите следующую систему линейных неравенств:

Хорошая вещь в данной задаче состоит в том, что все переменные y уже находятся в левой части символа неравенства.В таком виде мы можем легко определить, какую область заштриховать относительно границы.

• Изобразите первое неравенство y ≤ x — 1 . Поскольку у нас есть символ «меньше или равно», граница будет сплошной, и мы закрасим область под линией.

• Изобразите второе неравенство y <–2 x + 1 . Символ просто «меньше», поэтому граничная линия будет пунктирной или пунктирной, и мы закрасим область под ней.

• Окончательным решением системы линейных неравенств будет область, в которой два неравенства пересекаются, как показано справа.

Мы называем эту область решения «неограниченной», потому что на самом деле область постоянно расширяется в нисходящем направлении.

В следующем примере вы увидите пример «ограниченной» области.

---

Пример 2: Изобразите следующую систему линейных неравенств:

Система содержит три неравенства, это означает, что мы собираемся построить график трех из них.Обратите внимание, что все символы неравенства имеют компонент «равно». Это говорит нам о том, что все граничные линии будут сплошными.

• Вот график первого неравенства, где граничная линия сплошная, а заштрихованная область находится под ней.

• Второе неравенство будет иметь сплошную границу и заштрихованную область над ней.

• Наконец, третье неравенство также будет иметь сплошную границу и затемненную область над ней.

• Как видите, заштрихованные области трех линейных неравенств перекрываются прямо в средней части.

Мы называем эту систему «ограниченной», потому что область, в которой лежат все решения, ограничена тремя сторонами, идущими от граничных линий линейных неравенств.

---

Пример 3: Изобразите следующую систему линейных неравенств:

Когда я смотрю на три неравенства, включенные в систему, мне нужно учитывать три вещи:

• Перепишите первое неравенство x + 2 y <2 так, чтобы переменная « y » оставалась одна с левой стороны.Если вы правильно это сделаете, чтобы выделить « y », это неравенство эквивалентно выражению.
• Неравенство y > –1 будет иметь горизонтальную границу.
• Неравенство x ≥ –3 будет иметь вертикальную границу.

Если вам нужна помощь в построении вертикальных и горизонтальных линий, ознакомьтесь с этим отдельным уроком.

Теперь мы готовы построить график каждого из них.

• График будет пунктирной линией границы с заштрихованной областью, находящейся под ней.

• График y > –1 представляет собой горизонтальную пунктирную линию, проходящую через точку пересечения оси y в точке -1 с заштрихованной областью над ней.

• График x ≥ –3 представляет собой сплошную линию, проходящую через точку пересечения x -3 с заштрихованной областью справа.

• Решение этой системы — это общая область, в которой пересекаются все три неравенства.

Это также «ограниченная система», в которой область решения ограничена двумя сегментами пунктирной линии и одним сегментом сплошной линии.

---

Пример 4: Изобразите следующую систему линейных неравенств:

Оба неравенства нужно переписать, чтобы переменная « y » располагалась слева сама.

Вот и первая. Обязательно меняйте направление символа неравенства всякий раз, когда вы делите неравенство на отрицательное число.

А вот и второе неравенство. На этот раз мы не делим неравенство на отрицательное число, поэтому ориентация или направление символа неравенства остается прежним.

Давайте продолжим и построим их график.

• График y > –2 x + 1 представляет собой пунктирную или «ломаную» линию с заштрихованной областью над ней.

• График y ≤ –2 x — 3 представляет собой сплошную линию с заштрихованной областью под ней.

Поскольку две заштрихованные области не пересекаются и не перекрываются, это говорит нам о том, что данная система неравенств не имеет НЕТ РЕШЕНИЯ .

Вы также могли заметить, что граничные линии имеют одинаковый уклон, обе м = –2, что означает, что они параллельны и, следовательно, не пересекаются.

---

Вас также может заинтересовать:

Решение линейных неравенств

Шаги по построению графика линейных неравенств

Графики примеров линейных неравенств

Решение сложных неравенств

Систем неравенств, решаемых графически

Графическое решение систем неравенств

Чтобы построить график решений системы неравенств, нанесите на график каждое неравенство и найдите пересечения двух графиков.

Пример 1

Изобразите графики решений для следующей системы.

• (1)

  x ² + y ² ≤ 16

• (2)

  y ≤ x ² + 2

Уравнение (1) — это уравнение круга с центром в точке (0, 0) и радиусом 4. Постройте график круга; затем выберите контрольную точку не на круге и поместите ее в исходное неравенство.Если результат верный, закрасьте область, где находится контрольная точка. В противном случае закрасьте другую область. Используйте (0, 0) в качестве тестовой точки.

Это верное заявление. Поэтому внутренняя часть круга растушевывается. На рисунке 1 (а) эта штриховка выполнена горизонтальными линиями.

Уравнение (2) — это уравнение параболы, раскрывающейся вверх с вершиной в точке (0, 2). Используйте (0, 0) в качестве тестовой точки.

Это верное заявление. Поэтому заштрихуйте внешнюю часть параболы.На рисунке 1 (а) эта штриховка выполнена вертикальными линиями. Обе области, отмеченные штриховкой, представляют собой решения систем неравенств. Это решение показано затенением в правой части рисунка 1 (b).

Рисунок 1. Затенением показаны решения.

Пример 2

Решите следующую систему неравенств графически.

• (1)

• (2)

Уравнение (1) представляет собой уравнение эллипса с центром в (0, 0) с основными пересечениями в точках (6, 0) и (–6, 0) и второстепенными пересечениями в точках (0, 5) и (0, –5). ).Используйте (0, 0) в качестве тестовой точки.

Это верное заявление. Поэтому заштрихуйте внутреннюю часть эллипса. На рисунке 2 (а) эта штриховка сделана горизонтально.

Уравнение (2) — это уравнение гиперболы с центром в точке (0, 0), открывающейся вертикально с вершинами в точках (0, 2) и (0, –2). Используйте (0, 0) в качестве тестовой точки.

Это неправда. Поэтому заштрихуйте область внутри изгибов гиперболы. На рисунке 2 (а) эта штриховка сделана вертикально.Обе области, отмеченные штриховкой, представляют собой решение системы неравенств. Это решение показано затенением на рисунке 2 (b).

Рисунок 2. Решение примера.

.