Содержание
Неравенства
Отметим множество решений неравенства на числовой прямой и запишем ответ в виде числового промежутка.
Алгебраические неравенства.
Квадратные неравенства. Рациональные неравенства высших степеней.
Дробно-рациональные неравенства.
Методы решения неравенств зависят в основном от того, к какому классу относятся функции, составляющие неравенство.
- I. Квадратные неравенства, то есть неравенства вида
ax2 + bx + c > 0 (< 0), a ≠ 0.
Будем считать, что a>0. Если это не так, то умножив обе части неравенства на -1 и изменив знак неравенства на противоположный, получим желаемое.
Чтобы решить неравенство можно:
- Квадратный трехчлен разложить на множители, то есть неравенство записать в виде
a (x — x1) (x — x2) > 0 (< 0).
- Корни многочлена нанести на числовую ось.
 Корни разбивают множество действительных чисел на промежутки, в каждом из которых соответствующая квадратичная функция будет знакопостоянной.
Корни разбивают множество действительных чисел на промежутки, в каждом из которых соответствующая квадратичная функция будет знакопостоянной. - Определить знак a (x — x1) (x — x2) в каждом промежутке и записать ответ.
Если квадратный трехчлен не имеет корней, то при D<0 и a>0 квадратный трехчлен при любом x положителен.
Примеры:
- Решить неравенство. x2 + x — 6 > 0.
Решение.
Разложим квадратный трехчлен на множители (x + 3) (x — 2) > 0
Ответ: x (-∞; -3) (2; +∞).
2) (x — 6)2 > 0
Решение:
Это неравенство верно при любом х, кроме х = 6.
Ответ: (-∞; 6) (6; +∞).
3) x² + 4x + 15 < 0.
Решение:
Здесь D < 0, a = 1 > 0. Квадратный трехчлен положителен при всех х.
Ответ: x Î Ø.
Решить неравенства:
- 1 + х — 2х² < 0. Ответ:
- 3х² — 12х + 12 ≤ 0.
 Ответ:
Ответ: - 3х² — 7х + 5 ≤ 0. Ответ:
- 2х² — 12х + 18 > 0. Ответ:
- При каких значениях a неравенство
x² — ax > выполняется для любых х? Ответ:
- II. Рациональные неравенства высших степеней, то есть неравенства вида
anxn + an-1xn-1 + … + a1x + a0 > 0 (<0), n>2.
Многочлен высшей степени следует разложить на множители, то есть неравенство записать в виде
an (x — x1) (x — x2) ·…· (x — xn) > 0 (<0).
Отметить на числовой оси точки, в которых многочлен обращается в нуль.
Определить знаки многочлена на каждом промежутке.
Примеры:
1) Решить неравенство x4 — 6x3 + 11x2 — 6x < 0.
Решение:
x4 — 6x3 + 11x2 — 6x = x (x3 — 6x2 + 11x -6) = x (x3 — x2 — 5x2 + 5x +6x — 6) =x (x — 1)( x2 -5x + 6) =
x (x — 1) (x — 2) (x — 3). Итак, x (x — 1) (x — 2) (x — 3)<0
Итак, x (x — 1) (x — 2) (x — 3)<0
Ответ: (0; 1) (2; 3).
2) Решить неравенство (x -1)5 (x + 2) (x — ½)7 (2x + 1)4 <0.
Решение:
Отметим на числовой оси точки, в которых многочлен обращается в нуль. Это х = 1, х = -2, х = ½, х = — ½.
В точке х = — ½ смены знака не происходит, потому что двучлен (2х + 1) возводится в четную степень, то есть выражение (2x + 1)4 не меняет знак при переходе через точку х = — ½.
Ответ: (-∞; -2) (½; 1).
3) Решить неравенство: х2 (х + 2) (х — 3) ≥ 0.
Решение:
Данное неравенство равносильно следующей совокупности
Решением (1) является х (-∞; -2) (3; +∞). Решением (2) являются х = 0, х = -2, х = 3. Объединяя полученные решения, получаем х Î (-∞; -2] {0} [3; +∞).
Ответ: х (-∞; -2] {0} [3; +∞).
Решить неравенства:
- (5х — 1) (2 — 3х) (х + 3) > 0. Ответ:
- x3 + 5x2 +3x — 9 ≤ 0.
 Ответ:
Ответ: - (x — 3) (x — 1)² (3x — 6 — x²) < 0. Ответ:
- (x² -x)² + 3 (x² — x) + 2 ≥ 0. Ответ:
III. Дробно-рациональные неравенства.
При решении таких неравенств можно придерживаться следующей схемы.
- Перенести все члены неравенства в левую часть.
- Все члены неравенства в левой части привести к общему знаменателю, то есть неравенство записать в виде
> 0 (<0).
- Найти значения х, при которых функция y=может менять свой знак. Это корни уравнений
- Нанести найденные точки на числовую ось. Эти точки разбивают множество действительных чисел на промежутки, в каждом их которых функция будет знакопостоянной.
- Определить знак в каждом промежутке, вычисляя, например, значение данного отношения в произвольной точке каждого промежутка.
- Записать ответ, обращая особое внимание на граничные точки промежутков. При решении строгого неравенства >0 (<0) граничные точки в ответ не включаются.
 При решении нестрогого неравенства ≥ 0 ( ≤ 0), если точка является корнем знаменателя, то она не включается в ответ (даже если она одновременно является корнем числителя). Если же точка является корнем одного числителя, то она включается в ответ.
При решении нестрогого неравенства ≥ 0 ( ≤ 0), если точка является корнем знаменателя, то она не включается в ответ (даже если она одновременно является корнем числителя). Если же точка является корнем одного числителя, то она включается в ответ.
Примеры.
1). Решить неравенство .
Решение: > 0, > 0, > 0
Найдем нули числителя и знаменателя. Это х = 3, х = 5, х=1. Наносим найденные точки на числовую ось и определяем знаки в каждом промежутке
Выбираем любой х(5; +), например х = 10. Тогда < 0.
Выбираем х = 4 (3; 5).
Получаем > 0. При х = 2 (1; 3). Получаем > 0.
Наконец, при х = 0 (-; 1). Вычисляем < 0.
Ответ: х (1; 3) (3; 5).
2). Найти сумму целых решений неравенства.
Решение. Найдем нули числителя и знаменателя дроби. Это х = -1, х=8, х = 3, х= 5.
Нанесем найденные точки на числовую ось и определим знак дроби в каждом промежутке, вычисляя значение этой дроби в произвольной точке каждого промежутка.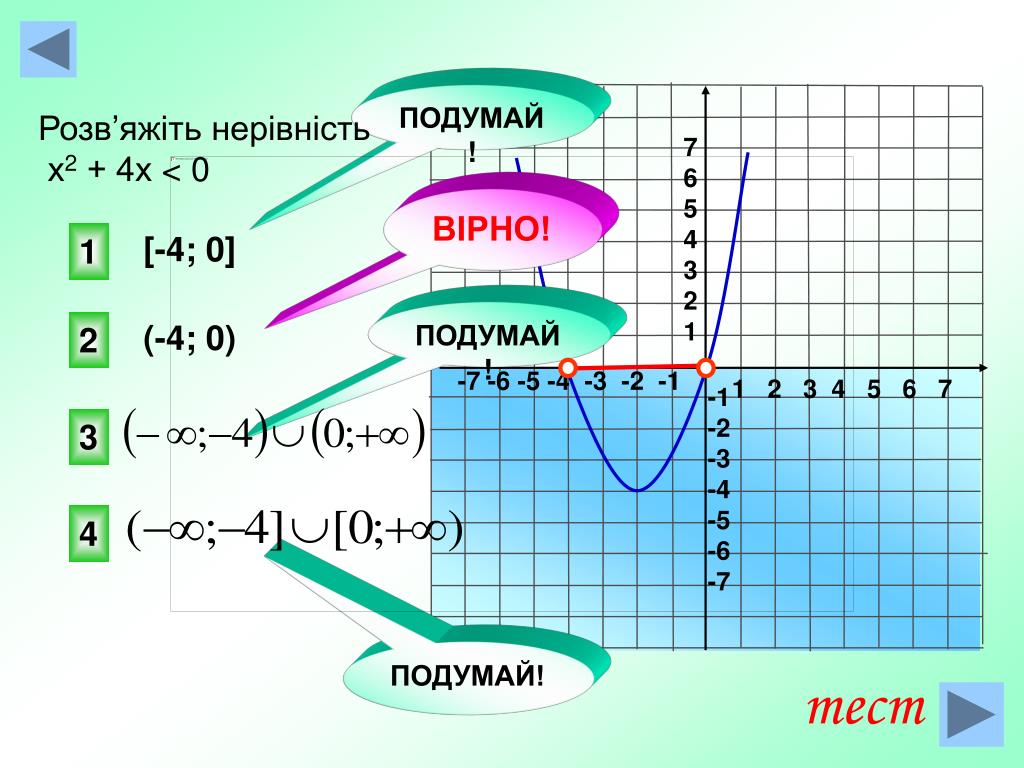
Решением исходного неравенства является
х [-1, 3) (3; 5) {8}. Найдем сумму целых решений: -1 +1+0+ 2 + 4 + 8 = =14.
Ответ: 14.
3.2.3. Иррациональные неравенства
Глава 3. Решение уравнений и неравенств
3.2.
3.2.3.
Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень: если в неравенство входит квадратный корень, то в квадрат; входит корень третьей степени − в куб и т. д. Однако, как было показано выше в правиле 4 преобразования неравенств, возводить в квадрат, не нарушая равносильности, можно только неравенство, у которого обе части неотрицательны. При возведении же в квадрат неравенств, части которых имеют разные знаки, могут получиться неравенства, как равносильные исходному, так и неравносильные ему. Простой пример: –1 < 3 − верное неравенство,
Простой пример: –1 < 3 − верное неравенство,
− тоже верное неравенство. Несмотря на то, что –4 < –1 − неравенство верное, неравенство
уже верным не является.
Покажем, как получить равносильные системы для некоторых часто встречающихся типов неравенств.
Неравенства вида
Если x лежит в ОДЗ: f (x) ≥ 0, то левая часть неравенства существует и неотрицательна. Поскольку для всех x, являющихся решением данного неравенства, правая часть больше левой, то g (x) > 0. Следовательно, обе части неравенства неотрицательны (для тех x, которые являются решениями неравенства, другие x нас не интересуют). Значит, возведение в квадрат не нарушает равносильности и можно записать равносильную нашему неравенству систему неравенств:
Пример 1
Решите неравенство
|
Сразу перейдём к равносильной системе:
Ответ.
|
Пример 2
Решите неравенство
|
Перейдём к равносильной системе:
Ответ.
|
Неравенства вида
ОДЗ данного неравенства f (x) ≥ 0. Пусть для каких-то x из ОДЗ g (x) < 0. Тогда, очевидно, все эти x − решения, так как при этих x левая часть определена (x ОДЗ) и неотрицательна, в то время как правая часть g (x) < 0.
Для других x из ОДЗ g (x) ≥ 0. Для них обе части неравенства неотрицательны, и его можно возвести в квадрат:
Значит, данное неравенство равносильно совокупности неравенств:
Заметим, что в последнюю систему не входит требование f (x) ≥ 0. Оно и не нужно, так как выполняется автоматически
Оно и не нужно, так как выполняется автоматически
ибо полный квадрат всегда неотрицателен.
Пример 3
Решите неравенство
Пример 4
Решите неравенство
Неравенства вида
ОДЗ данного неравенства:
Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему
Заметим, что из неравенства
следует, что
то есть дополнительно это требовать и включать это неравенство в систему не нужно.
Отметим полезное следствие. Предположим, что ОДЗ неравенства уже найдено, и мы будем отбирать решения только из ОДЗ (это разумно, поскольку вне ОДЗ решений нет). Тогда исходное неравенство равносильно следующему:
а та система, которой это неравенство равносильно, может быть представлена (для x из ОДЗ) в виде
Следовательно, в ОДЗ
Ясно, что те же рассуждения применимы и для знака неравенства ≥. Отсюда можно сделать полезное заключение:
Отсюда можно сделать полезное заключение:
Знак разности
совпадает со знаком выражения
Отсюда же получается ещё одно полезное следствие:
в ОДЗ:
Пример 5
Решите неравенство
|
Перейдём к равносильной системе:
Решая эту систему методом интервалов, сразу получаем: Ответ.
|
Пример 6
Решите неравенство
|
ОДЗ данного неравенства: Заметим, что в ОДЗ x ≥ 0, поэтому существует
Мы воспользовались здесь тем, что в ОДЗ x ≥ 0, (x – 5)(x – 6) ≥ 0 и потому существуют выписанные в последней строчке корни. Учтём теперь ОДЗ и получим: Ответ.
|
Неравенства вида
ОДЗ данного неравенства:
Предположим, что функции f (x) и g (x) не имеют общих корней. Рассмотрим вспомогательное неравенство
Рассмотрим вспомогательное неравенство
|
(*) |
1. Если g (x) < 0, то для любого x из ОДЗ выполнено
2. Если g (x) ≥ 0, то выражение
может иметь любой знак, но выражение
всегда строго положительно. Умножая обе части неравенства (*) на строго положительное число
не меняя знака неравенства, перейдём к равносильному неравенству
Таким образом, в ОДЗ
Значит, при g (x) ≥ 0, знак разности
совпадает со знаком разности
в ОДЗ.
Получаем следующие условия равносильности.
Запоминать приведённые системы неравенств не нужно, важно понимать, как они получаются.
Пример 7
Решите неравенство
Как решать систему неравенств 8 класс
Основные понятия
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Числовое неравенство — в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Типы неравенств
Строгие — используют только больше (>) или меньше (<)
- a < b — это значит, что a меньше, чем b.
- a > b — это значит, что a больше, чем b.
- a > b и b < a означают одно и тоже, то есть равносильны.
Нестрогие — используют сравнения ≥ (больше или равно) или ≤ (меньше или равно)
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
Другие типы
- a ≠ b — означает, что a не равно b.
- a ≫ b — означает, что a намного больше, чем b.
- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Система неравенств
Чтобы щелкать задачки, нам пригодятся свойства числовых неравенств. Вот они:
Если а > b , то b < а.
 Также наоборот: а < b, то b > а.
Также наоборот: а < b, то b > а.
Если а > b и b > c, то а > c. И также если а < b и b < c, то а < c.
Если а > b, то а + c > b+ c (и а – c > b – c).
Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям можно прибавлять или вычитать одну и ту же величину.
Если а > b и c > d, то а + c > b + d.
Если а < b и c < d, то а + c < b + d.
Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять, т.к. возможны исключения. Например, если из 12 > 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а > b и c < d, то а – c > b – d.
Если а < b и c > d, то а – c < b – d.
Из одного неравенства можно почленно вычесть другое противоположного смысла, оставляя знак того, из которого вычиталось.
Если а > b, m — положительное число, то mа > mb и
.
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
Если же а > b, n — отрицательное число, то nа < nb и.
Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.
Если а > b и c > d, где а, b, c, d > 0, то аc > bd.
Если а < b и c < d, где а, b, c, d > 0, то аc < bd.
Неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствием является: если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2. На множестве положительных чисел обе части можно возвести в квадрат.
- Если а > b, где а, b > 0, то .
Если а < b , то .
Таблица числовых промежутков
Полезна тем, что с ее помощью удобно записывать множество решений.
Неравенство | Графическое решение | Форма записи ответа |
x < c | x ∈ (−∞; c) | |
x ≤ c | x ∈ (−∞; c] | |
x > c | x ∈ (c; +∞) | |
x ≥ c | x ∈ (c; +∞) |
Еще один важный шаг — запись ответа. Вот, как правильно это делать:
- Если знак строгий (>, <), точка на оси будет не закрашена, а скобка — круглой.
- Если знак нестрогий (≥, ≤), точка на оси будет закрашена, а скобка — квадратной.
- Скобка, рядом со знаком бесконечности всегда круглая.

Решение системы неравенств
Линейное неравенство — то, в котором неизвестное представлено в первой степени. Для его решения нужно, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице. Алгоритм решения:
1. Раскрыть скобки, перенести неизвестное в левую часть, числа в правую и привести подобные слагаемые. Получится одно из следующих видов:
- ax < b,
- ax ≤ b,
- ax > b,
- ax ≥ b.
2. Если получилось ax ≤ b.Для его решения необходимо поделить левую и правую часть на коэффициент перед неизвестным a.
3. Если a > 0, то x ≤ ba.
Если a < 0, то знак меняется на противоположный.
Получаем x ≥ ba.
4. Записываем ответ как он есть или в соответствии с таблицей числовых промежутков.
Решим пример
3 * (2 − x) > 18
Как решаем
Ответ: x < −4 или в числовом промежутке x ∈ (−∞; −4). |
И еще один
Как решаем
Ответ: х < – 2. |
Последний, чтобы разобраться наверняка
Как решаем
Ответ: числовой промежуток x ∈ (– 2; 0]. |
Запомнить все правила и научиться быстро их применять помогут на уроках математики в детской школе Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.
Ошибки в неравенствах / math5school.ru
Неравенства по праву считаются одним из самых трудных разделов школьной математики, и при их решении допускается наибольшее количество ошибок. Рассмотрим наиболее часто встречающиеся из них.
Некоторые общие ошибки
K Упражнение | L Неправильно | J Правильно |
Указать наименьшее целое решение неравенства: x > 4 | х ∈ (4; +∞), наименьшее целое число 4. Ответ:x = 4 | х ∈ (4; +∞), наименьшее целое число 5. Ответ: x = 5. |
Решить неравенство: –х < 1 | x < –1 Ответ: (–∞; –1) | x > –1 Ответ: (–1; +∞) |
Сравнить a и b, если 1/a < 1/b | Ответ: если a и bположительные, то a > b; если a и b отрицательные, то a < b | Ответ: если a · b > 0, то a > b; |
Оценить х из 0,25 ≤ 1/x ≤ 2 | Ответ:4 ≥ х ≥ 0,5 | Ответ: 0,5 ≤ х ≤ 4 |
\[a< x< b\] | \[\left[\begin{matrix} x> a\\ x< b \end{matrix} \right. | \[\begin{cases} x> a\\ x< b \end{cases} \] |
Ошибки в квадратных неравенствах
Квадратные(квадратичные)неравенства – неравенства вида
aх2 + bx + c > 0, (< 0, ≥ 0, ≤ 0)
часто решаются разложением левой части на линейные множители, то есть
aх2 + bx + c = a (x – x1) (x – x2) > 0,
где x1 и x2 – корни квадратного трехчлена aх2 + bx +c. Это возможно сделать, когда корни квадратного трехчлена являются действительными числами. Однако в некоторых случаях при решении неравенств этим способом можно легко прийти к неверному заключению.
K Решить неравенство | L Неправильное решение | J Правильное решение |
– х2 + 5x– 6 < 0 | – (x – 2) (x – 3) < 0, х ∈ (2; 3). Ответ: (2; 3) | х2 – 5x + 6 < 0, (x – 2) (x – 3) > 0, х ∈ (–∞; 2)∪(3; +∞). Ответ: (–∞; 2)∪(3; +∞) |
х2 + 6x + 9 ≥ 0 | (х+ 3)2 ≥ 0, х + 3 ≥ 0, х ≥ –3. Ответ: [–3; +∞) | Неравенство (х + 3)2 ≥ 0 выполняется для всех значений х, значит х – любое число. Ответ: (–∞; +∞) |
х2 – 4x + 4 > 0 | Неравенство (х– 2)2 > 0 выполняется для всех значений х, значит х – любое число. Ответ: (–∞; +∞) | При х = 2 (х– 2)2 = 0, значит, х ≠ 2. Ответ: (–∞; 2)∪(2; +∞) |
х2 + 10x + 25 ≤ 0 | (х + 5)2 ≤ 0 – решений нет. Ответ: Ø | Неравенство (х + 5)2 ≤ 0
Ответ: –5 |
х2 + x + 2 > 0 | Так как D = 12 – 2·2 = –3 < 0, то решений нет. Ответ: Ø | Так как старший коэффициент положительный и D < 0, то при любом значении х левая часть неравенства положительна. Ответ: (–∞; +∞) |
х2 – 9 ≤ 0 | х2 ≤ 9, х ≤ 3. Ответ: (–∞; 3] | х2 ≤ 9, |х| ≤ 3, \[\begin{cases} x\geq -3,\\ x\leq +3. \end{cases}\] Ответ: [–3; 3] |
х2 – 9 ≥ 0 | х2 ≥ 9, х ≥ 3. Ответ: [3; +∞). Комментарий. Необходимо помнить, что, вообще говоря,
| х2 ≥ 9, |х| ≥ 3, \[\left[\begin{matrix} x\geq +3,\\ x\leq -3. Ответ: (–∞; –3]∪[3; +∞) |
Ошибки в дробно-рациональных неравенствах
Нередко ошибки появляются при сведении неравенств к системе неравенств, совокупности неравенств или совокупности систем неравенств.
K
Упражнение. Решить неравенство \(\large \frac{x+6}{x}>0.\)
L
Неправильное решение.
\(\begin{cases} x+6>0,\\ x>0; \end{cases}\;\;\; \begin{cases} x>-6,\\ x>0; \end{cases}\;\;\; x>0.\)
Ответ: (0; +∞).
Комментарий. Дробь может быть положительной в двух случаях: когда числитель и знаменатель одновременно положительны, и когда числитель и знаменатель отрицательны.
J
Правильное решение.
\(\left[\begin{matrix} \begin{cases} x + 6 > 0, \\ x > 0, \end{cases}\\ \begin{cases} x + 6 < 0,\\ x < 0; \end{cases} \end{matrix} \right.\;\;\;\;\left[\begin{matrix} \begin{cases} x > — 6,\\ x > 0, \end{cases}\\ \begin{cases} x < — 6,\\ x < 0; \end{cases} \end{matrix} \right.\;\;\;\;\left[\begin{matrix} x > 0,\;\;\\ x < -6.\end{matrix} \right.\)
Ответ: (–∞; –6)∪(0; +∞).
Часто учащиеся допускают ошибки при умножении неравенства на знаменатель, который не имеет определенного знака при любых значениях переменной.
K
Упражнение 1. Решить неравенство \(\large \frac{2x+3}{x-1}>1.\)
L
Неправильное решение.
2x + 3 > x – 1;
x > – 4.
Ответ: (–4; +∞).
Комментарий. Нельзя умножать обе части неравенства на знаменатель, который содержит неизвестное, если заранее не известен его знак. Если же вы все-таки не можете обойтись без умножения, то нужно рассматривать два варианта:
х –1 > 0 или х – 1 < 0.
J
Правильное решение.
Рассмотрим один из возможных способов решения данного неравенства:
\(\left[\begin{matrix} \begin{cases} 2 x + 3 > x — 1, \\ x — 1 > 0, \end{cases}\\ \begin{cases} 2 x + 3 < x — 1, \\ x — 1 < 0; \end{cases} \end{matrix} \right.2}>0.\)
L
Неправильное решение.
х2 + 81 > 0 при х ≠ ±2.
Ответ: (–∞; –2)∪(–2; 2)∪(2; +∞).
J
Правильное решение.
Так как дробь больше нуля, и числитель принимает положительные значения для любого допустимого значения х, то
4 –х2 > 0,
х2 < 4,
–2 < x < 2.
Ответ: (–2; 2).
K
Упражнение 3. Решить неравенство 1/x ≥ 2.
L
Неправильное решение.
2x ≤ 1;
x ≤ 1/2.
Ответ: (–∞; 1/2].
J
Правильное решение.
Так как обе части неравенства представлены стандартными функциями, то легко использовать графические метод решения неравенства:
Очевидно, что значения функции у = 1/x достигают 2 и более при х ∈ (0; 1/2].2}>0\), которое, очевидно, равносильно неравенству х2 – 81 > 0, полученному из первого умножением на положительное число 4 + х2.
Ошибки при использовании метода интервалов
Рассмотрим типичные ошибки, возникающие при решении неравенств с применением метода интервалов.
K
Упражнение 1. Решить неравенство х (х – 6) (х + 1) ≥ 0.
L
Неправильное решение.
Ответ: х ∈ (–∞; –1]∪[6; +∞).
Комментарий. В данном решении не учтено, что сравнивается с нулем произведение трех множителей, а не двух. Таким образом, получаются не три интервала, а четыре.
J
Правильное решение.
Ответ: х ∈ [–1; 0]∪[6; +∞).
K
Упражнение 2. Решить неравенство (х– 5) (х + 3) (2 – х) ≥ 0.
L
Неправильное решение.
Ответ: х ∈ [–3; 2]∪[5; +∞).
Комментарий. В данном примере знаки в интервалах проставлены неверно. Часто учащиеся не задумываясь проставляют знаки, чередуя их справа налево, начиная со знака +.
J
Правильное решение.
Числовая ось с проставленными знаками на промежутках должна выглядеть в данном случае следующим образом:
Ответ: х ∈ (–∞; –3]∪[2; 5].
K
Упражнение 3. Решить неравенство
| (х – 8) (х + 7) | ≥ 0. |
| х + 2 |
L
Неправильное решение.
Ответ: х ∈ [–7; –2]∪[8; +∞).
Комментарий. В дробно-рациональных неравенствах нули знаменателя на числовую ось наносятся пустыми(выколотыми)точками, и это не зависит от строгости неравенства.
J
Правильное решение.
Ответ: х ∈ [–7; –2)∪[8; +∞).
K
Упражнение 4. Решить неравенство (х – 5) (х + 3)2 ≤ 0.
L
Неправильное решение.
Ответ: х ∈ [–3; 5].
Комментарий. В данном упражнении знаки на интервалах проставлены неверно, так как при переходе через корень четной кратности знак не меняется.
J
Правильное решение.
Ответ: х ∈ (–∞; 5].
K
Упражнение 5. Решить неравенство (х – 1) (х – 10)2 > 0.
L
Неправильное решение.
Ответ: х ∈ (1; +∞).
Комментарий. При записи ответа к данному неравенству не учтено то, что в точке х = 10 левая часть неравенства обращается в ноль, что не соответствует знаку данного неравенства.
J
Правильный ответ: х ∈ (1; 10)∪(10; +∞).
K
Упражнение 6. Решить неравенство (х – 5)2 (х + 3) ≤ 0.
L
Неправильное решение.
Ответ: х ∈ (–∞; –3].
Комментарий. При решении данного неравенства потеряно одно решение. При х = 5 левая часть неравенства обращается в ноль, что тоже удовлетворяет данному неравенству.
J
Правильный ответ: х ∈ (–∞; –3]∪{5}.
Ошибки в иррациональных неравенствах
Самый распространенный вид ошибок при решении иррациональных неравенств связан с тем, что учащимися не учитывается область допустимых значений неизвестного для корня четной степени.
K
Упражнение. Решить неравенство √x – 5 < 2.
L
Неправильное решение.
x – 5 < 4;
x < 9.
Ответ: х ∈ (–∞; 9).
Комментарий. Неравенство имеет смысл лишь при x – 5 ≥ 0.
J
Правильное решение.
\(\begin{cases} x — 5 < 4,\\ x — 5 \geq 0; \end{cases}\;\;\;\; \begin{cases} x < 9,\\ x \geq 5; \end{cases}\;\;\;\; 5 \leq x < 9.\)
Ответ: х ∈ [5; 9).
Нередко учащиеся не учитывают ограничения, которые накладываются на выражения, стоящие вне знака корня четной степени и содержащие неизвестную величину.2-9x-10\leq 0,\\ x\geq -26,\\ x\geq 4; \end{cases} \\ \begin{cases} x\geq -26,\\ x < 4;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{cases} \end{matrix}\right.\;\;\; \left[\begin{matrix}\begin{cases} (x+1)(x-10)\leq 0,\\ x\geq -26,\\ x\geq 4; \end{cases} \\ \begin{cases} x\geq -26,\\ x < 4.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{cases} \end{matrix}\right.\;\;\;\)
Решением первой системы является промежуток [4; 10], решением второй – промежуток [–26; 4). Таким образом, решением совокупности систем является объединение этих промежутков.
Ответ: х ∈ [–26; 10].
Ошибки в показательных и логарифмических неравенствах
При решении показательных и логарифмических неравенств возникновение ошибок, как правило, вызвано тем, что учащиеся неверно применяют свойства показательной и логарифмической функции.
Например, не учитывают, что при положительном, меньшем единицы основании, и показательная, и логарифмическая функции являются убывающими.
K
Упражнение. Решить неравенство 0,8 х ≥ 0,8 – 1/3.
L
Неправильный ответ: х ≥ – 1/3.
Комментарий. Так как 0 < 0,8 < 1, то при переходе от неравенства степеней с одинаковыми основаниями к неравенству показателей необходимо было поменять знак основания.
J
Правильный ответ: х ≤ – 1/3.
Пренебрежение областью допустимых значений неизвестного – еще одна распространенная причина ошибок при решении показательных и, особенно, логарифмических неравенств.
K
Упражнение. Решить неравенство log4 (x2 + 3x) ≤ 1.
L
Неправильное решение.
x2 + 3x ≤ 4;
x2 + 3x – 4 ≤ 0;
(x – 1) (x + 4) ≤ 0;
х ∈ [–4; 1].
Ответ: [–4; 1].
J
Правильное решение.2-7x+6 \leq 0; \end{cases} \end{matrix} \right.\;\;\;\; \left[\begin{matrix} \begin{cases} 0 < x < 0,5, \\ (x-2)(x-3) > 0,\\ (x-1)(x-6) \geq 0; \end{cases}\\ \begin{cases} x > 0,5, \\ (x-2)(x-3) > 0,\\ (x-1)(x-6) \leq 0. \end{cases} \end{matrix} \right.\;\;\;\;\)
В первом случае решением системы является промежуток (0; 0,5), а во втором – объединение промежутков [1; 2)∪(3; 6].
Таким образом, после объединения ответов получим (0; 0,5)∪[1; 2)∪(3; 6].
Ответ: х ∈ (0; 0,5)∪[1; 2)∪(3; 6].
K
Упражнение 2. Решить неравенство х 3х + 1 > х 4.
L
Неправильное решение.
\(\begin{cases} x > 0, \\ 3x+1 > 4; \end{cases}\;\;\;\; \begin{cases} x > 0, \\ x > 1; \end{cases}\;\;\;\; x > 1.\)
Ответ: х ∈ (1; +∞).
J
Правильное решение.
\(\left[\begin{matrix} \begin{cases} 0 < x < 1, \\ 3x+1 < 4; \end{cases}\\ \begin{cases} x > 1, \\ 3x+1 > 4; \end{cases} \end{matrix} \right.\;\;\;\; \left[\begin{matrix} \begin{cases} 0 < x < 1, \\ x < 1; \end{cases}\\ \begin{cases} x > 1, \\ x > 1; \;\;\;\;\;\; \end{cases} \end{matrix} \right.\;\;\;\; \left[\begin{matrix} 0 < x < 1,\\ x > 1.\;\;\;\;\;\; \end{matrix} \right.\)
Ответ: х ∈ (0; 1)∪(1; +∞).
При решении неравенств методом замены переменной учащиеся достаточно часто путают, знак совокупности и знак системы, то есть не понимают, что в первом случае решением неравенства является объединение нескольких множеств, а во втором случае – их пересечение.
K
Упражнение 1. Решить неравенство lg2x + lg x – 2 ≥ 0.
L
Неправильное решение.
Пусть lg x = t, тогда
t 2 + t – 2 ≥ 0;
(t – 1) (t + 2) ≥ 0;
\(\begin{cases} t \geq 1, \\ t \leq -2; \end{cases}\;\;\;\; \begin{cases} \lg x \geq 1, \\ \lg x \leq -2; \end{cases}\;\;\;\; \begin{cases} x \geq 10, \\ x \leq 0,01. \end{cases}\;\;\;\;\)
Ответ: Ø.
Комментарий. Решение должно сводиться к объединению, а не к пересечению двух промежутков, то есть к решению совокупности неравенств.
J
Правильное решение.
\(\left[\begin{matrix} t \geq 1,\;\;\;\\ t \leq -2; \end{matrix} \right.\;\;\;\; \left[\begin{matrix} \lg x \geq 1,\;\;\;\\ \lg x \leq -2; \end{matrix} \right.\;\;\;\; \begin{cases} \left[\begin{matrix} x \geq 10,\;\;\;\\ x \leq 0,01; \end{matrix} \right. \\ \; x > 0. \end{cases}\)
Ответ: х ∈ (0; 0,01]∪[10; +∞).
K
Упражнение 2. Решить неравенство x – 3√x + 2 ≤ 0.
L
Неправильное решение.
Пусть √x =t; тогда
t 2 – 3t + 2 ≤ 0;
(t – 1) (t – 2) ≤ 0;
\(\left[\begin{matrix} t \geq 1,\\ t \leq 2; \end{matrix} \right.\;\;\;\; \left[\begin{matrix} \sqrt{x} \geq 1,\\ \sqrt{x} \leq 2; \end{matrix} \right.\;\;\;\; \left[\begin{matrix} x \geq 1,\\ x \leq 4; \end{matrix} \right.\;\;\;\; x\in (-\infty;\; +\infty).\)
Ответ: все числа.
Комментарий. Во-первых, в представленном решении не учтена область допустимых значений переменной, а во-вторых, решение должно сводиться к пересечению двух промежутков, а не к их объединению, то есть к решению системы неравенств или двойного неравенства.
J
Правильное решение.
1 ≤ t ≤ 2;
1 ≤ √x ≤ 2;
1 ≤ x ≤ 4.
Ответ: [1; 4].
Смотрите так же:
Ошибки в тождественных преобразованиях
Ошибки в уравнениях
Ошибки в системах уравнений
Ошибки в упражнениях с параметрами
Ошибки в упражнениях о функциях
Ошибки в упражнениях из начал анализа
Ошибки в геометрических задачах
Иррациональные неравенства. Исчерпывающий гид (ЕГЭ — 2021)
Определение
Иррациональное неравенство – это неравенство, содержащее переменную под корнем
Неравенства вида \( \sqrt{A}\ge \sqrt{B}\)
\( \sqrt{A}\ge \sqrt{B}\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}A\ge B\\B\ge 0\end{array} \right.\)
или
\( \sqrt{A}>\sqrt{B}\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}A>B\\B\ge 0\end{array} \right.\)
Неравенства вида \( A\sqrt{B}>0\) или \( A\sqrt{B}<0\)
\( A\sqrt{B}>0\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}B>0\\A>0\end{array} \right.\)
или
\( A\sqrt{B}<0\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}B>0\\A<0\end{array} \right.\)
Неравенства вида \( A\sqrt{B}\ge 0\)
\( A\sqrt{B}\ge 0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}B=0\\\left\{ \begin{array}{l}A\ge 0\\B\ge 0\end{array} \right.\end{array} \right.\)
или
\( A\sqrt{B}\le 0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}B=0\\\left\{ \begin{array}{l}A\le 0\\B\ge 0\end{array} \right.\end{array} \right.\)
Неравенства вида \( \sqrt{A}\ge B\)
\( \sqrt{A}\ge B\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}\left\{ \begin{array}{l}B\le 0\\A\ge 0\end{array} \right.{5}},\end{array}\) и т.д.
Примеры решения простейших тригонометрических неравенств
Часть 2.
Начало здесь.
Если вы беретесь за изучение темы «Простейшие тригонометрические неравенства», то должны прежде знать, где находятся оси тангенса и котангенса и уметь решать простейшие тригонометрические уравнения (часть III).
Кстати, для сдающих ЕГЭ по математике, – умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Примеры решения простейших тригонометрических неравенств
Пример 1.
Решить неравенство:
Решение:
Отмечаем на оси тангенсов 1. Указываем все значения тангенса, меньшие 1 – ниже 1.
Далее, отмечаем все точки тригонометрического круга, значение тангенса в которых будет меньше 1. Для этого мы мысленно соединяем каждую точку оси тангенсов ниже 1 с началом координат; тогда каждая проведенная прямая пересечет дважды тригонометрический круг. Вот эти-то точки круга нас и интересуют! Они выстраиваются в две дуги (точнее в две серии дуг). Значения тангенса в них – меньше 1.
Заметим, кстати, что дуга повторяет дугу равно через пол круга, то есть через (период функции – это ).
Все подходящие значения можно записать в виде следующего двойного неравенства:
или так
Пример 2.
Решить неравенство:
Решение:
Отмечаем на оси тангенсов . Указываем все значения тангенса, большие или равные – выше (включая саму точку).
«Транслируем» отмеченные точки оси тангенсов на тригонометрический круг.
Все подходящие значения можно записать в виде следующего двойного неравенства:
или такого (разницы – никакой):
Пример 3.
Решить неравенство:
Решение:
Отмечаем на оси котангенсов . Указываем все значения котангенса, большие или равные – правее (включая саму точку).
«Транслируем» отмеченные точки оси котангенсов на тригонометрический круг:
Все подходящие значения можно записать в виде следующего двойного неравенства:
Вы обратили внимание, решая тригонометрическое неравенство с тангенсом, – мы не включаем в ответ точки (значение тангенса в этих точках не определено)?
А, решая тригонометрическое неравенство с котангенсом, – мы не включаем в ответ точки (значение котангенса в этих точках не определено).
Пример 4.
Решить неравенство:
Решение:
Проверьте себя
Помните, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. (См., например, задание 2).
1. Решить неравенство:
Ответ: + показать
2. Решить неравенство:
Ответ: + показать
3. Решить неравенство:
Ответ: + показать
Если у вас есть вопросы, – пожалуйста, – пишите в комментариях!
Системы линейных неравенств с одной переменной
Предварительные навыки
Примеры решения систем линейных неравенств с одной переменной
Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.
Рассмотрим простейший пример. Система состоит из двух неравенств, которые уже решены.
Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.
Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:
Но дело в том, что неравенства x > 4 и x < 9 соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями, как захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.
Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.
Значит решениями системы являются числа от 4 до 9. Границы 4 и 9 не включаются во множество решений системы, поскольку неравенства x > 4 и x < 9 строгие. Ответ можно записать в виде числового промежутка:
x ∈ ( 4 ; 9 )
Также, нужно изобразить множество решений системы на координатной прямой.
Для системы линейных неравенств решение на координатной прямой изображают так:
Сначала указывают границы обоих неравенств:
На верхней области отмечают множество решений первого неравенства x > 4
На нижней области отмечают множество решений второго неравенства x < 9
Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 4 до 9. Для наглядности выделим эту область красным цветом:
Для проверки можно взять любое число из этого промежутка и подставить его в исходную систему . Возьмем, например, число 6
Видим, что решение 6 удовлетворяет обоим неравенствам. Возьмём ещё какое-нибудь число из промежутка (4; 9), например, число 8
Видим, что решение 8 удовлетворяет обоим неравенствам.
Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:
Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.
Пример 2. Решить систему неравенств
Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.
Решениями же обоих неравенств являются все числа, которые больше 17.
Изобразим множество решений системы на координатной прямой и запишем ответ в виде числового промежутка.
Для начала отметим на координатной прямой границы обоих неравенств:
На верхней области отметим множество решений первого неравенства x > 17
На нижней области отметим множество решений второго неравенства x > 12
Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы . Видно, что эта область располагается в промежутке от 17 до плюс бесконечности. Запишем ответ в виде числового промежутка:
x ∈ ( 17 ; +∞ )
Пример 3. Решить систему неравенств
Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок
Получили систему . На этом решение завершается. Осталось изобразить множество решений системы на координатной прямой и записать ответ в виде числового промежутка.
Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства (x > 6 и x > 3). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы
x ∈ ( 6 ; + ∞ )
Пример 4. Решить систему неравенств
Решим каждое неравенство по отдельности:
Изобразим множество решений системы на координатной прямой и запишем ответ в виде числового промежутка:
Пример 5. Решить неравенство
Решим каждое неравенство по отдельности:
Изобразим множество решений системы на координатной прямой и запишем ответ в виде числового промежутка:
Когда решений нет
Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.
Пример 1. Решить неравенство
Решим каждое неравенство по отдельности:
Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.
Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:
На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система
А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система
Ответ: решений нет.
Пример 2. Решить систему неравенств
Решим каждое неравенство по отдельности:
Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:
Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система
А если не имеет решений приведённая равносильная система , то не имеет решений и исходная система
Ответ: решений нет.
Пример 3. Решить систему неравенств
Решим каждое неравенство по отдельности:
Получили неравенства 0 < −0,2 и a > 5. Первое неравенство не является верным и не имеет решений. Решением второго неравенство a > 5 являются все числа, которые больше 5. Но поскольку первое неравенство не будет верным ни при каком a, то можно сделать вывод, что у неравенств нет общих решений. А значит не имеет решений исходная система
Ответ: решений нет.
Задания для самостоятельного решения
Задание 1. Решите неравенство:
Решение:
Задание 2. Решите неравенство:
Задание 3. Решите неравенство:
Задание 4. Решите неравенство:
Задание 5. Решите неравенство:
Задание 6. Решите неравенство:
Задание 7. Решите неравенство:
Задание 8. Решите неравенство:
Решение:
Решений нет
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Решайте неравенства с помощью программы «Пошаговое решение математических задач»
В главе 2 мы установили правила решения уравнений с использованием чисел арифметики. Теперь, когда мы изучили операции с числами со знаком, мы будем использовать те же правила для решения уравнений, содержащих отрицательные числа. Мы также изучим методы решения и построения графиков неравенств с одним неизвестным.
РЕШЕНИЕ УРАВНЕНИЙ НА ЗАПИСАННЫХ ЧИСЛАХ
ЗАДАЧИ
По завершении этого раздела вы сможете решать уравнения, содержащие числа со знаком.
Пример 1 Решите относительно x и проверьте: x + 5 = 3
Решение
Используя те же процедуры, что и в главе 2, мы вычитаем 5 из каждой части уравнения, получая
Пример 2 Решите относительно x и проверьте: — 3x = 12
Решение
Разделив каждую сторону на -3, получаем
| Всегда проверяйте исходное уравнение. |
| Другой способ решения уравнения 3x — 4 = 7x + 8 — сначала вычесть 3x из обеих сторон, получив -4 = 4x + 8, , затем вычесть 8 с обеих сторон и получить -12 = 4x . Теперь разделите обе стороны на 4, получив — 3 = x или x = — 3. |
| Сначала удалите круглые скобки. Затем следуйте процедуре, описанной в главе 2. |
ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите буквальное уравнение.
- Примените ранее изученные правила для решения буквальных уравнений.
Уравнение, состоящее из более чем одной буквы, иногда называют буквальным уравнением .Иногда бывает необходимо решить такое уравнение для одной из букв через другие. Пошаговая процедура, описанная и использованная в главе 2, остается действительной после удаления любых символов группировки.
Пример 1 Решите относительно c: 3 (x + c) — 4y = 2x — 5c
Решение
Сначала удалите круглые скобки.
Здесь мы отмечаем, что, поскольку мы решаем для c, мы хотим получить c с одной стороны и все другие члены с другой стороны уравнения.Таким образом, получаем
| Помните, abx — это то же самое, что 1abx. Делим на коэффициент при x, который в данном случае равен ab. |
| Решите уравнение 2x + 2y — 9x + 9a, сначала вычтя 2.v из обеих частей. Сравните полученное решение с полученным в примере. |
Иногда форму ответа можно изменить. В этом примере мы могли бы умножить числитель и знаменатель ответа на (- l) (это не меняет значения ответа) и получить
Преимущество этого последнего выражения перед первым в том, что в ответе не так много отрицательных знаков.
| Умножение числителя и знаменателя дроби на одно и то же число — это использование фундаментального принципа дробей. |
Наиболее часто используемые буквальные выражения — это формулы из геометрии, физики, бизнеса, электроники и т. Д.
Пример 4 — это формула площади трапеции. Решите для c.
| Трапеция имеет две параллельные стороны и две непараллельные стороны.Параллельные стороны называются основаниями. Удаление скобок не означает их простое стирание. Мы должны умножить каждый член в круглых скобках на множитель, стоящий перед скобками. Менять форму ответа не обязательно, но вы должны уметь распознать правильный ответ, даже если форма не та. |
Пример 5 — это формула, дающая проценты (I), полученные за период D дней, когда известны основная сумма (p) и годовая ставка (r).Найдите годовую ставку, когда известны сумма процентов, основная сумма и количество дней.
Решение
Задача требует решения для р.
Обратите внимание, что в этом примере r оставлено справа, и поэтому вычисление было проще. При желании мы можем переписать ответ по-другому.
ГРАФИЧЕСКИЕ НЕРАВЕНСТВА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Используйте символ неравенства для обозначения относительного положения двух чисел на числовой прямой.
- График неравенств на числовой прямой.
Мы уже обсуждали набор рациональных чисел как тех, которые могут быть выражены как отношение двух целых чисел. Существует также набор чисел, называемых иррациональными числами , , которые нельзя выразить как отношение целых чисел. В этот набор входят такие числа как и так далее. Набор, состоящий из рациональных и иррациональных чисел, называется действительными числами .
Учитывая любые два действительных числа a и b, всегда можно заявить, что Часто нас интересует только то, равны ли два числа или нет, но бывают ситуации, когда мы также хотим представить относительный размер чисел, которые не равны. равный.
Символы являются символами неравенства или отношениями порядка и используются для отображения относительных размеров значений двух чисел. Обычно мы читаем этот символ как «больше чем». Например, a> b читается как «a больше, чем b». Обратите внимание, что мы заявили, что обычно читаем
а
| Какое положительное число можно добавить к 2, чтобы получить 5? |
Проще говоря, это определение утверждает, что a меньше b, если мы должны что-то добавить к a, чтобы получить b.Конечно, «что-то» должно быть положительным.
Если вы думаете о числовой прямой, вы знаете, что добавление положительного числа равносильно перемещению вправо по числовой прямой. Это приводит к следующему альтернативному определению, которое может быть легче визуализировать.
Пример 1 3
| Мы также можем написать 6> 3. |
Пример 2 — 4
| Мы также можем написать 0> — 4. |
Пример 3 4> — 2, потому что 4 находится справа от -2 в числовой строке.
Пример 4 — 6
Математическое утверждение x
| Вы понимаете, почему невозможно найти наибольшее число меньше 3? |
На самом деле назвать число x, которое является наибольшим числом меньше 3, — невыполнимая задача. Однако это может быть указано в числовой строке.Для этого нам нужен символ, обозначающий значение такого оператора, как x
Символы (и), используемые в числовой строке, указывают на то, что конечная точка не включена в набор.
Пример 5 График x
Решение
Обратите внимание, что на графике есть стрелка, указывающая на то, что линия продолжается без конца влево.
| На этом графике представлено каждое действительное число меньше 3. |
Пример 6 График x> 4 на числовой прямой.
Решение
| На этом графике представлено каждое действительное число больше 4. |
Пример 7 График x> -5 на числовой прямой.
Решение
| На этом графике представлены все действительные числа больше -5. |
Пример 8 Постройте числовой график, показывающий, что x> — 1 и x
Решение
Выписка x> — 1 и x
| На этом графике представлены все действительные числа от -1 до 5. |
Пример 9 График — 3
Решение
Если мы хотим включить конечную точку в набор, мы используем другой символ:. Мы читаем эти символы как «равно или меньше» и «равно или больше».
Пример 10 x>; 4 обозначает число 4 и все действительные числа справа от 4 в числовой строке.
Символы [и], используемые в числовой строке, указывают на то, что конечная точка включена в набор.
| Вы обнаружите, что такое использование круглых и квадратных скобок согласуется с их использованием в будущих курсах математики. |
| На этом графике представлено число 1 и все действительные числа больше 1. |
| На этом графике представлено число 1 и все действительные числа, меньшие или равные — 3. |
Пример 13 Напишите алгебраическое утверждение, представленное следующим графиком.
Пример 14 Напишите алгебраическое выражение для следующего графика.
| На этом графике представлены все действительные числа от -4 до 5 , включая от -4 до 5. |
Пример 15 Напишите алгебраическое выражение для следующего графика.
| Этот график включает 4, но , а не -2. |
Пример 16 График на числовой прямой.
Решение
В этом примере возникает небольшая проблема. Как мы можем указать на числовой строке? Если мы оценим суть дела, то другой человек может неправильно истолковать это утверждение. Не могли бы вы сказать, представляет ли эта точка или может быть? Поскольку цель графика — прояснить, всегда обозначают конечную точку.
| График используется для передачи утверждения. Вы всегда должны называть нулевую точку, чтобы показать направление, а также конечную точку или точки, если быть точным. |
Устранение неравенств
ЗАДАЧИ
По завершении этого раздела вы сможете решать неравенства с одним неизвестным.
Решения неравенств обычно основаны на тех же основных правилах, что и уравнения. Есть одно исключение, которое мы скоро обнаружим. Однако первое правило аналогично тому, что используется при решении уравнений.
Если одно и то же количество добавляется к каждой стороне неравенства , результаты будут неравными в том же порядке.
Пример 1 Если 5
Пример 2 Если 7
Мы можем использовать это правило для решения определенных неравенств.
Пример 3 Решить относительно x: x + 6
Решение
Если мы прибавим -6 к каждой стороне, мы получим
Изобразив это решение на числовой прямой, получим
| Обратите внимание, что процедура такая же, как и при решении уравнений. |
Теперь мы воспользуемся правилом сложения, чтобы проиллюстрировать важную концепцию, касающуюся умножения или деления неравенств.
Предположим, что x> a.
Теперь добавьте — x к обеим сторонам по правилу сложения.
| Помните, добавление одинаковой величины к обеим сторонам неравенства не меняет его направления. |
Теперь добавьте -a с обеих сторон.
Последний оператор — a> -x можно переписать как — x <-a. Поэтому мы можем сказать: «Если x> a, то — x
Если неравенство умножается или делится на отрицательное число , результаты будут неравными в порядке , противоположном .
| Например: Если 5> 3, то -5 |
Пример 5 Решите относительно x и изобразите решение: -2x> 6
Решение
Чтобы получить x в левой части, мы должны разделить каждый член на — 2. Обратите внимание, что, поскольку мы делим на отрицательное число, мы должны изменить направление неравенства.
| Обратите внимание, что как только мы делим на отрицательную величину, мы должны изменить направление неравенства. |
Обратите внимание на этот факт. Каждый раз, когда вы делите или умножаете на отрицательное число, вы должны изменять направление символа неравенства. Это единственное различие между решением уравнений и решением неравенств.
| Когда мы умножаем или делим на положительное число, изменений нет. Когда мы умножаем или делим на отрицательное число, направление неравенства меняется. Будьте осторожны — это источник многих ошибок. |
После того, как мы удалили круглые скобки и остались в выражении только отдельные термины, процедура поиска решения стала почти такой же, как в главе 2.
Давайте теперь рассмотрим пошаговый метод из главы 2 и отметим разницу при решении неравенств.
Первые Исключите дроби, умножив все члены на наименьший общий знаменатель всех дробей. (Без изменений, когда мы умножаем на положительное число.)
Второй Упростите, комбинируя одинаковые члены с каждой стороны неравенства. (Без изменений)
Третий Сложите или вычтите количества, чтобы получить неизвестное с одной стороны и числа с другой.(Без изменений)
Четвертый Разделите каждый член неравенства на коэффициент неизвестной. Если коэффициент положительный, неравенство останется прежним. Если коэффициент отрицательный, неравенство будет отменено. (Это важное различие между уравнениями и неравенствами.)
| Единственное возможное отличие заключается в последнем шаге. |
| Что нужно делать при делении на отрицательное число? |
| Не забудьте пометить конечную точку. |
РЕЗЮМЕ
Ключевые слова
- Литеральное уравнение — это уравнение, состоящее из более чем одной буквы.
- Символы — это символы неравенства или отношения порядка .
- a a находится слева от b в строке действительного числа.
- Двойные символы: указывают, что конечные точки включены в набор решений .
Процедуры
- Чтобы решить буквальное уравнение для одной буквы через другие, выполните те же действия, что и в главе 2.
- Чтобы решить неравенство, используйте следующие шаги:
Шаг 1 Удалите дроби, умножив все члены на наименьший общий знаменатель всех дробей.
Шаг 2 Упростите, объединив одинаковые термины с каждой стороны неравенства.
Шаг 3 Сложите или вычтите количества, чтобы получить неизвестное с одной стороны и числа с другой.
Шаг 4 Разделите каждый член неравенства на коэффициент неизвестной. Если коэффициент положительный, неравенство останется прежним.Если коэффициент отрицательный, неравенство будет отменено.
Шаг 5 Проверьте свой ответ.
абсолютное значение — Вы можете мне помочь с этим неравенством? $ | x-1 |
Я нашел эту проблему в Precalculus 7-е изд, Джеймс Стюарт, глава 1.8, проблема 128.
«Напомним, что $ | ab | $ — это расстояние между a и b на числовой прямой. Что представляют собой $ | x-1 | $ и $ | x-3 | $ для любого числа x? Используйте эту интерпретацию для решения неравенство $ | x-1 | <| x-3 | $ геометрически.В общем случае, если a * Я знаю, что $ | x-1 | $ — это расстояние между x и 1, и геометрически, если $ x = 2 $, расстояние между 1 и x равно расстоянию между 3 и x, в этой точке мы Можно видеть, что для $ x <2 $ расстояние между x и 3 больше, чем расстояние между x и 1. Я хотел проверить это решение, используя формальный способ решения этого неравенства, поэтому я написал следующее решение, но я не был Я не могу это проверить, потому что, по-видимому, я сделал что-то не так и не могу понять, что было не так. $ | x-1 | <| x-3 | $ $ — | x-3 | долл. США $ — | x-3 | $ (- x + 1 $ (- x + 1 $ (4 <2x \ land -3 <-1) \ land (-1 <-3 \ lor 2x> 4) $ $ (2 У меня вопрос, что я сделал не так? и как улучшить мое формальное решение, заранее большое спасибо за то, что нашли время, чтобы прочитать это. РЕДАКТИРОВАТЬ: Прежде всего, спасибо всем за все ваши ответы, теперь я вижу различные способы решения этой проблемы. Что касается моего «громоздкого» решения, г-н @AnuragA указал на мою ошибку, и теперь я пришел с этим новым решением, надеюсь, теперь все в порядке, еще раз спасибо, и если вы можете указать на любую ошибку в этом новом решении, я буду признателен. $ | x-1 | <| x-3 | $ $ — | x-3 | долл. США $ [| x-3 | > -x + 1] \ land [x-1 <| x-3 |] $ $ [x-3> -x + 1 \ lor -x + 1 <- (x-3)] \ land [x-3> x-1 \ lor x-1 <- (x-3)] $ $ [2x> 4 \ lor 1 <3] \ land [-3> -1 \ lor 2x <4] $ $ [x> 2 \ lor \ {x \ in \ Bbb R \ Bbb \}] \ land [\ {x \ in \ emptyset \} \ lor x <2] $ $ [x \ in \ Bbb R \ Bbb] \ land [x <2] $ $ x <2 $ Прежде всего, обратите внимание, что ваше неравенство определяется только в том случае, если ваши знаменатели не равны нулю: # х + 1! = 0 <=> х! = -1 # #x — 2! = 0 <=> x! = 2 # Теперь ваш следующий шаг — «избавиться» от дробей.Это можно сделать, умножив обе части неравенства на # x + 1 # и # x-2 #. Однако вам нужно быть осторожным, поскольку, если вы умножаете неравенство на отрицательное число, вы должны перевернуть знак неравенства. ========================================= Рассмотрим разные случаи: корпус 1: # цвет (белый) (xxx) x> 2 #: Оба #x + 1> 0 # и #x — 2> 0 # удерживаются. Таким образом, вы получите: #x — 2> 3 (x + 1) # #x — 2> 3x + 3 # … вычислить # -3x # и # + 2 # с обеих сторон … # -2x> 5 # … разделить на # -2 # с обеих сторон. Поскольку # -2 # — отрицательное число, вы должны перевернуть знак неравенства … #x <- 5/2 # Однако не существует # x #, удовлетворяющего как условию #x> 2 #, так и #x <- 5/2 #. Таким образом, в данном случае решения нет. ========================================= случай 2: # цвет (белый) (xxx) -1 Здесь #x + 1> 0 #, но #x — 2 <0 #.Таким образом, вам нужно один раз перевернуть знак неравенства и вы получите: # цвет (белый) (i) x — 2 <3 (x + 1) # # цвет (белый) (x) -2x <5 # … разделить на # -2 # и снова перевернуть знак неравенства … # цвет (белый) (xxx) x> -5 / 2 # Неравенство #x> -5 / 2 # верно для всех # x # в интервале # -1 ========================================= случай 3: # цвет (белый) (xxx) x <-1 #: Здесь оба знаменателя отрицательны.Таким образом, если вы умножите неравенство на оба из них, вам нужно дважды перевернуть знак неравенства, и вы получите: #x — 2> 3x + 3 # # цвет (белый) (i) -2x> 5 # # цвет (белый) (xxi) x <- 5/2 # Поскольку условие #x <-5 / 2 # является более строгим, чем условие #x <-1 #, решение для этого случая - #x <- 5/2 #. ========================================= Всего решение #x <- 5/2 цвет (белый) (xx) # или # цвет (белый) (xx) -1 или, если вы предпочитаете другое обозначение, #x в (- oo, -5/2) uu (-1, 2) #. Иногда нам нужно решить такие неравенства: Обозначение слов Пример больше х + 3 > 2 менее 7x < 28 больше или равно 5 ≥ x — 1 меньше или равно 2 года + 1 ≤ 7 Наша цель — иметь x (или другую переменную) самостоятельно слева от знака неравенства: Мы называем это «решенным». Вычтем 2 с обеих сторон: х + 2 — 2> 12 — 2 Упростить: x> 10 Решено! Решение неравенств очень похоже на решение уравнений … мы делаем почти то же самое … … но мы также должны обратить внимание на направление неравенства . Направление: куда «указывает» стрелка Некоторые вещи могут изменить направление ! <становится> > становится < ≤ становится ≥ ≥ становится ≤ Эти вещи не влияют на направление неравенства: <7 + 3 Мы можем упростить 7 + 3, не влияя на неравенство: 3x <10 Но эти вещи действительно меняют направление неравенства (например, «<» становится «>»): <12 Когда мы меняем местами левую и правую части, мы также должны изменить направление неравенства : 12 > 2 года + 7 Вот подробности: Часто мы можем решить неравенства, добавляя (или вычитая) число с обеих сторон (точно так же, как во Введении в алгебру), например: <7 Если вычесть 3 с обеих сторон, мы получим: x + 3 — 3 <7 — 3 х <4 И вот наше решение: x <4 Другими словами, x может быть любым значением меньше 4. Мы пошли от этого: Кому: х + 3 <7 х <4 И это хорошо работает для , прибавляя и вычитая , потому что, если мы прибавляем (или вычитаем) одинаковую сумму с обеих сторон, это не влияет на неравенство Пример: У Алекса больше монет, чем у Билли.Если и Алекс, и Билли получат по три монеты больше, у Алекс все равно будет больше монет, чем у Билли. Неважно, просто поменяйте местами стороны, но переверните знак , чтобы он все еще «указывал» на правильное значение! Если вычесть 5 с обеих сторон, получим: 12 -5 7 <х Вот и решение! Но ставить «x» слева — это нормально… … так давайте обратим внимание (и знак неравенства!): x> 7 Вы видите, как знак неравенства все еще «указывает» на меньшее значение (7)? И вот наше решение: x> 7 Примечание: «x» может быть справа , но людям обычно нравится видеть его слева. Также мы умножаем или делим обе части на значение (как в алгебре — умножение). Но нам нужно быть немного осторожнее (как вы увидите). Положительные значения Все нормально, если мы хотим умножить или разделить на положительное число : <15 Если мы разделим обе стороны на 3, получим: 3 года /3 <15 /3 г <5 И вот наше решение: y <5 Отрицательные значения Почему? Ну, посмотрите на числовую строку! Например, от 3 до 7 это увеличение , Видите, как меняет знак неравенства (с <на>)? Давайте попробуем пример: <−8 Разделим обе части на −2… и отменяют неравенство ! −2 года <−8 −2y / −2 > −8 / −2 г> 4 И это правильное решение: y> 4 (Обратите внимание, что я перевернул неравенство в той же строке , разделенное на отрицательное число.) Итак, запомните: При умножении или делении на отрицательное число отменяет неравенство Вот еще один (хитрый!) Пример: <3b Кажется легко просто разделить обе стороны на b , что дает нам: x <3 … но подождите … если b равно отрицательное значение , нам нужно изменить неравенство следующим образом: x> 3 Но мы не знаем, положительное или отрицательное значение b, поэтому мы не можем ответить на этот ! Чтобы помочь вам понять, представьте, что замените b на 1 или −1 в примере bx <3b : Ответом может быть x <3 или x> 3 , и мы не можем выбрать, потому что не знаем b . Так: Не пытайтесь делить на переменную для решения неравенства (если вы не знаете, что переменная всегда положительна или всегда отрицательна). x − 3 2 <−5 Во-первых, давайте очистим «/ 2», умножив обе стороны на 2. Поскольку мы умножаем на положительное число, неравенства не изменятся. x − 3 2 × 2 <−5 × 2 х-3 <-10 Теперь прибавьте 3 к обеим сторонам: х − 3 + 3 <−10 + 3 х <−7 И это наше решение: x <−7 Как решить задачу с двумя неравенствами сразу? −2 < 6−2x 3 <4 Во-первых, давайте очистим «/ 3», умножив каждую часть на 3. Поскольку мы умножаем на положительное число, неравенства не меняются: −6 <6−2x <12 Теперь вычтите 6 из каждой части: −12 <−2x <6 Теперь разделите каждую часть на 2 (положительное число, чтобы неравенства снова не изменились): −6 <−x <3 Теперь умножьте каждую часть на -1. Поскольку мы умножаем на отрицательное число , неравенства изменяют направление . 6> х> −3 И это решение! Но для наглядности лучше иметь меньшее число слева, большее — справа. Так что давайте поменяем их местами (и убедимся, что неравенства указывают правильно): −3 <х <6 Слово неравенство означает математическое выражение, в котором стороны не равны друг другу.По сути, неравенство сравнивает любые два значения и показывает, что одно значение меньше, больше или равно значению на другой стороне уравнения. В основном, для представления уравнений неравенства используются пять символов неравенства. Эти символы неравенства: меньше ( <), больше (> ), меньше или равно ( ≤ ), больше или равно ( ≥ ) и символ неравенства ( ≠ ) . Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной. Операции с линейными неравенствами включают сложение, вычитание, умножение и деление. Общие правила этих операций показаны ниже. Хотя мы использовали символ <для иллюстрации, следует отметить, что те же правила применяются к>, ≤ и ≥. Подобно линейным уравнениям, неравенства можно решить, применяя аналогичные правила и шаги, за некоторыми исключениями. Единственная разница при решении линейных уравнений — это операция умножения или деления на отрицательное число.Умножение или деление неравенства на отрицательное число изменяет символ неравенства. Линейные неравенства можно решить с помощью следующих операций: Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию. Пример 1 Решите 3x — 5 ≤ 3 — x. Решение Начнем с того, что сложим обе части неравенства на 5 3x — 5 + 5 ≤ 3 + 5 — x 3х ≤ 8 — х Затем сложите обе стороны по x. 3х + х ≤ 8 — х + х 4x ≤ 8 Наконец, разделите обе части неравенства на 4, чтобы получить; х ≤ 2 Пример 2 Вычислите диапазон значений y, который удовлетворяет неравенству: y — 4 <2y + 5. Решение Сложите обе части неравенства на 4. л — 4 + 4 <2г + 5 + 4 лет <2лет + 9 Вычтем обе части на 2y. лет — 2 года <2 лет - 2 года + 9 Y <9 Умножьте обе части неравенства на -1 и измените направление символа неравенства. y> — 9 Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию. Пример 3 Решить x + 8> 5. Решение Выделите переменную x, вычтя 8 из обеих частей неравенства. х + 8-8> 5-8 => х> −3 Следовательно, x> −3. Пример 4 Решить 5x + 10> 3x + 24. Решение Вычтем 10 из обеих частей неравенства. 5x + 10–10> 3x + 24–10 5x> 3x + 14. Теперь вычтем обе части неравенства в 3 раза. 5x — 3x> 3x — 3x + 14 2x> 14 х> 7 Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию. Пример 5 Решить x / 4> 5 Решение: Умножим обе части неравенства на знаменатель дроби . 4 (х / 4)> 5 х 4 х> 20 Пример 6 Решить -x / 4 ≥ 10 Решение: Умножьте обе части неравенства на 4. 4 (-x / 4) ≥ 10 x 4 -x ≥ 40 Умножьте обе части неравенства на -1 и измените направление символа неравенства на противоположное. х ≤ — 40 Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию. Пример 7 Решите неравенство: 8x — 2> 0. Решение Прежде всего, сложим обе части неравенства на 2 8x — 2 + 2> 0 + 2 8x> 2 Теперь решите, разделив обе части неравенства на 8, чтобы получить; x> 2/8 х> 1/4 Пример 8 Решите следующее неравенство: −5x> 100 Решение Разделите обе части неравенства на -5 и измените направление символа неравенства = −5x / -5 <100 / -5 = х <- 20 Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию. Пример 9 Решить: 2 (x — 4) ≥ 3x — 5 Решение 2 (x — 4) ≥ 3x — 5 Примените свойство distributive, чтобы убрать круглые скобки. ⟹ 2x — 8 ≥ 3x — 5 Сложите обе стороны на 8. ⟹ 2x — 8 + 8 ≥ 3x — 5 + 8 ⟹ 2x ≥ 3x + 3 Вычтем обе части на 3. ⟹ 2x — 3x ≥ 3x + 3 — 3x ⟹ -x ≥ 3 ⟹ х ≤ — 3 Пример 10 Учащийся набрал 60 баллов за первый тест и 45 баллов за второй тест выпускного экзамена.Сколько минимальных баллов должен набрать ученик в третьем тесте, получив в среднем не менее 62 баллов? Решение Пусть в третьем тесте будет набрано x баллов. (60 + 45 + x) / 3 ≥ 62 Пример 11 Джастину требуется не менее 500 долларов на празднование дня рождения.Если он уже накопил 150 долларов, до этой даты осталось 7 месяцев. Какую минимальную сумму он должен откладывать ежемесячно? Решение Пусть минимальная сумма экономии ежемесячно = х 150 + 7x ≥ 500 Решить относительно x 150–150 + 7x ≥ 500–150 х ≥ 50 Следовательно, Джастин должен сэкономить 50 долларов или больше Пример 12 Найдите два последовательных нечетных числа, которые больше 10 и имеют сумму меньше 40. Решение Пусть меньшее нечетное число = x Следовательно, следующим числом будет x + 2 x> 10 ………. более 10 x + (x + 2) <40 …… сумма меньше 40 Решите уравнения. 2x + 2 <40 х + 1 <20 х <19 Объедините два выражения. 10 <х <19 Следовательно, последовательные нечетные числа — 11 и 13, 13 и 15, 15 и 17, 17 и 19. Лучшим инструментом для представления и визуализации чисел является числовая линия. Числовая линия определяется как прямая горизонтальная линия с числами, расположенными на равных отрезках или интервалах. У числовой прямой есть нейтральная точка в середине, известная как начало координат. Справа от начала координат на числовой прямой находятся положительные числа, а слева от начала координат — отрицательные числа. Линейные уравнения также могут быть решены графическим методом с использованием числовой прямой.Например, чтобы построить x> 1 на числовой прямой, вы обведите цифру 1 на числовой прямой и проведете линию, идущую от круга в направлении чисел, которые удовлетворяют утверждению о неравенстве. Пример 13 Если символ неравенства больше или равен или меньше или равен знаку (≥ или ≤), нарисуйте круг над числовым числом и закрасьте или закройте круг.Наконец, проведите линию, идущую от заштрихованного круга в направлении чисел, которая удовлетворяет уравнению неравенства. Пример 14 х ≥ 1 Та же процедура используется для решения уравнений, включающих интервалы. Пример 15 –2 < x <2 Как решить неравенство 1 / (x + 1)> 3 / (x-2)?
Устранение неравенств
> < ≥ ≤ Решение
Примерно так: х <5 или: г ≥ 11 Пример: x + 2> 12
Как решить
Безопасные дела
Пример: 3x
Пример: 2y + 7
Сложение или вычитание значения
Пример: x + 3
Что мы сделали?
Что, если я решу, но «x» справа?
Пример: 12
Умножение или деление на значение
Пример: 3y
Когда мы умножаем или делим на отрицательное число
, мы должны отменить неравенство.
, но от -3 до -7 это уменьшение. −7 <−3 7> 3 Пример: −2y
Умножение или деление на переменные
Пример: bx
Пример побольше
Пример:
Два неравенства сразу!
Пример:
Сводка
Устранение неравенств — объяснения и примеры
Что такое неравенство в математике?
Символы неравенства
Операции с неравенствами
Как устранить неравенство?
Решение линейных неравенств со сложением
Решение линейных неравенств с вычитанием
Решение линейных неравенств с умножением
Решение линейных неравенств с делением
Решение линейных неравенств с использованием распределительного свойства
105 + x ≥ 196
x ≥ 93
Следовательно, учащийся должен набрать 93 балла, чтобы поддерживать среднее значение не менее 62 баллов. Неравенства и числовая линия
Пример 16
–1 ≤ x ≤ 2
Пример 17
–1 < x ≤ 2
Практические вопросы
Решите следующие неравенства и запишите свой ответ на числовой прямой.
- 2x> 9
- х + 5> 13
- −3x <4
- 7x + 11> 2x + 5
- 2 (х + 3) <х + 1
- — 5 ≤ 2x — 7 ≤ 1
- 4x — 8 ≤ 12
ответы
- x> 9/2
- x> 8
- х> −4/3
- х> −6/5
- х <−5.
- 1 ≤ x ≤ 4.
- х ≤ 5
Предыдущий урок | Главная страница | Следующий урок
Литература: Устранение неравенств за один шаг | Конечная математика
Неравенства похожи на уравнения в том, что они показывают взаимосвязь между двумя выражениями.Мы решаем и графически изображаем неравенства аналогично уравнениям. Однако есть некоторые отличия, о которых мы поговорим в этой главе. Основное отличие состоит в том, что для линейных неравенств ответом является интервал значений, тогда как для линейного уравнения ответом чаще всего является одно значение.
При написании неравенств используются следующие символы
> больше
[латекс] \ ge [/ latex] больше или равно
<меньше
[латекс] \ le [/ latex] меньше или равно
Запишите и изобразите неравенства в одной переменной в числовой строке
Начнем с простого неравенства x> 3
Мы читаем это неравенство как «x больше 3.«Решение — это набор всех действительных чисел, которые больше трех. Мы часто представляем множество решений неравенства числовой линией.
Рассмотрим еще одно простое неравенство [латекс] x \ le4 [/ latex]
Мы читаем это неравенство как «x меньше или равно 4». Решение — это набор всех действительных чисел, которые равны четырем или меньше четырех. Построим это множество решений на числовой прямой.
В графе мы используем пустой кружок для конечной точки строгого неравенства (x> 3) и закрашенный кружок, если включен знак равенства (x [latex] \ le [/ latex] 4).
Пример 1
На числовой прямой нанесите следующие неравенства.
- х <−3
- [латекс] x \ ge6 [/ латекс]
- x> 0
- [латекс] x \ le8 [/ латекс]
Решения
- Неравенство x <−3 представляет все действительные числа, которые меньше −3. Число −3 не входит в решение и обозначено белым кружком на графике.
- Неравенство [латекс] x \ ge6 [/ latex] представляет все действительные числа, которые больше или равны шести.Число шесть включено в решение и обозначено на графике замкнутым кружком.
- Неравенство x > 0 представляет все действительные числа, которые больше нуля. Число ноль не входит в решение и обозначено белым кружком на графике.
- Неравенство [латекс] x \ le8 [/ latex] представляет все действительные числа, которые меньше или равны восьми. Число восемь включено в решение и обозначено на графике замкнутым кружком.
Пример 2
Напишите неравенство, которое представлено на каждом графике.
Решения
- x <−12
- x > 540
- x <65
- [латекс] x \ ge83 [/ латекс]
В реальной жизни неравенство проявляется повсюду. Вот несколько простых примеров реальных приложений.
Пример 3
Запишите каждое утверждение в виде неравенства и обозначьте его числовой прямой.
- Чтобы получить бесплатную проверку, вы должны поддерживать баланс не менее 2500 долларов на текущем счете.
- Чтобы кататься на американских горках «Тандерболт», вы должны быть ростом не менее 48 дюймов.
- Чтобы получить бесплатный вход в зоопарк Сан-Диего, вам должно быть меньше 3 лет.
- Ограничение скорости на межштатной автомагистрали составляет 65 миль в час.
Решения
- Неравенство записывается как [latex] x \ ge2500 [/ latex]. Слова «как минимум» означают, что в набор решений включена стоимость 2500 долларов.
- Неравенство записывается как [latex] x \ ge48 [/ latex]. Слова «по крайней мере» означают, что значение 48 дюймов включено в набор решений.
- Неравенство записывается как x <3.
- Ограничение скорости означает наивысшую допустимую скорость, поэтому неравенство записывается как [latex] x \ le65 [/ latex].
Чтобы решить неравенство, мы должны изолировать переменную с одной стороны от знака неравенства. Чтобы изолировать переменную, мы используем те же основные методы, которые используются при решении уравнений.Для неравенств этого типа:
x — a < b или x — a > b
Мы изолируем x, добавив константу a к обеим сторонам неравенства.
Пример 4
Решите каждое неравенство и изобразите набор решений.
- х − 3 <10
- х − 1> −10
- [латекс] x − 1 \ le − 5 [/ латекс]
- [латекс] x − 20 \ ge14 [/ латекс]
Решения
- Чтобы решить неравенство x- 3 <10 Упростите:
x <13 - Решить неравенство x — 1> -10
- Решить неравенство [латекс] x-1 \ le-5 [/ latex].Упростить:
[латекс] x \ le-4 [/ латекс] - Решить неравенство [латекс] x-20 \ le14 [/ latex]
Для неравенств этого типа:
x + 1 b
Мы выделяем x, вычитая константу a с обеих сторон неравенства.
Пример 5
Решите каждое неравенство и изобразите набор решений.
- [латекс] x + 2 <7 [/ латекс]
- [латекс] x + 8 \ le-7 [/ латекс]
- [латекс] x + 4> 13 [/ латекс]
Решения
- Чтобы решить неравенство x + 2 <7, вычтите 2 с обеих сторон неравенства. x + 2-2 <7-2
Упростить: x <5 - Чтобы решить неравенство [латекс] x + 8 \ le – 7 [/ latex], вычтите 8 с обеих сторон неравенства. [латекс] x + 8 — 8 \ le-7 — 8 [/ latex] Упростить:
[латекс] x \ ge – 15 [/ латекс] - Чтобы решить неравенство x + 4> 13, вычтите 4 с обеих сторон неравенства. x + 4-4> 13-4 Упростить:
x > 9
Рассмотрим проблему:
[латекс] \ frac {x} {5} \ le 3 [/ latex]
Чтобы найти решение, умножаем обе части на 5:
[latex] (5) \ frac {x} {5} \ le 3 (5) [/ latex]
Получаем
[латекс] х \ ле 15 [/ латекс].
Ответ неравенства может быть выражен четырьмя различными способами:
- Обозначение неравенства Ответ просто выражается как x <15.
- Обозначение набора Ответ: x | x <15. Вы читаете это как «набор всех значений x, таких, что x является действительным числом меньше 15».
- Интервальное обозначение использует скобки для обозначения диапазона значений в решении. Интервальное обозначение решения для нашей задачи — (−∞, 15). Обозначение интервалов также использует понятие бесконечности ∞ и отрицательной бесконечности −∞.Круглые или открытые скобки «(» и «)» означают, что число рядом со скобкой не входит в набор решений. Квадратные или закрытые скобки «[» и «]» означают, что число рядом со скобкой включено в набор решений.
- График решения показывает решение в виде вещественной числовой линии. Закрашенный кружок на номере указывает, что номер включен в набор решений. Белый кружок указывает на то, что номер не входит в набор. Для нашего примера здесь нарисован график решения.
Пример 6
- [−4,6] говорит, что решения — это все числа от −4 до 6 , включая −4 и 6.
- (8,24) говорит, что решением являются все числа от 8 до 24, но не включает числа 8 и 24.
- [3,12) говорит, что решением являются все числа от 3 до 12, включая 3, но не включая 12.
- (−5, ∞) говорит, что решением являются все числа больше −5, , исключая −5.
- (−∞, ∞) говорит, что решение — все действительные числа.
Решаем неравенство
[латекс] 2x \ ge 12 [/ latex] делением обеих сторон на 2:
[латекс] \ frac {2x} {2} \ ge \ frac {12} {2} [/ латекс]
Упростить:
[латекс] x \ ge 6 [/ латекс]
Давайте запишем решение в четырех различных обозначениях, которые вы только что выучили:
| Обозначение неравенства | [латекс] x \ ge 6 [/ латекс] |
| Обозначение набора | [латекс] {x | x \ ge 6} [/ латекс] |
| Обозначение интервалов | [латекс] [6, [/ латекс] ∞] |
| График решения |
Мы решаем неравенство аналогично решению обычного уравнения.Мы можем складывать или вычитать числа по обе стороны неравенства. Мы также можем умножать или делить положительные числа по обе стороны неравенства, не меняя решения.
Что-то другое происходит, если мы умножаем или делим на отрицательные числа. В этом случае знак неравенства меняет направление.
Например, чтобы решить −3x <9
Делим обе части на –3. Знак неравенства меняется с <на>, потому что мы делим на отрицательное число.
[латекс] \ frac {-3x} {- 3} \ gt \ 6 \ frac {9} {- 3} [/ латекс]
[латекс] x \ gt \ -3 [/ латекс]
Мы можем объяснить, почему это происходит, на простом примере.Мы знаем, что два меньше трех, поэтому можем записать неравенство.
2 <3
Если мы умножим оба числа на −1, мы получим −2 и −3, но мы знаем, что −2 больше −3.
−2> −3
Вы видите, что умножение обеих сторон неравенства на отрицательное число привело к изменению направления знака неравенства. Это также происходит, если мы делим на отрицательное число.
Пример 7
Решите каждое неравенство. Приведите решение в обозначениях неравенств и интервалов.
- [латекс] 4x \ lt 24 [/ латекс] [латекс] \ displaystyle {4} {x} lt {24} [/ latex]
- [латекс] -9x \ le \ frac {3} {5} [/ латекс]
- [латекс] \ displaystyle- {5} {x} \ le {21} [/ latex]
- [латекс] \ displaystyle {12} {x} \ gt- {30} [/ latex]
Решения
- [latex] \ displaystyle {4} {x} \ lt {24} [/ latex] Разделите обе стороны на 4: [latex] \ displaystyle \ frac {{{4} {x}}} {{4}} \ lt \ frac {{24}} {{4}} [/ latex] Упростите, чтобы получить ответ:
[latex] \ displaystyle {x} \ lt {6} [/ latex] - [латекс] \ displaystyle- {9} {x} \ le- \ frac {{3}} {{5}} [/ latex] Разделите обе стороны на –9:
[латекс] \ displaystyle \ frac {{- {9} {x}}} {{- {9}}} \ ge- \ frac {{3}} {{5}} (- \ frac {{1}} {{9}}) [/ latex] .Направление неравенства изменилось. Чтобы получить ответ, упростите:
[latex] \ displaystyle {x} \ ge \ frac {{1}} {{15}} [/ latex] - [латекс] \ displaystyle- {5} {x} \ le {21} [/ latex] Разделите обе стороны на –5:
[латекс] \ displaystyle \ frac {{- {5} {x}}} {{ — {{5}}}} \ ge \ frac {{21}} {{- {{5}}}} [/ latex] Направление неравенства изменено. Упростите, чтобы получить ответ
[latex] \ displaystyle {x} \ ge- \ frac {{21}} {{5}} [/ latex] - [latex] \ displaystyle {12} {x} \ gt- {30} [/ latex] Разделите обе стороны на 12: [latex] \ displaystyle \ frac {{{12} {x}}} {{12}} \ gt- \ frac {{30}} {{12}} [/ latex] Упростите, чтобы получить ответ
[latex] \ displaystyle {x} \ gt- \ frac {{5}} {{2}} [/ латекс]
Пример 8
Решите каждое неравенство.Приведите решение в обозначениях неравенств.
- [латекс] \ displaystyle \ frac {{x}} {{2}} \ gt {40} [/ latex]
- [латекс] \ displaystyle \ frac {{x}} {{- {3}}} \ le- {12} [/ latex]
- [латекс] \ displaystyle \ frac {{x}} {{25}} \ lt \ frac {{3}} {{2}} [/ latex]
- [латекс] \ displaystyle \ frac {{x}} {{- {7}}} \ ge {9} [/ latex]
Решения
- [латекс] \ displaystyle \ frac {{x}} {{2}} \ gt {40} [/ latex] Умножьте обе стороны на 2: [латекс] \ displaystyle {2} (\ frac {{x}} {{2}}) \ gt {40} ({2}) [/ latex] Упростить: [latex] \ displaystyle {x} \ gt {80} [/ latex]
- [латекс] \ displaystyle \ frac {{x}} {{- {3}}} \ le {12} [/ latex] Умножьте обе стороны на –3:
[латекс] \ displaystyle- {3} (\ frac {{x}} {{- {3}}}) \ ge- {12} (- {3}) [/ latex] Направление неравенства изменено.Упростить: [latex] \ displaystyle {x} \ ge {36} [/ latex] - [латекс] \ displaystyle \ frac {{x}} {{25}} \ lt \ frac {{3}} {{2}} [/ latex] Умножьте обе стороны на 25 [латекс] \ displaystyle {25} ( \ frac {{x}} {{25}}) \ lt \ frac {{3}} {{2}} ({25}) [/ latex] Упростить:
[латекс] \ displaystyle {x} \ lt \ гидроразрыв {{75}} {{2}} [/ latex] или 37,5 - [латекс] \ displaystyle \ frac {{x}} {{- {7}}} \ ge {9} [/ latex] Умножьте обе стороны на –7: [латекс] \ displaystyle (- {7}) \ frac {{x}} {{- {7}}} \ le {9} (- {7}) [/ latex] Направление неравенства изменено. Упростите: [latex] \ displaystyle {x} \ le- {63} [/ латекс]
.
- Ответом на неравенство часто бывает интервал значений.Распространенные неравенства:
- ge больше или равно
- le меньше или равно
- Решение неравенств с помощью сложения и вычитания работает так же, как решение уравнения. Чтобы решить, мы изолируем переменную на одной стороне уравнения.
- Есть четыре способа изобразить неравенство:
- Обозначение уравнения x ge 2
- Установить обозначение x ge 2
- Интервальное обозначение [2, ∞) Закрытые скобки «[» и «]» означают включение, круглые скобки «(« и »)» означают исключение.
- График решения
- При умножении или делении обеих сторон неравенства на отрицательное число необходимо обратить неравенство.
ck12, Algebra, Linear Inequalities, «
Solving One-Step Inequalities», под лицензией CC BY-NC 3.0.
Использование свойств неравенств
Когда мы работаем с неравенствами, мы обычно можем относиться к ним аналогично, но не точно так, как мы относимся к равенствам.Мы можем использовать свойство сложения и свойство умножения , чтобы помочь нам решить их. Единственное исключение — когда мы умножаем или делим на отрицательное число; при этом символ неравенства меняется на противоположное.
Общее примечание: свойства неравенств
[латекс] \ begin {array} {ll} \ text {Свойство добавления} \ hfill & \ text {If} a
Эти свойства также применимы к [latex] a \ le b [/ latex], [latex] a> b [/ latex] и [latex] a \ ge b [/ latex].
Пример 3: Демонстрация свойства сложения
Проиллюстрируйте свойство сложения неравенств, решив каждое из следующих решений:
а. [латекс] х — 15 <4 [/ латекс]
б. [латекс] 6 \ ge x — 1 [/ латекс]
c. [латекс] x + 7> 9 [/ латекс]
Решение
Свойство сложения для неравенств гласит, что если неравенство существует, добавление или вычитание одного и того же числа с обеих сторон не меняет неравенства.
а. [латекс] \ begin {array} {ll} x — 15 <4 \ hfill & \ hfill \\ x - 15 + 15 <4 + 15 \ hfill & \ text {Добавьте 15 с обеих сторон.} \ hfill \\ x <19 \ hfill & \ hfill \ end {array} [/ latex]
г. [латекс] \ begin {array} {ll} 6 \ ge x — 1 \ hfill & \ hfill \\ 6 + 1 \ ge x — 1 + 1 \ hfill & \ text {Добавить 1 с обеих сторон}. \ hfill \ \ 7 \ ge x \ hfill & \ hfill \ end {array} [/ latex]
г. [latex] \ begin {array} {ll} x + 7> 9 \ hfill & \ hfill \\ x + 7-7> 9-7 \ hfill & \ text {Вычтите 7 с обеих сторон}.\ hfill \\ x> 2 \ hfill & \ hfill \ end {array} [/ latex]
Попробовать 3
Решить [латекс] 3x — 2 <1 [/ латекс].
Решение
Пример 4: Демонстрация свойства умножения
Проиллюстрируйте свойство умножения неравенств, решив каждое из следующих решений:
- [латекс] 3x <6 [/ латекс]
- [латекс] -2x — 1 \ ge 5 [/ латекс]
- [латекс] 5-x> 10 [/ латекс]
Решение
а. [латекс] \ begin {array} {l} 3x <6 \ hfill \\ \ frac {1} {3} \ left (3x \ right) <\ left (6 \ right) \ frac {1} {3} \ hfill \\ x <2 \ hfill \ end {array} [/ latex]
г.[латекс] \ begin {array} {ll} -2x — 1 \ ge 5 \ hfill & \ hfill \\ -2x \ ge 6 \ hfill & \ hfill \\ \ left (- \ frac {1} {2} \ right) \ left (-2x \ right) \ ge \ left (6 \ right) \ left (- \ frac {1} {2} \ right) \ hfill & \ text {Умножить на} — \ frac {1} { 2}. \ Hfill \\ x \ le -3 \ hfill & \ text {Обратное неравенство}. \ Hfill \ end {array} [/ latex]
г. [латекс] \ begin {array} {ll} 5-x> 10 \ hfill & \ hfill \\ -x> 5 \ hfill & \ hfill \\ \ left (-1 \ right) \ left (-x \ right) > \ left (5 \ right) \ left (-1 \ right) \ hfill & \ text {Умножить на} -1.\ hfill \\ x <-5 \ hfill & \ text {Обратное неравенство}. \ hfill \ end {array} [/ latex]
Попробовать 4
Решить [латекс] 4x + 7 \ ge 2x — 3 [/ латекс].
Решение
Алгебраическое решение неравенств с одной переменной
Как показали примеры, мы можем выполнять те же операции с обеими сторонами неравенства, как и с уравнениями; совмещаем похожие сроки и выполняем операции. Чтобы решить, мы изолируем переменную.
Пример 5: Алгебраическое решение неравенства
Решите неравенство: [латекс] 13 — 7x \ ge 10x — 4 [/ латекс].
Решение
Решение этого неравенства аналогично решению уравнения до последнего шага.
[латекс] \ begin {array} {ll} 13 — 7x \ ge 10x — 4 \ hfill & \ hfill \\ 13 — 17x \ ge -4 \ hfill & \ text {Переместите переменные члены в одну сторону неравенства} . \ hfill \\ -17x \ ge -17 \ hfill & \ text {Изолировать термин переменной}. \ hfill \\ x \ le 1 \ hfill & \ text {Разделение обеих сторон на} -17 \ text {отменяет неравенство }. \ hfill \ end {array} [/ latex]
Множество решений задается интервалом [latex] \ left (- \ infty, 1 \ right] [/ latex] или всеми действительными числами, меньшими чем 1 включительно.
Попробуй 5
Решите неравенство и запишите ответ, используя интервальную запись: [latex] -x + 4 <\ frac {1} {2} x + 1 [/ latex].
Решение
Пример 6: Решение неравенства с дробями
Решите следующее неравенство и запишите ответ в интервальной записи: [latex] — \ frac {3} {4} x \ ge — \ frac {5} {8} + \ frac {2} {3} x [/ latex ].
Решение
Мы начинаем решать так же, как и при решении уравнения.
[латекс] \ begin {array} {ll} — \ frac {3} {4} x \ ge — \ frac {5} {8} + \ frac {2} {3} x \ hfill & \ hfill \\ — \ frac {3} {4} x- \ frac {2} {3} x \ ge — \ frac {5} {8} \ hfill & \ text {Поместите переменные члены в одну сторону}.\ hfill \\ — \ frac {9} {12} x- \ frac {8} {12} x \ ge — \ frac {5} {8} \ hfill & \ text {Запишите дроби с общим знаменателем}. \ hfill \\ — \ frac {17} {12} x \ ge — \ frac {5} {8} \ hfill & \ hfill \\ x \ le — \ frac {5} {8} \ left (- \ frac {12 } {17} \ right) \ hfill & \ text {Умножение на отрицательное число отменяет неравенство}. \ Hfill \\ x \ le \ frac {15} {34} \ hfill & \ hfill \ end {array} [/ латекс]
Набор решений — это интервал [latex] \ left (- \ infty, \ frac {15} {34} \ right] [/ latex].
Попробуй 6
Решите неравенство и запишите ответ в интервальной записи: [latex] — \ frac {5} {6} x \ le \ frac {3} {4} + \ frac {8} {3} x [/ latex].


 Кроме того, мы вынесли за скобку
Кроме того, мы вынесли за скобку



 \]
\]


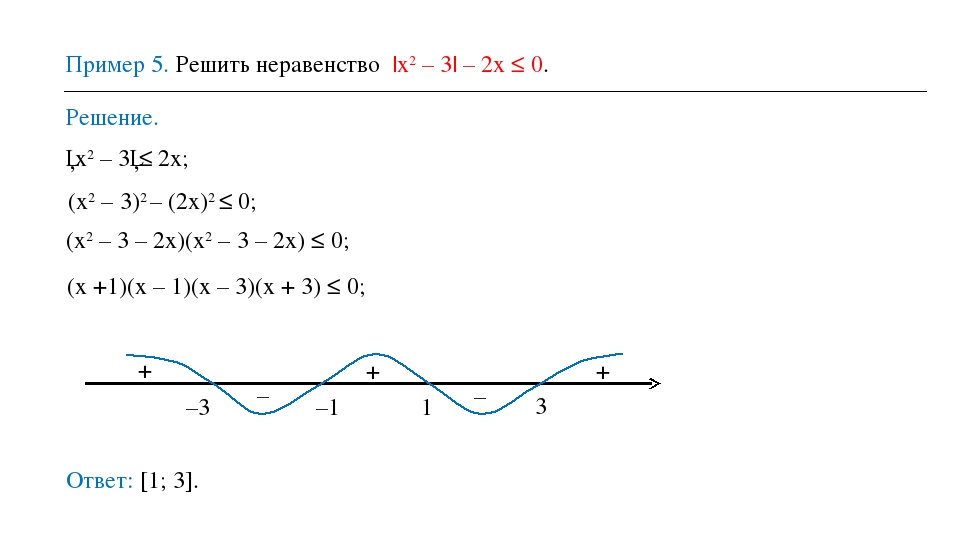 \end{matrix} \right.\]
\end{matrix} \right.\]