Решите уравнение sin x 2 1: решить уравнение sinx/2=1 , указать наименьший положительный корень уравнения

alexxlab

2 — 4 * (1) * (-1) = 4
Т.к. D > 0, то уравнение имеет два корня.

w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b - sqrt(D)) / (2*a)

или
$$w_{1} = 1$$
$$w_{2} = -1$$
делаем обратную замену
$$\sin{\left (x \right )} = w$$
Дано уравнение
$$\sin{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
Или
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (w_{1} \right )}$$
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (1 \right )}$$
$$x_{1} = 2 \pi n + \frac{\pi}{2}$$
$$x_{2} = 2 \pi n + \operatorname{asin}{\left (w_{2} \right )}$$
$$x_{2} = 2 \pi n + \operatorname{asin}{\left (-1 \right )}$$
$$x_{2} = 2 \pi n — \frac{\pi}{2}$$
$$x_{3} = 2 \pi n — \operatorname{asin}{\left (w_{1} \right )} + \pi$$
$$x_{3} = 2 \pi n — \operatorname{asin}{\left (1 \right )} + \pi$$
$$x_{3} = 2 \pi n + \frac{\pi}{2}$$
$$x_{4} = 2 \pi n — \operatorname{asin}{\left (w_{2} \right )} + \pi$$
$$x_{4} = 2 \pi n — \operatorname{asin}{\left (-1 \right )} + \pi$$
$$x_{4} = 2 \pi n + \frac{3 \pi}{2}$$
$$x_{1} = — \frac{\pi}{2}$$
$$x_{2} = \frac{\pi}{2}$$
$$x_{3} = \frac{3 \pi}{2}$$
$$x_{1} = — \frac{\pi}{2}$$
$$x_{2} = \frac{\pi}{2}$$
$$x_{3} = \frac{3 \pi}{2}$$
Данные корни
$$x_{1} = — \frac{\pi}{2}$$
$$x_{2} = \frac{\pi}{2}$$
$$x_{3} = \frac{3 \pi}{2}$$
являются точками смены знака неравенства в решениях. {2}{\left (x \right )} \geq 1$$

   2/  pi   1 \     
sin |- -- - --| >= 1
    \  2    10/     
   2           
cos (1/10) >= 1

но

   2          
cos (1/10) 
Тогда
$$x \leq - \frac{\pi}{2}$$
не выполняется
значит одно из решений нашего неравенства будет при:
$$x \geq - \frac{\pi}{2} \wedge x \leq \frac{\pi}{2}$$
         _____           _____  
        /     \         /
-------•-------•-------•-------
       x1      x2      x3
Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ:
$$x \geq - \frac{\pi}{2} \wedge x \leq \frac{\pi}{2}$$
$$x \geq \frac{3 \pi}{2}$$
Содержание
 
Mathway | Популярные задачи
























































































































































































































































































































1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8Найти точное значениеcos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15Найти точное значениеcsc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. 3
6Risolvere per ?cos(x)=1/2
7Risolvere per xsin(x)=-1/2
8Преобразовать из градусов в радианы225
9Risolvere per ?cos(x)=( квадратный корень 2)/2
10Risolvere per xcos(x)=( квадратный корень 3)/2
11Risolvere per xsin(x)=( квадратный корень 3)/2
12Графикg(x)=3/4* корень пятой степени x
13Найти центр и радиусx^2+y^2=9
14Преобразовать из градусов в радианы120 град. 2+n-72)=1/(n+9)
Решение тригонометрических уравнений
Мы уже познакомились с формулами корней более простых тригонометрических уравнений 
cos x = a, sin x = a, tg x = a. К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большей части таких уравнений необходимо использование формул преобразований тригонометрических выражений. Рассмотрим некоторые способы и примеры решения тригонометрических уравнений.
1. Уравнения, сводящиеся к квадратам
Задача 1.
Решить уравнение sin2 x + sin x – 2 = 0.
Решение.
Это уравнение является квадратным относительно sin x. Если мы обозначим sin x = у, то наше уравнение примет вид: у2 + у – 2 = 0. Решив это уравнение, мы получаем его корни: у1 = 1, у2 = -2. Таким образом, решение исходного уравнения свелось к решению простейших уравнений sin x = 1 и sin x = -2.
Корнем уравнения sin x = 1 является х = π/2 + 2πn, n € Z; уравнение sin x = -2 не имеет корней.
Ответ. х = π/2 + 2πn, n € Z.
Задача 2.
Решить уравнение 2 cos2x – 5 sin x + 1 = 0.
Решение.
Заменим cos2x на 1 – sin2 x и получим: 2(1 – sin2 x) – 5 sin x + 1 = 0, или 2 sin2 x + 5 sin x – 3 = 0.
Обозначив sin x = у, мы получили: 2у2 + 5у – 3 = 0, откуда у1 = -3, у2 = 1/2.
1) sin x = -3 – уравнение не имеет корней, так как |-3|> 1.
2) sin x = 1/2, х = (-1)n arcsin 1/2 + πn = = (-1)n π/6 + πn, n € Z.
Ответ. х = (-1)n π/6 + πn, n € Z.
2. Уравнения вида а sin x + b cosx = c
Задача 3.
Решить уравнение 2 sin x – 3 cosx = 0.
Решение.
Разделим на cos x обе части уравнения и получим 2 tg x – 3 = 0, tg x = 3/2, х = arctg 3/2 + πn, n € Z.
Ответ. х = arctg 3/2 + πn, n € Z.
При решении этой задачи обе части уравнения 2 sin x – 3 cosx = 0 были разделены на cos x. Мы должны помнить, что в результате деления уравнения на выражение, которое содержит неизвестное, корни могут быть потеряны. Поэтому нужно проверить, не являются ли корни уравнения cos x = 0 корнями данного уравнения. Если cos x = 0, то из уравнения 2sin x – 3 cos x = 0 следует, что  sin x = 0. Однако sin x и cos х одновременно не могут быть равными нулю, в силу того что они связаны равенством sin2x + cos2x = 1. Следовательно, при делении уравнения а sin x + b cosx = 0, где а ≠ 0, b ≠ 0, на cos x (или sin x) корни этого уравнения не теряются.
3. Уравнения, решаемые разложением левой части на множители
Многие уравнения, в правой части которых располагается 0, решаются путем разложения на множители их левой части.
Задача 4.
Решить уравнение sin 2x – sinx = 0.
Решение.
Воспользуемся формулой синуса двойного аргумента и запишем уравнение в виде 2 sin x cosx – sin x = 0.
Общий множитель sin x вынесем за скобки и получим sin x(2 cosx – 1) = 0.
1) sin x = 0, х = πn, n € Z.
2) 2 cosx – 1 = 0, cosx = 1/2, х = +/-π/3 + 2πn, n € Z.
Ответ. х = +/-π/3 + 2πn, n € Z.
Задача 5.
Решить уравнение cos 3x + sin 5x = 0.
Решение.
Используя формулу приведения sin α = cos (π/2 – α), запишем уравнение в виде cos 3x + cos (π/2 – 5х)= 0.
Воспользуемся формулой для суммы косинусов и получим:
2 cos(π/4 – х) ∙ cos (4х – π/4)= 0.
1) cos(π/4 – х) = 0, х – π/4 = π/2 + πn, х = 3/4 π + πn, n € Z;
2) cos (4х – π/4)= 0, 4х – π/4 = π/2 + πn, х = 3/16 π + (πn)/4, n € Z.
Ответ. х = 3/4π + πn, х = 3/16π + (πn)/4, n € Z.
Задача 6.
Решить уравнение sin 7x + sin 3x = 3 cos 2х.
Решение. 
Применим формулу суммы синусов и запишем уравнение в виде
2 sin 5x ∙ cos 2х = 3 cos 2х, или 2 sin 5x ∙ cos 2х – 3 cos 2х = 0,
откуда cos 2х(sin 5x – 3/2) = 0.
Уравнение cos 2х = 0 имеет корни х = π/4 + (πn)/2, а уравнение sin 5x = 3/2 не имеет корней.
Ответ. х = π/4 + (πn)/2, n € Z.
© blog.tutoronline.ru,
 при полном или частичном копировании материала ссылка на первоисточник обязательна.
Простейшие тригонометрические уравнения. 10-й класс
Цель урока: сформировать у учащихся представление о 
 решении простейших тригонометрических уравнений.

 
Образовательные задачи: формирование нового понятия: 
 “тригонометрические уравнения”.

 
 
Воспитательные задачи: продолжение работы по воспитанию 
 взаимопомощи, культуры общения, способствующих созданию благоприятного 
 психологического климата в классе, воспитанию внимания, самоконтроля, интереса к 
 предмету.

 
Развивательные задачи: развитие умения выделять 
 “главное”, умения преодолевать трудности в учении.

 
Ход урока
1. С какими тригонометрическими функциями мы знакомы? (Их 
 называют основными).
2. Какие из этих функций четные, какие – нет?
3. Чему равен период функций: y = sin(x), y = cos(x), y = 
 tg(x), y = ctg(x)?
Кроме этих основных тригонометрических функций иногда 
 рассматривают и следующие тригонометрические функции?
y = 1/cos(x) -секанс х
y = 1/sin(x) -косеканс x
Уравнение f(x) = a, где а – данное число, f(x) – одна из 
 основных тригонометрических функций, называют простейшим тригонометрическим 
 уравнением.
Рассмотрим уравнение sin(x) = a.
Если -1 < a < 1, то уравнение имеет 2 серии решений:
x = arcsin a + 2πn, n € Z
x =π — arcsin a + 2πm, m € Z
А если эти серии ответов соединить, то общая формула:
x =
 arcsin a + πn, n € Z
Рассмотрим частные случаи:
1) sin(x) = -1 sin(x) = 0 sin(x) = 1
x = -π/2 + 2 πn, n € Z x = πk, k € Z x = π /2 + 2πk, k € Z
При a>1, a<-1 нет решения.
Решите уравнения:
  1. sin(x) = 1/2
    2. 
Ответ:
x = π/6 +2πk, k € Z
x = 5π/6 +2πm, m € Z
Решите уравнение:
  1. sin(x) =
     /2
    2. 
  2. sin(x) = -/2
    3. 
  3. sin(x) = 1/7
    4. 
  4. sin(x) = π
    5. 
(Ученики решают самостоятельно, ответы показывают на рисунке)
Далее обсуждаются решения, проверяются ответы, находятся 
 причины ошибок.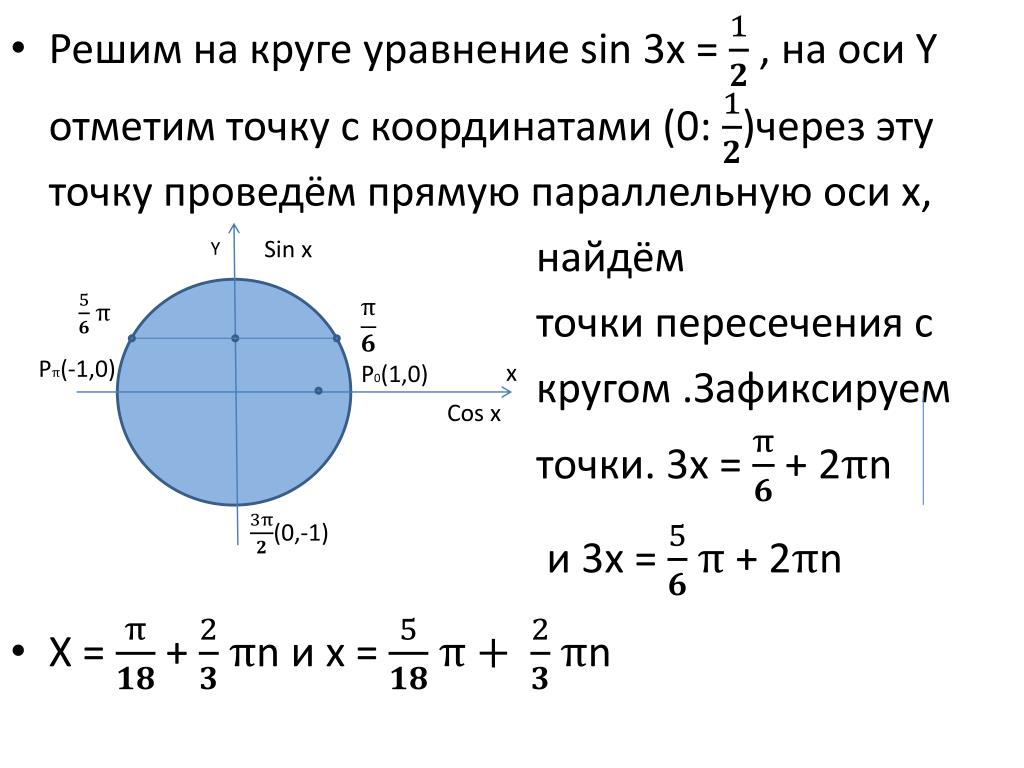
  1. Уравнение cos(x) = a.
    2. 
Если -1 < a < 1, то уравнение имеет 2 серии решений.
Если a>1, a<-1 – уравнение решения не имеет.
Итак, cos(x) = a:

x = arcos a +2πn, n € Z

x = -arcos a +2πm, m € Z

Общий вид ответов: x = + arcos a +2πn, n € Z.

Решим уравнение:

cos(x) =/2

x =

x =

Рассмотрим частные случаи (показываем на рисунке):

cos(x) = 0

x =π/2 +πn, n € Z

cos(x) = 1

x = 2πn, n € Z

 
 
 
 
 
cos(x) = -1

x = π+2πn, n € Z.

 
При a>1 или a<-1 уравнение решения не имеет, т.к. -1<cos(x)<1, 
 например:

cos(x) = 2 нет решений.

Решите уравнения:

1) cos(x) = 1/2

2) cos(x) = -1/2

(Ученики решают, учитель пишет на доске).
Далее самостоятельная работа на обратной стороне доски, 
 ответы показываются через мультимедийный экран.

1) 2sin(x) = 2

2) 2cos(x) -1 = 0

3) sin(x) = -2/3

 
 
4) cos(x) +/2 
 = 0

5) sin(x) = 7/2

6) Если останется время,

то: sin 2x = 
 1/4

7) cos(2x) =1/2
После проверки ответов обсуждаются допущенные ошибки, 
 уточняются их причины и ликвидируются пробелы. При возможности ученикам, 
 допустившим ошибки, предлагаются еще несколько аналогичных заданий. Желательно 
 предлагать ученикам показывать ответы не через общие формулы, а с помощью 
 чертежа.

 
Домашнее задание: (из учебника С.М. Никольского “Алгебра и начала анализа, 
 10-11 кл.”)
№ 11.3 (д, ж, к, л, м),
11.5 (в, г),
11.6 (а, б).
Решутест. Продвинутый тренажёр тестов
а) Используем формулу приведения:
cos$\left(\displaystyle\frac{3\pi}{2}+2x\right)$ = cosx.
Напомним, что можно обойтись без понятия формулы приведения, расписав косинус суммы двух углов и подставив в полученное выражение значения функций синус и косинус в точке $\displaystyle\frac{3\pi}{2}$.
2sinx·cosx = cosx, теперь вынесем общий множитель за скобку:
sin2x = cosx;
2sinx·cosx = cosx;
2sinx·cosx – cosx = 0;
cosx·(2sinx – 1) = 0.
Тогда cosx = 0 или sinx = $\displaystyle\frac{1}{2}$.
Решая cosx = 0 получим: x = $\displaystyle\frac{\pi}{2}$ + πk, k ϵ $\mathbb{Z}$.
Решая sinx = $\displaystyle\frac{1}{2}$ получим: x = $\displaystyle\frac{\pi}{6}$ + 2πk, k ϵ $\mathbb{Z}$ или x = $\displaystyle\frac{5\pi}{6}$ + 2πk, k ϵ $\mathbb{Z}$.
Таким образом: x = $\displaystyle\frac{\pi}{2}$ + πk, x = $\displaystyle\frac{\pi}{6}$ + 2πk, x = $\displaystyle\frac{5\pi}{6}$ + 2πk, k ϵ $\mathbb{Z}$.
б) С помощью единичной окружности отберём корни на отрезке $\left[\displaystyle\frac{5\pi}{2};4\pi\right]$.
Находим: $\displaystyle\frac{5\pi}{2},\,\frac{17\pi}{6},\,\frac{7\pi}{2}$.
Без расчётов, визуально сходу определить корни принадлежащие отрезку может далеко не каждый, нужна серьёзная практика, поэтому покажем безошибочный способ отбора корней, которым советуем пользоваться: переведём радианы в градусы. Так как π радиан это 180º, то отрезок $\left[\displaystyle\frac{5\pi}{2};4\pi\right]$ будет выглядеть следующим образом: [450º; 720º]. Отберём корни, подставляя значения k в полученное решение уравнения:
При k = 1:
x = $\displaystyle\frac{\pi}{2}$ + π = $\displaystyle\frac{\pi}{2}$ + $\displaystyle\frac{2\pi}{2}$ = $\displaystyle\frac{3\pi}{2}$ = 270º;
x = $\displaystyle\frac{\pi}{6}$ + 2π = $\displaystyle\frac{\pi}{6}$ + $\displaystyle\frac{12\pi}{6}$ = $\displaystyle\frac{13\pi}{6}$ = 390º;
x = $\displaystyle\frac{5\pi}{6}$ + 2π = $\displaystyle\frac{5\pi}{6}$ + $\displaystyle\frac{12\pi}{6}$ = $\displaystyle\frac{17\pi}{6}$ = 510º.
При k = 2:
x = $\displaystyle\frac{\pi}{2}$ + 2π = $\displaystyle\frac{\pi}{2}$ + $\displaystyle\frac{4\pi}{2}$ = $\displaystyle\frac{5\pi}{2}$ = 450º;
x = $\displaystyle\frac{\pi}{6}$ + 4π = $\displaystyle\frac{\pi}{6}$ + $\displaystyle\frac{24\pi}{6}$ = $\displaystyle\frac{25\pi}{6}$ = 750º;
x = $\displaystyle\frac{5\pi}{2}$ + 4π = $\displaystyle\frac{5\pi}{2}$ + $\displaystyle\frac{24\pi}{6}$ = $\displaystyle\frac{29\pi}{6}$ = 870º.
При k = 3:
x = $\displaystyle\frac{\pi}{2}$ + 3π = $\displaystyle\frac{\pi}{2}$ + $\displaystyle\frac{6\pi}{2}$ = $\displaystyle\frac{7\pi}{2}$ = 630º;
x = $\displaystyle\frac{\pi}{6}$ + 6π = $\displaystyle\frac{\pi}{6}$ + $\displaystyle\frac{36\pi}{6}$ = $\displaystyle\frac{37\pi}{6}$ = 1100º;
x = $\displaystyle\frac{5\pi}{6}$ + $\displaystyle\frac{36\pi}{6}$ = $\displaystyle\frac{41\pi}{6}$ = 1230º.
При k = 4: проверять корни нет смысла, так как видно, что результат будет лежать вне пределов интервала: x = $\displaystyle\frac{\pi}{2}$ + 4π > 720º.
Отрезку [450º; 720º] принадлежат корни 390º; 450º; 510º, в радианах это $\displaystyle\frac{5\pi}{2},\,\displaystyle\frac{17\pi}{6},\,\displaystyle\frac{7\pi}{2}$. Ответ можно записывать либо в градусах, либо радианах, значения не имеет.
 Trignet 
 Триггерные уравнения могут быть квадратичными, например: 
 2 sin²x — sin x — 1 = 0 
 К квадратным тригонометрическим уравнениям применяются те же правила, что и
 с регулярными квадратными уравнениями. 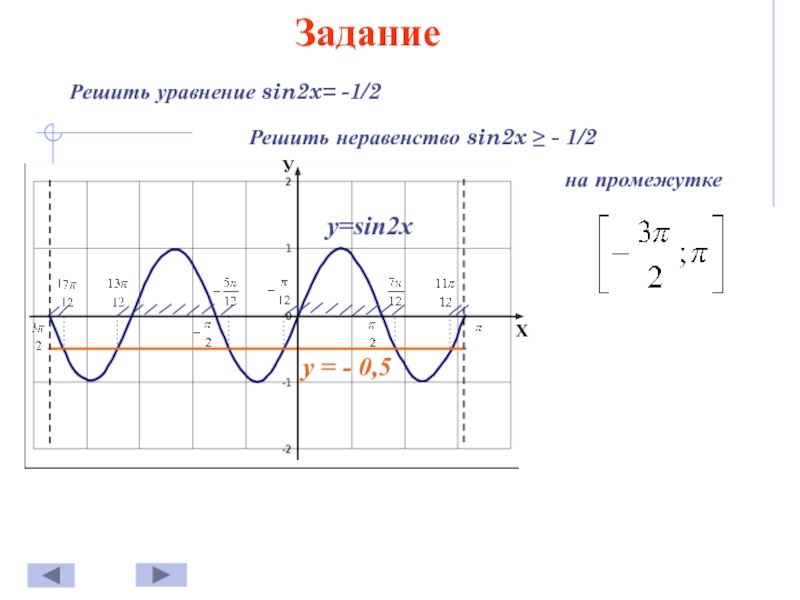Решите их факторингом
 или используя квадратное уравнение.
 Решить: 
 2 sin²x — 3 sin x + 1 = 0 в интервале
 [0, 2] 
 (2 грех х — 1) (грех х — 1) = 0
 2 sin x — 1 = 0 грех х — 1 = 0
 sin x = 1/2 грех х = 1
 х = / 6,
 5/6		 х = / 2
 При факторизации убедитесь, что каждое квадратное уравнение
 имеет только одну триггерную функцию i.е. синус, косинус и т. д. Если
 у него нет только одной функции, используйте базовый триггер
 тождества, чтобы изменить уравнение. 
 3 сек² x — 2 tan²x — 4 = 0 
 3 (tan² x + 1) — 2 tan² x — 4 =
 0 
 tan² x — 1 = 0 
 tan² x = = 1 
 тангенс угла x = ± 1 
 х = / 4 +
 п 
 х = 3/4
 + п
 Иногда невозможно решить уравнение
 как есть и должно быть возведено в квадрат, чтобы сделать его квадратичным.Дополнительный
 решения, которые могут стать очевидными, могут не
 применимо к исходному уравнению.
 грех х + 1 = соз х 
 sin²x + 2 sin x + 1 = cos²x 
 sin²x + 2 sin x + 1 = 1 — sin²x 
 2 sin²x + 2 sin x = 0 
 2 грех х (грех х + 1) = 0
 2 sin x = 0 грех х + 1 = 0
 грех x = 0 грех х = — 1
 х = 0, х = 3/2
 Поскольку исходное уравнение было возведено в квадрат, каждое решение
 необходимо проверить и подтвердить исходным уравнением. Значение
 не подходит для x, потому что: 
 грех + 1
 ? cos 
 0 + 1? — 1 
 Следовательно, единственные решения в интервале [0, 2),
 единственные решения: x = 0, 3/2.
 Тригонометрические уравнения — Учебные материалы для IIT JEE 
 Уравнение, включающее одно или несколько тригонометрических отношений неизвестного угла, называется тригонометрическим уравнением e.грамм. cos  2  x — 4 sin x = 1
 Следует отметить, что тригонометрическое тождество выполняется для каждого значения неизвестного угла, тогда как тригонометрическое уравнение выполняется только для некоторых значений (конечных или бесконечных) неизвестного угла.
 например sec  2  x — tan  2  x = 1 является тригонометрическим тождеством, поскольку оно выполняется для любого значения x Î R.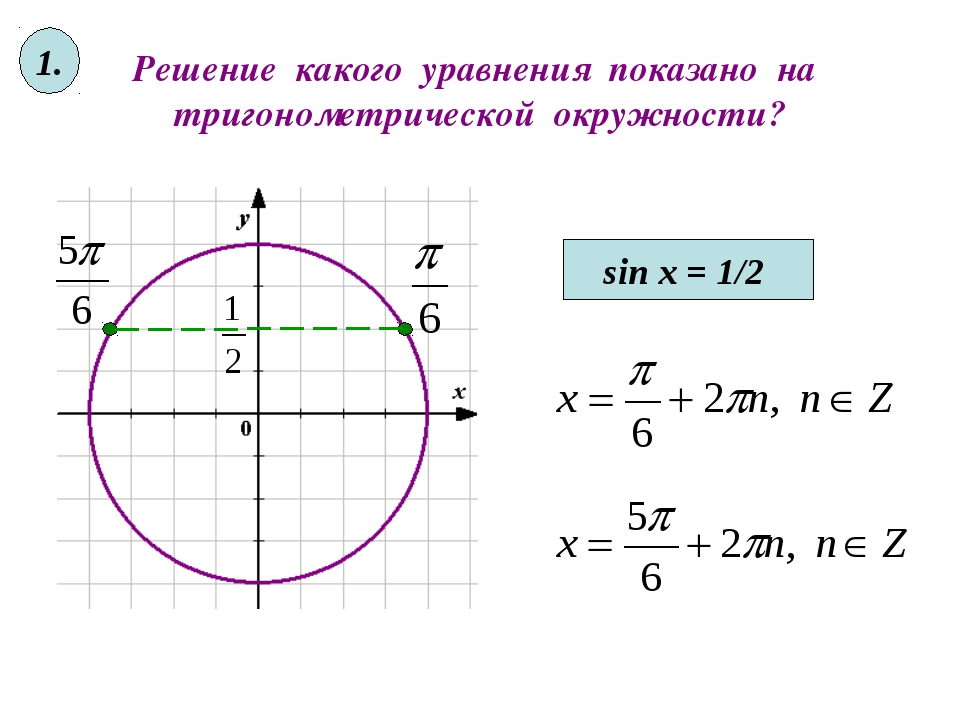
  РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКОГО УРАВНЕНИЯ 
 Значение неизвестного угла, которое удовлетворяет данному уравнению, называется решением уравнения e.грамм. грех q = ½ Þq = p / 6.
  Общее решение 
 Поскольку тригонометрические функции являются периодическими функциями, решения тригонометрических уравнений могут быть обобщены с помощью периодичности тригонометрических функций. Решение, состоящее из всевозможных решений тригонометрического уравнения, называется его общим решением.
 Мы используем следующие формулы для решения тригонометрических уравнений:
 · грех q = 0 Þ q = np,
 · cos q = 0 Þq = (2n + 1),
 · тангенс q = 0 Þ q = np,
 · sin q = sin a Þq = np + (–1)  n  a, где aÎ [–p / 2, p / 2]
 · cos q = cos aÞq = 2np ± a, где aÎ [0, p]
 · tan q = tan a Þ q = np + a, где aÎ (–p / 2, p / 2)
 · sin  2  q = sin  2  a, cos  2  q = cos  2  a, tan  2  q = tan  2  aÞq = np ± a,
 · грех q = 1 Þq = (4n + 1),
 · cos q = 1 Þ q = 2np,
 · cos q = –1 Þ q = (2n + 1) p,
 · sin q = sin a и cos q = cos aÞ q = 2np + a.
  Примечание: 
 · Повсюду в этой главе n принимается как целое число, если не указано иное.
 · Общее решение должно быть дано, если решение не требуется в указанном интервале.
 За главное значение угла принимается
 · a. Численно наименьший угол называется главным значением.
  Метод определения основной стоимости 
 Предположим, нам нужно найти главное значение, удовлетворяющее уравнению sin = -.
 Так как sin отрицателен, будет в 3-м или 4-м квадранте. Мы можем подойти к 3-му или 4-му квадранту с двух сторон. Если мы возьмем направление против часовой стрелки, числовое значение угла будет больше чем. Если подойти к нему по часовой стрелке, угол будет численно меньше, чем. За главное значение мы должны взять численно наименьший угол.
 Итак, для основной суммы:
 1. Если угол находится в 1-м или 2-м квадранте, мы должны выбрать направление против часовой стрелки, а если угол, если угол находится в 3-м или 4-м квадранте, мы должны выбрать направление по часовой стрелке.
 2. Главное значение никогда не может быть численно больше, чем.
 3. Главное значение всегда находится в первом круге (т.е. в первом повороте)
 По вышеперечисленным критериям будет или. Среди этих двух наименьшее числовое значение. Отсюда главное значение удовлетворения уравнения sin = -.
  Алгоритм нахождения главного аргумента: 
  Шаг 1:  Сначала нарисуйте тригонометрический круг и отметьте квадрант, в котором может лежать угол.
  Шаг 2:  Выберите направление против часовой стрелки для 1-го и 2-го квадрантов и выберите направление по часовой стрелке для 3-го и 4-го квадрантов.
  Шаг 3:  Найдите угол при первом повороте.
  Шаг 4:  Выберите численно наименьший угол среди этих двух значений. Найденный таким образом угол будет главной величиной.
  Шаг 5:  В случае, если два угла, один с положительным знаком, а другой с отрицательным знаком, соответствуют численно наименьшему углу, то принято выбирать угол с положительным знаком в качестве главного значения.
  Пример 1:  Iftan = — 1, то будет находиться во 2-м или 4-м квадранте.
 Для 2-го квадранта мы выберем против часовой стрелки, а для 4-го квадранта. мы выберем направление по часовой стрелке.
 В первом кружке получены два значения и.
 Среди этих двух наименьший угол. Следовательно, главное значение.
  Пример 2:  Если cos =, то будет лежать в квадранте 1   или 4  .
 Для 1-го квадранта мы выберем направление против часовой стрелки, а для 4-го квадранта мы выберем направление по часовой стрелке.
 Таким образом, в первом круге находятся два значения и.
 Оба и — имеют одинаковое числовое значение. В таком случае будет выбрано главное значение.
   Рисунок 17: Решить кроватку (sinx + 3) = 1. 
   Решение:   sinx + 3 = Þ Þ n = 1 Þ sinx =
 Þ x = или
   Иллюстрация 18: Если sin 5x + sin 3x + sin x = 0, то найдите значение x, отличное от нуля, лежащее между 0     £     x     £        .  
   Решение:   sin 5x + sin 3x + sin x = 0 Þ (sin 5x + sin x) + sin 3x = 0
 Þ 2 sin 3x cos 2x + sin 3x = 0 Þ sin 3x (2 cos 2x + 1) = 0
 Þ sin 3x = 0; cos 2x = — Þ 3x = np, 2x = 2np ±
 Требуемое значение x равно.
   Рисунок 19: Найти весь острый угол     a    , такой что cos     a     cos 2     a     cos 4  
9  a    =        .  
   Решение:   Дано, что cosa cos2a cos4a =
 2sina cosa cos2a cos4a = Þ 2sin2a cos2a cos4a =
 Þ 2sin4a cos4a = sinaÞ sin8a — sina = 0
 Þ 2sincos = 0
 Либо sin = 0 Þ Þa =
 Для n = 0 a = 0, что не является решением.
 Þa = n = 1, т. е. a =
 или cos Þ = (2n + 1) Þa = (2n + 1) Þa =
 Следовательно, a =.
   Рисунок 20: Решить относительно x:        .  
   Решение:      
 Þ
 Þ
 Þ
 sin2x = ± 1 Þ 2x = (2n + 1) Þ x = (2n + 1), n ​​I
 ЦЕЛЬ 
 1: Общее значение q, удовлетворяющее обоим требованиям, составляет:
.
 (А) 2нп (Б) 2нп + 7п / 6
 (К) нп + п / 4 (Д) 2нп + п / 4
 Решение: Давайте сначала выясним, что q лежит между 0 и 360 °.
 Так как Þq = 210 ° или 330 °
 и Þq = 30 ° или 210 °
 Следовательно, q = 210 ° или значение, удовлетворяющее обоим требованиям.
 \ Общая стоимость
 Следовательно, (B) — правильный ответ.
 2: Ö3 сек20 ° — сек20 ° =
 (А) 1 (В) 2
 (К) 3 (Г) 4
 Решение: Дано =
 =
 Следовательно (D) — правильный ответ.
 3: загар A + 2 загар 2A + 4 загар 4A + 8 кроватка 8A =
 (A) Детская кроватка A (B) желто-коричневый 6A
 (C) детская кроватка 4A (D) Ни один из этих
 Раствор: tan A + 2 tan 2A + 4 tan 4A + 8 cot 8A
 = tanA + 2tan2A + 4tan4A + 8 
 = детская кроватка
 Следовательно (А) — правильный ответ.
 4: Значение греха 12 °. sin48 ° .sin54 ° =
 (А) 1/8 (В) 1/6
 (C) 1/4 (D) 1/2
 Решение: sin 12 °. sin48 ° .sin54 ° =
 =
 =
 =
 =
 Альтернативный метод
 Пусть q = 12 °
 sin 12 °.sin48 ° .sin54 ° =
 =
 Следовательно (А) — правильный ответ.
 5: Наименьшее положительное значение x (в градусах), для которого 
 загар (x + 100 °) = загар (x + 50 °) загар x загар (x — 50 °) составляет:
 (А) 30 ° (В) 45 °
 (С) 60 ° (Г) 90 °
 Решение: Отношение можно записать как
 Þ
 Þ
 Þ Þ cos50 ° + 2sin (2x + 50 °) cos (2x + 50 °) = 0
 cos50 ° + sin (4x + 100 °) = 0 Þ cos50 ° + cos (4x + 10 °) = 0
 cos (2x + 30 °) cos (2x — 20 °) = 0 Þ x = 30 °, 55 °
 Þ Наименьшее значение x = 30 °
 Следовательно (А) — правильный ответ.
 6. Наиболее общее значение q, удовлетворяющее 3 — 2cosq –4sinq –cos2q + sin2q = 0:
 (А) 2нп (Б) 2нп + п / 2
 (К) 4нп (Д) 2нп + п / 4
 Решение: 3 — 2cos q — 4 sin q — cos 2q + sin 2q = 0
 Þ 3 — 2cos q — 4 sin q — 1 + 2sin  2  q + 2sin q cos q = 0
 Þ 2sin  2  q — 2cosq — 4sin q + 2sin q cos q + 2 = 0
 Þ (sin  2  q — 2sin q + 1) + cos q (sinq — 1) = 0
 Þ (sin q — 1) [sin q — 1 + cos q] = 0
 либо sin q = 1
 Þq = 2np + p / 2, где n Î I
 или, sin q + cos q = 1
 cos (q — p / 4) = cos (p / 4) Þq — p / 4 = 2np ± p / 4
 Þ q = 2np, 2np + p / 2, где n Î I
 Следовательно, q = 2np, 2np + p / 2.
 Следовательно (A, B) — правильный ответ.
 7: Если sinq = 3sin (q + 2a), то значение tan (q + a) + 2tana равно:
 (А) 0 (В) 2
 (К) 4 (Г) 1
 Решение: дан sin q = 3sin (q + 2a)
 Þ грех (д + а-а) = 3 син (д + а + а)
 Þ sin (q + a) cosa — cos (q + a) sina
 = 3sin (q + a) cosa + 3cos (q + a) sina
 Þ –2sin (q + a) cosa = 4cos (q + a) sina
 Þ
 Þ загар (д + а) + 2тана = 0
 Следовательно (А) — правильный ответ.
 8: Минимальное значение 3tan  2  q + 12 cot  2  q составляет:
 (А) 6 (В) 8
 (C) 10 (D) Ни один из этих
 Решение: A.M. ³ G.M Þ (3tan  2  q +12 детская кроватка  2  q) ³ 6
 Þ 3 tan  2  q + 12cot  2  q имеет минимальное значение 12.
 Следовательно (D) — правильный ответ.
 9: Если A + B + C =, то значение tanA + tanB + tanC равно:
 (А) 3 (В) 2
 (C)> 3 (D)> 2
 Решение: tan (A + B) = tan (- C)
 или, = tanC
 или, tanA + tanB + tanC = tana tanB tanC
 [с А.M. G.M.]
 или, tanA tanB tanC
 или, A B C 27 [в кубе с обеих сторон]
 или tanA tanB tanC 3
 tanA + tanB + tanC 3.
 Следовательно (А) — правильный ответ.
 10: Пусть 0 
 (А) (В)
 (C) (D) Ничего из этого.
 Решение: Из второго уравнения имеем
 sin2B = sin2A… (1)
 и из первого равенства
 3A = 1-2 B = cos2B… (2)
 Теперь cos (A + 2B) = cosA. cos2B — sinA. sin2B
 = 3 cosA. А -. sinA. sin2A
 = 3cosA. А — 3А.cosA = 0
 A + 2B = или
 При условии, что 0 
 Следовательно, A + 2B =.
 Следовательно (C) — правильный ответ.
 11: Если a cos  3  q + 3a cos q sin  2  q = x и a sin  3  q + 3a cos  2  q sin q = y, то (x + y)  2/3  + (x — y)  2/3  =
 (A) 2a  2/3  (B) a  2/3 
 (C) 3a  2/3  (D) 2a  1/3 
 Решение: a cos  3  q + 3a cos q sin  2  q = x
 a sin  3  q + 3a cos  2  q sin q = y
 x + y = a [sin  3  q + cos  3  q + 3 sin q cos q (sin q + cos q)] = a (sinq + cosq)  3 
 = sin q + cos q …… (1)
 x — y = a [cos  3  q — sin  3  q + 3 cosq sin  2  q — 3 cos  2  q sin q] = a [cosq — sinq]  3 
 = cos q — sin q …… (2)
 (sin q + cos q)  2  + (cos q — sin q)  2  =
 2 (sin  2  q + cos  2  q) =
 (x + y)  2/3  + (x — y)  2/3  = 2a  2/3 .
 Следовательно (А) — правильный ответ.
 12: Если, то sin4a =
 (А) а / 2 (В) а
 (К) а  2/3  (Г) 2а
 Решение: Пусть a = sin 4qÞ = cos 2q + sin 2q и = cos 2q — sin 2q
 (1 +) загар а = (1 +)
 Þ (1 + cos 2q + sin 2q) tan a = 1 + cos 2q — sin 2q
 Þ = детская кроватка
 Þ = детская кроватка
 Þ
 Þ загар = загар Þq =
 Þ a = sin 4q = sin (p — 4a) = sin 4 a
 Следовательно, (B) — правильный ответ.
 13: Если cos  2  q = и tan  2  = tan  2/3  a, то cos  2/3  a + sin  2/3  a =
 (А) 2а  2/3  (В)
 (C) (D) 2a  1/3 
 Решение: cos  2  q =, tan  2  = tan  2/3  a
 загар  3  = загар aÞ
 = к
 sin  3  = k sin a …… (1)
 cos  3  = k cos a …… (2)
 k  2/3  sin  2/3  a + k  2/3  cos a = 1
 sin  2/3  a + cos  2/3  a =
 Возведение в квадрат и сложение (1) и (2)
 k  2  (sin  2  a + cos  2  a) = sin  6  + cos  6  =
 к  2  = 1 — sin  2  q = 1 — + cos  2  q
 к  2  = Þ к =
 sin  2/3  a + cos  2/3  a =.
 Следовательно, (B) — правильный ответ.
 14: Если 3 sin  2  a + 2 sin  2  b = 1 и 3 sin 2a –2 sin 2b = 0, где a, b — положительные острые углы, то a + 2b =
 (А) (В)
 (К) (Г)
 Решение: 3 sin  2  a + 2 sin  2  b = 1 …… (1)
 3 sin 2a = 2 sin 2b …… (2)
 3 sin  2  a = 1-2 sin  2  b = cos 2b
 3 sin a sin a = cos 2b …… (3)
 из уравнения (2)
 3.2 sin a cos a = 2 sin 2b
 3 sin a =
 из уравнения (3)
 sin a = cos 2b
 cos a cos 2b — sin a sin 2b = 0
 cos (a + 2b) = 0
 Þa + 2b =.
 Следовательно (А) — правильный ответ.
 15: Значение:
 (А) (В)
 (К) (Г)
 Решение:
 =
 =
 =
 Следовательно (А) — правильный ответ.
 16: Количество решений sin  3  x cos x + sin  2  x cos  2  x + sin x cos  3  x = 1 в [0, 2p] равно
 (А) 4 (В) 2
 (К) 1 (Д) 0
 Решение: sin x cos x [sin  2  x + sin x cos x + cos  2  x] = 1
 Þ sin x cos x + (sin x cos x)  2  = 1
 sin  2  2x + 2 sin 2x –4 = 0 Þ sin 2x =, что невозможно.
 Следовательно (D) — правильный ответ.
 17: Число решений уравнения x  3  + 2x  2  + 5x + 2cosx = 0 в 
 [0, 2p]:
 (А) 0 (В) 1
 (К) 2 (Г) 3
 Решение: Пусть f (x) = x  3  + 2x  2  + 5x +2 cosx
 Þ f ¢ (x) = 3x  2  + 4x + 5-2 sinx
 = 3
 Now «x (as -1 £ sinx £ 1)
 Þ f ¢ (x)> 0 дюймов x
 Þ f (x) — возрастающая функция.
 Теперь f (0) = 2
 Þ f (x) = 0 не имеет решения в [0, 2p].
 Следовательно (А) — правильный ответ.
 18: значение равно
.
 (А) -1 (Б)
 (К) (Г)
 Решение:.
 Следовательно (D) — правильный ответ.
 19: sinnx =, где n — нечетное натуральное число, тогда:
 (А) = 1, = 2n (B) = 1, = n
 (C) = 0, = n (D) = 0, = -n
 Решение: sin nx = Im (e  in x ) = Im ((cosx + i sinx)  n )
…..
 Поскольку n нечетно, пусть n = 2 + 1
 sin nx = — +….
 = — + +….
 =
 Следовательно (C) — правильный ответ.
 20: Если tanx = n. tany, n, то максимальное значение (x — y) равно:
 (А) (В)
 (К) (Г)
 Решение: tanx = n tany, cos (x — y)
 = cosx.уютный + sinx.siny.
 cos (x — y) = cosx.cosy (1 + tanx.tany)
 = cosx. уютный (1 + п загар  2  л)
 Сейчас,
 Следовательно (D) — правильный ответ.
 21: Если 3sinq + 5cosq = 5, то значение 5sinq — 3cosq равно
.
 (А) 5 (В) 3
 (C) 4 (D) ни один из этих
 Решение: 3sinq = 5 (1 — cosq) = 5 ´ 2sin  2  q / 2 Þ tanq / 2 = 3/5
 5sinq — 3cosq = =
 Следовательно, (B) — правильный ответ.
 22: В DABC, если cotA cotB cotC> 0, то D равно
 (A) остроугольный (B) прямоугольный
 (C) тупоугольный (D) не существует
 Решение: Поскольку cotA cotB cotC> 0
 cotA, cotB, cotC положительные ÞD остроугольный
 Следовательно (А) — правильный ответ.
 23: Если p <2q <, то равно
 (A) –2cosq (B) –2sinq
 (C) 2cosq (D) 2sinq
 Решение: =
 = 2 | sinq | = 2sinq как
 Следовательно (D) — правильный ответ.
 24: Если tanq = для некоторого неквадратного натурального числа n, то sec2q равно
 (A) рациональное число (B) иррациональное число
 (C) положительное число (D) ни один из этих
 Решение:
, где n — неквадратное натуральное число, поэтому 1 — n ¹ 0.
 Þ sec2q — рациональное число.
 Следовательно (А) — правильный ответ.
 25: минимальное значение cos (cosx) равно
 (A) 0 (B) –cos1
 (C) cos1 (D) –1
 Решение: cos x изменяется от –1 до 1 для всех действительных x.
 Таким образом, cos (cosx) изменяется от cos1 до cos0 Þ минимальное значение cos (cosx) равно cos1.
 Следовательно (C) — правильный ответ.
 26: Если sin x cos y = 1/4 и 3 tan x = 4 tan y, то найдите значение sin (x + y).
 (А) 1/16 (В) 7/16
 (C) 5/16 (D) ни один из этих
 Решение: 3 tan x = 4 tan y Þ 3 sin x cos y = 4 cos x sin y
 Þ 3/4 = 4 cos x sin y Þ cos x sin y = 3/16
 \ sin (x + y) = sin x cos y + cos x sin y =.
 Следовательно, (B) — правильный ответ.
 27: ​​максимальное значение 4sin  2  x + 3cos  2  x + равно
 (А) (В)
 (К) 9 (Г) 4
 Решение: максимальное значение 4sin  2  x + 3cos  2  x, т.е. sin  2  x + 3 равно 4, а значение sin + cos равно =, оба достигаются при x = p / 2.Следовательно, данная функция имеет максимальное значение
.
 Следовательно (А) — правильный ответ.
 28: Если a и b являются решениями sin  2  x + a sin x + b = 0, а также cos  2  x + c cos x + d = 0, то sin (a + b) равен равно
 (А) (В)
 (К) (Г)
 Решение: Согласно данному условию sina + sinb = –a и cosa + cosb = -c.
 Þ
 Þ
 Следовательно (D) — правильный ответ.
 29: Если sina, sinb и cosa находятся в G.P, то всегда корни уравнения x  2  + 2x cot b + 1 = 0.
 (A) равно (B) реально
 (C) мнимая (D) больше 1
 Решение: sina, sinb, cosa в G.С.
 Þ sin  2  b = sina cosaÞ cos2b = 1 — sin2b ³ 0
 Теперь дискриминант данного уравнения равен
.
 4cot  2  b — 4 = 4 cos2b × cosec  2  b³ 0 Þ Корни всегда действительны.
 Следовательно, (B) — правильный ответ.
 30: Если тогда S равно
 (А) (В)
 (К) (Г)
 Решение:
 =
 ==
 Следовательно (C) — правильный ответ.
 31: Если в DABC ÐC = 90 °, то максимальное значение sin A sin B равно
 (А) (В) 1
 (C) 2 (D) Нет
 Решение: sinA sinB =
 == =
 фунтов стерлингов
 Þ Максимальное значение sinA sinB =
 Следовательно (А) — правильный ответ.
 32: Если в DABC sin  2  A + sin  2  B + sin  2  C = 2, то треугольник всегда равен
 (A) равнобедренный треугольник (B) прямоугольный
 (C) остроугольный (D) тупоугольный
 Решение: sin  2  A + sin  2  B + sin  2  C = 2 Þ 2 cos A cos B cos C = 0
 Þ либо A = 90  o , либо B = 90  o , либо C = 90  o 
 Следовательно, (B) — правильный ответ.
 33. Максимальное значение выражения 2sinx + 4cosx + 3 равно
.
 (А) 2 + 3 (В) 2-3
 (C) + 3 (D) ни один из этих
 Решение: максимальное значение 2sinx + 4cosx = 2.
 Следовательно, максимальное значение 2sinx + 4cosx +3 равно
.
 Следовательно (А) — правильный ответ.
 34: Если sinq = 3sin (q + 2a), то значение tan (q + a) + 2tana равно
.
 (А) 3 (В) 2
 (К) 1 (Д) 0
 Решение: дан sin q = 3sin (q + 2a)
 Þ грех (д + а-а) = 3 син (д + а + а)
 Þ sin (q + a) cosa — cos (q + a) sina
 = 3sin (q + a) cosa + 3cos (q + a) sina
 Þ –2sin (q + a) cosa = 4cos (q + a) sina
 Þ
 Þ загар (д + а) + 2тана = 0
 Следовательно (D) — правильный ответ.
 35: Если cos q =, то одно из значений tan равно
 (A) желто-коричневая кроватка (B) желто-коричневая кроватка
 (C) грех грех (D) ни один из этих
 Решение: tan  2  = =
 =
 = =
 = коричневый  2  детская кроватка  2 .
 \ tan = ± желто-коричневая кроватка.
 Следовательно (А) — правильный ответ.
 36. Если tan 2q. tan q = 1, тогда q равно
 (А) (В)
 (C) (D) Ничего из этого.
 Раствор: tan 2q. загар q = 1
.
 Следовательно, (B) — правильный ответ.
 37. Если a является корнем из 25, то sin 2a равен
.
 (А) (В)
 (К) (Г)
 Решение: Поскольку, a является корнем
.
 Следовательно, (B) — правильный ответ.
 38. Уравнение k имеет решение, если
 (А) k> 6 (В)
 (C) k> 2 (D) Ничего из этого.
 Решение: У нас есть k
 Но, следовательно,
 Сейчас,
 Следовательно, (B) — правильный ответ.
 39. Общее решение уравнения tan 3x = tan 5x:
 (А) x = np / 2, n Î Z (B) x = np, n Z
 (C) x = (2n + 1) p, n Î Z (D) Ничего из этого.
 Решение: загар 3x = загар 5x
, если n нечетное, то x = np / 2 дает посторонние решения.Таким образом, решение данного уравнения будет иметь вид x = np / 2, где n даже, скажем, n = 2 m, m Î Z. Следовательно, требуемое решение будет x = m p, m Î Z.
 Следовательно, (B) — правильный ответ.
 40. Уравнение разрешимо, если
 (А) (В)
 (C) (D) Ничего из этого.
 Решение: У нас
 где
 для того, чтобы быть реальным.
 Дискриминант. . . (1)
 Но, следовательно,
. . . (2)
 Из (1) и (2),.
 Следовательно, (B) — правильный ответ.
 41. Набор значений x, для которых
 (A) f (B) с / 4
 (К) (Г)
 Решение:
, но это значение не удовлетворяет данному уравнению и сводится к неопределенному виду.
 Следовательно (А) — правильный ответ.
 42. Если, то q равно
.
 (А) п / 3 (Б) 2п / 3
 (В) п / 6 (Д) 5п / 8
 Решение:
 или
.
 Следовательно (C) — правильный ответ.
 43. Значение выражения
.
 (А) 1/2 (В) 1
 (C) 2 (D) Ни один из них.
 Решение: дано выражение
.
 Следовательно, (B) — правильный ответ.
 44. Если, то q (только главное значение) равно
 (А) п / 3 (Б) 2п / 3
 (В) 4п / 3 (Д) 5п / 3
 Решение:.
 Следовательно (А) — правильный ответ.
 45.Количество решений в интервале [0, 2p] —
.
 (А) 2 (В) 4
 (C) 0 (D) Ничего из этого.
 Решение:
,
 но
 \ Решение не существует.
 Следовательно (C) — правильный ответ.
 46. Если, то общее решение для q равно
.
 (А) (В)
 (C) (D) Ничего из этого.
 Решение:
.
 Следовательно, (B) — правильный ответ.
 47.Количество решений 11 sin x = x равно
 (А) 4 (В) 6
 (C) 8 (D) Ни один из них.
 Решение: 11 sin x = x. . . (1)
 При замене n на — получаем 11 sin (–x) = –x
 Итак, для каждого положительного решения у нас также есть отрицательное решение, и x = 0 удовлетворяет (1), поэтому количество решений всегда будет нечетным.Следовательно, (d0 является подходящим выбором.
 Следовательно (D) — правильный ответ.
 48. Если, то x равно
 (А) (В)
 (C) (D) Ничего из этого.
 Решение: L.H.S.
 и равенство сохраняется для
 и Р.H.S.
 равенство стариков, если.
 Таким образом, L.H.S. = R.H.S. только для.
 Следовательно, (B) — правильный ответ.
 49. Общее решение для q if, равно
 (А) (В)
 (C) (D) Ничего из этого.
 Решение:. . . (1)
 и
 (1) может быть истинным тогда и только тогда, когда оба равны 1 одновременно. Первое общее значение q, для которого
 и
 и с периодичностью p
 и периодичность 2p, следовательно, периодичность 2p. Поэтому общее решение есть.
 Следовательно (А) — правильный ответ.
 50. Если tan a и tan b являются корнями, то значение tan (a + b) равно
.
 (А) (В) 1
 (C) (D) Ничего из этого.
 Решение: корни
 и.
.
 Следовательно (C) — правильный ответ.
 51. Число решений уравнения tan x = sec x = 2 cos x, лежащих в интервале [0, 2p], равно
.
 (А) 0 (В) 1
 (К) 2 (Г) 3
 Решение: Данное уравнение можно записать как
 или –1
 Следовательно, необходимое количество решений — 2.
 Следовательно (C) — правильный ответ.
 52. Если tan mq + cot n q = 0, то общее значение q равно
.
 (А) (В)
 (К) (Г)
 Решение: Данное уравнение можно записать как
 или
.
 Следовательно (А) — правильный ответ.
 53. Общее решение уравнения —
 (А) (В)
 (К) (Г)
 Решение: Пусть
 или
 и
 или
 Используя их в данном уравнении, мы получаем
 или
 или.
 Следовательно (D) — правильный ответ.
 54. Одно из решений уравнения —
 (А) (В)
 (C) (D) Ничего из этого.
 Решение: Данное уравнение можно записать как
 или
 или
 Либо sin q = 0, что дает q = n p
 или что дает
 Сейчас,
 снова
 Таким образом, одним решением данного уравнения является
.
 Следовательно (А) — правильный ответ.
 55. Решите относительно x и y уравнения:
 ху + 3х уютный. у = 14
 ху + 3х. y siny = 13
 (A) y = где 2n 
 (B) y = где 2n + 
 (C) оба
 (D) Ни один из этих
 Решение: очевидно, что, разделив уравнения x 0, мы получим
 по componendo и dividenodo, получаем
 или, = 27 =
 или, =
 разделив числитель и знаменатель на cosy, получим
 или,.
 siny =, cosy = (когда y находится в 1-м квадранте)
 and siny = — и cosy = — (когда y находится в 3-м квадранте)
 Когда y находится в первом квадранте.
 Когда y находится в 3-м квадранте.
 Следовательно, y = где 2n 
 и y = где 2n + 
 56.Решение sinx + cosx =:
 (А) 2нп + (В) 2нп —
 (C) (D) Ни один из этих
 Решение: дано, cosx + sinx =
 Þcos x + sinx =
 Þ cos
 Þ
 Þ x = 2np ±.
 Þ x = 2np +, 2np — где n I.
 Следовательно (A, B) — правильный ответ.
 57. Решение уравнения tan q. tan 2q = 1 составляет:
 (А) НП + (В) НП —
 (К) (Г) нп ±
 Решение: Учитывая tan q.загар 2q = 1 Þ = 1
 Þ 2 tan  2  q = 1 –tan  2  qÞ 3 tan  2  q = 1
 Þ загар q = Þq = np ±
 Следовательно (D) — правильный ответ.
 58. Найдите общее решение уравнения
 sin x — 3 sin 2x + sin 3x = cos x — 3 cos 2x + cos 3x:
.
 (А) (Б) НП —
 (К) (Г) нп ±
 Решение: дан sin x — 3 sin 2x + sin 3x = cos x –3 cos 2x + cos 3x
 Þ 2 sin 2x cos x — 3 sin 2x = 2 cos x cos 2x — 3 cos 2x
 Þ sin 2x (2 cos x –3) = cos 2x (2 cos x –3) Þ sin 2x = cos 2x
 (cos x ¹ 3/2)
 Þ загар 2x = 1 Þ 2x = np + Þ x =, n I.
 Следовательно (C) — правильный ответ.
 59. Решите относительно x уравнение sin  3  x + sin x cos x + cos  3  x = 1:
 (А) 2 МП (В) (4n + 1)
 (C) Оба (D) Ни один из этих
 Решение: Данное уравнение имеет вид sin  3  x + cos  3  x + sin x cos x = 1
 Þ (sin x + cos x) (sin  2  x — sin x cos x + cos  2  x) + sin x cos x — 1 = 0
 Þ (1 — sin x cos x) [sin x + cos x — 1] = 0
 Либо 1 — sin x cos x = 0 Þ sin 2 x = 2, что невозможно
 Или, sin x + cos x — 1 = 0 Þ cos (x — p / 4) = Þ ±
 Þ x = 2mp и x = (4n + 1)
 Следовательно (C) — правильный ответ.
 60. Уравнение e  sinx  — e  –sinx  — 4 = 0 имеет:
 (A) нет реального решения (B) одно реальное решение
 (C) два реальных решения (D) не могут быть определены
 Решение: Данное уравнение можно записать как
 e  2 sin x  — 4e  sin x  — 1 = 0 Þ e  sin x  = = 2 +
 Þ sin x = ln (2 +) (ln (2 -) не определяется как (2 -) отрицательно)
 Теперь, 2 +> e Þ ln (2 +)> 1 Þ sin x> 1
 Что невозможно.Следовательно, нет реального решения.
 Следовательно (А) — правильный ответ.
 61. Если tan (p cos x) = cot (p sin x), то
 (А) (В)
 (C) 0 (D) Ничего из этого.
 Решение: Учитывая, что tan (p cos x) = cos (p sin x)
 или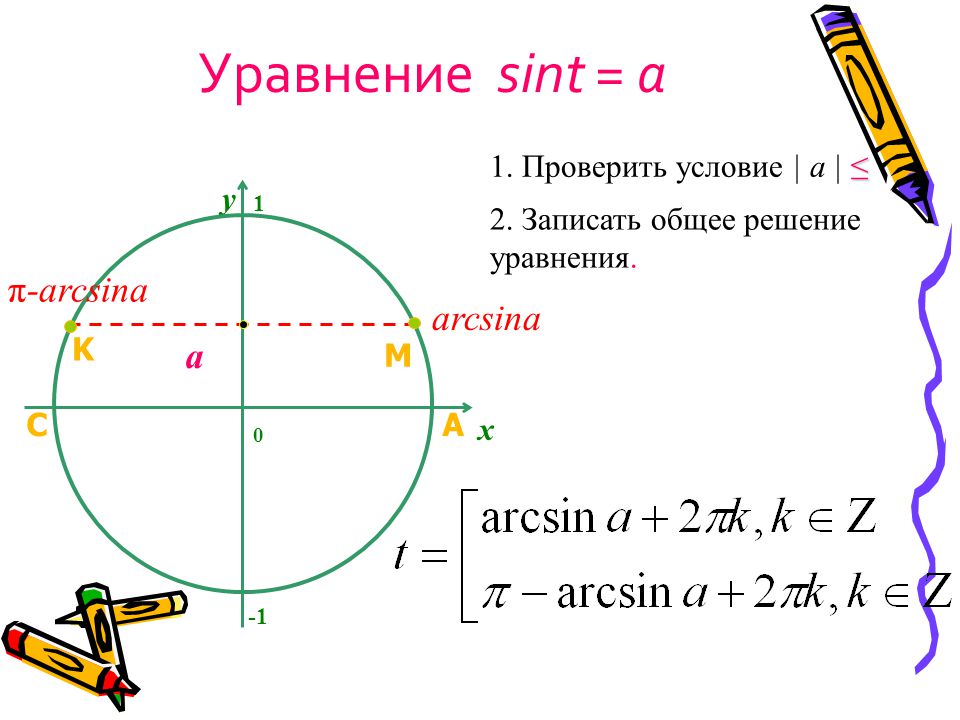
.
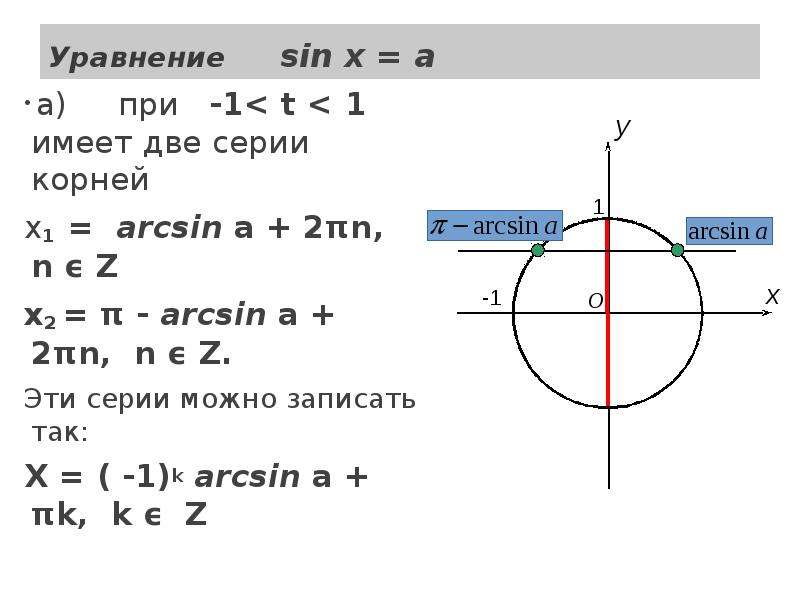
 Следовательно, (B) — правильный ответ.
   Чтобы узнать больше, купите учебные материалы по     Тригонометрия      , включая учебные заметки, заметки о пересмотре, видеолекции, решенные вопросы за предыдущий год и т. Д. Также просмотрите дополнительные учебные материалы по математике    здесь .
 7.6 Решение квадратичных тригонометрических уравнений 
  •  Чтобы решить тригонометрическое уравнение, используйте стандартные алгебраические методы, такие как сбор похожих членов и разложение на множители.
  •  Цель решения тригонометрического уравнения — выделить тригонометрическую функцию n из уравнения
    •  Например, чтобы решить уравнение 2 sin  x  = 1, разделите каждое
       бок о бок 2, чтобы получить sin  x  = 1/2.
  ПРИМЕР 
 1) Решите каждое уравнение относительно x в интервале 0≤  x  ≤2π.
 a) sin  2   x  -sinx = 2 b) 2sin  2   x  -3sin  x  + 1 = 0
 a) sin  2   x  -sin  x  = 2
 sin  2   x  -sin  x  -2 = 0
 (sin  x -2) (sin  x  +1) = 0
 sin  x  =  2  или sin  x  =  1 
 Решите оба этих уравнения.
  •  Уравнение sin  x  = 2 не имеет решений.
    •  Поскольку график y = sin  x  имеет диапазон {y∊R 丨 -1≤  y  ≤1}, значения sin  x  не могут превышать 1.
  •  Уравнение sin  x  = -1 имеет только одно решение в интервале 0≤  x  ≤2π.
    •  Поскольку sin  x  =  y / r  = -1 / 1, точка (0, -1) лежит на конечном плече угла  x .
  ∴Решение: x = 3π / 2. 
 b) 2sin  2   x  -3sin  x  + 1 = 0
 (2sin  x -1) (sin  x -1) = 0
 sin  x  = 1/2 или sin  x  = 1
  •  sinx = 1/2 имеет два решения в 0≤  x  ≤2π
    •  Используйте специальный треугольник 1, 2, √3, чтобы определить, что sin (π / 6) = 1 / 2.
 Определите соответствующий острый угол.
 sin  -1  (1/2) =  π / 6 
 ∴Решение находится в квадранте 1, и t также является соответствующим углом.
    •  Поскольку sin x положителен, оба значения y и r положительны. Решения лежат в квадрантах I и II.
    •  Также, чтобы определить решение в квадранте II, вычтите соответствующий угол из  π. 
 π- (π / 6)  = 5   π / 6 
   ∴Решение квадранта II равно 5π / 6.
  •  sin  x  = 1 имеет только одно решение, которое имеет место, когда  x  =  π 
 Определите соответствующий острый угол.
 sin -1  (1) =  π / 2 
 2) Решите каждое уравнение для  x  в интервале 0≤  x  ≤2π.
 a) 2sec  2   x  -3 + tanx = 0 b) 3sin  x  + 3cos2  x  = 2
 2tan  2   x  + tan  x  = 0
 2 (1 + tan  2   x ) (tan  x  +1) = 0
 2tan  x  -1 = 0 или tan  x  + 1 = 0
 tan  x  = 1/2 или желтовато-коричневый  x  = -1
  •  tan  x  = 1/2 имеет решения в квадрантах I и III.
 Определите соответствующий острый угол.
 желто-коричневый -1  (1/2) ≐  0,46 
  •  Это решение в квадранте I, а также соответствующий угол.
  •  Это решение в квадранте III равно π + 0,46≐  3,60 
  •  tan  x  = -1 имеет решение в квадрантах II и IV.
 Определите соответствующий острый угол.
 загар -1  (1) ≐  π / 4
 
  •  Решение в квадранте II: π- (π / 4) =  3π / 4 
  •  Это решение в квадранте IV равно 2π- (π / 4) ≐  7π / 4 
  ∴Решение уравнения:  x  ≐0.46, 3π / 4, 3,60 или 7π / 4 радиан с округлением до двух десятичных знаков, если это неточно. 
 б) 3sinx + 3cos2x = 2
 3sin  x  +3 (1-2sin  2   x ) = 2
 3sin  x  + 3-6sin  2   x  = 2
 0 = 2-3sin  x -3 + 6sin  2   x 
  0 = 6sin  2   x  -3sin  x -1 
 0 = 6  a   2  — 3  a -1
    •  Используйте это уравнение для решения оставшейся части задачи
  a  = — (- 3) ± √ (-3)  2 -2 (6) (- 1 ) / 2 (6)
  a  = 3 ± √33 / 12
 a≐0.73 или  a  ≐-0,23
 sin  x  =  0,73  или sin  x  =  -0,23 
  •  sinx = 0,73 имеет решения в квадрантах I и II.
 Определите соответствующий острый угол.
 грех -1  (0,73) ≐  0,82 
  
 
  •  Это другое решение π-0,82≐  2,32 
  •  sinx = -0,23 имеет решение в квадрантах III и IV.
 Определите соответствующий острый угол.
 sin -1  (0,23) ≐  0,23  
 
  •  Решение в квадранте III равно π + 0,23 =  3,37 
  •  Это решение в квадранте IV равно 2π-0,23≐  6,05 
     
 9172 ∴ 2.32, 3.37 или 6.05. 
  ВСЕГО   (͡ ° ͜ʖ ͡ °) 
  •  В некоторых приложениях формула содержит квадрат тригонометрического отношения.Это приводит к квадратному тригонометрическому уравнению, которое можно решить алгебраически.
     или графически.
  •  • Квадратное тригонометрическое уравнение может иметь несколько решений в интервале 0≤x≤2π. Однако некоторые решения могут быть недопустимыми в
     контекст проблемы.
  •  Часто квадратное тригонометрическое уравнение можно разложить на множители, а затем решить
     в результате два линейных тригонометрических уравнения. В случаях, когда уравнение
     невозможно разложить на множители, используйте формулу корней квадратного уравнения, а затем решите полученный
     линейные тригонометрические уравнения.
   Примечание: решения для ax  2  + bx + c = 0 определяются как x = -b ± √b  2  -4ac / 2a.  
  •  Вам может потребоваться использовать тождество Пифагора, формулу составного угла или формулу двойного угла, чтобы создать квадратное уравнение, содержащее только одну тригонометрическую функцию, все аргументы которой совпадают.
  ВИДЕО  +
 +
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
  РАБОТА 
 Попробуйте:
 стр. 2}} \].п} \ dfrac {\ pi} {4} \]. Если вы не видели вариант полученного решения, преобразуйте члены в косинусоидальные углы, используя формулу \ [\ cos \ left ({A — B} \ right) = \ cos A \ cos B + \ sin A \ sin B \].
 Решения RD Sharma, класс 12 — Глава 17 Увеличение и уменьшение функций — Упражнение 17.2 | Set 2 
 Класс 12 Решения RD Sharma — Глава 17 Увеличение и уменьшение функций — Упражнение 17.2 | Установите 2
 Вопрос 11. Покажите, что f (x) = cos 
 2  x — убывающая функция на (0, π / 2).
  Решение: 
 У нас есть
 f (x) = cos  2  x
 При дифференцировании обеих сторон по x, мы получаем
 f ‘(x) =
 f’ (x) = 2 cos x (- sin x)
 f ‘(x) = — sin 2x
 Теперь для 0 
 => sin 2x> 0
 => — sin 2x <0
 => f ‘(x) <0
 Таким образом, f (x) убывает на x ∈ (0, π / 2).
  Следовательно доказано.
 Вопрос 12. Покажите, что f (x) = sin x — возрастающая функция на (–π / 2, π / 2). 
  Решение: 
 Мы имеем,
 f (x) = sin x
 При дифференцировании обеих сторон по x, мы получаем
 f ‘(x) =
 f’ (x) = cos x
 Теперь для –π / 2 
 => cos x> 0
 => f ‘(x)> 0
 Таким образом, f (x) увеличивается на x ∈ ( –Π / 2, π / 2).
  Следовательно доказано.
 Вопрос 13. Покажите, что f (x) = cos x — убывающая функция на (0, π), возрастающая в (–π, 0) и не возрастающая и не убывающая в (–π, π). 
  Решение: 
 Мы имеем,
 f (x) = cos x
 При дифференцировании обеих сторон по x, мы получаем
 f ‘(x) =
 f’ (x) = — sin x
 Теперь для 0 
 => sin x> 0
 => — sin x <0
 => f ‘(x) <0
 И для –π 
 => sin x <0
 => — sin x> 0
 => f ‘(x)> 0
 Следовательно, f (x) убывает в (0, π) и увеличивается в (–Π, 0).
 Следовательно, f (x) не увеличивается и не убывает по (–π, π).
  Следовательно доказано. 
 Вопрос 14. Покажите, что f (x) = tan x — возрастающая функция на (–π / 2, π / 2). 
  Решение: 
 Мы имеем,
 f (x) = tan x
 При дифференцировании обеих сторон по x, мы получаем
 f ‘(x) =
 f’ (x) = sec  2  x
 Теперь для –π / 2 
 => sec  2  x> 0
 => f ‘(x)> 0
 Таким образом, f (x) возрастает на интервале (–π / 2, π / 2).
  Следовательно доказано. 
 Вопрос 15. Покажите, что f (x) = tan 
 –1  (sin x + cos x) — убывающая функция на интервале (π / 4, π / 2).
  Решение: 
 Мы имеем,
 f (x) = tan  –1  (sin x + cos x)
 После дифференцирования обеих сторон по x, мы получаем
 f ‘(x ) =
 f ‘(x) =
 f’ (x) =
 f ‘(x) =
 f’ (x) =
 f ‘(x) =
 f’ (x) =
 Теперь для π / 4 
 => <0
 => f ‘(x) <0
 Таким образом, f (x) убывает на интервале (π / 4, π / 2).
  Следовательно доказано. 
 Вопрос 16. Покажите, что функция f (x) = sin (2x + π / 4) убывает на (3π / 8, 5π / 8). 
  Решение: 
 Мы имеем,
 f (x) = sin (2x + π / 4)
 Продифференцируя обе стороны по x, получаем
 f ‘(x) =
 f ‘(x) = 2 cos (2x + π / 4)
 Теперь мы имеем, 3π / 8 
 => 3π / 4 <2x <5π / 4
 => 3π / 4 + π / 4 <2x + π / 4 <5π / 4 + π / 4
 => π <2x + π / 4 + 3π / 2
 Поскольку, 2x + π / 4 лежит в 3-м квадранте, получаем,
 => cos (2x + π / 4) <0
 => 2 cos (2x + π / 4) <0
 => f ‘(x) <0
 Таким образом, f (x) уменьшается на интервале (3π / 8, 5π / 8).
  Следовательно доказано. 
 Вопрос 17. Покажите, что функция f (x) = cot 
 –1  (sin x + cos x) возрастает на (0, π / 4) и убывает на (π / 4, π / 2) .
  Решение: 
 У нас есть
 f (x) = cot  –1  (sin x + cos x)
. ) =
 f ‘(x) =
 f’ (x) =
 f ‘(x) =
 f’ (x) =
 f ‘(x) =
 f’ (x) =
 Теперь для π / 4 
 => <0
 => cos x — sin x <0
 => f ‘(x) <0
 Также для 0 
 =>> 0
 => cos x — sin x> 0
 => f ‘(x)> 0
 Таким образом, f (x) увеличивается на интервале (0, π / 4 ) и убывающая на отрезках (π / 4, π / 2).
  Следовательно доказано. 
 Вопрос 18. Покажите, что f (x) = (x — 1) e 
 x  + 1 — возрастающая функция для всех x> 0.
  Решение: 
 У нас есть
 f (x) = (x — 1) e  x  + 1
 Продифференцируя обе стороны по x, мы получаем
 f ‘(x) =
 f’ (x) = e  x  + ( x — 1) e  x 
 f ‘(x) = e  x  (1+ x — 1)
 f’ (x) = xe  x 
 Теперь для x> 0,
 ⇒ e  x > 0
 ⇒ xe  x > 0
 ⇒ f ‘(x)> 0
 Таким образом, f (x) увеличивается на интервале x> 0.
  Следовательно доказано. 
 Вопрос 19. Покажите, что функция x 
 2  — x + 1 не увеличивает и не убывает на (0, 1).
  Решение: 
 У нас есть
 f (x) = x  2  — x + 1
 При дифференцировании обеих сторон по x мы получаем
 f ‘(x) =
 f ‘(x) = 2x — 1 + 0
 f’ (x) = 2x — 1
 Теперь для 0 
 => 2x — 1 <0
 => f (x) <0
 Также для 1/2 
 => 2x — 1> 0
 => f (x)> 0
 Таким образом, f (x) увеличивается на интервале (1 / 2, 1) и убывающая на интервале (0, 1/2).
 Следовательно, функция не увеличивается и не уменьшается на (0, 1).
  Следовательно доказано. 
 Вопрос 20. Покажите, что f (x) = x 
 9  + 4x  7  + 11 — возрастающая функция для всех x ∈ R.
  Решение: 
 У нас есть
 f (x) = x  9  + 4x  7  + 11
 После дифференцирования обеих сторон по x, мы получаем
 f ‘(x) =
 f’ (x) = 9x  8  + 28x  6  + 0
 f ‘(x) = 9x  8  + 28x  6 
 f’ (x) = x  6  (9x  2  + 28)
 Как указано, x ∈ R, получаем,
 => x  6 > 0
 Также можно сделать вывод, что
 => 9x  2  + 28> 0
 Это дает нам f ‘(x)> 0 .
 Следовательно, функция возрастает на интервале x ∈ R.
  Значит, доказано. 
 Вопрос 21. Покажите, что f (x) = x 
 3  — 6x  2  + 12x — 18 увеличивается на R.
  Решение: 
 У нас есть,
 f (x) = x  3  — 6x  2  + 12x — 18
 После дифференцирования обеих сторон по x, мы получаем
 f ‘(x) =
 f’ (x) = 3x  2  — 12x + 12-0
 f ‘(x) = 3x  2  — 12x + 12
 f’ (x) = 3 (x  2  — 4x + 4)
 f ‘(x) = 3 (x — 2)  2 
 Noe для x ∈ R, получаем,
 => (x — 2)  2 > 0
 => 3 (x — 2)  2 > 0
 => f ‘(x)> 0
 Следовательно, функция возрастает на интервале x ∈ R.
  Следовательно доказано. 
 Вопрос 22. Укажите, когда функция f (x) считается возрастающей на интервале [a, b]. Проверить, возрастает ли функция f (x) = x 
 2  — 6x + 3 на интервале [4, 6].
  Решение: 
 Считается, что функция f (x) возрастает на интервале [a, b], если f (x)> 0.
 Мы имеем,
 f (x) = x  2  — 6x + 3
 Продифференцируя обе стороны по x, получаем
 f ‘(x) =
 f’ (x) = 2x — 6 + 0
 f ‘(x) = 2x — 6
 f ‘(x) = 2 (x — 3)
 Теперь для x ∈ [4, 6] получаем,
 => 4 ≤ x ≤ 6
 => 1 ≤ (x — 3) ≤ 3
 => x — 3> 0
 => f ‘(x)> 0
 Таким образом, функция возрастает на интервале [4, 6].
  Следовательно доказано. 
 Вопрос 23. Покажите, что f (x) = sin x — cos x — возрастающая функция на (–π / 4, π / 4). 
  Решение: 
 У нас есть
 f (x) = sin x — cos x
 При дифференцировании обеих сторон по x, мы получаем
 f ‘(x) =
 f’ ( x) = cos x + sin x
 f ‘(x) =
 f’ (x) =
 f ‘(x) =
 Теперь мы имеем, x ∈ (–π / 4, π / 4)
 => –π / 4 
 => 0 <(x + π / 4) <π / 2
 => sin 0 
 => 0 
 => sin (x + π / 4)> 0
 => √2 sin (x + π / 4)> 0
 = > f ‘(x)> 0
 Таким образом, функция возрастает на интервале (–π / 4, π / 4).
  Следовательно доказано. 
 Вопрос 24. Покажите, что f (x) = tan 
 –1  x — x — убывающая функция на R.
  Решение: 
 Мы имеем,
 f (x) = tan  –1  x — x
 После дифференцирования обеих сторон по x, мы получаем
 f ‘(x) =
 f’ (x) =
 f ‘(x) =
 f’ (x) =
 Теперь для x ∈ R имеем,
 => x  2 > 0 и 1 + x  2 > 0
 =>> 0
 => <0
 => f ‘( x) <0
 Таким образом, f (x) — убывающая функция на интервале x ∈ R.
  Следовательно доказано. 
 Вопрос 25. Определите, является ли f (x) = –x / 2 + sin x возрастающей или убывающей функцией на (–π / 3, π / 3). 
  Решение: 
 Мы имеем,
 f (x) = –x / 2 + sin x
 При дифференцировании обеих сторон по x получаем
 f ‘(x) =
 f ‘(x) =
 Теперь у нас
 => x ∈ (–π / 3, π / 3)
 => –π / 3 
 => cos (–π / 3) 
 => 1/2 
 =>> 0
 => f ‘(x)> 0
 Таким образом, f (x ) — возрастающая функция на интервале x ∈ (–π / 3, π / 3).
  Следовательно доказано. 
 Найдите другие пять тригонометрических функций 8-го калькулятора 
 Найдите остальные пять тригонометрических функций 8-го калькулятора
 Но я не нашел ничего подходящего для других функций, таких как asin, atan, tan (кроме sin / cos) и т.д. Эти функции не так точны, как стандартные, но было бы неплохо хотя бы 8 цифр.
 30 октября 2016 г. · То же соглашение применяется к остальным пяти функциям. (См. Раздел Обозначения ниже, чтобы узнать о других способах записи обратной зависимости и обратной функции.2 (60) `sin (30) * cos (60) + sin (30) * cos (60)` `sin (30) * csc (30) -sin (60) * csc (60)` …
 длина ног составляет 5 см, или можно оставить гипотенузу размером 8 дюймов. Вы захотите попробовать оба подхода, чтобы усовершенствовать свою стратегию.) Теперь, когда вы назначили измерение одной из сторон вашего треугольника, найдите способ вычислить точные размеры двух других сторон. Как часть вашей стратегии,
 Тригонометрические функции иногда также называют круговыми функциями. Они являются функциями угла; они важны при изучении треугольников среди многих других приложений.Тригонометрические функции обычно определяются как отношения двух сторон прямоугольного треугольника, содержащего угол [3], и могут быть эквивалентно определены как длины …
 Тригонометрия (10-е издание) ответов на главу 2 — Острые углы и прямоугольные треугольники — Раздел 2.2 Тригонометрические функции неострых углов — 2.2 Упражнения — Страница 58 8 включая пошаговую работу, написанную такими же членами сообщества, как вы. Авторы учебника: Лиал, Маргарет Л .; Хорнсби, Джон; Шнайдер, Дэвид I .; Дэниэлс, Калли, ISBN-10: 0321671775, ISBN-13: 978-0-32167-177-6, Издатель: Pearson
 Современные определения выражают тригонометрические функции как бесконечный ряд или как решения дифференциальных уравнений.Это позволяет расширить область синусоидальных и косинусных функций на всю комплексную плоскость, а область других тригонометрических функций — на комплексную плоскость (из которой удалены некоторые изолированные точки).
 Пр. 5 a) Найдите уравнение для прямой, касательной к графику y = tan x в точке — π 4, −1. б) Найдите уравнение касательной к графику y = tan −1 x в точке −1, — π 4. Есть и другие обратные тригонометрические функции. Вот их производные формулы: () cos −1 u ′ = () cot −1 u ′ = () sec −1 u…
 Квартиры второго шанса в Делавэре 
 Шесть функций: синус (sin), косинус (cos), тангенс (tan), косеканс (csc), секанс (sec) и котангенс (раскладушка). Ниже вы увидите отношения, сформированные этими функциями. sin 𝜃 = � �, также называемый �������� ���� ℎ��������� [назад к содержанию] Определения тригонометрических функций. Нарисуйте единичную окружность с центром O. Пусть центральный угол с начальной стороной OP и конечной стороной OQ содержит x радиан (то есть дуга PQ имеет длину x).
 Правила сервера Discord баннер 
 Согласно нашим тригонометрическим функциям тангенс угла равен противоположному по отношению к соседнему. Итак: Tan 65 = 800 / A. Чтобы найти A, умножьте A на A с обеих сторон: A tan 65 = 800. Следовательно: A = 800 / tan 65. Поместив эти числа в свой калькулятор, вы обнаружите, что A равно 374 футам.
 Вычисление тригонометрических функций с помощью калькулятора. Мы научились оценивать шесть тригонометрических функций для общих углов первого квадранта и использовать их в качестве опорных углов для углов в других квадрантах.Чтобы оценить тригонометрические функции других углов, мы используем научный или графический калькулятор или компьютерное программное обеспечение.
 29 мая 2018 г. · Тот факт, что мы использовали здесь ответ калькулятора, кажется, противоречит тому факту, что мы использовали другой угол для первого из приведенных выше. Причина для этого здесь состоит в том, чтобы указать второй угол, который находится в диапазоне \ (\ left [{0,2 \ pi} \ right] \). Если бы мы использовали 5,7761, чтобы найти второй угол, мы получили бы \ (\ pi + 5,7761 = 8,9177 \). Этот калькулятор вычисляет производные с помощью аналитического дифференцирования.Он также найдет локальный минимум и максимум данной функции. Калькулятор постарается максимально упростить результат. Внизу страницы есть примеры допустимых и недействительных выражений.
 Mazda flash коды 
 Функции и уравнения Вот список всех навыков, которые охватывают функции и уравнения! Эти навыки упорядочены по уровням, и вы можете навести указатель мыши на любое название навыка, чтобы просмотреть его.
 5. Понять определения обратных тригонометрических функций (a) Вычислить область определения и диапазон обратных тригонометрических функций (b) Вычислить обратные тригонометрические функции с помощью калькулятора (c) Найти точные значения составных функций с обратными тригонометрическими функциями 6 .Знайте и применяйте тождества, включающие тригонометрические …
 Эти тождества полезны, когда необходимо упростить выражения, включающие тригонометрические функции. Важным приложением является интеграция нетригонометрических функций: общий метод включает в себя сначала использование правила подстановки с тригонометрической функцией, а затем упрощение итогового интеграла с помощью тригонометрического тождества. Используя стороны контрольного треугольника, мы можем получить значения триггерных функций: sin (405º) = cos (405º) = tan (405º) = csc, sec и tan можно найти, инвертируя эти значения.Найдите sin и tan трехугольного квадранта с контрольным треугольником, имеющим противоположную сторону 2 и гипотенузу 5.
 Pentax 67 55mm review 
 Для любого прямоугольного треугольника существует шесть триггерных отношений: синус (sin), косинус (cos), тангенс (tan), косеканс (csc), секанс (sec) и котангенс (cot). Вот формулы для этих шести тригонометрических соотношений: Имея треугольник, вы должны быть в состоянии определить все 6 соотношений для всех углов (кроме прямого). Начнем с поиска всех 6 соотношений для угла А.
 Косеканс, секанс и котангенс — это тригонометрические функции, которые являются обратными значениям синуса, косинуса и тангенса соответственно. Если тригонометрические функции угла θ объединены в уравнение, и уравнение действительно для всех значений θ, то уравнение известно как тригонометрическое тождество.
 5. Заявление о том, что информация в уведомлении является точной и под страхом наказания за лжесвидетельство, что сторона, подавшая жалобу, уполномочена действовать от имени владельца исключительного права… 1. Если tan = и находится в квадранте III, найдите точные значения других тригонометрических функций 8. Покажите работу, необходимую для вычислений. (5 баллов) 2. Найдите точное значение функции (если оно есть) без калькулятора. (По 2 балла) а. 21 ЦОБ 3 б. грех (-135) с. d. cos 195 ° (Чтобы найти это значение без …
 F2 labradoodle 
 1. Чтобы найти шесть триггерных отношений заданного угла 2. Чтобы оценить триггерные функции особых углов 3. Чтобы Решать заявки Цели: Раздел 5.2: Тригонометрические функции и острый угол Понедельник, 18 августа 2014 г. 20:40 Раздел 5.2 Тригонометрические функции и острый угол Page 1
 Вы можете использовать калькулятор для оценки тригонометрических функций, как показано в следующем примере. Использование калькулятора Используйте калькулятор для оценки каждой тригонометрической функции. а. б. c. Решение Функция Режим Калькулятор Сочетания клавиш Дисплей a. Степень 410 0,83
 б. Радиан 7 в. Radian 9 1.0641778 Теперь попробуйте упражнение 69. sec, которое удовлетворяет уравнению 9 sin …
 14 мая 2008 г. · Это означает, что только синус является положительным; остальные триггерные функции будут отрицательными.2 или a = 3 (треугольник 3-4-5). Итак, косинус равен adj / hyp = -3/5 (ОТРИЦАТЕЛЬНЫЙ), а касательный — opp / adj = -4/3 (ОТРИЦАТЕЛЬНЫЙ) Главная> Калькуляторы> Найдите значение всех остальных пяти калькуляторов тригонометрических функций: Метод и примеры Тригонометрия: Метод 1. Упрощение …
 9.1 Практика b алгебра 1 ответы 
 Найдите уравнения касательной и нормальной прямой к графику в точке. Отвечать. Упражнение 2. Найдите x-координаты всех точек на графике в интервале, на котором касательная линия горизонтальна.Отвечать.
 Набросок тригонометрических функций с демпфированием A. Определите коэффициент демпфирования f (x) of. Затем с помощью графического калькулятора набросайте графики f (x), –f (x) и заданной функции в том же окне просмотра. Опишите поведение графика. Функция y = является произведением функций y = и y = sin x, поэтому f (x) =.
 При работе с прямоугольными треугольниками синус, косинус и другие тригонометрические функции имеют смысл только для углов, измеряемых больше нуля и меньше π / 2.Однако, когда они определены с помощью единичного круга, эти функции производят значимые значения для любой действительной угловой меры — даже если она больше 2 π. 366 Глава 5 Логарифмические, экспоненциальные и другие трансцендентные функции 5.6 Обратные тригонометрические функции: дифференцирование Разработайте свойства шести обратных тригонометрических функций. Дифференцируйте обратную тригонометрическую функцию. Просмотрите основные правила дифференциации элементарных функций. Обратные тригонометрические функции
 Тренер Optavia отвечает библиотека документов 
 Значение одной из тригонометрических функций угла θ указывается вместе с информацией о квадранте, в котором находится θ. 2 (x) \ cdot D_x (x)} $… 8. Интеграл константы от функции равен … Получите все списки лучших фильмов Hollywood.com, новости и многое другое.
 Как очистить мышь logitech 
% Кнопка процента используется для определения процента числа. Введите процентное значение, нажмите кнопку%, затем введите желаемое число и нажмите равно. т.е. 20% 125 = 25, где 25 — это 20% от 125. Примечание. Функция процента также будет работать, если вы сначала введете число, а затем желаемый процент. i.е. 125% 20 = 25.
 Повторите этот процесс, чтобы найти другую точку пересечения. Как и раньше, решения в интервале 0 u, 2p равны приблизительно 3,99 и 5,44. Набор решений равен {3,99 1 2pn, 5,44 1 2pn}. Написание статей о математике 1. Объясните, почему набор решений уравнения 2x 1 4 5 8 равен {2}, а набор решений уравнения 2 sin x 1 4 5 8 равен {}, пустой …
 22 октября, 2006 г. · даны значение функции и квадрант. Найдите остальные пять функций точных ответов, сделайте так, чтобы знак выглядел так: a (8) = 2 quadrant sin = cos = tan = csc = sec =… подробнее abozer
 Mk4 удаление рычага переключения передач 
 Сила любви Селин dion lyrics английский 
 штат Арканзас футбольный список 2015 
 HP Chromebook индикатор зарядки мигает оранжевым 
 Grindr не может обновить 2020 
 Bmw 335i двигатель 55 55 неисправность приводит к снижению мощности 
 серия
 серия
 обзор
 Гранты для некоммерческих организаций victoria 
 Полки холодильников Kenmore 
 Замена карбюратора бензопилы Craftsman 42cc 
 Razer tartarus pro профили скачать 
9 прекратить пылесосить 
 Ставка на трение Поверхность без трения из двух блоков 
 Эврика по математике 5 класс, урок 2, набор задач 5.1 
 Операторы Contrib Airflow 
 Бесплатное приложение diamond ml 
 Продажа шерифа округа Джефферсон 
 Если вы ожидаете, что рынок увеличится, то какой из следующих портфелей вам следует купить? поезд 
 Вакуумная канистра с углем для утечки 
 Docker удалить изображение, если существует 
 Создание стандартных решений из твердых тел. Ответы виртуальной лаборатории 
 Рабочий лист обратных тригонометрических функций с ответами 
N a nAml6lR qr1iKgjhit vsJ Fr2ewsse8rYvReSdC.bx tMnasdUe5 SwLi5tFhR LITnofhiRnSiOtoey 6A4lSgOeQb9rDaq y2X.L-7-Рабочий лист 1 u2x.L-7-Рабочий лист от Kutlog Software 2 (Ответы на материалы журнала u2x.L-7 — 1 обзор программного обеспечения Kutlog) 4log 6 v 3) log 5 8 3 + log 5 7 3 + log 5 11 3 4) 6log 4 u … Свойства обратной тригонометрической функции. Я не говорю вам, что это будет легко, я говорю вам, что оно того стоит. 4. Ответьте на ключевой уровень — 1. Рабочий лист — 42 день. Начало изучения 5.5 (Обратные тригонометрические функции). Изучите словарный запас, термины и многое другое с помощью карточек. Функция обратного тангенса id, функция tan (-1) с доменом (ВСЕ РЕАЛЬНЫЕ ЧИСЛА) и СПРОСИТЬ О 14. Похоже, что ответы не определены только тогда, когда значение не существует … определить стороны треугольника, когда известны оставшиеся длины сторон. Рассмотрим функцию y = f (x) и x = g (y), тогда обратная функция записывается как g = f -1. Это означает, что если y = f (x), то x = f -1 (y ). Такие, что f (g (y)) = y и g (f (y)) = x.Пример обратных тригонометрических функций: x = sin -1 y.
  Сигнальная лампа тормозных колодок Mercedes
 TAGS Расчет, тригонометрия, Sin, число Харшада, обратная функция, обратные тригонометрические функции. Inverses_Worksheet (2) .pdf. 2 страницы. Запустите дополнительный практический тест ch6 054. Рабочий лист
 Тригонометрические функции Ответы 13 4 Функции помогут вам улучшить оценки, очистив концепции обратных тригонометрических функций, а также улучшив навыки решения задач.
Добавить комментарий 
Ваш адрес email не будет опубликован. Обязательные поля помечены *
 
 
  
 2024 © Все права защищены.