3
 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град.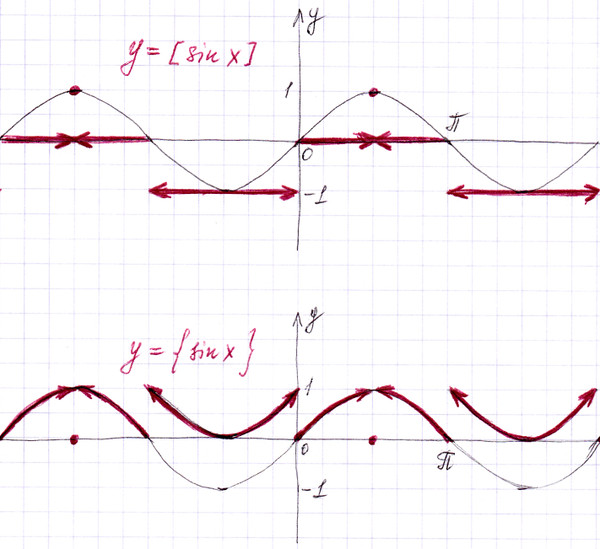 ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град.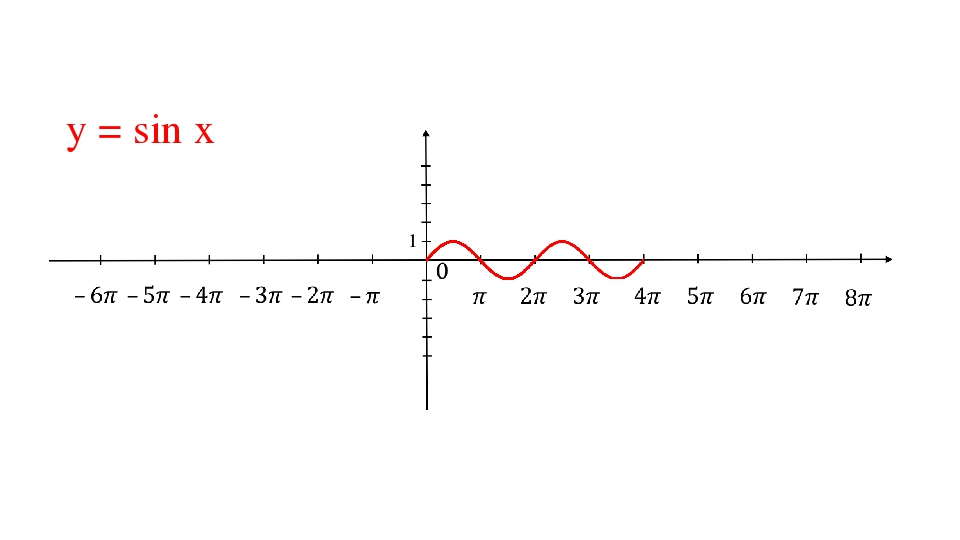 ) ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Тригонометрические уравнения с модулем
Раскрытие модуля по определению
Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а <
0.
Согласно этому определению, в уравнениях модуль можно раскрывать следующим образом:
№1. Решить уравнение.
№2. Решить уравнение.
Решаем уравнение первой системы:
2sin2x-sinx=0
sinx(2sinx-1)=0
sinx=0 или sinx= (оба уравнения удовлетворяют условию sinx≥0)
Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx<0,
получаем х =
Серии ответов можно записать объединяя
№3. Решить уравнение.
Решение. Раскрывая знак модуля, получаем системы:
Решая уравнение первой системы, получим Из значений нужно выбрать те, которые удовлетворяют неравенству системы х ≥ -3. Это при n=0, 1, 2, 3…
Решая уравнение второй системы, получим Из этого множества значений нужно выбрать те, которые удовлетворяют неравенству х < -3. Это значения при m= -1, -2, -3…
Ответ: при n=0, 1, 2, 3…; при m = -1, -2, -3…и х = -3
№4 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, поэтому, раскрывая знак модуля, получим только одну систему
Решаем уравнение системы:
соsx=cosx(x+1,5)2
cosx(1-(x+1,5)2)=0
cosx=0 или x+1,5=1 или x-1,5 = -1
х= -0,5 х = -2,5
Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)
Ответ:
№5. Найти все решения уравнения на отрезке [0;4].
Решение. Перепишем уравнение в виде
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим
Из серии в нужном промежутке [0;4] лежат точки 0 и ; , а из серии
Решая вторую систему, получим систему , которая не имеет решений.
Ответ:
№6 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и
левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия
правого модуля по определению рассматривается только один случай:
Если х-2≥0. то при раскрытия
правого модуля по определению рассматривается только один случай:
х=2
Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2
№7. Решить уравнение.
Решение. ОДЗ:
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим cos2x=0, и из решений надо выбрать те, при которых sinx>0. На круге видно, что это точки вида
Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.
Ответ:
№8. Решить уравнение.
Решение. Преобразуем уравнение следующим образом:
Обратная замена:
Ответ:
№9. Решить уравнение.
Решение. Выражение под первым модулем всегда неотрицательно, и его можно сразу отбросить. Второй модуль раскрываем по определению.
Решить уравнение первой система аналитически невозможно, исследуем поведение
левой и правой частей на данных промежутках. Функция f(x) =-x2+15x-45=(-x2+15x-44)-1≤-1
Функция f(x) =-x2+15x-45=(-x2+15x-44)-1≤-1
при причем, f(х)= -1 в точках 4 и 11.Левая часть cos при любых х, причем, в точках 4 и 11 не равна -1, значит, система решений не имеет.
При решении уравнения второй системы получается:
В промежутке только одно целое нечетное число 3, т.е
Ответ: 9
Другие способы раскрытия модулей.
Уравнения вида можно решать и следующим способом:
№10. Решить уравнение.
Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и правая часть, тогда cosx <0, тогда уравнение равносильно системе
Рассмотрим две системы:
Решая уравнение первой системы получим: cosx-2sinx=0
Учитывая, что cosx≤0, x = arctg Вторая система решений не имеет.
Ответ: x = arctg.
№11. Решить уравнение.
cosx
Решение.
№12. Решить уравнение.
Решение. Уравнение равносильно sinx = ± cosx
Ответ:
Задачи для самостоятельного решения:
y sin x модуль
Вы искали y sin x модуль? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y sin модуль x, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y sin x модуль».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y sin x модуль,y sin модуль x,y sinx модуль график,y модуль sin x,y модуль sinx,y модуль sinx график,график y sinx модуль,график модуль y sinx,график синус модуль х,модуль y sin x,модуль y sin модуль x,модуль синус х график,синус модуль х график. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y sin x модуль. Просто введите задачу в окошко и нажмите
«решить» здесь (например, y sinx модуль график).
Где можно решить любую задачу по математике, а так же y sin x модуль Онлайн?
Решить задачу y sin x модуль вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Модуль в тригонометрических уравнениях: найти и обезвредить
Достаточно часто в задачах повышенной сложности встречаются тригонометрические уравнения, содержащие модуль. Большинство из них требуют эвристического подхода к решению, который совсем не знаком большинству школьников.
Предлагаемые ниже задачи призваны познакомить вас с наиболее характерными приемами решения тригонометрических уравнений содержащих модуль.
Задача 1. Найти разность (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения 1 + 2sin x · |cos x| = 0.
Решение.
Раскроем модуль:
1) Если cos x ≥ 0, то исходное уравнение примет вид 1 + 2sin x · cos x = 0.
Воспользуемся формулой синуса двойного угла, получим:
1 + sin 2x = 0; sin 2x = -1;
2x = -π/2 + 2πn, n € Z;
x = -π/4 + πn, n € Z. Так как cos x ≥ 0, то x = -π/4 + 2πk, k € Z.
2) Если cos x < 0, то заданное уравнение имеет вид 1 – 2sin x · cos x = 0. По формуле синуса двойного угла, имеем:
1 – sin 2x = 0; sin 2x = 1;
2x = π/2 + 2πn, n € Z;
x = π/4 + πn, n € Z. Так как cos x < 0, то x = 5π/4 + 2πk, k € Z.
3) Наибольший отрицательный корень уравнения: -π/4; наименьший положительный корень уравнения: 5π/4.
Искомая разность: 5π/4 – (-π/4) = 6π/4 = 3π/2 = 3 · 180°/2 = 270°.
Ответ: 270°.
Задача 2. Найти (в градусах) наименьший положительный корень уравнения |tg x| + 1/cos x = tg x.
Решение.
Раскроем модуль:
1) Если tg x ≥ 0, тогда
tg x + 1/cos x = tg x;
1/cos x = 0.
В полученном уравнении корней нет.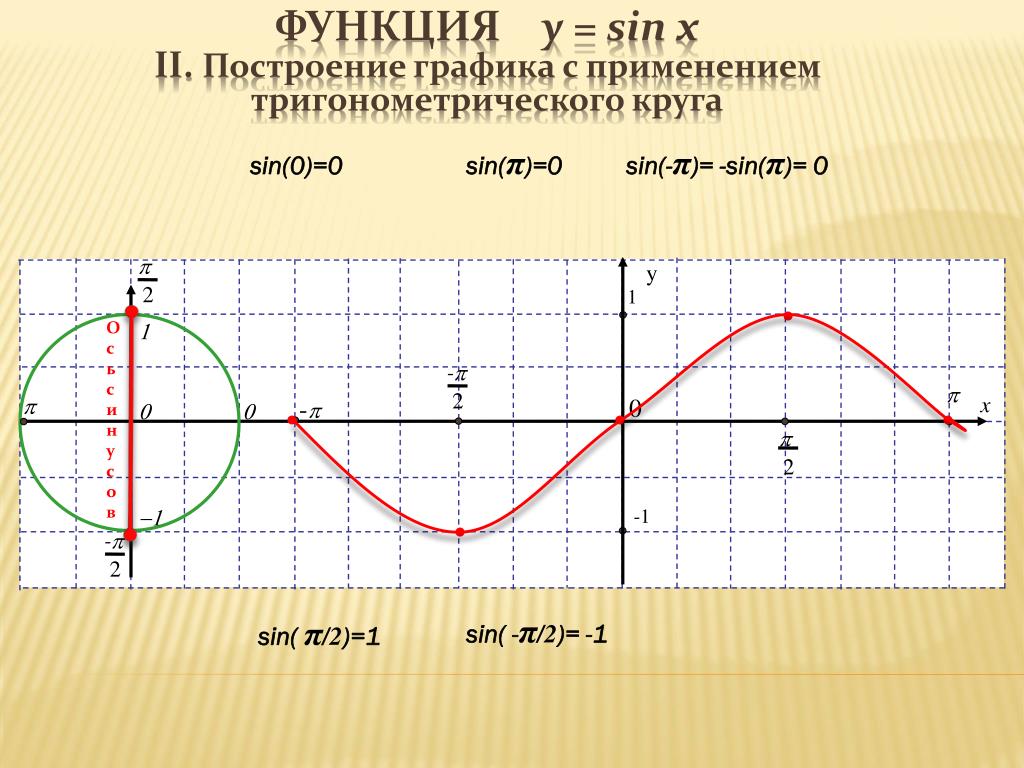
2) Если tg x < 0, тогда
-tg x + 1/cos x = tg x;
1/cos x – 2tg x = 0;
1/cos x – 2sin x / cos x = 0;
(1 – 2sin x) / cos x = 0;
1 – 2sin x = 0 и cos x ≠ 0.
С помощью рисунка 1 и условия tg x < 0 находим, что x = 5π/6 + 2πn, где n € Z.
3) Наименьший положительный корень уравнения 5π/6. Переведем это значение в градусы:
5π/6 = 5 · 180°/6 = 5 · 30° = 150°.
Ответ: 150°.
Задача 3. Найти количество различных корней уравнения sin |2x| = cos 2x на промежутке [-π/2; π/2].
Решение.
Запишем уравнение в виде sin|2x| – cos 2x = 0 и рассмотрим функцию y = sin |2x| – cos 2x. Так как функция является четной, то найдем ее нули при x ≥ 0.
sin 2x – cos 2x = 0; разделим обе части уравнения на cos 2x ≠ 0, получим:
tg 2x – 1 = 0;
tg 2x = 1;
2x = π/4 + πn, n € Z;
x = π/8 + πn/2, n € Z.
Воспользовавшись четностью функции, получим, что корнями исходного уравнения являются числа вида
± (π/8 + πn/2), где n € Z.
Промежутку [-π/2; π/2] принадлежат числа: -π/8; π/8.
Итак, два корня уравнения принадлежат заданному промежутку.
Ответ: 2.
Данное уравнения можно было бы решить и раскрытием модуля.
Задача 4. Найти количество корней уравнения sin x – (|2cos x – 1|)/(2cos x – 1) · sin2 x = sin2 x на промежутке [-π; 2π].
Решение.
1) Рассмотрим случай, когда 2cos x – 1 > 0, т.е. cos x > 1/2, тогда уравнение принимает вид:
sin x – sin2 x = sin2 x;
sin x – 2sin2 x = 0;
sin x(1 – 2sin x) = 0;
sin x = 0 или 1 – 2sin x = 0;
sin x = 0 или sin x = 1/2.
Используя рисунок 2 и условие cos x > 1/2, найдем корни уравнения:
x = π/6 + 2πn или x = 2πn, n € Z.
2) Рассмотрим случай, когда 2cos x – 1 < 0, т.е. cos x < 1/2, тогда исходное уравнение принимает вид:
sin x + sin2 x = sin2 x;
sin x = 0;
x = 2πn, n € Z.
Используя рисунок 2 и условие cos x < 1/2, находим, что x = π + 2πn, где n € Z.
Объединим два случая, получим:
x = π/6 + 2πn или x = πn.
3) Промежутку [-π; 2π] принадлежат корни: π/6; -π; 0; π; 2π.
Таким образом, заданному промежутку принадлежат пять корней уравнения.
Ответ: 5.
Задача 5. Найти количество корней уравнения (x – 0,7)2 |sin x| + sin x = 0 на промежутке [-π; 2π].
Решение.
1) Если sin x ≥ 0, то исходное уравнение принимает вид (x – 0,7)2 sin x + sin x = 0. После вынесения общего множителя sin x за скобки, получим:
sin x((x – 0,7)2 + 1) = 0; так как (x – 0,7)2 + 1 > 0 при всех действительных x, то sinx = 0, т.е. x = πn, n € Z.
2) Если sin x < 0, то -(x – 0,7)2 sin x + sin x = 0;
sin x((x – 0,7)2 – 1) = 0;
sinx = 0 или (x – 0,7)2 + 1 = 0.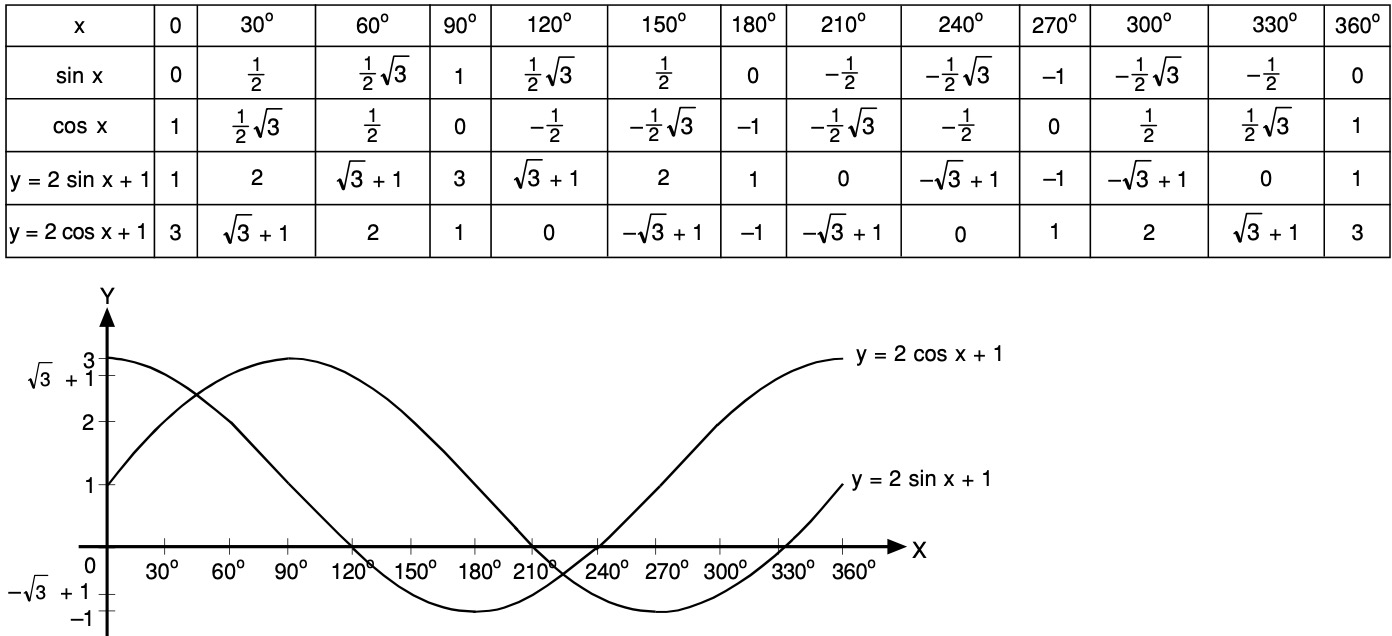 Так как sin x < 0, то (x – 0,7)2 = 1. Извлекаем квадратный корень из левой и правой частей последнего уравнения, получим:
Так как sin x < 0, то (x – 0,7)2 = 1. Извлекаем квадратный корень из левой и правой частей последнего уравнения, получим:
x – 0,7 = 1 или x – 0,7 = -1, а значит x = 1,7 или x = -0,3.
С учетом условия sinx < 0 получим, что sin (-0,3) ≈ sin (-17,1°) < 0 и sin (1,7) ≈ sin (96,9°) > 0, значит только число -0,3 является корнем исходного уравнения.
3) Промежутку [-π; 2π] принадлежат числа: -π; 0; π; 2π; -0,3.
Таким образом, уравнение имеет пять корней на заданном промежутке.
Ответ: 5.
Заняться подготовкой к урокам или экзаменам можно при помощи различных образовательных ресурсов, которые есть в сети. В настоящее время любому человеку просто необходимо использовать новые информационные технологии, ведь правильное, а главное уместное их применение будет способствовать повышению мотивации в изучении предмета, повысит интерес и поможет лучше усвоить необходимый материал. Но не стоит забывать о том, что компьютер не учит думать, полученную информацию обязательно необходимо обрабатывать, понимать и запоминать. Поэтому вы можете обратиться за помощью к нашим онлайн репетиторам, которые помогут вам разобраться с решением интересующих вас задач.
Поэтому вы можете обратиться за помощью к нашим онлайн репетиторам, которые помогут вам разобраться с решением интересующих вас задач.
Остались вопросы? Не знаете, как решать тригонометрические уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Модуль math | Python 3 для начинающих и чайников
Модуль math – один из наиважнейших в Python. Этот модуль предоставляет обширный функционал для работы с числами.
math.ceil(X) – округление до ближайшего большего числа.
math.copysign(X, Y) — возвращает число, имеющее модуль такой же, как и у числа X, а знак — как у числа Y.
math.fabs(X) — модуль X.
math.factorial(X) — факториал числа X.
math.floor(X) — округление вниз.
math.fmod(X, Y) — остаток от деления X на Y.
math.frexp(X) — возвращает мантиссу и экспоненту числа.
math.ldexp(X, I) — X * 2i. Функция, обратная функции math.frexp().
math.fsum(последовательность) — сумма всех членов последовательности. Эквивалент встроенной функции sum(), но math.fsum() более точна для чисел с плавающей точкой.
math.isfinite(X) — является ли X числом.
math.isinf(X) — является ли X бесконечностью.
math.isnan(X) — является ли X NaN (Not a Number — не число).
math.modf(X) — возвращает дробную и целую часть числа X. Оба числа имеют тот же знак, что и X.
math.trunc(X) — усекает значение X до целого.
math.exp(X) — eX.
math.expm1(X) — eX — 1. При X → 0 точнее, чем math.exp(X)-1.
math.log(X, [base]) — логарифм X по основанию base. Если base не указан, вычисляется натуральный логарифм.
Если base не указан, вычисляется натуральный логарифм.
math.log1p(X) — натуральный логарифм (1 + X). При X → 0 точнее, чем math.log(1+X).
math.log10(X) — логарифм X по основанию 10.
math.log2(X) — логарифм X по основанию 2. Новое в Python 3.3.
math.pow(X, Y) — XY.
math.sqrt(X) — квадратный корень из X.
math.acos(X) — арккосинус X. В радианах.
math.asin(X) — арксинус X. В радианах.
math.atan(X) — арктангенс X. В радианах.
math.atan2(Y, X) — арктангенс Y/X. В радианах. С учетом четверти, в которой находится точка (X, Y).
math.cos(X) — косинус X (X указывается в радианах).
math.sin(X) — синус X (X указывается в радианах).
math.tan(X) — тангенс X (X указывается в радианах).
math.hypot(X, Y) — вычисляет гипотенузу треугольника с катетами X и Y (math.sqrt(x * x + y * y)).
math.degrees(X) — конвертирует радианы в градусы.
math.radians(X) — конвертирует градусы в радианы.
math.cosh(X) — вычисляет гиперболический косинус.
math.sinh(X) — вычисляет гиперболический синус.
math.tanh(X) — вычисляет гиперболический тангенс.
math.acosh(X) — вычисляет обратный гиперболический косинус.
math.asinh(X) — вычисляет обратный гиперболический синус.
math.atanh(X) — вычисляет обратный гиперболический тангенс.
math.erf(X) — функция ошибок.
math.erfc(X) — дополнительная функция ошибок (1 — math.erf(X)).
math.gamma(X) — гамма-функция X.
math.lgamma(X) — натуральный логарифм гамма-функции X.
math.pi — pi = 3,1415926…
math.e — e = 2,718281…
Графики,содержащие знак модуля.Построение графиков,содержащих знак модуля. | Учебно-методический материал по алгебре (10 класс) по теме:
Исследовательская работа
«Построение графиков
функций, аналитическое выражение которых содержит знак абсолютной величины»
2008
Оглавление.
I. Введение——————————————————————————1
II. Основная часть.——————————————————————-1-13
1. Историческая справка——————————————————- -3-4
2. Геометрическая интерпретация понятия |а|—————————- -4-5
3. График функции у=f |(х)|——————————————————5-8
4. График функции у = | f (х)| —————————————————8-10
5. График функции у=|f |(х)| | — —- ——————————————10-13
III. Заключение.————————————————————————-13
IV. Список литературы —————————————————————14
I. Введение.
Построение графиков функций одна их интереснейших тем в школьной математике.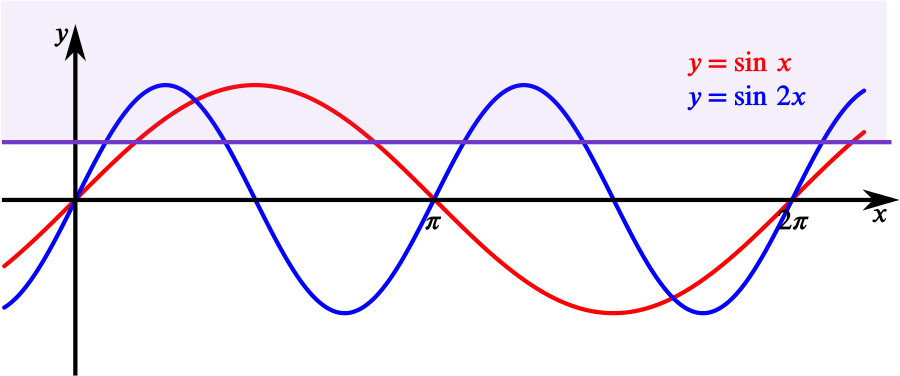 Один из крупнейших математиков нашего времени Израиль Моисеевич Гельфанд писал: «Процесс построения графиков является способом превращения формул и описаний в геометрические образы. Это – построение графиков – является средством увидеть формулы и функции и проследить, каким образом эти функции меняются. Например, если написано , то вы сразу видите параболу; если , вы видите параболу, опущенную на четыре единицы; если же , то вы видите предыдущую параболу, перевернутую вниз. Такое умение видеть сразу формулу, и ее геометрическую интерпретацию – является важным не только для изучения математики, но и для других предметов. Это умение, которое остается с вами на всю жизнь, подобно умению ездить на велосипеде, печатать на машинке или водить машину».
Один из крупнейших математиков нашего времени Израиль Моисеевич Гельфанд писал: «Процесс построения графиков является способом превращения формул и описаний в геометрические образы. Это – построение графиков – является средством увидеть формулы и функции и проследить, каким образом эти функции меняются. Например, если написано , то вы сразу видите параболу; если , вы видите параболу, опущенную на четыре единицы; если же , то вы видите предыдущую параболу, перевернутую вниз. Такое умение видеть сразу формулу, и ее геометрическую интерпретацию – является важным не только для изучения математики, но и для других предметов. Это умение, которое остается с вами на всю жизнь, подобно умению ездить на велосипеде, печатать на машинке или водить машину».
Хотя уравнения с модулями мы начали изучать уже с 6-го – 7-го класса, где мы проходили самые азы уравнений с модулями, я выбрала именно эту тему, потому что считаю, что она требует более глубокого и досконального исследования. Я хочу получить более широкие знания о модуле числа, различных способах построения графиков, содержащих знак абсолютной величины.
Цель работы: изучить соответствующие теоретические материалы, выявить алгоритм построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины.
Объект исследования: линейные функции, аналитическое выражение которых содержит знак абсолютной величины.
Методы исследования: построение графиков функций.
II. Основная часть.
1. Историческая справка.
В первой половине ХVII века начинает складываться представление о функции как о зависимости одной переменной величины от другой. Так, французские математики Пьер Ферма (1601-1665) и Рене Декарт (1596-1650) представляли себе функцию как зависимость ординаты тоски кривой от ее абсциссы. А английский ученый Исаак Ньютон (1643-1727) понимал функцию как изменяющуюся в зависимости от времени координату движущейся точки.
Термин «функция» (от латинского function – исполнение , совершение) впервые ввел немецкий математик Готфрид Лейбниц(1646-1716). У него функция связывалась с геометрическим образом (графиком функции). В дальнейшем швейцарский математик Иоганн Бернулли(1667-1748) и член Петербургской Академии наук знаменитый математик XVIII века Леонард Эйлер(1707-1783) рассматривали функцию как аналитическое выражение. У Эйлера имеется и общее понимание функции как зависимости одной переменной величины от другой.
У него функция связывалась с геометрическим образом (графиком функции). В дальнейшем швейцарский математик Иоганн Бернулли(1667-1748) и член Петербургской Академии наук знаменитый математик XVIII века Леонард Эйлер(1707-1783) рассматривали функцию как аналитическое выражение. У Эйлера имеется и общее понимание функции как зависимости одной переменной величины от другой.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово (омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.
В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и . т.п.
т.п.
Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению.
Определение. Модуль числа a или абсолютная величина числа a равна a, если a больше или равно нулю и равна -a, если a меньше нуля:
Из определения следует, что для любого действительного числа a,
2. Геометрическая интерпретация понятия модуля |а|
Каждому действительному числу можно поставить в соответствие точку числовой прямой, это точка будет геометрическим изображением данного действительного числа. Каждой точке числовой прямой соответствует её расстояние от начало отсчета, или длина отрезка, начало которого в точке начала отсчета, а конец – в данной точке. Длина отрезка всегда рассматривается как величина неотрицательная. Геометрической интерпретацией действительного числа служит вектор, выходящий из начала отсчета и имеющий конец в точке, изображающей данное число. Длина этого вектора будет геометрической интерпретацией модуля данного действительного числа.
-а 0 а
3. График функции у=f |(х)|
у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| = f | х |
График этой функции симметричен относительно оси координат.
Следовательно, достаточно построить график функции у=f(х) для х>0,а затем достроить его левую часть, симметрично правой относительно оси координат.
Например, пусть графиком функции у=f(х) является кривая, изображенная на рис.1, тогда графиком функции у=f |(х)| будет кривая, изображенная на рис.2.
Рис.1
Рис.2.
1. Построить график функции у= |х|
- Если х≥0, то |х| =х и наша функция у=х, т.
 е. искомый график совпадает с биссектрисой первого координатного угла.
е. искомый график совпадает с биссектрисой первого координатного угла. - Если х
Таким образом, искомый график есть ломанная, составленная из двух полупрямых. (Рис.3)
Из сопоставления двух графиков: у=х и у= |х|, я сделала вывод, что второй получается из первого зеркальным отображением относительно ОХ той части первого графика, которая лежит под осью абсцисс. Это положение вытекает из определения абсолютной величины.
Можно ли применять этот метод построения графиков дл квадратичной функции, для графиков обратной пропорциональности, содержащие абсолютную величину? Для этого я рассмотрела несколько функций, и сделала для себя вывод.
2. Например: у=х2 — |х| -3
а) Строю у=х2 -х -3 для х>0.
Квадратичная функция, графиком является парабола, ветви которой направлены вверх, т.к. а = , а > 0
- х0 = —
у0 =-4
(2; -4) – координаты вершины параболы.
- х=0, у= -3
(0; — 3) координаты точки пересечения графика функции с осью ОУ.
- у =0, х2 -х -3 = 0
х2 -4х -12 = 0 Имеем, х1= — 2; х2 = 6.
(-2; 0) и (6; 0) – координаты точки пересечения графика функции с осью ОХ.
Если х
Значит, часть требуемого графика, соответствующая значениям х0.
б) Поэтому достраиваю для х
Вывод: Для построения графика функции у=f |(х)|
- Достаточно построить график функции у=f(х) для х>0;
- Строить для х
4. График функции у = | f (х)|
По определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий:
у=f(х), если f(х) ≥0; у = — f(х), если f(х)
Для любой функции у = f(х), если f(х) >0, то | f (х)| = f(х), значит в этой части график функции у = | f (х)| совпадает с графиком самой функции у=f(х). Если же f(х) f (х)| = — f(х),т.е. точка (х; | f (х)| ) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ «отрицательную» часть графика.
1. Построить график функции у= | х2 – х – 6 |.
а) Построить график функции у= х2 – х – 6 . Квадратичная функция, графиком является парабола, ветви направлены вверх, т.к. а = 1, а >1.
х0 = —
у0 = — (1/2; — 6,25) координаты вершины
х=0; у = -6 (0; -6) координаты точки пересечения с осью ОУ.
у= 0, х2 – х – 6=0
х1 = -2; х2 = 3. (-2;0) и (3;0) –координаты точек пересечения с осью ОХ
б) Часть графика, расположенного в нижней полуплоскости, отобразить симметрично оси ОХ. (Рис.5)
Вывод: Для построения графика функции у=|f(х) |
1.Построить график функции у=f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)
(Рис.6, 7.)
5. График функции у=|f |(х)| |
Применяя, определение абсолютной величины и исследуя, графиков функции
у = | 2 · |х | — 3|
у = | х2 – 5 · |х| |
у = | |х3 | — 2 |, я нашла алгоритм построения графиков.
Для того чтобы построить график функции у=|f |(х)| | надо:
1. Построить график функции у=f(х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
1. у = | 2 · |х | — 3|
1) Строю у = 2х-3, для х>0. (1; -1) (; 0)
2) Строю прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ. Рис.8
2. у = | х2 – 5 · |х| |
а) Строю график функции у = х2 – 5 х для х>0.
Квадратичная функция, графиком является парабола, ветви направлены, т.к. а=1, а>0
х0 = -;
у0 = 6,25 -12,5 = -6,25 (2,5; -6,25) – координаты вершины
х=0; у=0; (0; 0) – координаты точки пересечения с осью ОУ
у=0; х2 – 5 х =0 (0; 0) и ( 5; 0) – координаты точек пересечения с осью ОХ.
х1 =0; х2=5
(Рис.9)
б) Строю часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.
3. у =| |х|3 | — 2 |
а) Строю у=х3 -2 для х > 0.
х1= 0; у1= -2
у2 = 0; х3 -2 =0
х2 =
б) Строю часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ. (Рис.10)
III. Заключение.
При выполнении исследовательской работы я делала такие выводы:
— сформировала алгоритмы построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины.
Алгоритм построения графика функции у=f |(х)|
1.Построить график функции у=f(х) для х>0;
2.Построить для х
Алгоритм построения графика функции у=|f(х) |
1. Построить график функции у=f(х) ;
Построить график функции у=f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)
Алгоритм построения графика функции у=|f |(х)| |
1. Построить график функции у=f(х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
— приобрела опыт построения графиков таких функций, как:
у=f |(х)|; у = | f (х)|; у=|f |(х)| |;
— научилась работать с дополнительной литературой и материалами, производить отбор
научных сведений;
— приобрела опыт выполнения графических работ на компьютере.
Список литературы:
- И. М.Гельфанд, Е.Г. Глаголева. Функции и графики. Издательство «Наука»
- Р.А. Калнин. Алгебра и элементарные функции. Издательство «Наука»
- М.
 К. Потапов, С.Н. Олехник. Конкурсные задачи по математики, Москва. «Наука»
К. Потапов, С.Н. Олехник. Конкурсные задачи по математики, Москва. «Наука» - Ю. Н.Макарычев, Н.Г. Миндюк. Дополнительные главы к школьному учебнику.
Москва, «Просвещение».
у
0
х
0
у
х
х
у
х
у
Рис 3.
0
6
-6
-3
х
у
Рис.4
0
6
-6
-2
3
х
у
Рис.5
у
х
Рис.6
у
х
Рис.7
0
у
х
-3/2
3/2
-3
3
Рис.8
1
-1
-6
-6
0
5
5
Рис.9
-2
0
1
2
2
-2
у
х
Рис.10
Python | Функция math.sin () — GeeksforGeeks
Python | math.sin () function
В Python модуль math содержит ряд математических операций, которые можно легко выполнить с помощью модуля. math.sin () функция возвращает синус значения, переданного в качестве аргумента. Значение, передаваемое в эту функцию, должно быть в радианах.
Значение, передаваемое в эту функцию, должно быть в радианах.
Синтаксис: math.sin (x)
Параметр:
x: значение, передаваемое в sin ()Возвращает: Возвращает синус значения, переданного в качестве аргумента
Код # 1:
|
Выход:
Значение синуса числа пи / 6 составляет: 0,49999999999999994.
Код # 2:
диапазон |
Вывод:
in_array: [-3.14159265, -2.57039399, -0.28559933, 0.28559933, 2.57039399, 3.14159265] —
-out_array: [-3.516811930e 0,2817325547837714, 0,2817325547837714, 0.5406408168673427, 3.5897
8416118e-09]
Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS . И чтобы начать свое путешествие по машинному обучению, присоединяйтесь к курсу Машинное обучение — базовый уровень
Функция Python sin (): объяснение с помощью 4 примеров
Функция sin ():
- Принимает аргумент (x = число)
- и возвращает его синус в радианах.

- Это часть математического модуля, поэтому эту функцию нельзя использовать напрямую.
- Вам необходимо импортировать математический модуль в вашу программу Python, как показано в примерах ниже.
- Чтобы получить результат в градусах, вы можете использовать функцию радиан () вместе с sin (), как показано в примере в следующем разделе этого руководства.
Синтаксис функции sin ()
Вот как используется функция sin ():
sin (x)
Например:
математ.грех (3)
Полный код см. В примерах ниже.
Что такое функция синуса в математике? Синус — одна из самых распространенных тригонометрических функций в математике. Два других — это функции косинуса (или cos) и тангенса (tan). Синусоидальная функция основана на прямоугольном треугольнике. Вы можете узнать больше о синусоидальной функции здесь.
Пример функции sin ()
Пример ниже показывает использование функции sin () для получения синуса нескольких чисел.Мы получим синус в радианах для 30, 45 и 60:
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 14 18 19 | # Демонстрация функции sin () из импорта математики sin sine_30 = sin (30) sine_45 = sin (45) 9000 60) print («Синус 30 =», sine_30) print («Синус 45 =», sine_45) print («Синус 60 = «, Sine_60) |
Результат:
В приведенном выше примере мы использовали сокращение для использования функции sin ().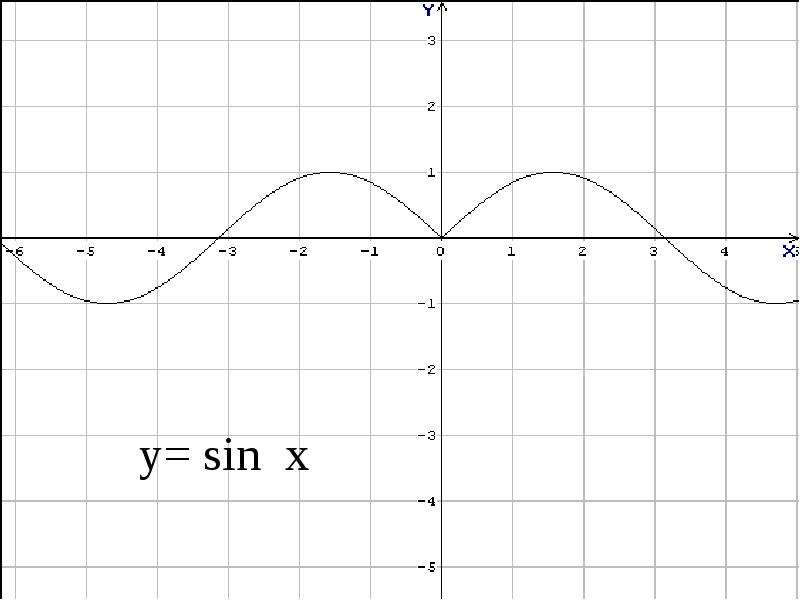 Этот код даст тот же результат:
Этот код даст тот же результат:
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 14 | import math sine_30 = math.sin (30) sine_45 = math.sin (45) sine_60 = math.sin (60) print («Синус 30 =», sine_302) print («Синус 45 =», sine_45) print («Синус 60 =», sine_60) |
Результат:
Синус 30 = -0,9880316240
8Синус 45 = 0,850
45341184
Синус 60 = -0.3048106211022167
Как получить градус синуса?
Вам может быть интересно, почему эти ответы отличаются от ответов калькулятора для получения синуса числа? Это потому, что функция Python sin () возвращает синус в радианах.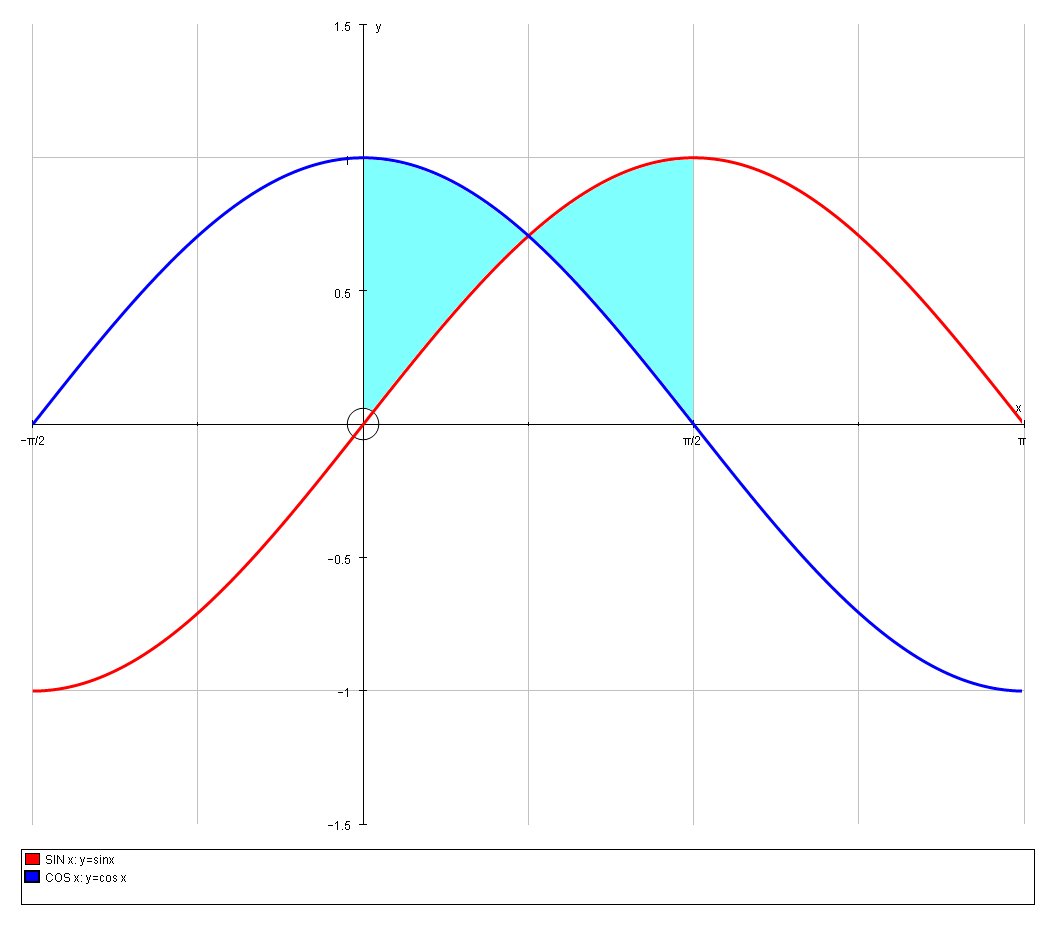
В математическом модуле есть еще одна функция radians (), которую вы можете использовать для преобразования радианов в градусы.
В приведенном ниже примере используются те же значения, что и в приведенных выше примерах, а также используется функция radians () для преобразования возвращаемого результата функцией sin () и получения значений синуса в градусах:
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 14 | import math sine_30 = math.sin (math.radians (30)) sine_45 = math.sin (math.radians (45)) sine_60 = math.sin (math.radians (60)) print («Синус 30 в градусах =», sine_30) print («Синус 45 в градусах =», sine_45) print («Синус 60 в градусах =», sine_60 ) |
Вывод:
Синус 30 в градусе = 0.
49999999999999994
Синус 45 в градусе = 0,7071067811865475
Синус 60 в градусе = 0,8660254037844386
Пример округления результата
В приведенном ниже примере используются три функции вместе; sin (), радианы () и round (). Функция round округляет результат, возвращаемый функцией radians (), до одинарной точности. См. Код и вывод:
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 14 | import math sine_30 = round (math.sin (math.radians (30)), 1) sine_45 = round (math.sin (math.radians (45)), 1) sine_60 = round (math.sin (math.radians ( 60)), 1) print («Синус 30 градусов с одинарной точностью =», sine_30) print («Синус 45 градусов с одинарной точностью =», sine_45) print («Синус 60 в градусах с одинарной точностью =», sine_60) |
Вывод:
Синус 30 градусов с одинарной точностью = 0.
5
Синус 45 градусов с одинарной точностью = 0,7
Синус 60 градусов с одинарной точностью = 0,9
Узнайте больше о круглой функции в ее руководстве: Python round function.
math — Математические функции — документация Python 3.9.5
Этот модуль обеспечивает доступ к математическим функциям, определенным C
стандарт.
Эти функции нельзя использовать с комплексными числами; использовать функции
то же имя из модуля cmath , если вам требуется поддержка сложных
числа.Различие между функциями, поддерживающими комплексные числа, и
те, которые не делаются, поскольку большинство пользователей не хотят учиться так много
математика, необходимая для понимания комплексных чисел. Получение исключения
вместо сложного результата позволяет раньше обнаруживать неожиданный комплекс
число, используемое в качестве параметра, чтобы программист мог определить, как и почему он
был создан в первую очередь.
Этот модуль предоставляет следующие функции. За исключением случаев, когда явно
в противном случае все возвращаемые значения являются числами с плавающей запятой.
Теоретико-числовые функции и функции представления
-
математика.потолок( x ) Вернуть потолок x , наименьшее целое число, большее или равное x .
Если x не является числом с плавающей запятой, делегируетx .__ ceil __ (), который должен вернуть
Интегральное значение.
-
математика.гребень( n , k ) Вернуть количество способов выбора k элементов из n элементов без повторения
и без заказа.Оценивается как
n! / (k! * (n - k)!), когдаk <= nи оценивает
к нулю, когдаk> n.Также называется биномиальным коэффициентом, потому что он эквивалентен
к коэффициенту k-го члена в полиномиальном разложении
выражение(1 + x) ** n.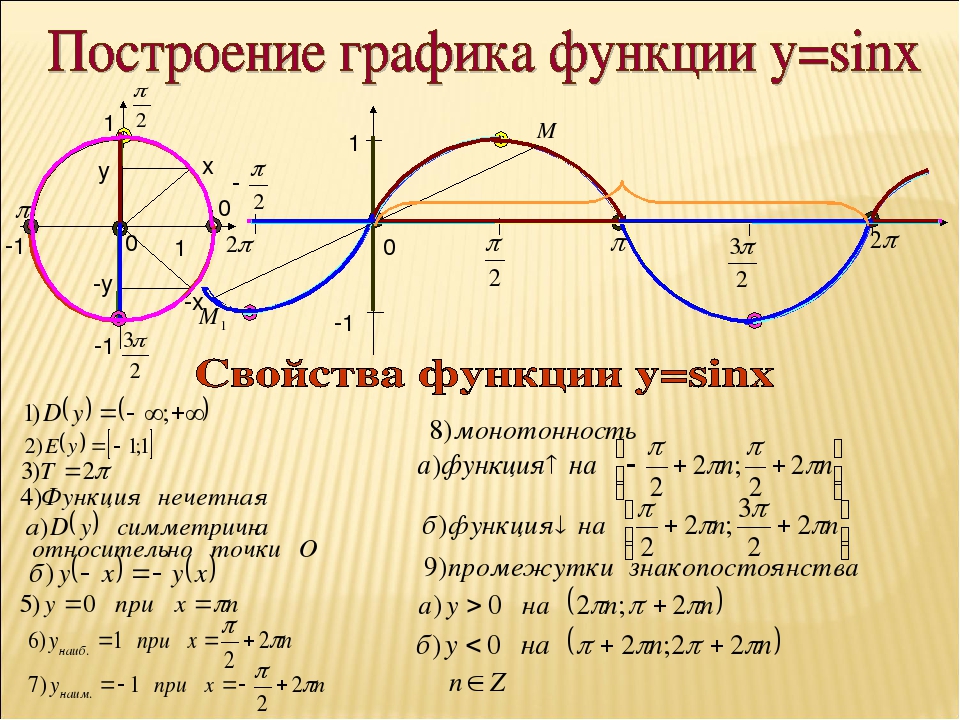
Вызывает
TypeError, если какой-либо из аргументов не является целым числом.
ВызываетValueError, если любой из аргументов отрицательный.
-
математика.копия( x , y ) Вернуть число с плавающей запятой с величиной (абсолютным значением) x , но со знаком
y . На платформах, поддерживающих нули со знаком,copysign (1.0, -0.0)
возвращает -1,0 .
-
математика.фабрик( x ) Вернуть абсолютное значение x .
-
математика.факториал( x ) Вернуть факториал x как целое число.Вызывает
ValueError, если x не является целым или
отрицательный.Не рекомендуется, начиная с версии 3.9: прием чисел с плавающей запятой с целыми значениями (например,
5.) не рекомендуется.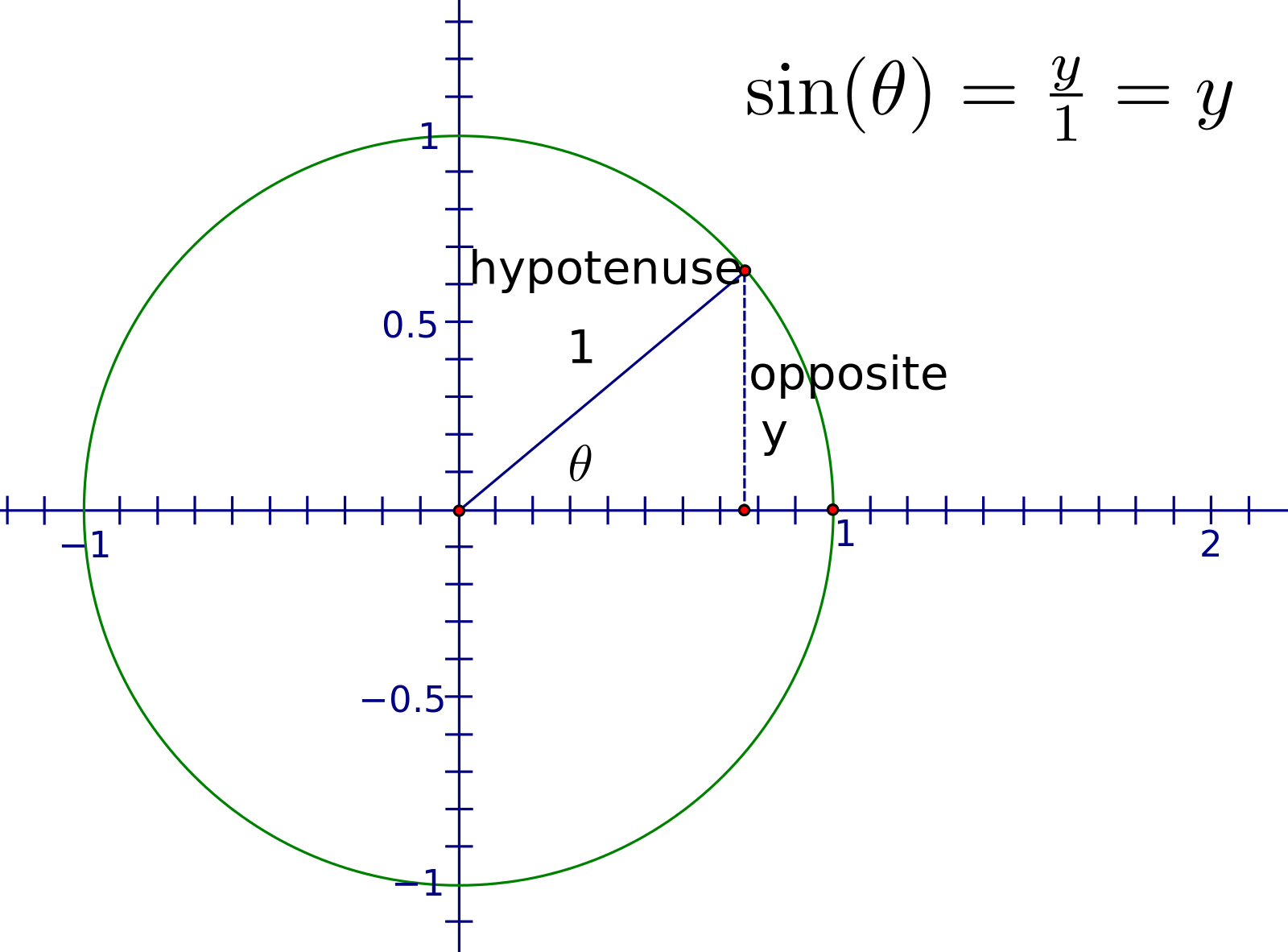 0
0
-
математика.этаж( x ) Вернуть нижний предел x , наибольшее целое число, меньшее или равное x .
Если x не является плавающим, делегируетx .__ floor __ (), который должен вернуть
Интегральное значение.
-
математика.fmod( x , y ) Вернуть
fmod (x, y), как определено библиотекой платформы C. Обратите внимание, что
Выражение Pythonx% yможет не возвращать тот же результат. Намерение C
стандартным является то, чтоfmod (x, y)должно быть точно (математически; до бесконечности
точности), равногоx - n * yдля некоторого целого числа n , так что результат имеет
тот же знак, что и x , и величина меньшеабс (y).Pythonx% y
вместо этого возвращает результат со знаком y и может быть неточно вычислимым
для аргументов с плавающей запятой. Например,
Например, fmod (-1e-100, 1e100)это-1e-100, но
результат Python-1e-100% 1e100будет1e100-1e-100, что не может быть
представлен в точности как поплавок и округляется до удивительного1e100. Для
по этой причине функцияfmod ()обычно предпочтительнее при работе с
float, тогда как Pythonx% yпредпочтительнее при работе с целыми числами.
-
математика.frexp( x ) Вернуть мантиссу и показатель степени x как пару
(m, e). м - поплавок
а e - целое число, такое чтоx == m * 2 ** eточно. Если x равно нулю,
возвращает(0,0, 0), иначе0,5 <= abs (m) <1. Это используется, чтобы «выбрать
отдельно »внутреннее представление поплавка портативным способом.
-
математика.fsum( итерация ) Вернуть точную сумму значений с плавающей запятой в итерируемом объекте.
 Избегает
Избегает
потеря точности из-за отслеживания нескольких промежуточных частичных сумм:>>> sum ([. 1, .1, .1, .1, .1, .1, .1, .1, .1, .1]) 0,9999999999999999 >>> fsum ([. 1, .1, .1, .1, .1, .1, .1, .1, .1, .1]) 1.0
Точность алгоритма зависит от арифметических гарантий IEEE-754 и
типичный случай, когда режим округления половинный.На некоторых не-Windows
сборки, базовая библиотека C использует сложение с расширенной точностью и может
иногда дважды округляют промежуточную сумму, в результате чего она
младший значащий бит.Для дальнейшего обсуждения и двух альтернативных подходов см. Поваренную книгу ASPN.
рецепты точного суммирования с плавающей запятой.
-
математика.gcd( * целые числа ) Вернуть наибольший общий делитель указанных целочисленных аргументов.Если какой-либо из аргументов отличен от нуля, то возвращаемое значение является наибольшим.
положительное целое число, которое является делителем всех аргументов. Если все аргументы
Если все аргументы
равны нулю, то возвращается значение0.gcd ()без аргументов
возвращает0.Изменено в версии 3.9: Добавлена поддержка произвольного количества аргументов. Раньше всего два
аргументы были поддержаны.
-
математика.isclose( a , b , * , rel_tol = 1e-09 , abs_tol = 0.0 ) Вернуть
Истина, если значения a и b близки друг к другу и
Неверноиначе.Считаются ли два значения близкими или нет, определяется в соответствии с
даны абсолютные и относительные допуски.rel_tol - относительный допуск - это максимально допустимая разница.
между a и b относительно большего абсолютного значения a или b .Например, чтобы установить допуск 5%, передайтеrel_tol = 0,05. По умолчанию
допуск1e-09, что гарантирует, что два значения совпадают
с точностью до 9 десятичных цифр. rel_tol должен быть больше нуля.
rel_tol должен быть больше нуля.abs_tol - минимальный абсолютный допуск - полезно для сравнений около
нуль. abs_tol должен быть не меньше нуля.Если ошибок не возникает, результатом будет:
абс (a-b) <= max (rel_tol * max (abs (a), abs (b)), abs_tol).Специальные значения IEEE 754:
NaN,infи-infбудут
обрабатывается в соответствии с правилами IEEE. В частности,NaNне считается
близко к любому другому значению, включаяNaN.infи-infтолько
считается близким к себе.См. Также
PEP 485 - Функция проверки примерного равенства
-
математика.исфинит( x ) Return
True, если x не является ни бесконечностью, ни NaN, и
Неверноиначе.(Обратите внимание, что0,0- это , считающееся конечным. )
)
-
математика.isinf( x ) Вернуть
Истинно, если x - положительная или отрицательная бесконечность, и
Неверноиначе.
-
математика.иснан( x ) Вернуть
Истина, если x - NaN (не число), иЛожьв противном случае.
-
математика.isqrt( n ) Вернуть квадратный корень целого неотрицательного целого числа n . Это
пол из точного квадратного корня из n , или, что эквивалентно, наибольшего целого числа
a таким образом, что a ² ≤ n .Для некоторых приложений может быть удобнее иметь наименьшее целое число
a таким образом, чтобы n ≤ a ², или, другими словами, потолок
точный квадратный корень из n .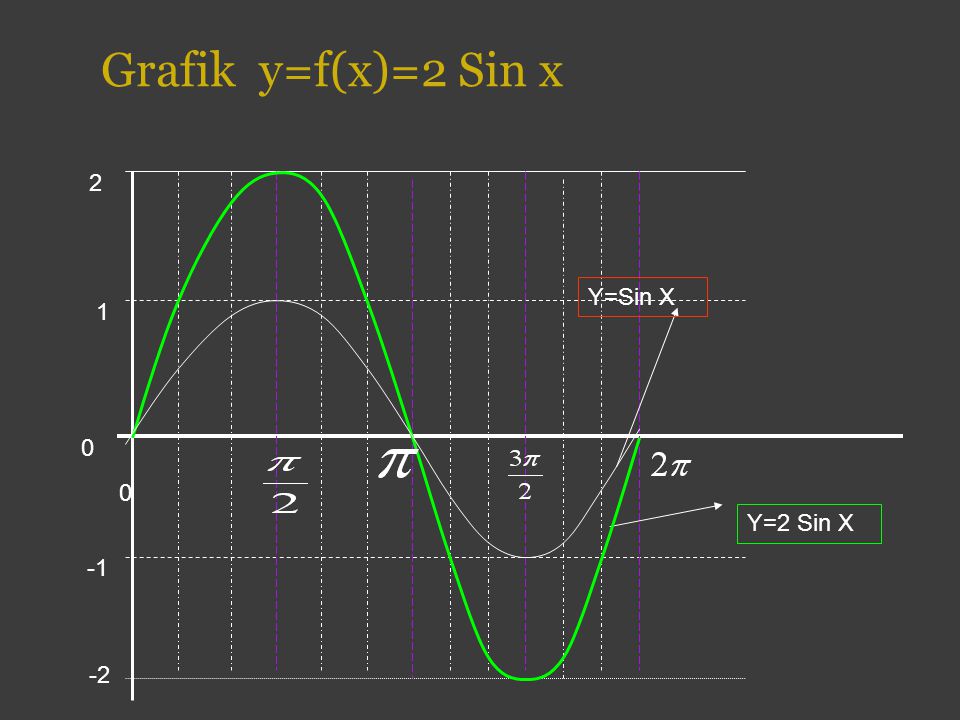 Для положительного n это можно вычислить, используя
Для положительного n это можно вычислить, используя
a = 1 + isqrt (n - 1).
-
математика.л / см( * целые числа ) Возвращает наименьшее общее кратное указанных целочисленных аргументов.
Если все аргументы отличны от нуля, то возвращаемое значение является наименьшим.
положительное целое число, кратное всем аргументам. Если какой-либо из аргументов
равно нулю, то возвращается значение0.лкм ()без аргументов
возвращает1.
-
математика.ldexp( x , и ) Возврат
x * (2 ** i). По сути, это обратная функция
frexp ().
-
математика.мод( x ) Вернуть дробную и целую части x . Оба результата несут знак
размером x и являются плавающими.
-
математика.далее после( x , y ) Вернуть следующее значение с плавающей запятой после x по направлению к y .
Если x равно y , вернуть y .
Примеры:
math.nextafter (x, math.inf)идет вверх: в сторону положительной бесконечности.math.nextafter (x, -math.inf)идет вниз: в сторону минус бесконечности.математ.nextafter (x, 0.0)стремится к нулю.math.nextafter (x, math.copysign (math.inf, x))уходит от нуля.
См. Также
math.ulp ().
-
математика.пермь( n , k = нет ) Вернуть количество способов выбора k элементов из n элементов
без повторов и по порядку.Оценивается как
n! / (п - к)!, когдаk <= nи оценивает
к нулю, когдаk> n.Если k не указан или None, то k по умолчанию n
и функция возвращаетn!.Вызывает
TypeError, если какой-либо из аргументов не является целым числом.
ВызываетValueError, если любой из аргументов отрицательный.
-
математика.prod( итераций , * , start = 1 ) Вычислить произведение всех элементов на входе итерация .Значение по умолчанию начало для продукта
1.Когда итерация пуста, вернуть начальное значение. Эта функция
предназначен специально для использования с числовыми значениями и может отклонять
нечисловые типы.
-
математика.остаток( x , y ) Вернуть остаток в стиле IEEE 754 x относительно y .
 Для
Для
конечное x и конечное ненулевое y , это разницаx - n * y,
гдеn- ближайшее целое число к точному значению частногоx /.Если
yx / yнаходится ровно посередине между двумя последовательными целыми числами,
ближайшее , четное целое число используется дляn. Остатокr = остаток (x,, таким образом, всегда удовлетворяет
y)abs (r) <= 0,5 * abs (y).Особые случаи соответствуют IEEE 754: в частности, остаток
(x, math.inf)- это
x для любых конечных x иостаток (x, 0)и
остаток (math.inf, x)поднятьValueErrorдля любых не-NaN x .Если результат операции с остатком равен нулю, этот ноль будет иметь
тот же знак, что и x .На платформах, использующих двоичные числа с плавающей запятой IEEE 754, результат этого
операция всегда точно представима: ошибка округления не вводится.
-
математика.усечение( x ) Вернуть значение
Realx , усеченное до
Integral(обычно целое число). Делегаты
х.__trunc __ ().
-
математика.ulp( x ) Вернуть значение младшего бита числа с плавающей запятой x :
Если x - NaN (не число), верните x .
Если x отрицательное, вернуть
ulp (-x).Если x является положительной бесконечностью, верните x .
Если x равно нулю, вернуть наименьшее положительное значение.
денормализованное представимое число с плавающей запятой (меньше минимального положительного
нормализованное с плавающей запятой,sys.float_info.min).Если x равно наибольшему положительному представимому веществу с плавающей запятой,
вернуть значение младшего бита x , так что первый
float меньше x равенx - ulp (x).
В противном случае ( x - положительное конечное число) вернуть значение наименьшего
значащий бит x , так что первое число с плавающей запятой больше x
равноx + ulp (x).
ULP означает «Единица на последнем месте».
См. Также
math.nextafter ()иsys.float_info.epsilon.
Обратите внимание, что frexp () и modf () имеют другой шаблон вызова / возврата
чем их эквиваленты в C: они принимают единственный аргумент и возвращают пару
значения, вместо того, чтобы возвращать их второе возвращаемое значение через "output"
параметр ’(в Python такого нет).
Для функций ceil () , floor () и modf () обратите внимание, что все
числа с плавающей запятой достаточно большой величины являются точными целыми числами.Поплавки Python обычно несут не более 53 бит точности (такая же, как у
платформа C двойного типа), в этом случае любой поплавок x с абс (x)> = 2 ** 52
обязательно не имеет дробных битов.
Степенные и логарифмические функции
-
математика.эксп.( x ) Возврат e в степени x , где e = 2,718281… это основание
натуральных логарифмов. Обычно это более точно, чем математика.e ** x
илиpow (math.e, x).
-
математика.экспм1( x ) Возврат e в степени x , минус 1. Здесь e - основание натурального
логарифмы. Для малых чисел с плавающей запятой x , вычитание вexp (x) - 1
может привести к значительной потере точности;expm1 ()
функция предоставляет способ вычислить это количество с полной точностью:>>> из математического импорта exp, expm1 >>> exp (1e-5) - 1 # дает результат с точностью до 11 разряда 1.0000050000069649e-05 >>> expm1 (1e-5) # результат с полной точностью 1.0000050000166668e-05
-
математика.
журнал( x [, основание ]) С одним аргументом верните натуральный логарифм x (с основанием e ).
С двумя аргументами вернуть логарифм x к заданному основанию ,
рассчитывается какlog (x) / log (base).
-
математика.log1p( x ) Вернуть натуральный логарифм 1 + x (основание e ). В
результат рассчитывается с точностью до x , близких к нулю.
-
математика.журнал2( x ) Вернуть логарифм по основанию 2 x . Обычно это более точно, чем
журнал (x, 2).См. Также
int.bit_length ()возвращает количество битов, необходимых для представления
целое число в двоичном формате, исключая знак и ведущие нули.
-
математика.
лог10( x ) Вернуть десятичный логарифм x . Обычно это более точно
чемlog (x, 10).
-
математика.pow( x , y ) Возврат
xв степениy. Далее следуют исключительные случаи
Приложение «F» стандарта C99, насколько это возможно. В частности,
мощь (1.0, x)иpow (x, 0.0)всегда возвращают1.0, даже
когдаx- это ноль или NaN. Если иx, иyконечны,
xотрицательно, аyне целое, тогдаpow (x, y)
не определено и вызываетValueError.В отличие от встроенного оператора
**,math.pow ()преобразует оба
его аргументы для типас плавающей запятой. Используйте**или встроенный
pow ()функция для вычисления точных целочисленных степеней.
-
математика.кв.( x ) Возвратите квадратный корень из x .
Тригонометрические функции
-
математика.acos( x ) Вернуть арккосинус x в радианах. Результат находится между
0и
пи.
-
математика.asin( x ) Вернуть арксинус x в радианах.Результат находится между
-pi / 2и
пи / 2.
-
математика.атан( x ) Вернуть арктангенс x в радианах. Результат находится между
-pi / 2и
пи / 2.
-
математика.атан2( y , x ) Вернуть
atan (y / x)в радианах. Результат находится между
Результат находится между -piиpi.Вектор в плоскости от начала координат до точки(x, y)составляет этот угол
с положительной осью X. Смыслatan2 ()в том, что признаки обоих
ему известны входные данные, поэтому он может вычислить правильный квадрант для угла.
Например,atan (1)иatan2 (1, 1)оба равныpi / 4, ноatan2 (-1,- это
-1)-3 * pi / 4.
-
математика.cos( x ) Вернуть косинус x радиан.
-
математика.расстояние( p , q ) Вернуть евклидово расстояние между двумя точками p и q , каждая
заданная как последовательность (или итерация) координат. Две точки
должен иметь такой же размер.Примерно эквивалентно:
sqrt (сумма ((px - qx) ** 2,0 для px, qx в zip (p, q)))
-
математика.
гипотеза( * координаты ) Вернуть евклидову норму,
sqrt (сумма (x ** 2 для x в координатах)).Это длина вектора от начала координат до точки
задается координатами.Для двумерной точки
(x, y)это эквивалентно вычислению
гипотенуза прямоугольного треугольника с использованием теоремы Пифагора,
sqrt (x * x + y * y).Изменено в версии 3.8: Добавлена поддержка n-мерных точек. Раньше только двое
размерный случай был поддержан.
-
математика.sin( x ) Вернуть синус x радиан.
-
математика.желто-коричневый( x ) Вернуть тангенс x радиан.
Угловое преобразование
-
математика.градусов( x ) Преобразование угла x из радианов в градусы.
-
математика.радиан( x ) Преобразование угла x из градусов в радианы.
Гиперболические функции
Гиперболические функции
являются аналогами тригонометрических функций, основанных на гиперболах
вместо кружков.
-
математика.acosh( x ) Вернуть обратный гиперболический косинус x .
-
математика.асинь( x ) Вернуть обратный гиперболический синус x .
-
математика.атанх( x ) Вернуть арктангенс гиперболического значения x .
-
математика.cosh( x ) Вернуть гиперболический косинус x .
-
математика.
sinh( x ) Вернуть гиперболический синус x .
-
математика.танх( x ) Вернуть гиперболический тангенс x .
Специальные функции
-
математика.эрф( x ) Вернуть функцию ошибки в
х .Функцию
erf ()можно использовать для вычисления традиционных статистических
такие функции, как кумулятивное стандартное нормальное распределение:деф фи (х): 'Кумулятивная функция распределения для стандартного нормального распределения' return (1.0 + erf (x / sqrt (2.0))) / 2.0
-
математика.erfc( x ) Вернуть дополнительную функцию ошибок при x . Дополнительная ошибка
функция определяется как
1.0 - erf (x). Он используется для больших значений x , где вычитание
Он используется для больших значений x , где вычитание
от одного вызовет потерю значимости.
-
математика.гамма( x ) Вернуть гамма-функцию в
х .
-
математика.lgamma( x ) Вернуть натуральный логарифм абсолютного значения гаммы.
функция при x .
Константы
-
математика.пи Математическая константа π = 3,141592…, с доступной точностью.
-
математика.e Математическая константа e = 2,718281…, с доступной точностью.
-
математика.тау Математическая константа τ = 6,283185…, с доступной точностью.
Тау - это постоянная окружности, равная 2 π , отношение длины окружности к
его радиус. Чтобы узнать больше о Тау, посмотрите видео Ви Харта Pi is (still)
Чтобы узнать больше о Тау, посмотрите видео Ви Харта Pi is (still)
Неправильно, и начни праздновать
Тау день, съев в два раза больше пирога!
-
математика.инф. Положительная бесконечность с плавающей запятой.(Для отрицательной бесконечности используйте
-math.inf.) Эквивалент выходуfloat ('inf').
-
математика.нан Значение с плавающей запятой, «не число» (NaN). Эквивалентно выходу
с плавающей запятой ('nan').
Детали реализации CPython: Модуль math состоит в основном из тонких оберток вокруг платформы C.
математические библиотечные функции. Поведение в исключительных случаях соответствует Приложению F к
стандарт C99, где это необходимо.Текущая реализация повысит
ValueError для недопустимых операций, таких как sqrt (-1. или 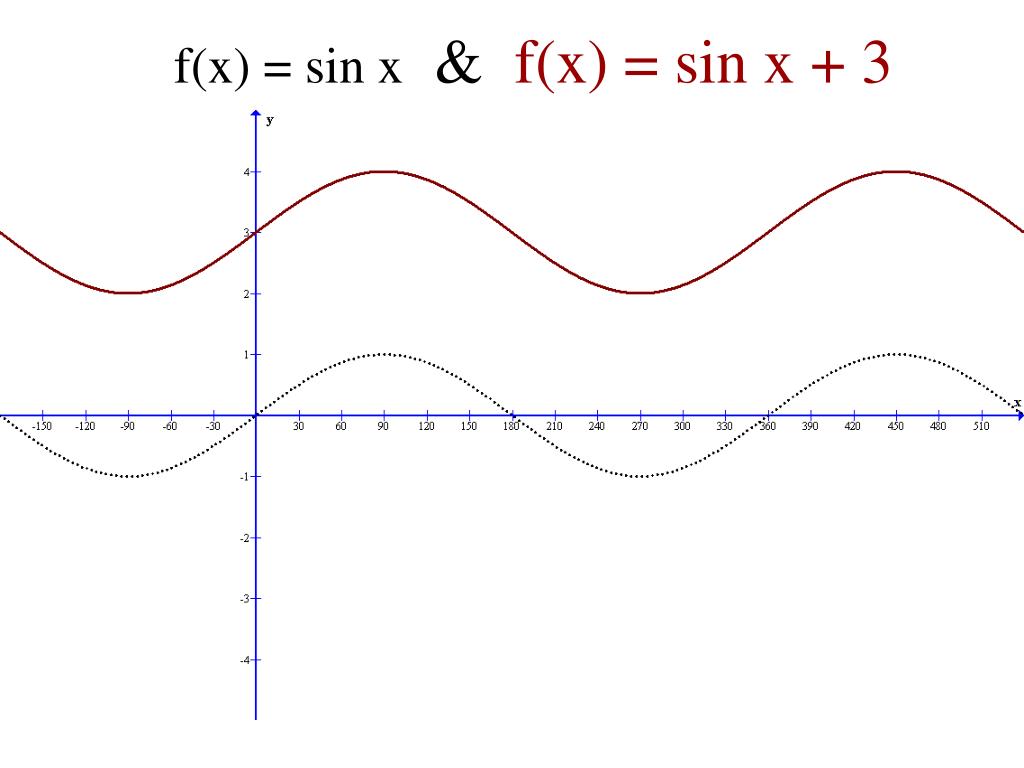 0)
0) log (0.0)
(где Приложение F C99 рекомендует сигнализировать о недопустимой операции или делении на ноль),
и OverflowError для результатов, которые переполняются (например,
exp (1000.0) ). NaN не будет возвращено ни одной из функций.
выше, если только один или несколько входных аргументов не были NaN; в этом случае,
большинство функций вернут NaN, но (опять же после приложения F C99) там
есть некоторые исключения из этого правила, например pow (float ('nan'), 0.0) или
гипотеза (float ('nan'), float ('inf')) .
Обратите внимание, что Python не пытается отличить сигнальные NaN от
тихие NaN, и поведение для передачи сигналов NaN остается неопределенным.
Типичное поведение - рассматривать все NaN, как если бы они были тихими.
См. Также
- Модуль
cmath Версии многих из этих функций с комплексными числами.
Модуль 4 - Параметрические уравнения, тригонометрические и обратные тригонометрические функции
Изучение x = cos t , y = sin t
Прежде чем исследовать взаимосвязь между синусоидальной функцией и единичной окружностью, изучите параметрические уравнения, показанные ниже.
Для
, спрогнозируйте форму кривой, которая создается параметрическими уравнениями
x = cos t
y = sin t
4.2.1 Убедитесь, что ваш калькулятор находится в режиме радиан, проверив меню РЕЖИМ. Изобразите параметрические уравнения, чтобы проверить свой прогноз. Нажмите здесь, чтобы получить ответ.
| |||
Синусоидальная функция
Синусоидальную функцию можно определить несколькими способами. Один из способов - позволить sin t быть координатой y точки на единичной окружности, длина пересекаемой дуги которой составляет t единиц, что является другим способом сказать, что соответствующий центральный угол равен t радиан.
Напомним, что синусоида имеет следующую форму:
Связь между графиком y = sin x и значениями единичного круга y можно проиллюстрировать, построив оба графика одновременно.
Последовательный и одновременный режимы построения графиков
В шестой строке меню РЕЖИМ доступны следующие варианты: Последовательный или Одновременный ( Simul ).(См. Экран ниже.) В последовательном режиме графики рисуются по одному в порядке, указанном в редакторе Y =. В одновременном режиме все графики в редакторе Y = рисуются одновременно, а не последовательно.
Выберите следующие настройки в меню РЕЖИМ для одновременного построения графиков параметрических уравнений.
Разворачивание синусоидальной волны
4.2.2. Опишите связь, которую вы видите между кругом и синусоидой. Нажмите здесь, чтобы получить ответ.
Периодическая функция и ее период
Периодическая функция имеет значения y , которые повторяются через определенные интервалы значений x . Период периодической функции - это длина интервала x , в течение которого значения y составляют один полный цикл. Синусоидальная функция имеет период 2
, который представляет собой количество радианов за один полный оборот.
Преобразованная синусоида
График y = A sin [ B ( x + C )] + D является преобразованной версией графика y = sin ( x ). Ниже перечислены эффекты каждого из значений A , B , C и D . Преобразования обсуждались в Модуле 3.
обеспечивает вертикальное растяжение или сжатие с коэффициентом A ; и отражение относительно оси x , если A отрицательно.
также называется амплитудой синусоидальной волны, которая составляет половину расстояния между самым высоким и самым низким значениями y на графике.
B производит горизонтальное растяжение или сжатие, которое изменяет период кривой.Период преобразованной синусоиды равен
. Если B отрицательное, значит, есть отражение относительно оси y .
C производит сдвиг по горизонтали.
D производит вертикальный сдвиг.
График y = 5sin [
( x - 1)] + 2 - это преобразованный график y = sin x , который имеет следующие характеристики:
Амплитуда 5 (растянута по вертикали в 5 раз)
Время
(сжато по горизонтали в
)
Смещен вправо по горизонтали на 1 шт.
Сдвинут по вертикали на 2 единицы
4.2.3. Опишите преобразования y = sin ( x ), которые дают график y = -3sin [2 ( x + 1)] -4, а затем изобразите уравнение на своем калькуляторе. Нажмите здесь, чтобы получить ответ.
Модуль 19 - Приложения интеграции
В этом уроке исследуется поиск общей площади, ограниченной кривой и осью x на заданном интервале. Он также исследует область между двумя кривыми.
Общая площадь области, которая находится как выше, так и ниже оси x , находится путем отделения положительных частей графика от отрицательных частей.Каждая часть интегрирована, и абсолютных значений результатов складываются вместе, чтобы найти общую площадь.
Изучите график y = sin x от 0 до 2.
очередной раз.
Как показано в Уроке 19.1,
, а также
.
Общая площадь, ограниченная y = sin x и осью x на интервале [0, 2
] равно 2+ | -2 | = 4 квадратных единицы.
Использование абсолютного значения для определения общей площади
Другой метод, используемый для определения общей площади, - это интегрирование абсолютного значения функции. Вы можете найти абсолютное значение abs (), нажав
.
Сравните графики y = sin ( x ) и y = | sin ( x ) | показано ниже в [0,2
] x [-2, 2] окно.Обратите внимание, что абсолют имеет эффект отражения части графика sin (x), которая находится ниже оси x , так что она находится выше оси x . Интеграл от | sin ( x ) | от 0 до 2
дает общую площадь, ограниченную кривой y = sin ( x ) и осью x между x = 0 и x = 2
.
Оценивать
и интерпретировать результат.
- Очистите главный экран.
- Введите fnInt (abs (sin (X)), X, 0,2
).
Общая площадь, ограниченная y = sin x и осью x на интервале [0, 2
] составляет 4 кв.
19.2.1 Найдите общую площадь, ограниченную x = x 3 - 3 x 2 - x + 3 и осью x на интервале [0, 4] путем интегрирования абсолютное значение y = x 3 - 3 x 2 - x + 3.Нажмите здесь, чтобы получить ответ.
Нахождение области между двумя кривыми
Интегралы могут использоваться для определения площади между двумя кривыми путем вычисления интеграла от значения верхней кривой за вычетом нижней кривой между их точками пересечения. Найдите область между y = 4 - x 2 и y = x , следуя приведенной ниже процедуре.
- Изобразите две функции y = 4 - x 2 и y = x в окне [-3, 3, 1] x [-5, 5, 1].
Верхняя кривая равна y = 4 - x 2 , а нижняя кривая - y = x .
Найдите точки пересечения кривых.
- Выберите 5: пересечение из меню CALC на экране графика.
- Выберите две кривые и переместите курсор ближе к левой точке пересечения.
- Пресс
найти левую точку пересечения.
- Повторите этот процесс для правой точки пересечения.
19.2.2 Какова приблизительная координата x правой точки пересечения?
Нажмите здесь, чтобы получить ответ.
Теперь нам нужно интегрировать верхнюю кривую за вычетом нижней кривой. Примерная площадь между кривыми определяется выражением
19.2.3 Оцените интеграл, указанный выше, на вашем TI-83 и интерпретируйте результат.
Нажмите здесь, чтобы получить ответ.
тригонометрических функций в Python - sin, cos, tan и т. Д.
Математическая библиотека на python имеет множество тригонометрических функций , которых достаточно для выполнения различных тригонометрических вычислений с помощью минимальных строк кода.Эти функции можно использовать после импорта математического модуля или путем обращения к математической библиотеке с помощью оператора dot следующим образом:
math.function_name (параметр)
# или импортируйте математический модуль
импорт математики Есть 2 вспомогательных метода, которые помогают преобразовывать значения из радианов в градусы и наоборот, так что вы можете проверить значение в любом формате.
градусов (значение) : этот метод преобразует переданное ему значение из радиан в градусы.
радиан (значение) : этот метод преобразует переданное ему значение из градусов в радианы.
Краткий факт: Все тригонометрические функции в Python предполагают, что входной угол выражается в радианах .
Кроме того, поскольку мы изучаем математику, пи / 2 составляет 90 градусов и пи / 3 составляет 60 градусов , математический модуль в Python предоставляет константу пи , которая представляет пи , что можно использовать с тригонометрической функцией.
Время для примера:
В приведенном ниже примере кода мы использовали методы градусов () и радиан () ,
импорт математики
печать (math.degrees ((math.pi / 2)))
печать (математические радианы (60)) Выход :
90,0 1.0471975511965976
Теперь давайте посмотрим на различные тригонометрические функции в действии, одну за другой.
sin (x) Функция
Эта функция возвращает синус переданного значения (здесь x).Входные данные x должны быть углом , указанным в терминах радиан (пи / 2, пи / 3 / пи / 6 и т. Д.).
cos (x) Функция
Эта функция возвращает косинус переданного значения (здесь x). Входные данные x - это угол, представленный в радианах .
tan (x) Функция
Эта функция возвращает тангенс переданного ей значения, то есть синус / косинус угла.Здесь вводится угол в радиан .
Пример кода для
sin , cos и tan :
Ниже у нас есть простой пример кода для трех тригонометрических функций, определенных выше,
импорт математики
print (math.sin (math.pi / 3)) # pi / 3 радиан преобразуется в 60 градусов
печать (math.tan (math.pi / 3))
печать (math.cos (math.pi / 6)) Выход:
0.8660254037844386 1.7320508075688767 0,8660254037844387
asin (x) Функция
Эта функция возвращает , обратный синусу , который также известен как арксинус комплексного числа . Входные данные выражаются в радианах и должны находиться в диапазоне от -1 до 1 . Он возвращает число с плавающей запятой в качестве вывода .
acos (x) Функция
Эта функция возвращает косинус , обратный параметра x в радианах.Это также известно как арккосинус комплексного числа . Значение x должно находиться в диапазоне от -1 до 1 . На выходе он возвращает число с плавающей запятой.
atan (x) Функция
Эта функция возвращает , обратное касательной , в радианах. Он известен как арктангенс комплексного числа . Значение параметра находится в пределах -1 и 1 . Его также можно представить как (математ.грех (math.pi / 4)) / (math.cos (math.pi / 4)) . На выходе он возвращает число с плавающей запятой.
Пример кода для
asin , acos и atan с углами в радианах:
импорт математики
печать (math.asin (1))
печать (math.acos (0))
печать (math.atan (1)) Выход:
1,5707963267948966 1,5707963267948966 0,7853981633974483
В примере ниже показано, как функции asin , acos и atan могут использоваться с комплексными числами в формате x + iy .
импорт cmath
х = 1,0
у = 1,0
г = комплекс (х, у)
print ("Арксинус равен:", cmath.asin (z))
print ("Арккосинус:", cmath.acos (z))
print ("Арктангенс равен:", cmath.atan (z)) Выход:
Арксинус: (0,66623943243 + 1,06127506157j) Арккосинус: (0,
68943023814-1.06127506157j) Арктангенс равен: (1.0172219678978514 + 0.40235947810852507j)
sinh (x) Функция
Этот метод возвращает гиперболический синус угла переданного комплексного числа.
cosh (x) Функция
Этот метод возвращает гиперболический косинус угла переданного комплексного числа.
tanh (x) Функция
Этот метод возвращает гиперболический тангенс угла переданного комплексного числа.
Пример кода для
sinh , cosh и tanh с комплексными числами:
импорт cmath
х = 1.0
у = 1,0
г = комплекс (х, у)
print ("Гиперболический синус:", cmath.sinh (z))
print ("Гиперболический косинус равен:", cmath.cosh (z))
print ("Гиперболический тангенс равен:", cmath.tanh (z)) Выход:
Гиперболический синус: (0,63496347361 + 1,2984575814159773j)
Гиперболический косинус: (0,8337300251311491 + 0,9888977057628651j)
Гиперболический тангенс: (1.08373386946 + 0.2717525853195118j) asinh (x) Функция
Возвращает , обратный гиперболическому синусу угла / комплексного числа.
acosh (x) Функция
Возвращает , обратное гиперболическому косинусу угла / комплексного числа.
atanh (x) Функция
Возвращает , обратный гиперболическому тангенсу угла / комплексного числа.
Пример кода для методов
asinh , acosh и atanh с комплексными числами:
импорт cmath
х = 1.0
у = 1,0
г = комплекс (х, у)
print ("Обратный гиперболический синус:", cmath.asinh (z))
print ("Обратный гиперболический косинус равен:", cmath.acosh (z))
print ("Обратный гиперболический тангенс равен:", cmath.atanh (z)) Выход:
Обратный гиперболический синус: (1.06127506157 + 0.6662394324
3j) Обратный гиперболический косинус равен: (1.06127506157 + 0.
68943023813j) Обратный гиперболический тангенс равен: (0.40235947810852507 + 1.0172219678978514j)
atan2 (y, x) Функция
Это переводится в atan2 (y / x) , где y и x являются числовыми значениями. Он возвращает значение в диапазоне от –pi до pi . Он представляет собой угол между положительной осью x и координатами (x, y).
печать (math.atan2 (1.2,1.3)) Выход:
0,7454194762741583
гипотеза (x, y) Функция
Эта функция возвращает гипотенузу , т.е.e Евклидова норма . Это означает, что он возвращает расстояние между началом координат и точками (x, y). Это указывает длину вектора в двумерном пространстве. Евклидова норма также известна как «величина» вектора. Это числовое значение вектора (поскольку у векторов есть величина, а также направление).
Если передано более 2 аргументов, он корректно возвращает TypeError .
печать (математ. Гипотеза (2,2)) Выход:
2.8284271247461903
ПРИМЕЧАНИЕ: Когда эти значения сравниваются с числовыми значениями углов, может быть несколько различий в десятичных разрядах, которые можно безопасно игнорировать. Например, tan (pi / 3) преобразуется в tan 60 , что эквивалентно sqrt (3) . Если используется функция tan , вывод будет 1.7320508075688767 , тогда как sqrt (3) даст 1.7320508075688772 .
Это так просто? А как насчет исключений и ошибок?
Что ж, вы совершенно правы.Есть два вида исключений, которые потенциально могут возникнуть из-за неправильного использования этих методов:
TypeError : Этот вид ошибки возникает, когда значение, не являющееся числом, передается в качестве параметра одному из тригонометрических методов.
ValueError : Возникает такая ошибка, в метод передается недопустимое значение / параметр.
Пример, демонстрирующий оба исключения:
импорт математики
# Он передается как строка, а не как число,
# отсюда и ошибка.печать (math.sin ('2'))
# Значение, обратное синусоидальному углу, можно найти для параметров
# которые указаны только в радианах и являются инверсией синуса целого числа
# математически не определено, что приводит к ошибке
печать (math.asin (5)) Выход:
TypeError: должно быть действительное число, а не str ValueError: ошибка математического домена
Заключение
Мы узнали о том, как можно использовать различные тригонометрические методы, импортировав модуль math в python.Не забудьте всегда передавать параметр в радианах или преобразовывать градусов в радиан , а затем передавать его как параметр.
Elementary - документация SymPy 1.8
Возвращает, если возможно, максимальное значение списка.
Если количество аргументов равно единице, то
вернуть этот аргумент.
Если количество аргументов равно двум, то
верните, если возможно, значение из (a, b), которое> = другое.
В общем случае, когда длина списка больше 2, задача
сложнее. Вернуть только те аргументы, которые больше
чем другие, если возможно определить направленность.
Если невозможно определить такую связь, вернуть частично
оценил результат.
Допущения также используются для принятия решения.
Также разрешены только сопоставимые аргументы.
Он называется Max , а не max , чтобы избежать конфликтов.
со встроенной функцией max .
Примеры
>>> из sympy import Max, Symbol, oo
>>> из sympy.abc import x, y, z
>>> p = символ ('p', положительный результат = True)
>>> n = Символ ('n', отрицательное значение = Истина)
>>> Макс (x, -2) Макс (-2; x) >>> Макс (x, -2) .subs (x, 3) 3 >>> Макс (p, -2) п >>> Макс (x, y) Макс (x, y) >>> Макс (x, y) == Макс (y, x) Правда >>> Макс (x, Макс (y, z)) Макс (x, y, z) >>> Макс (n, 8, p, 7, -oo) Макс (8, п) >>> Макс (1, x, oo) оо
Задачу можно рассматривать как поиск супремумов в
направленные полные частичные порядки [R280].
Исходные значения последовательно распределяются изолированными подмножествами
в котором выполняется поиск супремумов и получается максимальное количество аргументов.
Если полученный супремум один, он возвращается.
Изолированные подмножества - это наборы значений, которые являются только сопоставимыми
друг с другом в текущем наборе. Например. натуральные числа сопоставимы с
друг друга, но не сравнимы с символом \ (x \). Другой пример:
символ \ (x \) при отрицательном предположении сравним с натуральным числом.
Также есть «наименьшие» элементы, которые сопоставимы со всеми остальными,
и иметь нулевое свойство (максимум или минимум для всех элементов).

 pyplot as plt
pyplot as plt  plot (in_ray
plot (in_ray