3

6

Risolvere per ?

cos(x)=1/2

7

Risolvere per x

sin(x)=-1/2

8

Преобразовать из градусов в радианы

225

9

Risolvere per ?

cos(x)=( квадратный корень 2)/2

10

Risolvere per x

cos(x)=( квадратный корень 3)/2

11

Risolvere per x

sin(x)=( квадратный корень 3)/2

12

График

g(x)=3/4* корень пятой степени x

13

Найти центр и радиус

x^2+y^2=9

14

Преобразовать из градусов в радианы

120 град. 2+n-72)=1/(n+9)

sin x a

Вы искали sin x a? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и sin x найти x, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «sin x a».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как sin x a,sin x найти x,sinx a,корни синуса,решение уравнения x sin x,син х,уравнение sinx a,уравнение синус х равно а. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и sin x a. Просто введите задачу в окошко и нажмите
«решить» здесь (например, sinx a).

Где можно решить любую задачу по математике, а так же sin x a Онлайн?

Решить задачу sin x a вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Уравнение sin x = a

Значения синуса заключены в промежутке [-1; 1], т.е. -1 ≤ sin α ≤ 1. Поэтому если |а| > 1, то уравнение sin x = a не имеет корней.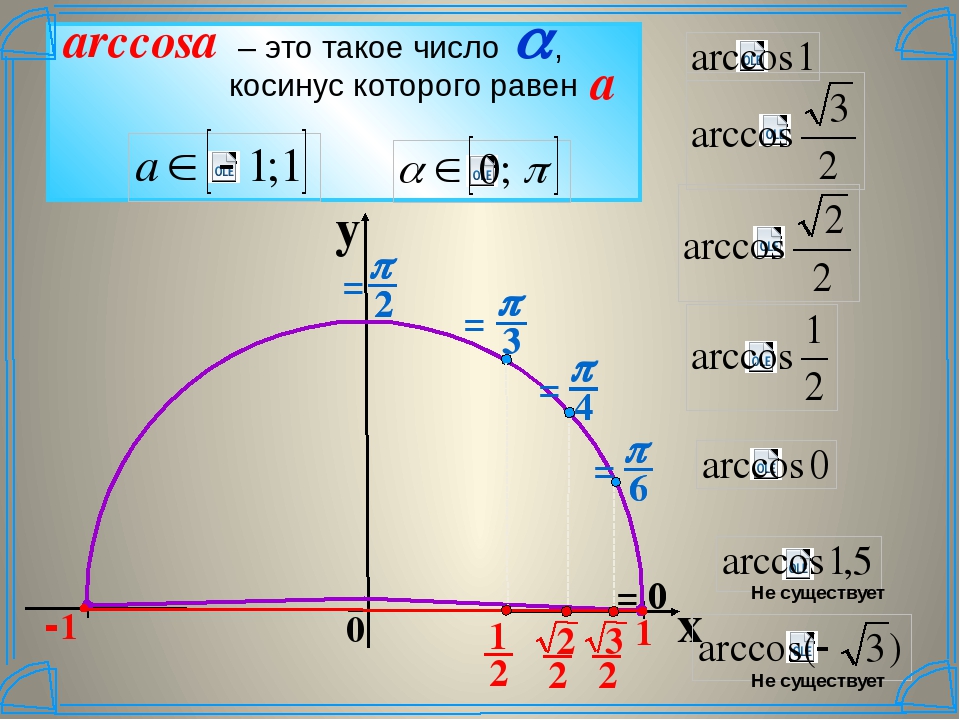 Например, уравнение sin x = 2 корней не имеет.

Обратимся к некоторым задачам.

Задача 1.

Решить уравнение sin x = 1/2.

Решение.

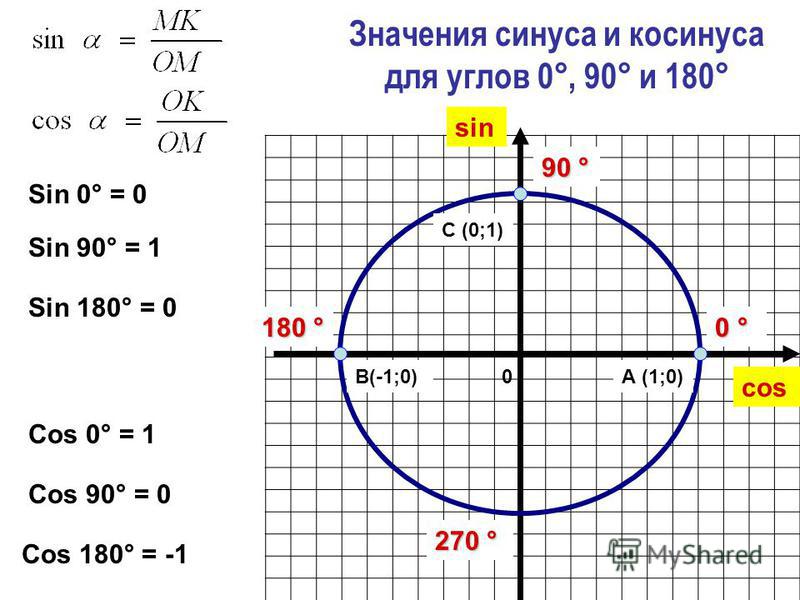
Отметим, что sin x – это ордината точки единичной окружности, которая получена в результате поворота точки Р (1; 0) на угол х вокруг начала координат.

Ордината, равная ½, присутствует у двух точек окружности М₁ и М₂.

Так как 1/2 = sin π/6, то точка М₁ получается из точки Р (1; 0) посредством поворота на угол х₁ = π/6, а также на углы х = π/6 + 2πk, где k = +/-1, +/-2, …

Точка М₂ получается из точки Р (1; 0) в результате поворота на угол х₂ = 5π/6, а также на углы х = 5π/6 + 2πk, где k = +/-1, +/-2, …, т.е. на углы х = π – π/6 + 2πk, где k = +/-1, +/-2, ….

Итак, все корни уравнения sin х = 1/2 можно найти по формулам х = π/6 + 2πk, х = π – π/6 + 2πk, где k € Z.

Эти формулы могут объединиться в одну: х = (-1)ⁿ π/6 + πn, где n € Z     (1).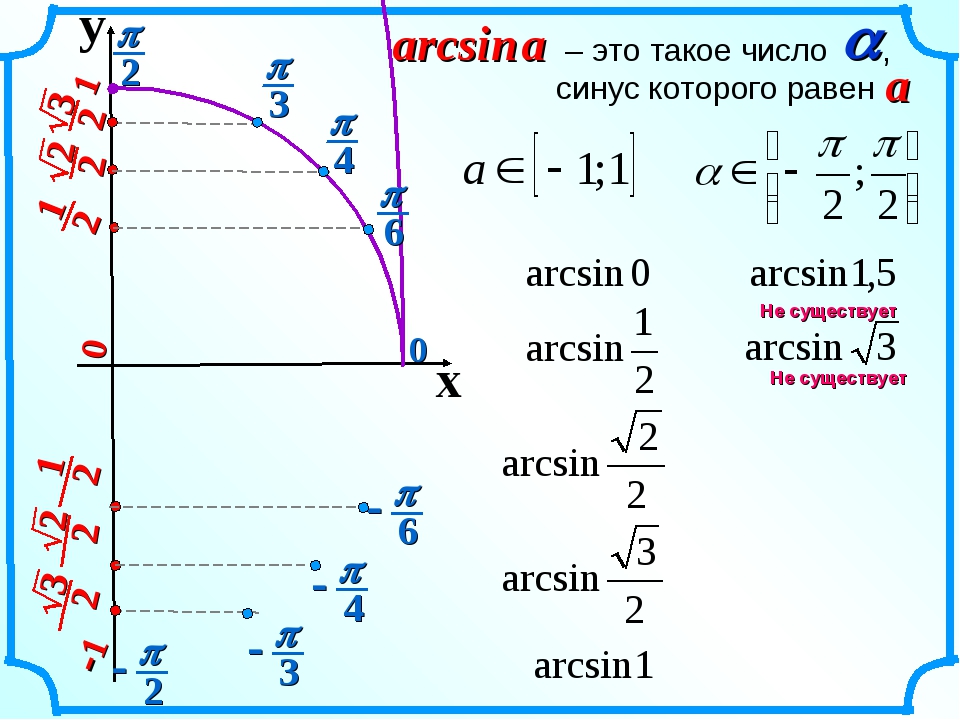

Действительно, если n – четное число, т.е. n = 2k, то из формулы (1) получаем х = π/6 + 2πk, а если n – нечетное число, т.е. n = 2k + 1, то из формулы (1) получаем х = π – π/6 + 2πk.

Ответ. х = (-1)ⁿ π/6 + πn, где n € Z.

Задача 2.

Решить уравнение sin x = -1/2.

Решение.

Ординату -1/2 имеют две точки единичной окружности М₁ и М₂, где х₁ = -π/6, х₂ = -5π/6. Следовательно, все корни уравнения sin x = -1/2 можно найти по формулам х = -π/6 + 2πk, х = -5π/6 + 2πk, k € Z.

Эти формулы мы можем объединить в одну: х = (-1)ⁿ (-π/6) + πn, n € Z    (2).

Действительно, если n = 2k, то по формуле (2) получаем х = -π/6 + 2πk, а если n = 2k – 1, то по формуле (2) находим х = -5π/6 + 2πk.

Ответ. х = (-1)ⁿ (-π/6) + πn, n € Z.

Таким образом, каждое из уравнений sin x = 1/2 и sin x = -1/2 имеет бесконечное множество корней.

На отрезке -π/2 ≤ х ≤ π/2 каждое из этих уравнений имеет только один корень:
х₁ = π/6 – корень уравнения sin x = 1/2 и х₁ = -π/6 – корень уравнения sin x = -1/2.

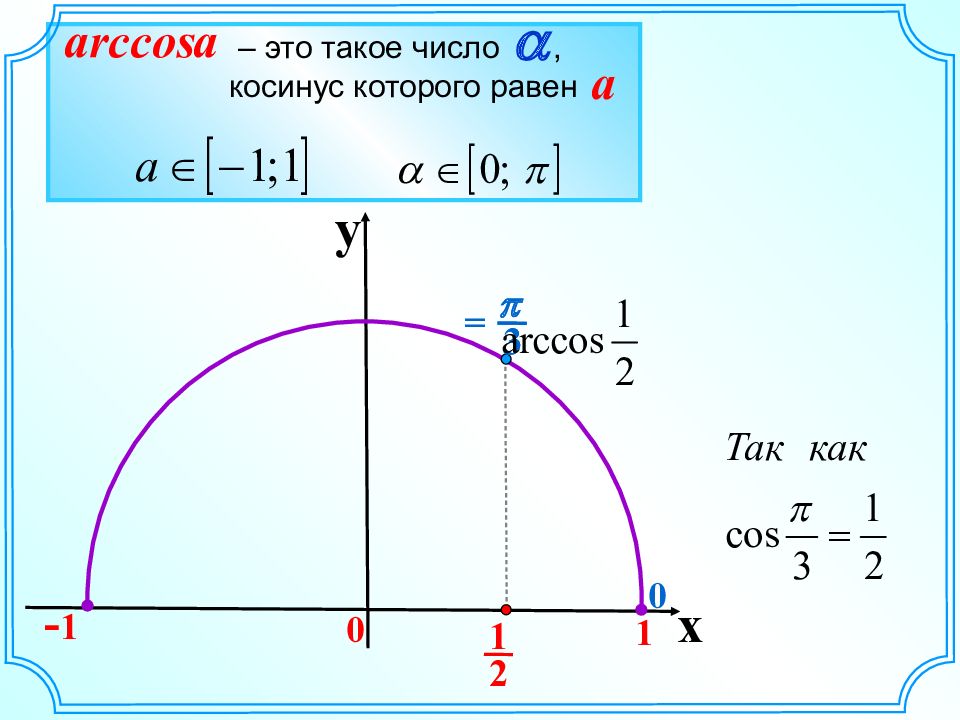
Число π/6 называют арксинусом числа 1/2 и записывают: arcsin 1/2 = π/6; число -π/6 называют арксинусом числа -1/2 и пишут: arcsin (-1/2) = -π/6.

Вообще уравнение sin x = а, где -1 ≤ а ≤ 1, на отрезке -π/2 ≤ х ≤ π/2 имеет лишь один корень. Если а ≥ 0, то корень заключен в промежутке [0; π/2]; если а < 0, то в промежутке [-π/2; 0). Этот корень называют арксинусом числа а и обозначают arcsin а.

Таким образом, арксинусом числа а € [–1; 1] называется такое число а € [–π/2; π/2], синус которого равен а.

аrcsin а = α, если sin α = а и -π/2 ≤ х ≤ π/2        (3).

Например, аrcsin √2/2 = π/4, так как sin π/4 = √2/2 и – π/2 ≤ π/4 ≤ π/2;
аrcsin (-√3/2) = -π/3, так как sin (-π/3) = -√3/2 и – π/2 ≤ – π/3 ≤ π/2.

Аналогично тому, как это сделано при решении задач 1 и 2, можно показать, что корни уравнения sin х = а, где |а| ≤ 1, выражаются формулой

х = (-1)ⁿ аrcsin а + πn, n € Z          (4).

Также мы можем доказать, что для любого а € [-1; 1] справедлива формула аrcsin (-а) = -аrcsin а.

Из формулы (4) следует, что корни уравнения
sin х = а при а = 0, а = 1, а = -1 можно находить по более простым формулам:

sin х = 0           х = πn, n € Z                        (5)

sin х = 1           х = π/2 + 2πn, n € Z          (6)

sin х = -1        х = -π/2 + 2πn, n € Z          (7)

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Производная синуса — sin x

Производная по переменной x от синуса x равна косинусу x:
( sin x )′ = cos x.

Доказательство

Для вывода формулы производной синуса, мы воспользуемся определением производной:
.

Чтобы найти этот предел, нам нужно преобразовать выражение таким образом, чтобы свести его к известным законам, свойствам и правилам. Для этого нам нужно знать четыре свойства.
1) Значение первого замечательного предела:
(1)   ;
2) Непрерывность функции косинус:
(2)   ;
3) Тригонометрические формулы. Нам понадобится следующая формула:
(3)   ;
4) Арифметические свойства предела функции:
Если    и  , то
(4)   .

Применяем эти правила к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим формулу
(3)   .
В нашем случае
; . Тогда
;
;
;
.

Теперь сделаем подстановку . При , . Применим первый замечательный предел (1):
.

Сделаем такую же подстановку и используем свойство непрерывности (2):
.

Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):

.

Формула производной синуса доказана.

Примеры

Рассмотрим простые примеры нахождения производных от функций, содержащих синус. Мы найдем производные от следующих функций:
y = sin 2x;   y = sin ² x   и   y = sin ³ x.

Пример 1

Найти производную от sin 2x.

Решение

Сначала найдем производную от самой простой части:
( 2x )′ = 2( x )′ = 2 · 1 = 2.
Применяем формулу производной сложной функции.
.
Здесь .

Ответ

( sin 2x )′ = 2 cos 2x.

См. также
Все примеры вычисления производных с решениями > > >

Пример 2

Найти производную от синуса в квадрате:
y = sin ² x.

Решение

Перепишем исходную функцию в более понятном виде:
.
Найдем производную от самой простой части:
.
Применяем формулу производной сложной функции.

.
Здесь .

Можно применить одну из формул тригонометрии. Тогда
.

Ответ

.

Пример 3

Найти производную от синуса в кубе:
y = sin ³ x.

Решение > > >

Производные высших порядков

Заметим, что производную от sin x первого порядка можно выразить через синус следующим образом:
.

Найдем производную второго порядка, используя формулу производной сложной функции:

.
Здесь  .

Теперь мы можем заметить, что дифференцирование sin x приводит к увеличению его аргумента на . Тогда производная n-го порядка имеет вид:
(5)   .

Докажем это, применяя метод математической индукции.

Мы уже проверили, что при , формула (5) справедлива.

Предположим, что формула (5) справедлива при некотором значении . Докажем, что из этого следует, что формула (5) выполняется для .

Выпишем формулу (5) при :
.
Дифференцируем это уравнение, применяя правило дифференцирования сложной функции:

.
Здесь .
Итак, мы нашли:
.
Если подставить , то эта формула примет вид (5).

Формула доказана.

Автор: Олег Одинцов.     Опубликовано: 04-03-2017

Внеклассный урок — Простейшие тригонометрические уравнения cos t = a, sin t = a, tg x = a, ctg x = a

Простейшие тригонометрические уравнения 

Тригонометрическое уравнение – это уравнение, содержащее неизвестное под знаком тригонометрической функции.

Простейшими тригонометрическими уравнениями называют уравнения вида
sin x = a, cos x = a, tg x = a, ctg x = a, где a – действительное число (a ∈ R).

 

Уравнение cos x = a.

Принцип:

arccos a = x. Следовательно, cos x = a. Условия: модуль а не больше 1;  x не меньше 0, но не больше π (| a | ≤ 1;  0 ≤ x  ≤ π)

 

Формулы:

x = ± arccos a  +  2πk,     где k – любое целое число                                            arccos (-a) = π – arccos a,    где 0 ≤ a ≤ 1

 

Пример 1: Решим уравнение

                √3
cos x  =  ——.
                 2

Решение.

Применим первую формулу:

                      √3
x = ± arccos —— + 2πk
                      2

Сначала находим значение арккосинуса:

             √3       π
arccos —— = —
              2        6

Осталось подставить этот число в нашу формулу:

            π
x = ± —— + 2πk
            6

Пример решен.

 

Пример 2: Решим уравнение

                  √3
cos x  =  – ——.
                   2

Решение.

Сначала применим первую формулу из таблицы:

                        √3
x = ± arccos (– —) + 2πk
                         2

Теперь с помощью второго уравнения вычислим значение арккосинуса:

                 √3                         √3                 π        π        π       6π       π         5π
arccos (– ——) = π – arcos ——  =  π  –  —  =  —  –  —  =  —  –  —  =  ——
                  2                           2                   6        1        6        6        6          6

Применяя формулу для —а, обращайте внимание на знак а: он меняется на противоположный.

Осталось подставить значение арккосинуса и решить пример:

           5π
x = ± —— + 2πk
            6

Пример решен.

 

Уравнение sin x = a.

Принцип:

arcsin a = x, следовательно sin x = a. Условия: модуль а не больше 1;  x в отрезке [-π/2; π/2] (| a | ≤ 1;  –π/2 ≤ x  ≤ π/2)

 

Формулы.

(1 из 3)

x = arcsin a  +  2πk x = π – arcsin a  +  2πk   Эти две формулы можно объединить в одну: x = (–1)narcsin a + πn   (k – любое целое число;  n – любое целое число; | a | ≤ 1) Значение четного n: n = 2k Значение нечетного n: n = 2k + 1 Если n – четное число, то получается первая формула. Если n – нечетное число, то получается вторая формула.

                                                                  √3
Пример 1: Решить уравнение sin x  =  ——
                                                                  2

Решение.

Применяем первые две формулы:

                        √3
1) x  =  arcsin —— + 2πk
                         2

                              √3
2) x  =  π – arcsin —— + 2πk
                               2

Находим значение арксинуса:

             √3        π
arcsin ——  =  —
             2          3

Осталось подставить это значение в наши формулы:

            π
1) x =  — + 2πk
           3

 

                 π                   2π
2) x =  π – —  + 2πk = —— + 2πk
                 3                    3

Пример решен.

 

Пример 2: Решим это же уравнение с помощью общей формулы.

Решение.

               π
x = (–1)ⁿ — + πn
               3

Пояснение: если n будет четное число, то решение примет вид № 1; если n будет нечетным числом – то вид №2.

Пример решен.

 

(2 из 3)
Для трех случаев есть и более простые решения:

Если sin x = 0,  то x = πk Если sin x = 1,  то x = π/2 + 2πk Если sin x = –1,  то x = –π/2 + 2πk

 

Пример 1: Вычислим arcsin 0.

Решение.

Пусть arcsin 0 = x.

Тогда sin x = 0, при этом x ∈ [–π/2; π/2].

Синус 0 тоже равен 0. Значит:

x = 0.

Итог:

arcsin 0 = 0.

Пример решен.

 

Пример 2: Вычислим arcsin 1.

Решение.

Пусть arcsin 1 = x.

Тогда sin x = 1.

Число 1 на оси ординат имеет имя π/2. Значит:

arcsin 1 = π/2.

Пример решен.

 

(3 из 3)

arcsin (–a) = –arcsin a

 

Пример: Решить уравнение

                √3
sin x = – ——
                2

Решение.

Применяем формулы:

                          √3
1) x = arcsin (– ——) + 2πk
                           2

                                √3
2) x = π – arcsin (– ——) + 2πk
                                 2

Находим значение арксинуса:

                 √3                        √3           π
arcsin (– ——) = – arcsin (——) = – —
                  2                          2             3

Подставляем это значение arcsin в обе формулы:

              π
1) x = – — + 2πk
              3
                     π                         π                    4π
2) x = π – (– —) + 2πk = π +  —  +  2πk = ——  +  2πk
                     3                         3                     3

Пример решен.

 

Уравнение tg x = a.

Принцип:

arctg a = x, следовательно tg x = a. Условие: x больше –π/2, но меньше π/2 (–π/2 < x < π/2)

 

Формулы.

(1)

x = arctg a + πk где k – любое целое число (k ∈ Z)

 

(2)

arctg (–a) = –arctg a

Пример 1: Вычислить arctg 1.

Решение.

Пусть arctg 1 = x.

Тогда tg x = 1,  при этом x ∈ (–π/2; π/2)

Следовательно:

       π                       π
x = —    при этом  — ∈ (–π/2; π/2)
       4                       4

                            π
Ответ: arctg 1 = —
                            4

 

Пример 2: Решить уравнение tg x = –√3.

Решение.

Применяем формулу:

x = arctg (–√3) + πk

Решаем:

arctg (–√3) = –arctg √3 = –π/3.

Подставляем:

x = –π/3 + πk.

Пример решен.

 

Уравнение ctg x = a.

Принцип:

arcctg a = x, следовательно ctg x = a. Условие: x больше 0, но меньше π (0 < x < π)

 

Формулы.

(1)

x = arcctg a + πk (k ∈ Z)

 

(2)

arcctg (–a) = π – arcctg а

                                                 
Пример 1: Вычислить arcctg √3.

Решение.

Следуем принципу:

arcctg √3 = х

ctg х = √3.

х = π/6.

Ответ: arcctg √3 = π/6

Пример 2: Вычислить arcctg (–1).

Решение.

Применяя формулу (2), обращайте внимание на знак а: он меняется на противоположный. В нашем примере –1 меняется на 1:

arcctg (–1) = π – arcctg 1 = π – π/4 = 3π/4.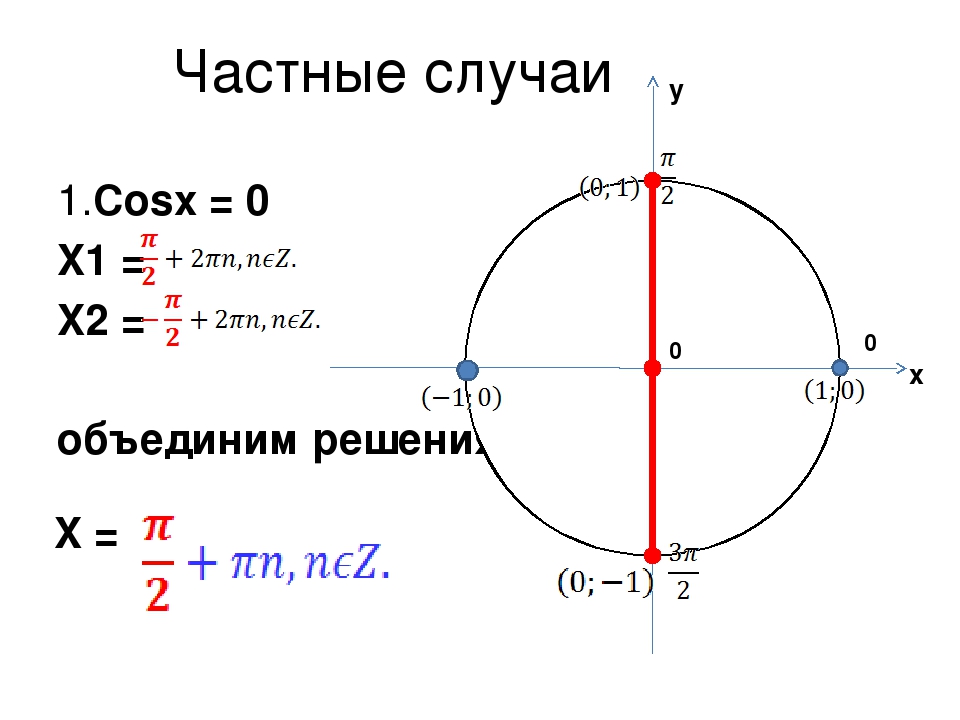

Пример решен.

 

ЦТ-2015, В9 — Живая Геометрия — LiveJournal

Мы должны знать.
Мы будем знать.

Д. Гильберт

Дасканалыя моманты

Абитуриенту
10 класс
9 класс

Консультация Справочники:
Алгебра Геометрия WolframAlpha
Geogebra online Блог
Избранные тестовые задания
Памятка для абитуриента Актуальные ссылки
Новая задача Катрионы

ЦТ — избранное

---

ЦТ-2021 РТ1 РТ 20-21 2-1
ЦТ-2020 v1 DRT РТ-2 PT-3
ЦТ-2018 PT-1 ДРТ PT-2
ЦТ-2017 РТ-1 Demo PT-2 PT-3
ЦТ-2016 РТ-1 РТ-2 РТ-3
ЦТ-2015 РТ-1 РТ-2 РТ-3
ЦТ-2014 РТ-1 РТ-2 РТ-3
ЦТ-2013 РТ-1 PT-2 РТ-3
ЦТ-2012 PТ-1 PТ-2 PТ-3
ЦТ-2011 PT-1 PT-2 PT-3
ЦТ-2010 РТ-1 PT-2 PT-3
ЦТ-2009 PT-1 ЦТ-2008 ЦТ-2007 ЦТ-2006 ЦТ-2005 ЦТ-2004 ЦТ-2003 ЦТ-2002
Демо-2017 ДемоЦТ-2016 ДемоЦТ-2015 Демо-2016, р Демо-2015, р

Темы ЦТ
1. Числа и вычисления
Целые числа
2. Тождественные преобразования
3. Квадратный трехчлен
4. Треугольники Метод площадей
5. Рациональные уравнения
6. Рациональные неравенства
7. Стереометрия Сечения
Круглые тела
8. Задачи с модулем
9. Иррациональные уравнения
10. Четырехугольники
11. Текстовые задачи
12. Прогрессии
13. Окружность Геометрические преобразования
14. Тригонометрия Триг_выражения Триг_уравнения
15. Показательная функция (уравнения и неравенства)
16. Логарифмы Тренажер
17. Функция Графики и координаты Диаграммы Параметры Подобие и пропорции

---

Тест-экзамены ФПМИ БГУ: 2017 2016 2015 2014 2013 2019

Моўкнасць

Эвристика Д. Пойа
Эссе. Поиск интерпретации
Пошук інтэрпрэтацыі
Ностальгия по параметрам
Памежныя задачы
Конфигурационный подход
ЖГ-технология абитуриенту
Введение в университет
Библиотека Видео Мары
Аудиокниги

ЖГ-пособия абитуриенту
Векторы
Комплексные числа
Графики. Справочник
Числа и вычисления
Квадратный трехчлен
Треугольники
Четырехугольники
Окружность. Многоугольники
Тригонометрия
Функции

РИКЗ ЕГЭ ЗНО Матура
GSP in China Математика из Франции Динамические
модели

---

Тест: Параметры и графики
Эволюция конфигурации
Диалог задач
Тест, 11 класс
Тест для абитуриента
Экстремумы функции
Показательная функция
Логарифмическая линейка
Вечно живая теорема
Параллельный перенос
Четырехугольники
Построение трапеции
Наибольший угол
Эволюция конфигурации
Площадь и радиус
Число π
Стереометрия-0
Сечение куба
Развертки куба
Выход в 4D
Площадь сечения
Классика на РТ
Объём пирамиды и призмы
Это не забывается
Формулы приведения
Тригонометрическая машина
Построение синусоиды
Тригонометрические уравнения
График уравнения
Корни уравнений
Задача о двух квадратах
Инвариант
Неподвижная точка
Параллельный перенос
Треугольник Рело
Квадратное колесо
Колбасная синусоида
Сумма квадратов
Теорема Монжа
Теорема Дезарга
Лента Мёбиуса
Мориц Эшер
Паркет: тип 15

Генератор тестов (сайт Ларина)
Экзаменационный сборник по математике, 11 класс SB ∼

▼ Вставка символов ▼

---

➀➁➂➃➄➅➆➇➈➉ ⇐⇑ ⇒⇓ ⇔ ∞ · ± ∼ ≠ ∈ ∉ ∅ ∃ ∀ ∆ ∠ ∩ ∪ ⊂ ≤ ≥ ⊥ ½⅓ ↻ ▼◄►§ ✏ ‣ 2° ² ³ ✅ ✌ 👍▶🔽α β γ θ π
≠≤≥≈±⋅≡≢×∘∞√°∠⊥∈∉∋∀∃∄∅∼ ¼½¾÷∫∂∇∝∧∨∩∪∴≅⊂⊃⊄⊆⊇⊕⊗ƒ ₀₁₂₃₄₅₆₇₈₉₊₋₍₌₎⁰¹²³⁴⁵⁶⁷⁸⁹⁺⁻⁽⁼⁾ⁿ

Решение уравнения sin x — cos x = 1.

Урок-семинар

Цели урока:

Главная дидактическая цель: рассмотреть все
возможные способы решения данного уравнения.

Обучающие: изучение новых приемов решения
тригонометрических уравнений на примере данного
в творческой ситуации урока-семинара.

Развивающие: формирование общих приемов
решения тригонометрических уравнений;
совершенствование мыслительных операций
учащихся; развитие умений и навыков устной
монологической математической речи при
изложении решения тригонометрического
уравнения.

Воспитывающие: развивать самостоятельность
и творчество; способствовать выработке у
школьников желания и потребности обобщения
изучаемых фактов.

Вопросы для подготовки и
дальнейшего обсуждения на семинаре.

1. Приведение уравнения к однородному
   относительно синуса и косинуса.
2. Разложение левой части уравнения на множители.
3. Введение вспомогательного угла.
4. Преобразование разности (или суммы)
   тригонометрических функций в произведение.
5. Приведение к квадратному уравнению
   относительно одной из функций.
6. Возведение обеих частей уравнения в квадрат.
7. Выражение всех функций через tg x (универсальная
   подстановка).
8. Графическое решения уравнения.

Все учащиеся разбиваются на группы (по 2-4
человека) в зависимости от общего количества
учащихся и их индивидуальных способностей и
желания. Самостоятельно определяют для себя тему
для подготовки и выступления на уроке-семинаре.
Выступает один человек от группы, а остальные
учащиеся принимают участие в дополнениях и
исправлениях ошибок, если в этом возникнет
необходимость.

Организационный момент.

Учащимся сообщаются:

Тема урока:

“Различные способы решения
тригонометрического уравнения sin x — cos x = 1

Форма проведения: урок – семинар.

Эпиграф к уроку:

“Крупное научное открытие дает решение
крупной проблемы, но и в решении любой задачи
присутствует крупица открытия. Задача, которую
вы решаете, может быть скромной, но если она
бросает вызов вашей любознательности и
заставляет вас быть изобретательными и если вы
решаете ее собственными силами, то вы сможете
испытать ведущее к открытию напряжение ума и
насладиться радостью победы”

(Д. Пойа)

Задачи урока:

а) рассмотреть возможность решения одного и
того же уравнения различными способами;

б) познакомиться с различными общими приемами
решения тригонометрических уравнений;

в) изучение нового материала (введение
вспомогательного угла, универсальная
подстановка).

План семинара

1. Приведение уравнения к однородному
   относительно синуса и косинуса.
2. Разложение левой части уравнения на множители.
3. Введение вспомогательного угла.
4. Преобразование разности (или суммы)
   тригонометрических функций в произведение.
5. Приведение к квадратному уравнению
   относительно одной из функций.
6. Возведение обеих частей уравнения в квадрат.
7. Выражение всех функций через tg x (универсальная
   подстановка).
8. Графическое решения уравнения.

Содержание.

1. Слово предоставляется первому участнику.

Приведение уравнения sin x — cos x = 1 к
однородному относительно синуса и косинуса.

Разложим левую часть по формулам двойного
аргумента, а правую часть заменим
тригонометрической единицей, используя основное
тригонометрическое тождество:

2 sin cos — cos + sin = sin + cos ;

2 sin cos — cos =0 ;

cos = 0;

Произведение равно нулю, если хотя бы один из
множителей равен нулю, а другие при этом не
теряют смысла, поэтому следует

cos =0 ; =

= 0 -
однородное уравнение первой степени.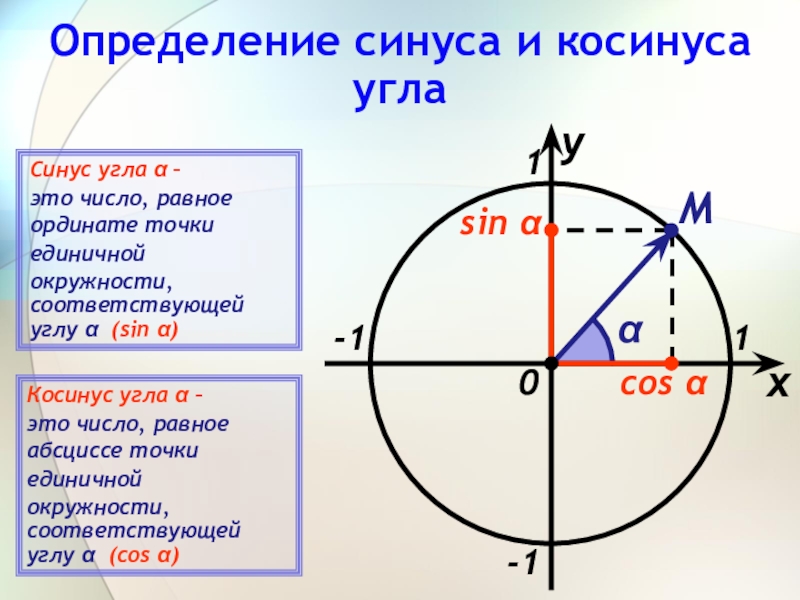 Делим обе
части уравнения на cos . (cos 0, так как если
cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит
тригонометрическому тождеству sin + cos = 1).

Получим tg -1
= 0 ; tg = 1 ; =
Ответ:

2. Слово предоставляется второму участнику.

Разложение левой части уравнения sin x — cos x = 1
на множители.

sin x – (1+ cos x ) = 1; используем формулы 1+ cos x = 2 , получим ;
далее аналогично:

произведение равно нулю, если хотя бы один из
множителей равен нулю, а другие при этом не
теряют смысла, поэтому следует

cos =0 ; =
= 0 -
однородное уравнение первой степени. Делим обе
части уравнения на cos . (cos 0, так как если
cos = 0 , то sin — 0 = 0 sin = 0, а это противоречит
тригонометрическому тождеству sin + cos = 1)

Получим tg -1
= 0 ; tg = 1 ; =
Ответ:

3. Слово предоставляется третьему участнику.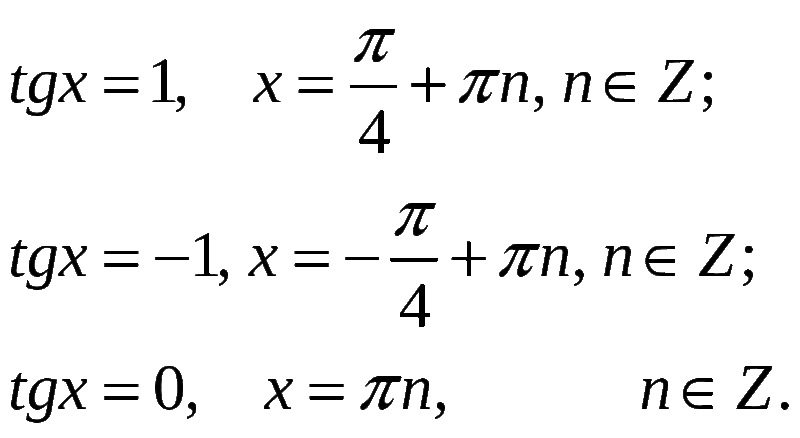

Решение уравнения sin x — cos x = 1 введением
вспомогательного угла.

Рассмотрим уравнение sin x — cos x = 1. Умножим и
разделим каждое слагаемое левой части

уравнения на .
Получим и
вынесем в левой части уравнения за скобку. Получим ; Разделим обе
части уравнения на и используем табличные значения
тригонометрических функций. Получим ; Применим
формулу синус разности.
;

Легко установить(с помощью тригонометрического
круга), что полученное решение распадается на два
случая:

;

Ответ:

4. Слово предоставляется четвертому участнику.

Решение уравнения sin x — cos x = 1 способом
преобразования разности (или суммы)
тригонометрических функций в произведение.

Запишем уравнение в виде , используя формулу приведения . Применяя
формулу разности двух синусов, получим

;

и так далее, аналогично предыдущему способу.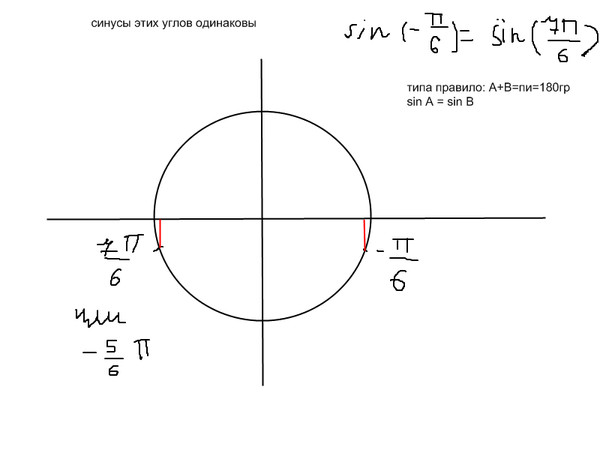

Ответ:

5. Слово предоставляется пятому участнику.

Решение уравнения sin x — cos x = 1 способом
приведения к квадратному уравнению относительно
одной из функций.

Рассмотрим основное тригонометрическое
тождество ,
откуда следует
подставим
полученное выражение в данное уравнение.

sin x — cos x = 1 ,

Возведем обе части полученного уравнения в
квадрат:

В процессе решения обе части уравнения
возводились в квадрат, что могло привести к
появлению посторонних решений, поэтому
необходима проверка. Выполним ее.

Полученные решения эквивалентны объединению
трех решений:

Первое и второе решения совпадают с ранее
полученными, поэтому не являются посторонними.
Остается проверить третье решение Подставим.

Левая часть:

Правая часть: 1.

Получили: ,
следовательно, – постороннее решение.

Ответ:

6. Слово предоставляется шестому участнику.

Возведение обеих частей уравнения sin x — cos x =
1 в квадрат.

Рассмотрим уравнение sin x — cos x = 1. Возведем обе
части данного уравнения в квадрат.

;

;

Используя основное тригонометрическое
тождество и формулу синуса двойного угла,
получим ; sin 2x = 0 ; .

Полученное решение эквивалентно объединению
четырех решений:

(эти решения можно нанести на единичную
окружность). Проверка показывает, что первое и
четвертое решения — посторонние.

Ответ:

7. Слово предоставляется седьмому участнику.

Использование универсальной подстановки в
решении уравнения sin x — cos x = 1. Выражение всех
функций через tg x по формулам:

Запишем данное уравнение с учетом приведенных
формул в виде .
,

получим

ОДЗ данного уравнения – все множество R. При
переходе к
из рассмотрения выпали значения, при которых не имеет
смысла, т. е.
или .

Следует проверить, не являются ли решениями данного
уравнения. Подставим в левую и правую часть
уравнения эти решения.

Левая часть: .

Правая часть: 1.

Получили 1=1. Значит, — решение данного уравнения.

Ответ:

8. Слово предоставляется восьмому участнику.

Рассмотрим графическое решение уравнения
sin x — cos x = 1.

Запишем рассматриваемое уравнение в виде sin x = 1
+ cos x.

Построим в системе координат Оxy графики
функций, соответствующих левой и правой частям
уравнения. Абсциссы точек пересечения графиков
являются решениями данного уравнения.

y = sin x – график: синусоида.

y = cos x +1 – график: косинусоида y = cos x, смещенная на 1
вверх по оси Oy. Абсциссы точек пересечения
являются решениями данного уравнения.

Ответ:

Итог урока.

• Учащиеся научились решать тригонометрические
  уравнения вида , освоили новый материал.
• На примере одного уравнения рассмотрели
  несколько способов решения.
• Учащиеся были непосредственными участниками
  урока, была задействована обратная связь в
  системе ученик-учитель.
• Учащиеся получили навыки самостоятельной
  работы с дополнительной литратурой.

Список использованной литературы:

1. Татарченкова С.С. Урок как педагогический
   феномен – Санкт-Петербург: Каро, 2005
2. Выгодский Н.В. Справочник по элементарной
   математике.-М.: Наука, 1975.
3. Виленкин Н.Я. и др. За страницами учебника
   математики: Арифметика. Алгебра. Геометрия: Книга
   для учащихся 10-11 класса – М.: Просвещение, 1996.
4. Гнеденко Б. В. Очерки по истории математики в
   России – М.: ОГИЗ, 1946.
5. Депман И.Я. и др. За страницами учебника
   математики – М.: Просвещение, 1999.
6. Дорофеев Г.В. и др. Математика: для поступающих в
   вузы – М.: Дрофа, 2000.
7. Математика: Большой энциклопедический словарь.
   – М.: БСЭ, 1998.
8. Мордкович А.Г. и др. Справочник школьника по
   математике. 10-11кл. Алгебра и начала анализа. – М.:
   Аквариум, 1997.
9. 300 конкурсных задач по математике. – М.: Рольф,
   2000.
10. 3600 задач по алгебре и началам анализа. – М.:
    Дрофа, 1999.
11. Школьная программа в таблицах и формулах.
    Большой универсальный справочник. – М.: Дрофа, 1999.
12. Торосян В.Г. История образования и
    педагогической мысли: учеб. для студентов вузов. -
    М.: Изд-во ВЛАДОС-ПРЕСС, 2006.- 351 с.
13. Крылова Н.Б. Педагогическая, психологическая и
    нравственная поддержка как пространство
    личностных изменений ребёнка и взрослого. //
    Классный руководитель.- 2000.- №3. –С.92-103.

грех (х) | функция синуса

sin (x), синусоидальная функция.

Определение синуса

В прямоугольном треугольнике ABC синус α, sin (α) определяется как отношение между стороной, противоположной углу α, и
сторона, противоположная прямому углу (гипотенуза):

sin α = a / c

Пример

a = 3 дюйма

c = 5 дюймов

sin α = a / c = 3/5 = 0.6

График синуса

TBD

Синус-правила

Название правила	Правило
Симметрия	sin (- θ ) = -sin θ
Симметрия	sin (90 ° — θ ) = cos θ
Пифагорейская идентичность	sin 2 α + cos 2 α = 1
	sin θ = cos θ × tan θ
	sin θ = 1 / csc θ
Двойной угол	sin 2 θ = 2 sin θ cos θ
Сумма углов	sin ( α + β ) = sin α cos β + cos α sin β
Разница углов	sin ( α-β ) = sin α cos β — cos α sin β
Сумма к продукту	sin α + sin β = 2 sin [( α + β ) / 2] cos [( α — β ) / 2]
Отличия от продукта	sin α — sin β = 2 sin [( α-β ) / 2] cos [( α + β ) / 2]
Закон синусов	a / sin α = b / sin β = c / sin γ
Производная	sin ‘ x = cos x
Интегральный	∫ sin x d x = — cos x + C
Формула Эйлера	sin x = ( e ix — e — ix ) / 2 i

Функция обратной синусоиды

Арксинус x определяется как функция, обратная синусу x, когда -1≤x≤1.

Когда синус y равен x:

sin y = x

Тогда арксинус x равен функции обратного синуса x, которая равна y:

arcsin x = sin ^-1 ( x ) = y

См .: функция Arcsin

Таблица синусов

x (°)	x (рад)	грех x
-90 °	-π / 2	-1
-60 °	-π / 3	-√3 / 2
-45 °	-π / 4	-√2 / 2
-30 °	-π / 6	-1/2
0 °	0	0
30 °	π / 6	1/2
45 °	π / 4	√2 / 2
60 °	π / 3	√3 / 2
90 °	π / 2	1

---

См. Также

1.

2 + 3)`.2 + 3) `

ВАЖНО:

cos x ² + 3

не равно

cos ( x ² + 3).

Кронштейны имеют большое значение. У многих студентов с этим возникают проблемы.

Вот графики y = cos x ² + 3 (зеленый) и y = cos ( x ² + 3) (показаны синим).

Первый, y = cos x ² + 3 или y = (cos x ² ) + 3, означает взять кривую y = cos x ² и переместите его вверх на «3» единицы.2sin x`

6. Найдите производную неявной функции

x cos 2 y + sin x cos y = 1.

Ответ

Неявная функция:

`x \ cos 2y + sin x \ cos y = 1`

Мы дифференцируем каждый термин слева направо:

`x (-2 \ sin 2y) ((dy) / (dx))` `+ (cos 2y) (1)` `+ sin x (-sin y (dy) / (dx))` `+ cos у \ соз х`

`= 0`

Так

`(-2x \ sin 2y-sin x \ sin y) ((dy) / (dx))` = -cos 2y-cos y \ cos x`

Решение для dy / dx дает:

`(dy) / (dx) = (- cos 2y-cos y \ cos x) / (- 2x \ sin 2y-sin x \ sin y)`

`= (cos 2y + cos x \ cos y) / (2x \ sin 2y + sin x \ sin y)`

7.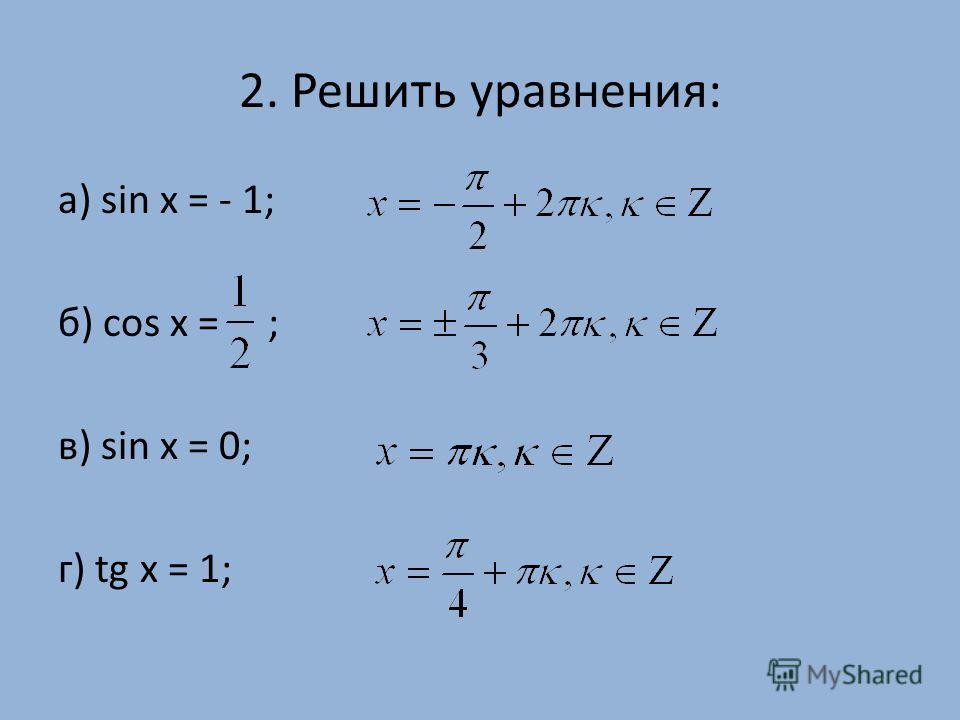 2`

Когда x = 0,15 (конечно, в радианах), это выражение (которое дает нам
наклон) равен «-2,65».

Вот график нашей ситуации. Показана касательная к кривой в точке, где x = 0,15. Его наклон равен «-2,65».

8. Ток (в амперах) в цепи усилителя как функция времени t (в секундах) определяется как

`i = 0.10 cos (120πt + π / 6)`.

Найдите выражение для напряжения на 2.2x + загар x`

См. Также: Производная квадратного корня из синуса x по первым принципам.

Тригонометрических функций

В

тригонометрические соотношения

также может рассматриваться как функция переменной, которая является мерой угла.

Эту угловую меру можно указать в

градусы

или же

радианы

. Здесь мы будем использовать радианы. Поскольку любой угол с мерой больше, чем

2

π

радианы или меньше

0

эквивалентен некоторому углу с мерой

0

≤

θ

< 2 π , все тригонометрические функции равны периодический .

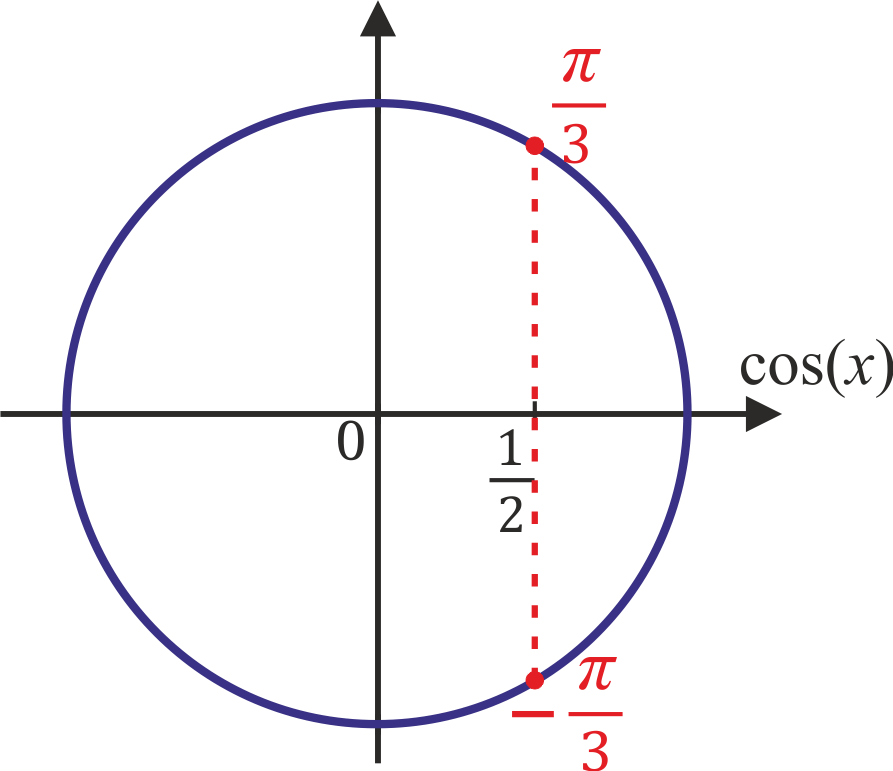
График

синус

функция выглядит так:

Обратите внимание, что

домен

функции

y

знак равно

грех

(

Икс

)

) — все действительные числа (синус определен для любой угловой меры),

диапазон

является

—

1

≤

y

≤

1

.

График

косинус

функция выглядит так:

Область определения функции

y

знак равно

потому что

(

Икс

)

все действительные числа (косинус определяется для любой угловой меры), диапазон равен

—

1

≤

y

≤

1

.

График

касательная

функция выглядит так:

Область определения функции

y

знак равно

загар

(

Икс

)

) все действительные числа

Кроме

значения, где

потому что

(

Икс

)

равно

0

, то есть значения

π

2

+

π

п

для всех целых чисел

п

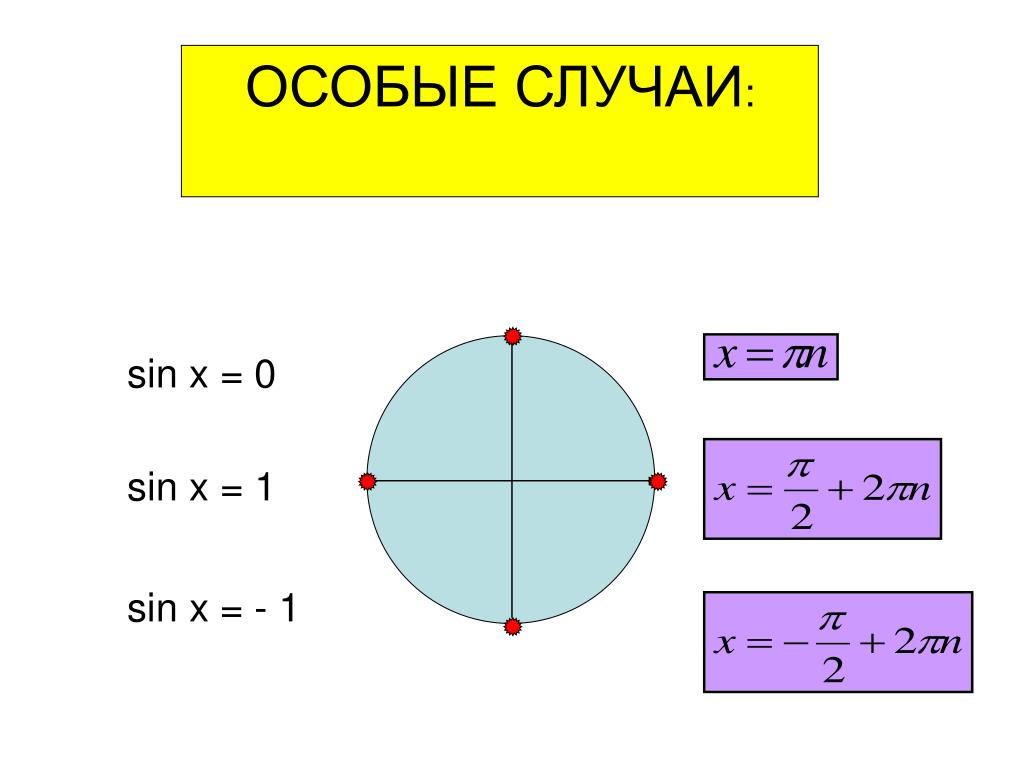. Диапазон касательной функции — это все действительные числа.

График функции секанса выглядит так:

Область определения функции

y

знак равно

сек

(

Икс

)

знак равно

1

потому что

(

Икс

)

снова все действительные числа, кроме значений, где

потому что

(

Икс

)

равно

0

, то есть значения

π

2

+

π

п

для всех целых чисел

п

.Диапазон функции:

y

≤

—

1

или же

y

≥

1

.

График функции косеканса выглядит так:

Область определения функции

y

знак равно

csc

(

Икс

)

знак равно

1

грех

(

Икс

)

это все действительные числа, кроме значений, где

грех

(

Икс

)

равно

0

, то есть значения

π

п

для всех целых чисел

п

. Диапазон функции:

y

≤

—

1

или же

y

≥

1

.

График функции котангенса выглядит так:

Область определения функции

y

знак равно

детская кроватка

(

Икс

)

знак равно

потому что

(

Икс

)

грех

(

Икс

)

это все действительные числа, кроме значений, где

грех

(

Икс

)

равно

0

, то есть значения

π

п

для всех целых чисел

п

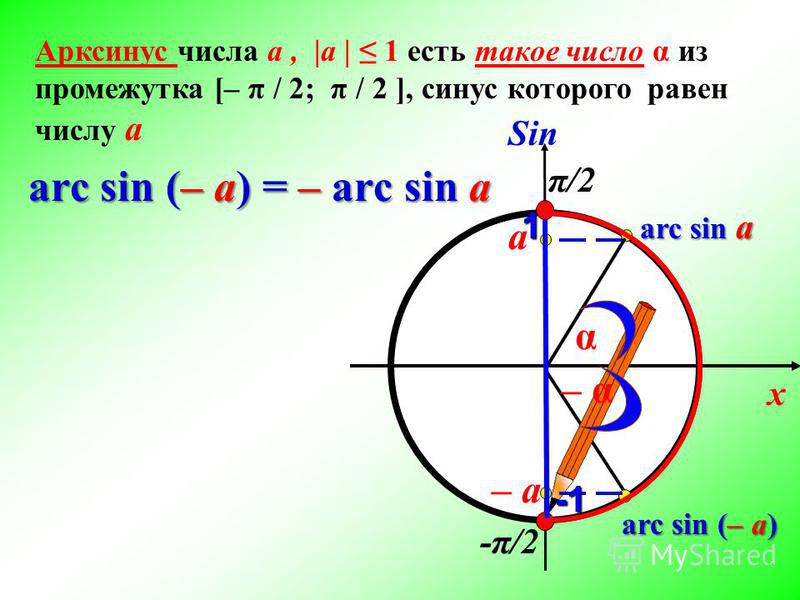. Диапазон функции — все действительные числа.

Исчисление

— интуитивное понимание производных от $ \ sin x $ и $ \ cos x $

Как специалист по физике, я хотел бы предложить ответ, который исходит из моего понимания синуса и косинуса в реальном мире.

При этом я исследую равномерное круговое движение.

Из-за определения синуса и косинуса точка на единице круга, мы можем сказать, что:

  r (t) = 
  

Это подходящая параметрическая функция для описания точки, движущейся по единичной окружности.

Давайте посмотрим, какой должна быть первая производная в физическом контексте. Первая производная от позиции должна представлять , в идеале, , скорость точки.

В физическом контексте мы ожидаем, что скорость будет касательной к направлению движения в данный момент времени t . Исходя из этого, он будет касаться окружности под углом t . Кроме того, поскольку угловая скорость постоянна, величина скорости также должна быть постоянной.2 = 1
| r ‘(t) | = 1

Как и ожидалось, скорость постоянна, поэтому производные синуса и косинуса ведут себя должным образом.

Мы также можем подумать о том, каким будет направление скорости по сравнению с вектором положения.

Я не уверен, является ли это «обманом» в рамках вопроса, но визуализировав график, мы можем увидеть, что скорость, по своей природе касательная к окружности, должна быть перпендикулярна вектору положения.

Если это правда, то позиция * скорость = 0 (скалярное произведение).

  г (т) * г '(т) = 0
   * <-sin (t), cos (t)> = 0
(cos (t) * -sin (t)) + (sin (t) * cos (t)) = 0
              -sin (t) cos (t) + sin (t) cos (t) = 0
                                         0 = 0
  

Жизнь хороша. Если мы предположим, что определение cos (t) равно -sin (t), а определение sin (t) равно cos (t), мы обнаружим, что физическое поведение точно соответствует ожидаемому: постоянная скорость, которая всегда перпендикулярна вектор положения.

Мы можем пойти дальше и посмотреть на ускорение. В физике мы бы назвали это восстанавливающей силой. Какое ускорение должно существовать в круге, чтобы точка двигалась по кругу?

Более конкретно, в каком направлении должно быть это ускорение?

Не нужно долго думать, чтобы прийти к мысли, что ускорение должно быть направлено к центру и направлено к центру. Итак, если мы сможем найти, что ускорение равно в направлении, противоположном , как вектор положения, мы можем быть почти уверены в производных синуса и косинуса.2) = -1
-1 * 1 = -1
-1 = -1

Сдвиг и фазовые сдвиги синусоидальных и косинусоидальных графиков. Как уравнение соотносится с графиком. Иллюстрированные демонстрации и примеры

Перевод — это вид преобразования, который является изометрическим (изометрический означает, что форма никоим образом не искажается). Перевод графика, будь то синус или косинус или что-то еще, можно рассматривать как «слайд».Чтобы перевести график, все, что вам нужно сделать, это переместить или сдвинуть весь график в другое место.

Вертикальные переводы синусов и косинусов

Пример

Проблема 1

На основе приведенного выше примера вы можете понять, как будет выглядеть график следующего перевода y = sin (x) — 1.

Покажи ответ

Этот перевод выражает вертикальный сдвиг вниз на 1.

Проблема 2

Как бы выглядел график следующего уравнения:
$$
\ frac {1} {2} sin (2x) — \ frac {1} {2}
$$
?

(Обратите внимание, что этот вопрос предполагает, что вы изучили амплитуду синусоидальных уравнений, а также периоды синусоидальных и косинусоидальных графиков).

Покажи ответ

Проблема 3

Каким будет график функции $$ g (x) = \ sin (-x) $$ по сравнению с графиком $$ f (x) = \ sin (x) $$?

Покажи ответ

График f (x) = sin (-x) является отражением графика f (x) = sin (x) относительно оси x.

Каждая пара соответствующих точек на графиках находится на одинаковом расстоянии от оси абсцисс.

Например, точки A и B — это две соответствующие точки на графиках, и они находятся на одинаковом расстоянии от оси x. То есть AM = BM.

Проблема 4

Каким будет график функции $$ g (x) = \ sin \ left (x + \ frac {5 \ pi} {4} \ right) $$ по сравнению с графиком $$ f (x) = \ sin \ left (x + \ frac {\ pi} {4} \ right) $$?

Покажи ответ

Разница между переменными двух функций:

$$ \ left (x + \ frac {5 \ pi} {4} \ right) — \ left (x + \ frac {\ pi} {4} \ right) $$

= $$ x + \ frac {5 \ pi} {4} -x- \ frac {\ pi} {4} $$

= $$ \ frac {5 \ pi} {4} — \ frac {\ pi} {4} $$

= $$ \ frac {4 \ pi} {4} $$

= $$ \ pi $$

Итак, график f (x) переносится на $$ \ pi $$ единиц влево, чтобы создать график g (x).

Проблема 5

Как график функции $$ f (x) = \ sin \ left (3x- \ frac {\ pi} {3} \ right) $$ переносится на график $$ g (x) = \ sin \ left ( 3x + \ frac {\ pi} {3} \ right) $$?

Покажи ответ

Разница между переменными двух функций:

$$ \ left (3x + \ frac {\ pi} {3} \ right) — \ left (3x- \ frac {\ pi} {3} \ right) $$

= $$ 3x + \ frac {\ pi} {3} -3x + \ frac {\ pi} {3} $$

= $$ \ frac {\ pi} {3} + \ frac {\ pi} {3} $$

= $$ \ frac {2 \ pi} {3} $$

Следовательно, график f (x) переносится на $$ \ frac {2 \ pi} {3} $$ единиц влево, чтобы сгенерировать график g (x)

Проблема 6

Каким будет график функции $$ g (x) = \ sin (-x) -3 $$ по сравнению с графиком $$ f (x) = \ sin (-x) $$?

Покажи ответ

Разница между значениями f (x) и g (x) составляет -3. Следовательно, g (x) получается перемещением f (x) на 2 единицы вниз.

Проблема 7

Как можно было бы перенести график функции $$ f (x) = \ sin (x) $$ на график $$ g (x) = \ sin (x + 2) + 2 $$?

Покажи ответ

Первый график $$ f (x) = \ sin (x) $$ переносится на график $$ h (x) = \ sin (x + 2) $$ путем перемещения на 2 единицы влево, как показано на график ниже.

Тогда график g (x) получается перемещением графика h (x) вверх на 2 единицы.

Проблема 8

Каким будет график функции $$ f (x) = \ cos (-x) $$ по сравнению с графиком $$ g (x) = — \ cos (x) $$?

Покажи ответ

График cos (-x) точно такой же, как график cos (x).

Итак, g (x) — это в точности отражение f (x) относительно оси x.

Проблема 9

Как график функции $$ f (x) = \ cos \ left (x- \ frac {5 \ pi} {3} \ right) $$ переносится на график $$ g (x) = \ cos \ left (x- \ frac {5 \ pi} {3} \ right) — \ frac {5 \ pi} {3} $$?

Покажи ответ

$$ g (x) -f (x) = \ left [\ cos \ left (x- \ frac {5 \ pi} {3} \ right) — \ frac {5 \ pi} {3} \ right] — \ cos \ left (x- \ frac {5 \ pi} {3} \ right) $$

= $$ \ cos \ left (x- \ frac {5 \ pi} {3} \ right) — \ frac {5 \ pi} {3} — \ cos \ left (x- \ frac {5 \ pi} { 3} \ right) $$

= $$ — \ frac {5 \ pi} {3} $$

Итак, график f (x) перемещается на $$ \ frac {5 \ pi} {3} $$ единиц вниз, чтобы создать график g (x).

Проблема 10

Каким будет график функции $$ g (x) = — \ cos \ left (x- \ pi \ right) $$ по сравнению с графиком $$ f (x) = \ cos \ left (\ pi — x \ right) $$?

Покажи ответ

$$ f (x) = \ cos \ left (\ pi -x \ right) $$ — это то же самое, что $$ f (x) = \ cos \ left (x- \ pi \ right) $$.Итак, $$ g (x) = — \ cos \ left (x- \ pi \ right) $$ — это отражение f (x) относительно оси x.

Проблема 11

Как бы график функции $$ f (x) = \ cos \ left (x- \ frac {\ pi} {3} \ right) $$ переносился на график $$ g (x) = \ cos \ left (\ frac {\ pi} {3} \, \, — \, \, x \ right) \, \, — \, \, \ frac {\ pi} {3} $$?

Покажи ответ

$$ g (x) = \ cos \ left (\ frac {\ pi} {3} \, \, — \, \, x \ right) \, \, — \, \, \ frac {\ pi} { 3} $$ — это то же самое, что $$ g (x) = \ cos \ left (x- \ frac {\ pi} {3} \, \, \ right) \, \, — \, \, \ frac { \ pi} {3} $$.
Итак, f (x) перемещается вниз на $$ \ frac {\ pi} {3} $$ единиц.

Проблема 12

Каким будет график функции $$ g (x) = \ cos (3x + 3 \ pi) $$ по сравнению с графиком $$ f (x) = \ cos (3x-2 \ pi) $$?

Покажи ответ

$$ (3x + 3 \ pi) — (3x-2 \ pi) $$

= $$ 3x + 2 \ pi -3x + 3 \ pi $$

= $$ 2 \ pi +3 \ pi $$

= $$ 5 \ pi $$

Итак, график f (x) переместился на $$ 5 \ pi $$ единиц влево, чтобы создать график g (x).

Ошибка: Нажмите «Не робот» и повторите попытку.

Функция в кубе синуса — Исчисление

Эта статья посвящена конкретной функции от подмножества действительных чисел до действительных чисел.Информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференциации и интеграции, представлена ​​в статье.
Посмотреть полный список определенных функций в этой вики

Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. Д.), Мы следуем соглашению, что все углы измеряются в радианах. Так, например, угол измеряется как.

Определение

Эта функция, обозначенная, определяется как комбинация функции куба и функции синуса. Явно это карта:

Для краткости пишем или.

Ключевые данные

Арт.	Значение
Домен по умолчанию	все действительные числа, т.е. весь диапазон
	закрытый интервал, то есть абсолютное максимальное значение: 1, абсолютное минимальное значение: -1
период	, т.е.
локальные максимальные значения и точки достижения	Все локальные максимальные значения равны 1, и они достигаются во всех точках формы, где изменяется по целым числам.
локальные минимальные значения и точки достижения	Все локальные минимальные значения равны -1, и они достигаются во всех точках формы, где изменяется целыми числами.
точек перегиба (обе координаты)	Все точки формы, а также точки формы и where варьируются в зависимости от целых чисел.
производная
вторая производная
первообразные
важные симметрии	нечетная функция (следует из сочетания нечетных функций является нечетным и того факта, что функция куба и синусоидальная функция являются нечетными) полуоборотная симметрия относительно всех точек формы зеркальная симметрия относительно всех линий.

Удостоверения

Имеем удостоверение:

График

Вот основной график, построенный на интервале:

Вот более крупный график, нарисованный на интервале. Толстые черные точки соответствуют локальным экстремальным значениям, а толстые красные точки соответствуют точкам перегиба.

Дифференциация

Первая производная

Чтобы дифференцировать один раз, мы используем цепное правило дифференциации.Явно мы рассматриваем функцию как композицию функции куба и функции синуса, поэтому функция куба — это внешняя функция , а функция синуса — внутренняя функция .

Получаем:

[ПОКАЗАТЬ БОЛЬШЕ]

Интеграция

Первая первообразная: стандартный метод

Переписываем, а затем интегрируем u-заменой где. Ясно:

Сейчас ставлю. У нас есть, поэтому мы можем заменить на, и мы получаем:

Путем полиномиального интегрирования получаем:

Вставляя обратно, получаем:

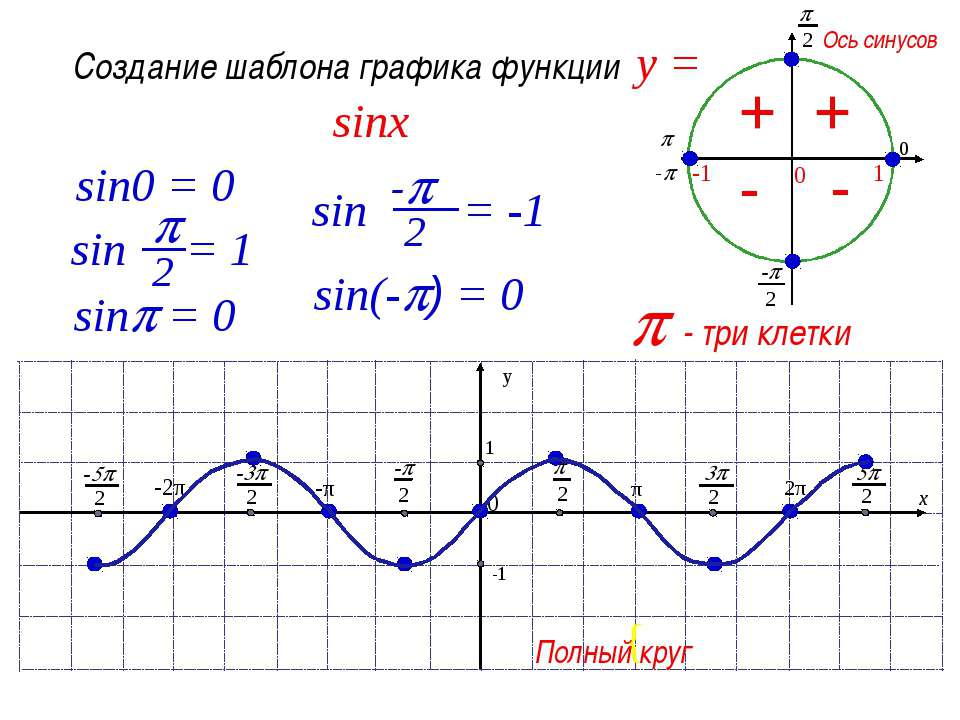. 3 и sin.Таким образом, мы можем антидифференцировать (то есть интегрировать) функцию любое количество раз, при этом первообразное выражение чередуется между кубической функцией синуса и кубической функцией косинуса.

Серия

Power и серия Тейлора

Вычисление степенного ряда

Мы можем использовать удостоверение личности:

У нас есть силовой ряд:

Таким образом, получаем степенной ряд:

Подставляя в формулу, получаем:

Первые несколько терминов следующие:

Почему предел, когда x приближается к нулю синуса x над x, равен 1 | Али | Тем не менее, Mathematics

На этот раз я хотел поделиться с вами одним моим любимым доказательством предела.

Заявление: Предел, когда «x» приближается к нулю синуса «x» по сравнению с «x», равен единице.

Мы можем начать с тригонометрической конструкции, представленной ниже. Итак, нам нужен единичный круг в начале.

Определение : Единичная окружность — это окружность с радиусом, равным единице. Единичная окружность — это окружность радиуса один с центром в начале координат (0, 0) в декартовой системе координат в евклидовой плоскости.

Ниже будут два треугольника.

— Маленький прямоугольный треугольник имеет зеленые и черные стороны и оранжевую гипотенузу.

— Большой треугольник с черными и красными ножками и оранжевой гипотенузой.

Определение: «Гипотенуза» — это самая длинная сторона прямоугольного треугольника, противоположная прямому углу.

Хорошо, а как насчет этой зеленой линии? Эта линия будет координатой y того места, где этот радиус пересекает единичный круг. Итак, по определению единичной окружности длина этой линии должна быть синусом x.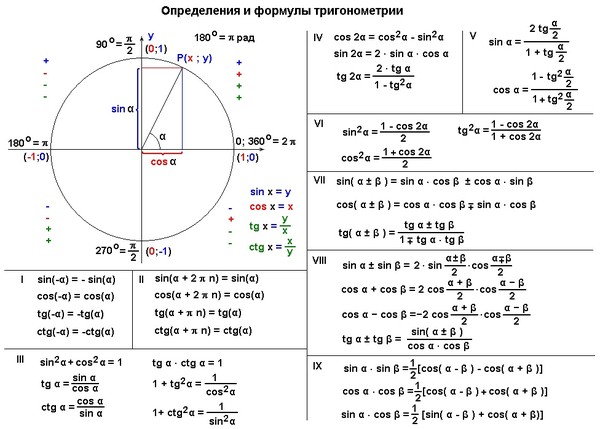

Примечание : Если мы хотим убедиться, что это также работает для xs, которые попадают в четвертый квадрант, мы можем просто убедиться, что это абсолютное значение синуса x.

А что насчет этой красной ножки большого треугольника? Нам нужно также выразить это в терминах тригонометрической функции. Хм, а какой будет тангенс x?

Примечание: Касательная «x» равна противоположной по соседнему.

Другое примечание: Соседняя сторона — это сторона без гипотенузы, которая находится рядом с данным углом.

Итак, если мы посмотрим на больший треугольник (черная линия + оранжевая линия + красная линия) прямо там, это наш угол «x» в радианах. Красная сторона — это противоположная сторона.

Соседняя сторона тоже радиусная и только имеет длину, равную единице. Не забывайте, это единичный круг.

Таким образом, тангенс «x» — противоположная сторона.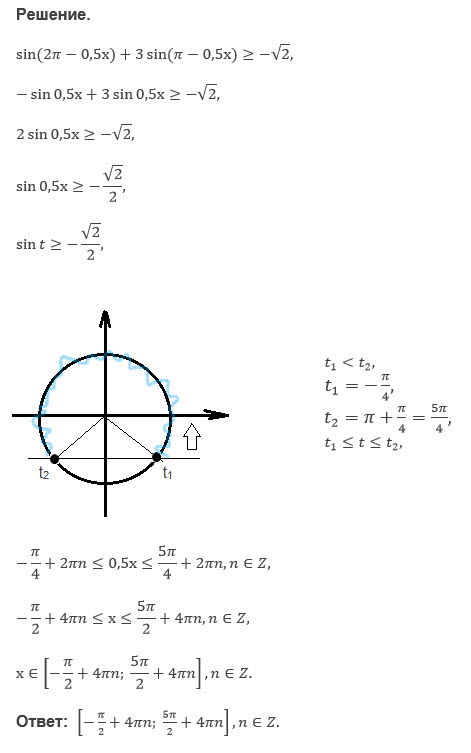 Противоположная сторона равна тангенсу «х».И, как и раньше, это будет положительным моментом для сидения здесь, в первом квадранте. Однако мы хотим, чтобы все работало как в первом, так и в четвертом квадранте ради нашего доказательства. Вот почему мы должны указывать абсолютное значение. Хороший. Что следующее?

Думаю, надо подумать об этом районе. Давайте разберемся с площадью треугольников и единичного круга. На этом этапе нам нужно нарисовать еще один треугольник, который находится в срезе части круга внутри круга.

А теперь пора поговорить о затененной зеленым области ниже.

Как мы можем выразить эту область? Очевидно, это треугольник.

Площадь треугольника равна половине основания, умноженного на высоту.

Мы только что узнали красивую информацию о треугольниках. Теперь нам просто нужно заменить. Мы знаем, что высота — это абсолютное значение синуса «x», и мы также знаем, что основание равно 1. Таким образом, площадь должна быть равна 1/2 от нашего основания, что равно 1, умноженному на нашу высоту, который является абсолютным значением синуса «x».Это просто абсолютное значение синуса «х» над двумя.

Теперь пора найти участок апельсинового пирога. Прежде всего, мы должны запомнить площадь круга.

Площадь круга равна пи умноженному на квадрат радиуса.

Но нам не нужна вся территория. Нам просто нужна область кусочка апельсинового пирога. Хм, значит, нам нужна дробь. Итак, какая часть всего круга это будет?

Примечание: Если бы мы обошли весь круг, получилось бы два радиана пи, так что это «x», равное двум пи всего круга

Хорошо, это хорошо, потому что мы знаем площадь круга.Это единичный круг с радиусом один. Таким образом, это умноженная на площадь круга, которая будет равна пи, умноженному на квадрат радиуса. Если вы замените радиус на единицу, мы получим всего 1, умноженное на пи. Он равен пи.

Истина: Площадь единичного квадрата равна пи.

А теперь нам просто нужно применить к коэффициенту. Это означает, что площадь ломтика апельсинового пирога будет «x» больше 2 пикселей. И снова, если бы мы хотели, чтобы это сработало для «x» в четвертом квадранте, мы могли бы просто написать знак абсолютного значения прямо там, потому что мы говорим о положительной области.

И, наконец, мы можем подумать о большем треугольнике синего цвета, и, конечно, это довольно просто.

Площадь здесь будет в 1/2 раза больше базовой, умноженной на высоту. Таким образом, площадь большего треугольника будет в 1/2 раза больше нашего основания, что равно единице нашей высоты, которая является абсолютным значением тангенса «x». Мы можем просто записать это как абсолютное значение тангенса теты над двумя.

B eautiful . Пришло время сравнить площади.Но как? Как бы вы сравнили площади треугольников и кусочка апельсинового пирога? Я думаю, это настолько очевидно, что площадь маленького треугольника меньше или равна площади ломтика апельсинового пирога, а площадь ломтика меньше или равна площади большого треугольника.

Пока все хорошо. Теперь нам нужно сделать какие-то шансы, не меняя неравенства. Все, что нам нужно, — это немного алгебраических манипуляций. Начнем все умножать на два. И тогда эта операция поможет мне переписать неравенство.Абсолютное значение синуса x меньше или равно абсолютному значению x, которое меньше или равно абсолютному значению тангенса x.

Примечание : Мы можем переписать абсолютное значение тангенса x как абсолютное значение синуса x над абсолютным значением косинуса x.

Это будет то же самое, что и абсолютное значение тангенса «x». И причина, по которой я это сделал, заключается в том, что теперь мы можем разделить все на абсолютное значение синуса «x».

Поскольку мы делим на положительную величину, это не изменит направления неравенств.

Итак, давайте разделим все члены на абсолютное значение синуса «x».

А что мы получаем? Что ж, как вы можете видеть ниже, мы получаем единицу и абсолютное значение x над синусом «x» с правой стороны, а также мы получаем единицу над абсолютным значением косинуса «x».

И снова красиво.

Помните, мы хотим доказать «синус x над x».И мы получаем «x по синусу x». Эта ситуация должна что-то напоминать. Да, взаимно.

Обратный : Мультипликативный обратный. Если вы возьмете обратную дробь a / b, вы получите b / a.

Итак, когда мы возьмем

, обратное всему , это фактически переключит неравенства.

Обратное значение единицы по-прежнему будет равно единице. Поскольку мы взяли обратную величину от членов, знак «меньше или равно» превратится в знак «больше или равно».Таким образом, абсолютное значение синуса «x» над абсолютным значением «x» больше или равно , обратная величина на единицу над абсолютным значением косинуса «x» является абсолютным значением косинуса «x». ».

Нам действительно важны только первый и четвертый квадранты. В первом квадранте синусы «x» и «x» положительны. В четвертом квадранте они оба отрицательные, но когда вы разделите их, вы получите положительное значение.