Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень 3)
24	Найти точное значение	csc(60 град. )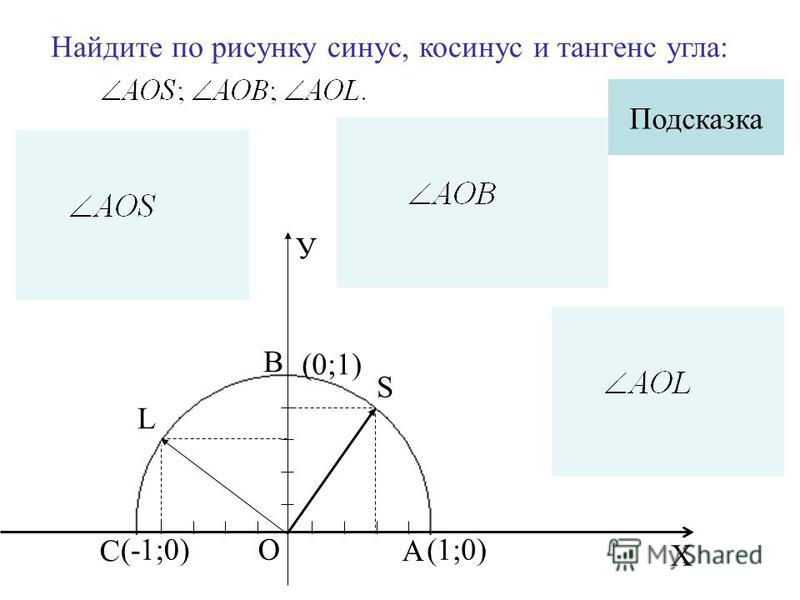
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )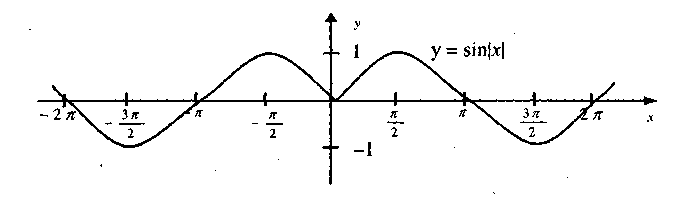
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )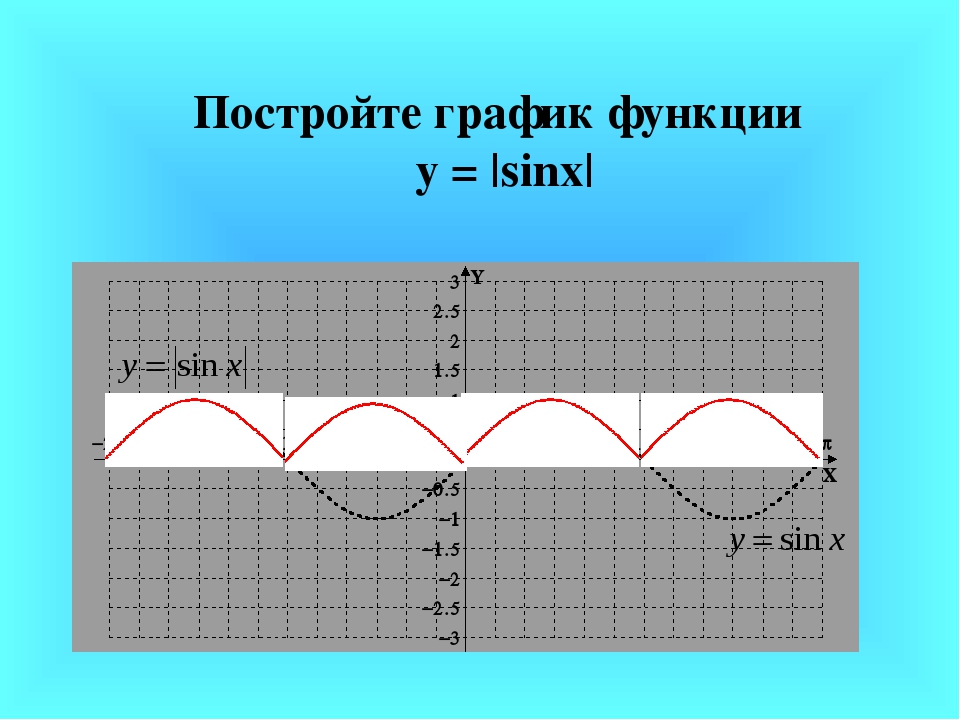
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )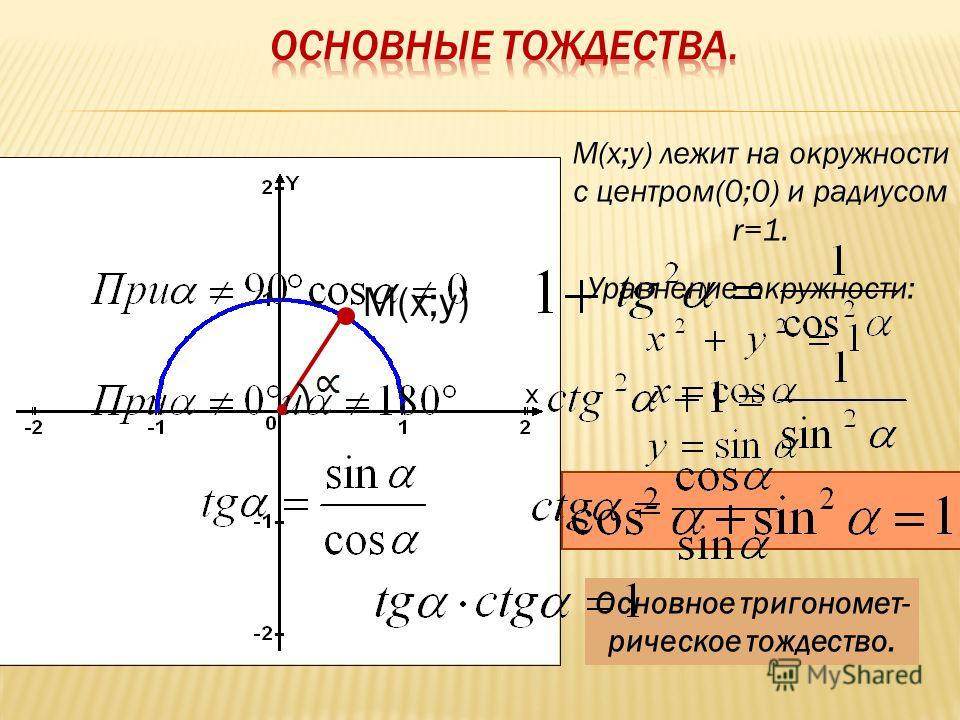
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Модуль в тригонометрических уравнениях: найти и обезвредить

Достаточно часто в задачах повышенной сложности встречаются тригонометрические уравнения, содержащие модуль. Большинство из них требуют эвристического подхода к решению, который совсем не знаком большинству школьников.

Предлагаемые ниже задачи призваны познакомить вас с наиболее характерными приемами решения тригонометрических уравнений содержащих модуль.

Задача 1. Найти разность (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения 1 + 2sin x · |cos x| = 0.

Решение.

Раскроем модуль:

1) Если cos x ≥ 0, то исходное уравнение примет вид 1 + 2sin x · cos x = 0.

Воспользуемся формулой синуса двойного угла, получим:

1 + sin 2x = 0; sin 2x = -1;

2x = -π/2 + 2πn, n € Z;

x = -π/4 + πn, n € Z. Так как cos x ≥ 0, то x = -π/4 + 2πk, k € Z.

2) Если cos x < 0, то заданное уравнение имеет вид 1 – 2sin x · cos x = 0. По формуле синуса двойного угла, имеем:

1 – sin 2x = 0; sin 2x = 1;

2x = π/2 + 2πn, n € Z;

x = π/4 + πn, n € Z. Так как cos x < 0, то x = 5π/4 + 2πk, k € Z.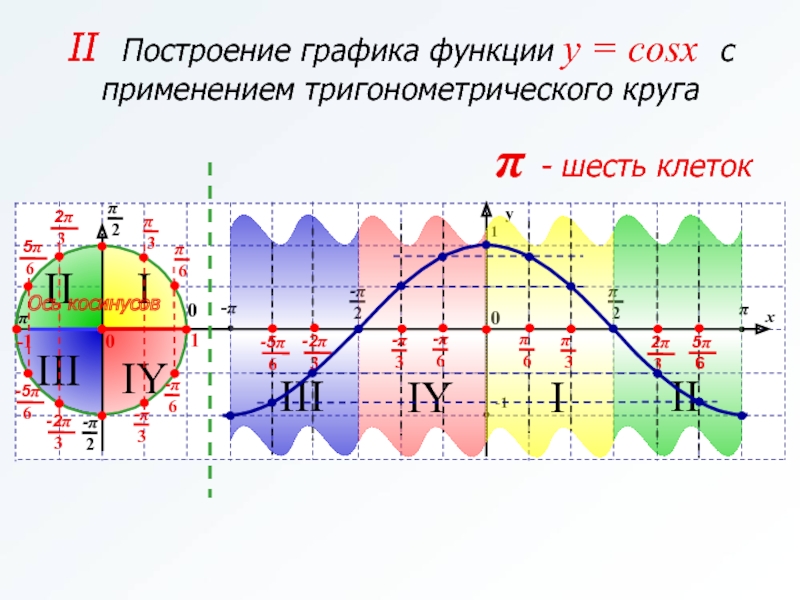

3) Наибольший отрицательный корень уравнения: -π/4; наименьший положительный корень уравнения: 5π/4.

Искомая разность: 5π/4 – (-π/4) = 6π/4 = 3π/2 = 3 · 180°/2 = 270°.

Ответ: 270°.

Задача 2. Найти (в градусах) наименьший положительный корень уравнения |tg x| + 1/cos x = tg x.

Решение.

Раскроем модуль:

1) Если tg x ≥ 0, тогда

tg x + 1/cos x = tg x;

1/cos x = 0.

В полученном уравнении корней нет.

2) Если tg x < 0, тогда  

-tg x + 1/cos x = tg x;

1/cos x – 2tg x = 0;

1/cos x – 2sin x / cos x = 0;

(1 – 2sin x) / cos x = 0;

 1 – 2sin x = 0 и cos x ≠ 0.

С помощью рисунка 1 и условия tg x < 0 находим, что x = 5π/6 + 2πn, где n € Z.

3) Наименьший положительный корень уравнения 5π/6. Переведем это значение в градусы:

 5π/6 = 5 · 180°/6 = 5 · 30° = 150°.

Ответ: 150°.

Задача 3.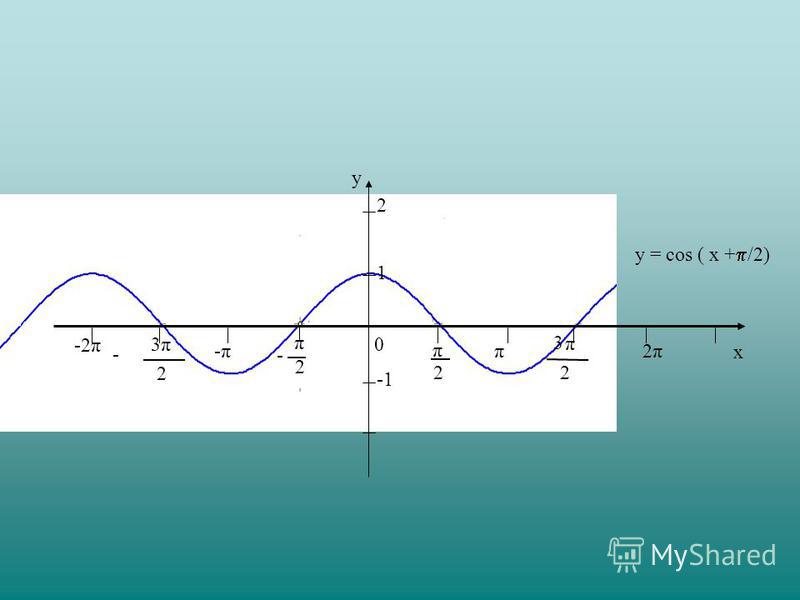 Найти количество различных корней уравнения sin |2x| = cos 2x на промежутке [-π/2; π/2].

Решение.

Запишем уравнение в виде sin|2x| – cos 2x = 0 и рассмотрим функцию y = sin |2x| – cos 2x. Так как функция является четной, то найдем ее нули при x ≥ 0.

sin 2x – cos 2x = 0; разделим обе части уравнения на cos 2x ≠ 0, получим:

tg 2x – 1 = 0;

tg 2x = 1;

2x = π/4 + πn, n € Z;

x = π/8 + πn/2, n € Z.

Воспользовавшись четностью функции, получим, что корнями исходного уравнения являются числа вида

± (π/8 + πn/2), где n € Z.

Промежутку [-π/2; π/2] принадлежат числа: -π/8; π/8.

Итак, два корня уравнения принадлежат заданному промежутку.

Ответ: 2.

Данное уравнения можно было бы решить и раскрытием модуля.

Задача 4. Найти количество корней уравнения sin x – (|2cos x – 1|)/(2cos x – 1) · sin² x = sin² x на промежутке [-π; 2π].

Решение.

1) Рассмотрим случай, когда 2cos x – 1 > 0, т.е. cos x > 1/2, тогда уравнение принимает вид:

sin x – sin² x = sin² x;

sin x – 2sin² x = 0;

sin x(1 – 2sin x) = 0;

sin x = 0 или 1 – 2sin x = 0;

sin x = 0 или sin x = 1/2.

Используя рисунок 2 и условие cos x > 1/2, найдем корни уравнения:

x = π/6 + 2πn или x = 2πn, n € Z.

2) Рассмотрим случай, когда 2cos x – 1 < 0, т.е. cos x < 1/2, тогда исходное уравнение принимает вид:

sin x + sin² x = sin² x;

sin x = 0;

x = 2πn, n € Z.

Используя рисунок 2 и условие cos x < 1/2, находим, что x = π + 2πn, где n € Z.

Объединим два случая, получим:

x = π/6 + 2πn или x = πn.

3) Промежутку [-π; 2π] принадлежат корни: π/6; -π; 0; π; 2π.

Таким образом, заданному промежутку принадлежат пять корней уравнения.

Ответ: 5.

Задача 5. Найти количество корней уравнения (x – 0,7)² |sin x| + sin x = 0 на промежутке [-π; 2π].

Решение.

1) Если sin x ≥ 0, то исходное уравнение принимает вид (x – 0,7)² sin x + sin x = 0. После вынесения общего множителя sin x за скобки, получим:

sin x((x – 0,7)² + 1) = 0; так как (x – 0,7)² + 1 > 0 при всех действительных x, то sinx = 0, т.е.  x = πn, n € Z.

2) Если sin x < 0, то -(x – 0,7)² sin x + sin x = 0;

sin x((x – 0,7)² – 1) = 0;

sinx = 0 или (x – 0,7)² + 1 = 0. Так как  sin x < 0, то (x – 0,7)² = 1. Извлекаем квадратный корень из левой и правой частей последнего уравнения, получим:

x – 0,7 = 1 или x – 0,7 = -1, а значит x = 1,7 или x = -0,3.

С учетом условия sinx < 0 получим, что sin (-0,3) ≈ sin (-17,1°) < 0 и sin (1,7) ≈ sin (96,9°) > 0, значит только число -0,3 является корнем исходного уравнения.

3) Промежутку [-π; 2π] принадлежат числа: -π; 0; π; 2π; -0,3.

Таким образом, уравнение имеет пять корней на заданном промежутке.

Ответ: 5.

Заняться подготовкой к урокам или экзаменам можно при помощи различных образовательных ресурсов, которые есть в сети. В настоящее время любому человеку просто необходимо использовать новые информационные технологии, ведь правильное, а главное уместное их применение будет способствовать повышению мотивации в изучении предмета, повысит интерес и поможет лучше усвоить необходимый материал. Но не стоит забывать о том, что компьютер не учит думать, полученную информацию обязательно необходимо обрабатывать, понимать и запоминать. Поэтому вы можете обратиться за помощью к нашим онлайн репетиторам, которые помогут вам разобраться с решением интересующих вас задач.

 Остались вопросы? Не знаете, как решать тригонометрические уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.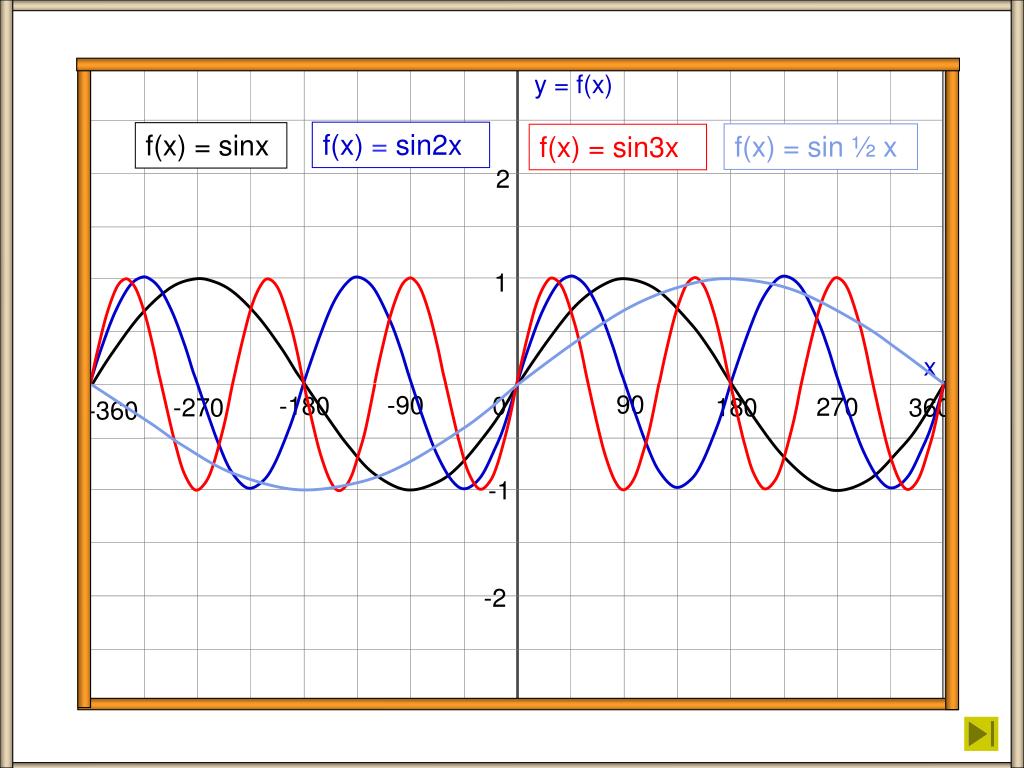
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

y sin x модуль

Вы искали y sin x модуль? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y sin модуль x, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «y sin x модуль».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y sin x модуль,y sin модуль x,y sinx модуль график,y модуль sin x,y модуль sinx,y модуль sinx график,график y sinx модуль,график модуль y sinx,график синус модуль х,модуль y sin x,модуль y sin модуль x,модуль синус х график,синус модуль х график. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y sin x модуль. Просто введите задачу в окошко и нажмите
«решить» здесь (например, y sinx модуль график).

Где можно решить любую задачу по математике, а так же y sin x модуль Онлайн?

Решить задачу y sin x модуль вы можете на нашем сайте https://pocketteacher. ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Функции и методы модуля math в python ~ PythonRu

Эта статья посвящена математическим функциям в Python. Для выполнения математических операций необходим модуль math.

Что такое модуль?

В C и C++ есть заголовочные файлы, в которых хранятся функции, переменные классов и так далее. При включении заголовочных файлов в код появляется возможность не писать лишние строки и не использовать одинаковые функции по несколько раз. Аналогично в Python для этого есть модули, которые включают функции, классы, переменные и скомпилированный код. Модуль содержит группу связанных функций, классов и переменных.

Есть три типа модулей в Python:

1. Модули, написанные на Python (.py).
2. Модули, написанные на C и загружаемые динамически (.dll, .pyd, .so, .sl и так далее).
3. Модули, написанные на C, но связанные с интерпретатором.

   import sys
   print(sys.builtin_module_names)
   

   ('_ast', '_bisect', '_codecs', '_codecs_cn', '_codecs_hk', '_codecs_iso2022', 
   '_codecs_jp', '_codecs_kr', '_codecs_tw', '_collections', '_csv', '_datetime', 
   '_functools', '_heapq', '_imp', '_io', '_json', '_locale', '_lsprof', '_md5', 
   '_multibytecodec', '_opcode', '_operator', '_pickle', '_random', '_sha1', 
   '_sha256', '_sha512', '_sre', '_stat', '_string', '_struct', '_symtable', '_thread', 
   '_tracemalloc', '_warnings', '_weakref', '_winapi', 'array', 'atexit', 'audioop', 
   'binascii', 'builtins', 'cmath', 'errno', 'faulthandler', 'gc', 'itertools', 'marshal', 
   'math', 'mmap', 'msvcrt', 'nt', 'parser', 'signal', 'sys', 'time', 'winreg', 
   'xxsubtype', 'zipimport', 'zlib'). 
   

Для получения списка модулей, написанных на C, но связанных с Python, можно использовать следующий код.

Как видно из списка выше, модуль math написан на C, но связан с интерпретатором. Он содержит математические функции и переменные, о которых дальше и пойдет речь.

Функции представления чисел

ceil() и floor() — целая часть числа

Сeil() и floor() — функции общего назначения. Функция ceil округляет число до ближайшего целого в большую сторону. Функция floor убирает цифры десятичных знаков. Обе принимают десятичное число в качестве аргумента и возвращают целое число.

Пример:

import math


number=8.10


print("Верхний предел 8.10 это:",math.ceil(number))


print("Нижний предел 8.10 это:",math.floor(number))

Вывод:

Верхний предел 8. 10 это: 9
Нижний предел 8.10 это: 8

Функция fabs() — абсолютное значение

Функция fabs используется для вычисления абсолютного значения числа. Если число содержит любой отрицательный знак (-), то функция убирает его и возвращает положительное дробное число.

Пример:

import math

number = -8.10

print(math.fabs(number))

Вывод:

8.1

factorial() — функция факториала

Эта функция принимает положительное целое число и выводит его факториал.

Пример:

import math    

number = 5

print("факториала числа", math.factorial(number))

Вывод:

факториала числа 120

Примечание: при попытке использовать отрицательное число, возвращается ошибка значения (Value Error).

Пример:

import math    

number = -5

print("факториала числа", math.factorial(number))

Вывод:

ValueError: factorial() not defined for negative values

Функция fmod() — остаток от деления

Функция fmod(x,y) возвращает x % y. Разница в том, что выражение x % y работает только с целыми числами, а эту функцию можно использовать и для чисел с плавающей точкой.

Пример:

import math  

print(math.fmod(5,2))  
print(math.fmod(-5,2))  
print(math.fmod(-5.2,2))  
print(math.fmod(5.2,2))  

Вывод:

1.0
-1.0
-1.2000000000000002
1.2000000000000002

Функция frexp()

Эта функция возвращает мантиссу и показатель степени в виде пары (m,n) любого числа x, решая следующее уравнение. x.

Пример:

import math   
    
print("e в степени 5 ", math.exp(5))
print("e в степени 2.5", math.exp(2.5))  

Вывод:

e в степени 5  148.4131591025766
e в степени 2.5 12.182493960703473

Функция expm1()

Эта функция работает так же, как и exp, но возвращает exp(x)-1. Здесь, expm1 значит exm-m-1, то есть, exp-minus-1.

Пример:

import math   
    
print(math.exp(5)-1)
print(math.expm1(5))

Вывод:

147.4131591025766
147.4131591025766

Функция log() — логарифм числа

Функция log(x[,base]) находит логарифм числа x по основанию e (по умолчанию). base— параметр опциональный. Если нужно вычислить логарифм с определенным основанием, его нужно указать.

Пример:

import math  
	  

print(math.log(2))  
	  

print(math.log(64,2)) 

Вывод:

0.6931471805599453
6.0

Функция log1p()

Эта функция похожа на функцию логарифма, но добавляет 1 к x. log1p значит log-1-p, то есть, log-1-plus.

Пример:

import math  
	  
print(math.log1p(2))

Вывод:

1.0986122886681098

Функция log10()

Вычисляет логарифм по основанию 10.

Пример:

import math  

print(math.log10(1000))

Вывод:

3.0

Функция pow() — степень числа

Используется для нахождение степени числа. Синтаксис функции pow(Base, Power). Она принимает два аргумента: основание и степень.

Пример:

import math  

print(math.pow(5,4))

Вывод:

625.0

Функция sqrt() — квадратный корень числа

Эта функция используется для нахождения квадратного корня числа. Она принимает число в качестве аргумента и находит его квадратный корень.

Пример:

import math  

print(math.sqrt(256))

Вывод:

16.0

Тригонометрические функции

В Python есть следующие тригонометрические функции.

Функция	Значение
sin	принимает радиан и возвращает его синус
cos	принимает радиан и возвращает его косинус
tan	принимает радиан и возвращает его тангенс
asin	принимает один параметр и возвращает арксинус (обратный синус)
acos	принимает один параметр и возвращает арккосинус (обратный косинус)
atan	принимает один параметр и возвращает арктангенс (обратный тангенс)
sinh	принимает один параметр и возвращает гиперболический синус
cosh	принимает один параметр и возвращает гиперболический косинус
tanh	принимает один параметр и возвращает гиперболический тангенс
asinh	принимает один параметр и возвращает обратный гиперболический синус
acosh	принимает один параметр и возвращает обратный гиперболический косинус
atanh	принимает один параметр и возвращает обратный гиперболический тангенс

Пример:

import math  
  

print("синус PI/2 :", math.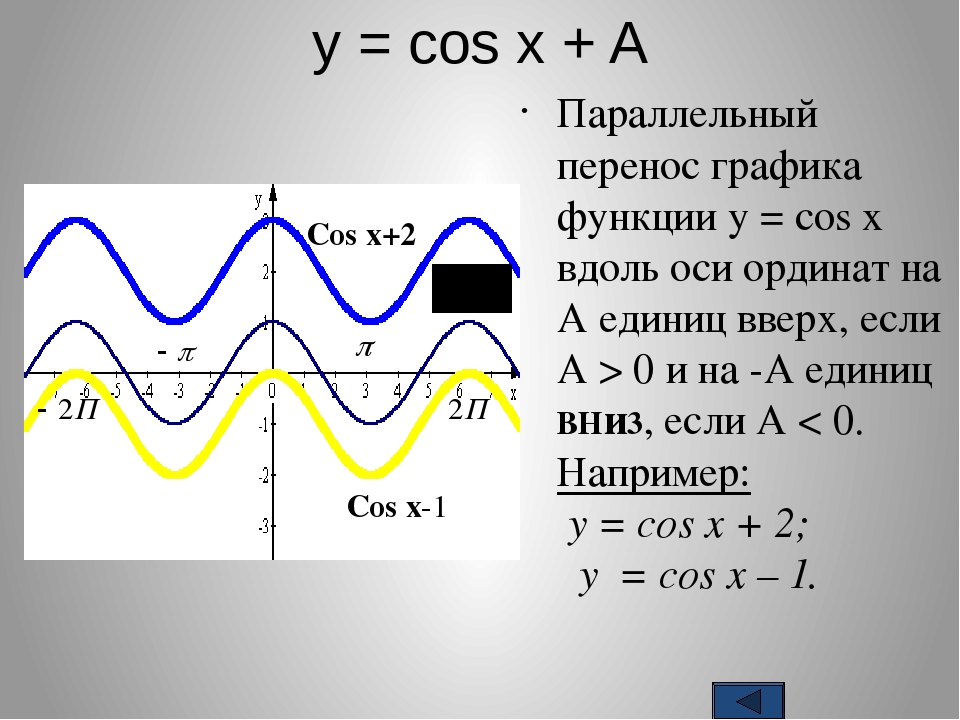 sin(math.pi/2))  

print("косинус 0 :", math.cos(0))  

print("тангенс PI/4 :", math.tan(math.pi/4))  
  
print()  
  

print("арксинус 0 :", math.acos(0))  

print("арккосинус 1 :", math.acos(1))  

print("арктангенс 0.5 :", math.atan(0.5))  
  
print()  
  

print("гиперболический синус 1 :", math.sinh(1))  

print("гиперболический косинус 0 :", math.cos(0))  

print("гиперболический тангенс 1 :", math.tan(1))  
  
print()  
  

print("обратный гиперболический синус 1 :", math.acosh(1))  

print("обратный гиперболический косинус 1 :", math.acosh(1))  

print("обратный гиперболический тангенс 0.5 :", math.atanh(0.5))  

Вывод:

синус PI/2 : 1.0
косинус 0 : 1.0
тангенс PI/4 : 0.9999999999999999

арксинус 0 : 1.5707963267948966
арккосинус 1 : 0.0
арктангенс 0.5 : 0.4636476090008061

гиперболический синус 1 : 1.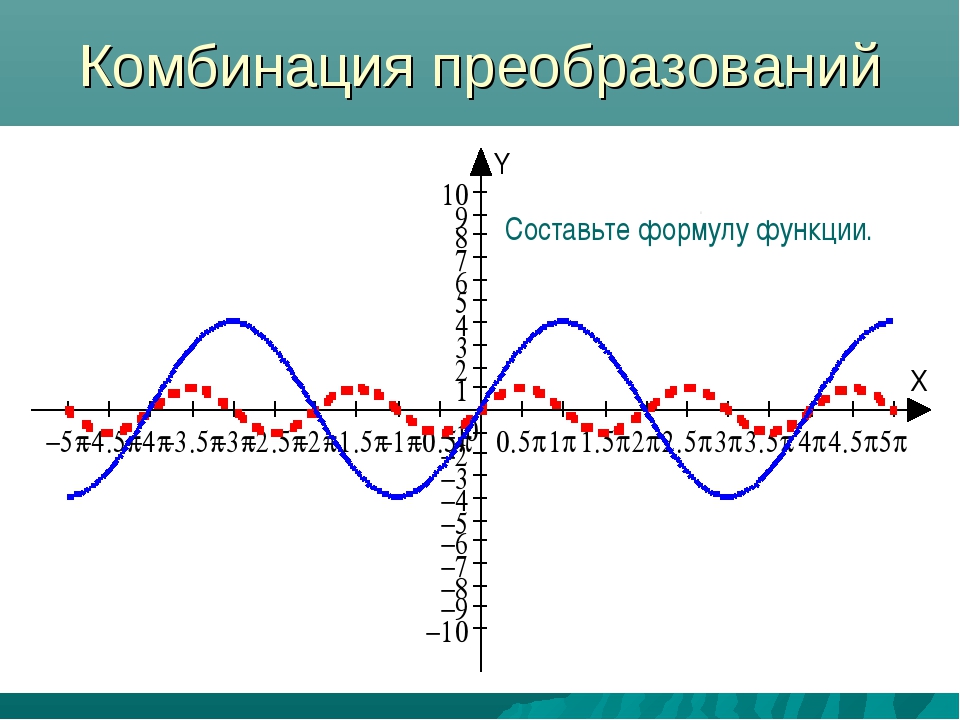 1752011936438014
гиперболический косинус 0 : 1.0
гиперболический тангенс 1 : 1.5574077246549023

обратный гиперболический синус 1 : 0.0
обратный гиперболический косинус 1 : 0.0
обратный гиперболический тангенс 0.5 : 0.5493061443340549

Функция преобразования углов

Эти функции преобразуют угол. В математике углы можно записывать двумя способами: угол и радиан. Есть две функции в Python, которые конвертируют градусы в радиан и обратно.

• degrees(): конвертирует радиан в градусы;
• radians(): конвертирует градус в радианы;

Пример:

import math  

print(math.degrees(1.57))
print(math.radians(90))

Вывод:

89.95437383553924
1.5707963267948966

Математические константы

В Python есть две математические константы: pi и e.

1. pi: это математическая константа со значением 3.1416..
2. e: это математическая константа со значением 2.7183..

Пример:

import math  


print("значение PI", math.pi)


print("значение e", math.e)

Вывод:

значение PI 3.141592653589793
значение e 2.718281828459045

Python. Модуль math. Тригонометрические функции. Примеры

---

Содержание

---

Поиск на других ресурсах:

1. Особенности применения тригонометрических функций. Преобразование радиан в градусы и наоборот

Чтобы использовать тригонометрические функции в программе, нужно подключить модуль math

import math

Все тригонометрические функции оперируют радианами. Зависимость между радианами и градусами определяется по формуле:

1 радиан = 180°/π = 57.2958°

Если известен угол в градусах, то для корректной работы тригонометрических функций, этот угол нужно преобразовать в радианы.

Например. Задан угол, имеющий n градусов. Найти арккосинус этого угла. В этом случае формула вычисления результата будет следующей:

...
n_rad = n*3.1415/180 # получить угол в радианах
ac = math.acos(n_rad) # вычислить арккосинус
...

Чтобы получить более точное значение результата, в программе можно использовать константу math.pi, которая определяет число π. В этом случае текст программы будет иметь следующий вид

n_rad = n*math.pi/180 # получить угол в радианах
ac = math.acos(n_rad) # вычислить арккосинус

  ⇑

2. Средства языка Python для конвертирования из градусов в радианы и наоборот. Функции math.degrees(x) и math.radians(x)

В языке Python существуют функции преобразования из градусов в радианы и, наоборот, из радиан в градусы.

Функция math.degrees(x) конвертирует значение параметра x из радиан в градусы.
Функция math.radians(x) конвертирует значение параметра x из градусов в радианы.

Пример.

# Функция math.degrees(x)
import math

x = 1 # x - угол в радианах
y = math.degrees(x) # y = 57.29577951308232 - угол в градусах

x = math.pi # x = 3.1415...
y = math.degrees(x) # y = 180.0

# Функция math.radians(x)
x = 180.0/math.pi
y = math.radians(x) # y = 1.0

x = 45 # x - угол в градусах
y = math.radians(x) # y = 0.7853981633974483

  ⇑

3. Ограничения на использование тригонометрических функций

При использовании тригонометрических функций следует учитывать соответствующие ограничения, которые следуют из самой сущности этих функций. Например, не существует арксинуса из числа, которое больше 1.
Если при вызове функции задать неправильный аргумент, то интерпретатор выдаст соответствующее сообщение об ошибке

ValueError: math domain error

  ⇑

---

---

4. Функция math.acos(x). Арккосинус угла

Функция acos(x) возвращает арккосинус угла x. Аргумент x задается в радианах и может быть как целым числом, так и вещественным числом.

Пример.

# Функция math.acos(x)
import math

n = float(input('n = ')) # ввести n

n_rad = n*math.pi/180 # получить угол в радианах
ac = math.acos(n_rad) # вычислить арккосинус

print('n_rad = ', n_rad)
print('ac = ', ac)

Результат работы программы

n = 35
n_rad = 0.6108652381980153
ac = 0.913643357298706

  ⇑

5. Функция math.asin(x). Арксинус

Функция math.asin(x) вычисляет арксинус угла от аргумента x. Значение аргумента x задается в радианах.

Пример.

# Функция math.asin(x)
import math

n = 10 # n - угол в градусах

# конвертировать из градусов в радианы
n_rad = n*math.pi/180 # n_rad = 0.17453292519943295

# вычислить арксинус
asn = math.asin(n_rad) # asn = 0.17543139267904395

  ⇑

6. Функция math.atan(x). Арктангенс

Функция math.atan(x) возвращает арктангенс аргумента x, значение которого задается в радианах. При использовании функции важно помнить допустимые значения x, которые можно задавать при вычислении арктангенса.

Пример.

# Функция math.atan(x)
import math

n = 60 # n - угол в градусах

# конвертировать из градусов в радианы
n_rad = n*math.pi/180 # n_rad = 1.0471975511965976

# вычислить арктангенс
atn = math.atan(n_rad) # atn = 0.808448792630022

  ⇑

7. Функция math.atan2(x, y). Арктангенс от x/y

Функция math.atan2(x, y) вычисляет арктангенс угла от деления x на y. Функция возвращает результат от —π до π. Аргументы x, y определяют координаты точки, через которую проходит отрезок от начала координат. В отличие от функции atan(x), данная функция правильно вычисляет квадрант, влияющий на знак результата.

Пример.

# Функция math.atan2(x,y)
import math

x = -2
y = -1

res = math.atan2(x, y) # res = -2.0344439357957027

  ⇑

8. Функция math.cos(x). Косинус угла

Функция math.cos(x) вычисляет косинус угла для аргумента x. Значение аргумента x задается в радианах.

Пример.

# Функция math.cos(x)
import math

x = 0
y = math.cos(x) # y = 1.0

x = math.pi
y = math.cos(x) # y = -1.0

x = 2 # 2 радианы
y = math.cos(x) # y = -0.4161468365471424

  ⇑

9. Функция math.sin(x)

Функция math.sin(x) возвращает синус угла от аргумента x, заданного в радианах.

Пример.

# Функция math.sin(x)
import math

x = math.pi
y = math.sin(x) # y = 1.2246467991473532e-16

x = 0
y = math.sin(x) # y = 0.0

x = 2 # 2 радиана
y = math.sin(x)

  ⇑

10. Функция math.hypot(x, y). Евклидовая норма (Euclidean norm)

Функция возвращает Евклидовую норму, которая равна длине вектора от начала координат до точки x, y и определяется по формуле

Пример.

# Функция math.hypot(x, y)
import math

x = 1.0
y = 1.0
z = math.hypot(x, y) # z = 1.4142135623730951

x = 3.0
y = 4.0
z = math.hypot(x, y) # z = 5.0

  ⇑

11. Функция math.tan(x). Тангенс угла x

Функция math.tan(x) возвращает тангенс от аргумента x. Аргумент x задается в радианах.

Пример.

# Функция math.tan(x, y)
import math

x = 1.0
y = math.tan(x) # y = 1.5574077246549023

x = 0.0
y = math.tan(x) # y = 0.0

  ⇑

---

Связанные темы

  ⇑

---

 

Модули. Курс «Python. Введение в программирование»

Встроенные в язык программирования функции доступны сразу. Чтобы их вызвать, не надо выполнять никаких дополнительных действий. Однако за время существования любого популярного языка на нем было написано столько функций и классов, которые оказались востребованными множеством программистов и в разных областях, что включить весь этот объем кода в сам язык если возможно, то нецелесообразно.

Чтобы разрешить проблему доступа к дополнительным возможностям языка, в программировании стало общепринятой практикой использовать так называемые модули, пакеты и библиотеки. Каждый модуль содержит коллекцию функций и классов, предназначенных для решения задач из определенной области. Так в модуле math языка Python содержатся математические функции, модуль random позволяет генерировать псевдослучайные числа, в модуле datetime содержатся классы для работы с датами и временем, модуль sys предоставляет доступ к системным переменным и т. д.

Количество модулей для языка Python огромно, что связано с популярностью языка. Часть модулей собрана в так называемую стандартную библиотеку. Стандартная она потому, что поставляется вместе с установочным пакетом. Однако существуют сторонние библиотеки. Они скачиваются и устанавливаются отдельно.

Для доступа к функционалу модуля, его надо импортировать в программу. После импорта интерпретатор «знает» о существовании дополнительных классов и функций и позволяет ими пользоваться.

В Питоне импорт осуществляется командой import. При этом существует несколько способов импорта. Рассмотрим работу с модулем на примере math. Итак,

Ничего не произошло. Однако в глобальной области видимости появилось имя math. Если до импорта вы упомянули бы имя math, то возникла бы ошибка NameError. Теперь же

>>> math
<module 'math' (built-in)>

В программе завелся объект math, относящийся к классу module.

Чтобы увидеть перечень функций, входящих в этот модуль, воспользуемся встроенной в Python функцией dir(), передав ей в качестве аргумента имя модуля:

>>> dir(math)
['__doc__', '__loader__', '__name__', 
'__package__', '__spec__', 'acos', 'acosh',
'asin', 'asinh', 'atan', 'atan2', 'atanh', 
'ceil', 'copysign', 'cos', 'cosh',
'degrees', 'e', 'erf', 'erfc', 'exp', 
'expm1', 'fabs', 'factorial', 'floor',
'fmod', 'frexp', 'fsum', 'gamma', 'gcd',
 'hypot', 'inf', 'isclose', 'isfinite',
'isinf', 'isnan', 'ldexp', 'lgamma', 'log', 
'log10', 'log1p', 'log2', 'modf',
'nan', 'pi', 'pow', 'radians', 'sin', 'sinh', 
'sqrt', 'tan', 'tanh', 'trunc']

Проигнорируем имена с двойными подчеркиваниями. Все остальное – имена функций и констант (переменных, которые не меняют своих значений), включенных в модуль math. Чтобы вызвать функцию из модуля, надо впереди написать имя модуля, поставить точку, далее указать имя функции, после чего в скобках передать аргументы, если они требуются. Например, чтобы вызвать функцию pow из math, надо написать так:

Обратите внимание, эта другая функция pow(), не та, что встроена в сам язык. «Обычная» функция pow() возвращает целое, если аргументы целые числа:

Для обращения к константе скобки не нужны:

>>> math.pi
3.141592653589793

Если мы не знаем, что делает та или иная функция, то можем получить справочную информацию о ней с помощью встроенной в язык Python функции help():

>>> help(math.gcd)
Help on built-in function gcd in module math:

gcd(...)
    gcd(x, y) -> int
    greatest common divisor of x and y

Для выхода из интерактивной справки надо нажать клавишу q. В данном случае сообщается, что функция возвращает целое число, и это наибольший общий делитель для чисел x и y. Описание модулей и их содержания также можно посмотреть в официальной документации на сайте python.org.

Второй способ импорта – это когда импортируется не сам модуль, а только необходимые функции из него.

>>> from math import gcd, sqrt, hypot

Перевести можно как «из модуля math импортировать функции gcd, sqrt и hypot«.

В таком случае при их вызове не надо перед именем функции указывать имя модуля:

>>> gcd(100, 150)
50
>>> sqrt(16)
4.0
>>> hypot(3, 4)
5.0

Чтобы импортировать сразу все функции из модуля:

Импорт через from не лишен недостатка. В программе уже может быть идентификатор с таким же именем, как имя одной из импортируемых функций или констант. Ошибки не будет, но одно из них окажется «затерто»:

>>> pi = 3.14
>>> from math import pi
>>> pi
3.141592653589793

Здесь исчезает значение 3.14, присвоенное переменной pi. Это имя теперь указывает на число из модуля math. Если импорт сделать раньше, чем присвоение значения pi, то будет все наоборот:

>>> from math import pi
>>> pi = 3.14
>>> pi
3.14

В этой связи более опасен именно импорт всех функций. Так как в этом случае очень легко не заметить подмены значений идентификаторов.

Однако можно изменить имя идентификатора из модуля на какое угодно:

>>> from math import pi as P
>>> P
3.141592653589793
>>> pi
3.14

В данном случае константа pi из модуля импортируется под именем P. Смысл подобных импортов в сокращении имен, так как есть модули с длинными именами, а имена функций и классов в них еще длиннее. Если в программу импортируется всего пара сущностей, и они используются в ней часто, то имеет смысл переименовать их на более короткий вариант. Сравните:

>>> import calendar
>>> calendar.weekheader(2)
'Mo Tu We Th Fr Sa Su'

и

>>> from calendar import weekheader as week
>>> week(3)
'Mon Tue Wed Thu Fri Sat Sun'

Во всех остальных случаях лучше оставлять идентификаторы содержимого модуля в пространстве имен самого модуля и получать доступ к ним через имя модуля, то есть выполнять импорт командой import имя_модуля, а вызывать, например, функции через имя_модуля.имя_функции().

Практическая работа. Создание собственного модуля

Программист на Python всегда может создать собственный модуль, чтобы использовать его в нескольких своих программах или даже предоставить в пользование всему миру. В качестве тренировки создадим модуль с функциями для вычисления площадей прямоугольника, треугольника и круга:

from math import pi, pow
 
def rectangle(a, b):
    return round(a * b, 2)
 
def triangle(a, h):
    return round(0.5 * a * h, 2)
 
def circle(r):
    return round(pi * pow(r, 2), 2) 

Здесь также иллюстрируется принцип, что один модуль может импортировать другие. В данном случае импортируются функции из модуля math.

Поместите данный код в отдельный файл square.py. Однако куда поместить сам файл?

Когда интерпретатор Питона встречает команду импорта, то просматривает на наличие файла-модуля определенные каталоги. Их перечень можно увидеть по содержимому sys.path:

>>> import sys
>>> sys.path
['', '/usr/lib/python35.zip', 
'/usr/lib/python3.5', 
'/usr/lib/python3.5/plat-x86_64-linux-gnu',
'/usr/lib/python3.5/lib-dynload', 
'/home/pl/.local/lib/python3.5/site-packages',
'/usr/local/lib/python3.5/dist-packages', 
'/usr/lib/python3/dist-packages']

Это список адресов в Linux. В Windows он будет несколько другим. Первый элемент – пустая строка, что обозначает текущий каталог, то есть то место, где сохранена сама программа, импортирующая модуль. Если вы сохраните файл-модуль и файл-программу в одном каталоге, то интерпретатор без труда найдет модуль.

Также модуль можно положить в любой другой из указанных в списке каталогов. Тогда он будет доступен для всех программ на Python, а также его можно будет импортировать в интерактивном режиме.

Можно добавить в sys.path свой каталог. Однако в этом случае либо код программы должен содержать команды изменения значения sys.path, либо надо править конфигурационный файл операционной системы. В большинстве случаев лучше так не делать.

Поместите файл square.py в тот же каталог, где будет исполняемая программа. Ее код должен включать инструкцию импорта модуля square (при импорте расширение файла не указывается) и вызов той функции и с теми параметрами, которые ввел пользователь. То есть у пользователя надо спросить, площадь какой фигуры он хочет вычислить. Далее запросить у него аргументы для соответствующей функции. Передать их в функцию из модуля square, а полученный оттуда результат вывести на экран.

Примечание. Исполнение модуля как самостоятельного скрипта, а также создание строк документации, которые отображает встроенная в Python функция help(), будут рассмотрены в курсе объектно-ориентированного программирования.

Примеры решения и дополнительные уроки в android-приложении и pdf-версии курса

Python | Модуль math

Модуль math

Последнее обновление: 02.05.2017

Встроенный модуль math в Python предоставляет набор функций для выполнения математических, тригонометрических и
логарифмических операций. Некоторые из основных функций модуля:

• pow(num, power): возведение числа num в степень power

• sqrt(num): квадратный корень числа num

• ceil(num): округление числа до ближайшего наибольшего целого

• floor(num): округление числа до ближайшего наименьшего целого

• factorial(num): факториал числа

• degrees(rad): перевод из радиан в градусы

• radians(grad): перевод из градусов в радианы

• cos(rad): косинус угла в радианах

• sin(rad): синус угла в радианах

• tan(rad): тангенс угла в радианах

• acos(rad): арккосинус угла в радианах

• asin(rad): арксинус угла в радианах

• atan(rad): арктангенс угла в радианах

• log(n, base): логарифм числа n по основанию base

• log10(n): десятичный логарифм числа n

Пример применения некоторых функций:

import math

# возведение числа 2 в степень 3
n1 = math.pow(2, 3)
print(n1)  # 8

# ту же самую операцию можно выполнить так
n2 = 2**3
print(n2)

# возведение в квадрат
print(math.sqrt(9))  # 3

# ближайшее наибольшее целое число
print(math.ceil(4.56))  # 5

# ближайшее наименьшее целое число
print(math.floor(4.56))  # 4

# перевод из радиан в градусы
print(math.degrees(3.14159))  # 180

# перевод из градусов в радианы
print(math.radians(180))   # 3.1415.....
# косинус
print(math.cos(math.radians(60)))  # 0.5
# cинус
print(math.sin(math.radians(90)))   # 1.0
# тангенс
print(math.tan(math.radians(0)))    # 0.0

print(math.log(8,2))    # 3.0
print(math.log10(100))    # 2.0

Также модуль math предоставляет ряд встроенных констант, такие как PI и E:

import math
radius = 30
# площадь круга с радиусом 30
area = math.pi * math.pow(radius, 2)
print(area)

# натуральный логарифм числа 10
number = math.log(10, math.e)
print(number)

Python | Функция math.sin () — GeeksforGeeks

Python | math.sin () function

В Python модуль math содержит ряд математических операций, которые можно легко выполнить с помощью модуля. math.sin () функция возвращает синус значения, переданного в качестве аргумента. Значение, передаваемое в эту функцию, должно быть в радианах.

Синтаксис: math.sin (x)

Параметр:
x: значение, передаваемое в sin ()

Возвращает: Возвращает синус значения, переданного в качестве аргумента

Код # 1:

импорт математика a = математика.pi / 6 print ( "Значение синуса pi / 6:" , конец = 0003 ") (math.sin (a))

Выход:

Значение синуса числа пи / 6 составляет: 0,49999999999999994.
 

Код # 2:

импорт математика импорт matplotlib.pyplot as plt in_array = [ - 3.14159265 , - 2.57039399 0,28559933 , 2,57039399 , 3,14159265 ] out_array = 0005 0005 диапазон ( len (in_array)): out_array.append (math.sin (in_array [i])) i + = 1 "печать " ( "печать , in_array) print ( "\ nout_array:" , out_array) plt.plot (in_ray = красный, цвет , маркер = "o" ) plt.title ( "math.sin ()" ) plt.xlabel ( "X" ) plt.ylabel ( "Y" ) ) plt.show ()

Вывод:

in_array: [-3.14159265, -2.57039399, -0.28559933, 0.28559933, 2.57039399, 3.14159265] —

-out_array: [-3.516811930e 0,2817325547837714, 0,2817325547837714, 0.5406408168673427, 3.5897

8416118e-09]

Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.

Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS . И чтобы начать свое путешествие по машинному обучению, присоединитесь к Машинное обучение — курс базового уровня

Python sin () function: объяснено с помощью 4 примеров

Функция sin ():

• Принимает аргумент (x = число)
• и возвращает его синус в радианах.
• Это часть математического модуля, поэтому эту функцию нельзя использовать напрямую.
• Вам необходимо импортировать математический модуль в вашу программу Python, как показано в примерах ниже.
• Чтобы получить результат в градусах, вы можете использовать функцию радиан () вместе с sin (), как показано в примере в последнем разделе этого руководства.

Синтаксис функции sin ()

Вот как используется функция sin ():

sin (x)

Например:

математ.грех (3)

Полный код см. В примерах ниже.

Что такое функция синуса в математике? Синус — одна из самых распространенных тригонометрических функций в математике. Два других — это функции косинуса (или cos) и тангенса (tan). Синусоидальная функция основана на прямоугольном треугольнике. Вы можете узнать больше о синусоидальной функции здесь.

Пример функции sin ()

В приведенном ниже примере показано использование функции sin () для получения синуса нескольких чисел.Мы получим синус в радианах для 30, 45 и 60:

1 2 3 4 5 6 7 8 9 10 11 12 13 140002 18 19

# Демонстрация функции sin () из импорта математики sin sine_30 = sin (30) sine_45 = sin (45) 9000 60) print («Синус 30 =», sine_30) print («Синус 45 =», sine_45) print («Синус 60 = «, Sine_60)

Результат:

В приведенном выше примере мы использовали сокращение для использования функции sin ().Этот код даст тот же результат:

1 2 3 4 5 6 7 8 9 10 11 12 13 140002

import math sine_30 = math.sin (30) sine_45 = math.sin (45) sine_60 = math.sin (60) print («Синус 30 =», sine_302) print («Синус 45 =», sine_45) print («Синус 60 =», sine_60)

Результат:

Синус 30 = -0,9880316240

8

Синус 45 = 0,850

45341184

Синус 60 = -0.3048106211022167

Как получить градус синуса?

Вам может быть интересно, почему эти ответы отличаются от ответов калькулятора для получения синуса числа? Это потому, что функция Python sin () возвращает синус в радианах.

В математическом модуле есть еще одна функция radians (), которую вы можете использовать для преобразования радианов в градусы.

В приведенном ниже примере используются те же значения, что и в приведенных выше примерах, а также используется функция radians () для преобразования возвращаемого результата функцией sin () и получения значений синуса в градусах:

1 2 3 4 5 6 7 8 9 10 11 12 13 140002

import math sine_30 = math.sin (math.radians (30)) sine_45 = math.sin (math.radians (45)) sine_60 = math.sin (math.radians (60)) print («Синус 30 в градусах =», sine_30) print («Синус 45 в градусах =», sine_45) print («Синус 60 в градусах =», sine_60 )

На выходе:

Синус 30 в градусе = 0.49999999999999994

Синус 45 в градусе = 0,7071067811865475

Синус 60 в градусе = 0,8660254037844386

Пример округления результата

В приведенном ниже примере используются три функции вместе; sin (), радианы () и round (). Функция round округляет результат, возвращаемый функцией radians (), до одинарной точности. См. Код и вывод:

1 2 3 4 5 6 7 8 9 10 11 12 13 140002

import math sine_30 = round (math.sin (math.radians (30)), 1) sine_45 = round (math.sin (math.radians (45)), 1) sine_60 = round (math.sin (math.radians ( 60)), 1) print («Синус 30 градусов с одинарной точностью =», sine_30) print («Синус 45 градусов с одинарной точностью =», sine_45) print («Синус 60 в градусах с одинарной точностью =», sine_60)

На выходе:

Синус 30 градусов с одинарной точностью = 0.5

Синус 45 градусов с одинарной точностью = 0,7

Синус 60 градусов с одинарной точностью = 0,9

Узнайте больше о круглой функции в ее руководстве: Python round function.

тригонометрических функций в Python — sin, cos, tan и т. Д.

Математическая библиотека на python имеет множество тригонометрических функций , которых достаточно для выполнения различных тригонометрических вычислений с помощью минимальных строк кода.Эти функции можно использовать после импорта математического модуля или путем обращения к математической библиотеке с помощью оператора dot следующим образом:

  math.function_name (параметр)

# или импортируйте математический модуль

импорт математики  

Есть 2 вспомогательных метода, которые помогают преобразовывать значения из радианов в градусы и наоборот, так что вы можете проверять значение в любом формате.

градусов (значение) : этот метод преобразует переданное ему значение из радиан в градусы.

радиан (значение) : этот метод преобразует переданное ему значение из градусов в радианы.

Краткий факт: Все тригонометрические функции в Python предполагают, что входной угол выражается в радианах .

Кроме того, поскольку мы изучаем математику, пи / 2 составляет 90 градусов и пи / 3 составляет 60 градусов , математический модуль в Python предоставляет константу пи , которая представляет пи , что можно использовать с тригонометрической функцией.

---

Время для примера:

В приведенном ниже примере кода мы использовали методы градусов () и радиан () ,

  импорт математики

печать (math.degrees ((math.pi / 2)))
печать (математические радианы (60))  

Выход :

 90,0
1.0471975511965976 

Теперь давайте посмотрим на различные тригонометрические функции в действии, одну за другой.

---

sin (x) Функция

Эта функция возвращает синус переданного значения (здесь x).Вход x должен быть углом , указанным в терминах радиан (пи / 2, пи / 3 / пи / 6 и т. Д.).

cos (x) Функция

Эта функция возвращает косинус переданного значения (здесь x). Входные данные x — это угол, представленный в радианах .

tan (x) Функция

Эта функция возвращает тангенс переданного ей значения, то есть синус / косинус угла.Здесь вводится угол в радиан .

Пример кода для

sin , cos и tan :

Ниже у нас есть простой пример кода для трех тригонометрических функций, определенных выше,

  импорт математики

print (math.sin (math.pi / 3)) # pi / 3 радиан преобразуется в 60 градусов
печать (math.tan (math.pi / 3))
печать (math.cos (math.pi / 6))  

Выход:

 0.8660254037844386
1.7320508075688767
0,8660254037844387 

---

asin (x) Функция

Эта функция возвращает , обратный синусу , который также известен как арксинус комплексного числа . Входные данные выражаются в радианах и должны находиться в диапазоне от -1 до 1 . Он возвращает число с плавающей запятой в качестве вывода .

acos (x) Функция

Эта функция возвращает косинус , обратный параметра x в радианах.Это также известно как арккосинус комплексного числа . Значение x должно находиться в диапазоне от -1 до 1 . На выходе он возвращает число с плавающей запятой.

atan (x) Функция

Эта функция возвращает , обратное касательной , в радианах. Он известен как арктангенс комплексного числа . Значение параметра находится в пределах -1 и 1 . Его также можно представить как (математ.грех (math.pi / 4)) / (math.cos (math.pi / 4)) . На выходе он возвращает число с плавающей запятой.

Пример кода для

asin , acos и atan с углами в радианах:

  импорт математики

печать (math.asin (1))
печать (math.acos (0))
печать (math.atan (1))  

Выход:

 1,5707963267948966
1,5707963267948966
0,7853981633974483 

В примере ниже показано, как функции asin , acos и atan могут использоваться с комплексными числами в формате x + iy .

  импорт cmath

х = 1,0
у = 1,0
г = комплекс (х, у)

print ("Арксинус равен:", cmath.asin (z))
print ("Арккосинус:", cmath.acos (z))
print ("Арктангенс равен:", cmath.atan (z))  

Выход:

 Арксинус: (0,6662394324
3 + 1,061275061
57j)
Арккосинус: (0,68943023814-1.061275061
57j)
Арктангенс равен: (1.0172219678978514 + 0.40235947810852507j) 
 
 
 
 sinh (x)  Функция 
 Этот метод возвращает гиперболический синус  угла  переданного комплексного числа.
 
 
 cosh (x)  Функция 
 Этот метод возвращает гиперболический косинус  угла  переданного комплексного числа. 
 
 
 tanh (x)  Функция 
 Этот метод возвращает гиперболический тангенс  угла  переданного комплексного числа. 
 
 Пример кода для 
 sinh ,  cosh  и  tanh  с комплексными числами: 
  импорт cmath

х = 1.0
у = 1,0
г = комплекс (х, у)
print ("Гиперболический синус:", cmath.sinh (z))
print ("Гиперболический косинус равен:", cmath.cosh (z))
print ("Гиперболический тангенс равен:", cmath.tanh (z))  
   Выход:   
 Гиперболический синус: (0,63496347361 + 1,2984575814159773j)
Гиперболический косинус: (0,8337300251311491 + 0,9888977057628651j)
Гиперболический тангенс: (1.08373386946 + 0.2717525853195118j) 
 
 
 
 asinh (x)  Функция 
 Возвращает , обратный гиперболическому синусу  угла / комплексного числа.
 
 
 acosh (x)  Функция 
 Возвращает , обратное гиперболическому косинусу  угла / комплексного числа. 
 
 
 atanh (x)  Функция 
 Возвращает , обратный гиперболическому тангенсу  угла / комплексного числа. 
 
 Пример кода для методов 
 asinh ,  acosh  и  atanh  с комплексными числами: 
  импорт cmath

х = 1.0
у = 1,0
г = комплекс (х, у)

print ("Обратный гиперболический синус:", cmath.asinh (z))
print ("Обратный гиперболический косинус равен:", cmath.acosh (z))
print ("Обратный гиперболический тангенс равен:", cmath.atanh (z))  
   Выход:   
 Обратный гиперболический синус: (1.061275061
57 + 0.6662394324
3j)
Обратный гиперболический косинус равен: (1.061275061
57 + 0.
68943023813j)
Обратный гиперболический тангенс равен: (0.40235947810852507 + 1.0172219678978514j) 
 

 
 
 atan2 (y, x)  Функция 
 Это переводится в  atan2 (y / x) , где y и x являются числовыми значениями. Он возвращает значение в диапазоне от  –pi  до  pi . Он представляет собой угол между положительной осью x и координатами (x, y). 
  печать (math.atan2 (1.2,1.3))  
   Выход:   
 0,7454194762741583 
 

 
 
 гипотеза (x, y)  Функция 
 Эта функция возвращает гипотенузу  , т.е.e  Евклидова норма . Это означает, что он возвращает расстояние между началом координат и точками (x, y). Это указывает длину вектора в двумерном пространстве. Евклидова норма также известна как «величина» вектора. Это числовое значение вектора (поскольку у векторов есть величина, а также направление). 
 Если передано более 2 аргументов, он корректно возвращает  TypeError . 
  печать (математ. Гипотеза (2,2))  
   Выход:   
 2.8284271247461903 
   ПРИМЕЧАНИЕ:   Когда эти значения сравниваются с числовыми значениями углов, может быть несколько различий в десятичных разрядах, которые можно безопасно игнорировать. Например,  tan (pi / 3)  преобразуется в  tan 60 , что эквивалентно  sqrt (3) . Если используется функция  tan , вывод будет  1.7320508075688767 , тогда как  sqrt (3)  даст  1.7320508075688772 . 
 

 
 Это так просто? А как насчет исключений и ошибок? 
 Что ж, вы совершенно правы.Есть два вида исключений, которые потенциально могут возникнуть из-за неправильного использования этих методов: 
  TypeError : Этот вид ошибки возникает, когда значение, не являющееся числом, передается в качестве параметра одному из тригонометрических методов. 
  ValueError : Возникает такая ошибка, в метод передается недопустимое значение / параметр. 
 
 
 Пример, демонстрирующий оба исключения:  
  импорт математики

# Он передается как строка, а не как число,
# отсюда и ошибка.печать (math.sin ('2'))

# Значение, обратное синусоидальному углу, можно найти для параметров
# которые указаны только в радианах и являются инверсией синуса целого числа
# математически не определено, что приводит к ошибке
печать (math.asin (5))  
   Выход:   
 TypeError: должно быть действительное число, а не str
ValueError: ошибка математического домена
 
 

 
 
 Заключение  
 Мы узнали о том, как можно использовать различные тригонометрические методы, импортировав модуль  math  в python.Не забудьте всегда передавать параметр в  радианах  или преобразовывать  градусов  в  радиан , а затем передавать его как параметр. 
 math - Математические функции - документация Python 3.9.4 

 Этот модуль обеспечивает доступ к математическим функциям, определенным C

стандарт. 
 Эти функции нельзя использовать с комплексными числами; использовать функции

то же имя из модуля  cmath , если вам требуется поддержка сложных

числа.Различие между функциями, поддерживающими комплексные числа, и

те, которые не делаются, поскольку большинство пользователей не хотят учиться так много

математика, необходимая для понимания комплексных чисел. Получение исключения

вместо сложного результата позволяет раньше обнаруживать неожиданный комплекс

число, используемое в качестве параметра, чтобы программист мог определить, как и почему он

был создан в первую очередь. 
 Этот модуль предоставляет следующие функции. За исключением случаев, когда явно

в противном случае все возвращаемые значения являются числами с плавающей запятой.
 Теоретико-числовые функции и функции представлений 


 математика.   потолок  ( x ) 

 Вернуть потолок  x , наименьшее целое число, большее или равное  x .

Если  x  не является числом с плавающей запятой, делегирует  x .__ ceil __ () , который должен вернуть

 Интегральное значение . 




 математика.   гребень  ( n ,  k ) 

 Вернуть количество способов выбора  k  элементов из  n  элементов без повторения

и без заказа.
 Оценивается как  n! / (k! * (n - k)!) , когда  k <= n  и оценивает

к нулю, когда  k> n . 
 Также называется биномиальным коэффициентом, потому что он эквивалентен

к коэффициенту k-го члена в полиномиальном разложении

выражение  (1 + x) ** n . 
 Вызывает  TypeError , если какой-либо из аргументов не является целым числом.

Вызывает  ValueError , если любой из аргументов отрицательный. 




 математика.  копия  ( x ,  y ) 

 Вернуть число с плавающей запятой с величиной (абсолютным значением)  x , но со знаком

 y . На платформах, поддерживающих нули со знаком,  copysign (1.0, -0.0) 

возвращает  -1,0 . 




 математика.   фабрик  ( x ) 

 Вернуть абсолютное значение  x . 




 математика.   факториал  ( x ) 

 Вернуть факториал  x  как целое число.Вызывает  ValueError , если  x  не является целым или

отрицательный. 
 Не рекомендуется, начиная с версии 3.9: прием чисел с плавающей запятой с целыми значениями (например,  5.0 ) не рекомендуется. 




 математика.   этаж  ( x ) 

 Вернуть нижний предел  x , наибольшее целое число, меньшее или равное  x .

Если  x  не является числом с плавающей запятой, делегирует  x .__ floor __ () , который должен вернуть

 Интегральное значение .




 математика.   fmod  ( x ,  y ) 

 Вернуть  fmod (x, y) , как определено библиотекой платформы C. Обратите внимание, что

Выражение Python  x% y  может не возвращать тот же результат. Намерение C

стандартным является то, что  fmod (x, y)  должно быть точно (математически; до бесконечности

точности), равного  x - n * y  для некоторого целого числа  n , такое, что результат имеет

тот же знак, что и  x , и величина меньше  абс (y) .Python  x% y 

вместо этого возвращает результат со знаком  y  и может быть неточно вычислимым

для аргументов с плавающей запятой. Например,  fmod (-1e-100, 1e100)  это  -1e-100 , но

результат Python  -1e-100% 1e100  будет  1e100-1e-100 , что не может быть

представлен в точности как поплавок и округляется до удивительного  1e100 . Для

по этой причине функция  fmod ()  обычно предпочтительнее при работе с

float, тогда как Python  x% y  предпочтительнее при работе с целыми числами.




 математика.   frexp  ( x ) 

 Вернуть мантиссу и показатель степени  x  как пару  (m, e) .  м  - поплавок

и  e  - целое число, такое что  x == m * 2 ** e  точно. Если  x  равно нулю,

возвращает  (0,0, 0) , иначе  0,5 <= abs (m) <1 . Это используется, чтобы «выбрать

отдельно »внутреннее представление поплавка портативным способом.




 математика.   fsum  ( итерация ) 

 Вернуть точную сумму значений с плавающей запятой в итерируемом объекте. Избегает

потеря точности из-за отслеживания нескольких промежуточных частичных сумм: 
 >>> sum ([. 1, .1, .1, .1, .1, .1, .1, .1, .1, .1])
0,9999999999999999
>>> fsum ([. 1, .1, .1, .1, .1, .1, .1, .1, .1, .1])
1.0
 
 Точность алгоритма зависит от арифметических гарантий IEEE-754 и

типичный случай, когда режим округления половинный.На некоторых не-Windows

сборки, базовая библиотека C использует сложение с расширенной точностью и может

иногда двойное округление промежуточной суммы, в результате чего ее

младший бит. 
 Для дальнейшего обсуждения и двух альтернативных подходов см. Поваренную книгу ASPN.

рецепты точного суммирования с плавающей запятой. 




 математика.   gcd  ( * целые числа ) 

 Возвращает наибольший общий делитель указанных целочисленных аргументов.Если какой-либо из аргументов отличен от нуля, то возвращаемое значение является наибольшим.

положительное целое число, которое является делителем всех аргументов. Если все аргументы

равны нулю, то возвращается значение  0 .  gcd ()  без аргументов

возвращает  0 . 
 Изменено в версии 3.9: Добавлена ​​поддержка произвольного количества аргументов. Раньше всего два

аргументы были поддержаны. 




 математика.   isclose  ( a ,  b ,  * ,  rel_tol = 1e-09 ,  abs_tol = 0.0 ) 

 Вернуть  Истина , если значения  a  и  b  близки друг к другу и

 Неверно  в противном случае. 
 Считается ли два значения близкими или нет, определяется в соответствии с

даны абсолютные и относительные допуски. 
  rel_tol  - относительный допуск - это максимально допустимая разница.

между  a  и  b  относительно большего абсолютного значения  a  или  b .Например, чтобы установить допуск 5%, передайте  rel_tol = 0,05 . По умолчанию

допуск  1e-09 , что гарантирует, что два значения совпадают

с точностью до 9 десятичных цифр.  rel_tol  должен быть больше нуля. 
  abs_tol  - минимальный абсолютный допуск - полезно для сравнений около

нуль.  abs_tol  должен быть не меньше нуля. 
 Если ошибок не возникает, результатом будет:

 абс (a-b) <= max (rel_tol * max (abs (a), abs (b)), abs_tol) .
 Специальные значения IEEE 754:  NaN ,  inf  и  -inf  будут

обрабатывается в соответствии с правилами IEEE. В частности,  NaN  не считается

близко к любому другому значению, включая  NaN .  inf  и  -inf  только

считается близким к себе. 
 См. Также 
  PEP 485  - Функция проверки примерного равенства 




 математика.   исфинит  ( x ) 

 Return  True , если  x  не является ни бесконечностью, ни NaN, и

 Неверно  в противном случае.(Обратите внимание, что  0,0   - это , считающееся конечным.) 




 математика.   isinf  ( x ) 

 Вернуть  Истинно , если  x  является положительной или отрицательной бесконечностью, и

 Неверно  в противном случае. 




 математика.   иснан  ( x ) 

 Вернуть  Истина , если  x  - NaN (не число), и  Ложь  в противном случае.




 математика.   isqrt  ( n ) 

 Вернуть квадратный корень целого неотрицательного целого числа  n . Это

пол из точного квадратного корня из  n  или, что эквивалентно, наибольшего целого числа

 a  таким образом, что  a  ² ≤  n . 
 Для некоторых приложений может быть удобнее иметь наименьшее целое число

 a  таким образом, чтобы  n  ≤  a  ², или, другими словами, потолок

точный квадратный корень из  n .Для положительного значения  n  это можно вычислить с помощью

 a = 1 + isqrt (n - 1) . 




 математика.   л / см  ( * целые числа ) 

 Возвращает наименьшее общее кратное указанных целочисленных аргументов.

Если все аргументы отличны от нуля, то возвращаемое значение является наименьшим.

положительное целое число, кратное всем аргументам. Если какой-либо из аргументов

равно нулю, то возвращается значение  0 .  лкм ()  без аргументов

возвращает  1 .




 математика.   ldexp  ( x ,  и ) 

 Возврат  x * (2 ** i) . По сути, это обратная функция

 frexp () . 




 математика.   мод  ( x ) 

 Вернуть дробную и целую части  x . Оба результата несут знак

размером  x  и являются плавающими. 




 математика.  далее после  ( x ,  y ) 

 Возвращает следующее значение с плавающей запятой после  x  по направлению к  y . 
 Если  x  равно  y , вернуть  y . 
 Примеры: 


  math.nextafter (x, math.inf)  идет вверх: в сторону положительной бесконечности. 


  math.nextafter (x, -math.inf)  идет вниз: в сторону минус бесконечности. 


  математ.nextafter (x, 0.0)  стремится к нулю. 


  math.nextafter (x, math.copysign (math.inf, x))  уходит от нуля. 


 См. Также  math.ulp () . 




 математика.   пермь  ( n ,  k = нет ) 

 Вернуть количество способов выбора  k  элементов из  n  элементов

без повторов и по порядку. 
 Оценивается как  n! / (п - к)! , когда  k <= n  и оценивает

к нулю, когда  k> n .
 Если  k  не указан или равно None, то  k  по умолчанию равно  n 

и функция возвращает  n! . 
 Вызывает  TypeError , если какой-либо из аргументов не является целым числом.

Вызывает  ValueError , если любой из аргументов отрицательный. 




 математика.   prod  ( итераций ,  * ,  start = 1 ) 

 Вычислить произведение всех элементов на входе  итерация .По умолчанию  начальное значение  для продукта  1 . 
 Когда итерация пуста, вернуть начальное значение. Эта функция

предназначен специально для использования с числовыми значениями и может отклонять

нечисловые типы. 




 математика.   остаток  ( x ,  y ) 

 Вернуть остаток в стиле IEEE 754  x  относительно  y . Для

конечное  x  и конечное ненулевое  y , это разница  x - n * y ,

где  n  - ближайшее целое число к точному значению частного  x /

y .Если  x / y  находится ровно посередине между двумя последовательными целыми числами,

ближайшее , четное целое число  используется для  n . Остаток  r = остаток (x,

y) , таким образом, всегда удовлетворяет  abs (r) <= 0,5 * abs (y) . 
 Особые случаи соответствуют IEEE 754: в частности, остаток  (x, math.inf)  - это

 x  для любых конечных  x  и  остаток (x, 0)  и

 остаток (math.inf, x)  поднять  ValueError  для любых не-NaN  x .Если результат операции с остатком равен нулю, этот ноль будет иметь

тот же знак, что и  x . 
 На платформах, использующих двоичные числа с плавающей запятой IEEE 754, результат этого

операция всегда точно представима: ошибка округления не вводится. 




 математика.   усечение  ( x ) 

 Вернуть значение  Real   x , усеченное до

 Integral  (обычно целое число). Делегаты

 х.__trunc __ () . 




 математика.   ulp  ( x ) 

 Вернуть значение младшего бита числа с плавающей запятой  x : 


 Если  x  является NaN (не числом), верните  x . 


 Если  x  отрицательное, вернуть  ulp (-x) . 


 Если  x  является положительной бесконечностью, верните  x . 


 Если  x  равно нулю, вернуть наименьшее положительное значение.

 денормализованный  представимое число с плавающей запятой (меньше минимального положительного

 нормализованное  с плавающей запятой,  sys.float_info.min ). 


 Если  x  равно наибольшему положительному представимому веществу с плавающей запятой,

вернуть значение младшего бита  x , так что первый

float меньше  x  равен  x - ulp (x) . 


 В противном случае ( x  - положительное конечное число) вернуть значение наименьшего

значащий бит  x , так что первое число с плавающей запятой больше  x 

равно  x + ulp (x) .


 ULP означает «Единица на последнем месте». 
 См. Также  math.nextafter ()  и  sys.float_info.epsilon . 


 Обратите внимание, что  frexp ()  и  modf ()  имеют другой шаблон вызова / возврата

чем их эквиваленты в C: они принимают единственный аргумент и возвращают пару

значения, вместо того, чтобы возвращать их второе возвращаемое значение через "output"

параметр ’(в Python такого нет). 
 Для функций  ceil () ,  floor ()  и  modf ()  обратите внимание, что  все 

числа с плавающей запятой достаточно большой величины являются точными целыми числами.Поплавки Python обычно несут не более 53 бита точности (такая же, как у

платформа C двойного типа), в этом случае любой поплавок  x  с  абс (x)> = 2 ** 52 

обязательно не имеет дробных битов. 
 Степенные и логарифмические функции 


 математика.   эксп.  ( x ) 

 Возврат  e  в степени  x , где  e  = 2,718281… - основание

натуральных логарифмов. Обычно это более точно, чем математика .e ** x 

или  pow (math.e, x) . 




 математика.   экспм1  ( x ) 

 Возврат  e  в степени  x , минус 1. Здесь  e  - основание натурального

логарифмы. Для малых чисел с плавающей запятой  x , вычитание в  exp (x) - 1 

может привести к значительной потере точности;  expm1 () 

функция предоставляет способ вычислить это количество с полной точностью: 
 >>> из математического импорта exp, expm1
>>> exp (1e-5) - 1 # дает результат с точностью до 11 разряда
1.0000050000069649e-05
>>> expm1 (1e-5) # результат с полной точностью
1.0000050000166668e-05
 




 математика.   журнал  ( x  [,  основание ]) 

 С одним аргументом верните натуральный логарифм  x  (с основанием  e ). 
 С двумя аргументами вернуть логарифм  x  к заданному основанию  ,

рассчитывается как  log (x) / log (base) . 




 математика.  log1p  ( x ) 

 Вернуть натуральный логарифм  1 + x  (основание  e ). В

результат рассчитывается с точностью до  x , близких к нулю. 




 математика.   журнал2  ( x ) 

 Вернуть логарифм по основанию 2  x . Обычно это более точно, чем

 журнал (x, 2) . 
 См. Также 
  int.bit_length ()  возвращает количество битов, необходимых для представления

целое число в двоичном формате, исключая знак и ведущие нули.




 математика.   лог10  ( x ) 

 Вернуть десятичный логарифм  x . Обычно это более точно

чем  log (x, 10) . 




 математика.   pow  ( x ,  y ) 

 Возврат  x  в степени  y . Далее следуют исключительные случаи

Приложение «F» стандарта C99, насколько это возможно. В частности,

 мощь (1.0, x)  и  pow (x, 0.0)  всегда возвращают  1.0 , даже

когда  x  - это ноль или NaN. Если и  x , и  y  конечны,

 x  отрицательно, а  y  не целое, тогда  pow (x, y) 

не определено, и вызывает  ValueError . 
 В отличие от встроенного оператора  ** ,  math.pow ()  преобразует оба

аргументы типа  с плавающей запятой . Используйте  **  или встроенный

 pow ()  функция для вычисления точных целочисленных степеней.




 математика.   кв.  ( x ) 

 Возвратите квадратный корень из  x . 


 Тригонометрические функции 


 математика.   acos  ( x ) 

 Вернуть арккосинус  x  в радианах. Результат находится между  0  и

 пи . 




 математика.   asin  ( x ) 

 Вернуть арксинус  x  в радианах.Результат находится между  -pi / 2  и

 пи / 2 . 




 математика.   атан  ( x ) 

 Вернуть арктангенс  x  в радианах. Результат находится между  -pi / 2  и

 пи / 2 . 




 математика.   атан2  ( y ,  x ) 

 Вернуть  atan (y / x)  в радианах. Результат находится между  -pi  и  pi .Вектор в плоскости от начала координат до точки  (x, y)  составляет этот угол

с положительной осью X. Смысл  atan2 ()  в том, что признаки обоих

ему известны входные данные, поэтому он может вычислить правильный квадрант для угла.

Например,  atan (1)  и  atan2 (1, 1)  оба равны  pi / 4 , но  atan2 (-1,

-1)  - это -3 * pi / 4 . 




 математика.   cos  ( x ) 

 Вернуть косинус  x  радиан.




 математика.   расстояние  ( p ,  q ) 

 Возвратите евклидово расстояние между двумя точками  p  и  q , каждая

заданная как последовательность (или итерация) координат. Две точки

должен иметь такой же размер. 
 Примерно эквивалентно: 
 sqrt (сумма ((px - qx) ** 2,0 для px, qx в zip (p, q)))
 




 математика.   гипотеза  ( * координаты ) 

 Вернуть евклидову норму,  sqrt (сумма (x ** 2 для x в координатах)) .Это длина вектора от начала координат до точки

задается координатами. 
 Для двумерной точки  (x, y)  это эквивалентно вычислению

гипотенуза прямоугольного треугольника по теореме Пифагора,

 sqrt (x * x + y * y) . 
 Изменено в версии 3.8: Добавлена ​​поддержка n-мерных точек. Раньше только двое

размерный случай был поддержан. 




 математика.   sin  ( x ) 

 Вернуть синус  x  радиан.




 математика.   желто-коричневый  ( x ) 

 Вернуть тангенс  x  радиан. 


 Угловое преобразование 


 математика.   градусов  ( x ) 

 Преобразование угла  x  из радианов в градусы. 




 математика.   радиан  ( x ) 

 Преобразование угла  x  из градусов в радианы.


 Гиперболические функции 
 Гиперболические функции

являются аналогами тригонометрических функций, основанных на гиперболах

вместо кружков. 


 математика.   acosh  ( x ) 

 Вернуть обратный гиперболический косинус  x . 




 математика.   асинь  ( x ) 

 Вернуть обратный гиперболический синус  x . 




 математика.  атанх  ( x ) 

 Вернуть обратный гиперболический тангенс  x . 




 математика.   cosh  ( x ) 

 Вернуть гиперболический косинус  x . 




 математика.   sinh  ( x ) 

 Вернуть гиперболический синус  x . 




 математика.   танх  ( x ) 

 Вернуть гиперболический тангенс  x .


 Специальные функции 


 математика.   эрф  ( x ) 

 Вернуть функцию ошибки в

 х . 
 Функцию  erf ()  можно использовать для вычисления традиционных статистических

такие функции, как кумулятивное стандартное нормальное распределение: 
 деф фи (х):
    'Кумулятивная функция распределения для стандартного нормального распределения'
    return (1.0 + erf (x / sqrt (2.0))) / 2.0
 




 математика.  erfc  ( x ) 

 Вернуть дополнительную функцию ошибок  x . Дополнительная ошибка

функция определяется как

 1.0 - erf (x) . Он используется для больших значений  x , где вычитание

от одного вызовет потерю значимости. 




 математика.   гамма  ( x ) 

 Вернуть гамма-функцию в

 х . 




 математика.  lgamma  ( x ) 

 Вернуть натуральный логарифм абсолютного значения гаммы.

функция  x . 


 Константы 


 математика.   пи  

 Математическая константа  π  = 3,141592…, с доступной точностью. 




 математика.   e  

 Математическая константа  e  = 2,718281…, с доступной точностью.




 математика.   тау  

 Математическая константа  τ  = 6,283185…, с доступной точностью.

Тау - это постоянная окружности, равная 2  π , отношение длины окружности к

его радиус. Чтобы узнать больше о Тау, посмотрите видео Ви Харта Pi is (still)

Неправильно, и начни праздновать

Тау день, съев в два раза больше пирога! 




 математика.   инф  

 Положительная бесконечность с плавающей запятой.(Для отрицательной бесконечности используйте

 -math.inf .) Эквивалент выходу  float ('inf') . 




 математика.   нан  

 Значение с плавающей запятой, «не число» (NaN). Эквивалентно выходу

 с плавающей запятой ('nan') . 


  Детали реализации CPython:  Модуль  math  состоит в основном из тонких оберток вокруг платформы C.

математические библиотечные функции. Поведение в исключительных случаях соответствует Приложению F к

стандарт C99, где это необходимо.Текущая реализация повысит

 ValueError  для недопустимых операций, таких как  sqrt (-1.0)  или  log (0.0) 

(где Приложение F C99 рекомендует сигнализировать о недопустимой операции или делении на ноль),

и  OverflowError  для результатов, которые переполняются (например,

 exp (1000.0) ). NaN не будет возвращено ни одной из функций.

выше, если один или несколько входных аргументов не были NaN; в этом случае,

большинство функций вернут NaN, но (опять же после приложения F C99) там

есть некоторые исключения из этого правила, например  pow (float ('nan'), 0.0)  или

 гипотеза (float ('nan'), float ('inf')) . 
 Обратите внимание, что Python не пытается отличить сигнальные NaN от

тихие NaN, и поведение для передачи сигналов NaN остается неопределенным.

Типичное поведение - рассматривать все NaN, как если бы они были тихими. 
 См. Также 

 Module  cmath  

 Версии многих из этих функций с комплексными числами. 


 Построение синуса и косинуса, модуль numpy 
  Приключения в

Python: построение синуса и косинуса,

numpy Module 
Эта программа потребует, чтобы у вас были как numpy, так и

matplotlib.Если вы работаете с

Pythonista для iOS, два модуля включены. Другие версии Python требуют, чтобы вы

загрузите matplotlib и numpy отдельно.
1. Модуль numpy работает с функциями со списками как

аргументы. Есть математическая функция

связанный с numpy. См. Раздел

о функциях numpy ниже.
2. Полезно

настройте все параметры построения графика перед отображением графика с помощью pylplot.show ().
3. Цветовые строки представляют собой шестизначные шестнадцатеричные целые числа с

формат ‘#RRGGBB’ (R = красный, G = зеленый, B = синий)
4.Чтобы повернуть сюжет

сетка, используйте pyplot.legend (). Чтобы включить легенду, используйте pyplot.legend (). Ярлыки определены в pyplot.plot.
# для этого потребуется

matplotlib
Режим # радиан

по умолчанию
из matplotlib

импортировать пиплот
# потребуется numpy для

создавать списки
# нам понадобится математика

модуль для пи
х =

numpy.linspace (-2 * math.pi, 2 * math.pi, 50)
# sin и cos

включен в numpy
y3 =

numpy.sin (x) + numpy.cos (x)
# alt для y3:

numpy.add (y1, y2)
pyplot.plot (x, y1, цвет

= '# 228b22', label = 'sin x')
пиплот.сюжет (x, y2, цвет

= '# ffa500', label = 'cos x')
pyplot.plot (x, y3, цвет

= '# 1', метка = 'sin x + cos x')
pyplot.title ('Триггер

Сюжеты 007 ')
numpy.add (список 1, список 2)

Добавляет два списка поэлементно.
numpy.subtract (list 1, list 2) Вычитает список 2 из списка 1, элемент по

элемент.
numpy.mutiply (list 1, list 2) Умножает два списка, элемент за элементом.
numpy.divide (список 1, список 2) Делит список 1 на список 2, элемент на

элемент.
numpy.power (список 1, список 2) Вычисляет список 1 ** список 2.numpy.maximum (список 1, список 2) Принимает максимум каждой соответствующей пары.
numpy.minimum (список 1, список 2) Принимает минимум каждой соответствующей пары.
numpy.round (список, количество десятичных знаков) Округлить каждый элемент.
Другие операции по элементам: (один список аргументов -

Радианы - это угловая мера по умолчанию)




















тупой.радианы (преобразовать в радианы)










numpy.degrees (скрытые в градусах)




















numpy.i0 (первый вид Бесселя, порядок 0)





Этот блог является собственностью Эдварда Шора, 2017 г.
 math - математические функции - MicroPython 1.15 документация 
  Этот модуль реализует подмножество соответствующего модуля  CPython ,

как описано ниже. Для получения дополнительной информации обратитесь к оригиналу

Документация CPython:   math . 
 Модуль  math  предоставляет некоторые основные математические функции для

работа с числами с плавающей запятой. 
  Примечание:  На pyboard числа с плавающей запятой имеют 32-битную точность. 
 Доступность: недоступно на WiPy.Требуется поддержка с плавающей запятой

для этого модуля. 
 Функции 


 математика.   acos  ( x ) 

 Вернуть обратный косинус  x . 




 математика.   acosh  ( x ) 

 Вернуть обратный гиперболический косинус  x . 




 математика.   asin  ( x ) 

 Вернуть обратный синус  x .




 математика.   асинь  ( x ) 

 Вернуть обратный гиперболический синус  x . 




 математика.   атан  ( x ) 

 Вернуть арктангенс  x . 




 математика.   атан2  ( y ,  x ) 

 Вернуть главное значение арктангенса  y / x .




 математика.   атанх  ( x ) 

 Вернуть арктангенс гиперболического  x . 




 математика.   потолок  ( x ) 

 Вернуть целое число  x , округленное до положительной бесконечности. 




 математика.   копия  ( x ,  y ) 

 Вернуть  x  со знаком  y .




 математика.   cos  ( x ) 

 Вернуть косинус  x . 




 математика.   cosh  ( x ) 

 Вернуть гиперболический косинус  x . 




 математика.   градусов  ( x ) 

 Вернуть радианы  x , преобразованные в градусы. 




 математика.  эрф  ( x ) 

 Вернуть функцию ошибок  x . 




 математика.   erfc  ( x ) 

 Вернуть дополнительную функцию ошибок  x . 




 математика.   эксп.  ( x ) 

 Вернуть экспоненту  x . 




 математика.   экспм1  ( x ) 

 Возврат  exp (x) - 1 .




 математика.   фабрик  ( x ) 

 Вернуть абсолютное значение  x . 




 математика.   этаж  ( x ) 

 Вернуть целое число  x , округленное до отрицательной бесконечности. 




 математика.   fmod  ( x ,  y ) 

 Вернуть остаток от  x / y .




 математика.   frexp  ( x ) 

 Разлагает число с плавающей запятой на мантиссу и показатель степени.

Возвращаемое значение - это кортеж  (m, e) , такой, что  x == m * 2 ** e 

точно. Если  x == 0 , функция возвращает  (0,0, 0) , иначе

выполняется соотношение  0,5 <= abs (m) <1 . 




 математика.   гамма  ( x ) 

 Вернуть гамма-функцию  x .




 математика.   исфинит  ( x ) 

 Вернуть  Истинно , если  x  конечно. 




 математика.   isinf  ( x ) 

 Вернуть  Истинно , если  x  бесконечно. 




 математика.   иснан  ( x ) 

 Вернуть  Истинно , если  x  не является числом 




 математика.  ldexp  ( x ,  эксп. ) 

 Возврат  x * (2 ** exp) . 




 математика.   lgamma  ( x ) 

 Вернуть натуральный логарифм гамма-функции  x . 




 математика.   журнал  ( x ) 

 Вернуть натуральный логарифм  x . 




 математика.  лог10  ( x ) 

 Вернуть десятичный логарифм  x . 




 математика.   журнал2  ( x ) 

 Вернуть логарифм по основанию 2  x . 




 математика.   мод  ( x ) 

 Вернуть кортеж из двух чисел с плавающей запятой, являющихся дробной и целой частями

 х . Оба возвращаемых значения имеют тот же знак, что и  x .




 математика.   pow  ( x ,  y ) 

 Возвращает  x  в степень  y . 




 математика.   радиан  ( x ) 

 Возвращает градусы  x , преобразованные в радианы. 




 математика.   sin  ( x ) 

 Вернуть синус  x . 




 математика.  sinh  ( x ) 

 Вернуть гиперболический синус  x . 




 математика.   кв.  ( x ) 

 Возвратите квадратный корень из  x . 




 математика.   желто-коричневый  ( x ) 

 Вернуть тангенс  x . 




 математика.   танх  ( x ) 

 Вернуть гиперболический тангенс  x .




 математика.   усечение  ( x ) 

 Вернуть целое число  x  с округлением до 0. 


 Константы 


 математика.   e  

 основание натурального логарифма 




 математика.   пи  

 отношение длины окружности к ее диаметру 


 Все математические функции, определенные в модуле Math в Python 3 
 Что такое математический модуль в Python? 
 Модуль  math  является стандартным модулем Python и всегда доступен.Чтобы использовать математические функции в этом модуле, вы должны импортировать модуль, используя  import math . 
 Предоставляет доступ к базовым функциям библиотеки C. Например, 
  # Расчет квадратного корня

импортная математика
math.sqrt (4)  
 Этот модуль не поддерживает  сложных типов данных . Модуль cmath - сложный аналог. 

 Функции в математическом модуле Python 
 Вот список всех функций и атрибутов, определенных в модуле  math , с кратким объяснением того, что они делают.
.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.


 Список функций в математическом модуле Python 


 Функция 
 Описание 


 ceil (x) 
 Возвращает наименьшее целое число, большее или равное x. 


 копия (x, y) 
 Возвращает x со знаком y 


 фабрики (x) 
 Возвращает абсолютное значение x 


 факториал (x) 
 Возвращает факториал x 


 этаж (х) 
 Возвращает наибольшее целое число, меньшее или равное x 


 fmod (x, y) 
 Возвращает остаток от деления x на y 


 frexp (х) 
 Возвращает мантиссу и показатель степени x как пару (m, e) 


 fsum (итерация) 
 Возвращает точную сумму значений с плавающей запятой в итерируемом 


 исфинит (x) 
 Возвращает True, если x не является ни бесконечностью, ни NaN (не числом) 


 isinf (x) 
 Возвращает True, если x является положительной или отрицательной бесконечностью 


 иснан (х) 
 Возвращает True, если x - NaN 


 ldexp (x, i) 
 Возвращает x * (2 ** i) 


 мод (х) 
 Возвращает дробную и целую части x 


 усечение (x) 
 Возвращает усеченное целое число x 


 эксп. (X) 
 Возвращает e ** x 


 экспм1 (х) 
 Возврат e ** x - 1 


 лог (x [, b]) 
 Возвращает логарифм  x  к основанию  b  (по умолчанию e) 


 log1p (x) 
 Возвращает натуральный логарифм 1 + x 


 журнал2 (x) 
 Возвращает логарифм по основанию 2 x 


 лог10 (x) 
 Возвращает десятичный логарифм x 


 pow (x, y) 
 Возвращает x в степени y 


 sqrt (x) 
 Возвращает квадратный корень из x 


 acos (x) 
 Возвращает арккосинус x 


 asin (x) 
 Возвращает арксинус x 


 атан (х) 
 Возвращает арктангенс x 


 atan2 (y, x) 
 Возвращает атан (г / х) 


 cos (x) 
 Возвращает косинус x 


 гипотеза (x, y) 
 Возвращает евклидову норму, sqrt (x * x + y * y) 


 грех (х) 
 Возвращает синус x 


 желто-коричневый (x) 
 Возвращает тангенс x 


 градусов (x) 
 Преобразует угол x из радиан в градусы 


 радиан (x) 
 Преобразует угол x из градусов в радианы 


 acosh (x) 
 Возвращает обратный гиперболический косинус x 


 asinh (х) 
 Возвращает обратный гиперболический синус x 


 атан (х) 
 Возвращает обратный гиперболический тангенс x 


 cosh (х) 
 Возвращает гиперболический косинус x 


 sinh (х) 
 Возвращает гиперболический косинус x 


 tanh (x) 
 Возвращает гиперболический тангенс x 


 эрф (х) 
 Возвращает функцию ошибки в x 


 erfc (x) 
 Возвращает дополнительную функцию ошибки в x 


 гамма (x) 
 Возвращает гамма-функцию при x 


 lgamma (х) 
 Возвращает натуральный логарифм абсолютного значения гамма-функции в x 


 pi 
 Математическая константа, отношение длины окружности к ее диаметру (3.14159 ...) 


 e 
 математическая константа e (2,71828 ...) 



 Посетите эту страницу, чтобы узнать обо всех математических функциях, определенных в Python 3.