| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.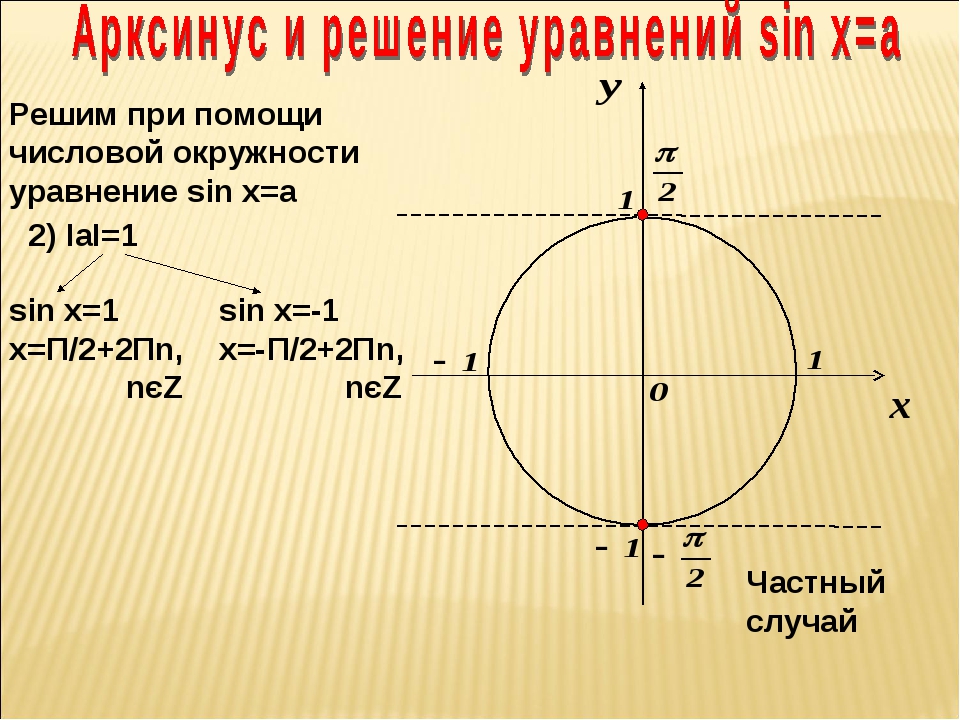 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.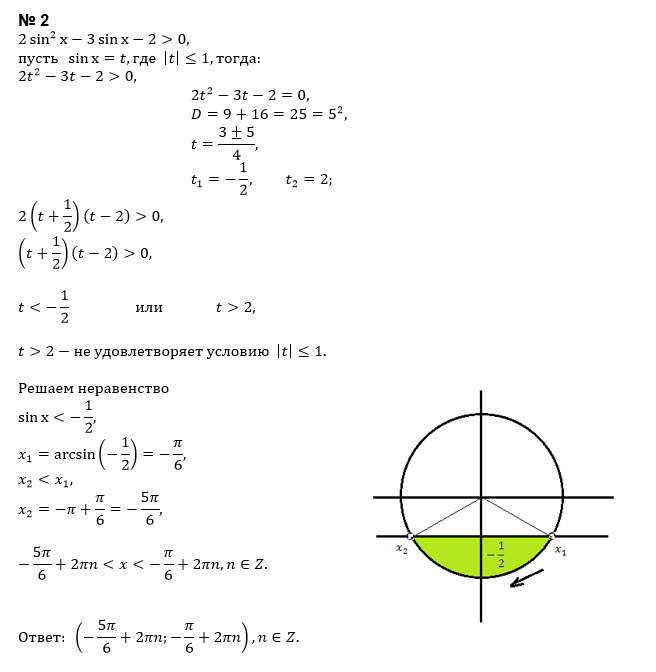 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град.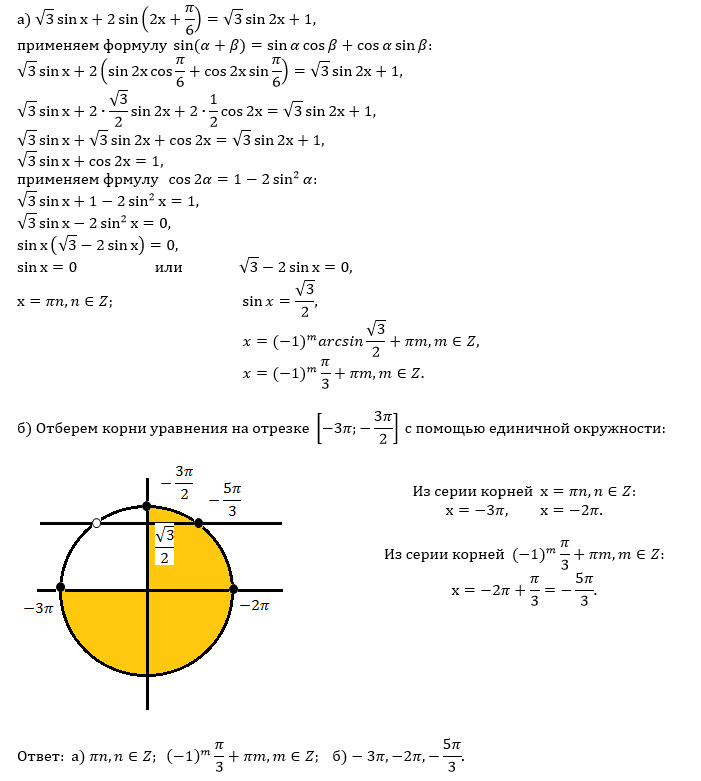 ) ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град.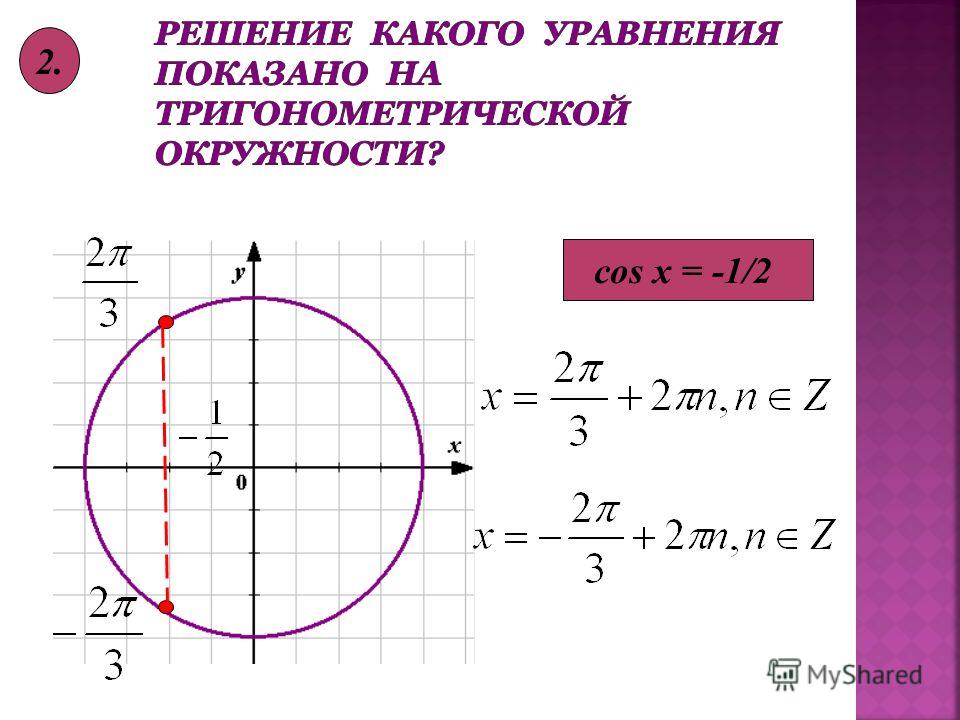 ) ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
cos x sin x 0
Вы искали cos x sin x 0? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и cos x sin x решите уравнение, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «cos x sin x 0».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как cos x sin x 0,cos x sin x решите уравнение,cosx sinx 0 решение,sin x 0 cos x 0,sin x cos x 0,решите уравнение sin x cos x,решить cosx sinx 0. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и cos x sin x 0.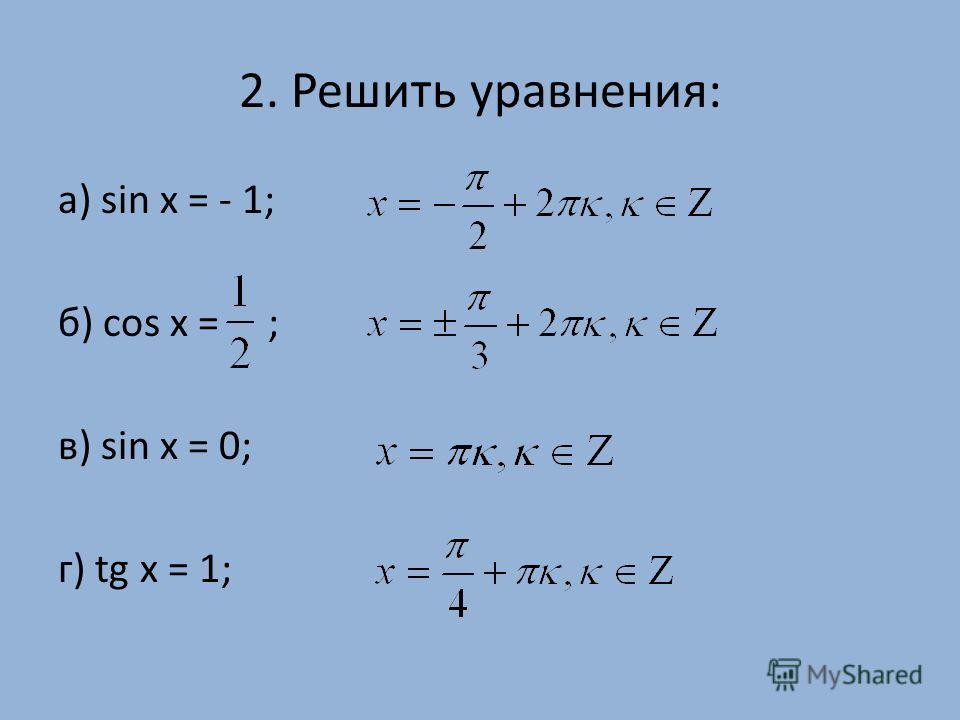 Просто введите задачу в окошко и нажмите
Просто введите задачу в окошко и нажмите
«решить» здесь (например, cosx sinx 0 решение).
Где можно решить любую задачу по математике, а так же cos x sin x 0 Онлайн?
Решить задачу cos x sin x 0 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
§1 Тригонометрические уравнения — ЗФТШ, МФТИ
Чтобы решить тригонометрическое уравнение надо путём тригонометрических преобразований свести его к простейшему тригонометрическому уравнению. Напомним формулы решений простейших тригонометрических уравнений. n arcsin a+pi n, n in Z`.
n arcsin a+pi n, n in Z`.
Отметим, что последнюю формулу иногда удобнее расписать отдельно для чётных `(n=2k, k in Z)` и нечётных `(n=2k+1, k in Z)n`. А именно
$$ x=\left[\begin{array}{l}\mathrm{arc}\mathrm{sin}a+2\pi k,\\ \pi -\mathrm{arc}\mathrm{sin}a+2\pi k, k\in Z.\end{array}\right.$$
2. `cosx=a`. Если `|a|>1`, решений нет. Если `|a|<=1`, то
`x=+- arccosa+2pin, n in Z`.
3. `»tg»x=a`. При любом `a` `x=»arctg»a+pin, n in Z`.
4. `»ctg»x=a`. При любом `a` `x=»arcctg»a+pin, n in Z`.
Отметим несколько частных случаев простейших тригонометрических уравнений, в которых ответ можно записать более просто, чем по общим формулам.
а) `sinx=1`. Тогда `x=pi/2+2pin,n in Z`.
б) `sinx=-1`. Тогда `x=-pi/2+2pin, n in Z`.
в) `cosx=0`. Тогда `x=pi/2+pin, n in Z`.
г) `cosx=-1`. Тогда `x=pi+2pin, n in Z`.
Рассмотрим несколько типовых способов решения тригонометрических уравнений.
I. 2 4x-1)-2cos4x=0`, `2cos4x(cos4x-1)=0 iff` $$ \iff \left[\begin{array}{l}\mathrm{cos}4x=1.\\ \mathrm{cos}4x=0.\end{array}\right.$$
2 4x-1)-2cos4x=0`, `2cos4x(cos4x-1)=0 iff` $$ \iff \left[\begin{array}{l}\mathrm{cos}4x=1.\\ \mathrm{cos}4x=0.\end{array}\right.$$
Если `cos4x=1`, то `4x=2pin,x=(pin)/2,ninZ`.
1. Изображаем точки
`x=(pin)/2,ninZ`, (3)
на тригонометрическом круге (рис. 4а). Геометрически их `4` штуки (для `n=0,1,2,3` – далее они повторяются).
2. Изображаем точки
`x=(pim)/3,m inZ` (4)
которые не удовлетворяют ОДЗ на тригонометрическом круге (4б). Их `6` штук (для `m=0,1,2,3,4,5` – далее они повторяются).
Видно, что совпадения точек в `(3)` и `(4)` будут при `x=pin,ninZ`. Эти значения надо исключить из решения, т. е. в ответ пойдут точки
`x=pi/2+pin,ninZ`.
С решениями уравнения
`cos4x=0`, `4x=pi/2+pin,ninZ`,
или `x=pi/8+(pin)/4,ninZ`, можно поступить аналогично, сделав отбор на тригонометрическом круге. Но когда точек–решений на тригонометрическом круге много, и много точек, не входящих в ОДЗ, то удобнее воспользоваться аналитическим способом отбора решений. В данном случае точек — решений на тригонометрическом круге в серии `x=pi/8+(pin)/4,ninZ`, будет `8` штук (различные при `n=0, 1, 2, 3, 4, 5, 6, 7` – далее они повторяются), а точек, не входящих в ОДЗ на тригонометрическом круге `6`. Посмотрим, есть ли совпадения, т. е. существуют ли целые `m` и `n` такие, что
Но когда точек–решений на тригонометрическом круге много, и много точек, не входящих в ОДЗ, то удобнее воспользоваться аналитическим способом отбора решений. В данном случае точек — решений на тригонометрическом круге в серии `x=pi/8+(pin)/4,ninZ`, будет `8` штук (различные при `n=0, 1, 2, 3, 4, 5, 6, 7` – далее они повторяются), а точек, не входящих в ОДЗ на тригонометрическом круге `6`. Посмотрим, есть ли совпадения, т. е. существуют ли целые `m` и `n` такие, что
`pi/8+(pin)/4=(pim)/3 iff 1/8+n/4=m/3 iff`
`iff 3+6n=8m iff 3=2(4m-3n)`.
Последнее равенство невозможно, т. к. слева стоит нечётное число, а справа чётное.
Отметим, что и для решений уравнения `cos4x=1` отбор можно было сделать аналитически. А именно смотрим, существуют ли целые `m` и `n` такие, что `(pin)/2=(pim)/3 iff 3n=2m`. Видим, что `n` делится на `2`. Тогда `n=2k` и `m=3k,kinZ`. Т. е. из решения уравнения `cos4x=1` надо исключить `x=(pin)/2`, где `n=2k`, т. е. оставить `x=(pin)/2` с `n=2k+1,kinZ`. 2-t-3=0`. Его решение `t_1=-1` и `t_2=3/2`.
2-t-3=0`. Его решение `t_1=-1` и `t_2=3/2`.
1) `»tg»x=-1`. Следовательно, `x=-pi/4+pin,ninZ`.
2) `»tg»x=2/3`. Тогда `x=»arctg»2/3+pin,ninZ`.
б) Сделаем отбор корней, принадлежащих отрезку `[-(3pi)/2; -pi/2]`.
1) Решаем неравенство `-(3pi)/2<=-pi/4+pin<=-pi/2`. Оно равносильно неравенству `-5/4<=n<=-1/4`. Т. к. `ninZ`, то последнему неравенству удовлетворяет только `n=-1`. Итак, из серии решений `x=-pi/4+pin,ninZ`, только корень `x=-(5pi)/4 in [-(3pi)/2; -pi/2]`.
2) Аналогично решаем неравенство
`-(3pi)/2<=»arctg»2/3+pin<=-pi/2`. (5)
Т. к. `ninZ`, то в силу правого неравенства `n<0`. Число `n=-1` подходит, т. к. неравенство (5) в этом случае преобразуется в неравенство `-pi/2<=»arctg»2/3<=pi/2`, что верно, `n=-2` не удовлетворяет (5), т. к. в этом случае получим `pi/2<=»arctg»2/3`, что неверно. Аналогично не подходит `n< -2`. Итак, из серии решений `x=»arctg»2/3+pin,ninZ`, только корень `(«arctg»2/3-pi)in[-(3pi)/2; -pi/2]`.
а) `x=-pi/4+pin,ninZ`; `x=»arctg»2/3+pin,ninZ`.
б) `x=-(5pi)/4` и `x=»arctg»2/3-pi`.
Найти наименьший корень уравнения `»ctg»6x-«tg»5x=1/(cos5x)`,
принадлежащий отрезку `[(8pi)/17; (40pi)/17]`.
Преобразуем данное уравнение
`(cos6x)/(sin6x)-(sin5x)/(cos5x)=1/(cos5x)`,
`(cos6x*cos5x-sin6x*sin5x)/(sin6x*cos5x)=1/(cos5x)`,
`(cos11x)/(sin6x*cos5x)=1/(cos5x)`.
Последнее уравнение равносильно `cos11x=sin6x` при условии `sin6x*cos5x!=0`.
Решаем уравнение `cos11x-sin6x=0`. Преобразуем его:
`cos11x-cos(6x-pi/2)=0` или `-2sin((17x)/2-pi/4)sin((5x)/2+pi/4)=0`.
1) Если `sin((5x)/2+pi/4)=0` то `(5x)/2+pi/4=pin,ninZ`, откуда `5x=-pi/2+2pin,ninZ`.
Эти числа не являются корнями исходного уравнения, т. к. нарушается условие `cos5x!=0`.
2) Если `sin((17x)/2-pi/4)=0`, то `x=(pi(1+4n))/(34),ninZ`. Находим, при каких `ninZ`, эти числа лежат на отрезке `[(8pi)/17;(40pi)/17]`. Решаем неравенства
`(8pi)/(17)<=(pi(1+4n))/34<=(40pi)/17 iff 15/4<=n<=79/4`. 2x)=0` или `sin2x+cos2x=0`.
2x)=0` или `sin2x+cos2x=0`.
Это однородное уравнение 1-го порядка. Оно эквивалентно уравнению `»tg»2x=-1`.
Отсюда `2x=-pi/4+pin,ninZ`, или `x=-pi/8+(pin)/2,ninZ`.
Изобразим решения на тригонометрическом круге (рис. 6). Это `4` точки (`n=0,1,2,3` — далее они повторяются).
Для этих точек надо проверить неравенство `cosx-3sinx>=0`. Ясно, что точка `x_1` удовлетворяет этому неравенству, т. к. `cosx_1>0` и `sinx_1<0`. Для точки `x_3`, диаметрально противоположной точке `x_1`, `sinx` и `cosx` меняют знак, меняет знак и выражение `(cosx-3sinx)`, и, следовательно, для `x_3` неравенство не выполняется. Точка `x_2` не удовлетворяет неравенству, т. к. `sinx_2>0`, `cosx_2>0`, но `sinx_2>cosx_2` в виду того, что `pi/4<x_2<pi/2`, так что выражение `cosx_2-3sinx_2<0`. Точка `x_4` диаметрально противоположна `x_2`. Следовательно,
`cosx_4-3sinx_4=-(cosx_2-3sinx_2)>0`,
и, значит, это решение. Учитывая, что решения имеют период `2pi`, получаем
`x=-pi/8+2pin,ninZ`; `x=11/8pi+2pin,ninZ`.
VII. Уравнения с модулем
Решить уравнение `sin3x+|sinx|=sin2x`.
Решение уравнения сводится к объединению решений двух систем.
1) $$ \left\{\begin{array}{l}\mathrm{sin}x\ge 0,\\ \mathrm{sin}3x+\mathrm{sin}x=\mathrm{sin}2x.\end{array}\right.$$
2) sinx0,sin3x-sinx=sin2x.\left\{\begin{array}{l}\sin x
Решаем первую систему. Уравнение `sin3x+sinx=sin2x` преобразуем:
`2sin2xcosx=sin2x` или `sin2x(2cosx-1)=0`.
Значит,
$$ \left[\begin{array}{l}\mathrm{sin}2x=0,\\ \mathrm{cos}x=\frac{1}{2}.\end{array}\right.$$
Изображаем решения уравнения `sin2x=0` на тригонометрическом круге: `x=(pin)/2,ninZ`, (рис. 7). В силу неравенства `sinx>=0` не подходит нижняя точка, т. е. в решения системы входят
`x=pin,ninZ`, и `x=pi/2+2pin,ninZ`.
Аналогично, изображаем на тригонометрическом круге (рис. 8) решения уравнения `cosx=1/2`. Нижняя точка не удовлетворяет неравенству `sinx>=0`. 2x-cosx-1=0`.
2x-cosx-1=0`.
Отсюда `cosx=1` или `cosx=-1/2`. На тригонометрическом круге этим уравнениям удовлетворяют соответственно точки (рис. 9 и рис. 10). Неравенству `sinx<0` удовлетворяет только одна из этих трёх точек, находящаяся в нижней полуплоскости, а именно
`x=pi/3+pi+2pin,ninZ`.
В ответе две серии решений
`x=pi/3+2pin,ninZ` и `x=pi/3+pi+2pin,ninZ`,
соответствующие двум диаметрально противоположным точкам тригонометрического круга, можно задать одной формулой:
`x=pi/3+pin,ninZ` (но это не обязательно).
`x=pin`; `x=pi/2+2pin`; `x=pi/3+pin,ninZ`.
Калькулятор
— equal_solver (sin (x) = 0) — Solumaths
Резюме:
Решатель уравнений позволяет решать уравнения с неизвестной с шагами вычисления: линейное уравнение,
квадратное уравнение, логарифмическое уравнение, дифференциальное уравнение.
Equation_solver онлайн
Описание:
Уравнение — это алгебраическое равенство, включающее одно или несколько неизвестных.
Решение уравнения — это то же самое, что и определение неизвестных или неизвестных.Неизвестное также называют переменной.
Этот калькулятор уравнений может решать уравнения с неизвестными,
Калькулятор может решать уравнений с переменными с обеих сторон , а также уравнений с круглыми скобками :
- Решение линейного уравнения
- Решение квадратного уравнения
- Решение кубического уравнения
- Решение уравнения нулевого произведения
- Решение уравнения абсолютного значения (уравнения с функцией abs)
- Решение экспоненциального уравнения
- Решение логарифмического уравнения (уравнения, включающего логарифмы)
- Решение тригонометрического уравнения (уравнения с косинусом или синусом)
- Решить онлайн дифференциальное уравнение первой степени
- Решить онлайн дифференциальное уравнение второй степени
Решение линейного уравнения онлайн
Уравнение первой степени — это уравнение вида «ax = b». Этот тип уравнения также называется линейным уравнением .
Этот тип уравнения также называется линейным уравнением .
Для решения этих уравнений мы используем следующую формулу `x = b / a`.
линейное решение уравнения вида ax = b s выполняется очень быстро,
если переменная не является неоднозначной, просто введите , уравнение с по , решите , а затем нажмите «Решить»,
затем результат возвращается решателем .
Также отображаются подробности расчетов, которые привели к разрешению линейного уравнения.Чтобы решить линейное уравнение после 3x + 5 = 0, просто введите выражение
3х + 5 = 0
в области вычислений, затем нажмите кнопку «решить», возвращается результат `[x = -5 / 3]`.
также можно решить уравнения в форме `(ax + c) / g (x) = 0` или уравнения, которые могут быть в этой форме
, g (x) представляет функцию.
Когда вы вводите выражение без знака ‘=’; функция возвращает, когда возможны значения, для которых выражение равно нулю.
Например, введите x + 5, вернитесь к x + 5 = 0 и решите.2-4ac`.
Дискриминант — это число, определяющее количество решений уравнения.
- При положительном дискриминанте уравнение второй степени допускает два решения, которые даются формулой
`(-b-sqrt (Delta)) / (2a)` и `(-b + sqrt (Delta)) / (2a)`; - Когда дискриминант равен нулю, квадратное уравнение допускает только одно решение, оно называется двойным корнем, который задается формулой
`(-b) / (2a)`; - Когда дискриминант отрицательный, полиномиальное уравнение степени 2 не допускает решения.2-1) / (x-1) = 0` возвращает -1, все определение принимается во внимание для вычисления числителя допускает два корня 1
и -1, но знаменатель равен нулю для x = 1, 1 не может быть решением уравнения.
Решение кубического уравнения
Калькулятор уравнений решает некоторые кубические уравнения . 3 = 0`).
3 = 0`).
Опять же, решения кубического уравнения будут сопровождаться пояснениями, которые позволили найти результат.
Решите уравнение, используя свойство нулевого произведения
Свойство нулевого произведения используется для решения уравнений вида A * B = 0, что это уравнение равно нулю, только если A = 0 или B = 0.
Чтобы решить , этот тип уравнения может быть выполнен, если A и B являются многочленами степени меньше или равной 2.
Также отображаются сведения о расчетах, которые привели к разрешению уравнения.2-1) (x + 2) (x-3) = 0` возвращает `[1; -1; -2; 3]`.
Решите уравнение абсолютного значения
Решатель позволяет решить уравнение с использованием абсолютного значения
он может решать линейные уравнения, используя абсолютные значения,
квадратные уравнения, включающие абсолютные значения, но также и другие многие типы уравнений
с абсолютными значениями.
Вот два примера использования калькулятора уравнений для решения уравнения с абсолютным значением:
- `abs (2 * x + 4) = 3`, решатель показывает детали вычисления линейного уравнения с абсолютным значением.2-4) = 4`, решатель показывает шаги расчета для решения квадратного уравнения с абсолютным значением.
Решите экспоненциальное уравнение
Калькулятор уравнений позволяет решать уравнение с использованием экспоненты
он может решать линейные уравнения с использованием экспоненты,
квадратные уравнения, включающие экспоненциальные, но также и другие многие типы уравнений
с экспоненциальной.
Вот два примера использования калькулятора для решения уравнения с экспонентой:
- `exp (2 * x + 4) = 3`, решатель показывает детали вычисления линейного уравнения с экспонентой.2-4) = 4`, решатель показывает этапы расчета для решения квадратного уравнения с экспонентой.

Решите логарифмическое уравнение
Решите логарифмическое уравнение , т.е. возможно несколько уравнений, включающих логарифмы.
Калькулятор не только предоставляет результат, но и предоставляет подробные шаги и расчеты, которые привели к
к разрешению логарифмического уравнения.
Чтобы решить следующее логарифмическое уравнение ln (x) + ln (2x-1) = 0,
просто введите выражение в области расчета и нажмите кнопку «Рассчитать».
Решение тригонометрического уравнения
Калькулятор уравнений позволяет решать круговые уравнения , он может
решить уравнение с косинусом
вида cos (x) = a или уравнение с синусом вида sin (x) = a .
Расчеты для получения результата детализированы, поэтому можно будет решать такие уравнения, как
`cos (x) = 1 / 2`
или же
`2 * sin (x) = sqrt (2)`
с шагами расчета.
Решение линейного дифференциального уравнения первого порядка
Функция Equation_solver может решать линейные дифференциальные уравнения первого порядка в режиме онлайн ,
решить следующее дифференциальное уравнение:
y ‘+ y = 0, вы должны ввести формул_переход (`y’ + y = 0; x`).
Решение дифференциального уравнения второго порядка
Функция Equation_solver может решать дифференциальное уравнение второго порядка в режиме онлайн ,
решить следующее дифференциальное уравнение:
y » — y = 0, вы должны ввести формулу_ползания (`y ‘- y = 0; x`).
Решатель уравнений позволяет решать уравнения с неизвестными с шагами вычисления: линейное уравнение,
квадратное уравнение, логарифмическое уравнение, дифференциальное уравнение.
Синтаксис:
Equation_solver (уравнение; переменная), переменный параметр может быть опущен, если нет неоднозначности.
Примеры:
Разрешение уравнения первой степени
Решение квадратных уравнений
Решение кубических уравнений
Решить дифференциальное уравнение
Рассчитывайте онлайн с помощью Equation_solver (решателя уравнений)
Решите уравнение.
 (sin (x)) (cos (x)) = 0 на [0, 2π)
(sin (x)) (cos (x)) = 0 на [0, 2π)
Аарон Т.
задано • 30.01.18
2 ответа опытных преподавателей
От:
Марк М.
ответил • 30.01.18
Учитель математики — Высшая квалификация NCLB
Для чего x является грехом x = 0?
Для какого x cos x = 0?
грех х соз х = 0
=> 2 sin x cos x = 0
=> грех 2x = 0
=> 2x = 0, π, 2π
=> х = 0, π / 2, π
Все еще ищете помощь? Получите правильный ответ быстро.

ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и познакомьтесь онлайн.
Никаких пакетов или подписок, платите только за необходимое время.
¢
€
£
¥
‰
µ
·
•
§
¶
SS
‹
›
«
»
<
>
≤
≥
—
—
¯
‾
¤
¦
¨
¡
¿
ˆ
˜
°
—
±
÷
⁄
×
ƒ
∫
∑
∞
√
∼
≅
≈
≠
≡
∈
∉
∋
∏
∧
∨
¬
∩
∪
∂
∀
∃
∅
∇
*
∝
∠
´
¸
ª
º
†
‡
А
Á
Â
Ã
Ä
Å
Æ
Ç
È
É
Ê
Ë
Я
Я
Я
Я
Ð
Ñ
Ò
Ó
Ô
Õ
Ö
Ø
Œ
Š
Ù
Ú
Û
Ü
Ý
Ÿ
Þ
à
á
â
ã
ä
å
æ
ç
è
é
ê
ë
я
я
я
я
ð
ñ
ò
ó
ô
х
ö
ø
œ
š
ù
ú
û
ü
ý
þ
ÿ
Α
Β
Γ
Δ
Ε
Ζ
Η
Θ
Ι
Κ
Λ
Μ
Ν
Ξ
Ο
Π
Ρ
Σ
Τ
Υ
Φ
Χ
Ψ
Ω
α
β
γ
δ
ε
ζ
η
θ
ι
κ
λ
μ
ν
ξ
ο
π
ρ
ς
σ
τ
υ
φ
χ
ψ
ω
ℵ
ϖ
ℜ
ϒ
℘
ℑ
←
↑
→
↓
↔
↵
⇐
⇑
⇒
⇓
⇔
∴
⊂
⊃
⊄
⊆
⊇
⊕
⊗
⊥
⋅
⌈
⌉
⌊
⌋
〈
〉
◊
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Примечание: Если вы хотите получить обзор тригонометрии, нажмите на
тригонометрия.
Задача 9.7c: Решите относительно x в уравнении
Ответ: точные ответы
где n — целое число.
Приблизительные значения этих решений:
, где n — целое число.
Решение:
Есть бесконечное множество решений этой проблемы.
В уравнении
есть два разных
тригонометрические термины. Чтобы упростить решение, преобразуйте уравнение в
эквивалентное уравнение с синусами и косинусами.Который из
это будет? Самый простой способ — преобразовать тригонометрические члены в синус.
условия, потому что вы можете решить для
в личности
Заменять
для
в
исходное уравнение.
Перепишите уравнение
в факторизованном виде и решить
для
.
Единственный способ, при котором произведение двух множителей равно нулю, — это если хотя бы один из
множители равны нулям. Это значит, что
если
или же
Мы превратили сложную проблему в две проблемы. Чтобы найти
Чтобы найти
решения исходного уравнения,
,
мы сначала решаем для
в уравнениях
а также
а также
Чтобы найти x, мы должны изолировать x. Как мы это делаем? Мы могли бы взять tex2 html c omment m ark >
арксинус с обеих сторон. Однако функция sine не является взаимно однозначной.
функция.
Мы можем ограничить область определения
функция, так что это один к одному на
ограниченный домен при сохранении исходного диапазона.Функция синус взаимно однозначна на интервале
Если мы ограничим область определения функции синус этим
интервал, мы можем взять арксинус обеих частей каждого уравнения.
Мы знаем это
Следовательно,
если
,
тогда
С периода
равно,
эти решения будут повторяться
каждый
единицы измерения. Точные решения
где n — целое число.
Приблизительные значения этих решений:
где n — целое число.
Вы можете проверить каждое решение алгебраически, подставив каждое решение в
исходное уравнение. Если после подстановки левая часть
исходное уравнение равно правой части исходного уравнения,
решение действительно.
Вы также можете проверить решения графически, построив график функции, сформированной
левой частью исходного уравнения и построив график функции, образованной
правой частью исходного уравнения. X-координаты точек
пересечения являются решениями.Правая часть уравнения равна 0 и tex2 html c omment m ark >
f ( x ) = 0 — ось абсцисс. Итак, на самом деле то, что вы ищете, — это
x-пересекает функцию, образованную левой частью уравнения.
Алгебраическая проверка:
Проверить решение
Левая сторона:
Правая сторона:
Поскольку левая часть исходного уравнения равна правой части
исходное уравнение при замене
0.52359878 для x, тогда
0. 52359878 — это решение.
52359878 — это решение.
Проверить решение
Левая сторона:
Правая сторона:
Поскольку левая часть исходного уравнения равна правой части
исходное уравнение, когда вы подставляете 2,6179939 вместо x, тогда 2,6179939 будет
решение.
Точные решения
а также
и эти
решения повторяются каждые
единицы измерения. Примерные значения этих
решения
и 2.6179939 и эти решения
повторять каждые
единицы измерения.
Графическая проверка:
Изобразите уравнение
Обратите внимание, что график
много раз пересекает ось абсцисс, указывая на множество решений.
Убедитесь, что график пересекает ось x в
0,52359878. Поскольку период
,
график также снова пересекает ось x при
tex2 html c omment m ark >
0,52359878 + 6,2831853 = 6,806784 и при
,
и т.п.
Убедитесь, что график пересекает ось x в
.
Поскольку период
,
график также снова пересекает ось x при
tex2 html c omment m ark >
2,6179939 + 6,2831853 = 8,
9 и при
,
и т. п.
п.
Примечание: если проблема заключалась в том, чтобы найти решение в интервале
,
затем вы выбираете эти решения из множества бесконечных
решения, принадлежащие множеству
а также
Если вы хотите просмотреть решение другой проблемы, щелкните
Вернитесь к Решениям, а затем нажмите на
слово решение напротив проблемы, которую вы хотите рассмотреть.
Если вы хотите перейти к следующему разделу, нажмите «Далее».
Если вы хотите вернуться к предыдущему разделу, нажмите
предыдущее .
Если вы хотите вернуться к оглавлению уравнения, щелкните
Содержание.
[Алгебра]
[Тригонометрия]
[Геометрия]
[Дифференциальные уравнения]
[Исчисление]
[Комплексные переменные]
[Матричная алгебра]
S.O.S MATHematics — домашняя страница
Автор:Нэнси Маркус
Авторские права 1999-2021 MathMedics, LLC.Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П. О. Box 12395 — El Paso TX 79913 — США
О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час
5. Тригонометрические уравнения
М. Борна
Тригонометрические уравнения могут быть решены с помощью
алгебраические методы и тригонометрические тождества и ценности
обсуждалось в предыдущих разделах. Возможно, вы захотите вернуться и взглянуть на тригонометрические функции любого угла, где мы видим предысторию следующих решений.
Безболезненный способ решить эти проблемы — использовать график.Там, где график пересекает ось x , вы найдете свои решения (значения x , которые «работают»). Графики также помогают понять, почему иногда есть один ответ, а иногда — много ответов. Я использую Scientific Notebook или аналогичную математическую программу для построения графиков функций.
Вы можете использовать этот онлайн-калькулятор для построения графиков, чтобы решить следующие уравнения (или проверить свои решения).
Пример 1
Решите уравнение 2 cos θ — 1 = 0 для 0 ≤ θ <2 π .
Ответ
Преобразуя приведенное выше уравнение, получаем:
`cos theta = 1 / 2`
Нам известно следующее:
с
`cos (pi / 3) = 1/2`
и `cos θ` положителен в первом и четвертом квадрантах, мы имеем:
`тета = пи / 3`
или
`theta = 2pi-pi / 3 = (5pi) / 3`
Итак, `theta = pi / 3` или` theta = (5pi) / 3`
Пример 2
Решите графически
уравнение
2 cos 2 x — sin x — 1 = 0
такой, что 0 ≤ θ <2 π .
Ответ
Используя программное обеспечение для построения графиков, мы рисуем кривую y = 2 cos 2 x — sin x — 1 в области 0 ≤ θ <2π. Везде, где кривая пересекает ось x , будет решением нашего уравнения.
Мы видим из графика, что решения примерно:
x = 0,5
x = 2,6
x = 4,7
Для получения более точных решений мы просто увеличим масштаб графика.
На этом следующем графике я увеличил масштаб до второго корня (около x = 2,6). Мы видим, что этот корень равен x = 2,618 с точностью до 3 знаков после запятой.
Мы можем продолжать увеличивать изображение настолько близко, насколько захотим, чтобы получить требуемую точность.
Решение уравнений, кратных
θ
Пример 3
Решите
уравнение sin 2 θ = 0,8 для 0 ≤ θ <2π.
Ответ
Если проблема касается только θ , мы ожидаем 2 решения; один
в первом квадранте и один во втором квадранте.
Но здесь наша проблема связана с `2θ`, поэтому нам нужно удвоить
область ( θ значений) для учета всех
возможные решения.
Действуем следующим образом:
Решаем
`sin 2θ = 0,8` для 0 ≤ 2 θ <4 π .
Базовый угол
`α = arcsin 0,8 = 0,9273`
Значит, значения для 2 θ будут в квадрантах I, II, V, VI.
2 θ = 0.9273, или π — 0,9273, или 2 π + 0,9273, или 3 π — 0,9273
То есть
`2θ = 0,9273, 2,2143, 7,2105, 8,4975`
Но нам нужны значения для θ , а не 2 θ ,
поэтому делим на 2:
θ = 0,4637, 1,1072, 3,6053, 4,2488`
Верны ли наши ответы? В виде
обычно, мы проверим, построив график исходного выражения:
Из графика видно, что
наши 4 значения разумны, так как это единственные 4 значения
которые удовлетворяют `sin 2θ = 0.2theta = 1/16`
для 0 ≤ θ <2π.
Ответ
Решение для cos θ дает:
`cos theta = + — 1 / 4`
Если cos alpha = 1/4, то ссылка
угол α = 1,3181.
Итак, для cos theta = 1/4 мы имеем θ в первом и четвертом квадрантах. Итак
` θ = 1,3181 или 4,9651`
Для cos theta = -1 / 4, мы имеем θ во 2-м и 3-м квадрантах. 2θ — грех θ — 1 = 0`
2θ — грех θ — 1 = 0`
`(2 sin θ — 1) (3 sin θ + 1) = 0`
Так либо
`2 sin θ — 1 = 0`
`грех θ = 1 / 2`
θ будет в 1-м и 2-м квадрантах.
`θ = 0,52360, 2,6180` (то есть` пи / 6` или `(5pi) / 6`)
ИЛИ
`3 грех θ + 1 = 0`
`sin θ = — 1 / 3`
θ будет в 3-м и 4-м квадрантах.
`θ = 3. 4814, 5. 9433`
Проверка нашего решения на
график:
Так что `θ =
0.2 \ х + 3 \ соз х + 1 = 0`
`(2 \ co \ s x + 1) (cos x + 1) = 0`
Решая, получаем
`cos x = — 0,5` или` cos x = — 1`
Теперь `cos x = -1 / 2` дает` x = (2pi) / 3, (4pi) / 3`.
Однако при проверке исходного уравнения ,
отметим, что
`» LHS «= cos ((4pi) / 3xx1 / 2)` `= cos ((2pi) / 3)` = -1 / 2`
но
«» RHS «= 1 + cos (4pi) / 3 = + 1 / 2`
Таким образом, единственное решение для этой части — `x = (2pi) / 3. 2 2θ = 1`
2 2θ = 1`
`tan 2θ = ± 1`
Так как `0 ≤ θ <2π`, нам нужно рассмотреть значения` 2theta` такие, что `0 ≤ 2θ <4π`.Следовательно, решение в приведенном выше уравнении имеем:
`2 theta = pi / 4, (3pi) / 4, (5pi) / 4 (7pi) / 4,` `(9pi) / 4, (11pi) / 4,` `(13pi) / 4, (15pi) ) / 4`
Деление на 2 дает нам полный набор решений в требуемой области, `0 <= theta <2pi`:
`theta = pi / 8, (3pi) / 8,` `(5pi) / 8, (7pi) / 8, » (9pi) / 8, (11pi) / 8,` `(13pi) / 8, (15pi) / 8`
Упражнения
Примечание 1: «Аналитически» означает использование методов и формул из предыдущих разделов.Это означает, что для ее решения нельзя просто использовать график.
Примечание 2: Однако я всегда использую график для проверки своей аналитической работы. Я сразу вижу, произошла ли какая-то ошибка. Я призываю вас поступить так же!
1. 2x) = 0`
2x) = 0`
Умножение на `cos x`:
`4 \ sin x \ cos x = 1`
Делим обе стороны на 2:
`2 \ sin x \ cos x = 1 / 2`
Распознавание LHS — это `sin 2x`, от до:
`sin 2x, = 0.5`
При 0 ≤ x <2π нам нужно
найти значения 2 x такие, что
0 ≤ 2 x <4π. (В два раза больше исходного домена.)
Значит, 2x:
.
`2x = pi / 6, (5pi) / 6, (13pi) / 6, (17pi) / 6`
Если разделить на 2, то получим требуемые значения для `x`:
`x = pi / 12, (5pi) / 12, (13pi) / 12, (17pi) / 12`
или в десятичной форме:
`х = 0,2618, 1,309, 3.403, 4.451`
2. Решите тригонометрическое уравнение
аналитически для 0 ≤ x <2 π :
sin 2 x cos x
— cos 2 x sin x = 0
Ответ
Мы узнаем, что левая сторона находится в
форма:
`sin (a — b) =` sin a cos b — cos a sin b, `
, где `a = 2x` и` b = x`.
Так
`sin 2x \ cos x — cos 2x \ sin x`
`= sin (2x — x)`
`= грех x`
Теперь мы знаем решения `sin x = 0`
быть:
`x = 0, π`.
[Почему?]
3. Решите данное тригонометрическое уравнение.
аналитически и графическим методом (для 0 ≤ x <2 π ):
sin 4 x — cos 2 x = 0
Ответ
sin 4 x — cos 2 x = 0
2sin 2 x cos 2 x — cos 2 x
= 0
Факторинг дает:
cos 2 x (2 sin 2 x — 1) = 0
ЛИБО
`cos 2x = 0`
`2x = pi / 2, (3pi) / 2, (5pi) / 2, (7pi) / 2`
`x = pi / 4, (3pi) / 4, (5pi) / 4, (7pi) / 4`
ИЛИ
`грех 2x = 1/2`
`2x = pi / 6, (5pi) / 6, (13pi) / 6, (17pi) / 6`
`x = pi / 12, (5pi) / 12, (13pi) / 12, (17pi) / 12`
Или в десятичной форме:
`х = 0. 26, 0,79, «1,31, 2,36,« 3,40, 3,93,
26, 0,79, «1,31, 2,36,« 3,40, 3,93,
«4.45, 5.50.»
График y = sin 4x− cos 2x выглядит следующим образом. Мы можем видеть, откуда график пересекает ось x , что наши ответы являются разумными.
Решение сложных триггерных уравнений | Purplemath
Purplemath
Решите sin (
x /2) = cos ( x /2) в полной общности.
Есть разные способы сделать это, но я думаю, что выберу простой выход. Разделив на косинус, я получу тангенс:
(Почему это деление приемлемо? Я не могу делить на ноль, поэтому это деление допустимо только в том случае, если косинус не равен нулю. Но в исходном уравнении синус и косинус равны, и они никогда не равны нулю. то же место.И тангенс никогда не равен единице, где косинус равен нулю. Так что в этом случае не было проблемы с делением на ноль. Но всегда не забывайте проверять себя, чтобы быть уверенным.)
то же место.И тангенс никогда не равен единице, где косинус равен нулю. Так что в этом случае не было проблемы с делением на ноль. Но всегда не забывайте проверять себя, чтобы быть уверенным.)
MathHelp.com
Тангенс равен 1 для
x /2 = 45 °, 225 ° в первом периоде.Но это упражнение требует ответа «в полной общности». Очевидно, я не могу перечислить все значения решения, потому что их бесконечно много. Так что мне придется использовать формулу.
Из того, что я знаю о графике касательной, я знаю, что касательная будет равна 1 при 45 ° через каждые 180 °. Эти решения для
Эти решения для
tan ( x /2) находятся при 0 ° + 45 °, 180 ° + 45 °, 360 ° + 45 ° и т. Д. Чтобы дать ответ «в общих чертах», я воспользуюсь формулой:
x /2 = (180 × n ) ° + 45 °, для всех целых чисел n
Теперь мне нужно решить для самого x .Умножу на 2:
В радианах приведенное выше решение будет иметь вид
x /2 = π / 4, 5π / 4, 9π / 4 и т. Д .; и общее решение будет x = 2π n + π / 2
Решите 3tan
3 ( x ) — 3tan 2 ( x ) — tan ( x ) + 1 = 0 в полной общности.
Я могу разделить это попарно:
3tan 2 ( x ) [tan ( x ) — 1] — 1 [tan ( x ) — 1] = 0
[tan ( x ) — 1] [3tan 2 ( x ) — 1] = 0
желтовато-коричневый ( x ) = 1 или коричневый 2 ( x ) = 1/3
загар ( x ) = 1 или загар ( x ) = ± 1/ sqrt [3]
Первое уравнение решает в первом периоде как:
Вторая решает в первом периоде как:
x = 30 °, 150 °, 210 °, 330 °
Чтобы сделать решение «общим», мне нужно сформулировать приведенные выше решения в виде формулы, чтобы учесть каждый период.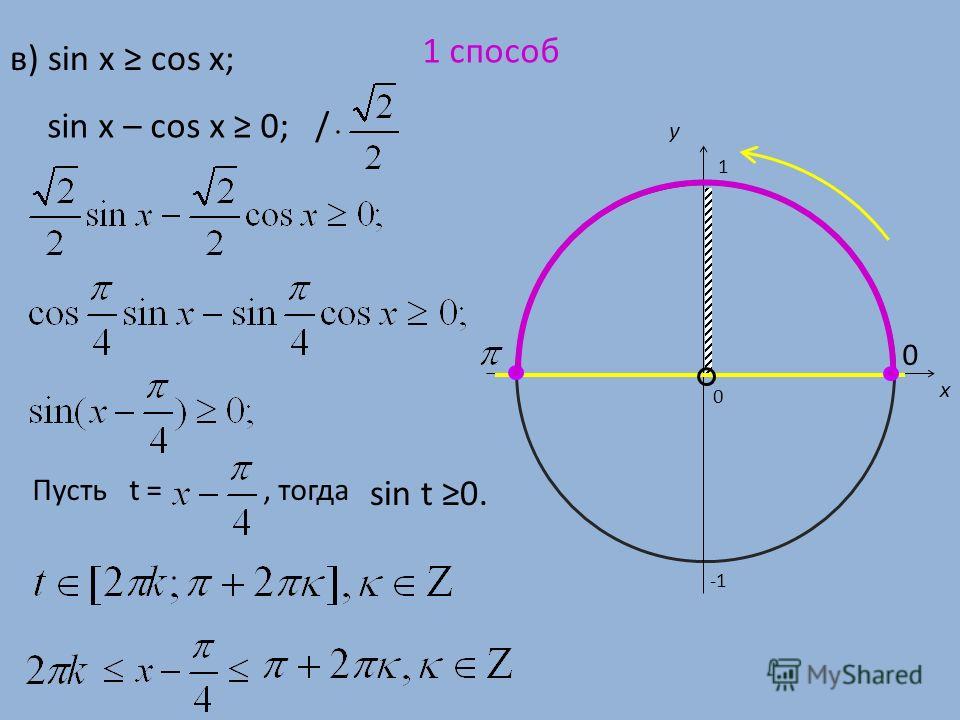
Первое решение на 45 ° больше, чем кратное 180 °, поэтому подойдет (180 n ) ° + 45 °. Второе решение — на 30 ° больше, чем кратное 180 °, и (из-за «плюс / минус») также на 30 ° меньше, чем того же кратного, поэтому (180 n ) ° ± 30 ° покроет эту часть .
x = (180 n ) ° ± 30 °, (180 n ) ° + 45 ° для всех целых чисел n
Решить на [0, 2π)
Что за черт…?!?
Когда похоже, что ничего не работает, иногда помогает выразить все в терминах синуса и косинуса. Этот процесс, примененный к этому уравнению, дает мне:
Это не намного лучше … но первые два члена имеют общий множитель 2. Если я конвертирую последний член в общий знаменатель с третьим членом, что это даст мне?
Если я разложу на множители 2 из первых двух членов и квадратный корень из 3 и косинус из вторых двух членов, я получу:
Теперь я могу вынести общий множитель:
Уф! Это действительно сработало! Хорошо, теперь мне нужно решить факторы.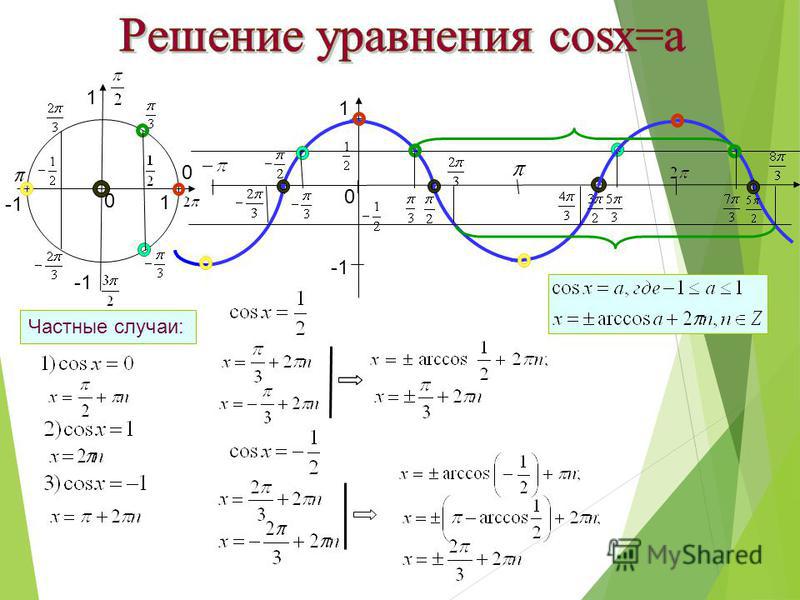 Первый множитель составляет:
Первый множитель составляет:
Это уравнение верно при x = 60 ° и, в силу симметрии касательной кривой, также при x = 180 ° + 60 ° = 240 °. В радианах это
.
Второй множитель решает как:
Косинус принимает это значение при x = 30 ° и, в силу симметрии кривой косинуса, также при x = 360 ° — 30 ° = 330 °.В радианах это
. Итак, мое решение:
Решить ln (2 — sin
2 ( x )) = 0 при 0 ° < x <360 °
Натуральный логарифм (ну, любой логарифм ) равен нулю, когда аргумент равен 1, поэтому это дает мне:
2 — грех 2 ( x ) = 1
1 — грех 2 ( x ) = 0
(1 — грех ( x )) (1 + sin ( x )) = 0
1 = грех ( x ) или 1 = –sin ( x )
Исходя из того, что я знаю о синусоиде, мое решение:
Журнал решения
3 (2sin ( x )) = 1/2 на [0, 2π)
По природе логарифмов эквивалентное экспоненциальное уравнение:
Синус принимает это значение при
, а также при. Тогда мое решение:
Тогда мое решение:
Ожидайте, что потребуется фактор (особенно квадратичный) для решения некоторых тригонометрических уравнений, а также ожидайте, что потребуется использовать триггерные тождества. Не бойтесь пробовать разные методы; иногда ваш первый импульс не приводит ни к чему полезному, но ваше второе предположение может сработать. И обратите особое внимание на любые необычно сложные примеры в вашем учебнике, так как они могут содержать подсказки о том, какие уловки вам понадобятся, особенно в следующем тесте.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении тригонометрических уравнений. Попробуйте выполнить указанное упражнение или введите свое собственное. (Если вам не сказали решать «в общих чертах», не забудьте указать интервал, как показано ниже.) Затем нажмите кнопку и, для получения наилучших результатов, выберите «Решить через интервал», чтобы сравнить свой ответ с ответом Mathway.
Примечание: решающая программа может предоставить только «точные» решения, а иногда и любое решение, если вы в радианах.Используйте дипломы на свой страх и риск!
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/solvtrig2.htm
Вся элементарная математика — Учебное пособие — Тригонометрия
Вся элементарная математика — Учебное пособие — Тригонометрия — Тригонометрические неравенства…
|
| Главная | О нас | Ссылки |
Свяжитесь с нами |
Авторские права 2002-2007 гг.

