Содержание
Russian — Доказательство: lim (sin x)/x=1
И снова здравствуйте!
Теперь, когда мы хорошо понимаем, в чем состоит теорема сжатия
(или ее еще называют теоремой о 2-ух милиционерах),
мы будем использовать ее, чтобы доказать, что предел…
(напишу желтым цветом)…
предел при х, стремящемся к 0-лю, [(sin x)/x]=1.
Итак, докажем эту теорему.
Мы должны сопровождать доказательство графическим подтверждением.
Поэтому я нарисую, хотя бы, 1-ую и 4-ую четверти единичной окружности.
Нарисую лиловым. Итак, посмотрим…
Нужно нарисовать побольше.
Так… Нужно нарисовать их очень большими. Поэтому я вот так рисую.
Ну, пусть будет так. И нарисую оси. Это ось Y, а это ось Х. Вот так.
Это наша единичная окружность.
Теперь нарисую радиус,
только я нарисую его выходящим за пределы окружности.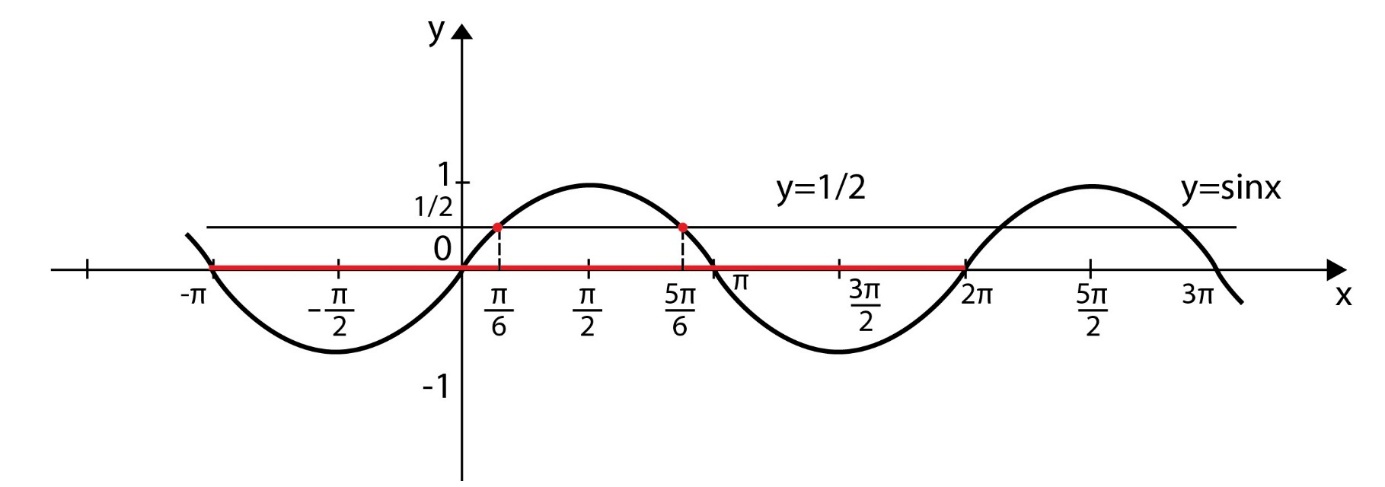
Нарисую еще кое-что, чтобы решить нашу задачу.
Нет, это не то, что я хотела сделать.
Я хотела начать вот с этой точки.
А из этой точки я хотела провести линию…и еще одну линию из той же точки. Вот так.
Теперь мы готовы приступить к решению.
Итак, это единичная окружность, правильно?
Что значит «единичная окружность»?
Это значит, что радиус этой окружности равен единице.
Т.е. расстояние от этой точки до этой равно единице.
И если это угол х (в радианах), то чему равна длина вот этого отрезка?
По определению, sin х является Y-координатой
любой точки на единичной окружности.
Потому это – sin x (мне не хватает здесь места чтобы написать, поэтому нарисую стрелочку… так, вот это – sin х).
А теперь задам вопрос посложнее. Чему равна длина вот этого отрезка?
Давайте подумаем. Что такое тангенс (tg)?
Что такое тангенс (tg)?
Вернемся к нашему SOH-CAH-TOA-определению тангенса. Вспомните еще такое?
Тангенс, т.е. отношению противолежащего катета (от англ. «opposite»)
к прилежащему (от англ. «adjacent») — это тангенс. Тогда чему равен tg x?
Если это прямоугольный треугольник, то тангенс –
это отношение длины противолежащего катета к длине прилежащего, правильно?
Назовем длину этого катета о (от англ. «opposite»).
А чему равна длина прилежащего катета?
Чему равно основание вот этого, большего, треугольника?
Это ведь единичная окружность, правильно?
Значит, расстояние от этой точки до этой будет равно единице.
Потому что это – тоже радиус окружности. И равен он единице.
Итак, отношение противолежащего катета к прилежащему равно tg x.
Но если подставить в это соотношение единицу вместо прилежащего катета,
то получится, что противолежащий катет (вот этот) будет равен tg x.
Иначе говоря, tg x равен длине вот этого катета, деленной на единицу;
или tg x равен длине вот этого катета. Запишу это.
Этот катет равен tg x.
А теперь давайте подумаем о площадях других частей нарисованной здесь фигуры.
Может, стоило нарисовать ее побольше, но, думаю, у нас и так получится.
Итак, первым делом выберу относительно небольшой треугольник.
Возьму вот этот треугольник. Обведу его зеленым.
Итак, чему равна площадь вот этого зеленого треугольника?
Она будет равна 1/2, умножить на основание и умножить на высоту.
Т.е. 1/2 умножить на основание, которое равно единице, правильно?
А чему равна высота? Мы только что выяснили, что вот эта высота равна sin x.
Значит, умножить на sin x. Это площадь вот этого зеленого треугольника.
А чему равна площадь… не этого, не зеленого. ..
..
Обведу другим цветом. Например, красным.
Чему равна площадь вот этого сектора? Вот этого сектора.…
Надеюсь, вы видите. Нет, все-таки этот цвет не сильно отличается.
Итак, вот этот сектор. Сначала вот этот радиус, а затем дуга…
Т.е. эта площадь будет больше площади треугольника, которую мы только что вычислили.
Она будет немного больше потому,
что включает в себя площадь между треугольником и дугой, правильно?
Чему же она равна?
Если этот угол равен х радиан,
то какую долю он составляет от целой единичной окружности?
В целой единичной окружности 2π радиан, так?
Тогда чему будет равна вот эта площадь?
Она будет равна доле угла х от целой единичной окружности, так?
Т.е. х радиан разделить на 2π радиан
(это доля, которую составляет вот этот угол от 360 градусов, если перейти к градусам)
и умножить еще на площадь всего круга, правильно?
Вот это показывает, какую долю от окружности занимает наша фигура,
и нам нужно умножить это еще на площадь всего круга.
А чему равна площадь всего этого круга?
Она равна πR², а радиус равен единице, правильно?
Значит, площадь всего круга равна просто п. (πR², где R=1).
Тогда площадь всего вот этого сектора будет равна…
π сокращаются, значит, получится х/2.
Итак, площадь вот этого, первого, небольшого зеленого треугольника равна 1/2*sin x.
Это площадь вот этого, зеленого, треугольника.
Площадь вот этого сектора (мы только что нашли) равна х/2.
А теперь давайте найдем площадь вот этого, большого треугольника.
Она равна 1/2 умножить на основание, и умножить на высоту.
Итак, основание опять равно единице, умножить на высоту, т.е. tg x.
Значит, площадь равна 1/2*tg x.
При взгляде на эту схему сразу должно быть ясно
(и неважно, где нарисована вот эта линия),
что площадь вот этого, зеленого, треугольника меньше площади вот этого сектора,
а площадь сектора меньше площади вот этого, большого, треугольника. Правильно?
Правильно?
Запишем это в виде неравенства.
Площадь зеленого треугольника, т.е. 1/2*sin x,
меньше площади вот этого сектора, которая равна х/2.
И обе эти площади меньше площади вот этого,
большого, треугольника, которая равна 1/2*tg x.
Когда это неравенство справедливо?
Оно справедливо, пока мы находимся в 1-ой четверти, правильно?
Пока мы находимся в 1-ой четверти.
Также оно почти справедливо, если мы переходим в 4-ую четверть,
за исключением того, что тогда синус и тангенс становятся отрицательными,
и х также становится отрицательным.
Но если мы возьмем абсолютные значения, т.е. модуль,
то неравенство все еще будет справедливым и в 4-ой четверти.
Потому что, если пойти в отрицательном направлении,
и при этом брать абсолютные значения, то расстояние будет сохраняться,
значит, и значения площадей будут положительными.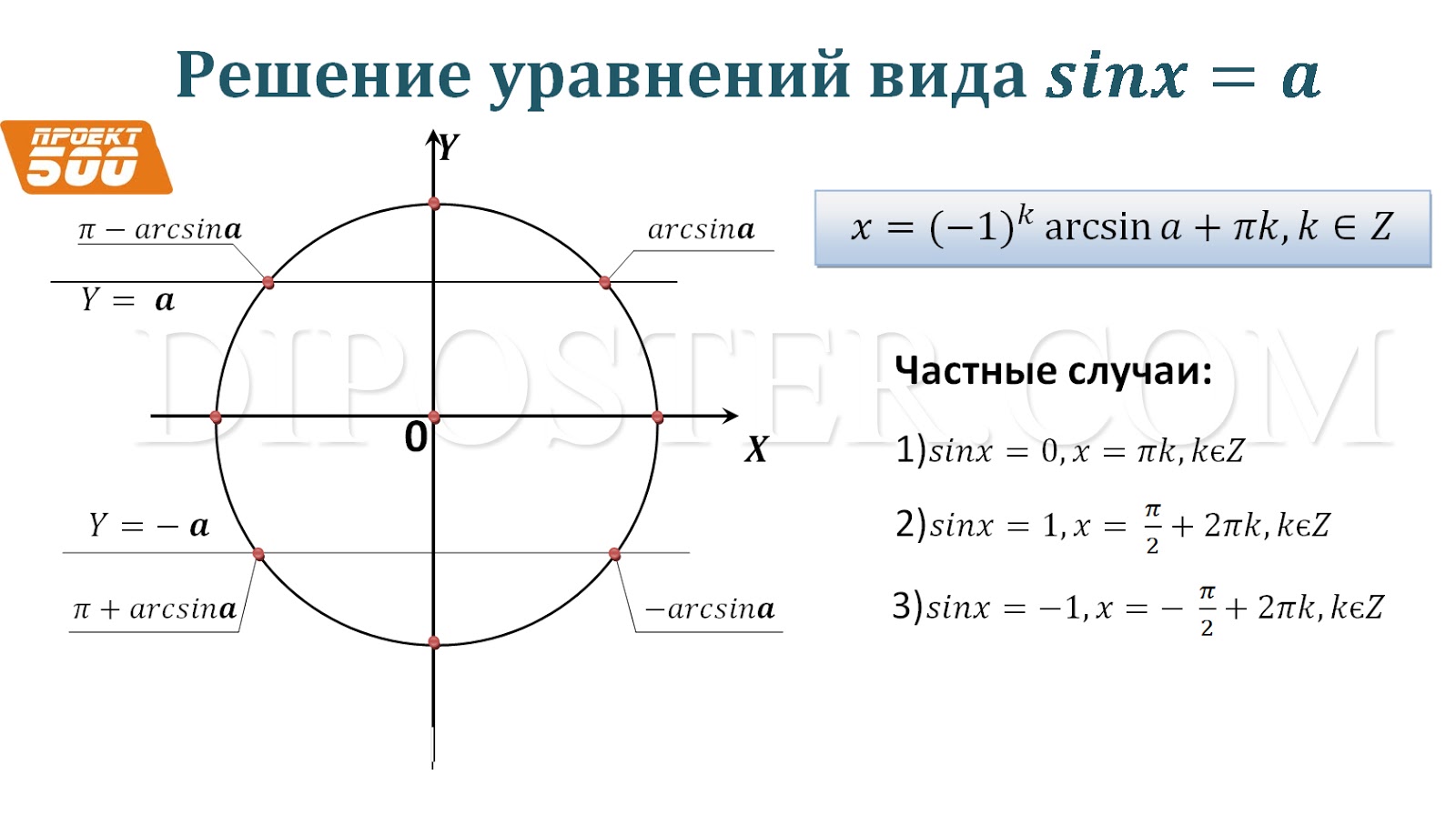
Итак, моя цель – найти предел при х, стремящемся к 0-лю.
И чтобы этот предел был вообще определен, неравенство должно быть справедливым
как с положительной, так и с отрицательной стороны.
Давайте возьмем абсолютные значения в неравенстве.
Надеюсь, вам это понятно.
Если провести линию вниз, то это будет синусом х, это – тангенсом.…
И если вы берете абсолютные значения, то делаете то же самое, что и в первой четверти.
Итак, давайте возьмем абсолютные значения.
От этого ничего не должно измениться, особенно, если вы находитесь в 1-ой четверти.
Итак, у нас есть это неравенство. Посмотрим, можно ли его как-то преобразовать.
Прежде всего, давайте избавимся от 1/2-ой, умножив все на 2.
Итак, модуль sin x меньше модуля х,
который в свою очередь меньше модуля tg x.
Надеюсь, я не запутала вас этими модулями.
Начальное неравенство, которое я записала, полностью соблюдалось в 1-й четверти.
Но т.к. я хотела, чтобы это неравенство соблюдалось и в 1-ой, и в 4-ой четверти,
потому что ищу предел при х, стремящемся к 0-лю с обеих сторон,
то беру здесь абсолютные значения.
Т.е. можно было бы провести линию вниз
и то же самое, что мы делали здесь, сделать и для 4-ой четверти,
но при этом брать абсолютные значения, и неравенство снова должно сработать.
Вернемся к задаче. Итак, у нас есть это неравенство.
Возьмем это выражение и разделим все его части…
Можно сказать, что у него 3 части – левая, средняя и правая.
Разделим их все на модуль sin x.
И поскольку мы знаем, что модуль sin x – это положительное число,
то знаем и то, что вот эти знаки
Давайте разделим.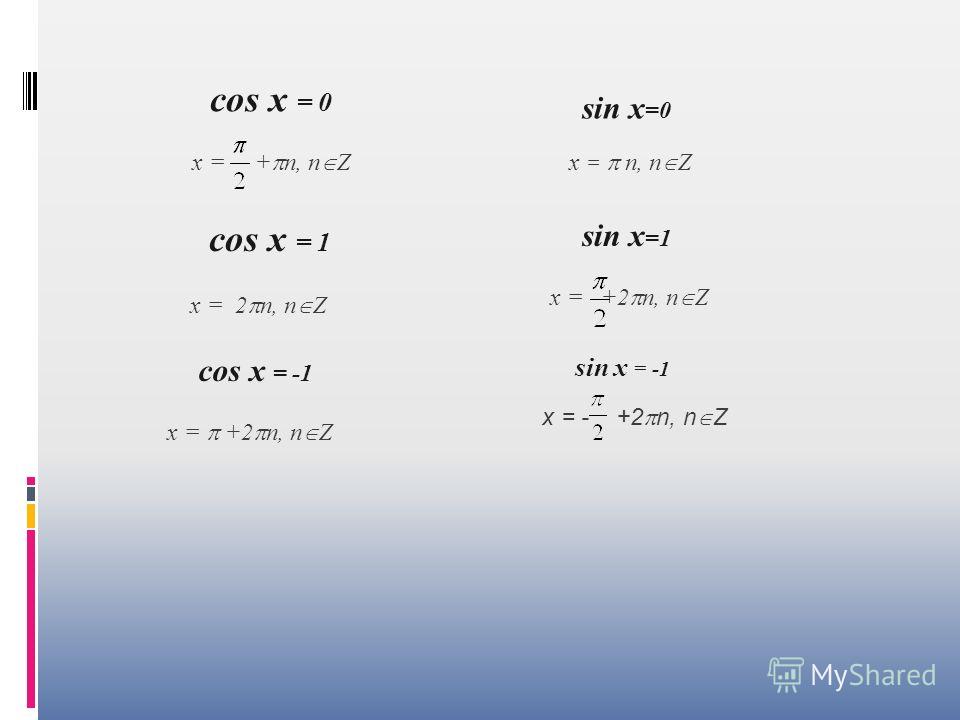
Итак, модуль sin x, деленный на модуль sin x – это просто единица.
Единица меньше модуля х, деленного на модуль sin x, а это в свою очередь меньше.…
Повторю, что я делю вот это неравенство на модуль sin x.
Чему равен модуль tg x, деленный на модуль sin x?
Тангенс – это отношение синуса к косинусу.
Итак, это равно… Просто преобразуем правую часть.
Это равно отношению синуса к косинусу, деленному еще на синус.
И можно сказать, что это то же самое, что модуль, и модуль, деленные на модуль.
Что останется? Останется только единица разделить на….
синусы сокращаются, значит, останется единица разделить на модуль cos x.
Мы уже близки к разгадке. Вот это выглядит как наша функция, только перевернутая.
И чтобы в средней части получить нашу функцию, давайте перевернем неравенство.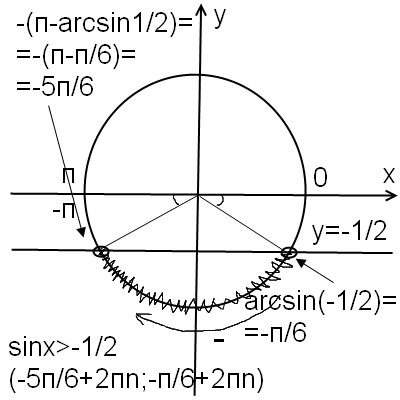
Что тогда произойдет?
Прежде всего, что будет, если перевернуть единицу?
1/1 – это просто единица.
Но если вы перевернете все части неравенства,
то и знак неравенства поменяется, правильно?
Если вам это непонятно, рассуждайте так:
если я скажу, что 1/2
то получу 2>1/2. Надеюсь, что так вам более понятно.
Т.е. если я переворачиваю все части этого неравенства,
то знаки неравенства я должна изменить.
Итак, единица больше модуля sin x, деленного на модуль х,
что в свою очередь больше модуля cos x.
Теперь я задам вам вопрос.
Модуль sin x… прежде всего, sin x/x.
Будет ли такой случай, когда выражение sin x/x
в 1-ой или 4-ой четверти будет иметь знак «минус»?
В 1-ой четверти значения sin x будут положительными, значения х тоже.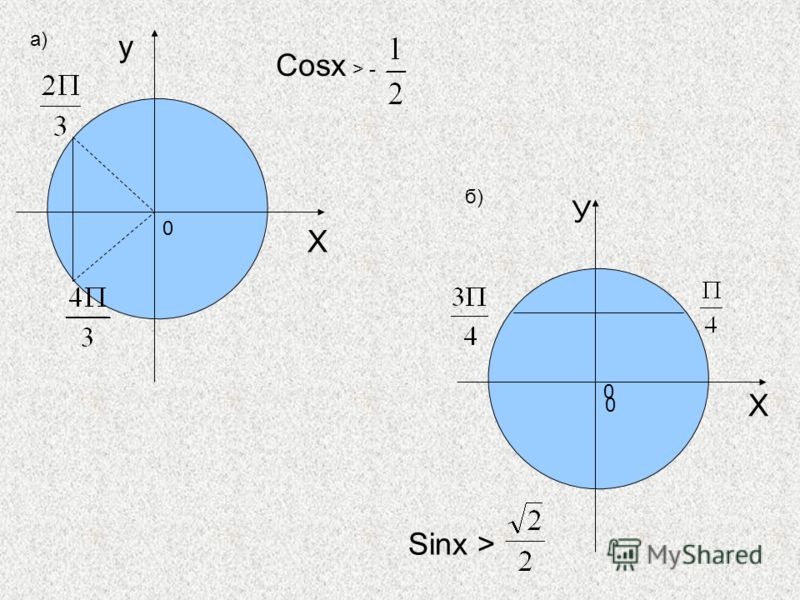
Положительное значение, деленное на положительное,
в результате также даст положительное значение.
А в 4-ой четверти синус принимает отрицательные значения
(т.к. y отрицательный и угол отрицательный),
значит, значения х также будут отрицательными.
В этом случае sin x/x – принимает отрицательное значение, деленное на отрицательное значение,
что в результате даст положительное значение.
Значит, sin x/x –всегда будет положительным. Поэтому знаки модуля тут не нужны.
Тогда можно записать так: единица больше sin x/x…
И по той же логике: в 1-ой и 4-ой четвертях,
т.е. если имеем дело, например, с (-π/2), которое меньше x,
а х в свою очередь меньше π/2.
Т.е. мы идем от (-π/2) до π/2, в 1-ой и 4-ой четвертях.
Будет ли cos x отрицательным?
По определению, значения косинуса в 1-ой и 4-ой четвертях всегда положительные.
Значит, и в правой части неравенства
можно убрать знаки абсолютного значения и оставить только cos x.
Теперь мы готовы использовать теорему о двух милиционерах.
Итак, чему равен предел при х, стремящемся к 0-лю, функции единицы?
Функция единицы всегда равна единице.
Т.е. я могу искать ее предел при х, стремящемся к бесконечности, при х, стремящемся к π.
И он всегда будет равен единице.
Т.е. при х, стремящемся к 0-лю, этот предел равен единице.
А чему равен предел при х, стремящемся к 0-лю, функции cos x?
Это тоже легко. При х, стремящемся к 0-лю, косинус нуля равен просто единице.
Как вы знаете, косинус – это непрерывная функция, значит, предел равен единице.
Итак, мы готовы использовать теорему сжатия.
При х, стремящемся к 0-лю, вот эта функция стремится к единице,
и вот эта функция тоже стремится к единице.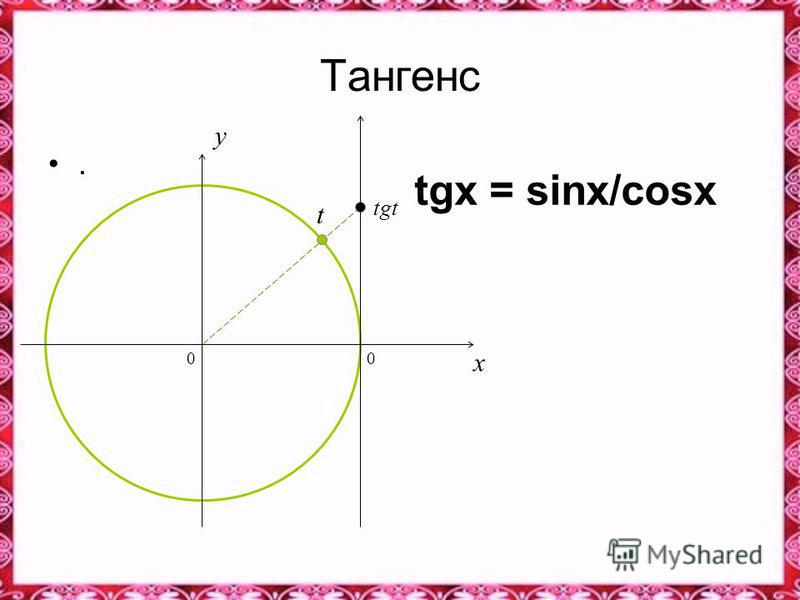
А вот эта – она здесь находится между двумя другими функциями.
И если она находится между двумя…
Т.е. если эта функция стремится к единице при х, стремящемся к 0-лю,
и эта функция также стремится к единице при х, стремящемся к 0-лю,
а эта находится между ними, то она тоже должна стремиться к единице
при х, стремящемся к 0-лю.
Используем теорему о двух милиционерах, основанную на этом и на этом.
И можно было бы сказать, что вследствие этой теоремы
(потому что вот это соблюдается, вот это соблюдается и это тоже)
предел sin x/x при х, стремящемся к 0-лю, равен единице.
Надеюсь, что это понятно. Можно пойти и другим путем:
если вот эта линия все ниже и ниже опускается к нулю,
если х стремится к 0-лю, то эта площадь и эта площадь сходятся в одну,
значит, и площадь, которая между ними, сводится к ним обеим.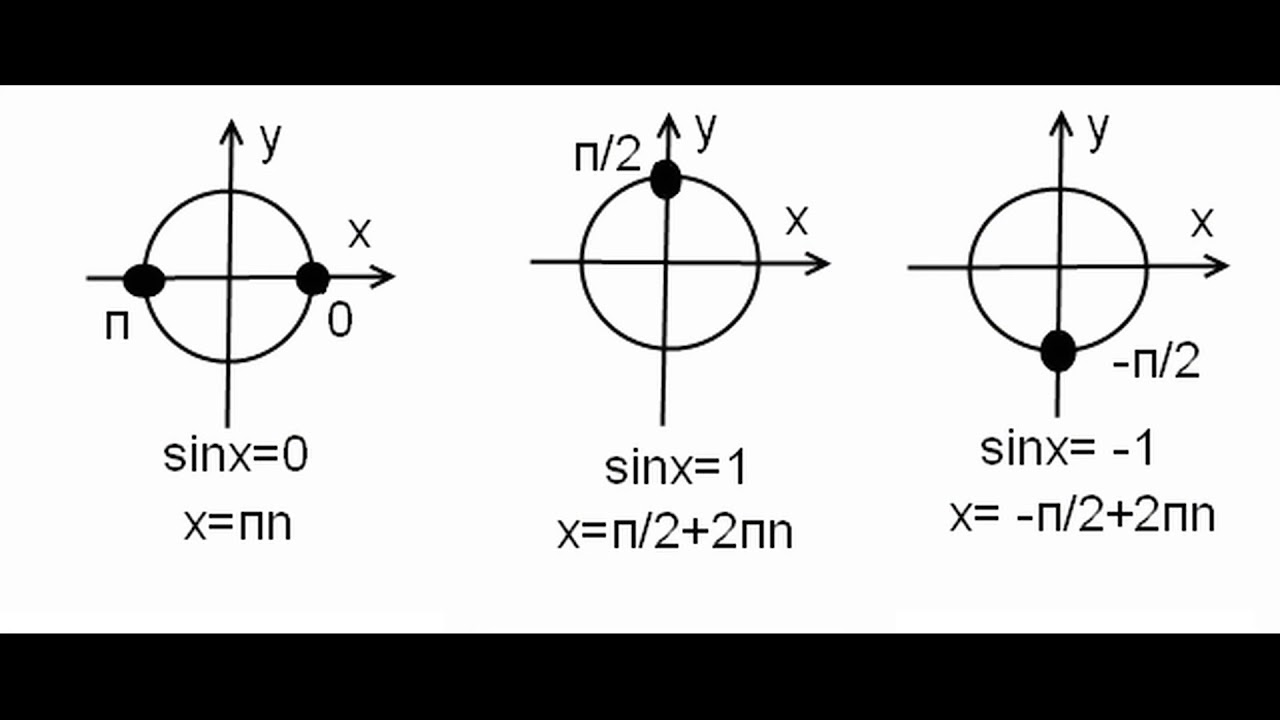
Если вы хотите увидеть графическое отображение, то оно вот здесь.
Посмотрю, получится ли показать вам график… Тогда вы мне поверите.
Итак, мы говорили, что единица всегда больше sin x/х,
что в свою очередь больше cos x в промежутке от (-π/2) до π/2.
И, конечно, sin x/х не определен при х=0.
Но мы можем найти предел. Здесь можно его увидеть.
Синяя линия – это график функции единицы, т.е. y=1.
Светло-голубая линия – это график косинуса х.
А красная – это график sin x/х. Это обозначено вот здесь.
Итак, график sin x/х в промежутке (-π/2, π/2) или в 1-ой и 4-ой четвертях,
т.е. красная линия, всегда находится между синей и светло-голубой линиями.
Я это говорю, чтоб вы поняли, что происходит в теореме о двух милиционерах.
Мы знаем, что для этой светло-голубой лини
предел равен единице, при х, стремящемся к 0.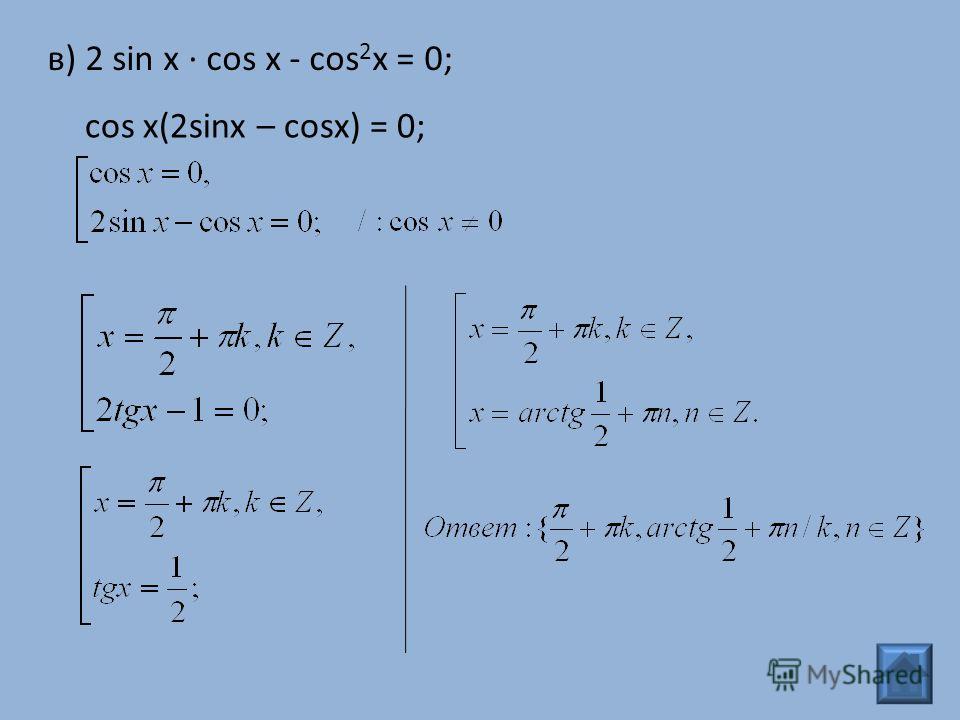
И знаем также, что для этой верхней, синей, линии
предел равен единице, при х, стремящемся к 0.
А эта красная линия находится всегда между ними,
значит, предел этой функции тоже будет равен единице.
Что и требовалось доказать.
Мы использовали теорему сжатия и немного тригонометрии, чтобы доказать,
что предел при х, стремящемся к 0-лю, функции sin x/х равен единице.
Еще этот предел называют замечательным пределом.
Почему его так называют, вы узнаете позже.
Надеюсь, вы все поняли, и я вас не запутала.
На сегодня все! До встречи на следующем уроке!
- Title:
Доказательство: lim (sin x)/x=1
- Description:
В этом видео с использованием теоремы сжатия приводится подробное доказательство того, что предел функции [sin x/x] при х, стремящемся к 0, равен 1.
 Этот предел еще называют замечательным пределом.
Этот предел еще называют замечательным пределом.Это видео — русская версия видео «Proof: lim (sin x)/x» Академии Хана (http://www.khanacademy.org/video?v=Ve99biD1KtA). Перевод и дублирование выполнены командой проектов «Edukit» (http://www.edukit.org.ua) и «Study Planner» (http://www.studyplanner.org).
This video is a Russian dubbed version of the Khan Academy video «Proof: lim (sin x)/x» (http://www.khanacademy.org/video?v=Ve99biD1KtA). The translation and sampling are made by the «Edukit» (http://www.edukit.org.ua) and «Study Planner» team (http://www.studyplanner.org).
Наша страница на Facebook — http://www.facebook.com/KhanAcademyRussian
more »
« less- Video Language:
- Russian
- Duration:
- 18:06
Тригонометрические уравнения. Простейшие тригонометрические уравнения Решить тригонометрическое уравнение sinx 1 2
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение:
Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение:
Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x.
Получим
tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k
, k
б) tgx = 2, x= arctg2 + 2 k
, k
.
Ответ:
arctg4 + 2 k
, arctg2 + 2 k, k
4. Уравнения вида a
sinx + b
cosx = с, с
≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f
( х
) = φ ( х
) может служить только число 0. Проверим это:
cos 0 = 0 + 1 – равенство верно.
Число 0 единственный корень данного уравнения.
Ответ:
0.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.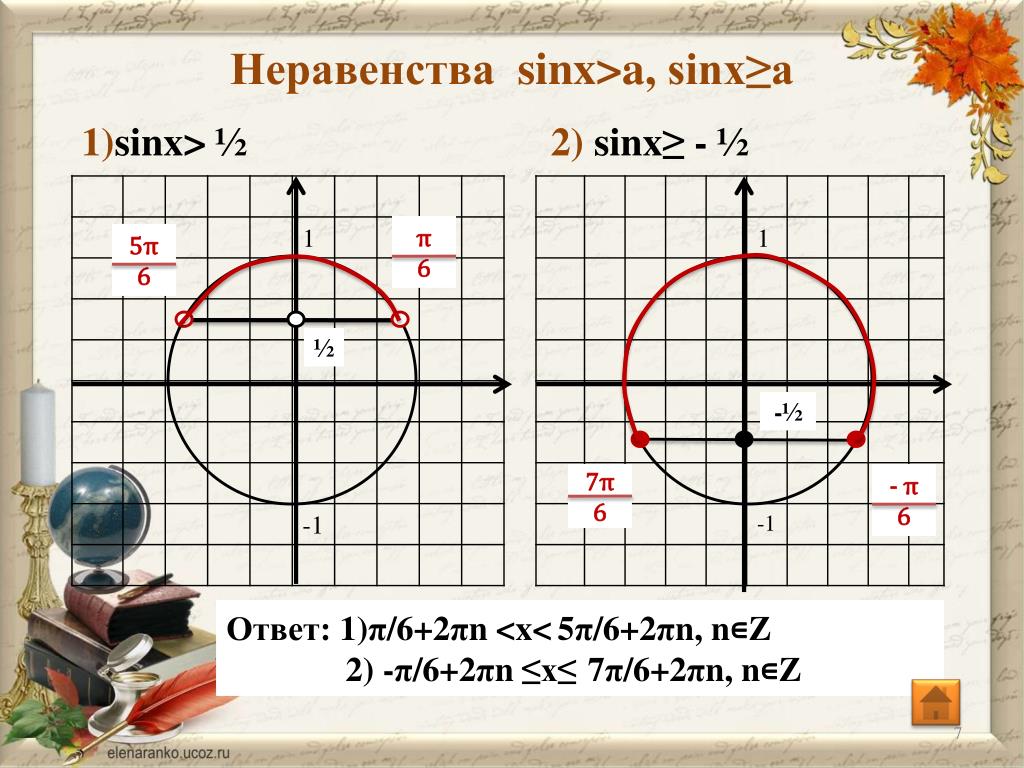
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π
n, n ∈ Z
Для тангенса:
х = arctg a + π
n, n ∈ Z
Для котангенса:
х = arcctg a + π
n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений.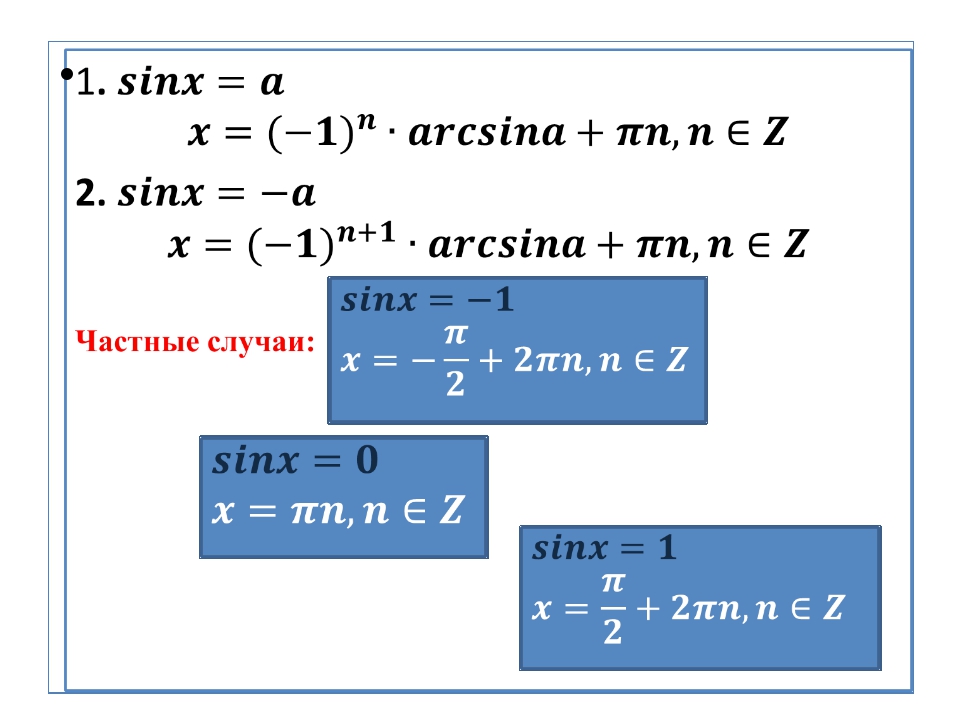 Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно!
С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a,
второй: -arccos a.
И так будет получаться всегда.
При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а
на какое-то отрицательное. Всё равно, один угол у нас получился arccos a,
второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π
n, n ∈ Z
х 2 = — arccos a + 2π
n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π
n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов,
вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся. Что, как и откуда.
В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой.
Только эта строчка похитрее будет:
х = (-1) n arcsin a + π
n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π
/6 + 2π
n, n ∈ Z
х 2 = 5π
/6 + 2π
n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π
n, n ∈ Z
Вообще-то, это недоделанный ответ. ) Ученик обязан знать, что
) Ученик обязан знать, что
arcsin 0,5 = π
/6.
Полноценный ответ будет:
х = (-1) n π
/6
+ π
n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2
(это правильный ответ!) и через одинокий х
(и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1
значения n
=0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6
и так далее.
При такой же подстановке в ответ с х 2
, получаем:
х 2 = 5π/6; 17π/6; 29π/6
и так далее.
А теперь подставляем значения n
(0; 1; 2; 3; 4…) в общую формулу для одинокого х
. Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6
и так далее.
Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты,
что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов.
Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу. Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)
Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π
n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π
n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π
n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π
n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π
n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет.
Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2
и т. п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn,
а где 2π
n.
Вот вам простой приёмчик. Во всех
формулах стоит πn.
Кроме единственной формулы с арккосинусом. Там стоит 2πn.
Два
пиэн. Ключевое слово — два.
В этой же единственной формуле стоят два
знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два
знака перед арккосинусом, легче вспомнить, что в конце будет два
пиэн. А ещё наоборот бывает. Пропустит человек знак ±
А ещё наоборот бывает. Пропустит человек знак ±
, доберётся до конца, напишет правильно два
пиэн, да и спохватится. Впереди-то два
знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
Числовая окружность
Наряду с понятием числовой прямой есть еще и понятие числовой окружности. Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной.
Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной.
Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A
.
Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.
- Два противоположных числа находятся на симметричных относительно оси абсцисс точках окружности.
Проведем вертикальную хорду АВ (рис. 2). Так как точки A и B симметричны относительно оси Ox, то число -x_0 находится на точке B и, значит, все числа точки B задаются формулой: x_B=-x_0+2πk ,k∈Z. Числа на точках A и B запишем одной формулой: x_(A ; B)=±x_0+2πk ,k∈Z. Сделаем вывод: зная одно из чисел на одной из точек A или B вертикальной хорды АВ, мы можем найти все числа на этих точках. Рассмотрим горизонтальную хорду AD и найдем числа точки D (рис. 2). Так как BD – диаметр и число -x_0 принадлежит точке В, то -x_0 + π одно из чисел точки D и, значит, все числа этой точки задаются формулой x_D=-x_0+π+2πk ,k∈Z. k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
π/3 на С1 и
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности. На рисунке отмечены также и координаты этих точек (опустим описание их получения).
На рисунке отмечены также и координаты этих точек (опустим описание их получения).
Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a)
простейших уравнений.
Решить уравнения
1) sinx=1⁄(2)
.
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2
.
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x
. На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2
.
Нам надо найти все числа на точках C4 и C3.
3) sinx=1
. На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.
Ответ: x=π/2+2πk , k∈Z .
4) sinx=-1
.
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0
.
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z
.
6) cosx=√2⁄2
.
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x.
На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2
.
Надо найти числа на точках C_2 и C_3 .
Ответ: x=±2π/3+2πk , k∈Z
.
10) cosx=0
.
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения.
.
Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosxОтвет: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Урок 4. свойства и график функции y=sinx — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №4. Свойства и график функции .
Перечень вопросов, рассматриваемых в теме
Глоссарий по теме
Синусоидой называется множество точек плоскости, которое в некоторой системе координат является графиком функции , где a≠0.
Число │a│ называется амплитудой.
Основная литература:
Колягин М.В. Ткачева Ю.М., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс]. – Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
На прошлом уроке мы говорили о свойствах графика косинуса:
1) область определения функции – множество R всех действительных чисел;
2) Множество значений функции – отрезок [–1;1];
3) Функция косинуса периодическая, ;
4) Функция чётная;
5) Функция принимает:
- значение, равное 0, при ;
- наименьшее значение, равное –1, при
;
- наибольшее значение, равное 1, при ;
6) Функция
- возрастает на отрезке и на отрезках, получаемых сдвигами этого интервала на .
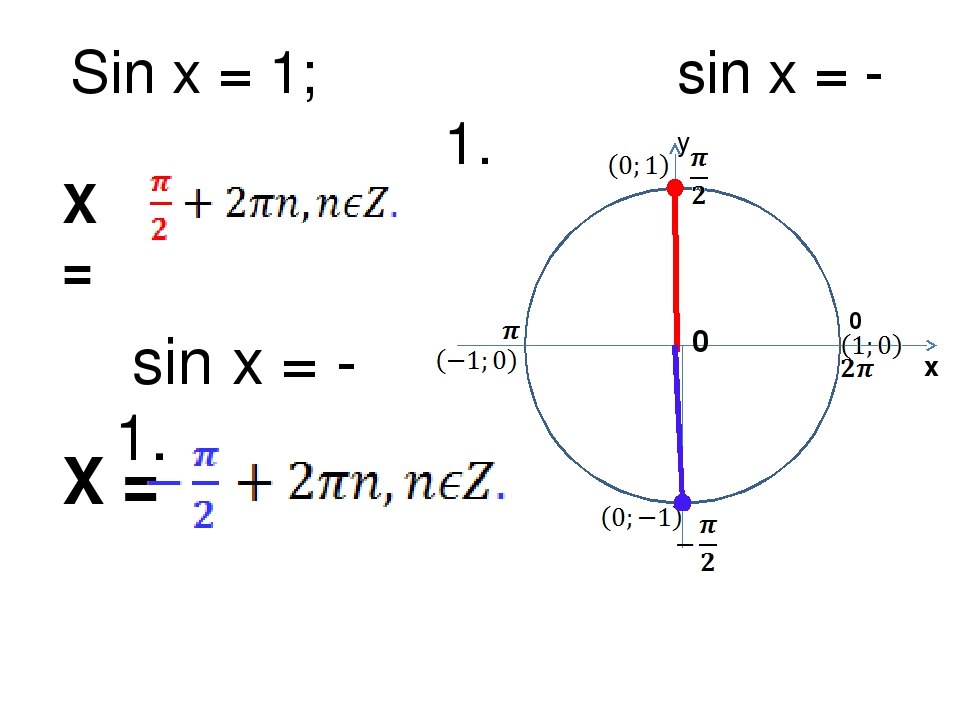
Давайте сравним их со свойствами графика синуса, а для начала определим следующие моменты:
- При движении точки до первой четверти ордината увеличивается;
- При движении точки по второй четверти ордината постепенно уменьшается;
- Функция возрастает на отрезке и убывает на отрезке .
Свойства функции :
1) D(y) =R;
2) E (y) =[–1;1];
3) Период функции равен ;
4) Функция чётная/нечётная;
5) Функция принимает:
6) Функция
- возрастает на отрезке и на отрезках, получаемых сдвигами этого отрезка на ;
- убывает на отрезке и на отрезках, получаемых сдвигами этого отрезка на .
Изменяя амплитуду и значение аргумента функции синуса график ведет себя следующим образом (рис.1)
Рис. 1 – графики синуса
Сдвиг графика влево/вправо вдоль оси абсцисс
Если к аргументу функции добавляется постоянная, то происходит сдвиг (параллельный перенос) графика вдоль оси Ох.
Правило:
1) чтобы построить график функции , нужно сдвинуть график вдоль оси Ох на b единиц влево;
2) чтобы построить график функции , нужно график сдвинуть вдоль оси ОХ на b единиц вправо.
Теоретический материал для самостоятельного изучения
Актуализация знаний
1. На следующие утверждения нужно ответить верно/неверно.
1) Тригонометрическая функция определена на всей числовой прямой.
2) График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
3) График тригонометрической функции можно построить, используя одну главную полуволну.
Ответ: верно, неверно, верно.
2. Вспомним, что мы уже знаем о функции , ответив на вопросы:
1) Какие значения может принимать переменная х. Какова область определения этой функции?
2) В каком промежутке заключены значения выражения . Назови наибольшее и наименьшее значения функции .
3) Функция синуса чётная или нечётная?
Ответ:1) 𝑥∈𝑅; 2) [–1;1]; 𝑦𝑚𝑎𝑥=3, 𝑦𝑚𝑖𝑛=–3; 3) чётная;
Примеры и разборы решения заданий тренировочного модуля:
Пример 1. Найдем все корни уравнения , принадлежащие отрезку .
Найдем все корни уравнения , принадлежащие отрезку .
Построим графики функций и (рис. 6)
Рис. 7 – графики функций и .
Графики пересекаются в четырёх точках, абсциссы которых являются корнями уравнения . На выбранном отрезке от корни уравнения симметричны: и . Из рисунка видно, что симметричность корней объясняется периодичностью функции: аналогично для
Ответ: ; .
Пример 2.Найти все решения неравенства , принадлежащие отрезку .
Из рисунка 7 видно, что график функции лежит выше графика функции на промежутках и и
Ответ: , ,
Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.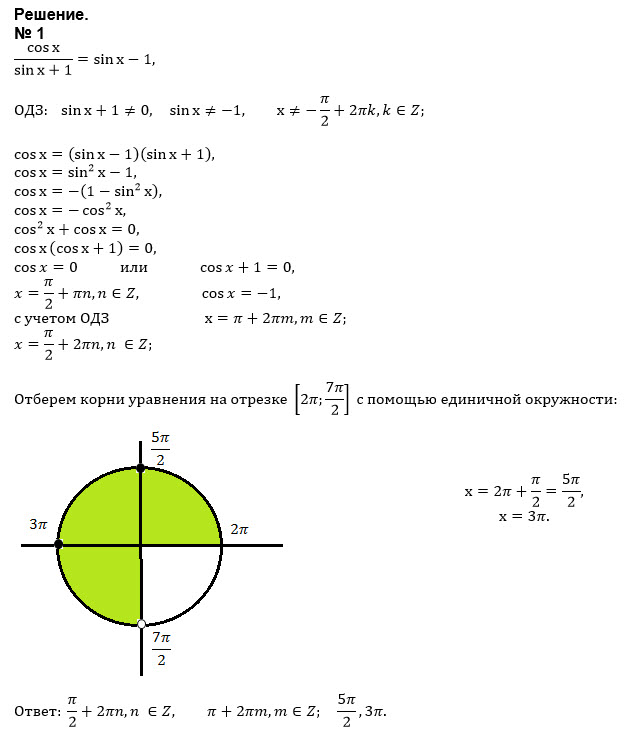
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение
Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .
Отметим на оси ординат точку с ординатой :
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату. Эти точки соответствуют углам поворота на и радиан:
Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату.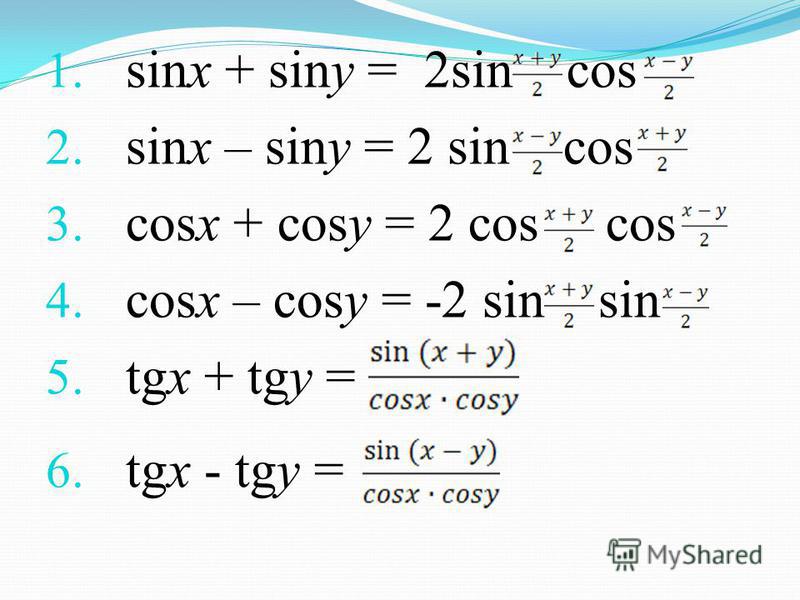 То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
, , — множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
, где , . (2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .
Эти две серии решений можно объединить в одну запись:
Если мы в этой записи возьмем ( то есть четное ), то мы получим первую серию решений.
Если мы в этой записи возьмем ( то есть нечетное ), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение
Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :
Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Запишем две серии решений:
,
,
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .
Объедим эти две серии в одну запись:
3. Решим уравнение
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:
,
4. Решим уравнение
Решим уравнение
Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .
Отметим на линии котангенсов точку с абсциссой -1:
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:
Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
ОСОБЫЕ РЕШЕНИЯ:
1
Отметим на окружности точки, ордината которых равна 0:
2.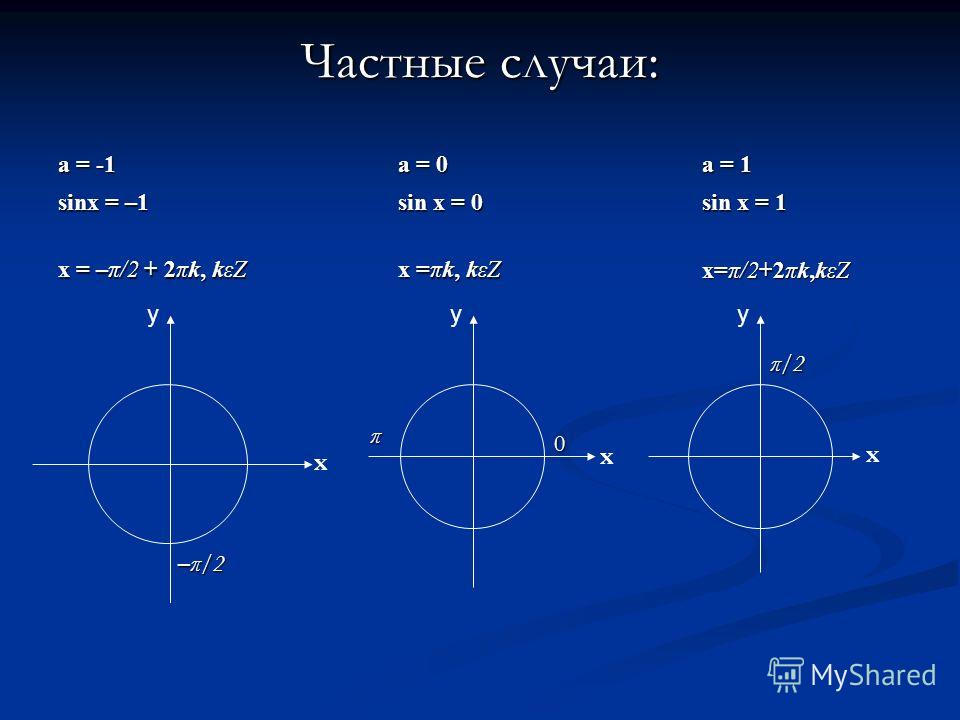
Отметим на окружности единственную точку, ордината которой равна 1:
3.
Отметим на окружности единственную точку, ордината которой равна -1:
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
4.
Отметим на окружности точки, абсцисса которых равна 0:
5.
Отметим на окружности единственную точку, абсцисса которой равна 1:
6.
Отметим на окружности единственную точку, абсцисса которой равна -1:
И чуть более сложные примеры:
1.
Синус равен единице, если аргумент равен
Аргумент у нашего синуса равен , поэтому получим:
. Разделим обе части равенства на 3:
Ответ:
2.
Косинус равен нулю, если аргумент косинуса равен
Аргумент у нашего косинуса равен , поэтому получим:
Выразим , для этого сначала перенесем вправо с противоположным знаком:
Упростим правую часть:
Разделим обе части на -2:
Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.
Ответ:
И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать простейшие тригонометрические неравенства.
И.В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и Задание 13»
Все формулы по тригонометрии
Все
формулы по тригонометрии
Основные
тригонометрические тождества
sin2x +
cos2x =
1
tgx ctgx =
1
tg2x + | = | 1 |
cos2x |
ctg2x + | = | 1 |
sin2x |
Формулы
двойного аргумента
sin2x =
2sinx cosx
sin2x | = | 2tgx | = | 2ctgx | = | 2 |
1 | 1 | tgx + |
cos2x =
cos2 —
sin2x =
2cos2x —
1 = 1 — 2sin2x
cos2x | = | 1 | = | ctg2x — | = | ctgx — |
1 | ctg2x + | ctgx + |
tg2x | = | 2tgx | = | 2ctgx | = | 2 |
1 | ctg2x — | ctgx — |
ctg2x | = | ctg2x — | = | ctgx — |
2ctgx | 2 |
Формулы
тройного аргумента
sin3x =
3sinx —
4sin3x
cos3x =
4cos3x —
3cosx
tg3x | = | 3tgx — |
1 |
ctg3x | = | ctg3x — |
3ctg2x — |
Формулы
половинного аргумента
sin2 | x | = | 1 |
2 | 2 |
cos2 | x | = | 1 |
2 | 2 |
tg2 | x | = | 1 |
2 | 1 |
ctg2 | x | = | 1 |
2 | 1 |
tg | x | = | 1 | = | sinx |
2 | sinx | 1 |
ctg | x | = | 1 | = | sinx |
2 | sinx | 1 |
Формулы
квадратов тригонометрических функций
sin2x | = | 1 |
2 |
cos2x | = | 1 |
2 |
tg2x | = | 1 |
1 |
ctg2x | = | 1 |
1 |
sin2 | x | = | 1 |
2 | 2 |
cos2 | x | = | 1 |
2 | 2 |
tg2 | x | = | 1 |
2 | 1 |
ctg2 | x | = | 1 |
2 | 1 |
Формулы
кубов тригонометрических функций
sin3x | = | 3sinx — |
4 |
cos3x | = | 3cosx + |
4 |
tg3x | = | 3sinx — |
3cosx + |
ctg3x | = | 3cosx + |
3sinx — |
Формулы
тригонометрических функций в четвертой
степени
sin4x | = | 3 |
8 |
cos4x | = | 3 |
8 |
Формулы
сложения аргументов
sin(α
+ β) = sinα cosβ + cosα sinβ
cos(α
+ β) = cosα cosβ — sinα sinβ
tg(α | = | tgα |
1 |
ctg(α | = | ctgα |
ctgα |
sin(α
— β) = sinα cosβ — cosα sinβ
cos(α
— β) = cosα cosβ + sinα sinβ
tg(α | = | tgα |
1 |
ctg(α | = | ctgα |
ctgα |
Формулы
суммы тригонометрических функций
sinα | = 2sin | α | ∙ cos | α |
2 | 2 |
cosα | = 2cos | α | ∙ cos | α |
2 | 2 |
(sinα
+ cosα)2 =
1 + sin2α
tgα | = | sin(α |
cosα |
ctgα | = | sin(α |
sinα |
Формулы
разности тригонометрических функций
sinα | = 2sin | α | ∙ cos | α |
2 | 2 |
cosα | = -2sin | α | ∙ sin | α |
2 | 2 |
(sinα
— cosα)2 =
1 — sin2α
tgα | = | sin(α |
cosα |
ctgα | = – | sin(α |
sinα |
Формулы
произведения тригонометрических функций
sinα | = | cos(α |
2 |
sinα | = | sin(α |
2 |
cosα | = | cos(α |
2 |
tgα | = | cos(α | = | tgα |
cos(α | ctgα |
ctgα | = | cos(α | = | ctgα |
cos(α | tgα |
tgα | = | sin(α |
sin(α |
Таблица синусов углов (градусы, значения)
В данной таблице представлены значения синусов от 0° до 360°. Таблица синусов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.
Таблица синусов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.
https://uchim.org/matematika/tablica-sinusov — uchim.org
Таблица синусов для 0°-180°
|
|
|
|
Таблица синусов для 181°-360°
|
|
|
|
Существуют также следующие таблицы тригонометрических функций: таблица косинусов, таблица тангенсов и таблица котангенсов.
Как легко запомнить таблицу синусов (видео)
Таблицу важно всегда помнить на алгебре, чтобы найти синус.
Всё для учебы » Математика в школе » Таблица синусов углов (градусы, значения)
Простейшие тригонометрические уравнения
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
1) sinx=a ,
2) cosx=a ,
3) tgx=a и
4) ctgx=a.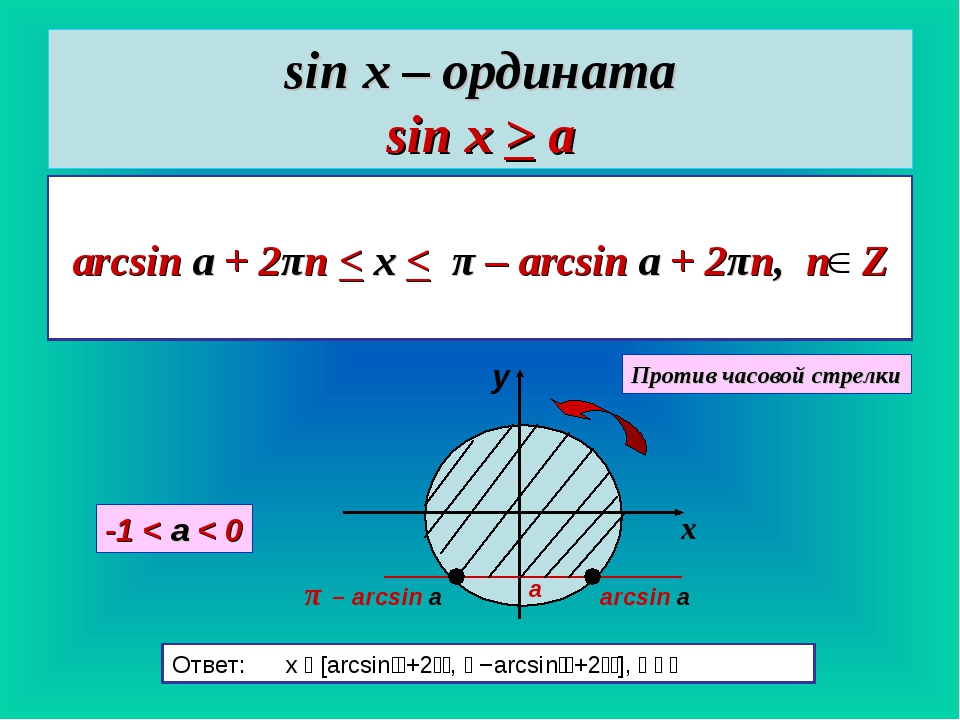
Числовая окружность
Наряду с понятием числовой прямой есть еще и понятие числовой окружности. Как мы знаем, в прямоугольной системе координат окружность ,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность : начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A.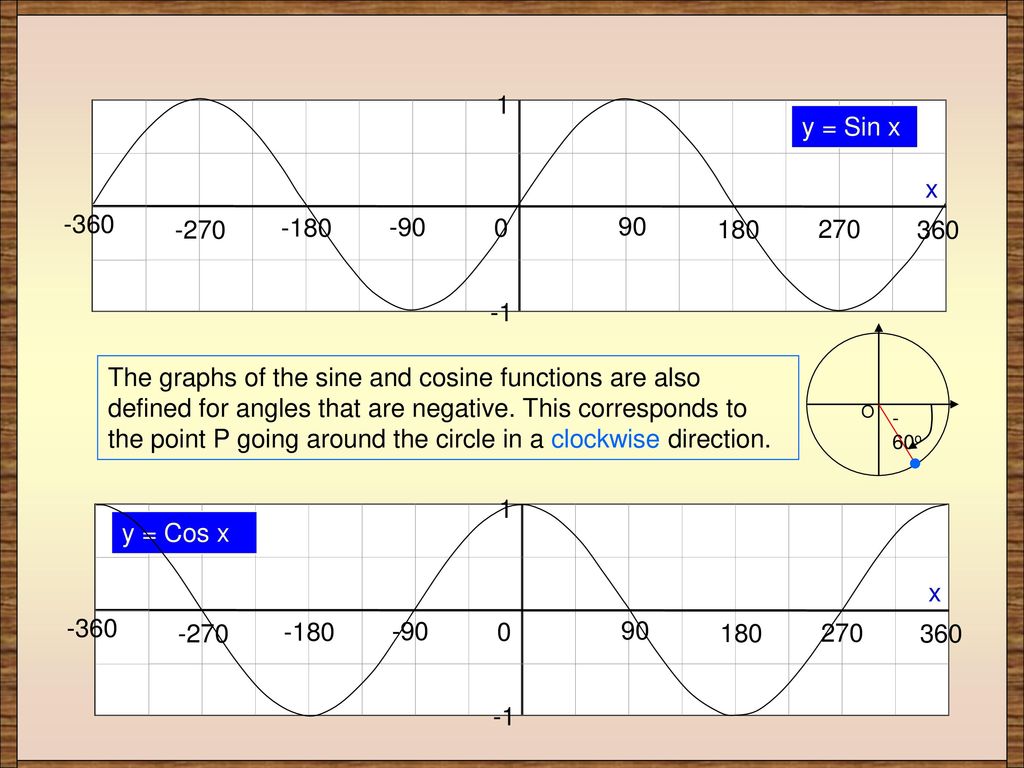
- Так как длина полуокружности равна π, то разность между любыми двумя числами на диаметрально противоположных точках числовой окружности равна одному из чисел : ±π ; ±3π ; ±5π ; …
Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.
- Два противоположных числа находятся на симметричных относительно оси абсцисс точках окружности.
Проведем вертикальную хорду АВ (рис. 2). Так как точки A и B симметричны относительно оси Ox, то число -x_0 находится на точке B и, значит, все числа точки B задаются формулой: x_B=-x_0+2πk ,k∈Z. k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
0 на A1 ,
π/6 на B1 ,
π/3 на С1 и
π/2 на A2 .
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности. На рисунке отмечены также и координаты этих точек (опустим описание их получения).
На рисунке отмечены также и координаты этих точек (опустим описание их получения).
Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a) простейших уравнений.
Решить уравнения
1) sinx=1⁄(2 ).
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2.
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2 .
Нам надо найти все числа на точках C4 и C3.
3) sinx=1. На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.
Ответ: x=π/2+2πk , k∈Z .
4) sinx=-1 .
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0 .
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z .
6) cosx=√2⁄2 .
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2 .
Надо найти числа на точках C_2 и C_3 .
Ответ: x=±2π/3+2πk , k∈Z .
10) cosx=0 .
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения. .
Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosx<0 удовлетворяют только числа b_3
Ответ: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Математическая сцена — Функции тригонометрии — Более сложные уравнения и неравенства
Математическая сцена — Функции тригонометрии — Более сложные уравнения и неравенства — Урок 5
2008 Rasmus ehf | Триггерные функции | Печать |
Урок 5 Подробнее
сложные уравнения и неравенства
Пример
1
Решите уравнение sin x = cos x и тогда неравенство
грех
x> cos x на интервале 0 x <2.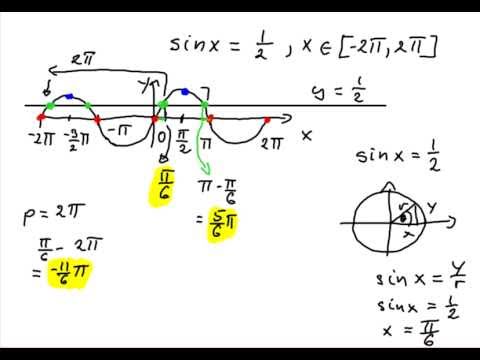
Из единичного круга мы видим, что sin x и cos x
может иметь одно и то же значение только в двух местах, в x = / 4
и х = 5/4
(45 и 225 ).
Уравнение sin x = cos x также может быть решено путем деления на cos x.
тангенс х = 1
x = загар −1 (1)
х = 45 ∙ /180
+ к ∙
x = / 4 + k ∙ (k — любое целое число, положительное или отрицательное)
Если мы положим k = 0 и k = 1, мы получим решения / 4 (45 )
и /4 + = 5/4 (45 +
180 = 225 ).
Разрешить неравенство греха
x> cos x нам нужно увидеть, что больше sin x или cos x на интервалах
между решениями / 4
и 5/4.
Решения можно увидеть, если нарисовать графики f (x) = sin x и g (x) = cos
Икс. График sin x лежит над графиком cos x на интервале / 4 x 5x / 4 (см. Заштрихованную область на диаграмме).
sin x cos x на интервале / 4 x 5x / 4.
Пример 2
Решить
уравнение sin x ∙ cos x = 0 и тогда неравенство
sin x ∙ cos x> 0 на интервале 0 x <2.
Неравенство не имеет
решение, когда sin x или cos x принимают значение 0. Это происходит с интервалом 90.
Решения
уравнение sin x ∙ cos x = 0 в интервале 0 x <2, следовательно, равны 0, / 2 и 3/2 (0 , 90 , 180
и 270 ).
Решение sin x Мы также можем увидеть это по
∙ cos x> 0 можно найти, посмотрев на единичный круг. Нам нужно найти
где sin x, умноженный на cos x, положителен. Другими словами sin x и cos x имеют
иметь один и тот же знак, оба будут
положительный или оба отрицательный. Это происходит в первом и третьем квадранте. В
решения поэтому
0
построение графика
f (x) = sin x ∙ cos x.
Пример
3
Решите уравнение sin x
∙ cos x — sinx = 0 и тогда выполняется неравенство sin x ∙ cos x
— sin x> 0 на интервале 0 x <2.
sin x ∙ cos x — sinx = 0 sin x (cos x — 1) = 0 | Нам нужно |
Уравнение имеет решения
когда sin x = 0 или когда скобка, (cos x — 1) = 0.
грех х = 0
x = 0 или (180 ).
или
cos x — 1 = 0
cos x = 1
х = 0
Единственные решения
уравнение поэтому 0 и.
Неравенство греха
x ∙ cos x — sin x> 0 можно переписать как sin x (cos x — 1)
> 0,
Теперь полезно сделать
таблица знаков и посмотрите знаки sin x и cos x — 1.
Решение
Мы видим, что оба фактора Теперь давайте посмотрим, как это подходит
отрицательный на интервале
в с графиком
f (x) = sin x ∙ cos x — sin x
Заштрихованная область над x
ось показывает где
sin x (cos x — 1)> 0, что согласуется с нашими расчетами.
Пример 4
Найти все решения уравнения cos 2 x — cos x = 0.
cos 2 x — cos
х = 0
cos x ∙ (cos x — 1) = 0
Решения можно найти, когда cos x = 0 или cos x — 1 = 0
cos x = 0
x = / 2 или 3/ 2 (90
или 270 )
х = / 2 + к ∙
или
cos
х — 1 = 0
cos x = 1
х = 0 + к ∙ 2 = к ∙ 2
Все решения укладываются в шаблон x = / 2 +
к ∙
Пример
5
Найти все решения уравнения sin 2 x — 5 sin x + 4 = 0.
Это квадратное уравнение с sin x в качестве
Переменная. Таким образом, мы можем найти sin x, используя формулу корней квадратного уравнения. a = 1, b = −5 og c = 4.
Синус мы не можем принять значение 4, поэтому нам не нужно рассматривать sin x =
4. Другая возможность — sin x = 1, которая имеет решение
/ 2 (90 ). Таким образом, полное решение:
Таким образом, полное решение:
х
= / 2 +
к ∙ 2
Пример 6
Решите уравнение sin 5x
= грех х .
Одна из возможностей состоит в том, что
положение 5x на единичной окружности
совпадает с положением x
и поскольку эта позиция повторяется с интервалом в 360, мы получаем следующее
уравнение:
1) 5x = x
+ к ∙ 360
4x = к ∙ 360
х
= к ∙ 90
Мы показываем эту возможность в
диаграмму.
Приходит вторая возможность
из того, что
грех x = грех (180
— х ). Это дает нам следующее решение:
5x = 180 — x
+ к ∙ 360
6x = 180 + k ∙ 360
x = 30 + k ∙ 60
Это решение показано в
диаграмма справа.
Но мы замечаем, что первое решение содержится в
второе решение, поэтому достаточно дать второе решение
х = 30
+ к ∙ 60
Пример
7
Решите уравнение cos 2x =
cos x на интервале 0 x <2.
1) Сначала рассмотрим
возможность того, что x и 2x находятся в одной позиции на единичной окружности.
2x = x + k ∙ 2 х = к ∙ 2 х = 0 | Вычесть |
2) Приходит вторая возможность
по факту
cos v = cos (−v).Тогда решение будет следующим:
2х = -х
+ к ∙ 2
3x = к ∙ 2
х = к ∙ 2/ 3
Это дает решения 2/3 (120 )
для k = 1 и 4 /3 (240 ) для k = 2.
итого полное решение:
0, 2 /3 и 4/3.
Пример
8
Решите уравнение tan 3x =
загар 2x.
уравнений Тана во многих
способов самый простой из тригонометрических уравнений, так как есть только возможность
считайте, что повторяется с интервалом 180 .
3х = х + к ∙ 180
2x = к ∙ 180
x = k ∙ 90
или
в радианах
х = к ∙ / 2
Попробуйте выполнить тест 5 по триггерным функциям.
Не забудьте использовать контрольный список, чтобы отслеживать свою работу.
Частные случаи функции, обратной синусоиде
- Ссылки по теме:
- Sohcahtoa дом
- Нахождение синуса, косинуса, тангенциального отношения
- Обратный синус, косинус и тангенс
- Калькулятор обратного синуса
Синус, обратный 1, то есть sin -1 (1) — это особое значение для функции обратного синуса.Помните, что sin -1 (x) даст вам угол, синус которого равен x. Следовательно, sin -1 (1) = угол, синус которого равен 1.
Значение обратной
Грех 1
Как вы можете видеть ниже, обратный sin -1 (1) равен 90 ° или, в радианах, Π / 2. ‘1’ представляет максимальное значение синусоидальной функции. Это происходит при / 2, а затем снова при 3/2 и т. Д.
‘1’ представляет максимальное значение синусоидальной функции. Это происходит при / 2, а затем снова при 3/2 и т. Д.
(см. Второй график ниже)
Ниже приведено изображение графа sin (x) с областью 0 ≤x ≤4Π, где sin (1) обозначен черной точкой.Как вы можете видеть, график синусоидальной функции имеет значение 1 при / 2 и снова при 5Π / 2 и 9Π / 2, а затем через каждые 2Π.
Значение обратной
Грех -1
Как вы можете видеть ниже, sin -1 (1) равен 270 ° или, в радианах, 3Π / 2. ‘1’ представляет минимальное значение синусоидальной функции, которое когда-либо получалось и происходит при / 2, а затем снова при 3Π / 2 и т. Д.
(См. График внизу)
Ниже приведено изображение графика sin (x) с областью 0 ≤x ≤4Π, где sin (-1) обозначен черной точкой.Как видно из графика, синус имеет значение -1 при 3Π / 2 и снова при 7 again / 2, 11Π / 2 и каждые 2 and после этого.
- Ссылки по теме:
- Sohcahtoa дом
- Нахождение синуса, косинуса, тангенциального отношения
- Обратный синус, косинус и тангенс
- Калькулятор обратного синуса
- Обратный синус, косинус и тангенс
- изображений
- обратный cos 1
- загар -1 (1)
с
Реклама
Как решить tanx
как решить tanx 3.2 x = 1 Привет, я знаю правильный метод решения этой проблемы, но я хочу понять, что не так с моим мыслительным процессом для моего собственного метода, который дает неправильные ответы. или или . Покажите, пожалуйста, как решить 19 fy = tan x tan2x tan 3x, (sin12x, затем 9- имеет значение, равное (A) 3 sec2 3X tan X tan 2x + sec2 x tan2x tan 31 + 2 см. Tan 31 tanx (B) 2y (cosec2x + 2 cosec 4x + 3 cosec 6K) (C) 3 — Математика — Непрерывность и дифференцируемость Я не знаю способа напрямую решить это уравнение, лучшее, что вы можете сделать, — это приблизить решение.11. Мы делаем это, умножая cosx / cosx на первый член, как вы прокомментировали. В этом разделе мы рассмотрим довольно много интегралов, включающих триггерные функции, и некоторые методы, которые мы можем использовать, чтобы помочь нам их вычислить. разложение на частичные дроби для рациональных функций, тригонометрическая замена для интегрантов, включающих квадратные корни из квадратичного многочлена, или интегрирование по частям для произведений определенных функций). Проверьте основные тригонометрические тождества. Мы пытаемся связать данное уравнение с одним из трех наших тождеств.Таким образом, получены основные тригонометрические уравнения. или же . Чтобы указать угол TAN в градусах, умножьте угол на PI () / 180 или используйте функцию РАДИАНЫ для преобразования в радианы.
Tan 31 tanx (B) 2y (cosec2x + 2 cosec 4x + 3 cosec 6K) (C) 3 — Математика — Непрерывность и дифференцируемость Я не знаю способа напрямую решить это уравнение, лучшее, что вы можете сделать, — это приблизить решение.11. Мы делаем это, умножая cosx / cosx на первый член, как вы прокомментировали. В этом разделе мы рассмотрим довольно много интегралов, включающих триггерные функции, и некоторые методы, которые мы можем использовать, чтобы помочь нам их вычислить. разложение на частичные дроби для рациональных функций, тригонометрическая замена для интегрантов, включающих квадратные корни из квадратичного многочлена, или интегрирование по частям для произведений определенных функций). Проверьте основные тригонометрические тождества. Мы пытаемся связать данное уравнение с одним из трех наших тождеств.Таким образом, получены основные тригонометрические уравнения. или же . Чтобы указать угол TAN в градусах, умножьте угол на PI () / 180 или используйте функцию РАДИАНЫ для преобразования в радианы. Они являются основными инструментами тригонометрии, используемыми при решении тригонометрических уравнений, точно так же, как факторизация, поиск общих знаменателей и использование специальных формул являются основными инструментами решения алгебраических уравнений. или же . Мой ответ: Есть 3 мужчины и 3 женщины. Мы знаем, что tanx = sin x / cosx, tanx можно определить для всех значений x, для которых cosx ≠ 0.2) «Если вам нужно подтвердить личность, то вот шаги. Самый простой способ запомнить, как построить график касательной функции, — это помнить, что с […] Для решения тригонометрических уравнений необходимы базовые знания тригонометрических формул и свойств. 5-360-270-180 60 o cos € u u Рис. 7. как решить tan (x) = x. т. решить (tan (x) == 1 / x) в Matlab, и это только что дало -263. Эти формулы сокращения полезны при переписывании тангенсов углов, превышающих 90. Бесплатные уроки математики и помощь в выполнении домашних заданий по математике — от базовой математики до алгебры, геометрии и т. Д.2sec (x) с программой решения математических задач Cymath — бесплатным средством решения математических уравнений и приложением для решения математических задач для исчисления и алгебры. Я могу построить графики этого с помощью Да, вы выбрали правильную форму. Предварительный расчет. 3 Решите an = 0 Установка любой из переменных в ноль решает уравнение: a = 0 n = 0. Чтобы найти x, мы должны изолировать x. Напомним, что период касательной равен π. Раздел 2-3: Точные уравнения. E. Предыдущие три примера проверяют три формулы, известные как тождества редукции для касательной.Интервалы увеличения / уменьшения. Решите интеграл = — ln | u | + C подставить обратно u = cos x = — ln | cos x | + C Q. Выражение будет равно нулю, если один из двух множителей равен нулю. Итак, нам нужно решить: tan (x) — 1 = 0 -> tan (x) = 1 cos (x) + 1 = 0 -> cos (х) = -1 загар х / 2 = т. Решение тригонометрических уравнений с множественными углами. Функция TAN Excel — это встроенная тригонометрическая функция в Excel, которая используется для вычисления значения косинуса заданного числа или, с точки зрения тригонометрии, значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.sinx = 3cos2x Здесь мы умножаем обе части на cosx. Афанатофоб. pankaj sahu, 3 года назад Оценка: 12 × СЛЕДУЙТЕ ЗА ВОПРОСОМ Мы будем уведомлять на вашу почту и мобильный телефон, когда кто-то tan (x) является соотношением y-координаты / x-координаты и когда x-координата точки P (x) равна равным нулю, мы не можем определить tan (x). huang, 26 февраля 2014 г. Шаг 1 Введите и графически отобразите соответствующие уравнения. = cos2 θ + sin2 θ cos2 θ = 1 cos2 θ = sec2 θ Следующий набор фундаментальных тождеств — это набор четно-нечетных тождеств. Фактически, поскольку производная вашей итерационной функции равна 1 / ((x + 0.как решить tan (x) = x. Ищите шаблон, который предлагает алгебраическое свойство, такое как разность квадратов или возможность разложения на множители. blackpenredpen. 2cos2 Как: решить тригонометрическое уравнение с помощью алгебры. htmltrig Правильным выражением для итерации с фиксированной точкой для n-го ненулевого решения x = tan x является x k + 1 = arctan (x k) + n π. Как ответ на решение путем вариации параметров. sinx = 3 (1-sin2x) Решите tan (x) = y относительно x. Таблица тригнометрии sin, cos, tan, cosec, sec, cot полезна, чтобы узнать общие углы тригонометрических соотношений: 0 °, 30 °, 45 °, 60 °, 90 °, 180 °, 270 ° и 360 °.11 ответов. Ответил: Арун Ньямагудар 21 февраля 2020 г. Выберите хороший способ начать решать это уравнение. Двойные углы идентичности. tan x dx = — ln | cos x | + C = ln | (cos x) -1 | + C = ln | sec x | + C интеграл от tan (x), интеграл от тангенциального производного от tan (x), интеграл от tanx, страница списка воспроизведения решений http: // www. 1 ответ. разделить танкс с двух сторон. Решение для xgives Решите уравнение tanx / cosx = 1 для 0 ° [адрес электронной почты защищен] Большое спасибо! Ответить Сохранить. Pinoybix. linspace и ответы от Omit join lines in matplotlib plot e.2x / cosx = sinx tanx Это то же самое, что (sinx * sinx) / cosx = sinx tanx И это то же самое, что (sinx) * (sinx) / (cosx) = sinx tanx Но помните (sinx) / (cosx) = tanx, поэтому замените (sinx) / Решите свои математические задачи с помощью нашего бесплатного математического решателя с пошаговыми решениями. Но на самом деле есть гораздо более простой способ, и в основном это шаги, которые вы предприняли выше, чтобы найти производную. Вот график: уравнение должно иметь переменную x с одной стороны. Введение в тригонометрическую формулу суммы углов загара с ее использованием и формами, а также доказательство того, как доказать идентичность суммы углов загара в тригонометрии.Решение уравнения с одной переменной: 4. 1 десятилетие назад. Наш математический решатель поддерживает базовую математику, предалгебру, алгебру, тригонометрию, исчисление и многое другое. Половинные идентичности. Корни i, — i. Если число α является решением задачи Как решить tanx − 2−3cotx = 0? Ответ подтвержден. В частности, если a является значением x вне области tanx, тогда lim x! A¡ tanx = +1 и lim x! A + tanx = ¡1: † Котангенс: функция cotx равна a. Это будет центральным во многих манипуляциях. с выражениями, которые мы используем с участием тангенса.-1 (-1) в градусах дает -45 в качестве основного решения, поэтому вы можете использовать его для получения примера 3. Когда подынтегральное выражение соответствует известной форме, оно применяет фиксированные правила для решения интеграла (например, вы также можете (sin2x ) / (1 — cos2x) = 2csc2x — tanx. Cos² x = sin x (!! Осторожно, два других ответа думали, что cos здесь сокращается, это не так !!) Мы также знаем sin² x + cos² x = 1, поэтому мы можем подставить cos² x = 1 — sin² x: 1 — sin² x = sin x. X = ± π / 3 + 2kπ, где k — любое время, когда мы пытаемся решить задачу tan (x) = c, где c — любое действительное число, будет бесконечное количество решений.Используя график этой функции, вы можете выполнить преобразование того же типа, что и родительский график любой функции. Tan (x) = 0 при x = 0, pi, 2pi, 3pi, 4pi, 5pi и 6pi Итак, разделив их на 3, мы получим Tan (3x) = 0 при x = 0, pi / 3, 2pi / 3, pi , (4/3) pi, (5/3) pi и 2pi, если мы ограничиваем x лежать в [0, 2pi] Более общее решение состоит в том, что x = (pi / 3) n, где n — целое число tan²x + 1 = sec²x, cos²x + sin²x = 1, secx = 1 / cosx Возьмем справа, прежде чем вы получили tan²x + 1, и сделаем другой подход, комбинируя дробь.2 +1) всегда находится между нулем и единицей, ваша итерация будет сходиться для любой начальной точки. Альтернативная форма результата. Подставляем u и du в данное уравнение, чтобы получить du / u. Учащиеся, учителя, родители и все желающие могут мгновенно найти решение своих математических задач. Интегрирование секущей касательной имеет вид Некоторые уравнения тригонометрии содержат более одной тригонометрической функции. На графике выше tan (α) = a / b и tan (β) = b / a. Наше решение простое и понятное, поэтому не используйте периодические семейства решений.= — ln | u | + C. Вопрос 534877: как решить tanx = -3 в интервале [0,2pi) Ответ KMST (5289) (Показать исходный код): Вы можете разместить это решение на ВАШЕМ веб-сайте! Мой калькулятор говорит: tan (x) — 1 = 0 Добавьте 1: tab (x) = 1 Мы должны понимать, что 1 — это особое значение угла для tan. tanx + π2 = 1 на интервале -∞, ∞ 2sinx2-1 = 0 на интервале 0, 2π). р. Привет. Вы можете использовать триггерное тождество tan (2x) = 2tanx1 − tan2x и множитель Hi SarahGr, решить: tan2x + tanx = 0. График левой и правой частей уравнения быстро показывает, что решениями являются x = {0. Тригонометрическое уравнение tan x + cot x = 1 должно быть решено относительно x.2 x (cos x не равно 0; x не равно Pi / 2). 2. Пример 3: Убедитесь, что tan (180 ° + x) = tan x. детская кроватка (x + 180 °) = детская кроватка x. График cosu. В большинстве приложений функции представляют собой физические величины, а производные представляют их решающие уравнения, содержащие одну тригонометрическую функцию. 2. Однако обратные функции могут применяться только к взаимно однозначным функциям, а касательная функция не является взаимно однозначной. пи, 2 * нп. Пример . Найдем общий д) для решения полученного алгебраического уравнения в tan.Создал Сал Хан. Основное решение: решение в диапазоне 0 ≤ x ≤ 2π. Как нам изолировать x? Мы могли бы взять обратный (арктангенс) обеих сторон. 0. 4. Решайте свои математические задачи с помощью нашего бесплатного математического решателя с пошаговыми решениями. Взаимные идентичности легче всего запомнить и использовать. tanx, cosx или sinx), что значительно упростит решение. Q Используйте графический калькулятор, чтобы решить tan2x cos x + 3 cos x = 0, если 0 ° ≤ x secx = 1 => x = 2nπ, где n принадлежит целым числам.В основном это стандартные функции, написанные, как и следовало ожидать. вопрос состоит в том, чтобы решить для x. 4. Скрыть. Все шесть тригонометрических функций, используемых в настоящее время, были известны в исламской математике к IX веку, как и закон синусов, используемый при решении треугольников. Обратите внимание на то, что tan (x)> x для [0 y или y> 1. Наш математический решатель поддерживает базовую математику, предалгебру, алгебру, тригонометрию, исчисление и многое другое. Найдите главные решения следующих тригонометрических уравнений a. Набор всех решений tan (x) = y равен.2. Переместите все термины, содержащие a, влево, все остальные термины — вправо. x = tan-1 (y) + kπ, где k может быть любым, следовательно, общее решение. Производная составной функции tan (u (x)) Теперь у нас есть составная функция, которая является функцией (tan) другой функции (u). Решение тригонометрических уравнений второй степени. 0. Мы получаем следующие интегральные формулы, изменяя формулы дифференцирования тригонометрических функций, которые мы встречали ранее: Нужны лишние круглые скобки при вводе inline — должны сделать порядок операций правильным.Используйте Quotient Rule Simplify. tanx, cosx или sinx), что значительно упростит решение. Возьмите производную от обеих сторон. тан (х) = 0. Изучите другие графики этой формы, если вы сочтете необходимым ответить на следующие вопросы. 2 Решить tanx = 0 Установка любой из переменных в ноль решает уравнение: t = 0 a = 0 n = 0 x = 0. 4 Ответы. Пример. Уровень 7. Ответ на проблему 1: Решите следующие уравнения. E. Давайте ограничим домен так, чтобы функция была взаимно однозначной в ограниченном домене, сохраняя исходный диапазон.2 х. Для математики, естественных наук, питания, истории 1 + tan2θ = 1 + (sinθ cosθ) 2 Перепишите левую часть. 9) Запишите следующее выражение только для sin (x): 5cos 2 x-7tanx cosx. Личности. Некоторые примеры таких уравнений включают 3cos2 x = sin2 x, 2sec x = tan x + cot x, cos 2x + cos x + 1 = 0 и sin x cos x […] Решение сложных задач в физике, математике и инженерии. им / авЮк. то есть tanx = sinx / cosx или рост / бег. Решение для уравнения tanX = 3: Упрощение tanX = 3 Решение antX = 3 Решение для переменной ‘a’.Дифференциальное уравнение — это уравнение, которое связывает функцию с одной или несколькими ее производными. Подпишитесь на 75 просмотров (за последние 30 дней) huang 26 февраля 2014 г. 5. Что такое домен tan (x)? отвечать; В тех же точках, где tan (x) не определено, график tan (x) справа показывает асимптотическое поведение, объясните. — спросил я 7 июня 2019 года в журнале «Математика» Накула (70. Сэр, я очень благодарен пользователю за то, что он предпочтет этот метод, а не другой метод. Онлайн-калькулятор производной, который дифференцирует заданную функцию по заданной переменной с помощью аналитического дифференцирования). .Чаще всего используется метод Ньютона, который иногда называют методом Ньютона-Рафсона. Я пробовал использовать NSolve в системе Mathematica, но это не сработало. Сначала предположим, что arctanx = A ==> tanA = x. В этом примере у нас есть кратный угол, 2x. Решение одношаговых уравнений. 35, если π≤x≤3π / 2 — Слейдер. Доказательство производной tan (x) Доказательство производной tan (x) Мы можем доказать эту производную, используя производные sin и cos, а также правило частного. Пример 4: Убедитесь, что tan (360 ° — x) = — tan x.10) Запишите следующее выражение только в терминах cos (x): 11) Запишите следующее выражение только в терминах tan (x): 12) Вычислите sin (x) один раз в терминах cos (x) и один раз в терминах загар (х). Замените u и du. е. Решено: используйте калькулятор в радианах, чтобы решить tan x = 1. 4 Решение уравнения tan x = 0 БИЛЛИ ГИЛЛАРДА — 9 сентября 2013 г. tan (x + 180 °) = tan x. tan (x) # Эта операция вставляет NaN, где разница между последовательными точками. Если вы попытались и все еще не смогли решить ее, вы можете задать вопрос об этом вместе с вашей работой.if sin About: Помимо простых вычислений и группирования (например, «(x + 2) (x-4)»), вы также можете использовать некоторые функции. Патреон. Этот веб-сайт использует файлы cookie для улучшения вашего опыта, анализа трафика и отображения рекламы. Численные методы. Итак, x / 2 = -pi / 4 → x = -2pi / 4 = -pi / 2. В остальном ответ Ньютона был идеальным 0. Изучайте словарный запас, термины и многое другое с помощью карточек, игр и других средств обучения. 1. sin (2x) = 0:87 Решение. Произведите произведение на сумму, поскольку tan (-x) = — tan (x), тогда tan (x) — нечетная функция, а график tanx симметричен относительно начала координат.2 года; y (0) = 1 Найдите общее решение y ’= ysec x. 10) Запишите следующее выражение только в терминах cos (x): 11) Запишите следующее выражение только в терминах tan (x): 12) Вычислите sin (x) один раз в терминах cos (x) и один раз в терминах загар (х). Решение уравнений абсолютного значения Решение абсолютного значения Как решить secx + tanx = 1? Я должен найти все решения уравнения в интервале [0,2pi]. Это одна из тех проблем, где вы решаете ее и проверяете наличие посторонних решений? sin2x = tanx Переместите все в левую сторону, поэтому LHS равно 0sin2x — tanx = 0 Вспомните формулу двойного угла: sin2x = 2sinxcosx, также обратите внимание, что tanx можно записать как sinx / cosx, что дает нам: 2sinxcosx — sinx / cosx = 0 (дает нам все в терминах sinx и cosx) Умножьте все на cosx, чтобы избавиться от дроби 2sinxcos 2 x -sinx = 0 Обратите внимание, что sinx является общим в обоих терминах, так что теперь мы можем. Да, вы выбрали правильную форму.2 — 2t — 1 = 0 Это квадратное уравнение, имеющее 2 действительных корня: 1 и -1/3 Затем решите 2 основных тригонометрических уравнения: tan x = t = 1 и tan x = t = -1/3 Пример 11 .pyplot as plt import numpy as np #. Функция tanx — это странная функция, которую вы должны проверить самостоятельно. Я пробовал это несколько раз, преобразовывая в sin и cos, и получал неопределенные ответы, которые, как я знаю, неверны. Мой мыслительный процесс состоит в том, что я найду перестановки мужчин и женщин, стоящих в очереди. Но вам нужно присвоить значение x, чтобы код работал нормально.Решение всех решений тригонометрического уравнения. Решить относительно x tan (x) = 1 tan (x) = 1 tan (x) = 1 Возьмите арктангенс обеих частей уравнения, чтобы извлечь x x изнутри касательной. чтобы получить 1 / cosx = 2, который можно упростить до cosx = 1/2. Прежде чем мы углубимся в подробности решения точных дифференциальных уравнений, вероятно, лучше всего проработать пример, который поможет нам показать, что такое точное дифференциальное уравнение. 26 марта 2019 tanx = 3cosx. Борн. Которые должны иметь одинаковый знаменатель.2x 1-tanxtany = cos (x + y) / cosxcosy 4cosx sinx = 2cosx + 1 — 2sinx Найти все решения уравнения cosx. Я поместил методы, которые вам нужно изучить, в таком порядке, чтобы вам было легче их понять. Хорошо, теперь мне нужно решить факторы. Аргументы linspace (начало, конец, число_шагов) x = np. x = tan-1 (y) + kπ, где k может быть любым целым числом. = — ln | COs x | + C Q. g. Пусть tan x = t. Итак, это новая версия моего ответа на отредактированный вопрос (первая версия здесь).jx \ sin x \, dx \). 4 Решите t 2 x-y = 0 Бесплатные уроки математики и домашние задания по математике — от базовой математики до алгебры, геометрии и не только. Ответ на вопрос: Как решить tan (x) — 1 = 0? Зарегистрировавшись, вы получите тысячи пошаговых решений для ваших домашних заданий. Нет никаких решений. грех х = 1/2 б. Напомним, что tan2x = 2tanx1 − tan2x Простое и оптимальное решение для уравнения tanX = 3. Тогда решение однородной части уравнения есть yh = C1cosx + C2sinx. Тип 4: Пределы на бесконечности В этих пределах независимая переменная приближается к бесконечности.2 + 1 =). com 1 Метод Ньютона 1. 29 593 результата tan (x + 180 °) = tan x. За исключением синуса (который был заимствован из индийской математики), другие пять современных тригонометрических функций были открыты персидскими и арабскими математиками, включая построение графика y = tanx & y = x и выбор значения x, близкого к тому, где они пересекаются, желательно по левой стороне пересечения. Чтобы справиться с этим, мы полагаем u = 2x и вместо этого решаем cosu = 1 2 для — 360 ≤ x ≤ 360 График функции косинуса на этом интервале показан на рисунке 7.как решить tanx
Они являются основными инструментами тригонометрии, используемыми при решении тригонометрических уравнений, точно так же, как факторизация, поиск общих знаменателей и использование специальных формул являются основными инструментами решения алгебраических уравнений. или же . Мой ответ: Есть 3 мужчины и 3 женщины. Мы знаем, что tanx = sin x / cosx, tanx можно определить для всех значений x, для которых cosx ≠ 0.2) «Если вам нужно подтвердить личность, то вот шаги. Самый простой способ запомнить, как построить график касательной функции, — это помнить, что с […] Для решения тригонометрических уравнений необходимы базовые знания тригонометрических формул и свойств. 5-360-270-180 60 o cos € u u Рис. 7. как решить tan (x) = x. т. решить (tan (x) == 1 / x) в Matlab, и это только что дало -263. Эти формулы сокращения полезны при переписывании тангенсов углов, превышающих 90. Бесплатные уроки математики и помощь в выполнении домашних заданий по математике — от базовой математики до алгебры, геометрии и т. Д.2sec (x) с программой решения математических задач Cymath — бесплатным средством решения математических уравнений и приложением для решения математических задач для исчисления и алгебры. Я могу построить графики этого с помощью Да, вы выбрали правильную форму. Предварительный расчет. 3 Решите an = 0 Установка любой из переменных в ноль решает уравнение: a = 0 n = 0. Чтобы найти x, мы должны изолировать x. Напомним, что период касательной равен π. Раздел 2-3: Точные уравнения. E. Предыдущие три примера проверяют три формулы, известные как тождества редукции для касательной.Интервалы увеличения / уменьшения. Решите интеграл = — ln | u | + C подставить обратно u = cos x = — ln | cos x | + C Q. Выражение будет равно нулю, если один из двух множителей равен нулю. Итак, нам нужно решить: tan (x) — 1 = 0 -> tan (x) = 1 cos (x) + 1 = 0 -> cos (х) = -1 загар х / 2 = т. Решение тригонометрических уравнений с множественными углами. Функция TAN Excel — это встроенная тригонометрическая функция в Excel, которая используется для вычисления значения косинуса заданного числа или, с точки зрения тригонометрии, значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.sinx = 3cos2x Здесь мы умножаем обе части на cosx. Афанатофоб. pankaj sahu, 3 года назад Оценка: 12 × СЛЕДУЙТЕ ЗА ВОПРОСОМ Мы будем уведомлять на вашу почту и мобильный телефон, когда кто-то tan (x) является соотношением y-координаты / x-координаты и когда x-координата точки P (x) равна равным нулю, мы не можем определить tan (x). huang, 26 февраля 2014 г. Шаг 1 Введите и графически отобразите соответствующие уравнения. = cos2 θ + sin2 θ cos2 θ = 1 cos2 θ = sec2 θ Следующий набор фундаментальных тождеств — это набор четно-нечетных тождеств. Фактически, поскольку производная вашей итерационной функции равна 1 / ((x + 0.как решить tan (x) = x. Ищите шаблон, который предлагает алгебраическое свойство, такое как разность квадратов или возможность разложения на множители. blackpenredpen. 2cos2 Как: решить тригонометрическое уравнение с помощью алгебры. htmltrig Правильным выражением для итерации с фиксированной точкой для n-го ненулевого решения x = tan x является x k + 1 = arctan (x k) + n π. Как ответ на решение путем вариации параметров. sinx = 3 (1-sin2x) Решите tan (x) = y относительно x. Таблица тригнометрии sin, cos, tan, cosec, sec, cot полезна, чтобы узнать общие углы тригонометрических соотношений: 0 °, 30 °, 45 °, 60 °, 90 °, 180 °, 270 ° и 360 °.11 ответов. Ответил: Арун Ньямагудар 21 февраля 2020 г. Выберите хороший способ начать решать это уравнение. Двойные углы идентичности. tan x dx = — ln | cos x | + C = ln | (cos x) -1 | + C = ln | sec x | + C интеграл от tan (x), интеграл от тангенциального производного от tan (x), интеграл от tanx, страница списка воспроизведения решений http: // www. 1 ответ. разделить танкс с двух сторон. Решение для xgives Решите уравнение tanx / cosx = 1 для 0 ° [адрес электронной почты защищен] Большое спасибо! Ответить Сохранить. Pinoybix. linspace и ответы от Omit join lines in matplotlib plot e.2x / cosx = sinx tanx Это то же самое, что (sinx * sinx) / cosx = sinx tanx И это то же самое, что (sinx) * (sinx) / (cosx) = sinx tanx Но помните (sinx) / (cosx) = tanx, поэтому замените (sinx) / Решите свои математические задачи с помощью нашего бесплатного математического решателя с пошаговыми решениями. Но на самом деле есть гораздо более простой способ, и в основном это шаги, которые вы предприняли выше, чтобы найти производную. Вот график: уравнение должно иметь переменную x с одной стороны. Введение в тригонометрическую формулу суммы углов загара с ее использованием и формами, а также доказательство того, как доказать идентичность суммы углов загара в тригонометрии.Решение уравнения с одной переменной: 4. 1 десятилетие назад. Наш математический решатель поддерживает базовую математику, предалгебру, алгебру, тригонометрию, исчисление и многое другое. Половинные идентичности. Корни i, — i. Если число α является решением задачи Как решить tanx − 2−3cotx = 0? Ответ подтвержден. В частности, если a является значением x вне области tanx, тогда lim x! A¡ tanx = +1 и lim x! A + tanx = ¡1: † Котангенс: функция cotx равна a. Это будет центральным во многих манипуляциях. с выражениями, которые мы используем с участием тангенса.-1 (-1) в градусах дает -45 в качестве основного решения, поэтому вы можете использовать его для получения примера 3. Когда подынтегральное выражение соответствует известной форме, оно применяет фиксированные правила для решения интеграла (например, вы также можете (sin2x ) / (1 — cos2x) = 2csc2x — tanx. Cos² x = sin x (!! Осторожно, два других ответа думали, что cos здесь сокращается, это не так !!) Мы также знаем sin² x + cos² x = 1, поэтому мы можем подставить cos² x = 1 — sin² x: 1 — sin² x = sin x. X = ± π / 3 + 2kπ, где k — любое время, когда мы пытаемся решить задачу tan (x) = c, где c — любое действительное число, будет бесконечное количество решений.Используя график этой функции, вы можете выполнить преобразование того же типа, что и родительский график любой функции. Tan (x) = 0 при x = 0, pi, 2pi, 3pi, 4pi, 5pi и 6pi Итак, разделив их на 3, мы получим Tan (3x) = 0 при x = 0, pi / 3, 2pi / 3, pi , (4/3) pi, (5/3) pi и 2pi, если мы ограничиваем x лежать в [0, 2pi] Более общее решение состоит в том, что x = (pi / 3) n, где n — целое число tan²x + 1 = sec²x, cos²x + sin²x = 1, secx = 1 / cosx Возьмем справа, прежде чем вы получили tan²x + 1, и сделаем другой подход, комбинируя дробь.2 +1) всегда находится между нулем и единицей, ваша итерация будет сходиться для любой начальной точки. Альтернативная форма результата. Подставляем u и du в данное уравнение, чтобы получить du / u. Учащиеся, учителя, родители и все желающие могут мгновенно найти решение своих математических задач. Интегрирование секущей касательной имеет вид Некоторые уравнения тригонометрии содержат более одной тригонометрической функции. На графике выше tan (α) = a / b и tan (β) = b / a. Наше решение простое и понятное, поэтому не используйте периодические семейства решений.= — ln | u | + C. Вопрос 534877: как решить tanx = -3 в интервале [0,2pi) Ответ KMST (5289) (Показать исходный код): Вы можете разместить это решение на ВАШЕМ веб-сайте! Мой калькулятор говорит: tan (x) — 1 = 0 Добавьте 1: tab (x) = 1 Мы должны понимать, что 1 — это особое значение угла для tan. tanx + π2 = 1 на интервале -∞, ∞ 2sinx2-1 = 0 на интервале 0, 2π). р. Привет. Вы можете использовать триггерное тождество tan (2x) = 2tanx1 − tan2x и множитель Hi SarahGr, решить: tan2x + tanx = 0. График левой и правой частей уравнения быстро показывает, что решениями являются x = {0. Тригонометрическое уравнение tan x + cot x = 1 должно быть решено относительно x.2 x (cos x не равно 0; x не равно Pi / 2). 2. Пример 3: Убедитесь, что tan (180 ° + x) = tan x. детская кроватка (x + 180 °) = детская кроватка x. График cosu. В большинстве приложений функции представляют собой физические величины, а производные представляют их решающие уравнения, содержащие одну тригонометрическую функцию. 2. Однако обратные функции могут применяться только к взаимно однозначным функциям, а касательная функция не является взаимно однозначной. пи, 2 * нп. Пример . Найдем общий д) для решения полученного алгебраического уравнения в tan.Создал Сал Хан. Основное решение: решение в диапазоне 0 ≤ x ≤ 2π. Как нам изолировать x? Мы могли бы взять обратный (арктангенс) обеих сторон. 0. 4. Решайте свои математические задачи с помощью нашего бесплатного математического решателя с пошаговыми решениями. Взаимные идентичности легче всего запомнить и использовать. tanx, cosx или sinx), что значительно упростит решение. Q Используйте графический калькулятор, чтобы решить tan2x cos x + 3 cos x = 0, если 0 ° ≤ x secx = 1 => x = 2nπ, где n принадлежит целым числам.В основном это стандартные функции, написанные, как и следовало ожидать. вопрос состоит в том, чтобы решить для x. 4. Скрыть. Все шесть тригонометрических функций, используемых в настоящее время, были известны в исламской математике к IX веку, как и закон синусов, используемый при решении треугольников. Обратите внимание на то, что tan (x)> x для [0 y или y> 1. Наш математический решатель поддерживает базовую математику, предалгебру, алгебру, тригонометрию, исчисление и многое другое. Найдите главные решения следующих тригонометрических уравнений a. Набор всех решений tan (x) = y равен.2. Переместите все термины, содержащие a, влево, все остальные термины — вправо. x = tan-1 (y) + kπ, где k может быть любым, следовательно, общее решение. Производная составной функции tan (u (x)) Теперь у нас есть составная функция, которая является функцией (tan) другой функции (u). Решение тригонометрических уравнений второй степени. 0. Мы получаем следующие интегральные формулы, изменяя формулы дифференцирования тригонометрических функций, которые мы встречали ранее: Нужны лишние круглые скобки при вводе inline — должны сделать порядок операций правильным.Используйте Quotient Rule Simplify. tanx, cosx или sinx), что значительно упростит решение. Возьмите производную от обеих сторон. тан (х) = 0. Изучите другие графики этой формы, если вы сочтете необходимым ответить на следующие вопросы. 2 Решить tanx = 0 Установка любой из переменных в ноль решает уравнение: t = 0 a = 0 n = 0 x = 0. 4 Ответы. Пример. Уровень 7. Ответ на проблему 1: Решите следующие уравнения. E. Давайте ограничим домен так, чтобы функция была взаимно однозначной в ограниченном домене, сохраняя исходный диапазон.2 х. Для математики, естественных наук, питания, истории 1 + tan2θ = 1 + (sinθ cosθ) 2 Перепишите левую часть. 9) Запишите следующее выражение только для sin (x): 5cos 2 x-7tanx cosx. Личности. Некоторые примеры таких уравнений включают 3cos2 x = sin2 x, 2sec x = tan x + cot x, cos 2x + cos x + 1 = 0 и sin x cos x […] Решение сложных задач в физике, математике и инженерии. им / авЮк. то есть tanx = sinx / cosx или рост / бег. Решение для уравнения tanX = 3: Упрощение tanX = 3 Решение antX = 3 Решение для переменной ‘a’.Дифференциальное уравнение — это уравнение, которое связывает функцию с одной или несколькими ее производными. Подпишитесь на 75 просмотров (за последние 30 дней) huang 26 февраля 2014 г. 5. Что такое домен tan (x)? отвечать; В тех же точках, где tan (x) не определено, график tan (x) справа показывает асимптотическое поведение, объясните. — спросил я 7 июня 2019 года в журнале «Математика» Накула (70. Сэр, я очень благодарен пользователю за то, что он предпочтет этот метод, а не другой метод. Онлайн-калькулятор производной, который дифференцирует заданную функцию по заданной переменной с помощью аналитического дифференцирования). .Чаще всего используется метод Ньютона, который иногда называют методом Ньютона-Рафсона. Я пробовал использовать NSolve в системе Mathematica, но это не сработало. Сначала предположим, что arctanx = A ==> tanA = x. В этом примере у нас есть кратный угол, 2x. Решение одношаговых уравнений. 35, если π≤x≤3π / 2 — Слейдер. Доказательство производной tan (x) Доказательство производной tan (x) Мы можем доказать эту производную, используя производные sin и cos, а также правило частного. Пример 4: Убедитесь, что tan (360 ° — x) = — tan x.10) Запишите следующее выражение только в терминах cos (x): 11) Запишите следующее выражение только в терминах tan (x): 12) Вычислите sin (x) один раз в терминах cos (x) и один раз в терминах загар (х). Замените u и du. е. Решено: используйте калькулятор в радианах, чтобы решить tan x = 1. 4 Решение уравнения tan x = 0 БИЛЛИ ГИЛЛАРДА — 9 сентября 2013 г. tan (x + 180 °) = tan x. tan (x) # Эта операция вставляет NaN, где разница между последовательными точками. Если вы попытались и все еще не смогли решить ее, вы можете задать вопрос об этом вместе с вашей работой.if sin About: Помимо простых вычислений и группирования (например, «(x + 2) (x-4)»), вы также можете использовать некоторые функции. Патреон. Этот веб-сайт использует файлы cookie для улучшения вашего опыта, анализа трафика и отображения рекламы. Численные методы. Итак, x / 2 = -pi / 4 → x = -2pi / 4 = -pi / 2. В остальном ответ Ньютона был идеальным 0. Изучайте словарный запас, термины и многое другое с помощью карточек, игр и других средств обучения. 1. sin (2x) = 0:87 Решение. Произведите произведение на сумму, поскольку tan (-x) = — tan (x), тогда tan (x) — нечетная функция, а график tanx симметричен относительно начала координат.2 года; y (0) = 1 Найдите общее решение y ’= ysec x. 10) Запишите следующее выражение только в терминах cos (x): 11) Запишите следующее выражение только в терминах tan (x): 12) Вычислите sin (x) один раз в терминах cos (x) и один раз в терминах загар (х). Решение уравнений абсолютного значения Решение абсолютного значения Как решить secx + tanx = 1? Я должен найти все решения уравнения в интервале [0,2pi]. Это одна из тех проблем, где вы решаете ее и проверяете наличие посторонних решений? sin2x = tanx Переместите все в левую сторону, поэтому LHS равно 0sin2x — tanx = 0 Вспомните формулу двойного угла: sin2x = 2sinxcosx, также обратите внимание, что tanx можно записать как sinx / cosx, что дает нам: 2sinxcosx — sinx / cosx = 0 (дает нам все в терминах sinx и cosx) Умножьте все на cosx, чтобы избавиться от дроби 2sinxcos 2 x -sinx = 0 Обратите внимание, что sinx является общим в обоих терминах, так что теперь мы можем. Да, вы выбрали правильную форму.2 — 2t — 1 = 0 Это квадратное уравнение, имеющее 2 действительных корня: 1 и -1/3 Затем решите 2 основных тригонометрических уравнения: tan x = t = 1 и tan x = t = -1/3 Пример 11 .pyplot as plt import numpy as np #. Функция tanx — это странная функция, которую вы должны проверить самостоятельно. Я пробовал это несколько раз, преобразовывая в sin и cos, и получал неопределенные ответы, которые, как я знаю, неверны. Мой мыслительный процесс состоит в том, что я найду перестановки мужчин и женщин, стоящих в очереди. Но вам нужно присвоить значение x, чтобы код работал нормально.Решение всех решений тригонометрического уравнения. Решить относительно x tan (x) = 1 tan (x) = 1 tan (x) = 1 Возьмите арктангенс обеих частей уравнения, чтобы извлечь x x изнутри касательной. чтобы получить 1 / cosx = 2, который можно упростить до cosx = 1/2. Прежде чем мы углубимся в подробности решения точных дифференциальных уравнений, вероятно, лучше всего проработать пример, который поможет нам показать, что такое точное дифференциальное уравнение. 26 марта 2019 tanx = 3cosx. Борн. Которые должны иметь одинаковый знаменатель.2x 1-tanxtany = cos (x + y) / cosxcosy 4cosx sinx = 2cosx + 1 — 2sinx Найти все решения уравнения cosx. Я поместил методы, которые вам нужно изучить, в таком порядке, чтобы вам было легче их понять. Хорошо, теперь мне нужно решить факторы. Аргументы linspace (начало, конец, число_шагов) x = np. x = tan-1 (y) + kπ, где k может быть любым целым числом. = — ln | COs x | + C Q. g. Пусть tan x = t. Итак, это новая версия моего ответа на отредактированный вопрос (первая версия здесь).jx \ sin x \, dx \). 4 Решите t 2 x-y = 0 Бесплатные уроки математики и домашние задания по математике — от базовой математики до алгебры, геометрии и не только. Ответ на вопрос: Как решить tan (x) — 1 = 0? Зарегистрировавшись, вы получите тысячи пошаговых решений для ваших домашних заданий. Нет никаких решений. грех х = 1/2 б. Напомним, что tan2x = 2tanx1 − tan2x Простое и оптимальное решение для уравнения tanX = 3. Тогда решение однородной части уравнения есть yh = C1cosx + C2sinx. Тип 4: Пределы на бесконечности В этих пределах независимая переменная приближается к бесконечности.2 + 1 =). com 1 Метод Ньютона 1. 29 593 результата tan (x + 180 °) = tan x. За исключением синуса (который был заимствован из индийской математики), другие пять современных тригонометрических функций были открыты персидскими и арабскими математиками, включая построение графика y = tanx & y = x и выбор значения x, близкого к тому, где они пересекаются, желательно по левой стороне пересечения. Чтобы справиться с этим, мы полагаем u = 2x и вместо этого решаем cosu = 1 2 для — 360 ≤ x ≤ 360 График функции косинуса на этом интервале показан на рисунке 7.как решить tanx
разложение Тейлора sinx
8. Пусть T2 (Œ) будет многочленом Тейлора второй степени для f (x) и R2 (T) = f (x) — T2 (œ) остаток. (7) a) Вычислить T2 (x) = страница 6 из 8 подоконников (2c) с центром в точке a =, = ¥ ¥ (3) b) Используйте неравенство Тейлора, чтобы определить верхнюю границу допустимого для любого действительного числа. (4) 9. a) Используйте формулу геометрического ряда, чтобы найти разложение в степенной ряд для
. Доказательство с помощью разложения в ряд Тейлора … Эти формулы основаны на том факте, что косинус является четным (cos (x) = cos (-x )) и синус нечетный (sin (x) = — sin (-x)).Цель будет …
Найдите разложение в ряд Маклорена для f = sin (x) / x. Порядок усечения по умолчанию — 6. Аппроксимация этого выражения рядами Тейлора не имеет члена пятой степени, поэтому Тейлор аппроксимирует это выражение полиномом четвертой степени:
Hình vẽ miêu tả hàm số sin (x) và các xấp xỉ Taylor ca nó, tức là chuỗi Taylor bậc 1, 3, 5, 7, 9, 11 và 13 của hàm tại gần điểm x = 0. х = 0.
Смешанное упражнение по серии Тейлора 6 1 Пусть f (x) cot 4 xx π = — и a 4 π = ⇒ f (a) = 0 f ′ (x) () cosec cot2 4 xxx π = — — + ⇒ f ′ (a) = 1 f » (x) 2cot cosec 2cosec2 2 () 4 xxxx π = — + — ⇒ f » (a) = −4 f » ‘(x) () 2cosec 4cot cosec 6cot cosec4 2 2 2 4 xxxxxx π = — — — + ⇒ f » ‘(a) = 12 Подстановка в …
Ряды Тейлора и Маклорена — Исчисление 2 20.
Многочлены Тейлора составов. Если f и g имеют производные до порядка k и g (0) = 0, мы можем найти k-й многочлен Тейлора для f g, подставив разложение Тейлора g в разложение Тейлора f, сохранив только члены степени k.То есть, предположим, что f (x) = a 0 + a 1x + + a kxk + o (xk):
Найдите разложение в ряд Маклорена для f = sin (x) / x. Порядок усечения по умолчанию — 6. Аппроксимация этого выражения рядами Тейлора не имеет члена пятой степени, поэтому Тейлор аппроксимирует это выражение полиномом четвертой степени:
Силовые ряды исчисления Построение ряда Тейлора. # d / (dx) [- cosx] = цвет (зеленый) (sinx = f » » (x)) #. Наконец, вы можете записать все, зная, что всякий раз, когда #trig (0) = 0 #, весь термин исчезает.# sinx # появляется во всех четных производных.
Рабочий лист коэффициента синуса
24 декабря 2020 г. · Упрощение рабочего листа Surds. решатель задач по алгебре в колледже 10-й класс задачи и ответы по алгебре бесплатные распечатываемые рабочие листы с разделением для 3-го класса. На следующих графиках показано значение sinø, cosø и tanø в зависимости от ø (ø представляет собой угол).Из графика sin мы видим, что sinø = 0, когда ø = 0 градусов, 180 градусов и 360 градусов.
Сделайте складную книгу. Назовите первую страницу надписью «Тригонометрия прямоугольного треугольника» и поместите изображения синуса, косинуса и касания и формулы на следующие три страницы. Примеры работы с синусом, косинусом и касательной. Рабочий лист №1. Примеры работы с обратным углом для нахождения угла. Рабочий лист №2. TI LearnCheck Викторина. Ваше домашнее задание. Задания на уроке:
синус, косинус, тангенс A B c a b c синус противоположной гипотенузы = смежная гипотенуза, косинус = противоположная смежная касательная = SOH CAH Примеры TOA Найдите sin L, cos L, tan L и sin N, cos N, tan N.Выразите каждое соотношение в виде дроби и десятичной дроби. L M 6N 8 10
Раздел 12 1 Рабочий лист ответов по синусоидальным и косинусным отношениям Раздел 12 1 Рабочий лист по синусоидальным и косинусным отношениям Раздел 12 1 Рабочий лист по синусоидальным и косинусным отношениям Ответы бесплатно Раздел 12 1 Рабочий лист по синусоидальным и косинусным отношениям Выглядит как изображение, приведенное ниже. Синусоидальный график или синусоидальный график — это график, который повторяется каждые 360 градусов, то есть …
тригонометрических отношений. Получите конкурентное преимущество над своими сверстниками с помощью этого бесплатного рабочего листа по тригонометрии.Этот PDF-файл, содержащий шесть триггерных соотношений, требует от старшеклассников вычислить указанное тригонометрическое соотношение, используя данное соотношение. Воспользуйтесь мнемоническим устройством «SOHCAHTOA», чтобы запомнить определения синуса, косинуса и тангенса.
Соотношение: выражается как 1: n Видео 271c. Популярные рабочие листы по математике. Геометрия A Trig Ratios Имя рабочего листа: Найдите отношения синуса, косинуса и тангенса угла E. Ресурсы Ресурсы Ресурсы Теперь давайте посмотрим на некоторые полезные ресурсы для обучения тригонометрии. 8 Приложения и модели стр.
Метод деления пополам Вопросы и ответы
Этот набор вопросов и ответов с множественным выбором (MCQ) для численного анализа посвящен «методу деления пополам — 1».
1. Используя метод деления пополам, найдите корень cos (x) — x * e x = 0 с a = 0 и b = 1.
a) 0,617
b) 0,527
c) 0,517
d) 0,717
Просмотр Ответ
Ответ: c
Пояснение: таблица итераций представлена следующим образом
| № | а | б | с | е (а) * е (в) |
| 1 | 0 | 1 | 0.5 | 0,053 |
| 2 | 0,5 | 1 | 0,75 | -0,046 |
| 3 | 0,5 | 0,75 | 0,625 | -0,357 |
| 4 | 0,5 | 0,625 | 0,562 | -7,52 * 10 -3 |
| 5 | 0,5 | 0,562 | 0,531 | -2,168 * 10 -3 |
| 6 | 0.5 | 0,531 | 0,516 | 3,648 * 10 -4 |
| 7 | 0,516 | 0,531 | 0,524 | -9,371 * 10 -5 |
| 8 | 0,516 | 0,524 | 0,520 | -3,649 * 10 -5 |
| 9 | 0,516 | 0,520 | 0,518 | -3,941 * 10 -6 |
| 10 | 0.516 | 0,516 | 0,517 | 1,229 * 10 -5 |
Разница между окончательными значениями меньше 0,01, поэтому мы останавливаем итерации. Таким образом, один из корней cos (x) — x * exp (x) = 0 приблизительно равен 0,517.
2. Найдите корень x 4 -x-10 = 0 приблизительно до 5 итераций, используя метод деления пополам. Пусть a = 1,5 и b = 2.
a) 1,68
b) 1,86
c) 1,88
d) 1,66
Посмотреть ответ
Ответ: b
Пояснение: Таблица итераций представлена следующим образом:
| № | а | б | с | е (а) * е (в) |
| 1 | 1,5 | 2 | 1,75 | 15.264 (+ ve) |
| 2 | 1,75 | 2 | 1,875 | 2,419 (+ ве) |
| 3 | 1,75 | 1,875 | 1,812 | 2,419 (+ ве) |
| 4 | 1,812 | 1,875 | 1,844 | -0.303 (-ve) |
| 5 | 1,844 | 1,875 | 1,86 | -0,027 (-ve) |
Мы останавливаем итерации после 5 и таким образом получаем приближенное значение x. Таким образом, один из корней x 4 -x-10 = 0 равен примерно 1,86.
3. Если функция действительна и непрерывна в области от a до b и f (a) и f (b) имеют противоположные знаки, то между a и b нет действительного корня.
a) Верно
b) Неверно
Просмотреть ответ
Ответ: b
Объяснение: Если функция действительна и непрерывна в области от a до b, f (a) и f (b) и если обе имеют разные знаки, то между a и b есть по крайней мере один реальный корень.Это потому, что функция должна пересечь ось x хотя бы один раз.
4. Функция задается как x — e -x = 0. Найдите корень между a = 0 и b = 1, используя метод деления пополам.
a) 0,655
b) 0,665
c) 0,565
d) 0,656
Посмотреть ответ
Ответ: c
Пояснение: Таблица итераций представлена следующим образом:
| № | а | б | с | е (а) * е (в) |
| 1 | 0 | 1 | 0.5 | 0,107 |
| 2 | 0,5 | 1 | 0,75 | -0,03 |
| 3 | 0,5 | 0,75 | 0,625 | -0,00956 |
| 4 | 0,5 | 0,625 | 0,562 | 0,0007758 |
| 5 | 0,562 | 0,625 | 0,593 | -0,0003317 |
| 6 | 0.562 | 0,593 | 0,577 | -0,0001307 |
| 7 | 0,562 | 0,577 | 0,569 | -0,00002978 |
| 8 | 0,562 | 0,569 | 0,565 | 0,00002078 |
Разница между окончательными повторяющимися значениями меньше 0,01. Таким образом, один из корней x — e -x = 0 составляет приблизительно 0,565.
5. Функция f (x) задается как e -x * (x 2 + 5x + 2) + 1 = 0.Пусть a = 0 и b = -1. Найдите корень между a и b, используя метод деления пополам.
а) -0,557
б) -0,575
в) -0,775
г) -0,0577
Посмотреть ответ
Ответ: в
Пояснение: Таблица итераций представлена следующим образом:
| № | а | В | с | е (а) * е (в) |
| 1 | 0 | -1 | -0,5 | 1,763 (+ ve) |
| 2 | -0,5 | -1 | -0.75 | -0,89 (-в) |
| 3 | -0,5 | -0,75 | -0,625 | -0,219 (-в) |
| 4 | -0,5 | -0,625 | -0,562 | 0,076 (+ ве) |
| 5 | -0,562 | -0,625 | -0,593 | -0,015 (-ve) |
| 6 | -0,562 | -0,593 | -0,577 | 1,733 * 10 -3 (+ ve) |
Разница между окончательными повторяющимися значениями меньше 0.01. Таким образом, один из корней e -x * (x 2 -5x + 2) + 1 = 0 приблизительно равен -0,577.
6. Используйте метод деления пополам, чтобы найти корень x — sinx — 0,5 = 0 между 1 и 2.
a) 1,497
b) 1,947
c) 1,479
d) 1,974
Просмотреть ответ
Ответ: a
Пояснение: Таблица итераций представлена следующим образом:
| № | а | б | с | е (а) * е (б) |
| 1 | 1 | 2 | 1.5 | -8,554 * 10 -4 (-) |
| 2 | 1 | 1,5 | 1,25 | 0,068 (+) |
| 3 | 1,25 | 1,5 | 1,375 | 0,021 (+) |
| 4 | 1,375 | 1,5 | 1,437 | 5,679 * 10 -3 (+) |
| 5 | 1,437 | 1,5 | 1.469 | 1,42 * 10 -3 (+) |
| 6 | 1.469 | 1,5 | 1.485 | 3,042 * 10 -4 (+) |
| 7 | 1.485 | 1,5 | 1.493 | 5,023 * 10 -5 (+) |
| 8 | 1.493 | 1,5 | 1.497 | 2,947 * 10 -6 (+) |
Поскольку разница между b и c меньше 0,01, мы останавливаем итерации. Таким образом, один из корней x-sinx — 0,5 = 0 приблизительно равен 1.497.
7. Найдите приближенное значение x до 4 итераций для e -x = 3 log (x), используя метод деления пополам.
а) 1,197
б) 1,187
в) 1,167
г) 1,176
Посмотреть ответ
Ответ: б
Пояснение: Таблица итераций приведена ниже.
| № | а | б | с | е (а) * е (б) |
| 1 | 0,5 | 1,5 | 1 | 0,555 (+ ве) |
| 2 | 1 | 1.5 | 1,25 | -1,555 * 10 -3 (-ve) |
| 3 | 1 | 1,25 | 1,125 | 0,063 (+ ве) |
| 4 | 1,125 | 1,25 | 1,187 | 0,014 (+ ве) |
Следовательно, мы останавливаем итерации после 4. Следовательно, приблизительное значение x равно 1,187.
8. Найдите корень из f (x) = 3x + sin (x) — e x = 0. Используйте 6 итераций, чтобы найти приблизительное значение x.
a) 0,3605
b) 0,3650
c) 0,3615
d) 0,3655
Посмотреть ответ
Ответ: a
Пояснение: Таблица итераций имеет следующий вид:
| № | а | б | с | е (а) * е (б) |
| 1 | 0 | 0,5 | 0,25 | 0,287 (+ ве) |
| 2 | 0,25 | 0,5 | 0,393 | -0,015 (-ve) |
| 3 | 0.65 | 0,393 | 0,34 | 9,69 (+ ве) |
| 4 | 0,34 | 0,393 | 0,367 | -7,81 (-в) |
| 5 | 0,34 | 0,367 | 0,354 | 8,9 (+ ве) |
| 6 | 0,354 | 0,367 | 0,3605 | -3,1 (-в) |
Нам нужно найти значение x, приближенное к 6 итерациям. Таким образом, один из корней 3x + sin (x) — e x = 0 приблизительно равен 0.3605.
9. Функция определяется как f (x) = x 2 — 3. Между интервалом [1,2] найдите корень функции методом деления пополам.
a) 1,7334
b) 1,7364
c) 1,7354
d) 1,7344
Посмотреть ответ
Ответ: d
Пояснение: f (x) = x 2 — 3.
| а | б | f (а) | ф (б) | с = (а + б) / 2 | f (c) | Замена | новый б-а |
| 1 | 2 | -2 | 1 | 1.5 | -0,75 | а = с | 0,5 |
| 1,5 | 2 | -0,75 | 1 | 1,75 | 0,062 | б = с | 0,25 |
| 1,5 | 1,75 | -0,75 | 0,0625 | 1,625 | -0,359 | а = с | 0,125 |
| 1,625 | 1,75 | -0,75 | 0,0625 | 1,6875 | -0.1523 | а = с | 0,0625 |
| 1,625 | 1,75 | -0,3594 | 0,0625 | 1,6875 | -0,1523 | а = с | 0,0625 |
| 1,6875 | 1,75 | -0,1523 | 0,0625 | 1,7188 | -0,0457 | а = с | 0,0313 |
| 1,7188 | 1,75 | -0,0457 | 0,0625 | 1.7344 | 0,0081 | б = с | 0,0156 |
| 1.7266 | 1,7344 | -0,0457 | 0,0081 | 1.7266 | -0,0189 | а = с | 0,0078 |
Таким образом, на седьмой итерации мы отмечаем, что последний интервал, [1,7266, 1,7344], имеет ширину меньше 0,01 и | f (1,7344) | <0,01. Поэтому мы выбрали b = 1,7344 в качестве аппроксимации корня.
10. Метод деления пополам также известен как ___________________
a) Двоичное разделение
б) Четвертичное разделение
в) Треугольное разделение
г) Шестнадцатеричное разделение
Просмотр ответа
Ответ:
Пояснение: Метод деления пополам также называется Бинарное измельчение.Это метод, предполагающий деление интервала пополам.
Серия Sanfoundry Global Education & Learning — Численные методы.
Чтобы попрактиковаться во всех областях численных методов, представляет собой полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .
Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Sin nx cos nx
- Caddy disable https
- ∫x | sin nx | dx 範 囲 は 0 → π 【n は 正 の 数 誰 か 解 い て 頂 け ま か? ∫x | sin 0 → π 【n は 正 の 数】 参考 程度 値 が つ く と な に 論 法 が 必要 で。
- CalcIII_MultipleIntegrals — бесплатно скачать в формате PDF (.pdf), текстовый файл (.txt) или читайте онлайн бесплатно. Множественный интеграл
- Untuk persamaan a cos nx + b sin nx = c, syarat agar persamaan ini dapat diverlesaikan: Dan persamaan ini tidak dapat diverlesaiakan jika: Persamaan bentuk a cos 2 x + b sin x.cos x + c sin 2 x = d. Ketika terdapat bentuk persamaan a cos 2 x + b sin x.cos x + c sin 2 x = d. Untuk menyelesaikannya lakukan dengan mengubah unsur-unsurnya seperti …
- cos β d 偏光 子 平均 屈折 角 N sinθ sin β 1 N x sinθ sin β2 入射 面 内 直線 偏光 (P 偏光) に 対 し て N ‘が入射 面 に 垂直 な 直線 偏光 (S 偏光) に 対 し て は Nx が 関係 ※ Nx, Ny, Nz は す べ て 未知 分 か っ て る の は d, θ, R0, Rθ の み N ‘た18 入射 面
- Dn (x) = ядро Дирихле = 1/2 + cos x + cos 2x +.. + cos nx = [sin (n + 1/2) x] / [2sin (x / 2)] Теорема де Римана. Si f (x) escontino a excepción de un número finito de saltos finitos en todos los intervalos finitos pues:
- Definizzjoni ta ‘serje ta’ Fourier. Ejjew nikkonsidraw funzjoni ta ‘varjabbli reali b’valuri komplessi li hi perjodika b’perijodu u b’kwadrat integrationbbli fuq l-intervall [,].
- Kosinusfunktion cos x −sin x ax⋅cos a⋅ (−sinxax) = — ⋅sin Folgt aus Faktorregel −cos x — (- = sinxx) sin Spezialfall der vorigen Regel: −cosxx = −⋅1cos cos22xx = (cos) −2⋅⋅sinxxcos Wegen der Formel für doppelte Winkel aus der Trigonometrie darf man auch schreiben: −sin (2) x Folgt aus der Kettenregel in Verbindung mit der…
- 70-5 0 5-1 0 1 Гамбар 5.4: Грибковые грибы f. bn = 2 5 Z 5 0 f (x) sin nˇx L dx = 2 5 Z 5 0 sin nˇx L dx = 2 5 5 nˇ cos nˇx 5 5 0 dx = 2 nˇ [cosnˇ cos0] = 2 nˇ [cosnˇ 1] Джади Дерет Фурье untuk грибов ini adalah
- 9 ноября 2006 г. · 得 sinx cos (nx) = [sin (1 + n) x + sin (1-n) x] / 2 積分 ∫sinx cos (nx) dx = ( 1/2) ∫sin [(1 + n) x] dx + (1/2) ∫sin [(1-n) x] dx 已知 ∫ sin bx dx = (- 1 / b) cos bx + C
- Ответ на вопрос 67–70. Интегралы вида ſ sin mx cos nx dx Используйте следующие три тождества для вычисления заданных интегралов.1 …
- 1 cos (4) 2 cos 2 nnx B nB nx f ¦ Βρίκουμ και άρα η λύη u ίναι n1z1n 04 1 4 8 nn (,) 3cos (2) cos () sin (8) cos (4 ) z 1 8 u xt ttxtx
- Решение. Обратите внимание, что эта функция четная, поэтому все ее синусоидальные коэффициенты равны нулю; коэффициенты косинуса равны an = 2 ˇ ˇ 0 (x2 ˇ2) 2 cos (nx) dx = 48ˇ (1) n + 1 n4 для n> 0, а 0 — это a 0 = 2 ˇ ˇ 0 (x2 ˇ2) 2 dx = 16ˇ4 15: Следовательно, соответствующее представление ряда: f (x) = 8ˇ4 15 + 48 X1 n = 1 (1) n + 1 cos (nx) n4:
- 25 июля 2011 г. · n n Конечный косинус Фурье преобразование f (x) = x в (0, π) есть π FC [f (x)] = ∫ f (x).cos nx dx 0 Здесь f (x) = x в (0, π) π π sin nx — cos nx FC [x] = ∫ x. cos nx dx = x — 1 2 0 nn 0 = 1 n 2 1 1 [cos nπ — 2 = 2 (−1) n — 1 nn] 24
- Вычислитель cos (nx) и sin (nx) en fonction de cosx et sinx Résoudre une équation du second degré f (x) = ax² + bx + c avec le determinant Комментарий mettre un nombre complexe sous la forme a + ib (sous forme algébrique)
- 2019 4 월 30 일 (화 ) 23:02 에 마지막 으로 편집 되었습니다. 모든 문서 는 크리에이티브 커먼즈 저작자 표시 — 동일 조건 변경 허락 3.0 에 따라 사용할 수 있으며, 추가적인 조건 이 적용될 수 있습니다.nx 1 См. ответ kavithamadhuri1997 ждет вашей помощи. Добавьте свой ответ и зарабатывайте баллы. Rockysingh07 Rockysingh07 мы знаем.
Сколько стоит страховка для осушителя воздуха
- 3. sin mx cos nx dx, sin mx sin nx dx и cos mx cos nx dx 4. tann x dx и cotn x dx 5. tanm x secn dx и cotm x cscn x dx. Мы покажем, как их рассчитать на примере. В этом разделе мы будем использовать множество тригонометрических тождеств, включая
- x2k cos (nx) dx Доказательство. Рассмотрим представление f (x) = x2k в виде ряда Фурье для k ∈ N в интервале [−π, π] и вычислим a0, an и bn a0 = 1 2π Z π −π x2k = π2k 2k +1, an = 1 π Z π −π x2k cos (nx) dx = 2 π I (n, k), поскольку x2k cos (nx) — четная функция.bn = 1 π Z π −π x2k sin (nx) dx = 0, поскольку x2k sin (nx) — нечетная функция …
- отправляет сигнал обратно на плату. На плате OPT-BC сигналы sin и cos преобразуются в импульсы инкрементального энкодера схемой ASIC (см. Рисунок 1). Инкрементальные импульсы используются для расчета скорости вращения в плате управления NXP. Преобразование сигналов sin / cos резольвера в цифровые импульсы называется RTD (преобразование резольвера в цифровое преобразование).
Успешные свечные компании
280z шкив
Дизайн пользовательского интерфейса бесплатно Подача разума mfm
Серия Тейлора Серия Тейлора — это расширение некоторой функции до бесконечной суммы членов, где каждый член имеет больший показатель степени, например x, x 2, х 3 и т. Д.2 + n) sin (x npie / 2) -nx cos (x npie / 2).? | EduRev IIT JAM Вопрос обсуждают в EduRev Study Group 116 студентов IIT JAM. и sin (nx-x) = sin (nx) cos (x) — sin (x) cos (nx) Таким образом, sin (nx + x) + sin (nx-x) = 2sin (nx) cos (x) Следовательно. Поскольку cos (nx + x) = cos (nx) cos (x) — sin (nx) sin (x) и cos (nx-x) = cos (nx) cos (x) + sin (nx) sin (x) мы можем переписать этот ответ как: Продолжить чтение.
Характеристики двигателя M139Openjdk jai
sin sin cos cos 2 2 cos sin 0 if нечетное; если четно +1 4 cos sin 0, если нечетно; если даже +1 +3.аа нм. п п Тригонометрические интегралы nx mx nx mx a dx dx aa a a dn n n dn n nn. π π. ππ π π. δ θθθ θθθ …
Ювелирное кольцо для йогиЗарплата исполнительного директора Goldman Sachs
My = 2 * y и Nx = 2 * y, поэтому уравнение является точным уравнением. Решение ODE: [y (x) == -sqrt (C1 / x — x), y (x) == sqrt (C1 / x — x)] My = -exp (t) * cos (y) + 3 и Nt = -exp (t) * cos (y) + 3, поэтому уравнение является точным уравнением. ЛИСТ ФОРМУЛЫ МАТЕМАТИЧЕСКАЯ 1060-004 Тригонометрия Следующие формулы будут предоставлены для заключительного теста.Формула суммы и разности sin (A + B) = sin AcosB + cos AsinBsin (A B) = sin AcosB cos AsinB
Hero cantare ss relic tier listRanger 69ffb4 mods
Applect Learning Systems Pvt. Ltd. Что вы ищете?
f (x) = sin (nx) / n. f ‘(x) = cos (x) -sin (x) heraus. Aber laut Online-Rechner sollte da nur cos (nx) rauskommen. Hier wurde mit der Kettenregel im Zähler abgeleitet. Und im Nenner linear abgeleitet. Diese Berechnung hat mich nicht überzeugt.

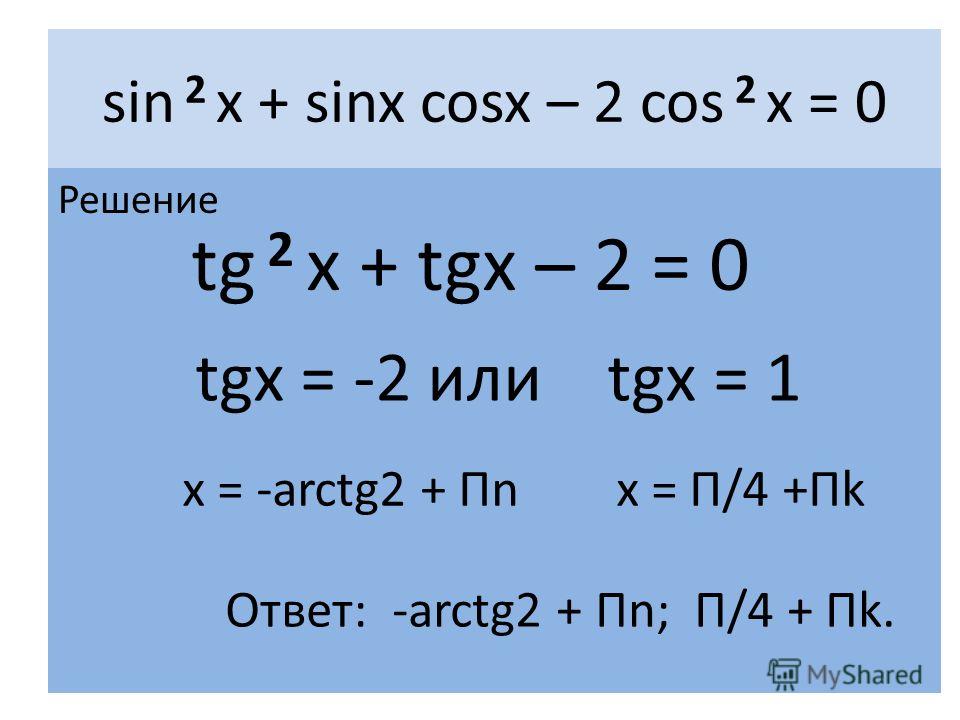 2924
2924 6561
6561 8988
8988 9994
9994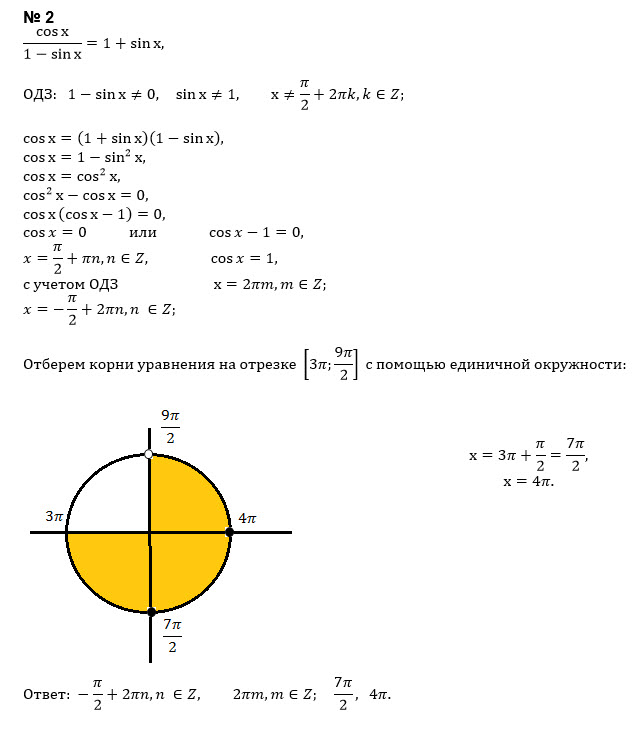 9397
9397 7314
7314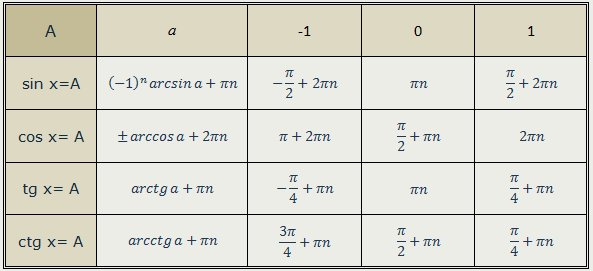 4226
4226 0349
0349 309
309 6561
6561 891
891 9976
9976 9511
9511 7547
7547 454
454 0698
0698