Содержание
Матричный метод решения систем линейных уравнений
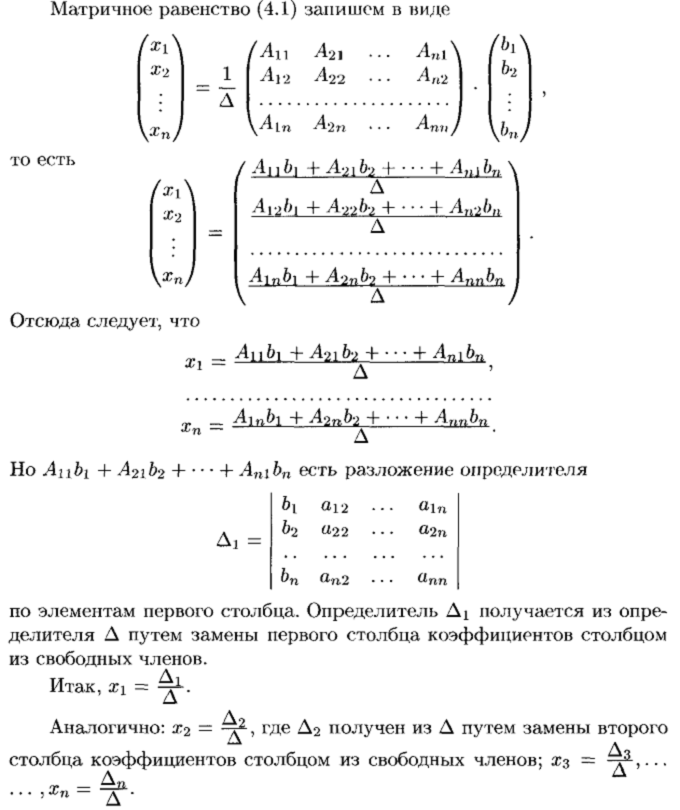
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов
Найдем произведение
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
или короче A∙X=B.
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A: . Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A-1B.
Примеры. Решить системы уравнений.
1.
Найдем матрицу обратную матрице A.
,
Таким образом, x = 3, y = – 1.
2.
Итак, х1=4,х2=3,х3=5.
Решите матричное уравнение: XA+B=C, где
Выразим искомую матрицу X из заданного уравнения.
Найдем матрицу А-1.
Проверка:
Решите матричное уравнение AX+B=C, где
Из уравнения получаем .
Следовательно,
МЕТОД ГАУССА
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:
Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования: перестановка строк или столбцов; умножение строки на число, отличное от нуля; прибавление к одной строке другие строки.
Примеры: Решить системы уравнений методом Гаусса.
1.
Вернувшись к системе уравнений, будем иметь
2
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.
Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
3.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
Вернемся к системе уравнений.
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
Таким образом, система имеет бесконечное множество решений.
Решение СЛАУ матричным методом — презентация онлайн
1.
 Решение СЛАУ матричным методом
Решение СЛАУ матричным методом
2. Матричный метод решения СЛАУ
Матричный метод – это метод решения
через обратную матрицу квадратных
(с числом уравнений, равным числу
неизвестных) систем линейных
алгебраических уравнений с
ненулевым определителем.
3. Пусть дана система линейных уравнений с n неизвестными
Пусть дана система линейных уравнений с n неизвестными
Запишем ее в матричной форме:
A — основная матрица системы, состоящая из
коэффициентов при неизвестных.
B — вектор — столбец свободных членов (слагаемых)
X — вектор – столбец решений системы
4. Запишем СЛАУ в виде матричного уравнения и решим его
AX = B
Умножим это матричное уравнение слева на A − 1 — матрицу,
обратную матрице A:
Так как A − 1A = E по определению обратной матрицы, получаем
E X = A − 1B
X = A − 1B
где A – 1=1/∆ (A*)Т ,
∆≠0
(A*)Т — транспонированная матрица алгебраических дополнений
соответствующих элементов матрицы A.
5. Пример Решить СЛАУ матричным методом:
Сначала убедимся в том, что определитель матрицы из
коэффициентов при неизвестных СЛАУ не равен нулю.
6. Вычислим алгебраические дополнения для элементов основной матрицы
Вычислим алгебраические дополнения для
элементов основной матрицы
7. Найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы
Найдём союзную матрицу, транспонируем её и подставим
в формулу для нахождения обратной матрицы
8. Найдем неизвестные, перемножив обратную матрицу и столбец свободных членов
Найдем неизвестные, перемножив обратную
матрицу и столбец свободных членов
Ответ: x=2; y=1; z=4.
9. Отдохнем на песочке…
11. Самостоятельная работа
1 вариант
2 вариант
Решить СЛАУ:
Решить СЛАУ:
2 x1 3 x2 x3 7
3 x1 2 x2 x3 5
4 x 7 x 3 x 4
2
3
1
x1 2x 2 — x 3 4
3×1 2 x 3 8
4x — 2x 5x 0
1
2
3
12.
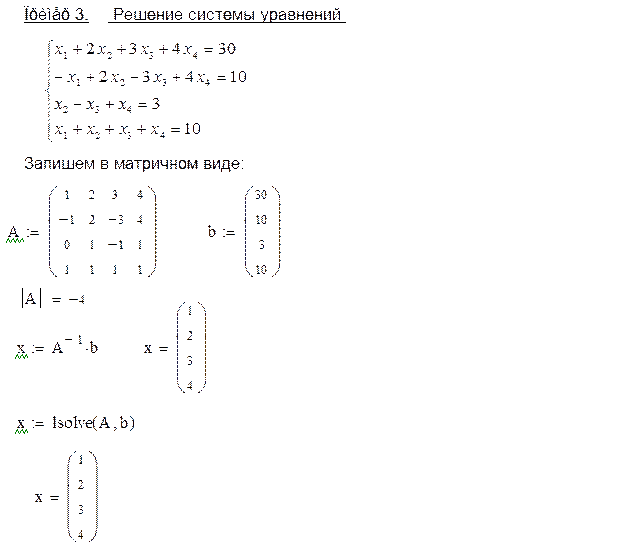 Домашнее задание
Домашнее задание
Решить СЛАУ:
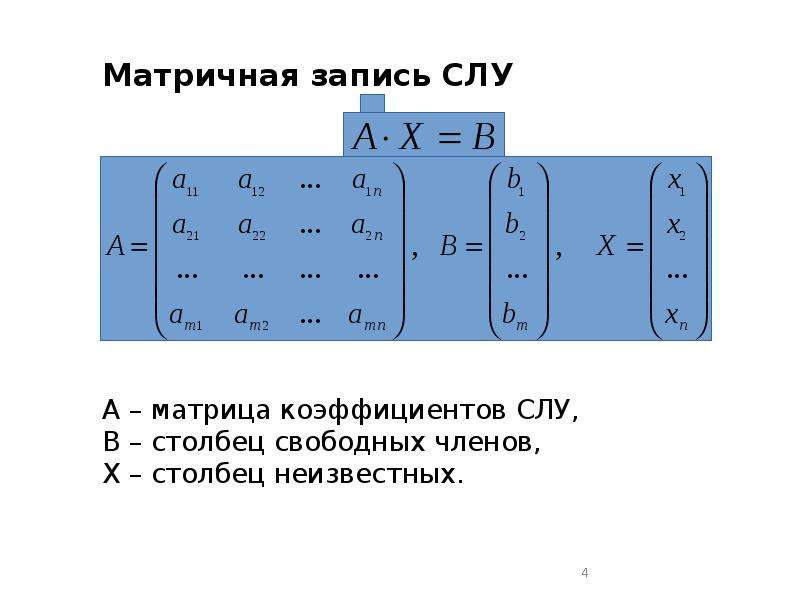
Матричный метод решения системы линейных алгебраических уравнений
Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.
Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.
Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.
Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.
Матричный метод решения — метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.
Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A-1 · B, где A-1 — обратная матрица.
Матричный метод решения состоит в следующем.
Пусть дана система линейных уравнений с nнеизвестными:
Её можно переписать в матричной форме: AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A-1 — матрицу, обратную к матрице A: A-1 (AX) = A-1B
Так как A-1A = E, получаем X = A-1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: detA≠ 0.
Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Пример решения неоднородной системы линейных алгебраических уравнений.
Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.
Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они понадобятся для нахождения обратной матрицы.
Теперь найдём союзную матрицу и транспонируем её, потом подставим в формулу для нахождения обратной матрицы.
Подставляя переменные в формулу, получаем:
Найдем неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.
Для этого перемножим обратную матрицу и столбец свободных членов.
Итак, x=2; y=1; z=4.
Если у Вас есть вопросы или Вам нужна помощь в решении линейных уравнений или систем, записывайтесь на мои занятия. Буду рад Вам помочь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решение систем дифференциальных уравнений матричным способом — справочник студента
Матричный метод может применяться в решении систем линейных уравнений, в которых число неизвестных равно числу уравнений, то есть систем линейных уравнений с квадратной матрицей коэффициентов при неизвестных.
Другое условие применимости матричного метода — невырожденность матрицы коэффициентов при неизвестных, то есть неравенство нулю определителя этой матрицы.
Узнай стоимость своей работы
Бесплатная оценка заказа!
Систему линейных уравнений, при выполнении вышеназванных условий, можно представить в матричном виде, а затем решить её путём отыскания обратной матрицы к матрице системы.
Решение систем линейных уравнений матричным методом основано на следующем свойстве обратной матрицы: произведение обратной матрицы и исходной матрицы равно единичной матрице. Обратная матрица обозначается символом .
Пусть нужно решить систему линейных уравнений:
Запишем эту систему уравнений в матричном виде:
Обозначим отдельно как A матрицу коэффициентов при неизвестных и как B матрицу неизвестных и матрицу свободных членов
Тогда
Узнай стоимость своей работы
Бесплатная оценка заказа!
То есть, для нахождения решений системы нужно обе части уравнения умножить на матрицу, обратную матрице коэффициентов при неизвестных и приравнять соответствующие элементы полученных матриц.
Алгоритм решения системы линейных уравнений матричным методом разберём на следующем примере системы линейных уравнений второго порядка.
- Пример 1. Решить матричным методом систему линейных уравнений:
- Решение состоит из следующих шагов.

Шаг 1. Составляем следующие матрицы.
- Матрица коэффициентов при неизвестных:
- Матрица неизвестных:
- Матрица свободных членов:
- Это сделано для того, чтобы применить в решении уже записанные закономерности, основанные на свойстве обратной матрицы:
По выведенному выше последнему равенству и будем вычислять решения данной системы.
Но сначала проверим, не является ли матрица коэффициентов при неизвестных вырожденной, то есть можем ли вообще применять матричный метод:
Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.
Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:
Шаг 3. Находим матрицу неизвестных:
Итак, получили решение:
Сделаем проверку:
Следовательно, ответ правильный.
Для второго примера выберем систему линейных уравнений третьего порядка.
Пример 2. Решить матричным методом систему линейных уравнений:
Шаг 1. Составляем следующие матрицы.
- Матрица коэффициентов при неизвестных:
- Матрица неизвестных:
- Матрица свободных членов:
- Проверим, не является ли матрица коэффициентов при неизвестных вырожденной:
- .
- Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.
- Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:
- .
- Шаг 3. Находим матрицу неизвестных:
- Итак, получили решение:
- .
- Сделаем проверку:
- Следовательно, ответ правильный.
Решить систему уравнений матричным методом самостоятельно, а затем посмотреть решение
Нет времени вникать в решение? Можно заказать работу! Пройти тест по теме Системы линейных уравнений
Всё по теме «Системы уравнений и неравенств»
Решение систем линейных уравнений методом подстановки и методом сложения Решение систем линейных уравнений методом Крамера Решение систем линейных уравнений методом Гаусса Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли Решение систем линейных уравнений матричным методом (обратной матрицы) Системы линейных неравенств и выпуклые множества точек
Теорема Кронекера-Капелли Решение систем линейных уравнений матричным методом (обратной матрицы) Системы линейных неравенств и выпуклые множества точек
Начало темы «Линейная алгебра»
Поделиться с друзьями
Источник: https://function-x.ru/systems_matrix_method.html
Матричный метод онлайн
Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Рассмотрим следующую систему линейных уравнений:
| (1) |
Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:
где
| (3) |
Мы будем предполагать, что матрица A имеет обратное, т. е. определитель матрицы A не равен нулю.
е. определитель матрицы A не равен нулю.
- Умножим матричное уравнение (2) на обратную матрицу A−1. Тогда
- Учитывая определение обратной матрицы, имеем A−1A=E, где E— единичная матрица. Следовательно (4) можно записать так:
- или, учитывая, что Ex=x:
- Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
- Пример 1. Решить следующую систему линейных уравнений матричным методом:
Матричный вид записи системы линейных уравнений: Ax=b, где
| . |
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
| . |
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:
| . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
| . |
Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:
| . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
Делим каждую строку матрицы на ведущий элемент соответствующей строки:
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
Ответ:
Пример 2. Решить следующую систему линейных уравнений матричным методом:
Матричный вид записи системы линейных уравнений: Ax=b, где
Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :
Вычислим определитель матрицы A :
Вычислим все алгебраические дополнения матрицы A:
Обратная матрица вычисляется из следующего выражения:
где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.
Используя формулу обратной матрицы, получим:
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
Ответ:
Источник: https://matworld.ru/calculator/matrix-method-online.php
Глава 4. Матрицы и дифференциальные уравнения
где – постоянный коэффициент; – непрерывная функция времени, определенная на некотором интервале . Решением уравнения является функция , подстановка которой в это уравнение обращает его в тождество. При уравнение называется однородным и его общее решение выражается как , где – произвольная постоянная. Общее решение исходного неоднородного уравнения ( ) выражается формулой
.
Это решение представляет собой сумму общего решения однородного и частного решения неоднородного дифференциальных уравнений. Оно удовлетворяет начальному условию при , т. е.
- .
- Переходя к системам дифференциальных уравнений, рассмотрим их представление в нормальной форме:
- ,
- к которой, как известно, можно привести любую систему линейных дифференциальных уравнений. В матричной записи эта система представляется одним уравнением
- ,
- где – вектор (столбец) неизвестных функций ; – вектор (столбец) задающих функций и – квадратная матрица постоянных коэффициентов :
- ; ; .
Задачу об отыскании решения системы дифференциальных уравнений, удовлетворяющих заданным начальным значениям скаляра и вектора , называют задачей Коши. По аналогии с дифференциальным уравнением первого порядка можно записать искомое решение для вектора неизвестных функций в виде: .
Необходимо установить допустимость такого представления решения, а также выяснить смысл и способы определения входящей в него матрицы .
В матричной форме нормальная однородная система дифференциальных уравнений ( ) имеет вид: . Будем искать ее решение в виде где вектор (столбец) произвольных постоянных. Подставляя в исходное уравнение, получаем или после сокращения на скаляр и перенесения в левую часть равенства: .
Заметим, что сокращать на вектор нельзя, так как операция деления на вектор в общем случае не имеет смысла. Вынося за скобки вектор , необходимо умножить предварительно на единичную матрицу . Уравнение имеет нетривиальные решения при условии, что определитель матрицы обращается в нуль, т. е.
или
.
Так как порядок матрицы равен , то является многочленом -й степени относительно , т. е. . Корни уравнения (нули многочлена ), число которых равно , дадут значения при которых исходная система имеет нетривиальные решения.
Рассмотрим наиболее простой случай, когда все корни уравнения простые (попарно различные). Тогда при имеем однородное уравнение , из которого можно определить вектор . Таким образом, решение нормальной системы дифференциальных уравнений, соответствующее корню , будет .
Таким образом, решение нормальной системы дифференциальных уравнений, соответствующее корню , будет .
Всего получим таких решений, соответствующих корням .
Для любой квадратной матрицы по установившейся терминологии называется характеристической матрицей, а – характеристическим уравнением. Корни уравнения называются собственными значениями (характеристическими числами), а векторы собственными векторами матрицы . Совокупность собственных значений называется спектром матрицы .
- Множество всех решений однородной системы дифференциальных уравнений образует -мерное линейное пространство с базисом . Общее решение имеет следующий вид:
- .
- Это выражение может быть представлено в матричной форме
- .
- В свою очередь матрица выражается следующим образом
- .
- Здесь через обозначена матрица -го порядка, называемая модальной и состоящая из столбцов , а элементами диагональной матрицы являются экспоненциальные функции .

Итак, решение нормальной однородной системы линейных дифференциальных уравнений представляется в виде .
При матрица равна единичной матрице, следовательно, начальное условие , откуда . Подставляя это значение в общее решение, получаем . Матрица -го порядка называется фундаментальной матрицей. Ее вычисление сводится к определению собственных значений и собственных векторов матрицы системы дифференциальных уравнений.
- Рассмотрим в качестве примера однородную систему дифференциальных уравнений:
- .
- Для этой системы
- ; .
- Поскольку для вычисления необходимы алгебраические дополнения какой-либо строки матрицы , то определитель этой матрицы удобно получать разложением по элементам той же строки.
- Алгебраические дополнения элементов первой строки:
- ;
- ;
- .
- Характеристический многочлен и собственные значения:
- ;
- ; ; .
- Собственные векторы : ; ; .

- Принимая (эти значения произвольны и выбираются по соображениям удобства), получаем модальную матрицу, а также обратную к ней:
- ;
- Фундаментальная матрица
- ,
- что после перемножения матриц приводит к следующему результату
- .
- Таким образом, в соответствии с соотношением общее решение рассматриваемой однородной системы дифференциальных уравнений:
- ,
- где элементы вектора , равные начальным значениям соответствующих переменных при .
- Выясним характер фундаментальной матрицы . Подставляя решение в однородное дифференциальное уравнение , получаем тождества:
- ; .
Так как в этих тождествах – вектор начальных значений не зависящий от времени, то , т. е. – это такая матрица, производная которой по времени равна произведению матрицы на саму матрицу. Аналогичными свойствами обладает единственная скалярная функция , поэтому по аналогии можно записать следующие соотношения:
- .

- Через экспоненциальную функцию выражаются также другие функции от матриц:
- Следует иметь в виду, что , а соотношение имеет смысл только в случаях, когда и – перестановочные матрицы.
- Решение неоднородной системы дифференциальных уравнений может быть записано в матричной форме , где – векторная функция времени, подлежащая определению. Подставляя выражение для и ее производной в исходное уравнение, имеем:
- или после очевидных упрощений
- .
- При начальных условиях начальное значение искомой функции . Интегрированием получаем
- .
- Используя это выражение, находим решение неоднородного уравнения, удовлетворяющее начальному условию :
- ,
которое называется формулой Коши. Его можно рассматривать как сумму решения соответствующего однородного уравнения (при ) и решения неоднородного уравнения при нулевых начальных условиях ( ).
- Пусть дана неоднородная система дифференциальных уравнений в нормальной форме:
- .

- Для этой системы:
- ; ; ;
- ;
- .
- Полагая для удобства , находим модальную матрицу и обратную к ней матрицу :
- ,
- после чего определяется фундаментальная матрица:
- .
- Решение задачи Коши для однородной системы:
- .
- Найдем интеграл в выражении для частного решения неоднородной системы при :
- Частное решение неоднородной системы:
- .
- Таким образом, решение неоднородной системы, удовлетворяющей начальным условиям , запишется следующим образом:
- .
- Контрольные вопросы к лекции 12
12-1. Как записывается система уравнений в матричном виде?
12-2. Как решается матричное уравнение ?
12-3. Что представляет собой определитель матрицы?
12-4. Как вычисляется определитель второго порядка?
12-5. Как вычисляется определитель третьего порядка?
12-6. В чем состоит свойство антисимметрии определителя?
12-7. В каком случае определитель равен нулю?
В каком случае определитель равен нулю?
12-8. Как изменяется определитель матрицы -го порядка при умножении ее на скаляр?
12-9. Как вычисляется алгебраическое дополнение?
12-10. Как вычисляется обратная матрица?
12-11. Опишите алгоритм вычисления обратной матрицы методом исключения.
12-12. Какие матрицы называются особенными?
12-13. Для каких матриц существуют обратные матрицы?
12-14. Какая матрица называется инволютивной?
12-15. Что называется рангом матрицы?
12-16. Что называется дефектом матрицы?
12-17. Какая система уравнений называется совместной?
12-18. В чем состоит суть теоремы Кронекера – Капелли?
12-19. Какая система уравнений называется неопределенной?
12-20. Опишите алгоритм Гаусса для решения неоднородных систем линейных уравнений -го порядка?
12-21. Опишите алгоритм Гаусса – Жордана для решения неоднородных систем линейных уравнений -го порядка?
12-22. Какая система уравнений называется однородной?
12-23. Как определяется характеристическая матрица для квадратной матрицы ?
Как определяется характеристическая матрица для квадратной матрицы ?
12-24. Как определяется характеристическое уравнение?
12-25. Что называется характеристическими числами квадратной матрицы ?
12-26. Что называется спектром квадратной матрицы ?
12-27. Какая матрица называется модальной?
12-28. Какая матрица называется фундаментальной?
12-29. Что представляет собой решение неоднородного дифференциального уравнения в форме Коши?
Дата добавления: 2016-09-06; просмотров: 5982;
Источник: https://poznayka.org/s59823t1.html
Исследование методов решения системы дифференциальных уравнений с постоянной матрицей (стр. 1 из 3)
- Содержание
- 1. Введение
- 2. Постановка задачи
3. Нахождение собственных чисел и построение ФСР
6. Построение общего решения матричным методом
7. Задача Коши для матричного метода
8. Решение неоднородной системы
Графики
Заключение
1. Введение
Введение
Рассмотрим систему линейных уравнений первого порядка, записанную в нормальной форме:
(1)
где коэффициенты аij, i=1,2,…..,n, к=1,2,…,n, являются постоянными величинами;
- yi=yi(t), i=1,2,…,n — неизвестные функции переменной t.
- Если все bi(t) (i=1,2,…,n) положить равным нулю (bi(t)=0), то получится однородная система, соответствующая неоднородной системе (1).
- Обозначая матрицу системы через А(х), а вектор
через тогда систему (1) можем переписать в матричной форме (1а)
- Если
- Всякая совокупность n функций
- определенных и непрерывно дифференцируемых в интервале (a;b), называется решением системы (1) в этом интервале, если она обращает все уравнения системы (1) в тождества:
, то получаем соответствующую систему однородных уравнений . (2)
справедливые при всех значениях x из интервала (a, b). Общее решение неоднородной системы представляет собой сумму общего решения соответствующей однородной системы и частного решения неоднородной.
2. Постановка задачи
Цель работы: исследование методов решения системы дифференциальных уравнений с постоянной матрицей:
; ;
1. Найти собственные числа и построить фундаментальную систему решений (ФСР).
2. Построить фундаментальную матрицу методом Эйлера.
3. Найти приближенное решение в виде матричного ряда.
4. Построить общее решение матричным методом. Исследовать зависимость Жордановой формы матрицы А от ее собственных чисел.
5. Решить задачу Коши.
- Начальные условия:
- Вектор начальных условий: [1, 2, 3, 4]
- t = 0
Однородной линейной системой дифференциальных уравнений называется система уравнений вида:
(3)
Если в матрице системы
все =const, то данная система называется системой с постоянными коэффициентами или с постоянной матрицей.
Фундаментальной системой решений однородной линейной системы уравнений называется базис линейного пространства решений a, т. е. n линейно независимых решений этой системы.
е. n линейно независимых решений этой системы.
Для построения фундаментальной системы решений дифференциального уравнения необходимо найти собственные числа характеристического полинома, так как в зависимости от их вида (характеристические числа могут быть действительными разными, кратными, комплексными) строится фундаментальная система решений.
Для того чтобы эта система n линейных однородных уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы определитель системы (вронскиан) был равен нулю:
(4)
Из этого уравнения степени n определяется значение k, при которых система имеет нетривиальные решения. Уравнение (4) называется характеристическим.
Запишем характеристический полином, для этого воспользуемся функцией CHARPOLY
- Для нахождения собственных чисел воспользуемся функцией SOLVE(U, l), которая возвращает характеристические числа матрицы А в вектор l. Получим:
- Получилось два действительно корня
- Матрицу y(x), столбцами которой являются решения, образующие фундаментальную систему, называют фундаментальной матрицей.

- И общее решение системы будет выглядеть следующим образом:
- Найдем решение данной системы с помощью метода Эйлера.
и два комплексно-сопряженных корня . Следовательно, вектора, образующие фундаментальную матрицу, для данного типа корней будут находиться отдельно для и отдельно для . Запишем ФСР для данных для полученных характеристических чисел:
4. Построение фундаментальной матрицы решений методом Эйлера
- Метод Эйлера заключается в следующем.
- Решение системы (1) находится в виде:
- Функция (5) является решением системы (1), если
(5) – собственное значение матрицы А, а а – собственный вектор этой матрицы, соответствующей числу .
Если собственные значения 1, 2, … , n матрицы А попарно различны и a1, a2, …, anсоответствующие собственные векторы этой матрицы, то общее решение системы уравнений (1) определяется формулой :
- где С1, С2, … , Сn – произвольные числа.
- Для случая кратных корней решение системы принимает вид
(6)
где Pi(x)-полиномы степени не выше, чем (к-1), имеющих в совокупности к произвольных коэффициентов. Так что среди коэффициентов этих полиномов к коэффициентов являются произвольными, а оставшиеся к·n-k выражаются через них.
Так что среди коэффициентов этих полиномов к коэффициентов являются произвольными, а оставшиеся к·n-k выражаются через них.
Для отыскания коэффициентов полиномов подставим решение (6) в исходную систему уравнений, приравняем коэффициенты при одинаковых функциях. Решим систему по отношению к (k·n-k) коэффициентов. Получим выражение всех коэффициентов через свободные.
- Если для кратного собственного значения
- Если для собственного значения
- Чтобы найти векторы
- Для данного задания были найдены следующие собственные значения:
- Построили фундаментальную систему решений:
- Найдем 1 строку фундаментальной матрицы решений для характеристического числа
матрицы А имеется столько линейно независимых собственных векторов , какова его кратность, то ему соответствует k независимых решений исходной системы: кратности k имеется только m (m
Источник: https://mirznanii.com/a/313656/issledovanie-metodov-resheniya-sistemy-differentsialnykh-uravneniy-s-postoyannoy-matritsey
Решение систем дифференциальных уравнений матричным способом
Матричная запись системы обыкновенных дифференциальных уравнений (СОДУ) с постоянными коэффициентами
Линейную однородную СОДУ с постоянными коэффициентами $\left\{\begin{array}{c} {\frac{dy_{1} }{dx} =a_{11} \cdot y_{1} +a_{12} \cdot y_{2} +\ldots +a_{1n} \cdot y_{n} } \\ {\frac{dy_{2} }{dx} =a_{21} \cdot y_{1} +a_{22} \cdot y_{2} +\ldots +a_{2n} \cdot y_{n} } \\ {\ldots } \\ {\frac{dy_{n} }{dx} =a_{n1} \cdot y_{1} +a_{n2} \cdot y_{2} +\ldots +a_{nn} \cdot y_{n} } \end{array}\right. $,
$,
где $y_{1} \left(x\right),\; y_{2} \left(x\right),\; \ldots ,\; y_{n} \left(x\right)$ — искомые функции независимой переменной $x$, коэффициенты $a_{jk} ,\; 1\le j,k\le n$ — заданные действительные числа представим в матричной записи:
- матрица искомых функций $Y=\left(\begin{array}{c} {y_{1} \left(x\right)} \\ {y_{2} \left(x\right)} \\ {\ldots } \\ {y_{n} \left(x\right)} \end{array}\right)$;
- матрица производных решений $\frac{dY}{dx} =\left(\begin{array}{c} {\frac{dy_{1} }{dx} } \\ {\frac{dy_{2} }{dx} } \\ {\ldots } \\ {\frac{dy_{n} }{dx} } \end{array}\right)$;
- матрица коэффициентов СОДУ $A=\left(\begin{array}{cccc} {a_{11} } & {a_{12} } & {\ldots } & {a_{1n} } \\ {a_{21} } & {a_{22} } & {\ldots } & {a_{2n} } \\ {\ldots } & {\ldots } & {\ldots } & {\ldots } \\ {a_{n1} } & {a_{n2} } & {\ldots } & {a_{nn} } \end{array}\right)$.
Теперь на основе правила умножения матриц данную СОДУ можно записать в виде матричного уравнения $\frac{dY}{dx} =A\cdot Y$. {k\cdot x} \cdot \left(\begin{array}{c} {\alpha _{1} } \\ {\alpha _{2} } \\ {\ldots } \\ {\alpha _{n} } \end{array}\right)$.
{k\cdot x} \cdot \left(\begin{array}{c} {\alpha _{1} } \\ {\alpha _{2} } \\ {\ldots } \\ {\alpha _{n} } \end{array}\right)$.
Отсюда получаем:
Теперь матричному уравнению данной СОДУ можно придать вид:
Полученное уравнение можно представить так:
Последнее равенство показывает, что вектор $\alpha $ с помощью матрицы $A$ преобразуется в параллельный ему вектор $k\cdot \alpha $. Это значит, что вектор $\alpha $ является собственным вектором матрицы $A$, соответствующий собственному значению $k$.
Число $k$ можно определить из уравнения$\left|\begin{array}{cccc} {a_{11} -k} & {a_{12} } & {\ldots } & {a_{1n} } \\ {a_{21} } & {a_{22} -k} & {\ldots } & {a_{2n} } \\ {\ldots } & {\ldots } & {\ldots } & {\ldots } \\ {a_{n1} } & {a_{n2} } & {\ldots } & {a_{nn} -k} \end{array}\right|=0$.
Это уравнение называется характеристическим.
Пусть все корни $k_{1} ,k_{2} ,\ldots ,k_{n} $ характеристического уравнения различны. {9\cdot x} } \end{array}\right. $.
{9\cdot x} } \end{array}\right. $.
Матричный способ решения систем линейных алгебраических уравнений
Запрос solve, который был использован ранее, чтобы получить решение системы линейных алгебраических уравнений (СЛАР) в Wolfram|Alpha, на самом деле является универсальным запросом для решения уравнений и их систем в Wolfram|Alpha. Собственно для решения системы линейных алгебраических уравнений он применяется лишь тогда, когда эта система задана в естественном виде: после запроса solve все уравнения системы перечисляются через запятую. Этот способ хорош тем, что позволяет решать не только определенные, но также и неопределенные системы — в общем виде.
Для решения определенных систем линейных алгебраических уравнений применяется также матричный способ.
В Wolfram|Alpha для решения систем линейных алгебраических уравнений матричным способом служит специальный запрос LinearSolve, после которого указываем матрицу коэффициентов системы и вектор (матрицу-столбец) свободных членов.
Чтобы понять особенности синтаксиса запроса LinearSolve, изучите следующие примеры.
Для начала рассмотрим решение однородных систем линейных алгебраических уравнений. После запроса LinearSolve вводим матрицу коэффициентов системы и нулевой вектор свободных членов. Получаем:
LinearSolve[{{a, b}, {c, d}}, {0, 0}]
Здесь Wolfram|Alpha дает тривиальное решение {0, 0}.
Точно также легко Wolfram|Alpha выводит тривиальное решение и для однородных систем линейных алгебраических уравнений более высокой размерности.
LinearSolve[{{1, 1, 1, -1}, {2, 1, 1, -2}, {1, 1, 2, 1}, {1, 1, 2, 4}}, {0, 0, 0, 0}]
Теперь взглянем на решение неоднородных систем линейных алгебраических уравнений.
После запроса LinearSolve вводим матрицу коэффициентов системы и ненулевой вектор свободных членов. В ответ получаем вектор неизвестных. Вот два примера.
LinearSolve[{{a, b}, {c, d}}, {1, 2}]
LinearSolve[{{1, 1, 1, -1}, {2, 1, 1, -2}, {1, 1, 2, 1}, {1, 1, 2, 4}}, {1, 1, 1, 2}]
Решение системы из двух однородных диофантовых уравнений
Рассматривается оригинальный алгоритм решения двух произвольных однородных линейных уравнений в целых числах. Автоматический расчет матрицы решений.
Автоматический расчет матрицы решений.
Пусть Нам надо решить систему из двух диофантовых уравнений
Несомненно можно решать эту систему так как делают все.
— Умножив первое уравнение на 31 и вычтя из второго мы получим классическое диофантовое уравнение с двумя переменными.
— Решив которое можно найти все целочисленные значения системы
Схема рабочая, несмотря на множество ручных вычислений
Мне такой подход не нравится и для решения мы будем использовать другой метод.
Он красив и понятен даже для школьников, знающих про вектора и матрицы.
Частично использован алгоритм, описанный вот в этой статье ( стр 36,37)
Он доработан, приведен к матричным операциям и обобщен на любые значения.
Алгоритм и его работу мы будем изучать на примере.
Решаем следующую систему диофантовых уравнений
Мы этот пример взяли по причине, что в интернете его решали и для него вывели общее решение. Так что есть с чем сравнивать.
1. Находим общее решения первого уравнения из заданной системы. Например пусть будет такое
8 14 20 -19 -30 -44 -1 1 0
Как проверим что это верное равенство? Да просто умножим вектор коэффициентов первого уравнения на полученную матрицу
Как видим ответ совпадает со свободным членом первого уравнения.
2. Теперь, раз мы нашли общее решение первого уравнения, давайте его подставим во второе.
То есть в уравнение подставим наши значения
Можно руками подставлять и сокращать подобное, но в матричном исчислении мы лишь умножаем вектор {70,-31,9} на нашу матрицу.
То есть мы получили уравнение
Но, обратите внимание, что во втором уравнении свободный член равен не нулю, а девяти.
То есть мы переписываем
Переносим свободные члены в правую часть и получаем классическое диофантовое уравнение, которое можем решать легко.
Общее решение такое
3. А теперь делаем обратное преобразование.
А теперь делаем обратное преобразование.
То есть
вот в эту систему
мы вместо неизвестных подставляем найденные m и p.
В матричном исчислении это решается так:
Убираем из матрицы последний столбец. Это свободные члены и они нам пока мешаются.
получили
Умножаем эту матрицу на матрицу созданную из этих уравнений
получаем
Последняя колонка это свободные члены, прибавим к ней ту колонку которую убирали в начале этого пункта
то есть к вектору {-22 36 -11} прибавляем {20 -44 0}
Получаем систему
А следовательно общее решение системы двух диофантовых уравнений
приобретает вид
Проверим, правильно ли посчитали
Для первого уравнения
Для второго
Как видим значения свободных членов совпадают с значениями в правой части уравнений, а следовательно мы получили общее решение.
Но радоваться рано, несмотря на то, что мы получили общее решение, мы получаем не все возможные значения.
Почему? Да потому что вектор {-608 -2261 -3059} имеет НОД =19
и фактически наше общее решение имеет вид
Так как числа в скобках должны быть целыми, то обозначим их t и наше, уже точно окончательное общее решение системы двух диофантовых уравнений имеет вид
Еще несколько примеров, и небольшие ремарки к алгоритму.
ответ
еще пример
ответ
Как видите можно решать неограниченные по числу переменных диофантовые уравнения.
Теперь что калькулятор не может.
Очень сильно не любит уравнения с нулевыми коэффициентами. Особенно первое. Например, вот такую систему
калькулятор не решит.
Ну как не решит? Решит, если прибегнем к уловке, и постараемся убрать все нулевые коэффициенты
Прибавим к первому уравнению, второе. Таким образом в первом уравнении исчезают все нулевые коэффициенты и калькулятор сможет решить эту систему
| Система двух диофантовых уравнений |
| Матрица общего решения |
Проверка показывает что общее решение корректно.
И еще пример
| Система двух диофантовых уравнений |
| Матрица общего решения |
Удачи в расчетах!!
Решить систему линейных уравнений методом обратной матрицы онлайн
Одним из известных методов решения систем линейных алгебраических уравнений (СЛАУ) является
метод обратной матрицы .
Предположим, у нас есть СЛАУ двух уравнений с двумя неизвестными.
a11xa12yb1a21xa22yb2
Введите обозначения:
А
— Матрица СЛАУ вида:
Aa11a12a21a22
Икс
— вектор-столбец неизвестных, которые необходимо найти:
Xxy
B
— векторный столбец свободных коэффициентов:
Bb1b2
Итак, исходную СЛАУ можно переписать в матричных обозначениях:
AXB
Чтобы решить это матричное уравнение, умножьте обе его части слева на
Матрица -1 :
A1AXA1B
Здесь,
А -1
— обратная матрица матрицы
А.Такая матрица существует для любой квадратной невырожденной матрицы (т.е. ее определитель не равен нулю).
Приведенные выше условия показывают границы применения метода обратной матрицы для решения СЛАУ. Прежде всего: матрица СЛАУ
А
должен быть квадратным. Это означает, что количество уравнений должно быть равно количеству переменных. Во-вторых: определитель матрицы
А
не должно быть равно нулю:
A0
Кроме того, у обратной матрицы есть замечательная особенность: ее произведение на исходную матрицу коммутативно и
равно единичной матрице:
A1AAA1E
Возвращаясь к решению нашего матричного уравнения, получаем:
EXXA1B
Итак, чтобы решить СЛАУ методом обратной матрицы, в первую очередь нужно проверить, существует ли обратная матрица, а затем найти ее и умножить на вектор
Б.
Наш онлайн-калькулятор предназначен для
решает СЛАУ методом обратной матрицы .
Калькулятор находит пошаговое решение. Уравнения СЛАУ вводятся в их естественном виде. Коэффициент уравнения может быть не только числом и дробью, но и параметрами — в этом случае калькулятор дает решение общепринятого вида.
Калькулятор Системы линейных уравнений
Этот калькулятор решает систему линейных уравнений любого вида с указанными шагами, используя либо метод исключения Гаусса-Жордана, либо правило Крамера.
Связанный калькулятор:
Калькулятор системы уравнений
Через запятую, например, x + 2y = 5,3x + 5y = 14.
Оставьте поле пустым для автоматического определения или укажите такие переменные, как x, y (через запятую).
Метод:
Исключение Гаусса-Джордана Правило Крамера
Если калькулятор что-то не вычислил, или вы определили ошибку, или у вас
предложение / отзыв, напишите в комментариях ниже.
Ваш ввод
Решите $$$ \ begin {case} 5 x — 2 y = 1 \\ x + 3 y = 7 \ end {cases} $$$ для $$$ x $$$, $ $$ y $$$ с использованием метода исключения Гаусса-Джордана.
Решение
Запишите расширенную матрицу: $$$ \ left [\ begin {array} {cc | c} 5 & -2 & 1 \\ 1 & 3 & 7 \ end {array} \ right] $ $$.
Выполните исключение Гаусса-Жордана (шаги см. В калькуляторе исключения Гаусса-Жордана): $$$ \ left [\ begin {array} {cc | c} 5 & -2 & 1 \\ 0 & \ frac {17 } {5} & \ frac {34} {5} \ end {array} \ right] $$$
Обратная замена:
$$$ y = \ frac {\ frac {34} {5}} { \ frac {17} {5}} = 2 $$$
$$$ x = \ frac {1 — \ left (-2 \ right) \ left (2 \ right)} {5} = 1 $$$
Ответ
$$$ x = 1 $$$, $$$ y = 2 $$$ A
Решение систем линейных уравнений с использованием матриц
Если нужно, просмотрите
матрицы
,
матричные операции со строками
а также
решение систем линейных уравнений
перед прочтением этой страницы.
В
матричный метод
решения систем линейных уравнений — это просто
метод устранения
в маскировке. При использовании матриц запись становится немного проще.
Предположим, у вас есть система линейных уравнений, например:
{
3
Икс
+
4
y
знак равно
5
2
Икс
—
y
знак равно
7
Первый шаг — преобразовать это в матрицу.Убедитесь, что все уравнения имеют стандартную форму
(
А
Икс
+
B
y
знак равно
C
)
, и используйте коэффициенты каждого уравнения для формирования каждой строки матрицы. Это может помочь вам разделить правый столбец пунктирной линией.
[
3
4
2
—
1
|
5
7
]
Далее мы используем
матричные операции со строками
изменить
2
×
2
матрицу слева на
единичная матрица
.Во-первых, мы хотим получить ноль в строке
1
, Столбец
2
. Итак, добавляем
4
раз Строка
2
грести
1
.
[
11
0
2
—
1
|
33
7
]
→
добавлен
(
4
×
Строка
2
)
к
Строка
1
Далее мы хотим
1
в верхнем левом углу.
[
1
0
2
—
1
|
3
7
]
→
разделенный
Строка
1
от
11
Теперь нам нужен ноль в нижнем левом углу.
[
1
0
0
—
1
|
3
1
]
→
добавлен
(
—
2
×
Строка
1
)
к
Строка
2
Наконец, мы хотим
1
в строке
2
, Столбец
2
.
[
1
0
0
1
|
3
—
1
]
→
умноженный
Строка
2
от
—
1
Теперь, когда у нас есть
2
×
2
Слева единичная матрица, мы можем считать решения из правого столбца:
Икс
знак равно
3
y
знак равно
—
1
Тот же метод можно использовать для
п
линейные уравнения в
п
неизвестные; в этом случае вы создадите
п
×
(
п
—
1
)
матрица и используйте операции со строками матрицы, чтобы получить тождество
п
×
п
матрица слева.
Важная заметка:
Если уравнения, представленные вашей исходной матрицей, представляют собой параллельные линии, вы не сможете получить единичную матрицу, используя операции со строками. В этом случае решения либо не существует, либо существует бесконечно много решений системы.
Решение системы линейных уравнений с использованием обратной матрицы
Решение системы линейных уравнений с использованием обратной матрицы требует определения двух новых матриц: [latex] X [/ latex] — это матрица, представляющая переменные системы, а [latex] B [/ latex] — это матрица матрица, представляющая константы.Используя умножение матриц , мы можем определить систему уравнений с таким же количеством уравнений в качестве переменных, как
[латекс] AX = B [/ латекс]
Чтобы решить систему линейных уравнений с использованием обратной матрицы , пусть [latex] A [/ latex] будет матрицей коэффициентов , пусть [latex] X [/ latex] будет переменной матрицей, и пусть [latex] B [/ latex] — постоянная матрица. Таким образом, мы хотим решить систему [латекс] AX = B [/ latex]. Например, посмотрите на следующую систему уравнений.
[латекс] \ begin {array} {c} {a} _ {1} x + {b} _ {1} y = {c} _ {1} \\ {a} _ {2} x + {b} _ {2} y = {c} _ {2} \ end {array} [/ latex]
Из этой системы матрица коэффициентов равна
[латекс] A = \ left [\ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ конец {массив} \ справа] [/ латекс]
Матрица переменных —
[латекс] X = \ left [\ begin {array} {c} x \\ y \ end {array} \ right] [/ latex]
А постоянная матрица
[латекс] B = \ left [\ begin {array} {c} {c} _ {1} \\ {c} _ {2} \ end {array} \ right] [/ latex]
Тогда [latex] AX = B [/ latex] выглядит как
[латекс] \ left [\ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end { массив} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {c} {c} _ {1 } \\ {c} _ {2} \ end {array} \ right] [/ latex]
Вспомните обсуждение ранее в этом разделе относительно умножения действительного числа на обратное, [латекс] \ left ({2} ^ {- 1} \ right) 2 = \ left (\ frac {1} {2} \ right) 2 = 1 [/ латекс].{-1} \ right) b \ end {array} [/ latex]
Единственное различие между решением линейного уравнения и системой уравнений , записанной в матричной форме, состоит в том, что поиск обратной матрицы более сложен, а умножение матриц — более длительный процесс. Однако цель та же — изолировать переменную.
Мы рассмотрим эту идею подробно, но полезно начать с системы [латекс] 2 \ times 2 [/ latex], а затем перейти к системе [латекс] 3 \ times 3 [/ latex].{-1} \ right) B \ end {array} [/ latex]
Вопросы и ответы
Если матрица коэффициентов не имеет обратной, означает ли это, что у системы нет решения?
Нет, если матрица коэффициентов необратима, система может быть несовместимой и не иметь решения, или быть зависимой и иметь бесконечно много решений.
Пример 7: Решение системы 2 × 2 с использованием обратной матрицы
Решите данную систему уравнений, используя обратную матрицу.
[латекс] \ begin {массив} {r} \ hfill 3x + 8y = 5 \\ \ hfill 4x + 11y = 7 \ end {array} [/ latex]
Решение
Запишите систему в виде матрицы коэффициентов, матрицы переменных и постоянной матрицы. {- 1} [/ latex].{-1} \ right) B \ hfill \\ \ left [\ begin {array} {rr} \ hfill 11 & \ hfill -8 \\ \ hfill -4 & \ hfill 3 \ end {array} \ right] \ text { } \ left [\ begin {array} {cc} 3 & 8 \\ 4 & 11 \ end {array} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {rr} \ hfill 11 & \ hfill -8 \\ \ hfill -4 & \ hfill 3 \ end {array} \ right] \ text {} \ left [\ begin {array } {c} 5 \\ 7 \ end {array} \ right] \ hfill \\ \ left [\ begin {array} {cc} 1 & 0 \\ 0 & 1 \ end {array} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {r} \ hfill 11 \ left (5 \ right) + \ left (-8 \ right) 7 \\ \ hfill -4 \ left (5 \ right) +3 \ left (7 \ right) \ end {array} \ right] \ hfill \\ \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {r} \ hfill -1 \\ \ hfill 1 \ end {array} \ right] \ hfill \ end {array} [/ latex ]
Решение [латекс] \ left (-1,1 \ right) [/ latex].{-1} [/ latex] находился слева от [latex] A [/ latex] с левой стороны и слева от [latex] B [/ latex] с правой стороны. Поскольку умножение матриц не коммутативно, порядок имеет значение.
Пример 8: Решение системы 3 × 3 с использованием обратной матрицы
Решите следующую систему, используя обратную матрицу.
[латекс] \ begin {array} {r} \ hfill 5x + 15y + 56z = 35 \\ \ hfill -4x — 11y — 41z = -26 \\ \ hfill -x — 3y — 11z = -7 \ end { array} [/ latex]
Решение
Напишите уравнение [латекс] AX = B [/ латекс].
[латекс] \ left [\ begin {array} {ccc} 5 & 15 & 56 \\ -4 & -11 & -41 \\ -1 & -3 & -11 \ end {array} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \\ z \ end {array} \ right] = \ left [\ begin {array} {r} \ hfill 35 \\ \ hfill -26 \\ \ hfill -7 \ конец {массив} \ справа] [/ латекс]
Во-первых, мы найдем инверсию [latex] A [/ latex] путем добавления идентификатора.
[латекс] \ left [\ begin {array} {rrr} \ hfill 5 & \ hfill 15 & \ hfill 56 \\ \ hfill -4 & \ hfill -11 & \ hfill -41 \\ \ hfill -1 & \ hfill -3 & \ hfill -11 \ end {array} | \ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] [/ latex]
Умножьте строку 1 на [latex] \ frac {1} {5} [/ latex].
[латекс] \ left [\ begin {array} {ccc} 1 & 3 & \ frac {56} {5} \\ -4 & -11 & -41 \\ -1 & -3 & -11 \ end {array} | \ begin { массив} {ccc} \ frac {1} {5} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] [/ latex]
Умножить строку 1 на 4 и прибавить к строке 2.
[латекс] \ left [\ begin {array} {ccc} 1 & 3 & \ frac {56} {5} \\ 0 & 1 & \ frac {19} {5} \\ -1 & -3 & -11 \ end {array} | \ begin {array} {ccc} \ frac {1} {5} & 0 & 0 \\ \ frac {4} {5} & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] [/ latex]
Добавьте строку 1 к строке 3.
[латекс] \ left [\ begin {array} {ccc} 1 & 3 & \ frac {56} {5} \\ 0 & 1 & \ frac {19} {5} \\ 0 & 0 & \ frac {1} {5} \ конец {массив} | \ begin {array} {ccc} \ frac {1} {5} & 0 & 0 \\ \ frac {4} {5} & 1 & 0 \\ \ frac {1} {5} & 0 & 1 \ end {array} \ right] [/ latex]
Умножить строку 2 на −3 и прибавить к строке 1.
[латекс] \ left [\ begin {array} {ccc} 1 & 0 & — \ frac {1} {5} \\ 0 & 1 & \ frac {19} {5} \\ 0 & 0 & \ frac {1} {5} \ end {array} | \ begin {array} {ccc} — \ frac {11} {5} & -3 & 0 \\ \ frac {4} {5} & 1 & 0 \\ \ frac {1} {5} & 0 & 1 \ end {array} \ right] [/ latex]
Умножить строку 3 на 5.
[латекс] \ left [\ begin {array} {ccc} 1 & 0 & — \ frac {1} {5} \\ 0 & 1 & \ frac {19} {5} \\ 0 & 0 & 1 \ end {array} | \ begin {array} {ccc} — \ frac {11} {5} & -3 & 0 \\ \ frac {4} {5} & 1 & 0 \\ 1 & 0 & 5 \ end {array} \ right] [/ latex]
Умножьте строку 3 на [latex] \ frac {1} {5} [/ latex] и прибавьте к строке 1.
[латекс] \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & \ frac {19} {5} \\ 0 & 0 & 1 \ end {array} | \ begin {array} {ccc} — 2 & -3 & 1 \\ \ frac {4} {5} & 1 & 0 \\ 1 & 0 & 5 \ end {array} \ right] [/ latex]
Умножьте строку 3 на [latex] — \ frac {19} {5} [/ latex] и добавьте к строке 2.{-1} B: [/ латекс]
[латекс] \ left [\ begin {array} {rrr} \ hfill -2 & \ hfill -3 & \ hfill 1 \\ \ hfill -3 & \ hfill 1 & \ hfill -19 \\ \ hfill 1 & \ hfill 0 & \ hfill 5 \ end {array} \ right] \ text {} \ left [\ begin {array} {rrr} \ hfill 5 & \ hfill 15 & \ hfill 56 \\ \ hfill -4 & \ hfill -11 & \ hfill -41 \\ \ hfill -1 & \ hfill -3 & \ hfill -11 \ end {array} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \\ z \ end {array} \ right] = \ left [\ begin {array} {rrr} \ hfill -2 & \ hfill -3 & \ hfill 1 \\ \ hfill -3 & \ hfill 1 & \ hfill -19 \\ \ hfill 1 & \ hfill 0 & \ hfill 5 \ end {array} \ right] \ text {} \ left [\ begin {array} {r} \ hfill 35 \\ \ hfill -26 \\ \ hfill -7 \ end {array} \ right] [/ latex]
Таким образом,
[латекс] {A} ^ {- 1} B = \ left [\ begin {array} {r} \ hfill -70 + 78-7 \\ \ hfill -105 — 26 + 133 \\ \ hfill 35 + 0 — 35 \ end {array} \ right] = \ left [\ begin {array} {c} 1 \\ 2 \\ 0 \ end {array} \ right] [/ latex]
Решение [латекс] \ left (1,2,0 \ right) [/ latex].
Попробовать 4
Решите систему, используя обратную матрицу коэффициентов.
[латекс] \ begin {array} {l} \ text {} 2x — 17y + 11z = 0 \ hfill \\ \ text {} -x + 11y — 7z = 8 \ hfill \\ \ text {} 3y — 2z = -2 \ hfill \ end {array} [/ latex]
Практическое руководство. Для данной системы уравнений решите с использованием обратных матриц с помощью калькулятора.
- Сохраните матрицу коэффициентов и постоянную матрицу как матричные переменные [latex] \ left [A \ right] [/ latex] и [latex] \ left [B \ right] [/ latex].
- Введите умножение в калькулятор, вызывая при необходимости каждую матричную переменную.
- Если матрица коэффициентов обратима, калькулятор представит матрицу решения; если матрица коэффициентов необратима, калькулятор выдаст сообщение об ошибке.
Пример 9: Использование калькулятора для решения системы уравнений с обратными матрицами
Решите систему уравнений с обратными матрицами с помощью калькулятора
[латекс] \ begin {array} {l} 2x + 3y + z = 32 \ hfill \\ 3x + 3y + z = -27 \ hfill \\ 2x + 4y + z = -2 \ hfill \ end {array} [/ латекс]
Решение
На странице матрицы калькулятора введите матрицу коэффициентов как матричную переменную [latex] \ left [A \ right] [/ latex] и введите постоянную матрицу как матричную переменную [latex] \ left [B \ right] [/ латекс].{-1} \ times \ left [B \ right] [/ латекс]
Вычислите выражение.
[латекс] \ left [\ begin {array} {c} -59 \\ -34 \\ 252 \ end {array} \ right] [/ latex]
Решение системы линейных уравнений с использованием матриц
Мы видели, как написать систему уравнений с расширенной матрицей , а затем как использовать строковые операции и обратную подстановку для получения эшелонированной формы . Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3.Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Пример 6: Решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
[латекс] \ begin {массив} {c} \ begin {array} {l} \ hfill \\ \ hfill \\ x-y + z = 8 \ hfill \ end {array} \\ 2x + 3y-z = -2 \\ 3x — 2y — 9z = 9 \ end {array} [/ latex]
Решение
Сначала мы пишем расширенную матрицу.
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill -1 \\ \ hfill 3 & \ hfill -2 & \ hfill -9 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 8 \\ \ hfill -2 \\ \ hfill 9 \ end {array} \ right] [/ latex]
Затем мы выполняем операции со строками для получения формы «строка-эшелон».
[латекс] \ begin {array} {rrrrr} \ hfill -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} { rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 3 & \ hfill & \ hfill -2 & \ hfill & \ hfill -9 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill 9 \ end {массив} \ right] & \ hfill & \ hfill & \ hfill & \ hfill -3 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill -15 \ end {array} \ right] \ end {array} [/ latex]
Самый простой способ получить 1 в строке 2 столбца 1 — это поменять местами [латекс] {R} _ {2} [/ latex] и [latex] {R} _ {3} [/ latex].
[латекс] \ text {Interchange} {R} _ {2} \ text {и} {R} _ {3} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill — 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 8 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill & \ hfill -15 \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill & \ hfill -18 \ end {array} \ right] [/ latex]
Затем
[латекс] \ begin {array} {l} \\ \ begin {array} {rrrrr} \ hfill -5 {R} _ {2} + {R} _ {3} = {R} _ {3} \ в \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 57 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \\ \ hfill & \ hfill 57 \ end {array} \ right] & \ hfill & \ hfill & \ hfill & \ hfill — \ frac {1} {57} {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \ \ \ hfill & \ hfill 1 \ end {array} \ right] \ end {array} \ end {array} [/ latex]
Последняя матрица представляет собой эквивалентную систему.
[латекс] \ begin {массив} {l} \ text {} x-y + z = 8 \ hfill \\ \ text {} y — 12z = -15 \ hfill \\ \ text {} z = 1 \ hfill \ end {array} [/ latex]
Используя обратную подстановку, мы получаем решение как [latex] \ left (4, -3,1 \ right) [/ latex].
Пример 7: Решение зависимой системы линейных уравнений с использованием матриц
Решите следующую систему линейных уравнений, используя матрицы.
[латекс] \ begin {array} {r} \ hfill -x — 2y + z = -1 \\ \ hfill 2x + 3y = 2 \\ \ hfill y — 2z = 0 \ end {array} [/ latex]
Решение
Запишите расширенную матрицу.
[латекс] \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill -2 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill -2 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill 2 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Сначала умножьте строку 1 на [latex] -1 [/ latex], чтобы получить 1 в строке 1, столбце 1. Затем выполните операции со строкой , чтобы получить форму строки-эшелона.
[латекс] — {R} _ {1} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 & \ hfill & \ hfill 2 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill & \ hfill 0 \ end {array} \ справа] [/ латекс]
[латекс] {R} _ {2} \ leftrightarrow {R} _ {3} \ to \ left [\ begin {array} {rrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 \ \ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 \ end {array} \ text {} | \ begin {array} { rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 2 \ end {array} \ right] [/ latex]
[латекс] -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -1 & \ hfill & \ hfill 2 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]
[латекс] {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 0 & \ hfill \ end { array} | \ begin {array} {rr} \ hfill & \ hfill 2 \\ \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]
Последняя матрица представляет следующую систему.
[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y — 2z = 0 \ hfill \\ \ text {} 0 = 0 \ hfill \ конец {array} [/ latex]
По тождеству [latex] 0 = 0 [/ latex] мы видим, что это зависимая система с бесконечным числом решений. Затем мы находим общее решение. Решив второе уравнение для [латекс] y [/ латекс] и подставив его в первое уравнение, мы можем решить для [латекс] z [/ латекс] через [латекс] x [/ латекс].
[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y = 2z \ hfill \\ \ hfill \\ x + 2 \ left (2z \ справа) -z = 1 \ hfill \\ \ text {} x + 3z = 1 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \ end {array} [/ latex]
Теперь мы подставляем выражение для [latex] z [/ latex] во второе уравнение, чтобы решить для [latex] y [/ latex] через [latex] x [/ latex].
[латекс] \ begin {массив} {l} \ text {} y — 2z = 0 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \\ \ hfill \\ y — 2 \ left (\ frac {1-x} {3} \ right) = 0 \ hfill \\ \ text {} y = \ frac {2 — 2x} {3} \ hfill \ end {array} [/ latex ]
Общее решение — [latex] \ left (x, \ frac {2 — 2x} {3}, \ frac {1-x} {3} \ right) [/ latex].
Попробуй 5
Решите систему, используя матрицы.
[латекс] \ begin {array} {c} x + 4y-z = 4 \\ 2x + 5y + 8z = 15 \ x + 3y — 3z = 1 \ end {array} [/ latex]
Вопросы и ответы
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Практическое руководство. Для данной системы уравнений решите с помощью матриц с помощью калькулятора.
- Сохраните расширенную матрицу как матричную переменную [latex] \ left [A \ right], \ left [B \ right], \ left [C \ right] \ text {,} \ dots [/ latex].
- Используйте функцию ref ( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.
Пример 8: Решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
[латекс] \ begin {array} {r} \ hfill 5x + 3y + 9z = -1 \\ \ hfill -2x + 3y-z = -2 \\ \ hfill -x — 4y + 5z = 1 \ end { array} [/ latex]
Решение
Напишите расширенную матрицу для системы уравнений.
[латекс] \ left [\ begin {array} {rrr} \ hfill 5 & \ hfill 3 & \ hfill 9 \\ \ hfill -2 & \ hfill 3 & \ hfill -1 \\ \ hfill -1 & \ hfill -4 & \ hfill 5 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 5 \\ \ hfill -2 \\ \ hfill -1 \ end {array} \ right] [/ latex]
На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную [latex] \ left [A \ right] [/ latex].
[латекс] \ left [A \ right] = \ left [\ begin {array} {rrrrrrr} \ hfill 5 & \ hfill & \ hfill 3 & \ hfill & \ hfill 9 & \ hfill & \ hfill -1 \\ \ hfill — 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill -1 & \ hfill & \ hfill -2 \\ \ hfill -1 & \ hfill & \ hfill -4 & \ hfill & \ hfill 5 & \ hfill & \ hfill 1 \ end {массив } \ right] [/ latex]
Используйте функцию ref ( в калькуляторе, вызывая матричную переменную [latex] \ left [A \ right] [/ latex].
[латекс] \ text {ref} \ left (\ left [A \ right] \ right) [/ латекс]
Оценить.
[латекс] \ begin {array} {l} \ hfill \\ \ left [\ begin {array} {rrrr} \ hfill 1 & \ hfill \ frac {3} {5} & \ hfill \ frac {9} {5 } & \ hfill \ frac {1} {5} \\ \ hfill 0 & \ hfill 1 & \ hfill \ frac {13} {21} & \ hfill — \ frac {4} {7} \\ \ hfill 0 & \ hfill 0 & \ hfill 1 & \ hfill — \ frac {24} {187} \ end {array} \ right] \ to \ begin {array} {l} x + \ frac {3} {5} y + \ frac {9} {5} z = — \ frac {1} {5} \ hfill \\ \ text {} y + \ frac {13} {21} z = — \ frac {4} {7} \ hfill \\ \ text {} z = — \ frac {24} {187} \ hfill \ end {array} \ hfill \ end {array} [/ latex]
При использовании обратной подстановки решение: [latex] \ left (\ frac {61} {187}, — \ frac {92} {187}, — \ frac {24} {187} \ right) [/ latex] .
Пример 9: Применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?
Решение
У нас есть система двух уравнений с двумя переменными. Пусть [latex] x = [/ latex] сумма, инвестированная под 10,5% годовых, и [latex] y = [/ latex] сумма, инвестированная под 12% годовых.
[латекс] \ begin {array} {l} \ text {} x + y = 12 000 \ hfill \\ 0.105x + 0.12y = 1335 \ hfill \ end {array} [/ latex]
В качестве матрицы имеем
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0.105 & \ hfill 0.12 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 12,000 \\ \ hfill 1,335 \ end {array} \ right] [/ latex]
Умножьте строку 1 на [latex] -0.105 [/ latex] и прибавьте результат к строке 2.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0 & \ hfill 0.015 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 12,000 \\ \ hfill 75 \ end {array} \ right] [/ latex]
Затем,
[латекс] \ begin {array} {l} 0,015y = 75 \ hfill \\ \ text {} y = 5,000 \ hfill \ end {array} [/ latex]
Итак [латекс] 12 000 — 5 000 = 7 000 [/ латекс].
Таким образом, 5000 долларов были инвестированы под 12% годовых и 7000 долларов под 10,5%.
Пример 10: Применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5%, другой — 8%, а третий — 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
Решение
У нас есть система трех уравнений с тремя переменными. Пусть [latex] x [/ latex] будет сумма, инвестированная под 5% годовых, пусть [latex] y [/ latex] будет суммой, инвестированной под 8%, и пусть [latex] z [/ latex] будет инвестированной суммой. под 9% годовых. Таким образом,
[латекс] \ begin {array} {l} \ text {} x + y + z = 10 000 \ hfill \\ 0.05x + 0,08y + 0,09z = 770 \ hfill \\ \ text {} 2x-z = 0 \ hfill \ end {array} [/ latex]
В качестве матрицы имеем
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 1 & \ hfill 1 \\ \ hfill 0,05 & \ hfill 0,08 & \ hfill 0,09 \\ \ hfill 2 & \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 10,000 \\ \ hfill 770 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Теперь мы выполняем исключение Гаусса, чтобы получить форму строки-эшелон.
[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ -0.05 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 2 & \ hfill & \ hfill 0 & \ hfill & \ hfill -1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill 0 \ end {array} \ right] \ hfill \ end {array} \ hfill \\ -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ \ frac {1} {0.03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ 2 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill — \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end {array} \ right] \ hfill \ end {array} [/ latex]
Третья строка сообщает нам [латекс] — \ frac {1} {3} z = -2,000 [/ latex]; таким образом [латекс] z = 6,000 [/ латекс].
Вторая строка сообщает нам [латекс] y + \ frac {4} {3} z = 9000 [/ latex]. Подставляя [латекс] z = 6,000 [/ latex], получаем
[латекс] \ begin {array} {r} \ hfill y + \ frac {4} {3} \ left (6000 \ right) = 9000 \\ \ hfill y + 8000 = 9000 \\ \ hfill y = 1000 \ end {array} [/ latex]
Первая строка сообщает нам [латекс] x + y + z = 10,000 [/ latex]. Подставляя [латекс] y = 1000 [/ latex] и [latex] z = 6000 [/ latex], получаем
[латекс] \ begin {array} {l} x + 1 000 + 6 000 = 10 000 \ hfill \\ \ text {} x = 3 000 \ text {} \ hfill \ end {array} [/ latex]
Ответ: 3000 долларов вложены под 5%, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.
Попробуй 6
Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своих запасов. Часть денег была взята под 7%, часть — под 8%, часть — под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.
Решение
Решатель линейных уравнений
| Система m линейных уравнений от n неизвестных имеет решение тогда и только тогда, когда ранг r расширенной матрицы равен рангу матрицы коэффициентов. Если две матрицы имеют одинаковый ранг r и r = n, решение уникально. Если две матрицы имеют одинаковый ранг r и r
| |||||||||
| Другой способ решения линейной системы уравнений — это правило Крамера, которое включает только детерминанты. Рассмотрим систему уравнений:
| |||||||
Поскольку r n = 4 2 = 2, две переменные зависят от двух других переменных, и мы должны выбрать определенные значения для двух переменных
например: w = a и y = b (a, b — любое число), тогда:
| z = 1 + 2a |
| x = 4 2b + a |
Вектор пространства решений (4 + a 2b, b, 1 + 2a, a)
например, если мы выберем: a = 1 b = 1, то решение будет:
(7, 1, 3, 1).
Решатель матричных уравнений
22 марта, 2019 · В общем, вычисление обратной известной невырожденной матрицы размера N × N эквивалентно одновременному решению N линейных уравнений. Таким образом, этот процесс также можно реализовать с помощью нашей платформы, поскольку он решает эквивалентную систему уравнений, связанную с данным линейным интегральным уравнением в уравнении (2). 1.
одновременный решатель уравнений квадратичные 3 неизвестных, целочисленное сложение, вычитание, умножение, деление рабочего листа, поиск алгебры наименьшего общего знаменателя, интерактивные игры решают квадратное уравнение путем заполнения квадрата, справочный лист, объясняющий, как решать уравнения путем их балансировки, квадратичный онлайн-калькуляторы вершинных уравнений и стандартной формы, решение читов для линейных уравнений…
Основной подход, используемый для решения уравнения с одной переменной, заключается в манипулировании уравнением до тех пор, пока переменная не будет изолирована с одной стороны уравнения, а все остальное — с другой. В случае линейного уравнения это может быть сделано путем добавления или вычитания равных с каждой стороны, умножения обеих сторон на равные или деления обоих …
14 ноября 2012 г. · Привет, у меня есть куча замкнутых дифференциальных уравнений что я хочу решить. Переменные DE представляют собой матрицы 2×2.Итак, я хочу ввести несколько матриц переменных 2×2, а затем использовать NDSolve для получения решения.