Самостоятельная работа «Степень числа», 5 класс

Просмотр
содержимого документа

Самостоятельная работа по теме: «Степень числа» Вариант I Запишите выражение и найдите его значение: а) три в четвертой степени; б) восемь в квадрате.   Запишите число, которое представлено в виде суммы разрядных слагаемых:   Найдите значение выражения:   Какой показатель надо вписать вместо звездочки, чтобы получилось верное равенство:   Найдите значение выражения:	Самостоятельная работа по теме: «Степень числа» Вариант II Запишите выражение и найдите его значение: а) два в пятой степени; б) пять в кубе.   Запишите число, которое представлено в виде суммы разрядных слагаемых:   Найдите значение выражения:   Какой показатель надо вписать вместо звездочки, чтобы получилось верное равенство:   Найдите значение выражения:
Самостоятельная работа по теме: «Степень числа» Вариант I Запишите выражение и найдите его значение: а) три в четвертой степени; б) восемь в квадрате.   Запишите число, которое представлено в виде суммы разрядных слагаемых:   Найдите значение выражения:   Какой показатель надо вписать вместо звездочки, чтобы получилось верное равенство:   Найдите значение выражения:	Самостоятельная работа по теме: «Степень числа» Вариант II Запишите выражение и найдите его значение: а) два в пятой степени; б) пять в кубе.   Запишите число, которое представлено в виде суммы разрядных слагаемых:   Найдите значение выражения:   Какой показатель надо вписать вместо звездочки, чтобы получилось верное равенство:   Найдите значение выражения:

 

«Степень числа».

Урок математики 5 класс

Дата: _______

Класс: 5

Предмет: математика

Тема: «Степень числа. Квадрат и куб числа».

Цель: ознакомление с понятием степень числа, куб и квадрат числа совершенствование навыков чтения степеней.

Задачи:

1. Образовательные: сформировать понятие степени; научиться: читать и записывать степень; называть компоненты степени; заменять произведение степенью; представлять степень в виде произведения; объяснить, что называется квадратом и кубом числа.

2. Развивающие: развивать логическое мышление, память, внимание.

3. Воспитательные: воспитывать ответственность и аккуратность, интерес к предмету.

Тип урока: урок «открытия» нового знания.

Ход урока

1. Орг. Момент

— Здравствуйте.

— Какие вопросы по контрольной работе?

— С какими проблемами вы столкнулись?

— Сегодня на уроке мы сначала восхитимся нашими умениями вычислять, для этого проведем устный счет.

1. Речевая разминка

-C-

—СТА-, -СТО-, -СТУ-.

Степень

В степень.

1. Актуализация знаний:

Устный счет. “Круговые” примеры.

— Ответ первого выражения является началом в записи следующего.

— Вычислите. Соедините выражения стрелочками.

35+35+35+35+35

51+51+51+51

7*13+37*7

150+270/90

204-104-65

175/25

350-50*4

153/3

— В каких выражениях можно одно действие заменить другим?

— Запишите, полученные выражения.

1. Изучение новой темы:

— На доске записаны выражения. 

2 + 2 + 2 + 2 + 2 и 2 · 2 · 2 · 2 · 2

— Как вы думаете, что общего у них?

— Чем они отличаются?

— Мы с вами уже повторили, как сумму 2 + 2 + 2 + 2 + 2 записать короче.

2 + 2 + 2 + 2 + 2=2 · 5.

— А как вы думаете, можно ли произведение 2 · 2 · 2 · 2 · 2 записать короче?

— Оказывается можно. И вот как: 2 · 2 · 2 · 2 · 2 =2 ⁵.

Тема нашего урока “Степень числа. Квадрат и куб числа”.

— Запись 2⁵ читают “два в пятой степени”. (Запись в тетрадь и проговорить). 

2 – основание степени;

5 – показатель степени;

2 ⁵ – степень.

— Прочитайте выражения, назовите в каждом основание и показатель степени: 

6⁷, 12³, 4¹⁰, 15², 3⁵, 8¹

— Запишем произведения в виде степени:

а) 4 · 4 · 4; б) 3 · 3 · 3; в) 2 · 2 · 2 · 2 · 2 · 2.

Г) 5* 5 д) 7* 7* 7* 7 е)6*6

— Вторую степень числа принято называть иначе.

— Произведение 5 · 5 называют квадратом числа 5 и обозначают 5².

n² = n · n (Чтение правила в учебнике).

— Рассмотрим таблицу квадратов первых десяти натуральных чисел. Как получены числа второй строки?

— Третья степень числа также имеет свое особое название.

— Произведение 7 · 7 · 7 называют кубом числа 7 и обозначают 7³.

n³ = n · n · n (чтение правила в учебнике).

— Рассмотрим таблицу кубов первых десяти натуральных чисел. Как получены числа второй строки?

— Квадрат числа в пределах 10 вычислить легко, это примеры из таблицы умножения, а вот квадрат чисел в пределах 20 помещены на форзаце учебника. Откройте эту таблицу. Чему равен квадрат 11, 12, 13. Для удобства здесь размещена таблица кубов, чтобы не искать ее в учебнике.

— Найдите значения выражений:

3¹ =? 15¹ =? 1¹=?

— Показатель степени 1 обычно не пишут.

1. Физминутка

2. Закрепление изученного материала

№ 653 у доски.

№ 654 4 столбика

2 столбика

3 столбика

1. Итог урока:

Назовите основание степени и показатель степени:

34, 57, 93, 158, 132.

Что такое “квадрат числа”?

Что такое “куб числа”?

Выставляются отметки за урок.

1. Домашнее задание:

С. 101 № 666.

Дата: ______

Класс: 6

Предмет: математика

Тема урока: «Сложение и вычитание рациональных чисел. Длина отрезка на координатной прямой».

Цель: Формирование навыков сложения и вычитания рациональных чисел

Задачи:

1. -закрепить навыки сложения и вычитания положительных и отрицательных чисел, проверить знания учащихся по данной теме;

2. -развивать навыки беглого устного счета, логическое мышление учащихся; развитие воли через задание посильной сложности, развитие интеллекта через заучивание математических терминов;

3. -воспитывать у учащихся интерес к математике и сознательную дисциплину.

Ход урока:

1. Организационный момент.

Думать — коллективно!

Решать — оперативно!

Отвечать — доказательно!

Бороться — старательно!

И открытия нас ждут обязательно!

1 препятствие.

Математика – царица наук,

Арифметика – царица математики

(К.Гаусс)

1.Сформулируйте правило сложения двух отрицательных чисел.

2.Сумма двух отрицательных чисел отрицательное или положительное число?

3.Что больше, сумма двух отрицательных чисел или одно из них?

4. Сформулируйте правило сложения чисел с разными знаками.

5.Если из двух слагаемых больший модуль имеет отрицательное число, то какой знак будет иметь сумма данных чисел?

6.Чему равна сумма противоположных чисел?

7.По какому правилу выполняется вычитание рациональных чисел?

8.Как вычитаются числа с разными знаками?

9. Как вычитаются числа с одинаковыми знаками?

10.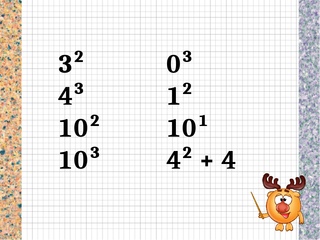 Как найти длину отрезка на координатной прямой?

11. Сформулируйте правило раскрытия скобок, перед которыми стоит знак «+».

Знак «плюс» не изменяет знака числа, поэтому, если перед скобкой стоит плюс, то знак в скобках не меняется.

+ (+ a) = + a
+ (- a) = — a

12. Сформулируйте правило раскрытия скобок, перед которыми стоит знак «-».

Знак «минус» перед скобками меняет знак числа в скобках на противоположный.

— (+ a) = — a
— (- a) = + a

Правило знаков для чисел

+ (+) = +

+ (-) = —
— (-) = +	— (+) = —

Или выучить простое правило.

2 препятствие.

Тот, кто не знает математики , не может узнать никакой другой науки.

(Роджер Бэкон)

Устный счет.

1) 15 – (- 58) = 4) 28 – 100 = 7) 75 – 90 =

2) – 36 – 24 = 5) – 20 + 6 = 8) – 189 + 64 =

3) -70 + 16= 6) – 75 + 75 = 9) -35 – 28 =

3 препятствие.

Математика – точильный камень способностей.

Работа в тетрадях.

1. Упростите сумму:

-8+х+(-22).

1. Упростите сумму:

-10+а+34.

1. Разность у и 6 равна 12. Найдите у.

1. Решите уравнение: 5-с=12.

1. Найдите длину отрезка с концами в точках с координатами 3 и -7.

4 препятствие.

Математика черпает свою силу в умении исключать все лишнее в процессе мышления. (Э.Мах)

Работа над нестандартными заданиями.

Связь математики с живой природой.

На островах Тихого океана живут черепахи-гиганты. Они такой величины, что дети могут кататься сидя у них на панцире. Название этих черепах мы узнаем после того, как выполним следующее задание:

Решая примеры, определите название этой черепахи.

-42 + 18=

0	Е
-3,91 + 3,91 =	-5	Л
15,3 + (- 2,3) =	19	О
-12 – (-2) =	-24	Д
31 – 12 =	-102,08	С
-48 – 23 =	14	М
-6,1 + 6,1 + 0 =	-71	Х
15 – 20 =	13	Р
-25 – (-5) =	-20	И
-102,08 – 0 =

(Дермохелис)

5. Препятствие.В мире интересного.

Только забавляясь и учимся. (Анатоль Франс)

а).На земном шаре обитают птицы – безошибочные определители прогноза погоды на лето. Название этих птиц зашифровано в примерах, которые нам предстоит решить. (Решаем письменно с комментарием).

Выполните действия.

-379 + 948 =

-0,15	Л
-0,81 + 0,66 =	-1000,7	Н
-7,6 + 19,2 =	-24,3	О
-2,6 – (-1,4) =	-1,2	М
3,2 – 6,28 =	569	Ф
-1408,7 + 408 =	0	Г
-817 + 817 =	-3,08	И
-13,25 – 11,05 =	11,6	А

(Фламинго)

– «Это интересно!»

Фламинго строят из песка гнезда в форме усеченного конуса, в верхнем основании его делают углубления, в которые складывают яйца. Если лето будет дождливым, то гнезда строятся высокими, чтобы их не могла затопить вода, а если засушливым – то более низкими.

б). Самое маленькое государство – Ватикан. Какова его площадь?

– 189 + 233 =?

в). Материк с наибольшим числом границ – Африка. Каково число границ?

– 75 +? = 33

6.Препятствие.

МИР построен на силе ЧИСЕЛ.

(Пифагор)

а).Математические знаки.

1). *6 *8 =-14

2). *29 * 50=+21

б).Какая рыба без чешуи?

1).Щука-5, 2).Сом-7, 3).Карась-9.

–15+у=-8

в).Какое озеро самое красивое?

1).Чудское-2, 20.Ильмень-4, 3).Байкал-6.

m+(-14)=-8

г). Сколько учеников вашего класса пробовали курить?

– 6 + ? = -4

д). Во сколько лет они попробовали курить?

1).– 15 – (-21)= ?

2)? –16= – 8;

7. Препятствие.

Мы с наслаждением познаем математику…

Она восхищает нас, как цветок лотоса.

(Аристотель)

Задание:

Расположите числа в порядке убывания:

— —Р; — И; 6,1 – Ф; 16 –П; -0,2 –Г; 0,2 –А; -0,6 – О.

(ответ: Пифагор)

Пифагор (1- призер Олимпийских Игр, 2- победитель в кулачных боях, 3- “Царица геометрии” – теорема Пифагора)

Самостоятельная работа

Вариант № 1

1.Сравните значения выражений: 3,87 + (-2,63) и 5,29 + (-3,59) (3 б)

2. Вычислите: 5,4 + (- 3,7) + (- 4,2) (3 б)

3. Вычислите: 3,7 – х = -2,3 (3 б)

4. Замените звездочки знаками «+» или « — » так, чтобы получились верные равенства: — 6,1 * (- 2,3)* 3,8 = 0 (3 б)

Вариант № 2

1. Сравните значения выражений: — 7,35 +4,54 и -4,68 + 3,46 (3 б)

2. Вычислите: 12,8 + (- 3,5) + (- 7,6) (3 б)

3. Вычислите: х – 3,9 = -2,7 (3 б)

4. Замените звездочки знаками «+» или « — » так, чтобы получились верные равенства: 3,9 * 7,4 * (- 9,3) = — 12,8 (3 б)

Проверка самостоятельной работы по образцу.

Вариант № 1

1.Сравните значения выражений: 3,87 + (-2,63)

3. Вычислите: 3,7 – х = -2,3 х = 6

4. Замените звездочки знаками «+» или « — » так, чтобы получились верные равенства: — 6,1 — (- 2,3) + 3,8 = 0

Вариант № 2

1.Сравните значения выражений: — 7,35 +4,54

2. Вычислите: 12,8 + (- 3,5) + (- 7,6) = 1,7

3.Вычислите: х – 3,9 = -2,7 х = 1,2

4. Замените звездочки знаками «+» или « — » так, чтобы получились верные равенства: 3,9 — 7,4 + (- 9,3) = — 12,8

8.Заключение.

Числа отрицательные – новые для нас
Лишь совсем недавно их узнал наш класс
Сразу поприбавилось всем теперь мороки
Учим – учим правила, готовимся к урокам!

Школьные дни-

Быстры они,

К финишу мчатся как птицы

Помни везде-

Помни всегда,

Что без труда

В учебе побед не добиться!

9. Подведение итогов урока. Выставление оценок.

— Что есть больше всего на свете? – Пространство.

— Что быстрее всего? – Ум.

— Что мудрее всего? – Время.

— Что приятнее всего? – Достичь желаемого.

Слова древнегреческого математика Фалеса.

10.Домашнее задание:

Найти сумму всех целых чисел от – 499 до 501.

«Степень числа» 5 класс (А.Г. Мерзляк) | Презентация к уроку по математике (5 класс) по теме:

Слайд 1

Степень числа 5 класс учитель: Елена Владимировна Куслина МБОУ СОШ № 206 Новосибирск, 2018

Слайд 2

5+5+5+5+5+5 = 10+10+10+10 = 7+7+7+7+7+7 = 2+2+2+2+2+2+2 = 30+30+30 = 34+34+34+34 = 9+9+9+9+9+9+9+9+9 = Замените действие сложение умножением

Слайд 3

5 6 = 30 10 4 = 40 7 6 = 42 2 7 = 14 30 3 = 90 34 4 = 136 9 9 = 81 Проверьте себя

Слайд 4

5 5 5 = 3 3 3 = 10 10 10 = 2 2 2 2 2 = 4 4 4 = 50 50 = 7 7 7 = Запишите задания! Существует ли действие, которым можно заменить умножение одинаковых множителей ??? Чтобы это узнать, прочитайте § 20 учебника

Слайд 5

400 лет назад французский математик Рене Декарт предложил такой способ записи произведения нескольких одинаковых множителей 5 · 5 · 5 · 5 = 5 4 Запись 5 4 читают « пять в четвёртой степени»

Слайд 6

Потренируемся! 7 ⁵ «семь в пятой степени» 9⁴ «девять в четвёртой степени» 8³ «восемь в кубе» 6 ¹ «шесть в первой степени или просто шесть» 5 ² «пять в квадрате» 10 ⁸ «десять в восьмой степени»

Слайд 7

Почему «квадрат» и «куб»? S = 3 ∙ 3 = 3² = 9 см² V = 2 ∙ 2 ∙ 2 = 2³ = 8 см³ 3 см 2 см Скоро узнаете ответ на этот вопрос

Слайд 8

Составьте конспект по основным понятиям и правилам темы, проговорите вслух 3 раза! Расскажите соседу по парте! Объединившись в группы по 4 человека, ответьте на вопросы в конце параграфа и замените умножение степенью числа (слайд №4)

Слайд 9

Показатель степени Основание степени 5 4 Выражение 5 4 называют степенью Ничего не упустили?

Слайд 10

Свойства степени Первая степень любого числа равна самому числу: Вторую степень числа называют «квадратом»: Третью степень числа называют «кубом»:

Слайд 11

Степень – действие III ступени 2 ступень 1 ступень 3 ступень степень

Слайд 12

5 ³ 3 ³ 10 ³ 2 ⁵ 4 ³ 50 ² 7 ³ Проверь себя

Слайд 13

Устно отвечаем по цепочке по рядам «Кто быстрее» № 548, № 549, № 550 (страница учебника 136) Работаем с таблицей квадратов и кубов натуральных чисел на форзаце учебника Фронтальная работа

Слайд 14

Самостоятельная работа Применим навыки работы с таблицами и новые знания о степени и порядке действий в вычислительных примерах со степенями выполняя № 552 (нечётные номера примеров) Взаимопроверка №552

Слайд 15

Самостоятельная работа № 551 № 553 (чётные номера примеров) № 554 коллективное обсуждение способа вычисления значения выражения, выполнение номера по заданному правильному алгоритму

Слайд 16

Физкультминутка для глаз

Слайд 17

Запомни простую истину! Почему называется: КВАДРАТ и КУБ числа! Найдите площадь квадрата со стороной 9 см Найдите объем куба со стороной 3 см

Слайд 18

Вычислите устно (работаем в группах) 3² 4³ 10² 10³ 0³ 1² 10¹ 4² + 8

Слайд 19

Проверьте себя (работаем в группах) 3²=3 3=9 4³= 4 4 4=64 10²= 10 10=100 10³=10 10 10=1000 0³=0 0 0=0 1²=1 1=1 10¹=10 4² + 8=4 4+8=24 3

Слайд 20

Контроль знаний (выполните задания под копирку, оригинал сдайте учителю, а копию оставляете у себя для самопроверки) Задание №1 Ответьте письменно на вопросы Когда произведение чисел можно записать короче? Приведите свои примеры Что такое квадрат числа? Приведите свои примеры Что такое куб числа? Приведите свои примеры

Слайд 21

5 4 6 5 7 8 Что означают записи ? Назовите основание и показатель степени. Задание №2

Слайд 22

Расставьте порядок действий и вычислите: 3² ; 4 ³; 6 ²; 7 ³; 0 ²; 1²; 8 ¹ 3²+1 7³-100:2 4) 10²+ 10²-2*100 5) (5² + 12-4 ¹):11 6) 5*2³ Задание №3

Слайд 23

Какое наибольшее число можно написать тремя 5 и знаками действий? 5+5 5 ? 55 5 ? Задание №4* Творческое

Слайд 24

Итого : Сегодня на уроке мы повторили… Сегодня на уроке мы узнали…. Сегодня на уроке мы научились… Что запомнили? Что вызвало затруднения?

Слайд 25

Самокоррекция , работа над ошибками, самооценка деятельности на уроке по десятибалльной шкале Как я усвоил материал ? Прочно 9-10 баллов Частично 7-8 баллов Мало что понял, надо еще поработать 4-6 баллов Как я работал ? Сам справился со всеми заданиями 9-10 баллов Допускал ошибки 7-8 баллов Сделал много ошибок 4-6 баллов

Слайд 26

Домашнее задание: № 553 (чётные номера примеров) или Написать небольшое сообщение на тему: Квадраты и кубы чисел в жизни. (библиотека, интернет, помощь родителей) Или* (забегая вперёд) Начертить квадрат со стороной 4 см и рассчитать его площадь, применяя знания о степени числа ; начертить куб и обозначив длину ребра каким-нибудь числом, вычислить объём куба

Конспект урока математики в 5-м классе «Степень с натуральным показателем»

 Конспект урока математики в 5-м классе «Степень с натуральным показателем»

Тип урока: Урок первичного предъявления новых знаний и универсальных учебных действий.

Образовательные: Создавать условия для усвоения учащимися понятия степень числа. Организовать деятельность учащихся по овладению умениями и навыками находить значения числовых выражений, содержащих степень. 

Развивающие: Способствовать развитию умения анализировать, делать выводы, развитию познавательной активности, формированию интереса к предмету.

Этап 1: Организационный момент и устный счет.

Здравствуйте, ребята. Я рада вас видеть. Откройте тетради и подпишите число и классная работа. Какую тему мы изучали на прошлом уроке? (Умножение чисел) Как вы думаете, чем мы будем заниматься сегодня? (Учащиеся предлагают варианты) Вам бы хотелось узнать что-либо новое?

Начнем урок с устной разминки. «Не зевай, быстрей считай!»

75+97

83-18

68*5

23*5

25*36

15*8

(Учащиеся используют приемы рационального устного счета)

Этап 2: Актуализация знаний и фиксация затруднений деятельности.

4+4+4

5*5*5*5

7*7

7+7+7+7

10*10*10

2+2+2+2+2+2+2

Найдите сходство и различие в примерах.

Разбейте выражения на группы и укажите принцип разбиения (разбейте выражения на две группы так, чтобы примеры каждой группы имели общий признак, были похожи друг на друга и укажите, что объединяет примеры каждой группы).

Сумма нескольких одинаковых слагаемых	Произведение нескольких одинаковых множителей
4+4+4 7+7+7+7 2+2+2+2+2+2+2	5*5*5*5 7*7 10*10*10

Как можно представить сумму нескольких одинаковых слагаемых? Вычислите удобным способом примеры из первой группы.

(Сумму одинаковых слагаемых можно представить в виде произведения:

4+4+4=4*3=12

7+7+7+7=7*4=28

2+2+2+2+2+2+2=2*7=14)

Обратите внимание на вторую группу примеров. Еще раз скажем, что их объединяет? (Это произведение одинаковых множителей) А если я попрошу вас записать произведение 1000 одинаковых множителей, какое выражение получиться? (Длинное) Удобно пользоваться такими длинными записями? (Нет) А знаем ли мы способ, который позволит сделать эту запись короче? (Нет)

Этап 3: Построение проекта выхода из затруднения.

Итак, как вы думаете, что мы должны узнать сегодня на уроке? (Как записать произведение одинаковых множителей короче) Правильно, сегодня на уроке мы узнаем новый способ записи произведения нескольких одинаковых множителей. Этот способ, 400 лет назад предложил французский математик Рене Декарт. Посмотрите, как Декарт предложил записать произведение 4 множителей, каждый из которых равен 5: 5*5*5*5=54. Как вы думаете, что означает 5 в данной записи? (Повторяющийся множитель) Что означает число 4? (Количество множителей)

Попробуйте записать оставшиеся произведения. (7*7=72) (В случае затянувшейся паузы вернуться к предыдущему примеру: Обратите внимание, в записи участвуют два числа, одно — повторяющийся множитель, число 5, другое, которое показывает количество множителей , число 4 записывают мелким шрифтом сверху и справа) Что означает число 7 в данной записи? (Повторяющийся множитель) Что означает число 2? (Количество множителей) Обратите внимание, в записи участвуют два числа, одно — повторяющийся множитель, число 7, другое, которое показывает количество множителей, число 2 записывают мелким шрифтом сверху и справа.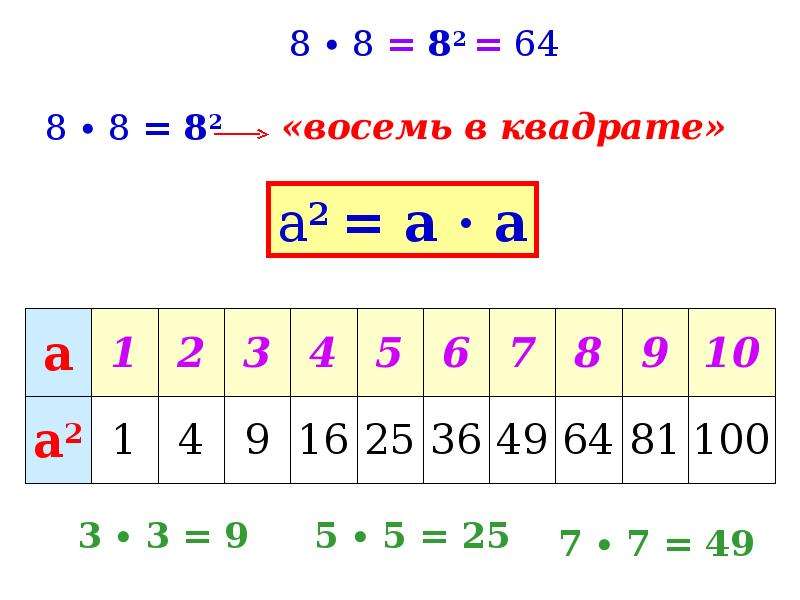 n=а*а*а*…*а)

                                                                                                    

                                                                                                         n раз

Мы получили произведение, которое состоит, из n множителей, каждый из которых равен а.

Степенью числа а с натуральным показателем n (n>1) называется произведение n множителей каждый из которых равен а.

Давайте сравним полученный вывод с текстом в учебнике. Прочитаем определение степени, которое дается в нашем учебнике на странице 38.

Совпадает ли, сформулированное нами определение с определением в учебнике? (Да)

Выделим ключевые слова. Определение какой величины мы сформулировали? (Степени) Подчеркнем слова – степенью числа а с показателем n.

Результат какого действия называется степенью? (Умножения) То есть произведение, подчеркнем слово произведение.

Сколько множителей содержит это произведение? (n) Чему равен каждый множитель? (а)

(Запись на доске: Степенью числа а с натуральным показателем n (n>1) называется произведение n множителей каждый из которых равен а)

Обратите внимание на условие: n>1. 3 читаем «девять в степени три», 9 – основание, 3 – показатель)

Вторую степень числа называют также квадратом числа и читают 6 в квадрате. Третью степень числа называют кубом числа и читают 9 в кубе. О происхождении этих названий мы узнаем позже.

Этап 4: Физкультминутка.

Раз – поднялись, потянулись,

Два – согнулись, разогнулись,

Три в ладоши три хлопка,

На четыре – три кивка,

Пять руками помахать,

Шесть – тихонько сесть.

Этап 5: Первичное закрепление.

Задание № 1.

8*8*8

8+8+8

8*3

8*8

Какие выражения можно представить в виде степени? (Первое и четвертое) Почему? (Это произведение одинаковых множителей) Почему второе выражение нельзя представить в виде степени? (Это сумма одинаковых слагаемых, а не произведение) Почему третье выражение нельзя представить в виде степени? (Это произведение разных множителей, а не одинаковых) Представьте первое произведение в виде степени и прочитайте степень. 7

Прочитайте степень и назовите основание и показатель степени. (4 в кубе. 4-основание, 3 – показатель) Что показывает основание 4? (Число 4 мы будем умножать само на себя) Что показывает показатель 3? (Число 4 мы будем умножать само на себя 3 раза) (Запись на доске: 43=4*4*4) Выполните вычисления, сколько получиться? (64)

Следующий пример. Какое число мы будем умножать само на себя? (3) Почему? (Основание степени равно 3) Сколько раз мы умножим число 3 само на себя? (4 раза) Почему? (Показатель равен 4) Выполните вычисления, сколько получиться? (81) Следующий пример. Какое число мы будем умножать само на себя и сколько раз? (Два раза умножим само на себя число 15) Выполните вычисления, сколько получиться? (225)

03. Как представить в виде произведения? (Три раза умножим число 0 само на себя) Выполните вычисления, сколько получиться? (0)

17. Как представить в виде произведения? (7 раз умножим число 1 само на себя) Давайте не будем записывать, вычислим сразу. 3 = 5 · 5 · 5 = 125

в) 112=11 · 11 =121)

Проверим работу. Подпишите оценочные листы.

Оценочный лист.                                                          Фамилия:

ЗАДАНИЕ	ВЫПОЛНЕНО ВЕРНО	ИСПРАВЛЕНО ПО ОБРАЗЦУ
№1(а)
№1(б)
№2(а)
№2(б)
№2(в)

Если задание выполнено верно, вы выставляете себе +. Если же вы допустили ошибки, мы постараемся их исправить при проверке.

Давайте выясним, в чем причины ошибок.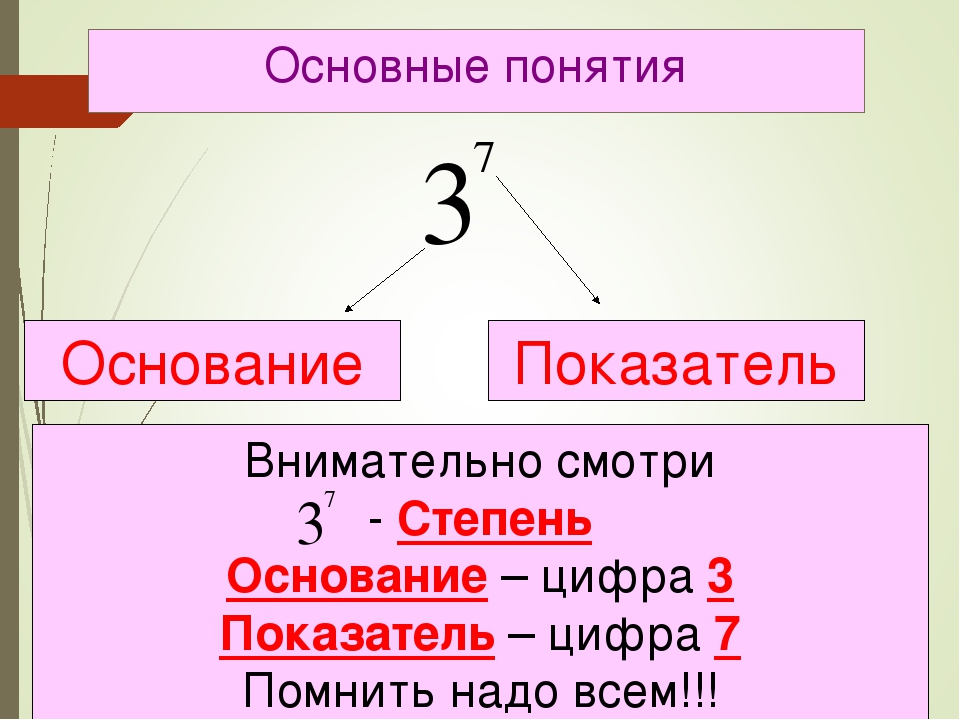 3)

Задание № 3.

Упростите запись, используя понятие степени:

3*3*5*5*5;

13*6*6*6*6*13;

а*а*12*а*12.

Если в произведении есть одинаковые множители, то пользуясь переместительным и сочетательным законами умножения, их можно сгруппировать вместе и заменить степенью.

Этап 8: домашнее задание.

I уровень: П. 1.11, № 159(1 строка), 163 (1 строка), 167.

Если сегодня на уроке вам было все понятно, вы легко справлялись со всеми заданиями без затруднений, то на дом вы записываете задания первого уровня.

II уровень: П. 1.11, № 154, 156 (2 строка), 163 (1 строка).

Если сегодня на уроке при выполнении заданий вы испытывали затруднения, то записываете задания второго уровня.

Этап 9: рефлексия деятельности.

Что нового и полезного вы узнали сегодня на уроке? С каким новым понятием познакомились? (С понятием степени)

Зачем нужны эти знания? (Понятие степени позволяет короче записывать произведения одинаковых множителей, упрощать записи)

Итак, что мы учились делать сегодня? (Записывать произведения одинаковых множителей в виде степени)

Еще чему учились? Учились ли мы вычислять значения степени? (Да)

На оценочном листе с помощью смайлика оцените свою работу сегодня на уроке.

Оценить работу класса.

Библиографический список

Математика. Учебник. 5 класс. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. – М: «Просвещение», 2014,-272 с.

Математика. Методические рекомендации. 5 класс : пособие для учителей общеобразоват. учреждений / М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2012.

Презентация «Степень числа — Квадрат и куб числа»

Текст этой презентации

Слайд 1

Степень числа. Квадрат и куб числа.
5 класс
Учитель : Исакова Маргарита Владимировна

Слайд 2

«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает в себе настойчивость и упорство в достижении цели.» А.И. Маркушевич.

Слайд 3

Устный счет «Круговые примеры»
15+15+15+15
41+41+41
350-50∙3
200 :2-59
60∙5+50
(140-100) :8
123-23+40
60
200
123
41
5
140
350

Слайд 4

1
2
3
4
15
15
15
15
+

+
+
15
4
×
41
41
41
+
+
41
3
×
Повторяющееся Сложение
Повторение арифметики
Повторяющееся Умножение
41

?

Слайд 5

Текст внимательно прочтем,все в порядок приведем !
Вопросы: Как называют это выражение: ? Сколько участвует чисел в записи степени? Назовите основание степени? Что показывает основание степени? Назовите показатель степени? Что показывает показатель степени? Приведи свои примеры.
3
9

Слайд 6

Основание
Показатель
3
Умножить 9 раз 3 между собой.
Основание = 3
показатель = 9
Показатель говорит сколько раз нужно умножить основание.

Слайд 7

1
2
3
4
15
15
15
15
+

+
+
15
4
×
41
41
41
+
+
41
3
×
= 60
= 123
Повторяющееся Сложение
Повторение арифметики
Повторяющееся Умножение
15
15
15
15
×
×
×
×
×
41
41
41
41

1
2
3
4

Слайд 8

9
3
“Три в девятой степени”
5
4
“Пять в четвертой степени”
7
2
“Семь во второй степени”
10
3
“Десять в третьей степени”
Как читать степень

Слайд 9

Математический диктант

Слайд 10

Найдите значения:
32
= 3 ∙3 = 9
53
= ∙5∙5∙5 = 125
13
103
=10∙10∙10 =1 000
151
= 15
19
= 1
34
= 3∙3∙3∙3 = 81
142
= 14∙14= 196
=17∙ 17 =289
172
=1∙1∙1 =1
61
= 6

Слайд 11

Работа в парах
Стр. 99 первый абзац до таблицы
Стр. 99 со второго абзаца до таблицы
Вариант 1
Вариант 2
Расскажи соседу по парте о том, что узнал.

Слайд 12

Квадрат числа
Произведение n и n называют квадратом числа записывают

Слайд 13

Куб числа
Произведение n, n и n называют кубом числа записывают

Слайд 14

Игра « Молчанка»
102
7∙9
23
24
9 ∙ 8
и
82
и
32
и
42
и
>
=

Слайд 15

Давным-давно в Древней Греции, для того, чтобы умножать числа, люди использовали счёт на камушках. Они рисовали многоугольники, выкладывали их стороны из камней и подсчитывали их число. В результате этого появились числа, называемые квадратными и кубическими. С помощью такого метода можно вычислить площади и объём любой фигуры, а также решать практические задачи на нахождение объёма воды в любом бассейне. В наше время не используют метод древних греков, так как он трудоёмкий и занимает много времени, для этого используют математические формулы.

Слайд 16

S = a ∙ a
a
= a ²

Слайд 17

Домашнее задание
Стр.98-99 правило №667, № 666,
№ 672.
№ 666,
№ 670.

Слайд 18

Итог урока
«Сегодня на уроке я узнал…» «Сегодня на уроке я научился…» «Сегодня на уроке я повторил…»

Слайд 19

Тестирование
Вариант 1
Вариант 2
1.Как называется число 4 записи 254 ? 1).основание степени 2).показатель степень 3).степень
2.Как называется число 8 в записи 87 ? 1). степень 2).основание степени 3). показатель степени
3. Как правильно записать в виде степени 3 ∙3 ∙3 ∙3 ∙3? 1). 35 2). 53
3. Как правильно записать в виде степени 7 ∙7 ∙7 ∙7? 1). 47 2). 74
4. Чему равно значение степени 102 ? 1). 20 3).100 2). 12 4).10
4. Чему равно значение степени 82 ? 1). 10 3).64 2). 16 4).8
2. Как называется число 6 в записи 96 ? 1). степень 2).основание степени 3). показатель степени
1.Как называется число 20 в записи 203 ? 1).основание степени 2).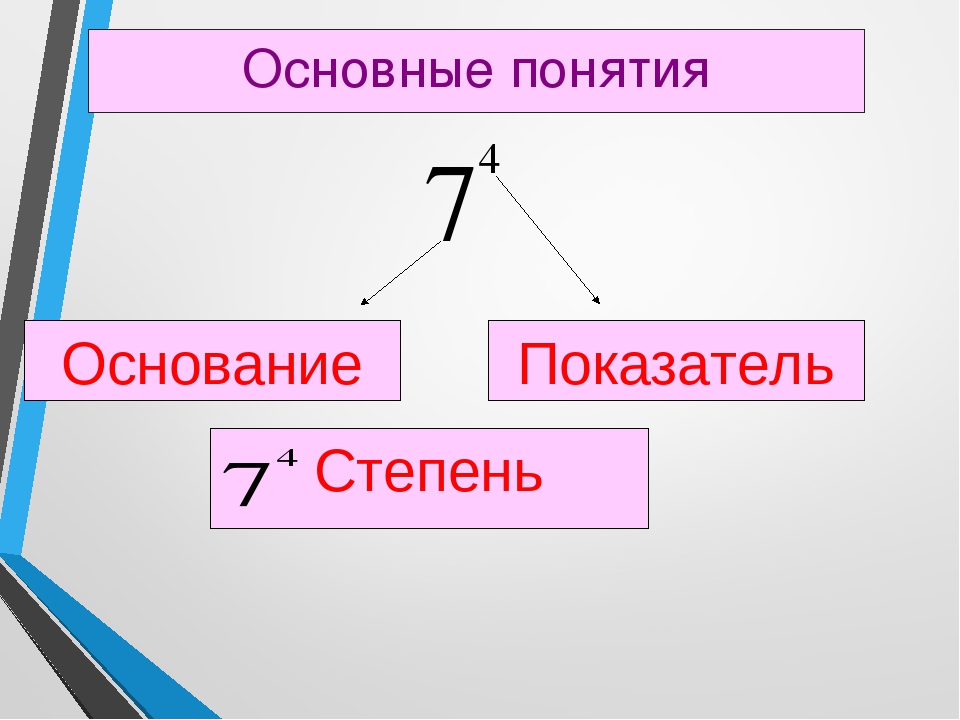 показатель степень 3).степень

Слайд 20

Что это?
Основание
Степени: Итоги и Повторение
Что это?
Показатель
= 3×3×3×3
“Три в четвертой степени”
“Три в кубе”
“Три в квадрате”

основание и показатель степени. Онлайн калькулятор

Степень числа — это выражение, обозначающее краткую запись произведения одинаковых сомножителей.

Рассмотрим умножение одинаковых чисел, например:

5 · 5 · 5 = 125.

Произведение  5 · 5 · 5  можно записать так:  5³  (пять в третьей степени). Выражение  5³  — это степень. Следовательно,

5 · 5 · 5 = 5³ = 125.

Рассмотрим выражение  5³ . В этом выражении число  5  — основание степени, а число  3  — показатель степени.

Основание степени — это повторяющийся множитель. Показатель степени — это число, указывающее количество повторений, то есть показатель степени показывает сколько одинаковых множителей содержится в произведении.

Читаются степени так:

• 7²  —  семь во второй степени.

  Вторую степень числа также называют квадратом этого числа. Следовательно, выражение 7² можно прочесть так: семь в квадрате или квадрат числа семь.




• 2³  —  два в третьей степени.

  Третью степень числа также называют кубом этого числа. Следовательно, выражение 2³ можно прочесть так: два в кубе или два куб.




• 6⁴  —  шесть в четвёртой степени.




• 10¹⁵  —  десять в пятнадцатой степени.




• aⁿ  —  a  в энной степени  или  a  в степени эн.

Пример. Записать в виде степени:

a) 5 · 5;

б) 10 · 10 · 10 · 10;

в) 8 · 8 · 8.

Решение:

a) 5 · 5 = 5²;

б) 10 · 10 · 10 · 10 = 10⁴;

в) 8 · 8 · 8 = 8³.

Возведение в степень

Возведение числа в степень — это вычисление произведения одинаковых множителей. Например, возвести число  2  в третью степень  (2³)  — это значит найти произведение  2 · 2 · 2 , то есть

2³ = 2 · 2 · 2 = 8.

Результат возведения в степень называется степенью (также как и само выражение, значение которого вычисляется). В выражении:

2³ = 8,

2  — это основание степени,  ³  — показатель степени,  8  — степень.

Пример. Вычислите:

a) 11²;

б) 2⁵;

в) 10⁴.

Решение:

a) 11² = 11 · 11 = 121;

б) 2⁵ = 2 · 2 · 2 · 2 · 2 = 32;

в) 10⁴ = 10 · 10 · 10 · 10 = 10000.

Выражения со степенями. Порядок действий

Если выражение не содержит скобки и содержит степени, то сначала выполняется возведение в степень в порядке следования степеней (слева направо), а затем все остальные арифметические действия.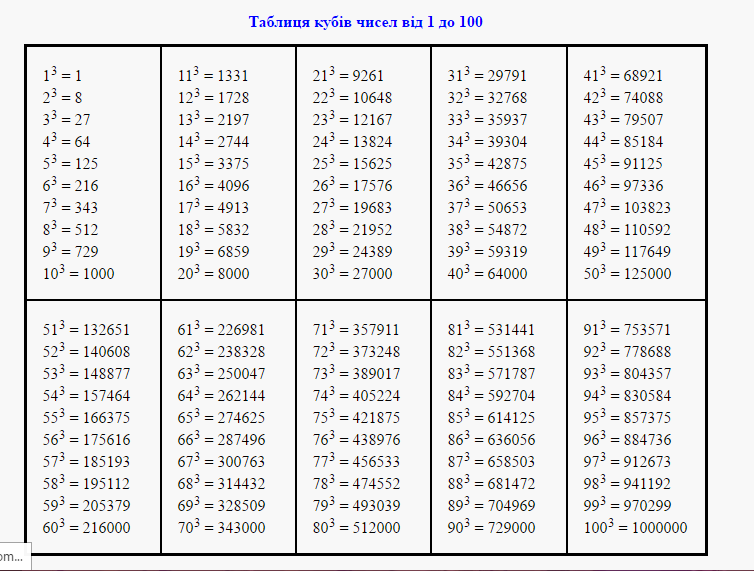 Если выражение содержит скобки, то сначала выполняются действия в скобках, с учётом всех правил порядка выполнения действий.

Рассмотрим два выражения:

5² + 2²

и

(5 + 2)²

В соответствии с порядком выполнения действий в первом случае сначала выполняется возведение в степень, а затем вычисляется сумма. Во втором случае сначала вычисляется сумма, а затем результат возводится в квадрат.

5² + 2² = 25 + 4 = 29,

(5 + 2)² = 7² = 49.

Пример 1. Найти значение выражения:

5 · (10 — 8)³.

Решение: Сначала выполняется действие, заключённое в скобки:

1) 10 — 8 = 2.

Затем, по правилам порядка действий, выполняется возведение в степень:

2) 2³ = 2 · 2 · 2 = 8.

И последним действием вычисляется произведение:

3) 5 · 8 = 40.

Ответ:  5 · (10 — 8)³ = 40.

Пример 2. Вычислить:

a) (4 + 2) · 3²;

б) 3 · 5² — 50;

в) 3 · 4 + 6².

Решение:

a) (4 + 2) · 3² = 54

1. 4 + 2 = 6
2. 3² = 9
3. 6 · 9 = 54

б) 3 · 5² — 50 = 25

1. 5² = 25
2. 3 · 25 = 75
3. 75 — 50 = 25

в) 3 · 4 + 6² = 48

1. 6² = 36
2. 3 · 4 = 12
3. 12 + 36 = 48

Калькулятор возведения в степень

Данный калькулятор поможет вам выполнить возведение в степень. Просто введите основание с показателем степени и нажмите кнопку Вычислить.

Что такое степень числа Возведение в степень отрицательного…

Привет, мой друг, тебе интересно узнать все про что такое степень числа возведение в степень отрицательного числа порядок действий в ах со степенями, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
что такое степень числа возведение в степень отрицательного числа порядок действий в ах со степенями , настоятельно рекомендую прочитать все из категории Арифметика

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулем.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберемся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращенное обозначение. Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 • 4 • 4 пишут 4⁶ и произносят «четыре в шестой степени».

4 • 4 • 4 • 4 • 4 • 4 = 4⁶

Выражение 4⁶ называют степенью числа, где:

• 4 — основание степени;
• 6 — показатель степени.

В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения :

 

Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».

Запись aⁿ читается так: «а в степени n» или «n-ая степень числа a».

Исключение составляют записи:

• a² — ее можно произносить как «а в квадрате»;
• a³ — ее можно произносить как «а в кубе».

Конечно, выражения выше можно читать и по определению степени:

• a² — «а во второй степени»;
• a³ — «а в третьей степени».

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).

 

Степенью числа «а» с показателем n = 1 является само это число :

a¹ = a

Любое число в нулевой степени равно единице.

a⁰ = 1

Ноль в любой натуральной степени равен нулю.

0ⁿ = 0

Единица в любой степени равна 1.

1ⁿ = 1

Выражение 0⁰ (ноль в нулевой степени) считают лишенным смыслом.

• (-32)⁰ = 1
• 0²⁵³ = 0
• 1⁴ = 1

При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.

Пример . Об этом говорит сайт https://intellect.icu . Возвести в степень.

• 5³ = 5 • 5 • 5 = 125
• 2.5² = 2.5 • 2.5 = 6.25
• (
  
  )⁴ = 
  
   • 
  
   • 
  
   • 
  
   = 

  
  

  
  

  3 • 3 • 3 • 3

  4 • 4 • 4 • 4

  
   = 

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулем.

 

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того четным или нечетным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечетную степень, то получается отрицательное число. Так как произведение нечетного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в четную степень, то получается положительное число. Так как произведение четного количество отрицательных сомножителей положительно.

 

Отрицательное число, возведенное в четную степень, есть число положительное.

Отрицательное число, возведенное в нечетнуюстепень, — число отрицательное.

Квадрат любого числа есть положительное число или нуль, то есть:

a² ≥ 0 при любом a.

• 2 • (- 3)² = 2 • (- 3) • (- 3) = 2 • 9 = 18
• — 5 • (- 2)³ = — 5 • (- 8) = 40

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (- 5)⁴ и -5⁴ это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (- 5)⁴ означает найти значение четвертой степени отрицательного числа.

(- 5)⁴ = (- 5) • (- 5) • (- 5) • (- 5) = 625

В то время как найти -5⁴ означает, что пример нужно решать в 2 действия:

1. Возвести в четвертую степень положительное число 5. 
   5⁴ = 5 • 5 • 5 • 5 = 625
2. Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание ). 
   -5⁴ = — 625

Пример. Вычислить: — 6² — (- 1)⁴

— 6² — (- 1)⁴ = — 37

1. 6² = 6 • 6 = 36
2. -6² = — 36
3. (- 1)⁴ = (- 1) • (- 1) • (- 1) • (- 1) = 1
4. — (- 1)⁴ = — 1
5. — 36 — 1 = — 37

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

 

В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем  умножение и деление , а в конце  сложение и вычитание.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Пример. Вычислить:

Для облегчения решения примеров полезно знать и пользоватьсятаблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про что такое степень числа возведение в степень отрицательного числа порядок действий в ах со степенями Надеюсь, что теперь ты понял что такое что такое степень числа возведение в степень отрицательного числа порядок действий в ах со степенями
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Арифметика

Классифицирующие полиномы

Полиномы можно классифицировать двумя разными способами — по количеству членов и по их степени.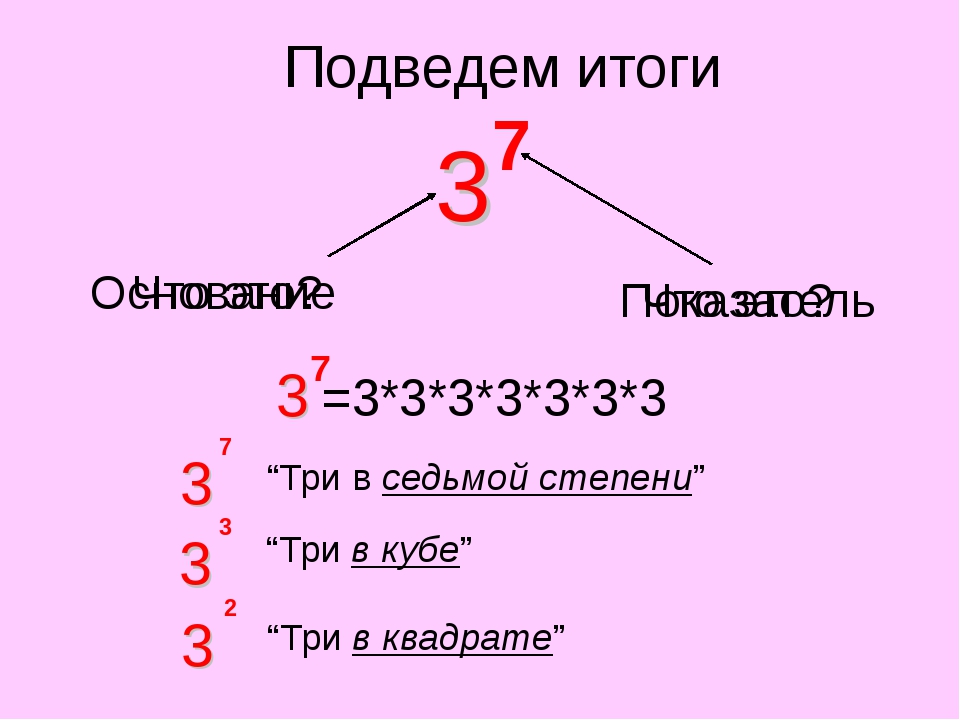 1. Количество терминов. Моном состоит только из одного члена. Например, 4x 2 . Помните, что термин содержит как переменную (и), так и ее коэффициент (число перед ним). Таким образом, это всего лишь один член. Бином имеет два члена.Например: 5x 2 -4x Трехчлен имеет три члена. Например: 3y 2 + 5y -2 Любой многочлен с четырьмя или более членами просто называется многочленом. Например: 2y 5 + 7y 3 — 5y 2 + 9y -2 Практикуйте классификацию этих многочленов по количеству членов: 1.5y 2. 3x 2 -3x + 1 3. 5y-10 4. 8xy 5. 3x 4 + x 2 -5x + 9 Ответы: 1) Моном 2) Трехчлен 3) Бином 4) Моном 5) Многочлен 2. Степень. Степень полинома определяется путем рассмотрения члена с наибольшим показателем его переменной (ей) . Примеры: 5x 2 -2x + 1 Наивысший показатель степени равен 2, так что это трехчлен 2 и градусов. 3x 4 + 4x 2 Наивысший показатель степени равен 4, так что это бином 4 th градусов. 8x-1 Хотя кажется, что показатель степени отсутствует, у x есть понятый показатель степени 1; следовательно, это бином 1 st градусов. 5 Переменной нет вообще. Следовательно, это моном 0 степени. Это 0 градусов, потому что x 0 = 1. Таким образом, технически 5 может быть записано как 5x 0 . 3x 2 y 5 Поскольку обе переменные являются частью одного и того же члена, мы должны сложить их показатели вместе, чтобы определить степень.2 + 5 = 7, так что это моном степени 7 th . Классифицируйте эти многочлены по степени. 1,7x 3 +5 2 +1 2,6y 5 + 9y 2 -3y + 8 3,8x-4 4,9x 2 y + 3 5,12x 2 Ответы 1) 3 rd градусов 2) 5 th градусов 3) 1 st градусов 4) 3 rd градусов 5) 2 и градусов

Классификация многочленов — MathsTips.com

Многочлен классифицируется в соответствии с количеством членов и имеющейся степенью. Полиномиальные уравнения — это уравнение, которое содержит одночлен, двучлен, трехчлен, а также многочлен более высокого порядка. Форма одночлена — это выражение, где n — неотрицательное целое число. Переменная «a» называется коэффициентом, а n — степенью монома. В зависимости от значения один член называется мономом (когда n = 1), многочленом двух степеней (когда n = 2) и многочленом трех степеней (когда n = 3).

Пример : Многочлен классифицируется по количеству членов как:

1. Мономиал — Один член — 3x
2. Биномиальный — двухчленный — 7a-5
3. Трехчлен — Трехчленный —

Типы многочленов

1. Monomial = Многочлен, состоящий только из одного члена, называется одночленом. Число или произведение числа и переменной. Пример: -2x ,, — одночлены.
2. Binomial = Многочлен с двумя членами называется биномиальным.Два одночлена соединены знаком + или -. Пример: , являются двучленами.
3. Трехчлен = Трехчлен полином называется трехчленным. Три одночлена соединены знаком + или -. Пример: — трехчлены.
4. Постоянный многочлен: многочлен, содержащий только постоянный член, является постоянным многочленом. Пример: 45, -78 — постоянный многочлен.
5. Полином: Если выражение содержит более трех членов, то выражение называется полиномом. Более трех одночленов, соединенных знаком + или -. Пример: — многочлен.

Пример: Определите типы многочленов:

6. -89

Решение: 1. Моном, 2. Трехчлен, 3. Бином, 4. Моном, 5. Полином, 6. Константа.

Степень полиномов

Наибольшее значение показателя степени в выражении называется степенью полинома.Степень полинома — это наибольший показатель. Он также известен как порядок полинома. При нахождении степени полинома степени полинома переменных должны быть в порядке возрастания или убывания.

1. Линейный многочлен: Если выражение имеет степень один, оно называется линейным многочленом. Например, 5x + 2,50z + 3.
2. Квадратичный многочлен: Если выражение имеет степень два, то оно называется квадратичным многочленом. Например.
3. Кубический многочлен: Если выражение имеет степень три, оно называется кубическим многочленом. Например .

Пример: Классифицируйте эти многочлены по степени:

Решение: 1. 3-я степень, 2. 1-я степень, 3. 5-я степень, 4. 2-я степень.

Упражнение

Определите типы многочленов:

3. 10 штук
6. -59

Классифицируйте эти многочлены по степени:

Идентификационные характеристики многочленов | Математика для гуманитарных наук Corequisite

Результаты обучения

• Определите, является ли многочлен одночленом, двучленом или трехчленом
• Определить степень многочлена

Определение многочленов, одночленов, биномов и трехчленов

В разделе «Оценить, упростить и преобразовать выражения» вы узнали, что термин является константой или произведением константы и одной или нескольких переменных. {m} [/ latex], где [latex] a [/ latex] — константа, а [latex] m [/ latex] — целое число, это называется мономом. Моном или сумма и / или разность мономов называется многочленом.

Полиномы

Полином

— одночлен, или два или более одночленов, объединенные сложением или вычитанием.
одночлен — многочлен с одним членом.
двучлен — многочлен с ровно двумя членами.

Обратите внимание на корни:

• poly — значит много
• mono — значит один
• bi — значит два
• tri — значит три

Вот несколько примеров многочленов:

{3} + a [/ latex]

Обратите внимание, что каждый одночлен, двучлен и трехчлен также является многочленом.{3} [/ латекс] [латекс] 2 [/ латекс] Биномиальное 5. [латекс] н [/ латекс] [латекс] 1 [/ латекс] Моном

Определение степени полиномов

В этом разделе мы будем работать с многочленами, у которых есть только одна переменная в каждом члене. Степень многочлена и степень его членов определяются показателями переменной.

Моном без переменной, только с константой, является особым случаем.Степень константы [латекс] 0 [/ латекс] — не имеет переменной.

Степень полинома

Степень члена — это показатель степени его переменной.
Степень константы [латекс] 0 [/ латекс].
Степень многочлена — это наивысшая степень всех его членов.

Давайте посмотрим, как это работает, посмотрев на несколько многочленов. Мы рассмотрим это шаг за шагом, начиная с одночленов, а затем перейдем к многочленам с большим количеством членов.

Помните: любая основа, написанная без показателя степени, имеет подразумеваемый показатель степени [латекс] 1 [/ латекс].{2} + 9х — 3 [/ латекс] Наивысшая степень из всех терминов — [латекс] 2 [/ латекс]. Степень [латекс] 2 [/ латекс]. 5. [латекс] 8x + 2 [/ латекс] Наивысшая степень из всех терминов — [латекс] 1 [/ латекс]. Степень [латекс] 1 [/ латекс].

Работать с многочленами проще, если вы перечисляете члены в порядке убывания степеней. Когда полином записывается таким образом, говорят, что он имеет стандартную форму.Вернитесь к многочленам из предыдущего примера. Обратите внимание, что все они написаны в стандартной форме. Возьмите за привычку сначала писать термин с наивысшей степенью.

Степень многочлена — определение и примеры

Степень полинома — это очень простое понятие, которое на самом деле нетрудно понять.

Определение : Степень — это член с наибольшим показателем.

Напомним, что для y ² y — основание, а 2 — показатель степени.

Еще примеры, показывающие, как найти степень многочлена.

Пример № 1 :

4x ² + 6x + 5

Этот многочлен состоит из трех членов. Первый — 4x ² , второй — 6x, а третий — 5.

Показатель первого члена равен 2.

Показатель второго члена равен 1, потому что 6x = 6x ¹ .

Показатель третьего члена равен 0, потому что 5 = 5x ⁰ .

Что? 5x ⁰ = 5?

Ну, все с показателем 0 всегда равно 1.

Таким образом, 5x ⁰ = 5 × x ⁰ = 5 × 1 = 5

Поскольку старший показатель равен 2, степень 4x ² + 6x + 5 равна 2.

Пример 2 :

2y ⁶ + 1y ⁵ + -3y ⁴ + 7y ³ + 9y ² + y + 6

Этот многочлен состоит из семи членов. Первый — 2y ² , второй — 1y ⁵ , третий — -3y ⁴ , четвертый — 7y ³ ,
пятый — 9y ² , шестой — y, а седьмой — 6.

Показатель степени первого члена равен 6.

Показатель степени второго члена равен 5.

Показатель степени третьего члена равен 4.

Показатель степени четвертого члена равен 3.

Показатель степени пятый член равен 2.

Показатель шестого члена равен 1, потому что y = y ¹ .

Показатель последнего члена равен 0, потому что 6 = 6x ⁰ .

Поскольку старший показатель равен 6, степень 2y ⁶ + 1y ⁵ + -3y ⁴ + 7y ³ + 9y ² + y + 6 равна 6.

Напишите полином для следующих описаний

1)

Бином от z со степенью 10

2)

Трехчлен от c со степенью 4

3)

Бином по y со степенью 1

4)

Моном в b со степенью 3

Ответы:

1)

2z ¹⁰ -4

2)

c ⁴ + c ² — 8

3)

y + 4

4)

b ³

Чтобы найти степень многочлена или монома с более чем одной переменной для одного и того же члена, просто сложите показатели для каждой переменной, чтобы получить степень.

Найдите степень x ³ y ² + x + 1.

Степень этого многочлена — это степень одночлена x ³ y ²

Поскольку степень x ³ y ² равно 3 + 2 = 5, степень x ³ y ² + x + 1 равна 5

Степень полиномиальной викторины.

Степени и показатели (предалгебра, Откройте дроби и множители) — Mathplanet

Мы знаем, как вычислить выражение 5 x 5.{3}

$

абстрактная алгебра — есть ли простое объяснение, почему полиномы 5-й степени (и выше) неразрешимы?

Пусть корнями уравнения являются A, B, C и т. Д. Нам говорят, что неразрешимость общего уравнения пятой степени связана с неразрешимостью ассоциированной группы Галуа, симметрической группы из пяти элементов. Думаю, я могу сказать вам, что это значит, на интуитивном уровне.

Для трех элементов A, B и C вы можете создать эти две функции:

AAB + BBC + CCA

ABB + BCC + CAA

У этих функций есть интересное свойство: независимо от того, как вы перетасовываете буквы A, B и C, вы получаете те же функции, с которых начинали.Вы можете перевернуть их (как если бы вы просто поменяли местами A и B), или они оба могли бы остаться на месте (как если бы вы повернули A на B на C), но в любом случае вы их вернете.

Для четырех элементов нечто подобное происходит с этими тремя функциями:

AB + CD

AC + BD

г. н.э. +

г. до н.э.

Независимо от того, как вы перетасовываете A, B, C и D, вы получаете эти три функции обратно. Они могут быть переставлены, или все они могут остаться на месте, но в любом случае вы их вернете.

Для пяти элементов такой группы функций не существует. Ну, не совсем так … есть пара огромных функций, каждая из которых состоит из шестидесяти членов, которые похожи на те, которые я нарисовал для кубического уравнения . .. но это все. Не существует групп функций с тремя или особенно четырьмя элементами, чего вы действительно хотели бы.

Если вы попытаетесь создать функции для пяти букв с этим свойством симметрии, вы убедитесь, что это невозможно. Но как доказать, что это невозможно? Для этого вам, вероятно, понадобится немного больше теории групп.Но что касается «простого» объяснения того, почему вы не можете решить пятую степень, на самом деле все дело в этих функциях.

Чтобы уточнить это более подробно: Для уравнения третьей степени я определил следующие функции:

AAB + BBC + CCA = p

ABB + BCC + CAA = q

A, B и C — корни кубики, но p и q — корни квадратичной. Вы можете видеть это, потому что если вы посмотрите на pq и (p + q), элементарные симметричные многочлены от p и q, вы увидите, что они симметричны по A, B и C.Таким образом, их легко выразить через коэффициенты нашего исходного кубического уравнения. Вот почему p и q являются ступенькой, ведущей к корням кубики.

Аналогичным образом для четвертой степени мы выделили следующие функции:

AB + CD = p

AC + BD = q

г. н.э. + г. до н.э. =

г.

Вы можете переписать предыдущий абзац слово в слово, но просто поднимите все на одну ступень выше, и это останется верным. A, B, C и D — корни квартики, но p, q и r — корни кубики.Вы можете видеть, что они должны быть такими, потому что если вы посмотрите на элементарные симметричные многочлены от p, q и r, вы увидите, что они симметричны по A, B, C и D. Таким образом, их легко выразить в терминах коэффициентов нашего оригинала. уравнение четвертой степени. Вот почему они являются ступенькой, ведущей к истокам квартики.

И простая причина, по которой уравнение пятой степени неразрешимо, заключается в том, что не существует аналогичного набора из четырех функций в A, B, C, D и E, который сохраняется при перестановках этих пяти букв.

Это было довольно хорошо понято Лагранжем за пятьдесят лет до того, как теория Галуа сделала его «строгим». Это связано с алгебраическими уловками, с помощью которых вы перешли, скажем, от A B и C к p и q. Он включает в себя взятие линейных функций, которые смешивают AB и C с кубическими корнями из единицы, и исследование куба этих функций. Это обратимый процесс, поэтому вы можете работать в обратном направлении другим способом (взяв кубические корни функций в p и q), чтобы решить кубику. Очень похожий прием работает с четвертой степенью.Я думаю, Лагранж смог убедительно показать, что тот же трюк не работает для пятой степени … это «интуитивное» доказательство. «Строгое» доказательство должно было бы показать, что в отсутствие очевидных уловок (аналогичных 3-й и 4-й степени) не было других возможных уловок, которые вы могли бы придумать.

4. Силы, корни и радикалы

На этой странице

Связанный раздел

Не пропустите главу «Экспоненты и радикалы», где мы более подробно рассмотрим эти
темы.

На этой странице мы продолжим рассмотрение того, как работают числа, прежде чем применять процедуры к алгебре. Все работает так же, за исключением того, что в алгебре мы используем буквы
для обозначения чисел.

Индексы

Индексы (или степеней , или степеней ) очень полезны в математике. Индексы — удобный
способ записи умножения, в котором есть много повторяющихся членов.

Пример индекса

Для примера 5 ³ мы говорим, что:

5 — это база и

3 — это индекс (или в степени , или в степени в степени ).

5 ³ означает «умножить 5 на себя 3 раза».

[Или, точнее, «многократно умножить 5 на себя так, чтобы в умножении было три 5», или
даже лучше, «три пятерки, перемноженные вместе». См. Обсуждение этого вопроса в разделе «Камни преткновения в математике».]

То есть 5 ³ означает

5 ³ = 5 × 5 × 5

Примеры целочисленных показателей

Что произойдет, если у нас будет индекс 1, может быть 0 или даже -2?

Давайте создадим шаблон, используя наш пример выше, чтобы мы могли видеть, что означают эти особые случаи.-1 = 1 / 5`

Эти легко испортить, и они могут лишить вас сна без надобности, когда вы позже будете заниматься алгеброй.

Как правило, любое число a (кроме 0) в степени 1 равно a .

a ¹ = a

Кроме того, любое число a (кроме 0) в степени 0 равно 1.

a ⁰ = 1

И любое число a (кроме 0) в степени -1 равно «1 / a».-1 = 1 / а`

Умножение чисел с одинаковым основанием

Нам часто нужно умножить что-то вроде следующего:

4 ³ × 4 ⁵

Мы замечаем, что числа имеют одинаковое основание (то есть 4), и мы думаем об этом так:

4 ³ × 4 ⁵ `= \ underbrace {(4 xx 4 xx 4)} _ {3″ из них «} xx \ underbrace {(4 xx 4 xx 4 xx 4 xx 4)} _ {5 «из них»} `

Мы получаем 3 четверки из первой сетки и 5 четверок из второй, так что в сумме у нас будет 3 + 5 = 8 четверок, умноженных вместе. 2}` = {(3xx3xx3xx3xx3xx3)} / (3xx3) `= 3 × 3 × 3 × 3 = 3 ⁴ = 81

Мы вычли 2 тройки наверху и 2 тройки внизу дроби, оставив 4 тройки наверху (и цифру 1 на
Нижний).(m-n) `

Возведение индексного выражения в индекс

В качестве примера возведем число 4 ² в степень 3:

(4 ² ) ³ = 4 ² × 4 ² × 4 ²

Из приведенного выше примера умножения мы видим, что это даст нам 4 ⁶ . Мы могли бы это сделать
как:

(4 ² ) ³ = 4 ^{2 × 3} = 4 ⁶

В общем у нас для любой базы a и индексов m и n :

( a ^м ) ⁿ = a ^mn

Повышение эффективности продукта

Пример числа:

(5 × 2) ³ = 5 ³ × 2 ³

В этом случае с числами лучше сначала произвести умножение в скобках, а затем возвести наш ответ в степень 3. n, (ane0)`

ПРИМЕЧАНИЕ 1: Эти правила применяются, когда a и b положительные и m и n — целых .7`

, потому что это , в отличие от (буквенная часть возведена в другую степень). (Мы можем разложить это на множители, но не можем каким-либо образом расширить или добавить термины.)

Чтобы узнать, как все это используется в алгебре, перейдите по ссылке:

Корни и радикалы

Мы используем радикальный знак : `sqrt (\ \)`

Означает «квадратный корень». Квадратный корень на самом деле является дробным индексом и эквивалентен возведению числа в
мощность 1/2.(1/2) = sqrt (25) = 5`

Также можно получить

Кубический корень: `root (3) x` (что эквивалентно возведению в степень 1/3) и

Корень четвертой степени: `root (4) x` (степень 1/4) и так далее.

См. Больше в разделе «Дробные экспоненты».

Основные моменты, на которые следует обратить внимание:

Связанный раздел

Как упоминалось выше, если вам нужна дополнительная информация по этой теме, перейдите в: Показатели и
Радикалы.

Если a ≥ 0 и b ≥ 0, имеем:

`sqrt (axxb) = sqrt (a) xxsqrt (b)`

Однако это работает только для умножения.2) = а`

Это смущает многих студентов. Но это просто означает:

1. Начать с номера
2. Квадрат
3. Найдите квадратный корень из результата
4. Закончите с номером, который вы начали с

Например, начать с 3.

Квадрат, вы получите 9.

Извлеките квадратный корень и получите 3, то есть с того места, где вы начали.

Почему это важно? Часто нам нужно «отменить» квадрат при решении уравнения, поэтому мы находим квадратный корень из обоих
стороны.