Степенная функция и показательная функция: Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Степенные функции

Определение 1. Степенной функцией называют функцию

y = x^p ,

где p – любое действительное число, отличное от нуля.

С понятиями степени с рациональным показателем и степени с иррациональным показателем можно ознакомиться в разделе нашего справочника «Степень с рациональным показателем».

Графики степенных функций при различных значениях p представлены в следующей таблице.

Графики степенных функций

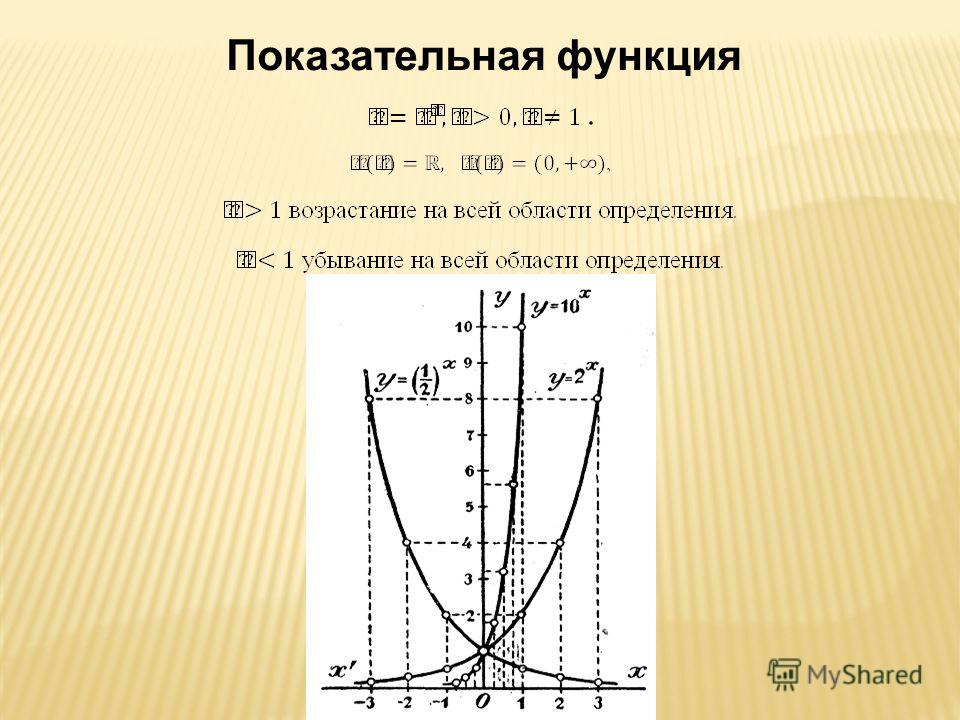
Показательные функции

Определение 2. Показательной функцией называют функцию

y = a^x ,

где a – любое положительное число, отличное от 1 .

Графики показательных функций при различных значениях a представлены в следующей таблице.

Графики показательных функций

Логарифмические функции

Определение 3. Логарифмической функцией называют функцию

y = log_a x ,

где a – любое положительное число, отличное от 1 .

С определением и свойствами логарифмов можно ознакомиться в разделе нашего справочника «Логарифмы».

Графики логарифмических функций при различных значениях a представлены в следующей таблице.

Графики логарифмических функций

y = ln x

y = lg x

y = log₂x

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Внеклассный урок — Показательная функция (экспонента)

Показательная функция (экспонента)

Показательная функция – это функция вида y = a^x, где a > 0, a ≠ 1.

Следует различать показательную функцию y = a^x и степенную функцию y = xⁿ. Это совершенно разные функции.

Разница – в местоположении аргумента х. В показательной функции он является степенью, в степенной – основанием. Соответственно в показательной функции изменяется значение степени, в степенной – значение основания.

Пример-пояснение.

Сначала найдем координаты точек показательной функции y = 2^x.

Пусть х = 1, 2, 3, 4, 5.

Тогда мы получим следующие значения у:

2¹ = 2,

2² = 4

2³ = 8,

2⁴ =16,

2⁵ = 32.

Итак, у имеет следующие точки: 2, 4, 8, 16, 32.

Обратите внимание: в показательной функции основание неизменно (в нашем случае оно равно 2). Разные значения присваиваются степени.

Теперь найдем координаты точек степенной функции у = х².

Пусть х имеет те же значения, что и в первом случае:

х = 1, 2, 3, 4, 5.

Тогда мы получим следующие значения у:

1² = 1;

2² = 4,

3² = 9,

4² = 16,

5² = 25.

Таким образом, у имеет следующие точки: 1, 4, 9, 16, 25.

Обратите внимание: в степенной функции степень неизменна (в нашем случае она равна 2). Разные значения присваиваются основанию.

Как видите, разница между двумя функциями существенная.

Есть еще функция вида x^x. Она не является ни показательной, ни степенной. Иногда ее называют показательно-степенной.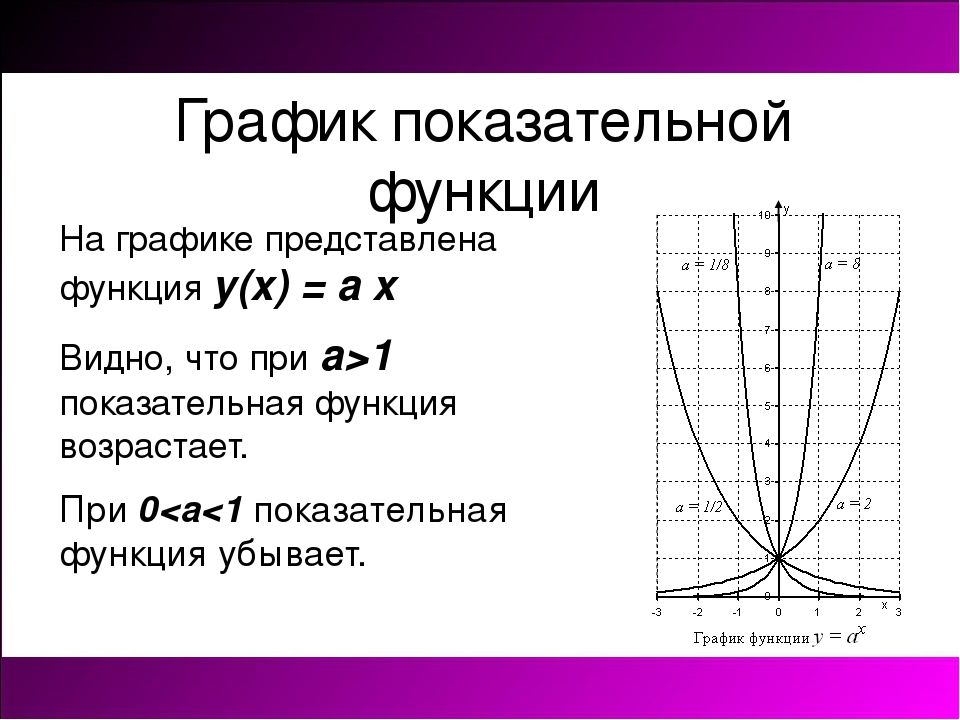

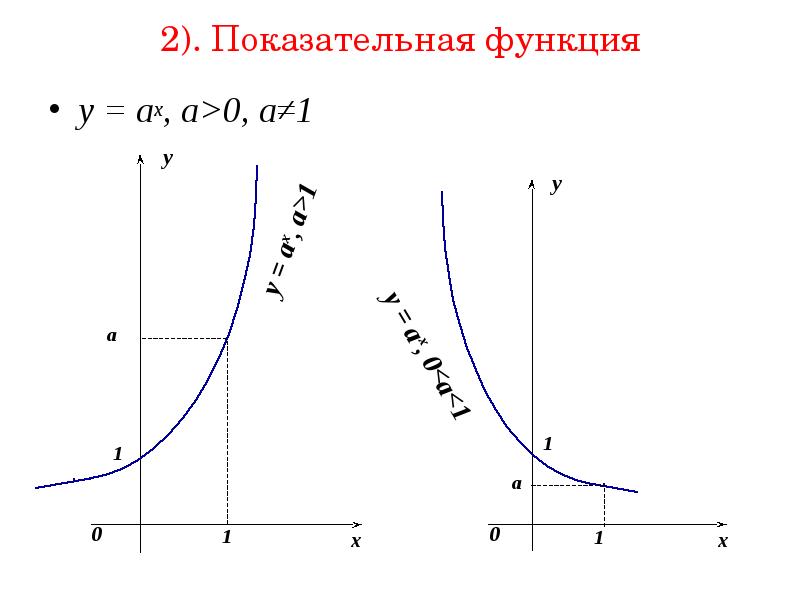
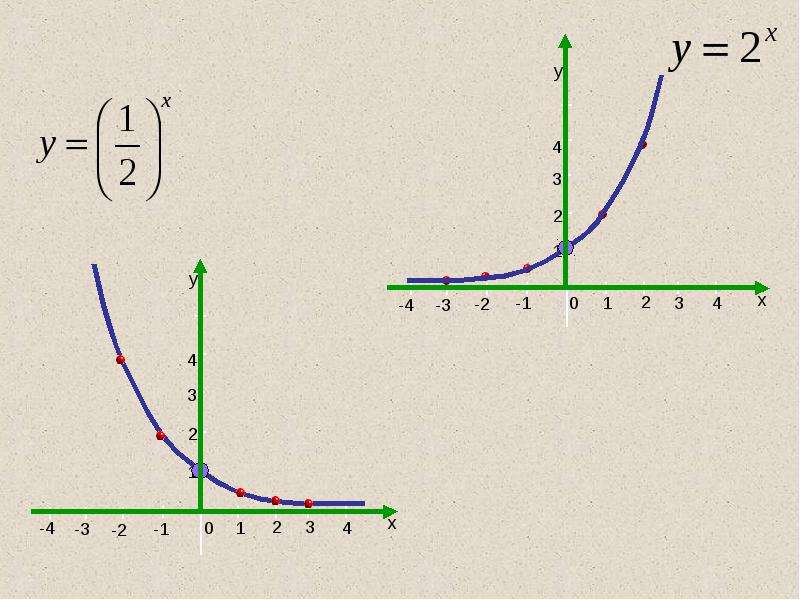
График показательной функции y = a^x.

Графиком функции является кривая, которую называют экспонентой. Этим словом принято называть и саму функцию. Таким образом, экспонента – это показательная функция y = a^x.

При a > 1 экспонента возрастает. При 0 < a < 1 экспонента убывает.

В обоих случаях экспонента выпукла вниз.

Горизонтальной асимптотой функции является ось x
(при х → –∞, если a > 1, и при х → +∞, если 0 < a < 1).

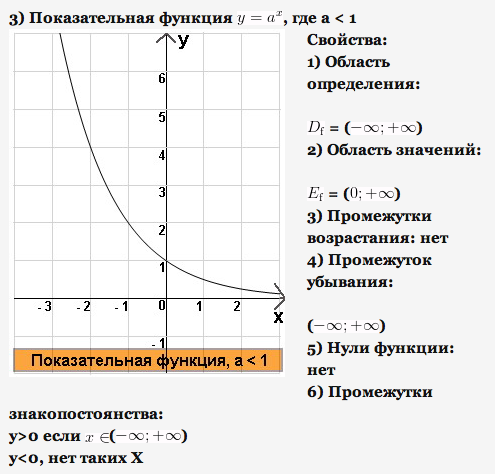
Основные свойства показательной функции y = a^x.

1) Область определения функции – множество всех чисел:

D(f) = (–∞; +∞)

2) Область значений функции – все положительные числа:

E(f) = (0; +∞)

3) Функция ни четная, ни нечетная.

4) При a > 1 функция возрастает.
При 0 < a < 1 функция убывает.

5) Не ограничена сверху, ограничена снизу.

6) Не имеет ни наибольшего, ни наименьшего значений.

7) Непрерывна.

Степенная функция (доказательство непрерывности и свойств)

Определение степенной функции

Определение
Степенная функция с показателем степени p – это функция f(x) = x^p, значение которой в точке x равно значению показательной функции с основанием x в точке p.
Кроме этого, f(0) = 0^p = 0 при p > 0.

Степенную функцию можно выразить через показательную и логарифм:
.
В качестве основания a можно взять любое действительное число . В математическом анализе наиболее удобно использовать число e:
2,718281828459045….
Тогда ,
.

Выше мы представили степенную функцию как сложную, составленную из логарифмической и показательной функций. Поэтому ее свойства можно получить из свойств этих функций.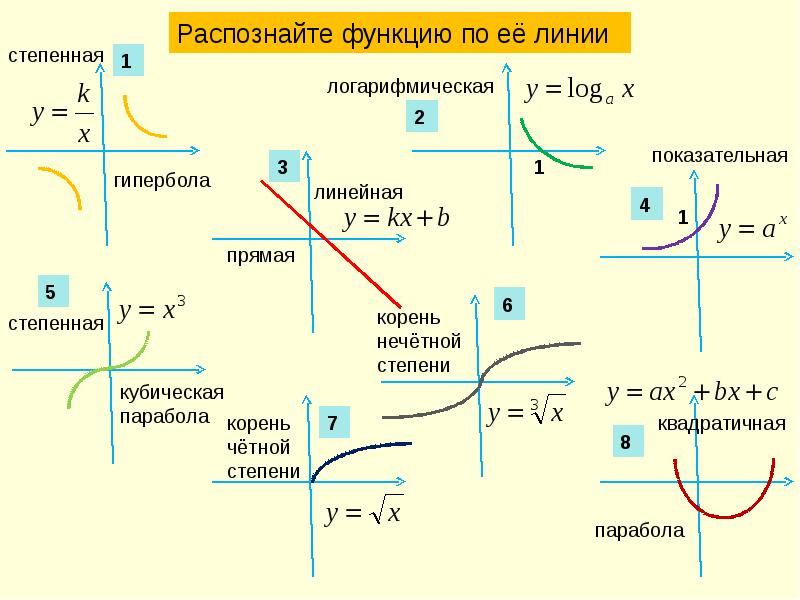

Свойства степенной функции

Графики степенной функции y = x^p при различных значениях показателя p.

Здесь мы рассмотрим свойства степенной функции y = x^p при неотрицательных значениях аргумента . Для рациональных , при нечетных m, степенная функция определена и для отрицательных x. В этом случае, ее свойства можно получить, используя четность или нечетность. Так, при четных функция четна:
.
При нечетных – нечетна:
.
Эти случаи подробно рассмотрены и проиллюстрированы на странице «Степенная функция, ее свойства и графики».

Теорема. Свойства степенной функции (x ≥ 0)
Степенная функция, y = x^p, с показателем p имеет следующие свойства:
(1.1) определена и непрерывна на множестве
при ,
при ;
(1.2) имеет множество значений
при ,
при ;
(1.3) строго возрастает при ,
строго убывает при ;
(1.4) при ;
при ;
(1.5) ;
(1. 5*) ;
(1.6) ;
(1.7) ;
(1.7*) ;
(1.8) ;
(1.9) .

Доказательство свойств

Для доказательства свойств, представим степенную функцию как сложную:
(2) .
Используем следующие обозначения:
(3) , где .
В качестве a возьмем произвольное число . При доказательстве будем использовать свойства показательной функции и логарифмической.

1.1. Найдем область определения. Логарифмическая функция определена при . Показательная функция определена для всех t. Поэтому степенная функция (2) определена при . Кроме этого, согласно определению, при , степенная функция определена в точке .

Исследуем на непрерывность. Поскольку логарифм и показательная функция непрерывны на своих областях определения, то, по теореме о непрерывности сложной функции, степенная функция непрерывна при .

Рассмотрим случай . Покажем, что показательная функция непрерывна в точке слева. Применяя теорему о пределе сложной функции, имеем:
.
Здесь мы использовали общепринятые обозначения:
.
Таким образом, . Непрерывность в точке слева доказана.

1.4. Найдем пределы на границе области определения.
Пусть .
По определению, .
Находим предел при , аналогично предыдущему:
.
Пусть . Тогда
;
.

1.3. Докажем, что степенная функция строго монотонна на области определения.
При , функции и строго возрастают. Поэтому сложная функция также строго возрастает.
Поскольку и при , , то степенная функция строго возрастает на области определения .
При , функция строго убывает, а функция строго возрастает. Поэтому сложная функция строго убывает на области определения .

1.2. Найдем множество значений степенной функции .
Для этого рассмотрим ее на отрезке , где . Поскольку функция на этом отрезке строго монотонна, то она достигает минимума и максимума на его концах – в точках и . Как мы уже доказали, степенная функция непрерывна на своей области определения.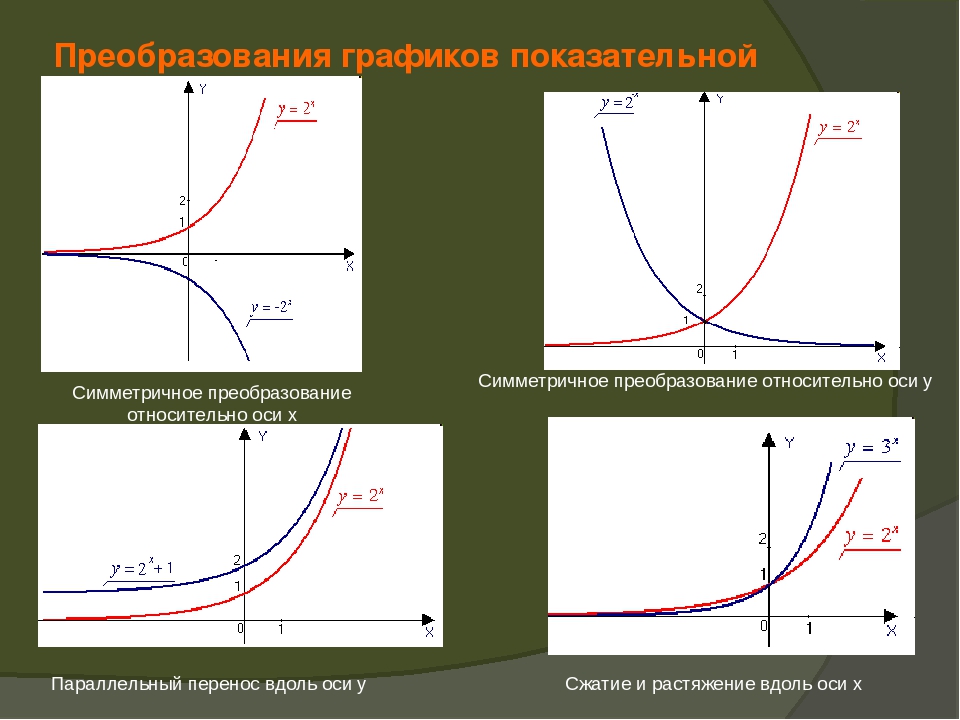 Тогда, согласно теореме Больцано – Коши о промежуточном значении, она принимает все значения из отрезка , если и , если . Устремляя и , и используя найденные выше пределы получаем, что множеством значений показательной функции является множество неотрицательных чисел при , и множество положительных чисел при .

Свойства (1.1-4) доказаны.

1.5-9. Доказательство свойств (1.5-9) приводится на странице «Определение и доказательство свойств показательной функции»

Автор: Олег Одинцов. Опубликовано: 09-12-2018

Степенная функция и ее свойства

Функция вида:

у = хⁿ

называется степенной функцией с натуральным показателем.

При n=1 получаем функцию вида у = х

Рассмотрим свойства функции у = kx:

Область определения — D(f)=(-∞; +∞).
Область значения — E(f)=(0; +∞).
Нечетная, так как f( — kх) = k ( — х)= — kx = -f(x)
При k > 0 функция возрастает, а при k < 0 функция убывает на всей числовой прямой.

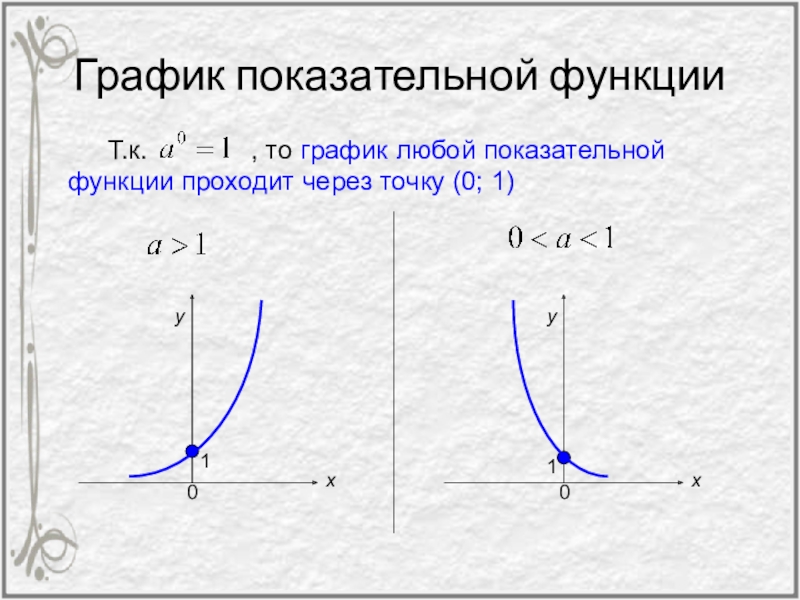
График линейной функции y=x

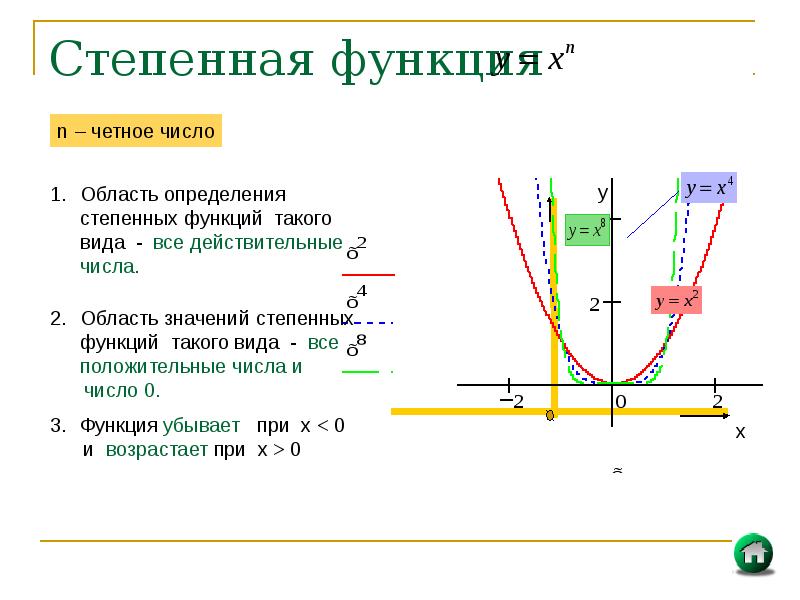
При n=2 получаем функцию вида у = х²— эта функция называется параболой.

Рассмотрим свойства функции у =х²:

Область определения — D(f)=(-∞; +∞).
Область значения E(f) y∈[0; +∞).
Чётная, так как f( — х) = ( — x)²= x² = f (х)
На промежутке (—∞; 0] функция убывает, а на промежутке [0; +∞) функция возрастает.
Корень x=0
Экстремумы функции — min при x=0.

График параболы y=x²

При n=3 получаем функцию вида у = х³— эта функция называется кубической параболой.

Рассмотрим свойства функции у = х³:

Область определения — D(f)=(-∞; +∞).
Область значения — E(f)=(-∞; +∞).
Нечётная, так как f( — х) = ( — x)³= —x³ = —f (х)

Функция возрастает на всей числовой прямой.

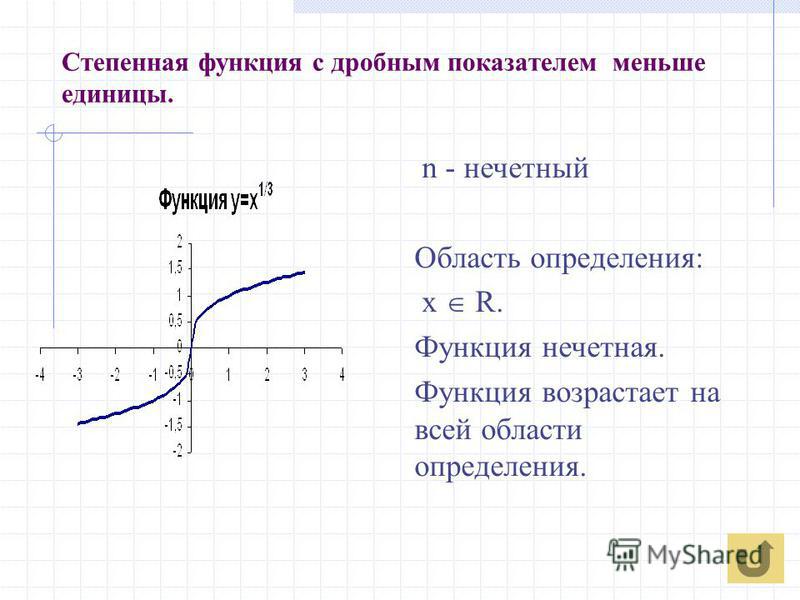
2}}}$

Рассмотрим элементарную функцию с корнем $y = \sqrt x $

Свойства функции $y = \sqrt x $:

Область определения — D(f)=[0; +∞).
Область значения — E(f)=[0; +∞).
Функция ни чётная, ни нечётная.
Функция возрастает на [0; +∞).
Экстремумов нет.
Корень x=0
Экстремумы функции — min при x=0.

Страница не найдена — ПриМат

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Юлия Стерлянко (8), Денис Стехун (8), Елизавета Савицкая (8), Игорь Любинский (8), Олег Шпинарев (7), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2),

Показательная функция, отличие ее от степенной функции, основные свойства, график

Урок 127. Тема: Показательная функция, отличие ее от степенной функции, основные свойства, график

Тип урока: Ознакомление с новым материалом

Форма урока: лекция – диалог

Продолжительность: 1 урок — 45 мин

Цель: — ознакомиться с понятием показательной функции;

— рассмотреть отличие показательной функции от степенной;

— рассмотреть свойства показательной функции;

— научиться строить график функции

Ход урока:

1.Организационный момент — 2мин

2. Проверка домашнего задания – 5 мин

У доски ученик

3. Сообщение темы и целей урока – 2 мин

4.АБЗ – 3мин

, ,y = , , , , .

Из функций записанных на доске укажите известные вам функции. К какому виду функции все они относятся? Какая новая для вас функция? (, , ). Именно сегодня на уроке и будем изучать эту функцию

5. Организация восприятия новой информации — 20мин

Введение определения показательной функции

аргумент – показатель степени

На доске:

у = а ^х

основание степени – заданное число

Этим и объясняется название функции. Итак, что называется показательной функцией?

Показательной функцией называется функция вида , где а – заданное число, а>0, .

Записать определение в тетрадь.

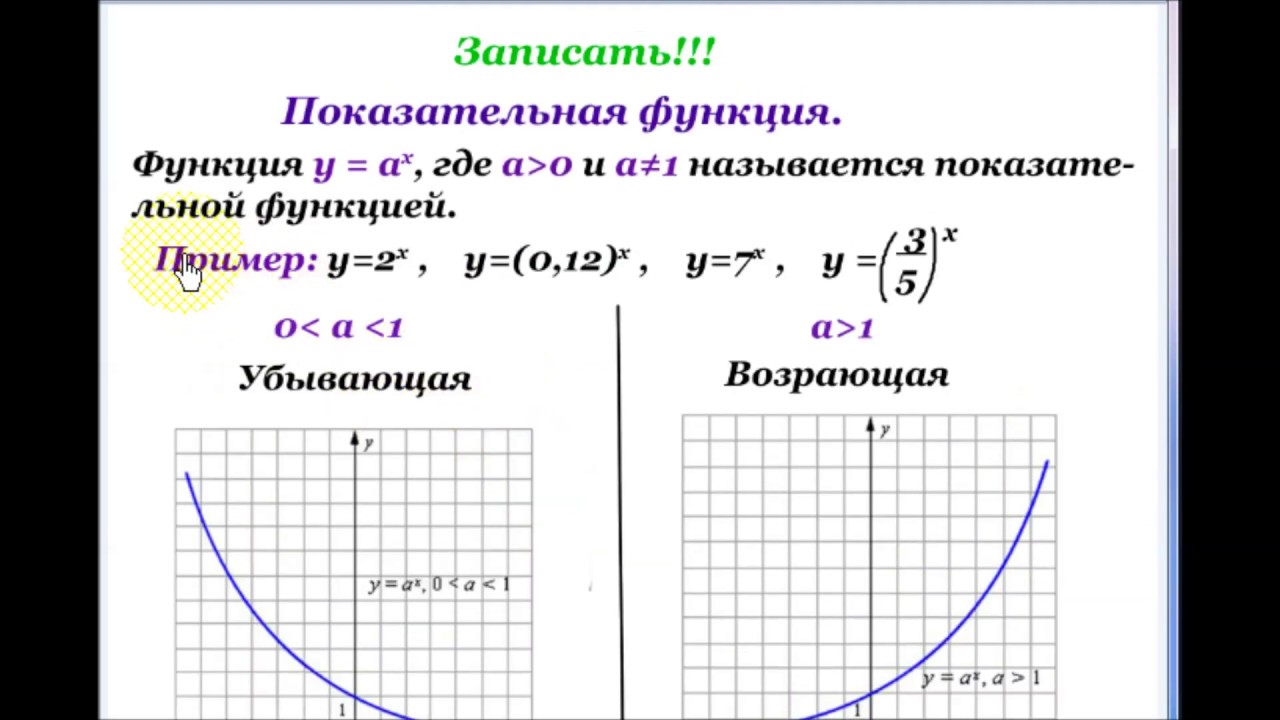
Графики показательной функции

Построим в одной системе координат графики функции и.

На заранее приготовленной системе координат строим два графика (), весь класс работает по вариантам.

У=(1/3)^х

У=3^х

Что общего в расположении графиков данных функций? Опишите расположение графиков данных функций относительно оси Оу. Запишите выводы в тетрадях:

По графикам рассмотрим свойства показательных функций.

Область определения показательной функции: D (y)=R – множество всех действительных чисел.
Область значений показательной функции: E (y)=R₊ — множество всех положительных чисел.
Показательная функция y=a^x возрастает при a>1.
Показательная функция y=a^x убывает при 0.

6. Первичная проверка понимания – 5мин

Сравнить:

А) 2³ и 2², т.к. а=2, 2>1, функция возрастающая и 3>2, то 2³>2².

Б) и, т.к. а=, , функция убывающая и 2>1, то <.

7.Домашнее задание –2мин

Перечислите свойства функции и постройте ее график:

А) у = 0,5^х

Б) у = 4^х

9.Итог урока, выставление оценок -4 мин

Свойства показательной функции представлены в опорном конспекте.

Учитель открывает опорный конспект и вместе с учащимися отвечают на вопросы:

Сформулируйте определение показательной функции.

Приведите примеры показательной функции.

Перечислите свойства показательной функции

7.Рефлексия – 2мин

Ребята на опорных конспектах высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:

сегодня я узнал…

было интересно…

было трудно…

я выполнял задания…

я понял, что…

теперь я могу…

я почувствовал, что…

я приобрел…

я научился…

у меня получилось …

я смог…

я попробую…

меня удивило…

урок дал мне для жизни…

мне захотелось…

Исследование простейших показательно-степенных функций

Гибадуллин А.А. , студент НВГУ

Аннотация: в работе исследуются простейшие показательно-степенные функции.

Ключевые слова: показательно-степенная функция, сложно-показательная функция, факториал.

Показательно-степенной функцией называется функция вида y=[f(x)]^g⁽^x⁾, где f(x) и g(x) – функции от некоторой переменной x. То есть неизвестная содержится и в основании, и в показателе степени.

Существует общая формула для нахождения производных таких функций y’= (g’ ln f + f’ g / f) f^g

Она находится следующим образом

ln y = ln f^g

ln y = g ln f

(ln y)’ = (g ln f)’

(1/y) y’ = g’ ln f + (ln f)’ g

(1/y) y’ = g’ ln f + (1/f) f’ g

y’= (g’ ln f + f’ g / f) y

В работе исследованы следующие функции: x^x и x^1/^x.

Подставляя функции в основании и показателе, получаем значение производных:

(x^x)’= (ln x + 1) x^x

(x^1/x)’= ((-1/x²) ln^{x + 1/x² ) x^1/x = (1 – ln x) x^-2+1/x}

Для обеих функций невозможно найти неопределенный интеграл, выраженный через элементарные функции.

Интересно поведение функций при отрицательных значениях аргумента, так как в этом случае меняется их знак, значения функций могут уходить в комплексную область.

В положительной области обе функции имеют положительное значение. В единице графики функций пересекаются в точке (1,1).

Функция x^x

— предел при стремлении значения аргумента к нулю справа равен единице,

— возрастает на знакоположительной области,

— предел при стремлении к бесконечности равен бесконечности.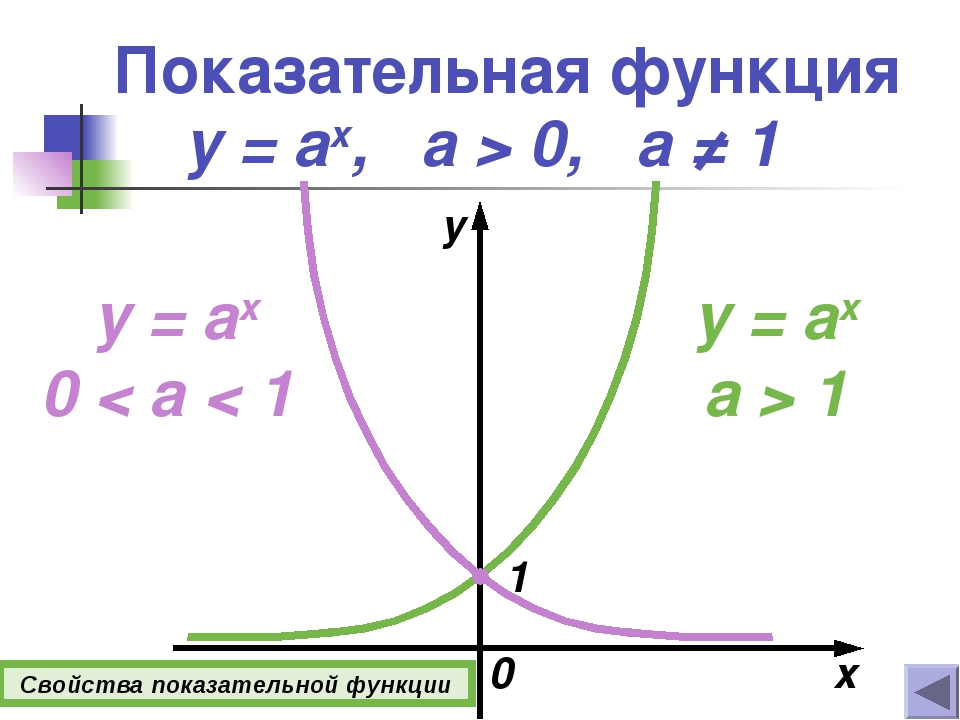

Функция x^1/^x

— предел при стремлении значения аргумента к нулю справа равен нулю,

— возрастает от нуля до e и убывает после,

— значение на знакоположительной области не превышает e^1/^e,

— предел при стремлении к бесконечности равен единице.

Если сравнить функцию x^x и x! при неотрицательных целых значениях аргумента, то обнаружим, что функция x^x возрастает быстрее. Также при x равном степени основания системы счисления, получается значение, которое легко записать в используемой системе счисления.

Например, 10¹⁰ = 10 000 000 000 в десятичной.

Литература

1. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. М.: Изд-во МГУ. Ч.1: 2-е изд., перераб., 1985. – С. 212-213

Сравнение экспоненциальной и степенной функций

Экспоненциальные функции и степенные функции сравниваются в интерактивном режиме с помощью апплета. В этом упражнении сравниваются такие свойства, как домен, диапазон, точки пересечения по осям x и y, интервалы увеличения и уменьшения графиков двух типов функций.

Питание экспоненциальных функций

Свойства экспоненциальных функций вида

f (x) = B ^x
и степенные функции вида

g (x) = x ^P
сравниваются в интерактивном режиме, используя апплет html5, путем изменения основания B экспоненциальной функции и степени P степенной функции.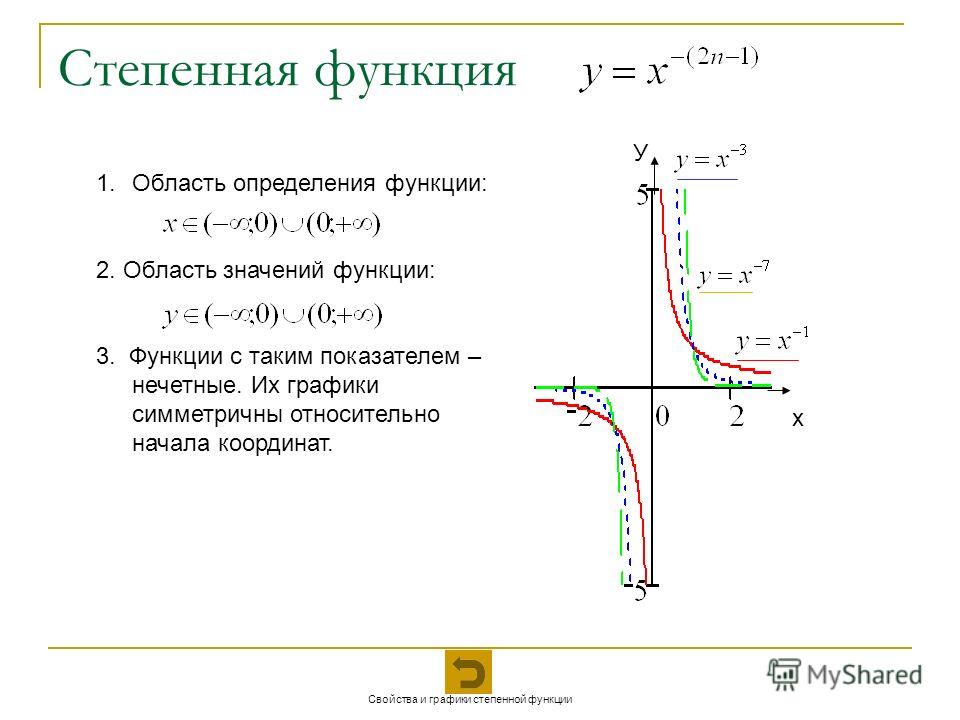

Интерактивное учебное пособие

Измените параметры B и P и сравните домены обеих функций.
Измените параметры B и P и сравните диапазоны обеих функций.
Используйте разные значения B и P и объясните, какой из двух типов функций растет быстрее, когда x принимает большие положительные значения.
Измените B и P и изучите интервалы увеличения и уменьшения двух типов функций. Сделайте вывод.
Есть ли у экспоненциальной функции точку пересечения по оси x? Измените P и исследуйте точку пересечения x степенной функции.
Сравните точку пересечения оси y графиков двух типов функций.

сообщить об этом объявлении

BioMath: функции мощности

Определение

Степенная функция — это функция вида,

f ( x ) = ax ^p ,

, где a ≠ 0 — постоянная величина, а p — действительное число. Некоторые примеры власти
функции включают:

Корневые функции, такие как примеры мощности
функции. Графически степенные функции могут напоминать экспоненциальные или логарифмические
функции для некоторых значений x . Однако, поскольку x становится очень большим, функции мощности
и экспоненциальные или логарифмические функции начинают расходиться друг от друга.
Экспоненциально растущая функция обгонит растущую мощь
функция для больших значений x . С другой стороны, растущие степенные функции будут
перегнать логарифмические функции для больших значений x .

Домен и диапазон

Область степенной функции зависит от значения мощности p . Мы будем
рассмотрим каждый случай отдельно.

1 . p — неотрицательное целое число
Домен состоит из действительных чисел (т. Е. (- ∞, ∞)).
2. p — отрицательное целое число
Домен — это все действительные числа, кроме нуля (т. Е.е. (−∞, 0) ∪ (0, ∞)
или { x | x ≠ 0}). Мы вернемся к этому случаю, когда будем изучать рациональные функции.
3 . p — рациональное число, выраженное в наименьших значениях как r /
с и с это даже
А . п. > 0
Домен — неотрицательные действительные числа (т.е.е. [0, ∞) или { x | x ≥ 0}).
Б. p <0
Домен — положительные действительные числа (т. Е. (0, ∞) или { x | x > 0}).
4. p — рациональное число, выраженное наименьшими значениями: r / s и s — нечетное
А . п. > 0
В домене все реальные числа.
Б . п. <0
Домен — это все действительные числа, кроме нуля.
5. p — иррациональное число
А . п. > 0
Домен — все неотрицательные действительные числа.
Б. p <0
Домен состоит только из положительных вещественных чисел.

*****

В следующем разделе мы изучим графики степенных функций.

График функций мощности

Экспоненциальная функция — Техническая математика, шестое издание [Книга]

18.1. Экспоненциальная функция

18.1.1. Определение

Показательная функция — это функция, в которой независимая переменная появляется в экспоненте. Величина, возведенная в степень, называется базой.

Следующие функции являются экспоненциальными, если a, b и e представляют собой положительные константы:

y = 5 ^x	y = b ^x	y = e ^x	y = 10 ^x
y = 3a ^x	y = 7 ^{x − 3}	y = 5e ^−2x

Поймите, что эти экспоненциальные функции отличаются от степенной функции, y = ax ⁿ. В степенной функции показатель степени постоянен. Здесь неизвестное находится в экспоненте. Мы увидим, что e, как и π, имеет определенное значение, которое мы обсудим позже в этой главе.

18.1.2. График экспоненциальной функции

▪ Разведка:

Попробуйте это. Используйте свой графический калькулятор, чтобы построить график экспоненциальной функции

y = 2 ^x

Для сравнения изобразите степенную функцию y = x ² в том же окне просмотра.Обе функции содержат одни и те же три величины: y, x и 2. Обе кривые одинаковы? Какие важные отличия?

Графики y = 2 ^x (сплошные) и y = x ² (пунктирные). Отметки на горизонтальной оси разнесены на 1 единицу.

Обратите внимание на экран, показанный слева, что график экспоненциальной функции полностью отличается от графика степенной функции. График степенной функции представляет собой параболу, симметричную относительно оси y, в то время как экспоненциальная функция не имеет симметрии. 4 $$
$$ B (4) = 100 * 1,12 * 1,12 * 1,12 * 1,12 $$
$$ B (4) = 157,35 … $$

На самом деле в числе много цифр после десятичной точки. В реальной проблеме обычно указывается, где следует округлить ответ, но в этом случае имеет смысл округление до ближайшего ВСЕГО числа. Почему? Потому что здесь мы имеем дело с бактериями. Бактерий может быть только целое количество, поэтому ответ лучше всего выразить как 157 после 4 часов роста.

Что такое экспоненциальная функция? — Видео и стенограмма урока

Пример функции

Всякий раз, когда появляется новая технология, люди не спешат заполучить ее сразу.Он начинается с нескольких человек, затем постепенно набирает популярность все больше и больше, а затем все его используют.

Эй, это похоже на экспоненциальную функцию!

Для примера возьмем сотовые телефоны. Во времена пещерного человека, также известные как 1980-е, сотовые телефоны были довольно редкостью. Не вдаваясь в точные цифры, предположим, что в 1980 году у пяти человек в вашем городе были мобильные телефоны.

В течение того года каждый из этих людей уговорил одного друга купить телефон, так что через год у вас было десять человек с телефонами.Затем каждый из этих людей уговорил друга купить телефон, так что через два года их стало 20 человек.

Если бы вы удваивали число каждый год, вы бы очень быстро получили действительно огромное число — в этом весь смысл экспоненциальной функции. С каждым годом количество увеличивается на все большую величину.

Теперь вернемся к нашему уравнению для экспоненциальной функции: y = ab x .

Y — это количество людей с телефонами, потому что это наша зависимая переменная. X — это количество лет, прошедших с 1980 года, потому что это наша независимая переменная.

У нас было всего пять человек с мобильными телефонами, поэтому 5 — это наше начальное значение , начальное значение функции, представленное константой a . В первый год мы умножили это число на 2.

Во второй год мы взяли наше число из первого года и умножили , что на 2. Это дает нам 5 x 2 x 2, что равно 5 умноженным на 2 в квадрате. Получилось 20 человек.На третий год каждый из этих 20 человек убедил друга купить телефон, поэтому нам просто пришлось снова умножить на 2. Это дало нам 5 x 2 x 2 x 2, или 5 умножить на 2 в третьей степени, которая равна 40. Здесь вы можете увидеть схему: мы добавляем 1 к показателю степени каждый год, что означает, что мы умножаем 2 на себя. один раз в год. В этом примере 2 представляет , число, многократно умножаемое на каждом этапе , значение, возведенное в степень x , представленное константой b .

Вот почему нам нужны две константы в уравнении: одна для исходного значения, а другая для значения, возведенного в степень x . Это может немного сбивать с толку, потому что многие экспоненциальные функции начинаются с одного, поэтому a = 1. 1 умноженное на любое число — это то же самое число, поэтому похоже, что функция просто y = b x . Но не путайте: все еще там! Оно просто равно 1.

Другой пример

Обычный способ увидеть экспоненциальные функции, описанные словами, — это фраза типа «увеличивается или уменьшается на _____% в год».«Например, стоимость инвестиции увеличивается на один процент в год. Если вы рассчитываете проценты по ссуде, вы должны использовать такое уравнение.

Давайте рассмотрим пример проблемы, чтобы увидеть, как она работает.

Инвестор покупает недвижимость в перспективном районе города. По мере того, как территория становится лучше, стоимость недвижимости увеличивается. Стоимость недвижимости увеличивается на два процента в год. Если инвестор изначально купил его за 500 000 долларов, то сколько он будет стоить через пять лет?

Давайте подставим это в нашу формулу экспоненциальной функции, y = ab x .

X — количество лет после первоначальной покупки. Y — стоимость имущества. Это наши входные и выходные переменные.

A представляет начальное значение функции. Начальное значение этого свойства — 500 000, поэтому мы подставим его для и . Теперь самая сложная часть — вычислить b .

В первой задаче b было 2, потому что у нас в два раза больше пользователей сотовых телефонов каждый год.В этом случае недвижимость стоит всего два процента, или на 0,02 доллара больше, поэтому ее стоимость растет медленнее. У вас может возникнуть соблазн вставить 0,02 для b , но просто посмотрите и посмотрите, что произойдет, когда вы построите график.

Сразу видно, что это не рост стоимости! Это дает нам функцию, показывающую, сколько будет стоить недвижимость, если бы каждый год ее оценивали в два процента от ее стоимости годом ранее. Но мы не хотим двух процентов от его стоимости годом ранее; мы хотим, чтобы на два процента больше, чем на год назад.Чтобы получить это, нам нужно умножить на 1,02.

y = 500000 * 1.02 x

Если мы определим некоторые из значений этой функции, мы получим:

Вот как это выглядит на графике.

А, вот и лучше! Вы не можете увидеть, как наклон становится все круче, потому что числа такие большие, но обратите внимание, как y увеличивается каждый раз немного больше — сначала увеличивается на 10 000, затем на 10 200, затем на 10 404 и т. Д. .

Вы можете видеть, что если вы выполните математические вычисления вручную, они получат те же значения, которые вы получаете от функции; умножив значение каждого года на 1,02, чтобы найти увеличение на два процента, вы получите одинаковые значения для каждого года. Итак, для пятого года, о котором изначально был задан вопрос, стоимость будет 552 020,40 долларов. Наш сообразительный инвестор заработал 52 000 долларов!

Резюме урока

На этом уроке вы узнали об экспоненциальных функциях. Показательная функция записывается в виде y = ab x .

y представляет результат
a представляет начальное значение функции
b представляет собой темп роста
x представляет вход

В экспоненциальной функции a умножается на b x раз, чтобы получить y . {a} $ (
Инжир.{- \ pi / 2}.
$$

Список литературы

[a1]	K.R. Стромберг, «Введение в классический реальный анализ», Wadsworth (1981) стр. 318ff
[a2]	К. Кнопп, «Theorie und Anwendung der unendlichen Reihen», Springer (1964) (английский перевод: Blackie, 1951 & Dover, перепечатка, 1990 г.)
[a3]	Дж. Марсден, «Базовый комплексный анализ», Freeman (1973)

Как процитировать эту запись:
Степенная функция. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Power_function&oldid=48271

Справочник по экспоненциальной функции

Это общая экспоненциальная функция (см. Ниже e ^x):

f (x) = a ^x

a — любое значение больше 0

Свойства зависят от значения «а»

Когда a = 1 , график представляет собой горизонтальную линию при y = 1

Кроме того, есть два случая, на которые стоит обратить внимание:

a от 0 до 1

Пример: f (x) = (0.5) ^х

Для a от 0 до 1

a выше 1

Пример: f (x) = (2) ^x

Для и и выше 1:

Постройте график здесь (используйте ползунок «a»)

В целом:

Это всегда больше 0 и никогда не пересекает ось x
Он всегда пересекает ось Y при y = 1 … другими словами, он проходит через (0,1)
При x = 1 , f (x) = a … другими словами он проходит через (1, а)
Это инъективная (однозначная) функция

Его домен — действительные числа:

Его диапазон — положительные действительные числа: (0, + ∞)

обратная

Таким образом, экспоненциальная функция может быть «обращена» логарифмической функцией.

Естественная экспоненциальная функция

Это экспоненциальная функция «Natural » :

f (x) = e ^x

Где e — «Число Эйлера» = 2.718281828459 … и т. Д.

График f (x) = e ^x

Значение e важно, потому что оно создает следующие полезные свойства:

В любой момент наклон e ^x равен значению e ^x:

, когда x = 0, значение e ^x = 1 и наклон = 1
, когда x = 1, значение e ^x = e и наклон = e
и т. Д…

Область от до любое значение x также равно e ^x: