Решение задач на применение аксиом стереометрии и их следствий

Слайд №2
	Цели: Повторить аксиомы стереометрии: — о взаимном расположении точек, — о взаимном расположении прямых, — о взаимном расположении плоскостей в пространстве. Повторить следствия из аксиом стереометрии. Формировать навык применения аксиом стереометрии и их следствий при решении задач. 2 10.03.2014 www.konspekturoka.ru
Слайд №3
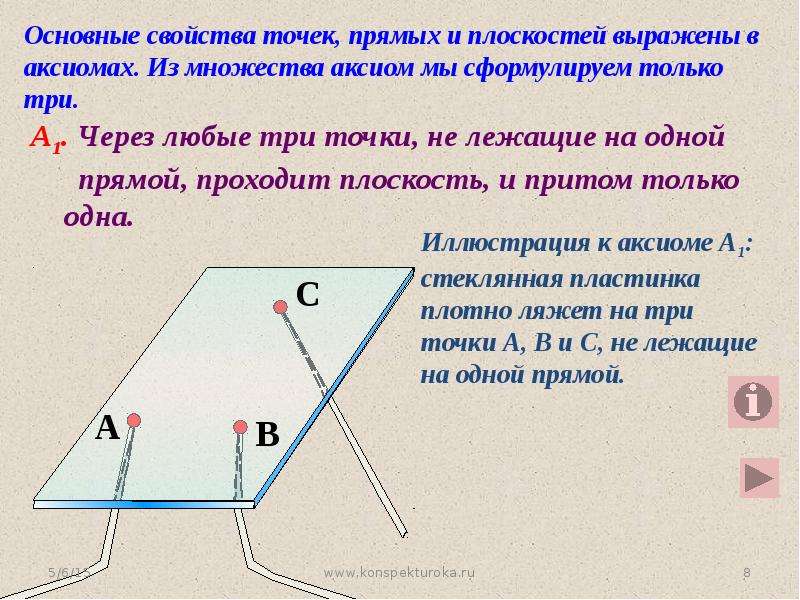
	А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. 10.03.2014 3 www.konspekturoka.ru Вспомним!
Слайд №4
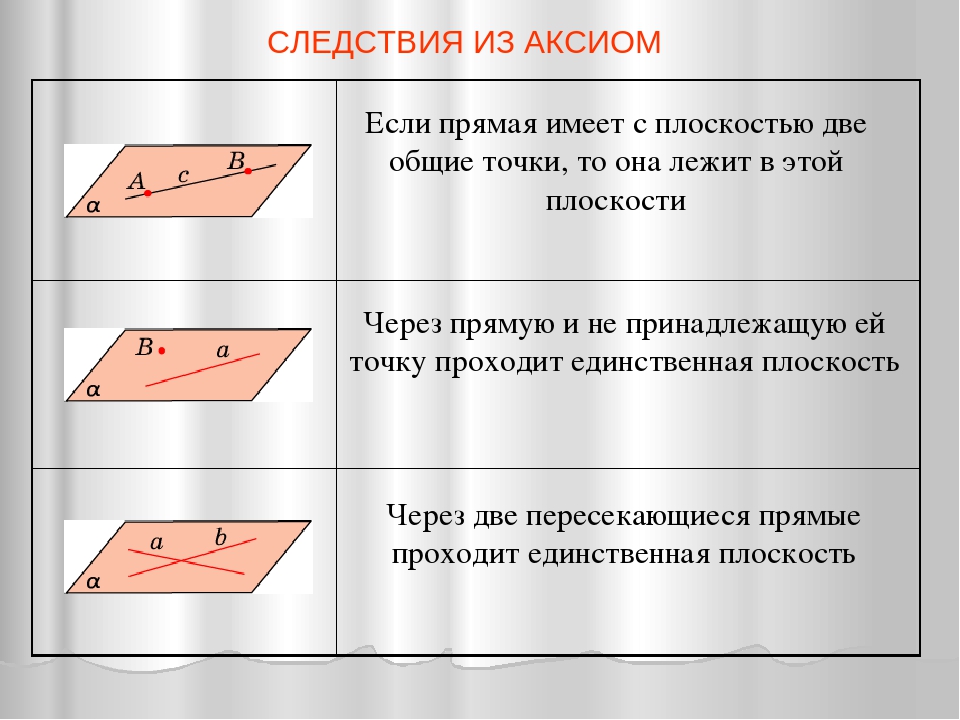
	Некоторые следствия из аксиом. Теорема Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. М a 10.03.2014 4 www.konspekturoka.ru Вспомним!
Слайд №5
	Теорема Через две пересекающиеся прямые проходит плоскость, и притом только одна М a b N 10. 03.2014 5 www.konspekturoka.ru Некоторые следствия из аксиом. Вспомним!
Слайд №6
	P A B C D A1 B1 C1 D1 M K Q Назовите точки, лежащие в плоскости ? 10.03.2014 6 www.konspekturoka.ru Куб АВСДА?В?С?Д?. Закрепление изученного материала. 1
Слайд №7
	P A B C D A1 B1 C1 D1 M K Q Назовите точки, не лежащие в плоскости ? Закрепление изученного материала. 10.03.2014 7 www.konspekturoka.ru Куб АВСДА?В?С?Д?. 2
Слайд №8
	P A B C D A1 B1 C1 D1 M K Q Назовите прямые, которые лежат в плоскости ? 10.03.2014 8 www.konspekturoka.ru Куб АВСДА?В?С?Д?. Закрепление изученного материала. 3
Слайд №9
	P A B C D A1 B1 C1 D1 M K Q Назовите прямые, которые не лежат в плоскости ? 10. 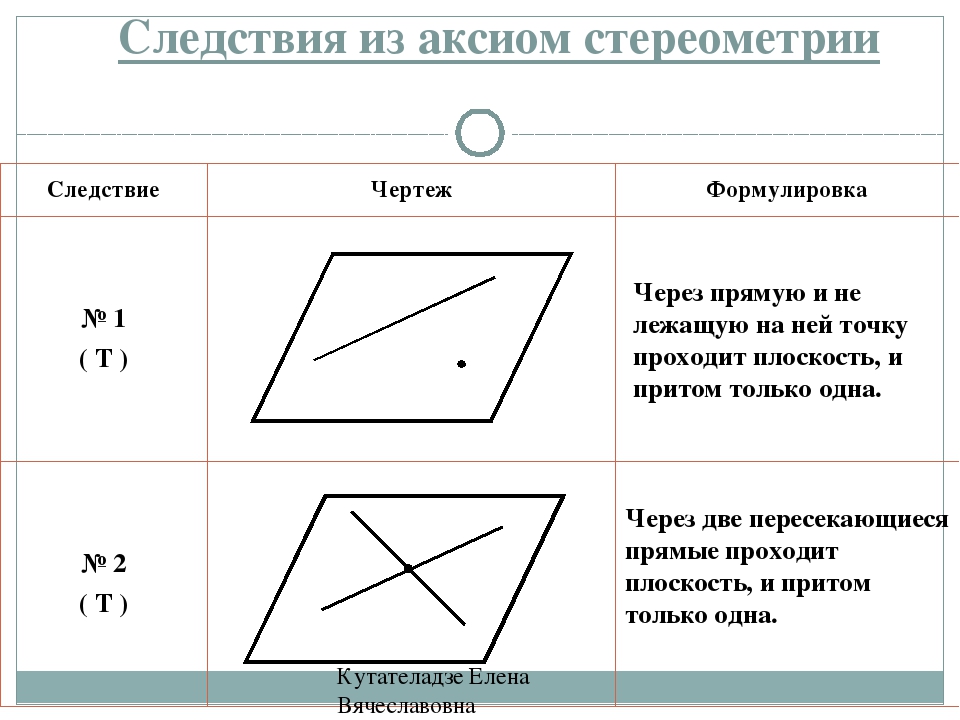03.2014 9 www.konspekturoka.ru Куб АВСДА?В?С?Д?. 4
Слайд №10
	P A B C D A1 B1 C1 D1 M K Q Назовите прямые, которые пересекают прямую ВС 10.03.2014 10 www.konspekturoka.ru Куб АВСДА?В?С?Д?. 5
Слайд №11
	P A B C D A1 B1 C1 D1 M K Q Назовите прямые, которые не пересекают прямую ВС 10.03.2014 11 www.konspekturoka.ru Куб АВСДА?В?С?Д?. 6
Слайд №12
	P A B C D A1 B1 C1 D1 M K Q Назовите точки, лежащие в плоскости ? 10.03.2014 12 www.konspekturoka.ru Куб АВСДА?В?С?Д?. 7
Слайд №13
	10.03.2014 www.konspekturoka.ru 13 Задача Две прямые пересекаются в точке М. 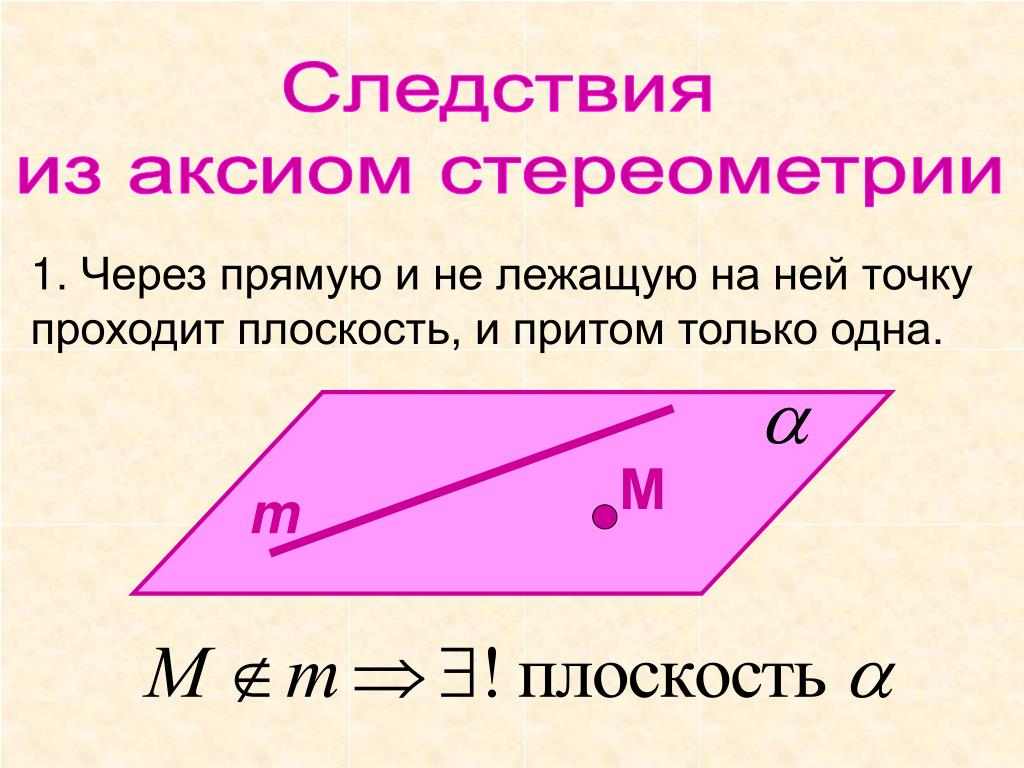Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости. Лежат ли в одной плоскости все прямые, проходящие через точку М? Пусть l? ? l? = M n – произвольная прямая M ? n, n — пересекает l? и l? в точках А и К, Значит через точку А и прямую l? можно провести единственную плоскость (по теореме). Поэтому отрезки АМ, АК и КМ лежат в одной плоскости (по аксиоме А?) и прямые , которым принадлежат эти отрезки, лежат в одной плоскости. Все прямые, проходящие через М не лежат в одной плоскости. Например, прямая т. т Решение Закрепление изученного материала.
Слайд №14
	10.03.2014 www.konspekturoka.ru 14 Задача Три прямые проходят через одну точку. Через каждые две из них проведена плоскость. Сколько всего проведено плоскостей? 1 случай Все прямые a, b, c — лежат в одной плоскости. В этом случае (по следствию 2) можно провести плоскости, и через три прямые проходит одна плоскость. Закрепление изученного материала.
Слайд №15
	10.03.2014 www.konspekturoka.ru 15 2 случай с Одна из трех прямых (с) не лежит в плоскости ?, определяемой другими прямыми a и b. В этом случае через заданные три прямые проходят три различные плоскости, определяемые парами прямых : a и b a и c b и c Ответ: или три или одну плоскость
Слайд №16
	10.03.2014 www.konspekturoka.ru 16 Верно ли, что прямая лежит в плоскости данного треугольника, если она: а) пересекает две стороны треугольника; б) проходит через одну из вершин треугольника? Решение a) Если MN пересекает стороны ?АВС, а ?АВС ? ?, то М ? ? и N ? ? . Из аксиомы А? прямая М N ? ? . б) Если l пересекает ? в точке В, то не обязательно будет лежать в ней. Ответ: а) да; б) нет. l Закрепление изученного материала.
Слайд №17
	Ответить на вопросы: 10. 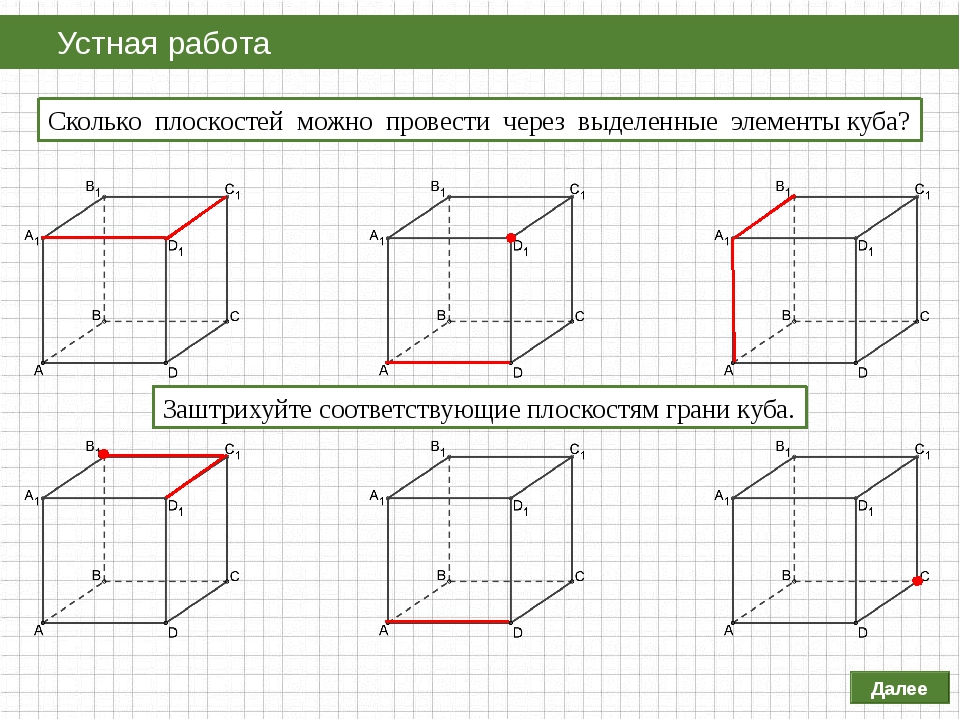03.2014 17 www.konspekturoka.ru Назвать аксиомы стереометрии: — о взаимном расположении точек, — о взаимном расположении прямых, — о взаимном расположении плоскостей в пространстве. Назвать следствия из аксиом стереометрии.

10 класс. Геометрия. Аксиомы стереометрии и их следствия. — Решение задач на применение аксиом и их следствий (в параллелепипеде)

Комментарии преподавателя

Аксиома 1 (А1)

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. 

Иллюстрация аксиомы А1.

Рис. 1.

Рассмотрим три точки: А, В, С, причем точка С не принадлежит прямой АВ: (Рис. 1.). Тогда через три точки А, В, С, не лежащие на одной прямой, проходит плоскость , и притом только одна. Плоскость  можно также обозначить через три точки АВС.

Аксиома 2 (А2)

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.  

Иллюстрация аксиомы А2.

Рассмотрим плоскость , точки А,  В  прямой  принадлежат плоскости  (Рис. 2.).

Рис. 2.

Аксиома утверждает – все точки прямой  (прямой АВ) принадлежат плоскости , т.е. вся прямая лежит в плоскости  или плоскость  проходит через прямую .

Аксиома 3 (А3).

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (плоскости пересекаются по прямой).

Иллюстрация аксиомы А3.

Имеем разные плоскости: плоскость , плоскость . Известно, что они имеют общую точку М, точка М принадлежит плоскости и плоскости . (Рис. 3.)

Рис. 3.

Третья аксиома утверждает, что они имеют прямую, на которой лежат все их общие точки. Прямую мы обозначили за l, т.е. плоскости  и  пересекаются по прямой l, проходящей через точку М.

Повторение теорем, которые следуют из аксиом стереометрии.

Теорема 1

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Иллюстрация теоремы 1.

Рис. 4. 

Даны прямая а и точка М, не лежащая на данной прямой (Рис. 4.). Теорема утверждает, что существует такая единственная плоскость , которая проходит и через прямую а, и через точку М, и что эта плоскость  – единственная. Это можно записать таким образом:

   единственная

Теорема 2

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Иллюстрация теоремы 2.

Рис. 5.

Даны прямые а и b, они пересекаются, т.е. имеют единственную общую точку М (Рис. 5.). Теорема утверждает, что существует единственная плоскость  – такая, которая проходит и через прямую а, и через прямую b, что можно записать таким образом:

Теперь применим аксиомы 1, 2, 3 и теоремы 1, 2 для задач в параллелепипеде.

Дан параллелепипед  (Рис. 6.). Точка L лежит на продолжении прямой AA1. Точка К лежит на продолжении прямой AD. Прямая LK пересекает ребра в точках N и M.

По какой прямой пересекаются плоскости:

1) АВС и 

2)  и 

3)  и ?

Рис. 6.

 Решение:

1) Плоскость АВС – плоскость нижней грани. Плоскость  – плоскость боковой грани. У них общая прямая DC, по ней эти плоскости пересекаются.

2) Плоскость  – это плоскость задней грани. Плоскость  – это плоскость грани . Они пересекаются по прямой .  – это общая прямая плоскостей  и .

3) Плоскость , можно обозначить как LAK. — плоскость передней грани .  – это плоскость нижней грани. Они пересекаются по прямой АD. Прямая АD входит и в переднюю грань  и в нижнюю грань .

Ответ: 1) DC, 2) , 3) АD.

Дан параллелепипед  (Рис. 6.). Точка L лежит на продолжении прямой AA1. Точка К лежит на продолжении прямой AD. Прямая LK пересекает ребра в точках N и M.

Назовите три разные плоскости, которые пересекаются:

1) в точке А

2) в точке С

Напоминание: В вершине сходятся три плоскости, так как первые две плоскости пересекаются по прямой линии, вторые две плоскости пересекаются по второй прямой линии. Прямые пересекаются в точке. Значит, три плоскости могут пересекаться в одной точке.

Решение: 

1) В точке А пересекаются плоскости АВС – плоскость нижней грани, плоскость  – плоскость передней грани, плоскость  – плоскость левой грани. Эти три плоскости пересекаются в точке А.

2) Какие плоскости пересекаются в точке С? Первая плоскость СВD, т.е. это плоскость нижнего основания, вторая плоскость  и третья плоскость .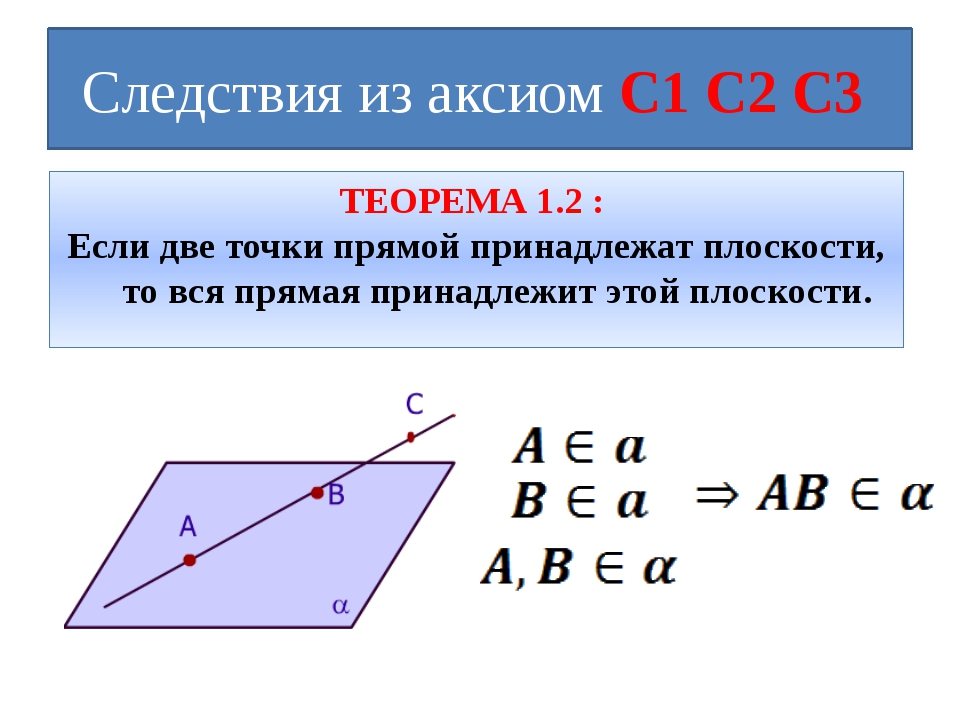

Ответ: 1) АВС; ; 2) СВD; ; .

Дан параллелепипед  (Рис. 6.). Точка L лежит на продолжении прямой AA1. Точка К лежит на продолжении прямой AD. Прямая LK пересекает ребра в точках N и M.

По какой прямой пересекаются плоскости  и ?

Плоскость – это плоскость передней грани. Заметим, что в ней расположены и точка М, и точка N. Обе точки расположены в этой плоскости, значит, в этой плоскости по аксиоме расположена вся прямая МN. И вторая плоскость  содержит прямую МN. Значит, прямая МN является линией пересечения двух этих плоскостей.

Ответ: MN 

Итак, мы рассмотрели применение аксиом стереометрии и следствие из них для решения задач в параллелепипеде. А именно: задач на расположение точек, прямых и плоскостей.

Эти сведения будут использованы для решения других задач в следующих уроках.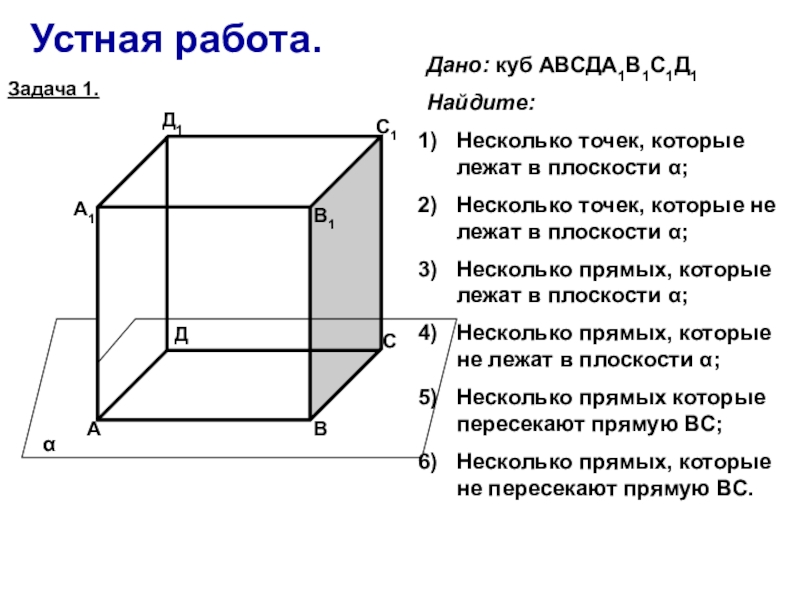

http://interneturok.ru/ru/school/geometry/10-klass/aksiomy-stereometrii-i-ih-sledstviya/reshenie-zadach-na-primenenie-aksiom-i-ih-sledstviy-v-parallelepipede?seconds=0&chapter_id=209

http://www.youtube.com/watch?v=75t-pn-XMiY

http://mathematichka.ru/ege/problems/b9_images/b9_par0.jpg

http://matematikalegko.ru/formuli/zadachi-v11-obshhij-obzor-formuly.html

http://www.otbet.ru/book/class-10/geometria/uchebnik-glazkov-yu-a-testy-po-geometrii/

Решение задач на применение аксиом стереометрии и их следствий

10 класс геометрия

Решение задач на применение аксиом стереометрии и их следствий.

Урок 1

Учитель : Олейникова И.В.

C

Вспомним!

B

А 1 .

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

A

a

B

А 2 .

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

A

А 3 .

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

a

2

Вспомним!

Некоторые следствия из аксиом.

Теорема

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Q

P

М

a

3

Вспомним!

Некоторые следствия из аксиом.

Теорема

Через две пересекающиеся прямые проходит плоскость, и притом только одна

b

N

М

a

3

Закрепление изученного материала.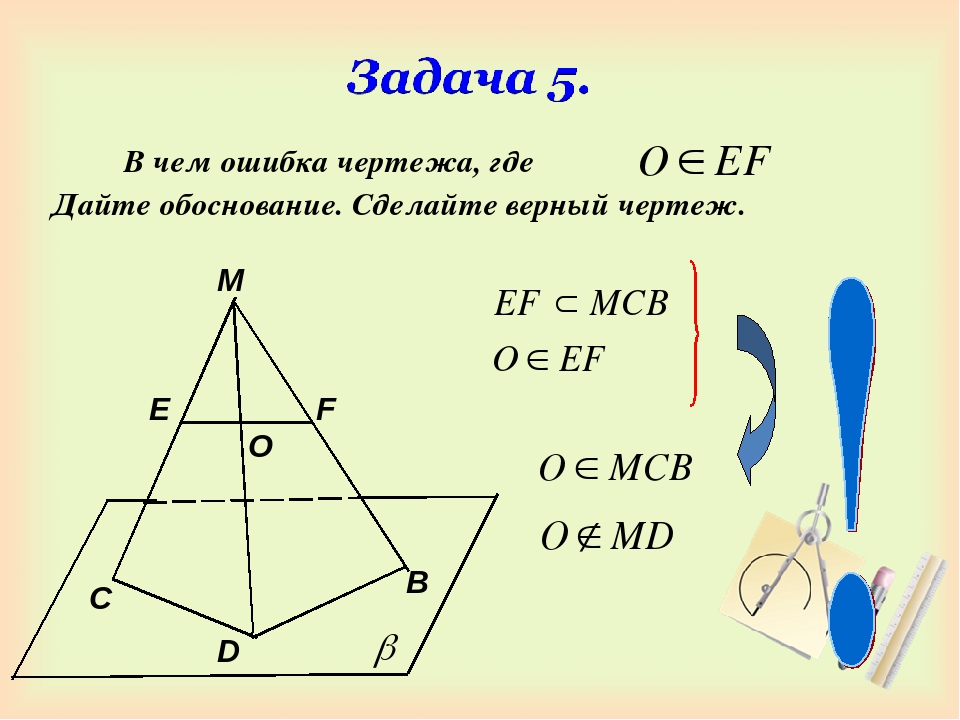

Задача

Две прямые пересекаются в точке М. Докажите, что все прямые,

не проходящие через точку М и пересекающие данные прямые,

лежат в одной плоскости. Лежат ли в одной плоскости все прямые,

проходящие через точку М?

Решение

l ₂

n

Пусть l ₁ ∩ l₂ = M

А

n – произвольная прямая

M

M  n,

n — пересекает l ₁ и l₂ в точках А и К,

Значит через точку А и прямую l₂

можно провести единственную

плоскость (по теореме).

l ₁

№ 7. А. С. Атанасян

К

т

Поэтому отрезки АМ, АК и КМ лежат в одной плоскости (по аксиоме А ₂) и прямые , которым принадлежат эти отрезки, лежат в одной плоскости.

Все прямые, проходящие через М не лежат в одной плоскости.

Например, прямая т.

3

5

Закрепление изученного материала.

Задача

Три прямые проходят через одну точку. Через каждые две из них

проведена плоскость. Сколько всего проведено плоскостей?

а

c

1 случай

O

b

№ 14. А. С. Атанасян

Все прямые a, b, c — лежат в одной плоскости.

В этом случае (по следствию 2) можно провести плоскости, и через три прямые проходит одна плоскость.

5

6

2 случай

Одна из трех прямых (с) не лежит в плоскости  , определяемой другими прямыми a и b.

В этом случае через заданные три прямые проходят три

различные плоскости, определяемые парами прямых :

а

a и b

a и c

O

b и c

b

№ 14.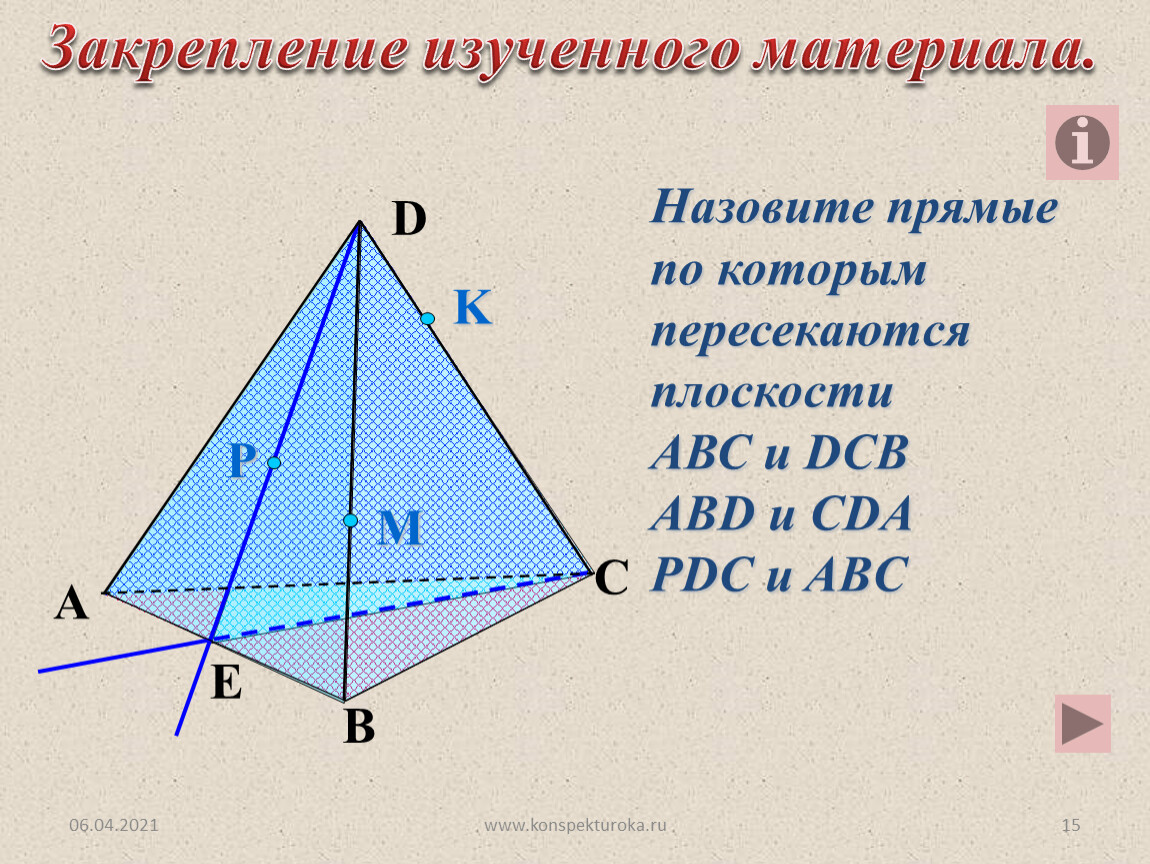 А. С. Атанасян

с

Ответ:

или три или одну плоскость

6

7

Закрепление изученного материала.

Верно ли, что прямая лежит в плоскости данного треугольника,

если она: а) пересекает две стороны треугольника;

б) проходит через одну из вершин треугольника?

l

B

М

Решение

С

A

N

№ 14. А. С. Атанасян

a) Если MN пересекает стороны ∆АВС, а ∆АВС   , то М   и N   .

Из аксиомы А ₂ прямая М N   .

б) Если l пересекает  в точке В, то не обязательно будет лежать в ней.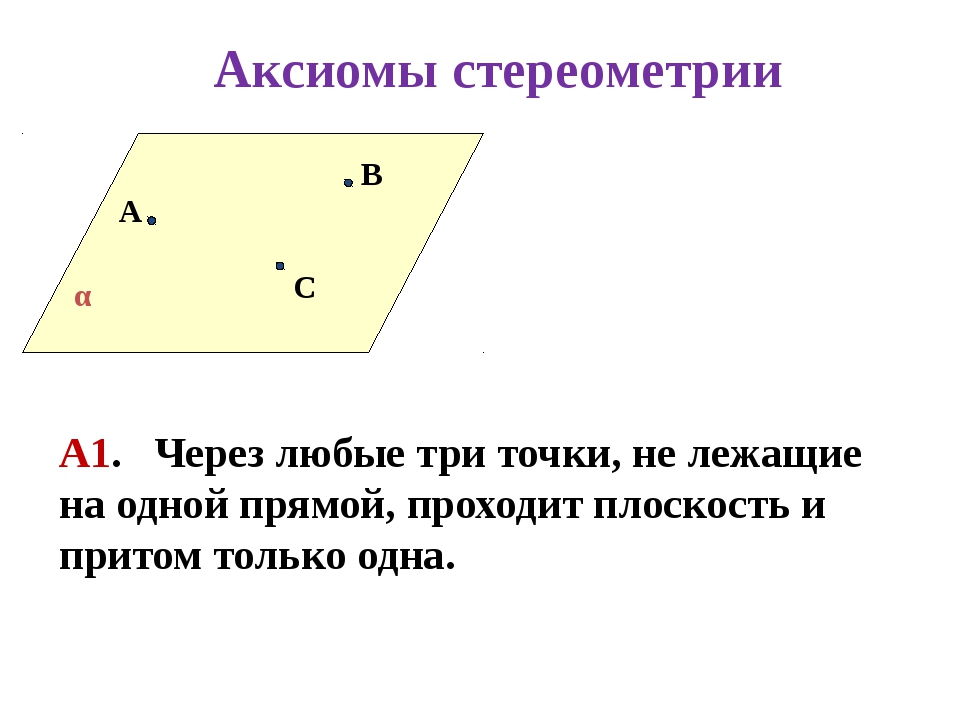

Ответ: а) да; б) нет.

7

8

Аксиомы стереометрии и их следствия. | Презентация к уроку по геометрии (10 класс) на тему:

Слайд 1

Аксиомы стереометрии и их следствия

Слайд 2

Тема урока: «Аксиомы стереометрии и их следствия. Решение задач»

Слайд 3

Цель урока: обобщение и применение аксиом и их следствий к решению задач

Слайд 4

Математический диктант 1). Сформулируйте аксиомы стереометрии: Аксиома 1. через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна _____________________________________________ Аксиома 2. если две точки прямой лежат в плоскости, то и все точки этой прямой лежат в этой плоскости __________________________________________________________ _ Аксиома 3. если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все_общие точки этих плоскостей

Слайд 5

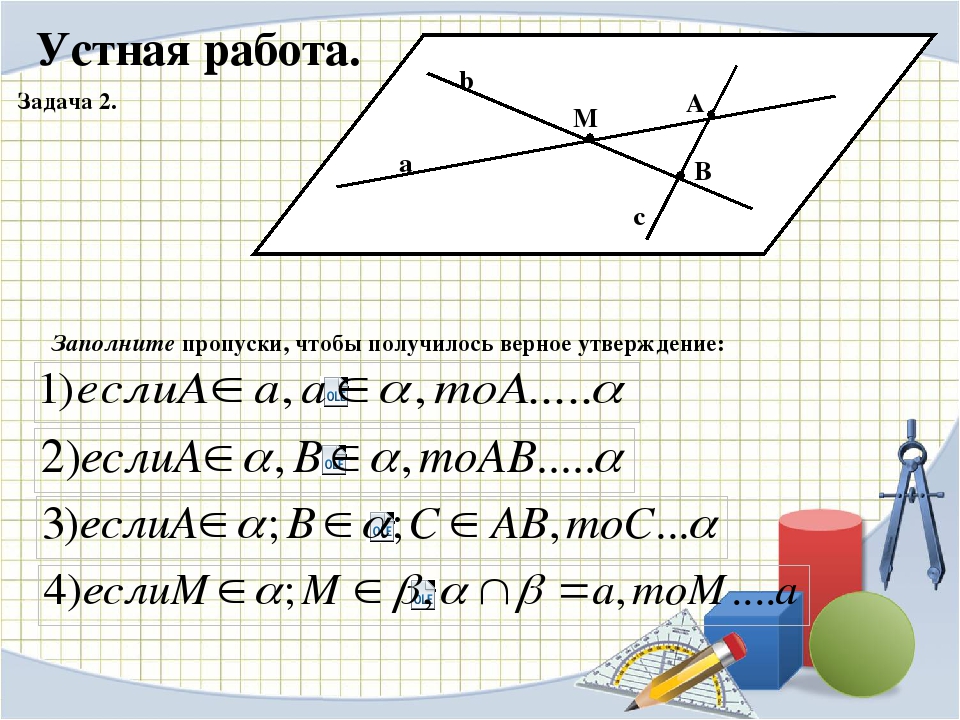
2). Заполните пропуски, чтобы получилось верное утверждение: а). Для любой прямой существуют точки, принадлежащие ей, и ______________ ____________________________________________________________________ б). Через прямую и не лежащую на ней точку проходит плоскость, и притом ____________________________________________________________________ в). Через две пересекающиеся прямые проходит плоскость, и притом _________ _____________________________________________ г). Если А  а, а   , то А …  . д). Если А   , В   , С  АВ, то С …  .

Слайд 6

АВСД – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в плоскости ромба. Точки А, Д, О лежат в плоскости α . Определить и обосновать: 1. Какие еще точки лежат в плоскости α ? Лежат ли в плоскости α точки В и М? Лежит ли в плоскости МОД точка В? Назовите линию пересечения плоскостей МОС и АДО. Точка О – общая точка плоскостей МОВ и МОС. Верно ли что эти плоскости пересекаются по прямой МО? Назовите три прямые, лежащие в одной плоскости; не лежащие в одной плоскости. А В С Д М О Задача (устно)

Слайд 7

Задача 1. Сколько плоскостей можно провести через выделенные элементы куба? Заштрихуйте соответствующие плоскостям грани куба. ● ● ●

Слайд 8

Проверь себя!

Слайд 9

Задача №2 Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в одной плоскости. Лежат ли две другие вершины параллелограмма в этой плоскости? Ответ объясните.

Слайд 10

Задания разного уровня сложности Уровень 1: Точка С – общая точка плоскости альфа и бета. Прямая с проходит через точку С. Верно ли, что плоскости альфа и бета пересекаются по прямой с. Ответ объясните. Уровень 2: Прямые а, в и с имеют общую точку. Верно ли, что данные прямые лежат в одной плоскости? Ответ объясните Уровень 3: Четыре прямые попарно пересекаются. Верно ли, что если любые три из них лежат в одной плоскости, то все четыре прямые лежат в одной плоскости? Ответ объясните

Слайд 11

Синквейн Аксиома

Слайд 12

Домашнее задание Пункты 1 – 3 Задачи : на карточках

Презентация на тему: Аксиомы стереометрии
10 класс геометрия
3.

Решение задач на применение аксиом

1

Первый слайд презентации

Аксиомы стереометрии
10 класс геометрия
3. Решение задач на применение аксиом стереометрии и их следствий
1
04.07.2012
www.konspekturoka.ru

Изображение слайда

2

Слайд 2

Цели:
Повторить аксиомы стереометрии:
— о взаимном расположении точек,
— о взаимном расположении прямых,
— о взаимном расположении плоскостей
в пространстве.
Повторить следствия из аксиом стереометрии.
Формировать навык применения аксиом стереометрии и их следствий при решении задач.
2
04.07.2012
www.konspekturoka.ru

Изображение слайда

3

Слайд 3

А 1.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
C
A
B
А 2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
a
A
B
a
А 3.
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
04.07.2012
3
www.konspekturoka.ru
Вспомним!

Изображение слайда

4

Слайд 4

Некоторые следствия из аксиом.
Теорема
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
М
a
Q
P
04.07.2012
4
www.konspekturoka.ru
Вспомним!

Изображение слайда

5

Слайд 5

Теорема
Через две пересекающиеся прямые проходит плоскость, и притом только одна
М
a
b
N
04.07.2012
5
www.konspekturoka.ru
Некоторые следствия из аксиом.
Вспомним!

Изображение слайда

6

Слайд 6

P
A
B
C
D
A 1
B 1
C 1
D 1
M
K
Q
Назовите точки, лежащие в
плоскости 
04. 07.2012
6
www.konspekturoka.ru
Куб АВСДА ₁ В ₁ С ₁ Д ₁.
Закрепление изученного материала.
1

Изображение слайда

7

Слайд 7

P
A
B
C
D
A 1
B 1
C 1
D 1
M
K
Q
Назовите точки, не лежащие в плоскости 
Закрепление изученного материала.
04.07.2012
7
www.konspekturoka.ru
Куб АВСДА ₁ В ₁ С ₁ Д ₁.
2

Изображение слайда

8

Слайд 8

P
A
B
C
D
A 1
B 1
C 1
D 1
M
K
Q
Назовите прямые, которые лежат в плоскости 
04. 07.2012
8
www.konspekturoka.ru
Куб АВСДА ₁ В ₁ С ₁ Д ₁.
Закрепление изученного материала.
3

Изображение слайда

9

Слайд 9

P
A
B
C
D
A 1
B 1
C 1
D 1
M
K
Q
Назовите прямые, которые не лежат в плоскости 
04.07.2012
9
www.konspekturoka.ru
Куб АВСДА ₁ В ₁ С ₁ Д ₁.
4

Изображение слайда

10

Слайд 10

P
A
B
C
D
A 1
B 1
C 1
D 1
M
K
Q
Назовите прямые, которые пересекают
прямую ВС
04. 07.2012
10
www.konspekturoka.ru
Куб АВСДА ₁ В ₁ С ₁ Д ₁.
5

Изображение слайда

11

Слайд 11

P
A
B
C
D
A 1
B 1
C 1
D 1
M
K
Q
Назовите прямые, которые не пересекают
прямую ВС
04.07.2012
11
www.konspekturoka.ru
Куб АВСДА ₁ В ₁ С ₁ Д ₁.
6

Изображение слайда

12

Слайд 12

P
A
B
C
D
A 1
B 1
C 1
D 1
M
K
Q
Назовите точки, лежащие в плоскости 
04. 07.2012
12
www.konspekturoka.ru
Куб АВСДА ₁ В ₁ С ₁ Д ₁.
7

Изображение слайда

13

Слайд 13

04.07.2012
www.konspekturoka.ru
13
Задача
Две прямые пересекаются в точке М. Докажите, что все прямые,
не проходящие через точку М и пересекающие данные прямые,
лежат в одной плоскости. Лежат ли в одной плоскости все прямые,
проходящие через точку М?
l ₁
l ₂
Пусть l ₁ ∩ l₂ = M
M
n – произвольная прямая
n
M  n,
n — пересекает l ₁ и l₂ в точках А и К,
А
К
Значит через точку А и прямую l₂
можно провести единственную
плоскость (по теореме).
Поэтому отрезки АМ, АК и КМ лежат в одной плоскости (по аксиоме А ₂) и прямые, которым принадлежат эти отрезки, лежат в одной плоскости.
Все прямые, проходящие через М не лежат в одной плоскости.
Например, прямая т.
т
Решение
Закрепление изученного материала.

Изображение слайда

14

Слайд 14

04.07.2012
www.konspekturoka.ru
14
Задача
Три прямые проходят через одну точку. Через каждые две из них
проведена плоскость. Сколько всего проведено плоскостей?
1 случай
Все прямые a, b, c — лежат в одной плоскости.
В этом случае (по следствию 2) можно провести плоскости, и через три прямые проходит одна плоскость.
а
b
c
O
Закрепление изученного материала.

Изображение слайда

15

Слайд 15

04. 07.2012
www.konspekturoka.ru
15
2 случай
а
b
O
с
Одна из трех прямых (с) не лежит в плоскости , определяемой другими прямыми a и b.
В этом случае через заданные три прямые проходят три
различные плоскости, определяемые парами прямых :
a и b
a и c
b и c
Ответ:
или три или одну плоскость

Изображение слайда

16

Слайд 16

04.07.2012
www.konspekturoka.ru
16
Верно ли, что прямая лежит в плоскости данного треугольника,
если она: а) пересекает две стороны треугольника;
б) проходит через одну из вершин треугольника?
Решение
A
B
С
М
N
a) Если MN пересекает стороны ∆АВС, а ∆АВС  , то М   и N  .
Из аксиомы А ₂ прямая М N  .
б) Если l пересекает  в точке В, то не обязательно будет лежать в ней.
Ответ: а) да; б) нет.
l
Закрепление изученного материала.

Изображение слайда

17

Последний слайд презентации: Аксиомы стереометрии
10 класс геометрия
3. Решение задач на применение аксиом

Ответить на вопросы:
04.07.2012
17
www.konspekturoka.ru
Назвать аксиомы стереометрии:
— о взаимном расположении точек,
— о взаимном расположении прямых,
— о взаимном расположении плоскостей
в пространстве.
Назвать следствия из аксиом стереометрии.

Изображение слайда

Решение задач на применение аксиом стереометрии и их следствий

Текст этой презентации

Слайд 1

Презентация урока по геометрии Тема: «Решение задач на применение аксиом стереометрии и их следствий»

Слайд 2

Данная презентация посвящена аксиомам стереометрии и следствиям из них. Может быть использована: в виде диагностики знаний обучающихся при завершении темы «Аксиомы стереометрии и следствия из них»; при организации работы по готовому чертежу, что способствует развитию быстрого интуитивного логического мышления; для развития устной и письменной математической речи.

Слайд 3

Решение задач на применение аксиом стереометрии и их следствий Выполнила: Соломина Наталья Васильевна преподаватель математики и информатики ГБПОУ «Вышневолоцкий медицинский колледж»

Слайд 4

Цель урока: Закрепить усвоение вопросов теории в процессе решения; Проверить уровень подготовленности обучающихся: — при решении задач на готовом чертеже; — путём проведения самостоятельной работы контролирующего характера

Слайд 5

Ход урока Ι. Организационный момент. ΙΙ. Устная работа.

Слайд 6

П о в т о р я е м
Каковы аксиомы стереометрии?

Слайд 7

А
В
С
ɑ
Аксиома 1 Через любые 3 точки, не лежащие на одной прямой, проходит плоскость и притом только одна

Слайд 8

Верно ли, что: Любые три точки лежат в одной плоскости; Да Любые четыре точки лежат в одной плоскости; Нет

Слайд 9

Любые четыре точки не лежат в одной плоскости; Нет Через любые три точки проходит плоскость, и притом только одна? Нет

Слайд 10

А
В
ɑ
Аксиома 2 Если 2 точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

Слайд 11

Верно ли, что прямая лежит в плоскости данного треугольника, если она ( ответ обоснуйте): пересекает две стороны треугольника; проходит через одну из вершин треугольника?

Слайд 12

А
а
ɑ
ß
Аксиома 3 Если 2 плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей

Слайд 13

В 1
С 1
А 1
Д 1
А
Д
В
С
К
М
Назовите плоскости, в которых лежат точка К, точка М.

Слайд 14

Каковы следствия из аксиом?

Слайд 15

ɑ
а
М
Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна

Слайд 16

а
с
ɑ
Теорема 2. Через 2 пересекающиеся прямые проходит плоскость, и притом только одна

Слайд 17

ΙΙΙ. Решение задач на готовом чертеже

Слайд 18

Сколько плоскостей можно провести через выделенные элементы куба? Заштрихуйте соответствующие плоскостям грани куба.

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

Сколько граней проходит через: а) одну, б) две, в) три, г) четыре точки, выделенные на рисунке куба? Сколько плоскостей можно провести через те же точки? Определится ли при этом положение плоскости однозначно? Ответ обоснуйте.

Слайд 25

Слайд 26

Слайд 27

Слайд 28

Слайд 29

Слайд 30

Слайд 31

Ι/. Самостоятельная работа контролирующего характера Оценка «3» – пять любых заданий Оценка «4» – семь любых заданий Оценка «5» – девять любых заданий

Слайд 32

1.Какое из следующих утверждений верно? а) любые четыре точки лежат в одной плоскости; б) любые три точки не лежат в одной плоскости; в) любые четыре точки не лежат в одной плоскости; г) через любые три точки проходит плоскость; д) через любые три точки проходит плоскость, и притом только одна. Д

Слайд 33

2. Сколько общих точек могут иметь две различные плоскости? а) 2; б) 3; в) несколько; г) бесконечно много; д) бесконечно много или ни одной. Д

Слайд 34

3. Точки А, В, С лежат на одной прямой, точка Д не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных плоскостей при этом получилось? а) 2; б) 3; в) 1; г) 4; д) бесконечно много. В

Слайд 35

4. Если три точки не лежат на одной прямой, то положение плоскости в пространстве они: а) не определяют в любом случае; б) определяют, но при дополнительных условиях; в) определяют в любом случае; г) ничего сказать нельзя; д) другой ответ. В

Слайд 36

5. Выберите верное утверждение: а) если одна точка прямой лежит в плоскости, то все точки прямой лежат в этой плоскости; б) через прямую и не лежащую на ней точку проходит плоскость, и притом только одна; в) через две пересекающиеся прямые плоскость провести нельзя; г) любые две плоскости не имеют общих точек; д) если четыре точки не лежат в одной плоскости, то какие-нибудь три из них лежат на одной прямой. Б

Слайд 37

6. Назовите общую прямую плоскостей РВМ и МАВ: а) РМ; б) АВ; в) РВ; г) ВМ; д) определить нельзя. Г
В 1
С 1
В
А 1
Д 1
С
А
Д
Р
7.Какую из перечисленных плоскостей пересекает прямая РМ? а) Д Д 1 С 1 ; б) Д 1 РМ; в) В 1 РМ; г) АВС; д) САД. А
М

Слайд 38

8. Две плоскости пересекаются по прямой с. Точка М лежит только в одной из плоскостей. Что можно сказать о взаимном положении точки М и прямой с? а) никакого вывода нельзя сделать; б) на прямой с лежит точка М; в) через точку М прямая с не проходит; г) другой ответ. Г

Слайд 39

9. Прямые а и в пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и в. Что можно сказать о взаимном положении прямых а, в и с? а) все прямые лежат в разных плоскостях; б) прямые а и в лежат в одной плоскости, а прямая с в ней не лежит; в) все прямые лежат в одной плоскости; г) ничего сказать нельзя; д) прямая с совпадает с одной из прямых: или са, или св. В

Слайд 40

10. Точки А, В, С не лежат на одной прямой. МϵАВ, КϵАС, ХϵМК. Выберите верное утверждение: а) ХϵАВ, б) ХϵАС, в) ХϵАВС; г) точки Х и М совпадают; д) точки Х, К совпадают В

Слайд 41

/. Подведение итогов. 1.Собрать тетради с самостоятельной работой. 2.Оценки за урок. /Ι. Домашнее задание. Постройте изображение тетраэдра (треугольной призмы, четырёхугольной пирамиды, четырёхугольной призмы). Отметьте произвольно точки М, Н, К на рёбрах многогранника. Постройте сечение многогранника плоскостью (МНК).

Слайд 42

Спасибо за урок

Презентация «Решение задач на применение аксиом стереометрии и их следствий» по математике – проект, доклад

Презентацию на тему «Решение задач на применение аксиом стереометрии и их следствий»
можно скачать абсолютно бесплатно на нашем сайте. Предмет
проекта: Математика. Красочные слайды и иллюстрации помогут вам
заинтересовать своих одноклассников или аудиторию.
Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад — нажмите на
соответствующий текст под плеером. Презентация
содержит 9 слайд(ов).

Слайд 1

Урок 3.

Решение задач на применение аксиом стереометрии и их следствий.

Слайд 2

Устная работа. А В С Д А1 В1 С1 Д1 α

Дано: куб АВСДА1В1С1Д1 Найдите: Несколько точек, которые лежат в плоскости α; Несколько точек, которые не лежат в плоскости α; Несколько прямых, которые лежат в плоскости α; Несколько прямых, которые не лежат в плоскости α; Несколько прямых которые пересекают прямую ВС; Несколько прямых, которые не пересекают прямую ВС.

Задача 1.

Слайд 3

Задача 2. М а b c

Заполните пропуски, чтобы получилось верное утверждение:

Слайд 4

Прямые АА1, АВ, АД проходят через точку А, но не лежат в одной плоскости

Лежат ли прямые АА1, АВ, АД в одной плоскости?

Слайд 5

Решите задачи из учебного пособия: стр. 8 № 7, 10, 14.

Работа учащихся на доске и в тетрадях:

Слайд 6

Задача 1 N F К

Дано: куб АВСДА1В1С1Д1 т.М лежит на ребре ВВ1, т.N лежит на ребре СС1 и точка К лежит на ребре ДД1

а) назовите плоскости, в которых лежат точки М; N.

б) найдите т.F-точку пересечения прямых МN и ВС. Каким свойством обладает точка F?

в) найдите точку пересечения прямой КN и плоскости АВС

О

г) найдите линию пересечения плоскостей МNК и АВС

Слайд 7

Повторение.

Формула для вычисления площади четырехугольника.

Слайд 8

Задача 2

Докажите, что все вершины четырехугольника АВСД лежат в одной плоскости, если его диагонали АС и ВД пересекаются. Вычислите площадь четырехугольника, если АС┴ВД, АС = 10см, ВД = 12см.

Доказательство:

1. (АС ∩ ВД) =α АС α, ВД α, (А, В, С, Д ) α

2. SАВСД = АС · ВД · sin90º = 10 · 12 = 120 (см2)

Ответ: 120 см2

Слайд 9

Домашнее задание: Пункты 1-3 прочитать Решить задачи № 9; 13 Дополнительно № 11; 15 ( по желанию)

Calculus — Проблемы с аксиомами

Как прямой ответ, исчисление не имеет присущих себе аксиом . Теоремы исчисления вытекают из аксиом действительной, рациональной, целочисленной и натуральной систем счисления, а также теории множеств.

Большинство дисциплин современной математики демонстрируют такое поведение, при котором дисциплина не имеет присущих самой себе аксиом . Современные математические дисциплины обычно работают в рамках единой аксиоматической системы, наиболее распространенной из которых является теория множеств Цермело-Френкеля с аксиомой выбора (ZFC).ZFC достаточно мощный, чтобы кодировать наши наиболее часто встречающиеся структуры, включая наши различные системы счисления.

Что же тогда изучают различные математические дисциплины, работающие в соответствии с аксиомами ZFC? Ответ — различные структуры , которые могут быть построены с использованием аксиом ZFC. Например, исчисление одной переменной можно (очень) широко охарактеризовать как исследование функций с действительными значениями в реальной области . Такие функции могут быть определены в ZFC, потому что система действительных чисел может быть аксиоматизирована в ZFC.

Аналогичным образом теоретики групп изучают алгебраические структуры, называемые группами, которые определены в ZFC как набор (строительные блоки теории набора Цермело-Френкеля ) и бинарную операцию над набором, которая представляет собой функцию (которая также определяется в ZFC с использованием только наборов ), подчиняющихся определенным свойствам. В некотором смысле можно было бы интерпретировать эти свойства как аксиомы теории групп, но на самом деле они являются просто определениями — лежащие в основе аксиомы — аксиомы ZFC.

Вопрос об истине немного сложнее для понимания, и существует множество различных точек зрения. Вопрос усложняется тем, что можно принять аксиоматическую систему, отличную от ZFC. Если вы примете точку зрения, что истинные предложения — это те, которые могут быть доказаны в вашей любимой аксиоматической системе, то вполне может оказаться, что математик, который верит в ZFC, не согласится с истинностью предложения с математиком, который принимает другую систему. И разные аксиоматические системы не являются странными или неестественными — они действительно составляют один из основных объектов изучения математической логики.

Можно также принять точку зрения, что аксиомы не являются самоочевидными истинами, и поэтому не следует верить или не верить какой-либо конкретной аксиоматической системе. Для многих из этих людей набор аксиом — это список бессмысленных правил, которым нужно следовать, а математика — это игра манипулирования символами в соответствии с этими бессмысленными правилами. (Это формалистическая точка зрения Гильберта.) Истина, таким образом, является бессмысленной концепцией: все предложения являются результатами некоторой игры с некоторыми конкретными правилами.

Есть и другие точки зрения на истину, многие из которых мне неизвестны. Но это должно убедить вас, что концепция «математической истины» более тонкая, чем вы, вероятно, думаете, и действительно варьируется от человека к человеку.

Что касается моего личного мнения: я склоняюсь к формализму, поэтому для меня бессмысленно говорить о том, «дает ли исчисление мне истину». Будучи склонным к анализу и топологии, я рассматриваю исчисление как невероятно важный и полезный инструмент, который согласуется с моим интуитивным пониманием мира, но я рассматриваю лежащие в его основе аксиомы как просто список правил, с которыми мне разрешено играть, независимо от того, Я верю в их «правду».«

справочный запрос — Что такое современная аксиоматизация (евклидовой) плоской геометрии?

Следующая аксиоматизация евклидовой плоскости может быть найдена, начиная со стр. 168 из Элементарная геометрия Агриколы и Фридриха:

Геометрическая плоскость состоит из

• набор $ \ mathcal {P} $, элементы которого мы называем точками,
• набор $ \ mathcal {Z} \ subset \ mathcal {P} \ times \ mathcal {P} \ times \ mathcal {P} $. Если тройка $ (A, B, C) $ точек в $ \ mathcal {P} $ лежит в $ \ mathcal {Z} $, мы будем говорить, что точка $ B $ находится на между точками $ A $ и $ C $.

Такая плоскость удовлетворяет аксиомам:

1. Существуют три различные точки $ A_0, B_0, C_0 \ in \ mathcal {P} $, которые не , а принадлежат отношению промежуточности $ \ mathcal {Z} $ в любом порядке, другими словами $ $ (A_0, B_0, C_0) \ not \ in \ mathcal {Z}, \ quad (A_0, C_0, B_0) \ not \ in \ mathcal {Z}, \ quad (B_0, A_0, C_0) \ not \ in \ mathcal {Z}, \ quad (B_0, C_0, A_0) \ not \ in \ mathcal {Z}, \ quad (C_0, A_0, B_0) \ not \ in \ mathcal {Z}, \ quad (C_0, B_0 , A_0) \ not \ in \ mathcal {Z} $$

2. Если одна из точек $ A, B, C $ лежит между другими, то эти три точки различны.

3. Для двух различных точек $ A $ и $ B $ существует точка $ C $ такая, что $ B $ лежит между $ A $ и $ C $.

4. Если $ B $ находится между $ A $ и $ C $, тогда $ B $ находится между $ C $ и $ A $.

5. Если $ A, B, C $ — три точки в $ \ mathcal {P} $, то не более одной из этих точек находится между двумя другими.

6. Если одна из точек $ A, B, C $ лежит между двумя другими и одна из точек $ A, B, D $ также находится между двумя другими, то одна из точек $ B, C, D $ также находится между двумя другими.

Пусть $ A, B \ in \ mathcal {P} $ — две различные точки. Сегмент $ AB $ состоит из $ A, B $ и всех точек, лежащих между $ A $ и $ B $.

Пусть $ A $ и $ B $ — две разные точки. Линия $ \ mathcal {L} (A, B) $ состоит из $ A $, $ B $ и всех точек $ C $ со свойством, что одна из точек $ A, B, C $ лежит между два других.

Две прямые $ \ mathcal {L} $ и $ \ mathcal {L ‘} $ называются параллелью , если они совпадают или имеют пустое пересечение $ \ mathcal {L} \ cap \ mathcal {L’} = \ emptyset $.

7. Если $ A, B, C $ — три разные точки, не входящие в какое-либо отношение промежуточности, $ S $ — точка отрезка $ AB $, а $ T $ — точка прямой $ \ mathcal { L} (A, C) $, не лежащего в отрезке $ AC $, то прямая $ \ mathcal {L} (S, T) $ содержит хотя бы одну точку отрезка $ BC $.

8. Если $ A, B, C $ — три различные точки, не находящиеся в каком-либо отношении промежуточности, то объединение $$ \ mathcal {P} = \ bigcup_ {S \ in BC} \ mathcal {L} (A , S) \ cup \ bigcup_ {T \ in AC} \ mathcal {L} (B, T) \ cup \ bigcup_ {U \ in AB} \ mathcal {L} (C, U) $$ всех строк, содержащих вершина треугольника $ \ Delta (A, B, C) $ и точка соответствующей противоположной стороны равна всей плоскости $ \ mathcal {P} $.

Мы постулируем новый базовый объект $$ d: \ mathcal {P} \ times \ mathcal {P} \ to [0, \ infty). $$ Число $ d (A, B) $ называется расстоянием от точки $ A $ до точки $ B $ . Расстояние $ d (A, B) = 0 $ обращается в нуль именно тогда, когда точки $ A $ и $ B $ равны. Расстояние, кроме того, должно быть симметричным, $ d (A, B) = d (B, A) $, и удовлетворять неравенству треугольника $$ d (A, B) \ le d (A, C) + d (В, В).

$

9. Точка $ C $ лежит в отрезке $ AB $ тогда и только тогда, когда $$ d (A, B) = d (A, C) + d (C, B).

$

10. Пара $ (\ mathcal {P}, d) $ — полное метрическое пространство; т.е. каждая последовательность Коши в $ \ mathcal {P} $ сходится к точке в $ \ mathcal {P} $.

11. Пусть $ \ mathcal {L} $ и $ \ mathcal {L ‘} $ — две прямые, пересекающие друг друга в точке $ P $. Далее, пусть $ A, A_1 \ in \ mathcal {L} $ и $ B, B_1 \ in \ mathcal {L ‘} $ — две точки на этих прямых, так что $ P $ лежит между $ A $ и $ A_1 $ на $ \ mathcal {L} $ и между $ B $ и $ B_1 $ на $ \ mathcal {L ‘} $. Если $ d (P, A) = d (P, A_1) $ и $ d (P, B) = d (P, B_1) $, то $ d (A, B) = d (A_1, B_1) $.

12. Если $ A, B, C $ — три разные точки, не входящие в какое-либо отношение промежуточности, и если $ A_1, B_1 $ — две другие точки с $ d (A, B) = d (A_1, B_1) $ , то существует точка $ C_1 $ с $ d (A, C) = d (A_1, C_1) $ и $ d (B, C) = d (B_1, C_1) $.

Изометрия геометрической плоскости $ \ mathcal {P} $ — это биективное отображение $ f: \ mathcal {P} \ to \ mathcal {P} $, сохраняющее расстояния; т.е. $ d (f (A), f (B)) = d (A, B) $. Два подмножества $ \ mathcal {P} $ называются конгруэнтными , если существует изометрия, которая биективно отображает эти множества одно на другое.

13. Если $ A, B, C $ и $ A_1, B_1, C_1 $ представляют собой наборы из трех точек $ \ mathcal {P} $ и если $$ d (A, B) = d (A_1, B_1 ), \ quad d (A, C) = d (A_1, C_1), \ quad d (B, C) = d (B_1, C_1), $$, то существует изометрия $ f $ с $ f (A) = A_1, f (B) = B_1 $ и $ f (C) = C_1 $.

Евклидова плоскость — геометрическая плоскость, удовлетворяющая этой следующей аксиоме, называемой постулатом параллельности :

14. Для каждой прямой $ \ mathcal {L} $ и каждой точки $ A $, не лежащей на ней, существует уникальных прямых, параллельных $ \ mathcal {L} $ и проходящих через точку $ A $.

Обратите внимание, что существование такой линии следует из первых 13 аксиом, но уникальность линии должна быть дополнительной аксиомой — например, гиперболическая геометрия удовлетворяет первым 13 аксиомам, но не удовлетворяет параллельному постулат. Первые 13 аксиом необходимо несколько изменить для неевклидовой геометрии (например, сферической геометрии), где существование параллельной линии не гарантируется.

% PDF-1.2
%
2862 0 объект
>
эндобдж
xref
2862 72
0000000016 00000 н.
0000001795 00000 н.
0000001898 00000 н.
0000002989 00000 н.
0000003347 00000 н.
0000003716 00000 н.
0000004011 00000 н.
0000004135 00000 п.
0000005256 00000 н.
0000005385 00000 п.
0000005409 00000 п.
0000005530 00000 н.
0000006838 00000 н.
0000006862 00000 н.
0000008040 00000 н.
0000008064 00000 н.
0000009228 00000 п.
0000009252 00000 н.
0000010401 00000 п.
0000010425 00000 п.
0000011575 00000 п.
0000011599 00000 п.
0000011722 00000 п.
0000012875 00000 п.
0000012899 00000 н.
0000013167 00000 п.
0000013460 00000 п.
0000014619 00000 п.
0000014643 00000 п.
0000014665 00000 п.
0000014687 00000 п.
0000015910 00000 п.
0000015933 00000 п.
0000016509 00000 п.
0000016533 00000 п.
0000018100 00000 п.
0000018124 00000 п.
0000019433 00000 п.
0000019457 00000 п.
0000020921 00000 п.
0000020945 00000 п.
0000022549 00000 п.
0000022573 00000 п.
0000023831 00000 п.
0000023855 00000 п.
0000025977 00000 п.
0000026001 00000 п.
0000031192 00000 п.
0000031216 00000 п.
0000036569 00000 п.
0000036593 00000 п.
0000037946 00000 п.
0000037969 00000 п.
0000038981 00000 п.
0000039005 00000 п.
0000043221 00000 п.
0000043245 00000 п.
0000047406 00000 п.
0000047430 00000 п.
0000051358 00000 п.
0000051382 00000 п.
0000055322 00000 п.
0000055346 00000 п.
0000059936 00000 н.
0000059960 00000 н.
0000062061 00000 п.
0000062084 00000 п.
0000062910 00000 п.
0000062934 00000 п.
0000064825 00000 п.
0000001964 00000 н.
0000002966 00000 н.
трейлер
]
>>
startxref
0
%% EOF

2863 0 объект
>
эндобдж
2864 0 объект
>
эндобдж
2932 0 объект
>
поток
Hc`pc`_Щ

Домашние задания 3

Домашние задания 3

Ответы на домашние задания

( стр.15, Smart, Modern Geometries, 4-е изд. .)

1 . Запишите плоскость, двойственную аксиомам трехточечной геометрии из раздела 1.2

Решение :

1. В этой геометрии существует ровно 3 линии.
2. Две разные линии имеют ровно одну общую точку.
3. Не все линии геометрии проходят через одну и ту же точку.

Упражнения 3–9 относятся к четырехлинейной геометрии .

3 . Какие аксиомы также являются истинными утверждениями в евклидовой геометрии?

Ответ : Нет. Решение : В евклидовой геометрии существует бесконечное количество линий. В евклидовой геометрии существуют параллельные прямые. Каждая точка находится на бесконечном количестве линий евклидовой геометрии.

5 . Лежат ли каждые две точки геометрии на одной общей линии? .

Ans : No. Решение : В этой геометрии 6 точек, и каждая линия имеет 3 точки.Количество пар точек C (6,2) = 15, и каждая линия добавляет 3 пары к этой сумме. Таким образом, на каждую пару точек на l
т.е. на общей линии, а в геометрии всего 4 линии. На рис. 1.6 (стр. 13) точки C и D не лежат на одной прямой.

7 . Сколько других прямых параллельно каждой прямой?

Ответ : Нет. Решение : Согласно Аксиоме 2 любая пара отдельных прямых пересекается, а значит, не параллельна.

9 . Докажите, что набор из двух линий не может содержать все точки геометрии.

Решение : На каждой линии есть три точки. В геометрии шесть точек. Учитывая две различные прямые, они имеют общую точку по аксиоме 2. Таким образом, на любых двух прямых есть только 5 различных точек, поэтому никакие две строки не могут содержать все
точки геометрии.

Упражнения 11-19 относятся к четырехточечной геометрии .

11 . Нарисуйте другую модель для этой геометрии, отличную от показанной на рис. 1.7.

Решение :

13 . Перепишите набор аксиом для этой геометрии, используя дерево для точки и строку для строки .

Решение :

1. Количество деревьев в этой геометрии — четыре.
2. Любые два различных дерева содержатся ровно в одной строке.
3. Каждая строка содержит ровно два дерева.

15 . Если точки — A, B, C, D, назовите все наборы параллельных прямых.

Решение : Так как линия имеет только две точки на ней (аксиома 3), после получения двух точек две другие точки должны образовать линию, параллельную линии, определяемой первыми двумя точками (аксиома 2). Итак, параллельными линиями являются: AB и CD, AC и BD и AD.
и до н.э.

17 . Докажите, не используя идею двойственности, что геометрия включает ровно 6 линий.

Решение : Так как имеется 4 точки, количество пар точек равно C (4,2) = 6. Каждая пара точек определяет уникальную линию (аксиома 2), поэтому имеется не менее 6 линий. Если была другая линия, то по аксиоме 3 она содержит две точки, т. Е. Пару
точек, и у нас уже есть линия, соединяющая эту пару точек. Согласно аксиоме 2, не может быть двух прямых через две точки, поэтому имеется ровно 6 прямых.

19 . Докажите, что существует набор из двух прямых, содержащий все точки геометрии.

Решение : любая линия содержит две точки (аксиома 3), назовите их A и B. Две другие точки (так как их всего 4 — аксиома 1) будут называться C и D. Есть строка, содержащая C и D (аксиома 2). Эта строка и первая строка содержат
n все точки геометрии.

% PDF-1.4
%
7 0 объект
>
эндобдж
10 0 obj
(Передний вопрос)
эндобдж
11 0 объект
>
эндобдж
14 0 объект
(PG Boilerplate)
эндобдж
15 0 объект
>
эндобдж
18 0 объект
(Биографический очерк: Кавальери)
эндобдж
19 0 объект
>
эндобдж
22 0 объект
(Примечание транскрибера)
эндобдж
23 0 объект
>
эндобдж
26 0 объект
(Предисловие)
эндобдж
27 0 объект
>
эндобдж
30 0 объект
(Оглавление)
эндобдж
31 0 объект
>
эндобдж
34 0 объект
(Вступление)
эндобдж
35 0 объект
>
эндобдж
38 0 объект
(Космические концепции)
эндобдж
39 0 объект
>
эндобдж
42 0 объект
(Аксиомы и теоремы из плоской геометрии)
эндобдж
43 0 объект
>
эндобдж
46 0 объект
(Свойства плоскости)
эндобдж
47 0 объект
>
эндобдж
50 0 объект
(Перпендикулярные плоскости и линии)
эндобдж
51 0 объект
>
эндобдж
54 0 объект
(Параллельные плоскости и линии)
эндобдж
55 0 объект
>
эндобдж
58 0 объект
(Двугранные углы)
эндобдж
59 0 объект
>
эндобдж
62 0 объект
(Конструкции из плоскостей и линий)
эндобдж
63 0 объект
>
эндобдж
66 0 объект
(Многогранные углы)
эндобдж
67 0 объект
>
эндобдж
70 0 объект
(Биографический очерк: Фалес)
эндобдж
71 0 объект
>
эндобдж
74 0 объект
(Правильные многогранники)
эндобдж
75 0 объект
>
эндобдж
78 0 объект
(Построение правильных многогранников)
эндобдж
79 0 объект
>
эндобдж
82 0 объект
(Призмы и цилиндры)
эндобдж
83 0 объект
>
эндобдж
86 0 объект
(Свойства призм)
эндобдж
87 0 объект
>
эндобдж
90 0 объект
(Свойства цилиндров)
эндобдж
91 0 объект
>
эндобдж
94 0 объект
(Пирамиды и конусы)
эндобдж
95 0 объект
>
эндобдж
98 0 объект
(Свойства пирамид)
эндобдж
99 0 объект
>
эндобдж
102 0 объект
(Свойства шишек)
эндобдж
103 0 объект
>
эндобдж
106 0 объект
(Биографический очерк: Архимед)
эндобдж
107 0 объект
>
эндобдж
110 0 объект
(Сфера)
эндобдж
111 0 объект
>
эндобдж
114 0 объект
(Сферические углы и треугольники)
эндобдж
115 0 объект
>
эндобдж
118 0 объект
(Площадь сферы)
эндобдж
119 0 объект
>
эндобдж
122 0 объект
(Объем сферы)
эндобдж
123 0 объект
>
эндобдж
126 0 объект
(Биографический очерк: Лежандр)
эндобдж
127 0 объект
>
эндобдж
130 0 объект
(Приложение I)
эндобдж
131 0 объект
>
эндобдж
134 0 объект
(Подобные твердые тела)
эндобдж
135 0 объект
>
эндобдж
138 0 объект
(Приложение II)
эндобдж
139 0 объект
>
эндобдж
142 0 объект
(Приложения проекции)
эндобдж
143 0 объект
>
эндобдж
146 0 объект
(Приложение III)
эндобдж
147 0 объект
>
эндобдж
150 0 объект
(Теория пределов)
эндобдж
151 0 объект
>
эндобдж
154 0 объект
(Индекс)
эндобдж
155 0 объект
>
эндобдж
158 0 объект
(Back Matter)
эндобдж
159 0 объект
>
эндобдж
162 0 объект
(Заметки транскрибера)
эндобдж
163 0 объект
>
эндобдж
166 0 объект
(Лицензия PG)
эндобдж
167 0 объект
>
эндобдж
170 0 obj>
поток
х ڝ Tr0ʀ
@h !! [[WVP: I + j [+ \ Qȵ | ۙ + zBlϚbE ܍2
ܡ Vf3.