Стереометрические задачи: Zadachi po stereometrii. — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

ЕГЭ. Задание 14. Стереометрия — Сайт Трушина Б.В.

Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по стереометрии, видеоразборы задач и подборка заданий прошлых лет.

Полезные материалы

Подборки видео и онлайн-курсы

Как решать стереометрию

Теорема о трёх перпендикулярах

Как найти объем. Принцип Кавальери

Видеоразборы задач

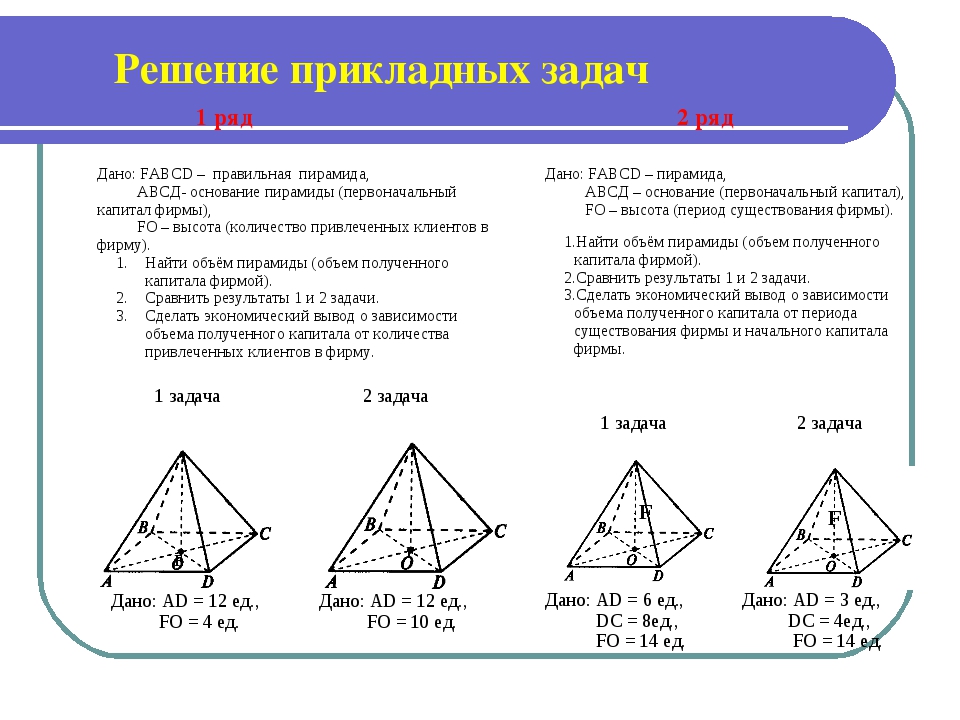
В треугольной пирамиде $SABC$ $SB=SC=AC=AB=\sqrt{17}$, $SA= BC = 2\sqrt5$.

а) Докажите, что прямые $BC$ и $SA$ перпендикулярны.

б) Найдите расстояние между прямыми $BC$ и $SA$.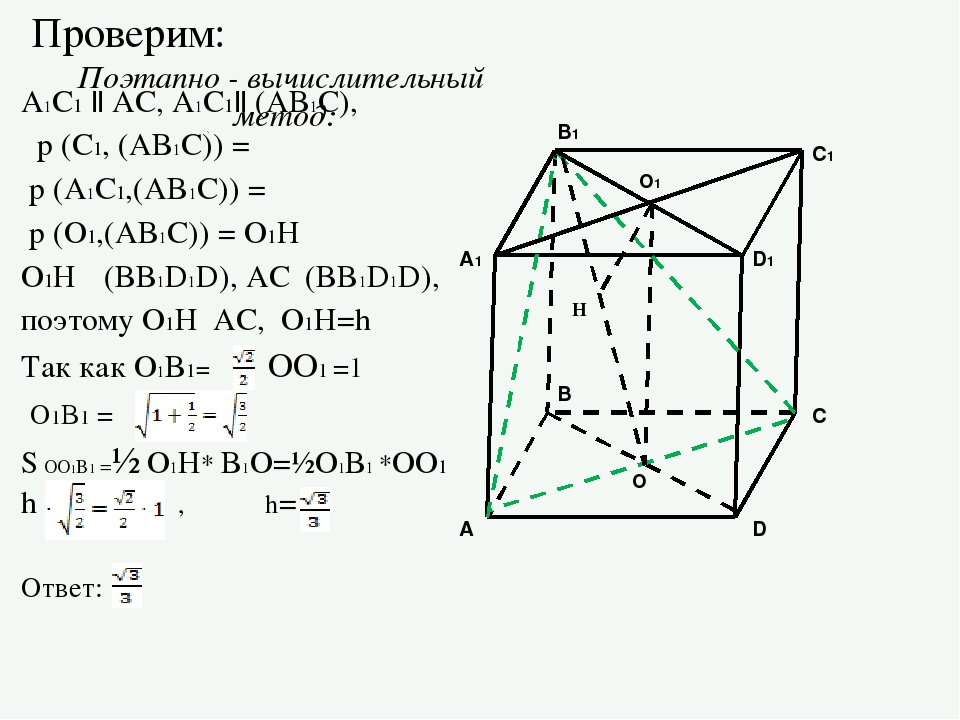

В прямом круговом конусе с вершиной $S$ и центром основания $O$ радиус основания равен 13, а высота равна $3\sqrt{41}$. Точки $A$ и $B$ — концы образующих, $M$ — середина $SA$, $N$ — точка в плоскости основания такая, что прямая $MN$ параллельна прямой $SB$.

а) Докажите что угол $ANO$ — прямой.

б) Найдите угол между $MB$ и плоскостью основания, если дополнительно известно что $AB = 10$.

В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны 2. Точка $M$ — середина ребра $AA_1$.

а) Докажите, что прямые $MB$ и $B_1C$ перпендикулярны.

б) Найдите расстояние между прямыми $MB$ и $B_1C$.

На окружности одного из оснований прямого кругового цилиндра выбраны точки $A$ и $B$, а на окружности другого основания — точки $B_1$ и $C_1$, причём $BB_1$ — образующая цилиндра, а отрезок $AC_1$ пересекает ось цилиндра.

а) Докажите, что угол $C_1BA$ прямой.

б) Найдите расстояние от точки $B$ до прямой $AC_1$, если $AB=12$, $BB_1=4$ и $B_1C_1 = 3$.

Дана правильная четырехугольная призма $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $K$ так, что $AK : KA_1 = 1 : 2$. Плоскость $\alpha$ проходит через точки $B$ и $K$ параллельно прямой $AC$. Эта плоскость пересекает ребро $DD_1$ в точке $M$.

а) Докажите, что $DM : MD_1 = 2 : 1$.

б) Найдите площадь сечения, если $AB = 4$, $AA_1 = 6$.

Длина диагонали куба $ABCDA_1B_1C_1D_1$ равна 3. На луче $A_1C$ отмечена точка $P$ так, что $A_1P = 4$.

a) Докажите, что грань $PBDC_1$ — правильный тетраэдр.

б) Найдите длину отрезка $AP$.

Сечением прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$ плоскостью $\alpha$, содержащей прямую $BD_1$ и параллельной прямой $AC$, является ромб.

a) Докажите, что грань $ABCD$ — квадрат.

б) Найдите угол между плоскостями $\alpha$ и $BCC_1$, если $AA_1 = 6$, $AB = 4$.

В правильной треугольной призме $ABCA_1B_1C_1$ сторона основания $AB$ равна 6, а боковое ребро $AA_1$ равно 3. На ребре $AB$ отмечена точка $K$ так, что $AK = 1$. Точки $M$ и $L$ — середины ребер $A_1C_1$ и $B_1C_1$ соответственно. Плоскость $\gamma$ параллельна прямой $AC$ и содержит точки $K$ и $L$.

а) Докажите, что прямая $BM$ перпендикулярна плоскости $\gamma$;

б) Найдите расстояние от точки $C$ до плоскости $\gamma$.

Подборка заданий прошлых лет

В прямом круговом конусе с вершиной $S$ и центром основания $O$ радиус основания равен 13, а высота равна $3\sqrt{41}$. Точки $A$ и $B$ — концы образующих, $M$ — середина $SA$, $N$ — точка в плоскости основания такая, что прямая $MN$ параллельна прямой $SB$.

а) Докажите что угол $ANO$ — прямой.

б) Найдите угол между $MB$ и плоскостью основания, если дополнительно известно что $AB = 10$.

(ЕГЭ-2019, досрочная волна, резервный день)

В треугольной пирамиде $SABC$ $SB=SC=AC=AB=\sqrt{17}$, $SA= BC = 2\sqrt5$.

а) Докажите, что прямые $BC$ и $SA$ перпендикулярны.

б) Найдите расстояние между прямыми $BC$ и $SA$.

(ЕГЭ-2019, досрочная волна)

В треугольной пирамиде $SABC$ $SB=SC=\sqrt{17}$, $AB=AC=\sqrt{29}$, $SA= BC = 2\sqrt5$.

а) Докажите, что прямые $BC$ и $SA$ перпендикулярны.

б) Найдите угол между прямой $SA$ и плоскостью $SBC$.

(ЕГЭ-2019, досрочная волна)

Дана правильная четырехугольная призма $ABCDA_1B_1C_1D_1$. На ребре $AA_1$ отмечена точка $K$ так, что $AK : KA_1 = 1 : 2$. Плоскость $\alpha$ проходит через точки $B$ и $K$ параллельно прямой $AC$. Эта плоскость пересекает ребро $DD_1$ в точке $M$.

а) Докажите, что $DM : MD_1 = 2 : 1$.

б) Найдите площадь сечения, если $AB = 4$, $AA_1 = 6$.

(ЕГЭ-2018, досрочная волна)

В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны~2. Точка $M$ — середина ребра $AA_1$.

а) Докажите, что прямые $MB$ и $B_1C$ перпендикулярны.

б) Найдите расстояние между прямыми $MB$ и $B_1C$.

(ЕГЭ-2018, досрочная волна, резервный день)

На окружности одного из оснований прямого кругового цилиндра выбраны точки $A$ и $B$, а на окружности другого основания — точки $B_1$ и $C_1$, причём $BB_1$ — образующая цилиндра, а отрезок $AC_1$ пересекает ось цилиндра.

а) Докажите, что угол $C_1BA$ прямой.

б) Найдите расстояние от точки $B$ до прямой $AC_1$, если $AB=12$, $BB_1=4$ и $B_1C_1 = 3$.

(ЕГЭ-2018, основная волна)

На окружности одного из оснований прямого кругового цилиндра выбраны точки $A$ и $B$, а на окружности другого основания — точки $B_1$ и $C_1$, причём $BB_1$ — образующая цилиндра, а отрезок $AC_1$ пересекает ось цилиндра. {\circ}$.

б) Найдите расстояние между прямыми $AC$ и $BC_1$.

(ЕГЭ-2018, основная волна)

На ребре $AB$ правильной четырёхугольной пирамиды $SABCD$ с основанием $ABCD$ отмечена точка $Q$, причём $AQ:OB=1:2$. Точка $P$ — середина ребра $AS$.

а) Докажите, что плоскость $DPQ$ перпендикулярна плоскости основания пирамиды.

б) Найдите площадь сечения $DPQ$, если площадь сечения $DSB$ равна 6.

(ЕГЭ-2018, основная волна, резервный день)

В правильном тетраэдре $ABCD$ точка $H$ — центр грани $ABC$, а точка $M$ — середина ребра $CD$.

а) Докажите, что прямые $AB$ и $CD$ перпендикулярны.

б) Найдите угол между прямыми $DH$ и $BM$.

(ЕГЭ-2018, основная волна, резервный день)

Основанием прямой четырехугольной призмы $ABCDA_1B_1C_1D_1$ является ромб $ABCD$, $AB = AA_1$.

а) Докажите, что прямые $A_1C$ и $BD$ перпендикулярны.

б) Найдите объем призмы, если $A_1C = BD = 2$.

(ЕГЭ-2017, основная волна, резервный день)

В правильной четырехугольной пирамиде $SABCD$ все ребра равны 5. На ребрах $SA$, $AB$, $BC$ взяты точки $P$, $Q$, $R$ соответственно так, что $PA = AQ = RC = 2$.

а) Докажите, что плоскость $PQR$ перпендикулярна ребру $SD$.

б) Найдите расстояние от вершины $D$ до плоскости $PQR$.

(ЕГЭ-2017, основная волна, резервный день)

В треугольной пирамиде $PABC$ с основанием $ABC$ известно, что $AB = 17$, $PB = 10$, $\cos \angle PBA = \dfrac{32}{85}$. Основанием высоты этой пирамиды является точка $C$. Прямые $PA$ и $BC$ перпендикулярны.

а) Докажите, что треугольник $ABC$ прямоугольный.

б) Найдите объем пирамиды $PABC$.

(ЕГЭ-2017, основная волна, резервный день)

Ребро куба $ABCDA_1B_1C_1D_1$ равно 6. Точки $K$, $L$ и $M$ — центры граней $ABCD$, $AA_1D_1D$ и $CC_1D_1D$ соответственно.

а) Докажите, что $B_1KLM$ — правильная пирамида.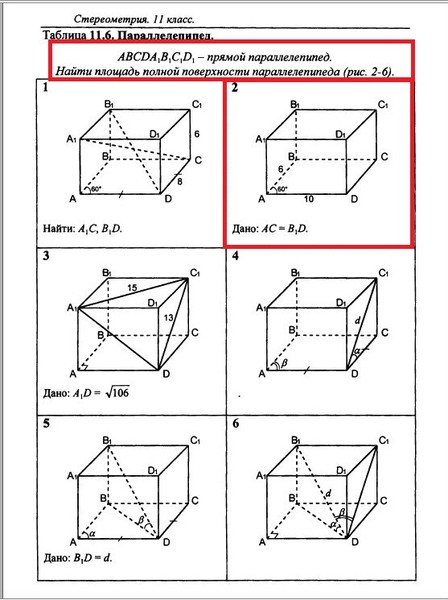

б) Найдите объём $B_1KLM$.

(ЕГЭ-2017, основная волна)

В треугольной пирамиде $SABC$ известны боковые рёбра: $SA = SB = 7$, $CS = 5$. Основанием высоты этой пирамиды является середина медианы $CM$ треугольника $ABC$. Эта высота равна 4.

а) Докажите, что треугольник $ABC$ равнобедренный.

б) Найдите объём пирамиды $SABC$.

(ЕГЭ-2017, основная волна)

Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Диагонали боковых граней $AA_1B_1B$ и $BB_1C_1C$ равны 15 и 9 соответственно, $AB = 13$.

а) Докажите, что треугольник $BA_1C_1$ прямоугольный.

б) Найдите объём пирамиды $AA_1C_1B$.

(ЕГЭ-2017, основная волна)

Основанием прямой треугольной призмы $ABCA_1B_1C_1$ является прямоугольный треугольник $ABC$ с прямым углом $C$. Прямые $CA_1$ и $AB_1$ перпендикулярны.

а) Докажите, что $AA_1 = AC$.

б) Найдите расстояние между прямыми $CA_1$ и $AB_1$, если $AC = 6$, $BC = 3$.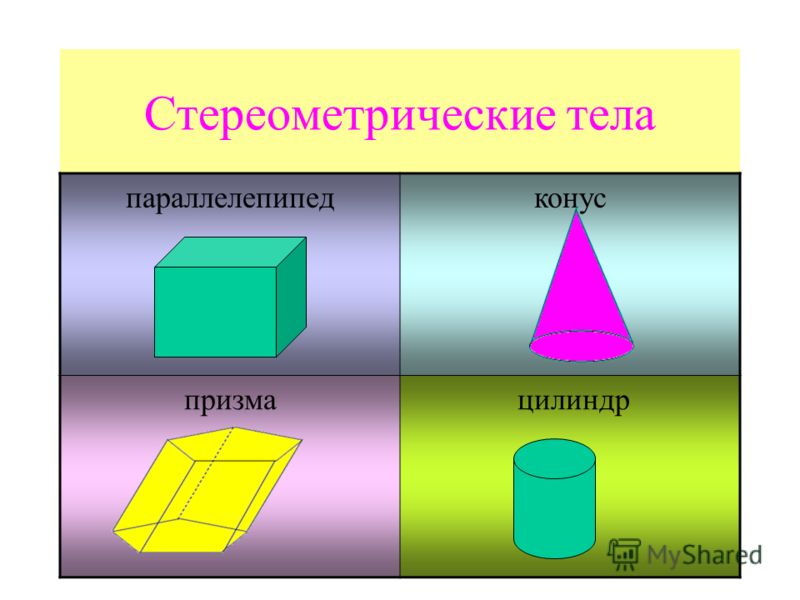

(ЕГЭ-2017, основная волна)

На ребрах $AB$ и $BC$ треугольной пирамиды $ABCD$ отмечены точки $M$ и $N$ соответственно, причём $AM:MB = CN:NB = 1:3$. Точки $P$ и $Q$ — середины сторон $DA$ и $DC$ соответственно.

а) Доказать, что $P$, $Q$, $M$ и $N$ лежат в одной плоскости.

б) Найти отношение объемов многогранников, на которые плоскость $PQM$ разбивает пирамиду.

(ЕГЭ-2017, основная волна)

Сечением прямоугольного параллелепипеда $ABCDA_1B_1C_1D_1$ плоскостью $\alpha$ содержащей прямую $BD_1$ и параллельной прямой $AC$, является ромб.

а) Докажите, что грань $ABCD$ — квадрат.

б) Найдите угол между плоскостями $\alpha$ и $BCC_1$, если $AA_1 = 6$, $AB = 4$.

(ЕГЭ-2017, досрочная волна)

В правильной треугольной призме $ABCA_1B_1C_1$ сторона $AB$ основания равна 12, а высота призмы равна 2. На рёбрах $B_1C_1$ и $AB$ отмечены точки $P$ и $Q$ соответственно, причём $PC_1 = 3$, а $AQ = 4$. Плоскость $A_1PQ$ пересекает ребро $BC$ в точке $M$.

а) Докажите, что точка $M$ является серединой ребра $BC$.

б) Найдите расстояние от точки $B$ до плоскости $A_1PQ$.

(ЕГЭ-2016, основная волна)

На рёбрах $DD_1$ и $BB_1$ куба $ABCDA_1B_1C_1D_1$ с ребром 12 отмечены точки $P$ и $Q$ соответственно, причём $DP = 10$, а $B_1Q = 4$. Плоскость $A_1PQ$ пересекает ребро $CC_1$ в точке $M$.

а) Докажите, что точка $M$ является серединой ребра $CC_1$.

б) Найдите расстояние от точки $C_1$ до плоскости $A_1PQ$.

(ЕГЭ-2016, основная волна)

В правильной четырёхугольной пирамиде $SABCD$ сторона $AB$ основания равна $2\sqrt{3}$, а высота $SH$ пирамиды равна 3. Точки $M$ и $N$ — середины рёбер $CD$ и $AB$, соответственно, а $NT$ — высота пирамиды $NSCD$ с вершиной $N$ и основанием $SCD$.

а) Докажите, что точка $T$ является серединой $SM$.

б) Найдите расстояние между $NT$ и $SC$.

(ЕГЭ-2016, основная волна)

В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона $AB$ основания равна 6, а боковое ребро $AA_1$ равно $3\sqrt2$. 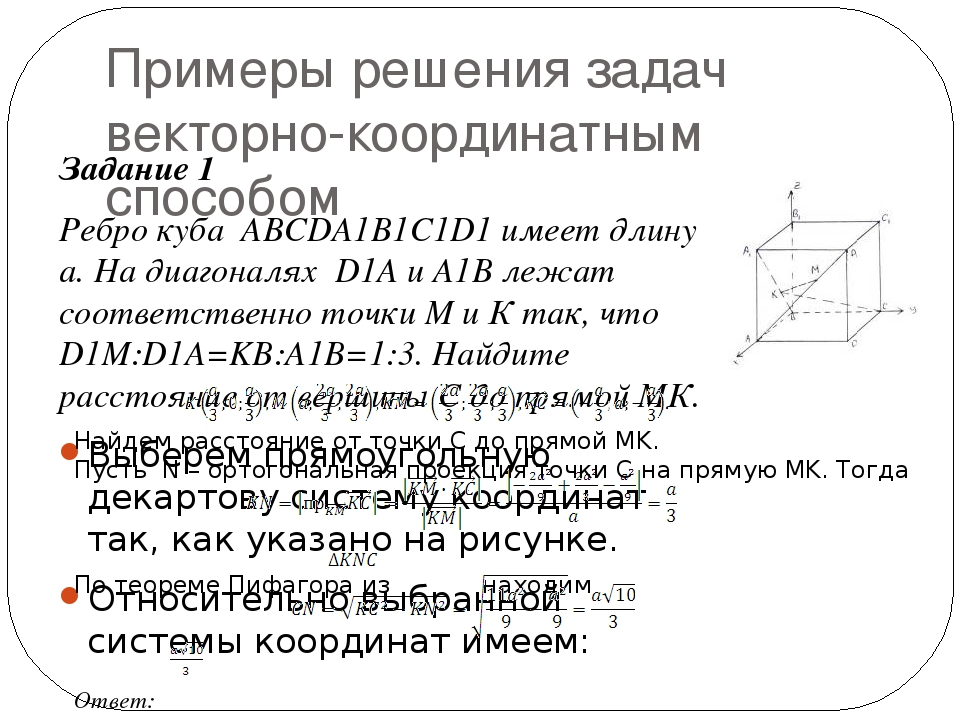На ребрах $BC$ и $C_1D_1$ отмечены точки $K$ и $L$ соответственно, причём $BK = 4$, $C_1L = 5$. Плоскость $\gamma$ параллельна прямой $BD$ и содержит точки $K$ и $L$.

а) Докажите, что прямая $AC_1$ перпендикулярна плоскости $\gamma$;

б) Найдите расстояние от точки $B_1$ до плоскости $\gamma$.

(ЕГЭ-2016, основная волна)

В правильной четырёхугольной пирамиде $SABCD$ сторона $AB$ основания равна 16, а высота пирамиды равна 4. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $M$, $N$ и $K$ соответственно, причём $AM = DN = 4$ и $AK = 3$.

а) Докажите, что плоскости $MNK$ и $SBC$ параллельны.

б) Найдите расстояние от точки $M$ до плоскости $SBC$.

(ЕГЭ-2016, основная волна)

В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны 8. На рёбрах $AA_1$ и $CC_1$ отмечены точки $M$ и $N$ соответственно, причём $AM = 3$, $CN = 1$.

а) Докажите, что плоскость $MNB_1$ разбивает призму на два многогранника, объёмы которых равны.

б) Найдите объём тетраэдра $MNBB_1$.

(ЕГЭ-2016, досрочная волна)

В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона $AB$ основания равна 6, а боковое ребро $AA_1$ равно $3\sqrt2$. На ребрах $BC$ и $C_1D_1$ отмечены точки $K$ и $L$ соответственно, причём $BK = 4$, $C_1L = 5$. Плоскость $\gamma$ параллельна прямой $BD$ и содержит точки $K$ и $L$.

а) Докажите, что прямая $AC_1$ перпендикулярна плоскости $\gamma$;

б) Найдите расстояние от точки $B_1$ до плоскости $\gamma$.

(ЕГЭ-2016, основная волна)

В правильной четырёхугольной пирамиде $SABCD$ сторона $AB$ основания равна 16, а высота пирамиды равна 4. На рёбрах $AB$, $CD$ и $AS$ отмечены точки $M$, $N$ и $K$ соответственно, причём $AM = DN = 4$ и $AK = 3$.

а) Докажите, что плоскости $MNK$ и $SBC$ параллельны.

б) Найдите расстояние от точки $M$ до плоскости $SBC$.

(ЕГЭ-2016, основная волна)

В правильной треугольной призме $ABCA_1B_1C_1$ все рёбра равны 8. На рёбрах $AA_1$ и $CC_1$ отмечены точки $M$ и $N$ соответственно, причём $AM = 3$, $CN = 1$.

а) Докажите, что плоскость $MNB_1$ разбивает призму на два многогранника, объёмы которых равны.

б) Найдите объём тетраэдра $MNBB_1$.

(ЕГЭ-2016, досрочная волна)

Дана правильная треугольная призма $ABCA_1B_1C_1$, все рёбра которой равны 6. Через точки $A$, $C_1$ и середину $T$ ребра $A_1B_1$ проведена плоскость.

а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.

б) Найдите угол между плоскостью сечения и плоскостью $ABC$.

(ЕГЭ-2016, досрочная волна)

В правильной четырёхугольной призме $ABCDA_1B_1C_1D_1$ сторона основания $AB = 6$, а боковое ребро $AA_1 = 4\sqrt3$. На рёбрах $AB$, $A_1D_1$ и $C_1D_1$ отмечены точки $M$, $N$ и $K$ соответственно, причём $AM = A_1N = C_1K = 1$.

а) Пусть $L$ — точка пересечения плоскости $MNK$ с ребром $BC$. Докажите, что $MNKL$ — квадрат.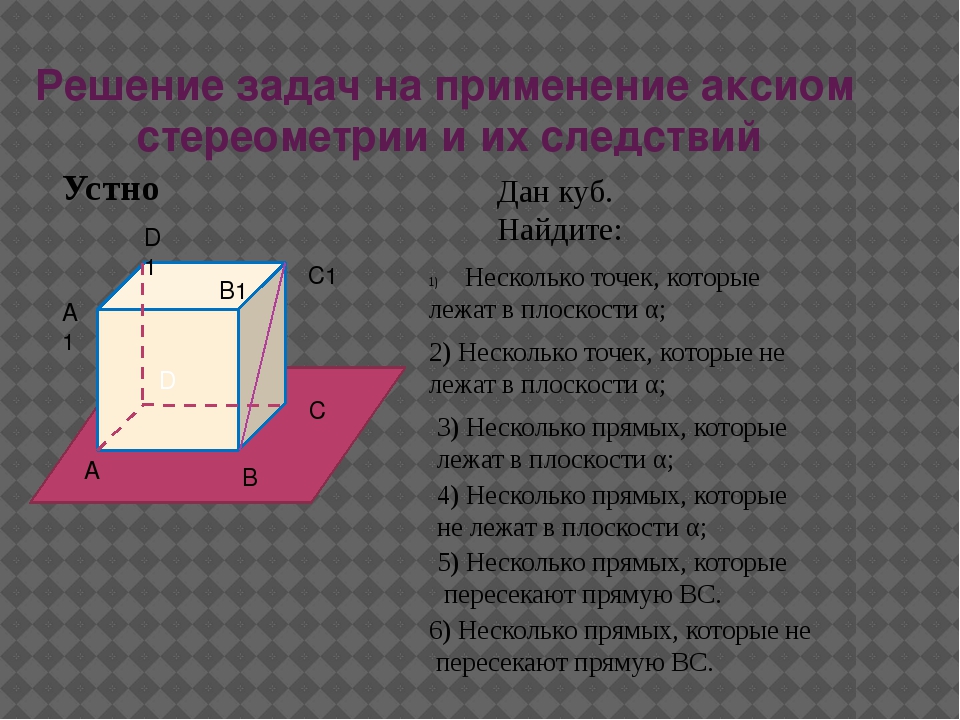

б) Найдите площадь сечения призмы плоскостью $MNK$.

(ЕГЭ-2016, досрочная волна)

В правильной треугольной пирамиде $SABC$ сторона основания $AB$ равна 24, а боковое ребро $SA$ равно 19. Точки $M$ и $N$ — середины рёбер $SA$ и $SB$ соответственно. Плоскость $\alpha$ содержит прямую $MN$ и перпендикулярна плоскости основания пирамиды.

а) Докажите, что плоскость $\alpha$ делит медиану $CE$ основания в отношении $5 : 1$, считая от точки $C$.

б) Найдите площадь многоугольника, являющегося сечением пирамиды $SABC$ плоскостью $\alpha$.

(ЕГЭ-2015, основная волна)

В кубе $ABCDA_1B_1C_1D_1$ все рёбра равны 4. На его ребре $BB_1$ отмечена точка $K$ так, что $KB = 3$. Через точки $K$ и $C_1$ проведена плоскость $\alpha$, параллельная прямой $BD_1$.

а) Докажите, что $A_1P: PB_1 = 2:1$, где $P$ — точка пересечения плоскости $\alpha$ с ребром $A_1B_1$.

б) Найдите угол наклона плоскости $\alpha$ к плоскости грани $BB_1C_1C$.

(ЕГЭ-2015, досрочная волна)

Задачи по стереометрии

Задачи по стереометрии. Друзья! В предыдущей статье были представлены основные формулы, которые необходимы для решения задач по стереометрии на экзамене по математике, и не только. Эти формулы знать НЕОБХОДИМО! Если вас интересует какая либо задача — вы можете ввести начало условия в строку ПОИСКА на карте блога или пройтись по рубрикам «СТЕРЕОМЕРИЯ». В этой публикации некоторые теоретические факты.

По ходу учебного процесса, при систематическом решении задач, все они запоминаются и откладываются в памяти крепко и надолго. Учите их, практикуйтесь в решении задач, они запомнятся, ни куда не денутся ;). К домашнему заданию добавляйте ещё пару задач самостоятельно. Понимаю, что никому не хочется создавать себе дополнительную работу, но ваш результат на будущем ЕГЭ целиком зависит только от вас.

В этой статье хочу напомнить вам некоторые моменты, которые необходимы для решения ряда задач по стереометрии.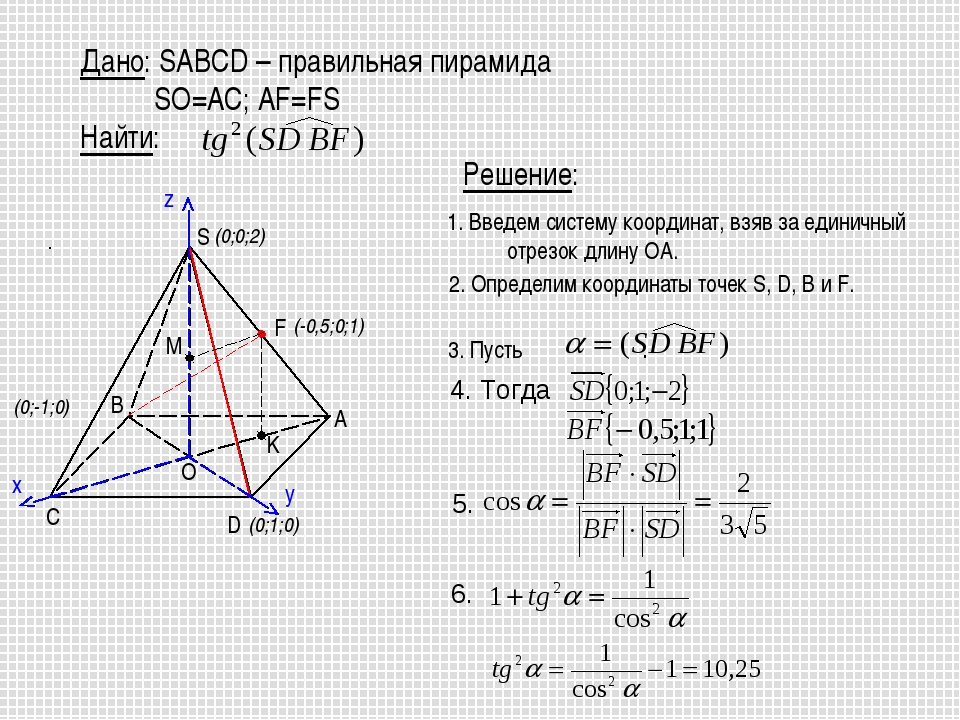 В этих примерах речь идёт о площади поверхности тел и объёме (относится к призме, параллелепипедам и другим телам). Данные факты используются во многих типах заданий. Уверен, представленная ниже информация вам известна, но всё же…

Не буду их здесь делить на теоремы, свойства, следствия и объяснять что из чего исходит. Предлагаю вам освежить их в памяти и запомнить именно как факты.

Немало задач, где при решении необходимо помнить, что:

1. У прямоугольного треугольника вписанного в окружность гипотенуза совпадает с диаметром. Центр этой окружности совпадает с серединой гипотенузы.

Если в окружность вписан треугольник и одна его сторона совпадает с диаметром этой окружности, то треугольник является прямоугольным.

То есть, если мы на диаметре окружности построим треугольник, вершина которого будет лежать на любой точке окружности, то такой треугольник будет являться прямоугольным.

2. Во многих типах задач часто говорится об отрезке, который соединяет середины двух соседних сторон треугольника. Понятно, что речь идёт о средней линии треугольника. Что мы о ней знаем?

Средняя линия треугольника – это отрезок, концы которого лежат на серединах двух соседних сторон данного треугольника, она параллельна третьей стороне и равна её половине

Что нам это даёт?

— Она отсекает от исходного треугольника подобный ему.

— Коэффициент подобия равен k = 0,5. Так как стороны отсечённого треугольника равны половине сторон исходного.

— Все линейные элементы отсечённого треугольника равны половине соответствующих им элементам исходного (стороны, высоты, медианы, биссектрисы, а также периметр треугольника).

— Площадь отсечённого треугольника равна одной четвёртой площади исходного треугольника. Это подтверждается формулой взаимосвязи площадей подобных фигур:

*А также равенством треугольников, посмотрите рисунок:

AD = DB, BE = EC, AF = FC, DE = AF, EF = AD, DF= EC

Треугольники равны по третьему признаку (по трём сторонам). Хотя и остальные признаки равенства треугольников также применимы.

4. Есть не мало задач, где речь идёт об изменения объёма (пирамиды, куба, параллелепипеда, шара), путём увеличения или уменьшения рёбер (радиуса) в определённое количество раз. То есть речь идёт о подобных телах. Помните о том, что есть формула, которая связывает объёмы подобных тел:

Пример подобных тел:

*Ещё пример: плоскость параллельная основанию конуса и проходящая перпендикулярно его высоте отсекает конус подобный исходному

5. Кроме того, есть много задач, в которых фигурируют правильные пирамиды. Напомню, что это пирамиды в основании которых лежит правильный многоугольник (в наших задачах – правильный треугольник, квадрат, правильный шестиугольник). Что необходимо запомнить здесь?

Высота опущенная из вершины к основанию пирамиды проходит через середину этого основания

или

Отрезок соединяющий вершину правильной пирамиды и середину её основания является высотой пирамиды

6. Есть группа задач, где речь идёт о правильной шестиугольной призме (в основании лежит правильный шестиугольник). Условия и вопросы различные, но знание следующих фактов о правильном шестиугольнике считаю необходимым:

1. Стороны правильного шестиугольника равны.

2. Углы при вершинах равны 120 градусам.

3. Около правильного шестиугольника можно описать окружность.

4. Радиус окружности описанной около правильного шестиугольника равен сторонам этого шестиугольника.

5. Расстояние между двумя диаметрально противоположными вершинами (это диаметр описанной окружности) равно двум сторонам этого шестиугольника.

*Правильный шестиугольник как бы состоит из шести сложенных друг с другом равносторонних треугольников.

Ещё стоит отметить некоторые моменты. Их нетрудно вывести, но предлагаю запомнить их и положить в копилку ваших математических навыков. Простыми словами можно сказать так:

Отрезок соединяющий две вершины правильного шестиугольника (при чём этот отрезок не проходит через центр), отсекает треугольник площадь которого равна одной шестой площади данного шестиугольника

Нетрудно сделать и следующие выводы:

Я не говорю о том, что если вы не запомните представленную информацию, то задачи вам этой группы не решить. Нет! При наличии хорошей математической базы, и владения навыками решения стереометрических и планиметрических задач проблем при решении не будет никаких. Вы с лёгкостью вспомните теорию и быстро сделаете необходимые выводы. Но помня указанные выше моменты, вы сэкономите время и проведёте решение в два раза быстрее.

Отмечу, что для решения ряда задач, связанных с увеличением (уменьшением) ребра в параллелепипеде, пирамиде, кубе, либо радиуса конуса или шара, и стоит вопрос об изменении объёма, существует более рациональный метод, чем тот который используется при обучении в школьной программе. Мы с вами его изучим. Вы удивитесь простоте подхода, задачи решаются практически в одну строчку, не пропустите!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Две интересные стереометрические задачи

В этой статье я привела решения двух задач по стереометрии. Задачи принес ученик, поэтому источника не знаю.

Задача 1. Дана треугольная пирамида с основанием , в которой , , . Расстояния от точки до , и одинаково и равно 5. Найти радиус вписанной в эту пирамиду сферы.

Решение. Воспользуемся довольно редко используемым, но очень полезным соотношением:

Где – радиус вписанной сферы, – объем пирамиды, – аолная площадь поверхности пирамиды.

Начнем с полной поверхности пирамиды. Расстояния от точки до , и – не что иное, как длина апофем. Поэтому площадь боковой поверхности пирамиды

Площадь основания определим по формуле Герона:

Полная площадь поверхности пирамиды равна

Так как апофемы одинаковы, то центр пирамиды проецируется в центр вписанной в основание пирамиды окружности (треугольники , , равны по гипотенузе и катету). Радиус этой вписанной окружности

Рисунок к первой задаче

Таким образом, высота пирамиды может быть найдена как

Определяем объем пирамиды:

И, наконец, можем найти радиус вписанной сферы:

Ответ: .

Задача 2. В правильной четырехугольной пирамиде центр вписанной в нее сферы делит высоту в отношении , считая от вершины. Найти угол между боковыми гранями.

Рисунок ко второй задаче

Решение. Если сфера вписана в пирамиду, то она касается всех ее граней. Рассмотрим осевое сечение пирамиды.

Осевое сечение

Треугольники и подобны. Пусть сторона основания пирамиды , высота – . Тогда ,

Для указанных подобных треугольников составим отношение сходственных сторон:

Перепишем с четом :

Теперь поработаем с этим равенством, выразим из него высоту пирамиды.

Определим площадь боковой грани, например, .

Теперь, чтобы найти угол между гранями – угол – рассмотрим треугольник . Нам понадобится рассчитать его по теореме косинусов, а для этого надо знать его сторону . – высота, проведенная в грани к . Найдем ее через площадь боковой грани, которую мы нашли ранее. В треугольнике :

Теперь определим :

Наконец, для расчета собственно угла применяем к треугольнику теорему косинусов:

Ответ:

Решение задач по стереометрии. Практикум. Подготовка к ЕГЭ., Потоскуев Е.В. | ISBN: 978-5-89237-352-4

Потоскуев Е.В.

есть в наличии

Аннотация

Отличительная особенность геометрии состоит в том, что при ее изучении неразрывно связаны два взаимоисключающих элемента познания истины: наглядность и воображение, с одной стороны, и строгая логика рассуждений, с другой. В этой связи, в пособии большое внимание уделено как вопросам верного и наглядного изображения пространственных фигур на плоскости, так и методике выработки умений корректно аргументировать утверждения, возникающие по ходу решения любой геометрической задачи.Рассматривается решение задач на построение сечений многогранников различными способами, при этом проиллюстрирована динамика построения сечения, процесс его «рождения».Используя изображения правильного тетраэдра, куба и правильной шестиугольной призмы, предлагаются методические рекомендации решения опорных задач метрической стереометрии о нахождении расстояний и углов между прямыми и плоскостями. Задачи подобраны по принципу: «от простого — к сложному», что позволяет методически обоснованно реализовывать принцип дифференциации обучения геометрии.Пособие адресовано учителям математики и учащимся школ, лицеев, гимназий, колледжей.

Дополнительная информация

Регион (Город/Страна где издана):	Москва
Год публикации:	2012
Тираж:	2000
Страниц:	108
Ширина издания:	150
Высота издания:	220
Вес в гр. :	92
Язык публикации:	Русский
Тип обложки:	Мягкий / Полужесткий переплет
Цвета обложки:	Зелёный

Методические подходы к организации пошагового решения обучающимися средней школы задач по стереометрии Текст научной статьи по специальности «Математика»

УДК 514.1 ББК 22.151.1

МЕТОДИЧЕСКИЕ ПОДХОДЫ К ОРГАНИЗАЦИИ ПОШАГОВОГО РЕШЕНИЯ ОБУЧАЮЩИМИСЯ СРЕДНЕЙ ШКОЛЫ ЗАДАЧ ПО СТЕРЕОМЕТРИИ

СЕРЮКОВА А.С., ПОДПЯТНИКОВА С. А. ФГБОУВО ЮУрГГПУ, Челябинск, Россия e-mail: [email protected], [email protected].

Аннотация

В статье рассмотрены проблемы, возникающие при решении стереометрических задач и предложены пути их решения на основе выделенных этапов по организации работы с требованиями задачи. На конкретных примерах показана структура деятельности учителя и обучающихся при формировании умения пошагового решения задач по стереометрии.

Ключевые слова: методика обучения математики, стереометрия, пространственное воображение, этапы решения.

Актуальность. Стереометрия формирует и развивает у обучающихся пространственные представления и воображение, логическое мышление, формирует умение выделять пространственные свойства и отношения объектов и оперировать ими в процессе решения задачи. Умение решать стереометрические задачи является одним из основных показателей уровня сформированности у выпускников школ математического мышления и глубины понимания изученного учебного материала. Поэтому контрольно-измерительные материалы (КИМ) по математике содержат задачу повышенного и высокого уровня сложности по стереометрии. На едином государственном экзамене (ЕГЭ) около 98% старшеклассников допускают ошибки при решении весьма несложной стереометрической задачи [2]. Многие обучающиеся испытывают большие трудности не только в поиске решения задачи, дополнительных построениях

пространственных объектов с учетом предлагаемых задач, но и в понимании методов построения объемных фигур, их взаимного расположения в трехмерном пространстве [5]. Отсутствие понимания объясняется тем, что на уроках многие учащиеся стремятся просто выучить изучаемый материал, не желая понимать его полностью [4, 10].

По мнению Саниной Е. И.: «Проведение определения стереометрических отношений должно основываться не просто на изучении наглядного материала, а в совокупности с интенсивным обдумыванием и перестройкой имеющихся данных, т.е. осуществление

определенной «интеллектуализации» [6]. В данном ракурсе под образом следует понимать определенную единицу пространственного мышления. Такие расчеты основываются на активной мыслительной деятельности, позволяющей создать ряд пространственных образов, которые лежат в рамках плоскости решения задач. Сам процесс осуществления разбора и решения задач, связанных с расположением пространственных фигур основан на мыслительных действия по формированию в сознании образов стереометрического расположения в пространстве фигур с определением взаимосвязи между двумерным образом и реальным положением фигур в пространстве. В процессе такой деятельности может возникнуть проблемы, не позволяющие довести решение до логического завершения.

Учитывая, что решение некоторых задач ученые-математики искали несколько лет. Но также есть некоторые задачи, которые, спустя не один десяток лет, до сих пор небыли решены. Одним из ярких примеров таких задач является Гипотеза Берча и Суиннертон-Дайера, которой не одна сотня лет. За доказательство данной гипотезы в США математический институт Клэя намерен вручить один миллион долларов. Сущность гипотезы основана на том, что ранг кривой можно определить, зная порядок нуля дзета-функции. За счет доказательства данной гипотезы современная наука может далеко продвинуться вперед. Большого прогресса в доказательстве достигли несколько математиков из США и Англии в 1977 году. Но они смогли

найти доказательство лишь для единственного частного случая [7]. На этапе стимулирования преодоления трудностей при решении стереометрических задач можно привести данные исторические сведения или использовать другие методические подходы.

Цель работы. Выявить и описать методические подходы к организации пошагового решения обучающимися средней школы задач по стереометрии.

Во время изучения стереометрии принято выделять следующие этапы:

1. в 1-9 классах создание условий для формирования начальных представлений о пространственных фигурах;

2. в 10-11 классах ведение систематического курса стереометрии.

В систематический курс стереометрии входят следующие темы:

1. Аксиомы стереометрии и их простейшие следствия.

2. Параллельность прямых и плоскостей в пространстве.

3. Перпендикулярность прямых и плоскостей в пространстве.

4. Координаты, векторы, геометрические преобразования в пространстве.

5. Многогранники.

6. Тела вращения.

7. Площадь поверхностей и объем геометрических тел.

8. Изображение пространственных фигур на плоскости.

Для достижения планируемых результатов изучения раздела «Стереометрия» учителю необходимо:

— использовать различные формы организации учебно-познавательной деятельности обучающихся;

— сконструировать банк заданий, способствующих формированию у обучающихся умения решать задачи, в том числе представленные в КИМ ЕГЭ;

— применять алгоритмическое предписание по этапному решению задач, развивая тем самым аналитические и логические умения обучающихся, расширяя их познавательный интерес и формируя у них творческие способности.

Материалы и методы. С целью ликвидации причин, связанных с неумением обучающимися решать стереометрические задачи высокой сложности без вмешательства педагога, необходимо определить алгоритм решения.

Следует выделить основные этапы обучения и разложить сложное решение на несколько более простых задач. Также нужно чтобы обучающиеся смогли научиться решать трудные задачи не только без посторонней помощи, но и без применения аналогий.

Обучение учащихся старших классов самостоятельному решению сложных стереометрических задач возможно через формирование у них навыков, нацеленных на применение общего подхода и адаптацию его под ту или иную задачу с правильным выбором направлений поиска способа решения неизвестных им ранее алгоритмов решения, для чего необходимо:

1. Сформировать у учащихся глубокие знания по теории решения задач. При этом преподнесение теории не должно отрываться от практики. Не стоить выделять отдельные теоретические темы, необходимо вводить теоретические знания вместе с решением задач на протяжении всего периода обучения, но при этом регулярно возвращаться к тому или иному понятию и повторять его.

2. Выработать у учеников и закрепить на практике четкие умения и навыки для реализации простых действий, выступающих частью решения сложных стереометрических задач, к которым следует отнести такие этапы работы: проведение анализа условий задачи, построение чертежей стереометрических фигур, поиск способа решения через систематизацию условий, проверку полученного результата, конечный анализ полученного решения.

3. Проработать с учениками основные способы решения стереометрических задач высокой сложности с обязательным закреплением полученных умений через решение ряда геометрических задач с применением каждого способа [8, 9, 10].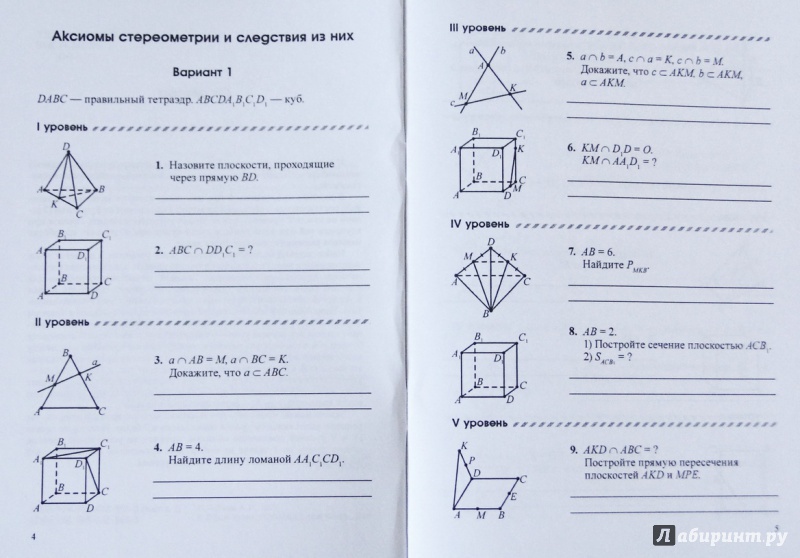

Управление процессом решения

стереометрических задач основывается на ряде поэтапных действий, которые берут свою основу в геометрии, но в первую очередь до учащихся необходимо довести информацию по разделу стереометрии, т.е. необходимо разложить весь сложный мыслительный процесс решения стереометрических задач на более простые подзадачи [1]. В качестве первого этапа решения задач выступает анализ условия задачи, который можно разделить на несколько более простых действия: а) определение точной области условий задачи с выявлением всех ее структурных элементов; б) определение

зависимостей элементов каждой области задачи и их свойств; в) выявление сути условий задачи. На втором этапе решения стереометрической задачи определяется план ее решения, а также формируется основная идея ее решения. К тому же второй этап решения задачи выступает ведущим в определении искомых величин и выборе направлений и способов решения, построение стратегии.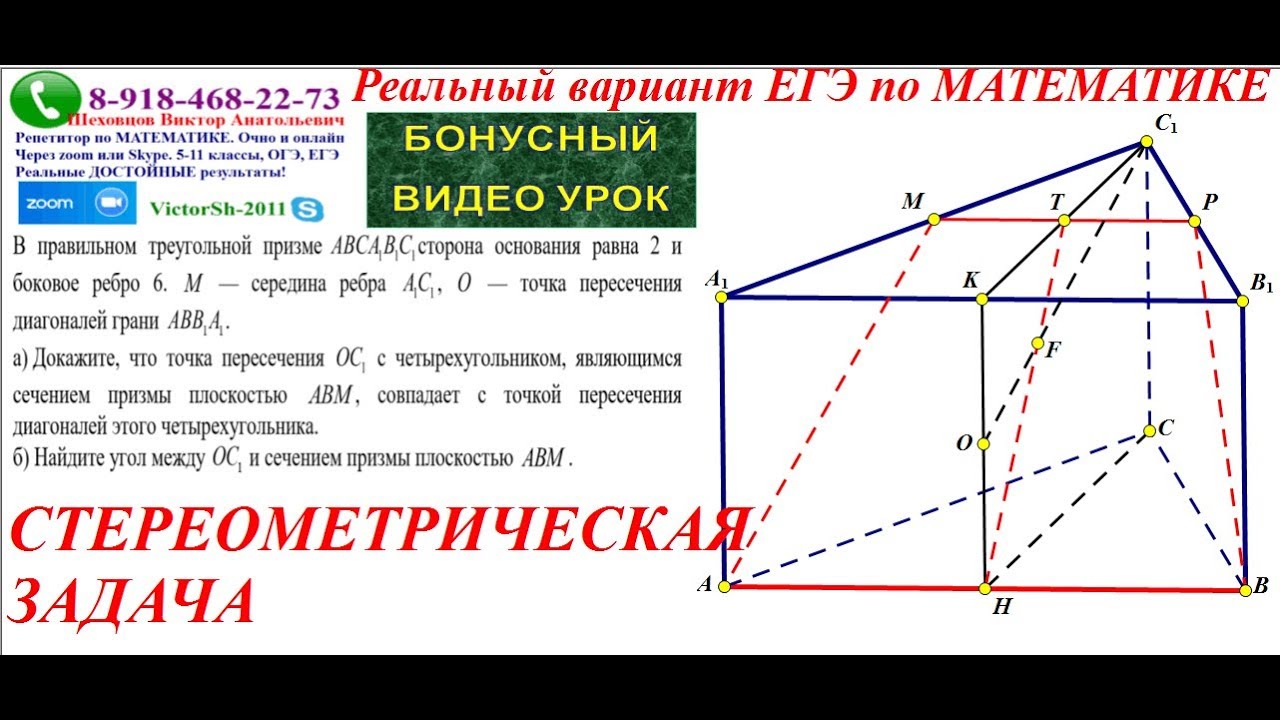 Переходя к третьему этапу решения стереометрических задач в работу включается уже выстроенный план решения, т.е. план получает реализацию на практике. Подробно описывается решение, при необходимости корректируется, выбирается методика решения, решение задачи записывается и оформляется. Четвертый этап деятельности, направленной на решение стереометрической задачи, направлен на обсуждение и анализ процесса решения. Приводится итоговое решение задачи, осуществляется анализ решения и систематизация полученных в процессе решения знаний. На основе описанного алгоритма решения стереометрической задачи можно более четко выделить следующие этапы: этап 1 — осуществление анализа условий задачи;

этап 2 — построение схемы условий задачи; этап 3 — выбор способов решения задачи; этап 4 — осуществление деятельности по решению задачи;

этап 5 — проведение проверки полученного решения;

этап 6 — окончательное формулирование ответа задачи.

Обратим внимание на первый этап. При внимательном прочтении любой задачи по геометрии, можно заметить, что в задаче прослеживается либо требование, либо вопрос, требующий ответа, основываясь на условиях, которые указаны в задаче. Поэтому при изучении условий стереометрической задачи, необходимо провести анализ ее условий, определить поставленные требования, на основе которых задача и будет решена. Приведем пример стереометрической задачи:

Задача 1. Найдите катеты прямоугольного треугольника, в котором гипотенуза в точке касания с вписанной окружностью делится на отрезки длинной 7 см и 10 см [3].

После прочтения задачи сразу же можно заметить, что в ней присутствует определенное утверждение, а именно: «в прямоугольном треугольнике гипотенуза в точке касания с

вписанной окружностью делится на отрезки длинной 7 см и 10 см». Далее необходимо выяснить, что надо найди или доказать. Требование данной стереометрической задачи заключается в том, что нужно найти катеты прямоугольного треугольника. Теперь на основе формулировки задачи необходимо вывести ее условия. Особенностью стереометрической задачи выступает то, что ее условие содержит несколько условий по решению отдельных элементарных задач, т.е. исходное задание подлежит расчленению на несколько более простых заданий. Поэтому утверждение и требования, установленные в условиях задачи, необходимо разделить на более простые условия и элементарные части.

В рассматриваемом варианте задачи можно выделить ряд следующих простых условий:

1) рассматриваемый треугольник является прямоугольным;

2) в данный треугольник вписана окружность;

3) гипотенуза точкой касания с окружностью делится на два отрезка;

4) длина первого отрезка составляет 7 см;

5) длина второго отрезка 10 см.

Требование данной задачи можно разделить

на два простых:

1) найти длину первого катета треугольника;

2) найти длину второго катета треугольника.

Глубина анализа в основном зависит от того,

знаком ли учащийся со стереометрическими задачами, и знает ли он общий способ их решения. Если да, то достаточно провести простой анализ, который сводится к определению вида задачи; если нет, то для отыскания решения стереометрической задачи необходим более подробный анализ.

В некоторых случаях анализ решения задачи должен быть оформлен письменно. В данном случае следует использовать различные схемы, позволяющие представить условия задачи в более простом виде. Схематическая запись решения стереометрических задач представляет собой второй этап. Схематическая запись стереометрических задач заключается в необходимости использования чертежа той фигуры, которая рассматривается в задаче. В момент построения такого чертежа нужно придерживаться следующих требований.

В основе чертежа лежит схематический рисунок основного объекта задачи, т.е. рисунок геометрической фигуры, нескольких фигур или их частей, которые имеют буквенное

обозначение или иных знаков, используемых для обозначения частей рисунка, представленного на схеме. Если в условиях задачи присутствуют обозначения фигуры или какой-либо ее части, то данные обозначения также переносятся на чертеж, если же обозначения специально не введены, то на чертеже используются произвольные обозначения, которые могут быть основаны на наборе наиболее распространенных опознавательных знаков.

Рассмотрим на примере одной из стереометрических задач, как строятся их схематические записи при помощи чертежей.

Задача 2. Представлена трапеция, диагональ которой проходит перпендикулярно к основаниям. Большое основание имеет длину 13 см, а тупой угол, который принадлежит ей составляет 120о. К тупому углу принадлежит боковая сторона, равная также 13 см. Необходимо определить среднюю линию трапеции [3].

Рис. Трапеция

Проводя анализ условий задачи, необходимо отметить, что основным объектом задачи является трапеция, в которой одна диагональ имеет перпендикулярное положение по отношению к ее основаниям. Следует обратить внимание, что при начертании трапеции, начав ее построение с боковых сторон, обязательно будет допущена ошибка. Поэтому построение чертежа трапеции необходимо начать с начертания диагонали, указанной в условиях задачи, так как она перпендикулярна основаниям трапеции. Обозначение диагонали можно осуществить через указание прописной буквы «а». Данную диагональ следует определить как вертикальный отрезок, из концов которого выходят основания трапеции -два горизонтальных отрезка. При таком алгоритме начертания трапеции видно, что углы, принадлежащие вершинам трапеции -тупые. На основе условий задачи можно определить, что тупой угол, принадлежащий

большому основанию, имеет 120о. Также отражено, что вершина данного угла выступает одновременно и одним из концов построенной диагонали. С данного момента построить трапецию становится намного проще. Далее необходимо обозначить все вершины трапеции, провести в ней среднюю линию, а данный в задаче тупой угол отметить дугой и подписать градусную меру (рис.).

После этого необходимо записать все условия и требования данной задачи, пользуясь принятыми на рисунке 1 буквенными обозначениями. Дано:

1) ADHCB;

2) AD±AC;

3) АС±СВ;

4) ^DAB = 120°;

5) AD = 13 см;

6) АВ = 6 см;

7) АМ = MB. DN = NC.

Найти: MN.

Сразу же после того, как были сделаны анализ задачи и ее чертеж, которые считаются обязательными этапами для нахождения способа решения стереометрической задачи, необходимо осуществить сам поиск способа ее решения. Это и есть третий этап процесса решения стереометрической задачи. Рассмотрим его на примере последней задачи. Прежде чем приступить к поиску способа решения данной задачи, необходимо вспомнить, средняя линия трапеции расположена параллельно к основаниям. Поэтому MN параллельна AD и MN параллельна ВС. При дальнейшем решении необходимо применение теоремы о средней линии трапеции: средняя линия трапеции параллельна ее основаниям, и длина ее равна полу сумме длин оснований. Данная теорема выступит основным правилом для решения рассматриваемой задачи.

Нахождение способа решения задачи становится переходом к следующему, четвертому этапу решения задачи по стереометрии. 5С = 0,5 •б см = 3 см.

= (££+££)= (3+13) = 8 см.

2 2

В процессе решения задач учащиеся совершают многочисленные ошибки, исправление которых часто вызывает большие затруднения. Основной причиной является не столько непонимание учащимся сути допущенной ошибки, сколько неумение их обнаружить. В связи с этим, после решения задачи нужно удостовериться в том, что найденное решение верное, что оно соответствует и удовлетворяет всем условиям и требованиям задачи. Это и есть пятый этап процесса решения стереометрических задач. В методической литературе всего существует два способа проверки стереометрических задач:

— составить и решить обратную задачу;

— решить данную задачу совершенно другим способом.

Для проверки задачи чаще всего используют первый способ. Данный метод довольно универсален, так как для любой задачи возможно составить обратную. Решение задачи другим способом — метод довольно сложный, потому что данная работа является по большей мере творческой, помимо этого не каждый учащийся способен найти хотя бы один способ решения стереометрической задачи.

Рассмотрим на примере второй задачи другой способ ее решения. Для отыскания другого способа решения стереометрической задачи, существуют различные методы: построение другой модели задачи, отличной от используемой; дополнение условия задачи сведениями, которые не повлияют на конечный результат; описание практического решения ситуации, представленной в задаче. В данной задаче возможно дополнение сведеньями. Изначально решить вторую задачу нам помогло свойство средней линии трапеции. Также осуществить решение данной задачи возможно, воспользовавшись теоремой Пифагора и синусом угла. Это и будет другой способ решения.

2 способ решения. ЛС = •

cos 30° = 7 • — = 3,5V3.

Из прямоугольного А ЛСД: ЛД2 = CD2 ЛС2 = 144 — 36,75 = 107,75 ЛД = 0,5 • V429 см.

„ (ВС+ЛО) 3,5+0,5 • V429

Средняя линия =-=-=

1,75 + 0,25 • V429 = 6,9 см.

Проверив решение и определив его верность, необходимо четко сформулировать и записать его. Данный этап является завершающим в решении стереометрической задачи (шестой этап).

Если учащиеся будут придерживаться данных этапов, то это даст им возможность узнать приемы решения стереометрических задач, сформировать умение использовать полученные знания в » измененных» ситуациях, «нетипичных» задачах. Процесс решения по данным, рассмотренный в разрезе приведенных этапов, дает возможность формирования и развития таких качеств у обучающихся, которые формируют аналитическую склонность, развивают способность освоения новой информации, логическое мышление,

основанное на алгоритмах исследовательской работы. К тому же приобретенные при решении стереометрических задач навыки, позволят повысить эффективность подготовки к ЕГЭ по геометрии, а также при определении профессиональных интересов учащихся, связанных с математикой.

Стремление к введению инновационных

методов обучения подталкивает педагогов к созданию более эффективных и продуктивных способов решения задач по данному разделу. Данный метод обосновывается своей структурированностью. Использование этого алгоритма на уроках по геометрии в 10 классе поможет педагогу научить решать стереометрические задачи более эффективно и

быстро, так как данный способ позволяет выстраивать новую программу обучения для старшеклассников.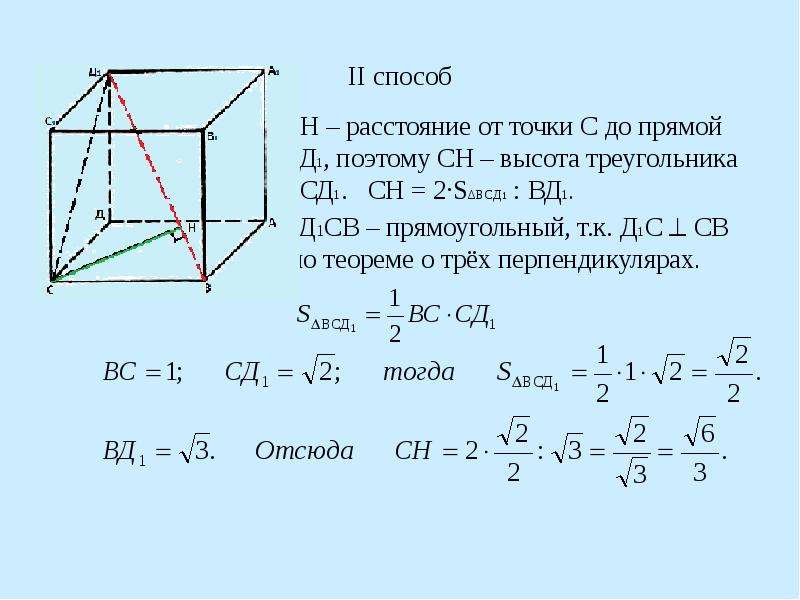 Главная идея данного метода направлена на результат более детального способа изучения и решения геометрических задач, путем их непосредственного поэтапного анализа.

Список литературы

1. Бордовская Н.В. Педагогика: учебное пособие /Н.В. Бордовская, А.А. Реан. — СПб.: Питер, 2006. — 304 с.

2. Журавлева Н.А. Интерпретация критериев проверки заданий с параметром ЕГЭ по математике /Н.А. Журавлева // Современная система образования: опыт прошлого, взгляд в будущее. — 2013. — №2. — С. 62-67.

3. Зив Б.Г. Геометрия. Дидактические материалы. 10 класс: базовый и профил. уровни / Б.Г. Зив. — М.: Просвещение, 2011. — 159 с.

4. Крайнева С.В. Психологические особенности процесса решения прикладных естественнонаучных задач / С.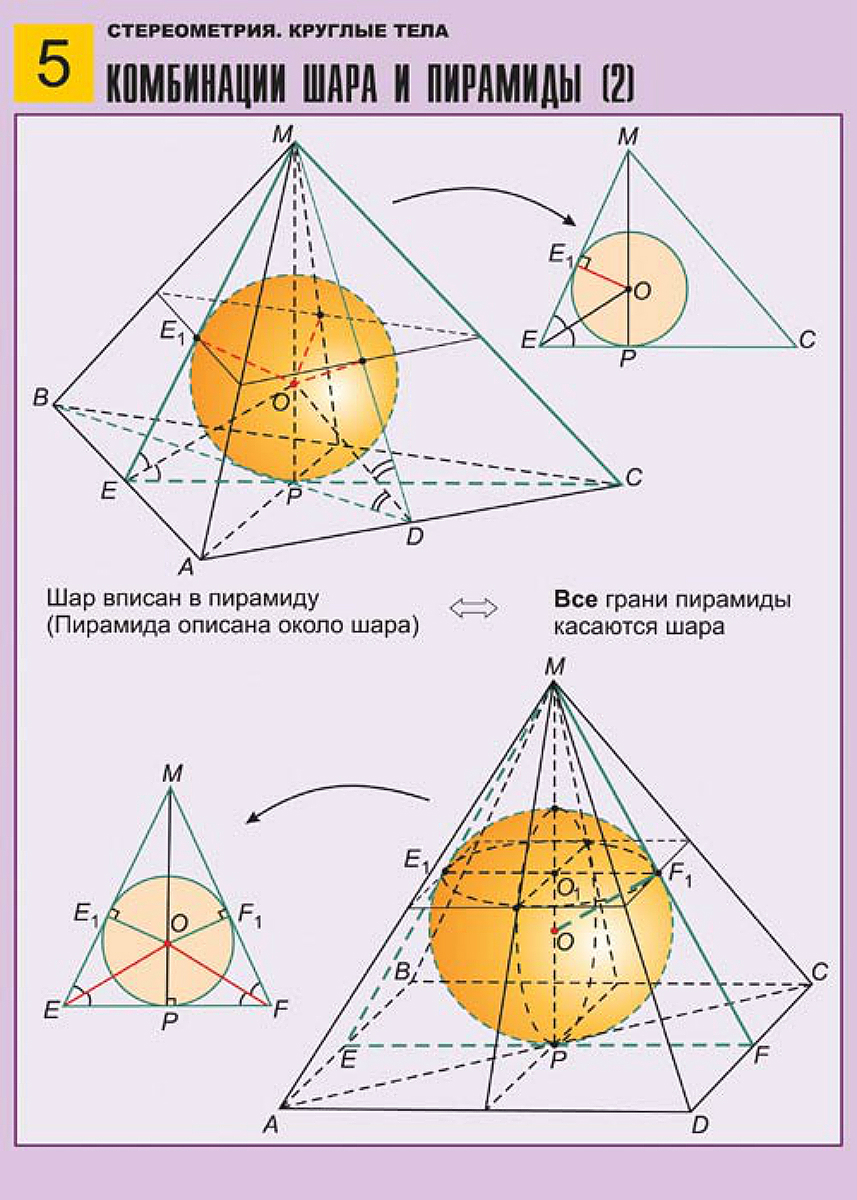 В. Крайнева, О.Р. Шефер //Психология обучения. — 2018. — №6. — С. 139-145.

5. Макарченко М.Г. Контекстуальный анализ учебных текстов по математике / М.Г. Макарченко // Известия Российского государственного педагогического университета имени А.И. Герцена. — 2008. — №11. — С. 268-276.

6. Санина Е.И. Развитие пространственного мышления в процессе обучения стереометрии /Е.И. Санина, О.А. Гришина // Вестник Российского университета дружбы народов. Серия: Психология и педагогика. — 2013. — №4. — С. 99-102.

7. Фильчев Э.Г. Гипотеза Берча и Свиннертон-Дайера / Э.Г. Фильчев //Проблемы науки. — 2016. — №4. — С. 19-21.

8. Фридман Л.М. Как научиться решать задачи /Л.М. Фридман, Е.Н. Турецкий. — М.: Просвещение. 1989. — 192 с.

9. Фридман Л. М. Теоретические основы методики обучения математике: учеб. пособ. /Л.М. Фридман. -М.: Едиториал УРСС, 2005. — 248 с.

10. Шефер О.Р. Комплексные задачи по физике как средства достижения обучающимися метапредметных и предметных результатов: монография / О.Р. Шефер, Ю.Г. Ваганова. — Челябинск: Край Ра, 2014. — 196 с.

METHODICAL APPROACHES TO ORGANIZING A STEP-BY-STEP SOLUTION FOR STUDENTS OF SECONDARY SCHOOL OF PROBLEMS BY STEREOMETRY

SERYUKOVA A.S., PODPYATNIKOVA S.A. FSBEI HE SUSHPU, Chelyabinsk, Russia e-mail: [email protected], [email protected].

Abstract

The article discusses the problems that arise when solving stereometric problems and suggests ways to solve them based on the steps outlined for organizing work with the requirements of the problem. The concrete examples show the structure of the teacher and students in the formation of the ability to step-by-step solving problems in stereometry.

Keywords: mathematics teaching methodology, stereometry, spatial imagination, solution steps.

Презентация — Решение задач B9

Слайды и текст этой онлайн презентации

Слайд 1

1
© Богомолова ОМ

Слайд 2

1. Диагональ куба равна . Найдите его объем
2
Богомолова ОМ

Слайд 3

2. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба
3
Богомолова ОМ

Слайд 4

3. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60о. Одно из ребер параллелепипеда составляет с этой гранью угол в 60о и равно 2. Найдите объем параллелепипеда
4
Богомолова ОМ

Слайд 5

4. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы
5
Богомолова ОМ

Слайд 6

5. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
6
Богомолова ОМ

Слайд 7

6. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности пирамиды
7
Богомолова ОМ

Слайд 8

7. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые
8
Богомолова ОМ

Слайд 9

8. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3
9
Богомолова ОМ

Слайд 10

9. В цилиндрический сосуд, в котором находится 6 дм3 воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали?
10
Богомолова ОМ

Слайд 11

10. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей
11
Богомолова ОМ

Слайд 12

11. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда
12
Богомолова ОМ

Слайд 13

12. В куб с ребром 6 вписан шар. Найдите объем шара, деленный на π
13
Богомолова ОМ

Слайд 14

13. В конус, радиус основания которого равен 2, вписан шар радиуса 1. Найдите объем конуса
14
Богомолова ОМ

Слайд 15

14. В сферу радиуса 5 вписан конус, высота которого равна 8. Найдите объем конуса
15
Богомолова ОМ

Слайд 16

15. Два противоположных ребра тетраэдра образуют угол 60о и равны 2. Расстояние между ними равно 3. Найдите объем тетраэдра
16
Богомолова ОМ

Слайд 17

16. Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом 30о. Диагонали ромба равны 10 см и 24 см. Найдите объем пирамиды
17
Богомолова ОМ

Слайд 18

17. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 600. Высота пирамиды равна 3 см. Найдите объем пирамиды
18
Богомолова ОМ

Слайд 19

18. Найдите объем правильной треугольной призмы, описанной около единичной сферы
19
Богомолова ОМ

Слайд 20

19. Боковые ребра наклонной треугольной призмы равны 15 см, а расстояния между ними равны 26 см, 25 см и 17 см. Найдите объем призмы
20
Богомолова ОМ

Стереометрия (Геометрия в пространстве) — Все свойства, теоремы, аксиомы и формулы — Математика

Базовые теоремы, аксиомы и определения стереометрии

Вводные определения и аксиомы стереометрии

К оглавлению. ..

Некоторые определения:

Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.

Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.

Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.

Параллелепипед – это многогранник, у которого шесть граней и каждая из них – параллелограмм. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. 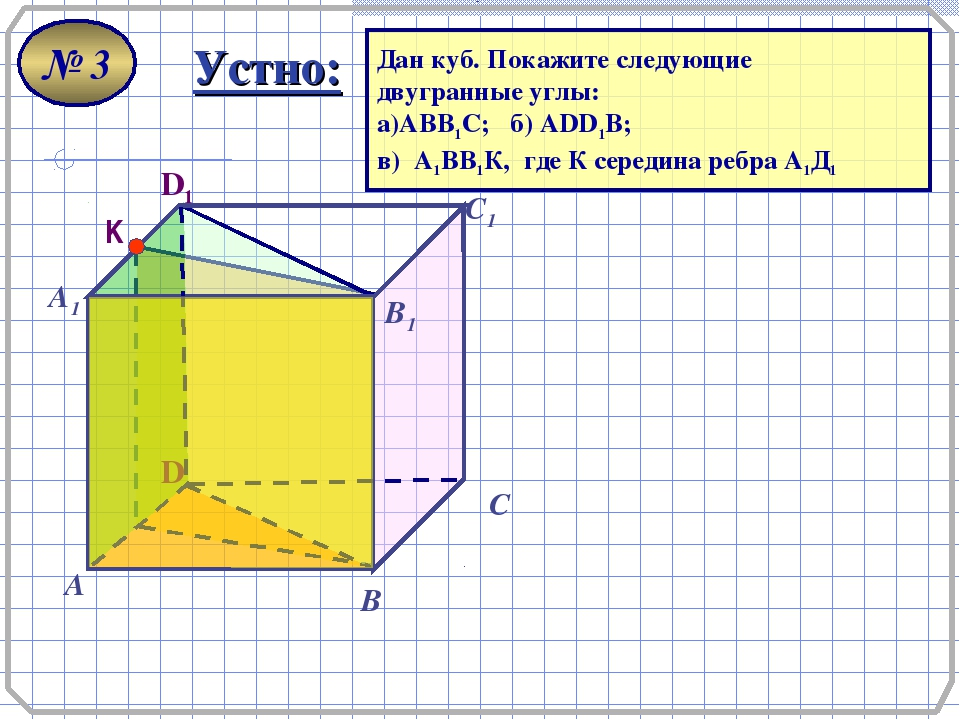Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра, а имеющие общее ребро называются смежными. Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми ребрами.

Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники. Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.

Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.

Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются основаниями, а параллелограммы – боковыми гранями призмы. Прямая призма – это такая призма, у которой боковые грани – прямоугольники. Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники.

Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается S_бок). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается S_полн).

Пирамида (n-угольная) – это многогранник, у которого одна грань – какой-нибудь n-угольник, а остальные n граней – треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды. 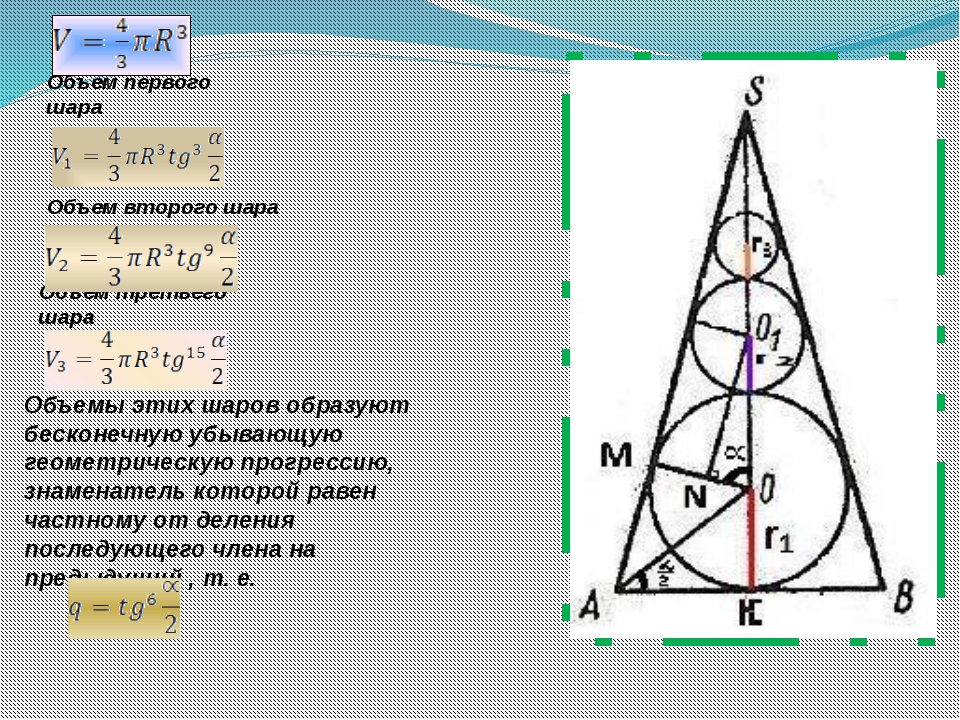Стороны граней пирамиды называются ее ребрами, а ребра, сходящиеся в вершине, называются боковыми.

Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается S_бок). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается S_полн).

Правильная n-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой. У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.

Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).

Аксиомы стереометрии:

Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.

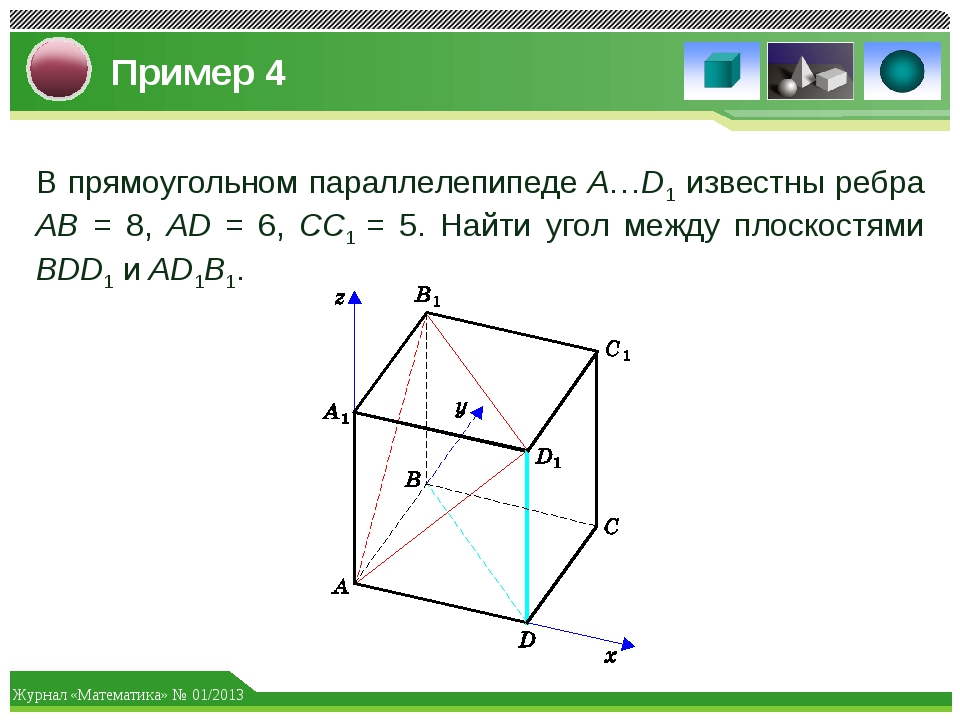
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Следствия из аксиом стереометрии:

Теорема 1. Через прямую и не лежащую на ней точку проходит единственная плоскость.

Теорема 2. Через две пересекающиеся прямые проходит единственная плоскость.

Теорема 3. Через две параллельные прямые проходит единственная плоскость.

Построение сечений в стереометрии

К оглавлению…

Для решения задач по стереометрии остро необходимо умение строить на рисунке сечения многогранников (например, пирамиды, параллелепипеда, куба, призмы) некоторой плоскостью. Дадим несколько определений, поясняющих, что такое сечение:

Секущей плоскостью пирамиды (призмы, параллелепипеда, куба) называется такая плоскость, по обе стороны от которой есть точки данной пирамиды (призмы, параллелепипеда, куба).

Сечением пирамиды (призмы, параллелепипеда, куба) называется фигура, состоящая из всех точек, которые являются общими для пирамиды (призмы, параллелепипеда, куба) и секущей плоскости.

Секущая плоскость пересекает грани пирамиды (параллелепипеда, призмы, куба) по отрезкам, поэтому сечение есть многоугольник, лежащий в секущей плоскости, сторонами которого являются указанные отрезки.

Для построения сечения пирамиды (призмы, параллелепипеда, куба) можно и нужно построить точки пересечения секущей плоскости с ребрами пирамиды (призмы, параллелепипеда, куба) и соединить каждые две из них, лежащие в одной грани. Заметим, что последовательность построения вершин и сторон сечения не существенна. В основе построения сечений многогранников лежит две задачи на построение:

Линии пересечения двух плоскостей.

Для построения прямой, по которой пересекаются некоторые две плоскости α и β (например, секущая плоскость и плоскость грани многогранника), нужно построить две их общие точки, тогда прямая, проходящая через эти точки, есть линия пересечения плоскостей α и β.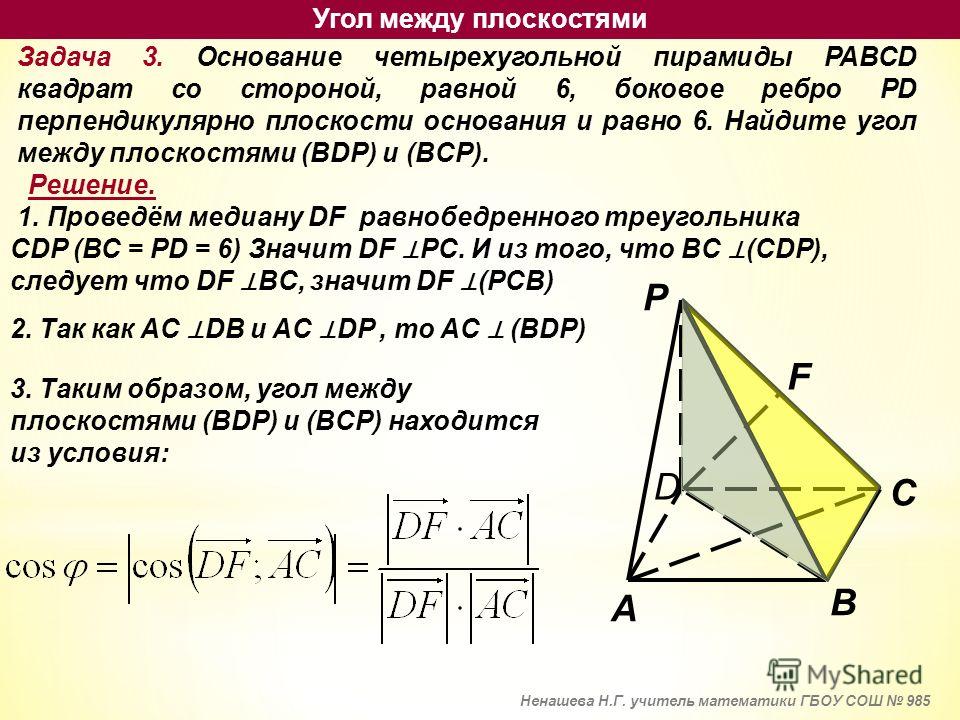

Точки пересечения прямой и плоскости.

Для построения точки пересечения прямой l и плоскости α нужно построить точку пересечения прямой l и прямой l₁, по которой пересекаются плоскость α и любая плоскость, содержащая прямую l.

Взаимное расположение прямых и плоскостей в стереометрии

К оглавлению…

Определение: В ходе решения задач по стереометрии две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Если прямые а и b, либо AB и CD параллельны, то пишут:

Несколько теорем:

Теорема 1. Через любую точку пространства, не лежащую на данной прямой, проходит единственная прямая, параллельная данной прямой.

Теорема 2. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

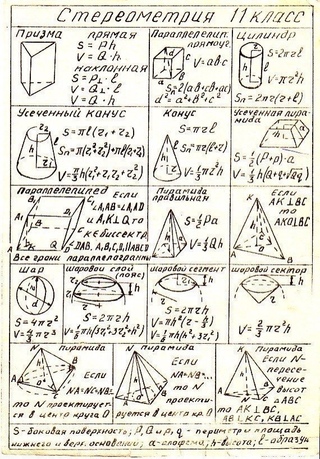
Теорема 3 (признак параллельности прямых). Если две прямые параллельны третьей прямой, то они параллельны между собой.

Теорема 4 (о точке пересечения диагоналей параллелепипеда). Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Возможны три случая взаимного расположения прямой и плоскости в стереометрии:

Прямая лежит в плоскости (каждая точка прямой лежит в плоскости).

Прямая и плоскость пересекаются (имеют единственную общую точку).

Прямая и плоскость не имеют ни одной общей точки.

Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая а параллельна плоскости β, то пишут:

Теоремы:

Теорема 1 (признак параллельности прямой и плоскости). Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Теорема 2. Если плоскость (на рисунке – α) проходит через прямую (на рисунке – с), параллельную другой плоскости (на рисунке – β), и пересекает эту плоскость, то линия пересечения плоскостей (на рисунке – d) параллельна данной прямой:

Если две различные прямые лежат в одной плоскости, то они либо пересекаются, либо параллельны. Однако, в пространстве (т.е. в стереометрии) возможен и третий случай, когда не существует плоскости, в которой лежат две прямые (при этом они и не пересекаются, и не параллельны).

Определение: Две прямые называются скрещивающимися, если не существует плоскости, в которой они обе лежат.

Теоремы:

Теорема 1 (признак скрещивающихся прямых). Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещивающиеся.

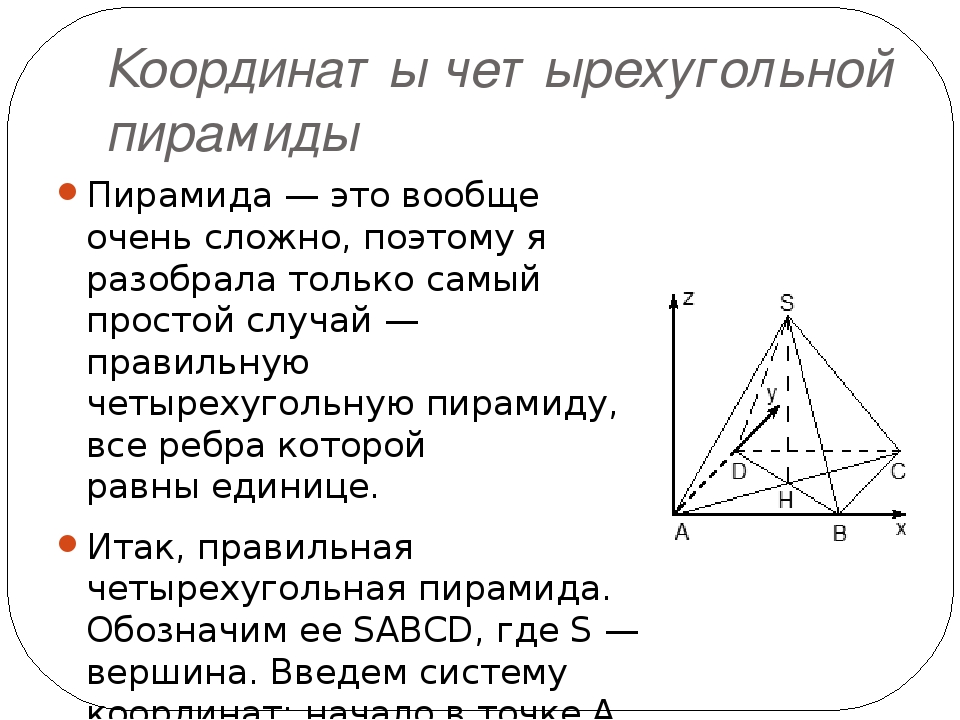
Теорема 2. Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой.

Теперь введем понятие угла между скрещивающимися прямыми. Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O в пространстве и проведем через нее прямые a₁ и b₁, параллельные прямым a и b соответственно. Углом между скрещивающимися прямыми a и b называется угол между построенными пересекающимися прямыми a₁ и b₁.

Однако на практике точку O чаще выбирают так, чтобы она принадлежала одной из прямых. Это обычно не только элементарно удобнее, но и рациональнее и правильнее с точки зрения построения чертежа и решения задачи. Поэтому для угла между скрещивающимися прямыми дадим такое определение:

Определение: Пусть a и b – две скрещивающиеся прямые. Возьмем произвольную точку O на одной из них (в нашем случае, на прямой b) и проведем через неё прямую параллельную другой из них (в нашем случае a₁ параллельна a). Углом между скрещивающимися прямыми a и b называется угол между построенной прямой и прямой, содержащей точку O (в нашем случае это угол β между прямыми a₁ и b).

Определение: Две прямые называются взаимно перпендикулярными (перпендикулярными), если угол между ними равен 90°. Перпендикулярными могут быть как скрещивающиеся прямые, так и прямые лежащие и пересекающиеся в одной плоскости. Если прямая a перпендикулярна прямой b, то пишут:

Определение: Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют общих точек. Если две плоскости α и β параллельны, то, как обычно, пишут:

Теоремы:

Теорема 1 (признак параллельности плоскостей). Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Теорема 2 (о свойстве противолежащих граней параллелепипеда). Противолежащие грани параллелепипеда лежат в параллельных плоскостях.

Теорема 3 (о прямых пересечения двух параллельных плоскостей третьей плоскостью). Если две параллельные плоскости пересечены третьей, то прямые их пересечения параллельны между собой.

Теорема 4. Отрезки параллельных прямых, расположенные между параллельными плоскостями, равны.

Теорема 5 (о существовании единственной плоскости, параллельной данной плоскости и проходящей через точку вне ее). Через точку, не лежащую в данной плоскости, проходит единственная плоскость, параллельная данной.

Определение: Прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости. Если прямая a перпендикулярна плоскости β, то пишут, как обычно:

Теоремы:

Теорема 1. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой.

Теорема 2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.

Теорема 3 (о параллельности прямых, перпендикулярных плоскости). Если две прямые перпендикулярны одной плоскости, то они параллельны.

Теорема 4 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.

Теорема 5 (о плоскости, проходящей через данную точку и перпендикулярной данной прямой). Через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.

Теорема 6 (о прямой, проходящей через данную точку и перпендикулярной данной плоскости). Через любую точку пространства проходит единственная прямая, перпендикулярная данной плоскости.

Теорема 7 (о свойстве диагонали прямоугольного параллелепипеда). Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, имеющих общую вершину:

Следствие: Все четыре диагонали прямоугольного параллелепипеда равны между собой.

Теорема о трех перпендикулярах

К оглавлению…

Пусть точка А не лежит на плоскости α. Проведем через точку А прямую, перпендикулярную плоскости α, и обозначим буквой О точку пересечения этой прямой с плоскостью α. Перпендикуляром, проведенным из точки А к плоскости α, называется отрезок АО, точка О называется основанием перпендикуляра.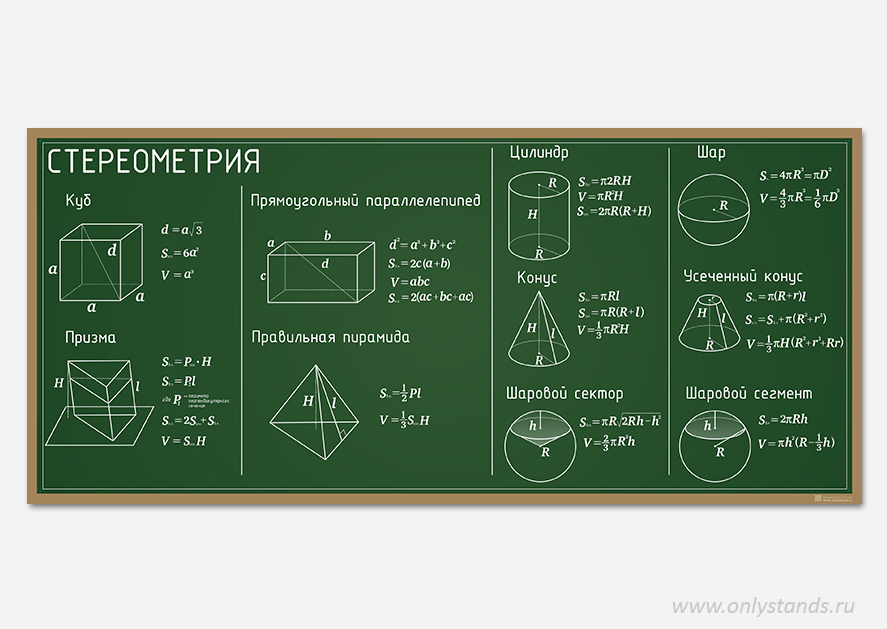 Если АО – перпендикуляр к плоскости α, а М – произвольная точка этой плоскости, отличная от точки О, то отрезок АМ называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Отрезок ОМ – ортогональная проекция (или, короче, проекция) наклонной АМ на плоскость α. Теперь приведем теорему, которая играет важную роль при решении многих задач.

Теорема 1 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной. Верно и обратное утверждение:

Теорема 2 (о трех перпендикулярах): Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость. Данные теоремы, для обозначений с чертежа выше можно кратко сформулировать так:

Теорема: Если из одной точки, взятой вне плоскости, проведены к этой плоскости перпендикуляр и две наклонные, то:

две наклонные, имеющие равные проекции, равны;

из двух наклонных больше та, проекция которой больше.

Определения расстояний объектами в пространстве:

Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к данной плоскости.

Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.

Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до плоскости.

Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до плоскости, проходящей через другую прямую и параллельной первой прямой.

Определение: В стереометрии ортогональной проекцией прямой a на плоскость α называется проекция этой прямой на плоскость α в случае, если прямая, определяющая направление проектирования, перпендикулярна плоскости α.

Замечание: Как видно из предыдущего определения, проекций бывает много.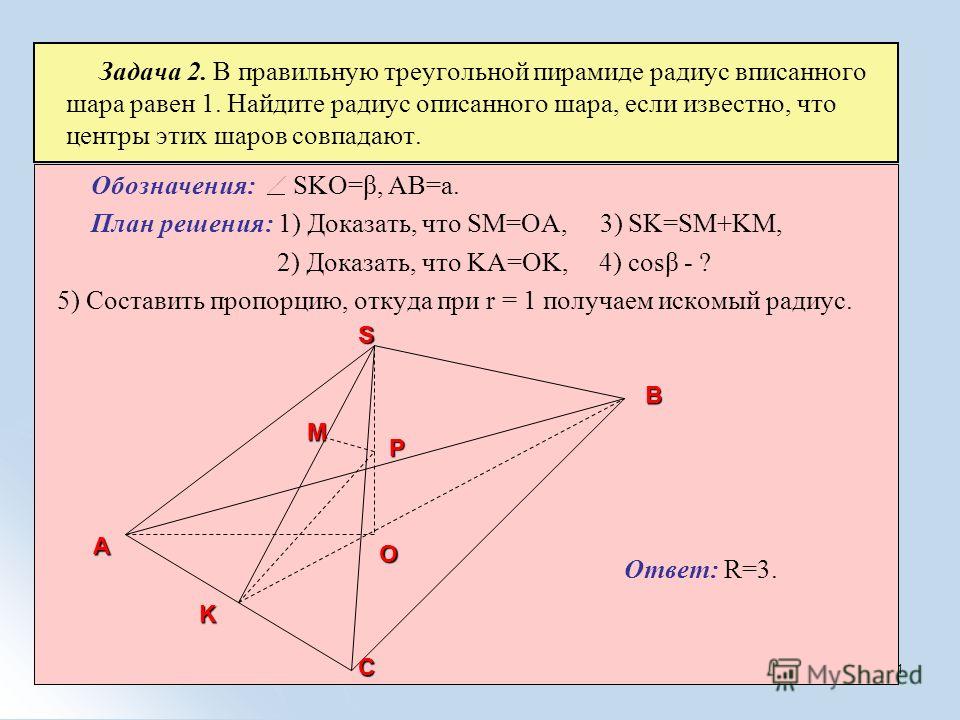 Другие (кроме ортогональной) проекции прямой на плоскость можно построить если прямая определяющая направление проецирования будет не перпендикулярна плоскости. Однако, именно ортогональную проекцию прямой на плоскость в будущем мы будем встречать в задачах. А называть ортогональную проекцию будем просто проекцией (как на чертеже).

Определение: Углом между прямой, не перпендикулярной плоскости, и этой плоскостью называется угол между прямой и ее ортогональной проекцией на данную плоскость (угол АОА’ на чертеже выше).

Теорема: Угол между прямой и плоскостью является наименьшим из всех углов, которые данная прямая образует с прямыми, лежащими в данной плоскости и проходящими через точку пересечения прямой и плоскости.

Двугранный угол

К оглавлению…

Определения:

Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой и частью пространства, для которой эти полуплоскости служат границей.

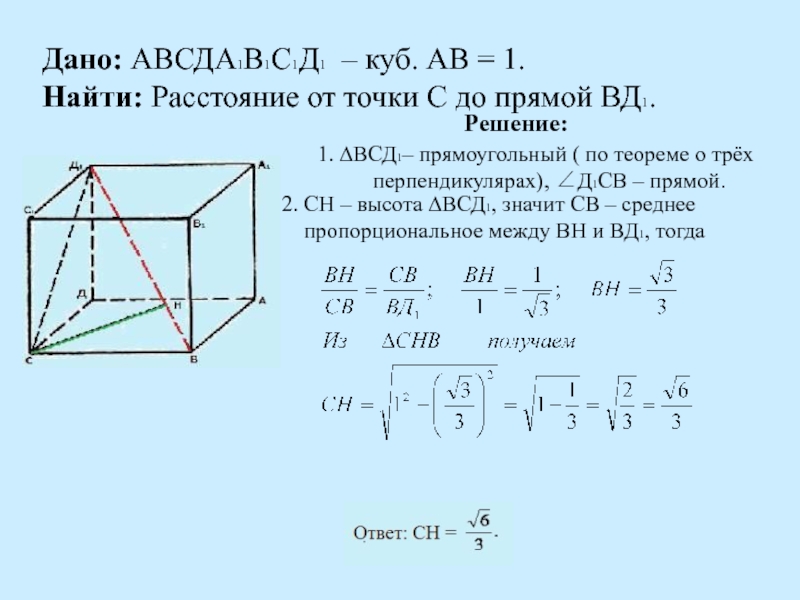
Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.

Таким образом, линейный угол двугранного угла – это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру. Все линейные углы двугранного угла равны между собой. Градусной мерой двугранного угла называется градусная мера его линейного угла.

Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°). В дальнейшем, при решении задач по стереометрии, под двугранным углом будем понимать всегда тот линейный угол, градусная мера которого удовлетворяет условию:

Определения:

Двугранным углом при ребре многогранника называется двугранный угол, ребро которого содержит ребро многогранника, а грани двугранного угла содержат грани многогранника, которые пересекаются по данному ребру многогранника.

Углом между пересекающимися плоскостями называется угол между прямыми, проведенными соответственно в данных плоскостях перпендикулярно их линии пересечения через некоторую ее точку.

Две плоскости называются перпендикулярными, если угол между ними равен 90°.

Теоремы:

Теорема 1 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Теорема 2. Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, по которой они пересекаются, перпендикулярна другой плоскости.

Симметрия фигур

К оглавлению…

Определения:

Точки M и M₁ называются симметричными относительно точки O, если O является серединой отрезка MM₁.

Точки M и M₁ называются симметричными относительно прямой l, если прямая l проходит через середину отрезка MM₁ и перпендикулярна ему.

Точки M и M₁ называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка MM₁ и перпендикулярна этому отрезку.

Точка O (прямая l, плоскость α) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно точки O (прямой l, плоскости α) некоторой точке этой же фигуры.

Выпуклый многогранник называется правильным, если все его грани – равные между собой правильные многоугольники и в каждой вершине сходится одно и то же число ребер.

Призма

К оглавлению. ..

Определения:

Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.

Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.

Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.

Боковая поверхность – объединение боковых граней.

Полная поверхность – объединение оснований и боковой поверхности.

Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.

Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.

Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.

Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:

Основания призмы являются равными многоугольниками.

Боковые грани призмы являются параллелограммами.

Боковые ребра призмы параллельны и равны.

Объём призмы равен произведению её высоты на площадь основания:

где: S_осн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:

Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A₂B₂C₂D₂E₂).

Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.

Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.

Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: S_сеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA₁ или BB₁ и так далее).

Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: P_сеч – периметр перпендикулярного сечения, l – длина бокового ребра.

Виды призм в стереометрии:

Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.

Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). 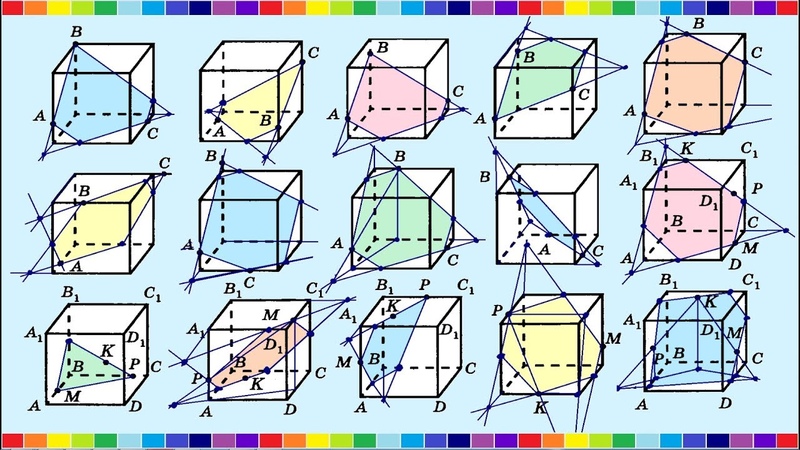Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):

где: P_осн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = S_осн∙h = S_осн∙l.

Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

Свойства правильной призмы:

Основания правильной призмы являются правильными многоугольниками.

Боковые грани правильной призмы являются равными прямоугольниками.

Боковые ребра правильной призмы равны между собой.

Правильная призма является прямой.

Параллелепипед

К оглавлению…

Определение: Параллелепипед – это призма, основания которой параллелограммы. В этом определении ключевым словом является «призма». Таким образом, параллелепипед – это частный случай призмы, которая отличается от общего случая только тем, что в основании у нее не произвольный многоугольник, а именно параллелограмм. Поэтому все приведенные выше свойства, формулы и определения касающиеся призмы остаются актуальными и для параллелепипеда. Однако, можно выделить несколько дополнительных свойств характерных для параллелепипеда.

Другие свойства и определения:

Две грани параллелепипеда, не имеющие общего ребра, называются противолежащими, а имеющие общее ребро – смежными.

Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.

Отрезок, соединяющий противолежащие вершины, называется диагональю параллелепипеда.

Параллелепипед имеет шесть граней и все они – параллелограммы.

Противоположные грани параллелепипеда попарно равны и параллельны.

У параллелепипеда четыре диагонали; они все пересекаются в одной точке, и каждая из них делится этой точкой пополам.

Если четыре боковые грани параллелепипеда – прямоугольники (а основания – произвольные параллелограммы), то он называется прямым (в этом случае, как и у прямой призмы, все боковые ребра перпендикулярны основаниям). Все свойства и формулы для прямой призмы актуальны для прямого параллелепипеда.

Параллелепипед называется наклонным, если не все его боковые грани являются прямоугольниками.

Объем прямого или наклонного параллелепипеда рассчитывается по общей формуле для объема призмы, т.е. равен произведению площади основания параллелепипеда на его высоту (V = S_осн∙h).

Прямой параллелепипед, у которого все шесть граней – прямоугольники (т.е. кроме боковых граней еще и основания являются прямоугольниками), называется прямоугольным. Для прямоугольного параллелепипеда актуальны все свойства прямого параллелепипеда, а также:
- Диагональ прямоугольного параллелепипеда d и его рёбра a, b, c связаны соотношением:

d² = a² + b² + c².

- Из общей формулы для объема призмы можно получить следующую формулу для объема прямоугольного параллелепипеда:

Прямоугольный параллелепипед, все грани которого являются равными квадратами, называется кубом. Помимо прочего, куб является правильной четырехугольной призмой, и вообще правильным многогранником. Для куба справедливы все свойства прямоугольного параллелепипеда и свойства правильных призм, а также:
- Абсолютно все рёбра куба равны между собой.
- Диагональ куба d и длина его ребра a связаны соотношением:

Из формулы для объема прямоугольного параллелепипеда можно получить следующую формулу для объема куба:

Пирамида

К оглавлению…

Определения:

Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и так далее. На рисунке приведены примеры: четырёхугольная и шестиугольная пирамиды.

Основание – многоугольник, которому не принадлежит вершина пирамиды. На чертеже основание это BCDE.

Грани, отличные от основания, называются боковыми. На чертеже это: ABC, ACD, ADE и AEB.

Общая вершина боковых граней называется вершиной пирамиды (именно вершиной всей пирамиды, а не просто вершиной, как все остальные вершины). На чертеже это A.

Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми. На чертеже это: AB, AC, AD и AE.

Обозначая пирамиду, сначала называют ее вершину, а затем – вершины основания. Для пирамиды с чертежа обозначение будет таким: ABCDE.

Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание. Длина этого перпендикуляра обозначается буквой H. На чертеже высота это AG. Обратите внимание: только в случае если пирамида является правильной четырехугольной пирамидой (как на чертеже) высота пирамиды попадает на диагональ основания. В остальных случаях это не так. 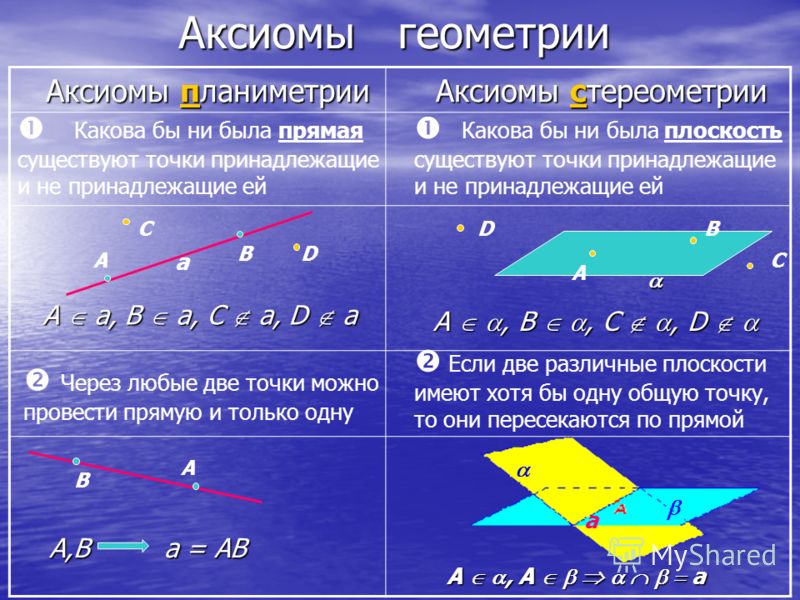В общем случае у произвольной пирамиды, точка пересечения высоты и основания может оказаться где угодно.

Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины. На чертеже это, например, AF.

Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину пирамиды и диагональ основания. На чертеже это, например, ACE.

Еще один стереометрический чертеж с обозначениями для лучшего запоминания (на рисунке правильная треугольная пирамида):

Если все боковые ребра (SA, SB, SC, SD на чертеже ниже) пирамиды равны, то:

Около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр (точка O). Иными словами, высота (отрезок SO), опущенная из вершины такой пирамиды на основание (ABCD), попадает в центр описанной вокруг основания окружности, т. е. в точку пересечения посерединных перпендикуляров основания.

Боковые ребра образуют с плоскостью основания равные углы (на чертеже ниже это углы SAO, SBO, SCO, SDO).

Важно: Также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

Если боковые грани наклонены к плоскости основания под одним углом (углы DMN, DKN, DLN на чертеже ниже равны), то:

В основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр (точка N). Иными словами, высота (отрезок DN), опущенная из вершины такой пирамиды на основание, попадает в центр вписанной в основание окружности, т.е. в точку пересечения биссектрис основания.

Высоты боковых граней (апофемы) равны. На чертеже ниже DK, DL, DM – равные апофемы.

Площадь боковой поверхности такой пирамиды равна половине произведения периметра основания на высоту боковой грани (апофему).

где: P – периметр основания, a – длина апофемы.

Важно: Также верно и обратное, то есть если в основание пирамиды можно вписать окружность, причем вершина пирамиды проецируется в её центр, то все боковые грани наклонены к плоскости основания под одним углом и высоты боковых граней (апофемы) равны.

Правильная пирамида

К оглавлению…

Определение: Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:

Все боковые ребра правильной пирамиды равны.

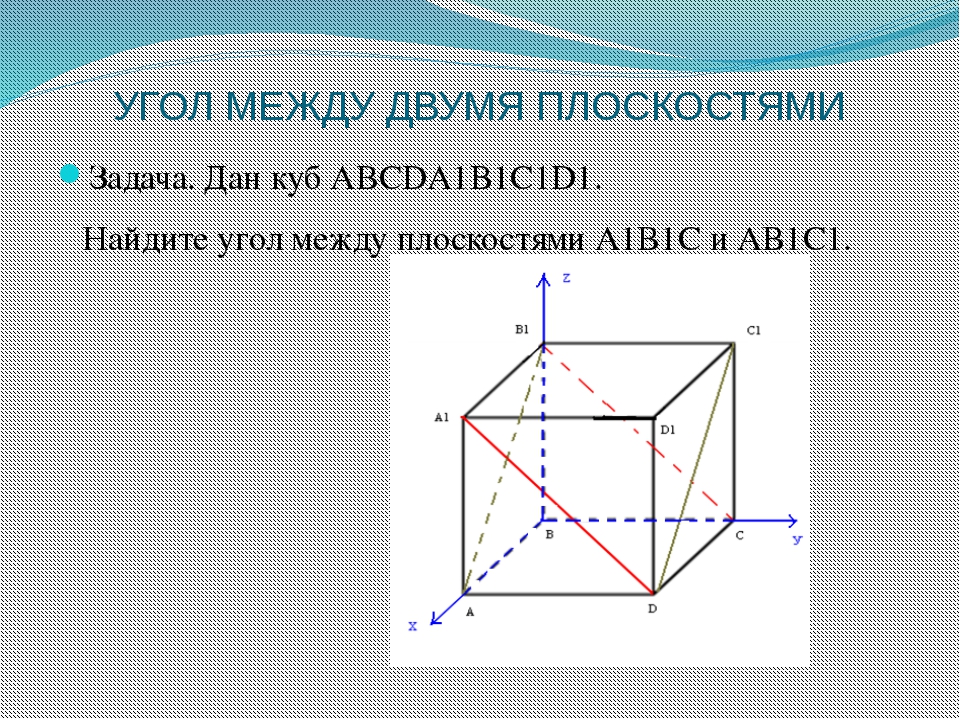
Все боковые грани правильной пирамиды наклонены к плоскости основания под одним углом.

Важное замечание: Как видим правильные пирамиды являются одними из тех пирамид к которым относятся свойства, изложенные чуть выше. Действительно, если основание правильной пирамиды – это правильный многоугольник, то центр его вписанной и описанной окружностей совпадают, а вершина правильной пирамиды проецируется именно в этот центр (по определению). Однако важно понимать, что не только правильные пирамиды могут обладать свойствами, о которых говорилось выше.

В правильной пирамиде все боковые грани – равные равнобедренные треугольники.

В любую правильную пирамиду можно как вписать сферу, так и описать около неё сферу.

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Формулы для объема и площади пирамиды

К оглавлению. ..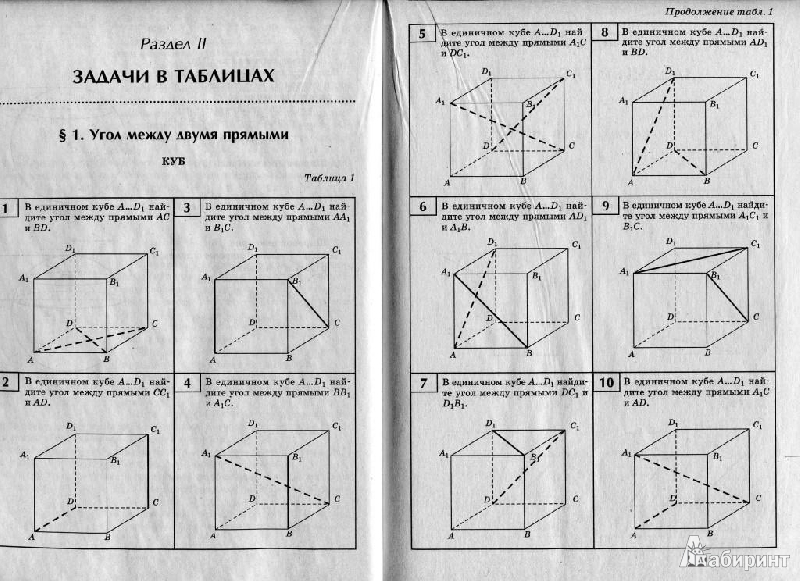

Теорема (об объеме пирамид, имеющих равные высоты и равные площади оснований). Две пирамиды, имеющие равные высоты и равные площади оснований, имеют равные объемы (Вы конечно, наверняка уже знаете формулу для объема пирамиды, ну или видите ее несколькими строчками ниже, и Вам кажется это утверждение очевидным, но на самом деле, если судить «на глаз», то данная теорема не так уж и очевидна (см. рисунок ниже). Это относится кстати и к другим многогранникам и геометрическим фигурам: их внешний вид обманчив, поэтому, действительно – в математике нужно доверять только формулам и правильным расчетам).

Объём пирамиды может быть вычислен по формуле:

где: S_осн – площадь основания пирамиды, h – высота пирамиды.

Боковая поверхность пирамиды равна сумме площадей боковых граней. Для площади боковой поверхности пирамиды можно формально записать такую стереометрическую формулу:

где: S_бок – площадь боковой поверхности, S₁, S₂, S₃ – площади боковых граней.

Полная поверхность пирамиды равна сумме площади боковой поверхности и площади основания:

Тетраэдр

К оглавлению…

Определения:

Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника, иными словами, треугольная пирамида. Для тетраэдра любая из его граней может служить основанием. Всего у тетраэдра 4 грани, 4 вершины и 6 рёбер.

Тетраэдр называется правильным, если все его грани – равносторонние треугольники. У правильного тетраэдра:
1. Все ребра правильного тетраэдра равны между собой.
2. Все грани правильного тетраэдра равны между собой.
3. Периметры, площади, высоты и все остальные элементы всех граней соответственно равны между собой.

На чертеже изображен правильный тетраэдр, при этом треугольники ABC, ADC, CBD, BAD – равны. Из общих формул для объема и площадей пирамиды, а также знаний из планиметрии не сложно получить формулы для объема и площадей правильного тетраэдра (а – длина ребра):

Прямоугольная пирамида

К оглавлению…

Определение: При решении задач по стереометрии, пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В таком случае, это ребро и является высотой пирамиды. Ниже примеры треугольной и пятиугольной прямоугольных пирамид. На рисунке слева SA – ребро, являющееся одновременно высотой.

Усечённая пирамида

К оглавлению…

Определения и свойства:

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Фигура, полученная на пересечении секущей плоскости и исходной пирамиды, также называется основанием усеченной пирамиды. Итак, у усеченной пирамиды на чертеже два основания: ABC и A₁B₁C₁.

Боковые грани усечённой пирамиды являются трапециями. На чертеже это, например, AA₁B₁B.

Боковыми ребрами усеченной пирамиды называются части ребер исходной пирамиды, заключенные между основаниями. На чертеже это, например, AA₁.

Высотой усеченной пирамиды называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания к плоскости другого основания.

Усеченная пирамида называется правильной, если она является многогранником, который отсекается плоскостью, параллельной основанию правильной пирамиды.

Основания правильной усеченной пирамиды – правильные многоугольники.

Боковые грани правильной усеченной пирамиды – равнобедренные трапеции.

Апофемой правильной усеченной пирамиды называется высота ее боковой грани.

Площадью боковой поверхности усеченной пирамиды называется сумма площадей всех ее боковых граней.

Формулы для усеченной пирамиды

Объём усечённой пирамиды равен:

где: S₁ и S₂ – площади оснований, h – высота усечённой пирамиды. Однако на практике, удобнее искать объем усеченной пирамиды так: можно достроить усечённую пирамиду до пирамиды, продлив до пересечения боковые рёбра. Тогда объём усечённой пирамиды можно найти, как разность объёмов всей пирамиды и достроенной части. Площадь боковой поверхности также можно искать как разность между площадями боковой поверхности всей пирамиды и достроенной части. Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы:

где: P₁ и P₂ – периметры оснований правильной усеченной пирамиды, а – длина апофемы. Площадь полной поверхности любой усеченной пирамиды, очевидно, находится как сумма площадей оснований и боковой поверхности:

Пирамида и шар (сфера)

К оглавлению…

Теорема: Около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит вписанный многоугольник (т.е. многоугольник около которого можно описать сферу). Данное условие является необходимым и достаточным. Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им.

Замечание: Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу. Однако, список пирамид около которых можно описать сферу не исчерпывается этими типами пирамид. На чертеже справа, на высоте SH надо выбрать точку О, равноудалённую от всех вершин пирамиды: SO = OВ = OС = OD = OA.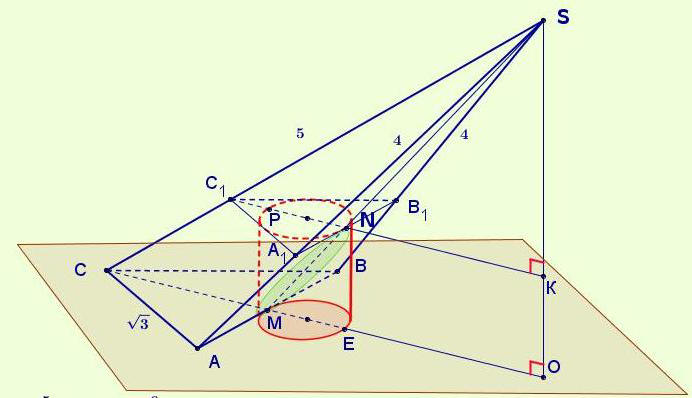 Тогда точка О – центр описанного шара.

Теорема: В пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.

Замечание: Вы, очевидно, не поняли того, что прочитали строчкой выше. Однако, главное запомнить, что любая правильная пирамида является такой, в которую можно вписать сферу. При этом список пирамид, в которые можно вписать сферу не исчерпывается правильными.

Определение: Биссекторная плоскость делит двугранный угол пополам, а каждая точка биссекторной плоскости равноудалена от граней, образующих двугранный угол. На рисунке справа плоскость γ является биссекторной плоскостью двугранного угла, образованного плоскостями α и β.

На стереометрическом чертеже ниже изображен шар вписанный в пирамиду (или пирамида описанная около шара), при этом точка О – центр вписанного шара. Данная точка О равноудалена от всех граней шара, например:

ОМ = ОО₁

Пирамида и конус

К оглавлению…

В стереометрии конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие).

Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые ребра пирамиды равны между собой (необходимое и достаточное условие).

Важное свойство: Высоты у таких конусов и пирамид равны между собой.

Пирамида и цилиндр

К оглавлению…

Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.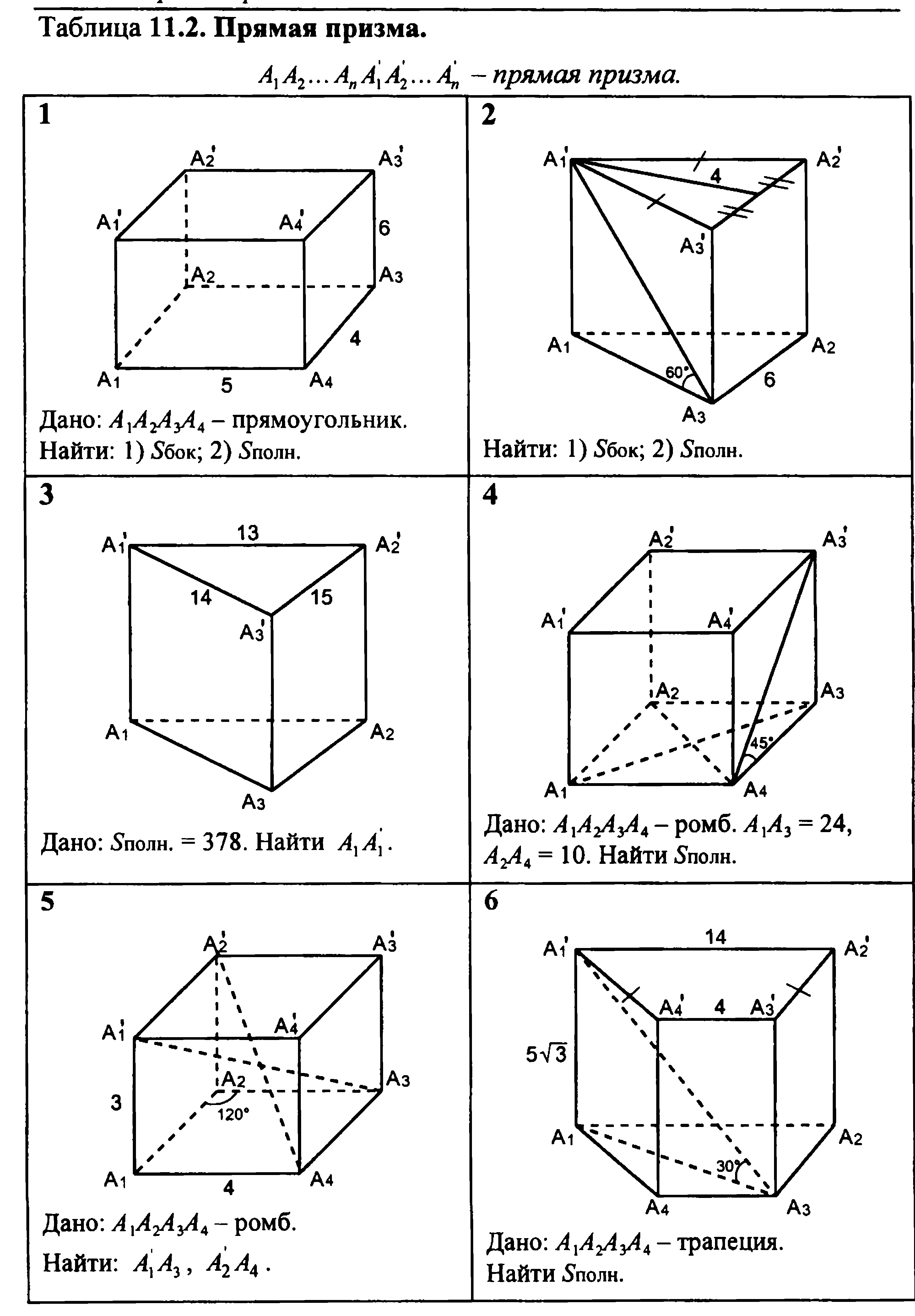

Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания пирамиды. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды – вписанный многоугольник (необходимое и достаточное условие).

Сфера и шар

К оглавлению…

Определения:

Сфера – замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Радиусом сферы называется отрезок, соединяющий центр сферы с какой-либо точкой сферы.

Хордой сферы называется отрезок, соединяющий две точки сферы.

Диаметром сферы называется хорда, проходящая через ее центр. 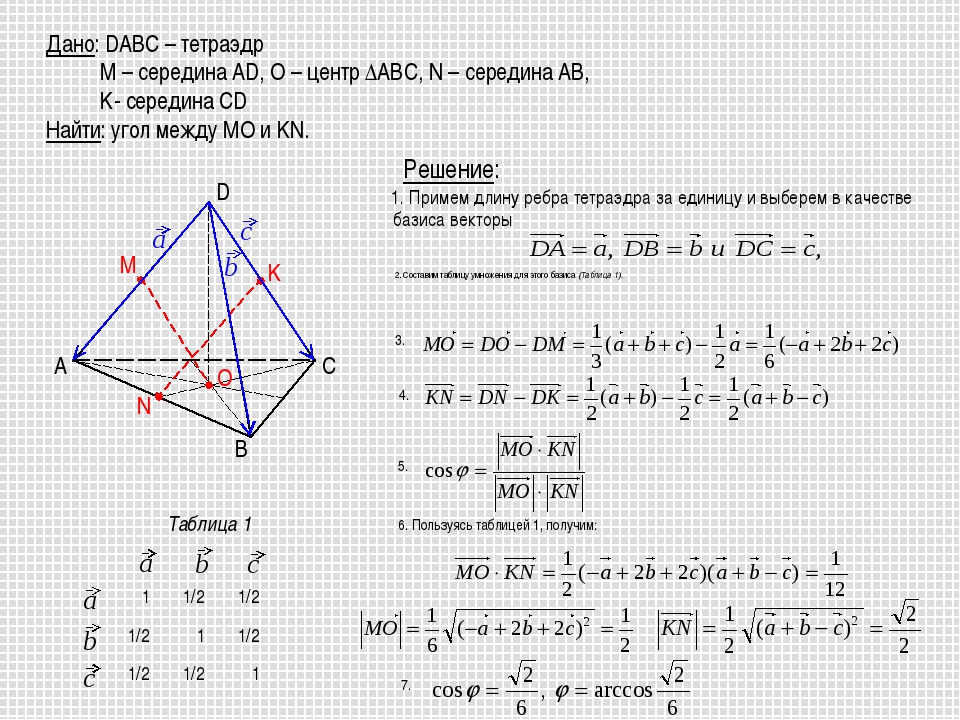Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R.

Шар – геометрическое тело; совокупность всех точек пространства, которые находятся на расстоянии не большем заданного от некоторого центра. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Обратите внимание: поверхность (или граница) шара называется сферой. Можно дать и такое определение шара: шаром называется геометрическое тело, состоящее из сферы и части пространства, ограниченного этой сферой.

Радиусом, хордой и диаметром шара называются радиус, хорда и диаметр сферы, которая является границей данного шара.

Разница между шаром и сферой аналогична разнице между кругом и окружностью. Окружность – это линия, а круг – это ещё и все точки внутри этой линии. Сфера – это оболочка, а шар – это ещё и все точки внутри этой оболочки.

Плоскость, проходящая через центр сферы (шара), называется диаметральной плоскостью.

Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).

Теоремы:

Теорема 1 (о сечении сферы плоскостью). Сечение сферы плоскостью есть окружность. Заметим, что утверждение теоремы остается верным и в случае, если плоскость проходит через центр сферы.

Теорема 2 (о сечении шара плоскостью). Сечение шара плоскостью есть круг, а основание перпендикуляра, проведенного из центра шара к плоскости сечения, есть центр круга, полученного в сечении.

Наибольший круг, из числа тех, которые можно получить в сечении данного шара плоскостью, лежит в сечении, проходящем через центр шара О. Он то и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара AB. Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. A и B), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.

Определения:

Касательной плоскостью к сфере называется плоскость, имеющая со сферой только одну общую точку, а их общая точка называется точкой касания плоскости и сферы.

Касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара.

Любая прямая, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной прямой к сфере (шару). По определению касательная плоскость имеет со сферой только одну общую точку, следовательно, касательная прямая также имеет со сферой только одну общую точку – точку касания.

Теоремы:

Теорема 1 (признак касательной плоскости к сфере). Плоскость, перпендикулярная радиусу сферы и проходящая через его конец, лежащий на сфере, касается сферы.

Теорема 2 (о свойстве касательной плоскости к сфере). Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.

Многогранники и сфера

К оглавлению…

Определение: В стереометрии многогранник (например, пирамида или призма) называется вписанным в сферу, если все его вершины лежат на сфере. При этом сфера называется описанной около многогранника (пирамиды, призмы). Аналогично: многогранник называется вписанным в шар, если все его вершины лежат на границе этого шара. При этом шар называется описанным около многогранника.

Важное свойство: Центр сферы, описанной около многогранника, находится на расстоянии, равном радиусу R сферы, от каждой вершины многогранника. Приведем примеры вписанных в сферу многогранников:

Определение: Многогранник называется описанным около сферы (шара), если сфера (шар) касается всех граней многогранника. При этом сфера и шар называются вписанными в многогранник.

Важно: Центр сферы, вписанной в многогранник, находится на расстоянии, равном радиусу r сферы, от каждой из плоскостей, содержащих грани многогранника. Приведем примеры описанных около сферы многогранников:

Объем и площадь поверхности шара

К оглавлению…

Теоремы:

Теорема 1 (о площади сферы). Площадь сферы равна:

где: R – радиус сферы.

Теорема 2 (об объеме шара). Объем шара радиусом R вычисляется по формуле:

Шаровой сегмент, слой, сектор

К оглавлению…

Шаровой сегмент

В стереометрии шаровым сегментом называется часть шара, отсекаемая секущей плоскостью. При этом соотношение между высотой, радиусом основания сегмента и радиусом шара:

где: h − высота сегмента, r − радиус основания сегмента, R − радиус шара. Площадь основания шарового сегмента:

Площадь внешней поверхности шарового сегмента:

Площадь полной поверхности шарового сегмента:

Объем шарового сегмента:

Шаровой слой

В стереометрии шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями. Площадь внешней поверхности шарового слоя:

где: h − высота шарового слоя, R − радиус шара. Площадь полной поверхности шарового слоя:

где: h − высота шарового слоя, R − радиус шара, r₁, r₂ − радиусы оснований шарового слоя, S₁, S₂ − площади этих оснований. Объем шарового слоя проще всего искать как разность объемов двух шаровых сегментов.

Шаровой сектор

В стереометрии шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше чем пол шара. Площадь полной поверхности шарового сектора:

где: h − высота соответствующего шарового сегмента, r − радиус основания шарового сегмента (или конуса), R − радиус шара. Объем шарового сектора вычисляется по формуле:

Цилиндр

К оглавлению…

Определения:

В некоторой плоскости рассмотрим окружность с центром O и радиусом R. Через каждую точку окружности проведем прямую, перпендикулярную плоскости окружности. Цилиндрической поверхностью называется фигура, образованная этими прямыми, а сами прямые называются образующими цилиндрической поверхности. Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости окружности.

Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые перпендикулярны образующим цилиндрической поверхности. Неформально, можно воспринимать цилиндр как прямую призму, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности цилиндра.

Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между секущими плоскостями, которые перпендикулярны ее образующим, а части (круги), отсекаемые цилиндрической поверхностью на параллельных плоскостях, называются основаниями цилиндра. Основания цилиндра – это два равных круга.

Образующей цилиндра называется отрезок (или длина этого отрезка) образующей цилиндрической поверхности, расположенный между параллельными плоскостями, в которых лежат основания цилиндра. Все образующие цилиндра параллельны и равны между собой, а также перпендикулярны основаниям.

Осью цилиндра называется отрезок, соединяющий центры кругов, являющихся основаниями цилиндра.

Высотой цилиндра называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания цилиндра к плоскости другого основания. В цилиндре высота равна образующей.

Радиусом цилиндра называется радиус его оснований.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

Цилиндр можно получить поворотом прямоугольника вокруг одной из его сторон на 360°.

Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие, а две другие – хорды оснований цилиндра.

Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований.

Если секущая плоскость, перпендикулярна оси цилиндра, то в сечении образуется круг равный основаниям. На чертеже ниже: слева – осевое сечение; в центре – сечение параллельное оси цилиндра; справа – сечение параллельное основанию цилиндра.

Цилиндр и призма

К оглавлению…

Призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра. В этом случае цилиндр называется описанным около призмы. Высота призмы и высота цилиндра в этом случае будут равны. Все боковые ребра призмы будут принадлежать боковой поверхности цилиндра и совпадать с его образующими. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать в такой цилиндр можно также только прямую призму. Примеры:

Призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра. В этом случае цилиндр называется вписанным в призму. Высота призмы и высота цилиндра в этом случае также будут равны. Все боковые ребра призмы будут параллельны образующим цилиндра. Так как под цилиндром мы понимаем только прямой цилиндр, то вписать такой цилиндр можно только в прямую призму. Примеры:

Цилиндр и сфера

К оглавлению…

Сфера (шар) называется вписанной в цилиндр, если она касается оснований цилиндра и каждой его образующей. При этом цилиндр называется описанным около сферы (шара). Сферу можно вписать в цилиндр, только если это равносторонний цилиндр, т.е. диаметр его основания и высота равны между собой. Центром вписанной сферы будет служить середина оси цилиндра, а радиус этой сферы будет совпадать с радиусом цилиндра. Пример:

Цилиндр называется вписанным в сферу, если окружности оснований цилиндра являются сечениями сферы. Цилиндр называется вписанным в шар, если основания цилиндра являются сечениями шара. При этом шар (сфера) называется описанным около цилиндра. Вокруг любого цилиндра можно описать сферу. Центром описанной сферы также будет служить середина оси цилиндра. Пример:

На основе теоремы Пифагора легко доказать следующую формулу, связывающую радиус описанной сферы (R), высоту цилиндра (h) и радиус цилиндра (r):

Объем и площадь боковой и полной поверхностей цилиндра

К оглавлению…

Теорема 1 (о площади боковой поверхности цилиндра): Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту:

где: R – радиус основания цилиндра, h – его высота. Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности прямой призмы.

Площадью полной поверхности цилиндра, как обычно в стереометрии, называется сумма площадей боковой поверхности и двух оснований. Площадь каждого основания цилиндра (т.е. просто площадь круга) вычисляется по формуле:

Следовательно, площадь полной поверхности цилиндра S_{полн. цилиндра} вычисляется по формуле:

Теорема 2 (об объеме цилиндра): Объем цилиндра равен произведению площади основания на высоту:

где: R и h – радиус и высота цилиндра соответственно. Эта формула также легко выводится (доказывается) на основе формулы для объема призмы.

Теорема 3 (Архимеда): Объём шара в полтора раза меньше объёма, описанного вокруг него цилиндра, а площадь поверхности такого шара в полтора раза меньше площади полной поверхности того же цилиндра:

Конус

К оглавлению…

Определения:

Конусом (точнее, круговым конусом) называется тело, которое состоит из круга (называемого основанием конуса), точки, не лежащей в плоскости этого круга (называемой вершиной конуса) и всех возможных отрезков, соединяющих вершину конуса с точками основания. Неформально, можно воспринимать конус как правильную пирамиду, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности конуса.

Отрезки (или их длины), соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Все образующие прямого кругового конуса равны между собой.

Поверхность конуса состоит из основания конуса (круга) и боковой поверхности (составленной из всех возможных образующих).

Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью.

Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом.

Наглядно прямой круговой конус можно представлять себе, как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси. При этом боковая поверхность конуса образуется вращением гипотенузы, а основание – вращением катета, не являющимся осью.

Радиусом конуса называется радиус его основания.

Высотой конуса называется перпендикуляр (или его длина), опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту, т.е. прямая проходящая через центр основания и вершину.

Если секущая плоскость проходит через ось конуса, то сечение равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Такое сечение называется осевым.

Если секущая плоскость проходит через внутреннюю точку высоты конуса и перпендикулярна ей, то сечением конуса является круг, центр которого есть точка пересечения высоты и этой плоскости.

Высота (h), радиус (R) и длина образующей (l) прямого кругового конуса удовлетворяют очевидному соотношению:

Объем и площадь боковой и полной поверхностей конуса

К оглавлению…

Теорема 1 (о площади боковой поверхности конуса). Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:

где: R – радиус основания конуса, l – длина образующей конуса. Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности правильной пирамиды.

Площадью полной поверхности конуса называется сумма площади боковой поверхности и площади основания. Площадь основания конуса (т.е. просто площадь круга) равна: S_осн = πR². Следовательно, площадь полной поверхности конуса S_{полн. конуса} вычисляется по формуле:

Теорема 2 (об объеме конуса). Объем конуса равен одной трети произведения площади основания на высоту:

где: R – радиус основания конуса, h – его высота. Эта формула также легко выводится (доказывается) на основе формулы для объема пирамиды.

Усеченный конус

К оглавлению…

Определения:

Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.

Основание исходного конуса и круг, получающийся в сечении этого конуса плоскостью, называются основаниями, а отрезок, соединяющий их центры — высотой усеченного конуса.

Прямая проходящая через высоту усеченного конуса (т.е. через центры его оснований) является его осью.

Часть боковой поверхности конуса, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конуса, расположенные между основаниями усеченного конуса, называются его образующими.

Все образующие усеченного конуса равны между собой.

Усеченный конус может быть получен при повороте на 360° прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.

Формулы для усеченного конуса:

Объем усеченного конуса равен разности объемов полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Объём усечённого конуса вычисляется по формуле:

где: S₁ = πr₁² и S₂ = πr₂² – площади оснований, h – высота усечённого конуса, r₁ и r₂ – радиусы верхнего и нижнего оснований усеченного конуса. Однако на практике, всё же удобнее искать объем усеченного конуса как разность объёмов исходного конуса и отсеченной части. Площадь боковой поверхности усеченного конуса также можно искать как разность между площадями боковой поверхности исходного конуса и отсеченной части.

Действительно, площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей полного конуса и конуса, отсекаемого плоскостью, параллельной основанию конуса. Площадь боковой поверхности усеченного конуса вычисляется по формуле:

где: P₁ = 2πr₁ и P₂ = 2πr₂ – периметры оснований усеченного конуса, l – длина образующей. Площадь полной поверхности усеченного конуса, очевидно, находится как сумма площадей оснований и боковой поверхности:

Обратите внимание, что формулы для объема и площади боковой поверхности усеченного конуса получены на основе формул для аналогичных характеристик правильной усеченной пирамиды.

Конус и сфера

К оглавлению…

Конус называется вписанным в сферу (шар), если его вершина принадлежит сфере (границе шара), а окружность основания (само основание) является сечением сферы (шара). При этом сфера (шар) называется описанной около конуса. Вокруг прямого кругового конуса всегда можно описать сферу. Центр описанной сферы будет лежать на прямой содержащей высоту конуса, а радиус этой сферы будет равен радиусу окружности, описанной около осевого сечения конуса (это сечение является равнобедренным треугольником). Примеры:

Сфера (шар) называется вписанной в конус, если сфера (шар) касается основания конуса и каждой его образующей. При этом конус называется описанным около сферы (шара). В прямой круговой конус всегда можно вписать сферу. Её центр будет лежать на высоте конуса, а радиус вписанной сферы будет равен радиусу окружности, вписанной в осевое сечение конуса (это сечение является равнобедренным треугольником). Примеры:

Конус и пирамида

К оглавлению…

Конус называется вписанным в пирамиду (пирамида – описанной около конуса), если основание конуса вписано в основание пирамиды, а вершины конуса и пирамиды совпадают.

Пирамида называется вписанной в конус (конус – описанным около пирамиды), если ее основание вписано в основание конуса, а боковые ребра являются образующими конуса.

Высоты у таких конусов и пирамид равны между собой.

Примечание: Подробнее о том, как в стереометрии конус вписывается в пирамиду или описывается около пирамиды уже говорилось в ранее здесь.

Stereometry (Геометрия в пространстве) — WhatMaster

Основные теоремы, аксиомы и определения стереометрии

Вводные определения и аксиомы стереометрии

Некоторые определения:

Многогранник — это геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имея общую сторону, не лежат в одной плоскости. Причем сами многоугольники называются гранями, их стороны — ребрами многогранника, а их вершины — вершинами многогранника.
Фигура, образованная всеми гранями многогранника, называется его поверхностью ( полной поверхности ), а сумма площадей всех его граней называется площадью (полной) поверхности .
Куб — это многогранник с шестью гранями, равными квадратам. Стороны квадратов называются ребрами куба, а вершины — вершинами куба.
Параллелепипед — это многогранник с шестью гранями, каждая из которых представляет собой параллелограмм.Стороны параллелограмма называются ребрами параллелепипеда, а их вершины — вершинами параллелепипеда. Две грани параллелепипеда называются напротив , если у них нет общего ребра, а те, которые имеют общее ребро, называются смежными . Иногда любые две противоположные грани параллелепипеда выделяются и называются основаниями , тогда другие грани являются боковыми гранями , а их стороны, соединяющие вершины оснований параллелепипеда, являются его боковыми сторонами .
Прямой параллелепипед — это параллелепипед, боковые грани которого являются прямоугольниками. Прямоугольный параллелепипед — это параллелепипед, все грани которого являются прямоугольниками. Обратите внимание, что каждый прямоугольный параллелепипед является прямым параллелепипедом, но не каждый прямой параллелепипед является прямоугольным.
Две вершины параллелепипеда, не принадлежащие одной грани, называются напротив . Отрезок, соединяющий противоположные вершины параллелепипеда, называется диагональю параллелепипеда .У параллелепипеда всего четыре диагонали.
Призма (угол n- ) представляет собой многогранник, две грани которого равны n -счетчиков, а другие n граней являются параллелограммами. Равные n -угольников называются основаниями , а параллелограммы называются боковыми гранями призмы . Прямая призма — это призма, боковые грани которой прямоугольные. Обычная призма n — это призма, у которой все боковые грани являются прямоугольниками, а ее основания — правильными счетчиками n .
Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначена S _{стороной}). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается S _full).
Пирамида ( n- угловая) — это многогранник с одной гранью, у некоторых n -угольник, а у другой n граней, треугольники с общей вершиной; An n -угольник называется base ; треугольники с общей вершиной называются боковыми гранями , а их общая вершина называется вершиной пирамиды .Стороны пирамиды называются ее ребер , а ребра, сходящиеся в вершине, называются боковыми .
Сумма площадей боковых сторон пирамиды называется площадью боковой поверхности пирамиды (обозначена S _{стороной}). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается как S _полная).
Обычная n -фунтовая пирамида — это такая пирамида, основание которой представляет собой правильный n -угольник, а все боковые грани равны между собой.У правильной пирамиды боковые грани представляют собой равнобедренные треугольники, равные друг другу.
Треугольная пирамида называется тетраэдром , если все ее грани равны правильным треугольникам. Тетраэдр — это частный случай правильной треугольной пирамиды (то есть не каждая правильная треугольная пирамида будет тетраэдром).

Аксиомы стереометрии:

Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.
Если две точки прямой лежат на плоскости, то все точки прямой лежат в этой плоскости.
Если две плоскости имеют общую точку, то у них есть общая линия, на которой лежат все общие точки этих плоскостей.

Последствия аксиом стереометрии:

Теорема 1. Отдельная плоскость проходит через линию, а не лежит на ней.
Теорема 2. Одна плоскость проходит через две пересекающиеся прямые.
Теорема 3. Одна плоскость проходит через две параллельные прямые.

Построение сечений в стереометрии

Для решения задач стереометрии необходимо срочно построить сечение многогранников (например, пирамиды, параллелепипеда, куба, призмы) на фигуре с определенной плоскостью. Дадим несколько определений, поясняющих, что такое секция:

Секущая плоскость пирамиды (призма, параллелепипед, куб) — это такая плоскость, по обе стороны от которой расположены точки данной пирамиды (призмы, параллелепипеда, куба).
Сечение пирамиды (призма, параллелепипед, куб) — это фигура, состоящая из всех точек, общих для пирамиды (призма, параллелепипед, куб), и плоскости отсечения.
Режущая плоскость пересекает грани пирамиды (параллелепипед, призма, куб) по сегментам, поэтому сечение представляет собой многоугольник, лежащий в плоскости сечения, стороны которого являются указанными сегментами.

Для построения сечения пирамиды (призмы, параллелепипеда, куба) можно и нужно построить точки пересечения секущей плоскости с гранями пирамиды (призма, параллелепипед, куб ) и соедините каждые два из них, лежащие на одной грани. Обратите внимание, что последовательность построения вершин и сторон сечения не имеет значения. Построение поперечных сечений многогранников основано на двух конструктивных задачах:

Линии пересечения двух плоскостей.

Чтобы построить прямую, по которой пересекаются две плоскости α и β (например, секущая плоскость и плоскость грани многогранника), нужно построить две общие точки, затем прямую, проходящую через эти точки являются линией пересечения плоскостей α и β .

Точки пересечения прямой и плоскости.

Для построения точки пересечения прямой l и плоскости α, необходимо построить точку пересечения прямой l и прямой l ₁, вдоль которой расположена плоскость α. и любая плоскость, содержащая линию l , пересекаются.

Взаимное расположение прямых и плоскостей в стереометрии

Определение: При решении задач стереометрии две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются.Если строки a и b или AB и CD параллельны , то напишите:

Некоторые теоремы:

Теорема 1. Через любую точку пространства, которая не лежит на данной прямой, проходит единственная прямая линия, параллельная этой прямой.
Теорема 2. Если одна из двух параллельных прямых пересекает эту плоскость, то другая прямая пересекает эту плоскость.
Теорема 3 (знак параллельных прямых). Если две прямые параллельны третьей прямой, то они параллельны друг другу.
Теорема 4 (о точке пересечения диагоналей параллелепипеда). Диагональ параллелепипеда пересекается в одной точке и делит эту точку пополам.

Существует три случая взаимного расположения линии и плоскости в стереометрии:

Прямая лежит на плоскости (каждая точка прямой лежит на плоскости).
Прямая и плоскость пересекаются (имеют общую точку).
Прямая линия и плоскость не имеют общих точек.

Определение: Прямая и плоскость называются параллельными , если у них нет общих точек. Если линия a является параллельной плоскости β , то напишите:

Теоремы:

Теорема 1 (признак параллельности прямой и плоскости).Если прямая, не лежащая в этой плоскости, параллельна любой прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
Теорема 2. Если плоскость (на рисунке — α ) проходит через прямую (на рисунке — c ) параллельную другой плоскости (на рисунке — β ) и пересекает эту плоскость, то линия пересечения плоскостей (на рисунке — d ) параллельна этой прямой:

Если две разные прямые лежат в одной плоскости, то они либо пересекаются, либо параллельны.Однако в пространстве (т.е. в стереометрии) возможен и третий случай, когда нет плоскости, в которой лежат две прямые (они не пересекаются и не параллельны).

Определение: Две прямые называются пересеченными , если нет плоскости, в которой они обе лежат.

Теоремы:

Теорема 1 (знак пересечения линий). Если одна из двух прямых лежит в определенной плоскости, а другая прямая линия пересекает эту плоскость в точке, которая не принадлежит первой прямой, то эти прямые пересекаются.
Теорема 2. Через каждую из двух пересеченных прямых проходит одна плоскость, параллельная другой прямой.

Теперь мы вводим понятие угла между пересекающимися прямыми линиями. Пусть a и b будут двумя наклонными линиями. Возьмем произвольную точку O в пространстве и проведем через нее прямые a ₁ и b ₁, параллельные прямым a и b, соответственно.Угол между линиями пересечения a и b — это угол между построенными линиями пересечения a ₁ и b ₁.

Однако на практике точку O чаще выбирают так, чтобы она принадлежала одной из прямых. Обычно это не только элементарно удобнее, но и рациональнее и правильнее с точки зрения построения чертежа и решения задачи. Поэтому для угла между пересеченными прямыми дадим следующее определение:

Определение: Пусть a и b будут двумя наклонными линиями.Возьмем произвольную точку O на одном из них (в нашем случае на прямой b ) и проведем через нее прямую, параллельную другому из них (в нашем случае a _{1 — это} параллель. до a ). Угол между пересекающимися прямыми a и b — это угол между построенной прямой и прямой, содержащей точку O (в нашем случае это угол β между прямыми a ₁ и b ).

Определение: Две прямые называются взаимно перпендикулярными (перпендикулярными), если угол между ними равен 90 °. И пересекающиеся прямые, и прямые, лежащие и пересекающиеся в одной плоскости, могут быть перпендикулярными. Если линия a находится на перпендикулярно линии b , то напишите:

Определение: Две плоскости называются параллельными , если они не пересекаются, т.е.е. не имеют общих точек. Если две плоскости α и β параллельны , то, как обычно, пишут:

Теоремы:

Теорема 1 (признак параллельности плоскостей). Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым линиям другой плоскости, то эти плоскости параллельны.
Теорема 2 (о свойстве противоположных граней параллелепипеда). Противоположные грани параллелепипеда лежат в параллельных плоскостях.
Теорема 3 (о прямых пересечениях двух параллельных плоскостей третьей плоскостью). Если две параллельные плоскости пересекаются третьей, то их прямые пересечения параллельны друг другу.
Теорема 4. Отрезки параллельных прямых, расположенных между параллельными плоскостями, равны.
Теорема 5 (о существовании единственной плоскости, параллельной данной плоскости и проходящей через точку за ее пределами). Через точку, не лежащую в этой плоскости, проходит единственная плоскость, параллельная этой.

Определение: Линия, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости. Если линия a расположена на перпендикулярно плоскости β , то напишите, как обычно:

Теоремы:

Теорема 1. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то другая прямая перпендикулярна этой прямой.
Теорема 2. Если одна из двух параллельных прямых перпендикулярна плоскости, то другая прямая перпендикулярна этой плоскости.
Теорема 3 (о параллельных прямых, перпендикулярных плоскости). Если две прямые перпендикулярны одной плоскости, то они параллельны.
Теорема 4 (признак перпендикулярности прямой и плоскости). Если прямая линия перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Теорема 5 (на плоскости, проходящей через данную точку и перпендикулярной данной прямой). Через любую точку пространства проходит единственная плоскость, перпендикулярная этой прямой.
Теорема 6 (о прямой, проходящей через заданную точку и перпендикулярной этой плоскости). Через любую точку пространства проходит единственная прямая, перпендикулярная этой плоскости.
Теорема 7 (о свойстве диагонали прямоугольного параллелепипеда).Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, имеющих общую вершину:

Следствие: Все четыре диагонали прямоугольного параллелепипеда равны друг другу.

Теорема о трех перпендикулярах

Пусть точка A не лежит в плоскости α . Проведите прямую линию через точку A , перпендикулярную плоскости α , и обозначьте буквой O точку пересечения этой линии с плоскостью α .Перпендикуляр, проведенный из точки A к плоскости α , называется отрезком AO , точка O называется основанием перпендикуляра. Если AO перпендикулярно плоскости α , а M — произвольная точка этой плоскости, отличная от точки O , то отрезок AM называется наклонным, проведенный от точки И до плоскость α , а точка M — основание наклонное.Отрезок OM — это ортогональная проекция (или, короче, проекция) наклонного AM на плоскость α . Приведем теорему, которая играет важную роль в решении многих задач.

Теорема 1 (о трех перпендикулярах): прямая линия, проведенная на плоскости и перпендикулярная проекции, наклоненной на эту плоскость, перпендикулярна наиболее наклонной. Верно и обратное:

Теорема 2 (о трех перпендикулярах): прямая линия, проведенная на плоскости и перпендикулярная наклонной, также перпендикулярна своей проекции на эту плоскость. Эти теоремы для обозначений на рисунке выше можно резюмировать следующим образом:

Теорема: Если из одной точки, взятой за пределами плоскости, провести к этой плоскости перпендикуляр и две наклонные линии, то:

два косых, имеющих равные выступы, равны;
из двух наклонных больше, чем тот, у которого выступ больше.

Определение расстояний по объектам в космосе:

Расстояние от точки до плоскости — это длина перпендикуляра, проведенного из этой точки в эту плоскость.
Расстояние между параллельными плоскостями — это расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.
Расстояние между прямой линией и параллельной ей плоскостью — это расстояние от произвольной точки прямой линии до плоскости.
Расстояние между пересекающимися линиями — это расстояние от одной из пересекающихся линий до плоскости, проходящей через другую прямую и параллельную первой прямой.

Определение: В стереометрии ортогональная проекция линии a на плоскость α является проекцией этой линии на плоскость α , если линия, определяющая направление проектирования, перпендикулярна плоскости α .

Примечание: Как видно из предыдущего определения, существует множество прогнозов. Другие (кроме ортогональной) проекции прямой на плоскость могут быть построены, если прямое, определяющее направление проекции, не перпендикулярно плоскости. Однако именно с ортогональной проекцией прямой на плоскость в будущем мы столкнемся в задачах. А ортогональную проекцию мы будем называть просто проекцией (как на рисунке).

Определение: Угол между прямой линией, не перпендикулярной плоскости, и этой плоскостью — это угол между прямой линией и ее ортогональной проекцией на эту плоскость (угол AOA на рисунке выше).

Теорема: Угол между прямой линией и плоскостью — это наименьший из всех углов, которые данная прямая образует с прямыми, лежащими в данной плоскости и проходящими через точку пересечения прямой и плоскости.

Двугранный угол

Определения:

Двугранный угол — это фигура, образованная двумя полуплоскостями с общей линией границы и частью пространства, для которой эти полуплоскости служат границей.
Линейный угол двугранного угла — это угол, стороны которого представляют собой лучи с общим началом на краю двугранного угла, которые удерживаются в его гранях перпендикулярно краю.

Таким образом, линейный угол двугранного угла — это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его краю.Все линейные углы двугранного угла равны между собой. Градусная мера двугранного угла — это градусная мера его линейного угла.

Двугранный угол называется прямым углом (острым, тупым), если его градус составляет 90 ° (менее 90 °, более 90 °). В дальнейшем при решении задач стереометрии под двугранным углом всегда будем понимать тот линейный угол, градусная мера которого удовлетворяет условию:

Определения:

Двугранный угол на краю многогранника — это двугранный угол, ребро которого содержит ребро многогранника, а грани двугранного угла содержат грани многогранника, которые пересекаются по этому ребру многогранника.
Угол между пересекающимися плоскостями — это угол между линиями, проведенными, соответственно, в этих плоскостях, перпендикулярными линии их пересечения через некоторые из ее точек.
Две плоскости называются перпендикулярными, если угол между ними составляет 90 °.

Теоремы:

Теорема 1 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую линию, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Теорема 2. Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, на которой они пересекаются, перпендикулярна другой плоскости.

Формы симметрии

Определения:

Точки M и M ₁ называются симметричными относительно точки O , если O является средней точкой сегмента MM ₁.
Точки M и M ₁ называются симметричными относительно прямой l , если прямая l проходит через середину отрезка MM ₁ и перпендикулярна к нему.
Точки M и M ₁ называются симметричными относительно плоскости α , если плоскость α проходит через середину сегмента MM ₁ и перпендикулярна ему. сегмент.
Точка O (линия l , плоскость α ) называется центром (ось, плоскость) симметрии фигуры , если каждая точка фигуры симметрична относительно точки O (линия l , плоскость α ) до определенной точки того же рисунка.
Выпуклый многогранник называется правильным , если все его грани — правильные многоугольники, равные друг другу и одинаковое количество ребер сходится в каждой вершине.

Призма

Определения:

Призма — это многогранник, две грани которого представляют собой равные многоугольники, лежащие в параллельных плоскостях, а другие грани являются параллелограммами, имеющими общие стороны с этими многоугольниками.
Основания — это две грани, которые представляют собой равные многоугольники, лежащие в параллельных плоскостях. Чертеж: ABCDE и KLMNP .
Боковые грани — все грани, кроме оснований.Каждая боковая грань обязательно представляет собой параллелограмм. Чертеж: ABLK , BCML , CDNM , DEPN и EAKP .
Боковая поверхность — соединение боковых граней.
Полная поверхность — совмещает основание и боковую поверхность.
Боковые кромки являются общими сторонами боковых граней. Чертеж: AK , BL , CM , DN и EP .
Высота — отрезок, соединяющий основания призм и перпендикулярный им. На чертеже, например, KR .
Диагональ — это сегмент, соединяющий две вершины призмы, которые не принадлежат одной грани. На чертеже это, например, BP .
Диагональная плоскость — это плоскость, проходящая через боковой край призмы и диагональ основания. Другое определение: диагональная плоскость — это плоскость, проходящая через два боковых края призмы, которые не принадлежат одной грани.
Диагональное сечение — пересечение призмы и диагональной плоскости. В поперечном сечении образуется параллелограмм, в том числе иногда его частные случаи — ромб, прямоугольник и квадрат. На чертеже, например, это EBLP .
Перпендикулярное (ортогональное) сечение — это пересечение призмы и плоскости, перпендикулярной ее боковому краю.

Свойства и формулы для призмы:

Основания призмы — равные многоугольники.
Боковые грани призмы — параллелограммы.
Боковые края призмы параллельны и равны.
Объем призмы равен произведению ее высоты на площадь основания:

где: S _D — площадь основания (на чертеже это, например, ABCDE ), h — высота (на чертеже это MN ).

Общая площадь призмы равна сумме площади ее боковой поверхности и площади двойного основания:

Перпендикулярное сечение перпендикулярно всем боковым краям призмы (на рисунке ниже перпендикулярное сечение составляет A ₂ B ₂ C ₂ D ₂ E ₂).
Углы перпендикулярного сечения — это линейные углы двугранных углов на соответствующих боковых кромках.
Перпендикулярное (ортогональное) сечение, перпендикулярное всем боковым граням.
Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину боковой грани:

где: S _Sich — площадь перпендикулярного сечения, l — длина боковой кромки (на рисунке ниже это, например, AA ₁ или BB ₁ и так далее).

Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину боковой грани:

где: P _Sech — периметр перпендикулярного сечения, l — длина боковой кромки.

Типы призм в стереометрии:

Если боковые грани не перпендикулярны основанию, то такая призма называется наклонной (показана выше).Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые грани не перпендикулярны этим плоскостям, а параллельны друг другу. Боковые грани — параллелограммы.
Прямая призма — это призма, у которой все боковые грани перпендикулярны основанию. В прямой призме боковые грани имеют высоту. Боковые грани прямой призмы — прямоугольники. А площадь и периметр основания равны, соответственно, площади и периметру перпендикулярного сечения (для прямой призмы, вообще говоря, перпендикулярное сечение полностью совпадает с фигурой основания).Следовательно, площадь боковой поверхности прямой призмы равна произведению периметра основания и длины бокового края (или, в данном случае, высоты призмы):

где: P _bas — периметр основания прямой призмы, l — длина бокового края, равная высоте призмы ( h ). Объем прямой призмы находится по общей формуле: V = S _{основание} ∙ h = S _{основание} ∙ л .

Правильная призма — это призма, в основании которой лежит правильный многоугольник (то есть такой, у которого все стороны и все углы равны друг другу), а боковые грани перпендикулярны плоскостям основания. Примеры правильных призм:

Свойства правильной призмы:

Основания правильной призмы — правильные многоугольники.
Боковые грани правильной призмы представляют собой равные прямоугольники.
Боковые края обычной призмы равны.
Правильная призма прямая.

Параллелепипед

Определение: Параллелепипед — это призма, основание которой — параллелограмм. В этом определении ключевое слово — «призма». Таким образом, параллелепипед — это частный случай призмы, который отличается от общего случая только тем, что у него в основании не произвольный многоугольник, а параллелограмм. Поэтому все приведенные выше свойства, формулы и определения, касающиеся призмы, остаются актуальными для параллелепипеда.Однако есть несколько дополнительных свойств, характерных для параллелепипеда.

Прочие свойства и определения:

Две грани параллелепипеда, у которых нет общего ребра, называются напротив , а те, которые имеют общий край, — , смежные .
Две вершины параллелепипеда, не принадлежащие одной грани, называются напротив .
Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда .
У параллелепипеда шесть граней, и все они параллелограммы.
Противоположные грани параллелепипеда попарно равны и параллельны.
У параллелепипеда четыре диагонали; все они пересекаются в одной точке, и каждая из них делится этой точкой пополам.
Если четыре боковые грани параллелепипеда представляют собой прямоугольники (а основания — произвольные параллелограммы), то он называется прямым (в этом случае, как и в случае с прямой призмой, все боковые грани перпендикулярны основаниям).Все свойства и формулы прямой призмы актуальны для прямого параллелепипеда.
Параллелепипед называется косым , если не все его боковые грани являются прямоугольниками.
Объем прямого или наклонного параллелепипеда равен , рассчитанному по общей формуле для объема призмы, т.е. равному произведению площади основания параллелепипеда на его высоту ( V = S _база ∙ ч ).
Прямой параллелепипед, у которого все шесть граней — прямоугольники (то есть, кроме боковых граней, тоже прямоугольники), называется прямоугольником . Для прямоугольного параллелепипеда актуальны все свойства прямого параллелепипеда, а также:
Диагональ прямоугольного параллелепипеда d и его края a , b , c связаны соотношением:

d ² = a ² + b ² + c ².

- Из общей формулы для объема призмы можно получить следующую формулу для объема прямоугольного параллелепипеда :

Прямоугольный параллелепипед, все грани которого равны квадратам, называется кубом . Помимо прочего, куб — это правильная четырехугольная призма и, как правило, правильный многогранник. Для куба действуют все свойства прямоугольного параллелепипеда и свойства правильных призм, а также:
Абсолютно все грани куба равны друг другу.
Диагональ куба d и длина его ребра a связаны соотношением:

Из формулы объема прямоугольного параллелепипеда можно получить следующую формулу для объема куба :

Пирамида

Определения:

Пирамида — это многогранник, основание которого — многоугольник, а остальные грани — треугольники с общей вершиной.По количеству углов основания пирамиды различают треугольные, четырехугольные и так далее. На рисунке показаны примеры: четырехугольная и шестиугольная пирамиды.

Основание — это многоугольник, не принадлежащий вершине пирамиды. На чертеже базой является BCDE .
Края, отличные от основания, называются стороной . Чертеж: ABC , ACD , ADE и AEB .
Общая вершина боковых граней называется вершиной пирамиды (а именно вершиной всей пирамиды, а не только вершиной, как все остальные вершины). Чертеж A .
Ребра, соединяющие вершину пирамиды с вершинами основания, называются стороной . Чертеж: AB , AC , AD и AE .
Обозначая пирамиду, сначала назовите ее вершину, а затем — вершину основания.Для пирамиды с чертежа обозначение будет: ABCDE .

Высота пирамиды называется перпендикулярной и проводится от вершины пирамиды к ее основанию. Длина этого перпендикуляра обозначается буквой H . На чертеже высота AG . Примечание: только если пирамида является правильной четырехугольной пирамидой (как на рисунке), высота пирамиды приходится на диагональ основания.В других случаях это не так. В общем случае для произвольной пирамиды точка пересечения высоты и основания может находиться где угодно.
Апофема — высота боковой грани правильной пирамиды , начерченная с ее вершины. На чертеже это, например, AF .
Диагональное сечение пирамиды — это сечение пирамиды, проходящее через вершину пирамиды и диагональ основания. На чертеже это, например, ACE .

Другой стереометрический рисунок с обозначениями для лучшего запоминания (на рисунке правильная треугольная пирамида):

Если все боковые грани ( SA , SB , SC , SD на рисунке ниже) пирамиды равны, то:

Окружность может быть описана около основания пирамиды, причем вершина пирамиды проецируется в ее центр (точка O ).Другими словами, высота (сегмент SO ), опущенная от вершины такой пирамиды к основанию ( ABCD ), попадает в центр описанной окружности, т.е. база.
Боковые кромки образуют равные углы с базовой плоскостью (на рисунке ниже это углы SAO , SBO , SCO , SDO ).

Важно: Верно и обратное, то есть, если боковые края образуют равные углы с базовой плоскостью или если можно описать круг около основания пирамиды, а вершина пирамиды проецируется в ее центр, тогда все боковые грани пирамиды равны.

Если боковые грани наклонены к базовой плоскости на один угол (углы DMN , DKN , DLN на чертеже равны ниже), то:

В основании пирамиды можно вписать круг, причем вершина пирамиды проецируется в ее центр (точка N ). Другими словами, высота (сегмент DN ), опущенная от вершины такой пирамиды к основанию, попадает в центр круга, вписанного в основание, т.е.е. на пересечении биссектрис основания.
Высота боковых граней (апофем) равна. На рисунке ниже DK , DL , DM являются равными апофемами.
Площадь боковой поверхности такой пирамиды равна половине произведения периметра основания на высоту боковой грани (апофемы).

, где: P — периметр основания, a — длина апофемы.

Важно: Верно и обратное, то есть если круг может быть вписан в основание пирамиды и вершина пирамиды проецируется в ее центр, то все боковые грани наклонены к плоскости основания одновременно. угол и высота боковых граней (апофемы) равны.

Правильная пирамида

Определение: пирамида называется правильная , если ее основание является правильным многоугольником, а вершина проецируется в центр основания.Тогда он имеет следующие свойства:

Все боковые грани правильной пирамиды равны.
Все боковые грани правильной пирамиды наклонены к плоскости основания под одним углом.

Важное примечание: Как видите, правильные пирамиды — это одна из тех пирамид, с которыми связаны описанные выше свойства. Действительно, если основание правильной пирамиды — правильный многоугольник, то центры вписанной и описанной окружностей совпадают, и вершина правильной пирамиды проецируется в этот центр (по определению).Однако важно понимать, что , а не только обычные пирамиды могут обладать указанными выше свойствами.

В правильной пирамиде все боковые грани представляют собой равнобедренные треугольники.
В любой обычной пирамиде вы можете войти в сферу или описать сферу рядом с ней.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания и апофемы.

Формулы объема и площади пирамиды

Теорема (об объеме пирамид, имеющих одинаковую высоту и равные площади оснований).Две пирамиды, которые имеют равную высоту и равные площади основания, имеют равные объемы (конечно, вы, вероятно, уже знаете формулу объема пирамиды, ну или видите ее несколькими строками ниже, и вы думаете, что это утверждение очевидно, но на самом деле, судя по «глазу», эта теорема не так очевидна (см. рисунок ниже). Это касается и других многогранников и геометрических фигур: их внешний вид обманчив, поэтому в математике нужно доверять только формулам и правильным вычислениям.

Объем пирамиды можно рассчитать по формуле:

где: S _осн — площадь основания пирамиды, h — высота пирамиды.

Боковая поверхность пирамиды равна сумме площадей боковых граней. Для площади боковой поверхности пирамиды формально можно записать следующую стереометрическую формулу:

где: S _{сторона} — площадь боковой поверхности, S ₁, S ₂, S ₃ — площадь боковых граней.

Общая площадь пирамиды равна сумме площади боковой поверхности и площади основания:

Тетраэдр

Определения:

Тетраэдр — простейший многогранник, грани которого представляют собой четыре треугольника, другими словами, треугольную пирамиду.Для тетраэдра любая его грань может служить основанием. Всего у тетраэдра 4 грани, 4 вершины и 6 ребер.
Тетраэдр называется правильным , если все его грани представляют собой равносторонние треугольники. В правильном тетраэдре:
Все ребра правильного тетраэдра равны.
Все грани правильного тетраэдра равны.
Периметры, площади, высоты и все остальные элементы всех граней соответственно равны друг другу.

На чертеже показан правильный тетраэдр, в котором треугольники ABC , ADC , CBD , BAD равны .Из общих формул для объема и площади пирамиды, а также знаний из планиметрии несложно получить формулы для объема и площади правильного тетраэдра ( a — длина ребра ):

Прямоугольная пирамида

Определение: При решении задач стереометрии пирамида называется прямоугольной , если одна из боковых сторон пирамиды перпендикулярна основанию. В данном случае это ребро — высота пирамиды.Ниже приведены примеры треугольных и пятиугольных прямоугольных пирамид. На рисунке слева SA — это край, который также является высотой.

Усеченная пирамида

Определения и свойства:

Усеченная пирамида — это многогранник, заключенный между основанием пирамиды и секущей плоскостью, параллельной ее основанию.
Форма, полученная на пересечении плоскости сечения и исходной пирамиды, также называется основанием усеченной пирамиды .Итак, усеченная пирамида на чертеже имеет два основания: ABC и A ₁ B ₁ C ₁.
Боковые грани усеченной пирамиды — трапеции. Чертеж имеет вид, например, AA ₁ B ₁ B .
Боковые края усеченной пирамиды — это части краев исходной пирамиды, заключенные между основаниями. На чертеже, например, AA ₁.
Высотой усеченной пирамиды называется перпендикуляр (или длина этого перпендикуляра), проведенный из некоторой точки плоскости одного основания в плоскость другого основания.
Усеченная пирамида называется правильной , если это многогранник, обрезанный плоскостью, параллельной основанию правильной пирамиды .
Основания правильной усеченной пирамиды — правильные многоугольники.
Боковые грани правильной усеченной пирамиды — равнобедренные трапеции.
Высота его боковой грани называется апофемой правильной усеченной пирамиды .
Площадь боковой поверхности усеченной пирамиды — это сумма площадей всех ее боковых граней.

Формулы усеченной пирамиды

Объем усеченной пирамиды:

где: S ₁ и S ₂ — площади основания, h — высота усеченной пирамиды.Однако на практике объем усеченной пирамиды удобнее искать так: можно завершить усеченную пирамиду до пирамиды, расширив боковые грани до пересечения. Тогда объем усеченной пирамиды можно найти как разницу между объемами всей пирамиды и завершенной части. Площадь боковой поверхности также можно искать как разность между площадями боковых поверхностей всей пирамиды и завершенной части. Площадь боковой поверхности правильной усеченной пирамиды равна полусумме периметров ее оснований и апофемы:

, где: P ₁ и P ₂ — периметры основания регулярной усеченной пирамиды , и — длина апофемы.Общая площадь любой усеченной пирамиды, очевидно, определяется как сумма площадей основания и боковой поверхности:

Пирамида и шар (сфера)

Теорема: Вокруг пирамиды можно описать сферу , когда вписанный многоугольник лежит в основании пирамиды (то есть многоугольник, около которого можно описать сферу). Это условие необходимо и достаточно. Центром сферы будет точка пересечения плоскостей, проходящих через середины ребер пирамиды, перпендикулярных им.

Примечание: Из этой теоремы следует, что сферу можно описать как около любого треугольника, так и около любой правильной пирамиды. Однако список пирамид, вокруг которых можно описать объем, не ограничивается этими типами пирамид. На рисунке справа на высоте SH, необходимо выбрать точку O , равноудаленную от всех вершин пирамиды: SO = OB = OС = OD = ОА .Тогда точка O является центром описываемого шара.

Теорема: Сфера может быть вписана в пирамиду , когда биссектрисы внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.

Примечание: Вы явно не поняли то, что прочитали в строке выше. Однако главное помнить, что любая правильная пирамида — это пирамида, в которую можно вписать сферу .Более того, список пирамид, в которые можно войти в сферу, не исчерпывается правильными.

Определение: Биссектриса делит двугранный угол пополам, и каждая точка биссектрисы равноудалена от граней, образующих двугранный угол. На рисунке справа плоскость γ является биссектрисой двугранного угла, образованного плоскостями α и β .

На стереометрическом рисунке ниже показан шар, вписанный в пирамиду (или пирамиду, описанную рядом с шаром), а точка O является центром вписанного шара.Эта точка O находится на равном расстоянии от всех граней шара, например:

OM = OO ₁

Пирамида и конус

К оглавлению…

В стереометрии конус называется вписанным в пирамиду , если их вершины совпадают, а его основание вписано в основание пирамиды. Причем вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны друг другу (необходимое и достаточное условие).

Конус описывается так, как описано около пирамиды , когда их вершины совпадают, а его основание описывается возле основания пирамиды. Более того, описать конус возле пирамиды можно только тогда, когда все боковые грани пирамиды равны между собой (необходимое и достаточное условие).

Важное свойство: Высота таких конусов и пирамид равна друг другу.

Пирамида и цилиндр

Цилиндр называется вписанным в пирамиду , если его одно основание совпадает с кругом, вписанным в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.

Цилиндр описывается так, как описано рядом с пирамидой , если вершина пирамиды принадлежит ее одному основанию, а его другое основание описывается рядом с основанием пирамиды. Более того, описать цилиндр возле пирамиды можно только при наличии вписанного многоугольника в основание пирамиды (необходимое и достаточное условие).

Сфера и шар

Определения:

Сфера — это замкнутая поверхность, геометрическое место точек в пространстве, которые равноудалены от данной точки, называемая центром сферы .Сфера — это также тело вращения, образованное вращением полукруга вокруг своего диаметра. Радиус сферы — это сегмент, соединяющий центр сферы с точкой сферы.
Хорда сферы — это отрезок, соединяющий две точки сферы.
Диаметр сферы называется хордой, проходящей через ее центр. Центр сферы делит любой ее диаметр на два равных сегмента. Любой диаметр шара радиусом R равен 2 R .
Мяч представляет собой геометрическое тело; совокупность всех точек пространства, находящихся на расстоянии не более заданного от некоторого центра. Это расстояние называется радиусом шара . Шар формируется путем вращения полукруга около фиксированного диаметра. Обратите внимание, что поверхность (или граница) шара называется сферой. Можно дать такое определение шара: шар — это геометрическое тело, состоящее из сферы и части пространства, ограниченного этой сферой.
Радиус , хорда , диаметр и шара называются радиусом, хордой и диаметром сферы, которая является границей шара.
Разница между шаром и сферой аналогична разнице между кругом и кругом. Круг — это линия, а круг — это все точки внутри этой линии. Сфера — это оболочка, а шар — это все точки внутри этой оболочки.
Плоскость, проходящая через центр сферы (шара), называется диаметральной плоскостью .
Поперечное сечение сферы (шара) с диаметральной плоскостью называется большим кругом ( большой круг ).

Теоремы:

Теорема 1 (о сечении сферы плоскостью). Поперечное сечение шара плоскостью представляет собой круг. Отметим, что утверждение теоремы остается верным, даже если плоскость проходит через центр сферы.
Теорема 2 (о сечении шара плоскостью).Сечение мяча плоскостью представляет собой окружность, а основанием перпендикуляра, проведенного из центра шара к плоскости сечения, является центр окружности, полученной в сечении.

Самый большой круг из числа тех, которые можно получить в сечении плоскости сферы, лежит в сечении, проходящем через центр шара O . Затем он созвал большой круг. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара AB .Этот диаметр также является диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. A и B ), можно провести бесконечное количество больших окружностей. Например, через полюса Земли можно провести бесконечное количество меридианов.

Определения:

Касательная плоскость к сфере — это плоскость, которая имеет только одну общую точку со сферой, и их общая точка называется точкой касания плоскости и сферы.
Касательная плоскость к шару называется касательной плоскостью к сфере, которая является границей этого шара.
Любая прямая линия, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной к сфере (шару) . По определению касательная плоскость имеет только одну общую точку со сферой, следовательно, касательная линия также имеет только одну общую точку со сферой — точку касания.

Теоремы:

Теорема 1 (признак касательной плоскости к сфере).Плоскость, перпендикулярная радиусу сферы и проходящая через ее конец, лежащий на сфере, касается сферы.
Теорема 2 (о свойстве касательной плоскости к сфере). Касательная плоскость к сфере перпендикулярна радиусу, проведенному до точки касания.

Многогранники и сфера

Определение: В стереометрии многогранник (например, пирамида или призма) называется , вписанный в сферу , если все его вершины лежат на сфере.В этом случае сфера называется описанной возле многогранника (пирамиды, призмы). Аналогично: многогранник называется вписанным в шар , если все его вершины лежат на границе этого шара. Более того, шар описывается так, как описано рядом с многогранником.

Важное свойство: центр сферы, описанной рядом с многогранником, находится на расстоянии, равном радиусу R сферы от каждой вершины многогранника. Приведем примеры вписанных в сферу многогранников:

Определение: Многогранник — это , описанный как , описанный рядом со сферой (шаром) , если сфера (шар) касается всех граней многогранника.В этом случае шар и шар называются вписанными в многогранник.

Важно: центр сферы, вписанной в многогранник, находится на расстоянии, равном радиусу r сферы от каждой из плоскостей, содержащих грани многогранника. Приведем примеры многогранников, описываемых около сферы:

Объем и площадь мяча

Теоремы:

Теорема 1 (о площади сферы).Площадь сферы:

где: R — радиус сферы.

Теорема 2 (об объеме шара). Объем шара радиуса R равен , рассчитывается по формуле:

Сегмент шара, пласт, сектор

Сегмент шариковый

В стереометрии сферический сегмент — это часть шара, отрезанная режущей плоскостью. Соотношение между высотой, радиусом основания сегмента и радиусом шара:

где: h — высота сегмента, r — радиус основания сегмента, R — радиус шара.Площадь основания сегмента шара:

Площадь внешней поверхности сегмента шара:

Общая площадь сегмента шара:

Объем сегмента шара:

Слой шарика

В стереометрии сферический слой — это часть сферы, заключенная между двумя параллельными плоскостями. Площадь внешней поверхности слоя шара:

где: h — высота слоя шара, R — радиус шара.Общая площадь слоя шара:

где: h — высота сферического слоя, R — радиус шара, r ₁, r ₂ — радиусы оснований сферического слоя, S ₁, S ₂ — это площади этих баз. Объем слоя шара проще всего определить по разнице объемов двух сегментов шара.

Сектор шара

В стереометрии сферический сектор — это часть сферы, состоящая из сферического сегмента и конуса, вершина которого находится в центре сферы, а основание совпадает с основанием сферического сегмента. Это означает, что сегмент шара меньше половины шара. Общая площадь сектора шара:

где: h — высота соответствующего сегмента шара, r — радиус основания сегмента шара (или конуса), R — радиус шара.Объем сектора шара рассчитывается по формуле:

Цилиндр

Определения:

В некоторых рассмотрим плоскую окружность с центром O и радиусом R . Через каждую точку круга проводим прямую линию, перпендикулярную плоскости круга. Цилиндрическая поверхность — это фигура, образованная этими линиями, а сами линии называются образующими цилиндрической поверхности .Все они образуют цилиндрические поверхности, параллельные друг другу, так как они перпендикулярны плоскости круга.

Прямой круговой цилиндр или просто цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, перпендикулярными формирующей цилиндрической поверхности. Неформально цилиндр можно представить как прямую призму с кругом в основании. Это поможет легко понять и при необходимости вывести формулы для объема и площади боковой поверхности цилиндра.
Боковая поверхность цилиндра — это часть цилиндрической поверхности, расположенная между плоскостями резания, перпендикулярными его образующим, а части (окружности), отрезанные цилиндрической поверхностью по параллельным плоскостям, называются основаниями цилиндра. цилиндр . Основания цилиндра — две равные окружности.
Формирование цилиндра называется сегментом (или длиной этого сегмента), образующим цилиндрическую поверхность, расположенную между параллельными плоскостями, в которых лежит основание цилиндра.Все образующие цилиндры параллельны и равны друг другу, а также перпендикулярны основанию.
Ось цилиндра — это отрезок, соединяющий центры окружностей, которые являются основаниями цилиндра.
Высота цилиндра называется перпендикуляром (или длиной этого перпендикуляра), проведенным из некоторой точки плоскости одного основания цилиндра в плоскость другого основания. В цилиндре высота равна генератору.
Радиус цилиндра — это радиус его основания.
Цилиндр называется равносторонним , если его высота равна диаметру основания.
Цилиндр можно получить, повернув прямоугольник вокруг одной из его сторон на 360 °.
Если плоскость сечения параллельна оси цилиндра, то сечение цилиндра представляет собой прямоугольник, две стороны которого являются образующими, а две другие — хордами оснований цилиндра.
Осевое сечение цилиндра называется сечением цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра представляет собой прямоугольник, две стороны которого образуют цилиндр, а две другие — диаметры его оснований.
Если плоскость разреза перпендикулярна оси цилиндра, то поперечное сечение образует окружность, равную основаниям. На рисунке ниже: слева — осевой разрез; в центре — участок, параллельный оси цилиндра; справа — сечение, параллельное основанию цилиндра.

Цилиндр и призма

Призма называется вписанной в цилиндр , если ее основания вписаны в основания цилиндра. В этом случае цилиндр называется описываемым возле призмы. Высота призмы и высота цилиндра в этом случае будут равны. Все боковые грани призмы будут принадлежать боковой поверхности цилиндра и совпадать с его формовкой. Поскольку мы понимаем под цилиндром только прямой цилиндр, мы также можем включить в такой цилиндр только прямую призму.Примеры:

Призма описывается как описанная рядом с цилиндром , если ее основания описываются возле оснований цилиндра. В этом случае цилиндр называется вписанным в призму. Высота призмы и высота цилиндра в этом случае также будут равны. Все боковые грани призмы будут параллельны цилиндру. Поскольку под цилиндром мы понимаем только прямой цилиндр, такой цилиндр можно ввести только в прямую призму. Примеры:

Цилиндр и сфера

Сфера (шар) называется вписанной в цилиндр , если он касается оснований цилиндра и каждого из его образующих.В этом случае цилиндр описывается так, как описано около сферы (шара). Сфера может быть вписана в цилиндр только в том случае, если это равносторонний цилиндр, т.е. диаметр его основания и высота равны между собой. Центр вписанной сферы будет серединой оси цилиндра, а радиус этой сферы будет совпадать с радиусом цилиндра. Пример:

Говорят, что цилиндр вписан в сферу , если окружности оснований цилиндра являются частями сферы.Говорят, что цилиндр вписан в шар, если его основания являются частями шара. В этом случае шар (сфера) называется описываемым возле цилиндра. Вокруг любого цилиндра можно описать сферу. Центр описываемой сферы также будет серединой оси цилиндра. Пример:

На основе теоремы Пифагора легко доказать следующую формулу, связывающую радиус описанной сферы ( R ), высоту цилиндра ( h ) и радиус цилиндра ( r ):

Объем и площадь боковой и полной поверхностей цилиндра

где: R — радиус основания цилиндра, h — его высота.Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности прямой призмы.

Площадь полной поверхности цилиндра , как обычно в стереометрии, представляет собой сумму площадей боковой поверхности и двух оснований. Площадь основания каждого цилиндра (то есть просто площадь круга) рассчитывается по формуле:

Следовательно, площадь полной поверхности цилиндра S составляет _{заполненных. цилиндр} рассчитывается по формуле:

Теорема 2 (об объеме цилиндра): Объем цилиндра равен произведению площади основания на высоту:

где: R и h — радиус и высота цилиндра соответственно.Эта формула также легко выводится (доказывается) на основе формулы для объема призмы.

Теорема 3 (Архимед): Объем шара в полтора раза меньше, чем описанный вокруг него объем цилиндра, а площадь поверхности такого шара в полтора раза меньше общей площадь того же цилиндра:

Конус

Определения:

Конус (точнее, круговой конус) — это тело, состоящее из круга (называемого основанием конуса ) , точка , не лежащая в плоскости этого круга (называемая вершиной конуса ) и всевозможные отрезки, соединяющие вершину конуса с точками основания.Неформально конус можно воспринимать как правильную пирамиду, в основании которой находится круг. Это поможет легко понять и при необходимости вывести формулы для определения объема и площади боковой поверхности конуса.

Отрезки (или их длины), соединяющие вершину конуса с точками окружности основания, называются конусовидными . Все образующие прямого кругового конуса равны между собой.
Поверхность конуса состоит из основания конуса (круг) и боковой поверхности (состоит из всех возможных форм).
Объединение образующей конуса называется образующей (или стороной) конуса . Поверхность, образующая конус, представляет собой коническую поверхность.
Конус называется прямым , если прямая линия, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. Далее мы будем рассматривать только прямой конус, для краткости назовем его просто конусом.
Визуально прямой круговой конус можно представить себе как тело, полученное вращением прямоугольного треугольника вокруг его ноги в качестве оси.В этом случае боковая поверхность конуса образуется вращением гипотенузы, а основание — вращением ножки, не являющейся осью.
Радиус конуса — это радиус его основания.
Высота конуса называется перпендикуляром (или его длиной), опущенным от его вершины к плоскости основания. У прямого конуса основание высоты совпадает с центром основания. Ось правого кругового конуса называется прямой линией, содержащей его высоту, т.е.е. прямое прохождение через центр основания и верх.
Если режущая плоскость проходит через ось конуса, то поперечное сечение представляет собой равнобедренный треугольник, основанием которого является диаметр основания конуса, а сторонами — образующий конус. Эта секция называется осевой .

Если секущая плоскость проходит через внутреннюю точку высоты конуса и перпендикулярна ей, то сечение конуса представляет собой окружность, центр которой является точкой пересечения высоты и этой плоскости.
Высота ( h ), радиус ( R ) и длина образующей ( l ) правого кругового конуса удовлетворяют очевидному соотношению:

Объем и площадь боковой и полной поверхностей конуса

Теорема 1 (о площади боковой поверхности конуса). Площадь боковой поверхности конуса равна произведению генератора на половину длины окружности основания:

где: R — радиус основания конуса, l — длина образующей конуса.Эта формула легко выводится (или доказывается) на основе формулы для площади боковой поверхности правильной пирамиды.

Площадь полной поверхности конуса — это сумма площади боковой поверхности и площади основания. Площадь основания конуса (т.е.просто площадь круга) равна: S _{основание} = πR ². Следовательно, площадь полной поверхности конуса S составляет _{полных. конус} рассчитывается по формуле:

Теорема 2 (об объеме конуса).Объем конуса равен одной трети произведения площади основания на высоту:

где: R — радиус основания конуса, h — его высота. Эта формула также легко выводится (доказывается) на основе формулы объема пирамиды.

Фрустум

Определения:

Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус.Остальное называется усеченным конусом .

Основание исходного конуса и окружность, образующая поперечное сечение этого конуса плоскостью, называются основаниями , а отрезок, соединяющий их центры, равен высоте усеченного конуса .
Прямая линия, проходящая через высоту усеченного конуса (т. Е. Через центры его оснований), является его осью .
Часть боковой поверхности конуса, ограничивающая усеченный конус, называется его боковой поверхностью , а сегменты, образующие конус, расположенные между основаниями усеченного конуса, называются его константами .
Все, образующие усеченный конус, равны между собой.
Усеченный конус можно получить, повернув прямоугольную трапецию на 360 ° вокруг своей стороны, перпендикулярно основанию.

Формулы усеченного конуса:

Объем усеченного конуса равен разности объемов полного конуса и конуса, отсеченного плоскостью, параллельной основанию конуса. Объем усеченного конуса рассчитывается по формуле:

где: S ₁ = π r ₁ ² и S ₂ = π r ₂ ² — площади оснований, h — высота усеченного конуса, r ₁ и r ₂ — радиусы верхнего и нижнего оснований усеченного конуса.Однако на практике объем усеченного конуса все же удобнее искать как разность объемов исходного конуса и отрезанной части. Площадь боковой поверхности усеченного конуса также можно искать как разницу между площадями боковой поверхности исходного конуса и обрезанной части.

Действительно, площадь боковой поверхности усеченного конуса равна разности площадей боковых поверхностей полного конуса и конуса, срезанного плоскостью, параллельной основанию конуса. Площадь боковой поверхности усеченного конуса равна , рассчитывается по формуле:

где: P ₁ = 2 π r ₁ и P ₂ = 2 π r ₂ — периметры оснований усеченного конуса, l — длина генератора. Общая площадь усеченного конуса , очевидно, определяется как сумма площадей основания и боковой поверхности:

Обратите внимание, что формулы для объема и площади боковой поверхности усеченного конуса получены из формул для аналогичных характеристик правильной усеченной пирамиды.

Конус и сфера

Конус называется вписанным в сферу (шар), если его вершина принадлежит сфере (границе шара), а базовая окружность (сама основа) является частью сферы (шара). В этом случае сфера (шар) описывается так, как описано рядом с конусом. Вокруг прямого кругового конуса всегда можно описать сферу. Центр описываемой сферы будет лежать на прямой, содержащей высоту конуса, а радиус этой сферы будет равен радиусу описанной окружности около осевого сечения конуса (это сечение представляет собой равнобедренный треугольник). .Примеры:

Сфера (шар) называется вписанной в конус , если сфера (шар) касается основания конуса и каждого из его образующих. В этом случае конус называется описанным около сферы (шара). В прямой круговой конус всегда можно войти в сферу. Его центр будет лежать на высоте конуса, а радиус вписанной сферы будет равен радиусу окружности, вписанной в осевое сечение конуса (это сечение — равнобедренный треугольник).Примеры:

Конус и пирамида

Конус называется вписанным в пирамиду (пирамида — описывается рядом с конусом), если основание конуса вписано в основание пирамиды, а вершины конуса и пирамиды совпадают.
Пирамида называется вписанной в конус (конус — описывается возле пирамиды), если ее основание вписано в основание конуса, а боковые грани образуют конус.
Высота таких конусов и пирамид равна.

Примечание: Более подробно о том, как конус вписывается в пирамиду в стереометрии или как он описывается рядом с пирамидой, уже упоминалось здесь ранее.

(PDF) Дидактические явления необычной геометрии Задачи в обучении стереометрии

355

Люсия Руманова и др. / Процедуры — Социальные и поведенческие науки 186 (2015) 354 — 358

Национальная программа обучения математике в Словакии (ISCED 3A) определяет математические стандарты

и количество уроков в словацких школах.Обучение стереометрии особенно сложно для пространственного и геометрического воображения учащихся. По этой причине у учащихся возникают проблемы с заданиями такого типа. Мы сосредоточились на

плоских секциях не только кубов, но и на секциях куба, состоящих из специальных тел, состоящих из нескольких кубов.

Для того, чтобы учащиеся усвоили вышеуказанный вопрос, необходимо соблюдать принцип иллюстративного обучения

, для которого целесообразно использовать ИКТ — компьютерную визуализацию с дидактическим программным обеспечением.

2. Теоретические основы

Анализ конкретной дидактической проблемы образовательного процесса с разных сторон является целью исследования

многих дидактических школ мира. Одна из таких школ — французская дидактическая школа, которую представляют Гай

Брюссо, Ив Шеваллар и Анна Серпинская. Исследовательская база теории дидактической ситуации (TDS), выпущенная

из этой дидактической школы, представляет собой анализ проблемы на отдельных уровнях дидактических ситуаций (Brousseau, 1998;

Chevallard, 1992; Sierpinska, 2001)

Базовый Понятием этой теории является дидактическая среда.Бруссо, следуя теории Пиаже, утверждал, что

среда является источником противоречий и нестабильных состояний учащегося (субъекта) в процессе адаптации

(по Бруссо, 1986, это ассимиляция и приспособление).

Согласно Бруссо (1998), априорный анализ является одним из инструментов, которые учитель может использовать при планировании своих собственных уроков

. Перед решением конкретной проблемы необходим априорный анализ, потому что учитель может подготовиться к

фону или различным возможностям, которые учитель может наблюдать на уроках.Хороший априорный анализ является предпосылкой успешного развития дидактической ситуации. Следовательно, это поможет учителю подготовить хорошую дидактическую ситуацию

, ситуацию, когда учащиеся получают знания самостоятельно. (Novotná et al., 2010)

Мы применяем принципы TDS, подтверждающие важность априорного анализа и апостериорных результатов

студентов. Мы сформулировали априорный анализ перед решениями учеников (исследование), и анализ включает

нисходящий анализ (анализ работы учителя) и восходящий анализ (анализ работы учеников).

3. Методология исследования

В нашем исследовании мы сосредоточились на анализе решения геометрических задач — плоских сечений кубических построек. В школе

принято решать задачи плоского сечения одного куба сверху и справа. В нашей статье мы продолжаем уже проведенное исследование

. Мы подробно анализируем выводы

словацких и чешских математиков и преподавателей университетов, чьи исследования направлены на развитие пространственного и

геометрического воображения.Основываясь на выводах о том, что предметная область развивается в основном за счет плоских секций из

тел, мы предлагаем новый вдохновляющий тип задач на секциях куба, строящих специальные тела, построенные из

составных кубов — кубические здания.

Итак, основной целью данного исследования было проанализировать связь между

x Стратегиями решения задачи

x Ошибками в решениях учащихся

x Окончательными результатами задачи.

После завершения исследования мы сравнили наш прогноз на основе априорного анализа решений студентов и получили

результатов в апостериорном анализе.

3.1. Априорный анализ задания

В соответствии с положениями структуры TDS: в рамках дидактической ситуации Noosferic мы

проанализировали школьные учебники математики и различные математические материалы. Мы выбрали геометрическую задачу, которой нет в учебниках по математике

, но которую студенты должны уметь решать с помощью своих знаний.

Геометрическое задание было дано студентам CPU в Нитре. Мы решили проверить их геометрические знания.

Некоторые из них решили аналогичную геометрическую задачу в рамках уже проведенного эксперимента, поэтому мы ожидали, что стереометрия

— перевод на японский язык

стереометрия

естественные и прикладные науки / химия — cjki.org

▷ Мультифрактальное описание морфологии трещин: квази-трехмерный анализ поверхности трещины … Ключевые слова: трещина; поверхность; стереометрия ; перекрытия; профиль; мультифрактал; ширина спектра 1 ▷ Дидактические явления необычных геометрических задач в обучении стереометрии … В учебную программу стереометрия тема плоских сечений твердых тел включена в связи с развитием пространственного воображения учащихся …

общие — core.ac.uk —

▷ Конкретный метод решения selected стереометрия задач в учебном процессе … На основании выводов этих экспертов мы представляем нашу оригинальную методику решения конкретной позиционной и метрической стереометрии тоже задач …

общие — core.ac.uk —

▷ стереометрия пустот в межсоединении припоя между печатной платой и корпусом… Стереометрия пустот и морфология сустава были исследованы с помощью трехмерного стереологического микроскопа (IFM) ® … ▷ Улучшение пространственного воображения школьников с помощью действий в приложениях 3d elica В статье представлены исследования, проведенные в рамках DALEST Developing Среда активного обучения для изучения стереометрии ) … ▷ Динамическая стереометрия височно-нижнечелюстного сустава …. Динамическая стереометрия показала, что поля напряжения перемещаются в медиолатеральном направлении во время открытия / закрытия, протрузии и латеротрузии, а также что их поступательная скорость варьируется внутри человека и со скоростью движения мыщелка… ▷ Проблемы в стереометрии … Перед заданиями приводится теоретическое резюме, которое знакомит читателя с основными характеристиками стереометрии … ▷ Разработка активной обучающей среды для изучения стереометрии В данной статье сообщается по разработке динамической среды для изучения стереометрии (DALEST) и преподавания пространственной геометрии и визуального мышления … ▷ Разработка активной учебной среды для изучения стереометрии В этой статье сообщается о дизайне динамическая среда для изучения стереометрии (DALEST) и обучения пространственной геометрии и визуальному мышлению…

1 миллиард переводов с разбивкой по видам деятельности на 28 языках

Наиболее частые запросы Английский: 1-200, -1k, -2k, -3k, -4k, -5k, -7k, -10k, -20k, — 40k, -100k, -200k, -500k,

Наиболее частые запросы Японский: 1-200, -1k, -2k, -3k, -4k, -5k, -7k, -10k, -20k, -40k, — 100k, -200k, -500k,

Traduction Перевод Traducción Übersetzung Tradução Traduzione Traducere Vertaling Tłumaczenie Mετάφραση Oversættelse Översättning Käännös Aistriúchán Traduzzjoni Prevajanje Vertimas Tõlge Preklad Fordítás Tulkojumi Превод Překlad Prijevod 翻訳 번역 翻译 Перевод

Разработано для TechDico

Издатель Условия и условия

Политика конфиденциальности

© techdico

geometry — Упражнение: Стереометрия> Линии и плоскости> Параллельные линии и плоскости

Вот несколько советов, которые, надеюсь, укажут вам правильное направление.

Как бы вы определили пару косых линий? Это свойство необходимо для работы. В зависимости от того, какие термины вы бы использовали для такого определения, я бы предложил использовать те же термины для формулировки доказательства уникальности. (Вероятно, термины включают понятия «векторов» или «направлений».) Если этих терминов недостаточно, добавьте термины, которые вы бы использовали для определения параллельных плоскостей.

Какой шаг вашего алгоритма завершится ошибкой, если две линии не скошены, а параллельны? Какое неявное предположение, сделанное в вашем доказательстве, было бы неудовлетворительным в этой ситуации? Обязательно сделайте предположение явным и покажите, что оно справедливо в случае косых линий.Проделайте такой же анализ и обоснование для случая пересечения линий.

Изменить: На основе вашего комментария я предполагаю, что вы определяете наклонные линии как линии без общей плоскости, параллельные линии как линии в общей плоскости, но без общей точки, и пересекающиеся линии на линиях, которые имеют ровно одну точку в общий. Точно так же параллельные плоскости будут плоскостями без общих точек, в то время как непараллельные плоскости пересекаются по линии. Поскольку такой формализм, основанный на инцидентности, не включает много понятий направлений, мне придется подумать о другом.

Практический подход к доказательству уникальности — доказательство от противного. Предположим, что пара $ (P, Q) $ была , а не уникальной. По сути, есть два возможных случая, которые следует рассмотреть. В одном случае у вас есть один выбор для одного из самолетов и как минимум два для другого. Итак, предположим, что $ (P, Q_1) $ и $ (P, Q_2) $ — это решения вашей проблемы. Тогда $ Q_1 \ parallel P $ и $ P \ parallel Q_2 $, поэтому $ Q_1 \ parallel Q_2 $ по транзитивности параллелизма (что вам, возможно, придется сначала показать). Следовательно (и поскольку $ Q_1 $ и $ Q_2 $ различны) $ Q_1 $ и $ Q_2 $ не имеют общих точек (это может быть ваше определение параллелизма или что-то вроде леммы), но поскольку оба должны содержать $ b $ у вас есть противоречие.

Другой случай — две пары попарно различных параллельных плоскостей, а именно $ (P_1, Q_1) $ и $ (P_2, Q_2) $. Тогда $ P_1 $ и $ P_2 $ должны пересекаться в $ a $, а $ Q_1 $ и $ Q_2 $ должны пересекаться в $ b $. Интуитивно понятно, что это может произойти, только если $ a \ parallel b $, но как это показать? Что ж, представьте, что ваш самолет $ M $ включает в себя все $ a $ и одну точку $ B $ из $ b $. Если бы $ M $ пересекали $ Q_1 $ и $ Q_2 $ в одной строке, эта линия была бы $ b $, поэтому $ M $ содержала бы все $ b $, поэтому $ a $ и $ b $ были бы параллельны не перекосить линии.Итак, $ M $ должен пересекать $ Q_1 $ и $ Q_2 $ по различным прямым, пересекающимся в точке $ B $. Назовем эти строки $ q_1 $ и $ q_2 $. С другой стороны, $ M $ пересекает $ P_1 $ и $ P_2 $ в $ a $. Теперь, поскольку пара параллельных плоскостей пересекает любую другую непараллельную плоскость в паре параллельных прямых, у вас есть $ a \ parallel q_1 $ (из-за $ P_1 \ parallel Q_1 $) и $ a \ parallel q_2 $ (из $ P_2 \ parallel Q_2 $), что по транзитивности (на этот раз на плоскости) влечет $ q_1 \ parallel q_2 $. Это противоречит тому факту, что $ q_1 $ и $ q_2 $ должны пересекаться в $ B $, поэтому все предположение о двух различных парах решений было опровергнуто.

Нобелевская премия по химии 1901 — Речь на церемонии награждения

Презентационная речь профессора Hj. Теэль, президент Шведской королевской академии наук, 10 декабря 1902 г.

Ваше Величество, Ваши Королевские Высочества, дамы и господа.

Королевская академия наук приняла решение присудить Нобелевскую премию по химии 1902 года доктору Эмилю Фишеру, профессору Берлинского университета и Гехаймрата, за «выдающиеся заслуги, которые он оказал своей работой по синтезу сахара и пуринов».

Одна из основных задач органической химии — исследовать и искусственно воспроизводить те процессы, которые происходят в живом веществе, как животном, так и растительном, чтобы тем самым обеспечить прочную основу для представлений о биологических явлениях. Помимо белковых веществ, нет более важной для органической жизни группы углеродных соединений, чем углеводы. По этой причине углеводы, и в особенности сахара, были объектом бесчисленных исследований с самого начала органической химии.Из-за природы этих веществ их изучение было сопряжено с большими трудностями и еще несколько лет назад казалось невыполнимой задачей.

На основе своего открытия производных гидразина, значительного открытия, профессору Фишеру удалось найти блестящее решение проблемы. С удивительно острым рассудком и блестящей проницательностью в выборе своих путей и средств Фишер не только воспроизвел синтетически натуральные виноградные и фруктовые сахара, но также около тридцати других сахаров и множество близкородственных соединений.В то время как из встречающихся в природе простых сахаров были обнаружены только сахара с 5-6 атомами углерода, Фишер синтезировал непрерывный ряд, содержащий от 2 до 9 атомов углерода. Кроме того, своим элегантным методом искусственного получения глюкозидов он также добавил к достижениям органического синтеза эту группу, которая так чрезвычайно важна для физиологии овощей.

Эти исследования особенно важны для теории пространственного расположения атомов, разработанной Вант-Хоффом и Ле Беллом.В случае обсуждаемых соединений Фишеру удалось полностью определить не только способ, которым атомы связаны в атомных комплексах, молекулах, но и положение атомов относительно друг друга, или, другими словами, стереометрические конфигурация молекул. Поскольку степень сложности здесь велика и теория поддается проверке до мельчайших деталей, наша концепция атомной группировки достигла такой степени определенности благодаря этим исследованиям, что мы можем быть убеждены, что эта концепция никогда не будет существенно ослаблена, даже если бы она была представление о природе атомов и особенно валентностей, которые претерпят радикальные изменения в будущем.

Эти исследования были не менее важны для физиологии.

Один из самых замечательных процессов, происходящих в природе, — это образование углеводов в зеленых частях растений. Фактически, этот процесс является первоисточником любого органического вещества, следовательно, его выяснение является одной из ключевых задач науки. Еще в 1870 г. А. фон Байер сформулировал гипотезу о том, что углекислый газ и вода восстанавливаются до формальдегида (формалина) в клетках, содержащих хлорофилл, и что он немедленно конденсируется с образованием сахара.Поскольку Фишеру теперь удалось получить из формальдегида как виноградный, так и фруктовый сахар, которые повсеместно встречаются в растениях и, несомненно, являются исходными веществами для других углеводов, рассматриваемая гипотеза тем самым получила экспериментальное подтверждение очевидной ценности. Эти синтезы сахаров, кроме того, связаны с неорганическим углеродом, водородом и кислородом через формальдегид.

Действия ферментов, которые имеют такое глубокое влияние на жизненно важные процессы, предстают в совершенно новой перспективе в результате этих исследований.Было обнаружено, что синтетические сахара с тремя и девятью атомами углерода превращаются дрожжами в спирт и углекислый газ так же легко, как виноградный сахар, содержащий шесть атомов углерода, но что после небольшого изменения стереометрической конфигурации молекулы последний полностью не подвержены влиянию того же фермента. Здесь мы сталкиваемся с важным открытием, что жизненно важная функция больше зависит от геометрической конфигурации молекулы питательного вещества, чем от состава в других отношениях .Фишер определил аналогичную чувствительность к так называемой асимметричной структуре и для других ферментов, и для глюкозидов. Благодаря этому наблюдению молекулярная асимметрия приобрела ранее неожиданное значение. Было обнаружено, что сами ферменты, вместе с наиболее важными продуктами жизнедеятельности растений, углеводами, белками, гранулами хлорофилла и самой протоплазмой, без исключения являются оптически активными веществами или состоят из них, и что все необходимые химические вещества трансформации в организме зависят от асимметрии .Таким образом, наше понимание природы и условий, регулирующих жизненно важные функции, значительно улучшилось. Эти синтезы сахара действительно являются самыми первыми процессами, в которых действие ферментов может быть проверено подробно и с точностью. Таким образом, для физиологии эти исследования открыли новую область, лечение которой уже началось и последствия которой еще не могут быть полностью поняты.

Одновременно с этими исследованиями и особенно после того, как были получены наиболее важные результаты, профессор Фишер завершил еще одно исследование, которое является одним из лучших и, с точки зрения результатов, одним из самых плодотворных, когда-либо проводившихся в органической химии.

Для жизни животных азотистые вещества, присутствующие в организме, являются наиболее важными. Помимо белковых веществ, в организме животного содержится значительное количество других азотистых веществ. Их исследования имеют большое значение для физиологической химии, потому что они либо являются продуктами, возникающими в результате использования белков, либо вместе с простыми белками содержатся в качестве компонентов в самых сложных соединениях организма, протеидов, , как их называют.

Даже с 1776 года, когда Шееле обнаружил мочевую кислоту в мочевом камне, в выделениях животных было обнаружено несколько тесно связанных с ней веществ, таких как ксантин , аденин и гуанин и т. Д. В эту же группу входят теобромин , теофиллин и кофеин , которые встречаются в растительном мире и являются стимуляторами в наших основных напитках какао, кофе и чае. Благодаря тонкому восприятию выдающегося ученого и мастерской технике профессор Фишер внес порядок и ясность и в эту область.Он продемонстрировал, что все эти вещества являются производными того же исходного вещества, пурина, которое он открыл. Он успешно приготовил их друг из друга и из более простых компонентов таким образом, что и здесь синтезированная цепь восходит к неорганическому углероду, водороду и кислороду, и, кроме них, он приготовил большое количество новых, тесно связанных веществ, так что производных пурина, изученных Фишером, должно быть теперь около 150. Внутренний состав каждого полностью определен.

Для физиологии экспериментальное доказательство того, что мочевая кислота и ксантины происходят от одной и той же исходной формы, имеет огромное значение, поскольку оно предоставило сильнейшую поддержку современной теории образования мочевой кислоты из нуклеопротеидов ядра клетки и из содержащихся в нем пуринов.

Поскольку некоторые представители этой группы — кофеин и теобромин — ценятся не только в форме напитков, но также использовались в медицине на протяжении веков, разумно ожидать, что некоторые из новых производных пурина окажутся имеющими лекарственную ценность .Химическая промышленность тоже уже предприняла первые попытки разработать для своих целей синтез Фишера этих веществ, которые так высоко ценятся в повседневной жизни.

Особый тип исследований, который характеризовал органическую химию в последние десятилетия только что завершившегося столетия, достиг зенита своего развития и своей лучшей формы в исследованиях Фишера сахара и пуринов. С экспериментальной точки зрения они непревзойденные.

Из Нобелевских лекций по химии 1901-1921 гг. , Elsevier Publishing Company, Амстердам, 1966 г.

Для цитирования этого раздела
Стиль MLA: Речь на церемонии награждения.NobelPrize.org. Nobel Media AB 2021. Сб. 22 мая 2021 г.

Вернуться наверх
Вернуться к началу Возвращает пользователей к началу страницы

Нетрадиционные подходы к избранным стереометрическим задачам с помощью DGS.

Страница / Ссылка:

URL страницы:

HTML-ссылка:
Бабкен Борисович Нерсисян

кандидат педагогических наук

[email protected]

Кандидат педагогических наук

Образование

1979-1983 гг. АГПУ им. К.Х. Абовян, математический факультет, учитель математики по специальности

Ученая степень
2005-по настоящее время АГПУ им. К.Х.Абовяна, 020 решение профсоюза кандидат педагогических наук
2001-2005 гг. АГПУ им. К.Х. Абовян, соискатель

Опыт работы
2011 г. по настоящее время АГПУ им. Х. Абовян, старший преподаватель кафедры математики и методики начального обучения
2005-10 АГПУ им. Х. Абовян, ассистент кафедры математики и методики начального обучения
2002 — 2005 АГПУ им. Х. Абовян, преподаватель кафедры математики и методики элементарного обучения
2001 — 2005 АГПУ им. Х.Абовян, соискатель кафедры математики и методики начального обучения
1983 по настоящее время Школа №2 Масис Араратской области, учитель математики

Курсы
Бакалавриат
Математика-B
Математика и методы обучения

Публикация
2003 по настоящее время
Автор около 40 научных статей и работ
1. Распределение натуральных чисел по группам и Выявление закономерностей в этих группах как фактор развития творческого мышления.
2. Бесконечно убывающая геометрическая прогрессия как ядро для изучения стереометрических задач.
3. Изучение геометрии как способ развить математическое мышление учащихся в основной школе.
4. Математические олимпиады в начальной школе.
5. Пример исследовательского проекта по курсу геометрии в основной школе.

Награды
2014 Заслуженный педагог РА
2008 АГПУ им. К.Х. Абовян, Диплом за многолетнюю трудовую деятельность и достижения в науке
1998, 1997 Учитель года от Союза помощи Армении
1994 Министерство образования РА Аттестационная Центральная Комиссия (АКК) Умелый учитель

Языки: русский, английский

ЕГЭ. Задание 14. Стереометрия — Сайт Трушина Б.В.

Полезные материалы

Подборки видео и онлайн-курсы

Как решать стереометрию

Теорема о трёх перпендикулярах

Как найти объем. Принцип Кавальери

Видеоразборы задач

Подборка заданий прошлых лет

Задачи по стереометрии

Две интересные стереометрические задачи

Решение задач по стереометрии. Практикум. Подготовка к ЕГЭ., Потоскуев Е.В. | ISBN: 978-5-89237-352-4

Аннотация

Дополнительная информация

Методические подходы к организации пошагового решения обучающимися средней школы задач по стереометрии Текст научной статьи по специальности «Математика»

Презентация — Решение задач B9

Слайды и текст этой онлайн презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Стереометрия (Геометрия в пространстве) — Все свойства, теоремы, аксиомы и формулы — Математика

Оглавление:

Базовые теоремы, аксиомы и определения стереометрии

Вводные определения и аксиомы стереометрии

Построение сечений в стереометрии

Взаимное расположение прямых и плоскостей в стереометрии

Теорема о трех перпендикулярах

Двугранный угол

Симметрия фигур

Призма

Параллелепипед

Пирамида

Правильная пирамида

Формулы для объема и площади пирамиды

Тетраэдр

Прямоугольная пирамида

Усечённая пирамида

Пирамида и шар (сфера)

Пирамида и конус

Пирамида и цилиндр

Сфера и шар

Многогранники и сфера

Объем и площадь поверхности шара

Шаровой сегмент, слой, сектор

Цилиндр

Цилиндр и призма

Цилиндр и сфера

Объем и площадь боковой и полной поверхностей цилиндра

Конус

Объем и площадь боковой и полной поверхностей конуса

Усеченный конус

Конус и сфера

Конус и пирамида

Stereometry (Геометрия в пространстве) — WhatMaster

Основные теоремы, аксиомы и определения стереометрии

Вводные определения и аксиомы стереометрии

Построение сечений в стереометрии

Взаимное расположение прямых и плоскостей в стереометрии

Теорема о трех перпендикулярах

Двугранный угол

Формы симметрии

Призма

Параллелепипед

Пирамида