Содержание
формула и примеры решения задач
Содержание:
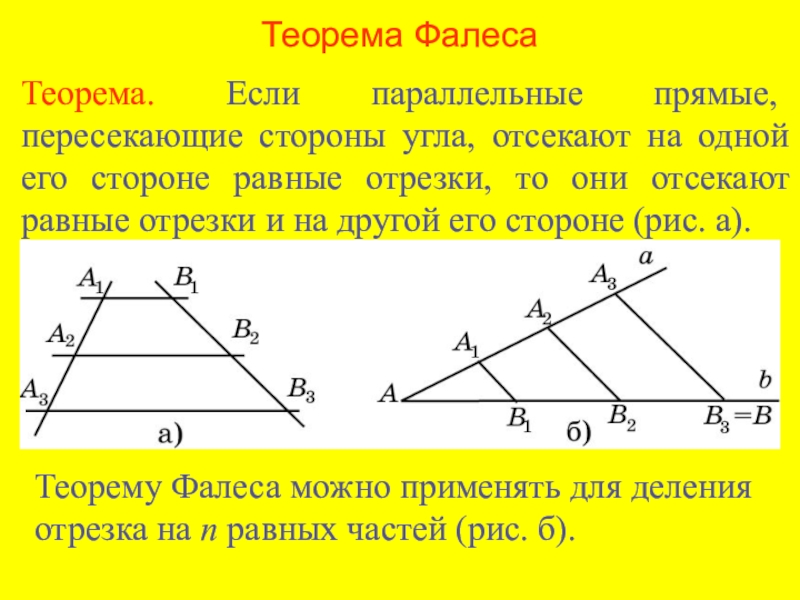
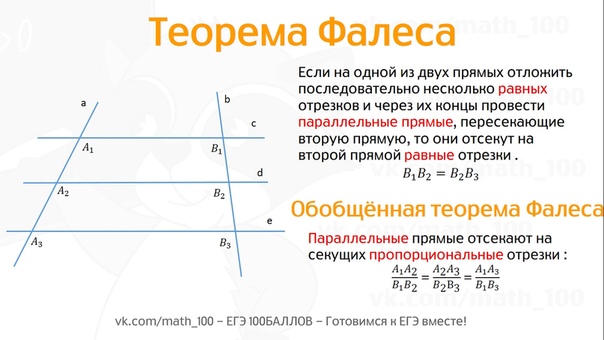
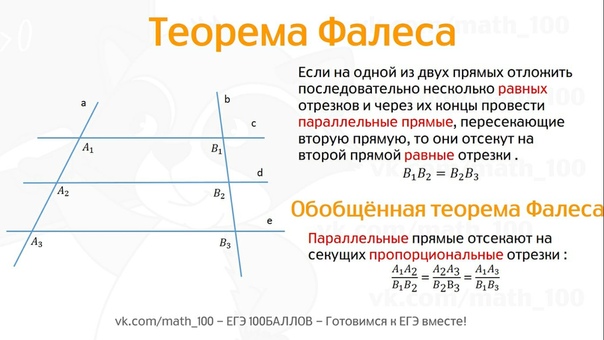
Формулировка теоремы Фалеса
Теорема
Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые,
пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки (рис. 1).
В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и
для параллельных). Также не важно, где находятся отрезки на секущих.
Теорема
Обобщённая теорема Фалеса
Параллельные прямые отсекают на секущих пропорциональные отрезки (рис. 1):
$$\frac{A_{1} A_{2}}{B_{1} B_{2}}=\frac{A_{2} A_{3}}{B_{2} B_{3}}=\frac{A_{1} A_{3}}{B_{1} B_{3}}$$
Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать
пропорциональными отрезками с коэффициентом пропорциональности, равным 1.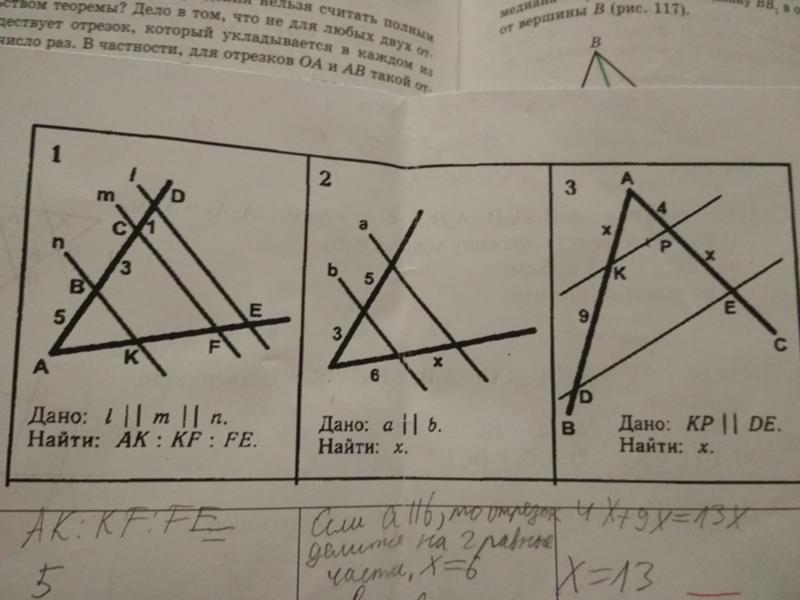
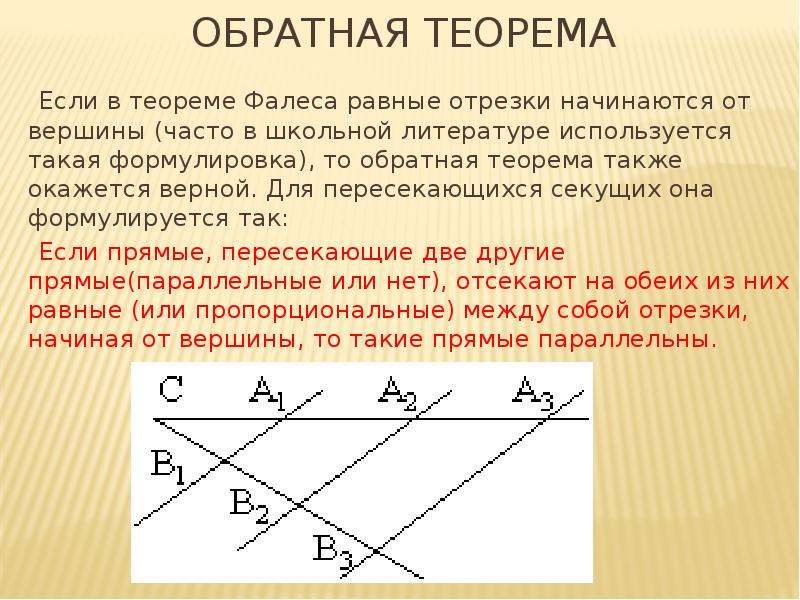
Теорема
Обратная теорема Фалеса
Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные
(или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны (рис. 2).
Замечание. В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины.
Примеры решения задач
Пример
Задание. Разделить данный отрезок на четыре равные части.
Решение. Пусть
$AB$ — заданный отрезок (рис. 3),
который необходимо разделить на четыре равные части.
Через точку $A$ проведем произвольную полупрямую
$a$ и отложим на ней последовательно четыре
равных между собой отрезка $AC, CD, DE, EK$ .
Соединим точки $B$ и $K$ отрезком и проведем через оставшиеся точки
$C$, $D$ и $E$ прямые, параллельные прямой
$BK$ так, чтобы они пересекли отрезок
$AB$ .
Согласно теореме Фалеса отрезок
$AB$ разделится на четыре равные части.
Слишком сложно?
Теорема Фалеса не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. На стороне $AB$ треугольника
$ABC$ отмечена точка
$K$. Отрезок
$CK$ пересекает медиану
$AM$ треугольника в точке
$P$, причем
$AK = AP$. Найти отношение
$BK : PM$ .
Решение. Проведем через точку
$M$ прямую, параллельную
$CK$, которая пересечет
$AB$ в точке
$D$ (рис. 4).
По теореме Фалеса $BD = KD$ .
По теореме о пропорциональных отрезках имеем, что
$$P M=K D=\frac{B K}{2} \Rightarrow B K: P M=2: 1$$
Ответ. $B K: P M=2: 1$
Историческая справка
Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между
отрезками. Очень часто при этом приходится проводить дополнительный отрезок.
Аргентинская музыкальная группа представила песню, посвящённую теореме. В видеоклипе для этой песни приводится доказательство
для прямой теоремы для пропорциональных отрезков.
Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с
постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что
вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу,
о чём есть свидетельство Прокла.
Задачи на применение теоремы Фалеса. 18 Список литературы. 21
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РФ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Управление образования Советского
района г. Красноярска
Использование
теоремы Фалеса в современном мире
(Исследовательско – реферативная
работа)
Работу выполнили:
Ученик 9 класса
Баландин Александр
Ученик 9 класса
Кузьмин Александр
Научные руководители:
Учитель математики Мальцева Т. Г
Г
Учитель информатики Заболотникова
Е.Ю.
Красноярск 2011
Содержание:
Цели и задачи проекта. 3
Аннотация 4
Введение 4
Теоретическая часть. 5
Исторические и биографические
факты из жизни Фалеса.Чем знаменит Фалес?
Практическая часть
Доказательство теоремы
Фалеса. 17Задачи на применение теоремы
Фалеса. 18
Список литературы. 21
Цели и задачи проекта
Методические задачи:
Научиться работать в паре,
Научиться обрабатывать и
обобщать полученную информацию,Научиться быстро и эффективно
работать в сети Интернет,Научиться создавать законченные
информационные продукты.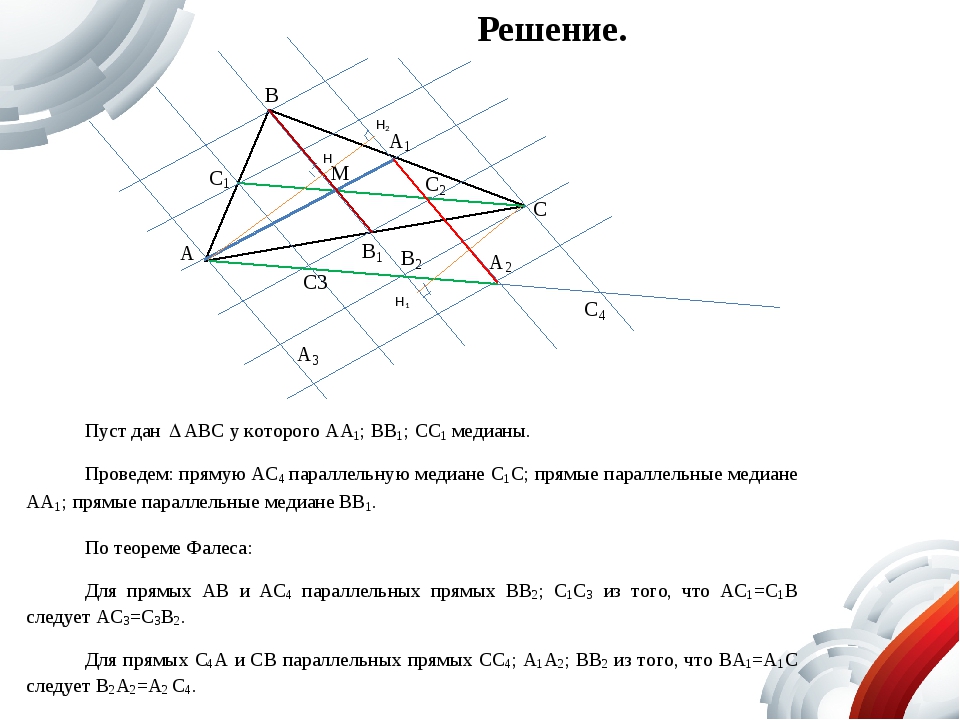
Дидактические цели проекта:
С помощью дополнительной
литературы, основанной на исторических
фактах, познакомиться с открытиями и
жизнью Фалеса и его последователей с
точки зрения истории развития математики
и других наук;Рассмотреть теорему Фалеса,
как источник замечательных математических
открытий;Изучение возможностей программы
Power
Point.
Аннотация.
Великий учёный Фалес
Милетский основал
одну из прекраснейших наук- геометрию.
Известно, что Фалес Милетский имел титул
одного из семи мудрецов Греции, что он
был поистине первым философом, первым
математиком, астрономом и вообще первым
по всем наукам в Греции. Он был то же для
Греции, что Ломоносов для России.
Введение.
Наиболее знаменитым из семи
мудрецов был Фалес из Милета,
ионийского города, греческой колонии
в Малой Азии(ок. 627-ок.547г. до н.э.).Фалеса
627-ок.547г. до н.э.).Фалеса
также считают и первым философом,
основателем Ионийской школы. Поскольку
Фалес жил в Ионии, школа его была названа
Ионийской.
Он умер в 546 году до н.э., и ему
наследовал Анаксимандр, а вслед за ним
шли Анаксимен, Анаксагор; Архелай, на
ком И. ш. и закончилась.
Сочинения представителей
Ионийской школы написаны на ионическом
диалекте, в отличие от аттического
диалекта произведений Платона и
Аристотеля.
Ионийская школа –
стихийно-материалистическое направление
древнегреческой философии, возникшее
и развившееся в ионийских колониях
Греции в 6-4вв. до н.э.. Зародилась в г.
Милет; её представители – Фалес,
Анаксимандр и Анаксимен (милетская
школа), Гераклит Эфесский. И. ш. принято
противопоставлять пифагорейской,
элейской и аттийской школам. Одна из
основных идей, впервые выдвинутых
философами И. ш. – мысль о единстве всего
сущего, о происхождении всех вещей из
некоторого единого первоначала, которое
понималось при этом как та или иная
вещественная стихия или как «беспредельное»,
из которого выделились основные
противоположности тёплого и холодного.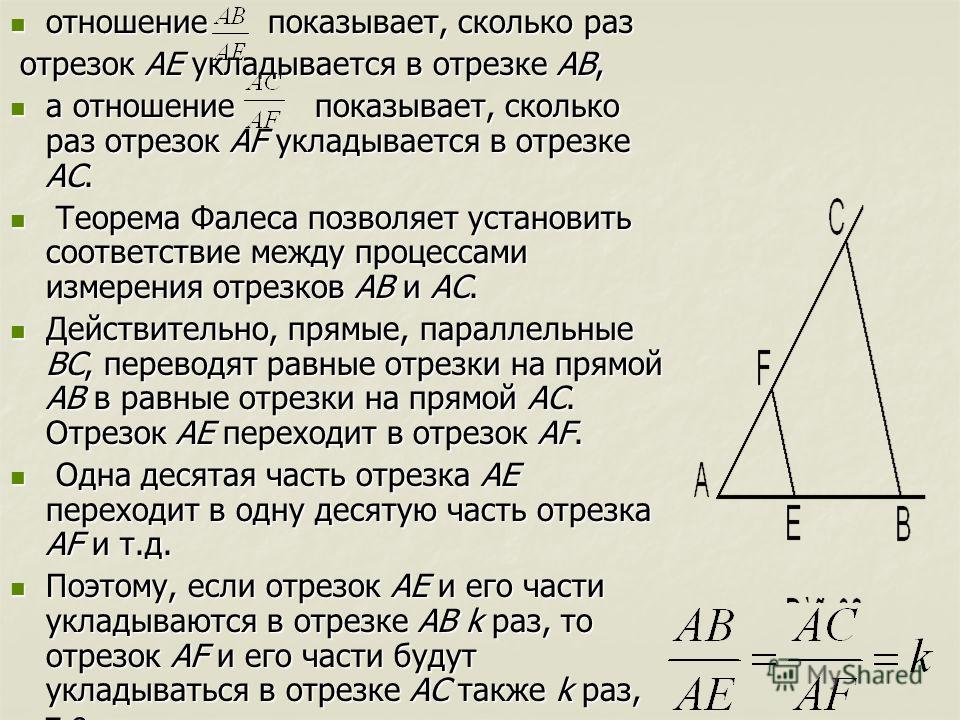
Теоретическая часть.
Вода, по Фалесу, является первичным
принципом или элементом, и на ней плавает
Земля подобно кораблю, и землетрясение
происходят из-за волнений этого
вселенского моря.
В дерзновении своём он как бы
сдвигает целые плиты и меняет демаркационные
линии между реальным и мнимым,
действительностью и грезой, ведь вопрошая
обо всём мыслитель как бы выносит себя
за пределы «всего», рассматривает его
со стороны и ставит его под вопрос,
выделяя себя, мыслящую в себе инстанцию
из «всего», само «всё» как предмет уже
в чём-то единиться, как бы округляется
в «извне» взгляде философа. Ахиллес и
Агамемнон – литература, как бы говорит
Фалес, а я – Гомер, как автор я вижу нить
сюжета, скрытую до поры от читателя и
отдающую непрояснённостью судьбы
героев. Так и Фалес, отстраняясь от
всего, старается разглядеть сюжетную
нить и драматургию, лицо, «физиономию»
«всего», вставая на беспрецедентную
точку «вне всего». Встав «по ту сторону»
только и можно сказать о мире «всё».
Фалес отверг всякую мысль о мнимости
мира, его неподлинности, а значит и
непознаваемости, сказав «есть» «всему»,
Фалес утвердил и свою позицию как
наличествующую, сущую. Э.Р.Ф. как математик
и астроном. В своё время Фалес был едва
ли не единственным во всей Греции
человеком, отдавшимся чистой науки и
абстрактному мышлению без преследования
каких-нибудь практических целей.
Важнейшей заслугой Фалеса в области
математики должно быть считаемо
перенесение им из Египта в Грецию первых
начал теоретической элементарной
геометрии. Эвдем, по свидетельству
Прокла, приписывает Фалес открытие
следующих предложений. Вертикальные
углы равны. Углы при основании
равнобедренного треугольника равны.
Треугольник определяется стороною и
прилежащими к ней двумя углами. Диаметр
делит круг на две равные части. Диоген
Лаерний, в основании слов Памфилия,
прибавляет к этому списку предложений
ещё вписывание в круг прямоугольного
треугольника. Что бы дать полный очерк
геометрических знаний Фалеса, необходимо
присоединить ещё ряд таких предложений,
без которых приобретение первых делается
невозможным, а именно предложений о
параллельных линиях, о равносторонних,
равнобедренных и разносторонних
треугольниках, о параллелограммах и
прочих сверх перечисленных «открытий»
Фалеса в области теоретической геометрии,
ему приписывается греческими писателями
ещё решение двух геометрических задач
практического характера, из которых
одна состояла в определении расстояния
корабля на море от Милетской гавани, а
другая – в определении высоты пирамиды
по длине её тени, а именно измеряя тень
в тот час, когда она бывает равна своему
телу.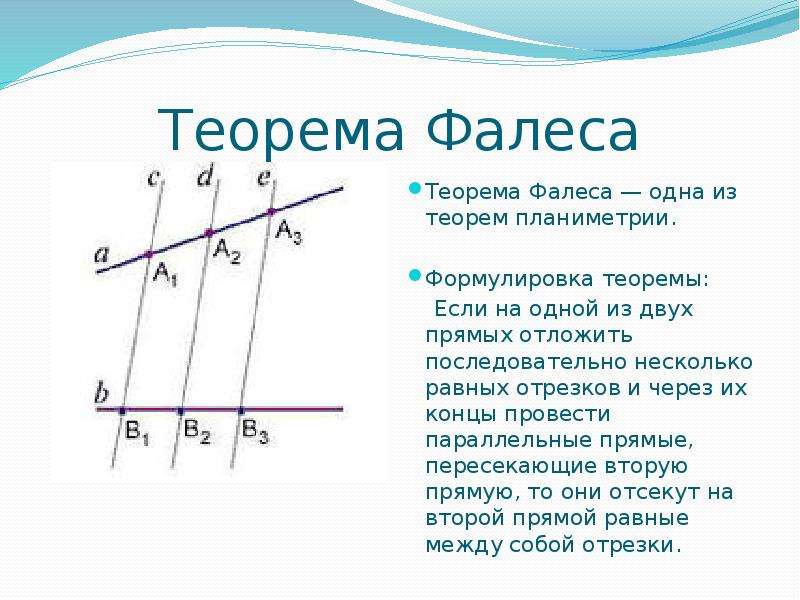 Поставив палку на конце тени,
Поставив палку на конце тени,
образуемой пирамидою, так что от
солнечного света образовалось два
треугольника, он показал, что отношение
между величиною пирамиды и палки такое
же, какое было между тенью пирамиды и
тенью палки. В настоящее время в истории
математики уже не существует никаких
сомнений относительно того, что всё
приписываемое Фалесу его соотечественниками
геометрические «открытия» были в
действительности простыми заимствованиями
из египетской науки.
С именем Фалеса связывают многие
остроумные и часто парадоксальные
высказывания и ответы, которые так
ценились греками. Так рассказывают, что
он оставался неженатым: когда его мать
в молодости побуждала его жениться, он
отвечал « Слишком рано!», в зрелом
возрасте «Слишком поздно!». А когда у
него спрашивали, почему у него нет детей,
он отвечал «Потому что люблю их». Фалес
так же утверждал, что между жизнью и
смертью нет разницы, а когда его
спрашивали: «Почему ты в таком случае
не умрёшь?», он отвечал «Именно поэтому».
Фалес был младше Солона
лет на 10-15, но они были очень дружны, что
видно, в частности, из письма, отправленного
Фалесом Ферекиду. Этого письма,
приведённого Диогеном Лаэрцким, могло
и не быть, но описанные в нём события и
отношения между людьми вполне
правдоподобны. Фалес пишет: «После того
как мы с Соломоном Афинским плавали на
Крит ради наших там изысканий и плавали
в Египет ради бесед с египетскими жрецами
и звездочётами, право, мы были бы
безумцами, если бы не поплыли и к тебе;
говорю «мы», ибо и Солон приедет, если
ты на то согласишься. Ты ведь домосед,
в Ионии бываешь редко, новых людей видеть
не будешь, и одна у тебя, как я полагаю,
забота – о том, что ты пишешь. Мы же не
пишем ничего, но зато странствуем по
всей Элладе и Азии». О дружбе между
Фалесом и Солоном свидетельствует и
сам Плутарх, который, который рассказал
о любопытном розыгрыше. «Когда Солон
прибыл к Фалесу в Милет,- пишет Плутарх,
— он удивлялся полному его равнодушию
к браку и рождению детей.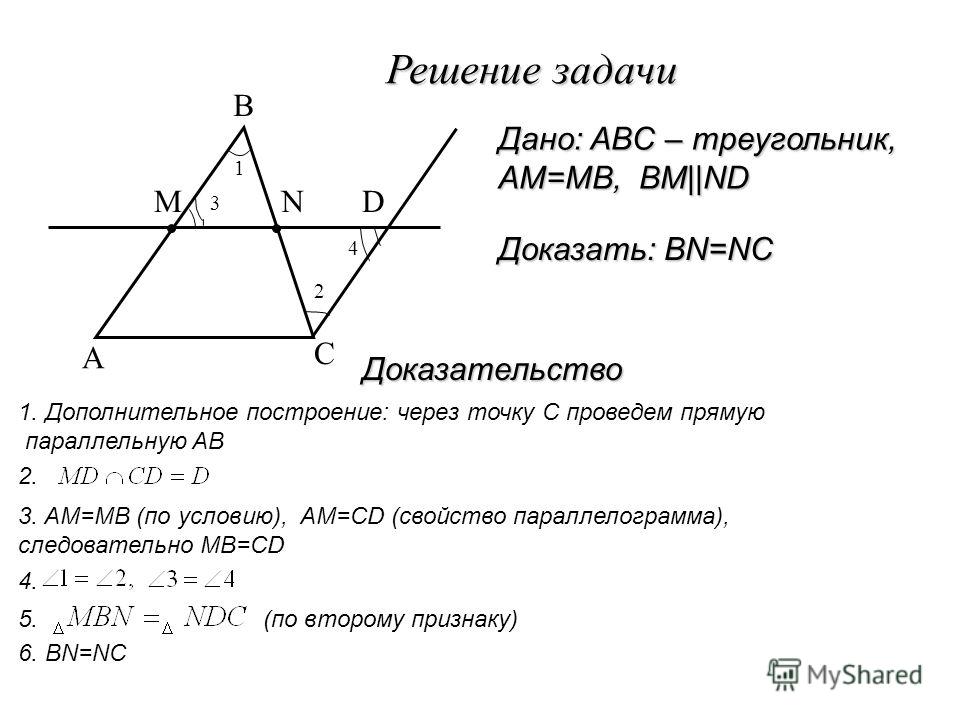 Фалес на этот
Фалес на этот
раз промолчал, а спустя несколько дней
подговорил одного приезжего рассказать,
будто он недавно, десять дней назад,
приехал из Афин. Солон спросил его, нет
ли чего нового в Афинах. Приезжий,
подученный Фалесом, сказал: «Ничего,
только клянусь Зевсом, были похороны
одного молодого человека, и провожал
его весь город. Это был, как говорили,
сын человека известного, первого в
городе по своим нравственным качествам.
Его самого не было; говорили, что он уже
давно находится за границей».- «Какой
несчастный!.. – воскликнул Солон. – А
как его называли?» «Я слышал его имя, —
отвечал тот, — да не помню; только много
было разговоров об его уме и справедливости».
Так при каждом ответе у Солона всё
возрастал. Наконец, уже в полной тревоге
он подсказал приезжему имя и спросил,
не называли ли умершего Сыном Солона.
Тот ответил утвердительно. Тогда Солон
стал бить себя по голове, делать и
говорить всё сказал: «Вот это, и удерживает
меня от брака и рождения детей, что валит
с ног и тебя, такого сильного человека.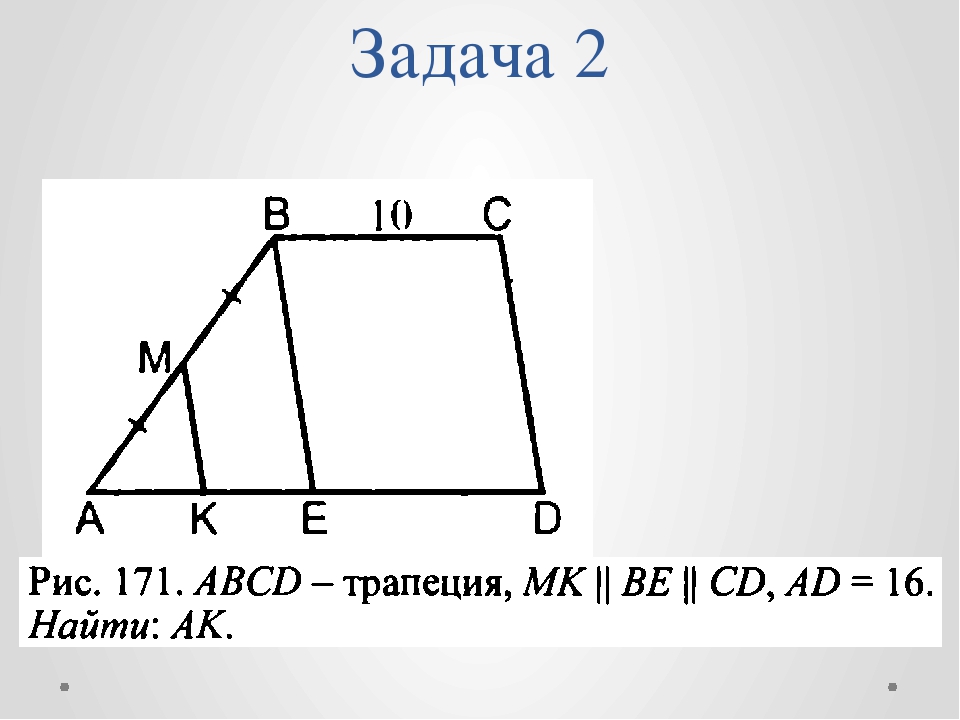
Что же касается этого рассказа, не бойся:
это неправда». Отсюда, между прочим,
следует, что семьи у Фалеса не было. Как
сообщил Плутарх, Фалес усыновил ребёнка
своей сестры, по имени Кабиста. Фалеса,
же всегда считали естествоиспытателем,
астрономом и математиком, изображали
с циркулем в руке.
Народ говорил о семи мудрецах,
к коим причислил Фалеса, Солона, Бианта,
Питтака, Периандра, Клеобула и Хилона.
В отношении первых трёх ни у кого сомнений
не было, но с причислением остальных к
лику мудрых велись ожесточённые споры.
Одни называли либо Ферекида Сиросского,
либо тирана Писистрата или какое-либо
другое лицо, выдвигавшееся на соискание
этого звания скорее из лести, чем по
истинным достоинствам. Платон в
«Протагоре» из названного списка убрал
тирана Периандра, добавив Мисона,
которому он, очевидно симпатизировал.
Писал Фалес или нет, этого мы уже никогда
не узнаем, но заслуги его перед наукой
огромны, хотя и не всё время он ей
посвятил. Находясь на службе у тирана
Трасибула , Фалес плавал по Средиземному
морю с торговой, а возможно, и
государственно-дипламатической миссией.
Сам он, скорее всего, в торговых сделках
не участвовал, так как у него, похоже,
не было устойчивого интереса к коммерческим
делам. В древности говорили: «Ну, сущий
Фалес», т.е. не от мира сего, отрешённый
от повседневной суеты, думающий только
о научных проблемах. Однако Аристотель
рассказал один забавный случай,
произошедший с Фалесом, который, будучи
увлечённым и занятым учёным, тем не
менее, мог провести успешную коммерческую
сделку. «Этот рассказ о некоем, предвидении,
— пишет Аристотель в «Политике», —
использованном для того, чтобы нажить
состояние, и его приписывают Фалесу,
имея в виду его мудрость, но её можно
рассматривать и с общей точки зрения.
Когда его попрекали бедностью, утверждая,
будто занятия философией никакой выгоды
не приносят.
То, рассказывают, он, предвидя
на основании астрономических данных
богатый урожай оливок, ещё до истечения
зимы роздал в задаток имевшуюся у него
небольшую сумму денег всем владельцам
маслобоен в Милете и на Хиосе, законтрактован
их дёшево, так как никто с ним не
конкурировал. Когда наступило время
Когда наступило время
сбора оливок и сразу многим одновременно
потребовались маслобойни, он, отдавая
маслобойни на откуп на желательных ему
условиях и собрав много денег, доказал,
что философам при желании легко
разбогатеть, но не это является предметом
их стремлений. Так, говорят, Фалес дал
доказательство своей мудрости. Этот
случай, произошедший с Фалесом, вероятно,
ещё в молодости, скорее подчёркивает
его непрактичность, поскольку выставляется
как исключение из правила, которому
была подчинена его натура.
Платон, Аристотель и Плутарх,
кивая на Фалеса, в унисон говорили, что
мудрость надо отличать от рассудительности:
первое касается знания природы, второе
— выгоды для себя; Фалес был мудрым, но
не рассудительным, (сейчас бы сказали,
не расчётливым). Его жизнь в чём-то
напоминает жизнь Галилея, который тоже
по молодости торговал циркулями и
подзорными трубами. Это занятие его
увлекало так, что трудно было сказать,
чем больше занята его голова — коммерцией
или наукой.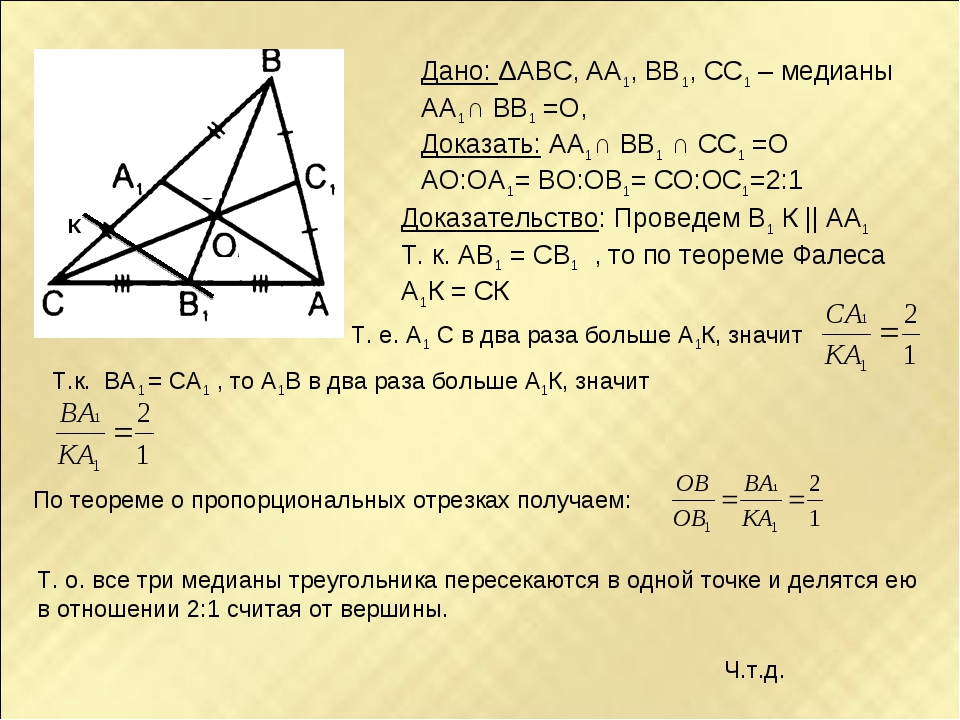 Но постепенно итальянского
Но постепенно итальянского
Фалеса – Галилея нередко сравнивают
с античным мудрецом – захватила наука:
все ночи напролёт он смотрел на звёзды,
пока не ослеп.
Естественно, рано или поздно,
знатному и мудрому Фалесу, на голову
возвышающемуся над всеми остальными,
чтобы не потерять её, пришлось «удалиться
от государственных дел» и заняться
науками. Знания качеств личности
Писистрата и Трасибула помогает понять
сложную политическую обстановку, в
которой жил Фалес. Слава учёного пришла
к Фалесу после предсказанного им
солнечного затмения, которое описал
Геродот: «Так как Алиатт, несмотря на
требования Киаксара, не захотел выдать
скифов, то у лидийцев с мидянами началась
война. Пять лет длилась эта война, причём
верх одерживали то мидяне, то побеждали
лидийцы и однажды – даже в какой-то
ночной битве. Так с переменным успехом
продолжалась эта затяжная война, и на
шестой год во время одной битвы внезапно
день превратился в ночь. Это солнечное
затмение предсказал ионянам Фалес
Милетский и даже точно определил заранее
год, в котором оно и наступило. Когда
Когда
лидийцы и мидяне увидели, что день
обратился в ночь, то прекратили битву
и поспешно заключили мир». Нечего
говорить о том, что занятия Фалеса в
Египте также трактуются очень серьёзно.
Это – крайне пессимистический взгляд
на успехи Фалеса и, вообще, достижения
всей античной науки.
Как показывает история исследования
некоторых математических алгоритмов
решения задач, которыми пользовались
древние вавилоняне и египтяне, современные
учёные не могут взять в толк, каким
образом они могли быть найдены. Нашим
современникам кажется, что для решения
задач по нахождению площадей геометрических
фигур, объёмов тел и прочих параметров
требуются знания высших разделов
математики – алгебры интегрально-дифферециального
исчисления. Однако вполне работоспособные
алгоритмы были найдены, причём некоторые
из них три-четыре тысячи лет назад – мы
просто не умеем их реконструировать.
Может быть, не Фалес первый разделил
год на365 дней, дал определение числа,
как совокупности единиц и понял, что
вписанный в круг треугольник, опирающийся
на диаметр, всегда будет прямым, как об
этом упоминается в различных древних
источниках, но, по крайней мере, в его
время об этом уже знали. Они говорят об
Они говорят об
уровне развития знаний той эпохи, в
которой жил самый выдающийся учёный.
Следовательно, мы смело можем говорить:
Фалес или кто-то из его современников
вполне понимал, что во всяком равнобедренном
треугольников углы при основании равны,
при пересечении двух прямых вертикальные
углы равны, два треугольника равны, если
два угла и одна сторона одного из них
равны углам и одной стороне другого.
Последняя теорема, как предполагается,
использовалась Фалесом для нахождения
расстояния до кораблей, находящихся в
море. Нахождение Фалесом определенных
отношений между элементами равнобедренного
треугольника, ничем принципиальным не
отличается от нахождений законов физики:
и математические(стороны, углы, площади),
и физические(сила, ускорение, масса)
величины измеряются эмпирически, т.е.
пришли к нам из опыта и используются
нами в практической жизни. Интеллектуальные
и чувственные образы тесно взаимосвязаны,
так что разъединять их какой-либо
преградой ненужно. Таким образом,
математические объекты вполне можно
отнести к естественнонаучным и
рассматривать математику и естествознание,
как одну рациональную науку, в которой
используется один и тот же конструктивный
подход. Нейгебауэр критиковал Фалеса
Нейгебауэр критиковал Фалеса
за неудачное предположение, что причиной
разлива Нила являются ветер, дующий с
моря против его течения. Да, конечно,
эта гипотеза ошибочна, но важно, что он
над этим явлением размышлял и предложил
рациональное объяснение, а не сводил
дело к божественному гневу или милости,
как это делали до него. Начиная с Фалеса
люди повсеместно стали задаваться
вопросами: почему сверкает молния, как
возникает гром, что такое огонь, как
связан он с теплом, откуда берётся ветер,
что такое снег и лёд, как связаны они с
холодом, из чего земля, животные и
растительные ткани, какие причины
приводят к землетрясению, наступлению
холодов, образованию облаков и т.д. и т.
д. Наука начинается там, где религии
говорят «Нет!», где ищут решения, не
прибегая к силам какого-либо Высшего
Существа. И вот в этом Фалес был Первым!
«Он первый нашёл путь Солнца от
солнцестояния до солнцестояния; он
первый ( по мнению некоторых) объявил,
что размер Солнца составляет 1/720 часть
[солнечного пути, а размеры Луны – такую
же часть] лунного пути [ т. е. оба светила
е. оба светила
видны под углом 0,5 гр.]. Он первый назвал
последний день месяца «тридесятым»,
[т.е. разделил год на 12 месяцев, в каждом
из них было по 30 дней]. Он первый, как
говорят иные, стал вести беседы о
природе». Главное геометрическое
достижение Фалеса состояла в том, что
ему удалось открыть пропорциональность
сторон подобных треугольников. Теперь
на основе пропорции a/b=c/d, он мог производить
измерение неизвестной величины по трём
известным. Именно с помощью этой пропорции
он нашёл высоту египетских пирамид.
Измерение расстояния до корабля,
находящегося далеко в море, производилось
тоже на основе этой пропорции. Выбрав
на берегу базиса и вымерив с крайних
его точек углы до корабля, геометр затем
вычерчивал подобный треугольник
небольших размеров и измерял у него две
стороны, скажем, c и d; после этого ничего
не стоило найти неизвестное расстояние
до корабля – сторону b. Такого рода
задачи и даже более сложного( нахождение
площади круга, объём усечённой пирамиды
и т.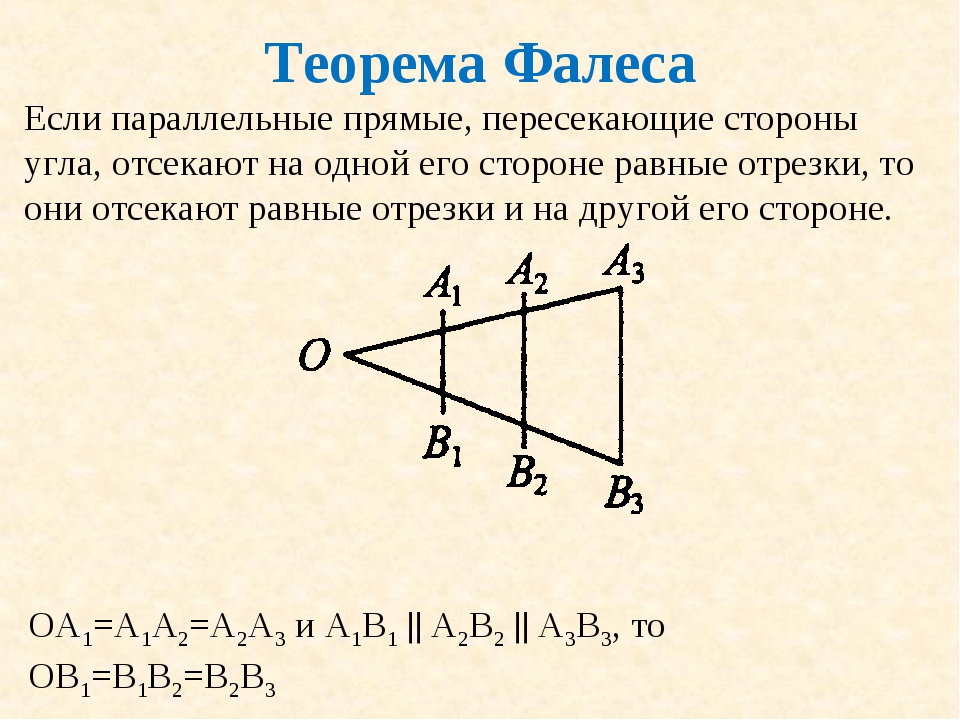 д.) умели решать в Египте. Это стало
д.) умели решать в Египте. Это стало
известно из найденных Московского и
Риндовского папирусов, написанных около
2000 году до н.э. Однако этими знаниями
овладел мудрый человек, живущий в
ответственный для науки период. Далее
можно пронаблюдать, как пропорция a/b =
c/d
через Пифагора, Демокрита и Архимеда
легла в основу науки эпохи Зарождения
и Итальянского Возрождения. Простота
и универсальность пропорции позволило
сделать множество математических и
естественнонаучных открытий. Всё это
говорит о том, что Фалес был не столько
первым философом, сколько первым учёным,
т.е. тем первым профессионалом, который
все явления природы пытался Объяснить
рациональными средствами. Но было в его
объяснениях физического мира и такое,
что отнести к рациональным соображениям
можно лишь с изрядной натяжкой. Время
жизни Фалеса, по Дильсу, 624 – 547 г. до
н.э., расцвет сил (акме) 585г., дата славы
585г., предсказанное им солнечное затмение
28 мая 585г. По Таннери, время жизни Фалеса
637-558г. акме 597г., дата славы 586г.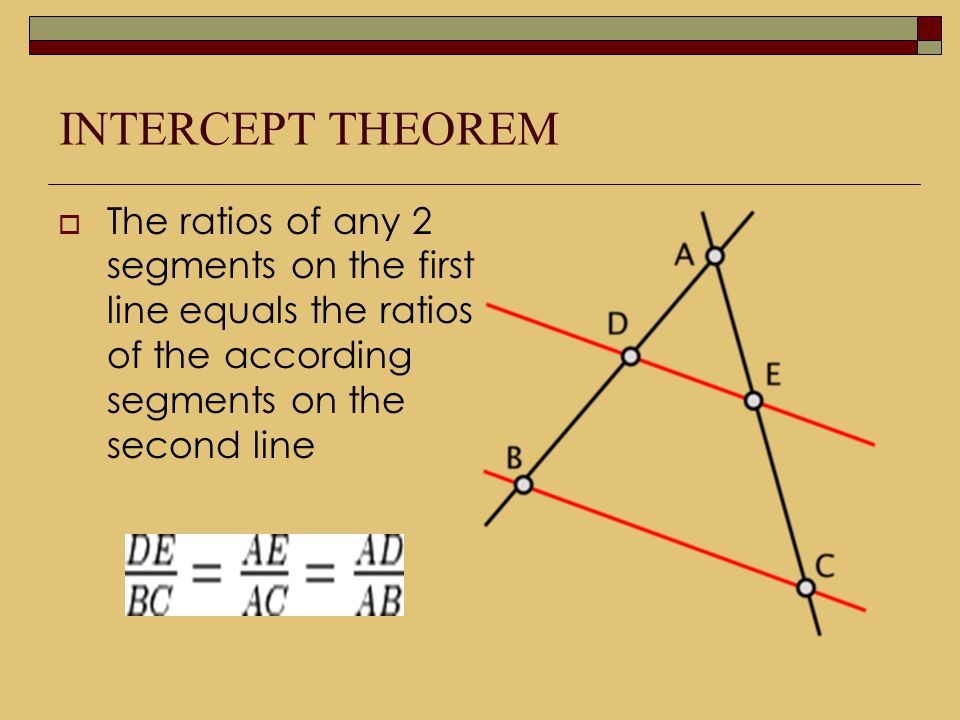 , предсказанное
, предсказанное
им солнечное затмение 30 сентября 610г.
Заслуги, которые приписывали Фалесу
историки в новое время, можно резюмировать
так: Фалес – родоначальник европейской
науки, он перенёс с Востока в Грецию
богатый запас эмпирических наблюдений
и на основании этого обширного собрания
фактов создал первые в истории мысли
научно-теоритические построения. В
частности, он – первый математик и
создатель научной геометрии (преобразовал
египетское искусство измерения в
дедуктивную геометрию, покоящуюся на
общих основаниях), астроном (предсказал
полное затмение; открыл, что из созвездий
наиболее точно север определяется Малой
Медведицей, и т. д.), метеоролог (удачное
предсказание урожая оливок), физик (ряд
объяснений физических явлений). Как
философов, он глава милетской школы и
отец греческой философии. Точность его
научных открытий, его деятельность не
ограничивалась научно-теоретической
областью, он также практически деятель
с обширной сферой интересов: он –
путешественник, купец (торгует солью),
инженер, политик и государственный
деятель.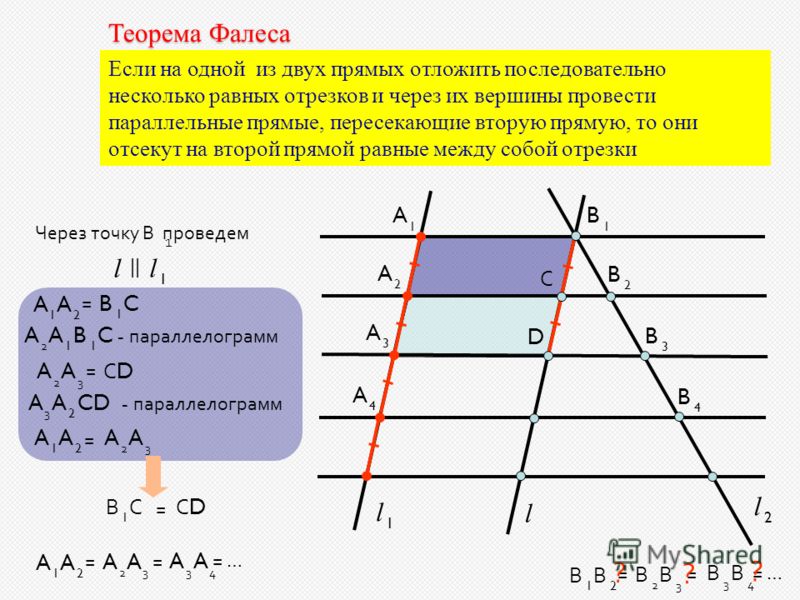 Наконец, известны его краткие
Наконец, известны его краткие
изречения – практические советы
морального характера. Основное положение
Фалеса: вода есть начало всего. Нам
неизвестно в точности, какой смысл
заключён в этом положении. Прежде всего,
идёт ли здесь речь о возникновении во
времени или в вечной основе всего
существующего? Говорит ли Фалес, что
всё возникло из воды (учение, которое в
16 веке повторил Парацельс), или он
указывает в воде постоянное начало,
неизменно лежащее в основе изменчивых
разнообразных форм природы? Далее, эта
первая стихия есть ли вода, как одно из
веществ природы, или под водой здесь
разумеется всякая жидкость (т.е. первичным
признаётся известное состояние матери),
или, наконец, вода здесь есть объектированное
качеств: влажность? Так расходятся
взгляды учёных в истолковании положения
Фалеса «вода есть начало всего», в
котором, таким образом, и субъект и
предикат двусмысленны для нас. Как
говорит Дмитрий Фалерский в «Списке
архонтов», Фалес был назван первым
мудрецом в тот год, когда в Афинах был
архонтом Дамасия, при котором были
названы мудрецами известные семь.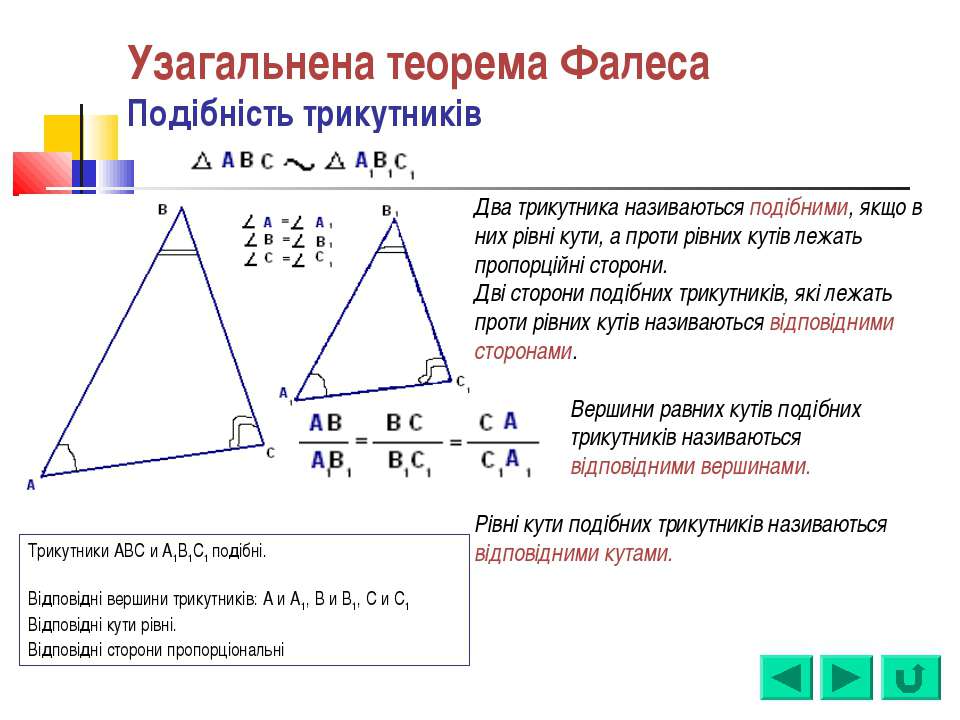 Принят
Принят
же в число граждан Фалес был в Милете,
куда он прибыл с Нейлеем, изгнанным из
Финикии. Впрочем, по свидетельству
большинства, он был природный милетец
и знатного рода. Почти все философы
древней Греции тщательно занимались
математикой, в частности геометрией.
Фалесу Мелецкому Прокл приписывает
открытие или доказательство теорем о
том, что диаметр делит круг пополам, что
угол, вписанный в полуокружность, прямой,
о равенстве вертикальных углов, о
равенстве углов при основании
равнобедренного треугольника и др. Эти
положения были частично известны ещё
вавилонянам и египтянам. Однако в отличии
от вавилонской и египетской геометрии,
имевшей преимущественно практический
и прикладной характер, греческая
геометрия характеризуется стремлением
установить, что геометрические факты
верны не только для отдельных частных
случаев, а справедливы в любом случае.
При помощи общих доказательств, с
постепенным переходим от одной истины
к другой, греческие математики создали
геометрию как науку.
Направление строгой логической
последовательности в геометрии первыми
заложили геометры греческой ионийской
школы, основателем которой был Фалес.
Фалес был знаком и с вавилонской
астрономией. Платон, знаменитый греческий
философ четвёртого века до нашей эры,
рассказывает, что Фалес, наблюдая звёзды,
упал в колодец, а стоявшая рядом женщина
посмеялась над ним, сказав: «Хочет знать,
что делается на небе, а что у него под
ногами, не видит…». Фалес сделал ряд
открытий в области астрономии: установил
время равноденствий и солнцестояний,
определил продолжительность года,
впервые наблюдал Малую Медведицу и т.п.
Особенную славу ему принесло предсказание
солнечного затмения, произошедшего в
585 году до н.э. Фалес был не только
философом и учёным, но также государственным
и общественным деятелем. Вот почему он
был причислен к группе «семи мудрецов»
древности.
Существуют разные версии смерти
Фалеса.
1. Диоген Лаэрцкий в своём известном
сочинении «О жизни, учёниях и изречениях
знаменитых философов», появившемся
где-то во 2-3вв., привёл письмо Анаксимена,
посланное Пифагору, где сообщает о
смерти своего учителя и друга. «Фалес,
«Фалес,
сын Эксамия, достигнув преклонных лет,
несчастным образом скончался. Ночью он
по своему обыкновению вышел со служанкой
из дома, чтобы посмотреть на звёзды, и,
созерцая их, свалился в канаву, о котором
совсем запамятовал. Вот каков, по словам
милетских жителей, был конец этого
небоведца. Мы же, его собеседники, и
сами, и дети наши, и коллеги наши по
занятиям, сохранили память об этом муже
и блюдем его заветы. Пусть же всякая
наша речь начинается именем Фалеса».
Во втором письме к Пифагору, который
бежал от тирана Поликрата с острова
Самос, расположенного недалеко от
Милета, в италийский город Кратон,
Анаксимен, жалуясь на тяжёлую жизнь,
обронил такую фразу: «Как же помышлять
Анаксимену о делах небесных, когда
приходится страшиться гибели или рабства
[на земле]. Возможно, в людской памяти
как-то соединилась эта фраза с личностью
Фалеса, но не с его гибелью.
2. В античности была распространена
легенда, будто мудрец скончался от зноя,
жажды и давки, когда смотрел на солнцепёке,
как состязаются молодые и сильные
гимнасты.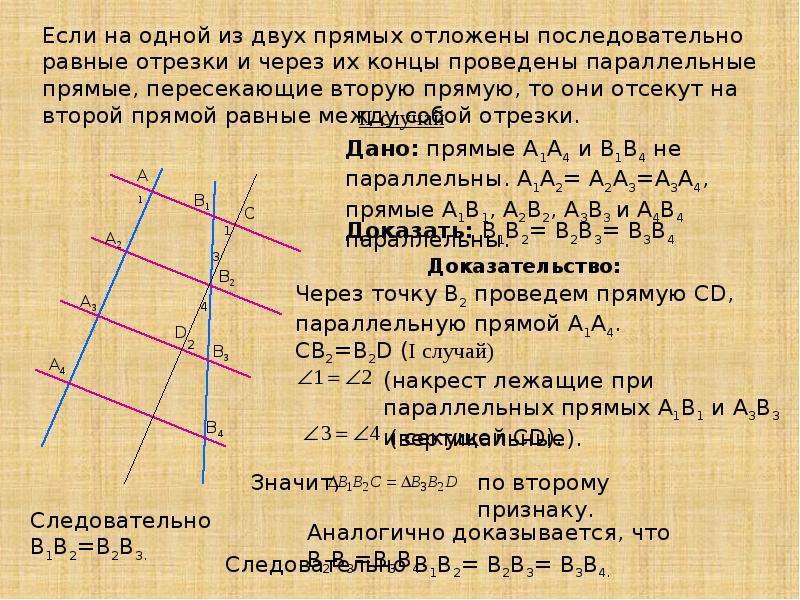 Старик слишком приблизился
Старик слишком приблизился
к соревнующимся, пишет Диоген Лаэрцкий,
и возбужденная толпа задавила его
насмерть. Однако такой печальный финиш
жизни этого выдающегося человека кажется
маловероятным. Вряд ли могло так
случиться, чтобы известного всей Элладе
мыслителя задавила толпа болельщиков?
Так что малопочётная гибель в канаве
здесь кажется более предпочтительной,
если только она действительно была
вызвана желанием смотреть на звёзды.
3..Мудрец Фалес скончался в то
время, когда смотрел гимнастическое
состязание, от жары, жажды и бессилия,
будучи уже престарелым. И на памятнике
его написано: «Взирай на эту действительно
малую могилу весьма мудрого Фалеса
(слава же его достигает небес)». Имеется
и у нас в первой из «Надписей», или в
«Написанной в различных размерах»,
следующая надпись, относящаяся к нему:
«Некогда смотревшего гимнастическое
состязание мудреца Фалеса ты, о солнце
Зевс, похитил из ристалища. Я восхваляю
тебя за то, что увёл его поближе к небу,
ибо, в самом деле, старик уже не мог более
с земли видеть звёзды.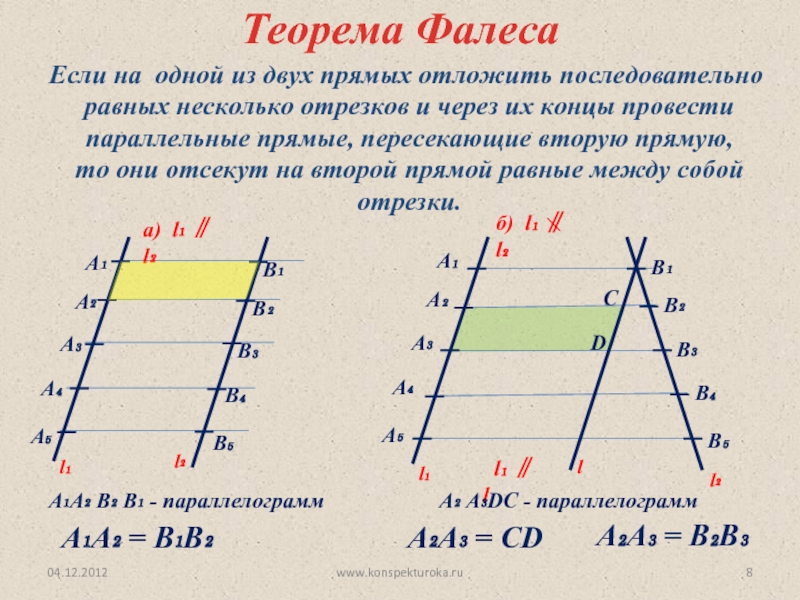 Фалесу принадлежит
Фалесу принадлежит
изречение: «Познай самого себя», о
котором Антисфен в «Диадохах» говорит,
что оно принадлежит Фемоною и что его
присвоил себе Хилон..
Сочинения Фалеса до нашего
времени не сохранились.
Практическая часть.
Теорема
Докажем теорему
Фалеса: если
на одной из двух прямых отложить
последовательно несколько равных
отрезков и через их концы провести
параллельные прямые, пересекающие
вторую прямую, то они отсекут на второй
прямой равные между собой отрезки.
Решение:
Пусть на прямой l1
отложены равные отрезки
А1А2,
А2А3,
А3А4,
…и через их концы проведены параллельные
прямые, которые пересекают прямую l2
в точках В1,
В2, В3,
В4, … (рис.1).
Требуется доказать, что отрезки В1В2,
В2В3,
В3В4,
… равны друг другу.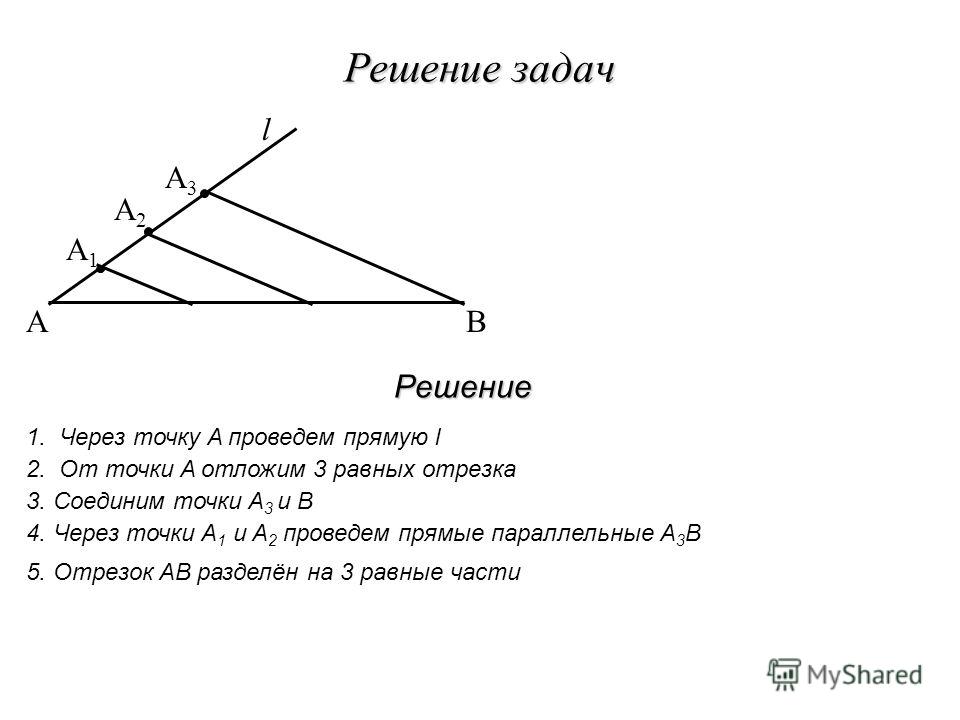 Докажем, например,
Докажем, например,
что В1В2
= В2В3.
Рассмотрим сначала случай, когда
прямые l1
и l2
параллельны (рис. 1, а). тогда А1А2
= В1В2
и А2А3
= В2В3
как противоположные стороны параллелограммов
А1В1В2А2
и А2В2В3А3.
так как А1А2
= А2А3,
то и В1В2
= В2В3
если прямые l1
и l2
не параллельны, то через точку
В1
проведем прямую l,
параллельную прямой l1
(рис.1, б). Она пересечет прямые А2В2
и А3В3
в некоторых точках С и D.
Так как А1А2
= А2А3,
то по доказанному В1С
= СD.
Отсюда получаем В1В2
= В2В3.
Аналогично можно доказать, что В2В3
= В3В4
и т.д.
Задача
Через середину М стороны АВ
треугольника АВС проведена прямая,
параллельная стороне ВС. Эта прямая
пересекает сторону АС в точке N.
Докажите, что
AN
= NC.
Решение:
Через точку С проведем прямую,
параллельную прямой АВ и обозначим
буквой D
точку пересечения этой прямой с прямой
MN
(рис. 2). Так как AM
= МВ по условию, а MB
= CD
как противоположные стороны параллелограмма
BCDM,
то АМ = DC.
Треугольники АМN
и CDN
равны по второму признаку равенства
треугольников (АМ=CD,
Задача
Разделите данный отрезок АВ на
n
равных частей.
Решение:
Проведен луч АХ, не лежащий на
прямой АВ, и на нем от точки А отложим
последовательно n
равных отрезков АА1,
А1А2,
…, Аn-1Аn
(рис.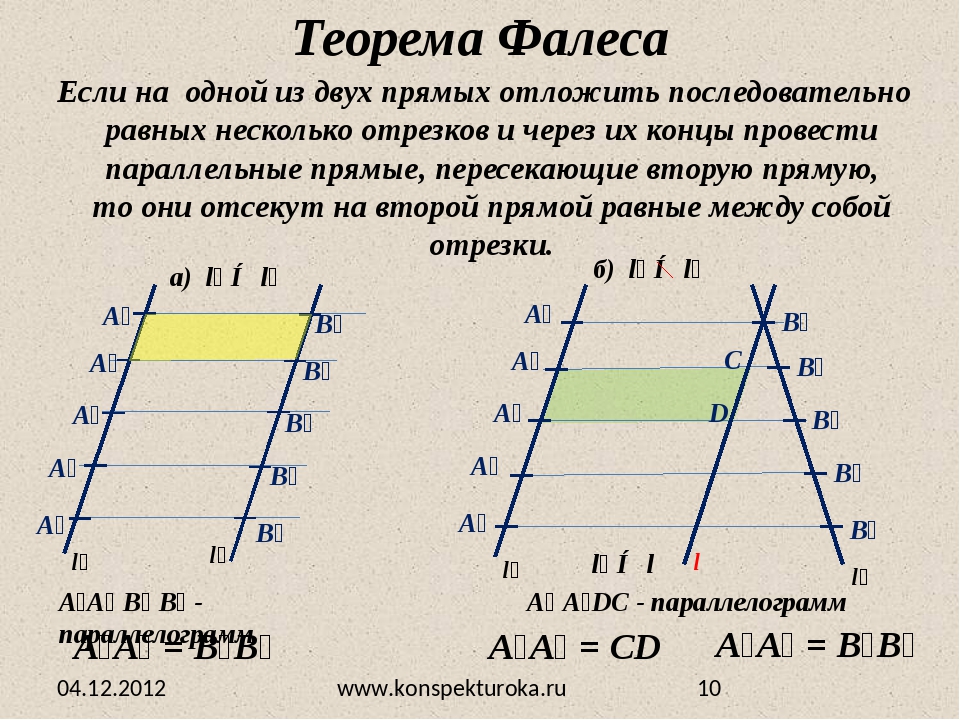 3), т.е. столько равных отрезков, на
3), т.е. столько равных отрезков, на
сколько равных частей нужно разделить
данный отрезок АВ (на рис. 3 n=5).
Проведем прямую АnВ
(точка Аn
– конец последнего отрезка) и построим
прямые, проходящие через точки А1
, А2 ,
…, Аn-1
и параллельные прямой
АnВ.
Эти прямые пересекают отрезок АВ в
точках В1 ,
В2 , …, Вn-1,
которые по теореме Фалеса делят отрезок
АВ на n
равных частей.
Задача
Разделите данный отрезок АВ на
8 равных частей.
Решение:
Проведен луч АХ, не лежащий на
прямой АВ, и на нем от точки А отложим
последовательно 8 равных отрезков АА1,
А1А2,
…, А7А8
(рис.3), т.е. столько равных отрезков, на
сколько равных частей нужно разделить
данный отрезок АВ (рис. 4). Проведем прямую
А8В (точка
А8 – конец
последнего отрезка) и построим прямые,
проходящие через точки А1
, А2 ,
…, А7 и
параллельные прямой А8В.
Эти прямые пересекают отрезок АВ в
точках В1 ,
В2 , …, В7,
которые по теореме Фалеса делят отрезок
АВ на 8 равных частей.
Литература
Атанасян Л.С. и др. Геометрия.
7—9 классы : учеб. для общеобразоват.
учреждений / [Л. С. Атанасян, В. Ф. Бутузов,
С. Б. Кадомцев и др.],М. : Просвещение,
1999.Глейзер Г.И. История в математики
в школе. Москва: Просвещение, 1983.Малыгин К.Л. Элементы историзма
в преподавании математики в средней
школе. М: Учпедгиз 1963г.Погорелов А.В. Геометрия 7 – 11
класс. Москва.: «Просвещение», 1995Рыбников Л.А. История математики.
Издательство МГУ, 1974 г.Интернет ресурсы.
Планиметрия /wiki/
Милетская школа
/wiki/Теорема Фалеса
/wiki/
Теорема Фалеса и отношение отрезков в задачах ОГЭ и ЕГЭ.
Теорема Фалеса и отношение отрезков в задачах ОГЭ и ЕГЭ.
Выступление учителя математики
МБОУ «СОШ №10» РТ г.Елабуги
Санникова Г.И.
Елабуга, 2020год
Содержание
«Человек… родился быть господином, повелителем, царём природы, но мудрость с которой он должен править, не дана ему от рождения: она приобретается с учением»
Н. И. Лобачевский
Эта работа , посвящённая задачам на отношение отрезков, адресована учащимся 8-11 классов для подготовки к ОГЭ и ЕГЭ .
Почему мы обращаемся к этому методу? Задачи на данную тему вызывают затруднения у учащихся привыполнений задач второй части (задания повышенной сложности) на выпускных экзаменах. Именно данная проблема и дала импульс к началу работы по изучению и освоению теоремы Фалеса, обобщенной теоремы Фалеса и метода подобия.
Идея самого метода построена на использовании обобщенной теоремы Фалеса. Теорема Фалеса изучается в восьмом классе, ее обобщение и тема «Подобие фигур» в девятом и только в десятом классе, в ознакомительном плане, изучаются две важные теоремы Чевы и Менелая, с помощью которых относительно легко решается ряд задач на нахождение отношения длин отрезков. Поэтому на ступени основного образования мы можем решать довольно узкий круг задач по данному учебному материалу. Хотя на итоговой аттестации за курс основной школы и на ЕГЭ по математике задачи по данной теме (Теорема Фалеса. Подобие треугольников, коэффициент подобия. Признаки подобия треугольников) предлагаются во второй части экзаменационной работы и относятся к высокому уровню сложности.
В процессе данной работы стало возможным углубление наших знаний по теме. Доказательство теоремы Фалеса входит в учебную программу — геометрия Л.С. Атанасяна в качестве задачи под №385, но вызывает затруднения у большинства учащихся. В результате подбора ряда задач мы смогли научиться решать более широкий круг математических заданий на отношение длин отрезков. В этом и заключается актуальность нашей работы.
В этом и заключается актуальность нашей работы.
Помимо обучающей функции Теорема Фалеса используется в практических вычислениях морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
Данная цель достигается по средствам:
1. Изучение биографии Фалеса, его теоремы и доказательства;
2. Разбор и решение конкретных задач в формате ОГЭ и ЕГЭ;
3. Теоритическая трактовка и компьютерная трансляция.
При изучении темы опорой служили следующие источники.
Биографическая литература:
Асмус В. Ф. Античная философия. — М.: Высшая школа, 1998. — С. 10—13.
Панченко Д. В. Фалес: рождение философии и науки // Некоторые проблемы истории античной науки : Сборник научных трудов / Отв. ред. А. И. Зайцев, Б. И. Козлов. — Л.: Главная астрономическая обсерватория, 1989. — С. 16—36.
Храмов Ю. А. Фалес Милетский (Θαλῆς ὁ Μιλήσιος, ThalestheMilesian, ThalesofMiletus) // Физики: Биографический справочник / Под ред.
 А. И. Ахиезера. — Изд. 2-е, испр. и дополн. — М.: Наука, 1983. — 400 с. — 200 000 экз. (в пер.)
А. И. Ахиезера. — Изд. 2-е, испр. и дополн. — М.: Наука, 1983. — 400 с. — 200 000 экз. (в пер.)Авторские учебно-тренировачные тесты по математике:
ГИА математика: типовые экзаминационные варианты, 30 вариантов под редакцией А.Л.Семёнова, И.В.Ященко; издательство «Муниципальное образование», 2012-1015гг (ФИПИ-школе).
Математика. Подготовка к ЕГЭ 2014 год под редакцией Ф.Ф.Лысенко и др. ООО «Легион»-готовимся к ЕГЭ.
ЕГЭ 2013; математика С4. Геометрия. Планиметрия под редакцией А.Л.Семёнова и И.В. Ященко.
Ссылки:
https://ru.wikipedia.org/wiki/Фалес_Милетский
www.physchem.chimfak.rsu.ru/Source/History/Persones/Thales.html
internat.msu.ru/…/Математика-ЗШ-9-032013-Задачи-для-самостоятел…
Фалес Милетский-греческийфилосов, самый древний из ученых, один из семи мудрецов, вошедших в историю геометрии, считают греческого философа Фалеса Милетского.
Будущий ученый родился в городе Милете, находившемся в западной части побережья Малой Азии. Фалес предсказал солнечное затмение 585г. до н. э. Он сделал немало важных открытий в различных областях науки. Его считают отцом греческой математики.
Однажды Фалес отправился по торговым делам в Египет. Там он пробыл несколько лет и настолько глубоко изучил достижения египетских жрецов, что вскоре превзошел их в значениях.
Рассказывают, что фараон пожелал узнать высоту пирамиды, но никто не мог ее определить.
Фалес легко справился с этой задачей. Он выбрал день и час, когда его собственная тень стала равной его росту. Измерив тень, которую отбрасывала пирамида, он установил, что длина тени от центра основания пирамиды до ее вершины была равна высоте этой пирамиды. Фараон и его приближенные были изумлены, как точно, быстро, без специальных приборов северный пришелец решил трудную задачу.
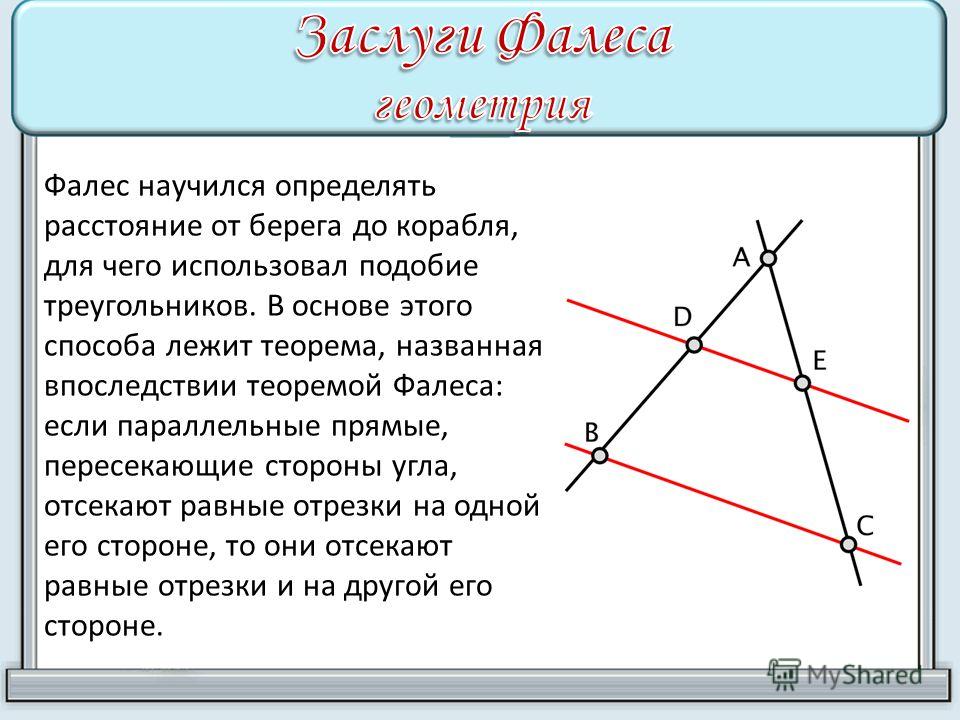
Однако, прежде чем сделать такое простое измерение, Фалес должен был открыть и доказать, что углы при основании равнобедренного треугольника равны и что против равных углов в треугольнике лежат равные стороны, а также, что сумма углов любого треугольника равна двум прямым углам.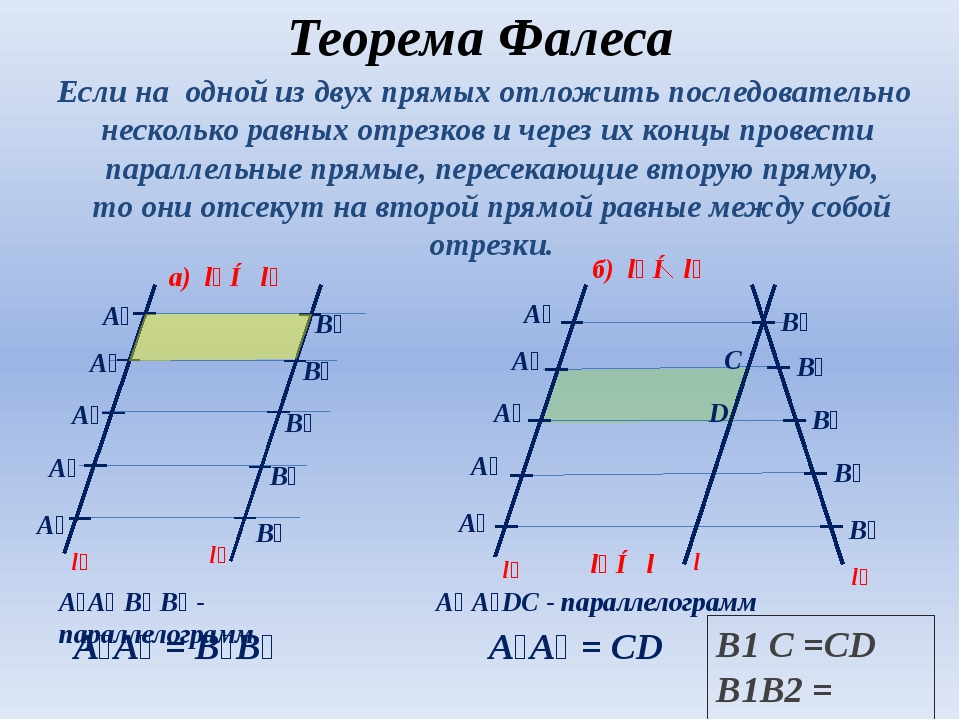 Фалес доказал также теорему о равенстве двух треугольников, если сторона и два прилежащих к ней угла треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника. На основании этой теоремы Фалес Милетский определил, как измерить расстояние от конкретного места на берегу до корабля, находящегося недалеко в море.
Фалес доказал также теорему о равенстве двух треугольников, если сторона и два прилежащих к ней угла треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника. На основании этой теоремы Фалес Милетский определил, как измерить расстояние от конкретного места на берегу до корабля, находящегося недалеко в море.
Некоторые из этих утверждений были известны вавилонам и египтянам и до Фалеса, но до него их не доказывали. Фалес же указанные положения доказывал и только после этого применял их на практике. Введя в практику доказательство теорем, Фалес заложил основы создания геометрии как науки. После него каждое открытие в геометрии древние ученые стремились обосновывать доказательством и только после этого считали его истинным.
Теорема:
Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие вторую сторону угла, то на второй стороне отложатся также равные отрезки.
Доказательство:
Через точки A, B, C и D, расположенные на одной стороне угла, проведены параллельные прямые, которые пересекают другую сторону в точках A1, B1,C1,D1 соответственно. АВ=СD.
АВ=СD.
Проведем через точки А и С прямые, параллельные другой стороне угла. Получим два параллелограмма АВ2В1А1 и CD2D1C1. Согласно свойству параллелограмма, AB2=A1B1 и CD2=C1D1. Осталось доказать AB2=CD2. ∆ABB2=∆СВВ2 (по 2 признаку) АВ=CD согласно условию теоремы; ∟АВВ2=∟CDD2 как соответственные углы, образовавшиеся при пересечении параллельных прямых ВВ1, DD1 и секущей BD. ∟ВАВ2=∟DCD2=∟DOD1 как соответственные при OD1llAB2llCD2 и секущей ОВ.
Ч.Т.Д.
① Задача № 26 (ГИА, ФИПИ)
На биссектрисе BD треугольника ABC отмечена точка М так, что BM/MD=5/4. Прямая АМ пересекает сторону ВС в точке К. Найти отношение ВК/KC, если AB/BC=3/2.
Решение:
Проведём через точку D прямую, параллельную прямой AK. Она пересекает BC в точке P. Воспользуемся обобщённой теоремой Фалеса: отрезки BM и MD пропорциональны отрезкам BK и KP, следовательно BK/KP=BM/MD=5/4. Пусть 1 часть будет Х следовательно BK=5X, KP=4X.
Отрезки AD и DC пропорциональны отрезкам KP и PC то есть KP/PC=AD/DC. Но AD/DC=AB/BC=3/2 (по свойству биссектрисы в треугольнике ABC)
Но AD/DC=AB/BC=3/2 (по свойству биссектрисы в треугольнике ABC)
Пусть 1 часть- Y, тогда AD=3Y, DC=2Y =>
Y/2Y=4X/PC, PC=8X/3, KC=KP+PC=4X+8X/3=20X/3.
Имеем BK/KC=5X/20X/3=15X/20X=3/4
Ответ: BK/KC=3/4.
② Задача № 26 (ГИА, ФИПИ)
На сторонах AC и BC треугольника ABC отмечены точки K и M так, что AK/KC=2/3, BM/MC=6/8. Отрезки AM и BK пересекаются в точке О.
Найти отношения: 1)AO/OM 2)BO/OK.
Решение:
1.Проведём через точку М прямую, параллельную BK. Она пересекает AC в точке D. Согласно обобщенной теоремы Фалеса KD/DC=BM/MC=6/8; AK/KC=2/3. AO/OM=AK/KD. Пусть 1 часть будет Х, тогда AK=2X, KC=3X => BM/MC=KD/DC=6/8,
6/8=KD/(3X-KD),
8KD=18X-6KD,
14KD=18X,
KD=18X/14,
KD=9X/7, DC=3X-9X/7=(21X-9X)/7=12X/7. Значит,
AO/OM=AK/KD= 2X/(9X/7)=(2x*7)/9X=14/9
=>AO/OM=14/9.
Ответ:14/9.
2.Проведём через точку К прямую параллельную АМ. Она пересекает ВС, в точке Р. Согласно обобщенной теоремы Фалеса CP/PM=KC/AK=3/2, BM/MC=6/8. Пусть 1 часть будет Y, тогда BM=6Y, MC=8Y, AK/KC=MD/DC, 2/3=MP/(MC-MP), 2/3=MP/(8Y-MP)
Пусть 1 часть будет Y, тогда BM=6Y, MC=8Y, AK/KC=MD/DC, 2/3=MP/(MC-MP), 2/3=MP/(8Y-MP)
2*(8Y-MP)=3MP
16Y-2MP=3MP
5MP=16Y
MP=16Y/5
Имеем BO/OK=BM/MP=6Y/(16Y/5)=30Y/16Y=15/8.
Ответ:15/8.
③ Задача №26 (ОГЭ, ФИПИ)
Биссектриса угла А треугольника ABC делит медиану, проведённую из вершины В, в отношении 5/4 , считая от вершины В. В каком отношении, считая от вершины С, эта биссектриса делит медиану, проведённую из вершины С?
Найти:CO/OK.
Решение:
Согласно обобщенной теоремы Фалеса, в треугольнике АВМ, AD-биссектриса, (по св-ву биссектрисы) АВ:АМ=ВD:DМ=5:4. В треугольнике АВС, AN-биссектриса АВ:АС=BN:CN=5:8. Проведем через точку К прямую КТ-параллельную АN. Имеем АК:ВК=NT:ВТ=>ВТ=TN, АК=ВК. Значит, СО:ОК=CN:TN=8:2,5=8:5/2=16:5.
Ответ: 16:5
④ Задача С4 (ЕГЭ)
В треугольнике АВС биссектриса AD делит сторону ВС в отношении BD:DC=2:1. В каком отношении медиана СЕ делит эту биссектрису.
Найти: АО:ОD
Решение:
AD-биссектриса(по св-ву биссектрисы) BD:CD=AB:AC=2:1, CE-биссектриса. Через точку D, проведем прямую DP, параллельную СЕ. Согласно обобщенной теоремой Фалеса имеем, CD:BD=ЕР:ВР=1:2, тогда АЕ:ЕР=АО:ОD=3:1.
Через точку D, проведем прямую DP, параллельную СЕ. Согласно обобщенной теоремой Фалеса имеем, CD:BD=ЕР:ВР=1:2, тогда АЕ:ЕР=АО:ОD=3:1.
Ответ: 3:1
⑤ Задача С4 (ЕГЭ)
На сторонах AB и BC параллелограмма ABCD расположены точки N и M соответственно, причём AN:NB=3:2, BM:MC=2:5.Прямая АМ и DN пересекаются в точке О.
Найти: АО:ОМ
Решение:
Проведём через точку В прямую ВК, параллельную DN, AM пересекается с BK в точке Т.
AN/BN=AO/OT=3/2; через точку М проведём прямую MP, параллельную BK; BM/MC=PK/CP=2/5; Пусть 1 часть-y, тогда BM=2y, MC=5y, CK=3x.
2/5=PK/(CK-PK), 2/5=PK/(3x-PK)
5PK=6x-2PK
7PK=6x
PK=6x/7, CP=3x=6x/7=(21x-6x)/7=15x/7, Значит, AO/OM=3x/(2x+6x:7)=21x/20x=21/20.
Ответ: 21/20.
⑥ Задача № 26 (ГИА,ФИПИ 2015)
В параллелограмме АВСD биссектриса тупого угла В пересекает сторону AD в точке F. Найдите периметр параллелограмма, если АВ=12 и AF:FD=4:3.
Решение:
По условию, BF-биссектриса угла В, угол CBF=углу ABF, угол BFA=углу CBF как накрест лежащие углы при ВСllAD, секущей BF, значит треугольник ABF-равнобедренный, т.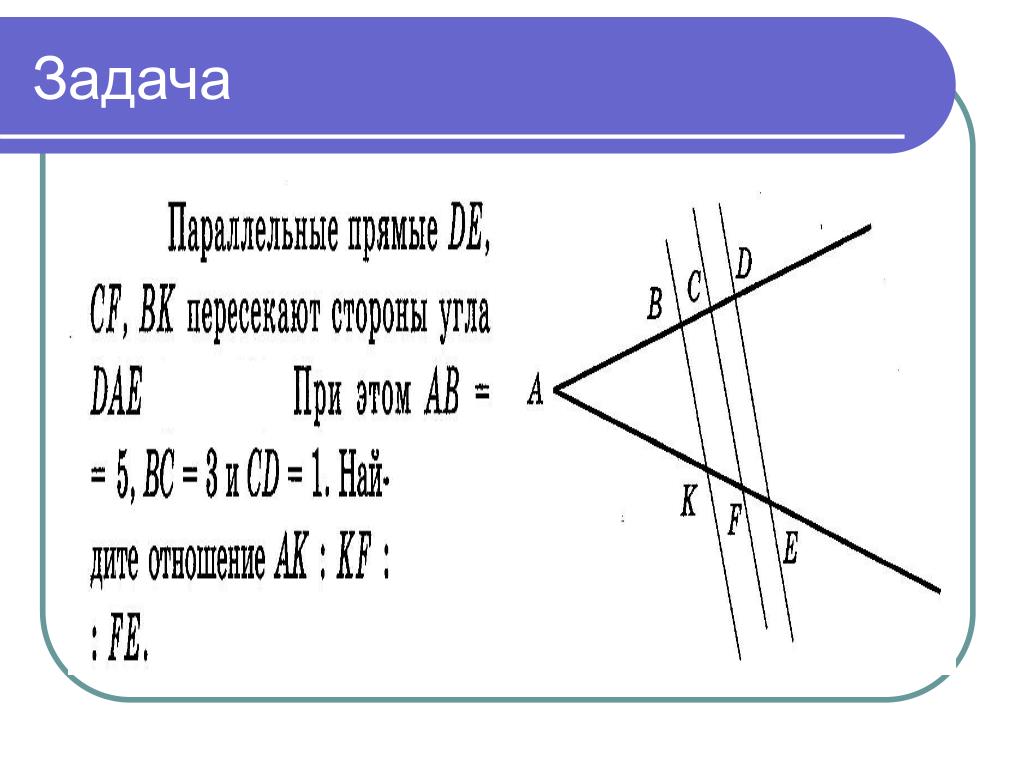 е. AF=AB=12. Пусть AF=AB=4x, FD=3x. По условию, АВ=12, т.е. 4х=12; х=3, AD=AF+FD=4x+3x=7x =>AD=7*3=21, следовательно РABCD=2(AB+AD)=2(12+21)=66
е. AF=AB=12. Пусть AF=AB=4x, FD=3x. По условию, АВ=12, т.е. 4х=12; х=3, AD=AF+FD=4x+3x=7x =>AD=7*3=21, следовательно РABCD=2(AB+AD)=2(12+21)=66
Ответ:66
⑦Задача №26 (ОГЭ, ФФ Лысенко)
Найдите длину отрезка, который соединяет боковые стороны трапеции и параллелен ее основаниям, если известно, что он делит сторону трапеции в отношении 2/3, считая от меньшего основания к большему. Основания трапеции равны 5 и 15.
Решение:
ABCD-данная трапеция, ВС=5, AD=15. Пусть MN-искомый отрезок, MNllBC, MNllAD, BC и CH-высоты трапеции.
1 случай:
AD=АК+КН+HD=АК+ВС+HD(т.к.BCHK-прямоугольник, ВС=КН) 15=5+АК+HD, АК+HD=10. Треугольник BMQ подобен треугольнику BAK(угол АВК- общий, угол BMQ=углу BAK как соответственные углы при секущей АВ, MNllAD). MQ/AK=BQ/BK=2/5, MQ=2/5АК, аналогично PN=2/5HD => MQ+PN=2/5AK +2/5HD=2/5(ak+MD)=2/5*10=4 => MN=4+5=9.
2 случай:
AD=AK+KH-DH=AK+BC-DH. 15=AK+5-DH, AK-DH=10. MQ=2/5AK, PN=2/5DH, MN=MQ+QP=MQ+QP-MP=5+MQ-NP=5+2/5*(AK-DH)=5+2/5*10=9.
Ответ:9
Интересное решение данной задачи с помощью метода площадей и подобия треугольников.
Задачи служат для отработки техники применения признаков подобия, теоремы об отношении площадей треугольников, имеющих по равному углу
(если угол одного треугольника соответственно равен углу другого треугольника, то площади этих треугольников относятся как произведении сторон, заключающих равные углы)
и теоремы площадей подобных треугольников
(отношение площадей двух подобных треугольников равно квадрату коэффициента подобия).
⑧Задача №26 (ГИА 2013, ФИПИ)
Площадь треугольника АВС равна 60. Биссектриса AD пересекает медиану ВК в точке Е, при этом BD:CD=1:2. Найдите площадь четырехугольника EDCK.
Решение:
SEDCK=SADC-SAEK. По теореме об отношении площадей треугольников, имеющих по равному углу (угол BAD= углу CAD, AD-бисс. треугольника АВС). SABD:SACD=(AB*AD)(AC*AD)=AB:AC. По свойству биссектрисы AD BD/DC=AB/AC=1/2=> SABD/SACD=1/2=> SABC=60.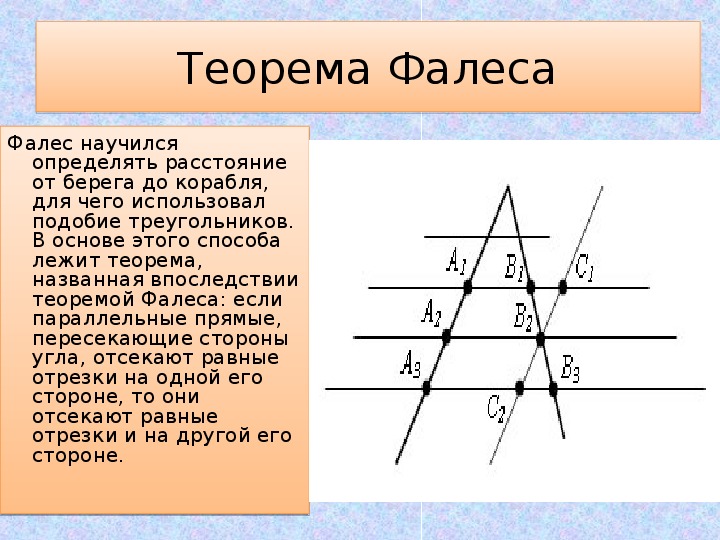 SABD=1/3*SABC= 60/3=20. В треугольнике АВК, АЕ –мед., АВ/АК=ВЕ/ЕК=АВ/0,5АС=2АВ/АС=2*1/2=1/1=1. SABE/SAEK=(AB*AE)/(AK*AE)=AB/AK=1 => SABK=1/2SABC, SABK=0,5AK*BH=0,5*0,5AC*BH=0,5SABC=30. SAEK=0,5SABK=0,5*30=15 => SEDCK=40-15=25.
SABD=1/3*SABC= 60/3=20. В треугольнике АВК, АЕ –мед., АВ/АК=ВЕ/ЕК=АВ/0,5АС=2АВ/АС=2*1/2=1/1=1. SABE/SAEK=(AB*AE)/(AK*AE)=AB/AK=1 => SABK=1/2SABC, SABK=0,5AK*BH=0,5*0,5AC*BH=0,5SABC=30. SAEK=0,5SABK=0,5*30=15 => SEDCK=40-15=25.
Ответ:25.
⑨ Задача №26 (ГИА 2013, ФИПИ)
Прямая пересекает стороны АВ и АС треугольника АВС в точках Р и М соответственно. Найдите отношение площади треугольника АРМ к площади четырехугольника МСВР, если АР:РВ=2:5, АМ:МС=1:4.
Решение:
В треугольнике АМР и треугольнике АВС, угол А-общий, по теореме об отношении площадей треугольников, имеющих по равному углу, имеем SAMP/SABC=(AM*AP)/(AC*AB), т.к. АР/РВ=2/5, АР=2/7АВ, АВ=7/2АР, АМ/МС=1/4, АМ=1/5АС, АС=5АМ, следовательно, SAMP/SABC=(АМ*АР):(5АМ*3,5АР)=2/35. Пусть 1часть=S. SAPM=28, SABC=35S, значит, SMCBP=35S-28=33S. Имеем, SAPM/SMCBP=28/33S=2/33.
Ответ:2/33.
⑩ Задача №26
Точки M и N-середины сторон соответственно BC и CD параллелограмма ABCD. Отрезки AM и BN пересекаются в точке О.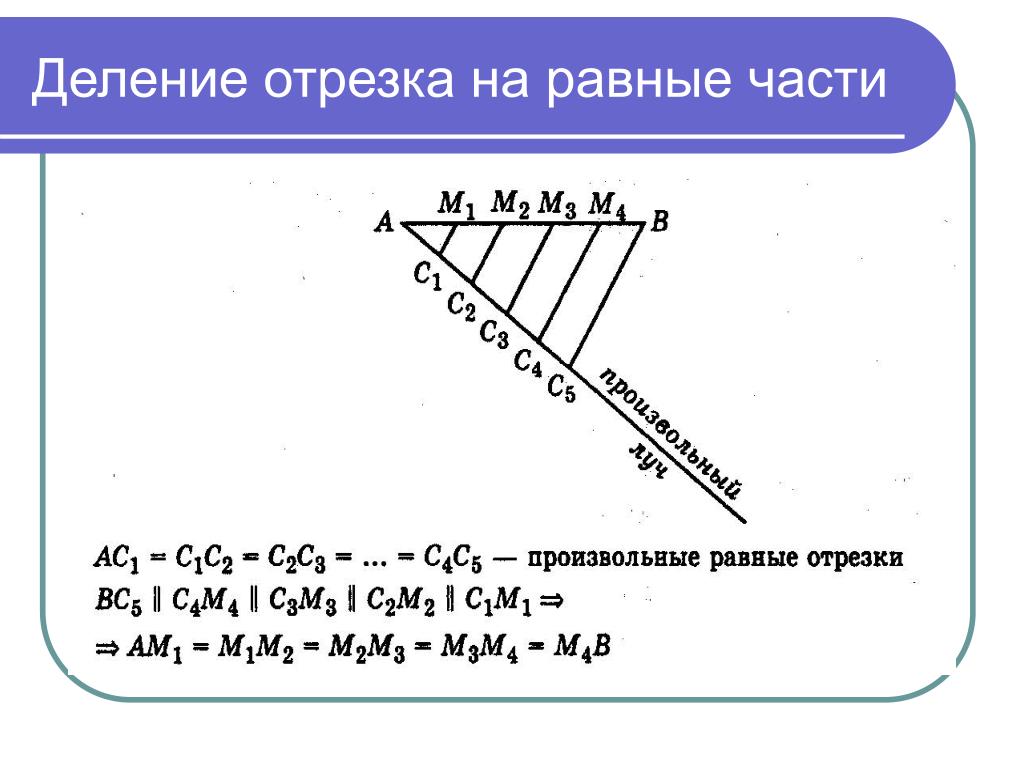 Найдите отношение MO:OA.
Найдите отношение MO:OA.
Решение:
Пусть продолжение отрезков BN и AD пересекаются в точке E. Обозначим BM=CM=a. Тогда AD=BC=2a. Треугольник DNE=треугольнику CNB по стороне и прилежащим к ней углам, поэтому DC=BC=2a. Значит, AE=AD+DE=2a+2a=4a. треугольник BOM подобен треугольнику BOA, следовательно MO:OA=BM:AE=a:4a=1:4=0,25.
Ответ: 0,25.
⑪ Задача №26
Дан треугольник АВС. На продолжении стороны АС за точку С взята точка N, причем АС=2CN. Точка М находится на стороне ВС, причем ВМ:МС=1:3. В каком отношении взята прямая MN, которая делит сторону АВ?
Решение:
Через точку В проведем прямую, параллельную АС. Пусть MN пересекает ее в точке Т, а прямую АВ-в точке . Обозначим АС=а. Тогда CN=1/2а, а N=3/2а. Из подобия треугольников, TBM и MCN (К=1/3) находим, что ТВ=1/3, CN=1/6a, а из подобия треугольника TBK и треугольника NAK- ВК:АК=ТВ:AN=1/6а:(3/2а)=1/9
Ответ: 1/9
На сторонах АВ и АС треугольника АВС расположены точки K и L, причём АК:КВ=4:7 и AL:LC=3:2.
 Прямая KL пересекает продолжение стороны ВС в точке М. Найдите отношение СМ:ВС.
Прямая KL пересекает продолжение стороны ВС в точке М. Найдите отношение СМ:ВС.На сторонах АВ и АС треугольника АВС расположены точки N и M, причём АN:NВ=3:2 и AM:MC=4:5. Прямая BM и СN пересекаются в точке O. Найдите отношение ОМ:ОВ и ON:ОС.
В равнобедренном треугольнике АВС (АВ=ВС) на стороне ВС взята точка D так, что BD/DC=1/4. В каком отношении прямая AD делит высоту ВЕ треугольника АВС, считая от вершины В.
В треугольнике АВС известно, что АВ=с, ВС=а, АС=в. В каком отношении центр вписанной окружности треугольника делит биссектрису CD?
В треугольник АВС биссектриса AD делит сторону ВС в отношении BD/DC=2/1. В каком отношении медиана СЕ делит эту биссектрису?
Дан треугольник АВС. Известно, что АВ=4, АС=2, ВС=3.Биссектриса угла ВАС пересекает сторону ВС в точке К. Прямая, проходящая через точку В параллельно АС, пересекает продолжение биссектрисы АК в точке М. Найдите КМ.
При каком отношении оснований трапеции существует прямая, на которой 6 точек пересечения с диагоналями, боковыми сторонами и продолжениями оснований трапеции высекают 5 равных отрезков?
Цель обозначенная в творческой работе-приобретение навыка решения задач на отношение отрезков в формате ОГЭ и ЕГЭ, достигнута по средствам :
Изучения биографии Фалеса, его теоремы и доказательства;
Разбора и решения ряда конкретных задач в формате ОГЭ и ЕГЭ и
Теоритической и компьютерной трансляции.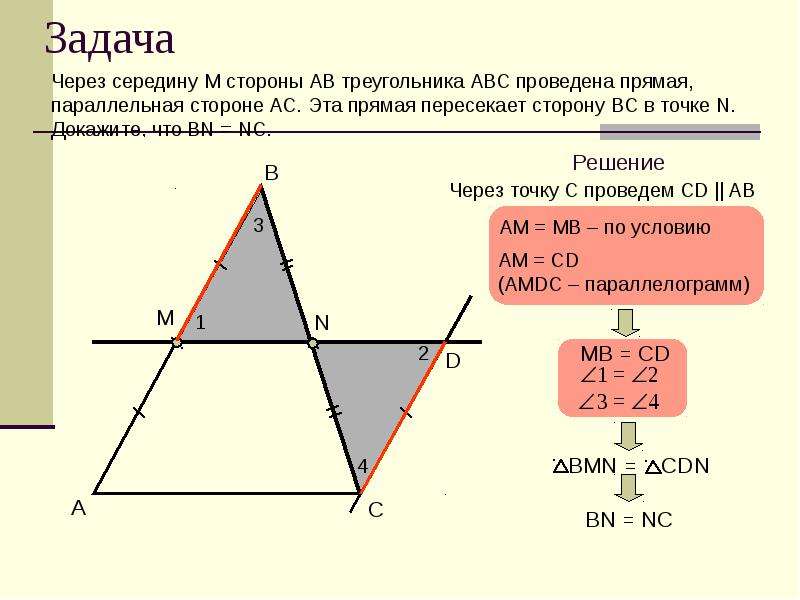
Данный материал можно использовать на уроках, консультациях и при самоподготовке к экзамену по математике для достижения наивысшего бала.
ГИА математика: типовые экзаминационные варианты, 30 вариантов под редакцией А.Л.Семёнова, И.В.Ященко; издательство «Муниципальное образование», 2012-1015гг (ФИПИ-школе).
Математика. Подготовка к ЕГЭ 2014 год под редакцией Ф.Ф.Лысенко и др. ООО «Легион»-готовимся к ЕГЭ.
ЕГЭ 2013; математика С4. Геометрия. Планиметрия под редакцией А.Л.Семёнова и И.В. Ященко.
Асмус В. Ф. Античная философия. — М.: Высшая школа, 1998. — С. 10—13.
Панченко Д. В. Фалес: рождение философии и науки // Некоторые проблемы истории античной науки : Сборник научных трудов / Отв. ред. А. И. Зайцев, Б. И. Козлов. — Л.: Главная астрономическая обсерватория, 1989. — С. 16—36.
Храмов Ю. А. Фалес Милетский (Θαλῆς ὁ Μιλήσιος, ThalestheMilesian, ThalesofMiletus) // Физики: Биографический справочник / Под ред.
 А. И. Ахиезера. — Изд. 2-е, испр. и дополн. — М.: Наука, 1983. — 400 с. — 200 000 экз. (в пер.)
А. И. Ахиезера. — Изд. 2-е, испр. и дополн. — М.: Наука, 1983. — 400 с. — 200 000 экз. (в пер.)Авторские учебно-тренировачные тесты по математике:
ГИА математика: типовые экзаминационные варианты, 30 вариантов под редакцией А.Л.Семёнова, И.В.Ященко; издательство «Муниципальное образование», 2012-1015гг (ФИПИ-школе).
Математика. Подготовка к ЕГЭ 2014 год под редакцией Ф.Ф.Лысенко и др. ООО «Легион»-готовимся к ЕГЭ.
ЕГЭ 2013; математика С4. Геометрия. Планиметрия под редакцией А.Л.Семёнова и И.В. Ященко.
Рис.1
Рис.2
Рис.3
Рис.4
Рис.5
Рис.6
Рис.7
Рис.8
Рис.9
Рис.10
Рис.11
«Теорема Фалеса» 8 класс. Урок №9 по геометрии
1. Теорема Фалеса
Урок №9 по геометрии в 8
классе
Учитель: Федорова Т.Ф.
2009-2010 уч.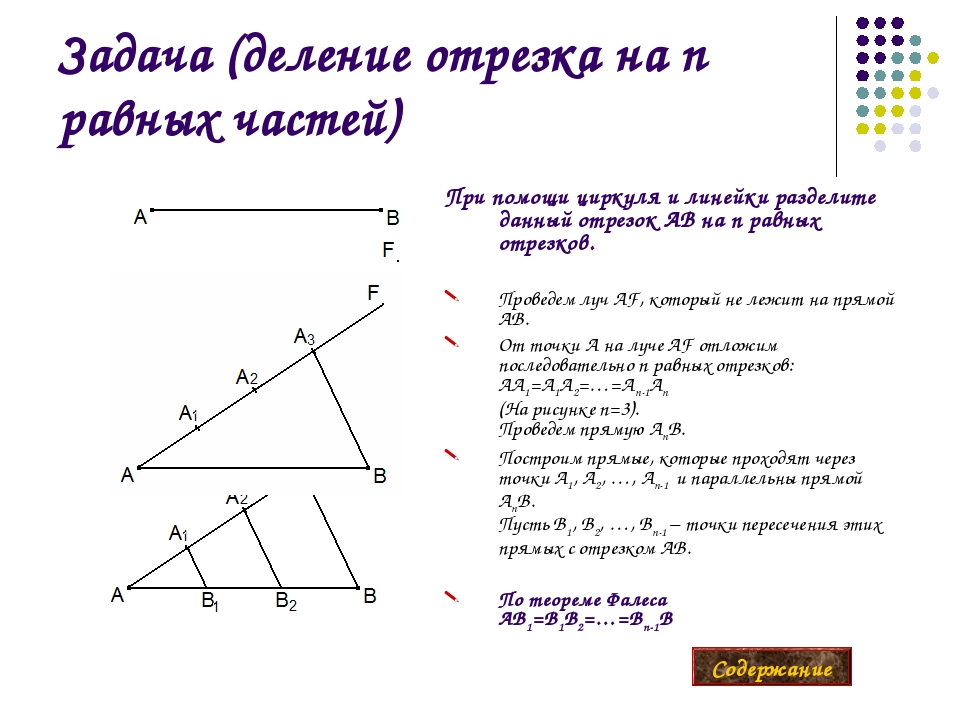 год.
год.
5klass.net
2. Цели урока:
• Рассмотреть теорему Фалеса и
закрепить ее в процессе решения
задач.
Совершенствовать навыки решения
задач на применение свойств
равнобедренной трапеции, ее
признаков, а также на применение
знаний по теме « Трапеция»
3. Задачи на готовых чертежах
В
В
С
С
75
40
А
D
Найти углы трапеции
В
А
BC║CD
Е
Найти углы трапеции
В
С
60
50
А
Найти С
D
А
5
D
С
60
Р
К
AD=7.Найти: СМ
D
В
С
х
Составим уравнение:
2х +х+90 = 180
3х = 180 — 90
х
х
3х = 90
2х
А
D
Х = 30
C = 30 + 90 = 120 .
Найти углы трапеции
Ответ:
А = D = 60 ,
C = B = 120 .
5. Ответы к задачам
1. A = D = 60 , B = C =120 .
2. A=40 , D=65 , C=115 , B=140 .
3. C = 100 .
4. CM =2.
Фалес Милетский
624-547г.г. до н.э.
Великий учёный Фалес
Милетский основал одну из
прекраснейших наукгеометрию. Известно, что
Фалес Милетский имел титул
одного из семи мудрецов
Греции, что он был поистине
первым философом, первым
математиком, астрономом и
вообще первым по всем наукам
в Греции. Короче: он был то
же для Греции, что Ломоносов
для России.
Карьеру он начинал как купец и ещё в
молодости попал в Египет. В Египте
Фалес застрял на много лет, изучая
науки в Фивах и Мемфисе.
Считается, что геометрию и
астрономию в Грецию привёз он.
Фалес- математик. Он измерил по
тени высоту пирамиды; установил,
что окружность диаметром
делится пополам, что углы при
основании равнобедренного
треугольника равны. Ему же
принадлежит теорема, что
вписанный угол, опирающийся на
диаметр окружности- прямой
До наших дней дошли изречения Фалеса, вот некоторые из них:
.
Фалес известен как геометр. Ему приписывают открытие и доказательство
ряда теорем: о делении круга диаметром пополам, о равенстве углов при
основании равнобедренного треугольника, о равенстве вертикальных
углов, один из признаков равенства прямоугольных треугольников и
другие. Он открыл любопытный способ определения расстояния от берега
до видимого корабля.
Столь же остроумно Фалес предложил измерять высоту предметов. Став недалеко
от предмета, надо дождаться пока тень человека не сделается равной его росту.
Измерив тогда длину тени предмета, можно заключить, что она равно длине
предмета. Говорят, что таким способом он измерял высоту египетских пирамид.
13. Задача № 384
В
1
М
3
Дано: тр-к АВС
АМ =МВ
N
4 D
МN || АС
Доказать: ВN =NC
2
А
С
Теорема: если параллельные прямые, пересекающие стороны
угла, отсекают на одной его стороне равные отрезки, то они
отсекают равные отрезки и на другой его стороне.
Дано: угол, параллельные прямые
пересекают стороны угла, А1А2=А2А3
В2
F
Доказать: В1В2=В2В3
В3
Доказательство.
E
1. Проведём через точку В2 прямую ЕF,
параллельную прямой А1А3.
В1
А1
А2
А3
2. По свойству параллелограмма
А1А2=FВ2, А2А3=В2Е.
3. Так как А1А2=А2А3, то FВ2=В2Е
4. Треугольники В2В1F и В2В3Е равны по
второму признаку ( у них В2F=В2Е по
доказанному. Углы при вершине В2
равны как вертикальные, а углы
В2FВ3равны как внутренние накрест
лежащие при параллельных А1В1 и А3В3
и секущей ЕF.)
5. Из равенства треугольников следует
16. Задача № 385
А1
А2
А3
А4
А1
А2
А3
А4
В1
В2
В3
В4
С
D
В1
В2
В3
В4
а
в
а
с
в
ЗАДАЧА: РАЗДЕЛИТЕ ДАННЫЙ ОТРЕЗОК НА n
РАВНЫХ ЧАСТЕЙ
Вn-1
В1
В2
В
2.Отложим на луче АО
равные отрезки:АА1,
А1А2, А2А3, …, Аn-1Аn.
В3
А
А1
А2
А3
1.Проведём из точки А
луч АО, не лежащий на
отрезке АВ.
Аn-1
Аn
О
3.Соединим отрезком
точку Аn с точкой В.
4.Через точки А1,А2, …
Аn-1проведём прямые,
параллельные АnВ.
5.По теореме Фалеса
отрезки АВ1, В1В2, …,Вn1В равны.
18. Задачи на готовых чертежах
B
Задачи на готовых чертежах
A
A1 A2 A3 A4
F
E
B1
5
4
12
A
C
EF║AC. Найти:РАВС
В
B3
B4
АВ4=20. Найти:В2В3.
С
10
В
С
М
N
М
B2
O
А
Доказать:АО = СО
D
А
К
Е
МК║ВЕ║СD, AD=16.
Найти:АК.
D
19. Задача №386
• Докажите, что отрезок, соединяющий середины
боковых сторон трапеции, параллелен
основаниям трапеции.
В
M
А
С
N
D
20. Задача № 393 б)
d1
d2
Дано:d1-диагональАС
d2- диагональ ВD
а- угол между диагоналями
a
Построить:
АВСD
21.
 Анализ
Анализ
В
С
О
А
D
Допустим, что АВСD построен. СО = 0,5d1, ОD = 0,5d2,
значит, треугольник СОD можем построить по двум
сторонам и углу между ними, а затем достроим его до
параллелограмма.
22. Доказательство
В четырёхугольнике АВСD диагонали точкой
пересечения делятся пополам, значит АВСDпараллелограмм. АС=d1, ВD = d2 ,
угол СОD=a, значит АВСD – искомый
параллелограмм.
23. Исследование
Задача имеет одно решение и всегда возможна.
24. Домашнее задание
Задачи № 391, № 392
Дополнительная задача:
В равнобедренной трапеции острый
угол равен 60 . Докажите, что меньшее
основание равно разности большего
основания и боковой стороны.
Планиметрия в тезисах и решениях. 9 класс
Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок. Идеи использования теоремы Фалеса хорошо видны на следующих примерах.
Примеры решения задач
102. Докажите, что медианы в треугольнике делятся в отношении 2:1, считая от вершины (известная теорема школьного курса математики). (2)
Самый простой путь решения (рис. 173):
Рис. 173.
Проведем медианы AM и ВК, а также отрезок МТ, параллельный ВК. Имеем: т. к. ВМ = МС, то КТ = ТС. Но тогда АК = КС = 2КТ и, значит, АО: ОМ = АК: КТ = 2, что и требовалось доказать.
103. В треугольнике ABC на стороне ВС взята точка М так, что MB = МС, а на стороне АС взята точка К так, что АК = 3 ? КС. Отрезки ВК и АМ пересекаются в точке О. Найдите AO/OM (рис. 174). (2)
Рис. 174.
Решение. Обозначим длину отрезка КС через а, тогда АК = За. Проведём MP||ВК По теореме Фалеса КР = РС = a/2. По теореме о пропорциональных отрезках имеем:
Ответ: 6.
104. В треугольнике ABC на стороне АВ взята точка К так, что АК: ВК = 1:2, а на стороне ВС взята точка L так, что CL: BL = 2:1. Пусть Q – точка пересечения прямых AL и СК. Найти площадь треугольника ABC, если дано, что площадь треугольника BQC равна 1 (рис. 175). (3)
Рис. 175.
Решение. Проведём через точку L прямую LM параллельно прямой СК. Из подобия треугольников MBL и КВС следует, что
Из подобия треугольников AKQ и AML находим:
Кроме того, имеем следующие равенства:
Ответ: 7/4.
Задачи для самостоятельной работы
105. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC(рис. 176). (2)
Рис. 176.
106. На сторонах АВ и АС треугольника ABC взяты точки M и N, такие, что AM/MB = CN/NA = 1/2.
Отрезки BN и СМ пересекаются в точке К. Найти отношения отрезков BK/KN и CK/KM.(2)
Математика. Основы геометрии: Обобщенная теоремы Фалеса. Пропорции. Масштаб
Главная >
Образование >
Математика >
МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Пропорции
Равенство вида
x1 | = | y1 |
x2 | y2 |
называется пропорцией. При этом говорят, что:
x1 относится к x2 как y1 относится к y2,
или
отношение чисел x1 и x2 равно отношению чисел y1 и y2,
или же
числа x1 и x2 соотносятся так же, как числа y1 и y2,
или, наконец,
числа x1 и y1 (!) пропорциональны числам x2 и y2 (то есть числители пропорциональны знаменателям).
Входящие сюда числа x1, x2, y1 и y2 называются членами пропорции. Обычно все они положительны, но это необязательно. Предполагается, однако, что ни одно из них не равно нулю. Особого названия это равенство удостоилось по той причине, что оно часто встречается при решении разных математических задач.
Пропорции можно преобразовывать, перенося члены «с верху» одной части равенства «в низ» другой части равенства и наоборот. Эту процедуру легко обосновать следующим образом. Допустим мы хотим перенести x1 из левой части в правую. Для этого умножим обе части пропорции на 1/x1:
1 |
| x1 | = | 1 |
| y1 | . |
x1 | x2 | x1 | y2 |
В результате получаем
1 | = | y1 | , |
x2 | x1y2 |
то есть переменная x1 у нас переместилась «по диагонали сверху вниз». Перенесем теперь «влево наверх» переменную y2. Это достигается умножением на нее обеих частей данного равенства. В результате имеем
y2 | = | y1 | . |
x2 | x1 |
Мы получили новую пропорцию, которая отличается от исходной перестановкой членов, расположенных «по диагонали». Таким образом, в первоначальном равенстве
x1 | = | y1 |
x2 | y2 |
числители x1 и y1 соотносятся между собой точно так же, как и соответствующие им знаменатели x2 и y2.
Обобщенная теорема Фалеса
Теорема Фалеса, рассмотренная в прошлый раз, допускает следующее обобщение.
Пусть две произвольные прямые x и y пересекаются тремя параллельными прямыми n1, n2 и n3 в точках X1, X2, X3 и Y1, Y2, Y3, как показано на рисунке:
Тогда длины отсекаемых отрезков образуют следующую пропорцию
|Y1Y2| | = | |X1X2| | . |
|Y1Y3| | |X1X3| |
Докажем эту теорему в случае, когда отношение длин
представляет собой рациональное число, то есть может быть выражено в виде несократимой дроби
|X1X2| | = | a | , |
|X1X3| | b |
где a и b — некоторые натуральные числа, a < b. Разобьем отрезок X1X3 на b одинаковых частей. (При этом точка X2 окажется одной из точек деления.) Проведем через каждую точку деления прямые, параллельные n1, n2 и n3. (Одна из этих прямых совпадет с прямой n2.)
По теореме Фалеса (в ее первоначальном варианте), отрезок Y1Y3 также делится этими прямыми на b равных частей, из которых a частей составляют отрезок Y1Y2. Следовательно,
|Y1Y2| | = | a | = | |X1X2| | , |
|Y1Y3| | b | |X1X3| |
что и требовалось доказать. Из нашего построения следует также, что
|Y2Y3| | = | b − a | = | |X2X3| |
|
|Y1Y3| | b | |X1X3| |
и
|Y2Y3| | = | b − a | = | |X2X3| | . |
|Y1Y2| | a | |X1X2| |
Пользуясь свойствами пропорций, эти равенства можно переписать в виде одной цепочки:
|Y1Y2| | = | |Y2Y3| | = | |Y1Y3| | . |
|X1X2| | |X2X3| | |X1X3| |
Таким образом, отрезки отсекаемые на прямой y пропорциональны соответствующим отрезкам на прямой x.
Теоретически возможна также ситуация, когда отношение длин
не является рациональным числом, поскольку длины отрезков |X1X2| и |X1X3| могут, в принципе, выражаться иррациональными числами. Однако на практике такой случай никогда не встречается. Для определения длин отрезков мы всегда пользуемся каким-либо измерительным прибором (например, школьной линейкой), который выдает лишь округленные результаты в виде конечной десятичной дроби.
Важное следствие
Пусть даны несовпадающие прямые x и y, которые пересекаются в точке O, и еще — две параллельные прямые n1 и n2, которые пересекают прямую x в точках X1 и X2 и прямую y в точках Y1 и Y2, как показано на рисунке.
Введем обозначения:
x1 = |OX1|, x2 = |OX2|;
y1 = |OY1|, y2 = |OY2|;
z1 = |X1Y1|, z2 = |X2Y2|.
Тогда
x1 | = | y1 | = | z1 | . |
x2 | y2 | z2 |
Действительно, оба равенства в этой цепочке непосредственно следует из обобщенной теоремы Фалеса. Для первого равенства это ясно сразу, а для второго это становится очевидным после того, как мы через точку Y1 проведем прямую m, параллельную прямой x.
Верно и обратное утверждение. Пусть дана та же геометрическая конструкция и известно, что
x1 | = | y1 | . |
x2 | y2 |
Тогда прямые n1 и n2 параллельны. В самом деле, проведем через точку X1 вспомогательную прямую, параллельную прямой n2. По обобщенной теореме Фалеса, эта вспомогательная прямая проходит через точку Y1. Следовательно, она совпадает с прямой n1. Таким образом, прямая n1 параллельна прямой n2.
Масштаб
Выйдем на улицу, прихватив с собой лист бумаги и карандаш. Расположим наш лист горизонтально и поставим на нем приблизительно посередине точку O. Из этой точки проведем мысленно лучи в направлении различных примечательных точек на местности, расположенных в радиусе примерно ста метров, — деревьев, столбов, углов зданий и того подобного.
Допустим, у нас есть возможность измерить расстояния до этих примечательных точек. Пусть, например, расстояние до ближайшего дерева равно 10 м. Мысленно отложим от точки O в направлении этого дерева отрезок, длина которого в 1000 раз меньше данного расстояния, и отметим карандашом на бумаге положение второго его конца. Нетрудно рассчитать, что расстояние от точки O до отметки составит 10 м/1000 = 1 см.
Подобным же образом, пусть расстояние до какого-то другого примечательного объекта равно x1. Умножим это расстояние на число k, равное 1/1000. Мысленно отложим от точки O отрезок длиной x2 = kx1 вдоль луча, направленного на данный объект. В том месте на бумаге, где находится второй конец отрезка, сделаем отметку карандашом. Проделаем такую процедуру со всеми примечательными точками на местности, используя всё время одно и то же значение параметра k. Если какие-либо из этих точек соединены между собой забором или стеной или же чем-то подобным, то между соответствующими метками на бумаге также проведем линии.
В результате на нашем листе бумаги получится карта местности. В силу теоремы Фалеса и свойств пропорций, все соотношения между расстояниями на бумаге будут в точности такими же, как и в действительности. Более того, все линии на бумаге окажутся параллельны соответствующим линиям на местности. Эта параллельность, конечно, нарушится, когда мы унесем наш лист куда-нибудь в другое место, однако углы между линиями сохранятся.
Параметр k, который мы использовали в нашем построении, называется масштабным коэффициентом или просто масштабом. Разумеется, он необязательно должен быть равен 1/1000. Он может, в принципе, принимать любое значение, важно лишь, чтобы это значение оставалось всё время неизменным в процессе построения карты.
На настоящих географических картах масштаб обязательно указывается в легенде, при этом вместо дробной черты обычно используется двоеточие. Например, масштаб 1:100 000 означает, что один сантиметр на карте соответствует 100000 сантиметрам (то есть одному километру) на местности.
Технические чертежи также всегда выполняются, как говорят, в определенном масштабе. Масштаб 1:1 означает, что деталь начерчена в натуральную величину. А масштаб 10:1 говорит о том, что чертеж выполнен с десятикратным увеличением.
Замечание о параллельных прямых
Мы назвали параллельными такие несовпадающие прямые, угол между которыми равен нулю. Мы отметили, что такие прямые нигде не пересекаются. Докажем теперь, что если прямые лежат в одной плоскости и не параллельны (то есть угол между ними отличен от нуля), то тогда они обязательно где-нибудь пересекутся.
Пусть на плоскости даны две прямые — x и n. Отметим на них произвольные точки — O и Y — и проведем через эти точки третью прямую — y. Если исходить из того, что угол между прямыми x и n не равен нулю, то смежные углы должны оказаться не равны друг другу. Пусть для определенности α1 > α2, как показано на рисунке.
Проведем через точку O прямую n1, параллельную прямой n. Отметим на ней со стороны угла α1 произвольную точку N1 и проведем через эту точку прямую y1, параллельную прямой y. При этом образуется параллелограмм, обозначенный на рисунке серым фоном.
Это значит, что прямая y1 пересекает прямую n в некоторой точке, которую мы обозначим через N. Прямая x, заходя на «территорию» параллелограмма в точке O, обязательно должна где-то оттуда выйти. Она может это сделать либо через отрезок YN, либо через отрезок N1N. В первом случае сразу становится очевидно, что прямая x пересекает прямую n. Рассмотрим второй случай. Обозначим точку пересечения прямой x и отрезка N1N через X1. Проведем через нее прямую n2, параллельную прямой n. Эта прямая разбивает параллелограмм ON1NY на два новых параллелограмма и пересекает прямую y в некоторой точке Y1. Отметим на прямой x такую точку X, для которой выполняется соотношение
|OY1| | = | |OX1| | . |
|OY| | |OX| |
Проведем через точки X и Y прямую. Согласно рассмотренному выше следствию из теоремы Фалеса, эта прямая параллельна прямой n2, а значит, образует нулевой угол с прямой n. Следовательно, новая прямая совпадает с прямой n, которая, таким образом, пересекает прямую x в точке X.
Мы теперь можем утверждать, что следующие три утверждения о несовпадающих прямых a и b, лежащих в одной плоскости, означают в точности одно и то же:
(1) Угол между прямыми a и b равен нулю.
(2) Прямые a и b нигде не пересекаются.
(3) Прямые a и b параллельны.
В традиционных курсах геометрии определением параллельности прямых служит утверждение 2. Мы выбрали для этих целей утверждение 1. Ведь гораздо проще определить угол между двумя прямыми, чем удостовериться, что они нигде не пересекаются на всём своем бесконечном протяжении.
Конспект
1. Равенство вида x1/x2 = y1/y2 называется пропорцией. Числители пропорциональны знаменателям. Числитель и знаменатель одной дроби соотносятся так же, как числитель и знаменатель другой дроби. Эквивалентное равенство: x1/y1 = x2/y2.
2. Обобщенная теорема Фалеса. Пусть две произвольные прямые a и b пересекаются тремя параллельными прямыми. Тогда отрезки, отсекаемые на прямой a, пропорциональны соответствующим отрезкам, отсекаемым на прямой b.
3. Следствие 1. Пусть стороны угла с вершиной в точке O пересекаются двумя параллельными прямыми n1 и n2. Тогда отрезки, отсекаемые на прямых n1 и n2, соотносятся так же, как отрезки, отложенные на любой из сторон угла от точки O до соответствующих точек пересечения с прямыми n1 и n2.
4. Следствие 2. Пусть на сторонах угла отложены от вершины отрезки таким образом, что отрезки на одной стороне пропорциональны отрезкам на другой. Тогда прямые, проходящие через соответствующие концы этих отрезков, параллельны друг другу.
5. На карте сохраняются все соотношения между расстояниями и все углы. Отношение расстояния между некоторыми двумя точками на карте к расстоянию между соответствующими точками на местности не зависит от выбора точек и называется масштабом.
6. Если угол между двумя прямыми, лежащими в одной плоскости, не равен нулю, то такие прямые обязательно пересекаются.
Методическая разработка урока по теме «Теорема Фалеса»
Теорема Фалеса
Фале́с (640/624 — 548/545 до н. э.) —древнегреческий философ и математик из Милета (Малая Азия).
ПЛАН УРОКА
Определение и свойства параллелограмма и трапеции
ПОВТОРИМ
Теорему Фалеса
УЗНАЕМ
Решать задачи с применением теоремы Фалеса
НАУЧИМСЯ
AN=NC ч.т.д. М 3 1 А N 2 C D «
В
Задача:
Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N .
Доказать: AN=NC
1. Через точку С проведем прямую, С D || АВ
2. АМ=МВ по условию , МВ=С D как противоположные стороны параллелограмма
ВС D М, то АМ= D С
3. ∆АМ N =∆С DN по второму признаку равенства ∆.
Так как АМ= D С, ∠1= ∠2, ∠3= ∠4, как накрест лежащие углы при пересечении С D || АВ секущими
АС и М D . = AN=NC ч.т.д.
М
3
1
А
N
2
C
D
AN=NC ч.т.д. М 3 1 А N 2 C 4 D «
В
Задача:
Через середину М стороны АВ треугольника АС проведена прямая, параллельная стороне ВС. Эта прямая пересекает сторону АС в точке N .
Доказать: AN=NC
1. Через точку С проведем прямую, С D || АВ
2. АМ= по условию , МВ= как противоположные стороны параллелограмма
ВС D М, то АМ= D С
3. ∆АМ N =∆ по второму признаку равенства ∆.
Так как АМ= , ∠1= ∠ , ∠3= ∠ как накрест лежащие углы при пересечении С D || секущими
АС и . = AN=NC ч.т.д.
М
3
1
А
N
2
C
4
D
Теорема Фалеса
Теорема. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне
В режиме слайдов ответы появляются после кликанья мышкой
В теореме нет ограничений на взаимное расположение прямых (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на прямых.
В 1 В 2 = В 2 В 3 ч.т.д. n m «
Теорема Фалеса : Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Дано : ∠ nm , прямые В 1 А 1 ∥ В 2 А 2 ∥ В 3 А 3 пересекают стороны ∠ nm , А 1 А 2 = А 2 А 3
Доказать : В 1 В 2 = В 2 В 3
Доказательство :
1. Проведем через точку В 2 прямую EF || A 1 A 3
2. По свойству параллелограмма А 1 А 2 = EB 2 ,
A 2 A 3 = FB 2
3 . ∆ В 2 В 1 Е= ∆ В 2 В 3 F по
второму признаку равенства ∆ :
1)А 1 А 2 = А 2 А 3 по условию и А 1 А 2 = EB 2 ,
A 2 A 3 = FB 2 из пункта 2) В 2 F = В 2 Е
2) ЕВ 2 В 1 = B 3 B 2 F как вертикальные
3) В 1 ЕВ 2 = B 3 FB 2 , как внутренние накрест лежащие при прямых А 1 В 1 ∥ А 3 В 3 и секущей EF
5. Из равенства треугольников следует равенство соответствующих элементов = В 1 В 2 = В 2 В 3 ч.т.д.
n
m
Задача 1
Доказать, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции
Доказательство:
Задача 1
Доказать, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции
Доказательство:
Пусть К–середина АВ.
Проведем KL || BC ||AD .
Тогда по теореме Фалеса L – середина CD
Докажем, что К L — единственный.
Через точки К и L можно провести только одну прямую(аксиома), т.е. отрезок, соединяющий середины боковых сторон трапеции ABCD параллелен основаниям. ч.т.д.
Задача 2
Дано: МК || ВЕ || С D , AD=16 см, ВС=8 см
Найти:АК
в
C
M
D
A
E
K
Задача 2
Дано: МК || ВЕ || С D , AD=16 см, ВС=8 см
Найти: АК
в
C
M
Решение:
По теореме Фалеса АК=КЕ, т.к.
АМ=МВ и МК || ВЕ
ВС=Е D , т.к. BCD Е- параллелограмм по определению
АК=0.5∙АЕ= 0.5∙(А D- Е D)=
= 0.5∙ (16-8)=4 см
Ответ: 4 см
D
A
E
K
Следствие
Прямая, проведенная через середину стороны треугольника параллельно другой его стороне, делит третью сторону пополам
Дано: ∆ АВС, ВМ=МА, М € АВ, MN || АС
Доказать: BN=NC
Доказательство:
Следствие
Прямая, проведенная через середину стороны треугольника параллельно другой его стороне, делит третью сторону пополам
Дано: ∆ АВС, ВМ=МА, М € АВ, MN || АС
Доказать: BN=NC
Доказательство:
По теореме Фалеса для угла В имеем
BN=NC ч.т.д.
Деление отрезка на равные части
AC 1 =C 1 D 1 =D 1 E 1 =E 1 B
E 1
C 1
D 1
А
В
•
C
•
D
•
Пусть отрезок АВ требуется разделить например на 4 равных части.
- Для этого из любого конца отрезка (из точки А ) проведем под острым углом к отрезку прямую линию АС,
- на которой от точки А измерительным циркулем откладываем 4 равных отрезка произвольной величины.
- Точку F соединяем с точкой В (концом данного отрезка) прямой.
- Из точек C, D, E проведем ряд прямых параллельных прямой FB , которые пересекая отрезок АВ разделят его на 4 равных части.
E
•
F
С
Задача 1
Решение:
По теореме Фалеса для угла А
АК=КЕ;
ДОМАШНЕЕ ЗАДАНИЕ
Выучить теорему Фалеса и решить
задачи на готовых чертежах
1.
2.
Интересные факты
Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
Теорема Фалеса. Решенные упражнения. Как нанести пошагово
Хотите узнать, как решать задачи ТЕОРЕМЫ ТАЛИИ ?
Далее я объясню, как понять теорему Фалеса и как применять ее с определенными упражнениями шаг за шагом.
В чем причина двух сегментов
Чтобы понять теорему Фалеса, вам нужно очень хорошо понимать, в чем причина между двумя сегментами.
Например, у нас есть эти два сегмента:
Как вы знаете, сегменты разделены двумя крайними точками и названы по крайним значениям, которые их ограничивают.Красный сегмент, который начинается в конце A и заканчивается в конце B, называется сегментом AB.
Если два сегмента связаны между собой, для их имен используются одни и те же буквы, но, поскольку они не могут повторяться, используется одинарная кавычка рядом с каждой буквой, а кавычка читается как «прима». Итак, А ‘читал бы «А прима».
Таким образом, синий сегмент, который начинается в A ’и заканчивается в B’, будет называться сегментом A ’B’.
Box] Соотношение (или соотношение) двух сегментов является результатом деления длины этих двух сегментов .[/коробка]
Если размер сегмента AB составляет 5 см, а сегмента A ’B’ — 10 см, в чем причина появления этих двух сегментов?
Все, что нам нужно сделать, это разделить длину сегмента AB на длину сегмента A ’B’:
Отношение этих двух сегментов составляет 0,5, что означает, что AB вдвое меньше, чем A ’B’.
Мы также можем рассчитать соотношение, разделив длину сегмента A ’B’ на длину сегмента AB:
В этом случае соотношение равно 2, или, другими словами, сегмент A ’B’ в два раза выше сегмента AB.
Если вы заметили, сказать, что сегмент AB вдвое меньше сегмента A ’B’, значит сказать, что сегмент A ’B’ вдвое больше, чем сегмент AB.
Следовательно, нет необходимости рассчитывать соотношение обоими способами. Достаточно рассчитать его одним из двух способов.
Пропорциональность между парами сегментов
Теперь у нас есть два сегмента:
Красный сегмент CD имеет размер 3 см, а синий сегмент C ’D’ — 6 см.
Давайте выясним его причину:
Соотношение сегментов CD и C ’D’ такое же, как соотношение сегментов AB и A ’B’.
Когда две пары сегментов имеют одинаковую причину, они считаются пропорциональными.
Следовательно, сегменты AB и A ’B’ пропорциональны CD и C ’D’:
Две пары сегментов пропорциональны, если их соотношение одинаково
Теорема Фалеса
После того, как я объяснил рассуждения между двумя сегментами и пропорциональность между двумя парами сегментов, давайте взглянем на теорему Фалеса.
У нас есть две секущие (непараллельные) прямые. Одна называется прямой линией r (красный цвет), а другая — прямой s (синий цвет):
К этим двум прямым линиям мы разрезаем их несколькими параллельными линиями (зеленого цвета), как показано ниже:
В точках, где они разрезают линии, параллельные прямой, я назову их A, B и C, а в точках, где они разрезают линии, параллельные прямой, я назову их A ‘, B’ и C. ‘:
Зеленые линии разделили прямую r на два сегмента: отрезок AB и отрезок BC.У нас также есть третий сегмент, если мы рассмотрим первую и последнюю параллельную линию, т.е. е. сегмент переменного тока.
Они также разделили линию s на два сегмента A ’B’ и B ’C’, и если мы рассмотрим первую и последнюю параллельную линию, есть третий сегмент A ’C’.
Теорема Фалеса говорит нам следующее:
Box] Когда любые две прямые, r и s, разделены несколькими параллельными линиями, сегменты, составляющие линию r, пропорциональны сегментам, составляющим линию s .[/коробка].
А что это значит?
Итак, если вы разделите длины сегментов, которые находятся в противоречии, т.е. е. сегмент AB на сегмент A ’B’, они имеют ту же причину, как если бы вы делили сегмент BC на сегмент B ’C’:
Поскольку у них одна и та же причина, AB и A ’B’ пропорциональны BC и B ’C’.
Если мы рассмотрим отрезок, образованный первой и последней параллельными линиями, т.е. е. сегмент AC, он также пропорционален сегменту AB:
И, следовательно, все отрезки прямой r пропорциональны отрезкам прямой s:
Для чего нужна теорема Фалеса?
Теорема
Фалеса позволяет вычислить длину отрезка, зная значения всех других отрезков двух прямых линий, находящихся в положении Фалеса.
Находиться в позиции Фалеса означает, что прямые линии должны быть такими, как говорит теорема Фалеса, то есть двумя прямыми линиями, пересеченными несколькими параллельными прямыми линиями.
Решим несколько упражнений, чтобы было понятнее.
Решенные упражнения по теореме Фалеса
Упражнение 1
Линии a и b на чертеже параллельны. Проверьте по теореме Фалеса, верна ли линия c.
Как доказать, что прямая c параллельна?
Ибо мы должны доказать, что прямые находятся в положении Фалеса и что теорема Фалеса выполняется, проверяя, имеют ли сегменты обеих прямых одну и ту же причину и что между ними они пропорциональны.
Рассчитываем причину первых сегментов:
И причина следующих двух сегментов:
Причина та же, поэтому обе пары сегментов пропорциональны.
Тогда выполняется теорема Фалеса и, как следствие, прямая c параллельна.
Упражнение 2
Сколько измеряет отрезок x на этом чертеже?
Мы знаем, что измеряют два сегмента r, но нам остается знать, сколько измеряет один из сегментов s, поэтому мы называем этот сегмент x.
Тогда, согласно теореме Фалеса, секции, которые находятся в противоречии, имеют одну и ту же причину, поэтому их деления должны быть одинаковыми, и поэтому мы можем сопоставить их:
У нас осталось одно уравнение первой степени, из которого мы должны очистить x.
При решении уравнений такого типа возникает большая путаница.
Чтобы решить это уравнение, мы передаем знаменатели каждого члена, умножая числитель противоположного члена (умножаем крестиком).
5, которая делит 8 в первом члене, проходит, умножая 6 во втором члене, а x, который делит 6 во втором члене, проходит, умножая 8 в первом члене, и мы остаемся вот так:
У нас больше нет знаменателей. Уберем x.
Теперь 8, которая умножает x, переходит ко второму члену деления:
И, наконец, мы вычисляем значение x:
Если вы отметите галочку, пары сегментов будут пропорциональными.
Геометрия
— Пропорциональность и теорема Фалеса
Я думаю, что у вас должно быть два соображения, и они заключаются в том, где находится точка $ P $, в которой они пересекаются (внутри или вне параллелей). Я думаю (я не совсем уверен) это зависит от того, как вы расставляете очки. Я просто дам вам одно соображение, и это то, что точка $ P $ находится внутри параллелей.
Здесь я просто поставил пять точек ($ A, C, A ‘, C’, P $), я знаю, что я не поставил две другие точки, но я уже могу сказать, что это точка $ P $, где они пересекаются.Могу сказать, что некоторые углы, например (угол $ CAA ‘\ cong AA’C’ $, потому что это углы между параллелями), равны другим. Я хотел бы назвать их точными названиями, но, поскольку я не говорю по-английски, я не знаю, что они из себя представляют (я бы хотел, чтобы вы их отредактировали и поместили). А теперь могу сказать, что треугольники $ ACP \ sim A’C’P $ by $ AAA $.
Итак, теперь, рисуя этот второй рисунок, я получаю несколько пар углов, которые равны (углы, которые измеряют то же самое, имеют одинаковые цвета), потому что они являются углами между линиями (напротив вершины? Это правильное слово? А также я получаю другие похожие треугольники.И поскольку они похожи, я могу установить следующие пропорции:
$ 1) $ $$ \ frac {| AB |} {| A’B ‘|} = \ frac {| BP |} {| B’P |} $$
$ 2) $ $$ \ frac {| BC |} {| B’C ‘|} = \ frac {| BP |} {| B’P |} $$
Следовательно,
$$ \ frac {| AB |} {| A’B ‘|} = \ frac {| BC |} {| B’C’ |} = \ frac {| BP |} {| B’P |} $ $
Итак, имеем:
$$ \ frac {| AB |} {| A’B ‘|} = \ frac {| BC |} {| B’C’ |} $$
А затем, если я умножу на $ | A’B ‘| $ и $ \ frac {1} {| BC |} $, я получу:
$$ \ frac {| AB |} {| BC |} = \ frac {| A’B ‘|} {| B’C’ |} $$, что вы просите.
Но тот, кто задавал этот вопрос, мог сказать вам, что они имели в виду не это, потому что, когда они задавали вопрос, они не указали порядок точек. Итак, здесь было бы другое решение (конечно, для этого требуется новая графика):
(разница в порядке точек)
Итак, здесь у нас также есть похожие треугольники, которые технически такие же, как и раньше.
Так, например, $ ACP \ sim PA’C ‘$ by $ AA $. Итак, я могу установить следующую пропорцию S:
$ 1) $ $$ \ frac {| AC |} {| A’C ‘|} = \ frac {| CP |} {| C’P |} $$
$ 2) $ $$ \ frac {| CB |} {| C’B ‘|} = \ frac {| CP |} {| C’P |} $$
Следовательно:
$$ \ frac {| AC |} {| A’C ‘|} = \ frac {| CB |} {| C’B’ |} $$
(Я собираюсь решить эту проблему, используя свойство пропорций, которое я также продемонстрирую, но вы можете решить ее геометрически.)
Итак, я применю то, что только что продемонстрировал:
$$ \ frac {| AC | + | CB |} {| A’C ‘| + | C’B’ |} = \ frac {| AC |} {| A’C ‘|} = \ frac {| CB |} {| C’B ‘|} $$
$$ \ frac {| AB |} {| A’B ‘|} = \ frac {| CB |} {| C’B’ |} $$
А мы попадаем в:
$$ \ frac {| A’B ‘|} {| C’B’ |} = \ frac {| AB |} {| CB |} $$. И, я бы сказал, в данном случае это два решения. Я не делал случаев, когда $ P $, где они пересекаются, находятся вне параллелей, но я думаю (я не совсем уверен), что должно быть также два решения (изменение порядка).=)
Упражнение 4.2: Теорема Фалеса и теорема о биссектрисе угла — проблемные вопросы с ответом, решение
Упражнение 4.2
1. В Δ ABC , D и E — точки на сторонах AB и AC соответственно такое, что DE || BC
(i) Если AD / DB = 3/4 и AC = 15 см, найдите AE .
(ii).Если AD = 8 x -7, DB = 5 x -3, AE = 4 x — 3 и EC = 3 x −1, найдите значение х .
2. ABCD представляет собой трапецию, в которой AB || DC и P, Q — это точки на AD и BC соответственно, так что PQ || DC , если PD = 18 см, BQ = 35 см и QC = 15 см, найдите AD .
3. In Δ ABC , D и E — точки на сторонах AB и AC соответственно. Для каждого из следующих случаев покажите, что DE || BC
(i) AB = 12 см, AD = 8 см, AE = 12 см и AC = 18 см.
(ii) AB = 5,6 см, AD = 1,4 см, AC = 7,2 см и AE = 1,8 см.
4.На рис. если PQ || BC и PR || CD доказывает, что
5. Ромб PQRB вписан в Δ ABC , так что ∠ B составляет на один из его углов. P , Q и R лежат на AB , AC и BC соответственно. Если AB = 12 см и BC = 6 см, найдите стороны PQ , RB ромба.
6.В трапеции ABCD , AB || DC , E и F — это точки на непараллельных сторонах AD и BC соответственно, так что EF || AB . Покажи это .
7. На рисунке DE || BC и CD || EF . Докажите, что AD 2 = AB × AF .
8. In Δ ABC , AD — это биссектриса ∠ A сторона встречи BC на D, если AB 10 см, AC = 14 см и BC = 6 см, найдите BD и DC
9.Проверьте, является ли AD биссектрисой ∠ A из Δ ABC в каждом из следующих
(i) AB = 5 см, AC = 10 см, BD = 1,5 см и CD = 3,5 см.
(ii) AB = 4 см, AC = 6 см, BD = 1,6 см и CD = 2,4 см.
10. На рисунке ∠ QPR = 90 °, PS — его биссектриса. Если ST ┴ PR , докажите, что ST × ( PQ + PR ) = PQ × PR.
11. ABCD — четырехугольник, в котором AB = AD, биссектриса ∠ BAC и ∠ CAD пересекаются со сторонами и . CD в точках E и F соответственно. Докажите, что EF || БД .
12. Постройте Δ PQR , у которого основание PQ = 4,5 см, ∠ R = 35 и медиана от R до RG равна 6 см.
13. Постройте Δ PQR , в котором QR = 5 см, ∠ P = 40 ° и медиана PG от P до QR составляет 4,4 см. Найдите длину высоты от P до QR .
14. Постройте Δ PQR так, чтобы QR = 6,5 см, ∠ P = 60 ° и высота от P до QR имела длину 4,5 см.
15.Постройте Δ ABC так, чтобы AB = 5,5 см, ∠ C = 25 ° и высота от C до AB была 4 см.
16. Нарисуйте треугольник ABC из основания BC = 5,6 см, ∠ A = 40 ° и биссектрису ∠ A пересекает BC на D , так что CD = 4 см.
17. Нарисуйте Δ PQR так, чтобы PQ = 6,8 см, вертикальный угол составлял 50 °, а биссектриса вертикального угла пересекалась с основанием в точке D , где PD = 5.2 см.
Ответы:
1. (i) 6,43 см (ii) 1
2. 60 см
5. 4 см, 4 см
8. 2,5 см, 3,5 см
9. (i ) Не является биссектрисой (ii) Биссектриса
13. 2,1 см
Теорема Фалеса — GeeksforGeeks
Формулировка теоремы: Теорема Фалеса или основная теорема пропорциональности утверждает, что если линия проводится параллельно одной стороне треугольника, пересекая две другие стороны в разных точках, то две другие стороны делятся в одинаковом соотношении.
Доказательство основной теоремы о пропорциональности
Предположим, у нас есть треугольник ABC, если мы проведем линию LM, параллельную стороне BC, то теорема утверждает, что
В треугольнике ABC соедините вершину B к M на прямой AC и соединить вершину C на прямой AB. Затем опустите перпендикуляр MX на линию AB и перпендикуляр LY на линию AC. На приведенной ниже диаграмме показана конструкция того же самого.
Так как площадь треугольника =
Площадь ALM =
Площадь LBM =
Площадь ALM =
Площадь LMC =
Отношение площадей ALM5 и
:
:
—- (1)
Соотношение площадей ALM и LMC:
—- (2)
Согласно свойству треугольников, треугольники на одном основании и между одинаковыми параллельными линиями имеют равные площади.
Следовательно, LBM и LMC имеют равные площади .—- (3)
Из уравнений (1), (2) и (3) мы можем заключить:
Следовательно, основная теорема пропорциональности доказано.
Решенные примеры основной теоремы о пропорциональности
Пример 1. В ∆ABC стороны AB и AC пересекаются линией в точках D и E соответственно, которая параллельна стороне BC. Докажите, что AD / AB = AE / AC.
Решение:
Дано: DE || ДО Н.Э.Итак, AD / DB = AE / EC
или путем замены соотношений как => DB / AD = EC / AE
Теперь добавьте 1 с обеих сторон => (DB / AD) + 1 = (EC / AE) + 1
(DB + AD) / AD = (EC + AE) / AE
AB / AD = AC / AE
Если мы снова поменяем отношения местами, мы получим => AD / AB = AE / AC
Значит, доказано.
Пример 2. В треугольнике ABC, где DE — линия, проведенная из средней точки AB и заканчивающаяся средней точкой AC в E.AD / DB = AE / EC и ∠ADE = ∠ACB. Затем докажите, что ABC — равнобедренный треугольник.
Решение:
Дано: AD / DB = AE / EC
Обращаясь к основной теореме пропорциональности, получаем => DE || BC
Согласно вопросу => ∠ADE = ∠ACB
Следовательно, ABC = ∠ACB
Сторона, противоположная равным углам, также равна AB = AC
Следовательно, ABC — равнобедренный треугольник.
Вниманию читателя! Не прекращайте учиться сейчас.Освойте все важные концепции DSA с помощью курса DSA Self Paced Course по доступной для студентов цене и будьте готовы к работе в отрасли.
Проблемы и вопросы по свободной геометрии с решениями
Бесплатные учебники по геометрии по таким темам, как отражение, серединный перпендикуляр, центральный и вписанный углы, описанные окружности, закон синуса и свойства треугольника для решения задач треугольника. Также включены геометрические задачи с подробными решениями для треугольников, многоугольников, параллелограммов, трапеций, пирамид и конусов.Также включены уравнения полярных координат, преобразование и построение графиков. Также включены более сложные геометрические задачи.
Проблемы геометрии
- Прямоугольник. Прямоугольные задачи по площади, размерам, периметру и диагонали с подробными решениями.
- Задачи геометрии на квадратах. Квадратные задачи по площади, диагонали и периметру, с подробными решениями.
- Проблемы с полигонами. Проблемы, связанные с правильными многоугольниками.
- Проблемы с параллельными линиями и углами.Проблемы, связанные с параллельными линиями и чередующимися и соответствующими углами.
- Проблема перекрывающихся кругов. Найдите область перекрытия двух кругов: проблема с подробными решениями.
- Проблемы секторов и кругов. Проблемы, с подробными решениями, относящиеся к секторам и кругу.
- Проблемы закона косинуса. Закон косинуса используется для решения словесных задач.
- Проблемы закона синуса. Синус-закон используется для решения словесных задач.
- Проблемы треугольника.Проблемы треугольника с подробным решением.
- Задачи о равносторонних треугольниках с решениями.
- Равнобедренные треугольники. Задачи с решениями.
- Проблемы объема трехмерных фигур. 3D-формы, такие как призмы, проблемы объема с подробными решениями.
- Площадь восьмиугольника — проблема с решением. Найдите длину одной стороны, периметр и площадь правильного восьмиугольника, учитывая расстояние между двумя противоположными сторонами (пролет).
- Площадь и периметр прямоугольных треугольников. Задачи с решением.
- Два квадрата и круг — проблема с решением. Представлена задача с подробным решением о круге, вписанном в один квадрат и описанном в другом.
- Два круга и квадрат — проблема с решением. Представлена проблема с подробным решением на квадрате, вписанном в один круг и описанном в другом.
- Треугольник, вписанный в круг — проблема с решением. Вписанная задача прямоугольного треугольника с подробным решением.
- Примеры подобных треугольников и проблемы с решениями.Определение и теоремы о подобных треугольниках, включая примеры и задачи с подробными решениями.
- Круг, касающийся прямоугольного треугольника — проблема с решением. Решите прямоугольный треугольник, все стороны касаются окружности. Представлены как проблема, так и ее подробное решение.
- Примеры конгруэнтных треугольников и задачи с решениями.
- Сравните объемы трехмерных фигур. Задача сравнить объемы конуса, цилиндра и полусферы.
- Как построить усеченную пирамиду ?.Если отрезать верхнюю часть конуса плоскостью, перпендикулярной высоте конуса, получится усеченный конус. Как построить усеченную пирамиду с учетом радиуса основания, радиуса вершины и высоты?
- Задачи параллелограмма. Проблемы со словами, относящиеся к параллелограммам, представлены вместе с подробными решениями.
- Проблемы с конусом. Представлены проблемы, связанные с площадью поверхности и объемом конуса, с подробными решениями.
- Проблемы пирамиды.Проблемы пирамиды, связанные с площадью и объемом поверхности, с подробными решениями.
- Проблемы трапеции. Проблемы трапеции представлены вместе с подробными решениями.
- Решите трапецию с учетом ее оснований и ножек.
- Проблемы ромба. Описание и свойства ромба представлены вместе с проблемами с подробными решениями.
Вызов задач геометрии
Учебные пособия по геометрии
- Простые доказательства теоремы Пифагора и проблемы с решениями.
- Треугольники. Определения и свойства треугольников в геометрии.
- Вписанные и центральные углы в кругах. Определения и теоремы, относящиеся к вписанным и центральным углам в кругах, обсуждаются с использованием примеров и задач.
- Области треугольников. Задачи с решениями. Используйте разные формулы площади треугольника, чтобы вычислить площади треугольников и фигур.
- Параллельные линии и углы. Этот урок посвящен соответствующим внутренним и внешним углам, которые образуются при пересечении поперечной линией двух параллельных линий.
- Свойства треугольников. Апплет используется для интерактивного исследования свойств треугольников.
- Теорема Фалеса. Аплет используется для проверки теоремы Фалеса: угол, вписанный в полукруг, является прямым углом.
- Правильные многоугольники. Учебник по разработке полезных формул для площади правильных многоугольников.
- Симметрия вращения в правильных многоугольниках. Интерактивное руководство для изучения симметрии вращения правильных многоугольников и вывода формулы для угла поворота.
- Симметрия вращения геометрических фигур. Интерактивное руководство для изучения симметрии вращения геометрических фигур.
- Углы в геометрии. Определения и свойства углов в геометрии.
- Закон синуса — неоднозначный случай — апплет. Неоднозначный случай синусоидального закона при решении задач треугольника исследуется в интерактивном режиме с помощью апплета.
- Высота, медиана и биссектриса угла треугольника.
- Центральные и вписанные углы — Интерактивный апплет.Свойства центрального и вписанного углов, пересекающих общую дугу в окружности, исследуются с помощью апплета интерактивной геометрии.
- Перпендикулярная биссектриса — интерактивный апплет. Определение и свойства серединного перпендикуляра исследуются с помощью апплета геометрии.
- Треугольники, биссектрисы и окружности — интерактивный апплет. Свойства серединных перпендикуляров в треугольниках и описанных окружностях исследуются в интерактивном режиме с помощью геометрического Java-апплета.
- Таблица формул для геометрии. Представлена таблица формул геометрии, относящаяся к площади и периметру треугольников, прямоугольников, окружностей, секторов и объему сферы, конуса, цилиндра.
Полярные координаты
Геометрические преобразования
Геометрические калькуляторы и рабочие таблицы
Автор —
e-mail
Домашняя страница сообщить об этом объявлении
теорем о круге
Некоторые интересные вещи об углах и окружностях.
Угол с надписью
Во-первых, определение:
Inscribed Angle : угол, образованный точками, лежащими на окружности круга.
A и C — «конечные точки»
B — «вершины»
Поиграйте с этим здесь:
Когда вы перемещаете точку «B», что происходит с углом?
Теоремы о вписанных углах
Вписанный угол a ° равен половине центрального угла 2a °
(называется углом в центральной теореме )
и (с фиксированными конечными точками) …
… угол a ° равен всегда один и тот же ,
независимо от того, где он находится на той же дуге между конечными точками:
Угол а ° то же .
(так называемые углы , подчиненные теореме о той же дуге )
Пример: Каков размер POQ Angle? (О — центр круга)
Угол POQ = 2 × Угол PRQ = 2 × 62 ° = 124 °
Пример: Какой размер Angle CBX?
Угол ADB = 32 ° также равен углу ACB.
А Angle ACB также равен Angle XCB.
Итак, в треугольнике BXC мы знаем, что угол BXC = 85 °, а угол XCB = 32 °.
Теперь используем углы треугольника и прибавляем к 180 °:
Угол CBX + Угол BXC + Угол XCB = 180 °
Угол CBX + 85 ° + 32 ° = 180 °
Угол CBX = 63 °
Угол в полукруге (теорема Фалеса)
Угол , вписанный поперек диаметра круга , всегда является прямым углом:
(Конечные точки — это любой конец диаметра круга,
точка вершины может находиться в любом месте окружности.)
Почему? Потому что: Вписанный угол 90 ° составляет половину центрального угла 180 ° (с использованием «теоремы об угле в центре» выше) |
Еще одна веская причина, почему это работает
Мы также можем повернуть фигуру на 180 °, чтобы получился прямоугольник!
Это — это прямоугольник, потому что все стороны параллельны и обе диагонали равны.
Итак, его внутренние углы прямые (90 °).
Итак, поехали! Независимо от того, где , этот угол на окружности равен
, это всегда 90 °
Пример: Какой размер Angle BAC?
Угол в теореме о полукруге говорит нам, что угол ACB = 90 °
Теперь используйте углы треугольника и прибавьте к 180 °, чтобы найти угол ВАС:
.
Угол ВАС + 55 ° + 90 ° = 180 °
Угол ВАС = 35 °
В поисках центра круга
Мы можем использовать эту идею, чтобы найти центр круга:
- нарисуйте прямой угол из любого места на окружности круга, затем нарисуйте диаметр, в котором две ножки соприкасаются с окружностью
- сделайте это снова, но для другого диаметра
Где крест диаметров — центр!
Циклический четырехугольник
«Циклический» четырехугольник имеет каждую вершину на окружности: | |
Противоположные углы циклического четырехугольника складываются в 180 ° :
|
Пример: Каков размер угла WXY?
Сумма противоположных углов вписанного четырехугольника дает 180 °
Угол WZY + Угол WXY = 180 °
69 ° + угол WXY = 180 °
Угол WXY = 111 °
Касательный уголКасательная линия касается окружности в одной точке. Всегда образует прямой угол с радиусом круга. |
Рабочий лист практических вопросов по основной теореме пропорциональности
(1) В ΔABC, D и E — точки на сторонах AB и AC соответственно, такие, что DE ∥ BC
(i) Если AD / DB = 3/4 и AC = 15 см, найдите AE. Решение
(ii) Если AD = 8x −7, DB = 5x −3, AE = 4x −3 и EC = 3x −1, найдите значение x. Решение
(2) ABCD — это трапеция, в которой AB || DC и P, Q — точки на AD и BC соответственно, такие что PQ || DC, если PD = 18 см, BQ = 35 см и QC = 15 см, найдите AD
Решение
(3) В ΔABC, D и E — точки на сторонах AB и AC соответственно.Для каждого из следующих случаев покажите, что DE || BC
(i) AB = 12 см, AD = 8 см, AE = 12 см и AC = 18 см.
(ii) AB = 5,6 см, AD = 1,4 см, AC = 7,2 см и AE = 1,8 см.
Раствор
(4) На рис. если PQ || БК и PR || CD доказать, что
(i) AR / RD = AQ / AB
(ii) QB / AQ = DR / AR Решение
(5) Ромб PQRB вписан в ΔABC, так что ÐB является одним из его углов. P, Q и R лежат на AB, AC и BC соответственно. Если AB = 12 см и BC = 6 см, найти стороны PQ, RB ромба
.
Раствор
(6) В форме трапеции ABCD, AB || DC, E и F — точки на непараллельных сторонах AD и BC соответственно, такие что EF || AB.Покажите, что AE / ED = BF / FC
Раствор
(7) На рисунке DE || BC и CD || EF. Докажите, что AD 2 = AB × AF
Решение
