Содержание
Теорема Пифагора: формула, доказательство. Обратная теорема
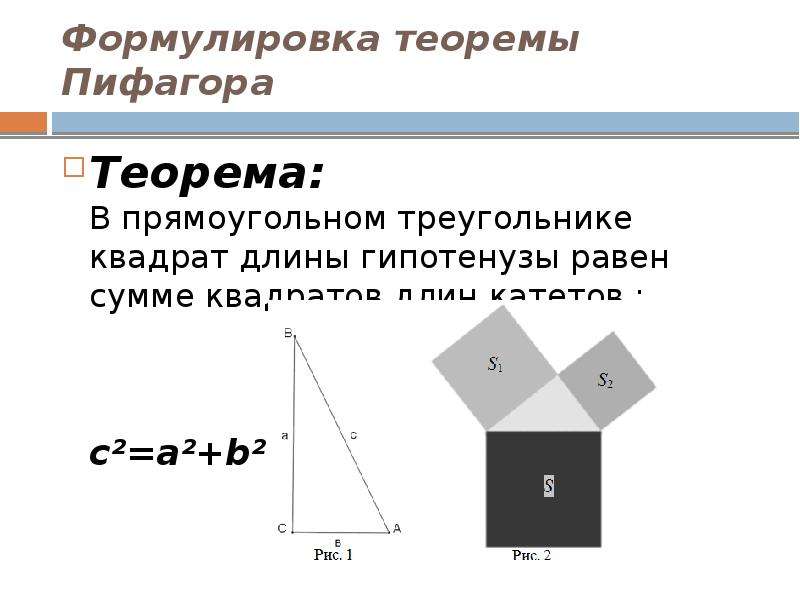
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Если ∠A = 90°, то a2 + b2 = c2.
Доказательство:
Возьмём прямоугольный треугольник с катетами a, b и гипотенузой c:
Достроим этот треугольник до квадрата со стороной a + b:
Площадь данного квадрата S будет равна (a + b)2:
S = (a + b)2.
С другой стороны, площадь этого квадрата состоит из четырёх одинаковых треугольник, площадь каждого из которых равна половине произведения их катетов (ab : 2), и квадрата со стороной c, поэтому:
S = (a + b)2
или
| S = 4 · ( | ab | ) + c2 = 2ab + c2 |
| 2 |
Таким образом:
(a + b)2 = 2ab + c2.
Так квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(a + b)2 = a2 + 2ab + b2,
то для того, чтобы наше равенство было верным c2 должен быть равен a2 + b2. Таким образом,
(a + b)2 = 2ab + c2, где c2 = a2 + b2.
Теорема доказана.
Обратная теорема Пифагора
Обратная теорема Пифагора:
Если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других сторон, то этот треугольник – прямоугольный.
Если a2 + b2 = c2, то треугольник ABC — прямоугольный.
Доказательство:
Возьмём треугольник ABC со сторонами a, b и c, у которого c2 = a2 + b2. Докажем, что ∠A = 90°:
Рассмотрим прямоугольный треугольник A1B1C1 с прямым углом A1, у которого A1B1 = a и A1C1 = b:
По теореме Пифагора:
B1C12 = A1B12 + A1C12.
Значит B1C12 = a2 + b2. Но a2 + b2 = c2 по условию теоремы. Следовательно B1C12 = c2, откуда можно сделать вывод B1C1 = c.
Треугольники ABC и A1B1C1 равны по трём сторонам, поэтому ∠A = ∠A1 = 90°, то есть треугольник ABC является прямоугольным. Теорема доказана.
Теорема пифагора и обратная ей. Урок «теорема, обратная теореме пифагора». Обратная теорема Пифагора
Теорема Пифагора
— одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение
между сторонами прямоугольного треугольника .
Считается, что доказана греческим математиком Пифагором, в честь которого и названа.
Геометрическая формулировка теоремы Пифагора.
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата , построенного на гипотенузе , равна сумме площадей квадратов ,
построенных на катетах.
Алгебраическая формулировка теоремы Пифагора.

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c
, а длины катетов через a
и b
:
Обе формулировки теоремы Пифагора
эквивалентны, но вторая формулировка более элементарна, она не
требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и
измерив только длины сторон прямоугольного треугольника .
Обратная теорема Пифагора.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то
треугольник прямоугольный.
Или, иными словами:
Для всякой тройки положительных чисел a
, b
и c
, такой, что
существует прямоугольный треугольник с катетами a
и b
и гипотенузой c
.
Теорема Пифагора для равнобедренного треугольника.
Теорема Пифагора для равностороннего треугольника.

Доказательства теоремы Пифагора.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема
Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие
можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:
доказательства методом площадей
, аксиоматические
и экзотические доказательства
(например,
с помощью дифференциальных уравнений
).
1. Доказательство теоремы Пифагора через подобные треугольники.
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся
напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC
есть прямоугольный треугольник с прямым углом C
. Проведём высоту из C
Проведём высоту из C
и обозначим
её основание через H
.
Треугольник ACH
подобен треугольнику AB
C по двум углам. Аналогично, треугольник CBH
подобен ABC
.
Введя обозначения:
получаем:
,
что соответствует —
Сложив a
2 и b
2 , получаем:
или , что и требовалось доказать.
2. Доказательство теоремы Пифагора методом площадей.
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они
используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.
- Доказательство через равнодополняемость.
Расположим четыре равных прямоугольных
треугольника так, как показано на рисунке
справа.
Четырёхугольник со сторонами c
— квадратом,
так как сумма двух острых углов 90°, а
развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны,
площади квадрата со стороной (a+b
), а с другой стороны, сумме площадей четырёх треугольников и
Что и требовалось доказать.
3. Доказательство теоремы Пифагора методом бесконечно малых.
Рассматривая чертёж, показанный на рисунке, и
наблюдая изменение стороны
a
, мы можем
записать следующее соотношение для бесконечно
малых
приращений сторон
с
и
a
(используя подобие
треугольников):
Используя метод разделения переменных, находим:
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:
Интегрируя данное уравнение и используя начальные условия, получаем:
Таким образом, мы приходим к желаемому ответу:
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной
пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми
вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения
(в данном случае катет b
). Тогда для константы интегрирования получим:
Тогда для константы интегрирования получим:
Замечательно, что свойство указанное в теореме Пифагора, является характеристическим свойством прямоугольного треугольника. Это следует из теоремы, обратной теореме Пифагора.
Теорема: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Выведем формулу, выражающую плоскость треугольника через длины его сторон. Эту формулу связывают с именем Герона александрийского — древнегреческого математика и механика, жившего, вероятно в 1 в.н.э. Герон много уделял внимания практическим приложениям геометрии.
Теорема. Площадь S треугольника, стороны которого равны a , b , c , вычисляется по формуле S=, где p — полупериметр треугольника.
Доказательство.
Дано: ?ABC, АВ= с, ВС= а, АС= b.Углы А и В, острые. СН — высота.
Доказать:
Доказательсво:
Рассмотрим треугольник ABC, в котором AB=c , BC=a, AC=b. Во всяком треугольнике, по крайней мере, два угла острые.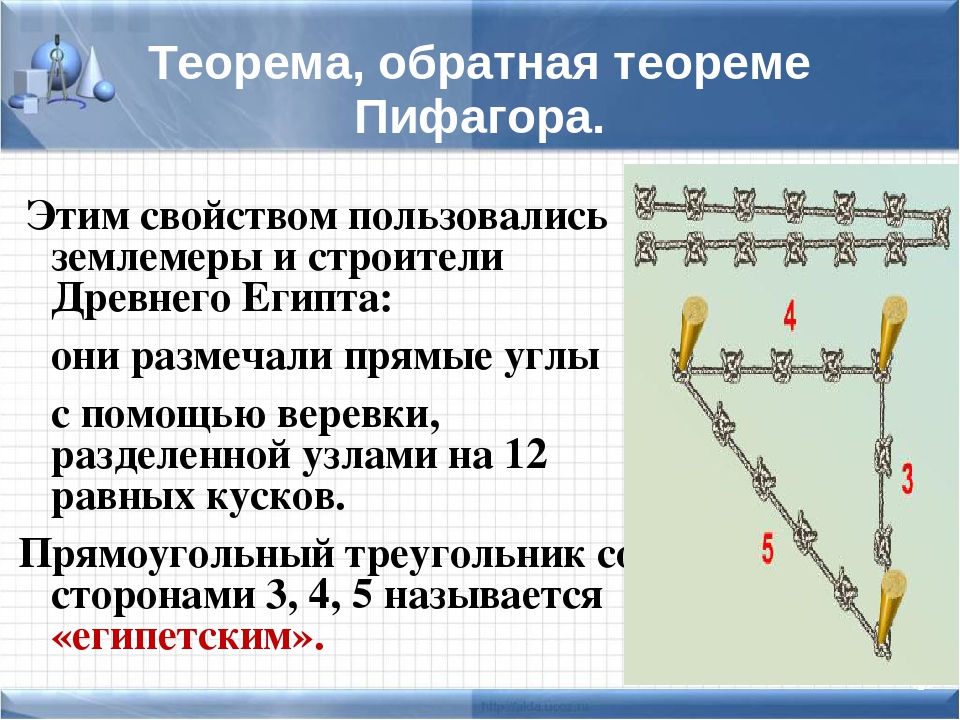 Пусть А и В — острые углы треугольника АВС. Tогда основание H высоты CH треугольника лежит на стороне AB. Введем обозначения: CH = h, AH=y, HB=x. по теореме Пифагора a 2 — x 2 = h 2 =b 2 -y 2 , откуда
Пусть А и В — острые углы треугольника АВС. Tогда основание H высоты CH треугольника лежит на стороне AB. Введем обозначения: CH = h, AH=y, HB=x. по теореме Пифагора a 2 — x 2 = h 2 =b 2 -y 2 , откуда
Y 2 — x 2 = b 2 — a 2 , или (y — x) (y + x) = b 2 — a 2 , а так как y + x = c, то y- x = (b2 — a2).
Складывая два последних равенства, п олучаем:
2y = +c, откуда
y=,и, значит, h 2 = b 2 -y 2 =(b — y)(b+y)=
Следовательно, h = .
Цели урока:
общеобразовательные:
- проверить теоретические знания учащихся
(свойства прямоугольного треугольника, теорема
Пифагора), умение использовать их при решении
задач; - создав проблемную ситуацию, подвести учащихся к
“открытию” обратной теоремы Пифагора.
развивающие:
- развитие умений применять теоретические знания
на практике; - развитие умения формулировать выводы при
наблюдениях; - развитие памяти, внимания, наблюдательности:
- развитие мотивации учения через эмоциональное
удовлетворение от открытий, через введение
элементов истории развития математических
понятий.
воспитательные:
- воспитывать устойчивый интерес к предмету
через изучение жизнедеятельности Пифагора; - воспитание взаимопомощи и объективного
оценивания знаний одноклассников через
взаимопроверку.
Форма урока: классно-урочная.
План урока:
- Организационный момент.
- Проверка домашнего задания. Актуализация
знаний. - Решение практических задач с использованием
теоремы Пифагора. - Новая тема.
- Первичное закрепление знаний.
- Домашнее задание.
- Итоги урока.
- Самостоятельная работа (по индивидуальным
карточкам с отгадыванием афоризмов Пифагора).
Ход урока.
Организационный момент.
Проверка домашнего задания. Актуализация
знаний.
Учитель:
Какое задание вы
выполняли дома?
Ученики:
По двум данным
сторонам прямоугольного треугольника найти
третью сторону, ответы оформить в виде таблицы.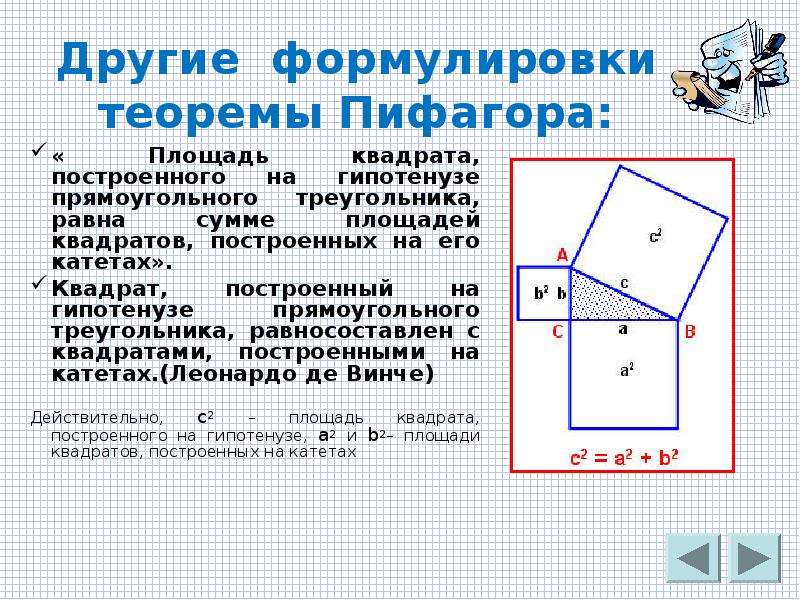
Повторить свойства ромба и прямоугольника.
Повторить, что называется условием, а что
заключением теоремы. Подготовить сообщения о
жизни и деятельности Пифагора. Принести веревку
с 12-ю завязанными на ней узлами.
Учитель:
Ответы к домашнему
заданию проверьте по таблице
(черным цветом выделены данные,
красным – ответы).
Учитель:
На доске
записаны утверждения. Если вы согласны с ними на
листочках напротив соответствующего номера
вопроса поставьте “+”, если не согласны, то
поставьте “–”.
На доске заранее написаны
утверждения.
- Гипотенуза больше катета.
- Сумма острых углов прямоугольного треугольника
равна 180 0 . - Площадь прямоугольного треугольника с катетами
а
и в
вычисляется по формуле S=ab/2
. - Теорема Пифагора верна для всех равнобедренных
треугольников. - В прямоугольном треугольнике катет, лежащий
напротив угла 30 0 , равен половине
гипотенузы.
- Сумма квадратов катетов равна квадрату
гипотенузы. - Квадрат катета равен разности квадратов
гипотенузы и второго катета. - Сторона треугольника равна сумме двух других
сторон.
Проверяются работы с помощью
взаимопроверки. Утверждения, вызвавшие споры, –
обсуждаются.
Ключ к теоретическим вопросам.
Учащиеся ставят друг другу оценки по следующей
системе:
8 правильных ответов “5”;
6-7 правильных ответов “4”;
4-5 правильных ответов “3”;
меньше 4 правильных ответов “2”.
Учитель:
О чем мы говорили на
прошлом уроке?
Ученик:
О Пифагоре и его теореме.
Учитель:
Сформулируйте
теорему Пифагора. (Несколько учеников читают
формулировку, в это время 2-3 ученика доказывают
ее у доски, 6 учеников – за первыми партами на
листочках).
На магнитной доске на карточках
написаны математические формулы. Выберите те из
них, которые отражают смысл теоремы Пифагора, где
а
и в
– катеты, с
–
гипотенуза.
| 1) с 2 = а 2 + в 2 | 2) с = а + в | 3) а 2 = с 2 – в 2 |
| 4) с 2 = а 2 – в 2 | 5) в 2 = с 2 – а 2 | 6) а 2 = с 2 + в 2 |
Пока учащиеся, доказывающие теорему у
доски и на местах, не готовы, слово
предоставляется тем, кто подготовил сообщения о
жизни и деятельности Пифагора.
Школьники, работающие на местах, сдают
листочки и слушают доказательства тех, кто
работал у доски.
Решение практических задач с использованием
теоремы Пифагора.
Учитель:
предлагаю вам
практические задачи с применением изучаемой
теоремы. Побываем сначала в лесу, после бури,
потом на загородном участке.
Задача 1
. После бури сломалась ель.
Высота оставшейся части 4,2 м. Расстояние от
основания до упавшей макушки 5,6 м. Найти высоту
ели до бури.
Задача 2
. Высота дома 4,4 м Ширина
Высота дома 4,4 м Ширина
газона вокруг дома 1,4 м. Какой длины надо
изготовить лестницу, чтобы она не заступала на
газон и доставала до крыши дома?
Новая тема.
Учитель:
(звучит музыка)
Закройте глаза, на несколько минут мы окунемся в
историю. Мы с вами в Древнем Египте. Вот на верфях
египтяне строят свои знаменитые корабли. А вот
землемеры, они измеряют участки земли, границы
которых смылись после разлива Нила. Строители
строят грандиозные пирамиды, которые до сих пор
поражают нас своим великолепием. Во всех этих
видах деятельности египтянам необходимо было
использовать прямые углы. Они умели строить их с
помощью веревки с 12 ю завязанными на
одинаковом расстоянии друг от друга узелками.
Попробуйте и вы, рассуждая как древние египтяне,
построить с помощью своих веревок прямоугольные
треугольники. (Решая эту проблему, ребята
работают в группах по 4 человека. Через некоторое
время на планшете у доски кто-то показывает
построение треугольника).
Стороны полученного треугольника 3, 4 и
5. Если между этими узлами завязать еще по одному
узлу, то его стороны станут 6, 8 и 10. Если по два – 9,
12 и 15. Все эти треугольники являются
прямоугольными т. к.
5 2 = 3 2 + 4 2 , 10 2
= 6 2 + 8 2 , 15 2 = 9 2 + 12 2
и т.д.
Каким свойством должен обладать
треугольник, чтобы быть прямоугольным? (Учащиеся
пытаются сами сформулировать обратную теорему
Пифагора, наконец, у кого-то это получается).
Чем эта теорема отличается от теоремы
Пифагора?
Ученик:
Условие и
заключение поменялись местами.
Учитель:
Дома вы повторяли,
как называются такие теоремы. Так с чем мы сейчас
познакомились?
Ученик:
С обратной
теоремой Пифагора.
Учитель:
Запишем в
тетради тему урока. Откройте учебники на стр. 127
прочитайте еще раз это утверждение, запишите его
себе в тетрадь и разберите доказательство.
(После нескольких минут
самостоятельной работы с учебником по желанию
один человек у доски приводит доказательство
теоремы).
- Как называется треугольник со сторонами 3, 4 и 5?
Почему? - Какие треугольники называются пифагоровыми?
- С какими треугольниками вы работали в домашнем
задании? А в задачах с сосной и лестницей?
Первичное закрепление знаний
.
Эта теорема помогает решать задачи, в
которых надо выяснить, будут ли треугольники
прямоугольными.
Задания:
1) Выясните, является ли треугольник
прямоугольным, если его стороны равны:
а) 12,37 и 35; б) 21, 29 и 24.
2) Вычислите высоты треугольника со сторонами 6,
8 и 10 см.
Домашнее задание
.
Стр.127:обратная теорема Пифагора. № 498(а,б,в) № 497.
Итоги урока.
Что нового узнали на уроке?
Пифагора?
Самостоятельная работа (проводится по
индивидуальным карточкам).

Учитель:
Дома вы повторяли
свойства ромба и прямоугольника. Перечислите их
(идет беседа с классом). На прошлом уроке мы
говорили о том, что Пифагор был разносторонней
личностью. Он занимался и медициной, и музыкой, и
астрономией, а так же был спортсменом и
участвовал в олимпийских играх. А еще Пифагор был
философом. Многие его афоризмы и сегодня
актуальны для нас. Сейчас вы будете выполнять
самостоятельную работу. К каждому заданию дано
несколько вариантов ответов, рядом с которыми
записаны фрагменты афоризмов Пифагора. Ваша
задача – решив все задания, составить из
полученных фрагментов высказывание и записать
его.
Тема:
Теорема, обратная теореме Пифагора.
Цели урока:
1) рассмотреть теорему, обратную теореме Пифагора; ее применение в процессе решения задач; закрепить теорему Пифагора и совершенствовать навыки решения задач на ее применение;
2) развивать логическое мышление, творческий поиск, познавательный интерес;
3) воспитывать у учащихся ответственного отношения к учению, культуры математической речи.
Тип урока.
Урок усвоения новых знаний.
Ход урока
І.
Организационный момент
ІІ.
Актуализация
знаний
Урок мне
бы
хотелось
начать с четверостишья.
Да, путь познания не гладок
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!
Итак, на прошлом уроке вы выучили теорему Пифагора. Вопросы:
Теорема Пифагора справедлива для какой фигуры?
Какой треугольник называют прямоугольным?
Сформулируйте теорему Пифагора.
Как запишется теорема Пифагора для каждого треугольника?
Какие треугольники называются равными?
Сформулируйте признаки равенства треугольников?
А теперь проведем небольшую самостоятельную работу:
Решение задач по чертежам.
№1
(1 б.) Найти: АВ.
№2
(1 б.) Найти: ВС.
№3
(
2
б.)
Найти: АС
№4
(1 б.)
Найти: АС
№5
Дано: АВС
D
ромб
(2 б.) АВ = 13 см
АС = 10 см
Найти: В
D
Самопроверка №1. 5
№2. 5
№3. 16
№4. 13
№5. 24
ІІІ.
Изучение
нового
материала.
Древние египтяне строили прямые углы на местности таким образом: делили узлами веревку на 12 равных частей, связывали ее концы, после чего веревку растягивали так на земле, чтобы образовался треугольник со сторонами 3, 4 и 5 делений. Угол треугольника, который лежал против стороны с 5 делениями, был прямой.
Можете ли вы объяснить правильность этого суждения?
В результате поиска ответа на вопрос учащиеся должны понять, что с математической точки зрения вопрос ставится: будет ли треугольник прямоугольным.
Ставим проблему: как, не делая измерений, определить, будет ли треугольник с заданными сторонами прямоугольным. Решение этой проблемы и есть цель урока.
Решение этой проблемы и есть цель урока.
Запишите тему урока.
Теорема. Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник прямоугольный.
Самостоятельно доказывают теорему (составляют план доказательства по учебнику).
Из этой теоремы следует, что треугольник со сторонами 3, 4, 5 – прямоугольный (египетский).
Вообще, числа, для которых выполняется равенство
, называют пифагоровыми тройками. А треугольники, длины сторон которых выражаются пифагоровыми тройками (6, 8, 10), — пифагоровы треугольники.
Закрепление.
Т.к.
, то треугольник со сторонами 12, 13, 5 не является прямоугольным.
Т.к.
, то треугольник со сторонами 1, 5, 6 является прямоугольным.
№ 430 (а, б, в)
(
— не является)
По мнению Ван-дер-Вардена , очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.
Приблизительно в 400 году до н. {2}}
{2}}
, существует прямоугольный треугольник с катетами
a
{\displaystyle a}
и
b
{\displaystyle b}
и гипотенузой
c
{\displaystyle c}
.
Доказательства
В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора , что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия ), метод площадей , существуют также различные экзотические доказательства (например, с помощью дифференциальных уравнений).
Через подобные треугольники
Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами.
Конструкция, используемая для доказательства следующая: для прямоугольного треугольника с прямым углом
C
{\displaystyle C}
, квадратов над катетами и и квадрата над гипотенузой
A
B
I
K
{\displaystyle ABIK}
строится высота
C
H
{\displaystyle CH}
и продолжающий её луч
s
{\displaystyle s}
, разбивающий квадрат над гипотенузой на два прямоугольника и .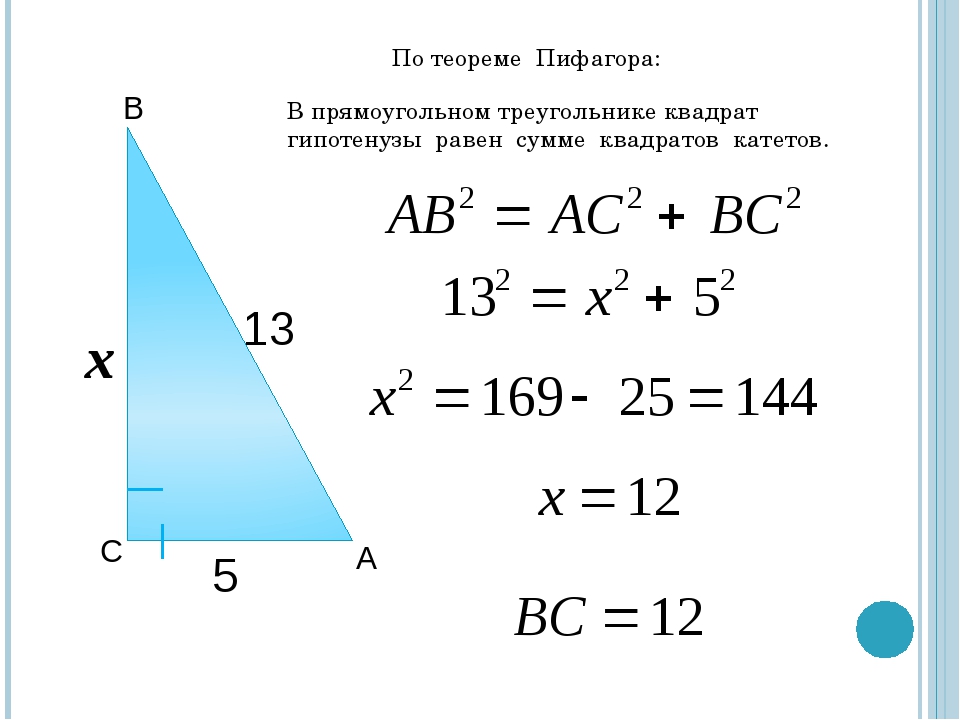 Доказательство нацелено на установление равенства площадей прямоугольника
Доказательство нацелено на установление равенства площадей прямоугольника
A
H
J
K
{\displaystyle AHJK}
с квадратом над катетом
A
C
{\displaystyle AC}
; равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом устанавливается аналогичным образом.
Равенство площадей прямоугольника
A
H
J
K
{\displaystyle AHJK}
и
A
C
E
D
{\displaystyle ACED}
устанавливается через конгруэнтность треугольников
△
A
C
K
{\displaystyle \triangle ACK}
и
△
A
B
D
{\displaystyle \triangle ABD}
, площадь каждого из которых равна половине площади квадратов
A
H
J
K
{\displaystyle AHJK}
и
A
C
E
D
{\displaystyle ACED}
соответственно в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если у фигур есть общая сторона, а высота треугольника к общей стороне является другой стороной прямоугольника. Конгруэнтность треугольников следует из равенства двух сторон (стороны квадратов) и углу между ними (составленного из прямой угла и угла при
A
{\displaystyle A}
.
Таким образом, доказательством устанавливается, что площадь квадрата над гипотенузой, составленного из прямоугольников
A
H
J
K
{\displaystyle AHJK}
и
B
H
J
I
{\displaystyle BHJI}
, равна сумме площадей квадратов над катетами.
Доказательство Леонардо да Винчи
К методу площадей относится также доказательство, найденное Леонардо да Винчи . Пусть дан прямоугольный треугольник
△
A
B
C
{\displaystyle \triangle ABC}
с прямым углом
C
{\displaystyle C}
и квадраты
A
C
E
D
{\displaystyle ACED}
,
B
C
F
G
{\displaystyle BCFG}
и
A
B
H
J
{\displaystyle ABHJ}
(см. рисунок). В этом доказательстве на стороне
H
J
{\displaystyle HJ}
последнего во внешнюю сторону строится треугольник, конгруэнтный
△
A
B
C
{\displaystyle \triangle ABC}
, притом отражённый как относительно гипотенузы, так и относительно высоты к ней (то есть
J
I
=
B
C
{\displaystyle JI=BC}
и
H
I
=
A
C
{\displaystyle HI=AC}
). Прямая
C
I
{\displaystyle CI}
разбивает квадрат, построенный на гипотенузе на две равные части, поскольку треугольники
△
A
B
C
{\displaystyle \triangle ABC}
и
△
J
H
I
{\displaystyle \triangle JHI}
равны по построению.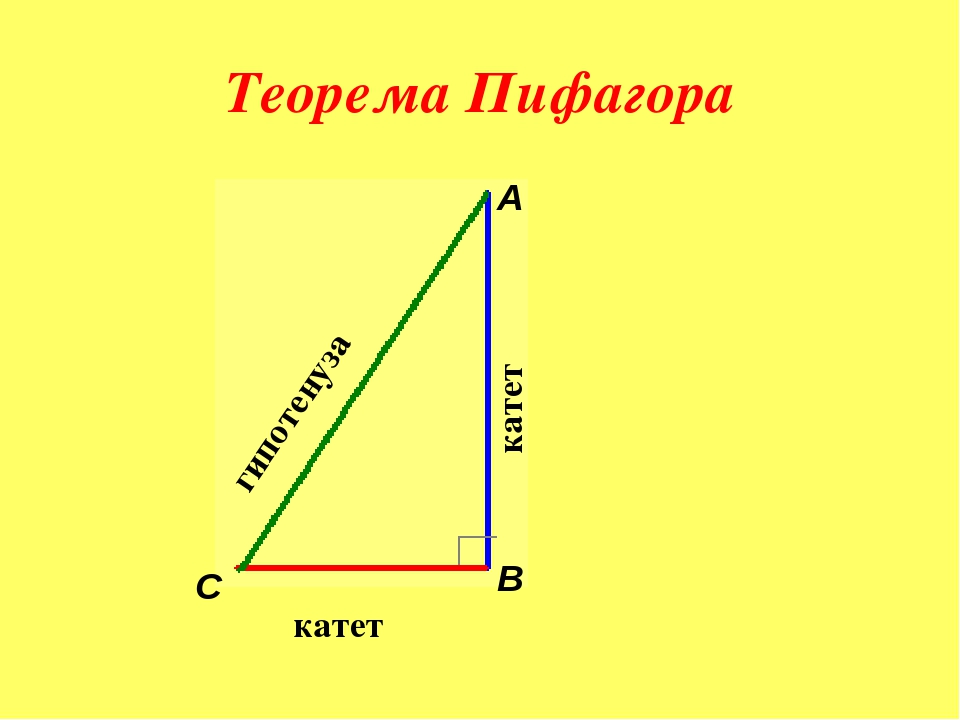 Доказательство устанавливает конгруэнтность четырёхугольников
Доказательство устанавливает конгруэнтность четырёхугольников
C
A
J
I
{\displaystyle CAJI}
и
D
A
B
G
{\displaystyle DABG}
, площадь каждого из которых, оказывается, с одной стороны, равной сумме половин площадей квадратов на катетах и площади исходного треугольника, с другой стороны — половине площади квадрата на гипотенузе плюс площадь исходного треугольника. Итого, половина суммы площадей квадратов над катетами равна половине площади квадрата над гипотенузой, что равносильно геометрической формулировке теоремы Пифагора.
Доказательство методом бесконечно малых
Существует несколько доказательств, прибегающих к технике дифференциальных уравнений . В частности, Харди приписывается доказательство, использующее бесконечно малые приращения катетов
a
{\displaystyle a}
и
b
{\displaystyle b}
и гипотенузы
c
{\displaystyle c}
, и сохраняющие подобие с исходным прямоугольником, то есть, обеспечивающие выполнение следующих дифференциальных соотношений:
d
a
d
c
=
c
a
{\displaystyle {\frac {da}{dc}}={\frac {c}{a}}}
,
d
b
d
c
=
c
b
{\displaystyle {\frac {db}{dc}}={\frac {c}{b}}}
. {2}+\mathrm {Const} }
{2}+\mathrm {Const} }
. Применение начальных условий
a
=
b
=
c
=
0
{\displaystyle a=b=c=0}
определяет константу как 0, что в результате даёт утверждение теоремы.
Квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.
Вариации и обобщения
Подобные геометрические фигуры на трёх сторонах
Важное геометрическое обобщение теоремы Пифагора дал Евклид в «Началах », перейдя от площадей квадратов на сторонах к площадям произвольных подобных геометрических фигур : сумма площадей таких фигур, построенных на катетах, будет равна площади подобной им фигуры, построенной на гипотенузе.
Главная идея этого обобщения заключается в том, что площадь подобной геометрической фигуры пропорциональна квадрату любого своего линейного размера и в частности квадрату длины любой стороны. Следовательно, для подобных фигур с площадями
A
{\displaystyle A}
,
B
{\displaystyle B}
и
C
{\displaystyle C}
, построенных на катетах с длинами
a
{\displaystyle a}
и
b
{\displaystyle b}
и гипотенузе
c
{\displaystyle c}
соответственно, имеет место соотношение:
A
a
2
=
B
b
2
=
C
c
2
⇒
A
+
B
=
a
2
c
2
C
+
b
2
c
2
C
{\displaystyle {\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,\Rightarrow \,A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C}
. {2}}
{2}}
, то выполнено .
Кроме того, если возможно доказать без привлечения теоремы Пифагора, что для площадей трёх подобных геометрических фигур на сторонах прямоугольного треугольника выполнено соотношение
A
+
B
=
C
{\displaystyle A+B=C}
, то с использованием обратного хода доказательства обобщения Евклида можно вывести доказательство теоремы Пифагора. Например, если на гипотенузе построить конгруэтный начальному прямоугольный треугольник площадью
C
{\displaystyle C}
, а на катетах — два подобных ему прямоугольных треугольника с площадями
A
{\displaystyle A}
и
B
{\displaystyle B}
, то оказывается, что треугольники на катетах образуются в результате деления начального треугольника его высотой, то есть сумма двух меньших площадей треугольников равна площади третьего, таким образом
A
+
B
=
C
{\displaystyle A+B=C}
и, применяя соотношение для подобных фигур, выводится теорема Пифагора.
Теорема косинусов
Теорема Пифагора — это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике :
a
2
+
b
2
−
2
a
b
cos
θ
=
c
2
{\displaystyle a^{2}+b^{2}-2ab\cos {\theta }=c^{2}}
,
где — угол между сторонами
a
{\displaystyle a}
и
b
{\displaystyle b}
. Если угол равен 90°, то
cos
θ
=
0
{\displaystyle \cos \theta =0}
, и формула упрощается до обычной теоремы Пифагора.
Произвольный треугольник
Существует обобщение теоремы Пифагора на произвольный треугольник, оперирующее исключительно соотношением длин сторон, считается, что оно впервые было установлено сабийским астрономом Сабитом ибн Куррой . В нём для произвольного треугольника со сторонами в него вписывается равнобедренный треугольник с основанием на стороне
c
{\displaystyle c}
, вершиной, совпадающей с вершиной исходного треугольника, противолежащей стороне
c
{\displaystyle c}
и углами при основании, равными углу
θ
{\displaystyle \theta }
, противолежащему стороне
c
{\displaystyle c}
. В результате образуются два треугольника, подобных исходному: первый — со сторонами
a
{\displaystyle a}
, дальней от неё боковой стороной вписанного равнобедренного треугольника, и
r
{\displaystyle r}
— части стороны
c
{\displaystyle c}
; второй — симметрично к нему от стороны
b
{\displaystyle b}
со стороной
s
{\displaystyle s}
— соответствующей частью стороны
c
{\displaystyle c}
.{2}}
.
Теорема Паппа о площадях
Неевклидова геометрия
Теорема Пифагора выводится из аксиом евклидовой геометрии и недействительна для неевклидовой геометрии — выполнение теоремы Пифагора равносильно постулату Евклида о параллельности .
В неевклидовой геометрии соотношение между сторонами прямоугольного треугольника обязательно будет в форме, отличной от теоремы Пифагора. Например, в сферической геометрии все три стороны прямоугольного треугольника, которые ограничивают собой октант единичной сферы, имеют длину
π
/
2
{\displaystyle \pi /2}
, что противоречит теореме Пифагора.
При этом теорема Пифагора справедлива в гиперболической и эллиптической геометрии, если требование о прямоугольности треугольника заменить условием, что сумма двух углов треугольника должна равняться третьему .
Сферическая геометрия
Для любого прямоугольного треугольника на сфере радиусом
R
{\displaystyle R}
(например, если угол в треугольнике прямой) со сторонами
a
,
b
,
c
{\displaystyle a,b,c}
соотношение между сторонами имеет вид :
cos
(c
R)
=
cos
(a
R)
⋅
cos
(b
R)
{\displaystyle \cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\cdot \cos \left({\frac {b}{R}}\right)}
.
Это равенство может быть выведено как особый случай сферической теоремы косинусов , которая справедлива для всех сферических треугольников:
cos
(c
R)
=
cos
(a
R)
⋅
cos
(b
R)
+
sin
(a
R)
⋅
sin
(b
R)
⋅
cos
γ
{\displaystyle \cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\cdot \cos \left({\frac {b}{R}}\right)+\sin \left({\frac {a}{R}}\right)\cdot \sin \left({\frac {b}{R}}\right)\cdot \cos \gamma }
.
ch
c
=
ch
a
⋅
ch
b
{\displaystyle \operatorname {ch} c=\operatorname {ch} a\cdot \operatorname {ch} b}
,
где
ch
{\displaystyle \operatorname {ch} }
— гиперболический косинус . Эта формула является частным случаем гиперболической теоремы косинусов, которая справедлива для всех треугольников :
ch
c
=
ch
a
⋅
ch
b
−
sh
a
⋅
sh
b
⋅
cos
γ
{\displaystyle \operatorname {ch} c=\operatorname {ch} a\cdot \operatorname {ch} b-\operatorname {sh} a\cdot \operatorname {sh} b\cdot \cos \gamma }
,
где
γ
{\displaystyle \gamma }
— угол, вершина которого противоположна стороне
c
{\displaystyle c}
.{2}}}}
.
Для комплексных чисел теорема Пифагора даёт естественную формулу для нахождения модуля комплексного числа — для
z
=
x
+
y
i
{\displaystyle z=x+yi}
он равен длине
Теорема, обратная теореме Пифагора
На предыдущем уроке мы с вами познакомились с теоремой
Пифагора, которая звучит следующим образом: в прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов катетов.
На этом уроке мы сформулируем и докажем теорему,
обратную теореме Пифагора.
Теорема. Если квадрат
одной стороны треугольника равен сумме квадратов двух других сторон, то этот
треугольник – прямоугольный.
Доказательство.
Пусть ABC
– треугольник, для которого справедливо равенство: .
,
Докажем, что –
прямой.
–
прямоугольный.
–
прямой, ,.
,
.
Следовательно, ,то
есть,.
по
третьему признаку.
Тогда .
Значит, –
прямоугольный.
Что и требовалось доказать.
Прямоугольные треугольники, у которых длины сторон
выражаются целыми числами, называются пифагоровыми треугольниками. Так
каждый из приведённых треугольников является пифагоровым.
В Древнем Египте для построения прямого угла строили
прямоугольный треугольник при помощи кольев и натянутых на них верёвок длиной
три, четыре и пять единиц.
Тогда угол между сторонами, равными трём и четырём,
получался прямым.
Задача. Выясните,
является ли треугольник прямоугольным, если его стороны выражаются числами: а) ,
,
;
б) ,
,
;
в) ,
,
.
Решение.
Задача. Найдите площадь
треугольника, если его стороны равны см,
см
и см.
Решение.
,
тогда –
прямоугольный, .
,
(см2).
Ответ: см2.
Задача. В равнобедренном
треугольнике длина
боковой стороны равна
см,
а основание –
см.
Найдите .
Решение.
см.
,следовательно,
–
прямоугольный, .
Так как –
равнобедренный, то .
,тогда
.
Ответ: .
Итак, на этом уроке мы вспомнили теорему Пифагора и
познакомились с обратной ей: если квадрат одной стороны треугольника равен
сумме квадратов двух других сторон, то этот треугольник – прямоугольный.
Отметили, что прямоугольные треугольники, у которых
длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.
А также мы поговорили о египетском треугольнике,
который представляет собой треугольник со сторонами три, четыре, пять. При этом
если пропорционально увеличивать стороны такого треугольника, то полученные
треугольники, например, со сторонами шесть, восемь, десять; девять, двенадцать,
пятнадцать и так далее также будут прямоугольными.{2}
Обратная теорема Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. То есть для всякой тройки положительных чисел a, b
и c
, такой, что
a 2 + b 2 = c 2
,
существует прямоугольный треугольник с катетами a
и b
и гипотенузой c
.
Теорема Пифагора
— одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Доказана она ученым математиком и философом Пифагором.
Значение теоремы
в том, что с ее помощью можно доказать другие теоремы и решать задачи.
Дополнительный материал:
Теорема Пифагора
— одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение
между сторонами прямоугольного треугольника .
Считается, что доказана греческим математиком Пифагором, в честь которого и названа.
Геометрическая формулировка теоремы Пифагора.
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата , построенного на гипотенузе , равна сумме площадей квадратов ,
построенных на катетах.
Алгебраическая формулировка теоремы Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c
, а длины катетов через a
и b
:
Обе формулировки теоремы Пифагора
эквивалентны, но вторая формулировка более элементарна, она не
требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и
измерив только длины сторон прямоугольного треугольника .
Обратная теорема Пифагора.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то
треугольник прямоугольный.
Или, иными словами:
Для всякой тройки положительных чисел a
, b
и c
, такой, что
существует прямоугольный треугольник с катетами a
и b
и гипотенузой c
.
Теорема Пифагора для равнобедренного треугольника.
Теорема Пифагора для равностороннего треугольника.
Доказательства теоремы Пифагора.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема
Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие
можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:
доказательства методом площадей
, аксиоматические
и экзотические доказательства
(например,
с помощью дифференциальных уравнений
).
1. Доказательство теоремы Пифагора через подобные треугольники.
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся
напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC
есть прямоугольный треугольник с прямым углом C
. Проведём высоту из C
и обозначим
её основание через H
.
Треугольник ACH
подобен треугольнику AB
C по двум углам. Аналогично, треугольник CBH
подобен ABC
.
Введя обозначения:
получаем:
,
что соответствует —
Сложив a
2 и b
2 , получаем:
или , что и требовалось доказать.
2. Доказательство теоремы Пифагора методом площадей.
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они
используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.
- Доказательство через равнодополняемость.
Расположим четыре равных прямоугольных
треугольника так, как показано на рисунке
справа.
Четырёхугольник со сторонами c
— квадратом,
так как сумма двух острых углов 90°, а
развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны,
площади квадрата со стороной (a+b
), а с другой стороны, сумме площадей четырёх треугольников и
Что и требовалось доказать.
3. Доказательство теоремы Пифагора методом бесконечно малых.
Рассматривая чертёж, показанный на рисунке, и
наблюдая изменение стороны
a
, мы можем
записать следующее соотношение для бесконечно
малых
приращений сторон
с
и
a
(используя подобие
треугольников):
Используя метод разделения переменных, находим:
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:
Интегрируя данное уравнение и используя начальные условия, получаем:
Таким образом, мы приходим к желаемому ответу:
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной
пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми
вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения
(в данном случае катет b
). Тогда для константы интегрирования получим:
Цели урока:
общеобразовательные:
- проверить теоретические знания учащихся
(свойства прямоугольного треугольника, теорема
Пифагора), умение использовать их при решении
задач; - создав проблемную ситуацию, подвести учащихся к
“открытию” обратной теоремы Пифагора.
развивающие:
- развитие умений применять теоретические знания
на практике; - развитие умения формулировать выводы при
наблюдениях; - развитие памяти, внимания, наблюдательности:
- развитие мотивации учения через эмоциональное
удовлетворение от открытий, через введение
элементов истории развития математических
понятий.
воспитательные:
- воспитывать устойчивый интерес к предмету
через изучение жизнедеятельности Пифагора; - воспитание взаимопомощи и объективного
оценивания знаний одноклассников через
взаимопроверку.
Форма урока: классно-урочная.
План урока:
- Организационный момент.
- Проверка домашнего задания. Актуализация
знаний. - Решение практических задач с использованием
теоремы Пифагора. - Новая тема.
- Первичное закрепление знаний.
- Домашнее задание.
- Итоги урока.
- Самостоятельная работа (по индивидуальным
карточкам с отгадыванием афоризмов Пифагора).
Ход урока.
Организационный момент.
Проверка домашнего задания. Актуализация
знаний.
Учитель:
Какое задание вы
выполняли дома?
Ученики:
По двум данным
сторонам прямоугольного треугольника найти
третью сторону, ответы оформить в виде таблицы.
Повторить свойства ромба и прямоугольника.
Повторить, что называется условием, а что
заключением теоремы. Подготовить сообщения о
жизни и деятельности Пифагора. Принести веревку
с 12-ю завязанными на ней узлами.
Учитель:
Ответы к домашнему
заданию проверьте по таблице
(черным цветом выделены данные,
красным – ответы).
Учитель:
На доске
записаны утверждения. Если вы согласны с ними на
листочках напротив соответствующего номера
вопроса поставьте “+”, если не согласны, то
поставьте “–”.
На доске заранее написаны
утверждения.
- Гипотенуза больше катета.
- Сумма острых углов прямоугольного треугольника
равна 180 0 . - Площадь прямоугольного треугольника с катетами
а
и в
вычисляется по формуле S=ab/2
. - Теорема Пифагора верна для всех равнобедренных
треугольников. - В прямоугольном треугольнике катет, лежащий
напротив угла 30 0 , равен половине
гипотенузы. - Сумма квадратов катетов равна квадрату
гипотенузы. - Квадрат катета равен разности квадратов
гипотенузы и второго катета. - Сторона треугольника равна сумме двух других
сторон.
Проверяются работы с помощью
взаимопроверки. Утверждения, вызвавшие споры, –
обсуждаются.
Ключ к теоретическим вопросам.
Учащиеся ставят друг другу оценки по следующей
системе:
8 правильных ответов “5”;
6-7 правильных ответов “4”;
4-5 правильных ответов “3”;
меньше 4 правильных ответов “2”.
Учитель:
О чем мы говорили на
прошлом уроке?
Ученик:
О Пифагоре и его теореме.
Учитель:
Сформулируйте
теорему Пифагора. (Несколько учеников читают
формулировку, в это время 2-3 ученика доказывают
ее у доски, 6 учеников – за первыми партами на
листочках).
На магнитной доске на карточках
написаны математические формулы. Выберите те из
них, которые отражают смысл теоремы Пифагора, где
а
и в
– катеты, с
–
гипотенуза.
| 1) с 2 = а 2 + в 2 | 2) с = а + в | 3) а 2 = с 2 – в 2 |
| 4) с 2 = а 2 – в 2 | 5) в 2 = с 2 – а 2 | 6) а 2 = с 2 + в 2 |
Пока учащиеся, доказывающие теорему у
доски и на местах, не готовы, слово
предоставляется тем, кто подготовил сообщения о
жизни и деятельности Пифагора.
Школьники, работающие на местах, сдают
листочки и слушают доказательства тех, кто
работал у доски.
Решение практических задач с использованием
теоремы Пифагора.
Учитель:
предлагаю вам
практические задачи с применением изучаемой
теоремы. Побываем сначала в лесу, после бури,
потом на загородном участке.
Задача 1
. После бури сломалась ель.
Высота оставшейся части 4,2 м. Расстояние от
основания до упавшей макушки 5,6 м. Найти высоту
ели до бури.
Задача 2
. Высота дома 4,4 м Ширина
газона вокруг дома 1,4 м. Какой длины надо
изготовить лестницу, чтобы она не заступала на
газон и доставала до крыши дома?
Новая тема.
Учитель:
(звучит музыка)
Закройте глаза, на несколько минут мы окунемся в
историю. Мы с вами в Древнем Египте. Вот на верфях
египтяне строят свои знаменитые корабли. А вот
землемеры, они измеряют участки земли, границы
которых смылись после разлива Нила. Строители
строят грандиозные пирамиды, которые до сих пор
поражают нас своим великолепием. Во всех этих
видах деятельности египтянам необходимо было
использовать прямые углы. Они умели строить их с
помощью веревки с 12 ю завязанными на
одинаковом расстоянии друг от друга узелками.
Попробуйте и вы, рассуждая как древние египтяне,
построить с помощью своих веревок прямоугольные
треугольники. (Решая эту проблему, ребята
работают в группах по 4 человека. Через некоторое
время на планшете у доски кто-то показывает
построение треугольника).
Стороны полученного треугольника 3, 4 и
5. Если между этими узлами завязать еще по одному
узлу, то его стороны станут 6, 8 и 10. Если по два – 9,
12 и 15. Все эти треугольники являются
прямоугольными т. к.
5 2 = 3 2 + 4 2 , 10 2
= 6 2 + 8 2 , 15 2 = 9 2 + 12 2
и т.д.
Каким свойством должен обладать
треугольник, чтобы быть прямоугольным? (Учащиеся
пытаются сами сформулировать обратную теорему
Пифагора, наконец, у кого-то это получается).
Чем эта теорема отличается от теоремы
Пифагора?
Ученик:
Условие и
заключение поменялись местами.
Учитель:
Дома вы повторяли,
как называются такие теоремы. Так с чем мы сейчас
познакомились?
Ученик:
С обратной
теоремой Пифагора.
Учитель:
Запишем в
тетради тему урока. Откройте учебники на стр. 127
прочитайте еще раз это утверждение, запишите его
себе в тетрадь и разберите доказательство.
(После нескольких минут
самостоятельной работы с учебником по желанию
один человек у доски приводит доказательство
теоремы).
- Как называется треугольник со сторонами 3, 4 и 5?
Почему? - Какие треугольники называются пифагоровыми?
- С какими треугольниками вы работали в домашнем
задании? А в задачах с сосной и лестницей?
Первичное закрепление знаний
.
Эта теорема помогает решать задачи, в
которых надо выяснить, будут ли треугольники
прямоугольными.
Задания:
1) Выясните, является ли треугольник
прямоугольным, если его стороны равны:
а) 12,37 и 35; б) 21, 29 и 24.
2) Вычислите высоты треугольника со сторонами 6,
8 и 10 см.
Домашнее задание
.
Стр.127:обратная теорема Пифагора. № 498(а,б,в) № 497.
Итоги урока.
Что нового узнали на уроке?
Пифагора?
Самостоятельная работа (проводится по
индивидуальным карточкам).
Учитель:
Дома вы повторяли
свойства ромба и прямоугольника. Перечислите их
(идет беседа с классом). На прошлом уроке мы
говорили о том, что Пифагор был разносторонней
личностью. Он занимался и медициной, и музыкой, и
астрономией, а так же был спортсменом и
участвовал в олимпийских играх. А еще Пифагор был
философом. Многие его афоризмы и сегодня
актуальны для нас. Сейчас вы будете выполнять
самостоятельную работу. К каждому заданию дано
несколько вариантов ответов, рядом с которыми
записаны фрагменты афоризмов Пифагора. Ваша
задача – решив все задания, составить из
полученных фрагментов высказывание и записать
его.
Тема:
Теорема, обратная теореме Пифагора.
Цели урока:
1) рассмотреть теорему, обратную теореме Пифагора; ее применение в процессе решения задач; закрепить теорему Пифагора и совершенствовать навыки решения задач на ее применение;
2) развивать логическое мышление, творческий поиск, познавательный интерес;
3) воспитывать у учащихся ответственного отношения к учению, культуры математической речи.
Тип урока.
Урок усвоения новых знаний.
Ход урока
І.
Организационный момент
ІІ.
Актуализация
знаний
Урок мне
бы
хотелось
начать с четверостишья.
Да, путь познания не гладок
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!
Итак, на прошлом уроке вы выучили теорему Пифагора. Вопросы:
Теорема Пифагора справедлива для какой фигуры?
Какой треугольник называют прямоугольным?
Сформулируйте теорему Пифагора.
Как запишется теорема Пифагора для каждого треугольника?
Какие треугольники называются равными?
Сформулируйте признаки равенства треугольников?
А теперь проведем небольшую самостоятельную работу:
Решение задач по чертежам.
№1
(1 б.) Найти: АВ.
№2
(1 б.) Найти: ВС.
№3
(
2
б.)
Найти: АС
№4
(1 б.)
Найти: АС
№5
Дано: АВС
D
ромб
(2 б.) АВ = 13 см
АС = 10 см
Найти: В
D
Самопроверка №1. 5
№2. 5
№3. 16
№4. 13
№5. 24
ІІІ.
Изучение
нового
материала.
Древние египтяне строили прямые углы на местности таким образом: делили узлами веревку на 12 равных частей, связывали ее концы, после чего веревку растягивали так на земле, чтобы образовался треугольник со сторонами 3, 4 и 5 делений. Угол треугольника, который лежал против стороны с 5 делениями, был прямой.
Можете ли вы объяснить правильность этого суждения?
В результате поиска ответа на вопрос учащиеся должны понять, что с математической точки зрения вопрос ставится: будет ли треугольник прямоугольным.
Ставим проблему: как, не делая измерений, определить, будет ли треугольник с заданными сторонами прямоугольным. Решение этой проблемы и есть цель урока.
Запишите тему урока.
Теорема. Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник прямоугольный.
Самостоятельно доказывают теорему (составляют план доказательства по учебнику).
Из этой теоремы следует, что треугольник со сторонами 3, 4, 5 – прямоугольный (египетский).
Вообще, числа, для которых выполняется равенство
, называют пифагоровыми тройками. А треугольники, длины сторон которых выражаются пифагоровыми тройками (6, 8, 10), — пифагоровы треугольники.
Закрепление.
Т.к.
, то треугольник со сторонами 12, 13, 5 не является прямоугольным.
Т.к.
, то треугольник со сторонами 1, 5, 6 является прямоугольным.
№ 430 (а, б, в)
(
— не является)
Замечательно, что свойство указанное в теореме Пифагора, является характеристическим свойством прямоугольного треугольника. Это следует из теоремы, обратной теореме Пифагора.
Теорема: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Выведем формулу, выражающую плоскость треугольника через длины его сторон. Эту формулу связывают с именем Герона александрийского — древнегреческого математика и механика, жившего, вероятно в 1 в.н.э. Герон много уделял внимания практическим приложениям геометрии.
Теорема. Площадь S треугольника, стороны которого равны a , b , c , вычисляется по формуле S=, где p — полупериметр треугольника.
Доказательство.
Дано: ?ABC, АВ= с, ВС= а, АС= b.Углы А и В, острые. СН — высота.
Доказать:
Доказательсво:
Рассмотрим треугольник ABC, в котором AB=c , BC=a, AC=b. Во всяком треугольнике, по крайней мере, два угла острые. Пусть А и В — острые углы треугольника АВС. Tогда основание H высоты CH треугольника лежит на стороне AB. Введем обозначения: CH = h, AH=y, HB=x. по теореме Пифагора a 2 — x 2 = h 2 =b 2 -y 2 , откуда
Y 2 — x 2 = b 2 — a 2 , или (y — x) (y + x) = b 2 — a 2 , а так как y + x = c, то y- x = (b2 — a2).
Складывая два последних равенства, п олучаем:
2y = +c, откуда
y=,и, значит, h 2 = b 2 -y 2 =(b — y)(b+y)=
Следовательно, h = .
Теорема Пифагора — формула, доказательство, задачи
Основные понятия
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
a2 + b2 = c2,
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
- a = √c2 − b2
- b = √c2 − a2
- c = √a2 + b2
Запоминаем
в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.
Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:
- если c2 < a2 + b2 , значит угол, обращенный к стороне c, является острым.
- если c2 = a2 + b2 , значит угол, обращенный к стороне c, является прямым.
- если c2 > a2 +b2 , значит угол, обращенный к стороне c, является тупым.
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: ∆ABC, в котором ∠C = 90º.
Доказать: a2 + b2 = c2.
Пошаговое доказательство:
- Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
- Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:
∠ACB =∠CHA = 90º,
∠A — общий.
- Также прямоугольная фигура ∆CBH подобна ∆ABC:
∠ACB =∠CHB = 90º,
∠B — общий.
- Введем новые обозначения: BC = a, AC = b, AB = c.
- Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.
- Значит a2 = c * HB, b2 = c * AH.
- Сложим полученные равенства:
a2 + b2 = c * HB + c * AH
a2 + b2 = c * (HB + AH)
a2 + b2 = c * AB
a2 + b2 = c * c
a2 + b2 = c2
Теорема доказана.
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такая фигура является прямоугольной.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
- Построим прямой угол с вершиной в точке C₁.
- Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.
- Проведём отрезок A₁B₁.
- Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.
- В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁2 = A₁C₁2 + B₁C₁2.
- Таким образом получится:
- Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:
- C₁A₁ = CA и C₁B₁ = CB по результату построения,
- A₁B₁ = AB по доказанному результату.
- Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
- Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см. Какое значение у гипотенузы?
Как решаем:
значит c2 = a2 + b2 = 62 + 102 = 36 + 100 = 136
Ответ: 11,7.
Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?
Как решаем:
- Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:
112 = 82 + 92
121 ≠ 146
Ответ: треугольник не является прямоугольным.
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до теоремы Пифагора — и ответят на вопросы, которые бывает неловко задать перед всем классом.{2}$ было известно уже египтянам ещё около
2300 г. до н.э. По мнению ученого, строители строили тогда прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте приводится приближённое вычисление гипотенузы равнобедренного
прямоугольного треугольника.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является
единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным
значением теоремы для геометрии.
ФИО | Козлова Лидия Николаевна | ||
Место работы | Тенистовская СОШ | ||
Должность | Учитель математики | ||
Предмет | География | ||
Класс | 8 | ||
Тема и номер урока | Теорема обратная теореме Пифагора. Решение задач | ||
Базовый учебник | Геометрия 8: учебник для 8 кл. образоват. организаций с приложением на электронном носителе /Л.С. Анатасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина.– М.: Просвещение, 2013. | ||
а) разности гипотенузы и катета | б) сумме квадратов гипотенузы и катета | в) разности квадратов гипотенузы и катета | г) нет правильного ответа |
2. Если в треугольнике квадрат одной стороны равен разности квадратов двух других сторон, то эта сторона лежит напротив…………………………………………………………… | |||
а) острого угла | б) прямого угла | в) тупого угла | г) нет правильного ответа |
3.Квадрат гипотенузы равен сумме квадратов катетов в треугольнике с углами ………….. | |||
а) 60º и 60º | б) 37º и 53º | в) 45º и 50º | г) нет правильного ответа |
4. Какой из треугольников с указанными сторонами – прямоугольный? | |||
а) 5; 4; 2 | б) 8; 8; 8 | в) 12; 5; 13 | г) нет правильного ответа |
5. Угол А в треугольнике АВС равен В А С 2 | |||
60º | б) 45º | в) 30º | г) нет правильного ответа | 2. |
3. | 4. При построении | 2. Найти: АС | |
3. Дано: ABCD – квадрат Найти: АО. | 4. Дано: АВСD – ромб; АС = 2; DВ = 4. Найти: ВС. | 1. Диагонали ромба равны 14 и 28 см. Найдите сторону ромба. 2. В треугольнике два угла равны 45º и 90º, а большая сторона – 20 см. Найдите две другие стороны треугольника. | |
«4» | 1. Найдите диагональ ромба, если вторая диагональ и сторона ромба соответственно равны 12 и 10 см. 2. Основания равнобокой трапеции равны 4 и 12 см, а боковая сторона равна 5. Найдите высоту и диагональ трапеции. | ||
«5» | 1. Найдите диагонали равнобокой трапеции, если ее высота равна 6 см, а средняя линия, равна 8 см. 2. В параллелограмме ABCD BD = 2 см, АС= 26 см, АD= 16 см. Через точку О – точку пересечения диагоналей параллелограмма проведена прямая, перпендикулярная стороне ВС. Найдите отрезки, на которые эта прямая разделила сторону АD. | ||
Обращение теоремы Пифагора
Мы предполагаем, что вы знакомы с теоремой Пифагора.
Обратное к теореме Пифагора:
Если квадрат длины самой длинной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
То есть в
ΔABC, если c2 = a2 + b2, то
∠C — прямоугольный треугольник,
ΔPQR — прямой угол.
Мы можем доказать это от противного.
Предположим, что c2 = a2 + b2 в ΔABC и треугольник , а не прямоугольный.
Теперь рассмотрим другой треугольник.
ΔPQR.
Мы строим
ΔPQR так, чтобы
PR = a, QR = b и ∠R — прямой угол.
По теореме Пифагора (PQ) 2 = a2 + b2.
Но мы знаем, что a2 + b2 = c2, a2 + b2 = c2 и c = AB.
Итак, (PQ) 2 = a2 + b2 = (AB) 2.
То есть (PQ) 2 = (AB) 2.
Так как PQ и AB — длины сторон, мы можем взять положительные квадратные корни.
PQ = AB
То есть, все три стороны ΔPQR конгруэнтны трем сторонам ΔABC.
Итак, два треугольника конгруэнтны по свойству конгруэнтности сторона-сторона-сторона.
Поскольку ΔABC конгруэнтно ΔPQR, а ΔPQR — прямоугольный треугольник, ΔABC также должен быть прямоугольным треугольником.
Получили противоречие. Следовательно, наше предположение должно быть неверным.
Пример 1:
Проверьте, является ли треугольник со сторонами 6 см, 10 см и 8 см прямоугольным.
Проверьте, является ли квадрат длины самой длинной стороны суммой квадратов двух других сторон.
(10) 2 =? (8) 2+ (6) 2100 =? 64 + 36 100 = 100
Примените обратную теорему Пифагора.
Поскольку квадрат длины самой длинной стороны является суммой квадратов двух других сторон, согласно обратной теореме Пифагора, треугольник является прямоугольным.
Следствие теоремы подразделяет треугольники на острые, правые и тупые.
В треугольнике с длинами сторон a, b и c, где c — длина самой длинной стороны,
, если c2 если c2> a2 + b2, то треугольник тупой. Пример 2: Проверьте, является ли треугольник с длинами сторон 5, 7 и 9 единиц острым, прямым или тупым треугольником. Самая длинная сторона треугольника имеет длину 9 единиц. Сравните квадрат длины самой длинной стороны и сумму квадратов двух других сторон. Квадрат длины самой длинной стороны 92 = 81 кв. Ед. Сумма квадратов двух других сторон равна 52 + 72 = 25 + 49 = 74 кв. Единицы То есть 92> 52 + 72. Следовательно, согласно следствию, обратному теореме Пифагора, треугольник является тупым треугольником. Уже поздний вечер, на самом деле уже за полночь, поэтому текст поста буду кратким.Сегодня был хороший день, и сегодня вечером я сварил 23-ю партию пива, известную как «Спин-полпиво». (Я назвал его так, потому что он содержит только половину темного солода, который я использую в пиве, известного как темная материя…;), поэтому он не имеет ничего общего с электронами). Это очень простой пост о некоторой «обратной теореме Пифагора», пролетевшей в каком-то математическом видео. Я был довольно удивлен, что не видел этого раньше, но существует так много теорем, использующих эту старомодную евклидову геометрию, что я мог бы совсем забыть об этом. В течение 10 минут у меня было хорошее доказательство 2D-версии этой «обратной теоремы Пифагора». Вы можете найти его на первой картинке ниже. Однажды спустя, когда я немного катался, я попытался найти более многомерный аналог этого простого для понимания 2D утверждения или теоремы. И поэтому мне пришла в голову важная роль, которую число расстояния d сыграло в моем доказательстве общей теоремы Пифагора, которая действует на симплексы, которые являются более высокоразмерным аналогом двумерных треугольников. Придя домой, было легко записать детали, но для меня все было настолько просто, что заслуживает ли этот материал названия «теорема»? Что ж, примите решение по этому поводу, но если это не очень сложная теорема, это все равно хороший и милый результат … Этот пост состоит из шести изображений (все 550 × 775 пикселей, кроме последнего, которое потребовало немного расширения, потому что математика не подошла должным образом, поэтому одно изображение имеет размер 600 × 775 пикселей). Иногда это может показаться трудным, но это только потому, что в общих настройках, когда дело доходит до количества измерений, основная идея заключается в простых вещах, таких как взятие внутреннего продукта с нормализованным вектором нормали. Вот шесть картинок: Что такое обратная теорема Пифагора?
Это прекрасный результат, но для меня вектор нормали такой же милый, но только немного сложнее для записи, потому что эта часть имеет дело с общими настройками, где размерность n не фиксирована.
На этом пост пока заканчивается. Увидимся, мой дорогой читатель.
__________
Приложение добавлено 30 марта 2018 г .: В предыдущем посте я забыл разместить ссылку на доказательство общей теоремы Пифагора, которое я когда-то создавал давным-давно.
Перед этой ссылкой я хотел бы еще раз показать вам, как доказать общую теорему Пифагора для трехмерного случая, используя только двумерную теорему.
В конце концов, это первый основной шаг в моем доказательстве общей теоремы Пифагора…
Вот два дополнительных изображения, показывающих, как проходит этот основной шаг от двухмерной плоскости к трехмерному пространству:
Вот ссылка на доказательство общей теоремы Пифагора:
Общая теорема Пифагора (второй и последний пост).
Общая теорема Пифагора (второй и последний пост).
Ладно, до обновлений.
Теорема Пифагора и ее обратное
На рисунке 1 CD — это высота до гипотенузы AB.
Рис. 1 Высота, проведенная к гипотенузе прямоугольного треугольника, чтобы помочь в выводе теоремы Пифагора .
Из свойства сложения уравнений в алгебре мы получаем следующее уравнение.
Если вычесть c с правой стороны,
Но x + y = c (Постулат сложения сегментов) ,
Этот результат известен как теорема Пифагора .
Теорема 65 (теорема Пифагора): В любом прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы (катет 2 + катет 2 = гипотенуза 2 ).На рисунке 2 показаны части прямоугольного треугольника.
Рисунок 2 Части прямоугольного треугольника.
Пример 1: На рисунке 3 найдите x , длину гипотенузы.
Рисунок 3 Использование теоремы Пифагора для нахождения гипотенузы прямоугольного треугольника.
Пример 2: Используйте рисунок 4, чтобы найти x .
Рис. 4 Использование теоремы Пифагора для нахождения гипотенузы прямоугольного треугольника.
Любые три натуральных числа a, b, c , составляющие предложение a 2 + b 2 = c 2 , называются тройкой Пифагора. Поэтому 3-4-5 называется пифагоровой тройкой. Некоторые другие значения для a , b и c , которые будут работать, — это 5-12-13 и 8-15-17. Любое кратное одной из этих троек также будет работать. Например, использование 3-4-5: 6-8-10, 9-12-15 и 15-20-25 также являются троек Пифагора.
Пример 3: Используйте рисунок 5, чтобы найти x .
Рис. 5 Использование теоремы Пифагора для нахождения катета прямоугольного треугольника.
Если вы узнаете, что числа x , 24, 26 кратны 5-12-13 тройке Пифагора, ответ для x будет быстро найден. Поскольку 24 = 2 (12) и 26 = 2 (13), тогда x = 2 (5) или x = 10. Вы также можете найти x , используя теорему Пифагора .
Пример 4: Используйте рисунок 6, чтобы найти x .
Рисунок 6 Использование теоремы Пифагора для поиска неизвестных частей прямоугольного треугольника.
Вычтем x 2 + 12 x + 36 с обеих сторон.
Но x — это длина, поэтому она не может быть отрицательной. Следовательно, x = 9.
Обратное (обратное) утверждение теоремы Пифагора также верно.
Теорема 66: Если треугольник имеет стороны длиной a, b, и c , где c — самая длинная длина, а c 2 = a 2 + b 2 , то треугольник представляет собой прямоугольный треугольник с гипотенузой c .
Пример 5: Определите, могут ли следующие наборы длин быть сторонами прямоугольного треугольника: (a) 6-5-4, (b), (c) 3 / 4-1-5 / 4.
(a) Поскольку 6 — самая длинная длина, выполните следующую проверку.
Итак, 4-5-6 не являются сторонами прямоугольного треугольника.
(b) Поскольку 5 — самая длинная длина, выполните следующую проверку.
Таковы стороны прямоугольного треугольника, а 5 — длина гипотенузы.
(c) Поскольку 5/4 — самая длинная длина, выполните следующую проверку.
Итак, 3 / 4-1-5 / 4 — стороны прямоугольного треугольника, а 5/4 — длина гипотенузы.
Что обратное для теоремы Пифагора?
Обращение теоремы Пифагора говорит нам, что, сравнивая сумму квадратов двух сторон треугольника с квадратом его третьей стороны, мы можем определить, является ли этот треугольник острым, прямым или тупым.
Напомним, что теорема Пифагора — одна из самых известных теорем тригонометрии, которая помогает нам определять стороны прямоугольного треугольника. Некоторые другие формулы, которые могут вам понадобиться для треугольника, относятся к нахождению основания треугольника и площади. Вот дополнительные статьи о том, как найти площадь прямоугольного треугольника, и одна о том, как найти третью сторону треугольника.
Прочтите, чтобы понять, как работает обратная теорема Пифагора!
Теорема Пифагора, обратная
Теорема Пифагора говорит нам, что для прямоугольного треугольника сумма квадратов катетов треугольника эквивалентна квадрату третьей стороны:
Обратное утверждение теоремы Пифагора гласит, что если квадрат третьей стороны треугольника эквивалентен сумме двух его более коротких сторон, то это должен быть прямоугольный треугольник.Другими словами, обратная теорема Пифагора — это та же теорема Пифагора, но с другой стороны. Это дает нам простой способ доказать, является ли треугольник прямоугольным (определение ниже).
Но подождите, это еще не все!
Обратное к теореме Пифагора также говорит нам, является ли треугольник острым, тупым или прямым, сравнивая сумму квадратов более коротких сторон с квадратом самой длинной стороны треугольника.
- Если они эквивалентны, треугольник прямоугольный .Это означает, что самая длинная сторона треугольника лежит напротив 90 градусов или прямого угла.
- Если сумма квадратов более коротких сторон больше, чем квадрат самой длинной стороны, то треугольник является острым треугольником . Угол, образованный двумя сторонами, должен быть меньше 90 градусов.
- Если сумма квадратов более коротких сторон меньше квадрата самой длинной стороны, то треугольник является тупым треугольником . Угол, образованный двумя сторонами, должен быть больше 90 градусов.
Сравнивая квадрат гипотенузы с суммой квадратов двух более коротких сторон, обратная теорема Пифагора также говорит нам, к какому типу треугольника это относится. Давайте посмотрим на треугольники ниже.
Треугольник 1 прямоугольный, потому что:
9 + 16 = 25
25 = 25
Треугольник 2 — тупой треугольник, потому что:
16 + 16 <49
32 <49
Треугольник 3 острый, потому что:
9 + 20.25> 25
29,25> 25
Обращение теоремы Пифагора
Обратное к теореме Пифагора — это логика теоремы Пифагора, примененная наоборот. Возможны три случая.
Если сумма квадратов двух сторон треугольника равна квадрату гипотенузы, равному квадрату гипотенузы, то треугольник будет прямоугольным треугольником .
Если сумма квадратов двух сторон треугольника на меньше, чем квадрата гипотенузы, треугольник является тупым треугольником .
Если сумма квадратов двух сторон треугольника на больше, чем квадрата гипотенузы, треугольник будет острым треугольником .
Если вы воспользуетесь этим рассуждением, будет легко определить, какой у вас тип треугольника.
Теорема Пифагора — обзор
Длина вектора
Вспомните формулу расстояния на плоскости; расстояние между двумя точками x1, y1 и x2, y2 равно d = x2 − x12 + y2 − y12 (см. рисунок 1.3). Эта формула возникает из теоремы Пифагора для прямоугольных треугольников. 2-вектор между точками равен [ a 1 , a 2 ], где a 1 = x 2 — x 1 и a 2 = y 2 — y 1 , поэтому d = a12 + a22. Эта формула мотивирует следующее определение:
Рисунок 1.3. Отрезок (и вектор), соединяющий точки A и B , с длиной x2 − x12 + (y2 − y1) 2 = a12 + a22
Определение
Длина (также известная как norm или величина ) вектора a = [ a 1 , a 2 ,…, a n ] в Rn равно a = a12 + a22 + ⋯ + an2.
Пример 1
Длина вектора a = [4, −3, 0, 2] равна
a = 42 + (- 3) 2 + 02 + 22 = 16 + 9 + 0 + 4 = 29.
Упражнение 21 просит вас показать, что длина любого вектора в Rn всегда неотрицательна (то есть ≥ 0), а также что единственный вектор с длиной 0 в Rn является нулевым вектором [0,0,…, 0].
Векторы длины 1 играют важную роль в линейной алгебре.
Определение
Любой вектор длины 1 называется единичным вектором .
В R2 вектор 35, −45 является единичным вектором, потому что 352 + −452 = 1. Аналогично, -12,12,12, -12 — единичный вектор в R4. Некоторые единичные векторы особенно полезны: те, у которых одна координата равна 1, а все другие координаты равны 0. В R2 эти векторы представлены как i = [1, 0] и j = [0,1]; в R3 они представлены как i = [1,0,0], j = [0,1,0] и k = [0,0,1]. {2}} [/ latex].
Ключевые термины
- ножки : стороны, прилегающие к прямому углу в прямоугольном треугольнике.
- прямоугольный треугольник : [латекс] 3 [/ латекс] -сторонняя форма, где один угол имеет значение [латекс] 90 [/ латекс] градусов
- гипотенуза : сторона, противоположная прямому углу треугольника, и самая длинная сторона прямоугольного треугольника.
- Теорема Пифагора : Сумма площадей двух квадратов на ножках ([латекс] a [/ латекс] и [латекс] b [/ латекс]) равна площади квадрата на гипотенузе ([ латекс] с [/ латекс]).\ circ [/ latex]). Прямоугольный треугольник — это треугольник, в котором один угол является прямым. Соотношение сторон и углов прямоугольного треугольника является основой тригонометрии.
Сторона, противоположная прямому углу, называется гипотенузой (на рисунке сторона [латекс] c [/ латекс]). Боковые стороны, прилегающие к прямому углу, называются ножками (стороны [латекс] a [/ латекс] и [латекс] b [/ латекс]). Сторона [латекс] a [/ латекс] может быть идентифицирована как сторона, прилегающая к углу [латекс] B [/ латекс] и противоположная (или противоположная) углу [латекс] A [/ латекс].Сторона [латекс] b [/ латекс] — это сторона, прилегающая к уголку [латекс] A [/ латекс] и противоположная уголку [латекс] B [/ латекс].
Прямой треугольник: Теорема Пифагора может использоваться, чтобы найти значение длины недостающей стороны в прямоугольном треугольнике.
Если длины всех трех сторон прямоугольного треугольника являются целыми числами, треугольник называется треугольником Пифагора, а длины его сторон в совокупности известны как тройка Пифагора.
Теорема Пифагора
Теорема Пифагора, также известная как теорема Пифагора, является фундаментальным соотношением в евклидовой геометрии.{2}} [/ латекс]
В этом уравнении [латекс] c [/ латекс] представляет длину гипотенузы, а [латекс] a [/ латекс] и [латекс] b [/ латекс] — длины двух других сторон треугольника. {\ circ} [/ latex]) Три тригонометрические функции, наиболее часто используемые для поиска недостающей стороны прямоугольного треугольника, следующие: [latex ] \ Displaystyle {\ грех {т} = \ гидроразрыва {противоположный} {гипотенуза}} [/ латекс], [латекс] \ displaystyle {\ соз {т} = \ гидроразрыва {прилегающий} {гипотенуза}} [/ латекс], и [латекс] \ Displaystyle {\ загар {т} = \ гидроразрыва {противоположный} {смежный}} [/ латекс]
Тригонометрические функции
Мы можем определить тригонометрические функции через угол [латекс] t [/ латекс] и длины сторон треугольника.Соседняя сторона — это сторона, ближайшая к углу. («Соседний» означает «рядом».) Противоположная сторона — это сторона, противоположная углу. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.
Прямой треугольник: Стороны прямоугольного треугольника относительно угла [латекс] t [/ латекс].
При поиске недостающей стороны прямоугольного треугольника, но единственной информацией, которая дается, является измерение острого угла и длина стороны, используйте тригонометрические функции, перечисленные ниже:
- Синус [латекс] \ displaystyle {\ sin {t} = \ frac {напротив} {гипотенуза}} [/ латекс]
- Косинус [латекс] \ displaystyle {\ cos {t} = \ frac {соседний} {гипотенуза}} [/ латекс]
- Касательная [латекс] \ Displaystyle {\ tan {t} = \ frac {напротив} {смежный}} [/ латекс]
Тригонометрические функции равны отношениям, которые связывают определенные длины сторон прямоугольного треугольника.При поиске отсутствующей стороны первым делом необходимо определить, какие стороны и под каким углом даны, а затем выбрать соответствующую функцию, которая будет использоваться для решения проблемы.
Вычисление тригонометрической функции прямоугольного треугольника
Иногда вы знаете длину одной стороны треугольника и угол, и вам нужно найти другие измерения. Используйте одну из тригонометрических функций ([latex] \ sin {} [/ latex], [latex] \ cos {} [/ latex], [latex] \ tan {} [/ latex]), определите стороны и заданный угол , составьте уравнение и воспользуйтесь калькулятором и алгеброй, чтобы найти недостающую длину стороны.{\ circ} [/ latex] и длина гипотенузы [latex] 25 [/ latex] футов, найдите длину стороны, противоположной острому углу (округлите до ближайшей десятой):
Прямой треугольник: Для прямоугольного треугольника с острым углом [латекс] 34 [/ латекс] градуса и длиной гипотенузы [латекс] 25 [/ латекс] футов найдите длину противоположной стороны.
Глядя на рисунок, решите для стороны, противоположной острому углу [латекса] 34 [/ латекса] градуса. Соотношение сторон будет равняться противоположной стороне и гипотенузе .{\ circ} [/ latex] и длина гипотенузы [latex] 300 [/ latex] футов, найдите длину гипотенузы (округлите до десятых):
Прямой треугольник: Для прямоугольного треугольника с острым углом [латекс] 83 [/ латекс] градуса и длиной гипотенузы [латекс] 300 [/ латекс] футов найдите длину гипотенузы.
Глядя на рисунок, решите гипотенузу острого угла [латекс] 83 [/ латекс] градуса. Соотношение сторон будет равняться смежной стороне и гипотенузе .{\ circ} \ right)}} \\ x & = \ frac {300} {\ left (0,1218 \ dots \ right)} \\ x & = 2461,7 ~ \ mathrm {feet} \ end {align}} [/ латекс]
Синус, косинус и тангенс
Мнемоника
SohCahToa может использоваться для определения длины стороны прямоугольного треугольника.
Цели обучения
Используйте аббревиатуру SohCahToa для определения синуса, косинуса и тангенса в терминах прямоугольных треугольников.
Основные выводы
Ключевые моменты
- Распространенный мнемоник для запоминания отношений между функциями синуса, косинуса и тангенса — SohCahToa.
- SohCahToa образован из первых букв « S INE — o pposite более часов ypotenuse ( Soh ), C osine — a djacent over h ypotenuse». ), Касательная противоположна соседней ( Тоа ) ».
Определения тригонометрических функций
Для прямоугольного треугольника с острым углом [латекс] t [/ латекс] первые три тригонометрические функции:
- Синус [латекс] \ displaystyle {\ sin {t} = \ frac {напротив} {гипотенуза}} [/ латекс]
- Косинус [латекс] \ displaystyle {\ cos {t} = \ frac {смежный} {гипотенуза}} [/ латекс]
- Касательная [латекс] \ Displaystyle {\ tan {t} = \ frac {напротив} {смежный}} [/ латекс]
Распространенный мнемоник для запоминания этих отношений — SohCahToa , образованный из первых букв « S ine is o pposite over h ypotenuse ( Soh ), C osine is a a . более ч ypotenuse ( Cah ), касательная противоположна соседней ( Toa ).{\ circ} [/ latex] и прилегающую сторону [latex] 45 [/ latex] ножек, решите для длины противоположной стороны. (округляем до десятых)
Прямой треугольник: Дан прямоугольный треугольник с острым углом [латекс] 62 [/ латекс] градуса и прилегающей стороной [латекс] 45 [/ латекс] ступней, решите для длины противоположной стороны.
Сначала определите, какую тригонометрическую функцию использовать при заданной соседней стороне, и вам нужно найти противоположную сторону. Всегда определяйте, какая сторона дана, а какая неизвестна под острым углом ([латекс] 62 [/ латекс] градуса).\ circ [/ latex], гипотенуза составляет 30 футов, а длина отсутствующей стороны — это противоположная ножка, [latex] x [/ latex] футов.
Определите, какую тригонометрическую функцию использовать при заданной гипотенузе, и вам нужно найти противоположную сторону. Вспоминая мнемонику « S ohCahToa», указанные стороны представляют собой гипотенузу и противоположные «h» и «o», что означает использование «S» или тригонометрической функции синуса. {\ circ} \ right)} \\ x & = 30 \ cdot \ left (0.5299 \ dots \ right) \\ x & = 15.9 ~ \ mathrm {feet} \ end {align}} [/ latex]
Нахождение углов по отношениям: обратные тригонометрические функции
Обратные тригонометрические функции можно использовать для определения острого угла прямоугольного треугольника.
Цели обучения
Использование обратных тригонометрических функций при решении задач с прямоугольными треугольниками
Основные выводы
Ключевые моменты
- Отсутствующее значение острого угла прямоугольного треугольника можно найти, если заданы две длины сторон.{-1} [/ латекс].
Использование тригонометрических функций для поиска отсутствующей стороны при заданном остром угле так же просто, как определение сторон относительно острого угла, выбор правильной функции, создание уравнения и решение. Так же просто найти недостающий острый угол при наличии двух сторон прямоугольного треугольника. {- 1} [/ latex] на калькуляторе), чтобы найти угол ([latex] A [/ latex]) с двух сторон.\ circ [/ latex] с противоположной длиной стороны [латекс] 12 ~ \ mathrm {feet} [/ latex], найдите острый угол с точностью до градуса:
Прямой треугольник: Найдите угол [латекс] A [/ латекс], если задана противоположная сторона и гипотенуза.
От угла [латекс] A [/ латекс] даны стороны напротив и гипотенузы . Поэтому используйте тригонометрическую функцию синуса. ( Soh от SohCahToa) Напишите уравнение и решите его, используя обратный ключ для синуса.{\ circ} \ end {align}} [/ латекс]
Что такое теорема Пифагора? [Видео и практика]
Теорема Пифагора
Привет, и добро пожаловать в этот обзор теоремы Пифагора! Мы рассмотрим, как его правильно использовать, а также рассмотрим некоторые специальные треугольники , называемые «пифагоровыми тройками», которые могут сэкономить вам время при прохождении тестов. Итак, приступим!
Прежде всего: что такое теорема Пифагора? Теорема Пифагора :
a 2 + b 2 = c 2
Теперь это используется, чтобы найти длину стороны прямоугольного треугольника, когда мы знаем длину другой стороны. две стороны.Треугольник должен быть прямоугольным, а это значит, что у него угол, равный 90 градусам, как у этого.
Теорема очень легко запомнить и столь же проста в использовании! В теореме a , b и c — длины трех сторон треугольника. Но что есть что? Давайте начнем с выяснения, где найти a , b и c в треугольнике:
Для начала вы можете сказать, что имеете дело с прямоугольным треугольником, потому что вы можете увидеть этот маленький квадрат в одном треугольнике. из уголков .Это символ прямого угла (или угла 90˚), и любой треугольник с прямым углом должен быть прямоугольным. Итак, теперь мы должны решить, где разместить три стороны. Ключ в том, чтобы начать с буквы c, которая всегда находится сбоку от прямого угла. Это называется гипотенузой, и это всегда самая длинная сторона.
Вы можете спросить себя: «Если c всегда находится напротив прямого угла, как мне определить, какой из двух других является a, а какой — b?» Хороший вопрос, и ответ — неважно! Любую из этих двух сторон, которые называются ножками, можно использовать как a, а затем просто использовать другую как b.Возьмем 3 см для a и используем 4 см для b. Вот как выглядит наша теорема, когда мы ее заполнили.
3 2 + 4 2 = c 2
Теперь мы просто можем вычислить 3 в квадрате и 4 в квадрате, что означает умножение в 3 раза 3 и 4 умножьте на 4, чтобы получить следующее:
Итак, теперь у нас есть
9 + 16 = c 2
Итак, что это?
Небольшое дополнение говорит нам, что
25 = c 2 или c 2 = 25
А вот где это немного сложно.Теперь мы знаем, что c 2 = 25, но мы хотим знать, что такое c, а не то, что такое c в квадрате! Так как же нам избавиться от этой маленькой двойки? Что ж, мы используем обратную или противоположную операцию возведения чего-либо в квадрат! И эта обратная операция — квадратный корень! Поскольку это уравнение, все, что мы делаем с одной стороной уравнения, мы должны делать с другой, поэтому я извлечу квадратный корень из обеих сторон.
√c 2 = √25
Квадратный корень из c 2 равен c, а квадратный корень из 25 равен 5.Посмотри на это. Всегда полезно проверить наш ответ, чтобы понять, имеет ли он смысл. Поскольку мы находим c, оно должно быть длиннее любой из двух других сторон, а 5 больше, чем 4 или 3. Кроме того, из-за теоремы о неравенстве треугольника , к которой мы вернемся позже. видео гипотенуза должна быть меньше суммы двух других сторон, что означает, что 5 должно быть меньше 3 + 4. Так оно и есть.
Итак, вы могли заметить, что ответом на эту проблему было красивое аккуратное целое число (5).Это действительно редкость, если мы посмотрим на случайные треугольники. Но это не редкость в математической задаче, которую вы можете увидеть на тесте. Это происходит всякий раз, когда в задаче используется тройка Пифагора . Треугольник, который мы только что рассмотрели, является наиболее распространенным видом прямоугольного треугольника 3-4-5. Ноги имеют размер 3 и 4, а гипотенуза равна 5. Иногда это будет замаскировано, умножив все числа на 2, что означает, что мы получим (6-8-10) или умножим на 10, что означает, что у нас будет ( 30-40-50) длины или любое другое число.Вам не нужно знать это, чтобы решить задачу по теореме Пифагора, но это хороший способ сэкономить время или проверить свой ответ другим способом. Другие тройки Пифагора включают 5-12-13, 8-15-17 и 7-24-25. Их гораздо больше, но это те, которые вы увидите чаще всего.
Конечно, есть прямоугольные треугольники, которые не являются троек по Пифагору. Давайте посмотрим на один, чтобы увидеть, как будет выглядеть ответ.
Мы снова решаем гипотенузу (самую длинную сторону, противоположную 90˚ или прямому углу.) Это длина c. Когда мы вставляем 5 и 7 для a и b, мы получаем следующее:
5 2 + 7 2 = c 2
2 5 + 4 9 = c 2
Итак, добавим 25 + 49, чтобы получить 74, что равно c 2
74 = c 2
Затем мы извлекаем квадратный корень из каждой стороны и получаем, что c = √74 , теперь, несмотря на то, что 74 — не идеальный квадрат. Это — это ответ.Если вы извлечете квадратный корень на калькуляторе, вы получите только приблизительный ответ (который составляет около 8,60232526…). Мы можем использовать это приближение для проверки: оно больше любой из двух других сторон и меньше, чем две стороны, сложенные вместе. Но при написании ответа следует использовать форму квадратного корня.
Спасибо за просмотр и приятной учебы!
.
