5 Метод Гаусса и теорема Крамера

Лекция 5

ТЕМА: Построение
решений систем линейных уравнений

Пусть задана
система линейных уравнений

(4.1)

Если в заданной
системе
,
то берут любой отличный от нуля минор
основной матрицы порядка

и рассматривают

уравнений, коэффициенты которых входят
в этот базисный минор, а остальные
уравнения отбрасывают. Неизвестные,
которые входят в выбранный минор
объявляют главными,
а остальные неизвестные – свободными.
Новую систему переписывают так, что в
левых частях уравнений остаются только
члены, содержащие

главных неизвестных, а остальные члены
уравнений, содержащие

неизвестных, переносятся в правые части
уравнений (выражаются через главные),
затем находят главные неизвестные
(например, по правилу Крамера). При этом
главные неизвестные выражаются через
свободные, каждое из которых может
принимать любое числовое значение.

Полученные решения
новой системы с

главными неизвестными называется общим
решением системы
(4.1).

Придавая свободным
неизвестным некоторые числовые значения,
из общего решения находят соответствующие
значения главных неизвестных и тем
самым находят частное
решение
исходной системы уравнений (4.1).

Пример 4.1

Решить систему
линейных уравнений:

,
найдем ранг матрицы методом «окаймляющих
миноров»:

Рассмотрим
миноры третьего порядка:

;

система
совместна,

—
базисный минор;

x,
y
– главные переменные,

z
– свободная переменная.

решим
систему по правилу Крамера.

,

.

Общим решением
исходной системы является бесконечное
множество наборов

вида

Частным решением
будет, например, числовой набор
,
получающийся при t=o.

Метод Гаусса

(метод
последовательного исключения переменных)

На практике чаще
всего применяется метод Гаусса –
построения решения систем линейных
уравнений.

При исследовании
и решении систем линейных уравнений
производятся элементарные преобразования
строк расширенной матрицы
,
в результате которых получится ступенчатая
расширенная матрица некоторой новой
системы, эквивалентной данной:

,

(5.1).

Выберем в матрице

ненулевой минор порядка
,
т.е. базисный минор (его можно выбрать
на пересечении первых

строк и столбцов, с которых начинаются
ненулевые элементы строк). Будем считать,
что этот минор расположен в левом верхнем
углу матрицы

Этот минор является
верхнетреугольным и равен произведению
.

Нулевые строки
матрицы отбросим

(им соответствуют
уравнения
).

(5.2)

(отбросили нулевые
столбцы и перенумеровали переменные).

Все элементы
базисного минора выше главной диагонали
можно сделать равными нулю, а элементы
главной диагонали равными единице.
Таким образом, исходная система (4.1)
приведена к эквивалентной системе:

(5.3),

или к системе
(5.4)

из которой видно,
что если
,
то система (5.4) имеет единственное
решение:

,
…,
.

Если
,
то переменные

– базисные,

– свободные и придавая им произвольные
значения
,
…,
,
можно записать общее решение системы
в виде:

(5.5).

Итак, метод Гаусса
состоит в следующем:

1. расширенную
   матрицу системы элементарными
   преобразованиями приводят к ступенчатому
   виду;

2. сравнивают ранги
   основной и расширенной матриц и делают
   вывод о совместности или несовместности
   системы;

3. в случае совместности
   системы в основной матрице выбирают
   базисный минор и дальнейшими элементарными
   преобразованиями строк добиваются
   того, чтобы в этом миноре все элементы
   вне главной диагонали стали равными
   нулю, а элементы главной диагонали
   стали равными единице;

4. выписывают систему,
   соответствующую полученной расширенной
   матрице, после чего переписывают
   систему, оставляя базисные неизвестные
   слева и переведя остальные слагаемые
   в правую часть;

5. если
   ,то
   в правой части стоят только свободные
   члены и получено единственное решение;

6. если
   ,
   то в правой части есть свободные
   неизвестные.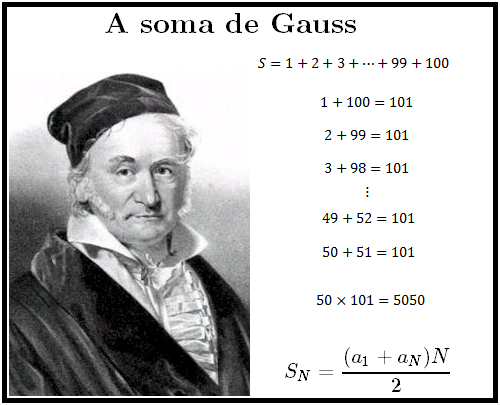 Придавая им произвольные
   значения, получаем общее решение по
   формуле (5.5).

Пример 5.2






.

Теорема Крамера
5.1

Линейная система
(4.2) с квадратной матрицей

имеет решение,
притом единственное,
тогда и только тогда, когда
.

Доказательство

Пусть система
(4.2) имеет и притом единственное решение.
Допустим, что
.
Это значит, что единственный минор
-го
порядка в основной матрице (который
является ее определителем), равен нулю,
и потому

(т.е. ранг матрицы меньше числа неизвестных).
Но согласно следствию (2) теоремы (4.1) в
этом случае система имеет бесконечное
множество решений, что противоречит
условию. Значит допущенное

неверно, и потому
.

Пусть
.
Тогда
,
а так как
,
то и
.
Но по теореме (4.1) это означает, что СЛУ
(4.2) имеет решение, а так как ранг основной
матрицы системы равен числу неизвестных,
то в силу следствия (1) теоремы (4. 1) это
решение единственное.

Нахождение
обратной матрицы методом Гаусса

Напомним, что
матрица

называется обратной к
,
если
.
Обратные матрицы существуют лишь для
невырожденных матриц, т.е.
.
Было показано, что
,
где

– присоединенная матрица, полученная
из алгебраических дополнений, т. е.
вычислением определителей
-ого
порядка. Вместе с тем, операция вычисления
определителя, запрограммированная в
ЭВМ, требует больших машинных ресурсов.
Поэтому более предпочтительным выглядит
вычисление обратной матрицы с помощью
метода Гаусса.

Для этого
воспользуемся определением обратной
матрицы

…

.

Таким образом,
матричное уравнение

эквивалентно системе линейных уравнений,
состоящей из

систем, каждая из которых является
системой из

переменных и все они имеют одну и ту же
основную матрицу системы:

;
;
…;

Все эти системы
объединим в одной расширенной матрице:

.

Приведение этой
матрицы к ступенчатому виду должно
обозначать приведение к ступенчатому
виду всех расширенных матриц подсистем.
Так как

она может быть приведена к следующему
виду:

.

Решение каждой из
подсистем имеет вид:

,

,
…,

матрица
,
стоящая за вертикальной чертой, является
обратной матрицей
.

Пример 5.3










.

7

Применение метода Гаусса в электротехнике Текст научной статьи по специальности «Математика»

128 ИНТЕЛЛЕКТУАЛЬНЫЙ ПОТЕНЦИАЛ XXI ВЕКА: СТУПЕНИ ПОЗНАНИЯ

ПРИМЕНЕНИЕ МЕТОДА ГАУССА В ЭЛЕКТРОТЕХНИКЕ

© Ерёмкин Д.С.*, Лисицын Н.С.*

Дальневосточный федеральный университет, г. Владивосток

В данной статье рассматривается тема прикладного значения метода Гаусса в электротехнике. Представлена теория, охватывающая данную тему. Проведен анализ основных вопросов. Приведены примеры, демонстрирующие практическое использование метода Гаусса при расчетах электротехнических величин.

Ключевые слова метод Гаусса, электротехника.

В современном мире математика и технические науки развиваются в тесном взаимодействии и сотрудничестве друг с другом. Сегодня трудно представить научно-техническую деятельность, где бы не использовались фундаментальные исследования в области математики. Все технические инновации, которые окружают нас в повседневной жизни, есть результат плодотворного сотрудничества техники с математикой. Взаимодействие математических и прикладных дисциплин приводит к их двустороннему обогащению. С одной стороны мы наблюдаем это в применении математического аппарата для решения технических задач. С другой стороны, инженерная практика в существенной мере определяет и стимулирует развитие самой математики. Такой симбиоз математики и технических наук уже весьма высоко зарекомендовал себя и открывает далекие перспективы в будущем.

Математика является фундаментом в инженерном деле. Инженерное дело, в ходе своего развития постоянно расширяет сферу своего приложения, и, тем самым, отвечает все более обширным и сложным техническим задачам. Также, стоит отметить, что вместе с расширением прикладной сферы инженерного дела происходит усиление его специализации. Вследствие развития науки и техники происходит расщепление основных специальностей, появляются новые, ориентированные на более узкий круг практических задач. Таким образом, инженер, являясь специалистом в узкой области, должен базировать свои знания на прочном фундаменте математических и естественных наук. Благодаря различным методам решения технических задач, математический аппарат инженера легко приспосабливается к решению задач в конкретной области.

* Кафедра Электроэнергетики и электротехники. Научный руководитель: Дмух Г.Ю., доцент кафедры Алгебры, геометрии и анализа ШЕН ДВФУ, кандидат педагогических наук.

Важнейшую роль играет умение инженера выбрать соответствующий его задаче математический аппарат и наиболее эффективно использовать его для получения требуемого результата.

В данной статье мы рассмотрим прикладное значение одного из важнейших разделов математики, а именно метода Гаусса в электротехнике. Современный инженер-электротехник должен в совершенстве обладать методом Гаусса для решения конкретных практических задач в своей профессиональной сфере. Например, к ним относятся: определение тока и сопротивления, в ветвях схемы электрической цепи и т.д.

Метод Гаусса — это метод решения систем линейных алгебраических уравнений, состоящий в последовательном исключении неизвестных, и приведению системы уравнений к ступенчатому виду, из которых последовательно, начиная с последних переменных, находятся все последующие переменные системы. X—

ак1Х1 + ак 2 х2 + … + а кпхп = Ьк

Преобразуем систему, исключив неизвестное х во всех уравнениях системы, кроме первого. Для этого умножим обе части первого уравнения

на —— и сложим со вторым уравнением системы. Затем умножим обе час-

ти первого уравнения на

и сложим с третьим уравнением системы.

Продолжаем этот процесс, пока система не примет вид:

а11х1 + а12х2 + … + а1п Хп = Ь1

а*2х2 + … + а2п Хп = Ь2

а*2 х2 + … + а*пХп = Ьк

Затем процесс повторяется уже делением второй строки на а 22, столбец за столбцом, в итоге, матрица приводится к верхнетреугольному виду.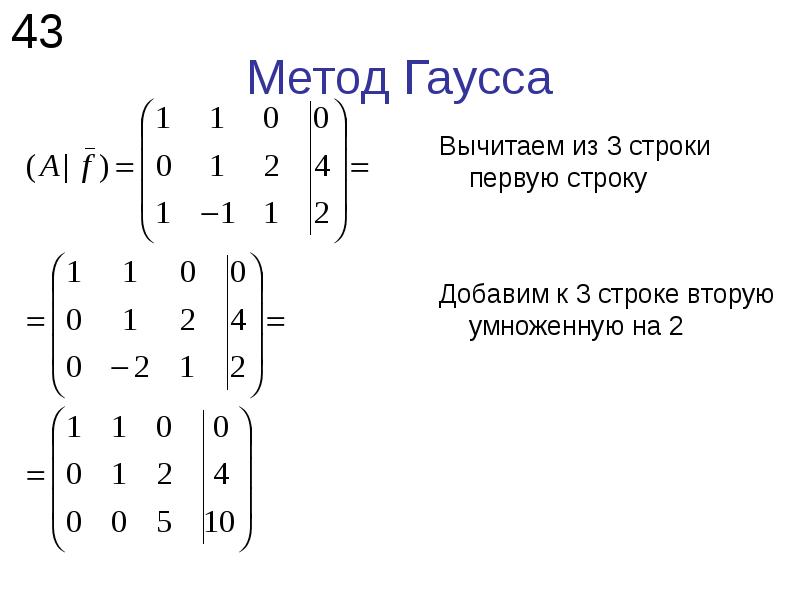

Второй этап решения заключается в решении ступенчатой системы, просто находя неизвестные х:

а

31

а

130 ИНТЕЛЛЕКТУАЛЬНЫЙ ПОТЕНЦИАЛ XXI ВЕКА: СТУПЕНИ ПОЗНАНИЯ

= й*

Хп-1 = Ьп-1 ап-1пХп

Хп-2 = Ьп-2 — ап-2пХп — ап-2п-1Хп-1

Рассмотрим на примере применение метода Гаусса в электротехнике. Для этого решим задачу по нахождению тока. Пример 1:

Схема постоянного тока содержит три замкнутых контура. Используя известный многим закон Кирхгофа для данной задачи, а именно для замкнутых контуров, получаем систему уравнений для тока в миллиамперах:

I + 212 + 313 = 20 41 — 6/2 + 8/3 =-52 -91 + 2/2 — 4/3 = 12

(1) (2) (3)

1. Вычтем из уравнения (2) уравнение (1), умножая его на 4:

0 -14/2 — 4/3 =-132

(4)

Из уравнения (3) вычтем уравнение (1), домноженное на -9:

0 + 20/2 + 23/3 = 192

2. Вычтем из уравнения (5) уравнение (4), умноженное на

0 + 0 + 17.3/3 = 4

20 -14 ‘

(5)

(6)

3. Из уравнения (6) находим /3 = = 0.2 мА, затем последовательно , -132 + 0.8

вычисляем 12 =-—-= 9.37 мА из уравнения (4), откуда находим

11 = 0,66 мА, подставляя известные нам переменные 12 и 13 в уравнение (1). — 4Д2 — 5Д3 =-15

(7)

(8) (9)

1. Вычтем из уравнения (8) уравнение (7), умножая его на 8:

0 — 39Л2 -18Я3 =-184 (10)

Из уравнения (9) вычтем уравнение (7), домноженное на 6:

0 — 34Д2-17Я3 =-165 (11)

-34

2. Вычтем из уравнения (11) уравнение (10), умноженное на -—:

0 — 0-1.308Д3 =-4.59 (12)

-4.59

3. Из уравнения (12) находим Л3 =—= 351 Ом, затем последовательно вычисляем Л2 =-— = 3.098 « 3. 1 Ом из уравнения (10), откуда находим Я-[ = 2,49 Ом, подставляя известные нам переменные Я2 и Я3 в уравнение (7).

Список литературы:

1. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть. -изд. 5-е. — М.: Айрис-пресс, 2005. — 279 с.

2. Сигорский В.П. Математический аппарат инженера. — изд. 2-е, стереотип. — «Техтка», 1977. — 753 с.

АНАЛИЗ СУЩЕСТВУЮЩИХ ПРОЦЕССНЫХ ПОДХОДОВ К УПРАВЛЕНИЮ ИНЦИДЕНТАМИ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ

© Костомаров В.А.*

Московский государственный университет экономики, статистики и информатики (МЭСИ), г. Москва

Рассматриваются процессные подходы, принятые в международных и национальных стандартах в области информационной безопасности и проводится сравнительный анализ представленных процессных подходов.

Ключевые слова: управление информационной безопасностью, процессный подход, менеджмент инцидентов ИБ.

* Магистрант кафедры Автоматизированных систем обработки информации и управления. Научный руководитель: Микрюков А.А. заведующий кафедрой Автоматизированных систем обработки информации и управления МЭСИ, кандидат технических наук, доцент.

Занимательная математика: правило Гаусса

Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.

Первая статья из этого цикла посвящена правилу Гаусса.

Немного истории

Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.

Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:

Найти сумму всех натуральных чисел от 1 до 100.

Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.

Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.

Гаусс сгруппировал числа следующим образом:

(1+10) + (2+9) + (3+8) + (4+7) + (5+6)

Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11.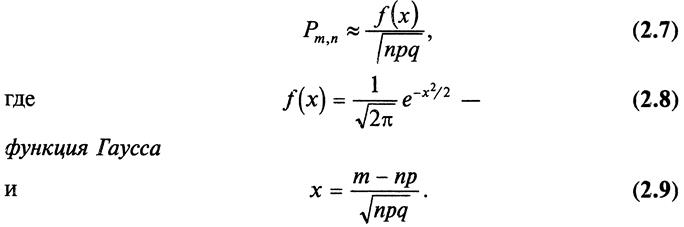 Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо

5 * 11 = 55

Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:

1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100

1. Находим количество пар в ряде натуральных чисел. В данном случае их 50.

2. Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.

3. Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050

Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.

Задачи на использование правила Гаусса

А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.

Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.

В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.

Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.

Задача 1

Найти сумму чисел:

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
• 1 + 2 + 3 + … + 14 + 15 + 16;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.

Решение.

Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
• 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050

Задача 2

Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?

Решение.

С помощью правила Гаусса находим сумму всех весов:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)

Далее смотрим, можно ли этот вес разбить на три равных веса:

45 : 3 = 15 (г)

Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.

Один из вариантов:

• 9г, 6г
• 8г, 7г
• 5г, 4г, 3г, 2г, 1г

Другие возможные варианты найдите сами с ребенком.

Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).

Задача 3

Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?

Решение.

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

Значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.

Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.

Задача 4

Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?

Решение.

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.

Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.

Задача 5

Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?

Решение.

Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:

1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.

Задача 6

Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?

Решение.

Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:

• первая клетка — 1,
• вторая — 2,
• третья — 3,
• …
• восьмая — 8,
• девятая — 9.

Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.

Задача 7

Вычислить сумму, используя прием Гаусса:

• 31 + 32 + 33 + … + 40;
• 5 + 10 + 15 + 20 + … + 100;
• 91 + 81 + … + 21 + 11 + 1;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
• 1 + 2 + 3 + 4 + 5 + 6;
• 4 + 6 + 8 + 10 + 12 + 14;
• 4 + 6 + 8 + 10 + 12;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.

Решение.

• 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
• 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
• 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
• 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
• 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
• 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.

Задача 8

Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?

Решение.

Применяем правило Гаусса, чтобы найти общую массу гирек:

1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)

Вычисляем массу гирек, которые убрали:

78 : 3 = 26 (г)

Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.

Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.

Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):

1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.

Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.

Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.

Удачи в развитии Ваших детей.

Теорема Гаусса • Джеймс Трефил, энциклопедия «Двести законов мироздания»

В науке часто бывает, что один и тот же закон можно сформулировать по-разному. По большому счету, от формулировки закона ничего не меняется с точки зрения его действия, однако новая формулировка помогает теоретикам несколько иначе интерпретировать закон и испытать его применительно к новым природным явлениям. Именно такой случай мы и наблюдаем с теоремой Гаусса, которая, по существу, является обобщением закона Кулона, который, в свою очередь, явился обобщением всего, что ученые знали об электростатических зарядах на момент, когда он был сформулирован.

Вообще говоря, в математике, физике и астрономии найдется немного областей, развитию которых не посодействовал замечательный гений Карла Фридриха Гаусса. В 1831 году он вместе со своим молодым коллегой Вильгельмом Вебером (Wilhelm Weber, 1804–1891) занялся изучением электричества и магнетизма и вскоре сформулировал и доказал теорему, названную его именем. Чтобы понять, в чем заключается ее смысл, представьте себе изолированный точечный электрический заряд q. А теперь представьте, что он окружен замкнутой поверхностью. Форма поверхности в теореме не важна — это может быть пусть даже сдутый воздушный шарик. В каждой точке окружающей заряд поверхности, однако, наблюдается электрическое поле, образованное зарядом, а произведение напряженности этого электрического поля на сколь угодно малую единицу площади окружающей заряд поверхности, через которую проходят силовые линии поля, называется потоком напряженности электрического поля, и можно рассчитать поток напряженности, приходящийся на каждый элемент поверхности. Теорема Гаусса как раз и гласит, что суммарный поток напряженности электрического поля, проходящий через окружающую заряд поверхность, пропорционален величине заряда.

Связь между законом Кулона и теоремой Гаусса станет очевидной на простом примере. Предположим, что заряд q окружен сферой радиуса r. На удалении r от заряда напряженность электрического поля, которая определяется силой притяжения или отталкивания единичного заряда, помещенного в соответствующую точку, составит, согласно закону Кулона:

    E = kq/r²

И то же самое значение мы получим для любой точки сферы заданного радиуса. Следовательно, суммарный поток напряженности электрического поля будет равен значению напряженности поля на удалении r от заряда, помноженному на площадь сферы (которая, как известно, равняется 4πr²). Иными словами, суммарный поток будет равен:

    4πr² × kq/r² = 4πkq

Это и есть теорема Гаусса.

Интересное следствие из нее получается, если применить эту теорему к сплошному металлу. Представьте себе цельнометаллический предмет и воображаемую замкнутую поверхность внутри него. Полный электрический заряд внутри такой поверхности будет нулевым, поскольку внутри окажется равное число положительных и отрицательных зарядов — протонов атомных ядер и электронов соответственно. Следовательно, поток напряженности электрического поля, проходящий через такую замкнутую поверхность, также будет равен нулю. Поскольку это верно для любой замкнутой поверхности внутри металла, это означает, что внутри металла не существует и не может существовать электрического поля.

Это свойство металлов часто используется экспериментаторами и инженерами-связистами для защиты высокочувствительных приборов от наведенных извне электрических помех. Обычно прибор просто окружается защитным медным экраном. Согласно теореме Гаусса, внешние электрические поля просто не в состоянии проникнуть внутрь такой оболочки и создать помехи работе прибора.

Другое интересное следствие теоремы Гаусса заключается в том, что если в дороге вас застала гроза, самое безопасное для вас — не выходить из машины, поскольку там вы окружены цельнометаллическим экраном. Даже если в ваш автомобиль ударит молния, внутри вам ничего не будет угрожать, поскольку весь разряд пройдет по корпусу и уйдет в землю. Резина, скорее всего, сгорит, зато сами вы останетесь в целости и сохранности.

См. также:

МЕТОД ГАУССА В РЕШЕНИИ СЛАУ В ШКОЛЕ. Ключевые слова: СЛАУ, метод Гаусса, матрица, ступенчатый вид.

Аналитическая геометрия. Лекция 1.3

Московский Государственный Технический Университет им. Н.Э. Баумана Факультет Фундаментальные науки Кафедра Высшая математика Аналитическая геометрия Модуль 1. Матричная алгебра. Векторная алгебра Лекция

Подробнее

Решение систем линейных уравнений

Решение систем линейных уравнений Л. В. Калиновская, Ю. Л. Калиновский Министерство образования Московской области Государственное бюджетное образовательное учреждение высшего образования Московской области

Подробнее

РАЗДЕЛ 1. Линейная алгебра.

-й семестр. РАЗДЕЛ. Линейная алгебра. Основные определения. Определение. Матрицей размера mn где m- число строк n- число столбцов называется таблица чисел расположенных в определенном порядке. Эти числа

Подробнее

Тема: Системы линейных уравнений

Линейная алгебра и аналитическая геометрия Тема: Системы линейных уравнений (Метод Гаусса. Системы линейных однородных уравнений) Лектор Рожкова С.В. 0 г. Метод Гаусса (метод исключения неизвестных) Две

Подробнее

Линейная алгебра Лекция 6. Метод Гаусса

Линейная алгебра Лекция 6 Метод Гаусса В свободной энциклопедии Википедии написано: «Метод Гаусса классический метод решения системы линейных алгебраических уравнений (СЛАУ) Этот метод последовательного

Подробнее

Семинар 7. Линейная алгебра

1 Семинар 7. Линейная алгебра Теоретические вопросы для самостоятельного изучения: 1. Определители и их свойства. 2. Матрица. Виды матриц. 3. Действия над матрицами 4. Обратная матрица. Решение матричных

Подробнее

Практикум по линейной алгебре

Министерство образования и науки РФ Нижегородский государственный университет им. Н.И. Лобачевского В.К. Вильданов Практикум по линейной алгебре Учебно-методическое пособие Нижний Новгород Издательство

Подробнее

ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

УНИВЕРСИТЕТСКИЙ УЧЕБНИК ВЫСШАЯ МАТЕМАТИКА И ЕЕ ПРИЛОЖЕНИЯ К ХИМИИ А. А. МИХАЛЕВ, И. Х. САБИТОВ ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ Допущено Учебно-методическим объединением по классическому университетскому

Подробнее

Линейная алгебра Вариант 4

Линейная алгебра Вариант Задание. Систему уравнений привести к равносильной разрешенной системе, включив в набор разрешенных неизвестных,,. Записать общее решение, найти соответствующее базисное решение:

Подробнее

ТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ

Лекции по Математике. Вып. ТММ-1 Ю. В. Чебраков ТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ Санкт-Петербург, 2010 УДК 511+512 ББК 22 Ч45 Р е ц е н з е н т ы: Доктор физико-математических наук, профессор С.-Петерб. техн.

Подробнее

Линейная алгебра 12(6) 18(9)

Линейная алгебра Краткий конспект лекций Составитель В.А.Чуриков Кандидат физ.-мат. наук, доцент кафедры Высшей математики Томского политехнического университета. E-mail: [email protected]. 1 Линейная

Подробнее

МАТЕМАТИКА ЛИНЕЙНАЯ АЛГЕБРА

ООО «Резольвента», wwwresolventru, resolvent@listru, (95) 509-8-0 Учебный центр «Резольвента» Доктор физико-математических наук, профессор К Л САМАРОВ МАТЕМАТИКА Учебно-методическое пособие по разделу

Подробнее

1. Линейные системы и матрицы

1. Линейные системы и матрицы 1. Дать определение умножения матриц. Коммутативна ли эта операция? Ответ пояснить. Произведение C матриц A и B определяется как m p m p A B ij = A ik B kj. Операция не коммутативна.

Подробнее

Примеры решений контрольных работ

Примеры решений контрольных работ Л.И. Терехина, И.И. Фикс 1 Контрольная работа 1 Линейная алгебра Решить матричное уравнение ( ( 3 1 2 1 X + 2 4 2 3 3 ( 1 0 = 3 2 3 Выполним вначале умножение матриц на

Подробнее

1 ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ

1 ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ Цели курса. Целью изучения курса является освоение основных понятий и основных методов линейной алгебры, что поможет использовать их в области будущей деятельности студентов.

Подробнее

1. Требования к знаниям, умениям, навыкам

ПРИЛОЖЕНИЯ Требования к знаниям умениям навыкам Страницы даны по учебнику «Математика в экономике» [] Дополнительные задачи по данному курсу можно найти в учебных пособиях [ 6] Векторы Владеть понятиями:

Подробнее

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ После изучения данной темы вы сможете: проводить численное решение задач линейной алгебры. К решению систем линейных уравнений сводятся многочисленные практические задачи, решение

Подробнее

ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ. I часть

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный университет путей сообщения» Институт экономики и финансов Кафедра «Математика»

Подробнее

1. Линейная алгебра. a21x1 a12 x2 a13 x3 b2

1. Линейная алгебра 1.1. В 1 представлены задачи на решение линейных алгебраических крамеровских систем с определителем, отличным от нуля, вычисление определителей и действий с матрицами. Линейные алгебраические

Подробнее

ТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ

Лекции по Математике. Вып. ТММ-1 Ю. В. Чебраков ТЕОРИЯ МАГИЧЕСКИХ МАТРИЦ Санкт-Петербург, 2010 УДК 511+512 ББК 22 Ч345 Р е ц е н з е н т ы: Доктор физико-математических наук, профессор С.-Петерб. техн.

Подробнее

Линейная алгебра в примерах и задачах

Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая математика» И Н Пирогова О В Куликова Линейная алгебра в примерах и задачах Сборник

Подробнее

Три случая из жизни короля математики Карла Гаусса, которые перевернули науку — Наука

В память о Карле Фридрихе Гауссе король Ганновера Георг V выпустил медаль с надписью «король математики». С этим титулом знаменитый немец и остался в истории. До и после Гаусса жили великие ученые, но что выделяло его среди остальных — это всеохватность ума. Математика развивается благодаря задачам, которые возникают из разных источников. Одни, фундаментальные, остались от прошлых поколений, другие поставили естествознание и инженерные науки, третьи появились благодаря открытию глубоких взаимосвязей разных разделов математики. Гений Гаусса заключался в том, что он принимал любые вызовы, если они были ему интересны.

Как Гаусс нашел неуловимую планету

1 января 1801 года итальянский астроном Джузеппе Пиацци открыл новую «звезду» в созвездии Тельца. В последующие две ночи этот объект менял положение странным образом, а потом погода испортилась, и в следующий раз Пиацци заметил свою находку только 23 января. Вскоре Пиацци решил, что это вовсе не звезда, а комета: ее размер и блеск были меньше, чем первое время. Затем он передумал еще раз и признал в небесном теле планету.

Весной Пиацци разослал данные наблюдений коллегам в Милан, Париж и Берлин и попросил называть находку Церерой Фердинандой в честь римской богини плодородия и короля Сицилии. Церера тем временем скрылась в лучах Солнца, и никто не понимал, где она появится в следующий раз. Об этом прознал Гаусс, и ему захотелось придумать новый метод определения орбит небесных тел. Метод Гаусса отличался от других и только предполагал, что орбита должна быть эллиптической, а чтобы высчитать положение тела, ему было достаточно трех наблюдений.

Когда ученый сопоставил выкладки Пиацци с собственными расчетами, данные почти совпали. Спустя несколько месяцев астрономы из Гринвичской обсерватории еще раз подтвердили правоту Гаусса. История Цереры на этом не закончилась. Долгое время ее считали планетой между Марсом и Юпитером, потом — астероидом, и наконец ученые сошлись во мнении, что это карликовая планета.

Как Гаусс помог придумать новую геометрию

Одна из заслуг Гаусса — построение новой геометрической теории. В школе проходят геометрию Евклида, сформулированную еще в III веке до н.э. Это в ней говорится, что через точку на плоскости можно провести только одну прямую, параллельную данной. В течение двух тысячелетий не прекращались попытки исключить эту вроде бы очевидную вещь — пятый постулат Евклида — из аксиом и вывести как теорему, то есть как утверждение, требующее доказательства. Все эти попытки оканчивались неудачей.

Кроме Гаусса, создателями неевклидовой геометрии считаются Николай Лобачевский, Фаркаш Бойяи и его сын Янош. Янош был талантливым юношей и тоже решил пересмотреть пятый постулат Евклида. Фаркаш отговаривал его от этого занятия, но тот все-таки представил результат. Тогда старший Бойяи послал работу на оценку своему другу Гауссу в надежде, что он возьмет Яноша в ученики.

Сначала Гаусс долго не отвечал приятелю, а когда все-таки созрел, ответ его был не из лестных. Знаменитый ученый сказал, что в работе для него нет ничего нового и что он уже сам все это придумал, а не обнародовал свои выкладки потому, что не хотел шумихи. Даже такой великий ум трепетал перед задачей, не решенной за две тысячи лет.  

Примерно в то же время пятый постулат Евклида пытался перевернуть Николай Лобачевский. Он верил, что добился не просто абстрактного результата, и представил доклад в Казанском университете. Но когда статья Лобачевского попала в печать, его поднял на смех авторитетный математик Михаил Остроградский. А через два года публицист Фаддей Булгарин выпустил пасквиль о профессорах, которые публикуют чушь. Зато работу Лобачевского высоко оценил Гаусс. В 1842 году по его рекомендации Лобачевского избрали членом-корреспондентом Геттингенского королевского научного общества как «одного из отличнейших математиков Российской империи». 

Впоследствии «воображаемая геометрия» Лобачевского, в которой сумма углов треугольника меньше 180°, была признана в научном мире. Это раскрепостило ученика Гаусса Бернхарда Римана, и он создал геометрию, где сумма углов треугольника больше 180°. Позже обе теории понадобились Альберту Эйнштейну, чтобы построить теорию относительности. Эффект, связанный с неевклидовой геометрией, может заметить каждый: если бы его не учитывали в системе GPS, из-за большой скорости спутников на орбите в определении местоположения объекта всего за сутки накопилась бы погрешность около 10 км.

Как Гаусс измерил королевство

В 1818 году Гаусс был живой легендой и, к удивлению коллег, согласился организовать геодезическую съемку недавно образованного королевства Ганновер, чтобы составить подробную карту. Эта задача выглядела слишком приземленной, но не для Гаусса. Во-первых, для этого требовалось оборудование, и Гаусс сконструировал гелиотроп — цилиндр с зеркалом, чтобы направлять луч солнечного света на расстояние и тем самым определять положение в пространстве. Гелиотропы использовали в геодезии вплоть до появления спутниковой навигации.

Во-вторых, перенести кривую поверхность ландшафта на плоскую карту не так-то просто. Гауссу пришлось разработать собственную теорию поверхностей и придумать новые вычислительные методы. Эйнштейн сказал об этом: «Если бы Гаусс не создал геометрию поверхностей, которую взял за основу Риман, трудно представить, что это сделал бы кто-то другой. Значение Гаусса для современной физики и особенно для математических оснований теории относительности поистине огромно».

Марат Кузаев

Редакция благодарит за помощь в подготовке материала профессора Виктора Матвеевича Бухштабера из Математического института имени В.А. Стеклова.

Первая теорема «короля математики» – Наука – Коммерсантъ

В этот день в своем личном «Дневнике открытий» Гаусс записал: «Heureka! num= треугольник + треугольник + треугольник» (в оригинале записи вместо слова «треугольник», разумеется, стоял маленький рисунок треугольника). Это означало: «Эврика! Любое натуральное число может быть представлено как сумма не более чем трех треугольных чисел». Гауссу был 19 лет, он учился в Геттингенском университете и писал капитальный труд по теории чисел, который через пять лет был опубликован под названием «Арифметические исследования».

Сами треугольные числа заняли в этой монографии Гаусса довольно скромное место. Ведь что такое треугольные числа? Это простейшая разновидность фигурных чисел из трудов древнегреческих математиков пифагорейской школы, которые помимо решения чисто практических задач любили пофилософствовать насчет «магии чисел». Сколько нужно одинаковых камешков, чтобы сложить треугольник? Три камешка. А чтобы сложить квадрат? Четыре. А чтобы увеличить в размерах треугольник из трех камешков? Шесть. И так далее. Набрав побольше монет одного достоинства, например, в один рубль, любой может выложить из них самые разные правильные многоугольники.

В XVII веке Ферма сформулировал свою великую теорему. Но только сформулировал, а не доказал, что всякое натуральное число — либо треугольное, либо сумма двух или трех треугольных чисел; всякое натуральное число — либо квадратное, либо сумма двух, трех или четырех квадратных; всякое натуральное число — либо пятиугольное, либо сумма от двух до пяти пятиугольных чисел; и так далее. Вот ее Гаусс и доказал относительно треугольных чисел (полностью она была доказана только в 1994 году англичанином Эндрю Уайлсом, ставшим за это сэром Эндрю).

Наверное, в 19 лет Гаусс гордился, что смог доказать то, что не смогли доказать Ферма, Паскаль, Эйлер. Но наверняка понимал, что этой теоремой лишь залатал небольшую прореху в математике прошлого, и надо идти дальше. В своих «Арифметических исследованиях» Гаусс собрал воедино результаты Ферма, Эйлера, Лагранжа и других своих предшественников и добавил к ним собственные. Монография принесла Гауссу мировую известность и легла в основу современной теории чисел — одного из основных разделов математики.

Сегодня с его юношеской теоремой о треугольных числах знакомы, наверное, только ученики математических спецшкол. Но именно с нее начался путь Гаусса к его неофициальному, но общепризнанному в мировой науке титулу «короля математики».

Сергей Петухов

Карл Фридрих Гаусс | Биография, открытия и факты

Карл Фридрих Гаусс , оригинальное имя Иоганн Фридрих Карл Гаусс , (родился 30 апреля 1777 года, Брауншвейг [Германия] — умер 23 февраля 1855 года, Геттинген, Ганновер), немецкий математик, в целом считается одним из величайших математиков всех времен за его вклад в теорию чисел, геометрию, теорию вероятностей, геодезию, планетарную астрономию, теорию функций и теорию потенциала (включая электромагнетизм).

Популярные вопросы

Чем известен Карл Фридрих Гаусс?

Каким было детство Карла Фридриха Гаусса?

Гаусс был единственным ребенком в семье бедных. Он был расчетливым вундеркиндом с даром к языкам. Его учителя и преданная мать порекомендовали его герцогу Брауншвейгскому в 1791 году, который предоставил ему финансовую помощь для продолжения учебы на месте, а затем для изучения математики в Геттингенском университете.

Какие награды получил Карл Фридрих Гаусс?

Гаусс получил медаль Копли, самую престижную научную награду в Соединенном Королевстве, ежегодно присуждаемую Лондонским королевским обществом в 1838 году «за изобретения и математические исследования в области магнетизма.«За изучение карт, сохраняющих угол обзора, он был удостоен премии Датской академии наук в 1823 году.

Какое влияние оказал Карл Фридрих Гаусс?

Гаусс написал первый систематический учебник по алгебраической теории чисел и заново открыл астероид Церера. Он опубликовал работы по теории чисел, математической теории построения карт и многим другим предметам. После смерти Гаусса в 1855 году открытие многих новых идей среди его неопубликованных работ расширило его влияние на оставшуюся часть века.

Гаусс был единственным ребенком в семье бедных родителей. Среди математиков он был редкостью, поскольку был вундеркиндом и большую часть жизни сохранял способность производить сложные вычисления в уме. Впечатленные его способностями и даром к языкам, его учителя и его преданная мать порекомендовали его герцогу Брауншвейгскому в 1791 году, который предоставил ему финансовую помощь для продолжения учебы на месте, а затем для изучения математики в Геттингенском университете с 1795 по 1798 г.Новаторская работа Гаусса постепенно сделала его выдающимся математиком того времени, сначала в немецкоязычном мире, а затем и в более отдаленных уголках мира, хотя он оставался отстраненной и отстраненной фигурой.

Первое важное открытие Гаусса в 1792 году заключалось в том, что правильный многоугольник с 17 сторонами можно построить только с помощью линейки и компаса. Его значение заключается не в результате, а в доказательстве, основанном на глубоком анализе факторизации полиномиальных уравнений и открывшем дверь для более поздних идей теории Галуа.Его докторская диссертация 1797 г. дала доказательство основной теоремы алгебры: каждое полиномиальное уравнение с действительными или комплексными коэффициентами имеет столько корней (решений), сколько его степень (наивысшая степень переменной). Доказательство Гаусса, хотя и не совсем убедительное, отличалось критикой более ранних попыток. Позднее Гаусс дал еще три доказательства этого важного результата, последнее — в честь 50-летия первого, что показывает важность, которую он придавал этой теме.

Узнайте о жизни и карьере математического гения Карла Фридриха Гаусса

Вопросы и ответы о Карле Фридрихе Гауссе.

Encyclopædia Britannica, Inc. Посмотреть все видео к этой статье

Признание Гаусса поистине выдающимся талантом стало результатом двух крупных публикаций в 1801 году. Прежде всего, он опубликовал первый систематический учебник по алгебраической теории чисел, Disquisitiones Arithmeticae . Эта книга начинается с первого изложения модулярной арифметики, дает подробный отчет о решениях квадратичных многочленов от двух переменных в целых числах и заканчивается теорией факторизации, упомянутой выше.Этот выбор тем и его естественные обобщения определили повестку дня теории чисел на протяжении большей части XIX века, и постоянный интерес Гаусса к этому предмету стимулировал множество исследований, особенно в немецких университетах.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас

Вторая публикация была его повторным открытием астероида Церера. Его первоначальное открытие итальянским астрономом Джузеппе Пиацци в 1800 году произвело сенсацию, но оно исчезло за Солнцем прежде, чем удалось провести достаточно наблюдений, чтобы вычислить его орбиту с достаточной точностью, чтобы знать, где он появится снова.Многие астрономы боролись за честь снова найти его, но победил Гаусс. Его успех был основан на новом методе работы с ошибками в наблюдениях, который сегодня называется методом наименьших квадратов. После этого Гаусс много лет работал астрономом и опубликовал крупную работу по вычислению орбит — численная сторона такой работы была для него гораздо менее обременительной, чем для большинства людей. Будучи чрезвычайно лояльным подданным герцога Брауншвейгского и после 1807 года, когда он вернулся в Геттинген в качестве астронома герцога Ганноверского, Гаусс чувствовал, что работа имеет социальную ценность.

Подобные мотивы побудили Гаусса принять вызов исследования территории Ганновера, и он часто бывал в полевых условиях, отвечая за наблюдения. Проект, продолжавшийся с 1818 по 1832 год, столкнулся с многочисленными трудностями, но привел к ряду успехов. Одним из них было изобретение Гауссом гелиотропа (инструмента, отражающего солнечные лучи сфокусированным лучом, который можно наблюдать с расстояния в несколько миль), который повысил точность наблюдений. Другим было открытие им способа сформулировать понятие кривизны поверхности.Гаусс показал, что существует внутренняя мера кривизны, которая не изменяется, если поверхность изгибается без растяжения. Например, круговой цилиндр и плоский лист бумаги имеют одинаковую внутреннюю кривизну, поэтому точные копии фигур на цилиндре могут быть сделаны на бумаге (как, например, при печати). Но сфера и плоскость имеют разную кривизну, поэтому невозможно составить полностью точную плоскую карту Земли.

Гаусс опубликовал работы по теории чисел, математической теории построения карт и многим другим предметам.В 1830-х годах он заинтересовался земным магнетизмом и участвовал в первом всемирном исследовании магнитного поля Земли (для его измерения он изобрел магнитометр). Вместе со своим коллегой из Геттингена, физиком Вильгельмом Вебером, он создал первый электрический телеграф, но определенная ограниченность помешала ему энергично заняться этим изобретением. Вместо этого он сделал важные математические выводы из этой работы для того, что сегодня называется теорией потенциала, важной области математической физики, возникающей при изучении электромагнетизма и гравитации.

Гаусс также писал о картографии, теории картографических проекций. За свое исследование карт, сохраняющих угол, он был награжден премией Датской академии наук в 1823 году. Эта работа была близка к предположению, что сложные функции комплексной переменной обычно сохраняют угол, но Гаусс не дал этого фундаментального решения. Понимание явным, оставив его Бернхарду Риману, который глубоко ценил работу Гаусса. У Гаусса также были другие неопубликованные идеи о природе сложных функций и их интегралов, некоторые из которых он поделился с друзьями.

Фактически, Гаусс часто отказывался от публикации своих открытий. Будучи студентом Геттингена, он начал сомневаться в априорной истинности евклидовой геометрии и подозревал, что ее истинность может быть эмпирической. Для этого должно существовать альтернативное геометрическое описание пространства. Вместо того, чтобы опубликовать такое описание, Гаусс ограничился критикой различных априорных защит евклидовой геометрии. Казалось бы, постепенно он убедился, что существует логическая альтернатива евклидовой геометрии.Однако, когда около 1830 г. венгр Янош Бойяи и россиянин Николай Лобачевский опубликовали свои отчеты о новой, неевклидовой геометрии, Гаусс не смог дать связного изложения своих собственных идей. Эти идеи можно собрать во впечатляющее целое, в котором его концепция внутренней кривизны играет центральную роль, но Гаусс никогда этого не делал. Некоторые приписывают эту неудачу его врожденному консерватизму, другие — его непрекращающейся изобретательности, которая всегда влекла его к следующей новой идее, третьи — его неспособности найти центральную идею, которая управляла бы геометрией, когда евклидова геометрия перестанет быть уникальной.У всех этих объяснений есть свои достоинства, хотя ни одного из них недостаточно, чтобы быть полным объяснением.

Другой темой, по которой Гаусс в значительной степени скрывал свои идеи от современников, были эллиптические функции. В 1812 году он опубликовал отчет об интересной бесконечной серии, и он написал, но не опубликовал отчет о дифференциальном уравнении, которому удовлетворяет бесконечный ряд. Он показал, что ряд, называемый гипергеометрическим рядом, можно использовать для определения многих знакомых и многих новых функций.Но к тому времени он уже знал, как использовать дифференциальное уравнение для создания очень общей теории эллиптических функций и полностью освободить теорию от ее истоков в теории эллиптических интегралов. Это было большим прорывом, потому что, как обнаружил Гаусс в 1790-х годах, теория эллиптических функций естественным образом рассматривает их как комплексные функции комплексного переменного, но современная теория комплексных интегралов была совершенно неадекватной для этой задачи. Когда часть этой теории была опубликована норвежцем Нильсом Абелем и немцем Карлом Якоби около 1830 года, Гаусс сказал другу, что Абель прошел треть пути.Это было верно, но это печальная мера личности Гаусса, поскольку он по-прежнему отказывался от публикации.

Гаусс доставил меньше, чем мог бы, и многими другими способами. Геттингенский университет был маленьким, и он не стремился ни расширять его, ни привлекать дополнительных студентов. К концу его жизни математики уровня Рихарда Дедекинда и Римана прошли через Геттинген, и он был полезен, но современники сравнивали его стиль письма с жидкой кашей: он ясен и устанавливает высокие стандарты строгости, но ему не хватает мотивации и может быть медленным и утомительным.Он переписывался со многими, но не со всеми людьми, достаточно опрометчиво писать ему, но мало что делал, чтобы поддержать их публично. Редким исключением были случаи, когда на Лобачевского нападали другие россияне за его идеи о неевклидовой геометрии. Гаусс достаточно выучил русский язык, чтобы следить за спорами и предложил Лобачевского в Геттингенскую академию наук. Напротив, Гаусс написал Бойяи письмо, в котором сообщил ему, что он уже обнаружил все, что Бойяи только что опубликовал.

После смерти Гаусса в 1855 году открытие множества новых идей среди его неопубликованных статей расширило его влияние на оставшуюся часть века.Принятие неевклидовой геометрии не было связано с оригинальными работами Бойяи и Лобачевского, но вместо этого оно пришло с почти одновременной публикацией общих идей Римана о геометрии, явного и строгого изложения этого итальянца Эудженио Бельтрами, а также личных заметок Гаусса и переписка.

Карл Фридрих Гаусс: принц математики

Биография

Иоганн Карл Фридрих Гаусс иногда называют « принцем математиков » и «величайшим математиком со времен античности».Он оказал заметное влияние во многих областях математики и науки и считается одним из самых влиятельных математиков в истории.

Гаусс был вундеркиндом. Есть много анекдотов о его раннем детстве, и он сделал свои первые революционные математические открытия еще подростком.

Всего в три года он исправил ошибку в расчетах заработной платы отца, и к пяти годам он регулярно следил за счетами отца.Сообщается, что в возрасте 7 лет он поразил своих учителей, суммировав целые числа от 1 до 100 почти мгновенно (быстро обнаружив, что на самом деле сумма составляла 50 пар чисел, каждая пара в сумме составила 101, всего 5050). К 12 годам он уже посещал гимназию и критиковал геометрию Евклида.

Хотя его семья была бедной и принадлежала к рабочему классу, интеллектуальные способности Гаусса привлекли внимание герцога Брауншвейгского, который отправил его в Коллегиум Каролинум в 15 лет, а затем в престижный Геттингенский университет (который он посещал с 1795 по 1798 год). .Еще будучи подростком, посещающим университет, Гаусс открыл (или независимо переоткрыл) несколько важных теорем.

В 15 лет Гаусс первым обнаружил какую-либо закономерность в появлении простых чисел — проблема, которая с древних времен занимала умы лучших математиков. Хотя появление простых чисел казалось почти полностью случайным, Гаусс подошел к проблеме с другой точки зрения, построив график частоты появления простых чисел по мере увеличения числа.Он заметил грубую закономерность или тенденцию: по мере того, как числа увеличиваются на 10, вероятность выпадения простых чисел уменьшается примерно в 2 раза (например, шанс получить простое число в числе от 1 до 100 составляет 1 из 4, 1 из 6 шансов выпадения простого числа от 1 до 1000, 1 из 8 шансов от 1 до 10 000, 1 из 10 от 1 до 100 000 и т. Д.). Однако он прекрасно понимал, что его метод просто дает приблизительное значение и, поскольку он не может окончательно доказать свои выводы, держал их в секрете до гораздо более поздних лет.

В annus mirabilis Гаусса 1796 года, всего в 19 лет, он построил неизвестную до сих пор правильную семнадцатигранную фигуру, используя только линейку и циркуль, что стало большим достижением в этой области со времен греческой математики, сформулировав свою теорему о простых числах. о распределении простых чисел среди целых и доказал, что каждое положительное целое число можно представить в виде суммы не более трех треугольных чисел.

Теория Гаусса

Хотя он внес вклад почти во все области математики, теория чисел всегда была любимой областью Гаусса, и он утверждал, что «математика — королева наук, а теория чисел — королева математики». Пример того, как Гаусс произвел революцию в теории чисел, можно увидеть в его работе с комплексными числами (комбинациями действительных и мнимых чисел).

Гаусс дал первое четкое изложение комплексных чисел и исследования функций комплексных переменных в начале 19 века.Хотя мнимые числа, состоящие из и (мнимая единица, равная квадратному корню из -1), использовались еще в 16 веке для решения уравнений, которые нельзя было решить никаким другим способом, и несмотря на новаторские идеи Эйлера. Работая над мнимыми и комплексными числами в 18 веке, до начала 19 века не было четкой картины того, как мнимые числа связаны с действительными числами. Гаусс был не первым, кто интерпретировал комплексные числа графически (Жан-Робер Арган создал свои диаграммы Аргана в 1806 году, а датчанин Каспар Вессель описал аналогичные идеи еще до начала века), но Гаусс, безусловно, был ответственен за популяризацию этой практики и также формально введены стандартные обозначения a + b i для комплексных чисел.В результате теория комплексных чисел получила заметное расширение, и ее потенциал начал раскрываться в полной мере.

В возрасте всего 22 лет он доказал то, что сейчас известно как основная теорема алгебры (хотя на самом деле это не касалось алгебры). Теорема утверждает, что каждый непостоянный многочлен от одной переменной над комплексными числами имеет по крайней мере один корень (хотя его первоначальное доказательство не было строгим, он улучшил его позже). Он также показал, что поле комплексных чисел алгебраически «замкнуто» (в отличие от действительных чисел, где решение многочлена с действительными коэффициентами может дать решение в поле комплексных чисел).

Затем, в 1801 году, в возрасте 24 лет он опубликовал свою книгу «Disquisitiones Arithmeticae», которая сегодня считается одной из самых влиятельных когда-либо написанных книг по математике и заложила основы современной теории чисел. Среди прочего, книга содержала ясное изложение метода модулярной арифметики Гаусса и первое доказательство закона квадратичной взаимности (впервые высказанное Эйлером и Лежандром).

На протяжении большей части своей жизни Гаусс также сохранял сильный интерес к теоретической астрономии и много лет занимал пост директора астрономической обсерватории в Геттингене.Когда планетоид Церера находился в процессе идентификации в конце 17 века, Гаусс сделал предсказание ее положения, которое сильно отличалось от предсказаний большинства других астрономов того времени. Но когда в 1801 году Церера была наконец открыта, это было почти точно так, как предсказывал Гаусс. Хотя он не объяснил свои методы в то время, это было одно из первых применений метода аппроксимации наименьших квадратов, обычно приписываемого Гауссу, хотя также заявленного французом Лежандром.Гаусс утверждал, что производил логарифмические вычисления в уме.

Однако по мере того, как слава Гаусса распространилась и он стал известен по всей Европе как человек, умеющий решать сложные математические вопросы, его характер ухудшался, и он становился все более высокомерным, горьким, пренебрежительным и неприятным, а не просто застенчивым. Существует множество историй о том, как Гаусс отверг идеи молодых математиков или, в некоторых случаях, объявил их своими собственными.

В области вероятности и статистики Гаусс ввел то, что теперь известно как распределение Гаусса, функцию Гаусса и кривую ошибки Гаусса.Он показал, как вероятность может быть представлена ​​колоколообразной или «нормальной» кривой, которая достигает пика около среднего или ожидаемого значения и быстро спадает в сторону плюс / минус бесконечности, что является основным для описания статистически распределенных данных.

Он также провел первое систематическое исследование модульной арифметики — с использованием целочисленного деления и модуля — которая теперь находит применение в теории чисел, абстрактной алгебре, информатике, криптографии и даже в визуальном и музыкальном искусстве.

Выполняя довольно банальную геодезическую работу для Королевского дома Ганновера в годы после 1818 года, Гаусс также изучал форму Земли и начал размышлять о революционных идеях, таких как форма самого пространства.Это заставило его усомниться в одном из центральных принципов всей математики, евклидовой геометрии, которая явно исходила из плоской, а не искривленной Вселенной. Позже он утверждал, что рассматривал неевклидову геометрию (к которой, например, не применима параллельная аксиома Евклида), которая была внутренне последовательной и свободной от противоречий еще в 1800 году. решил не развивать и не публиковать какие-либо из его авангардных идей в этой области, оставив поле открытым для Бойяи и Лобачевского, хотя некоторые до сих пор считают его пионером неевклидовой геометрии.

Исследования в Ганновере также подогрели интерес Гаусса к дифференциальной геометрии (область математики, имеющая дело с кривыми и поверхностями) и к тому, что стало известно как гауссова кривизна (внутренняя мера кривизны, зависящая только от того, как измеряются расстояния на поверхность, а не то, как она встроена в пространство). В целом, несмотря на довольно скучный характер его работы, обязанности по уходу за больной матерью и постоянные ссоры с его женой Минной (которая отчаянно хотела переехать в Берлин), это был очень плодотворный период его академической жизни. и он опубликовал более 70 статей между 1820 и 1830 годами.

Однако достижения Гаусса

не ограничивались чистой математикой. В годы геодезии он изобрел гелиотроп, инструмент, который использует зеркало для отражения солнечного света на больших расстояниях, чтобы отмечать позиции при съемке местности. Позже он сотрудничал с Вильгельмом Вебером в измерениях магнитного поля Земли и изобрел первый электрический телеграф. В знак признания его вклада в теорию электромагнетизма международная единица магнитной индукции известна как гаусс.

Гаусс

Карл Фридрих Гаусс — биография, факты и изображения

Жил 1777 — 1855.

Карл Фридрих Гаусс был последним человеком, который знал всю математику.

Он был, вероятно, величайшим математиком, которого когда-либо знал мир — хотя, возможно, Архимед, Исаак Ньютон и Леонард Эйлер также имеют законные права на этот титул.

Примечательны опубликованные работы

Гаусса. В возрасте всего 21 года он написал книгу Disquisitiones Arithmeticae , важность которой для теории чисел приравнивается к важности для геометрии книги Евклида Elements .

Помимо математики, Гаусс внес весомый вклад в широкий спектр математических и физических наук, включая астрономию, оптику, электричество, магнетизм, статистику и геодезию.

Объявления

Начало

Иоганн Карл Фридрих Гаусс родился 30 апреля 1777 года в городе Брауншвейг, Германия.Его матерью была Доротея Бенце, а отцом — Гебхард Дитрих Гаусс.

Мать Карла была умной, но неграмотной; до замужества она не получала образования, работала домработницей.

Отец Карла сводил концы с концами, как мог, работая в разное время продавцом, мясником, каменщиком, садовником и казначеем в местной страховой компании. Денег всегда не хватало. У Карла был старший сводный брат Георг от первого брака отца, который распался, когда умерла его первая жена.

С самого начала Карл проявил необычный талант к числам; он умел вычислять, прежде чем научился говорить.

Школа

В 1782 году, в возрасте семи лет, Карл поступил в государственную школу Святой Екатерины. В более поздней жизни он рассказывал юмористические истории о том, как сбивал с толку своего учителя, считая быстрее, чем мог бы более образованный г-н Бюттнер. Г-н Бюттнер имел благородство и заказал учебник по арифметике, и 8-летний Карл быстро проглотил его упражнения.

Хотя Карл происходил из простой крестьянской семьи, г-н Бюттнер признал, что однажды мальчик может стать профессором в большом университете — если кто-то даст ему шанс.

Г-н Бюттнер пригласил отца Карла в школу, чтобы обсудить будущее своего сына. Отца Карла это не убедило — его кругозор был очень ограничен. Он надеялся, что Карл станет чернорабочим и поможет содержать семью. Г-н Бюттнер заверил его, что таланты его сына настолько необычны, что у богатого спонсора будут найдены деньги для продолжения образования мальчиком.

Отец Карла согласился на это, освободив мальчика от работы прядением льна на полставки.

Расширяя горизонты

Карла начал обучать Мартин Бартельс, его старший на восемь лет, хорошо образованный и талантливый математик.Вскоре Бартельс был вдохновлен своим учеником полностью посвятить свою карьеру математике и в конечном итоге стал профессором. Эти двое будут друзьями на всю жизнь.

К 10 годам Карл независимо вывел биномиальную теорему — поистине выдающийся подвиг.

Весть о юном гении достигла ушей герцога Брауншвейгского, который великодушно согласился профинансировать его образование.

В 1788 году, в возрасте 11 лет, Карл поступил в гимназию Мартино-Катаринеум, где он преуспел в математике, древнегреческом, латинском и современных языках.

Колледж

В 1792 году, в возрасте 15 лет, при поддержке герцога Карл поступил в Кэролайн-колледж. К 18 годам он получил степень по математике.

Он необычно глубоко погрузился в тему. Он был особенно увлечен разработками Исаака Ньютона, Леонарда Эйлера и Жозефа-Луи Лагранжа. Его героем был Архимед.

Докторантура

Гаусс учился в докторантуре Геттингенского университета в течение трех лет, начиная с октября 1795 года.

Он уже намного опередил большинство профессоров математики как по широте, так и по глубине знаний. Геттинген с его великолепными библиотечными коллекциями был его идеальным домом.

Он погрузился в современную математику. Он также посещал лекции по лингвистике, физике и астрономии. На самом деле он взял из библиотеки больше книг по гуманитарным наукам, чем по математике.

Хотя он знал, что его способности были особенными, его сокурсники не считали его полностью преданным и блестящим математиком, каким он был.Они считали его скромным и нормальным.

Карл Фридрих Гаусс, математика и естественные науки

Во время учебы в Геттингене излияние новых идей Гауссом навсегда изменило математику.

Строительство Heptadecagon

A Heptadecagon

Всего через шесть месяцев Гаусс решил задачу, которая ставила математиков в тупик на 2000 лет, — построение правильной 17-гранной фигуры, семиугольника, с помощью только линейки и циркуля.

Древние греки показали, что правильные 3-, 5- и 15-сторонние многоугольники могут быть построены с использованием только линейки и циркуля, но не смогли обнаружить больше таких форм.

Фактически, Гаусс вышел даже за пределы семиугольника. Он открыл математическую формулу, чтобы найти все правильные многоугольники, которые можно построить, используя только линейку и циркуль — и нашел 31. После 17-сторонней фигуры идут фигуры с 51, 85, 255, 257,… .. и 4 294 967 295 сторонами.

Самый замечательный математический дневник

Открыв конструкцию семиугольника, Гаусс понял, что ему обеспечено место в истории как математика высочайшего ранга.

Он вел дневник своих открытий, начиная с семиугольника. Дневник, содержащий 146 открытий, был утерян более 40 лет после его смерти.

1796 год был годом чудес, в нем было 49 записей, некоторые из которых настолько короткие или загадочные, что их значение неясно.

Запись 18, значение которой известно, относится к 10 июля 1796 года. Это открытие Гаусса о том, что любое целое число может быть образовано путем суммирования не более трех треугольных чисел. Наклоняя шляпу перед Архимедом, Гаусс записал в своем дневнике:

Ε Υ Ρ Η Κ Α! число = Δ + Δ + Δ

Естественно, освоив древнегреческий язык, 19-летний Гаусс произнес слово «Эврика», как это сделал бы Архимед.

Гаусс был, пожалуй, последним человеком, овладевшим всеми аспектами математики. Сегодня даже такой одаренный человек, как Гаусс, не может знать всю математику; тема стала слишком большой.

Теория чисел

Будучи студентом, Гаусс сделал много важных открытий в теории чисел, таких как одно из вышеперечисленных.

Теория чисел была его любимой областью. Позже он сказал бы классную фразу:

.
«Математика — королева наук, а теория чисел — королева математики.”

Карл Фридрих Гаусс

Gauss zum Gedächtniss , 1856

Disquisitiones Arithmeticae — Исследования по арифметике

Герцог Брауншвейгский продолжал финансировать работу Гаусса, поэтому он мог свободно копаться в любых областях, которые его интересовали.

В 1801 году, когда ему было 24 года, он опубликовал одну из величайших работ в истории математики — Disquisitiones Arithmeticae . Он решил написать книгу на совершенной классической латыни, написав большую часть за три года до публикации.В нем он записал формальные доказательства многих своих более ранних открытий.

Disquisitiones Arithmeticae объединили отдельные направления теории чисел. Здесь начинается современная теория чисел. Гаусс задокументировал значительные прорывы, такие как закон квадратичной взаимности, его формулировку современной модульной арифметики и конгруэнтность — идею, лежащую в основе его единого подхода к теории чисел. Поклонники говорили, что Гаусс сделал для теории чисел то же, что Евклид сделал для геометрии.

Вы можете представить себе восхищение Гаусса, когда великий Жозеф-Луи Лагранж, работы которого Гаусс усердно изучал в колледже, отправил ему сообщение:

«Ваша [книга] возвела вас в ранг выдающихся математиков; содержание последнего раздела — прекраснейшее аналитическое открытие, сделанное за долгое время.”

Жозеф-Луи Лагранж

Открытие карликовой планеты Церера

1 января 1801 года Джузеппе Пьяцци в Италии открыл новое небесное тело. Он не знал, что он нашел, кроме того, что это было очень тусклым, звездным, и не было в его звездном каталоге. В течение следующих нескольких ночей он наблюдал, как объект слегка перемещается среди звезд на заднем плане.

Джузеппе Пиацци был единственным человеком, когда-либо наблюдавшим за Церерой, но он потерял ее. Он был обнаружен снова после того, как Гаусс, используя свои собственные математические методы, вычислил его местоположение.Изображение предоставлено NASA / JPL-Caltech.

Он начал верить, что открыл комету, но к 24 января был озадачен. Объект не был похож на комету и двигался слишком медленно.

Пиацци наблюдал за ним в течение 6 недель, за это время он переместился на 3 градуса по небу. Затем он серьезно заболел. К тому времени, когда он выздоровел, он его потерял. К сожалению, ни один астроном не смог найти его снова, поэтому они попросили математической помощи.

В конце концов, помочь мог только один человек — 24-летний Гаусс, который изобрел новый метод вычисления орбит по минимальному количеству наблюдений.Гаусс не только нашел потерянное тело, но и показал, что его орбита была почти круглой, как у планеты, и вычислил, как далеко объект находится от Солнца.

Объект, названный Церера, оказался совершенно новым классом объектов — астероидом, или, на современном жаргоне, карликовой планетой.

Слава, скромность и стойкие научные методы

С повторным открытием Цереры Гауссом пришла заслуженная международная известность.

Гаусс скромно похвалил новое открытие теории тяготения Исаака Ньютона и книги Ньютона Principia .Гаусс считал Ньютона величайшим математиком всех времен.

Но Гаусс вышел за рамки Ньютона. В ходе своей обширной программы работы по разгадке тайны Цереры он применил два очень мощных новых математических метода, которые он изобрел: метод наименьших квадратов и быстрое преобразование Фурье. Спустя более двух веков эти методы все еще остаются важными научными инструментами.

Профессор, избегавший преподавания

В 1806 году умер герцог Брауншвейгский. Его финансовая поддержка Гаусса тоже умерла.

В следующем году Гаусс принял кафедру астрономии в Геттингене, которую он занимал до конца своей жизни.

Гаусс серьезно относился к своей новой работе в астрономии, регулярно используя свой телескоп для наблюдений за ночным небом — ему это очень нравилось. Он внес несколько практических усовершенствований в астрономические инструменты и руководил строительством новой обсерватории.

Гаусс согласился с позицией астрономии главным образом потому, что она предполагала минимальное обучение на уровне бакалавриата.Он выразил свое презрение к обучению одного из своих друзей:

«Я испытываю истинное отвращение к преподаванию. Постоянное занятие профессора математики — преподавать азбуку своей науки… И с этой неблагодарной работой профессор теряет свое благородное время ».

Карл Фридрих Гаусс

Письмо Генриху Ольберсу, 26 октября 1802 г.

Гаусс избегал преподавания не только из учеников Геттингена. Его основные работы, такие как Disquisitiones Arithmeticae , были трудны для всех, кроме лучших математиков, и предлагали мало подсказок относительно того, откуда пришли его идеи.Ссылаясь на эту привычку, Гаусс сказал:

«Когда архитектор завершает красивое здание, он снимает строительные леса».

Карл Фридрих Гаусс

Блестящие студенты

В более поздние годы Гаусс начал получать удовольствие от обучения студентов — не потому, что его взгляды изменились, а потому, что качество студентов улучшилось; он преподавал не только азбуку. Его присутствие в Геттингене действовало как магнит, привлекая таких элитных студентов, как Бернхард Риманн и Рихард Дедекинд.

Со временем Геттинген стал центром математики не только в Германии, но и во всем мире.

«Нам казалось, что Гаусс, несмотря на то, что ранее он не проявлял интереса к чтению курса, теперь получает удовольствие от своей преподавательской деятельности».

Ричард Дедекинд

1901

Астрономия, математика и физика

Подход Гаусса к выпуску научных работ был «немногочисленным, но зрелым». Он был перфекционистом и публиковал только те работы, которые, по его мнению, были безупречными.Многие очень важные открытия, которые он совершил, оставались неопубликованными до его смерти.

В первые годы работы профессором он опубликовал статьи, посвященные рядам, интегралам и статистике. Он также начал очень серьезно относиться к теории потенциала и решению уравнений в частных производных — эти уравнения имеют множество приложений в физике, включая электромагнетизм и гравитацию.

В 1809 году он опубликовал важный двухтомный труд о движении небесных тел — Теория движения небесных тел .

Изобретение гелиотропа

Гелиотроп Гаусса

Гаусс изобрел гелиотроп в 1821 году. Он принимал участие в съемке земли для составления карт и понял важность записи удаленных друг от друга положений с большой точностью.

Гелиотроп — это зеркало, которое отражает солнечные лучи на очень большие расстояния.

Его недостаток в том, что его можно использовать только при ярком солнечном свете.

Гелиотропы использовались при геодезии в Германии более 150 лет. Они также использовались для обследования США.

Споры с глупыми людьми — пустая трата времени

В молодости Гаусс обнаружил, что не может угнаться за потоком математических идей, неослабевающим в его сознании.

Он решил не публиковать некоторые материалы, которые, по его мнению, слишком опережали свое время, например, неевклидова геометрия.

Гаусс сказал, что не хотел тратить свое драгоценное время на бессмысленные споры с людьми, которые не могли полностью понять его работу.

Электричество и магнетизм

В 1831 году Гаусс начал применять математическую теорию потенциала к реальному миру.54-летний математик помог 27-летнему физику Вильгельму Веберу получить кафедру физики в Геттингене, а затем работал с ним над электричеством и магнетизмом.

Магнитное поле и единицы СИ

В 1832 году с помощью Вебера Гаусс провел эксперименты, результаты которых позволили ему определить магнитное поле Земли в миллиметрах, граммах и секундах. Другими словами, он показал, что магнитное поле Земли можно определить с помощью чисто механических параметров — массы, длины и времени.

Работа дала сильный толчок к использованию единиц СИ.

Телеграф

В 1833 году Гаусс и Вебер изобрели одну из первых в мире телеграфных систем. Они также изобрели двоичный алфавитный код, обеспечивающий связь между физическим корпусом Вебера и астрономической обсерваторией Гаусса на расстоянии примерно 1,5 мили (2,5 км) друг от друга. К 1835 году их телеграфные линии были проложены рядом с первой железной дорогой Германии.

Окружные законы Кирхгофа

В 1833 году Гаусс и Вебер обнаружили, как напряжение и ток распределяются в ветвях электрических цепей: напряжение регулируется законом сохранения энергии, а ток — законом сохранения заряда.Густав Кирхгоф заново открыл законы в 1845 году, и теперь они носят его имя.

Закон Гаусса и закон Гаусса для магнетизма

Гаусс использовал свой огромный математический арсенал для анализа поведения электрических и магнитных полей. Используя свою теорему о расходимости, которую он открыл независимо от Жозефа-Луи Лагранжа, он сформулировал два закона в 1835 году:

• Закон Гаусса, который связывает электрическое поле с распределением электрических зарядов, которые его вызывают
• Закон Гаусса для магнетизма, который гласит, что магнитных монополей не существует

Закон Гаусса (для электрических полей и зарядов) и Закон Гаусса для магнетизма.

Написанные математически, эти законы образуют два из четырех уравнений, необходимых для объединения электрического и магнитного полей в единое электромагнитное поле. Объединение было достигнуто Джеймсом Клерком Максвеллом в 1864 году.

«Гаусс … реконструировал всю магнитную науку в том, что касается используемых инструментов, методов наблюдения и расчета результатов …»

Джеймс Клерк Максвелл, 1873 г.

Трактат об электричестве и магнетизме, 1873 г.

Но подождите, есть еще

Для документирования всего вклада Гаусса в математику и физические науки потребуется книга.Гаусс может претендовать на гораздо большее количество достижений, чем указано выше. Например,

• Невероятная вычислительная сила Гаусса позволила ему находить закономерности в числах с большей готовностью, чем большинство математиков. Это позволило ему открыть теорему о простых числах, когда он был подростком. Как это часто бывает, он не опубликовал свое открытие.
• нормальное распределение / колоколообразную кривую часто называют распределением Гаусса, потому что его открыл Гаусс.
• хотя и не был первым, кто использовал комплексные числа, он определил их, установив современные обозначения, и применил комплексные числа для решения научных задач.
• он открыл область дифференциальной геометрии и опубликовал «Теорему Egregium », связывающую кривизну поверхности с расстояниями и углами.
• он стал финансовым волшебником после того, как принял на себя общественную обязанность управлять фондом вдов Геттингена. В результате своей финансовой изобретательности он разбогател, оставив имение, стоимость которого почти в 200 раз превышает его годовую зарплату. Если рассматривать это в современном контексте, тот, кто сегодня зарабатывает, например, 50 000 долларов в год, в конечном итоге получит активы в размере почти 10 миллионов долларов.

Некоторые личные данные и конец

Образ жизни

Гаусс был в целом добродушным человеком. Он жил просто, несмотря на накопленное богатство. Он ненавидел путешествия и, став заведующим кафедрой астрономии, уезжал из Геттингена только один раз за 48 лет — чтобы поехать на конференцию в Берлин.

Он был страстно увлечен литературой и сбором фактов, и единственным его удовольствием была личная библиотека, в которой находилось 6000 книг, написанных на языках, которые он освоил, включая датский, английский, французский, греческий, латинский, русский и его родной немецкий.

Семья

Гаусс был дважды женат.

В октябре 1805 года, в возрасте 28 лет, он женился на Йоханне Остхофф. У них было трое детей: Иосиф, который стал армейским офицером; Вильгельмина, вышедшая замуж за академика, и Луи, умерший в возрасте 5 месяцев. К сожалению, жена Гаусса Джоанна умерла в октябре 1809 года, через месяц после рождения Луи.

В октябре 1810 года Гаусс женился на лучшей подруге Джоанны Вильгельмине. У них было трое детей: Юджин, который стал бизнесменом в Америке; Вильгельм, который также стал бизнесменом в Америке; и Тереза, которая до конца жизни вела дом для своего отца, затем вышла замуж за художника.

Любимая мать Гаусса дожила до 97 лет. Последние 20 лет своей жизни она жила в доме своего сына, получая от него личную заботу.

Мемориал гептадекагона (и маринованный мозг!)

Карл Фридрих Гаусс мирно скончался во сне в Геттингене 23 февраля 1855 года. Ему было 77 лет. Он был похоронен без мозга на кладбище Альбанифридхоф в Геттингене, недалеко от университета. Его мозг был сохранен и хранится в физиологическом отделении Геттингена.Он все еще там.

В последние годы своей жизни Гаусс так гордился своим юношеским достижением в области семиугольника, что попросил вырезать форму на его надгробии, точно так же, как у Архимеда была сфера внутри цилиндра, вырезанная на его надгробии.

К сожалению, его желание не исполнилось — каменщик сказал, что будет слишком сложно вырезать семиугольник, не напоминающий круг.

Тем не менее, в его родном городе Брансуик воздвигнут мемориал в честь Гаусса, и на этом и есть гептадекагон.

Объявления

Автор этой страницы: The Doc
Изображения, улучшенные и раскрашенные в цифровом виде с помощью этого веб-сайта. © Все права защищены.

Процитируйте эту страницу

Используйте следующую ссылку, соответствующую требованиям MLA:

 «Карл Фридрих Гаусс». Известные ученые. famousscientists.org. 25 июля 2016 г. Web.
. 

Опубликовано FamousScientists.org

Дополнительная литература
Марк Литтманн
Запредельные планеты: открытие внешней Солнечной системы
John Wiley & Sons, Inc., 1990

Джордж М. Рассиас
Математическое наследие К. Ф. Гаусса
World Scientific, 1991

Г. Уолдо Даннингтон, Джереми Грей, Фриц-Эгберт Дозе
Карл Фридрих Гаусс: Титан науки
MAA, 2004

Стивен Хокинг
Бог создал целые числа
Running Press, 2005

Стюарт Холлингдейл
Создатели математики
Dover Publications, 2011

Гаусс: Принц математики

Одной из причин, по которой Гаусс смог так много заниматься математикой в ​​течение своей жизни, было то, что он очень рано начал.Есть много историй о его раннем детстве. Самый известный анекдот молодого Гаусса — это время, когда он нашел ярлык для вычисления суммы арифметической прогрессии в нежном возрасте 10 лет.

В анекдоте рассказывается о его школьном учителе, который хотел отдохнуть и попросил учеников суммировать целые числа от 1 до 100 как занятую работу. Через несколько секунд учитель увидел, что Гаусс сидит без дела. Когда Гаусс спросили, почему он не прибавил в суматохе, он быстро ответил, что сумма составляет 5050.Его одноклассники и учитель были поражены, и Гаусс оказался единственным учеником, который вычислил правильный ответ.

История может быть апокрифической и рассказывается по-разному в разных источниках. Никто не знает, какой метод суммирования арифметической последовательности придумал Гаусс в детстве. Хотя есть несколько способов, которыми мог бы ее решить молодой Гаусс, один из них имеет краткое, интуитивно понятное и элегантное визуальное представление.

1 + 2 + 3 + ⋯ + (n − 1) + n =? 1 + 2 + 3 + \ cdots + (n-1) + n =? 1 + 2 + 3 + ⋯ + (n − 1) + n =?

Рис.1: Арифметическая прогрессия

Рассмотрим два набора шариков, как показано на рисунке 1.\ text {th} j-я строка содержит n + 1 − j n + 1-jn + 1 − j шариков.

Общее количество синих шариков равно

.

1 + 2 + 3 + ⋯ + (n − 1) + n, 1 + 2 +3+ \ cdots + (n-1) + n, 1 + 2 + 3 + ⋯ + (n − 1) + n,

, а общее количество красных шариков равно

.

n + (n − 1) + (n − 2) + ⋯ + 2 + 1, n + (n-1) + (n-2) + \ cdots + 2 + 1, n + (n − 1) + (n− 2) + ⋯ + 2 + 1,

, и очевидно, что оба содержат одинаковое количество шариков. Теперь, если бы мы сложили эти стопки вместе, как показано на рисунке 2, мы получили бы стопку из n nn строк, где каждая строка содержит n + 1 n + 1n + 1 шарик:

Рис 2: Арифметическая прогрессия

Общее количество шариков в добавленной стопке будет n (n + 1) n (n + 1) n (n + 1).Поскольку и красная, и синяя кучки содержат одинаковое количество шариков, каждая куча должна содержать n (n + 1) 2 \ frac {n (n + 1)} {2} 2n (n + 1) шариков. Отсюда получаем

1 + 2 + 3 + … + (n — 1) + n = n (n + 1) 2. 1 + 2 + 3 + … + (n-1) + n = \ frac {n (n + 1)} {2}. 1 + 2 + 3 + … + (n − 1) + n = 2n (n + 1).

Чтобы просуммировать все числа от 1 до 100, Гаусс просто вычислил 100 × (100 + 1) 2 = 5050 \ frac {100 \ times (100 + 1)} {2} = 50502100 × (100 + 1) = 5050. , что намного проще, чем сложение всех чисел от 1 до 100. Обратите внимание, что 1 + 2 + 3 + ⋯ + (n − 1) + n 1 + 2 + 3 + \ cdots + (n-1) + n1 + 2 + 3 + ⋯ + (n − 1) + n всегда должно быть положительным целым числом.Несмотря на то, что приведенная выше формула делится на 2, результат всегда будет положительным целым числом. Это потому, что числитель всегда будет удобен даже из-за умножительных свойств четности. Например, n nn может быть четным или нечетным. Если n nn четно, то n + 1 n + 1n + 1 нечетно и, следовательно,

n × (n + 1) = четное × нечетное = четное. n \ times (n + 1) = четное \ times odd = четное. n × (n + 1) = четное × нечетное = четное.

Аналогично, если n nn нечетное, то n + 1 n + 1n + 1 четное и, следовательно,

n × (n + 1) = нечетное × четное = четное.n \ times (n + 1) = нечетное \ times even = четное. n × (n + 1) = нечетное × четное = четное.

Следовательно, числитель всегда четный, а n (n + 1) 2 \ frac {n (n + 1)} 22n (n + 1) всегда является положительным целым числом.

Числа вида n (n + 1) 2 \ frac {n (n + 1)} {2} 2n (n + 1) называются треугольными числами по причинам, хорошо показанным на рисунках выше. Первые несколько треугольных чисел —

.

1,3,6,10,15,21,28,36,…. 1,3,6,10,15,21,28,36, \ ldots. 1,3,6,10,15,21,28,36,….

Часто можно встретить применение суммирования арифметической последовательности как в школьных задачах, так и при описании более широкого мира.Реже можно встретить 10-летних детей, которые сами придумывают уловки арифметической прогрессии. Еще реже рано развившийся 10-летний ребенок вырастает почти таким же плодовитым, как Гаусс.

ГАУСС — ИОГАНН КАРЛ ФРИДРИХ ГАУСС — математик тысячелетия

Иоганн Карл Фридрих Гаусс

Иоганн Карл Фридрих Гаусс (30 апреля 1777 г. — 23 февраля 1855 г.) был немецким математиком, астрономом и физиком. Хотя Гаусс внес большой вклад в науку и понимание природы электричества и магнетизма, его настоящей страстью была математика.Он называл математику «королевой наук», и его влияние на математику было огромным. Гаусс был, например, первым математиком, доказавшим основную теорему алгебры, и он доказал ее четырьмя различными способами в течение своей жизни. Гаусс широко известен как один из величайших математиков в истории.

Гаусс родился в Брансуике, Германия, в семье рабочего. Его родители практически не имели формального образования, но их сын пошел в школу в возрасте семи лет и сразу же проявил себя как вундеркинд, который умел вычислять сложные математические решения в своей голове.Он выучил немецкий и латынь и получил стипендию от герцога Брауншвейгского на обучение в академии, где изучал астрономию, математику и геометрию.

Самостоятельно, будучи подростком, он начал открывать передовые математические принципы, а в 1795 году — в возрасте 18 лет — Гаусс стал первым, кто доказал закон квадратичной взаимности, математическую теорию, которая позволяет нам определить, является ли квадратичная взаимность. уравнения могут быть решены. В том же году он поступил в Геттингенский университет.

Во время учебы в университете он сделал одно из самых важных открытий.Используя линейку и циркуль, он построил правильный 17-гранный многоугольник или семиугольник. Исследуя теорию, лежащую в основе этой конструкции, Гаусс обнаружил важную связь между алгеброй и геометрическими формами, которая успешно завершила работу, начатую классическими греческими математиками. Таким образом, Гаусс изменил мир современной математики, а также внес свой вклад в исследования, начатые французским философом и математиком 16 века Рене Декарт.

После трех лет в университете Гаусс ушел, не получив диплома, и вернулся в Брауншвейг.Гаусс получил докторскую степень, защитив диссертацию по алгебре в Университете Хельмштедта.

В 1801 году Гаусс написал статью, в которой попытался предсказать орбитальный путь карликовой планеты или астероида Церера, который был недавно открыт в то время. Его выводы радикально отличались от выводов других специалистов в области астрономии, но оказались наиболее точными. Для расчета траектории Цереры Гаусс использовал метод «наименьших квадратов», который он открыл, но еще не открыл другим.Его метод наименьших квадратов был официально опубликован в 1809 году, получил широкое распространение и сегодня используется всеми отраслями науки для контроля и минимизации влияния ошибок измерения.

В 1805 году Гаусс женился на Йоханне Остофф, а в 1807 году они переехали в Геттинген из Брауншвейга, где он стал директором Геттингенской обсерватории. Гаусс был очень счастлив в то время своей жизни. У них было трое детей, но вскоре случилась трагедия, оставившая его убитым горем. В 1808 году умер отец Гаусса; в 1809 году умерла новая жена Гаусса; за смертью Джоанны сразу же последовала смерть второго сына Гаусса.Гаусс страдал от депрессии после этой череды событий, но позже снова женился и имел троих детей от Минны Вальдек.

В 1818 году Гаусс начал работу, которая привела к исследованиям в области дифференциальной геометрии и написанию важных теорий, связанных с природой кривых и кривизны. За следующие 12 лет он опубликовал более 70 статей, в том числе одну, получившую премию Копенгагенского университета.

В 1831 году Гаусс начал сотрудничать с физиком Вильгельмом Вебером.Гаусс и Вебер провели обширные исследования природы электричества и магнетизма, создав простой телеграфный аппарат и открыли законы Кирхгофа, набор правил, применимых к электрическим цепям.