Содержание
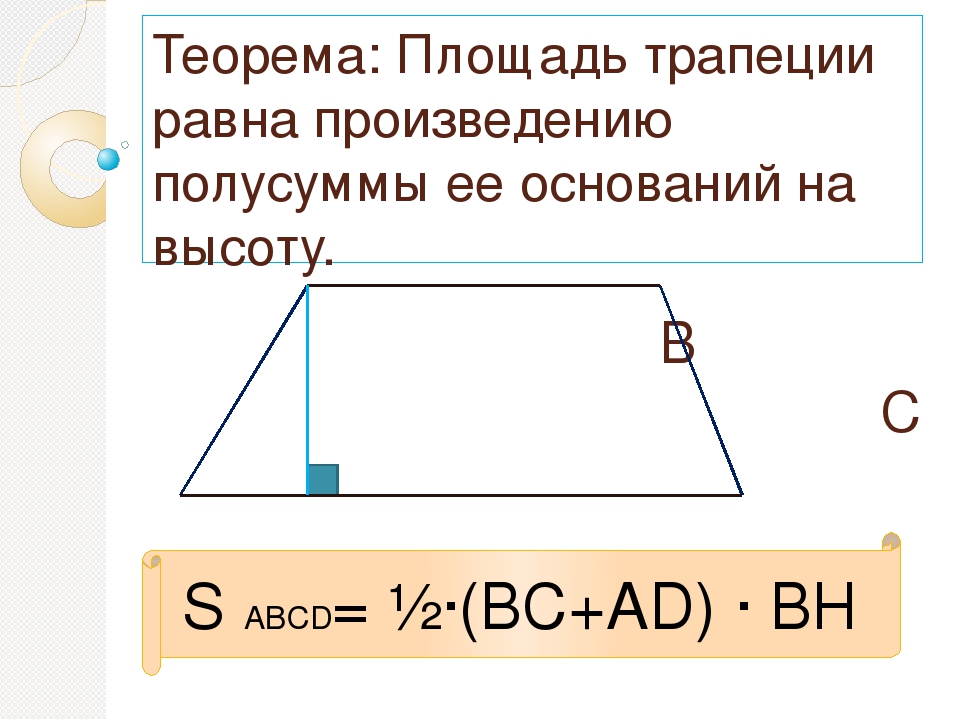
Прямоугольная трапеция
См. также: трапеция и ее свойства.
Прямоугольная трапеция — это трапеция, у которой хотя бы один из углов прямой (классическое определение)
Примечание. На самом деле, у прямоугольной трапеции, как минимум, два прямых угла (см. ниже — свойства)
Другие определения:
- Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Формулы для прямоугольной трапеции
Обозначения формул даны на чертеже выше.
Соответственно:
a и b — основания трапеции
с — боковая сторона прямоугольной трапеции, перпендикулярная основаниям
d — боковая сторона трапеции, не являющаяся перпендикулярной основаниям
α — острый угол при большем основании трапеции
m — средняя линия трапеции
Интерпретация формул:
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна высоте трапеции (Формула 1)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна произведению синуса острого угла при большем основании на длину второй боковой стороны.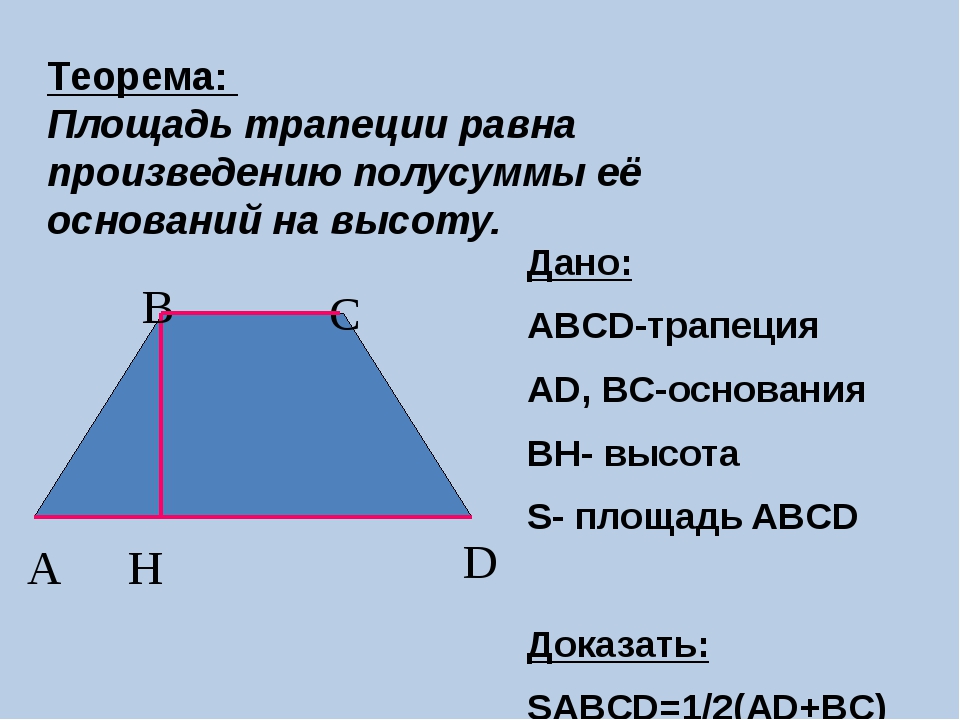 (Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
(Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
Боковая сторона, перпендикулярная основаниям, равна произведению разности оснований на тангенс острого угла при большем основании. (Треугольник CKD — прямоугольный. Поскольку трапеция — прямоугольная, то длина KD — это и есть разность оснований, а h/KD=tgα по определению тангенса, а c=h, откуда с/KD=tgα) (Формула 3)
Боковая сторона, которая не перпендикулярна основаниям, равна частному разности оснований к косинусу острого угла при большем основании или частному высоты трапеции и синуса острого угла при большем основании. (разность оснований равна KD. В прямоугольном треугольнике CKD по определению косинуса cos α = KD / d, откуда и проистекает искомая формула) (Формула 4)
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна корню квадратному из разности квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
(Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна корню квадратному из суммы квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, прямоугольный, далее — следствие из теоремы Пифагора — находим сумму квадратов катетов и извлекаем из полученного выражения квадратный корень) (Формула 6)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна частному от деления двойной площади трапеции на сумму ее оснований. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 7)
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна частному от деления двойной площади трапеции на произведение суммы ее оснований и синуса острого угла при основании.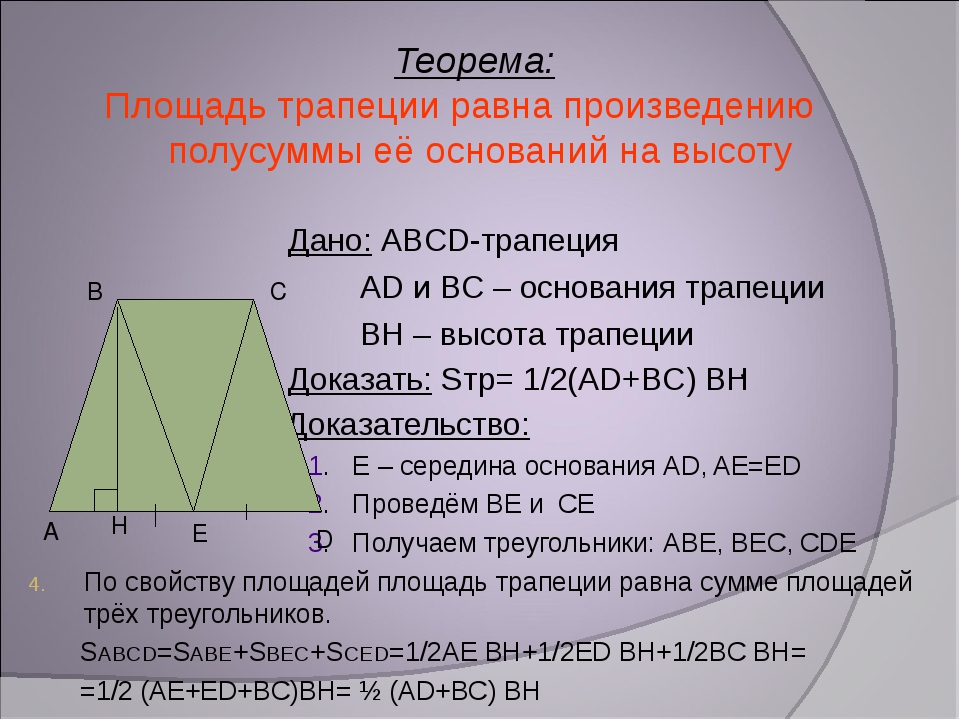 (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
(Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
Так как прямоугольная трапеция — это частный случай трапеции, то остальные формулы и свойства можно посмотреть в разделе «Трапеция».
Свойства прямоугольной трапеции
- У прямоугольной трапеции два угла обязательно прямые
- Оба прямых угла прямоугольной трапеции обязательно принадлежат смежным вершинам
- Оба прямых угла в прямоугольной трапеции обязательно прилежат к одной и той же боковой стороне
- Диагонали прямоугольной трапеции образуют с одной из боковых сторон прямоугольный треугольник
- Длина боковой стороны трапеции, перпендикулярной основаниям равна ее высоте
- У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям
- У прямоугольной трапеции два угла прямые, а два других – острый и тупой
Задача
В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см.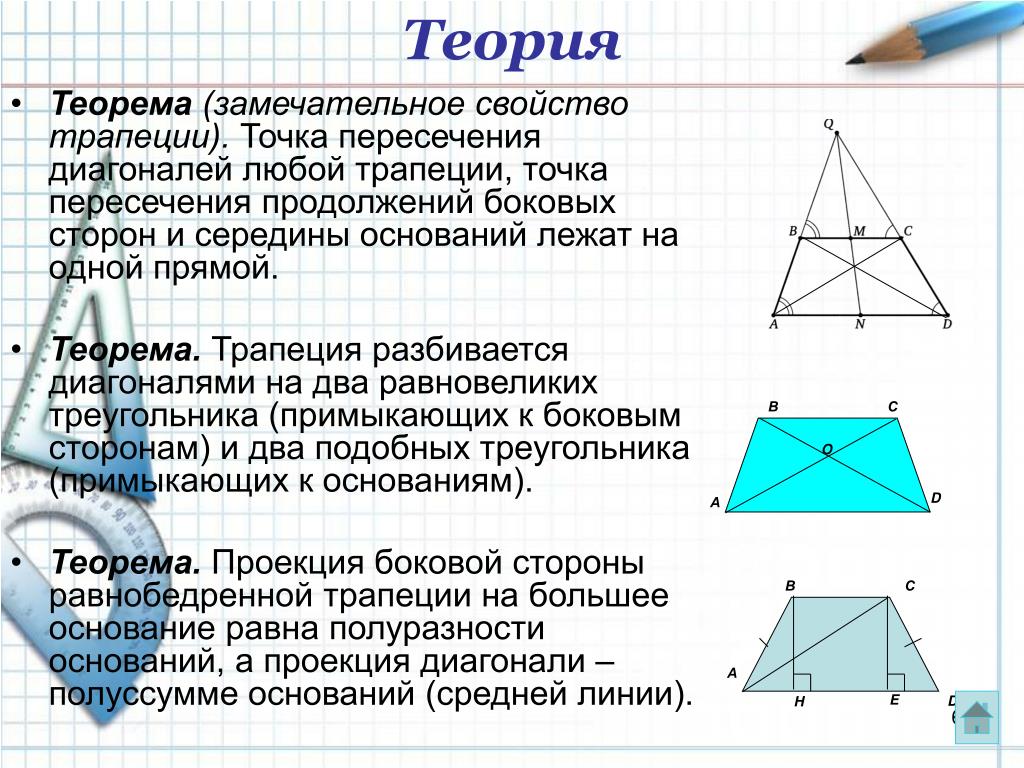 Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Решение.
Обозначим трапецию как ABCD. Обозначим длины оснований трапеции как a (большее основание AD) и b (меньшее основание BC). Пусть прямым углом будет
∠A.
Площадь прямоугольника, стороны которого равны основаниям трапеции, будет равна
S = ab
Из вершины C верхнего основания трапеции ABCD опустим на нижнее основание высоту CK. Высота трапеции известна по условию задачи. Тогда, по теореме Пифагора
CK2 + KD
2 = CD2
Поскольку большая боковая сторона трапеции по условию равна сумме оснований, то CD = a + b
Поскольку трапеция прямоугольная, то высота, проведенная из верхнего основания трапеции разбивает нижнее основание на два отрезка
AD = AK + KD. Величина первого отрезка равна меньшему основанию трапеции, так как высота образовала прямоугольник ABCK, то есть BC = AK = b, следовательно, KD будет равен разности длин оснований прямоугольной трапеции KD = a — b.
то есть
122 + (a — b)2 = (a + b)2
откуда
144 + a2 — 2ab + b2 = a2+ 2ab + b2
144 = 4ab
Поскольку площадь прямоугольника S = ab (см. выше), то
144 = 4S
S = 144 / 4 = 36
Ответ: 36 см
2 .
| Слайд №2 | |
| 04.12.2012 www.konspekturoka.ru 2 Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. АВСD – трапеция, если ВС?AD, АВ и СD – боковые стороны, ВС и AD – основания. | |
| Слайд №3 | |
| 04.12.2012 www.konspekturoka.ru 3 Трапеция называется равнобедренной, если ее боковые стороны равны. АВСD – равнобедренная трапеция, если ВС? AD, АВ = СD – боковые стороны. | |
| Слайд №4 | |
04. 12.2012 12.2012www.konspekturoka.ru 4 Трапеция называется прямоугольной, если один из углов прямой. АВСD – прямоугольная трапеция, если ВС? AD, ?А = 90° или ?В= 90°. | |
| Слайд №5 | |
| 04.12.2012 www.konspekturoka.ru 5 М – середина АВ N – середина CD MN – средняя линия трапеции | |
| Слайд №6 | |
| 04.12.2012 www.konspekturoka.ru 6 ВD = AC – диагонали трапеции ?А = ?D, ?В = ?С – углы при основаниях Свойства равнобедренной трапеции 2. В равнобедренной трапеции углы при каждом основании равны. 1. В равнобедренной трапеции диагонали равны. | |
| Слайд №7 | |
| 04.12.2012 www.konspekturoka.ru 7 ВD = AC – диагонали трапеции ?А = ?D, ?В = ?С – углы при основаниях Признаки равнобедренной трапеции 2. Если углы при основании трапеции равны, то она равнобедренная. 1. 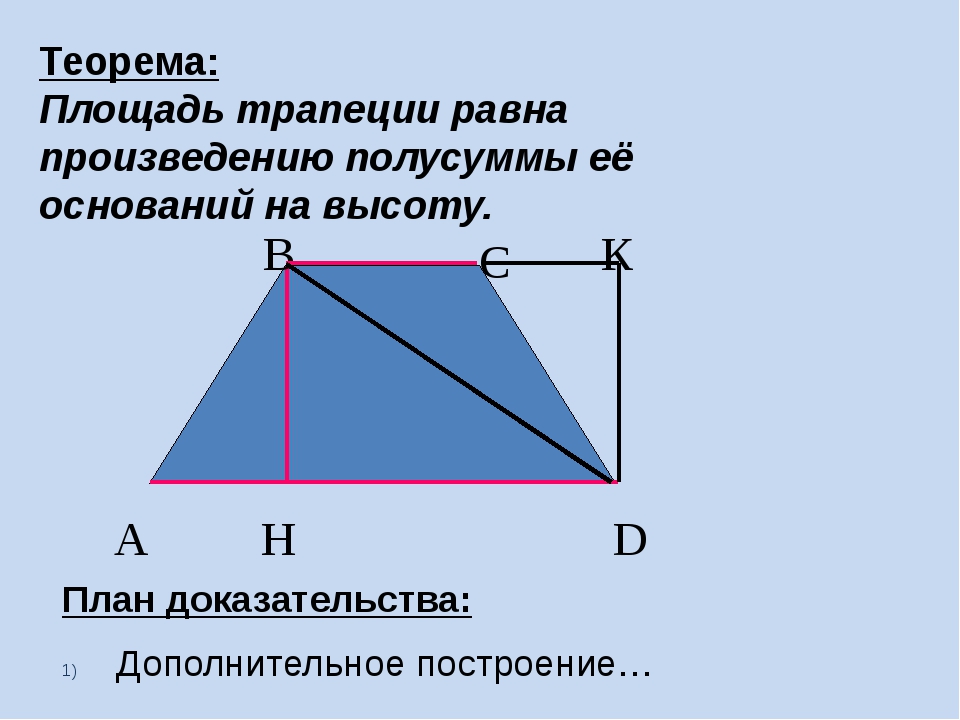 Если диагонали трапеции равны, то она равнобедренная. Если диагонали трапеции равны, то она равнобедренная. | |
| Слайд №8 | |
| 04.12.2012 www.konspekturoka.ru 8 Теорема Фалеса Если на одной из двух прямых отложить последовательно равных несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. а) l? ? l? б) l? ? l? А?А? = В?В? l? l? l? l? А?А? В? В? — параллелограмм l? ? l А? А?DC — параллелограмм А?A? = CD А?A? = В?B? | |
| Слайд №9 | |
| 04.12.2012 www.konspekturoka.ru 9 Задача 1 Доказательство Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции. Пусть Е – середина АВ. Проведем ЕF ? BC ? AD. Точка F – середина CD (по теореме Фалеса). Докажем, что ЕF — единственный Через точки Е и F можно провести только одну прямую (аксиома) т. 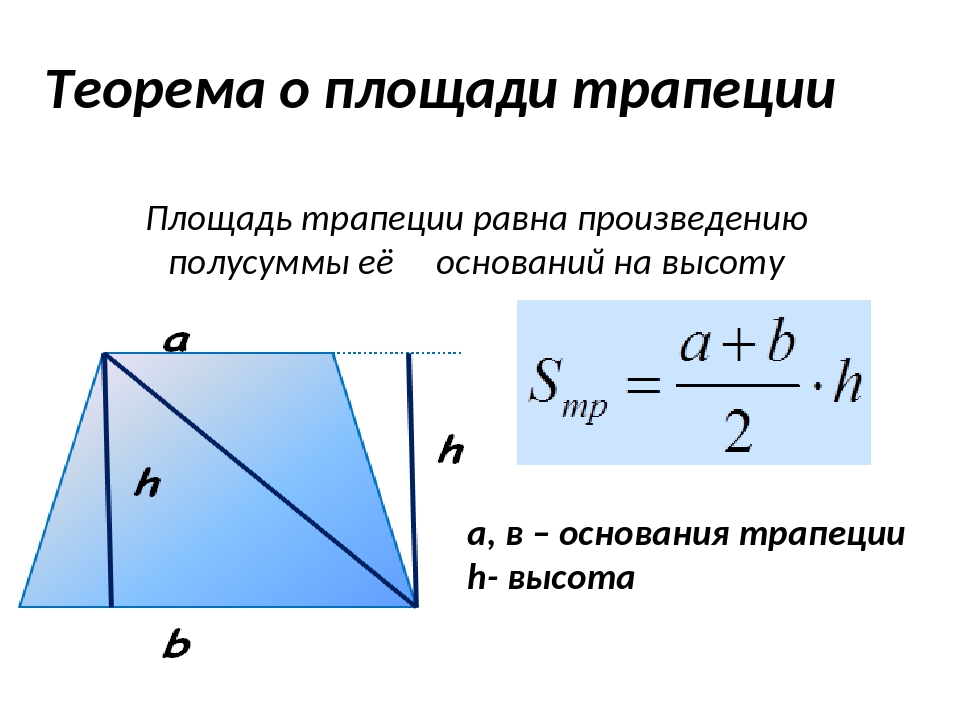 е. отрезок, соединяющий середины боковых е. отрезок, соединяющий середины боковыхсторон трапеции ABCD параллелен основаниям, ч. т. д. | |
| Слайд №10 | |
| 04.12.2012 www.konspekturoka.ru 10 Задача 2 АВСD – трапеция, ?A = 36°, ?C = 117° ?В = ?, ?D = ? 36° 117° Решение АВСD – трапеция, то ВС? AD. ?А + ?В = 180° 36° + ?В = 180° ?В = 180° — 36° ?В = 144° ?С + ?D = 180° ?117° + ?D = 180° ?D = 180° — ?117° ?D = 63° Ответ: ?В = 144°, ?D = 63° | |
| Слайд №11 | |
| 04.12.2012 www.konspekturoka.ru 11 Задача 3 АВСD – равнобокая трапеция, ?A = 68°, ?В = ?, ?С -?, ?D = ? Решение Если АВСD – равнобокая трапеция, то ?A = ?D = 68°, 68° 68° ? 68°+ ?В = 180° ?В = 180° — ? 68° ?В = 112° ?В = ?С = 112°, Ответ: | |
| Слайд №12 | |
04. 12.2012 12.2012www.konspekturoka.ru 12 Задача 4 АВСD – прямоугольная трапеция, ?D = 90°, BC = 4 см, AD = 7 см, ?A = 60° АВ — ? | |
| Слайд №13 | |
| 04.12.2012 13 Ответить на вопросы: www.konspekturoka.ru Спасибо за внимание! Какой четырехугольник называется трапецией? Как называются стороны трапеции? Какая трапеция называется прямоугольной? Равнобедренной? Сформулируйте свойства равнобедренной трапеции. Сформулируйте признаки равнобедренной трапеции. Что такое средняя линия трапеции? Свойство средней линии трапеции. | |
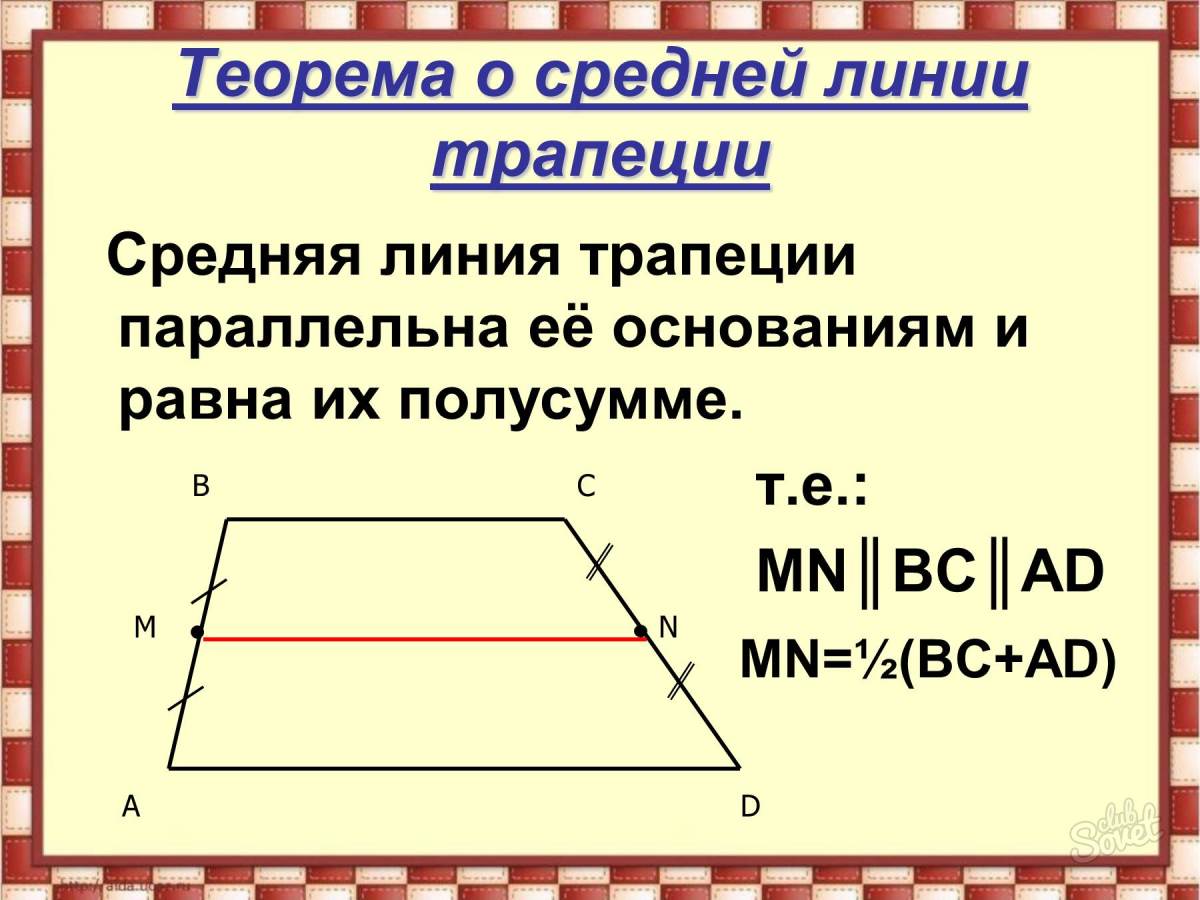
Трапеция. Теорема о средней линии трапеции
1.
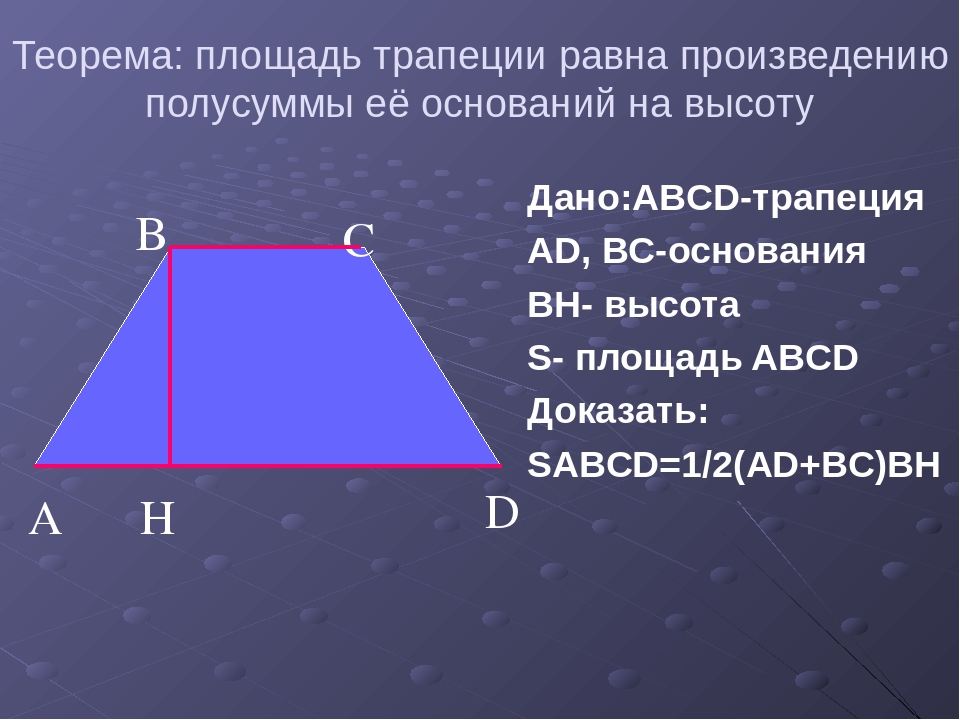 Трапеция
Трапеция
Трапецией называется четырехугольник, у которого две
стороны параллельны, а две другие не параллельны.
Параллельные стороны трапеции называются ее
основаниями, а непараллельные стороны – боковыми
сторонами.
Трапеция называется равнобедренной, если ее боковые
стороны равны.
Трапеция называется прямоугольной, если один из ее
углов прямой.
2. Средняя линия трапеции
Средней линией трапеции называется
соединяющий середины ее боковых сторон.
отрезок,
3. Теорема о средней линии трапеции
Теорема. Средняя линия трапеции параллельна основаниям и
равна их полусумме.
Доказательство. Пусть EF – средняя
линия трапеции ABCD (AB || CD).
Проведем прямую DF и ее точку
пересечения с прямой AB обозначим G.
Треугольники DFC и GFB равны по второму признаку равенства
треугольников (CF = BF по условию, угол 1 равен углу 2, как
вертикальные, угол 3 равен углу 4, как накрест лежащие углы). Из
Из
равенства этих треугольников следует, что DF = GF и, значит, EF средняя линия треугольника AGD. Из теоремы о средней линии
треугольника следует, что EF параллельна AB и EF = AG. Так как
AB || CD, то EF будет параллельна обоим основаниям и кроме того,
EF = AG/2 = (AB + BG)/2 = (AB + CD)/2.
4. Вопрос 1
Какой четырехугольник называется трапецией?
Ответ: Трапецией называется четырехугольник,
у которого две стороны параллельны, а две
другие не параллельны.
5. Вопрос 2
Какие стороны трапеции называются:
основаниями; б) боковыми сторонами?
а)
Ответ: а) Основаниями трапеции называются ее
параллельные стороны;
б) боковыми сторонами трапеции
называются ее непараллельные стороны.
6. Вопрос 3
Какая трапеция называется: а) равнобедренной;
б) прямоугольной?
Ответ: а) Трапеция называется равнобедренной,
если ее боковые стороны равны;
б) трапеция называется прямоугольной,
если один из ее углов прямой.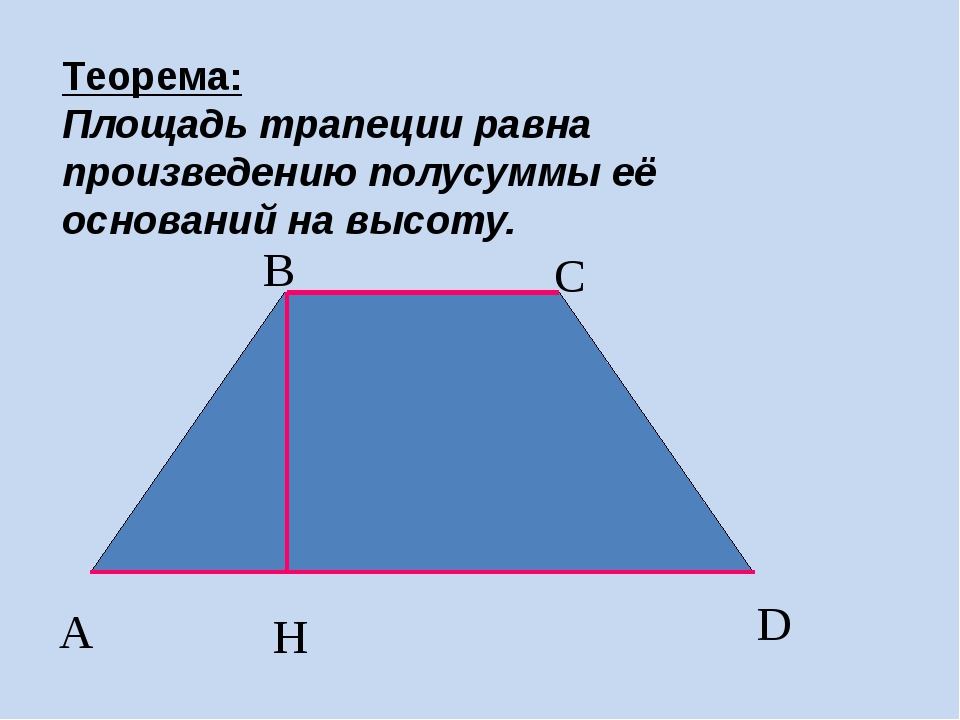
7. Вопрос 4
Что называется средней линией трапеции?
Ответ: Средней линией трапеции называется
отрезок, соединяющий середины ее боковых
сторон.
8. Вопрос 5
Сформулируйте
трапеции.
Вопрос 5
теорему
о
средней
линии
Ответ: Средняя линия трапеции параллельна
основаниям и равна их полусумме.
9. Упражнение 1
Изобразите равнобедренную трапецию ABCD,
три вершины которой даны на рисунке, а
четвертая находится в одном из узлов сетки.
Ответ:
10. Упражнение 2
Изобразите прямоугольную трапецию ABCD,
три вершины которой даны на рисунке, а
четвертая находится в одном из узлов сетки.
Ответ:
11. Упражнение 3
Могут ли углы, прилежащие к основанию
трапеции, быть один острым, а другой тупым?
Ответ: Да.
12. Упражнение 4
Может ли у трапеции быть: а) три прямых угла;
б) три острых угла?
Ответ: а) Нет; б) нет.
13. Упражнение 5
Докажите,
что
углы
при
равнобедренной трапеции равны.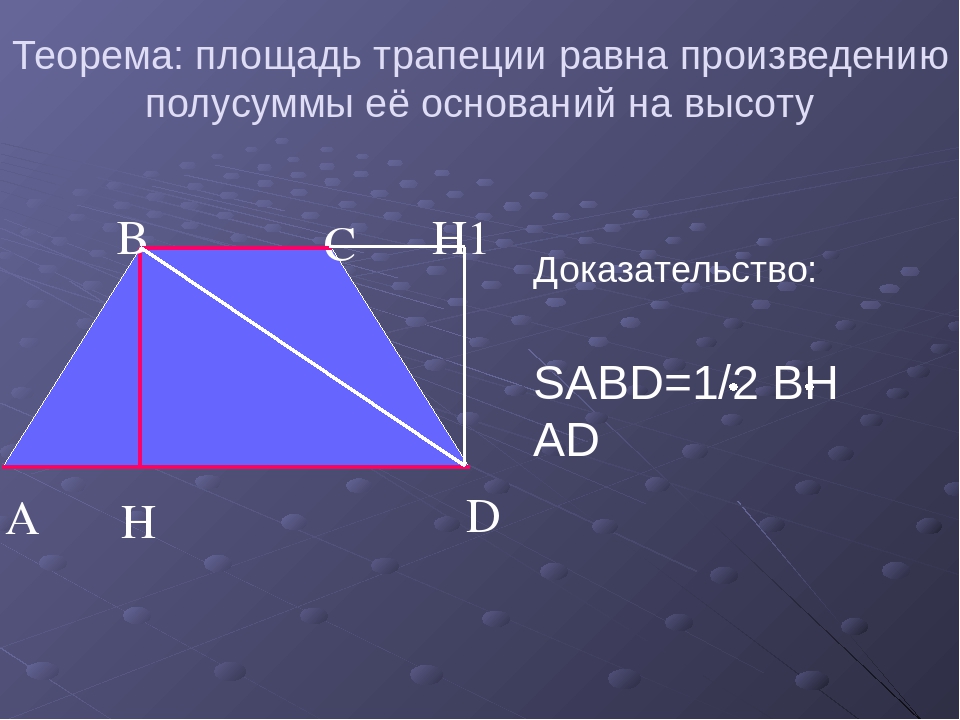
основании
Доказательство. Пусть ABCD –
трапеция, AD не параллельна BC.
Докажем, что углы A и B равны.
Через вершину C проведем прямую, параллельную AD и
обозначим E ее точку пересечения с прямой AB.
Четырехугольник AECD – параллелограмм,
следовательно, угол BAD равен углу BEC. Треугольник
BCE – равнобедренный, следовательно, угол BCE равен
углу BEC. Таким образом, в трапеции ABCD угол A равен
углу B.
14. Упражнение 6
Верно ли, что если два угла трапеции равны, то
она равнобедренная?
Ответ. Нет, она может быть прямоугольной.
15. Упражнение 7
Верно ли, что если два угла при основании
трапеции равны, то она равнобедренная?
Ответ. Да.
16. Упражнение 8
Докажите, что сумма двух противоположных
углов равнобедренной трапеции равна 180о.
Доказательство. Пусть ABCD – трапеция, AD не
параллельна BC. Докажем, что сумма углов A и С равна
180о. Действительно, Сумма углов B и C равна 180о.
Угол A равен углу B. Следовательно, сумма углов A и С
равна 180о.
17. Упражнение 9
Чему равны углы равнобедренной трапеции,
если известно, что разность противолежащих
углов равна 40о?
Ответ: 70о, 110о, 70о, 110о.
18. Упражнение 10
Докажите, что
трапеции равны.
диагонали
равнобедренной
Доказательство. Пусть ABCD – равнобедренная
трапеция. Треугольники ABC и BAD равны (AB –
общая сторона, BC = AD, угол ABC равен углу
BAD. Следовательно, AC = BD.
19. Упражнение 11
Верно ли, что если диагонали трапеции равны,
то она равнобедренная?
Ответ. Да.
20. Упражнение 12
Определите вид четырехугольника, который
получится, если последовательно соединить
отрезками середины сторон равнобедренной
трапеции.
Ответ: Ромб.
21. Упражнение 13
Прямая, проведенная параллельно боковой
стороне трапеции через конец меньшего
основания, равного 3 см, отсекает треугольник,
периметр которого равен 15 см.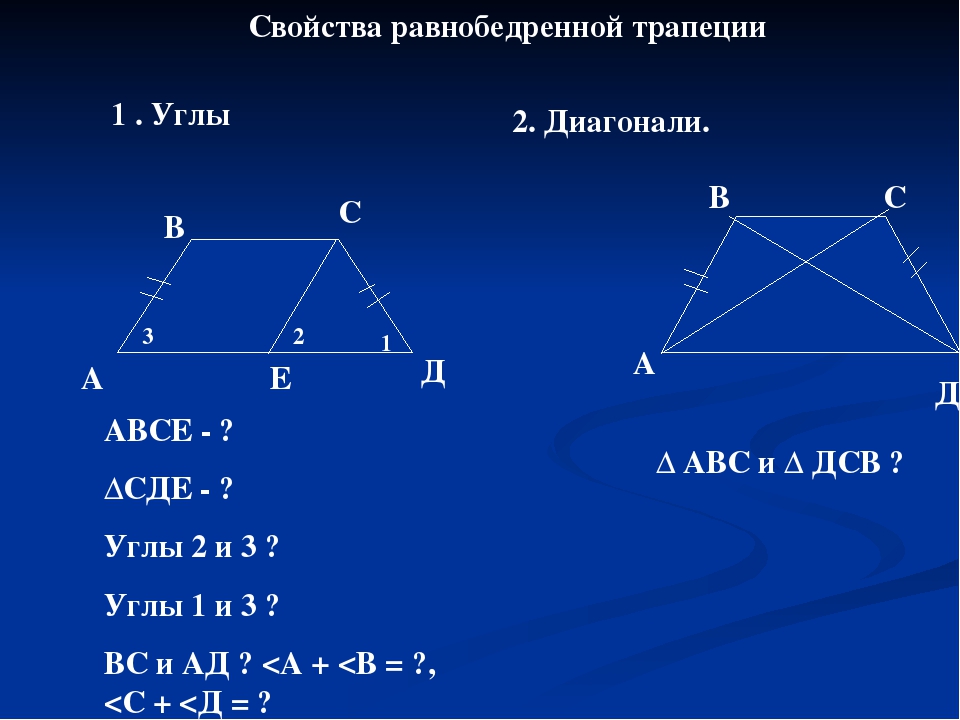 Найдите
Найдите
периметр трапеции.
Ответ: 21 см.
22. Упражнение 14
Проведите
среднюю
линию
изображенной на рисунке.
Ответ:
трапеции,
23. Упражнение 15
Проведите
среднюю
линию
изображенной на рисунке.
Ответ:
трапеции,
24. Упражнение 16
Основания трапеции относятся как 5:2, а их
разность равна 18 см. Найдите среднюю линию
трапеции.
Ответ: 21 см.
25. Упражнение 17
Периметр трапеции равен 50 см, а сумма
непараллельных сторон равна 20 см. Найдите
среднюю линию трапеции.
Ответ: 15 см.
26. Упражнение 18
Средняя линия трапеции равна 30 см, а меньшее
основание равно 20 см. Найдите большее
основание.
Ответ: 40 см.
27. Упражнение 19
Периметр равнобедренной трапеции равен 80 см,
ее средняя линия равна боковой стороне.
Найдите боковую сторону данной трапеции.
Ответ: 20 см.
28. Упражнение 20
Средняя линия трапеции равна 7 см, а одно из ее
оснований больше другого на 4 см.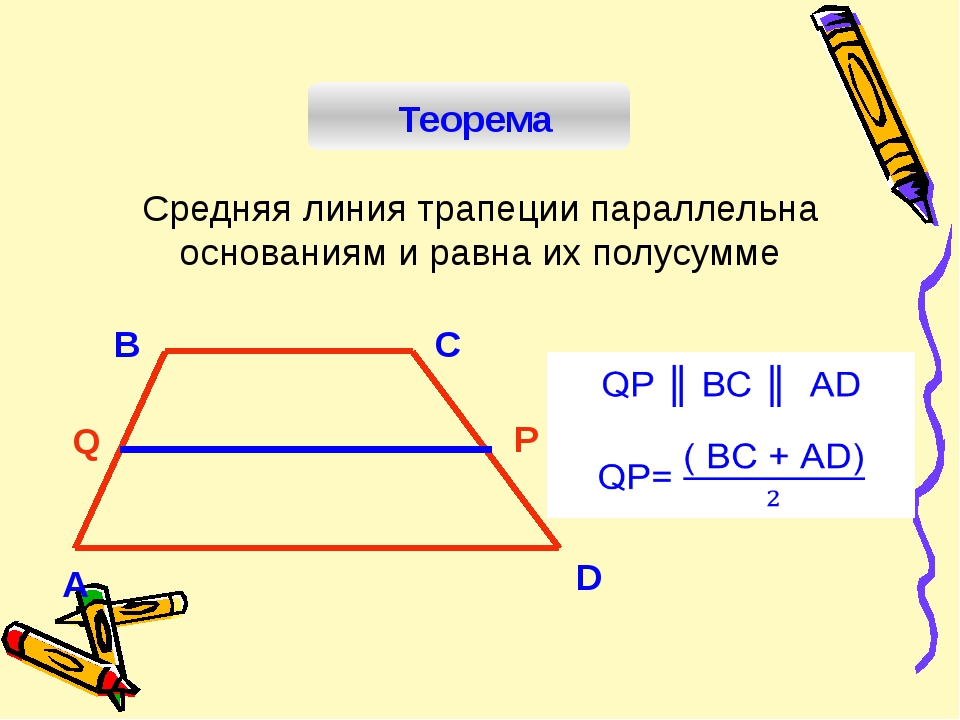 Найдите
Найдите
основания трапеции.
Ответ: 5 см и 9 см.
29. Упражнение 21
Основания трапеции относятся как 2 : 3, а
средняя линия равна 5 м. Найдите основания.
Ответ: 4 м и 6 м.
30. Упражнение 22
Перпендикуляр, опущенный из вершины тупого
угла на большее основание равнобедренной
трапеции, делит его на части, имеющие длины 5
см и 2 см. Найдите среднюю линию этой
трапеции.
Ответ: 5 см.
31. Упражнение 23
В равнобедренной трапеции большее основание
равно 2,7 м, боковая сторона равна 1 м, угол
между ними 60о. Найдите меньшее основание.
Ответ: 1,7 м.
32. Упражнение 24
Cредняя линия трапеции равна 10 см. Одна из
диагоналей делит ее на два отрезка, разность
которых равна 2 см. Найдите основания этой
трапеции.
Ответ: 8 см и 12 см.
33. Упражнение 25
Основания трапеции равны 4 см и 10 см.
Найдите отрезки, на которые делит среднюю
линию этой трапеции одна из ее диагоналей.
Ответ: 2 см и 5 см.
34. Упражнение 26
Меньшее основание равнобедренной трапеции
равно
боковой
стороне,
а
диагональ
перпендикулярна боковой стороне. Найдите углы
трапеции.
Ответ: 60о, 120о, 60о, 120о.
35. Упражнение 27*
Может ли средняя линия трапеции пройти через
точку пересечения диагоналей?
Решение: Нет. Действительно, пусть ABCD – трапеция, EF
– средняя линия, G, H – ее точки пересечения с
диагоналями. Тогда EG – средняя линия треугольника
ACD и, следовательно, равна половине CD. FH – средняя
линия треугольника BCD и, следовательно, равна
половине CD. Если бы точки G и H совпадали, то средняя
линия EF была бы равна CD. В этом случае трапеция была
бы параллелограммом.
36. Упражнение 28*
В выпуклом пятиугольнике ABCDE AE = 4.
Середины сторон AB и CD, BC и ED соединены
отрезками. Середины H и K этих отрезков снова
соединены отрезками. Найдите длину отрезка
HK.
Решение: Пусть M, N, P, R, L – середины
соответствующих сторон. Тогда HK = 1 ML = 1 AE = 1.
2
4
Подготовка к ОГЭ и ЕГЭ. «Формулы и свойства трапеции»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 5
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ город – курорт АНАПА
Рассмотрено и
рекомендовано к использованию
на заседании МО от _______________
Протокол №______
Подготовка к ОГЭ и ЕГЭ.
«Формулы и свойства трапеции»
Методическая разработка
учителя математики
Снегуровой Амины Мугиновны
2018 год.
Оглавление
Введение 3
Определения 4
Частные случаи трапеции 5
Свойства произвольной трапеции 6-7
Свойства равнобедренной трапеции 8-10
Свойства биссектрисы угла трапеции 10-12
Свойства треугольников, образованных диагоналями трапеции 12-13
Формулы нахождения диагоналей трапеции 13-14
Трапеция и окружность 14-17
Дополнительные построения в трапеции 17-23
Для тех, кому интересно.
 Теоремы. 23-27
Теоремы. 23-27Задачи с решениями.27-35
Список используемой литературы.
Введение
Дорогой ученик!
В материалах различных контрольных работ и экзаменов очень часто встречаются задачи на трапецию, решение которых требует от учащихся знаний «непрограммных» свойств трапеции. (Программными считаются свойство средней линии трапеции, свойства диагоналей и углов равнобедренной трапеции.) Свойства, необходимые для решения задач, отсутствуют в учебниках или перенесены в задачи и не воспринимаются как теоретические положения.
Какими же замечательными свойствами обладает трапеция? Как решать геометрические задачи, требующие глубоких знаний? Трапеция обладает рядом интересных и полезных для решения задач свойствами. Если овладеть ими и рассмотреть дополнительные построения в трапеции, то возникает объективная возможность для решения задач повышенной сложности.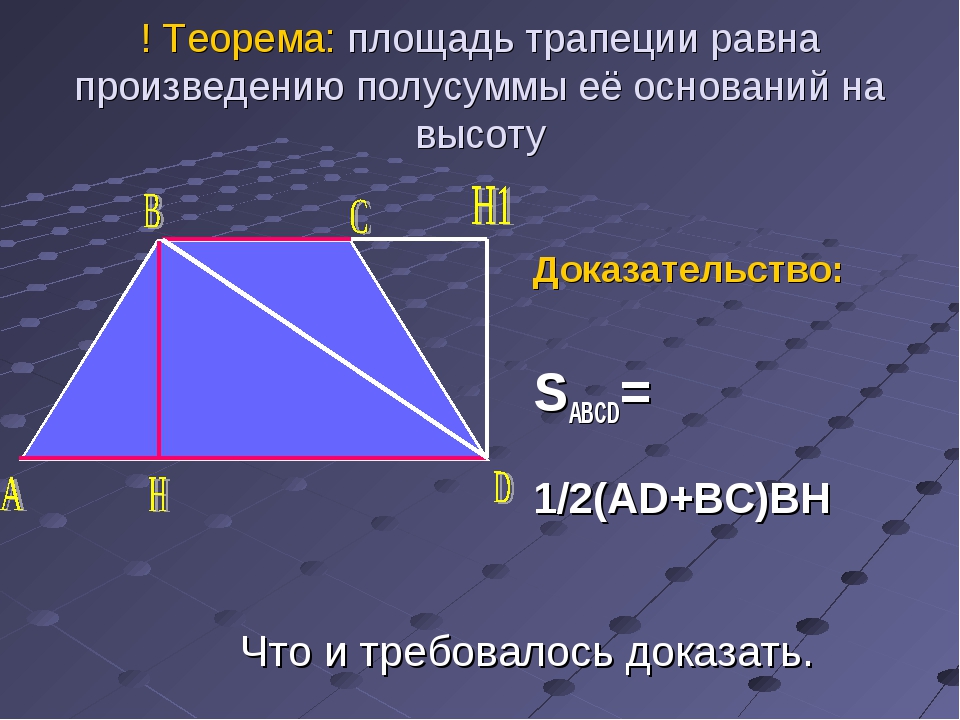
В планиметрии существует целый класс таких задач, к которым традиционные методы (метод цепочек равных треугольников, метод геометрических преобразований, векторный метод и др.) либо вовсе не применимы, либо дают сложные и громоздкие решения. Во многих случаях решать такого рода задачи помогает введение в чертеж дополнительных линий – так называемое дополнительное построение. В одних случаях эти построения напрашиваются сами собой, в других они не так очевидны и требуют от решающего достаточно большого опыта, изобретательности, геометрической интуиции.
Так, чертеж данной в задаче фигуры можно достраивать до фигуры другого типа, можно с многоугольной фигурой связывать окружность, а можно целью дополнительного построения ставить выделение на чертеже равных, равновеликих или подобных фигур.
Знание метода дополнительных построений в большинстве случаев позволяет решать, казалось бы, сложные геометрические задачи просто, понятно и красиво.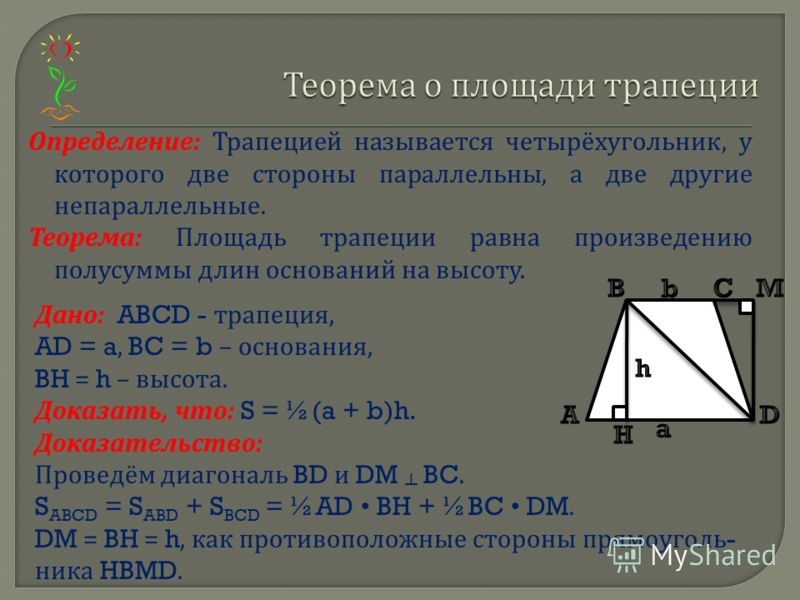
В этой разработке собраны формулы, свойства и подсказки для решения задач связанных с трапецией. Надеюсь, что ты здесь найдешь для себя много полезной информации.
1.Определения.
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
Параллельные стороны
называются её основаниями, а две другие стороны — боковыми
сторонами.
Высотой трапеции называется расстояние между основаниями.
Kаждый из этих отрезков EF, BM, DK, PQ является высотой трапеции ABCD.
В формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
h— высота.
2.Частные случаи трапеции.
Прямоугольной трапецией называется трапециия, в которой одна из боковых сторон перпендикулярна основаниям.
У нее два прямых угла при меньшей боковой стороне.
Эта сторона одновременно является и высотой трапеции.
произвольная
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
У равнобедренной трапеции так же, как и у равнобедренного треугольника, углы при основании равны.
Трапеция, у которой боковые стороны равны, называется равнобедренной
(равнобокой, равнобочной).
3.Свойства произвольной трапеции.
1. Во всякой трапеции сумма углов , прилежащих к одной ее боковой стороне, равна 1800.
2. Во всякой трапеции средняя линия параллельна ее основаниям, равна полусумме этих оснований и делит диагонали трапеции пополам.
MК =
3.Четыре замечательные точки трапеции:
Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.
4. Во всякой трапеции если сумма углов при большем основании равна 900, то боковые стороны лежат на перпендикулярных прямых. Длина отрезка, соединяющего середины оснований, равна полуразности оснований.
5. Свойства отрезка, соединяющего основания трапеции
Отрезок, соединяющий основания всякой трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции.
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношение составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции:
6.Свойства отрезка, параллельного основаниям всякой трапеции.
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
*Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам, то есть КО=ОМ
*Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна
KM = .
7.Во всякой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему геометрическому оснований, если он делит трапецию на две трапеции, подобные между собой.
8. Во всякой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему квадратичному оснований, если он делит трапецию на две трапеции равной площади (равновеликие).
9.Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований.
d12 + d22 = c2 + d2+ 2ab, d- боковая сторона. d1 и d2 – диагонали.
Свойства равнобедренной трапеции.
Трапеция является равнобедренной тогда и только тогда, когда
*углы, прилежащие к одному основанию, равны
*сумма противолежащих углов 1800;
*диагонали равны;
AC = BD
*отрезки диагоналей, соединяющих точку пересечения с концами одного основания, равны; BO = OC, AO = OD.
*вокруг этой трапеции можно описать окружность.
BC // AD, AB = CD. ABCD – вписанная трапеция.
* высота, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
*если в равнобедренной трапеции диагонали перпендикулярны, то
1)квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
2)высота трапеции равна полусумме оснований.
3)ее высота равна средней линии.
4) площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты.
(или квадрату полусуммы оснований, или квадрату средней линии).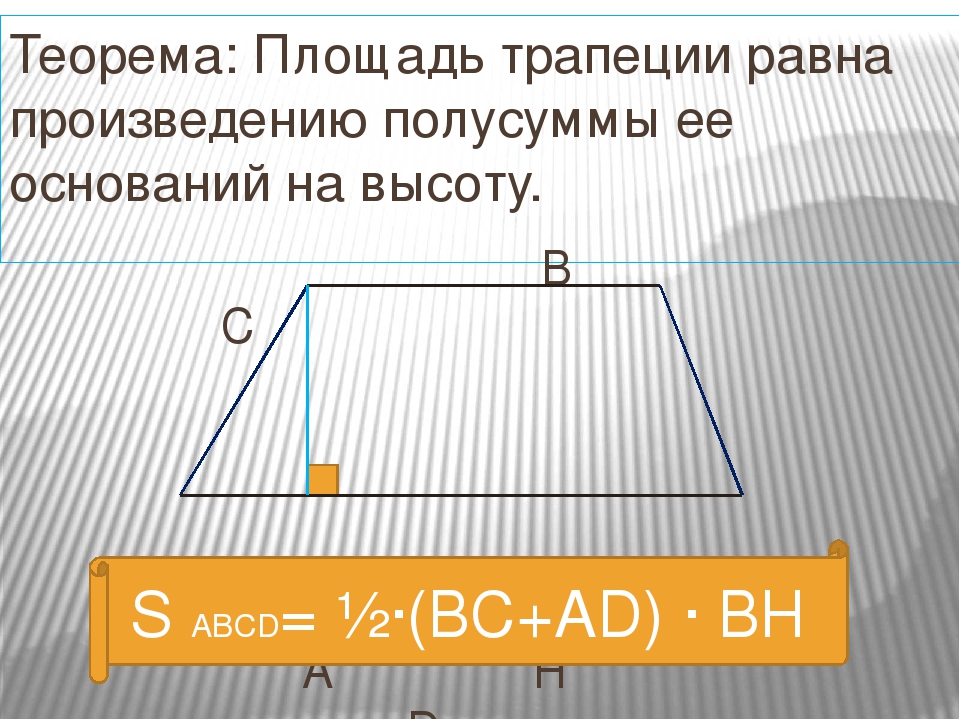
*если в равнобокой трапеции высота равна средней линии, то диагонали трапеции взаимно перпендикулярны.
BH = HD = h =.
*высота, проведённая через точку пересечения диагоналей, в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
*в равнобедренной трапеции прямая, проходящая через середины оснований, перпендикулярна им и является осью симметрии трапеции.
*отрезки, последовательно соединяющие середины смежных сторон равнобедренной трапеции, образуют ромб.
MNKE – ромб, то есть
MN=NK=KE= ME.
*в равнобедренной трапеции квадрат диагонали равен квадрату его боковой стороны плюс произведение оснований: d2 = c2 + a b
*площадь равнобедренной трапеции с радиусом вписанной окружности равным r и углом при основании α:
S =
Свойства биссектрисы угла трапеции.
*биссектриса угла отсекает от трапеции равнобедренный треугольник.
*точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
*если диагональ трапеции является биссектрисой ее острого угла, то меньшее основание равно боковой стороне трапеции, прилежащей к этому углу.
*биссектриса угла трапеции, пересекающая основание, отсекает от трапеции равнобедренный треугольник.
*биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
* точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
*если биссектриса тупого угла трапеции является диагональю, то боковая сторона равна большему основанию трапеции.
*если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.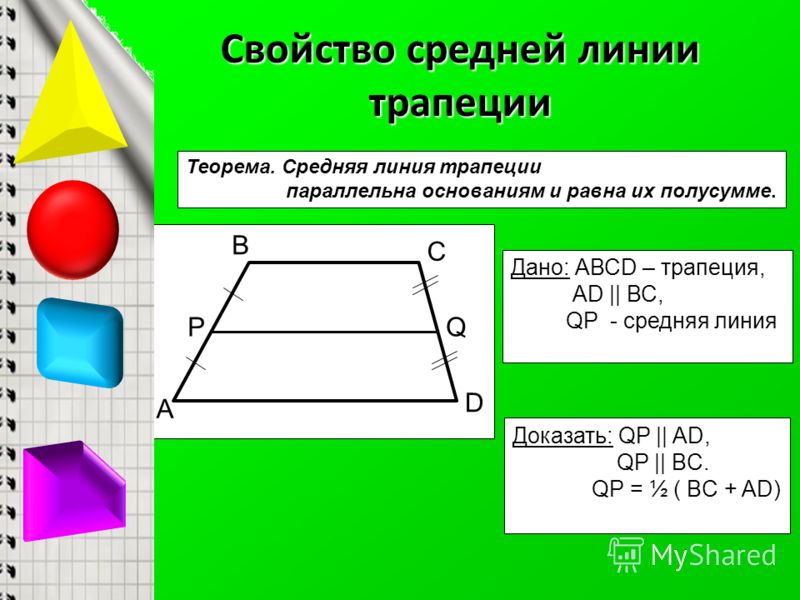
Если в условии задачи сказано, что основание трапеции равно ее боковой стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее угла.
*если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
*если большее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне тупого угла.
*если большее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к меньшему основанию.
* если меньшее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к большему основанию.
* если меньшее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне острого угла.
* если большее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне тупого угла.
*если меньшее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой острого угла трапеции.
* если большее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой тупого угла трапеции.
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом.
*Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
*В подобных треугольниках длины всех линейных элементов пропорциональны, а именно:
отношения периметров, радиусы вписанных окружностей, радиусы описанных окружностей, соответствующих высот, биссектрис, медиан (проведенных из равных углов) подобных треугольников равны отношению соответствующих сторон (лежащих против равных углов) или равны коэффициенту подобия.
*Площади подобных треугольников относятся как квадраты соответствующих сторон или равно квадрату коэффициента подобия.
*Площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
S12= S2 S3
S3: S2 = 2
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»
Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»
Далее, в формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
h— высота
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Эта группа формул отражает одно из основных свойств диагоналей трапеции:
*Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Используем теорему косинусов.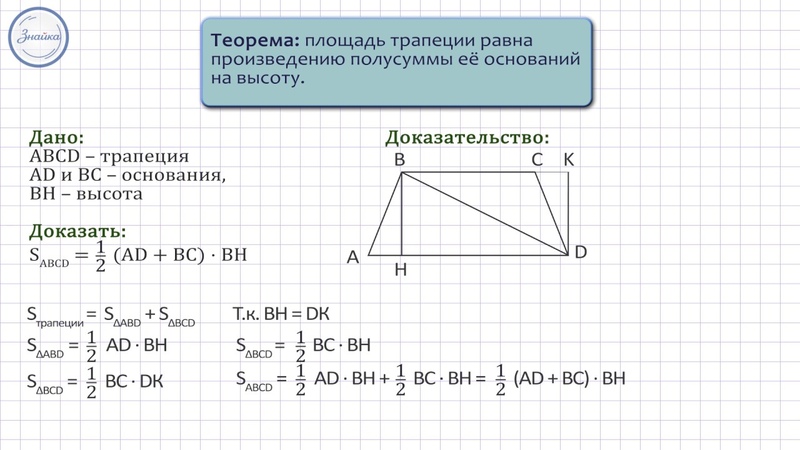
*Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
*Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
4.В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований
d12 — d22 = a2 – b2
*Если диагонали трапеции взаимно перпендикулярны, то длина отрезка, соединяющего середины оснований трапеции равна полусумме оснований.
MH =
BDCE и FAOD прямоугольники, а диагонали прямоугольника равны.
Трапеция и окружность.
1) Если в равнобокую трапецию можно вписать окружность, то средняя линия трапеции равна боковой стороне.
Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим её оснований
h2 = a ∙ b
2) Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна средней линии. Площадь трапеции определяется произведением средней линии на высоту трапеции.
3. Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.
MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности.
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
. CF =m, FD =n, OF = r.
∠COD=90º, т.к. ∠ADC+∠BCD=180º — так
как сумма внутренних односторонних углов при параллельных прямых AD и BC и секущей CD равна 1800.
Отсюда радиус вписанной в трапецию окружности выражается через длины отрезков, как которые боковая сторона делится точкой касания, как r = .
А так как высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через длины этих отрезков: h = 2 .
5.Если в трапецию можно вписать окружность и около трапеции можно описать окружность, то проекция диагонали на большее основание, равна боковой стороне и равна средней линии трапеции.
Если в трапецию вписана окружность, в задаче появляется несколько путей, по которым можно повести рассуждение.
1.В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.
AB+CD=AD+BC
2. Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что
AL=AK BL=BM
CM=CF DF=DK
Описанная окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
1)Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания.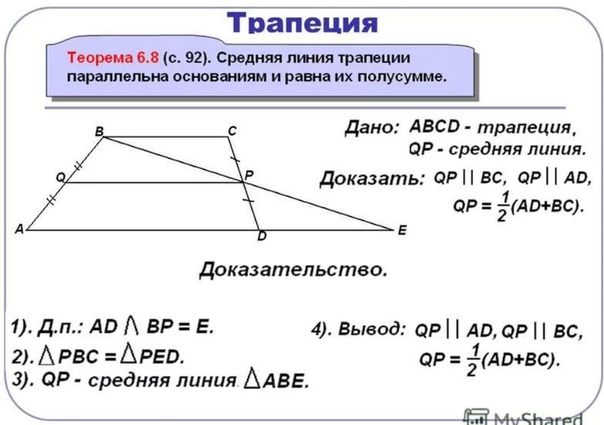 Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
2) Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции.
3) Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
4)Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла.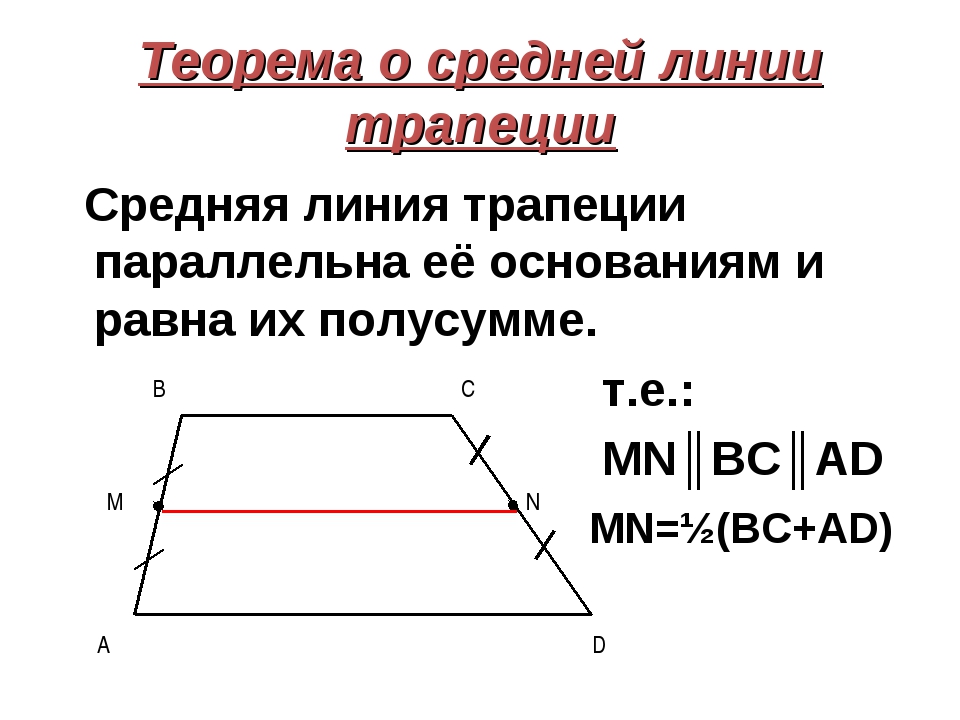 Например,
Например,
Использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
5)Если диагонали вписанной в окружность трапеции (четырехугольника) взаимно перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности или удвоенному квадрату боковой стороны:
a2 + b2 = 4R2 = 2c2.
6) Если в трапецию вписана окружность, то вершина трапеции, центр вписанной в нее окружности и основание перпендикуляра, опущенного из другой вершины на основание, лежат на одной прямой.
Дополнительные построения как прием при решении задач
Дополнительные построения являются эффективным методом решения геометрических задач.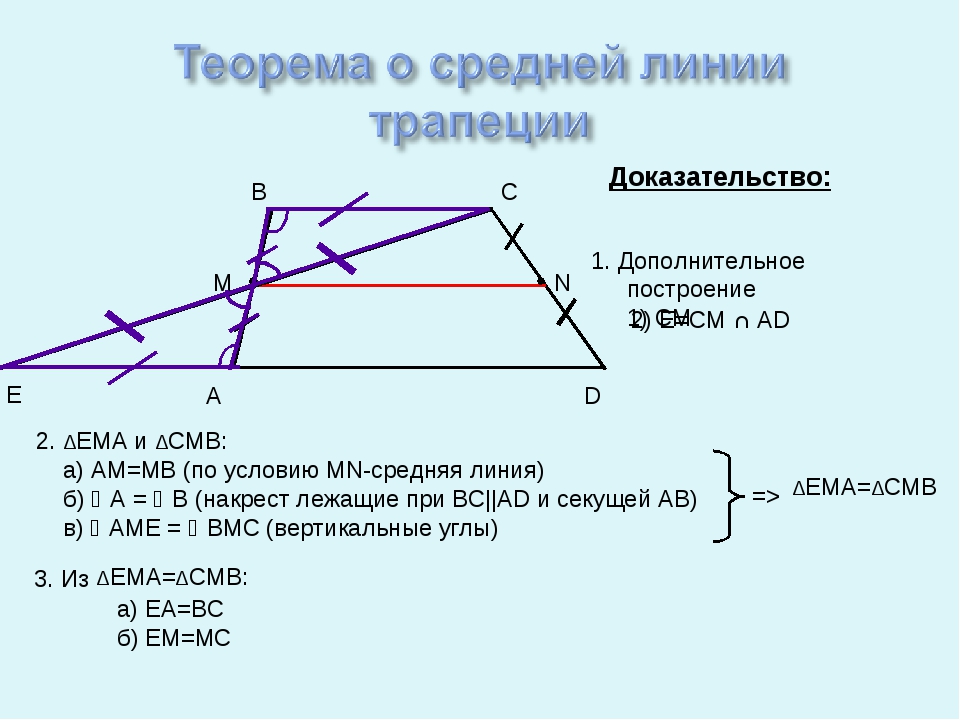 Наиболее часто используются при решении задач:
Наиболее часто используются при решении задач:
1. Опускание высот из концов одного основания на другое основание
2. Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину
3. Проведение через середину меньшего основания прямых, параллельных боковым сторонам
4. Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину .
5. Продолжение боковых сторон до пересечения.
Рассмотрим каждое их них.
При решении задач на отыскание площади дополнительным построением считается построение ее высоты или высот. Если построение высоты не помогает решить задачу, то нужно построить прямую, параллельную одной из ее диагоналей. Потом найти площадь полученного треугольника, который будет равновеликим исходной трапеции.
1. Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину.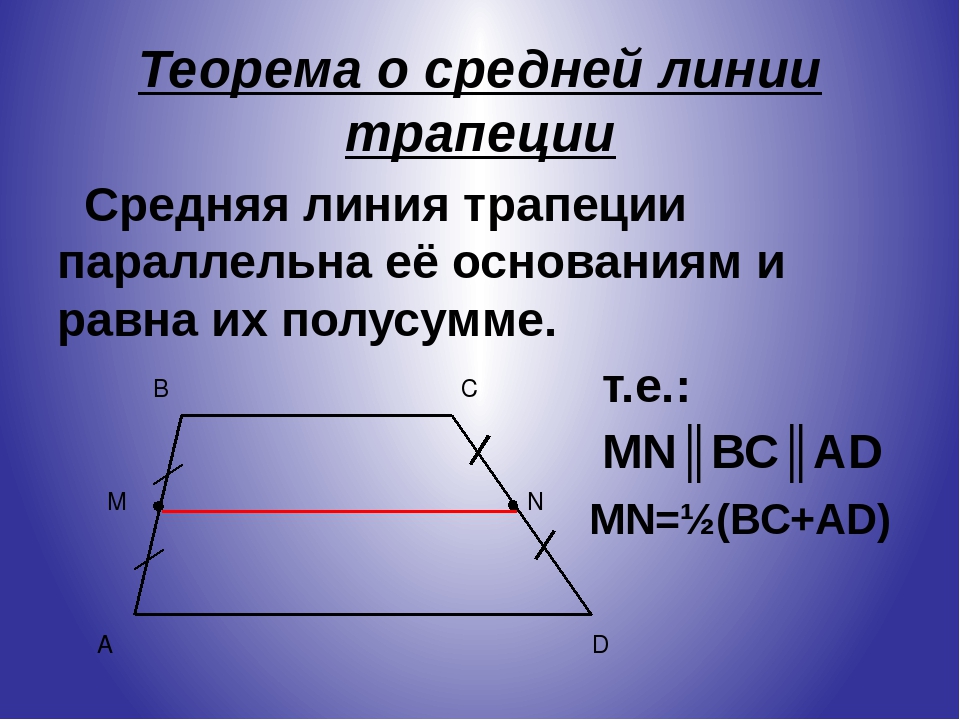
При дополнительном построении, когда переносится диагональ, образуется треугольник, площадь которого равна площади трапеции.
S1 = S2
Задача.
Найдите площадь трапеции, дмагонали которой равны 8 и 15, а средняя линия равна 8,5.
Решение.
Построим CF // BD и получим SACF = SABCD. Почему?
ABC = CDF, так как DF = BC и эти треугольники имеют одинаковую высоту.
Значит, для того, чтобы найти площадь трапеции нам достаточно найти площадь ACF.
АF = АD + ВС — сумма оснований трапеции. По условию задачи средняя линия трапеции 8,5. Значит сумма оснований АF = 8,52=17.
Рассмотрим ACF. Проверим, является ли он прямоугольным? В этом нам поможет теорема Пифагора:
172 = 82 + 152
289 = 64 + 225.
289 = 289.
ACF – прямоугольный. SACF = AC*CF = 8*15 = 60. SABCD= 60.
Если ACF разносторонний, то его площадь вычислим по формуле Герона.
Ответ:60.
2. Продолжение боковых сторон до пересечения.
Свойства трапеции, достроенной до треугольника
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
*Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
*Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника.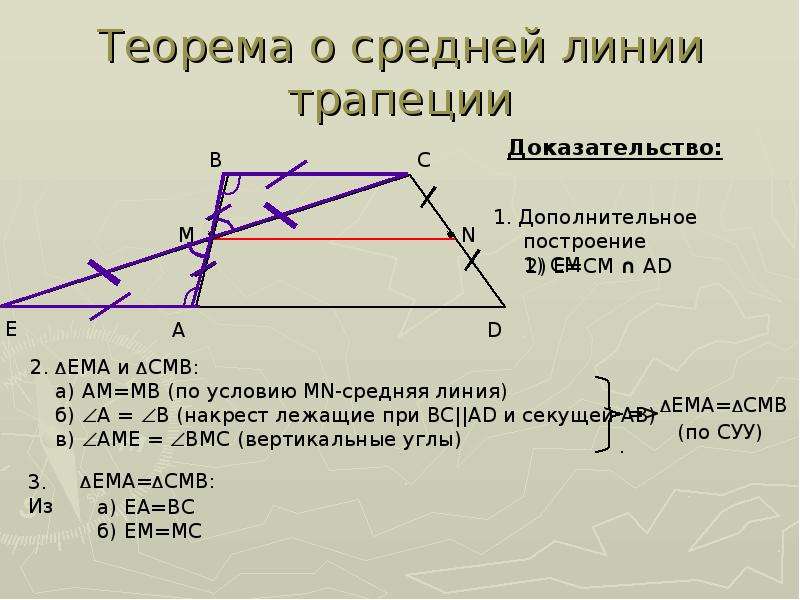
*Если ABCD равнобедренная трапеция, то KL является биссектрисой, медианой и высотой одновременно.
Это дополнительное построение позволяет перейти от трапеции к треугольнику. Если сумма углов при большем основании равна 900, топродолжив боковые стороны мы получим прямоугольный треугольник.
Задача.
В трапеции ABCD основания АD и ВС равны соответственно 72 и 18, а сумма углов при основании АD равна 900. Найдите радиус окружности, проходящей через точки А и В и касающейся прямой CD, если АВ = 18.
Решение.
Центром О данной окружности будет точка пересечения серединного перпендикуляра к АВ и перпендикуляра, возведенного к стороне CD из точки касания окружности. АВО равнобедренный: АО = ВО. Продлим боковые стороны трапеции и получим прямоугольный треугольник АМD. KMNO – прямоугольник, где KM = MN = NO =КО = R.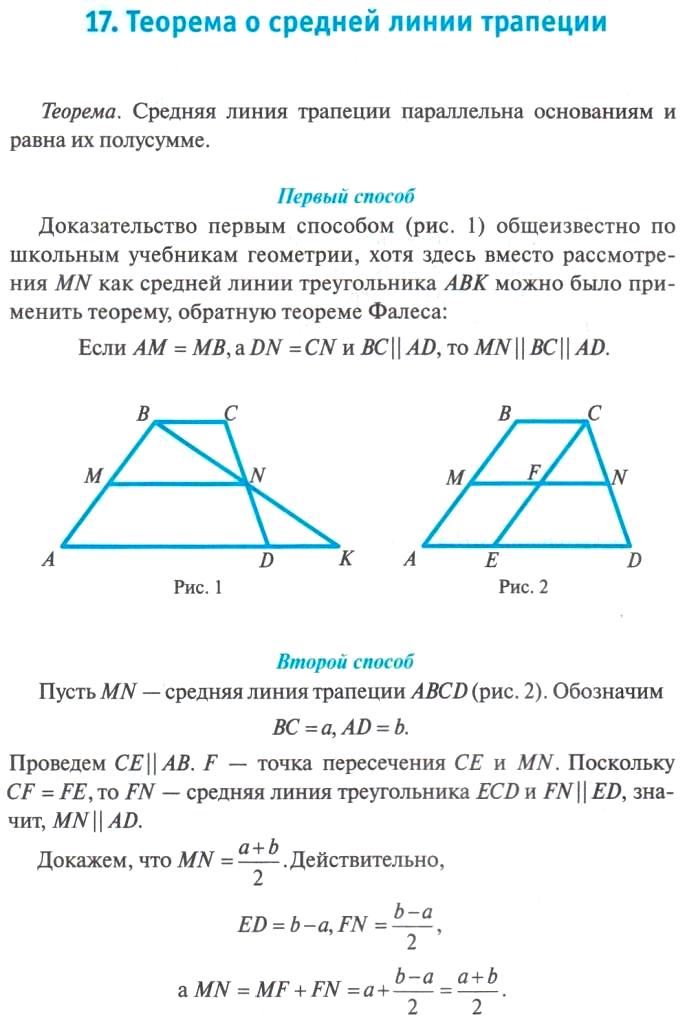
BMC AMD.
= , то есть и x = 6. Тогда R = КВ + 6 = 9 + 6 = 15.
Ответ:15.
3. Опускание высот из концов одного основания на другое основание.
Дополнительное построение 1,2 позволяет разбить трапецию на прямоугольник (стороны которого — одно из оснований и высота трапеции) и два прямоугольных треугольника (в которых один из катетов – высота трапеции, а гипотенузы – боковые стороны трапеции)
Построение 1 Построение 2
Задача. Найдите площадь трапеции с основаниями 8 и 13 и боковыми сторонами 3 и 4.
Решение.
Проведем ВН и СM — высоты и получим ABD (египетский треугольник) со сторонами 3,4,5, так как АD – ВС=13 – 8=5.
S= АВ* BD= 6.
Найдем высоту трапеции: h= 2S:5 = 2*6:5= 2,4.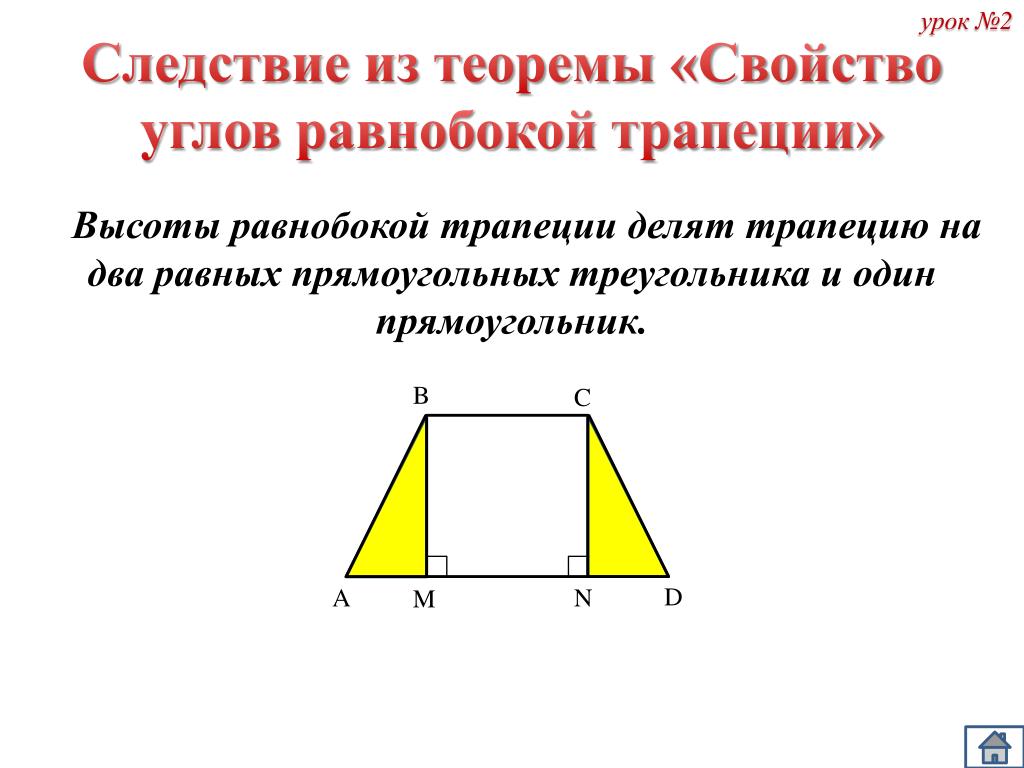
SABCD= 6+2,4*8=25,2. Ответ:25,2.
4. Проведение через середину меньшего основания прямых, параллельных боковым сторонам.
Дополнительное построение 4 делит трапецию на параллелограммы и треугольник. Боковые стороны соединяются в треугольник.
5. Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину.
Задача. Основания трапеции равны 30см и 15см, а боковые стороны равны 9 см и 12 см. Найдите высоту трапеции.
Решение. Пусть АВСД трапеция, заданная в условии.
Проведем через вершину С прямую, которая параллельна АВ. Пусть эта прямая пересекает АД в точке М.
Тогда АВСМ – параллелограмм и СМ=9, АМ=ДМ=15.
Так как 92+122=152, то, применив обратную теорему Пифагора, приходим к выводу, что СМ перпендикулярна СД.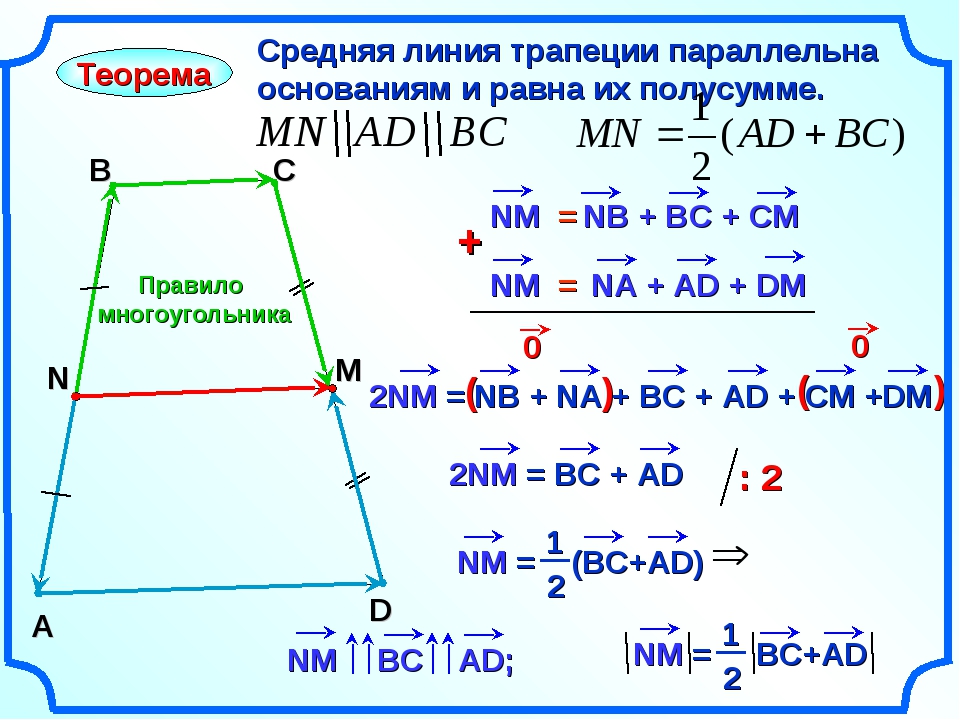
Заметим, что высота трапеции и треугольника МСД, проведенная из вершины С, совпадают. Для определения искомой высоты применим метод площадей. Пусть искомая высота равна х. Тогда для определения х составим уравнение, дважды вычислив площадь треугольника МСД:
.
Решив это уравнение находим: х=7,2. Ответ: 7,2.
Задача. Боковые стороны AB и CD трапеции ABCD равны 15 и 12 соответственно. Найдите градусную величину угла D, если одно из оснований трапеции на 9 больше другого.
Решение.
Из вершины угла проведем прямую линию, параллельную стороне. Трапеция разделена данной прямой линией на параллелограмм и треугольник. Противоположные стороны параллелограмма равны, значит, длина стороны треугольника равна разности длин оснований трапеции. Данный треугольник определен по трем сторонам. По теореме косинусов определим искомый угол. Вычисления показывают, что боковая сторона перпендикулярна к основанию, искомый угол прямой.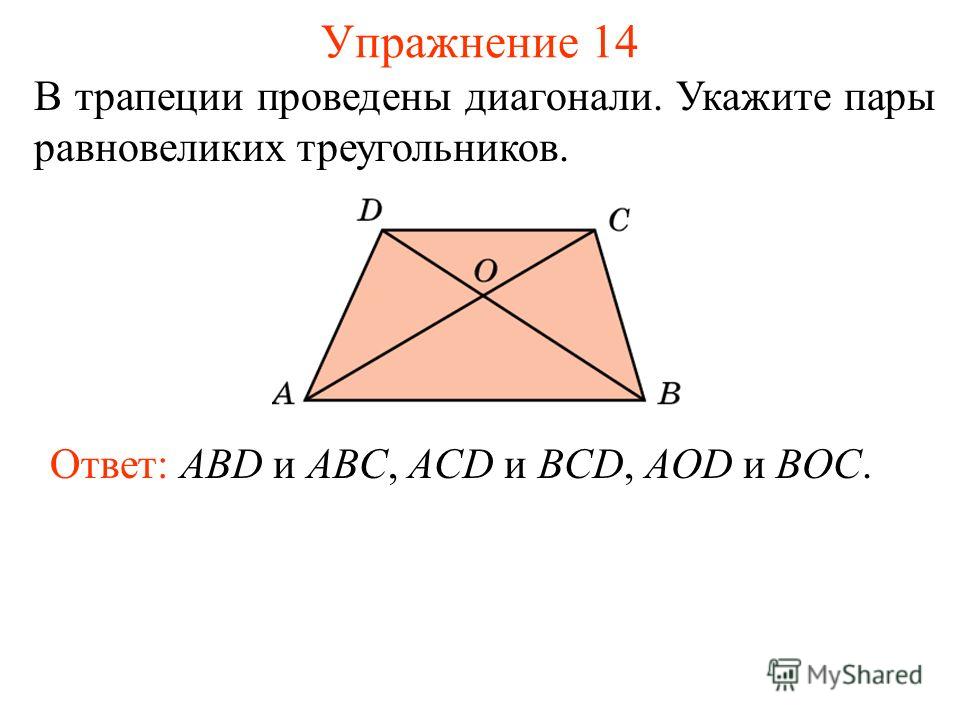
Ответ:
Для тех, кому интересно.
Теорема.
Задачи с решениями.
Пример 1.Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
Решение.
Дано: ABCD — равнобедренная трапеция, r = 4, AB = 10
Найти: SABCD
AB = CD = 10 по условию.
AB + CD = AD + BC по свойству вписанной окружности.
AD + BC = 10 + 10 = 20.
FE = 2r = 2 · 4 = 8.
SABCD=1/2(BC + AD)·FE, SABCD = 1/2 · 20 · 8 = 20/2 · 8 = 10 · 8 = 80.
Пример 2.Основания трапеции равны 10 м и 31 м, а боковые стороны — 20 м и 13 м. Найдите высоту трапеции.
Решение.
Пусть HK = BC = 10 м, BH = CK = x, AH = y, тогда KD = 21 – y
По теореме Пифагора:x2 + y2 = 132x2 + (21 – y)2 = 202x2 + y2 = 169 (1)
x2 + 441 – 42y + y2 = 400 (2)
Вычтем из (2) уравнения (1):441 – 42y = 23142y = 210y = 5AH = 5 м
По теореме Пифагора:BH2 = AB2 – AH2BH2 = 132 – 52BH2 = 169 – 25BH2 = 144
BH = 12
Пример 3. Большее основание трапеции равно 24. Найдите длину меньшего основания, если расстояние между серединами диагоналей равно 4.
Большее основание трапеции равно 24. Найдите длину меньшего основания, если расстояние между серединами диагоналей равно 4.
Решение.
Пример 4.Диагонали AC и BD трапеции ABCD пересекаются в точке O.
Найдите площадь трапеции, если BC < AD и площади треугольников BOC и ABO равны соответственно равны 2 и 8.
Анализ.
Рассмотреть подобие треугольников.
Квадраты соответствующих сторон относятся как площади треугольников.
Введем параметры треугольников: стороны оснований и высоты треугольников.
Площади трапеции и треугольников определим по известным формулам.
Решение.
Ответ:
Пример 5.В трапеции большее основание равно 10. Диагонали трапеции, равные 8, перпендикулярны боковым сторонам. Найдите площадь трапеции.
Найдите площадь трапеции.
Анализ.
Длины диагоналей равны и перпендикулярны боковым сторонам. Имеем равенство прямоугольных треугольников по катету и гипотенузе: ABD = ACD, поэтому трапеция равнобедренная, т.е. АВ = СD.
Применим теорему Пифагора для определения боковой стороны трапеции.
Высоту трапеции определим из равенства площадей.
Проекцию боковой стороны на большее основание легче определить из подобия треугольников, чем по теореме Пифагора.
Длину средней линии в равнобокой трапеции можно определять как разность большего основания и проекции боковой стороны на основание.
Площадь трапеции находим как площадь прямоугольника АМСК, который получим, если достроим трапецию.
Пример 6.Диагонали трапеции взаимно перпендикулярны, а длина ее средней линии равна 9. Найдите длину отрезка, соединяющего середины оснований трапеции.
Найдите длину отрезка, соединяющего середины оснований трапеции.
Анализ.
Задача решается построением.
Достроим прямоугольники и используем свойство прямоугольника: диагонали прямоугольника равны и в точке пересечения делятся пополам.
Длина средней линии равна полусумме длин оснований.
Длина отрезка, соединяющая середины оснований, равна полусумме длин диагоналей двух построенных треугольников.
Пример 7.Длины оснований трапеции равны 1 и 7. Найдите длину отрезка, параллельного основаниям и заключенного между боковыми сторонами, который делит трапецию на две равновеликие части.
Анализ.
Провести из вершины тупого угла трапеции прямую линию, параллельную боковой стороне.
Рассмотреть отношение площадей трапеций.
Определить отношение при подобии треугольников.
Рациональные алгебраические преобразования приведут к результату.
Решение.Ответ:
Пример 11.Равнобедренная трапеция ABCD описана около окружности. Боковая сторона трапеции равна 10, а основания относятся как 1: 4. Найдите площадь трапеции.
Анализ.
Сумма противоположных сторон трапеции равна между собой — свойство описанного четырехугольника.
Трапеция равнобедренная.
Боковая сторона равна длине средней линии.
Применяем теорему Пифагора для нахождения высоты трапеции.
Площадь трапеции определяем по доступной формуле.
Пример 8.Длины боковых сторон трапеции равны 6 и 10. Известно, что в трапецию можно вписать окружность, а средняя линия делит ее на части, площади которых относятся как 5: 11.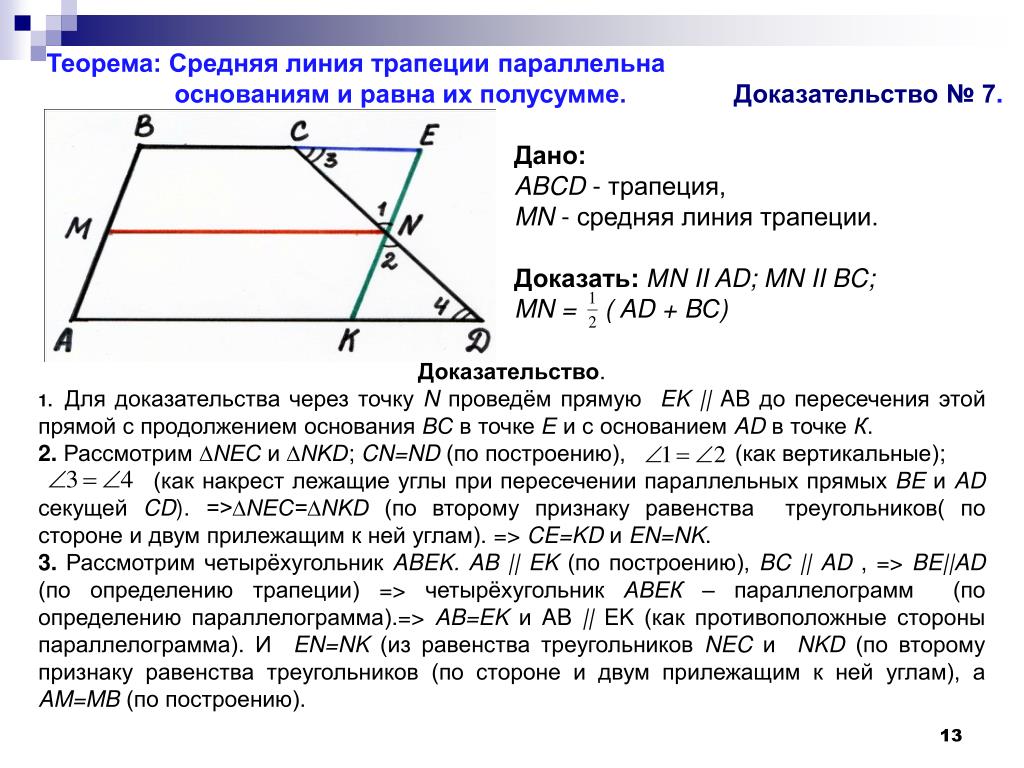 Найдите длину большего основания трапеции.
Найдите длину большего основания трапеции.
Анализ.
Трапеция является описанной.
Сумма длин оснований равна сумме боковых сторон.
Средняя линия делит трапецию на две трапеции, высоты которых равны.
Задача сводится к системе уравнений.
Длина средней линии равна половине суммы длин боковых сторон.
Пример 9.Площадь равнобедренной трапеции, описанной около окружности равна 15. Найдите среднюю линию трапеции, если косинус острого угла при ее основании равен 4/5.
Анализ.
Трапеция равнобедренная.
Длина средней линии равна боковой стороне.
Площадь трапеции определяется произведением средней линии на высоту трапеции.
Опустим высоту трапеции из тупого угла. Через заданный косинус угла определим синус угла.
По синусу угла выразим высоту трапеции через боковую сторону.
Пример 10.В прямоугольной трапеции, описанной около окружности, большая боковая сторона равна 13, а средняя линия равна 12,5. Найдите меньшее основание трапеции.
Анализ.
Необходимо использовать свойство сторон четырехугольника, описанной около окружности: сумма длин противоположных сторон равна между собой.
Кроме того, длина средней линии равна полусумме длин сторон оснований.
Проведем из вершины тупого угла высоту трапеции.
Воспользуемся теоремой Пифагора и определим проекцию наклонной боковой стороны на основание.
Пример 11.В равнобедренную трапецию, один из углов которой равен 60°, а площадь равна , вписана окружность. Найдите радиус этой окружности.
Анализ.
Важное положение, что трапеция является равнобедренной и имеет ось симметрии. Тогда длина боковой стороны равна длине средней линии.
Введем параметр боковой стороны, из прямоугольного треугольника по заданному углу определим высоту трапеции, которая является диаметром вписанной окружности. Площадь трапеции определяется как произведение средней линии на высоту трапеции.
.
Пример 12.Найдите площадь равнобедренной трапеции, у которой большее основание равно 13, средняя линия равна 8, а биссектриса тупого угла является диагональю трапеции.
Анализ.
При проведении биссектрисы тупого угла боковая сторона равна большему основанию трапеции. Проекция боковой стороны равнобедренной трапеции равна полуразности длин оснований.
По теореме Пифагора найдем высоту трапеции.
Площадь трапеции находим по формул.
Список используемой литературы
4.
5.
6.
7.
8.
Средняя линия трапеции / Векторы / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Векторы
- Средняя линия трапеции
Средняя линия трапеции — это отрезок, который соединяет середины её боковых сторон.
Теорема
Доказательство
Дано: ABCD — трапеция, MN — средняя линия ABCD
Доказать: MN AD,
Доказательство:
По правилу многоугольника = + + и = + + . Сложив эти равенства, получим:
2 = ( + ) + ( + ) + ( + ).
Но M и N — середины сторон АВ и CD, поэтому + = и + = (так как сумму составляют противоположные векторы, а сумма противоположных векторов равна нулевому вектору) . Следовательно, 2 = + , откуда = ( + ).
Так как векторы и сонаправлены, то векторы и также сонаправлены, а длина вектора ( + ) равна AD + ВС. Отсюда следует, что MN AD, . Теорема доказана.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Сумма двух векторов
Законы сложения векторов. Правило параллелограмма
Сумма нескольких векторов
Вычитание векторов
Произведение вектора на число
Применение векторов к решению задач
Векторы
Правило встречается в следующих упражнениях:
7 класс
Задание 793,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 795,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 797,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 20,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 810,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 974,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5.com, 2021
Пользовательское соглашение
Copyright
Определение, признаки и свойства произвольной, равнобедренной и прямоугольной трапеции
В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.
Определение и виды
В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Различные виды указаны на рисунке ниже.
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Важнейшие свойства и формулы
Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.
В её состав входят:
- основания BC и AD — две стороны, параллельные по отношению друг к другу,
- боковые стороны AB и CD — два непараллельных элемента,
- диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры,
- высота трапеции CH — перпендикулярный основаниям отрезок,
- средняя линия EF — линия, соединяющая середины боковых сторон.
Основные свойства элементов
Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:
- Средняя линия всегда проходит параллельно обоим основаниям фигуры и численно равна их полусумме: EF = (BC + AD)/2.
- Точка пересечения диагоналей фигуры разделяет их с таким же соотношением длины, с каким относятся основания трапеции: AD : BC = AO : CO = DO : BO.
- Основание можно вычислить, зная длину второго основания и средней линии: BC = 2 · EF — AD, AD = 2 · EF — BC.
- Боковые стороны вычисляются, если известна высота фигуры и синус угла при основании: AB = CH / sinA, CD = CH / sinD.
- Для расчёта высоты необходимо знать, чему равна боковая сторона и прилегающий угол: CH = AB · sinA = CD · sinD.
Кроме того, часто полезно знать и применять следующие утверждения:
- Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.
- При проведении диагоналей образуются 4 треугольника, из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
- Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.
Вычисление периметра и площади
Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):
P = AD + BC + AB + CD.
Есть несколько способов, как можно рассчитать площадь трапеции по формуле. Следует выбрать из них наиболее подходящий вариант, опираясь на то, какие данные известны по условию задачи.
Вписанная и описанная окружность
Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.
Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2.
Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен r = h/2.
Частные случаи
Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения, которые характерны для произвольной трапеции. Другие свойства равнобедренной трапеции:
- Прямая, которая проходит через середины оснований фигуры, пересекает их под углом 90 градусов.
- Углы, лежащие при любых основаниях, попарно равны.
- Длины диагоналей совпадают.
- Высота будет равна средней линии, если диагонали проходят перпендикулярно друг к другу.
- Высота, опущенная из вершины к основанию, делит его на 2 отрезка, длина большего вычисляется как половина суммы оснований, а длина меньшего — как половина разности.
Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.
Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.
формулы и примеры. Трапеция решение задач по геометрии Как решать трапецию
Добрый день, дорогие друзья! Сегодня у нас тема — трапеция решение задач по геометрии.
Прежде чем начинать разбирать задачи, давайте вспомним, что такое трапеция, и какие у неё есть элементы.
Трапеция — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие — не параллельны.
Параллельные стороны называют основаниями, а непараллельные — боковыми сторонами.
Трапеции бывают прямоугольные, равнобедренные и простые.
В прямоугольных трапециях есть 2 прямых угла.
В равнобедренных трапециях, как в равнобедренных треугольниках, углы при основаниях равны, равны так же и боковые стороны.
В трапеции имеется средняя линия, которая соединяет середины боковых сторон.
А теперь задачи.
Острый угол равнобедренной трапеции равен 60°. Доказать, что основание ВС = AD — AB.
Доказательство.
Опустим из вершин трапеции высоты BM и CN на нижнее основание AD.
Получим два прямоугольных треугольника ABM и DCN, а также прямоугольник BCNM.
Поскольку в прямоугольных треугольниках один угол равен 60°, то второй, согласно следствию из теоремы о сумме внутренних углов треугольника,
равен 30°.
А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы.
Т.е. АМ= с/2.
То же самое и в правом треугольнике — ND = с/2.
Получается, что нижнее основание можно представить в виде суммы трёх отрезков, а именно AM, MN, ND, где AM=ND=c/2.
MN=BC, или верхнему основанию.
Отсюда можно написать MN=BC=AD — AM — ND = AD — c/2 — c/2 = AD — AB.
Мы доказали, что верхнее основание равно разности нижнего основания и боковой стороны.
Основания трапеции равны AD и BC. Найти длину отрезка KP, который соединяет середины диагоналей трапеции.
Решение:
На основании теоремы Фалеса отрезок KP принадлежит большему отрезку MN, который является средней линией трапеции.
Средняя линия трапеции
, как мы знаем, равна полу-сумме оснований трапеции
, или (AD+BC)/2.
В то же время, рассматривая треугольник ACD и его среднюю линию KN, можно понять, что KN=AD/2.
Рассматривая другой треугольник BCD и его среднюю линию PN, можно увидеть, что PN=BC/2.
Отсюда, KP=KN-PN = AD/2 — BC/2 = (AD-BC)/2.
Мы доказали, что отрезок, который соединяет середины диагоналей трапеции, равен полу-разности оснований данной трапеции
.
Задача 3.
Найти меньшее основание ВС равнобедренной трапеции, если высота СK, проведённая из конца C меньшего основания, делит большее основание на отрезки AK и KD, разность которых равна 8 см.
Решение:
Сделаем дополнительное построение. Проведём высоту ВМ.
Рассмотрим треугольники ABM и DCK. Они равны по гипотенузе и катету
— AB=CD, как боковые стороны равнобедренной трапеции.
Высоты трапеции BM и CK тоже равны, как перпендикуляры, расположенные между двумя параллельными прямыми
.
Следовательно, AM=KD. Получается, что разность между AK и KD равна разности между AK и AM.
А это есть отрезок MK. Но MK равен ВС, поскольку BCKM — прямоугольник.
Отсюда меньшее основание трапеции равно 8 см.
Задача 4.
Найти отношение оснований трапеции, если её средняя линия делится диагоналями на 3 равные части.
Решение:
Поскольку MN — средняя линия трапеции, то она параллельна основаниям и делит боковые стороны пополам
.
По теореме Фалеса MN делит также и стороны AC и BD пополам.
Рассматривая треугольник АВС можно видеть, что MO в нём — средняя линия. А средняя линия треугольника параллельна основанию и равна его половине
. Т.е. если MO=Х, то ВС=2Х.
Из треугольника ACD имеем ON — средняя линия.
Она тоже параллельна основанию и равна его половине.
Но, поскольку OP+PN= Х+Х=2Х, тогда AD=4Х.
Получается, что верхнее основание трапеции равно 2Х, а нижнее — 4Х.
Ответ: отношение оснований трапеции равно 1:2.
Задачи с трапецией не кажутся сложными в ряде фигур, которые изучены ранее. Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а боковые стороны могут иметь произвольное значение углов к ним. Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Другие углы в прямоугольной трапеции − это всегда острый и тупой. Причем их сумма всегда будет равна 180 градусам.
Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения приняты в представленных формулах?
Все величины, используемые в разных выражениях, которые описывают трапецию, удобно сразу оговорить и представить в таблице:
Формулы, которые описывают элементы прямоугольной трапеции
Самая простая из них связывает высоту и меньшую боковую сторону:
Еще несколько формул для этой стороны прямоугольной трапеции:
с = d *sinα;
c = (a — b) * tg α;
c = √ (d 2 — (a — b) 2).
Первая вытекает из прямоугольного треугольника. И говорит о том, что катет к гипотенузе дает синус противолежащего угла.
В том же треугольнике второй катет равен разности двух оснований. Поэтому справедливо утверждение, которое приравнивает тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основываясь на знании теоремы Пифагора. Это третье записанное выражение.
Можно записать формулы для другой боковой стороны. Их тоже три:
d = (a — b) /cosα;
d = c / sin α;
d = √ (c 2 + (а — b) 2).
Первые две опять получаются из соотношения сторон в том же прямоугольном треугольнике, а вторая выводится из теоремы Пифагора.
Какой формулой можно воспользоваться для расчета площади?
Той, что дана для произвольной трапеции. Только нужно учесть, что высотой является сторона, перпендикулярная к основаниям.
S = (a + b) * h / 2.
Эти величины не всегда даны явно. Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Как быть, если нужно вычислить диагонали?
В этом случае нужно увидеть, что они образуют два прямоугольных треугольника. Значит, всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражаться так:
d1 = √ (с 2 + b 2)
или по-другому, заменив «с» на «h»:
d1 = √ (h 2 + b 2).
Аналогичным образом получаются формулы для второй диагонали:
d2 = √ (с 2 + b 2)
или d 2 = √ (h 2 + а 2).
Задача №1
Условие
. Площадь прямоугольной трапеции известна и равна 120 дм 2 . Ее высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Решение.
Поскольку дана прямоугольная трапеция, в которой известна высота, то сразу же можно сказать о том, что одна из сторон равна 8 дм, то есть меньшая боковая сторона.
Теперь можно сосчитать другую: d = √ (с 2 + (а — b) 2). Причем здесь сразу даны и сторона с, и разность оснований. Последнее равно 6 дм, это известно из условия. Тогда d будет равняться квадратному корню из (64 + 36), то есть из 100. Так найдена еще одна боковая сторона, равная 10 дм.
Сумму оснований можно найти из формулы для площади. Она будет равна удвоенному значению площади, разделенному на высоту. Если считать, то получается 240 / 8. Значит, сумма оснований — это 30 дм. С другой стороны, их разность равна 6 дм. Объединив эти уравнения, можно сосчитать оба основания:
а + b = 30 и а — b = 6.
Можно выразить а как (b + 6), подставить его в первое равенство. Тогда получится, что 2b будет равняться 24. Поэтому просто b окажется 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ.
Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
Условие.
Дана прямоугольная трапеция. Ее большая боковая сторона равняется сумме оснований. Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Решение.
Начать нужно с искомого. Нужная площадь определится как произведение a и b. Обе эти величины не известны.
Потребуется использовать дополнительные равенства. Одно из них построено на утверждении из условия: d = а + b. Необходимо воспользоваться третьей формулой для этой стороны, которая дана выше. Получится: d 2 = с 2 + (a — b) 2 или (a + b) 2 = с 2 + (a — b) 2 .
Необходимо сделать преобразования, подставив вместо с его значение из условия — 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
В начале решения шла речь о том, что а*b дает искомую площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см 2 .
Ответ.
Искомая площадь 36 см 2 .
Задача №3
Условие.
Площадь прямоугольной трапеции 150√3 см². Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Решение.
Из свойства углов трапеции получается, что ее тупой угол равен 120º. Тогда диагональ делит его на равные, потому что одна его часть уже 60 градусов. Тогда и угол между этой диагональю и вторым основанием тоже 60 градусов. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нужно рассмотреть прямоугольный треугольник. В нем третий угол равен 30 градусам. Значит катет, лежащий против него, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. Из него же нужно найти высоту, равную боковой стороне, перпендикулярной основаниям. Сторона с здесь катет. Из теоремы Пифагора:
с = (a/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Решение этого уравнения дает корень 20
Ответ.
Меньшая диагональ имеет длину 20 см.
В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания . На блоге уже рассмотрены задачи условия которых связаны с , а также . Кратко о средней линии:
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.
Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:
Можем теперь выразить отрезок KL через основания:
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Вычисляем по формуле:
27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:
Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
Таким образом DC=6. Вычисляем:
27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.
Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
Следовательно меньшее основание равно 2∙2=4.
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
Исходя из условия можем записать:
Если обозначить среднюю линию через величину х, то получится:
Второе уравнение уже можно записать в виде:
27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
Получили, что меньшее основание рано пяти, значит большее равно 9.
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:
Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
27848. Найдите среднюю линию трапеции ABCD
, если стороны квадратных клеток равны 1.
Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией
называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h
.
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h
. Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα
.
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2
.
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα
. Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2
.
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2
.
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a)
. В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1:
Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение:
Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2:
Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение:
Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Использование теоремы о трапецеидальном срединном сегменте — математический класс [видео 2021 года]
Средний сегмент
Давайте назовем две стороны треугольника, которые не параллельны, ногами . Две другие параллельные стороны будут называться основаниями .
Средний сегмент трапеции — это линия, проходящая от середины одной ноги до середины другой ноги.Средний сегмент пересекает каждую ногу посередине. Средняя точка находится на одинаковом расстоянии от обоих концов линий ног.
На координатной плоскости
Можно использовать все, что мы узнали, когда у нас есть трапеция на координатной плоскости. Допустим, вам даны следующие четыре балла:
- (0, 0) (5, 0) (1, 4) (5, 4)
Вы можете изобразить их на координатной плоскости, проведя линии между точками, чтобы найти трапецию.
Эта трапеция выглядит немного иначе, чем та, которую мы видели ранее, но вы все равно можете видеть, что основания параллельны, а ножки — нет. Здесь мы можем легко нарисовать средний сегмент. Помните, что средний сегмент должен начинаться посередине каждой ноги.
Поскольку обе наши ноги начинаются с 0 на оси y и заканчиваются на 4 на оси y , легко увидеть, что средние точки должны находиться на 2 на оси y для обеих сторон. .Затем мы просто проводим линию через середину сегмента.
Теорема о среднем сегменте трапеции
Теперь, когда мы понимаем некоторые основы трапеций, давайте поговорим о теореме о срединном сегменте о трапеции , в которой говорится, что длина среднего сегмента равна сумме базовых длин, деленной на 2 Другими словами, средний сегмент — это средняя длина двух оснований.
Итак, допустим, мы смотрим на трапецию, у которой длина основания наверху равна 2, а длина основания внизу равна 4. Чтобы найти длину среднего сегмента, мы просто сложим длину основания базы:
Затем разделите сумму на 2:
Таким образом, длина среднего сегмента равна 3.
Некоторые примеры
На этот раз длины двух оснований составляют 8,975 см и 3,4 см. Какова длина среднего сегмента?
Начните с сложения двух оснований:
- 8.975 см + 3,4 см = 12,375 см
Затем разделите сумму на 2:
- 12,375 см / 2 = 6,1875 см
Просто! Длина миделя составляет всего 6,1875 см.
Теперь предположим, что вам дали задачу, где вам дали:
- Длина среднего сегмента = 14
- Длина одной из баз = 16,5
Какова длина другой базы? Можем ли мы использовать теорему таким образом? Что ж, давайте посмотрим на пример.
При решении подобных задач проще всего начать с уравнения и заполнить то, что мы знаем:
- Средний сегмент = (base1 + base2) / 2
Так как мы знаем длину среднего сегмента, давайте заполним это:
Затем мы заполним известную базовую длину:
Теперь мы будем использовать обратные операции для решения для base2.Начните с умножения обеих сторон на 2:
Затем вычтите 16,5 с обеих сторон, чтобы выделить base2:
Таким образом, длина второго основания равна 11,5.
Итоги урока
Хорошо, давайте сделаем небольшой обзор. Как мы узнали, трапеции — это 4-сторонние фигуры (четырехугольники), пара сторон которых параллельна, а другая пара — нет. У них одна пара параллельных сторон, называемая основаниями , и другая пара непараллельных сторон, называемая ножками .
Средний сегмент трапеции проходит поперек трапеции, начиная с середины каждой ноги, при этом средняя точка находится на равном расстоянии от обоих концов линий ног. Длину среднего сегмента можно рассчитать с помощью теоремы о срединном сегменте трапеции , которая гласит, что длина среднего сегмента равна сумме базовых длин, деленной на 2. Следовательно, ее можно рассчитать, сложив длину каждого сегмента. base и разделив сумму на 2.
Пифагорейская Теорема
Пифагорейская Теорема
пифагорейский
Теорема
по
Грег Хуберти
У теоремы Пифагора было несколько различных
доказательства, многие из которых очень похожи. На этом я обнаружил, что очень
иным и интересным является доказательство того, что бывший президент
Соединенных Штатов Джеймсу Гарфилду приписывают находку.
Это не похоже на другие доказательства тем, что в нем не используются квадраты
стороны, скорее, он использует два треугольника сторон a, b и c вдоль
с треугольником с ногами c, чтобы получилась трапеция.Вот это
доказательство
Сначала сделаем трапецию. Вы начинаете с треугольника
стороны a, b и c, где стороны a и b встречаются, чтобы образовать правую
угол.
Затем поместите второй треугольник ниже первого так, чтобы сторона a
является продолжением стороны b другого треугольника.
Затем соедините конец стороны a вверху со стороной b на
снизу, чтобы создать трапецию.
Запомните формулу площади трапеции, равную
.
формула для площади этой трапеции будет.Этот
площадь будет такой же, как сумма площадей трех треугольников
которые расположены внутри трапеции
Установив эти значения равными, вы получите
Упрощая обе стороны, вы придете к
Умножая обе стороны на два, получаем
Затем вычитая обе стороны на 2ab, конечный результат
это теорема Пифагора.
Еще одно доказательство этой теоремы — доказательство Да Винчи использования площадей.
и вырезать и приклеить их, чтобы показать равные области.Щелкните здесь .
Чтобы узнать больше о теореме Пифагора, попробуйте следующие:
Вот
Пифагор
Леонардо
да Пифагор
Озадаченный
Пифагор
Сдвиг
Пифагор
Это еще одно место, где можно увидеть больше
о теореме Пифагора. Щелкните здесь .
Вернуться к Грегу
Дано: Трапеция РОЗА с диагоналями RS и EO, пересекающимися в точке M Теперь моя книга дает мне все шаги; однако один шаг, я не понимаю. Я надеюсь, что вы можете помочь. Я дам вам шаг: Они сначала доказали, что треугольник I конгруэнтен треугольнику II с помощью SAS, используя косвенное доказательство. Я это понимаю. Но тогда они говорят, что ИЛИ параллельно SE, и причина в том, что «если две линии пересекаются поперечным и чередующиеся внутренние углы совпадают, то линии параллельны». И затем они продолжают говорить, что трапеция имеет только одну пара параллельных сторон, и мы только что увидели, что есть 2 пары параллельных сторон, если диагонали RS и EO делят друг друга пополам, поэтому они не могут делить друг друга пополам. Мой вопрос: как узнать, что происходит с переменными внутренними углами? Вы могли бы сказать, что OS параллельна RE, потому что если 2 линии, OS и RE, пересекаются поперечным, RS и альтернативные внутренние углы совпадают, тогда линии SO и RE параллельны. Откуда вы знаете, что линии SE и OR пересекаются поперечной RS; таким образом, параллельна и противоречит тому, что фигура является трапецией? | Привет Авраам, Ниже я воспроизвел диаграмму, которую вы прислали. Ваша книга дает доказательство от противоречия. Авторы сначала предполагают, что диагонали действительно делят друг друга пополам. То есть они предполагают, что
Затем они утверждают, используя SAS, что треугольники I и II конгруэнтны, это треугольники ORM и ESM. На этом этапе вы должны быть несколько осторожны, поскольку диаграмма может вводить в заблуждение. Предполагается, что | OM | = | ME | даже если они не выглядят одинаково на диаграмме.Также | RM | = | MS | и, следовательно, совпадение треугольников ORM и ESM подразумевает, что углы ORM и ESM совпадают. Следовательно, RS — это линия, которая пересекает OR и ES, а альтернативные внутренние углы (ORM и ESR) совпадают. Следовательно, OR параллельно ES. Мне не нравится эта проблема. Я предпочитаю определение, что «трапеция — это четырехугольник с парой параллельных сторон», а не «трапеция — это четырехугольник с ровно одной парой параллельных сторон». С моим определением параллелограмм — это трапеция, и проблема, которую вы задали, может быть переформулирована как Дано: Трапеция РОЗА с диагоналями RS и EO, пересекающимися в точке M Харлей |
Математическое сокровище: доказательство теоремы Пифагора Джеймсом А. Гарфилдом
Рис. 1. Carte de visite (CDV) или визитная карточка с фотографией (сделанной W. D. Gates & Co.) Джеймса А. Гарфилда около 1881 года из коллекции автора. CDV были популярны в то время. Показанная здесь карта была изготовлена после смерти Гарфилда в 1881 году, предположительно как памятный сувенир.В то время были также популярны похожие, но более крупные CDV.
Краткая биография
Джеймс А. Гарфилд (1831–1881) был двадцатым президентом Соединенных Штатов. После того, как он окончил Уильямс-колледж в 1856 году, он преподавал греческий, латынь, математику, историю, философию и риторику в Western Reserve Eclectic Institute, ныне Hiram College, в Хираме, штат Огайо, частном институте гуманитарных наук. Помимо преподавания, он также занимался юридической практикой, был бригадным генералом во время Гражданской войны, был президентом Западного резерва и был избран в U.С. Конгресс.
Инаугурация
Гарфилда состоялась 4 марта 1881 года. Он был популярным президентом, поддерживавшим процесс удержания на государственной службе. Он был последним из семи президентов, родившихся в бревенчатой хижине, и первым президентом, который остался левшой. Он был обоюдоострым и, как известно, развлекал друзей тем, что одновременно писал одной рукой на латыни, а другой — на греческом. Президент Гарфилд был убит выстрелом в спину 2 июля 1881 года Чарльзом Гито, которому Гарфилд отказал в просьбе о приеме на государственную службу.Александр Грэм Белл сконструировал электрический зонд, чтобы найти пулю, застрявшую в позвоночнике Гарфилда (подробности см. В примечании ), но после нескольких недель страданий 19 сентября 1881 года Гарфилд умер от инфекции и заражения крови. убили его, но нестерилизованные руки и оборудование врачей.
Гарфилд внес оригинальное доказательство теоремы Пифагора в сотни, записанные на протяжении веков. Хранилище оригинальных доказательств теоремы Пифагора см. В книге Элиша Лумиса «Предложение Пифагора». Гарфилд разработал свое доказательство в 1876 году, будучи членом Конгресса; Это был год, когда Александр Грэм Белл разработал телефон. Это «очень красивое доказательство теоремы Пифагора», как его описал Говард Ивс, было опубликовано в выпуске New-England Journal of Education от 1 апреля 1876 года. Очевидно, редактор журнала ошибочно (или, возможно, из политической шутки) назвал теорему Pons Asinorum или «Мост ослов», на самом деле прозвище теоремы о равнобедренном треугольнике (Элементы Евклида , Книга I, Предложение 5).Последняя теорема, возможно, получила свое название из-за того, что многие исследователи средневековья испытывали трудности с пониманием доказательства, диаграмма которого несколько напоминает мост, и поэтому не могли перейти через мост к последующим доказательствам в «Элементах » Евклида.
Рис. 2. Исаак Барроу, Элементы Евклида, (1686) из коллекции доктора Ф.Сид Колпас. Предложение 5 книги I (Евклид I-5) показано справа. Студент конца 17 века написал на полях: «Мост ослов» (сейчас он очень потускневший, выделен розовым).
Доказательство теоремы Пифагора Гарфилдом по существу состоит из диаграммы трапеции с основаниями \ (a \) и \ (b \) и высотой \ (a + b. \). Он смотрел на площадь диаграммы двумя разными способами. : как у трапеции и как у трех прямоугольных треугольников, два из которых конгруэнтны.
Доказательство Гарфилда
Рисунок 3. С титульного листа New-England Journal of Education (Том 3, № 14, 1 апреля 1876 г.) (изображение из Google Книги)
Рис. 4. Доказательство теоремы Пифагора Гарфилдом на странице 161 журнала New-England Journal of Education, 1 апреля 1876 г. (изображение из Google Книги)
Модернизированная версия доказательства Гарфилда из авторского Теорема Пифагора: восемь классических доказательств следует.
Рис. 5. Современная диаграмма, иллюстрирующая доказательство Гарфилда (из авторской книги Теорема Пифагора: восемь классических доказательств )
Более подробная версия приведенного выше доказательства приводится ниже.
- Начните с прямоугольного треугольника с катетами \ (a \) и \ (b \) и гипотенузой \ (c. \)
- Вытяните ногу \ (a \) на единицы \ (b \) и постройте дублирующий прямоугольный треугольник вдоль этого расширения.
- Верхняя нога \ (a \) параллельна исходной ноге \ (b \), поскольку на плоскости, если прямая перпендикулярна каждой из двух прямых, то эти две прямые параллельны.
- Нарисуйте сегмент XY, чтобы закрыть фигуру.
- Получившийся четырехугольник представляет собой трапецию с основаниями \ (a \) и \ (b \) и высотой \ (a + b. \)
- Трапеция состоит из двух равных прямоугольных треугольников и прямоугольного треугольника XYZ. Треугольник XYZ равнобедренный, так как две его стороны имеют длину \ (c. \). Угол XZY — прямой угол, так как угол 1 + угол XZY + угол 2 = 180 o и угол 1 + угол 2 = 90 o . (Острые углы прямоугольного треугольника дополняют друг друга.)
- Следовательно, площадь трапеции равна сумме площадей трех прямоугольных треугольников, из которых она составлена, два из которых совпадают.
- Выражая это соотношение алгебраически:
| Площадь трапеции | \ (= \) | \ (2 \, \) (площадь разностороннего прямоугольного треугольника) | \ (+ \) | площадь равнобедренного прямоугольного треугольника |
| \ (\ frac {1} {2} (a + b) (a + b) \) | \ (= \) | \ (2 \ влево (\ frac {1} {2} ab \ right) \) | \ (+ \) | \ (\ frac {1} {2} c ^ 2 \) |
| \ ((a + b) (a + b) \) | \ (= \) | \ (\, \, \, \, 2ab \) | \ (+ \) | \ (\, \, с ^ 2 \) |
| \ (а ^ 2 + 2ab + b ^ 2 \) | \ (= \) | \ (\, \, \, \, 2ab \) | \ (+ \) | \ (\, \, с ^ 2 \) |
| \ (а ^ 2 \, \, \, \, + \, \, \, \, b ^ 2 \) | \ (= \) | \ (\, \, с ^ 2 \) |
Примечание: Фильм PBS «Убийство президента» изображает врача, который посещал Гарфилда, как настаивающего на том, чтобы сам протянуть электронное устройство Александра Грэма Белла над животом Гарфилда, к большому неудовольствию Белла.Согласно программе, врач провел им только по правой стороне Гарфилда, настаивая на том, что пуля должна быть там. Оказалось, что пуля была на его левом боку, ближе к точке попадания. К тому времени безудержная инфекция охватила тело Гарфилда. Вернуться к биографии Гарфилда.
Список литературы
Кеннет Д. Акерман. Темная лошадка: неожиданные выборы и политическое убийство президента Джеймса А. Гарфилда. New York: Carroll & Graf Publishers, 2003 (теперь доступно в Viral History Press, Falls Church, Virginia, 2011).
Говард Ивс. Великие моменты в математике (до 1650 г.). Вашингтон, округ Колумбия: Математическая ассоциация Америки, 1983.
Джейн К. Финн. Малоизвестные факты о президентах США. Лэнхэм, Мэриленд: Rowman and Littlefield Publishing Group, 2016.
Джеймс А. Гарфилд. «Pons Asinorum». Журнал образования Новой Англии, Vol. 3, № 14, стр. 161. Бостон, Массачусетс: 1 апреля 1876 г. Доступно в Google Книгах.)
Дж. Л.Хейльброн. «Мост ослов». Британская энциклопедия. http://www.britannica.com/topic/The-Bridge-of-Asses
Сидней Дж. Колпас. Теорема Пифагора: восемь классических доказательств. Пало-Альто, Калифорния: Dale Seymour Publications, 1992 (все права принадлежат автору с 2011 года).
Элиша С. Лумис. Предложение Пифагора. Рестон, Вирджиния: Национальный совет учителей математики, 1968.
Джеймс Д. МакКейб. Наш мученик Президент.Жизнь и общественные службы генерала Джеймса А. Гарфилда. Филадельфия, Пенсильвания: National Publishing Company, 1881.
Роб Рэпли (режиссер, сопродюсер, автор телескрипта). «Убийство президента» в телесериале American Experience . PBS: первый эфир 2 февраля 2016 г. http://www.pbs.org/wgbh/americanexperience/films/garfield/
Указатель математических сокровищ
.
