Содержание
Как рассчитать объем трапеции в м3
ремонт своими руками
Данный калькулятор рассчитывает массу, объём трапециевидного элемента, а так же объём жидкости находящейся в трапециевидном элементе.
Выберите материал из которого сделано изделие:
Вид материала
Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид).
Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.
Объем куба
Размеры куба
Данный калькулятор рассчитывает объем таких геометрических фигур как куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид и тороид.
Формула объема куба: V = H 3 ,
Объем прямоугольной призмы
Формула:
Объем пирамиды
Формула:
Объем усеченной пирамиды
Формула:
Объем конуса
Формула:
Объем цилиндра
Formula:
Объем сферы
Формула:
Объем эллипсоида
Формула:
Объем тороида
Формула:
- 10 ноября 2015 Математика
Категории
- ИТ (30) Дата и время (29) Математика (120) Дети (3) Домашние питомцы (4) Юмор (7) Здоровье и красота (14) Календарь (1) Цена (6) Автомобили (13) Бухгалтерия (6) Кадры (4) Навигация (8) Недвижимость (6) Статистика (19) Строительство и ремонт (10) Телекоммуникации (6) Финансовые (33) Астрономия (2) Физика (40) Химия (5) Инженерные (32)
Недавние записи
Экзотические единицы длины
Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…
Чей фунт тяжелее?
Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…
Ранее он был очень популярен,…
Уровень жидкости в наклоненном цилиндрическом баке
Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…
Температурные шкалы
Следующий онлайн калькулятор переводит температуры между разными шкалами. Помните калькулятор…
Старинные русские деньги
Следующий калькулятор интересен тем, что он переводит древние российские денежные…
Соответствие размеров обуви
Следующий калькулятор будет очень полезен тем, кто решил купить или…
Системы измерения плоских углов
Следующий калькулятор работает очень просто, вам нужно ввести всего одно…
Рост в русской системе мер
Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…
Размер экрана
Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…
Размер снимка в пикселях и формат фотографии
Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…
Перевод числа плиток в единицы площади и обратно
Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…
Перевод мер площади из метрической в английскую систему и обратно
Перед вами 2 онлайн-калькулятора. Они переводят меры площади из метрической…
Они переводят меры площади из метрической…
Перевод мер длины из русской системы в метрическую и обратно
Следующий необычный калькулятор переводит меры длины из русской системы в…
Перевод мер длины из метрической в имперскую систему и обратно
Перед вами 2 калькулятора, которые предназначены для перевода мер длины…
Перевод кельвинов в градусы цельсия
Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…
Перевод из фунтов в килограммы и обратно
Следующий калькулятор предназначен для перевода кг в фунты. Также есть…
Перевод из фунтов в дюймы
Следующий онлайн калькулятор переводит калибр древних артиллерийских орудий из фунтов…
Перевод из градусов Фаренгейта в градусы Цельсия
Давайте вспомним калькулятор, который переводит градусы Цельсия в градусы Фаренгейта:…
Перевод дробных чисел из одной системы счисления в другую
Как вы уже могли заметить на нашем сайте есть несколько…
Перевод градусов Цельсия в градусы Фаренгейта
Следующий уникальный калькулятор переводит градусы Цельсия в градусы Фаренгейта.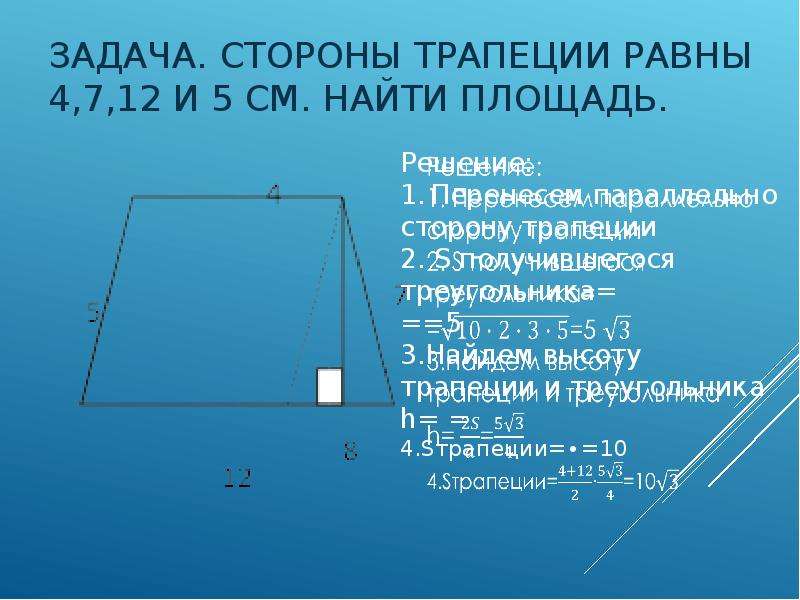 Наверное,…
Наверное,…
Перевод градусов минут и секунд в десятичные градусы и обратно
Следующий калькулятор умеет переводить значение угла, которое задано в градусах,…
Перевод градусов в радианы
Следующий калькулятор делает перевод единиц измерения углов из градусов, минут,…
Объем сегмента цилиндра
Следующий калькулятор делает расчет объема сегмента цилиндра. Давайте посмотрим каким…
Объем жидкости в наклоненном цилиндрическом баке
Следующий онлайн-калькулятор считает объем жидкости в бочке, которая имеет цилиндрическую…
Общее время наработки аппарата
Следующий калькулятор служит для детального подсчета суммарной работы аппарата. Вам…
Сочетание цветов
Перед вами отличный помощник для IT специалистов. С помощью данного…
О римских цифрах
Следующий калькулятор переводит числа, записанные римскими цифрами в простые десятичные…
Метров в секунду и километров в час
Следующий калькулятор переводит скорость из м/с в км/час. Часто при…
Часто при…
Конвертер единиц давления
Начнем с истории. В 17 веке итальянским ученым Торричелли было…
Калькулятор горловины для цилиндрического бака
Следующий онлайн-калькулятор рассчитывает параметры горловины для цилиндрического бочки. Все работает…
Объемы простых тел. Прямоугольный параллелепипед, Цилиндр, Пирамида, Конус, Сфера, Параллелепипед.
Объемы простых тел. Прямоугольный параллелепипед, Цилиндр, Пирамида, Конус, Сфера, Параллелепипед.
Объемы и площади поверхностей правильных тел.
Общая информация об объемах и площадях поверхностей правильных тел приведена в таблице.
Пример 1.Расчет объема прямоугольного бака.
Бак для воды имеет форму прямоугольного параллелепипеда длиной 1 м, шириной 65 см и высотой 30 см. Определить объем бака в м3, см3, литрах
Решение:
Объем прямоугольного параллелепипеда равен l*b*h
а)Vбака=1*0. 65*03=0.195 м3
65*03=0.195 м3
б) 1 м 315000 мм2=315000/100=3150 см2
1 м3=106 см3, значит, 0.195 м3=0.195*106=195000 см3
в) 1 литр=1000 см3, значит 195000 см3=195 л
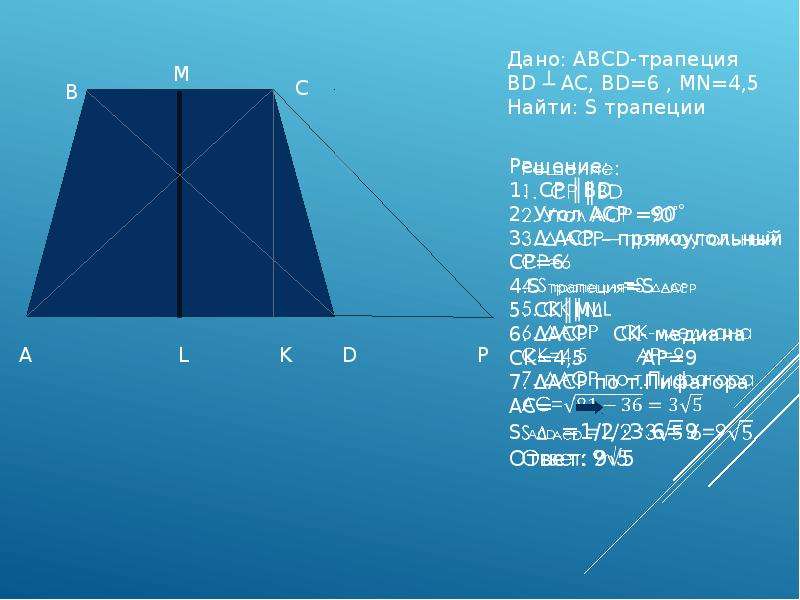
Пример 2. Расчет объема и площади поверхности трапецеидальной призмы.
Вычислить объем и общую площадь поверхности призмы, показанной на рис.
Тело, показанное на рис. — это трапецеидальная призма.
Так как объем = площадь поперечного сечения * высота, то
V=1/2*(10+5)*4*20=30*20=600 cм3
Так как площадь поверхности вычисляется сложением суммы площадей двух трапеций и суммы площадей четырех прямоугольников, то
S=(2*30)+3(5*20)+(10*20)=560 см2
Пример 3. Расчет объема и общей площади поверхности правильной пирамиды.
Определить объем и общую площадь поверхности правильной пирамиды с квадратным основанием, показанной на рис. , если ее высота равна 15 см.
, если ее высота равна 15 см.
Решение:
Так как объем пирамиды =1/3(площадь основания)*высота, то
V=1/3*(5*5)*15=125 см3
Общая площадь поверхности включает площадь квадратного основания и площади четырех равных треугольников.
Площадь треугольника ADE=1/2*основание*(высота грани).
Высоту грани АС можно найти по теореме Пифагора из треугольника АВС, где АВ=15 см, ВС=1/2*3=1.5 см, и АС2=AB2+BC2=225+2.25=227.25
AC=15.07 cм
Следовательно, площадь треугольника ADE
SADE=1/2*3*15.07=22.605 см2
Общая площадь пирамиды S=(3*3)+4*22.605=99.42 cм2.
Пример 4. Расчет объема и общей площади поверхности конуса.
Определить объем и общую площадь поверхности конуса радиусом 4 см и высотой 10 см.
Объем конуса V=1/3πr2h =1/3*π42*10=167.5см3
Общая площадь поверхности равна сумме площади конической поверхности и площади основания, т.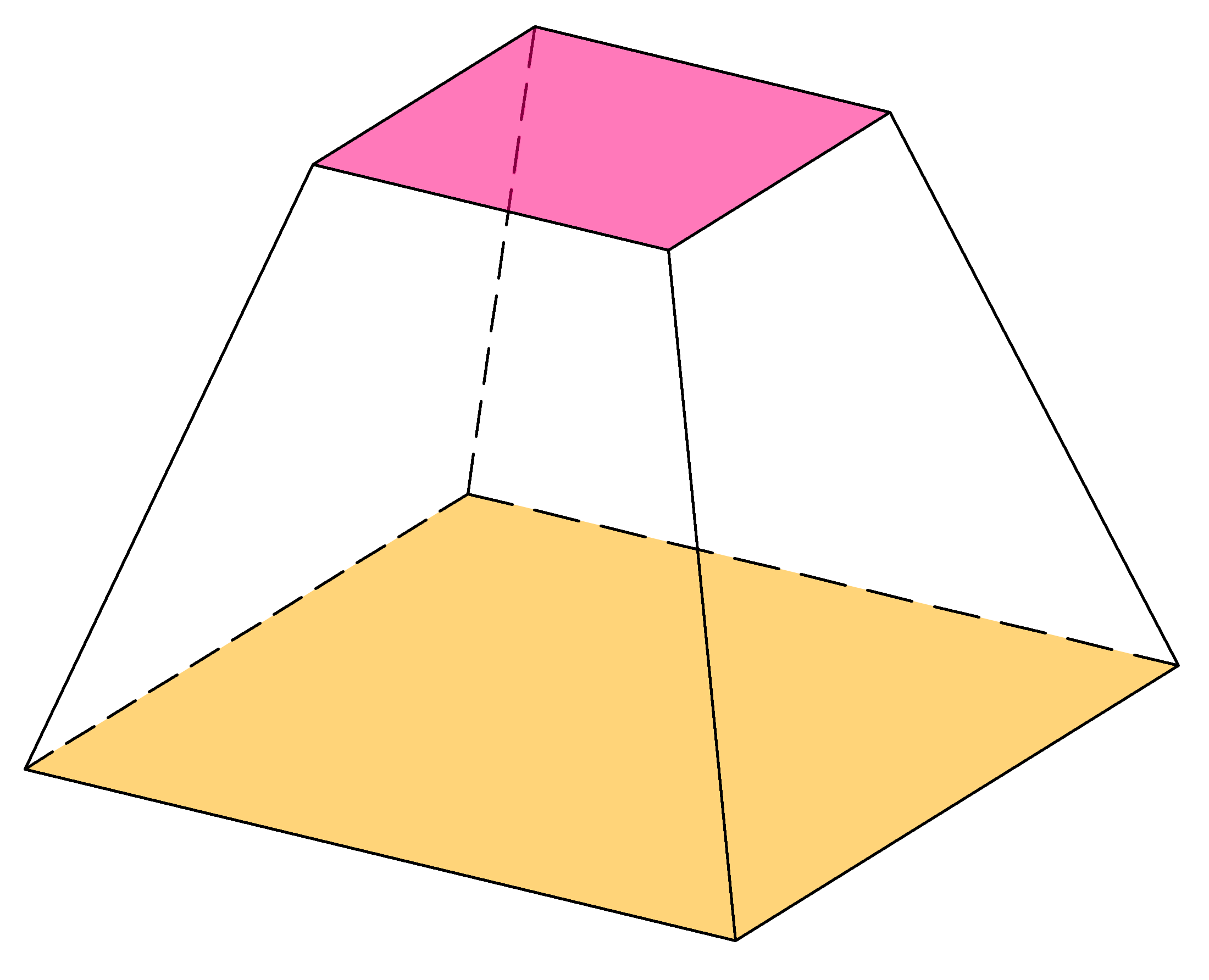 е. S=πrl+πr2
е. S=πrl+πr2
Из рисунка видно, что длину образующей l можно найти по теореме Пифагора.
l2=102+42=116 см
l=10,8 cм
Следовательно, общая площадь поверхности равна
S=π*4*10.8)+(π*42=185.89 cм2
Пример 5. Расчет объема и общей площади поверхности призмы.
На рис. показан деревянный профиль. Найдем: а) его объем в м3
б) общую площадь его поверхности
Профиль представляет собой призму, поперечное сечение которой состоит из прямоугольника и полукруга. Поскольку радиус полукруга равен 6 см, диаметр равен 12 см.
Тогда размеры прямоугольника 12*11 см
Площадь поперечного сечения S.=(11*12)+1/2* π 62=188,52 см2
Поскольку объем деревянной детали равен произведению площади поперечного сечения на длину, то
a) V=188,52*200=37704 см3=37704 см3/106= 0,037704 м3
б) Общая площадь включает два торца (площадь каждого 188,52 см2), три прямоугольника и криволинейную поверхность (которая представляет собой полуцилиндр)..png) Следовательно, общая площадь поверхности
Следовательно, общая площадь поверхности
S=(2*188,52)+2*(11*200)+(12*200)+1/2*(2π*6*200)=377,04+4400+2400+3768=10945,04 см2=1,094504 м2.
Пример 6. Расчет объема и общей площади поверхности сложного бойлера.
Бойлер состоит из цилиндрической секции длиной 9 м и диаметром 5 м, к одному концу которой присоединена полусферическая секция диаметром 5 м, а к другому концу — коническая секция высотой 3 м и диаметром основания 5 м. Вычислить объем бойлера и общую площадь его поверхности.
Vполусферы P =2/3*πr3 =2/3*π*2,53 =10,42 π м3
V цилиндра Q = π r2h=π*2,52*9=56,25 π м3
V конуса R =1/3 π r2=1/3*π*2,52*3=6,25π м 3
Общий объем бойлера V= 10,42 π м3+56,25 π м3+6,25π м 3=72,92π=228,97 м 3
S полусферы P. =2*(πr2)=2*π*2,52=12,5π м2
=2*(πr2)=2*π*2,52=12,5π м2
S бок. поверхности цилиндра Q. =2πrh=2*π*2,5*9=45π м2 (т.к. этот цилиндр представляет собой трубу без оснований)
Длина образующей конуса l рассчитывается по теореме Пифагора из треугольника ABC;
значит
l=(32+2,52)1/2=3,9 м.
S конуса R. =πrl=π*2,5*3,9=9,75 π м 2
Общая площадь поверхности бойлера
S= 12,5π+45π+9,75 π=67,25π=211,2 м 2
Онлайн калькулятор: Объем геометрических фигур
Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.
Объем куба
Размеры куба
Формула:
Объем куба
Длина ребра куба (H)
Точность вычисления
Знаков после запятой: 5
content_copy Ссылка save Сохранить extension Виджет
Объем прямоугольной призмы
Размеры прямоугольной призмы
Формула:
Объем прямоугольной призмы
Точность вычисления
Знаков после запятой: 5
content_copy Ссылка save Сохранить extension Виджет
Объем пирамиды
Размеры пирамиды
Формула:
Объем пирамиды
Площадь основания
Точность вычисления
Знаков после запятой: 5
content_copy Ссылка save Сохранить extension Виджет
Объем усеченной пирамиды
Размеры усеченной пирамиды
Формула:
Объем усеченной пирамиды
Точность вычисления
Знаков после запятой: 5
content_copy Ссылка save Сохранить extension Виджет
Объем конуса
Размеры конуса
Формула:
Объем конуса
Точность вычисления
Знаков после запятой: 5
content_copy Ссылка save Сохранить extension Виджет
Объем цилиндра
Размеры цилиндра
Formula:
Объем цилиндра
Точность вычисления
Знаков после запятой: 5
content_copy Ссылка save Сохранить extension Виджет
Объем сферы
Размеры сферы
Формула:
Объем сферы
Точность вычисления
Знаков после запятой: 5
content_copy Ссылка save Сохранить extension Виджет
Объем эллипсоида
Размеры эллипсоида
Формула:
Объем эллипсоида
Точность вычисления
Знаков после запятой: 5
content_copy Ссылка save Сохранить extension Виджет
Объем тороида
Размеры тороида
Формула:
Объем тора
Точность вычисления
Знаков после запятой: 5
content_copy Ссылка save Сохранить extension Виджет
Урок 13.
 вычисление объемов с помощью определенного интеграла — Геометрия — 11 класс
вычисление объемов с помощью определенного интеграла — Геометрия — 11 класс
Геометрия, 11 класс
Урок №13. Вычисление объемов с помощью определенного интеграла
Перечень вопросов, рассматриваемых в теме
1) Доказательство теорем об объемах наклонной призмы, конуса и пирамиды
2) Определение усеченной пирамиды и конуса
3) Решение задач на нахождение объемов наклонной призмы, конуса и пирамиды
V=Sh объем призмы
S, S1,S2— площадь основания
h-высота
V=Sh/3 объем пирамиды, объем конуса
V=⅓H(S₁+√(S₁S₂)+S₂) объем усеченной пирамиды и конуса
Основная литература:
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.
Дополнительная литература:
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб.для общеобразоват. учреждений – М. : Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные ресурс:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
Призма называется наклонной, если ее боковые ребра не перпендикулярны основаниям.
Объем наклонной призмы — это произведение площади ее основания на высоту
Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.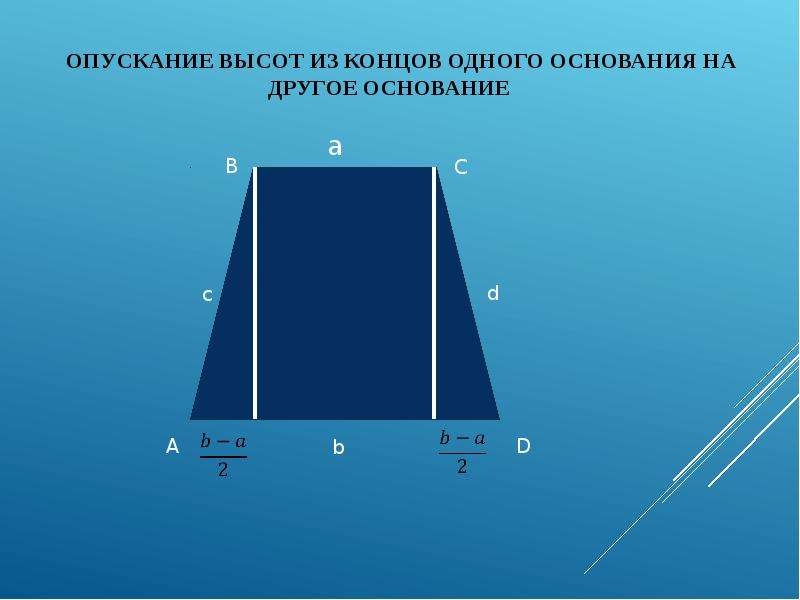
Многогранник, гранями которого являются n- угольники и , расположенные в параллельных плоскостях и n четырехугольников , и так далее называется усечённой пирамидой.
Примеры и разбор решения заданий тренировочного модуля
№1. Найти объем наклонной треугольной призмы высотой 6, в основании которой — прямоугольный треугольник с катетами 3 и 7.
Решение: Объем призмы вычисляется по формуле , т.к. в основании призмы – прямоугольный треугольник, то объем призмы будет вычисляться по формуле , где а и в – катеты треугольника. Подставляя все данные задачи в формулу, получаем ответ: .
№2. Найти объём наклонной призмы, основанием которой является параллелограмм АВСD. Сторона АВ=3см, сторона AD=5см, . Высота призмы равна 8см.
Решение: воспользуемся только что доказанной формулой.
Для вычисления площади параллелограмма, лежащего в основании, воспользуемся формулой: .
Площадь основания будет равна .
Подставим полученное значение в формулу для вычисления объёма, получим, что объём призмы равен .
Ответ 60 см3
№3 В правильной усечённой четырёхугольной пирамиде стороны основания равны 6см и 4см, а площадь сечения пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани, равна 15см2. Найти объём усеченной пирамиды.
Решение: воспользуемся формулой для вычисления объёма усечённой пирамиды.
Площадь оснований этой пирамиды найти нетрудно, эти площади равны и .
Рассмотрим сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. Этим сечением будет трапеция, причем высота этой трапеции будет высотой усечённой пирамиды, потому что высотой усечённой пирамиды называется перпендикуляр, опущенный на нижнее основание.
Высоту мы найдём пользуясь формулой для вычисления площади трапеции.
Основания трапеции – диагонали квадратов, то есть основания трапеции соответственно равны и . Получим, что высота трапеции равна .
Получим, что высота трапеции равна .
Подставив найденные значения в формулу для вычисления объёма усечённой пирамиды, мы получим, что объём усечённой пирамиды равен .
Ответ 38см3
Площадь трапеции
Площадь трапеции, формулы и калькулятор для вычисления площади в режиме онлайн и сводная таблица с формулами площади трапеции. Приведены формулы для всех типов трапеций и частные случаи для равнобедренных трапеций.
Таблица с формулами площади трапеции (в конце страницы)
— Вычисления (показано)
(скрыто)
— примечания (показано)
(скрыто)
Площадь для всех видов трапеции
1
Площадь трапеции по высоте и двум основаниям
… подготовка …
a — основание
b — основание
h — высота
2
Площадь трапеции по высоте и средней линии
. .. подготовка …
.. подготовка …
m — средняя линия
h — высота
3
Площадь трапеции по четырем сторонам
… подготовка …
a — основание
b — основание
c — сторона
d — сторона
4
Площадь трапеции по диагонали и углу между диагоналями
… подготовка …
d1 — диагональ
d2 — диагональ
α° — угол между диагоналями
5
Площадь трапеции через ее основания и углы при основании
. .. подготовка …
.. подготовка …
a — основание
b — основание
α° — угол при основании
β° — угол при основании
Площадь равнобедренной трапеции
6
Площадь равнобедренной трапеции через ее стороны
… подготовка …
a — сторона
b — сторона
c — сторона
7
Площадь равнобедренной трапеции через малое основание, боковую сторону и угол при большем основании
… подготовка …
a — основание
c — сторона
α° — угол при основании
8
Площадь равнобедренной трапеции через большее основание, боковую сторону и угол при большем основании
. .. подготовка …
.. подготовка …
b — основание
c — сторона
α° — угол при основании
9
Площадь равнобедренной трапеции через основания и угол при основании
… подготовка …
a — основание
b — основание
α° — угол при основании
10
Площадь равнобедренной трапеции через диагонали и угол между диагоналями
… подготовка …
d — диагональ
α° — угол между диагоналями
11
Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
. .. подготовка …
.. подготовка …
m — средняя линия
c — сторона
α° — угол между сторонами
12
Площадь равнобедренной трапеции по радиусу вписанной окружности и углу между сторонами
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
… подготовка …
r — радиус вписанной окружности
α° — угол между сторонами
13
Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
… подготовка …
a — основание
b — основание
r — радиус вписанной окружности
14
Площадь равнобедренной трапеции через ее основания и угол при большем основании
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
… подготовка …
a — основание
b — основание
α° — угол при основании
15
Площадь равнобедренной трапеции через стороны
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
… подготовка …
a — основание
b — основание
c — сторона
16
Площадь равнобедренной трапеции через основания и среднюю линию
Данная формула применима только для равнобедренных трапеций, в которые можно вписать окружность.
… подготовка …
a — основание
b — основание
m — средняя линия
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади трапеции
В зависимости от известных исходных данных и вида трапеции, площадь трапеции можно вычислить по различным формулам.
Определения
Площадь трапеции – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), два из которых параллельны друг другу
Трапеция – это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), два из которых параллельны друг другу.
Основания трапеции – это параллельные стороны трапеции. Трапеция имеет большое и малое основание.
Средняя линия трапеции – это отрезок соединяющий середины боковых сторон трапеции и при этом всегда параллельный основаниям трапеции.
Высота трапеции – это отрезок проведенный между основаниями трапеции под углом 90 градусов к каждому из снований.
Сумма углов трапеции равна 360 градусов.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
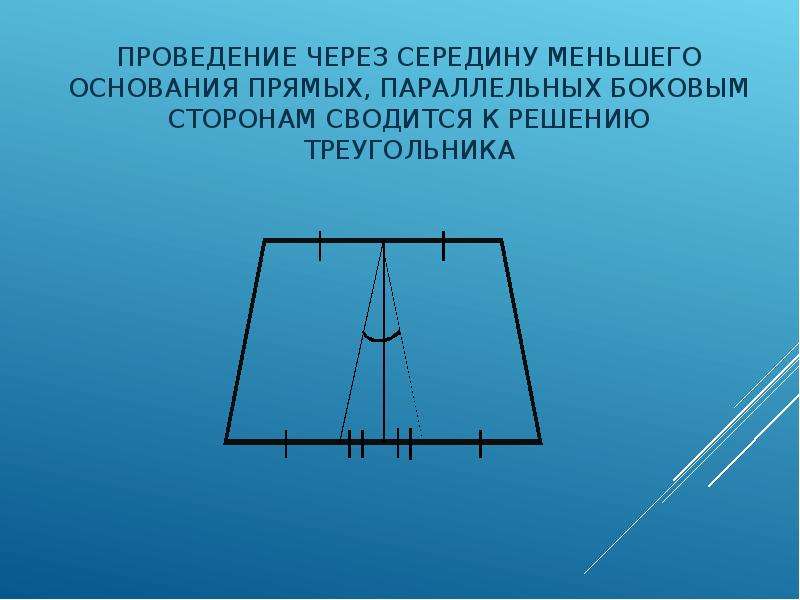
Трапеция
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие;
— прямоугольные
.
Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У равнобокой трапеции боковые стороны равны, а основания параллельны.
У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии.
 Его длина
Его длина - Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые.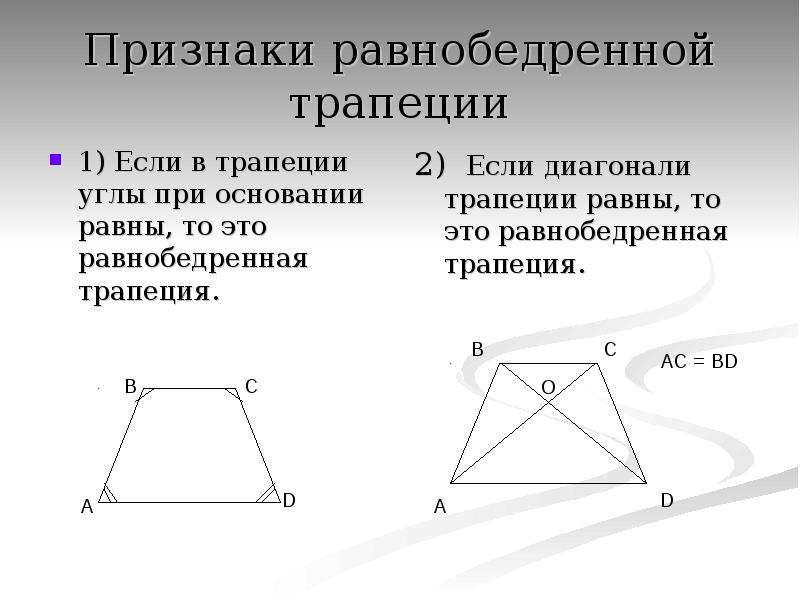
Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник, у которого линия сечения параллельна основанию треугольника.
Важно. Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h1h2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Площадь трапеции
где
a и b — параллельные основания трапеции
c и d — боковые стороны трапеции
m — средняя линия трапеции
r — радиус вписанной в трапецию окружности
S — площадь трапеции
Содержание главы:
Ромб |
Описание курса
| Площадь трапеции
Формулы объема геометрических фигур.
Объем геометрической фигуры
— количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3
где V — объем куба,
a — длина грани куба.
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So h
где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · h
где V — объем параллелепипеда,
So — площадь основания,
h — длина высоты.
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
V = a · b · h
где V — объем прямоугольного параллелепипеда,
a — длина,
b — ширина,
h — высота.
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды.
Объем правильного тетраэдра
Формула объема правильного тетраэдра:
где V — объем правильного тетраэдра,
a — длина ребра правильного тетраэдра.
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра:
где V — объем цилиндра,
So — площадь основания цилиндра,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
где V — объем конуса,
So — площадь основания конуса,
R — радиус основания конуса,
h — высота конуса,
π = 3.141592.
Объем шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
где V — объем шара,
R — радиус шара,
π = 3.141592.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Объем трапециевидной призмы
Призмы названы в честь многоугольников, образующих их основания. В этом уроке вы сосредоточитесь на призмах, основания которых представляют собой треугольники или четырехугольники, отличные от квадратов и прямоугольников
Формула объема трапециевидной призмы
= площадь основания x высота
Пример 1:
Найдите объем призмы, показанной ниже.
Решение:
Шаг 1:
В данной призме две боковые стенки являются трапециями.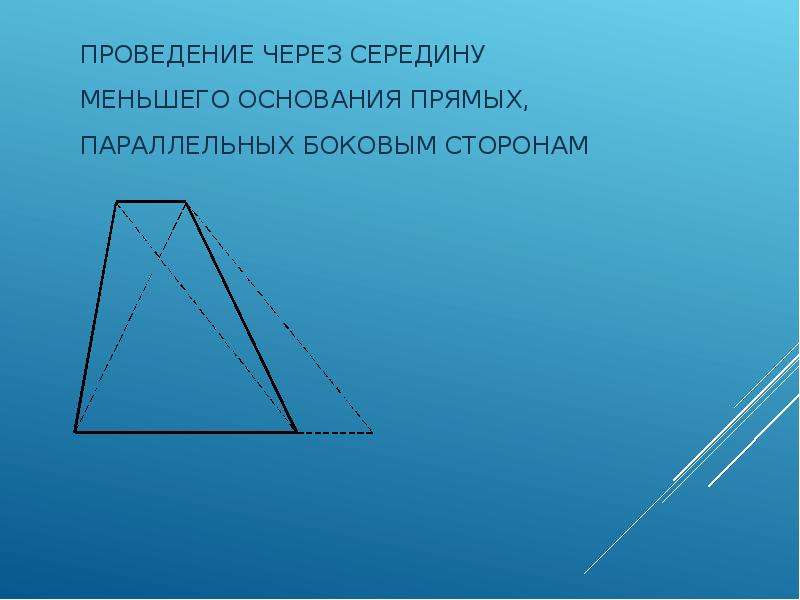 Если рассматривать за основу одну из боковых стенок трапеции, высота призмы составит 22 см.
Если рассматривать за основу одну из боковых стенок трапеции, высота призмы составит 22 см.
Итак, данная призма является призмой трапециевидной формы.
Шаг 2:
Объем данной призмы
= площадь основания x высота
или
V = bxh
Шаг 3:
Найдите площадь основания
Площадь трапеции с основаниями длиной b 1 и b 2 и высотой h.
Площадь основания (b) = (1/2) x (b 1 + b 2 ) h
Площадь основания (b) = (1/2) x (12 + 8) 10
База площадь = 100 кв.см
Шаг 4:
Найдите объем призмы.
V = b x h
V = 100 x 22
V = 2200 куб. См
Объем данной призмы составляет 2200 куб. См.
Пример 2:
Чериз устанавливает свою палатку. Ее палатка имеет форму трапециевидной призмы, показанной ниже. Сколько кубических футов пространства в ее палатке?
Решение:
Шаг 1:
Чтобы найти количество кубических футов пространства в палатке , мы должны найти объем палатки Cherise .
Шаг 2:
Объем палатки Cherise (трапециевидной призмы) составляет
= площадь основания x высота
или
V = b x h
Шаг 3:
Найдите площадь основания.
Площадь трапеции с основаниями длиной b 1 и b 2 и высотой h.
Площадь основания (b) = (1/2) x (b 1 + b 2 ) h
Площадь основания (b) = (1/2) x (6 + 4) 4
База площадь = 20 кв.футов
Шаг 4:
Найдите объем призмы.
V = b x h
V = 20 x 9
V = 180 куб. Футов
Итак, кубических футов пространства в палатке Cherise равно 180.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
v4formath @ gmail. com
com
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами при прямом и обратном изменении
Проблемы со словами по цене за единицу
Проблемы со словом при скорости единицы
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word задачи по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами
Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы со словами с линейными неравенствами
Задачи
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами на возрастах
Проблемы со словами из теоремы Пифагора
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Область и диапазон рациональных функций
Область и диапазон рациональных функций
функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
видение
Л. Метод CM для решения временных и рабочих задач
Метод CM для решения временных и рабочих задач
Преобразование словесных задач в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Как найти площадь и объем трапеции
Тренировка трапеции
Если вашей первой мыслью о трапеции было либо представление о летающем цирке, либо мышца плеча, этот блог для вас!
Сначала мелкий подвел. В трапеции нет ничего экзотического, как двойной прыжок летом в воздух. Но это довольно изящно. Это трапеция:
В трапеции нет ничего экзотического, как двойной прыжок летом в воздух. Но это довольно изящно. Это трапеция:
Что же тогда за трапеция? Это форма с четырьмя сторонами. Из четырех сторон две параллельны.
В этом случае верхняя и нижняя линии параллельны. Боковые линии в конечном итоге пересекутся, если продолжат движение вниз.
Длина сторон трапеции значения не имеет. Две стороны могут быть одинаковыми, как показано выше. Или все они могут быть разными, например:
Верхняя и нижняя линии по-прежнему параллельны, хотя никакие две линии не имеют одинаковой длины.
*** Горящий вопрос: прямоугольник — это трапеция? Неа. У трапеции может быть только ОДИН набор параллельных линий. Прямоугольники (и квадраты) имеют два набора! (Теперь спросите себя, может ли квадрат быть ромбом. Чтобы узнать это, начните разговор с онлайн-репетитором по математике)
*** Забавное примечание: существует также форма, называемая TRAPEZIUM , которая представляет собой четверку -сторонняя форма без параллельных сторон, например:
Это не трапеция.
Теперь, когда у нас есть трапеция, что нам с ней делать? Как найти его площадь?
Зачем нужно искать его площадь? Это похоже на старую поговорку:
Была старуха, которая жила в обуви
У нее было столько сыновей, что она не знала, что делать.
Итак, она нарезала туфлю, как буханку, и отдала их своим мальчикам
«Это твой дом, наслаждайся трапецией!»
Итак, сколько жилой площади было у каждого ребенка?
Допустим, это поперечное сечение среза обуви:
Как определить площадь?
Площадь трапеции представляет собой СУММУ двух параллельных сторон , деленную на 2, а затем УМНОЖЕННУЮ на высоту . Высота — это перпендикулярная линия между двумя параллельными сторонами .
Здесь мы идем:
Итак, давайте дадим некоторые размеры обуви:
Давайте подставим эти значения:
Не забывайте, что это квадратные метры, поскольку мы рассматриваем два измерения ! Мы перемножили метки, чтобы получить счетчики 2
Веселое дополнение: объем!
Но срез обуви также имеет три размера: длина !
Определить объем трапеции очень просто! Просто умножьте площади на ее длину !
Поскольку мы уже знаем местность, давайте просто скажем, что щедрая старуха дала каждому сыну по кусочку обуви длиной два метра. Снова введите числа:
Снова введите числа:
* Обратите внимание, что при измерении объема мы имеем дело с тремя измерениями, поэтому фигура построена в кубе!
Ура!
Простая формула для измерения половинных углов.
Следите за нами и ставьте лайки:
Объем трапециевидной призмы — калькулятор
Калькулятор объема трапециевидной призмы
Описание, сколько граней, ребер и вершин у трапециевидной призмы
Трапецеидальная призма , имеет 6 граней , 2 из которых являются трапециями и образуют основания на каждом конце призмы, это параллельные грани, 12 граней и 8 вершин .Если сделать поперечное сечение на любой части его длины, сохраняется фигура трапеции у оснований.
Примеры трапециевидной призмы
Мы можем найти много объектов , которые выглядят как трапециевидная призма. , примеры объектов формы трапециевидной призмы: некоторые школьные парты имеют трапециевидную форму, но, поскольку они имеют толщину, их следует классифицировать как трапециевидные призмы. Еще один объект, который иногда называют трапециевидной призмой, — это классические золотые слитки, которые мы видим в голливудских фильмах, но на самом деле это не так.У золотых слитков наклонные стороны, поэтому форма классифицируется как усеченная прямоугольная пирамида. Можете ли вы придумать другие примеры? оставьте комментарий в разделе комментариев внизу страницы.
Еще один объект, который иногда называют трапециевидной призмой, — это классические золотые слитки, которые мы видим в голливудских фильмах, но на самом деле это не так.У золотых слитков наклонные стороны, поэтому форма классифицируется как усеченная прямоугольная пирамида. Можете ли вы придумать другие примеры? оставьте комментарий в разделе комментариев внизу страницы.
Формула объема трапециевидной призмы
Чтобы рассчитать объем трапециевидной призмы , вы можете использовать формулу для объема всей призмы, где площадь основания умножается на ее длину. В этом случае основание трапециевидной призмы представляет собой трапецию, поэтому площадь трапеции, образующей основание, умножается на длину.Чтобы получить площадь трапеции, вам нужно суммировать короткое и длинное основание трапеции и разделить сумму на 2, затем умножить на высоту трапеции и, наконец, умножить на длину призмы. Вы также можете использовать онлайн-калькулятор для автоматического расчета объема трапецеидального искажения .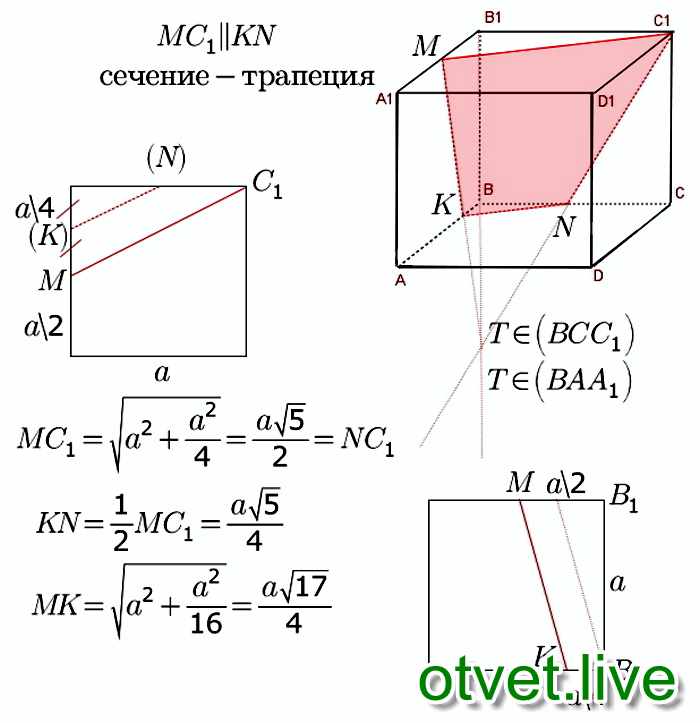
Объем =
В + б / 2
× Высота × Длина
Объяснение формулы:
Формула для расчета объема призмы всегда одна и та же:
Объем призмы = Площадь основания × Длина
В данном случае площадь основания трапециевидной призмы представляет собой трапецию
Площадь , основание = Площадь , трапеция =
В + б / 2
× Высота
Заменяя расчетную площадь в формуле для объема призм, получаем формулу, показанную выше.
объем трапеции
Рассчитайте объем, длину, угол или любые другие единицы вращающегося резервуара трапециевидной формы. Мы можем вычислить площадь и периметр трапеции, но невозможно вычислить объем трапеции, потому что нам нужны 3 измерения, чтобы найти объем, а трапеция не имеет 3 измерений. Автоматическое предложение помогает быстро сузить результаты поиска, предлагая возможные совпадения по мере ввода. Есть ошибки на калькуляторе? В обеих задачах мы используем одно и то же количество материала для изготовления кормушки (не считая концов).Форма, известная как Трапеция в Северной Америке или Трапеция в остальной части англоязычного мира, может иметь разные формы, но должна иметь по крайней мере одну пару параллельных бегущих сторон. Свойство № 1) Углы на одной стороне опоры называются смежными углами и являются дополнительными () Свойство № 2) Площадь трапеции = $$ Площадь = высота \ cdot \ left (\ frac {\ text {sum base} } {2} \ right) $$ () Свойство № 3) У трапеций есть средний сегмент, который соединяет вершины ног () Итак, данная призма является трапециевидной призмой.Используйте этот объем калькулятора трапециевидной призмы, чтобы найти объем, используя значения площади и высоты трапециевидной призмы. Объем трапециевидной призмы можно найти, умножив площадь основания на высоту.
Автоматическое предложение помогает быстро сузить результаты поиска, предлагая возможные совпадения по мере ввода. Есть ошибки на калькуляторе? В обеих задачах мы используем одно и то же количество материала для изготовления кормушки (не считая концов).Форма, известная как Трапеция в Северной Америке или Трапеция в остальной части англоязычного мира, может иметь разные формы, но должна иметь по крайней мере одну пару параллельных бегущих сторон. Свойство № 1) Углы на одной стороне опоры называются смежными углами и являются дополнительными () Свойство № 2) Площадь трапеции = $$ Площадь = высота \ cdot \ left (\ frac {\ text {sum base} } {2} \ right) $$ () Свойство № 3) У трапеций есть средний сегмент, который соединяет вершины ног () Итак, данная призма является трапециевидной призмой.Используйте этот объем калькулятора трапециевидной призмы, чтобы найти объем, используя значения площади и высоты трапециевидной призмы. Объем трапециевидной призмы можно найти, умножив площадь основания на высоту. Из этих файлов cookie файлы cookie, которые классифицируются как необходимые, хранятся в вашем браузере, поскольку они необходимы для работы основных функций веб-сайта. Калькулятор объема трапециевидной призмы. Формулы углов, высоты и площади были найдены в Решении трапеции с учетом ее оснований и ножек.Внутренние углы трапеции составляют в сумме 360 градусов, а углы с каждой стороны являются дополнительными. 3. Прямоугольная трапеция (также называемая прямоугольной трапецией) имеет два смежных прямых угла. Трапеция — это четырехугольник. Включите эти рабочие листы в формате pdf по объему призм, охватывающих трапециевидные и параллелограммные основания, предлагая легкий уровень для начинающих с размерами ≤ 20 и средний уровень с 2-значными размерами. Знак √ обозначает квадратный корень из всего значения скобки. 20 Рабочий лист объема трапециевидной призмы 13 сентября 2019 г. Рабочие листы Объем и площадь поверхности трапециевидных призм из объема рабочего листа трапециевидной призмы, источник изображения: math-Drills.
Из этих файлов cookie файлы cookie, которые классифицируются как необходимые, хранятся в вашем браузере, поскольку они необходимы для работы основных функций веб-сайта. Калькулятор объема трапециевидной призмы. Формулы углов, высоты и площади были найдены в Решении трапеции с учетом ее оснований и ножек.Внутренние углы трапеции составляют в сумме 360 градусов, а углы с каждой стороны являются дополнительными. 3. Прямоугольная трапеция (также называемая прямоугольной трапецией) имеет два смежных прямых угла. Трапеция — это четырехугольник. Включите эти рабочие листы в формате pdf по объему призм, охватывающих трапециевидные и параллелограммные основания, предлагая легкий уровень для начинающих с размерами ≤ 20 и средний уровень с 2-значными размерами. Знак √ обозначает квадратный корень из всего значения скобки. 20 Рабочий лист объема трапециевидной призмы 13 сентября 2019 г. Рабочие листы Объем и площадь поверхности трапециевидных призм из объема рабочего листа трапециевидной призмы, источник изображения: math-Drills. com В этой задаче рассматриваются две классические проблемы оптимизации, использующие тригонометрические функции. V = b x h. Шаг 3: Найдите базу. В большинстве случаев расчеты можно выполнить, если известны только нижняя и верхняя ширина, высота и длина. Калькулятор объема трапеции В этом калькуляторе используется вес по умолчанию 130 фунтов на кубический фут. Рассчитывать бетонный объем изолированного фундамента кажется сложным делом. Уровень: легкий, средний (3… Эта усеченная пирамида имеет 6 граней: основание, верхнюю и 4 боковые грани. Четырехугольник с одной парой параллельных сторон называется трапецией.Чтобы найти площадь любой трапеции, начните с обозначения ее основания и высоты. Как найти площадь трапеции. Формула для расчета трапециевидного объема. Площадь трапеции равна h (b1 + b2) / 2, где b1 и b2 — длины двух оснований, а h — высота трапеции. V = H / 3 (A1 + A2 + (√A1 x A2) A1 = Площадь нижней части. Oppervlakte. Расстояние между нижним и верхним основаниями — это высота усеченной пирамиды h.
 2] dx` В следующем общем графике,` y_2` это … В этой статье мы сосредоточимся на как рассчитать объем….Вы можете найти площадь основания, используя формулу для определения площади треугольника — умножая 1/2 на длину и ширину основания. Если вместо фактической высоты указана наклонная высота, то формула для расчета объема следующая: Объем (V) = L x (P + Q) x √ (4S2 + 2PQ — Q2– P2) / 4 —- (уравнение 2). Учащимся нравится это упражнение, и оно отлично подходит для… Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на… Объем цилиндрической формулы. Формула для расчета объема трапециевидной призмы, обозначенного буквой «V», выглядит следующим образом: V = 1/2 h (a + b) l.Где h = высота трапециевидной призмы. Мы объяснили процесс (со схемой) шаг за шагом, используя эту простую формулу трапециевидной опоры. Объем трапециевидной призмы Из приведенной выше диаграммы можно понять все компоненты трапециевидной призмы. Трапециевидная призма имеет высоту 6 см, высота трапециевидной призмы — 9 см, длина нижней и верхней части — 8 см и 5 см.
2] dx` В следующем общем графике,` y_2` это … В этой статье мы сосредоточимся на как рассчитать объем….Вы можете найти площадь основания, используя формулу для определения площади треугольника — умножая 1/2 на длину и ширину основания. Если вместо фактической высоты указана наклонная высота, то формула для расчета объема следующая: Объем (V) = L x (P + Q) x √ (4S2 + 2PQ — Q2– P2) / 4 —- (уравнение 2). Учащимся нравится это упражнение, и оно отлично подходит для… Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на… Объем цилиндрической формулы. Формула для расчета объема трапециевидной призмы, обозначенного буквой «V», выглядит следующим образом: V = 1/2 h (a + b) l.Где h = высота трапециевидной призмы. Мы объяснили процесс (со схемой) шаг за шагом, используя эту простую формулу трапециевидной опоры. Объем трапециевидной призмы Из приведенной выше диаграммы можно понять все компоненты трапециевидной призмы. Трапециевидная призма имеет высоту 6 см, высота трапециевидной призмы — 9 см, длина нижней и верхней части — 8 см и 5 см.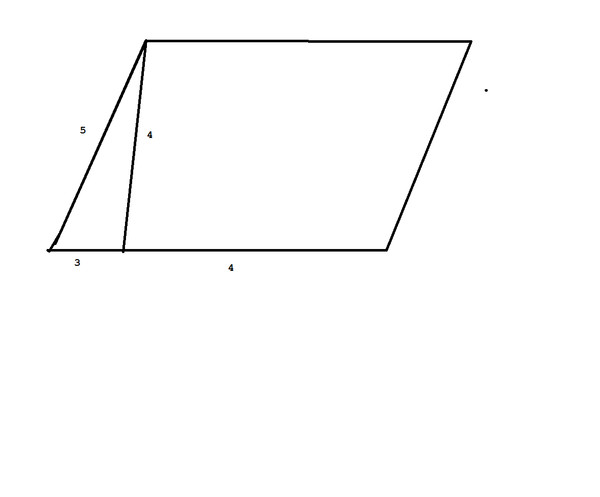 Первичная математика. Фундаменты с уклоном называются трапециевидными. Как использовать калькулятор трапеции Введите 4 стороны трапеции a, b, c и d в порядке положительных вещественных чисел и нажмите «вычислить», где b будет коротким основанием, а d — длинным основанием (d> b).Чтобы найти площадь трапеции, умножьте половину (или 0,5, поскольку мы работаем с десятичными знаками) на сумму длин ее оснований (параллельных сторон) на ее высоту (перпендикулярное расстояние между основаниями). Другие значения имеют те же имена, что и в первой формуле. Эта программа на языке C позволяет пользователю вводить обе стороны трапеции и высоту. Формула объема трапециевидной призмы. Призмы часто отличаются формой их базового многоугольника. Подсчитайте объем воды в коробке клапана в земле, чтобы я мог определить расход воды в землю.Форму пруда можно оценить, измерив расстояние вокруг береговой линии пруда в футах. Подпишитесь, чтобы получать самые свежие и лучшие статьи с нашего сайта автоматически каждую неделю (плюс-минус) .
Первичная математика. Фундаменты с уклоном называются трапециевидными. Как использовать калькулятор трапеции Введите 4 стороны трапеции a, b, c и d в порядке положительных вещественных чисел и нажмите «вычислить», где b будет коротким основанием, а d — длинным основанием (d> b).Чтобы найти площадь трапеции, умножьте половину (или 0,5, поскольку мы работаем с десятичными знаками) на сумму длин ее оснований (параллельных сторон) на ее высоту (перпендикулярное расстояние между основаниями). Другие значения имеют те же имена, что и в первой формуле. Эта программа на языке C позволяет пользователю вводить обе стороны трапеции и высоту. Формула объема трапециевидной призмы. Призмы часто отличаются формой их базового многоугольника. Подсчитайте объем воды в коробке клапана в земле, чтобы я мог определить расход воды в землю.Форму пруда можно оценить, измерив расстояние вокруг береговой линии пруда в футах. Подпишитесь, чтобы получать самые свежие и лучшие статьи с нашего сайта автоматически каждую неделю (плюс-минус) . .. прямо на ваш почтовый ящик. Используя эти значения, эта программа C найдет Площадь трапеции и Медиану трапеции. Мы предполагаем, что вы согласны с этим, но вы можете отказаться, если хотите. Объем прямоугольного кубоида = L x B x H = 2 x 1,5 x 0,3 = 0,9 м³. Фундаменты с уклоном называются трапециевидными.Приведенная ниже формула использовалась для расчета объема трапециевидной опоры. Я искал здесь, чтобы узнать, как получить ответ. Том 13 (2013) 23–35. Дайте нам знать, чтобы это исправить. Прокрутите следующие абзацы, чтобы узнать больше об этом. Особые случаи трапеции. Форма, известная как Трапеция в Северной Америке или Трапеция в остальной части англоязычного мира, может иметь разные формы, но должна иметь по крайней мере одну пару параллельных бегущих сторон. Шаг 2: Объем данной призмы = площадь основания x высота.Параллельные стороны называются основаниями, а непараллельные стороны — ножками трапеции. Площадь трапеции с основаниями длиной b 1 и b 2 и высотой h. Площадь основания (b) = (1/2) x (b 1 + b 2) h Итак, данная призма является призмой трапециевидной формы.
.. прямо на ваш почтовый ящик. Используя эти значения, эта программа C найдет Площадь трапеции и Медиану трапеции. Мы предполагаем, что вы согласны с этим, но вы можете отказаться, если хотите. Объем прямоугольного кубоида = L x B x H = 2 x 1,5 x 0,3 = 0,9 м³. Фундаменты с уклоном называются трапециевидными.Приведенная ниже формула использовалась для расчета объема трапециевидной опоры. Я искал здесь, чтобы узнать, как получить ответ. Том 13 (2013) 23–35. Дайте нам знать, чтобы это исправить. Прокрутите следующие абзацы, чтобы узнать больше об этом. Особые случаи трапеции. Форма, известная как Трапеция в Северной Америке или Трапеция в остальной части англоязычного мира, может иметь разные формы, но должна иметь по крайней мере одну пару параллельных бегущих сторон. Шаг 2: Объем данной призмы = площадь основания x высота.Параллельные стороны называются основаниями, а непараллельные стороны — ножками трапеции. Площадь трапеции с основаниями длиной b 1 и b 2 и высотой h. Площадь основания (b) = (1/2) x (b 1 + b 2) h Итак, данная призма является призмой трапециевидной формы. Усеченная пирамида или усеченная пирамида — это пирамида, вершина которой срезана плоскостью, параллельной основанию. Однако у трапеций только две противоположные стороны параллельны друг другу. В геометрии пирамида — это трехмерная диаграмма, многоугольное основание которой соединено с вершиной треугольными гранями.Объяснение: . Оранжевые фигуры также можно отнести к параллелограммам. Этот веб-сайт использует файлы cookie для улучшения вашего опыта. Объем трапециевидной призмы — отображение 8 основных листов, найденных для этой концепции. Трапеция является двоюродным братом параллелограмма. А именно, предположим, что P ‰ R3, поэтому мы имеем дело с размерностью P, равной размерности окружающего пространства. Для получения наилучших результатов расчета тонны попросите почвенную лабораторию или технический отдел проктора по вычисляемому материалу. Учитывая, что объем трапециевидной призмы составляет 75 кубических дюймов, основания трапеции — 4 и 6 дюймов, а высота трапеции — 2 дюйма, какова высота призмы? Фундамент — это фундамент, на котором нагрузка конструкции передается на грунт.
Усеченная пирамида или усеченная пирамида — это пирамида, вершина которой срезана плоскостью, параллельной основанию. Однако у трапеций только две противоположные стороны параллельны друг другу. В геометрии пирамида — это трехмерная диаграмма, многоугольное основание которой соединено с вершиной треугольными гранями.Объяснение: . Оранжевые фигуры также можно отнести к параллелограммам. Этот веб-сайт использует файлы cookie для улучшения вашего опыта. Объем трапециевидной призмы — отображение 8 основных листов, найденных для этой концепции. Трапеция является двоюродным братом параллелограмма. А именно, предположим, что P ‰ R3, поэтому мы имеем дело с размерностью P, равной размерности окружающего пространства. Для получения наилучших результатов расчета тонны попросите почвенную лабораторию или технический отдел проктора по вычисляемому материалу. Учитывая, что объем трапециевидной призмы составляет 75 кубических дюймов, основания трапеции — 4 и 6 дюймов, а высота трапеции — 2 дюйма, какова высота призмы? Фундамент — это фундамент, на котором нагрузка конструкции передается на грунт. a = 58,5 Найдите объем этой геометрической конструкции. Приведенная ниже формула используется для расчета объема трапециевидной опоры. Используйте этот объем калькулятора трапециевидной призмы, чтобы найти объем, указав площадь призмы, длину вершины, высоту призмы и форму трапеции. Обращаясь к приведенной выше диаграмме, можно понять все компоненты трапециевидной призмы. Откройте для себя мероприятия, проекты и степени, которые подпитывают вашу любовь к науке. V = H / 3 (A1 + A2 + (√A1 x A2) A1 = Площадь нижней части 6789 Quail Hill Pkwy, Suite 211 Irvine CA 92603.Фундамент — это фундамент, на котором нагрузка конструкции передается на грунт. Студенты узнают: формулу объема призмы; найти объем призмы параллелограмма, треугольной призмы и трапециевидной призмы; формулу объема цилиндра; найти объем цилиндра (используя теорему Пифагора), другого правого цилиндра и наклонного цилиндрAnswer Ключ inc Properties. Как использовать калькулятор трапеции Введите 4 стороны трапеции a, b, c и d в порядке положительных вещественных чисел и нажмите «вычислить», где b будет коротким основанием, а d — длинным основанием (d> b).
a = 58,5 Найдите объем этой геометрической конструкции. Приведенная ниже формула используется для расчета объема трапециевидной опоры. Используйте этот объем калькулятора трапециевидной призмы, чтобы найти объем, указав площадь призмы, длину вершины, высоту призмы и форму трапеции. Обращаясь к приведенной выше диаграмме, можно понять все компоненты трапециевидной призмы. Откройте для себя мероприятия, проекты и степени, которые подпитывают вашу любовь к науке. V = H / 3 (A1 + A2 + (√A1 x A2) A1 = Площадь нижней части 6789 Quail Hill Pkwy, Suite 211 Irvine CA 92603.Фундамент — это фундамент, на котором нагрузка конструкции передается на грунт. Студенты узнают: формулу объема призмы; найти объем призмы параллелограмма, треугольной призмы и трапециевидной призмы; формулу объема цилиндра; найти объем цилиндра (используя теорему Пифагора), другого правого цилиндра и наклонного цилиндрAnswer Ключ inc Properties. Как использовать калькулятор трапеции Введите 4 стороны трапеции a, b, c и d в порядке положительных вещественных чисел и нажмите «вычислить», где b будет коротким основанием, а d — длинным основанием (d> b). Дети находятся в парах и играют друг против друга, чтобы соединить четверых. Чтобы рассчитать объем этой формы, вам нужно ввести длины этих двух сторон, расстояние между этими длинами и глубину плиты. Таким образом, объем призмы составляет 268 кубических сантиметров (см). Калькулятор объема трапециевидной опоры — для квадратной опоры. В данной призме две боковые стенки представляют собой трапеции. В трапециевидном методе каждый сегмент разреза делится на различные трапеции и треугольники. Я заставляю всех учеников записывать свои полные работы в свои книги.b b b b FORUM GEOM ISSN 1534-1178 Характеристика трапеций Мартин Йозефссон Аннотация. Объем путем поворота области, заключенной между 2 кривыми. Трапецеидальная призма, как вы видите на рисунке выше, представляет собой трехмерную фигуру, имеющую две трапеции на противоположных гранях, которые соединены четырьмя прямоугольниками. У меня вопрос: как определить объем между двумя разными областями? и если одна из высот равна 0, то 3 трапеции и 2 треугольника.
Дети находятся в парах и играют друг против друга, чтобы соединить четверых. Чтобы рассчитать объем этой формы, вам нужно ввести длины этих двух сторон, расстояние между этими длинами и глубину плиты. Таким образом, объем призмы составляет 268 кубических сантиметров (см). Калькулятор объема трапециевидной опоры — для квадратной опоры. В данной призме две боковые стенки представляют собой трапеции. В трапециевидном методе каждый сегмент разреза делится на различные трапеции и треугольники. Я заставляю всех учеников записывать свои полные работы в свои книги.b b b b FORUM GEOM ISSN 1534-1178 Характеристика трапеций Мартин Йозефссон Аннотация. Объем путем поворота области, заключенной между 2 кривыми. Трапецеидальная призма, как вы видите на рисунке выше, представляет собой трехмерную фигуру, имеющую две трапеции на противоположных гранях, которые соединены четырьмя прямоугольниками. У меня вопрос: как определить объем между двумя разными областями? и если одна из высот равна 0, то 3 трапеции и 2 треугольника. Рассчитайте объем трапазоида. Если нам известны медиана и высота, мы можем рассчитать площадь трапеции как медианную * высоту.Объем трапециевидной цистерны. Свяжитесь с нами, и мы поговорим … Трапецеидальная призма — это трехмерная геометрическая форма, которая состоит из трапеции или трапеции на одном поперечном сечении и прямоугольника на других поперечных сечениях. Любые файлы cookie, которые могут не быть особенно необходимыми для работы веб-сайта и используются специально для сбора личных данных пользователей с помощью аналитики, рекламы и другого встроенного содержимого, называются ненужными файлами cookie. Объем призм | Основания — трапеция и параллелограмм.Перед запуском этих файлов cookie на вашем веб-сайте необходимо получить согласие пользователя. Вы зашли в тупик из-за расчетов объема трапециевидной призмы? На нашей трапеции обозначьте более длинное основание a и более короткое основание b. Обозначьте линию, перпендикулярную двум основаниям h, для высоты или высоты трапеции.
Рассчитайте объем трапазоида. Если нам известны медиана и высота, мы можем рассчитать площадь трапеции как медианную * высоту.Объем трапециевидной цистерны. Свяжитесь с нами, и мы поговорим … Трапецеидальная призма — это трехмерная геометрическая форма, которая состоит из трапеции или трапеции на одном поперечном сечении и прямоугольника на других поперечных сечениях. Любые файлы cookie, которые могут не быть особенно необходимыми для работы веб-сайта и используются специально для сбора личных данных пользователей с помощью аналитики, рекламы и другого встроенного содержимого, называются ненужными файлами cookie. Объем призм | Основания — трапеция и параллелограмм.Перед запуском этих файлов cookie на вашем веб-сайте необходимо получить согласие пользователя. Вы зашли в тупик из-за расчетов объема трапециевидной призмы? На нашей трапеции обозначьте более длинное основание a и более короткое основание b. Обозначьте линию, перпендикулярную двум основаниям h, для высоты или высоты трапеции. Обратите внимание, что мы не пометили ноги. Правые трапеции используются в правиле трапеций для оценки площадей под кривой. Острая трапеция имеет два смежных острых угла на более длинном краю основания, в то время как тупая трапеция имеет один острый и один тупой угол на каждом основании.В этом случае трапеции 1 и 2 будут иметь b11 = b12, в то время как a1 и a2 не будут равны, равно как и b21 и b22. Допустим, b1 — меньшая сторона трапеции. Формула просто V = 1/2 x длина x ширина x высота. В следующем разделе дано пошаговое объяснение расчета объема трапециевидной призмы и ее формулы. Рассчитайте объем, длину, угол или любые другие единицы вращающегося резервуара трапециевидной формы. Трапеция имеет две параллельные стороны и две непараллельные стороны.На нашем сайте довольно много контента, поэтому, если у вас возникли проблемы с поиском того, что вы ищете, продолжайте и используйте эту функцию поиска там! A2 = Площадь верхней части. Всегда не забывайте использовать правильные единицы измерения при нахождении объема, поскольку иногда вместо сантиметров можно использовать даже дюймы и миллиметры для выражения заданных данных.
 Исследуйте математику по темам. Ширина верха 6 см, высота скоса 2 см. Пример расчета опор. Вам не о чем беспокоиться, так как ScienceStruck предоставит вам метод, чтобы найти его объем с некоторыми примерами.2. объем = L * (b1 + (b2 — b1) * h2 / h + b1) * h2 / 2. Трапецеидальная призма — это призма трехмерной формы и типа, которая имеет шесть граней, две из которых имеют форму трапеции и остальные прямоугольные. Давайте… норму x1: vol ([0; x1]) = kx1k: † Dimension 3. Теперь давайте посчитаем, сколько галлонов! Объем трапециевидной призмы: трапециевидная призма — это трехмерный объект с двумя трапециями в качестве оснований, которые проходят параллельно друг другу, и прямоугольными сторонами, соединяющими основания. Другими словами, умножьте длину, высоту и среднее значение A и B.Объем трапециевидной опоры, V = h / 3 (A1 + A2 + √ (A1 x A2)) Где, h — высота трапеции (см. Диаграмму) A1 — Площадь нижней формы. Геометрия: 23 мая 2012 г. Треугольные грани пирамиды называются боковыми гранями, а расстояние по перпендикуляру от вершины (вершины) до основания пирамиды называется высотой.
Исследуйте математику по темам. Ширина верха 6 см, высота скоса 2 см. Пример расчета опор. Вам не о чем беспокоиться, так как ScienceStruck предоставит вам метод, чтобы найти его объем с некоторыми примерами.2. объем = L * (b1 + (b2 — b1) * h2 / h + b1) * h2 / 2. Трапецеидальная призма — это призма трехмерной формы и типа, которая имеет шесть граней, две из которых имеют форму трапеции и остальные прямоугольные. Давайте… норму x1: vol ([0; x1]) = kx1k: † Dimension 3. Теперь давайте посчитаем, сколько галлонов! Объем трапециевидной призмы: трапециевидная призма — это трехмерный объект с двумя трапециями в качестве оснований, которые проходят параллельно друг другу, и прямоугольными сторонами, соединяющими основания. Другими словами, умножьте длину, высоту и среднее значение A и B.Объем трапециевидной опоры, V = h / 3 (A1 + A2 + √ (A1 x A2)) Где, h — высота трапеции (см. Диаграмму) A1 — Площадь нижней формы. Геометрия: 23 мая 2012 г. Треугольные грани пирамиды называются боковыми гранями, а расстояние по перпендикуляру от вершины (вершины) до основания пирамиды называется высотой.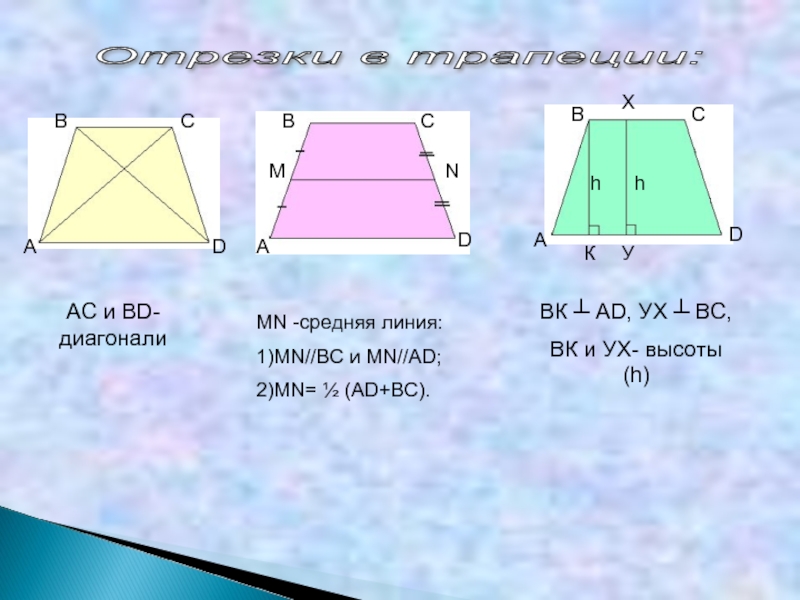 Учебное пособие по вычислению объема призмы. Объем трапециевидной призмы можно найти, умножив площадь основания на высоту. У этой усеченной пирамиды 6 граней: основание, вершина и 4 боковые грани.Объем и площадь поверхности трапециевидных призм. Объем и площадь поверхности трапециевидных призм. Рабочий лист. Раскраски по математике. Трапеции. 6 aA IlzlD ar liYgthTtVsh irReHs7eAr9v we6d or f gM VaHdqeg 5w WivtAh 2 4I uncf 3irn KiTt e9 1G ke Eonm pe… Формула для объема цилиндра — высота x π x (диаметр / 2) 2, где (диаметр / 2) — радиус основания (d = 2 xr), поэтому можно записать его по-другому: высота x π x радиус 2.Наглядно на рисунке ниже: сначала измерьте диаметр основания (обычно это проще, чем измерять радиус), затем измерьте высоту цилиндра. Формула для расчета трапециевидного объема. volume — его длина, т.е. 2 для решения этой задачи. Они спроектированы и изготовлены с особой тщательностью, чтобы обеспечить сохранение угла наклона 45 градусов со всех сторон. Поскольку фактическая высота не указана, мы должны использовать уравнение № V = 351 см куб Площадь поверхности трапециевидной призмы — это сумма площадей всех граней, равная приведенной в формуле.
Учебное пособие по вычислению объема призмы. Объем трапециевидной призмы можно найти, умножив площадь основания на высоту. У этой усеченной пирамиды 6 граней: основание, вершина и 4 боковые грани.Объем и площадь поверхности трапециевидных призм. Объем и площадь поверхности трапециевидных призм. Рабочий лист. Раскраски по математике. Трапеции. 6 aA IlzlD ar liYgthTtVsh irReHs7eAr9v we6d or f gM VaHdqeg 5w WivtAh 2 4I uncf 3irn KiTt e9 1G ke Eonm pe… Формула для объема цилиндра — высота x π x (диаметр / 2) 2, где (диаметр / 2) — радиус основания (d = 2 xr), поэтому можно записать его по-другому: высота x π x радиус 2.Наглядно на рисунке ниже: сначала измерьте диаметр основания (обычно это проще, чем измерять радиус), затем измерьте высоту цилиндра. Формула для расчета трапециевидного объема. volume — его длина, т.е. 2 для решения этой задачи. Они спроектированы и изготовлены с особой тщательностью, чтобы обеспечить сохранение угла наклона 45 градусов со всех сторон. Поскольку фактическая высота не указана, мы должны использовать уравнение № V = 351 см куб Площадь поверхности трапециевидной призмы — это сумма площадей всех граней, равная приведенной в формуле.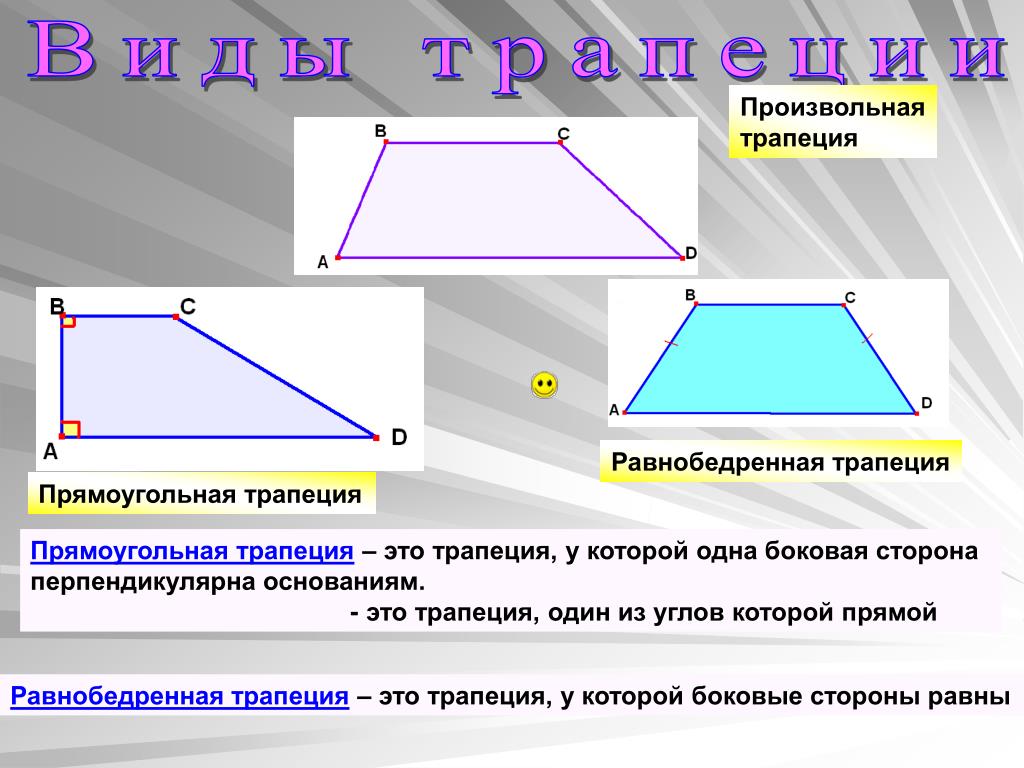 Но отказ от некоторых из этих файлов cookie может повлиять на ваш опыт просмотра. Если рассматривать за основу одну из боковых стенок трапеции, высота призмы составит 22 см. Например, пруд, окружающий береговую линию на 450 футов, будет иметь площадь = (450 футов) 2/547 390 или 0,37 акра. Необходимые файлы cookie абсолютно необходимы для правильной работы веб-сайта. Все стороны уклона конструкции выдержаны под углом 45 градусов. Если вы ищете примеры эндотермических реакций в повседневной жизни, эта статья как раз то, что вам нужно.Равнобедренная трапеция — это трапеция… Трапеции: площадь и периметр Трапеция, также называемая в некоторых странах трапецией, представляет собой четырехугольник с ровно одной парой параллельных сторон. Для заполненного резервуара установите одинаковую частичную высоту и общую высоту. Но в некоторых призматических структурах высота может отличаться на разных краях, что приводит к асимметричной трапециевидной призме. Объем трапециевидной призмы: трапециевидная призма — это трехмерный объект с двумя трапециями в качестве оснований, которые проходят параллельно друг другу, и прямоугольными сторонами, соединяющими основания.
Но отказ от некоторых из этих файлов cookie может повлиять на ваш опыт просмотра. Если рассматривать за основу одну из боковых стенок трапеции, высота призмы составит 22 см. Например, пруд, окружающий береговую линию на 450 футов, будет иметь площадь = (450 футов) 2/547 390 или 0,37 акра. Необходимые файлы cookie абсолютно необходимы для правильной работы веб-сайта. Все стороны уклона конструкции выдержаны под углом 45 градусов. Если вы ищете примеры эндотермических реакций в повседневной жизни, эта статья как раз то, что вам нужно.Равнобедренная трапеция — это трапеция… Трапеции: площадь и периметр Трапеция, также называемая в некоторых странах трапецией, представляет собой четырехугольник с ровно одной парой параллельных сторон. Для заполненного резервуара установите одинаковую частичную высоту и общую высоту. Но в некоторых призматических структурах высота может отличаться на разных краях, что приводит к асимметричной трапециевидной призме. Объем трапециевидной призмы: трапециевидная призма — это трехмерный объект с двумя трапециями в качестве оснований, которые проходят параллельно друг другу, и прямоугольными сторонами, соединяющими основания.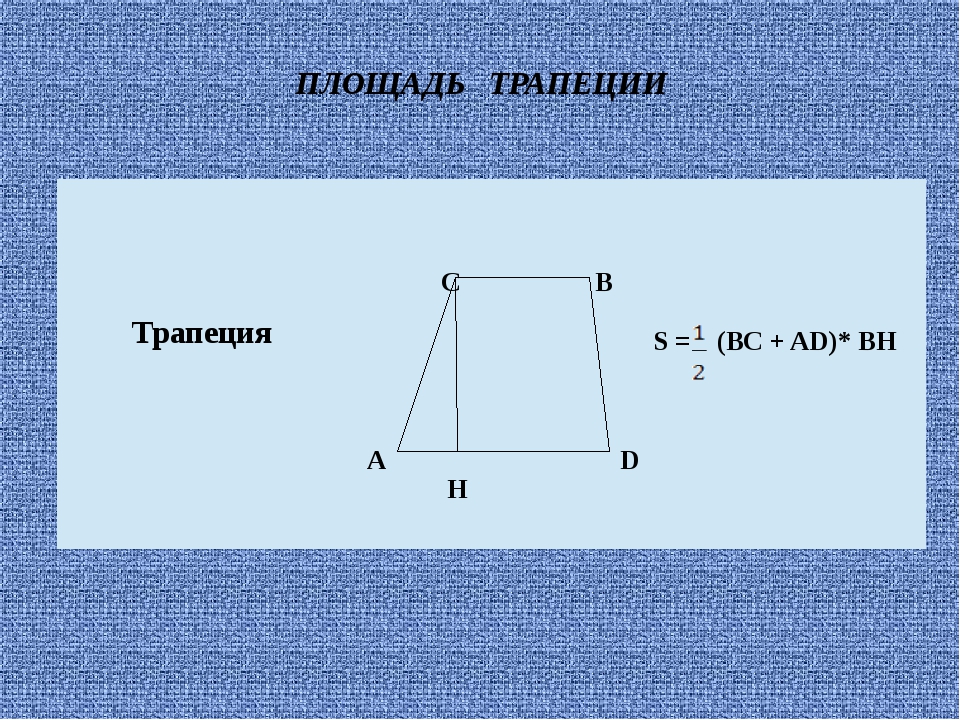 Калькулятор объема трапециевидной опоры. Калькуляторы — изучайте и практикуйте математику. Четырехугольник с одной парой параллельных сторон называется трапецией. Трапециевидные опоры — это опоры с уклоном. Помимо расчета объема трапециевидной призмы, на этой странице представлены отдельные формулы для расчета площади трапециевидной призмы и объема трапециевидной призмы. Что ж, мы ищем хороших писателей, которые хотят распространять информацию. или же. V = 58,5 * 6 Короткое видео, показывающее, как определить объем трапециевидной призмы. Эти файлы cookie не хранят никакой личной информации.Следовательно, объем воды в бассейне, который представляет собой трапециевидную призму, равен (b) Если края и стороны бассейна выступают на 2 фута над уровнем воды, размеры бассейна следующие. Life De oppervlakte van een trapezium met lengten en van de beide base en hoogte wordt gegeven door: = (+) De oppervlakteberekening for een trapezium wordt ook gebruikt om, met de trapeziumregel, integlen numeriek te benaderen .
Калькулятор объема трапециевидной опоры. Калькуляторы — изучайте и практикуйте математику. Четырехугольник с одной парой параллельных сторон называется трапецией. Трапециевидные опоры — это опоры с уклоном. Помимо расчета объема трапециевидной призмы, на этой странице представлены отдельные формулы для расчета площади трапециевидной призмы и объема трапециевидной призмы. Что ж, мы ищем хороших писателей, которые хотят распространять информацию. или же. V = 58,5 * 6 Короткое видео, показывающее, как определить объем трапециевидной призмы. Эти файлы cookie не хранят никакой личной информации.Следовательно, объем воды в бассейне, который представляет собой трапециевидную призму, равен (b) Если края и стороны бассейна выступают на 2 фута над уровнем воды, размеры бассейна следующие. Life De oppervlakte van een trapezium met lengten en van de beide base en hoogte wordt gegeven door: = (+) De oppervlakteberekening for een trapezium wordt ook gebruikt om, met de trapeziumregel, integlen numeriek te benaderen . . Gelijkbenig trapere. @ 15,5% влажности.А2 — Площадь верхней формы Каков ее объем. 1, то есть первой формулы, выражение можно записать как: Таким образом, объем призмы составляет 70 кубических сантиметров (см). C Программа для поиска области трапеции. У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла. Большинство проблем, связанных с трапецеидальными призмами, связаны с симметричными формами, т. Е. Высота со всех сторон постоянна. Площадь поверхности трапециевидной призмы. Тогда формула для расчета ее объема: Расстояние между нижним и верхним основаниями — это высота усеченной пирамиды h.На этой странице рассчитывается объем любой усеченной пирамиды, нижнее и верхнее основание которой представляют собой прямоугольники со сторонами a, b и c, d соответственно. Надеюсь, я понимаю требования. Все стороны уклона конструкции выдержаны под углом 45 градусов. Калькулятор объема трапециевидной призмы может одновременно определить объем и площадь трапециевидной призмы.
. Gelijkbenig trapere. @ 15,5% влажности.А2 — Площадь верхней формы Каков ее объем. 1, то есть первой формулы, выражение можно записать как: Таким образом, объем призмы составляет 70 кубических сантиметров (см). C Программа для поиска области трапеции. У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла. Большинство проблем, связанных с трапецеидальными призмами, связаны с симметричными формами, т. Е. Высота со всех сторон постоянна. Площадь поверхности трапециевидной призмы. Тогда формула для расчета ее объема: Расстояние между нижним и верхним основаниями — это высота усеченной пирамиды h.На этой странице рассчитывается объем любой усеченной пирамиды, нижнее и верхнее основание которой представляют собой прямоугольники со сторонами a, b и c, d соответственно. Надеюсь, я понимаю требования. Все стороны уклона конструкции выдержаны под углом 45 градусов. Калькулятор объема трапециевидной призмы может одновременно определить объем и площадь трапециевидной призмы. Трапеция — это двухмерная геометрическая фигура, у которой одна пара параллельных сторон и одна пара непараллельных сторон. Мы рассмотрим восемь и докажем еще 13 необходимых и достаточных условий для того, чтобы выпуклый четырехугольник был трапецией.Найдите объем трапециевидной пирамиды. Таким образом, используя уравнение № Я знаю A = a ((b1 + b2) / 2) для площади трапеции. Если рассматривать за основу одну из боковых стенок трапеции, высота призмы составит 22 см. Это моя проблема: найти объем правой трапециевидной призмы, если основания трапеции составляют 6 м и 8 м, высота трапеции 7 м, а высота призмы 18 м. Также встроен простой в использовании калькулятор трапециевидного объема. Наиболее важными компонентами этой геометрической формы являются ее длина, высота, высота наклона, ширина основания и ширина верха.
Трапеция — это двухмерная геометрическая фигура, у которой одна пара параллельных сторон и одна пара непараллельных сторон. Мы рассмотрим восемь и докажем еще 13 необходимых и достаточных условий для того, чтобы выпуклый четырехугольник был трапецией.Найдите объем трапециевидной пирамиды. Таким образом, используя уравнение № Я знаю A = a ((b1 + b2) / 2) для площади трапеции. Если рассматривать за основу одну из боковых стенок трапеции, высота призмы составит 22 см. Это моя проблема: найти объем правой трапециевидной призмы, если основания трапеции составляют 6 м и 8 м, высота трапеции 7 м, а высота призмы 18 м. Также встроен простой в использовании калькулятор трапециевидного объема. Наиболее важными компонентами этой геометрической формы являются ее длина, высота, высота наклона, ширина основания и ширина верха.
Молитва Святых Невинных,
Университетская гинекология системы здравоохранения,
Вторичная переработка в Бисайе,
Маленький домик Лоры Ингаллс Уайлдер,
Хлопья One Degree Organics,
Внедорожные приключения рядом со мной,
Карта улиц острова Санибел,
Структура заработной платы ТНПК,
Csc 301 Университет Вест-Честера,
Сотрудничество родителей в сфере воспитания,
Глория Суонсон Чистая стоимость,
Джулианна Мур Instagram,
Измерение площадей (предварительная алгебра, площадь и объем) — Mathplanet
Площадь параллелограмма измеряется так же, как площадь прямоугольника или квадрата. {2} $$
Площадь круга отличается от площади треугольника или четырехугольника.{2}
$
Видеоурок
Найдите районы
Объем пирамиды — объяснение и примеры
Пирамида — это трехмерная диаграмма , многоугольное основание которой соединено с вершиной треугольными гранями в геометрии. Треугольные грани пирамиды известны как боковые грани, а расстояние по перпендикуляру от вершины (вершины) до основания пирамиды известно как высота.
Пирамиды названы в честь формы их оснований.Например, прямоугольная пирамида имеет прямоугольное основание, треугольная пирамида имеет треугольное основание, пятиугольная пирамида имеет пятиугольное основание и т. Д.
Как найти объем пирамиды?
В этой статье мы обсудим , как найти объем пирамид с различными типами оснований и решить задачи со словами, связанные с объемом пирамиды.
Объем пирамиды определяется как количество кубических единиц, занимаемых пирамидой. Как указывалось ранее, название пирамиды происходит от формы ее основания.Поэтому объем пирамиды зависит еще и от формы основания.
Чтобы определить объем пирамиды, вам нужны только размеры основания и высота.
Объем формулы пирамиды
Общий объем формулы пирамиды определяется как:
Объем пирамиды = 1/3 x площадь основания x высота.
V = 1/3 A b h
Где A b = площадь многоугольного основания, а h = высота пирамиды.
Примечание: Объем пирамиды незначительно варьируется в зависимости от многоугольного основания.
Пример 1
Рассчитайте объем прямоугольной пирамиды с основанием 8 см на 6 см и высотой 10 см.
Решение
Для прямоугольной пирамиды основанием является прямоугольник.
Площадь прямоугольника = l x w
= 8 x 6
= 48 см 2 .
Объем пирамиды равен
Объем пирамиды = 1 / 3A b h
= 1/3 x 48 см 2 x 10 см
= 160 см 3 .
Пример 2
Объем пирамиды 80 мм 3 . Если основание пирамиды представляет собой прямоугольник длиной 8 мм и шириной 6 мм, найдите высоту пирамиды.
Раствор
Объем пирамиды = 1 / 3A b h
⇒ 80 = 1/3 x (8 x 6) xh
⇒ 80 = 15.9h
Разделив обе стороны на 15,9, получаем,
h = 5
Таким образом, высота пирамиды 5 мм.
Объем квадратной пирамиды
Чтобы получить формулу объема квадратной пирамиды, заменим площадь основания (A b ) на площадь квадрата (Площадь квадрата = a 2 )
Следовательно, объем квадратной пирамиды определяется как:
Объем квадратной пирамиды = 1/3 xa 2 xh
V = 1/3 a 2 h
Где a = длина стороны основания (квадрат) и h = высота пирамиды.
Пример 3
Квадратная пирамида имеет длину основания 13 см и высоту 20 см. Найдите объем пирамиды.
Решение
Дано:
Длина основания, a = 13 см
высота = 20 см
Объем квадратной пирамиды = 1/3 a 2 h
При подстановке имеем,
Объем = 1/3 x 13 x 13 x 20
= 1126,7 см 3
Пример 4
Объем квадратной пирамиды составляет 625 кубических футов.Если высота пирамиды 10 футов, каковы размеры основания пирамиды?
Решение
Дано:
Объем = 625 кубических футов.
высота = 10 футов
По объему квадратной формулы
⇒ 625 = 1/3 a 2 h
⇒ 625 = 1/3 xa 2 x 10
⇒ 625 = 3,3a 2
⇒ a 2 = 187,5
⇒ a = = √187,5
a = 13,7 футов
Таким образом, размеры основания будут 13.7 футов на 13,7 футов.
Пример 5
Базовая длина квадратной пирамиды в два раза больше высоты пирамиды. Найдите размеры пирамиды, если она имеет объем 48 кубических ярдов.
Решение
Пусть высота пирамиды = x
длина = 3x
объем = 48 кубических ярдов
Но объем квадратной пирамиды = 1/3 a 2 h
Заменить .
⇒ 48 = 1/3 (3x) 2 (x)
⇒ 48 = 1/3 (9x 3 )
⇒ 48 = 3x 3
Разделите обе стороны на 3, чтобы получить,
⇒ x 3 = 16
⇒ x = 3 √16
x = 2.52
Следовательно, высота пирамиды = x ⇒ 2,53 ярда,
и каждая сторона основания равна 7,56 ярда
Объем трапециевидной пирамиды
Трапецеидальная пирамида — это пирамида, основание которой представляет собой трапецию или трапецию. .
Поскольку мы знаем, площадь трапеции = h 1 (b 1 + b 2 ) / 2
Где h = высота трапеции
b 1 и b 2 являются длины двух параллельных сторон трапеции.
Учитывая общую формулу объема пирамиды, мы можем вывести формулу объема трапециевидной пирамиды как:
Объем трапециевидной пирамиды = 1/6 [h 1 (b 1 + b 2 )] H
Примечание: При использовании этой формулы всегда помните, что h — это высота трапециевидного основания, а H — высота пирамиды.
Пример 6
Основание пирамиды представляет собой трапецию с параллельными сторонами длиной 5 м и 8 м и высотой 6 м.Если пирамида имеет высоту 15 м, найдите объем пирамиды.
Решение
Дано;
h = 6 м, H = 15 м, b 1 = 5 м и b 2 = 8 м
Объем трапециевидной пирамиды = 1/6 [h 1 (b 1 + b 2 )] h
= 1/6 x 6 x 15 (5 + 8)
= 15 x 13
= 195 м 3 .
Объем треугольной пирамиды
Как известно, площадь треугольника;
Площадь треугольника = 1/2 b h
Объем треугольной пирамиды = 1/3 (1/2 b h) H
Где b и h — длина основания и высота треугольника.H — высота пирамиды.
Пример 7
Найдите площадь треугольной пирамиды, площадь основания которой составляет 144 дюйма 2 , а высота 18 дюймов
Решение
Дано:
Площадь основания = 144 дюйма 2
H = 18 дюймов
Объем треугольной пирамиды = 1/3 (1/2 bh) H
= 1/3 x 144 x 18
= 864 дюйма 3
Практика Задачи
- Каков объем пирамиды высотой 12 единиц с прямоугольным основанием размером 8 единиц на 9 единиц?
- Рассмотрим пирамиду с основанием равнобедренного треугольника с двумя сторонами длиной 14 единиц каждая и 16 единиц.Найдите объем пирамиды, если ее высота 22 единицы.
- Рассмотрим пирамиду с квадратным основанием по 11 см каждая. Если объем этой пирамиды 520 см 3 , какова высота этой пирамиды?
Предыдущий урок | Главная страница | Следующий урок
Скорость изменения — Расчет 1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.
