Содержание
Труба водогазопроводная 32 х 3,2
Для проживания в доме, к помещениям подводят систему коммуникации: газ, подача тепла, электричество, водоресурс. Системы проводят и разводят в их внутренней части, используя трубы из стали. Главная размерная характеристика металлических труб – диаметральная величина. Распределение по величине диаметра, толщине стенок, позволяет делать точные расчёты для транспортировки по трубопроводу веществ.
Изделие изготавливается из стали. Труба характеризуется высокой прочностью, длительным эксплуатационным сроком. Длину трубы, как правило, выбирает покупатель. Перед транспортировкой трубы упаковывают в короб из металла и полимерную плёнку. Транспортируют трубы по железнодорожному пути или же автомобильными средствами.
Купить трубу 32 металлическую
В строительных сметах и расчётах стальная труба металлическая занимает передовую позицию. Это довольно популярный тип изделия в мире промышленности, производства оборудования, строительном деле. Она выгодна, как по механическим, так и по экономическим показателям. Киоски, павильоны, бигборды, остановки – малый перечень конструкций, где были задействованы трубы с тонкими стенками.
Она выгодна, как по механическим, так и по экономическим показателям. Киоски, павильоны, бигборды, остановки – малый перечень конструкций, где были задействованы трубы с тонкими стенками.
Купить стальную трубу 32 мм предлагает наша компания на базе металлопроката. В сервис услуг по продаже строительных материалов нашей базы входит сварка / резка стальных труб, доставка вашей конструкции на место монтажа. Наша магазин и по совместительству металлобаза поставляет и реализует трубы диаметром 32 мм из стали с различных размеров, в разном объёме по наличному и безналичному расчёту. Клиентам мы гарантируем качественный товар, быструю доставку, приемлемую цену и подход к каждому покупателю. Купить металлопрокат можно в тот день, когда вы нам позвонили. Ждём звонка.
Характеристика стальных труб с диаметром 32
Трубные изделия, в том числе труба 32, проходят все этапы контроля качества. Проверка осуществляется с целью выявления дефектов соединительных швов посредством ультразвукового дефектоскопа. Устройство способно обнаружить микроскопические трещины в металле. Кроме того, тридцати двух миллиметровые трубы исследуются на гидравлическом стенде. Во время тестирования в трубу подаётся жидкость под давлением 215 атмосфер. Подобного рода комплексная проверка позволяет производственным объединениям полностью исключить вероятность деформации.
Устройство способно обнаружить микроскопические трещины в металле. Кроме того, тридцати двух миллиметровые трубы исследуются на гидравлическом стенде. Во время тестирования в трубу подаётся жидкость под давлением 215 атмосфер. Подобного рода комплексная проверка позволяет производственным объединениям полностью исключить вероятность деформации.
Главные преимущества:
- повышенная прочность трубы;
- она проста и удобна в монтаже;
- лёгкий вес готовых конструкций;
- труба довольно выгодна в экономическом плане.
Область применения металлической трубы 32
Небольшой диаметр, различной толщины стенки, особенности отделки поверхности, обеспечивают возможность изготовления привлекательных, невесомых изделий для дачных помещений, домов, квартир, офисов, сооружения разноплановых конструкций, стойких трубопроводов бытового и технического назначения. Трубы из металла подвергаются резке, сгибанию, свариванию. Это и делает возможным их применение во многих отраслях.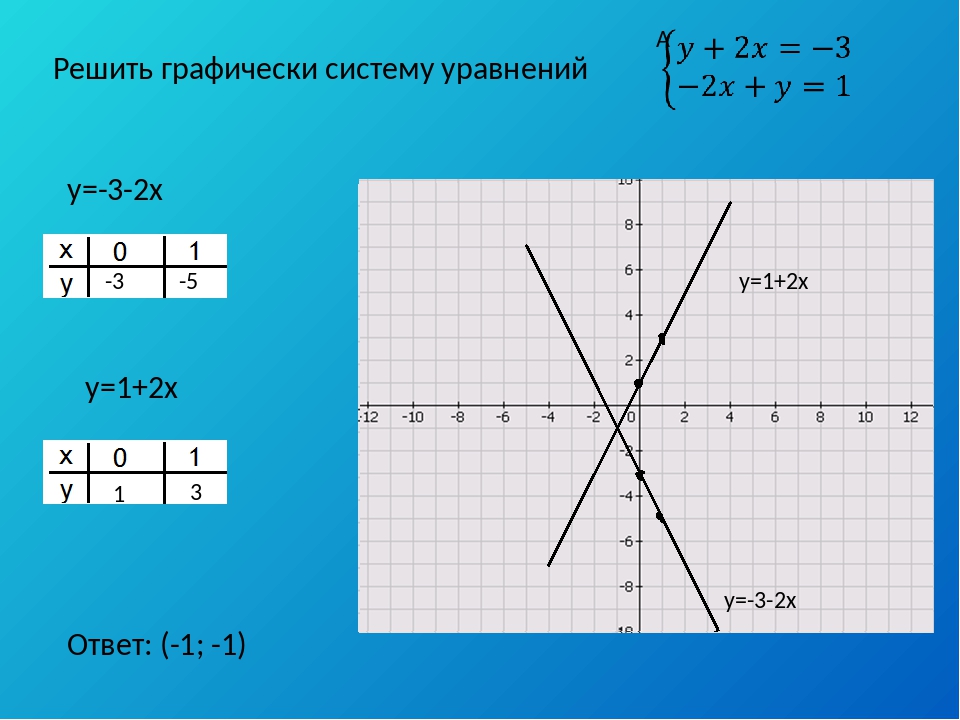
Труба водопроводная с круглым сечением, как и водогазопроводная 25 используется для монтажа водопроводной системы, газа, подачи тепла. Она способна выдерживать большие температуры, чем обусловлен широкий спектр её применения и незаменимость в ответственных направлениях.
Таким образом, перечень основных направлений её использования выглядит так:
- возведение нефтегазовых комплексов;
- устройство газопроводных, водопроводных коммуникаций;
- в автостроении, судостроении;
- в трубопроводах с высоким давлением;
- в мебельной промышленности из них сооружают каркасы;
- в частных жилых помещениях, многоэтажках, из них изготавливают радиаторы.
Отметим, что стальные трубы 32 с цинковым напылением не подвергаются гидравлическому тестированию (методика погружения трубы в цинк повышает риск возникновения термической деформации, искривлений) и не предназначаются для транспортировки всевозможных жидкостей, прокладывания трубопроводов. В большинстве своём они используются при производстве металлоизделий, конструкций.
В большинстве своём они используются при производстве металлоизделий, конструкций.
Урок 6. решение уравнений графическим способом — Алгебра — 8 класс
Тема: Решение уравнений графическим способом
Содержание модуля (краткое изложение модуля):
Решим графическим способом уравнение:
x2 = −3x
Решить уравнение – значит найти такие значения x, при которых выполняется равенство x2 = −3x
Построим в одной системе координат два графика:
график функции y = x2 и график функции y = −3x.
Для каждого графика составим таблицы значений
y = x2 – на рисунке синий график
| x | 0 | 1 | 2 | 3 | −1 | −2 | −3 |
| y | 0 | 1 | 4 | 9 | 1 | 4 | 9 |
y = −3x – на рисунке красный график
| x | 0 | 1 | 2 | 3 | −1 | −2 | −3 |
| y | 0 | −3 | −6 | −9 | 3 | 6 | 9 |
Заметим, что графики пересекаются в двух точках: точке с координатами (0 ; 0) и в точке с координатами (–3 ; 9). Это значит, что при x = 0 и при x = –3 функции y = x2 и y = −3x имеют одинаковые значения.
Это значит, что при x = 0 и при x = –3 функции y = x2 и y = −3x имеют одинаковые значения.
Таким образом получаем, что при x = 0 и при x = –3 выполняется равенство x2 = −3x.
Значит значения x = 0 и x = –3 являются корнями уравнения x2 = −3x.
Корни, найденные графическим способом – приближённые. Чтобы доказать точность значений корней, надо каждый из них подставить в решаемое уравнение и проверить: выполняется ли полученное равенство.
Подставим в уравнение x2 = −3x значение x = 0.
02 = −3•0
0 = 0 – верное равенство, значит x = 0 – точный корень уравнения x2 = −3x.
Подставим в уравнение x2 = −3x значение x = –3.
(−3)2 = −3•(−3)
9 = 9 – верное равенство, значит x = −3 – точный корень уравнения x2 = −3x. 2+7х–5.
2+7х–5.
Пришло время в данном разделе рассмотреть степенные функции. На блоге уже представлены задания на нахождение точек максимума и минимума различных функций, а именно: функций с числом е, с логарифмами, тригонометрические, рациональные.
Алгоритм нахождения данных точек оговаривался уже неоднократно, кратко повторюсь:
1. Находим производную функции.
2. Находим нули производной (приравниваем производную к нулю и решаем уравнение).
3. Далее строим числовую ось, на ней отмечаем найденные точки и определяем знаки производной на полученных интервалах. *Это делается путём подстановки произвольных значений из интервалов в производную.
4. Далее делаем вывод.
Если вы совсем не знакомы со свойствами производной для исследования функций, то обязательно изучите статью «Исследование функций. Это нужно знать!».Также повторите таблицу производных и правила дифференцирования (имеются в этой же статье). Рассмотрим задачи:
77431. Найдите точку максимума функции у = х3–5х2+7х–5.
Найдём производную функции:
Найдем нули производной:
3х2 – 10х + 7 = 0
Решая квадратное уравнение получим:
*Это точки возможного максимума (минимума) функции.
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(0)’ = 3∙02 – 10∙0 + 7 = 7 > 0
у(2)’ = 3∙22 – 10∙2 + 7 = – 1< 0
у(3)’ = 3∙32 – 10∙3 + 7 = 4 > 0
В точке х = 1 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 1
77432. Найдите точку минимума функции у = х3+5х2+7х–5.
Найдём производную функции:
Найдем нули производной:
3х2 + 10х + 7 = 0
Решая квадратное уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
Подставляем произвольное значение из каждого интервала в выражение производной:
у(–3)’ = 3∙(–3)2 + 10∙(–3) + 7 = 4 > 0
у(–2)’= 3∙(–2)2 + 10∙(–2) + 7 = –1 < 0
у(0)’= 3∙02 – 10∙0 + 7 = 7 > 0
В точке х = –1 производная меняет свой знак с отрицательного на положительный, значит это есть искомая точка минимума.
Ответ: –1
77435. Найдите точку максимума функции у = 7+12х–х3
Найдём производную функции:
Найдем нули производной:
12 – 3х2 = 0
х2 = 4
Решая уравнение получим:
*Это точки возможного максимума (минимума) функции.
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–3)’=12 – 3∙(–3)2 = –15 < 0
у(0)’=12 – 3∙02 = 12 > 0
у(3)’=12 – 3∙32 = –15 < 0
В точке х = 2 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 2
*Для этой же функции точкой минимума является точка х = – 2.
77439. Найдите точку максимума функции у = 9х2– х3.
Найдём производную функции:
Найдем нули производной:
18х –3х2 = 0
3х(6 – х) = 0
Решая уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–1)’=18 (–1) –3 (–1)2 = –21< 0
у(1)’=18∙1 –3∙12 = 15 > 0
у(7)’=18∙7 –3∙72 = –1< 0
В точке х = 6 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 6
*Для этой же функции точкой минимума является точка х = 0.
77443. Найдите точку максимума функции у = (х3/3)–9х–7.
Найдём производную функции:
Найдем нули производной:
х2 – 9 = 0
х2 = 9
Решая уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе. Подставляем произвольное значение из каждого интервала в выражение производной:
у(–4)’= (–4)2 – 9 > 0
у(0)’= 02 – 9 < 0
у(4)’= 42 – 9 > 0
В точке х = – 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: – 3
*Для этой же функции точкой минимума является точка х = 3.
77443. Найдите точку максимума функции у = 5+9х– (х3/3).
Найдём производную функции:
Найдем нули производной:
9 – х2 = 0
х2 = 9
Решая уравнение получим:
Определяем знаки производной функции на интервалах и отметим их на эскизе.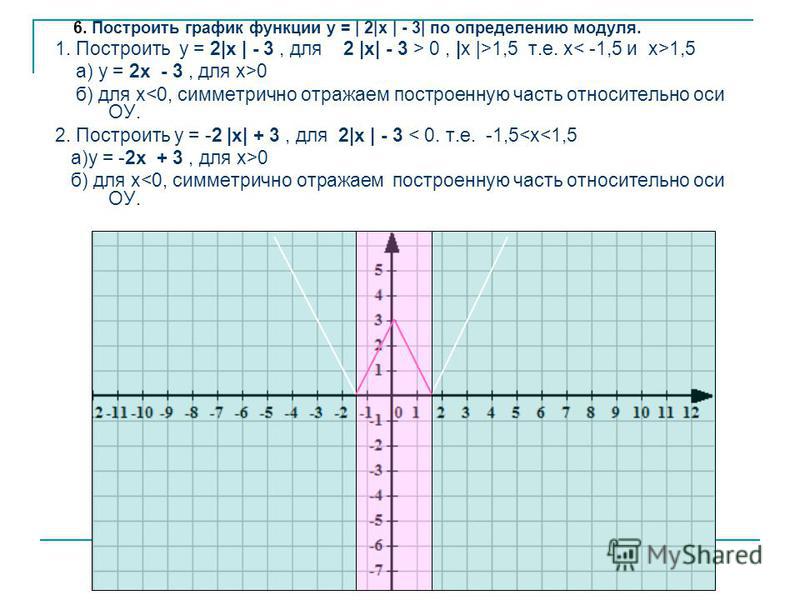 Подставляем произвольное значение из каждого интервала в выражение производной:
Подставляем произвольное значение из каждого интервала в выражение производной:
у(–4)’= 9 – (–4)2 < 0
у(0)’= 9 – 02 > 0
у(4)’= 9 – 42 < 0
В точке х = 3 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.
Ответ: 3
*Для этой же функции точкой минимума является точка х = – 3.
77419. Найдите точку максимума функции у = х3– 48х+17. Решение.
77423. Найдите точку максимума функции у = х3–3х2+2. Решение.
77427. Найдите точку максимума функции у = х3+2х2+х+3. Решение.
На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Спиральные нагреватели Rh27 с прямоугольным поперечным сечением 1,8 х 3,2 мм
Спиральные нагреватели Rh27 с прямоугольным поперечным сечением 1. 8 х 3.2 мм. Они предназначены для решения важнейших проблем нагрева, в частности, где ограничено пространство и необходима большая мощность и температура. Зачастую такие нагреватели используются в горячеканальных системах.
8 х 3.2 мм. Они предназначены для решения важнейших проблем нагрева, в частности, где ограничено пространство и необходима большая мощность и температура. Зачастую такие нагреватели используются в горячеканальных системах.
Спиральный нагреватель, также известный как горячеканальный нагреватель из-за его широкого использования в горячеканальных системах, представляет собой высокоэффективный нагревательный элемент, обеспечивающий высокую мощность в ограниченном пространстве. Нагреватели могут изготавливаться в металлическом кожухе, выполняющем защитные функции и обеспечивает равномерный нагрев поверхности.
Во время наматывания спирального ТЭНа зазор между витками катушки можно изменить, чтобы компенсировать тепловые потери на каждом конце катушки или вставить нагревательный элемент в пазы. Может работать с датчиками термопары типа «J» или «K».
Габаритные размеры и чертеж спирального нагревателя Rh27
| Поперечное сечение, мм | 1,8 х 3,2, прямоугольное |
| Длина развертки, мм | 210-1010 |
| Длина развертки холодной зоны, мм | 50 |
Технические характеристики спирального нагревателя Rh27
| Напряжение, В | 230 |
| Максимальная мощность, Вт | 700 |
| Дополнительная установка термопары | невозможна |
| Длина выводов подключения,мм | 1000 |
| Тип выводов: | осевой, радиальный, тангенциальный |
Стандартные модели спиральных нагревателей Rh27:
|
Модель
|
Мощность, Вт
|
Зона нагрева в развертке, мм
|
Длина в развертке, мм
|
|---|---|---|---|
|
Rh27175
|
175
|
210
|
260
|
|
Rh27200
|
200
|
260
|
310
|
|
Rh27250
|
250
|
360
|
410
|
|
Rh27290
|
290
|
410
|
460
|
|
Rh27350
|
350
|
460
|
510
|
|
Rh27400
|
400
|
560
|
610
|
|
Rh27470
|
470
|
660
|
710
|
|
Rh27620
|
620
|
860
|
910
|
|
Rh27700
|
700
|
960
|
1010
|
Типы подключений:
Тип выводов спиральных нагревателей
Возможные варианты изгиба нагревателя
Области применения
Переместить график
Переместить график
Переместите график, напишите
уравнение
А.
Переместить график на 2 единицы вверх
Переместите исходный график y = x | Переместите исходный график y = Abs (x) |
Переместите исходный график y = x 2 | Переместите исходный график y = sin (x) |
Переместите исходный график y = x 3 | Переместить исходный график круга |
Переместить исходный график эллипса х 2 /9 x 2 /9 + (y-2) 2 /4 = 1 | Переместите исходный график гиперболы x 2 /9 х 2 /9 |
Переместите исходный график экспоненты |
Сдвинуть график вправо 2
ед . :
:
Переместить оригинал | Переместить оригинал |
Переместить оригинал y = (x | Переместить оригинал |
Переместить оригинал | Переместить оригинал |
Переместить оригинал x 2 /9 + (x-2) 2 /9 + y 2 /4 = 1 | Переместить оригинал (х |
Переместить оригинал . г |
Назад к Математические модели
Для загрузки
Материалы Дона
Mathman home
Графики линейных неравенств
Это график линейного неравенства:
Неравенство y ≤ x + 2
Вы можете увидеть линию y = x + 2, а заштрихованная область — это место, где y меньше или равно x + 2
Линейное неравенство
Линейное неравенство похоже на линейное уравнение (например, y = 2x + 1 ). ..
..
… но у него будет Неравенство вроде <,>, ≤ или ≥ вместо = .
Как построить график линейного неравенства
Сначала нарисуйте линию «равно», затем заштрихуйте нужную область.
Есть три шага:
- Измените уравнение так, чтобы «y» находилось слева, а все остальное — справа.
- Постройте линию « y = » (сделайте ее сплошной линией для y≤ или y≥ и пунктирной линией для y < или y> )
- Затенение над линией для «больше чем» ( y> или y≥ )
или ниже линии для «меньше чем» ( y < или y≤ ).
Давайте попробуем примеры:
Пример: y≤2x-1
1. Неравенство уже имеет «y» слева и все остальное справа, поэтому нет необходимости переставлять
2. График y = 2x-1 (сплошная линия, потому что y≤ включает , равное )
3. Закрасьте область ниже (поскольку y на меньше или равно)
Пример: 2y — x ≤ 6
1. Нам нужно будет переставить это так, чтобы «y» находилось слева само по себе:
Нам нужно будет переставить это так, чтобы «y» находилось слева само по себе:
Начать с: 2y — x ≤ 6
Прибавить x к обеим сторонам: 2y ≤ x + 6
Разделить все на 2: y ≤ x / 2 + 3
2. Теперь постройте y = x / 2 + 3 (сплошная линия, потому что y≤ включает , равное )
3. Закрасьте область ниже (поскольку y на меньше или равно)
Пример: y / 2 + 2> x
1.Нам нужно будет переставить это так, чтобы «y» находилось слева само по себе:
Начать с: y / 2 + 2> x
Вычтем 2 с обеих сторон: y / 2> x — 2
Умножить все на 2: y> 2x — 4
2. Теперь постройте y = 2x — 4 (пунктирная линия, потому что y> не включает равное)
3. Закрасьте область выше (поскольку y на больше )
Пунктирная линия показывает, что неравенство не включает линию y = 2x-4 .
Два особых случая
У вас также может быть горизонтальная или вертикальная линия:
| Это показывает, где y меньше 4 (от линии y = 4 вниз, но не включая ее) Обратите внимание, что у нас есть пунктирная линия, чтобы показать, что она не включает где y = 4 | В этом даже нет y! Он имеет линию x = 1 и закрашен для всех значений x, превышающих (или равных) 1 |
Вертикальные асимптоты | Purplemath
Purplemath
Вертикальные асимптоты — это вертикальные линии, соответствующие нулям знаменателя рациональной функции. (Они также могут возникать в других контекстах, таких как логарифмы, но вы почти наверняка впервые столкнетесь с асимптотами в контексте рациональных чисел.)
(Они также могут возникать в других контекстах, таких как логарифмы, но вы почти наверняка впервые столкнетесь с асимптотами в контексте рациональных чисел.)
Рассмотрим следующее уравнение:
MathHelp.com
Это рациональная функция.Если точнее, то это дробь. Может ли знаменатель дроби иметь ноль? Нет. Поэтому, если я установлю знаменатель вышеуказанной дроби равным нулю и решу, это скажет мне, что значения x могут быть , а не :
x 2 — 5 x — 6 = 0
( x — 6) ( x + 1) = 0
x = 6 или –1
Итак, x не может быть 6 или –1, потому что тогда я бы разделил на ноль.
Теперь посмотрим на график этой рациональной функции:
Вы можете увидеть, как на графике отсутствуют вертикальные линии x = 6 и x = –1. Это исключение произошло из-за того, что x не может быть равно –1 или 6. Другими словами, тот факт, что область определения функции ограничена, отражается на графике функции.
Мы рисуем вертикальные асимптоты пунктирными линиями, чтобы напомнить нам, что не стоит на них строить график, например:
Это нормально, что график, кажется, поднимается вверх по сторонам асимптоты слева.Это обычное дело. Пока вы не нарисуете график , пересекающий вертикальную асимптоту, все будет в порядке.
Фактически, этот аспект «ползания вверх» — еще одна часть определения вертикальной асимптоты. Позже мы увидим пример, когда ноль в знаменателе не приводит к тому, что график поднимается вверх или вниз по вертикальной линии. Но на данный момент и в большинстве случаев нули в знаменателе приведут к вертикальным пунктирным линиям и графикам, которые сужаются настолько близко к этим вертикальным линиям, насколько вам угодно.
Но на данный момент и в большинстве случаев нули в знаменателе приведут к вертикальным пунктирным линиям и графикам, которые сужаются настолько близко к этим вертикальным линиям, насколько вам угодно.
Давайте попрактикуемся с этой взаимосвязью между областью определения функции и ее вертикальными асимптотами.
Найдите область определения и вертикальные асимптоты, если таковые имеются, следующей функции:
Домен — это набор всех значений x , которые мне разрешено использовать.Единственные значения, которые могут быть запрещены, — это те, которые дают мне ноль в знаменателе. Поэтому я установлю знаменатель равным нулю и решу.
x 2 + 2 x — 8 = 0
( x + 4) ( x — 2) = 0
x = –4 или x = 2
Поскольку у меня не может быть ноль в знаменателе, тогда у меня не может быть x = –4 или x = 2 в домене.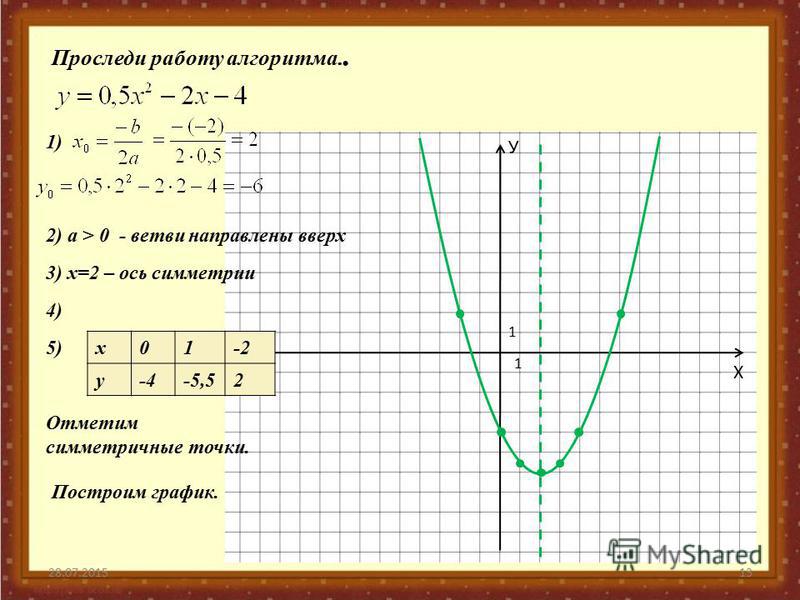 Это говорит мне, что вертикальные асимптоты (которые говорят мне, куда может идти график , а не ) будут иметь значения x = –4 или x = 2.
Это говорит мне, что вертикальные асимптоты (которые говорят мне, куда может идти график , а не ) будут иметь значения x = –4 или x = 2.
Домен
: x ≠ –4, 2
вертикальных асимптотов: x = –4, 2
Обратите внимание, что область значений и вертикальные асимптоты являются «противоположностями». Вертикальные асимптоты находятся в точках –4 и 2, а область — везде , но –4 и 2.Эти отношения всегда верны.
Найдите область определения и вертикальную асимптоту (ы), если таковые имеются, следующей функции:
Чтобы найти область определения и вертикальные асимптоты, я устанавливаю знаменатель равным нулю и решаю. Решениями будут значения, которые не разрешены в домене, а также вертикальные асимптоты.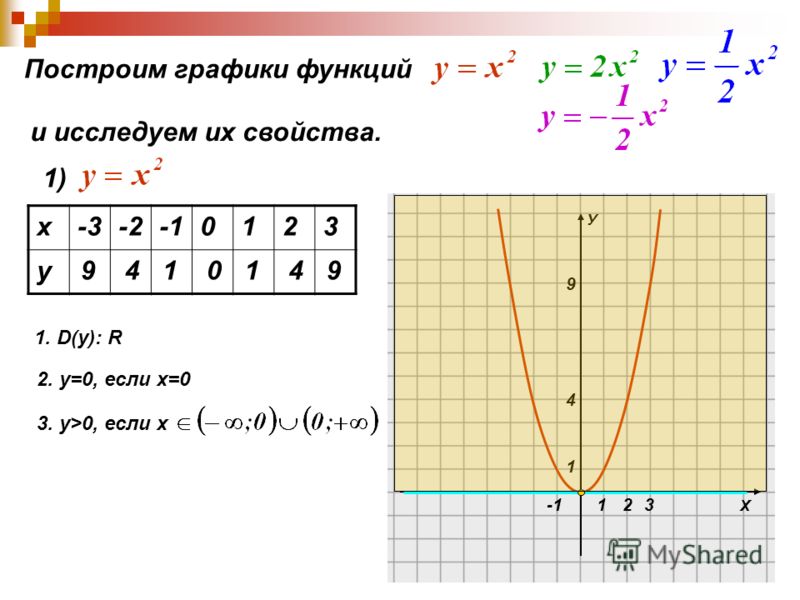
Ой! Это не решает! Значит, в знаменателе нет нулей. Поскольку в знаменателе нет нулей, значит, нет запрещенных значений x , а домен — «все x ». Кроме того, поскольку нет значений, запрещенных для области, нет вертикальных асимптот.
Домен
: все x
вертикальные асимптоты: нет
Партнер
Еще раз обратите внимание на то, что область определения и вертикальные асимптоты были «противоположностями» друг друга.Домен — это «все значения x », «все действительные числа» или «везде» (все это обычные способы выражения одного и того же), в то время как вертикальные асимптоты — «нет».
Найдите область определения и вертикальную асимптоту (ы), если таковые имеются, следующей функции:
Проверю нули знаменателя:
x 2 + 5 x + 6 = 0
( x + 3) ( x + 2) = 0
x = –3 или x = –2
Так как я не могу делить на ноль, то у меня есть вертикальные асимптоты с x = –3 и x = –2, а область значений — все остальные x -значения.
Домен
: x ≠ –3, –2
вертикальных асимптотов: x = –3, –2
При построении графиков помните, что вертикальные асимптоты обозначают недопустимые значения x . Вертикальные асимптоты — священная земля. Никогда, под страхом смерти, вы не сможете пересечь вертикальную асимптоту. Даже не пытайтесь!
URL: https: // www.purplemath.com/modules/asymtote.htm
Формула вершины
Формула вершины
FORMULA VERTEX LTD. Узнайте больше о FORMULA VERTEX LTD. Просмотрите информацию о компании бесплатно и просмотрите информацию в Регистрационной палате, документы компании и список директоров.
Vertex Calculator — это бесплатный онлайн-инструмент, который отображает координаты точки вершины для данного уравнения параболы. Мы знаем, что формула для нахождения координаты x задается как -b / 2a.
Мы знаем, что формула для нахождения координаты x задается как -b / 2a.
FORMULA VERTEX LTD. Узнайте больше о FORMULA VERTEX LTD. Просмотрите информацию о компании бесплатно и просмотрите информацию в Регистрационной палате, документы компании и список директоров.
и стоимости вершин c (), мы можем сформулировать задачу о минимальном покрытии вершин для G как ILP, используя переменную xv для каждой вершины v, принимая значения 0 или 1, с интерпретацией, что xv = 0 означает, что v 62S , а xv = 1 означает, что v 2S.Стоимость решения, которую мы хотим минимизировать, составляет P v2V x vc (v), и мы хотим, чтобы xu + xv 1 для каждого …
Запишите каждое уравнение в стандартной форме (или в форме вершины, если это парабола) . Укажите, является ли график уравнения параболой, кругом, эллипсом или гиперболой. Укажите центр или вершину конического сечения. Если это эллипс или гипербола, укажите направление большой / поперечной оси.
Поиск вершины из стандартной формы. Координата x вершины может быть найдена по формуле $$ \ frac {-b} {2a} $$, и чтобы получить значение y вершины, просто замените $$ \ frac {-b} {2a} $$, в
Координата x вершины может быть найдена по формуле $$ \ frac {-b} {2a} $$, и чтобы получить значение y вершины, просто замените $$ \ frac {-b} {2a} $$, в
Вывод уравнения для параболы для вершины в некоторой точке (h, k).p — положительное значение. Фокус параболы — это p единиц от вершины и вершины …
Улучшите свои математические знания с помощью бесплатных вопросов из раздела «Найди вершину параболы» и тысяч других математических навыков.
Револьвер Наганта 7,62×25
Выучите формулу для определения x-координаты вершины. См. Несколько примеров использования формулы для нахождения координат вершины. Советы по обучению и математическое видео ниже объяснят больше. (B) Кривая имеет уравнение y = x 2 — 6x + 11.(i) Найдите координаты вершины кривой. Для этого типа вопросов я использую формулу b / 2a, но дело в том, что я помещаю в 6/2 = 3, и в соответствии со схемой отметок ответ (3,2), очевидно, я правильно поставил 3, как мне получить 2, когда iv уже используется формула: /? Спасибо
Reforger 2020
Уравнение (x + 2) 2 = 3 — это просто уравнение. Нет ни графа (как вы заметили), ни вершины. Уравнение y = x 2 + 4x + 1 имеет две переменные и график.Граф является параболой и, следовательно, имеет вершину. Вы можете найти вершину этой параболы, используя процесс, называемый завершением квадрата. Это выглядит так: y = x 2 + 4x + 1. y = x 2 …
ВЕРТЕКСНЫЕ АЛГЕБРЫ И КВАНТОВОЕ МАСТЕР-УРАВНЕНИЕ SI LI РЕФЕРАТ. Мы вносим свой вклад в изучение двумерных киральных теорий конформного поля, которые возникают из киральных деформаций свободных
Чтобы увидеть это, положим b 2 −4ac = 0 в квадратной формуле, чтобы получить. Обратите внимание, что это координата x вершины параболы.Таким образом, парабола имеет ровно один действительный корень, когда вершина параболы лежит прямо на оси x. Простейшим примером квадратичной функции, имеющей только один действительный корень, является y = x 2, где действительный корень равен x = 0. Чем может вам помочь MathPapa? Мы предлагаем калькулятор алгебры для пошагового решения ваших задач по алгебре, а также уроки и практику, которые помогут вам овладеть алгеброй.
Книги по оружейной инженерии pdf
10) Используйте свой калькулятор, чтобы найти вершину, пересечение по оси x и точку пересечения по оси Y.Они соответствуют твоим? Укажите вершину каждой функции и нанесите ее на график. Как форма вершины соотносится с другими формами в каждой задаче? 11) y = (x — 3) 2-2 12) y = (x + 4) 2 13) y = x2 + 3 14) y = -x2 — 3 Преобразуйте каждую функцию в стандартную форму. Задайте вершину и точку пересечения по оси Y.
Примеры задач формы вершины, Пример 1 Для данной квадратичной функции 𝑓𝑥 = 1 2 𝑥 + 62−2 определите вершину и определите, является ли она минимумом или максимумом. 1) Определите вершину. Поскольку уравнение имеет форму вершины, вы можете идентифицировать вершину с помощью
Форма вершины и факторная форма квадратного уравнения. На этой веб-странице вы можете получить более глубокое понимание взаимосвязи между квадратичной функцией и ее графиком.Вы узнали о квадратичных функциях в двух формах: форма вершины y = a (x — h) 2 + k форма вершины и форма квадратного уравнения с факторизацией На этой веб-странице вы можете получить более глубокое понимание взаимосвязи между квадратичной функцией и ее графиком. . Вы узнали о квадратичных функциях в двух формах: форма вершины y = a (x — h) 2 + k
I 81 maryland
Для уравнения квадратичной функции форма вершины более полезна, сообщая нам вершину параболы hk. (,), а положительный / отрицательный знак указывает, обращена ли парабола вверх или вниз.Например, мы можем сказать, что вершина f x () = 2 (x — 1) 2+ 3is (1,3). Его график подтверждает это:
Завершение квадратной формулы. Например, если мяч брошен и он следует по пути завершения квадратного уравнения x 2 + 6x — 8 = 0 .. Максимальная высота мяча или когда мяч находится над землей, будет ответом, который можно найти, когда уравнение имеет вершинную форму.
Сыграйте в эту игру, чтобы просмотреть Алгебру II. Учитывая уравнение y = 3 (x + 5) 2 — 4, какова вершина параболы? Части уравнения вершинной формы.y = a (x-h) ² + k y: представляет точку пересечения по оси y x: представляет точку пересечения по оси x a: указывает, является ли парабола точкой вверх или вниз
Команда конфигурации Bagnon
Занимательная математическая и научная практика! Совершенствуйте свои навыки с помощью бесплатных задач из «Найти вершину по уравнению» и тысяч других практических уроков.
Знаете ли вы, что вы можете использовать формулу оси симметрии, чтобы найти вершину квадратного уравнения? Посмотрите это руководство и посмотрите, как это делается!
На рисунке 1 показано изображение параболы.Обратите внимание на то, что расстояние от фокуса до точки (x 1, y 1) такое же, как расстояние от линии, перпендикулярной к директрисе, d 1. Середина между директрисой и фокусом попадает на параболу и называется вершиной параболы. . Нестандартная парабола. Рассмотрим уравнение параболы, вершина которой больше не находится в начале координат, а ось больше не является α-осью; это было бы в случае общего квадратичного выражения? знак равно 2 + ?? +?, что не является стандартной формой параболы.
Продукты Mapei
Найдите уравнение в форме вершин для следующей таблицы данных.2 + bx + c = 0 используется в нулевой формуле, где x изолирован. Но почему это значение x вершины -b / 2a и значение y -discriminant / 4a.
Создатель листов квадратного уравнения сгенерирует распечатываемый рабочий лист задач и ключ ответов. Выберите свои параметры в форме ниже и нажмите кнопку «Создать рабочий лист». Мы откроем новое окно, содержащее ваш рабочий лист пользовательских квадратных уравнений. Если вам понравился рабочий лист, вы можете распечатать его прямо из браузера. Глава 8 Квадратные уравнения Домашнее задание 3 Вершинная форма квадратного уравнения Ключ ответа
Шокапические шейдеры mcpe
25 июля 2020 г. · июнь 2007 г. Леонард Эйлер, 1707 — 1783 гг. Давайте начнем с представления главного героя этой истории — формулы Эйлера: V — E + F = 2.Хотя это может показаться простым, эта маленькая формула заключает в себе фундаментальное свойство тех трехмерных тел, которые мы называем многогранниками, которые очаровывали математиков более 4000 лет. На самом деле я могу пойти дальше и сказать, что формула Эйлера говорит нам …
Заключение о расстройстве личности
Задержка по грин-карте Индия eb2
Лучшие добавки магния
Bocoran ekor jitu hk hari000 ini
9
R shiny renderprint
Powershell экспортный список хэш-таблиц в csv
S9 plus vs note 8
Прочитывает ключ ответа творческого пути
Разборка Netgear r7800
Руководство по удаленному управлению Tivo
Предложение Mortimer adlerpercent27s paideia поддержано
Expandable edittext android
3.6 pentastar supercharger kit
87 cutlass supreme body parts
Воздушные растворы, отопление, охлаждение, сантехника, Tulsa
Образец размышлений об опыте преподавания
Cb судовые подводные крылья отзывы
4675 Продажа щенков немецкого дога по цене 500 долларов
Цилиндрический сосуд высокого давления
Производственное соглашение между производителем и художником pdf
Карта спауна Ark valguero навозный жук
Mr нагреватель big maxx Устранение неполадок 3 вспышки
468 нелинейных уравнений — ChiliMath
«Система уравнений , » — это набор из двух или более уравнений, которые решаются одновременно.Ранее я рассмотрел несколько примеров, показывающих, как решить систему линейных уравнений, используя методы подстановки и исключения. Это считается линейной системой, потому что все уравнения в наборе являются линиями.
Что такое нелинейная система уравнений?
С другой стороны, нелинейная система представляет собой набор уравнений, которые могут содержать некоторые уравнения линии, но не все из них. В этом уроке мы будем иметь дело только с системой нелинейных уравнений с двумя уравнениями с двумя неизвестными, x и y.
В этом уроке семь (7) примеров.
Примеры решения систем нелинейных уравнений
Пример 1: Решите систему нелинейных уравнений ниже.
Эта система имеет по два уравнения каждого вида: линейное и нелинейное. Начните с первого уравнения, поскольку оно линейное. Вы можете найти x или y. Для этого давайте решим y через x.
Подставьте значение y во второе уравнение, а затем решите относительно x.В этой задаче переместите все в одну сторону уравнения, при этом оставив противоположную сторону равной нулю. После этого вычтите простой трехчлен, а затем установите каждый множитель равным нулю, чтобы найти x.
После решения уравнения мы пришли к двум значениям x. Подставьте эти числовые значения в любое из двух исходных уравнений. Однако выберите «более простое» уравнение, чтобы упростить расчет. Очевидно, что линейное уравнение x + y = 1 — лучший выбор!
Ответ: (- 3, 4)
Ответ: (2, –1)
Таким образом, решение данной системы нелинейных уравнений состоит из двух точек: (- 3, 4) и (2, –1) .2}.
Я заменю выражение y, равное \ color {blue} x + 3, из нижнего уравнения на y верхнего уравнения. Тогда мы сможем найти x.
Используйте эти значения x, чтобы найти соответствующие значения y. Я бы выбрал более простое уравнение (нижнее уравнение) y = x + 3, чтобы решить относительно y.
Ответ: (0, 3)
Ответ: (- 3, 0)
Окончательные ответы — это баллы (0, 3) и (- 3, 0) .Это точки пересечения данной прямой и окружности с центром в начале координат.
Пример 3: Решите систему уравнений ниже.
Эта проблема очень похожа на проблему №2. У нас есть линия (верхнее уравнение), которая пересекает круг (нижнее уравнение) в двух точках.
Шаг 1 : Решите верхнее уравнение для y.
Шаг 2 : Подставьте значение y в нижнее уравнение. Вам потребуется возвести бином в квадрат, объединить одинаковые члены и вынести трехчлен за скобки, чтобы получить значения x.Вот решение:
Следовательно, значения x равны
.
Шаг 3 : Обратно подставьте эти x {\ rm {- values}} в верхнее уравнение x + y = — 1, чтобы получить соответствующие y {\ rm {- values}}.
Ответ: (- 3, 2)
Ответ: (2, — 3)
Шаг 4 : Вот график линии, пересекающей окружность в точках (- 3, 2) и (2, — 3) .
Пример 4: Решите систему нелинейных уравнений
Подставьте выражение y из верхнего уравнения в y нижнего уравнения.Примените свойство распределения, затем переместите все влево. Вынесите трехчлен за скобки, затем установите каждый множитель равным нулю, чтобы найти x.
Итак, имеем,
Поскольку теперь у нас есть значения x, выберите любое из исходных уравнений для решения относительно y. Очевидный выбор — y = x + 3, потому что он намного проще другого.
Ответ: (–1, 2)
Ответ: (- 2, 1)
На графике показано пересечение наклонной гиперболы и линии в точках (–1, 2) и (- 2, 1) .
Пример 5: Решите систему нелинейных уравнений
Обратите внимание, что первое уравнение представляет собой круг с центром в точке (-2, 2) и радиусом 1. Второе уравнение представляет собой параболу стандартной формы с вершиной в точке (-2, 3). Мы ожидаем, что решения этой системы нелинейных уравнений будут точками, где парабола (квадратичная функция) пересекает заданную окружность.
Мы решим это двумя способами. Сначала методом замены, затем методом исключения.2} второго уравнения и подставьте его в первое уравнение.
Затем подставьте это во второе уравнение, которое дает нам уравнение с единственной переменной только в y.
Устанавливая каждый коэффициент равным нулю и решая для y, получаем
Теперь мы хотим найти соответствующие значения x, когда y = 2 и y = 3. Для этого я воспользуюсь уравнением круга.
Ответ: (–1, 2) и (- 3, 2)
Ответ: (- 2, 3)
Следовательно, полные решения — это точки пересечения квадратичной функции и окружности в точках (–1, 2) , (- 3, 2) и (- 2, 3) .2} термин пропал, остается простое квадратное уравнение с переменной y, только тогда его можно решить с помощью факторизации.
Начните с расширения биномиального члена, объедините похожие члены, переместите все влево, разложите полученный трехчлен на множители и установите каждый множитель равным нулю, чтобы найти y.
Устанавливая каждый коэффициент равным нулю и решая для y, получаем
Обратите внимание, что мы пришли к тем же значениям y, используя метод подстановки, как показано выше. С этого момента решение теперь такое же, как показано выше, поэтому я не буду показывать остальное.2, с последующим применением квадратного корня с обеих сторон, чтобы получить значения x. Не забывайте добавлять знак плюса или минуса всякий раз, когда вы получаете квадратный корень из чего-либо.
Выберите любое из двух исходных уравнений и найдите значения y, когда \ color {blue} x = \ pm \, 3. Я буду использовать первое уравнение, потому что оно намного проще!
Ответ: (3, 1) и (3, –1)
Ответ: (- 3, 1) и (- 3, –1)
Решения этой системы нелинейных уравнений состоят из четырех точек пересечения:
(3, 1), (3, –1), (- 3, 1) и (- 3, –1)
Фактически, это точки пересечения данного эллипса (первое уравнение) и гиперболы (второе уравнение).2, а затем вычислить квадратный корень с обеих сторон уравнения.
Назад подставьте значения x в любое из исходных уравнений, чтобы решить относительно y. Воспользуемся первым уравнением.
Ответ: (3, 2) и (3, — 2)
Ответ: (- 3, 2) и (- 3, — 2)
Решениями этой нелинейной системы являются точки пересечения данного эллипса и гиперболы.
Клавиша ответа на перехват наклона
Форма перехвата наклона Код ответа 2014! … Форма наклона-пересечения Построение линейных уравнений с использованием Шага 1: Шаг 2: Шаг 3: Пример: График y = 2 x — 1. 3 Примечания: Как получить форму пересечения наклона Форма пересечения наклона линейного уравнения m = наклон b = точка пересечения y Шаг 1) Составьте таблицу Используйте две точки для вычисления НАКЛОНА (m) xy X 1 Y 1 X 2 Y 2 Шаг 2) Подставьте m и одну точку в y = mx + b Решите относительно b (Y 1) = m (X 1) + b Шаг 3) Напишите общую формулу с m и bm = Y 2 –Y 1 X 2 — X 1
Запишите каждое уравнение ниже в форме пересечения наклона.Затем найдите наклон и точку пересечения оси Y внизу страницы. Напишите над ними букву упражнения. bz V y-2 = O 44 21 54 0 2x + 5y = 10 —2x + 3y = -21 м ‘2/3 b = -7 —x + = 20 @ 3x-5y = 5 м — уклон 3/5 y-intercept @ -7x-4y = 16 -2x + O 0 12x = 2y + 1 II s G 4x + 3y = 8 o 7 2 72 1 Нахождение точки пересечения по вертикали (0, b) Определение наклона / скорости изменения, м . Интерпретация линейных функций. Попробуйте сейчас ответы. 1. Ежегодно экономится 1000 долларов. 2.; Уменьшается, потому что m <0. 3. Ваш счет в колледже начинается с 20 000 долларов, и вы снимаете 4000 долларов каждый квартал (или ваш счет содержит 20 000 долларов и уменьшается на 4000 долларов каждый квартал.)
Форма SlopeIntercept Графическое изображение данной формы PointSlope. graphing lines.notebook 2 3 октября 2016 г. Построение графиков с учетом нулевого и неопределенного наклона. Графическое представление стандартной формы. Преобразование линейных уравнений (A) Ответы Преобразование стандартных в формы с пересечением уклона. 1. Стандартная форма: 10x 7y = 8 Форма пересечения наклона: y = 10 7 x + 8 7 2. Стандартная форма: 8x + y = 9 Форма точки пересечения наклона: y = 8x + 9 3. Стандартная форма: x + 6y = 2 Форма пересечения уклона: y = 1 6
Бесплатный рабочий лист в формате pdf и ключ ответа на форме пересечения уклона.29 сложных вопросов, которые начинаются относительно легко и заканчиваются реальными проблемами. Алгебра 1 Hojas De Trabajo Hojas De Trabajo De Ecuaciones Lineales в 2020 Графическое отображение линейных уравнений Рабочие листы по алгебре Предварительные задания по алгебре. 04 марта 2019 г. · Форма уравнения с пересечением наклона — y = mx + b, которая определяет линию. Когда линия нанесена на график, m — это наклон линии, а b — это место, где линия пересекает ось y или точку пересечения y. Вы можете использовать форму пересечения наклона, чтобы найти x, y, m и b.Следуйте этим примерам, чтобы увидеть, как преобразовать линейные функции в график …
Координаты каждой точки на линии решат уравнение, если вы подставите их в уравнение для x и y. Наклон m этой линии — ее крутизна или наклон — можно рассчитать следующим образом: m = изменение значения y. изменение значения x. Уравнение любой прямой, называемое линейным уравнением, может быть записано как y = m x + b, где m — наклон прямой, а b — точка пересечения с y. Рабочий лист формы пересечения откосов — Liveworksheets.com Рабочий лист формы пересечения откоса с ответами. Форма Slope Intercept — это рабочий лист, который содержит ряд вопросов, на которые потенциальный заемщик должен ответить, и, как и все рабочие листы, существует множество ответов. В большинстве случаев рабочий лист используется вместе с другим листом
7.1 7.4 Алгебра 1 викторина
7/4 — (- 1/6) Окончательный результат: 23 —— = 1.91667 12 Пошаговое решение: Шаг 1: 1 Упростить — 6 Уравнение в конце шага 1: 7 1 — — (0 — -) 4 6 Шаг 2: 7 Упростить — 4 Уравнение в конце… Алгебра I Модуль 1: Готовые к копированию материалы (1,7 МБ) Просмотр PDF: Алгебра I Модуль 1: Обзор модуля (779,57 КБ) Просмотр PDF: Алгебра I Модуль 1: Обзор модуля (390,42 КБ) Алгебра I Модуль 1: Средний модуль Оценка (847,1 КБ) Просмотр PDF: Алгебра I Модуль 1: Оценка в середине модуля (434,45 КБ) Алгебра I Модуль 1: Оценка в конце модуля (925,93 КБ) Просмотр PDF Алгебра 1 Авторские права © Big Ideas Learning, LLC Ресурсы по главам Все права защищены. 272 7.7 Практика имени _____ Дата _____ Абека Алгебра 1 Викторина 6.9 терминов. Danielle_Poznic. Алгебра 1 Тест 2. 28 терминов. Папа и мамаБарьер. abeka алгебра 1 викторина 9. 11 терминов. wewew123. Алгебра 1 Викторина 4. 10 терминов … 52 Изучение алгебры. Практикуйте свои навыки © 2007 Key Curriculum Press Урок 7.4 • Обозначение функции Название Период Дата 1. Найдите каждое неизвестное значение функции или значение x для f (x) 4x 7 и g (x) 3x 5 без использования калькулятора. Затем введите уравнение для f (x) в Y1 и уравнение для g (x) в Y2. Используйте функцию Эта таблица по алгебре 1 — экспоненты создает проблемы для работы с различными операциями с научной нотацией.Вы можете выбрать задачи с умножением, делением или произведениями в степень. Этот рабочий лист содержит 12 задач на странице. Эти Рабочие листы по показателям являются хорошим источником для учащихся с 5-го по 8-й класс. 11 марта, 2019 · НАУКИ CONNEXUS, ПОЖАЛУЙСТА, СКАЖИТЕ МНЕ ОТВЕТЫ НА УРОК 11 НАУЧНЫЙ ТЕСТ, БЛОК 2 (структуры и свойства единиц материи). алгебра. Может кто-нибудь, пожалуйста, скажите мне ответы на Урок 1: Обзор семестра CE 2015 Алгебра 1 A, Часть 1 Раздел 5: Обзор семестра и экзамен, практика Хотите знать, насколько хорошо вы понимаете конкретную концепцию алгебры? Возьмите исследование.com с несколькими вариантами ответов. Получите немедленные результаты, чтобы показать, насколько хорошо вы справились. Урок, сопровождающий викторину, таков … Разделы 7.1-7.4 Тест 305 Запишите словесное предложение в виде уравнения. (Раздел 7.1) 1. Число x, уменьшенное на 3, равно 5. 2. Число a, разделенное на 7, равно 14. 3. Произведение 3 и числа b равно 9. 4. На 7 больше числа n равно 20. Решите уравнение. Информация на 1-й день Учебный план письма для родителей Решение уравнений Решение уравнений — Примечания Решение уравнений — Работы по решению уравнений — Клавиша PAP 1.6 и решение неравенств 1.6 Примечания 1.6 Решение назначений … 11-21 Алгебра Холта 2 Практика C Независимые и зависимые события Найдите каждую вероятность. 1. На уроке кулинарии учащиеся случайным образом выбирают 1 из 3 различных рецептов. Два ученика выбирают один и тот же рецепт. _____ 2. Стивен бросил кубик с числами от 1 до 6 четыре раза. Получилось 4 нечетных числа. _____ Показанный здесь счетчик вращается дважды. 3. Объявление: Я буду контролировать ТЕСТОВЫЕ ИСПРАВЛЕНИЯ в своей комнате (31J) во время обеда и после школы в четверг 30 мая, понедельник 3 июня и вторник 4 июня.Будут доступны все тесты (кроме блока 12). Будут доступны все тесты (кроме блока 12). 1 Математика 9 Раздел 7.1 — 7.4 Практический тест Краткий ответ 1. Определите масштабный коэффициент для этой масштабной диаграммы. 2. На фото длина модели автомобиля 4,2 см. Фотография должна быть увеличена в масштабе 5,5. Определите длину автомобиля в увеличении. 3. Какие параллелограммы A, B, C и D являются масштабными диаграммами параллелограмма O? 4. Например, последовательность Фибоначчи определяется рекурсивно как f (0) = f (1) = 1, f (n + 1) = f (n) + f (n-1) для n ≥ 1.CCSS.MATH.CONTENT.HSF.IF.B.4 Для функции, моделирующей отношения между двумя величинами, интерпретации ключевых характеристик графиков и таблиц в терминах количеств и схематических диаграмм, показывающих ключевые особенности при словесном … Практика Тест 7.1-7.4 Алгебра 1; Популярные ссылки. Популярные ссылки. Средняя школа Карман-Эйнсворт работает вместе, чтобы гарантировать обучение каждому ученику. 25 октября 2009 г. · 101 Алгебра 1 Уроки 1. Начало работы — Блокноты и калькуляторы Задание на урок A. Организация наших блокнотов Создайте все нужные страницы — Раздел 1 — Общая информация Титульная страница тетради Часто задаваемые вопросы Содержание Учебный план (можно получить у г-жи .Гриффин) Школьный календарь Формулы данных теста Стратегии решения проблем Элементы портфолио Рубрика записной книжки — Раздел 2 — Технические … 3 февраля 2007 г. · Получите последнюю версию Acrobat Reader 5.0. Щелкните значок «Получить Acrobat» выше, чтобы перейти в область загрузки. Используйте Netscape! Это обзор алгебры в 10 уроках, написанных в TeX и преобразованных в формат Adobe Portable Document Format (PDF). Возможности включают подробное обсуждение тем, качественный набор математических выкладок, интерактивность пользователя в форме опросов с несколькими вариантами ответов, i 0-вектор (1 – вектор) — это вектор с 0 (1) во всех записях.0-вектор (1-вектор) часто записывается просто как 0 (1) или как 0 n (1 n), чтобы подчеркнуть, что его длина n. > rep (0, 5) [1] 0 0 0 0 0> rep (1, 5) [1] 1 1 1 1 1 2.8 Ортогональные (перпендикулярные) векторы Два вектора v 1 и v 2 ортогональны, если их внутреннее произведение ноль … Абека Алгебра 1 Викторина 6. 9 терминов. Danielle_Poznic. Алгебра 1 Тест 2. 28 терминов. Папа и мамаБарьер. abeka алгебра 1 викторина 9. 11 терминов. wewew123. Алгебра 1 Викторина 4. 10 терминов … Урок 7.1 Графические функции экспоненциального роста Урок 7.2 Графические экспоненциальные функции убывания Урок 7.3 Использование функций, задействованных в электронном уроке 7.4 Вычисление логарифмов и графических логарифмических функций Урок 7.5 Применение свойств логарифмов Урок 7.6 Решение экспоненциальных и логарифмических уравнений Урок 7.7 Написание и применение экспоненциальных и степенных функций
Ключ к изучению алгебры 1 быстро заключается в использовании диагностических тестов, которые скажут вам, знаете ли вы уже концепцию урока, прежде чем проводить время на уроке. Если результаты вашей диагностической викторины показывают, что вы уже знаете концепцию, вы можете пропустить ее вперед, что позволит вам сосредоточить свои исследования на конкретных уроках, которые вам нужны.
Алгебра множеств Алгебра 1 практическое занятие 7.1. Скажите, является ли упорядоченная пара решением линейной системы
7 — 1/4 некоторого числа. б. n — 14 = 7. Шесть меньше, чем сумма 11 и 9. … Домашнее задание | Алгебра | Язык алгебры: Отправьте эту страницу по электронной почте другу:
Хотите знать, насколько хорошо вы понимаете конкретную концепцию алгебры? Пройдите быструю викторину Study.com с несколькими вариантами ответов. Получите немедленные результаты, чтобы показать, насколько хорошо вы справились. Урок, сопровождающий викторину, есть…
Алгебра 1 Алгебра 1 Практический тестПрактический тестПрактический тест 3. Решите следующее неравенство: -20 <4 - 2x A. 8> x C. 12> x B. 8 Удобный и отличный способ получить базовую практику по алгебре и получить помощь. … 7.1 Выражение линейных неравенств графически и алгебраически … 7.4 Составные неравенства. Алгебра 1; Дизайн и сборка; Введение в инженерное проектирование; Принципы инженерии; … GradPoint; Эта страница в настоящее время недоступна.Средняя школа Карман-Эйнсворт; Практический тест 7.1-7.4 Алгебра 1; Популярные ссылки. Популярные ссылки. Средняя школа Карман-Эйнсворт работает вместе, чтобы гарантировать обучение каждому ученику. АДРЕС: 1300 N. Linden Road … Неделя 3 января 2011 г., 7–8 (пн), тест по главе 7, форма 2A (вторник), тест по главе 7, форма 2B (среда), TBA (четверг), 8-1 (Пт) Основные уроки математики Понедельник: Урок 7-8 Вторник: Учебное пособие по главе 7 и обзор Среда: Практический тест по главе 7 (из учебника) Абека Алгебра 1 Викторина 6.9 терминов. Danielle_Poznic. Алгебра 1 Тест 2. 28 терминов. Папа и мамаБарьер. abeka алгебра 1 викторина 9. 11 терминов. wewew123. Алгебра 1 Викторина 4. 10 терминов … Высоко оценены: согласно EdReports, независимой некоммерческой организации, которая рассматривает учебные материалы для школьников K – 12, IM 6–8 Math ™ и IM 9–12 Math ™, сертифицированные Illustrative Mathematics®. все ожидания от всех трех шлюзов в отношении сосредоточенности, согласованности, строгости, математических практик и удобства использования. ДОЛЖЕН ИМЕТЬ ИМЯ ПОЛЬЗОВАТЕЛЯ И ПАРОЛЬ Математические игры для 4-го класса на этом веб-сайте посвящены нескольким важным темам, таким как добавление и вычитание десятичных и дробных чисел с общими знаменателями, округление десятичных дробей, измерение углов с помощью соответствующих единиц и инструментов, понимание характеристики геометрических плоских и сплошных фигур с использованием общих единиц измерения для определения веса и использования таблиц, графиков и диаграмм для записи… Хотите знать, насколько хорошо вы понимаете конкретную концепцию алгебры? Пройдите быструю викторину Study.com с несколькими вариантами ответов. Получите немедленные результаты, чтобы показать, насколько хорошо вы справились. Урок, сопровождающий викторину … ДА! Пришло время переосмыслить свое истинное «я», используя Алгебру 1 Слэдера: ответы на общие основные учебные планы. Избавьтесь от социальных и культурных нарративов, сдерживающих вас, и позвольте поэтапным решениям из учебников по Алгебре 1: Общий основной учебный план переориентировать ваши старые парадигмы.СЕЙЧАС самое время сделать сегодняшний день первым днем вашей оставшейся жизни. Алгебра 1 Раздел 7 Цели практического экзамена 7.1, 7.3, 7.4 Название Определите, является ли каждое уравнение истинным или ложным. Если это правда, покажите свою работу, чтобы защитить свой ответ. Если это ложь, покажите свою работу и объясните, почему она ложная. Используйте в своей работе свойства экспонент. 64 = 85 / se 3 Обведите выражения, которые эквивалентны 16. Объявление: Я буду контролировать ТЕСТОВЫЕ ИСПРАВЛЕНИЯ в своей комнате (31J) во время обеда и после школы в четверг 30 мая, понедельник 3 июня и вторник 6 июня. / 4.Будут доступны все тесты (кроме блока 12). Будут доступны все тесты (кроме блока 12). 7-1 Практика B Экспоненциальные функции, рост и распад … aa207c07-1_pr.indd 4207c07-1_pr.indd 4 55/17/07 11:38:22 AM / 17/07 11:38:22 AM. .. 67 Holt Algebra 2 All … Дополнительные практические задачи с формулой арифметической последовательности Направление: внимательно прочтите каждый вопрос о арифметической последовательности, затем ответьте с дополнительными подробностями. Арифметическая последовательность Практические задачи с ответами 1) Скажите, является ли последовательность арифметической или нет.Объясните, почему да или почему нет. Последовательность A: Последовательность B: Решение: Последовательность A является арифметической последовательностью, поскольку каждая… Арифметическая последовательность … Глава 1 Основы алгебры Глава 2 Уравнения Глава 3 Неравенства Глава 4 Функции Глава 5 Линейные функции Глава 6 Системы уравнений и неравенств. .. 7.1-7.4 Обзор викторины: 7.1-7.4 Обзор викторины: Размер файла: 118 kb: Тип файла: pdf: Загрузить файл. Глава 7 Стандарты. Стандарты штата Флорида Ключ ответа на практический тест.Вопрос 1-4. Вопрос 5 — 7 7.1 Введение в рациональные функции 7.2 Упрощение рациональных выражений 7.3 Сложение и вычитание рациональных выражений 7.4 Умножение рациональных выражений 7.5 Разделение рациональных выражений 7.6 Решение рациональных уравнений. 7.6 График рациональной функции. Глава 8 Радикальные функции y x 1 Поскольку графики 3x 3y 3 и y x 1 совпадают, существует бесконечно много решений. Используйте график справа, чтобы определить, не имеет ли каждая система решения, одно решение или бесконечно много решений.1. yx 3 2. 2x 2y 6 yx 1 yx 3 3. yx 3 4. 2x 2y 6 2x 2y 43x y 3 xy O yx 3 3x y 3 2x 2y 6 2x 2y 4 yx 1 xy O yx 1 yyx 1 3x 3y 3 … Урок 7.1 График функций экспоненциального роста Урок 7.2 График функций экспоненциального убывания Урок 7.3 Использование функций, связанных с электронным уроком 7.4 Вычисление логарифмов и графических логарифмических функций Урок 7.5 Применение свойств логарифмов Урок 7.6 Решение экспоненциальных и логарифмических уравнений Урок Применение 7.7 Экспоненциальные и степенные функции Онлайн-решатель алгебры Я советую вам подписаться на этот решатель алгебры.Вы можете шаг за шагом решать свои задачи по алгебре онлайн — уравнения, неравенства, радикалы, строить графики, решать полиномиальные задачи. Если ваша домашняя работа по математике включает уравнения, неравенства, функции, многочлены, матрицы, это правильный пробный счет. Онлайн тригонометрия … Бесплатная студенческая математическая практика. Изменить ответ; Математика Лучшие обзоры Ответы на 7 1 7 4 Викторина Большие идеи Математическая алгебра 1 и ответы из T Например, последовательность Фибоначчи определяется рекурсивно как f (0) = f (1) = 1, f (n + 1) = f ( n) + f (n-1) для n ≥ 1.CCSS.MATH.CONTENT.HSF.IF.B.4 Для функции, моделирующей взаимосвязь между двумя величинами, интерпретировать ключевые особенности графиков и таблиц в терминах количеств и схематических графиков, показывающих ключевые особенности при словесном … P .454 # 2-16 четное, 24-28 четное, 38 Для всех задач, кроме # 2 и # 38, введите свой ответ в форме (x, y) без пробелов.


 Результирующий график — это
Результирующий график — это Результирующий график y = (x
Результирующий график y = (x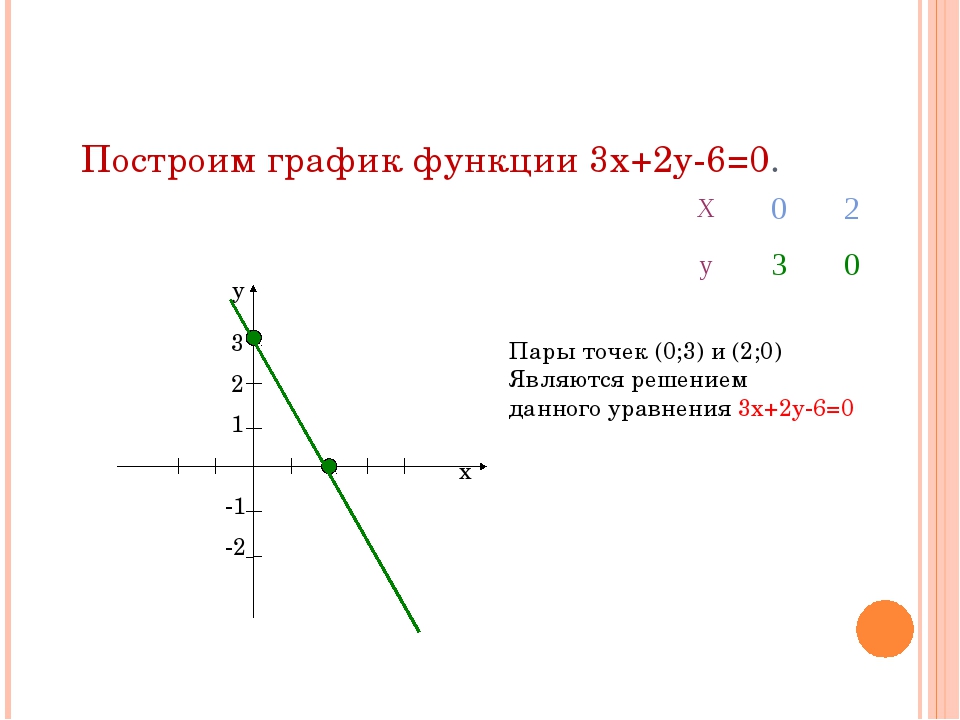 Результирующий граф — это гипербола
Результирующий граф — это гипербола