Содержание
Урок 5. измерение углов — Геометрия — 7 класс
Геометрия
7 класс
Урок №5
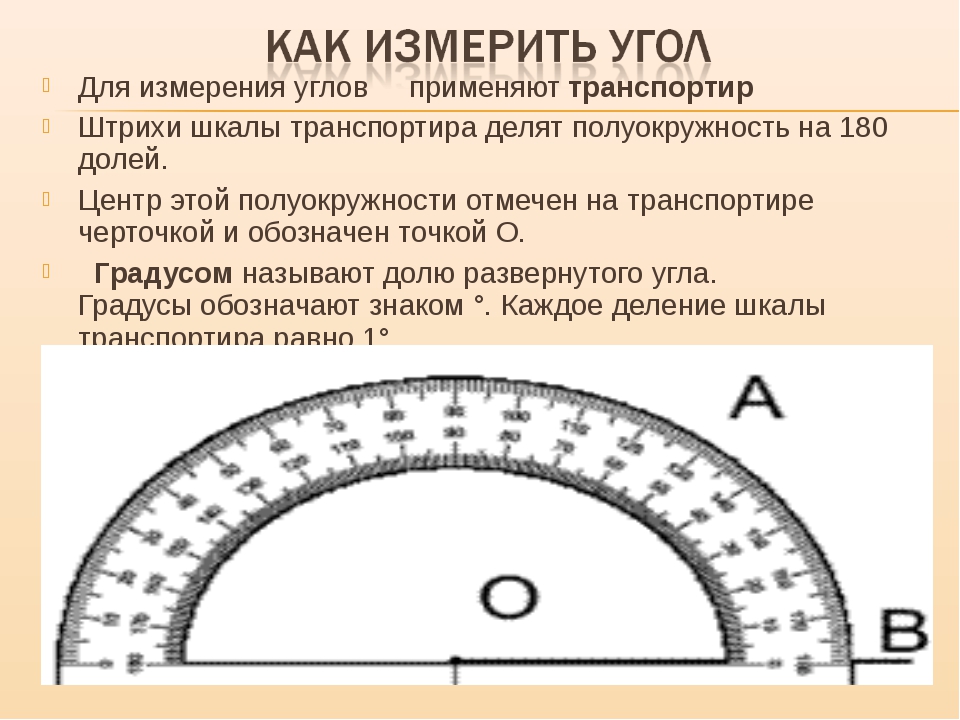
Измерение углов
Перечень рассматриваемых вопросов:
- Измерительные инструменты.
- Градусная мера угла; биссектриса.
- Транспортир.
- Классификация углов.
Тезаурус:
Градус – угол, равный одной сто восьмидесятой части развернутого угла.
Градусная мера угла – положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Минута – 1/60 часть градуса.
Секунда – 1/60 часть минуты.
Луч – часть прямой, состоящий из всех точек, лежащих по одну сторону от заданной точки, которая является началом луча.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Стороны угла – лучи, из которых состоит угол.
Вершина угла – общее начало сторон угла.
Биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.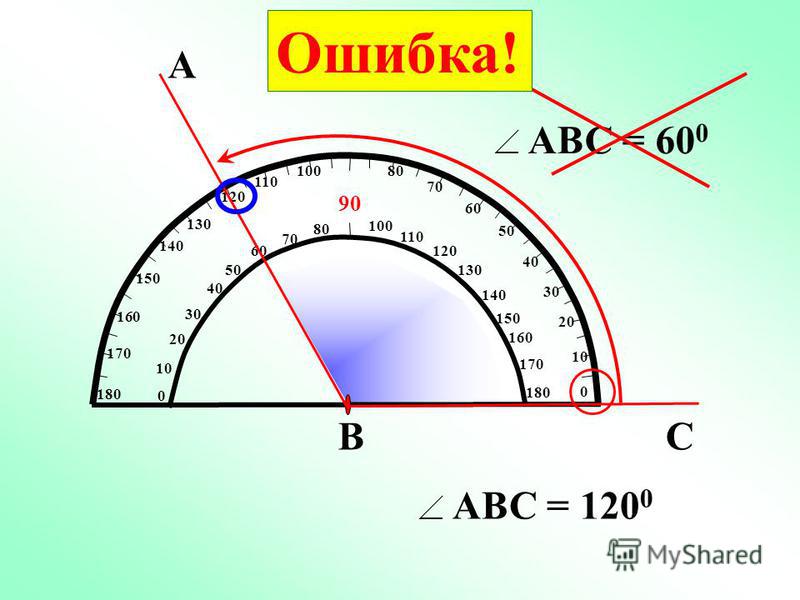
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее вы уже познакомились с геометрической фигурой – уголи его составными элементами.
Сегодня мы продолжим изучать углы, познакомимся с их классификацией и будем измерять углы с помощью транспортира.
Измерение углов аналогично измерению отрезков – оно основано на сравнении, только отрезки сравнивались с отрезком, принятым за единицу измерения, а углы с углом, тоже принятым за единицу измерения.
Обычно за единицу измерения углов принимают градус.
Градус – угол, равный 1/180 части развёрнутого угла.
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу, называется градусной мерой угла.
Для измерения углов используют транспортир. Вспомним, как проводить измерение углов с помощью транспортира.
Транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах на той же шкале.
Например:
∠О = 50°
Но обычно говорят кратко – угол О равен 50 градусам.
Если масштабныйугол не укладываетсяцелое число раз в измеряемом угле, тоединицу измерения делят ещё на части.
Определённые части градуса носят специальные названия.
Части градуса.
Минута – 1/60 часть градуса.
Обозначается «´».
Секунда – 1/60 часть минуты.
Обозначается «´´».
Например:
∠А = 40 ° 15´ 16 ´´
Далее, аналогично понятию равные отрезки, ведём понятие равные углы.
Дваугла считаются равными, если градус и его части укладываются в этих углах одинаковое число раз, т.е. равные углы имеют равные градусные меры.
Если один угол меньше другого, то градус в нём (или его часть) укладываются в этом углу меньшее число раз, чем в другом, т.е. меньший угол имеет меньшую градусную меру.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
∠АОС =∠АОL + ∠LОС,
∠АОL = 64°,
∠LОС = 64°,
∠АОС = 64° + 64° = 128°.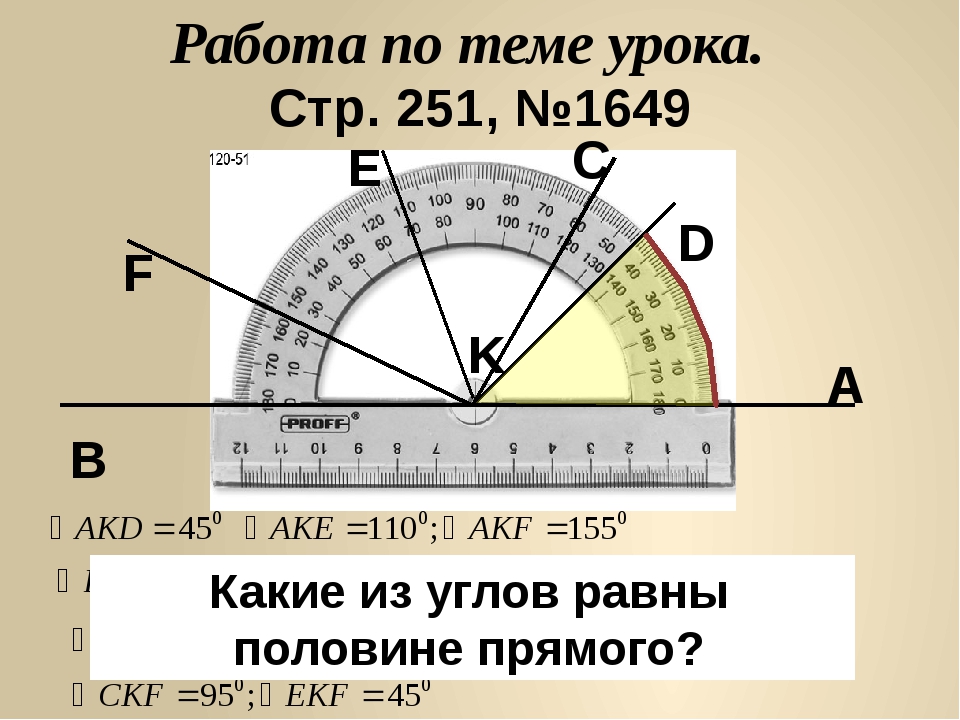
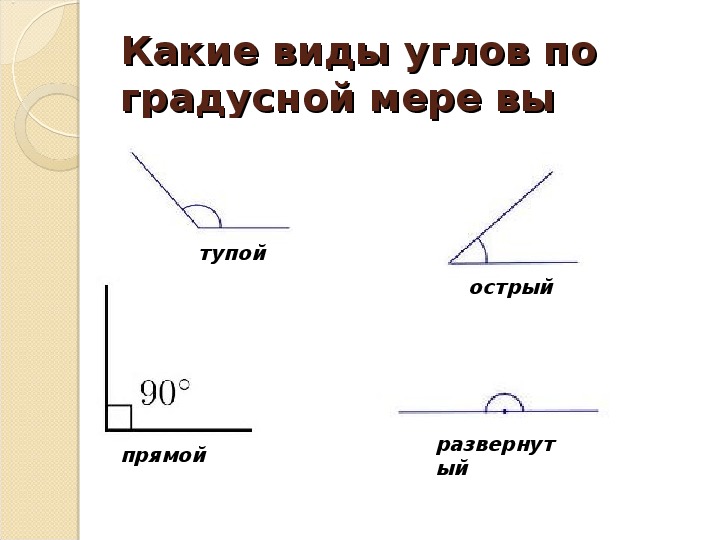
Далее рассмотрим классификацию углов.
Мы уже знаем, что есть развёрнутый угол, его градусная мера сто восемьдесят градусов.
Но есть и другие углы.
Например, прямой угол, его градусная мера девяносто градусов;
острый угол, его градусная мера меньше девяноста градусов;
тупой угол, его градусная мера больше девяноста градусов, но меньше ста восьмидесяти.
Выполним практическое задание – построим биссектрису угла с помощью транспортира.
Мы знаем, что биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
∠АОС = 128°,
128° : 2 = 64°,
OL – биссектриса ∠АОС.
Поэтому для начала определим градусную меру ∠АОС, она составляет 128°, тогда биссектриса этого угла, исходя из определения, составит 64 °.
Итак, сегодня получили представление о том, как измерять и изображать угол с помощью транспортира. Перейдем к практическим заданиям.
Способы измерения на местности.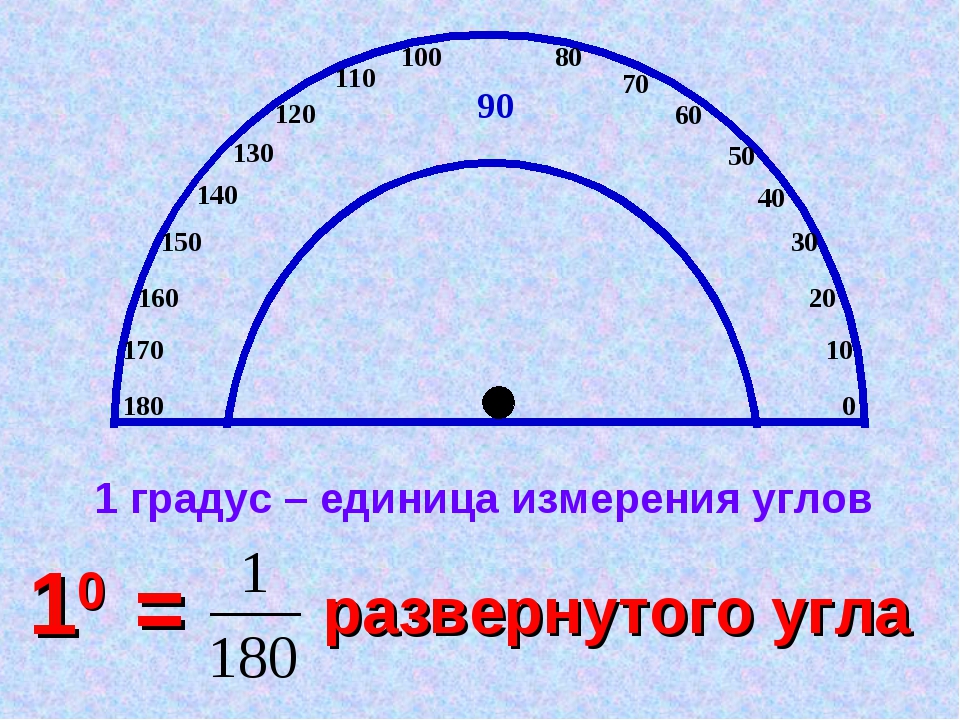
Измерение углов на местности проводят с помощью различных приборов. Один из таких – астролябия, она состоит из диска (лимб), разбитого на градусы и вращающейся вокруг центра диска линейки (алидады). На концах алидады есть окошечки, которые нужны, чтобы устанавливать её в определённом направлении.
Опишем, как происходит измерение углов с помощью этого прибора. При измерении углов астролябию устанавливают в его вершине, например, точке О, при этом лимб должен находится горизонтально плоскости угла, а отвес, в центе диска, совпадать с вершиной угла.
Затем устанавливаем алидаду вдоль одной из сторон угла, например, АО, отмечаем деление, напротив которого находится указатель алидады.
Далее поворачиваем алидаду по часовой стрелке, пока она не совпадёт со второй стороной угла, у нас это сторона ОВ, отмечаем деление, напротив которого оказался указатель алидады. Теперь можно найти градусную меру измеряемого угла, как разность второго и первого измерения.
Тренировочные задания.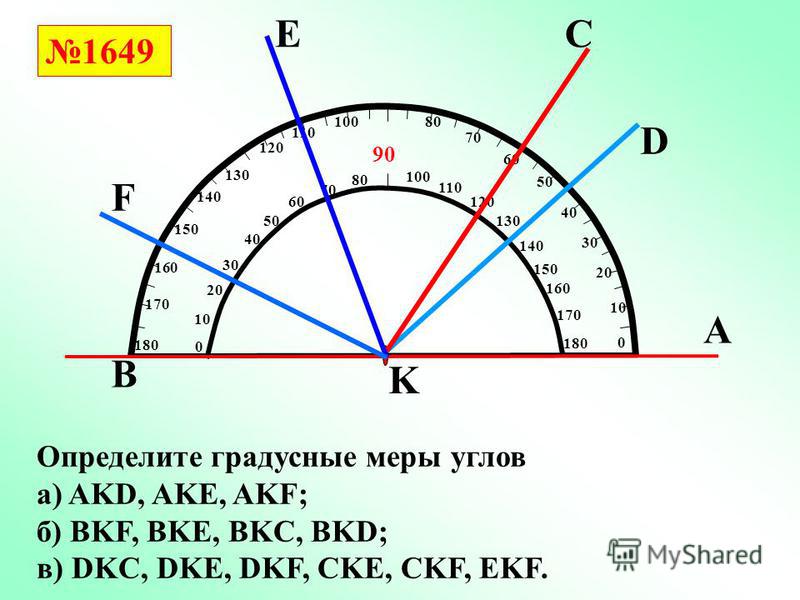
1. Луч ВК делит развернутый ∠ОВС на два угла, разность которых равна 56°. Найдите образовавшиеся углы.
Решение: нарисуем рисунок, исходя из условия задачи.
Обозначим ∠СВК за х, тогда ∠ОВК= х + 56°, исходя из условия задачи (разность углов равна 56°). Развёрнутый угол равен 180°. Составим уравнение и решим его.
х + х +56 =180,
2х= 180 – 56,
2х= 124,
х = 124:2,
х = 62° (∠СВК).
Тогда ∠ОВК= х + 56°= 62° +56° = 118°.
Ответ: ∠СВК = 62°; ∠ОВК = 118°.
2. Чему равен ∠ЕОА, если ∠ВОА = 130° 54´, а ∠ВОЕ = 105° 76´?
Решение: Найдём ∠ЕОА = ∠ВОА – ∠ВОЕ, т.к. ОЕ – луч, проведённый из вершины ∠ВОА и делящий этот угол на 2 части. Подставим в выражение градусные меры углов и найдём градусную меру ∠ЕОА. Так как в градусе 60 минут, то 105° 76´ = 106° 16´.
∠ЕОА = 130° 54´ – 106° 16´ = 24° 38´.
Ответ: ∠ЕОА = 24° 38´.
Измерение углов. Транспортир. Виды углов
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Измерение углов.
 Транспортир. Виды углов
Транспортир. Виды углов
Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом, записывают так 1°.
Градусная мера угла — это число, которое показывает, сколько раз градус и его части укладываются в данном угле.
Пример:
Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .
Транспортир — это измерительный инструмент, который используется для измерения и построения углов.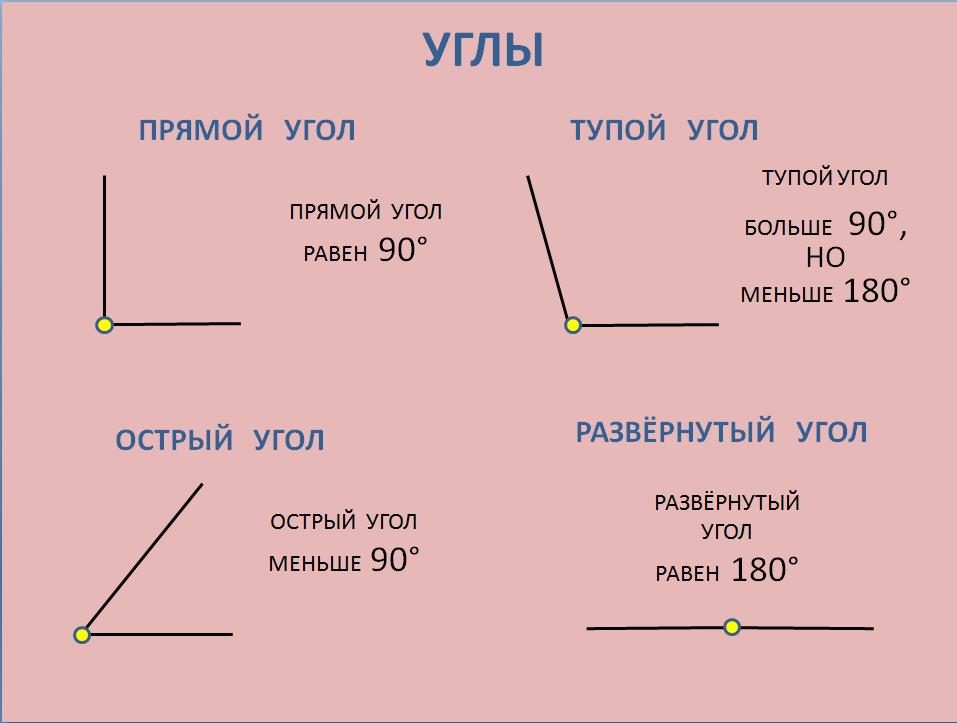 Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .
Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .
Свойства:
- Равные углы имеют равные градусные меры.
- Меньший угол имеет меньшую градусную меру.
- Развернутый угол равен .
- Неразвернутый угол меньше .
- Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов, т.е. на рисунке ниже
АОС = АОВ + ВОС.
Виды углов:
- Острый угол — угол, градусная мера которого меньше 90°.
- Прямой угол — угол, градусная мера которого равна 90°.

- Тупой угол — угол, градусная мера которого больше 90°, но меньше 180°.
- Развернутый угол — угол, градусная мера которого равна 180°.
Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 900.
АОС — развернутый, ОВ — биссектриса, АОВ = ВОС = 900.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.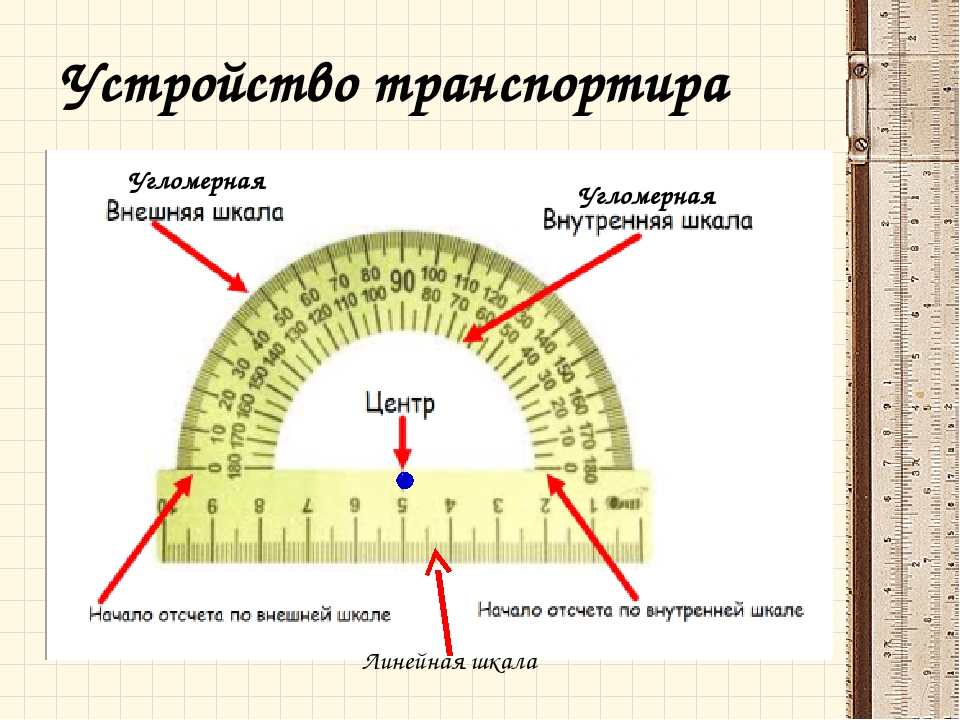
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Треугольник и его виды
Окружность, круг, шар
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 1662,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1686,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1773,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1774,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1847,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
Номер 298,
Мерзляк, Полонский, Якир, Учебник
Номер 314,
Мерзляк, Полонский, Якир, Учебник
Номер 354,
Мерзляк, Полонский, Якир, Учебник
Номер 500,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 220,
Мерзляк, Полонский, Якир, Учебник
Номер 391,
Мерзляк, Полонский, Якир, Учебник
Номер 433,
Мерзляк, Полонский, Якир, Учебник
Номер 495,
Мерзляк, Полонский, Якир, Учебник
Задание 738,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 837,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1375,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1425,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1534,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1545,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© budu5. com, 2021
com, 2021
Пользовательское соглашение
Copyright
В градусах
Вы не задавались вопросом, почему в градусах измеряют настолько не связанные между собой вещи — углы и температуру? Скажем больше, градусами меряют плотность жидкости и качество молока и (да, мы не забыли) долю спирта. Gradus — латинское слово, означающее шаг, ступень или степень. Иными словами, у градуса, в отличие от метрических единиц измерения, нет конкретной величины, и он не соответствует никакому эталону, привязанному к тем или иным физическим параметрам. При этом размер градуса можно всякий раз устанавливать по-разному, и ничего не изменится. Кому и зачем могла понадобиться такая единица измерения? Давайте разбираться.
Углы
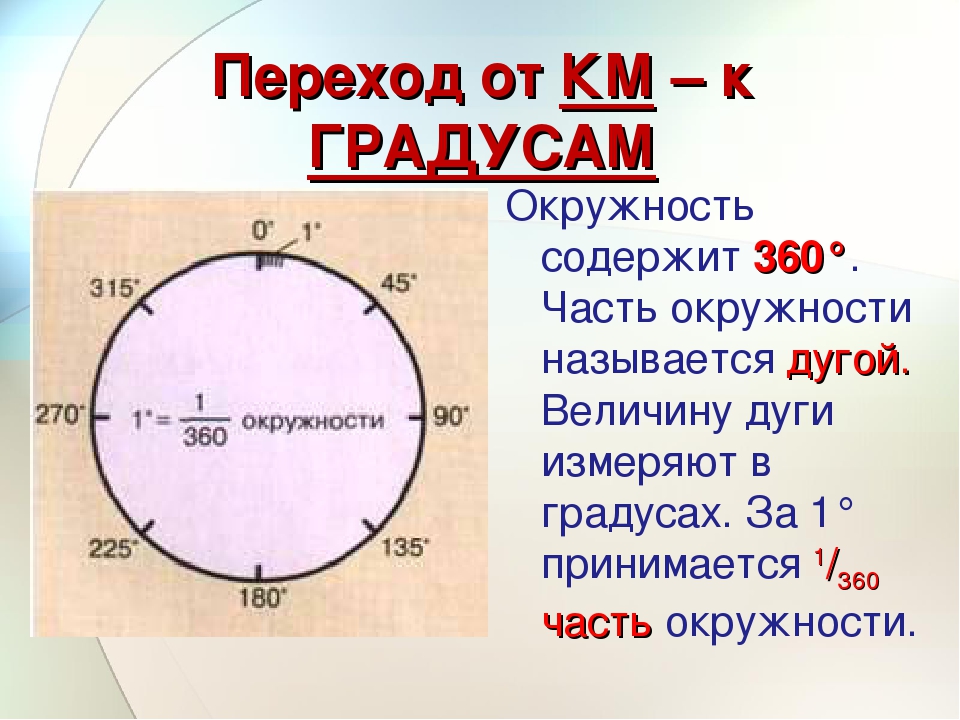
Со школы все мы знаем, что в окружности содержится ровно 360 градусов.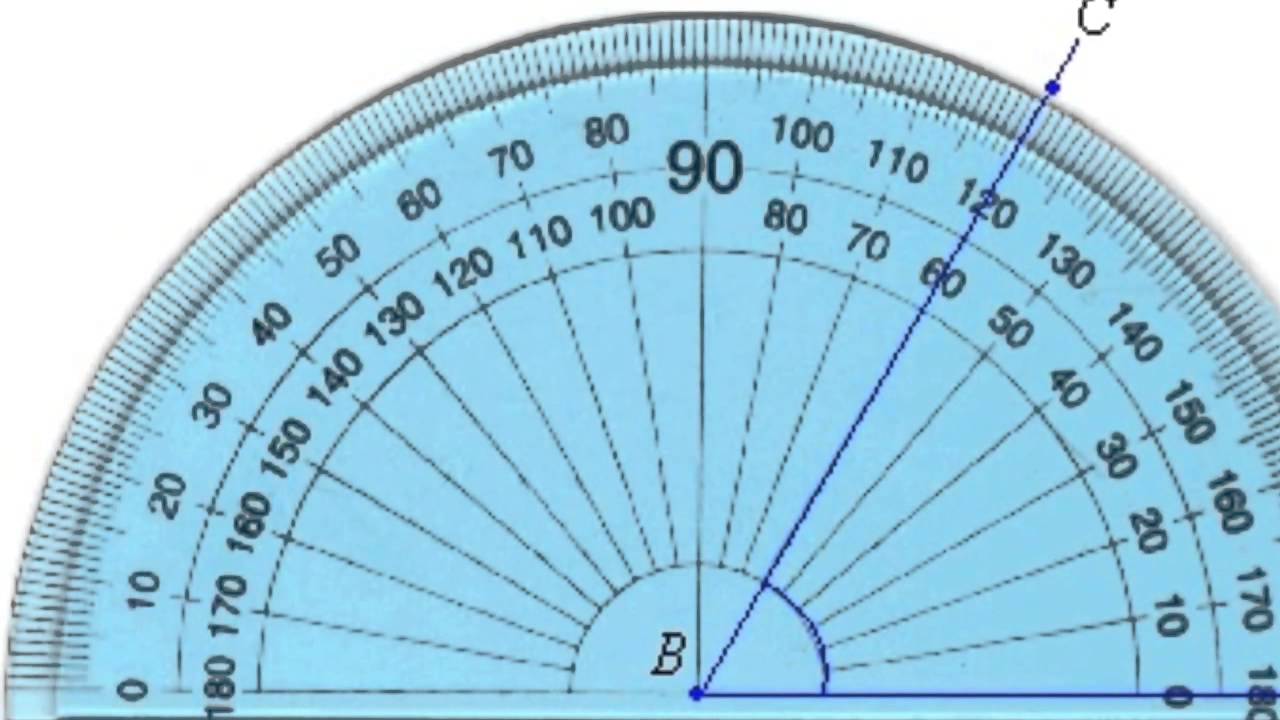 Но почему именно 360? Ответить на этот вопрос можно по-разному.
Но почему именно 360? Ответить на этот вопрос можно по-разному.
По одной версии, древние астрономы, скорее всего персы и каппадокийцы, заметили, что солнце оказывается в одной и той же точке небосвода лишь один раз в 365 дней. Они объяснили это тем, что солнце совершает полный оборот вокруг земли за год и возвращается в исходную точку.
Возможно, они округлили число 365, а может, и просто пропустили пять дней, но в итоге заключили: солнце сдвигается на одну трехсот шестидесятую долю окружности в день.
Другая теория объясняет 360-градусный полный угол совсем другими причинами. Шумеры и вавилоняне пользовались (не самой удобной) шестидесятеричной системой счисления. Большие числа они считали шестидесятками (например, число 1020 это 17 шестидесятков).
Знаки шумерской шестидесятиричной системы счисления
Wikimedia commons
Вписав в окружность правильный шестиугольник, вавилоняне заметили, что в круг отлично помещаются шесть равносторонних треугольников. Каждому треугольнику они приписывали по шестидесятку. В итоге, шесть треугольников по шестидесятку дали известные 360 градусов.
Каждому треугольнику они приписывали по шестидесятку. В итоге, шесть треугольников по шестидесятку дали известные 360 градусов.
Шестидесятизначная система объясняет и деление градуса на 60 минут (‘) и 3600 секунд (“). Знак, которым мы сегодня обозначаем градусы (°), впервые был использован в математике в 1569 году, по аналогии с верхним штриховым индексом для минут и секунд.
Независимо от истории, полный угол в 360 градусов — лучший вариант из возможных, ведь 360 — сверхсоставное число (натуральное число, с бoльшим числом делителей, чем все предыдущие). Оно делится на все числа от 1 до 10 за исключением семи, а еще и на: 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 и 180. На такое количество частей вы можете разделить окружность простым вычислением в уме.
Геометрические градусы прошли проверку временем и оказались самой удобной единицей измерения углов. Но есть и другие.
Так, если у вас есть инженерный калькулятор, то, переключаясь между градусами (DEG) и радианами (RAD), вы, возможно, попадали в режим GRAD — это исчисление в градах (или гонах). Один град — это одна сотая часть прямого угла, а значит, полный угол равен 400 град.
Один град — это одна сотая часть прямого угла, а значит, полный угол равен 400 град.
Такая единица измерения появилась во времена Французской революции вместе с метрической системой и быстро всех запутала. Кроме проблем с названием, — в некоторых странах grad обозначали привычные градусы, — возникли трудности и с вычислением.
Например, как известно, углы равностороннего треугольника равны друг другу и составляют 60 градусов. Переведем это в грады — 66 целых и шесть в периоде, ужасно неудобно.
В отличие от метрической системы, без которой трудно представить нашу жизнь, вычисления в градах оказались не самыми простыми, сейчас их практически нигде не используют.
Но свой след в истории они оставили — именно благодаря градам стоградусная температурная шкала получила название шкалы Цельсия.
Температура
Как ни странно, температурные шкалы появились гораздо раньше термометров. Создателем первой шкалы можно считать Галена — древнеримского медика, хирурга и философа.
Гален утверждал, что существует некая нейтральная температура — он определил ее как температуру смеси одинакового количества кипящей воды и льда. От нейтральной температуры он отсчитал по четыре шага (ступени) в сторону тепла и холода.
Шведский теолог и физик Иоганн Хаслер на основании работ Галена построил таблицу температуры, опубликованную на страницах труда «De Logistica Medica problematis novem» в 1578 году. Он отложил те же четыре шага тепла и холода по разные стороны от нейтральной температуры, а также заметил, что шкалу можно заменить на последовательность чисел от единицы до девяти.
В таблице значения температуры называются просто «номерами», но в тексте Хаслер использует слово «градус». Нейтральная температура в его системе будет соответствовать числу пять.
Таблица температуры Иоганна Хаслера. Слева направо: первый столбец — шкала Хаслера, второй — шкала Галена, следующие столбцы связаны с рецептами лекарств
Wikimedia commons
Первое устройство, похожее на современный термометр, создал Галилео Галилей приблизительно в 1597 году. Вслед за этим ученые почти 200 лет искали универсальную, удобную и точную шкалу температур.
Вслед за этим ученые почти 200 лет искали универсальную, удобную и точную шкалу температур.
Например, в 1701 году Исаак Ньютон в опубликованной анонимно работе (в ней он уже использует слово gradus для обозначения единиц тепла) предлагат 18 реперных точек, часть из которых формирует геометрическую, а другая — арифметическую прогрессии. В градусах Ньютона точка замерзания воды равна 0 градусов, а температура человеческого тела — 12 градусов.
В том же году известный астроном Оле Ремер (первым измеривший скорость света) предложил свой вариант. Нулем своей шкалы он выбрал температуру соленой воды со льдом, а вот температуру кипения воды — снова это магическое число — он обозначил как 60 градусов. Эту шкалу позаимствовал знакомый Ремера, Габриэль Фаренгейт.
Фаренгейт избавился от неудобных дробей, возникавших при измерении температуры человеческого тела (22,5 градуса) и замерзания пресной воды (7,5 градуса), заменив их на 24 и 8 градусов соответственно. Вода стала кипеть при 64 градусах Фаренгейта.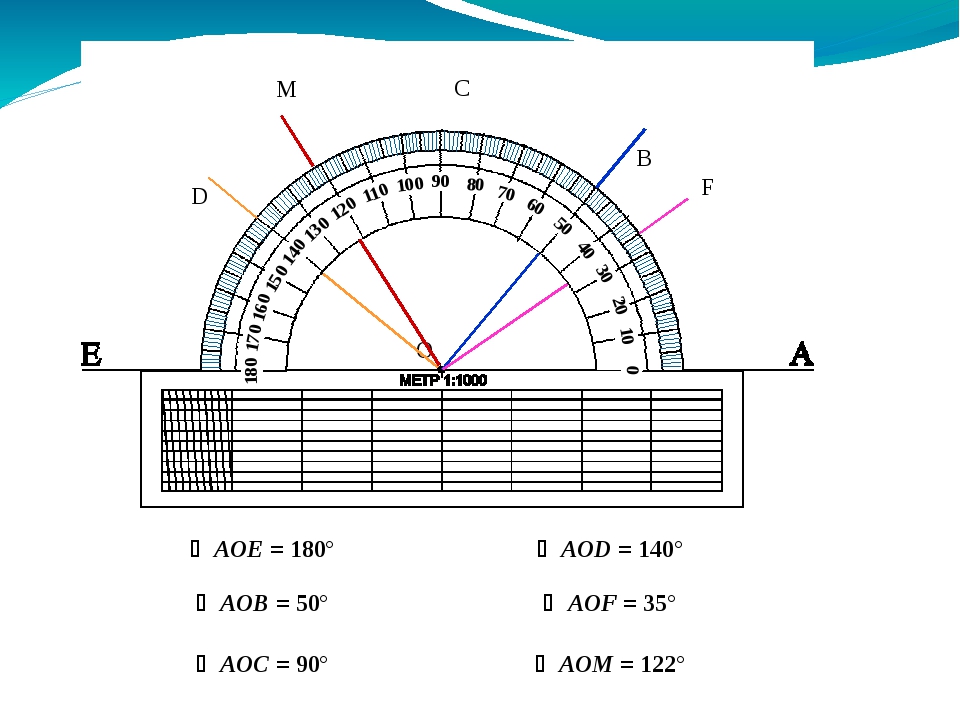
Некоторое время он производил термометры с такой шкалой, но потом, в 1724 году, умножил ее на 4. По одной версии, Фаренгейт просто хотел сделать шкалу точнее, поэтому увеличил количество рисок на градуснике, по другой — он сделал это, чтобы увеличение температуры на один Фаренгейт приводило к увеличению объема ртути ровно на одну десятитысячную.
Так появилась знаменитая шкала Фаренгейта, которой люди пользуются и сегодня. Некоторое время она была лучшей из возможных, но затем ей смену пришел более совершенный вариант. Хотя жители США навряд ли согласились бы с нами.
Жозеф Николя Делиль пошел несколько другим путем. Он выбрал всего одну реперную точку, температуру кипения воды, и обозначил ее за ноль. Градуировать шкалу он решил по расширению ртути в термометре — понижение температуры, приводящее к уменьшению объема ртути на одну стотысячную, Делиль обозначил за один градус.
Температура замерзания воды в таком случае — 2400 градусов, шкала оказалась излишне мелкой, поэтому в 1738 году Иосия Вейтбрехт изменил ее. Он задал температуру замерзания воды в 150 градусов.
Он задал температуру замерзания воды в 150 градусов.
Такие термометры стали удобными и получили широкое распространение. Ими примерно сто лет пользовались в России, Ломоносов использовал термометр Делиля (правда, перевернув шкалу) в своих опытах.
Только в этот момент на сцене появляется Андерс Цельсий. В 1741 году он наносит на термометр Делиля свою шкалу — 0 градусов в точке кипения и 100 градусов в точке замерзания воды. Перевернули шкалу (скорее всего, это сделал Карл Линней) через год после смерти Цельсия (он умер в 1744 году от туберкулеза).
Кстати, к 1745 году уже существовал термометр с нулем в точке замерзания и сотней градусов в точке кипения воды. Он называется термометром Лиона, его изобретатель — французский физик Жан-Пьер Кристен.
Заслуга Цельсия в другом — он провел эксперименты, продемонстрировавшие, что температура плавления льда практически не зависит от давления. Более того, он с высокой точностью определил, как температура кипения воды изменяется в зависимости от атмосферного давления.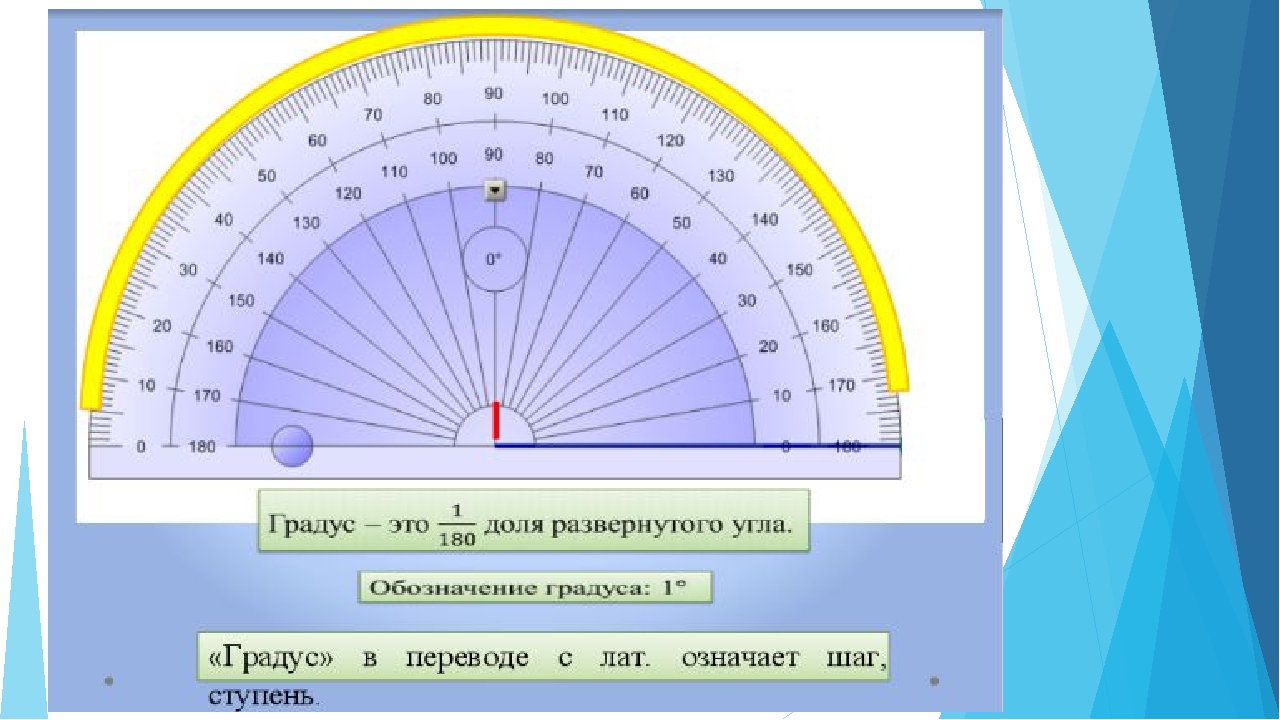
Цельсий предложил калибровать ноль своей температурной шкалы (в тот момент, точку кипения воды) по атмосферному давлению, определить которое можно по среднему уровню моря.
Эта калибровка наконец сделала термометры по-настоящему универсальными. Вероятно, именно поэтому прогноз погоды, который вы смотрели сегодня утром, был в градусах Цельсия.
Но стоградусную температурную шкалу назвали в честь Цельсия только в 1948 году. До этого она так и называлась — стоградусной температурной (centigrade temperature scale). Но во французском (где использовали грады) термин centigrade уже был занят в геометрии.
Чтобы избежать путаницы, Международное бюро мер и весов переименовало шкалу в честь Андерса Цельсия. Так градусы температуры стали градусами Цельсия.
Диаграмма перевода температур, на которой указаны основные температурные шкалы
Wikimedia commons
Шкала Цельсия оказалась идеальной для применения в быту, но физики остались ею недовольны.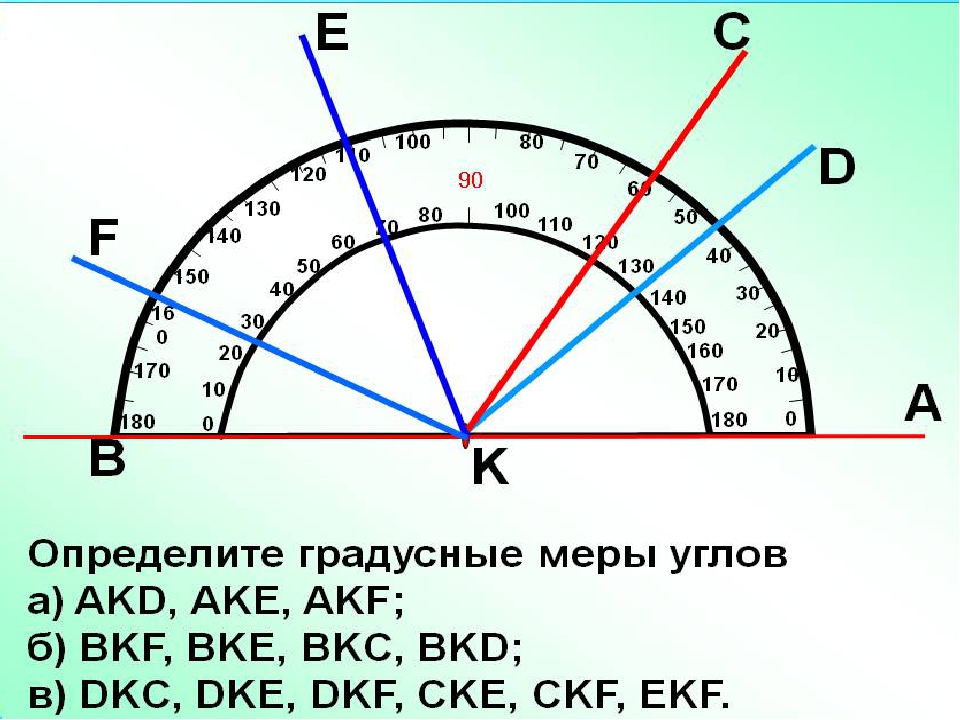
Привязка реперных точек к свойствам воды очень удобна для экспериментов, ведь воду можно найти практически где угодно. А вот для теоретических вычислений, например, связи энергии молекул с температурой, требовалось найти абсолютную шкалу.
Ее создал Уильям Томсон в 1848 году — нулевая точка его шкалы соответствует абсолютному нулю, а цена деления равна градусу Цельсия. Новую шкалу назвали в честь Томсона (ставшего лордом Кельвином), а градус Цельсия в ней превратился в Кельвин. Но почему Кельвин — это не градус?
Дело в том, что шкала Кельвина — это шкала абсолютной температуры. Все шкалы, о которых шла речь выше — произвольные, ведь для их градуировки были выбраны произвольные точки.
Шкалу Кельвина отсчитывают от абсолютного нуля — минимального предела температуры во Вселенной, она тесно связана с энергией молекул через постоянную Больцмана. Чтобы подчернуть, что речь идет об абсолютной температуре, Кельвин не называют градусом.
Цвет
Получается, температура в Кельвинах нужна только физикам? Нет, вы наверняка пользовались Кельвинами в бытовом отделе супермаркета, просто не подозревали об этом.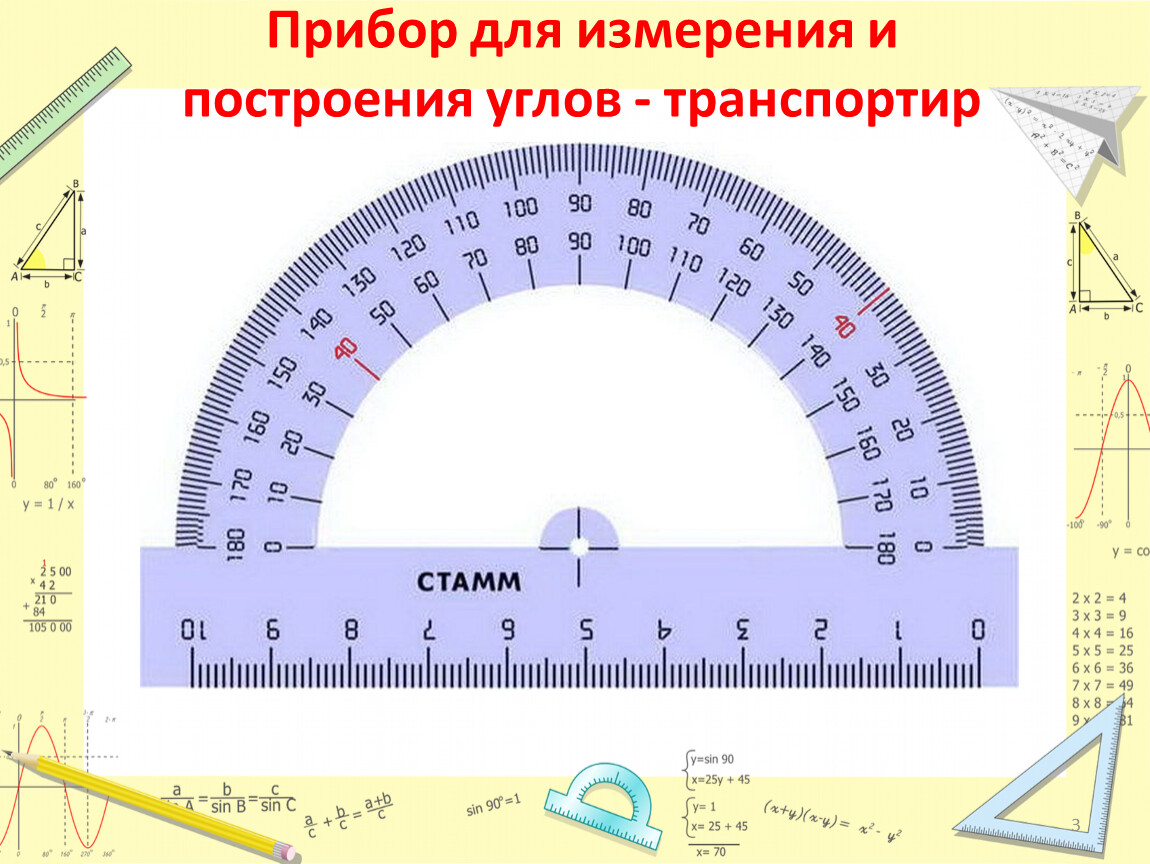
Выбирая оттенок света лампочки, мы обращаем внимание на цветовую температуру (например, 2800К), она измеряется в Кельвинах.
Такой свет будет испускать абсолютно черное тело, нагретое до указанной температуры. Так цвет измеряют температурой, а не в длинной волны, ведь излучение нагретого тела, как и лампочки, не монохроматично (состоит из множества частот).
Алкоголь
Из бытового отдела переместимся в отдел алкоголя и снова увидим там градусы. А точнее — объемные проценты, называемые градусами.
В России крепость алкогольных напитков в градусах Гесса стали измерять с 1847 года, когда академик Герман Гесс выпустил книгу «Учет спиртов».
В этой книге Гесс приводил спиртовые таблицы и инструкции по использованию спиртомера. А сам спиртомер Гесса показывал «не содержание алкоголя, а число ведер воды, имеющей температуру 12,44 Р[еомюра], которое надобно добавить к 100 ведрам испытываемого спирта, чтобы получить полугар, то есть такую смесь, которая содержит 38% алкоголя».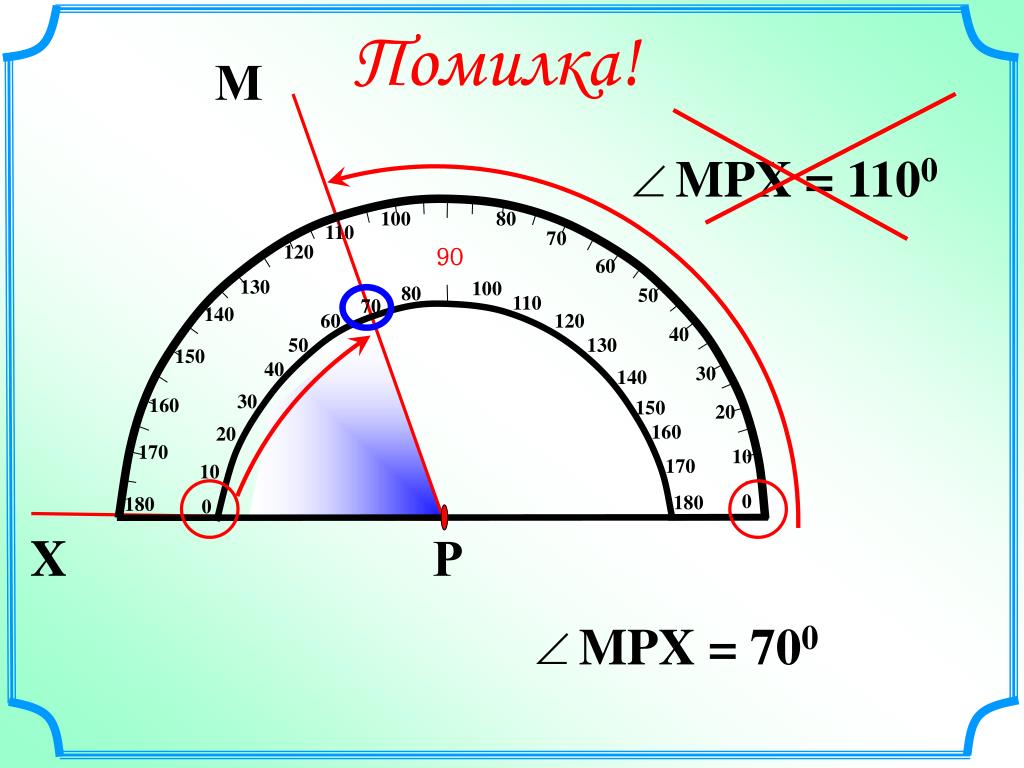 Например, к 100 ведрам водки нужно добавить примерно пять ведер воды для получения полугара.
Например, к 100 ведрам водки нужно добавить примерно пять ведер воды для получения полугара.
Официально перестали оценивать крепость в градусах Гесса уже в 1863 году, когда на их место пришли объемные проценты — отношение объема этилового спирта к общему объему напитка. А слово «градус» осталось.
Кстати, английское degree (градус) не имеет никакого отношения к алкоголю, а вот во Франции скажут, что в коньяке 40 градусов Гей-Люссака.
Плотность, кислотность молока
До середины XX века в химии и фармакологии широко использовались градусы Боме, предложенные Антуаном Боме в 1768 году для измерения плотности жидкости.
В физике и химии градусы Боме были вытеснены нынешней единицей СИ — килограммом на метр в кубе, но их продолжают использовать в пивоварении, переработке сахарной свеклы и других областях.
Кислотность молока также измеряют в градусах — в градусах Тернера. Это число миллилитров децинормального (0,1 н.) раствора гидроксида натрия, необходимое для нейтрализации 100 миллилитров молока.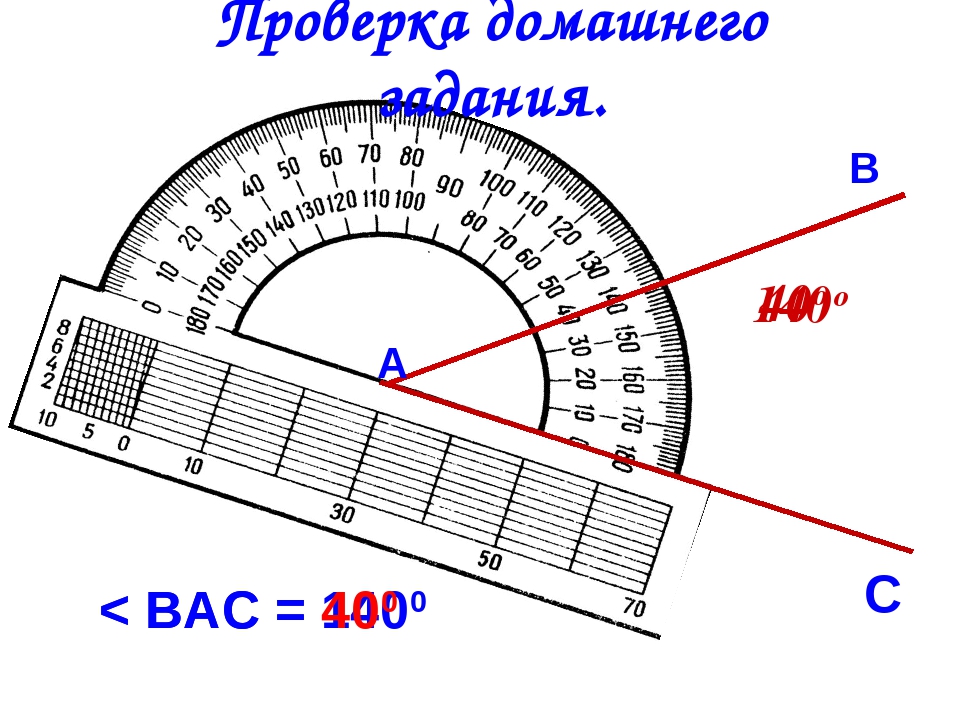 Молоко высшего сорта должно обладать градусом Тернера в пределах от 16 до 18.
Молоко высшего сорта должно обладать градусом Тернера в пределах от 16 до 18.
Олег Макаров
|
Таблица . Единицы измерения углов (плоских) вводятся как:
Таблица 1. Перевод угловых градусов, минут, секунд, радиан, оборотов в тысячные.
Таблица 2. Перевод тысячных, угловых градусов, минут, радиан, оборотов в угловые секунды.
Таблица 3. Перевод тысячных, угловых градусов, секунд, радиан, оборотов в угловые минуты.
Таблица 4. Перевод тысячных, угловых минут, секунд, радиан, оборотов в угловые градусы.
Таблица 5. Перевод тысячных, угловых градусов, минут, секунд, оборотов в радианы.
Таблица 6. Перевод тысячных, угловых градусов, минут, секунд, радиан в обороты.
| ||
|
Точно в оборотах |
Численное значение | |
|
1 тысячная (артиллерийская РФ) |
1/6000 |
0,00016666667…оборотов |
|
1 угловая секунда = 1» |
1/360/60/60=1/1296000 |
0,00000077160….оборотов |
|
1 угловая минута = 1′ |
1/360/60=1/21600 |
0,00004629630…оборотов |
|
1 угловой градус = 1° |
1/360 |
0,00277777778. |
|
1 радиан = 1 рад |
1/2π |
0,15915494309 … оборотов |
- Почему 360°? или почему круг стали делить на 360° частей?:
- Как заметили вавилонские жрецы, солнечный диск укладывается по дневному пути солнца 180 раз .»Солнце делает за световой день 180 шагов.“ Тогда путь за сутки равен 360 шагам. Латинское слово gradus как раз и означает «шаг». Они-то были уверены, что солнце крутится вокруг земли, хотя и сейчас многие…
- Источник: Александрова,Н.В. Математические термины. Справочник. Москва: Высшая школа, 1978.
Виды углов. Измерение углов
На каждом из рисунков 82, a − г изображены два луча. На каком из рисунков пара лучей образует угол, сторонами которого являются эти лучи?
Поскольку на рисунках 82, а − в начала лучей не совпадают, то они не могут служить сторонами угла.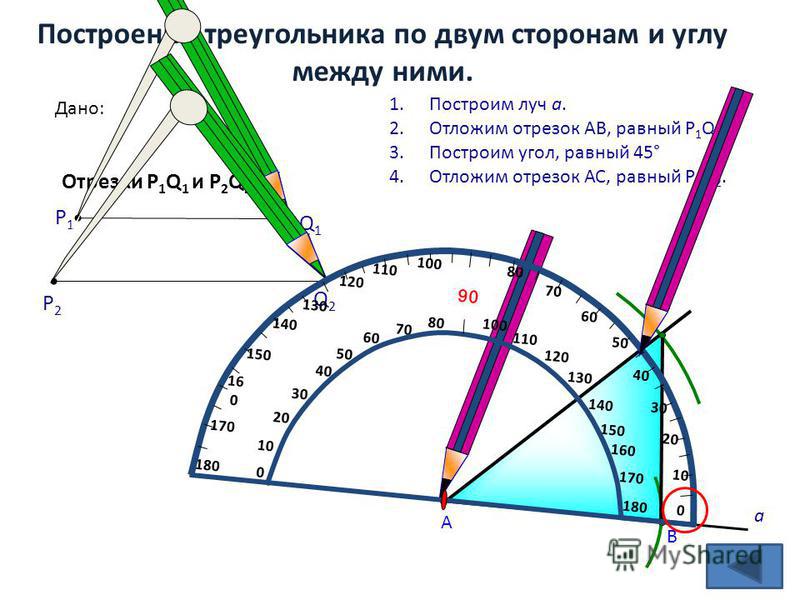 Лучи на рисунке 82, г образуют прямую. При этом начала лучей совпадают, а следовательно, они образуют угол. Такой угол называт развернутым.
Лучи на рисунке 82, г образуют прямую. При этом начала лучей совпадают, а следовательно, они образуют угол. Такой угол называт развернутым.
Угол, стороны которого образуют прямую, нахывают развернутым.
Углы, как и отрезки, можно измерять. Напомним, что для измерения отрезков мы использовали единичный отрезок (1 мм, 1 см и т.п.).
Однако для измерения углов мы пока не имеем такого единичного угла.
Создать его можно, например, так. Разделим развернутый угол на 180 равных углов (рис. 83). Угол, образованный двумя соседними лучами, выбирают за единицу измерения. Его величину называют градусом (от лат. gradus − «шаг», «ступенька») и записывают 1°.
Измерить угол − значит подсчитать, сколько единичных углов в нем помещается.
Тогда величина или, как еще принято говорить, градусная мера развернутого угла равна 180°.
Для измерения углов используют специальный прибор − транспортир (рис. 84). Он состоит, как правило, из полукольца, соединенного с линейкой. Его шкала содержит 180 делений.
Чтобы измерить угол, совместим его вершину с центром транспортира таким образом, чтобы одна из сторон угла прошла по линейке (рис. 85).
Тогда штрих на шкале, через который пройдет вторая сторона, укажет градусная (величину) этого угла.
Так, на рисунке 85 градусная мера угла AOB равна 55°. Пишут: ∠AOB = 55°. На рисунке 86 имеем: ∠MON = 134°.
Равные углы имеют равные градусные меры. Из двух неравных углов бОльшим будем считать тот, градусная мера которого больше. Например, из трех углов, изображенных на рисунке 87, ∠MON − наибольший. В этом легко убедиться, измерив углы транспортиром.
Величина угла обладает следующим свойством.
Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC (рис.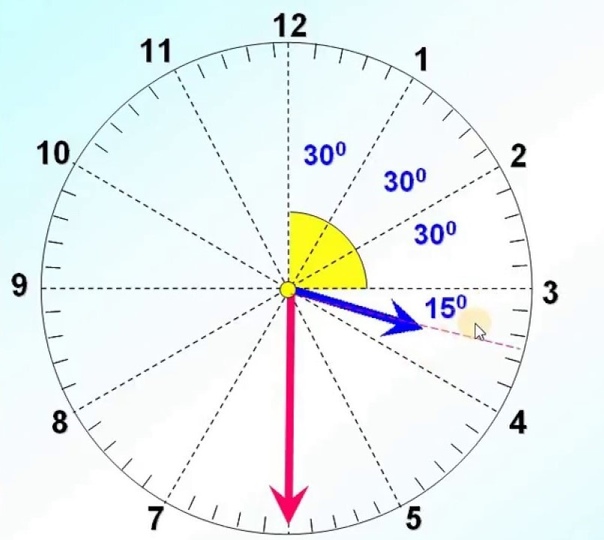 88), т.е.
88), т.е.
∠ABC = ∠ABD + ∠DBC.
Угол, градусная мера которого меньше 90°, называют острым (рис. 89, a).
Угол, градусная мера которого равна 90°, называют прямым (рис. 89, б).
На рисунке прямой угол обозначает так: ∟.
Угол, градусная мера которого больше 90°, но меньше 180° называют тупым (рис. 89, в).
Отметим, что биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90°. Следовательно, биссектриса развернутого угла делит его на два прямых угла (рис. 90).
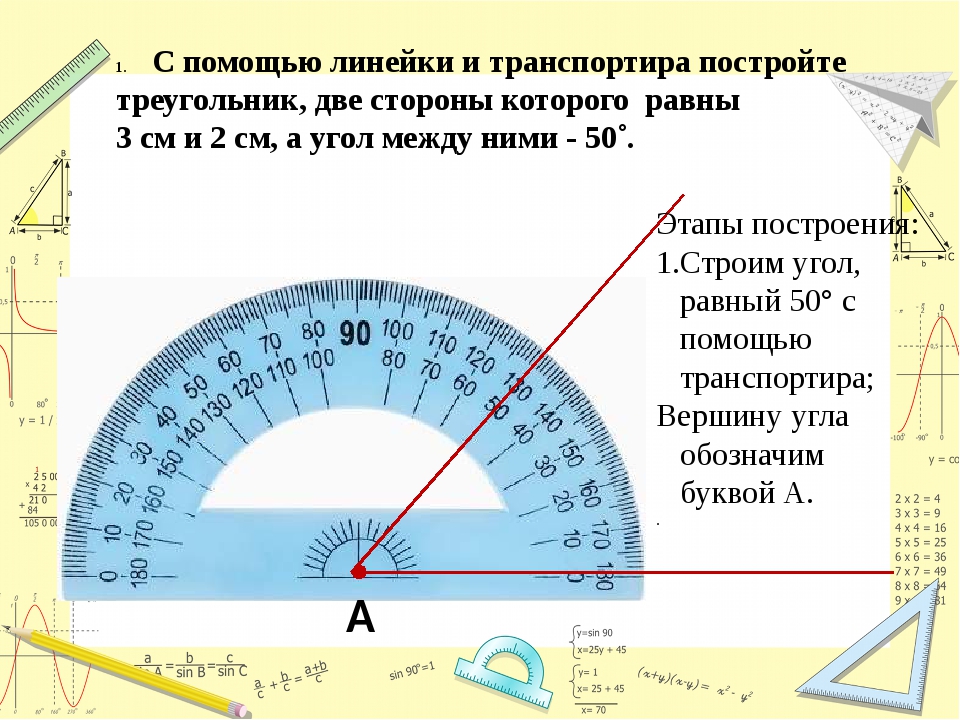
Пример 1. Дан луч OA. Постройте угол BOA, равный 72°.
Решение.
Совместим центр транспортира с точкой O так, чтобы луч OA прошел по линейке. Выберем на кольце транспортира штрих, который соответствует 72°. Возле этого штриха отметим точку B (рис. 91). Проведем луч OB. Угол BOA − искомый.
Если дан луч OA и построен угол BOA, то говорят, что от луча OA отложен угол BOA.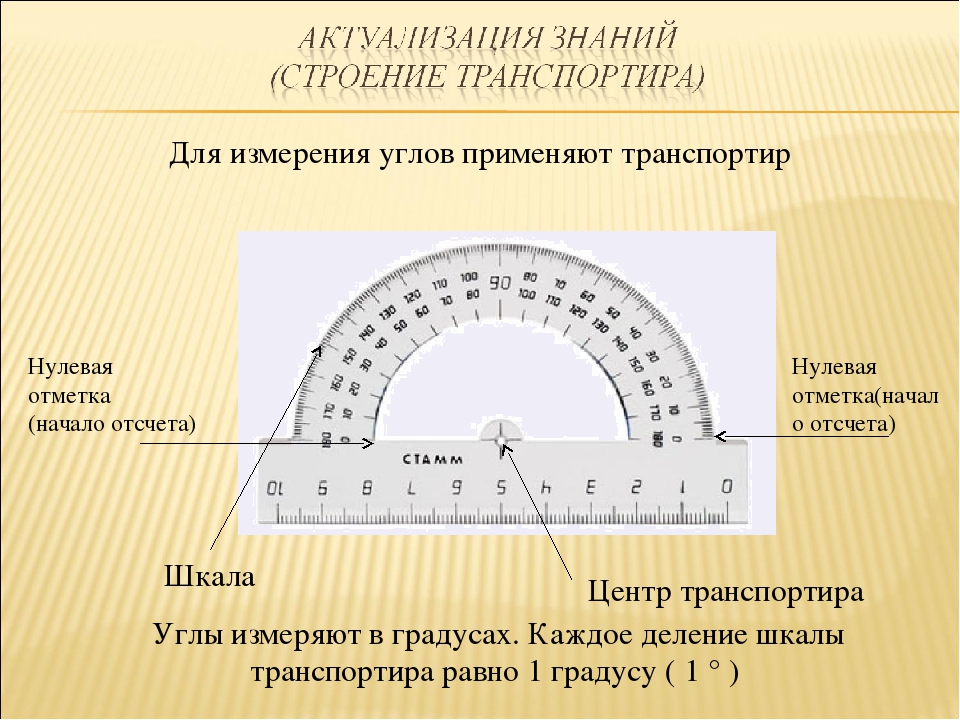
Пример 2. Из вершины угла ABC проведены два луча BK и BM так, что ∠ABK = 48°, ∠CBM = 72° (рис. 92).
Вычислите величину угла ABC, если ∠MBK = 16°.
Решение.
Имеем: ∠ABM = ∠ABK − ∠MBK, ∠ABM = 48° − 16° = 32°;
∠ABC = ∠ABM + ∠СBM, ∠ABC = 32° + 72° = 104°.
Ответ: 104°.
Функция ГРАДУСЫ для выполнения геометрических расчетов в Excel
Функция ГРАДУСЫ в Excel используется для преобразования радианной меры угла в соответствующей величину, выраженную в градусах, и возвращает полученное значение.
Примеры использования функции ГРАДУСЫ в Excel
Пример 1. Для определения количества оборотов вала электродвигателя используется датчик, который определяет и возвращает значение угла в радианах. Спустя минуту работы двигателя было получено значение 2350π. Определить количество оборотов за 1 минуту.
Исходные данные:
Для расчета используем формулу:
=ГРАДУСЫ(2350*ПИ())/360
Описание составляющих:
- 2350*ПИ() – функция, преобразует радианную меру угла 2350*ПИ() и возвращающая значение, выраженное в градусах.

- 360 – полное количество градусов в окружности.
В результате получим:
То есть, двигатель сделал 1175 оборотов за 1 минуту.
Расчет траектории движения с помощью функции ГРАДУСЫ в Excel
Пример 2. Автомобиль движется по круговой трассе. Определить, на какой угол он отклонится относительно начальной точки пути через 17 минут, если за 10 минут он проехал расстояние, равное радиусу окружности трассы.
Исходные данные:
Для определения угловой скорости разделим количество радиан на время пути. Известно, что за 10 минут был пройден путь, равный радиусу окружности. Из этого следует, что автомобиль отклонился на 1 радиан от начальной точки пути. Искомая угловая скорость:
- 1 – количество радиан;
- 10 – время пути в минутах.
Результат:
То есть, 1 рад/мин. Для нахождения искомого угла используем формулу:
Описание:
- B3 – скорость в рад/мин;
- 17 – время пути в минутах.
Результат вычислений:
То есть, автомобиль отклонится примерно на 97°.
Как перевести радианы в градусы в Excel
Пример 3. Определить угол (в градусах), который проходит минутная стрелка механических часов, если часовая успела отклониться от момента отсчета на 0,05236 радиана?
Исходные данные:
Описание величин:
- B3 – количество делений для минутной стрелки.
- B3/B2 – количество делений, которые проходит часовая стрелка за полный оборот минутной. То есть, выражение B3/(B3/B2) определяет, во сколько раз скорость минутной стрелки превышает скорость часовой стрелки.
- B4 – отклонение часовой стрелки в радианах.
Полученный результат:
Минутная стрелка отклонится на 36°.
Особенности использования функции ГРАДУСЫ в Excel
Функция ГРАДУСЫ имеет следующую синтаксическую запись:
=ГРАДУСЫ(угол)
Единственным аргументом данной функции является угол (обязательный для заполнения). Он характеризует величину угла, выраженную в радианах.
Примечания 1:
- Excel выполняет автоматическое преобразование данных к требуемому типу в тех случаях, где это возможно.
 Например, запись типа =ГРАДУСЫ(ИСТИНА) соответствует записи =ГРАДУСЫ(1) и вернет значение 57,29577951, то есть количество градусов в 1 радиане.
Например, запись типа =ГРАДУСЫ(ИСТИНА) соответствует записи =ГРАДУСЫ(1) и вернет значение 57,29577951, то есть количество градусов в 1 радиане. - Рассматриваемая функция может принимать в качестве аргумента числа из диапазона отрицательных значений. Например, если в аргументе функции указано значение (-1,5), тогда результат равен -85,94366927.
- Функция вернет код ошибки #ЗНАЧ!, если в качестве аргумента была передана текстовая строка, которая не может быть преобразована в числовой тип данных.
Примечания 2:
- В геометрии углом считается фигура, образованная двумя лучами, которые проведены из одной точки (точки их пересечения), при этом данные лучи называются сторонами угла, а точка – его вершиной.
- Градусы и радианы являются двумя количественными характеристиками размера угла.
- 1 градус соответствует 1/180 развернутого угла, то есть угла, стороны которого лежат на одной прямой.
- Если точка пересечения сторон угла (вершина) является центром окружности, а его стороны – радиусы данной окружности, то радиан – центральный угол, радиусы и длина образованной данным углом дуги являются равными величинами (AO=BO=AmB):
- Между градусной и радианной мерами угла установлена следующая взаимосвязь: град=2π*рад/360°, где рад – количество радиан, а град – рассчитываемое количество градусов.

| Фрирайдер Анна Ханкевич пошагово объясняет, как определить угол склона и потенциальную лавиноопасность с помощью простых лыжных палок. | ||||||||||
|
Хочу рассказать про то, как измерять угол склона.
У меня есть волшебный бипер PIEPS DSP Prо, у которого есть функция измерения наклона. Она включается нажатием кнопки Scan (сканирование) и работает в режиме передачи. Но он есть не у всех. Поэтому я хочу рассказать о методе маятника (который к своему стыду, узнала совсем недавно из методички Сергея Веденина).
Многим известно, что приблизительно можно прикинуть угол склона по расстоянию от вытянутой руки стоящего человека до склона.
| ||||||||||
Но этот способ подходит только для грубой оценки. Однако зачастую нам надо узнать угол более точно. Диапазон от 25 до 40 является самым лавиноопасным, и умение анализировать наклон важно. Однако зачастую нам надо узнать угол более точно. Диапазон от 25 до 40 является самым лавиноопасным, и умение анализировать наклон важно. | ||||||||||
|
Также для скитура умение на взгляд точно определить угол склона крайне важно, ведь при углах выше 20-25 градусов мы начинаем проскальзывать при движении прямо вверх и нужно перейти к траверсам.
Однако, нам надо определять угол со стороны, заранее. Поэтому рекомендую постоянно тренироваться, прикидывая угол на взгляд и потом проверяя свою оценку с помощью метода маятника.
Также для передачи информации необходимо точно знать численные значения. (И скептически улыбаться, когда твой приятель уверяет, что катал по 55-градусному склону).
| ||||||||||
|
Метод маятника позволяет определить угол склона с точностью до нескольких градусов и не требует никаких специальных приспособлений, кроме обычных палок, которые у лыжника всегда с собой=) Только палки должны быть одной длины.
Шаг первый
Находясь на склоне, положите палку вниз по линии падения воды ручкой вниз. Можно провести засечку на снегу у конца ручки.
| ||||||||||
Шаг второй
Теперь поднимайте эту палку вверх, оставляя острие палки на снегу. Подставьте вторую палку, соединив их рукоятками, при этом вторая палка должна прийти в вертикальное положение (можно представить вторую палку как отвес).
| ||||||||||
|
Засеките расстояние от засечки на снегу до острия второй палки. Если расстояние равно нулю, то есть если острие вертикальной палки воткнулось точно в отметку — угол склона равен 30 градусам.
Если острие выше по склону, чем засечка — то угол меньше 30 градусов.
Если острие ниже по склону, чем засечка — то угол больше 30 градусов.
Но я обещала точное количественное значение градусов. Наконец, мы увидим пример, который позволяет нам выражать в градусах величины, выраженные в секундах или минутах. Если у нас есть $$ 460 $$ секунд, то мы имеем: Если мы хотим выразить это в градусах: Измерение углов натяженияУглы можно измерять с помощью таких инструментов, как гониометр, квадрант, секстант, поперечина или транспортир.\ circ $$. Интуитивное руководство по углам, градусам и радианам — лучшее объяснение Очевидно, что окружности должны иметь 360 градусов. Неправильно. Большинство из нас не понимают , почему в круге 360 градусов. Мы запоминаем магическое число как «размер круга» и вводим себя в заблуждение при изучении продвинутой математики или физики с их так называемыми «радианами». «Радианы упрощают математику!» эксперты говорят, без простой причины (дискуссии с участием серии Тейлора непростые).Сегодня мы узнаем, что такое радианы на самом деле и почему они упрощают математику. Откуда берутся ученые степени?До чисел и языка у нас были звезды. Древние цивилизации использовали астрономию, чтобы отмечать времена года, предсказывать будущее и умиротворять богов (при принесении человеческих жертв, , им лучше быть вовремя, ). Как это относится к углам? Ну, дружище, дайте мне загадку: разве не странно, что у круга 360 градусов, а в году 365 дней? И разве не странно, что созвездия просто кружат по небу в течение года? В отличие от пирата, держу пари, сухопутные жители не могут определять времена года по ночному небу. Созвездия каждый день делают круг (видео). Если вы смотрите в одно и то же время каждый день (полночь), они также будут образовывать круг в течение года. Вот теория о том, как стали поступать ученые степени:
Но, но… почему не 365 градусов по кругу? Немного расслабиться: у них было солнечные часы, и они не знали, что год должен иметь удобные 365.242199 градусов как у вас. 360 достаточно близко для работы правительства. Оно прекрасно вписывается в вавилонскую систему счисления с основанием 60 и хорошо делится (на 2, 3, 4, 6, 10, 12, 15, 30, 45, 90… вы поняли). Основание математики на Солнце кажется совершенно разумным Земле повезло: ~ 360 — большое количество дней в году. Многие объяснения на этом заканчиваются: «Ну, степень произвольна, но нам нужно выбрать или ». Не здесь: мы увидим, что вся предпосылка степени находится в обратном направлении . Правило радианов, градусы слюниГрадус — это величина, на которую мне, наблюдателю, нужно наклонить голову, чтобы увидеть вас, движущегося человека. Он немного эгоцентричен, тебе не кажется? Предположим, вы увидели, как друг бежит по большой трассе:
Эгоистичный, правда? Вот как мы занимаемся математикой! Мы пишем уравнения в виде «Эй, как далеко я повернул голову, чтобы увидеть, как движется планета / маятник / колесо?». Бьюсь об заклад, вы никогда не задумывались о чувствах, надеждах и мечтах маятника. Как вы думаете, уравнения физики должны быть простыми для движущегося или наблюдателя? Радианы: Бескорыстный выборБольшая часть физики (и жизни!) Включает в себя выход из вашей системы отсчета и взгляд на вещи с другой точки зрения.Вместо того чтобы гадать, как далеко мы наклонили голову, подумайте, как далеко переместился другой человек . градуса измеряют углы по тому, насколько мы наклонили голову. Радианы измеряют углы как пройденное расстояние . Но абсолютная дистанция не так полезна, поскольку пробег 10 миль — это разное количество кругов в зависимости от трассы. . Вы часто видите это как или угол в радианах (тета) — длина дуги, деленная на радиус (r). Круг имеет 360 градусов или 2 радиана на дюйм — полный круг равен 2 * пи * r / r. Таким образом, радиан составляет около 360 / (2 * пи) или 57,3 градуса. А теперь не будьте похожи на меня, запоминая эту мысль: «Отлично, еще одна единица. 57,3 градуса — это так странно ». Потому что это странно, когда все еще думаешь о себе! Перемещение 1 радиан (единица) — это совершенно нормальное расстояние для путешествия. Другими словами, наша идея «чистого угла в 90 градусов» означает, что движитель проходит очень нечистых единиц пи / 2.Подумайте об этом — «Эй, Билл, ты можешь пробежать для меня на 90 градусов? Это что? Ах да, с твоей точки зрения это будет пи / 2 мили. Странность двусторонняя. Радианы — это чуткий способ делать математические вычисления — переход от наклона головы к точке зрения движущегося. Что в имени?Радианы — это количество расстояний в «единицах радиуса», и я думаю, что радиан — это сокращение для этого понятия. Строго говоря, радианы — это просто число вроде 1.5 или 73 и не имеют единиц измерения (при вычислении «радианы = пройденное расстояние / радиус» мы видим, что длина делится на длину, поэтому любые единицы будут отменены). Но с практической точки зрения мы не математические роботы, и радианы можно рассматривать как «расстояние», пройденное по единичной окружности. Использование радиановЯ все еще привыкаю думать в радианах. Но мы довольно часто сталкиваемся с понятием «расстояние движущегося»:
Эта формула работает, только если x выражается в радианах! Почему? Ну, синус в основном связан с расстоянием , пройденным на , а не с наклоном головы.Но мы отложим это обсуждение на другой день. Radian Пример 1: Колеса автобусаРассмотрим реальный пример: у вас есть автобус с радиусом колес 2 метра (это автобус-монстр-грузовик). Я скажу, с какой скоростью вращаются колеса, а вы скажете, с какой скоростью движется автобус. Готовый? «Колеса вращаются на 2000 градусов в секунду». Вы бы подумали:
Ок. А теперь представьте себе машину с колесами радиусом 2 метра (тоже монстра). «Колеса машины вращаются на 6 радиан в секунду». Вы бы подумали:
Ух ты, в машине было легче разобраться, чем в автобусе! Никаких сумасшедших формул, никакого плавающего числа Пи — просто умножьте , чтобы преобразовать скорость вращения в линейную.Все потому, что радианы говорят о двигателе. Обратное тоже легко. Предположим, вы едете со скоростью 90 футов в секунду по шоссе (60 миль в час) на колесах диаметром 24 дюйма (радиус 1 фут). Как быстро вращаются колеса? Ну, 90 футов в секунду / радиус 1 фут = 90 радиан в секунду. Это было легко. Я подозреваю, что рэперы поют около 24-дюймовых дисков именно по этой причине. Радиан Пример 2: sin (x) Пришло время более крутого примера. Выберите число градусов (x) и поместите sin (x) в свой калькулятор: Когда вы делаете x маленьким, например, 0,01, sin (x) также становится малым. И отношение sin (x) / x кажется примерно 0,017 — что это значит? Еще более странно, что значит умножать или делить на градус? У вас могут быть квадратные или кубические градусы? Радианы спешат на помощь! Зная, что они относятся к пройденному расстоянию (это не просто соотношение!), Мы можем интерпретировать уравнение следующим образом:
Итак, sin (x) / x — это отношение того, как высоко вы находитесь, к тому, как далеко вы зашли: количество энергии, ушедшее в «восходящем» направлении.Если вы двигаетесь вертикально, это соотношение составляет 100%. Когда что-то перемещается на небольшое расстояние, например, от 0 до 1 градуса с нашей точки зрения, оно в основном идет прямо вверх. Если пойти еще на меньшую величину, от 0 до 0,00001 градуса, получится , на самом деле идет прямо вверх. Пройденное расстояние (x) очень близко к высоте (sin (x)). По мере уменьшения x соотношение приближается к 100% — больше движения идет прямо вверх. Радианы помогают нам интуитивно понять, почему sin (x) / x приближается к 1, когда x становится крошечным.Мы просто немного продвигаемся в вертикальном направлении. Кстати, это также объясняет, почему sin (x) ~ x для малых чисел. Конечно, вы можете строго доказать это с помощью исчисления, но интуиция в радианах поможет вам понять это. Помните, что эти отношения работают только при измерении углов в радианах. В градусах вы сравниваете свой рост на окружности (sin (x)) с тем, насколько наблюдатель наклонил голову (x градусов), и быстро становится уродливо. Так в чем же смысл?У градусов есть свое место: в нашей жизни мы являемся фокусом и хотим видеть, как вещи влияют на нас. Насколько я наклоняю телескоп, вращаю сноуборд или поворачиваю рулевое колесо? В соответствии с законами природы мы — наблюдатели, описывающие движение других. Радианы о них, а не о нас. Мне потребовалось много лет, чтобы понять, что:
Равные углы можно увидеть с нескольких точек зрения, а понимание радианов делает математические и физические уравнения более интуитивно понятными. Счастливая математика. Другие сообщения этой серии
Опорный угол. Калькулятор | ОпределениеБазовый угол для 1 °: 1 ° Базовый угол для 2 °: 2 ° Базовый угол для 3 °: 3 ° Базовый угол для 4 °: 4 ° Базовый угол для 5 °: 5 ° Базовый угол для 6 °: 6 ° Базовый угол для 7 °: 7 ° Базовый угол для 8 °: 8 ° Базовый угол для 9 °: 9 ° Базовый угол для 10 °: 10 ° Базовый угол для 15 °: 15 ° Базовый угол для 20 °: 20 ° Базовый угол для 25 °: 25 ° Базовый угол для 30 °: 30 ° (π / 6) Базовый угол для 35 °: 35 ° Базовый угол для 40 °: 40 ° Базовый угол для 45 °: 45 ° (π / 4) Базовый угол для 50 °: 50 ° Базовый угол для 55 °: 55 ° Базовый угол для 60 °: 60 ° (π / 3) Базовый угол для 65 °: 65 ° Базовый угол для 70 °: 70 ° Базовый угол для 75 °: 75 ° Базовый угол для 80 °: 80 ° Базовый угол для 85 °: 85 ° Базовый угол для 90 °: 90 ° (π / 2) Базовый угол для 95 °: 85 ° Базовый угол для 100 °: 80 ° Базовый угол для 105 °: 75 ° Базовый угол для 110 °: 70 ° Базовый угол для 115 °: 65 ° Базовый угол для 120 °: 60 ° (π / 3) Базовый угол для 125 °: 55 ° Базовый угол для 130 °: 50 ° Базовый угол для 135 °: 45 ° (π / 4) Базовый угол для 140 °: 40 ° Базовый угол для 145 °: 35 ° Базовый угол для 150 °: 30 ° (π / 6) Базовый угол для 155 °: 25 ° Базовый угол для 160 °: 20 ° Базовый угол для 165 °: 15 ° Базовый угол для 170 °: 10 ° Базовый угол для 175 °: 5 ° Базовый угол для 180 °: 0 ° Базовый угол для 185 °: 5 ° Базовый угол для 190 °: 10 ° Базовый угол для 195 °: 15 ° Базовый угол для 200 °: 20 ° Базовый угол для 205 °: 25 ° Базовый угол для 210 °: 30 ° (π / 6) Базовый угол для 215 °: 35 ° Базовый угол для 220 °: 40 ° Базовый угол для 225 °: 45 ° (π / 4) Базовый угол для 230 °: 50 ° Базовый угол для 235 °: 55 ° Базовый угол для 240 °: 60 ° (π / 3) Базовый угол для 245 °: 65 ° Базовый угол для 250 °: 70 ° Базовый угол для 255 °: 75 ° Базовый угол для 260 °: 80 ° Базовый угол для 265 °: 85 ° Базовый угол для 270 °: 90 ° (π / 2) Базовый угол для 275 °: 85 ° Базовый угол для 280 °: 80 ° Базовый угол для 285 °: 75 ° Базовый угол для 290 °: 70 ° Базовый угол для 295 °: 65 ° Базовый угол для 300 °: 60 ° (π / 3) Базовый угол для 305 °: 55 ° Базовый угол для 310 °: 50 ° Базовый угол для 315 °: 45 ° (π / 4) Базовый угол для 320 °: 40 ° Базовый угол для 325 °: 35 ° Базовый угол для 330 °: 30 ° (π / 6) Базовый угол для 335 °: 25 ° Базовый угол для 340 °: 20 ° Базовый угол для 345 °: 15 ° Базовый угол для 350 °: 10 ° Базовый угол для 355 °: 5 ° Базовый угол для 360 °: 0 ° Измерьте и классифицируйте угол (геометрия, точки, линии, плоскости и углы) — Mathplanet Линия, имеющая одну определенную конечную точку, называется лучом и продолжается бесконечно в одном направлении. $$ \ overset {\ rightarrow} {AB} $$ Угол, который образуется между двумя лучами с одинаковой конечной точкой, измеряется в градусах. Точка называется вершиной . Вершина записывается как $$ \ Измеренный угол CAB $$ В алгебре мы использовали координатную плоскость для построения графиков и решения уравнений. Вы можете наносить линии, отрезки, лучи и углы на координатную плоскость. В координатной плоскости выше у нас есть два луча $$ \ overset {\ rightarrow} {BA} \: \: и \: \: \ overset {\ rightarrow} {BD} $$ образуют угол с вершиной в точке B. Вы можете использовать координатную плоскость для измерения длины отрезка. Точка B находится в точках (-2, -2) и C (1,2). Расстояние между двумя точками составляет 1 — (-2) = 3 единицы. Углы могут быть прямыми, прямыми, острыми или тупыми. Угол — это часть окружности, в которой весь круг равен 360 °. Вы измеряете угол с помощью транспортира. Два угла с одинаковой мерой называются конгруэнтными углами. Конгруэнтные углы обозначены как . $$ \ угол A \ конг \ угол B $$ Или может быть показан дугой на рисунке, чтобы указать, какие углы совпадают. Два угла, общая длина которых составляет 180 °, называются дополнительными e.{\ circ} $$ Видеоурок Измерьте размер уголка
Как найти измерения углов треугольникаСумма трех углов в треугольнике всегда равна 180 градусам. Треугольник может быть прямым, равнобедренным, острым, тупым, равносторонним или разносторонним, но сумма всех углов по-прежнему составляет 180 градусов. Используйте свойства треугольников каждого типа для решения вопроса об измерении углов. Определение углов по градусам: два известных углаНарисуйте треугольник, если изображение не предоставлено. Обозначьте каждый известный угол соответствующими размерами. Сложите два измерения вместе. 30 градусов + 45 градусов = 75 градусов Найдите величину угла C, вычитая сумму двух измерений из 180 градусов, чтобы найти величину третьего угла. Добавьте ответ и два предоставленных угловых измерения, чтобы проверить точность. Сумма всех трех углов должна равняться 180 градусам. 30 градусов + 45 градусов + 105 градусов = 180 градусов Определение углов по градусам: один известный угол Нарисуйте треугольник, если изображение не предоставлено. Сформируйте уравнение, используя свойства типа треугольника, представленного в задаче, который равен 180 градусам. Равнобедренные треугольники содержат равные угловые размеры, прилегающие к равным по длине сторонам, а прямоугольные треугольники содержат один угол в 90 градусов. Угол A (рядом с равным боковым углом) = x Угол B (рядом с равным боковым углом) = x x + x + 80 градусов = 180 градусов Угол A = прямой угол = 90 градусов 90 градусов + 15 градусов + x = 180 градусов Решите уравнение для значения «x», вычитая цифры из 180 градусов. 90 + 15 + x = 180 градусов Добавьте вычисленные и предоставленные угловые измерения, чтобы убедиться, что он равен 180 градусам. Пример равнобедренного сустава: 50 + 50 + 80 = 180 градусов Пример прямоугольного треугольника: 90 + 15 + 75 = 180 градусов Определение углов по градусам: без известных углов Нарисуйте равносторонний треугольник, который представляет собой многоугольник с тремя равными сторонами и тремя равными углами. Составьте уравнение, складывающее три неизвестных измерения, равных 180 градусам, которые являются суммой всех трех углов в треугольнике любого типа. Решите уравнение для «x», объединив три значения в «3x». А затем разделите каждую сторону знака «равно» на три. Проверьте свою работу, сложив каждое измерение угла вместе, и убедитесь, что сумма этих трех углов равна 180 градусам. 60 + 60 + 60 = 180 градусов Тригонометрия Обзор градусов, радиан и измерение угловОбзор Хотя многие студенты лучше всего знакомы с измерением углов по градусам, существуют и другие способы измерения углов.В исчислении, продвинутой тригонометрии и приложениях исчисления в науке углы измеряются в радианах. Град — это единица измерения угла, используемая при геодезии и как часть метрической системы, а угловые минуты и секунды используются для измерения углов для навигации и в астрономии. ГрадусовМногие люди знакомы с измерением угла в градусах с помощью транспортира. Один градус равен 1/360 окружности, так как у окружности 360 градусов. Углы меньше 90 o — острые, углы 90 o — прямые, а углы больше 90 o — тупые.Измерение полного круга как 360 o происходит от вавилонян, которые использовали в своей математической системе число, кратное 60. РадианыРадианы менее знакомы. Они измеряют длину дуги, деленную на ее радиус. Они являются частью системы СИ и используются во многих научных приложениях, а также в математике. Один радиан равен 180 / π градусов, поэтому, чтобы преобразовать градусы в радианы, умножьте градус на π / 180. Чтобы преобразовать радианы в градусы, умножьте радиан на 180 / π градусов.Например, 1 радиан, умноженный на 180 / π, равен примерно 57,296 o . Угол 23 o составляет около 0,401 рад. Грады Грады, сокращенно от градиана, тесно связаны с радианами. Arc MinutesУгловая минута равна 1/60 th одного градуса, а секунда дуги равна 1/60 th угловой минуты. Он используется в приложениях, требующих очень малых углов, таких как астрономия, оптика, офтальмология, оптометрия и навигация. Заинтересованы в услугах репетиторства по тригонометрии? Узнайте больше о том, как мы помогаем тысячам студентов каждый учебный год. SchoolTutoring Academy — ведущая компания по оказанию образовательных услуг для школьников и школьников. Мы предлагаем учебные программы для учащихся K-12, AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и ученикам в Ливане, NH: посетите: Репетиторство в Ливане, NH Углы Угол — это мера поворота.Углы измеряются в градусах . Один полный оборот измеряется как 360 °. Угол может быть положительным или отрицательным, в зависимости от направления вращения. Угловая мера — это величина поворота между двумя лучами, образующими угол. Вращение измеряется от начальной стороны к конечной стороне угла . Положительные углы (рисунок a) возникают в результате поворота на против часовой стрелки на , а отрицательные углы (рисунок b) возникают в результате поворота на по часовой стрелке и на .Угол с его начальной стороной на оси x считается стандартным положением . Рисунок 1 Углы, которые находятся в стандартном положении, называются квадрантными , если их конечная сторона совпадает с координатной осью. Углы в стандартном положении, которые не являются квадрантами, попадают в один из четырех квадрантов, как показано на рисунке 2. Пример 1: Следующие углы (стандартное положение) заканчиваются в указанном квадранте.
Два угла в стандартном положении, которые имеют общую клеммную сторону, называются на конце. Все углы, совпадающие с углом d °, можно записать как , где n — целое число (положительное, отрицательное или ноль). Пример 2: Угол 200 ° совпадает с углом 940 °? Если угол 940 ° и угол 200 ° совпадают, то Поскольку 740 не кратно 360, эти углы не совпадают. Пример 3: Назовите 5 углов, которые совпадают с −70 °. Угловые измерения не всегда являются целыми числами. Дробный градус может быть выражен либо в виде десятичной части градуса, например 34,25 °, либо с помощью стандартных делений градуса, называемых минутами и секундами. Между градусами, минутами и секундами существуют следующие отношения: Пример 4: Запишите 34 ° 15 ′ в десятичных градусах Пример 5: Запишите 12 ° 18′44 ″ в десятичных градусах. |

 Транспортир. Виды углов
Транспортир. Виды углов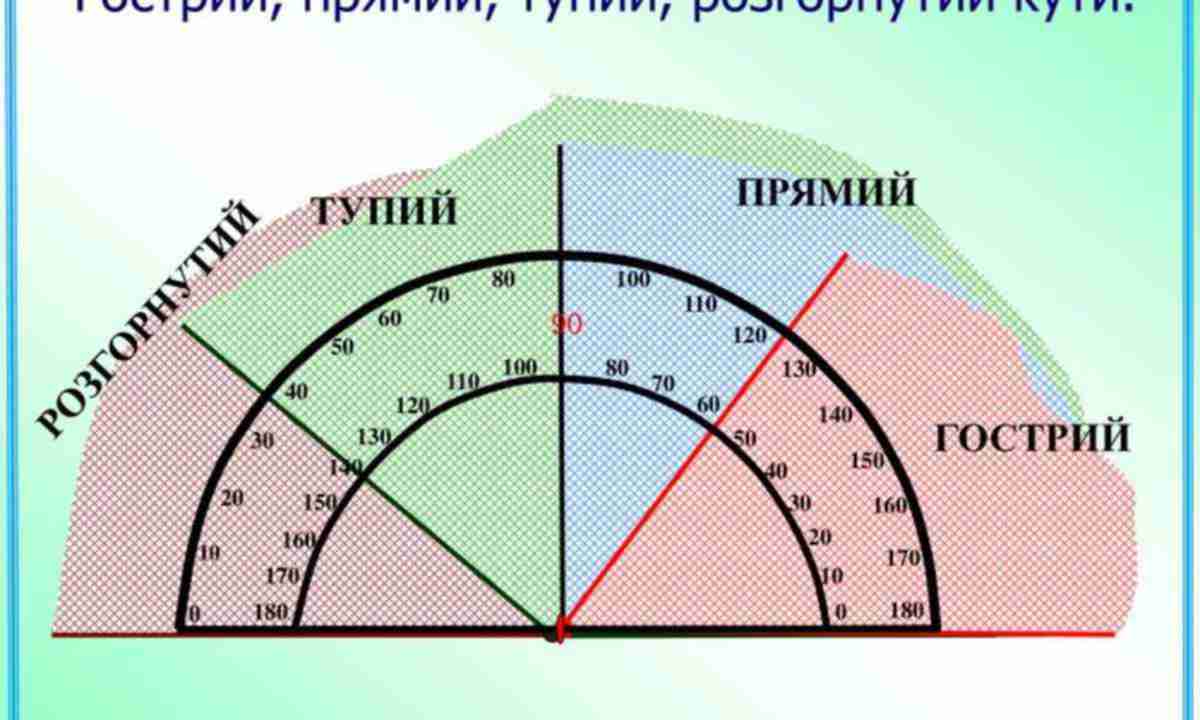
 .. тысячных
.. тысячных ..угловых секунд
..угловых секунд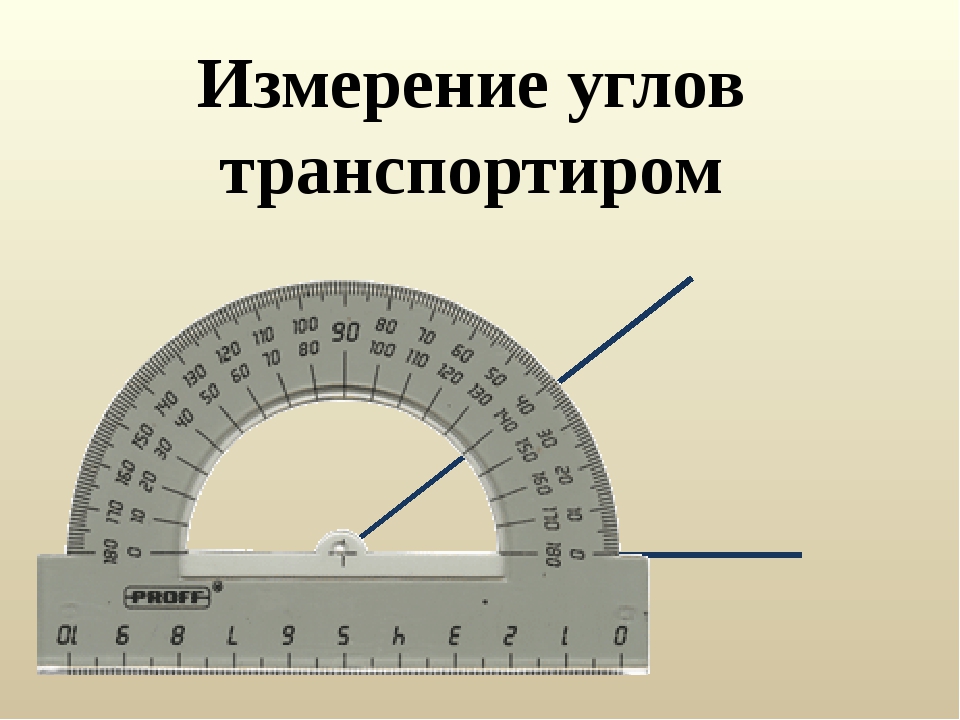 ..угловых минут
..угловых минут .. угловых градусов
.. угловых градусов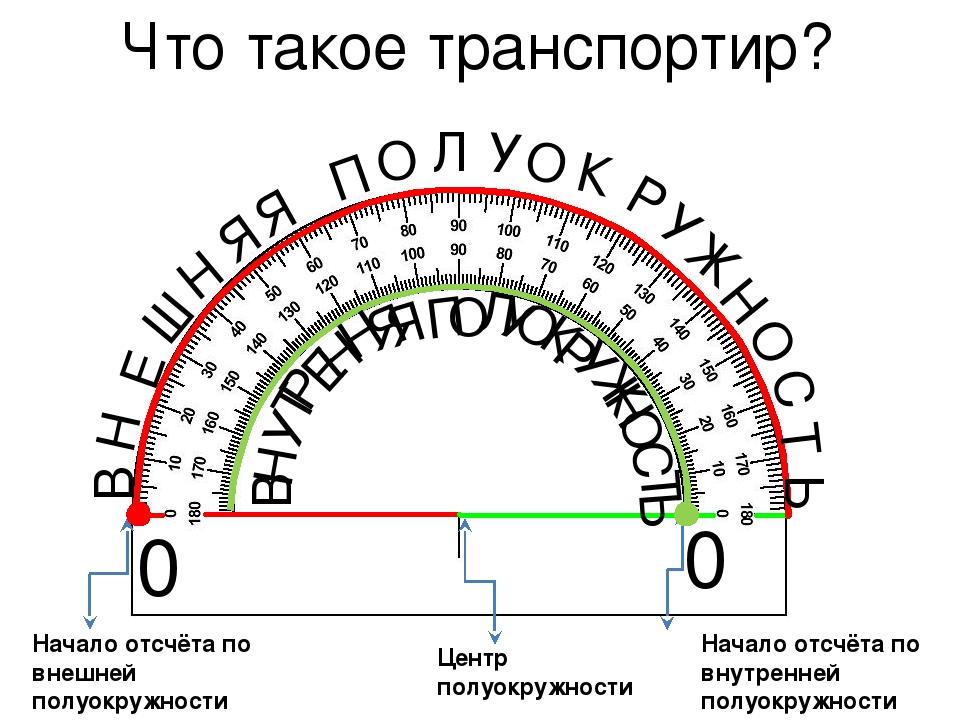 .. радиан
.. радиан .. оборотов
.. оборотов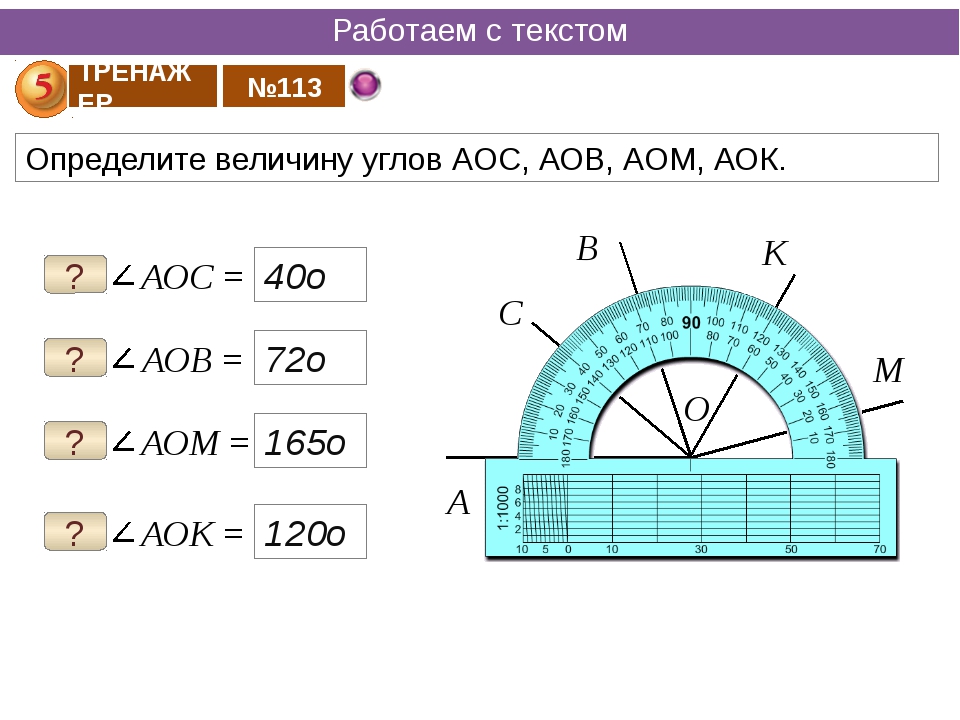
 Например, запись типа =ГРАДУСЫ(ИСТИНА) соответствует записи =ГРАДУСЫ(1) и вернет значение 57,29577951, то есть количество градусов в 1 радиане.
Например, запись типа =ГРАДУСЫ(ИСТИНА) соответствует записи =ГРАДУСЫ(1) и вернет значение 57,29577951, то есть количество градусов в 1 радиане.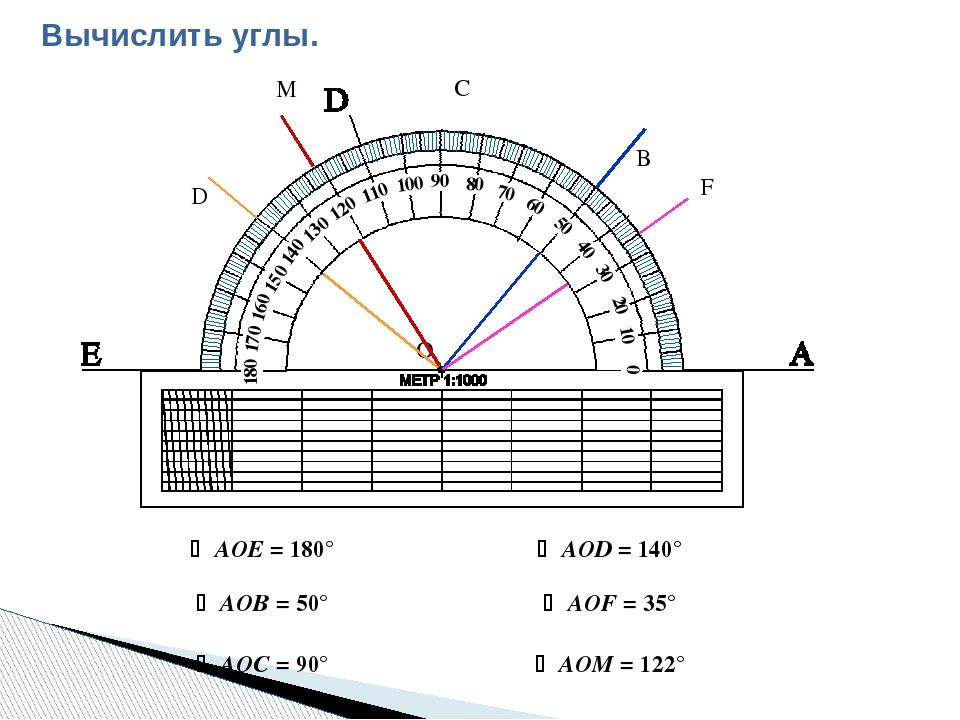
 \ circ $$.\ circ} \ cdot \ frac {60 \ \ mbox {секунды}} {1 \ \ mbox {minute}} = 21 \ cdot 60 \ cdot 60 \ \ mbox {секунды} = 75600 \ \ mbox {секунды} $$$
\ circ $$.\ circ} \ cdot \ frac {60 \ \ mbox {секунды}} {1 \ \ mbox {minute}} = 21 \ cdot 60 \ cdot 60 \ \ mbox {секунды} = 75600 \ \ mbox {секунды} $$$ Верно?
Верно? Вид на Большую Медведицу из Нью-Йорка в 2008 году (попробуйте любой город):
Вид на Большую Медведицу из Нью-Йорка в 2008 году (попробуйте любой город):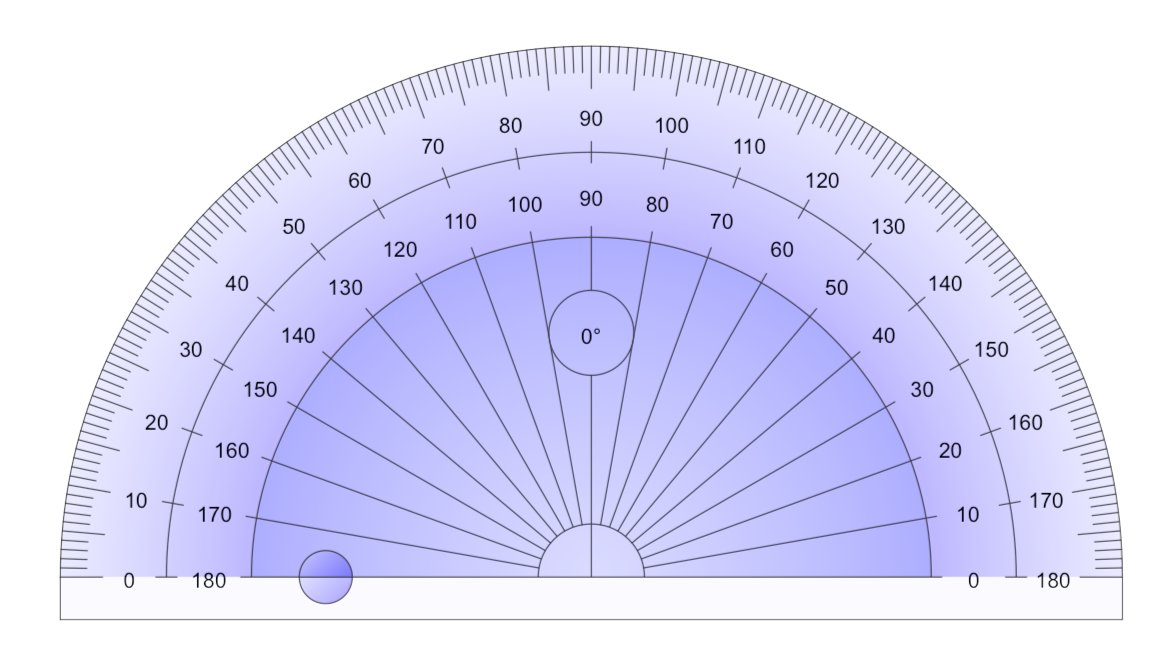 Но это кажется произвольным: на Марсе у нас будет примерно ~ 680 градусов по кругу в течение более длительного марсианского года. А в некоторых частях Европы использовали градианы, когда круг делится на 400 частей.
Но это кажется произвольным: на Марсе у нас будет примерно ~ 680 градусов по кругу в течение более длительного марсианского года. А в некоторых частях Европы использовали градианы, когда круг делится на 400 частей.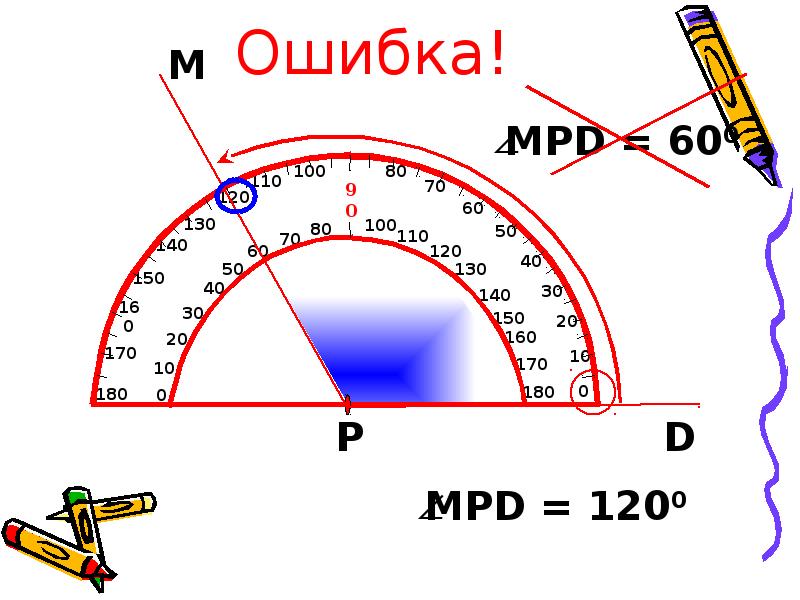 Я посреди трассы. Вы бегали. Насколько… сильно… я… повернул… свою… голову? »
Я посреди трассы. Вы бегали. Насколько… сильно… я… повернул… свою… голову? »
 Теперь разделите на расстояние до спутника, и вы получите орбитальную скорость в радианах в час.
Теперь разделите на расстояние до спутника, и вы получите орбитальную скорость в радианах в час.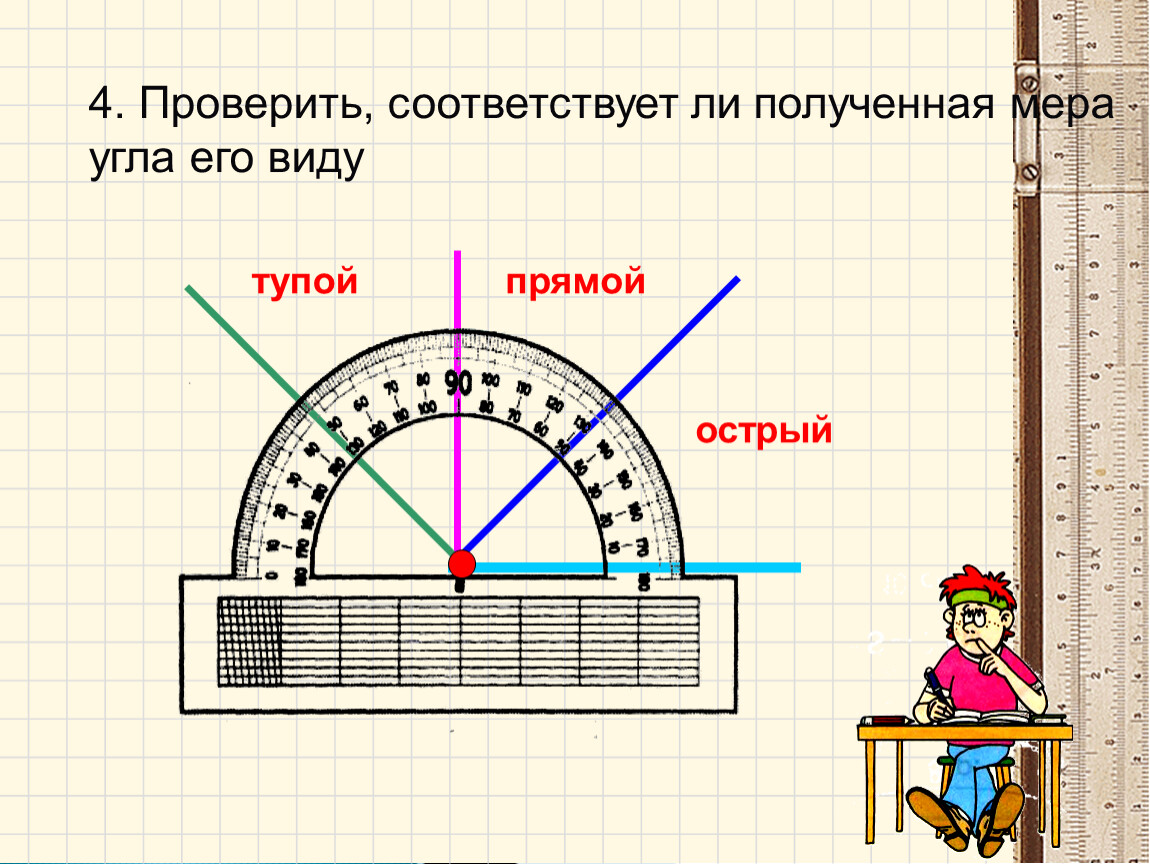 ..
.. Исчисление касается многих вещей, и одна из них — это то, что происходит, когда числа становятся действительно большими или очень маленькими.
Исчисление касается многих вещей, и одна из них — это то, что происходит, когда числа становятся действительно большими или очень маленькими.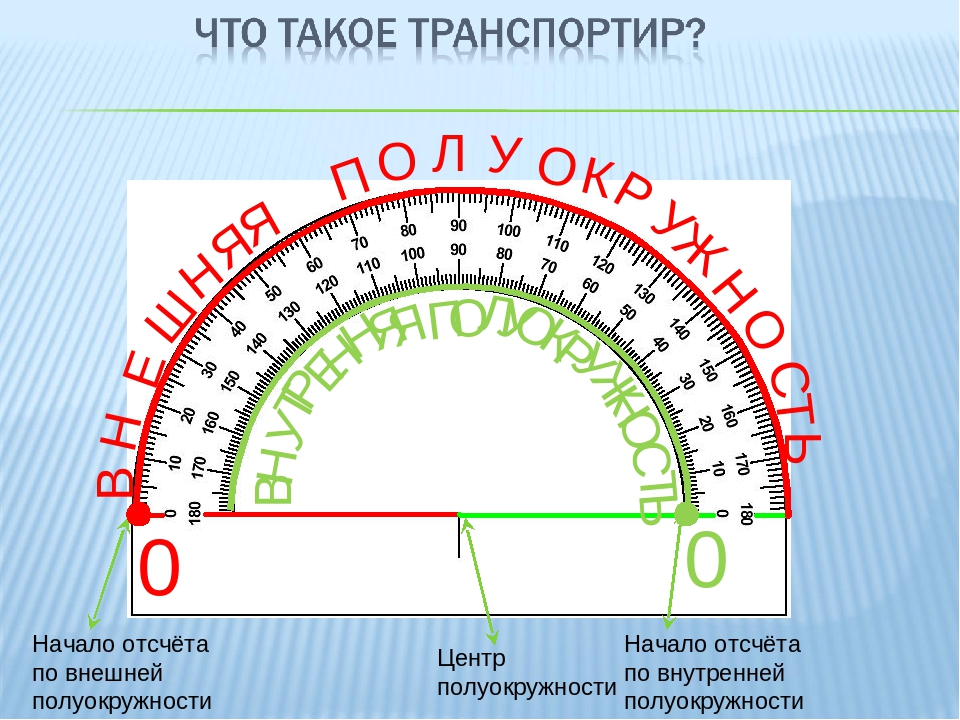 Если вы двигаетесь по горизонтали, это соотношение составляет 0%.
Если вы двигаетесь по горизонтали, это соотношение составляет 0%.
 Мнимые экспоненты
Мнимые экспоненты Луч назван в честь конечной точки и другой точки на луче, например.
Луч назван в честь конечной точки и другой точки на луче, например. Прямой угол равен половине круга и равен 180 °, тогда как прямой угол равен четверти круга и равен 90 °.
Прямой угол равен половине круга и равен 180 °, тогда как прямой угол равен четверти круга и равен 90 °. Когда вы помните об этих конкретных характеристиках, это вопрос точного вычисления углового измерения для определения углов по градусам.
Когда вы помните об этих конкретных характеристиках, это вопрос точного вычисления углового измерения для определения углов по градусам.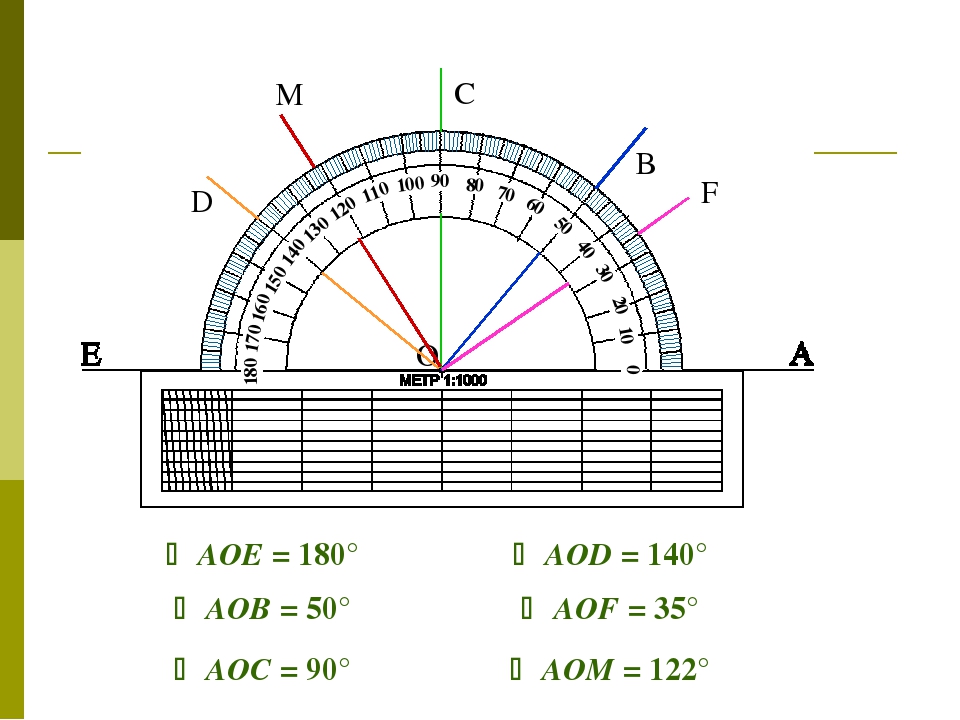 Равнобедренный и прямоугольный треугольники являются общими треугольниками, которые используются при измерении одного угла. Пометьте каждый известный угол прилагаемым размером.
Равнобедренный и прямоугольный треугольники являются общими треугольниками, которые используются при измерении одного угла. Пометьте каждый известный угол прилагаемым размером.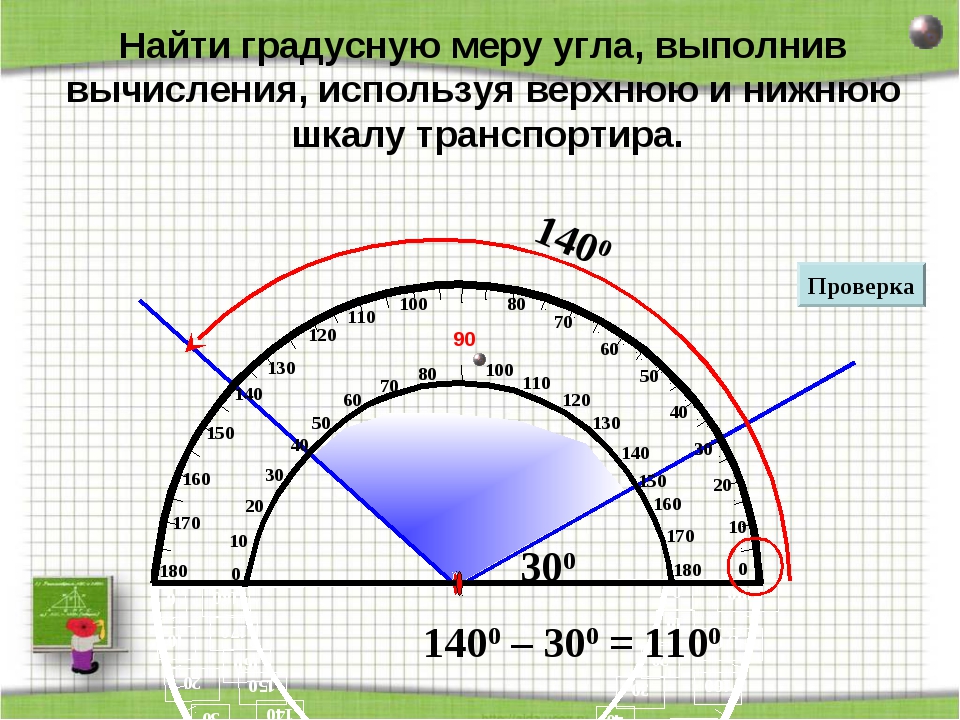 Обозначьте каждое измерение угла знаком «x», представляющим неизвестное измерение, поскольку равносторонние треугольники имеют три угла, которые эквивалентны друг другу (отсюда и название).
Обозначьте каждое измерение угла знаком «x», представляющим неизвестное измерение, поскольку равносторонние треугольники имеют три угла, которые эквивалентны друг другу (отсюда и название).
 Полный оборот или 2π равен 400 градусам. Это альтернативная мера углов, используемая во Франции и некоторых других европейских странах, и используется геодезистами. Угол 45 o равен 50 градусам, угол 90 o равен 100 градусам, угол 135 o равен 150 градусам, а прямая линия составляет 180 o или 200 градусов.Во Франции общепринятой мерой угла является сантиград или 1/100 градуса. Этот термин настолько похож на термин для шкалы Цельсия для измерения температуры, что название шкалы температуры было изменено на Цельсий, чтобы отметить ее разработчика и избежать путаницы.
Полный оборот или 2π равен 400 градусам. Это альтернативная мера углов, используемая во Франции и некоторых других европейских странах, и используется геодезистами. Угол 45 o равен 50 градусам, угол 90 o равен 100 градусам, угол 135 o равен 150 градусам, а прямая линия составляет 180 o или 200 градусов.Во Франции общепринятой мерой угла является сантиград или 1/100 градуса. Этот термин настолько похож на термин для шкалы Цельсия для измерения температуры, что название шкалы температуры было изменено на Цельсий, чтобы отметить ее разработчика и избежать путаницы.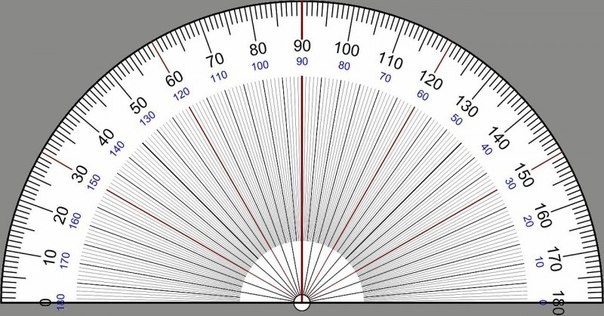

 Все углы на Рисунке 3 совпадают с углом 30 °.
Все углы на Рисунке 3 совпадают с углом 30 °.