Упрощение выражений с корнями и степенями: Упрощение выражений, содержащих корни и степени — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Упрощение выражений, содержащих корни и степени

При упрощении выражений, содержащих корни и степени, прежде чем воспользоваться свойствами степени, полезно совершить такие предварительные действия:

1. Записать корни в виде степени. Для этого нужно воспользоваться следующим свойством:

2. Десятичную дробь записать в виде обыкновенной.

Например:

3. Смешанные числа записать в виде неправильных дробей.

Например:

4. Разложить основания степеней на простые множители. Или, по крайней мере, разложить на множители так, чтобы количество различных оснований было минимальным.

Решим несколько задач из Задания В11 из Открытого банка заданий для подготовки к ЕГЭ по математике , воспользовавшись этим правилом.

1. Задание В10 ( 26745) Найдите значение выражения .

Запишем корни в виде степени и воспользуемся свойствами степеней с одинаковым основанием:

Ответ: 1.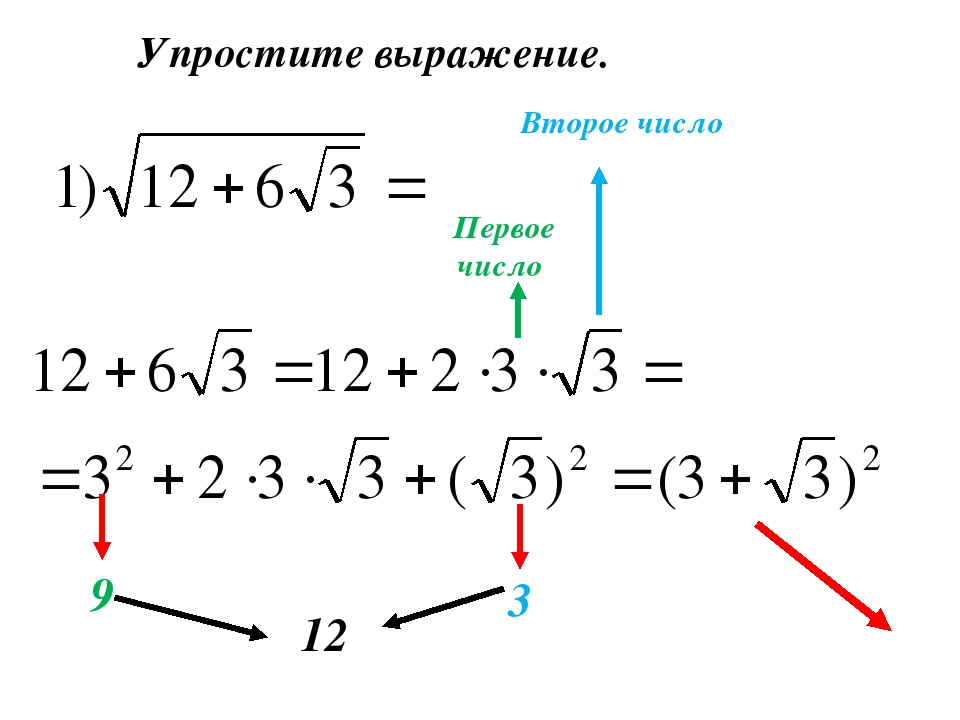

2. Задание В10 ( 26748) Найдите значение выражения

Разложим число 10 в знаменателе дроби на простые множители и воспользуемся свойствами степеней:

Ответ: 5.

3. Задание В10( 26749) Найдите значение выражения .

Представим число 0,8 в виде обыкновенной дроби, разложим число 20 на множители и воспользуемся свойствами степеней:

Ответ: 20.

4. Задание В10 ( 26749) Найдите значение выражения .

Разложим число 42 на множители и воспользуемся свойствами степеней.

Ответ: 42.

5. Задание В10 ( 26749) Найдите значение выражения при .

1. Запишем корни в виде степени:

2. Воспользуемся свойствами степени, получим:

Ответ: 0,25

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать
Firefox

И. В. Фельдман, репетитор по математике.

Упрощение выражения содержащего корень вида

Упрощение
выражения, содержащего корень вида

Способ
1(представление подкоренного выражения
в виде квадрата двучлена)

Рассмотрим на примере.

Пример
1. Упростить выражение

Решение.

Пусть
.

Тогда
.
Приравняв, свободные от квадратного
корня числа и коэффициенты, стоящие
перед корнем получим систему уравнений:

или

Так как числа х, у – натуральные,
то получим следующие системы:

или

и тем самым только система (3) имеет
натуральные решения:
.

Следовательно
.

Ответ:
.

Способ
2 (формула сложного радикала)

Пример 2. Разность
является целым числом. Найти это число.

Решение.

Ответ:

Пример
3. Упростить выражение

Решение.

Упростим корень

по формуле сложного радикала:

Тогда

Упростим корень
по формуле сложного радикала:

Поэтому получим
.

Ответ:
.

Из ЕГЭ-2008г

Пример
4. Упростить выражение

Решение.

Способ 1 (формула сложного
радикала).

Способ 2 (выделение полного
квадрата). Пример 1.

Способ 3.

Пусть

т.к.

Очевидно, что
.

Возведем равенство

в квадрат:

и т.к.
,
по
.

(представление подкоренного выражения
в виде куба двучлена)

Рассмотрим на примере.

Пример
4. Упростить выражение

Решение.

Пусть
.

Тогда
.
Приравняв, свободные от квадратного
корня числа и коэффициенты, стоящие
перед корнем получим систему уравнений

или

Решать данную систему будем в натуральных
числах
.

Рассмотрим второе уравнение. С учетом
условия
,
причем
,
получим следующие системы:

или

и тем самым только система (1) имеет
натуральные решения:
.

Следовательно
.

Пример
5. Упростить выражение

Решение.

Упростим
каждый корень.

Для упрощения квадратного корня
воспользуемся формулой сложного
радикала:
.

Для упрощения кубического корня
представим подкоренное выражение в
виде куба двучлена:
.
Тогда
.

Тем
самым получим, что:

Ответ:

Обобщение понятия степени и решение примеров со степенями

Здравствуйте. Многие ученики испытывают сложности при решении заданий, в которых встречаются выражения с корнями. В данной статье я попытаюсь обобщить материал по темам «Радикал» и «Степень». Покажу как решать некоторые задания. Если у Вас во время прочтения статьи появятся вопросы, Вы можете записаться ко мне на занятие, я с радостью помогу Вам во всем разобраться, помогу с решением именно Ваших задач!

1. Свойства степеней и корней

Степенью числа а с натуральным показателем n называется произведение n множителей, каждый из которых равняется а.
Степень числа а с показателем n обозначают aⁿ, например:

В общем случае при n > 1 имеем

Число a называется основой степени, число n — показателем степени.

Приведем основные свойства действий со степенями.

Приведенные свойства обобщаются для любых показателей степени

Часто в вычислениях используются степени с рациональным показателем. При этом удобным оказалось такое обозначение:

Корнем n— ой степени из числа а называется число b, n— я степень которого равняется a:

Корень также называется радикалом.

Корень нечетной степени n всегда существует. Корень четной степени 2n из отрицательного числа не существует. Существуют два противоположных числа, которые являются корнями четной степени из положительного числа а > 0. Положительный корень n— ой степени из положительного числа называют арифметическим корнем.

Из формул (3), (4) вытекают такие свойства радикалов

Если степень корня n = 2, то показатель корня обычно не пишется.

Пример 1.1. Найти значение выражения

Подкоренное выражение разложим на простые множители:

Пример 1.2. Упростить выражение

Имеем:

Пример 1.3. Извлечь корень

Имеем:

Пример 1.4. Упростить выражение

Поскольку при

2. Действия с радикалами

1) Преобразование корня по формуле называется внесением множителя под знак радикала.

Пример 2.1. Внести множитель под знак корня 5√2.

Исходя из формулы (7) получим

Пример 2.2. Внести множитель под знак радикала x√y при x< 0.

Имеем равенство

2) Преобразование корня исходя из формулы называется вынесением множителя из-под знака радикала.

Пример 2.3. Вынести множитель из-под знака корня в выражении

Получим:

Пример 2.4. Вынести множитель из-под знака корня

Имеем:

Пример 2.5. Вынести множитель из-под знака корня:

Радикалы вида , где a, b — рациональные числа, называются подобными. Их можно прибавлять и отнимать:

Пример 2. 6. Упростить:

Пример 2.7. Сложить радикалы:

Пример 2.8. Выполнить действие:

Заметим, что равенство не выполняется. В этом можно убедиться на таком примере:

Приведем примеры умножения радикалов.

Пример 2.9.

Аналогично освобождаются от кубических иррациональностей в знаменателе:

Рассмотрим более сложные примеры рационализации знаменателей:

Чтобы перемножить радикалы с разными степенями, их сначала превращают в радикалы с одинаковыми степенями.

Пример 2.10. Перемножим радикалы:

Во время умножения радикалов можно использовать формулы сокращенного умножения. Например:

Если радикалы находятся в знаменателе дроби, то, используя свойства радикалов, можно избавиться от иррациональности.

Пример 2.11. Рационализируем знаменатели дробей

Выражения называются сопряженными. Произведение сопряженных выражений не содержит радикалов:

Это свойство используется для рационализации знаменателей.

Пример 2.12. Избавиться от иррациональности в знаменателе:

Избавимся от иррациональности в знаменателе дроби:

3. Вычисление иррациональных выражений

С помощью свойств корней можно упрощать и вычислять иррациональные выражения.

Пример 3.1. Вычислить

Выполним последовательно действия:

Пример 3.2. Вычислить:

Выполним действия.

Часто используется формула двойного радикала:

Пример 3.3. Исходя из формулы (8) находим:

Пример 3. 4. Вычислить

Исходя из формулы (8) находим:

Окончательно получаем:

Аналогично вычисляются кубические корни. Имеем:

Возводим обе части равенства в куб:

Сравнивая выражения при √с, получаем однородную систему уравнений:

Поделив уравнение почленно, приходим к уравнению для z = y/x:

Пример 3.5. Вычислить значение радикала

После возведения в куб уравнения приходим к системе уравнений:

Поделив почленно первое уравнение на второе, получим уравнение для z= y/x:

По схеме Горнера находим корень z = — ½

Из системы уравнений и уравнения y/x = — ½ находим x = 2, y = -1. Итак,

Пример 3.6. Вычислить .

Возьмем .

Возведя обе части уравнения в куб, получаем откуда вытекает система уравнений

Система уравнений имеет очевидное решение x= 1, y= 1.

Поэтому .

Вычисляем радикал

Окончательно имеем a = — 1.

Пример 3.7. Вычислить

Поскольку

Дальше имеем:

Итак, a = — 2.

Пример 3.8. Вычислить

Возведем уравнение в куб, воспользовавшись равенством .

Получили для x кубическое уравнение

или x³ – 3x – 18 = 0,

имеет корни

Во множестве действительных чисел имеем корень x = 3.

4. Оценки для радикалов

Если

Это неравенство можно использовать для доведения неровностей, которые содержат радикалы.

Пример 4.1. Доказать, что .

Возведя неравенство в шестую степень, получим очевидное неравенство

Можно приводить радикалы к одной и то й же самой степени :

Пример 4.2. Оценим .

Поскольку

При преобразовании неравенств можно использовать символ V, понимая под ним знаки « > », « < », или « ».

Пример 4.3. Какое число больше

Поскольку

На этом все. Напоминаю, что Вы можете записываться ко мне на занятия в расписании, я с радостью помогу Вам с любыми вопросами по математике или высшей математике.

Урок 47. преобразование выражений — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №47. Преобразование выражений.

Перечень вопросов, рассматриваемых в теме:

Преобразование рациональных выражений;
Преобразование иррациональных выражений;
Преобразование логарифмических выражений.

Глоссарий по теме

Алгебраическая сумма — это запись, состоящая из нескольких алгебраических выражений, соединенных знаком «+» или «-».

Одночлен – это произведение числовых и буквенных множителей, являющихся степенями с натуральными показателями.

Многочлен – это алгебраическая сумма нескольких одночленов.

Алгебраическая дробь – это дробь, числитель и знаменатель которой являются алгебраическими выражениями.

Степень с натуральным и целым показателем. Степень числа a с натуральным показателем n, большим 1, — это произведение n множителей, равных a , , где a — основание степени, n — показатель степени, – степень.

Если и n — натуральное число, то ,

если . то .

Арифметический корень. Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a. Обозначается , где a — подкоренное выражение.

Степень с рациональным показателем. Если n — натуральное число, m — целое число и частное является целым числом, то при справедливо равенство

Логарифмом положительного числа в по основанию а, где a > 0, a ≠ 1, называется показатель степени, в которую надо возвести а, чтобы получить в.

Основная литература:

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege. sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Выделение полного квадрата или куба. под знаком корня. Например, необходимо упростить выражение:

Предположим, что под корнем стоит полный квадрат.

Тогда

Так как сумма квадратов не может равняться иррациональному числу, то в нашем случае сумма квадратов равна четырнадцати, а удвоенное произведение равно шесть корней из пяти.

Мы получили систему, которую можно решить методом подстановки

Решая первое уравнение как биквадратное, получим

Так как в формуле квадрат суммы переменные a и b равноправны, получаем

Аналогично

Итак, заданное выражение

Аналогично можно выделять полный куб под корнем.

В некоторых случаях выделить полный куб не представляется возможным, тогда можно поступить следующим образом:

Обозначим указанное выражение буквой А и получим равенство

возведем обе части равенства в куб.

Учитывая, что сумму кубических корней равна А, получим

A = 3

Таким образом, найдено значение выражения

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Упростить выражение и найти его значение при заданном значении переменной:

при

Варианты ответа: 0,2; 4; 0,4; 0,04;

Решение.

Обозначим , тогда наше выражение будет иметь вид:

Вернемся к первоначальной переменной

Вычислим при заданном значении переменной

Пример 2. Упростите и вычислите: при a = 125.

Варианты ответов: 125; 3,2; 6,4; 32; 62,5;

Решение.

Найдем значение при заданном значении переменной

1 упростите выражение

Вы искали 1 упростите выражение? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 2 упростите выражение, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 упростите выражение».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 упростите выражение,2 упростите выражение,2 упростить выражение 1 2,3 4x 2 5 упростить,3 упростить выражение,4 упростите выражение,4 упростить выражение,7 класс алгебра упростить выражение онлайн калькулятор,x y x упростить,алгебра как упростить выражение,алгебра упрощение выражений,алгебраическое выражение упростить,вы упростите,выражение онлайн,выражение решить онлайн,выражения решение онлайн,выразить из формулы онлайн,выразить онлайн,выразить онлайн переменную,выразить формулу онлайн,дроби упростить выражение,дробное выражение как упростить,как правильно упрощать выражения,как решать упростите выражение,как решать упростить выражение,как упростить,как упростить выражение,как упростить выражение алгебра,как упростить выражение дробное,как упростить выражения,как упростить дробное выражение,как упростить пример,как упростить уравнение,как упрощать,как упрощать выражение,как упрощать выражения,как упрощать уравнения,калькулятор алгебраических выражений,калькулятор алгебраических выражений онлайн калькулятор,калькулятор алгебраических выражений с буквами,калькулятор буквенных выражений,калькулятор буквенных выражений онлайн,калькулятор выражений,калькулятор выражений с буквами,калькулятор для упрощения выражений,калькулятор для упрощения выражений с дробями,калькулятор дробей упрощение выражений,калькулятор онлайн буквенных выражений,калькулятор онлайн подобные слагаемые,калькулятор онлайн упростить выражение,калькулятор онлайн упрощение выражений,калькулятор онлайн упрощение дробных выражений,калькулятор онлайн упрощения выражений,калькулятор подобных слагаемых,калькулятор преобразования выражений,калькулятор раскрытие скобок,калькулятор раскрытие скобок онлайн,калькулятор раскрытия скобок онлайн,калькулятор рациональных выражений с решением онлайн,калькулятор тождественных выражений,калькулятор упростите выражение,калькулятор упростите выражение с дробями,калькулятор упростите выражение с корнями,калькулятор упростить,калькулятор упростить выражение,калькулятор упростить выражение онлайн с дробями,калькулятор упростить выражение онлайн с дробями с буквами,калькулятор упрощение выражений,калькулятор упрощение выражений дробей,калькулятор упрощение выражений онлайн,калькулятор упрощение выражений с дробями,калькулятор упрощение выражений со степенями онлайн,калькулятор упрощение многочлена онлайн,калькулятор упрощения,калькулятор упрощения выражений,калькулятор упрощения выражений онлайн,калькулятор упрощения выражений онлайн калькулятор,калькулятор упрощения выражений с буквами,калькулятор упрощения выражений с буквами и степенями и дробями,калькулятор упрощения выражений с дробями,калькулятор упрощения выражений с дробями и степенями и буквами,калькулятор упрощения выражений с дробями и степенями и с буквами,калькулятор упрощения выражения,калькулятор упрощения дробей с буквами и степенями,математика выражение упростить,онлайн выражение,онлайн выражение формул,онлайн выразить,онлайн калькулятор буквенных выражений,онлайн калькулятор преобразование рациональных выражений,онлайн калькулятор раскрытие скобок,онлайн калькулятор раскрытия скобок,онлайн калькулятор спростить вираз,онлайн калькулятор упростите выражение,онлайн калькулятор упростить выражение,онлайн калькулятор упрощение выражений,онлайн калькулятор упрощение выражений с дробями,онлайн калькулятор упрощение выражений со степенями,онлайн калькулятор упрощение дробных выражений,онлайн калькулятор упрощение многочлена,онлайн калькулятор упрощения выражений,онлайн преобразование выражений,онлайн преобразование тригонометрических выражений,онлайн преобразователь в многочлен,онлайн преобразователь формул,онлайн раскройте скобки,онлайн раскрытие скобок,онлайн решение алгебраических выражений,онлайн решение выражений,онлайн решение выражения,онлайн решение рациональных выражений,онлайн решения выражений,онлайн сокращение выражений,онлайн сокращение многочленов,онлайн упроститель выражений,онлайн упростить,онлайн упростить выражение со степенями,онлайн упростить дробное выражение,онлайн упрощение выражений с дробями,онлайн упрощение выражений с корнями,онлайн упрощение выражений со степенями,онлайн упрощение дробных выражений,онлайн упрощение многочленов,онлайн упрощения выражений,подобные слагаемые калькулятор онлайн,подобные слагаемые онлайн калькулятор,преобразование выражений онлайн,преобразование иррациональных выражений онлайн калькулятор,преобразование рациональных выражений калькулятор онлайн,преобразование рациональных выражений онлайн калькулятор,преобразование формул онлайн,преобразования выражений калькулятор,преобразовать в многочлен выражение онлайн,преобразовать выражение в многочлен онлайн,преобразовать выражение онлайн,преобразовать многочлен в выражение онлайн,преобразуйте в дробь выражение онлайн,преобразуйте в многочлен выражение онлайн калькулятор,преобразуйте дробь в выражение онлайн,приведи подобные слагаемые онлайн калькулятор,пример упростить,пример упростить выражение,примеры упростите выражение,примеры упрощение выражений,примеры упрощения,раскрытие скобок калькулятор,раскрытие скобок калькулятор онлайн,раскрытие скобок онлайн,раскрытие скобок онлайн калькулятор,раскрытия скобок онлайн калькулятор,раскрыть скобки онлайн,раскрыть скобки онлайн калькулятор,рациональных выражений онлайн калькулятор с решением,решение алгебраических выражений онлайн,решение выражений,решение выражений онлайн,решение выражения,решение выражения онлайн,решение онлайн алгебраических выражений,решение онлайн выражения,решение примеров на упрощение выражений,решение упростите выражение,решения выражений онлайн,решите выражение,решить выражение,решить выражение онлайн,решить выражение онлайн со степенями,решить онлайн выражение,сократить выражение,сократить выражение онлайн,сократить выражение онлайн с подробным решением,сократить многочлен онлайн,сократить онлайн выражение,сократить уравнение онлайн,сокращение выражений,сокращение выражений онлайн,сокращение многочленов онлайн,сокращение уравнений онлайн,способы упрощения выражений,спростити вираз,спростити вираз онлайн,спростити вираз онлайн калькулятор,спростити вираз приклади,спростить вираз,спростить вираз онлайн калькулятор,спростіть вираз,спрощення виразів,упрости,упрости выражение,упрости выражения,упростите,упростите 3 4х 2 5,упростите алгебраическое выражение,упростите вы,упростите выражение,упростите выражение 1,упростите выражение 2,упростите выражение 2 3x 2,упростите выражение 3,упростите выражение a,упростите выражение x,упростите выражение x 2 x 8 x,упростите выражение x 3 x 4,упростите выражение а,упростите выражение дроби,упростите выражение дробное,упростите выражение дробь,упростите выражение и,упростите выражение калькулятор,упростите выражение калькулятор онлайн,упростите выражение калькулятор онлайн с решением,упростите выражение калькулятор с дробями,упростите выражение калькулятор с дробями и степенями,упростите выражение калькулятор с степенями,упростите выражение калькулятор с степенями и дробями,упростите выражение онлайн,упростите выражение онлайн калькулятор,упростите выражение онлайн калькулятор с решением,упростите выражение онлайн с дробями,упростите выражение онлайн с дробями и степенями,упростите выражение онлайн с дробями и степенями с решением,упростите выражение онлайн с корнями,упростите выражение примеры,упростите выражение решение,упростите выражение с дробями,упростите выражение с дробями онлайн,упростите выражение с корнями калькулятор,упростите выражение с корнями онлайн,упростите выражения,упростите выражения а,упростите выражения калькулятор,упростите выражения калькулятор онлайн,упростите выражения онлайн,упростите дробное выражение,упростите уравнение,упростите уравнение онлайн,упроститель выражений,упроститель выражений онлайн,упростить 2x 4 6x 6,упростить x 2 x,упростить алгебраическое выражение,упростить векторное выражение онлайн,упростить выражение,упростить выражение 3,упростить выражение алгебра как,упростить выражение алгебраическое,упростить выражение дроби,упростить выражение дробное,упростить выражение дробное онлайн,упростить выражение дробное онлайн калькулятор с решением,упростить выражение как решать,упростить выражение калькулятор,упростить выражение калькулятор онлайн,упростить выражение онлайн,упростить выражение онлайн калькулятор,упростить выражение онлайн калькулятор с дробями,упростить выражение онлайн калькулятор с дробями и буквами,упростить выражение онлайн калькулятор с корнями,упростить выражение онлайн калькулятор с решением,упростить выражение онлайн калькулятор с решением с дробями,упростить выражение онлайн калькулятор с решением с дробями и буквами,упростить выражение онлайн калькулятор с решением с дробями и корнями,упростить выражение онлайн калькулятор с решением с корнями,упростить выражение онлайн калькулятор с решением со степенями,упростить выражение онлайн калькулятор со степенями,упростить выражение онлайн калькулятор со степенями с решением,упростить выражение онлайн с дробями,упростить выражение онлайн с дробями буквами и степенями онлайн,упростить выражение онлайн с дробями и буквами,упростить выражение онлайн с дробями и буквами 8 класс,упростить выражение онлайн с дробями и буквами калькулятор,упростить выражение онлайн с дробями и степенями,упростить выражение онлайн с дробями калькулятор,упростить выражение онлайн с корнями,упростить выражение онлайн с корнями и степенями,упростить выражение онлайн с корнями калькулятор,упростить выражение онлайн с решением,упростить выражение онлайн со степенями,упростить выражение примеры,упростить выражение с дробями,упростить выражение с дробями и буквами,упростить выражение с дробями и буквами 8 класс онлайн,упростить выражение с дробями и буквами онлайн калькулятор,упростить выражение с дробями и с степенями онлайн,упростить выражение с дробями и степенями онлайн,упростить выражение с дробями онлайн,упростить выражение с дробями онлайн калькулятор,упростить выражение с дробями онлайн калькулятор с решением,упростить выражение с корнями онлайн,упростить выражение с корнями онлайн калькулятор,упростить выражение с корнями онлайн калькулятор с решением,упростить выражение с корнями онлайн калькулятор с решением с дробями,упростить выражение со степенями онлайн,упростить выражение со степенями онлайн калькулятор,упростить выражение со степенями онлайн калькулятор с решением,упростить выражение что такое,упростить выражения,упростить выражения онлайн,упростить дробное выражение,упростить дробное выражение онлайн,упростить дробное выражение онлайн калькулятор с решением,упростить дробь онлайн с буквами,упростить дробь онлайн с буквами и степенями,упростить дробь с буквами онлайн,упростить как,упростить калькулятор,упростить многочлен онлайн,упростить онлайн,упростить онлайн выражение с корнями,упростить онлайн выражение со степенями,упростить тригонометрическое выражение онлайн,упростить тригонометрическое выражение онлайн калькулятор с решением,упростить уравнение,упростить уравнение онлайн,упростить уравнение онлайн с решением,упрощать как,упрощение алгебраические выражения,упрощение алгебраических выражений,упрощение выражений,упрощение выражений алгебра,упрощение выражений дробей,упрощение выражений дробей калькулятор,упрощение выражений дробных,упрощение выражений дробных онлайн,упрощение выражений калькулятор,упрощение выражений калькулятор онлайн,упрощение выражений калькулятор онлайн с корнями,упрощение выражений онлайн,упрощение выражений онлайн калькулятор,упрощение выражений онлайн калькулятор с дробями,упрощение выражений онлайн калькулятор с решением,упрощение выражений онлайн калькулятор со степенями,упрощение выражений онлайн с дробями,упрощение выражений онлайн с корнями,упрощение выражений онлайн с решением,упрощение выражений примеры,упрощение выражений с дробями,упрощение выражений с дробями калькулятор,упрощение выражений с дробями онлайн,упрощение выражений с дробями онлайн калькулятор,упрощение выражений с корнями онлайн,упрощение выражений с решением онлайн,упрощение выражений со степенями калькулятор онлайн,упрощение выражений со степенями онлайн калькулятор,упрощение дробей онлайн с буквами,упрощение дробей онлайн со степенями и буквами,упрощение дробей с буквами онлайн,упрощение дробных выражений,упрощение дробных выражений калькулятор онлайн,упрощение дробных выражений онлайн,упрощение дробных выражений онлайн калькулятор,упрощение корней онлайн,упрощение многочленов онлайн,упрощение онлайн,упрощение тригонометрических выражений онлайн,упрощение уравнений,упрощение уравнений онлайн,упрощение уравнения,упрощения,упрощения выражений,упрощения выражений онлайн калькулятор,упрощения выражений примеры,упрощения выражения калькулятор,формула упрощения выражения,формулы для упрощения выражений,формулы упрощения,формулы упрощения выражений,формулы упрощения выражения,что такое упростить выражение. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 упростите выражение. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 2 упростить выражение 1 2).

Где можно решить любую задачу по математике, а так же 1 упростите выражение Онлайн?

Решить задачу 1 упростите выражение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

С1 ГИА по математике — упрощение выражений, содержащих корни

Рассмотрим задачи, связанные с упрощением выражений, содержащих иррациональные числа.

10.

11.

Решим несколько задач из задания С1:

1.Найдите значение выражения:

Избавимся от иррациональности в знаменателе. У нас там присутствует разность двух чисел, одно из которых иррациональное. Умножим дробь на сумму этих чисел, тогда в знаменателе окажется разность квадратов, что и позволит избавиться от иррациональности. Этот метод – умножения на сопряженное – используется также и в теории комплексных чисел.

Раскрываем скобки в числителе:

Ответ: -2

2.Найдите значение выражения:

Так же, домножая на сопряженное, избавляемся от иррациональности в знаменателе:

Ответ:1

В заданиях также часто встречаются такие:

3. Укажите наибольшее из следующих чисел:

а)

б)

в)

г)

Способ решения может быть таким: возведем все эти числа в квадрат. Наибольший квадрат соответствует наибольшему числу:

а)

б)

в)

г)

Осталось выбрать из чисел б) и г). Здесь нужно вспомнить, что

Тогда

Значит, среди представленных чисел число – наибольшее.

Ответ: б)

Решим еще одно такое задание:

4. Укажите наибольшее из следующих чисел:

а)

б)

в)

г)

Возводим в квадраты:

а)

б)

в)

г)

Подумаем, к какому числу близко число ? Оно меньше 9, но больше 8, так как

Тогда , и .

Число 6 – наибольшее.

Ответ: в)

Попробуем теперь упрощать выражения, содержащие корни.

5. Упростите выражение:

Воспользуемся свойствами корня. “Втащим” все под один корень:

Ответ:

6. Найдите значение выражения:

Представим число 46 как 23*2:

Теперь переставим сомножители:

Ответ: 460.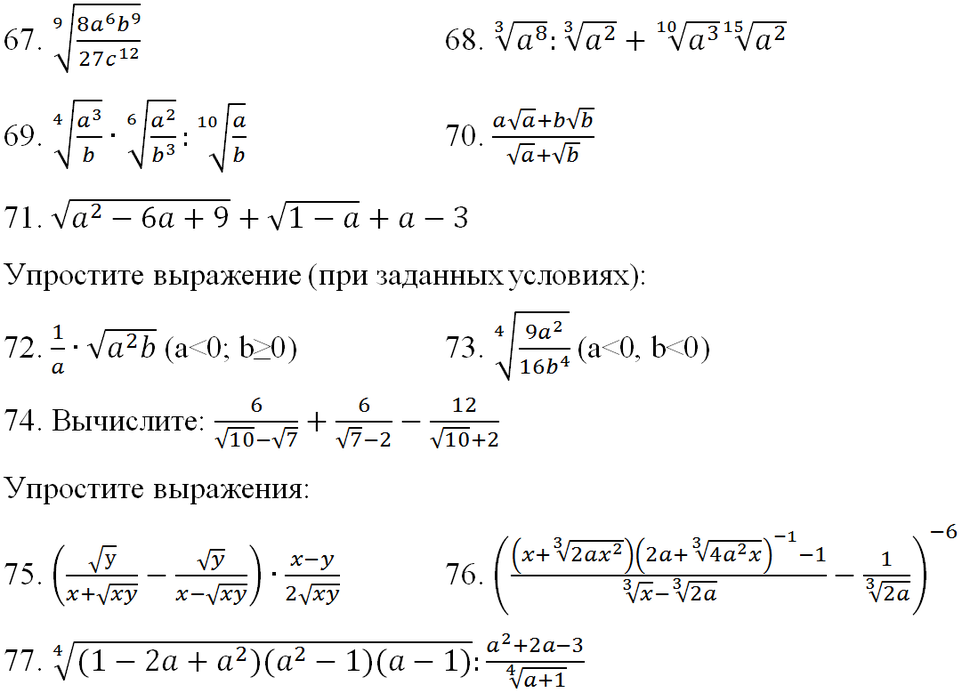

Еще один тип заданий:

7. Какое из чисел является рациональным?

Рациональным является число, представимое сократимой дробью. Попробуем записать наши числа иначе:

Ни первое, ни третье числа не являются сократимыми дробями, значит, они иррациональны.

Ответ:

Сложение ⚠️ корней, вычитание корней с одинаковыми и разными показателями

Определение

Действие сложения и вычитания квадратных корней возможно лишь при условии одинаковости подкоренных выражений слагаемых.

Сложение корней, формулы

Складывать подобные квадратные корни, то есть иррациональные выражения с одинаковым основанием, очень просто. Для этого суммируют множители слагаемых, а подкоренное число остается неизменным:

$m\sqrt a+n\sqrt a=\left(m+n\right)\sqrt a$

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В случае со сложением корней с разными подкоренными значениями нужно привести их к подобию. Упрощение корневых чисел выполняют по следующему алгоритму:

Раскладывание подкоренного числа на два множителя так, чтобы один из них являлся числом, из которого извлекается целый квадратный корень.

Извлечение корня из квадратного числа, запись ответа перед символом корня. Второй множитель остается под знаком корня.

Упрощенные корни с одинаковым основанием можно складывать как подобные.

Пример

$3\sqrt{50}+2\sqrt8+\sqrt{12}$

$3\sqrt{50}=3\sqrt{25\times2}=3\times5\sqrt2=15\sqrt2$

$2\sqrt8=2\sqrt{4\times2}=2\times2\sqrt2=4\sqrt2$

$\sqrt{12}\;=\sqrt{4\times3}=2\times1\sqrt2=2\sqrt2$

После упрощения исходное выражение приобретает вид:

$15\sqrt2+4\sqrt2+2\sqrt2=21\sqrt2$

Примечание

Подкоренные выражения между собой не суммируются и не вычитаются. При этом выражения под одним корнем складываются и вычитаются как обычные числа.

Вычитание корней, формулы

При вычитании подобных корней вычитаются их множители, а подкоренное выражение не меняется:

$m\sqrt a-n\sqrt a=\left(m-n\right)\sqrt a$

Чтобы узнать разность иррациональных чисел с разным основанием, нужно привести уменьшаемое и вычитаемое к единому образцу. Для этого используют тот же алгоритм, что и перед сложением.

Пример

$4\sqrt{75}-3\sqrt{24}$

$4\sqrt{75}=4\sqrt{25\times3}=4\times5\sqrt3=20\sqrt3$

$3\sqrt{12}=3\sqrt{4\times3}=3\times2\sqrt3=6\sqrt3$

Упростив, получаем:

$20\sqrt3-6\sqrt3=14\sqrt3$

Сложение корней со степенями

Складывание и вычитание корней с разными степенями, но одинаковым основанием имеет следующую последовательность:

Допустим, надо решить данное выражение:

$\sqrt[3]а+\sqrt[4]а$

Для начала проведем процедуру упрощения:

$\sqrt[3]а+\sqrt[4]а=12\times\sqrt a^4+12\times\sqrt a^3$

$12\times\sqrt a^4+12\times\sqrt a^3=12\times\sqrt{a^4+a^3}$

При приведении двух подобных членов к общему показателю корневого числа применяется одно из свойств корней.2}=\left|а-2\right|+\left|а-4\right|\)

Раскроем модули в промежутке $2\leq а\leq4$:

$\vert а-2\vert=а-2,\;т.к.\;а-2\geq0$

$\vert а-4\vert=4-а,\;т.к.\;а-4\leq0$

Следовательно, $\vert а-2\vert+\vert а-4\vert=а-2+4-а=2$

Ответ: 2.

8.1 Упрощение выражений с помощью корней — промежуточная алгебра 2e

Задачи обучения

К концу этого раздела вы сможете:

Упростить выражения с корнями
Оценочные и приблизительные корни
Упростить выражения переменных с помощью корней

Будьте готовы 8.1

Перед тем, как начать, пройдите тест на готовность.

Упростить: ⓐ (−9) 2 (−9) 2 ⓑ −92−92 ⓒ (−9) 3. (- 9) 3.
Если вы пропустили эту проблему, просмотрите Пример 2.21.

Будьте готовы 8.2

Округлите 3,8463,846 до сотых.
Если вы пропустили эту проблему, просмотрите Пример 1.34.

Будьте готовы 8,3

Упростить: ⓐ x3 · x3x3 · x3 ⓑ y2 · y2 · y2y2 · y2 · y2 ⓒ z3 · z3 · z3 · z3.z3 · z3 · z3 · z3.
Если вы пропустили эту проблему, просмотрите Пример 5.12.

Упростите выражения с помощью корней

В разделе «Основы» мы вкратце рассмотрели квадратные корни. Помните, что когда действительное число n умножается само на себя, мы пишем n2n2 и читаем его как « n в квадрате».Это число называется квадратом n , а n называется квадратным корнем. Например,

132 читается как «13 в квадрате» 169 называется квадратом 13, так как 132 = 16913 квадратный корень 1691 32 читается «13 в квадрате» 169 называется квадратом 13, поскольку 132 = 16913 квадратный корень 169

Квадратный и квадратный корень числа

Квадрат

Если n2 = m, то m — квадрат n. Если n 2 = m, то m квадрат n.

Квадратный корень

Если n2 = m, то корень равен квадратному.Если n2 = m, то корень равен квадратному.

Замечание (−13) ² = 169 также, поэтому −13 также является квадратным корнем из 169. Следовательно, и 13, и −13 являются квадратными корнями из 169.

Итак, каждое положительное число имеет два квадратных корня — один положительный и один отрицательный. Что, если бы нам нужен был только положительный квадратный корень из положительного числа? Мы используем знак корня и пишем m, m, что означает положительный квадратный корень из m . Положительный квадратный корень также называется главным квадратным корнем.Этот символ, а также другие радикалы, которые будут введены позже, являются символами группировки.

Мы также используем знак корня для квадратного корня из нуля. Поскольку 02 = 0,02 = 0, 0 = 0,0 = 0. Обратите внимание, что у нуля есть только один квадратный корень.

Квадратный корень

неправильно прочитано «квадратный корень из m». Если n2 = m, то n = m, для n ≥ 0. m читается «квадратный корень из m». Если n 2 = m, то n = m, для n ≥ 0.

Мы знаем, что каждое положительное число имеет два квадратных корня, а знак корня указывает на положительный. Мы пишем 169 = 13.169 = 13. Если мы хотим найти отрицательный квадратный корень из числа, мы помещаем минус перед знаком корня. Например, −169 = −13. − 169 = −13.

Пример 8.1

Упростить: ⓐ 144144 ⓑ −289. − 289.

Решение

ⓐ

144144

Так как 122 = 144,122 = 144.

1212

Ⓑ

	−289−289
Так как 172 = 289172 = 289 и отрицательный знак стоит перед радикальным знаком.	−17−17

Попробуйте 8.1

Упростить: ⓐ −64−64 ⓑ 225,225.

Попробовать 8.2

Упростить: ⓐ 100100 ⓑ −121. − 121.

Можно ли упростить −49? −49? Есть ли число, квадрат которого равен -49? -49?

Любое положительное число в квадрате положительно. Любое отрицательное число в квадрате положительно. Не существует действительного числа, равного -49.-49. Квадратный корень отрицательного числа не является действительным числом.

Пример 8.2

Упростить: ⓐ −196−196 ⓑ −64. − 64.

Решение

ⓐ

	−196−196
Не существует действительного числа, квадрат которого равен −196. −196.	−196 не является действительным числом. −196 не является действительным числом.

Ⓑ

04″ summary=»Table 6.1 » data-label=»»>

	−64−64
Негатив перед радикалом.	−8−8

Попробуй 8.3

Упростить: ⓐ −169−169 ⓑ −81. − 81.

Попробовать 8.4

Упростить: ⓐ −49−49 ⓑ −121. − 121.

До сих пор мы говорили только о квадратах и квадратных корнях. Теперь давайте расширим нашу работу, включив в нее высшие силы и высшие корни.

Давайте сначала просмотрим словарный запас.

Мы пишем: Мы говорим: n2nsquaredn3ncubedn4в четвертой степени n5на пятой степени Мы пишем: Мы говорим: n2nsquaredn3ncubedn4в четвертой степениn5в пятой степени

Термины «квадрат» и «куб» происходят от формул для площади квадрата и объема куба.

Было бы полезно иметь таблицу степеней целых чисел от −5 до 5. См. Рис. 8.2.

Рисунок 8.2

Обратите внимание на знаки в таблице. Конечно, все степени положительных чисел положительны. Но когда у нас есть отрицательное число, четных степеней положительны, а нечетных степеней отрицательны. Мы скопируем строку со степенью −2, чтобы вы в этом убедились.

Теперь мы расширим определение квадратного корня на более высокие корни.

n ^th Корень числа

Если bn = a, то бис корень a. Основной корень записанного называется индексом радикала. Если b n = a, то является корнем корня a. Основной корень письменного называется индексом радикала.

Точно так же, как мы используем слово «кубический» для b ³, мы используем термин «кубический корень» для a3.a3.

Мы можем обратиться к рисунку 8.2, чтобы найти более высокие корни.

43 = 6434 = 81 (−2) 5 = −32643 = 4814 = 3−325 = −243 = 6434 = 81 (−2) 5 = −32643 = 4814 = 3−325 = −2

Может ли у нас быть четный корень отрицательного числа? Мы знаем, что квадратный корень отрицательного числа не является действительным числом.То же верно и для любого четного корня. Даже корней отрицательных чисел не являются действительными числами. Нечетные корней отрицательных чисел — действительные числа.

Недвижимость анана

Когда n — четное число и

a≥0, a≥0, тогда anan — действительное число.
a <0, a <0, тогда anan не является действительным числом.

Когда n является нечетным числом, anan является действительным числом для всех значений a .

Мы применим эти свойства в следующих двух примерах.

Пример 8.3

Упростить: 643643 ⓑ 814814 325,325.

Решение

ⓐ

	643643
Так как 43 = 64,43 = 64.	44

Ⓑ

	814814
Поскольку (3) 4 = 81, (3) 4 = 81.	33

Ⓒ

325325

Поскольку (2) 5 = 32.(2) 5 = 32.

Попробуй 8,5

Упростить: ⓐ 273273 ⓑ 25642564 ⓒ 2435,2435.

Попробуйте 8.6

Упростить: ⓐ 1000310003 ⓑ 164164 ⓒ 10245.10245.

В этом примере будьте внимательны к отрицательным знакам, а также к четным и нечетным степеням.

Пример 8.4

Упростить: ⓐ −1253−1253 ⓑ -164-164 ⓒ −2435. − 2435.

Решение

ⓐ

	−1253−1253
Так как (−5) 3 = −125.(−5) 3 = −125.	−5−5

Ⓑ

	−164−164
Подумайте, (?) 4 = −16. (?) 4 = −16. Никакое действительное число в четвертой степени не является отрицательным.	Неверное число.

Ⓒ

	−2435−2435
Так как (−3) 5 = −243. (- 3) 5 = −243.	−3−3

Попробуй 8.7

Упростить: ⓐ −273−273 ⓑ −2564−2564 ⓒ −325. − 325.

Попробовать 8,8

Упростить: ⓐ −2163−2163 ⓑ −814−814 ⓒ −10245. − 10245.

Оценка и приблизительные корни

Когда мы видим число со знаком радикала, мы часто не задумываемся о его числовом значении. Хотя мы, вероятно, знаем, что 4 = 2,4 = 2, каково значение 2121 или 503? 503? В некоторых ситуациях имеет смысл быстрая оценка, а в других удобно использовать десятичное приближение.

Чтобы получить численную оценку квадратного корня, мы ищем точные квадратные числа, наиболее близкие к подкоренному выражению. Чтобы найти оценку 11,11, мы видим, что 11 находится между точными квадратными числами 9 и 16, ближе к 9. Тогда его квадратный корень будет между 3 и 4, но ближе к 3.

Точно так же, чтобы оценить 913 913, мы видим, что 91 находится между числами идеального куба 64 и 125. Тогда кубический корень будет между 4 и 5.

Пример 8.5

Оцените каждый корень между двумя последовательными целыми числами: ⓐ 105105 ⓑ 433.433.

Попробовать 8.9

Оцените каждый корень между двумя последовательными целыми числами:

3838 933 933

Попробуйте 8.10

Оцените каждый корень между двумя последовательными целыми числами:

ⓐ 8484 15231523

Существуют математические методы для вычисления квадратного корня, но в настоящее время большинство людей используют калькулятор для нахождения квадратного корня. Чтобы найти квадратный корень, воспользуйтесь клавишей xx на калькуляторе. Чтобы найти корень куба или любой корень с более высоким индексом, вы будете использовать ключ xyxy.

При использовании этих ключей вы получаете приблизительное значение. Это приблизительное значение, соответствующее количеству цифр, отображаемых на экране калькулятора. Символ приблизительного значения ≈ ≈ читается как «приблизительно».

Предположим, ваш калькулятор имеет 10-разрядный дисплей. Вы бы увидели, что

5≈2,236067978, округленное до двух десятичных знаков, 5≈2,24934≈3,105422799, округленное до двух десятичных знаков: 934≈3,115≈2,236067978, округленное до двух десятичных знаков, 5≈2,24934≈3,105422799, округленное до двух десятичных разрядов 934≈3.11

Откуда мы знаем, что эти значения являются приблизительными, а не точными? Посмотрите, что получится, когда мы возведем их в квадрат:

(2,236067978) 2 = 5,000000002 (2,24) 2 = 5,0176 (3,105422799) 4 = 92,999999991 (3,11) 4 = 93,54951841 (2,236067978) 2 = 5,000000002 (2,24) 2 = 5,0176 (3,105422799) 4 = 92,99999419991 (3495)

Их квадраты близки к 5, но не в точности равны 5. Четвертая степень близка к 93, но не равна 93.

Пример 8.6

Округляем до двух десятичных знаков: ⓐ 1717 ⓑ 493493 ⓒ 514.514.

Решение

ⓐ

	1717
Воспользуйтесь ключом вычисления квадратного корня калькулятора.	4,123105626… 4,123105626…
Округление до двух десятичных знаков.	4.124.12
	17≈4,1217≈4,12

Ⓑ

	493493
Используйте кнопку xyxy калькулятора.	3.65 10… 3.65 10…
Округление до двух десятичных знаков.	3,663,66
	493≈3,66493≈3,66

Ⓒ

	514514
Используйте кнопку xyxy калькулятора.	2.6723451177… 2.6723451177…
Округление до двух десятичных знаков.	2,672,67
	514≈2.67514≈2,67

Попробуйте 8.11

Округление до двух десятичных знаков:

1111 713713 1274.1274.

Попробуйте 8.12

Округление до двух десятичных знаков:

1313 843843 984,984.

Упростите выражения переменных с помощью корней

Нечетный корень числа может быть положительным или отрицательным. Например,

А как насчет ровного рута? Нам нужен главный корень, поэтому 6254 = 5,6254 = 5.

Но обратите внимание,

Как мы можем убедиться, что корень четвертой степени из −5 в четвертой степени равен 5? Мы можем использовать абсолютное значение. | −5 | = 5. | −5 | = 5. Итак, мы говорим, что когда n четное ann = | a | .ann = | a |. Это гарантирует, что главный корень положителен.

Упрощение четных и нечетных корней

Для любого целого числа n≥2, n≥2,

когда indexnis oddann = когда indexnis evenann = | a | когда indexnis oddann = когда indexnis evenann = | a |

Мы должны использовать знаки абсолютного значения, когда мы извлекаем четный корень из выражения с переменной в корне.

Пример 8.7

Упростить: ⓐ x2x2 ⓑ n33n33 ⓒ p44p44 ⓓ y55.y55.

Решение

ⓐ Мы используем абсолютное значение, чтобы гарантированно получить положительный корень.

	x2x2
Поскольку индекс nn четный, ann = \| a \| .ann = \| a \|.	\| x \|\| x \|

ⓑ Это нечетный индексированный корень, поэтому знак абсолютного значения не требуется.

	м33м33
Поскольку индекс nn нечетный, ann = a.ann = а.	мм

ⓒ

	п44п44
Так как индекс nis evenann = \| a \| .nis evenann = \| a \|.	\| p \|\| p \|

ⓓ

	y55y55
Поскольку индекс nn нечетный, ann = a.ann = a.	г.г

Попробуйте 8.13

Упростить: ⓐ b2b2 ⓑ w33w33 ⓒ m44m44 ⓓ q55.q55.

Попробуйте 8.14

Упростить: ⓐ y2y2 ⓑ p33p33 ⓒ z44z44 ⓓ q55.q55.

А как насчет квадратных корней из высших степеней переменных? Свойство степени экспоненты говорит: (am) n = am · n. (Am) n = am · n. Итак, если возвести в квадрат и ^м , показатель степени станет 2 м .

Теперь посмотрим на квадратный корень,

a2mПоскольку (am) 2 = a2m. (Am) 2Sincenis evenann = | a |. | Am | Soa2m = | am | .a2mПоскольку (am) 2 = a2m. (Am) 2Sincenis evenann = | a |. | Am | Soa2m = | утра |.

Мы применим эту концепцию в следующем примере.

Пример 8.8

Упростить: ⓐ x6x6 ⓑ y16.y16.

Решение

ⓐ

	x6x6
Поскольку (x3) 2 = x6. (X3) 2 = x6.	(x3) 2 (x3) 2
Так как индекс nn четный an = \| a \| .an = \| a \|.	\| x3 \|\| x3 \|

Ⓑ

	y16y16
Поскольку (y8) 2 = y16.(у8) 2 = у16.	(y8) 2 (y8) 2
Так как индекс nn четный ann = \| a \| .ann = \| a \|.	y8y8
В этом случае знак абсолютного значения не нужен, так как y8y8 положителен.

Попробуйте 8.15

Упростить: ⓐ y18y18 ⓑ z12.z12.

Попробуйте 8.16

Упростить: ⓐ m4m4 ⓑ b10.b10.

В следующем примере используется та же идея для более высоких корней.

Пример 8.9

Упростить: ⓐ y183y183 ⓑ z84.z84.

Решение

ⓐ

	y183y183
Поскольку (y6) 3 = y18. (Y6) 3 = y18.	(y6) 33 (y6) 33
Поскольку nn нечетно, ann = a.ann = a.	y6y6

Ⓑ

z84z84

Так как (z2) 4 = z8. (Z2) 4 = z8.	(z2) 44 (z2) 44
Поскольку z2z2 положительно, знак абсолютного значения нам не нужен.	z2z2

Попробуйте 8.17

Упростить: ⓐ u124u124 ⓑ v153.v153.

Попробуйте 8.18

Упростить: ⓐ c205c205 ⓑ d246d246

В следующем примере у нас теперь есть коэффициент перед переменной. Понятие a2m = | am | a2m = | am | работает примерно так же.

16r22 = 4 | r11 | потому что (4r11) 2 = 16r22. 16r22 = 4 | r11 | потому что (4r11) 2 = 16r22.

Но обратите внимание, 25u8 = 5u425u8 = 5u4, и знак абсолютного значения не требуется, так как u ⁴ всегда положительный.

Пример 8.10

Упростить: ⓐ 16n216n2 ⓑ −81c2. − 81c2.

Решение

ⓐ

	16n216n2
Поскольку (4n) 2 = 16n2, (4n) 2 = 16n2.	(4н) 2 (4н) 2
Так как индекс nn четный ann = \| a \| .ann = \| a \|.	4 \| n \| 4 \| n \|

Ⓑ

−81c2−81c2

Поскольку (9c) 2 = 81c2.(9c) 2 = 81c2.	— (9c) 2- (9c) 2
Так как индекс nn четный ann = \| a \| .ann = \| a \|.	−9 \| c \| −9 \| c \|

Попробуйте 8.19

Упростить: ⓐ 64x264x2 ⓑ −100p2. − 100p2.

Попробовать 8.20

Упростить: ⓐ 169y2169y2 ⓑ −121y2. − 121y2.

Этот пример просто развивает идею, поскольку он имеет корни с более высоким индексом.

Пример 8.11

Упростить: ⓐ 64p6364p63 ⓑ 16q124.16q124.

Решение

ⓐ

64p6364p63

Записать 64p664p6 как (4p2) 3. (4p2) 3.	(4п2) 33 (4п2) 33
Возьмите кубический корень.	4п24п2

Ⓑ

	16q12416q124
Записываем подкоренное выражение в четвертой степени.	(2q3) 44 (2q3) 44
Извлечь корень четвертой степени.	2 \| q3 \| 2 \| q3 \|

Попробуйте 8.21

Упростить: ⓐ 27x27327x273 ⓑ 81q284.81q284.

Попробовать 8.22

Упростить: ⓐ 125q

q93 ⓑ 243q255.243q255.

В следующих примерах есть две переменные.

Пример 8.12

Упростить: ⓐ 36x2y236x2y2 ⓑ 121a6b8121a6b8 ⓒ 64p63q93.64p63q93.

Решение

ⓐ

	36x2y236x2y2
Поскольку (6xy) 2 = 36x2y2 (6xy) 2 = 36x2y2	(6xy) 2 (6xy) 2
Извлеките квадратный корень.	6 \| xy \| 6 \| xy \|

Ⓑ

	121a6b8121a6b8
Поскольку (11a3b4) 2 = 121a6b8 (11a3b4) 2 = 121a6b8	(11a3b4) 2 (11a3b4) 2
Извлеките квадратный корень.	11 \| a3 \| b411 \| a3 \| b4

Ⓒ

64p63q9364p63q93

Поскольку (4p21q3) 3 = 64p63q9 (4p21q3) 3 = 64p63q9	(4п21q3) 33 (4п21q3) 33
Возьмите кубический корень.	4p21q34p21q3

Попробовать 8.23

Упростить: ⓐ 100a2b2100a2b2 ⓑ 144p12q20144p12q20 ⓒ 8x30y1238x30y123

Попробуйте 8,24

Упростить: ⓐ 225m2n2225m2n2 ⓑ 169x10y14169x10y14 ⓒ 27w36z15327w36z153

Раздел 8.1 Упражнения

Практика ведет к совершенству

Упростить выражения с помощью корней

В следующих упражнениях упростите.

ⓐ 169169 ⓑ −100−100

ⓐ 144144 ⓑ −121−121

ⓐ 4949 ⓑ −0,01−0,01

ⓐ 6412164121 ⓑ −0,16−0,16

ⓐ −121−121 ⓑ −289−289

ⓐ −400−400 ⓑ −36−36

ⓐ −225−225 ⓑ −9−9

10.

ⓐ −49−49 ⓑ −256−256

11.

21632163 25642564

12.

273273 164164 24352435

13.

51235123 ⓑ 814814 ⓒ 1515

14.

12531253 ⓑ 1296412964 10 1024510245

15.

ⓐ −83−83 ⓑ −814−814 ⓒ −325−325

16.

ⓐ −643−643 ⓑ −164−164 ⓒ −2435−2435

17.

ⓐ −1253−1253 ⓑ −12964−12964 ⓒ −10245−10245

18.

ⓐ −5123−5123 ⓑ −814−814 ⓒ −15−15

Оценка и приблизительные корни

В следующих упражнениях оцените каждый корень между двумя последовательными целыми числами.

В следующих упражнениях округлите каждый корень до двух десятичных знаков.

23.

ⓐ 1919 ⓑ 893893 974974

24.

25.

26.

4747 ⓑ 16331633 52745274

Упростить выражения переменных с помощью корней

В следующих упражнениях упростите использование абсолютных значений по мере необходимости.

36.

ⓐ a105a105 ⓑ b273b273

38.

ⓐ r126r126 ⓑ s303s303

39.

ⓐ 49x249x2 ⓑ −81×18−81×18

40.

ⓐ 100y2100y2 ⓑ −100m32−100m32

41.

ⓐ 121m20121m20 ⓑ −64a2−64a2

42.

ⓐ 81x3681x36 ⓑ −25×2−25×2

43.

ⓐ 16x8416x84 ⓑ 64y12664y126

44.

ⓐ −8c93−8c93 ⓑ 125d153125d153

45.

216a63216a63 ⓑ 32b20532b205

46.

ⓐ 128r147128r147 ⓑ 81s24481s244

47.

48.

49.

50.

Письменные упражнения

51.

Почему нет действительного числа, равного -64? -64?

52.

В чем разница между 9292 и 9? 9?

53.

Объясните, что означает корень числа n ^th .

54.

Объясните разницу в нахождении корня n ^-го из числа, когда индекс четный, по сравнению с тем, когда индекс нечетный.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

ⓑ Если бы большинство ваших чеков было:

… уверенно. Поздравляем! Вы достигли целей в этом разделе. Поразмышляйте над своими учебными навыками, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы убедиться в своей способности делать эти вещи? Быть конкретным.

… с некоторой помощью. Эту проблему нужно решать быстро, потому что темы, которые вы не освоили, становятся ухабами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе.Прежде чем двигаться дальше, важно убедиться, что у вас есть прочный фундамент. К кому вы можете обратиться за помощью? Ваши одноклассники и инструктор — хорошие помощники. Есть ли в кампусе место, где доступны репетиторы по математике? Можно ли улучшить свои учебные навыки?

… нет, не понимаю! Это предупреждающий знак, игнорировать его нельзя. Вам следует немедленно обратиться за помощью, иначе вы быстро не справитесь. Как можно скорее обратитесь к своему инструктору, чтобы обсудить вашу ситуацию. Вместе вы сможете составить план оказания вам необходимой помощи.

Упрощение радикальных выражений — ChiliMath

Радикальное выражение состоит из трех частей:

радикальный символ , подкоренный символ и индекс

В этом руководстве основное внимание уделяется упрощению радикальных выражений с индексом 2. Этот тип радикала обычно известен как квадратный корень.

Компоненты радикального выражения

Начав с одного радикального выражения, мы хотим разбить его на части «меньших» радикальных выражений.Мы надеемся, что некоторые из этих фигур можно еще больше упростить, потому что подкоренные выражения (элементы внутри символа) представляют собой идеальные квадраты. Помните, что квадратный корень из полных квадратов получается очень хорошо!

Нам нужно понять, как может выглядеть идеальное квадратное число или выражение. {16}}

Что делает их идеальными квадратами?

Обратите внимание, что квадратный корень из каждого числа выше дает целочисленный ответ.Думайте о них как о числах с идеальным поведением.

Кроме того, эти числа представляют собой точные квадраты, потому что все они могут быть выражены как экспоненциальные числа с четной степенью. Степень не обязательно должна быть постоянно равной «2». Пока степени являются четными числами, такими как 2, 4, 6, 8 и т. Д., Они считаются полными квадратами. С одной стороны, пара любых чисел — это идеальный квадрат!

Более того, приведенные выше выражения переменных также являются точными квадратами, потому что все переменные имеют четные показатели или степени.

Примеры упрощения радикальных выражений

Пример 1: Упростите радикальное выражение \ sqrt {16}.

Это легкий! Число 16, очевидно, является точным квадратом, потому что я могу найти целое число, которое при умножении само на себя дает целевое число. Должно быть 4, так как (4) (4) = 4 ² = 16. Таким образом, ответ будет

Ниже приведен снимок экрана с ответом калькулятора, который подтверждает наш ответ.

Пример 2: Упростите радикальное выражение \ sqrt {60}.

Вы можете методом проб и ошибок найти число, когда возведение в квадрат дает 60. Перебирая некоторые квадраты натуральных чисел…

Ответом должно быть некоторое число n , которое находится между 7 и 8. Таким образом, мы ожидаем, что квадратный корень из 60 должен содержать десятичные значения. Чтобы упростить это радикальное число, попробуйте разложить его на множители так, чтобы один из множителей был точным квадратом. При беглом осмотре число 4 представляет собой идеальный квадрат, на который можно разделить 60.

Итак, наш ответ…

А для нашего калькулятора проверьте…

Какое правило я использовал, чтобы разбить их как произведение квадратных корней? Вот!

Запомните приведенное ниже правило, поскольку вы будете использовать его снова и снова.

ПРОДУКТ ПРАВИЛО КВАДРАТНЫХ КОРНЕЙ

Это означает, что квадратный корень из произведения a и b равен произведению их индивидуальных квадратных корней.

Пример 3: Упростите радикальное выражение \ sqrt {72}.

Всегда ищите точный квадрат подкоренного выражения. После проб и ошибок я обнаружил, что любой из идеальных квадратов 4, 9 и 36 может разделить 72.Итак, что мне выбрать? На самом деле должен работать любой из трех коэффициентов точного квадрата. Однако лучший вариант — это максимально возможный, потому что это значительно сокращает количество шагов в решении.

Сравните, что произойдет, если я упросту радикальное выражение, используя каждый из трех возможных абсолютных квадратов. Выбор самого большого делает решение очень коротким и точным.

Ничего страшного, если вы когда-нибудь начнете с меньших коэффициентов точного квадрата. Вам просто нужно убедиться, что вы еще больше упростили оставшееся подкоренное выражение (содержимое внутри радикального символа).Повторяйте процесс до тех пор, пока подкоренное выражение не перестанет иметь точный квадратный множитель.

Похоже, калькулятор согласен с нашим ответом. Большой!

Пример 4: Упростите радикальное выражение \ sqrt {48}.

Другой способ решить эту проблему — выполнить разложение на простые множители для подкоренного выражения. Затем выразите простые числа как можно точнее. Парные простые числа выйдут из символа квадратного корня, а простое простое число останется внутри.

И он проверяет, когда решается в калькуляторе.

Пример 5: Упростите радикальное выражение \ sqrt {200}.

Давайте найдем квадратный множитель подкоренного выражения. Хотя 25 может делить 200, наибольшее число равно 100. Затем выразите подкоренное выражение как произведение квадратных корней и упростите. 4}}.

Подкоренное выражение содержит как числа, так и переменные. Разберемся с ними отдельно.

Для числового члена 12 его наибольший коэффициент полного квадрата равен 4. Теперь что касается переменных, мне нужно разбить их на пары, поскольку квадратный корень любой парной переменной — это просто сама переменная. Решение этой проблемы должно выглядеть примерно так…

Стандартный способ записать окончательный ответ — поместить все термины (как числа, так и переменные), которые находятся за пределами радикального символа , перед терминами, остающимися внутри.7}}.

Для этой проблемы мы собираемся решить ее двумя способами. Цель состоит в том, чтобы показать, что есть более простой способ приблизиться к этому, особенно когда показатели переменных становятся больше.

Метод сопряжения : Это обычный способ, при котором мы группируем переменные в две, а затем применяем операцию извлечения квадратного корня, чтобы вывести переменную за пределы радикального символа. Вы увидите, что для больших мощностей этот метод может быть утомительным и трудоемким.

«Разделение четных степеней» Метод : Вы не можете найти это имя ни в одном учебнике алгебры, потому что я его придумал.Однако ключевая концепция есть. Основной подход состоит в том, чтобы выразить каждую переменную как произведение членов с четными и нечетными показателями. Если термин уже имеет равную силу, вам нечего делать. В противном случае вам нужно выразить это как некоторую четную степень плюс 1 .

Помните, что получение квадратного корня из «чего-то» эквивалентно возведению этого «чего-то» в дробную степень {1 \ более 2}.

Проще говоря, разделите показатель этого «чего-то» на 2.

Вот почему мы хотим выразить их с четной степенью, поскольку любое четное число делится на 2 .{13}}}.
Практика с рабочими листами
Вас может заинтересовать:
Решение радикальных уравнений
Сложение и вычитание радикальных выражений
Умножение радикальных выражений
Рационализация знаменателя
Упростите радикальные выражения | Промежуточная алгебра
Результаты обучения
- Упростите радикальные выражения с помощью факторизации
- Упростите радикальные выражения, используя рациональные показатели и законы показателей
- Определите [латекс] \ sqrt {x ^ 2} = | x | [/ latex] и примените его при упрощении радикальных выражений
Радикальные выражения — это выражения, содержащие радикалы.{\ frac {1} {2}}} [/ латекс]
И поскольку вы знаете, что возведение числа в степень [latex] \ frac {1} {2} [/ latex] — это то же самое, что извлечение квадратного корня из этого числа, вы также можете записать это так.
[латекс] \ sqrt {3x} = \ sqrt {3} \ cdot \ sqrt {x} [/ латекс]
Посмотрите на это — вы можете думать о любом числе под радикалом как о произведении отдельных множителей , каждый под собственным радикалом.
Продукт, возведенный в правило степени или иногда называемый квадратным корнем правила продукта
Для любых действительных чисел a и b , [латекс] \ sqrt {ab} = \ sqrt {a} \ cdot \ sqrt {b} [/ latex].{2}}} [/ латекс].
Квадратный корень из правила произведения поможет нам упростить корни, которые не идеальны, как показано в следующем примере.
Пример
Упростить. [латекс] \ sqrt {63} [/ латекс]
Показать решение
[latex] 63 [/ latex] не является точным квадратом, поэтому мы можем использовать квадратный корень из правила произведения, чтобы упростить любые множители, которые являются точными квадратами. 2 [/ latex], поэтому мы можем переписать подкоренное выражение.{2} [/ латекс].
[latex] \ sqrt {7} \ cdot 3 [/ latex]
Поменяйте местами множители так, чтобы целое число стояло перед корнем, а затем умножьте. Это сделано для того, чтобы было ясно, что под радикалом находится только [латекс] 7 [/ латекс], а не [латекс] 3 [/ латекс].
[латекс] 3 \ cdot \ sqrt {7} [/ latex]
Ответ [латекс] 3 \ sqrt {7} [/ latex].
Окончательный ответ [latex] 3 \ sqrt {7} [/ latex] может выглядеть немного странно, но в упрощенной форме. Вы можете прочитать это как «три корня из семи» или «три раза больше квадратного корня из семи».{2}} [/ латекс] [латекс] \ слева | x \ справа | [/ латекс] [латекс] -5 [/ латекс] [латекс] 25 [/ латекс] [латекс] 5 [/ латекс] [латекс] 5 [/ латекс] [латекс] -2 [/ латекс] [латекс] 4 [/ латекс] [латекс] 2 [/ латекс] [латекс] 2 [/ латекс] [латекс] 0 [/ латекс] [латекс] 0 [/ латекс] [латекс] 0 [/ латекс] [латекс] 0 [/ латекс] [латекс] 6 [/ латекс] [латекс] 36 [/ латекс] [латекс] 6 [/ латекс] [латекс] 6 [/ латекс] [латекс] 10 [/ латекс] [латекс] 100 [/ латекс] [латекс] 10 [/ латекс] [латекс] 10 [/ латекс]
Примечание — в случаях, когда x является отрицательным числом, [latex] \ sqrt {x ^ {2}} \ neq {x} [/ latex]! Однако во всех случаях [латекс] \ sqrt {x ^ {2}} = \ left | x \ right | [/ latex].2 [/ latex] всегда будет неотрицательным. Один совет, чтобы знать, когда применять абсолютное значение после упрощения любого даже индексированного корня, — это посмотреть на конечный показатель степени в ваших переменных условиях. Если показатель нечетный, включая [латекс] 1 [/ латекс], добавьте абсолютное значение. Это относится к упрощению любого корня с помощью четного индекса, как мы увидим в следующих примерах.
В следующем видео вы увидите больше примеров того, как упрощать радикальные выражения с помощью переменных.

Мы покажем другой пример, где упрощенное выражение содержит переменные как с нечетной, так и с четной степенью.{4}} [/ латекс]
Упростите корни куба
Мы можем использовать те же методы, которые мы использовали для упрощения квадратных корней, чтобы упростить корни более высокого порядка. Например, чтобы упростить кубический корень, цель состоит в том, чтобы найти множители под радикалом, которые являются идеальными кубами, чтобы вы могли извлечь их кубический корень. Нам больше не нужно беспокоиться о том, идентифицировали ли мы главный корень, поскольку теперь мы находим кубические корни. По мере упрощения сосредоточьтесь на поиске одинаковых трех факторов.
Пример
Упростить.{2}}} [/ латекс]
В следующем видео мы покажем больше примеров упрощения кубических корней.

Упрощение четвертых корней
Теперь перейдем к упрощению корней четвертой степени. Независимо от того, какой корень вы упрощаете, применяется одна и та же идея: найти кубы для кубических корней, степени четырех для корней четвертой степени и т. Д. Вспомните, что когда ваше упрощенное выражение содержит четный индексированный радикал и переменный множитель с нечетной степенью, вам нужно применить абсолютное значение.{2}}} [/ латекс]
Ну, это заняло время, но вы сделали это. Вы применили то, что знаете о дробных показателях, отрицательных показателях и правилах экспонент, чтобы упростить выражение.
В нашем последнем видео мы показываем, как использовать рациональные показатели для упрощения радикальных выражений.

Сводка
Радикальное выражение — это математический способ представления корня n -й степени числа. Квадратные корни и кубические корни являются наиболее распространенными радикалами, но корень может быть любым числом.{n}}} = \ left | х \ право | [/ латекс]. (Абсолютное значение учитывает тот факт, что если x отрицательно и возведено в четную степень, это число будет положительным, как и главный корень n -го числа этого числа.)

Упрощение выражений с квадратными корнями

Результаты обучения

Упростите выражения с квадратными корнями, используя порядок операций
Упростите выражения с квадратными корнями, которые содержат переменные

Квадратные корни и порядок операций

При использовании порядка операций для упрощения выражения, имеющего квадратные корни, мы рассматриваем знак корня как символ группировки.Перед выполнением других операций мы упрощаем любые выражения под знаком радикала.

, пример

Упростите: ⓐ [латекс] \ sqrt {25} + \ sqrt {144} [/ latex] ⓑ [латекс] \ sqrt {25 + 144} [/ latex].

Решение

ⓐ Используйте порядок операций.
[латекс] \ sqrt {25} + \ sqrt {144} [/ латекс]
Упростите каждый радикал.	[латекс] 5 + 12 [/ латекс]
Доп.	[латекс] 17 [/ латекс]

ⓑ Используйте порядок операций.
[латекс] \ sqrt {25 + 144} [/ латекс]
Добавить под знаком корня.	[латекс] \ sqrt {169} [/ латекс]
Упростить.	[латекс] 13 [/ латекс]

Обратите внимание на разные ответы в частях ⓐ и ⓑ приведенного выше примера. Важно правильно соблюдать порядок действий. В ⓐ мы сначала взяли каждый квадратный корень, а затем сложили его. В ⓑ мы сначала добавили под знаком корня, а затем нашли квадратный корень.{2} [/ латекс] [латекс] 6xy [/ латекс]

Упростите радикальные, рациональные выражения с помощью программы «Пошаговое решение математических задач»

В разделе 3 главы 1 есть несколько очень важных определений, которые мы использовали много раз. Поскольку эти определения приобретают новое значение в этой главе, мы повторим их.

Когда алгебраическое выражение состоит из частей, соединенных знаками + или -, эти части вместе с их знаками называются членами выражения.

a + b состоит из двух членов.
2x + 5y — 3 состоит из трех членов.

В a + b термины a и b. В 2x + 5y — 3 термины 2x, 5y и -3.

Когда алгебраическое выражение состоит из частей, которые нужно умножить, эти части называются коэффициентами выражения.

ab имеет факторы a и b.

Очень важно уметь различать термины и факторы. Правила, применяемые к условиям, в целом не применяются к факторам.Называя термины или факторы, необходимо учитывать все выражение.

С этого момента во всей алгебре вы будете использовать слова , термин и фактор , . Убедитесь, что вы понимаете определения.

Показатель — это число, которое указывает, сколько раз коэффициент должен использоваться в продукте. Показатель степени обычно записывается как меньшее (по размеру) число немного выше и правее множителя, на который влияет показатель степени.

Показатель степени иногда называют «степенью». Например, 5 ³ можно обозначить как «пятерка в третьей степени».

Обратите внимание на разницу между 2x ³ и (2x) ³. Используя круглые скобки в качестве группирующих символов, мы видим, что

2x ³ означает 2 (x) (x) (x), тогда как (2x) ³ означает (2x) (2x) (2x) или 8x ³.

Если не используются скобки, показатель степени влияет только на множитель, непосредственно предшествующий ему.

В таком выражении, как 5x ⁴
5 — коэффициент ,
x — основание ,
4 — показатель степени .
5x ⁴ означает 5 (x) (x) (x) (x).

Обратите внимание, что экспонента влияет только на основание.

Многие студенты совершают ошибку, умножая основание на показатель степени. Например, они скажут 3 ⁴ = 12 вместо правильного ответа,
3 ⁴ = (3) (3) (3) ( 3) = 81.

Когда мы пишем буквальное число, такое как x, будет понятно, что коэффициент равен единице, а показатель степени равен единице. Это может быть очень важно во многих операциях.

x означает 1x ¹.

Также понятно, что письменная цифра, такая как 3, имеет показатель степени 1. Мы просто не утруждаемся записывать показатель степени 1.

ЗАКОН УМНОЖЕНИЯ ЭКСПОНЕНТОВ

ЗАДАЧИ

По завершении этого раздела вы сможете правильно применить первый закон экспонент.

Теперь, когда мы рассмотрели эти определения, мы хотим установить очень важные законы экспонент. Эти законы вытекают непосредственно из определений.

Первый закон экспонент Если a и b — натуральные числа, а x — действительное число, то

Чтобы умножить множители с одинаковым основанием, сложите экспоненты.

В отношении любого правила, закона или формулы мы всегда должны быть очень осторожны, чтобы выполнить требуемые условия, прежде чем пытаться применить их.Обратите внимание, что в приведенном выше законе база одинакова для обоих факторов. Этот закон применяется только при соблюдении этого условия.

Эти факторы не имеют одинакового основания.

Показатель 1 обычно не записывается. Когда мы пишем x, предполагается экспонента: x = x1. Это необходимо для применения законов экспонент.

Если выражение содержит результат различных оснований, мы применяем закон к одинаковым основаниям.

УМНОЖЕНИЕ МОНОМОВ

ЗАДАЧИ

По завершении этого раздела вы сможете:

Распознать моном.
Найдите произведение нескольких одночленов.

Моном — это алгебраическое выражение, в котором буквальные числа связаны только операцией умножения.

не является мономом, поскольку задействована операция сложения.

предполагает операцию разделения.

Чтобы найти произведение двух одночленов , умножьте числовые коэффициенты и примените первый закон экспонент к буквальным множителям.

Вы помните первый закон экспонентов?

Умножьте 5 на 3 и сложите показатели x.
Помните, что если показатель не записан, подразумевается показатель, равный единице.

МОНОМИЛЫ, УМНОЖЕННЫЕ НА ПОЛИНОМИКИ

ЗАДАЧИ

По завершении этого раздела вы сможете:

Распознавать многочлены.
Определение биномов и трехчленов.
Найдите произведение одночлена на двучлен.

Многочлен — это сумма или разность одного или нескольких одночленов.

Обычно, если существует более одной переменной, многочлен записывается в алфавитном порядке.

Для некоторых многочленов используются специальные имена. Если полином состоит из двух членов, он называется биномом .

Если многочлен состоит из трех членов, он называется трехчленом .

В процессе удаления скобок мы уже отметили, что на все термины в скобках влияет знак или число, стоящее перед скобками. Теперь мы расширим эту идею, чтобы умножить одночлен на многочлен.

Размещение 2x непосредственно перед скобками означает умножение выражения в скобках на 2x. Обратите внимание, что каждый член умножается в 2 раза.

Опять же, каждый член в скобках умножается на 3y ²

И снова каждый член в круглых скобках умножается на 3y ².
В каждом из этих примеров мы используем распределительное свойство .

ПОЛИНОМИЧЕСКИЕ ТОВАРЫ

ЗАДАЧИ

По завершении этого раздела вы сможете:

Найдите произведение двух биномов.
Используйте свойство распределения, чтобы умножить любые два полинома.

В предыдущем разделе вы узнали, что произведение A (2x + y) расширяется до A (2x) + A (y).

Теперь рассмотрим произведение (3x + z) (2x + y).

Поскольку (3x + z) находится в круглых скобках, мы можем рассматривать его как единственный множитель и расширять (3x + z) (2x + y) так же, как A (2x + y).Это дает нам

Если мы теперь расширим каждый из этих терминов, у нас будет

Обратите внимание, что в окончательном ответе каждый член одной круглой скобки умножается на каждый член других скобок.

Обратите внимание, что это приложение свойства распределения.

Поскольку — 8x и 15x — похожие термины, мы можем объединить их, чтобы получить 7x.

В этом примере мы смогли объединить два термина, чтобы упростить окончательный ответ.

Здесь мы снова объединили некоторые термины, чтобы упростить окончательный ответ. Обратите внимание, что порядок терминов в окончательном ответе не влияет на правильность решения.

Свойство коммутативности позволяет изменять порядок.

Попытайтесь создать систему для умножения каждого члена одной круглой скобки на каждый член другой.В этих примерах мы взяли первый член в первом наборе круглых скобок и умножили его на каждый член во втором наборе круглых скобок. Затем мы взяли второй член первого набора и умножили его на каждый член второго набора, и так далее.

ПОЛНОМОЧИЯ И КВАДРАТНЫЕ КОРНИ

ЗАДАЧИ

По завершении этого раздела вы сможете:

Правильно применяйте второй закон экспонент.
Найдите квадратные корни и главные квадратные корни чисел, являющихся точными квадратами.

Теперь мы хотим установить второй закон экспонент. Обратите внимание на следующие примеры, как этот закон выводится с использованием определения показателя степени и первого закона экспоненты.

по значению показателя 3.

Теперь по первому закону экспонент имеем

В целом отметим, что

Это означает, что ответ будет

Помните, чтобы умножить общее основание, добавьте экспоненты.

Если мы просуммируем член a b раз, мы получим произведение a и b. Отсюда мы видим, что

Второй закон экспонент Если a и b — натуральные числа, а x — действительное число, то
.

Другими словами, «чтобы возвести степень основания x в степень, умножьте степень».

Обратите внимание, что каждый показатель должен быть умножен на 4.

Обратите внимание, что когда факторы сгруппированы в скобках, на каждый фактор влияет показатель степени.

Опять же, каждый множитель должен быть возведен в третью степень.

Используя определение показателей, (5) ² = 25. Мы говорим, что 25 — это квадрат 5. Теперь мы вводим новый термин в наш алгебраический язык. Если 25 равно квадрату 5, то говорят, что 5 является квадратным корнем из 25.

Если x ² = y, то x представляет собой квадратный корень из y.

Обратите внимание, мы говорим, что 5 — это квадратный корень , а не квадратный корень .Вы скоро поймете, почему.

Из последних двух примеров вы заметите, что 49 имеет два квадратных корня, 7 и — 7. Это правда, что на самом деле каждое положительное число имеет два квадратных корня.

Фактически, один квадратный корень положительный, а другой отрицательный.

Каковы квадратные корни из 36?

Главный квадратный корень положительного числа является положительным квадратным корнем.

Символ «» называется радикальным знаком и обозначает основную часть

обозначает главный квадратный корень или положительный квадратный корень из 9.

Обратите внимание на разницу в этих двух задачах.

а. Найдите квадратные корни из 25.
b. Находить .

Очень важно понимать разницу между этими двумя утверждениями.

Для а. ответ будет +5 и -5, поскольку (+ 5) ² = 25 и (- 5) ² = 25.
Для б. ответ будет +5, поскольку знак корня представляет собой главный или положительный квадратный корень.
Целые числа, такие как 16, 25, 36 и т. Д., Квадратные корни которых являются целыми числами, называются полными квадратными числами . В настоящее время нас интересуют только квадратные корни из полных квадратных чисел. В следующей главе мы будем иметь дело с оценкой и упрощением указанного квадратного корня из чисел, которые не являются точными квадратными числами.

Иногда вы можете увидеть символ +/-.Это означает, что требуются оба квадратных корня из числа. Например,

+/- 5 — это краткое обозначение + 5 и -5.

ЗАКОН ПОДРАЗДЕЛЕНИЯ ЭКСПОНЕНТОВ

ЗАДАЧИ

По завершении этого раздела вы сможете правильно применить третий закон экспонент.

Прежде чем приступить к установлению третьего закона экспонент, мы сначала рассмотрим некоторые факты о действии деления.

Разделение двух чисел можно обозначить знаком деления или написанием одного числа поверх другого с полосой между ними.Шесть, разделенная на два, записывается как

Деление связано с умножением по правилу, если тогда a = be. Это проверка для всех проблем с разделением. Например, мы знаем это, потому что 18 = (6) (3).
Деление на ноль невозможно. Для оценки нам необходимо найти число, которое при умножении на ноль даст 5. Такого числа не существует.
Ненулевое число, разделенное на себя, равно 1.

. Умножьте значения в кружках, чтобы получить.
Это очень важно! Если a — любое ненулевое число, оно не имеет значения.

Из (3) мы видим, что выражение, подобное как, не имеет смысла, если мы не знаем, что y In 0. В этом и будущих разделах всякий раз, когда мы пишем дробь, будет предполагаться, что знаменатель не равен нулю. Теперь, чтобы установить закон деления показателей, воспользуемся определением показателей.

Важно! Прочтите этот абзац еще раз!

Мы знаем, что = 1.Мы также предполагаем, что x представляет собой ненулевое число.

В таком примере нам не нужно разделять количества, если мы помним, что количество, разделенное само на себя, равно единице. В приведенном выше примере мы могли бы написать

Три x в знаменателе делят три x в числителе.

Помните, что 1 должна быть записана, если это единственный член в числителе.

Из предыдущих примеров мы можем обобщить и прийти к следующему закону:

Третий закон экспонент Если a и b — натуральные числа, а x — ненулевое действительное число, то

Если мы попытаемся использовать только ту часть закона, которая указывает на такое выражение, как, например, мы получим
На данный момент отрицательные показатели не определены.Мы обсудим их позже.

РАЗДЕЛЕНИЕ МОНОМИАЛА НА МОНОМИАЛ

ЗАДАЧИ

По завершении этого раздела вы сможете упростить выражение, уменьшив дробь, включающую коэффициенты, а также используя третий закон экспонент.

Мы должны помнить, что коэффициенты и показатели управляются разными законами, потому что они имеют разные определения. При делении одночленов коэффициенты делятся, а показатели вычитаются согласно закону деления показателей.

Если деление невозможно или если с помощью коэффициентов возможно только уменьшение дроби, это не влияет на использование закона экспонент для деления.

Уменьшите этот тип дроби в два этапа:
1. Уменьшите коэффициенты.
2. Используйте третий закон экспонент.

РАЗДЕЛЕНИЕ ПОЛИНОМА НА МОНОМИАЛ

ЗАДАЧИ

По завершении этого раздела вы сможете разделить многочлен на одночлен.

Разделение многочлена на одночлен включает в себя еще один очень важный факт в дополнение к тому, что мы уже использовали. Дело в том, что если в числителе дроби несколько членов, то каждый член нужно разделить на знаменатель.

Таким образом, мы фактически используем в этом процессе свойство дистрибуции.

РАЗДЕЛЕНИЕ ПОЛИНОМА НА БИНОМИЧЕСТВО

ЗАДАЧИ

По завершении этого раздела вы сможете правильно применить алгоритм деления в столбик для деления полинома на бином.

Процесс деления многочлена на другой многочлен будет ценным инструментом в последующих разделах. Здесь мы разработаем методику и обсудим причины, по которым она работает в будущем.

Этот метод называется алгоритмом деления в столбик . Алгоритм — это просто метод, которому необходимо точно следовать. Поэтому представим его в пошаговом формате и на примере.

Вспомните три выражения в разделе:

Если нас попросят расположить выражение в порядке убывания, мы напишем.Нулевой коэффициент дает 0x ³ = 0. По этой причине член x ³ отсутствовал или не был записан в исходном выражении.

Решение

Шаг 1: Расположите как делитель, так и делимое в порядке убывания переменной (это означает, что сначала наивысший показатель степени, затем следующий наивысший второй и т. Д.) И укажите нулевой коэффициент для любых пропущенных членов. (В этом примере нет необходимости менять расположение и отсутствуют пропущенные термины.) Затем расположите делитель и делимое следующим образом:

Шаг 2: Чтобы получить первый член частного, в данном случае разделите первый член делимого на первый член делителя. Мы записываем это следующим образом:

Шаг 3: Умножьте весь делитель на член, полученный на шаге 2. Вычтите результат из делимого следующим образом:

Убедитесь, что вы указываете частное непосредственно над количеством, на которое делите.В этом случае x делится на x ² x раз.

Шаг 4: Разделите первый член остатка на первый член делителя, чтобы получить следующий член частного. Затем умножьте весь делитель на полученный член и снова вычтите следующим образом:

Первый член остатка (-2x — 14) равен -2x.
Умножьте (x + 7) на -2.

Этот процесс повторяется до тех пор, пока остаток не станет равен нулю (как в этом примере) или степень первого члена остатка не станет меньше степени первого члена делителя.

Как и в арифметике, деление проверяется умножением. Мы должны помнить, что (частное) X (делитель) + (остаток) = (делимое).

Чтобы проверить этот пример, мы умножаем (x + 7) и (x — 2), чтобы получить x ² + 5x — 14.

Так как это дивиденд, ответ правильный.

Опять же, (частное) X (делитель) + (остаток) = (делимое)

Ответ: x — 3. Проверяя, находим (x + 3) (x — 3)

Распространенная ошибка — забыть написать пропущенный член с нулевым коэффициентом.

РЕЗЮМЕ

Ключевые слова

Моном — это алгебраическое выражение, в котором буквальные числа связаны только операцией умножения.
Многочлен — это сумма или разность одного или нескольких одночленов.
Бином — это многочлен, состоящий из двух членов.
Трехчлен — это многочлен, состоящий из трех членов.
Если x ² = y, то x представляет собой квадратный корень из y.
Главный квадратный корень положительного числа является положительным квадратным корнем.
Этот символ называется радикальным знаком и указывает на главный квадратный корень из числа.
Полноквадратное число имеет целые числа в качестве квадратных корней.

Процедуры

Первый закон экспонент: x ^a x ^b = x ^{a + b}.
Чтобы найти произведение двух одночленов, умножьте числовые коэффициенты и примените первый закон экспонент к буквальным множителям.
Чтобы умножить многочлен на другой многочлен, умножьте каждый член одного многочлена на каждый член другого и объедините одинаковые члены.
Второй закон экспонент (x ^a) ^b = x ^ab.
Третий закон экспонент:
Чтобы разделить одночлен на одночлен, разделите числовые коэффициенты и используйте третий закон экспонент для буквальных чисел.
Чтобы разделить многочлен на одночлен, разделите каждый член многочлена на одночлен.{\ frac {1} {2}} $$
Если мы объединим эти две вещи, мы получим свойство произведения радикалов и факторное свойство радикалов. Эти два свойства говорят нам, что квадратный корень из произведения равен произведению квадратных корней из множителей.
$$ \ sqrt {xy} = \ sqrt {x} \ cdot \ sqrt {y} $$
$$ \ sqrt {\ frac {x} {y}} = \ frac {\ sqrt {x}} {\ sqrt {y}} $$
$$ где \: \: x \ geq 0, y \ geq 0 $$
Ответ не может быть отрицательным, а x и y не могут быть отрицательными, так как в этом случае мы не получим реального ответа.{2}}} = \ frac {\ sqrt {xy}} {y} $$
Биномы как
$$ x \ sqrt {y} + z \ sqrt {w} \: \: и \: \: x \ sqrt {y} -z \ sqrt {w} $$
называются конъюгатами друг с другом. Произведение двух конъюгатов всегда является рациональным числом, что означает, что вы можете использовать конъюгаты для рационализации знаменателя, например.
$$ \ frac {x} {4+ \ sqrt {x}} = \ frac {x \ left ({\ color {green} {4- \ sqrt {x}}} \ right)} {\ left (4 + \ sqrt {x} \ right) \ left ({\ color {green} {4- \ sqrt {x}}} \ right)} = $$
$$ = \ frac {x \ left (4- \ sqrt {x} \ right)} {16- \ left (\ sqrt {x} \ right) ^ {2}} = \ frac {4x-x \ sqrt {x}} {16-x} $$
Видеоурок
Упростить радикальное выражение
$$ \ frac {x} {5- \ sqrt {x}} $$

Упрощение радикальных выражений
Мы знаем, что квадратный корень не является действительным числом, когда подкоренное выражение x отрицательно.Следовательно, мы заключаем, что область состоит из всех действительных чисел, больших или равных 0. Здесь мы выбираем 0 и некоторые положительные значения для x , вычисляем соответствующие значения y и строим полученные упорядоченные пары.
После нанесения точек мы можем нарисовать график функции квадратного корня.
Пример 11: Для функции f (x) = x + 2 найдите f (−2), f (2) и f (6).
Решение: Замените x каждым из указанных значений.
Поскольку корень куба может быть как отрицательным, так и положительным, мы заключаем, что область состоит из всех действительных чисел. Для полноты выберите несколько положительных и отрицательных значений для x , а также 0, а затем вычислите соответствующие значения y .
Постройте точки и нарисуйте график функции кубического корня.
Пример 12: Для функции g (x) = x − 13 найдите g (−7), g (0) и g (55).
Решение: Замените x каждым из указанных значений.
Тематические упражнения
Часть A: Упрощение радикальных выражений
Упростить. ( Предположим, что все переменные представляют собой положительные числа. )
1. 36a2
2. 121b2
3. x2y2
4. 25x2y2z2
5. 180×3
6. 150y3
7. 49a3b2
8.4a4b3c
9. 45x5y3
10. 50x6y4
11. 64р2с6т5
12. 144р8с6т2
13. (x + 1) 2
14. (2х + 3) 2
15. 4 (3x − 1) 2
16. 9 (2х + 3) 2
17. 9x325y2
18. 4x59y4
19. m736n4
20. 147м9н6
21. 2р2с525т4
22.36р5с2т6
23. 27a33
24. 125b33
25. 250x4y33
26. 162a3b53
27. 64x3y6z93
28. 216x12y33
29. 8x3y43
30. 27x5y33
31. a4b5c63
32. a7b5c33
33. 8x427y33
34. x5125y63
35. 360р5с12т133
36.540р3с2т93
37. 81×44
38. x4y44
39. 16x4y84
40. 81x12y44
41. a4b5c64
42. 54a6c84
43. 128×64
44. 243y74
45. 32м10н55
46. 37м9н105
47. −34×2
48. 79y2
49. −5x4x2y
50.−3y16x3y2
51. 12aba5b3
52. 6a2b9a7b2
53. 2x⋅8×63
54. −5×2⋅27×33
55. 2ab⋅ − 8a4b53
56. 5a2b⋅ − 27a3b33
Запишем следующее в виде радикального выражения с коэффициентом 1.
57. 52x
58. 23лет
59. 2×3
60. 3y2
61.ab10a
62. 2ab2a
63. m2nmn
64. 2м2н33н
65,5 2×3
66. 3 5y3
67. 2x⋅33
68. 3 года⋅23
Предположим, что переменная может представлять любое действительное число, а затем упростить.
69. 4х2
70. 25y2
71. 8y33
72.125a33
73. 64×44
74. 81y44
75. 36a4
76. 100a8
77. 4a6
78. a10
79. 18a4b5
80. 48a5b3
81. 128x6y86
82. a6b7c86
Часть B: Формулы, включающие радикалы
Перехваты y для любого графа будут иметь форму (0, y ), где y — действительное число.Следовательно, чтобы найти y -перехват, установите x = 0 и решите относительно y . Найдите перехватчики y для следующего.
83. у = х + 4−1
84. у = х + 1−3
85. у = х − 13 + 2
86. у = х + 13−3
Используйте формулу расстояния, чтобы вычислить расстояние между заданными двумя точками.
87.(5, −7) и (3, −8)
88. (−9, 7) и (−8, 4)
89. (−3, −4) и (3, −6)
90. (−5, −2) и (1, −6)
91. (-1, 1) и (-4, 10)
92. (8, −3) и (2, −12)
Разложите на множители подкоренное выражение и затем упростите. ( Предположим, что все выражения положительны. )
93. x2−6x + 9
94. x2−10x + 25
95.4×2 + 12x + 9
96. 9×2 + 6x + 1
97. Скорость транспортного средства до того, как были задействованы тормоза, можно оценить по длине следов заноса, оставленных на дороге. На сухом асфальте скорость v в милях в час можно оценить по формуле v = 5d, где d представляет собой длину следов заноса в футах. Оцените скорость транспортного средства перед тем, как задействовать тормоз на сухом асфальте, если оставленные следы заноса составляют 36 футов.
98.Радиус сферы, r , можно рассчитать по формуле r = 6π2V32π, где V представляет собой объем сферы. Каков радиус сферы, если ее объем составляет 36π кубических сантиметров?
Период маятника T в секундах определяется формулой
Т = 2πL32
, где L — длина в футах. Рассчитайте период, учитывая следующие значения длины.Укажите точное значение и округлите приблизительное значение с точностью до десятых долей секунды.
99,8 футов
100. 32 фута
101. 1/2 фута
102. 1/8 фута
Время, t , в секундах, в течение которого объект находится в свободном падении, определяется формулой
т = s4
, где s представляет собой расстояние в футах, на которое он упал.Рассчитайте время, за которое объект упадет, учитывая следующие расстояния. Укажите точное значение и округлите приблизительное значение с точностью до десятых долей секунды.
103. 48 футов
104. 80 футов
105,192 футов
106. 288 футов
Часть C: Радикальные функции
Для данной функции вычислите следующее.
107.f (x) = x − 1, найти f (1), f (2) и f (5)
108. f (x) = x + 5, найти f (−5), f (−1) и f (20)
109. f (x) = x + 3, найти f (0), f (1) и f (16)
110. f (x) = x − 5, найти f (0), f (1) и f (25)
111. g (x) = x3, найти g (−1), g (0) и g (1)
112. g (x) = x + 73, найти g (−15), g (−7) и g (20)
113. g (x) = x3−2, найти g (−1), g (0) и g (8)
114. g (x) = x − 13 + 2, найти g (0), g (2) и g (9)
Для каждой функции заполните таблицу.
115. f (x) = x + 1
116. f (x) = x − 2
117. f (x) = x3 + 1
118. f (x) = x + 23
Часть D: Обсуждение
119. Задайте для x такое значение, чтобы x2 ≠ x. Объясните, почему важно предполагать, что переменные представляют собой положительные числа.
120. Изучите и обсудите достижения Кристофа Рудольфа. За что ему приписывают?
121. Изучите и обсудите методы, используемые для вычисления квадратных корней, прежде чем электронные калькуляторы станут повсеместно использоваться.
122. Что такое surd и откуда взялось это слово?
.

Упрощение выражений, содержащих корни и степени

Упрощение выражения содержащего корень вида

Обобщение понятия степени и решение примеров со степенями

Урок 47. преобразование выражений — Алгебра и начала математического анализа — 11 класс

1 упростите выражение

Где можно решить любую задачу по математике, а так же 1 упростите выражение Онлайн?

С1 ГИА по математике — упрощение выражений, содержащих корни

Сложение ⚠️ корней, вычитание корней с одинаковыми и разными показателями

Сложение корней, формулы

Вычитание корней, формулы

Сложение корней со степенями

8.1 Упрощение выражений с помощью корней — промежуточная алгебра 2e

Задачи обучения

Упростите выражения с помощью корней

Квадратный и квадратный корень числа

Квадратный корень

Пример 8.1

Решение

Пример 8.2

Решение

Недвижимость анана

Пример 8.3

Решение

Пример 8.4

Решение

Оценка и приблизительные корни

Пример 8.5

Пример 8.6

Решение

Упростите выражения переменных с помощью корней

Упрощение четных и нечетных корней

Пример 8.7

Решение

Пример 8.8

Решение

Пример 8.9

Решение

Пример 8.10

Решение

Пример 8.11

Решение

Пример 8.12

Решение

Раздел 8.1 Упражнения

Практика ведет к совершенству

Письменные упражнения

Самопроверка

Упрощение радикальных выражений — ChiliMath

Компоненты радикального выражения

Примеры упрощения радикальных выражений

Практика с рабочими листами

Упростите радикальные выражения | Промежуточная алгебра

Результаты обучения

Продукт, возведенный в правило степени или иногда называемый квадратным корнем правила продукта

Пример

Упростите корни куба

Пример

Упрощение четвертых корней

Сводка

Упрощение выражений с квадратными корнями

Результаты обучения

Квадратные корни и порядок операций

, пример

Упростите радикальные, рациональные выражения с помощью программы «Пошаговое решение математических задач»

ЗАКОН УМНОЖЕНИЯ ЭКСПОНЕНТОВ

ЗАДАЧИ

УМНОЖЕНИЕ МОНОМОВ

ЗАДАЧИ

МОНОМИЛЫ, УМНОЖЕННЫЕ НА ПОЛИНОМИКИ

ЗАДАЧИ

ПОЛИНОМИЧЕСКИЕ ТОВАРЫ

ЗАДАЧИ

ПОЛНОМОЧИЯ И КВАДРАТНЫЕ КОРНИ

ЗАДАЧИ

ЗАКОН ПОДРАЗДЕЛЕНИЯ ЭКСПОНЕНТОВ

ЗАДАЧИ

РАЗДЕЛЕНИЕ МОНОМИАЛА НА МОНОМИАЛ

ЗАДАЧИ

РАЗДЕЛЕНИЕ ПОЛИНОМА НА МОНОМИАЛ

ЗАДАЧИ