Содержание
Онлайн калькулятор: Кубическое уравнение
Сегодня выполняем запрос пользователя Решение кубического уравнения.
Канонический вид кубического уравнения:
Решать кубическое уравнение мы будем по формуле Виета.
Формула Виета — способ решения кубического уравнения вида
Соответственно, чтобы привести к этому виду оригинальное уравнение первым шагом все введенные коэффициенты делятся на коэффициент а:
Калькулятор ниже, а описание формулы Виета — под ним
Кубическое уравнение
Точность вычисления
Знаков после запятой: 2
content_copy Ссылка save Сохранить extension Виджет
Кстати сказать, на других сайтах почему-то для решения кубических уравнений используют формулу Кардано, однако я согласен с Википедией в том, что формула Виета более удобна для практического применения. Так что почему везде формула Кардано — непонятно, разве что лень людям Гиперболические функции и Обратные гиперболические функции реализовывать. Ну мне не лень было.
Ну мне не лень было.
Итак, формула Виета (из Википедии)
Обратите внимание, что по представлению формулы Виета а — второй коэффициент, а коэффициент перед x3 всегда считается равным 1. Калькулятор позволяет ввести а как коэффициент перед х3, но сразу же на него и делит уравнение, чтобы получить 1
Вычисляем:
Вычисляем:
Если S > 0, то вычисляем:
и имеем три действительных корня:
Если S < 0, то заменяем тригонометрические функции гиперболическими. Здесь возможны два случая в зависимости от знака Q
Q > 0:
(действительный корень)
(пара комплексных корней)
Q < 0:
(действительный корень)
(пара комплексных корней)
Если S = 0, то уравнение вырождено и имеет меньше 3 различных решений (второй корень кратности 2):
По этим формулам калькулятор и работает. Решает вроде правильно, хотя решения с мнимой частью не проверял. Если что, пишите.
Если что, пишите.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени (кубических уравнений)
| a0x3 + a1x2 + + a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа,
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями.
Такие кубические уравнения называют трёхчленными кубическими уравнениями.
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x3 + ax2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
| (3) |
Тогда, поскольку
то уравнение (2) примет вид
В результате уравнение (2) примет вид
| (4) |
Если ввести обозначения
то уравнение (4) примет вид
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями, у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
| (6) |
где t – новая переменная.
Поскольку
то выполнено равенство:
Следовательно, уравнение (5) переписывается в виде
| (7) |
Если теперь уравнение (7) умножить на t, то мы получим квадратное уравнение относительно t :
| (8) |
Формула Кардано
Решение уравнения (8) имеет вид:
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
| (9) |
В развернутой форме эти решения записываются так:
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
Действительно,
С другой стороны,
Таким образом,
и для решения уравнения (5) мы получили формулу
которая и называется «Формула Кардано».
Замечание. Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Пример решения кубического уравнения
Пример. Решить уравнение
| x3 – 6x2 – 6x – 2 = 0. | (13) |
Решение. Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
Тогда получим
x3 – 6x2 – 6x – 2 =
= (y + 2)3– 6(y + 2)2 –
– 6(y + 2) – 2 =
= y3 + 6y2 + 12y + 8 – 6y2 –
– 24y – 24 – 6y – 12 – 2 =
= y3 – 18y – 30.
Следовательно, уравнение (13) принимает вид
| y3 – 18y – 30 = 0. | (15) |
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
| (16) |
Тогда поскольку
то уравнение (15) примет вид
| (17) |
Далее из (17) получаем:
Отсюда по формуле (16) получаем:
Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
или использовали формулу
Далее из равенства (18) в соответствии с (14) получаем:
Таким образом, мы нашли у уравнения (13) вещественный корень
Замечание 1. У уравнения (13) других вещественных корней нет.
У уравнения (13) других вещественных корней нет.
Замечание 2. Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Об уравнениях высших степеней / Хабр
Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.
Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:
Уравнением высшей степени, называется уравнение вида:
В этой статье я рассмотрю:
1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.
Кубические уравнения
Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:
Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:
В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.
Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.
Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и.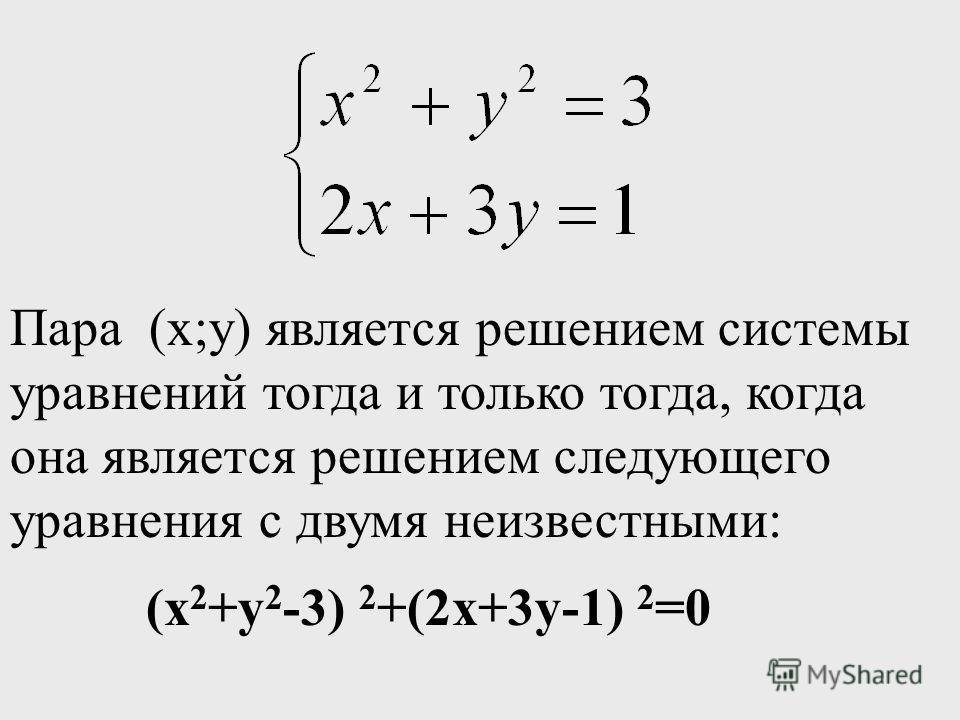 т. д.
т. д.
Возвратные кубические уравнения
Возвратные кубические уравнения имеют вид:
Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:
Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.
Теорема Безу и схема Горнера
Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:
Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.
Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.
Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.
Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:
И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:
(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. 2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).
2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).
Область применения
В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.
Заключение
В этой статье я рассмотрел только кубические и биквадратные уравнения. Однако рассмотренная теорема Безу (и схема Горнера) могут быть задействованы и для решения уравнений 5, 6, 7 и других степеней, даже несмотря на ограниченность их применения.
Алгебраические уравнения и способы их решения. Уравнения третьей и четвертой степени
Что делать, если вам – например, на Профильном ЕГЭ по математике – встретилось не квадратное уравнение, а кубическое? Или даже уравнение четвертой степени? Ведь для уравнений третьей, четвертой и более высоких степеней нет таких простых формул, как для квадратного уравнения.
В этой статье – способы решения сложных алгебраических уравнений. Замена переменной, использование симметрии и даже деление многочлена на многочлен.
Вспомним основные понятия.
Корень уравнения – такое число, которое мы можем подставить вместо переменной в уравнение и получить истинное равенство.
Например, число 3 – корень уравнения 2x = 6.
Решить уравнение – значит найти его корни или доказать, что их нет.
Равносильными называются уравнения, множества решений которых совпадают. Другими словами, у них одни и те же корни.
Например, уравнения и равносильны. Их корни совпадают: или
Замена переменной – ключ к решению многих задач.
Решим уравнение:
Если приводить обе части к одному знаменателю, получим уравнение четвертой степени. Вряд ли мы с ним справимся.
Сделаем замену Тогда
С новой переменной уравнение стало проще:
Умножим обе части на 10t. Получим квадратное уравнение:
Получим квадратное уравнение:
Корни этого уравнения: или
Вернемся к переменной
Если , то
Отсюда
Дискриминант этого уравнения отрицателен, корней нет.
Если , то Получим квадратное уравнение для :
У этого уравнения два корня: или Это ответ.
Решим уравнение
Не будем спешить раскрывать скобки. Ведь раскрыв их, мы получили бы уравнение четвертной степени.
Посмотрим на уравнение внимательно.
На координатной прямой точки 1; 3; –5; –7 расположены симметрично относительно точки
Сделаем замену , тогда .
Тогда:
Мы выразили все «скобки», то есть все множители, через новую переменную. Вот что это дает:
И еще одна замена: .
Обычное квадратное уравнение. Замечательно!
Подберем его корни по теореме Виета. Заметим, что
; отсюда , .
Если , то нет решений.
Если , то Тогда или
Если , то .
Если , то .
Ответ: 4; –8.
Дальше – еще интереснее.
3. Решите уравнение
Сделаем замену . То, что в правой части в скобках, заменили на новую переменную.
.
Получили квадратное уравнение:
Если , то
Если , то
Ответ:
Следующее уравнение решим с помощью группировки слагаемых.
4. Решите уравнение
Разложим левую часть уравнения на множители. Сгруппируем слагаемые:
Первые два слагаемых – сумма кубов. Применим формулу: . Получим:
.
Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Записывается это так:
Ответ: -2; 1; 4.
У нас появилось новое обозначение: — знак совокупности.
Такой знак означает «или».
Запись читается как « или или ».
Решая уравнения и особенно неравенства, мы будем постоянно пользоваться знаками системы и совокупности. Мы записываем решения в виде цепочки равносильных переходов. Для сложных уравнений и неравенств это единственный способ прийти к ответу и не запутаться.
Мы записываем решения в виде цепочки равносильных переходов. Для сложных уравнений и неравенств это единственный способ прийти к ответу и не запутаться.
5. Решите уравнение
Разложить левую часть на множители с первой попытки не удается.
Оказывается, если уравнение третьей (четвертой, пятой…) степени имеет целые корни, то находятся они среди делителей свободного члена (слагаемого, не содержащего x). В данном случае – среди целых делителей числа 24.
Выпишем целые делители числа 24:
1; –1; 2; –2; 3; –3; 4; –4; 6; –6; 8; –8; 12; –12; 24; –24
Подставляя их по очереди в уравнение, при получаем верное равенство:
Это значит, что левую часть уравнения можно разложить на множители:
, где .
Чтобы найти , поделим выражение на . В столбик. Так же, как мы делим друг на друга числа.
Немного непривычно, да? Потренируйтесь – у вас получится!
Ответ: 2; 3; 4.
6. Решите уравнение
группируем слагаемые:
А если сделать замену ?
Тогда .
Получаем квадратное уравнение: . Удачная замена!
Если , то , нет решений.
Если , то
, .
Ответ: .
7. Решите уравнение
Разложить на множители? Но как? И замена не видна сразу. Посмотрим на уравнение внимательно. Его коэффициенты: 1, — 5, 4, — 5, 1.
Такое уравнение называется симметрическим.
Разделим обе его части на . Мы можем это сделать, поскольку не является корнем нашего уравнения.
Теперь группируем слагаемые:
Сделаем замену .
Тогда
Получили уравнение . Легко!
Ответ:
Решение кубических уравнений методом разложения на множители
Пример 2. Решить уравнение -2x3 + 3x2 — 4x — 9 = 0.
Решение.
Делителями свободного члена являются числа: ±1, ±3, ±9. Делителями старшего коэффициента являются числа: ±1, ±2.
Значит, корни исходного уравнения могут быть среди чисел: ±1, ±3, ±9,
.
Снова простой подстановкой убеждаемся, что -1 является корнем уравнения. С помощью схемы Горнера делим левую часть исходного уравнения на x + 1.
Таким образом, -2x3 + 3x2 — 4x — 9 = (x + 1)(-2x2 + 5x — 9). Следовательно, исходное уравнение эквивалентно (x + 1) (-2x2 + 5x — 9)=0. Решая квадратное уравнение -2x2 + 5x — 9 = 0, получаем, что его дискриминант
Ответ: -1.
Пример 3. Решить уравнение 2x3 — x2 — 8x + 4 = 0.
Решение.
Делителями свободного члена являются числа: ±1, ±2, ±4. Делителями старшего коэффициента являются числа: ±1, ±2.
Значит, корни исходного уравнения могут быть среди чисел: ±1, ±2, ±4.
Простой подстановкой убеждаемся, что 2 является корнем уравнения. С помощью схемы Горнера делим левую часть исходного уравнения на x — 2.
Таким образом, 2x3 — x2 — 8x + 4 = (x — 2)(2x2 + 3x — 2). Следовательно, исходное уравнение эквивалентно (x — 2) (2x2 + 3x — 2) = 0. Решая квадратное уравнение 2x2 + 3x — 2 = 0, получаем,
Решая квадратное уравнение 2x2 + 3x — 2 = 0, получаем,
Ответ: -2,
, 2.
Еще один способ разложения на множители многочлена третьей степени — метод неопределенных коэффициентов. Он довольно громоздкий, но иногда бывает очень полезным при решении разного рода задач, а не только в случае разложения на множители. Разложение на множители любого многочлена третьей степени можно представить следующим образом a(x) = (x-x0)*(a3x2 + bx + c).
Раскрывая скобки, получим a(x) = a3x3 + x2(b — a3x0) + x*(c — bx0) — cx0.
Приравнивая теперь коэффициенты при одинаковых степенях x и свободные члены в исходном многочлене и в многочлене a(x), получим систему из четырех уравнений и четырех неизвестных a3,b,c и x0. Рассмотрим применение метода неопределенных коэффициентов на примерах.
Пример 4. Решить уравнение x3 + 2x2 — 5x — 6 = 0.
Решение.
Так как любой многочлен 3 степени можно представить в виде a3x3 + x2(b — a3x0) + x*(c — bx0) — cx0, то приравнивая коэффициенты при одинаковых степенях x, получаем следующую систему уравнений:
Выразим из первого уравнения x0 = b — 2 и подставим в два оставшихся. Получим
Теперь выразим переменную c из первого уравнения и подставим во второе.
Раскрывая скобки во втором уравнении и решая его, находим b:
Если b=4, то c=3, x0 = 2. Следовательно, x3 + 2x2 — 5x — 6 = (x — 2)(x2 — 4x + 3)=(x — 2)(x + 1)(x + 3).
Если b = 1, то c = -6, x0 = -1. Следовательно, x3 + 2x2 — 5x — 6 = (x + 1)(x2 + x — 6)=(x + 1)(x + 3)(x — 2).
Если b = -1, то c = -2, x0 = -3. Следовательно, x3 + 2x2 — 5x — 6=(x + 3)(x2 — x — 2) = (x + 3)(x — 2)(x + 1).
Таким образом, исходное уравнение эквивалентно уравнению (x + 3)(x — 2)(x + 1) = 0.
Приравнивая к нулю каждый из множителей, получаем корни уравнения x = -3, x = 2, x = -1.
Ответ: -3, -1, 2.
Пример 5. Решить уравнение 2x3 + x2 — 5x + 2 = 0.
Решение.
Приравнивая соответствующие коэффициенты при одинаковых степенях x, получаем следующую систему уравнений:
Выразим из первого уравнения x0 =
и подставим в два оставшихся. Получим
Теперь из первого уравнения выразим переменную c и подставим во второе.
Умножая левую и правую части второго уравнения на 4 и раскрывая скобки, находим b:
Если b=2, то c=-4, x0 =
. Следовательно, 2x3 + x2 — 5x + 2 = (x — )(2x2 + 2x — 4) = 2(x — )(x — 1)(x + 2).
Если b = 3, то c = -2, x0 = 1. Следовательно, 2x3 + x2 — 5x + 2 = (x — 1)(2x2 + 3x — 2)=2(x — 1)(x —
)(x + 2).
Если b = -3, то c = 1, x0 = -2. Следовательно, 2x3 + x2 — 5x + 2 = (x + 2)(2x2 — 3x + 1) = 2(x + 2)(x —
)(x — 1).
Следовательно, исходное уравнение эквивалентно уравнению 2(x + 2)(x —
)(x — 1) = 0.
Приравнивая к нулю каждый из множителей, получаем корни уравнения x = -2, x =
, x = 1.
Ответ: -2,
, 1.
Урок 12. решение алгебраических уравнений разложением на множители — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №12. Решение алгебраических уравнений разложением на множители.
Перечень вопросов, рассматриваемых в теме
1) типы алгебраических уравнений;
2) решение алгебраические уравнения методом разложения на множители;
3) методы решения алгебраических уравнений.
Глоссарий по теме
Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x1, x2, …, xn)=0, где P — многочлен от переменных x1, x2, …, xn, которые называются неизвестными.
Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнение над множеством F.
Степенью алгебраического уравнения называют степень многочлена P.
Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
Биквадратными называются уравнения вида ах4 + bх2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.
Симметрическим уравнением 3-ей степени называют уравнение вида: ax3 + bx2 + bx + a = 0, где a, b – заданные числа.
Уравнение вида anxn+an-1xn-1+…+a1x+a0=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. an-1=ak, при k=0, 1, …, n.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Давайте вспомним, что такое алгебраическое уравнение?
Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x1, x2, …, xn)=0, где P — многочлен от переменных x1, x2, …, xn, которые называются неизвестными.
Коэффициенты многочлена P обычно берутся из некоторого поля F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнение над полем F.
Степенью алгебраического уравнения называют степень многочлена P.
Например, уравнение
является алгебраическим уравнением седьмой степени от трёх переменных (с тремя неизвестными) над полем вещественных чисел.
Связанные определения. Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.
Примеры и разбор решения заданий тренировочного модуля
- Алгебраические уравнения, решаемые разложением на множители:
Пример 1.
x3 – 3x – 2 = 0.
Решение: I способ
D(–2) : ,
Можно догадаться, что число х1 = –1 является корнем этого уравнения, так как –1 + 3 – 2 = 0.
(х + 1)( х2 –х–2) = 0;
х + 1 = 0 или х2 –х–2 = 0;
х1 = –1 х2,3 = ;
х2,3 = ;
х2 = –1, х3 = 2
Ответ: –1; 2.
II способ
x3 + х2 – х2 – х – 2x – 2 = 0;
(x3 + х2) – (х2 + х) – 2(x + 1) = 0;
х2(х + 1) – х(х + 1) – 2(х + 1) = 0;
(х + 1) (х2 –х–2) = 0;
(х + 1) (х + 1) (х –2) = 0;
(х –2) = 0;
х1 = –1, х2 = 2
Ответ: –1; 2.
- Уравнения, сводящиеся к алгебраическим
- Биквадратные уравнения
На прошлом уроке мы познакомились с данным видом уравнений
Определение. Биквадратными называются уравнения вида ах4 + bх2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.
Метод решения
Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки у=х2.
Новое квадратное уравнение относительно переменной у: ay2+by+c=0.
Решая это уравнение, мы получаем корни квадратного уравнения
y1 и y2.
Решая эти два уравнения (y1=x12 и y2=x12) относительно переменной x, мы получаем корни данного биквадратного уравнения.
Порядок действий при решении биквадратных уравнений
- Ввести новую переменную у=х2
- Подставить данную переменную в исходное уравнение
- Решить квадратное уравнение относительно новой переменной
- После нахождения корней (y1; y2) подставить их в нашу переменную у=х2 и найти исходные корни биквадратного уравнения
Пример 2.
х4 – 8х2 – 9 = 0.
Решение: Пусть у = х2, где у 0; у2 – 8у – 9 = 0;
По формулам Виета:
у1 = –1; у2 = 9;
Первое решение отбрасываем ( у 0),
а из второго находим х1 = –3; х2 = 3.
Ответ: х1 = –3; х2 = 3.
2 Симметрические уравнения
Решение симметрических уравнений рассмотрим на примере симметрических уравнений третьей степени.
Симметрическим уравнением 3-ей степени называют уравнение вида ax3 + bx2 + bx + a = 0, где a, b – заданные числа.
Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства симметрических уравнений:
10. У любого симметрического уравнения нечетной степени всегда есть корень, равный -1.
Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е.
(х + 1)(ах2 + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах2 + (b – а)x + а = 0,
первое уравнение и доказывает интересующее нас утверждение.
20. У симметрического уравнения корней, равных нулю, нет.
30. При делении многочлена нечетной степени на (х + 1) частное является снова симметрическим многочленом.
Пример 3.
х3 + 2x2 + 2х + 1 = 0.
Решение: У исходного уравнения обязательно есть корень х = –1.
Разлагая далее левую часть на множители, получим
(х + 1)(x2 + х + 1) = 0.
Квадратное уравнение
x2 + х + 1 = 0 не имеет корней.
Ответ: –1.
2 Возвратные уравнения
Уравнение вида anxn+an-1xn-1+…+a1x+a0=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. an-1=ak, при k=0, 1, …, n.
Рассмотрим возвратное уравнение четвёртой степени вида
ax⁴ + bx³ + cx² + bx + a = 0, где a, b и c — некоторые числа, причём a ≠ 0. Оно является частным случаем уравнения ax⁴ + bx³ + cx² + kbx + k²a = 0 при k = 1.
Порядок действий при решении возвратных уравнений вида ax4 + bx3 + cx2 + bx + a = 0:
- разделить левую и правую части уравнения на . При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
- группировкой привести полученное уравнение к виду
- ввести новую переменную , тогда выполнено
, то есть ;
в новых переменных рассматриваемое уравнение является квадратным: at2 +bt+c–2a=0;
- решить его относительно t, возвратиться к исходной переменной.
Пример 4
2x4 – 3x3 – 7x2 –15x + 50 = 0.
Решение: Разделим на x2, получим:
Введем замену:
Пусть
тогда 2t2 – 3t – 27 = 0
t=-3 x2+3x+5=0 D<0 | 2×2-9x+10=0 x=2; x=2,5 |
Ответ: .
§7. Уравнения третьей степени.
Уравнение третьей
степени
x3+ax2+bx+c=0 (1)
подстановкойx=y–приводится кприведенному кубическому
уравнению
y3+py+q=0. (2)
Корни
такого уравнения можно найти по формулам
Кардано:y=u+v=, (3)
гдеu=,v=и
они связаны соотношениемuv=. (4)
С
учётом (4) формулу Кардано (3) можно
использовать и в таком виде:y=u,
гдеu=. (5)
Здесь
можно брать любое (одно из двух) значение
квадратного корня; три значения
кубического корня дают три корня
приведенного уравнения (2). Заметим, чтоu0,
еслиp0;
еслиp=0, то никакая
специальная формула не нужна (имеемдвучленное уравнение).
Чтобы не запоминать
формулу, можно пользоваться методом
решения, по сути повторяющим вывод
формул Кардано. Чтобы найти корни
уравнения (2) (считаем р0),
пологаяy=u+v,
подставляем его в уравнение:
(u+v)3+p(u+v)+q=0.
Раскрыв
скобки, и перегруппировав члены,
получим:
(u3+v3+q)+(
3uv+p)(u+v)=0.
Для
уничтожения второго слагаемого подберёмu, vтак, чтобы 3uv+p=0
илиuv=.
Тогда уравнение (2) приводится к системе
уравнений:Замечаем,
чтоu3,v3– корни квадратного уравненияz2+qz=0.
Затем, выбираем
один (любой) корень z1этого квадратного уравнения. Берём
в качествеu1одно (любое) значение кубического корня
изz1и вычисляем
корни кубического уравнения (1) по
следующей схеме:
u1,
v1=,y1=u1+v1,x1=y1–;u2=
u11,
v2=
v12,y2=u2+v2,x2=y2–;u3=
u12,
v3=
v11,y3=u3+v3,x3=y3–;
где1,2=
невещественные кубические корни из
единицы. Заметим, что2=(1)2=и1=(2)2=,
это позволяет варьировать нахождениеu2, v2,
u3, v3.
При исследовании
уравнений третьей степени используют
теорему:
Теорема. Пустьx3+px+q=0
неполное кубическое уравнение с
действительными коэффициентами.
Обозначим
∆=.
Если ∆>0, то
уравнение имеет один действительный
и два мнимых сопряжённых корня.Если ∆=0, то корни
уравнения действительны и хотя бы один
из них кратный.Если ∆<0, то все
корни действительны и различны.
Если не все
коэффициенты уравнения (2) действительны,
то для упрощения вычислений можно
вычислить ∆. Если ∆=0 (p0,q0),
тогда уравнение (2) имеет два равных
корняy2=y3,
и в этом случае корни уравнения (2)
можно найти, не прибегая к извлечению
корней второй и третьей степени, а
именноy1=; y2=y3=. (6)
Если
же ∆0, то уравнение
(2) имеет три различных корня, для
нахождения которых, используют один
из вышеописанных способов.
Пример 1. Решить
уравнение:
x3–6x+9=0.
Решение.Уравнение
приведенное (отсутствует член сx2).
Используем модифицированную формулу
Кардано (5):
∆===>0.(берём
только одно значение квадратного
корня). Тогдаu=.
Одно
из значенийестьu1=–1, ещё
два значения получим, умножаяu1на1,2
– кубические корни из единицы. Итак,
u1=–1
,
x1=
u1–=–1–=–3;
u2=
u11=–1,
x2=
u2–=–1+=–1–2/1=
=–1–22=.
Так
как коэффициенты данного уравнения
действительны и ∆>0, тоx3=(x3не нужно
вычислять по формуле).
Ответ:x1=–3,
x2,3=.
Пример 2. Решить
уравнение:x3+9x2+18x+28=0.
Решение.
Сделаем подстановкуx=y–=y–3.
Получим уравнениеy3–9y+28=0.
Полагаемy=u+v:
(u+v)3–9(u+v)+28=0,
(u3+v3+28)+(3uv–9)(u+v)=0.
Откуда,
или,
гдеu3,v3– корни квадратного уравненияz2+28z+27=0.
Один из корней
последнего уравнения z1=–1,
тогдаu1=–1,
v1==–3,y1=–4,x1=–7;u2=
u11=,v2=
v12=,y2=,x2=;
Поскольку коэффициенты уравнения
действительны и ∆>0, тоx3=.
Ответ: x1=–7,
x2,3=.
Пример 3. Решить
уравнение:x3+3x–2i=0.
Решение. Данное
уравнение приведенное, и не все его
коэффициенты действительны, поэтому
вычислим ∆.
∆===–1+1=0
Таким
образом корни уравнения можно вычислить
по формулам (6).x1==; x2=x3==.
Ответ:
x1=–2i,
x2,3=i.
Пример 4. Решить
уравнение:x3–3abx+
a3+b3=0
Решение.
Пологаяx=u+v,
получим
(u+v)3–3ab(u+v)+
a3+b3=0
или (u3+v3+
a3+b3)+(3uv–3ab)(u+v)=0.
ОткудаОдно
из решений последней системы
Тогда
u1=–a,
v1=–b,
x1=–a–b;
u2=
u11=,
v2=
v12=,
x2=.
Ответ:
x1=–a–b,
x2,3=.
Замечание:
При выписывании ответа воспользовались
тем, что при вещественныхa,bне надо вычислять x3.
Но если выписанное значениеx3есть корень уравнения при (любых)
вещественныхa иb, то ясно, чтоx3
будет корнем при любыхa,b.
Для самостоятельного
решения.
Решить уравнения:
x3+6x2–12x+32=0
x3+9x2–18x+44=0
x3–3x2–6x+36=0
x3–12x2+24x–40=0
x3–6ix+4(1–i)=0
x3+(3–3i)x–9=0
x3+3ax+1–a3=0
Ответы:
(–8;
)(–11;
)(–3;
)(10;
)(2+2i;
–1–i;
–1–i)(i;
(a–1;
Решение кубических уравнений — методы и примеры
Решение полиномиальных уравнений высшего порядка — важный навык для любого, кто изучает естественные науки и математику. Однако понять, как решать такие уравнения, довольно сложно.
В этой статье будет обсуждаться, как решать кубические уравнения, используя различные методы, такие как метод деления, теорема о множителях и разложение на множители по группировке.
Но прежде чем перейти к этой теме, давайте обсудим , что такое полиномиальное и кубическое уравнение.
Многочлен — это алгебраическое выражение с одним или несколькими членами, в которых знак сложения или вычитания разделяет константу и переменную.
Общая форма многочлена: ax n + bx n-1 + cx n-2 +…. + kx + l, где каждая переменная сопровождается константой в качестве коэффициента. Различные типы полиномов включают в себя; двучлены, трехчлены и четырехчлены. Примеры полиномов: 3x + 1, x 2 + 5xy — ax — 2ay, 6x 2 + 3x + 2x + 1 и т. Д.
Кубическое уравнение — это алгебраическое уравнение третьей степени.
Общий вид кубической функции: f (x) = ax 3 + bx 2 + cx 1 + d. Кубическое уравнение имеет вид ax 3 + bx 2 + cx + d = 0, где a, b и c — коэффициенты, а d — постоянная.
Как решать кубические уравнения?
Традиционный способ решения кубического уравнения состоит в том, чтобы свести его к квадратному уравнению, а затем решить его либо факторизацией, либо квадратной формулой.
Подобно тому, как квадратное уравнение имеет два действительных корня , кубическое уравнение может иметь три действительных корня. Но в отличие от квадратного уравнения, которое может не иметь реального решения, кубическое уравнение имеет по крайней мере один действительный корень.
Два других корня могут быть действительными или мнимыми.
Всякий раз, когда вам задают кубическое уравнение или какое-либо уравнение, вы всегда должны сначала преобразовать его в стандартную форму.
Например, если вам дано что-то вроде этого, 3x 2 + x — 3 = 2 / x, вы перегруппируете его в стандартную форму и запишете это как, 3x 3 + x 2 — 3х — 2 = 0.Тогда вы сможете решить эту проблему любым подходящим способом.
Давайте рассмотрим несколько примеров ниже для лучшего понимания:
Пример 1
Определите корни кубического уравнения 2x 3 + 3x 2 — 11x — 6 = 0
Решение
Поскольку d = 6, тогда возможными множителями являются 1, 2, 3 и 6.
Теперь примените теорему о факторах, чтобы проверить возможные значения методом проб и ошибок.
f (1) = 2 + 3 — 11 — 6 ≠ 0
f (–1) = –2 + 3 + 11 — 6 ≠ 0
f (2) = 16 + 12 — 22 — 6 = 0
Следовательно, x = 2 — первый корень.
Остальные корни уравнения можно получить, используя метод синтетического деления.
= (x — 2) (ax 2 + bx + c)
= (x — 2) (2x 2 + bx + 3)
= (x — 2) (2x 2 + 7x + 3 )
= (x — 2) (2x + 1) (x +3)
Следовательно, решения следующие: x = 2, x = -1/2 и x = -3.
Пример 2
Найдите корни кубического уравнения x 3 — 6x 2 + 11x — 6 = 0
Решение
x 3 — 6x 2 + 11x — 6
(x — 1) — один из факторов.
Разделив x 3 — 6x 2 + 11x — 6 на (x — 1),
⟹ (x — 1) (x 2 — 5x + 6) = 0
⟹ (x — 1) (x — 2) (x — 3) = 0
Это решение кубического уравнения: x = 1, x = 2 и x = 3.
Пример 3
Решить x 3 — 2x 2 — x + 2
Решение
Факторизуйте уравнение.
x 3 — 2x 2 — x + 2 = x 2 (x — 2) — (x — 2)
= (x 2 — 1) (x — 2)
= (x + 1) (x — 1) (x — 2)
x = 1, -1 и 2.
Пример 4
Решите кубическое уравнение x 3 — 23x 2 + 142x — 120
Решение
Сначала разложите полином на множители.
x 3 — 23x 2 + 142x — 120 = (x — 1) (x 2 — 22x + 120)
Но x 2 — 22x + 120 = x 2 — 12x — 10x + 120
= x (x — 12) — 10 (x — 12)
= (x — 12) (x — 10)
Следовательно, x 3 — 23x 2 + 142x — 120 = ( x — 1) (x — 10) (x — 12)
Приравнять каждый множитель к нулю.
x — 1 = 0
x = 1
x — 10 = 10
x — 12 = 0
x = 12
Корни уравнения: x = 1, 10 и 12.
Пример 5
Решите кубическое уравнение x 3 — 6 x 2 + 11x — 6 = 0.
Решение
Чтобы решить эту задачу методом деления, возьмите любой множитель константы 6 ;
let x = 2
Разделим полином на x-2 до
(x 2 — 4x + 3) = 0.
Теперь решите квадратное уравнение (x 2 — 4x + 3) = 0, чтобы получить x = 1 или x = 3
Следовательно, решениями являются x = 2, x = 1 и x = 3.
Пример 6
Решите кубическое уравнение x 3 — 7x 2 + 4x + 12 = 0
Решение
Пусть f (x) = x 3 — 7x 2 + 4x + 12
Поскольку d = 12, возможные значения — 1, 2, 3, 4, 6 и 12.
Методом проб и ошибок мы находим, что f (–1) = –1 — 7 — 4 + 12 = 0
Итак, (x + 1) является множителем функции.
x 3 — 7x 2 + 4x + 12
= (x + 1) (x 2 — 8x + 12)
= (x + 1) (x — 2) (x — 6)
Следовательно, x = –1, 2, 6
Пример 7
Решите следующее кубическое уравнение:
x 3 + 3x 2 + x + 3 = 0.
Решение
x 3 + 3x 2 + x + 3
= (x 3 + 3x 2 ) + (x + 3)
= x 2 (x + 3) + 1 (x + 3 )
= (x + 3) (x 2 + 1)
Следовательно, x = -1, 1-3.
Пример 8
Решить x 3 — 6x 2 + 11x — 6 = 0
Решение
Разложить на множители
x 3 — 6x 2 + 11x — 6 = 0 ⟹ (x — 1) (x — 2) (x — 3) = 0
Приравнивание каждого множителя к нулю дает;
x = 1, x = 2 и x = 3
Пример 9
Решить x 3 — 4x 2 — 9x + 36 = 0
Решение
Разложите каждый набор два срока.
x 2 (x — 4) — 9 (x — 4) = 0
Извлеките общий множитель (x — 4), чтобы получить
(x 2 — 9) (x — 4) = 0
Теперь разложите разность двух квадратов на множители
(x + 3) (x — 3) (x — 4) = 0
Приравнивая каждый множитель к нулю, мы получаем;
x = −3, 3 или 4
Пример 10
Решите уравнение 3x 3 −16x 2 + 23x — 6 = 0
Решение
Divide 3x 3 −16x 2 + 23x — 6 на x -2, чтобы получить 3x 2 — 1x — 9x + 3
= x (3x — 1) — 3 (3x — 1)
= (x — 3) ( 3x — 1)
Следовательно, 3x 3 −16x 2 + 23x — 6 = (x- 2) (x — 3) (3x — 1)
Приравняем каждый множитель к нулю, чтобы получить,
x = 2, 3 и 1/3
Пример 11
Найдите корни 3x 3 — 3x 2 — 90x = 0
Решение
разложите на множители 3x
3x 3 — 3x 2 — 90x ⟹3x (x 2 — x — 30)
Найдите пару множителей, произведение которых равно −30, а сумма равна −1.
⟹- 6 * 5 = -30
⟹ −6 + 5 = -1
Перепишите уравнение, заменив член «bx» на выбранные множители.
⟹ 3x [(x 2 — 6x) + (5x — 30)]
Разложите уравнение на множители;
⟹ 3x [(x (x — 6) + 5 (x — 6)]
= 3x (x — 6) (x + 5)
Приравнивая каждый множитель к нулю, получаем:
x = 0, 6, -5
Решение кубических уравнений с использованием графического метода
Если вы не можете решить кубическое уравнение ни одним из вышеперечисленных методов, вы можете решить его графическим способом.Для этого вам необходимо иметь точный набросок данного кубического уравнения.
Точка (точки), где его график пересекает ось x, является решением уравнения. Количество реальных решений кубических уравнений равно количеству пересечений его графиком оси абсцисс.
Пример 12
Найдите корни x 3 + 5x 2 + 2x — 8 = 0 графически.
Решение
Просто нарисуйте график следующей функции, подставив случайные значения x:
f (x) = x 3 + 5x 2 + 2x — 8
. График отсекает ось абсцисс в 3 точках, следовательно, существует 3 реальных решения.
На графике решения следующие:
x = 1, x = -2 & x = -4.
Практические вопросы
Решите следующие кубические уравнения:
- x 3 — 4x 2 — 6x + 5 = 0
- 2x 3 — 3x 2 — 4x — 35 = 0
- x 3 — 3x 2 — x + 1 = 0
- x 3 + 3x 2 — 6x — 8 = 0
- x 3 + 4x 2 + 7x + 6 = 0
- 2x 3 + 9x 2 + 3x — 4 = 0
- x 3 + 9x 2 + 26x + 24 = 0
- x 3 — 6x 2 — 6x — 7 = 0
- x 3 — 7x — 6 = 0
- x 3 — 5x 2 — 2x + 24 = 0
- 2x 3 + 3x 2 + 8x + 12 = 0
- 5x 3 — 2x 2 + 5x — 2 = 0
- 4x 3 + x 2 — 4x — 1 = 0
- 5x 3 — 2x 2 + 5x — 2 = 0
- 4x 3 900 17 — 3x 2 + 20x — 15 = 0
- 3x 3 + 2x 2 — 12x — 8 = 0
- x 3 + 8 = 0
- 2x 3 — x 2 + 2x — 1 = 0
- 3x 3 — 6x 2 + 2x — 4 = 0
- 3x 3 + 5x 2 — 3x — 5 = 0
Предыдущий урок | Главная страница | Следующий урок
Кубическая формула
Кубическая формула
Кубическая формула
(Решите любое полиномиальное уравнение 3-й степени)
Я размещаю это в Интернете, потому что некоторые студенты могут
нахожу это интересным.Это легко можно было бы упомянуть в
много курсов математики бакалавриата, хотя это не кажется
появиться в большинстве учебников, используемых для этих курсов.
Ни один из этих материалов я не обнаружил. —
ES
Вы должны знать, что решение ax 2 + bx + c = 0 равно
Аналогичная формула существует для многочленов степени
три: Решение ax 3 + bx 2 + cx + d = 0 является
(Подобная формула была впервые опубликована Кардано в 1545 году.)
Или, короче,
х = {q + [q 2
+ (р-п 2 ) 3 ] 1/2 } 1/3
+ {Q — [q 2
+ (р-п 2 ) 3 ] 1/2 } 1/3
+ П
где
p = -b / (3a), q = p 3 + (bc-3ad) / (6a 2 ), r = c / (3a)
Но я не , а не рекомендую вам запомнить эти формулы.
Помимо того, что это слишком сложно, там
другие причины, по которым мы не обучаем этой формуле
студентам-математикам.Одна из причин в том, что
мы стараемся не учить их сложным
числа. Комплексные числа (т. Е. Точки лечения
в самолете цифрами) — это более сложная тема,
лучше оставить для более продвинутого курса. Но тогда
только числа, которые нам разрешено использовать в расчетах
являются действительными числами (т. е. точками на линии).
Это накладывает на нас некоторые ограничения — например,
мы не можем извлечь квадратный корень из отрицательного
номер. Теперь у формулы Кардана есть недостаток
что он может принести в игру такие квадратные корни
на промежуточных этапах вычислений, даже если те
числа не фигурируют в задаче или ответе на нее.
Например, рассмотрим кубическое уравнение
х 3 -15x-4 = 0. (Этот пример был
упомянутый Бомбелли в его книге в 1572 году.)
У этой проблемы есть настоящая
коэффициенты, и он имеет три действительных корня
за его ответы. (Подсказка: один из корней
небольшое положительное целое число; теперь ты можешь найти все
три корня?)
Но если мы применим к этому примеру формулу Кардано,
мы используем a = 1, b = 0, c = -15, d = -4, и мы находим, что
нам нужно извлечь квадратный корень из -109 в
итоговое вычисление.В конечном счете,
квадратные корни отрицательных чисел сократят
позже в вычислении, но это вычисление
не может быть понят изучающим математику без
дополнительное обсуждение комплексных чисел.
Аналогичная формула существует и для многочленов от
степень 4, но записывать гораздо хуже; Я не буду
даже попробуйте здесь.
Не существует аналогичной формулы для многочленов степени
5.Я не имею в виду, что никто не нашел формулы
еще; Я имею в виду, что в 1826 году Абель доказал, что не может
быть такой формулой. Проблема в том, что функции
не делай достаточно того, что тебе нужно
решение всех уравнений 5-й степени. (Представьте себе калькулятор
в нем не хватает нескольких кнопок; есть несколько видов
расчеты, которые вы не можете сделать на нем.) Вам нужно как минимум
еще одна функция. Одна из таких функций, например,
функция, обратная f (x) = x 5 + x.(Есть
другие функции, которые также будут работать, и некоторые из них
математикам интереснее по разным
причины, но мне нравится этот, потому что его можно описать
в довольно элементарных терминах.) Эта функция вместе
с функциями
и сложение, вычитание,
умножения и деления достаточно, чтобы получить формулу
для решения общего многочлена 5-й степени
уравнение через коэффициенты многочлена
— я.е., аналог квадратичной формулы 5-й степени.
Но это ужасно сложно; Я даже не хочу думать
о записи.
Как решать кубические уравнения
Обновлено 30 ноября 2018 г.
Ли Джонсон
Решение полиномиальных функций — ключевой навык для любого, кто изучает математику или физику, но для того, чтобы справиться с процессом, особенно когда речь идет о высшем — функции заказа — может быть довольно сложно. Кубическая функция — один из самых сложных типов полиномиальных уравнений, которые вам, возможно, придется решать вручную.1 + d = 0
Каждое решение для x называется «корнем» уравнения. Кубические уравнения имеют либо один действительный корень, либо три, хотя они могут повторяться, но всегда есть хотя бы одно решение.
Тип уравнения определяется наивысшей степенью, поэтому в приведенном выше примере это не было бы кубическим уравнением, если бы a = 0 , потому что член наивысшей степени будет bx 2 , и он будет — квадратное уравнение. 2 = 0
Решение с использованием Теорема о факторах и синтетическое деление
Самый простой способ решить кубическое уравнение включает в себя немного догадок и процесс алгоритмического типа, называемый синтетическим делением.2 — 2x + 24 = 0
Вы должны угадать одно из значений для x , но, поскольку a = 1, в этом случае вы знаете, что какое бы значение ни было, оно должно быть множителем 24. сначала такой множитель равен 1, но это оставит:
Что не равно нулю, а −1 оставит:
Что снова не равно нулю. Затем x = 2 даст:
Еще одна ошибка. Попытка x = −2 дает:
Это означает, что x = −2 является корнем кубического уравнения.Это показывает преимущества и недостатки метода проб и ошибок: вы можете получить ответ, не задумываясь, но это требует много времени (особенно если вам нужно перейти к более высоким коэффициентам, прежде чем найти корень). К счастью, когда вы нашли один корень, вы можете легко решить остальную часть уравнения.
Ключевым моментом является включение теоремы о множителях. Это означает, что если x = s является решением, то ( x — s ) является фактором, который может быть исключен из уравнения.2 + ax + b) = 0
Члены во второй группе скобок имеют форму квадратного уравнения, поэтому, если вы найдете подходящие значения для a и b , уравнение можно решить.
Этого можно достичь с помощью синтетического разделения. Сначала запишите коэффициенты исходного уравнения в верхней строке таблицы с разделительной линией и затем известным корнем справа:
\ def \ arraystretch {1.5} \ begin {array} {cccc: c} 1 & -5 & -2 & 24 & x = -2 \\ & & & & \\ \ hline & & & & \ end {array}
Оставьте одну свободную строку, а затем добавьте горизонтальную линию под ней.Сначала возьмите первое число (в данном случае 1) до строки под горизонтальной линией
\ def \ arraystretch {1.5} \ begin {array} {cccc: c} 1 & -5 & -2 & 24 & x = -2 \\ & & & & \\ \ hline 1 & & & & \ end {array}
Теперь умножьте полученное вами число на известный корень. В этом случае 1 × −2 = −2, и это записывается под следующим числом в списке, как показано ниже:
\ def \ arraystretch {1.5} \ begin {array} {cccc: c} 1 & -5 & -2 & 24 & x = -2 \\ & -2 & & & \\ \ hline 1 & & & & \ end {array}
Затем сложите числа во втором столбце и поместите результат под горизонтальной линией :
\ def \ arraystretch {1.5} \ begin {array} {cccc: c} 1 & -5 & -2 & 24 & x = -2 \\ & -2 & & & \\ \ hline 1 & -7 & & & \ end {array}
Теперь повторите процесс, который вы только что прошли, с новым числом под горизонтальной линией: умножьте на корень, поместите ответ в пустое место в следующем столбце, а затем добавьте столбец, чтобы получить новое число в Нижний ряд. Это оставляет:
\ def \ arraystretch {1.5} \ begin {array} {cccc: c} 1 & -5 & -2 & 24 & x = -2 \\ & -2 & 14 & & \\ \ hline 1 & -7 & 12 & & \ end {array}
И затем пройдите процесс в последний раз.2 — 7x + 12) = (x — 3) (x — 4)
Вы можете умножить это, чтобы проверить, если хотите. Не расстраивайтесь, если вы не можете сразу увидеть факторизацию; это требует немного практики. Это оставляет исходное уравнение как:
(x + 2) (x — 3) (x — 4) = 0
, которое, как вы можете сразу увидеть, имеет решения при x = −2, 3 и 4 (все из которых множители 24, исходная константа). Теоретически можно также увидеть всю факторизацию, начиная с исходной версии уравнения, но это намного сложнее, поэтому лучше найти одно решение методом проб и ошибок и использовать описанный выше подход, прежде чем пытаться обнаружить причину. факторизация.2}
r = {c \ above {1pt} 3a}
Использование этой формулы требует много времени, но если вы не хотите использовать метод проб и ошибок для решения кубического уравнения, а затем квадратную формулу, это действительно работает, когда вы проходите через все это.
Комплексные числа: квадратные и кубические уравнения
Комплексные числа: квадратные и кубические уравнения
Математика возродилась в Западной Европе в 13 веке. В то время работы по математике были переведены с арабского на латынь, что позволило западноевропейским ученым узнать о средневековой арабоязычной математике и более древней греческой математике, такой как «Элементы » Евклида.Во всей этой математике числами считались только положительные числа. Отрицательные числа еще не были приняты как юридические лица.
(Некоторые древние культуры, в том числе Китай и Индия, принимали отрицательные числа, но не упомянутые выше.)
Решение квадратиков.
Под отрицательными числами мы понимаем, что каждое квадратное уравнение в переменной x можно записать в виде
топор 2 + bx + c = 0,
где a, b, и c — константы.Мы также знаем, что общее решение дается квадратной формулой:
где есть два различных реальных решения, если дискриминант b 2 — 4 ac положительный, одно двойное действительное решение, если дискриминант равен 0, и нет реальных решений, если дискриминант отрицательный.
Еще в 15 веке этого не понимали. Вместо этого квадратные уравнения были разделены на четыре различных типа в зависимости от знаков коэффициентов a, b, и c. Поскольку старший коэффициент a не равен нулю в квадратном уравнении, вы всегда можете разделить на него, чтобы получить эквивалентное квадратное уравнение, где a равно 1, то есть x 2 + bx + с = 0.
Эта одна форма порождает четыре формы, когда вы перемещаете отрицательные члены на другую сторону уравнения и когда вы отбрасываете ноль членов из уравнения:
| x 2 | = | c | ||
| x 2 + bx | = | 900 + c | = | bx |
| x 2 | = | bx + c |
Существуют и другие формы, но либо они не имеют решений среди положительных чисел, либо их можно свести к линейным уравнениям.Каждая из этих форм требовала разных форм решения. Оглядываясь назад, мы видим, что решения XV века — это всего лишь частные случаи формулы квадратиков. Можно было бы подумать, что объединение четырех случаев в один может быть достаточным оправданием для принятия отрицательных чисел, но, очевидно, это не так. Похоже, пройдет много времени, прежде чем люди расширят свое понятие числа, включив в него новые сущности.
Раствор кубиков.
Уравнения третьей степени называются кубическими уравнениями.Общая форма кубики после деления на старший коэффициент:
x 3 + bx 2 + cx + d = 0,
Как и в случае с квадратным уравнением, существует несколько форм кубического уравнения, когда отрицательные члены перемещаются на другую сторону уравнения, а нулевые члены отбрасываются.
Еще в 16 веке решение кубических уравнений было большим делом. В Италии между Кардано (1501–1576) и Тартальей (1499–1557) велись большие разногласия по поводу того, кому следует отдать должное за решение кубического уравнения.Любая книга по истории математики подробно расскажет об этом увлекательном споре. Однако для нас интересно то, что отрицательные числа стали узаконенными, было разработано более глубокое понимание уравнений и появилось первое подозрение на комплексное число. Кстати, в то время символическая алгебра еще не была развита, поэтому все уравнения записывались не символами, а словами!
Кардано в своей книге Artiss Magnæ или Great Art нашел отрицательные решения уравнений и назвал эти числа «фиктивными».Он также отметил важный факт, связывающий решения кубического уравнения с его коэффициентами, а именно, сумма решений представляет собой отрицание b, — коэффициент при члене x 2 . В другом месте он упоминает, что проблема деления 10 на две части, чтобы их произведение равнялось 40, должна быть 5 + √ (–15) и 5 - √ (–15).
Исследования комплексных чисел Бомбелли
Кардано не стал углубляться в то, что позже стало называться комплексными числами, чем это наблюдение, но несколько лет спустя Бомбелли (1526–1572) привел несколько примеров с участием этих новых зверей.Вот один пример.
Одна из кубических формул Кардано дает решение уравнения x 3 = cx + d как
где e = ( d /2) 2 — ( c /3) 3 ). Бомбелли использовал это, чтобы решить уравнение x 3 = 15 x + 4, чтобы получить решение
Итак, квадратный корень из –121 не является действительным числом; он ни положительный, ни отрицательный, ни нулевой.Бомбелли продолжал работать с этим выражением, пока не нашел уравнения, которые привели его к решению 4. Он определил, что
и, следовательно, решение x = 4. Вы можете проверить правильность этих уравнений, построив куб 2 & pm; √ – 1, чтобы получить 2 & pm; 11√ – 1.
Этот пример приведен не для того, чтобы показать, что Бомбелли знал все, что нужно знать о комплексных числах, только то, что он начал их понимать.
Математическая сцена — Уравнения III — Урок 2
Математическая сцена — Уравнения III — Урок 2 — Квадратные уравнения
| 2008 Rasmus ehf и Jhann sak Ptursson | Уравнения III |
Урок 2 Уравнения кубической и четвертой степени
Как мы можем решить уравнения, такие как кубическое уравнение
показано здесь?
x 3 — x 2 4x + 4 = 0
Существует чрезвычайно сложная формула решения
кубические уравнения.Некоторые калькуляторы имеют встроенную формулу и поэтому могут
использоваться для решения кубических уравнений.
Мы собираемся узнать, как эти уравнения могут быть решены с помощью
факторизация. Если уравнение имеет решения, которые являются целыми числами a,
b и c, то мы можем разложить уравнение на множители следующим образом:
x 3 — x 2 4x + 4 = (x
— а) (х — б) (х — в) = 0
Умножая скобки, видим, что константа
член 4 должен быть числом, которое мы получаем, когда мы умножаем a, b и c вместе.
abc = 4
Все решения a, b и c должны быть множителями 4, поэтому
не так много целых чисел, которые нам нужно учитывать.
У нас есть только следующие возможности:
1, 2 и 4
Хорошо изучите каждое из этих чисел, чтобы найти, какие из них
являются решениями уравнения.
f (1) = 1 3 — 1 2 4 × 1 +
4 = 0 1 — решение
f (-1) = (-1) 3 — (-1) 2
4 × (-1) + 4 = 6
f (2) = 2 3 — 2 2 4 × 2 +
4 = 0 2 — решение
f (−2) = (−2) 3 — (−2) 2
4 × (−2) + 4 = 0 −2 — решение
Мы нашли три решения, поэтому нам не нужно
попробуйте 4 и −4 как кубический
уравнение имеет максимум три решения.
Эти три числа дают нам значения a, b и c и
мы можем факторизовать уравнение.
x 3 — x 2 4x + 4 = (x
— 1) (х — 2) (х + 2) = 0
Этот метод включает поиск целых чисел, которые являются множителями
(можно разделить на) постоянный член, а затем проверить, действительно ли эти
целые числа являются решениями уравнения.
К сожалению, мы не можем предполагать, что решения уравнения третьей степени являются
все целые числа.
Однако, если мы можем найти одно целочисленное решение, допустим, что это x = a, тогда
Теорема остатка, мы знаем, что (x — a) является фактором уравнения. Мы
можно найти другой множитель, квадратичный множитель, путем деления. Затем мы можем решить квадратное уравнение, используя
формула решения квадратичных.
Пример 1
Решите уравнение x 3 — 3x 2 2x + 4 = 0
Ставим числа, кратные 4
в уравнение, чтобы увидеть, верны ли какие-либо из них.
f (1) = 1 3 — 3 × 1 2
2 × 1 + 4 = 0 1 — решение
f (−1) = (−1) 3 — 3 × (−1) 2
2 × (-1) + 4 = 2
f (2) = 2 3 — 3 × 2 2
2 × 2 + 4 = −4
f (−2) = (−2) 3 — 3 × (−2) 2
2 × (−2) + 4 = −12
f (4) = 4 3 — 3 × 4 2
2 × 4 + 4 = 12
f (−4) = (−4) 3 — 3 × (−4) 2
2 × (−4) + 4 = −100
Единственное целочисленное решение — x = 1.Когда мы
нашли одно решение, нам действительно не нужно проверять другие числа, потому что
теперь мы можем решить уравнение, разделив на (x — 1) и попытавшись решить
квадратичный получаем из деления.
Теперь мы можем разложить наши
выражение следующим образом:
x 3 — 3x 2 2x + 4 =
(х — 1) (х 2 —
2х — 4) = 0
Теперь нам остается решить квадратичную
уравнение.
x 2 — 2x — 4 = 0
Используем формулу квадратиков с a = 1, b =
−2 и c = −4.
Мы нашли все три решения
уравнение x 3 — 3x 2 2x + 4 =
0. Это: эфтирфаранди:
.
х = 1
x = 1 + 5
x = 1 — 5
Пример 2
Мы можем легко использовать тот же метод для решения
уравнение четвертой степени или уравнения еще более высокой степени.Решите уравнение f (x) = x 4 — x 3 — 5x 2 + 3x + 2 = 0.
Сначала мы находим целые множители
постоянный член, 2. Целочисленные множители 2 равны 1
и 2.
f (1) = 1 4 — 1 3 — 5 × 1 2 + 3 × 1 + 2 = 0
1 — это решение
f (−1) = (−1) 4 — (−1) 3 — 5 × (−1) 2 + 3 × (−1) + 2 = −4
f (2) = 2 4 — 2 3 — 5 × 2 2 + 3 × 2 + 2 = −4
f (−2) = (−2) 4 — (−2) 3 — 5 × (−2) 2 + 3 × (−2) + 2 = 0 ср. нашли вторую
решение.
Два найденных нами решения 1 и −2 означают, что мы можем разделить на x —
1 и x + 2 и остатка не будет. Сделайте это в два этапа.
Сначала разделим на x + 2
Теперь разделите полученное
кубический коэффициент по x — 1.
Теперь мы разложили на множители
f (x) = x 4 — x 3 — 5x 2 + 3x + 2 в
f (x) = (x + 2) (x — 1) (x 2 — 2x — 1) и только
Осталось решить квадратное уравнение
x 2 — 2x — 1 = 0.Мы используем
формула с a = 1, b = −2 и c = −1.
Всего найдено четыре решения.
Их:
х = 1
х = -2
х = 1 +
х = 1 —
Иногда мы можем решить
уравнение третьей степени, заключив в скобки члены два на два и найдя множитель
что у них общего.Давайте посмотрим на это на примере.
Пример 3.
Решите уравнение x 3 — 2x 2 — 4x + 8 = 0
x 3 — 2x 2 — 4x + 8 = 0 (x 3 — 2x 2 ) [x 2 (x — 2) — 4 (x — 2)] = 0 (x — 2) [x 2 — 4] = 0 (х — 2) (х | Здесь скобка (x — 2) является общим множителем и может быть вынесена за пределы общая скобка. |
Обратите внимание, что скоба (x
— 2) происходит дважды, когда мы закончили факторизацию. x = 2 — это
поэтому двойное решение, и у нас есть только два разных. Это:
х = 2 и х = -2 .
Лауснир: x = 2 og x = −2 .
Примеры, которые мы рассмотрели до сих пор, являются
уравнения, в которых член с наибольшей степенью имеет коэффициент 1.
Как мы
иметь дело с уравнениями, где этот коэффициент — какое-то другое число?
Общая форма — f (x)
= ax 3 + bx 2 + cx + d, где a, b, c и d — целые числа.
Мы можем искать целочисленные решения в том же
как и раньше, проверяя множители постоянного члена d. Если мы найдем
целочисленное решение, тогда мы можем разделить и найти другие решения, как и раньше.
Если ни один из факторов d не дает нам решения
затем мы ищем решения, которые являются дробями.
Предположим, есть дробное решение, и назовем его
решение x = t / n.
Это означает, что x — t / n является фактором
f (x), или, если мы умножаем на n, то xn — t является множителем.
Теперь предположим, что мы разделили f (x) на xn.
— t и нашли квадратичный множитель, мы можем назвать его
Ax 2 + Bx + C.
Теперь у нас есть результат
ax 3 + bx 2 + cx + d = (xn
— t) (Ax 2 + Bx + C)
сравнение коэффициентов х 3 на
обе стороны уравнения мы видим, что a = nA и, следовательно, n должно быть множителем
а.
Аналогично, сравнивая постоянные члены, мы видим, что
d = −tC и, следовательно, t является множителем d.
Мы заключаем, что любая дробь является решением
кубическое уравнение ax 3 +
bx 2 + cx + d должен иметь вид t / n, где t — множитель числа d, а n —
фактор числа a.
Обобщение для функции степени n:
ф (х)
= a n x n + a n − 1 x n − 1 +
× × × × + а 1 х
+ 0
с коэффициентами a 0 ,
а 1 , а 2 , × × × × × а n − 2 ,
n − 1 и n .
Если эта функция имеет рациональное решение,
скажем, t / n, тогда t — коэффициент 0 , а n — коэффициент n .
Пример 4
Решите уравнение f (x) = 2x 3 — 7x 2 + 4x + 3 = 0.
Возможные целые корни f (x) — это
делители 3, они равны 1
и 3.
Дроби, которые могут быть корнями, — это эти четыре числа, разделенные на множители
2.Итак, полный список рациональных чисел, которые нам нужно рассмотреть, — это , 1, 3 / 2 и 3.
Сразу видно, что нам не нужно
рассмотрите любые отрицательные значения, поскольку все они будут давать отрицательные значения для f (x), а не
0.
Теперь попробуем другие возможности
f () = 2 () 3 — 7 () 2 + 4 × + 3 = 3
f (1) = 2 × 1 3 — 7 × 2 + 4 × 1 + 3 = 2
ф ( 3 / 2 )
= 2 ( 3 / 2 ) 3 — 7 ( 3 / 2 ) 2 + 4 × 3 / 2 + 3 = 0, поэтому мы нашли решение.
x = 3 / 2 — решение, поэтому (x — 3 / 2 ) является множителем.
Разделение на (x — 3 / 2 ) может быть затруднено. Поэтому мы умножаем на 2 и вместо этого делим на (2x — 3). Если (x
— 3 / 2 ) является
фактор
, то (2x — 3).
Теперь нам нужно решить уравнение x 2 — 2x — 1 = 0.Мы уже решили это уравнение в примере 2.
Решения: 1 + 2 og 1 — 2.
Итак, мы нашли три решения. Их:
х = 3 / 2 = 1
х = 1 + 2
х = 1 — 2
Попробуйте пройти тест 2 по уравнениям III.
Не забудьте использовать контрольный список для
следите за своей работой.
«Кубическая формула»
«Кубическая формула»
Введение.
Знание квадратичной формулы старше пифагорейской
Теорема. С другой стороны, решение кубического уравнения было первой важной задачей.
история успеха математики эпохи Возрождения в Италии.
Решение было впервые опубликовано
Джироламо Кардано (1501-1576) в своей книге по алгебре Ars Magna .
Наша цель — найти действительный корень кубического уравнения
ax 3 + bx 2 + cx + d = 0.
Два других корня (действительный или комплексный) затем можно найти с помощью полиномиального деления и квадратичной формулы. Решение состоит из двух этапов. Во-первых, кубическое уравнение «подавлено»; затем решается угнетенная кубическая.
Угнетая кубическое уравнение.
Этот трюк, который преобразует общее кубическое уравнение в новое кубическое уравнение
с отсутствующими x 2 — срок обусловлен
Николь Фонтана Тарталья (1500–1557). Применяем замену
к кубическому уравнению, чтобы получить:
Умножая и упрощая, получаем «вдавленную» кубическую
Давайте попробуем это на примере
2 x 3 -30 x 2 +162 x -350 = 0.
Наша замена будет x = y +5; расширяя и упрощая, получаем депрессивное кубическое уравнение
y 3 +6 y -20 = 0.
Решение депрессивного кубика.
Остается решить депрессивное кубическое уравнение вида
y 3 + Ay = B .
Как это сделать, было обнаружено ранее
Сципионе дель Ферро (1465-1526).
Найдем s и t , так что
| 3 ул | = | А | (1) |
| с 3 — т 3 | = | В . | (2) |
Получается, что y = s — t будет решением депрессивной кубики. Проверим, что:
Замена A , B и y , как показано, преобразует наше уравнение в
( s — t ) 3 +3 st ( s — t ) = s 3 — t 3 .
Это верно, поскольку мы можем упростить левую часть, используя биномиальную формулу, чтобы:
( s 3 -3 s 2 t +3 st 2 — t 3 ) + (3 s 2 t -3 st 2 ) = с 3 — т 3 .
Как мы можем найти s и t , удовлетворяющие (1) и (2)? Решение первого уравнения для s и подстановка в (2) дает:
При упрощении получается «триквадратичное» уравнение
которое с помощью замены u = t 3 становится квадратным уравнением
Отсюда мы можем найти значение для и по формуле корней квадратного уравнения, затем получить t , затем s , и все готово.
Выполним вычисления для нашего примера
y 3 +6 y = 20.
Нам нужны s и t , чтобы удовлетворить
| 3 ул | = | 6 | (3) |
| с 3 — т 3 | = | 20. | (4) |
Решение для с в (3) и замена результата в (4) дает:
которая умножается на т 3 становится
т 6 +20 т 3 -8 = 0.
Используя формулу корней квадратного уравнения, получаем, что
Мы отбросим отрицательный корень, затем возьмем кубический корень и получим t :
По уравнению (4)
Наше решение y для депрессивного кубического уравнения представляет собой разность s и t :
Решение нашего исходного кубического уравнения
2 x 3 -30 x 2 +162 x -350 = 0
дан кем-то
Заключительные замечания.
Я не буду обсуждать небольшую проблему, с которой вы можете столкнуться, если будете следовать изложенному маршруту. О какой проблеме я говорю?
Вскоре после открытия метода решения кубического уравнения
Лодовико Феррари (1522-1565), ученик Кардано, нашел аналогичный метод решения уравнения четвертой степени.
Этот раздел в общих чертах основан на главе из книги Путешествие через гений
пользователя Уильям Данхэм.
Упражнение 1.
Покажите, что y = 2 является решением нашей угнетенной кубической
y 3 +6 y -20 = 0.
Затем найдите два других корня. Какой из корней соответствует нашему решению
Ответ.
Упражнение 2.
Преобразуйте кубическое уравнение
x 3 -6 x 2 +14 x -15 = 0
в депрессивный куб.
Ответ.
Упражнение 3.
Найдите действительный корень кубического уравнения в упражнении 2.
(Это только для практических целей; чтобы сделать вычисления менее беспорядочными, корень окажется целым числом, поэтому вместо этого можно использовать тест Rational Zero.)
Ответ.
[Назад]
[Далее: Геометрия кубической формулы]
[Алгебра]
[Тригонометрия]
[Комплексные переменные]
[Исчисление]
[Дифференциальные уравнения]
[Матричная алгебра] Домашняя страница S.O.S MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем
S.O.S. Математика CyberBoard.
Гельмут Кнауст98-05-20
Авторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователей онлайн за последний час
формул для решения уравнений 3-й степени (или кубиков).
Формулы для решения уравнений 3-й степени (или кубиков).
<---- Назад
Обратите внимание, что может быть
Другие
методы, помимо этой большой формулы для решения кубиков и
квартики. Но я хотел показать здесь, что формулы действительно существуют.
Общий вид 3-й степени
уравнение (или
Кубический ) это: ax 3
+ bx 2 + cx
+ д
= 0
Кубики имеют 3 корней.
3 корня можно представить следующим образом:
Первый корень (из трех):
Второй корень (из трех):
Третий корень (из трех):
Вторая и третья формулы равны, за исключением знака «+ или -» на
в начале и еще один знак «+» или «-» посередине. Обратите внимание, что
вторая и третья формулы содержат мнимую единицу « i ».
Теперь те же три формулы в ASCII .(1/3) * а)
Формулы вверху были получены с помощью
Программа Вольфрама Mathematica . Казалось, что не было
вариант, поэтому я скопировал их вручную в ASCII.
