Уравнения с одной переменной [wiki.eduVdom.com]

Уравнение с одной переменной — это равенство, содержащее переменную.

Корень уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.

Решить уравнение означает найти все его корни или доказать, что корней нет.

Равносильные уравнения — уравнения с одними и теми же корнями.

Следующие преобразования: перенос слагаемого из одной части в другую с изменением знака этого слагаемого; умножение или деление обеих частей уравнения на одно и то же не равное нулю число приводят уравнение к равносильному ему уравнению.

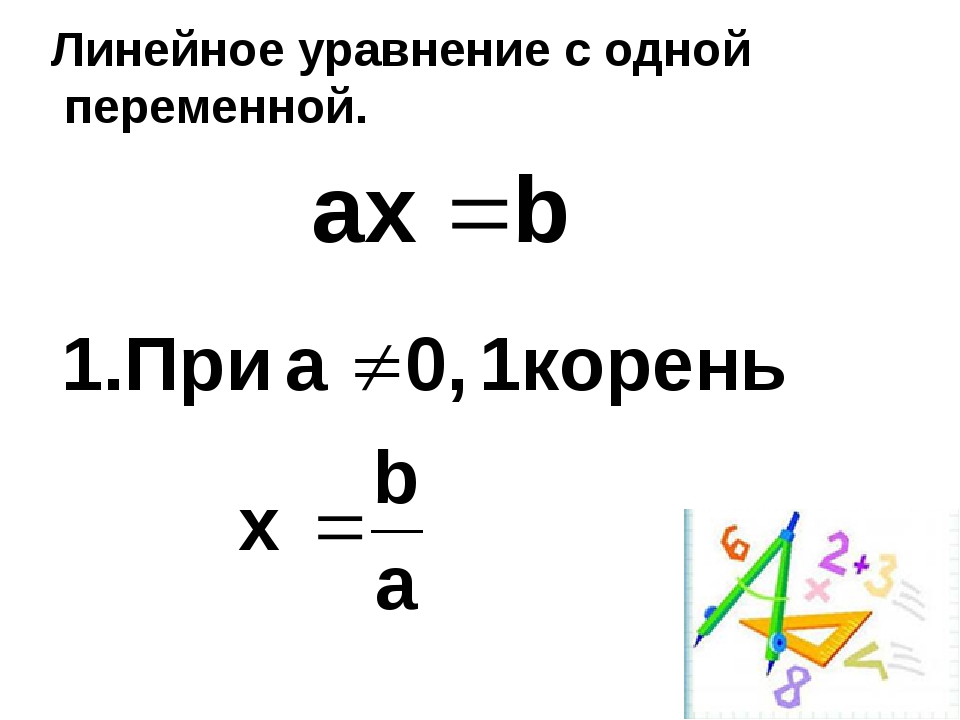
Линейное уравнение с одной переменной — это уравнение вида a*x = b, где х — переменная, а и b — некоторые числа.

1. Если а = 0 и b = 0, то это уравнение имеет бесконечно много решений;

2. Если а ≠ 0, то это уравнение имеет один корень: $x = \frac{b}{a}$

3. Если а = 0 и b ≠ 0, то это уравнение не имеет корней.

—-
Пример 1. Решите уравнение $\frac{2x-1}{3} — \frac{x+1}{2} = 2$

Решение:

• $\frac{2x-1}{3} — \frac{x+1}{2} = 2$

• $\frac{(2x-1)*2}{3*2} — \frac{(x+1)*3}{2*3} = 2$

• $\frac{(4x-2) — (3x+3)}{6} = 2$

• $\frac{4x-2 — 3x-3}{6} = 2$

• $\frac{x — 5}{6} = 2$

• $x — 5 = 2*6$

• $x — 5 = 12$

• $x = 12 + 5$

• $x = 17$

Ответ: 17.

Пример 2. Решите уравнение $5x + \frac{2x+3}{4} = \frac{3x-1}{2} + 4x$

Решение:

• $5x + \frac{2x+3}{4} = \frac{3x-1}{2} + 4x$

• $\frac{20x+2x+3}{4} = \frac{3x-1+8x}{2}$

• $\frac{22x+3}{4} = \frac{11x-1}{2}$

• $22x+3 = 22x-2$

• $22x-22x = -2-3$

• $0 = -5$, но такого быть не может, значит данное уравнение не имеет корней.

Ответ: нет корней.

subjects/mathematics/уравнения_с_одной_переменной.txt · Последние изменения: 2013/02/02 17:42 — ¶

Уравнения с одной переменной

Уравнение — это равенство, которое имеет неизвестное число, обозначенное буквой. Неизвестное число называют переменной.

Например: $4x-9=x,\ \ 2\left(y+8\right)=5y-8,\ \ 3z-18=-\left(z+2\right).$

Уравнения могут иметь разное количество корней. Решить уравнение — означает найти все его корни либо доказать, что их нет.

Если уравнения имеет одни и те же корни, то они называются равносильными. Равносильными считаются и те уравнения, которые не имею решения.

При решении равнений используют такие свойства:

1. Если в любой из частей уравнения раскрыть скобки или свести подобные слагаемые, то получим уравнение, равносильное данному.
2. Если в уравнении перенести слагаемое с одной части в другую, сменив знак на противоположный, то получим уравнение, равносильное данному. 2-ac}}{a}$, где $k=\frac{b}{2}.$

   Уравнения с параметрами

   Если в уравнении $ax=b\ \ \ \ x-$переменная, а буква $a$ обозначает какое либо число, то говорят, что это уравнение с параметром. Что б решить такое уравнение, необходимо рассмотреть такие случаи:

   1. При $a=0$ получаем уравнение $0x=b$

   Имеем два случая:

   1. При $b=0$ корнем будет любое число
   2. При $b\ne 0$ уравнение корней не имеет
   2. При $a\ne 0$ делим обе части уравнения на $a$ (которое не равняется нулю) и получаем $x=\frac{b}{a}.$

   Уравнение с параметром можно решать так само, как и обычные уравнения, но только до тех пор, пока каждое перевоплощение можно выполнить однозначно. Если же какое-то перевоплощение нельзя выполнить однозначно, то решение надо разбить на несколько случаев.

   Пример 4

   Решить уравнение $5ax+3a=2ax+9a,$ где $x-$переменная.

   Решение. Перенесем члены со сменной $x$ в одну часть, а без $x-$ в другую:

   \[5ax-2ax=9a-3a\]

   Сведем подобные слагаемые

   \[3ax=6a\]

   Для нахождения переменной $x$ мы б хотели поделить обе части уравнения на $3a,\ $но при $a=0$ мы будем делить на $0,$ что невозможно. Значит, начиная с этого момента, надо рассматривать два случая. Можем записать так:

   \[5ax-2ax=9a-3a\]

   \[3ax=6a\]

   Если $a=0,$ то $0\cdot x=0$, значит $x-$ любое число;

   Если $a\ne 0,$ то $x=2.$

   Ответ. При $a=0-$любое число; при $a\ne 0\ \ \ \ x=2.$

   Уравнения с одной переменной

   • Главная
   • Справочник
   • Алгебра
   • Уравнения с одной переменной

   На предыдущих занятиях мы знакомились с выражениями, а также учились их упрощать и вычислять. Теперь переходим к более сложному и интересному, а именно к уравнениям.

   
   

   Уравнение и его корни

   Равенство, содержащие переменную (-ые) называются уравнениями. Решить уравнение, значит найти значение переменной, при котором равенство будет верным. Значение переменной называют корнем уравнения.

   Уравнения могут иметь, как один корень, так и несколько или вообще ни одного.

   При решении уравнений используются следующие свойства:

   • если в уравнении перенести слагаемое из одной части уравнения в другую, поменяв при этом знак на противоположный, то получится уравнение равносильное данному. 2=10-3x \) являются числа -2 и 2.

     Линейное уравнение с одной переменной

     Линейное уравнение с одной переменной — это уравнения вида ax = b, где x — переменная, а a и b — некоторые числа.

     Существует большое количество видов уравнений, но решение многих из них сводится именно к решению линейных уравнений, поэтому знание этой темы обязательно для дальнейшего обучения!

     Пример №2 Решить уравнение: 4(x+7) = 3-x

     Для решения данного уравнения, в первую очередь, нужно избавиться от скобки, а для этого домножим на 4 каждое из слагаемых в скобке, получаем:

     4х + 28 = 3 — х

     Теперь нужно перенести все значения с «х» в одну сторону, а все остальное в другую сторону (не забывая менять знак на противоположный), получаем:

     4х + х = 3 — 28

     Теперь вычитаем значение слева и справа:

     5х = -25

     Чтобы найти неизвестный множитель (х) нужно произведение (25) разделить на известный множитель (5):

     х = -25:5

     х = -5

     Ответ х = -5

     Если сомневаетесь в ответе можно проверить, подставив полученное значение в наше уравнение вместо х:

     4(-5+7) = 3-(-5)

     4*2 = 8

     8 = 8 — уравнение решено верно!

     Решить теперь что-нибудь по-сложнее:

     Пример №3 Найти корни уравнения: \( (y+4)-(y-4)=6y \)

     В первую очередь, также избавимся от скобок:

     \( y+4-y+4=6y \)

     Сразу видим в левой части y и -y, а значит их можно просто вычеркнуть, а полученные числа просто сложить, и записать выражение:

     \( 8 = 6y \)

     Теперь можно перенести значения с «y» в левую сторону, а значения с числами в правую. Но ведь это не обязательно, ведь не важно с какой стороны находятся переменные, главное, чтобы они были без чисел, а значит, ничего переносить не будем. Но для тех кто не понял, то сделаем, как гласит правило и разделим обе части на (-1), как гласит свойство:

     \( 6y=8 \)

     Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель:

     \( y=\frac{8}{6} = \frac{4}{3} = 1\frac{1}{3} \)

     Ответ: y = \( 1\frac{1}{3} \)

     Также можно проверить ответ, но сделайте это самостоятельно.

     Пример №4 \( (0,5x+1,2)-(3,6-4,5x)=(4,8-0,3x)+(10,5x+0,6) \)

     Теперь я просто решу, без объяснений, а вы посмотрите на ход решения и правильную запись решения уравнений:

     \( (0,5x+1,2)-(3,6-4,5x)=(4,8-0,3x)+(10,5x+0,6) \)

     \( 0,5x+1,2-3,6+4,5x=4,8-0,3x+10,5x+0,6 \)

     \( 0,5x+4,5x+0,3x-10,5x=4,8+0,6-1,2+3,6 \)

     \( -5,2x=7,8 \)

     \( x=\frac{7,8}{-5,2}=\frac{3}{-2} =-1,5 \)

     Ответ: x = -1,5

     Если что-то не понятно по ходу решения пишите в комментариях

     Решение задач с помощью уравнений

     Зная что такое уравнения и научившись их вычислять — вы также открываете себе доступ к решению множества задач, где для решения используются именно уравнения.

     Не буду вдаваться в теорию, лучше показать все и сразу на примерах

     Пример №5 В корзине было в 2 раза меньше яблок, чем в ящике. После того, как из корзины переложили в ящик 10 яблок, в ящике их стало в 5 раз больше, чем в корзине. Сколько яблок было в корзине, а сколько в ящике?

     В первую очередь нужно определить, что мы примем за «х», в данной задаче можно принять и ящики, и корзины, но я возьму яблоки в корзине.

     Значит, пусть в корзине было x яблок, так как в ящике яблок было в два раза больше, то возьмем это за 2х. После того, как  из корзины яблоки переложили в ящик в корзине яблок стало: х — 10,  а значит, в ящике стало — (2х + 10) яблок.

     Теперь можно составить уравнение:

     5(х-10) — в ящике стало в 5 раз больше яблок, чем в корзине.

     Приравняем первое значение и второе:

     2x+10 = 5(x-10) и решаем:

     2х + 10 = 5х — 50

     2х — 5х = -50 — 10

     -3х = -60

     х = -60/-3 = 20 (яблок) — в корзине

     Теперь, зная сколько яблок было в корзине, найдем сколько яблок было в ящике — так как их было в два раза больше, то просто результат умножим на 2:

     2*20 = 40 (яблок) — в ящике

     Ответ:  в ящике — 40 яблок, а в корзине — 20 яблок.

     Я понимаю, что многие из вас, возможно, не до конца разобрались в решении задач, но уверяю к этой теме мы вернемся и еще не раз на наших уроках, а пока если у вас остались вопросы — задавайте их в комментариях.

     Под конец еще несколько примеров на решения уравнений

     Пример №6 \( 2x — 0,7x = 0 \)

     \( 1,3x = 0 \)

     \( x=0/1,3 \)

     \( x = 0 \)

     Пример №7 \( 3p — 1 -(p+3) = 1 \)

     \( 3p-1-p-3=1 \)

     \( 3p-p=1+1+3 \)

     \( 2p=5 \)

     \( p=5/2 \)

     \( p=2,5 \)

     Пример №8 \( 6y-(y-1) = 4+5y \)

     \( 6y-y+1=4+5y \)

     \( 6y-y-5y=4-1 \)

     \( 0y=3 \) — корней нет, т.к. на ноль делить нельзя!

      

     Всем спасибо за внимание. Если что-то непонятно спрашивайте в комментариях.

      

      

     В вашем браузере отключен Javascript.
     Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

     Источник

     Больше интересного в телеграм @calcsbox

     Линейное уравнение с одной переменной.

     Алгоритм решения. Алгебра, 7 класс: уроки, тесты, задания.

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     
     

     1.	Корень линейного уравнения Сложность: лёгкое	1
     2.	Решение линейного уравнения Сложность: лёгкое	1
     3.	Линейное уравнение, схема решения Сложность: лёгкое	1
     4.	Линейное уравнение (коэффициент при x дробный) Сложность: лёгкое	1
     5.	Составление и решение линейного уравнения Сложность: лёгкое	2
     6.	Линейное уравнение вида x + a = b Сложность: лёгкое	1
     7.	Линейное уравнение вида x + a = 0 Сложность: лёгкое	1
     8.	Линейное уравнение вида ax + b = 0 Сложность: лёгкое	1
     9.	Линейное уравнение (с дробями) Сложность: среднее	2
     10.	Линейное уравнение вида a — kx = c Сложность: среднее	3
     11.	Линейное уравнение вида a — b + kx = c + d — mx Сложность: среднее	4
     12.	Задача на движение Сложность: среднее	3
     13.	Задача на движение, скорость по течению и против течения Сложность: среднее	4
     14.	Задача на движение, две лодки Сложность: среднее	4
     15.	Задача на движение в одном направлении Сложность: среднее	4
     16.	Задача на движение, скорость течения реки Сложность: сложное	5
     17.	Решение уравнения, записанного в виде пропорции Сложность: сложное	3
     18.	Определение книг на полках Сложность: сложное	6

     Внеклассный урок — Уравнение с одной переменной.

     Корень уравнения. Уравнения n-й степени. Уравнение с одной переменной.

     Уравнение с одной переменной. Корень уравнения. Уравнения n-й степени

       

     Уравнение – это равенство, содержащее переменную, обозначенную буквой.

     Корень уравнения (или решение уравнения) – это такое значение переменной, при котором уравнение превращается в верное равенство.

      

     Пример: решим уравнение (то есть найдем корень уравнения): 4x – 15 = x + 15

     Итак:
     4х – х = 15 + 15
     3х = 30
     х = 30 : 3
     х = 10

     Результат: уравнение имеет один корень – число 10.

     Уравнение может иметь и два, три, четыре и более корней. Например, уравнение (х-4)(х-5)(х-6) = 0 имеет три корня: 4, 5 и 6.

     Уравнение может вовсе не иметь корней. Например, уравнение х+2=х не имеет корней, т.к. при любом значении х равенство невозможно.

      

     Равносильность уравнений.

     Два уравнения являются равносильными, если они имеют одинаковые корни либо если оба уравнения не имеют корней.

     Пример1:

     Уравнения х + 3 = 5 и 3х – 1 = 5 равносильны, так как в обоих уравнениях х=2.

     Пример 2:

     Уравнения х⁴ + 2 = 1 и х² + 5 = 0 равносильны, так как оба уравнения не имеют корней.

      

     Целое уравнение с одной переменной

     Целое уравнение с одной переменной – это уравнение, левая и правая части которого являются целыми выражениями (о целых выражениях см.раздел «Рациональные выражения»).

     Уравнение с одной переменной может быть записано в виде P(x) = 0, где P(x) – многочлен стандартного вида.

     Например:
     y² + 3y – 6 = 0
     (здесь P(x) представлен в виде многочлена y² + 3y – 6).

     В таком уравнении степень многочлена называют степенью уравнения.

     В нашем примере представлено уравнение второй степени (так как в нем многочлен второй степени).

      

     Уравнение первой степени.

     Уравнение первой степени можно привести к виду:

     ax + b = 0,

     где x – переменная, a и b – некоторые числа, причем a ≠ 0.

     Отсюда легко вывести значение x:

                b
     x = – —
               a

     Это значение x является корнем уравнения.

     Уравнения первой степени имеют один корень.

      

     Уравнение второй степени.

     Уравнение второй степени можно привести к виду:

     ax² + bx + c = 0,

     где x – переменная, a, b, c – некоторые числа, причем a ≠ 0.

     Число корней уравнения второй степени зависит от дискриминанта:

     — если D > 0, то уравнение имеет два корня;

     — если D = 0, то уравнение имеет один корень;

     — если D < 0, то уравнение корней не имеет.

     Уравнение второй степени может иметь не более двух корней.

     (о том, что такое дискриминант и как находить корни уравнения, см.разделы «Формулы корней квадратного уравнения. Дискриминант» и «Другой способ решения квадратного уравнения»).

      

     Уравнение третьей степени.

     Уравнение третьей степени можно привести к виду:

     ax³ + bx² + cx + d = 0,

     где x – переменная, a, b, c, d – некоторые числа, причем a ≠ 0.

     Уравнение третьей степени может иметь не более трех корней.

      

     Уравнение четвертой степени.

     Уравнение четвертой степени можно привести к виду:

     ax⁴ + bx³ + cx² + dx + e  = 0,

     где x – переменная, a, b, c, d, e – некоторые числа, причем a ≠ 0.

     Уравнение третьей степени может иметь не более четырех корней.

      

     Обобщение:

     1) уравнение пятой, шестой и т.д. степеней можно легко вывести самостоятельно, следуя приведенной выше схеме;

     2) уравнение n-й степени может иметь не более n корней.

      

     Пример 1: Решим уравнение

     x³ – 8x² – x + 8 = 0.

     Мы видим, что это уравнение третьей степени. Значит, у него может быть от нуля до трех корней.
     Найдем их и тем самым решим уравнение.
     Разложим левую часть уравнения на множители:

     x²(x – 8) – (x – 8) = 0.

     Применим правило разложения многочлена способом группировки его членов. Для этого поставим перед вторыми скобками число 1:

     x²(x – 8) – 1(x – 8) = 0.

     Теперь сгруппируем многочлены x² и –1, являющиеся множителями многочлена x–8.
     Получим две группы многочленов: (x² –1) и (x – 8). Следовательно, наше уравнение примет новый вид:

     (x – 8)(x² – 1) = 0.

     Здесь выражение x² – 1 можно представить в виде x² – 1².
     А значит, можем применить формулу сокращенного умножения: x² – 1² = (x – 1)(x + 1).
     Подставим в наше уравнение это выражение и получим:

     (x – 8)(x – 1)(x + 1) = 0.

     Дальше все просто. При x – 8 = 0 всё уравнение тоже равно нулю.
     И так – в случае и с двумя остальными выражениями x – 1 и x + 1. Таким образом:

     x – 8 = 0

     x – 1 = 0

     x + 1 = 0

     Осталось найти корни нашего уравнения:

     x₁ = 0 + 8 = 8

     x₂ = 0 + 1 = 1

     x₃ = 0 – 1 = –1.

     Уравнение решено. Оно имеет три корня: 8, 1 и –1.

      

     Пример 2: Решим уравнение

     (x² – 5x + 4)(x² – 5x +6) = 120.

     Это уравнение сложнее. Но его можно упростить оригинальным образом – методом введения новой переменной.
     В нашем уравнении дважды встречается выражение x² – 5x.
     Мы можем обозначить его переменной y. То есть представим, что x² – 5x = y.

     Тогда наше уравнение обретает более простой вид:

     (y + 4)(y + 6) = 120.

     Раскроем скобки:

     y² + 4y + 6y + 24 = 120

     y² + 10y + 24 = 120

     Приравняем уравнение к нулю:

     y² + 10y + 24 – 120 = 0

     y² + 10y – 96 = 0

     Мы получили обычное квадратное уравнение. Найдем его корни. Нет необходимости производить расчеты: о том, как решать подобные уравнения, подробно написано в разделах «Квадратные уравнения» и «Формулы корней квадратного уравнения. Дискриминант». Здесь же мы сразу выведем результат. Квадратное уравнение y² + 10y – 96 = 0 имеет два корня:

     y₁ = -16

     y₂ = 6

     Буквой y мы заменили выражение x² – 5x. А значит, мы уже можем подставить значения y и найти корни заданного уравнения, тем самым решив задачу:

     1) Сначала применяем значение y₁ = –16:

     x² – 5x = –16

     Чтобы решить это уравнение, превращаем его в квадратное уравнение:

     x² – 5x + 16 = 0

     Решив его, мы обнаружим, что оно не имеет корней.

     2) Теперь применяем значение y₂ = 6:

     x² – 5x = 6

     x² – 5x – 6 = 0

     Решив это квадратное уравнение, мы увидим, что у него два корня:

     x₁ = –1

     x₂ = 6.

     Уравнение решено. Оно имеет два корня: –1 и 6.

      

     Метод введения новой переменной позволяет легко решать уравнения четвертой степени, которые являются квадратными относительно x² (такие уравнения называют биквадратными).

     Как решать линейное уравнение с одной переменной?

     ☰

     Линейное уравнение с одной переменной имеет общий вид
     ax + b = 0.
     Здесь x — это переменная, a и b – коэффициенты. По-другому a называют «коэффициент при неизвестной», b – «свободный член».

     Коэффициенты это какие-то числа, а решить уравнение — это значит найти значение x, при котором выражение ax + b = 0 верно. Например, имеем линейное уравнение 3x – 6 = 0. Решить его – это значит найти, чему должен быть равен x, чтобы 3x – 6 было равно 0. Выполняя преобразования, получим:
     3x = 6
     x = 2

     Таким образом выражение 3x – 6 = 0 верно при x = 2:
     3 * 2 – 6 = 0
     2 – это корень данного уравнения. Когда решают уравнение, то находят его корни.

     Коэффициенты a и b могут быть любыми числами, однако бывают такие их значения, когда корень линейного уравнения с одной переменной не один.

     Если a = 0, то ax + b = 0 превращается в b = 0. Здесь x «уничтожается». Само же выражение b = 0 может быть истинным только в том случае, если знание b – это 0. То есть уравнение 0*x + 3 = 0 неверно, т. к. 3 = 0 – это ложное утверждение. Однако 0*x + 0 = 0 верное выражение. Отсюда делается вывод, если a = 0 и b ≠ 0 линейное уравнение с одной переменной корней не имеет вообще, но если a = 0 и b = 0, то корней у уравнения бесконечное множество.

     Если b = 0, а a ≠ 0, то уравнение примет вид ax = 0. Понятно, что если a ≠ 0, но в результате умножения получается 0, то значит x = 0. То есть корнем этого уравнения является 0.

     Если же ни a, ни b не равны нулю, то уравнение ax + b = 0 преобразовывается к виду
     x = –b / a.
     Значение x в данном случае будет зависеть от значений a и b. При этом оно будет одним единственным. То есть нельзя при одних и тех же коэффициентах получить два или более разных значений x. Например,
     –8.5x – 17 = 0
     x = 17 / –8.5
     x = –2
     Никакое другое число, кроме –2 нельзя получить, деля 17 на –8.5.

     Бывают уравнения, которые с первого взгляда непохожи на общий вид линейного уравнения с одной переменной, однако легко преобразуются к нему. Например,
     –4.8 + 1.3x = 1.5x + 12

     Если перенести все в левую часть, то в правой останется 0:
     –4.8 + 1.3x – 1.5x – 12 = 0

     Далее надо привести подобные члены:
     –0.2x – 16.8 = 0

     Теперь уравнение приведено к стандартному виду и можно его решить:
     x = 16.8 / 0.2
     x = 84

     Уравнение. Линейное уравнение с одной переменной. Решение задач с помощью уравнений 7 класс онлайн-подготовка на

     Уравнение. Линейное уравнение с одной переменной. Решение задач с помощью уравнений

     Равенство, содержащее переменную, называют уравнением.

     Значение переменной, при которой уравнение обращается в верное равенство, называют корнем уравнения.

     Решить уравнение – это значит найти все его корни или доказать, что корней нет.

     Решим уравнение

     (х-10)(х+5)(х-7) = 0

     Произведение равно нулю, когда хотя бы один из множителей равен нулю. Приравняем к нулю каждый множитель и найдем корни уравнения

     Х-10 = 0               х+5 = 0               х-7 = 0

     Х1 = 10               х2 = -5               х3 = 7

     Это уравнение имеет три корня.

     А вот уравнение

     0*х = 10 корней не имеет, поскольку для того, чтобы найти х нужно 10:0, а на ноль, как вы о делить нельзя.

     Уравнения, имеющие одинаковые корни, называют равносильными уравнениями. Также равносильными считаются уравнения, не имеющие корней.

     Например, уравнения 3*х = 9 и х-3 = 0

     Уравнение вида ах = b, где х – переменная, а а и b – некоторые числа, называется линейным уравнением с одной переменной.

     Выразим неизвестный множитель х.

     х = ab

     Если а≠0 и b≠0, то уравнение имеет единственный корень.

     Если а≠0 и b = 0, то уравнение не имеет корней, ведь на ноль делить нельзя.

     Если а = 0 и b = 0, то уравнение имеет бесконечное множество корней. Действительно, равенство

     0*х = 0 верно при любых значениях х.

     Часто мы используем уравнения для решения задач. При этом, как показывает практика, самое сложное – это правильно составить уравнение.

     Пожалуй, основное, от чего надо отталкиваться при составлении уравнения – это небольшое правило: обозначь за х то, что нужно найти в задаче. Если надо найти несколько величин, то обозначь за х меньшую из них.

     Рассмотрим задачу:

     За 9 часов теплоход проходит тот же путь по течению реки, что и за 11 часов против течения. Найдите собственную скорость теплохода, если скорость течения реки 2 км/ч.

     Итак, обозначим за х км/ч собственную скорость теплохода.

     Тогда скорость теплохода, когда он плывет по течению реки, будет (х+2) км/ч, а скорость теплохода, когда он плывет против течения реки – (х-2) км/ч.

     По течению реки теплоход шел 9 часов, значит за 9 часов он пройдет (х+2)*9 км.

     Против течения реки теплоход шел 11 часов. За 11 часов он пройдет (х-2)*11 км.

     В задаче сказано, что эти расстояния одинаковы, давай приравняем выражение для пути по течению к выражению для пути против течения. Получим такое уравнение:

     (х+2)*9 = (х-2)*11

     9х+18 = 11х-22

     11х-9х = 18+22

     2х = 40

     х = 20

     За х мы обозначали собственную скорость теплохода. Значит, собственная скорость теплохода – 20 км/ч. Это и есть ответ на вопрос задачи.

     Уравнений с одной переменной в алгебре: математические стратегии ACT

     Уравнения с одной переменной являются одними из наиболее распространенных типов задач в разделе математики ACT. Вы должны знать, как составлять, использовать и манипулировать такими уравнениями, поскольку они являются фундаментальным элементом математики, на котором основаны более сложные выражения (множественные переменные, квадраты и т. Д.).

     Поэтому убедитесь, что вы готовы заняться тонкостями уравнений с одной переменной (независимо от того, как они представлены в ACT), прежде чем приступить к некоторым из более сложных элементов математики ACT.

     Это руководство будет вашим полным пошаговым руководством по уравнениям с одной переменной для ACT — что они собой представляют, как вы увидите их в тесте, а также как их составить и решить.

     
     И тайна раскрывается.

     Что такое уравнения с одной переменной?

     Чтобы понять уравнение с одной переменной, давайте разберем его на две составляющие: переменную и уравнение.

     Переменная является символическим заполнителем для числа, которое мы еще не знаем.Очень часто в математических задачах используются переменные $ x $ или $ y $, но переменные могут быть представлены любым символом или буквой.

     $ x + 4 = 14 $

     В данном случае $ x $ — наша переменная. Он представляет собой число, которое в настоящее время неизвестно.

     
     

     Уравнение устанавливает два равных друг другу математических выражения. Это равенство представлено знаком равенства (=), и каждая сторона выражения может быть простой, как одно целое число, или сложной, как выражение с несколькими переменными, показателями степени или чем-либо еще.2}) / 14 — 65 (x — 3) = 2

     долларов США

     Выше приведен пример уравнения. Каждая сторона выражения равна другой.

     Итак, если мы сложим наши определения, мы узнаем, что:

     
     

     Уравнение с одной переменной — это уравнение, в котором используется только одна переменная . (Примечание: переменную можно использовать несколько раз и / или использовать с любой стороны уравнения; важно только то, что переменная остается той же.)

     $ {(x + 4)} / 2 = 12

     $

     $ 6x + 3 — 2x = 19 $

     $ 4y — 2 = y + 7 $

     Это все примеры уравнений с одной переменной. Вы можете увидеть, как некоторые выражения использовали переменную несколько раз или использовали переменную в и обоих выражениях (по обе стороны от знака равенства).

     Независимо от того, сколько раз используется переменная, они все равно считаются проблемами с одной переменной, потому что переменная остается постоянной и других переменных нет.

     Нахождение пропавшей переменной похоже на поиск последнего недостающего фрагмента головоломки.

     Типичные уравнения с одной переменной на ACT

     Уравнения с одной переменной попадают в две широкие категории в уравнениях, заданных в ACT, и в задачах со словами. Давайте посмотрим на каждый тип.

     
     

     Данные уравнения

     Данное уравнение даст вам уравнение, которое нужно использовать для решения проблемы.В следующем разделе мы рассмотрим точные процессы, необходимые для решения такого рода проблем, а пока просто поймите, что ваша цель — изолировать переменную.

     (мы рассмотрим, как решить этот вопрос позже в руководстве)

     Как видно из этой задачи, изолированная переменная не может быть вашим окончательным ответом . Иногда вам будет предложено решить для $ x $, иногда вам будет предложено решить для $ x $ с другим термином (как в этом случае, когда они просят вас найти $ 2x $).

     Всегда обращайте пристальное внимание на именно на то, что просит вас найти! Вам нужно сначала изолировать свои $ x $, чтобы решить проблему, но если вы остановитесь на этом, вы получите неправильный окончательный ответ.

     
     

     Проблемы Word

     Словесная задача описывает сцену, в которой вы должны создать собственное уравнение с одной переменной для ее решения. Опять же, вашим окончательным ответом может быть значение вашей переменной ($ x $ или $ y $ и т. Д.) или ваша переменная перенесена в другой термин ($ 2x $, $ y / 2 $ и т. д.).

     (мы рассмотрим, как решить этот вопрос позже в руководстве)

     
     

     Как управлять уравнением с одной переменной

     Чтобы решить уравнение с одной переменной, мы должны изолировать нашу переменную с одной стороны уравнения. И мы делаем это, сдвигая остальные члены на другую сторону уравнения.

     Чтобы сдвинуть наши термины (числа), мы должны сократить их на их исходную сторону, выполнив функцию, противоположную термину.

     Противоположные пары функций:

     Сложение и вычитание

     Умножение и деление

     
     

     Итак, если у нас есть член на одной стороне со знаком плюс (сложение), мы должны вычесть на ту же сумму с обеих сторон.

     $ x + 2 = 6 $

     $ x + 2 — 2 = 6 — 2 $

     долл. США x = 4 долл. США

     долл. США

     Если у нас есть член, который умножается, мы должны разделить на ту же сумму с обеих сторон.

     $ 3x = 18 $

     $ {3x} / 3 = 18/3 $

     $ x = 6 $

     И так далее.

     
     

     Что бы вы ни делали с одной стороны уравнения, вы должны делать с другой. Это отменяет одинаковые члены и по существу перемещает ваши члены из одной части уравнения в другую.

     Уравнения с одной переменной предназначены для поддержания баланса.

     Шаги к решению проблемы с одной переменной

     Давайте возьмем типичное выражение переменной и разберем его на шаги, необходимые для его решения.

     $ 3г — 10 + 2г = 15 $. Найдите $ y $.

     
     

     1) Объедините похожие термины

     Если существует более одного термина с одной и той же переменной, мы должны объединить их, чтобы в конечном итоге изолировать эту переменную. Мы можем складывать или вычитать члены одной и той же переменной так же, как и любые другие числа.

     Здесь у нас есть 3y $ и 2y $. Они оба положительные, поэтому мы складываем их вместе.

     Итак, теперь наше уравнение выглядит так:

     
     

     2) Изолировать термин с вашей переменной

     После того, как мы объединили наши переменные, мы должны изолировать член переменной.Если термин — это просто сама переменная (например, $ y $), то мы можем пропустить этот шаг. Но поскольку наш термин her составляет $ 5y $, мы должны сначала выделить весь термин.

     Итак, мы должны добавить 10 к любой части нашего уравнения. Почему? Потому что у нас отрицательное число 10, а сложение противоположно вычитанию. И мы должны сделать это с любой стороны, чтобы отменить 10 в первом выражении, чтобы изолировать нашу переменную.

     $ 5лет — 10 + 10 = 15 + 10 $

     $ 5лет = 25 $

     
     

     3) Изолировать вашу переменную

     Теперь, когда мы изолировали наш термин ($ 5y $), мы можем дополнительно изолировать саму переменную.

     Опять же, мы выполняем функцию, противоположную термину. В этом случае у нас есть $ 5y $, в котором используется умножение. Следовательно, чтобы изолировать переменную, мы должны использовать деление (противоположное умножению) путем деления на обе стороны.

     $ 5лет = 25 $

     $ {5y} / 5 = 25/5

     $

     $ y = 5 $

     
     

     4) Еще раз проверьте переменную, вставив ее обратно в

     Теперь, когда мы решили для нашей переменной, давайте проверим, чтобы убедиться, что она верна, вставив ее обратно в исходное уравнение.

     $ y = 5 $

     $ 3y — 10 + 2y = 15 $

     $ 3 (5) — 10 + 2 (5) = 15 $

     15–10 + 10 = 15

     15 долларов = 15

     долларов

     Успех! Мы правильно изолировали переменную и нашли ее значение.

     
     

     5) И, наконец, перепроверьте, чтобы убедиться, что вы отвечаете на правильный вопрос!

     В этом случае мы закончили, потому что наш первоначальный вопрос просил нас найти значение $ y $. Но вы всегда должны перепроверять, чтобы убедиться, что отвечаете на правильный вопрос.Если бы они спросили у нас значение $ 5y $ или $ y / 3 $, то мы бы получили неправильный ответ, если бы остановились на этом значении на $ y = 5 $.

     Всегда перепроверяйте, что ваша переменная верна и что вы отвечаете на вопрос, на который вас просят ответить.

     
     

     Теперь давайте попробуем еще раз с нашей предыдущей проблемой:

     У нас есть $ 7 + 3x = 22 $, и мы должны изолировать нашу переменную, чтобы в конечном итоге найти $ 2x $

     .

     Шаг 1, объедините похожие термины:

     Нет подобных терминов для объединения, поэтому мы можем пропустить шаг 1.

     
     

     Шаг 2, выделите переменный член:

     $ 7 + 3x = 22 $

     $ 7-7 + 3x = 22-7 $

     $ 3x = 15 $

     
     

     Шаг 3, изолировать переменную:

     $ 3x = 15 $

     $ {3x} / 3 = 15/3 $

     $ x = 5 $

     
     

     Шаг 4, проверьте ответ еще раз:

     $ 7 + 3 (5) = 22 $

     $ 7 + 15 = 22 $

     22 доллара = 22

     доллара
     
     

     Успех.Но ждать! Мы еще не закончили.

     
     

     Шаг 5, посмотрите, что задает последний вопрос:

     Мы должны закончить вопрос, найдя $ 2x $

     $ x = 5 $

     $ 2 (5) = 10 $

     Итак, , наш окончательный ответ — G , $ 2x = 10 $

     .

     
     Может показаться, что выполнение уравнения с одной переменной требует большого количества шагов, но чем больше вы практикуетесь, тем проще и инстинктивнее станет этот процесс.
     

     Проверьте свои знания

     
     

     Ответы: C, G, B, G, E

     
     

     Объяснение ответа:

     1) Мисс Льюис начинает с проезда 900 миль со скоростью 50 миль в час, и мы хотим выяснить, насколько быстрее она должна ехать, чтобы преодолеть такое же количество миль за три часа меньше времени. Поскольку она ведет такую ​​же сумму, мы можем установить эти условия равными.

     Мы также работаем только с переменной в милях в час, так что это уравнение с одной переменной.

     Теперь две стороны уравнения имеют дело с милями и милями в час. Первая половина нашего уравнения будет выглядеть так:

     $ (900/50) — 3 $

     Почему? Поскольку мисс Льюис проезжает 900 миль со скоростью 50 миль в час, поэтому нам нужно разделить мили на мили в час, чтобы узнать время ее поездки. И , а затем , мы должны уменьшить это количество на 3, потому что нам сказали, что ее новое время в пути будет на 3 мили меньше этого.

     Это означает, что другая половина нашего уравнения будет выглядеть так:

     900 долл. США / x 9 000 долл. США 3

     Почему? Потому что мы знаем, что количество миль, которые она проезжает, будет таким же, но нам неизвестно ее количество миль в час.

     Теперь давайте соединим их и решим для нашей переменной.

     $ (900/50) — 3 = 900 / x

     $

     $ 18 — 3 = 900 / x

     $

     15 долларов = 900 / x

     долларов

     Теперь мы должны выделить наше значение $ x $. Поскольку он действует как знаменатель, мы должны умножить обе части уравнения на $ x $.

     долл. США x * 15 = (900 / x) * x

     долл. США

     $ 15x = 900 $

     Теперь мы можем разделить обе стороны на 15, чтобы выделить наше значение $ x $.

     $ 15x = 900 $

     $ {15x} / 15 = 900/15 $

     $ х = 60 $

     Наконец, давайте снова подставим это значение в исходное уравнение, чтобы перепроверить наш ответ.

     $ (900/50) — 3 = 900 / x

     $

     $ (900/50) — 3 = 900/60 $

     15 долларов = 15

     долларов

     Мы успешно нашли наше значение $ x $, которое представляет собой новый пробег в час, который г-жа.Льюис должен путешествовать.

     Но подождите, мы еще не закончили! В вопросе нам предлагалось выяснить, насколько быстрее она должна проехать, а не новые мили в час, с которыми она должна ехать. Это означает, что мы должны взять разницу между исходными милями в час и новыми милями в час.

     60–50 долларов = 10

     Она должна ехать на 10 миль в час быстрее, чтобы проехать столько же за три часа меньше времени.

     Итак, , наш окончательный ответ — C , 10.

     2) Здесь у нас есть две кабельные компании, и нам сказали, что мы должны решить, когда их ставки станут равными по прошествии равного количества месяцев.Это означает, что у нас есть одна переменная (количество месяцев), и у нас есть уравнение, потому что мы устанавливаем каждую сторону равной (поскольку в вопросе указано, что их цены будут равны через неизвестное количество месяцев).

     Uptown Cable имеет фиксированную плату в размере 120 долларов и дополнительную плату в размере 25 долларов в месяц. Фиксированная плата не изменится (это происходит только один раз), но 25 долларов будут зависеть от количества месяцев. Поскольку количество месяцев — наша неизвестная переменная, давайте присвоим ей значение $ x $.

     Итак, наше первое выражение будет выглядеть так:

     120 $ + 25x $

     Now Downtown Cable имеет фиксированную плату в размере 60 долларов (происходит только один раз) и 35 долларов в месяц. Мы пытаемся найти , равное количеству месяцев для пакета Downtown Cable и пакета Uptown Cable, поэтому наша переменная $ x $ останется прежней. Итак, наше второе выражение будет выглядеть так:

     $ 60 + 35x $

     Теперь мы устанавливаем два выражения равными друг другу. (Почему? Потому что нам говорят, что через определенное количество месяцев цены будут равны.)

     120 + 25x = 60 + 35x

     Теперь мы решаем, сдвигая члены с каждой стороны уравнения. Во-первых, давайте объединим наши переменные члены, вычтя 25x с каждой стороны.

     120 + 25x — 25x = 60 + 35x — 25x

     долларов США

     120 долларов = 60 + 10x 9000 долларов 3

     Теперь вычтем по 60 с каждой стороны.

     120–60 долларов = 60–60 + 10x

     долларов США

     60 долларов = 10x

     долларов

     И, наконец, выделим нашу переменную.

     60 долл. США / 10 = {10x} / 10

     долл. США

     6 долларов = x

     доллара

     Итак, наш окончательный ответ — G , ровно через 6 месяцев цены на каждый пакет кабеля будут равны.

     
     

     3) Этот вопрос основан на манипулировании дробями. Если этот процесс вам незнаком, обязательно ознакомьтесь с нашим руководством по фракциям и соотношениям ACT. Если этот вам знаком , то давайте продолжим.

     $ {1/3} k + {1/4} k = 1 $

     Мы должны найти общий знаменатель двух дробей, чтобы объединить наши одинаковые термины. В этом случае наименьший общий множитель 3 и 4 равен 12. (Подробнее об этом процессе читайте в нашем руководстве по фракциям и соотношениям ACT.)

     $ {4/12} k + {3/12} k = 1 $

     долл. США {7/12} k = 1

     долл. США

     Теперь у нас есть число (7), деленное на другое число (12). Мы знаем, что деление противоположно умножению, поэтому мы должны умножить каждую сторону на 12.

     12 долларов США * {7/12} k = 1 * 12

     долларов США

     7 тыс. = 12

     И, наконец, мы должны разделить каждую сторону на 7, чтобы изолировать нашу переменную.

     7 тыс. = 12

     {7 тыс.} Долл. США / 7 = 12/7

     долл. США

     $ k = 12/7

     $

     Итак, , наш окончательный ответ — B , $ 12/7 $

     .
     
     

     4) У нас есть консультант с фиксированной (единовременной) оплатой 30 долларов и дополнительной оплатой 45 долларов в час.Поскольку 45 долларов почасовая, она меняется в зависимости от нашей переменной (количества часов). Мы не знаем, сколько часов она работает, но знаем, что ее окончательный заработок составлял 210 долларов. Итак, давайте представим это в виде уравнения.

     30 долл. США + 45x = 210 долл. США

     Подобных терминов нет, поэтому мы можем начать изолировать нашу переменную.

     30–30 долларов США + 45x = 210–30 долларов США

     $ 45x = 180 $

     $ {45x} / 45 = 180/45 $

     долл. США x = 4 долл. США

     долл. США

     Итак, , наш окончательный ответ — G , она проработала 4 часа, чтобы заработать 210 долларов.

     
     

     5) Это проблема с одной переменной, которую можно решить одним из двух способов: вы можете сначала распределить, а затем решить, или вы можете решить без необходимости распространения. Здесь мы пойдем обоими путями.

     Решить с разводкой:

     $ 9 (x — 9) = -11 $

     Сначала распределите ваши 9 по выражению $ (x — 9) $

     $ 9 (x) — 9 (9) = -11 $

     $ 9x — 81 = -11 $

     Теперь, как обычно, изолируйте свой переменный член.

     $ 9x — 81 + 81 = -11 + 81 $

     $ 9x = 70 $

     И, наконец, изолируйте свою переменную.

     $ 9x = 70 $

     $ {9x} / 9 = 70/9 $

     Итак, , наш окончательный ответ — E , 70/9.

     
     

     В качестве альтернативы вы можете решить эту проблему без необходимости распределять число 9 по выражению (x — 9)

     Решить без разводки:

     $ 9 (x — 9) = -11 $

     Разделим каждую сторону на 9

     $ {9 (x — 9)} / 9 = -11 / 9 $

     $ x — 9 = -11 / 9 $

     Теперь мы должны добавить по 9 с каждой стороны.

     $ x — 9 + 9 = -11/9 + 9 $

     $ x = -11/9 + 9

     $

     Чтобы сложить -11 / 9 $ и 9, мы должны дать им общий знаменатель. Опять же, ознакомьтесь с руководством по дробям и отношениям, если этот процесс вам незнаком.

     $ x = -11/9 + 9/1 (9/9)

     $

     $ x = -11/9 + 81/9

     $

     $ x = 70/9 $

     Итак, , наш ответ — E , 70/9.

     
     Уф! Я думаю, это требует десерта.
     

     Итоги

     Отдельные вариации составляют основу многих других проблем ACT.Зная, как манипулировать такими выражениями, вы сможете использовать эти методы для решения гораздо более сложных задач и уравнений.

     Просто не забывайте всегда выполнять одно и то же действие с каждой стороной уравнения и сохранять изоляцию переменной напоследок. Теперь возьмите свои знания об одной переменной и изучите остальные наши руководства по математике. У тебя есть это.

     
     

     Что дальше?

     Вы создали свой математический фундамент, и теперь вам не терпится заняться чем-нибудь еще.Прежде чем приступить к изучению другого руководства по математической теме ACT, убедитесь, что у вас есть хорошее представление обо всех темах, охватываемых математикой ACT.

     Думаете, вам может понадобиться репетитор? Узнайте, как лучше всего найти учителя, который соответствует вашим потребностям, онлайн или лично.

     Сдали практический тест и не знаете, как вы подходите к школе? Убедитесь, что вы хорошо представляете, какой на самом деле ваш идеальный результат.

     И если вы чувствуете, что разбираетесь в самой математике, но боретесь с расчетом времени , то обязательно ознакомьтесь с нашей статьей о том, как перестать не хватать времени на ACT.

     Хотите улучшить свой результат ACT на 4 балла?

     Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к ACT. Мы гарантируем возврат ваших денег , если вы не улучшите свою оценку ACT на 4 или более балла.

     Наша программа полностью интерактивна, и она адаптирует то, что вы изучаете, к вашим сильным и слабым сторонам. Если вам понравился этот урок математики, вам понравится наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по индивидуальным навыкам, чтобы вы могли учиться наиболее эффективно.Мы также дадим вам пошаговую программу, которой нужно следовать, чтобы вы никогда не запутались, что изучать дальше.

     Воспользуйтесь нашей 5-дневной бесплатной пробной версией:

     Решение линейных уравнений с одной переменной

     Линейные уравнения с одной переменной — это уравнения, в которых переменная имеет показатель степени 1, который обычно не отображается (это понятно). Примером может быть что-то вроде \ (12x = x — 5 \). Для решения линейных уравнений есть одна основная цель: изолировать переменную .В этом уроке мы рассмотрим, как это делается, на нескольких примерах.

     Содержание

     1. Примеры решения одношаговых уравнений
     2. Примеры решения двухэтапных уравнений
     3. Примеры уравнений, в которых сначала необходимо упростить
     4. Бесконечно много или нет решений
     5. Сводка

     реклама

     Примеры решения одношаговых линейных уравнений

     После всей вашей тяжелой работы над решением уравнения вы знаете, что хотите получить окончательный ответ, например \ (x = 5 \) или \ (y = 1 \).В обоих случаях переменная изолирована или сама по себе.

     Итак, нам нужно выяснить, как изолировать переменную. Как мы это сделаем, зависит от самого уравнения! Если его на что-то умножили, поделим. Если к нему что-то добавили, мы вычтем. Поступая так, мы постепенно будем получать переменную сама по себе.

     Давайте рассмотрим пример, чтобы увидеть, как это работает.

     Пример

     Решите уравнение: \ (4x = 8 \)

     Решение

     В этом примере 4 — это умножение на \ (x \).Следовательно, чтобы изолировать \ (x \), вы должны разделить эту сторону на 4. Делая это, вы должны помнить одно важное правило: что бы вы ни делали с одной стороной уравнения, вы должны делать с другой стороной. Итак, мы разделим обе стороны на 4.

     \ (\ begin {align} 4x & = 8 \\ \ dfrac {4x} {\ color {red} {4}} & = \ dfrac {8} {\ color {red} {4}} \ end {align} \)

     Упрощение:

     \ (х = \ в коробке {2} \)

     Вот и все, один шаг, и готово. (Вот почему подобные уравнения часто называют «одношаговыми» уравнениями)

     Чек

     Каждый раз, когда вы решаете линейные уравнения, вы всегда можете проверить свой ответ, подставив его обратно в уравнение.Если вы получите верное утверждение, значит, ответ правильный. Это не обязательно на 100% для каждой задачи, но это хорошая привычка, поэтому мы сделаем это для наших уравнений.

     В этом примере наше исходное уравнение было \ (4x = 8 \). Чтобы проверить это, убедитесь, что верно следующее:

     \ (\ begin {align} 4x & = 8 \\ 4 (2) & = 8 \\ 8 & = 8 \ end {align} \)

     Это верное утверждение, поэтому наш ответ правильный.

     Для любого уравнения любая операция, которую вы выполняете с одной стороной, должна выполняться и с другой стороной.

     Давайте попробуем еще пару примеров, прежде чем переходить к более сложным уравнениям.

     Пример

     Решить: \ (3x = 12 \)

     Решение

     Поскольку \ (x \) умножается на 3, план состоит в том, чтобы разделить на 3 с обеих сторон:

     \ (\ begin {align} 3x & = 12 \\ \ dfrac {3x} {\ color {red} {3}} & = \ dfrac {12} {\ color {red} {3}} \\ x & = \ в штучной упаковке {4} \ end {align} \)

     Чек

     Чтобы проверить наш ответ, мы позволим \ (x = 4 \) и подставим его обратно в уравнение:

     \ (\ begin {align} 3x & = 12 \\ 3 (4) & = 12 \\ 12 & = 12 \ end {align} \)

     Как и раньше, поскольку это верное утверждение, мы знаем, что наш ответ правильный.

     В следующем примере вместо умножения переменной на значение из переменной вычитается значение. Чтобы «отменить» это, мы добавим это значение обеим сторонам.

     Пример

     Решить: \ (y-9 = 21 \)

     Решение

     На этот раз из y вычитается 9. Итак, мы отменим это, добавив 9 к обеим сторонам.

     \ (\ begin {align} y-9 & = 21 \\ y-9 \ color {red} {+ 9} & = 21 \ color {red} {+ 9} \\ y & = 30 \ end {align} \)

     Далее мы рассмотрим то, что обычно называют «двухшаговыми» уравнениями.В этих уравнениях нам нужно будет отменить две операции, чтобы изолировать переменную.

     Примеры двухшаговых уравнений

     В каждом из приведенных выше примеров нужно было выполнить один шаг, прежде чем мы получили ответ. В следующих примерах вы увидите, как работать с уравнениями, которые вместо этого состоят из двух шагов. Если выполняется более одной операции, важно помнить порядок операций PEMDAS. Поскольку вы отменяете операции с \ (x \), вы будете работать «снаружи внутрь».Это легче понять, когда вы увидите это на примере.

     Пример

     Решить: \ (2x-7 = 13 \)

     Решение

     Обратите внимание на две операции, происходящие с \ (x \): он умножается на 2, а затем вычитается 7. Нам нужно будет отменить это. Но только \ (x \) умножается на 2, поэтому первым шагом будет прибавление 7 к обеим сторонам. Тогда мы можем разделить обе части на 2.

     Добавление 7 к обеим сторонам:

     \ (\ begin {align} 2x-7 & = 13 \\ 2x-7 \ color {red} {+ 7} & = 13 \ color {red} {+ 7} \\ 2x & = 20 \ end {align} \ )

     Теперь разделите обе стороны на 2:

     \ (\ begin {align} 2x & = 20 \\ \ dfrac {2x} {\ color {red} {2}} & = \ dfrac {20} {\ color {red} {2}} \\ x & = \ в штучной упаковке {10} \ end {align} \)

     Чек

     Как и в случае с более простыми задачами, вы можете проверить свой ответ, подставив свое значение \ (x \) обратно в исходное уравнение.

     \ (\ begin {align} 2x-7 & = 13 \\ 2 (10) — 7 & = 13 \\ 13 & = 13 \ end {align} \)

     Это правда, значит, у нас есть правильный ответ.

     Давайте рассмотрим еще один пример с двумя шагами, прежде чем мы снова будем преодолевать трудности. Убедитесь, что вы понимаете каждый показанный шаг и также работаете над проблемой.

     Пример

     Решить: \ (5w + 2 = 9 \)

     Решение

     Как и выше, есть две операции: \ (w \) умножается на 5, а затем к нему прибавляется 2.Мы отменим их, сначала вычтя 2 с обеих сторон, а затем разделив на 5.

     \ (\ begin {align} 5w + 2 & = 9 \\ 5w + 2 \ color {red} {- 2} & = 9 \ color {red} {- 2} \\ 5w & = 7 \\ \ dfrac { 5w} {\ color {red} {5}} & = \ dfrac {7} {\ color {red} {5}} \\ w = \ boxed {\ dfrac {7} {5}} \ end {align} \)

     Дробь справа не может быть упрощена, так что это наш окончательный ответ.

     Чек

     Пусть \ (w = \ dfrac {7} {5} \). Тогда:

     \ (\ begin {align} 5w + 2 & = 9 \\ 5 \ left (\ dfrac {7} {5} \ right) + 2 & = 9 \\ 7 + 2 & = 9 \\ 9 & = 9 \ конец {align} \)

     Итак, мы снова получили правильный ответ!

     Упрощение перед решением

     В следующих примерах есть больше изменяемых терминов и, возможно, необходимо некоторое упрощение.В каждом случае шаги будут заключаться в том, чтобы сначала упростить обе стороны, а затем использовать то, что мы делали, чтобы изолировать переменную. Сначала мы подробно рассмотрим пример, чтобы увидеть, как все это работает.

     Чтобы понять этот раздел, вам должно быть удобно комбинировать похожие термины.

     Пример

     Решить: \ (3x + 2 = 4x-1 \)

     Решение

     Поскольку обе части упрощены (нет скобок, которые нам нужно вычислять, и нет одинаковых членов для объединения), следующим шагом будет получение всех x на одной стороне уравнения и всех чисел на другой стороне.Применяется то же правило — что бы вы ни делали с одной стороной уравнения, вы должны делать и с другой стороной!

     Можно перемещать \ (3x \) или \ (4x \). Предположим, вы переместили \ (4x \). Поскольку он положительный, вы должны вычесть его с обеих сторон:

     \ (\ begin {align} 3x + 2 & = 4x-1 \\ 3x + 2 \ color {red} {- 4x} & = 4x-1 \ color {red} {- 4x} \\ -x + 2 & = -1 \ end {align} \)

     Теперь уравнение выглядит так, как раньше. Следующим шагом будет вычитание 2 с обеих сторон:

     \ (\ begin {align} -x + 2 \ color {red} {- 2} & = -1 \ color {red} {- 2} \\ — x = -3 \ end {align} \)

     Наконец, поскольку \ (- x = -1x \) (это всегда верно), разделите обе стороны на \ (- 1 \):

     \ (\ begin {align} \ dfrac {-x} {\ color {red} {- 1}} & = \ dfrac {-3} {\ color {red} {- 1}} \\ x & = 3 \ end {выровнять}\)

     Чек

     Вы должны воспользоваться моментом и убедиться, что следующее утверждение является верным:

     \ (3 (3) + 2 = 4 (3) — 1 \)

     В следующем примере нам нужно будет использовать свойство распределения перед решением.Здесь легко ошибиться, поэтому убедитесь, что вы распределили число перед круглыми скобками для всех терминов внутри.

     Пример

     Решить: \ (3 (x + 2) -1 = x-3 (x + 1) \)

     Решение

     Сначала разложите 3 и –3 и соберите одинаковые термины.

     \ (\ begin {align} 3 (x + 2) -1 & = x-3 (x + 1) \\ 3x + 6-1 & = x-3x-3 \\ 3x + 5 & = — 2x-3 \ end {выровнять}\)

     Теперь мы можем прибавить 2x к обеим сторонам. (Помните, что вы получите тот же ответ, если вместо этого вычтете 3x с обеих сторон)

     \ (\ begin {align} 3x + 5 \ color {red} {+ 2x} & = — 2x-3 \ color {red} {+ 2x} \\ 5x + 5 & = -3 \ end {align} \)

     Отсюда мы можем решить, как и с другими двухэтапными уравнениями.

     \ (\ begin {align} 5x + 5 \ color {red} {- 5} & = — 3 \ color {red} {- 5} \\ 5x & = — 8 \\ \ dfrac {5x} {\ color { красный} {5}} & = \ dfrac {-8} {\ color {red} {5}} \\ x & = \ dfrac {-8} {5} \\ & = \ boxed {- \ dfrac {8 } {5}} \ end {align} \)

     Чек

     Это был сложный вопрос, поэтому не забудьте проверить свой ответ и убедиться, что не было допущено никаких ошибок. Для этого вы убедитесь, что следующее утверждение является верным:

     \ (3 \ left (- \ dfrac {8} {5} +2 \ right) -1 = \ left (- \ dfrac {8} {5} \ right) -3 \ left (- \ dfrac {8} { 5} +1 \ вправо) \)

     (Примечание: это работает, но вы должны быть очень осторожны с скобками!)

     Бесконечно много решений и нет решений

     Бывают случаи, когда вы выполняете все эти шаги, и возникает действительно странное решение.Например, при решении уравнения \ (x + 2 = x + 2 \) с использованием описанных выше шагов в итоге получается \ (0 = 0 \). Это, конечно, правда, но что хорошего в этом?

     Если вы получите подобное утверждение, это означает, что уравнение имеет бесконечно много решений. Любой \ (x \), о котором вы можете подумать, удовлетворял бы уравнению \ (x + 2 = x + 2 \). Подходящий ответ в этом случае — «бесконечно много решений».

     Другая ситуация возникает, когда вы упрощаете уравнение до утверждения, которое никогда не бывает истинным, например \ (3 = 4 \) или \ (0 = 1 \).Это происходит с уравнением \ (x + 5 = x-7 \), которое приводит к \ (5 = -7 \), что, конечно, никогда не бывает истинным. Это означает, что никакое \ (x \) не удовлетворяет этому уравнению. Другими словами «нет решения». Итого:

     • Если вы получите утверждение, которое всегда истинно, например \ (5 = 5 \) или \ (0 = 0 \), то существует бесконечно много решений.
     • Если вы получаете утверждение, которое всегда ложно, например \ (10 ​​= 11 \) или \ (1 = 5 \), то решений нет.

     реклама

     Сводка

     Решение линейных уравнений сводится к выделению переменной.В зависимости от уравнения это может занять всего один шаг или намного больше. Всегда проверяйте, нужно ли вам сначала упростить одну или обе стороны уравнения, и всегда проверяйте свой ответ.

     Подпишитесь на нашу рассылку новостей!

     Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

     Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

     Связанные

     Промежуточная алгебра Урок 7: Линейные уравнения в одной переменной WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня Цели обучения После изучения этого руководства вы сможете: Знайте, что такое линейное уравнение. Знайте, является ли значение решением или нет. Используйте свойства сложения, вычитания, умножения и деления равенств для решения линейных уравнений. Знайте, когда уравнение не имеет решения. Знайте, когда в уравнении все действительные числа являются решением. Введение Здесь мы начинаем вникать в суть того, что алгебра о — решение уравнений.В этом уроке мы будем искать конкретно при линейных уравнениях и их решениях. Мы начнем медленно а также решать уравнения, использующие только одно свойство, чтобы убедиться, что у вас есть физическое лицо понятий вниз. Тогда мы наберем темп и смешаем их там, где вам нужно использовать несколько свойств и шагов, чтобы выполнить работу. Уравнения могут быть использованы для решения различных проблемы. Позже учебные пособия, мы будем использовать их для решения текстовых задач.потом ты может ответить на эти сложные математические вопросы. Учебник Уравнение Два выражения равны друг другу Линейное уравнение Уравнение, которое можно записать в виде ax + b = c где a, b и c — константы Ниже приведен пример линейного уравнения: 3 x — 4 = 5 Решение Значение, такое, что при замене переменной на оно, это делает уравнение верно. (левая сторона выходит равной правой) Набор решений Набор всех решений Пример 1 : Определите, соответствуют ли какие-либо из следующих значений x решения к данному уравнению. 3 х — 4 знак равно 5; x = 3, 5. Проверка 3 3 x — 4 = 5 3 (3) — 4 = 5 9–4 = 5 5 = 5 Истинно 3 это решение Проверка 5 3 x — 4 = 5 3 (5) — 4 = 5 15–4 = 5 11 = 5 Ложь 5 не решение Решение линейного уравнения в целом Получите переменную, которую вы решаете, в одиночку с одной стороны и все else на другой стороне, используя ОБРАТНЫЕ операции. Ниже приведены инструменты, необходимые для решать линейные уравнения. Сложение и вычитание Свойства равенства Если a = b, то a + c = b + c Если a = b, то a — c = b — c Другими словами, если два выражения равны каждому другой и ты прибавлять или вычитать одно и то же к обеим сторонам, обе стороны будут оставаться равными. Обратите внимание, что сложение и вычитание являются обратными операции каждого Другие. Например, если у вас есть добавляемый номер, вам нужно перейти к другой стороне уравнения, тогда вы бы вычесть это с обеих сторон этого уравнения. Пример 2 : Найдите переменную. x — 5 = 2. x — 5 = 2 x — 5 + 5 = 2 + 5 x = 7 * Обратное от sub. 5 — доп. 5 Обратите внимание, что если вы вернете 7 для x дюймов исходной проблемы вы увидите, что 7 — это решение нашей проблема. Пример 3 : Найдите переменную. y + 4 = -7. y + 4 = -7 y + 4-4 = -7-4 y = -11 * Инверсия доп.4 является суб. 4 Обратите внимание, что если вы вернете -11 для y в исходной задаче, вы увидите, что -11 — это решение, которое мы находятся ищу . Умножение и деление Свойства равенства Если a = b, то a (c) = b (c) Если a = b, то a / c = b / c, где c — не равно 0. Другими словами, , если два выражения равны друг друга и ты умножить или разделить (кроме 0) одну и ту же константу на оба стороны, обе стороны останутся равными. Обратите внимание, что умножение и деление являются обратными операции каждого Другие.Например, если у вас есть число, которое умножается что вам нужно перейти к другой стороне уравнения, тогда вы бы разделите его с обеих сторон этого уравнения. Обратите внимание, что для умножения и деления это не гарантировал, что если вы умножаете на переменную, которую вы решаете, чтобы две стороны будет равным. Но гарантировано, что обе стороны пойдут быть равным, если вы умножаете или делите на константу или другое переменная, для которой вы не решаете.Мы поговорим подробнее о это в более позднем руководстве. Для этого урока просто обратите внимание, что вы можете использовать это свойство с константами и переменными, для которых вы не ищите. Пример 4 : Найдите переменную. х /2 = 5. * Обратно дел.на 2 это мульт. по 2 Если вы вернете 10 для x дюймов оригинал проблема, вы увидите, что 10 — это решение, которое мы ищем. Пример 5 : Найдите переменную.5 x = 7. * Инверсная по отношению к мульт. на 5 дел. по 5 Если вы вставите 7/5 обратно для x в оригинале проблема, вы увидите, что 7/5 — это решение, которое мы ищем. В приведенных выше примерах использовались только одно свойство за раз, чтобы помочь вам понять различные свойства, которые мы используем к решать уравнения.Однако в большинстве случаев нам приходится использовать несколько характеристики чтобы выполнить свою работу. Ниже приводится стратегия, которую вы можете использовать. чтобы помочь вам решить более сложные линейные уравнения. Стратегия решения линейной Уравнение Обратите внимание, что ваш учитель или книга ты Возможно, using сформулировал эти шаги немного иначе, чем я, но Это все сводится к одной и той же концепции — включите свою переменную один сторона и все остальное с другой, используя обратные операции. Шаг 1. При необходимости упростите каждую сторону. Это может включать в себя такие вещи, как удаление (), удаление дробей, добавление как термины и т. д. Чтобы удалить (): Просто используйте дистрибутив свойство, найденное в Уроке 5: Свойства действительных чисел. Для удаления дробей : Поскольку дроби другой способ написать деление, а обратное деление — умножение, вы удаляете фракции умножив обе части на ЖК-дисплей всех ваших дробей. Шаг 2: Используйте Добавить./ Sub. Свойства для переместить переменную срок в одну сторону и все остальные условия в другую сторону. Шаг 3: Используйте Mult./Div. Свойства для удалить любые значения которые находятся перед переменной. Шаг 4. Проверьте свой ответ. Я считаю, что это самый быстрый и Самый простой способ приблизиться к линейным уравнениям. Пример 6 : Найдите переменную. 10 — 3 x = 7. * Инверсия доп. 10 является суб. 10 * Инверсная по отношению к мульт.на -3 — это div. по -3 Будьте осторожны, начиная со строки 4 к строке 5. Да, есть отрицательный знак. Но операция между -3 и x — это умножение, а не вычитание. Итак, если бы вы Добавлять 3 в обе стороны вы бы получили -3 x + 3 вместо желаемых x . Если вы вернете 1 вместо x в исходной задаче, вы увидим, что 1 это решение, которое мы ищем. Пример 7 : Найдите переменную. 2 ( x + 5) — 7 = 3 ( x — 2). * Удалить () с помощью dist.опора * Получить все условия x с одной стороны * Инверсия доп. 3 является суб. 3 * Инверсная по отношению к мульт. на -1 — это div. по -1 Если вы вернете 9 вместо x в исходной задаче, вы увидим, что 9 — это решение, которое мы ищем. Пример 8 : Найдите переменную:. * Чтобы избавиться от дроби, мульт. с обеих сторон ЖК-дисплеем 4 * Получить все термины x на одной стороне * Инверсия доп.2 является суб. 2 * Инверсная по отношению к мульт. на -3 — это div. по -3 Если вы вернете 4/3 вместо x в исходной задаче вы увидите, что 4/3 это решение, которое мы ищем. Противоречие Противоречие — это уравнение с одной переменной, которая не имеет решения. Пример 9 : Найдите переменную. 4 x — 1 = 4 ( x + 3). * Удалить () с помощью dist. опора * Получить все термины x на одной стороне Куда делась наша переменная, x, ??? Он исчез на нас.Также обратите внимание, как мы получили ЛОЖЬ утверждение, -1 не равно 12. Это не означает, что x = 12 или x = -1. Когда ваша переменная падает из И вы закончите с ложным утверждением, то после всей вашей тяжелой работы есть НЕТ РЕШЕНИЕ. Итак, ответ — нет решения. Личность Идентификатор — это уравнение с одной переменной который имеет все действительные числа как решение. Пример 10 : Найдите переменную. 5 x + 10 = 5 ( x + 2). * Удалить () с помощью dist. опора * Получить все термины x на одной стороне На этот раз, когда наша переменная выпал, мы закончил с ИСТИННЫМ заявлением.Когда бы это ни случилось, твой ответ ВСЕ РЕАЛЬНЫЕ ЧИСЛА. Итак, ответ — все действительные числа . Практические задачи Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Math работает так же, как что-нибудь иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшим спортсменам и музыкантам помогали на протяжении всего пути. практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики. Чтобы получить от них максимальную отдачу, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, щелкнув ссылку для ответ / обсуждение для этой проблемы .По ссылке вы найдете ответ а также любые шаги, которые позволили найти этот ответ. Практика Задачи 1a — 1e: Решите для переменной. Нужна дополнительная помощь по этим темам? Последняя редакция 1 июля 2011 г. Ким Сьюард. Авторские права на все содержимое (C) 2002 — 2011, WTAMU и Kim Seward. Все права защищены.

     Линейные уравнения с одной переменной | Алгебра | Решенные примеры

     Линейное уравнение с одной переменной — это основное уравнение, используемое для представления и решения неизвестных величин. Линейное уравнение с одной переменной можно легко представить графически, и это всегда прямая линия. Линейное уравнение — это простой способ представить математическое утверждение.Любая переменная или символ могут использоваться для представления неизвестных величин, но обычно переменная «x» используется для представления неизвестной величины в линейном уравнении в одной переменной.

     Решение линейного уравнения включает набор простых методов. Переменные изолированы с одной стороны уравнения, а константы изолированы с другой стороны уравнения, чтобы получить окончательное значение величины. Давайте узнаем больше о линейных уравнениях с одной переменной и методах их решения в этом уроке.

     Что такое линейные уравнения с одной переменной?

     Прежде чем изучать линейные уравнения с одной переменной, давайте быстро разберемся в значении линейных уравнений. Линейное уравнение — это тип уравнения, в котором степень каждой переменной в уравнении точно равна единице. Когда он нарисован на графике, он выглядит как прямая линия по горизонтали или вертикали. Линейные уравнения с одной переменной — это те уравнения, в которых присутствует только одна переменная и есть только одно решение уравнения.

     Линейное уравнение с одной переменной имеет вид ax + b = 0, где a и b — любые два целых числа, а x — неизвестная переменная, имеющая только одно решение. Давайте разберемся в этом на примере. «4, добавленные к определенному числу, дает 10». Найдите этот номер. Как можно проще представить эту проблему? Можно сказать, x + 4 = 10, найти x. Мы присвоили этому номеру переменную; это называется уравнением. Это помогает нам писать такие большие задачи короче. Это уравнение имеет одну переменную — x, а наибольшая степень x равна единице.Эти виды уравнений известны как линейных уравнений с одной переменной , потому что степень переменной x равна единице.

     Как решить линейные уравнения с одной переменной?

     Общая форма линейного уравнения с одной переменной: Ax + B = 0. Здесь A — коэффициент при x, x — переменная, а B — постоянный член. Чтобы найти окончательное решение этого линейного уравнения, необходимо разделить коэффициент и постоянный член.

     Теперь давайте посмотрим, как решить линейное уравнение с одной переменной.Уравнение похоже на весы с одинаковыми весами с обеих сторон.

     Если мы прибавим или вычтем одно и то же число из обеих частей уравнения, оно все равно останется в силе. Точно так же, если мы умножим или разделим одно и то же число в обеих частях уравнения, оно все равно останется в силе. Рассмотрим уравнение 3x-2 = 4. Мы будем выполнять математические операции с LHS и RHS, чтобы не нарушить баланс. Добавим 2 с обеих сторон, чтобы уменьшить левую до 3х. Это не нарушит равновесия.Новое значение LHS равно 3x-2 + 2 = 3x, а новое значение RHS равно 4 + 2 = 6. Теперь давайте разделим обе стороны на 3, чтобы уменьшить LHS до x. Таким образом, мы имеем 3x / 3 = 6/3. Отсюда x = 2.

     Вышеупомянутые шаги для решения линейных уравнений с одной переменной можно кратко изложить в перечисленных ниже пунктах.

     • Сохраните переменный член с одной стороны, а константы с другой стороны уравнения, добавляя или вычитая с обеих сторон уравнения.
     • Упростите постоянные члены.
     • Выделите переменную с одной стороны, умножив или разделив ее на обе части уравнения.
     • Упростите и напишите ответ.

     Сравнение линейных уравнений с одной переменной и нелинейных уравнений

     Помимо линейных уравнений с одной переменной, у нас есть другие нелинейные уравнения, которые имеют множество приложений в геометрии, тригонометрии, математическом анализе. Линейные уравнения с одной переменной являются уравнениями с одной степенью и представлены в виде линии в осях координат. С другой стороны, нелинейное уравнение — это кривая или одно линейное представление на оси координат.Нелинейное уравнение более высокой степени. Примером нелинейного уравнения является уравнение кривой, такой как окружность, парабола, эллипс, гипербола.

     Некоторые примеры линейных уравнений: x = 5, 3x + 7 = 9, 4x + 2y = 11. И некоторые из примеров нелинейных уравнений — это уравнение круга — x ² + y ² = 25, уравнение эллипса — x ² /9 + y ² /16 = 1, уравнение гиперболы — x ² /16 — y ² /25 = 1.

     Следующие пункты помогают нам четко обобщить концепции, связанные с линейными уравнениями с одной переменной.

     1. Степень переменной в линейных уравнениях должна быть точно равна единице.
     2. График линейного уравнения с одной переменной представляет собой прямую линию.
     3. На решение линейного уравнения не повлияет добавление, вычитание, умножение или деление любого числа с обеих сторон уравнения.

     ---

     Часто задаваемые вопросы о линейных уравнениях с одной переменной

     Какие типы линейных уравнений?

     Типы линейных уравнений классифицируются на основе ряда переменных в уравнении.В основном есть три типа линейных уравнений:

     • Линейное уравнение с одной переменной.
     • Линейное уравнение с двумя переменными.
     • Линейное уравнение с тремя переменными.

     Какие три типа решений линейных уравнений?

     Три типа решений линейных уравнений даются как:

     • Одно уникальное решение.
     • Нет решения.
     • Бесконечное количество решений.

     Что такое линейное уравнение с одной переменной с примером?

     Линейное уравнение с одной переменной имеет вид ax + b = 0.Линейное уравнение с одной переменной — это уравнения, в которых наивысшая степень каждого члена равна единице, есть одно возможное решение уравнения и в нем присутствует только одна переменная. Пример линейного уравнения с одной переменной: 3y + 2 = 0.

     Какова наибольшая степень линейного уравнения?

     Линейное уравнение имеет наивысшую степень 1. Ссылаясь на пример линейного уравнения, 3x + 4 = 11, степень переменной ‘x’ равна 1.

     Может ли линейное уравнение иметь более одной переменной?

     Да, линейные уравнения могут иметь более одной переменной.Мы называем такие уравнения линейными уравнениями с двумя переменными или линейными уравнениями с тремя переменными. Линейные уравнения с двумя переменными имеют вид ax + by + c = 0, а линейное уравнение с тремя переменными имеет вид ax + by + cz + d = 0. Здесь x, y, z — переменные, а a , b и c — коэффициенты, а d — постоянная.

     Как решить линейные уравнения с одной переменной?

     Шаги для решения линейных уравнений с одной переменной перечислены ниже:

     • Сохраните переменный член с одной стороны, а константы с другой стороны уравнения, добавляя или вычитая с обеих сторон уравнения.
     • Упростите постоянные члены.
     • Изолируйте переменную с одной стороны, умножив или разделив обе стороны уравнения.
     • Упростите и напишите ответ.

     Как решить линейные уравнения с переменными с обеих сторон?

     Чтобы решить линейные уравнения с переменными с обеих сторон, мы сначала приводим все члены с переменными с одной стороны и константы с другой стороны уравнения. Затем мы упрощаем уравнение, выделяем переменную и записываем окончательный ответ уравнения.Давайте посмотрим на простое уравнение, чтобы понять это. 4х + 1 = 2х + 7; 4х — 2х = 7 — 1; 2х = 6; х = 6/2; х = 3.

     Каковы правила решения линейных уравнений?

     Наиболее общее правило для решения линейных уравнений состоит в том, что мы можем складывать, вычитать, умножать или делить один и тот же член с обеих сторон уравнения, чтобы мы могли найти значение переменной, присутствующей в нем.

     Как узнать, является ли система линейной или зависимой?

     Уравнение является линейным, если в нем присутствует только одна переменная, тогда как в зависимых уравнениях присутствуют как минимум две переменные, а значение одной зависит от значений других переменных.

     ---

     Простые уравнения в одной переменной — MathsTips.com

     Когда одно выражение равно другому, равенство этих выражений может выполняться либо для всех значений задействованных неизвестных переменных, либо для некоторых конкретных значений задействованных переменных. В первом случае это называется тождеством. Например, это верно для всех значений и. В последнем случае это называется уравнением. Например, что верно только тогда, когда.

     Определение

     Уравнение — это утверждение, в котором два алгебраических выражения связаны знаком равенства (=).Каждое выражение по обе стороны от знака равенства называется стороной или членом уравнения.

     Например, если выражения и равны по значению, то есть, то это алгебраическое утверждение называется уравнением, где, и являются членами уравнения. Решить уравнение — значит найти значение буквы. Эта буква называется переменной, неизвестной величиной или корнем уравнения. Переменные обычно представлены алфавитами, например,. Уравнение, в котором переменная первого порядка, т.е.е. уравнение, в котором наивысшая степень участвующих переменных равна 1, называется простым или линейным уравнением.

     Решение линейного уравнения:

     Решение линейного уравнения подчиняется следующим правилам:

     1. Если к двум выражениям по обе стороны от знака равенства добавляется одна и та же величина, то есть равные величины, то суммы равны.
     2. Если из двух выражений по обе стороны от знака равенства убрать одну и ту же величину, т. Е. Равные величины, то разности равны.
     3. Если два выражения по обе стороны от знака равенства умножить на одно и то же количество, то произведения равны.
     4. Если два выражения по обе стороны от знака равенства разделить на одинаковую величину, то частные равны.

     Следствие 1:

     Из правил 1 и 2 мы можем вывести важный принцип, то есть любой член может быть перенесен с одной стороны знака равенства на другую, просто изменив его знак.

     Например, пусть

     Складывая с обеих сторон, получаем,

     [Правило 1]

     Опять же, вычитая с обеих сторон, получаем

     [Правило 2]

     Таким образом, мы видим, что удаленное с левой стороны выглядит как с правой стороны.Опять же, удаленное с правой стороны выглядит так же, как с левой стороны.

     Следовательно, если получим,

     Это называется транспонированием.

     Следствие 2:

     Знак каждого члена уравнения может быть изменен без нарушения равенства.

     Например, пусть

     [Правило 3]

     Шаги для решения простого уравнения:

     1. При необходимости упростите все скобки, дроби и т. Д.
     2. Перенесите все члены, содержащие переменные, с одной стороны, и все постоянные члены, с другой стороны.
     3. Решите уравнение, полученное на шаге 2, чтобы получить значение его переменной.

     Простые уравнения в различных формах

     Простые уравнения, как правило, бывают трех типов:

     1. Неизвестная величина или переменная с любым коэффициентом равна известной величине (т. Е. Константе). Например, . Общий вид этого типа уравнения:. Корень этого типа уравнения получается делением известной величины на коэффициент неизвестной величины и.
     2. Сумма неизвестной величины с любым коэффициентом и известной величины равна известной величине. Например, . Общая форма этого типа уравнения: При решении уравнения, необходимо транспонировать в правую часть, и уравнение обозначается как. Корень находится делением алгебраической разности известных величин на коэффициент неизвестной величины и составляет.
     3. В уравнениях этого типа есть известные и неизвестные величины с обеих сторон.Например, . Общая форма этого типа уравнения: Чтобы решить простое уравнение этого типа, неизвестные величины должны быть сгруппированы с одной стороны, а известные величины должны быть сгруппированы с другой стороны. Тогда уравнение обозначается как или, а корень определяется путем деления алгебраической разности известных величин на алгебраическую разность коэффициентов неизвестной величины. Вот рут.

     Примечание: Совершенно очевидно, что все простые уравнения сводятся к Типу 1.

     Пример: Решить

     Решение:

     Пример: Решить

     Решение:

     Пример: Если и; найти значение.

     Решение:

     Дано:

     и

     Пример: Решить

     Левая сторона

     Правая сторона

     Следовательно,

     Снимаем с двух сторон имеем,

     Следовательно, путем транспонирования,

     или,

     Таким образом, требуемое значение -4.

     Пример: Решить:

     Поскольку«

     умножив обе части на 12, что является L.C.M знаменателей, мы получим

     или,

     Следовательно, путем транспонирования,

     или,

     или, (разделив обе стороны на -5)

     Таким образом, искомый корень уравнения равен 12.

     Примечание: При решении уравнений, когда обнаружен корень, то есть значение переменной, его можно проверить, поместив это значение переменной в уравнение.Если обнаруживается, что равенство обеих сторон сохраняется, когда мы помещаем это значение переменной в уравнение, то мы можем сделать вывод, что корень правильный.

     Упражнение

     Решите следующие уравнения:

     4. Найдите значение, которое делает два выражения равными друг другу.
     5. Решить для:

     Решение уравнений с одной переменной: TEAS || Зарегистрированныйorg

     Основные термины и терминология, относящиеся к решению уравнений с одной переменной

     • Алгебра: раздел математики, в котором есть хотя бы одно неизвестное число или переменная.
     • Переменная: неизвестное число в алгебраическом уравнении
     • Обратные математические вычисления: Противоположные вычисления
     • Обратный математический расчет для сложения: Вычитание
     • Обратный математический расчет для вычитания: сложение
     • Обратный математический расчет для умножения: Деление
     • Обратный математический расчет для деления: Умножение

     Алгебраические уравнения

     Обозначение алгебраических выражений:

     1 — степень (показатель степени)
     2 — коэффициент
     3 — член
     4 — оператор
     5 — постоянный член
     x y c — переменные / константы

     Проще говоря, алгебра — это раздел математики, в котором есть по крайней мере одно неизвестное число или переменная.

     Переменная в алгебре — это неизвестное число в алгебраическом уравнении. Переменные выражаются любой буквой, но x — это наиболее часто используемая буква переменной, которая используется в алгебре с одной неизвестной переменной, а любые другие буквы используются, когда в алгебраическом уравнении есть более одного неизвестного числа или переменной, например показано на картинке выше. Наиболее часто используемая буква для второй переменной — y, однако, как указано выше, может использоваться любая буква.

     В этом разделе вы узнаете, как решать алгебраические уравнения только с одним неизвестным числом или переменной в алгебраическом уравнении, поэтому в этом разделе мы будем использовать только x в качестве неизвестного числа или переменной в алгебраическом уравнении, хотя любая буква может быть используется, как указано выше.

     Решение алгебраических уравнений

     Процедура решения алгебраических уравнений следующая:

     1. Поместите все неизвестные переменные (x) в левую часть знака равенства (=)
     2. Поместите все константы или известные числа справа от знака равенства (=)
     3. Выполните обратные математические вычисления для всех неизвестных или x, пока только 1 x или x не окажется слева от знака равенства (=)

     Обратные математические вычисления — это противоположные вычисления.

     Например:

     • Обратным математическим вычислением для сложения является вычитание.
     • Обратным математическим вычислением для вычитания является сложение.
     • Обратным математическим вычислением умножения является деление.
     • Обратным математическим вычислением деления является умножение.

     Обратные математические вычисления важны и необходимы в алгебре, но они также полезны при проверке ваших ответов на вычисления сложения, вычитания, умножения и деления.

     Вот несколько примеров того, как вычисления сложения могут быть проверены и проверены с помощью обратного математического вычисления вычитания:

     Расчет сложения:

     24 + 56 = 80

     Обратное вычисление вычитания:

     80–24 = 56

     80–56 = 24

     Расчет сложения:

     2 + 560 = 562

     Обратное вычисление вычитания:

     562 — 2 = 560

     562–560 = 2

     Вот несколько примеров того, как вычисления вычитания могут быть проверены и подтверждены с помощью обратного математического вычисления сложения:

     Расчет вычитания:

     35–27 = 8

     Обратный расчет сложения:

     8 + 27 = 35

     Расчет вычитания:

     55-20 = 35

     Обратный расчет сложения:

     35 + 25 = 55

     Вот несколько примеров того, как вычисления умножения могут быть проверены и проверены с помощью обратного математического вычисления деления:

     Расчет умножения:

     35 х 50 = 1750

     Обратное вычисление деления:

     1750 ÷ 50 = 35

     1750 ÷ 35 = 50

     Расчет умножения:

     2.7 х 8,4 = 22,68

     Обратное вычисление деления:

     22,68 ÷ 2,7 = 8,4

     22,68 ÷ 8,4 = 2,7

     Вот несколько примеров того, как вычисления деления могут быть проверены и проверены с помощью обратного математического вычисления умножения:

     Расчет отдела:

     722 ÷ 4 = 180,5

     Обратное вычисление умножения:

     180,5 x 4 = 722

     Расчет отдела:

     82.6 ÷ 4 = 20,65

     Обратное вычисление умножения:

     20,65 x 4 = 82,6

     Построение и решение алгебраических уравнений

     Вот несколько примеров составления алгебраических уравнений с x в левой части и константами в правой части алгебраического уравнения:

     Пример 1: Постановка и обработка алгебраических уравнений

     11 х + 2 = 46

     • Установите с x слева и константой справа от знака =:

     11 х + 2 = 46

     Пример 2: Постановка и обработка алгебраических уравнений

     х + 30 = 110

     • Установите с x слева и константой справа от знака =:

     х + 30 = 110

     Пример 3: Постановка и обработка алгебраических уравнений

     14-3 = 3 х + 2

     • Установите с x слева и константой справа от знака =:

     3 х + 2 = 14 — 3

     Пример 4: Установка и обработка алгебраических уравнений

     46 -2 = 11 х

     • Установите с x слева и константой справа от знака =:

     11 x = 46 — 2

     Пример 5: Установка и обработка алгебраических уравнений

     33.3 х + 7 = 276

     • Установите с x слева и константой справа от знака =:

     33,3 х + 7 = 276

     Теперь, когда уравнения составлены, как указано выше, пришло время решить уравнение и узнать точное значение неизвестного x. Процедура для этого показана ниже для каждого из пяти приведенных выше уравнений.

     Пример 1: Решение алгебраического уравнения
     

     1. 11 х + 2 = 46
     2. 11 х = 46 — 2
     3. 11 х = 44
     4. х = 44 ÷ 11
     5. х = 4

     Ответ: 4

     Пример 2: Решение алгебраического уравнения

     • х + 30 = 110
     • х = 110-30
     • х = 80

     Ответ: 80

     Пример 3: Решение алгебраического уравнения

     • 3 х + 2 = 14 — 3
     • 3 х = 14 — 3 — 2
     • 3 х = 9
     • х = 9 ÷ 3
     • х = 3

     Ответ: 3

     Пример 4: Решение алгебраического уравнения

     • 11 x = 46 — 2
     • 11 х = 44
     • х = 44 ÷ 11
     • х = 4

     Ответ: 4

     Пример 5: Решение алгебраического уравнения

     • 33.3 х + 7 = 276
     • 33,3 х = 276-7
     • 33,3 х = 269
     • х = 269 ÷ 33,3
     • x = 8,08 с округлением до сотых

     Ответ: 8.08

     Вот несколько примеров выполнения обратных или противоположных вычислений для неизвестных (x) в алгебраическом уравнении:

     Пример 1

     Алгебраическое уравнение: 2 x + 7 = 19

     Решение уравнения с обратными вычислениями:

     Выполните обратный расчет.Вычтем 7 из обеих частей знака равенства (=)

     • 2 х + 7-7 = 19-7
     • 2 х = 12
     • Разделите обе части знака равенства (=) на 2.

     Ответ: x = 6

     Чтобы проверить этот ответ, подставьте 6 вместо каждого x в исходном алгебраическом уравнении, как показано ниже:

     • 2 (6) + 7 = 19
     • 12 + 7 = 19
     • 19 = 19

     Когда числа (19) одинаковы по обе стороны от знака равенства, вычисление x как 6 является правильным.Когда числа различны для каждой стороны знака равенства, расчет неверен и неверен.

     Пример 2

     Алгебраическое уравнение: 2 x — 7 = 19

     Решение уравнения с обратными вычислениями:

     Выполните обратный расчет. Добавьте 7 к обеим сторонам знака равенства (=)

     • 2 х — 7 + 7 = 19 + 7
     • 2 х = 26
     • Разделите обе части знака равенства (=) на 2.

     Ответ: x = 13

     Чтобы проверить этот ответ, подставьте 13 вместо каждого x в исходном алгебраическом уравнении, как показано ниже:

     • 2 х — 7 = 19
     • 2 (13) — 7 = 19
     • 26-7 = 19
     • 19 = 19

     Когда числа (19) одинаковы по обе стороны от знака равенства, вычисление x как 13 является правильным.Когда числа различны для каждой стороны знака равенства, расчет неверен и неверен.

     Упрощенные алгебраические уравнения

     Помимо решения алгебраических уравнений, как вы узнали выше, вы также можете увидеть другие типы алгебраических вычислений на вашем TEAS. Например, вы можете получить упрощенные вычисления алгебры и решение для x с помощью задачи со словом.

     Вас могут спросить, каково решение или ответ для вычисления алгебры, такого как приведенные ниже.

     Пример 1

     Каков ответ на 2 x + 6 x — 2, когда x равно 4?

     • 2 (4) + 6 (4) — 2
     • 8 + 24-2 = 30

     Ответ: 30

     Пример 2

     Каков ответ на 3 x + 2 x + 2, когда x равно 8?

     • 3 (8) + 2 (8) + 2
     • 24 + 16 + 2 = 42

     Ответ: 42

     Пример 3

     Каков ответ на 3 ² x + 2 x + 2, когда x равен 5?

     • 9 (5) + 2 (5) + 2
     • 45 + 10 + 2 = 57

     Ответ: 57

     Пример 4

     Каков ответ на 2 ² x — 2 x / 2, когда x равно 8?

     • 4 (8) — 2 (8) / 2
     • 32-16 ÷ 2
     • 16 ÷ 2 = 8

     Ответ: 8

     Алгебраические задачи со словами

     У вас могут быть проблемы со словами на экзамене TEAS, которые необходимо решить и вычислить с помощью алгебры.

     Самый простой способ определить, нужно ли решать проблему со словами и вычислять ее с помощью алгебры, — это задать вопрос: «Есть ли какие-нибудь неизвестные в этой задаче со словами?» Если ответ на этот вопрос утвердительный, то эту словесную задачу необходимо решить и вычислить с помощью алгебры. Если ответ на этот вопрос отрицательный, то эту словесную задачу НЕ нужно решать и вычислять с помощью алгебры.

     Ниже приведены некоторые алгебраические задачи со словами:

     Задача с алгебраическими словами № 1:

     Сколько вам нужно было бы положить на свой сберегательный счет, чтобы утроить свои деньги на этом счете, если в настоящее время у вас есть 657 долларов.

     Ответ: Вам нужно будет положить 1971 доллар на свой сберегательный счет.

     Задача с алгебраическими словами № 2:

     Что на 5 больше, чем на 2 дюжины?

     • х = 2 (12) + 5
     • х = 24 + 5
     • х = 29

     Ответ: 29 — это 5 больше, чем 2 десятка. Их 12 в одной дюжине.

     Задача с алгебраическими словами № 3:

     Что составляет 2/7 (одна седьмая) веса объекта, когда 3/7 (три седьмых) составляет 68 фунтов? (Этот расчет представляет собой двухэтапный расчет.Сначала вы должны вычислить, что такое 1/7, а затем вы должны вычислить, что составляет 2/7 веса объекта.

     Узнаем, что такое 1/7:

     • 3/7: 68 = 2/7: x
     • 3/7 x = 68 x 2/7
     • 3 х = 68
     • x = 19,43 с округлением до сотых
     • 1/7 веса составляет 19,43 фунта, когда 3/7 веса составляет 68 фунтов
     • Следующий шаг — определить 2/7 веса, когда 1/7 равна 19,43.
     • х = 2 (19,43)
     • х = 38.86

     Ответ: На 2/7 общего веса приходится 38,86 фунта, тогда как общий вес для 3/7 общего веса составляет 68 фунтов.

     ЧИСЛА СВЯЗАННЫХ TEAS И СОДЕРЖАНИЕ АЛГЕБРЫ :

     Alene Burke, RN, MSN

     Alene Burke RN, MSN является национально признанным преподавателем сестринского дела. Она начала свою карьеру учителем начальной школы в Нью-Йорке, а затем поступила в общественный колледж Квинсборо, чтобы получить степень младшего специалиста по медсестринскому делу. Она работала дипломированной медсестрой в отделении интенсивной терапии местной общественной больницы, и в то время она решила стать преподавателем медсестер.Она получила степень бакалавра наук по медсестринскому делу в колледже Excelsior, который входит в состав Университета штата Нью-Йорк, и сразу после его окончания поступила в аспирантуру в университете Адельфи на Лонг-Айленде, штат Нью-Йорк. Она закончила Summa Cum Laude в Адельфи со степенью двойного магистра в области сестринского образования и сестринского администрирования и сразу же получила докторскую степень по сестринскому делу в том же университете. Она является автором сотен курсов для медицинских работников, включая медсестер, работает медсестрой-консультантом в медицинских учреждениях и частных корпорациях, она также является утвержденным поставщиком непрерывного образования для медсестер и других дисциплин, а также была членом Американской ассоциации медсестер. Целевая группа ассоциации по компетентности и обучению членов медсестер.

     Последние сообщения Alene Burke, RN, MSN (посмотреть все)

     Решение алгебраического линейного уравнения с одной переменной, Рон Куртус

     SfC Home> Арифметика> Алгебра>

     Рон Куртус (отредактировано 17 августа 2012 г.)

     Линейное уравнение с одной переменной состоит из чисел или констант и умножений переменной. Стандартная форма такого уравнения — ax + b = 0 , где a и b — константы, а x — переменная.Часто уравнение имеет более сложную форму. Решение уравнения находится, оперируя обеими сторонами уравнения, чтобы привести его к форме, подобной x = −b / a .

     Вопросы, которые могут у вас возникнуть:

     • Как вы оперируете уравнением?
     • Как найти x ?
     • Что произойдет, если уравнение будет иметь более сложную форму?

     Этот урок ответит на эти вопросы.

     ---

     ---

     Правила раствора

     Когда у вас есть линейное уравнение с одной переменной, ваша цель — манипулировать выражениями так, чтобы вы получили переменную x слева от знака равенства и константы справа.Это решение уравнения.

     Например, решение уравнения 4a = 3 — x равно x = 3 — 4a .

     Основное правило

     Основное правило, используемое при решении уравнений алгебры:

     То, что вы делаете слева от знака равенства, вы должны делать справа.

     Если вы добавляете термин с левой стороны, вы должны добавить тот же термин с правой стороны. Если вы умножаете член в левой части, вы должны умножать такой же член в правой части.

     Примеры

     В уравнении 4a = 3 — x вы хотите получить x слева, а остальные элементы — справа. Вы выполняете следующие операции:

     Добавьте x к обеим частям уравнения.

     4a + x = 3 — x + x

     4a + x = 3

     Вычтем 4a из обеих частей уравнения.

     4a — 4a + x = 3 — 4a

     x = 3 — 4a , что является решением уравнения.

     Решение путем объединения одинаковых терминов

     Вы можете решить уравнение типа 2x + 3 = −4x — 7 , получив сначала все члены x в левой части и все постоянные члены в правой части. Затем вы комбинируете похожие термины. Затем вы делите на x , чтобы получить решение.

     Пример

     Рассмотрим уравнение:

     2x + 3 = −4x — 7

     Добавьте 4x с обеих сторон.

     2x + 4x + 3 = −4x + 4x — 7

     Объедините похожие термины.

     6x + 3 = −7

     Вычтем 3 с обеих сторон.

     6x + 3 — 3 = −7 — 3

     Объедините похожие термины.

     6x = −10

     Разделите обе стороны на 6 .

     6x / 6 = −10/6

     Упростите дробь.

     x = −5/3 или x = −1 2/3

     Примечание : Лучше идти пошагово, чем пытаться делать несколько дел одновременно или делать что-то в уме.

     Другой пример

     Рассмотрим уравнение:

     2x / 3 + 3 — x = 2 (x + 2) — 5

     Умножьте, чтобы избавиться от скобок.

     2x / 3 + 3 — x = 2x + 4-5

     2x / 3 + 3 — x = 2x — 1

     Избавьтесь от дроби, умножив обе части на 3.

     3 (2x / 3 + 3 — x) = 3 (2x — 1)

     Умножьте, чтобы избавиться от скобок.

     2x + 9 — 3x = 6x — 3

     Объедините похожие термины.

     9 — х = 6х — 3

     Вычтем 9 с обеих сторон.

     −x = 6x — 12

     Вычтем 6x с обеих сторон.

     −7x = −12

     Разделим на −7 .

     x = 12/7 или x = 1 5/7

     Дробная переменная

     Существуют уравнения, в которых член x является частью знаменателя уравнения. В таком случае вы должны умножить обе части уравнения на член x , чтобы оно не содержало переменных дробей. Точно так же вы хотите удалить любые дроби в уравнении, но умножая их на знаменатель уравнения.

     Пример

     Рассмотрим уравнение:

     2x / (x + 1) = 7/12

     Умножьте обе стороны на (x + 1) .

     2x (x + 1) / (x + 1) = 7 (x + 1) / 12

     Упростим дробь (x + 1) / (x + 1) = 1 .

     2x = 7 (x + 1) / 12

     Умножьте обе стороны на 12 .

     24x = 7 (x + 1)

     Умножьте в соответствии с законом распределения или умножьте, чтобы избавиться от скобок.

     24x = 7x + 7

     Вычтем 7x с обеих сторон.

     24x — 7x = 7x — 7x + 7

     Объедините похожие термины.

     17x = 7

     Разделите на 17 , чтобы получить решение уравнения.

     x = 7/17

     Другой пример

     Рассмотрим уравнение:

     1 / (5x — 3) = 3 / x

     Умножьте обе стороны на (5x — 3) .

     1 = 3 (5x — 3) / x

     Умножьте обе стороны на x .

     x = 3 (5x — 3)

     Обратите внимание на , что иногда эти два шага объединяются и называются «перекрестным умножением» уравнения. Одна из проблем заключается в том, что сокращение может привести к ошибкам. Кроме того, для лучшего понимания лучше знать, что вы делаете и почему.

     Умножить с распределительным законом (убрать скобки).

     x = 15x — 9

     Вычтите 15x с обеих сторон.

     −14 x = −9

     Разделите обе стороны на −14 x .

     x = 9/14

     Сводка

     Линейное уравнение с одной переменной состоит из чисел или констант и умножений переменной. Стандартная форма такого уравнения — ax + b = 0 , где a и b — константы, а x — переменная.Часто уравнение имеет более сложную форму.

     Решение уравнения находится, оперируя уравнением, чтобы привести его к форме, подобной x = −b / a . Другими словами, вам нужно только x в левой части, а остальные элементы в правой части уравнения. Правило: то, что вы делаете с левой стороны, вы делаете с правой стороны.

     ---

     Пошаговая инструкция

     ---

     Ресурсы и ссылки

     Полномочия Рона Куртуса

     Сайтов

     Ресурсы по алгебре

     Книги

     (Примечание: Школа чемпионов может получать комиссионные от покупки книг)

     Книги по алгебре с самым высоким рейтингом

     ---

     Вопросы и комментарии

     Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.