Содержание
Простейшие тригонометрические уравнения с косинусом и синусом. Часть 1
Ключ к решению простейших тригонометрических уравнений – в отличном знании тригонометрического круга. Если вы знаете значения стандартных точек и их синусы и косинусы, то проблем с уравнениями не будет. А если пробелы все-таки есть, то восполнить их можно в статье «Как запомнить тригонометрический круг?».
Эта статья состоит из двух частей:
Решение простейших уравнений с косинусом
Решение простейших уравнений с синусом
Алгоритм решения простейших уравнений с косинусом
Любой алгоритм проще всего понять на конкретных примерах, поэтому сразу с них и начнем.
Пример №1. Решить уравнение \(\cosx=\frac{1}{2}\).
Шаг 1. Построить окружность и оси синусов и косинусов.
Шаг 2. Отметить на оси косинусов значение, которому косинус должен быть равен.
Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Шаг 4. Найти по одному значению для каждой из полученных точек на круге. Для уравнений с косинусом значения в верхней и нижней точках всегда будут отличаться только знаком.
Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn,n∈Z\) (подробнее о формуле в этом видео), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.
Возможно, у вас возник вопрос, почему мы в ответ добавляем \(+2πn\), \(n∈Z\). Дело в том, что у каждой точки на тригонометрическом круге есть множество значений, и каждое значение будет решением уравнения, а значит все они обязательно должны быть в ответе.
Но проблема в том, что значений этих бесконечно много, и просто в строчку их не запишешь. Поэтому и придумали такую формулу записи, в которой содержатся все значения одной точки на тригонометрическом круге (подробнее смотрите в этом и этом видео).
Поэтому и придумали такую формулу записи, в которой содержатся все значения одной точки на тригонометрическом круге (подробнее смотрите в этом и этом видео).
Пример №2. Решить уравнение \(\cosx=-\frac{\sqrt{3}}{2}\).
С 1-3 шагом всё понятно, а вот над 4 шагом надо подумать. Как найти значения полученных точек? Можно заметить, что дуга между точкой со значением \(π\) и найденной точкой равняется π/6 (см. картинку ниже). И чтоб из точки π прийти к верхней найденной точке надо пройти в отрицательную сторону расстояние \(\frac{π}{6}\), то есть значение верхней точки равно \(π-\frac{π}{6}=\frac{5π}{6}\). Значит значение нижней \(-\frac{5π}{6}\).
Пример №3. Решить уравнение \(\cosx=1\).
Видно, что в этом случае у косинуса только одна точка на круге будет решением, и эта точка совпадает с нулём на окружности. Т.е. по формуле получим \(x=0+2πn\), \(n∈Z\). Однако добавление нуля ничего не меняет, поэтому ответ можно записать проще: \(x=2πn\), \(n∈Z\).
Т.е. по формуле получим \(x=0+2πn\), \(n∈Z\). Однако добавление нуля ничего не меняет, поэтому ответ можно записать проще: \(x=2πn\), \(n∈Z\).
Пример №4. Решить уравнение \(\cosx=-\frac{7}{6}\).
Значения косинуса (как и синуса) для любого аргумента всегда лежат между \(-1\) и \(1\) включительно, поэтому равняться \(-\frac{7}{6}\) косинус никак не может. Значит такое уравнение не имеет решений.
Вот так решаются простейшие тригонометрические уравнения вида \(\cosx=a\). Для наглядности мы все рассказанное выше объединили на одной инфографике — взглянув на нее вы сразу вспомните суть. Пользуйтесь на здоровье.
Алгоритм решения простейших уравнений с синусом
Пример №5. Решить уравнение \(\sinx=\frac{\sqrt{3}}{2}\).
Шаг 1. Построить окружность и оси синусов и косинусов.
Шаг 2. Отметить на оси синусов, значение, которому синус должен быть равен.
Отметить на оси синусов, значение, которому синус должен быть равен.
Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Шаг 4. Найти по одному значению каждой из полученных точек на круге. Для уравнений с синусом значение второй точки можно найти, если вычесть из π значение первой точки.
Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn\), \(n∈Z\), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.
Пример №6. Решить уравнение \(\sinx=-\frac{\sqrt{2}}{2}\).
Так как суть, думаю, вам уже ясна, дальнейшие объяснения мы опускаем.
Пример №7. Решить уравнение \(\sinx=0\). {n}}\cdot 1+\pi n,~n\in Z\)
{n}}\cdot 1+\pi n,~n\in Z\)
Так как \( \displaystyle \sin \left( \frac{\pi }{2} \right)=1\)
Но ты же внимательно читал мои пространные рассуждения, не так ли? И ты ведь не напишешь такую чушь? И ты понял, в чем здесь подвох?
А подвох вот в чем:
\( \displaystyle \frac{\pi }{2}\approx \frac{3,14}{2}>1\)
А мы помним, что если правая часть тригонометрического уравнения больше \( \displaystyle 1\) (или меньше \( \displaystyle -1\)), то такое уравнение решений не имеет в принципе!!
Второе рассуждение тем более ересь: \( \displaystyle \arcsin \left( \frac{\pi }{2} \right)\) надо понимать как угол, синус которого равен \( \displaystyle \frac{\pi }{2}\).
А ну-ка попытайся в таблице найти такой угол, синус которого равен \( \displaystyle \frac{\pi }{2}\)?!
Не нашёл? То-то же!
В общем, из того, что \( \displaystyle \sin \left( \frac{\pi }{2} \right)=1\) никак не следует, что и \( \displaystyle \arcsin \left( \frac{\pi }{2} \right)=1\)!!
Из этого только следует, что \( \displaystyle \arcsin 1=\frac{\pi }{2}\)!
4. {n+1}}\arcsin \left( 0,1 \right)+\pi n,~n\in Z\)
{n+1}}\arcsin \left( 0,1 \right)+\pi n,~n\in Z\)
5. \( \displaystyle cos\left( x \right)=1\)
И снова по определению (теперь для уравнения другого вида)
\( \displaystyle x=\pm arccos1+2\pi n,~n\in Z\)
Чему равен угол, косинус которого равен \( \displaystyle 1\)?
Этот угол равен\( \displaystyle 0\)!
\( \displaystyle x=\pm 0+2\pi n,~n\in Z\)
Тогда нет смысла прибавлять или вычитать ноль, всё равно это ноль.
\( \displaystyle x=2\pi n,~n\in Z\)
Получили формулу, которая есть в таблице решений тригонометрических уравнений!
Ответ: \( \displaystyle x=2\pi n,~n\in Z\)
6. \( \displaystyle cos\left( x \right)=-\frac{1}{\sqrt{2}}\)
По определению:
\( \displaystyle x=\pm \arccos \left( -\frac{1}{\sqrt{2}} \right)+2\pi n,~n\in Z\)
Прежде всего вынесем «минус» по правилам для арккосинуса:
\( \displaystyle x=\pm \left( \pi -\arccos \left( \frac{1}{\sqrt{2}} \right) \right)+2\pi n,~n\in Z\)
Вот так и никак иначе выносится минус, запомни это!
Теперь арккосинус.
Не во всех таблицах есть значение \( \displaystyle \frac{1}{\sqrt{2}}\), но во всех есть \( \displaystyle \frac{\sqrt{2}}{2}\)!!!
А теперь, внимание, ловкость рук и никакого мошенничества!
\( \displaystyle \frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{\sqrt{2}\cdot \sqrt{2}}=\frac{\sqrt{2}}{2}\)
Единица деленная на корень из двух равно корень из двух деленное на два!
Я не зря выделил это замечание жирным шрифтом, запомни это тождество хорошенько! Оно спасёт тебя в очень многих случаях!!
Итак, чему же равен угол, косинус которого равен \( \displaystyle \frac{1}{\sqrt{2}}\)(или одно и то же \( \displaystyle \frac{\sqrt{2}}{2}\))?
Верно, это угол \( \displaystyle \frac{\pi }{4}\).
Тогда:
\( \displaystyle x=\pm \left( \pi -\text{ }\!\!~\!\!\text{ }\frac{\pi }{4} \right)+2\pi n,~n\)
\( \displaystyle x=\pm \left( \frac{4\pi }{4}-\text{ }\!\!~\!\!\text{ }\frac{\pi }{4} \right)+2\pi n,~n\in Z\)
\( \displaystyle x=\pm \frac{3\pi }{4}+2\pi n,~n\in Z\)
Ответ: \( \displaystyle x=\pm \frac{3\pi }{4}+2\pi n,~n\in Z\)
7._1-228x228.jpg) \( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
\( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
\( \displaystyle cos\left( x \right)=\frac{\pi }{4}\)
Ещё один пример-обманка! Хотя данное уравнение решения имеет, ибо:
\( \displaystyle \frac{\pi }{4}=\frac{3,14}{4}<1\)
Тогда по определению:
\( \displaystyle x=\pm \arccos \left( \frac{\pi }{4} \right)+2\pi n,~n\in Z\)
Но из этого никак не следует, что \( \displaystyle \arccos \left( \frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)=\frac{\sqrt{2}}{2}\)!!!!!!
Запомни, арккосинус – это угол, его аргумент (начинка) – это число, а выход – угол!!!
Ты когда-нибудь встречал в своей практике такой странный угол как \( \displaystyle \frac{\sqrt{2}}{2}\)?!
Вот и я нет.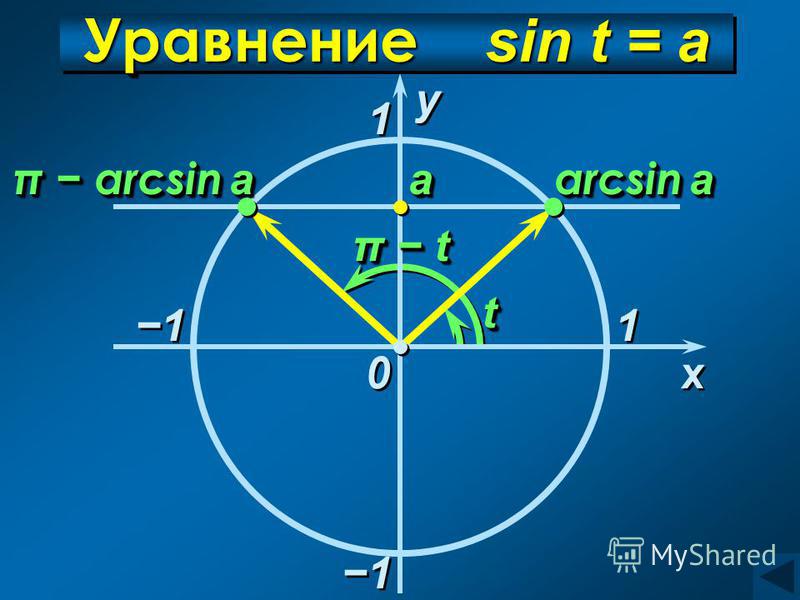 Поэтому оставим как есть!
Поэтому оставим как есть!
Ответ: \( \displaystyle x=\pm \arccos \left( \frac{\pi }{4} \right)+2\pi n,~n\in Z\)
8. \( \displaystyle cos\left( x \right)=-\sqrt{2}\)
Всё просто: \( \displaystyle -\sqrt{2}<-1\)
… и решений данное уравнение не имеет.
9. \( \displaystyle tg\left( x \right)=\sqrt{2}\)
Запишем по определению:
\( \displaystyle x=arctg\sqrt{2}+\pi n,~n\in Z\)
\( \displaystyle arctg\sqrt{2}\) – не табличное значение, поэтому ответ сохраняем неизменным.
Обрати внимание, что в отличие от уравнений с синусом и косинусом, здесь мне не уже важно, какое у меня число стоит в правой части уравнения.
10. \( \displaystyle ctg\left( x \right)=-\sqrt{3}\)
Снова по определению:
\( \displaystyle x=arсctg\left( -\sqrt{3} \right)+\pi n,~n\in Z\)
Без проблем выносим минус из арккотангенса:
\( \displaystyle x=\pi-arcctg\left( \sqrt{3} \right)+\pi n,~n\in Z\)
Вычисляем: котангенс какого угла равен \( \displaystyle \sqrt{3}\)?
Это угол \( \displaystyle \frac{\pi }{6}\).
Ответ: \( \displaystyle x=\pi-\frac{\pi }{6}+\pi n = \frac{5\pi}{6}+\pi n,~n\in Z\).
11. \( \displaystyle ctg\left( x \right)=1\)
По формуле: \( \displaystyle x=arcctg1+\pi n,~n\in Z\).
Котангенс какого угла равен \( \displaystyle 1\)?
Это угол \( \displaystyle \frac{\pi }{4}\).
Ответ: \( \displaystyle x=\frac{\pi }{4}+\pi n,~n\in Z\).
Ну как, материал не кажется тебе слишком сложным? Я надеюсь, что нет. Теперь давай порешаем для закрепления чуть более сложные задачки.
Тригонометрические уравнения | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
Ну что, перечисляем обе серии (1) и (2) в ответе через запятую? Нет! Серия (2) является в данном случае частью серии (1). Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).
Поэтому ответ:
3. Бывает, что перед разложением суммы или разности тригонометрических функций в произведение надо проделать обратную процедуру: превратить произведение в сумму (разность).
Решим уравнение:
Домножаем обе части на 2, преобразуем левую часть в разность косинусов, а правую часть — в сумму косинусов:
Ответ:
4. Ещё пример, где финальное разложение на множители поначалу замаскировано:
Здесь используем формулу понижения степени:
(которая является ни чем иным, как переписанной в другом виде формулой косинуса двойного
угла). Получаем:
и дальше ясно.
5. Многие оказываются в ступоре при виде следующего уравнения:
Переносим косинус влево и применяем формулу приведения
Дальше — дело техники.
6. А в этом примере нужны совсем другие манипуляции:
Раскладываем синус двойного угла, всё собираем в левой части и группируем:
Цель достигнута.
Рассмотрим уравнение:
Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене
степень каждого слагаемого равна двум (степень одночлена — это сумма степеней входящих в него сомножителей).
Поскольку степени всех слагаемых одинаковы, такое уравнение называют однородным. Для однородных уравнений существует стандартный приём решения — деление обеих его частей на . Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?
Следующий абзац предлагаем выучить наизусть и всегда прописывать его при решении однородных уравнений.
Предположим, что . Тогда в силу уравнения и , что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию , и мы можем поделить обе его части на .
В результате деления приходим к равносильному квадратному уравнению относительно тангенса:
и дальнейший ход решения трудностей не представляет
1. Рассмотрим уравнение
Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение :
и дело сделано.
2. Неожиданным образом сводится к однородному следующее уравнение:
Казалось бы, где тут однородность? Переходим к половинному углу!
откуда
| (3) |
Мы не случайно довели это уравнение до ответа. В следующем разделе оно будет решено другим методом, и ответ окажется внешне непохожим на этот.
Введение дополнительного угла
Этот метод применяется для уравнений вида . Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.
1. Рассмотрим уравнение
Делим обе части на 2:
Замечаем, что :
В левой части получили синус суммы:
,
откуда и
2. Другой пример:
Делим обе части на
Сделаем теперь для разнообразия в левой части косинус разности:
3. Рассмотрим теперь общий случай — уравнение
Делим обе части на :
| (4) |
Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:
Легко видеть, что сумма их квадратов равна единице:
Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла :
Соотношение (4) тогда приобретает вид:
,
или
Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол .
4. Снова решим уравнение
Делим обе части на :
Существует угол такой, что . Например, . Получаем:
,
,
,
,
В предыдущем разделе мы решили это уравнение, сведя его к однородному, и получили в качестве ответа выражение (3). Сравните с полученным только что выражением. А ведь это одно и то же множество решений!
Универсальная подстановка
Запомним две важные формулы:
Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной подстановки. Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.
Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.
1. Решим уравнение
Выражаем , используя универсальную подстановку:
Делаем замену :
Получаем кубическое уравнение:
Оно имеет единственный корень . Стало быть, , откуда .
Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало .
2. Рассмотрим уравнение
А вот здесь использование универсальной подстановки сужает ОДЗ. Поэтому сначала непосредственно подставляем в уравнение и убеждаемся, что это — решение.
Теперь обозначаем и применяем универсальную подстановку:
После простых алгебраических преобразований приходим к уравнению:
Следовательно, и .
Ответ: .
Метод оценок
В некоторых уравнениях на помощь приходят оценки .
3. Рассмотрим уравнение
Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в
том случае, когда они равны единице одновременно:
Таким образом, должны одновременно выполняться следующие равенства:
Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем:
Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем:
Умножаем обе части на 90 и сокращаем на π:
Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где. Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.
Искать k, в принципе, уже не нужно. Сразу находим x:
Ответ: .
4. Рассмотрим уравнение
Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.
Лучше поступить по-другому: умножим обе части на 2 и преобразуем левую часть в разность косинусов:
Тем самым мы сокращаем работу вдвое, получая лишь одну систему:
Имеем:
Ищем пересечение:
Умножаем на 21 и сокращаем на π:
Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.
Ответ: решений нет.
5. Страшное с виду уравнение
также решается методом оценок. В самом деле, из неравенств следует, что . Следовательно, , причём равенство возможно в том и только в том случае, когда
Остаётся решить полученную систему. Это не сложно.
Учёт тригонометрических неравенств
Рассмотрим уравнение:
Перепишем его в виде, пригодном для возведения в квадрат:
Тогда наше уравнение равносильно системе:
Решаем уравнение системы:
,
,
Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:
Теперь нужно произвести отбор решений в соответствии с неравенством . Серия не удовлетворяет этому неравенству, а серия удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия .
Ответ: .
Специальные приёмы
В этом разделе рассматриваются некоторые типы уравнений, приёмы решения которых нужно знать обязательно.
1. Рассмотрим уравнение
Это сравнительно редкий случай, когда используется исходная формула косинуса двойного угла:
,
,
,
Каждое из уравнений полученной совокупности мы решать умеем.
2. Теперь рассмотрим такое уравнение:
Метод решения будет совсем другим. Сделаем замену . Как выразить через t? Имеем:
,
откуда . Получаем:
,
,
,
Как действовать дальше, мы знаем.
3. Надо обязательно помнить формулы косинуса и синуса тройного угла (чтобы не изобретать их на экзамене):
,
Вот, например, уравнение:
Оно сводится к уравнению относительно :
,
,
Дальше всё понятно.
4. Как бороться с суммой четвёртых степеней синуса и косинуса? Рассмотрим уравнение
Выделяем полный квадрат!
,
,
,
,
,
,
5. А как быть с суммой шестых степеней? Рассмотрим такое уравнение:
Раскладываем левую часть на множители как сумму кубов: .
Получим:
,
С суммой четвёртых степеней вы уже умеете обращаться.
Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.
Знать их нужно обязательно, это — необходимая база.
В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.
решить уравнение sin 7x/2 sin x/2 + cos 7x/2 cos x/2 = cos23x
Записи с меткой «решить уравнение sin 7x/2 sin x/2 + cos 7x/2 cos x/2 = cos23x»
Пример 1.
а) Решить уравнение cos4x+cos2x=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [-π; π/3].
Решение.
а) Решаем уравнение cos4x+cos2x=0.
Применим формулу
Tогда данное уравнение примет вид: 2cos3x⋅cosx=0. Отсюда следует, что либо cos3x=0 либо cosx=0.
- Если cos3x=0, то 3х=π/2+πn, отсюда х=π/6+πn/3, где nϵZ.
- Если cosx=0, то х=π/2+πn, где nϵZ.
Заметим, что решения уравнения cosx=0 входят в решения уравнения cos3x=0, поэтому общим решением данного уравнения будут числа x=π/6+πn/3, где nϵZ.
б) Найдём все корни этого уравнения, принадлежащие отрезку [-π; π/3].
Рассмотрим общее решение x=π/6+πn/3, где nϵZ на единичной окружности. Здесь значение πn/3 означает, что нужно брать n раз угол π/3. Отмечаем угол π/6, а затем углы, полученные поворотом угла π/6 на π/3, полученный таким образом угол π/2 опять повернём на π/3, получится угол 5π/6, затем угол 5π/6+ π/3=7π/6, следующий угол
7π/6+ π/3=9π/6=3π/2, и, наконец, 3π/2+ π/3=11π/6. Смотрите рисунок 1.
Все отмеченные углы рассмотрим на отрезке [-π; π/3]. Смотрим рисунок 2. Получились числа -5π/6; -π/2; -π/6; π/6.
Ответ: а) π/6+πn/3, где nϵZ; б) -5π/6; -π/2; -π/6; π/6.
Пример 2.
а) Решить уравнение cos4x-sin2x=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [0; π].
Решение.
а) Применим формулу 1-cos2α=2sin2α; тогда данное уравнение примет вид:
1-2sin22x-sin2x=0; 2sin22x+sin2x-1=0. Сделаем замену: sin2x=t.
Сделаем замену: sin2x=t.
Получаем равенство: 2t2+t-1=0.
У нас a-b+c=0, поэтому по методу коэффициентов t1=-1, t2=1/2.
- При sin2x=-1 получаем 2х=-π/2+2πn, отсюда х=-π/4+πn, где nϵZ.
- При sin2x=1/2 получаем 2х=π/6+2πn и 2х=5π/6+2πn, где nϵZ.
Тогда х=π/12+πn и х=5π/12+πn, где nϵZ.
Рассмотрим решения 2х=-π/2+2πn, 2х=π/6+2πn и 2х=5π/6+2πn на единичной окружности. Возьмём значения 2х при n=0. Углы -π/2, π/6 и 5π/6 отличаются друг от друга на значение 2π/3. Тогда общим решением будут являться числа
2х=π/6+(2π/3)n, отсюда общим решением данного уравнения будут
значения х=π/12+(π/3)n, где nϵZ.
б) Найдём все корни этого уравнения, принадлежащие отрезку [0; π]. Для этого в общее решение х=π/12+(π/3)n, где nϵZ будем подставлять такие целые значения nϵZ,
чтобы хϵ[0; π].
Возьмём n=0, тогда х=π/12 ϵ[0; π].
При n=1 получим х= π/12+π/3= π/12+4π/12=5π/12 ϵ[0; π].
При n=2 получим х= π/12+2π/3= π/12+8π/12=9π/12=3π/4 ϵ[0; π].
При n=3 получим х= π/12+π, и это значение не входит в заданный отрезок [0; π].
Ответ: а) π/12+(π/3)n, где nϵZ; б) π/12, 5π/12, 3π/4.
Пример 3.
а) Решить уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 3π/2].
Решение.
а) Применим формулу cos(α-β)=cosα∙cosβ+sinα∙sinβ; тогда данное уравнение примет вид:
cos3x=cos23x; cos23x-cos3x=0; cos3x(cos3x-1)=0;
cos3x=0 или cos3x-1=0.
- Если cos3x=0, то 3х=π/2+πn, тогда х= π/6+(π/3)n, где nϵZ.
- Если cos3x-1=0, то cos3x=1, тогда 3х=2πm, тогда х=(2π/3)m, где mϵZ.
Общие решения данного уравнения: х=π/6+(π/3)n, где nϵZ и х=(2π/3)m, где mϵZ.
б) Найдём все корни этого уравнения, принадлежащие отрезку [π; 3π/2].
Мы получили значения 3х=π/2+πn и 3х=2πm. Отметим их на единичной окружности, сделав замену 3х=t. Смотрите рисунок 3.
Необходимо выполнение условие хϵ[π; 3π/2]. 3
3
 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)
ЕГЭ. Задание 13. Тригонометрические (и не только) уравнения
Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по тригонометрии, большие теоретические видеолекции, видеоразборы задач и подборка заданий прошлых лет.
Полезные материалы
Подборки видео и онлайн-курсы
Тригонометрические формулы
Геометрическая иллюстрация тригонометрических формул
Арк-функции. Простейшие тригонометрические уравнения
Тригонометрические уравнения
а) Решите уравнение $\sin x + \left(\cos \dfrac{x}{2} — \sin \dfrac{x}{2}\right)\left(\cos \dfrac{x}{2} + \sin \dfrac{x}{2}\right) = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\pi; \dfrac{5\pi}{2}\right]$.
а) Решите уравнение $\log_4 (\sin x + \sin 2x + 16) = 2$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$.
Подборка заданий прошлых лет
- а) Решите уравнение $\dfrac{\sin x}{\sin^2\dfrac{x}{2}} = 4\cos^2\dfrac{x}{2}$.
 2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
2 x + \sin x = \sqrt2 \sin\left( x + \dfrac{\pi}{4} \right)$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2 \sin\left( 2x + \dfrac{\pi}{3} \right) — \sqrt{3} \sin x = \sin 2x + \sqrt3$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2\sqrt3 \sin\left( x + \dfrac{\pi}{3} \right) — \cos 2x = 3\cos x — 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2\sin\left( 2x + \dfrac{\pi}{6} \right) — \cos x = \sqrt3\sin 2x — 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2}; 4\pi \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $\sqrt2\sin\left( \dfrac{\pi}{4} + x \right) + \cos 2x = \sin x — 1$.
 2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -5\pi; \ — \dfrac{7\pi}{2}\right]$. (ЕГЭ-2012, вторая волна)
Уравнение синус-Гордона
Уравнение синус-Гордона — это нелинейное гиперболическое уравнение в частных производных в 1 + 1 измерениях, включающее в себя оператор Даламбера и синус неизвестной функции. Изначально оно было рассмотрено в XIX веке в связи с изучением поверхностей постоянной отрицательной кривизны. Это уравнение привлекло много внимания в 1970-х из-за наличия у него солитонных решений.
Происхождение уравнения и его названия
Существует две эквивалентные формы уравнения синус-Гордона. В (вещественных) координатах пространство-время, обозначенных (x, t), уравнение имеет вид:
φ t t − φ x x + sin φ = 0. {displaystyle varphi _{tt}-varphi _{xx}+sin varphi =0.}
{displaystyle varphi _{tt}-varphi _{xx}+sin varphi =0.}
При переходе к координатам светового конуса (u, v), близким к асимптотическим координатам, где
u = x + t 2 , v = x − t 2 , {displaystyle u={frac {x+t}{2}},quad v={frac {x-t}{2}},}
уравнение принимает вид:
φ u v = sin φ . {displaystyle varphi _{uv}=sin varphi .}
Это исходная форма уравнения синус-Гордона, в которой оно было рассмотрено в XIX веке в связи с изучением поверхностей постоянной гауссовой кривизны K = −1, также называемых псевдосферами. {2},}
{2},}
где φ — угол между асимптотическими линиями, и для второй квадратичной формы, L = N = 0. Тогда уравнение Петерсона ― Кодацци, отражающее условие совместимости между первой и второй квадратичными формами, приводит к уравнению синус-Гордона. Изучение этого уравнения и соответствующих преобразований псевдосфер в XIX веке Бьянки и Бэклундом привели к открытию преобразований Бэклунда.
Название «уравнение синус-Гордона» — каламбур на тему хорошо известного в физике уравнения Клейна — Гордона:
φ t t − φ x x + φ = 0. {displaystyle varphi _{tt}-varphi _{xx}+varphi =0.}
Уравнение синус-Гордона является уравнением Эйлера — Лагранжа для лагранжиана
L sine–Gordon ( φ ) := 1 2 ( φ t 2 − φ x 2 ) − 1 + cos φ . {n}}{(2n)!}}}
{n}}{(2n)!}}}
в данном лагранжиане, он может быть записан как лагранжиан Клейна — Гордона плюс члены более высокого порядка
L sine–Gordon ( φ ) = 1 2 ( φ t 2 − φ x 2 ) − φ 2 2 + ∑ n = 2 ∞ ( − φ 2 ) n ( 2 n ) ! = 2 L Klein–Gordon ( φ ) + ∑ n = 2 ∞ ( − φ 2 ) n ( 2 n ) ! . {2}}}.}
{2}}}.}
односолитонное решение, для которого мы выбрали положительный корень для γ {displaystyle gamma } , называется кинк и представляет виток по переменной φ {displaystyle varphi } , который переводит одно решение φ = 0 {displaystyle varphi =0} в смежное φ = 2 π {displaystyle varphi =2pi } . Состояния φ = 0 ( mod 2 π ) {displaystyle varphi =0({ extrm {mod}}2pi )} известны как вакуумные, так как они постоянные решения нулевой энергии. Односолитонное решение, в котором мы взяли отрицательный корень для γ {displaystyle gamma } , называется антикинк. Форма односолитонных решений может быть получена посредством применения преобразования Бэклунда к тривиальному (постоянному вакуумному) решению и интегрированию получившихся дифференциальных уравнений первого порядка:
φ ′ u = φ u + 2 β sin ( φ ′ + φ 2 ) , {displaystyle {varphi ^{prime }}_{u}=varphi _{u}+2eta sin left({frac {varphi ^{prime }+varphi }{2}}
ight),} φ ′ v = − φ v + 2 β sin ( φ ′ − φ 2 ) with φ = φ 0 = 0 {displaystyle {varphi ^{prime }}_{v}=-varphi _{v}+{frac {2}{eta }}sin left({frac {varphi ^{prime }-varphi }{2}}
ight){ ext{ with }}varphi =varphi _{0}=0}
Односолитонные решения могут быть визуализированы посредством синус-гордоновской модели упругой ленты. Примем виток упругой ленты по часовой стрелке (левовинтовой) за кинк с топологическим зарядом ϑ K = − 1 {displaystyle vartheta _{ extrm {K}}=-1} . Альтернативный виток против часовой стрелки (правовинтовой) с топологическим зарядом ϑ AK = + 1 {displaystyle vartheta _{ extrm {AK}}=+1} будет антикинком.
Примем виток упругой ленты по часовой стрелке (левовинтовой) за кинк с топологическим зарядом ϑ K = − 1 {displaystyle vartheta _{ extrm {K}}=-1} . Альтернативный виток против часовой стрелки (правовинтовой) с топологическим зарядом ϑ AK = + 1 {displaystyle vartheta _{ extrm {AK}}=+1} будет антикинком.
Двухсолитонные решения
Многосолитонные решения могут быть получены посредством непрерывного применения преобразования Бэклунда к односолитонному решению, как предписывается решёткой Бьянки, соответствующей результатам преобразования. 2-солитонные решения уравнения синус-Гордона проявляют некоторые характерные свойства солитонов. Бегущие синус-гордоновские кинки и/или антикинки проходят сквозь друг друга как полностью проницаемые, и единственный наблюдаемый эффект — фазовый сдвиг. Так как сталкивающиеся солитоны сохраняют свою скорость и форму, такой вид взаимодействия называется упругим столкновением.
Так как сталкивающиеся солитоны сохраняют свою скорость и форму, такой вид взаимодействия называется упругим столкновением.
Другие интересные двухсолитонные решения возникают из возможности спаренного кинк-антикинкового поведения, известного как бризер. Известно три типа бризеров: стоячий бризер, бегущий высокоамплитудный бризер и бегущий малоамплитудный бризер.
Трёхсолитонные решения
Трёхсолитонные столкновения между бегущим кинком и стоячим бризером или бегущим антикинком и стоячим бризером приводят к фазовому сдвигу стоячего бризера. В процессе столкновения между движущимся кинком и стоячим бризером сдвиг последнего Δ B {displaystyle Delta _{ extrm {B}}} даётся соотношением:
Δ B = 2 arctanh ( 1 − ω 2 ) ( 1 − v K 2 ) 1 − ω 2 {displaystyle Delta _{B}={frac {2{ extrm {arctanh}}{sqrt {(1-omega ^{2})(1-v_{ ext{K}}^{2})}}}{sqrt {1-omega ^{2}}}}}
где v K {displaystyle v_{ ext{K}}} — скорость кинка, а ω {displaystyle omega } — частота бризера. Если координата стоячего бризера до столкновения — x 0 {displaystyle x_{0}} , то после столкновения она станет x 0 + Δ B {displaystyle x_{0}+Delta _{ ext{B}}} .
Если координата стоячего бризера до столкновения — x 0 {displaystyle x_{0}} , то после столкновения она станет x 0 + Δ B {displaystyle x_{0}+Delta _{ ext{B}}} .
Связанные уравнения
Уранение cинус-Гордона:
φ x x − φ t t = sinh φ . {displaystyle varphi _{xx}-varphi _{tt}=sinh varphi .}
Это уравнения Эйлера — Лагранжа для лагранжиана
L = 1 2 ( φ t 2 − φ x 2 ) − cosh φ .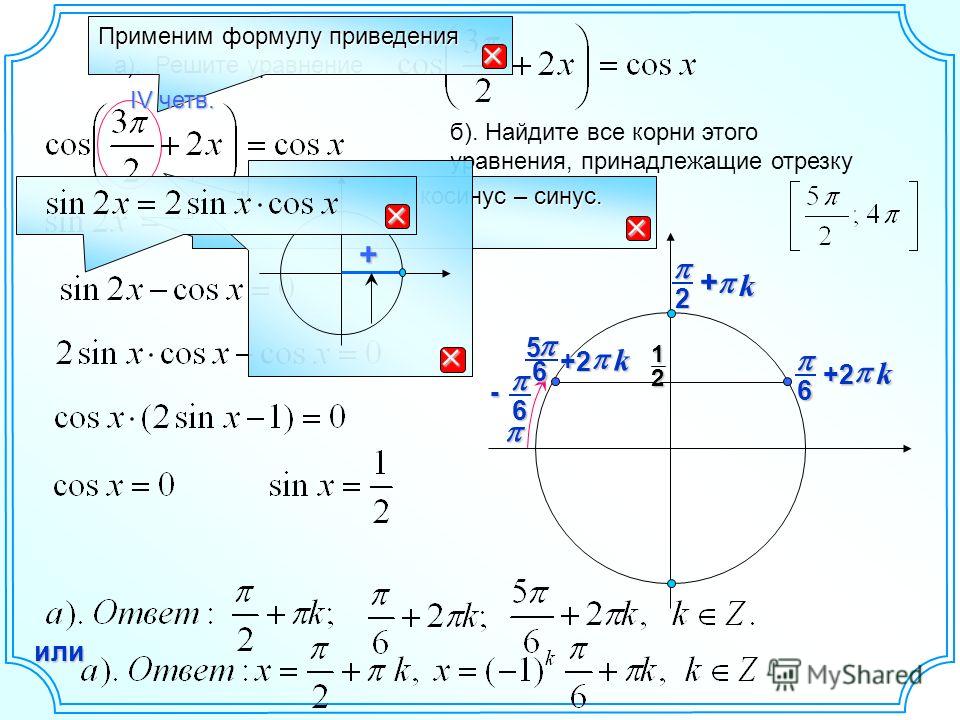 {2})-cosh varphi .}
{2})-cosh varphi .}
Другое тесно связанное с уравнением синус-Гордона — это эллиптическое уравнение синус-Гордона:
φ x x + φ y y = sin φ , {displaystyle varphi _{xx}+varphi _{yy}=sin varphi ,}
где φ {displaystyle varphi } — функция переменных x и y. Это уже не солитонное уравнение, но оно имеет много похожих свойств, так как оно связано с уравнением синус-Гордона аналитическим продолжением (или поворотом Вика) y = it.
Эллиптическое уранение шинус-Гордона может быть определено аналогичным образом. Обобщение даётся теорией поля Тоды.
Квантовая версия
В квантовой теории поля модель синус-Гордона содержит параметр, который может быть отождествлён с постоянной Планка. Спектр частиц состоит из солитона, антисолитона и конечного (возможно, нулевого) числа бризеров. Число бризеров зависит от данного параметра. Множественные рождения частиц сокращаются на уравнениях движения. Квазиклассическое квантование модели синус-Гордона было осуществлено Людвигом Фаддеевым и Владимиром Корепиным, см. Physics Reports том 42(1), стр. 1-87, июнь 1978. Точная квантовая матрица рассеяния была открыта Александром и Алексеем Замолодчиковыми. Данная модель s-дуальна модели Тирринга.
Спектр частиц состоит из солитона, антисолитона и конечного (возможно, нулевого) числа бризеров. Число бризеров зависит от данного параметра. Множественные рождения частиц сокращаются на уравнениях движения. Квазиклассическое квантование модели синус-Гордона было осуществлено Людвигом Фаддеевым и Владимиром Корепиным, см. Physics Reports том 42(1), стр. 1-87, июнь 1978. Точная квантовая матрица рассеяния была открыта Александром и Алексеем Замолодчиковыми. Данная модель s-дуальна модели Тирринга.
В конечном объёме и на луче
Также рассматривают модель синус-Гордона на круге, отрезке прямой или луче. Возможно подобрать граничные условия, которые сохраняют интегрируемость данной модели. На луче спектр частиц содержит пограничные состояния кроме солитонов и бризеров.
Суперсимметричная модель синуса-Гордона
Суперсимметричный аналог модели синус-Гордона также существует. С таким же успехом для него могут быть найдены сохраняющие интегрируемость граничные условия.
Амплитуда, период, фазовый сдвиг и частота
Некоторые функции (например, синус и косинус) повторяются вечно
и называются периодическими функциями .
Период переходит от одного пика к следующему (или от любой точки до следующей точки совпадения):
Амплитуда — это высота от центральной линии до пика (или до впадины). Или мы можем измерить высоту от самой высокой до самой низкой точки и разделить ее на 2.
Phase Shift показывает, насколько функция сдвинута на горизонтально на от обычного положения.
Вертикальный сдвиг показывает, насколько функция сдвинута на вертикально на от обычного положения.
Теперь все вместе!
Мы можем получить все в одном уравнении:
y = грех (B (x + C)) + D
- амплитуда А
- период 2π / B
- фазовый сдвиг C (положительный — слева )
- вертикальное смещение D
А вот как это выглядит на графике:
Обратите внимание, что здесь мы используем радианы, а не градусы, а полный оборот равен 2π радианам.
Пример: sin (x)
Это основная неизмененная формула синуса. A = 1, B = 1, C = 0 и D = 0
Итак, амплитуда 1 , период 2π , нет сдвига фазы или вертикального сдвига:
Пример: 2 sin (4 (x — 0,5)) + 3
- амплитуда A = 2
- период 2π / B = 2π / 4 = π / 2
- фазовый сдвиг = -0.5 (или 0,5 вправо)
- вертикальный сдвиг D = 3
Прописью:
- 2 говорит нам, что он будет в 2 раза выше, чем обычно, поэтому Amplitude = 2
- , обычный период — 2 π , но в нашем случае он «ускорен» (сокращен) на 4 в 4 раза, поэтому Период = π / 2
- и −0,5 означает, что он будет сдвинут на вправо на 0.5
- , наконец, +3 говорит нам, что центральная линия y = +3, поэтому вертикальный сдвиг = 3
Вместо x мы можем иметь t (для времени) или, возможно, другие переменные:
Пример: 3 sin (100t + 1)
Сначала нам нужны скобки вокруг (t + 1), поэтому мы можем начать с деления 1 на 100:
3 sin (100t + 1) = 3 sin (100 (t + 0,01))
Теперь мы видим:
- амплитуда А = 3
- равен 2π / 100 = 0.
 02 π
02 π - фазовый сдвиг C = 0,01 (влево)
- вертикальный сдвиг D = 0
Период
И получаем:
Частота
Частота — это то, как часто что-то происходит в единицу времени (на «1»).
Пример: Здесь синусоидальная функция повторяется 4 раза от 0 до 1:
Таким образом, частота равна 4
И период
1
4
Фактически Период и Частота связаны:
Частота =
1
Период
Период =
1
Частота
Пример из предыдущего: 3 sin (100 (t + 0.01))
Период 0,02 π
Итак, частота
1
0,02π
знак равно
50
π
Еще несколько примеров:
| Период | Частота |
|---|---|
| 1 10 | 10 |
| 1 4 | 4 |
| 1 | 1 |
| 5 | 1 5 |
| 100 | 1 100 |
При частоте в секунду называется «Герц».
Пример: 50 Гц означает 50 раз в секунду
Чем быстрее он отскакивает, тем больше у него «Герц»!
Анимация
Синус, косинус, тангенс
Три функции, но та же идея.
Прямой треугольник
Синус, косинус и тангенс — основные функции, используемые в тригонометрии, они основаны на прямоугольном треугольнике.
Прежде чем углубляться в функции, полезно присвоить имя каждой стороне прямоугольного треугольника:
- «Противоположно» противоположно углу θ
- «Соседний» примыкает (рядом) к углу θ
- «Гипотенуза» — длинная
Соседний всегда находится рядом с углом
И Напротив находится напротив угла
Синус, косинус и тангенс
Синус , Косинус и Касательная (часто сокращается до sin , cos и tan ) — это отношение сторон прямоугольного треугольника:
.
Для заданного угла θ каждое отношение остается неизменным
, независимо от того, насколько большой или малый треугольник
Для их расчета:
Разделите длину одной стороны на другую
Пример: Что такое синус 35 °?
Используя этот треугольник (длины до одного десятичного знака):
| sin (35 °) | = Напротив Гипотенуза |
| = 2.8 4,9 | |
| = 0,57 … | |
| cos (35 °) | = Соседний Гипотенуза |
| = 4,0 4,9 | |
| = 0,82 … | |
| желто-коричневый (35 °) | = Напротив Соседний |
= 2. 8 4,0 8 4,0 | |
| = 0,70 … |
Размер не имеет значения
Треугольник может быть большим или маленьким, а соотношение сторон остается неизменным .
Только угол меняет соотношение.
Попробуйте перетащить точку «A», чтобы изменить угол, и точку «B», чтобы изменить размер:
На хороших калькуляторах есть sin, cos и tan, чтобы облегчить вам задачу.Просто вставьте угол и нажмите кнопку.
Но вам все равно нужно запомнить , что они означают !
В форме изображения:
Практика здесь:
Sohcahtoa
Как запомнить? Подумайте «Sohcahtoa» !
Работает так:
Soh … | S ine = O pposite / H ypotenuse |
…ка … | C осин = A djacent / H ypotenuse |
. | T angent = O pposite / A djacent |
Вы можете узнать больше о sohcahtoa … запомните, это может помочь на экзамене!
Углы от 0 ° до 360 °
Перемещайте мышь, чтобы увидеть, как разные углы (в радианах или градусах) влияют на синус, косинус и тангенс.
На этой анимации гипотенуза равна 1, образуя единичную окружность.
Обратите внимание, что смежная сторона и противоположная сторона могут быть положительными или отрицательными, что также приводит к изменению синуса, косинуса и тангенса между положительными и отрицательными значениями.
| «Почему sin и tan не пошли на вечеринку?» «… всего cos !» |
Примеры
Пример: каковы синус, косинус и тангенс 30 °?
Классический треугольник 30 ° имеет гипотенузу длины 2, противоположную сторону длины 1 и прилегающую сторону
√3:
Теперь мы знаем длины, можем вычислить функции:
Синус | sin (30 °) = 1/2 = 0.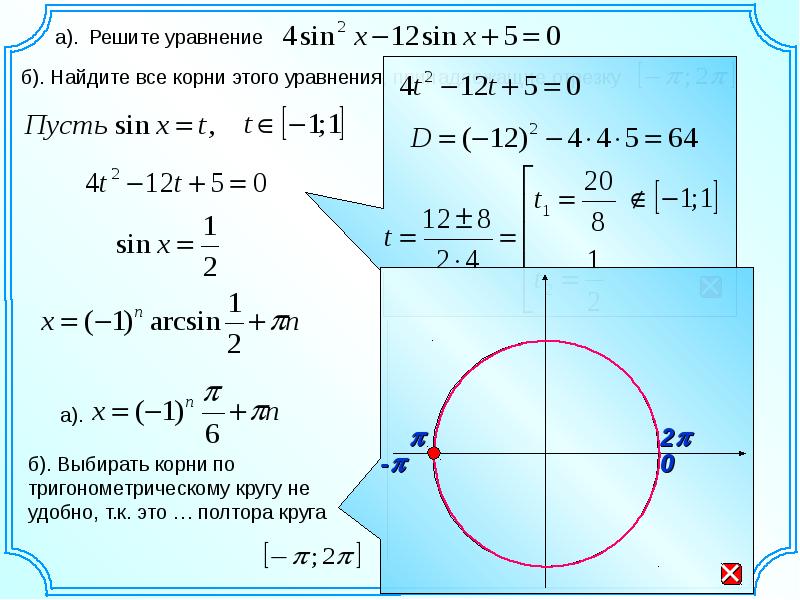 5 5 | |
Косинус | cos (30 °) = 1,732 / 2 = 0,866 … | |
Касательная | тангенс угла (30 °) = 1 / 1,732 = 0,577 … |
(возьмите калькулятор и проверьте его!)
Пример: каковы синус, косинус и тангенс угла 45 °?
Классический треугольник 45 ° имеет две стороны 1 и гипотенузу √2:
Синус | sin (45 °) = 1/1.414 = 0,707 … | |
Косинус | cos (45 °) = 1 / 1,414 = 0,707 … | |
Касательная | тангенс угла (45 °) = 1/1 = 1 |
Почему?
Почему эти функции важны?
- Потому что они позволяют нам вычислять углы, когда мы знаем стороны
- И они позволяют нам определять стороны, когда мы знаем углы
Пример: используйте синусоидальную функцию
, чтобы найти «d»
Мы знаем:
- Кабель образует угол 39 ° относительно морского дна
- Кабель длиной 30 метров .

И мы хотим знать «d» (расстояние вниз).
Начать с: sin 39 ° = противоположно / гипотенуза
sin 39 ° = d / 30
Поменять местами стороны: d / 30 = sin 39 °
С помощью калькулятора найдите sin 39 °: d / 30 = 0,6293 …
Умножаем обе стороны на 30: d = 0,6293… x 30
d = 18,88 с точностью до 2 знаков после запятой.
Глубина «d» 18,88 м
Упражнение
Попробуйте это бумажное упражнение, в котором вы можете вычислить синусоидальную функцию.
для всех углов от 0 ° до 360 °, а затем нарисуйте результат.Это поможет вам понять эти относительно
простые функции.
Вы также можете увидеть графики синуса, косинуса и тангенса.
И поиграйте с пружиной, создающей синусоидальную волну.
Менее распространенные функции
Чтобы завершить картину, есть еще 3 функции, в которых мы разделяем одну сторону на другую, но они не так часто используются.
Они равны 1, деленному на cos , 1, деленному на sin , и 1, деленному на tan :
Секущая функция: | сек ( θ ) = Гипотенуза Соседний | (= 1 / cos) | ||
Косеканс Функция: | csc ( θ ) = Гипотенуза Напротив | (= 1 / sin) | ||
Котангенс Функция: | детская кроватка ( θ ) = Соседний Напротив | (= 1 / tan) |
графиков функции синуса и косинуса
График изменения y = sin (x) и y = cos (x)
Напомним, что функции синуса и косинуса связывают значения действительных чисел с координатами x и y точки на единичной окружности. Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции . Мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения синусоидальной функции на единичной окружности.
Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции . Мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения синусоидальной функции на единичной окружности.
| x | 0 | [латекс] \ frac {π} {6} \\ [/ латекс] | [латекс] \ frac {π} {6} \\ [/ латекс] | [латекс] \ frac {π} {3} \\ [/ латекс] | [латекс] \ frac {π} {2} \\ [/ латекс] | [латекс] \ frac {2π} {3} \\ [/ латекс] | [латекс] \ frac {3π} {4} \\ [/ латекс] | [латекс] \ frac {5π} {6} \\ [/ латекс] | π |
| sin (x) | 0 | [латекс] \ frac {1} {2} \\ [/ latex] | [латекс] \ frac {\ sqrt {2}} {2} \\ [/ латекс] | [латекс] \ frac {\ sqrt {3}} {2} \\ [/ латекс] | 1 | [латекс] \ frac {\ sqrt {3}} {2} \\ [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} \\ [/ латекс] | [латекс] \ frac {1} {2} \\ [/ латекс] | 0 |
Построение точек из таблицы и продолжение по оси x дает форму синусоидальной функции. См. Рисунок 2.
См. Рисунок 2.
Рисунок 2. Синусоидальная функция
Обратите внимание, что значения синуса положительны между 0 и π, что соответствует значениям функции синуса в квадрантах I и II на единичной окружности, а значения синуса отрицательны между π и 2π, которые соответствуют значениям функция синуса в квадрантах III и IV на единичной окружности. См. Рисунок 3.
Рисунок 3. График значений синусоидальной функции
Теперь давайте аналогичным образом посмотрим на функцию косинуса .Опять же, мы можем создать таблицу значений и использовать их для построения графика. В таблице ниже перечислены некоторые значения функции косинуса на единичной окружности.
| x | 0 | [латекс] \ frac {π} {6} \\ [/ латекс] | [латекс] \ frac {π} {4} \\ [/ латекс] | [латекс] \ frac {π} {3} \\ [/ латекс] | [латекс] \ frac {π} {2} \\ [/ латекс] | [латекс] \ frac {2π} {3} \\ [/ латекс] | [латекс] \ frac {3π} {4} \\ [/ латекс] | [латекс] \ frac {5π} {6} \\ [/ латекс] | π |
| cos (x) | 1 | [латекс] \ frac {\ sqrt {3}} {2} \\ [/ латекс] | [латекс] \ frac {\ sqrt {2}} {2} \\ [/ латекс] | [латекс] \ frac {1} {2} \\ [/ латекс] | 0 | [латекс] — \ frac {1} {2} \\ [/ latex] | [латекс] — \ frac {\ sqrt {2}} {2} \\ [/ латекс] | [латекс] — \ frac {\ sqrt {3}} {2} \\ [/ латекс] | -1 |
Как и в случае с функцией синуса, мы можем построить точки для построения графика функции косинуса, как показано на рисунке 4.
Рисунок 4. Функция косинуса
Поскольку мы можем вычислять синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Если рассматривать значения синуса и косинуса как координаты точек на единичной окружности, становится ясно, что диапазон обеих функций должен быть интервалом [-1,1].
На обоих графиках форма графика повторяется после 2π, что означает, что функции являются периодическими с периодом 2π. Периодическая функция — это функция, для которой определенный горизонтальный сдвиг , P , приводит к функции, равной исходной функции: f ( x + P ) = f ( x ) для всех значений x в области f .Когда это происходит, мы называем наименьший такой горизонтальный сдвиг с P > 0 периодом функции. На рисунке 5 показаны несколько периодов функций синуса и косинуса.
Рисунок 5
Еще раз взглянув на функции синуса и косинуса в области с центром на оси y , можно выявить симметрии. Как мы видим на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомните из «Других тригонометрических функций», что мы определили с помощью единичного круга, что синусоидальная функция является нечетной функцией, потому что [latex] sin (−x) = — sinx [/ latex].Теперь мы можем ясно видеть это свойство на графике.
Как мы видим на рисунке 6, синусоидальная функция симметрична относительно начала координат. Вспомните из «Других тригонометрических функций», что мы определили с помощью единичного круга, что синусоидальная функция является нечетной функцией, потому что [latex] sin (−x) = — sinx [/ latex].Теперь мы можем ясно видеть это свойство на графике.
Рисунок 6. Нечетная симметрия синусоидальной функции
На рисунке 7 показано, что функция косинуса симметрична относительно оси y . Опять же, мы определили, что функция косинуса является четной функцией. Теперь мы можем видеть из графика, что [латекс] \ cos (−x) = \ cos x \\ [/ latex].
Рисунок 7. Четная симметрия функции косинуса
Общее примечание: характеристики функций синуса и косинуса
Функции синуса и косинуса имеют несколько отличительных характеристик:
- Это периодические функции с периодом 2π.
- Область определения каждой функции — (−∞, ∞), а диапазон — [−1,1].

- График y = sin x симметричен относительно начала координат, потому что это нечетная функция.
- График y = cos x симметричен относительно оси y , потому что это четная функция.
Исследование синусоидальных функций
Как мы видим, функции синуса и косинуса имеют постоянный период и диапазон. Если мы посмотрим на океанские волны или рябь на пруду, мы увидим, что они напоминают функции синуса или косинуса.Однако они не обязательно идентичны. Некоторые из них выше или длиннее других. Функция, которая имеет ту же общую форму, что и функция синуса или косинуса , известна как синусоидальная функция . Общие формы синусоидальных функций:
y = A sin ( Bx — C ) + D
и
y = A cos ( Bx — C ) + D
Определение периода синусоидальной функции
Глядя на формы синусоидальных функций, мы видим, что они являются преобразованиями функций синуса и косинуса. Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
Мы можем использовать то, что мы знаем о преобразованиях, для определения периода.
В общей формуле B связано с периодом соотношением [latex] \ text {P =} \ frac {2π} {| B |} [/ latex]. Если | B | > 1, то период меньше 2π и функция испытывает сжатие по горизонтали, а если | B | <1, то период больше 2π и функция растягивается по горизонтали. Например, f ( x ) = sin ( x ), B = 1, поэтому период равен 2π, который мы знали.Если f ( x ) = sin (2 x ), то B = 2, поэтому период равен π и график сжат. Если [латекс] \ text {f (x) = sin} (\ frac {x} {2}) [/ latex], то [latex] B = \ frac {1} {2} [/ latex], поэтому период равен 4π, и график растянут. Обратите внимание на рис. 8, как период косвенно связан с | B |.
Рисунок 8
Общее примечание: период синусоидальной функции
Если положить C = 0 и D = 0 в уравнениях синуса и косинуса в общем виде, мы получим формы
Период [латекс] \ frac {2π} {| B |} [/ латекс].
Пример 1: Определение периода функции синуса или косинуса
Определите период функции [latex] f (x) = \ sin (\ frac {π} {6} x) \\ [/ latex].
Решение
Начнем с сравнения уравнения с общей формой [latex] y = Asin (Bx) [/ latex].
В данном уравнении [latex] B = \ frac {π} {6} [/ latex], поэтому период будет
[латекс] \ begin {array} P = \ frac {\ frac {2} {\ pi}} {| B |} \ hfill \\ = \ frac {2 \ pi} {\ frac {x} {6} } \ hfill \\ = 2 \ pi \ times \ frac {6} {\ pi} \ hfill \\ = 12 \ hfill \ end {array} \\ [/ latex]
Попробуйте 1
Определите период функции [latex] g (x) = \ cos (\ frac {x} {3}) \\ [/ latex].
Решение
Определение амплитуды
Возвращаясь к общей формуле синусоидальной функции, мы проанализировали, как переменная B связана с периодом. Теперь давайте обратимся к переменной A , чтобы мы могли проанализировать, как она связана с амплитудой , или наибольшим расстоянием от покоя. A представляет коэффициент вертикального растяжения и его абсолютное значение | A | это амплитуда. Локальные максимумы будут на расстоянии | A | над вертикальной средней линией графика, которая представляет собой линию x = D ; поскольку D = 0 в этом случае, средняя линия является осью x .Локальные минимумы будут на таком же расстоянии ниже средней линии. Если | A | > 1 функция растягивается. Например, амплитуда f ( x ) = 4 sin x в два раза больше амплитуды
A представляет коэффициент вертикального растяжения и его абсолютное значение | A | это амплитуда. Локальные максимумы будут на расстоянии | A | над вертикальной средней линией графика, которая представляет собой линию x = D ; поскольку D = 0 в этом случае, средняя линия является осью x .Локальные минимумы будут на таком же расстоянии ниже средней линии. Если | A | > 1 функция растягивается. Например, амплитуда f ( x ) = 4 sin x в два раза больше амплитуды
f ( x ) = 2 sin x .
Если | A | <1, функция сжимается. На рисунке 9 сравниваются несколько синусоидальных функций с разными амплитудами.
Рисунок 9
Общее примечание: амплитуда синусоидальных функций
Если положить C = 0 и D = 0 в уравнениях синуса и косинуса общего вида, мы получим формы
[латекс] y = A \ sin (Bx) \\ [/ latex] и [латекс] y = A \ cos (Bx) \\ [/ latex]
Амплитуда равна A, а высота по вертикали от средней линии равна | A |. Кроме того, обратите внимание на пример, что
Кроме того, обратите внимание на пример, что
[латекс] | A | = \ text {амплитуда} = \ frac {1} {2} | \ text {maximum} — \ text {minimum} | \\ [/ latex]
Пример 2: Определение амплитуды функции синуса или косинуса
Какова амплитуда синусоидальной функции [латекс] f (x) = — 4 \ sin (x) \\ [/ latex]? Функция растягивается или сжимается по вертикали?
Решение
Начнем с сравнения функции с упрощенной формой y = A sin ( Bx ).
В данной функции A = −4, поэтому амплитуда | A | = | −4 | = 4. Функция растягивается.
Анализ решения
Отрицательное значение A приводит к отражению по оси x синусоидальной функции , как показано на рисунке 10.
Рисунок 10
Попробуйте 2
Какова амплитуда синусоидальной функции f ( x ) = 12 sin ( x )? Функция растягивается или сжимается по вертикали?
Решение
Анализ графиков вариаций
y = sin x и y = cos x
Теперь, когда мы понимаем, как A и B связаны с уравнением общей формы для функций синуса и косинуса, мы исследуем переменные C и D . Напомним общую форму:
Напомним общую форму:
[латекс] y = A \ sin (Bx-C) + D \\ [/ latex] и [латекс] y = A \ cos (Bx-C) + D \\ [/ latex]
или
[латекс] y = A \ sin (B (x− \ frac {C} {B})) + D \\ [/ latex] и [латекс] y = A \ cos (B (x− \ frac {C } {B})) + D \\ [/ latex]
Значение [latex] \ frac {C} {B} \\ [/ latex] для синусоидальной функции называется фазовым сдвигом , или горизонтальным смещением основного синуса или функции косинуса . Если C> 0, график сдвигается вправо. Если C <0, график сдвигается влево.Чем больше значение | C |, тем больше смещается график. На рисунке 11 показано, что график [latex] f (x) = \ sin (x − π) \\ [/ latex] сдвигается вправо на π единиц, что больше, чем мы видим на графике [latex] f. (x) = \ sin (x− \ frac {π} {4}) \\ [/ latex], который сдвигается вправо на единицы [latex] \ frac {π} {4} \\ [/ latex].
Рисунок 11
В то время как C относится к горизонтальному смещению, D указывает вертикальное смещение от средней линии в общей формуле для синусоидальной функции. Функция [latex] y = \ cos (x) + D \\ [/ latex] имеет среднюю линию в [latex] y = D [/ latex].
Функция [latex] y = \ cos (x) + D \\ [/ latex] имеет среднюю линию в [latex] y = D [/ latex].
Рисунок 12
Любое значение D , кроме нуля, сдвигает график вверх или вниз. На рисунке 13 [latex] f (x) = \ sin x \\ [/ latex] сравнивается с [latex] f (x) = \ sin x + 2 \\ [/ latex], который сдвинут на 2 единицы вверх на графике. .
Рисунок 13
Общее примечание: Вариации функций синуса и косинуса
Дано уравнение в виде [латекс] f (x) = A \ sin (Bx − C) + D \\ [/ latex] или [латекс] f (x) = A \ cos (Bx − C) + D \\ [/ latex], [latex] \ frac {C} {B} \\ [/ latex] — это фазовый сдвиг , а D — вертикальный сдвиг .
Пример 3: Определение фазового сдвига функции
Определите направление и величину фазового сдвига для [латекса] f (x) = \ sin (x + \ frac {π} {6}) — 2 \\ [/ latex].
Решение
Начнем с сравнения уравнения с общей формой [латекс] y = A \ sin (Bx − C) + D \\ [/ latex].
В данном уравнении обратите внимание, что B = 1 и [латекс] C = — \ frac {π} {6} \\ [/ latex]. Итак, фазовый сдвиг
[латекс] \ begin {array} \ frac {C} {B} = — \ frac {\ frac {x} {6}} {1} \ hfill \\ = — \ frac {\ pi} {6} \ hfill \ end {array} \\ [/ latex]
или [latex] \ frac {\ pi} {6} \\ [/ latex] единиц слева.
Анализ решения
Обязательно обратите внимание на знак в уравнении общего вида синусоидальной функции. Уравнение показывает знак минус перед C . Следовательно, [latex] f (x) = \ sin (x + \ frac {π} {6}) — 2 \\ [/ latex] можно переписать как [latex] f (x) = \ sin (x — (- \ гидроразрыв {π} {6})) — 2 \\ [/ latex]. Если значение C отрицательное, сдвиг влево.
Попробовать 3
Определите направление и величину фазового сдвига для [latex] f (x) = 3 \ cos (x− \ frac {\ pi} {2}) \\ [/ latex].
Решение
Пример 4: Определение вертикального сдвига функции
Определите направление и величину вертикального сдвига для [латекса] f (x) = \ cos (x) −3 \\ [/ latex].
Решение
Начнем с сравнения уравнения с общей формой [латекс] y = A \ cos (Bx − C) + D \\ [/ latex]
Попробовать 4
Определите направление и величину вертикального сдвига для [латекса] f (x) = 3 \ sin (x) +2 \\ [/ latex].
Решение
Практическое руководство. Учитывая синусоидальную функцию в форме [латекс] f (x) = A \ sin (Bx − C) + D [/ latex], определите среднюю линию, амплитуду, период и фазовый сдвиг.
- Определите амплитуду как | A |.
- Определите период как [латекс] P = \ frac {2π} {| B |} \\ [/ latex].
- Определите фазовый сдвиг как [latex] \ frac {C} {B} \\ [/ latex].
- Определите среднюю линию как y = D.
Пример 5: Определение вариаций синусоидальной функции из уравнения
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции [латекс] y = 3 \ sin (2x) +1 \\ [/ latex].
Решение
Начнем с сравнения уравнения с общей формой [латекс] y = A \ sin (Bx − C) + D \\ [/ latex]. A = 3, поэтому амплитуда | A | = 3.
A = 3, поэтому амплитуда | A | = 3.
Затем B = 2, поэтому период равен [latex] \ text {P} = \ frac {2π} {| B |} = \ frac {2π} {2} = π \\ [/ latex].
В скобках нет добавленной константы, поэтому C = 0, а фазовый сдвиг равен [latex] \ frac {C} {B} = \ frac {0} {2} = 0 \\ [/ latex].
Наконец, D = 1, поэтому средняя линия составляет y = 1.
Анализ решения
Изучая график, мы можем определить, что период равен π, средняя линия равна y = 1, а амплитуда равна 3.См. Рисунок 14.
Рисунок 14
Попробовать 5
Определите среднюю линию, амплитуду, период и фазовый сдвиг функции [латекс] y = \ frac {1} {2} \ cos (\ frac {x} {3} — \ frac {π} {3}) \ \[/латекс].
Решение
Пример 6: Определение уравнения для синусоидальной функции из графика
Определите формулу для функции косинуса на рисунке 15.
Рисунок 15
Решение
[латекс] f (x) = \ sin (x) +2 \\ [/ latex]
Попробовать 6
Определите формулу синусоидальной функции на рисунке 16.
Рисунок 16
Решение
Пример 7: Определение уравнения для синусоидальной функции из графика
Определите уравнение для синусоидальной функции на рисунке 17.
Рисунок 17
Решение
При максимальном значении 1 и минимальном значении −5 средняя линия будет находиться посередине между −2. Итак, D = −2.
Расстояние от средней линии до самого высокого или самого низкого значения дает амплитуду | А | = 3.
Период графика равен 6, и его можно измерить от пика при x = 1 до следующего пика при x = 7 или от расстояния между самыми низкими точками. Следовательно, [latex] \ text {P} = \ frac {2 \ pi} {| B |} = 6 [/ latex]. Используя положительное значение для B , находим
[латекс] B = \ frac {2π} {P} = \ frac {2π} {6} = \ frac {π} {3} \\ [/ latex]
Пока что наше уравнение выглядит так: [latex] y = 3 \ sin (\ frac {\ pi} {3} x − C) −2 \\ [/ latex] или [latex] y = 3 \ cos (\ frac {\ pi} {3} x − C) −2 \\ [/ латекс]. Для формы и сдвига у нас есть несколько вариантов. Мы могли бы записать это как любое из следующих:
Для формы и сдвига у нас есть несколько вариантов. Мы могли бы записать это как любое из следующих:
- косинус, смещенный вправо
- отрицательный косинус, сдвинутый влево
- синус смещен влево
- отрицательный синус смещен вправо
Хотя любой из них был бы правильным, в этом случае с косинусоидальными сдвигами работать легче, чем с синусоидальными сдвигами, поскольку они включают целочисленные значения. Таким образом, наша функция становится
[латекс] y = 3 \ cos (\ frac {π} {3} x− \ frac {π} {3}) — 2 \\ [/ latex] или [латекс] y = −3 \ cos (\ frac {π} {3} x + \ frac {2π} {3}) — 2 \\ [/ латекс]
Опять же, эти функции эквивалентны, поэтому обе дают один и тот же график.
Попробовать 7
Напишите формулу функции, показанной на рисунке 18.
Рисунок 18
Решение
Графические вариации
y = sin x и y = cos x
В этом разделе мы узнали о типах вариаций функций синуса и косинуса и использовали эту информацию для написания уравнений из графиков.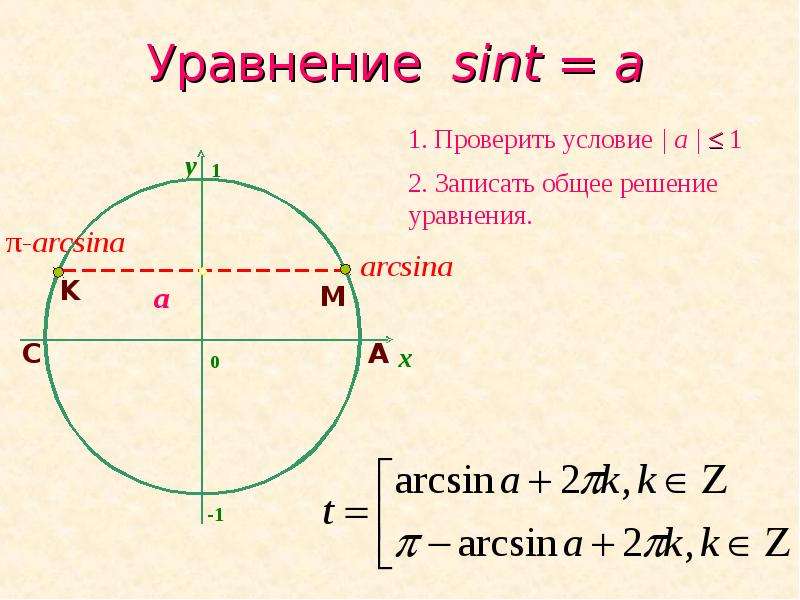 Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Теперь мы можем использовать ту же информацию для создания графиков из уравнений.
Вместо того, чтобы сосредоточиться на уравнениях общего вида
[латекс] y = A \ sin (Bx-C) + D \\ [/ latex] и [латекс] y = A \ cos (Bx-C) + D \\ [/ latex],
мы положим C = 0 и D = 0 и будем работать с упрощенной формой уравнений в следующих примерах.
Практическое руководство. Для функции [latex] y = Asin (Bx) \\ [/ latex] нарисуйте ее график.
- Определите амплитуду, | A |.
- Определите период, [латекс] P = \ frac {2π} {| B |} \\ [/ latex].
- Начать с начала координат, функция увеличивается вправо, если A положительна, или уменьшается, если A отрицательна.
- В [latex] x = \ frac {π} {2 | B |} \\ [/ latex] существует локальный максимум для A > 0 или минимум для A <0, при y = А .
- Кривая возвращается к оси x в точке [латекс] x = \ frac {π} {| B |} \\ [/ latex].

- Существует локальный минимум для A > 0 (максимум для A <0) при [latex] x = \ frac {3π} {2 | B |} \\ [/ latex] при y = — А .
- Кривая снова возвращается к оси x в точке [latex] x = \ frac {π} {2 | B |} \\ [/ latex].
Пример 8: Построение графика функции и определение амплитуды и периода
Нарисуйте график [латекса] f (x) = — 2 \ sin (\ frac {πx} {2}) \\ [/ latex].
Решение
Начнем с сравнения уравнения с формой [латекс] y = A \ sin (Bx) \\ [/ latex].
Шаг 1. Из уравнения видно, что A = −2, поэтому амплитуда равна 2.
| A | = 2
Шаг 2. Уравнение показывает, что [latex] B = \ frac {π} {2} \\ [/ latex], поэтому период равен
[латекс] \ begin {array} \ text {P} = \ frac {2 \ pi} {\ frac {\ pi} {2}} \\ = 2 \ pi \ times \ frac {2} {\ pi} \\ = 4 \ end {array} \\ [/ latex]
Шаг 3. Поскольку A отрицательное значение, график опускается вниз по мере того, как мы перемещаемся вправо от начала координат.
Поскольку A отрицательное значение, график опускается вниз по мере того, как мы перемещаемся вправо от начала координат.
Шаг 4–7. Интерпретации x находятся в начале одного периода, x = 0, горизонтальные средние точки находятся на уровне x = 2 и в конце одного периода при x = 4.
Четверть точки включают минимум x = 1 и максимум x = 3. Локальный минимум будет на 2 единицы ниже средней линии при x = 1, а локальный максимум будет на 2 единицах. над средней линией при x = 3. На рисунке 19 показан график функции.
Рисунок 19
Попробовать 8
Нарисуйте график [латекс] g (x) = — 0,8 \ cos (2x) \\ [/ latex]. Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Решение
Практическое руководство. Для синусоидальной функции со сдвигом фазы и вертикальным сдвигом нарисуйте ее график.
- Выразите функцию в общем виде [латекс] y = A \ sin (Bx − C) + D [/ latex] или [latex] y = A \ cos (Bx − C) + D \\ [/ latex] .

- Определите амплитуду, | A |.
- Укажите период, [латекс] P = 2π | B | [/ латекс].
- Определите фазовый сдвиг, [latex] \ frac {C} {B} \\ [/ latex].
- Нарисуйте график [латекс] f (x) = A \ sin (Bx) \\ [/ latex], сдвинутый вправо или влево на [латекс] \ frac {C} {B} \\ [/ latex] и вверх или вниз на D .
Пример 9: Построение преобразованной синусоиды
Нарисуйте граф [латекс] f (x) = 3 \ sin (\ frac {π} {4} x− \ frac {π} {4}) \\ [/ latex].
Решение
Шаг 1. Функция уже записана в общем виде: [latex] f (x) = 3 \ sin (\ frac {π} {4} x− \ frac {π} {4}) \\ [/ латекс]. Этот график будет иметь форму синусоидальной функции , начиная со средней линии и увеличиваясь вправо.
Шаг 2. | А | = | 3 | = 3. Амплитуда 3.
Шаг 3. Поскольку [latex] | B | = | \ frac {π} {4} | = \ frac {π} {4} \\ [/ latex], мы определяем период следующим образом.
[латекс] \ text {P} = \ frac {2π} {| B |} = \ frac {2π} {\ frac {π} {4}} = 2π \ times \ frac {4} {π} = 8 \\ [/ латекс]
Период 8.
Шаг 4. Поскольку [latex] \ text {C} = \ frac {π} {4} \\ [/ latex], фазовый сдвиг равен
[латекс] \ frac {C} {B} = \ frac {\ frac {\ pi} {4}} {\ frac {\ pi} {4}} = 1 \\ [/ latex].
Фазовый сдвиг — 1 ед.
Шаг 5. На рисунке 20 показан график функции.
Рисунок 20. Синусоида, сжатая по горизонтали, растянута по вертикали и смещена по горизонтали
Попробовать 9
Нарисуйте график [латекс] g (x) = — 2 \ cos (\ frac {\ pi} {3} x + \ frac {\ pi} {6}) \\ [/ latex]. Определите среднюю линию, амплитуду, период и фазовый сдвиг.
Решение
Пример 10: Определение свойств синусоидальной функции
Учитывая [латекс] y = −2 \ cos (\ frac {\ pi} {2} x + \ pi) +3 \\ [/ latex], определите амплитуду, период, фазовый сдвиг и горизонтальный сдвиг.Затем изобразите функцию.
Решение
Начните со сравнения уравнения с общей формой и выполните шаги, описанные в Примере 9.
[латекс] y = A \ cos (Bx − C) + D \\ [/ латекс]
Шаг 1. Функция уже написана в общем виде.
Шаг 2. Поскольку A = −2, амплитуда | A | = 2.
Шаг 3. [latex] | B | = \ frac {\ pi} {2} \\ [/ latex], поэтому период равен [latex] \ text {P} = \ frac {2π} {| B |} = \ frac {2 \ pi} {\ frac {\ pi} {2}} \ times2 \ pi = 4 \\ [/ latex].Период 4.
Шаг 4. [latex] C = — \ pi \\ [/ latex], поэтому мы вычисляем фазовый сдвиг как [latex] \ frac {C} {B} = \ frac {- \ pi} {\ frac {\ pi} {2}} = — \ pi \ times \ frac {2} {\ pi} = — 2 \\ [/ latex]. Сдвиг фазы равен -2.
Шаг 5. D = 3, поэтому средняя линия составляет y = 3, а вертикальный сдвиг увеличивается 3.
Поскольку A отрицательное, график функции косинуса отражается относительно оси x .
На рисунке 21 показан один цикл графика функции.
Рисунок 21
Использование преобразований функций синуса и косинуса
Мы можем использовать преобразования функций синуса и косинуса во многих приложениях. Как упоминалось в начале главы, круговое движение можно смоделировать с помощью функции синуса или косинуса .
Пример 11: Нахождение вертикальной составляющей кругового движения
Точка вращается по окружности радиуса 3 с центром в начале координат.Нарисуйте график координаты y точки как функции угла поворота.
Решение
Напомним, что для точки на окружности радиуса r координата y точки равна [латекс] y = r \ sin (x) [/ latex], поэтому в этом случае мы получаем уравнение [латекс] у (х) = 3 \ грех (х) [/ латекс]. Константа 3 вызывает растяжение значений y функции в 3 раза по вертикали, что мы можем видеть на графике на рисунке 22.
Рисунок 22
Анализ решения
Обратите внимание, что период функции по-прежнему равен 2π; путешествуя по кругу, мы возвращаемся в точку (3,0) для x = 2π, 4π, 6π,….Поскольку выходные данные графика теперь будут колебаться между –3 и 3, амплитуда синусоиды равна 3.
Попробовать 10
Какова амплитуда функции [латекс] f (x) = 7 \ cos (x) [/ latex]? Нарисуйте график этой функции.
Решение
Пример 12: Нахождение вертикальной составляющей кругового движения
Круг радиусом 3 фута устанавливается с центром в 4 футах от земли. Ближайшая к земле точка обозначена P , как показано на рисунке 23.Нарисуйте график высоты над землей точки P при вращении окружности; затем найдите функцию, которая дает высоту через угол поворота.
Рисунок 23
Решение
Набрасывая высоту, мы отмечаем, что она начинается на высоте 1 фута над землей, затем увеличивается до 7 футов над землей и продолжает колебаться на 3 фута выше и ниже центрального значения в 4 фута, как показано на Рисунке 24.
Рисунок 24
Хотя мы могли бы использовать преобразование функции синуса или косинуса, мы начнем с поиска характеристик, которые сделают использование одной функции проще, чем другой.Давайте использовать функцию косинуса, потому что она начинается с самого высокого или самого низкого значения, а функция синуса начинается со среднего значения. Стандартный косинус начинается с самого высокого значения, а этот график начинается с самого низкого значения, поэтому нам нужно включить вертикальное отражение.
Во-вторых, мы видим, что график колеблется на 3 выше и ниже центра, в то время как основной косинус имеет амплитуду 1, поэтому этот график был растянут по вертикали на 3, как в последнем примере.
Наконец, чтобы переместить центр круга на высоту 4, график был сдвинут по вертикали на 4.Собирая эти преобразования вместе, получаем, что
[латекс] y = −3 \ cos (x) +4 [/ латекс]
Попробуй 11
К пружине прикрепляется груз, который затем подвешивается к доске, как показано на рисунке 25. Когда пружина колеблется вверх и вниз, положение и груза относительно доски изменяется в диапазоне от –1 дюйма (при время x = 0) до –7 дюймов. (в момент времени x = π) под доской. Предположим, что положение y задано как синусоидальная функция x .Нарисуйте график функции, а затем найдите функцию косинуса, которая дает положение y в единицах x .
Рисунок 25
Решение
Пример 13: Определение роста всадника на колесе обозрения
Лондонский глаз — это огромное колесо обозрения диаметром 135 метров (443 фута). Он совершает один оборот каждые 30 минут. Всадники садятся на платформу на высоте 2 метров над землей. Выразите высоту всадника над землей как функцию времени в минутах.
Решение
При диаметре 135 м колесо имеет радиус 67,5 м. Высота будет колебаться с амплитудой 67,5 м выше и ниже центра.
Пассажирский борт на высоте 2 м над уровнем земли, поэтому центр колеса должен находиться на высоте 67,5 + 2 = 69,5 м над уровнем земли. Средняя линия колебания составит 69,5 м.
Колесо совершает 1 оборот за 30 минут, поэтому высота будет колебаться с периодом 30 минут.
Наконец, так как райдерские борта находятся в самой нижней точке, высота будет начинаться с наименьшего значения и увеличиваться по форме вертикально отраженной косинусоидальной кривой.
- Амплитуда: 67,5, поэтому A = 67,5
- Средняя линия: 69,5, поэтому D = 69,5
- Период: 30, поэтому [латекс] B = \ frac {2 \ pi} {30} = \ frac {\ pi} {15} [/ latex]
- Форма: −cos ( t )
Уравнение для роста всадника будет
[латекс] y = -67,5 \ cos (\ frac {\ pi} {15} t) +69,5 [/ латекс]
, где t в минутах, а y в метрах.
Ключевые уравнения
| Синусоидальные функции | [латекс] f (x) = A \ sin (Bx − C) + D [/ латекс] |
| [латекс] f (x) = A \ cos (Bx-C) + D [/ латекс] |
- Периодические функции повторяются после заданного значения.Наименьшее из таких значений — период. Основные функции синуса и косинуса имеют период 2π.
- Функция sin x нечетная, поэтому ее график симметричен относительно начала координат. Функция cos x четная, поэтому ее график симметричен относительно оси y .
- График синусоидальной функции имеет ту же общую форму, что и синусоидальная или косинусная функция.
- В общей формуле для синусоидальной функции период равен [latex] \ text {P} = \ frac {2 \ pi} {| B |} [/ latex].
- В общей формуле синусоидальной функции | A | представляет амплитуду. Если | A | > 1 функция растягивается, а если | A | <1, функция сжимается.
- Значение [latex] \ frac {C} {B} [/ latex] в общей формуле для синусоидальной функции указывает фазовый сдвиг.
- Значение D в общей формуле для синусоидальной функции указывает вертикальное смещение от средней линии.
- Комбинации вариаций синусоидальных функций могут быть обнаружены с помощью уравнения.
- Уравнение для синусоидальной функции может быть определено из графика.
- Функцию можно изобразить, указав ее амплитуду и период.
- Функцию также можно изобразить, указав ее амплитуду, период, фазовый сдвиг и горизонтальный сдвиг.
- Синусоидальные функции могут использоваться для решения реальных проблем.
Глоссарий
- амплитуда
- вертикальная высота функции; константа A , фигурирующая в определении синусоидальной функции
- средняя линия
- горизонтальная линия y = D , где D появляется в общем виде синусоидальной функции
- периодическая функция
- функция f ( x ), которая удовлетворяет [latex] f (x + P) = f (x) [/ latex] для конкретной константы P и любого значения x
- сдвиг фазы
- горизонтальное смещение основной функции синуса или косинуса; константа [латекс] \ frac {C} {B} [/ latex]
- синусоидальная функция
- любая функция, которая может быть выражена в форме [латекс] f (x) = A \ sin (Bx − C) + D [/ latex] или [latex] f (x) = A \ cos (Bx − C) + D [/ латекс]
Упражнения по разделам
1.Почему функции синуса и косинуса называются периодическими функциями?
2. Как график [латекса] y = \ sin x [/ latex] соотносится с графиком [латекса] y = \ cos x [/ latex]? Объясните, как можно горизонтально перевести график [latex] y = \ sin x [/ latex], чтобы получить [latex] y = \ cos x [/ latex].
3. Какие константы влияют на диапазон функции и как они влияют на диапазон для уравнения [латекс] A \ cos (Bx + C) + D [/ latex]?
4. Как диапазон преобразованной синусоидальной функции соотносится с уравнением [латекс] y = A \ sin (Bx + C) + D [/ latex]?
5.Как можно использовать единичный круг для построения графика [латекса] f (t) = \ sin t [/ latex]?
6. [латекс] f (x) = 2 \ sin x [/ латекс]
7. [латекс] f (x) = \ frac {2} {3} \ cos x [/ латекс]
8. [латекс] f (x) = — 3 \ sin x [/ латекс]
9. [латекс] f (x) = 4 \ sin x [/ латекс]
10. [латекс] f (x) = 2 \ cos x [/ латекс]
11. [латекс] f (x) = \ cos (2x) [/ латекс]
12. [латекс] f (x) = 2 \ sin (\ frac {1} {2} x) [/ latex]
13. [латекс] f (x) = 4 \ cos (\ pi x) [/ латекс]
14. [латекс] f (x) = 3 \ cos (\ frac {6} {5} x) [/ latex]
15.[латекс] y = 3 \ sin (8 (x + 4)) + 5 [/ латекс]
16. [латекс] y = 2 \ sin (3x − 21) +4 [/ латекс]
17. [латекс] y = 5 \ sin (5x + 20) -2 [/ латекс]
Для следующих упражнений нарисуйте один полный период каждой функции, начиная с [latex] x = 0 [/ latex]. Для каждой функции укажите амплитуду, период и среднюю линию. Укажите максимальное и минимальное значения y и соответствующие им значения x на одном периоде для [latex] x> 0 [/ latex]. Укажите фазовый сдвиг и вертикальный сдвиг, если применимо.При необходимости округлите ответы до двух десятичных знаков.
18. [латекс] f (t) = 2 \ sin (t− \ frac {5 \ pi} {6}) [/ latex]
19. [латекс] f (t) = — \ cos (t + \ frac {\ pi} {3}) + 1 [/ latex]
20. [латекс] f (t) = 4 \ cos (2 (t + \ frac {\ pi} {4})) — 3 [/ латекс]
21. [латекс] f (t) = — \ sin (12t + \ frac {5 \ pi} {3}) [/ latex]
22. [латекс] f (x) = 4 \ sin (\ frac {\ pi} {2} (x − 3)) + 7 [/ latex]
23. Определите амплитуду, среднюю линию, период и уравнение, включающее синусоидальную функцию, для графика, показанного на рисунке 26.
Рисунок 26
24. Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 27.
Рисунок 27
25. Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 28.
Рисунок 28
26. Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на рисунке 29.
Рисунок 29
27.Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 30.
Рисунок 30
28. Определите амплитуду, период, среднюю линию и уравнение, включающее синус, для графика, показанного на рисунке 31.
Рисунок 31
29. Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 32.
Рисунок 32
30. Определите амплитуду, период, среднюю линию и уравнение с синусом для графика, показанного на рисунке 33.
Рисунок 33
Для следующих упражнений пусть [latex] f (x) = \ sin x [/ latex].
31. На [0,2π) решите [латекс] f (x) = \ frac {1} {2} [/ latex].
32. Вычислить [латекс] f (\ frac {\ pi} {2}) [/ latex].
33. На [0,2π), [латексе] f (x) = \ frac {\ sqrt {2}} {2} [/ latex]. Найдите все значения x .
34. На [0,2π) максимальное значение (я) функции встречается (а) при каких значениях x ?
35. На [0,2π) встречается минимальное значение (я) функции, при каком значении (ах) x ?
36.Покажите, что [latex] f (−x) = — f (x) [/ latex]. Это означает, что [latex] f (x) = \ sin x [/ latex] является нечетной функцией и обладает симметрией относительно ________________ .
Для следующих упражнений пусть [latex] f (x) = \ cos x [/ latex].
37. На [0,2π) решите уравнение [латекс] f (x) = \ cos x = 0 [/ latex].
38. На [0,2π) решите [латекс] f (x) = \ frac {1} {2} [/ latex].
39. На [0,2π) найдите x -перехваты [latex] f (x) = \ cos x [/ latex].
40. На [0,2π) найдите значения x , при которых функция имеет максимальное или минимальное значение.
41. На [0,2π) решите уравнение [латекс] f (x) = \ frac {\ sqrt {3}} {2} [/ latex].
42. График [латекс] h (x) = x + \ sin x \ text {on} [0,2 \ pi] [/ latex]. Объясните, почему график выглядит именно так.
43. График [латекс] h (x) = x + \ sin x [/ latex] на [−100,100]. График выглядел так, как было предсказано в предыдущем упражнении?
44. Изобразите [латекс] f (x) = x \ sin x [/ latex] на [0,2π] и вербализируйте, как график отличается от графика [латекса] f (x) = \ sin x [/ latex ].
45. Изобразите [латекс] f (x) = x \ sin x [/ latex] в окне [-10,10] и объясните, что показывает график.
46. Изобразите [латекс] f (x) = \ frac {\ sin x} {x} [/ latex] в окне [−5π, 5π] и объясните, что показывает график.
47. Колесо обозрения имеет диаметр 25 метров и поднимается на него с платформы, находящейся на высоте 1 метра над землей. Шесть часов на колесе обозрения находится на уровне погрузочной платформы. Колесо совершает 1 полный оборот за 10 минут. Функция h ( t ) дает высоту человека в метрах над землей t минуту после начала вращения колеса.
а. Найдите амплитуду, среднюю линию и период ч ( t ).
г. Найдите формулу для функции высоты h ( t ).
г. Как высоко над землей окажется человек через 5 минут?
Графическая функция синуса
В
тригонометрические соотношения
также может рассматриваться как функция переменной, которая является мерой угла. Эту угловую меру можно указать в
градусы
или же
радианы
. Здесь мы будем использовать радианы.
График
синус
функция
y
знак равно
грех
(
Икс
)
выглядит так:
Свойства синусоидальной функции,
y
знак равно
грех
(
Икс
)
Домен
:
(
—
∞
,
∞
)
Диапазон
:
[
—
1
,
1
]
или же
—
1
≤
y
≤
1
y
-перехват
:
(
0
,
0
)
Икс
-перехват
:
п
π
, где
п
целое число.
Период:
2
π
Непрерывность: непрерывно горит
(
—
∞
,
∞
)
Симметрия: происхождение (нечетная функция)
Максимальное значение
y
знак равно
грех
(
Икс
)
происходит, когда
Икс
знак равно
π
2
+
2
п
π
, где
п
целое число.
Минимальное значение
y
знак равно
грех
(
Икс
)
происходит, когда
Икс
знак равно
3
π
2
+
2
п
π
, где
п
целое число.
Амплитуда и период функции с момента
Амплитуда графика
y
знак равно
а
грех
(
б
Икс
)
это величина, на которую он изменяется выше и ниже
Икс
-ось.
Амплитуда = |
а
|
Период синусоидальной функции — это длина самого короткого интервала на
Икс
-ось, по которой график повторяется.
Период =
2
π
|
б
|
Пример:
Нарисуйте графики
y
знак равно
грех
(
Икс
)
а также
y
знак равно
2
грех
(
Икс
)
.Сравните графики.
Для функции
y
знак равно
2
грех
(
Икс
)
, график имеет амплитуду
2
. С
б
знак равно
1
, график имеет период
2
π
.
Таким образом, он проходит один цикл от
0
к
2
π
с одним максимумом
2
, и один минимум
—
2
.
Обратите внимание на графики
y
знак равно
грех
(
Икс
)
а также
y
знак равно
2
грех
(
Икс
)
. У каждого такое же
Икс
-перехватывает, но
y
знак равно
2
грех
(
Икс
)
имеет амплитуду, в два раза превышающую амплитуду
y
знак равно
грех
(
Икс
)
.
Также см
Тригонометрические функции
.
Найдите период функции синуса или косинуса
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Задание 1: Изучение синусоидальных кривых
Задание 1: Изучение синусоидальных кривых
Задание 1. Изучение синусоидальных кривых
Кристина Данбар, UGA
В этом задании мы будем
исследуя график уравнения
y = грех (bx + c)
, используя разные значения для a, b,
и c.
В приведенном выше уравнении
- а есть
амплитуда синусоидальной кривой - b есть
период синусоидальной кривой - c есть
фаза сдвиг синусоидальной кривой
Что такое
амплитуда синусоидальной кривой?
Амплитуда синусоиды — это ее высота.
Что такое период гг.
синусоида?
Период синусоиды — это длина
одного цикла кривой. Естественный период синуса
кривая равна 2π. Итак, коэффициент b = 1
эквивалентен периоду 2π. Чтобы получить
период синусоиды для любого коэффициента b , просто разделите 2π на
коэффициент b , чтобы получить новый период кривой.
Коэффициент b и
период синусоиды имеет обратную зависимость, так как b получает
чем меньше, тем больше длина одного цикла кривой.Точно так же, как
увеличиваешь на , период уменьшится.
Что такое фазовый сдвиг из
синусоида?
Фазовый сдвиг синусоидальной кривой на сколько
кривая смещается от нуля. Если фазовый сдвиг равен нулю,
кривая начинается в начале координат, но может двигаться влево или вправо
в зависимости от фазового сдвига. Отрицательный фазовый сдвиг указывает на
движение вправо, а положительный фазовый сдвиг указывает
движение влево.
Давайте посмотрим на график y = sin x.
Глядя на график, помните, что
числовое значение π
приблизительно равно 3,1416, поэтому 2π приблизительно равно 6,2832.
На графике выше
Амплитуда a равна 1.
Это означает, что высота графика будет равна 1, а вершина первого
«горб» равен 1.Период b имеет
коэффициент 1, поэтому период равен (2π) / 1, или просто 2π.Фазовый сдвиг c равен
ноль, поэтому кривая начинается в начале координат.
Вернуться на мою домашнюю страницу.
Рассмотрим синусоидальную кривую с разными
амплитуды.
Мы уже видели
случай, когда амплитуда равна 1; это в приведенном выше графике. А как насчет других
амплитуды?
y = 2 sin x
у = 5 грехов x
y = -1 грех x
Чем отличается приведенный выше график? Это
имеет коэффициент a = -1.Что это обозначает? Мы видим, что
наивысшая точка кривой по-прежнему равна 1, но первый горб находится на уровне -1 вместо 1.
Мы существенно перевернули график.
Теперь давайте посмотрим на несколько разных синусоидальных графиков.
все вместе.
Вернуться на мою домашнюю страницу.
Рассмотрим синусоидальную кривую с разными
периоды.
Мы уже видели
случай, когда коэффициент b равен 1; это в приведенном выше графике.Как насчет
другие периоды?
Помните, б
коэффициент и период кривой имеют обратную зависимость.
у = грех (2х)
Коэффициент b на приведенном выше графике равен 2, поэтому
период синусоиды изменился в 1/2 раза, в результате чего новый период
π, или около 3,14.
y = sin (0,5x)
Для приведенного выше графика коэффициент b = 1/2,
поэтому период синусоиды будет вдвое больше, чем обычно, или 4π.
у = грех (3х)
Обратите внимание, что новый период составляет 1/3 от первоначального.
период 2π / 3, что
примерно 2,09.
Теперь рассмотрим несколько разных синусов.
графики вместе, с разными периодами.
Вернуться на мою домашнюю страницу.
Рассмотрим синусоидальную кривую с фазой
сдвиг.
Обычно синусоида не имеет фазы
shift, поэтому переменная c равна 0.Это означает, что синусоида начинается с
происхождение, как показано на первом графике вверху этой страницы.
Что делать, если c не равно нулю?
y = sin (x +
π)
На приведенном выше графике y = sin (x +
π) , график был
сдвинут влево на единицу π .
Фактически положительный
фазовый сдвиг c фактически указывает на сдвиг влево.Давайте посмотрим на некоторые
другие примеры:
у = грех (х + 1)
Синусоидальная кривая сдвинута на одну единицу к
оставил.
у = грех (х + π / 2)
Кривая сдвинута
π / 2 единицы слева. Напомним, что
π / 2 составляет приблизительно 1,57.
Что делать, если переменная c
отрицательный?
у = грех (х — 1)
Кривая сместилась на 1 единицу вправо.
у = грех (х —
π / 2)
Давайте вместе посмотрим на несколько фазовых сдвигов:
Примечание: Фазовый сдвиг
π будет выглядеть точно так же, как
фазовый сдвиг -π.
y = sin (x +
π)
y = sin (x —
π)
Вернуться на мою домашнюю страницу.
В приведенных выше упражнениях мы исследовали, что
происходит с синусоидой, когда мы меняем коэффициенты a, b и c
индивидуально. Что, если вы меняли более одного за раз?
y = 2 sin (2x)
а = 2 б = 2
с = 0
Амплитуда 2, период 2π / 2,
или π. Фазового сдвига нет.
y = 2 sin (2x -1)
а = 2 б = 2
с = -1
Амплитуда 2, период 2π / 2,
или π.Вся кривая сдвинута на одну единицу вправо.
y = 3 sin (2x + 2)
а = 3 б = 2
с = 2
Амплитуда, как и следовало ожидать, равна 3. В
период графика равен 2π / 2 или π.
Мы ожидаем, что сдвиг фазы будет на две единицы влево, но мы видим, что
Это не относится к делу. Почему? Поскольку фазовый сдвиг зависит от
Период. Период графика равен 1/2 его первоначального размера, и
следовательно, фазовый сдвиг также будет 1/2 коэффициента c, или 1.
Это показано на графике выше.
y = 0,5 sin (0,5x -3)
а = 0,5 Ь = 0,5
с = -3
Амплитуда 0,5, что мы ясно видим на
график. Коэффициент b равен 0,5, поэтому период синусоиды вдвое больше.
как обычно, или 4π
(примерно 12,57). Поскольку период кривой вдвое больше,
как правило, фазовый сдвиг будет вдвое больше коэффициента c, или 6 единиц от
верно.
Вернуться на мою домашнюю страницу.
Хотите поработать несколько практических задач?
Кликните сюда.
Функция синуса — определение математического слова
Функция синуса — определение слова в математике — открытый справочник по математике
Попробуй это
Перетащите любой
вершину треугольника и посмотрите, как вычисляются синусы A и C.
Функция синуса, наряду с косинусом и тангенсом, является одной из трех наиболее распространенных
тригонометрические функции.В любом прямоугольном треугольнике
синус угла x — это длина противоположной стороны (O), деленная на длину
гипотенуза (H).
В формуле это пишется как «грех» без «е»:
Часто вспоминается как «SOH» — что означает
Синус
Напротив
Гипотенуза.
См. SOH CAH TOA.
В качестве примера предположим, что мы хотим найти синус угла C на рисунке выше (сначала нажмите «сбросить»).
Из приведенной выше формулы мы знаем, что синус угла — это сторона, противоположная делению гипотенузы.Противоположная сторона — AB и имеет длину 15. Гипотенуза — это AC длиной 30. Таким образом, мы можем написать
что составляет 0,5.
Таким образом, мы можем сказать: « Синус 30 ° равен 0,5 », или
Воспользуйтесь калькулятором, чтобы найти синус 30 °. Должно получиться 0,5, как указано выше.
(Если нет — убедитесь, что калькулятор настроен на работу в градусах, а не
радианы).
Пример — использование синуса для нахождения гипотенузы
Если мы посмотрим на общее определение —
мы видим, что есть три переменные: мера угла x и длины двух сторон (противоположность и гипотенуза).Итак, если у нас есть какие-то два из них, мы можем найти третий.
На рисунке выше нажмите «Сброс». Представьте, что мы не знаем длины гипотенузы H.
Мы знаем, что синус A (60 °) — это противоположная сторона (26), деленная на H.
Из нашего калькулятора мы находим, что sin60 равен 0,866, поэтому мы можем написать
Транспонирование:
что выходит на 30.02 *
* Примечание:
Длины и углы на рисунке выше округлены для ясности.
Используя калькулятор, они будут немного отличаться. Калькулятор верен.
Обратная функция синуса — arcsin
Для каждой тригонометрической функции, такой как sin, существует обратная функция, которая работает в обратном порядке.
Эти обратные функции имеют то же имя, но с дугой впереди.
(На некоторых калькуляторах кнопка arcsin может быть помечена как asin, а иногда
грех -1 .)
Итак, обратное к греху — это arcsin и т. Д. Когда мы видим «arcsin A», мы понимаем его как «угол, грех которого равен A».
| sin30 = 0,5 | Означает: синус 30 градусов равен 0.5 |
| arcsin0.5 = 30 | Означает: Угол, грех которого равен 0,5, равен 30 градусам. |
Используйте его, если вы знаете синус угла и хотите узнать фактический угол.
См. Также определение арксинуса и
Обратные функции — тригонометрия
Большие и отрицательные углы
В прямоугольном треугольнике два переменных угла всегда меньше 90 °.
(См. Внутренние углы треугольника).
Но мы можем найти синус любого угла, независимо от его размера, а также синус отрицательных углов.Подробнее об этом см. Функции больших и отрицательных углов.
Построение синусоиды
Когда синус угла отображается в зависимости от угла, в результате получается форма, аналогичная приведенной выше:
называется синусоидальной волной.
Для получения дополнительной информации см. График синусоидальной функции.
Производная sin (x)
В расчетах производная sin (x) равна cos (x) .
Это означает, что при любом значении x скорость изменения или наклон sin (x) составляет cos (x) .Подробнее об этом см.
Производные тригонометрических функций вместе с производными других тригонометрических функций.
См. Также Оглавление по исчислению.
Другие темы по тригонометрии
Уголки
Тригонометрические функции
Решение задач тригонометрии
Исчисление
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
.

 .. тоа
.. тоа