Показательные уравнения. Решения

Решение множества показательных уравнений не обходится без замен, квадратных уравнений и сложных преобразований. Приведенные ниже примеры помогут Вам в этом быстро разобраться и научат решать самые сложные из них. Также Вы сможете выучить некоторые свойства логарифмов без которых показательные уравнения в простой способ не решить. Начнем с самых азов — теоретического материала об уравнениях.
Показательными называют уравнения в которых неизвестная величина содержится в показателе степени, при этом основа степени не содержит неизвестной величины. Самое простое показательных уравнения a^x=b решают логарифмированием x=log[a](b).

При решении показательных уравнений используют свойство показателей: если в уравнение степени с одной и той же основой то равные показатели степени или основание равно единице.
Из равенства следует или .

Некоторые уравнения требуют замены переменной и сводится к решению степенного уравнения. Например уравнения
легко сводится к квадратному если сделать замену
При этом исходное уравнение примет вид
После его решения нужно вернуться к замене и решить полученное уравнение.
Если показательной уравнение содержит две различные показательные функции ( основы не сводятся к одной) , то выполняют деления уравнения на одну из основ в соответствующей степени и переход до показательного уравнения которое содержит функцию с дробной основой.
Находя решения показательных уравнений следует помнить что показательная функция принимает только положительные значения. Отрицательные значения или нули замененной переменной не принимаются к рассмотрению.

На этом необходимый теоретический материал заканчивается и переходим к рассмотрению распространенных примеров.

Пример 1.Решить показательное уравнение

Решение. Перепишем уравнение к следующему виду

Второе слагаемое распишем как произведение

и сделаем замену в уравнении

Исходное уравнение преобразуем к следующему

Областью допустимых значений будет действительная ось за исключением точки y=0.
Умножим его на y и переносим все в левую сторону

Получили квадратное уравнение корни которого находим по теореме Виета. Нетрудно убедиться что они принимают значения

Возвращаемся к замене и находим решения

Выполняем проверку

Итак оба решения удовлетворяют уравнению.

Пример 2. Решить показательное уравнение

Решение. Используя одну из свойств логарифма записываем правую сторону уравнения в виде

Приравнивая показатели находим

Пример 3. Решить уравнение

Решение. Такого сорта примеры решают логарифмированием обеих сторон что приводит к сведению показательного уравнения к простому виду.

Полученное уравнение относительно переменной решаем через дискриминант

Корни уравнения приобретут значения

Другого метода позволяющего аналитически получить решения Вы не найдете ни в интернете, ни на форумах.

Пример 4. Решить уравнение

Решение. Выполним некоторые преобразования с показателями чтобы упростить уравнение

Эквивалентные значения подставим в уравнение, в результате получим

Выполняем замену

Уравнение превратится к квадратному

Вычисляем дискриминант

Найденное значение подставляем в формулу корней

Возвращаемся к замене и находим

Задача решена.

Пример 5.Решить уравнение

Решение. Такого типа уравнения решают с постоянной основой . За основу классически берут 10 , однако , если взять другую (для данного примера 5 или 9 ) то решение примет компактный вид
Рассмотрим оба метода.
1. Прологарифмируем обе части равенства

Раскрываем скобки и группируем слагаемые при неизвестных

Такой интересный результат.

2. Прологарифмируем обе части равенства по основанию 9

Группируя слагаемые содержащие переменную получим

Оба метода достаточно быстрые и эффективные, для себя выбирайте который Вам больше подходит.

Пример 6.Решить уравнение

Решение.Такого рода задачи решают по следующей схеме. Показательное уравнения превращают к виду

Все слагаемые разделяем на величину чтобы свести к дробному виду

После этого выполняем замену

Уравнение переписываем в виде

Умножаем на переменную и решаем квадратное уравнение

Дискриминант принимает нулевое значение, при етом корни уравнения совпадают

Возвращаемся к замене и решаем

Итак x=2 — единственное решение.
Используйте приведенную схему в подобных задач и гарантированно получите верный результат.

Пример 7. Решить уравнение

Решение. На первый взгляд уравнения достаточно сложное и неизвестно как его упрощать, однако схема решения данного примера и подобных довольно проста и интересна. Выполним над уравнением преобразования

Нужно это уравнение преобразовать к квадратному

Выполним замену

и перепишем уравнение в виде следуещого

Вычисляем дискриминант

и корни уравнения

Возвращаемся к совершенной замене

Такое уравнение сводим к квадратному, выполнив замену

В результате получим

Решаем через дискриминант

Возвращаемся к замене и определяем переменную x

Второе значение рассматривать не будем, поскольку оно отрицательное, а показательная функция всюду положительная.
Решаем вторую половину задачи

Используя предыдущую замену получим

Дискриминант примет значение

Находим корни уравнения

Первый корень имеет место бить, второй — отрицательный и не подходит.

Получили два решения показательного уравнения

Хорошо разберитесь с приведенными методами решения показательных уравнений, возможно некоторые из них пригодятся при прохождении ВНО, экзамене или контрольной работе. Будьте внимательны при упрощении, первое время используйте подстановку для проверки результатов.

Похожие материалы:

Степень уравнения | Математика

Кроме разделения уравнений по количеству неизвестных, уравнения также разделяются по степеням неизвестных: уравнения первой степени, уравнения второй степени и так далее.

Чтобы определить степень уравнения, в нём нужно предварительно сделать следующие преобразования:

• раскрыть скобки,
• освободить уравнение от дробных членов,
• перенести все неизвестные члены в одну из частей уравнения,
• сделать приведение подобных членов.

После выполнения всех этих преобразований, степень уравнения определяется по следующим правилам:

Степенью уравнения с одним неизвестным называется показатель при неизвестном в том члене уравнения, в котором этот показатель наибольший.

Примеры:

10 — x = 2  — уравнение первой степени с одним неизвестным;

x² + 7x = 16  — уравнение второй степени с одним неизвестным;

x³ = 8  — уравнение третьей степени с одним неизвестным.

Степенью уравнения с несколькими неизвестными называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая.

Для примера возьмём уравнение

3x²y + xy + 25 = 0.

Для наглядности расставим показатели первой степени (которые обычно не ставят):

3x²y¹ + x¹y¹ + 25¹ = 0.

Теперь посчитаем суммы показателей для тех членов уравнения, в которых присутствуют неизвестные:

3x²y¹  — сумма показателей равна  2 + 1 = 3;

x¹y¹  — сумма показателей равна  1 + 1 = 2.

Сумма показателей у первого члена уравнения больше, чем у второго, значит, при определении степени уравнения будем ориентироваться на сумму показателей первого члена. Это значит, что про данное уравнение можно сказать, что это уравнение третьей степени с двумя неизвестными.

Примеры:

2xy — x = 25  — уравнение второй степени с двумя неизвестным,

xy² — 2xy + 8y = 0  — уравнение третьей степени с двумя неизвестными.

Дети и учеба — Информационный портал

В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.

Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.

Уравнения высшей степени с целыми коэффициентами

Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x:

a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · (a n) n — 1 · x + a 0 · (a n) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0

Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .

Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 (x) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 (x) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .

Подставляем остальные выписанные делители в P n — 1 (x) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде (x — x 1) (x — x 2) · P n — 2 (x) = 0 .Здесь P n — 2 (x) будет частным от деления P n — 1 (x) на x — x 2 .

Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m (x) = 0 . Здесь P n — m (x) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.

Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.

У нас в итоге получилось уравнение P n — m (x) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.

Покажем на конкретном примере, как применяется такая схема решения.

Пример 1

Условие:
найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .

Решение

Начнем с нахождений целых корней.

У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.

При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.

Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на (х — 1) в столбик:

Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .

1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 · (- 1) 2 + 4 · — 1 + 3 = 0

У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .

Делим многочлен x 3 + 2 x 2 + 4 x + 3 на (х + 1) в столбик:

Получаем, что

x 4 + x 3 + 2 x 2 — x — 3 = (x — 1) (x 3 + 2 x 2 + 4 x + 3) = = (x — 1) (x + 1) (x 2 + x + 3)

Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1:

1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0

Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.

Оставшиеся корни будут корнями выражения x 2 + x + 3 .

D = 1 2 — 4 · 1 · 3 = — 11

Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .

Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.

В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .

После нахождения следующего корня, равного — 1 , мы получаем следующее:

Ответ:
х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .

Пример 2

Условие:
решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .

Решение

У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .

Проверяем их по порядку:

1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 (- 1) 4 — (- 1) 3 — 5 · (- 1) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0

Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:

В итоге мы получим x — 2 (x 3 + x 2 — 3 x — 6) = 0 .

2 3 + 2 2 — 3 · 2 — 6 = 0

Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2:

В итоге получим (x — 2) 2 · (x 2 + 3 x + 3) = 0 .

Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.

Решим квадратное уравнение:

x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3

Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .

Ответ
: x = — 3 2 ± i 3 2 .

Пример 3

Условие:
найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.

Решение

x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0

Выполняем домножение 2 3 обеих частей уравнения:

2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0

Заменяем переменные y = 2 x:

2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0

В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .

Ответ:
x 1 = — 1 , x 2 = 3 2

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Рассмотрим решения уравнений с одной переменной степени выше второй.

Степенью уравнения Р(х) = 0 называется степень многочлена Р(х), т.е. наибольшая из степеней его членов с коэффициентом, не равным нулю.

Так, например, уравнение (х 3 – 1) 2 + х 5 = х 6 – 2 имеет пятую степень, т.к. после операций раскрытия скобок и приведения подобных получим равносильное уравнение х 5 – 2х 3 + 3 = 0 пятой степени.

Вспомним правила, которые понадобятся для решения уравнений степени выше второй.

Утверждения о корнях многочлена и его делителях:

1.
Многочлен n-й степени имеет число корней не превышающее число n, причем корни кратности m встречаются ровно m раз.

2.
Многочлен нечетной степени имеет хотя бы один действительный корень.

3.
Если α – корень Р(х), то Р n (х) = (х – α) · Q n – 1 (x), где Q n – 1 (x) – многочлен степени (n – 1).

4.

5.
Приведенный многочлен с целыми коэффициентами не может иметь дробных рациональных корней.

6.
Для многочлена третьей степени

Р 3 (х) = ах 3 + bx 2 + cx + d возможно одно из двух: либо он разлагается в произведение трех двучленов

Р 3 (x) = а(х – α)(х – β)(х – γ), либо разлагается в произведение двучлена и квадратного трехчлена Р 3 (x) = а(х – α)(х 2 + βх + γ).

7.
Любой многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов.

8.
Многочлен f(x) делится на многочлен g(х) без остатка, если существует многочлен q(x), что f(x) = g(x) · q(x). Для деления многочленов применяется правило «деления уголком».

9.
Для делимости многочлена P(x) на двучлен (x – c) необходимо и достаточно, чтобы число с было корнем P(x) (Следствие теоремы Безу).

10.
Теорема Виета: Если х 1 , х 2 , …, х n – действительные корни многочлена

Р(х) = а 0 х n + а 1 х n — 1 + … + а n , то имеют место следующие равенства:

х 1 + х 2 + … + х n = -а 1 /а 0 ,

х 1 · х 2 + х 1 · х 3 + … + х n – 1 · х n = a 2 /а 0 ,

х 1 · х 2 · х 3 + … + х n – 2 · х n – 1 · х n = -a 3 / а 0 ,

х 1 · х 2 · х 3 · х n = (-1) n a n / а 0 .

Решение примеров

Пример 1.

Найти остаток от деления Р(х) = х 3 + 2/3 x 2 – 1/9 на (х – 1/3).

Решение.

По следствию из теоремы Безу: «Остаток от деления многочлена на двучлен (х – с) равен значению многочлена от с». Найдем Р(1/3) = 0. Следовательно, остаток равен 0 и число 1/3 – корень многочлена.

Ответ: R = 0.

Пример 2.

Разделить «уголком» 2х 3 + 3x 2 – 2х + 3 на (х + 2). Найти остаток и неполное частное.

Решение:

2х 3 + 3x 2 – 2х + 3| х + 2

2х 3 + 4
x 2
2x 2 – x

X 2 – 2
x

Ответ: R = 3; частное: 2х 2 – х.

Основные методы решения уравнений высших степеней

1. Введение новой переменной

Метод введения новой переменной уже знаком на примере биквадратных уравнений. Он заключается в том, что для решения уравнения f(x) = 0 вводят новую переменную (подстановку) t = x n или t = g(х) и выражают f(x) через t, получая новое уравнение r(t). Решая затем уравнение r(t), находят корни:

(t 1 , t 2 , …, t n). После этого получают совокупность n уравнений q(x) = t 1 , q(x) = t 2 , … , q(x) = t n , из которых находят корни исходного уравнения.

Пример 1.

(х 2 + х + 1) 2 – 3х 2 – 3x – 1 = 0.

Решение:

(х 2 + х + 1) 2 – 3(х 2 + x) – 1 = 0.

(х 2 + х + 1) 2 – 3(х 2 + x + 1) + 3 – 1 = 0.

Замена (х 2 + х + 1) = t.

t 2 – 3t + 2 = 0.

t 1 = 2, t 2 = 1. Обратная замена:

х 2 + х + 1 = 2 или х 2 + х + 1 = 1;

х 2 + х — 1 = 0 или х 2 + х = 0;

Ответ: Из первого уравнения: х 1, 2 = (-1 ± √5)/2, из второго: 0 и -1.

2. Разложение на множители методом группировки и формул сокращенного умножения

Основа данного метода также не нова и заключается в группировке слагаемых таким образом, чтобы каждая группа содержала общий множитель. Для этого иногда приходится применять некоторые искусственные приемы.

Пример 1.

х 4 – 3x 2 + 4х – 3 = 0.

Решение.

Представим — 3x 2 = -2x 2 – x 2 и сгруппируем:

(х 4 – 2x 2) – (x 2 – 4х + 3) = 0.

(х 4 – 2x 2 +1 – 1) – (x 2 – 4х + 3 + 1 – 1) = 0.

(х 2 – 1) 2 – 1 – (x – 2) 2 + 1 = 0.

(х 2 – 1) 2 – (x – 2) 2 = 0.

(х 2 – 1 – х + 2)(х 2 – 1 + х — 2) = 0.

(х 2 – х + 1)(х 2 + х – 3) = 0.

х 2 – х + 1 = 0 или х 2 + х – 3 = 0.

Ответ: В первом уравнении нет корней, из второго: х 1, 2 = (-1 ± √13)/2.

3. Разложение на множитель методом неопределенных коэффициентов

Суть метода состоит в том, что исходный многочлен раскладывается на множители с неизвестными коэффициентами. Используя свойство, что многочлены равны, если равны их коэффициенты при одинаковых степенях, находят неизвестные коэффициенты разложения.

Пример 1.

х 3 + 4x 2 + 5х + 2 = 0.

Решение.

Многочлен 3-й степени можно разложить в произведение линейного и квадратного множителей.

х 3 + 4x 2 + 5х + 2 = (х – а)(x 2 + bх + c),

х 3 + 4x 2 + 5х + 2 = х 3 +bx 2 + cх – ax 2 – abх – ac,

х 3 + 4x 2 + 5х + 2 = х 3 + (b – a)x 2 + (cх – ab)х – ac.

Решив систему:

{b – a = 4,
{c – ab = 5,
{-ac = 2,

{a = -1,
{b = 3,
{c = 2, т.е.

х 3 + 4x 2 + 5х + 2 = (х + 1)(x 2 + 3х + 2).

Корни уравнения (х + 1)(x 2 + 3х + 2) = 0 находятся легко.

Ответ: -1; -2.

4. Метод подбора корня по старшему и свободному коэффициенту

Метод опирается на применение теорем:

1)
Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.

2)
Для того, чтобы несократимая дробь p/q (p – целое, q – натуральное) была корнем уравнения с целыми коэффициентами, необходимо, чтобы число p было целым делителем свободного члена а 0 , а q – натуральным делителем старшего коэффициента.

Пример 1.

6х 3 + 7x 2 – 9х + 2 = 0.

Решение:

6: q = 1, 2, 3, 6.

Следовательно, p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.

Найдя один корень, например – 2, другие корни найдем, используя деление уголком, метод неопределенных коэффициентов или схему Горнера.

Ответ: -2; 1/2; 1/3.

Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

На канал на youtube нашего сайта сайт, чтобы быть в курсе всех новых видео уроков.

Для начала вспомним основные формулы степеней и их свойства.

Произведение числа a
само на себя происходит n раз, это выражение мы можем записать как a a … a=a n

1. a 0 = 1 (a ≠ 0)

3. a n a m = a n + m

4. (a n) m = a nm

5. a n b n = (ab) n

7. a n /a m = a n — m

Степенные или показательные уравнения
– это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.

Примеры показательных уравнений:

В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x
степенью или показателем.

Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0

Теперь разберем как решаются показательные уравнения?

Возьмем простое уравнение:

2 х = 2 3

Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:

2 х = 2 3
х = 3

Для того, чтобы решить такое уравнение, мы убрали одинаковые основания
(то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.

Теперь подведем итоги нашего решения.

Алгоритм решения показательного уравнения:

1. Нужно проверить одинаковые
ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем
степени и решаем полученное новое уравнение.

Теперь прорешаем несколько примеров:

Начнем с простого.

Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.

x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2

В следующем примере видно, что основания разные это 3 и 9.

3 3х — 9 х+8 = 0

Для начала переносим девятку в правую сторону, получаем:

Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n) m = a nm .

3 3х = (3 2) х+8

Получим 9 х+8 =(3 2) х+8 =3 2х+16

3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.

3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.

Смотрим следующий пример:

2 2х+4 — 10 4 х = 2 4

В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n) m = a nm .

4 х = (2 2) х = 2 2х

И еще используем одну формулу a n a m = a n + m:

2 2х+4 = 2 2х 2 4

Добавляем в уравнение:

2 2х 2 4 — 10 2 2х = 24

Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х,вот и ответ — 2 2х мы можем вынести за скобки:

2 2х (2 4 — 10) = 24

Посчитаем выражение в скобках:

2 4 — 10 = 16 — 10 = 6

Все уравнение делим на 6:

Представим 4=2 2:

2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.

Решим уравнение:

9 х – 12*3 х +27= 0

Преобразуем:
9 х = (3 2) х = 3 2х

Получаем уравнение:
3 2х — 12 3 х +27 = 0

Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены
. Число с наименьшей степенью заменяем:

Тогда 3 2х = (3 х) 2 = t 2

Заменяем в уравнении все степени с иксами на t:

t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t 1 = 9
t 2 = 3

Возвращаемся к переменной x
.

Берем t 1:
t 1 = 9 = 3 х

Стало быть,

3 х = 9
3 х = 3 2
х 1 = 2

Один корень нашли. Ищем второй, из t 2:
t 2 = 3 = 3 х
3 х = 3 1
х 2 = 1
Ответ: х 1 = 2; х 2 = 1.

На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.

Вступайте в группу

Судя по началу публикации, которое мы здесь опустим, текст писал Юрий Игнатьевич. И написано хорошо, и проблематика злободневная, вот только так называть Россию, как это делает Мухин…

Как бы кто ни относился к антинародной власти, Россия выше неё и не заслуживает оскорблений. Даже от талантливого разоблачителя лжи американского агенства НАСА.

*

Обращение к тов. Мухину Ю.И.

Уважаемый Юрий Игнатьевич!
Я знаю, что вы посещаете эти страницы. Поэтому обращаюсь к вам напрямую.

Мы все ценим ваш подвижнический труд на ниве разоблачения лжи Запада, лжи Америки, лжи псевдоучёных, лжи либералов. Мы с удовольствием и пользой для себя и общества задумываемся над серьёзными темами, которые вы нам время от времени подбрасываете, будь то меритократия или метафизика, любовь к отечественной истории или восстановление справедливости.

Однако ваши определения нашей общей с вами Родины вызывают недоумение и сильно огорчают.

Впрочем, посудите сами: как бы вы охарактеризовали человека, который стал оскорблять свою заболевшую и от этого временно переставшую работать мать?

А ведь Россия, как бы она ни именовалась, и какой бы хорошей или отвратительной ни была власть, — Россия это наша Родина. Родина-мать.
За неё наши деды проливали кровь и клали свои жизни.

Поэтому ставить её в один ряд с властью — это опускать духовное возвышенное на уровень материального, да ещё и низкого. Т.е. вы проводите сравнение совершенно различных категорий. Вещь, недопустимая для любого вменяемого человека.

Прошу вас, уважаемый тов. Мухин, серьёзно задуматься над этим.

**

…А с уравнениями (я этого и не знал) положение таково. Как найти корни квадратного уравнения догадались ещё в древнем Египте
.

Как найти корни кубического уравнения и уравнения четвёртой степени, нашли в шестнадцатом веке, а вот найти корни уравнения пятой степени до 2016 года не могли. А пытались далеко не простые люди.

В шестнадцатом веке найти корни уравнения пятой степени пытался основоположник символической алгебры Франсуа Виет, в девятнадцатом веке это пытался сделать основатель современной высшей алгебры французский математик Эварист Галуа, после него найти корни уравнений пятой степени пробовал норвежский математик Нильс Хенрик Абель, который, в конце концов, сдался и доказал невозможность решения уравнения пятой степени в общем виде.

Читаем в Википедии о заслугах Абеля: «Абель закончил блестящее исследование древней
проблемы:
доказал невозможность решить в общем виде (в радикалах) уравнение 5-й степени…

В алгебре Абель нашёл необходимое условие для того, чтобы корень уравнения выражался «в радикалах» через коэффициенты этого уравнения. Достаточное условие вскоре открыл Галуа, чьи достижения опирались на труды Абеля.

Абель привёл конкретные примеры уравнения 5-й степени, чьи корни нельзя выразить в радикалах, и тем самым в значительной степени закрыл древнюю проблему».

Как видите, если теорему Пуанкаре доказать пытались всё время и Перельман оказался удачливее остальных математиков, то после Абеля за уравнения пятой степени математики и не брались.

А в 2014 году математик из Томска
Сергей Зайков
, о котором по фото можно судить, что он уже в годах, а по данным из статьи о нём, что он выпускник факультета прикладной математики и кибернетики Томского государственного университета, в ходе своей работы получил уравнения пятой степени. Тупик? Да, тупик! Но Сергей Зайков взялся его проломить.

И в 2016 году он нашёл способы решений уравнений пятой степени в общем виде! Сделал то, невозможность чего доказали математики Галуа и Абель.

Я попытался найти сведения о Сергее Зайкове в Википедии, но хрен вам! О математике Сергее Зайкове и о нахождении им решения уравнений пятой степени сведений нет!

Пикантность делу придаёт и то, что для математиков существует аналог Нобелевской премии — Абелевская премия
(Нобель запретил давать премию математикам и теперь её дают за математические испражнения, называя их «физикой
»).

Эта математическая премия в честь того самого Абеля, который доказал невозможность того, что сделал Зайков
. Однако, самовыдвижение на эту премию не допускается. А Зайков математик-одиночка и нет никаких организаций, которые могли бы предложить его кандидатуру на соискание этой премии.

Правда у нас есть Академия наук, но ведь там академики сидят не для развития математики, а «бабло пилить». Кому там нужен этот Зайков?

Ну а для новостных агентств Зайков — это вам не Перельман! Посему открытие Зайкова для СМИ — это не сенсация.

Вот то, что Порошенко дверью ошибся — это да! Это настоящая сенсация!

Томский математик решил проблему, которую не могли решить двести лет

С появлением алгебры ее основной задачей считалось решение алгебраических уравнений. Решение уравнения второй степени было известно еще в Вавилоне и Древнем Египте. Мы проходим такие уравнения в школе. Помните уравнение x2
+ ax + b = 0, и дискриминант?

Сергей Зайков с книгой

Решение алгебраических уравнений третьей и четвертой степени было найдено в шестнадцатом веке. Но решить уравнение пятой степени не удалось. Причину нашел Лагранж. Он показал, что решение уравнений третьей и четвертой степени стало возможным потому, что их можно свести к уравнениям, ранее уже решенным. Уравнение третьей степени можно свести к уравнению второй степени, а уравнение четвертой — к уравнению третьей. Но уравнение пятой степени сводится к уравнению шестой, т. е. более сложному, поэтому традиционные методы решения не применимы.

Вопрос о решении уравнения пятой степени сдвинулся с места лишь двести лет назад, когда Абель доказал, что не все уравнения пятой степени можно решить в радикалах, т. е. в квадратных, кубических и иных корнях, известных нам по школе. А Галуа вскоре, т. е. двести лет назад, нашел критерий, позволяющий определить, какие уравнения пятой степени можно решить в радикалах, а какие нет. Он заключается в том, что группа Галуа, разрешимых в радикалах уравнения пятой степени, должна быть либо циклической или метациклической. Но Галуа не нашел способ решения в радикалах тех уравнений пятой степени, которые разрешимы в радикалах. Теория Галуа очень известна, о ней написано много книг.

До сих пор находились лишь частные решения для разрешимых в радикалах уравнений пятой степени. И только в этом году томский математик Сергей Зайков решил задачу, которую не могли решить двести лет. Опубликовал книгу «Как решаются в радикалах алгебраические уравнения пятой степени», в которой указал способ решения для любых уравнений пятой степени, которые разрешимы в радикалах. Зайков — выпускник факультета прикладной математики и кибернетики Томского государственного университета. Нам удалось взять у него интервью.

— Сергей, почему Вы стали решать эту задачу?

— Мне нужно было решение уравнения пятой степени для решения задачи из другого раздела математики. Я начал выяснять, как его найти, и узнал, что не все из них решаются в радикалах. Тогда я попытался найти в научной литературе способ решения тех уравнений, которые разрешимы в радикалах, но нашел лишь критерий, по которому можно определить, какие разрешимы, а какие нет. Я не алгебраист, но, разумеется, как выпускник ФПМК, умею применять и алгебраические методы. Поэтому я с 2014 г. всерьез начал искать решение и нашел его сам.

Способ был найден мной два года назад, я подготовил книгу, в которой был описан не только он, но и способы решения некоторых уравнений степеней больше пятой. Но у меня не было денег для ее издания. В этом году я решил, что проще опубликовать лишь часть этой работы, и взял только ее половину, посвященную способу решения уравнения пятой степени в радикалах.

Я поставил своей целью публикацию что-то вроде руководства по решению этой задачи, понятной для математиков, которым необходимо решить конкретное уравнение. Поэтому упростил ее, убрав множество длинных формул и значительную часть теории, урезав более чем наполовину, оставив только необходимое. Поэтому у меня получилось что-то вроде книжки «для чайников», по которой математики, не знакомые с теорией Галуа, могут решить нужное им уравнение.

— За это большое спасибо Владиславу Бересневу, с которым мы знакомы много лет. Он проспонсировал издание книги.

— Возможно ли получение Вами какой-либо премии по математике за решение этой задачи? Например, Вы упоминали Абеля. А ведь есть Абелевская премия по математике, которую считают аналогом нобелевской?

— Полностью исключить такую возможность нельзя. Но и надеяться на это не стоит.

Например, заявки на кандидатов на Абелевскую премию 2019 г. подаются до 15 сентября. Причем самовыдвижение не допускается. А я математик-одиночка. Нет никаких организаций или известных математиков, которые предложат мою кандидатуру. Поэтому она не будет рассматриваться независимо от того, заслуживает ли моя работа этой премии, и насколько соответствует духу этой премии вручение ее тем, кто продолжает работы Абеля. Но даже в случае, если она будет представлена, все зависит еще и от уровня работ других кандидатов.

Книга рассчитана на тех, кто не знаком с теорией Галуа. Основы теории Галуа даются только в той части, в которой они необходимы для решения уравнения, детально описан способ решения, показаны приемы, упрощающие решение. Значительная часть книги посвящена примеру решения конкретного уравнения. Рецензентами книги являются доктор технических наук Геннадий Петрович Агибалов и доктор физ. мат. наук, профессор Петр Андреевич Крылов.

ПОДГОТОВИЛА АНАСТАСИЯ СКИРНЕВСКАЯ

Формула решения уравнения 4 степени / Хабр

Существует несколько методов нахождения корней полиномиального уравнения 4-ой степени.

Однако они не очень удобны при решении уравнений с коэффициентами, которые представляют собой выражения с параметрами.

Инстаграм

1. Формула решения уравнения 4 степени

Рассмотрим уравнение 4-ой степени, сумма корней которого равна нулю. Коэффициенты могут быть вещественными или комплексными.

Произведение следующих двух квадратов тождественно рассматриваемому уравнению 4-ой степени.

Значение R является решением следующего кубического уравнения.

Почти такое же уравнение появляется при решении уравнения 4-ой степени путем разложения на разность полных квадратов. Будем называть данное кубическое уравнение вспомогательным.

Вычислим произведение двух квадратов new.

То же самое, но в форме коэффициентов при степенях x (в порядке убывания степеней).

Упростим выражения для коэффициентов при второй и первой степени x.

Приведенное выражение для первой степени x.

В итоге получаем k1. 3 заменяется на

Получается выражение

В общем описанные в п.2 преобразования не являются тождественными. Но если считать интересными только значения x, которые являются корнями исходного уравнения, то данные преобразования можно считать квазитождественными. И тогда y представляется выражением, соответствующим корням исходного уравнения.

3. Для кубического уравнения операция в п.2 производится еще один раз. В итоге получается система из 3 уравнений по x, которая имеет три ненулевых решения, соответствующих корням исходного уравнения. Из коэффициентов x формируем матрицу

4. Находим определитель матрицы, который представляется кубическим выражением по y.

Вычисляем значения, обеспечивающие равенство определителя нулю.

5. В уравнении по y имеются два параметра P и Q. Вычислим их так, чтобы нулю равнялись коэффициенты при второй и первой степени y.

Любое P

, где

6. В итоге имеем уравнение c тремя кратными корнями для y

7. Остается решить квадратное уравнение с известными y, P, Q

Одно из решений будет решением исходного уравнения.

3. Параметры решения вспомогательного кубического уравнения

Для конкретных значений коэффициентов все выглядит не таким страшным образом.

Отметим, что для формулы решения уравнения 4-ой степени требуется только один корень R вспомогательного кубического уравнения.

Для конкретных коэффициентов вспомогательного уравнения имеем

При использовании формулы решения уравнения 4-ой степени необходимо ссылаться — «Метод ftvmetrics».

Интересные задачи присылайте в Direct Инстаграмм.

Степенные или показательные уравнения.

Приветствую вас дорогие учащиеся!

Рекомендуем подписаться на канал на youtube нашего сайта TutoMath.ru, чтобы быть в курсе всех новых видео уроков.

Для начала вспомним основные формулы степеней и их свойства.

Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=aⁿ

1. a⁰ = 1 (a ≠ 0)

2. a¹ = a

3. aⁿ • a^m = a^{n + m}

4. (aⁿ)^m = a^nm

5. aⁿbⁿ = (ab)ⁿ

6. a^-n= 1/aⁿ

7. aⁿ/a^m= a^{n — m}

Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.

Примеры показательных уравнений:

6^x=36

В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.

Приведем еще примеры показательных уравнений.
2^x*5=10
16^x — 4^x — 6=0

Теперь разберем как решаются показательные уравнения?

Возьмем простое уравнение:

2^х = 2³

Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:

2^х = 2³
х = 3

Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.

Теперь подведем итоги нашего решения.

Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.

Теперь прорешаем несколько примеров:

Начнем с простого.

2^х+2 = 2⁴

Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.

x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2

В следующем примере видно, что основания разные это 3 и 9.

3^3х — 9^х+8 = 0

Для начала переносим девятку в правую сторону, получаем:

3^3х = 9^х+8

Теперь нужно сделать одинаковые основания. Мы знаем что 9=3² . Воспользуемся формулой степеней (aⁿ)^m = a^nm.

3^3х = (3²)^х+8

Получим 9^х+8 =(3²)^х+8 =3 ^2х+16

3^3х = 3 ^2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.

3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.

Смотрим следующий пример:

2^2х+4 — 10•4^х = 2⁴

В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (aⁿ)^m = a^nm.

4^х = (2²)^х = 2^2х

И еще используем одну формулу aⁿ • a^m = a^{n + m}:

2^2х+4 = 2^2х•2⁴

Добавляем в уравнение:

2^2х•2⁴ — 10•2^2х = 24

Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2^2х ,вот и ответ — 2^2х мы можем вынести за скобки:

2^2х(2⁴ — 10) = 24

Посчитаем выражение в скобках:

2⁴ — 10 = 16 — 10 = 6

6•2^2х = 24

Все уравнение делим на 6:

2^2х = 4

Представим 4=2²:

2^2х = 2² основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.

Решим уравнение:

9^х – 12*3^х +27= 0

Преобразуем:
9^х = (3²)^х = 3^2х

Получаем уравнение:
3^2х — 12•3^х +27 = 0

Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:

3^х = t

Тогда 3^2х = (3^х)² = t²

Заменяем в уравнении все степени с иксами на t:

t² — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t₁ = 9
t₂ = 3

Возвращаемся к переменной x.

Берем t₁:
t₁ = 9 = 3^х

Стало быть,

3^х = 9
3^х = 3²
х₁ = 2

Один корень нашли.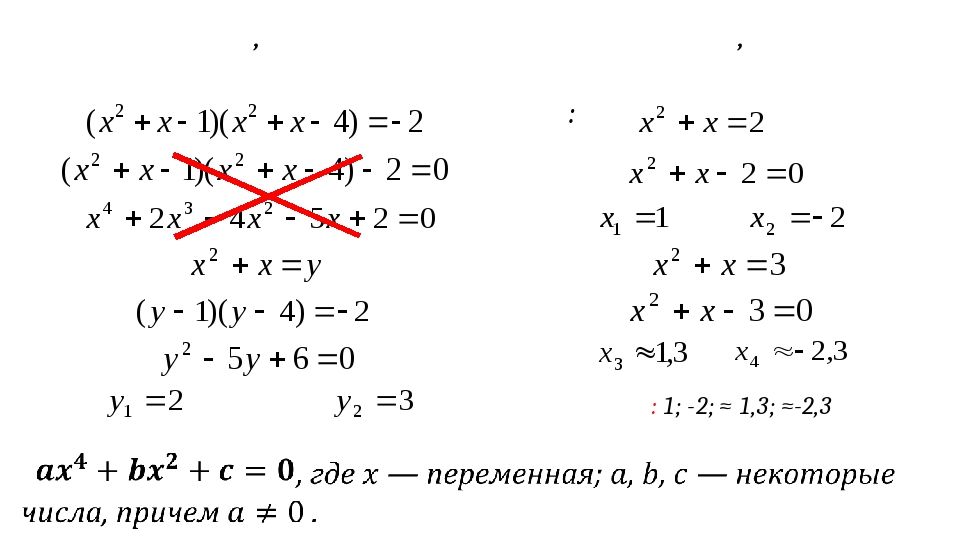 Ищем второй, из t₂:
t₂ = 3 = 3^х
3^х = 3¹
х₂ = 1
Ответ: х₁ = 2; х₂ = 1.

На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.

Вступайте в группу ВКОНТАКТЕ

“Методы решения уравнений четвертой степени”

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №1 г. Южи Ивановской области

Педагогический проект по теме:

“Методы решения уравнений четвертой степени”

Выполнила Чурина

Елена Вениаминовна,

учитель математики первой

квалификационной категории

Г. Южа

2021 год

Содержание

Актуальность

Цель и задачи работы:………………………………

1. Исторические сведения об уравнениях четвёртой степени……стр.

2. Определение уравнения 4 степени………………………….стр.

3. Способы решения уравнений 4 степени……………………………стр.

3.1. Схема метода Феррари……………………….стр.

3.2. Разложение на множители. Кубическая резольвента……………стр.

3.3. Теорема Виета для уравнения 4 степени……………………..стр.

3.4. Решение уравнений 4 степени по схеме Горнера……………………стр.

4.Решение некоторых уравнений 4 степени……………………………стр.

4.1. Решение биквадратного уравнения………………………………стр.

4.2. Решение уравнения способом группировки………………….стр.

4.3. Решение уравнения по свободному члену……………………стр.

4.4. Графический метод………………………………………..стр.

4.5. Применение формул сокращенного умножения. Выделение полного квадрата………………………………………………..стр.

5. Исследование………………………………………………стр.

6. Выводы

7. Заключение

8. Тренировочные задания для отработки различных способов решения уравнений высших степеней……………………………………………стр.

Список литературы

Актуальность

Как все знают, в математике одна из важнейших вещей — это уравнения. Чаще всего решаются линейные либо квадратные уравнения, но не мало важны уравнения 4 степени, которые решить сможет не каждый учащийся 9 класса. Чтобы решать такие уравнения было проще, нужно выбрать тот способ, который тебе более понятен.

Задания с уравнениями высших степеней есть в контрольных измерительных материалах  при проведении государственной итоговой аттестации. Значит, ученики должны уметь решать уравнения не только 2 степени, но и выше. А это умеет делать далеко не каждый.

Цель работы: узнать и разобрать методы решения уравнений высших степеней.

Задачи:

Изучить литературу по истории приемов решения уравнений 4-й стпени

Обобщить накопленные знания об уравнениях4-й степени и способах их решения.

Сделать выводы.

Разработать дидактический материал для проведения практикума по решению уравнений 4-й степени с использованием новых приемов в помощь ученикам, увлеченным математикой и учителям, ведущим факультативные занятия.

Проблемный вопрос: существуют ли кроме общепринятых приемов решения квадратных уравнений другие, которые позволяют быстро и рационально решать уравнения 4-й степени?

Гипотеза: существует универсальный способ для решения всех видов уравнений 4-степеней.

Объект исследования: уравнения 4-й степени

Предмет изучения: методы и приемы решениях уравнений 4-й степени, в том числе

1.Исторические сведения об уравнениях четвёртой степени

Решение уравнений высших степеней – история полная драматизма, разочарования и радости открытия. В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.

Необходимость решать уравнения не только первой, но и второй и высших степеней ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне.

Однако уже при решении уравнений третей степени математики столкнулись с большими трудностями. История открытия способа решения кубических уравнений полна тайн, так как в древности учёные часто на открытых диспутах соревновались в решении трудных задач. От исхода этих состязаний зависела их научная репутация и материальное благополучие.

Тот, кто первым овладел решением кубических уравнений, мог легко победить своих соперников давая им задачи, сводящиеся к кубическим уравнениям. Поэтому способы решения уравнения тщательно скрывались. Историки полагают, что первым нашёл способ решения кубических уравнений известный итальянский алгебраист Специна дель Ферро (1465-1576), но впервые опубликовал общую формулу решения кубических уравнений итальянский математик Джераламо Кордано (1501-1576г.). Эта формула носит теперь название формулы Кордано, хотя предполагают, что эту формулу ему передал итальянский математик Николо Тарталья ( 1500-1557). С именами этих же математиков связано открытие способов решения уравнений четвёртой степени.

В дальнейшем математики активно пытались найти формулы вычисления корней уравнений пятой и более степени. И только почти через три столетия впервые итальянский учёный Паоло Руффини (1765-1822), а затем норвежский математик Нильс Хенрих Абель (1802-1829г.) доказали, что не  существует формулы, выражающей корни любого целого уравнения пятой степени через конечное число алгебраических операций над его коэффициентами. Да и найденные формулы вычисления корней для уравнений третьей и четвёртой степени столь сложны, что ими практически не пользуются. Поэтому в современной математике разработаны методы, позволяющие находить с любой степенью точности приближенные значения корней уравнений. Использование компьютеров значительно облегчают эту работу.

2. Определение уравнения 4 степени

Уравнение четвёртой степени —алгебраическое уравнение вида:

,

при этом a≠0 и где a,b,c,d,e- любые числа.

Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любых значениях коэффициентов).

3. Способы решения уравнений 4 степени.

3.1 Схема метода Феррари

где a0, a1, a2, a3, a4 –  произвольные вещественные числа, причем 

      Метод Феррари состоит из двух этапов.

      На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.

      На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.

Приведение уравнений 4-ой степени

      Разделим уравнение (1) на старший коэффициент a0 .  Тогда оно примет вид

где a, b, c, d –  произвольные вещественные числа.

      Сделаем в уравнении (2) замену

где y –  новая переменная.

      Тогда, поскольку

то уравнение (2) принимает вид

      Если ввести обозначения

то уравнение (4) примет вид

где p, q, r –  вещественные числа.

      Первый этап метода Феррари  завершён.

3.2.Разложение на множители. Кубическая резольвента

      Добавив и вычитая в левой части уравнения (5) выражение

2sy2 + s2,

где s –  некоторое число, которое мы определим чуть позже, из (5) получим

      Следовательно, уравнение (5) принимает вид

      Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения

то уравнение (6) примет вид

      Избавляясь от знаменателя, уравнение (7) можно переписать в виде

или, раскрыв скобки, — в виде

      Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).

      Если какое-нибудь решение  кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».

      Действительно,

      Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение

а также квадратное уравнение

      Вывод метода Феррари завершен.

Пример решения уравнения 4-ой степени

      Пример. Решить уравнение

      Решение. В соответствии с (3) сделаем в уравнении (12) замену

      Поскольку

x4 + 4×3 – 4×2 – 20x – 5 = (y – 1)4 + 4(y – 1)3 – 4(y – 1)2 – 20(y – 1)– 5 = 
= y4 – 4y3 + 6y2 – 4y + 1 + 4y3 – 12y2 + 12y – 4 – 4y2 + 8y – 4 – 20y + 20 – 5 =
= y4 – 10y2 – 4y + 8,

то в результате замены (13) уравнение (12) принимает вид

      В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства

      В силу (9)  и (15) кубической резольвентой для уравнения (14) служит уравнение

2s3 + 10s2 – 16s – 84 = 0,

которое при сокращении на 2 принимает вид:

      Проверяя, какой из делителей свободного члена уравнения (16) является целым корнем этого уравнения, находим, что целым корнем кубической резольвенты является число

      Подставляя значения (15) и (17) в формулу (10), получаем уравнение

y2 – 2y – 4 = 0,

корни которого имеют вид:

      Подставляя значения (15) и (17) в формулу (11), получаем уравнение

y2 + 2y – 2 = 0,

корни которого имеют вид:

      В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):

      Ответ.  

Но эти способы очень сложны. Рассмотрю более простые способы, с помощью которых можно решить некоторые уравнения 4-й четверти.

3.3Теорема Виета для уравнения четвёртой степени

Корни уравнения четвёртой степени {\displaystyle x_{1},\,x_{2},\,x_{3},\,x_{4}} связаны с коэффициентами {\displaystyle a,\,b,\,c,\,d,\,e}следующим образом:

{\displaystyle x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}},}

3.4.Решение уравнений четвертой степени по схеме Горнера

2x4 + 5x3 — 11x2 — 20x + 12 = 0

Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди:

1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1 не является корнем многочлена

-1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена

2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена

Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:

В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления.

Они считаются так:

Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.

Таким образом, мы исходный многочлен разложили на множители и переходим к уравнению.

(х-2)(2х3+9х2+7х-6)=0

Многочлен, являющийся вторым множителем попробуем разложить на множители подобным образом.

Отыщем опять делители свободного члена. В данном случае делителями числа -6: ±1, ±2, ±3, ±4, ±6.

Число -2 является корнем многочлена. Напишем найденный корень в схему Горнера и начнем заполнять ячейки:

Таким образом, мы исходный многочлен разложили на множители и переходим к уравнению.{2}-4ac}}}{2a}}}.}

Пример.

Решить уравнение

Замена

из этого следует, что уравнение имеет два корня.

Обратная замена

т.е. невозможно

Ответ: .

4.2. Решение уравнения способом группировки

Способом группировки можно решить уравнение 4 степени.

Чтобы разложить уравнение на множители, надо сгруппировать слагаемые по парам. Мы должны сгруппировать слагаемые по парам таким образом, чтобы при вынесении общего множителя за скобки у слагаемых был одинаковый множитель.

Решим на примере.

2х4-5х3+2х2-5х=0

(2х4-5х3)+( 2х2-5х)=0

х3(2х-5)+х(2х-5)=0

(2х-5)(х3-х)=0

х(2х-5)(х2-1)=0

х(2х-5)(х-1)(х+1)=0

х=0 или 2х-5=0 или х-1=0 или х+1=0

х1=0 х2=2,5 х3=1 х4=-1

4.3. Решение уравнения по свободному члену

Любое уравнение вида   можно свести к приведенному уравнению той же степени, домножив обе его части на  и выполнив замену переменной вида :

Полученные коэффициенты   тоже будут целыми.

Таким образом, будем решать приведенное уравнение степени n с целыми коэффициентами вида  .

Алгоритм решения.

Находим целые корни уравнения.

Целые корни уравнения  , i=1, 2, …, m (m – количество целых корней уравнения) находятся среди делителей свободного члена . То есть, первым делом выписываем делители свободного члена и подставляем их по очереди в исходное равенство для проверки. Перебираем их по очереди, пока не получим тождество. Как только тождество получено, то первый целый корень уравнения найден и уравнение предстает в виде  , где  — корень уравнения, а  — частное от деления  на .

Продолжаем подставлять выписанные ранее делители в уравнение , начиная с  (так как корни могут повторяться). Как только получаем тождество, то корень  найден и уравнение предстает в виде , где  — частное от деления  на .

И так продолжаем перебор делителей, начиная с . В итоге найдем все m целых корней уравнения и оно представится в виде , где  — многочлен степени n-m. Весь этот процесс удобно проводить по схеме Горнера.

Дробных корней приведенное уравнение с целыми коэффициентами иметь не может.

Находим оставшиеся корни (иррациональные и/или комплексные) из уравнения  любым способом.

Решить уравнение .

Во-первых, найдем все целые корни данного уравнения.

Свободным членом является -3. Его делителями являются числа 1, -1, 3 и -3.

Будем подставлять их по очереди в исходное равенство до получения тождества.

При х=1 имеем . То есть х=1 является корнем уравнения.

Разделим многочлен  на (х-1) столбиком:

Следовательно, .

Продолжим перебор делителей, но уже для равенства :

При х = -1 получили верное равенство, следовательно, -1 является корнем уравнения.

Разделим  на (х+1) столбиком:

Таким образом,

Продолжаем перебор делителей для равенства , начиная с х = -1:

Получили неверные равенства, следовательно, целых корней уравнение больше не имеет.

Оставшиеся корни исходного уравнения являются корнями квадратного трехчлена .

, то есть, действительных корней трехчлен не имеет, но имеет пару комплексно сопряженных.

4.4.Графический метод.

Иногда полезно рассмотреть эскизы графиков функций у=ƒ(x) и у=g(x), входящих в уравнение ƒ(x) = g(x). Это может помочь выяснить:

1) на какие множества надо разбить числовую ось, чтобы на каждом из этих множеств использовать свой способ решения;

2) наличие или отсутствие корней, их количество.

Пример: (материал взят из ОГЭ 2016г.)

x4=(3x-10)2

Решение №3: x4=(3x-10)2

1) Рассмотрим две функции: у = х4 и у =(3х-10)2.

2) Построим график функции у = х4 — график парабола ветви направлены вверх.

3) Построим график линейной функции у = (3х-10)2. Это парабола ветви, которой направлены вверх.

4) В данном примере наглядно видна только одна точка пересечения В(2;16) (см. приложение рис.3), хотя очевидно, что графики пересекаются еще в одной точке (т.е. имеется еще одно решение).

Как видим, что графический способ в данном случае не удобен, так как ограниченный размер листа тетради не позволяет увидеть все точки пересечения.

Графическое решение уравнения- наглядный способ, он хорош при необходимости определения наличия или отсутствия корней и их количества.

4.5. Применение формул сокращенного умножения. Выделение полного квадрата.

Этот метод основан на использовании формул: 

а2-b2=(а-b)(а+b)a2+2ab+b2=(a+b)2a2−2ab+b2=(a−b)2

а3+b3=(а+b)(а2-аb+b2)а3-b3=(а-b)(а2+аb+b2)(а+b)3=а3+3а2b+3аb2+b3

(а-b)3= а3-3а2b+3аb2-b3,

Пример: х4=(3х-10)2

Способ 1: Используем формулу сокращенного умножения х4-(3х-10)2=0

(х2-3х+10)(х2+3х-10)=0

х2-3х+10=0 или х2+3х-10=0

D=9-40=-31 D=9+40=49

корней нет х1=-5, х2=2.

Ответ: х1=-2, х2=5.

6. Выводы:

1. Уравнения высших степеней решали еще более 500 тыс. лет назад.

2. Есть много способов решения уравнений 4-й степеней. Некоторые из них довольно сложные, а некоторые помогут быстро решить задания на ОГЭ.

3. Уравнения 4-й степеней играют немалую роль в развитии математики. Лишь немногие из учащихся умеют решать такие уравнения. Эти методы решения уравнений высших степеней непросты в применении, но они всё равно могут заинтересовать увлекающихся математикой учеников.

7. Заключение

В данной работе рассмотрены способы решения уравнений 4-й степени.

А также рассмотрены приёмы решения уравнений 4-й степени, которые позволяют быстрее и проще решить такие уравнения.

Данные приёмы решения заслуживают внимания, поскольку каждые из них интересны и уникальны. Овладение данными приёмами поможет экономить время и эффективно решать уравнения. Потребность в быстром и упрощенном решении обусловлена применением этих навыком на экзаменах.

Таким образом, цель работы — узнать и разобрать методы решения уравнений высших степеней- достигнуты. Гипотеза доказана, существует универсальный способ решения уравнений 4-й степени. Это способ Феррари.

Источники:

Алгебра. 9 класс:учебник для общеобразовательных организаций / А45 Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под редакцией С. А. Теляковского. – 4-е издание – М.: Просвещение, 2017. – 287 с.: ил. – ISBN 978-5-09-046396-6.

. М.Л. Галицкий, А.М. Гольдман, Л.М. Звавич «Сборник задач по алгебре для 8-9 классов». Учебное пособие для учащихся школ и классов с углубленным изучением математики -Москва «Просвещение», 1999.

 В.В. Бардушкин, И.Б. Кожухов, А.А. Прокофьев, А.М. Ревякин,
А.М. Терещенко «Письменный вступительный экзамен по математике» — Москва «Лист», 1998.

 Н.В. Бурмистрова, Н.Г. Старостенкова «Функции и их графики». Учебное пособие — Саратов «Лицей», 2003.

 М.А.Еремин «Уравнения высших степеней» — Арзамас, 2003.

А.Г.Курош «Алгебраические уравнения произвольных степеней» — М.:Наука, 1975.

Л.М.Лоповок «1000 проблемных задач по математике» — М.: Просвящение, 1995.

 И.Р.Шафаревич «Популярные лекции по математике. О решении уравнений высших степеней» Вып.15 – М.: Наука, 1954.

10.https://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/

11. http://www.cleverstudents.ru/equations/equations_of_higher_degree.html

12. https://ru.wikipedia.org/wiki/Уравнение_четвёртой_степени

Приложение 1

Тренировочные задания для отработки различных способов решения уравнений 4-й степени.

№1 Решите уравнения способом замены: , б) X4-2×2-8=0,

в) x4-8×2-9=0, г) x4-7×2+12=0, д) 3×4-13×2+4=0, е) 2×4-19×2+9=0,

ж) 3×4-13×2+4=0, з) (x2+4x)(x2+4x-17)=60=0, и) (x2-5x)(x2-5x+10)+24=0,

к)(x2-3x)2-2(x2-3x)=8, л) (x2+x)2-11(x2+x)=12, 1

м) ()+10=0, н) ()=3; о)

№2 Решите уравнения, раскладывая левую часть на множители способом группировки:

а) 2×4-5×3+2×2-5x=0,

б) 6×4-3×3+12×2-6x=0,

в) 2×4+3×3-8×2-12x=0,

г) 2×4-5×3-18×2+45x=0.4+b=0$

Корни уравнения такой разновидности находятся с помощью применения формул сокращённого умножения.

Степень уравнения

градус уравнения описывает то, что наивысшее
power любая переменная в уравнении возводится в. А 1 ^ул
Уравнение степени используется для описания уравнения, в котором наивысшая степень
любая переменная — «1». Уравнение 2 ^nd градусов используется для
описать тот, у которого наивысшая степень любой переменной равна «2». Это продолжается для
3 градусов, 4 градусов и т. Д.

Возьмем, к примеру, это уравнение:

В этом уравнении есть только один член, который имеет переменную
или местоимение в нем — термин «х».Наличие там просто «х» означает, что
возведен в первую степень, поскольку мы знаем, что:

Итак, уравнение является уравнением первой степени. Но что насчет
это уравнение:

В этом уравнении много членов и два типа
переменная — «а» и «б». Наивысшая степень любого «а» равна 3, а наивысшая степень
степень любого «b» равна 2.Поскольку a имеет наивысшую степень, он определяет, в какой степени
уравнение есть. Поскольку в степени «3» возведена буква «а», это означает, что
уравнение представляет собой уравнение 3 ^rd градусов .

Решение уравнений первой степени

Решить уравнения первой степени довольно просто, достаточно
нужно помнить, что что бы вы ни делали с одной стороны уравнения, вы должны делать
на другую сторону тоже. Если умножить одну сторону на 5, нужно умножить
с другой стороны тоже на 5.Если вы вычтете «2x» с одной стороны, вам нужно будет
вычтите «2x» и с другой стороны. Довольно простая вещь. Вот
главное, что вы можете сделать, чтобы решить уравнение:

·
Умножьте или и разделите обеих частей уравнения на число
или местоимение.

·
Добавьте или вычтите что-нибудь из обеих частей уравнения.

·
Умножьте слова в квадратных скобках.

·
Сделайте так, чтобы у всех дробей был общий знаменатель , чтобы вы могли
расчеты с ними.

·
В качестве альтернативы полностью избавьтесь от дробей, умножив обе
стороны уравнения на произведение их знаменателей.

Помните, что ваша конечная цель, когда вы решаете
значение конкретной переменной или местоимения состоит в том, чтобы получить уравнение в
форма:

Например, вот типичный первой степени
уравнение:

После небольшой практики с их решением вы должны
Вы сразу заметите, что можно разделить обе стороны на «4»:

Теперь скобки можно умножать:

Ваша конечная цель — получить «x = что-то…» На данный момент,
у нас есть члены с буквой «x» по обе стороны уравнения.Мы можем решить
это, избавившись от символа «x» на L.H.S. путем вычитания «x» из обоих
сторон:

Теперь у нас есть только «x» на одной стороне уравнения, но
у нас также есть надоедливое «–9». Давайте избавимся от этого, добавив «9» к
обе стороны:

Теперь единственное, что нам нужно сделать, это сократить его до на один
x, мы можем сделать это, разделив обе части уравнения на «2»:

Степень уравнения

Решение уравнений

Что такое квадратное уравнение?

Квадратное уравнение — это полиномиальное уравнение второй степени.2 + bx + c = 0`. Постоянная a называется квадратичным коэффициентом, и она не может быть равна нулю (иначе это будет линейное уравнение). Константа b обозначается как линейный коэффициент. Наконец, константа c известна как постоянный коэффициент или независимый член. Если уравнение второй степени не имеет констант «b» или «c», оно называется неполным квадратным уравнением, в противном случае оно будет полным уравнением.

Почему это уравнение так важно?

Его график представляет собой параболу и описывает движение баскетбольного мяча в корзину.Но вы можете спросить: насколько важен этот расчет? Видимо это неважно. Однако вместо того, чтобы думать о баскетбольном мяче, если мы думаем о траектории пули из пушки, пока она не достигнет поля противника, это все меняет. Что касается последнего примера, вам важно точно рассчитать место, где пуля нанесет урон, чтобы не тратить зря снаряды или, что еще хуже, поразить наших союзников.

И как вы решите этот расчет?

Расчет места попадания пули в землю производится путем изучения нулей функции, которые также называют корнями уравнения.2 — 4ac)) / (2a) `

Что делать, если мне не нужно рассчитывать траекторию выстрелов из пушки?

Студентам часто трудно понять полезность того, что они изучают. Один из наиболее часто задаваемых вопросов в классе: для чего это нужно? Это справедливый вопрос, на который, к сожалению, многие учителя не затрудняются ответить. Помимо этого примера, квадратное уравнение имеет множество других приложений в нескольких областях, таких как физика, инженерия, экономика и так далее.Если мы посмотрим на крыши наших домов, мы заметим, что многие из них имеют антенны-тарелки. Эти антенны были построены на основе важного свойства этих функций, которое позволяет электромагнитным волнам, собранным антенной, отражаться в простую точку, где находится приемник, и это является фокусом цифровой антенны.

Ознакомьтесь с нашим Списком вопросов, чтобы узнать немного больше о самых разных темах, связанных с математикой. Если у вас есть подходящий (математический) вопрос, ответ на который нелегко найти, отправьте нам электронное письмо с вопросом на странице «Контакты».2 + cz + 2fyz + 2gzx + 2hxy + 2ux + 2vy + 2wz ​​+ d = 0 \ label {4.8.1} \ tag {4.8.1} \]

Может представлять собой плоскость или пару плоскостей (которые, если они не параллельны, определяют прямую линию), или эллипсоид, параболоид, гиперболоид, цилиндр или конус. Уравнение, если это удобно, можно разделить на \ (d \) (или любую другую константу), и в действительности существует только девять независимых констант. Следовательно, девяти точек в пространстве достаточно, чтобы определить поверхность второй степени, на которой они лежат.

Если \ (d \) равно нулю, поверхность содержит начало координат. Если \ (u \), \ (v \) и \ (w \) все равны нулю, а поверхность является эллипсоидом, гиперболическим параболоидом или гиперболоидом, начало координат находится в центре фигуры. Если фигура является эллиптическим параболоидом, начало координат находится в вершине. Если \ (u \), \ (v \), \ (w \) и \ (d \) все равны нулю, поверхность является конусом с оговоркой, упомянутой в разделе 4. 2 + 8yz — 2zx + 4xy + 14x — 10y — 4z + 5 = 0 \ label {4.8.2} \ tag {4.8.2} \]

Что это за поверхность?

Нам нужно сделать две вещи. Сначала нам нужно повернуть оси координат так, чтобы они были параллельны осям фигуры. Уравнение, относящееся к осям фигуры, не будет иметь членов в \ (yz \), \ (zx \) или \ (xy \). Затем нам нужно переместить оси так, чтобы начало координат было в центре фигуры (или в вершине, если это эллиптический параболоид).

Математически нам нужно найти собственные векторы матрицы

\ [\ begin {vmatrix}
a & h & g \\
h & b & f \\
g & f & c \\
\ end {vmatrix}
=
\ begin {vmatrix}
3 & 2 & -1 \\
2 & -4 & 4 \\
-1 & 4 & 6 \\
\ end {vmatrix}
\ label {4.8.3} \ tag {4.8.3} \]

Некоторые читатели легко знают, как это сделать. Другие могут не знать и даже не совсем уверены в том, что такое собственный вектор. Раздел 4.9 может быть интересен любой группе читателей. В любом случае собственные векторы оказываются равными

\ [\ pmatrix {l_ {11} \\ l_ {12} \\ l_ {13}} = \ pmatrix {-0.069 \ 5481 \\ +0.318 \ 8310 \\ +0.945 \ 2565} \ quad \ pmatrix {l_ {12} \\ l_ {22} \\ l_ {32}} = \ pmatrix {-0.240 \ 6405 \\ +0.914 \ 2071 \\ -0.326 \ 0635} \ quad \ pmatrix {l_ {13} \\ l_ { 23} \\ l_ {33}} = \ pmatrix {-0.968 \ 1194 \ -0,2501441 \ +0,013 \ 1423} \]

с соответствующими собственными значениями \ (7.422 \ 7590, \ 5.953 \ 0969, \ 3.530 \ 3380 \).

Элементы собственных векторов являются направляющими косинусами текущей координатной оси по отношению к осям фигуры. Чтобы выразить Уравнение поверхности относительно осей координат, параллельных осям фигуры, заменим

\ [x \ text {by} l_ {11} x + l_ {12} y + l_ {13} z \]

\ [y \ text {by} l_ {21} x + l_ {22} y + l_ {23} z \]

\ [z \ text {by} l_ {31} x + l_ {32} y + l_ {33} z \]

Это приведет к исчезновению членов в \ (yz \), \ (zx \) и \ (xy \); это следует проверить численно, особенно потому, что оси легко повернуть в неправильном направлении.2 — 7.9430994x — 11.206 7840 y — 11. 2) = — 0.2, \ quad b

не является одной из квадратичных поверхностей. Если квадратный корень изолирован и возведен в квадрат, полученное уравнение будет содержать члены четвертой степени. Поверхность довольно знакома, и читатель должен попытаться представить, что это такое. В противном случае, если ваши компьютерные навыки соответствуют этому, вы можете попытаться нарисовать поверхность в трехмерном пространстве. Единственный совет, который я даю, — это предложить вам поместить \ (y = 0 \) в уравнение \ (\ ref {4.8.7} \), чтобы увидеть, что это за раздел в \ (z \) — \ (x \) самолет.

Авторы и авторство

4. Корни полиномиального уравнения

Вот три важные теоремы, касающиеся корней полиномиального уравнения:

(a) Многочлен n -й степени может быть разложен на n линейных множителей.

(b) Полиномиальное уравнение степени n имеет ровно n корней.

(c) Если `(x — r)` представляет собой множитель полинома, то `x = r` является корнем соответствующего полиномиального уравнения.

Давайте рассмотрим несколько примеров, чтобы понять, что это означает.

Пример 1

Кубический многочлен f ( x ) = 4 x ³ -3 x ² -25 x -6 имеет степень `3` (так как максимальная степень x — это `3`).

Мы обсуждали этот пример в разделе 3. Как разложить многочлены на множители и нашли, что множители будут следующими:

4 x ³ -3 x ² -25 x -6 = ( x -3) (4 x + 1) ( x + 2)

Напомним, что многочлен 3-й степени имеет 3 корня.

Соответствующее полиномиальное уравнение формируется путем установки полинома равным нулю:

f ( x ) = 4 x ³ — 3 x ² -25 x — 6 = 0

В факторизованном виде это:

`(x — 3) (4x + 1) (x + 2) = 0`

Из выражений в скобках и использования третьей теоремы сверху видно, что существует 3 корня: `x = 3`,` x = -1 / 4` и `x = −2`.

В этом примере все 3 корня нашего полиномиального уравнения степени 3 действительны.

Поскольку `(x — 3)` является множителем, то `x = 3` является корнем.

Поскольку `(4x + 1)` является множителем, то `x = -1 / 4` является корнем.

Поскольку `(x + 2)` является множителем, то `x = −2` является корнем.

Вот график нашего полинома, показывающий x -перехватов , которые являются корнями:

График f ( x ) = 4 x ³ — 3 x ² -25 x — 6

Пример 2

Уравнение x ⁵ -4 x ⁴ — 7 x ³ + 14 x ² -44 x + 120 = 0 можно разложить на множители (с использованием Wolfram | Alpha) и записывается как:

( x — 2) ( x — 5) ( x + 3) ( x ² + 4) = 0

Мы видим, что имеется 3 действительных корней `x = 2, 5, -3,` и 2 комплексных корней `x = ± 2j` (где` j = sqrt (-1) `).

Итак, у нашего уравнения 5-й степени всего 5 корней, как и ожидалось.

На графике мы видим только три настоящих корня:

График y = x ⁵ — 4 x ⁴ — 7 x ³ + 14 x ² — 44 x + 120

[Вам нужна доработка комплексных чисел? Перейти к комплексным числам.]

Пример 3

В предыдущем разделе 2.2− 5x — 6 = 0`.

Чтобы проверить это, подставьте в полином `x = -1`. Если это корень, то при подстановке вы должны получить значение «0».

Другой способ увидеть, что происходит, — это построить график полинома.

График y = x ³ + 2 x ² — 5 x — 6

График показывает нам два других корня, −3 и 2.

Пример 4

Следующее полиномиальное уравнение было бы довольно сложно решить с помощью теорем об остатке и множителях.Решим это с помощью Wolfram | Alpha:

x ⁴ + 0,4 x ³ — 6,49 x ² + 7,244 x — 2,112 = 0

Ответ

Wolfram | Результат Alpha:

Решить: x ⁴ + 0,4 x ³ — 6,49 x ² + 7,244 x — 2,112 = 0,

Решение: {`x = -3.2`}, {` x = 1.2`}, {`x = 0.5`}, {`x = 1.1`}

Вот график:

График y = x ⁴ + 0,4 x ³ — 6,49 x ² + 7,244 x — 2,112

Трудно увидеть три положительных корня. Вот эта часть снова, увеличенная для более четкого обзора:

График y = x ⁴ + 0,4 x ³ — 6,49 x ² + 7.244 х — 2,112

Примечание: Полиномиальные уравнения не всегда имеют «хорошие» решения! (Под «хорошими решениями» я подразумеваю решения, которые являются целыми числами или простыми дробями.) Вот почему я считаю, что теоремы об остатках и факторах следует рассматривать как исторический подход, потому что вы можете использовать их только в том случае, если хотя бы некоторые из решений являются целыми числами. или простые дроби.

Если вы используете систему компьютерной алгебры (например, Wolfram | Alpha для решения этих проблем, вы можете сделать это за секунды и перейти к чему-то более значимому, например к приложениям.

Пример 5

Решите следующее полиномиальное уравнение с помощью системы компьютерной алгебры:

3 x ³ — x ² — x + 4 = 0.

Ответ

3 x ³ — x ² — x + 4, Решение: {`x = -1,0914`,` x≈0,71237 — 0,84509 i`, `x≈0,71237 + 0,84509 i` }

Мы видим, что есть одно реальное решение и 2 комплексных решения.

Проверив это графически, имеем:

График y = 3 x ³ — x ² — x + 4

Мы видим, что существует только один (реальный) корень, около `x = -1`, как и ожидалось.

Использование системы компьютерной алгебры для поиска корней

Мы использовали технологии, чтобы найти большинство вышеперечисленных корней. Это лучше, чем пытаться угадывать решения и затем делить многочлены. Используя компьютер, мы можем быстро найти корни либо графически, либо с помощью встроенного средства поиска корней, если оно доступно.

Используя график, мы можем легко найти корни полиномиальных уравнений, у которых нет «хороших» корней, например, следующее:

x ⁵ + 8,5 x ⁴ + 10 x ³ — 37,5 x ² — 36 x + 54 = 0.

Корни уравнения — это просто интервалы x (т.е. где функция имеет значение «0»). Вот график функции:

График y = x ⁵ + 8.5 x ⁴ + 10 x ³ — 37,5 x ² — 36 x + 54.

Мы можем видеть решения: `x = -6`,` x = -3`, `x = -2`,` x = 1` и `x = 1.5`. (Увеличение масштаба близко к этим корням на графике подтверждает эти значения.)

Сложные корни

Относительно комплексных корней применима следующая теорема:

Если коэффициенты уравнения `f (x) = 0` действительны и` a + bj` является комплексным корнем, то сопряженное ему `a — bj` также является корнем.

Подробнее о комплексных числах см .: Комплексные числа

Пример 6

В примере (2) выше у нас было 3 действительных корня и 2 комплексных корня. Эти сложные корни образуют комплексно-сопряженную пару,

x = 0-2 j и x = 0 + 2 j

Пример 7

Коэффициенты полинома x ³ + 7 x ² + 17 x + 15 находятся с использованием системы компьютерной алгебры следующим образом:

x ³ + 7 x ² + 17 x + 15 = ( x + 3) ( x + 2- j ) ( x + 2 + j )

Итак, корни

`x = −3`

`x = −2 + j` и

`x = −2 — j`

Имеется один действительный корень, а оставшиеся 2 корня образуют комплексно сопряженную пару.